1. INTRODUCTION
The problem of stochastic heating was recently discussed (Patin et al., 2006, 2005a, 2005b). The effect of a constant homogeneous magnetic field is studied in the first part of this paper. Then, in the case of nonmagnetized plasma interacting with several electromagnetic waves, the use of Chirikov criterion (Chirikov, 1979) to predict the conditions when this heating takes place is emphasized.
A large number of issues remain open in the study of laser-matter interaction at very high intensities. Recently, particle-in-cell (PIC) code simulations results published by Tajima et al. (2001) and also experimental results obtained by Mulser et al. (2005) have shown that the irradiation of very high intensity lasers on clustered matter leads to a very efficient heating of electrons. Tajima et al. (2001) and Kanapathipillai (2006) have shown that chaos seems to be the origin of the strong laser coupling with clusters. It was confirmed in PIC code simulations, in the case of two counter propagating laser pulses, that the stochastic motion of electrons can lead to their acceleration (Sheng et al., 2002, 2004) of electrons. Therefore, the issue that we will address below is the stability of electron motion in the fields of one electromagnetic wave, and a constant homogeneous magnetic field, and in those of several waves.
At very high intensities, the motion of a charged particle in a wave is highly nonlinear. The situations when the motion is integrable are exceptional. The solutions corresponding to these situations deserve to be studied as they are strong as predicted by KAM theorem (Lichtenberg & Liebermann, 1983; Arnold, 1988; Rasband, 1983; Ott, 1993; Tabor, 1989; Walker & Ford, 1969). Moreover, they are useful to predict resonances when a perturbing wave is considered (Lichtenberg & Liebermann, 1983; Arnold, 1988; Rasband, 1983; Ott, 1993; Tabor, 1989).
First, the dynamic of a charged particle in a linearly or almost linearly polarized traveling high intensity wave is studied when it propagates along a constant homogeneous magnetic field in a vacuum, or in low density plasma. A certain number of results already published are recalled in order to make this paper easy to read. In the first part, the electromagnetic wave is assumed to propagate in a vacuum. Roberts and Buchsbaum (1964) have already explored this problem in the case of a circularly polarized wave. They found a “synchronous” solution in which the particle gains energy indefinitely. In this paper, it is shown that the synchronous solution still exists when the wave is linearly polarized. One of the constants of motion appears in the resonance condition (Davydovski, 1963). This means that when a particle is initially resonant it remains resonant forever. Two constants which are canonically conjugate are found. This property is used to reduce the initially three degrees of freedom problem to two degrees of freedom problem. The system is integrated and is shown to be integrable (Lichtenberg & Liebermann, 1983; Arnold, 1988; Rasband, 1983; Ott, 1993; Tabor, 1989; Bouquet & Bourdier, 1998). Then, in order to study the plasma response in the case of a very high intensity wave propagating in low-density plasma, it is assumed that the wave remains linearly polarized. Performing a Lorentz transformation eliminates the space variable corresponding to the direction of propagation of the wave (Winkles & Eldridge, 1972). Just like in the previous case, two canonically conjugate constants are used to reduce the initially three degrees of freedom problem to two degrees of freedom problem. Thus, Poincaré maps are performed. Lyapunov exponents are also calculated to confirm the chaotic nature of some trajectories (Lichtenberg & Liebermann, 1983; Ott, 1993; Tabor, 1989; Bourdier & Michel-Lours, 1994). Chaos appears when a secondary resonance and a primary resonance overlap (Van Der Weele et al., 1998; Kwon & Lee, 1999; Bourdier et al., 2005). Consequently, the system is not integrable and chaos may appear as soon as the plasma response is taken into account. The overlap of the two resonances can generate some stochastic heating.
Finally, the motion in a high intensity plane wave propagating in a nonmagnetized vacuum, perturbed by one or two electromagnetic plane waves is studied. The solution of Hamilton–Jacobi equation, in the case of one wave, is used to identify resonances. The effect of the different parameters is described by using the Chirikov (1979) criterion. Above the Chirikov threshold and for electron trajectories with their initial conditions in the overlapping region of two or more resonances, stochastic heating is evidenced by computing single particle energies. Finally, PIC code simulations results obtained with the code CALDER (Lefebvre et al., 2003) are presented in order to validate the theoretical model.
2. DYNAMICS OF A CHARGED PARTICLE IN A LINEARLY POLARIZED ELECTROMAGNETIC TRAVELING WAVE PROPAGATING ALONG A CONSTANT HOMOGENEOUS MAGNETIC FIELD
2.1. The wave propagates in vacuum
2.1.1. Hamiltonian structure of the problem
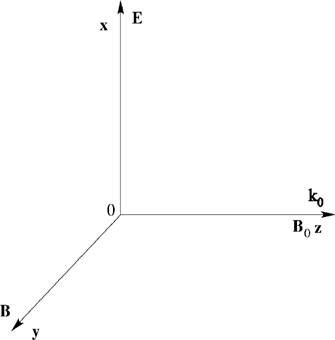
The constant magnetic field B0 is supposed to be along the z-axis. The traveling wave is assumed to be linearly polarized. It has a propagation vector k0 parallel to B0 (Fig. 1). The following vector potential is chosen for the electromagnetic field
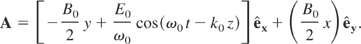
The scalar potential is assumed to vanish. The relativistic Hamiltonian for the motion is
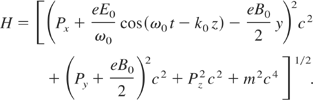
This is a time-dependent system with three degrees of freedom. It can be easily checked that
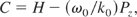
is a constant of motion for this system. Combining the equations of Hamilton allows us to easily find two other constants of motion
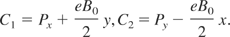
These two constants are such that
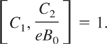
The three constants just found are not in involution, and at this stage, one cannot conclude that the problem is integrable.
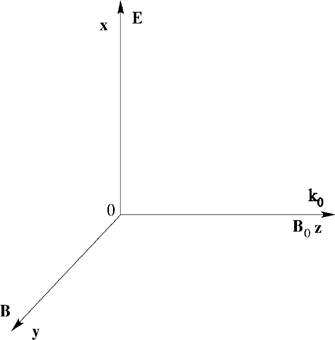
Frame of reference.
The normalized equations of motion are obtained by introducing new normalized variables and parameters
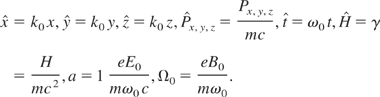
The following three normalized constants are also introduced,
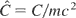
,
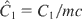
and
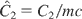
.
2.1.2. Integration of the system
The canonical transformation
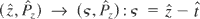
, defined by type-2 generating function:
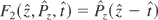
is performed first (Lichtenberg & Liebermann, 1983; Arnold, 1988; Rasband, 1983; Ott, 1993; Tabor, 1989; Bourdier & Gond, 2000, 2001). The normalized Hamiltonian is given by
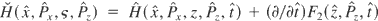
, that is to say,

In this new system, ς plays the part of a space coordinate. The new Hamiltonian is a constant as it does not depend explicitly on time.
The fact that the two constants,
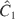
and
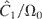
, are canonically conjugate, is used now to reduce the system. To do so, a canonical transformation, which is the product of two canonical transformations, defined by the following type-2 generating functions:
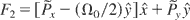
and
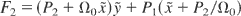
given by
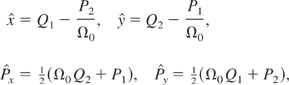
is performed (Bourdier et al., 1996; Bourdier & Gond, 2000). The degree of freedom associated with the conjugate variables (Q2,P2) is eliminated. Thus, the initially three degrees of freedom system is reduced to two degrees of freedom system. In terms of the new conjugate variables: (Q1,P1) and
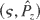
, the Hamiltonian is

The equations of Hamilton are

The equation of Hamilton for ς [Eq. (10)], can be put in the form
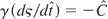
. As a consequence, indicating differentiation with respect to ς by a prime in this paragraph, we can write
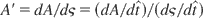
, which implies that
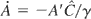
. Thus, the equations of Hamilton (Eq. (10)) become


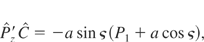
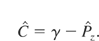
Differentiating a second time the second equation leads to the following equation of motion for Q1
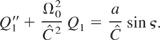
The following equation for P1 is obtained in the same way
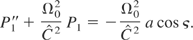
These two equations (12a and 12b) are the equations of two driven oscillators. One has a resonance when
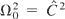
(Davydovski, 1963). This resonance condition contains a first integral of the system; this implies that when the particle is initially resonant, it remains resonant forever. These equations can be easily solved analytically whether the resonance condition is satisfied or not. Then Eq. (11c) is used to determine Pz and γ is derived through Eq. (11d).
2.1.3. Liouville inerrability
Inerrability can also be demonstrated by using Liouville's theorem. Let us consider the following Hamiltonian
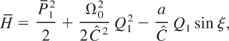
where P1 will be defined further. Assuming that ξ plays the part of time, the equations of Hamilton read
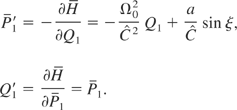
Taking the derivative of the second equation of Eq. (14) and combining it with the first one, leads to Eq. (12a) after replacing ξ by ς. In the same way, taking the derivative of the first equation gives
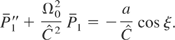
One finds Eq. (12b) again by letting
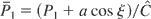
and ς = ξ. A constant
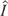
of the system defined by Eq. (13) becomes a constant I of the initial system defined by Hamiltonian Eq. (9); one has:
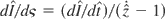
, which implies that when
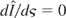
, then
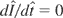
and
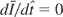
. Taking the total derivative of Eq. (13) with respect to ξ gives

If f (Q1,P1,ξ) can be such that

then the quantity: I = H + f (Q1,P1,ξ) is a first integral of the system. Eq. (17) is integrated
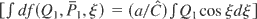
by performing two integrations by parts and using the equations of Hamilton. We find
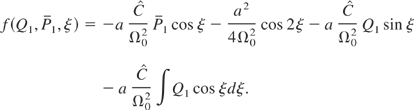
The last term of this equation is proportional to f, thus
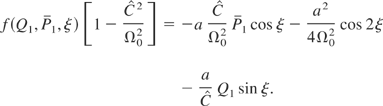
As a consequence, a first integral of the system is given by
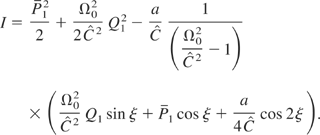
The following constant:
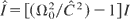
is held, as it has no singularity at
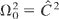
. It can be verified easily that, in any case, one has:
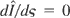
. When replacing P1 by its expression in function of P1 and
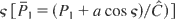
, one obtains a constant of motion
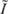
for the initial two degrees of freedom system, thus showing that the system defined by Hamiltonian (Eq. (9)) is Liouville integrable.
As we have shown, the system is integrable when the wave is assumed to propagate along a constant homogeneous magnetic field in a vacuum by different methods, no chaos can take place, and consequently all trajectories are regular.
2.2. The wave propagates in plasma
In this part of our paper, the influence of the plasma is taken into account. The wave is assumed to remain linearly polarized. The wave vector potential for the electromagnetic field is supposed to be given by Eq. (1). The dimensionless variables and parameters previously defined are used again. The normalized Hamiltonian of the system reads
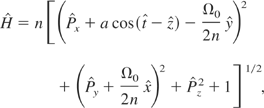
where n is the index of refraction of the plasma. The Hamilton equations allow us to readily find two constants of motion
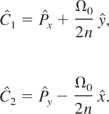
It can be noted that the two constants
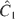
and
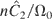
are canonically conjugate.
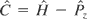
is still a constant of motion. These three constants of motion are not in involution and one cannot conclude that the problem is integrable.
We have solved the equations of Hamilton numerically. When the wave propagates in a medium, with an index of refraction inferior to unity (n < 1), the trajectories spiral outward and inward just as in the none resonant case when the wave propagates in a vacuum.
2.2.1. Introduction of a simplifying Lorentz transformation
A new frame (L*) which moves uniformly along the z-axis with velocity U relative to the laboratory frame is introduced. The Lorentz transformation of the four-momentum is given by Jackson (1975) and Landau and Lifshitz (1975).

where Γ = (1 − U2/c2)−1/2, and E = γmc2 is the energy of the charged particle.
In the extended phase space, where time is treated on a common basis with other coordinates, a fully covariant Hamiltonian formulation of the problem can be constructed. In this space, the Lorentz transformation defined above is identical to the canonical transformation generated by the following type-2 generating function
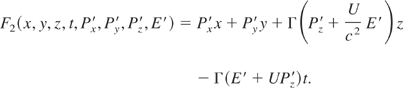
As a consequence, if the problem is integrable in the frame (L*), it is also integrable in the laboratory frame.
The phase of the wave which is an invariant takes, in the moving frame, the following form (Jackson, 1975; Landau & Lifshitz, 1975).
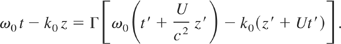
When the phase velocity of the wave is greater than the speed of light, there exists one special frame (L*) in which the phase does not depend on the variable z′. This frame can be defined by its drift velocity (Winkles & Eldridge, 1972)
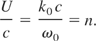
In (L*), the vector potential is (Landau & Lifshitz, 1975)
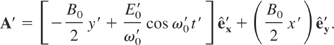
Within the new frame (L*), the equations of motion are generated by the following Hamiltonian.

Let us now introduce the following dimensionless variables and parameters
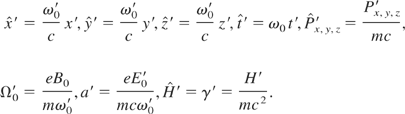
The following normalized Hamiltonian
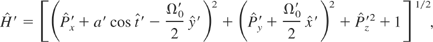
leads to the normalized equations of motion.
Dropping the primes for convenience, it can be shown very easily that this system has three constants of motion
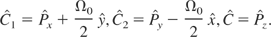
The first two constants (
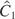
and

) are canonically conjugate.
2.2.2. Reduction to a two-dimensional problem and chaos in the new frame
Let us reduce the system in order to perform Poincaré maps. To do so, let us choose the two constants
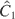
and
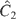
as new momentum and coordinate conjugate. The canonical transformation defined by Eq. (8) is performed. The new Hamiltonian is
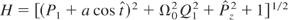
This is a time-dependent system with only two degrees of freedom. As
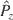
is an obvious first integral, one can evacuate the conjugate variable

and say, even if it is not academic, that we have a time-dependent system with one degree of freedom.
Let us perform now the following canonical transformation
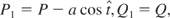
generated by
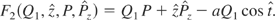
The Hamiltonian in terms of the new variables is
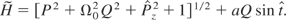
This is still a time-dependent system with only two degrees of freedom.
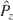
is still a constant of motion. The equations of Hamilton read
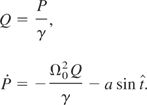
This set of equations is similar to the one found by Kwon and Lee to describe the motion of a particle in a constant and homogeneous magnetic field and an oscillating electric field of arbitrary polarization (Kwon & Lee, 1999).
These equations of motion are solved numerically. We have assumed that
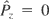
in every case. Chaos is evidenced first by performing Poincaré maps. The plane P-Q with
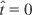
(mod2π) is chosen to be the Poincaré surface of section. Figure 2 shows Poincaré maps for only one trajectory. The Lyapunov exponent for this trajectory has also been calculated by using Benettin's method (Lichtenberg & Liebermann, 1983; Ott, 1993; Tabor, 1989; Bourdier & Michel-Lours, 1994). To do so, two very close trajectories are considered, the very small distance between them being initially d0. A sequence dn corresponding to these trajectories is calculated numerically. For every fixed time Δt, or for every fixed distance ratio d/d0, dn is renormalized to d0. The two ways to renormalize are used and compared, Figure 2b shows the good agreement obtained for the Lyapunov exponents when using the two renormalization techniques. The fact that we have chaotic trajectories shows that the system is not integrable.

(A) Surface of section plots for one trajectory. a = 4.03, Ω0 = 2. (B) Lyapunov exponent calculated with the same trajectory as in Figure 2b, the two renormalization methods are compared.
Performing Poincaré maps, one can check that the primary resonance (3,1) exists for all none zero values of the dimensionless electric field, a, while the secondary (3,1) resonance appears when a is greater that some threshold for one given value of Ω0. When Ω0 = 2, the secondary resonance is born when a is in the range 3.33–3.34 (Figs. 3b and 3c). As a grows, the central island is squeezed by the hyperbolic fixed points of the secondary (3,1) resonance until the fixed points are absorbed by the elliptic fixed point of the (1,1) resonance (Figs. 3c and 3d). When a increases, the hyperbolic fixed points reappear and move outward (Fig. 3e). When a is in the range 3.38–4, the primary (3,1) resonance and the secondary (3,1) resonance overlap, and chaotic trajectories cover the overlapped region (Fig. 3f) (Van Der Weele et al., 1998).

Surface of section plot Ω0 = 2. (A): a = 3.3, (B): a = 3.33, (C): a = 3.34, (D): a = 3.35, (E): a = 3.38, (F): a = 4.
2.2.2. Reduction to a two-dimensional problem and chaos in the laboratory frame
When going back to the laboratory frame, the equations of Hamilton must be derived through Eq. (21). Performing the canonical transformation:
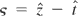
, the following Hamiltonian is obtained
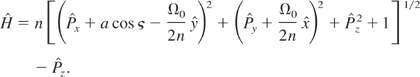
In order to reduce the system, two canonical transformations defined by the following type-2 generating functions
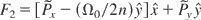
and
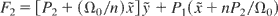
are performed. The new Hamiltonian reads
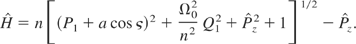
The equations of Hamilton are
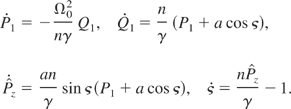
When the index of refraction is very close to unity, performing Poincaré maps and calculating Lyapunov exponents evidenced chaotic trajectories (Figs. 4a, 4b, 5).

Surface of section plots for one trajectory in the laboratory frame. a = 4.03 (A): Ω0 = 0.1997, n = 0.995. (B): Ω0 = 0.282, n = 0.99.

Lyapunov exponent calculated for one trajectory in the laboratory frame. Ω0 = 0.282, n = 0.99.
It has been shown in the last two paragraphs that, as soon as the phase velocity is higher than the speed of light, chaotic trajectories can exist due to the overlap of only two resonances. Then, some particles can move in a larger phase space and take more energy from the wave than in the integrable case. The situation studied next seems to be more promising as there will be an infinite number of resonances, thus leading to a very large space possibly opened to the charged particle.
3. DYNAMICS OF A CHARGED PARTICLE IN ONE OR SEVERAL LINEARLY POLARIZED TRAVELING ELECTROMAGNETIC WAVES PROPAGATING IN A NONMAGNETIZED VACUUM
3.1. Dynamics of one particle in one wave propagating in vacuum. Hamiltonian formulation of the problem
Let us consider a charged particle in an electromagnetic plane wave propagating along the z direction (the wave vector k0 is parallel to the z direction). The following four-potential is chosen
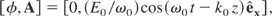
where E0, ω0, and k0 are constants. When time t is treated as a parameter entirely distinct from the spatial coordinates, the relativistic Hamiltonian of a particle in the electromagnetic wave is given by Eq. (2) in which B0 equals zero. This system has three degrees of freedom. H0 − (ω0 /k0)Pz, Px and Py are three constants of motion, which are independent and in involution. As a consequence, the system is completely integrable (Lichtenberg & Liebermann, 1983; Bouquet & Bourdier, 1998). Let us introduce the following dimensionless variables and parameter:
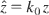
,

,
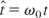
,
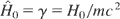
, a = eE0/mcω0. The new Hamiltonian, which describes the system, expressed in terms of these new variables, is:
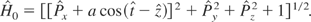
When using the proper time of the particle to parameterize the motion in the extended phase space, and the dimensionless variables and parameter just introduced above, the normalized Hamiltonian in the extended phase space reads (Jackson, 1975; Rax, 1992)
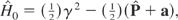
where
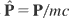
and
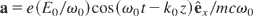
. A normalized proper time:
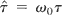
is introduced next. The y degree of freedom is assumed not to be excited. We look for a set of actions (P⊥,P∥,E) and angles (θ,φ,φ), instead of the configuration (r,t), and momentum, (P,−γ) in the
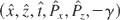
phase space. This comes out to seek a canonical transformation
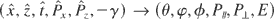
, such that the new momenta are constants of motion. Following Landau and Lifshitz (1975) and Rax (1992), the Hamilton–Jacobi equation is solved. The Hamiltonian in terms of action-angle variables reads
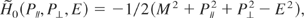
where M2 = 1 + a2/2. As
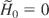
, the energy momentum dispersion relation is given by the following expression
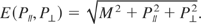
The solution of the equations of motion is in terms of these variables
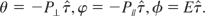
This solution is necessary to predict resonances when a perturbing mode is considered.
3.2. Dynamics of a charged particle in two or three linearly polarized traveling waves
The perturbing waves are assumed to have their electric fields in the polarization plane of the high intensity wave
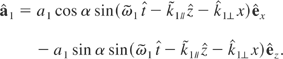
The perturbing Hamiltonian is approximated by:
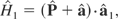
one has
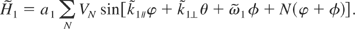
When the phase of the sine is stationary, the perturbation calculation fails to converge because of the occurrence of a small denominator. On the basis of the solution of Hamilton-Jacobi in the case of one wave, this stationary condition gives the Compton resonance condition
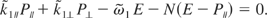
Figure 6 displays P⊥ versus P∥ restricted to the energy surface equation.

Compton resonances. α = 5π/6, a = 1, .
3.3. Influence of the different parameters. Chirikov criterion
Let us show how to choose the different parameters in order to optimize the stochastic heating. Trajectories are chaotic when their initial conditions stand in the overlapping region of two or several resonances. Extended chaos takes place when many resonances overlap. For the sake of simplicity, we shall consider two resonances only, and check if the Chirikov threshold is reached, that is to say when the ratio RN,N′ = (ΔP⊥,∥,N + ΔP⊥,∥,N′)/dN,N′, where ΔP⊥,∥,N + ΔP⊥,∥,N′ is the sum of the half-widths of the resonances and dN,N′ is the distance which separates them, is larger than unity.
Figure 7 displays the Compton resonances (P⊥ versus P∥) for different situations. They show their influence on the resonance pattern. Only the first resonances are shown in these figures. Resonances become closer for higher values of α and
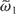
and when a decreases. The resonance lines become symmetric with respect to the P∥ axis when α grows. Figures 6 and 7 seem to show that chaos will be optimum when α is close to π. They show that the resonance lines become closer for growing values of
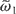
. They also show that higher values of a have the opposite effect.

Compton resonances for different values of the parameters. (A): α = π/6, a = 1, , (B): α = π/4, a = 1, , (C): α = π/6, a = 4, , (d): α = π/6, a = 1, .
At this level, one cannot come to a conclusion as these behaviors must be compared to the resonance widths. Only the ratio of the sum of the half-widths of two resonances over the distance separating them allows a conclusion.
Figure 8 show that the Chirikov criterion is better satisfied when α in is close to π, in the range [5π/6, 7π/6]. The best choice is for resonances N = −1 and N = −2, when
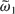
is in the range [1, 2]. The criterion is also satisfied when
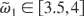
and α ∈ [9π/10,11π/10]. With respect to the resonances N = −2 and N = −3, a higher value of
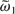
must be considered, one must have
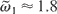
.

Chirikov criterion: RN,N′ as a function of different parameters when P⊥ = 0. a = 1, a1 = 0.1, (A) Resonances N = −1 and N = −2, (B): N = −2 and N = −3.
Figure 9 show the influence on the Chirikov criterion of a and a1. When α = π/6 (Fig. 4a), the Chirikov threshold can be reached only outside the scope of this model (a1 < a). It can be reached, for instance, for a = 4 and a1 = 0.4 when α = 5π/6 (Fig. 9b).

Chirikov criterion: RN,N′ in function of electric field amplitudes when P⊥ = 0. Resonances N = −1 and N = −2. (A): , α = π/6, (B): , α = 5π/6.
In summary, the Chirikov criterion will be satisfied when α is close to π, and almost only the resonances N = −1 and N = −2 can overlap when P⊥ does not equal zero. Extended chaos can take place in a banana-like surface in the (P⊥,P∥) phase place.
3.4. Numerical results for one or several particles
First, stochastic acceleration was evidenced by considering one particle only. Figure 10 shows the evolution of the energy of one particle. These results were obtained with a fourth order Runge–Kutta considering one and two waves.

Energy of one particle versus time. (A): one wave case, , a = 4, a1 = 0.1. (B): two waves case, , a = 4, a1 = 0.1.
Then, using the integrator of the PIC code CALDER (Lefebvre et al., 2003), the dynamics of five particles was studied. The case of one wave was compared to the case of three waves for which an “anomalous” heating was evidenced. The two perturbing waves are symmetric with respect to the propagation direction of the high intensity wave. Figure 11 shows that this heating takes place when the trajectories become “chaotic.”

Trajectories of five particles in the phase space [Px, Pz]. (A): one wave case, a = 3.922. (B): three waves case, a = 4.12.
As it was shown that stochastic heating grows with α, and the plasma density, the case of two counter propagating waves was considered. To study this specific problem, one-dimensional simulations were achieved. The laser pulses are two stepwise, 1 ps, long pulses with the same frequency. The plasma occupies a 100 μm region, the laser wave length is 1 μm and the maximum intensity is I = 1.24 × 1019 W/cm2 (a = 3) for the high intensity wave, and I = 1.38 × 1016 W/cm2 (a1 = 0.1) for the low intensity wave. The initial temperature of the plasma is 1 keV. The energy carried by all the waves was kept constant. The case when the plasma interacts with two waves is compared to the one when it interacts with one wave only. It shows that stochastic heating can be very important in the two waves case (Fig. 12)

Evolution of the plasma kinetic energy in the case of one wave and two counter propagating waves, ne = 0.01 nc(nc is the critical density).
4. CONCLUSIONS
The stability of a charged particle in the fields of one wave traveling along a constant homogeneous magnetic field or several waves propagating in nonmagnetized plasma was explored within the framework of a Hamiltonian analysis. In the first part of this paper, it was shown that the motion of one particle in a wave propagating along a magnetic field in a vacuum is integrable. When a plasma index of refraction is considered, it has been shown that the problem is nonintegrable; it becomes chaotic when a primary and a secondary resonance overlap.
Then, a high intensity plane wave propagating in nonmagnetized plasma was perturbed by one or two electromagnetic plane waves. The solution of the Hamilton–Jacobi equation was used to identify resonances. The Chirikov criterion was applied to two resonances corresponding to two or three (symmetric) perturbing waves. Stochastic heating was evidenced considering single trajectories and computing the energy of the charged particle. PIC code simulations were performed to confirm the occurrence of stochastic heating.