Published online by Cambridge University Press: 30 August 2005
Stochastic instabilities are studied considering the motion of one particle in a very high intensity wave perturbed by one or two low intensity traveling waves. Resonances are identified and conditions for resonance overlap are studied. PIC code simulation results confirm the stochastic heating.This paper was presented at the 28th ECLIM conference in Rome, Italy.
A large number of issues remain open in the study of laser-matter interaction at very high intensities. Recently, particle-in-cell (PIC) code simulations results have shown that the irradiation of very high intensity lasers on clustered matter leads to a very efficient heating of electrons (Tajima et al., 2001). They show that chaos seems to be the origin of the strong laser coupling with clusters. More recently, it was confirmed in PIC code simulations, in the case of two counter-propagating laser pulses, that stochastic heating can lead to an efficient acceleration of electrons (Sheng et al., 2002, 2004). Therefore, the issue that we will address is the stability of electron motion in the fields of several waves. We study this motion in a high intensity plane wave, perturbed by one or two electromagnetic plane waves. The solution of Hamilton-Jacobin equation is used to identify resonances. The Chirikov (1979) criterion is applied to two resonances corresponding to two symmetric perturbing waves. Above the Chirikov threshold, and for electron trajectories with their initial conditions in the overlapping region, stochastic heating is evidenced by computing single particle energies.
Finally, PIC code simulations results obtained with the code CALDER (Lefebvre et al., 2003; Pommier & Lefebvre, 2003) are presented in order to validate the theoretical model, for experimentally relevant parameters.
Let us consider a charged particle in an electromagnetic plane wave propagating along the z direction (the wave vector k0 is parallel to the z direction). The following four-potential is chosen:

where E0, ω0, and k0 are constants.
When time t is treated as a parameter entirely distinct from the spatial coordinates, the relativistic Hamiltonian of a particle in the wave is
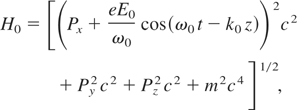
where −e, m, and Pi(i = x, y, z) are, respectively, the particle's charge, its rest mass, and its canonical momentum components. This system has three degrees of freedom. We next introduce the following dimensionless variables and parameter
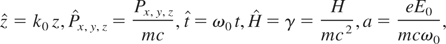
and perform the canonical transformation,
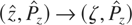
, given by the type-2 generating function:

. This canonical transformation keeps
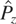
unchanged and yields:

. The new Hamiltonian expressed in terms of the new conjugate variables, is:
(Lichtenberg & Liebermann, 1983). This Hamiltonian,
are three constants of motion, which are independent and in involution. As a consequence, the system is completely integrable (Lichtenberg & Liebermann, 1983).
When using the proper time of the particle to parameterize the motion in the extended phase space, the Hamiltonian of the charged particle in the wave reads (Jackson, 1975): H0 = (1/2)mc2γ2 − (1/2m)(P + eA)2 − (1/2)mc2. When the dimensionless variables and parameter (Eq. 2) are used again, the normalized Hamiltonian is:
. A normalized proper time:
is also introduced.
Although the electron motion is not restricted to the plane of polarization of the wave (the y degree of freedom is assumed to be excited), we look for a set of actions (P⊥,P//,E) and angles (θ,φ,φ), instead of the configuration (r,t), and momentum, (P,−γ) in the
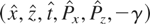
phase space. This comes out to say that we seek a canonical transformation
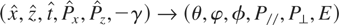
, such that the new moments are constants of motion. Following Landau and Lifshitz (1975), the following type-2 generating function is obtained (Rax, 1992)
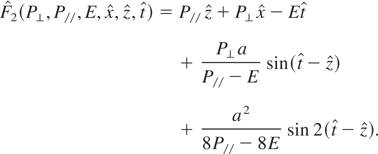
The Hamiltonian in terms of the action variables is:
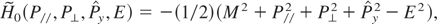
where M2 = 1 + a2/2 (Rax, 1992). As

, the energy momentum dispersion relation is given by the following expression:
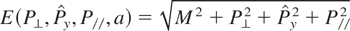
.
The solution of Hamilton-Jacobin equation is
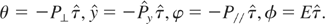
This solution is necessary to predict resonances when a perturbing mode is considered.
In this section, the stability of a charged particle in two or three linearly polarized waves is studied. One of the waves is assumed to have an ultra-high intensity. The second and third perturbing wave can represent other laser beams.
When the two waves propagate in the same direction and have the same phase velocity (V = ω0 /k0 = ω1 /k1), one still has
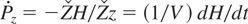
. Thus, C = H − VPz, is a first integral of the system, and consequently, the problem is integrable. When, ω0 /k0 ≠ ω1 /k1, we have shown numerically that trajectories can become chaotic. When the directions of propagation of the two waves are different, the problem is not integrable. Chaotic trajectories were also evidenced in this case.
In this article, we focus on the case of waves propagating in different directions and assume that the second and third waves are perturbing transverse electromagnetic waves.
Let us consider a transverse perturbation polarized perpendicularly to the plane of polarization of the high intensity wave. The wave vector of the perturbing mode with vector potential A1 is assumed to be at some angle α with respect to the wave vector of the high intensity wave, one has:
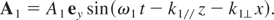
In the extended phase space, when using the proper time of the particle to parameterize the motion, the Hamiltonian of the particle can be put in the following form (Jackson, 1975; Rax, 1992)

or, neglecting terms in A12:
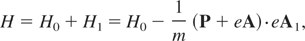
where H0 is the Hamiltonian of the system when the perturbation, H1, is neglected. We know that this problem is integrable. We chose:

.
The dimensionless variable
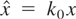
is added to the dimensionless variables and parameter defined by equations (2). They are used to normalize the equations of motion. A normalized vector potential for the perturbation A1, a1 = eA1 /mc = eE1 /mcω1, and a normalized proper time,
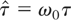
, are also introduced. The normalized Hamiltonian is given by:

, the normalized perturbing vector potential is:
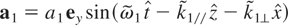
, with
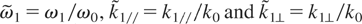
. We have assumed that

, which means that we consider that
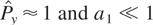
.
First, the phase,
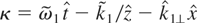
, is expressed in terms of the coordinates defined by the transformation generated by (4). We have: κ = κ′ − δ sin ζ − β sin 2ζ, with:
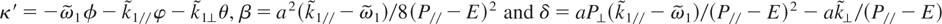
. Then, one obtains
The generalized Bessel function which is usually defined as
is introduced (Nikishov & Ritus, 1964). Letting N = (n + 2m), one obtains the Hamiltonian expressed as a sum of harmonic interactions
with VN(δ,β) = (−1)NC−N(δ,β). When the zero-order solution (4) is plugged in the argument of the perturbation sines, the stationary phase condition leads to the following resonance condition (Rax, 1992)

This resonance condition when restricted to the energy surface equation given by the following expression:
gives P⊥ versus P//. We have plotted these resonances in the case when
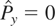
in (9). Considering that
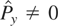
comes out to assuming a higher value of

, given by

. When
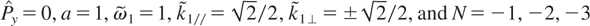
, Figure 1 shows P⊥ versus P// when the resonance condition is satisfied, for α = π/4 and α = 3π/4. The solid lines are obtained when assuming that the perturbation is such that
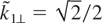
. The dashed lines correspond to the situation when

. Figure 1 shows that the lines are quite far from each other when considering one perturbing wave only. One can conclude that a second perturbing wave is necessary so that many resonances overlap. As a consequence, two perturbing waves were considered in order to define conditions when efficient stochastic heating takes place. We consider that the two wave-vectors of the perturbation are symmetric with respect to the direction of propagation of the very intense wave.

Resonances in the (P//,P⊥) plane, . (a): α = π/4, (b): α = 3π/4.
The whole numerical results obtained show that the resonance overlap seems to be easier (as the resonances get closer to each other) when
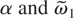
go to higher values.
In order to calculate the width of the Nth resonance, following Rax (1992), a resonant torus (P//c, P⊥c, Ec) verifying the resonance condition Eq. (9) for a certain value of N is isolated. The following new variables are introduced next:

Then, the perturbed motion is described by a one-dimensional oscillator. The half-width of this resonance is given by:
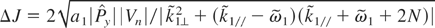
(Lichtenberg & Liebermann, 1983). Consequently, the half-width in terms of the action variables is given by
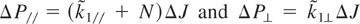
. Then, the sum of the half-widths of the two resonances N and N′, corresponding to modes with wave vectors
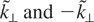
, can be calculated. The following quantities: ΔPN⊥ + ΔPN′⊥ and ΔPN// + ΔPN′// can be estimated in order to apply Chirikov criterion.
Let us consider now, the overlap of resonances N = −1 corresponding to the two modes with wave vector components
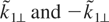
when
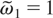
. The quantities V−1,k⊥ and V−1,−k⊥ are evaluated by using the following Taylor expansion relevant for small δ and β (Rax, 1992; Ritus, 1985): C1(δ,β) = δ/2 + δβ/4 − δ3/16. In the situations considered here, the results obtained when using this expansion are in good agreement with those obtained through a numerical evaluation of the series representation of this generalized Bessel function. The Chirikov (1979) criterion is satisfied for two resonances when their unperturbed separatices touch or overlap. In this case, a trajectory is no longer locked within one of the resonance, and it can pass from one resonance to the other. In other words the Chirikov threshold is reached when ΔP−1⊥ + ΔP−1⊥′ and is ΔP−1// + ΔP−1//′ are larger than the distance between the two resonances in term of P⊥ and P//, respectively. The values of the quantities and which are used in our numerical estimates verify the resonance condition (9).
When assuming that
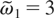
, the resonance overlap seems to be easier to achieve. Then, the most dangerous resonance is N = −3. In order to calculate the resonance half-widths of each resonance, the generalized Bessel function, C3(δ,β), is estimated through its series representation.
When
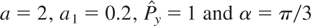
, considering P// = 0.4 and P⊥ = ±0.231, we are well above the Chirikov threshold for the resonance N = −3. Figure 2 shows the evolution of the energy of one particle in the case when it interacts with the three modes and in the case when all the intensity is in one mode. This figure shows that there is stochastic heating for realistic laser parameters.

Normalized energy of the charged particle versus time. . (α) a = 2, a1 = 0.2, (β) the total intensity is in one wave: a = 2.176, a1= 0.
The normalized vector potential is assumed to be
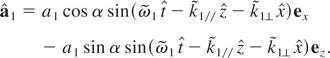
The perturbing Hamiltonian is still approximated by:
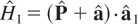
.
The same calculations as in the previous chapter were performed. The same resonance condition was obtained (Eq. 9). Stochastic heating was also evidenced considering one particle only.
PIC code simulations were performed in order to confirm stochastic heating. As we used the CALDER code in its two-dimension version, only the case when the electric fields of the perturbation are in the plane of polarization of the high intensity wave was considered (Lefebvre et al., 2003; Pommier & Lefebvre, 2003). The simulation box is 9.55 × 15.9 μm2 with homogeneous plasma. Laser parameters typical of current terawatt facilities were considered to study the influence of the angle
. The wavelength is λ0 = 1 μm, the length of the pulse is Δτ = 0.3 ps, and the maximum intensity is: I = 5.53 × 1018 W/cm2. The initial plasma temperature was assumed to be 1 keV.
First, stochastic heating was evidenced considering the energy carried by all the waves is the same in all cases. The case when the plasma interacts with three waves was compared to the one when it interacts with one wave only. Both electron temperature and total kinetic energy are higher in the cases with three waves (Fig. 3a). As the ponderomotive force is almost the same in the two situations, one can conclude that this is due to stochastic heating. The effect of stochastic heating will appear more clearly when considering two counter-propagating long pulses.

Evolution of the plasma kinetic energy. (a): ne = 0.01nc; (1): a =2, a1 = 0.1, α = 5π/6; (2): a = 2, a1 = 0.1, α = π/6; (3): one wave case, a = 2.002. (b): ne = 0.05nc; a = 2, a1 = 0.1; (1): α = 5π/6; (2): α = π/6.
Figure 3a and 3b show that stochastic heating grows with α and the plasma density. As a consequence, the best way to obtain efficient stochastic heating is to consider two counter-propagating waves. To study this specific problem, one-dimensional (1D) simulations were achieved. The laser pulses are two stepwise 1.59 ps long pulses with the same frequency. The plasma occupies a 100 μm region, the laser wave length is 1 μm and the maximum intensity for the high intensity wave is I = 1.24 × 1019 W/cm2 (a = 3), and for the low intensity wave I1 = 1.38 × 1016 W/cm2 (a1 = 0.1). The initial temperature of the plasma is still 1 keV. The energy carried by all the waves was kept constant. The case when the plasma interacts with three waves is compared to the one when it interacts with one wave only (Fig. 4). The difference between the one wave case and the two wave's case shows that stochastic heating can be very important when considering a high intensity long pulse. These results show that stochastic heating can be predicted with a plane wave approach.
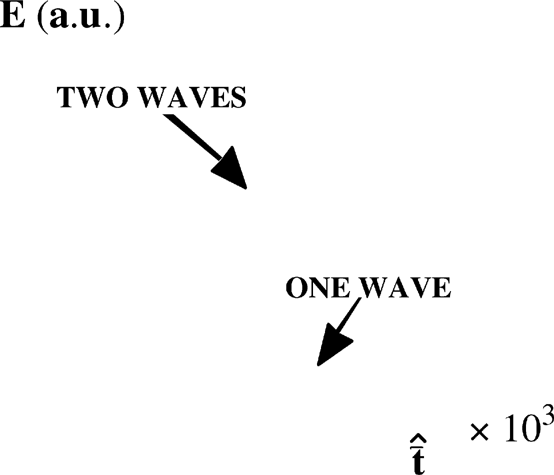
Evolution of the plasma kinetic energy in the case of one wave and two counter-propagating waves. a = 3, a1 = 0.1, ne = 0.01nc.
The dynamics of a charged particle in a high intensity linearly polarized traveling wave (above 1018 W/cm2) was investigated within the framework of a Hamiltonian analysis.
The stability of a charged particle in the fields of several waves was explored. A high intensity plane wave was perturbed by one or two electromagnetic plane waves. The solution of Hamilton-Jacobin equation was used to identify resonances. The Chirikov criterion was applied to two resonances corresponding to two symmetric perturbing waves. Stochastic heating was evidenced considering single trajectories and computing the energy of the charged particle. PIC code simulations were performed to confirm the occurrence of stochastic heating.

Resonances in the (P//,P⊥) plane, . (a): α = π/4, (b): α = 3π/4.

Normalized energy of the charged particle versus time. . (α) a = 2, a1 = 0.2, (β) the total intensity is in one wave: a = 2.176, a1= 0.

Evolution of the plasma kinetic energy. (a): ne = 0.01nc; (1): a =2, a1 = 0.1, α = 5π/6; (2): a = 2, a1 = 0.1, α = π/6; (3): one wave case, a = 2.002. (b): ne = 0.05nc; a = 2, a1 = 0.1; (1): α = 5π/6; (2): α = π/6.
Evolution of the plasma kinetic energy in the case of one wave and two counter-propagating waves. a = 3, a1 = 0.1, ne = 0.01nc.