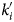Introduction
Technological development in the field of laser physics has ushered a new era where highly intense lasers are available. The interaction of these intense laser radiations with plasma has been known to produce various nonlinear phenomena such as self-focusing, self-phase modulation (SPM), harmonic generations, etc. Theoretical and experimental study of these nonlinear phenomena is an active area of research due to its importance in potential applications such as plasma-based accelerators (Sarkisov et al., Reference Sarkisov, Bychenkov, Novikov, Tikhonchuk, Maksimchuk, Chen, Wagner, Mourou and Umstadter1999), inertial confinement fusion (ICF) (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Regan et al., Reference Regan, Bradley, Chirokikh, Craxton, Meyerhofer, Seka, Short, Simon, Town and Yaakobi1999), ionospheric modification (Guzdar et al., Reference Guzdar, Chaturvedi, Papadopoulos and Ossakow1998; Gondarenko et al., Reference Gondarenko, Ossakow and Milikh2005), and other applications (Askar'yan, Reference Askar'yan1962; Parashar et al., Reference Parashar, Pandey and Tripathi1997; Honda et al., Reference Honda, Meyer-Ter-Vehn and Pukhov2000; Liu and Tripathi, Reference Liu and Tripathi2001; Mulser and Bauer, Reference Mulser and Bauer2004; Gupta and Suk, Reference Gupta and Suk2007; Hora, Reference Hora2007; Winterberg, Reference Winterberg2008; Uhm et al., Reference Uhm, Nam and Suk2012). In order to practically realize these applications, it is important that a laser beam should propagate hundreds of Rayleigh lengths. The development of high-intensity laser beams makes the investigations of such nonlinear effects feasible. When high power intense laser beam/pulse propagates through a plasma medium, many instabilities and nonlinear phenomena such as the SPM, the filamentation instability, the group velocity dispersion (GVD), the finite pulse effects, and the relativistic and ponderomotive self-focusing effects, become important. Therefore, it is important to study analytically and numerically some of these effects. This leads us to understand physical insight of basic and fundamental processes.
Among the fundamental processes, the self-focusing and self-trapping are genuinely nonlinear phenomena which have become a fascinating field in the modern plasma physics research. For the first time, these two mechanisms were reported by Askar'yan (Reference Askar'yan1962) and Chiao et al. (Reference Chiao, Garmire and Townes1964), respectively, and had been focus of attention for nearly five decades because of their relevance to a number of newly discovered processes. The self-focusing is a process in which a beam of light comes to focus as consequences of a nonlinear response of a material medium. In a nonlinear medium, a high power electromagnetic beam creates a refractive index profile across its cross-section corresponding to its own intensity profile. The refractive index of the medium increases with the beam intensity. As a result, the beam focuses of its own. In laser–plasma interaction, the generic process of the self-focusing of laser beams (Chiao et al., Reference Chiao, Garmire and Townes1964; Kelley, Reference Kelley1965; Sodha et al., Reference Sodha, Ghatak and Tripathi1974, Reference Sodha, Ghatak and Tripathi1976; Milchberg et al., Reference Milchberg, Durfee III and Mcllrath1995; Saini and Gill, Reference Saini and Gill2006; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007; Gill et al., Reference Gill, Kaur and Mahajan2010a, Reference Gill, Mahajan and Kaur2010b, Reference Gill, Mahajan and Kaur2010c, Reference Gill, Mahajan and Kaur2011; Kaur et al., Reference Kaur, Gill and Mahajan2010, Reference Kaur, Gill and Mahajan2011; Mahajan et al., Reference Mahajan, Gill and Kaur2010) has been focus of attention as it affects many other nonlinear processes. It plays crucial role in the beam propagation.
The self-focusing of laser beams in different plasma environments using a fundamental Gaussian beam has been confined mostly to the classical regimes. With the advent of ultra-high-intensity laser pulses, the study of laser–plasma interactions has undergone a paradigm shift. The relativistic nonlinearity is a fundamental nonlinear effect which occurs in highly intense field. This nonlinearity is particularly interesting when laser power is sufficiently large. The electric field associated with high power laser pulses leads to a quiver motion of electrons of the order of the speed of light in vacuum. The quiver motion of electrons leads to their expulsion from the region of high intensity. The expulsion due to ponderomotive force sets up a space charge field that retards electrons and eventually a quasi-steady state is reached. The effect of quiver motion of electrons modifies the refractive index. The transverse gradient of the nonlinear refractive index is responsible for the relativistic self-focusing (Zhou et al., Reference Zhou, Wang, Yuan and Du2011; Patil et al., Reference Patil, Takale, Navare and Dongare2012; Niknam et al., Reference Niknam, Barzegar and Hashemzadeh2013; Bokaei and Niknam, Reference Bokaei and Niknam2014). The relativistic self-focusing is counterbalanced by the tendency of the beam to spread because of diffraction. In the absence of nonlinearities, the beam will spread substantially in a Rayleigh length, R d (~![]() $ka_0^2 $), where k is the wavenumber and a 0 is the spot size of laser beam.
$ka_0^2 $), where k is the wavenumber and a 0 is the spot size of laser beam.
The relativistic self-focusing is not limited to low density and high temperature plasma. Last decades have witnessed an increasing interest in propagation of laser beams in dense plasmas where the quantum effects are important (Manfredi, Reference Manfredi2005; Shukla et al., Reference Shukla, Ali, Stenflo and Marklund2006; Shukla and Eliasson, Reference Shukla and Eliasson2010, Reference Shukla and Eliasson2011; Haas, Reference Haas2011; Habibi and Ghamari, Reference Habibi and Ghamari2012a, Reference Habibi and Ghamari2012b, Reference Habibi and Ghamari2015a, Reference Habibi and Ghamari2015b; Patil and Takale, Reference Patil and Takale2013; Patil et al., Reference Patil, Takale, Navare, Fulari and Dongare2013a, Reference Patil, Takale, Navare, Dongare and Fulari2013b). The combined effects of the relativistic variation of mass and quantum correction would significantly change the dielectric function and hence modify the nonlinear behavior of electromagnetic wave (EMW) propagation in the quantum plasmas. In principle, the classical plasma is identified by virtue of high temperature and low density, while the quantum plasma is characterized by high density and low temperature (Shukla and Eliasson, Reference Shukla and Eliasson2010, Reference Shukla and Eliasson2011). The parameter χ = T F/T is often used to characterize the relevance of quantum effects. Here T F is the Fermi temperature and T is the corresponding plasma temperature. For χ ≥ 1, the quantum effects are dominant and Fermi–Dirac distribution statistics is relevant for description of plasma. The quantum effects can also be measured by the thermal de-Broglie wavelength ![]() $\lambda _{\rm B} = \hbar /((m_{\rm e}k_{\rm B}T)^{1/2})$ where
$\lambda _{\rm B} = \hbar /((m_{\rm e}k_{\rm B}T)^{1/2})$ where ![]() $\hbar $ is the rationalized Planck's constant, k B is the Boltzmann constant, and m e is the electron mass. Here λB is the measure of spatial extension of the particle wave function. Thus, the quantum effects are relevant when λB of the electrons is equal or greater than the average inter-electron distance
$\hbar $ is the rationalized Planck's constant, k B is the Boltzmann constant, and m e is the electron mass. Here λB is the measure of spatial extension of the particle wave function. Thus, the quantum effects are relevant when λB of the electrons is equal or greater than the average inter-electron distance ![]() $n_{\rm e}^{ - 1/3} $. Further in the classical regime, λB is small enough to ignore the overlapping of wave functions and quantum interferences. Eliasson and Shukla (Reference Eliasson and Shukla2012) have presented a quantum relativistic model for nonlinear interaction between the large amplitude waves and quantum plasmas. The relativistic effects in such plasmas arise due to an increase in fermion number density in the case of degenerate plasma and influence the dynamics of high power EMWs. The plasma dielectric function for an unmagnetized and collisionless electron quantum plasma including the fermion gas pressure and Bohm potential has been derived by Ali and Shukla (Reference Ali and Shukla2006). Na and Jung (Reference Na and Jung2009) extended this model to study the ponderomotive magnetization in quantum plasma. The significant research work on different aspects of nonlinear wave propagation in quantum plasmas has been reported (Kremp et al., Reference Kremp, Bornath, Bonitz and Schlanges1999; Andreev, Reference Andreev2000; Azechi and FIREX Project, Reference Azechi2006; Marklund and Shukla, Reference Marklund and Shukla2006; Shukla et al., Reference Shukla, Ali, Stenflo and Marklund2006; Shukla and Eliasson, Reference Shukla and Eliasson2007; Glenzer and Redmer, Reference Glenzer and Redmer2009). With the progress in technology of short-pulse and high-intensity radiation, creation and diagnosis of dense quantum plasmas with X-ray-free electron lasers (FELs) and modern high power lasers is possible (Peyrusse et al., Reference Peyrusse, Busquet, Kieffer, Jiang and Cote1995; Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001; Neumayer et al., Reference Neumayer, Gregori, Ravasio, Koenig, Price, Widmann, Bastea, Landen and Glenzer2006; Vinko et al., Reference Vinko, Ciricosta, Cho, Engelhorn, Chung, Brown, Burian, Chalpusky, Falcone, Graves, Hajkova, Higginbotham, Juha, Krzywinski, Lee, Messerschmidt, Murphy, Ping, Scherz, Schlotter, Toleikis, Turner, Vysin, Wang, Wu, Zastrau, Zhu, Lee, Heimann, Nagler and Wark2012). Powerful X-ray sources (Landen et al., Reference Landen, Farley, Glendinning, Logory, Bell, Koch, Lee, Bradley, Kalantar, Back and Tarner2001; Lee et al., Reference Lee, Moon, Chung, Rozmus, Baldis, Gregori, Cauble, Landen, Wark, Ng, Rose, Lewis, Riley, Gauthier and Audebert2003; Faenov et al., Reference Faenov, Colgan, Hansen, Zhidkov, Pikuz, Nishiuchi, Pikuz, Skobelev, Abdallah, Sakaki, Sagisaka, Pirozhkov, Ogura, Fukuda, Kanasaki, Hasegawa, Nishikino, Kando, Watanabe, Kawachi, Masuda, Hosokai, Kodama and Kondo2015) replaced the optical lasers in penetrating dense or compressed matter and access the dense plasma physics regimes with electron density of the solid. Kodama et al. (Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001) have reported that in laser-driven implosion of spherical polymer shells, an increase in density of 1000 times relative to the solid state (Azechi et al., Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi, Yamanaka and Yamanaka1991) has been achieved. These densities are large enough to enable controlled fusion provided the compressed fuel is heated to a temperature of about 108 K. The X-ray-FELs explore matter on the scale of a few angstroms and the quantum effects which play an important role in the degenerate electron gas and the warm dense matter (Glenzer et al., Reference Glenzer, Landen, Neumayer, Lee, Widmann, Pollaine, Wallace, Gregori, Höll, Bornath, Thiele, Schwarz, Kraeft and Redmer2007; Glenzer and Redmer, Reference Glenzer and Redmer2009; Neumayer et al., Reference Neumayer, Fortmann, Döppner, Davis, Falcone, Kritcher, Landen, Lee, Lee, Niemann, Le Pape and Glenzer2010) have been measured experimentally. The quantum plasmas are encountered in many environments such as in quantum dots (Shpatakovskaya, Reference Shpatakovskaya2006), astrophysical systems (Opher et al., Reference Opher, Silva, Dauger, Decyk and Dawson2001), and neutron stars (Chabrier et al., Reference Chabrier, Douchin and Potekhin2002). Further, it has been recognized that the quantum mechanical effects play an important role in the intense laser solid density plasma interaction experiments (Andreev, Reference Andreev2000; Marklund and Shukla, Reference Marklund and Shukla2006; Mourou et al., Reference Mourou, Tajima and Bulanov2006). It has been noticed that X-ray lasers and the FELs also undergo compression (Malkin and Fisch, Reference Malkin and Fisch2007; Malkin et al., Reference Malkin, Fisch and Wurtele2007). Propagation losses, deflection, and critical issues of relativistic ultra-intense laser–plasma interactions along with energy transport from interaction region to core plasma are the key issues of ICF-related research (Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001; Lindl et al., Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter2004; Azechi and FIREX Project, Reference Azechi2006; Remington et al., Reference Remington, Drake and Ryutov2006).
$n_{\rm e}^{ - 1/3} $. Further in the classical regime, λB is small enough to ignore the overlapping of wave functions and quantum interferences. Eliasson and Shukla (Reference Eliasson and Shukla2012) have presented a quantum relativistic model for nonlinear interaction between the large amplitude waves and quantum plasmas. The relativistic effects in such plasmas arise due to an increase in fermion number density in the case of degenerate plasma and influence the dynamics of high power EMWs. The plasma dielectric function for an unmagnetized and collisionless electron quantum plasma including the fermion gas pressure and Bohm potential has been derived by Ali and Shukla (Reference Ali and Shukla2006). Na and Jung (Reference Na and Jung2009) extended this model to study the ponderomotive magnetization in quantum plasma. The significant research work on different aspects of nonlinear wave propagation in quantum plasmas has been reported (Kremp et al., Reference Kremp, Bornath, Bonitz and Schlanges1999; Andreev, Reference Andreev2000; Azechi and FIREX Project, Reference Azechi2006; Marklund and Shukla, Reference Marklund and Shukla2006; Shukla et al., Reference Shukla, Ali, Stenflo and Marklund2006; Shukla and Eliasson, Reference Shukla and Eliasson2007; Glenzer and Redmer, Reference Glenzer and Redmer2009). With the progress in technology of short-pulse and high-intensity radiation, creation and diagnosis of dense quantum plasmas with X-ray-free electron lasers (FELs) and modern high power lasers is possible (Peyrusse et al., Reference Peyrusse, Busquet, Kieffer, Jiang and Cote1995; Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001; Neumayer et al., Reference Neumayer, Gregori, Ravasio, Koenig, Price, Widmann, Bastea, Landen and Glenzer2006; Vinko et al., Reference Vinko, Ciricosta, Cho, Engelhorn, Chung, Brown, Burian, Chalpusky, Falcone, Graves, Hajkova, Higginbotham, Juha, Krzywinski, Lee, Messerschmidt, Murphy, Ping, Scherz, Schlotter, Toleikis, Turner, Vysin, Wang, Wu, Zastrau, Zhu, Lee, Heimann, Nagler and Wark2012). Powerful X-ray sources (Landen et al., Reference Landen, Farley, Glendinning, Logory, Bell, Koch, Lee, Bradley, Kalantar, Back and Tarner2001; Lee et al., Reference Lee, Moon, Chung, Rozmus, Baldis, Gregori, Cauble, Landen, Wark, Ng, Rose, Lewis, Riley, Gauthier and Audebert2003; Faenov et al., Reference Faenov, Colgan, Hansen, Zhidkov, Pikuz, Nishiuchi, Pikuz, Skobelev, Abdallah, Sakaki, Sagisaka, Pirozhkov, Ogura, Fukuda, Kanasaki, Hasegawa, Nishikino, Kando, Watanabe, Kawachi, Masuda, Hosokai, Kodama and Kondo2015) replaced the optical lasers in penetrating dense or compressed matter and access the dense plasma physics regimes with electron density of the solid. Kodama et al. (Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001) have reported that in laser-driven implosion of spherical polymer shells, an increase in density of 1000 times relative to the solid state (Azechi et al., Reference Azechi, Jitsuno, Kanabe, Katayama, Mima, Miyanaga, Nakai, Nakai, Nakaishi, Nakatsuka, Nishiguchi, Norrays, Setsuhara, Takagi, Yamanaka and Yamanaka1991) has been achieved. These densities are large enough to enable controlled fusion provided the compressed fuel is heated to a temperature of about 108 K. The X-ray-FELs explore matter on the scale of a few angstroms and the quantum effects which play an important role in the degenerate electron gas and the warm dense matter (Glenzer et al., Reference Glenzer, Landen, Neumayer, Lee, Widmann, Pollaine, Wallace, Gregori, Höll, Bornath, Thiele, Schwarz, Kraeft and Redmer2007; Glenzer and Redmer, Reference Glenzer and Redmer2009; Neumayer et al., Reference Neumayer, Fortmann, Döppner, Davis, Falcone, Kritcher, Landen, Lee, Lee, Niemann, Le Pape and Glenzer2010) have been measured experimentally. The quantum plasmas are encountered in many environments such as in quantum dots (Shpatakovskaya, Reference Shpatakovskaya2006), astrophysical systems (Opher et al., Reference Opher, Silva, Dauger, Decyk and Dawson2001), and neutron stars (Chabrier et al., Reference Chabrier, Douchin and Potekhin2002). Further, it has been recognized that the quantum mechanical effects play an important role in the intense laser solid density plasma interaction experiments (Andreev, Reference Andreev2000; Marklund and Shukla, Reference Marklund and Shukla2006; Mourou et al., Reference Mourou, Tajima and Bulanov2006). It has been noticed that X-ray lasers and the FELs also undergo compression (Malkin and Fisch, Reference Malkin and Fisch2007; Malkin et al., Reference Malkin, Fisch and Wurtele2007). Propagation losses, deflection, and critical issues of relativistic ultra-intense laser–plasma interactions along with energy transport from interaction region to core plasma are the key issues of ICF-related research (Kodama et al., Reference Kodama, Norreys, Mima, Dangor, Evans, Fujita, Kitagawa, Krushelnick, Miyakoshi, Miyanaga, Norimatsu, Rose, Shozaki, Shigemori, Sunahara, Tampo, Tanaka, Toyama, Yamanaka and Zepf2001; Lindl et al., Reference Lindl, Amendt, Berger, Glendinning, Glenzer, Haan, Kauffman, Landen and Suter2004; Azechi and FIREX Project, Reference Azechi2006; Remington et al., Reference Remington, Drake and Ryutov2006).
During the past few years, theoretical work on the quantum plasmas has staged an impressive comeback due to their tendency to behave as an active nonlinear medium. Ali and Shukla (Reference Ali and Shukla2006) presented analytical and numerical studies of potential distributions around a moving test charge in quantum plasmas. They used quantum hydrodynamic (QHD) and Poisson equations to obtain the potential, which depends on the dielectric susceptibility of quantum plasmas. Ren et al. (Reference Ren, Wu and Chu2007) derived the dispersion relation of linear waves in uniform cold quantum plasma (CQP) using the QHD with the magnetic field of the Wigner–Poisson system. The quantum effects on the magnetization due to ponderomotive force are investigated by Jung and Murakami (Reference Jung and Murakami2009). The results showed that the quantum effects cause the magnetization and cyclotron motion in quantum plasmas. The temperature effects on the nonstationary Karpman–Washimi ponderomotive magnetization are investigated in quantum Fermi plasmas by Na and Jung (Reference Na and Jung2009). It has been observed that the frequency dependence on the ponderomotive magnetization diminishes with an increase in the Fermi temperature. Hefferon et al. (Reference Hefferon, Sharma and Kourakis2010) studied the beam dynamics of a Gaussian laser pulse propagating through quantum plasma. They applied a quantum fluid model and Maxwell's equations for the beam dynamics and the quantum dielectric response (Jung and Murakami, Reference Jung and Murakami2009; Na and Jung, Reference Na and Jung2009) to derive a nonlinear Schrödinger equation for the electromagnetic (EM) field envelope. The results showed a longitudinal compression and stronger beam localization due to quantum effects. Habibi and Ghamari (Reference Habibi and Ghamari2012a) studied the self-focusing of an electromagnetic Gaussian beam in an inhomogeneous CQP. A better self-focusing with higher oscillations is obtained because of the quantum effects and upward density profile. In addition to the ramp density profile, the role of relativistic nonlinearity on nonstationary self-focusing of intense laser beam in the CQP has been reported in another investigation (Habibi and Ghamari, Reference Habibi and Ghamari2012b). Stronger self-focusing at the rear part of the pulse is obtained. Further, Patil et al. (Reference Patil, Takale, Navare, Fulari and Dongare2013a, Reference Patil, Takale, Navare, Dongare and Fulari2013b) have studied the self-focusing of a Gaussian laser beam in the relativistic cold quantum (RCQ) plasma. Additional self-focusing using the CQP has been observed in comparison with the classical relativistic (CR) case. Similar results were reported by the relativistic self-focusing of a Gaussian laser beam in collisional quantum plasma by Zare et al. (Reference Zare, Rezaee, Yazdani, Anvari and Sadighi-Bonabi2015). Improved focusing of a cosh-Gaussian laser beam in the CQP using higher order paraxial ray approximation (PRA) is presented in a recent investigation by Habibi and Ghamari (Reference Habibi and Ghamari2015a). Further, they studied the significant enhancement in the relativistic self-focusing of a cosh-Gaussian laser beam in dense plasmas using the ramp density profile (Habibi and Ghamari, Reference Habibi and Ghamari2015b). They used modified refractive index of an inhomogeneous CQP with quantum correction in the relativistic regime. In relatively recent studies, the stationary self-focusing of a Gaussian laser beam in the relativistic thermal quantum plasma (TQP) has been studied in detail (Patil and Takale, Reference Patil and Takale2013). Patil and Takale (Reference Patil and Takale2014) further provided the evidence of strong self-focusing in the TQP as compared with the case of the CQP. The relativistic self-focusing of ultra-high-intensity X-ray laser beams using upward density profile in the warm quantum plasma is reported by Habibi and Ghamari (Reference Habibi and Ghamari2014). It is observed that the quantum effects enhance the self-focusing of laser beams.
There are several approximate analytical approaches to describe the effects of self-focusing such as the PRA (Sodha et al., Reference Sodha, Ghatak and Tripathi1974, Reference Sodha, Ghatak and Tripathi1976), the moment theory approach (Firth, Reference Firth1977; Lam et al., Reference Lam, Lippmann and Tappert1977), and the source-dependent expansion (SDE) method (Sprangle et al., Reference Sprangle, Hafizi and Penano2000). Each of these theories has limitations in describing completely the experimental/computer simulation results. Most of the investigations related to the self-focusing are based on Wentzel–Kramers–Brillouin (WKB) approximation and PRA given by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and developed by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976). This theory being local in character overemphasizes the field closest to the beam axis and lacks global pulse dynamics. Furthermore, it also predicts the unphysical phase relationship (Karlsson et al., Reference Karlsson, Anderson, Desaix and Lisak1991). However, study of certain moments is done by the moment theory approach. The moment theory is not applicable for the beams of all types of irradiance and it also lacks the phase description. It has also been pointed out that the PRA is not applicable when high power laser beams are used (Subbarao et al., Reference Subbarao, Uma and Singh1998). Another global approach is the variational approach (Firth, Reference Firth1977; Anderson and Bonnedal, Reference Anderson1979), though crude to describe the singularity formation and collapse dynamics, it is fairly general in nature to study the propagation of laser beam and also correctly predicts the phase.
Several research investigations on the self-focusing of laser beams have been confined to the cylindrically symmetric Gaussian beams symmetry (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997; Sharma et al., Reference Sharma, Verma and Sodha2004), a very few have been reported on Hermite-sinusoidal-Gaussian (HSG) laser beams in the turbulent atmosphere (Baykal, Reference Baykal2004), Hermite–Gaussian beams (Takale et al., Reference Takale, Navare, Patil, Fulari and Dongare2009), and Hermite-cosh-Gaussian (HChG) laser beams (Belafhal and Ibnchaikh, Reference Belafhal and Ibnchaikh2000; Patil et al., Reference Patil, Takale, Fulari, Gupta and Suk2010). Apart from these, great interest has been evinced in the cosh-Gaussian beams. This is due to the fact that the propagation properties of the cosh-Gaussian laser beams have important technological issues as these beams possess high power in comparison with that of a circular Gaussian laser beam. A review of the literature highlights the fact that the propagation characteristics of the cosh-Gaussian laser beams in the TQP have not been studied to a significant extent. The objective of the present research work is to investigate the self-focusing of a cosh-Gaussian laser beam in the relativistic TQP by making use of the variational approach.
This paper has been structured as follows: in the section Basic formulation, a brief description of the effective plasma permittivity is given and the evolution equations governing the beam width parameter and the longitudinal phase are derived. In the section Self-trapping, authors have studied the self-trapped mode, and the section Numerical results and discussion is devoted to discussion. The stability characteristics of cosh-Gaussian laser beams are studied in the section Stability criterion of beam dynamics. Conclusions of the present analysis are presented in the last section.
Basic formulation
The present model is set up in an unmagnetized and collisionless TQP considering the relativistic nonlinearity. Assuming wave propagation in the z − direction, the electric vector of laser beam E satisfies the following wave equation:
which may be derived directly from Maxwell's equations by neglecting the term ![]() $\nabla (\nabla \times E)$. The effective dielectric constant of homogeneous gaseous plasma can be expressed as:
$\nabla (\nabla \times E)$. The effective dielectric constant of homogeneous gaseous plasma can be expressed as:
where ![]() ${\rm \epsilon} _0 = 1 - (\omega _{\rm p}^2 /\omega ^2)$ and Φ are the linear and nonlinear parts of the dielectric constant respectively.
${\rm \epsilon} _0 = 1 - (\omega _{\rm p}^2 /\omega ^2)$ and Φ are the linear and nonlinear parts of the dielectric constant respectively. ![]() $\omega _{\rm p}^2 = 4\pi n_0e^2/m_0$ is the plasma frequency and e and m 0 are charge and rest mass of electron, respectively.
$\omega _{\rm p}^2 = 4\pi n_0e^2/m_0$ is the plasma frequency and e and m 0 are charge and rest mass of electron, respectively.
Starting by considering the dielectric constant in an unmagnetized and collisionless electron quantum plasmas including the Fermi gas pressure term as well as the Bohm potential effect caused by the collective interactions (Ali and Shukla, Reference Ali and Shukla2006; Na and Jung, Reference Na and Jung2009):
where ![]() $\beta = k^2v_{{\rm Fe}}^2 /\omega ^2$,
$\beta = k^2v_{{\rm Fe}}^2 /\omega ^2$, ![]() $v_{{\rm Fe}} = \surd (2k_{\rm B}T_{{\rm Fe}}/m_0)$ is the Fermi speed,
$v_{{\rm Fe}} = \surd (2k_{\rm B}T_{{\rm Fe}}/m_0)$ is the Fermi speed, ![]() $\delta = 4\pi ^4h^2/m_0^2 \omega ^2\lambda ^4$,
$\delta = 4\pi ^4h^2/m_0^2 \omega ^2\lambda ^4$, ![]() $\gamma = \surd 1 + \alpha EE^ * $ is the relativistic factor with
$\gamma = \surd 1 + \alpha EE^ * $ is the relativistic factor with ![]() $\alpha = e^2/m_0^2 \omega ^2c^2$, and λ is the wavelength of the laser used. It may be mentioned that simple expressions can be found only in the limiting cases: T ≫ T Fe (corresponding to the classical regime) and T ≪ T Fe (corresponding to the fully degenerate quantum plasma case). A smooth transition cannot be achieved in a straightforward manner (Manassah et al., Reference Manassah, Baldeck and Alfano1988) using dimensional arguments. However, the thermal speed becomes meaningless in very low temperature limit and should be replaced by the Fermi velocity. The nonlinear part of the dielectric constant can be written as:
$\alpha = e^2/m_0^2 \omega ^2c^2$, and λ is the wavelength of the laser used. It may be mentioned that simple expressions can be found only in the limiting cases: T ≫ T Fe (corresponding to the classical regime) and T ≪ T Fe (corresponding to the fully degenerate quantum plasma case). A smooth transition cannot be achieved in a straightforward manner (Manassah et al., Reference Manassah, Baldeck and Alfano1988) using dimensional arguments. However, the thermal speed becomes meaningless in very low temperature limit and should be replaced by the Fermi velocity. The nonlinear part of the dielectric constant can be written as:
 $$\Phi (EE^ {^\ast} ) = \displaystyle{{\omega _{\rm p}^2} \over {\omega ^2}}\left[ {1 - \displaystyle{1 \over \gamma} {\left( {1 - \displaystyle{\delta \over \gamma} - \beta} \right)}^{ - 1}} \right]$$
$$\Phi (EE^ {^\ast} ) = \displaystyle{{\omega _{\rm p}^2} \over {\omega ^2}}\left[ {1 - \displaystyle{1 \over \gamma} {\left( {1 - \displaystyle{\delta \over \gamma} - \beta} \right)}^{ - 1}} \right]$$The amplitude of the electric field of laser beam is given by:
where ψ(r, z) is a complex function of its argument. Substituting the above expression for E into Eq. (1), one may neglect ∂2ψ/∂z 2 and obtain the envelop equation governing the propagation of the beam in nonlinear media as shown below:
 $$\eqalign{\left[ { - 2\iota k\displaystyle{\partial \over {\partial z}} + \nabla_ \bot^2 + \displaystyle{{\omega^2} \over {c^2}}\left( {\displaystyle{{\omega_{\rm p}^2} \over {\omega^2}}\left( {1 - \displaystyle{1 \over \gamma} {\left( {1 - \displaystyle{\delta \over \gamma} - \beta} \right)}^{ - 1}} \right)} \right)} \right]\psi (r,z) = 0$$
$$\eqalign{\left[ { - 2\iota k\displaystyle{\partial \over {\partial z}} + \nabla_ \bot^2 + \displaystyle{{\omega^2} \over {c^2}}\left( {\displaystyle{{\omega_{\rm p}^2} \over {\omega^2}}\left( {1 - \displaystyle{1 \over \gamma} {\left( {1 - \displaystyle{\delta \over \gamma} - \beta} \right)}^{ - 1}} \right)} \right)} \right]\psi (r,z) = 0$$where ![]() $\nabla _ \bot ^2 = \displaystyle{{\partial ^2} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}$.
$\nabla _ \bot ^2 = \displaystyle{{\partial ^2} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}$.
Equation (5) is a nonlinear parabolic partial differential equation. The variational approach, which has rigorous basis, is employed here to investigate nonlinear wave propagation. The exact solution to Eq. (5) is not available and we therefore seek numerical or approximate analytical methods. Further, we choose the latter using a powerful variational method that has been used in several similar investigations (Anderson and Bonnedal, Reference Anderson1979; Gill et al., Reference Gill, Kaur and Mahajan2010a, Reference Gill, Mahajan and Kaur2010b, Reference Gill, Mahajan and Kaur2011; Kaur et al., Reference Kaur, Gill and Mahajan2010, Reference Kaur, Gill and Mahajan2011; Mahajan et al., Reference Mahajan, Gill and Kaur2010). Following the procedure of Anderson and Bonnedal (Reference Anderson1979), we reformulate Eq. (5) into a variational problem corresponding to a Lagrangian L to make (δL/δz) = 0. Solving Eq. (5) is equivalent to making a certain function an extremum. Lagrangian L corresponding to Eq. (5) is given by:
 $$\eqalign{L & = \iota k\left( {\psi \displaystyle{{\partial \psi^ {^\ast}} \over {\partial z}} - \psi^ {^\ast} \displaystyle{{\partial \psi} \over {\partial z}}} \right) - \left[ {\left \vert {\displaystyle{{\partial \psi} \over {\partial r}}} \right \vert} \right]^2 \cr & \quad\, + \displaystyle{{\omega _{\rm p}^2} \over {c^2}}\left[ { - (\delta + \beta )\alpha \vert \psi \vert^2 + 0.5(\alpha \vert \psi \vert^2)^2\left( {\delta - \displaystyle{1 \over 2}} \right)} \right. \cr & \quad\,\, \left. { + \displaystyle{\beta \over 4}{(\alpha \vert \psi \vert^2)}^2 - \displaystyle{1 \over {12}}\delta {(\alpha \vert \psi \vert^2)}^3} \right]} $$
$$\eqalign{L & = \iota k\left( {\psi \displaystyle{{\partial \psi^ {^\ast}} \over {\partial z}} - \psi^ {^\ast} \displaystyle{{\partial \psi} \over {\partial z}}} \right) - \left[ {\left \vert {\displaystyle{{\partial \psi} \over {\partial r}}} \right \vert} \right]^2 \cr & \quad\, + \displaystyle{{\omega _{\rm p}^2} \over {c^2}}\left[ { - (\delta + \beta )\alpha \vert \psi \vert^2 + 0.5(\alpha \vert \psi \vert^2)^2\left( {\delta - \displaystyle{1 \over 2}} \right)} \right. \cr & \quad\,\, \left. { + \displaystyle{\beta \over 4}{(\alpha \vert \psi \vert^2)}^2 - \displaystyle{1 \over {12}}\delta {(\alpha \vert \psi \vert^2)}^3} \right]} $$Thus, the solution to the variational problem
also solves the nonlinear Schrödinger Eq. (5). We use the cosh-Gaussian field distribution ansatz for the amplitude ψ as trial function:
 $$\eqalign{\psi (r,z) & = \displaystyle{{\psi _0(z)} \over 2}\hbox{exp}\left( {\displaystyle{{b^2} \over 4} - 2k_iz} \right) \cr & \quad \times \left( {\hbox{exp}\left[ { - {\left( {\displaystyle{r \over {a(z)}} + \displaystyle{b \over 2}} \right)}^2} \right] + \hbox{exp}\left[ { - {\left( {\displaystyle{r \over {a(z)}} - \displaystyle{b \over 2}} \right)}^2} \right]} \right) \cr & \quad \times \hbox{exp}(\iota {q}^{\prime}(z)r^2 + \iota \phi (z))} $$
$$\eqalign{\psi (r,z) & = \displaystyle{{\psi _0(z)} \over 2}\hbox{exp}\left( {\displaystyle{{b^2} \over 4} - 2k_iz} \right) \cr & \quad \times \left( {\hbox{exp}\left[ { - {\left( {\displaystyle{r \over {a(z)}} + \displaystyle{b \over 2}} \right)}^2} \right] + \hbox{exp}\left[ { - {\left( {\displaystyle{r \over {a(z)}} - \displaystyle{b \over 2}} \right)}^2} \right]} \right) \cr & \quad \times \hbox{exp}(\iota {q}^{\prime}(z)r^2 + \iota \phi (z))} $$where a(z) is the beam width of the Gaussian amplitude distribution, ψ 0 is the amplitude at the central position, k i is the absorption coefficient, b the decentered parameter, also termed the normalized modal parameter, q′(z) is the spatial chirp, and ϕ(z) is the phase of laser beam. Using the expression for ψ as trial function into the Lagrangian L of Eq. (6) and after integrating L, we obtain:
The reduced variational problem is obtained by solving the integration in Eq. (9) using some standard integrals to get:
 $$\eqalign{\lt L \gt & = \displaystyle{{\iota ka\surd \pi } \over {8\surd 2}}e^{ - 4k_iz}(b^2 + 8)\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) \cr & \quad + \displaystyle{{k \vert \psi _0 \vert ^2} \over {32\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^3\surd \pi e^{ - 4k_iz}(b^2 + 8) \cr & \quad + \displaystyle{{k \vert \psi _0 \vert ^2} \over {4\surd 2}}\displaystyle{{d\phi } \over {dz}}a\surd \pi e^{ - 4k_iz}(b^2 + 8) \cr & \quad - \displaystyle{{ \vert \psi _0 \vert ^2} \over {4\surd 2}}e^{ - 4k_iz}\surd \pi \left[ {\displaystyle{2 \over a} + \displaystyle{{b^4} \over {2a}} + 2{{q}^{\prime}}^2a^3 + \displaystyle{{{{q}^{\prime}}^2b^2a^3} \over 4}} \right.\left. { - \displaystyle{{7b^2} \over {4a}}} \right] \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {8\surd 2}}(\delta + \beta )e^{ - 4k_iz}\surd \pi (b^2 + 8) \cr & \quad + \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 8k_iz}\surd \pi (b^2 + 8) \cr & \quad + \displaystyle{{\omega _{\rm p}^{\rm 2} } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ - {{b^2} \over 2} - 8k_iz}\surd \pi (b^2 + 8) \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 12k_iz}\surd \pi \left( {\displaystyle{{10} \over {\surd 6}} + \displaystyle{{1.5b^2} \over {\surd 6}}} \right) \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 12k_iz}\surd \pi \left( {\displaystyle{3 \over {\surd 6}} + 6 + \displaystyle{{3b^2} \over 4}} \right)} $$
$$\eqalign{\lt L \gt & = \displaystyle{{\iota ka\surd \pi } \over {8\surd 2}}e^{ - 4k_iz}(b^2 + 8)\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) \cr & \quad + \displaystyle{{k \vert \psi _0 \vert ^2} \over {32\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^3\surd \pi e^{ - 4k_iz}(b^2 + 8) \cr & \quad + \displaystyle{{k \vert \psi _0 \vert ^2} \over {4\surd 2}}\displaystyle{{d\phi } \over {dz}}a\surd \pi e^{ - 4k_iz}(b^2 + 8) \cr & \quad - \displaystyle{{ \vert \psi _0 \vert ^2} \over {4\surd 2}}e^{ - 4k_iz}\surd \pi \left[ {\displaystyle{2 \over a} + \displaystyle{{b^4} \over {2a}} + 2{{q}^{\prime}}^2a^3 + \displaystyle{{{{q}^{\prime}}^2b^2a^3} \over 4}} \right.\left. { - \displaystyle{{7b^2} \over {4a}}} \right] \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {8\surd 2}}(\delta + \beta )e^{ - 4k_iz}\surd \pi (b^2 + 8) \cr & \quad + \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 8k_iz}\surd \pi (b^2 + 8) \cr & \quad + \displaystyle{{\omega _{\rm p}^{\rm 2} } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ - {{b^2} \over 2} - 8k_iz}\surd \pi (b^2 + 8) \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 12k_iz}\surd \pi \left( {\displaystyle{{10} \over {\surd 6}} + \displaystyle{{1.5b^2} \over {\surd 6}}} \right) \cr & \quad - \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 12k_iz}\surd \pi \left( {\displaystyle{3 \over {\surd 6}} + 6 + \displaystyle{{3b^2} \over 4}} \right)} $$ We differentiate < L > with respect to the variables ψ 0 and ![]() $\psi _0^ * $. Using the Euler–Lagrange's equations, we arrive at two equations. Further, we multiply these two equations with variables ψ 0 and
$\psi _0^ * $. Using the Euler–Lagrange's equations, we arrive at two equations. Further, we multiply these two equations with variables ψ 0 and ![]() $\psi _0^ * $. On adding the resultant equations, we arrive at Eq. (11). The variation of < L >, i.e., (δ< L >/δS) = 0 where S denotes
$\psi _0^ * $. On adding the resultant equations, we arrive at Eq. (11). The variation of < L >, i.e., (δ< L >/δS) = 0 where S denotes ![]() $\displaystyle{{\partial \psi _0} / {\partial z}},\displaystyle{{\partial \psi _0 ^{*} } / {\partial z}},a,{q}{\prime},\displaystyle{{d{q}{\prime}} / {dz}}$ etc., and following the procedure of Anderson and Bonnedal (Reference Anderson1979) and Saini and Gill (Reference Saini and Gill2006), we arrive at the following equations:
$\displaystyle{{\partial \psi _0} / {\partial z}},\displaystyle{{\partial \psi _0 ^{*} } / {\partial z}},a,{q}{\prime},\displaystyle{{d{q}{\prime}} / {dz}}$ etc., and following the procedure of Anderson and Bonnedal (Reference Anderson1979) and Saini and Gill (Reference Saini and Gill2006), we arrive at the following equations:
 $$\eqalign{& \displaystyle{{\iota ka} \over {4\surd 2}}\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) = - \displaystyle{{k \vert \psi _0 \vert ^2} \over {16\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^3 - \displaystyle{{k \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{{d\phi } \over {dz}}a \cr & + \displaystyle{{ \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{1 \over {(b^2 + 8)}}\left( {\displaystyle{2 \over a} + \displaystyle{{b^4} \over {2a}} + 2{{q}^{\prime}}^2a^3 + \displaystyle{{{{q}^{\prime}}^2b^2a^3} \over 4} - \displaystyle{{7b^2} \over {4a}}} \right) \cr & + \displaystyle{{\omega _p^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {4\surd 2}}(\delta + \beta )e^{ - 4k_iz} - \displaystyle{{\omega _{\rm p}^2 } \over {16c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 4k_iz} \cr & - \displaystyle{{\omega _{\rm p}^2 } \over {16c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ -{{b^2} \over 2} - 4k_iz} \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {128c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 8k_iz}\left( {\displaystyle{{10} \over {\surd 6}} + {{1.5b^2} \over {\surd 6}}} \right) \cr & + \displaystyle{{\omega _p^2 } \over {128c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 8k_iz}\left( {\displaystyle{3 \over {\surd 6}} + 0.75b^2 + 6} \right)} $$
$$\eqalign{& \displaystyle{{\iota ka} \over {4\surd 2}}\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) = - \displaystyle{{k \vert \psi _0 \vert ^2} \over {16\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^3 - \displaystyle{{k \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{{d\phi } \over {dz}}a \cr & + \displaystyle{{ \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{1 \over {(b^2 + 8)}}\left( {\displaystyle{2 \over a} + \displaystyle{{b^4} \over {2a}} + 2{{q}^{\prime}}^2a^3 + \displaystyle{{{{q}^{\prime}}^2b^2a^3} \over 4} - \displaystyle{{7b^2} \over {4a}}} \right) \cr & + \displaystyle{{\omega _p^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {4\surd 2}}(\delta + \beta )e^{ - 4k_iz} - \displaystyle{{\omega _{\rm p}^2 } \over {16c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 4k_iz} \cr & - \displaystyle{{\omega _{\rm p}^2 } \over {16c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ -{{b^2} \over 2} - 4k_iz} \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {128c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 8k_iz}\left( {\displaystyle{{10} \over {\surd 6}} + {{1.5b^2} \over {\surd 6}}} \right) \cr & + \displaystyle{{\omega _p^2 } \over {128c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 8k_iz}\left( {\displaystyle{3 \over {\surd 6}} + 0.75b^2 + 6} \right)} $$and
(δ<L>/δa) = 0 gives,
 $$\! \eqalign{&\displaystyle{{\iota k} \over {8\surd 2}}\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) = - \displaystyle{3 \over {32}}\displaystyle{{k \vert \psi _0 \vert ^2} \over {\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^2 \cr & \! - \displaystyle{{k \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{{d\phi } \over {dz}} + \displaystyle{{ \vert \psi _0 \vert ^2} \over {4\surd 2}}\displaystyle{1 \over {(b^2 + 8)}}\left( {\displaystyle{{ - 2} \over {a^2}} - \displaystyle{{b^4} \over {2a^2}} + 6{{q}^{\prime}}^2a^2 + \displaystyle{{3{{q}^{\prime}}^2b^2a^2} \over 4} - \displaystyle{{2b^2} \over {4a^2}}} \right) \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {8\surd 2}}(\delta + \beta ) - \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 4k_iz} \cr & - \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ - {{b^2} \over 2} - 4k_iz} \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 8k_iz}\left( {\displaystyle{{10} \over {\surd 6}} + 1.5b^2} \right) \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 8k_iz}\left( {\displaystyle{3 \over {\surd 6}} + 0.75b^2 + 6} \right)} $$
$$\! \eqalign{&\displaystyle{{\iota k} \over {8\surd 2}}\left( {\psi _0\displaystyle{{\partial \psi _0^ * } \over {\partial z}} - \psi _0^ * \displaystyle{{\partial \psi _0} \over {\partial z}}} \right) = - \displaystyle{3 \over {32}}\displaystyle{{k \vert \psi _0 \vert ^2} \over {\surd 2}}\displaystyle{{d{q}^{\prime}} \over {dz}}a^2 \cr & \! - \displaystyle{{k \vert \psi _0 \vert ^2} \over {2\surd 2}}\displaystyle{{d\phi } \over {dz}} + \displaystyle{{ \vert \psi _0 \vert ^2} \over {4\surd 2}}\displaystyle{1 \over {(b^2 + 8)}}\left( {\displaystyle{{ - 2} \over {a^2}} - \displaystyle{{b^4} \over {2a^2}} + 6{{q}^{\prime}}^2a^2 + \displaystyle{{3{{q}^{\prime}}^2b^2a^2} \over 4} - \displaystyle{{2b^2} \over {4a^2}}} \right) \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {c^2}}\displaystyle{{ \vert \alpha ^2\psi _0 \vert ^2} \over {8\surd 2}}(\delta + \beta ) - \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2(\delta - 0.5)e^{ - {{b^2} \over 2} - 4k_iz} \cr & - \displaystyle{{\omega _{\rm p}^2 } \over {64c^2}}a(\alpha ^2 \vert \psi _0 \vert ^2)^2\beta e^{ - {{b^2} \over 2} - 4k_iz} \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{ - 8k_iz}\left( {\displaystyle{{10} \over {\surd 6}} + 1.5b^2} \right) \cr & + \displaystyle{{\omega _{\rm p}^2 } \over {768c^2}}a\delta (\alpha ^2 \vert \psi _0 \vert ^2)^3e^{{{b^2} \over 2} - 8k_iz}\left( {\displaystyle{3 \over {\surd 6}} + 0.75b^2 + 6} \right)} $$(δ<L>/δq′) = 0 gives;
Substituting Eq. (11) into Eq. (13) and using Eqs. (14) and (15), we arrive at the following equation for a:
 $$\eqalign{\displaystyle{{d^2a} \over {dz^2}} & = \displaystyle{{32} \over {k^2a^3(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & \quad + \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad + \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}} (\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} \cr & \quad - \surd 2 \displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_iz - {{b^2} \over 2}}} $$
$$\eqalign{\displaystyle{{d^2a} \over {dz^2}} & = \displaystyle{{32} \over {k^2a^3(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & \quad + \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad + \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}} (\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} \cr & \quad - \surd 2 \displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_iz - {{b^2} \over 2}}} $$ Finally, the phase ϕ(z) of amplitude ψ 0(z) is obtained by using ![]() $\psi _0(z) = \vert \psi _0 \vert e^{\iota \phi} $ and also using Eq. (16):
$\psi _0(z) = \vert \psi _0 \vert e^{\iota \phi} $ and also using Eq. (16):
 $$\eqalign{\displaystyle{{d\phi} \over {dz}} & = \displaystyle{2 \over {ka^2(b^2 + 8)}}\left( {1 - \displaystyle{{7b^2} \over 8} + \displaystyle{{b^4} \over 4}} \right) \cr & \quad + \left( {\displaystyle{1 \over {384\surd 3}} + \displaystyle{1 \over {128}}} \right)\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}\,\,(1.5b^2 + 10) \cr & \quad + \displaystyle{{\omega _{\rm p}^2} \over {4kc^2}}(\delta + \beta )e^{ - 4k_iz} + \displaystyle{{\surd 2} \over {96}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}} \cr & \quad \times \! \left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2) \cr & \quad \times \beta e^{ - 4k_iz - {{b^2} \over 2}}} $$
$$\eqalign{\displaystyle{{d\phi} \over {dz}} & = \displaystyle{2 \over {ka^2(b^2 + 8)}}\left( {1 - \displaystyle{{7b^2} \over 8} + \displaystyle{{b^4} \over 4}} \right) \cr & \quad + \left( {\displaystyle{1 \over {384\surd 3}} + \displaystyle{1 \over {128}}} \right)\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}\,\,(1.5b^2 + 10) \cr & \quad + \displaystyle{{\omega _{\rm p}^2} \over {4kc^2}}(\delta + \beta )e^{ - 4k_iz} + \displaystyle{{\surd 2} \over {96}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}} \cr & \quad \times \! \left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2}}(\alpha ^2 \vert \psi _0 \vert ^2) \cr & \quad \times \beta e^{ - 4k_iz - {{b^2} \over 2}}} $$ After normalization using ![]() $\eta = cz/\omega a_0^2 $, we arrive at the following equations for a n and ϕ:
$\eta = cz/\omega a_0^2 $, we arrive at the following equations for a n and ϕ:
 $$\eqalign{\displaystyle{{d^2a_n} \over {d\eta ^2}} & = \displaystyle{{32} \over {a_n^3 (b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & \quad + \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_i^{\prime}\eta}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad + \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}\,(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_i^{\prime}\eta + \displaystyle{{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \surd 2\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_i^{\prime}\eta + \displaystyle{{b^2} \over 2}} \cr & \quad - \surd 2 \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_i^{\prime}\eta - \displaystyle{{b^2} \over 2}}} $$
$$\eqalign{\displaystyle{{d^2a_n} \over {d\eta ^2}} & = \displaystyle{{32} \over {a_n^3 (b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & \quad + \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_i^{\prime}\eta}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad + \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}\,(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_i^{\prime}\eta + \displaystyle{{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad - \surd 2\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_i^{\prime}\eta + \displaystyle{{b^2} \over 2}} \cr & \quad - \surd 2 \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2a_n}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_i^{\prime}\eta - \displaystyle{{b^2} \over 2}}} $$ $$\openup6pt\eqalign{\displaystyle{{d\phi} \over {d\eta}} & = \displaystyle{2 \over {a_n^2 (b^2 + 8)}}\left( {1 - \displaystyle{{7b^2} \over 8} + \displaystyle{{b^4} \over 4}} \right) \cr &\quad + \left( {\displaystyle{1 \over {384\surd 3}} + \displaystyle{1 \over {128}}} \right)\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\displaystyle{{e^{ - 8k{\rm ^{\prime}}_i\eta}} \over {(b^2 + 8)}}\,(1.5b^2 + 10) \cr &\quad + \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {4c^2}}\delta e^{ - 4k{\rm ^{\prime}}_i\eta} + \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {4c^2}}\beta e^{ - 4k{\rm ^{\prime}}_i\eta} \cr &\quad + \displaystyle{{\surd 2} \over {96}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k{\rm ^{\prime}}_i\eta + {{b^2} \over 2}}} \over {(b^2 + 8)}}\,\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k{\rm ^{\prime}}_iz + {{b^2} \over 2}} \cr &\quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k{\rm ^{\prime}}_i\eta - {{b^2} \over 2}}} $$
$$\openup6pt\eqalign{\displaystyle{{d\phi} \over {d\eta}} & = \displaystyle{2 \over {a_n^2 (b^2 + 8)}}\left( {1 - \displaystyle{{7b^2} \over 8} + \displaystyle{{b^4} \over 4}} \right) \cr &\quad + \left( {\displaystyle{1 \over {384\surd 3}} + \displaystyle{1 \over {128}}} \right)\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\displaystyle{{e^{ - 8k{\rm ^{\prime}}_i\eta}} \over {(b^2 + 8)}}\,(1.5b^2 + 10) \cr &\quad + \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {4c^2}}\delta e^{ - 4k{\rm ^{\prime}}_i\eta} + \displaystyle{{\omega _{\rm p}^2 a_0^2} \over {4c^2}}\beta e^{ - 4k{\rm ^{\prime}}_i\eta} \cr &\quad + \displaystyle{{\surd 2} \over {96}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k{\rm ^{\prime}}_i\eta + {{b^2} \over 2}}} \over {(b^2 + 8)}}\,\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k{\rm ^{\prime}}_iz + {{b^2} \over 2}} \cr &\quad - \displaystyle{{5\surd 2} \over {64}}\displaystyle{{\omega _{\rm p}^2 a_0^2} \over {c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k{\rm ^{\prime}}_i\eta - {{b^2} \over 2}}} $$with ![]() ${k}^{\prime}_i = k_iR_d$,
${k}^{\prime}_i = k_iR_d$, ![]() ${k}^{\prime}_i$ is the normalized absorption coefficient.
${k}^{\prime}_i$ is the normalized absorption coefficient.
Self-trapping
For an initially plane wave front, a = a 0 = a e, da/dz = 0, and a = 1 at z = 0, the condition d 2a/dz 2 = 0 leads to propagation of a cosh-Gaussian laser beam without any change in its beam width. This is known as the uniform waveguide propagation. If we put ![]() $\displaystyle{{d^2a} \over {dz^2}} = 0$ in Eq. (16), we obtain a relation between the dimensionless initial beam width parameter (ρ0) and critical values of the intensity parameter Π (= α2|ψ 0|2). The following general expression is obtained for determination of critical threshold for various values of b:
$\displaystyle{{d^2a} \over {dz^2}} = 0$ in Eq. (16), we obtain a relation between the dimensionless initial beam width parameter (ρ0) and critical values of the intensity parameter Π (= α2|ψ 0|2). The following general expression is obtained for determination of critical threshold for various values of b:
 $$\openup6pt\eqalign{&\displaystyle{{32} \over {k^2a^2(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & = - \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad - \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} \cr & \quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_iz - {{b^2} \over 2}}} $$
$$\openup6pt\eqalign{&\displaystyle{{32} \over {k^2a^2(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr & = - \displaystyle{1 \over {6\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr & \quad - \displaystyle{{\surd 2} \over 6}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr & \quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)(\delta - 0.5)e^{ - 4k_iz + {{b^2} \over 2}} \cr & \quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2}}(\alpha ^2 \vert \psi _0 \vert ^2)\beta e^{ - 4k_iz - {{b^2} \over 2}}} $$where ρ0 = a eω/c, is the initial dimensionless beam width parameter. The results are shown in the form of graphs. Such graphs are called the critical curves and these curves characterize the self-focusing region in the ![]() $\rho _0^2 - \Pi $ plane. The region below the critical curve corresponds to propagation of a cosh-Gaussian beam with self-focusing whereas the region above the critical curve corresponds to either oscillatory or steady state self-focusing of a cosh-Gaussian beam.
$\rho _0^2 - \Pi $ plane. The region below the critical curve corresponds to propagation of a cosh-Gaussian beam with self-focusing whereas the region above the critical curve corresponds to either oscillatory or steady state self-focusing of a cosh-Gaussian beam.
Numerical results and discussion
Equations (18) and (19) are nonlinearly coupled ordinary second order differential equations governing the normalized beam width parameter a n and the phase ϕ as a function of distance of propagation η. These equations cannot be solved analytically. Therefore, we employ numerical computational techniques to study the dynamics of the beam. The first term on right hand side (R.H.S.) of Eq. (18) has its origin in the Laplacian ![]() $(\nabla _ \bot ^2 )$ appearing in the evolution Eq. (5) and it leads to the diffractional divergence of laser beam. The other terms in Eq. (18) arise due to the relativistic nonlinear effect when laser beam of high intensity is used. This effect arises due to the relativistic mass correction and it depends on various factors such as the intensity parameter (Π = α2|ψ 0|2), relative plasma density, etc. The second, third, and the fourth terms have dependence on the cold quantum contribution δ as well as on the decentered parameter, b. However, the last term (fifth) is dominated by the TQP whose contribution comes from the term proportional to β which contains quantum effects via the Fermi temperature. A similar explanation can be given for the terms appearing in Eq. (19). The first term leads to the diffractional divergence of laser beam. The other terms in Eq. (19) appear because of the relativistic effects. The third term has dependence on the cold quantum contribution δ, the fifth and the sixth terms depend on δ as well as on the decentered parameter, b. The contribution of the fourth term comes from the term proportional to β which consists of the quantum effects. The last term is proportional to β, the decentered parameter, b and Π. The self-focusing/defocusing of laser beam is determined by the competing mechanisms on the R.H.S. of Eq. (18). The normalized beam width parameter, a n < 1 corresponds to the self-focusing and a n > 1 is the result of diffractional dominance over all the other terms leading to the defocusing of laser beam. If we set δ and β to zero, i.e., ignoring quantum effects, one obtains a differential equation for the normalized beam width parameter in the CR plasma. In Figure 1, the plot of normalized beam width parameter, a n as a function of the dimensionless distance of propagation, η is displayed for b = 0 at different values of absorption levels
$(\nabla _ \bot ^2 )$ appearing in the evolution Eq. (5) and it leads to the diffractional divergence of laser beam. The other terms in Eq. (18) arise due to the relativistic nonlinear effect when laser beam of high intensity is used. This effect arises due to the relativistic mass correction and it depends on various factors such as the intensity parameter (Π = α2|ψ 0|2), relative plasma density, etc. The second, third, and the fourth terms have dependence on the cold quantum contribution δ as well as on the decentered parameter, b. However, the last term (fifth) is dominated by the TQP whose contribution comes from the term proportional to β which contains quantum effects via the Fermi temperature. A similar explanation can be given for the terms appearing in Eq. (19). The first term leads to the diffractional divergence of laser beam. The other terms in Eq. (19) appear because of the relativistic effects. The third term has dependence on the cold quantum contribution δ, the fifth and the sixth terms depend on δ as well as on the decentered parameter, b. The contribution of the fourth term comes from the term proportional to β which consists of the quantum effects. The last term is proportional to β, the decentered parameter, b and Π. The self-focusing/defocusing of laser beam is determined by the competing mechanisms on the R.H.S. of Eq. (18). The normalized beam width parameter, a n < 1 corresponds to the self-focusing and a n > 1 is the result of diffractional dominance over all the other terms leading to the defocusing of laser beam. If we set δ and β to zero, i.e., ignoring quantum effects, one obtains a differential equation for the normalized beam width parameter in the CR plasma. In Figure 1, the plot of normalized beam width parameter, a n as a function of the dimensionless distance of propagation, η is displayed for b = 0 at different values of absorption levels ![]() ${k}^{\prime}_i$ considering the relativistic warm quantum plasma. In absence of the decentered parameter, a large value of
${k}^{\prime}_i$ considering the relativistic warm quantum plasma. In absence of the decentered parameter, a large value of ![]() ${k}^{\prime}_i$ is observed to weak the self-focusing effect. An analysis of evolution of the normalized beam width parameter as a function of distance of propagation, η is performed at b = 0, 1, 2 for three values of
${k}^{\prime}_i$ is observed to weak the self-focusing effect. An analysis of evolution of the normalized beam width parameter as a function of distance of propagation, η is performed at b = 0, 1, 2 for three values of ![]() $k_i^{\prime}$ with other parameters chosen as follows: a 0 = 0.002 cm, k = 0.53 × 104 cm−1, ωp = 2 × 10−6 × ω, ω = 1.778 × 1020(rad/sec), T Fe = 109 K, and λ = 0.0106 nm. Figure 2 plots a n as a function of η for b = 1 with different values of absorption levels
$k_i^{\prime}$ with other parameters chosen as follows: a 0 = 0.002 cm, k = 0.53 × 104 cm−1, ωp = 2 × 10−6 × ω, ω = 1.778 × 1020(rad/sec), T Fe = 109 K, and λ = 0.0106 nm. Figure 2 plots a n as a function of η for b = 1 with different values of absorption levels ![]() ${k}^{\prime}_i$. The beam propagates oscillatory over several number of Rayleigh lengths. However, the situation has changed significantly in Figure 3, where we have plotted a n as a function of η for b = 2 with varying
${k}^{\prime}_i$. The beam propagates oscillatory over several number of Rayleigh lengths. However, the situation has changed significantly in Figure 3, where we have plotted a n as a function of η for b = 2 with varying ![]() ${k}^{\prime}_i$. All curves are seen to exhibit sharp self-focusing effects.
${k}^{\prime}_i$. All curves are seen to exhibit sharp self-focusing effects.
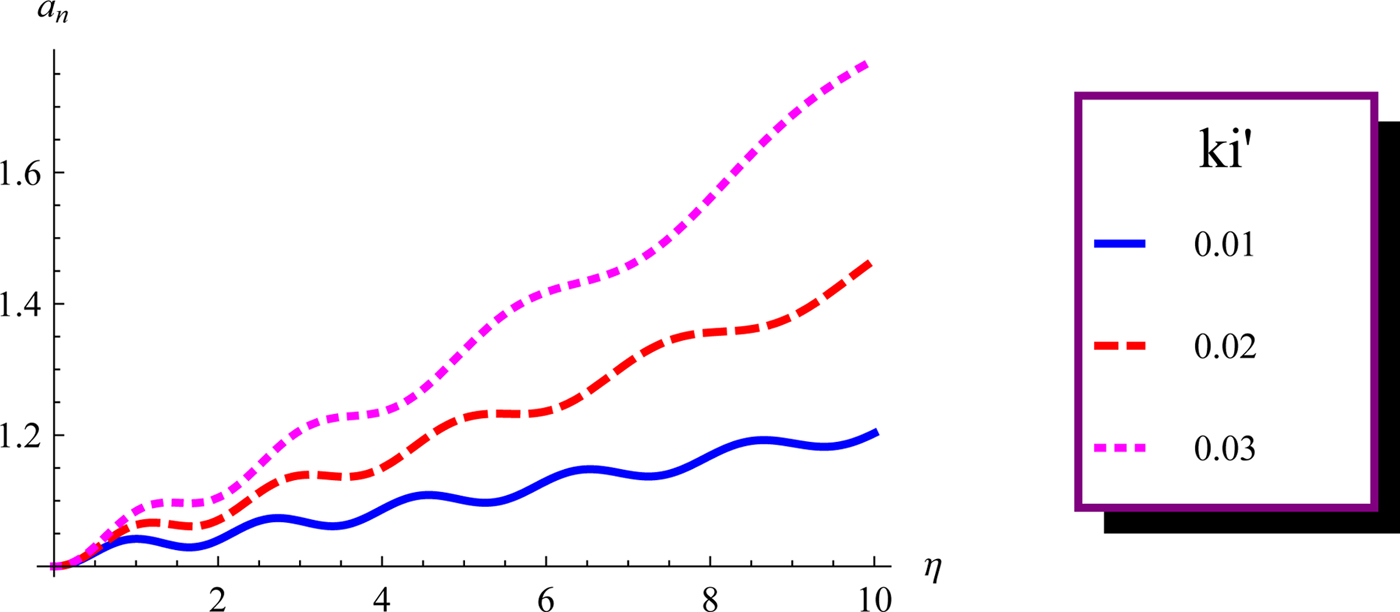
Fig. 1. Variation of normalized beam width parameter a n(η) as a function of dimensionless distance of propagation η considering relativistic nonlinearity for b = 0 with the following set of parameters for the various values of ![]() ${k}^{\prime}_i$: a 0 = 0.002 cm, ωp = 2 × 10−6 × ω, ω = 1.778 × 1020(rad/sec), k = 0.53 × 104 cm−1, and intensity parameter, Π = 0.1. Solid curve corresponds to
${k}^{\prime}_i$: a 0 = 0.002 cm, ωp = 2 × 10−6 × ω, ω = 1.778 × 1020(rad/sec), k = 0.53 × 104 cm−1, and intensity parameter, Π = 0.1. Solid curve corresponds to ![]() $k_i^{\prime} = 0.01$, dashed to
$k_i^{\prime} = 0.01$, dashed to ![]() ${k}^{\prime}_i = 0.02$, and dotted to
${k}^{\prime}_i = 0.02$, and dotted to ![]() ${k}^{\prime}_i = 0.03$.
${k}^{\prime}_i = 0.03$.
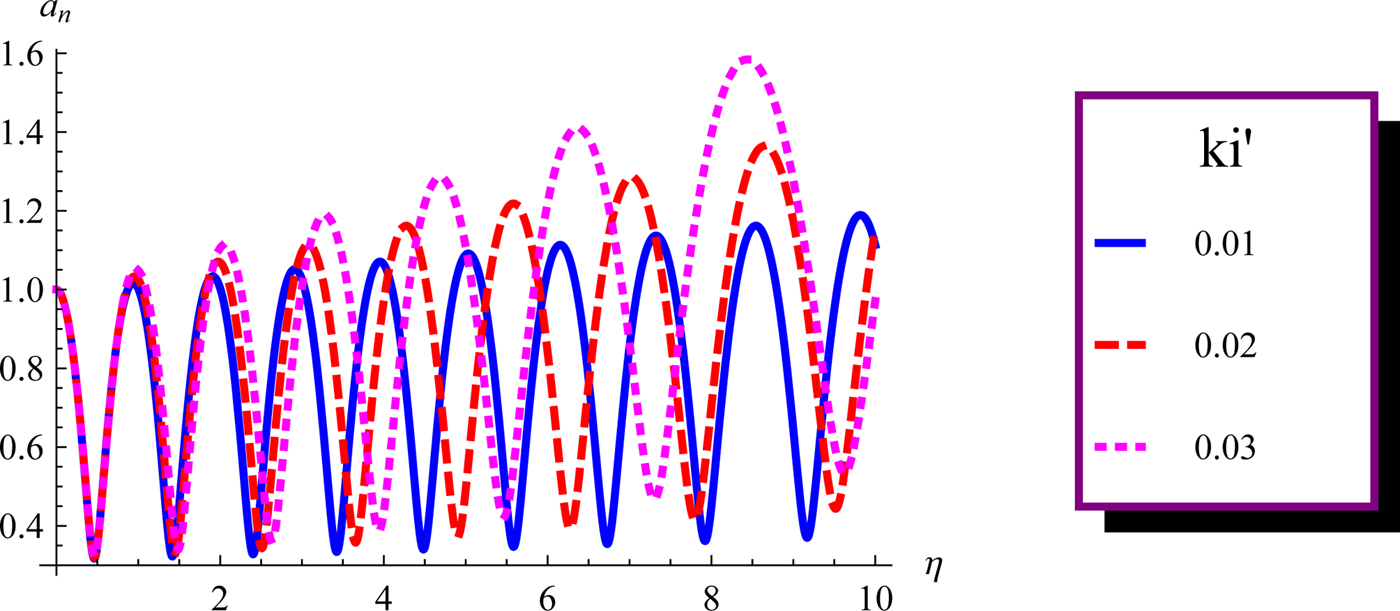
Fig. 2. Plot of a n(η) as a function of dimensionless distance of propagation η for b = 1 for the same set of parameters as in the caption of Figure 1.

Fig. 3. Variation of normalized beam width a n(η) as a function of dimensionless distance of propagation η for b = 2 for the same set of parameters as in the caption of Figure 1.
The variation of the normalized beam width parameter, a n as a function of the dimensionless distance of propagation, η with various intensity parameters (Π = α2|ψ 0|2), keeping b and ![]() ${k}^{\prime}_i$ fixed is displayed in Figure 4. It is observed from Figure 4 that the self-focusing takes place at lower values of Π in comparison with the earlier investigations (Gill et al., Reference Gill, Mahajan and Kaur2011). However, there is a substantial increase in the self-focusing with increase in Π. Figure 5 highlights the variation of the beam width parameter with η for the three cases of plasma. If we consider all the terms in Eq. (18), we obtain a plot between a n and η for the case of relativistic TQP (dotted curve). If we put β → 0, a curve for the RCQ plasma is obtained (dashed curve). Further if β → 0 and δ → 0, i.e., ignoring the quantum effects, one obtains a curve for the CR plasma (solid curve). The results show much higher oscillations and better self-focusing in the TQP than the RCQ and the CR cases. Another aspect of this phenomenon observed here is that there is a decrease in the focusing length for the TQP in comparison with the earlier RCQ and the CR cases. The stronger pinching effect offered by the quantum effects enhances laser self-focusing. The largest self-focusing length is observed in the CR regime. Further, Eq. (19) describes the evolution of the longitudinal phase, ϕ(η, α2|ψ 0|2) with the dimensionless distance of propagation (η) in Figure 6. The R.H.S. of Eq. (19) is a complicated function of b,
${k}^{\prime}_i$ fixed is displayed in Figure 4. It is observed from Figure 4 that the self-focusing takes place at lower values of Π in comparison with the earlier investigations (Gill et al., Reference Gill, Mahajan and Kaur2011). However, there is a substantial increase in the self-focusing with increase in Π. Figure 5 highlights the variation of the beam width parameter with η for the three cases of plasma. If we consider all the terms in Eq. (18), we obtain a plot between a n and η for the case of relativistic TQP (dotted curve). If we put β → 0, a curve for the RCQ plasma is obtained (dashed curve). Further if β → 0 and δ → 0, i.e., ignoring the quantum effects, one obtains a curve for the CR plasma (solid curve). The results show much higher oscillations and better self-focusing in the TQP than the RCQ and the CR cases. Another aspect of this phenomenon observed here is that there is a decrease in the focusing length for the TQP in comparison with the earlier RCQ and the CR cases. The stronger pinching effect offered by the quantum effects enhances laser self-focusing. The largest self-focusing length is observed in the CR regime. Further, Eq. (19) describes the evolution of the longitudinal phase, ϕ(η, α2|ψ 0|2) with the dimensionless distance of propagation (η) in Figure 6. The R.H.S. of Eq. (19) is a complicated function of b, ![]() ${k}^{\prime}_i$, the normalized beam width a n and the intensity parameter, α2|ψ 0|2. Though we can fix b,
${k}^{\prime}_i$, the normalized beam width a n and the intensity parameter, α2|ψ 0|2. Though we can fix b, ![]() ${k}^{\prime}_i$, and α2|ψ 0|2, the evolution of the normalized beam width parameter, a n significantly affects the longitudinal phase with η. The longitudinal phase may be positive or negative depending upon the value of α2|ψ 0|2 and
${k}^{\prime}_i$, and α2|ψ 0|2, the evolution of the normalized beam width parameter, a n significantly affects the longitudinal phase with η. The longitudinal phase may be positive or negative depending upon the value of α2|ψ 0|2 and ![]() ${k}^{\prime}_i$. It is positive for the present model and does not show an oscillatory character as the R.H.S. of Eq. (19) for b = 0 depends only on α2|ψ 0|2 and
${k}^{\prime}_i$. It is positive for the present model and does not show an oscillatory character as the R.H.S. of Eq. (19) for b = 0 depends only on α2|ψ 0|2 and ![]() ${k}^{\prime}_i$ maintaining a nonlinear relationship. The regularized phase, ϕ reg, is defined as:
${k}^{\prime}_i$ maintaining a nonlinear relationship. The regularized phase, ϕ reg, is defined as:

Fig. 4. Graph of a n(η) as a function of dimensionless distance of propagation η for b = 1 and ![]() ${k}^{\prime}_i = 0.01$ at varying values of intensity parameter for the same set of parameters as in the caption of Figure 1. Solid curve corresponds to Π = 0.09, dashed to Π = 0.1, and dotted to Π = 0.3.
${k}^{\prime}_i = 0.01$ at varying values of intensity parameter for the same set of parameters as in the caption of Figure 1. Solid curve corresponds to Π = 0.09, dashed to Π = 0.1, and dotted to Π = 0.3.
Fig. 5. Variation of a n(η) as a function of dimensionless distance of propagation η for b = 1, ![]() ${k}^{\prime}_i = 0.01$, and Π = 0.1 for different plasma regimes using same set of parameters as in the caption of Figure 1. Solid curve corresponds to CR region, dashed to RCQ, and dotted to TQP.
${k}^{\prime}_i = 0.01$, and Π = 0.1 for different plasma regimes using same set of parameters as in the caption of Figure 1. Solid curve corresponds to CR region, dashed to RCQ, and dotted to TQP.
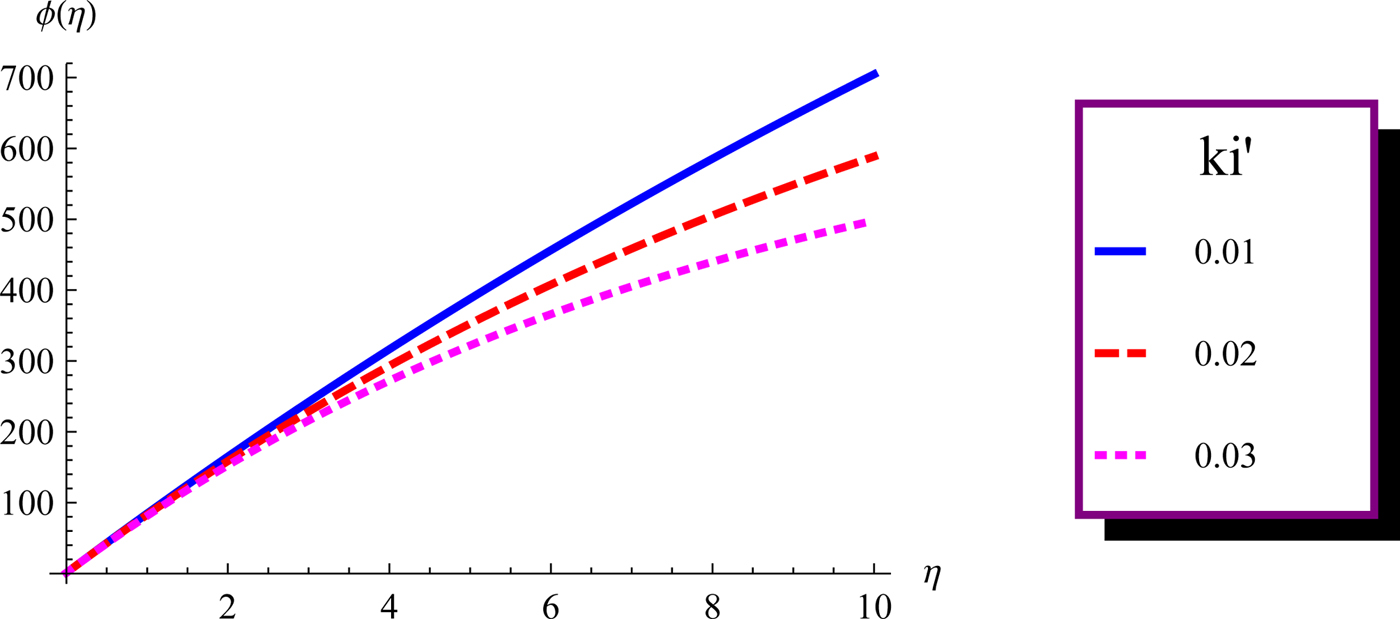
Fig. 6. Plot of longitudinal phase ϕ(η) versus dimensionless distance of propagation η for b = 0 for the same set of parameters as mentioned in the caption of Figure 1. Solid curve corresponds to ![]() ${k}^{\prime}_i = 0.01$, dashed to
${k}^{\prime}_i = 0.01$, dashed to ![]() ${k}^{\prime}_i = 0.02$, and dotted to
${k}^{\prime}_i = 0.02$, and dotted to ![]() ${k}^{\prime}_i = 0.03$.
${k}^{\prime}_i = 0.03$.
In the linear limit (α2|ψ 0|2 = 0), the phase will have a more rapid growth during the propagation. But the presence of nonlinear forces counteracts the diffraction and tends to keep the pulse intensity higher in the plasma medium. However, the regularized phase always has a negative value. This is a consequence of frequency chirp as the time derivative of the phase will have same sign as in the case of a conventional plane wave. Thus, the red will always lead blue in the super continuum. This aspect of the phase change is well presented using the variational approach in the present investigation. Figure 7 displays the plot of the regularized phase versus η. This feature confirms the finding of Karlsson et al. (Reference Karlsson, Anderson and Desaix1992) and is contrary to the results of Manassah et al. (Reference Manassah, Baldeck and Alfano1988). The latter predicted that the regularized phase may be positive or negative during the beam propagation. This inconsistent result stems from the fact that the PRA used by Manasaah et al., does not correctly predict the ϕ reg.
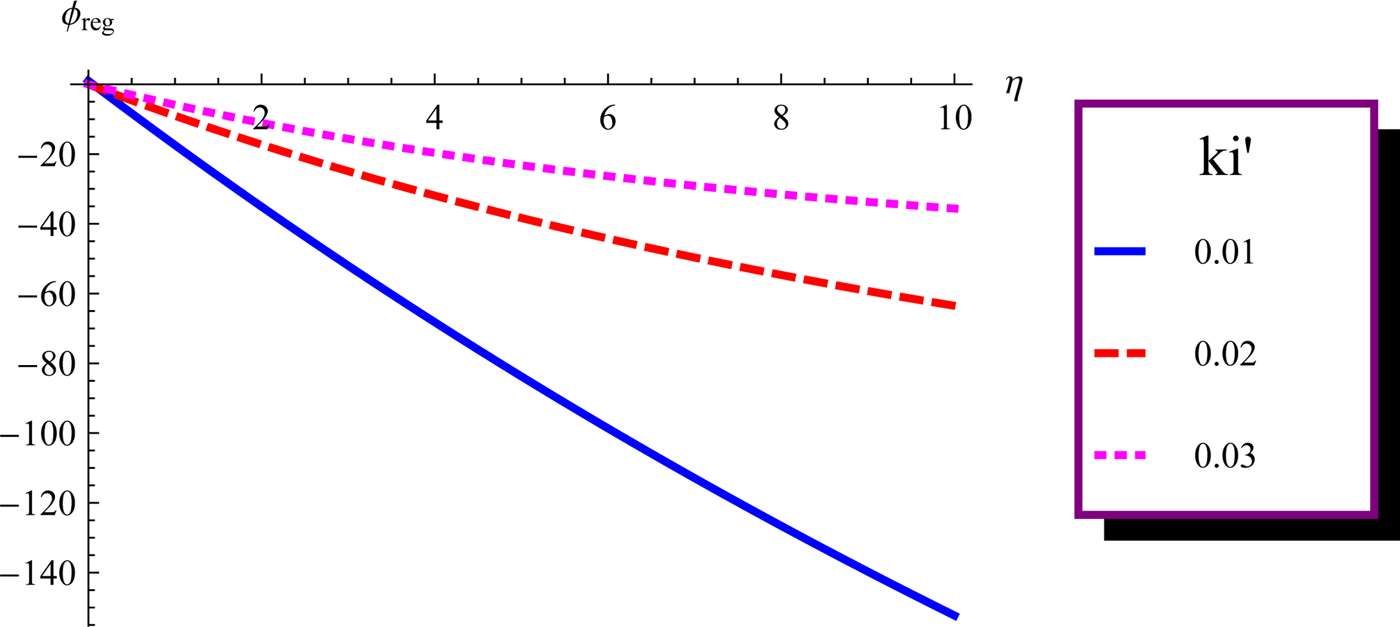
Fig. 7. Plot of regularized phase ϕ reg versus dimensionless distance of propagation η for b = 1 for the same set of parameters as mentioned in the caption of Figure 1. Solid curve corresponds to ![]() ${k}^{\prime}_i = 0.01$, dashed to
${k}^{\prime}_i = 0.01$, dashed to ![]() ${k}^{\prime}_i = 0.02$, and dotted to
${k}^{\prime}_i = 0.02$, and dotted to ![]() ${k}^{\prime}_i = 0.03$.
${k}^{\prime}_i = 0.03$.
To further elucidate the results for delineating the underlying physics for the propagation of a cosh-Gaussian laser beam in the TQP, we numerically analyze the dimensionless initial beam width parameter (ρ0) as a function of critical values of beam power Π (= α2|ψ 0|2) for different values of b when the relativistic nonlinearity is considered. The results are depicted in the form of graphs. The critical curves for a cosh-Gaussian laser beam characterize the self-focusing region in the ![]() $\rho _0^2 - \Pi $ space. In Figure 8,
$\rho _0^2 - \Pi $ space. In Figure 8, ![]() $\rho _0^2 $ versus Π is plotted for two values of b, i.e., b = 0 and b = 1. The solid curve corresponds to b = 0 and the dashed curve to b = 1. The solid curve depicts that the dependence of
$\rho _0^2 $ versus Π is plotted for two values of b, i.e., b = 0 and b = 1. The solid curve corresponds to b = 0 and the dashed curve to b = 1. The solid curve depicts that the dependence of ![]() $\rho _0^2 $ for b = 0 is much weaker on the high intensity, a result consistent with earlier calculations based on the variational approach (Anderson, Reference Anderson and Bonnedal1978). The initial beam width is much higher than the earlier investigations. Higher the value of b, the faster is the initial decrease in
$\rho _0^2 $ for b = 0 is much weaker on the high intensity, a result consistent with earlier calculations based on the variational approach (Anderson, Reference Anderson and Bonnedal1978). The initial beam width is much higher than the earlier investigations. Higher the value of b, the faster is the initial decrease in ![]() $\rho _0^2 $ with Π.
$\rho _0^2 $ with Π.

Fig. 8. Dependence of dimensionless initial beam width (ρ0) as a function of Π with b = 0 and b = 1. Solid curve corresponds to b = 0 and dashed curve to b = 1.
Lastly, Figure 9 depicts the variation of a n with η in the relativistic TQP for three different values of the Fermi temperature. It is observed that the self-focusing length decreases with an increase in the Fermi electron temperature. A propagation to several Rayleigh lengths is observed. Also, it occurs at much lower value of the intensity parameter in comparison with the earlier investigations. This is apparently a consequence of the variational approach where the contribution of the whole wave front is considered in the averaging process. On the other hand, the PRA takes into account only those rays which are very close to the beam-axis.
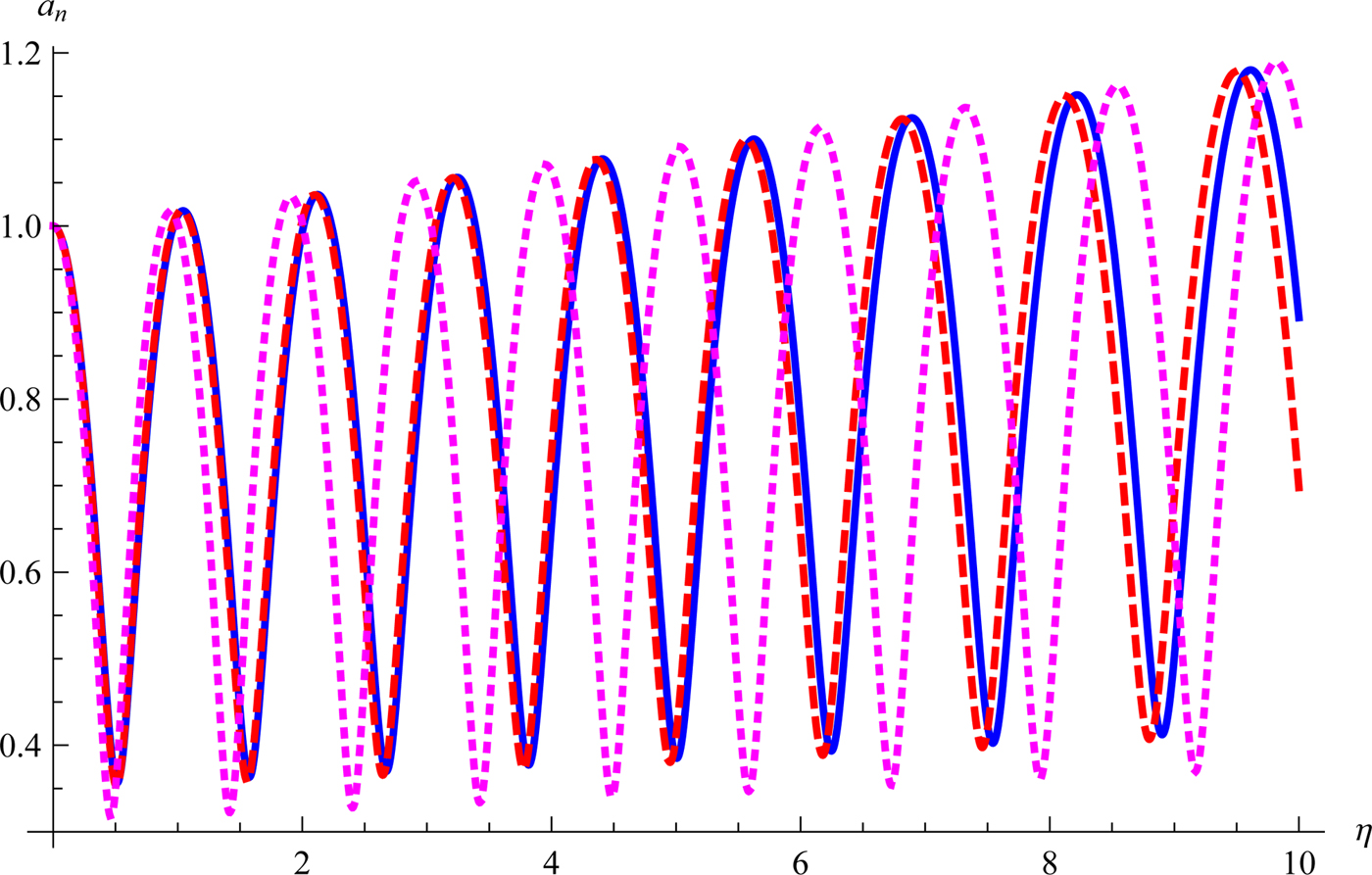
Fig. 9. Comparison of a n(η) with dimensionless distance of propagation η at different values of electron temperature (T Fe). Other parameters are same as in the caption of Figure 1. Solid curve corresponds to T Fe = 107 K, dashed to T Fe = 108 K, and dotted to T Fe = 109 K.
Stability criterion of beam dynamics
Variational method is used in several branches of physics and mathematics, can also be applied to study the stability characteristics of the evolution of cosh-Gaussian laser beam in TQP when relativistic effects are taken into account. The methods of nonlinear dynamics applied to dissipative solitons (Skarka et al., Reference Skarka, Berezhiani and Miklaszewski1997, Reference Skarka, Berezhiani and Miklaszewski1999; Skarka and Aleksic, Reference Skarka and Aleksic2006) can also be used to study stability properties in the present investigation. The Euler–Lagrange equations are the starting point to establish stability criterion. The dependent variables are disturbed about their equilibrium values and method of Lyapunov's exponents (Lakshman and Rajasekar, Reference Lakshman and Rajasekar2003; Skarka and Aleksic, Reference Skarka and Aleksic2006) is used. Thus, for stability characteristics of the system, the following Jacobi determinant is constructed from derivatives with respect to amplitude, width and curvature in terms of S, F, and G where
 $$\eqalign{G & = \displaystyle{{d{q}^{\prime}} \over {dz}} = \displaystyle{{4{{q}^{\prime}}^2} \over k} - \displaystyle{8 \over {ka^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad - \displaystyle{1 \over {24\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad - \displaystyle{{\surd 2} \over {24}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad + \displaystyle{{\surd 2} \over 4}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)e^{ - 4k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad + \displaystyle{{\surd 2} \over 4}\displaystyle{{\omega _{\rm p}^2 \beta} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)e^{ - 4k_iz - {{b^2} \over 2}}} $$
$$\eqalign{G & = \displaystyle{{d{q}^{\prime}} \over {dz}} = \displaystyle{{4{{q}^{\prime}}^2} \over k} - \displaystyle{8 \over {ka^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad - \displaystyle{1 \over {24\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad - \displaystyle{{\surd 2} \over {24}}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad + \displaystyle{{\surd 2} \over 4}\displaystyle{{\omega _{\rm p}^2} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)e^{ - 4k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad + \displaystyle{{\surd 2} \over 4}\displaystyle{{\omega _{\rm p}^2 \beta} \over {kc^2a^2}}(\alpha ^2 \vert \psi _0 \vert ^2)e^{ - 4k_iz - {{b^2} \over 2}}} $$ $$\openup6pt\hbox{det} \vert J - \lambda I \vert = \left \vert {\matrix{ {\displaystyle{{\partial S} \over {\partial \psi_0}} - \lambda} & {\displaystyle{{\partial S} \over {\partial a}}} & {\displaystyle{{\partial S} \over {\partial {q}^{\prime}}}} \cr {\displaystyle{{\partial F} \over {\partial \psi_0}}} & {\displaystyle{{\partial F} \over {\partial a}} - \lambda} & {\displaystyle{{\partial F} \over {\partial {q}^{\prime}}}} \cr {\displaystyle{{\partial G} \over {\partial \psi_0}}} & {\displaystyle{{\partial G} \over {\partial a}}} & {\displaystyle{{\partial G} \over {\partial {q}^{\prime}}} - \lambda} \cr}} \right \vert = 0$$
$$\openup6pt\hbox{det} \vert J - \lambda I \vert = \left \vert {\matrix{ {\displaystyle{{\partial S} \over {\partial \psi_0}} - \lambda} & {\displaystyle{{\partial S} \over {\partial a}}} & {\displaystyle{{\partial S} \over {\partial {q}^{\prime}}}} \cr {\displaystyle{{\partial F} \over {\partial \psi_0}}} & {\displaystyle{{\partial F} \over {\partial a}} - \lambda} & {\displaystyle{{\partial F} \over {\partial {q}^{\prime}}}} \cr {\displaystyle{{\partial G} \over {\partial \psi_0}}} & {\displaystyle{{\partial G} \over {\partial a}}} & {\displaystyle{{\partial G} \over {\partial {q}^{\prime}}} - \lambda} \cr}} \right \vert = 0$$This leads to the following characteristic equation cubic in λ:
where
 $$\eqalign{\alpha _2 & = \displaystyle{{ - 32{{q}^{\prime}}^2} \over {k^2}} + \displaystyle{{128} \over {k^2a^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad + \displaystyle{1 \over {\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - 4\surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad - 4\surd 2\displaystyle{{\omega _{\rm p}^2 \beta} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz -{{b^2} \over 2}}} $$
$$\eqalign{\alpha _2 & = \displaystyle{{ - 32{{q}^{\prime}}^2} \over {k^2}} + \displaystyle{{128} \over {k^2a^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad + \displaystyle{1 \over {\surd 3}}\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad + \surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - 4\surd 2\displaystyle{{\omega _{\rm p}^2} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad - 4\surd 2\displaystyle{{\omega _{\rm p}^2 \beta} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz -{{b^2} \over 2}}} $$ $$\eqalign{\alpha _3 & = \displaystyle{{ - 128{{q}^{\prime}}^3} \over {k^3}} + \displaystyle{{512{q}^{\prime}} \over {k^3a^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad + \displaystyle{4 \over {\surd 3}}\displaystyle{{\omega _{\rm p}^2 {q}^{\prime}} \over {k^3c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad + 4\surd 2\displaystyle{{\omega _{\rm p}^2 {q}^{\prime}} \over {k^3c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - 16\surd 2{q}^{\prime}\displaystyle{{\omega _{\rm p}^2} \over {k^3c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 8k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad - 16\surd 2{q}^{\prime}\displaystyle{{\omega _{\rm p}^2 \beta} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz - {{b^2} \over 2}}} $$
$$\eqalign{\alpha _3 & = \displaystyle{{ - 128{{q}^{\prime}}^3} \over {k^3}} + \displaystyle{{512{q}^{\prime}} \over {k^3a^4(b^2 + 8)}}\left( {2 - \displaystyle{{7b^2} \over 4} + \displaystyle{{b^4} \over 2}} \right) \cr &\quad + \displaystyle{4 \over {\surd 3}}\displaystyle{{\omega _{\rm p}^2 {q}^{\prime}} \over {k^3c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz}} \over {(b^2 + 8)}}(1.5b^2 + 10) \cr &\quad + 4\surd 2\displaystyle{{\omega _{\rm p}^2 {q}^{\prime}} \over {k^3c^2a^6}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)^2\delta \displaystyle{{e^{ - 8k_iz + {{b^2} \over 2}}} \over {(b^2 + 8)}}\left( {0.75b^2 + 6 + \displaystyle{3 \over {\surd 6}}} \right) \cr &\quad - 16\surd 2{q}^{\prime}\displaystyle{{\omega _{\rm p}^2} \over {k^3c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 8k_iz + {{b^2} \over 2}}(\delta - 0.5) \cr &\quad - 16\surd 2{q}^{\prime}\displaystyle{{\omega _{\rm p}^2 \beta} \over {k^2c^2a^4}}(\alpha ^2A_0^2 \vert \psi _{00} \vert ^2)e^{ - 4k_iz - {{b^2} \over 2}}} $$In order to have Lyapunov's stability, Hurwitz conditions must be fulfilled, i.e., α1α2 − α3 must be positive. According to the Routh–Hurwitz criterion, a necessary and sufficient condition for the stationary solutions to be stable is:
Equation (26) has a pair of purely imaginary roots at a critical point (Lugiato and Narducci, Reference Lugiato and Narducci1985):
Substituting Eq. (31) into Eq. (26), we get:
and
The critical condition of the Hopf-bifurcation is:
f > 0 is a necessary condition for the stationary solution to be stable, f < 0 is a necessary condition for the Hopf-bifurcation to emerge. It is observed that the condition f ≥ 0 is satisfied for chosen set of parameters in the present analysis and therefore Hopf-bifurcation, resulting from the unstable fixed point does not come into play and it leads to overall stability of the beam dynamics (Wang, Reference Wang1990).
Conclusions
In the present research work, authors have studied the evolution of a cosh-Gaussian laser beam in the TQP by taking into account the relativistic nonlinearity. An equation describing the envelope of the EM field is set up on prior knowledge based on the quantum fluid model, Maxwell's equations, and the earlier results of the quantum dielectric response and solved by using the variational approach. Approximate trial function for describing a cosh-Gaussian beam is used and equations for the beam width parameter and phase are derived and solved numerically for suitable set of parameters. It is observed that the combined quantum effects and the relativistic nonlinearity lead to a stronger self-focusing. The results are supported on the basis of comparison between the TQP, the CQP, and the CR regimes. The decentered parameter plays a crucial role in the beam dynamics. It is observed that the large value of ![]() ${k}^{\prime}_i$, the normalized absorption coefficient, weakens the self-focusing effect in the absence of b. However, an oscillatory self-focusing takes place for higher value of the decentered parameter. The aspect of the longitudinal phase and the regularized phase is well displayed in the form of graphs using the variational approach in the present investigation. Some features describing the critical curves for b = 0, 1 are also obtained for the chosen set of parameters. A better evolution of laser beam to several Rayleigh lengths is obtained using the variational approach as compared with the PRA. Because integration over the whole wave front is considered in the variational approach whereas in the PRA, only those rays are considered which are very close to the beam axis. Further, a cosh-Gaussian beam can handle high power in comparison with a circular Gaussian beam, the present investigation may shed some light on key aspects such as propagation, losses, diffraction, and critical issues of the relativistic ultra-intense laser–plasma interaction physics relevant to the ICF as well as the intense laser-solid density plasma experiments where the quantum effects are important. Lastly, stability properties of beam dynamics are studied and it is found that beam is marginally stable in the absence of any dissipation.
${k}^{\prime}_i$, the normalized absorption coefficient, weakens the self-focusing effect in the absence of b. However, an oscillatory self-focusing takes place for higher value of the decentered parameter. The aspect of the longitudinal phase and the regularized phase is well displayed in the form of graphs using the variational approach in the present investigation. Some features describing the critical curves for b = 0, 1 are also obtained for the chosen set of parameters. A better evolution of laser beam to several Rayleigh lengths is obtained using the variational approach as compared with the PRA. Because integration over the whole wave front is considered in the variational approach whereas in the PRA, only those rays are considered which are very close to the beam axis. Further, a cosh-Gaussian beam can handle high power in comparison with a circular Gaussian beam, the present investigation may shed some light on key aspects such as propagation, losses, diffraction, and critical issues of the relativistic ultra-intense laser–plasma interaction physics relevant to the ICF as well as the intense laser-solid density plasma experiments where the quantum effects are important. Lastly, stability properties of beam dynamics are studied and it is found that beam is marginally stable in the absence of any dissipation.
Acknowledgement
One of the authors, Richa, is thankful to Dean RIC, I.K. Gujral Punjab Technical University for their valuable support.