1. INTRODUCTION
In a nonlinear medium like dielectrics, semiconductors, and plasmas, if a high power electromagnetic beam increases the electric susceptibility, and thus index of refraction with wave intensity, then in a region where the wave amplitude is amplified, the refractive index is also enhanced. The beam thus creates a refractive index profile across its wavefront corresponding to its own intensity profile and focuses of its own. Historically, this phenomenon was predicted by Askar'yan (1962) and named as self-focusing of radiation. The possibility of self-focusing or self-trapping of a laser beam in a solid has been further discussed by Chiao et al. (1964) and Raizer (1967). Hora (1969) treated the process of self-focusing in a plasma in terms of the ponderomotive acceleration due to the gradient of the light intensity. The focusing of the laser beam within the first minima of diffraction yields a lower limit to the laser power. The threshold power was of the order of 1 MW for lasers if cut-off density and plasma temperature of about 10 eV are considered. The value was confirmed by different derivations (Palmer, 1971; Shearer & Eddleman, 1973; Kaw et al., 1973) and in subsequent publications (Jones et al., 1982; Hauser et al., 1988, 1992; Bret et al., 2005; Beech & Osman, 2005; Anderson et al., 2005). It has been extensively studied in context of laser beam propagation since the earlier sixties (Askar'yan, 1962; Akhmanov et al., 1968; Sodha et al., 1976; Anderson et al., 1979; Berge, 1997). In the plasma based applications, it is required that intense laser light be propagated through thousands of wavelengths of underdense plasma. Such situation is prone to vigorous growth of laser plasma instabilities. Self-focusing and filamentation are the key issues to be resolved, understood, and controlled. Recently, these have attracted considerable attention and have been studied extensively for improvement of the uniformity in direct or indirect drive implosion (Young et al., 1995), applications to soft X-ray lasers (Clark & Milchberg, 1997), generation of high harmonics (Milchberg et al., 1995), and fast ignitor concept.
These detrimental processes are most violent in the so-called hot spots of the beam (Russell et al., 1999), where the laser intensity is significantly higher than the average over the focal spot. As far as hot spot dynamics is concerned, in the region of higher laser intensity, increased thermal electron pressure, and pondromotive force cooperate to expel the plasma, increasing the refractive index and leading to still higher intensity. Self-focusing and filamentation have been related to the inhomogeneity of the absorption of laser energy and to the nonuniformity in the target compression in laser induced fusion, latter this triggers the hydrodynamics instability of the target. Since very high power lasers are involved in laser-plasma interaction, controlling self-focusing is crucial to successful and sustainable laser fusion as well as for application to modified fast ignitor schemes for controlled fusion (Hora, 2004, 2005; Badziak et al., 2005).
Most of the theoretical investigations of self-focusing of laser beams in nonlinear media including plasmas, have been carried out for cylindrically symmetric Gaussian beam (Zakharov, 1972; Anderson et al., 1979; Anderson, 1983; Kruglov & Vlasov, 1985; Manassah et al., 1988; Karlsson et al., 1992; Subbarao et al., 1998). Only in a few publications, cylindrical off modes (Jones et al., 1988), spiral self-trapping (Kruglov & Vlasov, 1985), elliptic Gaussian beam (Anderson et al., 1980; Cornolti et al., 1990; Gill et al., 2000, 2004), and nonisotropic and gyrotropic media (Karpman & Shagalov, 1992) were taken into account. Cornolti et al. (1990) have used Wentzel-Krammers-Brillouin (WKB) and paraxial ray (PR) approximations for investigation of elliptic Gaussian beam in a Kerr-medium. The main drawback of this theory is that it over emphasizes the importance of field close to beam axis and lacks global pulse dynamics. It has been recently pointed out that paraxial ray theory (PRT) is not applicable when high power laser beams are used (Subbarao et al., 1998). Since intense laser beams are usually used in laser plasma experiments, it is pertinent to use some alternative approach based on the invariants. Furthermore, PRT does not correctly predicts the phase dynamics. The moment theory (Zakharov, 1972), although remedies this shortcoming but is neither generalized nor does it include the phase dynamics. Variational approach, although a crude one to describe, the singularity formation, and collapse, is fairly general in nature to describe the propagation and correctly predicts the self-phase modulation (Karlsson et al., 1992). We have used variational approach using elliptic Gaussian beam as a trial function. Since the laser systems usually generate a beam which is rather more elliptical than circular in cross-section, it is therefore worthwhile to undertake such realistic situation. In Section 2, we have set up and derived the equations for beam widths a and b using variational approach. Further, we have also set up the equation for longitudinal phase. Section 3 is devoted to the discussion of the important results.
2. BASIC FORMULATION
The fundamental equation which governs the evolution of the field in plasma medium is the nonlinear wave equation. In the slowly varying envelope approximation, the evolution of the electric field envelope in a collisionless magnetoplasma is given by
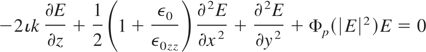
where z is the longitudinal coordinate,
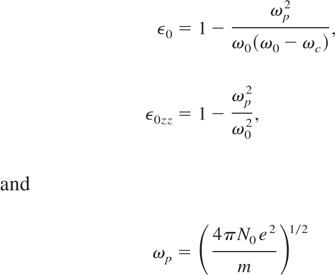
is the plasma frequency.
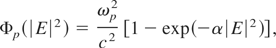
where
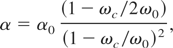
with
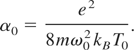
Here ω0 is the angular frequency of the wave, e and m are the electronic charge and mass, respectively, kB is the Boltzmann constant. We investigate elliptic Gaussian beam assuming aberrationless propagation.
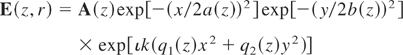
where a and b are the width parameters of the beam in the x and y directions, respectively. It may be noted that beam widths a and b are all real functions of z. The exact solution to Eq. (1) is not available and we, therefore, seek numerical or approximate analytical methods. We choose the latter approach in this paper, using a powerful variational method that has been used in several similar investigations (Anderson et al., 1979; Karlsson et al., 1992). We can reformulate Eq. (1) into a variational problem corresponding to a Lagrangian L so as to make δL/δz = 0 equivalent to Eq. (1), thus, Lagrangian L is given as
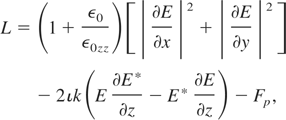
where
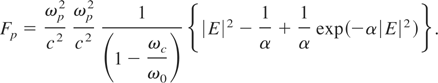
Thus, the solution to the variational problem

also solves the nonlinear Schrodinger equation (NLSE) (1). Using the ansatz, Eq. (3) as a trial function into the Lagrangian L, of Eq. (4), we can integrate L to obtain
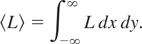
We have arrived at a reduced variational problem. We solve the integration in Eq. (6) to get
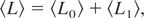
where

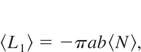
where
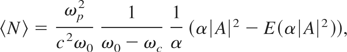
with exponential integral
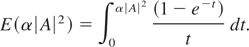
Variation with respect to A, A*, a, b, q1, q2 etc., and following approach of Anderson et al. (1979), we obtain the following equations for a, b, and φ

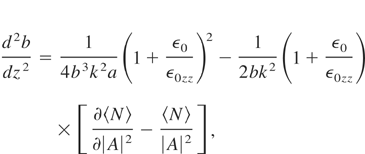
and
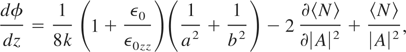
where
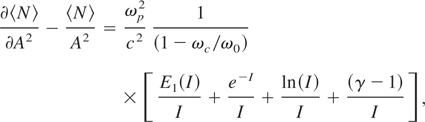
with γ = 0.57721 being a Euler's constant,
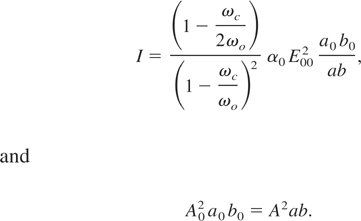
Subscripts on the left-side of the above equation denote the value at z = 0. Eqs. (10) and (11) can be manipulated algebraically in the following form:
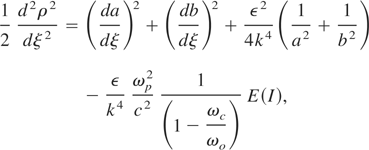
where
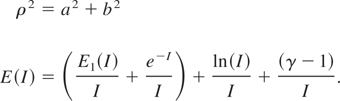
For an initially parallel beam, initial conditions are

implies
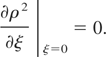
The condition for stationary self-trapping is
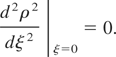
This leads to
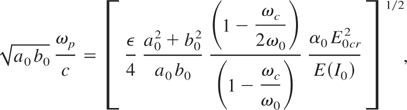
where

with
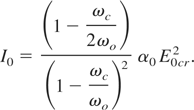
3. DISCUSSION
The first terms on the right-hand side of Eqs. (10) and (11) represent spatial dispersion and are responsible for diffractional divergence. On the other hand, second terms, respectively, are nonlinear in nature leading to self-focusing of the beam. Moreover, these equations are coupled and analytical solution for these equations is not possible. We seek numerical computation of these equations using Runge-Kutta method. The following parameters are chosen for the purpose of numerical calculation a0 = 0.002 cm, b0 = 0.0012 cm, WPO (= ωp /ω0) = 0.45, WCO (= ωc /ω0) = 0.1, α0 E002 = 1.64 and k = 1.3 × 103 cm−1. The results are plotted in the form of graphs. Figure 1 displays the variation of a and b with the normalized distance of propagation ξ (= kz). The phenomenon of cross focusing where focusing of a leads to defocusing of b and vice versa, is observed here for particular value of intensity parameter α0 E002 = 1.64 and magnetic field ωc /ω0 = 0.1. This value corresponds to critical value of field required for self-trapping. However, no self-trapping similar to cylindrically symmetric Gaussian beam is observed for the present case of elliptic Gaussian beam. As apparent from Figure 1, a as well as b keep on oscillating with the distance of propagation.

Variation of beam widths a and b with normalized distance of propagation ξ (= kz) for α0 E002 = 1.64, a0 = 2.0 × 10−3 cm, b0 = 1.2 × 10−3 cm, WCO (= ωc /ω0) = 0.1, WPO (= ωp /ω0) = 0.45 and k = 1.3 × 103 cm−1.
In Figure 2, we observe the effect of ellipticity on the self-focusing/defocusing of elliptic Gaussian beam with distance of propagation. We have chosen two different values of initial a0 and b0 indicating the effect of ellipticity. Increase in ellipticity results in large oscillatory self-focusing/defocusing behavior which emanates disturbed delicate balance between nonlinear term and diffraction term.

Variation of beam widths a and b with normalized distance of propagation ξ for different ratio of a0 and b0. Curves for a1 and b1 correspond to a0 = 2.0 × 10−3 cm, b0 = 1.2 × 10−3 cm. Curves for a2 and b2 correspond to a0 = 2.0 × 10−3 cm, b0 = 1.0 × 10−3 cm, and other parameters are same as mentioned in Figure 1 caption.
In Figure 3, we have shown the plots of beam width parameters a and b for fixed intensity parameter with the distance of propagation corresponding to two values of externally applied magnetic field ωc /ω0 = 0.01 and ωc /ω0 = 0.15, respectively. As obvious from the form of the graphs, higher the value of the applied magnetic field, more oscillatory self-focusing is observed. As obvious from Figure 3b, increase in magnetic field leads to enhanced self-focusing resulting in large intensity. Such situation has potential relevance to microwave emission in laser-plasma interaction and acting as a new source of radiation (Dorranian et al., 2005). Smaller value of magnetic field leads to oscillatory defocusing of the beam. The role of magnetic field is to trap carriers and inhibit the resulting transport. This decrease in ωc /ω0 results in decrease in nonlinear terms in Eqs. (10) and (11), leading to overall expansion of the beam with nonmonotonic evolution of the width parameters as shown in Figure 3.

a: Variation of a and b with ξ for WCO = 0.01 and other parameters are the same as mentioned in Figure 1 caption. b: Variation of a and b with ξ for WCO = 0.15 and other parameters are the same as mentioned in Figure 1 caption.
Eq. (12) represents the phase change with distance of propagation. As apparent from the form of this equation, both a, b, magnetic field, and intensity of beam appear in this equation. Since a and b are determined from Eqs. (10) and (11), therefore even though we can fix intensity and magnetic field, therefore evolution of beam width parameters significantly affect the longitudinal phase delay with ξ. Figure 4 displays such behavior where we have fixed externally applied but taken four different values of intensity parameter α0 E002. As apparent from the form of Eq. (12), we find that longitudinal phase increases whenever α0 E002 decreases. From the form of the graphs representing curve 1 (α0 E002 = 1.64), the phase is always positive with distance of propagation. However, when α0 E002 = 2.25 (curve 2), the phase changes its sign during the course of its propagation. Increase in intensity leads to decrease in nonlinear term with dominance of self-focusing term over the spatial dispersion. The overall effect is negative phase change with ξ (Fig. 4, curves 3 and 4 for other two values). Wiggles in φ with ξ are due to oscillatory focusing/defocusing associated with a and b. Almost similar behavior is observed when intensity parameter α0 E002 = 1.64 fixed but the value of magnetic field is increased, which is shown in Figure 5. The phase may be positive or negative depending on the value of intensity parameter α0 E002 and magnetic field (ωc /ω0) (Figs. 4 and 5). However, the regularised phase, φreg which is defined as
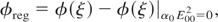
is always negative. This aspect of the phase change is well highlighted in Figure 6, where we have fixed the value of magnetic field but plotted φreg for three different values of α0 E002. This feature confirms the finding of Karlsson et al. (1992) and is contrary to the results of Manassah et al. (1988). The latter predicted results contrary to experimentally observed fact. They predicted that regularized phase may be positive or negative during the course of beam propagation. However, it could imply change in wave number shift leading to erroneous calculation that blue may lead the red in the supercontinuum. This inconsistent result stems from the fact that paraxial ray approximation used by Manassah et al. (1988) does not correctly predict the regularised φreg and our results also reciprocate the findings of Karlsson et al. (1992).

Plot of the longitudinal phase φ(ξ) versus ξ for different values of α0 E002 and other parameters are the same as mentioned in Figure 1 caption.

Plot of the longitudinal phase φ(ξ) versus ξ for different values of WCO and other parameters are the same as mentioned in Figure 1 caption.

Plot of the regularised phase φreg versus ξ for different values of α0 E002 and other parameters are the same as mentioned in Figure 1 caption.
ACKNOWLEDGMENT
Authors are thankful to Prof. D. Anderson, Department of Electromagnetics and EURATOM-VR Association, Chalmers University of Technology, SE-41296 Goteborg, Sweden for his valuable suggestions and comments.








