Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T01:49:28.833Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativistic self-focusing and self-phase modulation of cosh-Gaussian laser beam in magnetoplasma

Published online by Cambridge University Press:  22 March 2011

Tarsem Singh Gill ,
Ravinder Kaur  and
Ranju Mahajan
Tarsem Singh Gill*
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
Ravinder Kaur
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
Ranju Mahajan
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
*
Address correspondence and reprint requests to: Tarsem Singh Gill, Department of Physics, Guru Nanak Dev University, Amristar 143005, India. E-mail: gillsema@yahoo.co.in
Rights & Permissions [Opens in a new window]

Abstract

In this paper, we have investigated the propagation characteristics of cosh-Gaussian laser beam in magnetoplasma using relativistic nonlinearity. The field distribution in the medium is expressed in terms of beam width parameter an and decentred parameter b. An appropriate nonlinear Schräodinger equation has been solved analytically using variational approach. The behaviour of beam width parameter with dimensionless distance of propagation ξ for various b values is examined. Self-phase modulation and self-trapping is also studied under variety of parameters. Further, the effect of magnetic field on self-focusing of the beam have been explored.

Keywords

Cosh-Gaussian beamRelativistic and magnetoplasmaSelf-focusing and self-trappingSelf-phase modulation
Type
Research Article
Information
Laser and Particle Beams , Volume 29 , Issue 2 , June 2011 , pp. 183 - 191
Copyright
Copyright © Cambridge University Press 2011

1. INTRODUCTION

Technological development in the field of laser physics has ushered a new era where highly intense lasers are available. This has opened new vistas of novel applications not only in other fields but also in plasmas such as plasma based accelerators (Esarey et al., 1996; Hartemann et al., Reference Hartemann, Van Meter, Troha, Landahl, Luhmann, Baldis, Gupta and Kerman1998; Sarkisov et al., Reference Sarkisov, Bychenkov, Novikov, Tikhonchuk, Maksimchuk, Chen, Wagner, Mourou and Umstadter1999; Hora et al., Reference Hora1988, Reference Hora, Hoeless, Scheid, Wang, Ho, Osman and Castillo2000; Hauser et al., Reference Hauser, Scheid and Hora1994), advanced laser fusion schemes (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Deutsch et al., Reference Deutsch, Furkawa, Mima, Murakami and Nishihara1996; Regan et al., Reference Regan, Bradley, Chirokikh, Craxton, Meyerhofer, Seka, Short, Simon, Town and Yaakobi1999), ionospheric radio wave propagation, X-ray lasers (Lemoff et al., Reference Lemoff, Yin, Gordon, Barty and Harris1995), harmonic generation (Sprangle et al., Reference Sprangle and Esarey1990) and new radiation sources (Benware et al., Reference Benware, Macchietto, Moreno and Rocca1998; Foldes et al., Reference Foldes, Bakos, Bakonyi, Nagy and Szatmari1999; Fedotov et al., Reference Fedotov, Naumov, Silin, Uryupin, Zheltikov, Tarasevitch and Von der Linde2000). To make these applications feasible, it is desirable that laser beam should propagate several Rayleigh lengths (R d). But in vacuum, the laser beam propagation is limited by diffraction characteristic distance R d ~ k 0 + a 02 +, where k 0+ is wavenumber and a 0+ is laser spot size in vacuum.

In a nonlinear medium like dielectrics, semiconductors and plasmas, the phenomenon of self-focusing being genuinely nonlinear optical process is induced by modification of refractive index of material to intense electromagnetic/laser beam. The electronic nonlinear response of a medium leads to nonlinear polarization that influences the propagation of beam itself. Usually for an electromagnetic radiation such as laser characterized by Gaussian intensity distribution, the refractive index of the medium increases with electric field intensity, leading to self-focusing of the beam. Historically, this phenomenon was predicted by Kerr in 1960 (Askaryan, Reference Askaryan1962; Chiao, Reference Chiao, Garmire and Townes1964) and experimentally verified. In such medium, refractive index is described by the formulae n = n 0 = n 2I, where n 0 and n 2 are linear and nonlinear coefficient of refractive index and I is intensity of radiation. Kerr induced self-focusing is relevant to many applications in laser physics (Chen & Wang, Reference Chen and Wang1991; Herrmann, Reference Herrmann1994). This phenomenon also predicted by Askaryan (Reference Askaryan1962) and named as self-focusing of radiation. The possibility of self-focusing or self-trapping of a laser beam in a solid has been further discussed by Chiao (Reference Chiao, Garmire and Townes1964). This nonlinearly generic process had been focus of attention for nearly five decades and is still being actively persued by researchers worldwide because of their relevance to a number of newly discovered processes. Hora (Reference Hora1969) treated the process of self-focusing due to the gradient of the light intensity. Basic nonlinear physical mechanisms that play crucial role in self-focusing phenomenon are collisional, ponderomotive, relativistic, heating type as reported in the research work (Sodha et al., Reference Sodha, Singh, Singh and Sharma1981, Reference Sodha, Ghatak and Tripathi1976). For example, ponderomotive nonlinearity, resulting from intensity gradient of laser beam, is operational on the time scale of ${a_0 / v_s}$, where a 0 is the dimension of the beam, and v s is the ion acoustic speed. As very high power laser beams are used in experiments, the quiver motion also reduces the local plasma frequency, resulting in relativistic self-focusing (Sprangle et al., 1987; Chessa et al., Reference Chessa, Mora and Antonsen1998; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis-Jacquet, Malka and Miquel1995). Relativistic and ponderomotive self-focusing has been investigated by a number of researchers (Chen et al., Reference Chen, Sarkisov, Maksimchuk, Wagner and Umstadter1998; Krushelnick et al., Reference Krushelnick, Ting, Moore, Burris, Esarey, Sprangle and Baine1997). In a variety of applications, the fundamental TEM00 mode plays a vital role on account of its specific characteristics, and such mode produces the smallest beam divergence and the highest brightness with simple Gaussian intensity profile (Soudagar et al., Reference Soudagar, Bote, Wali and Khandekar1994). Most of the theoretical investigations of self-focusing of laser beam in nonlinear medium including plasmas have been carried out for simple Gaussian beam (Kaur et al., Reference Kaur, Gill and Mahajan2010a, Reference Kaur, Gill and Mahajan2010b; Gill et al., Reference Gill, Mahajan and Kaur2010a) and cylindrically symmetric Gaussian beam (Zakharov,Reference Zakharov1972; Anderson, et al., Reference Anderson, Bonnedal and Lisak1979, 1983; Kruglov & Vlasov, Reference Kruglov and Vlasov1985; Manassah et al., Reference Manassah, Baldeck and Alfano1988; Karlsson et al., 1992; Subbarao et al., Reference Subbarao, Uma and Singh1998). Only a few investigations have been reported on self-focusing of super Gaussian (Nayyar, Reference Nayyar1986; Grow et al., Reference Grow, Ishaaya, Vuong, Gaeta, Gavish and Fibich2006; Fibich, Reference Fibich, Boyd, Lukishova and Shen2007), self trapping of degenerate modes of laser beam (Karlsson, Reference Karlsson1992), self-trapping of Bessel beam (Johannisson et al., Reference Johannisson, Anderson, Lisak and Marklund2003), elliptic Gaussian beam (Anderson et al., Reference Anderson, Bonnedal and Lisak1980; Cornolti et al., Reference Cornolti, Lunches and Zambian1990; Gill et al., Reference Gill, Saini and Kaul2000, Reference Gill, Saini, Kaul and Singh2004; Saini & Gill, Reference Saini and Gill2006; Mahajan et al., 2009), hollow elliptic Gaussian beam (Cai & Lin, Reference Cai and Lin2004), Hermite-cosh-Gaussian beam (Patil et al., Reference Patil, Takale, Navare, Fulart and Dongare2007, Reference Patil, Takale, Fulart and Dongare2008, Reference Patil, Takale and Dongare2010) and cosh Gaussian spiral field (Konar et al., Reference Konar, Mishra and Jana2007). Focusing of dark hollow Gaussian electromagnetic beams in plasma has been reported (Gill et al., Reference Gill, Mahajan and Kaur2010b; Sodha et al., Reference Sodha, Mishra and Misra2009a, Reference Sodha, Mishra and Misra2009b). Ring formation in electromagnetic beams in relativistic magnetoplasma is given (Gill et al., Reference Gill, Kaur and Mahajan2010c). Recent investigations (Casperson et al., Reference Casperson, Hall and Tovar1997; Lu et al., Reference Lu, Ma and Zhang1999; Lu & Luo, Reference Lu and Luo2000; Eyyuboglu & Baykal, Reference Eyyuboglu and Baykal2004, Reference Eyyuboglu and Baykal2005; Konar et al., Reference Konar, Mishra and Jana2007) have focused on the cosh-Gaussian spiral field and its propagation characteristics highlighting potential applications. The propagation properties of cosh-Gaussian laser beams are important technological issues since these beams possesses high power in comparison to that of a Gaussian laser beam. With the availability of superintense laser pulse, the laser plasma interactions has undergone a paradigm shift. The electron oscillatory velocity at high laser intensity approaches the velocity of light and we enter a regime when relativistic effects are of paramount importance. The situation is more relevant in the fast ignition schemes of laser driven fusion. In such case, long laser pulse converts the pellet into plasma ball, heats the coronal region, and compresses the core to a superdense plasma. Propagation of intense laser in such plasma involves the relativistic mass effect and plasma frequency is lowered falling below the laser frequency, consequently making the plasma transparent. Several models for propagation in overdense plasma have been proposed (Vshivkov et al., Reference Vshivkov, Naumova, Pegoraro and Bulanov1998; Fuchs et al., Reference Fuchs, Adam, Amiranoff, Baton, Gallant, Gremillet, Héron, Kieffer, Laval, Malka, Miquel, Mora, Ppin and Rousseaux1998; Pandey et al., 2006; Cattani et al., Reference Cattani, Kim, Anderson and Lisak2000; Yu et al., Reference Yu, Yu, Zhang and Xu1998). Intense laser beam produce self induced strong magnetic field of several megagauss.

Mostly used model to study self-focusing is based on Wentzel-Kramer-Brillouin (WKB) and paraxial ray approximation (PRA) through a nonlinear parabolic wave equation (Akhmanov et al., Reference Akhmanov, Schnorkel and Chekhov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976). Liu and Tripathi (1994) used PRA and WKB approximation to study the competing physical process of self-focusing and diffraction. The main drawback of the PRA is that it overemphasizes the importance of field close to beam axis and lacks global pulse dynamics. Another global approach is variational approach, though crude to describe the singularity formation and collapse dynamics is fairly genuine in nature to study propagation and also it correctly predicts the phase. Variational approach is used in many other branches of science. In the present investigation, the attention is being paid to address the self-focusing and self-phase modulation of a beam having cosh-Gaussian field distribution. Also the present investigation extends to cover the effect of linear absorption on to self-focusing. The paper is structured as the following: In Section 2, we have given brief description of dielectric constant and derived the equation for the beam width parameter a n using Variational approach in relativistic magnetoplasma. In Section 3, we have introduced the concept of self-trapping. In Section 4, we presented a detailed discussion of numerical work carried out for the relevant parameters. Last, Section 5 is devoted to the conclusions of the present investigation.

2. BASIC FORMULATION

The wave equation governing the propagation of electromagnetic wave in extraordinary mode

(1)
{\rm \delta}_+ \nabla_{\bot}^2 A_{0+} - 2\iota k_{0+} {\partial A_{0+} \over \partial z} + {{\rm \omega}^2 \over c^2} \rm \epsilon_+ \lpar r\comma \; z\rpar A_{0+} = 0\comma \; \eqno\lpar 1\rpar

where ${\rm \delta}_+ = {\lpar1 / 2\rpar}\lpar 1 + {{\rm \epsilon}_{0+} / {\rm \epsilon}_{0zz}}\rpar $ and ${\rm \epsilon}_{0zz} = 1 - {{\lpar\rm \omega}_p^2 / {\rm \omega}^2\rpar}$. ɛ0zz is the dielectric tensor component along the z direction. ω is the wave frequency, c is the speed of light in free space, $k_{0+}^2 = {{\rm \epsilon}_0 {\lpar\rm \omega}^2 / c^2\rpar}\comma \; {\rm \epsilon}_0$ is the dielectric function on the axis of the beam and the effective plasma permittivity ɛ+ (r, z) (Pandey & Tripathi, Reference Pandey and Tripathi2009) is given by:

(2)
{\rm \epsilon}_+ \lpar r\comma \; z\rpar = 1 - {{\rm \omega}_p^2 \over \left({\rm \omega} - \displaystyle {{\rm \omega}_c \over {\rm \gamma}} \right){\rm \gamma} }. \eqno\lpar 2\rpar

Here

(3)
{\rm \omega}_c = {eB_0 \over m_0 c}\comma \; \eqno\lpar 3\rpar
(4)
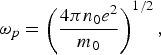
{\rm \omega}_p = \left({4{\rm \pi} n_0 e^2 \over m_0} \right)^{1 / 2}\comma \; \eqno\lpar 4\rpar

be the nonrelativistic plasma frequency and −e and m 0 are the electronic charge and rest mass, and the relativistic factor is

(5)
{\rm \gamma} = \left[1 +{e^2 \vert A_{0+}^2 \vert \over m_0^2 c^2 \left( {\rm \omega} - \displaystyle {{\rm \omega}_c \over {\rm \gamma}}\right) ^2 } \right]^{1 / 2}\comma \; \eqno\lpar 5\rpar
(6)
{\rm \gamma} = \left[1 + a^2 \left(1 - {{\rm \omega}_c \over {\rm \gamma} {\rm \omega}} \right)^{ - 2} \right]^{1 / 2}\comma \; \eqno\lpar 6\rpar

where

(7)
a^2 = {e^2 \vert A_{0+}^2 \vert \over m_0^2 c^2 {\rm \omega} ^2}. \eqno\lpar 7\rpar

For ${{\rm \omega}_c / {\rm \gamma} {\rm \omega}} \lt 1$, the equation can be solved iteratively. First we choose ωc = 0, then ${\rm \gamma} = \lpar 1 + a^2\rpar ^{1 / 2}$; by using this value of γ in the right hand side of Eq. (8), we obtain

(8)
{\rm \gamma} = \left[1 + a^2 \left(1 - {{\rm \omega}_c \over {\rm \omega} \lpar 1 + a^2 \rpar ^{1\ 2}} \right)^{- 2}\right]^{1 / 2}\comma \; \eqno\lpar 8\rpar
(9)
{\rm \gamma} = \left[1+ a^2 + 2a^2 {{\rm \omega}_c \over {\rm \omega}} \left({1 \over \lpar 1 + a^2 \rpar ^{1 / 2}}\right)+ 3a^2 {{\rm \omega}_c^2 \over {\rm \omega}^2}\left({1 \over \lpar 1 + a^2 \rpar } \right)\right]^{1 / 2}\comma \; \eqno\lpar 9\rpar

The exact solution of Eq. (1) is not available and we therefore seek either numerical or analytical approximate method. Although several approximate methods are available, we have used a powerful variational method, which have been used in several nonlinear wave problem in many physical systems (Anderson, Reference Anderson1983). The results of this approach agree quantitatively with that of moment theory and computer simulations (Arevalo, Reference Arevalo and Becker2005). In this approach, we can reformulate Eq. (1) into a variational problem corresponding to a Lagrangian L so as to make ${{\rm \delta} L / {\rm \delta} z} = 0$, is equivalent to Eq. (1). Following (Anderson et al., Reference Anderson, Bonnedal and Lisak1979; Karlsson, Reference Karlsson1992; Gill et al., Reference Gill, Saini and Kaul2001), the Lagrangian L is given by:

(10)
\eqalign {L = &\,\iota k_{0+} \left(A_{0+} {\partial A_{0+}^{\ast} \over \partial z} - A_{0+}^{\ast} {\partial A_{0+} \over \partial z} \right)- \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)\vert {\partial A_{0+} \over \partial r}\vert^2 \cr &+ {{\rm \omega}^2 \over c^2} \left({\rm \alpha} A_{0+}^2 - {{\rm \omega}_p^2 \over {\rm \omega}^2} {{\rm \omega}_c \over {\rm \omega}} {\rm \alpha} A_{0+}^2 - {{\rm \omega}_p^2 \over {\rm \omega}^2} {\rm \alpha} A_{0+}^2 +{{\rm \omega}_p^2 \over {\rm \omega}^2} \Bigg( 1 + 5{{\rm \omega}_c \over {\rm \omega}}\Bigg) \right. \cr &\quad \times \left.{\lpar {\rm \alpha} A_{0+}^2 \rpar ^2 \over 2} \Bigg( {1 \over 2} + {{\rm \omega}_c \over {\rm \omega}}\Bigg) - {{\rm \omega}_p^2 \over {\rm \omega}^2} \Bigg( 2 + {{\rm \omega}_c \over {\rm \omega}}\Bigg) {\lpar {\rm \alpha} A_{0+}^2\rpar ^3 \over 3} {{\rm \omega}_c \over {\rm \omega}} \right)\comma \; }

where ${\rm \alpha} = {e^2 / m_0^2 c^2 {\rm \omega}^2}$.

Thus, the solution to the variational problem:

(11)
{\rm \delta} \vint\hskip-1.2pt\vint Ldrdz = 0\comma \; \eqno\lpar 11\rpar

also solves the nonlinear Schrödinger Eq. (1). We can construct the following ansatz for the field distribution of cosh-Gaussian beam A0+ in extraordinary mode propagating along the z-axis.

(12)
\eqalign {A_{0+} \lpar r\comma \; z\rpar \, = \, & {A_{0+}^\prime \over 2} exp \left({b^2 \over 4}\right)exp\lpar\!\! -\! 2k_i z\rpar \cr &\left[exp - \left({r \over a_+} + {b \over 2}\right) ^2 + exp - \left({r \over a_+} - {b \over 2}\right)^2 \right]exp\left[\iota q_+^\prime r^2 + \iota {\rm \phi} \right]\comma \; } \fleqno\lpar 12\rpar

where ki is the absorption coefficient, q′+ is spatial chirp, and a + is the beam width parameter. Particularly, we have chosen extraordinary mode for the beam propagation as ɛ0+ should be positive for plasma to act as an overdense medium (Misra & Mishra, Reference Misra and Mishra2009). Using A 0+ given by Eq. (12) into L, we integrate L to obtain:

(13)
\lt L \gt = \vint_0^\infty \, Ldr\comma \; \eqno\lpar 13\rpar
(14)
\lt L \gt = \lt L_0\!\! \gt + \lt \!L_1 \!\gt. \eqno\lpar 14\rpar

Thus, we have arrived at reduced variational problem. We solve the above integral to give:

(15)
\eqalignno{\lt L_0 \gt = &{\iota k_{0+} \over 4}exp\left({b^2 \over 2} - 4k_i z \right)exp\left({- b^2 \over 2} \right)a_+ \surd {\rm \pi} \left({4 \over \surd 2} + {b^2 \over 2\surd 2} \right)\cr & \quad\times\left(A_{0+}^\prime {\partial A_{0+}^{\ast \prime} \over \partial z} - A_{0+}^{\ast \prime} {\partial A_{0+} \over \partial z} \right)+ {k_{0+} \over 2}exp\left( {b^2 \over 2} - 4k_i z\right) \cr &\quad\times\;\vert A_{0+}^\prime \vert^2 {d_+ \over dz}exp\left({- b^2 \over 2} \right){a_+^3 \surd {\rm \pi} \over 2\surd 2}\left(1 + {b^2 \over 8} \right)+ {k_{0+} \over 2} \cr &\quad\times\; exp\left({b^2 \over 2} - 4k_i z \right)\vert A_{0+}^\prime \vert^2 {d{\rm \phi} \over dz}exp\left({ - b^2 \over 2} \right)a_ + \surd {\rm \pi} \cr &\quad \times\left({4 \over \surd 2} + {b^2 \over 2\surd 2} \right) \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right){\vert A_{0+}^\prime \vert^2 \over 4}\cr &\quad \times exp\left({b^2 \over 2} - 4k_i z\right) exp\left( - b^2 \right)\cr &\quad\times \left({2 \surd {\rm \pi} \over a_+\surd 2} - {2b^2 \surd {\rm \pi} \over a_+\surd 2} + {b^2 \surd {\rm \pi} \over 8a_+\surd 2} + {b^4 \surd {\rm \pi} \over a_+2\surd 2} \right)\cr &\quad - \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right){4q_+^2 a_+^3 \surd {\rm \pi} exp\lpar {- b^2 / 2}\rpar \over 2\surd 2}\left(1 + {b^2 \over 8} \right)\cr & \quad \times\; exp\left({b^2 \over 2 - 4k_i z} \right){\vert A_{0+}^\prime \vert ^2 \over 4}\comma &\lpar 15\rpar}
(16)
\eqalign{\lt L_1 \gt = &{{\rm \omega} ^2 \over c^2 }{{\rm \alpha} \vert A_{0+}^\prime \vert ^2 \over 4}exp\left({b^2 \over 2} - 4k_i z \right)\left(1 - {{\rm \omega}_p^2 \over {\rm \omega} ^2 }{{\rm \omega}_c \over {\rm \omega} } - {{\rm \omega}_p^2 \over {\rm \omega}^2} \right)\cr & \quad \times exp\left({ - b^2 \over 2} \right)\left({4a_+\surd {\rm \pi} \over \surd 2} + {b^2 a_+\surd {\rm \pi} \over 2\surd 2} \right)+ {{\rm \omega} ^2 \over c^2 }{{\rm \omega}_p^2 \over 2{\rm \omega} ^2 } \cr &\quad \times \left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right){\lpar {\rm \alpha} \vert A_{0+}^\prime \vert^2 \rpar ^2 \over 4}exp2\left({b^2 \over 2} - 4k_i z \right)\cr &\quad \times exp \left(- b^2 \right)a_+\surd {\rm \pi} \left(8 + 2b^2 \right)- {{\rm \omega} ^2 \over c^2}{{\rm \omega}_p^2 \over 3{\rm \omega} ^2} \left(2 + {{\rm \omega}_c \over {\rm \omega}} \right){{\rm \omega}_c \over {\rm \omega} }\cr &\quad \times {\lpar {\rm \alpha} \vert A_{0+}^\prime \vert^2 \rpar ^3 \over 4} exp3\left({b^2 \over 2} - 4k_i z\right)a_+\surd {\rm \pi} \left({2exp\lpar {- 3b^2 / 2}\rpar \over \surd 6} \right.\cr & \left.\quad + {4exp\lpar {- 3b^2 / 2}\rpar \over 3\surd 6} + {15 \over 2}exp\lpar \!-\! b^2 \rpar + {3 \over 4}b^2 exp\lpar \!-\! b^2\rpar \right).}\eqno\lpar 16\rpar

We obtain Euler-Lagrange equations using ${{\rm \delta} \lt L \gt \!\!/ {\rm \delta} S} = 0$, where S denotes A′0+, A 0+*′, a +, q′+ etc. and following procedure of (Anderson et al., Reference Anderson, Bonnedal and Lisak1979), we get:

(17)
\vert A_0 + ^\prime\!\vert ^2 \,a_+^2 = A_+^2 a_{0+}^2\comma \; \eqno\lpar 17\rpar
(18)
q^\prime = - {k_{0+} \over 4a_+d\lpar z\rpar }{da_+ \over dz}\comma \; \eqno\lpar 18\rpar
(19)
\eqalign{{d^2 a_+ \over dz^2} &= {2\left(1 + ({{\rm \epsilon}_{0+} / {\rm \epsilon}_{0zz})} \right)^2 \over \bigg( 1 + \displaystyle {b^2 \over 8}\bigg )} {exp\lpar {- \lpar b\rpar ^2 / 2}\rpar \over k_{0+}^2 a_+^3 }\left(4 - 4b^2 + {b^2 \over 4} + b^4 \right)\cr & \quad- {\surd 2 \over a_+\bigg( 1 + {\displaystyle {b^2 \over 8}}\bigg ) }exp\left(b^2 /2 - 4k_i z \right)\lpar 8+2b^2\rpar \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)\cr &\quad \times {{\rm \omega}_p^2 \over {\rm \omega}^2} exp\left({- b^2 \over 2} \right)\left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right){\rm \alpha} \vert A_{0+}^\prime \vert^2 \cr &\quad + {4\surd 2 \over 3a_+} \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)exp\lpar 3{b^2 \over 2} - 8k_i z\rpar {1 \over \bigg( 1 + {\displaystyle {b^2 \over 8}}\bigg )}{{\rm \omega}_p^2 \over {\rm \omega} ^2}{{\rm \omega}_c \over {\rm \omega}} \cr &\quad \times\left(2 + {{\rm \omega}_c \over {\rm \omega}} \right)\lpar {\rm \alpha} \vert A_{0+}^{\prime} \vert^2\rpar^2 \left({2exp\lpar {- 3b^2 / 2}\rpar \over \surd 6} + {4exp\lpar { - 3b^2 / 2}\rpar \over 3 \surd 6} \right. \cr & \quad\left. + {15 \over 2} exp\lpar \!\!- \!b^2 \rpar + {3 \over 4}b^2 exp\lpar \!\!- \!b^2 \rpar \right)\comma} \eqno\lpar 19\rpar
(20)
\eqalign {{d{\rm \phi} \over dz} &= \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right){1 \over k_{0+} \bigg( 1 + {\displaystyle {b^2 \over 8}}\bigg ) }exp\left(- {b^2 \over 2}\right) \cr &\quad\times\left({1 \over 4a_+^2} - {b^2 \over 4a_+^2} + {b^2 \over 64a_+^2} + {b^4 \over 16a_+^2} \right)\cr &\quad- {{\rm \omega}^2 \over k_{0+} c^2}{5\surd 2 \over 64}{\rm \alpha} \vert A_{0+}^\prime \vert^2 exp\left(b^2/2 - 4k_i z \right)\cr &\quad \times {1 \over \bigg(1 + { \displaystyle {b^2 \over 8}}\bigg) } exp\left( - {b^2 \over 2}\right) \lpar 8+2b^2 \rpar {{\rm \omega}_p^2 \over {\rm \omega}^2}\left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right)\cr & \quad+ {{\rm \omega}^2 \over k_{0+} c^2} exp\left( 3{b^2 \over 2} - 4k_i z\right) {{\rm \omega}_p^2 \over {\rm \omega}^2}{{\rm \omega}_c \over {\rm \omega}}\lpar {\rm \alpha} \vert A_{0+}^\prime \vert^2 \rpar ^2 {1 \over \bigg( 1 + {\displaystyle {b^2 \over 8}}\bigg ) } \cr &\quad \times\left({\surd 2exp\lpar {- 3b^2 / 2}\rpar \over 24\surd 6} + {\surd 2 exp\lpar { - 3b^2 / 2}\rpar \over 36\surd 6} + {15 \surd 2 exp\lpar \!\!-\! b^2\rpar \over 96} \right. \cr & \quad\left.+ {3\surd 2b^2 exp\lpar \!\!-\! b^2 \rpar \over 48} \right)- {{\rm \omega}^2 \over k_{0+} c^2} {1 \over 4}\left(1 - {{\rm \omega}_p^2 \over {\rm \omega}^2}{{\rm \omega}_c \over {\rm \omega}} - {{\rm \omega}_p^2 \over {\rm \omega}^2} \right)\cr & \quad+ {\surd 2 \over 4} {{\rm \omega}_p^2 \over {\rm \omega}^2} {{\rm \omega}_c \over {\rm \omega}} \left(2 + {{\rm \omega}_c \over {\rm \omega}} \right){\rm \alpha} \vert A_{0+}^\prime \vert^2 {exp\lpar b^2 - 8k_i z\rpar \over \bigg( 1 + { \displaystyle{b^2 \over 8}}\bigg) } \cr &\quad + {4exp\lpar {- 3b^2 /2}\rpar \over 3\surd 6} + {15exp\lpar \!\!-\! b^2\rpar \over 2} + {3b^2 exp\lpar \!\!-\! b^2\rpar \over 4} \Bigg).} \eqno \lpar 20\rpar

We usually write the above equations in the dimensionless form using ${\rm \xi} = {zc / {\rm \omega}_0 a_0^2}$

(21)
\eqalign{{d^2 a_{n+} \over d{\rm \xi}^2} &= {2\left(1 + {\rm \epsilon}_{0+} / {\rm \epsilon}_{0zz} \right)^2 \over \bigg( 1 + {\displaystyle {b^2 \over 8}}\bigg ) } {exp\lpar { - \lpar b\rpar ^2 / 2}\rpar \over a_{n+}^3}\left(4 - 4b^2 + {b^2 \over 4} + b^4 \right)\cr &\quad- {\surd 2k_{0+}^2 a_0^2 \over a_{n+} \lpar 1 + {b^2 / 8}\rpar } exp\left(b^2 /2 - 4k_i {\rm \xi} \right)\lpar 8 + 2b^2\rpar \left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)\cr &\quad \times {{\rm \omega}_p^2 \over {\rm \omega} ^2}exp\left({ - b^2 \over 2} \right)\left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right){\rm \alpha} \vert A_{0+}^\prime \vert^2 \cr &\quad+ {4\surd 2k_{0+}^2 a_0^2 \over 3a_{n+}}\left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)exp\lpar 3{b^2 \over 2} - 8k_i^\prime {\rm \xi}\rpar {1 \over \bigg ( 1 + { \displaystyle {b^2 \over 8}}\bigg) } \cr & \quad \times{{\rm \omega}_p^2 \over {\rm \omega} ^2} {{\rm \omega}_c \over {\rm \omega}}\left(2 + {{\rm \omega}_c \over {\rm \omega}} \right)\lpar {\rm \alpha} \vert A_{0+}^\prime \vert^2\rpar ^2 \left({2exp\lpar {- 3b^2 / 2}\rpar \over \surd 6} \right. \cr & \quad\left. + {4exp\lpar {- 3b^2 / 2}\rpar \over 3\surd 6} + {15 \over 2} exp\lpar \!\!-\! b^2\rpar + {3 \over 4}b^2 exp\lpar \!\!- \!b^2 \rpar \right)\comma} \eqno\lpar 21\rpar
(22)
\eqalign{{d{\rm \phi} \over d{\rm \xi} } &=\left(1 + {{\rm \epsilon}_{0+} \over {\rm \epsilon}_{0zz}} \right)\left( 1 + {b^2 \over 8}\right) exp\left(- {b^2 \over 2}\right) \left({1 \over 4a_{n+}^2 a_0^2 } - {b^2 \over 4a_{n+}^2 a_0^2} \right. \cr &\quad \left. + {b^2 \over 64a_{n+}^2 a_0^2} + {b^4 \over 16a_{n+}^2 a_0^2}\right)- {k_{0+}^2 a_0^2 5\surd 2 \over 24}{\rm \alpha} \vert A_{0+}^\prime \vert ^2 \cr &\quad \times exp\left({b^2 /2 - 4k_i^\prime \xi} \right){1 \over \bigg( 1 + { \displaystyle{b^2 \over 8}}\bigg) } exp\left(- {b^2 \over 2}\right)\lpar 8 + 2b^2\rpar {{\rm \omega}_p^2 \over {\rm \omega} ^2}\cr &\quad \times\left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right)+ exp\lpar 3{b^2 \over 2} - 4k_i^\prime {\rm \xi}\rpar {{\rm \omega}_p^2 \over {\rm \omega} ^2}{{\rm \omega}_c \over {\rm \omega}}\cr &\quad \times \lpar {\rm \alpha} \vert A_{0+}^\prime \vert ^2\rpar ^2 {1 \over \bigg( 1 + { \displaystyle{b^2 \over 8}}\bigg) } \left({\surd 2exp\lpar {- 3b^2 / 2}\rpar \over 24\surd 6} + {\surd 2exp\lpar {- 3b^2 / 2}\rpar \over 36\surd 6} \right. \cr & \quad\left. + {15\surd 2exp\lpar \!\!-\! b^2\rpar \over 96} + {3\surd 2b^2 exp\lpar \!\!-\! b^2\rpar \over 48} \right)- {k_{0+}^2 a_0^2 \over 4}\cr & \quad \times\left(1 - {{\rm \omega}_p^2 \over {\rm \omega} ^2}{{\rm \omega}_c \over {\rm \omega}} - {{\rm \omega}_p^2 \over {\rm \omega} ^2} \right)+ k_{0+}^2 a_0^2 {\surd 2 \over 4} {{\rm \omega}_p^2 \over {\rm \omega} ^2} {{\rm \omega}_c \over {\rm \omega}}\left(2 + {{\rm \omega}_c \over {\rm \omega}} \right)\cr &\quad \times\lpar {\rm \alpha} \vert A_{0+}^\prime \vert ^2\rpar ^2 {exp\lpar b^2 - 8k_i^\prime {\rm \xi}\rpar \over \lpar 1 + {(b^2 / 8)}\rpar } \left({2exp\lpar {- 3b^2 / 2}\rpar \over \surd 6} + {4exp\lpar {- 3b^2 / 2}\rpar \over 3\surd 6} \right. \cr & \quad\left.+ {15exp\lpar \!\!-\! b^2\rpar \over 2} + {3b^2 exp\lpar \!\!-\! b^2\rpar \over 4} \right){{\rm \omega} ^2 \over c^2}\comma} \eqno \lpar 22\rpar

where k′i = k iR d is the normalized absorption coefficient.

3. SELF-TRAPPED MODE

For an initially plane wave front, ${\lpar da_+ / dz\rpar } = 0$ and a +=1 at z = 0, the condition ${\lpar d^2 a_+ / dz^2\rpar} = 0$ leads to the propagation of cosh-Gaussian beam in the uniform waveguide/self-trapped mode.

By putting ${\lpar d^2 a_+ / dz^2\rpar} = 0$ in Eq. (19), we obtain a relation between equilibrium beam width parameter $R\lpar ={{\rm \omega}_0 a_e / c}\rpar $ and intensity parameter α | A′0+ |2 taking into account relativistic type nonlinearity. The expression when simplified is given as follow:

(23)
\eqalign{\left({{\rm \omega}_0 a_e \over c} \right)^2 &= exp\left({- \lpar b\rpar ^2 \over 2} \right)\left(4 - 4b^2 + {b^2 \over 4} + b^4 \right)\left[\surd 2{\rm \alpha} \vert A_{0+}^\prime \vert ^2 \right. \cr &\quad \times\left. exp\left(b^2 /2 - 4k_i z \right)\lpar 8 + 2b^2\rpar {{\rm \omega}_p^2 \over {\rm \omega}^2 } exp\left({- \lpar b\rpar ^2 \over 2}\right) \left(1 + 5{{\rm \omega}_c \over {\rm \omega}} \right)\right. \cr &\quad\times \left.\left({1 \over 2} + {{\rm \omega}_c \over {\rm \omega}} \right)- {4 \over 3}\surd 2exp\bigg( 3{b^2 \over 2} - 8k_i z\bigg) {{\rm \omega}_p^2 \over {\rm \omega} ^2} {{\rm \omega}_c \over {\rm \omega}} \left(2 + {{\rm \omega}_c \over {\rm \omega}} \right)\right. \cr & \quad \times\left.\lpar {\rm \alpha} \vert A_{0+}^\prime \vert ^2\rpar ^2 \left({2exp\lpar {- 3b^2 / 2}\rpar \over \surd 6} + {4exp\lpar {- 3b^2 / 2}\rpar \over 3\surd 6} \right.\right. \cr & \quad \left.\left. + {15 \over 2} exp\lpar \!\!-\! b^2 \rpar + {3 \over 4}b^2 exp\lpar \!\!- \!b^2\rpar \right)\right]^{- 1}.} \eqno \lpar 23\rpar

4. DISCUSSION

For an initially plane wavefront of the beam, ${\lpar da_+ / dz\rpar } = 0$ at z = 0; hence initially beam width will decrease (focusing) or increase (divergence), when ${\lpar d^2 a_+ / dz^2\rpar } = 0$; a does not change (a + = 1) and beam is said to propagate in the uniform waveguide. Eqs. (21) and (22) are nonlinear ordinary differential equations governing the evolution of normalized beam width of the laser beam and phase developed during the propagation in magnetoplasma. It may further be mentioned that the right-hand side of Eq. (21) contains several terms, each representing some physical mechanism responsible for the evolution of beam during its propagation in plasma. First term on the right-hand side is diffraction term which leads to divergence of beam as the beam propagate in the medium whereas second and third term is due to relativistic nonlinearity which is responsible for the convergence of the beam. This nonlinear term oppose the phenomenon of diffraction and depending on its numerical value as compared to the diffractive terms, we can observe focusing/defocusing of the beam. It is the relative competition of the various terms which ultimately determines the fate of the beam width. Eq. (22) describe associative longitudinal phase change as the beam travel through medium. Eqs. (21) and (22) are coupled nonlinear ordinary differential equations and can not solved analytically. We therefore analyse them numerically and find the solution. To highlight propagation characteristics, we have performed numerical computation of Eqs. (21) and (22) for the following set of parameters:

k_0 = 1.25 \times 10^3cm^{- 1}\comma \; a_0 = 0.002cm\comma \; {\rm \alpha} \vert A_0^\prime \vert ^2 = 0.5\comma \; {{\rm \omega}_p^2 \over {\rm \omega}^2} = 5

In Figure 1, we have displayed the variation of the beam width parameter a n+ with normalized distance of propagation ξ for the chosen set of parameters. This figure displays the self-focusing effect for different values of absorption coefficient(k′i ). It is observed that large value of absorption coefficient weakens the self-focusing in the absence of decentred parameter (b = 0). Sharp self-focusing occurs up to k′i < 2, but beam width parameter first decreases and then increases slowly for k′i ≥ 2. If k′i increase, the minimum shift to the lower values of ξ occurs with increasing minimum dimension a n+ of the beam. However, there is substantial decrease in self-focusing length with increase in absorption coefficient (k′i). From Figure 2, it is observed that all curves are seen to exhibit sharp self-focusing for finite value of decentred parameter (b) but self-focusing length increases with absorption level (k′i). This occurs because of the decentred parameter that changes the nature of self-focusing/defocusing of the beam. Sharp self-focusing is observed in Figure 3 at finite value of decentred parameter (b), where decrease in magnetic field leads to increase in self-focusing. Eq. (22) represents the phase change with distance of propagation. As apparent from the form of this equation, beam width, magneticfield, absorption coefficient, decentred parameter, and intensity of the beam appear in this equation. Since a n+ is determined from Eq. (21), therefore even though we can fix absorption coefficient, intensity and magnetic field, the evolution of beam width parameter significantly affect the longitudinal phase delay with ξ. Figures 4 and 5 depicts such behavior where we have fixed magnetic field and intensity parameter but taken different values of absorption coefficient (k′i) for b = 0 and b = 1. It is observed that phase is positive or negative depending on the value of decentred parameter (b). In Figures 6 and 7, we have fixed k′i and intensity parameter but taken different values of magnetic field (${{\rm \omega} c /{\rm \omega}}$) for b = 0 and b = 1. From Figure 6 it is observed that phase decreases with increase in magnetic field when decentred parameter, b = 0. However, the contrasting behaviour is observed when finite value of decentred parameter (b) is considered as obvious from Figure 7.

Fig. 1. (Color online) Variation of normalized beam width parameter a n with dimensionless distance of propagation ξ with b = 0 (in the absence of decentred parameter) for different values of absorption coefficient k′i. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2\rpar } = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega\rpar }} = 0.4.$ Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 1, dotted curve correspond to when k′i = 2 and dotdashed curve correspond to when k′i = 3.

Fig. 2. (Color online) Variation of normalized beam width parameter a n with dimensionless distance of propagation ξ with b = 2 (finite value of decentred parameter) for different values of absorption coefficient k′i. The parametersused here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2\rpar} = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega \rpar}} = 0.4.$ Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 1, dotted curve correspond to when k′i = 2 and dotdashed curve correspond to when k′i = 3.

Fig. 3. (Color online) Dependence of normalized beam width parameter a n on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for finite value of b. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2 \rpar} = 5.$ Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.06$.

Fig. 4. (Color online) Variation of the longitudinal phase delay ϕ with dimensionless distance of propagation ξ with b = 0 (in the absence of decentred parameter) for different values of absorption coefficient k′i and with the otherparameters the same as mentioned in Figure 1. Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 0.3, dotted curve correspond to when k′i = 0.5 and dotdashed curve correspond to when k′i = 0.7.

Fig. 5. (Color online) Variation of the longitudinal phase delay ϕ with dimensionless distance of propagation ξ with b = 1 (finite value of decentred parameter) for different values of absorption coefficient k′i and with the other parameters the same as mentioned in Figure 1. Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 0.3, dotted curve correspond to when k′i = 0.5 and dotdashed curve correspond to when k′i = 0.7.

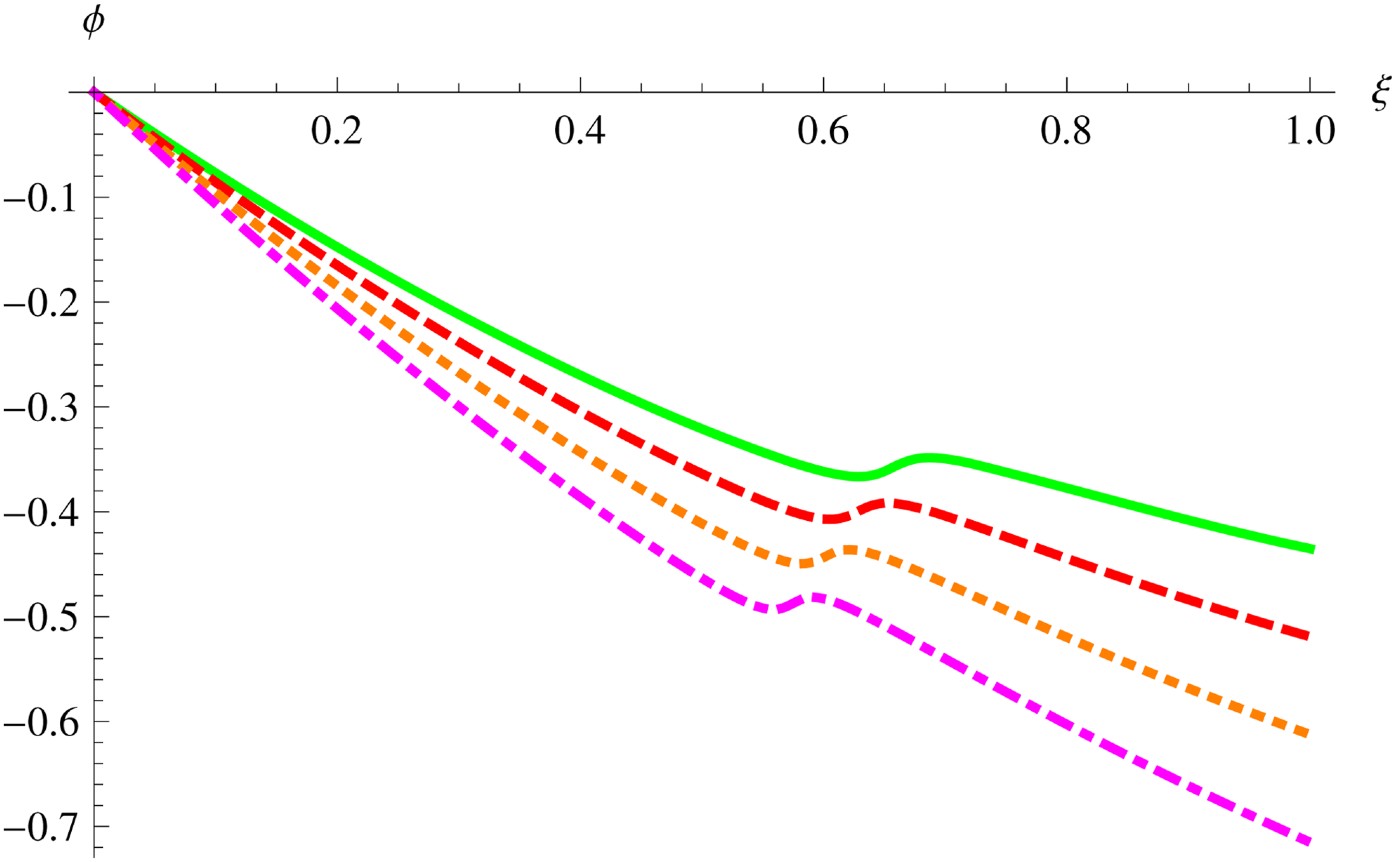
Fig. 6. (Color online) Dependence of longitudinal phase delay ϕ on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for b = 0. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2}\rpar = 5$. Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.06$.

Fig. 7. (Color online) Dependence of longitudinal phase delay ϕ on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for b = 1. The parameters usedhere are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega} ^2 \rpar} = 5$. Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.06$.

In self-trapped mode, we put d 2a +/dz 2 = 0 in Eq. (19) to highlight the features as how decentred parameter, b determines the behaviour of laser beam in magnetoplasma. Figure 8 depicts the dependence of equilibrium radii R as a function of A(=α |A′0|2) for three values of b. For low values of b, the present investigation predicts higher values of equilibrium radii with faster monotonic fall with increase in intensity. However, increase in values of b results in lower values of equilibrium radii as well as weaker dependence on intensity. The behaviour is quite similar to the earlier prediction based on variational approach (Anderson & Bonnedal, Reference Chessa, Mora and Antonsen1979; Anderson, Reference Anderson1978).

Fig. 8. (Color online) Plot of equilibrium beam width R as intensity parameter $A = {\rm \alpha} \vert A_{0+}^\prime \vert^2$ for different value of decentred parameter (b). The parameters used here are: ${{\lpar \rm \omega}_p^2 / {\rm \omega} ^2\rpar} = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.2$. Solid curve correspond to when b = 0, dashed curve corresponds to b = 0.5 and dotted curve correspond to b = 1.

5. CONCLUSIONS

In the present investigation, we have studied self-focusing and self-phase modulation of laser beam in relativistic magnetoplasma. Equation for beam width parameter is derived using variational approach. We find that study of cosh-Gaussian beams can be analyzed like Gaussian beam in plasma, but the decentred parameter and absorption coefficient are found to play key role on the nature of self-focusing/defocusing of the beam.

ACKNOWLEDGMENT

R. K. and R. M. gratefully acknowledge for financial support by Guru Nanak Dev University, Amritsar India.

References

REFERENCES

Akhmanov, S.A., Schnorkel, A.P. & Chekhov, R.V. (1968). Self-focusing and diffraction of light in a nonlinear medium. Sov. Phys. 10, 609–636.CrossRefGoogle Scholar
Anderson, D. (1978). Stationary self-trapped laser beams in plasma. Phys. Scripta 18, 35–36CrossRefGoogle Scholar
Anderson, D. (1983). Variational approach to nonlinear pulse propagation in optical fibers. Phys. Rev. A 27, 3135–3145.CrossRefGoogle Scholar
Anderson, D., Bonnedal, M. & Lisak, M. (1979). Self-trapped cylindrical laser beams. Phys. Fluids 22, 1838–1840.CrossRefGoogle Scholar
Anderson, D., Bonnedal, M. & Lisak, M. (1980). Nonlinear propagation of elliptically shaped Gaussian laser beams. J. Plasma Phys. 23, 115–127.CrossRefGoogle Scholar
Arevalo, E. & Becker, A. (2005). Theoretical analysis of fluorescence in fragmentation of nanosecond laser pulses in nitrogen molecular gas. Phys. Rev. A 72, 0438071–5.CrossRefGoogle Scholar
Askaryan, G.A. (1962). Effect of the gradient of a strong electromagnetic beam on electron and atoms. J. Exp. Their. Phys. 42, 1567–1570.Google Scholar
Benware, B.R., Macchietto, C.D., Moreno, C.H. & Rocca, J.J. (1998). Demonstration of a high average power tabletop soft X-ray laser. Phys. Rev. Lett. 81, 5804–5807.CrossRefGoogle Scholar
Cai, Y. & Lin, Q. (2004). Hollow elliptical Gaussian beam and its propagation through aligned and misaligned paraxial optical systems. J. Opt. Soc. Am. A 21, 1058–1065.CrossRefGoogle ScholarPubMed
Casperson, L.W., Hall, D.G. & Tovar, A.A. (1997). Sinusoidal-Gaussian beams in complex optical systems. J. Opt. Soc. Am. A 14, 3341–3348.CrossRefGoogle Scholar
Cattani, F., Kim, A., Anderson, D. & Lisak, M. (2000). Threshold of induced transparency in the relativistic interaction of an electromagnetic wave with overdense plasmas. Phys. Rev. E 62, 1234–1237.CrossRefGoogle ScholarPubMed
Chen, S.Y., Sarkisov, G.S., Maksimchuk, A., Wagner, R. & Umstadter, D. (1998). Evolution of a plasma waveguide created during relativistic-ponderomotive self-channeling of an intense laser pulse. Phys. Rev. Lett. 80, 2610–2613.CrossRefGoogle Scholar
Chen, S. & Wang, J. (1991). Self starting issues of passive self-focusing mode locking. Opt. Lett. 16, 1689–1691.CrossRefGoogle ScholarPubMed
Chessa, P., Mora, P. & Antonsen, T.M. (1998). Numerical simulation of short laser pulse relativistic self-focusing in underdense plasma. Phys. Plasma 5, 3451–3458.CrossRefGoogle Scholar
Chiao, R.Y., Garmire, E. & Townes, C.H. (1964). Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482.CrossRefGoogle Scholar
Cornolti, F., Lunches, M. & Zambian, B. (1990). Elliptic Gaussian beam of self-focusing in nonlinear media. Opt. Common. 75, 129–135.CrossRefGoogle Scholar
Deutsch, C., Furkawa, H., Mima, K., Murakami, M. & Nishihara, K. (1996). Interaction physics of the fast ignitor concept. Phys. Rev. Lett. 77, 2483–2486.CrossRefGoogle ScholarPubMed
Esarey, E., Sprangle, P., Krall, J. & Ting, A. (1997). Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quant. Electr. 33, 1879–1914.CrossRefGoogle Scholar
Eyyuboglu, H.T. & Baykal, Y. (2004). Analysis of reciprocity of cosh-Gaussian beams in turbulent atmosphere. Opt Exp 12, 4659–4674.CrossRefGoogle ScholarPubMed
Eyyuboglu, H.T. & Baykal, Y. (2005). Average intensity and spreading of cosh-Gaussian beams in a turbulent atmosphere. Appl Opt 44, 976–983.CrossRefGoogle Scholar
Fedotov, A.B., Naumov, A.N., Silin, V.P., Uryupin, S.A., Zheltikov, A.M., Tarasevitch, A.P. & Von der Linde, D. (2000). Third-harmonic generation in a laser-pre-excited gas: the role of excited-state neutrals. Phys. Lett. A 271, 407–412.CrossRefGoogle Scholar
Fibich, G. (2007). Some modern aspects of self-focusing theory, a chapter in self-focusing: Past and present (Boyd, R.W., Lukishova, S.G. & Shen, Y.R., eds.). New York: Springer Verlag.Google Scholar
Firth, W.J. (1977). Propagation of laser beams through inhomogeneous media. Opt. Commun. 22, 226–230.CrossRefGoogle Scholar
Foldes, I.B., Bakos, J.S., Bakonyi, Z., Nagy, T. & Szatmari, S. (1999). Harmonic generation in plasmas of different density gradients. Phys. Lett. A 258, 312–316.CrossRefGoogle Scholar
Fuchs, J., Adam, J.C., Amiranoff, F., Baton, S.D., Gallant, P., Gremillet, L., Héron, A., Kieffer, J.C., Laval, G., Malka, G., Miquel, J.L., Mora, P., Ppin, H. & Rousseaux, C. (1998). Transmission through highly overdense plasma slabs with a subpicosecond relativistic laser pulse. Phys. Rev. Lett. 80, 2326–2329.CrossRefGoogle Scholar
Gill, T.S., Saini, N.S. & Kaul, S.S. (2000). Dynamics of self-focusing and self-phase modulation of elliptic Gaussian laser beam in a Kerr-medium. Pramana J. Phys. 55, 423–431.Google Scholar
Gill, T.S., Saini, N.S. & Kaul, S.S. (2001). Two dimensional self-focusing of a laser beam in an inhomogeneous laser produced plasma. J. Plasma Phys. 66, 39–51.CrossRefGoogle Scholar
Gill, T.S., Saini, N.S., Kaul, S.S. & Singh, A. (2004). Propagation of elliptic Gaussian laser beam in a higher order non-linear medium. Optik 115, 493–498.CrossRefGoogle Scholar
Gill, T.S., Mahajan, R. & Kaur, R. (2010 a). Relativistic and ponderomotive effects on evolution of laser beam in a non-uniform plasma channel. Laser Part. Beams 28, 11–20.CrossRefGoogle Scholar
Gill, T.S., Mahajan, R. & Kaur, R. (2010 b). Relativistic and ponderomotive effects on evolution of dark hollow Gaussian electromagnetic beams in a plasma. Laser Part. Beams 28, 521–529.CrossRefGoogle Scholar
Gill, T.S., Kaur, R. & Mahajan, R. (2010 c). Propagation of high power electromagnetic beam in relativistic magnetoplasma: Higher order paraxial ray theory. Phys. Plasmas 17, 0931011–6.CrossRefGoogle Scholar
Grow, T.D., Ishaaya, A.A., Vuong, L.T., Gaeta, A.L., Gavish, N. & Fibich, G. (2006). Collapse dynamics of super-Gaussian beams. Opt. Express 14, 5468–5475.CrossRefGoogle ScholarPubMed
Hartemann, F.V., Van Meter, J.R., Troha, A.L., Landahl, E.C., Luhmann, N.C., Baldis, H.A., Gupta, A. & Kerman, A.K. (1998). Three-dimensional relativistic electron scattering in an ultrahigh-intensity laser focus. Phys. Rev. E 88, 5001–5012.CrossRefGoogle Scholar
Hauser, T., Scheid, W. & Hora, H. (1994). Acceleration of electrons by intense laser pulses in vacuum. Phys. Lett. A 186, 189–192.CrossRefGoogle Scholar
Herrmann, H. (1994). Theory of Kerr-lens mode locking: role of self-focusing and radially varying gain. J. Opt. Soc. Am. B 18, 498–512.CrossRefGoogle Scholar
Hora, H. (1969). Self-focusing of laser beams in a plasma by ponderomotive forces. Zeitschriftd. Physik 226, 156–159.CrossRefGoogle Scholar
Hora, H., Hoeless, M., Scheid, W., Wang, J.W., Ho, Y.K., Osman, F. & Castillo, R. (2000). Principle of high accuracy for the nonlinear theory of the acceleration of electrons in a vacuum by lasers at relativistic intensities. Laser Part. Beams 18, 135–144.CrossRefGoogle Scholar
Hora, H. (1988). Particle acceleration by superposition of frequency-controlled laser pulses. Nature(London) 333, 337–338.CrossRefGoogle Scholar
Johannisson, P., Anderson, D., Lisak, M. & Marklund, M. (2003). Nonlinear Bessel beams.Opt. Commun. 222, 107–115.CrossRefGoogle Scholar
Karlsson, M. (1992). Optical beams in saturable self-focusing media. Phys. Rev. A 46, 2726–2734.CrossRefGoogle ScholarPubMed
Kaur, R., Gill, T.S. & Mahajan, R. (2010). Steady state self-focusing, self-phase modulation of laser beam in an inhomogeneous plasma. Optik (In Press).Google Scholar
Kaur, R., Gill, T.S. & Mahajan, R. (2010). Self-focusing, self modulation and stability properties of laser beam propagating in plasma: A variational approach. JPCS 208, 0120861–10.Google Scholar
Konar, S., Mishra, M. & Jana, S. (2007). Nonlinear evolution of cosh-Gaussian laser beams and generation of flat top spatial solitons in cubic cuintic nonlinear media. Phys. Lett. A 362, 505–510.CrossRefGoogle Scholar
Kruglov, V.I. & Vlasov, R.A. (1985). Spiral self-trapping propagation of optical beams in media with cubic nonlinearity. Phys. Lett. A 111, 401–404.CrossRefGoogle Scholar
Krushelnick, K., Ting, A., Moore, C.I., Burris, H.R., Esarey, E., Sprangle, P. & Baine, M. (1997). Plasma channel formation and guiding during high intensity short pulse laser plasma experiments. Phys. Rev. Lett. 78, 4047–4050.CrossRefGoogle Scholar
Lemoff, B.E., Yin, G.Y., Gordon, C.L., Barty, C.P.J., & Harris, S.E. (1995). Demonstration of a 10-Hz femtosecond-pulse-driven XUV Laser at 41.8 nm in Xe IX. Phys. Rev. Lett. 74, 1574–1577.CrossRefGoogle Scholar
Lu, B., Ma, H. & Zhang, B. (1999). Propagation properties of cosh-Gaussian beams. Opt Commun 164, 269–276.CrossRefGoogle Scholar
Lu, B. & Luo, S. (2000). Beam propagation factor of hard-edged diffracted cosh-Gaussian beams. Opt Commun 178, 275–281.CrossRefGoogle Scholar
Mahajan, R., Gill, T.S. & Kaur, R. (2010). Nonlinear dynamics of intense EM pulses in plasma. JPCS 208, 0120871–11.Google Scholar
Misra, S. & Mishra, S.K. (2009). Ring formation in electromagnetic beams propagating in magnetoplasma. J. Plasma Phy. 75, 769–785.CrossRefGoogle Scholar
Monot, P., Auguste, T., Gibbon, P., Jakober, F., Mainfray, G., Dulieu, A., Louis-Jacquet, M., Malka, G. & Miquel, J.L. (1995). Experimental demonstration of relativistic self-channeling of a multiterawatt laser pulse in an underdense plasma. Phys. Rev. Lett. 74, 2953–2956.CrossRefGoogle Scholar
Manassah, J.T., Baldeck, P.L. & Alfano, R.R. (1988). Self-focusing and self-phase modulation in a parabolic graded-index optical fiber. Opt. Lett. 13, 589–591.CrossRefGoogle Scholar
Nayyar, V.P. (1986). Nonlinear propagation of degenerate modes of a laser cavity. J. Opt. Soc. Am. B 3, 711–714.CrossRefGoogle Scholar
Pandey, B.K. & Tripathi, V.K. (2009). Anomalous transmission of an intense short-pulse laser through a magnetized overdense plasma. Phys. Scr. 79, 025101.Google Scholar
Patil, S.D., Takale, M.V., Navare, S.T., Fulart, V.J. & Dongare, M.B. (2007). Analytical study of HChG- laser beams in collisional and collisionless plasma. J. Opt. 36, 136–144.CrossRefGoogle Scholar
Patil, S.D., Takale, M.V., Fulart, V.J. & Dongare, M.B. (2008). Propagation of Hermite-cosh-Gaussian laser beams in nondegenerate germanium having space charge neutrality. J. Mod. Opt. 55, 3529–3535.CrossRefGoogle Scholar
Patil, S.D., Takale, M.V. & Dongare, M.B. (2010). Focusing of Hermite-cosh-Gaussian laser beams in collisionless magnetoplasma. Laser Part. Beams 28, 343–349.CrossRefGoogle Scholar
Regan, S.P., Bradley, D.K., Chirokikh, A.V., Craxton, R.S., Meyerhofer, D.D., Seka, W., Short, R.W., Simon, A., Town, R.P.J. & Yaakobi, B. (1999). Laser-plasma interactions in long-scale-length plasmas under direct-drive national ignition facility conditions. Phys. Plasmas 6, 2072–2080.CrossRefGoogle Scholar
Saini, N.S. & Gill, T.S. (2006). Self-focusing and self-phase modulation of an elliptic Gaussian laser beam in collisionless magnetoplasma. Laser Part. Beams 24, 447–453.CrossRefGoogle Scholar
Sarkisov, G.S., Bychenkov, V.Yu., Novikov, V.N., Tikhonchuk, V.T., Maksimchuk, A., Chen, S.-Y., Wagner, R., Mourou, G. & Umstadter, D. (1999). Self-focusing, channel formation, and high-energy ion generation in interaction of an intense short laser pulse with a He jet. Phys. Rev. E 59, 7042–7054.CrossRefGoogle ScholarPubMed
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Progr. Optics 13, 169.Google Scholar
Sodha, M.S., Singh, T., Singh, D.P. & Sharma, R.P. (1981). Growth of laser ripple in a plasma and its effect on plasma wave excitation. Phys. Fluids 24, 914–919.CrossRefGoogle Scholar
Sodha, M.S., Mishra, S.K. & Misra, S. (2009 a). Focusing of dark hollow Gaussian electromagnetic beams in a magnetoplasma. J. Plasma Phys. 75, 731–748.CrossRefGoogle Scholar
Sodha, M.S., Mishra, S.K. & Misra, S. (2009 b). Focusing of dark hollow Gaussian electromagnetic beams in plasma. Laser Part.Beams 27, 57–68.CrossRefGoogle Scholar
Soudagar, M.K., Bote, S.R., Wali, A.A. & Khandekar, R.N. (1994). Propagation of TEMPO laser beams in a parabolic medium. Pure Appl Phys 30, 751–753.Google Scholar
Sprangle, P. & Esarey, E. (1990). Stimulated backscattered harmonic generation from intense laser interactions with beams and plasmas. Phys. Rev. Lett. 67, 2021–2024.CrossRefGoogle Scholar
Subbarao, D., Uma, R. & Singh, H. (1998). Paraxial theory of self-focusing of cylindrical laser beams. I. ABCD laws. Phys. Plasmas 5, 3440–3450.CrossRefGoogle Scholar
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Vshivkov, V.A., Naumova, N.M., Pegoraro, F. & Bulanov, S.V. (1998). Nonlinear electrodynamics of the interaction of ultra-intense laser pulses with a thin foil. Phys. Plasmas 5, 2727–2741.CrossRefGoogle Scholar
Yu, W., Yu, M.Y., Zhang, J. & Xu, Z. (1998). Model for the boring of ultraintense lasers into overdense plasmas. Phys. Rev. E 58, 6553–6556.CrossRefGoogle Scholar
Zakharov, V.I. (1972). Collapse of Langmuir waves. Sov. Phys. JETP 35, 908–914.Google Scholar
Figure 0

Fig. 1. (Color online) Variation of normalized beam width parameter an with dimensionless distance of propagation ξ with b = 0 (in the absence of decentred parameter) for different values of absorption coefficient k′i. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2\rpar } = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega\rpar }} = 0.4.$ Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 1, dotted curve correspond to when k′i = 2 and dotdashed curve correspond to when k′i = 3.

Figure 1

Fig. 2. (Color online) Variation of normalized beam width parameter an with dimensionless distance of propagation ξ with b = 2 (finite value of decentred parameter) for different values of absorption coefficient k′i. The parametersused here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2\rpar} = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega \rpar}} = 0.4.$ Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 1, dotted curve correspond to when k′i = 2 and dotdashed curve correspond to when k′i = 3.

Figure 2

Fig. 3. (Color online) Dependence of normalized beam width parameter an on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for finite value of b. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2 \rpar} = 5.$ Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0.06$.

Figure 3

Fig. 4. (Color online) Variation of the longitudinal phase delay ϕ with dimensionless distance of propagation ξ with b = 0 (in the absence of decentred parameter) for different values of absorption coefficient k′i and with the otherparameters the same as mentioned in Figure 1. Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 0.3, dotted curve correspond to when k′i = 0.5 and dotdashed curve correspond to when k′i = 0.7.

Figure 4

Fig. 5. (Color online) Variation of the longitudinal phase delay ϕ with dimensionless distance of propagation ξ with b = 1 (finite value of decentred parameter) for different values of absorption coefficient k′i and with the other parameters the same as mentioned in Figure 1. Solid curve correspond to when k′i = 0, dashed curve correspond to when k′i = 0.3, dotted curve correspond to when k′i = 0.5 and dotdashed curve correspond to when k′i = 0.7.

Figure 5

Fig. 6. (Color online) Dependence of longitudinal phase delay ϕ on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for b = 0. The parameters used here are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega}^2}\rpar = 5$. Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.06$.

Figure 6

Fig. 7. (Color online) Dependence of longitudinal phase delay ϕ on the magnetic field as a function of dimensionless distance of propagation ξ in a collisionless magnetoplasma with relativistic nonlinearity for b = 1. The parameters usedhere are: ${\rm \alpha} \vert A_{0+}^\prime \vert ^2 = 0.5\comma \; k_i^\prime = 0.5\comma \; {{\lpar \rm \omega}_p^2 / {\rm \omega} ^2 \rpar} = 5$. Solid curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega} \rpar} = 0$, dashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.02$ and dotted curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.04$, dotdashed curve correspond to when ${{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.06$.

Figure 7

Fig. 8. (Color online) Plot of equilibrium beam width R as intensity parameter $A = {\rm \alpha} \vert A_{0+}^\prime \vert^2$ for different value of decentred parameter (b). The parameters used here are: ${{\lpar \rm \omega}_p^2 / {\rm \omega} ^2\rpar} = 5\comma \; {{\lpar \rm \omega}_c / {\rm \omega}\rpar} = 0.2$. Solid curve correspond to when b = 0, dashed curve corresponds to b = 0.5 and dotted curve correspond to b = 1.