Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-06T04:36:11.813Z Has data issue: false hasContentIssue false
  • English
  • Français

Relativistic and ponderomotive effects on evolution of dark hollow Gaussian electromagnetic beams in a plasma

Published online by Cambridge University Press:  14 October 2010

T.S. Gill ,
R. Mahajan  and
R. Kaur
T.S. Gill*
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
R. Mahajan
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
R. Kaur
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar, India
*
Address correspondence and reprint requests to: Tarsem Singh Gill, Department of Physics, Guru Nanak Dev University, Amritsar-143005, India. E-mail: gillsema@yahoo.co.in
Rights & Permissions [Opens in a new window]

Abstract

Nonlinear parabolic partial differential equation governing the evolution of complex envelope in slowly varying envelope approximation is solved using variational approach. The basic nonlinear phenomena of relativistic and ponderomotive self-focusing in a plasma are taken into account. Self-focusing, self-phase modulation as well as self-trapping of dark hollow Gaussian beam is studied for higher orders of hollow Gaussian beam (n).

Keywords

Hollow Gaussian beamSelf-focusing and self-trappingSelf-phase modulationRelativistic and ponderomotive
Type
Research Article
Information
Laser and Particle Beams , Volume 28 , Issue 4 , December 2010 , pp. 521 - 529
Copyright
Copyright © Cambridge University Press 2010

1. INTRODUCTION

Theoretical and experimental study of the evolution of high power laser beams as they propagate through plasmas is an active area of research due to their potential relevance in plasma based accelerators (Sarkisov et al., Reference Sarkisov, Bychenkov, Novikov, Tikhonchuk, Maksimchuk, Chen, Wagner, Mourou and Umstadter1999), inertial confinement fusion (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell, Perry and Mason1994; Regan et al., Reference Regan, Bradley, Chirokikh, Craxton, Meyerhofer, Seka, Short, Simon, Town and Yaakobi1999), ionospheric modification (Perkins & Goldman, Reference Perkins and Goldman1981; Guzdar et al., Reference Guzdar, Chaturvedi, Papadopoulos and Ossakow1998; Gondarenko et al., Reference Gondarenko, Ossakow and Milikh2005), and new radiation sources (Suckewer & Skinner, Reference Suckewer and Skinner1990, Reference Suckewer and Skinner1995; Benware et al., Reference Benware, Macchietto, Moreno and Rocca1998; Foldes et al., Reference Foldes, Bakos, Bakonyi, Nagy and Szatmari1999; Fedotov et al., Reference Fedotov, Naumov, Silin, Uryupin, Zheltikov, Tarasevitch and Von der Linde2000). Specifically, in the laser plasma interaction, the generic process of the self-focusing of the laser beams (Chiao et al., Reference Chiao, Garmire and Townes1964; Kelley, Reference Kelley1965; Sodha et al., Reference Sodha, Ghatak and Tripathi1974, Reference Sodha, Ghatak and Tripathi1976; Milchberg et al., Reference Milchberg, Durfee and Mcllrath1995; Saini & Gill, Reference Saini and Gill2006; Gill & Saini, Reference Gill and Saini2007; Yu et al., Reference Yu, Yu, Xu, Tian, Chen and Wong2007; Gill et al., Reference Gill, Mahajan and Kaur2010; Kaur et al., Reference Kaur, Gill and Mahajan2010) has been focus of attention as it affects many other nonlinear processes. It plays crucial role in beam propagation and arises due to increase of the on-axis index of refraction relative to edge of the laser beam. For example, for ponderomotive force type nonlinearity, electrons are expelled from the region of high intensity laser field. On the other hand, relativistic self-focusing results from the effect of quiver motion leading to reduced local plasma frequency. The self-focusing is counterbalanced by the tendency of the beam to spread because of diffraction. In the absence of nonlinearities, the beam will spread substantially in a Rayleigh length, R d(~ka 02), where k is the wavenumber and a 0 is the initial spot size of the laser beam.

Self-focusing and filamentation are among the most dangerous nonlinear phenomena that destroy the uniformity of overall irradiation required for direct-drive fusion experiment as well as leads to seeding and growth of hydrodynamic instabilities. Experimental as well as theoretical observations of relativistic self-focusing and ponderomotive self-channeling have been reported in a number of investigations (Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, De Silvestri, Poletto, Villoresi and Andreev2007; Chessa et al., Reference Chessa, Mora and Antonsen1998; Kurki-Suonio et al., Reference Kurki-Suonio, Morrison and Tajima1989; Abramyan et al., Reference Abramyan, Litvak, Mironov and Sergeev1992; Tzeng & Mori, Reference Tzeng and Mori1998; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis-Jacquet, Malka and Miquel1995; Krushelnick et al., Reference Krushelnick, Ting, Moore, Burris, Esarey, Sprangle and Baine1997; Konar & Manoj, Reference Konar and Manoj2005; Wagner et al., Reference Wagner, Chen, Maksimuchuk and Umstadter1997; Chen et al., Reference Chen, Sarkisov, Maksimchuk, Wagner and Umstadter1998; Borisov et al., Reference Borisov, Longworth, Boyer and Rhodes1998). The dynamics of ponderomotive channeling in underdense plasma has recently been studied experimentally (Borghesi et al., Reference Borghesi, Kar, Romagnani, Toncian, Antici, Audebert, Brambrink, Ceccherini, Cecchetti, Fuchs, Galimberti, Gizzi, Grismayer, Lyseikina, Jung, Macchi, Mora, Osterholtz, Schiavi and Willi2007). Relativistic laser-plasma interaction physics has also been focus of attention as many nonlinear processes playing key roles in the generation of new ion sources as reported recently (Laska et al., Reference Laska, Badziak, Boody, Gammino, Jungwirth, Krasa, Krousky, Parys, Pfeifer, Rohlena, Ryc, Skala, Torrisi, Ullschmied and Wolowski2007; Strangio et al., Reference Strangio, Caruso, Neely, Andreoli, Anzalone, Clarke, Cristofari, DelPrete, Di Giorgio, Murphy, Ricci, Stevens and Tolley2007; Torrisi et al., Reference Torrisi, Margarone, Laska, Krasa, Velyhan, Pfeifer, Ullschmied and Ryc2008). Further, there have been a series of novel experiments to study rich physics issues in nuclear and particle physics, atomic physics (Stoehlker et al., Reference Stoehlker, Backe, Beyer, Bosch, Braeuning-Demian, Hagman, Ionescu, Jungmann, Kluge, Kozhuharov, Kuehl, Lisen, Mann, Mokler and Quint2003), plasma physics (Hoffmann et al., Reference Hoffmann, Blazevic, Ni, Rosmej, Roth, Tahir, Tauschwitz, Udrea, Varentsov, Weyrich and Maron2005; Schaumann et al., Reference Schaumann, Schollmeier, Rodriguez-Prieto, Blazevic, Brambrink, Geissel, Korostiy, Pirzadeh, Roth, Rosmej, Faenov, Pikuz, Tsigutkin, Maron, Tahir and Hoffmann2005) and applied sciences (Kuehl et al., Reference Kuehl, Ursescu, Bagnoud, Javorkova, Rosmej, Cassou, Kazamias, Klisnick, Ros, Nickles, Zielbauer, Dunn, Neumayer and Pert2007; Kasperczuk et al., Reference Kasperczuk, Pisarczyk, Kalal, Martinkova, Ullschmied, Krousky, Masek, Pfeifer, Rohlena, Skala and Pisarczyk2008). Such experiments have opened new vistas in this field and are supposed to pay rich dividents to multidisciplinary character of laser produced plasma.

Some of the approximate theories used to study self-focusing process are a paraxial ray approximation (PRA) (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1974, Reference Sodha, Ghatak and Tripathi1976), moment theory approach (Firth, Reference Firth1977; Lam et al., Reference Lam, Lippmann and Tappert1977), variational approach (Firth, Reference Firth1977; Anderson & Bonnedal, Reference Anderson and Bonnedal1979), and source-dependent expansion method (Sprangle et al., Reference Sprangle, Hafizi and Penano2000). Each of these theories has limitations in describing completely the experimental/computer simulation results. However, the most used theory based on Wentzel-Krammers-Brillouin approximation and paraxial ray approach (PRA) is given by Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and developed by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976). Due to its mathematical simplicity, it has been extensively used to account for general features of self-focusing as witnessed by the increasing number of publications. However, this theory being local in character overemphasizes the field closest to beam axis and lacks global pulse dynamics. Furthermore, it also predicts unphysical phase relationship (Karlsson et al., Reference Karlsson, Anderson, Desaix and Lisak1991). It has also been pointed out that PRA is not applicable when high power laser beams are used (Subbarao et al., Reference Subbarao, Uma and Singh1998). Another global approach is variational approach, though crude to describe the singularity formation and collapse dynamics, is fairly general in nature to describe the propagation and correctly predicts the phase.

Most of the research work on self-focusing of the laser beam has been confined to the cylindrically symmetric Gaussian beams symmetry (Kumar et al., Reference Kumar, Gupta and Sharma2006; Hora, Reference Hora1975; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997; Sharma et al., Reference Sharma, Verma and Sodha2004; Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968). Only a few investigations have been reported on the self-focusing of super-Gaussian beams (Grow et al., Reference Grow, Ishaaya, Vuong, Gaeta, Gavish and Fibich2006; Fibich, Reference Fibich, Boyd, Lukishova and Shen2007), self-trapping of degenerate modes of laser beams (Karlsson, Reference Karlsson1992), self-trapping of Bessel beams (Johannisson et al. Reference Johannisson, Anderson, Lisak and Marklund2003), elliptical Gaussian beam (Cornolti et al. Reference Cornolti, Lucchesi and Zambon1990), and hollow elliptical Gaussian beam (Cai & Lin, Reference Cai and Lin2004). These types of beams have different type of irradiance distribution. Recently, the optical beams with central shadow, generally known as dark hollow beams (DHB) have attracted the attention of the physics community because of their wide potential applications in the field of modern optics, atomic optics, and plasmas (Cai et al., Reference Cai, Lu and Lin2003; Yin et al., Reference Yin, Gao and Zhu2003; York et al., Reference York, Milchberg, Palastro and Antonsen2008). A DHB can be expressed as a finite sum of Laguerre Gaussian beams or Gaussian beams. DHBs have been widely studied both from experimental and theoretical aspect (Arlt & Dholakia, Reference Arlt and Dholakia2000; Zhang et al., Reference Zhang, Lu, Chen and He2004). For the explanation of dynamics and other propagation characteristics, several theoretical models for dark hollow Gaussian Beam (DHGB) like the TEM 01 mode doughnut beam, some higher order Bessel beams, superposition of off-axis Gaussian beams, and DHGB have been reported in several recent investigations (Arlt & Dholakia, Reference Arlt and Dholakia2000; Zhu et al., 2002; Deng et al., Reference Deng, Fu, Wei, Shao and Fan2005; Mei & Zhao, Reference Mei and Zhao2005). However, the propagation characteristics of coherent DHBs in a plasma or any other nonlinear media have received little attention. In recent investigations, Sodha et al. (Reference Sodha, Mishra and Misra2009a, Reference Sodha, Mishra and Misra2009b) have presented a modified paraxial like approach to study self-focusing of a HGB in plasma. In the present investigation, authors have studied evolution of DHGB in a plasma when relativistic and ponderomotive nonlinearities are considered.

The organization of the paper is as follows: In Section 2, a model is setup in a weakly relativistic regime in underdense plasma starting from Ampere's and Faraday's laws. These equations under approximate conditions leads to an evolution equation. Lagrangian for the problem is setup and variational approach is used. In Section 3, authors have studied the self-trapped mode, and Section 4 is devoted to discussion. In Section 5, conclusions of present investigation are presented.

2. BASIC FORMULATION

The present model is setup in a weakly relativistic regime in underdense plasma. Starting from Ampere's and Faraday's laws and in the absence of the external charge and current, we have the following set of equations:

(1)
{\vec \nabla}\times {\vec B}={1 \over c}{\partial {\vec D} \over \partial t} \comma
(2)
{\vec \nabla}\times {\vec E}= -{1 \over c}{\partial {\vec B} \over \partial t}.

where ${\vec E}$ and ${\vec B}$ are the electric and magnetic field vectors, respectively. ${\vec D} = \epsilon {\vec E}$ is the displacement vector. Also, the induced current density due to laser-plasma interaction exists in the dielectric permittivity, ε.

Combining the above two equations gives:

(3)
{\vec \nabla} \times {\vec \nabla} \times {\vec E} + {1 \over c^2} {\partial^2 {\vec D} \over \partial t^2} = 0.

Assuming wave propagation in z-direction and the electric and magnetic fields in the xy-plane, Eq. (3) is reduced to:

(4)
\nabla^2{\vec E} + {\omega^2 \over c^2} \epsilon {\vec E} = 0.

Further the relativistic ponderomotive force on the electrons modifies the electron density. The relativistic ponderomotive force on electrons is given by:

(5)
{\vec F}_{\,pe} = -m_{e0}c^2 \nabla \lpar \gamma - 1 \rpar \comma

where m e0 is the electron mass in the absence of the external field and γ is called the relativistic factor defined as follows:

(6)
\gamma = \surd{1 + \left({eE \over m_{0e} c \omega} \right)^2}.

Following Niknam et al. (Reference Niknam, Hashemzadeh and Shokri2009), the dielectric permittivity for the cold plasma is:

(7)
\epsilon = 1 - {\omega_{\,pe}^2 \over \gamma \omega^2} \comma
(8)
\epsilon = 1 - {\omega_{\,pe}^2 \over \gamma \omega^2} exp \left(-{m_{0e}c^2 \over T_e} \lpar \gamma -1\rpar \right)\comma

where

(9)
\omega_{\,pe0}^2 = {4\pi n_{e0} e^2 \over m_{e0}} \comma
(10)
n_e = n_{e0} exp \left(-{m_{0e}c^2 \over T_e} \lpar \gamma -1\rpar \right)\comma

where n e0 is the maximum electron density at the place in which the laser electric field is zero. We obtain the following evolution equation governing the electric field envelope in collisionless plasmas as follows:

(11)
\eqalign{&\left[\nabla_{\bot}^2- 2\iota k {\partial \over \partial z}+ {\omega^2 \over c^2}\left(1-{\omega_{\,pe}^2 \over \gamma \omega^2} \right. \right. \cr &\left. \left. \quad \times \,exp \left(-{m_{0e}c^2 \over T_e}\lpar \gamma -1\rpar \right)\right)\right]\psi\lpar r\comma \; z\rpar =0.}

Eq. (11) is a nonlinear parabolic partial differential equation in which the first term has its origin in diffractional divergence, in third term within parenthesis, “1” is the free space propagation term and rest corresponds to relativistic and ponderomotive self-focusing terms. Since relativistic and ponderomotive channeling occur together, we investigate their combined effects on the evolution of intense laser beam in a plasma. Variational approach that have rigorous basis, as applied in other fields, is used here to investigate nonlinear wave propagation. We use procedure of Anderson and Bonnedal (Reference Anderson and Bonnedal1979) to reformulate Eq. (11) into a variational problem corresponding to a Lagrangian L, so as to make ${\delta L \over \delta z} = 0$. Thus, Lagrangian L corresponding to Eq. (11) is given by:

(12)
\eqalign{L &= \iota k r\left(\psi{\partial\psi^{\ast} \over \partial z}-\psi^{\ast}{\partial\psi \over \partial z}\right)-r \left\vert{\partial\psi \over \partial r}\right\vert^2\cr &\quad + r\left[{\omega^2 \over c^2}\alpha^2 \vert\psi\vert^2 - {\omega_{\,pe0}^2 \over 52 c^2}\left(1-e^{-52 \alpha^2 \vert\psi\vert^2}\right)+ {\omega_{\,pe0}^2 \over 2704 c^2}\right. \cr &\quad \left. \times \left(1-e^{-52 \alpha^2 \vert \psi\vert^2}\right)-{\omega_{\,pe0}^2 \over 52 c^2} \alpha^2 \vert \psi\vert^2 e^{-52 \alpha^2 \vert \psi\vert^2} \right]\comma}

where $\alpha={e \over \surd2 m_{e0} c \omega}$

Thus, the solution to the variational problem

(13)
\delta \int\!\!\!\int\!\!\!\int L dx dy dz = 0\comma

also solves the nonlinear Schrödinger Eq. (11). Using the trial function as Gaussian beam of the form as follows:

(14)
\eqalign{\psi \lpar r \comma\ z \rpar &= \psi_{0} \lpar z \rpar \left({r^2 \over 2 a^2 \lpar z \rpar }\right)^n exp \cr &\quad \times \left(-{r^2 \over 2 a^2 \lpar z \rpar } + \iota b \lpar z \rpar r^2+\iota\phi \lpar z \rpar \right)\comma}

where a(z) is the beam width, b(z) is the spatial chirp, and ϕ(z) is the phase of the laser beam. Using the ansatz, with expression for ψ as a trial function, we can perform the integration to write:

(15)
\lt L\gt = \lt L_{0}\!\!\gt + \lt \!L_{1}\!\!\gt \comma

where

(16)
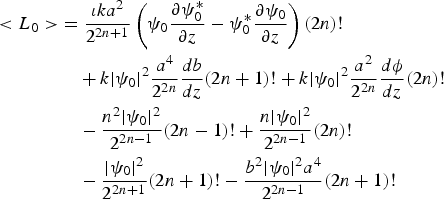
\eqalign{\lt L_{0}\gt &= {\iota k a^2 \over 2^{2n+1}}\left(\psi_{0}{\partial\psi_{0}^{\ast} \over \partial z}-\psi_{0}^{\ast}{\partial\psi_{0} \over \partial z}\right)\lpar 2n \rpar ! \cr &\quad + k \vert \psi_{0}\vert^2{a^{4} \over 2^{2n}}{d b \over d z} \lpar 2n+1 \rpar !+ k \vert\psi_{0}\vert^2{a^2 \over 2^{2n}}{d \phi \over d z} \lpar 2n \rpar ! \cr &\quad- {n^2\vert\psi_{0}\vert^2 \over 2^{2n-1}} \lpar 2n-1 \rpar !+ {n \vert \psi_{0}\vert^2 \over 2^{2n-1}} \lpar 2n \rpar ! \cr &\quad- {\vert\psi_{0}\vert^2 \over 2^{2n+1}} \lpar 2n+1 \rpar ! - {b^2\vert\psi_{0}\vert ^2a^{4} \over 2^{2n-1}} \lpar 2n+1 \rpar !}
(17)
\eqalign{\lt L_{1}\gt &= {\omega^2a^2 \over c^2}{\alpha^2 \vert \psi_{0} \vert ^2 \over 2^{2n+1}} \lpar 2n \rpar !+ {\omega_{\,pe0}^2a^2 \over 104 c^2}\cr & \quad \times \left[c^{\prime}-2n \lpar 1-n \rpar \left(c^{\prime}-{2 \over e}\right)Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2 \rpar \right]- \cr & \quad {\omega_{\,pe0}^2a^2 \over 5408 c^2} \left[c^{\prime}-2n \lpar 1-n \rpar \left(c^{\prime}-{2 \over e}\right)Log \right. \cr &\left. \quad \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2 \rpar \right]+ {\omega_{\,pe0}^2a^2 \over 5408 c^2} \lsqb 1- \lpar 2n-4 n^2 \rpar \cr &\quad \times \lpar c^{\prime}+ Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2 \rpar \rsqb \comma }

where c′ = 0.57721 is Euler's constant. Using the procedure of (Anderson & Bonnedal, Reference Anderson and Bonnedal1979; Saini & Gill, Reference Saini and Gill2006), we arrive at the following equation for a:

(18)
\eqalign{{d^2a \over d z^2} &= {2 \over k^2 a^{3}}-{4 n \over k^2 a^{3} \lpar 2n+1\rpar }+ {2^{2n+2} \over a \lpar 2n+1\rpar!}\cr &\quad \times\left[-{ \lpar 2n\rpar! \over 2^{2n+2}}+ {51 \omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar c^{\prime}-2n \lpar 1-n\rpar \right. \cr & \quad \times \left.\left(c^{\prime}-{2 \over e}\right)Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar\right.\cr &\quad \left. + {\omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar 1- \lpar 2n-4n^2\rpar \right. \cr & \quad\times \left.\lpar c^{\prime}+ Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar\rpar +{51 \omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\right. \cr & \quad \times\left.2n \lpar 1-n\rpar \left(c^{\prime}-{2 \over e}\right)+ {\omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\right. \cr & \quad \times \left. \lpar 2n-4 n^2\rpar \right].}

After normalization using $\eta={c z \over \omega a_{0}^2}$, we arrive at the following equations for a n, ϕ:

(19)
\eqalign{{d^2a_{n} \over d \eta^2} &= {2 \over a_{n}^{3}}-{4 n \over \lpar 2n+1\rpar a_n^{3}}+ {2^{2n+2} k^2 a_{0}^2 \over a_{n} \lpar 2n+1\rpar!}\cr &\quad \times\left[-{\lpar 2n\rpar! \over 2^{2n+2}}+ {51 \omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar c^{\prime}-2n\lpar 1-n\rpar \right. \cr &\quad \left.\left(c^{\prime}-{2 \over e}\right)Log\lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar + {\omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert^2} \right. \cr &\quad \left.\times\lpar 1-\lpar 2n-4n^2\rpar \lpar c^{\prime}+ Log\lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar\rpar \right. \cr & \left. \quad +{51 \omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}2n \lpar 1-n\rpar \left(c^{\prime}-{2 \over e}\right)+ {\omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\right. \cr & \left. \quad\lpar 2n-4 n^2\rpar \right]}
(20)
\eqalign{{d \phi \over d \eta} &= {n \over 2 a_{n}^2}+{2^{2n-1} k^2 a_{0}^2 \over \lpar 2n\rpar!} \left[-{\lpar 2n\rpar! \over 2^{2n+2}}+ {51 \omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\right. \cr & \quad \left.\times\left(c^{\prime}-2n\lpar 1-n\rpar \left(c^{\prime}-{2 \over e}\right)Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar \right. )\right. \cr & \quad \left. + {\omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar 1 - \lpar 2n - 4 n^2\rpar \right. \cr &\quad \left. \times \lpar c^{\prime}+ Log\lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar\rpar \Bigg ) + {51 \omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}2n\lpar 1-n\rpar \right. \cr & \quad \left. \lpar c^{\prime}-{2 \over e}\rpar + {\omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar 2n-4 n^2\rpar \right]\cr &\quad + {2^{2n-1} k^2 a_{0}^2 \over \lpar 2n\rpar !}\left[-{\lpar 2n\rpar! \over 2^{2n+1}}\alpha^2 \vert \psi_{0} \vert ^2+ {51 \over 5408} \right. \cr & \quad \left. {\omega_{\,pe0}^2} {\omega^2}2n\lpar 1-n\rpar \left(c^{\prime}-{2 \over e}\right)+ {\omega_{\,pe0}^2 \lpar 2n-4 n^2\rpar \over 5408 \omega^2}\right].}

3. SELF-TRAPPED MODE

For an initially plane wave front, ${da \over dz}=0$ and a = 1 at z = 0, the condition ${d^2 a \over d z^2}=0$ leads to the propagation of DHGB in the uniform waveguide/self-trapped mode. The conditions under which this occurs are termed as critical conditions and their graphical representation is known as the critical curve.

By putting ${d^2 a \over d z^2}=0$ in Eq. (18), we obtain a relation between dimensionless initial beam width parameter (ρ0) and critical values of power of the beam Π(=α2 |ψ0|2) taking into account relativistic-ponderomotive type nonlinearity. The critical condition leads to general expression for determination of critical threshold for various orders of n. The expression when simplified is given as follow:

(21)
\eqalign{1 &= {2 n \over \lpar 2n+1\rpar }- {2^{2n+1} \over \lpar 2n+1\rpar !} {\omega^2 a_{0}^2 \over c^2}\cr &\quad\times \left[{-\lpar 2n\rpar ! \over 2^{2n+2}}+ {51 \omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\lpar c^{\prime}-2n\lpar 1-n\rpar \right. \cr & \quad \left.\left(c^{\prime}-{2 \over e}\right)Log\lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar \right. \cr & \left. + {\omega_{\,pe0}^2 \over 10816 \omega^2\alpha^2 \vert \psi_{0} \vert ^2} \lpar 1-\lpar 2n-4n^2\rpar \right. \cr & \left. \times\, \lpar c^{\prime}+ Log \lpar 52 \alpha^2 \vert \psi_{0} \vert ^2\rpar\rpar +{51 \omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}2n \lpar 1-n\rpar \right. \cr & \left. \times \left(c^{\prime}-{2 \over e}\right)+ {\omega_{\,pe0}^2 \over 5408 \omega^2\alpha^2 \vert \psi_{0} \vert ^2}\lpar 2n-4 n^2\rpar \right],}

where $\rho_{0}={a_0 \omega \over c}$, is the initial dimensionless beam width parameter.

The nature of self-focusing is further highlighted through the critical curves. DHB undergoes self-focusing when the condition ${d^2 a \over d z^2}\lt 0$ is satisfied whereas for ${d^2 a \over d z^2}\gt 0$, HGB displays either oscillatory or steady state self-focusing.

4. DISCUSSION

Eq. (19) describes the beam dynamics in plasma with relativistic and ponderomotive nonlinearities taken into account. Eqs. (19) and (20) are nonlinearly coupled ordinary second order differential equations governing the normalized beam width parameter a n and phase ϕ. There are several terms appearing on right hand side (R.H.S.) of Eqs. (19) and (20). Analytical solutions to these equations are not possible. We therefore seek numerical computational techniques to study beam dynamics. Before that, it is worthnoting to understand the physical mechanisms and origin of various terms on R.H.S. of Eq. (19). The first and second terms on R.H.S of Eq. (19) are responsible for diffractional divergence of the laser beam which has its origin in the Laplacian (∇⊥2) appearing in the evolution Eq. (11). It is noteworthy to point out that the second term in Eq. (19) weakens the divergence of laser beam solely because of its sign. Further, within parenthesis, the first term comes from free space propagation and the rest of the terms represent the combined effects of ponderomotive self-channeling and relativistic self-focusing. Self-focusing/defocusing of laser beam in plasma is determined by the competing mechanisms on the R.H.S. of Eq. (19). The normalized beam width parameter, a n < 1 corresponds to self-focusing and a n > 1 is the result of diffractional dominance over all other terms leading to defocusing of laser beam. However, as mentioned in the Introduction, long distance of several Rayleigh lengths (R d) are prerequisite for novel applications of laser produced plasma. In Figure 1, the plot of normalized beam width parameter, a n with dimensionless distance of propagation, η is shown for various orders of n. In this case, free space propagation term on R.H.S of Eq. (19) within parenthesis is not taken into account. Further, it is observed that defocusing of the laser beam occurs for all n values but decrease with increase in n. However, situation changes drastically when the combined effects of both relativistic and ponderomotive nonlinearities along with free space propagation term are taken into account. It is observed from Figure 2 that oscillatory self-focusing takes place for all higher orders of n. It is also important to notice that beam propagates oscillatory and infinitely over several number of Rayleigh lengths. Inspite of higher order, defocusing is not observed for all powers. It is in contrast to the results of Sodha et al. (Reference Sodha, Mishra and Misra2009a) where defocusing is observed with increase in n. This is apparently a consequence of variational approach where in averaging process the contribution of whole wave front is considered. On the other hand, PRA takes into account only rays that are very close to the beam-axis. Another aspect of this phenomenon observed here is that oscillatory character becomes slow with increase in the value of n. We have numerically analyzed the evolution of normalized beam width as a function of distance of propagation, η for four values of n with other parameters chosen as follows:

\eqalign{a_{0} &= 0.002\, \hbox{cm}\comma \; k = 1.25 \times 10^3\, \hbox{cm}^{-1}\comma \; \cr \omega_{\,pe0} &= 0.01 \times \omega\comma \; \omega=1.778 \times10^{14}\, {{\rm rad} \over {\rm sec}}.}

Eq. (20) describes the evolution of longitudinal phase, ϕ with the dimensionless distance of propagation (η). As is apparent from the R.H.S of Eq. (20), which is a complicated function of n, normalized beam width a n and intensity parameter, α2 |ψ0|2 besides other parameters, determines the nature of phase. It is observed from Figure 3, the phase is negative for lower values of n (=0,1), but becomes positive with further increase in n. However, for lowest order of n, observed phase is negative and does not show oscillatory character. This is due to the fact that the R.H.S. of Eq. (20) for n = 0 depends only on α2 |ψ0|2 maintaining a linear relationship. However, oscillatory character is obtained for n ≠ 1, as self-focusing of the main beam enters into the picture. Wiggles observed in ϕ versus η graph are more pronounced for higher values of n.

Fig. 1. (Color online) Variation of normalized beam width a n(η) with dimensionless distance of propagation η for the case when free space propagation term is not taken into account with the following set of parameters for the various orders of n: a 0 = 0.002 cm, ωpe0 0.01 × ω, $\omega=1.778 \times10^{14}\, {{\rm rad} \over {\rm sec}}$, k = 1.25 × 103 cm−1, intensity parameter, α2|ψ0|2 = 0.8. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

Fig. 2. (Color online) Variation of normalized beam width a n(η) with dimensionless distance of propagation η for the case when both relativistic and ponderomotive nonlinearities alongwith free space propagation term are considered with the same set of parameters as in the caption of Figure 1 for the various orders of n. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

Fig. 3. (Color online) Plot of longitudinal phase ϕ(η) versus dimensionless distance of propagation η for the case when both the mechanisms (relativistic self-focusing and ponderomotive self-channeling) are considered for the same set of parameters as mentioned in the caption of Figure 1. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

To further elucidate the results for deleanating the underlying physics, we numerically analyze the dependence of dimensionless initial beam width parameter (ρ0) as a function of critical values of beam power Π (=α2|ψ0|2) for various orders of n when both relativistic and ponderomotive nonlinearities are taken into account. The results are depicted in the form of graphs. The critical curves for the propagation of the HGB in a plasma have been computed for a chosen set of parameters, n, c′ and $\Omega \lpar \!={\omega_{\,pe0} \over \omega}\rpar $. The critical curve for the DHGB characterizes the self-focusing region in ${1 / \rho_{0}^2}-\Pi$ space. Those points that lie below the critical power curve correspond to the propagation of the HGB with self-focusing whereas the points lying above the critical curve result in oscillatory or steady defocusing of HGB. Points on the critical curve lead to the propagation of the HGB in self-trapped mode. Figure 4 depicts such graph showing that the dependence of ${1 / \rho_{0}^2}$ for n = 0 is much weaker on the high intensity, a result consistent with earlier calculation based on variational approach (Anderson, Reference Anderson1978). However, initial beam width is much higher than the earlier investigations. Substantial decrease in dimensionless beam width as a function of Π is observed for higher order of n. Although the results corresponding to n = 4 in Figure 5 are quite similar to those obtained for n = 0, however, the following departure is observed:

Fig. 4. Variation of the dimensionless initial beam width (ρ0) as a function of measure of critical beam power (Π) for the case when both the mechanisms are present with n = 0.

Fig. 5. (Color online) Variation of the dimensionless initial beam width (ρ0) as a function of Π with n = 2 and n = 4. Solid curve corresponds to n = 2 and dashed to n = 4.

Dependence of ${1 / \rho_{0}^2}$ as a function of Π is initially fast which becomes slow for large Π. However, contrary results are observed for n = 2 in Figure 5, where ${1 / \rho_{0}^2}$ reaches maximum followed by steady decrease with Π. The result is quite similar to those of Misra and Mishra (Reference Misra and Mishra2009).

It is worthnoting that critical power curves exhibit some distinct features for different values of n, particularly for odd values of n. Both qualitatively as well as quantitatively different characteristics are obtained in critical curves. There is a sharp contrast witnessed for even and odd values of n shown in Figures 4–8 where ${1 / \rho_{0}^2}$ as a function of Π is displayed. Critical curves shown in Figures 7 and 8 are quite similar but with different trapped powers. However, behavior for n = 1 in Figure 6 is quite astonishing and interesting when significant departure is observed. There is a significant decrease in ${1 / \rho_{0}^2}$ with Π till minimum value is obtained. This is followed by increase in Π and finally exhibit a saturation behavior with Π (independent of Π).

Fig. 6. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 1.

Fig. 7. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 3.

Fig. 8. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 5.

5. CONCLUSIONS

In the present investigation, authors have studied the self-focusing and self-phase modulation of laser beam with relativistic and ponderomotive nonlinearities. Equation for normalized beam width and phase is derived using variational approach. When free space propagation term is not considered, the beam defocuses for all values of n. However, when relativistic as well as ponderomotive nonlinearities alongwith free space term are taken into account, oscillatory self-focusing is observed over several Rayleigh lengths. This result is in contrast to those of Sodha et al. (Reference Sodha, Mishra and Misra2009a). Phase exhibit peculiar behavior for different values of n as it becomes positive as well as negative. Lastly, we have studied some distinct features of critical power curves for even and odd values of n. Substantial decrease in dimensionless beam width (ρ0) as a function of Π is also observed for higher orders of n.

ACKNOWLEDGMENT

R. M. and R. K. gratefully acknowledge Guru Nanak Dev University, Amritsar India for providing Research Fellowship.

References

REFERENCES

Abramyan, L.A., Litvak, A.G., Mironov, V.A. & Sergeev, A.M. (1992). Self-focusing and relativistic waveguiding of an ultrashort laser pulse in a plasma. Sov. Phys. JETP 75, 978.Google Scholar
Akhmanov, S.A., Sukhorukov, A.P. & Khokhlov, R.V. (1968). Self-focusing and diffraction of light in a nonlinear medium. Sov. Phys. Usp. 10, 609–636.CrossRefGoogle Scholar
Anderson, D. (1978). Stationary self-trapped laser beams in plasma. Physica Scripta 18, 35–36.CrossRefGoogle Scholar
Anderson, D. & Bonnedal, M. (1979). Variational approach to nonlinear self-focusing of Gaussian laser beams. Phys. Fluids 22, 105–109.CrossRefGoogle Scholar
Arlt, J. & Dholakia, K. (2000). Generation of high order Bessel beams by use of an axicon. Opt. Commun. 177, 297–301.CrossRefGoogle Scholar
Benware, B.R., Macchietto, C.D., Moreno, C.H. & Rocca, J.J. (1998). Demonstration of a high average power tabletop soft X-ray laser. Phys. Rev. Lett. 81, 5804–5807.CrossRefGoogle Scholar
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C.A., Fuchs, J., Galimberti, M., Gizzi, L.A., Grismayer, T., Lyseikina, T., Jung, R., Macchi, A., Mora, P., Osterholtz, J., Schiavi, A. & Willi, O. (2007). Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25, 161–167.CrossRefGoogle Scholar
Borisov, A.B., Longworth, J.W., Boyer, K. & Rhodes, C.K. (1998). Stable relativistic/charge-displacement channels in ultrahigh power density (1021 W/cm3) plasmas. Proc. Natl. Acad. Sci. USA 95, 7854–7859.CrossRefGoogle ScholarPubMed
Cai, Y. & Lin, Q. (2004). Hollow elliptical Gaussian beam and its propagation through aligned and misaligned paraxial optical systems. J. Opt. Soc. Am. A 21, 1058–1065.CrossRefGoogle ScholarPubMed
Cai, Y., Lu, X. & Lin, Q. (2003). Hollow Gaussian beam and their propagation properties. Opt. Lett. 28, 1084–1086.CrossRefGoogle ScholarPubMed
Chen, S.Y., Sarkisov, G.S., Maksimchuk, A., Wagner, R. & Umstadter, D. (1998). Evolution of a plasma waveguide created during relativistic-ponderomotive self-channeling of an intense laser pulse. Phys. Rev. Lett. 80, 2610–2613.CrossRefGoogle Scholar
Chessa, P., Mora, P. & Antonsen, T.M. (1998). Numerical simulation of short laser pulse relativistic self-focusing in underdense plasma. Phys. Plasma 5, 3451–3458.CrossRefGoogle Scholar
Chiao, R.Y., Garmire, E. & Townes, C.H. (1964). Self-trapping of optical beams. Phys. Rev. Lett. 13, 479–482.CrossRefGoogle Scholar
Cornolti, F., Lucchesi, M. & Zambon, B. (1990). Elliptic Gaussian beam self-focusing in nonlinear media. Opt. Commun. 75, 129–135.CrossRefGoogle Scholar
Deng, D., Fu, X., Wei, C., Shao, J. & Fan, Z. (2005). Far field intensity distribution and M 2 factor of hollow Gaussian beams. Appl. Opt. 44, 7187–7190.CrossRefGoogle ScholarPubMed
Esarey, E., Sprangle, P., Krall, J. & Ting, A. (1997). Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE J. Quantum Electron 33, 1879–1914.CrossRefGoogle Scholar
Faenov, A.Y., Magunov, A.I., Pikuz, T.A., Skobelev, I.Y., Gasilov, S.V., Stagira, S., Calegari, F., Nisoli, M., De Silvestri, S., Poletto, L., Villoresi, P. & Andreev, A.A. (2007). X-ray spectroscopy observation of fast ions generation in plasma produced by short low-contrast laser pulse irradiation of solid targets. Laser Part. Beams 25, 267–275.CrossRefGoogle Scholar
Fedotov, A.B., Naumov, A.N., Silin, V.P., Uryupin, S.A., Zheltikov, A.M., Tarasevitch, A.P. & Von der Linde, D. (2000). Third-harmonic generation in a laser-pre-excited gas: the role of excited-state neutrals. Phys. Lett. A 271, 407–412.CrossRefGoogle Scholar
Fibich, G. (2007). Some Modern Aspects of Self-Focusing Theory, A Chapter in Self-Focusing: Past and Present (Boyd, R.W., Lukishova, S.G. & Shen, Y.R. eds.). New York: Springer Verlag.Google Scholar
Firth, W.J. (1977). Propagation of laser beams through inhomogeneous media. Opt. Commun. 22, 226–230.CrossRefGoogle Scholar
Foldes, I.B., Bakos, J.S., Bakonyi, Z., Nagy, T. & Szatmari, S. (1999). Harmonic generation in plasmas of different density gradients. Phys. Lett. A 258, 312–316.CrossRefGoogle Scholar
Gill, T.S., Mahajan, R. & Kaur, R. (2010). Relativistic and ponderomotive effects on evolution of laser beam in a non-uniform plasma channel. Laser Part. Beams 28, 11–20.CrossRefGoogle Scholar
Gill, T.S. & Saini, N.S. (2007). Nonlinear interaction of a rippled laser beam with an electrostatic upper hybrid wave in collisional plasma. Laser Part. Beams 25, 283–293.CrossRefGoogle Scholar
Gondarenko, N.A., Ossakow, S.L. & Milikh, G.M. (2005). Generation and evolution of density irregularities due to self-focusing in ionospheric modifications. J. Geophys. Res. 110, A093041–13.Google Scholar
Grow, T.D., Ishaaya, A.A., Vuong, L.T., Gaeta, A.L., Gavish, N. & Fibich, G. (2006). Collapse dynamics of super-Gaussian beams. Opt. Express 14, 5468–5475.CrossRefGoogle ScholarPubMed
Guzdar, P.N., Chaturvedi, P.K., Papadopoulos, K. & Ossakow, S.L. (1998). The thermal self-focusing instability near the critical surface in the high- latitude ionosphere. J. Geophys. Res. 103, 2231–2237.CrossRefGoogle Scholar
Hoffmann, D.H.H., Blazevic, A., Ni, P., Rosmej, O., Roth, M., Tahir, N., Tauschwitz, A., Udrea, S., Varentsov, D., Weyrich, K. & Maron, Y. (2005). Present and future perspective for high energy density physics with intense heavy ions and laser beams. Laser Part. Beams 23, 395–395.CrossRefGoogle Scholar
Hora, H. (1975). Theory of relativistic self focusing of laser radiations in plasmas. J. Opt. Soc. Am. 65, 882–886.CrossRefGoogle Scholar
Johannisson, P., Anderson, D., Lisak, M. & Marklund, M. (2003). Nonlinear Bessel beams. Opt. Commun. 222, 107–115.CrossRefGoogle Scholar
Karlsson, M., Anderson, D., Desaix, M. & Lisak, M. (1991). Dynamic effects of Kerr nonlinearity and spatial diffraction on self-phase modulation of optical pulses. Opt. Lett. 16, 1373–1375.CrossRefGoogle ScholarPubMed
Karlsson, M. (1992). Optical beams in saturable self-focusing media. Phys. Rev. A 46, 2726–2734.CrossRefGoogle ScholarPubMed
Kasperczuk, A., Pisarczyk, T., Kalal, M., Martinkova, M., Ullschmied, J., Krousky, E., Masek, K., Pfeifer, M., Rohlena, K., Skala, J. & Pisarczyk, P. (2008). PALS laser energy transfer into solid targets and its dependence on the lens focal point position with respect to the target surface. Laser Part. Beams 26, 189–196.CrossRefGoogle Scholar
Kaur, R., Gill, T.S. & Mahajan, R. (2010). Steady state self-focusing, self-phase modulation of laser beam in an inhomogeneous plasma. Optik (In Press).Google Scholar
Kelley, P.L. (1965). Self-focusing of laser beams and stimulated Raman gain in liquids. Phys. Rev. Lett. 15, 1010–1012.Google Scholar
Konar, S. & Manoj, M. (2005). Effect of higher order nonlinearities on induced focusing and on the conversion of circular Gaussian laser beams into elliptic Gaussian laser beam. J. Opt. A: Pure Appl. Opt. 7, 576.CrossRefGoogle Scholar
Krushelnick, K., Ting, A., Moore, C.I., Burris, H.R., Esarey, E., Sprangle, P. & Baine, M. (1997). Plasma channel formation and guiding during high intensity short pulse laser plasma experiments. Phys. Rev. Lett. 78, 4047–4050.CrossRefGoogle Scholar
Kuehl, Th., Ursescu, D., Bagnoud, V., Javorkova, D., Rosmej, O., Cassou, K., Kazamias, S., Klisnick, A., Ros, D., Nickles, P., Zielbauer, B., Dunn, J., Neumayer, P., Pert, G. & The Phelix Team. (2007). Optimization of non thermal incidence, transient pumped plasma X-ray laser for laser spectroscopy and plasma diagnostics at the facility for antiproton and ion research (FAIR). Laser Part. Beams 25, 93–97.CrossRefGoogle Scholar
Kumar, A., Gupta, M.K. & Sharma, R.P. (2006). Effect of ultraintense laser pulse on the propagation of electron plasma wave in relativistic and ponderomotive regime and particle acceleration. Laser Part. Beams 24, 403–409.CrossRefGoogle Scholar
Kurki-Suonio, T., Morrison, P.J. & Tajima, T. (1989). Self-focusing of an optical beam in a plasma. Phys. Rev. A 40, 3230–3239.CrossRefGoogle ScholarPubMed
Lam, J.F., Lippmann, B. & Tappert, F. (1977). Self-trapped laser beams in plasma. Phys. Fluids 20, 1176–1179.CrossRefGoogle Scholar
Laska, L., Badziak, J., Boody, F.P., Gammino, S., Jungwirth, K., Krasa, J., Krousky, E., Parys, P., Pfeifer, M., Rohlena, K., Ryc, L., Skala, J., Torrisi, L., Ullschmied, J. & Wolowski, J. (2007). Factor influencing parameters of laser ion sources. Laser Part. Beams 25, 199–205.CrossRefGoogle Scholar
Mei, Z. & Zhao, D. (2005). Controllable dark hollow beams and their propagation characteristics. J. Opt. Soc. Am. A 22, 1898–1902.CrossRefGoogle ScholarPubMed
Milchberg, H.M., Durfee, C.G. III. & Mcllrath, T.J. (1995). Highorder frequency conversion in the plasma waveguide. Phys. Rev. Lett. 75, 2494–2497.CrossRefGoogle ScholarPubMed
Misra, S. & Mishra, S.K. (2009). Focusing of dark hollow Gaussian electromagnetic beams in a plasma with relativistic-ponderomotive regime. Progress in electromagnetic research 16, 291–309.CrossRefGoogle Scholar
Monot, P., Auguste, T., Gibbon, P., Jakober, F., Mainfray, G., Dulieu, A., Louis-Jacquet, M., Malka, G. & Miquel, J.L. (1995). Experimental demonstration of relativistic self-channeling of a multiterawatt laser pulse in an underdense plasma. Phys. Rev. Lett. 74, 2953–2956.CrossRefGoogle Scholar
Niknam, A.R., Hashemzadeh, M. & Shokri, B. (2009). Weakly relativistic and ponderomotive effects on the density steepening in the interaction of an intense laser pulse with an underdense plasma. Phys. Plasmas 16, 033105/1–5.CrossRefGoogle Scholar
Perkins, F.W. & Goldman, M.V. (1981). Self-focusing of radio waves in an underdense ionosphere. J. Geophys. Res. 86, 600–608.CrossRefGoogle Scholar
Regan, S.P., Bradley, D.K., Chirokikh, A.V., Craxton, R.S., Meyerhofer, D.D., Seka, W., Short, R.W., Simon, A., Town, R.P.J. & Yaakobi, B. (1999). Laser-plasma interactions in long-scale-length plasmas under direct-drive National Ignition Facility conditions. Phys. Plasmas 6, 2072–2080.CrossRefGoogle Scholar
Saini, N.S. & Gill, T.S. (2006). Self-focusing and self-phase modulation of an elliptic Gaussian laser beam in collisionless magnetoplasma. Laser Part. Beams 24, 447–453.CrossRefGoogle Scholar
Sarkisov, G.S., Bychenkov, V.Yu., Novikov, V.N., Tikhonchuk, V.T., Maksimchuk, A., Chen, S.-Y., Wagner, R., Mourou, G. & Umstadter, D. (1999). Self-focusing, channel formation, and high-energy ion generation in interaction of an intense short laser pulse with a He jet. Phys. Rev. E 59, 7042–7054.CrossRefGoogle ScholarPubMed
Schaumann, G., Schollmeier, M.S., Rodriguez-Prieto, G., Blazevic, A., Brambrink, E., Geissel, M., Korostiy, S., Pirzadeh, P., Roth, M., Rosmej, F.B., Faenov, A.Y., Pikuz, T.A., Tsigutkin, K., Maron, Y., Tahir, N.A. & Hoffmann, D.H.H. (2005). High energy heavy ion jets emerging from laser plasma generated by long pulse laser beams from the NHELIX laser system at GSI. Laser Part. Beams 23, 503–512.CrossRefGoogle Scholar
Sharma, A., Verma, M.P. & Sodha, M.S. (2004). Self-focusing of electromagnetic beams in a collisional plasmas with nonlinear absorption. Phys. Plasmas 11, 4275–4279.CrossRefGoogle Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1974). Self-focusing of laser beams in dielectric plasma and semi conductors. New York: Tata McGra-Hill.Google Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Self-focusing of laser beams in plasmas and semiconductors. Prog. optics 13, 171–265.Google Scholar
Sodha, M.S., Mishra, S.K. & Misra, S. (2009a). Focusing of dark hollow Gaussian electromagnetic beams in a plasma. Laser Part. Beams 27, 57–68.CrossRefGoogle Scholar
Sodha, M.S., Mishra, S.K. & Misra, S. (2009b). Focusing of dark hollow Gaussian electromagnetic beam in a magnetoplasma. J. Plasma Phys. 75, 731–748.CrossRefGoogle Scholar
Sprangle, P., Hafizi, B. & Penano, J.R. (2000). Laser pulse modulation instabilities in plasma channels. Phys. Rev. E 61, 4381–4393.CrossRefGoogle ScholarPubMed
Stoehlker, T., Backe, H., Beyer, H., Bosch, F., Braeuning-Demian, A., Hagman, S., Ionescu, D., Jungmann, K., Kluge, H.-J., Kozhuharov, C., Kuehl, Th., Lisen, D., Mann, R., Mokler, P. & Quint, W. (2003). Status and perspectives of atomic physics research at GSI: The new GSI accelerator project. Nucl. Instr. Meth. B 205, 156.CrossRefGoogle Scholar
Strangio, C., Caruso, A., Neely, D., Andreoli, P.L., Anzalone, R., Clarke, R., Cristofari, G., DelPrete, E., Di Giorgio, G., Murphy, C., Ricci, C., Stevens, R. & Tolley, M. (2007). Production of multi-Mev per nucleon ions in the controlled amount of matter mode (CAM) by using casually isolated targets. Laser Part. Beams 25, 85–91.CrossRefGoogle Scholar
Subbarao, D., Uma, R. & Singh, H. (1998). Paraxial theory of self-focusing of cylindrical laser beams. I. ABCD laws. Phys. Plasmas 5, 3440–3450.CrossRefGoogle Scholar
Suckewer, S. & Skinner, C.H. (1990). Soft X-ray lasers and their applications. Science 247, 1553–1557.CrossRefGoogle ScholarPubMed
Suckewer, S. & Skinner, C.H. (1995). Comments At. Mol. Phys. 30, 331.Google Scholar
Tabak, M., Hammer, J., Glinsky, M.E., Kruer, W.L., Wilks, S.C., Woodworth, J., Campbell, E.M., Perry, M.D. & Mason, R.J. (1994). Ignition and high gain with ultrapowerful lasers. Phys. Plasmas 1, 1626–1634.CrossRefGoogle Scholar
Torrisi, L., Margarone, D., Laska, L., Krasa, J., Velyhan, A., Pfeifer, M., Ullschmied, J. & Ryc, L. (2008). Self-focusing effects in Au-target induced by high power pulsed laser at PALS. Laser Part. Beams 26, 379–387.CrossRefGoogle Scholar
Tzeng, K.C. & Mori, W.B. (1998). Suppression of electron ponderomotive blowout and relativistic self-focusing by the occurence of Raman scattering and plasma heating. Phys. Rev. Lett. 81, 104–107.CrossRefGoogle Scholar
Wagner, R., Chen, S.Y., Maksimuchuk, A. & Umstadter, D. (1997). Electron acceleration by a laser wakefield in a relativistically self-guided channel. Phys. Rev. Lett. 78, 3125–3128.CrossRefGoogle Scholar
Yin, J., Gao, W. & Zhu, Y. (2003). Propagation of various dark hollow beams in a turbulent atmosphere. Prog. Opt. 44, 119–204.CrossRefGoogle Scholar
York, A.G., Milchberg, H.M., Palastro, J.P. & Antonsen, T.M. (2008). Direct acceleration of electrons in a corrugated plasma waveguide. Phys. Rev. Lett. 100, 195001–7.CrossRefGoogle Scholar
Yu, W., Yu, M.Y., Xu, H., Tian, Y.W., Chen, J. & Wong, A.Y. (2007). Intense local plasma heating by stopping of ultrashort ultraintense laser pulse in dense plasma. Laser Part. Beams 25, 631–638.CrossRefGoogle Scholar
Zhang, L., Lu, X., Chen, X. & He, S. (2004). Generation of a dark hollow beam inside a cavity. Chin. Phys. Lett. 21, 298–301.Google Scholar
Figure 0

Fig. 1. (Color online) Variation of normalized beam width an(η) with dimensionless distance of propagation η for the case when free space propagation term is not taken into account with the following set of parameters for the various orders of n: a0 = 0.002 cm, ωpe0 0.01 × ω, $\omega=1.778 \times10^{14}\, {{\rm rad} \over {\rm sec}}$, k = 1.25 × 103 cm−1, intensity parameter, α2|ψ0|2 = 0.8. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

Figure 1

Fig. 2. (Color online) Variation of normalized beam width an(η) with dimensionless distance of propagation η for the case when both relativistic and ponderomotive nonlinearities alongwith free space propagation term are considered with the same set of parameters as in the caption of Figure 1 for the various orders of n. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

Figure 2

Fig. 3. (Color online) Plot of longitudinal phase ϕ(η) versus dimensionless distance of propagation η for the case when both the mechanisms (relativistic self-focusing and ponderomotive self-channeling) are considered for the same set of parameters as mentioned in the caption of Figure 1. Solid curve corresponds to n = 0, dashed curve to n = 1, dotted curve to n = 2 and dotdashed curve to n = 3.

Figure 3

Fig. 4. Variation of the dimensionless initial beam width (ρ0) as a function of measure of critical beam power (Π) for the case when both the mechanisms are present with n = 0.

Figure 4

Fig. 5. (Color online) Variation of the dimensionless initial beam width (ρ0) as a function of Π with n = 2 and n = 4. Solid curve corresponds to n = 2 and dashed to n = 4.

Figure 5

Fig. 6. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 1.

Figure 6

Fig. 7. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 3.

Figure 7

Fig. 8. Dependence of the dimensionless initial beam width (ρ0) as a function of Π with n = 5.