1. INTRODUCTION
High-power laser–matter interaction has many applications such as particle acceleration, laser-induced fusion, harmonic generation, X-ray generation, bio-medical application, electromagnetic radiation, etc. (Drake et al., Reference Drake, Lee, Nishikawa and Tsintsadze1976; Wilks et al., Reference Wilks, Kruer, Tabak and Langdon1992; Milchberg et al.,
Reference Milchberg, Durfee and Mcilrath1995; Pukhov & Meyer-Ter-vehn, Reference Pukhov and Meyer-Ter-vehn1998; Pukhov et al., Reference Pukhov, Sheng and Meyer-Ter-vehn1999; Gattass & Mazur, Reference Gattass and Mazur2008). At present, high-power laser systems are able to produce ultra-short pulses having intensities well above 1018 W cm−2. Such intense laser pulse can reveal numerous types of nonlinear phenomenon (Akhmanov et al.,
Reference Akhmanov, Sukhorukov and Khokhlov1968; Hora, Reference Hora1975; Sodha et al.,
Reference Sodha, Ghatak and Tripathi1976; Brandi et al.,
Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993), during propagation through the plasma. These nonlinearities include self-focusing/filamentation and self-compression, the growth of various parametric instabilities, plasma wave excitation, and harmonic generation (Hora, Reference Hora1975; Sodha et al.,
Reference Sodha, Ghatak and Tripathi1976; Kruer, Reference Kruer1988; Milchberg et al.,
Reference Milchberg, Durfee and Mcilrath1995; Lehner & Di Menza, Reference Lehner and Di Menza2000; Kumar et al.,
Reference Kumar, Gupta and Sharma2006; Purohit et al., Reference Purohit, Sharma and Sharma2012, Rawat et al., Reference Rawat, Chauhan and Purohit2013). Among all these nonlinearities, the prime importance goes to self-focusing and self-compression. These can enhance the intensity of the pulse many folds at the focused position and affects all other intensity-dependent complex processes in the plasma. In general, self-focusing of a laser beam depends on properties of the medium and laser pulse width. Self-focusing of intense laser beams propagating through the plasma can be attributed to various nonlinear processes such as collisional, ponderomotive, and relativistic nonlinearity. These nonlinearities have a strong dependence on laser beam intensity and setup in different time scales. In the case of intense and shorter laser pulses, relativistic and relativistic–ponderomotive nonlinearities are dominant. Both of these nonlinearities operate at distinct scales of time, (i)
![]() $t_0 \lt {t}^{\prime}_{{\rm pe}}$
or (ii)
$t_0 \lt {t}^{\prime}_{{\rm pe}}$
or (ii)
![]() ${t}^{\prime}_{{\rm pe}} \lt t_0 \lt {t}^{\prime}_{{\rm pi}}$
; where, t
0 is the duration of the laser pulse,
${t}^{\prime}_{{\rm pe}} \lt t_0 \lt {t}^{\prime}_{{\rm pi}}$
; where, t
0 is the duration of the laser pulse,
![]() ${t}^{\prime}_{{\rm pe}}$
the period of an electron in plasma and
${t}^{\prime}_{{\rm pe}}$
the period of an electron in plasma and
![]() ${t}^{\prime}_{{\rm pi}}$
period of ion in plasma. The former (relativistic) is set up instantly [case (i)], while relativistic–ponderomotive is set up at a later time [case (ii)] (Hora, Reference Hora1975; Brandi et al.,
Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993).
${t}^{\prime}_{{\rm pi}}$
period of ion in plasma. The former (relativistic) is set up instantly [case (i)], while relativistic–ponderomotive is set up at a later time [case (ii)] (Hora, Reference Hora1975; Brandi et al.,
Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993).
The relativistic nonlinearity comes into the picture because the mass of electron changes as the quiver velocity of electron approaches to the velocity of light. In ponderomotive nonlinearity, the change in refractive index arises due to the density variation induced by ponderomotive force, which expels electrons out of higher intensity zone. The gradient of intensity is the key cause for the ponderomotive force generation. When ponderomotive and relativistic nonlinearity work simultaneously, the density perturbation (extra term with relativistic nonlinearity) increases the weightage of this relativistic–ponderomotive nonlinearity and confirms the dominance of relativistic–ponderomotive nonlinearity over relativistic nonlinearity.
Drescher et al. (Reference Drescher, Hentschel, Kienberger, Uiberacker, Yakovlev, Scrinzi and Krausz2002) have successfully demonstrated the inner-shell decay process inside an atom of a noble gas by time resolved atomic inner-shell spectroscopy by using sub-femtosecond pulse. The main challenge to the laser science community is to generate the high-energy few-cycle pulses, which is required for time-domain spectroscopy. The few-cycle laser pulses can be easily achieved by a self-compression technique in the nonlinear media. But non-plasma-based materials busted when the power of laser exceeds a certain limit. To overcome the material busting issue, a novel scheme based on short pulse laser plasma interaction has been proposed. A laser pulse undergoes self-compression during its propagation through plasma due to the interplay between the self-phase modulations due to the nonlinearity of plasma and group velocity dispersion (GVD) (Mora & Antonsen, Reference Mora and Antonsen1997; Chessa et al., Reference Chessa, Mora and Antonsen1998; Hauri et al., Reference Hauri, Kornelis, Helbing, Heinrich, Couairon, Mysyrowicz and Keller2004). GVD is a process in which the group velocity of the electromagnetic wave in a medium becomes dependent on the wavelength. GVD is defined as the derivative of the inverse of the group velocity. It could be positive or negative depending on the medium. Ultrashort pulses are having broad spectral band width, which leads to material dispersion and hence the study of GVD becomes more important.
Now a days the development of chirped pulse amplification (CPA) technique is used to produce short laser pulse with the intensity of the order of 1022 watt/cm2, in which laser is first stretched, second amplified, and then recompressed. But, this technique is limited to the active medium amplifier (millimeter) having finite bandwidth Strickland & Mourou (Reference Strickland and Mourou1985). It has been found that relativistic mass variation may also serve as an ingredient for compression of the laser pulse. Shorokhov et al. (Reference Shorokhov, Pukhov and Kostyukov2003) have done one-dimensional particle-in-cell (1D PIC) and 3D PIC simulation of a 26 TW laser propagating in the plasma and reported the compression of a 30 fs long laser pulse to a 5 fs pulse by considering relativistic nonlinearity. A theoretical model was developed by Olumi and Maraghechi (Reference Olumi and Maraghechi2014) to investigate the self-compression of the relativistic Gaussian laser pulse in the presence of relativistic nonlinearity in magnetized plasma. They examined numerically that when the pulse is compressed, a hike in intensity could be achieved because of the coupling of relativistic nonlinearity and magnetic field. They further observed that the negative chirped leads to more compression of the pulse and positively chirped leads to decompression of the pulse. Karle and Spatschek (Reference Karle and Spatschek2008) have shown relativistic laser pulse self-compression in a plasma channel separated by vacuum in the weakly relativistic regime. Bokaei and Niknam (Reference Bokaei and Niknam2014) have reported self-compression and self-focusing of laser pulse propagation by considering weakly relativistic and ponderomotive nonlinearities, which work at larger time scale to establish ponderomotive nonlinearity. Compression of laser pulse using plasma as medium has been studied widely by many authors (Ren et al., Reference Ren, Duda, Hemker, Mori, Katsouleas, Antonsen and Mora2001; Avitzour & Shvets, Reference Avitzour and Shvets2008; Sharma & Kourakis, Reference Sharma and Kourakis2010; Liang et al., Reference Liang, Sang, Wan, Lv and Xie2015) by taking all spectrum of nonlinearities into account.
This paper presents the simultaneous study of self-focusing and self-compression of a Gaussian (spatiotemporal) laser pulse due to the combined effect of ponderomotive and relativistic nonlinearity. This paper is arranged as follows: In Section 2, we have developed the model equation of Gaussian laser beam and performed a numerical simulation to examine the pulse amplitude evolution and intensity enhancement of Gaussian laser pulses in plasma having relativistic–ponderomotive nonlinearity. Then in Section 3, a semi-analytical model is obtained for clear insight. Lastly, the conclusion and summary are given in Section 4.
2. Model Equation for Numerical Simmulation
A short pulse laser having electric field profile (space and time)
![]() $\vec E(x,z,t) = E_0(x,z,t)e^{i(kz - {\rm \omega} t)}$
moving in the z-direction over the plasma, the governing wave equation is given by,
$\vec E(x,z,t) = E_0(x,z,t)e^{i(kz - {\rm \omega} t)}$
moving in the z-direction over the plasma, the governing wave equation is given by,
where
![]() $\vec J = - N_{\rm e}e\vec v$
is current density, N
e represent the density of electron,
$\vec J = - N_{\rm e}e\vec v$
is current density, N
e represent the density of electron,
![]() $\vec v$
and e are the velocity and charge of an electron, respectively. The high intense laser pulse pushes the electrons from the central region of the pulse due to its ponderomotive force and relativistic mass variation because of electrons oscillates at relativistic frequency, so the density of plasma can further modify. The relativistic–ponderomotive force (Brandi et al.,
Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993) is,
$\vec v$
and e are the velocity and charge of an electron, respectively. The high intense laser pulse pushes the electrons from the central region of the pulse due to its ponderomotive force and relativistic mass variation because of electrons oscillates at relativistic frequency, so the density of plasma can further modify. The relativistic–ponderomotive force (Brandi et al.,
Reference Brandi, Manus, Mainfray, Lehner and Bonnaud1993) is,
where γ = (1 + (e 2|A|2/m2ω2 c 2))1/2.
Equation (2) shows the ponderomotive force in the relativistic regime, where the Lorentz factor becomes a function of the laser intensity. The high intense laser beam increases the mass of electron, which can strongly modify the laser beam propagation leading to strong self-focusing and self-compression of laser beam. The ponderomotive force induces density perturbation within time duration of
![]() ${\rm \omega} _{\rm p}^{ - 1} $
, due to the high intensity of laser pulse and very short time duration permits the movement of electrons only. Moreover, the ions are remains stationary. The density perturbation can be attributed by,
${\rm \omega} _{\rm p}^{ - 1} $
, due to the high intensity of laser pulse and very short time duration permits the movement of electrons only. Moreover, the ions are remains stationary. The density perturbation can be attributed by,
 $$\displaystyle{{N_{\rm e}} \over {N_0}} = 1 + \displaystyle{{c^2} \over {{\rm \omega} _{{\rm p}0}^{\rm 2}}} \left( {\nabla ^2{\rm \gamma} - \displaystyle{{{(\nabla {\rm \gamma} )}^2} \over {\rm \gamma}}} \right).$$
$$\displaystyle{{N_{\rm e}} \over {N_0}} = 1 + \displaystyle{{c^2} \over {{\rm \omega} _{{\rm p}0}^{\rm 2}}} \left( {\nabla ^2{\rm \gamma} - \displaystyle{{{(\nabla {\rm \gamma} )}^2} \over {\rm \gamma}}} \right).$$
The nonlinear Schrödinger equation can be written by using Eq. (1) and replacing the old variables by new variables t′ = (t − (z/v g)) and z′ = z, we get
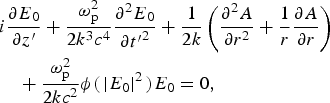 $$\eqalign{& i\displaystyle{{\partial E_0} \over {\partial z{\rm ^{\prime}}}} + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {2k^3c^4}}\displaystyle{{\partial ^2E_0} \over {\partial t{\rm ^{\prime}}^2}} + \displaystyle{1 \over {2k}}\left( {\displaystyle{{\partial ^2A} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A} \over {\partial r}}} \right) \cr & \quad + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {2kc^2}}{\rm \phi (}\left \vert {E_0} \right \vert ^2{\rm )}E_0 = 0,} $$
$$\eqalign{& i\displaystyle{{\partial E_0} \over {\partial z{\rm ^{\prime}}}} + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {2k^3c^4}}\displaystyle{{\partial ^2E_0} \over {\partial t{\rm ^{\prime}}^2}} + \displaystyle{1 \over {2k}}\left( {\displaystyle{{\partial ^2A} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A} \over {\partial r}}} \right) \cr & \quad + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {2kc^2}}{\rm \phi (}\left \vert {E_0} \right \vert ^2{\rm )}E_0 = 0,} $$
where ϕ(|E 0|2) = ((N e/γN 0) − 1). Since the z-variation of amplitude is linked with t variation the term (∂A/∂z) nearly as [(1/v g)(∂A/∂z)] (where v g is group velocity), we can replace the term (∂2 A/∂z 2) by [(1/v g)(∂2 A/∂z 2)] .We have normalized Eq. (4) by substituting the value of ϕ(|E 0|2) and using normalized parameters given as,
 $$\eqalign{& A = \displaystyle{{10eE_0} \over {m{\rm \omega} c}},\quad {\rm where}\quad A^2 = a^2\;\exp \left( { - \displaystyle{{t{\rm ^{\prime}}^2} \over {t_0^2}}} \right)\exp \left( { - \displaystyle{{r^2} \over {r_0^2}}} \right), \cr & \quad {\rm \varsigma} = \displaystyle{{z{\rm \omega} _{\rm p}^2} \over {2k^3c^4t_0^2}}, \quad {\rm \eta} = \displaystyle{r \over {r_0}},\quad {\rm \tau} = \displaystyle{{t{\rm ^{\prime}}} \over {t_0}},} $$
$$\eqalign{& A = \displaystyle{{10eE_0} \over {m{\rm \omega} c}},\quad {\rm where}\quad A^2 = a^2\;\exp \left( { - \displaystyle{{t{\rm ^{\prime}}^2} \over {t_0^2}}} \right)\exp \left( { - \displaystyle{{r^2} \over {r_0^2}}} \right), \cr & \quad {\rm \varsigma} = \displaystyle{{z{\rm \omega} _{\rm p}^2} \over {2k^3c^4t_0^2}}, \quad {\rm \eta} = \displaystyle{r \over {r_0}},\quad {\rm \tau} = \displaystyle{{t{\rm ^{\prime}}} \over {t_0}},} $$
where ω, r 0, and t 0 represent the laser pulse frequency, the initial beam radius, and pulse duration, respectively. Now the modified nonlinear Schrödinger equation is,
 $$\eqalign{& i\displaystyle{{\partial A} \over {\partial {\rm \varsigma}}} + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm dif}}}}\displaystyle{{\partial ^2A} \over {\partial \eta ^2}} + \displaystyle{{\partial ^2A} \over {\partial t{\rm ^{\prime}}^2}} + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm NL}}}}\displaystyle{{ \vert A \vert ^2} \over 2} \cr & \quad A + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm NL}}}}\left( {\left( {\displaystyle{{4c^2} \over {{\rm \omega} _{\rm p}^2 r_0^2}}} \right)\displaystyle{1 \over 2} - \displaystyle{{2c^2} \over {r_0^2 {\rm \omega} _{\rm p}}}{\rm \eta} ^2} \right)\left \vert A \right \vert ^2A = 0,} $$
$$\eqalign{& i\displaystyle{{\partial A} \over {\partial {\rm \varsigma}}} + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm dif}}}}\displaystyle{{\partial ^2A} \over {\partial \eta ^2}} + \displaystyle{{\partial ^2A} \over {\partial t{\rm ^{\prime}}^2}} + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm NL}}}}\displaystyle{{ \vert A \vert ^2} \over 2} \cr & \quad A + \displaystyle{{L_{{\rm disp}}} \over {L_{{\rm NL}}}}\left( {\left( {\displaystyle{{4c^2} \over {{\rm \omega} _{\rm p}^2 r_0^2}}} \right)\displaystyle{1 \over 2} - \displaystyle{{2c^2} \over {r_0^2 {\rm \omega} _{\rm p}}}{\rm \eta} ^2} \right)\left \vert A \right \vert ^2A = 0,} $$
where
![]() $L_{{\rm dif}} = kr_0^2 $
is called the diffraction length,
$L_{{\rm dif}} = kr_0^2 $
is called the diffraction length,
![]() $L_{{\rm disp}} =$
$L_{{\rm disp}} =$
![]() $(2k^3c^4t_0^2 /{\rm \omega} _{\rm p}^2 )$
indicates the dispersion length and
$(2k^3c^4t_0^2 /{\rm \omega} _{\rm p}^2 )$
indicates the dispersion length and
![]() $L_{{\rm NL}} = (2kc^2/$
$L_{{\rm NL}} = (2kc^2/$
![]() ${\rm \omega} _{\rm p}^{\rm 2} )$
represent the nonlinear length. These parameters will help to dictate the propagation of short pulse laser in plasma.
${\rm \omega} _{\rm p}^{\rm 2} )$
represent the nonlinear length. These parameters will help to dictate the propagation of short pulse laser in plasma.
While solving Eq. (5) numerically, the Pseudo spectral method along with a predictor corrector scheme have been employed to study. The spatiotemporal evolution for different plasma frequencies
![]() ${\rm \omega} _{\rm p}^2 = 0.83{\rm \omega} ^2$
,
${\rm \omega} _{\rm p}^2 = 0.83{\rm \omega} ^2$
,
![]() ${\rm \omega} _{\rm p}^2 = 0.85{\rm \omega} ^2,$
and
${\rm \omega} _{\rm p}^2 = 0.85{\rm \omega} ^2,$
and
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
have been seen when initial value of the normalized electric field a was kept as two. The assuming laser parameters are laser pulse duration t
0 = 30 fs, initial radius of the laser beam r
0 = 10 μm and wavelength λ= 1064 nm. We have also seen the intensity of the pulse at different values of normalized electric field a = 1.5 and 2.5 by keeping the plasma frequency constant
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
have been seen when initial value of the normalized electric field a was kept as two. The assuming laser parameters are laser pulse duration t
0 = 30 fs, initial radius of the laser beam r
0 = 10 μm and wavelength λ= 1064 nm. We have also seen the intensity of the pulse at different values of normalized electric field a = 1.5 and 2.5 by keeping the plasma frequency constant
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. Moreover, we have seen the intensities of pulse at a normalized distance (ξ = 0.2).
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. Moreover, we have seen the intensities of pulse at a normalized distance (ξ = 0.2).
When laser pulse propagates in plasma, it gets compressed and self-focused simultaneously because of the nonlinear role played by the plasma, which opposes the dispersion and diffraction of the laser pulse. This leads to the manifold intensity enhancement of laser beam. The compression of the pulse occurs due to interaction of self-phase modulation (arising due to nonlinearity) and GVD. The mass of electron varies due to intense laser pulse causing a modification in refractive index. A laser pulse having spatiotemporal Gaussian profile brings change in refractive index with a maximum value at maximum intensity and continuously falling in the radial direction. Hence, laser pulse gets self-focused due to alteration in refractive index. Short laser pulse increases the plasma refractive index through increasing intensity and decreases as laser pulse goes past. This will make time varying the index of refraction, which causes the time varying phase change leading to compression of the pulse in time domain.
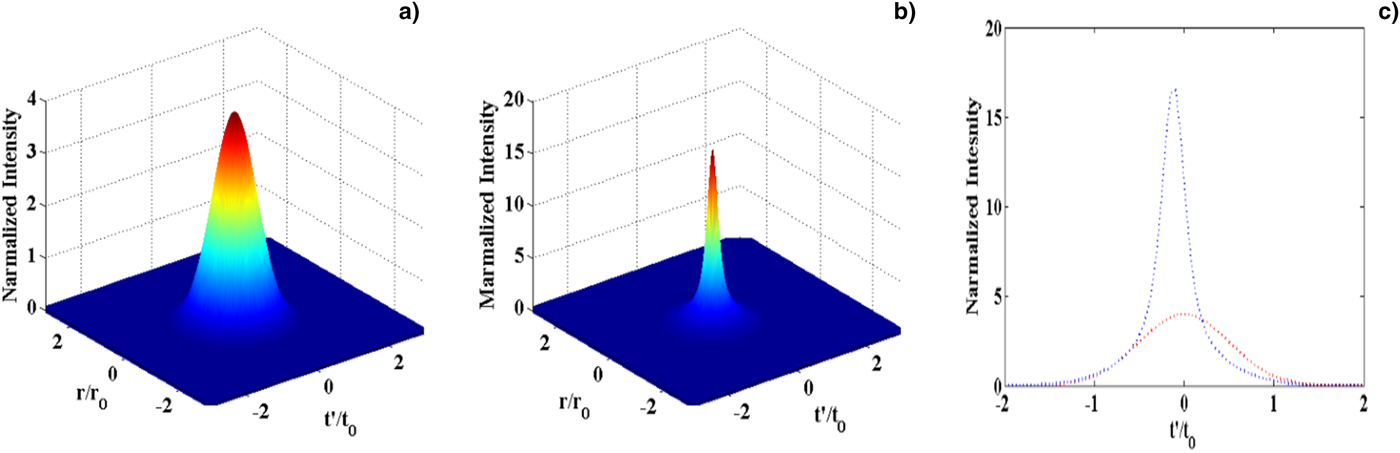
Figure 1a plots the initial laser pulse having the normalized intensity of 4 with normalized radial distance (r/r
0) and time (t′/t
0). Figure 1b presents the intensity and spatiotemporal pattern of the compressed laser pulse at z = 18.9 μm. Here the propagating laser pulse of initial time duration t
0 = 30 fs get compressed to 9.77 fs and Figure 1c represents the compressed and initial laser pulse in time domain for plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
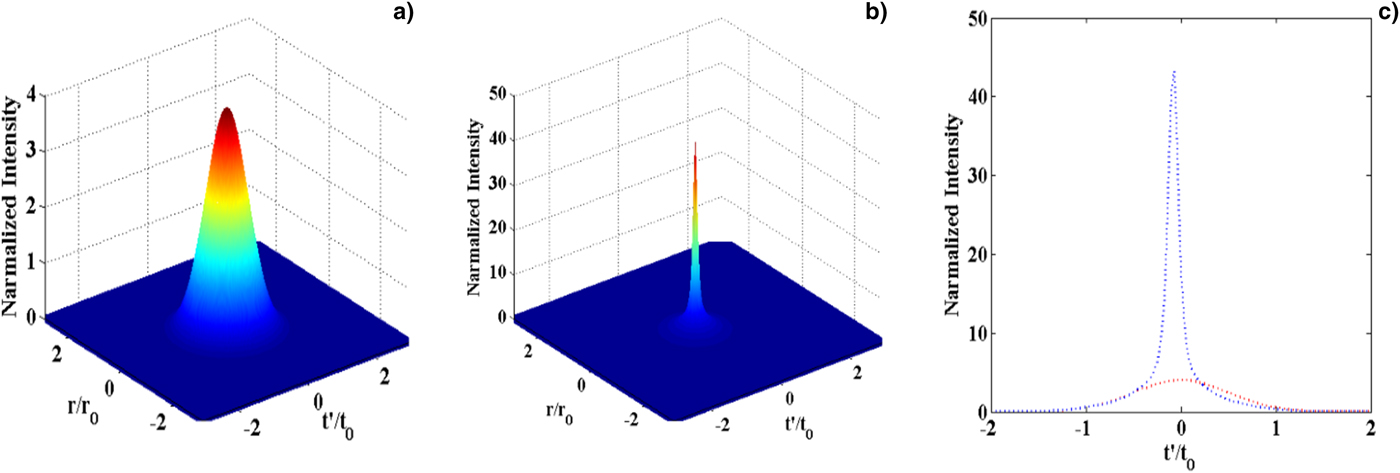
. Figures 2a–2c display the intensity and spatiotemporal pattern of the compressed laser pulse. When the initial laser pulse having pulse duration t
0 = 30 fs travels a distance z = 13.0 μm in plasma, initial pulse duration gets compressed to 8.45 fs at plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. Figures 2a–2c display the intensity and spatiotemporal pattern of the compressed laser pulse. When the initial laser pulse having pulse duration t
0 = 30 fs travels a distance z = 13.0 μm in plasma, initial pulse duration gets compressed to 8.45 fs at plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
. Figures 3a–3c represent the intensity pattern and compressed laser pulse at plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
. Figures 3a–3c represent the intensity pattern and compressed laser pulse at plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
and the duration of initial pulse get shorter to 5.86 fs at distance z = 10.4 μm.
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
and the duration of initial pulse get shorter to 5.86 fs at distance z = 10.4 μm.

Fig. 1. (a) Initial laser pulse intensity in 3D at (z = 0), (b) intensity of the compressed pulse in 3D at z = 18.9 μm, and panel (c) represents the initial and compressed pulse (at z = 18.9 μm) intensity in 2D on pulse duration scale for λ = 1064 nm,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 2 same for all.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 2 same for all.
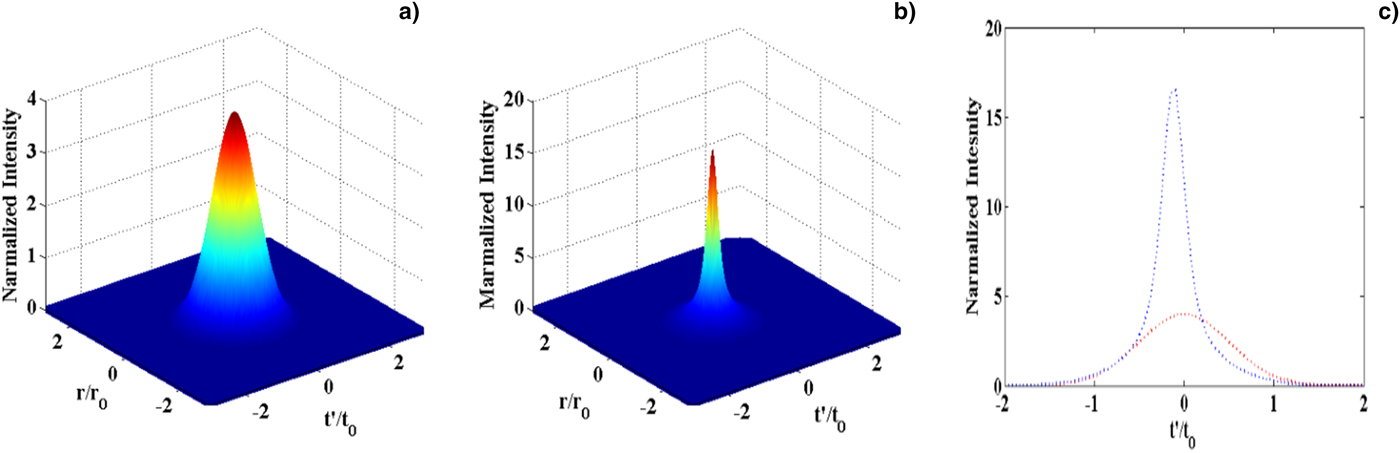
Fig. 2. (a) Initial laser pulse intensity in 3D at z = 0, (b) intensity of the compressed pulse in 3D at z = 13.0 μm and panel (c) represents the initial and compressed pulse (at z = 13.0 μm) intensity in 2D on pulse duration scale for λ= 1064 nm,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^{\rm 2},$
and a = 2 same for all.
${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^{\rm 2},$
and a = 2 same for all.

Fig. 3. (a) Initial laser pulse intensity in 3D at z = 0, (b) intensity of the compressed pulse in 3D at z = 10.4 μm, and panel (c) represents the initial and compressed pulse (at z = 10.4 μm) intensity in 2D on pulse duration scale for λ= 1064 nm,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2,$
and a = 2 same for all.
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2,$
and a = 2 same for all.
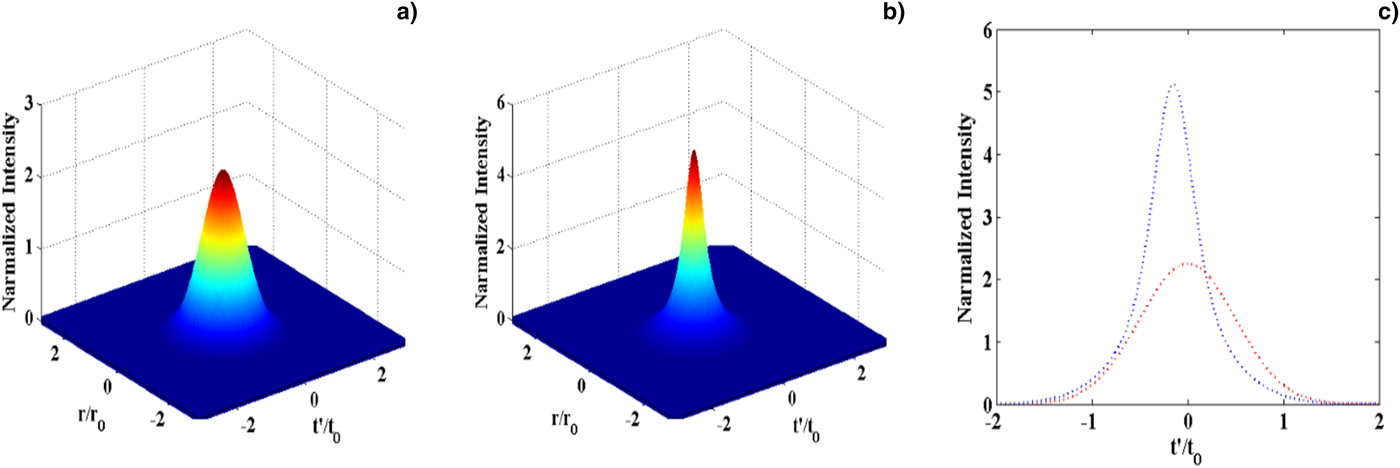
It has been observed that increasing the values of normalized electric field, strengthens compression mechanism in the plasma and an increment in intensity of the laser pulse could be achieved at constant
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
plasma frequency. Figures 4a–4c show intensity and pattern of compressed laser pulse at normalized electric field a = 1.5 and plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
plasma frequency. Figures 4a–4c show intensity and pattern of compressed laser pulse at normalized electric field a = 1.5 and plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^{\rm 2}$
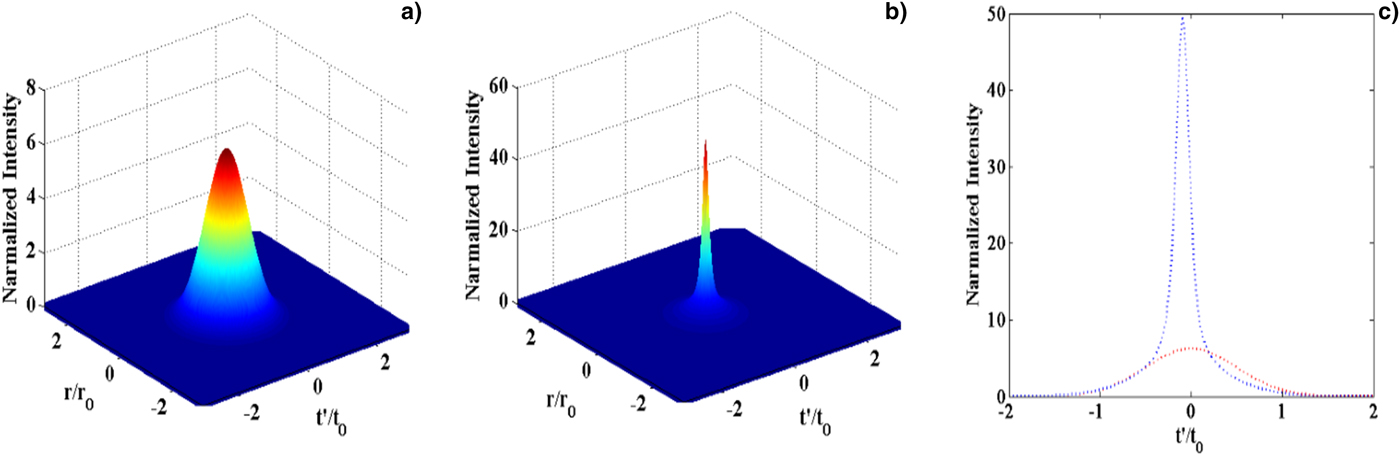
. However, the laser pulse travels to z = 16.2 μm distance inside plasma it get compressed to 14.44 fs. Figures 5a–5c present the intensity and pattern of compressed laser pulse at normalized value of electric field a = 2.5 and plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^{\rm 2}$
. However, the laser pulse travels to z = 16.2 μm distance inside plasma it get compressed to 14.44 fs. Figures 5a–5c present the intensity and pattern of compressed laser pulse at normalized value of electric field a = 2.5 and plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. However, the compression in laser pulse duration in plasma is about 4.66 fs at z = 16.2 μm distance. While the pulse propagates more in the plasma, both dispersion and diffraction circumstances are effective that can start chaotic shape.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. However, the compression in laser pulse duration in plasma is about 4.66 fs at z = 16.2 μm distance. While the pulse propagates more in the plasma, both dispersion and diffraction circumstances are effective that can start chaotic shape.
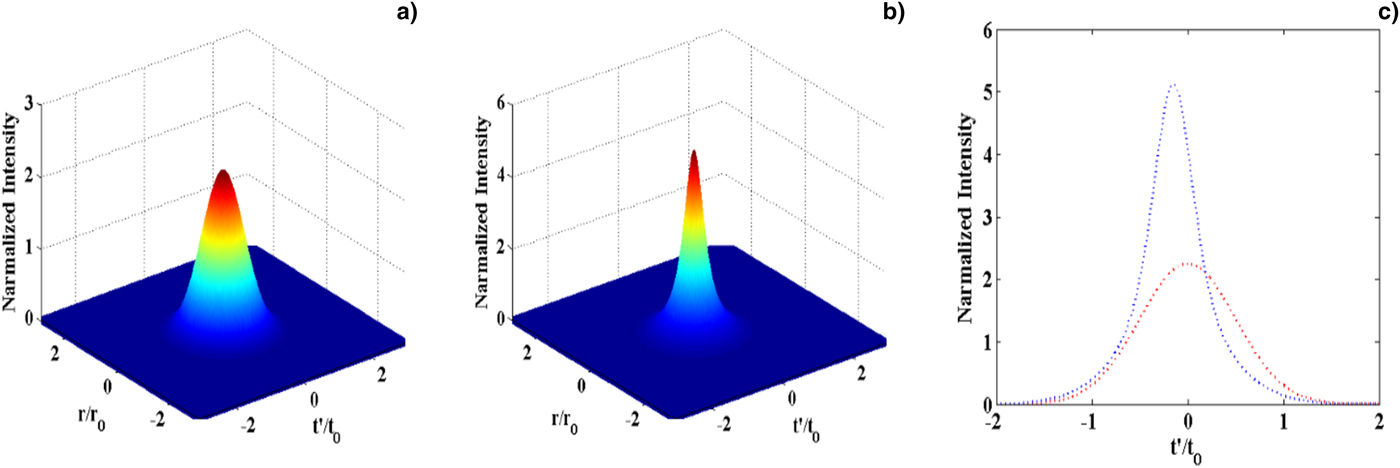
Fig. 4. (a) Initial laser pulse intensity in 3D at z = 0, (b) intensity of the compressed pulse in 3D at z = 16.2 μm, and panel (c) represents the initial and compressed pulse (at z = 16.2 μm) intensity in 2D on pulse duration scale for λ= 1064 nm,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 1.5 same for all.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 1.5 same for all.
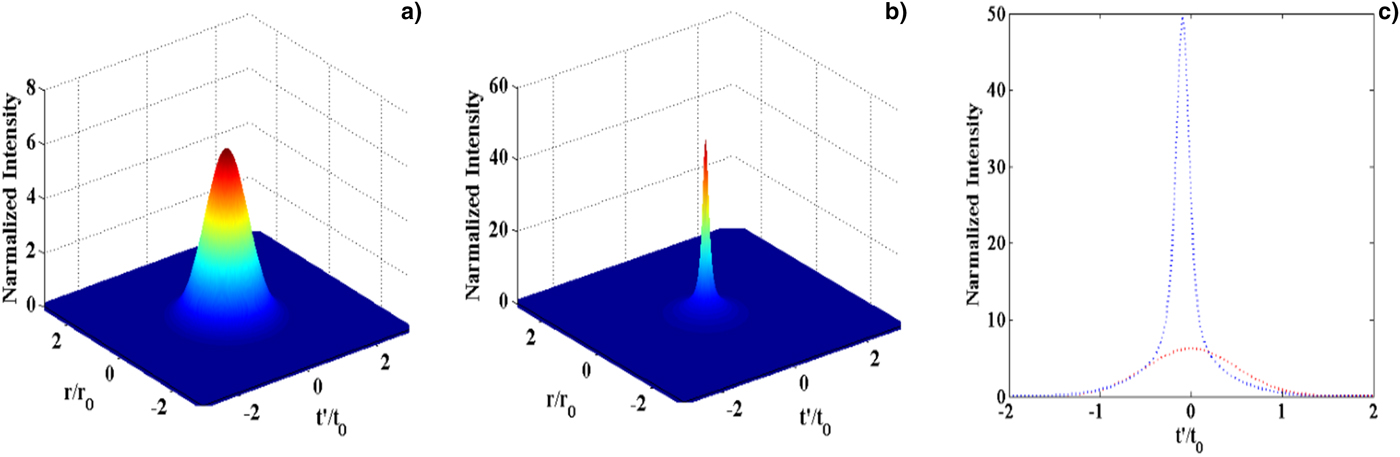
Fig. 5. (a) Initial laser pulse intensity in 3D at z = 0, (b) intensity of the compressed pulse in 3D at z = 16.2 μm, and panel (c) represents the initial and compressed pulse (at z = 16.2 μm) intensity in 2D on pulse duration scale for λ = 1064 nm,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 2.5 same for all.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2,$
and a = 2.5 same for all.
3. Model Equation for Semi-Analytical Method
Consider an approximate model to explain the physical significance of nonlinear evolution of spatiotemporal Gaussian laser pulse by using Eqs. (1)–(3) and introducing new dimensionless variable t′ = (t − (z/v g))(ω v g/ωp0) and z′ = z, one can get
 $$2ik\displaystyle{{\partial A} \over {\partial z{\rm ^{\prime}}}} + \displaystyle{{\partial ^2A} \over {\partial t{\rm ^{\prime}}^2}} + \left( {\displaystyle{{\partial ^2A} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A} \over {\partial r}}} \right) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {c^2}}\left( {\displaystyle{{N_{\rm e}} \over {{\rm \gamma} N_0}} - 1} \right)\,A.$$
$$2ik\displaystyle{{\partial A} \over {\partial z{\rm ^{\prime}}}} + \displaystyle{{\partial ^2A} \over {\partial t{\rm ^{\prime}}^2}} + \left( {\displaystyle{{\partial ^2A} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A} \over {\partial r}}} \right) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {c^2}}\left( {\displaystyle{{N_{\rm e}} \over {{\rm \gamma} N_0}} - 1} \right)\,A.$$
Equation (6) represents the nonlinear Schrödinger equation and it includes both transverse self-focusing and longitudinal compression terms. Now assuming the solution of Eq. (6) as,
where (A 0) is the amplitude and (S) is eikonal of the laser beam. The eikonal S is a parameter related to the curvature of the wave front and it has been used to study the converging or diverging behavior of the laser beam (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968). Using Eqs. (6) and (7) obtained the real and imaginary parts of Eq. (6) as,
 $$\eqalign{& \left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2 + \left( {\displaystyle{{\partial S} \over {\partial t{\rm ^{\prime}}}}} \right)^2 +\; 2\displaystyle{{\partial S} \over {\partial z{\rm ^{\prime}}}} = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {c^2\;k^2}}\left( {\displaystyle{1 \over {\rm \gamma}} \displaystyle{{N_{\rm e}} \over {N_0}} - 1} \right) \cr & \quad + \displaystyle{1 \over {k\,A}}_0\left[ {\displaystyle{{\partial ^2A_0} \over {\partial t{\rm ^{\prime}}^2}} + \left( {\displaystyle{{\partial ^2A_0} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A_0} \over {\partial r}}} \right)} \right]} $$
$$\eqalign{& \left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2 + \left( {\displaystyle{{\partial S} \over {\partial t{\rm ^{\prime}}}}} \right)^2 +\; 2\displaystyle{{\partial S} \over {\partial z{\rm ^{\prime}}}} = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {c^2\;k^2}}\left( {\displaystyle{1 \over {\rm \gamma}} \displaystyle{{N_{\rm e}} \over {N_0}} - 1} \right) \cr & \quad + \displaystyle{1 \over {k\,A}}_0\left[ {\displaystyle{{\partial ^2A_0} \over {\partial t{\rm ^{\prime}}^2}} + \left( {\displaystyle{{\partial ^2A_0} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial A_0} \over {\partial r}}} \right)} \right]} $$
and
 $$\eqalign{& \displaystyle{{\partial A_0^2} \over {\partial z{\rm ^{\prime}}}} + \left( {\displaystyle{{\partial A_0^2} \over {\partial r}}} \right)\left( {\displaystyle{{\partial S} \over {\partial r}}} \right) + A_0^2 \left( {\displaystyle{{\partial ^2S} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right) \cr & \quad + \left( {\displaystyle{{\partial S} \over {\partial t{\rm ^{\prime}}}}} \right)\left( {\displaystyle{{\partial A_0^2} \over {\partial t{\rm ^{\prime}}}}} \right) + A_0^2 \displaystyle{{\partial ^2S} \over {\partial t{\rm ^{\prime}}^2}} = 0.} $$
$$\eqalign{& \displaystyle{{\partial A_0^2} \over {\partial z{\rm ^{\prime}}}} + \left( {\displaystyle{{\partial A_0^2} \over {\partial r}}} \right)\left( {\displaystyle{{\partial S} \over {\partial r}}} \right) + A_0^2 \left( {\displaystyle{{\partial ^2S} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right) \cr & \quad + \left( {\displaystyle{{\partial S} \over {\partial t{\rm ^{\prime}}}}} \right)\left( {\displaystyle{{\partial A_0^2} \over {\partial t{\rm ^{\prime}}}}} \right) + A_0^2 \displaystyle{{\partial ^2S} \over {\partial t{\rm ^{\prime}}^2}} = 0.} $$
We have considered the solution of Eq. (9) as follows:
 $$A_0^2 = \displaystyle{{A_{00}^2} \over {g\,f^2}}\exp \left\{ { - \displaystyle{{r^2} \over {r_0^2 \,f^2}} - \displaystyle{{t{\rm ^{\prime}}^2} \over {t_0^2 \,g^2}}} \right\}$$
$$A_0^2 = \displaystyle{{A_{00}^2} \over {g\,f^2}}\exp \left\{ { - \displaystyle{{r^2} \over {r_0^2 \,f^2}} - \displaystyle{{t{\rm ^{\prime}}^2} \over {t_0^2 \,g^2}}} \right\}$$
and
where f(z′) and g(z′) are spatial beam width and temporal pulse width parameters respectively. The evolution of these parameters determines the laser pulse dynamics. Now using Eqs. (10) and (11) in Eq. (9) we get,
Now, using Eqs. (10)–(12b) in Eq. (8) and collecting the coefficient of (t′2) and (r 2) we get,
 $$\displaystyle{{\partial ^2f} \over {\partial {\rm \xi} ^2}} = \displaystyle{1 \over {r_0^4 \,f^3{\rm \varepsilon} _0{({\rm \omega} /c)}^4}} - \displaystyle{{{\rm \varepsilon} _{2r}({\rm \xi} )\,f} \over {{\rm \varepsilon} _0{({\rm \omega} /c)}^2}}$$
$$\displaystyle{{\partial ^2f} \over {\partial {\rm \xi} ^2}} = \displaystyle{1 \over {r_0^4 \,f^3{\rm \varepsilon} _0{({\rm \omega} /c)}^4}} - \displaystyle{{{\rm \varepsilon} _{2r}({\rm \xi} )\,f} \over {{\rm \varepsilon} _0{({\rm \omega} /c)}^2}}$$
and
 $$\displaystyle{{\partial ^2g} \over {\partial {\rm \xi} ^2}} = \displaystyle{1 \over {t_0^4 g^3{\rm \varepsilon} _0{({\rm \omega} /c)}^4}} - \displaystyle{{{\rm \varepsilon} _{2{\rm \tau}} ({\rm \xi} )\,g} \over {{\rm \varepsilon} _0{({\rm \omega} /c)}^2}}$$
$$\displaystyle{{\partial ^2g} \over {\partial {\rm \xi} ^2}} = \displaystyle{1 \over {t_0^4 g^3{\rm \varepsilon} _0{({\rm \omega} /c)}^4}} - \displaystyle{{{\rm \varepsilon} _{2{\rm \tau}} ({\rm \xi} )\,g} \over {{\rm \varepsilon} _0{({\rm \omega} /c)}^2}}$$
where ξ = ωz′/c. We have calculated the values of ε0(ξ), ε2r (ξ), and ε2τ(ξ) by considering relativistic–ponderomotive nonlinearity which are given below,
 $${\rm \varepsilon} _0({\rm \xi} ) = 1 - \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {{\rm \omega} ^2\,{\rm \gamma}}} + \displaystyle{{2c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,g\,r_0^2 f^4}},$$
$${\rm \varepsilon} _0({\rm \xi} ) = 1 - \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2}} \over {{\rm \omega} ^2\,{\rm \gamma}}} + \displaystyle{{2c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,g\,r_0^2 f^4}},$$
 $${\rm \varepsilon} _{2r}({\rm \xi} ) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2} a_0^2} \over {2{\rm \omega} ^2\,{\rm \gamma} ^3f^4g\,r_0^2}} + \displaystyle{{4c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,f^6g\,r_0^4}} - \displaystyle{{4c^2a_0^4} \over {{\rm \omega} ^2{\rm \gamma} ^4\,f^8\,g^2\,r_0^4}}, $$
$${\rm \varepsilon} _{2r}({\rm \xi} ) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2} a_0^2} \over {2{\rm \omega} ^2\,{\rm \gamma} ^3f^4g\,r_0^2}} + \displaystyle{{4c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,f^6g\,r_0^4}} - \displaystyle{{4c^2a_0^4} \over {{\rm \omega} ^2{\rm \gamma} ^4\,f^8\,g^2\,r_0^4}}, $$
 $${\rm \varepsilon} _{{\rm 2\tau}} ({\rm \xi} ) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2} a_0^2} \over {2{\rm \omega} ^2\,{\rm \gamma} ^3f^2g^3\,t_0^2}} + \displaystyle{{2c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,f^4g^3t_0^2 \,r_0^2}} - \displaystyle{{2c^2a_0^4} \over {{\rm \omega} ^2{\rm \gamma} ^4\,f^6\,g^4t_0^2 \,r_0^2}}, $$
$${\rm \varepsilon} _{{\rm 2\tau}} ({\rm \xi} ) = \displaystyle{{{\rm \omega} _{{\rm p0}}^{\rm 2} a_0^2} \over {2{\rm \omega} ^2\,{\rm \gamma} ^3f^2g^3\,t_0^2}} + \displaystyle{{2c^2a_0^2} \over {{\rm \omega} ^2{\rm \gamma} ^2\,f^4g^3t_0^2 \,r_0^2}} - \displaystyle{{2c^2a_0^4} \over {{\rm \omega} ^2{\rm \gamma} ^4\,f^6\,g^4t_0^2 \,r_0^2}}, $$
where a 0 ( = eA 00/mωc) is the normalized electric field.
We have solved Eqs. (13) and (14) to examine the self-focusing and pulse compression behavior of the spatiotemporal Gaussian laser pulse in plasma by using the Runge–Kutta method in MATLAB with f = g = 1 and (df/dξ) = (dg/dξ) = 0 at ξ = 0 as the initial boundary conditions. We have studied the dynamics of the Gaussian pulse using the following laser parameters: λ = 1064 nm, r 0 = 10 µm, and t 0 = 30 fs. The focusing/defocusing of the laser beam can be governed by Eq. (13) the first term on the right-hand side of the specified equation is called diffraction term, while the second term is answerable for self-focusing due to relativistic–ponderomotive nonlinearity. The compression of the laser pulse can be explained by Eq. (14), the first term appearing on the right-hand side represents the dispersion broadening term although the last term represents nonlinear term. The self-compression and self-focusing mechanism can occur when the magnitude of the second term goes larger than the first one. As the high intense Gaussian laser pulse propagates through the plasma, the dielectric constant get modified due to the combined effects of the ponderomotive and relativistic nonlinearity which in turn leads to the self-focusing as well as self-compression of the laser pulse.
Figure 6 shows the plot of dimensionless spatial beam width and temporal pulse width parameters as a function of the normalized distance of propagation at different values of plasma frequencies
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
, and
${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
, and
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
for constant value of normalized electric-field a
0 = 0.2. Solid curves show the variation of dimensionless spatial beam width parameter (f ), while the dot-dash curves show the variation of temporal pulse width parameters (g) with normalized distance (ξ). However, Figure 7 represents the variation of beam width and pulse width parameter for plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2$
for constant value of normalized electric-field a
0 = 0.2. Solid curves show the variation of dimensionless spatial beam width parameter (f ), while the dot-dash curves show the variation of temporal pulse width parameters (g) with normalized distance (ξ). However, Figure 7 represents the variation of beam width and pulse width parameter for plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
at different values of normalized electric field a = 0.15, 0.2, and 0.25. It is clear from the figure, as the laser beam propagates both spatial beam width parameter (f ) and temporal pulse width parameter (g) show an oscillatory behavior. It indicates the intensity of pulse will also oscillate and having a minimum beam width at one position and a minimum pulse width at another position.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
at different values of normalized electric field a = 0.15, 0.2, and 0.25. It is clear from the figure, as the laser beam propagates both spatial beam width parameter (f ) and temporal pulse width parameter (g) show an oscillatory behavior. It indicates the intensity of pulse will also oscillate and having a minimum beam width at one position and a minimum pulse width at another position.

Fig. 6. Variation of dimensionless beam width f (solid lines) and pulse width g (dot-dash lines) parameters of laser beam with normalized distance (ξ) for electric field a
0 = 0. 2, λ = 1064 nm, r
0 = 10 μm, τ0 = 30 fs at different plasma frequencies
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2,$
and
${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2,$
and
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2.$
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2.$

Fig. 7. Variation of dimensionless beam width f (solid lines) and pulse width g (dot-dash lines) parameters of laser beam with normalized distance (ξ) for plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
, λ = 1064 nm, r
0 = 10 μm, τ0 = 30 fs at different normalized electric field a
0 = 0.15, 0.2, and 0.25.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
, λ = 1064 nm, r
0 = 10 μm, τ0 = 30 fs at different normalized electric field a
0 = 0.15, 0.2, and 0.25.
4. DISCUSSION AND CONCLUSION
The propagation dynamics of spatiotemporal Gaussian laser pulse has been investigated by numerical simulation as well as semi-analytical. In numerical simulation method, we have obtained the different pulse duration at varying z. The pulse compression has been studied for both different values of plasma frequencies (by keeping normalized beam intensity constant at a
2 = 4) and varying beam intensities (by keeping plasma frequency constant at
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
). It was observed that the laser beam having initial pulse duration t
0 = 30 fs gets compressed to 9.77, 8.45, and 5.86 fs by varying plasma frequencies
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
). It was observed that the laser beam having initial pulse duration t
0 = 30 fs gets compressed to 9.77, 8.45, and 5.86 fs by varying plasma frequencies
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
,
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
, and
${\rm \omega} _{\rm p}^{\rm 2} = 0.85{\rm \omega} ^2$
, and
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2,$
respectively, at constant value of pulse intensity of 4. Here, absolute distance for compression comes out to be z = 18.9, 13.0, and 10.4 μm for above used parameters. However, we can also see the significant change in pulse duration of laser beam by varying normalized initial intensity from 2.25 to 6.25 at constant plasma frequency
${\rm \omega} _{\rm p}^{\rm 2} = 0.87{\rm \omega} ^2,$
respectively, at constant value of pulse intensity of 4. Here, absolute distance for compression comes out to be z = 18.9, 13.0, and 10.4 μm for above used parameters. However, we can also see the significant change in pulse duration of laser beam by varying normalized initial intensity from 2.25 to 6.25 at constant plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
, wherein the different values of pulse duration are 14.44 and 4.66 fsat a distance z = 16.2 μm.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
, wherein the different values of pulse duration are 14.44 and 4.66 fsat a distance z = 16.2 μm.
Although compression depend on plasma frequency and initial intensity. In this study, we have found that the optimum value of pulse duration is 4.66 at a distance z = 16.2μm for plasma frequency
![]() ${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. The intense, non-uniform laser intensity profile gives the relativistic and ponderomotive phenomenon together, resulting modification in electron plasma density and variation in relativistic mass. This leads to a stage where both relativistic and ponderomotive nonlinearity are simultaneously operative. In this scenario, the refractive index is the maximum along the propagation axis and decreases slowly in the radial direction. This spatial part of refractive index profile causes lowering of beam width parameter (f), and time-varying part of the refractive index will be responsible for lowering of pulse width parameter (g). Pulse width parameter (g) and beam width parameter (f) decrease from its initial value. Therefore, the transverse self-focusing in space and longitudinal self-compression in time take place.
${\rm \omega} _{\rm p}^{\rm 2} = 0.83{\rm \omega} ^2$
. The intense, non-uniform laser intensity profile gives the relativistic and ponderomotive phenomenon together, resulting modification in electron plasma density and variation in relativistic mass. This leads to a stage where both relativistic and ponderomotive nonlinearity are simultaneously operative. In this scenario, the refractive index is the maximum along the propagation axis and decreases slowly in the radial direction. This spatial part of refractive index profile causes lowering of beam width parameter (f), and time-varying part of the refractive index will be responsible for lowering of pulse width parameter (g). Pulse width parameter (g) and beam width parameter (f) decrease from its initial value. Therefore, the transverse self-focusing in space and longitudinal self-compression in time take place.
Ultrashort intense laser pulse invokes nonlinearity in the plasma, which gives rise to both time & space-varying refractive index that introduces chirping in the frequency spectrum and negative curvature in the wavefront of ultrashort pulse. This chirping has opposite sign than the normal GVD. This opposite nature of both chirpings is finally responsible for broadening or compression (depending on their strength) of the pulse. While negative curvature would be responsible for focusing of the pulse. Finally, these two phenomena will decide the intensity of the pulse.
It has been observed that the intensity of the pulse shows an oscillatory behavior. The results of semi-analytical model also show different focusing point for pulse width and beam width parameters. This oscillatory behavior gives the extra freedom to choose the intensity maxima either having minimum (t 0) or having minimum (r 0). The semi-analytical method is used to analyze the self-focusing and self-compression of the spatiotemporal Gaussian pulse. It is also found that the rate of variations of parameters governing the pulse width, the beam width of the laser pulse, and intensity of the laser pulse are different at a different normalized distance. Moreover, the plasma parameter such as density governs the GVD, which is a key parameter in our simulation. In addition, the results are significantly useful in the studies of short pulse laser propagation by application of sub-millimeter-scale plasmas where self-focusing and self-compression are involved.
ACKNOWLEDGMENT
This work was partially supported by University Grant Commission (UGC), India and Department of Science and Technology (DST), India.