Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-06T18:47:43.901Z Has data issue: false hasContentIssue false
  • English
  • Français

A new turbulent two-field concept for modeling Rayleigh–Taylor, Richtmyer–Meshkov, and Kelvin–Helmholtz mixing layers

Published online by Cambridge University Press:  03 March 2004

ANTOINE LLOR  and
PASCAL BAILLY
ANTOINE LLOR
Affiliation:
Commissariat à l'Energie Atomique, Bruyères le Châtel, France
PASCAL BAILLY
Affiliation:
Commissariat à l'Energie Atomique, Bruyères le Châtel, France
Rights & Permissions [Opens in a new window]

Abstract

An accurate turbulent mixing model for gravitationally induced instabilities with arbitrarily variable accelerations has been developed to capture the following physical aspects: (1) directed transport, (2) correct buoyancy forces, (3) turbulence diffusion, and (4) geometrical aspects. We present the two-structure two-fluid two-turbulence concept (2SFK), which consistently answers these requirements by identifying the large-scale transport structures in a statistical approach. An example of a 2SFK-based model is given and applied to the Rayleigh–Taylor case.

Keywords

Mixing instabilitiesRayleigh–TaylorRichtmyer–MeshkovSelf-similar flowsTurbulence modelingTwo-fluid flows
Type
Research Article
Information
Laser and Particle Beams , Volume 21 , Issue 3 , July 2003 , pp. 311 - 315
Copyright
© 2003 Cambridge University Press

1. INTRODUCTION

Turbulent mixing in Rayleigh–Taylor (RT) and Richtmyer–Meshkov (RM) instabilities has so far been modeled within two main different Reynolds-averaged Navier–Stokes (RANS)-based frameworks, which can be broadly designated by single and two-fluid approaches. Fluids transport is described in the former by a mass (or Favre) average velocity,

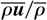
, and a concentration flux,

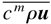
(.: ensemble average, ρ: density, u: velocity, cm: mass fraction of fluid m), whereas in the latter the velocities of each fluid,

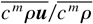
, are used. Although formally equivalent, some approaches implicitly bias the subsequent closure assumptions, leading sometimes to different, unreliable, or even unphysical model results in practical situations (Llor, 2003).

This situation has motivated the reassessment of the basic physical phenomena that are to be captured, and to design a new modeling approach to meet these requirements. Following the recent analysis of the RT and RM cases by Dimonte (2000), and of the self-similar variable acceleration RT flows (SSVARTs) by Llor (2002), we have considered it crucial to capture the following physical aspects by using the corresponding model features: (1) the directed transport by a two-fluid approach, (2) the correct buoyancy force by including mass transfer between fluids, (3) the turbulence diffusion by including most of the standard k–ε features, and (4) the geometrical aspects by consistent closures of the length scales.

Our strategy here is to combine and to adapt as much as possible the relevant features from simple and efficient existing models, such as the k–ε model (Hanjalic & Launder, 1972) for the turbulence dynamics, the two-fluid model of Youngs (1989) to match the directed transport that is dominant in RT and SSVARTs cases, and the mass exchange model of Youngs (1995) to generate appropriate buoyancy forces.

The model of Youngs (1995) meets most of the four conditions above and was used as a starting point for this study. Although it seems to be reasonably accurate and robust (Llor, 2002), it carries some clearly identified problems as detailed in Bailly & Llor (2002), among which the most important stands in the characteristic length scale, λ, and its phenomenological equation: It is not RANS based and overestimates the effective Knudsen numbera

Previously called Von Kármán number in Llor (2002) and Bailly & Llor (2002).

of the turbulent transport κT (defined as the ratio between the turbulent integral length scale and the thickness of the turbulent mixing zone (TMZ)) by a factor of 6.5 in the Rayleigh–Taylor instability, independently of acceleration history (Llor, 2002).

To consistently address these difficulties, it is necessary to answer to following questions: what are the transported/transporting structures in the TMZ, and what mechanisms control the size (and thus the drag) of the structures? We introduce here a general concept, called two-structure two-fluid two-turbulent (2SFK),b

Previously called TTT in Bailly and Llor (2002).

which provides these answers within a RANS-based framework. It thus permits calibrations on measured correlations and avoids phenomenological length equations.

The key features of a 2SFK-based model are given in Section 3 and preliminary numerical results are given in Section 4 to illustrate the relevance of the 2SFK concept (see Bailly and Llor, 2002, for more details).

2. THE 2SFK CONCEPT

Foremost to any modeling approach is the definition of transport structures associated with the motion of fluids at large scales across the TMZ. According to authors' preferences and emphasis on different phenomena, these can be designated and treated as bubbles, turbulent eddies, thermals, plumes, and so forth.

Here, we shall combine the basic aspects of turbulence and directed transport by assuming that their respective structures, namely large eddies and bubbles, actually describe identical fluid structures. This transport structure concept is central to the 2SFK modeling approach, and is experimentally and numerically supported by the observed identity of bubble sizes and integral length scales (Dalziel et al., 1999; Dimonte & Schneider, 2000). Intuitively, it means that separation of fluids inside bubbles is marginal because of the high turbulence level they contain and of the large drag of smaller structures.

The 2SFK concept is illustrated in Figure 1. The boundaries between upward and downward moving structures follow the turbulence field contrast, but not the distribution of the fluids. Mass transfer between structures is induced by turbulent diffusion, resulting in a nonuniform composition of the transport structures across the TMZ. The growth of the structures is controlled by the dynamics of turbulence and their motion by the buoyancy–drag balance as discussed by Dimonte (2000). A statistical model should then contain the following three basic elements: (1) two velocities to capture directed transport, (2) mass exchange to capture appropriate densities and buoyancy, and (3) two turbulence fields to define structures and capture their evolution.

Schematic representation of the 2SFK TMZ; dashed line: structure boundary; gray shading: fluid mass fraction levels.

The 2SFK approach can be readily adapted to a RANS-based model derivation. Let the structures, labeled + and −, be defined by the presence functions b± (= 0 or 1). In the initial state, the fluids are separated and c1 = b− and c2 = b+. The evolution of the structures is defined by a velocity w according to

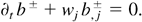
A generic quantity a evolves as ∂t(ρa) + (ρauj), j = s − (θj), j where a stands for c1,2 or the velocity u, s is the source term, and θ is the flux. The statistical RANS method consists here in the ensemble conditional averaging by b±, leading to

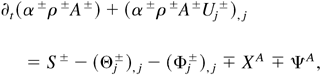
where the following structure characteristic quantities are thus defined:

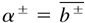
volume fractions,

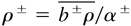
densities,

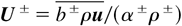
mean velocities, u± = u − U± velocity fluctuations, and

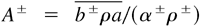
other mean quantities. Fluxes, turbulent fluxes, and source terms per structure are respectively

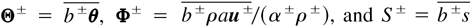
. Finally, fluxes and exchanges between structures are

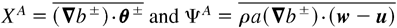
(for a = u, XA contains buoyancy and drag).

An important feature here is that turbulent kinetic energies of structures are defined as

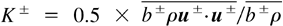
. Although it is not completely microscopically defined, b± can always be made to follow the large-scale contrast of velocity fluctuations. Therefore, the double K± description is able to capture the intermittency between laminar and turbulent zones at the edge of the TMZ.

3. THE 2SFK MODEL

Introducing the generalized derivative DA± = ∂t A± + (A±Uj±), j and assuming single pressure, the 2SFK incompressible model is derived from Eq. (2):

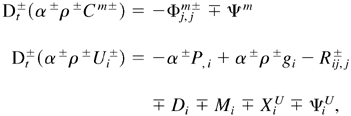
where Cm± is the averaged mass fraction of fluid m in structure ±, P is the mean pressure, g is the acceleration field, R± are the Reynolds stresses, D and M are the drag and the added mass forces respectively, XU is the turbulent buoyancy force, and ΨU is the momentum exchange term. The dissipative terms in the momentum equation lead to production terms of K±: (1) shear of structures Π±, (2) drag work Πd, and (3) loss of KD by mass exchange ΠΨ. The K± dissipation rates, ε±, are modeled assuming that general principles of the usual k–ε model (Hanjalic & Launder, 1972) hold. This is indeed appropriate because structures, as defined by b±, do match the large-scale turbulent motions. Spectral quasi-equilibrium is also assumed inside structures. Thus, production and dissipation terms of ε± equations are mirrored from the K± equations with Cε1 and Cε2 constants, so, Eqs. (3) are completed with:

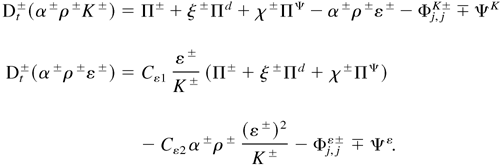
The unknown terms that appear in Eqs. (3) and (4) have to be closed. The simplest are deduced from classical single-fluid approaches, such as gradient laws for turbulent fluxes, closure relations for Reynolds stresses, turbulent viscosities, turbulent integral rates σ± = ε±/K±, and turbulent integral length scales λ± = (K±)3/2/ε±, and will not be discussed here. Eqs. (4) reduce to the usual k–ε equations in the pure structure limits, enabling application to shear layers such as the Kelvin–Helmholtz (KH) case.

The exchange process results from two simultaneous physical phenomena: turbulent diffusion and evolution of structure boundaries because laminar structures are absorbed progressively by turbulent ones. Extending the approach of Youngs (1995) and according to Figure 2, the exchange terms are proportional to an approximate interface density α+α− and the volume fractions per unit time affected by growth are proportional to σ±. The mixing layer thus defined is assumed to be homogeneous and the turbulent flux due to mass exchange is proportional to σ+ − σ−. Therefore, we write for the quantity A± = 1, Cm±, U±, K±, or ε±:

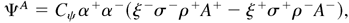
where ξ± = σ±/(σ+ + σ−). The constant Cψ is close to 1, in order to match the dissipation rate of density fluctuations in homogeneous isotropic turbulence (Mantel, 1993), and is independent of A± to ensure Galilean and thermodynamic invariance. The dissipation of KD by momentum exchange results in the total production of K± as

which is distributed on structures according to the ξ± and with δU = U+ − U−.

Schematic representation of inter-structure mass transfer and structure growth.

The analogy with the Πψ term suggests to close the drag force as

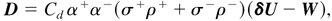
where Cd is the drag constant. This is a Stokes-like closure, because the structure turbulent Reynolds number is about 1.7. Moreover, it assumes that shear due to δU is evenly spread on structures, where the structure viscosities induce dissipation. The total production of K± by D is

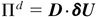
and spread on structures according to χ± = σ±ρ±/(σ+ρ+ + σ−ρ−). The dispersion drift velocity is given by:

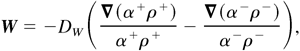
with the diffusion coefficient DW proportional to δU·δU.

4. RELEVANCE OF THE 2SFK APPROACH: NUMERICAL RESULTS

Some important features of the 2SFK concept are illustrated by the following one-dimensional (1D) self-similar RT flows at At = 0.2. Calculations were carried out using a simple 1D all-purpose test code (for more details, see Bailly and Llor, 2002, and Cournède, 2001) on a mesh of 100 equal cells spanning the [0,1] interval. Cells 1 to 49 and 52 to 100 were initialized with pure, at rest, and laminar, light and heavy fluids respectively. To mimic the expected self-similar RT parameters at the initial state, cells 50 and 51 were mixed and turbulent so that: (1) the turbulent energy was half of the gravitational energy loss (with respect to pure cells) and (2) the integral length scales were one-fifth of the cell size. The final observed self-similar behaviors did not depend significantly on the details of the initial condition.

The effect of mass transfer between structures is shown in Figure 3, where the profiles of α± are not linear in contrast with the profiles of the fluid volume fractions, as experimentally observed by Dimonte and Schneider (2000). Indeed a fraction of the laminar structure is absorbed by the turbulent structure along the relative motion.

Profiles of structure and fluid volume fractions in the RT TMZ.

Structure turbulent kinetic energy profiles, plotted versus position in Figure 4, show clearly that the laminar pure structures become turbulent when progressing across TMZ. The large-scale intermittency between laminar and turbulent zones at the edges of the TMZ is captured.

Profiles of K± in the RT TMZ.

The (single fluid) velocity fluctuations are here due to the superposition of the almost anisotropic Reynolds stress tensors per structure and to the purely axial directed energy KD = 0.5 × α+ρ+α−ρ−δU·δU/(α+ρ+ + α−ρ−). As shown in Figure 5, the profiles of K = α+ρ+K+ + α−ρ−K− and KD are very close, yielding a 4:1 ratio between longitudinal and transverse components of the overall Reynolds stress tensor. This is in reasonable agreement with the 3:1 available estimate of Youngs (1994). Previous estimates (Llor, 2002) of the directed energy were based on a two–fluid analysis KD f = 0.5 × α1ρ1α2ρ2(U2 − U1)·(U2 − U1)/(α1ρ1 + α2ρ2) that can be reconstructed from the 2SFK variables. As given in Figure 5, the ratio of KD f to Kf = K + KD − KD f is about 1:3, showing the importance of mass exchange and fluid entrainment in the longitudinal transport.

Profiles of mean turbulent kinetic and directed energies in the RT TMZ.

The 2SFK constants Cd and Cψ have been adjusted to match the growth rate of the TMZ and the molecular mixing fraction as in Youngs (1991). Remarkably, without any other adjustments, the effective Knudsen number is also correctly captured: κT = 0.14 compared to a value of 0.09 calculated by Llor (2002, 2003) from previous experimental results. This reflects the overall consistency of the dissipative processes in the 2SFK model. The residual discrepancy may be due to the crudeness of the closures in this first proposed model and to experimental errors in estimating κT.

The 2SFK model also gives appropriate results for both SSVART and RM flows, as shown in Bailly and Llor (2002).

5. CONCLUSIONS

The 2SFK concept based on a two-field RANS approach, has been introduced and shown to be physically consistent with the main known features of transport in RT-type mixing layers: directed transport, buoyancy, turbulence, and characteristic length scales. An explicit model has been developed within this framework, as described in Bailly and Llor (2002). With a limited number of constants, it appropriately captures the growth laws of the TMZ width, the TMZ average global energy balance, and the associated length scales such as the effective Knudsen number.

The 2SFK model will be improved regarding the influence of Atwood number, response to KH, and the consistency with simulated correlations, as currently explored by Youngs and Llor (2002).

ACKNOWLEDGMENTS

The authors gratefully acknowledge O. Simonin, A. Vallet, D.L. Youngs, P.H. Cournède, B. Desjardins and L. Chodorge.

References

REFERENCES

Bailly, P., & Llor, A. (2002). A new turbulent two-fluid RANS model for KH, RT and RM mixing layers. In Proc. Eighth Int. Workshop on the Physics of Compressible Turbulent Mixing ( Schilling, O., Ed.), Report UCRL-MI-146350. Livermore, CA: Lawrence Livermore National Laboratory.
Cournède, P.H. (2001). Un schéma bilagrange plus projection pour la simulation bifluide des instabilités de mélange. Ph.D. thesis, Ecole Centrale Paris, France.
Dalziel, S.B., Linden, P.F., & Youngs, D.L. (1999) Self-similarity and internal structure of turbulence induced by Rayleigh–Taylor instability. J. Fluid Mech. 399, 1–48.Google Scholar
Dimonte, G. (2000) Spanwise homogeneous buoyancy-drag model for Rayleigh–Taylor mixing and experimental evaluation. Phys. Plasmas 7(6), 2255–2269.Google Scholar
Dimonte, G., & Schneider, M. (2000) Density ratio dependence of Rayleigh–Taylor mixing for sustained and impulsive acceleration histories. Phys. Fluids. 12, 304–321.Google Scholar
Hanjalic, K., & Launder, B.E. (1972) A Reynolds stress model of turbulence and its application to thin shear flows. J. Fluid Mech. 52, 609–638.Google Scholar
Llor, A. (2002). Response of turbulent RANS models to self-similar variable acceleration RT mixing: An analytical “0D” analysis. In Proc. Eighth Int. Workshop on the Physics of Compressible Turbulent Mixing ( Schilling, O., Ed.), Report UCRL-MI-146350. Livermore, CA: Lawrence Livermore National Laboratory.
Llor, A. (2003) Bulk turbulent transport and structure in Rayleigh–Taylor, Richtmyer–Meshkov, and variable acceleration instabilities. Laser Part. Beams 21, 305–310.Google Scholar
Mantel, T. (1993). Contribution à la modélisation de la combustion dans les moteurs à allumage commandé avec prise en compte de la phase d'allumage. Ph.D. thesis, Université de Rouen, France.
Youngs, D.L. (1989) Modelling turbulent mixing by Rayleigh–Taylor instability. Physica D 37, 270–287.Google Scholar
Youngs, D.L. (1991) Three-dimensional numerical simulation of turbulent mixing by Rayleigh–Taylor instability. Phys. Fluids. A 3, 1312–1320.Google Scholar
Youngs, D.L. (1994) Numerical simulation of mixing by Rayleigh–Taylor and Richtmyer–Meshkov instabilities. Laser Part. Beams 12, 725–750.Google Scholar
Youngs, D.L. (1995). Representation of the molecular mixing process in a two-phase flow turbulent mixing model. Proc. Fifth Int. Workshop on the Physics of Compressible Turbulent Mixing, pp. 83–88. Singapore: World Scientific.
Youngs, D.L., & Llor, A. (2002). Preliminary results of LES simulations of self-similar variable acceleration RT mixing flows. In Proc. Eighth Int. Workshop on the Physics of Compressible Turbulent Mixing ( Schilling, O., Ed.), Report UCRL-MI-146350. Livermore, CA: Lawrence Livermore National Laboratory.
Figure 0

Schematic representation of the 2SFK TMZ; dashed line: structure boundary; gray shading: fluid mass fraction levels.

Figure 1

Schematic representation of inter-structure mass transfer and structure growth.

Figure 2

Profiles of structure and fluid volume fractions in the RT TMZ.

Figure 3

Profiles of K± in the RT TMZ.

Figure 4

Profiles of mean turbulent kinetic and directed energies in the RT TMZ.