Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T01:03:52.283Z Has data issue: false hasContentIssue false
  • English
  • Français

Nanoparticles and nanotubes induced by femtosecond lasers

Published online by Cambridge University Press:  02 June 2005

S. ELIEZER ,
N. ELIAZ ,
E. GROSSMAN ,
D. FISHER ,
I. GOUZMAN ,
Z. HENIS ,
S. PECKER ,
Y. HOROVITZ ,
M. FRAENKEL  and
S. MAMAN
...Show all authors
S. ELIEZER
Affiliation:
Soreq NRC, Yavne, Israel Institute of Nuclear Fusion, Polytechnic University of Madrid, Madrid, Spain
N. ELIAZ
Affiliation:
Tel Aviv University, Tel Aviv, Israel
E. GROSSMAN
Affiliation:
Soreq NRC, Yavne, Israel
D. FISHER
Affiliation:
Soreq NRC, Yavne, Israel Weizmann Institute of Science, Rehovot, Israel
I. GOUZMAN
Affiliation:
Soreq NRC, Yavne, Israel
Z. HENIS
Affiliation:
Soreq NRC, Yavne, Israel
S. PECKER
Affiliation:
Soreq NRC, Yavne, Israel
Y. HOROVITZ
Affiliation:
Soreq NRC, Yavne, Israel
M. FRAENKEL
Affiliation:
Soreq NRC, Yavne, Israel
S. MAMAN
Affiliation:
Soreq NRC, Yavne, Israel
V. EZERSKY
Affiliation:
Ben-Gurion University, Beer Sheva, Israel
D. ELIEZER
Affiliation:
Ben-Gurion University, Beer Sheva, Israel
Rights & Permissions [Opens in a new window]

Abstract

In this paper, we suggest the creation of a nanoparticles and nanotubes by using the interaction of a femtosecond laser with a solid target in a vacuum. A simple model is used to predict the optimal target and the laser parameters for the production of efficient nanoparticles. At the Soreq laboratory, experiments are performed with aluminium and carbon targets using a femtosecond laser. The irradiated targets are composed of either a thin layer of aluminium or of carbon, deposited on a transparent heat-insulating glass substrate. The nanoparticle debris is collected on a silicone wafer for X-ray diffraction (XRD), for scanning electron microscopy (SEM), and for atomic force microscopy (AFM). For transmission electron microscopy (TEM), the debris is caught on a copper grid covered on one side with a carbon membrane. Our experiments confirm the creation of crystal nanoparticles for aluminium and nanotubes for carbon experiments.

Keywords

Femtosecond lasersNanoparticlesNanotubes
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 1 , March 2005 , pp. 15 - 19
Copyright
2005 Cambridge University Press

1. INTRODUCTION

A particle with a dimension larger than about 1 nanometer (the size of one molecule) and smaller than 100 nanometers (order of magnitude for a wavelength of light) is defined as a nanoparticle. These particles are of great interest (Dresselhaus et al., 1996) because of the physics associated with them, namely, the nanoparticles are described by the intermediate regime between quantum physics and classical physics. Furthermore, they possess a large surface to volume ratio. These same particles may also prove important and useful to many industrial and biological applications.

Thus, the synthesis and study of nanoparticles (NP) of various elements and compounds is of great interest both in technological applications and for fundamental research. Traditionally, NPs are produced (Dutta & Hofmann, 2003) by techniques such as arc discharge, vapor deposition, electrochemical deposition, and laser ablation through long pulse duration (about a few ns) in an appropriate gas atmosphere. For example, it has also been suggested (Gamaly et al., 2000) that by using high repetition rate of ultrafast laser pulses, one can obtain carbon films in the presence of an argon gas. In this model, only a low number of atoms are evaporated per single laser pulse.

In our present work, we created nanoparticles (Eliezer et al., 2004) and for the first time nanotubes by a femtosecond laser; solid target interaction. These ultrashort laser pulses allow the completion of the energy deposition into the target well before the target expansion begins, thus effectively decoupling these two stages of the process. The laser energy is initially deposited in the electron subsystem, within a target surface layer of a few tens of nm thick. This stage continues during the laser pulse duration. After the pulse terminates and before the expansion sets in, the electrons in the surface layer undergo cooling by heat diffusion and by energy transfer to the ions. This stage continues for several picoseconds followed by a cooling process that lasts about 1 ns. If during this cooling, a mixture of liquid plus vapor is obtained, then the particles condensate into nanoparticles or nanotubes. The timescales and appropriate dimensions of this scenario can be described by the following:

where cs is of the order of speed of sound, taken in the above equation as 5 × 105 cm/s. Note that at room temperature, the speed of sound for aluminum is 5.4 × 105 cm/s, for graphite carbon it is 2.63 × 105 cm/s, while for diamond it is 1.96 × 105 cm/s. It is interesting to see that when a femtosecond laser interacts with a solid target, nanoparticles can be created in a few nanoseconds during which time the material expands into the vacuum at a distance of a few microns. For adiabatic expansion into the vacuum, one has to replace cs by a velocity of about ten times greater, thus increasing the estimations in Eq. (1) by a factor of ten. Even in this case, the nanoparticles and nanotubes are created during the plasma expansion in less than 100 μm.

2. THE LASER PLASMA INTERACTION

In our experiments, the nanoparticles are collected on a silicon crystal at a distance of about 3 cm from the target, therefore allowing free expansion of nanoparticles into the vacuum. These experiments, described schematically in Fig. 1, are carried out with a titanium sapphire laser with 0.8 μm wavelength, 50 fs pulse duration, 0.5 joule of energy, with intensities varying between 3 × 1012 W/cm2 and 5 × 1015 W/cm2 . The irradiated targets are composed of a 100 nm thick foil either of aluminum or of carbon, deposited on a transparent heat-insulating glass substrate (e.g., CaF2). The NP debris is collected on a silicone wafer.

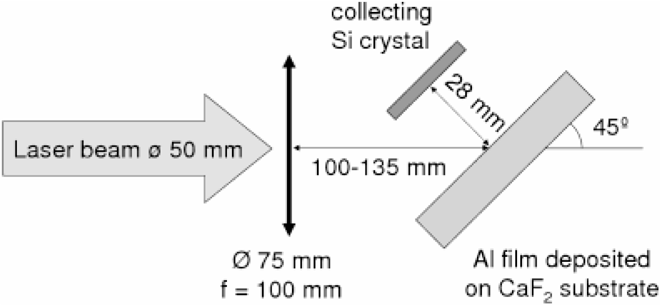
A schematic view with experimental description of the experiment.

Since the target does not change its density during the short laser plasma interaction, one can neglect the hydrodynamic effects and write the following energy conservation in order to calculate the plasma temperature (Fisher et al., 2001; Eliezer, 2002).

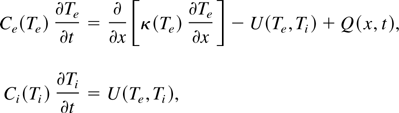
where Te and Ti is the electron and ion temperatures, Ce and Ci are the electron and ion heat capacities, κ is the electron heat conductivity, U is the heat transfer rate from electrons to ions, t is time, x is the distance from the target surface inward, and Q is the heat deposition rate due to the laser radiation absorption. The laser absorption changes significantly on the scale of the skin depth, in the order of 10 nm. The laser deposition energy Q is obtained from the solution from Maxwell equations. The detailed expressions for Ce, Ci, and U are given in Fisher et al. (2001).

3. THE EXPERIMENTAL RESULTS FOR ALUMINUM TARGETS

The experimental setup and conditions are described in Fig. 1. The pressure in the vacuum chamber is 10−4 Torr. The laser absorption coefficient changes between 16% to about 40% for laser irradiances of 5 × 1012 W/cm2 and 2 × 1014 W/cm2 accordingly.

The density and temperature (ρ, T) diagram of aluminum is presented in Fig. 2. Here we are using the accurate equation of state (EOS), similar to the one we developed when analyzing the ultimate strength of materials (Eliezer et al., 2002). The initial conditions of the laser created plasma is given by the solid density ρ0 and a temperature T0 determined by the laser plasma interaction. The area between the spinodal and binodal on the right side in Fig. 2 is the super heated liquid domain. If during the adiabatic expansion from the initial condition (ρ0 T0), the plasma enters the super heated liquid domain, then the liquid phase is achieved followed by a fast crystallization of the aluminum. Adiabatic paths starting at T0 in the domain of 0.2 eV to 4 eV are the most promising in the context of nanoparticle productions; since they reach the spinodal lower than the critical density where a large fraction of the material transforms into a liquid state. For initial temperatures T0 is larger than 10 eV, the plasma expands, cools, recombines into gas, and is eventually deposited on the vacuum vessel walls as individual atoms.

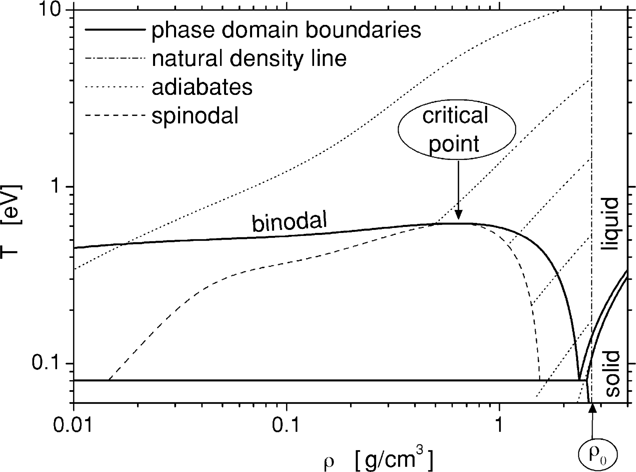
Phase diagram of Aluminum.

For the appropriate initial conditions, the nanoparticles are created during a period of the order of 1 nanosecond (see Introduction). These nanoparticles expand into the vacuum perpendicular to the aluminum target and are collected on a silicon wafer for X-ray diffraction (XRD), for scanning electron microscopy (SEM), and for atomic force microscopy (AFM). For transmission electron microscopy (TEM), the debris is caught on a copper grid covered on one side with a carbon membrane.

A typical atomic force microscope image (out of many images of different scales) of the nanoparticles deposited onto a silicone substrate is given in Fig. 3. In this particular figure, the scan size in the x − y is 250 × 250 nm, and 25 nm in the z direction. This image reveals particles ranging from 10 to 50 nm in diameter and from 2 to 10 nm in height.

An atomic force microscope (AFM) image for Aluminum nanoparticles.

The size distribution of the nanoparticles is determined with the aid of an image analysis software package based on the AFM data. The cumulative number density f(S) of nanoparticles with an area from ∞ to S (in units of nm2) fits well the following formula:

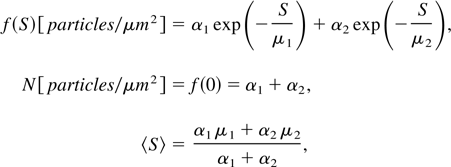
where N is the total number of particles per unit area and 〈S〉 is the average area of the nanoparticles.

Our experiments show the following data: N = 4, 300, 1000, and 30 [particles/μm2] for IL = 3 × 1012, 3.7 × 1013, 5.3 × 1013, and 5 × 1014 W/cm2, respectively. For the same laser irradiances we get appropriately 〈S〉 = 1.2 × 104, 4.2 × 102, 1.2 × 102, and 5 × 103 nm2. These experimental values are in agreement with the qualitative model described above.

The TEM data characterizes the structure and the composition of the nanoparticles at a subnanometer resolution. Line arrays of atoms are measured indicating the crystalline nature of the aluminum nanoparticles. The distance between the atomic layers of the crystal is found to be 2.354 ± 0.118 Å, which is in good agreement with the strongest reflection from the cubic Al phase (2.338 Å for planes {111}). It is important to point out that these crystals contain less than 10 atoms in each direction.

4. THE CARBON TARGETS

For carbon the EOS is more complicated and we do not have all of the necessary data and knowledge to make a rigorous analysis like the one for aluminum in the previous section. Therefore, a simplified analysis is done here for the carbon case.

The energy equation used in this simplified analysis equates the absorbed laser energy to the integrated heat capacity,

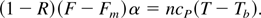
The nanotubes are obtained with a laser fluency of F = 7.5 J/cm2, implying a laser irradiance of I = 1.5 × 1014 W/cm2. The fluency of the femtosecond laser that melts (actually sublimates) the graphite is Fm J/cm2 = 0.13 (Reitze et al., 1992). From the reflection experiments, one gets for our case R = 0.2, namely 80% of the laser energy is absorbed. The α−1 = 10−5 cm is the carbon layer thickness, assumed to have an initial constant temperature T, Tb = 4500 K is the boiling temperature, cP = 3 kB (kB is the Boltzmann constant) is the Dulong-Petit value of the heat capacity and n = 1.12 × 1023 cm−3 is the initial density of the graphite plasma (for ρ0 = 2.25 g/cm3). Eq. (4) yields an initial temperature of T = 111,000 K

Our laser focal spot is large compared to the plasma expansion before it solidifies. Therefore, it is conceivable to assume a one dimensional (1D) adiabatic expansion described by the following equations:

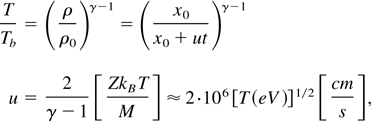
where x0 = α−1 is the graphite foil thickness, γ = 1.6 is the adiabatic constant, u is the plasma expansion velocity, Z = 4 is the appropriate ionization of carbon and M is the carbon mass. For the temperature derived in Eq. (4), one gets u = 6 × 106 cm/s. This value yields from Eq. (5) a time t = 0.35 ns, namely the plasma has cooled to the boiling temperature Tb in a time of 0.35 ns while expanding only 60 μm. We don't know the time required for the nanotube productions; however, it is estimated to be in the order of one to a few nanoseconds.

Figures 4 and 5 were taken with a TEM. Fig. 4 shows high resolution onion-like graphitic particles (Dresselhaus et al., 1996). The concentric spherical shells, the so called “onions,” constitute a form of carbon consisting of spherical concentric layers of carbon shells. In Fig. 5, about 10 concentric tubes are seen when the internal tube has a diameter of about 5 nm.

Onion like carbon structures as measured by TEM.

Nanotubes of carbon as measured by TEM.

5. CONCLUSIONS

The main methods used to synthesize nanotubes are by carbon arc discharge, chemical vapor deposition, and ion bombardment. Nanoparticles have also been achieved with these techniques and also by laser ablative deposition in an appropriate gas atmosphere. In this paper, it has been suggested to use the femtosecond lasers to create nanocrystals and nanotubes in a vacuum medium. One of the advantages of this scheme is that the interaction of the external field (the laser in our case) with the material under consideration during the nanoparticle or nanotube formation is non existent. The femtosecond laser is used only in order to achieve appropriate initial conditions. Therefore, in these experiments it might be easier to understand the mechanism of the production of nanotubes and nanocrystals. Furthermore, with the laser, there are no limits on the density and temperature of the initial conditions. Very high temperatures and solid densities can be easily achieved. More work and experiments are required in order to comprehend the new ideas suggested in this work.

References

REFERENCES

Dresselhaus, M.S., Dresselhaus, G. & Eklund, P.C. (1996). Science of Fullerenes and Carbon Nanotubes. San Diego, CA: Academic Press.Google Scholar
Dutta, J. & Hofmann, H. (2003). Nanomaterials. http://www.nano.ait.ac.ch.Google Scholar
Eliezer, S. (2002). The Interaction of High Power Lasers with Plasmas. Bristol, UK: Institute of Physics.CrossRefGoogle Scholar
Eliezer, S., Moshe, E. & Eliezer, D. (2002). Laser-induced tension to measure the ultimate strength of metals related to the equation of state. Laser Part. Beams 20, 87.CrossRefGoogle Scholar
Eliezer, S., Eliaz, N., Grossman, E., Fisher, D., Gouzman, I., Henis, Z., Pecker, S., Horovitz, Y., Fraenkel, M., Maman, S. & Lereah, Y. (2004). Synthesis of nanoparticles with femtosecond laser pulses. Phys. Rev. B 69, 144119.CrossRefGoogle Scholar
Fisher, D., Fraenkel, M., Henis, Z., Moshe, E. & Eliezer, S. (2001). Interband and intraband (Drude) contributions to femtosecond laser absorption in aluminum. Phys. Rev. E 65, 016409.Google Scholar
Gamaly, E.G., Rode, A.V. & Luther-Davies, B. (2000). Formation of diamond-like carbon films and carbon foam by ultrafast laser ablation. Laser Part. Beams 18, 245.CrossRefGoogle Scholar
Reitze, D.H., Ahn, H. & Downer, M.C. (1992). Optical properties of liquid carbon measured by femtosecond spectroscopy. Phys. Rev. B 45, 2677.Google Scholar
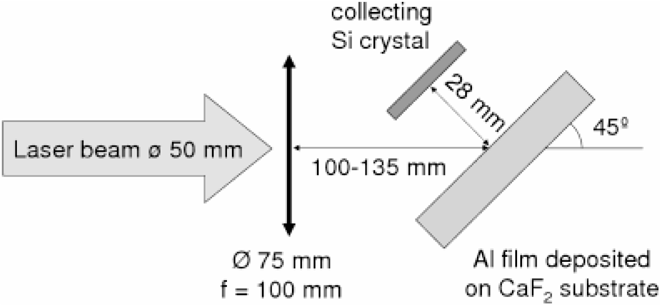
Figure 0

A schematic view with experimental description of the experiment.

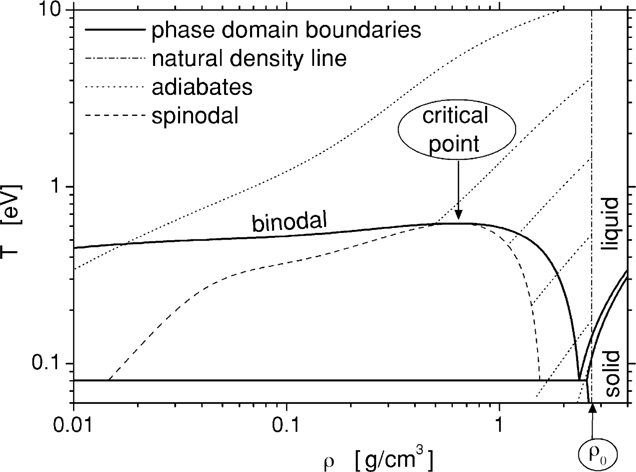
Figure 1

Phase diagram of Aluminum.

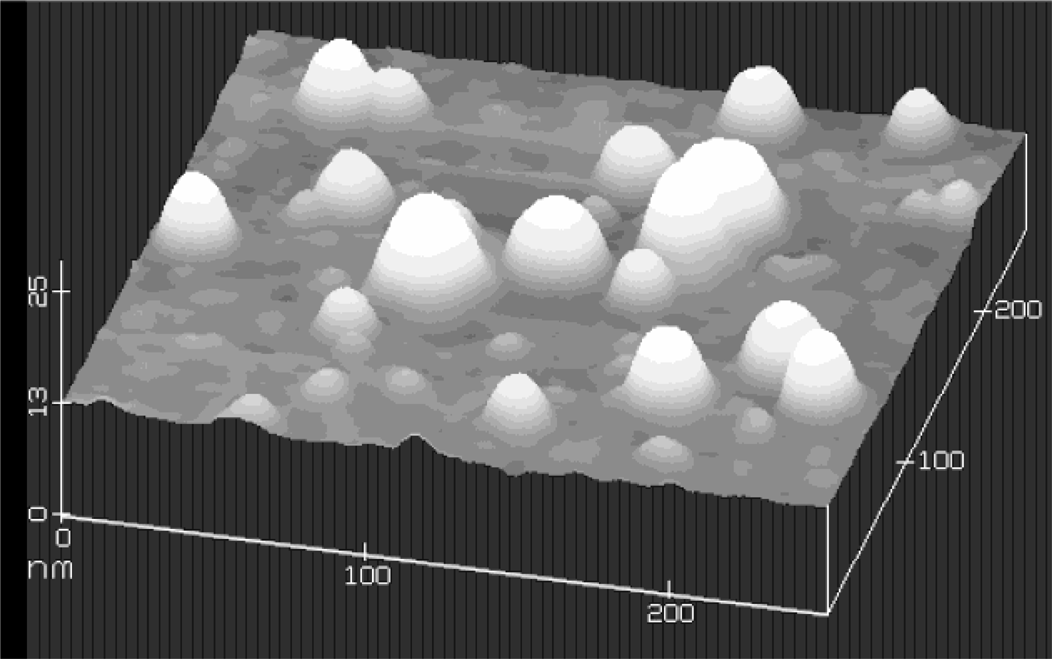
Figure 2

An atomic force microscope (AFM) image for Aluminum nanoparticles.

Figure 3

Onion like carbon structures as measured by TEM.

Figure 4

Nanotubes of carbon as measured by TEM.