2. ION BUBBLE IN A PREFORMED PLASMA CHANNEL: A DYNAMIC APPROACH

Consider a preformed plasma channel with ion (or electron) density profile,

(1)$$n_0 = n_0^0 \lpar 1 + r^2 /r_{ch}^2 \rpar \comma \;$$$n_0=n_0^0(1+r^2/r_{ch}^2),$

where r _ch is the radius of the channel and n ₀⁰ is the density at the channel axis. An intense short pulse laser propagates through it,

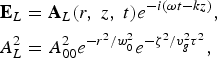(2)$$\eqalign{{\bf E}_L &= {\bf A}_L \lpar r\comma \; z\comma \; t\rpar e^{ - i\lpar {\rm \omega} t - kz\rpar }\comma \; \cr A_L^2 &= A_{00}^2 e^{-r^2 /w_0^2} e^{-{\rm \zeta}^2 /v_g^2 {\rm \tau}^2}\comma \;}$$$\begin{array}{cc}{E}_L& =A_L(r,z,t)e^{-i(\text{ω}t-kz)},\\ A_L^2& =A_{00}^2{e}^{-r^2/w_0^2}{e}^{-{\text{ζ}}^2/v_g^2{\text{τ}}^2},\end{array}$

where k = ω/c(1−ω_p²/ω²)^1/2 , v _g = c(1−ω_p²/ω²)^1/2 , ζ = z−v _gt, ${\rm \omega} _p = k_p c = \sqrt{4{\rm \pi} n_0^0 e^2 /m}$${\text{ω}}_p=k_{p}c=\sqrt{4\text{π}{n}_0^0{e}^2/m}$, −e and m are the electron charge and mass. It exerts a ponderomotive force on electrons,

(3)$${\bf F} = e\nabla {\rm \phi} _p = \displaystyle{{ma^2 c^2 \over 2{\rm \gamma}}} \left[\displaystyle{r \over w_0^2} \hat{r} + \displaystyle{{\rm \zeta} \over v_g^2 {\rm \tau} ^2} \hat{z} \right] \comma \;$$$F=e\nabla {\text{ϕ}}_p=\frac{{ma}^2{c}^2}{2\text{γ}}[\frac{r}{w_0^2}\hat{r}+\frac{\text{ζ}}{v_g^2{\text{τ}}^2}\hat{z}],$

where ϕ_p = −(mc ²/e) (γ−1), ${\rm \gamma} = \sqrt{1 + {{1 \over 2}}a^2}, a^2 = a_0^2 e^{ - r^2 /w_0^2 } e^{ - {\rm \zeta} ^2 /v_g^2 {\rm \tau} ^2 }$$\text{γ}=\sqrt{1+\frac{1}{2}{a}^2},a^2=a_0^2{e}^{-r^2/w_0^2}{e}^{-{\text{ζ}}^2/v_g^2{\text{τ}}^2}$, and a ₀ = eA ₀₀/mωc.

As the electron originated at r _i (initial point) at time t = 0 moves to a distance r, it sees the space charge field due to the ion space charge left behind. The net ion charge in a cylinder of radius r and unit axial length is 2π∫₀^rn ₀⁰e(1+r ²/r _ch²)rdr. Therefore, the space charge field may be approximated as,

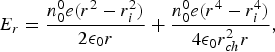(4)$$E_r = \displaystyle{{n_0^0 e \lpar r^2 - r_i^2 \rpar \over 2{\rm \epsilon} _0 r}} + \displaystyle{{n_0^0 e\lpar r^4 - r_i^4 \rpar \over 4{\rm \epsilon}_0 r_{ch}^2 r}} \comma \; $$$E_r=\frac{n_0^{0}e(r^2-r_i^2)}{2{\text{ε}}_{0}r}+\frac{n_0^{0}e(r^4-r_i^4)}{4{\text{ε}}_0{r}_{ch}^{2}r},$

while the longitudinal component of space charge field, which is Lorentz invariant, is E _z = E _z′ (where E _z′ is the field in moving frame, as calculated in Appendix A). In addition, to these transverse fields an azimuthal magnetic field B _ϕ = −E _r/c is also generated within the cavity moving with relativistic velocities (Lu et al., Reference Lu, Huang, Zhou, Tzoufras, Tsung, Mori and Katsouleas2006; Kostyukov et al., Reference Kostyukov, Pukhov and Kiselev2010; Lotov, Reference Lotov2004). In the quasi-equilibrium, as the laser bubble combine moves ahead, the plasma electrons must remain outside the bubble, at the bubble boundary or bit farther from it. Simulations reveal that the width of the region of electron build up at the boundary is significantly smaller than the radius of the bubble. Since the axial velocities of electrons in this layer are less than v _g (the velocity of the bubble), these electrons surge toward the stagnation point near the bubble. We may get a reasonable clue about the shape of the bubble by studying the trajectory of a test electron that originates at an off axis point at the front of the laser pulse. The equation of motion for the electron in the laboratory frame in component form can be written as,

(5)$$\displaystyle{{d\lpar {\rm \gamma} v_r \rpar \over dt}} = \displaystyle{{F_r \over m}} - \displaystyle{e\lpar E_r - v_z B_{\rm \phi} \rpar \over m}\comma \;$$$\frac{d\left(\text{γ}{v}_r\right)}{dt}=\frac{F_r}{m}-\frac{e(E_r-v_z{B}_{\text{ϕ}})}{m},$

(6)$$\displaystyle{{d\lpar {\rm \gamma} v_z \rpar \over dt}} = \displaystyle{{F_z \over m}} - \displaystyle{e\lpar E_z+v_r B_{\rm \phi} \rpar \over m}.$$$\frac{d\left(\text{γ}{v}_z\right)}{dt}=\frac{F_z}{m}-\frac{e(E_z+v_r{B}_{\text{ϕ}})}{m}.$

Writing $d\lpar {\rm \gamma} \vec{v}\rpar /dt = \vec{v}d{\rm \gamma} /dt + {\rm \gamma} d\vec{v}/dt$$d\left(\text{γ}\overrightarrow{v}\right)/dt=\overrightarrow{v}d\text{γ}/dt+\text{γ}d\overrightarrow{v}/dt$, where $\vec{v} = v_r \hat{r} + v_z \hat{z}$$\overrightarrow{v}=v_r\hat{r}+v_z\hat{z}$ and $d{\rm \gamma} /dt=- {\textstyle{{a^2 } \over {2{\rm \gamma} }}} \left[ {\textstyle{r \over {w_0^2 }}}{\textstyle{{dr} \over {dt}}}+{\textstyle{{\rm \zeta} \over {v_g^2 {\rm \tau} ^2 }}}\lpar v_z - v_g \rpar \right] $$d\text{γ}/dt=-\frac{a^2}{2\text{γ}}[\frac{r}{w_0^2}\frac{dr}{dt}+\frac{\text{ζ}}{v_g^2{\text{τ}}^2}(v_z-v_g\left)\right]$, one obtains,

(7)$$\displaystyle{{d^2 r} \over {dt^2 }}=\displaystyle{{F_r } \over {m{\rm \gamma} }} - \displaystyle{{e\lpar E_r - v_z B_{\rm \phi} \rpar } \over {m{\rm \gamma} }}+\displaystyle{{a^2 } \over {2{\rm \gamma} ^2 }}\displaystyle{{dr} \over {dt}} \left[ \displaystyle{r \over {w_0^2 }}\displaystyle{{dr} \over {dt}}+\displaystyle{{\rm \zeta} \over {v_g^2 {\rm \tau} ^2 }}\lpar v_z - v_g \rpar \right] \comma \;$$$\frac{d^{2}r}{{dt}^2}=\frac{F_r}{m\text{γ}}-\frac{e(E_r-v_z{B}_{\text{ϕ}})}{m\text{γ}}+\frac{a^2}{2{\text{γ}}^2}\frac{dr}{dt}[\frac{r}{w_0^2}\frac{dr}{dt}+\frac{\text{ζ}}{v_g^2{\text{τ}}^2}(v_z-v_g\left)\right],$

(8)$$\!\displaystyle{{d^2 z} \over {dt^2 }}=\displaystyle{{F_z } \over {m{\rm \gamma} }} - \displaystyle{{e\lpar E_z+v_r B_{\rm \phi} \rpar } \over {m{\rm \gamma} }}+\displaystyle{{a^2 } \over {2{\rm \gamma} ^2 }}\displaystyle{{dz} \over {dt}} \left[ \displaystyle{r \over {w_0^2 }}\displaystyle{{dr} \over {dt}}+\displaystyle{{\rm \zeta} \over {v_g^2 {\rm \tau} ^2 }}\lpar v_z - v_g \rpar \right] \comma \;$$$\frac{d^{2}z}{{dt}^2}=\frac{F_z}{m\text{γ}}-\frac{e(E_z+v_r{B}_{\text{ϕ}})}{m\text{γ}}+\frac{a^2}{2{\text{γ}}^2}\frac{dz}{dt}[\frac{r}{w_0^2}\frac{dr}{dt}+\frac{\text{ζ}}{v_g^2{\text{τ}}^2}(v_z-v_g\left)\right],$

where F _r and F _z are the radial components of ponderomotive force obtained from Eq. (3).

To estimate the efficacy of the dynamic approach, we numerically solved the coupled Eqs. (7) and (8) for the parameters used by Mora (Reference Mora2009), a ₀ = 5, the spot size k _pw ₀ = 2.5 and the pulse length k _pv _gτ = 6, where $v_g = c\sqrt{1 - \lpar 1/{\rm \gamma}_g^2 \rpar} \approx 0.995c$$v_g=c\sqrt{1-(1/{\text{γ}}_g^2)}\approx 0.995c$ for γ_g = 10. Mora used fully relativistic time-averaged particle code WAKE to study the radial wavebreaking of the density perturbation in the highly nonlinear laser wakefield regime in a uniform plasma. Figure 1a shows the contours of electron trajectories of analytically obtained by us for electrons starting from different radial positions k _pr _i = 0.3, 0.6, 0.8, and 1. One may note that the electrons (in the moving bubble) are streaming backward from right to left. All the trajectories tend to converge at the rear (at k _p(z−v _gt) = −11) and acquire a spherical shape. This is indicative of longitudinal wavebreaking. For comparison, we have in Figure 1b the trajectories obtained by Mora (Reference Mora2009) in their simulations. Their trajectories run from left to right due to horizontal axis being k _p(ct−z). For the electron originating near the axis, the trajectories diverge continuously away from the axis. For the electrons originating between k _pr _i ~ 1.3 and 3, the trajectories surge to a common radial point and then bend toward the z axis. The ones between k _pr _i = 1.3 and 1.8 reach the axis at k _p(ct−z) ≈ 10, which is comparable to axial span of trajectories inour case (Fig. 1a). The radial height of these trajectories (the radial breaking point) is k _pr _i ~ 3 that is close to the height of trajectories in our case. The major difference is in the trajectories of electrons for k _pr _i< 1.

Fig. 1. Contour of k _pr with k _p(z−v _gt) for a ₀ = 5, k _pw ₀ = 2.5, k _pv _gτ = 6 and k _pr _i = 0.3, 0.6, 0.8 and where v _g = 0.995c. Figure 1b is printed with permission from Patrick Mora (Eur. Phys. J. Special Topics 175, 97–104 (2009).

Similarly, Kim et al. (Reference Kim, Kim, Kim, Hafz, Lee and Suk2003) used a two-dimensional PIC simulation to study the electron trapping and acceleration of electrons in the bubble (wakefield) with parabolic density profile. The parameters used were: a ₀ = 2.27, the laser wavelength λ = 0.8 μm, the minimum density at the axis n ₀⁰ = 2.1 × 10¹⁸ cm⁻³, corresponding plasma wavelength λ_p = 23.21 µm, the pulse duration τ = 50 fs and the pulse length k _pv _gτ = 4, where v _g ≈ 0.998c for γ_g = λ_p/λ ≈ 30. The spot size at the centre of the channel is w ₀ = 10 µm (k _pw ₀ = 2.7) and the channel radius is r _ch = 160 µm (k _pr _ch = 43.3). The wake has taken the form of a bubble with longitudinal dimension Δz = 25 µm, where as the radius is ≈ 8 µm at z = 100 µm and the accelerated electron bunch gains energy in the ranges of 5 and 20 MeV.

Now we compare our result by solving the same coupled equations Eqs. (7) and (8) in the lab frame for the parameters mentioned above. Figure 2 shows the contour of electron trajectory for k _pr _i = 0.1. One may note that the radiusof the bubble is approximately equal to 9 µm and the longitudinal extent is ≈30 µm that are not too different from the value of 8 µm and 25 µm obtained in PIC simulations. A detailed analysis of energy gain of a test electron will be discussed later.

Fig. 2. Contour of k _pr with k _p(z−v _gt) for a ₀ = 2.27, k _pw ₀ = 2.7, k _pr _ch = 43.2, k _pv _gτ = 4 and k _pr _i = 0.1, where v _g = 0.998c.

The trajectory of the laser expelled electrons is entirely different in a frame moving parallel to the bubble. One may use the Lorentz transformation, z′ = γ_g(z−v _gt) and t = γ_g(t′+v _gz′/c ²) (primed variables representing the moving frame) to transform the equations Eqs. (7) and (8) from lab frame to Lorentz boosted frame. Therefore,

(9)$$\eqalign{{d^2 z^{\prime} \over dt^{{\prime}2}} &= {a^2 \over 2{\rm \gamma}^2} {\rm \gamma}_g^2 \left[{z^{\prime} \over L_p^2} \left( 1 + {v_g v_z^{\prime} \over c^2} \right)^3 + \left( {v_g \over c} \right)^2 \left( 1 + {v_z^{\prime} \over v_g} \right) \right. \cr &\quad \left. \times \left( {r \over R_0^2} {v_r^{\prime} \over v_g} + {z^{\prime} \over {\rm \gamma}_g^2\, L_p^2} {v_z^{\prime} \over v_g} \right) \right] - {\rm \gamma}_g^3 \left( 1 + {v_g v_z^{\prime} \over c^2} \right)^3 \cr &\quad \times \left( {eE_z^{\prime} \over m{\rm \gamma} {\rm \omega}_p c} - {v_r^{\prime} \over c} \left( {\lpar r^2 - r_{in}^2 \rpar \over 2{\rm \gamma} r} + {\lpar r^4 - r_{in}^4 \rpar \over 4{\rm \gamma} R_{ch}^2 r} \right) \right) \comma \;}$$$\begin{array}{cc}\frac{d^2{z}^{\text{'}}}{{dt}^{\text{'}2}}& =\frac{a^2}{2{\text{γ}}^2}{\text{γ}}_g^2[\frac{z^{\text{'}}}{L_p^2}{(1+\frac{v_g{v}_z^{\text{'}}}{c^2})}^3+{\left(\frac{v_g}{c}\right)}^2(1+\frac{v_z^{\text{'}}}{v_g})\\ & \times (\frac{r}{R_0^2}\frac{v_r^{\text{'}}}{v_g}+\frac{z^{\text{'}}}{{\text{γ}}_g^2{L}_p^2}\frac{v_z^{\text{'}}}{v_g})]-{\text{γ}}_g^3{(1+\frac{v_g{v}_z^{\text{'}}}{c^2})}^3\\ & \times (\frac{{eE}_z^{\text{'}}}{m\text{γ}{\text{ω}}_{p}c}-\frac{v_r^{\text{'}}}{c}(\frac{(r^2-r_{in}^2)}{2\text{γ}r}+\frac{(r^4-r_{in}^4)}{4\text{γ}{R}_{ch}^{2}r})),\end{array}$

(10)$$\eqalign{{d^2 r \over dt^{\prime 2}} &= {a^2 \over 2{\rm \gamma}^2} \left( {r \over R_0^2} \left( \left( 1 + {v_g v_z^{\prime} \over c^2} \right)^2 + {v_r^{\prime 2} \over c^2} \right) + {z^{\prime} \over {\rm \gamma}_g^2\, L_p^2} {v_r^{\prime} v_z^{\prime} \over c^2} \right) \cr &\quad + {v_r^{\prime} v_g \over c^2} {v_z^{\prime} \over \lpar 1 + {v_g v_z^{\prime} \over c^2} \rpar} - {\rm \gamma}_g^2 \left( 1 + {v_g v_z^{\prime} \over c^2 } \right)^2 \left( {\lpar r^2 - r_{in}^2 \rpar \over 2{\rm \gamma} r} \right. \cr &\left. \quad + {\lpar r^4 - r_{in}^4 \rpar \over 4{\rm \gamma} R_{ch}^2 r} \right) \left( 1 + {v_z^{\prime} \over c} \right) \comma \;}$$$\begin{array}{cc}\frac{d^{2}r}{{dt}^{\text{'}2}}& =\frac{a^2}{2{\text{γ}}^2}(\frac{r}{R_0^2}({(1+\frac{v_g{v}_z^{\text{'}}}{c^2})}^2+\frac{v_r^{\text{'}2}}{c^2})+\frac{z^{\text{'}}}{{\text{γ}}_g^2{L}_p^2}\frac{v_r^{\text{'}}{v}_z^{\text{'}}}{c^2})\\ & +\frac{v_r^{\text{'}}{v}_g}{c^2}\frac{v_z^{\text{'}}}{(1+\frac{v_g{v}_z^{\text{'}}}{c^2})}-{\text{γ}}_g^2{(1+\frac{v_g{v}_z^{\text{'}}}{c^2})}^2(\frac{(r^2-r_{in}^2)}{2\text{γ}r}\\ & +\frac{(r^4-r_{in}^4)}{4\text{γ}{R}_{ch}^{2}r})(1+\frac{v_z^{\text{'}}}{c}),\end{array}$

where r → k _pr, r _in → k _pr _i, R ₀ → k _pw ₀, R _ch → k _pr _ch, z′ → k _pz′, t′ → ω_pt′, v _r′ = dr/dt′, v _z′ = dz′/dt′, L _p = k _pv _gτ, γ_g = (1−v _g²/c ²)^−1/2, and v _g → v _g/c (v _g is the velocity of the frame moving parallel to the ion bubble). The coupled Eqs. (9) and (10) are numerically solved to obtain the trajectory of the electrons in the Lorentz boosted frame. Figure 3 represents the contour of the electron trajectory in the moving frame plotted for the parameters used by Kim et al. (Reference Kim, Kim, Kim, Hafz, Lee and Suk2003) From Figure 3 one may note that the longitudinal distance is approximately stretched to γ_g (≈30) times the transverse dimension of the bubble with maximum radius at the centre. Hence the ion bubble acquires an elliptic shape in the Lorentz boosted frame moving parallel to the bubble.

Fig. 3. Contour of k _pr with k _p(z−v _gt) in the Lorentz boosted frame for a ₀ = 2.27, k _pw ₀ = 2.7, k _pr _ch = 43.2, k _pv _gτ = 4 and k _pr _i = 0.1, where v _g = 0.998c.

Previous studies (Esarey et al., Reference Esarey, Schroeder and Leemans2009; Lu et al., Reference Lu, Huang, Zhou, Tzoufras, Tsung, Mori and Katsouleas2006; Kostyukov et al., Reference Kostyukov, Pukhov and Kiselev2010) have given an estimate of the radius of ion bubble by equating the laser ponderomotive force on a single electron and ion channel force for a uniform plasma. Following the same analysis, one may estimate the maximum radius of the non uniform ion bubble by balancing the two forces at the bubble boundary in the lab frame.

From the Poisson's equation ∇²ϕ = e(n _e−n ₀)/ε₀, on using ϕ = −ϕ_p and n _e = 0 (complete evacuation of electrons inside the ion bubble) one obtains the bubble boundary r ≡ R versus Z ₁ = ζ, ζ = z−v _gt,

(11)$$\eqalign{1 + {R^2 \over r_{ch}^2} &- {a^2 /2 \over \lpar 1 + a^2 /2\rpar ^{3/2}} \left[ \left( {\matrix{2\lpar 1 - R^2 /w_0^2 \rpar + \lpar a^2 /2\rpar \cr \lpar 2 - R^2 /w_0^2 \rpar} \over k_p^2 w_0^2} \right) - \right. \cr &\qquad \left. \left( {\matrix{\lpar 1 - 2Z_1^2 /\lpar v_g^2 {\rm \tau}^2 \rpar + \lpar a^2 /2\rpar \cr \lpar 1 - Z_1^2 /\lpar v_g^2 \tau^2 \rpar \rpar} \over k_p^2 \lpar v_g^2 {\rm \tau}^2 \rpar} \right) \right] = 0\comma \;}$$$\begin{array}{cc}1+\frac{R^2}{r_{ch}^2}& -\frac{a^2/2}{(1+a^2/2{)}^{3/2}}[\left(\frac{\begin{array}{c}2(1-R^2/w_0^2)+(a^2/2)\\ (2-R^2/w_0^2)\end{array}}{k_p^2{w}_0^2}\right)-\\ & \left(\frac{\begin{array}{c}(1-2Z_1^2/(v_g^2{\text{τ}}^2)+(a^2/2)\\ (1-Z_1^2/(v_g^2{\tau }^2\left)\right)\end{array}}{k_p^2\left(v_g^2{\text{τ}}^2\right)}\right)]=0,\end{array}$

where $a^2=a_0^2 e^{ - R^2 /w_0^2 } e^{ - Z_1^2 /\lpar v_g {\rm \tau} \rpar ^2 }$$a^2=a_0^2{e}^{-R^2/w_0^2}{e}^{-Z_1^2/(v_g\text{τ}{)}^2}$, R is the radius, and ϕ is the space charge potential of the ion bubble.

Inside the bubble ϕ ≠ −ϕ_p and imbalance of the ponderomotive and space charge forces does not matter as there are no electrons to feel the forces. The bubble surface in the moving frame is an ellipsoid with axial length L _z = γ_gζ(=z−v _gt) (at R = 0) and transverse length L _r = R (at Z ₁ = 0). Substituting Z ₁ = 0 and r = L _r in Eq. (11) we obtain,

(12)$$\eqalign{\left( 1 + {L_r^2 \over r_{ch}^2} \right) \lpar 2 + a^{\prime 2} \rpar^{1/2} &= \sqrt{2} {a^{\prime 2} \over k_p^2 w_0^2} \left[ 1 + {w_0^2 \over 2v_g^2 {\rm \tau}^2 } \right. \cr &\left. \quad - {L_r^2 \over 2w_0^2} {4 + a^{\prime 2} \over 2 + a^{\prime 2}} \right] \comma \;}$$$\begin{array}{cc}(1+\frac{L_r^2}{r_{ch}^2})(2+a^{\text{'}2}{)}^{1/2}& =\sqrt{2}\frac{a^{\text{'}2}}{k_p^2{w}_0^2}[1+\frac{w_0^2}{2v_g^2{\text{τ}}^2}\\ & -\frac{L_r^2}{2w_0^2}\frac{4+a^{\text{'}2}}{2+a^{\text{'}2}}],\end{array}$

where $a^{{\rm ^{\prime}}2}=a_0^2 e^{ - L_r^2 /w_0^2 } $$a^{{\prime }^{}2}=a_0^2{e}^{-L_r^2/w_0^2}$.

The transverse dimension L _r (maximum radius) of the ion bubble is a function of laser amplitude a ₀, spot size w ₀, channel dimension r _ch, and pulse width τ. For a long laser pulse w ₀/v _gτ ≪ 1, i.e., pulse length larger than the spot size, L _r is independent of τ. However, for a short pulse L _r has dependence on τ. Eq. (12) is transcendental equation and is numerically solved for L _r. Figure 4 shows the variation of transverse length L _r/w ₀ with a ₀ for k _pr _ch = 3 and w ₀/v _gτ = 0.32. The transverse size of the bubble initially rises almost linearly with a ₀ and then tends to saturate at a value comparable to laser spot size. For a ₀ = 3, k _pw ₀ = 2.1, and k _pr _ch = 3 the radius L _r turns out to be L _r = 1.5c/ω_p. For a constant value of L _r, i.e., to achieve a bubble of a given radius, the laser spot size k _pw ₀ varies linearly with a ₀.

Fig. 4. Variation of L _r/w ₀ with a ₀ for w ₀/r _ch = 0.7 (dot), 0.8 (dash) and 0.9 (solid), where k _pr _ch = 3 and w ₀/v _gτ = 0.32.

It is also possible to estimate the critical size k _pr _e of the electron sphere at the stagnation point by equating the potential energy (potential = n _eer _e²/3ε₀) of the electrons at the surface of the electron sphere to their initial kinetic energy at the bubble boundary (after emerging from the laser) (Liu & Tripathi, Reference Liu and Tripathi2010). So one obtains,

(13)$$\eqalign{&n_e r_e^2 e^2 /3{\rm \epsilon} _0=mc^2 \lpar {\rm \gamma} _{in} - 1\rpar \cr &\Rightarrow k_p r_e \sim \sqrt{3\lpar {\rm \gamma}_{in} - 1\rpar /n}\comma \;}$$$\begin{array}{cc}& n_e{r}_e^2{e}^2/3{\text{ε}}_0={mc}^2({\text{γ}}_{in}-1)\\ & \Rightarrow k_p{r}_e~\sqrt{3({\text{γ}}_{in}-1)/n},\end{array}$

where ${\rm \gamma}_{in}^2 = \lpar 1 - v_{in}^2 /c^2 \rpar^{ - 1}$${\text{γ}}_{in}^2=(1-v_{in}^2/c^2{)}^{-1}$, v _in/c is the initial velocity of the electron just after emerging from the laser and n = n _e/n ₀⁰. The critical size of electron sphere thus depends upon the initial energy and ratio of densities n. For v _in/c = 0.99, n = 100, one obtains k _pr _e = 0.5.

3. ENERGY GAIN

Now we calculate the energy gained by a test electron under the influence of the longitudinal field E _z^′ of the ion bubble in the Lorentz boosted frame. The longitudinal electric field E _z′ (see Appendix A) depends on radius R(a ₀, v _gτ, w ₀, r _ch) and z _m. Figure 5 shows the variation of E _z′ with z _m/γ_gR for different values of a ₀, where z _m is the distance (from the shifted origin) on the longitudinal axis of the ion bubble. The longitudinalfield is almost linear and symmetric about the center of the cavity. For a ₀ = 3.27, k _pw ₀ = 6.28, k _pv _gτ = 4.2, where v _g = 0.996c and γ_g = 16.3, the acceleration gradient is E _z′ ~ 6 GV/cm for uniform density 6.5×10¹⁸ cm⁻³ (parameters from Kalmykov et al. (Reference Kalmykov, Beck, Yi, Khudik, Downer, Lefebvre, Shadwick and Umstadter2011). Therefore, the bubble provides a huge space charge potential, which pulls the electrons from the stagnation point with a huge force eE _z′. Hence a test electron in the spherical electron cloud at the stagnation point can gain tremendous amount of energy.

Fig. 5. Variation of longitudinal field eE _z′/m ω _pc inside the uniform bubble with z _m/γ_gR for a ₀ = 3.27, k _pw ₀ = 6.28 and k _pv _gτ = 4.2, where v _g = 0.996c.

Using energy gain equation, one may write

(14)$${d{\rm \gamma}^{\prime} \over dt^{\prime}} = - {eE_z^{\prime} v_z \over m_0 c^2} \comma \;$$$\frac{d{\text{γ}}^{\text{'}}}{{dt}^{\text{'}}}=-\frac{{eE}_z^{\text{'}}{v}_z}{m_0{c}^2},$

where γ′, v _z = dz _m/dt′ (longitudinal velocity of electron inside the ion bubble) and t′ are measured in boosted frame. Transforming from moving frame to lab frame, using Lorentz transformations, we get

(15)$${\rm \gamma}_{lab} = {\rm \gamma}_g \left( {\rm \gamma}^{\prime} + \lpar v_g /c \rpar \sqrt{{\rm \gamma}^{\prime 2} - 1} \right) \comma \;$$${\text{γ}}_{lab}={\text{γ}}_g({\text{γ}}^{\text{'}}+(v_g/c\left)\sqrt{{\text{γ}}^{\text{'}2}-1}\right),$

(16)$$dt/dt^{\prime} = {\rm \gamma}_g .$$$dt/{dt}^{\text{'}}={\text{γ}}_g.$

Eq. (14) is numerically solved using fourth order Runga Kutta method and transformed to lab frame using Eqs. (15) and (16). Variation of electron energy (MeV) with z _m/γ_gR is plotted in Figure 6 for the parameters used by (Reference Kim, Kim, Kim, Hafz, Lee and Suk2003) (red) and Chen et al. (Reference Chen, Tai, Liu and Lin-Liu2010) (blue). Chen et al. (Reference Chen, Tai, Liu and Lin-Liu2010) performed 2D PIC simulation to obtain the dependence of the maximum energy of the electron beam on laser amplitude a ₀ and plasma density. Their simulation shows that the maximum energy of the electron beam varies from 90–200 MeV in the density range 3–4 × 10¹⁹ cm⁻³ for the initial laser amplitude a ₀ = 4, initial spot size w ₀ = 4 µm, pulse length cτ = 13.5 μm and laser wavelength λ = 0.8 µm. For a comparison we have in Figure 6 the energy gain of the test electron in the density regime of Chen's et al. (2010) simulation. Figure 6 shows the variation of energy gain of a test electron with z _m/γ_gR for uniform and nonuniform plasma density. One may note that the test electron gains a maximum energy of about 35 (dash) and ≈100 (Solid) MeV before entering the dephasing region of the ion bubble. Since the longitudinal field of the bubbleis approximately linear about the center of the bubble (shown in Fig. 5), the electron that crosses the center of the ion bubble are decelerated due to the reversal of sign of the longitudinal field. Hence the interaction must terminate there. The energygains obtained for the both cases are in reasonable agreement with the previous studies. Though the model which we use did not include the effects of laser pulse evolution nor self-focusing and electron beam loading on the plasma bubble, it gives an estimate of energy gain of electrons within a factor of 1.5 or 2 from simulation results.

Fig. 6. Variation of electron energy with z _m/γ_gR for uniform and non uniform plasma. The parameters for non uniform plasma (dash): a ₀ = 2.27, k _pw ₀ = 2.7, k _pr _ch = 43.2, k _pv _gτ = 4, v _g = 0.998c and laser wavelength λ = 0.8 μm. And for uniform plasma (solid): a ₀ = 4, k _pw ₀ = 4.48, k _pv _gτ = 15.45, v _g = 0.99c and laser wavelength λ = 0.8 μm.