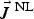1. INTRODUCTION
The generation of terahertz (THz) radiation by high power laser–surface interaction has attracted considerable attention in recent years. Structured metal surfaces, such as spoof, are employed for this purpose as they slow down the group velocity of surface plasmons (SPs) and bring the asymptotic SP frequency into the THz range (Schultz et al., Reference Schultz, Smith, Mock and Schultz2000; Jeon & Grischkowsky, Reference Jeon and Grischkowsky2006; Williams et al., Reference Williams, Andrews, Maier, Fernández-Domínguez, Martín-Moreno and García-Vidal2008). When a laser is impinged on the surface, its mode converts to SP and the latter produces photoelectrons. These electrons get accelerated in the ponderomotive potential associated with the evanescent field producing short pulse THz radiation. Kadlec et al. (Reference Kadlec, Kuzel and Coutaz2005) have experimentally observed THz generation in gold films of variable thickness. For thickness 
$\sim 150\,{\rm nm}$ and incident angle 
$\sim {45} $°, the measured THz field attains peak values of ~4 KV/cm. The experiments also reveal that emitted THz field is suppressed for thickness below 100 nm.
Welsh et al. (Reference Welsh, Hunt and Wynne2007) have reported THz emission from gold-coated glass gratings having a period suitable for phase matched excitation of SPs. Using 0.8 μm intense optical pulses they saw THz emission from nanostructured metal surfaces only for p-polarized pump light with a strong peak when the angle of incidence of the pump satisfied the k-matching condition for laser mode conversion into SPs. The pump energy density in their experiments reached values up to 3.5 mJ/cm2.
Kumar and Tripathi (Reference Kumar and Tripathi2013) have proposed a planar structure, comprising a dielectric plate coated on top with an ultra-thin metal film, for nonlinear mixing of lasers and the generation of THz surface plasma wave (SPW). The structure supports THz SPW with SP resonance, controllable by film thickness, in the THz domain. The lasers exert a beat frequency ponderomotive force on film electrons that drives the THz SPW. Suizu and Kawase (Reference Suizu and Kawase2007) have theoretically studied surface-emitted and collinear phase-matched THz generation in a conventional optical fiber. The third-order nonlinear effect, four-wave mixing, is used to generate THz that radiates out from the surface of the fiber, perpendicular to the direction of the optical beams.
Due to wide range of applications (Taton et al., Reference Taton, Mirkin and Letsinger2000; Kalkbrenner et al., Reference Kalkbrenner, Ramstein, Mlynek and Sandoghdar2001; Ditlbacher et al., Reference Ditlbacher, Krenn, Schider, Leitner and Aussenegg2002; Li et al., Reference Li, Stockman and Bergman2003) SPs have drawn vigorous attention in recent years. SPs are ideally suited as sensors, they propagate along the surface between a conductor and a dielectric or conductor and air with fields peaking at the interface and falling off exponentially away from it in either medium (Barnes et al., Reference Barnes, Dereux and Ebbesen2003; Steinhauer & Kimura, Reference Steinhauer and Kimura2003; Kalmykov et al., Reference Kalmykov, Polomarov, Korobkin, Otwinowski, Power and Shvets2006; Mork et al., Reference Mork, Chen and Heuck2014). A tiny trace of a gas or DNA on the interface produces a measurable change in the propagation constant when one uses the attenuated total reflection configuration (Kretschmann & Raether, Reference Kretschmann and Raether1968; Kretschmann, Reference Kretschmann1971).
In this paper, we examine the efficacy of capillary plasma for laser excitation of THz surface plasma wave. Capillary plasma could be produced in two ways (Kaganovich et al., Reference Kaganovich, Sasorov, Ehrlich, Cohen and Zigler1997; Nitikant & Sharma, Reference Nitikant and Sharma2005; Kameshima et al., Reference Kameshima, Kotaki, Kando, Daito, Kawase, Fukunda, Chen, Homma, Kondo, Esirkepov, Bobrova, Sasorov and Bulanov2009; Genoud et al., Reference Genoud, Cassou, Wojda, Ferrari, Kamperidis, Burza, Persson, Uhlig, Kneip, Mangles, Lifschitz, Cros and Wahlström2011) one, by electrical discharge of a hollow capillary filled with a gas and second, by the irradiation of a low spot size hollow capillary by a laser. In the second, hollow plasma waveguide is created naturally. The laser ionizes the capillary and laser ponderomotive force keeps the plasma away from the axial region. Thus we model the capillary as a hollow plasma cylinder. An electron depleted ion channel created by a laser irradiation of gas jet target has similar electron density profile. Gas filled metallic waveguide is not practical as it cannot sustain a plasma for long without suffering damage to its wall.
Two collinear Gaussian laser beams with frequencies much above the plasma frequency propagate along the cylinder axis and extending radially outward into the plasma region. The lasers impart oscillatory velocity to plasma electrons and exert a ponderomotive force on them at the beat frequency. The ponderomotive force has a transverse component that drives nonlinear current, producing THz radiation. The lasers also exert a static radial ponderomotive force that keeps the plasma from creeping in.
The situation resembles high power laser propagation in gas jet plasmas. The laser ponderomotive force pushes the electrons radially outward creating a fully electron evacuated channel (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1967, Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976; Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997). The space charge thus created holds the electrons and pulls the ions outward, causing ambipolar diffusion of the plasma. The plasma density is minimum on the laser axis and monotonically falls off away from it. In a two-stage acceleration process using three-dimensional particle in cell simulations Naseri et al. (Reference Naseri, Pesme, Rozmus and Popov2012) have shown that for laser powers above the threshold, the laser pulse propagates in a single mode through the electron-free channel for a time of the order of 1 picosecond, the steep laser front excites a surface wave along the boundaries of the ion channel. This surface wave traps the electrons at the channel wall and preaccelerates them to relativistic energies, after having gained sufficient energies these electrons are further accelerated by the longitudinal electric field of the surface wave.
A novel feature of the scheme is that the phase matching condition between the beating lasers and the THz is exactly satisfied in certain parameter regime. In Section 2, we derive the dispersion relation for SPW. In Section 3 we study SPW THz excitation and obtain the amplitude. The results are discussed in Section 4.
2. SPW DISPERSION RELATION
Consider a hollow plasma cylinder of inner radius a with electron density
$${n_0} = 0\;{\rm for}\;r \lt a,$$
$$\quad= {n_0}\;{\rm for}\;r \gt a.$$A SPW propagates over the inner surface with electric field
$${E_z} = A(r){e^{ - i({\rm \omega} t - {k_z}{\hat z})}}.$$Using this in the wave equation one obtains the equation governing A
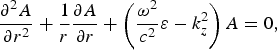$$\displaystyle{{{{\rm \partial} ^2}A} \over {{\rm \partial} {r^2}}} + \displaystyle{1 \over r}\displaystyle{{{\rm \partial} A} \over {{\rm \partial} r}} + \left( {\displaystyle{{{{\rm \omega} ^2}} \over {{c^2}}}{\rm \varepsilon} - k_z^2 } \right)A = 0,$$giving
$$A = {A_0}{I_0}({{\rm \alpha} _{\rm I}}r)\; {\rm for}\,r \lt a,$$
$$A = A_0^{\prime} {K_0}({{\rm \alpha} _{{\rm II}}}r)\,\; {\rm for}\,r \gt a,$$where
$${\rm \varepsilon} = 1\,\; {\rm for}\,r \lt a,$$
$${\rm \varepsilon} = {{\rm \varepsilon} _{\rm p}} = \left( {1 - {\rm \omega} _{\rm p}^2 /{{\rm \omega} ^2}} \right)\,{\rm for}\; r \gt a,$$
$${\rm \alpha} _{\rm I}^2 = k_z^2 - \displaystyle{{{{\rm \omega} ^2}} \over {{c^2}}},$$
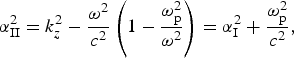$${\rm \alpha} _{{\rm II}}^2 = k_z^2 - \displaystyle{{{{\rm \omega} ^2}} \over {{c^2}}}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2}}}} \right) = {\rm \alpha} _{\rm I}^2 + \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{c^2}}},$$
where, ωp = (n 0e 2/mε0)1/2, −e, and m are the electronic charge and mass. Using E z in the relevant Maxwell's equations one obtains 
$\vec H = \hat{\rm \phi} \,{H_{\rm \phi}} $ and E r
$${H_{\rm \phi}} = \displaystyle{{\rm \omega} \over {{k_z}}}{{\rm \varepsilon} _0}{\rm \varepsilon} {E_{\rm r}}.$$
$${E_{\rm r}} = - \displaystyle{{i{k_z}} \over {(k_z^2 - {{\rm \omega} ^2}{\rm \varepsilon} /{c^2})}}\displaystyle{{\rm \partial} \over {{\rm \partial} r}}{E_z}.$$Employing the continuity of E z and H ϕ at r = a, we obtain the SPW dispersion relation
$$\displaystyle{{{I_1}({{\rm \alpha} _{\rm I}}a)} \over {{I_0}({{\rm \alpha} _{\rm I}}a)}} = - \displaystyle{{{{\rm \alpha} _{\rm I}}} \over {{{\rm \alpha} _{{\rm II}}}}}\displaystyle{{{K_1}({{\rm \alpha} _{{\rm II}}}a)} \over {{K_0}({{\rm \alpha} _{{\rm II}}}a)}}{{\rm \varepsilon} _{\rm p}}.$$For αIa ≫ 1 and αIIa ≫ 1, this dispersion relation reduces to the usual SP dispersion relation over a planar surface
$${k_z} = \displaystyle{{\rm \omega} \over c}{\left( {\displaystyle{{{{\rm \varepsilon} _{\rm p}}} \over {{{\rm \varepsilon} _{\rm p}} + 1}}} \right)^{1/2}},$$The power carried by the SPW is
$${P_{\rm s}} = {\rm \pi} \int {E_{\rm r}^{\ast}} {H_{\rm \phi}} \,rdr,$$
$$\eqalign{= \displaystyle{{{\rm \pi} {{\rm \varepsilon} _0}{k_z}{\rm \omega}} \over {{\rm \alpha} _{\rm I}^2}} A_0^2 \left[ {\int_0^a {I_1^2 \left( {{{\rm \alpha} _{\rm I}}r} \right)rdr + \displaystyle{{{{\rm \varepsilon} _{\rm p}}{\rm \alpha} _{\rm I}^2} \over {{\rm \alpha} _{{\rm II}}^2}} \displaystyle{{I_0^2 ({{\rm \alpha} _{\rm I}}a)} \over {K_0^2 ({{\rm \alpha} _{{\rm II}}}a)}}\int_a^\infty {K_1^2 \left( {{{\rm \alpha} _{{\rm II}}}r} \right)rdr}}} \right].}$$ We have solved Eq. (7) numerically for the following parameters: a = 2 μm, ωpa/c = 0.2, and εL = 9 (corresponding to gold). In Figure 1 we have plotted the dispersion relation; we see that the frequency asymptotically approaches 
${\rm \omega} = 0.71 {{\rm \omega} _{\rm p}}$.
Fig. 1. Plot of dispersion relation of SPW for the parameters a = 2 μm, ωpa/c = 0.2, and εL = 9.
3. EXCITATION OF THz SPW
Let two lasers propagate through the hollow plasma cylinder in the cylindrically symmetric fundamental mode (cf. Fig. 2). The axial components of the laser fields satisfying wave equation [Eq. (2)] can be written as
$${E_{{\rm j}z}} = {A_{\rm j}}{e^{ - i({{\rm \omega} _{\rm j}}t - {k_{{\rm j}z}}z)\,}},$$
$$\eqalign{{A_{\rm j}} & = {A_{0{\rm j}}}{J_0}({{\rm \delta} _{\rm j}}r),\; \;{\rm for}\;r \gt a, = {A_{0{\rm j}}}\displaystyle{{{J_0}({{\rm \delta} _{\rm j}}a)} \over {{K_0}({{\rm \beta} _{\rm j}}a)}}{K_0}({{\rm \beta} _{\rm j}}r), \cr & = {A_{0{\rm j}}}\displaystyle{{{J_0}({{\rm \delta} _{\rm j}}a)} \over {{K_0}({{\rm \beta} _{\rm j}}a)}}{K_0}({{\rm \beta} _{\rm j}}r),\,{\rm for}\,r \lt a,} $$where j = 1, 2 and 
${{\rm \delta} _{\rm j}} = {({\rm \omega} _{\rm j}^2 - k_{{\rm j}z}^2 {c^2})^{1/2}}/c,\;{{\rm \beta} _{\rm j}} = {({\rm \omega} _{\rm p}^2 + k_{{\rm j}z}^2 {c^2}}$
${- {\rm \omega} _{\rm j}^2 )^{1/2}} /c\; {{\rm \beta} _{\rm j}} = {({\rm \omega} _{\rm p}^2 + k_{{\rm j}z}^2 {c^2} - {\rm \omega} _{\rm j}^2 )^{1/2}}/c$. Using Maxwell's equations one can deduce E jr and H jϕ. These turn out to be the same as given by Eqs. (5) and (6) with ω, ε replaced by ωj, and 
${{\rm \varepsilon} _{\rm j}} = (1 - {\rm \omega} _{\rm p}^2 /{\rm \omega} _{\rm j}^2 )$. Employing the boundary conditions on E z, H ϕ, and H ϕ at r = a one obtains the dispersion relation, for laser of frequency 
${{\rm \omega} _{1}}$
$$\displaystyle{{J_0^{\prime} ({{\rm \delta} _1}a)} \over {{J_0}({{\rm \delta} _1}a)}} = - \displaystyle{{{{\rm \delta} _1}} \over {{{\rm \beta} _1}}}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} _{1}}}}} \right)\displaystyle{{K_0^{\prime} ({{\rm \beta} _1}a)} \over {{K_0}({{\rm \beta} _1}a)}}.$$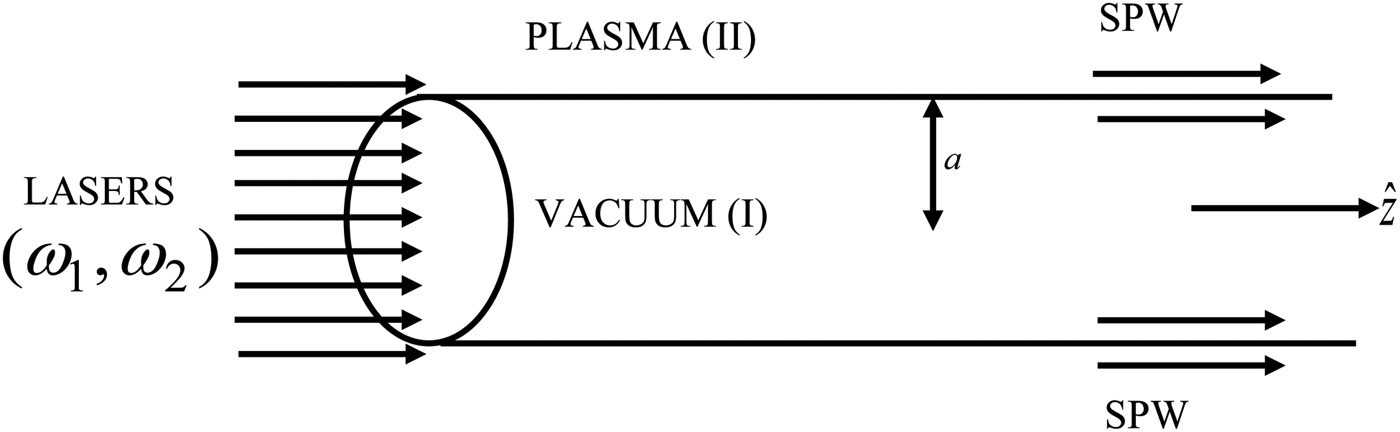
Fig. 2. Schematic of beat wave excitation of THz SPW over a hollow plasma cylinder.
From the expressions for δ1 and β1 one may write 
${\rm \beta} _1^2 = {\rm \omega} _{\rm p}^2 /$
${c^2} - {\rm \alpha} _1^2 $. Using this in Eq. (11) one gets an equation that determines δ1c/ωp explicitly in terms of 
$a{{\rm \omega}_{\rm p}}/c$ and ω1/ωp. For ω1/ωp ≫ 1, δ1c/ωp is fairly independent ω1/ωp. We call this value of δ1c/ωp as α⊥c/ωp, which is fixed for a particular mode, irrespective of ω1/ωp. Thus the dispersion relation for transverse magnetic (TM) mode reduces to 
${\rm \omega} _{\rm j}^2 = {\rm \alpha} _ \bot ^2 {c^2} + k_{{\rm j}z}^2 {c^2}$. For 
$a{{\rm \omega} _{\rm p}}/c = 4$, one obtains α⊥c/ωp = 0.7, hence 
${\rm \omega} _{\rm j}^2 /{\rm \omega} _{\rm p}^2 = 0.49 + k_{{\rm j}z}^2 {c^2}/{\rm \omega} _{\rm p}^2 $. The field structure is quite similar to Gaussian. The power carried by a laser is
$$\hskip-142pt{P_{\rm L}} = {\rm \pi} \int {E_{\rm r}^{\ast}} {H_{\rm \phi}} \,rdr,$$
$$\eqalign{\cong \displaystyle{{{\rm \pi} {{\rm \varepsilon} _0}{k_{1z}}{{\rm \omega} _1}} \over {{\rm \alpha} _ \bot ^2}} A_{01}^2 \left[ {\int_0^a {J_1^2 \left( {{{\rm \alpha} _ \bot} r} \right)rdr + \displaystyle{{{\rm \alpha} _ \bot ^2} \over {{\rm \beta} _{1}^2}} \displaystyle{{J_0^2 ({{\rm \alpha} _ \bot} a)} \over {K_0^2 ({{\rm \beta} _{1}}a)}}\int\limits_a^\infty {K_1^2 \left( {{{\rm \beta} _{1}}r} \right)rdr}}} \right].}$$The lasers impart oscillatory velocities to electrons
$${\vec v}_1 = \displaystyle{{e{{\vec E}_1}} \over {mi{{\rm \omega} _{\,1}}}},$$
$${\vec v}_2 = \displaystyle{{e{{\vec E}_2}} \over {mi{{\rm \omega} _{\,2}}}}.$$ They also exert a beat ponderomotive force on electrons at the beat frequency, that goes as e −i(ωt−k zz) with 
${\rm \omega} = {\rm \omega}_{1} - {{\rm \omega}_{2}},$
${k_z} = {k_{1z}} - {k_{2z}}$.
$${\vec F}_{{\rm p}_{{\rm \omega}_1 - {\rm \omega}_2}} = e\nabla {\rm \phi}_{\rm p} = - \displaystyle{m \over 2}\nabla ({\vec v}_1 \cdot {\vec v}_2^{\ast} ).$$The ponderomotive force imparts oscillatory velocity to electrons
$${\vec v}_{\rm \omega}^{{\,\rm NL}} = - \displaystyle{{{{\vec F}_{{{\rm p}_{{{\rm \omega_1 - {{\rm \omega} _2}}}}}}}} \over {mi{\rm \omega}}} = \displaystyle{{\nabla ({{\vec v}_1} \cdot {\vec v}_2^{{\,}\ast} )} \over {2i{\rm \omega}}}, $$giving a nonlinear current
$${{\vec J}^{{\,\rm NL}}} = - {n_e}e\,{\vec v}_{\rm \omega}^{{\, \rm NL}} \;\; {\rm for}\,r \gt a,$$
$$\hskip-23pt = 0\,{\rm for}\,r \lt a.$$The wave equation governing the propagation of THz SPW is
$${\nabla ^2}{\vec E} - \nabla (\nabla \cdot {\vec E}) + \left( {\displaystyle{{{{\rm \omega} ^2} - {\rm \omega} _p^2} \over {{c^2}}}} \right){\vec E} = - \displaystyle{{i{\rm \omega}} \over {{c^2}{{\rm \varepsilon} _0}}}{{\vec J}^{{\, \rm NL}}},$$
$\nabla \cdot $ of the above equation gives
$$\left( {\displaystyle{{{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2} \over {{c^2}}}} \right)\nabla \cdot {\vec E} = - \displaystyle{{i{\rm \omega}} \over {{c^2}{{\rm \varepsilon} _0}}}{{\vec J} ^{{\, \rm NL}}}.$$Hence the Z-component of Eq. (17) can be written as
$$\eqalign{{\nabla ^2}{E_z} & + \left( {\displaystyle{{{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2} \over {{c^2}}}} \right){E_z} = - \displaystyle{{i{\rm \omega}} \over {{c^2}{{\rm \varepsilon} _0}}}J_z^{{\rm NL}} \cr & + {\nabla _z}\left( { - \displaystyle{{i{\rm \omega} \,(\nabla \cdot {{\vec J}^{{\, \rm NL}}})} \over {{{\rm \varepsilon} _0}({{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 )}}} \right).}$$For k za > 1, this equation takes the form
$$\eqalign{{\nabla ^2}{E_z} & + \left( {\displaystyle{{{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2} \over {{c^2}}}} \right){E_z} = \displaystyle{{m{\rm \omega} c} \over e}\displaystyle{{{\rm \omega} _{\rm p}^2 \,i{k_z}({{\vec v}_1} \cdot {\vec v}_2^{{\,}\ast} )} \over {2{c^3}{\rm \omega} ({{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 )}} \cr & \quad \times\left( {{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 - k_z^2 {c^2} - \displaystyle{{8{c^2}} \over {r_0^2}} + \displaystyle{{16{c^2}} \over {r_0^4}}} \right),} $$where, k z = k 1z − k 2z and r 0 is the radial half width of the laser, for getting Eq. (19), we have used
$$\nabla \left( {{{\vec J}^{{\,\rm NL}}}} \right) \cong - \displaystyle{{{n_0}e} \over {2i{\rm \omega}}} {\nabla ^2}({\vec v}_1 \cdot {\vec v}_2^{{\,}\ast} ),$$
$$= - \displaystyle{{{n_0}e} \over {2i{\rm \omega}}} \left( - k_z^2 + \displaystyle{{{{\rm \partial} ^2}} \over {{\rm \partial} {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\rm \partial} \over {{\rm \partial} r}}\right)({\vec v}_1 \cdot {\vec v}_2^{{\,}\ast} ).$$ The z dependence of the right hand side (RHS) of Eq. (19) is 
$e^{i\lpar k_{1z}-k_{2z}\rpar z}$, for ω1, ω2 ≫ ωp, α⊥c, k 1z − k 2z = ω/v g1, where 
${v_{{\rm g1}}} = c\left( {1 - {\rm \alpha} _ \bot ^2 {c^2}/2{\rm \omega} _{\,1}^2} \right)$, thus
$${k_z} = {k_{1z}} - {k_{2z}} = \displaystyle{{\rm \omega} \over c}\left( {1 + \displaystyle{{{\rm \alpha} _ \bot ^2 {c^2}} \over {2{\rm \omega} _{\,1}^2}}} \right) = \displaystyle{{\rm \omega} \over c}{\left( {\displaystyle{{{{\rm \varepsilon} _{\rm p}}} \over {{{\rm \varepsilon} _{\rm p}} + 1}}} \right)^{1/2}}.$$ For phase matching k z must equal the parallel wave number of THz SPW. For 
${{\rm \alpha} _{\rm I}}a \gg 1,\;{I_0}({{\rm \alpha} _{\rm I}}a) = {e^{{{\rm \alpha} _{\rm I}}a}}/\sqrt {2{\rm \pi} {{\rm \alpha} _{\rm I}}a}, \;{I_0}({{\rm \alpha} _{\rm I}}a) = {I_0}$, and 
${K_0}({{\rm \alpha} _{{\rm II}}}a) = {e^{ - {{\rm \alpha} _{{\rm II}}}a}}\sqrt {{\rm \pi} /2{{\rm \alpha} _{{\rm II}}}a} $, so we have
$$1 = - \displaystyle{{{{\rm \alpha} _{\rm I}}} \over {{{\rm \alpha} _{{\rm II}}}}}{\rm \varepsilon},$$
$${k_z} = \displaystyle{{\rm \omega} \over c}{\left( {\displaystyle{{{{\rm \varepsilon} _{\rm p}}} \over {{{\rm \varepsilon} _{\rm p}} + 1}}} \right)^{1/2}},$$using this value of k z in Eq. (20) one obtains the requisite value of 
${{\rm \varepsilon} _{\rm p}},{{\rm \varepsilon} _{\rm p}} = - ({\rm \omega} _{\rm p}^2 /{\rm \alpha} _ \bot ^2 {c^2}) \cdot (2{\rm \omega} _1^2 /{\rm \omega} _{\rm p}^2 ) - 1$.
Thus the phase matching condition for resonant excitation of the THz SPW by the lasers turns out to be
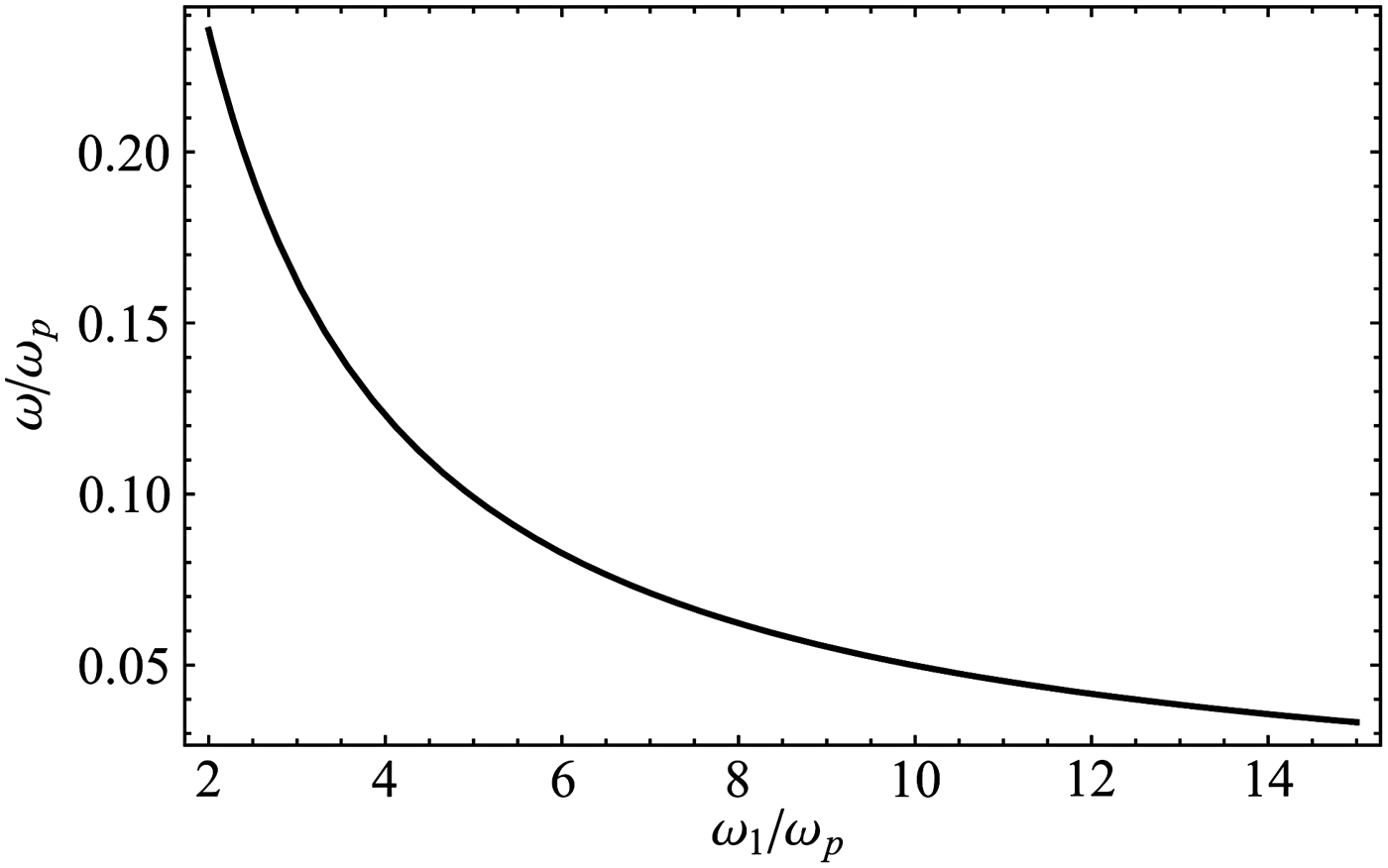
$$\displaystyle{{{\rm \omega} _{\rm p}^2} \over {{{\rm \omega} ^2}}} = 2 + \displaystyle{{4{\rm \omega} _{\,1}^2} \over {{\rm \omega} _{\rm p}^2}}. $$ From the above equation we plot ω/ωp versus 
${{\rm \omega} _{1}}/{{\rm \omega} _{\rm p}}$, in Figure 3, we see that the THz frequency falls off with the increasing laser frequency.
Fig. 3. Plot of ω/ωp versus 
${\rm \omega}_{1}/{{\rm \omega}_{\rm p}}$ (THz frequency vs., laser frequency).
Under exact phase matching we solve Eq. (17) iteratively. First we ignore the RHS, then solution of this equation is
$${E_z} = A{\vec F}(r){e^{ - i({\rm \omega} t - {k_z}z)}},$$where
$$F = {I_0}({{\rm \alpha} _{\rm I}}r)\,{\rm for}\,r \lt a,$$
$$F = \displaystyle{{{I_0}({{\rm \alpha} _{\rm I}}a)} \over {{K_0}({{\rm \alpha} _{{\rm II}}}a)}} \cdot {K_0}({{\rm \alpha} _{{\rm II}}}r)\,{\rm for}\,r \gt a.$$ Substituting E z from above in Eq. (17) and multiplying the resulting equation by 
$Frdr$ and integrating it from 0 to ∞. With finite RHS we assume that the radial mode structure remains the same but A becomes a function of z, from Eq. (16) we have
$$\eqalign{& 2i{k_z}{c^2}\displaystyle{{{\rm \partial} A} \over {{\rm \partial} z}} + A\left( {{{\rm \omega} ^2} - {\rm \omega} _{\rm m}^2} \right)\left( {{P_1} + \displaystyle{{I_0^2 ({{\rm \alpha} _{\rm I}}a)} \over {K_0^2 ({{\rm \alpha} _{{\rm II}}}a)}}{P_2}} \right) \cr & \quad = \displaystyle{{m{\rm \omega} c} \over e}\displaystyle{{{\rm \omega} _{\rm p}^2 i{k_z}\,} \over {2 {\rm \omega} ({{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 )}}\displaystyle{{{I_0}({{\rm \alpha} _{\rm I}}a)} \over {{K_0}({{\rm \alpha} _{{\rm II}}}a)}}\displaystyle{{{e^2}{A_{01}}{A_{02}}} \over {{m^2} {{\rm \omega} _1}{{\rm \omega} _2}}}\displaystyle{{{J_0}({{\rm \alpha} _1}a)} \over {{K_0}({{\rm \beta} _1}a)}}\displaystyle{{{J_0}({{\rm \alpha} _2}a)} \over {{K_0}({{\rm \beta} _2}a)}} \cr & \quad\quad\times\, \left[ {\left( {{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 - k_z^2 {c^2} - \displaystyle{{8{c^2}} \over {r_0^2}}} \right){P_3} + \displaystyle{{16{c^2}} \over {r_0^4}} {P_4}} \right],}$$
where ωm is the eigen frequency of the TM mode THz wave, 
${{\rm \omega} ^2} - {\rm \omega} _{\rm m}^2 \simeq {\rm \beta} {\rm \omega} _{\rm p}^2 $, where β ≤ 1 is a parameter that accounts for the waveguide effects.
$$\eqalign{\displaystyle{{eA} \over {m{\rm \omega} c}} & = \displaystyle{{z{\rm \omega}} \over c}\displaystyle{{{\rm \omega} _{\rm p}^2 \,} \over {4{c^2}{{\rm \omega} ^2}({{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 )}} \displaystyle{{{I_0}({{\rm \alpha} _{\rm I}}a)} \over {{K_0}({{\rm \alpha} _{{\rm II}}}a)}}\displaystyle{{{e^2}{A_{01}}{A_{02}}} \over {{m^2} {{\rm \omega} _1}{{\rm \omega} _2}}}\displaystyle{{{J_0}({{\rm \alpha} _1}a)} \over {{K_0}({{\rm \beta} _1}a)}}\displaystyle{{{J_0}({{\rm \alpha} _2}a)} \over {{K_0}({{\rm \beta} _2}a)}} \cr & \quad\times \left[ {\left( {{{\rm \omega} ^2} - {\rm \omega} _{\rm p}^2 - k_z^2 {c^2} - \displaystyle{{8{c^2}} \over {r_0^2}}} \right){P_3} + \displaystyle{{16{c^2}} \over {r_0^4}} {P_4}} \right],} $$where
$${P_1} = \int_0^a {I_0^2 ({{\rm \alpha} _{{\rm II}}}r)rdr},$$
$${P_2} = \int_a^\infty {K_0^2 ({{\rm \alpha} _{{\rm II}}}r)rdr},$$
$${P_3} = \int_a^\infty {\left[ {{K_0}({{\rm \beta} _1}r){K_0}({{\rm \beta} _2}r) + \displaystyle{{{k_{1z}}{k_{2z}}} \over {{{\rm \beta} _1}{{\rm \beta} _2}}}K_0^{\prime} ({{\rm \beta} _1}r)K_0^{\prime} ({{\rm \beta} _2}r)} \right]rdr}, $$
$${P_4} = \int_a^\infty {\left[ {{K_0}({{\rm \beta} _1}r){K_0}({{\rm \beta} _2}r) + \displaystyle{{{k_{1z}}{k_{2z}}} \over {{{\rm \beta} _1}{{\rm \beta} _2}}}K_0^{\prime} ({{\rm \beta} _1}r)K_0^{\prime} ({{\rm \beta} _2}r)} \right]rdr}.$$The power conversion efficiency may be written as
$$\eqalign{{\rm \eta} & = \displaystyle{{{P_{{\rm THz}}}} \over {{P_{\rm L}}}} = \displaystyle{{\displaystyle{{{\rm \pi} {{\rm \varepsilon} _0}{k_z}{\rm \omega}} \over {{\rm \alpha} _{\rm I}^2}} A_0^2 \left[ \matrix{\int_0^a {I_1^2 \left( {{{\rm \alpha} _{\rm I}}r} \right)rdr + \displaystyle{{{{\rm \varepsilon} _{\rm p}}{\rm \alpha} _{\rm I}^2} \over {{\rm \alpha} _{{\rm II}}^2}} \displaystyle{{I_0^2 ({{\rm \alpha} _{\rm I}}a)} \over {K_0^2 ({{\rm \alpha} _{{\rm II}}}a)}}} \hfill \cr \quad \times \int_a^\infty {K_1^2 \left( {{{\rm \alpha} _{{\rm II}}}r} \right)rdr} \hfill} \right]} \over {\displaystyle{{{\rm \pi} {{\rm \varepsilon} _0}{k_{1z}}{{\rm \omega} _1}} \over {{\rm \alpha} _ \bot ^2}} A_{01}^2 \left[ \matrix{\int_0^a {J_1^2 \left( {{{\rm \alpha} _ \bot} r} \right)rdr + \displaystyle{{{\rm \alpha} _ \bot ^2} \over {{\rm \beta} _{ 1}^2}} \displaystyle{{J_0^2 ({{\rm \alpha} _ \bot} a)} \over {K_0^2 ({{\rm \beta} _{ 1}}a)}}} \hfill \cr \quad \times \int_a^\infty {K_1^2 \left( {{{\rm \beta} _{ 1}}r} \right)rdr} \hfill} \right]}}.} $$We have carried out numerical calculations for Eq. (22) using MATHEMATICA with the parameters: a 1 = 0.1, a 2 = 0.1, k zc/ωp = 0.3, r 0ωp/c = 1, and zω/c = 100. In Figure 4 we have plotted the normalized SPW THz amplitude |eA/mω c| as a function of ωpa/c at ωpa/c = 0.3 (red line) and ωpa/c = 0.6 (green dashed). As the plasma frequency is raised the amplitude falls monotonically because of the low coupling at higher frequencies. The THz amplitude has an inverse relationship with the laser frequencies ω1 andω2, hence decreases as the laser frequencies increase. Also the variation of THz amplitude with the laser beam width is explicit from the figure as the radius of the plasma channel is of the order of the laser beam width. After solving Eq. (23), we plot the efficiency (P THz/P L) as a function of ωpa/c for the parameters: ω/ωp = 0.6 and ω1/ωp ≈ 100 (Fig. 5). We see that efficiency falls off as the normalized size of the capillary plasma increases. The reason is that the power of the laser increases as the square of the radius, whereas the power of the THz goes linearly with a.
Fig. 4. Normalized SPW THz amplitude |eA/mω c|2 as a function of ωpa/c for r 0ωp/c = 1 and k zc/ωp = 0.3 at ωpa/c = 0.3, 0.6.
Fig. 5. Power conversion efficiency (P THz/P L) as a function of ωpa/c for ω/ωp = 0.6 and ω1/ωp ≈ 100.
4. DISCUSSION
Laser beat wave excitation of SPW on a hollow plasma cylinder has several notable features. The processes is resonant (phase matched) when the phase velocity of the SPW equals the group velocity of lasers. This demands 
${{\rm \omega} _1}/{{\rm \omega} _{\rm p}}\sim {{\rm \omega} _{\rm p}}/{\rm \omega} $, as ω1 increases ω decreases Under phase matched condition, THz power scales linearly with distance, up to a distance of the order of attenuation length, (k zi)−1 and then saturates. The THz SPW amplitude decreases with increasing aω p/c as the evanescent laser field in the plasma decreases. However, the THz amplitude increases when THz frequency increases.
In the present formalism we have neglected the collisions in the electron response. If one includes the collisional effects, εeff gets modified to 
${{\rm \varepsilon} _{{\rm eff}}} = 1 - {\rm \omega} _{\rm p}^2 (1 - i{\rm \nu} /{\rm \omega} )/{{\rm \omega} ^2}$, where ν is the electron collision frequency, this leads to imaginary part in 
${k_{zi}}\sim({\rm \nu} /{\rm \omega} )({\rm \omega} _{\rm p}^2 /{{\rm \omega} ^2}){k_{zr}}$. For 
$z \gt k_{zi}^{ - 1} $, one must replace z by 
$k_{zi}^{ - 1} $ in Eq. (22). Thus the amplitude of THz saturates to this value.
ACKNOWLEDGEMENTS
The authors are grateful to Prof. C. S. Liu (University of Maryland) for valuable discussions.
