1. INTRODUCTION
Nowadays, sub-picosecond high intensity lasers can generate short bunches of energetic ion beams with good efficiency (Pegoraro et al., 2004; Roth et al., 2005). Many applications of these ion beams are emerging: (1) ignition of an inertial fusion target (Tahir et al., 1997; Roth et al., 2001; Deutsch, 2004), (2) ion radiography (King et al., 1999) or ion imaging (Borghesi et al., 2001, 2005; Breschi et al., 2004) of plasma targets, and (3) isochoric heating of solid into plasmas (Patel et al., 2003), etc. All of them require an accurate description of the interactions between the ion beam and the plasma target. This paper is focused on the effects of target plasma nuclei on correlated transport of the beam ions.
When the density of an atomic beam increases, the ions get closer, and new interactions take place between them. But these interactions can also be observed in low density molecular ion beams. These ions dissociate when entering the target, so that the resulting charged fragments are very close to each other and their motion is also highly correlated (Zwicknagel et al., 1995; Zwicknagel & Deutsch, 1996). Because the energy loss of molecular beams is higher than that of atomic beams, they have also been proposed as drivers for inertial confinement fusion (Deutsch, 1990, 1992; Eliezer et al., 1995). Regardless of the origin of the closeness of the charges, the interaction forces between them when they move through an electronic medium (plasma) are called vicinage forces (Neufeld & Ritchie, 1955). These vicinage forces change the movement of the ions giving rise to a correlated motion.
The correlated motion of the ions will be studied through a molecular dynamic method included in a computer code. Dielectric formalism has been used to describe the forces due to electronic excitations in the medium; the self-retarding ion force and the vicinage forces created by its partner ions. Nuclear collisions with target plasma nuclei are incorporated in the computer code through a Monte Carlo method.
In Section 2 we detail the dielectric formalism used to study the electronic stopping of cluster ions. This formalism has been successfully applied to the interaction of protons with plasmas (Barriga-Carrasco et al., 2004) and molecular protons with solid targets (Barriga-Carrasco & Garcia-Molina, 2004). Ion scattering due to target nuclei are treated in Section 3. The final purpose of this paper is to include our conclusions in the computer code, TAMIM (Transport of Atomic and Molecular Ions in Matter), former MBC-ITFIP (Barriga-Carrasco & Maynard, 2005).
2. ELECTRONIC STOPPING OF CLUSTER IONS
In the dielectric formalism, the dielectric function ε(k,ω) defines the target taking into account its response to electronic excitations induced by a charged ion that travels through it. This function depends on the momentum k and the energy ω of the produced excitation. To simplify theoretical calculations, atomic units (a.u.) will be used, except for results where plasma units will be stated. In the random phase approximation, the longitudinal dielectric function of a classical electron plasma is written as (Peter & Meyer-ter-Vehn, 1991):
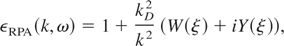
with
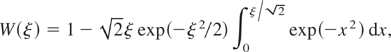
and
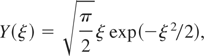
where ξ = ω/(kvth) with

the electron thermal velocity, kD = ωp /vth the inverse Debye length and
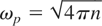
the plasma frequency. T and n are the temperature (in eV) and the electronic density (in a.u.) of the target plasma, respectively.
Following the dielectric formalism, the induced force produced by a point-like charge Zp1, moving at velocity v inside an uniform electron gas, on a neighbor charge Zp2 is (Barriga-Carrasco & Garcia-Molina, 2003):


where z and σ are the coordinates parallel and perpendicular of the neighbor projectile from the projectile that generates the potential in the reference frame of the motion of the last one. J0(x) and J1(x) are the zeroth and the first order Bessel functions. It is worthwhile to mention that the induced or vicinage forces in Eqs. (4) and (5) do not include the Coulomb force and they only depend on the target through the dielectric function ε(k,ω). As an example, Figure 1 shows the vicinage forces that one proton traveling with velocities vp = vth, 2vth and 3vth produces on another proton at a distance σ = 1/kD = λD, as a function of the longitudinal distance zkD.

Induced forces that one proton with velocity vp = vth, 2vth and 3vth produces on another proton at a distance σ = λD through a plasma with n = 1023 cm−3 and T = 10 eV, as a function of longitudinal distance zkD. Forces are normalized to F0 = Zp1 Zp2 /λD2.
Assigning z = σ = 0 and Zp1 = Zp2 to Eqs. (4) and (5) results Fσ = 0, and Fz yields the self-stopping particle force Fs. The variation of the projectile kinetic energy is dE = Fsvp1 dt, so the electronic stopping, Se, defined as the energy loss per unit path length, becomes
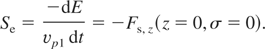
Then, the well-known electronic stopping formula for one projectile is recovered
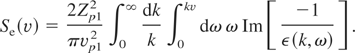
Thus, the sum of forces on projectile 1 and 2 are
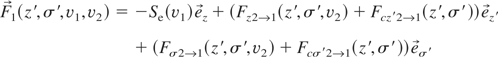
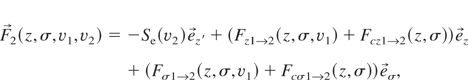
where the values without and with prima refer to the projectile 1 and to the projectile 2 movement frames, and v1 and v2 are their respective velocities. Coulomb forces are denoted by FC.
3. NUCLEAR SCATTERING MODEL
The classical dispersion theory will be used to treat projectile interactions with the target nuclei. Let us consider Ep = mp vp2/2, mp and Zp as the projectile energy, mass and charge; and mn and Zn as the target nucleus mass and charge, in the center of mass frame. The target nucleus produces a potential energy V(r) at the projectile position during the collision, so the projectile is scattered with an angle θ (Goldstein, 1980)
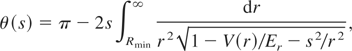
where Er = 4mp mn Ep /(mp + mn)2 is the maximum transferable energy in a collision, r is the distance between the projectile and the force center, Rmin is the minimum r, and s is the impact parameter.
The potential energy V(r) is written as
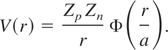
For a fully ionized plasma Φ is the Debye potential Φ(r/a) = exp(−r/a) and a is the dynamical adiabatic screening length, which depends on temperature
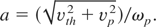
Φ and a are obtained from the average atom model (Maynard et al., 2002) for a partially ionized plasma.
The elastic collision transfers an energy ET to the nucleus which is lost by the projectile. The energy transferred is related to the scattering angle θ by
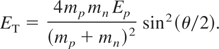
Therefore, the greater the scattering angle, the greater the energy loss. In our energy regime, Eq. (13) introduces only a small correction to the inelastic proton energy loss, Eq. (7). Nuclear collisions mainly produce changes on the movement direction of the projectiles, so they are not considered in Eqs. (8) and (9).
This nuclear scattering model is included in our computer code (TAMIM) through a binary collision model described by Möller et al. (1975) and using a Monte Carlo technique.
4. RESULTS
This section shows the effects of the nuclear scattering in the transport process of a fragmented H2+ ion. The interest in the study of these ions is that H2+ is the simplest molecular projectile and therefore, it can be used to test the effects due to the correlated motion of two charged particles through a target. But the same study can be done for other cluster ions.
The H2+ ion will lose its electron just entering the target and will dissociate into two protons, Zp1 = Zp2 = 1 and mp = 1 in proton units (p.u.), separated by an initial distance r0 = 1.08 × 10−8 cm (Garcia-Molina & Barriga-Carrasco, 2003). This gives two protons that move in close proximity, interacting between them and with the target electrons and nuclei. The target is considered to be deuterium, Zn = 1 and mn = 2 in p.u., in a plasma state characterized by its density, n = 1023 cm−3, and its temperature, T = 10 eV. The velocities of the H2+ projectiles impinging on the plasma target are low enough to see the effects of nuclear collisions in its slowing down, so vp ≈ vth.
The main difference on the transport between two correlated or isolated protons is due to the Coulomb and vicinage forces. Thus, we are going to analyze how nuclear collisions influence two fundamental quantities for calculating these forces: the interproton distance, r, and the angle between the interproton vector and the motion direction, α. It is worth to introduce here the logarithm of the dimensionless dwell time τ = log 10(t/tc), where tc = 1.47 fs is the characteristic Coulomb explosion time of the two protons fragmented from the H2+ ion.
Figure 2 shows the evolution of the adimensional interproton distance rkD as a function of the logarithm of the dwell time τ during the Coulomb explosion of H2+ protons traversing the target plasma with different velocities (a) vp = vth, (b) vp = 2vth and (c) vp = 3vth. Each graph represents this evolution taking into account only electronic stopping (square symbols), electronic stopping and Coulomb force (circle symbols), electronic stopping, Coulomb, and vicinage forces (up triangle symbols), and electronic stopping, Coulomb force, vicinage force, and nuclear collisions (down triangle symbols). We see that Coulomb repulsion separates the protons. When vicinage forces are also taken into account, the Coulomb repulsion is always delayed. This screening is a consequence of the asymmetry of vicinage forces that tries to join the two protons in σ and z direction. This is more significant in the late dwell times when the two protons are quite separated and the Coulomb force is smaller than the vicinage forces. These results are also more noticeable for low velocities. If nuclear collisions are considered, the delay produced by the vicinage forces is now canceled. Indeed, now r increases faster than for the bare Coulomb explosion. To check this, a new graph is plotted in Figure 2 for vp = 2vth. In this case, electronic stopping and nuclear collisions are only considered in the calculations. If it is compared with the graph of electronic stopping plus Coulomb force (circle symbols), it is concluded that nuclear collisions are more responsable of proton separation than Coulomb forces. This separation is faster for low impact projectile velocities as nuclear scattering effects are more significant.

Evolution of the adimensional interproton distance rkD as a function of the logarithm of dwell time τ during the Coulomb explosion of H2+ protons traversing the plasma with different velocities (a) vp = vth, (b) vp = 2vth and (c) vp = 3vth. Each graph represents this evolution taking into account only electronic stopping (square symbols), electronic stopping and Coulomb force (circle symbols), electronic stopping, Coulomb and vicinage forces (up triangle symbols), and electronic stopping, Coulomb force, vicinage force and nuclear collisions (down triangle symbols).
Many published works (see Arista (2000) for a complete list) have mentioned that vicinage forces tend to align the interproton vector in the motion direction due to its asymmetry. We studied this effect through the time evolution of the azimutal angle α between the interproton vector and the motion direction. Figure 3 shows the number of protons pairs with azimutal angle |α| ≤ 20° (Nal), as a function of the logarithm of dwell time τ for the same conditions as in Figure 2. When only self-stopping electronic forces are considered, the number of protons pairs aligned (Nal) does not vary as expected. Then adding Coulomb forces to the same calculations, the Nal slightly decreases for low velocities and slightly increases for high velocities, at long dwell times, because of the different self-stopping electronic force produced by these Coulomb forces in each proton of the same pair. Vicinage forces substantially increase the Nal percentage indicating that most part of protons pairs align their relative vectors along the motion direction. This also results from the asymmetry of the vicinage forces. In this case, the aligning of the interproton vector means that the relative averaged force Fσ is higher than the relative averaged Fz during protons flight. These effects are more significant at high velocities, as the ratio between the averaged Fσ and the averaged Fz forces is more important. When nuclear collisions are included in the calculations the interproton vector misaligns and the effects of the vicinage forces cancel. This cancellation happens more or less at the same dwell time, τ ≃ 1, for the three examined velocities.

Evolution of the number of aligned proton pairs (Nal) as a function of the logarithm of dwell time τ; for same conditions as in Figure 2.
5. CONCLUSIONS
In this work the correlated motion of two charged particles through a classical electron plasma has been studied. In particular, results have been shown for the case of two protons fragmented from a H2+ molecular ion in a Te = 10 eV and n = 1023 cm−3 deuterium plasma. The same study can be made for other correlated ions and target plasmas. The interest in the study of these ions is that H2+ is the simplest molecular projectile, and therefore, it can be used to investigate the correlated motion of two protons.
It has been shown that vicinage forces screen the Coulomb repulsion between the two protons and tend to align the interproton vector along motion direction. These effects are more important at low projectile velocities and for long dwell times. On the other hand, when proton collisions with target nuclei are considered, the effects of the vicinage forces are masked and surpassed: the relative proton distances increases more than for Coulomb repulsion and the number of proton pairs aligned decreases even more than in the initial percentage. The main conclusion of this work is that correlated motion of ions can not be investigated without considering vicinage forces and ion collisions with target nuclei.
ACKNOWLEDGMENT
This work was financed by he Spanish Ministerio de Educacion y Cultura.





