1. INTRODUCTION
The nonlinear interaction of highly intense laser beams with plasmas has recently received significant attention of a number of theoretical as well as experimental researchers due to its relevance to a wide range of applications including plasma based accelerators (Tajima & Dawson, Reference Tajima and Dawson1979; Singh et al., Reference Singh, Sharma and Tripathi2010a; Modena et al., Reference Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Malka, Darrow, Danson, Neely and Walsh2002; Hora et al., Reference Hora, Hoelss, Scheid, Wang, Ho, Osman and Castillo2000), laser plasma channeling (Borisov et al., Reference Borisov, Borovskiy, Korobkin, Prokhorov, Shiryaev, Shi, Luk, McPherson, Solem, Boyer and Rhodes1992; Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis-Jacquet, Malka and Miquel1995; Gibbon et al., Reference Gibbon, Monot, Auguste and Mainfray1995; Singh et al., Reference Singh and Walia2010b), X-ray lasers (Amendt et al., Reference Amendt, Eder and Wilks1991; Eder et al., Reference Eder, Amendt, DaSilva, London, MacGowan, Matthews, Penetrante, Rosen, Wilks, Donnelly, Falcone and Strobel1994; Faenov et al., Reference Faenov, Magunov, Pikuz, Skobelev, Gasilov, Stagira, Calegari, Nisoli, Silvestri, Poletto, Villoresi and Andreev2007), XUV beams (Burnett et al., Reference Burnett and Corkum1989), super continuum generation (Corkum et al., Reference Corkum, Rolland and Rao1986; Ting et al., Reference Ting, Krushelnick, Burris, Fisher, Manka and Moore1996), and fast ignition schemes for inertial confinement fusion (Tabak et al., Reference Tabak, Hammer, Glinsky, Kruer, Wilks, Woodworth, Campbell and Perry1994; Deutsch et al., Reference Deutsch, Bret, Firpo, Gremillet, Lefebvre and Lifschitz2008; Hora, Reference Hora2007; Seifter et al., Reference Seifter, Kyrala, Goldman, Hoffman, Kline and Batha2009). In all these applications, it is highly desirable that the laser beam propagate extended distances (many Rayleigh lengths) into plasma at high intensity and directionability. In the absence of an optical guiding mechanism, the propagation distance is limited to approximately to a Rayleigh (diffraction) length, due to diffraction divergence. In conventional optics, diffraction of laser beam can be prevented either by using optical fibers or relying on nonlinear self focusing. Laser propagation in a medium is often characterized by dielectric constant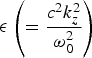 
${\rm \epsilon} \left( = {c^2 k_z^2 \over {\rm \omega}_0^2} \right) $; where ω0 is laser frequency and k z is propagation constant. Refractive guiding can occur when the transverse (radial) profile of the dielectric constant is peaked along the propagation axis. When this condition is satisfied, the phase velocity 
$v_p \lpar\!\! = {\textstyle{{\rm\omega _0 } \over {\rm k_z }}}\rpar $ becomes smaller on axis (r = 0) as compared to off axis and as a result phase fronts of the optical field become curved such that the laser beam focuses toward the axis. A plasma wave guide (channel) is formed by tailoring the transverse profile of the electron density N e(r) such that 
${\textstyle{{\partial N_e } \over {\partial r}}} \gt 0\comma \; $ i.e., 
${\textstyle{{\partial \rm\epsilon} \over {\partial r}}} \lt 0$. When intense laser beam propagates through such a plasma channel, various parametric instabilities such as self focusing, higher harmonic generation (HHG), stimulated raman scattering (SRS), stimulated Brillouin scattering (SBS), compton scattering, etc., come into play. However, self focusing continues to be a subject of great fascination due to its relevance to a wide range of applications including X-ray lasers, HHG, electron acceleration. The laser beams, having non-uniform intensity distribution along its wavefront, leads to change in dielectric constant of plasma by producing non-uniform redistribution of plasma electrons. In collisionless plasma, this redistribution of carriers take place on account of ponderomotive force that displaces electrons from high field region to low field region. Generation of higher harmonics of electromagnetic radiations in laser produced plasmas and laboratory plasmas is an important nonlinear process and has engaged the attention of a number of researchers due to its practical significance for many applications. Harmonic generation in laser plasma interaction has been studied extensively both experimentally as well as theoretically (Prashar et al., Reference Parashar and Pandey1992; Rax et al., Reference Rax and Fisch1992; Malka et al., Reference Malka, Modena, Najmudin, Dangor, Clayton, Marsh, Joshi, Danson, Neely and Walsh1997; Singh et al., Reference Singh and Walia2011a; Reference Singh and Walia2011b; Kant et al., (Reference Kant and Sharma2004; Reference Kant, Gupta and Suk2011; Reference Kant, Gupta and Suk2012); Rajput et al., Reference Rajput, Kant, Singh and Nanda2009). There are number of mechanisms through which one can generate higher harmonics of laser beam in plasmas. These mechanisms include resonance absorption (Erokhin et al., Reference Erokhin, Zakharov and Moiseev1969), parametric instabilities (Bobin, Reference Bobin1985), transverse density gradients associated with light filaments (Stamper et al., Reference Stamper, Lehmberg, Schmitt, Herbst, Young, Gardner and Obenshain1985), ionization fronts (Brunel, Reference Brunel1990), photon acceleration (Wilks et al., Reference Wilks, Dawson, Mori, Katsouleas and Jones1989), through excitation of plasma wave (Sodha et al., Reference Sodha, Sharma, Tewari, Sharma and Kaushik1978; Prashar et al., Reference Parashar and Pandey1992; Singh et al., Reference Singh and Walia2011a; Reference Singh and Walia2011b). The most common mechanism for HHG in plasmas is through the excitation of plasma wave at pump frequency by the laser beam. The process of HHG has strong influence on the nature of laser propagation through the plasma. It allows the penetration of laser power to over dense region and can provide valuable diagnostics information not only on plasma parameters such as local electron density, density gradients, expansion velocity, etc., but also on the presence of large electric and magnetic fields and plasma waves. (Teubner & Gibbon, Reference Teubner and Gibbon2009). This phenomenon presents new opportunities for applications such as nonlinear optics in the extreme ultraviolet region, photoelectron spectroscopy, and opacity measurements of high-density matter with high temporal and spatial resolution (Huillier et al., Reference Huillier, Descamps, Johansson, Norin, Mauritsson and Wahlstom2003).
Most of the theories of HHG are based on the assumption of a uniform laser beam or laser beam having Gaussian distribution of intensity along its wavefront. Since most of the laser beams used in experiments have non-uniform distribution of intensity along its wavefront, therefore it is necessary to take into account this non-uniformity in theory of HHG. A laser beam is usually assumed to be characterized by Gaussian intensity distribution function along its wavefront. In contrast to this picture, Patel et al. (Reference Patel, Key, Mackinnon, Berry, Borghesi, Chambers, Chen, Damian, Eagleton, Freeman, Glenzer, Gregori, Heathcote, Hey, Izumi, Kar, King, Nikroo, Niles, Park, Pasley, Patel, Shepherd, Snavely, Steinman, Stoeckl, Storm, Theobald, Town, Maren, Wilks and Zhang2005), measured the intensity profile for the Vulcan petawatt laser and found that intensity profile of the laser beam was not exactly Gaussian but was having deviation form Gaussian distribution. Further investigations of the laser beam spot profile of the Vulcan laser in Rutherford Appelton Laboratories by Nakatsutsumi et al. (Reference Nakatsutsumi, Davies, Kodama, Green, Lancaster, Akli, Beg, Chen, Clark, Freeman, Gregory, Habara, Heathcote, Hey, Highbarger, Jaanimagi, Key, Krushelnick, Ma, MacPhee, MacKinnon, Nakamura, Stephens, Storm, Theobald, Woerkom, Weber, Wei, Woolsey and Norreys2008), suggests that the beam intensity is characterized by function of the form
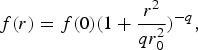$$\,f\lpar r\rpar = f\lpar 0\rpar \lpar 1 + \displaystyle{{r^2 } \over {qr_0^2 }}\rpar ^{ - q} \comma \; $$where the values of relevant parameters q and r 0 can be obtained by fitting the experimental data. Since, for a given power of laser beam, the average square of electric vector in the wavefront is much higher for q-Gaussian distribution than that for Gaussian distribution, the magnitude of generated harmonics is much higher in case of q-Gaussian irradiance. To the best of authors knowledge, no theoretical investigation on HHG by self focusing of q-Gaussian laser beams in preformed plasma channels has been carried out. This gives strong motivation for the study of HHG in preformed plasma channels by taking into consideration the deviation of intensity distribution of laser beam from Gaussian distribution.
In the present paper, electron plasma wave has been considered as a source for the generation of higher harmonics of the laser beam propagating through preformed collisionless plasma channel. In Section 2, moment theory has been developed to describe the evolution of spot size of q-Gaussian laser beam propagating through preformed collisionless plasma channel. In Section 3, source term for HHG has been setup. In Section 4, equation for yield of higher harmonics has been derived for q-Gaussian laser beam. In Section 5, detailed discussion of the results has been presented.
2. SELF FOCUSING OF LASER BEAM
Consider the propagation of an intense laser beam of frequency ω0 and wave vector k 0 having nonuniform intensity distribution (q-Gaussian) along its wavefront, through a preformed collisionless plasma channel having parabolic electron density distribution (Esarey et al., Reference Esaray, Sprangle, Krall and Ting1997)
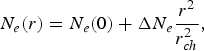$$N_e \lpar r\rpar = N_e \lpar 0\rpar + {\rm\Delta} N_e \displaystyle{{r^2 } \over {r_{ch}^2 }}\comma \; $$where N e(0) is the electron density on the axis of the channel, Δ N e = N e (r ch) − N e (0) is the depth of channel. The initial intensity distribution of the laser beam along its wavefront at z = 0 is given by (Sharma & Kourakis, Reference Sharma and Kourakis2010)
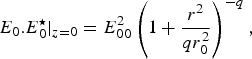$$E_0 .E_0^ \star \vert _{z = 0} = E_{00}^2 \left( 1 + \displaystyle{{r^2 } \over {qr_0^2 }}\right) ^{ - q} \comma \; $$where r 0 is the spot size of the laser beam at z = 0 and r is radial co-ordinate of the cylindrical co-ordinate system. The parameter ‘q’ describes the deviation of the intensity distribution of the laser beam from the Gaussian intensity distribution. As the value of q increases, the intensity distribution of the beam converges toward the Gaussian distribution and become exactly Gaussian for q = ∞. For z > 0, we assume an energy conserving q-Gaussian ansatz for the laser intensity.
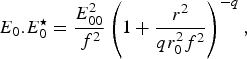$$E_0 .E_0^ \star = \displaystyle{{E_{00}^2 } \over {\,f^2 }}\left( 1 + \displaystyle{{r^2 } \over {qr_0^2 f^2 }}\right) ^{ - q} \comma \; $$where f is the dimensionless beam width parameter. The slowly varying electric field E of the pump beam satisfies the wave equation
$$\nabla ^2 {\bf E} - \nabla \lpar \nabla .{\bf E}\rpar + \displaystyle{{{\rm\omega} _0^2 } \over {c^2 }} {\rm\epsilon}{\bf E} = 0.$$In the Wentzel-Kramers-Brillouin approximation, the polarization term ∇ (∇.E) of Eq. (4) can be neglected, which is justified when
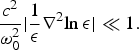$$\displaystyle{{c^2 } \over {{\rm\omega} _0^2 }}\vert \displaystyle{1 \over {\rm\epsilon}}\nabla ^2 {\rm ln} \,{\rm \epsilon} \vert \ll 1.$$Under this approximation wave Eq. (4) reduces to
$$\nabla ^2 {\bf E} + \displaystyle{{\rm \omega _0^2 } \over {c^2 }} {\rm \epsilon}{\bf E} = 0\comma \; $$and
$${\rm \epsilon} = {\rm \epsilon}_0 + \Phi \lpar E_0 E_0^ \star \rpar .$$
Here, ε0 = ε|r=0 is the axial dielectric constant of the channel and 
$\Phi \lpar E_0 E_0^ \star \rpar $ is the off axial part of the dielectric function. Due to non-uniform intensity distribution along the wavefront of the laser beam the plasma electrons experience ponderomotive force and hence get displaced from high field region to low field region, as a result the effective dielectric constant of the plasma get modified.The modified dielectric constant of the plasma channel is given by Sodha et al. (Reference Sodha, Ghatak and Tripathi1976)
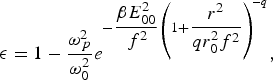$${\rm \epsilon} = 1 - \displaystyle{{\rm \omega^2}_{\!\!\!p } \over {{\rm \omega} _0^2 }}e^{ - {\displaystyle{{{\rm \beta} E_{00}^2 } \over {\,f^2 }}}\left( 1 + {\displaystyle{{r^2 } \over {qr_0^2 f^2 }}}\right) ^{\!\! - q} } \comma \; $$
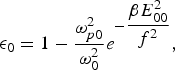$${\rm \epsilon}_0 = 1 - \displaystyle{{\rm \omega}_{p0}^2 \over {\rm \omega}_0^2} e^{ - \displaystyle{{\rm \beta} E_{00}^2 \over f^2}} \comma \; $$
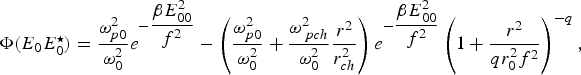$$\Phi \lpar E_0 E_0^{\star} \rpar = \displaystyle{{\rm \omega} _{p0}^2 \over {\rm \omega}_0^2} e^{ - \displaystyle{{\rm \beta} E_{00}^2 \over f^2}} - \left( \displaystyle{{\rm \omega}_{p0}^2 \over {\rm \omega}_0^2} + \displaystyle{{\rm \omega}_{\,pch}^2 \over {\rm \omega}_0^2} \displaystyle{r^2 \over r_{ch}^2} \right) e^{ - \displaystyle{{\rm \beta} E_{00}^2 \over f^2}}\left( 1 + \displaystyle{r^2 \over qr_0^2 f^2} \right)^{- q} \comma \; $$where
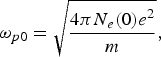$${\rm \omega} _{p0} = \sqrt{\displaystyle{4 {\rm \pi} N_e \lpar 0\rpar e^2 \over m}} \comma \;$$
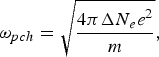$${\rm \omega}_{pch} = \sqrt {\displaystyle{{4 {\rm \pi\Delta} N_e e^2 } \over m}} \comma \;$$
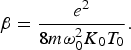$${\rm \beta} = \displaystyle{{e^2 } \over {8 m{\rm \omega} _0^2 K_0 T_0 }}.$$e and m are electronic charge and mass, T 0 is equilibrium temperature of plasma and K 0 is the Boltzmann constant. Taking E in Eq. (7) as
$${\bf E} = E_0 \lpar r\comma \; z\rpar \exp \lsqb \iota \lcub\omega _0 t - k_0 z\rcub\rsqb {\bf e}_{\bf x} \comma \; $$we get the following quasi optic equation
$$- 2\iota k_0 \displaystyle{{dE_0 } \over {dz}} + \nabla _ \bot ^2 E_0 + \displaystyle{{{\rm \omega} _0^2 {\rm \phi} } \over {c^2 }}E_0 = 0\comma \; $$
where we have neglected the term 
${\textstyle{{d^2 E_0 } \over {dz^2 }}}$ by assuming that variations in the z-direction are slower than those in radial direction. Eq. (13) can be written as
$$\iota \displaystyle{{dE_0 } \over {dz}} = \displaystyle{1 \over {2k_0 }}\nabla _ \bot ^2 E_0 + PE_0 \comma \; $$
where 
$P = {\textstyle{{k_0 } \over {2 {\rm \epsilon}_0 }}}{\rm \phi}$. Now from definition of second order moment, the mean square radius of the beam is given by
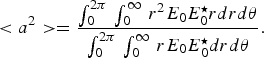$$\lt a^2 \gt = \displaystyle{{\vint_0^{2{\rm \pi }} \, \vint_0^\infty \, r^2 E_0 E_0^ \star rdrd\rm \theta } \over {\vint_0^{2{\rm \pi } } \, \vint_0^\infty \, rE_0 E_0^ \star drd\rm \theta }}.$$Following procedure of Lam et al. (Reference Lam, Lippmann and Tappert1977), we get the following differential equation governing the evolution of mean square radius of the laser beam with distance of propagation.
$$\displaystyle{{d^2 \lt a^2 \gt } \over {dz^2 }} = \displaystyle{{4I_2 } \over {I_0 }} - \displaystyle{4 \over {I_0 }}\vint_0^{2\rm \pi } \, \vint_0^\infty \, Q\lpar E_0 E_0^ \star \rpar rdrd\rm \theta .$$Where I 0 and I 2 are the invariants of Eq. (13)
$$I_0 = \vint_0^{2 \rm \pi} \, \vint_0^\infty \, \vert E_0 \vert ^2 rdrd\rm\theta \comma \; $$
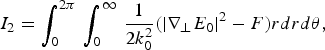$$I_2 = \vint_0^{2 \rm \pi} \, \vint_0^\infty \, \displaystyle{1 \over {2k_0^2 }}\lpar \vert \nabla _ \bot E_0 \vert ^2 - F\rpar rdrd\rm\theta \comma \; $$where,
$$F\lpar E_0 E_0^ \star \rpar = \displaystyle{1 \over {k_0 }}\vint_0^{E_0 E_0^ \star } \, P\lpar E_0 E_0^ \star \rpar d\lpar E_0 E_0^ \star \rpar \comma \; $$and
$$Q\lpar E_0 E_0^ \star \rpar = \left[{\displaystyle{{E_0 E_0^ \star P\lpar E_0 E_0^ \star \rpar } \over {k_0 }} - 2F\lpar E_0 E_0^ \star \rpar } \right].$$From Eqs. (4),(15), and (17) it can be shown that
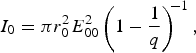$$I_0 = {\rm \pi} r_0^2 E_{00}^2 \left( 1 - \displaystyle{1 \over q}\right) ^{\!\! - 1} \comma \; $$
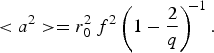$$\lt a^2 \gt = r_0^2 \,f^2 \left( 1 - \displaystyle{2 \over q}\right) ^{\!\! - 1} .$$Using Eqs. (11), (17)–(22) in (16), we get
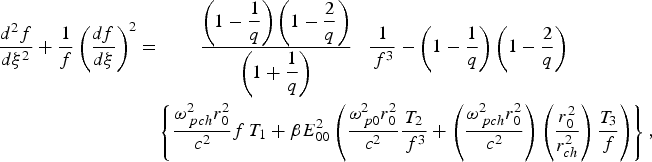$$\eqalign{\displaystyle{{d^2 f} \over {d\rm \xi ^2 }} + \displaystyle{1 \over f}\left( \displaystyle{{df} \over {d\rm \xi }}\right) ^2 &=\qquad \displaystyle{{\left( 1 - {\displaystyle{1 \over q}}\right) \left( 1 - {\displaystyle{2 \over q}}\right) } \over {\left( 1 + {\displaystyle{1 \over q}}\right) }}\;\;\;\displaystyle{1 \over {\,f^3 }} - \left( 1 - \displaystyle{1 \over q}\right) \left( 1 - \displaystyle{2 \over q}\right) \cr & \quad \left\{ \displaystyle{{\rm \omega}^2 _{{\,pch}} r_0^2 \over {c^2 }}f\,T_1 + {\rm \beta} E_{00}^2 \left( \displaystyle{{\rm \omega}^2 _{{\,p0}} r_0^2 \over {c^2 }}\displaystyle{{T_2 } \over {\,f^3 }} + \left( \displaystyle{{\rm \omega}^2 _{{\,pch}} r_0^2 \over {c^2 }}\right) \left( \displaystyle{{r_0^2 } \over {r_{ch}^2 }}\right) \displaystyle{{T_3 } \over f}\right) \right\} \comma \; }$$where ξ = (z/k 0r 02) is the dimensionless propagation distance, and
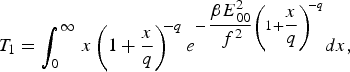$$T_1 = \vint_0^\infty \, x\left( 1 + \displaystyle{x \over q}\right) ^{\!\! - q} e^{ -\, {\displaystyle{{\rm \beta} {E_{00}^2 } \over {\,f^2 }}}\left( 1 + {\displaystyle{x \over q}}\right) ^{\!\! - q} } dx\comma \;$$
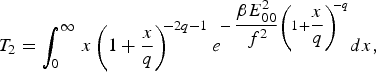$$T_2 = \vint_0^\infty \, x\left( 1 + \displaystyle{x \over q}\right) ^{\!\! - 2q - 1} e^{ -\, {\displaystyle{{\rm \beta} {E_{00}^2 } \over {\,f^2 }}}\left( 1 + {\displaystyle{x \over q}}\right) ^{\!\! - q} } dx\comma \;$$
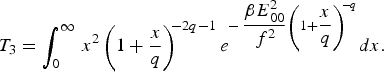$$T_3 = \vint_0^\infty \, x^2 \left( 1 + \displaystyle{x \over q}\right) ^{\!\! - 2q - 1} e^{ -\, {\displaystyle{{\rm \beta} {E_{00}^2 } \over {\,f^2 }}}\left( 1 + {\displaystyle{x \over q}}\right) ^{\!\! - q} } dx.$$
Initial conditions of plane wavefront are 
${\textstyle{{df} \over {d\rm \xi }}} = 0$ and f = 1 at ξ = 0. Eq. (23) describes the evolution of the spot size of a q-Gaussian laser beam with dimensionless distance of propagation as it propagate through a preformed collisionless plasma channel.
3. PLASMA WAVE GENERATION
The non-uniform q-Gaussian intensity distribution of the laser beam along its wavefront produces a transverse density gradient in the channel by exerting non-linear ponderomotive force on the electrons and hence displaces electrons from the high field region to the low field region. This density gradient in turn generate plasma wave at pump frequency. The plasma wave generated by the laser beam is governed by equation of continuity, equation of motion, equation of state and Poisson's equation.
$$\displaystyle{\partial N_e \over \partial t} + \nabla \lpar N_e {\bf v}\rpar = 0\comma \; $$
$$\displaystyle{\partial \lpar N_e {\bf v}\rpar \over \partial t} + \nabla \lpar N_e {\rm v}^2 \rpar + \displaystyle{1 \over m}\nabla P_e + \displaystyle{N_e eE_0 \over m} - 2\Gamma N_e {\bf v} = 0\comma \; $$
$$\displaystyle{{P_e } \over {N_e^{\rm \gamma}}} = constant\comma \; $$
$$\nabla E_0 = 4 {\rm \pi}\lpar ZN_{0i} - N_e \rpar e\comma \; $$where, v and P e, respectively, are velocity and pressure of electron fluid γ is degrees of freedom, Z is charge state of ions and N 0i is density of ions.
Using linear perturbation theory in which the physical quantities (N e, v) are expanded up to first order term about their equilibrium value, we get equation of plasma wave as follows
$$- {\rm \omega} _0^2 n + {\rm v}_{th}^2 \nabla ^2 n + {\rm \omega} _p^2 n = \displaystyle{e \over m}n_0 \nabla E.$$For q-Gaussian laser beam solution of this wave equation gives the higher harmonic source term
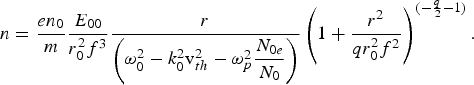$$n = \displaystyle{en_0 \over m}\displaystyle{E_{00} \over r_0^2 f^3} \displaystyle{r \over \left({\rm \omega}_0^2 - k_0^2 {\rm v}_{th}^2 - {\rm \omega}_p^2 \displaystyle{N_{0e} \over N_0} \right)} \left(1 + \displaystyle{r^2 \over qr_0^2 f^2} \right)^{\lpar - {q \over 2} - 1\rpar} .$$4. HIGHER HARMONIC GENERATION
The wave equation governing the electric field 
${\bf E}_{\bf l} $ of lth harmonic is given by
$$\nabla ^2 {\bf E}_{\bf l} + \displaystyle{{\rm \omega}^2 _{l} \over {c^2 }} {\rm \epsilon}_l \lpar {\rm \omega} _l \rpar {\bf E}_{\bf l} = \displaystyle{{\rm \omega}^2 _{p} \over {c^2 }}\displaystyle{n \over {n_0 }}{\bf E}_0 \comma \; $$where ω l = lω 0 is frequency of lth harmonic and εl is the effective dielectric constant at lth harmonic frequency. From the above equation we get expression for field E l of lth harmonic as
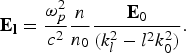$${\bf E}_{\bf l} = \displaystyle{{\rm\omega}^2 _{p} \over {c^2 }}\displaystyle{n \over {n_0 }}\displaystyle{{{\bf E}_0 } \over {\lpar k_l^2 - l^2 k_0^2 \rpar }}.$$Now the lth harmonic power can be written as
$$P_l = \vint_0^{2 \rm \pi} \, \vint_0^\infty \, E_l E_l^ \star rdrd\rm \theta \comma \; $$also, the power of initial pump beam is given by
$$P_0 = \vint_0^{2 \rm \pi} \, \vint_0^\infty \, E_0 E_0^ \star rdrd\rm \theta .$$Defining lth harmonic yield as
$$Y_l = \displaystyle{P_l \over P_0} = \displaystyle{8 \over \lpar l^2 - 1\rpar^2} \displaystyle{K_0 T_0 \over mc^2} \displaystyle{c^2 \over r_0^2 {\rm \omega}_{p0}^2} \displaystyle{{\rm \omega}^2 _{0} \over {\rm \omega}_{p0}^2} \displaystyle{{\rm \beta} E_{00}^2 \over f^4} \left( 1 - \displaystyle{1 \over q}\right) e^{2\left({{\rm \beta} E_{00}^2 \over f^2} \right)} H\comma \; $$where
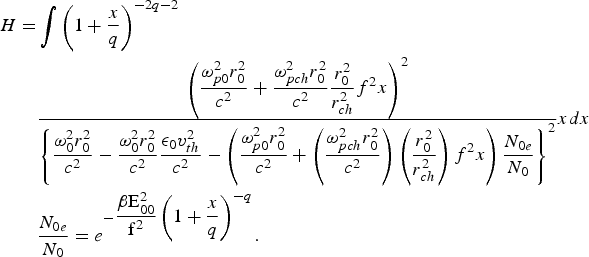$$\eqalign{H = & \int \left( 1 + \displaystyle{x \over q} \right) ^{- 2q - 2}\cr &\displaystyle{\left(\displaystyle{{\rm \omega}_{p0}^2 r_0^2 \over c^2} + \displaystyle{{\rm \omega}_{pch}^2 r_0^2 \over c^2} \displaystyle{r_0^2 \over r_{ch}^2} f^2 x\right)^{2} \over \left\{\displaystyle{{\rm \omega}_0^2 r_0^2 \over c^2} - \displaystyle{{\rm \omega}_0^2 r_0^2 \over c^2} \displaystyle{{\rm \epsilon}_0 v_{th}^2 \over c^2} - \left(\displaystyle{{\rm \omega}_{p0}^2 r_0^2 \over c^2} + \left(\displaystyle{{\rm \omega} _{pch}^2 r_0^2 \over c^2} \right) \left(\displaystyle{r_0^2 \over r_{ch}^2}\right) f^2 x \right) \displaystyle{N_{0e} \over N_0} \right\}^2} xdx \cr &\displaystyle{N_{0e} \over N_0} = e^{ - \displaystyle{{\rm \beta E_{00}^2 \over f^2}} \left( 1 + \displaystyle{x \over q} \right)^{ - q}}.} $$5. DISCUSSION
Eqs. (23) and (34), respectively, describe the variation of dimensionless beam width parameter f and harmonic yield Y l of a q-Gaussian laser beam with dimensionless distance of propagation ξ. These equations have been solved numerically for following set of parameters; q = 3.0, βE 002 = 0.50, 
${{\rm \omega}_{p0}^2 r_0^2 \over c^2} = 6.0$,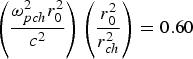 
$\left({{\rm \omega}_{pch}^2 r_0^2 \over c^2} \right) \left(\displaystyle{r_0^2 \over r_{ch}^2} \right) = 0.60$, ω0 = 1.78 × 1015 rad sec−1, λ = 1.06 μm, r 0 = 15 μm, r ch = 150 μm, T 0 = 106K and for different values of q, normalized intensity βE 002, normalized plasma density and normalized depth of channel. Effect of order of harmonicity on harmonic yield has been also analyzed.
The first term on the right-hand side of Eq. (23) represents diffractional divergence of the laser beam and the second term that arises due to radial inhomogeneity of plasma channel and pon-deromotive force exerted by the laser represents non linear refraction of the beam. Relative magnitude of these two terms determines the focusing/defocusing behavior of the beam.
Figure 1 describes the variation of magnitude of diffraction term at (ξ = 0) in Eq. (23) with q. It is observed that with increase in the value of q vacuum diffraction of the laser beam increases linearly and then almost saturates for higher values of q. This is due to the fact that with increase in the value of q the intensity of the beam shifts toward the axial region of the wavefront and the divergence of axial rays is stronger as compared to off axial rays.
Fig. 1. Variation of magnitude of diffraction term at ξ = 0 in eqn.(25) against q.
Figure 2 describes the variation of dimensionless beam width parameter f with normalized distance of propagation ξ for above mentioned set of parameters and for different values of q = 3,4,∞ From Figure 2, it is observed that with increase in the value of q there is decrease in the extent of self focusing of the laser beam as well as decrease in focusing length. This is due to the fact that with increase in the value of q the magnitude of diffractive term in Eq (23) increases as a result of which the diffractive term dominate over refractive term. So, increase in q leads to decrease in the extent of self focusing of the laser beam.
Fig. 2. Variation of beam with parameter f against the normalized distance of propagation ξ for different values of q viz. q = 3, 4, ∞ and at fixed values of the following set of parameters βE 002 = 0.50, 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0}$,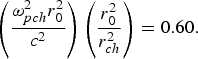 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60}.$
Figures 3, 4, 5 describe the variation of beam width parameter f against the normalized distance of propagation ξ for different values of normalized intensity of laser beam viz. βE 002 = 0.50, 0.55, 0.60, normalized plasma density 
${{\rm \omega}_{p0}^2 r_0^2 \over c^2} = 6.0\comma \; 6.5\comma \; 7.0$, normalized channel depth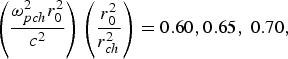 
$\left({{\rm \omega}_{pch}^2 r_0^2 \over c^2} \right) \left({r_0^2 \over r_{ch}^2} \right) = 0.60\comma 0.65\comma \; 0.70\comma \; $ respectively, for above mentioned set of parameters. From Figures 3, 4, 5 it is observed that with increase in the intensity of the laser beam, plasma density, and depth of channel there is increase in self focusing of the laser beam as well as decrease in focusing length. This is due to the fact that with increase in intensity of laser beam, plasma density, and depth of channel, nonlinear refraction dominate over natural diffraction which leads to increase in extent of self focusing of the laser beam as well as to decrease in focusing length.
Fig. 3. Variation of beam width parameter f against the normalized distance of propagation ξ for different values of normalized intensity of laser baeam viz. βE 002 = 0.50, 0.55, 0.60 and at fixed values of q = 3,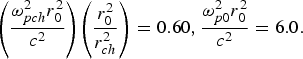 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right)} {\left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60 , \displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0.}$
Fig. 4. Variation of beam width parameter f against the normalized distance of propagation ξ for different values of normalized plasma density viz. 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0, 6.5, 7.0}$ and at fixed values of q = 3, βE 002 = 0.50,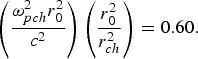 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60.}$
Fig. 5. Variation of beam width parameter f against the normalized distance of propagation ξ for different values of normalized depth of channel viz.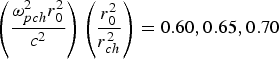 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60, 0.65, 0.70}$ and at fixed values of q = 3, βE 002 = 0.50, 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0.}$
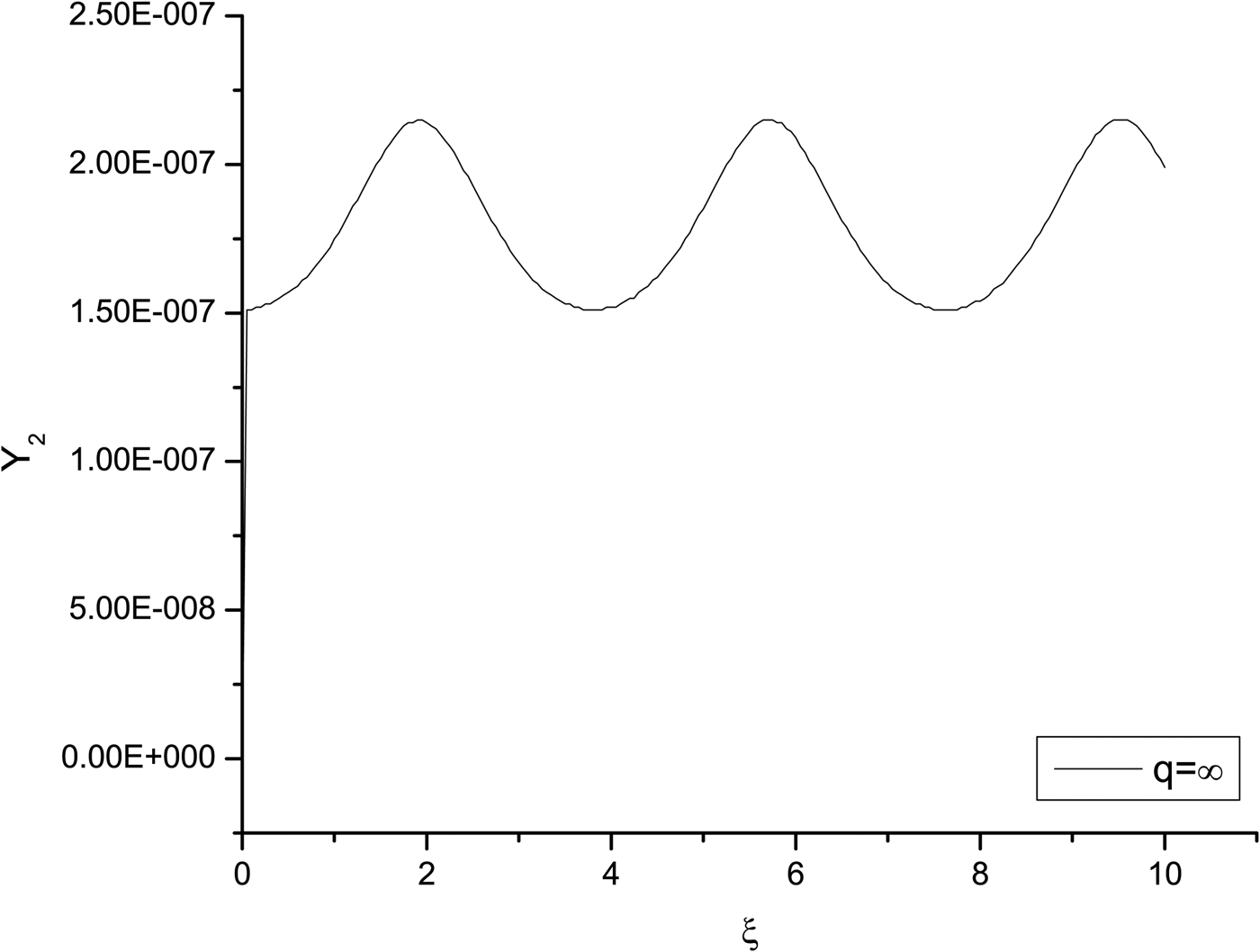
Figures 6 and 7 describe the variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of q = 3, 4, and ∞, respectively, for above mentioned set of parameters. From Figures 6 and 7, it is observed that with increase in the value of q there is decrease in harmonic yield. This is due to the fact that harmonic yield is very sensitive to the extent of self focusing of the laser beam. Greater is the extent of self focusing of the laser beam higher is transverse density gradient in the focal region and hence higher is the harmonic yield.
Fig. 6. Variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of q viz. q = 3, 4 and at fixed values of the following set of parameters βE 002 = 0.50,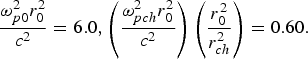 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0}, {\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60.}$
Fig. 7. Variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for q = ∞ and at fixed values of the following set of parameters βE 002 = 0.50,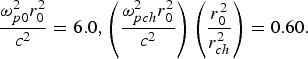 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0}, {\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60.}$
Figure 8 Depicts the variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of normalized intensity of laser beam βE 002 = 0.50, 0.55, 0.60 and for above mentioned set of parameters. It is observed that with increase in intensity of laser beam there is increase in harmonic yield. This is due to the fact that increase in intensity of the incident laser beam enhances the self focusing of the laser beam which further enhances the harmonic yield.
Fig. 8. Variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of normalized indensity of laser beam viz. βE 002 = 0.50, 0.55, 0.60 and at fixed values of the following set of parameters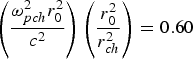 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60}$, q = 3, 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0.}$
Figures 9 and 10 describe the variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of normalized plasma density 
${{\rm \omega}_{p0}^2 r_0^2 \over c^2} = 6.0\comma \; 6.5\comma \; 7.0$ and normalized depth of channel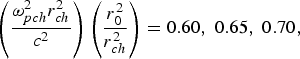 
$\left({{\rm \omega}_{pch}^2 r_{ch}^2 \over c^2} \right) \left({r_0^2 \over r_{ch}^2} \right) = 0.60\comma \; 0.65\comma \; 0.70\comma \; $ respectively, for above mentioned set of parameters. It is observed from Figures 9 and 10 that with increase in the plasma density and depth of the channel there is increase in harmonic yield. This is due to the fact that with the increase in plasma density and depth of channel, self focusing of the laser beam increases and therefore the transverse density gradient becomes very steep in the focal region, which leads to increase in amplitude of plasma wave and hence harmonic yield.
Fig. 9. Variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of normalized plasma density viz. 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0, 0.65, 0.70}$ and at fixed values of the following set of parameters βE 002 = 0.50, q = 3,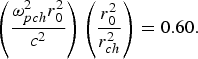 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60.}$
Fig. 10. Variation of second harmonic yield Y 2 against the normalized distance of propagation ξ for different values of normalized depth of channel viz.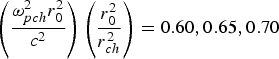 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60, 0.65, 0.70}$ and at fixed values of the following set of parameters βE 002 = 0.50, q = 3, 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0.}$
Figure 11 depicts variation of harmonic yield Y l against the normalized distance of propagation 
$\xi $ for different orders of harmonicity l = 2,3,4 and for above mentioned set of parameters. It is observed from Figure 11 that harmonic yield decreases with the increase in order of harmonicity. This is due to the fact that harmonic yield Y l of lth harmonic is inversely proportional to (l 2 − 1)2. Therefore, with increase in the value of order of harmonicity there is decrease in harmonic yield.
Fig. 11. Variation of second harmonic yield Y l against the normalized distance of propagation ξ for different values of harmonicity viz. l = 2, 3, 4 and at fixed values of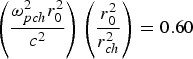 
${\left(\displaystyle{{{\rm \omega} _{pch}^2 } r_0^2 \over c^2 } \right) \left(\displaystyle{{r_0^2 \over {r _{ch}^2 }}} \right) = 0.60}$, q = 3, 
${\displaystyle{{{\rm \omega} _{p0}^2 } r_0^2 \over {{c^2 }}} = 6.0}$, βE 002 = 0.50.
CONCLUSION
In the present work, Self-focusing of q-Gaussian laser beam in collisionless plasma channel and its effect on higher harmonic generation has been studied by moment theory approach. Following important conclusions are drawn from present analysis.
• Diffraction divergence of axial rays is stronger as compared to off axial rays.
• Self focusing of q-Gaussian laser beam increases with decrease in q as well as with increase in intensity of laser beam, density of channel and depth of channel.
• Harmonic yield increases with decrease in q.
• Harmonic yield increases with increase in intensity of laser beam, density and depth of channel.
• Harmonic yield decreases with increase in order of harmonicity.
Harmonic generation is a useful diagnostic tool for filamentation. We know that filamentation in the underdense plasma corona of the fusion pellet destroy the symmetry of energy deposition on the target and therefore uneven compression of the target takes place, which leads to the premature end of the implosion. Moreover higher harmonic generation allows the penetration of laser power to overdense region of plasma corona of the fusion pellet. Therefore, the results of the present investigation are useful to understand the physics of laser induced fusion.
ACKNOWLEDGEMENT
The authors are thankful to the ministry of Human Resources and Development of India for providing financial assistance for carrying out this work.
