2. WAVE EQUATION

Consider a linearly polarized laser beam propagating along the z-direction in a tenuous clustered gas. The electric vector of the laser field is given by

(1)$$\vec{E}\left(r\comma \; z\comma \; t \right)= \displaystyle{1 \over 2}E_0 \left(r\comma \; z\comma \; t \right)\exp \left[i\left(k_0 z - {\rm \omega} _0 t \right)\right]\hat{x} + c.c.\comma \;$$

where E ₀ (r,z,t) is the amplitude of the radiation field and k ₀ (ω₀) is its wave number (angular frequency). Considering the individual cluster to behave like a dielectric sphere, the wave equation governing the propagation of a laser beam in clustered gas is given by

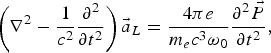(2)$$\left(\nabla^2 - \displaystyle{1 \over c^2} \displaystyle{\partial^2 \over \partial t^2} \right)\vec{a}_L = \displaystyle{4{\rm \pi} e \over m_e c^3 {\rm \omega}_0} \displaystyle{\partial ^2 \vec{P} \over \partial t^2}\comma \;$$

where $\vec{a}_L \left(= e\vec{E}\left(r\comma \; z\comma \; t \right)/ m_e c{\rm \omega}_0 \right)$ is the normalized electric vector of the laser field. The polarization field $\left(\vec{P} \right)$ arising due to the presence of the clusters may be written as

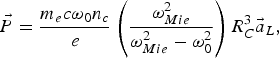(3)$$\vec{P} = \displaystyle{m_e c{\rm \omega}_0 n_c \over e} \left(\displaystyle{{\rm \omega}_{Mie}^2 \over {\rm \omega}_{Mie}^2 - {\rm \omega}_0^2} \right)R_C^3 \vec{a}_L\comma \;$$

where n _c is the cluster density and ${\rm \omega}_{Mie} \lpar \!\!= {\rm \omega}_p / \sqrt{3}\comma \; {\rm \omega}_p$ being the plasma frequency) is known as Mie frequency. The cluster radius (R _C) is a function of time t. The expansion of the cluster radius occurs on the time scale of ion motion (τ_i). Hence the change in cluster radius averaged over ion time scale is given (Mishra & Jha, Reference Mishra and Jha2011b)

(4)$$\left(\Delta R_C \right)_{avg}\, = \displaystyle{m_e^2 c^2 {\rm \omega}_0^6 {\rm \tau}_i^2 \left\vert a_0 \right\vert^2 \over {\rm \pi} e^2 M_i n_{i0} R_{C0} \left({\rm \omega}_{Mie}^2 - {\rm \omega}_0^2 \right)^2}.$$

R _C0, M _i, n _i0, and a ₀ (eE ₀/m _ecω₀) are initial cluster radius, ion mass, initial ion density, and normalized laser amplitude, respectively. Substituting the value of polarization vector $\vec{P}$ from Eq. (3) in Eq. (2) gives

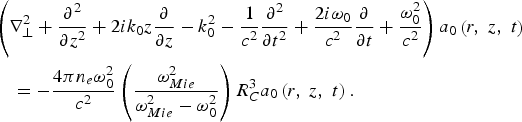(5)$$\eqalign{&\left(\nabla_{\bot}^2 + \displaystyle{\partial^2 \over \partial z^2} + 2ik_0 z \displaystyle{\partial \over \partial z} - k_0^2 - \displaystyle{1 \over c^2} \displaystyle{\partial^2 \over \partial t^2} + \displaystyle{2i{\rm \omega}_0 \over c^2} \displaystyle{\partial \over \partial t} + \displaystyle{{\rm \omega}_0^2 \over c^2} \right) a_0 \left(r\comma \; z\comma \; t \right)\cr &\quad =- \displaystyle{4{\rm \pi} n_e {\rm \omega}_0^2 \over c^2} \left(\displaystyle{{\rm \omega}_{Mie}^2 \over {\rm \omega}_{Mie}^2 - {\rm \omega}_0^2} \right)R_C^3 a_0 \left(r\comma \; z\comma \; t \right).}$$

With the help of the linear dispersion relation

(6)$$- k_0^2 + \displaystyle{{\rm \omega}_0^2 \over c^2} = - \displaystyle{4{\rm \pi} n_c {\rm \omega}_0^2 \over c^2} \left(\displaystyle{{\rm \omega}_{Mie}^2 \over {\rm \omega}_{Mie}^2 - {\rm \omega}_0^2} \right)R_{C0}^3\comma \;$$

and the transformation τ = t − z /v _g (v _g is the group velocity) and η = z, the wave Eq. (5) may be written as

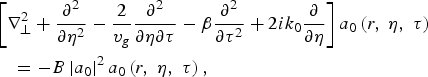(7)$$\eqalign{&\left[\nabla_{\bot}^2 + \displaystyle{\partial^2 \over \partial {\rm \eta}^2} - \displaystyle{2 \over v_g} \displaystyle{\partial^2 \over \partial {\rm \eta} \partial {\rm \tau}} - {\rm \beta} \displaystyle{\partial^2 \over \partial {\rm \tau}^2} + 2ik_0 \displaystyle{\partial \over \partial {\rm \eta}} \right]a_0 \left(r\comma \; {\rm \eta}\comma \; {\rm \tau} \right)\cr &\quad = - B\left\vert a_0 \right\vert^2 a_0 \left(r\comma \; {\rm \eta}\comma \; {\rm \tau} \right)\comma \;}$$

where B = 12n _cm _e²R _C0ω₀⁸ω_Mie²τ_i²/M _in _i0e ²(ω_Mie² − ω₀²)³ and β (=1/c ² − 1/v _g²) is the group velocity dispersion parameter.

Assuming slowly varying amplitude, the higher order diffraction term (∂²/∂η²~1/Z _R²) can be neglected in comparison to 2k ₀∂/∂η. The third and the fourth terms on the left side of Eq. (7) representing finite pulse length effects are about two orders of magnitude less than 2k ₀ (∂/∂η) and will therefore perturb the pulse amplitude. Also the propagation of a broad laser beam can be described with the help of a one-dimensional model. Therefore, the lowest order of Eq. (7) may be written as

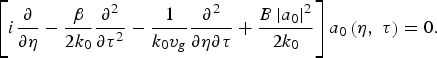(8)$$\left[i\displaystyle{\partial \over \partial {\rm \eta}} - \displaystyle{{\rm \beta} \over 2k_0} \displaystyle{\partial^2 \over \partial {\rm \tau}^2} - \displaystyle{1 \over k_0 v_g} \displaystyle{\partial^2 \over \partial {\rm \eta} \partial {\rm \tau}} + \displaystyle{B\left\vert a_0 \right\vert^2 \over 2k_0} \right]a_0 \left({\rm \eta}\comma \; {\rm \tau} \right)= 0.$$

Considering a Gaussian laser pulse profile, the field amplitude is represented by

(9)$$a_0 \left({\rm \eta}\comma \; {\rm \tau} \right)= b\left({\rm \eta}\comma \; {\rm \tau} \right)\exp \left(- \displaystyle{{\rm \tau}^2 \over {\rm \tau}_0^2} \right)\comma \;$$

where b(η, τ) is the pulse amplitude and τ₀ is the initial pulse duration. Substituting Eq. (9) into Eq. (8) and considering the variation in the pulse amplitude with respect to τ to be a higher order effect the lowest order evolution equation for the unperturbed pulse amplitude b ₀ is given by

(10)$$\eqalign{\left[\displaystyle{2 \over k_0 v_g {\rm \tau}_0} \displaystyle{{\rm \tau} \over {\rm \tau}_0} + i \right]\displaystyle{\partial b_0 \over \partial {\rm \eta}} &= - b_0 \left[\displaystyle{{\rm \beta} \over k_0 {\rm \tau}_0^2} \left\{1 - 2\displaystyle{{\rm \tau}^2 \over {\rm \tau}_0^2} \right\}\right. \cr &\quad \left. + \displaystyle{B\left\vert b_0 \right\vert^2 \over 2k_0}\exp \left(- 2\displaystyle{{\rm \tau}^2 \over {\rm \tau}_0^2} \right)\right].}$$

Solving Eq. (10) the lowest order, unperturbed amplitude is given by

(11)$$b_0 \left({\rm \eta}\comma \; {\rm \tau} \right)= a_{00} \exp \left[A\left({\rm \tau} \right)+ i\Phi \left({\rm \tau} \right)\right]\comma \;$$

where a ₀₀ (laser strength parameter) is the initial (η = 0) amplitude of the laser pulse, A(τ) and Φ(τ) are given by

$$A\left({\rm \tau} \right)= - {\displaystyle{2 \over k_0 v_g {\rm \tau}_0} \displaystyle{{\rm \tau} \over {\rm \tau}_0} \left[\matrix{\displaystyle{Ba_{00}^2 \over 2k_0} \exp \left(- \displaystyle{2{\rm \tau}^2 \over {\rm \tau}_0^2} \right) + \displaystyle{{\rm \beta} \over k_0 {\rm \tau}_0^2} \left(1 - \displaystyle{2{\rm \tau}^2 \over {\rm \tau}_0^2} \right)} \right]\over 1 + \left(\displaystyle{2 \over k_0 v_g {\rm \tau}_0} \displaystyle{{\rm \tau} \over {\rm \tau}_0} \right)^2},$$

and

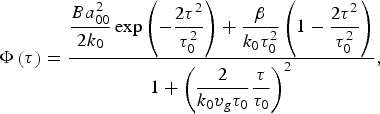$$\hskip-62pt\Phi \left({\rm \tau} \right)=\displaystyle{{\displaystyle{{Ba_{00}^2 } \over {2k_0 }}\exp \left({ - \displaystyle{{2{\rm \tau} ^2 } \over {{\rm \tau} _0^2 }}} \right)+\displaystyle{{\rm \beta} \over {k_0 {\rm \tau} _0^2 }}\left({1 - \displaystyle{{2{\rm \tau} ^2 } \over {{\rm \tau} _0^2 }}} \right)} \over {1+\left({\displaystyle{2 \over {k_0 v_g {\rm \tau} _0 }}\displaystyle{{\rm \tau} \over {{\rm \tau} _0 }}} \right)^2 }},$$

respectively. A(τ) leads to an exponential amplitude variation in the pulse frame while Φ(τ) is the self-induced phase shift (self-phase modulation) experienced by a laser pulse propagating in clustered gas. A(τ) is positive (negative) at the front (back) of the pulse, hence the amplitude of the laser pulse increases at the front while it decreases at the back of the pulse, while the self-induced phase shift Φ(τ) remains same at the front as well as back of the pulse. It may also be noted that variation in amplitude due to change in pulse length is such that for shorter pulse durations A(τ) is larger and vice-versa while the self-induced phase shift decreases with decrease in the pulse duration.

3. MODULATION INSTABILITY

Modulation instabilities are caused by the interplay between group velocity dispersion (GVD) and self-phase modulation (Sprangle et al., Reference Sprangle, Hafizi and Penano2000). Hence, the modulated amplitude of the laser pulse, due to GVD and finite pulse effects, may be written as the superposition of perturbed and unperturbed amplitudes, as

(12)$$\eqalign{a\left({\rm \eta}\comma \; {\rm \tau} \right)&= \left[a_{00} \exp \left\{A\left({\rm \tau} \right)\right\}+ a_{01} \left({\rm \eta}\comma \; {\rm \tau} \right)\right]\exp \left(- \displaystyle{2{\rm \tau}^2 \over {\rm \tau}_0^2} \right) \exp \left\{i\Phi \left({\rm \tau} \right){\rm \eta} \right\}\comma \; }$$

where a ₀₁(η, τ) is the complex perturbed beam amplitude. Substituting Eq. (12) into Eq. (8), considering |a ₀₁| <<|a ₀₀|, neglecting further variations in the pulse shape and considering the perturbed wave amplitude to be a sinusoidally varying function of η and τ, that is, a ₀₁ = exp{i(Kη − Ωτ)} + exp{−i(Kη − Ωτ)} (K and Ω are the wave number and frequency of the perturbed wave amplitude, respectively), the dispersion relation for the one-dimensional modulation instability is given by

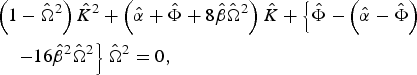(13)$$\eqalign{&\left(1 - \hat{\Omega}^2 \right)\hat{K}^2 + \left(\hat{{\rm \alpha}} + \hat{\Phi} + 8 \hat{{\rm \beta}} \hat{\Omega}^2 \right)\hat{K} + \left\{\hat{\Phi} - \left(\hat{{\rm \alpha}} - \hat{\Phi} \right)\right. \cr &\quad \left. - 16\hat{{\rm \beta}}^2 \hat{\Omega}^2 \right\}\hat{\Omega}^2 = 0\comma \;}$$

where $\hat{K} = KZ_R$ (Z_R being the Rayleigh length), $\hat{{\rm \beta}} = k_0 v_g^2Z_R {\rm \beta} / 8\comma$$ \hat{\Phi} = \Phi Z_R\comma \; \hat{\Omega} = \Omega / k_0 v_g$, and $\hat{{\rm \alpha}} = {\rm \alpha} Z_R \lpar {\rm \alpha} = \left(Ba_{00}^2 / 2k_0 \right)\exp $$\left\{2A\left({\rm \tau} \right){\rm \eta} \right\}\exp \left(- 2{\rm \tau}^2 / {\rm \tau}_0^2 \right)$ are dimensionless quantities. The imaginary part of $\hat{K}$, in Eq. (13), gives the growth rate of modulation instability as

(14)$${\Gamma = \displaystyle{\hat{\Omega} \over 2\left(1 - \hat{\Omega}^2 \right)}} \sqrt{\matrix{\left\{\left(\hat{{\rm \alpha}} - \hat{\Phi} \right)^2 + 2\left(2\hat{\Phi} + 8\hat{{\rm \beta}} \right)\left(\hat{{\rm \alpha}} - \hat{\Phi} \right)\right\}\cr + \left(2\hat{\Phi} + 8\hat{{\rm \beta}} \right)^2 \hat{\Omega}^2}}.$$

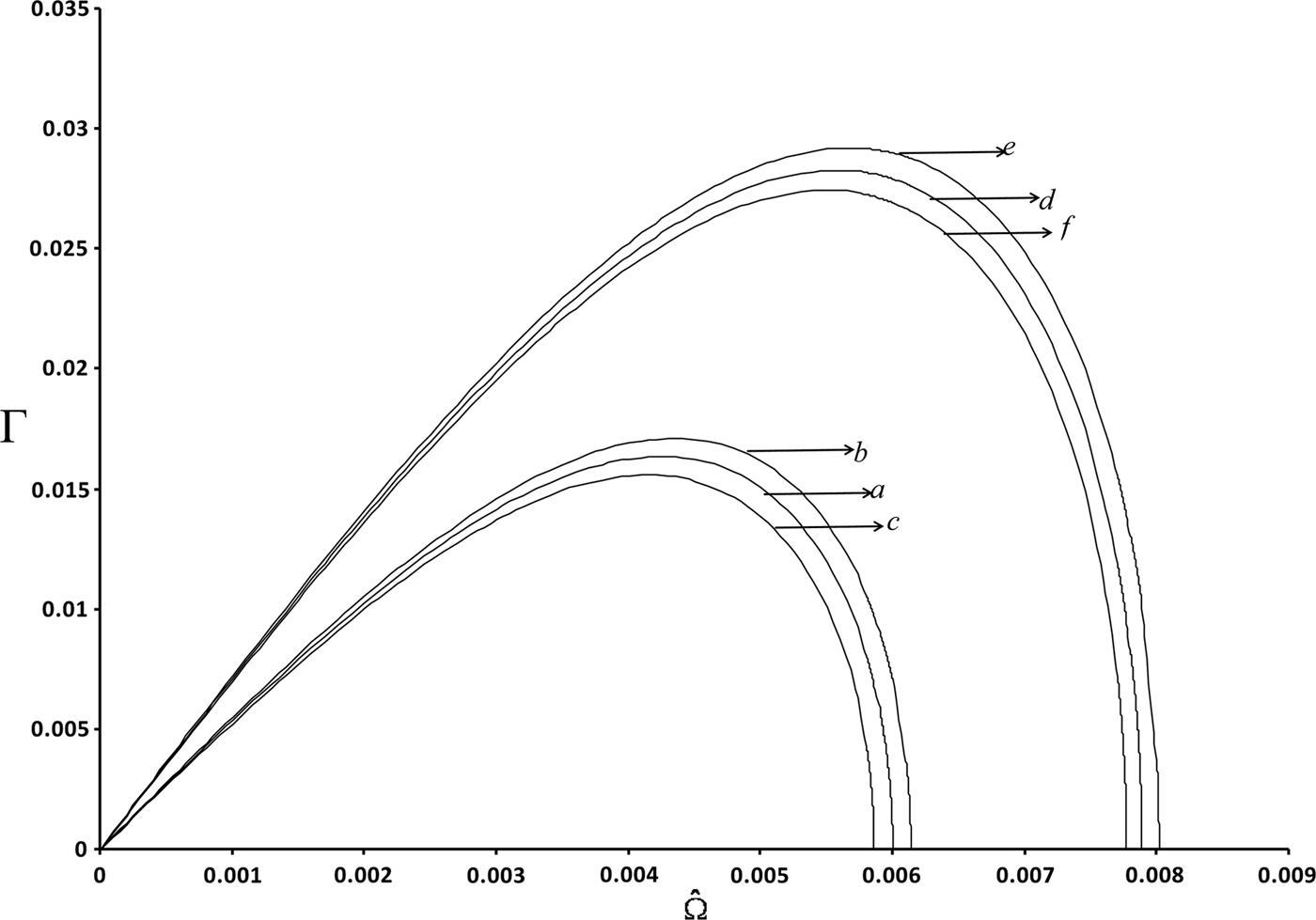
Variation in the growth rate of modulation instability (Γ) with respect to the normalized perturbed frequency $\left(\hat{\Omega} \right)$ is shown in the Figure 1. Figure 1 shows the growth rates of modulation instabilities at η = 0 as well as at the front (τ/τ₀ = −0.14) and back (τ/τ₀ = +0.14) of the pulse for 100 fs and 80 fs pulses with τ₀ = 100 fs, ω₀ = 2.36 × 10¹⁵s ⁻¹, λ₀ = 800 nm, r ₀ = 40 µm, a ₀₀² = 6.84 × 10⁻² (peak intensity = 1.46 × 10¹⁷ W/cm²), n _c = 8.0 × 10¹³ cm ⁻³, n ₀ = 1.8 × 10²² cm ⁻³, R _C0 = 30 nm and M _i = 1.39 × 10⁻¹² gm. Curves a (d), b (e), and c (f) show the growth rate of modulation instability at the centroid (η = 0), at the front and back of the pulse, respectively, for 100 fs (80 fs) pulse. For both the pulses, it is seen that exponential amplitude variation (A(τ)) is positive (negative) at the front (back) of the pulse that leads to increase in growth rate of modulation instability at the front and decrease at the back of the pulse.

Fig. 1. Variation in the growth rate of modulation instability (Γ) with $\hat{\Omega}$ after the pulse has traversed a distance of a Rayleigh length (Z_R) at the centroid of the pulse (η = 0) (Curve a (d)), at the front (τ/τ₀ = −0.14) of the 100 fs (Curve b) and 80 fs (Curve e) pulses. Curves ‘c’ and ‘f’ represent growth rate of modulation instability at the back (τ/τ₀ = +0.14) for 100 fs and 80 fs pulses, respectively. The parameters used are τ₀ = 100 fs, ω₀ = 2.36 × 10¹⁵s ⁻¹, λ₀–800 nm, r ₀ = 40 μm, a ₀₀² = 6.84 × 10⁻², n _c = 8.0 × 10¹³ cm⁻³, n ₀ = 1.8 × 10²²cm ⁻³, R _C0 = 30 nm and M _i = 1.39 × 10⁻¹²gm.

It is seen that as the pulse duration decreases the growth rate of modulation instability increases due to increase in the exponential amplitude variation (A(τ)) and decrease in the self-induced phase shift (Φ(τ)). Average enhancement in the growth rate of modulation instability of the shorter pulse is 73.17%. For 80 fs (100 fs) pulse growth rate of modulation instability increases by 3.30% (4.67%) at the front and decreases by 2.93% (4.63%) at the back of the pulse in comparison to η = 0 case. It is also seen that with decrease in the pulse duration the percentage variation in the growth rate of modulation instability at the front as well as at the back of the pulse decreases in comparison to the centroid of the pulse.

4. SUMMARY AND CONCLUSION

This paper deals with the analytical study of the growth rate of modulation instability as the laser pulse propagates in a clustered gas. It is shown that exponential amplitude variation (A(τ)) is positive (negative) at the front (back) of the pulse due to which the growth rate of modulation instability increases (decreases) at the front (back) of the laser pulse in comparison to the centroid of the pulse. It is seen that for 100 fs (80 fs) pulse the growth rate of modulation instability at the front of the pulse increases by 4.67% ( 3.30%) and decreases by 4.63% (2.93%) at the back of the pulse in comparison to that of the centroid of the pulse (η = 0). Also, with decrease in the pulse duration the peak value of the growth rate of modulation instability increases and for lower (higher) values of the pulse duration change in the growth rate at the front as well as at the back of the pulse in comparison to the centroid of the pulse is reduced (enhanced). Reason for this behavior may be attributed to the fact that with decrease in pulse duration the exponential amplitude variation (A(τ)) increases and the self-induced phase shift (Φ(τ)) decreases. The average enhancement in the growth rate of modulation instability at the front as well as at the back of the pulse is 73.17% by reducing the pulse duration from 100 fs to 80 fs. This analytical study shows the limitations of using short laser pulse propagating in clustered gas since decrease in the pulse duration causes sharp rise in growth rate of modulation instability. Hence an optimum value of pulse duration may be chosen for application based on interaction of short laser pulses with clustered gas.