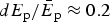1. INTRODUCTION
Extreme Light Infrastructure (ELI) (Danson et al., Reference Danson, Hillier, Hopps and Neely2015; https://www.eli-laser.eu) is a currently implemented large-scale European project that uses cutting-edge laser technologies to build multi-petawatt (PW) lasers generating femtosecond pulses of ultra-relativistic intensities ~1022–1023 W/cm2. The launch of ELI will open a doorway into new areas of fundamental research as well as establishing new technical developments and applications. Laser-driven ion/proton acceleration is a topical and rapidly developing research area stimulated by a variety of potential applications. The use of the ELI lasers to accelerate ions makes it possible to apply the produced intense ion beams of sub-GeV and GeV ion energies into various branches of nuclear physics (Ledingham & Galster, Reference Ledingham and Galster2010) and high-energy-density physics (Patel et al., Reference Patel, MacKinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003; Macchi et al., Reference Macchi, Borghesi and Passoni2013; Fernandez et al., Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014) as well as for medical applications such as the hadron cancer therapy (Bulanov et al., Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro2002; Ledingham & Galster, Reference Ledingham and Galster2010; Macchi et al., Reference Macchi, Borghesi and Passoni2013).
The mechanisms of ion acceleration and parameters of generated ion beams depend significantly on both the laser beam and irradiated target parameters, in particular on the laser beam intensity and the thicknesses and composition of the target. The ions can be accelerated by several laser-induced mechanisms such as: the TNSA (target normal sheath acceleration) (Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001; Borghesi et al., Reference Borghesi, Fuchs, Bulanov, Mackinnon, Patel and Roth2006; Badziak, Reference Badziak2007; Macchi et al., Reference Macchi, Borghesi and Passoni2013), the RPA (radiation pressure acceleration) (Esirkepov et al., Reference Esirkepov, Borghesi, Bulanov, Mourou and Tajima2004; Macchi et al., Reference Macchi, Cattani, Liseykina and Cornalti2005, Reference Macchi, Borghesi and Passoni2013; Liseykina et al., Reference Liseykina, Borghesi, Macchi and Tuveri2008; Robinson et al., Reference Robinson, Zepf, Kar, Evans and Bellei2008) [also known as the skin-layer ponderomotive acceleration (SLPA) (Badziak, Reference Badziak2007; Badziak et al., Reference Badziak, Antici, Fuchs, Jabłoński, Mancic, Parys, Rosiński, Suchańska, Szydłowski and Wołowski2008b )], the laser BOA (break-out afterburner) (Yin et al., Reference Yin, Albright, Hegelich and Fernandez2006, Reference Yin, Albright, Hegelich, Browers, Flippo, Kwan and Fernandez2007; Macchi et al., Reference Macchi, Borghesi and Passoni2013; Fernandez et al., Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014), the CESA (collisionless electrostatic shock acceleration) (Denavit, Reference Denavit1992; Silva et al., Reference Silva, Marti, Davies and Fonseca2004; Macchi et al., Reference Macchi, Borghesi and Passoni2013), or the LICPA (laser-induced cavity pressure acceleration) (Badziak et al., Reference Badziak, Borodziuk, Pisarczyk, Chodukowski, Krousky, Masek, Skala, Ullschmied and Rhee2010, Reference Badziak, Jabłoński, Pisarczyk, Rączka, Krousky, Liska, Kucharik, Chodukowski, Kalinowska, Parys, Rosiński, Borodziuk and Ullschmied2012). Since the dominant acceleration mechanism is determined by the laser–target interaction conditions, the laser beam parameters as well as the structure of the targets must be carefully selected to produce the ion beams of characteristics required for a particular application. Furthermore, the ion acceleration mechanisms should be well identified and controlled.
Previous studies presented in papers (Foord et al., Reference Foord, Mackinnon, Patel, MacPhee, Ping, Tabak and Town2008; Domański et al., Reference Domański, Badziak and Jabłoński2016a , Reference Domański, Badziak and Jabłoński b ) have shown a strong influence of the target composition on the ion beam parameters. It was proven that in the case of laser pulses produced by the PW titanium–sapphire laser facilities (laser intensity I L ≤ 1021 W/cm2, laser power P L < 1 PW), using hydride targets with heavy atoms, instead of commonly used hydrocarbon (CH) targets, allows for a considerable increase in all particular important parameters of the proton beams. In this paper, we deliver a comprehensive analysis of the effect of the target composition as well as the laser beam polarization and intensity for the laser beam parameters predicted for the ELI facilities. This research was performed using two-dimensional (2D) particle-in-cell (PIC) simulations, which are a convenient and effective tool for studies of laser-driven ion acceleration and for the prediction of parameters of laser-accelerated ion beams. The correctness of the PIC code used in the simulations was verified by a comparison of the results obtained using this code with the ones from the measurements presented in (Badziak et al., Reference Badziak, Jabłoński, Parys, Rosiński, Wołowski, Szydłowski, Antici, Fuchs and Mancic2008a ) as well as with the results of 3D simulations of carbon ion acceleration carried out in (Sgattoni et al., Reference Sgattoni, Sinigardi and Macchi2014).
The numerical simulations were performed for thin CH and heavy atoms erbium hydride (ErH3) targets irradiated by a 130 fs duration laser pulse of the intensity ranging from 1021 to 1023 W/cm2 and 800 nm wavelength. The laser pulse shape in time and space (along the y-axis) was described by a super-Gaussian function of the power index equal to 6 and the laser beam width (FWHM-Full Width Half Maximum) was assumed to be 8 µm. The transverse dimensions of the targets were equal to 12 µm and their areal mass density ranging from 0.06 to 0.8 mg/cm3. Molecular densities of the targets corresponded to solid-state densities and they were equal to 4.86 × 1022 molecules/cm3 for CH and 2.69 × 1022 molecules/cm3 for ErH3. The ionization degrees of target components were assumed to be 1 for hydrogen, 6 for carbon and 10 (Foord et al., Reference Foord, Mackinnon, Patel, MacPhee, Ping, Tabak and Town2008) for erbium. A pre-plasma layer of 0.25 µm thickness and the density shape described by an exponential function was placed in front of the target. The simulations were performed in the s, y space equal to 160 × 32 µm2 and the number of macroparticles (optimized) was assumed to be 5 × 106 for thinner targets (σt ≤ 0.2 mg/cm2) and 9 × 106 for thicker targets (σt > 0.2 mg/cm2).
2. RESULTS AND DISCUSSION
Figure 1 presents a 2D spatial distribution of charge density of erbium ions (a), carbon ions (c), and protons (b, d) generated from both types of investigated target. The targets were irradiated by the circularly polarized (CP) laser pulses of intensity equal to 1023 W/cm2 and the presented situation corresponds to the final stage of ion acceleration (the simulation time is equal to 0.4 ps). It can be observed that protons are clearly separated from the erbium ions which attain much lower velocities than protons. The difference between velocities of protons and carbon ions is much smaller, and some carbon ions move with the velocities close to the proton velocities. It is worth mentioning that the mean energy achieved by the protons generated from the CH target is higher than for those generated from the ErH3 target, and that the energy dispersion of protons emitted from the CH target is quite small. The analogical plot for the linearly polarized (LP) laser pulse is presented in Figure 2. It is clearly visible that the parameters of ion beams generated from both types of the target do not depend significantly on the state of polarization of the laser beam.
Fig. 1. The 2D spatial distributions of charge density of erbium ions (a), carbon ions (c), and protons (b, d) generated from the ErH3 (a, b) and CH (c, d) targets. I L = 1023 W/cm2, circular polarization.
Fig. 2. The 2D spatial distributions of charge density of erbium ions (a), carbon ions (c) and protons (b, d) generated from the ErH3 (a, b) and CH (c, d) targets. I L = 2 × 1023 W/cm2, linear polarization.
The weak influence of laser polarization on the acceleration process could be explained by the dominance of the RPA mechanism. In this mechanism the mean ion energy depends on the laser energy fluence and the target areal density. These parameters were identical for the considered cases with different polarizations.
Figure 3 presents a 2D spatial distribution of electric field component parallel to laser beam propagation direction for CP and for the initial and later stages of simulations. This component of the electric field is directly responsible for ion acceleration. It is visible that protons are accelerated by the RPA field. The difference between energies of proton beams generated using CH and ErH3 can be explained by the difference in the strength of interaction between heavier ions stored in the target and the electric field which accelerates these ions. The interaction between erbium ions and the field is much weaker than the interaction between the field and carbon ions due to the lower q/m value for the erbium ions (q is the ion charge and m is the ion mass). For this reason, the amount of energy transferred by the field to protons during the initial stage of acceleration is higher for the erbium–hydrogen plasma than for the CH plasma (Fig. 4). However, in the RPA mechanism the acceleration process is limited by the transparency of the plasma. The plasma becomes transparent for light when the density of electrons in plasma decreases below the critical density. In the case of ErH3 target, the electrons are concentrated both in the region of erbium ions and protons in later phases of acceleration, while in the case of polystyrene target the electrons achieve more or less the same velocity as protons and carbon ions and are concentrated in the same region. For this reason, in the case of CH target the dispersion of electron energy is smaller and the density of electrons is higher. Consequently, for the CH target the plasma becomes transparent later and the process of ion acceleration lasts longer than for the ErH3. As a result, after a sufficiently long time (>100 fs) the higher energies of protons are achieved for the polystyrene target (Fig. 4).
Fig. 3. The 2D spatial distributions of electric field component parallel to laser beam propagation direction for circular polarization in the initial (a) and later (b) stages of acceleration. I L = 1023 W/cm2.
Fig. 4. The time dependence of the mean energy of protons generated from CH and ErH3 targets. I L = 1023 W/cm2.
Figure 5 presents the energy spectra of protons accelerated forward from both types of investigated target by a CP or LP laser pulse for the early and late stages of simulation. As opposite to the previous studies for lower laser intensities (Domański et al., Reference Domański, Badziak and Jabłoński2016a
, Reference Domański, Badziak and Jabłoński
b
), the shapes of most of these spectra are rather similar to the Gaussian distribution. For this reason, the parameters appropriate to describe the spectra are the mean ion energy and the standard ion energy deviation. The mean energy of protons generated from the polystyrene target for both types of polarization is equal to 1.8 GeV. The proton energy dispersion is smaller for the CP than for the linear one and the standard deviation expressed in the mean energy units is equal to
$\; dE_{\rm p} /\bar E_{\rm p} = 0.19$
for CP and
$dE_{\rm p} /\bar E_{\rm p} = 0.3$
for LP. The mean energy of protons generated from the ErH3 target is equal to 0.7 GeV for CP and 0.6 GeV for LP, while the standard deviations of proton energies equal to 0.68 for CP and 0.71 for LP. The difference between energy dispersion of the proton beam generated from different targets could be explained by the higher penetration of the laser pulse into the proton sheet in case of the ErH3 target.
Fig. 5. The energy spectra of protons generated forward from the ErH3 target and the CH target for two different stages of the proton acceleration. I L = 1023 W/cm2 for CP and I L = 2 × 1023 W/cm2 for LP, (a) linear polarization, (b) circular polarization.
The following figures present the mean energy and the standard energy deviation of protons (Fig. 6) and heavy ions (Fig. 7) generated from both types of target and for both types of polarization as a function of laser beam intensity (the laser energy fluence is the same for both types of polarization, the laser intensities on the horizontal axis correspond to CP). It can be observed that the influence of the target's composition on the efficiency of ion acceleration significantly depends on the laser beam intensity. For high laser intensities ≥1022 W/cm2, the mean proton energies are higher for CH than for ErH3, while for the lower ones the higher proton energies are achieved for the ErH3 target. This effect could be explained by the fact that at lower laser intensities the influence of relativistic transparency on the acceleration process is low and the efficiency of proton acceleration is determined by the q/m value of the heavy ion component of the target [see the explanation related to Figure 4 and (Domański et al., Reference Domański, Badziak and Jabłoński2016b )].
Fig. 6. The mean energy (a) and the standard energy deviation (b) of protons generated from the ErH3 target and the CH target as a function of laser intensity for linear (LP) and circular (CP) polarization.
Fig. 7. The mean energy (a) and the standard energy deviation (b) of heavy ions generated from the ErH3 target and the CH target as a function of laser intensity for linear (LP) and circular (CP) polarization.
Both for CH and ErH3 the widths of the proton energy spectrum are smaller for CP than for LP. Additionally, for the CH target they decrease with an increase in laser intensity. The dispersion of proton energy for the ErH3 target is higher than that for the CH target and weakly depends on the laser intensity. The average energies per nucleon of heavy ions are much higher for the carbon ions than for the erbium ions. The energy spectra of both kinds of ions are broad (
$dE_i /\bar E_i \sim 1$
) and the widths of the spectra weakly depend on the intensity.
The quantitative values of the mean energy and the standard energy deviation for protons and heavy ions for the ErH3 and the CH targets as a function of the areal target density σt are shown in Figures 8 and 9. For thin targets of σt < 0.1 mg/cm2, the mean proton energies are higher for CH than for ErH3, while for thicker targets the higher efficiencies of the proton acceleration are achieved for the ErH3 target. Since the electron energy dispersion in the ErH3 target is higher than in the CH one, this type of target becomes transparent for the laser light earlier which results in lower proton energies when the target is thin. For thick targets the laser pulse cannot penetrate through the target and better results are achieved for ErH3.
Fig. 8. The mean energy (a) and the standard energy deviation (b) of protons generated from the ErH3 target and the CH target as a function of the target areal density for linear (LP) and circular (CP) polarization. I L = 1023 W/cm2 for CP and I L = 2 × 1023 W/cm2 for LP.
Fig. 9. The mean energy (a) and the standard energy deviation (b) of heavy ions generated from the ErH3 target and the CH target as a function of the target areal density for linear (LP) and circular (CP) polarization. I L = 1023 W/cm2 for CP and I L = 2 × 1023 W/cm2 for LP.
Such characteristics of ion beams as the beam intensity, the beam ion current density and the shape and duration of the ion pulse are important from the point of view of potential applications of laser-generated ion beams and in the applications such as the fast ignition of nuclear fusion, the production of high-energy-density matter or some nuclear physics experiments, they play a key role (Patel et al., Reference Patel, MacKinnon, Key, Cowan, Foord, Allen, Price, Ruhl, Springer and Stephens2003; Ledingham & Galster, Reference Ledingham and Galster2010; Macchi et al., Reference Macchi, Borghesi and Passoni2013; Fernandez et al., Reference Fernandez, Albright, Beg, Foord, Hegelich, Honrubia, Roth, Stephens and Yin2014). Figure 10 presents the temporal distributions of intensity of proton beams generated from the ErH3 target and the CH target for the linear (a) and circular (b) polarization. These distributions were detected 40 µm behind the rear surface of the target. The spatial (transverse) distributions of the proton beam intensity are shown in Figure 11. The weak influence of laser polarization on the temporal distribution of the proton beam can be observed. In turn, the target's composition strongly influences this characteristic. In the case of CH target, the proton pulse of duration equal to ~11 fs and intensity by an order of magnitude higher than in the case of CH target is produced. It is worth mentioning that the generated proton beams are much shorter and their intensities are much higher than those produced in classical accelerators. For ErH3, the waists of the ion beams are comparable to the waist of the laser pulse, while for CH, they are broader.
Fig. 10. The temporal distribution of intensity of proton beams generated from the ErH3 target and the CH target for linear (a) and circular (b) polarization. I L = 1023 W/cm2 for CP and I L = 2 × 1023 W/cm2 for LP.
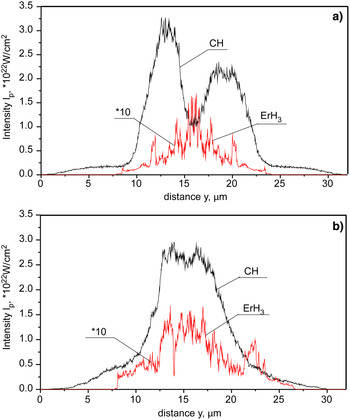
Fig. 11. The spatial distribution of intensity of proton beams generated from the ErH3 target and the CH target for linear (a) and circular (b) polarization. I L = 1023 W/cm2 for CP and I L = 2 × 1023 W/cm2 for LP.
Figure 12 presents the peak proton beam intensity (a) and the peak proton current density (b) as a function of laser beam intensity for the ErH3 and CH targets and for both types of laser beam polarization. In the case of higher laser intensities, the presented values are higher for the CH target, while in the case of lower laser intensities they are higher for the ErH3 target or are similar for both types of the targets. In particular, at the laser pulse intensity of 1023 W/cm2 and the polystyrene target the peak proton beam intensity and the peak proton current density reaches extremely high values, respectively, of 0.8 × 1022 W/cm2 (two orders of magnitude higher than for the ErH3 target) and of 4.5 × 1012 A/cm2 (one order of magnitude higher than for the ErH3 target).
Fig. 12. The peak proton beam intensity (a) and the peak proton current density (b) as a function of laser intensity for the ErH3 and CH targets and for both types of laser beam polarization.
3. CONCLUSIONS
It has been shown that the influence of the target's compositions on the parameters of the generated ion/proton beams significantly depends on other laser–target system parameters such as the laser pulse intensity and the target's thickness. In the case of laser intensities ≥1022 W/cm2 and CH and ErH3 targets with areal densities smaller than 0.1 mg/cm2 higher efficiency of proton acceleration is obtained for the CH targets, while in other cases the higher accelerations efficiency is achieved with the ErH3 targets. At the laser intensities predicted for the ELI lasers (~1023 W/cm2), both for the circular and the linear laser light polarization, the mean energies of protons generated for the CH target can reach values approaching 2 GeV; however, the proton energy spectrum is relatively broad (~0.2
$\bar E_{\rm p} $
for CP and ~0.3
$\bar E_{\rm p} $
for LP). At short distances from the irradiated target (<50 µm), the proton pulse is very short (<20 fs), and the proton beam intensities and the proton current densities reach extremely high values, >1021 W/cm2 and >1012 A/cm2, respectively, which are much higher than those attainable in conventional accelerators. Such proton beams can open the door for new areas of research in high-energy-density physics as well as nuclear physics and can also prove useful for some medical applications.
ACKNOWLEDGMENTS
The simulations were carried out with the support of the Interdisciplinary Centre for Mathematical and Computational Modelling (ICM), University of Warsaw under grant no. G57-20.
