2. DIFFICULTY TO PRODUCE THERMONUCLEAR PROPAGATION IN UNCOMPRESSED DT

The initial theory to find the conditions for the fusion flame generation (thermonuclear propagation) (Nuckolls & Wood, 2002) was published by Bobin (1971) and Chu (1972) as summarized (Bobin, 1974; Brueckner & Jorna, 1974) to arrive at the following:

Condition A: the necessary energy flux density for plane geometry has to be

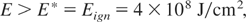
which is above the critical value E_crit = 1.2 × 10⁸ J/cm². This critical value does not change much for other geometries (cylindrical, spherical).

Condition B: if the flame is carried by and ion beam of the optimum DT reaction energy of 80 keV, the ion current density has to be

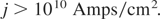
These conditions were indeed far above the possibilities the lasers offered in the 1970s. Considering the interpenetration of the hot plasma of the fusion flame when propagating into the cold solid state DT, a reduction of the condition (1) to

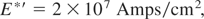
was considered (Hora, 1983).

In view of the present aspects to study the fusion flame generation, it is interesting to mention a number of corrections in the earlier theory which may relax the values of E* to lower values.

Thermal conductivity in the plasma was based—as correct inside of homogeneous plasmas—on the thermal conductivity κ_e of electrons. This is different at the conditions of inhomogeneous plasmas as realized from the double layers (Eliezer & Hora, 1989) and as measured from the field effects in the surface of laser produced plasmas recognized by computations as double layers and even as inverted double layers due to the nonlinear force driven cavities (Hora et al., 1984). This decrease of thermal conductivity was concluded indirectly when fitting measurements of laser produced fast pushers for DT fusion with numerical simulations. A fit was reached if an inhibition of the thermal conduction of electrons could be assumed by a factor up to about 70. From the double layer theory (Eliezer & Hora, 1989) it could be concluded, Figure 1, that the thermal conduction is performed only by the ions such that the thermal conductivity is then

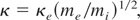
Electric double layer between hot and cold plasma: after the electrons with high energy have left the double layer as preheat towards the cold plasma, the remaining ions only can carry heat conduction at the (me /mi)1/2 times lower conductivity than electrons.

which value for the experiment is then close to 70 as expected. The omission of this double layer effect is the reason for misinterpretations of the otherwise very sophisticated fast pusher laser fusion experiments, e.g., about preheats.

Another effect not included in the theory (Bobin, 1974) is the quantum modification of the electron ion collision frequency. Based on work by Marshak (1941), the classical collision frequency ν_c has to be modified to

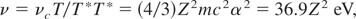
where Z is the ion charge, m the rest mass of the electron, c the speed of light, and α the fine structure constant. This fact has been recognized in several plasma experiments at sufficiently high temperatures and is the reason for the anomalous resistively, for the measured 20 times higher diffusion of deuterium against the magnetic field at 800 eV temperature (Grieger & Wendelstein VII Team, 1981), and the deviation of thermal conductivity (Razumova, 1983) from the classical value agreeing with the quantum corrected values (Hora, 1991: Section 2.6). This quantum modification causes a faster energy transfer form electrons to ions in the fusion flame than under the classical assumptions.

Another problem for the interpenetration process is, what to use for the stopping power of the energetic ions in the plasma flame region. There was a heated discussion (Stepanek, 1981) that the stopping length should be quite large as derived from binary collision models following the Bohr–Bethe-Bloch formulas. In contrast there are experiments by Kerns et al. (1972) as outlined by Guenther (1974) where 2 MeV–0.5 MAmp electron beams of 10 ns duration and 2 mm diameter were hitting deuterated polyethylene producing 10¹⁰ fusion neutrons. In order to measure the penetration depth of the electron beam, the thickness of the target was varied. The saturation of neutron emission at 3 mm proved this value as stopping length. The Bethe–Bloch formula would have arrived at more then 20 times larger stopping lengths. Following Bagge's model for cosmic radiation (Bagge & Hora, 1974) by using a plasma collective energy

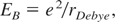
in the stopping power instead of the otherwise used 15.5 eV in the binary collision theory. This means that the fast particles are slowed down as if hitting the whole Debye spheres of the plasma. This model was introduced first by Gabor (1953) and was based on quantum electrodynamics (Ray & Hora, 1977) using an unpublished derivation of Max Born for the Fokker-Planck collisional term in the Boltzmann equation. With this collective collisions, the relativistic penetration of the 2 MeV electrons interactions with the deuterated polyethylene immediately resulted in a stopping length of 3 mm. This result again is reducing the theoretical value E* for the energy flux density.

3. NEW ASPECTS BY SKIN LAYER ACCELERATION OF PLASMA BLOCKS

There was an unexpected effect in the plasma block acceleration by the nonlinear force as first measured by Sauerbrey (1996) with completely unprepared 350 fs KrF laser pulses. Similar unpredicted results on ion emission appeared with ps neodymium glass laser pulses with sophisticated preparation for suppression of pre-pulses (contrast ratio 10⁷ or higher) in numerous details by Badziak et al. (2003, 2004a) as an expression of a skin layer acceleration process (Hora et al., 2002a; Hora, 2003a, 2003b). The uniqueness consists in the avoiding of relativistic self-focusing. Usually it was the experience since the 1070s that the plane geometry plasma blocks were never generated at interaction with powerful laser beams. It always happened that relativistic self-focusing (Hora, 1975, 1991, Section 12.2) appeared (Haseroth & Hora, 1996) and the generation of large numbers of highly charged ions of MeV energy nearly up to GeV were measured moving into a wide range of angles. The more were these relativistic self-focusing effects involved in most of the later ps interaction experiments with TW to PW power apart from many new relativistic effects of pair production (Roth et al., 2001), relativistic electron beams (Umstadter, 1996), gammas of more than 10 MeV energy with subsequent nuclear reactions (Ledingham et al., 2000; Clark et al., 2001; Wilks et al., 2001; Schwoerer et al., 2001; Leemans et al., 2001) etc.

In retrospect, we can consider the discovery of the plane wave geometry without self-focusing by Sauerbrey (1996) as a completely new phenomenon in contrast to all the other experiments known at this time. This is due to the fact—as we know now in retrospect from the work by Badziak et al. (2004a, 2005) as skin layer acceleration (Hora et al., 2002a)—that the 360 fs TW pulses of Schäfer's (1986, see also Teubner et al., 1993) KrF excimer laser were extremely clean, i.e., without prepulse, estimate with a contrast ratio of at least 10⁷. The fact that the Doppler acceleration measured by Sauerbrey (1996) was from a plane geometry plasma block moving against the laser light and that there was not the relativistic self focusing known from all the other observations, can be seen from the splendid agreement of the measured acceleration with the action of the nonlinear force (Hora, 1969, 1986, 1991).

Sauerbrey (1996) measured an acceleration A in a carbon plasma produced by a 350 fs TW KrF laser pulse at 3.5 × 10¹⁷ W/cm² of

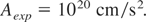
This corresponds to an electric field E² = 2.9 × 10¹⁵ erg/cm³ and a density n_i m_i of the accelerated plasma layer of 5.4 × 10⁻³ g/cm³ at the critical density n_i = 1.6 × 10²¹cm⁻³ for C⁺⁶ ions. The nonlinear force is

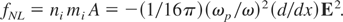
Assuming for simplification dx = Δx = 10 μm and a swelling S = 2 (the experiments Badziak et al., 2003 for ps pulses resulted in S = 3.5) we find the theoretical value

Since end of the 1970s, plane geometry numerical studies of the nonlinear force interaction led to results of interaction of few ps duration and with laser fields up to 10¹⁸ W/cm² which were then completely academic and too early in view of the just mentioned experiments during the last few years, but the results showed the plasma block acceleration which obviously was first observed in such a clear way by Sauerbrey (1996). Figure 2 shows results of these computations where a deuterium plasma block of several wave length thickness was accelerated against the laser light with velocities above 10⁹ cm/s at neodymium glass laser beam irradiation of 10¹⁸ W/cm² intensity.

Generation of blocks of deuterium plasma moving against the neodymium glass laser light (positive velocities v to the right) and moving into the plasma interior (negative velocities) at irradiation by a neodymium glass laser of 1015 to 1018 W/cm2 intensity onto an initially 100 eV hot and 100 μm thick bi-Rayleigh profile (Hora, 1991:Fig. 10.17) with minimum internal reflection at the beginning. The velocity profiles are shown at the same time for 1.5 ps after begin of the constant irradiation (Hora, 1991).

Another key experiment was that by Zhang et al. (1998) (see Wu et al., 2005) where 100 fs TW laser pulses were focused to about 30 wave lengths diameter onto a target and the X-ray emission was measured. The laser pulses produced very much lower X-rays than known from other experiments with the same intensities. The uniqueness of this experiment consists in the procedure, that a lower intensity similar pulse was irradiated on the target at varying times between 10 to 100 ps before the main pulse. At short time pre-irradiation, no change of the low X-ray emission was seen, but as soon as the pre-pulse time reached 70 ps and more, suddenly the very high X-ray emission appeared as known from all the usual main stream experiments. The later given explanation (Hora & Wang, 2001) was evident: thanks to the clean laser pulse technique where the contrast ratio for the main pulse was 10⁸ (ratio of suppression of any pre-pulse). When the 70 ps prepulse was incident, a plasma plum was generated of a depth about two times the focus diameter. This was sufficient that the main pulse was shrinking to about one wave length diameter by relativistic self-focusing such that the then very high X-ray intensities resulted as in the usual cases.

These both experiments (Sauerbrey, 1996; Zhang et al., 1998) were a clear confirmation of the plane wave plasma interaction, in agreement with the plane wave interaction theory, Figure 2, and the exclusion of the self-focusing theory (Hora, 1975; Jones et al., 1982; Häuser et al., 1992; Osman et al., 1999) was rather an unexpected surprise. The drastic difference against the usual observations appeared with the experiments by Badziak et al. (1999) from the studies of ion emission with high contrast ratio ps-TW laser pulses. This mutually confirmed the high contrast ratio of the excimer laser pulses (Sauerbrey, 1996) as well as the very clean techniques of the other experiments (Zhang et al., 1998; Hora & Wang, 2001).

The experiments (Badziak et al., 2003) with copper targets should have led to Cu⁺¹³ ion of 22 MeV energy due to relativistic self-focusing, but only 0.5 MeV ions were detected. Furthermore it was strange that the number of the fast ions did not change at all when the laser intensity was varying by a factor 30, while the energy of the fast ions was fully linear on the laser intensity as expected from nonlinear force acceleration. The measured X-ray emission, leading to a quiver energy swelled dielectrically by a factor three, fully explaining the measured ion energies from a plane wave interaction which was taking place within the skin depth of intensity of independent volume (Hora et al., 2002b). This confirmed the observation of the intensity independence of the fast ions. These experiments were repeated with gold targets confirming all the details of the skin layer mechanism (Badziak et al., 2003) including the generation of the plasma block moving into the target as experimentally confirmed from thin irradiated films (Badziak et al., 2004a, 2004b) and confirming an ion current density in the blocks above

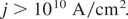
The measurements confirmed also (Badziak et al., 2003) that the ps-TW interaction resulted only in one narrow ion beam, Figure 3, accelerated against the laser light as expected from the nonlinear force acceleration while the use of longer laser pulses as usually resulted in several groups of ions (Ehler, 1975) moving into a wide angle against the laser light (Wolowski et al., 2003). The result of Eq. (10) was most intriguing since it opened the connection to the very early hope, that the plasma blocks from the skin layer acceleration using the nonlinear force can well provide the conditions from sub-relativistic laser plasma interaction with DT ion current densities exceeding 10¹⁰ Amps/cm² and optimum ion energies of 80 keV for initiation of a fusion flame according to Eq. (2). These high density ion currents move space charge neutral within the plasma blocks since their Debye length is more than 10 times smaller than the thickness of the blocks.

The rough angular distributions of mean velocity and peak current density at 1 m from Au target for backward-emitted fast ions driven by 1-ps laser pulses of intensity 7 × 1016 W/cm2 (Badziak et al., 2003).

Because of the importance of the very high current densities in the nonlinear force driven plasma bocks form the SLA process, extensive numerical calculations were performed using the genuine two fluid model with two different but very general codes (Badziak et al., 2004a, 2004b; Cang et al., 2005; Jablonski, 2005; Glowacz et al., 2006). Figure 4 shows the intensity dependence of the block velocities and current densities and Figure 5 is showing also the dependence of the interaction on the duration of the laser pulse.

The maximum ion velocities (a) and the maximum ion current densities (b) for backward-emitted (υb, jb) and forward-emitted (υf , jf ) ions as a function of laser intensity, (Badziak et al., 2004a).

The maximum ion velocities (a) and the maximum ion current densities (b) as a function of the laser pulse duration. IL = 1017W/cm2, Ln /λ = 1 (Badziak et al., 2004a).

It should be mentioned that PIC calculations for the SLA plasma block generation were performed (Klimo & Limpouch, 2006) with very similar results as the genuine two fluid computations showed. The insufficiency of the PIC codes for omitting collisions does not count so much for the laser intensities around 10¹⁷ W/cm² since the basic interaction is the nonlinear force which is essentially a collisionless interaction process. The careful inclusion of the collisions in the hydrodynamic codes is a point of safety for the studies, since it is well known from the theory of resonance absorption (Hora, 1991: Section 11.2) that the essential negative infinite pole of the collisionless theory changes to nearly positive infinite values if the slightest absorption is included.

4. PW-ps LASER PULSES FOR CONTROLLED IGNITION OF SOLID DT

The just presented results of nonlinear force driven plasma blocks by the TW or PW laser pulses of ps duration may open laser fusion by generating the fusion flame in uncompressed solid state density DT as envisaged by Bobin (1974). This alternative for laser fusion would very much simplify a laser fusion reactor avoiding the complicated compression of the DT fuel to several 1000 times the solid state density and may provide the controlled reaction with very high gain in the range of 10⁴ for a much lower cost competitive technological solution.

The result (10) of ion current densities above 10¹⁰ A/cm² for ion energies above 50 keV up to higher values from fast blocks driven into a target by the nonlinear (ponderomotive) force at laser interaction may permit an application to beam fusion as discussed before (Hora, 2004, Hora et al., 2004). Light ion beams for igniting nuclear fusion reactions in uncompressed solid deuterium-tritium targets were considered for years and the necessary conditions turned out to be far above the available technology for generating the ion beams. Nevertheless this scheme was studied in various experiments (Yonas, 1978; Ryutov et al., 2000). The difficulties with the necessary conditions were the two limits of Eqs. (1) and (2) of the energy flux density the ion current density for generating a thermonuclear propagation front (flame propagation) into uncompressed solid DT. Condition (2) can now be fulfilled with the ps laser pulses in the PW range with rather unfocussed beams in order to stay with the optimized DT energies of about 80 keV. We discuss now how the condition (1) may be fulfilled.

Specific studies of the interpenetration process (Hora, 1983) in view of the new knowledge of plasma theory may well permit that the threshold for E* may be further reduced

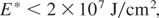
as explained in the preceding section. In the experiments (Badziak et al., 2004a; 2005) the energy flux density was nearly up to values of 10⁶ J/cm². In the following, we may concentrate on the more pessimistic value of Eq. (1).

For the physics—within many more problems to be clarified—it has to be shown that at least condition (1) has to be fulfilled where we are aware that this even may be considered as a pessimistic conclusion in view of the not yet exhausted theory about the threshold E* toward lower values. For the compressing block, the whole maximum quiver energy of the electron is converted into translation energy of the ions. The aim for the DT interaction, we use the oscillation energy of 80 keV of the resonance maximum of the DT reaction may not necessarily be the best choice. Since this is close to the relativistic threshold intensity I_rel we have to use the general quiver energy (Hora, 1991)

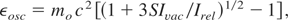
where the maximum intensity I_max = SI_vac due to the dielectric swelling near the critical density is expressed by the factor S with the laser intensity I_vac in vacuum at the target surface.

For the general analysis, we have to be flexible about the chosen values of the applied maximum (dielectrically swelled) oscillation energy ε_osc into the translation DT ion energy ε_trans in adjustment to fusion cross sections (Li et al., 2004). We further let open the value of the energy flux density E* = I_vacτ_L for the reaction conditions (2) or (10), or possibly even a lower value depending on the future research to find the correct value E* where the laser pulse duration τ_L will have to be in the range of ps. According to our numerical studies (Badziak et al., 2004a, 2004b; Jablonski et al., 2005, Glowacz et al., 2006; Cang et al., 2005) in agreement with summarizing estimations, this value could well be a few ps. From

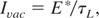
we arrive at the function for the laser wave length

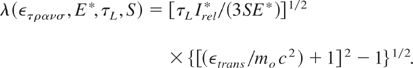
Using as a special case τ_L = 3ps, E* = 2 × 10⁷ J/cm², ε_trans = 80 keV, we arrive at

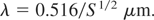
The nonlinear force driven two-block skin layer interaction model works for swelling S considerably larger than 1, as it was the case automatically from the detailed analysis of the measurements (Hora et al., 2002b; Badziak et al., 2003) with S = 3. The lowest possible case with S = 1, is that without any dielectric swelling where the whole laser pulse energy is transferred as in the simple case of radiation pressure (Hora, 1991) to the (nonlinear-force collisionless dominated) absorbing plasma. We conclude that the conditions of (1) or (11) could well be fulfilled for the ignition of uncompressed solid DT fuel when applying shorter laser wave length than that of the neodymium glass laser, which are well in the reach of present technology. For the pessimistic case of Bobin (1974), the numerical factor in (15) is 0.105 such that with S = 1, just the borderline of higher harmonics CPA or of excimer lasers would be covered. Further research on lower values of E* and numerical studies for a little bit longer laser pulses may further relax the conditions, and longer laser wave lengths would be possible. Figure 6 shows the dependence of the necessary laser wave length for a pulse length of 3 ps and swelling S = 1, which one needs for a desired ion translative energy in multiples of m_o c² (m_o is the rest mass of the electron) if the threshold E* is given. Maybe there is a narrow gap for successful conditions.

Relation between the laser wave length the aimed ion energy εtrans in multiples of mo c2 and the necessary energy flux density for ignition of uncompressed DT following Eq. (14) for S = 1 and a laser pulse length of 3 ps.

This study with several preliminary estimations on fusion apart from the solid experimental and theoretically based results on the plasma block generation, may provide the framework for further evaluation of the PIC results for generation of plasma blocks fully covering conditions (1) and (2) (Esirkepov et al., 2004). Attention has to be directed to how to avoid relativistic self-focusing and how to fit the optimum DT ion energies for the fusion flame. Our present position from the side of sub-relativistic conditions may be an alternative approach on the way to the very simplified low cost fusion reactor.