Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T14:53:07.510Z Has data issue: false hasContentIssue false
  • English
  • Français

Excitation of wakefield in a rectangular waveguide: Comparative study with different microwave pulses

Published online by Cambridge University Press:  08 January 2009

A.K. Aria ,
H.K. Malik  and
K.P. Singh
A.K. Aria
Affiliation:
Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology Delhi, Delhi, India
H.K. Malik*
Affiliation:
Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology Delhi, Delhi, India
K.P. Singh
Affiliation:
Simutech, Gainesville, Florida
*
Address correspondence and reprint requests to: H.K. Malik, Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology, Delhi 110016, India. E-mail: hkmalik@physics.iitd.ac.in
Rights & Permissions [Opens in a new window]

Abstract

A differential equation governing the wakefield potential (φ) in a plasma filled rectangular waveguide is derived analytically. This equation is solved numerically for the wakefield (Ew) generated with the help of three kinds of microwave pulses, namely sine pulse (SP), rectangular Gaussian pulse (RGP), and rectangular triangular pulse (RTP). The effect of microwave frequency (f), pulse duration (τ), waveguide width (b), equilibrium plasma density (n0), and microwave intensity (I) on the amplitude of the wakefield is studied. This amplitude is increased for the longer pulse duration and higher microwave intensity, but is decreased with growing waveguide width for all types of pulses. With regard to the variation of wakefield amplitude with plasma density, the RTP and SP behave in a similar fashion and the RGP behaves oppositely. The amplitude for the case of RGP gets increased with the plasma density. The amplitude is enhanced at larger microwave frequency for the cases of RGP and SP, but is decreased for the case of RTP. The comparative study of three types of pulses shows that the wakefield with larger amplitude is achieved with the help of rectangular triangular pulse, which is found to be sensitive with waveguide width, pulse duration and microwave intensity.

Keywords

Microwave pulsesPlasmawakefieldWaveguide
Type
Research Article
Information
Laser and Particle Beams , Volume 27 , Issue 1 , March 2009 , pp. 41 - 47
Copyright
Copyright © Cambridge University Press 2009

INTRODUCTION AND MOTIVATION

The interaction of electromagnetic waves with plasmas has been an interesting and growing field of research primarily due to the availability of very high power lasers and other radiation sources. This field has applications in laser induced fusion, beat wave acceleration, laser wakefield acceleration, harmonic generation, self focusing of laser light, nuclear physics etc. Wakefield generation for the purpose of charged particle acceleration using lasers has been widely studied experimentally, analytically, and using simulations. Efforts have been made related to wakefield excitation by relativistic electron bunch (Balakirev et al., Reference Balakirev, Karas, Karas and Levchenko2001; Baiwen et al., Reference Baiwen, Ishiguro, Skoric, Takamaru and Sato2004; Zhou et al., Reference Zhou, Yu and He2007), ion accelerators (Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007), coupling of longitudinal and transverse motion of accelerated electrons in laser wakefield (Reitsma & Jaroszynski, Reference Reitsma and Jaroszynski2004), and compact GeV plasma accelerator (Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006). Koyama et al. (Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006) experimentally generated a monoenergetic electron beam by focusing 2 TW laser pulses of 50 fs on supersonic gas jet targets. In another experiment, Chen et al. (Reference Chen, Unick, Vafaei-Najafabadi, Tsui, Fedosejevs, Naseri, Masson-Laborde and Rozmus2008) produced quasi-monoenergetic electron beams from 7 TW laser pulses in N2 and He gas targets. Lotov (Reference Lotov2001) analytically studied the laser wakefield acceleration in narrow plasma filled channels. The wakefield is reported to be enhanced by the nonlinearities in the response of the plasma to the ponderomotive force of a long smooth laser pulse of relativistic intensity, whose length is much larger than half of the plasma wavelength (Kingham & Bell, Reference Kingham and Bell1997). The amplitude of the laser wakefield has also been found to increase by the ionization processes of the gases at comparatively higher laser peak intensities (Andreev et al., Reference Andreev, Chegotov and Veisman2000). A capillary tube can be used as a waveguide in order to enhance the interaction length (Cros et al., Reference Cros, Courtois, Malka, Matthieussent, Marques, Dorchies, Amiranoff, Rebibo, Hamoniaux, Blanchot and Miquel2000). Tapered plasma channels have been proposed to achieve stronger electron acceleration in laser wakefield mechanism by enhancing the interaction length of the laser pulse with the plasma (Sprangle et al., Reference Sprangle, Hafizi, Peñano, Hubbard, Ting, Moore, Gordon, Zigler, Kaganovich and Antonsen2001). On the other hand, the polarization effect of fields in the vacuum laser accelerator has been discussed (Xu et al., Reference Yoder, Marshall and Hirshfield2007) including collimated GeV electron bunch generation (Karmakar & Pukhov, Reference Karmakar and Pukhov2007), and collimated proton beam generation from tantalum targets irradiated with circularly polarized laser pulses (Kado et al., Reference Kado, Daido, Fukumi, Li, Orimo, Hayashi, Nishiuchi, Sagisaka, Ogura, Mori, Nakamura, Noda, Iwashita, Shirai, Tongu, Takeuchi, Yamazaki, Itoh, Souda, Nemoto, Oishi, Nayuki, Kiriyama, Kanazawa, Aoyama, Akahane, Inoue, Tsuji, Nakai, Yamamoto, Kotaki, Kondo, Bulanov, Esirkepov, Utsumi, Nagashima, Kimura and Yamakawa2006).

Zhang et al. (Reference Zhou, Yu and He1997) have done calculations for a wakefield accelerator using a dielectric lined waveguide structure and showed that the acceleration gradient for electrons or positrons can be achieved in the range of 50–100 MV/m for a few nC driving bunches. Using a uniform circular waveguide with a helical wiggler and axial magnetic field, Yoder et al. (Reference Zhang, Hirshfield, Marshall and Hafizi2001) measured the energy gain of about 360 keV for a 6 MeV electron bunch and an accelerating gradient of 0.43 MV/m in a microwave inverse free electron laser accelerator. In another wakefield accelerator using a dielectric lined waveguide, a peak acceleration gradient of 155 MeV/m was predicted for a 2 nC rectangular drive bunch (Park & Hirshfield, Reference Park and Hirshfield1997). Jing et al. (Reference Jing, Liu, Xiao, Gai and Schoessow2003) have found transverse wakefields of about 0.13 MeV/mnC (0.2 MeV/mnC) due to X-dipole modes (Y-dipole modes) in an X-band structure generated by an electron bunch in dipole-mode wakefields in a waveguide accelerating structure. On the other hand, microwaves have been used in experiments for particle acceleration via resonance absorption during wave particle interaction (Nishida et al., Reference Nishida, Okazaki, Yugami and Nagasawa1991) and $\vec v_p \times \vec B$ process (Nishida et al., Reference Nishida, Yoshizumi and Sugihara1985; Nishida & Sato, Reference Nishida and Sato1987; Nishida & Shinozaki, Reference Nishida and Shinozaki1990), where $\vec v_p$ is the phase velocity of the microwave and $\vec B$ is the externally applied magnetic field. Short microwave pulses have also been used in some experiments to excite a nonlinear large amplitude ion wave at resonance absorption region (Nishida et al., Reference Nishida, Kusaka and Yugami1994).

It is clear from the literature that the lasers have been extensively used for the purpose of particle acceleration via wakefield generation and other methods. An appreciable amount of energy gain has also been achieved for the electrons and protons. However, these types of systems cost very much and very sophisticated instrumentation is required for the specific/accurate measurement on ultrafast time scale. Therefore, in view of low cost structure and effective acceleration by moderate intensity microwave radiation, we investigate in the present article the wakefield excited by three different types of microwave pulses in a rectangular waveguide filled with homogeneous plasma. We make a comparative study between the proposed pulses, namely sine pulse (SP), rectangular Gaussian pulse (RGP), and rectangular triangular pulse (RTP).

GOVERNING EQUATIONS

The present model consists of a waveguide of width b(m) and height h(m) filled with plasma of equilibrium density n 0. The wakefield is assumed to be generated by the microwave pulse having frequency f and pulse duration τ. The corresponding potential to this wakefield is φ. The plasma is assumed to be cold and collisionless and the motion of ions is neglected. We use the fluid approach and write below the basic fluid equations together with the Maxwell's equations describing the propagation of the microwave pulse in the plasma.

(1)
{{\partial n_e } \over {\partial t}}+\nabla \cdot \left({n_e \vec v} \right)=0\comma \;
(2)
{{d\vec p} \over {dt}}+n_e e\left({\vec E+\vec v \times \vec B} \right)=0.
(3)
\nabla \times \vec E+{{\partial \vec B} \over {\partial t}}=0\comma \;
(4)
\nabla \times \vec B - \mu _0 \vec J - {1 \over {c^2 }}{{\partial \vec E} \over {\partial t}}=0\comma \;
(5)
\nabla \cdot \vec B=0\comma \;
(6)
\nabla \cdot \vec E={e \over {\varepsilon _0 }}\left({n_i - n_e } \right).

Here n e and n i are the densities of the electrons and ions, respectively, The electric and magnetic fields associated with the microwave are given by $\vec E$ and $\vec B$, respectively, and $\vec J$ is the current density of the electrons in the plasma induced by the microwave field. Now we separate out the x-, y-, and z-components of the above equations as follows

(7)
{{\partial n_e } \over {\partial t}}+{{\partial n_e v_z } \over {\partial z}}=0\comma \;
(8)
{{\partial v_x } \over {\partial t}}+v_z {{\partial v_x } \over {\partial z}}+{e \over m}\left({v_y B_z } \right)=0\comma \;
(9)
{{\partial v_y } \over {\partial t}}+v_x {{\partial v_y } \over {\partial x}}+v_z {{\partial v_y } \over {\partial z}}+{e \over m}\left({E - v_x B_z+v_z B_x } \right)=0\comma \;
(10)
{{\partial v_z } \over {\partial t}}+v_x {{\partial v_z } \over {\partial x}}+v_z {{\partial v_z } \over {\partial z}} - {e \over m}\left({{{\partial \phi } \over {\partial z}}+v_y B_x } \right)=0\comma \;
(11)
{{\partial E} \over {\partial x}}+{{\partial B_z } \over {\partial t}}=0\comma \;
(12)
{{\partial E} \over {\partial z}} - {{\partial B_x } \over {\partial t}}=0\comma \;
(13)
- {{\partial B_z } \over {\partial x}}+{{\partial B_x } \over {\partial z}}+\mu _0 n_e ev_y - {1 \over {c^2 }}{{\partial E} \over {\partial t}}=0\comma \;
(14)
{{\partial B_x } \over {\partial x}}+{{\partial B_z } \over {\partial z}}=0\comma \;
(15)
{{\partial ^2 \phi } \over {\partial z^2 }}+{e \over {\varepsilon _0 }}\left({n_i - n_e } \right)=0.

Here v x, v y and v z are the x-, y-, and z-components of the velocity of the electron fluid and v x is taken to be uniform in the direction of the waveguide width (Aria & Malik, Reference Aria and Malik2008). It is assumed that the electric field is directed along the y-axis and $\vec \nabla$ is taken in the (x, z) plane.

Now we will express the density of the electrons as $n_e = n_0 + n_{e1}$, where n e1 is the density perturbation due to the microwave pulse. We are considering the system to be non-evolving, i.e., all the quantities are taken as a function of $\xi = z - v_g t$, where v g is the group velocity of the microwave pulse (Tajima & Dawson, Reference Xu, Kong, Chen, Wang, Wang, Lin and Ho1979; Sprangle et al., Reference Tajima and Dawson2001; Gorbunov et al., Reference Gorbunov, Mora and Ramazashvili2003a, Reference Gorbunov, Mora and Solodov2003b, Aria & Malik, Reference Aria and Malik2008; Malik, Reference Malik2008) and ${{\partial n_0 } / {\partial \xi }}=0$ is suggested for the homogeneous plasma. Therefore, Eqs. (7)–(15) take the form

(16)
- v_g {{\partial n_{e1} } \over {\partial \xi }}+n_0 {{\partial v_z } \over {\partial \xi }}+{{\partial n_e v_z } \over {\partial \xi }}=0\comma \;
(17)
- v_g {{\partial v_x } \over {\partial \xi }}+v_z {{\partial v_x } \over {\partial \xi }}+{e \over m}\left({v_y B_z } \right)=0\comma \;
(18)
- v_g {{\partial v_y } \over {\partial \xi }}+v_x {{\partial v_y } \over {\partial x}}+v_z {{\partial v_y } \over {\partial \xi }}+{e \over m}\left({E - v_x B_z+v_z B_x } \right)=0\comma \;
(19)
- v_g {{\partial v_z } \over {\partial \xi }}+v_x {{\partial v_z } \over {\partial x}}+v_z {{\partial v_z } \over {\partial \xi }} - {e \over m}\left({{{\partial \phi } \over {\partial \xi }}+v_y B_x } \right)=0\comma \;
(20)
{{\partial E} \over {\partial x}} - v_g {{\partial B_z } \over {\partial \xi }}=0\comma \;
(21)
{{\partial E} \over {\partial \xi }}+v_g {{\partial B_x } \over {\partial \xi }}=0\comma \;
(22)
- {{\partial B_z } \over {\partial x}}+{{\partial B_x } \over {\partial \xi }}+\mu _0 n_e ev_y+{{v_g } \over {c^2 }}{{\partial E} \over {\partial \xi }}=0\comma \;
(23)
{{\partial B_x } \over {\partial x}}+{{\partial B_z } \over {\partial \xi }}=0\comma \;
(24)
{{\partial ^2 \phi } \over {\partial \xi ^2 }} - {e \over {\varepsilon _0 }}n_{e1}=0\comma \;

where group velocity of the microwave pulse $v_g=c\, \left({1 - {{\omega _p ^2 }/{\omega ^2 }} - {{\pi ^2 c^2 }/{b^2 \omega ^2 }}} \right)^{1/2}$ coincides with the phase velocity of the wakefield.

For the rectangular waveguide, we have taken the distribution of the microwave field as $\vec E=\hat y\, E\left(\xi \right)\, \sin \left({{{\pi x} \over b}} \right)$, $\vec B=\hat x\, B_z \lpar \xi\rpar \, \, \sin \left({{\pi x} \over b} \right)\, \, +\hat z\, B_z \lpar \xi\rpar \, \cos \left({{\pi x} \over b} \right).$ By means of these relations, we integrate Eqs. (16)–(24) under the conditions that all the oscillating quantities tend to zero as $\xi \to \infty$ and that $n_{e1}\lt \lt n_0$. With this we get the following equation

(25)
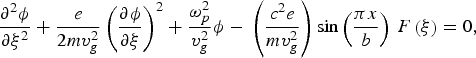
{{\partial ^2 \phi } \over {\partial \xi ^2 }}+{e \over {2mv_g ^2 }}\left({{{\partial \phi } \over {\partial \xi }}} \right)^2+{{\omega _p ^2 } \over {v_g^2 }}\phi - \, \left({{c^2 e} \over {mv_g ^2 }} \right)\sin \left({{\pi x} \over b} \right)\, F\left(\xi \right)=0\comma \;

where

F \lpar \xi\rpar = {1 \over 2}\left[{\left({{1 \over {v_g ^2 }} - {1 \over {c^2 }}} \right)E^2 \left(\xi \right)- B_z ^2 \left(\xi \right)} \right].

PULSE PROFILES FOR NUMERICAL CALCULATIONS

We can use the information related to the shape of the pulse through the last term of Eq. (25) via the coefficient F(ξ). In the present study, using the fourth-order Runge-Kutta method, we simulate Eq. (25) for three types of the pulse shapes, namely SP, RGP, and RTP by giving typical values to microwave intensity I, its frequency f(= ω/2π), pulse duration τ, equilibrium plasma density n 0 and waveguide width b. Here, we take different profiles for the electric field of the pulse, keeping in mind its shape and calculate B z(ξ) with the help of Eq. (20). The relation between B z(ξ) and E(ξ) thereby comes out to be

(26)
B_z \lpar \xi \rpar ={1 \over {v_g }}{\pi \over b}\vint {E\lpar \xi \rpar } d\xi.

Sine Pulse (SP)

This pulse is the simplest one whose profile is taken sinusoidal along with the following expression

E\lpar \xi \rpar = E_0 \, \sin \left({{{\pi \xi } /L}} \right)\quad \,\hbox{for} \ 0 \leq \xi \leq L

The profile of this pulse is shown in Figure 1a, where L is the length of the pulse.

Fig. 1. Profiles of three different types of the microwave pulses of length L.

Rectangular Gaussian pulse (RGP)

This pulse with length L is shown in Figure 1b. The field profile is taken as below

\matrix {E\left(\xi \right)=E_0 \hfill & \quad \,\hbox{for} \ 0 \leq \xi \leq L/2\comma \; \cr E\lpar \xi \rpar = E_0 \, \sin \left({{\pi \xi } / L} \right)& \enspace \ \,\hbox{for} \ L/2 \leq \xi \leq L.}

Rectangular Triangular Pulse (RTP)

Finally, we select the field profile so that it looks like a combination of rectangular and triangular pulses (Fig.1c). For the pulse length L, we take the following expressions for E(ξ)

\matrix {E\lpar \xi\rpar = E_0 \sqrt {1 - \cos \left({{2\pi \xi } / L} \right)} \hfill & \quad\,\hbox{for} \ 0 \leq \xi \leq L/4\comma \; \hfill \cr E\lpar \xi \rpar = E_0 \hfill & \quad\,\hbox{for} \ L/4 \leq \xi \leq 2L/3\comma \; \hfill \cr E\lpar \xi \rpar = E_0 \sqrt{\left\{1 + \cos \left(3 \pi \xi / L \right)\right\}/ 2} \hfill & \quad\,\hbox{for} \ 2L/3 \leq \xi \leq L.\hfill}

RESULTS AND DISCUSSION

So far we have derived a differential Eq. (25) for the wakefield potential φ induced by the microwave pulse in a waveguide filled with homogeneous plasma. For typical values of f, τ, b, n 0, and I, we solve this equation numerically and obtain the potential φ from which we look for the wakefield amplitude E W for the mentioned three types of the pulse shapes. Figures 2 to 4 show the profile of wakefield generated by SP, RGP, and RTP. Here, it can be easily seen that the amplitude of the wakefield is the largest in the case of RTP and is the least for the case of SP; in other words, wakefield amplitude follows the trend $E_{WRTP}\gt E_{WRGP}\gt E_{WSP}$.

Fig. 2. (Color online) Variation of wakefield generated by microwave SP in a waveguide for microwave intensity I = 2 GW/m2, frequency f = 30 GHz, pulse duration τ = 2 ns, plasma density n 0 = 4.5 × 1017 m−3 and waveguide width b = 0.03 m.

Fig. 3. (Color online) Variation of wakefield generated by microwave RGP in a waveguide for the same parameters as in Figure 2.

Fig. 4. (Color online) Variation of wakefield generated by microwave RTP in a waveguide for the same parameters as in Figure 2.

Figure 5 shows the dependence of the wakefield amplitude on the plasma density for two different pulse durations of 1.5 ns (left axis in the figure) and 3 ns (right axis in the figure). We find that the amplitude is increased for the higher plasma density in the waveguide for the case of RGP. However, the opposite trend is realized for the other types of the pulses (SP and RTP). Again, the amplitude of wakefield remains the largest in case of the rectangular triangular pulse. Moreover, when we compare the slopes of the graphs, we obtain that the RTP shows stronger dependence on the plasma density in comparison with the other types of the pulses. When we examine the effect of pulse duration on the wakefield, we notice that the larger wakefield is achieved for the case of longer pulse durations. This is true for all types of the pulses. Similar effect of pulse duration on the wakefield as well as on the wake potential was obtained in our recent work for Gaussian like pulse where the matching condition ($\tau = f_p^{-1}$) was maintained (Aria & Malik, Reference Aria and Malik2008).

Fig. 5. Dependence of wakefield amplitude on plasma density n 0 for two different microwave pulse durations τ = 1.5 ns (solid line graphs, left axis) and τ = 3.0 ns (dashed line graphs, right axis), when other parameters are the same as in Figure 2.

In Figure 6, we show the effect of microwave frequency and its intensity on the wakefield amplitude. Here, it is seen that an increase in microwave frequency leads to an enhancement in the wakefield amplitude for the cases of RGP and SP. However, the opposite is true for the RTP, which also shows a strong dependence (slope 0.097 at I = 2 × 109 W/m2) on the microwave frequency as compared with the other pulses (slope 0.064 for RGP and 0.024 for SP). When we analyze the effect of microwave intensity on the wakefield amplitude, we observe that the larger wakefield is obtained for the higher microwave intensity in the case of all types of the pulses. Also, it is evident from the figure that the amplitude is modified at a faster rate in the case of RTP in comparison with the other types of the pulses. Generally, we can conclude that the RTP is most sensitive with respect to microwave frequency and intensity. The increase of wakefield for the larger pulse intensity is consistent with the results obtained analytically for the rectangular, rectangular Gaussian, and rectangular triangular pulses (Malik, Reference Malik2008). Moreover, it is worth noticing from Figures 2–6 that tens of MV/m wakefield is attained with the use of moderate intensity microwave pulses. In view of the effect of microwave intensity (Fig. 6), it is therefore expected that the wakefield on the order of GV/m can be generated if the microwave pulses of intensity ~ TW/m2 are available. Since the wakefield on this order is generally obtained by ultra high intensity lasers in usual wakefield generation schemes (Lotov, Reference Lotov2001; Reitsma et al., 2004; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Nickles et al., Reference Nickles, Ter-Avetisyan, Schnuerer, Sokollik, Sandner, Schreiber, Hilscher, Jahnke, Andreev and Tikhonchuk2007), the present mechanism of exciting wakefield in the waveguide by microwave pulses seems to be more effective and feasible as it can reduce the cost of accelerator, and also it will provide an additional controlling parameter (the waveguide width).

Fig. 6. Variation of wakefield amplitude with microwave frequency f for two different microwave intensities I = 2 × 109 W/m2 (solid line graphs, left axis) and I = 1 × 109 W/m2 (dashed line graphs, right axis), when the other parameters are the same as in Figure 2.

Figure 7 shows the variation of the wakefield amplitude with the waveguide width for all types of the pulses. Interestingly, it is observed that the amplitude is decreased with the increase of waveguide width; same result was obtained in another calculation done analytically for a plasma filled rectangular waveguide (Malik, Reference Malik2008). It means the larger wakefield can be obtained for the case of plasma filled narrower waveguide. When we compare the slopes of the graphs in the figure, we notice that again the wakefield amplitude changes at a faster rate in the case of RTP. Therefore, the RTP is found to be more sensitive with the waveguide width. So, we can conclude that a plasma filled narrower waveguide is best suited for an effective wakefield excitation and the significant particle acceleration if the RTP is used.

Fig. 7. Variation of wakefield amplitude with waveguide width. The values of intensity, frequency, pulse duration, and plasma density are given in the caption of Figure 2.

CONCLUSIONS

In the present paper, we carried out numerical studies on the wakefield excitation by three types of the pulses in a rectangular waveguide filled with homogeneous plasma. Our analysis reveals that moderate intensity (~109 W/m2) microwave pulses can produce up to 100 MV/m wakefields in the waveguide if the nanosecond pulses are used. Since the wakefield amplitude changes at a faster rate with waveguide width, pulse duration, and microwave intensity, and it is larger for the smaller waveguide width, longer pulse duration and the higher microwave intensity in the case of RTP, it is concluded that the significant wakefield can be excited in the waveguide and effective particle acceleration can be achieved with the use of RTP for which the parameters can be optimized using the present study.

References

REFERENCES

Andreev, N.E., Chegotov, M.V. & Veisman, M.E. (2000). Wakefield generation by elliptically polarized femtosecond laser pulse in ionizing gases. IEEE Trans. Plasma Sci. 28, 1098–1105.CrossRefGoogle Scholar
Aria, A.K. & Malik, H.K. (2008). Wakefield generation in a plasma filled rectangular waveguide. Open Plasma Phys. J. 1, 1–8.CrossRefGoogle Scholar
Baiwen, L.I., Ishiguro, S., Skoric, M.M., Takamaru, H. & Sato, T. (2004). Acceleration of high-quality, well-collimated return beam of relativistic electrons by intense laser pulse in a low-density plasma. Laser Part. Beams 22, 307–314.CrossRefGoogle Scholar
Balakirev, V.A., Karas, V.I., Karas, I.V. & Levchenko, V.D. (2001). Plasma wakefield excitation by relativistic electron bunches and charged particle acceleration in the presence of external magnetic field. Laser Part. Beams 19, 597–604.CrossRefGoogle Scholar
Chen, Z.L., Unick, C., Vafaei-Najafabadi, N., Tsui, Y.Y., Fedosejevs, R., Naseri, N., Masson-Laborde, P.E. & Rozmus, W. (2008). Quasi-monoenergetic electron beams generated from 7 TW laser pulses in N2 and He gas targets. Laser Part. Beams 26, 147–155.CrossRefGoogle Scholar
Cros, B., Courtois, C., Malka, G., Matthieussent, G., Marques, J.R., Dorchies, F., Amiranoff, F., Rebibo, S., Hamoniaux, G., Blanchot, N. & Miquel, J.L. (2000). Extending plasma accelerators: Guiding with capillary tubes. IEEE Trans. Plasma Sci. 28, 1071–1077.CrossRefGoogle Scholar
Flippo, K., Hegelich, B.M., Albright, B.J., Yin, L., Gautier, D.C., Letzring, S., Schollmeier, M., Schreiber, J., Schulze, R. & Fernandez, J.C. (2007). Laser-driven ion accelerators: Spectral control, monoenergetic ions and new acceleration mechanisms. Laser Part. Beams 25, 3–8.CrossRefGoogle Scholar
Gorbunov, L.M., Mora, P. & Ramazashvili, R.R. (2003 a). Laser surface wakefield in a plasma column. Phys. Plasmas 10, 4563–4566.CrossRefGoogle Scholar
Gorbunov, L.M., Mora, P. & Solodov, A.A. (2003 b). Dynamics of a plasma channel created by the wakefield of a laser pulse. Phys. Plasmas 10, 1124–1134.CrossRefGoogle Scholar
Jing, C., Liu, W., Xiao, L., Gai, W. & Schoessow, P. (2003). Dipole-mode wakefields in dielectric-loaded rectangular waveguide accelerating structures. Phys. Rev. E. 6, 016502 (1–6).Google Scholar
Kado, M., Daido, H., Fukumi, A., Li, Z., Orimo, S., Hayashi, Y., Nishiuchi, M., Sagisaka, A., Ogura, K., Mori, M., Nakamura, S., Noda, A., Iwashita, Y., Shirai, T., Tongu, H., Takeuchi, T., Yamazaki, A., Itoh, H., Souda, H., Nemoto, K., Oishi, Y., Nayuki, T., Kiriyama, H., Kanazawa, S., Aoyama, M., Akahane, Y., Inoue, N., Tsuji, K., Nakai, Y., Yamamoto, Y., Kotaki, H., Kondo, S., Bulanov, S., Esirkepov, T., Utsumi, T., Nagashima, A., Kimura, T. & Yamakawa, K. (2006). Observation of strongly collimated proton beam from Tantalum targets irradiated with circular polarized laser pulses. Laser Part. Beams 24, 117–123.CrossRefGoogle Scholar
Karmakar, A. & Pukhov, A. (2007). Collimated attosecond GeV electron bunches from ionization of high-Z material by radially polarized ultra-relativistic laser pulses. Laser Part. Beams 25, 371–377.CrossRefGoogle Scholar
Kingham, R.J. & Bell, A.R. (1997). Enhanced wakefields for the 1D Laser wakefield Accelerator. Phys. Rev. Lett. 79, 4810–4813.CrossRefGoogle Scholar
Koyama, K., Adachi, M., Miura, E., Kato, S., Masuda, S., Watanabe, T., Ogata, A. & Tanimoto, M. (2006). Monoenergetic electron beam generation from a laser-plasma accelerator. Laser Part. Beams 24, 95–100.CrossRefGoogle Scholar
Lifschitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser plasma accelerator. Laser Part. Beams 24, 255–259.CrossRefGoogle Scholar
Lotov, K.V. (2001). Laser wakefield acceleration in narrow plasma-filled channels. Laser Part. Beams 19, 219–222.CrossRefGoogle Scholar
Malik, H.K. (2008). Analytical calculations of wake field generated by microwave pulses in a plasma filled waveguide for electron acceleration. J. Appl. Phys. 104, 053308(1–7).CrossRefGoogle Scholar
Nickles, P.V., Ter-Avetisyan, S., Schnuerer, M., Sokollik, T., Sandner, W., Schreiber, J., Hilscher, D., Jahnke, U., Andreev, A. & Tikhonchuk, V. (2007). Review of ultrafast ion acceleration experiments in laser plasma at Max Born Institute. Laser Part. Beams 25, 347–363.CrossRefGoogle Scholar
Nishida, Y. & Sato, N. (1987). Observation of high-energy electrons accelerated by electrostatic waves propagating obliquely to a magnetic field. Phys. Rev. Lett. 59, 653–656.CrossRefGoogle ScholarPubMed
Nishida, Y. & Shinozaki, T. (1990). Resonant wave-particle interaction in v p x B acceleration scheme. Phys. Rev. Lett. 65, 2386–2389.CrossRefGoogle ScholarPubMed
Nishida, Y., Kusaka, S. & Yugami, N. (1994). Excitation of wakefield and electron acceleration by short microwave pulse. Phys. Scripta T52, 65–68.CrossRefGoogle Scholar
Nishida, Y., Okazaki, T., Yugami, N. & Nagasawa, T. (1991). Excitation of large-amplitude ion-wave wake fields. Phys. Rev Lett. 66, 2328–2332.CrossRefGoogle ScholarPubMed
Nishida, Y., Yoshizumi, M. & Sugihara, R. (1985). Electron acceleration by electromagnetic waves in weakly magnetized inhomogeneous plasma. Phys. Fluids 28,1574–1576.CrossRefGoogle Scholar
Park, S.Y. & Hirshfield, J.L. (1997). Theory of wakefields in a dielectric-lined waveguide. Phys. Rev. E 62, p. 1266–1283.CrossRefGoogle Scholar
Reitsma, A.J.W. & Jaroszynski, D.A. (2004). Coupling of longitudinal and transverse motion of accelerated electrons in laser wakefield acceleration. Laser Part. Beams 22, 407–413.CrossRefGoogle Scholar
Sprangle, P., Hafizi, B., Peñano, J.R., Hubbard, R.F., Ting, A., Moore, C.I., Gordon, D.F., Zigler, A., Kaganovich, D. & Antonsen, T.M. Jr. (2001). Wakefield generation and GeV acceleration in tapered plasma channels. Phys. Rev. 63, 056405(1–11).Google ScholarPubMed
Tajima, T. & Dawson, J.M. (1979). Laser electron accelerator. Phys. Rev. Lett. 43, 267–270.CrossRefGoogle Scholar
Xu, J.J., Kong, Q., Chen, Z., Wang, P.X., Wang, W., Lin, D. & Ho, Y.K. (2007). Polarization effect of fields on vacuum laser acceleration. Laser Part. Beams 25, 253–257.CrossRefGoogle Scholar
Yoder, R.B., Marshall, T.C. & Hirshfield, J.L. (2001). Energy-gain measurements from a microwave inverse free-electron-laser accelerator. Phys. Rev. Lett. 86, 1765–1768.CrossRefGoogle ScholarPubMed
Zhang, T.B., Hirshfield, J.L., Marshall, T.C. & Hafizi, B. (1997). Stimulated dielectric wake-field accelerator. Phys. Rev. E 56, 4647–4655.CrossRefGoogle Scholar
Zhou, C.T., Yu, M.Y. & He, X.T. (2007). Electron acceleration by high current-density relativistic electron bunch in plasmas. Laser Part. Beams 25, 313–319.CrossRefGoogle Scholar
Figure 0

Fig. 1. Profiles of three different types of the microwave pulses of length L.

Figure 1

Fig. 2. (Color online) Variation of wakefield generated by microwave SP in a waveguide for microwave intensity I = 2 GW/m2, frequency f = 30 GHz, pulse duration τ = 2 ns, plasma density n0 = 4.5 × 1017 m−3 and waveguide width b = 0.03 m.

Figure 2

Fig. 3. (Color online) Variation of wakefield generated by microwave RGP in a waveguide for the same parameters as in Figure 2.

Figure 3

Fig. 4. (Color online) Variation of wakefield generated by microwave RTP in a waveguide for the same parameters as in Figure 2.

Figure 4

Fig. 5. Dependence of wakefield amplitude on plasma density n0 for two different microwave pulse durations τ = 1.5 ns (solid line graphs, left axis) and τ = 3.0 ns (dashed line graphs, right axis), when other parameters are the same as in Figure 2.

Figure 5

Fig. 6. Variation of wakefield amplitude with microwave frequency f for two different microwave intensities I = 2 × 109 W/m2 (solid line graphs, left axis) and I = 1 × 109 W/m2 (dashed line graphs, right axis), when the other parameters are the same as in Figure 2.

Figure 6

Fig. 7. Variation of wakefield amplitude with waveguide width. The values of intensity, frequency, pulse duration, and plasma density are given in the caption of Figure 2.