Instability analysis

Consider a plasma with equilibrium electron number density n _e0, ion number density n _i0, and dust grain number density n _d0. The dusty plasma is under the influence of the static magnetic field B _s in the z-direction. The electrons are defined by (−e, m _e, T _e), ions by (e, m _i, T _i) and dust particles by (−Q _d0, m _d, T _d). Consider an electrostatic wave, say, TG mode, propagating almost perpendicular to the external magnetic field (propagation vector k) in the x-z plane. The streaming ions are considered to be magnetized and moving parallel to applied magnetic field with velocity v _i, electrons are taken to be non-streaming and magnetized and dust grains are considered as negatively charged, non-streaming, and unmagnetized. Prior to the perturbation, plasma system is quasi-neutral such that − n _e0 + n _i0 − n _d0 ≈ 0. This equilibrium is perturbed due to electrostatic TG mode and potential associated with it is given by

(1)$${\rm \phi} = {\rm \phi} _0\exp [-i({\rm \omega} t-k_xx-k_zz)]{\rm.} $$

The plasma species are taken as fluids and governed by the equation of motion [$m(d\vec{v}/dt) = e\vec{E} + (e/c)\vec{v} \times \vec{B}_{\rm s}$] and equation of continuity [$(\partial n/\partial t) + \nabla. (n\vec{v}) = 0$]. On linearization, the equation of motion and the equation of continuity lead to the plasma electron, plasma ion, and dust grain density perturbations as:

(2)$$n_{1{\rm e}} = -\displaystyle{{n_{{\rm e}0}{\rm e}{\rm \phi}} \over {m_{\rm e}}}\left[ {\displaystyle{{k_x^2} \over {{\rm \omega}^2-{\rm \omega}_{{\rm ce}}^2}} + \displaystyle{{k_z^2} \over {{\rm \omega}^2}}} \right]{\rm,} $$

(3)$$n_{1{\rm i}} = \displaystyle{{n_{{\rm i}0}{\rm e}{\rm \phi}} \over {m_{\rm i}}}\left[ {\displaystyle{{k_x^2} \over {{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega}_{{\rm ci}}^2}} + \displaystyle{{k_z^2} \over {{({\rm \omega} -k_zv_{\rm i})}^2}}} \right]{\rm,} $$

(4)$$n_{1{\rm d}} = -\displaystyle{{n_{{\rm d}0}Q_{{\rm d}0}k^2{\rm \phi}} \over {m_{\rm d}{\rm \omega} ^2}}{\rm,} $$

where ω_ce( = eB _s/m _ec) is the electron-cyclotron frequency and ω_ci( = eB _s/m _ic) is the ion-cyclotron frequency.

In this case, dust is taken as unmagnetized since ω ≫ ω_cd with ω_cd(=Q _d0B _s/m _dc) (dust cyclotron frequency). Further applying the probe theory to a dust grain, Q _d is said to be well-balanced with the plasma currents present on the grain surface (Whipple et al., Reference Whipple, Northdrop and Mendis1985; Jana et al., Reference Jana, Sen and Kaw1993) and the dust grain charge fluctuation as

(5)$$Q_{1{\rm d}} = \displaystyle{{ \vert I_{{\rm e}0} \vert} \over {i({\rm \omega} + i{\rm \eta} )}}\left( {\displaystyle{{n_{1{\rm i}}} \over {n_{{\rm i}0}}}-\displaystyle{{n_{1{\rm e}}} \over {n_{{\rm e}0}}}} \right).$$

Substituting the values of n _1e and n _1i from Eqs. (2) and (3) in Eq. (5), we obtain

(6)$$\eqalign{Q_{1{\rm d}} & = \displaystyle{{ \vert I_{{\rm e0}} \vert} \over {i{\rm} ({\rm \omega} + i{\rm \eta} )}} \bigg[ \displaystyle{{k_x^2 {\rm \phi}} \over {[{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega}_{{\rm ci}}^2 ]m_{\rm i}}} \cr & \quad + \displaystyle{{k_z^2 {\rm \phi}} \over {{({\rm \omega} -k_zv_{\rm i})}^2m_{\rm i}{\rm \omega}^2}} + \displaystyle{{k_x^2 {\rm \phi}} \over {m_{\rm e}({\rm \omega}^2-{\rm \omega}_{{\rm ce}}^2 )}} + \displaystyle{{k_z^2 {\rm \phi}} \over {m_{\rm e}{\rm \omega}^2}} \bigg] {\rm.} } $$

Under the view of overall charge neutrality in equilibrium, we can write,

$$-en_{{\rm i}0} + en_{{\rm e}0} + Q_{{\rm d}0}n_{{\rm d}0} = 0\quad {\rm or}\quad n_{{\rm d}0}/n_{{\rm e}0} = ({\rm \delta} -1)(e/Q_{{\rm d}0}),$$

where δ = n _i0/n _e0 is the relative density of negatively charged dust grains.

Using Poisson's equation

(7)$$\nabla ^2{\rm \phi} = 4{\rm \pi} n_{1{\rm e}}e-4{\rm \pi} n_{1{\rm i}}e + 4{\rm \pi} n_{{\rm d}0}Q_{1{\rm d}} + 4{\rm \pi} Q_{{\rm d}0}n_{1{\rm d}}$$

and substituting the values from Eqs. (2)–(4) and (6) in (7), and taking ω ≪ ω_ce for TG mode, we obtain

(8)$$\eqalign{1 + &\displaystyle{{{\rm \omega} _{{\rm pe}}^2 \,} \over {{\rm \omega} ^2\,K}}\displaystyle{{k_z^2} \over {k^2}} + \displaystyle{{i{\rm \beta}} \over {({\rm \omega} + i{\rm \eta} )K}}\displaystyle{{{\rm \omega} _{{\rm pe}}^2 \,} \over {{\rm \omega} _{{\rm ce}}^2 \,}}\displaystyle{{k_x^2} \over {k^2}}-\displaystyle{{i{\rm \beta}} \over {({\rm \omega} + i{\rm \eta} )K}}\displaystyle{{m_{\rm e}} \over {m_{\rm i}}}\displaystyle{{{\rm \omega} _{{\rm pe}}^2 \,} \over {{\rm \omega} ^2\,}}\displaystyle{{k_z^2} \over {k^2}} \cr & + \displaystyle{{{\rm \omega} _{{\rm pd}}^2} \over {{\rm \omega} ^2K}} = \displaystyle{{{\rm \omega} _{{\rm pi}}^2 \,} \over {{({\rm \omega} -k_zv_{\rm i})}^2\,K}}\displaystyle{{k_z^2} \over {k^2}} + \displaystyle{{{\rm \omega} _{{\rm pi}}^2 \,} \over {[{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega} _{{\rm ci}}^2 ]\,K}}\displaystyle{{k_x^2} \over {k^2}} \cr & + \displaystyle{{i{\rm \beta}} \over {({\rm \omega} + i{\rm \eta} )K}}\displaystyle{{{\rm \omega} _{{\rm pe}}^2 \,} \over {[{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega} _{{\rm ci}}^2 ]\,}}\displaystyle{{k_z^2} \over {k^2}},} $$

where

$${\rm {\rm \omega}} _{{\rm pe}}^2 = \left( {\displaystyle{{4{\rm {\rm \pi}} n_{{\rm e}0}e^2} \over {m_{\rm e}}}} \right),\;{\rm {\rm \omega}} _{{\rm pi}}^2 = \left( {\displaystyle{{4{\rm {\rm \pi}} n_{{\rm i}0}e^2} \over {m_{\rm i}}}} \right)$$

and

$${\rm {\rm \omega}} _{{\rm pd}}^2 = \left( {\displaystyle{{4{\rm {\rm \pi}} n_{{\rm d}0}e^2} \over {m_{\rm d}}}} \right).\;{\rm {\rm \beta}} = \left( {\displaystyle{{ \vert I_{{\rm e}0} \vert} \over e}\displaystyle{{n_{{\rm d0}}} \over {n_{{\rm e}0}}}} \right)$$

is the dust plasma coupling parameter given as

(9)$${\rm \beta} = 0.397(1-(1/{\rm \delta} ))\,(a/v_{{\rm te}})(m_{\rm i}/m_{\rm e}){\rm \omega} _{{\rm pi}}^2, {\rm and}$$

(10)$${\rm \eta} = 10^{-2}{\rm \omega} _{{\rm pe}}\left( {\displaystyle{a \over {{\rm \lambda}_{{\rm De}}}}} \right)\displaystyle{1 \over {\rm \delta}}. $$

where, η is the time scale of delay and $v_{{\rm te}}( = \sqrt {2T_{\rm e}/m_{\rm e}} )$ is the thermal velocity of electrons (Prakash and Sharma, Reference Prakash and Sharma2009). For non-streaming ions v _i = 0 and for a plasma without dust grains δ = 1. Using the conditions for the existence of TG wave, that is, ω_pi ≪ ω ≪ ω_ce, we get ω = ω_pe(k _z/k) which is the standard dispersion relation of TG wave (Jain and Khristiansen, Reference Jain and Khristiansen1983; Jain and Khristiansen, Reference Jain and Khristiansen1984).

Equation (8) can be rewritten as

(11)$$\eqalign{&({\rm \omega} ^2-{\rm \alpha} ^2)({\rm \omega} + i{\rm \eta} + i({\rm \beta} _1 + {\rm \beta} _2)) \cr&\quad= \left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2 \,{\rm \omega}^3} \over {[{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega}_{{\rm ci}}^2 ]\,K}}\displaystyle{{k_x^2} \over {k^2}} + \displaystyle{{{\rm \omega}_{{\rm pi}}^2 \,{\rm \omega}^3} \over {{({\rm \omega} -k_zv_{\rm i})}^2}}\displaystyle{1 \over K}\displaystyle{{k_z^2} \over {k^2}}} \right] \cr &\quad + i\left[ \matrix{\displaystyle{{{\rm \omega}_{{\rm pi}}^2 \,{\rm \omega}^2} \over {[{({\rm \omega} -k_zv_{\rm i})}^2-{\rm \omega}_{{\rm ci}}^2 ]\,}}\displaystyle{1 \over K}\displaystyle{{k_x^2} \over {k^2}}({\rm \eta} + {\textstyle{{\rm \beta} \over {\rm \delta}}} ) + \,\displaystyle{{{\rm \omega}_{{\rm pi}}^2 \,{\rm \omega}^2{\rm \eta}} \over {{({\rm \omega} -k_zv_{\rm i})}^2\,}}\displaystyle{1 \over K}\displaystyle{{k_z^2} \over {k^2}} \hfill \cr -{\rm \alpha}^2({\rm \beta}_1 + {\rm \beta}_2) \hfill} \right],} $$

where

(12)$${\rm \alpha} ^2 = \displaystyle{1 \over K}\left( {{\rm \omega}_{{\rm pe}}^2 \displaystyle{{k_z^2} \over {k^2}}-{\rm \omega}_{{\rm pd}}^2} \right),$$

$${\rm \beta} _1 = {\rm \beta} \displaystyle{1 \over K}\displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \omega} _{{\rm ce}}^2}} \displaystyle{{k_x^2} \over {k^2}},$$

$${\rm \beta} _2 = \left( {-{\rm \beta} \displaystyle{1 \over K}{\rm \omega}_{{\rm pe}}^2 \displaystyle{{k_z^2} \over {k^2}}\left( {1 + \displaystyle{{m_{\rm e}} \over {m_{\rm i}}}} \right)} \right)/{\rm \omega} ^2,$$

and

$$K = 1 + \displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \omega} _{{\rm ce}}^2}}. $$

Equation (11) gives dispersion relation for the TG wave. The first bracket on the left-hand side of Eq. (11) associates with TG modes in a dusty plasma with frequency given by Eq. (12). The second bracket of Eq. (11) gives the damping mode due to dust charge fluctuations. From Eq. (11), in the absence of streaming ions and putting δ( = n _i0/n _e0) = 1, that is, β → 0, we obtain

$${\rm \omega} ^2 = {\rm \omega} _{{\rm tg}}^2 \left( {1 + \displaystyle{{m_{\rm i}} \over {m_{\rm e}}}\displaystyle{{k_z^2} \over {k^2}}} \right),$$

where

$${\rm \omega} _{{\rm tg}}^2 = {\rm \omega} _{{\rm pi}}^2 /\left( {1 + \displaystyle{{{\rm \omega}_{{\rm pe}}^2} \over {{\rm \omega}_{{\rm ce}}^2}} \displaystyle{{k_x^2} \over {k^2}}} \right),$$

which are the standard expressions for TG mode in plasma.

Further, solving Eq. (11) under three limits:

Case I: For fast cyclotron interaction between TG wave and streaming plasma ions, that is, when ω − k _zv _i = +ω_ci, Eq. (11) can be rewritten as

$$\Delta _1^2 = \left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2} \over {4K{\rm \omega}_{{\rm ci}}}}\displaystyle{{k_x^2} \over {k^2}}{\rm \alpha}} \right] + i\left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2} \over {4K{\rm \omega}_{{\rm ci}}}}\displaystyle{{k_x^2} \over {k^2}}\left( {{\rm \eta} + \displaystyle{{\rm \beta} \over {\rm \delta}}} \right)} \right],$$

where we have considered only the cyclotron interaction terms from RHS of Eq. (11). Δ₁ is the small frequency discrepancy due to the finite value on RHS of Eq. (11). This gives the growth rate of TG mode as

(13)$${\rm \gamma} _1 = {\mathop{\rm Im}\nolimits} (\Delta _1) = \displaystyle{{Q_1} \over {2\sqrt {P_1}}}, $$

where

$$P_1 = \displaystyle{{{\rm \omega} _{{\rm pi}}^2} \over {4K{\rm \omega} _{{\rm ci}}}}\displaystyle{{k_x^2} \over {k^2}}{\rm \alpha} $$

and

$$Q_1 = \displaystyle{{{\rm \omega} _{{\rm pi}}^2} \over {4K{\rm \omega} _{{\rm ci}}}}\displaystyle{{k_x^2} \over {k^2}}\left( {{\rm \eta} + \displaystyle{{\rm \beta} \over {\rm \delta}}} \right).$$

Case II: For slow cyclotron interaction between TG wave and streaming plasma ions, that is, when ω − k _zv _i = −ω_ci, Eq. (11) can be rewritten as

$$\Delta _2^2 = \left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2} \over {4K(-{\rm \omega}_{{\rm ci}})}}\displaystyle{{k_x^2} \over {k^2}}{\rm \alpha}} \right] + i\left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2} \over {4K(-{\rm \omega}_{{\rm ci}})}}\displaystyle{{k_x^2} \over {k^2}}\left( {{\rm \eta} + \displaystyle{{\rm \beta} \over {\rm \delta}}} \right)} \right],$$

where again we have considered only the cyclotron interaction terms from RHS of Eq. (11).

The growth rate of TG mode in this limit is obtained as

(14)$${\rm \gamma} _2 = {\mathop{\rm Im}\nolimits} (\Delta _2) = \displaystyle{{Q_2} \over {2\sqrt {P_2}}}, $$

where Δ₂ is the small frequency discrepancy,

$$P_2 = \displaystyle{{{\rm \omega} _{\,pi}^2} \over {4K(-{\rm \omega} _{ci})}}\displaystyle{{k_x^2} \over {k^2}}{\rm \alpha} $$

and

$$Q_2 = \displaystyle{{{\rm \omega} _{{\rm pi}}^2} \over {4K(-{\rm \omega} _{{\rm ci}})}}\displaystyle{{k_x^2} \over {k^2}}\left( {{\rm \eta} + \displaystyle{{\rm \beta} \over {\rm \delta}}} \right).$$

Case III: For Cerenkov interaction when ω = k _zv _i then Eq. (11) can be written as

$$\Delta _3^3 = \displaystyle{{{\rm \omega} _{{\rm pi}}^2} \over {2K}}\displaystyle{{k_z^2} \over {k^2}}({\rm \alpha} + i{\rm \eta} ),$$

where we have considered only the Cerenkov interaction terms from RHS of Eq. (11). Δ₃ is the small frequency discrepancy.

Therefore, the growth rate of TG mode in this case is given by

(15)$${\rm \gamma} _3 = {\mathop{\rm Im}\nolimits} (\Delta _3) = \displaystyle{{\rm \eta} \over {3{\rm \alpha}}} \left[ {\displaystyle{{{\rm \omega}_{{\rm pi}}^2} \over {2K}}\displaystyle{{k_z^2} \over {k^2}}{\rm \alpha}} \right]^{1/3}.$$

Numerical results and discussion

For numerical calculations, the plasma parameters are taken as: number density of plasma ions n _i0 = 10⁹ cm⁻³, number density of plasma electrons n _e0 = 0.2 × 10⁹ − 1 × 10⁹ cm⁻³, temperatures of electrons and ions are taken as 0.2 eV, external magnetic field is 3kG, number density of dust grains density is 10⁴ cm⁻³, and m _i/m _e = 7.16 × 10⁴ for potassium plasma and the average dust grain size a = 2 µm. Using Eq. (13), we have plotted the growth rate γ₁(s⁻¹) of TG mode during fast cyclotron interaction with plasma ions as a function of normalized parallel wave number k _z/k for different values of δ = (n _i0/n _e0) (relative density of negatively charged dust grains) (c.f. Fig. 1). It is observed that the growth rate decreases as the parallel wave number increases. This shows that the growth rate of unstable mode decreases in the direction of the applied magnetic field or the direction of streaming ions. Therefore, we can say that the TG wave grows with an increase in perpendicular wave number or the unstable mode grows along its direction of propagation, if the magnetized plasma ions undergo a normal cyclotron resonance interaction with the TG waves. It can also be inferred from Eq. (13) that the growth rate of TG mode increases with an increase in the value of magnetic field, as observed by Haas and Pascoal, (Reference Haas and Pascoal2017). The growth of TG waves across the magnetic field may be attributed to the fact that these waves have a frequency between ion and electron gyrofrequencies. Due to which electrons are strongly magnetized but ions do not feel the presence of the magnetic field and can oscillate freely across the field lines. Therefore, the ions interact with waves having phase velocities perpendicular to the magnetic field. During normal resonance, the fast parallel component waves give energy to the streaming ions and their velocity increases. The high-velocity plasma ions interact with the perpendicular component of waves and the wave grows across the magnetic field.

Fig. 1. Growth rate γ₁(s⁻¹) as a function of normalized parallel wave number k _z/k during fast cyclotron interaction for δ = 1, 2, 3, 4, 5.

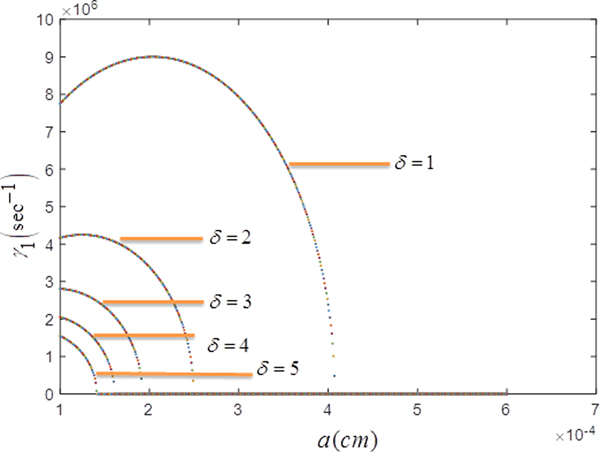
Figure 2 represents the growth rate γ₁(s⁻¹) as a function of dust grain size a (cm)for different values of δ keeping all the other parameters [c.f. Eq. (13)] same as used for plotting Figure 1. The growth rate of unstable mode first increases, reaches a maximum value, and then decreases to zero for δ = 1 and δ = 2. The reason for the above result is that as dust grains are added in the plasma, free electrons in the plasma approach it, increasing the surface potential of dust grains, further increasing the average dust grain charge Q _d0. Hence the number density of free electrons in the plasma reduces with respect to number density of plasma ions. Thus the ions have an effective mass m _ieff = (m _i/n _i0)n _e0, which is less than m _i and their greater mobility leads to wave generation along the magnetic field direction also. As the size of dust grain increases, more and more electrons approach it, and the growth rate of TG wave is enhanced. The growth rate shows a maxima and then decreases as observed in Figure 1 also. The parallel phase velocity of TG wave (ω/k _z) is more than the streaming ions velocity during normal cyclotron resonance. The relative motion of the waves and ions across the magnetic field causes a Doppler shift of the wave frequency up to the ion cyclotron frequency and the waves are generated across the magnetic field. Thus the growth rate of TG mode decreases with parallel wave number as shown in Figure 2. It is also observed that the peak value of growth rate decreases as δ increases. The critical value of dust grain size to obtain a maximum growth for δ = 1 is 2.5 × 10⁻⁴ cm. Our trend of growth rate is similar to the results of Tribeche and Zerguini (Reference Tribeche and Zerguini2001) for a dusty plasma.

Fig. 2. Growth rate γ₁(s⁻¹) as a function of size of dust grains a (cm) during fast cyclotron interaction, for δ = 1, 2, 3, 4, 5.

Again, using Eq. (13) we have plotted Figure 3 which shows the variation of growth rate γ₁(s⁻¹) as a function of δ = (n _i0/n _e0) for dust grain size a = 1.2 × 10⁻⁴ cm. The growth rate decreases with increase in the value of δ. As the value of δ increases, the relative density of electrons in dusty plasma decreases and the ambient plasma becomes deficient of electrons. Hence more and more energy will be supplied by the TG wave to the dusty plasma through dust grains, which decreases its growth.

Fig. 3. Growth rate γ₁(s⁻¹) during fast cyclotron interaction as a function of δ for a = 1.2 × 10⁻⁴ cm .

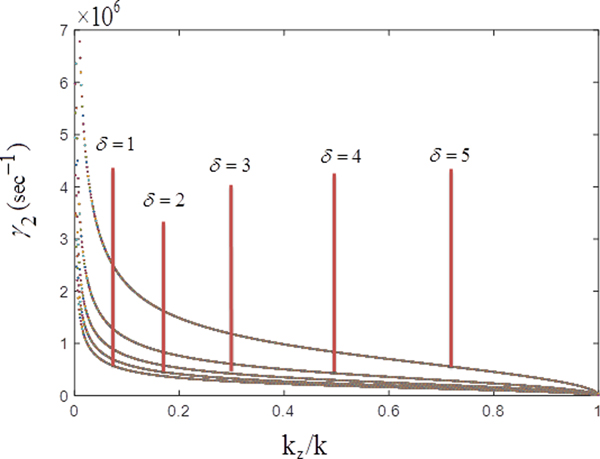
Using Eq. (14) we have plotted Figure 4 which shows the damping rate of TG mode in slow cyclotron interaction γ₂(s⁻¹) as a function of normalized parallel wave number k _z/k. Figure 4 indicates that damping rate of TG wave reduces with an increase in parallel wave number. This indicates that the TG wave damps with an increase in the parallel wave number during anomalous cyclotron resonance interaction with the streaming ions. It can also be inferred that the wave damping reduces along the magnetic field direction or along the direction of streaming ions but enhances in a direction perpendicular to the magnetic field. During anomalous resonance, the positive ions overtake the waves (ω − k _zv _i = −ω_ci) as phase velocity of waves is less than the streaming ions velocity. The Doppler shift decreases the wave frequency to that of ion cyclotron frequency. The waves gain energy from the ions, and the damping of waves is reduced along the magnetic field lines.

Fig. 4. Damping rate γ₂(s⁻¹) as a function of normalized parallel wave number k _z/k during slow cyclotron interaction for δ = 1, 2, 3, 4, 5.

Further, when the phase velocity of TG mode is equal to the streaming ions velocity, that is, for Cerenkov interaction between plasma ions and TG mode, using Eq. (15) Figure 5 is plotted, which shows the growth rate γ₃(s⁻¹) of unstable mode as a function of normalized parallel wave number k _z/k for different values of δ, keeping all other plasma parameters constant. It is observed that the growth rate of unstable mode increases with increase in parallel wave number for all the values of δ. In other words, the TG wave grows with an increase in parallel wave number during Cerenkov interaction with streaming ions. In this case, the phase velocity of TG wave is comparable to the streaming ions velocity, and therefore the wave grows due to inverse Landau damping. Due to cyclotron interactions, a situation is created, where in a given velocity interval around the phase velocity of the wave, there are more number of faster ions than of slower ions. Thus the waves grow by gaining energy from the ions, which corresponds to inverse Landau damping. The ions are thus decelerated and they lose their energy to the wave, synchronizing with the wave.

Fig. 5. Growth rate γ₃(s⁻¹) as a function of normalized parallel wave number k _z/k during Cerenkov interaction for δ = 1, 2, 3, 4, 5.

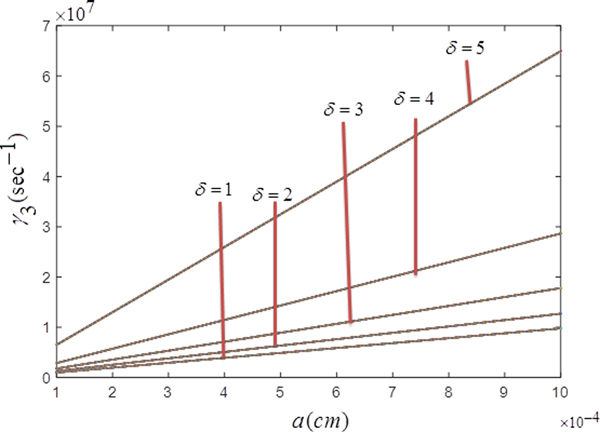
Figure 6 shows the variation of growth rate γ₃(s⁻¹) of unstable mode during Cerenkov interaction with respect to dust grain size a (cm) for different values of δ. It is found that growth rate of unstable TG mode increases (c.f. Eq. 15) with the increasing size of dust grains due to electron capturing ability. The dust grains capture electrons and wave will gain energy from these electrons through dust grains in the plasma which lead to the enhancement in the growth of TG wave, as obtained in the case of fast cyclotron interaction. In this case, a maxima in growth rate is not observed as the parallel phase velocity of wave is equal to the streaming ions velocity, due to which a strong interaction occurs between the two and the wave keeps growing along the ion streaming direction.

Fig. 6. Growth rate γ₃(s⁻¹) as a function of size of dust grains a (cm) during Cerenkov interaction for δ = 1, 2, 3, 4, 5.

Figure 7 displays the growth rate γ₃(s⁻¹) of unstable mode during Cerenkov interaction as a function of δ. The growth rate of the unstable mode increases with increase in the value of δ, as observed in Figures 5 and 6 also. In this case, the growth rate increases as the number of dust grains are increased in the plasma, which is in contrary to the growth rate variation with δ in case of cyclotron interactions. This is because more number of dust grains shield more plasma electrons, increasing the mobility of plasma ions. An increase in the number of fast ions leads to energy transfer from ions to the waves by inverse Landau damping.

Fig. 7. Growth rate γ₃(s⁻¹) during Cerenkov interaction as a function of δ for a = 1.2 × 10⁻⁴ cm.