1. INTRODUCTION
Laser generation of ultrashort particle beams is currently a topic of very intense research and has experienced much progress during recent years (Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006; Lifschitz et al., Reference Lifschitz, Faure, Glinec, Malka and Mora2006; Sakai et al., Reference Sakai, Miyazaki, Kawata, Hasumi and Kikuchi2006; Zhou et al., Reference Zhou, Yu and He2007; Flippo et al., Reference Flippo, Hegelich, Albright, Yin, Gautier, Letzring, Schollmeier, Schreiber, Schulze and Fernandez2007; Gupta & Suk Reference Gupta and Suk2007; Karmakar & Pukhov Reference Karmakar and Pukhov2007) because such beams can be very important for many applications. For example, the ultrashort energetic electron beams can be used for injection purposes in accelerators (Umstadter et al., Reference Umstadter, Kim and Dodd1996; Reitsma et al., Reference Reitsma, Goloviznin, Kamp and Schep2001), in femtosecond physics and chemistry (Barbara et al., Reference Barbara, Knox, Mourou and Zewail1994; Crowell et al., Reference Crowell, Gosztola, Shkrob, Oulianov, Jonah and Rajh2004), for generation of bright ultrashort X-ray pulses through Thomson backscattering of a probe laser pulse (Esarey et al., Reference Esarey, Ride and Sprangle1993), in technological applications, and in many other fields. Besides, engineering of an ultrashort electron beam with a predefined internal structure (i.e., the beam having fast longitudinal density modulation, which is called microbunching) can be interesting for application in free-electron lasers (Marshall, Reference Marshall1985; Brau, Reference Brau1990; Saldin et al., Reference Saldin, Schneidmiller and Yurkov1999), where the microbunching is an inherent feature vitally important for functioning of the device.
Due to progress in super-intense lasers during the last decade (Danson et al., Reference Danson, Brummitt, Clarke, Collier, Fell, Frackiewicz, Hawkes, Hernandez-Gomez, Holligan, Hutchinson, Kidd, Lester, Musgrave, Neely, Neville, Norreys, Pepler, Reason, Shaikh, Winstone, Wyatt and Wyborn2005; Neumayer et al., Reference Neumayer, Bock, Borneis, Brambrink, Brand, Caird, Campbell, Gaul, Goette, Haefner, Hahn, Heuck, Hoffmann, Javorkova, Kluge, Kuehl, Kunzer, Merz, Onkels, Perry, Reemts, Roth, Samek, Schaumann, Schrader, Seelig, Tauschwitz, Thiel, Ursescu, Wiewior, Wittrock and Zielbauer2005, Zvorykin et al., Reference Zvorykin, Didenko, Ionin, Kholin, Konyashchenko, Krokhin, Levchenko, Mavritskii, Mesyats, Molchanov, Rogulev, Seleznev, Sinitsyn, Tenyakov, Ustinovskii and Zayarnyi2007; Kalashnikov et al., Reference Kalashnikov, Osvay and Sandner2007; Canova et al., Reference Canova, Flacco, Canova, Clady, Chambaret, Ple, Pittman, Planchon, Silva, Benocci, Lucchini, Batani, Lavergne, Dovillaire and Levecq2007), high-density electron beams with linear dimensions of 10–20 µm became available in laboratories by using table-top laser-plasma accelerators (Mangles et al., Reference Mangles, Murphy, Najmudin, Thomas, Collier, Dangor, Divall, Foster, Gallacher, Hooker, Jaroszynski, Langley, Mori, Norreys, Tsung, Viskup, Walton and Krushelnick2004; Geddes et al., Reference Geddes, Toth, van Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Hafz et al., Reference Hafz, Choi, Sung, Kim, Hong, Jeong, Yu, Kulagin, Suk, Noh, Ko and Lee2007). Such a high-density electron beam can be additionally accelerated, compressed, and microbunched by a field of another super-intense laser pulse to improve the properties of the electron beam (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a, Reference Kulagin, Hur and Suk2006b). Alternatively, ordinary electron beams can be used for acceleration, compression, and microbunching by a super-intense laser pulse. After that, these preprocessed electron beams can be effectively utilized, e.g., for Thomson backscattering of a probe counter-streaming laser pulse with frequency up-shifting and amplitude enhancement (Cherepenin & Kulagin, Reference Cherepenin and Kulagin2004; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004a, Reference Kulagin, Cherepenin and Suk2004b). These two-pulse methods allow in principle to control all parameters of the converted electromagnetic pulse in a full extent (duration, frequency, shape of an envelope, carrier-envelope phase, etc.) in contrast with the case of one-pulse method of over critical plasma excitation (Baeva et al., Reference Baeva, Gordienko and Pukhov2007), or with the case of free electron lasers (Saldin et al., Reference Saldin, Schneidmiller and Yurkov2008), where it is not easy to change these parameters. In the two-pulse generation scheme, coherent properties of the electron beam directly influence the statistics of the generated high-frequency radiation. Therefore, an investigation of the dynamic behavior of the dense electron beam in the field of a high-intensity laser pulse is a very important issue, and we address it in this paper.
Having in mind the above mentioned application for the dense electron beam, one can define the differences of our problem from the usual study of the electron beams: high density of the beam, large energy spread of the electrons (sometimes reaching 100%), relatively short (with respect to the ordinary electron beams) propagation distance, for which the parameters of the electron beam should be calculated (for backscattering, the evolution time of the beam on the order of 0.3–0.5 ps is more than enough so that the required maximal propagation distance of the beam is less than 0.15 mm), and last, permanent action of an ultrastrong electromagnetic wave on the electron beam during evolution. Therefore, several analytic and numeric algorithms (Reiser, Reference Reiser1994; Lapostolle et al., Reference Lapostolle, Lombardi, Tanke, Valero, Garnett and Wangler1996; Wangler, Reference Wangler1998; Fubiani et al., Reference Fubiani, Qiang, Esarey, Leemans and Dugan2006) used so far for description of the electron beam evolution in the presence of the space-charge forces can be hardly applied to our case.
For a dense electron beam interacting with an ultraintense laser pulse, two extreme cases are possible. In the first case (case 1 below), the electromagnetic wave gives only small modification to the dynamics of the electron beam evolving under the space-charge forces. In the second case (case 2), which is considered below in details, the space-charge forces can be considered as a small perturbation (at least, within some initial interval of time) to the electron beam dynamics in the field of an ultraintense electromagnetic wave. The limiting situation of this second case, when space-charge forces and radiation of the electrons can be entirely omitted, was considered earlier (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a; Kulagin et al., Reference Kulagin, Hur and Suk2006b), and the solutions for the electron motion in a given laser field were utilized to study the evolution of low-density electron beams in the field of ultraintense laser pulses. It was shown that the laser pulse front compresses and accelerates the electron beam, and induces a density wave inside the beam producing characteristic microbunching. This spatial structure can be supported without change during all time of interaction. However, it is not evident beforehand, what value of the electron density for the electron beam with a certain initial length can be considered as low in our particular problem, besides, if the density is not low, then how will the dynamics of the electrons in a laser field be modified by the space-charge forces of the electron beam, and what new effects can arise? In this paper, the answers to these questions are presented.
The paper is organized as follows: the one-dimensional (1D) mathematical model with equations of motion for the electrons and exact analytical solutions to these equations are specified in Section 2. In Section 3, the characteristic parameters for the evolution of the high-density electron beam are investigated by an example of the laser pulse with a step-like envelope acting on the initially nonrelativistic electron beam. The analytical expression for the length of the electron beam as a function of time is derived. Taking into account the space-charge forces in the high-density electron beam results in a slow longitudinal spreading of the beam with corresponding decrease of an average electron density. However, the microbunching is still present here, and during the evolution, the total number of humps in the beam increases. In Section 4, the analytical expression for the longitudinal density profile of the electron beam as a function of time is derived and compared with the results of the 1D particle-in-cell (PIC) simulations showing good agreement. Also here, the other difference from the vanishingly low electron beam density case is revealed: it is the presence of a very short and very high frozen density peak in the front side of the electron beam (side illuminated with the laser pulse), which originates from the modulation of initial counter-velocities of the electrons that are accelerated by the space-charge forces. In Section 5, discussion of the results is presented and conclusions are derived.
2. MATHEMATICAL MODEL AND EQUATIONS OF MOTION FOR THE ELECTRONS
For description of the interaction of an intense laser pulse with an electron beam, a 1D model is used below. Formally, this model can be applicable in cases, where all variables depend only on one coordinate and time, i.e., diameters of laser and electron beams are infinite. In reality, 1D model can also be useful for a quasi-1D character of interaction of a laser pulse with an electron beam, when variables change along the transverse coordinates much slowly than along the longitudinal coordinate. For this case, a laser spot size and an electron beam diameter should be much larger than longitudinal (along the laser beam axis) dimensions of the electron medium (for example, this situation is realized quite well in laser pulse interaction with solid nanofilms (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2007a); for high-density electron beams from laser-plasma accelerators, the requirement for quasi-1D character of interaction can be fulfilled if the laser spot is larger than 20–30 µm).
The laser pulse is modeled below by a plane electromagnetic wave with amplitude E 0, frequency ω, and wave vector k(k = ω/c), which is running along the z axis and is linearly polarized with only E y = E 0e y non-zero component. The electron beam is modeled by a set of parallel electron sheets (ESs) each labeled by its initial position Z 0e (Lagrangian description). Each ES has infinite dimensions in x- and y-directions, besides, the motion of the ESs is assumed to be plane-parallel (one of the ESs is shown in Fig. 1).

Fig. 1. Geometry of the model.
Let us first consider only one ES. Charge and current densities for it are ρ(z, t) = σδ[z−Z(t)] and j(z, t) = σv(t)δ[z − Z(t)], where σ is the surface charge density, v and Z are the velocity and the coordinate of the ES. Then, formal solutions to the Maxwell's equations for the fields of the ES at coordinate z and time t can be obtained with the help of Green function and have the form (Il'in et al., Reference Il'in, Kulagin and Cherepenin1999; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b; Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2007b)
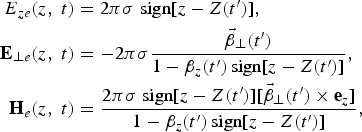
where ![]() , c is the velocity of light in vacuum, E⊥e = E xeex + E yeey, v⊥ = v xex + v yey, and t′ is the retarded time
, c is the velocity of light in vacuum, E⊥e = E xeex + E yeey, v⊥ = v xex + v yey, and t′ is the retarded time
Eq. (1) describe the field of an infinite ES, in which case the field components E ze and E⊥e can be interpreted as the longitudinal (Coulomb) field and the radiation field of the sheet, respectively.
The total fields of the electron beam can be considered as the sum of the fields of all ESs calculated in accordance with Eqs. (1) and (2) with proper time and space variables. In a general case, the total field can be calculated only numerically (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2007b). However, if the longitudinal dimension of the electron beam after compression (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a; Reference Kulagin, Hur and Suk2006b) is not very small (not less than the laser wavelength), a coherent part of the electron beam radiation in the laser field greatly reduces (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2007b), and the radiation reaction force due to E⊥e can be omitted in the model. This condition is fulfilled if the laser amplitude is not very high to compress the initial electron beam into a bunch with the length much smaller than the laser wavelength. Therefore, only static Coulomb forces due to E ze can be accounted for in the model (we will call this a Coulomb interaction below). For initially very thin targets such as foils, this approximation is not valid, and both components of the field for the ESs should be considered (Cherepenin & Kulagin, Reference Cherepenin and Kulagin2004; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b).
When calculating the Coulomb interaction between the ESs below, we suppose that there are no intersections of trajectories Z(t) of the ESs (none of the ESs overtakes the other ES, and the numbers of the ESs on the left and the right sides of a particular ES are constants in time). Then, the Coulomb force between each ES and other ESs can also be considered as constant in time. The equations of motion for the electrons, which belong to the ES with initial coordinate Z 0e, have the following form:

where p y and p z are the transversal and the longitudinal momenta of the electron, e and m are the charge and the rest mass of an electron, n 0 and l are the initial density and the initial length of the electron beam, and γ2 = 1 + p y2/(mc)2 + p z2/(mc)2. In Eq. (3), we suppose that initial coordinate for the left end of the electron beam is Z 0e = 0 and, for the right end, it is Z 0e = l (other configurations can be considered on the similar basis).
Below, it is convenient to use normalized momenta p y/(mc) → p y and p z/(mc) → p z. When the density of the electron beam is vanishing, n 0 → 0, and the field of an electromagnetic wave is the only present, the value
is invariant and is equal to unity for the electrons with the zero initial momenta (Landau & Lifshitz, Reference Landau and Lifshitz1975). In our case, the Coulomb forces are also present in the model, however, as we supposed, they give only some correction to the motion of the electrons in the ultraintense electromagnetic wave (cf. case 2 of the Introduction) so again it is convenient to transfer to the variable κ, which will be a slowly varying variable, instead of γ and p z, whose variations are fast. Then, introducing a new independent variable
which is different for the different ESs, one has the following equations of motion for the electrons with the initial coordinate Z 0e

where a 0 = |e|E 0/(mcω), ν = ωp2/(2ω2) = n 0r eλ2/(2π), ![]() is the characteristic plasma frequency, r e and λ are the classical radius of an electron and the laser wavelength correspondingly. Also, the variable γ and the longitudinal momentum p z can be defined from the usual expressions
is the characteristic plasma frequency, r e and λ are the classical radius of an electron and the laser wavelength correspondingly. Also, the variable γ and the longitudinal momentum p z can be defined from the usual expressions

General solutions to Eqs. (3) and (6) have the following parametric form
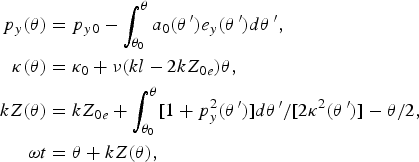
where θ0 = ωt 0 − kZ 0e, p y0 and κ0 are the initial values at the initial moment of time t = t 0 for the transversal momentum p y and the parameter κ, which depend on the initial position Z 0e of the electron and can be different for the electrons belonging to the different ESs.
From Eqs. (6) and (8), one can conclude that the motion of the central ES with the coordinate Z 0e = l/2 have no perturbation due to the Coulomb forces, so this ES is moving just as in the given field of the electromagnetic wave only, and κ(θ) = κ0. Besides, the outermost ESs feel the maximal Coulomb force, which is defined by all electrons in the electron beam and is proportional to a parameter α (Vshivkov et al., Reference Vshivkov, Naumova, Pegoraro and Bulanov1998; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b)
The parameter κ for the most left electrons is increasing with θ according to equation κl = κl0 + αθ, and, for the most right electrons, it is decreasing, κr = κr0 − αθ. For the first glance, for some value of θ, the parameter κr can become equal to zero, giving the divergence for p z and γ. However, it can be verified that this value of θ cannot be achieved for any finite time t.
General solutions (8) are valid for both cases 1 and 2 considered in the Introduction. The electron momentum p y has a period θp = 2π. If, during this time, a change in κ is small enough, i.e., 2πα << κ0 then the Coulomb forces give only some perturbation for the dynamics of the electron beam in the given external electromagnetic wave, and case 2 is realized. In the opposite situation, the dynamics of the electrons will be defined primarily by the Coulomb forces (case 1 in the Introduction). It is necessary to note, that parameter α depends not only on the density n 0 of the electron beam, but on the total length (l) of the beam also, so even in a long low-density electron beam, the Coulomb forces can be important (this conclusion is true if the 1D model is applicable, i.e., the diameter of the beam is considerably larger than its length). Below, only case 2 with 2πα << κ0 will be considered. For κ0 ≃ 1 and l = 10 µm, this condition corresponds to ν << 2.5×10−3 and n 0 << 5.5·1018cm−3.
3. CHARACTERISTIC PARAMETERS OF THE ELECTRON BEAM EVOLUTION FOR THE STEP-LIKE ENVELOPE OF THE LASER PULSE
3.1. Solutions for Equations of Motion for Initially Nonrelativistic Electron Beam
To study the characteristics of a dense electron beam evolution and to demonstrate the capabilities of the theory, it is useful to consider one of the simplest form for the laser pulse envelope, e.g., a step-like envelope, where the integral for p y can be calculated analytically (smooth envelope cases can be considered on the similar basis using Eq. (8)). Also, we will suppose initially nonrelativistic electron beam, which most prominently demonstrates the peculiarities of the evolution of the dense electron beam in the super-intense laser field (non-zero initial momenta for p y and p x lead only to the changes in numbers due to electron mass scaling and leave the qualitative results intact). Let us assume that the front of the laser beam touches the electron beam at point Z 0e = 0 when ωt = 0. Then, the laser field is E y(θ) = E 0 sin θ for θ ≥ 0 and zero for θ < 0, and for the transversal momentum p y, one has for θ ≥ 0 from Eq. (8)
and p y = 0 for θ < 0, if the zero initial value is supposed for p y. It is convenient to consider the evolution of the electron beam in two intervals, θ < 0 and θ > 0, separately. Laser pulse need some time to reach the ES with the initial coordinate Z 0e. During this time, this ES will move due to the space-charge (static Coulomb) forces, so when the laser pulse reaches it, this ES will have the following parameters of motion, which are the solutions of Eq. (3) with the zero amplitude of the electromagnetic field

where αkl < 1, and zero value for the initial longitudinal momentum p z is supposed (κ0 = 1). The values κin and kZ in are just the initial values for the evolution of the electron beam in the field of the laser pulse, and with this values as initial, the parameter θ0 in Eq. (8) should be considered as zero. Then, equation for the coordinate Z can be split into two equations for slow Z s and fast Z f parts according to the formulas
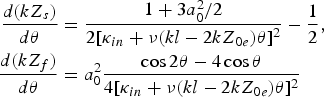
with correspondent solutions

where the solution for Z f is correct up to the first order in ν(kl − 2kZ 0e) (cf. 2πα = 2πνkl << κ0 and κin ≈ κ0 = 1).
From Eq. (13), one can conclude that |Z f| << Z s for not very small values of θ. Then, the slow evolution of the electron beam can be evaluated only using Z s, and the transition from parameter θ to the time ωt becomes simple
![\omega t = kZ_{in} + {\theta \over 2} \left[1 + {\lpar 1 + 3a_0^2/2\rpar \over \kappa_{in} \lpar \kappa_{in} + \nu \lpar kl - 2kZ_{0e}\rpar \theta\rpar }\right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000414_eqn14.gif?pub-status=live)
From the first equation of the system (12), one can conclude that the coordinate of the electron with the initial coordinate Z 0e ≥ l/2 will increase infinitely, while the electrons with the initial coordinates Z 0e < l/2 will turn back at point
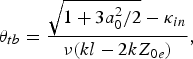
or, for laboratory time,
At this moment, the coordinate Z will have the value

and, for a 0 >> 1 supposed below, it is about kZ in + 3a 02/[4κinν(kl − 2kZ 0e)]. So the most left ES (Z in = Z 0e = 0, κin = 1) will turn first at

and this value of ωt can be considered as a time of coherent evolution for the beam. Actually, after the turning of the most left ES, electrons in the beam will move away with relativistic velocity so the total beam cannot be considered as a single whole (however, major part of the ESs continues to move relativistically at this time, so a truncated electron beam can still be used). The maximal coordinate of the most left ES is

Also, the most left ES returns to its initial point with the coordinate Z 0 = 0 at the moment
For the vanishingly small density of the electron beam, none of the ESs will return to the initial position.
3.2. Analysis of the Motion for the ESs
The motion of the ESs in the laser fields with large amplitudes consists of two parts (cf. Fig. 2): a long period of forward longitudinal movement with a relativistic velocity and a short period of movement with a small velocity in forward (for the right ESs) or in backward (for the left ESs) directions. During this short interval, the ES switches from one cycle of the laser field to the other. For n 0 → 0, the period of time between two successive switches, which is determined by successive vanishing of p y, i.e., for θn = 2πn and θn+1 = 2π(n + 1), does not depend on time and initial coordinate of the ES, and is equal to (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a)
Hence, the most left and the most right ESs in the electron beam with vanishingly small density switch within one cycle of the laser field, so the length of the electron beam does not grow in average. For the dense electron beam, this period depends on time. Moreover, T sw depends also on the initial coordinate Z 0e: it grows for the ESs with the initial coordinates Z 0e > l/2 and decreases for the ESs with Z 0e < l/2. For Z 0e = l/2, this period is constant and is determined by Eq. (21). So, the length of the high-density electron beam will grow in average. Actually, from Eq. (14), one has for the times of switching for the most right and the most left ESs
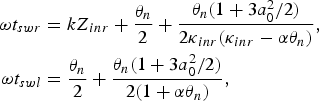
where one has now from Eq. (11) for the coordinate Z inr and the parameter κinr:

Fig. 2. (Color online) Trajectories of some ESs of the electron beam in the field of a super-intense laser pulse with the step-like envelope (a 0 = 5): (a) ν = 10−4 and n 0 = 2.2 × 1017 cm−3, (b) ν = 10−5 and n 0 = 2.2 × 1016 cm−3. In the insets, the zoomed views of the trajectories are shown: (a) multilayer structure of the beam and the third switching of the left ESs; (b) monolayer configuration of the beam (from ωt ≃ 470 to ωt ≃ 490) and switchings—third for the right ESs (below ωt ≃ 470) and forth for the left ESs (above ωt ≃ 490).
Depending on the values of ωt swr and ωt swl, the electron beam can exist either in a single layer (only one hump in the density distribution along z) or multilayer configurations. When the multilayer configuration is realized, the number of full layers in the electron beam at time ωt can be defined as the difference between the numbers of the switchings for the most left and for the most right ESs, which is given by the whole part of the value
where θr and θl are the corresponding values of θ for the most right and the most left ESs (we suppose that the front of the laser pulse already reached the most right ES, and all ESs are in motion, ωt ≥ kZ inr):

Then, for θr and θl, one has quadratic equations with the following solutions:

The length of the electron beam at time t is defined as l b(t) = Z r(t) − Z l(t) = Z r[θr(t)] − Z l[θl(t)]. Then from Eq. (5), one has
So the electron beam in the strong electromagnetic wave can be imagined as a set of N l layers each having the same full length equal to λ (may be, barring the boundary layers), and this length does not depend on time and the initial coordinate Z 0e. Actually, such a structure in space is defined by the electromagnetic wave itself, for which every two neighboring maxima or minima are separated just by the same distance λ.
For not very large time ωt long before the turning of the most left ES (2αωt << 3a 02/2, cf. Eqs. (18)), the length of the electron beam can be estimated from Eq. (26) as

So for ωt~kZ inr, the initial compression of the electron beam is defined by very similar formula as for α = 0 case (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a), however, the equivalent initial thickness of the beam now is Z inr, which is greater than Z 0e due to the action of the static Coulomb forces. For the vanishing density of the electron beam, Z inr = Z 0e and Eq. (28) gives exactly the same value for the length of the beam as in the paper by Kulagin et al. (Reference Kulagin, Cherepenin, Hur and Suk2006a).
The single-layer configuration after the nth switching is possible if ωt swl(θn+1) > ωt swr(θn), which gives the following condition for n
where the coefficients A, B, and C are the following

Realization of the single-layer configuration after the nth switching requires at least an existence of the single-layer configuration after the initial compression of the electron beam. Then, one has (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a) kZ inr < 2π(1 + 3a 02/4), and the coefficient C is negative, while A and B are positive. Then, for the maximal value of n, one has
and [x] means the whole part of x.
In Figure 2, the evolutions of the beams with l = 10 µm and ν = 10−4 (a) or ν = 10−5 (b) are presented (laser amplitude is a 0 = 5, laser wavelength is λ = 1 µm). The initial electron density for the ν = 10−4 case is n 0 = 2.2×1017 cm−3, and for the ν = 10−5 case, it is n 0 = 2.2×1016 cm−3. The trajectories of the ESs in Figure 2 were calculated with the help of 1D MATLAB code EXACT (Cherepenin et al., Reference Cherepenin, Il'in and Kulagin2001; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b, Reference Kulagin, Cherepenin, Hur and Suk2007b), which uses the exact expressions for the electromagnetic fields of the ESs and takes into account self-consistently the radiation of the electron beam. Also, the crossings of the trajectories are allowed in the code. In Figure 2a, the increase due to the static Coulomb forces of the coordinate of the right ESs before interaction with the laser pulse is evident (from kZ 0e ≃ 63 to kZ in = 84 for the most right ESs). For the smaller beam density ν = 10−5, the single-layer configuration still exists after the forth switching of the ESs; for ν = 10−4, it disappears after the first switching, and the single-layer configuration exists here only after the primary compression of the electron beam (from ωt ≃ 84 to ωt ≃ 120). In the inset of Figure 2a, the multilayer structure of the beam and the third switching of the left ESs are shown. In the inset of Figure 2b, the single-layer configuration of the beam after the third switching is shown (from ωt ≃ 470 to ωt ≃ 490), and also, third switching for the right ESs (below ωt ≃ 470) and forth switching for the left ESs (above ωt ≃ 490). All these switching times, numbers of layers and lengths of the electron beam coincide rather well with the analytic predictions from Eqs. (22)–(31).
In Figure 3, the lengths of the electron beam as a functions of time, which are calculated from Eq. (27), are presented for different laser pulse amplitudes a 0 and initial electron beam densities n 0 (the initial length of the electron beam is 10 µm). From these figures, one can conclude that, if the time of evolution is not too large (less than 1 ps), the electron beam with the initial density n 0 < 1015 cm−3 can be considered as a low-density beam in the fields of laser pulses with amplitudes a 0 > 3.

Fig. 3. (Color online) The length of the high-density electron beam (with initial length of 10 µm) as a function of time in the field of a super-intense laser pulse with the step-like envelope: (a) ν = 10−4 (n 0 = 2.2 × 1017 cm−3), (b) ν = 10−5 (n 0 = 2.2 × 1016 cm−3), (c) ν = 10−6 (n 0 = 2.2·1015 cm−3). Solid lines (red online) is for a 0 = 10, dash-dotted lines (green online) is for a 0 = 5, and dashed lines (blue online) is for a 0 = 3.
4. DENSITY DISTRIBUTION FOR THE DENSE ELECTRON BEAM
4.1. Analytical Expression for the Density Distribution of the Electron Beam
Let us now derive analytically the density distribution for the electron beam. For the constant initial density n 0 of the beam, one has, taking the conservation of charge into account

In our case, the coordinate Z of some ES depends on its initial coordinate Z 0e directly and, also, through the dependence of θ on Z 0e. So one has
Expression for ∂[kZ(Z 0e, θ)]/∂θ can be defined from Eq. (6), and ∂θ/∂(kZ 0e) can be evaluated from Eq. (5) with the help of the rule for the differentiation of implicit functions. Then, one has
Partial derivative ∂[kZ(Z 0e, θ)]/∂(kZ 0e) can be evaluated either from Eq. (8) using the rules for the differentiation of integrals depending on parameters, or, alternatively, directly from Eq. (13) (which will be different for different laser pulse envelopes). For the case of the step-like envelope of the laser pulse, one can obtain from Eq. (13) the following equations, which define analytically the density distribution for the high-density electron beam interacting with the ultra-intense laser pulse:
![\eqalign{n\lpar Z_{0e}\comma \, t\rpar &= {n_0 \lpar 1 + p_y^2 + \kappa^2\rpar \over 2\kappa^2} \cr &\quad \times \left\{{\partial \lsqb kZ_s \lpar Z_{0e}\comma \, \theta\rpar \rsqb \over \partial \lpar kZ_{0e}\rpar } + {\partial \lsqb kZ_f \lpar Z_{0e}\comma \, \theta\rpar \rsqb \over \partial \lpar kZ_{0e}\rpar }\right\}_{\theta = \theta \lpar Z_{0e}\comma t\rpar }^{-1}\comma \; \cr {\partial \lpar kZ_s\rpar \over \partial \lpar kZ_{0e}\rpar } &= {\partial \lpar kZ_{in}\rpar \over \partial \lpar kZ_{0e}\rpar } - {\lpar 1 + 3a_0^2/2\rpar \theta \over 2\kappa_{in} \kappa} \cr &\quad \times \left[\left({1 \over \kappa_{in}} + {1 \over \kappa}\right){\partial \kappa_{in} \over \partial \lpar kZ_{0e}\rpar } - {2\nu \theta \over \kappa}\right]\comma \; \cr {\partial \lpar kZ_f\rpar \over \partial \lpar kZ_{0e}\rpar } &= -a_0^2 {\sin 2\theta - 8\sin \theta \over 4\kappa^3} {\partial \kappa \over \partial \lpar kZ_{0e}\rpar } \cr &\quad - a_0^2 \nu {1 - cos2\theta + 16\lpar cos\theta - 1\rpar \over 8\kappa^3} \cr &\quad \times \left[2 + {3\lpar kl - 2kZ_{0e}\rpar \over \kappa} {\partial \kappa \over \partial \lpar kZ_{0e}\rpar }\right]\comma \; \cr {\partial \kappa_{in} \over \partial \lpar kZ_{0e}\rpar } &= \nu \lpar kl - 4kZ_{0e}\rpar \comma \; \cr {\partial \kappa \over \partial \lpar kZ_{0e}\rpar } &= {\partial \kappa_{in} \over \partial \lpar kZ_{0e}\rpar } - 2\nu \theta\comma \; \cr {\partial \lpar kZ_{in}\rpar \over \partial \lpar kZ_{0e}\rpar } &= 1 - {\kappa_{in} - 1 \over 2\kappa_{in}} - {kZ_{0e} \over 2\kappa_{in}^2} {\partial \kappa_{in} \over \partial \lpar kZ_{0e}\rpar }. \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160710064349-50708-mediumThumb-S0263034608000414_eqn35.jpg?pub-status=live)
4.2. PIC Simulations for the Density Distribution of the Electron Beam
To verify the predictions of the derived theory for the evolution of the dense electron beam in the super-intense laser field, the PIC simulations with the 1D version of the XOOPIC code were executed. Full details of this object-oriented fully relativistic PIC code are described by Usui et al. (Reference Usui, Verboncoeur and Birdsall2000). The main goal of the PIC simulations was to test the adequacy of the model, i.e., the possibility for omitting the radiation reaction force of the electrons and the importance of the supposition that the trajectories of the ESs do not cross.
In the simulations, the laser pulse had the step-like envelope with the amplitude a 0 = 5 and the wavelength λ = 1 µm. The length of the laser pulse was equal to 20 λ (actually, electron beam evolution will be the same for any step-like laser pulse with length greater than ≃8λ for considered time of interaction of ≃0.4 ps since only eight first laser pulse cycles interact with the electron beam during this time). In Figures 4 and 5, the electron density distributions inside the laser pulse are presented for different moments of time. The electron beam before interaction had the length of l = 10 µm, and two different electron densities, n 0 = 2.2×1017 cm−3 (ν = 10−4) in Figure 4 and n 0 = 2.2 × 1016 cm −3 (ν = 10−5) in Figure 5, were utilized. In both cases, initial velocity of the electrons was equal to zero. There were 2000 (Fig. 4) or 1100 (Fig. 5) spatial grid points on the laser wavelength λ, and there were 50 macroparticles in one grid cell. Since the left sharp peaks in the density distribution are considerably higher than smooth peaks to the right, the values for the maximal heights n max of the sharp density peaks obtained from the PIC simulation are indicated in Figure 4 also.

Fig. 4. (Color online) Evolution of the electron beam density distribution (n 0 = 2.2·1017 cm−3, ν = 10−4) in the field of an ultra-intense laser pulse with a step-like envelope and a 0 = 5 [black line—theory, grey line (cyan online)—PIC simulations]. The electron density (in units of the initial density n 0) is presented for different times: ωt ≃ 57, 138, 258, 377, 591, 748 for (a)–(f). Also, the maximal heights n max for the sharp density peaks, obtained in the PIC simulation, are indicated for these times. Note the different vertical scales for plots (a)–(f).

Fig. 5. (Color online) Same as in Figure 4, but for n 0 = 2.2 × 1016 cm−3, ν = 10−5 [black line—theory, grey line (cyan online)—PIC simulations]. The electron density (in units of the initial density n 0) is presented for the following times: ωt ≃ 57, 138, 396, 779 for (a)–(d). Note the different vertical scales for plots (a)–(f).
In the same figures, the results of calculations for the theoretical value of the electron density according to Eq. (35) are presented. Here, for every initial coordinate Z 0e of the ES (1000 in total), the value for parameter θ at some moment of time, t, was calculated from Eq. (5) using Eq. (13) for the value of the coordinate (the fast part Z f of the ES's coordinate was also taken into account). Then, these values for θ for all ESs were used for plotting the electron density distribution at this moment of time, t. When the density from Eq. (35) has negative and positive values simultaneously in some points Z (many-valued function, cf. Section 4.3), then for such points, the absolute values of positive and negative parts of the density distribution were added to calculate the total density.
From these figures, one can conclude that the theory gives good agreement with the PIC simulations. There is a small difference in the positions of the sharp peaks in calculated and simulated density distributions. This difference oscillates with time, and its maximal values are about λ for ν = 10−4 and about λ/10 for ν = 10−5 for ωt ≃ 750 (0.4 ps from the beginning of interaction). The difference in the positions of the sharp peaks can be explained by two reasons. The first reason is the physical one, i.e., the acceleration of the electrons by the radiation reaction force, which is omitted in the analytical calculations and is present in the PIC simulations. This radiation reaction force accelerates more effectively those electrons, which are incorporated into a very short bunch with length considerably smaller than the laser wavelength (Cherepenin et al., Reference Cherepenin, Il'in and Kulagin2001; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b). Therefore, the position of the sharp simulation peak changes with respect to the position of the theoretical peak due to this force, while the positions of the wide diffuse simulation peaks to the right of the sharp peak are almost unchanged with respect to their theoretical positions. The other reason is numerical, i.e., not high enough accuracy of the PIC simulations. Actually, if one takes 1000 grid points on the laser wavelength λ instead of 2000 (which was used for simulations in Fig. 4) with other parameters as in Figure 4, the discrepancy in the positions of calculated and simulated sharp peaks increases. An excess noise (around sharp peaks) of the PIC simulations at large times in Figures 4 and 5 can also be explained by not high enough accuracy of the PIC simulations (to remove the noise it is necessary to increase considerably the number of spatial grid points on the laser wavelength).
4.3. Sharp Density Peak frozen Into the Density Distribution of the Electron Beam
There is the sharp peak in the electron density distribution at the left end of the electron beam, where the laser pulse strikes first (cf. Figs. 4 and 5). Since the position of this peak does not change with time with respect to the electron beam, it can be considered as frozen into the density distribution. All other peaks are the peaks of the density wave inside the electron beam (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a) defined by the factor γ, and they change their position with time. The position of the frozen peak is defined by the factor ∂[kZ(Z 0e, θ)]/∂(kZ 0e) in the expression for the density distribution (34), more precisely, by the points, where this factor is close (or equal) to zero. To investigate the conditions for the appearance of the frozen density peak, let us consider more closely Eq. (35) for the density distribution in the field of the laser pulse with the step-like envelope. The height of the density peak changes slowly with time so the fast part kZ f of the coordinate of ESs can be disregarded, and only the slow part kZ s should be analyzed. Then, from the last equation of the system (35), one can estimate that ∂(kZ in)/∂(kZ 0e) ≃ 1 for reasonable parameters of the electron beam, and the only term, which can give the divergence of n, is the term proportional to ∂κin/∂(kZ 0e) in ∂(kZ s)/∂(kZ 0e). This means that, for the electron beams without initial modulation of velocity, there will be no frozen peak in the density distribution. For the dense electron beams, such a modulation is provided by the space-charge (Coulomb) forces in the beam. Also, since initial velocity modulation is strongly dependent on the initial conditions of the problem, the parameters of the frozen density peak will be varied for different initial conditions, e.g., will depend on the presence of focusing forces for the electron beam, etc. The parameters of the laser pulse front also influence on the appearance and characteristics of the sharp density peak.
From the physical point of view, the equality of the derivative d[kZ(Z 0e, t)]/d(kZ 0e) to zero, which causes the divergence of the density, means only the crossing of the trajectories of the ESs, i.e., after some time, two ESs with different initial coordinates arrive at the same point z cr. This, of course, does not mean any inconsistency in the approach since the surface charge density is limited for any layer with finite length around z cr (the infinity is “integrable”). On the other hand, our model and exact solutions (8) are based on the assumption that there are no crossings of the trajectories of ESs during evolution of the electron beam in the super-intense laser pulse. If such crossings occur then the Coulomb forces for the ESs with the crossed trajectories are calculated inaccurately, and the motion of these ESs is reproduced only approximately by the model. So, strictly speaking, Eq. (8) are valid only for such parameters of the electron beam and the laser pulse, for which there are no divergence of the electron beam density. However, if the number of crossings is not large (only small part of the trajectories of the ESs crosses), then Eq. (8) can be considered as the approximate solutions for those ESs, which suffer the crossings of the trajectories, and as exact solutions for the other ESs.
To derive approximate conditions for the appearance of the frozen density peak and the crossings of the trajectories, let us suppose that κ ≃ κin ≃ 1, that is, reasonable for not very large values of θ. Then, from the second equation of the system (35), one has
The electron beam density will be infinite in the points where this partial derivative is equal to zero. Then, from quadratic equation for θ, one can estimate two possible solutions
The frozen density peak can appear only during interaction of electromagnetic wave with the dense electron beam; when the beam evolves freely under the action of the Coulomb forces only, the density distribution has no sharp peaks. So for the parameter θ, only positive values are possible. Then, from Eq. (37), one can conclude that kZ 0e < kl/4. To have real solutions, the determinant should be non-negative, that gives together with the previous condition the following inequality ![]() , and the divergence in the density distribution of the electron beam is possible only for ν(kl)2(1 + 3a 02/2) = αkl(1 + 3a 02/2) ≥ 4.
, and the divergence in the density distribution of the electron beam is possible only for ν(kl)2(1 + 3a 02/2) = αkl(1 + 3a 02/2) ≥ 4.
The crossings of the trajectories begin first for the ESs with initial coordinates around Z 0e ≃ 0 (the left ESs, which are touched first by the laser pulse front). This occurs at
where (1 + 3a 02/2)αkl >> 4 is supposed, and for the transition from θ to ωt, Eq. (14) is utilized with the same assumptions that were used for deriving Eq. (36). Then, at time
the crossings of the trajectories for these ESs will disappear (however, the frozen density peak will die only when the condition θ >> θcr2 = kl is fulfilled for the left ESs). The value (39) for θcr2 is less accurate than Eq. (38) for θcr1 since, for such a large time, approximation of κ by unity can be invalid.
The initial coordinate Z 0e of the last (the most right) ES, which still suffer the crossings of the trajectories, is defined by expression
![kZ_{0max} = kl/4 - \left[2\sqrt{\nu \lpar 1 + 3a_0^2/2\rpar }\right]^{-1}.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000414_eqn40.gif?pub-status=live)
The value

gives just the part of the ESs, which outstrips the neighboring ESs. So in the worst case, this part is about 0.25. The ES with the initial coordinate kZ 0max will suffer the crossing of the trajectories, or, more exactly, touching of the trajectories as long as θcr1 = θcr2, at time
![\theta_t = \left[\sqrt{\lpar 1 + 3a_0^2/2\rpar \nu}\right]^{-1}\comma \; \quad \omega t_t \approx \sqrt{{3a_0^2 \over 8\nu}}.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021083621293-0637:S0263034608000414_eqn42.gif?pub-status=live)
It can be checked easily that ωt cr1 ≤ ωt t ≤ ωt cr2 for all parameters of the electron beam and the laser pulse.
Let us now make some estimates for the simulated electron beams with ν = 10−4 and ν = 10−5. For the ν = 10−5 case, αkl(1 + 3a 02/2) ≃ 1.5 < 4, and there are no crossings of the trajectories and divergence of the density distribution. However, the frozen peak still exists, because the value for αkl(1 + 3a 02/2) here is comparable with 4. For the ν = 10−4 case, αkl(1 + 3a 02/2) ≃ 15> > 4, and there are the crossings of the trajectories and the divergence of the density distribution. The first crossing takes place according to the estimate (38) at ωt cr1 ≃ 80, this value from numerical solutions of Eq. (6) is equal to 88. So in Figure 4a, there are no crossings of the trajectories. The crossings of the trajectories disappear at ωt cr2 ≃ 1180 (numerical value is about 950), and the time for the touching of the trajectories by the ES with the initial coordinate kZ 0max ≃ 0.12kl is ωt t ≃ 310 (numeric value is about 320). Therefore, in Fig. 4b to 4f, the trajectories are crossed near the left end of the electron beam, and the analytic expression for the electron beam density has the divergence here. However, from the calculations with the self-consistent MATLAB code EXACT (Cherepenin et al., Reference Cherepenin, Il'in and Kulagin2001; Kulagin et al., Reference Kulagin, Cherepenin and Suk2004b, Reference Kulagin, Cherepenin, Hur and Suk2007b), the results for which are presented in Figure 2a, one can conclude that all the ESs, which suffer the crossings of the trajectories, stay within the distance of λ/10 near the sharp density peak. In this case, the value, obtained from the PIC simulation for the maximal height ηmax of the sharp density peak, characterizes indirectly the part of the ESs with the crossed trajectories. So the estimates (38), (39), and (42) provide the reasonable approximations to the characteristic time points of the evolution for the frozen density peak.
5. DISCUSSION OF RESULTS AND CONCLUSIONS
The theory, presented above for the interaction of the high-density electron beam with the super-intense laser pulse, shows that there are two conditions, which define the characteristics for the evolution of the electron beam. The first condition is applicable to the initial period of motion of the electrons in the beam, when the laser pulse still have not reached them. This condition defines whether the space-charge (Coulomb) forces do or do not play a determinative role in the evolution of the electrons during this period. More exactly, when αkl = 2π2l 2/λp2 << 1, where λp = 2πc/ωp, or, equivalently, ![]() , the Coulomb forces do not change significantly the initial coordinates of the electrons before the laser pulse reaches them, so the electron beam can be considered as a low-density beam (with regard to this particular problem of interaction). In the opposite case, when αkl≲1, the Coulomb forces considerably change the initial coordinates of the electrons during the time, required for the laser pulse to reach them (Fig. 2a).
, the Coulomb forces do not change significantly the initial coordinates of the electrons before the laser pulse reaches them, so the electron beam can be considered as a low-density beam (with regard to this particular problem of interaction). In the opposite case, when αkl≲1, the Coulomb forces considerably change the initial coordinates of the electrons during the time, required for the laser pulse to reach them (Fig. 2a).
The second condition deals with the crossings of the electron trajectories resulting in the infinite analytical value for the electron density in the beam. This occurs when αkl(1 + 3a 02/2) ≥ 4. When the crossings of the trajectories start, some electrons in the electron beam become to participate in the multi-stream motion. The crossings of the trajectories result in appearance of the sharp high-density peak frozen into the density distribution at the side of the electron beam, which is touched first by the laser pulse front. The characteristics of this sharp density peak strongly depend on the initial conditions of the motion for the electrons, i.e., on initial modulation of velocity of the electrons, on the presence of the focusing forces, etc., and on the parameters of the laser pulse front.
It is necessary to note that both conditions depend not only on the initial density of the electron beam, but also on its length. So electron beams with relatively low density but large length can demonstrate the described effects. The second condition depends also on the amplitude of the laser pulse, therefore, for high enough amplitudes, the sharp peak of the density can appear in the low-density electron beams.
These sharp peaks in the electron beams can be effectively used as attosecond electron beams in different applications. Thus, estimates based on Figures 4 and 5 give the length of this peaks on the level of several nanometers, which results in the duration of about several attoseconds. Also, these sharp peaks can be used for the generation of coherent X-ray radiation, required in many applications (Barbara et al., Reference Barbara, Knox, Mourou and Zewail1994; Crowell et al., Reference Crowell, Gosztola, Shkrob, Oulianov, Jonah and Rajh2004).
If the laser pulse will have a smooth front, then the transverse momentum of the electrons will be determined by an expression different from Eq. (10). However, all parameters for the electron beam evolution can be easily recalculated for this case with the help of Eq. (8). Qualitatively, the main difference for the smooth front will be the other distance between the layers in the multilayer configuration - λ/2 instead of λ for the sharp front (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a, Reference Kulagin, Hur and Suk2006b). Spread of initial parameters for the electrons in the beam due to, e.g., thermal effects, can increase the sharp peak width. However, for high enough laser pulse amplitudes and not very large initial electron temperatures, this effect will be not prominent, at least, in the beginning of interaction. Note that the microbunching structure of the electron beam is extremely stable and does not depend on the thermal properties of the electrons since the microbunching is defined only by the distribution of the electromagnetic field in space.
Let us estimate at last some practical laser parameters required for realization of considered scheme for high-density electron beam preprocessing. If the longitudinal dimensions of the electron medium is about 10 µm (that is inherent for electron beams from laser-plasma accelerators, and can be achieved for focused ordinary electron beams in the scheme of perpendicular propagation of electron and accelerating laser beams) then the laser spot should be not less than 20 µm. For a 0 = 5, this requires the laser power of 50–100 TW that is easily accessible in experiment.
In summary, the evolution of the high-density electron beam in the field of the super-intense laser pulse was considered. The theory for the interaction was developed, and the exact solutions for the equations of motion of the electrons were found. The main differences of this high-density electron beam case from the low-density case (Kulagin et al., Reference Kulagin, Cherepenin, Hur and Suk2006a, Reference Kulagin, Hur and Suk2006b) are the slow increase of the electron beam length in time after initial compression of the beam and the appearance of the sharp density peak frozen into the density distribution of the electron beam. Characteristic parameters for the evolution of the electron beam were calculated by an example of a step-like envelope of the laser pulse. Comparison with the 1D PIC simulations shows that, for αkl(1 + 3a 02/2) < 4 the theory correctly describes the density of the electron beam inside the super-intense laser pulse. In the opposite case, αkl(1 + 3a 02/2) ≥ 4, the theory adequately describes the smooth part of the density distribution, where the trajectories of the electrons do not cross and approximately describe the density distribution around the sharp density peak, where the crossings of the electron trajectories exist (multi-stream region).
ACKNOWLEDGMENTS
This work was supported by the Ministry of Knowledge and Economy of Korea through the Ultrashort Quantum Beam Facility Program and the GIST Top Brand Project “Photonics 2020,” and by the RFBR project 05-02-17297-a.







