1. INTRODUCTION
The tremendous advancement of last two decades in laser and accelerator-plasma technologies has allowed the appearance of superpower laser sources of relativistic intensities and high brightness electron beams that predetermine the behavior of coherent interaction and multiphoton character of laser-induced processes with free electrons. Many classical, quantum-mechanical, and quantum electrodynamics (QED) effects, the observation of which seemed practically unreal because of small cross-section of electron–photon electromagnetic (EM) interaction and poor parameters of particle and photon beams, became observable with relativistic/ultrarelativistic laser and high brightness electron beams. Good example of the latter is electron diffraction effect on a standing EM wave lattice – Kapitza–Dirac effect (Kapitza & Dirac, Reference Kapitza and Dirac1933), the interest to which has been increased especially after the successful realization of experiment with high-intensity and strongly coherent laser beams-gratings by Freimund et al. (Reference Freimund, Aflatooni and Batelaan2001). For the acquaintance with the experimental situation in this area since the advent of Kapitza–Dirac effect up to the implemented experiment Freimund et al. (Reference Freimund, Aflatooni and Batelaan2001) and for detailed references on earlier work we refer the reader to review papers by Schwarz (Reference Schwarz1967, Reference Schwarz1973), Takeda and Matsui (Reference Takeda and Matsui1968), Bucksbaum et al. (Reference Bucksbaum, Schumacher and Bashkansky1988), Batelaan (Reference Batelaan2007).
The scope of the Kapitza–Dirac effect has been extended since 1975 in the works Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975), Avetissian (Reference Avetissian1976), Avetissian et al. (Reference Avetissian, Jivanian and Petrossian1981a ) for inelastic diffraction scattering of electrons on a slowed traveling wave propagating with the phase velocity smaller than light speed in vacuum in the induced Compton, Cherenkov, and undulator/wiggler processes. These are the processes of threshold nature, which possess an essential peculiarity consisted in the existence of a critical intensity of the effective wave-field at which electron's longitudinal velocity in the field reaches the resonance value (for an each induced process) irrespective of its initial value and stipulates non-linear resonance of threshold nature in the critical point that leads to electron-slowed-wave impact interaction [for electron scattering on a potential in the field of bichromatic waves, see, for example, Florescu & Cionga (Reference Florescu and Cionga2000)]. This radically changes the ordinary dynamics of electrons interaction with a periodic wave: the slowed traveling wave becomes a potential barrier for electrons at the intensities above critical values [in general case of arbitrary interaction angle these classical critical values are given in the works Avetissian (Reference Avetissian1978, Reference Avetissian1979, 1982–Reference Avetissian1983), Avetissian et al. (Reference Avetissian, Jivanian and Petrossian1981a , Reference Avetissian, Jivanian and Petrossian b )] that “reflects” the electrons (Haroutunian & Avetissian, Reference Haroutunian and Avetissian1972, Reference Haroutunian and Avetissian1976; Avetissian et al., Reference Avetissian, Jivanian and Petrossian1978) violating the synchronous motion of electrons with the effective slowed wave and, consequently, the necessary condition for diffraction scattering in these coherent processes. This concerns the multiphoton Kapitza–Dirac effect on a standing wave as well, as a particular case of induced Compton process Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975, Reference Haroutunian and Avetissian1976). So, at the consideration of electron diffraction effect on the strong waves-lattice/laser-beams-gratings the mentioned peculiarity – existence of critical intensity in the induced Cherenkov, Compton, and undulator processes cannot be neglected. Note that the term “strong wave” here is relative, since the mentioned non-linear resonance takes place even in the very weak wave-fields if the electrons initially are close to the resonance state, that is, the electrons’ initial longitudinal velocities are close to the phase velocity of the slowed wave, at which the critical field is also very small and, respectively, very low laser intensities may be above critical for such electrons (Avetissian, Reference Avetissian1997).
The Kapitza–Dirac effect has been predicted in 1933, so that for a long time it had been considered for the one-photon interaction in the low-intensity fields of common light sources because of the absence of high-intensity and coherent light sources. With the appearance of laser sources Kapitza–Dirac diffraction effect achieved multiphoton character. The Kapitza–Dirac effect in the strong counterpropagating laser beams has been considered in the papers Li et al. (Reference Li, Zhang, Xu, Fu, Guo and Freeman2004), Rosenberg (Reference Rosenberg2004), Smirnova et al. (Reference Smirnova, Freimund, Batelaan and Ivanov2004), Kaplan and Pokrovsky (Reference Kaplan and Pokrovsky2005), Dellweg and Muller (Reference Dellweg and Müller2015), as well as in the papers of relevant subject Eichmann et al. (Reference Eichmann, Nubbemeyer, Rottkel and Sandner2009), Gadway et al. (Reference Gadway, Pertot, Reimann, Cohen and Schneble2009), Eilzer et al. (Reference Eilzer, Zimmermann and Eichmann2014). The multiphoton probability of electron diffraction at Kapitza–Dirac effect in the field of strong counterpropagating laser beams has been done by Ehlotzky and Leubner in 1974 on the base of the Helmholtz–Kirchhoff diffraction theory Ehlotzky and Leubner (Reference Ehlotzky and Leubner1974, Reference Ehlotzky and Leubner1975) [see, also the papers by Fedorov (Reference Fedorov1967), Fedorov (Reference Fedorov1975), and Fedorov & McIver (Reference Fedorov and McIver1980) where theoretical analysis of electrons scattering by a strong standing wave in adiabatic switching of interaction regime is considered]. Then, in 1975 this phenomenon has been developed by Haroutunian and Avetissian for bichromatic counterpropagating waves and electron inelastic diffraction scattering on a slowed interference wave has been stated (Haroutunian & Avetissian, Reference Haroutunian and Avetissian1975). In this process, due to the induced Compton effect in the two wave fields electron absorbs s photons from the one wave and coherently radiates s photons into the other wave and vice versa. This is the condition of coherency in the induced Compton process corresponding to the resonance between the Doppler-shifted frequencies in the intrinsic frame of reference of an electron in the bichromatic counterpropagating waves at which the conservation of the number of photons in the induced Compton process takes place Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975), Fedorov and McIver (Reference Fedorov and McIver1980) in contrast to spontaneous Compton effect in the strong wave field, where after the multiphoton absorption, a single photon is emitted Goldman (Reference Goldman1964). Note that here we do not consider nonlinear optics effects of wave mixing – up- or down-conversion processes, when a single electron can be considered as a nonlinear medium in the high-intensity laser field, and matter wave of the electron may diffract from the stationary laser-grating to generate the new wave, etc. at which the conservation of the number of photons in the induced Compton process evidently does not take place [for diffraction effect in this case, see the paper by Batelaan (Reference Batelaan2007) and references therein]. The result of coherent scattering at the satisfaction of the condition of coherency in the induced Compton process is equivalent to diffraction of electrons on a slowed interference wave that has the form of a plane traveling wave.
The significance of Kapitza–Dirac effect, apart from its quantum-mechanical meaning as a best example of demonstration of electron matter wave diffracted by light and, moreover, as an unique sample of a diffraction system with reversed properties of the matter and light, is also conditioned by important applications since electron beams diffracted from highly coherent laser gratings are coherent with each other. Hence, the Kapitza–Dirac effect is a very convenient, even maybe an irreplaceable means to realize coherent electron beams. Such beams can serve as a basis for construction of new important tools of diverse species, for example, coherent beam splitters, new type electron interferometers, which would operate at rather low electron energies (typical for atomic physics) etc. Note also that the interference of above-threshold de Broglie waves – electrons matter waves may lead to formation of attosecond electron pulses, as it has been reported in the paper Varro and Farkas (Reference Varro and Farkas2007).
The present review article is devoted to comprehensive consideration of elastic and inelastic diffraction effects of electrons on the slowed traveling waves with the mentioned peculiarity stipulated by non-linear resonance in the induced coherent processes. We will specifically consider in detail electrons diffraction effect on a traveling wave in a dielectric medium because of confusion arisen in literature on this subject connected with the appearance recently of a paper in New Journal of Physics (Hayrapetyan et al., Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015). Therefore, apart from the pure scientific interest, in this paper we will clarify the state-of-the-art on the considering subject for last four decades in chronological order, to avoid the further confusions and misunderstandings in scientific literature.
Kapitza–Dirac effect is a particular case of the induced Compton process in the field of two counterpropagating EM waves of the same frequencies at which the scattering electron moves in perpendicular direction to wavevectors of counterpropagating waves, to exclude the Doppler shift of waves’ frequencies because of longitudinal component of electron velocity. Note that the perpendicular incidence of electron to counterpropagating waves corresponds to classical condition of coherence – resonance between the electron and two waves of the same frequencies in the induced Compton process, which is valid at the neglect of quantum recoil in the result of photons absorption–radiation by electron. At the quantum consideration, taking into account the quantum recoil as well, the exact condition of resonance is satisfied at the small angle to perpendicular direction that corresponds to elastic Bragg diffraction on the phase lattice of a standing wave Freimund and Batelaan (Reference Freimund and Batelaan2002). The Bragg regime of the two-particle Kapitza–Dirac effect is considered in the paper Sancho (Reference Sancho2011) [for two-particle Kapitza–Dirac diffraction effect see Sancho (Reference Sancho2010)]. However, the phase matching between the electron and counterpropagating waves in the induced Compton process can also be fulfilled in general case of bichromatic EM waves if electron moves at the certain angle with respect to wavevectors of counterpropagating waves at which the condition of coherency between the electron and waves of different frequencies is satisfied. It is evident that this is the condition of resonance between the Doppler shifted waves’ frequencies in the frame of reference moving with the electron. On the other hand, consideration of the dynamics of induced Compton process shows that coherent interaction of electron in this case occurs with the effective interference wave-field that has form of a slowed traveling wave propagating with the phase velocity smaller than the light speed in vacuum. In the frame of reference connected with the electron this slowed traveling wave at the satisfaction of resonance condition becomes a stationary phase lattice (standing light-wave structure) for electron, since this condition is equivalent to the condition of synchronous motion of electron with the slowed effective wave, and due to such phase matching a coherent scattering of electrons – diffraction on the slowed interference wave in the vacuum occurs Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975). In contrast to Kapitza–Dirac effect (Kapitza & Dirac, Reference Kapitza and Dirac1933), diffraction of electron in this case Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975) is inelastic.
The organization of the paper is as follows. In Section 2, the relativistic quantum theory of electron inelastic diffraction effect on a traveling EM wave (intense laser beam) in a dielectric medium is presented, which is the result of multiphoton-induced Cherenkov interaction of electron with a slowed plane EM wave-grating (“Cherenkov diffraction”). In Section 3, the formation of a slowed traveling wave in vacuum – responsible for electron diffraction effect at the induced coherent processes is considered. In Section 3.1, the effective interaction of electron with a slowed interference traveling wave formed by the two intense bichromatic counterpropagating waves in vacuum is considered. In Section 3.2, the electron effective interaction with a slowed in undulators/wiggler traveling wave formed in the result of interference of a laser radiation and undulators’ periodic electric or magnetic fields is presented. In Section 4, the quantum dynamics of relativistic electron in the induced Cherenkov, Compton, and undulator processes is investigated in diffraction and strongly quantum Bragg regimes – at the exact quantum resonance taking also into account the quantum recoil of electron because of photons absorption–radiation. Finally, conclusions are given in Section 5.
2. ELECTRON DIFFRACTION EFFECT ON A TRAVELING EM WAVE IN A DIELECTRIC MEDIUM
In this section, we will represent theoretical description of electron inelastic diffraction effect on a strong traveling EM wave in a dielectric medium in the original form corresponding to the paper Avetissian (Reference Avetissian1976) and monographs Avetissian (Reference Avetissian2006, Reference Avetissian2016) or the book Saakyan and Chubaryan (Reference Saakyan and Chubaryan1982) for its direct comparison with the result of the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) pretended to priority for proposed effect of electron diffraction on a traveling wave in a dielectric medium after four decades of the paper Avetissian (Reference Avetissian1976).
In general, we will start from the relativistic quantum equations of motion for electron wave function Ψ. As far as the spin interaction of an electron with a light-field is rather small compared with the charge interaction and by its nature is different than the considering diffraction dynamics, we can neglect the spin interaction, and then the Dirac equation in quadratic form passes to Klein–Gordon equation for electron in the field of a plane EM wave in a dielectric medium [e.g., regarding the spin dynamics in the Kapitza–Dirac effect – spin flips or spin rotation, see the papers of Ahrens et al. (Reference Ahrens, Bauke, Keitel and Müller2012, Reference Ahrens, Bauke, Keitel and Müller2013)]. So, we will consider diffraction problem on the basis of the Klein–Gordon equation:
$$- \hbar ^2 \displaystyle{{\partial ^2 {\rm \Psi}} \over {\partial t^2}} = \left\{ {c^2 \left[ { - i\hbar \nabla + \displaystyle{e \over c}{\bf A}} \right]^2 + m^2 c^4} \right\}{\rm \Psi}, $$
where
$\hbar $
is the Planck constant, e is the elementary charge, m is the electron mass, c is the light speed in vacuum, A = A(t, r) is the vector potential of a plane EM wave in a dielectric medium. A plane quasimonochromatic EM wave in a medium may be described by the vector potential
${\bf A}(t,{\bf r}) = $
${\bf A}(t - n{\rm \nu} _0 {\bf r}/c)$
, where n ≡ n(ω) is the refractive index of the medium at the carrier frequency ω of the wave (laser beam), ν0 is the unit vector along the wave propagation direction. We will assume that the frequency ω is far from the main resonance transitions between the atomic levels of the medium to prohibit the wave absorption and non-linear optical effects in the medium and consequently
$n = \sqrt {{\rm \varepsilon}_0 {\rm \mu}_0} =$
${\rm const}$
will correspond to the linear refractive index of the medium (ε0 and μ0 are the dielectric and magnetic permittivities of the medium, respectively).
Choosing a concrete polarization of the wave and directing vector ν0 along the OX-axis of a Cartesian coordinate system one can write:
$${\bf A} = \left\{ {0,A_0 ({\rm \tau} )\cos {\rm \omega} \left( {t - nx/c} \right),0} \right\},$$
where A 0(τ)is a slowly varying amplitude of the vector potential of a quasimonochromatic laser pulse, τ = t − nx/c is the plane wave coordinate. As the existence of a plane wave does not violate the homogeneity of the space in the plane of the wave polarization (r ⊥) the variables y and z are cyclic and the corresponding components of generalized momentum p ⊥ are conserved. Then the solution of Eq. (1) can be represented in the form:
$${\rm \Psi} \left( {x,y,z,t} \right) = {\rm \psi} (x,t)\exp \left\{ {\displaystyle{i \over \hbar} {\bf p}_ \bot {\bf r}_ \bot} \right\}.$$
Substituting Eq. (3) into (1) for the function Ψ(x, t) yields the equation
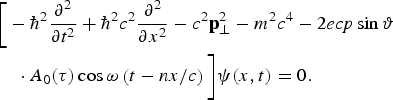$$\eqalign{&\bigg[ - \hbar ^2 \displaystyle{{\partial ^2} \over {\partial t^2}} + \hbar ^2 c^2 \displaystyle{{\partial ^2} \over {\partial x^2}} - c^2 {\bf p}_ \bot ^2 - m^2 c^4 - 2ecp\sin {\rm \vartheta} \cr & \quad \cdot A_0 ({\rm \tau} )\cos {\rm \omega} \left( {t - nx/c} \right) \bigg]{\rm \psi} (x,t) = 0.}$$
Here ϑ is the angle between the electron initial momentum (p) and wave propagation direction (OX-axis):
$p_ \bot = p\sin {\rm \vartheta} $
. In Eq. (4), we have neglected the term
${\rm \sim} A_0^2 ({\rm \tau} )$
since for actual values of parameters
$p\sin {\rm \vartheta} /mc{\rm \gg} {\rm \xi} _{\max} $
and to be below the ionization threshold of a dielectric medium too it should be ξmax <ξcr ≪ 1 (ξcr is the aforementioned critical intensity of the induced Cherenkov process above which diffraction effect cannot proceed). Here the quantity ξ ≡ eA
0/mc
2 = eE
0/mcω is the dimensionless relativistic invariant parameter of the wave intensity (E
0 is the amplitude of the wave electric field strength).
Equation (4) describes diffraction of electron on the phase lattice of a slowed traveling wave A 0 (τ)cosω(t − nx/c). To describe the multiphoton inelastic diffraction effect at the interaction of electron with strong laser field, Eq. (4) is solved in the eikonal approximation by electron wave function
$${\rm \Psi} (x,t) = \sqrt {\displaystyle{{N_0} \over {2{\rm \cal E}}}} \,f\,(x,t)\exp \left[ {\displaystyle{i \over \hbar} \left( {\,p_x x - {\rm \cal E}t} \right)} \right],$$
(
${\rm \cal E}$
is the electron initial energy) according to which f(x,t) is a slowly varying function with respect to free-electron wave function (the latter is normalized on N
0 particles per unit volume):
$$\left \vert {\displaystyle{{\partial f} \over {\partial t}}} \right \vert {\rm \ll} \displaystyle{ {\cal E} \over \hbar} \left \vert f \right \vert ;\quad \quad \left \vert {\displaystyle{{\partial f} \over {\partial x}}} \right \vert {\rm \ll} \displaystyle{{\,p_x} \over \hbar} \left \vert f \right \vert. $$
Choosing a concrete polarization of the wave (assume a linear one along the axis OY) and taking into account Eq. (4) for f(x,t) we will have a differential equation of the first order:
$${\displaystyle{{\partial f} \over {\partial t}} + v\cos {\rm \vartheta} \displaystyle{{\partial f} \over {\partial x}} = \displaystyle{i \over {\hbar {\cal E}}}\left[ {ecp\sin {\rm \vartheta} \cdot A_0 ({\rm \tau} )} \right. \left. { \times \cos {\rm \omega} \left( {t - nx/c} \right)} \right]f\,(x,t).} $$
Changing to characteristic coordinates
${\rm \tau} ^{\prime} = t - x/v\cos {\rm \vartheta} $
and η′ = t, it will be obvious that at the fulfillment of the induced Cherenkov condition
$$1 - n\displaystyle{v \over c}\cos {\rm \vartheta} _{{\rm ch}} = 0$$
the traveling wave in this frame of coordinates becomes a diffraction lattice over the coordinate τ′ and for the scattered amplitude of the electron wave function from Eq. (7) we have
$$f\,({\rm \tau} ^{\prime}) = \exp \left\{ {\displaystyle{{iecp\sin {\rm \vartheta} _{{\rm ch}}} \over {\hbar {\cal E}}}\cos {\rm \omega} {\rm \tau} ^{\prime}\int_{{\rm \eta} _1} ^{{\rm \eta} _2} A({\rm \eta} ^{\prime})d{\rm \eta} ^{\prime}} \right\},$$
where η1 and η2 are the moments of the electron entrance into the wave and exit, respectively. If one returns to coordinates x and t and expands the exponential (8) into a series by Bessel functions for the total wave function (5) we will have
$$\eqalign{{\rm \Psi} \left( {{\bf r},t} \right) = & \sqrt {\displaystyle{{N_0} \over {2 {\cal E}}}} \exp \left( {\displaystyle{i \over \hbar} yp\sin {\rm \vartheta} _{{\rm ch}}} \right)\sum\limits_{s = - \infty} ^{ + \infty} i^s J_s ({\rm \alpha} ) \cr & \times \exp \left[ {\displaystyle{i \over \hbar} \left( {\,p\cos {\rm \vartheta} _{{\rm ch}} - \displaystyle{{sn\hbar {\rm \omega}} \over c}} \right)x - \displaystyle{i \over \hbar} \left( { {\cal E} - s\hbar {\rm \omega}} \right)t} \right],} $$
where the argument of the Bessel function
$${\rm \alpha} = \displaystyle{{e{\rm v}\sin {\rm \vartheta} _{{\rm ch}}} \over {\hbar {\rm \omega}}} \int_{{\rm t}_1} ^{{\rm t}_2} E({\rm \eta} ^{\prime})d{\rm \eta} ^{\prime},$$
and E is the wave electric field strength (see the definition of amplitudes of electric field E 0 and vector potential A 0 for a monochromatic wave in the above-stated parameter ξ of the wave intensity: E 0 = A 0ω/c). The wave function (9) describes inelastic diffraction scattering of the electron on the slowed traveling wave in a dielectric-like medium. The electron's energy and momentum after the scattering are
$${{\cal E}^{\prime}} = {\cal E} - s\hbar {\rm \omega}, \quad p^{\prime}_x = p\cos {\rm \vartheta} _{{\rm ch}} - \displaystyle{{sn\hbar {\rm \omega}} \over c},$$
$$p_y = {\rm const};\quad s = 0, \pm 1, \ldots. $$
The probability of this process
$$W_s = J_s^2 \left[ {\displaystyle{{ec^2 p\sin {\rm \vartheta} _{{\rm ch}}} \over {\hbar {\rm \omega} {\cal E}}}\int_{{\rm t}_1} ^{{\rm t}_2} E({\rm \eta} ^{\prime})d{\rm \eta} ^{\prime}} \right].$$
The condition of the applied eikonal approximation (6) with Eq. (8) is equivalent to the conditions |p′
x
− p
x
| ≪ p
x
and
$\left\vert {{{\cal E}^{\prime}} - {\cal E}} \right\vert{\rm \ll {\cal E}}$
, which with Eq. (12) gives:
$\left\vert s \right \vert n\hbar {\rm \omega } /c \ll p$
.
In the case of a monochromatic wave from Eq. (13), we have
$$W_s = J_s^2 \left( {{\rm \xi} \displaystyle{{mc^2} \over \hbar} \displaystyle{{cp\sin {\rm \vartheta} _{{\rm ch}}} \over {\cal E}}t_0} \right),$$
where t 0 = t 2 − t 1 is the duration of the electron motion in the wave.
As is seen from Eq. (14) for the actual values of the parameters α ≫ 1, that is, the process is essentially multiphoton. The most probable number of absorbed/emitted Cherenkov photons is
$$\bar s\,{\rm \simeq}\, {\rm \xi} \displaystyle{{mc^2} \over \hbar} \displaystyle{v \over c}\sin {\rm \vartheta} _{{\rm ch}} \cdot t_0. $$
The energetic width of the main diffraction maximums
$\Gamma (\bar s){\rm \simeq} \bar s^{1/3} $
$\Gamma (\bar s){\rm \simeq} \bar s^{1/3} \hbar {\rm \omega} _0 $
and since
$\bar s{\rm \gg} 1,$
then
$\Gamma (\bar s){\rm \ll} \left\vert {{ {\cal E}^{\prime}} - {\cal E}} \right\vert$
.
The scattering angles of the s-photon Cherenkov diffraction are determined by Eq. (12):
$$\tan {\rm \vartheta} _s = \displaystyle{{sn\hbar {\rm \omega} \sin {\rm \vartheta} _{{\rm ch}}} \over {cp + sn\hbar {\rm \omega} \cos {\rm \vartheta} _{{\rm ch}}}}. $$
From Eq. (16) it follows that at the inelastic diffraction there is an asymmetry in the angular distribution of the scattered electron:
$\left\vert {{\rm \vartheta} _{ - s}} \right\vert \gt {\rm \vartheta} _s $
, that is, the main diffraction maximums are situated at different angles with respect to the direction of electron initial motion. However, in accordance with the condition
$\left\vert s \right \vert n\hbar {\rm \omega} /c{\rm \ll} p$
of the eikonal approximation this asymmetry is negligibly small and for the scattering angles of the main diffraction maximums from Eq. (16) we have
${\rm \vartheta} _{ - s} {\rm \simeq} - {\rm \vartheta} _s $
. Hence, the main diffraction maximums will be situated at the angles
$${\rm \vartheta} _{ \pm \bar s} = \pm \bar s\displaystyle{{n\hbar {\rm \omega}} \over {cp}}\sin {\rm \vartheta} _{{\rm ch}} $$
with respect to the direction of the electron initial motion.
Note that the formula (14) has been applied by Avetissian in 1977 for explanation of the experiment on energetic widening of an electron beam interacting with a laser beam at the induced Cherenkov process in a gaseous medium (Avetissian, Reference Avetissian1977, Reference Avetissian1982–1983) implemented in SLAC by the group Piestrup et al. (Reference Piestrup, Rothbart, Fleming and Pantell1975) (see, also the next experiment of this group Edighoffer et al. (Reference Edighoffer, Kimura, Pantell, Piestrup and Wang1981), made in the same conditions).
These results, in particular, inelastic Kapitza–Dirac effect and electron diffraction on a traveling wave in a dielectric medium, as was mentioned above, had been received 40 years ago and included in the monographs of Avetissian (Reference Avetissian2006, Reference Avetissian2016), as well as in the book of Saakyan and Chubaryan (Reference Saakyan and Chubaryan1982). Nevertheless, after the four decades, in 2015 a paper has been published in New Journal of Physics Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015), where authors report in the Abstract on the possibility of electrons diffraction scattering on a traveling EM wave in a dielectric medium: “We report on the possibility of diffracting electrons from light waves traveling inside a dielectric medium. We show that, in the frame of reference, which moves with the group velocity of light, the traveling wave acts as a stationary diffraction grating from which electrons can diffract, similar to the conventional Kapitza–Dirac effect” (citation from the Abstract). Here only the difference with the known results is in the physical characteristic “group velocity of light” which is a rough mistake repeated also in the text, even for a monochromatic wave. As it has been shown above, diffraction effect is thoroughly the result of the phase relations and is conditioned exceptionally by the phase velocity of light that must be smaller than c. Beside this incorrectness, authors of the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) ignored the existence of critical field in this process and influence of mentioned phenomenon of a particle “reflection” or capture on the diffraction effect. Meanwhile, one of the authors (Hayrapetyan et al., Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) is also a coauthor of both inelastic diffraction effect (Avetissian et al., Reference Avetissian, Jivanian and Petrossian1981a , Reference Avetissian, Jivanian and Petrossian b ) and “reflection” phenomenon in the undulators (Avetissian et al., Reference Avetissian, Jivanian and Petrossian1978). Concerning the citation of considered papers Avetissian (Reference Avetissian1976), Avetissian et al. (Reference Avetissian, Jivanian and Petrossian1981a , Reference Avetissian, Jivanian and Petrossian b ), devoted to diffraction effect on a traveling wave, these mechanically are included in the list of References of the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) in irrelevant context by footnote: “see, for example…”.
Regarding the method of calculation of the probability of multiphoton diffraction scattering, it is well known that there are two adequate methods – quantum-mechanical and Helmholtz–Kirchhoff diffraction theory. The second method has been proposed and applied by Ehlotzky and Leubner in 1974 just for the calculation of the multiphoton diffraction probability of Kapitza–Dirac effect in strong laser fields (Ehlotzky & Leubner, Reference Ehlotzky and Leubner1974), which in particular case of counterpropagating waves of the same frequencies (ω1 = ω2) coincides with the general formula obtained by Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975). Hence, the theories of multiphoton diffraction effect of Kapitza–Dirac and inelastic diffraction effect on bichromatic counterpropagating waves in general case of induced Compton process have been done firstly in the works Ehlotzky and Leubner (Reference Ehlotzky and Leubner1974) and Haroutunian and Avetissian (Reference Haroutunian and Avetissian1975), respectively.
Authors of the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) following to the method developed by Ehlotzky and Leubner (Reference Ehlotzky and Leubner1974), calculated the known formula for the probability of multiphoton diffraction scattering in a dielectric medium Eq. (14) and claim on the possibility of diffraction effect in a dielectric medium.
Thus, the probability of s-photon diffraction in the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) is given by the formula 16:
$${\cal I}_s = {\cal I}_{\rm i} J_s^2 \left( \Delta \right);\Delta = \displaystyle{{eA_0 d} \over {\hbar c}}.$$
The analogous expression for s-photon diffraction in the paper Avetissian (Reference Avetissian1976) is given by the formula 8 [which is the same Eq. (14) obtained above]:
$$W_s = J_s^2 \left( {\displaystyle{{ec^2 E_0 tP\sin {\rm \vartheta} _{{\rm ch}}} \over {\hbar {\rm \omega} {\cal E}}}} \right) = J_s^2 \left( {\displaystyle{{eE_0 d} \over {\hbar {\rm \omega}}}} \right),$$
where
$d \equiv tv\sin {\rm \vartheta} _{{\rm ch}} $
is the electron–wave interaction length.
Expressing the amplitude of the wave electric field strength E 0 by the amplitude A 0 of the wave vector potential (E 0 = A 0ω/c), Eq. (19) will have a form:
$$W_s = J_s^2 \left( \rm \Delta \right);\quad \Delta = \displaystyle{{eA_0 d} \over {\hbar c}};$$
that is, the formula (18) is the same as formula (19) or (20) except of undetermined in the paper Hayrapetyan et al. (Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) normalization constant
${\cal I}_{\rm i} $
, which should be
${\cal I}_{\rm i} = 1$
in accordance to the total probability norm of the process, and general formula for the Bessel functions:
$$\sum\limits_{s = - \infty} ^\infty J_s^2 \left( \Delta \right) = 1$$
(s > 0 – corresponds to photon radiation, s < 0 - to photon absorption in the wave field).
3. FORMATION OF SLOWED TRAVELING WAVE IN VACUUM
For the unified consideration of electron diffraction effect in the induced Compton and undulator/wiggler coherent processes, in this section we will describe the general picture of formation of a slowed traveling EM wave in vacuum corresponding to effective coherent interaction of electron with vacuum-traveling waves and responsible for electron inelastic diffraction effect on diverse moving light gratings. In other physical interpretation, just the slowed traveling EM wave can provide the satisfaction of conservation laws of energy–momentum for real radiation–absorption of photons propagating with phase velocity smaller c by a free electron. Hence, from the physical point of view the problem of electron inelastic diffraction effect reduces to fulfillment of conditions for real radiation–absorption of photons by electron in corresponding induced process.
Thus, the conservation laws of energy–momentum for real radiation–absorption of photons by a free electron after the interaction with a plane monochromatic wave propagating in general with phase velocity v
ph = c/n, where n is the effective refraction index (in case of a medium
$n = \sqrt {{\rm \varepsilon} _0 {\rm \mu} _0} $
where ε0 and μ0 are respectively dielectric and magnetic permittivities of the medium, as it was mentioned above; in other – vacuum cases see below) can be written in the form:
$$ {\cal E} = {\cal E}_0 + s\hbar {\rm \omega}, \quad {\bf p} = {\bf p}_0 + s\hbar {\bf k},\quad {\bf k} = n\displaystyle{{\rm \omega} \over c}{\rm \nu} _0, \quad \left \vert {{\rm \nu} _0} \right \vert = 1,$$
where
$ {\cal E}_0 $
, p
0 are electron initial energy and momentum,
$ {\cal E}$
, p are its final values after the absorption (s > 0) or radiation (s < 0) of photons with frequency ω and wavevector k. For a real particle after the absorption/radiation of photons the dispersion relation of energy–momentum must be satisfied. Hence, the dispersion law of relativistic electron
$ {\cal E}^2 = c^2 {\bf p}^2 + m^2 c^4 $
with Eq. (22) gives:
$$\left( { {\cal E}_0 + s\hbar {\rm \omega}} \right)^2 = c^2 \left( {{\bf p}_0 + s\hbar n\displaystyle{{\rm \omega} \over c}{\rm \nu} _0} \right)^2 + m^2 c^4. $$
From Eq. (23) we obtain the following relation:
$$1 - n\displaystyle{{v_0} \over c}\cos {\rm \vartheta} = \displaystyle{{s\hbar {\rm \omega} (n^2 - 1)} \over {2 {\cal E}_0}}, $$
where
$v_0 = \left\vert {c^2 {\bf p}_0 / {\cal E}_0} \right\vert$
is the electron initial velocity and
${\rm \vartheta} = \widehat{{{\bf v}_0 {\bf k}}}$
is the angle between the electron and photon propagation directions.
Equation (24) is the exact quantum conservation law for real absorption–radiation of photons by a free electron. The term in the right-hand side of Eq. (24) is the quantum recoil of electron acquired due to the photons absorption–radiation in each induced process. In case of a medium, Eq. (24) shows that the latter must be of dielectric character for satisfaction of conservation law of energy–momentum for real radiation–absorption of photons by electron that is must be n > 1. Thus, in vacuum – at n = 1 the right-hand side of Eq. (24) is zero, while the term in the left-hand side
$1 - (v_0 /c)\cos {\rm \vartheta} \gt 0$
always. In plasma – at n < 1 the left-hand side of Eq. (24)
$1 - n(v_0 /c)\cos {\rm \vartheta} \gt 0$
, but the right-hand side at s > 0 is negative: n
2 − 1 < 0, that is, the conservation law of energy–momentum does not satisfied again. However, at s < 0 though the right-hand side of Eq. (24) may be positive: s(n
2 − 1) > 0, nevertheless the dispersion relation of energy–momentum for final electron after the interaction that is equivalent to conservation law for real absorption–radiation process:
$$1 - n\displaystyle{v \over c}\cos {\rm \vartheta} = - \displaystyle{{s\hbar {\rm \omega} (n^2 - 1)} \over {2 {\cal E}}}$$
at s < 0 again cannot be satisfied.
Equations (24) and (25) in the plasma (n < 1) are satisfied for electron–positron pair production and annihilation processes when in Eq. (24) for initial electron one should assume an electron in the Dirac sea with negative energy
$ {\cal E}_0 \lt 0$
. Hence, the real radiation–absorption processes by a free electron proceed in dielectric media, the electron–positron pair production and annihilation processes – in the plasma.
In dielectric media, the conservation laws (24) and (25) correspond to induced multiphoton Cherenkov process with exact quantum description (taking into account the quantum recoil as well), which represent the condition of coherency for Bragg resonant scattering on the slowed traveling EM wave. As will be shown below, the diffraction effect takes place at the satisfaction of the classical condition of coherency:
$$1 - n\displaystyle{{v_0} \over c}\cos {\rm \vartheta} _{{\rm ch}} = 0,$$
when the quantum recoil of electron due to radiation–absorption of photons (the term in the right-hand side of Eq. (24) is neglected. It is just the condition of spontaneous Cherenkov radiation at the angle ϑch to rectilinear uniform motion of a charge at the absence of external EM wave.
Consider now the vacuum cases of formation of slowed traveling EM waves corresponding to induced Compton and undulator/wiggler coherent processes. As it is shown in the next subsection, the slowed traveling wave of frequency ω1 − ω2 formed at the interference of bichromatic counterpropagating waves in the induced Compton process [see Eq. (36)] propagates with the phase velocity v ph = c|ω1 − ω2|/(ω1 + ω2) <c [see Eq. (38)]. Consequently, the effective refraction index n including in the formulas Eqs (22)–(25) in this case has the form:
$$n_{\rm c} = \displaystyle{{{\rm \omega} _1 + {\rm \omega} _2} \over {\left \vert {{\rm \omega} _1 - {\rm \omega} _2} \right \vert}} \gt 1.$$
With Eq. (27) the exact quantum condition of coherency of the induced Compton process reads (without loss of generality let ω1 > ω2 when the slowed interference wave propagates along the wavevector k 1 of higher frequency wave ω1):
$${\rm \omega} _1 \left( {1 - \displaystyle{{v_0} \over c}\cos {\rm \vartheta}} \right) - {\rm \omega} _2 \left( {1 + \displaystyle{{v_0} \over c}\cos {\rm \vartheta}} \right) = 2\displaystyle{{s\hbar} \over { {\cal E}_0}} {\rm \omega} _1 {\rm \omega} _2. $$
The term in the right-hand side of Eq. (28) is the quantum recoil of electron acquired due to the photons absorption–radiation in the induced Compton process, which is responsible for strongly quantum regime of Bragg diffraction. At the neglect of the latter (because of smallness) we have the classical condition of coherency of the induced Compton process corresponding to electron diffraction on bichromatic counterpropagating waves:
$${\rm \omega} _1 \left( {1 - \displaystyle{{v_0} \over c}\cos {\rm \vartheta}} \right) = {\rm \omega} _2 \left( {1 + \displaystyle{{v_0} \over c}\cos {\rm \vartheta}} \right),$$
which is the condition of resonance between the Doppler-shifted counterpropagating waves of different frequencies ω1 and ω2 in the intrinsic frame of reference of relativistic electron, due to which the resulting from interference slowed EM wave turns to a standing wave-lattice with respect to the electron and diffraction like to Kapitza–Dirac effect (in the own –“R” frame of electron) on this phase-grating occurs. However, because of moving character of the grating diffraction effect in the laboratory – “L” frame is inelastic.
From the possible vacuum coherent processes in electric and magnetic undulators we will separate the magnetic undulator/wiggler as an important system with rather long coherent length (see below). The effective refraction index n, as it is seen from Eq. (46), is
$$n_{\rm u} = 1 + {\rm \lambda} /l \gt 1,$$
where l is the space period (step) of magnetic undulator/wiggler, λ = 2πc/ω – wavelength of a laser radiation. The exact quantum condition of coherency Eq. (24) in the induced undulator process with Eq. (30) turns to the following relation between the undulator step l and laser wavelength λ:
$$1 - \left( {\displaystyle{{l + {\rm \lambda}} \over l}} \right)\displaystyle{{v_0} \over c}\cos {\rm \vartheta} = s\displaystyle{{{\rm \pi} c\hbar} \over { {\cal E}_0}} \left( {\displaystyle{{2l + {\rm \lambda}} \over {l^2}}} \right),$$
at which the strongly quantum regime of Bragg diffraction in a magnetic undulator/wiggler is established. Electron inelastic diffraction in the magnetic undulator/wiggler takes place on the slowed wave [see Eq. (36)] at the satisfaction of classical condition of coherency that corresponds to the neglect of quantum recoil – the term in the right-hand side of Eq. (31):
$$\displaystyle{{v_0} \over c}\cos {\rm \vartheta} = \displaystyle{l \over {l + {\rm \lambda}}}. $$
Coherent scattering of electron on the moving phase-lattice at the fulfillment of Eq. (32) leads to multiphoton inelastic diffraction effect.
So, s-photons diffraction maxima/minima at the electron inelastic scattering on a slowed traveling EM wave corresponds to s-photons absorption/radiation by a free electron in corresponding coherent process, the multiphoton probability of which is the probability of s-photons diffraction (inelastic) of electron. So, the problem of description of electron inelastic diffraction effect on the moving phase-gratings eventually reduces to determination of the multiphoton probabilities of aforementioned coherent processes.
3.1. Electron effective interaction with slowed traveling wave formed in the field of bichromatic counterpropagating waves
Now let us consider the quantum dynamics of electron coherent interaction with the bichromatic counterpropagating waves (laser beams) in vacuum that is induced Compton process. Within the above justification concerning the electron spin interaction with optical fields in these processes we will start again from the relativistic quantum Eq. (1) (Dirac equation in quadratic form with neglect quantitatively the spin interaction because of its smallness does not mean to neglect the electron spin and for scalar particle use the Klein–Gordon equation). For actual quasimonochromatic laser beams with the vector potentials
$${\bf A}_1 = \left\{ {0,\displaystyle{{cE_1 (t - x/c)} \over {{\rm \omega} _1}} \cos {\rm \omega} _1 \left( {t - x/c} \right),0} \right\},$$
$${\bf A}_2 = \left\{ {0,\displaystyle{{cE_2 (t + x/c)} \over {{\rm \omega} _2}} \cos {\rm \omega} _2 \left( {t + x/c} \right),0} \right\},$$
E 1 (t − x/c), E 2 (t + x/c) are slowly varying amplitudes of electric field strengths of quasimonochromatic laser beams with carrier frequencies ω1 and ω2 propagating along and opposite to the OX-axis, respectively) we look for wave function in the form Eq. (3) and for the function Ψ(x, t) from Eq. (1) in the fields (33) and (34): A = A 1 + A 2 we obtain the following equation (for simplicity hereafter the arguments of slowly varying amplitudes of electric fields E 1 and E 2 will be omitted):
$$\left[ { - \hbar ^2 \displaystyle{{\partial ^2} \over {\partial t^2}} + \hbar ^2 c^2 \displaystyle{{\partial ^2} \over {\partial x^2}} - c^2 {\bf p}_ \bot ^2 - m^2 c^4 - {{\cal W}}_{\rm C} \left( {x,t} \right)} \right]{\rm \psi} (x,t) = 0,$$
where
$$\eqalign{{{\cal W}}_{\rm C} \left( {x,t} \right) = & \displaystyle{1 \over 2}\left( {\displaystyle{{eE_1 c} \over {{\rm \omega} _1}}} \right)^2 + \displaystyle{1 \over 2}\left( {\displaystyle{{eE_2 c} \over {{\rm \omega} _2}}} \right)^2 + \displaystyle{{e^2 E_1 E_2 c^2} \over {{\rm \omega} _1 {\rm \omega} _2}} \cos ({\rm \omega} _1 - {\rm \omega} _2 ) \cr & \quad \left( {t - \displaystyle{{{\rm \omega} _1 + {\rm \omega} _2} \over {{\rm \omega} _1 - {\rm \omega} _2}} \displaystyle{x \over c}} \right) + \displaystyle{{e^2 E_1 E_2 c^2} \over {{\rm \omega} _1 {\rm \omega} _2}} \cos ({\rm \omega} _1 + {\rm \omega} _2 ) \cr & \quad \left( {t - \displaystyle{{{\rm \omega} _1 - {\rm \omega} _2} \over {{\rm \omega} _1 + {\rm \omega} _2}} \displaystyle{x \over c}} \right) + \displaystyle{1 \over 2}\left( {\displaystyle{{eE_1 c} \over {{\rm \omega} _1}}} \right)^2 \cos 2{\rm \omega} _1 \left( {t - \displaystyle{x \over c}} \right) \cr & \quad + \displaystyle{1 \over 2}\left( {\displaystyle{{eE_2 c} \over {{\rm \omega} _2}}} \right)^2 \cos 2{\rm \omega} _2 \left( {t + \displaystyle{x \over c}} \right) \cr & \quad + ecp_y \left[ {\displaystyle{{E_1 c} \over {{\rm \omega} _1}} \cos {\rm \omega} _1 \left( {t - \displaystyle{x \over c}} \right) + \displaystyle{{E_2 c} \over {{\rm \omega} _2}} \cos {\rm \omega} _2 \left( {t + \displaystyle{x \over c}} \right)} \right].} $$
As is seen from Eq. (36), at the interaction with the counterpropagating waves of different frequencies two interference waves are formed – third and fourth terms on the right-hand side – which propagate with the phase velocities
$$v_{{\rm ph}} = c\displaystyle{{{\rm \omega} _1 + {\rm \omega} _2} \over {\left \vert {{\rm \omega} _1 - {\rm \omega} _2} \right \vert}} \gt c$$
and
$$v_{{\rm ph}} = c\displaystyle{{\left \vert {{\rm \omega} _1 - {\rm \omega} _2} \right \vert} \over {{\rm \omega} _1 + {\rm \omega} _2}} \lt c,$$
respectively. It is clear that the interaction of the electron with the wave propagating with the phase velocity v ph > c, as well as with the separate waves propagating in the vacuum with the phase velocity c cannot be coherent. These terms correspond to non-coherent scattering of the particle in the separate wave fields, which vanish after the interaction (in accordance with the violation of mentioned above conservation law of energy–momentum for real radiation–absorption of photons by free electron). Coherent interaction in this process occurs with the slowed interference wave. The first two terms can be cast into the mass term and for the coherent interaction process we obtain the following equation:
$$\eqalign{& \left[ - \hbar ^2 \displaystyle{\partial ^2 \over \partial t^2} + \hbar ^2 c^2 \displaystyle{\partial ^2 \over \partial x^2} - c^2 {\bf p}_ \bot ^2 - m_ {\ast} ^2 c^4 \right. \cr & \quad \left. - \displaystyle{e^2 c^2 E_1 E_2 \over {\rm \omega} _1 {\rm \omega} _2} \cos ({\rm \omega} _1 - {\rm \omega} _2 ) \left(t - \displaystyle{{\rm \omega} _1 + {\rm \omega} _2 \over {\rm \omega} _1 - {\rm \omega} _2} \displaystyle{x \over c} \right) \right]{\rm \psi} (x,t) = 0,}$$
where
$$m_ {\ast} = \sqrt {m^2 + \displaystyle{{e^2} \over {2c^2}} \left( {\displaystyle{{E_1^2} \over {{\rm \omega} _1^2}} + \displaystyle{{E_2^2} \over {{\rm \omega} _2^2}}} \right)} $$
is the effective mass of electron in the bichromatic counterpropagating waves.
3.2. Electron effective interaction with slowed traveling wave formed in undulators
Electron inelastic diffraction effect is also possible on a plane EM wave propagating in electric or magnetic undulator/wiggler Avetissian et al. (Reference Avetissian, Jivanian and Petrossian1981a , Reference Avetissian, Jivanian and Petrossian b ). In such space–time periodic structures like the considered induced Compton process a slowed interference wave is formed on which diffraction scattering of electron occurs by the described scheme, at the intensities below the corresponding critical values of electrons “reflection” or capture by a traveling wave in the electric and magnetic undulators [see Avetissian et al. (Reference Avetissian, Jivanian and Petrossian1978)]. As far as descriptions of electron inelastic diffraction scattering on a plane monochromatic wave in the electric and magnetic undulators are coincide in many features, here we will consider more important case of magnetic undulator/wiggler, which is currently the most perspective coherent tool with extremely large length of coherency, specifically due to which the x-ray free electron laser has been realized in the wiggler.
At the propagation of a plane quasimonochromatic wave of carrier frequency ω and slowly varying amplitude of electric field strength E(t − x/c) (let of linear polarization) in the linear undulator with the magnetic field
$$H_z (x) = H\cos \displaystyle{{2{\rm \pi}} \over l}x$$
the vector potential will be described by the equation
$$A_{2y} (x) = \displaystyle{{lH} \over {2{\rm \pi}}} \sin \displaystyle{{2{\rm \pi}} \over l}x,$$
and correspondingly the EM wave will be assumed linearly polarized along the axis OY
$$A_{1y} (t - x/c) = \displaystyle{{cE(t - x/c)} \over {\rm \omega}} \sin {\rm \omega} (t - x/c).$$
We look for wave function in the form Eq. (3) and for the function Ψ(x, t) from (1) in the fields (42) and (43): A y = A 1y + A 2y we obtain the following equation (hereafter the argument of slowly varying amplitude of the wave electric field E(t − x/c) will be omitted):
$$\left[ { - \hbar ^2 \displaystyle{{\partial ^2} \over {\partial t^2}} + \hbar ^2 c^2 \displaystyle{{\partial ^2} \over {\partial x^2}} - c^2 {\bf p}_ \bot ^2 - m^2 c^4 - {{\cal W}}_{\rm U} \left( {x,t} \right)} \right]{\rm \psi} (x,t) = 0,$$
where
$$\eqalign{{{\cal W}}_{\rm U} \left( {x,t} \right) = & \displaystyle{{e^2 E^2 c^2} \over {2{\rm \omega} ^2}} + \displaystyle{{e^2 l^2 H^2} \over {8{\rm \pi} ^2}} + \displaystyle{{e^2 lHEc} \over {2 {\rm \pi} {\rm \omega}}} \cos {\rm \omega} \left( {t - \left( {1 + \displaystyle{{\rm \lambda} \over l}} \right)\displaystyle{x \over c}} \right) \cr & - \displaystyle{{e^2 lHEc} \over {2 {\rm \pi} {\rm \omega}}} \cos {\rm \omega} \left( {t - \left( {1 - \displaystyle{{\rm \lambda} \over l}} \right)\displaystyle{x \over c}} \right) \cr & - \displaystyle{{e^2 E^2 c^2} \over {2{\rm \omega} ^2}} \cos 2{\rm \omega} \left( {t - \displaystyle{x \over c}} \right) - \displaystyle{{e^2 l^2 H^2} \over {8{\rm \pi} ^2}} \cos \displaystyle{{4{\rm \pi}} \over l}x \cr & + ecp_y \left[ {\displaystyle{{Ec} \over {\rm \omega}} \sin {\rm \omega} \left( {t - \displaystyle{x \over c}} \right) + \displaystyle{{lH} \over {2{\rm \pi}}} \sin \displaystyle{{2{\rm \pi}} \over l}x} \right].}$$
As is seen from Eq. (45), under the induced interaction in the undulator the traveling waves propagating with the phase velocities v ph = c/(1 + λ/l) <c and v ph = c/(1 -λ/l) >c arise. We will not repeat here the analogous interpretation of the terms in Eq. (36) which correspond to interaction of the particle with the waves propagating with the phase velocities v ph ⋝ c that has been done for the above-considered induced Compton process. Note only that coherent interaction in this process occurs with the slowed interference wave propagating with the phase velocity
$$v_{{\rm ph}} = \displaystyle{c \over {1 + {\rm \lambda} /l}} \lt c$$
and for the coherent interaction process we obtain the following equation:
$$\eqalign{& \left[ { - \hbar ^2\displaystyle{{\partial ^2} \over {\partial t^2}} + \hbar ^2c^2\displaystyle{{\partial ^2} \over {\partial x^2}} - c^2{\bf p}_{\bot} ^2 - m_{\ast} ^2 c^4} \right. \cr & \quad \left.{ - \displaystyle{{e^2lHEc} \over {2 {\rm \pi} {\rm \omega} }}\cos {\rm \omega }\left( {t - \left( {1 + \displaystyle{ {\rm \lambda} \over l}} \right)\displaystyle{x \over c}} \right)} \right] {\rm \psi} (x,t) = 0,} $$
where
$$m_{\ast} = \sqrt {m^2 + \displaystyle{{e^2 E^2} \over {2{\rm \omega} ^2 c^2}} + \displaystyle{{e^2 l^2 H^2} \over {8{\rm \pi} ^2 c^4}}} $$
is the effective mass of electron in the plane EM wave propagating in the magnetic undulator/wiggler.
4. QUANTUM DYNAMICS OF ELECTRON IN THE SLOWED TRAVELING WAVE
In this section, we will derive the theory for effective description of electron multiphoton coherent scattering in the induced Cherenkov, Compton, and undulator processes on the base of relativistic quantum equations of motion for unified consideration of diffraction and Bragg regimes on diverse type moving phase-gratings. As is seen from the previous section, electron inelastic diffraction effect on a slowed traveling wave in all three induced coherent processes can be described in the scope of relativistic quantum-mechanical consideration with the help of solution of the following wave equation:
$$\eqalign{&\Bigg[ - \hbar ^2 \displaystyle{{\partial ^2} \over {\partial t^2}} + \hbar ^2 c^2 \displaystyle{{\partial ^2} \over {\partial x^2}} - c^2 {\bf p}_{\bot}^2 - m_{\ast} ^2 c^4 \cr & \quad - {{\cal W}}_{{\rm eff}} \cos k\left( {x - v_{{\rm ph}} t} \right) \Bigg] {\rm \psi} (x,t) = 0,}$$
where k = |k| is the wavevector of the slowed traveling EM wave.
Here for an each concrete process one should specify the main interaction parameters, which is brought in Table 1 in accordance with the results of the previous sections.
Table 1. Main parameters of particle-slowed wave interaction in various coherent processes
The exact investigation of the classical dynamics of considered induced coherent processes Avetissian (Reference Avetissian2006, Reference Avetissian2016) reveals the existence of a critical value for effective interference wave field
${{\cal W}}_{{\rm eff}} $
:
$${\cal W}_{{\rm eff}}^{({\rm cr})} = \displaystyle{{ {\cal E}^2 (v_x - v_{{\rm ph}} )^2} \over {c^2 - v_{{\rm ph}}^2}} $$
that crucially affects on the particle dynamics in the induced Cherenkov, Compton, and undulator processes. If the amplitude of a slowed interference wave
${{\cal W}}_{{\rm eff}} $
exceeds this critical value Eq. (50):
${{\cal W}}_{{\rm eff}} \gt {{\cal W}}_{{\rm ef}f}^{({\rm cr})} $
, a nonlinear threshold phenomenon of particle “reflection” or capture by the slowed traveling wave occurs at which the periodic wave-field in the intrinsic frame of reference of the slowed interference wave becomes a potential barrier for a particle, instead of a standing phase lattice, and reflecting from this barrier electron abandons the wave. Therefore, the considering effect of electron diffraction on a traveling wave propagating with the phase velocity v
ph < c can occur only if
${{\cal W}}_{{\rm eff}} $
is smaller than the corresponding critical value (50).
Now let us proceed to the solution of Eq. (49). According to Floquet's theorem the solution of Eq. (49) may be sought in the form
$${\rm \psi} (x,t) = \sum\limits_s C_s \left( t \right)e^{i/{\hbar} (\,p_x + s{\hbar} k)x} e^{ - i/{\hbar} ( {\cal E} + s{\hbar} k{\rm v}_{{\rm ph}} ){\rm t}}. $$
Here
$ {\cal E} = \sqrt {c^2 {\bf p}^2 + m_{\ast} ^2 c^4} $
and we will assume that C
s
(t) are slowly varying functions:
$$\left \vert {\displaystyle{{\partial C_s} \over {\partial t}}} \right \vert {\rm \ll} \displaystyle{ {\cal E} \over \hbar} \left \vert {C_s} \right \vert, $$
and
${{\cal E} \gg} \left\vert s \right\vert\hbar k{\rm v}_{{\rm ph}} $
(this condition is always satisfied for optical photons). From Eqs (49) and (51) for the coefficients C
s
(t) we obtain the set of equation
$$i\displaystyle{{\partial C_s (t)} \over {\partial t}} + \Gamma _s C_s \left( t \right) = \displaystyle{{{{\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}\left( {C_{s - 1} \left( t \right) + C_{s + 1} \left( t \right)} \right),$$
where
$$\Gamma _s = \displaystyle{{2 {\cal E}s\hbar k(v_{{\rm ph}} - v_x ) + (v_{{\rm ph}}^2 - c^2 )(s\hbar k)^2} \over {2\hbar {\cal E}}}$$
is the resonance width. The wave function (51) at the initial condition
$$C_s \left( 0 \right) = {\rm \delta} _{s,0} $$
describes inelastic scattering of the electron on the slowed traveling wave. The energy and momentum of the electron after the scattering are:
$$\eqalign{& {\cal E}^{\prime} = {\cal E} + s\hbar kv_{{\rm ph}}, \quad p_x^{\prime} = p_x + s\hbar k, \cr & {\bf p}_ \bot = {\rm const};\quad s = 0, \pm 1, \ldots.} $$
The probabilities of these s-photon absorption–radiation processes are:
$$W_s = \left \vert {C_s} \right \vert ^2. $$
We will present the solution of equations Eq. (52) in the two interaction regimes: diffraction and Bragg resonance (see Fig. 1).
Fig. 1. Slowed wave–electron interaction is shown schematically in the frame of reference of the rest of the wave (frame moving with velocity V = v ph). On the left, diffraction regime of interaction is shown. Here we have many symmetric diffraction maxima. On the right, Bragg scattering with two maxima is shown.
4.1. Diffraction regime
For the finite interaction time the interaction energy is uncertain by the quantity
${\rm \delta} {{\cal E} \simeq} \hbar /t_{{\rm int}} $
. The diffraction regime corresponds to the short interaction times and intense wave fields [when the quantum recoil received by electron is neglected in the condition of coherency, see (26), (29), (32)]. Thus, at the fulfillment of the conditions
$${\rm \delta} {{\cal E} \gg} \hbar \left \vert {\Gamma _s} \right \vert ;\displaystyle{{{{\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}{\rm \gg} \left \vert {\Gamma _s} \right \vert, $$
one can neglect the term ~ Γ s C s (t) in Eq. (52) and the electron dynamics will be described by the following equation:
$$i\displaystyle{{\partial C_s (t)} \over {\partial t}} = \displaystyle{{{{\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}\left( {C_{s - 1} \left( t \right) + C_{s + 1} \left( t \right)} \right).$$
For the initial condition (54) taking into account recurrent relation of Bessel functions J s (x):
$$2\displaystyle{{dJ_s (x)} \over {dx}} = J_{s - 1} \left( x \right) - J_{s + 1} \left( x \right),$$
one can obtain the following solution:
$$C_s \left( t \right) = J_s \left( {\displaystyle{1 \over {2\hbar {\cal E}}}\int_0^{\rm t} {{\cal W}}_{{\rm eff}} dt^{\prime}} \right)e^{ - is({\rm \pi} /2)}. $$
Hence, the probability of this process is given by the formula:
$$W_s = J_s^2 \left[ {\displaystyle{1 \over {2\hbar {\cal E}}}\int_0^t {{\cal W}}_{{\rm eff}} dt^{\prime}} \right].$$
In the case of a monochromatic wave from Eq. (61), we have
$$W_s = J_s^2 \left( {\displaystyle{{{{\cal W}}_{{\rm eff}} t_{{\rm int}}} \over {2\hbar {\cal E}}}} \right),$$
where t
int is the time duration of the particle motion in the wave. As is seen from Eq. (62), in the diffraction regime the symmetric diffraction picture (
$J_s^2 = J_{ - s}^2 $
) into many momentum states is possible (see Fig. 1). The process dynamics is defined by the argument of the Bessel function
${\rm \alpha} = {{\cal W}}_{{\rm eff}}$
$t_{{\rm int}} /(2\hbar {\cal E})$
. For
${\rm \alpha} {\rm \mathbin{\lower.3ex\hbox{$\buildrel\prec\over {\smash{\scriptstyle\sim}\vphantom{_x}}$}}} 1$
only few diffraction maxima are possible, which is shown in Figure 2. For the values α > 1, the process is essentially multiphoton. The most probable number of absorbed/emitted Cherenkov photons is
$$\bar s\,{\rm \simeq}\, {\rm \alpha}. $$
Fig. 2. Diffraction of electron at
${{\cal W}}_{{\rm eff}} t_{{\rm int}} /2{\hbar} {\cal E} = 1$
in the rest frame of reference connected with the wave.
The width of the main diffraction maxima:
$\Delta (\bar s){\rm \simeq} \bar s^{1/3} \hbar k$
, and since
$\bar s{\rm \gg} 1$
then
$\Delta (\bar s){\rm \ll} \vert p_x^{\prime} - p_x \vert$
. The typical scattering picture is shown in Figure 3.
Fig. 3. Diffraction of electron at
${{\cal W}}_{{\rm eff}} t_{{\rm int}} /2{\hbar} {\cal E} = 50$
in the rest frame of reference connected with the wave.
For the concreteness let us explicitly write probability for the Cherenkov diffraction on a slowed wave in a dielectric medium and electron inelastic Kapitza–Dirac effect on the bichromatic counterpropagating waves. For the Cherenkov diffraction effect on a strong traveling wave from Eq. (62) and Table 1, we have the formula (14) already presented in Section 2:
$$W_s^{({\rm Cherenkov})} = J_s^2 \left( {{\rm \xi} \displaystyle{{mc^2} \over \hbar} \displaystyle{{cp\sin {\rm \vartheta} _{{\rm ch}}} \over {\cal E}}t_{{\rm int}}} \right),$$
which has been obtained by the author of this article in 1976 (Avetissian, Reference Avetissian1976).
For the Kapitza–Dirac effect, which is the particular case of induced Compton effect on the bichromatic counterpropagating waves at ω1 = ω2 ≡ ω, E 1 = E 2 = E 0, from Table 1 and Eqs (51) and (62) we can write:
$$\eqalign{{\rm \Psi} & = e^{{ - (i/\hbar)} {\cal E}t} e^{{ (i/\hbar)}{\bf p}_ \bot {\bf r}} \sum\limits_s e^{ - is({\rm \pi} /2)} J_s \left( {\displaystyle{{e^2 c^2 E_0^2 t_{{\rm int}}} \over {2 {\cal E}\hbar {\rm \omega} ^2}}} \right)\cr & \quad \times e^{{(i/\hbar)} (\,p_x + 2s{\hbar} ({\rm \omega} /c))x}. }$$
Hence, the probability of s-photons Kapitza–Dirac diffraction effect on the strong standing EM wave is determined by the formula:
$$W_s^{({\rm Kapitza - Dirac})} = J_s^2 \left( {\displaystyle{{e^2 c^2 E_0^2 t_{{\rm int}}} \over {2 {\cal E}\hbar {\rm \omega} ^2}}} \right).$$
Note that formula (65) for the nonrelativistic case
${{\cal E} \simeq} mc^2 $
coincides with analogous formula (7) of the paper Batelaan (Reference Batelaan2007) up to a factor of 1 = 2 [in the paper Batelaan (Reference Batelaan2007)] the factor 1/2 has been missed perhaps at the transformation of recurrent relation of Bessel functions J
s
(x) (59).
4.2. Bragg regime of exact quantum resonance
For the diffraction effect with sufficiently long interaction time one can fulfill resonance conditions with quantum recoil in each concrete process Eq. (24), Eq. (28), Eq. (31) for the concrete s
0:
$\Gamma _{s_0} = 0$
. The latter can be written as:
$$v_{{\rm ph}} - v_x = \left( {c^2 - v_{{\rm ph}}^2} \right)\displaystyle{{s_0 \hbar k} \over {2 {\cal E}}}.$$
The condition (66) has transparent physical in p′ x terpretation in the intrinsic frame of reference of the slowed wave. In this frame, due to the conservation of electron energy and transverse momentum the real transitions in this strongly quantum regime occur from a state to the − p′ x one and we reach the Bragg diffraction effect on a slowed traveling wave at the fulfillment of the condition:
$$2p_x^{\prime} = - s_0 \hbar k^{\prime} \quad \quad (s_0 = \pm 1; \pm 2 \ldots ).$$
The latter expresses the condition of exact resonance between the electron de Broglie wave and the “wave motionless lattice”. In particular, in this case when the above-mentioned particle capture regime by the slowed traveling wave (Haroutunian & Avetissian, Reference Haroutunian and Avetissian1972) takes place, we have the quantum effect of zone structure of particle states like the particle states in a crystal lattice, and at the condition (66) the diffraction maxima take place; see Figure 1. For acquaintance in detail with the different regimes of electron diffraction on a slowed traveling wave in a dielectric medium we refer the reader to the works Avetissian et al. (Reference Avetissian, Bagdasarian, Hatsagortsian and Mkrtchian1998a , Reference Avetissian, Bagdasarian, Hatsagortsian and Mkrtchian b , Reference Avetissian, Bagdasarian and Mkrtchian c ; Avetissian & Mkrtchian, Reference Avetissian and Mkrtchian2001) [regarding the Bragg diffraction effect see, also the paper Freimund and Batelaan (Reference Freimund and Batelaan2002)]. Here we just write the solution for the resonant case Γ1 = 0. At the condition
$${\rm \delta} {{\cal E} }\ll \hbar \left \vert {\Gamma _s} \right \vert, \displaystyle{{{{\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}{\rm \ll} \left \vert {\Gamma _s} \right \vert ;s \ne 0,1$$
from the set of equations (52) one can keep only resonant terms:
$$i\displaystyle{{\partial C_0 (t)} \over {\partial t}} = \displaystyle{{{ {\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}C_1 \left( t \right),$$
$$i\displaystyle{{\partial C_1 (t)} \over {\partial t}} = \displaystyle{{{ {\cal W}}_{{\rm eff}}} \over {4\hbar {\cal E}}}C_0 \left( t \right),$$
with the solution
$$\displaylines{C_0 \left( t \right) = \cos \left( {\displaystyle{1 \over {4\hbar {\cal E}}}\int_0^t {{\cal W}}_{{\rm eff}} dt^{\prime}} \right), \cr C_1 \left( t \right) = - i\sin \left( {\displaystyle{1 \over {4\hbar {\cal E}}}\int_0^t {{\cal W}}_{{\rm eff}} dt^{\prime}} \right).}$$
For the concreteness let us explicitly write probability for Kapitza–Dirac effect: ω1 = ω2 ≡ ω, E
1 = E
2 = E
0, vph = 0, k = 2ω/c). From Eq. (66) at s
0 = 1 we obtain resonant initial momentum
$p_x = - \hbar {\rm \omega} /c$
and electron wave function can be written as:
$$\Psi = e^{(i/{\hbar} ){\bf p}_ \bot {\bf r} - (i/{\hbar} ) {\cal E}t} \left[ {C_0 \left( t \right)e^{ - i({\rm \omega} /c)x} + C_1 \left( t \right)e^{i({\rm \omega} /c)x}} \right]$$
with the probabilities
$$\eqalign{& W_0 = \mathop {\cos} \nolimits^2 \left( {\displaystyle{{e^2 c^2 E_0^2 t_{{\rm int}}} \over {4 {\cal E}\hbar {\rm \omega} ^2}}} \right), \cr & W_1 = \mathop {\sin} \nolimits^2 \left( {\displaystyle{{e^2 c^2 E_0^2 t_{{\rm int}}} \over {4 {\cal E}\hbar {\rm \omega} ^2}}} \right).} $$
For the non-relativistic case
${{\cal E} \simeq} mc^2 $
Eq. (73) coincide with the results in Batelaan (Reference Batelaan2007). For comparison with Figure 3, in Figure 4, we illustrate the probabilities of diffraction in the Bragg regime.
Fig. 4. Bragg scattering with two maxima is shown at
${{\cal W}}_{{\rm eff}} t_{{\rm int}} /4{\hbar} {\cal E} = 1$
in the rest frame of reference connected with the wave.
5. CONCLUSION
With the successful implementation by Freimund et al. (Reference Freimund, Aflatooni and Batelaan2001) of the Kapitza–Dirac effect on high-intensity counterpropagating laser beams – standing phase-grating in 2001, after about 70 years since the prediction of this effect, the interest to this phenomenon has been increased by several important reasons. Note only two – fundamental and applied aspects of significance of the Kapitza–Dirac effect: this is a best example for demonstration of matter wave diffracted by light, especially, with reversed properties of the matter–light in quantum mechanics, and important applications connected with acquirement of coherent electron beams diffracted from laser gratings for construction of new important tools of diverse species, for example, coherent beam splitters, new type electron interferometers, which would operate at rather low electron energies than existing ones in atomic physics, etc. There was another motivation as well to discuss the main works regarding the elastic and inelastic diffraction of electron matter wave on the standing and moving light gratings because of confusion arisen in literature on this subject after appearance recently of a paper in New Journal of Physics (Hayrapetyan et al., Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) that required to clarify the state-of-the-art on the considering subject for last four decades in chronological order, to avoid the further confusions and misunderstandings in scientific literature.
In this review paper, we have represented comprehensive consideration of elastic and inelastic diffraction effects of electron on the standing and slowed traveling waves in the induced Cherenkov, Compton, and undulator/wiggler processes with the non-linear peculiarity of threshold nature – inherent to these coherent processes (a periodic wave above a certain intensity becomes a potential barrier for electron from which it is reflected) that may radically affect on the diffraction effect. It has been shown that to remove this negative factor for diffraction effect one should restrict waves’ intensities by critical values for an each induced process.
We have also considered the strongly quantum regime of Bragg diffraction – at the exact quantum resonance between the electron matter wave and light gratings taking also into account the quantum recoil of electron because of photons absorption–radiation.
We have specifically considered in detail electron diffraction effect on a traveling wave in a dielectric medium (“Cherenkov diffraction”) and have shown that the result of the paper and claim of the authors in the Abstract (Hayrapetyan et al., Reference Hayrapetyan, Grigoryan, Götte and Petrosyan2015) published in 2015 in New Journal of Physics is a direct repeat of the original paper Avetissian (Reference Avetissian1976) published in 1976 in “Physics Letters”.
Acknowledgment
This work was supported by the RA MES State Committee of Science.
