1. INTRODUCTION
Acceleration of electrons by laser Wakefield (Tajima & Dawson, Reference Tajima and Dawson1979) has been one of the most developed areas of interest during the past 20 years, leading to a number of theoretical and experimental efforts. In a laser Wakefield accelerator (LWFA), a high intensity laser pulse with duration approximately equal to plasma oscillation period, generates a large amplitude plasma wave with phase velocity that is close to the speed of light. A beam of electrons interacting with this wave can be effectively accelerated. The pioneering idea of Tajima and Dawson, has been theoretically explored and experimentally verified (Andreev et al., Reference Andreev, Gorbunov, Kirsonov and Pegosova1994; Balakirev et al., Reference Balakirev, Karas and Levchenko2001; Blumenfeld et al., Reference Blumenfeld, Clayton, Decker, Hogan, Huang, Ischebeck, Iverson, Joshi, Katsouleas, Kirby, Lu, Marsh, Mori, Muggli, Oz, Siemann, Walz and Zhou2007; Faure et al., Reference Faure, Glinec, Pukhov, Kiselev, Gordienko, Lefebvre, Rousseau, Burgy and Malka2004; Geddes et al., Reference Geddes, Toth, Tilborg, Esarey, Schroeder, Bruhwiler, Nieter, Cary and Leemans2004; Gorbunov et al., Reference Gorbunov, Mora and Solodov2003; Jha et al., Reference Jha, Kumar, Upadhyaya and Raj2005; Joshi, Reference Joshi2007; Kawata et al., Reference Kawata, Kong, Miyazaki, Miyauchi, Sonobe, Sakai, Nakashima, Masuda, Ho, Miyanakga, Limpouch and Andreev2005; Koyama et al., Reference Koyama, Adachi, Miura, Kato, Masuda, Watanabe, Ogata and Tanimoto2006; Leemans et al., Reference Leemans, Nager, Gonsalves, Toth, Nakamura, Geddes, Esarey, Schroeder and Hooker2006; Lifshitz et al., Reference Lifshitz, Faure, Glinec, Malka and Mora2006; Lourenco et al., Reference Lourenco, Nicolas, Werner and Wang2010; Lotov, Reference Lotov2001; Luttikhof et al., Reference Luttikhof, Khachatryan, Van Goor, Boller and Mora2009; Malka & Fritzler, Reference Malka and Fritzler2004; Malka et al., Reference Malka, Fritzler, Lefebvre, Aleonard, Burgy, Chambaret, Chemin, Krushelnick, Malka, Mangles, Najmudin, Pittman, Rousseau, Scheurer, Walton and Dangor2002; Mangles et al., 2004; Marques et al., Reference Marques, Geindre, Amiranoff, Audebert, Gauthier, Antonetti and Grillon1996; Masuda & Miura, Reference Masuda and Miura2009; Maltis et al., Reference Maltis, Reed, Bulanov, Chvykov, Kalintchenko, Matsuoka, Rousseau, Yanovsky, Maksimchuk, Kalmykov, Shvets and Downer2006; Phuoc et al., 2008; Pukhov & Meyer-ter-Vehn, Reference Pukhov and Meyer-Ter-Vehn2002; Schlenvoigt, 2008; Siders et al., Reference Siders, Le Blane, Fisher, Tajima, Downer, Babine, Stepanov and Sergreev1996; Takahashi et al., Reference Takahashi, Honda, Miura, Yugami, Nishida, Katsura and Kondo2004; Wang et al., Reference Wang, Sheng and Zhang2009; Xie et al., Reference Xie, Aimidula, Niu, Liu and Yu2009; Zhou et al., Reference Zhou, Yu and He2007).
Recently, studies concerning high-density plasmas (quantum plasma) that are created by high intensity laser pulses have received attention and pertinent research activities have been observed. Quantum affects appear in ultra-small electronic devices (Markowich et al., Reference Markowich, Ringhofer and Schmeiser1990), dense astrophysical plasmas (Jung, Reference Jung2001), and laser plasmas (Kremp et al., Reference Kremp, Bornath, Bonitz and Schlanges1999). The high-density, low-temperature quantum Fermi plasma is significantly different from the low-density, high temperature “classical plasma” obeying the Maxwell-Boltzmann distribution. In the dense Fermi plasma, the electron degeneracy leads to a consideration of the Fermi-Dirac electron distribution and electron tunneling through the quantum Bohm potential (Gardner & Ringhofer, Reference Gardner and Ringhofer1996; Manfredi, Reference Manfredi2005). The quantum statistical pressure and the quantum Bohm force affect the electron dynamics that results in collective interactions in dense quantum plasmas. The studies regarding Wakefield generation in quantum plasmas have been recently reported (Shukla et al., Reference Shukla, Brodin, Marklund and Stenflo2009).
In this work, we have carried out a detailed analytical study of plasma Wakefield generation in quantum plasma. We have used perturbative technique involving orders of the incident laser beam to obtain explicit electric and magnetic Wakefields. Further, the accelerating force acting on a test electron has been evaluated. The results show that the accelerating force is increased due to the collective contributions of statistical pressure and the quantum Bohm force. Such a study has not been reported in literature before.
In Section 2, the lowest order fast oscillating plasma electron velocities and density perturbations have been derived. Coupling the time averaged current densities with Maxwell's equations, the generated electric and magnetic Wakefields have been obtained in Section 3. In Section 4, the axial and radial forces acting on a moving test electron have been derived and analyzed graphically. Section 5 is devoted to summary and discussion.
2. LASER-PLASMA INTERACTION
We consider the propagation of linearly polarized laser beam represented by the electric vector ![]() (êx is the unit vector of polarization) propagating in an uniform quantum plasma of density n o. In quantum plasma, the electrons obey the equations
(êx is the unit vector of polarization) propagating in an uniform quantum plasma of density n o. In quantum plasma, the electrons obey the equations
![\eqalign{\displaystyle{{\partial \vec v} \over {\partial t}}&=- \displaystyle{e \over m}\left[\vec E+\displaystyle{1 \over c}\lpar \vec v \times \vec B\rpar \right]- \displaystyle{1 \over 2}\vec \nabla \lpar \vec v.\vec v\rpar +\vec v \times \lpar \vec \nabla \times \vec v\rpar \cr &\quad - \displaystyle{{v_F^2 } \over {3n_o^2 }}\displaystyle{{\vec \nabla n^3 } \over n}+\displaystyle{{\hbar ^2 } \over {2m^2 }}\vec \nabla \left(\displaystyle{1 \over {\sqrt n }}\vec \nabla ^2 \sqrt n \right)\comma \; }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn1.gif?pub-status=live)
and
![]() is the electron density, m is the electron rest mass, ħ is the Planck's constant divided by 2π, and v F is the Fermi velocity. The fourth term on the right-hand side of Eq. (1) denotes the Fermi electron pressure. The fifth term is the quantum Bohm potential and is due to the quantum corrections in the density fluctuation. The classical equations may be recovered in the limit of ħ = 0. The ponderomotive force of the high-frequency laser pulse drives longitudinal waves with a frequency much smaller than ω, but fast enough for the dynamics to take place on the electron timescale. The ions form a neutralizing background in dense plasma. A correct relativistic treatment of quantum effects should rely on the moments of a relativistic Wigner function (Bialynicki et al., Reference Bialynicki-Birula, Gornicki and Rafelski1991; Shin, Reference Shin1996). Perturbatively, expanding Eqs. (1) and (2) for the first order of the electromagnetic field, we get
is the electron density, m is the electron rest mass, ħ is the Planck's constant divided by 2π, and v F is the Fermi velocity. The fourth term on the right-hand side of Eq. (1) denotes the Fermi electron pressure. The fifth term is the quantum Bohm potential and is due to the quantum corrections in the density fluctuation. The classical equations may be recovered in the limit of ħ = 0. The ponderomotive force of the high-frequency laser pulse drives longitudinal waves with a frequency much smaller than ω, but fast enough for the dynamics to take place on the electron timescale. The ions form a neutralizing background in dense plasma. A correct relativistic treatment of quantum effects should rely on the moments of a relativistic Wigner function (Bialynicki et al., Reference Bialynicki-Birula, Gornicki and Rafelski1991; Shin, Reference Shin1996). Perturbatively, expanding Eqs. (1) and (2) for the first order of the electromagnetic field, we get
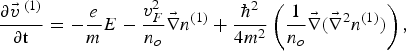
and
The last term in Eq. (4) has been obtained by using the perturbative expansion (Cao et al., Reference Cao, Ren, Wu and Chu2008),
![\eqalign{\vec{\nabla} \left( {1 \over \sqrt{n}} \vec{\nabla}^2 \sqrt{n} \right) &= {1 \over n} \left[{1 \over 2} \vec{\nabla} \vec{\nabla}^2 n^{\lpar 1\rpar}- {1 \over 2n_o} \vec{\nabla} n^{\lpar 1\rpar} \vec{\nabla}^2 n_o \right. \cr &\quad - {1 \over 2n_o} \vec{\nabla} n_o \vec{\nabla}^2 n^{\lpar 1\rpar }+\displaystyle{{n^{\lpar 1\rpar } } \over {2n_o^2 }}\vec \nabla n_o \vec \nabla ^2 n_o \cr &\quad - {1 \over 4n_o} \vec{\nabla} \lpar 2 \vec{\nabla} n_o .\vec{\nabla} n^{\lpar 1\rpar} \rpar + {1 \over 4n_o^2} n^{\lpar 1\rpar} \vec{\nabla} \lpar \vec{\nabla} n_o \rpar ^2\cr &\quad + {1 \over 2n_o^2} \lpar \vec{\nabla} n_o \rpar^2 \vec{\nabla} n^{\lpar 1\rpar } + {1 \over n_o^2} \lpar \vec{\nabla} n_o . \vec{\nabla} n^{\lpar 1\rpar} \rpar \vec{\nabla} n_o \cr &\left. \quad - {1 \over n_o^3}\lpar \vec{\nabla} n_o \rpar ^2 n^{\lpar 1\rpar } \vec \nabla n_o \right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU1.gif?pub-status=live)
Assuming the perturbed density to vary according to (Bret, Reference Bret2007) n (1) = ηexpi(kr − ωt), we get from Eqs.(3), (4), and (5),
where ![]() . High frequency laser pulse propagating in collisionless quantum plasma provides a periodic force due to which the plasma electrons oscillate with the frequency of the laser. This high frequency fluctuation in charge density becomes source of a longitudinal electric field and velocity in quantum plasma, which are given by
. High frequency laser pulse propagating in collisionless quantum plasma provides a periodic force due to which the plasma electrons oscillate with the frequency of the laser. This high frequency fluctuation in charge density becomes source of a longitudinal electric field and velocity in quantum plasma, which are given by
and
respectively, where ![]() (the electron plasma frequency),
(the electron plasma frequency), ![]() and
and ![]() .
.
3. WAKEFIELDS
To proceed with the study of excitation of plasma waves, we use the quasistatic approximation where the plasma fluid equations are written in terms of independent variables ξ = z − ct and τ = t. It is assumed that the laser does not evolve significantly as it transits a plasma electron (Esarey et al., Reference Esarey, Sprangle, Krall and Ting1997). Thus, plasma electrons experience a laser field that is a function of ξ and r variables only. Electric and magnetic Wakefields can be obtained using the time dependent Maxwell's equations
The radial profile of the laser field is Gaussian and the generated fields are assumed to be axisymmetric. The field components may be written as,
where J r and J z are transverse and axial current densities, respectively. In order to obtain the second order slow components of the plasma electron velocity, we substitute the first order quantities into the force equation, which gives
and
where, ![]() ; E r and E z represents the radial and axial electric Wakefields. The above equations have been obtained by substituting the value of v z(1) averaged over the polar angle θ. It is observable that the ponderomotive nonlinear effects contribute to transverse as well as longitudinal Wakefield generation. The ponderomotive force is modified due to the contribution of first order longitudinal velocity of plasma electrons. Further, the quantum effects appear significantly in both transverse and longitudinal velocities. From Eqs. (6) and (7), we get
; E r and E z represents the radial and axial electric Wakefields. The above equations have been obtained by substituting the value of v z(1) averaged over the polar angle θ. It is observable that the ponderomotive nonlinear effects contribute to transverse as well as longitudinal Wakefield generation. The ponderomotive force is modified due to the contribution of first order longitudinal velocity of plasma electrons. Further, the quantum effects appear significantly in both transverse and longitudinal velocities. From Eqs. (6) and (7), we get
![\left[\displaystyle{{\partial ^2 } \over {\partial {\rm \xi} ^2 }}+k_p^2 \right]E_z=- \displaystyle{{k_p^2 mc^2 \Omega ^2 \Omega _p^2 } \over {4e}}\displaystyle{{\partial a^2 } \over {\partial {\rm \xi} }} - \displaystyle{\partial \over {\partial {\rm \xi} }}\left(\displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\lpar rB_{\rm \theta} \rpar \right)\comma \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn9.gif?pub-status=live)
where
![k_p^2=k_{\,po}^2 \left[1+\displaystyle{{n^{\lpar 1\rpar } } \over {n_o }}\right].](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU7.gif?pub-status=live)
Combining Eqs. (6a) and (6b) and substituting in Eq. (8) gives

Eqs. (9) and (10) are the principal equations for generation of axial and transverse electric Wakefields in a dense quantum plasma. The magnetic Wakefields can be obtained from Eq. (6a). The radial dependence of transverse electric and magnetic Wakefields can be considered to be a higher order effect. The lowest order axial Wakefield is given as
![\left[\displaystyle{{\partial ^2 } \over {\partial {\rm \xi} ^2 }}+k_{\,po}^2 \right]E_z^{\lpar 0\rpar }=- \displaystyle{{k_{\,po}^2 mc^2 \Omega ^2 \Omega _p^2 } \over {4e}}\displaystyle{{\partial a^2 } \over {\partial {\rm \xi} }}.](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU8.gif?pub-status=live)
Considering a laser pulse ![]() , where a r2 = a o2 exp(−2r 2/r o2), the solution of the above equation, within the pulse (0 ≤ ξ ≤ L) and behind the pulse (ξ < 0) are,
, where a r2 = a o2 exp(−2r 2/r o2), the solution of the above equation, within the pulse (0 ≤ ξ ≤ L) and behind the pulse (ξ < 0) are,
![E_z^{\lpar 0\rpar }=\displaystyle{{{\rm \varepsilon} \Omega ^2 \Omega _p^2\, k_{\,po} \hskip 1pt f} \over 8}\left[\sin k_{\,po} \lpar L - {\rm \xi} \rpar +\displaystyle{{k_{\,po} L} \over {2{\rm \pi} }}.\sin \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}\right]\comma \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn11a.gif?pub-status=live)
and
where

Similarly, from Eq. (10) the lowest order transverse Wakefields within (0 ≤ ξ ≤ L) and behind (ξ < 0) the pulse are
![\eqalign{E_r^{\lpar 0\rpar }&=- \displaystyle{{{\rm \varepsilon} r} \over {2r_o^2 }}\left[\Omega ^2 \Omega _p^2 \hskip 1.5pt f\cos k_{\,po} \lpar L - {\rm \xi} \rpar \right. \cr &\left. \quad+\ \lpar \Omega _s^2 - \Omega ^2 \Omega _p^2 \hskip 1.5pt f\rpar \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L} - \Omega _s^2 \right]\comma \;}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn12a.gif?pub-status=live)
![\eqalign{E_r^{\lpar 0\rpar }&=- \displaystyle{{{\rm \varepsilon} r} \over {2r_o^2 }}\left[\Omega ^2 \Omega _p^2 \Big\{ f\cos k_{\,po} \lpar L - {\rm \xi} \rpar \right. \cr &\left. \quad - \,f\cos k_{\,po} {\rm \xi} \Big\} +\Omega _s^2 \left( \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L} - 1\right) \right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn12b.gif?pub-status=live)
The lowest order magnetic field, within (0 ≤ ξ ≤ L) and behind (ξ < 0) the pulse is obtained by substituting the value axial and transverse electric Wakefield from Eqs. (11) and Eq. (12) in Eq. (6a). The magnetic field within the pulse is B θ(0) = 0, while the magnetic field behind the pulse is
![\eqalign{B_{\rm \theta} ^{\lpar 0\rpar }&=- \displaystyle{{{\rm \varepsilon} r} \over {2r_o^2 }}\left[\Omega _s^2 \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}\right. \cr &\left. \quad \;- \, f\cos k_{\,po} {\rm \xi}+\Omega ^2 \Omega _p^2 \,f\cos k_{\,po} {\rm \xi} - \Omega _s^2+f\lpar 1 - \Omega ^2 \Omega _p^2 \rpar \right].}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn12c.gif?pub-status=live)
It is evident that the above field is zero for on-axis (r = 0) propagation.
On further perturbative expansion of Eq. (9), the equation for first order axial Wakefield comes out to be,
![\eqalign{\left[\displaystyle{{\partial ^2 } \over {\partial {\rm \xi} ^2 }}+k_{\,po}^2 \right]E_z^{\lpar 1\rpar }&=\Omega _k k_{\,po} E_z^{\lpar 0\rpar }+\displaystyle{{k_{\,po}^{} mc^2 \Omega ^2 \Omega _p^2 \Omega _k } \over {4e}}\cr &\quad a_r^2 \displaystyle{{\rm \pi} \over L}\sin \displaystyle{{2{\rm \pi} {\rm \xi} } \over L} - \displaystyle{\partial \over {\partial {\rm \xi} }}\left(\displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\lpar rB_{\rm \theta} ^{\lpar 0\rpar } \rpar \right)}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU10.gif?pub-status=live)
where, ![]() . In solving the above equation, the first order axial fields within and behind the pulse are found to be
. In solving the above equation, the first order axial fields within and behind the pulse are found to be
![\eqalign{E_z^{\lpar 1\rpar }&=- \displaystyle{{\Omega _k \Omega ^2 \Omega _p^2 {\rm \varepsilon} f} \over 8}\left[\displaystyle{{k_{\,po} } \over 2}\lpar L - {\rm \xi} \rpar \cos k_{\,po} \lpar L - {\rm \xi} \rpar \right. \cr &\left. \quad +\left(\,f - \displaystyle{1 \over 2}\right)\sin k_{\,po} \lpar L - {\rm \xi} \rpar +\displaystyle{{\,fk_{\,po} L} \over {2{\rm \pi} }}\sin \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}\right]}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn13a.gif?pub-status=live)
and
![\eqalign{E_z^{\lpar 1\rpar} &= {\rm \varepsilon} f \left[{\Omega_k \Omega^2 \Omega _p^2 \over 16} \sin k_{\,po} L\cos k_{\,po} {\rm \xi} \right. \cr & \quad \left. - {\Omega_k \Omega^2 \Omega_p^2 Lk_{\,po} \over 16} \cos k_{\,po} \lpar L - {\rm \xi} \rpar \right. \cr &\left. \quad + \left\{{\Omega_k \Omega^2 \Omega_p^2 Lk_{\,po} \over 16} - {1 \over 2r_o^2} \left( 1 - {2r^2 \over r_o^2} \right) \lpar \Omega^2 \Omega_p^2 - 1\rpar L \right\} \right. \cr &\left. \quad \cos k_{\,po} {\rm \xi} + \left\{- {5\Omega_k \Omega^2 \Omega_p^2 \over 32} +{1 \over 4k_{\,po} r_o^2} \left(1 - {2r^2 \over r_o^2} \right) \right. \right. \cr &\left. \left. \quad \lpar \Omega^2 \Omega_p^2 - 1\rpar + {\Omega_s^2 \over k_{\,po} r_o^2} \left(1 - {2r^2 \over r_o^2} \right) \right\} \sin k_{\,po} {\rm \xi} \right. \cr &\quad \left. + \left\{- {\Omega_k \Omega^2 \Omega_p^2 \over 32} + {1 \over 4k_{\,po} r_o^2} \left(1 - {2r^2 \over r_o^2} \right) \lpar \Omega^2 \Omega_p^2 - 1\rpar \right\} \right. \cr &\left. \quad \sin k_{\,po} \lpar 2L - {\rm \xi} \rpar + \left\{- {\Omega_k \Omega^2 \Omega_p^2 \over 8} + {\Omega_s^2 \over k_{\,po} r_o^2} \left(1 - {2r^2 \over r_o^2} \right) \right\} \right. \cr &\quad \sin k_{\,po} \lpar L - {\rm \xi} \rpar \bigg]\comma}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn13b.gif?pub-status=live)
respectively. The first order transverse electric Wakefields within and at the back of the pulse are obtained by substituting Eq. (13) into Eq. (10) as
![\eqalign {E_r^{\lpar 1\rpar }&=- \displaystyle{{{\rm \varepsilon} r\Omega ^2 \Omega _p^2 \Omega _k f} \over {2r_o^2\, k_{\,po}^2 }}\left[\displaystyle{{k_{\,po}^2 } \over 2}\lpar L - {\rm \xi} \rpar \sin k_{\,po} \lpar L - {\rm \xi} \rpar \right. \cr &\left. \quad \;- fk_{\,po} \cos k_{\,po} \lpar L - {\rm \xi} \rpar +fk_{\,po} \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}\right]\comma} \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqn14a.gif?pub-status=live)
and
![\eqalign {E_r^{\lpar 1\rpar } &=\displaystyle{{{\rm \varepsilon} fr} \over {r_o^2 }}\left[- \displaystyle{{\Omega _k \Omega ^2 \Omega _p^2 } \over {4k_{\,po} }} \sin k_{\,po} L \sin k_{\,po} {\rm \xi} - \displaystyle{{\Omega _k \Omega ^2 \Omega _p^2\, L_{} } \over 4}\right. \cr&\left. \quad \sin k_{\,po} \lpar L - {\rm \xi} \rpar +\left\{- \displaystyle{{\Omega _k \Omega ^2 \Omega _p^2\, L} \over 4}\right. \right. \cr&\left. \left. \quad +\displaystyle{1 \over {k_{\,po} r_o^2 }}\left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\lpar \Omega ^2 \Omega _p^2 - 1\rpar L\right\}\right. \cr &\left. \quad \sin k_{\,po} {\rm \xi} \rcub +\displaystyle{1 \over {k_{\,po} }}\left\{- \displaystyle{{5\Omega _k \Omega ^2 \Omega _p^2 } \over 8}+\displaystyle{{8\Omega _s^2 } \over {k_{\,po} r_o^2 }}\left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\right.\right. \cr &\left. \left.\quad +\displaystyle{{\lpar \Omega ^2 \Omega _p^2 - 1\rpar } \over {k_{\,po} }}\displaystyle{2 \over {r_o^2 }}\left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\right\}\cos k_{\,po} {\rm \xi} \right. \cr &\left.\quad +\left\{\displaystyle{{\Omega _k \Omega ^2 \Omega _p^2 } \over {8k_{\,po} }} - \displaystyle{1 \over {k_{\,po}^2 }}\displaystyle{2 \over {r_o^2 }}\left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\lpar \Omega ^2 \Omega _p^2 - 1\rpar \right\}\right. \cr &\left. \quad \cos k_{\,po} \lpar 2L - {\rm \xi} \rpar - \displaystyle{1 \over {k_{\,po} }}\left\{- \displaystyle{{\Omega _k \Omega ^2 \Omega _p^2 } \over 2}\right. \quad +\displaystyle{{8\Omega _s^2 } \over {k_{\,po} r_o^2 }}\left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\right\} \cr &\quad \cos k_{\,po} \lpar L - {\rm \xi} \rpar \bigg]\comma} \;](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary-alt:20160626081527-43507-mediumThumb-S026303461200002X_eqn14b.jpg?pub-status=live)
respectively. Substitution of Eqs. (13) and (14) into Eq. (6a) give the first order magnetic Wakefields within and behind the pulse.

and

The higher order (second and higher) Wakefields can be obtained similarly. It is evident that all the Wakefields are proportional to the intensity of the laser pulse.
4. ELECTRON ACCELERATION
The maximum axial Wakefields within and behind the pulse are obtained using Eqs. (11) and (13) evaluated in the limit L → λ p as
![\eqalign{E_{zm} & = E_{zm}^{\lpar 0 \rpar} + E_{zm}^{\lpar 1\rpar} = - {{\rm \varepsilon} \Omega^2 \Omega_p^2 {\rm \pi}^2 \over 4L} \left[\left(1 - {{\rm \xi} \over L} \right) \cos {2{\rm \pi} {\rm \xi} \over L} \right.\cr &\left. \quad +{1 \over 2{\rm \pi}} \sin {2{\rm \pi} {\rm \xi} \over L} \right]+ {{\rm \varepsilon} \Omega_k \Omega^2 \Omega_p^2 \over 64} \left[\left\{4{\rm \pi}^2 \left(1 - {{\rm \xi} \over L} \right)^2 + 1\right\} \right. \cr &\left. \quad \sin {2{\rm \pi} {\rm \xi} \over L} + 2{\rm \pi} \left(1 - {{\rm \xi} \over L} \right) \cos {2{\rm \pi} {\rm \xi} \over L} \right] \cr &\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \lpar 0 \leq {\rm \xi} \leq L\rpar}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU11.gif?pub-status=live)
![\eqalignno{E_{zm} &={\rm \varepsilon} \left[\displaystyle{{\Omega ^2 \Omega _p^2 {\rm \pi} ^2 } \over 4}\left\{\displaystyle{{\Omega _k } \over 2} - \displaystyle{{\rm \pi} \over L}\right\}\right. \cr &\left. \quad - \displaystyle{{{\rm \pi} ^2\, L} \over {r_o^2 }}\left(1 - \displaystyle{{2r^2 } \over {r_o^2 }}\right)\left\{\displaystyle{3 \over 8}\lpar \Omega ^2 \Omega _p^2 - 1\rpar +\displaystyle{{\Omega _s^2 } \over 2}\right\}\right]\cr &\quad \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}+\displaystyle{{{\rm \varepsilon} \Omega ^2 \Omega _p^2 \Omega _k {\rm \pi} ^2 } \over 8}\sin \displaystyle{{2{\rm \pi} {\rm \xi} } \over L} & \lpar {\rm \xi}\lt 0\rpar }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU12.gif?pub-status=live)
The maximum transverse electric Wakefield for L → λ p is
![\eqalign{E_{rm} & = E_{rm}^{\lpar 0\rpar } + E_{rm}^{\lpar 1\rpar } = {{\rm \varepsilon} r \over 2r_o^2} \left[\Omega^2 \Omega_p^2 {\rm \pi} \left(1 - {{\rm \xi} \over L} \right)\sin {2{\rm \pi} {\rm \xi} \over L} \right. \cr &\left. \quad - \Omega _s^2 \cos {2{\rm \pi} {\rm \xi} \over L} - {\Omega^2 \Omega_p^2 \Omega_k L \over 8} \left\{3 \left(1 - {{\rm \xi} \over L} \right) \sin {2{\rm \pi} {\rm \xi} \over L} \right. \right. \cr &\left. \left. \quad - 2{\rm \pi} \left(1 - {{\rm \xi} \over L} \right)^2 \cos {2{\rm \pi} {\rm \xi} \over L} \right\} \right] \qquad \qquad \qquad \lpar 0 \leq {\rm \xi} \leq L\rpar}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU13.gif?pub-status=live)
![\eqalignno { E_{rm} &=\displaystyle{{{\rm \varepsilon} {\rm \pi} r} \over {2r_o^2 }}\left[\Omega ^2 \Omega _p^2 \left(1 - \displaystyle{{L\Omega _k } \over {2{\rm \pi} }}\right)+L^2 \left(1 - \displaystyle{{r^2 } \over {r_o^2 }}\right)\right. \cr &\left. \quad \left\{\displaystyle{{4\Omega _s^2 } \over {{\rm \pi} ^2 r_o^2 }} +\lpar \Omega ^2 \Omega _p^2 - 1\rpar \left(2 - \displaystyle{1 \over {2r_o^2 }}\right)\right\}\right]\cr &\quad \sin \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}+\displaystyle{{{\rm \varepsilon} r} \over {2r_o^2 }}\left[\displaystyle{{{\rm \pi} \Omega ^2 \Omega _p^2 \Omega _k L} \over 2} - \Omega _s^2 \right]\cr &\quad \cos \displaystyle{{2{\rm \pi} {\rm \xi} } \over L}+\displaystyle{{r{\rm \varepsilon} \Omega _s^2 } \over {2r_o^2 }} & \hskip 15pt\lpar {\rm \xi}\lt 0\rpar }](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU14.gif?pub-status=live)
and the maximum magnetic Wakefield is found to be

![\eqalign{B_{{\rm \theta} m} & = {{\rm \varepsilon} r \over r_o^2} \left[{3L^2 \over 4{\rm \pi} r_o^2} \lpar \Omega^2 \Omega_p^2 - 1\rpar \left(1 - {r^2 \over r_o^2} \right)\sin {2{\rm \pi} {\rm \xi} \over L} \right. \cr &\left. \quad + {\Omega_s^2 \over 2} \left(\cos {2{\rm \pi} {\rm \xi} \over L} - 1\right) \right]. \qquad \qquad \lpar {\rm \xi}\lt 0\rpar}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151021072132278-0431:S026303461200002X_eqnU17.gif?pub-status=live)
In a LWFA, we consider a test electron moving along the z-direction of the laser plasma interaction region. The maximum longitudinal force experienced by test electron is given by,
The electron will be accelerated by this force if F z > 0. The maximum transverse force is,
The evolution of the normalized force within the pulse F z,r/mcωpo with ξ/L is shown in Figure 1 for no=1034m −3, a o2 = 0.05, r o = 15.0 µm and r = 4.0 µm. The solid curve represents the axial while the dotted line represents the transverse force. The force is greater in the axial direction in comparison to the transverse direction.

Fig. 1. Variation of the normalized force within the pulse F z,r/mcωpo with ξ/L for n o = 1034 m−3, a o2 = 0.05, r o = 15.0 μm and r = 4.0 μm.
The variation of the normalized force behind the pulse F z,r/mcωpo with ξ/L is shown in Figure 2 for the same parameters as in Figure 1. The solid line represents the axial white the dotted represents the transverse force. The force is greater in the axial direction then in the transverse direction. The accelerating force produced due to Wakefields in quantum plasma is greater than that produced in classical plasma for similar values of parameters.

Fig. 2. Variation of the normalized force behind the pulse F z,r/mcωpo with ξ/L for n o = 1034 m−3, a o2 = 0.05,r o = 15.0 μm and r = 4.0 μm.
5. SUMMARY AND DISCUSSION
We have studied in detail, the Wakefield generation by an intense laser pulse traveling through dense quantum plasma. We have used the electron continuity and electron momentum equation including the quantum statistical pressure and the quantum Bohm force, together with the Poisson equation to obtain the perturbed density and velocity. Equations for Wakefields are setup for radial Gaussian field amplitude. Electric and magnetic Wakefields have been derived with the help of time dependent Maxwell's equations using quasistatic approximation. It is found that ponderomotive nonlinear effects, quantum force and quantum statistical pressure contribute to transverse as well as longitudinal Wakefield generation. However, nonlinear terms representing vortex motion contribute only to transverse velocity components. The zeroth and first order electric and magnetic Wakefields (both transverse and longitudinal) within and behind the pulse have been obtained for a sinusoidal pulse profile.
The maximum axial and transverse forces acting on a test electron due to the Wakefields have been evaluated. The variation of these forces with ξ/L have been studied graphically. It is found that even weak short pulses are capable of generating considerable Wakefields. The force behind the pulse is greater than within the pulse. Wakefields generated within the pulse are of the same order, whereas behind the pulse, axial field is greater than transverse. Simultaneous acceleration focusing is observed in the regime where F Z > 0 and F r < 0. The laser induced Wakefields can trap electrons and accelerate them to high energies at nanoscales in dense plasmas, such as those in the next generation intense laser-solid density plasma experiments, free electron lasers, plasmonic devices and in compact astrophysical objects (Harding & Lai, Reference Harding and Lai2006).




