TIME EVOLUTION OF THE ION DENSITY

A temporal Gaussian profile of the electric field of the laser pulse with frequency ω, intensity, I ₀ (corresponding amplitude electric field E ₀) and pulse duration τ is considered to propagate in a homogenous plasma of density n _p,

(1)$$\vec E\lpar r\comma \; t\rpar = \vec E_0 \lpar r\comma \; t\rpar \exp \left({ - \displaystyle{{\lpar t - t_m \rpar ^2 } \over {{\rm \tau} ^2 }}} \right).$$

Where t _m is the time corresponding to maximum intensity, and we consider a monochromatic linearly polarized light plan wave propagating along the z-axis with $\vec E_0\lpar r\comma \; t\rpar =$$E_0 \cos \lpar {\rm \omega} t\rpar \hat x$ and the peak electric field $E_0 = \sqrt {140{\rm \pi} I} \lpar V/cm\rpar $. The intense electric field can ionize the neutral gas, and the numbers of electrons from the various charge states are created. If a stepwise production of multiply charge atomic ions is assumed, the evolution of ion density is given by a series of coupled equations, where the ground ion state plays the role of intermediate state. In this case, the rate equations take the form,

(2)$$\displaystyle{{dn_j \lpar t\rpar } \over {dt}} = \sum\limits_{\scriptstyle i = 0 \atop \scriptstyle i < j } {W_{i\comma j} \lpar t\rpar n_i \lpar t\rpar - \sum\limits_{k = j + 1}^{Z_{\max } } {W_{\,j\comma k} \lpar t\rpar n_j \lpar t\rpar } }$$

Here n _i(t), and n _j(t) are the number density of species i, j at a specific time t, and W _ij(t) is the ionization rate for production of a singly charged ion j from i. Z _max is the maximum produced charge state. The interaction of laser-plasma is governed by the Keldish parameter (Keldysh, Reference Keldysh1964) in practical unit,

(3)$${\rm \gamma} = \displaystyle{{2.31} \over {{\rm \lambda} [ {\rm \mu} m\rsqb }}\left({\displaystyle{{U_i [ eV\rsqb } \over {I_0 [ TW/cm^2 \rsqb }}} \right)^{1/2} .$$

Where U _i is the ionization potential of atom or ion with a charge state i, λ is the wavelength, and $I_0 \simeq \lpar c{\rm \eta} /8{\rm \pi} \rpar E_0^2 $ is the average intensity of electromagnetic field in a rare field gas. There are many theoretical methods used to treat the ionization processes of atoms for γ < 1, such as Keldish (Reference Keldysh1964), barrier suppression ionization (Augst et al., Reference Augst, Strickland, Meyerhofer, Chin and Eberly1989; Penetrante & Bardsley, Reference Penetrante and Bardsley1991), Amosov-Delone-Krainov (Ammosov et al., Reference Ammosov, Delone and Krainov1989) theory, and so on. In the quasistatic or high-filed limit, γ_k ≪ 1, from the general form of Keldish formula, the instantaneous ionization rate, W(t), may be expressed as,

(4)$$W\lpar t\rpar = 1.61{\rm \omega} _{au} \displaystyle{{Z^2 } \over {n_{eff}^{4.5} }}\left({10.87\displaystyle{{Z^3 } \over {n_{eff}^4 }}\displaystyle{{E_{au} } \over {E\lpar t\rpar }}} \right)^{2n_{eff} - 1.5} \exp \left({ - \displaystyle{2 \over 3}\displaystyle{{Z^3 } \over {n_{eff}^3 }}\displaystyle{{E_{au} } \over {E\lpar t\rpar }}} \right).$$

Where ω_au = 4.1 × 10¹⁶s ⁻¹ and E _au = 5.1 × 10⁹V/cm are the fundamental atomic frequency and field strength, respectively. $n_{eff} = Z/\sqrt {U_i [ eV\rsqb /13.6} $ is the effective principal quantum number for a hydrogenic atom, where U _i in eV is the ionization potential, and Z is the charge of the produced ion. It is worth notice that the laser pulse duration is much shorter than the recombination time. In fact, the recombination rate for an electron of several ten of eV and electron density below 10²⁰ cm⁻³ is on the order of nanosecond, so that during the pulse evolution, recombination terms in Eq. (2) could be neglected. The resulting set of ionization rate equations are stiff ordinary differential equations that may be solved routinely with standard initial value problem solvers (Byrne & Hindmarsh, Reference Byrne and Hindmarsh1987). Figure 1 shows the time evolution of the relative populations of the charge state oxygen ions for a pulse length τ = 100f _s (t_max = 200f _s) at wavelength ~ 532 nm for two different laser intensities; I₀ = 10¹⁷W/cm ² (1) and I₀ = 10¹⁸W/cm ² (2), respectively. The temporal variation of ionization population shows a step like behavior, because the electric field strength is sinusoidally oscillatory and the ionization rate depends strongly on the electric strength. Notice that the threshold laser intensity for OFI for hydrogenic ions is estimated by I _th = 4 × 10⁹U _i/Z ²W/cm ² (Chichkov et al., Reference Chichkov, Egbert, Eichmann, Momma, Nolte and Wellegehausen1995). Each new ion states are created when the laser intensity reaches the level of threshold intensity. In our calculation, the highest charge state was O⁶⁺. This is because the threshold intensity of the ions ≤ O⁶⁺ (~ 4 × 10¹⁶ W/cm²) (NIST) are significantly below the applied laser intensity. In addition, the lower ionization states (< 2 +) are produced in the first half cycle of pulse. They are then rapidly vanished when the higher ionization states are generated. This means, the electrons can be created at different times over the laser pulse. In the highly ionized plasma, the electron motion can affect the pulse propagation in the plasma, and consequently, it can change the electron residual energy. These electrons account for the average ATI energy.

Fig. 1. (Color online) Time history of the average residual energy of electrons for the first six charge states of oxygen during laser pulse evolution for two different intensities I ₀ = 10¹⁷W/cm ² (a) and I ₀ = 10¹⁸W/cm ² (b), when pulse duration τ = 100 fs, and wavelength λ = 532 nm.

AVERAGE RESIDUAL ENERGY

The numbers of charged particles are produced from the various charge state at different time scale. They are thus subject to different accelerations, and the interactions among them are complicated. The electron velocity in the laser field is determined by the momentum equation,

(5)$$\displaystyle{{d^2 \vec r} \over {dt^2 }} = - \displaystyle{e \over {m_e }}\vec E\lpar t\rpar + \vec F_{sch} \lpar t\rpar .$$

Where $\vec F_{sch} \lpar t\rpar = -{\rm \omega} _p^2 \vec r$ is the restoring force due to space charge effect, which can reduced the residual energy of electrons (Pulsifer et al., Reference Pulsifer, Apruzese, Davis and Kepple1994; Wilks et al., Reference Wilks, Kruer, Williams, Amendt and Eder1995). e and m _e are the electron charge and mass relatively, and ω_p is the plasma frequency as a harmonic restoring force for the space-charge effect. In order to keep the residual energy small, the electron must interact with the EM field in nearly adiabatic fashion as laser pulse passes.

At the time of ionization, we assume that electrons have zero energy (Burnett & Corkum, Reference Burnett and Corkum1989); therefore, they are classically accelerated by fields from the laser and from the surrounding plasma. Most of the electron energy during the laser pulse comes from the oscillatory quiver motion in the laser field, and is returned to the field when the pulse passed. In our calculation, the initial velocity of the ionized electron is taken to be zero at time t ₀ at the origin r ₀. t ₀ is the time at which the electron is ionized by OFI process. If an electron is created at rest at this time in a linearly polarized laser pulse, it has a later time, t, with velocity,

(6)$$\dot x\lpar t_0 \comma \; t\rpar = \displaystyle{{eE_0 } \over {m_e \lpar {\rm \omega} ^2 - {\rm \omega} _p^2 \rpar }}[ - {\rm \omega} \sin \lpar {\rm \omega} t\rpar + S_1 \lpar t_0 \rpar \cos \lpar {\rm \omega} _p t\rpar + S_2 \lpar t_0 \rpar \sin \lpar {\rm \omega} _p t\rpar \rsqb .$$

Where

$$\eqalign{S_1 \lpar t_0 \rpar &= \Big\{ {\rm \omega} \cos \lpar {\rm \omega} _p t_0 \rpar \sin \lpar {\rm \omega} t_0 \rpar\cr& - {\rm \omega} _p \cos \lpar {\rm \omega} t_0 \rpar \sin \lpar {\rm \omega} _p t_0 \rpar \Big\} \exp \left({ - \displaystyle{{\lpar t - t_m \rpar ^2 } \over {{\rm \tau} ^2 }}} \right)\comma \;}$$

(7)$$\eqalign{S_2 \lpar t_0 \rpar &= \Big\{ {\rm \omega} \sin \lpar {\rm \omega} t_0 \rpar \sin \lpar {\rm \omega} _p t_0 \rpar \cr&+ {\rm \omega} _p \cos \lpar {\rm \omega} t_0 \rpar \cos \lpar {\rm \omega} _p t_0 \rpar \Big\} \exp \left({ - \displaystyle{{\lpar t - t_m \rpar ^2 } \over {{\rm \tau} ^2 }}} \right).}$$

The single electron kinetic energy after interaction with laser pulse over laser frequency, 2π/ω, is then given by,

(8)$${\rm \epsilon} _{t_0 } = \displaystyle{{ \lt \dot x^2 \lpar t_0 \comma \; t\rpar \gt } \over {2m_e }} = {\rm \epsilon} _q + {\rm \epsilon} _{ATI} \lpar {\rm \omega} \comma \; {\rm \omega} _p \comma \; t_0\rpar .$$

Where 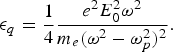${\rm \epsilon} _q = \displaystyle{1 \over 4}\displaystyle{{e^2 E_0^2 {\rm \omega} ^2 } \over {m_e \lpar {\rm \omega} ^2 - {\rm \omega} _p^2 \rpar ^2 }}.$ is the ponderomotive or quiver energy due to coherent oscillatory motion of electron, and the second term represents the excess energy of electron, and what has come to be known as the ATI energy.

(9)$$\eqalign {{\rm \epsilon} _{ATI} \lpar {\rm \omega} \comma \; {\rm \omega} _p \comma \; t_0 \rpar &= \displaystyle{1 \over 4}\displaystyle{{e^2 E_0^2 } \over {m_e \lpar {\rm \omega} ^2 - {\rm \omega} _p^2 \rpar ^2 }}\left\{{S_1 \lpar t_0 \rpar \left[{1 + \displaystyle{{\sin \left({\displaystyle{{4{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }} \right)} \over {\displaystyle{{4{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }}}} \right]}\right.\cr & \quad +\left.{ S_2^2 \lpar t_0 \rpar \left[{1 - \displaystyle{{\sin \left({\displaystyle{{4{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }} \right)} \over {\displaystyle{{4{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }}}} \right]- \displaystyle{4 \over {\rm \pi} }S_1 \lpar t_0 \rpar \displaystyle{{{\rm \omega} ^3 \sin \left({\displaystyle{{{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }} \right)} \over {{\rm \omega} ^2 - {\rm \omega} _p^2 }}}\right.\cr & \quad +\left.{ \displaystyle{2 \over {\rm \pi} }S_2 \lpar t_0 \rpar \displaystyle{{{\rm \omega} ^3 \sin ^2 \left({\displaystyle{{2{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }} \right)} \over {{\rm \omega} ^2 - {\rm \omega} _p^2 }}}\right.\cr & \quad +\left.{ S_1 \lpar t_0 \rpar S_2 \lpar t_0 \rpar \displaystyle{{\sin ^2 \left({\displaystyle{{2{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }} \right)} \over {\displaystyle{{{\rm \pi} {\rm \omega} _p } \over {\rm \omega} }}}} \right\}.}$$

Here we assumed the pulse length is much greater than an optical cycle time, τ_p ≫ 2π/ω, and the electric field envelope is relatively constant. That is, ATI energy of each electron depends only on its own ionization time, t ₀, when the electron becomes free of the atom. The average ATI or residual energy of all electrons by considering the number of electrons produced from the various charge states can be written,

(10)$$\bar {\rm \epsilon} _{ATI} \lpar {\rm \omega} \comma \; {\rm \omega} _p \rpar = \displaystyle{{\sum\limits_{k = 1}^{Z_{\max } } {\int\limits_0^{t_{\max } } {n_k \lpar t_0 \rpar W_k \lpar t_0 \rpar {\rm \epsilon} _{ATI} \lpar {\rm \omega} \comma \; {\rm \omega} _p \comma \; t_0 \rpar dt_0 } } } \over {\sum\limits_{k = 1}^{Z_{\max } } {\int\limits_0^{t_{\max } } {n_k \lpar t_0 \rpar W_k \lpar t_0 \rpar dt_0 } } }}.$$

Where the integration is taken over the pulse envelope. It is obvious that the plasma containing higher ionization state would have a larger average ATI energy.

RESULTS AND DISCUSSION

Effect of Plasma Density on Residual Energy

Figure 2 shows the dependence of the residual energy as a function of plasma frequency normalized by laser frequency, ω_p/ω, for three different pulse intensities of 10¹⁶, 10¹⁷, and 10¹⁸ W/cm², respectively. Duration of linear polarized laser pulse is τ = 100 fs at wavelength λ= 532 nm. The free electrons are coming from various charge state of oxygen. Clearly, the ATI energy gets larger with increasing laser intensity. If the density is so high that the effective plasma frequency ω_p approaches the laser frequency with increasing oxygen gas density, the resonance will occur; hence, the value of residual energy will become very large, as shown in figure. At electron densities close to the critical density, the plasma enhances the ATI energy by approximately a factor of 10. The non-uniform behavior of the curves is due to the modulation of the laser field amplitude. That is, large electron density corresponding to large plasma frequency produced effective electric field, which could alter the electric field of laser pulse. The fields then might cancel each other.

Fig. 2. (Color online) Dependence of average residual energy of electrons on plasma density (${\rm \omega}_p\over {\rm \omega} $) for three different laser pulse intensities I ₀ = 10¹⁶W/cm ² (■), I ₀ = 10¹⁷W/cm ² (▲) and I ₀ = 10¹⁸W/cm ² (●), when pulse duration τ = 100 fs, and wavelength λ = 532 nm.

However, an enlarged part of the figure shows the ATI energy slightly decrease as the plasma density approaches ω_p/ω ≈ 10⁻³. This minimum in the residual energy is less dependent of the peak intensity and could simply achieve when ω_p ≈ π/2τ as shown in Figure 3 for two pulse durations τ = 500 fs and τ = 500 fs. However, the values of the electron residual energy in OFI plasmas are increased for the higher laser intensity as shown in Figure 2. Beyond this point and point for critical plasma density, it is found that low energy electrons with < 60 eV for the pulse length τ = 500 fs can be produced in the density range of 10⁻⁴ < ω_p/ω < 10⁻¹. Rapid recombination process to achieve high gain in X-ray plasma is more effective in the low electron temperature, and then the plasma density is chosen so that the ratio ω_p/ω ≈ 10⁻³ is valid for the rest of our analysis.

Fig. 3. (Color online) Dependence of average residual energy of electrons on plasma density (${\rm \omega}_p\over {\rm \omega} $) for two different pulse durations τ = 50 fs (■), τ = 500 fs (▲), when laser intensity I ₀ = 10¹⁷W / cm ², and wavelength λ = 532 nm.

Effect of Laser Parameters on Residual Energy

The effect of laser intensity on average ATI energy of electrons in the three wavelengths, 266 nm, 532 nm, and 1064 nm, is shown in Figure 4, when the pulse duration is kept at 100 fs. The plasma frequency was about ω_p = 2.2 ×10⁻³ω, ω_p = 4.4 ×10⁻³ω, and ω_p = 6.6 ×10⁻³ω, respectively. It is clear from the figure that electron residual energy is larger with higher laser intensity. Further, a comparison between three wavelengths infers that largest energy is achieved for the longer wavelength.

Fig. 4. (Color online) Variation of average residual energy of electrons with laser pulse intensity I ₀ for three different light wavelength λ = 266 nm (■), λ = 532 nm (▲), and λ = 1064 nm (●) when pulse duration τ = 100 fs.

Figure 5 shows the effects of laser frequency and the intensity for the same pulse duration as used in Figure 4. The ATI energy is found to vary with the square of laser wavelength, because the ionization rate of Eq. (4) is independent of the wavelength while the electron quiver energy depends on the square of the wavelength. However, the ATI energy are enhanced when wavelength is increased for all laser intensities. When we compare the slopes of the graphs in the figure, we notice that the average residual energy of electrons changes at a faster rate in the case of I = 10¹⁸ W/cm². Therefore, the laser with higher intensity is found to be more sensitive with the wavelength. In the case of I = 10¹⁶ W/cm², ATI energy at 266 nm is about one order of magnitude smaller than that at 1064 nm. However, similar to the last results, the residual energy are increased for the higher laser intensity. So, we can conclude that plasma with higher frequency is best suited for a cold electron production in the plasma. The decreased residual energy for larger frequency can be explained on the basis of velocity term in Eq. (6). Actually, the group velocity v_g gets larger with the increasing frequency. This leads to weaker driven force in the plasma as the frequency is appearing in denominator in Eq. (9). Therefore, the electrons with smaller ATI energy are created in the plasma. It is worth to notice that a laser operating with I = 10¹⁶ W/cm², and I = 10¹⁷ W/cm² at 226 nm, will produce electrons having an average energy of 2 eV, and 15 eV respectively, which are much smaller than an ionization potential of O²⁺ (35 eV), and O³⁺ (55 eV). These values, however, are not low enough to produce population inversion with respect to the ground state by rapid recombination. In Figure 6, we investigate the effect of laser pulse duration on the average ATI energy of electrons for three cases of τ = 2π/ω_p, τ > 2π/ω_p and τ < 2π/ω_p when I = 10¹⁷W/cm ₂ and λ = 532nm. From the figure it is evident that the laser pulse with τ ≠ 2π/ω_p is less effective for the high energy electron production in the plasma. The residual energy for all three cases goes down with increasing pulse duration. Therefore, it can be concluded that the narrow laser pulses are more suitable for the high electron energy production. A comparison between the three graphs shows that the ATI energy changes at a faster rate with the pulse duration when the plasma density and pulse duration satisfy the condition τ < 2π/ω_p. It means long pulses would generate low residual energy of the electrons to facilitate recombination and suppress collisional excitation. It is worth to notice that when we compare these results with ones in Figures 2 and 3, we find that there are two regions where the residual energy is relatively high. At the high-density where the plasma and laser frequency are close (ω ≈ ω_p), and at the density where the plasma oscillation is approximately equal to laser pulse length (τ ≈ 2π/ω_p). It means the pulses with τ ≠ 2π/ω_p would generate low ATI electron energy if used in the low density plasma.

Fig. 5. (Color online) Variation of average residual energy of electrons with light wavelength for three different laser I ₀ = 10¹⁶W/cm ² (■), I ₀ = 10¹⁷W/cm ² (▲) and I ₀ = 10¹⁸W/cm ² (●), when λ = 532 nm, and pulse duration τ = 100 fs.

Fig. 6. (Color online) Variation of average residual energy of electrons with pulse duration τ for three different cases τ = 2π/ω_p (■), τ > 2π/ω_p (▲), and τ < 2π/ω_p (●) when, I ₀ = 10¹⁷W / cm ² and laser wavelength λ = 532 nm.

Electron Energy Distribution Function

Although the collisional heating is significant in high density plasmas, but electron energy distributions are determined mainly by the ATI energy in low density plasmas. So adequate control of electron energy distribution is a critical issue for developing the OFI X-ray lasers. Figure 7 shows the residual electron energy distribution function for two different wavelengths, 532 nm, and 1064 nm for a laser intensity of I = 10¹⁷W/cm ², τ = 100fs. ATI energy distribution of electrons produced by OFI from different ionization stages are obtained numerically by performing the summation indicated in the analytical form for the distribution function.

(11)$$\,f_k \lpar {\rm \epsilon} _k \rpar \Delta {\rm \epsilon} = \sum\limits_{k = 1}^{Z_{\max } } {\sum\limits_{t_0 = 0}^{t_{\max } } {n_t \lpar t_0 \rpar W_i \lpar t_0 \rpar \Delta t} }$$

Where ϵ_k = (ϵ_k+1 + ϵ_k)/2 and Δϵ = (ϵ_k+1 − ϵ_k)/2.

Fig. 7. (Color online) Electron energy distribution function versus ATI energy for two different wavelengths 532 nm (■), and 1064 nm (●). The laser conditions are I ₀ = 10¹⁷W/cm ² and τ = 100 fs.

For both case, the distribution function increases over the entire energy range as more and more electrons are released. It is evident that the calculated electron energy distribution is different from the Maxwellian distribution as reported by Mohideen et al. (Reference Mohideen, Sher, Tom, Aumiller, Wood, Freeman, Boker and Bucksbaum1993). The electron distribution gets decrease exponentially at the energy between 0–0.1 KeV, and 0–1 KeV at wavelength 523 nm, and 1064 nm, respectively. At the high energy, the distribution rather slowly decreases for both cases.

SUMMARY

In conclusion, a simple and effective approach to calculate the properties of OFI oxygen background gas has been presented. Numerical studies carried out in order to analyze the dependence of the ATI probabilities, as most important plasma heating mechanisms, on the laser field parameters (pulse duration, laser-field intensity, frequency), and background gas density. The presented results give indication that the laser-plasma parameters significantly alter the values of the electron residual temperature of the ionized neutrals in the plasma.

A careful investigation reveals that the effect of pulse duration could be stronger than that of the laser frequency on average ATI energy. In fact there are two regions where the residual energy is relatively high. At the high-density where the plasma and laser frequency are close (ω ≈ ω_p). At the density where the plasma oscillation is approximately equal to laser pulse length (τ ≈ 1/v _p). Based on our numerical studied we observed that slower electrons can be generated under the situation of pulse duration much smaller than the plasma period and lower wavelengths. In each case, higher intensity pulses produce higher ATI electron energy.

Therefore, a judicious choice of laser pulse parameters and the plasma density can lead to cold electrons for the effective role in realizing a recombination pumping X-ray laser in an OFI plasma (Burnett & Enright, Reference Burnett and Enright1990; Hulin et al., Reference Hulin, Auguste, D'Oliveira, Monot, Jacquemot, Bonnet and Lefebvre2000).