1. INTRODUCTION
The interaction of very intense laser beam with plasmas (Kruer, 1988) finds its application in laser-induced fusion for efficient coupling of laser beam energy to plasmas and particle acceleration by beat wave process (Tajima & Dawson, 1979; Esarey et al., 1988; Wurtele, 1994). In both the processes electron plasma wave and laser beam interaction is involved. For example, in laser induced fusion, electron plasma wave generated by stimulated Raman scattering process may generate hot electrons/energetic electrons by wave particle interaction. In beat wave process, the generated electron plasma wave leads to particle acceleration. Modena et al. (1995) and Malka (2002) investigated that the longitudinal electric field associated with electron plasma wave can be extremely large and this can be utilized for high energy electron acceleration, over very short distances. The wave breaking mechanism is used for this electron acceleration. This wave breaking occur by the Raman forward scattering instability induced by short, high intensity laser pulses, and they got maximum energy up to 44 MeV of accelerated plasma electrons. But they have not considered the self focusing of the laser beam. Pukhov and Meyer-ter-Vehn (1996) show three-dimensional (3D) particle-in-cell simulation of short-pulse laser propagation in near-critical plasma at relativistic intensities. This work shows that the incident laser beam creates a single propagation channel with considerably enhanced concentration of light on the axis. This beam also propagates through unstable filamentary stages. But Pukhov and Meyer-ter-Vehn (1996) have not considered the ponderomotive effects in self focusing process.
Most of these studies have been done by taking only relativistic nonlinearity. But ultra intense laser pulse can create different type of nonlinearities at different time scales, for example, case 1:
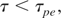
and case 2:
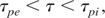
τ is the laser pulse duration, τpi is the ion plasma period, and τpe is the electron plasma period. In case (1), only relativistic nonlinearity is operative and in case (2), relativistic and ponderomotive nonlinearities are operative.
In this paper, we have studied the electron plasma wave coupling with an ultra intense laser beam and its effect on electron plasma wave excitation, and particle acceleration when relativistic and ponderomotive nonlinearities are operative. This coupling arises on account of the relativistic change in the electron mass and the modification of the background electron density due to ponderomotive nonlinearity. Therefore, the plasma wave dynamical equation gets significantly modified. This nonlinear evolution has been studied by using the paraxial ray approximation and the plasma wave intensity has been evaluated with and without coupling. For typical laser plasma parameters chosen here (please see Section 3), the maximum intensity in the laser beam filaments get enhanced by a factor of about 2.5 and the maximum intensity in the localized electron plasma waves enhanced by a factor of about 1.8 when compared to the coupling for relativistic case.
In Section 2, we have derived the expression for the effective dielectric constant of the plasma in the presence of a laser beam when relativistic and ponderomotive nonlinearities are operative. In Section 3, the solution for laser beam propagation has been presented and numerical results are given showing the laser intensity evolution in axial and transverse directions and the corresponding filamentation of the laser beam. In Section 4, first, the equation for electron plasma wave (in the presence of laser pulse propagation) is derived and then its solution is obtained in order to study the evolution/localization of the plasma wave. Using these results, particle acceleration has been studied in this section. The last section presents the conclusion drawn from this investigation and the consequences in laser plasma coupling and beat wave process.
2. EFFECTIVE DIELECTRIC CONSTANT OF THE PLASMA
Consider the propagation of a Gaussian laser beam of frequency ω0 along the z-direction. The initial intensity distribution of the beam is given by
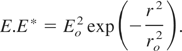
Where r is the radial coordinate of the cylindrical coordinate system and ro is the initial beam width. The dielectric constant of the plasma is given by
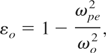
Where
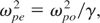
ωpo is the plasma frequency given by
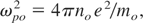
(with e being the charge of an electron, mo is the rest mass and no is the density of plasma electrons in the absence of laser beam) and relativistic factor is given by

The above expression is valid, when there is no change in the plasma density. The relativistic ponderomotive force is given by Borisov et al. (1992), Brandi et al. (1993a, 1993b), and Gupta et al. (2005)
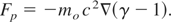
Using the electron continuity equation and current density equation for second order correction in the electron density equation (with the help of ponderomotive force) total, the density is given by Brandi et al. (1993a, 1993b)
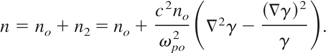
Now the effective dielectric constant of the plasma at frequency ω0 is given by

where

Expending dielectric constant in Eq. (4) around r = 0 by Taylor expansion, one can write
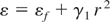
where

Here, a = αo Ao2 is the square of dimensionless vector potential (E = −∂A/∂(ct)), αo = e2/mo2 c4, fo is the beam width parameter at z as given by Eq. (10) in Section 3 and kp2 = ωpo2/c2.
3. LASER BEAM PROPAGATION
The wave equation governing the vector potential of the laser beam in plasma can be written as
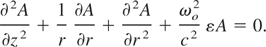
Following Akhmanov et al. (1968), we write
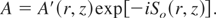
Using Eq. (7) into Eq. (6) and separating the real and imaginary parts we get

The solution of the above-coupled equations can be written as
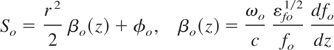
and the intensity of the laser beam
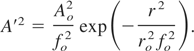
Using Eq. (9) in Eq. (8a), we get
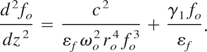
The above equation becomes as follows after putting the value of γ1 from Eq. (5) and using the normalized distance ξ = zc/ωo ro2, then we get
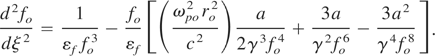
The intensity of the laser beam with relativistic and ponderomotive nonlinearities is given by Eqs. (9) and (10). In this paper first, we have studied the variation of laser beam intensity with distance along the laser beam propagation direction and radial distance. The results are presented in the form of Figures 1 and 2. The following set of parameters has been used in the numerical calculations: we used laser beam Nd: YAG (γ = 1064 nm), ro = 15 μm, ωpo = 0.03ωo, and vth = 0.1c.

(a) Variation in laser beam intensity with normalized distance (ξ) and radial distance (r) for a = 1.3, when relativistic and ponderomotive nonlinearities are operative. (b) Variation in laser beam intensity with normalized distance (ξ) and radial distance (r) for a = 1.3, when only relativistic nonlinearity is operative.

(a) Variation in laser beam intensity with normalized distance (ξ) and radial distance (r) for a = 2.0, when relativistic and ponderomotive nonlinearities are operative. (b) Variation in laser beam intensity with normalized distance (ξ) and radial distance (r) for a = 2.0, when only relativistic nonlinearity is operative.
For initial plane wave front of the beam, the initial conditions for fo are fo = 1 and dfo /dz = 0 at z = 0. When a laser beam propagates through the plasma, then density of the plasma will be varying through the channel due to ponderomotive force. But the relativistic and ponderomotive nonlinearities introduced in the plasma depend upon the total intensity of the beam; therefore, the intensity patterns in the relativistic case are different than the ponderomotive and relativistic case (combined) as shown in Figure 1. Here we have comparatively studied the variation in laser beam intensity with normalized distance and radial distance, when in Figure 1a, relativistic and ponderomotive nonlinearities are operative and in Figure 1b, only relativistic nonlinearity is operative. It is obvious that the maximum intensity in the laser beam filaments get enhanced by a factor of about 2.5 when both nonlinearities are present. Similarly, we plot in Figure 2 for different initial laser intensity and the maximum intensity in the laser beam filaments get enhanced by a factor of about 2.2, so when initial intensity is increasing then enhancement factor decreases.
4. PROPAGATION OF PLASMA WAVE
On account of the change in the background density due to ponderomotive force and the relativistic effects, the laser beam gets filamented as discussed above. In these filaments, the laser beam intensity is very intense and plasma density is also changed due to ponderomotive force. Therefore, the plasma wave amplitude, which depends upon the background density, gets strongly coupled to the laser beam in the filaments where the intensity is very large. In order to study the effect of this coupling on plasma wave excitation, we have first set up the equation of the plasma wave and then this nonlinear equation has been solved. Following standard procedure, the equation governing the electron plasma wave is given by
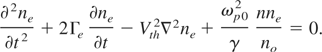
Where 2Γe is the Landau damping factor, Vth2 is the square of the electron thermal speed. Writing:
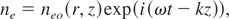
in Eq. (11), one gets

Further substituting neo = neoo exp(−ikS(r,z)) in Eq. (12) and equating real and imaginary parts, we obtain:
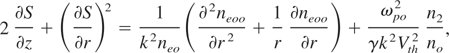
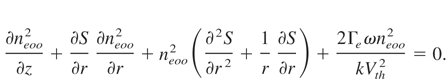
We assume initial density variation at z = 0 to be
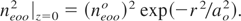
Here ao is the initial beam width of the plasma wave. Following Akhmanov et al. (1968), solution of Eqs. (13) and (14) can be written as,

where
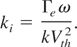
Using Eq. (15) in Eq. (13) and equating the coefficients of r2 on both sides, we obtain
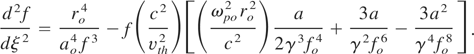
It is interesting to compare Eq. (16) with Eq. (10) of the laser beam. In the absence of coupling between the pump wave and the plasma wave, the second term in Eq. (16) is zero and f is given by:
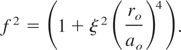
From Eq. (16), it is obvious that f depends on fo, hence an analytical solution for f cannot in general, be obtained. We can, however, obtain an analytical solution of Eq. (16) in a special case, viz., the diffraction term (i.e., the first term on the right-hand side) balances the nonlinear term in Eq. (10); this happens when the laser beam has critical power for self-focusing. Under such conditions (fo = 1), the main beam propagates without convergence or divergence. Therefore the solution for f is given by
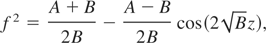
where
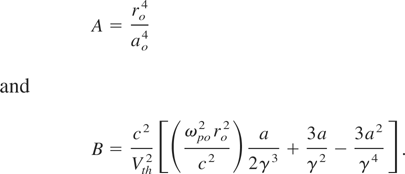
We have, however, solved Eq. (15) with the help of Eq. (16) numerically to obtain the amplitude of the density perturbation at finite ξ (when the laser beam power is more than its critical power and a = 1.3). The results are displayed in Figures 3, 4, and 5 for typical laser plasma parameters. The electron plasma wave excited due to nonlinear coupling by high power laser beam because of ponderomotive and relativistic effects, transfer its energy to electrons and accelerate them. In Figure 3, we have comparatively studied the variation in the intensity of electron plasma wave with normalized distance and radial distance, when relativistic and ponderomotive nonlinearities are operative (Fig. 3a) and only relativistic nonlinearity is operative (Fig. 3b). The maximum intensity of electron plasma wave filaments gets enhanced by a factor of about 1.8 in comparison to relativistic case. Similarly, we plot Figure 4 for different laser intensity. Here the maximum intensity of the electron plasma wave filaments get enhanced by a factor of about 1.9 in comparison to relativistic case. Figure 5 shows the variation in the plasma wave density with distance.

(a) Variation in electron plasma wave intensity with normalized distance (ξ) and radial distance (r) for a = 1.3, when relativistic and ponderomotive nonlinearities are operative. (b) Variation in electron plasma wave intensity with normalized distance (ξ) and radial distance (r) for a = 1.3, when only relativistic nonlinearity is operative.

(a). Variation in electron plasma wave intensity with normalized distance (ξ) and radial distance (r) for a = 2.0, when relativistic and ponderomotive nonlinearities are operative. (b) Variation in electron plasma wave intensity with normalized distance (ξ) and radial distance (r) for a = 2.0, when only relativistic nonlinearity is operative.

Variation in normalized density with normalized distance (ξ) for a = 1.3, solid line represent only relativistic nonlinearity and semi-dotted line represents both relativistic and ponderomotive nonlinearities case.
The electron plasma wave excited due to nonlinear coupling by high power laser beam because of ponderomotive and relativistic effects (last term on the left-hand side of the Eq. (11)) transfer its energy to electrons and accelerate them. The energy gain (energy per unit rest mass energy of electron) by the electron is given by
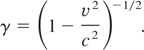
Differentiating and putting d(mv)/dt = ikmo c2φ1, then we get
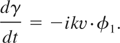
Here φ1(= eφ/mo c2) is the dimensionless electrostatic potential of the electron plasma wave and we get
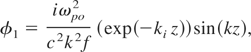
by using Poisson equation. This first order differential Eq. (18) has been solved numerically, where we have used f by Eq. (16). Figure 6 represents the variation of energy gain with the normalized distance (ξ). Here, solid line represents energy gain by electron when only relativistic nonlinearity is operative and semi-dotted line represent the gain when both relativistic and ponderomotive nonlinearities are operative. These results show that the maximum energy gain by electrons is significantly increased by the inclusion of ponderomotive nonlinearity. This is on account of the enhancement of plasma wave intensity in comparison to relativistic case. The following set of parameters has been used in the numerical calculations: we used laser beam Nd: YAG (λ = 1064 nm), ro = 15 μm, ao = 10 μm, ωpo = 0.03ωo, Vth = 0.1c, and initially we take γ = 1.

Variation in energy gain (γ) of electron with normalized distance (ξ) for a = 1.3, solid line represents only relativistic nonlinearity and semi-dotted line represents both relativistic and ponderomotive nonlinearities case.
5. RESULTS AND DISCUSSION
Here we have developed a model for electron plasma wave excitation by ultra intense laser beam. The excitation is on account of nonlinear coupling between the laser beam and the plasma wave. This coupling arises on account of ponderomotive and relativistic effects by the laser beam. The coupling is so strong that the initial plasma wave becomes highly localized as shown here. We investigated here the intensity variation of laser beam as well as electron plasma wave with normalized distance and radial distance, when only relativistic and both relativistic and ponderomotive nonlinearities are operative. In fact, the intensity of plasma wave exhibits oscillatory behavior. The oscillatory behavior may be understood as follows: Because of redistribution of charges, plasma frequency minimum is on the axis. According to the dispersion relation of plasma wave, the phase velocity of electron plasma wave minimum is on the axis and increases away from the axis. If we consider an initial plane wave front of electron plasma wave, then as the wave front advances in the plasma, focusing occurs and amplitude of density perturbation increases. When the spot size is considerably reduced, diffraction effects become important, and amplitude of density perturbation starts decreasing. Thus, we get oscillatory behavior with the distance of propagation. In these localized structures, the wave particle interaction should lead to particle acceleration. A crude estimate can also be made as presented here. In fact, these studies should be done by using Fokker Planck equation and using the velocity space diffusion coefficient in the localized structures of the electron plasmas wave packets. These rigorous estimates are in progress and will be a part of future publication. Such studies should be useful in hot electron generation by stimulated Raman scattering in laser plasma interaction and particle acceleration by beat wave process.
ACKNOWLEDGMENTS
This work was partially supported by DST India. One of the authors, Atul Kumar, is grateful to Dr. P.D. Gupta, Head, Laser Plasma Division and Dr. P.A. Naik (RRCAT) for their constant support and encouragement during this work. Manoj Kumar Gupta is grateful to the Council of Scientific and Industrial Research (CSIR), HRDG, Government of India, for granting the assistantship for the present research work.








