2. NONLINEAR WAVE EQUATION

Consider a non-Maxwellian two-component electron–ion plasma is immersed in the static magnetic field. The magnetic field is a constant and here we assume ${\bf B}_{\bf 0} = B_0 {\hat{\bf e}}_{\bf z} $. We assume that in the equilibrium state the distribution function of plasma particles is determined by Kappa distribution as following (Vasyliunas, Reference Vasyliunas1968):

(1)$$\eqalign{f_{\rm s} (v) & = \displaystyle{1 \over {({\rm \pi} {\rm \kappa} _{\rm s} {\rm \theta} _{\rm s} ^2 )^{3/2}}} \displaystyle{{{\rm \Gamma} ({\rm \kappa} _{\rm s} + 1)} \over {{\rm \Gamma} ({\rm \kappa} _{\rm s} - (1/2))}}\left( {1 + \displaystyle{{v^2} \over {{\rm \kappa} _{\rm s} {\rm \theta} _{\rm s} ^2}}} \right)^{ - ({\rm \kappa} _{\rm s} + 1)}, \cr & s = i,e,} $$

where for κ_s > 3/2, v is the velocity, indices i and e denote ion and electron, respectively, ${\rm \theta} _{\rm s} = [({\rm \kappa} _{\rm s} - (3/2))/{\rm \kappa} _{\rm s} ]^{1/2} v_{{\rm Ts}} $, v _Ts=(k _BT _s/m _s)^1/2 is the thermal velocity of s sort of plasma particles, k _B, T _s, and m _s are Boltzmann constant, temperature, and mass of s sort of plasma particles, respectively.

For describing nonlinear dynamics of an EM wave interaction with plasma, we define electric and magnetic fields of EM wave E, B through the vector and scalar potentials A, ϕ as below:

(2)$${\bf E} = - \displaystyle{1 \over c}\displaystyle{{{\partial} {\bf A}} \over {{\partial} t}} - {\rm \nabla} {\rm \phi}, \quad {\bf B} = {\rm \nabla} \times {\bf A}, $$

where c is the speed of light. In the Coulomb gauge (viz., ▿.A = 0), using Eq. (2) in the Maxwell equations, we can write

(3)$$\displaystyle{1 \over {c^2}} \displaystyle{{{\partial} ^2 {\bf A}} \over {{\partial} t^2}} - {\rm \nabla} ^2 {\bf A} = \displaystyle{{4 {\rm \pi}} \over c}{\bf J}, $$

where J=−n _ee v_e is the current density of electrons of plasma, and e, n _e, v_e are the electron charge, density, and fluid velocity, respectively.

To clarify this situation let us return to the similar condition in a Maxwellian plasma. In the non-equilibrium state of the Maxwellian magnetized plasma, which is irradiated by a weakly relativistic laser pulse, momentum of electron can be obtained as (Rao et al., Reference Rao, Shukla and Yu1984; Sepehri Javan, Reference Sepehri Javan2012; Reference Sepehri Javan2013)

(4)$${\bar{\bf p}}_{\rm e} = \displaystyle{{ {\bar{\bf A}}} \over {(1 - {\rm \sigma} {\rm \alpha} /{\rm \gamma} _{\rm e} )}}. $$

Here ${\bar{\bf p}}_{\rm e} = {\bf p}_{\rm e} /m_{\rm e} c$ is the normalized electron momentum, ${\bar{\bf A}} = (e/m_{\rm e} c^2 ){\bf A}$ is the normalized vector potential, ${\rm \gamma} _{\rm e} =$$\sqrt {1 + p_{\rm e}^2 /m_{\rm e} ^2 c^2} $ is the relativistic Lorentz factor of electron, m _e is the electron rest mass, α = ω_c/ω₀, ω₀ is the laser frequency, ω_c = eB ₀/m _ec is the electron cyclotron frequency and ${\rm \beta} _{\rm e} = c^2 /v_{{\rm Te}}^2 $. σ = +1, −1 denote the right- and left-hand circularly polarized waves, respectively. The form of the vector potential of circularly polarized radiation field, which propagates parallel to the direction of external magnetic field is assumed

(5)$${\bf A} = \displaystyle{1 \over 2}\tilde A({\hat{\bf e}}_{\bf x} + i{\rm \sigma} {\hat{\bf e}}_y )\,\exp ( - i{\rm \omega} _0 t + ik_0 z) + {\rm c}{\rm c}., $$

where k ₀ is the frequency and wave number and $\tilde A(z,t)$ is the slowly varying amplitude that satisfies the following condition:

(6)$$\left\vert {\displaystyle{1 \over {{\rm \omega} _0}} \displaystyle{{{\rm \partial} \tilde A} \over {{\rm \partial} t}}} \right\vert \ll \left\vert {\tilde A} \right\vert. $$

In this case, the density of electron is obtained (Sepehri Javan, Reference Sepehri Javan2012; Reference Sepehri Javan2013)

(7)$${\kern 1pt} n_{\rm e} = n_{0{\rm e}} \exp \left\{ {{\rm \Phi} - \beta _{\rm e} \left[ {{\rm \gamma} _{\rm e} - 1 - \displaystyle{{{\rm \sigma} {\rm \alpha} \vert {\bar{\bf p}}_{\bf e} \vert ^2} \over {2{\rm \gamma} _{\rm e} ^2}}} \right]} \right\}, $$

where Φ=eϕ/k _BT _e is the normalized scalar potential. To obtain Eq. (7), it is assumed that the plasma is unperturbed at infinity and therefore we have the boundary conditions n _e = n _0e, Φ→0, $\bar{\,p}_{\rm e} \to 0$ at |z|→∞. It is clear from comparing Eqs. (7) and (1) that for the non-Maxwellian magnetized plasma irradiated by the circularly polarized laser pulse, the distribution function should be modified as

(8)$$\eqalign{\,f_{\rm e} (v) &= \displaystyle{{n_{0{\rm e}}} \over {({\rm \pi} {\rm \kappa} _{\rm e} {\rm \theta} _{\rm e} ^2 )^{3/2}}} \displaystyle{{{\rm \Gamma} ({\rm \kappa} _{\rm e} + 1)} \over {{\rm \Gamma} ({\rm \kappa} _{\rm e} - (1/2))}}\cr & \times\quad\left[ {1 + \displaystyle{{v^2 - 2e{\rm \phi} /m_{\rm e} + 2c^2 \left( {{\rm \gamma} _{\rm e} - 1 - ({\rm \sigma} {\rm \alpha} /2{\rm \gamma} _{\rm e}^2 )\vert {\bar {\bf p}}_{\bf e} \vert ^2} \right)} \over {{\rm \kappa} _{\rm e} {\rm \theta} _{\rm e} ^2}}} \right]^{ - ({\rm \kappa} _{\rm e} + 1)}}. $$

By integrating Eq. (8) over all the velocity space, we can find the electron density distribution as following:

(9)$$n_{\rm e} = n_{0{\rm e}} \left[ {1 - \displaystyle{{{\rm \Phi} - {\rm \beta} _{\rm e} ({\rm \gamma} _{\rm e} - 1 - ({\rm \sigma} {\rm \alpha} /2{\rm \gamma} _{\rm e}^2 )\vert {\bar {\bf p}}_{\bf e} \vert ^2 )} \over {({\rm \kappa} _{\rm e} - 3/2)}}} \right]^{ - ({\rm \kappa} _{\rm e} - 1/2)}. $$

In this case for Maxwellian plasma, by considering non-relativistic behavior for the slow motion of ions, the ion density can be described by the relation

(10)$$n_i = n_{0{\rm i}} \,\exp ( - \rm \delta {\kern 1pt} {\rm \Phi} ), $$

where δ=T _e/T _i is the ratio of the electron temperature to the ion temperature. Then, in similar way, for the ion density of non-Maxwellian plasma, one can achieve

(11)$$n_{\rm i} = n_{0{\rm i}} \left[ {1 + \displaystyle{{{\rm \delta} {\rm \Phi}} \over {({\rm \kappa} _{\rm i} - 3/2)}}} \right]^{ - ({\rm \kappa} _{\rm i} - 1/2)}. $$

In the weakly relativistic regime by considering the quasi-neutrality condition n _e = n _i (and also n _e0 = n _i0 = n ₀), expanding Eqs. (9) and (11) and using Eq. (4) we can obtain

(12)$$n_{\rm e} = n_{\rm i} = n_0 \left( {1 - \displaystyle{1 \over 2}{\vert \bar{\bf A} \vert }^{\bf 2} Q} \right), $$

where

(13)$$\eqalign{Q & = \displaystyle{{({\rm \kappa} _{\rm i} - (1/2))({\rm \kappa} _{\rm e} - (1/2))} \over {{\rm \delta} ^{ - 1} ({\rm \kappa} _{\rm e} - (1/2))({\rm \kappa} _{\rm i} - (3/2)) + ({\rm \kappa} _{\rm i} - (1/2))({\rm \kappa} _{\rm e} - (3/2))}} \cr & \quad \times \displaystyle{{{\rm \beta} _{\rm e}} \over {(1 - {\rm \sigma} {\rm \alpha} )}}}. $$

In order to formulate nonlinear interaction of EM wave propagating along external magnetic field in the non-Maxwellian plasma let us obtain J. From Eq. (4) the electron velocity can be obtained

(14)$${\bf v}_{\rm e} = \displaystyle{e \over {m_{\rm e} c}}\displaystyle{{\bf A} \over {{\rm \gamma} _{\rm e} - {\rm \sigma} {\rm \alpha}}}. $$

Also, for electron Lorentz factor we can approximately write

$${\rm \gamma} _{\rm e} \approx \sqrt {1 + \displaystyle{{\vert {\bar{\bf A}}\vert ^2} \over {(1 - {\rm \sigma} {\rm \alpha} )^2}}}, $$

And in the weakly relativistic laser intensity, when $\vert {\bar{\bf A}}\vert ^2,$${\hskip-2pt\kern 1pt} \,\vert {\bar{\bf P}}_{\bf e} \vert ^2 \ll 1$we can expand it as

(15)$${\rm \gamma} _{\rm e} \approx 1 + \displaystyle{1 \over 2}\vert {\bar{\bf P}}_{\bf e} \vert ^2. $$

Using Eqs. (4), (12), (14), and (15) yields to the following nonlinear current:

(16)$$ - \displaystyle{{4 {\rm \pi}} \over c}{\bf J} = \displaystyle{{{\rm \omega} _{\rm p}^2} \over {c^2}} \displaystyle{{\bf A} \over {{\rm \gamma} _{\rm e} - {\rm \sigma} {\rm \alpha}}} \left( {1 - \displaystyle{1 \over 2}\vert {\bar{\bf A}}\vert ^2 Q} \right), $$

where ${\rm \omega} _{\rm p} = \sqrt {4\pi n_0 e^2 /m_{\rm e}} $ is the plasma frequency.

Expanding the nonlinear current density of Eq. (16) with respect to the normalized vector potential amplitude, saving only the second orders and substituting it in the wave equation of (3) yields

(17)$$\eqalign{& \left( \{ {\rm \nabla}^2 - \displaystyle{1 \over c^2} \displaystyle{{\partial}^2 \over {\partial} t^2} \right)ae^{i(k_0 z - {\rm \omega} _0 t)} = k_{\rm p}^2 \left[\displaystyle{1 \over 1 - {\rm \sigma} {\rm \alpha}} - \vert a \vert^2 \right. \cr & \left. \quad \times \quad \left(\displaystyle{1 \over 2} \displaystyle{Q \over (1 - {\rm \alpha} {\rm \sigma})} + \displaystyle{1 \over 2} \displaystyle{1 \over (1 - {\rm \alpha} {\rm \sigma})^4} \right) \right] ae^{i(k_0 z - {\rm \omega} _0 t)},}$$

here $a = e/m_{{\rm oe}} c^2 \tilde A$ is the normalized amplitude of vector potential (also $\vert a\vert = \vert {\bar{\bf A}}\vert $) and k _p = ω_p/c.

3. NONLINEAR DISPERSION RELATION AND MODULATION INSTABILITY

After mathematical simplifications, Eq. (17) can be presented in its new form

(18)$$\eqalign{& \displaystyle{{\partial}^2 a \over {\partial} t^2} - c^2 \displaystyle{{\partial}^2 a \over {\partial} z^2} - 2i{\rm \omega}_0 \displaystyle{{\partial} a \over {\partial} t} - 2ik_0 c^2 \displaystyle{{\partial} a \over {\partial} z} + \bigg \{- {\rm \omega} _0^2 + c^2 k_0^2 + {\rm \omega}_{pe}^{2} \cr & \quad \times\bigg[\displaystyle{1 \over 1 - {\rm \sigma} {\rm \alpha}} - \vert a\vert^2 \times \bigg(\displaystyle{1 \over 2} \displaystyle{Q \over (1 - {\rm \sigma} {\rm \alpha})} + \displaystyle{1 \over 2} \displaystyle{1 \over (1 - {\rm \sigma} {\rm \alpha})^4} \bigg) \bigg] \bigg \} a \cr & \quad = 0.} $$

The coefficient of a in the last term of Eq. (18) is the nonlinear dispersion relation. In the absence of interaction between EM wave and plasma, when amplitude is a real constant (a = a ₀), we can derive the nonlinear dispersion relation for non-Maxwellian magnetoplasma as following:

(19)$$\eqalign{& c^2 k_0^2 - {\rm \omega} _0^2 + {\rm \omega} _{\rm p}^2 \left[ {\displaystyle{1 \over {1 - {\rm \sigma} {\rm \alpha}}} - a_0 ^2 \,\left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right)} \right] \cr & \quad = 0.} $$

In the linear limit (when a ²→0) Eq. (19) can be reduced to the well-known linear dispersion relation of circularly polarized EM waves in magnetized plasma

(20)$$k_0 = \displaystyle{{{\rm \omega} _0} \over c}\left( {1 - \displaystyle{{{\rm \omega} _{\rm p}^2} \over {{\rm \omega} _0 ({\rm \omega} _0 - {\rm \sigma} {\rm \omega} _{\rm c} )}}} \right)^{1/2}. $$

By considering the condition of slowly varying amplitude [Eq. (6)] and assuming that ω₀ and k ₀ satisfy the linear dispersion of Eq. (20), Eq. (19) can be modified to the following equation

(21)$$\eqalign{& i \bigg( {\displaystyle{{{\rm \partial} a} \over {{\partial} t}} + v_{\rm g} \displaystyle{{{\partial} a} \over {{\partial} z}}} \bigg) + \displaystyle{{c^2} \over {2{\rm \omega} _0}} \displaystyle{{{\partial} ^2 a} \over {{\partial} z^2}} + \displaystyle{{{\rm \omega} _{{\rm pe}} ^2} \over {2{\rm \omega} _0}} \vert a\vert ^2 \cr & \quad \times \, \bigg( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \bigg)a = 0},$$

here v _g = k ₀c ²/ω₀ is the group velocity. Using the following dimensionless variables:

$${\rm \tau} = \displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \omega} _0}} t,\quad U_{\rm g} = \displaystyle{{{\rm \omega} _0} \over {{\rm \omega} _{{\rm pe}}}} \displaystyle{{v_{\rm g}} \over c},\quad {\rm \zeta} = \displaystyle{{{\rm \omega} _{{\rm pe}}} \over c}z - U_{\rm g} {\rm \tau}, $$

in Eq. (21), we can write

(22)$$i\displaystyle{{{\partial} a} \over {{\partial} {\rm \tau}}} + \displaystyle{1 \over 2}\displaystyle{{{\partial} ^2 a} \over {{\partial} {\rm \zeta} ^2}} + D_{\rm NL} a = 0, $$

where

$$D_{\rm NL} = \displaystyle{1 \over 2}\vert a\vert ^2 \,\left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - \sigma \alpha )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - \sigma \alpha )^4}}} \right).$$

Equation (22) is the well-known modified nonlinear Schrödinger equation and describes the nonlinear dynamics of slowly varying envelope of EM wave in the quasi-neutral limit. In the case of cold plasma and large amplitude fields this approximation is not valid (Shukla et al., Reference Shukla, Marklund and Eliasson2004).

To obtain the dispersion relation for MI, we use the usual method introduced by Shukla and Bharuthram (Reference Shukla and Bharuthram1987). In this approach, we suppose

(23)$$a = (a_0 + a_1 )\,\exp (i \Lambda {\rm \tau} ), $$

where a ₀ is a real constant parameter, a ₀≫|a ₁|, and

(24)$$\Lambda \equiv D_{{\rm NL}} (a = a_0 ) = \displaystyle{1 \over 2}a_0 ^2 \,\left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right). $$

By substituting Eq. (23) into (22) and linearizing this equation with respect to a ₁, we can achieve

(25)$$\eqalign{& i \displaystyle{{{\partial} a_1} \over {{\partial} {\rm \tau}}} + \displaystyle{1 \over 2}\displaystyle{{{\partial} ^2 a_1} \over {{\partial} {\rm \zeta} ^2}} + \displaystyle{1 \over 2}a_0 ^2 \,\left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right)\,(a_1 + a_1 ^{\ast} ) \cr & \quad = 0}. $$

Introducing a ₁=X+iY, inserting it into Eq. (25) and separating the real and imaginary parts of this equation yields

(26and27)$$\left\{ \matrix{\eqalign{&\displaystyle{{{\partial} X} \over {{\partial} {\rm \tau}}} + \displaystyle{1 \over 2}\displaystyle{{{\partial} ^2 Y} \over {{\partial} {\rm \zeta} ^2}} = 0, \cr & - \displaystyle{{{\partial} Y} \over {{\partial} {\rm \tau}}} + \displaystyle{1 \over 2}\displaystyle{{{\partial} ^2 X} \over {{\partial} {\rm \zeta} ^2}} + a_0^2 \left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right) = 0 }} \right. .$$

We consider the following oscillational form for X and Y

(28)$$\left( {\matrix{ X \cr Y \cr}} \right) = \left( {\matrix{ {\tilde X} \cr {\tilde Y} \cr}} \right)\,\exp ( - i{\rm \Omega} {\rm \tau} + iK{\rm \zeta} ), $$

where ${\tilde X},\,{\tilde Y}$ are real amplitudes, Ω is the modulation frequency normalized by ${\rm \omega} _{\rm p}^2, \,{\rm \omega} _0 $ and K is the modulation wave number normalized by ω_p/c. Constituting Eq. (28) into the set of Eqs. (26) and (27) we can obtain the nonlinear dispersion relation of MI

(29)$${\rm \Omega} ^2 = - \displaystyle{{K^2} \over 2}\left[ {a_0^2 \left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right) - \displaystyle{{K^2} \over 2}} \right]. $$

The temporal growth rate Γ=−iΩ can be extracted from Eq. (29) as below:

(30)$${\rm \Gamma} = \displaystyle{K \over {\sqrt 2}} \left[ {a_0^2 \left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right) - \displaystyle{{K^2} \over 2}} \right]^{1/2}. $$

The maximum growth rate of MI that occurs at $K = K_{\rm m} = $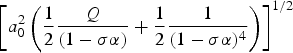$\left[ {a_0^2 \left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} \rm \alpha )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right)} \right]^{1/2} $, is

(31)$${\rm \Gamma} _{\max} = \displaystyle{{a_0^2} \over 2}\left( {\displaystyle{1 \over 2}\displaystyle{Q \over {(1 - {\rm \sigma} {\rm \alpha} )}} + \displaystyle{1 \over 2}\displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^4}}} \right). $$

We note that, for the Maxwellian plasma, when κ_e, κ_i → ∞, Eq. (12) reduces to

(32)$$Q = \displaystyle{{{\rm \beta} _{\rm e}} \over {(1 + {\rm \delta} ^{ - 1} )(1 - {\rm \sigma} {\rm \alpha} )}}, $$

and by substituting this equation into Eq. (30) we can derive the growth rate for the Maxwellian plasma

(33)$${\rm \Gamma} = \displaystyle{K \over {\sqrt 2}} \left[ {\displaystyle{{a_0^2} \over {2(1 - {\rm \sigma} {\rm \alpha} )^2}} \left( {\displaystyle{{{\rm \beta} _{\rm e}} \over {(1 + {\rm \delta} ^{ - 1} )}} + \displaystyle{1 \over {(1 - {\rm \sigma} {\rm \alpha} )^2}}} \right) - \displaystyle{{K^2} \over 2}} \right]^{1/2}. $$

4. RESULTS AND DISCUSSIONS

In this section, we could analyze the numerical results of Eqs (30), (31) and discuss the variation of the growth rate as a function of the physical parameters. The order of parameters in the figures is in accordance with the usual ranges of parameters used in the laser–plasma interaction experiments (Jha et al., Reference Jha, Kumar, Raj and Upadhyaya2005; Sepehri Javan, Reference Sepehri Javan2012). We suppose a Nd:YAG laser with frequency ω₀ = 1.88 × 10¹⁵ s⁻¹ (that corresponds to the laser wave length λ ≈ 1 μm) and intensity I ≈ 1.4 × 10¹⁶ W/cm² (or a ₀ = 0.1) for the all investigated cases. In addition, for all the cases, T _e = 10 keV, solid lines denote the unmagnetized plasma and dotted (dashed) lines are used to denote the propagation of the circularly polarized right(left)-hand laser in the magnetized plasma with α = 0.1 or ω_c = 1.88 × 10¹⁴ s⁻¹.

Figure 1 shows the variation of growth rate Γ with respect to K at four different values of κ_e and κ_i for magnetized (α = 0.1) and unmagnetized (α = 0) plasma, when δ = T _e/T _i = 1. In all the cases, it is shown that the growth rate increases by exerting the external magnetic field for the right-hand laser polarization. Inversely, the growth rate decreases by using the magnetic field for the left-hand polarization. This result can be explained as follows: By increasing the external magnetic field the transverse velocity of the electrons of plasma that is driven by the right-hand polarization wave in the direction of cyclotron motion, increases and it leads to the increase of the medium's nonlinearity. Oppositely, for the case of left-hand polarization, electrons are driven opposite to the cyclotron motion and increase in the external magnetic field leads to the decrease in the velocity of electrons and consequently to the decrease in the nonlinearity of plasma medium. In Figure 1 we set κ_e = κ_i = 100 and as we know for the large values of κ_e and κ_i the state of plasma thermodynamically tends to the Maxwellian. In Figure 1b electrons and ions are super-thermal and κ_e = κ_i = 2. It is clear that the existence of super-thermal particles leads to an increase in the nonlinearity and consequently to the substantial increase in the growth rate of MI. In Figure 1c, we choose the super-thermal electrons and Maxwellian ions (κ_e = 2 and κ_i = 100). Comparison of Figure 1b and 1c shows that the presence of Maxwellian ions causes the decrease in the growth rate. In Figure 1d, we exchange the values of kappa between electrons and ions and set κ_e = 100 and κ_i = 2. One can see that in Figure 1c and 1d situation is the same and interchanging of κ_e and κ_i does not affect on the growth rate. As a matter of fact, when the ions and electrons are equi-temperature, in Eq. (11) parameter Q is invariant with interchanging of indices i and e. To interpret these results, it is important to remember that the hydrodynamic pressure force created by the hot particles can extinguish the ponderomotive force induced by the nonlinear laser–plasma interaction (Sepehri Javan, Reference Sepehri Javan2012; Reference Sepehri Javan2013). Thermodynamic pressure force is proportional to the density gradient and the decrease in the slope of the density profile via presence of the super-thermal particles leads to the decrease in the pressure and consequently to the increase in the effective ponderomotive force in the medium. As a result, enhancement of the ponderomotive force for non-Maxwellian plasma leads to the increase in the growth rate.

Fig. 1. Variation of normalized growth rate Γ as a function of normalized wave number K for solid line unmagnetized plasma and dashed(dotted) line right(left-)-hand polarized laser in magnetized plasma (α = 0.1), when T _e = 10 keV and δ =T _e/T _i = 1, for four different values of κ_e and κ_i, (a) κ_e=κ_i = 100, (b) κ_e=κ_i = 2, (c)κ_e = 2 and κ_i = 100, and (d) κ_e = 100 and κ_i = 2.

In Figure 2, the effect of κ_e on the maximum growth rate is studied, numerically for δ =1. For all the cases, the increase of κ_e yields the decrease in the growth rate; however for large values of κ_e the growth rate (decreases at an infinitesimal constant rate) is saturated and tends to the value of growth rate in the Maxwellian state. Figure 3 demonstrates the effect of the decrease in the ion temperature on the growth rate. Here, we set δ = T _e/T _i = 10. We can see that the decrease in the ions temperature causes a significant enhancement of the growth rate for all the cases. Figure 3a reveals that in the case of super-thermal ions growth rate is a sharp decreasing function of κ_e and is very sensitive to the variation of κ_e, especially in the range κ_e < 2. From Figure 3b it is evident that in the case of super-thermal electrons with a fixed κ_e = 2, variation of growth rate respect to κ_i is very smooth. After value κ_i = 5 the growth rate practically (stops) saturates and becomes constant.

Fig. 2. Variation of normalized maximum growth rate Γ_max versus κ_e when κ_i = 2, T _e = 10 keV and δ =T _e/T _i = 1, solid line for unmagnetized plasma and dashed (dotted) line for right (left)-hand polarized laser in magnetized plasma (α = 0.1).

Fig. 3. Variation of normalized maximum growth rate Γ_max (a) versus κ_e when κ_i = 2 and (b) versus κ_i when κ_e = 2, when T _e = 10 keV and δ = T _e/T _i = 10, solid lines for unmagnetized plasma and dashed (dotted) lines for right(left)-hand polarized laser in magnetized plasma (α = 0.1).