Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-11T16:50:52.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of relativistic mutual interaction of two laser beams on the growth of laser ripple in plasma

Published online by Cambridge University Press:  02 June 2005

GUNJAN PUROHIT ,
P.K. CHAUHAN ,
R.P. SHARMA  and
H.D. PANDEY
GUNJAN PUROHIT
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi, India
P.K. CHAUHAN
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi, India
R.P. SHARMA
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi, India
H.D. PANDEY
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi, India
Rights & Permissions [Opens in a new window]

Abstract

This paper presents an effect of relativistic mutual interaction of two laser beams of different frequencies on the growth of a laser ripple in laser produced plasmas. The nonlinearity due to relativistic mass variation depends not only on the intensity of one laser but also on the second laser. Therefore, one laser beam affects the dynamics of the second beam and hence a mutual nonlinear interaction (cross-focusing) takes place. The dynamical equations governing the laser intensity of two laser beams and the perturbation present on one laser beam (ripple) have been set up and a numerical solution has been presented for typical laser plasma parameters. It is found that a change in the intensity of the second laser beam can affect the growth of the laser ripple significantly. This study is important in plasma beat wave excitation and collective laser particle accelerators.

Keywords

LasersNonlinearityRelativisticRipple
Type
Research Article
Information
Laser and Particle Beams , Volume 23 , Issue 1 , March 2005 , pp. 69 - 77
Copyright
2005 Cambridge University Press

1. INTRODUCTION

There has been considerable interest in the interaction of intense laser beam with plasmas on account of its relevance to laser fusion (Mulser & Bauer, 2004) and charged particle acceleration. Laser intensities have increased in the past few years to reach the enormous value of 1020 W/cm2 (peak power are currently exceeding tens of tera watts) and their electric field strength reaches 1010 V/cm, which is greater than that of characteristic inter-atomic fields (Joshi et al., 1981; Sprangle et al., 1987, 1990, 1992). The generation of a large electric field in plasmas by high power lasers has been studied (Wyrtele, 1993) for several years in the context of particle acceleration.

New techniques are being investigated for particle acceleration. Some of these techniques are beat wave (Tajima & Dawson, 1979; Katsouleas & Dawson, 1983; Darrow et al., 1986; Shukla et al., 1986; Kitagawa et al., 1992), Wakefield (Gorbunov & Kirsanov, 1987; Sprangle et al., 1988), and self modulated Wakefield accelerators (Krall, 1993; Nakajima et al., 1995). Large amplitude longitudinal fields can also be generated using intense positron beam for particle acceleration (Blue et al., 2003). The beating between two co-propagating laser beams in plasma can generate longitudinal plasma wave with high electric field and relativistic phase velocity. The mechanism is called beat wave accelerator. If the electron plasma frequency ωp is close to the difference frequency between the two laser beams, a resonance effect results and the charge separation produces a field up to several GV/cm. A relativistic particle with right phase can catch the wave and gain energy.

Filamentation instability (hot spot formation) and self focusing of laser beams in plasmas have been studied in detail in the past, and it is an area of continued interest. These studies are also relevant to laser electron acceleration and laser driven fusion. The relativistic filamentation instability can lead to modification of the propagation pulse by spatially modulating the laser intensity transverse to the direction of propagation. The relativistic filamentation and self focusing have been studied for number of years and are important, because one needs to understand laser propagation at high intensities before one can interpret the results from other nonlinear phenomena (Sprangle & Esarey, 1991; Manot, 1995).

A lot of theoretical and experimental work has been reported related to beat wave excitation (BWE), by two laser beams and laser induced parametric instabilities in plasmas like stimulated Raman scattering (SRS), and stimulated Brillioun scattering (SBS) by a single laser beam. But these studies used spatially smooth laser beam, which is not realistic. The direct and indirect experimental evidence (Toy & Shen, 1969) revels that the smooth looking laser beams have strong intensity ripples (spikes) which may lead to the formation of filaments (hot spots) in plasmas. Therefore, the parametric interaction and plasma beat wave excitation (PBWE) can be considered coherently only inside a spike. But the experimental observations, which generally reflect integrated quantity, results from an average over a statistical distribution of independent ripples with different intensities. One can use different models of a laser beam having single hot spot (Huller et al., 1996), two closely hot spots (Huller et al., 1997), and a randomized laser beam having ripples of different intensities (Berger et al., 1995).

The effect of speckle self-focusing on the SRS (Saini & Gill, 2004) and SBS have been studied but the effect of speckle self-focusing on BWE process has not been studied so far. For example, the work of (Ren et al., 2000; Mckinstrie & Bingham, 1989; Mckinstrie & Russell, 1988; Esarey et al., 1988) have considered two laser beams but without ripple superimposed on either of the laser beams. Therefore, these theories are not applicable in realistic case of PBWE where laser beams having ripples are frequently used. Actual realistic case will be when; both of the laser beams are having multiple ripples of different intensities. We have first considered a simple case in order to understand the physics of mutual interaction of two laser beams, when one of them is having a ripple present on it. In our earlier study (Purohit et al., 2003), we addressed the cross focusing of two laser beams on the growth of laser ripples in plasma, when the nonlinearity is due to pondermotive force exerted by laser beams on the plasma electrons. But this work can not be used when the laser beams are having very high powers (relativistic region) because in those situations nonlinearity arising on account of relativistic electron mass variation becomes important. In the present paper, we have studied the effect of cross focusing of the two laser beams on the growth of laser ripple in plasma, when the nonlinearity is due to relativistic mass variation of plasma electrons, depending on the intensity of both laser beams. Because of the relativistic nonlinearity, the dynamical equation governing the intensity of the laser ripple depends upon the total intensity of both lasers. Therefore, by changing the intensity of the second laser, one can control the growth of the ripple in the plasmas. One can also obtain the optimum intensity of the second laser beam, so that the growth rate of the ripple can be decreased. If we know the dynamics of a single ripple in the presence of the second laser beam, the PBWE process can be studied in each single intense hot spot, and by averaging over the hot spot intensity distribution, one can obtain the correct amplitude of the excited plasma wave and hence the acceleration of the particles.

In section 2, we will present an analysis of the nonlinear effective dielectric constant of the plasma and derive the differential equations governing the nature of the laser ripple intensity in plasma. In section 3, a brief discussion and conclusions of the numerical results of the present investigation are presented.

2. MODEL EQUATIONS

Consider the propagation of two coaxial Gaussian laser beams of frequencies ω1 and ω2 along the z direction. The initial intensity distributions of the beams are given by

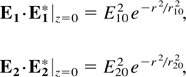
where r is the radial coordinate of the cylindrical coordinate system and r10 and r20 are their initial beamwidths. The dielectric constant of the plasma is given by

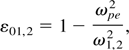
where ωpe is the plasma frequency, given by ωpe2 = 4πne e2/m (with e being the charge of an electron, m its rest mass, and ne the density of plasma electrons). The relativistic general expression for the plasma frequency is

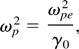
where

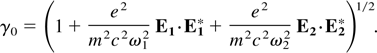
Using (3) and (2), the intensity dependent effective dielectric constant of the plasma can be expressed as

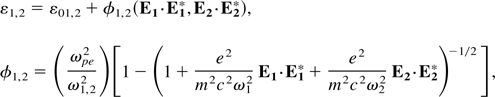
where φ1,2 is the nonlinear part of the dielectric constant. By Using a Taylor expansion of the dielectric constant around r = 0, the equation can be rewritten as

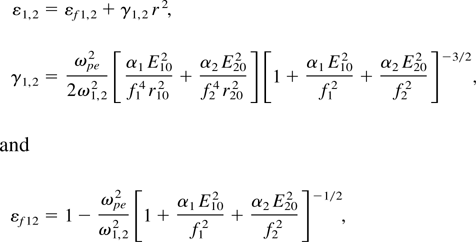
where f1 and f2 are the dimensionless beam width parameters of the laser beams and

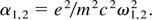
The wave equation governing the electric vectors of the two beams in plasma can be written as

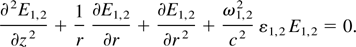
In writing Eq. (6), we have neglected the ∇(∇.E) term which is justified as long as (ωp02/ω1,22)(1/ε1,2)In ε1,2 ≤ 1. The solution for E1,2 can be written as (Sodha et al., 1976, 1979; Akhamanov et al., 1968)

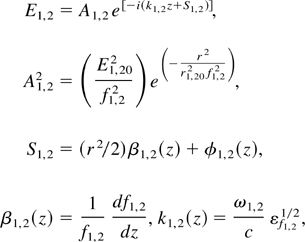
where the dimensionless beam width parameter f1,2 is given by the following equation

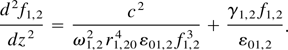
For initial plane wavefronts of the beams, the initial conditions on f1,2 are

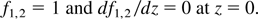
By using these initial conditions, one can solve numerically Eq. (8) and can evaluate the evaluation of f1,2 with the distance of propagation.

Let a perturbation be superimposed on the first beam such that its initial intensity distribution is given by

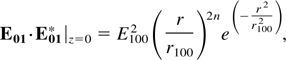
where n is a positive number and r100 is the width of the ripple. By changing the value of n the position of the ripple changes. However, more detailed information about the intensity distribution in the ripple is needed. But as a model of single ripple, we can consider it to be Gaussian. The total electric vector of the laser, having ripple superimposed on it can be written as

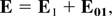
where E01 is the ripple superimposed on the first laser beam. The total electric vector E satisfies the wave equation

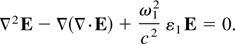
In the WKB approximation, the second term of Eq. (11) can be neglected, this is, justified since one has

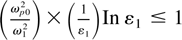
, and the electric vectors of the main beam E1 and the ripple E01 satisfy the equations

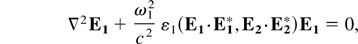
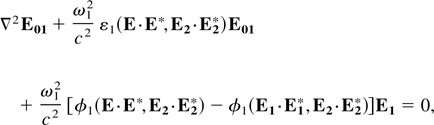
respectively. To obtain the solution of Eq. (13), we express

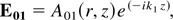
where A01(r,z) is a complex function of its argument. Substituting for E01 from Eq. (14) into Eq. (13) we get the following equation within the WKB approximation

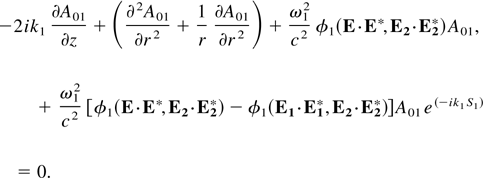
Further, substituting for A01 in Eq. (15)

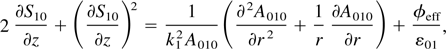
where

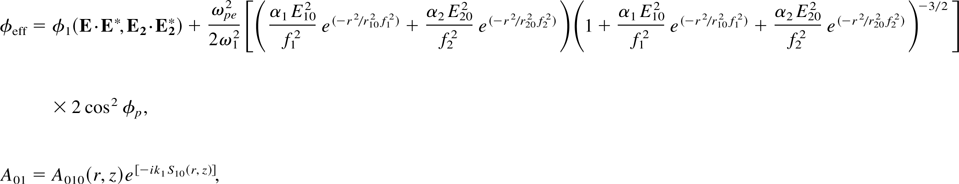
where A010(r,z) is a real function and S10 is the eikonal, we obtain the following equations after separating the real and imaginary parts

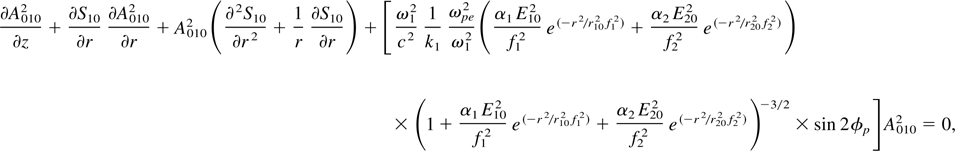
where φp is the angle between the electric vectors of the main laser beam (one) and the ripple. In writing Eq. (16) we have expanded

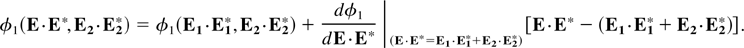
Following Akhamanov et al. (1968), the solutions to Eqs. (16a) and (16b) can be written as

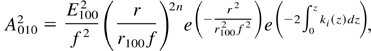
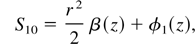
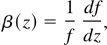
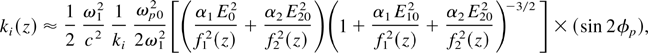
where f is the dimensionless beam width parameter of the ripple and φ(z) is a constant. For an initially plane wave front df/dz = 0 and f = 1 at z = 0. Substituting for A010 and S10 from Eq. (17) into Eq. (16a) and expanding around r = r100 fn1/2 by Taylor expansion, we get

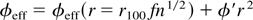
where

Using Eqs. 18a, 18b, and 16a, we get the following equation for f after equating the coefficient of r2

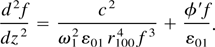
Equation (19) determines the focusing/defocusing of a ripple. It is apparent from the Eq. (17) for A0102 that the ripple grows/decays inside the plasma and the growth rate is ki. The growth rate depends on the intensity of the main beams, the phase angle φp, and parameters of the pump waves and plasma. But these solutions are valid in the neighborhood of r = r100fn1/2. The following set of parameters has been used in the numerical calculations: r10 = 15 μm, r20 = 20 μm, r100, = 10 μm, ω1 = 1.778 × 1015 rad/s, ω2 = 1.778 × 1014rad/s, ωpo = 0.04ω2, 2φp = 3π/2,n = 1.5 and 1.8.

3. DISCUSSION AND CONCLUSIONS

In the present analysis, the coupling between the ripple and main beams, which leads to growth/decay of the ripple inside the plasma, is studied. Due to this coupling, the ripple can grow in the plasma. The growth rate of the ripple (ki) is given by Eq. (17d), which depends on the effective intensity of the main beams in the plasma, electron density of the plasma, frequency of the laser beams, and the phase angle φp. It is clear from the equation, when sin 2φp is positive, the ripple will not grow and it will be attenuated at a distance on the order of 1/ki. The ripple will grow only when sin 2φp is negative.

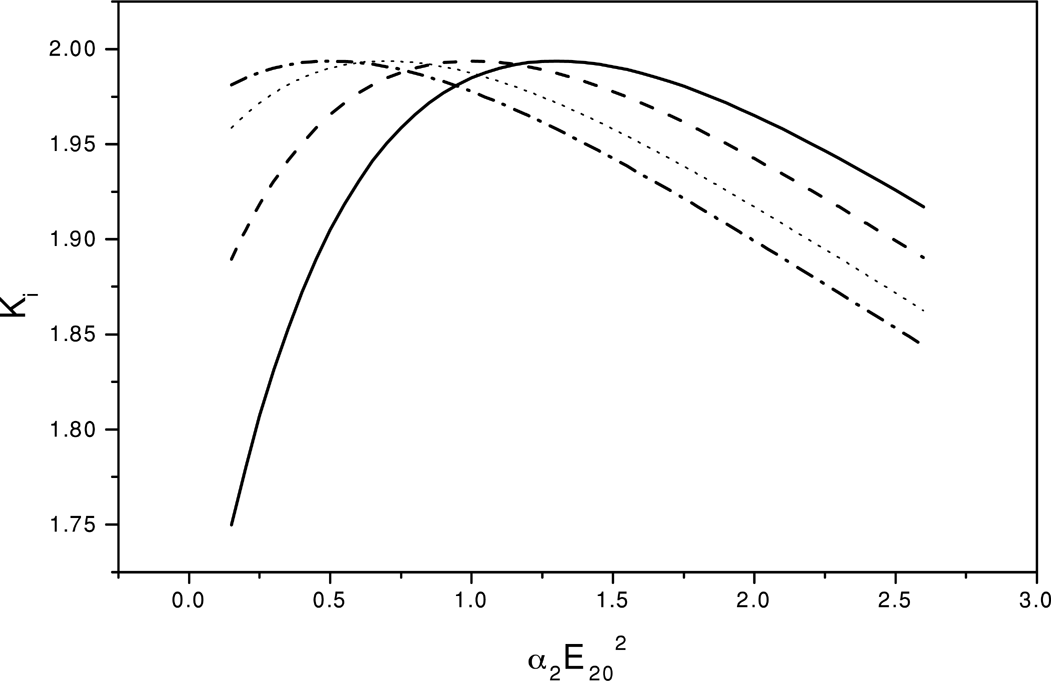
As mentioned in the Introduction, the real aberration is modeled, when the ripples are present on both the laser beams. The growth rate of the ripple as given by Eq. (17d) depends on the intensity of both laser beams. It is possible to find out the value of α1 E102 and α2 E202 such that the ripple has as minimum as possible growth rate. This can be obtained by studying the behavior of the growth rate ki of the ripple with the intensities of the laser beams as given in Fig. 1. Figure 1 represents the variation of the growth rate ki (Eq. 17d) at z = 0, with the change in the intensity of the second laser beam, when the intensity of the first laser beam is fixed. It is seen from Fig. 1, that first ki increases with the intensity of the second laser beam, but decreases after that. There is an optimum intensity of the second laser beam where the value of ki is maximum. This optimum value of the second laser beam decreases as we increase the intensity of the first laser beam. For example, for the value of α1 E102 = 0.7, 1.0 and 1.5 optimum value of α2 E202 is 1.3, 1.0, and 0.5, respectively. Similarly one can study the behavior of the ripple present on the second laser beam. Therefore, it is possible to find out the combination of intensities of laser one and laser two, such that the ripple riding on them are having the growth rate as minimum as possible.

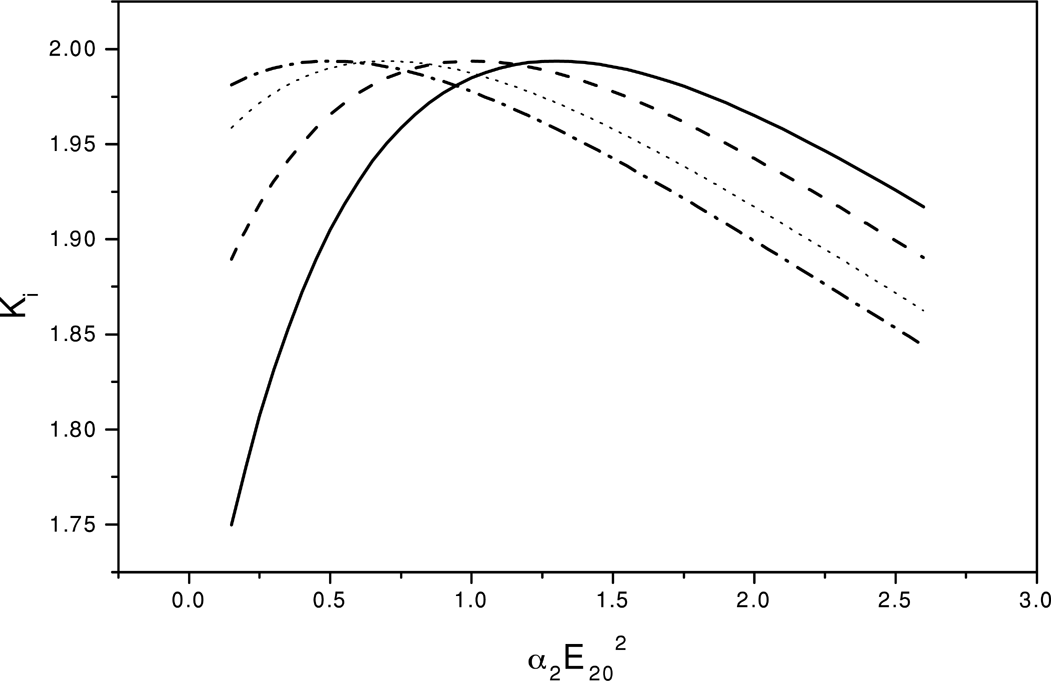
Variation of ki for the two beams with the power of the second laser beam (α2 E202) at z = 0. Solid line, dash line, dotted line and dash dotted line are for α1 E102 = 0.7, 1.0, 1.3, and, 1.5, respectively.

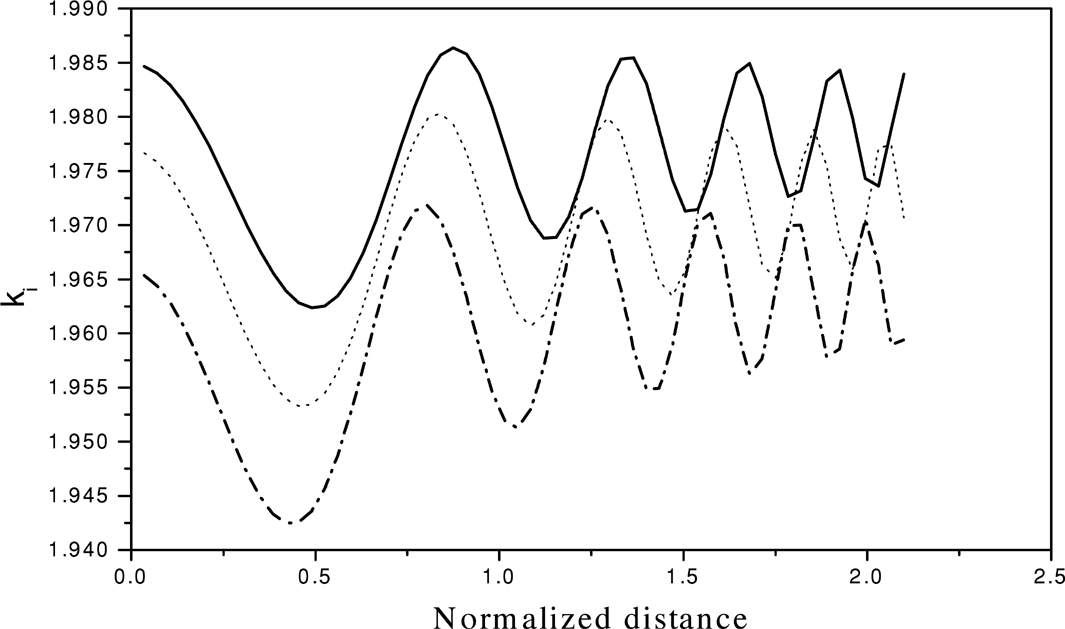
Figure 2 represents the variation of the growth rate (ki) with the distance of propagation, for different powers of the second laser beam. It is obvious from this graph that the growth rate of the ripple oscillates with the distance of propagation. When the power of the second laser beam is increased, similar effect has been found, but the over all growth rate is decreased. This behavior of ki with the distance of propagation is attributed to the fact that the growth rate depends on the intensity of two main laser beams (Eq. 17d), but the intensities of laser beams are also changing with the distance of propagation, therefore the change in ki.

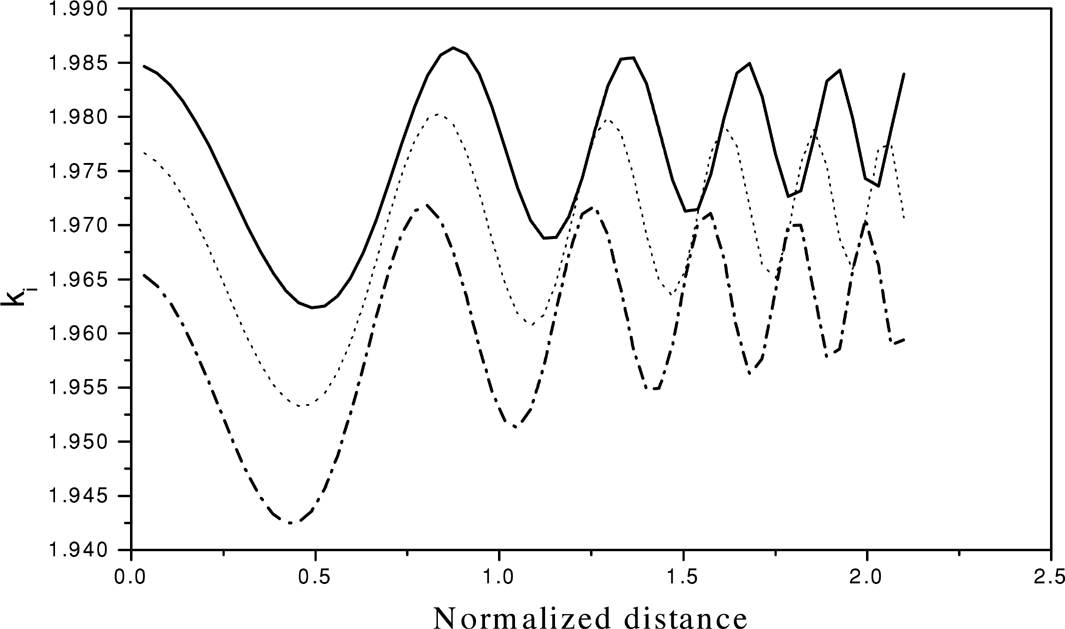
Variation of ki for the two beams with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively.

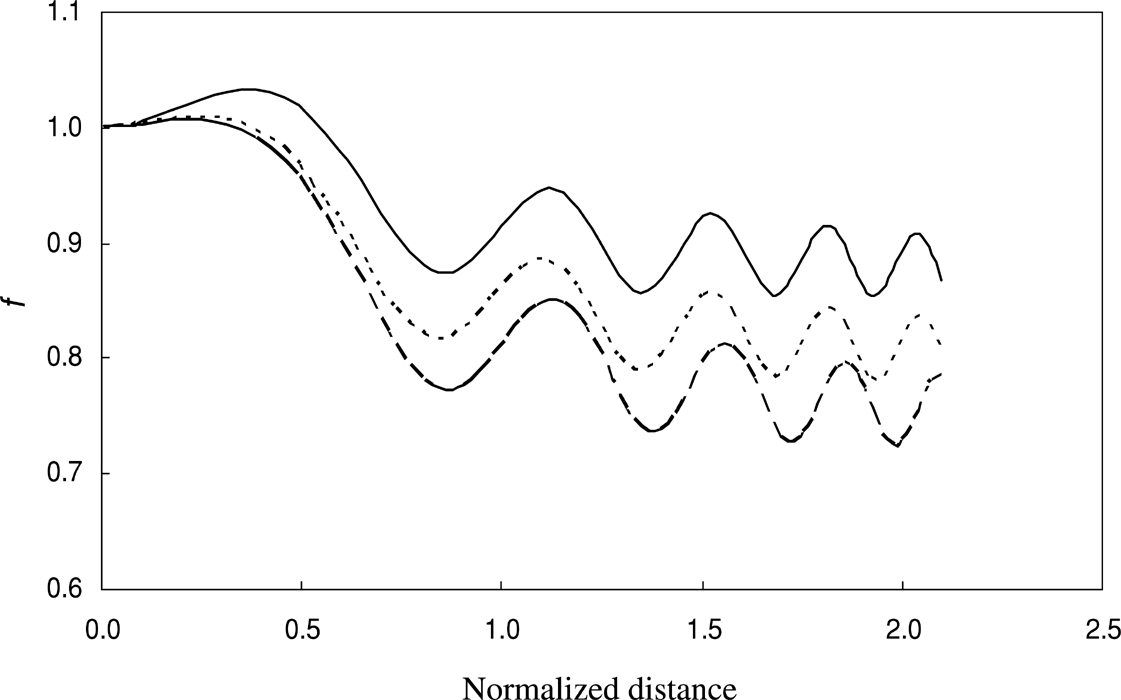
Equation (8) is the fundamental equation for cross focusing of two laser beams, when the ripple is not present on the laser beams. On neglecting the contribution of the second beam in Eq. (8), one can obtain the usual relativistic self-focusing of the first beam. With the simultaneous propagation of two laser beams, the relativistic nonlinearity introduced in the plasma depends upon the total intensity of the two beams, and the behavior of f1 is also governed by f2, and vice versa. In other words, the self-focusing of one beam is affected by the presence of another beam; this is referred to as cross-focusing. The first term on the right-hand side of Eq. (19) represents the diffraction phenomenon of the ripple. The second term, which arises from the relativistic nonlinearity, describes nonlinear refraction. The relative magnitude of these terms determines the focusing/defocusing behavior of the ripple. If the first term is large in comparison to the second term, the diffraction dominates over the nonlinear phenomena, leading to defocusing of the ripple. When the second term is large than the first term, self-focusing of the ripple is observed. The growth rate (ki) contributes significantly to focusing/defocusing of the ripple. The variations of the beam width parameter f of the ripple with the distance of propagation is illustrated in Fig. 3 for fixed 2φp = 3π/2, but for different powers of the second laser beam, when n = 1.5. When the power of the second laser beam is increased, the ripple shows focusing/defocusing behavior continuously. The focusing/defocusing of the ripple is found to be considerably affected by the power of the main beams, phase angle between the electric vectors of the first laser beam, and the parameter n.

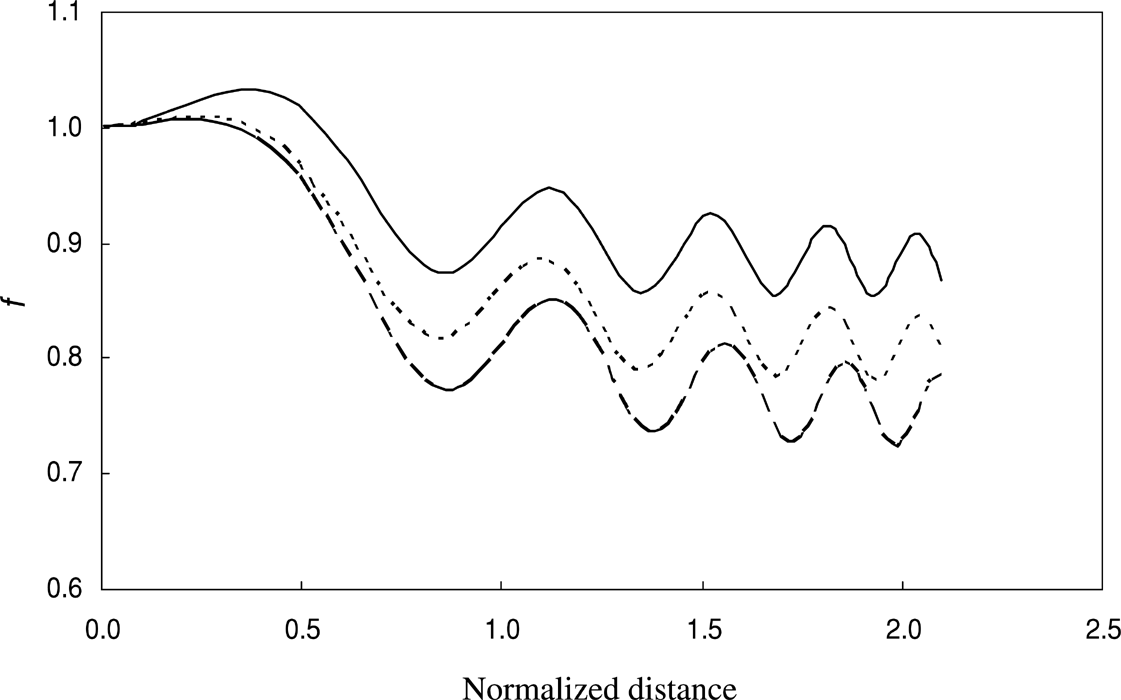
Variation of dimensionless beam width parameter (f) of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.5, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and, 2, respectively.

Figures 4(a) and 4(b) depict the variation of normalized intensity of the ripple at r = r100 fn1/2 in the plasma with the normalized distance of propagation for fixed 2φp = 3π/2, but for different values of the ripple position parameter n. For different powers of the second laser beam, intensity of the ripple oscillates with the distance of propagation. It is also obvious form the graphs that the intensity of the ripple is decreased by increasing the power of the second laser beam for the typical sets of parameter chosen here. This variation is having a complex dependence on the intensity of the laser beams, because the intensity of the ripple depends on the growth rate ki (Eq. 17d) and the parameter f (as given by Eq. 19). When the intensity of the second laser beam (Eq. 8) is changed, it changes the values of f1 and f2, therefore the value of ki and f also changes. Consequently the intensity of the ripple behaves as shown in Fig. 4, respectively.

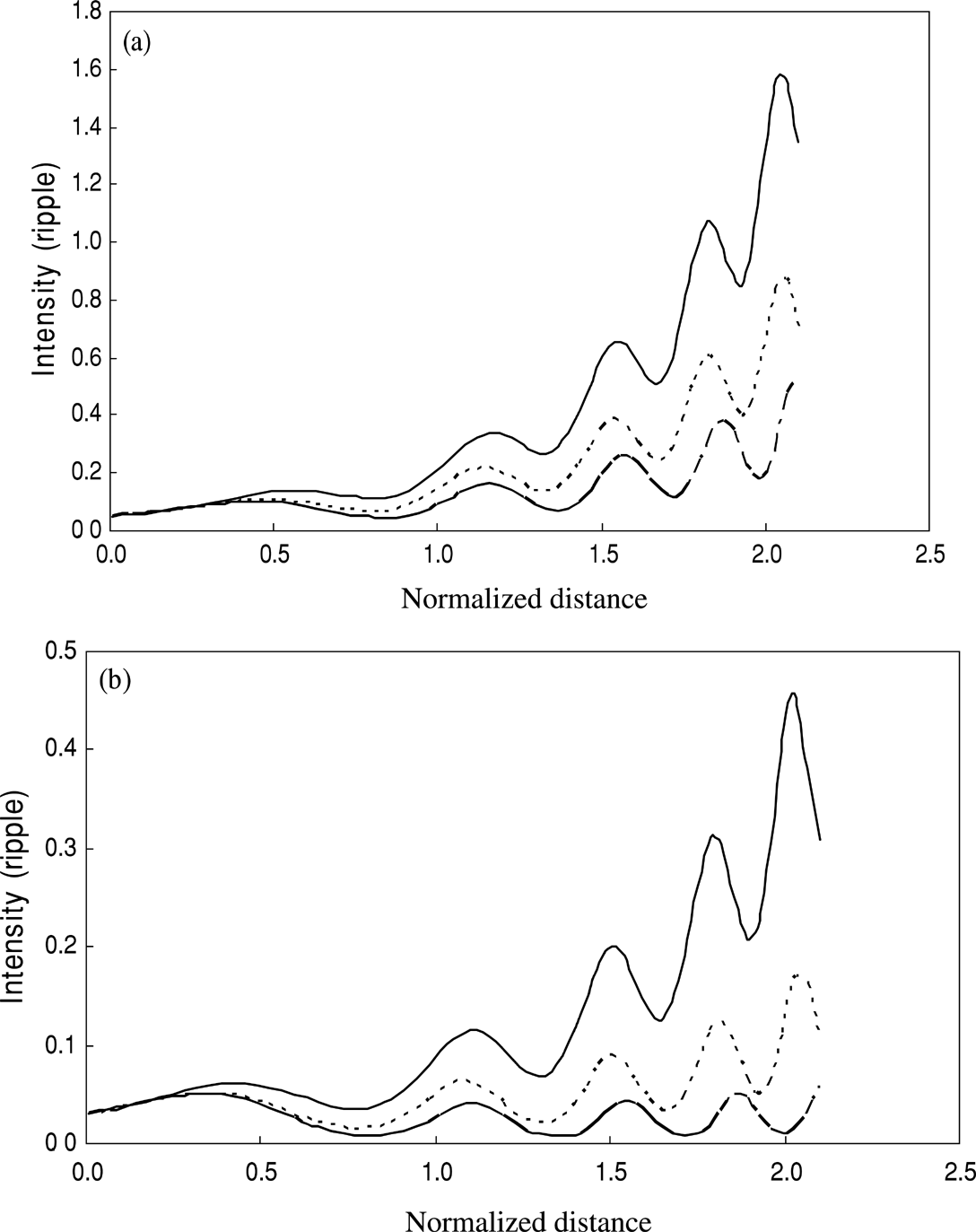
(a) Variation in intensity of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.5, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively. (b) Variation in intensity of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.8, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively.

To conclude, one of the important results to come out from the present analysis is that we can control the fluctuations on the first laser beam by increasing the power of the second laser beam. Similarly one can control the fluctuations on the second laser beam by increasing the intensity of first laser beam. The results are quite similar as in our previous study (Purohit et al., 2003); where the nonlinearity was due to pondermotive force, but both the effects occur at different time scales. Relativistic mutual interaction occurs at very short time scale, while nonlinearity due to pondermotive force occurs at long time scale. Moreover, due to the difference in the nonlinearity mechanism considered here and in our previous paper (Purohit et al., 2003), the growth rate ki is different and the threshold power (required for ripple to be self-focus) is also different. This study may be useful in understanding the mechanism of laser plasma coupling where filamentation process plays very important role. Specially, one can study the change in the magnitude of the plasma wave excited by beat wave process, when both the laser beams are having ripples present on them. Besides this we find that for the typical laser plasma parameters, ki Rd ≈ 14 (where Rd is Rayleigh length). Therefore, these studies may also be useful for beat wave excitation.

ACKNOWLEDGMENT

One of the authors, Mr. P.K. Chauhan, is grateful to the Indian Institute of Technology Delhi for providing the financial support.

References

REFERENCES

Akhamanov, S.A., Sukhorukov, A.P. & Khokhlov, R.V. (1968). Self-focusing and diffraction of light in nonlinear medium. Sov. Phys. Uspekhi 10, 609–635.CrossRefGoogle Scholar
Berger, R.L., Lasinski, B.F., Langdon, A.B., Kaiser, T.B., Afeyan, B.B., Cohen, B.I., Still, C.H. & Williams, E.A. (1995). Influence of spatial and temporal laser beam smoothing on stimulated Brillouin scattering in filamentarty laser light. Phys. Rev. Lett. 75, 1078.CrossRefGoogle Scholar
Blue, B.E., Clayton, C.E., O'Connell, C.L., Decker, F.J., Hogan, M.J., Huang, C., Iverson, R., Joshi, C., Katsouleas, T.C., Marsh, K.A., Mori, W.B. & Walz, D. (2003). Parametric exploration of intense positron beam-plasma interactions. Laser Part. Beams 21, 497–504.Google Scholar
Darrow, C., Umstadter, D., Katsouleas, T., Mori, W.B., Clayton, C.E. & Joshi, C. (1986). Saturation of beat-excited plasma waves by electrostatic mode coupling. Phys. Rev. Lett. 56, 2622–2632.CrossRefGoogle Scholar
Esarey, E., Ting, A. & Sprangle, P. (1988). Relativistic focusing and beat wave phase velocity control in plasma beat wave accelerator. Appl. Phys. Lett. 53, 1261–1268.Google Scholar
Gorbunov, L.M. & Kirsanov, V.I. (1987). Sov. Phys. JETP 66, 290.Google Scholar
Huller, S., Mounaix, Ph. & Pesme, D. (1996). Phys. Scr. T63, 151.Google Scholar
Huller, S., Mounaix, Ph., Pesme, D. & Tikhonchuk, V.T. (1997). Interaction of two neighboring laser beams taking in to account the effect of plasma hydrodynamics. Phys. Plasmas 4, 2670–2680.CrossRefGoogle Scholar
Joshi, C., Tajima, T., Dawson, J.M., Baldis, H.A. & Ebrahim, N.A. (1981). Forward Raman instability and electron acceleration. Phys. Rev. Lett. 47, 1285–1288.CrossRefGoogle Scholar
Katsouleas, T. & Dawson, J.M. (1983). Unlimited electron acceleration in laser driven plasma waves. Phys. Rev. Lett. 51, 392–395.CrossRefGoogle Scholar
Kitagawa, Y., Matsumoto, T., Minamihata, T., Sawai, K., Matsuo, K., Mima, K., Nishihara, K., Azechi, H., Tanaka, K.A., Tkaba, H. & Nakai, S. (1992). Beat wave excitation of plasma wave and observation of accelerated electron. Phys. Rev. Lett. 68, 48–51.CrossRefGoogle Scholar
Krall, J. (1993). Enhanced acceleration in a self modulated laser wake-field accelerator. Phys. Rev. A. 48, 2157–2161.Google Scholar
Manot, P. (1995). Experimental demonstration of relativistic self-channeling of a multi terawatt laser pulse in an under dense plasma. Phys. Rev. Lett. 74, 2953–2956.CrossRefGoogle Scholar
Mckinstrie, C.J. & Bingham, R. (1989). The modulation instability of coupled waves. Phys. Fluids B1, 230–237.CrossRefGoogle Scholar
Mckinstrie, C.J. & Russell, A. (1988). Nonlinear focusing of coupled waves. Phys. Rev. Lett 61, No.-21, 2929–2932.CrossRefGoogle Scholar
Mulser, P. & Bauer, D. (2004). Fast ignition of fusion pellets with super intense lasers: Concepts, problems, and prospective. Laser Part. Beams 22, 5–12.Google Scholar
Nakajima, K., Fisher, D., Kavakubo, T., Nakanishi, H., Ogata, A., Kato, Y., Kitagowa, Y., Kodama, P., Mima K., Sriraga, H., Suzuki, K., Yamakawa, K., Sakawa, Y., Shoji, T., Nishida, Y., Yugami, N., Downe, M., &Tajima, T. (1995). Observation of ultrahigh electron acceleration by a self modulated intense short laser pulse. Phys. Rev. Lett. 74, 4428–4431.CrossRefGoogle Scholar
Purohit, G., Pandey, H.D. & Sharma, R.P. (2003). Effect of cross focusing of two laser beams on the growth of laser ripple in plasma. Laser Part. Beams 21, 567–572.Google Scholar
Ren, C., Hemker, R.G., Fonseca, R.A., Duda, B.J. & Mori, W.B. (2000). Mutual interaction of laser beams: Braided light. Phys. Rev. Lett. 85, 2124–2127.CrossRefGoogle Scholar
Saini, N.S. & Gill, T.S. (2004). Enhanced Raman scattering of a rippled laser beam in a magnetized collisional plasma. Laser Part. Beams 22, 35–40.Google Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1976). Progress in Optics 13, 171, North–Holland Publishing Company–Amsterdam, Oxford.Google Scholar
Shukla, P.K., Rao, N.N., Yu, M.Y. & Tsintsadze, N.L. (1986). Relativistic non-linear effects in plasma. Phys. Report 138, 1–149.CrossRefGoogle Scholar
Sodha, M.S., Govind, Tewari, D.P., Sharma, R.P., &Kaushik, S.C. (1979). Excitation of a plasma wave by two coaxial Gaussian EM beams. J. Appl. Phys. 50(1), 158–164.CrossRefGoogle Scholar
Sprangle, P. & Esarey, E. (1991). Stimulated backscattered harmonic generation from intense laser interaction with beams and plasmas. Phys. Rev. Lett. 67, 2021–2024.CrossRefGoogle Scholar
Sprangle, P., Esarey, E., Krall, J. & Joyce, G. (1992). Propagation and guiding of intense laser pulse in plasmas. Phys. Rev. Lett. 69, 2200–2003.CrossRefGoogle Scholar
Sprangle, P., Esarey, E. & Tang, C.M. (1990). Phy. Rev. A 64, 2011.Google Scholar
Sprangle, P., Tang, C.M. & Esarey, E. (1987). IEEE Trans. Plasma Sci. 15, 145.CrossRefGoogle Scholar
Sprangle, P., Esarey, E., Ting, A. & Joyce, G. (1988). Laser wakefield acceleration and relativistic optical guiding. Appl. Phys. Lett. 53, 2146–2148.Google Scholar
Tajima, T. & Dawson, J.M. (1979). Laser electron accelerator. Phys. Rev. Lett. 43, 267–270.CrossRefGoogle Scholar
Toy, M.M. & Shen, Y.S. (1969). Phys. Rev. Lett. 22, 994.Google Scholar
Wyrtele, J.S. (1993). Advance accelerator Concepts, AIP, New York.Google Scholar
Figure 0

Variation of ki for the two beams with the power of the second laser beam (α2 E202) at z = 0. Solid line, dash line, dotted line and dash dotted line are for α1 E102 = 0.7, 1.0, 1.3, and, 1.5, respectively.

Figure 1

Variation of ki for the two beams with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively.

Figure 2

Variation of dimensionless beam width parameter (f) of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.5, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and, 2, respectively.

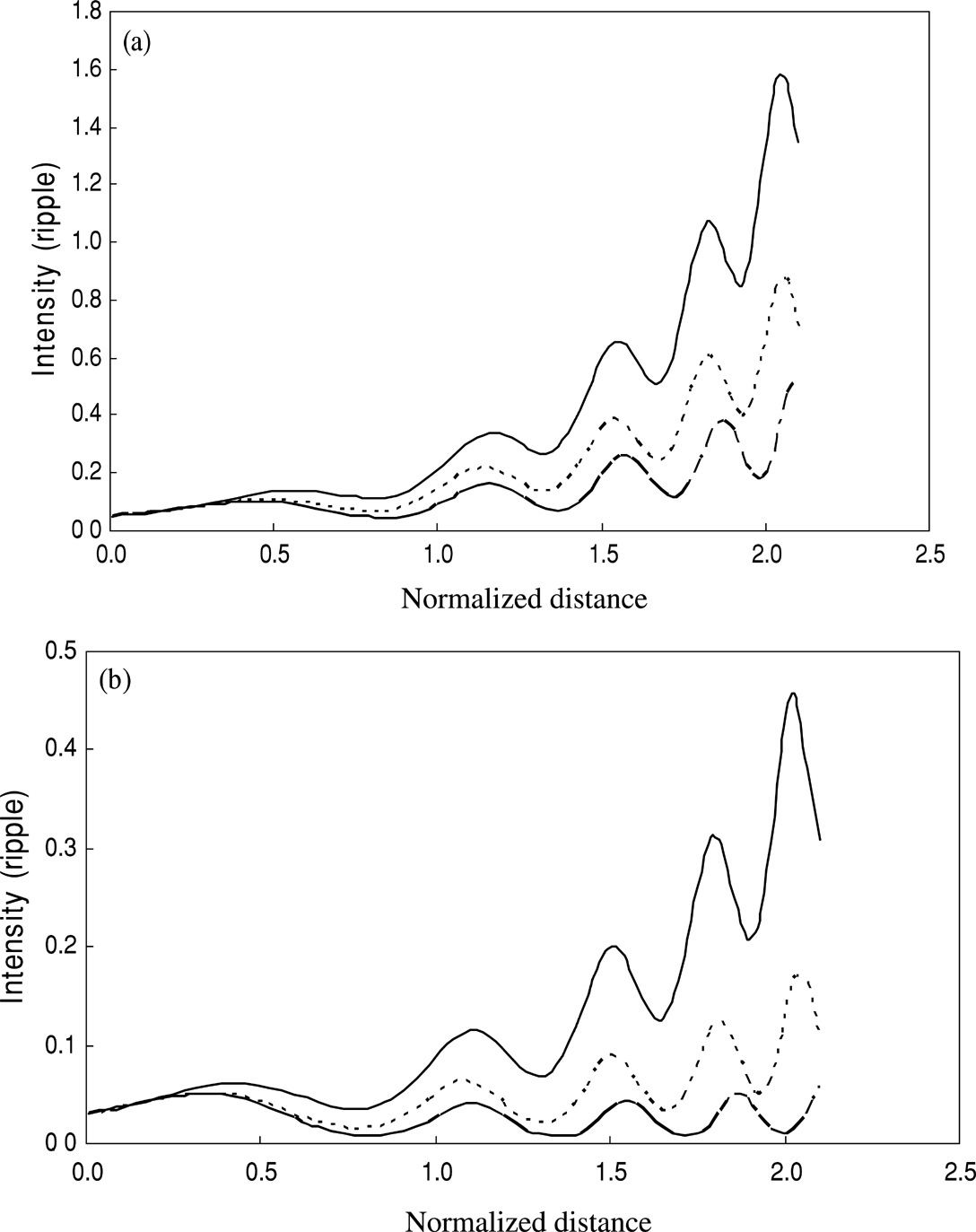
Figure 3

(a) Variation in intensity of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.5, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively. (b) Variation in intensity of the ripple with the normalized distance of propagation ξ (= zc/ω1 r102) for a fixed power of the first beam [α1 E102 = 0.7, n = 1.8, and 2φp = 3π/2] and different powers of the second beam. Solid line, dotted line and semi-dotted line are for α2 E202 = 1, 1.5, and 2, respectively.