Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T08:58:54.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Cross-focusing of two hollow Gaussian laser beams in plasmas

Published online by Cambridge University Press:  06 April 2011

Ruchika Gupta ,
Prerana Sharma ,
M. Rafat  and
R.P. Sharma
Ruchika Gupta*
Affiliation:
Department of Applied Sciences and Humanities, Jamia Millia Islamia, New Delhi, India
Prerana Sharma
Affiliation:
Government Ujjain Engineering College, Ujjain, Madhya Pradesh, India
M. Rafat
Affiliation:
Department of Applied Sciences and Humanities, Jamia Millia Islamia, New Delhi, India
R.P. Sharma
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi, India
*
Address correspondence and reprint requests to: Ruchika Gupta, Department of Applied Sciences and Humanities, Jamia Millia Islamia, New Delhi 110025, India. E-mail: ruchikaji81@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

This article presents the cross-focusing of two high power dark hollow Gaussian beams in plasma when relativistic nonlinearity is operative. A paraxial like approach has been used in the present analysis. In this study, the non-linear dielectric function has been expanded in terms of radial distance from the maximum of the irradiance, rather than from the axis, as is the case of Gaussian beams. The nature of propagation of a hollow Gaussian beam propagating in plasmas has been studied under the influence of relativistic non-linearity. The effect on the order (n) of hollow Gaussian beam on the cross-focusing of two beams has been explored in relativistic non-linearity in this publication.

Keywords

Cross-focusingHollow Gaussian beamLaser plasma interactionRelativistic nonlinearityRipple
Type
Research Article
Information
Laser and Particle Beams , Volume 29 , Issue 2 , June 2011 , pp. 227 - 230
Copyright
Copyright © Cambridge University Press 2011

1. INTRODUCTION

The interaction of laser beams with plasmas has gained a lot of interest worldwide because of its relevance to laser fusion (Imasaki & Li, Reference Imasaki and Li2009; Sullivan & Von Rosenberg, Reference Sullivan and Von Rosenberg1986) and charged particle acceleration (Giulietti et al., Reference Giulietti, Galimberti, Giulietti, Gizzi, Labate and Tomassini2005; Ogata & Nakajima, Reference Ogata and Nakajima1998; Kumar et al., Reference Kumar, Gupta and Sharma2006). In laser induced fusion, the most interesting phase is the efficient coupling of the laser beam to plasma to heat the latter. Hence in this process of coupling, many nonlinear processes such as, stimulated Raman scattering (Tajima et al., 1979), stimulated Brillioun scattering (Sharma & Kourakis, 2010), filamentation (Nicholas & Sajjadi, Reference Nicholas and Sajjadi1989) or hot spot formation and self-focusing (Sodha et al., Reference Sodha, Khanna and Tripathi1974d; Gill et al., Reference Gill, Mahajan and Kaur2010) play a vital role. Out of many non-linear processes in the laser-plasma interaction the phenomena of self-focusing (Sprangle et al., 1991; Hora, Reference Hora1991; Kruer, Reference Kruer1974; Sodha et al., Reference Sodha, Tripathi and Ghatak1976) is of notable attention to the physicists. It is so because of the fact that the non-linear effects are highly sensitive to the irradiance distribution along the wavefront of the beam, which is appreciably affected by self-focusing.

In recent studies, the intensity distribution has been taken in the form of zero central intensity called the dark hollow beams (DHBs), because beam dynamics depend on the non-linear propagation which is sensitive to transverse intensity distribution of the main beam. Various methods have been developed to generate DHBs such as Laguerre-Gaussian beams, high-order Bessel-Gaussian beams, high-order Mathieu beams, doughnut hollow beams, LP01-mode output hollow beam, localized hollow beams, and so on. This is the family of special light beams or DHBs (Yin et al., Reference Yin, Noh, Lee, Kim, Wang and Jhe1997). DHBs have some unique physical properties, such as a barrel-shaped intensity distribution, a helical wavefront, and center phase singularity, and may carry spin and orbital angular momentum and exhibit nondiffracting behavior on propagation. DHBs may be used as optical pipes, optical tweezers and spanners, and have become a powerful tool in the manipulation and control of microscopic particles (such as micrometer-sized particles, nanometer-sized particles, biological cells, and so on). Therefore, they have many important and extensive applications in laser optics, binary optics, computer-generated holography, optical trapping of particles, materials science, biological and medical sciences, and so on. They also provide a powerful tool to study the linear and non-linear particle dynamics (Patil et al., Reference Patil, Takale, Navare and Dongare2010) in a storage ring. (Hechenberg et al., Reference Heckenberg, McDuff, Smith and White1992). Several novel DHBs have been realized by various techniques like the transverse mode selection method, the geometrical optical method, the computer-generated hologram, and spatial filtering methods. The physical interpretation for DHBs have been given by various theoretical methods like higher-order Bessel beams, high-order Mathieu beams, TEM01 mode doughnut hollow beam. A DHB is designed in general as a ringed shaped light beam with null intensity center on the beam axis. A review of the literature throws light on the fact that the propagation characteristics of DHBs in a plasma or other non-linear media have not been studied to a significant extent; but to a good extent the beam propagation in the TEM10 mode has been done in plasma for regions around the axis and the maximum of irradiance, in the geometrical optics approximation (Sodha et al., 1974b, Reference Sodha, Tripathi and Ghatak1976).

The laser beam is influenced by the presence of another laser beam. One can control the focusing/ defocusing of laser beams by choosing the parameters of another beam. This behavior is known as a cross-focusing of the laser beams. Therefore, we have considered in the present paper the effect on laser beam dynamics in the cross-focusing of two laser beams where the two initial beams are having DHB distribution. The study of the cross-focusing of the laser beams having DHB distribution in relativistic nonlinearity has not been carried out so far. In this study, the authors have attempted to extend the understanding to cross focusing of dark cylindrical hollow Gaussian beams (DHGBs), where the irradiance along the axis is zero, and the maximum is away from the axis. Although the cylindrical geometry has certain limitations, but some of the interesting effects (Feit & Fleck, Reference Ffeit and Fleck1988; Johnston et al., Reference Johnston, Vidal and Fre'chette1997; Vidal & Johnston, Reference Vidal and Johnston1996) given by detailed numerical simulation like the breaking up into a number of beams cannot be tracked in cylindrical symmetry. So it is restricted for beams with powers above the critical value. However, since cylindrical beams are commonly used, a theory for cylindrical beams (even approximate) is in order. Taking the relativistic non-linearity (Sharma & Kourakis, Reference Sharma and Kourakis2010) into account, the present work is based on the modified approach followed by Sodha and Kourakis (2010). This paper investigates some of the interesting facts about the cross- focusing of the hollow Gaussian laser beams in the relativistic regime.

Fig. 1. (Color online) Illustrates the plot between dimensionless distance of propagation and the dimensionless beam width parameter with different orders of HGB.

2. CROSS-FOCUSING OF THE HOLLOW GAUSSIAN BEAMS (HGBS)

Consider the propagation of two coaxial Gaussian laser beams of frequencies ω 1 and ω 2 along the z direction. In a steady state, the electric field vector E 1,2 for such a beam may be expressed in a cylindrical coordinate system with azimuthal symmetry as

(1)
\left(E \right)_{Z=0}={\hat j} E_{1\comma 2} \left({r\comma \; z} \right)\exp \left({i{\rm \omega} _{1\comma 2} t} \right)\comma \; \eqno\lpar 1\rpar

where

(2)
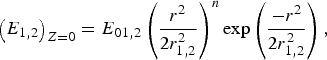
\left(E_{1\comma 2} \right)_{Z=0}=E_{01\comma 2} \left({r^2 } \over {2r_{1\comma 2}^2 } \right)^n \exp \left(- {r^2 } \over {2r_{1\comma 2}^2 } \right)\comma\eqno\lpar 2\rpar

where E 1,2 refers to the complex amplitude of the HGB of initial beam width r 1,2, E 01,2 is a real constant characterizing the amplitude of the HGB, n is the order of the HGB and a positive integer, characterizing the shape of the HGB and position of its irradiance maximum, ω 1,2 is the wave frequency, ${\hat j}$ is the unit vector along the y axis and E 01,2denotes the electric field maximum at $r_{10}=r_{20}=r_{\max}=r_{0}\sqrt{2n}$, corresponding to z = 0. For n = 0, Eq. (2) represents a fundamental Gaussian beam of width r 1,2; however, the interest of the present investigation lies in higher order HGBs (i.e., n > 0).

The electric field vector E 1,2 satisfies the wave equation (stationary frame),

(3)
\nabla ^2 E_{1\comma 2} - \nabla \left(\nabla .E_{1\comma 2} \right)+{{\rm \varepsilon} _{1\comma 2} \left({r\comma \; z} \right)\over c^2 }{\partial ^2 E_{1\comma 2} \over \partial t^2 }=0\comma \; \eqno\lpar 3\rpar

where ɛ 1,2is the effective dielectric function of the plasma and c is the speed of light in free space.

For transverse beams, the second term in Eq. (3) is zero. One can thus write the wave equation for the electromagnetic beam as,

(4)
\nabla ^2 E_{1\comma 2}+\left({\rm \omega} _{1\comma 2}^2 / {c^2 } \right){\rm \varepsilon} _{1\comma 2} \left({r\comma \; z} \right)E_{1\comma 2}=0.\eqno\lpar 4\rpar

Following Akhmanov et al. (Reference Akhmanov, Sukhorukov and Khokhlov1968) and Sodha et al. (Reference Sodha, Ghatak and Tripathi1974a, Reference Sodha, Tripathi and Ghatak1976), the solution of Eq. (4) can be shown as,

(5)
E_{1\comma 2} \left({r\comma \; z} \right)=jA_{1\comma 2} \left({r\comma \; z} \right)\exp \left({ - i\vint\! k_{1\comma 2} \left(z \right)dz } \right)\comma \; \eqno\lpar 5\rpar

where A 1,2 (r,z) is the complex amplitude of the electric field $E_{1\comma 2}\comma \; k_{1\comma 2}\left(z\right)={{\rm \omega} \over c} \sqrt{{\rm \varepsilon} _{0}\left(z\right)\comma \; {\rm \varepsilon} _{0}\left(z\right)}$ is the dielectric function, equivalent to the highest electric field on the wavefront of the HGB (Eq. (11)).

Substituting E 1,2 (r,z) from Eq. (5) into Eq. (4) and neglecting the term $\partial^2A_{1\comma 2}/ \partial z^2$, one obtains,

(6)
2ik_{1\comma 2} {\partial A_{1\comma 2} \over \partial z} + iA_{1\comma 2} {\partial k_{1\comma 2} \over \partial z} = \left({\partial ^2 A_{1\comma 2} \over \partial r^2 } + {1 \over r} {\partial A_{1\comma 2} \over \partial r} \right)+ {{\rm \omega} _{1\comma 2}^2 \over k_{1\comma 2} c^2 }\left({\rm \varepsilon} - {\rm \varepsilon}_0 \right).\eqno\lpar 6\rpar

The complex amplitude A 1,2(r,z) may be expressed as,

(7)
A_{1\comma 2} \left({r\comma \; z} \right)= A_{01\comma 2} \left({r\comma \; z} \right)\exp \left(- ik_{1\comma 2} \left(z \right)S_{1\comma 2} \left({r\comma \; z} \right)\right)\comma \; \eqno\lpar 7\rpar

where S 1,2(r,z) is the eikonal associated with the HGB. Now putting Eq. (7) into Eq. (6) and segregating the real and imaginary parts of the resulting equation, we get,

(8)
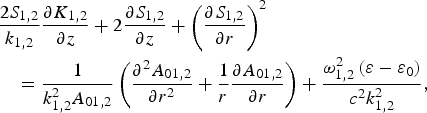
\eqalign{&{2S_{1\comma 2} \over k_{1\comma 2}} {\partial K_{1\comma 2} \over \partial z} + 2{\partial S_{1\comma 2} \over \partial z} + \left({\partial S_{1\comma 2} \over \partial r} \right)^2 \cr & \quad = {1 \over k_{1\comma 2}^2 A_{01\comma 2}} \left({\partial ^2 A_{01\comma 2} \over \partial r^2 } + {1 \over r} {\partial A_{01\comma 2} \over \partial r} \right)+ {{\rm \omega}_{1\comma 2}^2 \left({\rm \varepsilon} - {\rm \varepsilon} _0 \right)\over c^2 k_{1\comma 2}^2 }\comma \; } \eqno \lpar 8\rpar

and

(9)
\eqalign{&{\partial A_{01\comma 2}^2 \over \partial z} + A_{01\comma 2}^2 \left({\partial ^2 S_{1\comma 2} \over \partial r^2 } + {1 \over r} {\partial S_{1\comma 2} \over \partial r} \right)+ {\partial A_{01\comma 2}^2 \over \partial r} {\partial S_{1\comma 2} \over \partial r} \cr & \quad + {A_{01\comma 2}^2 \over k_{1\comma 2}} {\partial k_{1\comma 2} \over \partial z} = 0.} \eqno\lpar 9\rpar

To move further, one can adopt an approach, analogous to the paraxial approximation. Thus one may start with, expressing Eq. (8) and Eq. (9) in terms of variables η and z, as,

(10)
{\rm \eta} = \left[\left(r / r_{1\comma 2} f \right)- \sqrt {2n} \right]\eqno\lpar 10\rpar

r 1,2 (z) is the width of the beam, and $r = r_{1\comma 2}\;f \sqrt{2n}$ is the position of the maximum irradiance for the propagating beam. Since the irradiance of the beam is a function of r and z only, expansions of expressions for relevant parameters made along r, near the irradiance maximum via $r = r_{1\comma 2}\;f\lpar z\rpar \sqrt{2n}$, are certainly justified in the paraxial like approximation; for n = 0 (Gaussian beam ), the expansion is made (likewise) around r = 0(as usual). In the present analysis, the condition ${\rm \eta} \ll \sqrt {2n}$ is strictly applicable just like the paraxial theory. Therefore, we get the following using Eqs. (8), (9), and (10):

(11)
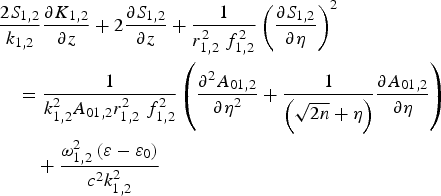
\eqalign{&{2S_{1\comma 2} \over k_{1\comma 2}} {\partial K_{1\comma 2} \over \partial z} + 2{\partial S_{1\comma 2} \over \partial z} + {1 \over r_{1\comma 2}^2 \;f_{1\comma 2}^2} \left({\partial S_{1\comma 2} \over \partial {\rm \eta} } \right)^2 \cr & \quad = {1 \over k_{1\comma 2}^2 A_{01\comma 2} r_{1\comma 2}^2\; f_{1\comma 2}^2 }\left({\partial ^2 A_{01\comma 2} \over \partial {\rm \eta} ^2 } + {1 \over \left({\sqrt {2n}+{\rm \eta} } \right)} {\partial A_{01\comma 2} \over \partial {\rm \eta}} \right) \cr &\quad\quad+ {{\rm \omega}_{1\comma 2}^2 \left({\rm \varepsilon} - {\rm \varepsilon}_0 \right)\over c^2 k_{1\comma 2}^2 }}\eqno\lpar 11\rpar

and

(12)
\eqalign{&{\partial A_{01\comma 2}^2 \over \partial z} + {A_{01\comma 2}^2 \over r_{1\comma 2}^2 f_{1\comma 2}^2}\left({\partial ^2 S_{1\comma 2} \over \partial {\rm \eta} ^2} + {1 \over \left(\sqrt {2n}+{\rm \eta} \right)} {\partial S_{1\comma 2} \over \partial {\rm \eta}} \right) \cr & \quad + {1 \over r_{1\comma 2}^2 f_{1\comma 2}^2} {\partial A_{01\comma 2}^2 \over \partial {\rm \eta} } {\partial S_{1\comma 2} \over \partial {\rm \eta}} + {A_{01\comma 2}^2 \over k_{1\comma 2}} {\partial k_{1\comma 2} \over \partial z} = 0.} \eqno\lpar 12\rpar

In the paraxial like approximation, the relevant parameters (i.e., the dielectric function ɛ(r,z), eikonal and irradiance) may be expanded around the maximum of the HGB, i.e., around η = 0. Thus, one can express the dielectric function ɛ(η,z) around the maximum (η = 0)of the HGB as

(13)
{\rm \varepsilon} \left({\rm \eta}\comma \; z \right)= {\rm \varepsilon}_0 \left(z \right)- {\rm \eta} ^2 {\rm \varepsilon}_2 \left(z \right)\comma \; \eqno\lpar 13\rpar

where ɛ 0(z) and ɛ2(z) are the coefficients associated with η 0and η 2 in the expansion of ɛ(η,z)around η = 0. Putting Eq. (13) into Eqs. (11) and (12) we get,

(14)
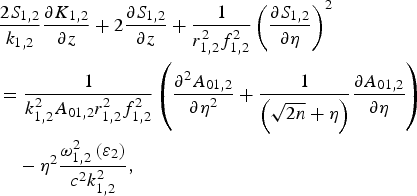
\eqalign{&{2S_{1\comma 2} \over k_{1\comma 2}} {\partial K_{1\comma 2} \over \partial z} + 2{\partial S_{1\comma 2} \over \partial z} + {1 \over r_{1\comma 2}^2 f_{1\comma 2}^2}\left({\partial S_{1\comma 2} \over \partial {\rm \eta}} \right)^2 \cr & = {1 \over k_{1\comma 2}^2 A_{01\comma 2} r_{1\comma 2}^2 f_{1\comma 2}^2}\left({\partial ^2 A_{01\comma 2} \over \partial {\rm \eta} ^2} + {1 \over \left(\sqrt {2n} + {\rm \eta} \right)} {\partial A_{01\comma 2} \over \partial {\rm \eta} } \right)\cr & \quad - {\rm \eta} ^2 {{\rm \omega} _{1\comma 2}^2 \left({{\rm \varepsilon} _2 } \right)\over c^2 k_{1\comma 2}^2}\comma \; } \eqno\lpar 14\rpar
(15)
\eqalign{&{\partial A_{01\comma 2}^2 \over \partial z} + {A_{01\comma 2}^2 \over r_{1\comma 2}^2 f_{1\comma 2}^2}\left({\partial ^2 S_{1\comma 2} \over \partial {\rm \eta} ^2} + {1 \over \left(\sqrt {2n} + {\rm \eta} \right)} {\partial S_{1\comma 2} \over \partial {\rm \eta} } \right)\cr & \quad + {1 \over r_{1\comma 2}^2 f_{1\comma 2}^2 } {\partial A_{01\comma 2}^2 \over \partial {\rm \eta} } {\partial S_{1\comma 2} \over \partial {\rm \eta}} + {A_{01\comma 2}^2 \over k_{1\comma 2}} {\partial k_{1\comma 2} \over \partial z} = 0.}\eqno\lpar 15\rpar

One can express the solution of Eq. (15), under the paraxial approximation ${\rm \eta} \ll \sqrt {2 n}$ as

(16)
A_{01\comma 2}^2 = {E_{1\comma 2}^2 \over 2^{2n} f_{1\comma 2}^2}\left(\sqrt {2n} + {\rm \eta} \right)^{4n} \exp \left(- \left(\sqrt {2n} + {\rm \eta} \right)^2 \right)\comma \; \eqno\lpar 16\rpar

with

(17)
S_{1\comma 2} \left({\rm \eta}\comma \; z \right)= {\left(\sqrt {2n} + {\rm \eta} \right)^2 \over 2}\beta \left(z \right)+ \varphi \left(z \right)\comma \; \eqno\lpar 17\rpar

where

\beta \left(z \right)= r_{1\comma 2}^2 f_{1\comma 2} {df_{1\comma 2} \over {dz}}\comma \;
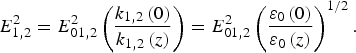
E_{1\comma 2}^2 = E_{01\comma 2}^2 \left({k_{1\comma 2} \left(0 \right)\over k_{1\comma 2} \left(z \right)} \right)= E_{01\comma 2}^2 \left({{\rm \varepsilon} _0 \left(0 \right)\over {\rm \varepsilon} _0 \left(z \right)} \right)^{1/2}.

Here ϕ(z) is an arbitrary function of z, and f 1,2(z)is the beam width parameter for the HGB. Most of the power of the beam is concentrated in the region aroundη = 0. There is certainly some power of the beam beyond this limitation, which is accounted for in an approximate manner by Eq. (16). Also, it tells that the nature of the r dependence is not affected by the change with propagation. Hence, power is conserved as the beam propagates.

Substituting from Eq. (16) and (17) into A 01,22 and S 1,2 into Eq. (14) and equating the coefficients of η 0and η 2on both sides of the resulting equation, one obtains

(18)
{\rm \varepsilon}_0 f_{1\comma 2} {d^2 f_{1\comma 2} \over d \xi ^2} = \left({4 \over f_{1\comma 2}^2 } - \rho_0^2 {\rm \varepsilon}_2\right)\comma \; \eqno\lpar 18\rpar

where ξ = (c/r 02ω)z is the dimensionless distance of propagation, ρ0 = (r 0ω/c) is the dimensionless initial beam width.

3. CONCLUSION AND DISCUSSION

The results of the present analysis may be appreciated through the numerical computation of the critical curve and the variation of the beam width parameter f with dimensionless distance of propagation ξ, for a chosen set of parameters for relativistic non-linearity. The computations have also been made to find the dependence of the beam width parameter associated with the propagation of the hollow Gaussian beam, on the dimensionless distance of propagation ξ in homogeneous plasmas. One can see from Eq. (2) that the radius of the bright ring increases when the order n of the HGB increases, this implies that the area of the dark region across the HGB increases as n increases. In conclusion, we have derived the focusing equation for two hollow gaussian laser beams interacting with each other in the cylindrical coordinate system. It is interesting to compare the propagation characteristics of the HGBs to those of the fundamental Gaussian beam. It is seen that the HGBs also exhibit three regions in the ρ0 - ∏0 space which follow a nature similar to that in the case of the Gaussian beam. The regions for self-focusing and steady divergence occupy larger areas while the oscillatory divergence becomes narrower with respect to the Gaussian beam in ρ0 - ∏0 space for higher order HGBs. The nature of the critical curve involves that self-focusing is more pronounced for lower orders of low power HGBs, while the trend just reverses for high power of the beam.

References

REFERENCES

Akhmanov, S.A., Sukhorukov, A.P. & Khokhlov, R.V. (1968). Self-focusing and diffraction of light in a non linear medium. Sov. Phys. Usp. 10, 609–636.CrossRefGoogle Scholar
Ffeit, M.D. & Fleck, J.A. Jr (1988). Beam non-paraxiality, filament formation and beam breakup in the self-focusing of optical beams. Opt. Soc. Am. B 5, 633–640.Google Scholar
Gill, T.S., Mahajan, R. & Kaur, R. (2010). Relativistic & Ponderomotive effects on evolution of dark hollow Gaussian electromagnetic beams in a plasma. Laser Part. Beams 28, 521–529.Google Scholar
Giulietti, D., Galimberti, M., Giulietti, A., Gizzi, L.A., Labate, L. & Tomassini, P. (2005). The laser-matter interaction meets the high energy physics: Laser-plasma accelerators and bright X/γ-ray source. Laser Part. Beams 23, 309–314.Google Scholar
Heckenberg, N.R., McDuff, R., Smith, C.P., White, A.G. (1992). Nonlinear rotation of 3D dark spatial solitons in a Gaussian laser beam. Opt. Lett. 17, 221.CrossRefGoogle Scholar
Hora, H. (1991). Plasmas at High Temperature and Density. Heidelberg: Springer.Google Scholar
Imasaki, K. & Li, D. (2009). Feasibility of new Laser Fusion by intense Laser Field. Laser Part. Beams 27, 273–279.Google Scholar
Johnston, T.W., Vidal, F. & Fre'chette, D. (1997). Laser plasma filamentation and spatially periodic non linear Schrodinger equation approximation. Phys. Plasmas 4, 1582–1588.CrossRefGoogle Scholar
Kruer, W.L. (1974). The physics of Laser Plasma Interaction. New York: Additison-Wesley.Google Scholar
Kumar, A., Gupta, M.K. & Sharma, R.P. (2006). Effect of ultra intense laser pulse on the propagation of electron plasma wave in relativistic and ponderomotive regime and particle acceleration. Laser Part. Beams 24, 403–409.Google Scholar
Nicholas, D.J. & Sajjadi, S.G. (1989). The effect of light filamentation on uniformity of energy deposition in laser plasmas. J. Plasma Phys. 41, 209–218.Google Scholar
Ogata, A. & Nakajima, K. (1998). Recent progress and perspectives of laser-plasma accelerators. Laser Part. Beams 16, 381–396.Google Scholar
Patil, S.D., Takale, M.V., Navare, S.T. & Dongare, M.B. (2010). Focusing of Hermite-cosh-Gaussian laser beams in collisionless magnetoplasma. Laser Part. Beams 28, 343–349.Google Scholar
Sharma, A. & Kourakis, I. (2010). Spatial evolution of a q-Gaussian Laser beam in relativistic Plasma. Laser Part. Beams 28, 479–489.Google Scholar
Sodha, M.S., Ghatak, A.K. & Tripathi, V.K. (1974a). Self-focusing of Laser Beams in Dielectrics, Semiconductors and Plasmas. Delhi: Tata-Mc Graw-Hill.Google Scholar
Sodha, M.S., Khanna, R.K. & Tripathi, V.K. (1974). The Self-focusing of electromagnetic beams in a strongly ionized magnetoplasma. J. Phys. D: Appl. Phys. 7, 2188.CrossRefGoogle Scholar
Sodha, M.S., Tripathi, V.K. & Ghatak, A.K. (1976). Self-focusing of laser beams in plasmas and semiconductors. Prog. Opt. 13, 169–265.CrossRefGoogle Scholar
Sparangle, P. & Esarey, E. (1991). Stimulated backscattered harmonic generation from intense laser interactions with beams and plasmas. Phys. Rev. Lett. 67, 2021–2024.Google Scholar
Sullivan, J.A. & Von Rosenberg, C.W. (1986). High energy Krypton fluoride amplifiers for laser-induced fusion. Laser Part. Beams 4, 91–105.Google Scholar
Tajmania, T. & Dawson, J.M. (1979). Experiments and simulations of tunnel-ionized plasmas. Phys. Rev. 46, 1091–1105.Google Scholar
Vidal, F. & Johnston, T.W. (1996). Electromagnetic beam breakup: Multi filaments, single beam equilibriya and radiation. Phys. Rev. Lett. 77, 1282–1285.CrossRefGoogle Scholar
Yin, J., Noh, H., Lee, K., Kim, K., Wang, Y. & Jhe, W. (1997). Generation of a dark hollow beam by a small hollow fiber. Opt. Commun. 138, 287.CrossRefGoogle Scholar
Figure 0

Fig. 1. (Color online) Illustrates the plot between dimensionless distance of propagation and the dimensionless beam width parameter with different orders of HGB.