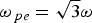1. INTRODUCTION
The interaction of intense short pulse laser with atomic clusters (Krainov & Smirnov, Reference Krainov and Smirnov2002; Ditmire et al., Reference Ditmire, Springate, Tisch, Shao, Mason, Hay, Marangos and Hutchinson1998; Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996; Reference Ditmire, Smith, Tisch and Hutchinision1997; Reference Ditmire, Zweiback, Yanovsky, Cowan, Hays and Wharton1999; Milchberg et al., Reference Milchberg, Mcnaught and Parra2001; Shokri et al., Reference Shokri, Niknam and Krainov2004; Mishra et al., Reference Mishra, Holkundkar and Gupta2011; Kanapathipillai et al., Reference Kanapathipillai2004, Kumar et al., Reference Kumar and Tripathi2013; Mulser et al., Reference Mulser, Kanapathipillai and Hoffmann2005) has become an important area of research with wide ranging applications from harmonic generation (Tiwari & Tripathi, Reference Tiwari and Tripathi2006; Shim et al., Reference Shim, Hays, Zgadzaj, Ditmire and Downer2007; Huillier & Balcou, Reference Huillier and Balcou1993; Para et al., Reference Para, Alexeev, Fan, Kim, Mcnaught and Milchberg2000) and X-ray generation (Shao et al., Reference Shao, Ditmire, Tisch, Springate, Marangos and Hutchinson1996; Liu et al., Reference Liu, Dong, Peng, Jin and Zhang2009; Fukuda et al., Reference Fukuda, Akahane, Aoyama, Inoue, Ueda, Kishimoto, Yamakawa, Faenov, Magunov, Pikuz, Skobelev, Abdallah, Csanak, Boldarev and Gasilov2004; Jha et al., Reference Jha, Mathur and Krishnamurthy2008; Kumarappan et al., Reference Kumarappan, Krishnamurthy, Mathur and Tribedi2001) to energetic neutron production (Ditmire et al., Reference Ditmire, Donnelly, Falcone and Perry1995; Hegelich et al., Reference Hegelich, Albright, Cobble, Flippo, Letzring, Paffett, Ruhl, Schreiber, Schulze and Fernandez2006). The clusters (Hagena & Obert, Reference Hagena and Obert1972) are the Vander-walls bonded assemblies of about 102–107 atoms that are formed during rapid cooling of supersonic gas flowing out of a nozzle. The cluster can be considered as small spherical balls of nanometer dimension, whose radius is much smaller than laser wavelength. The main characteristic of a gaseous cluster is the near solid density inside the cluster that results in an enhanced absorption of laser energy via collisional processes and consequently in an increase of X-ray conversion efficiency. This results in efficient generation of incoherent short wavelength light for application such as extreme ultraviolet (EUV) lithography, EUV and X-ray microscopy, and X-ray tomography.
The X-ray emission spectrum (Dorchies et al., Reference Dorchies, Blasco, Bonté, Caillaud, Fourment and Peyrusse2008; Mocek et al., Reference Mocek, Kim, Shin, Lee, Cha, Hong and Nam2002; Deiss et al., Reference Deiss, Rohringer and Burgdorfer2006; Smirnov & Becker, Reference Smirnov and Becker2006; Kumar & Tripathi, Reference Kumar and Tripathi2009; Issac et al., Reference Issac, Wirthig, Brunetti, Vieux, Ersfeld, Jamison, Jones, Bingham, Clark and Jaroszynski2003; Sailja et al., Reference Sailja, Khan, Naik and Gupta2005) is obtained from clusters irradiated by a femtosecond laser pulse. One can see a continuous Bremsstrahlung emission, and three different spectral structures identified as the K-shell emission, corresponding to transitions from the L, M, N-shells down to the K-shell. The nano-plasma model proposed first by Ditmire et al. (Reference Ditmire, Donnelly, Rubenchik, Falcone and Perry1996) and improved by Milchberg et al. (Reference Milchberg, Mcnaught and Parra2001) shows, that the laser absorption is enhanced during the cluster expansion when the electron density approaches thrice the critical density 
${\rm \omega} = {\rm \omega}_{\,pe} /\sqrt{3}$. Ditmire et al. (Reference Ditmire, Donnelly, Falcone and Perry1995) have reported that the enhanced absorption of laser by the clusters results in the production of high ion charge states via collisional ionization giving strong X-ray emission from the hot plasma. Dorchies et al. (Reference Dorchies, Blasco, Bonté, Caillaud, Fourment and Peyrusse2008) have reported the experimental evidence of sub-picosecond X-ray bursts produced by laser-cluster interaction in the multi-KeV range. The theoretical understanding of X-ray emission from clustered gases in these studies is primarily based on uniform laser intensity model. Kumar and Tripathi (Reference Kumar and Tripathi2009) have recently developed a theory of Rayleigh scattering of an intense laser, with Gaussian temporal and radial profiles, from expanding clusters.
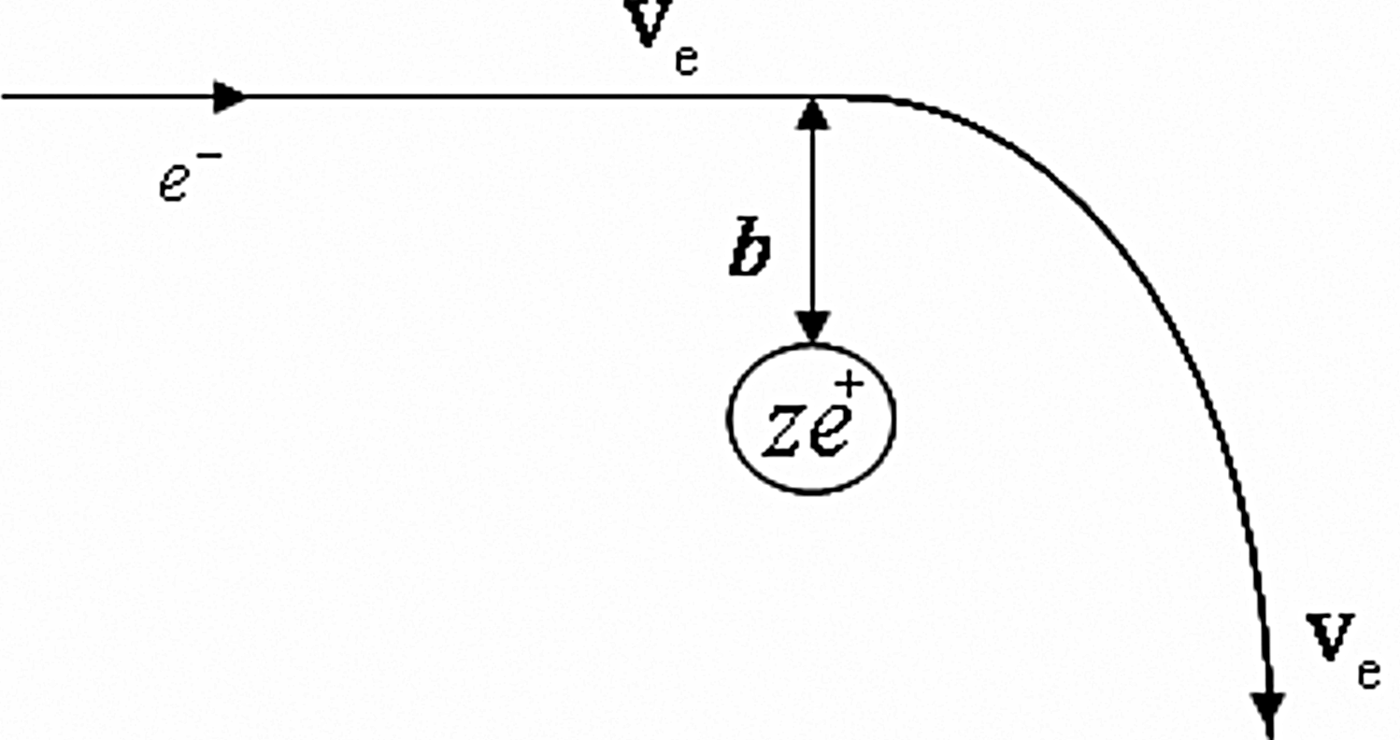
In this paper, we develop a theoretical model of cluster heating and X-ray emission by intense short pulse Gaussian laser beam. The physics of the problem is as follows. The laser quickly ionizes all the atoms of the clusters converting them into plasma balls and also heats the electrons inside them. The heating is faster on the laser axis and slower as one move radially away. The heated clusters expand on sub-picosecond time scale and their electron density decreases. As the plasma frequency approaches plasma resonance, 
${\rm \omega}_{\,pe} = \sqrt{3} {\rm \omega}$, electron temperature rises sharply. The free electrons get accelerated and emit radiation in the X-ray regime, when they pass through the vicinity of positive ions (Fig. 1). The sharp rise in X-ray emission rate is first expected from clusters in the axial region. However, when the cluster electron plasma frequency falls below the plasma resonance, the emission rate should slow down due to reduction in the rate of Bremstrahlung encounters. In Section 2, we calculate laser induced cluster heating and expansion. In Section 3, we study the Bremsstrahlung X-ray emission. In Section 4, we discuss the results.
Fig. 1. Schematic of the Bremsstrahlung process.
2. CLUSTER HEATING AND EXPANSION
Consider a gas jet target embedded with clusters of initial radius r c0 and density n c. Each cluster has free electron density n e0 inside it. A Gaussian laser beam is launched into it with electric field
$$\vec{E}_L = \hat{x}A_L \lpar z\comma \; t\rpar \exp \lpar \!\!- i\lpar {\rm \omega} t - kz\rpar \rpar \comma$$
where A L2 = A L02 exp(−r 2/r 02) exp(−(t − z/c)2/τL2) and magnetic field 
$\vec{B} = \lpar \vec{k} \times \vec{E}/{\rm \omega}\rpar $. We ignore the effects of diffraction and nonlinear refraction. The laser quickly ionizes all the atoms of the clusters converting them into plasma balls with overlapping electron and ion spheres. The electron sphere oscillates in the 
$\hat{x}$ direction due to the laser field. At any instant, the center of electron cloud is shifted by a distance Δ with respect to the center of the ion sphere. The equation of motion for the cluster electrons is
$$m\displaystyle{d^2 \Delta \over dt^2} = - \displaystyle{{\rm \omega}_{\,pe}^2\, m\Delta \over 3} - eE_L - m{\rm \nu} \displaystyle{d\Delta \over dt}\comma$$where ωpe = (4πn ee 2/m)1/2 is the cluster electron plasma frequency and −e, m, v, and n e are the electronic charge, mass, electron-ion collision frequency, and modified electron density (due to cluster expansion). The oscillatory velocity of the cluster electrons may be written as
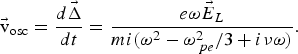$$\vec{\rm v}_{\rm osc} = \displaystyle{d\vec{\Delta} \over dt} = \displaystyle{e{\rm \omega} \vec{E}_L \over mi\lpar {\rm \omega}^2 - {\rm \omega}_{\,pe}^2 /3 + i{\rm \nu} {\rm \omega}\rpar }.$$The laser heats the electrons at an average rate
$$\displaystyle{d \over dt} \left[3T_e /2 \right]= - \lpar e/2\rpar \vec{E}_L^{\ast} . \vec{\rm v}_{\rm osc}\comma \;$$where the energy loss rate via collisions has been ignored which, is valid when pulse duration is shorter than the energy relaxation time. Following Kumar and Tripathi (Reference Kumar and Tripathi2009), we take ν = ν0 (T e/T 0)−3/2 and define ξ = T e/T 0, τ = ν0t′, t′ = (t − z/c), and write the temperature equation as,
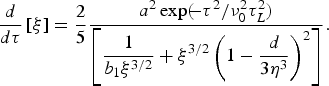$$\displaystyle{d \over d{\rm \tau}} \left[{\rm \xi} \right]= \displaystyle{2 \over 5} \displaystyle{a^2 \exp \lpar \!\!- {\rm \tau}^2 /{\rm \nu}_0^2 {\rm \tau}_L^2 \rpar \over \left[\displaystyle{1 \over b_1 {\rm \xi}^{3/2}} + {\rm \xi}^{3/2} \left(1 - \displaystyle{d \over 3{\rm \eta}^3} \right)^2 \right]}.$$where a 2 = a 02 exp (−r 2/r 02), a 02 = e 2A L02/3mω2T 0, b 1 = ω2/ν02, d = ωpe02/ω2, η = r c/r c0, r c is the modified cluster radius (due to expansion) and T 0 is the normalizing temperature. If one takes the expansion of cluster to be adiabatic, one must add a cooling term to Eq. (4). For adiabatic expansion in the absence of heating, T eV γ−1 = const., where V = 4π r c3 /3 is the volume of the cluster and γ is the ratio of specific heats, one may write,
$$\displaystyle{dT_e \over dt} = - \displaystyle{T_e \lpar {\rm \gamma} - 1\rpar \over V} \displaystyle{dV \over dt} = - \displaystyle{3T_e \lpar {\rm \gamma} - 1\rpar \over r_c} \displaystyle{dr_c \over dt}.$$For γ = 5/3. The rate of temperature decrease due to the cluster expansion is
$$\displaystyle{dT_e \over dt} = - 2\displaystyle{T_e \over r_c} \displaystyle{dr_c \over dt}.$$With this cooling rate Eq. (4) can be written as,
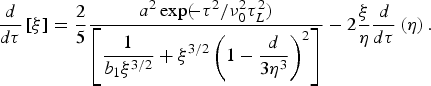$$\displaystyle{d \over d{\rm \tau}} \left[{\rm \xi} \right]= \displaystyle{2 \over 5} \displaystyle{a^2 \exp \lpar \!\!- {\rm \tau} ^2 /{\rm \nu}_0^2 {\rm \tau}_L^2\rpar \over \left[\displaystyle{1 \over b_1 {\rm \xi}^{3/2}} + {\rm \xi}^{3/2} \left(1 - \displaystyle{d \over 3{\rm \eta}^3} \right)^2 \right]} - 2\displaystyle{{\rm \xi} \over {\rm \eta}} \displaystyle{d \over d{\rm \tau}} \left({\rm \eta} \right).$$As a cluster gets heated, its radius r c expands with sound velocity (dr c/dt) = (T e/m i)1/2,
where m i is the mass of the ion. Defining vs0 = (T 0 /m i)1/2, η = r c/r c0, g = vs0/r c0ν0, we may write
$$\displaystyle{d \over d{\rm \tau}} \lpar {\rm \eta} \rpar = \lpar {\rm \xi} \rpar ^{1/2} g.$$ As the radius increases, plasma frequency decreases, keeping ωpe2r c3= constant, i.e., ωpe2r c3 = ωpe02r co3, where ωp0 is the value of ωpe at t = 0. Thus, ωpe2 = ωpe02 /η3. Eqs. (7)–(8) are coupled in ξ and η and can be solved numerically. One may note (cf. Kumar & Tripathi, Reference Kumar and Tripathi2009) that the heating rate rises sharply when the electron density in the cluster approaches three times that of the critical density, i.e., 
${\rm \omega}_{\,pe} = \sqrt{3} {\rm \omega}$. The timing of resonance would depend on the radial location of the cluster besides its size and ion mass. In Figures 2 and 3, we have plotted the variation of electron temperature and cluster radius with time for clusters located at r/r 0 = 0.1,1 when the parameters are: a 0 = 1, b = 105, d = 5, g = 0.3 and ν02τL2 = 1. One may note that initially the cluster radius expands slowly. As the plasma resonance is reached it rises sharply. The clusters near the axis expand more quickly and plasma resonance occurs earlier in time. For the off axis clusters, the laser field is weak and clusters expand slowly, taking longer time to reach the resonance.
Fig. 2. (Color online) Normalized temperature of cluster electrons (T e/T 0) as a function of normalized time (τ = ν0t′) for a 0 = 1.0 at radial locations.
Fig. 3. (Color online) Normalized cluster radius (r c /r c0) as a function of normalized time (τ = ν0t′) for the different values of radial locations at normalized axial laser amplitude a 0 = 1.0.
3. BREMSSTRAHLUNG X-RAY EMISSION
The free electrons of a cluster when pass through the vicinity of ions with initial velocity ve and impact parameter b get accelerated and emit radiation in the X-ray regime. The energy radiated by the electron, using the Larmor's formula (Jackson, Reference Jackson1962; Liu & Tripathi, Reference Liu and Tripathi1994; Landau & Lifshitz, Reference Landau and Lifshitz1975) is
$$U = \displaystyle{2 \over 3} \displaystyle{e^2 a_c^2 {\rm \tau}_c \over c^3} = \displaystyle{4 \over 3} \displaystyle{Ze^6 \over m^2 c^3 b^3 {\rm v}_{\rm e}}\comma$$where τc = 2b/ve is the collision time of the electron with the ion, a c = Ze 2/mb 2 is the maximum acceleration suffered by the electrons, Z is the ion charge state, and c is the speed of light. In the Bremsstrahlung process (Fig. 1) the acceleration is the function of time. For the frequency spectrum of the emitted radiation, it is necessary to Fourier analysis of the acceleration
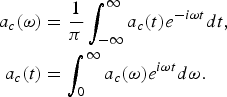$$\eqalign{a_c \lpar {\rm \omega} \rpar &= \displaystyle{1 \over {\rm \pi} } \int\nolimits_{ - \infty}^{\infty} a_c \lpar t\rpar e^{ - i{\rm \omega} t} dt\comma \; \cr a_c \lpar t\rpar &= \int\nolimits_0^{\infty} a_c \lpar {\rm \omega} \rpar e^{i{\rm \omega} t} d{\rm \omega}.}$$Using the Parseval's formula
$$\int\nolimits_{- \infty}^{\infty} \left[a_c \lpar t\rpar \right]^2 dt = {\rm \pi} \int\nolimits_0^{\infty} \left\vert a_c \lpar {\rm \omega}\rpar \right\vert^2 d{\rm \omega}.$$The energy emitted as the electron passes by the ion is
$$U\lpar {\rm \omega} \rpar = \int\nolimits_{ - \infty}^{\infty} P\lpar t\rpar = \displaystyle{2e^2 \over 3c^3} \int\nolimits_{ - \infty}^{\infty} \left[a_c \lpar t\rpar \right]^2 dt = \displaystyle{2{\rm \pi} e^2 \over 3c^3} \int\nolimits_0^{\infty} \left\vert a_c \lpar {\rm \omega}\rpar \right\vert^2 d{\rm \omega}.$$The two components of acceleration are;
$$\eqalign{a_{cx} \lpar t\rpar &= \displaystyle{Ze^2 \over m} \displaystyle{{\rm v}_{\rm e} t \over \left(b^2 - \lpar {\rm v}_{\rm e} t\rpar ^2 \right)^{3/2}}\comma \; \cr a_{cz} \lpar t\rpar &= \displaystyle{{Ze^2 } \over m}\displaystyle{{\rm b} \over {\left({b^2 - \lpar {\rm v}_{\rm e} t\rpar ^2 } \right)^{3/2} }}.}$$Their Fourier Transforms are:
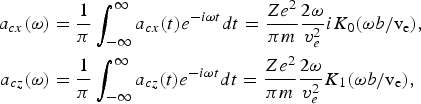$$\eqalign{a_{cx} \lpar {\rm \omega}\rpar &= \displaystyle{1 \over {\rm \pi}} \int\nolimits_{ - \infty}^{\infty} a_{cx} \lpar t\rpar e^{ - i{\rm \omega} t} dt = \displaystyle{Ze^2 \over {\rm \pi} m} \displaystyle{2{\rm \omega} \over v_e^2} iK_0 \lpar {\rm \omega} b/{\rm v}_{\rm e}\rpar \comma \; \cr a_{cz} \lpar {\rm \omega}\rpar &= \displaystyle{1 \over {\rm \pi}} \int\nolimits_{ - \infty}^{\infty} a_{cz} \lpar t\rpar e^{ - i{\rm \omega} t} dt = \displaystyle{Ze^2 \over {\rm \pi} m} \displaystyle{2{\rm \omega} \over v_e^2} K_1 \lpar {\rm \omega} b/{\rm v}_{\rm e}\rpar \comma \; }$$where K 0(ωb/ve) and K 1(ωb/ve) are the modified Bessel functions of argument (ωb/ve). Using these expressions in Eq. (10) we get
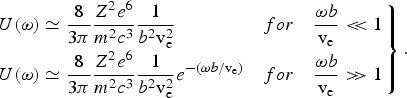$$\left. \matrix{U\lpar {\rm \omega} \rpar \simeq \displaystyle{8 \over 3{\rm \pi}} \displaystyle{Z^2 e^6 \over m^2 c^3} \displaystyle{1 \over b^2 {\rm v}_{\rm e}^{\rm 2}}\hfill &for \hfill &\displaystyle{{\rm \omega} b \over {\rm v}_{\rm e}} \lt\!\! \lt 1 \hfill \cr U\lpar {\rm \omega} \rpar \simeq \displaystyle{8 \over 3{\rm \pi}} \displaystyle{Z^2 e^6 \over m^2 c^3} \displaystyle{1 \over b^2 {\rm v}_{\rm e}^{\rm 2}} e^{ - \lpar {\rm \omega} b/{\rm v}_{\rm e}\rpar } \hfill &for \hfill &\displaystyle{{\rm \omega} b \over {\rm v}_{\rm e}} \gt\!\! \gt 1 \hfill} \right\}.$$The number of electron ion collisions per unit time with impact parameter ranging from b to b + db is n ive2πbdb. Hence, the power radiated per electron is
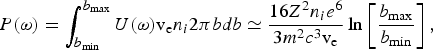$$P\lpar {\rm \omega}\rpar = \int_{b_{\min}}^{b_{\max}} U\lpar {\rm \omega} \rpar {\rm v}_{\rm e} n_i 2{\rm \pi} bdb \simeq \displaystyle{16Z^2 n_i e^6 \over 3m^2 c^3 {\rm v}_{\rm e}} \ln \left[\displaystyle{b_{\max} \over b_{\min}} \right]\comma$$
where b max ≈ (ve /ω) and 
$b_{\min }=\lpar \hbar /m{\rm v}_{\rm e}\rpar $. The contribution to the frequency comes ω only from those electrons that have velocity 
${\rm v}_{\rm e} \gt \lpar 2\hbar {\rm \omega} /{\rm m}\rpar ^{1/2}$. If we consider the electron velocity distribution function to be Maxwellian,
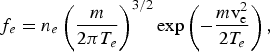$$\,f_e = n_e \left(\displaystyle{m \over 2{\rm \pi} T_e} \right)^{3/2} \exp \left(- \displaystyle{m{\rm v}_{\rm e}^{\rm 2} \over 2T_e} \right)\comma \;$$The total power radiated per unit frequency interval per unit volume is
$$\eqalign{P_B \lpar {\rm \omega} \rpar &= \int\nolimits_{\lpar 2\hbar {\rm \omega} /m\rpar ^{1/2}}^{\infty} Pf_e 4{\rm \pi} {\rm v}_{\rm e}^{\rm 2} d{\rm v}_{\rm e} \simeq \int\nolimits_{\lpar 2\hbar {\rm \omega} /m\rpar ^{1/2}}^{\infty} \displaystyle{64{\rm \pi} Z^2 n_i e^6 \over 3m^2 c^3} \cr &\quad \times {\rm v}_{\rm e} n_e \left(\displaystyle{m \over 2{\rm \pi} T_e} \right)^{3/2} \exp \lpar \!\!- m{\rm v}_{\rm e}^{\rm 2} /2T_e\rpar d{\rm v}_{\rm e}.}$$After solving the above equation we get
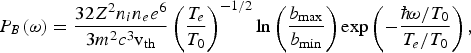$$\eqalign{P_B \lpar {\rm \omega} \rpar &= \displaystyle{32Z^2 n_i n_e e^6 \over 3m^2 c^3 {\rm v}_{\rm th}} \left(\displaystyle{T_e \over T_0} \right)^{ - 1/2} \ln \left(\displaystyle{b_{\max} \over b_{\min}} \right) \exp \left(- \displaystyle{\hbar \!{\rm \omega} /T_0 \over T_e /T_0} \right)\comma}$$where vth = (2T 0/m)1/2 is the thermal velocity of electrons and n eis the density of electrons. The total power radiated per unit frequency interval due to the clusters in
plasma channel of length L is
$$P_B^T \lpar {\rm \omega}\rpar = \int\nolimits_0^{\infty} \int\nolimits_0^L \displaystyle{4{\rm \pi} r_c^3 n_c \over 3} P_B 2{\rm \pi} rdrdz\comma$$For deuterium cluster Z = 1, n e = n i, Eq. (15) gives
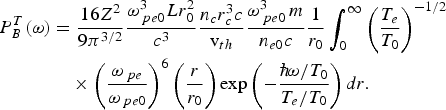$$\eqalign{P_B^T \lpar {\rm \omega} \rpar &= \displaystyle{16Z^2 \over 9{\rm \pi}^{3/2}} \displaystyle{{\rm \omega}_{\,pe0}^3 Lr_0^2 \over c^3} \displaystyle{n_c r_c^3 c \over {\rm v}_{th}} \displaystyle{{\rm \omega}_{\,pe0}^3\, m \over n_{e0} c} \displaystyle{1 \over r_0} \int\nolimits_0^{\infty} \left(\displaystyle{T_e \over T_0} \right)^{ - 1/2}\cr &\quad \times \left(\displaystyle{{\rm \omega}_{\,pe} \over {\rm \omega}_{\,pe0}} \right)^6 \left(\displaystyle{r \over r_0} \right)\exp \left(- \displaystyle{\hbar\! {\rm \omega} /T_0 \over T_e /T_0} \right)dr.}$$We may normalize Eq. (16) by the factor (mωpe03/n e0c), then we get
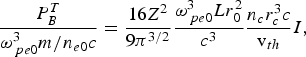$$\displaystyle{P_B^T \over {\rm \omega}_{\,pe0}^3 m/n_{e0} c} = \displaystyle{16Z^2 \over 9{\rm \pi} ^{3/2}} \displaystyle{{\rm \omega}_{\,pe0}^3 Lr_0^2 \over c^3} \displaystyle{n_c r_c^3 c \over {\rm v}_{th}} I\comma$$where
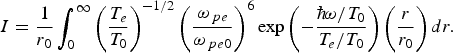$$I = \displaystyle{1 \over r_0} \int\nolimits_0^{\infty} \left(\displaystyle{T_e \over T_0} \right)^{ - 1/2} \left(\displaystyle{{\rm \omega}_{\,pe} \over {\rm \omega}_{\,pe0}} \right)^6 \exp \left(- \displaystyle{\hbar\! {\rm \omega} /T_0 \over T_e /T_0} \right)\left(\displaystyle{r \over r_0} \right)dr.$$ The integrand in I has explicit dependence on r/r 0. Implicit dependence on r/r 0 comes through cluster electron temperature and cluster electron plasma frequency. We have solved Eq. (17) numerically for the following parameters: a 0 = 1 r c0 = 10−6cm, n c = 1013/cm 3, r 0 = 10−2cm, vth = 107 cm/sec, ωpe0 = 5 × 1015 rad/sec, L = 0.01cm, c = 3 × 1010cm/sec, 
$\hbar {\rm \omega} /T_0=10$. Figure 4 shows the variation of the normalized total X-ray emission by the clusters (P BT/(mωpe03 /n e0c)) as a function of normalized time (τ = ν0t′). It shows rapid raise in X-ray emission at τ ~ 0.6. The emission attains a maximum at τ = 0.8 and then falls off. Figure 5 shows the spectrum of Bremsstrahlung X-ray radiation. The spectrum falls off exponentially at frequency 
$\hbar \!{\rm \omega}\gt\!\!\! \gt T_e$. Initially, X-ray emission rises slowly but rises resonantly when 
${\rm \omega} = {\rm \omega}_{\,pe} /\sqrt{3}$. After a while, when cluster expansion detunes the plasma resonance, X-ray emission falls off. At any given instant of time the total X-ray emission comes from all the clusters at the different radial locations. The plasma resonance first occurs in clusters at laser axis. However, their number is small; hence enhancement in X-ray emission rate is small. As the plasma resonance layer 
$\lpar{\rm \omega} = {\rm \omega}_{\,pe} /\sqrt{3}$) moves to high value of (r/r 0), the number of resonantly heated electrons goes up and the net value of Bremsstrahlung X-ray emission rate is enhanced.
Fig. 4. (Color online) Normalized total X-ray emission by all clusters (P BT /(mωpe03 /n e0c)) as a function of normalized time (τ = ν0t′) for a 0 = 1.0 and 
$\hbar {\rm \omega} /T_0 = 10$.
Fig. 5. (Color online) Bremsstrahlung soft X-ray spectrum of the emitted radiation.
4. DISCUSSION
The laser heated clusters emit X-rays via Bremsstrahlung process. When a Gaussian laser beam interacts with clusters, laser quickly ionizes all the atoms of cluster and electrons are set free in the cluster. These free electrons of a cluster when pass through the vicinity of ions get accelerated and emit radiation in the X-ray regime. The electrons in the cluster acquire energy and oscillate in the laser field. Due to electron-ion collision the cluster gets heated and begins to expand under hydrodynamic pressure. The heating rate of the cluster electrons is maximum on the axis and decreases away from the axis. As the clusters expand under hydrodynamic pressure, plasma frequency of the cluster electrons ωpe decreases. As a consequence, clusters in the axial region expand more rapidly and approach plasma resonance 
${\rm \omega}_{\,pe} = \sqrt{3} {\rm \omega}$ quickly, whereas the clusters at the larger r/r 0 attain the resonance at the later times. At any given instant of time the total X-ray emission comes to all the clusters at the different radial locations. As the plasma resonance layer move to high values of r/r 0, the number of resonantly heated electrons goes up and the net values of X-ray emission rate is enhanced. When the plasma frequency of cluster electrons falls down below the plasma resonance, the emission rate slows down due to reduction in the rate of Bremstrahlung encounters. The X-ray emission peak has a finite temporal width, of the order of the characteristic cluster expansion time (r c0/vs0) (n e/n cr)1/3. The X-ray emission peak thus turns out to be after order of picosecond, which is comparable to the time width of the peak of X- ray emission, reported by Ditmire et al. for the Argon and Xenon clusters. For the high cluster densities and longer plasma length absorption may become important.
ACKNOWLEDGMENTS
The authors are grateful to Prof. V. K. Tripathi, IIT Delhi for fruitful discussions. M. K. is thankful to the Strong Field Science (TIFR), India for financial support.
