Introduction
The excitation of collective modes in plasmas by beating intense electromagnetic beams has been studied extensively over the years (Tajima and Dawson, Reference Tajima and Dawson1979; Joshi et al., Reference Joshi, Mori, Katsouleas, Dawson, Kindel and Forslund1984; Clayton et al., Reference Clayton, Marsh, Dyson, Everett, Lal, Leemans, Williams and Joshi1993; Krall et al., Reference Krall, Ting, Esarey and Sprangle1993). The plasma waves excited by such schemes have proven useful for electron acceleration up to ultra-relativistic energies (Liu and Tripathi, Reference Liu and Tripathi1994; Nakajima et al., Reference Nakajima, Fisher, Kawakubo, Nakanishi, Ogata, Kato, Kitagawa, Kodama, Mima, Shiraga, Suzuki, Yamakawa, Zhang, Sakawa, Shoji, Nishida, Yugami, Downer and Tajima1995; Esarey et al., Reference Esarey, Sprangle, Krall and Krall1996; Ting et al., Reference Ting, Moorei, Krushelnick, Manka, Esarey, Sprangle, Hubbard, Burris, Fischer and Baine1997; Jarwal et al., Reference Jarwal, Sharma and Tripathi1999). In tokomak, radio frequency wave driven space charge modes are used for current drive, plasma heating, and diagnostics (Liu and Tripathi, Reference Liu and Tripathi1986).
The efficiency of mode coupling processes is significantly influenced by the presence of plasma density ripple. Experimental and analytical studies have demonstrated resonant enhancement in the efficiency of second and third harmonic generation and terahertz generation due to density ripples (Parashar and Pandey, Reference Parashar and Pandey1992; Liu and Tripathi, Reference Liu and Tripathi2008; Kumar and Tripathi, Reference Kumar and Tripathi2012. Vijay and Tripathi (Reference Vijay and Tripathi2016) found density ripple to be effective in laser beat frequency heating of unmagnetized plasma. Malik et al. (Reference Malik, Uma and Kumar2017) have reported resonant enhancement in two color laser excitation of terahertz radiation due to a density ripple.
In this paper, we study the beat frequency heating of a magnetized plasma in the presence of a density ripple. The magnetic field introduces cyclotron damping as an effective route to energy deposition where finite Larmor radius effects could also play a role. We employ two collinear lasers, with frequency difference near the electron cyclotron frequency, propagating along the static magnetic field but transverse to ripple wave vector. The beat frequency ponderomotive force by the laser drives an electrostatic Bernstein quasi-mode (Kumar and Tripathi, Reference Kumar and Tripathi2010). The mode is cyclotron damped on electrons and gives rise to strong electron heating. We employ fluid theory to obtain electron response to lasers and Vlasov theory to obtain the response of magnetized electrons at the beat frequency, including finite Larmor radius effects.
In Section “Excitation of Bernstein quasi-mode”, we deduce the beat frequency electric field produced by two collinear lasers in a rippled density plasma. In Section “Anomalous heating”, we obtain the anomalous heating rate of electrons and study the rise in electron temperature. In Section “Discussion”, we discuss the results.
Excitation of Bernstein quasi-mode
Consider a magnetized plasma of electron density n 0, electron temperature T e, and ambient magnetic field 
$\mathop B\nolimits_{\rm s} \hat{z}$. The plasma has a density ripple,
$$n_0 = n_0^0 + n_q$$
$$n_q = n_{q_0}e^{iqx}$$Two collinear lasers propagate through the plasma along the magnetic field (Fig. 1),
$$\vec{E}_j = \hat{x}A_je^{-i({\rm \omega} _jt-k_jz)},{\rm} \,j = 1,2$$
where ω1 − ω2 ≈ ωc, ω1 − ω2 ≫ ωp, ωc k 1 ≈ (ω1/c), k 2 ≈ (ω2/c), ωp = (n 0e 2/mε0)1/2 is the plasma frequency, ωc = eB s/m is the electron cyclotron frequency, -e and m are the electron charge and mass, and ε0 is the free space permittivity. The lasers impart oscillatory velocities to electrons 
$\vec{v}_1 = ((e\vec{E}_1)/(im{\rm \omega} _1))$, 
$\vec{v}_2 = ((e\vec{E}_2)/(im{\rm \omega} _2))$ and exert a ponderomotive force on them at ω = ω1 − ω2, 
$(k_1-k_2)\hat{z}$,
$$F_{{\rm p}z} = \displaystyle{{e\partial {\rm \phi} _{\rm p}} \over {\partial z}}$$where
$${\rm \phi} _{\rm p} = \displaystyle{{A_1A_2e} \over {\mathop {m{\rm \omega}} \nolimits_1 \mathop {\rm \omega} \nolimits_2}} e^{-i\lsqb {\lpar {{\rm \omega}_1-{\rm \omega}_2} \rpar t-\lpar {k_1-k_2} \rpar z} \rsqb }$$
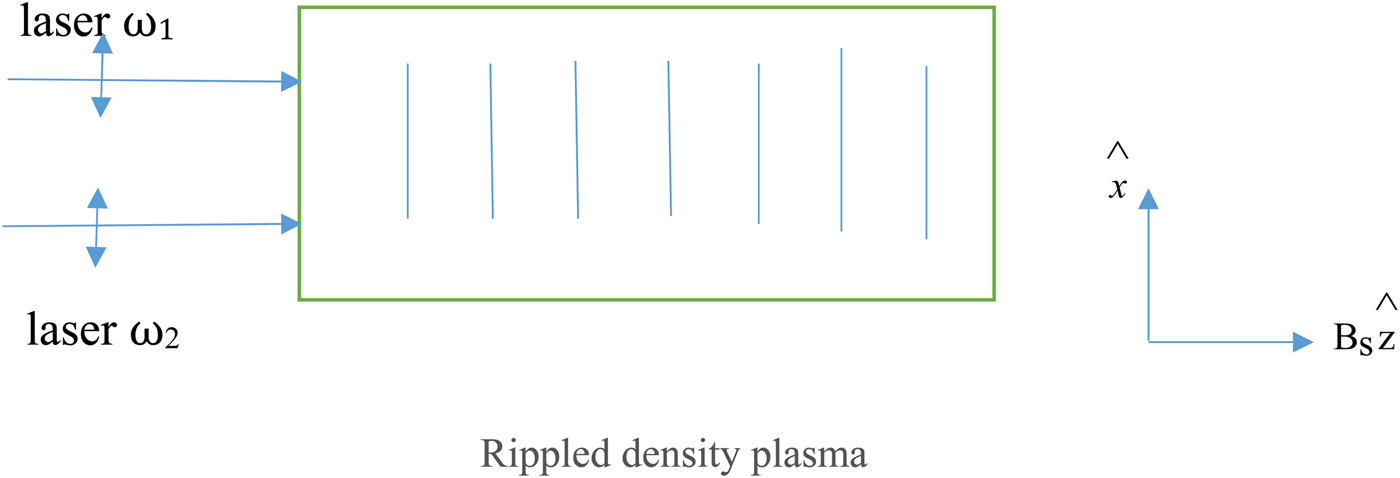
Fig. 1. Schematic of laser beat wave heating of electrons in rippled density plasma in the presence of a parallel static magnetic field.
The ponderomotive force creates a velocity perturbation
$$v_{{\rm \omega} z}^{{\rm NL}} = -\displaystyle{{F_{{\rm p}z}} \over {m_i\lpar {\mathop {\rm \omega} \nolimits_1 -\mathop {\rm \omega} \nolimits_2} \rpar }}$$ which beats with the density ripple n q to produce nonlinear density perturbation 
$n_{{\rm \omega}, k}^{{\rm NL}} $ at ω = ω1 − ω2, 
$\vec{k} = (k_1-k_2)\hat{z} + q\hat{x}$. Following Vijay and Tripathi (Reference Vijay and Tripathi2016), one may write
$$n_{{\rm \omega}, k}^{{\rm NL}} = -\displaystyle{{k_zn_qek_z{\rm \phi} _{\rm p}} \over {2{\rm \omega} m^2}}$$ The nonlinear density perturbation 
$n_{{\rm \omega}, k}^{{\rm NL}} $, produces space charge potential ϕ ω,k. This potential produces self-consistent electron density perturbation 
$n_{{\rm \omega}, k}^{\rm L} $, called linear density perturbation. Following Vlasov theory one may write 
$n_{{\rm \omega}, k}^{\rm L} $ in terms of ϕ ω,k and electron susceptibility χ e as
$${\rm \chi} _{\rm e} = \displaystyle{{2{\rm \omega} _{\rm p}^2} \over {k^2v_{{\rm th}}^2}} \left[ {1 + \displaystyle{{\rm \omega} \over {k_zv_{{\rm th}}}}\mathop {\mathop \sum \limits_l Z\left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_zv_{{\rm th}}}}} \right)I_l(b)e^{-b}}\limits_{}} \right]$$
where I l is the modified Bessel function of order l and argument 
$b = k_\bot ^2 v_{{\rm th}}^{\rm 2} /2{\rm \omega} _{\rm c}^2 $, v th = (2T e/m)1/2 is the electron thermal velocity, and ⊥ refers to the component perpendicular to magnetic field. From the Poisson's equation (assuming ions to be immobile),
$$\nabla ^2{\rm \phi} _{{\rm \omega}, k} = \displaystyle{e \over {{\rm \varepsilon} _0}}\lpar {n_{{\rm \omega}, k}^{\rm L} + n_{{\rm \omega}, k}^{{\rm NL}}} \rpar $$we obtain
$${\rm \phi} _{{\rm \omega}, k} = -\displaystyle{e \over {{\rm \varepsilon} _0k}}\left[ {\displaystyle{{k{\rm \varepsilon}_0{\rm \chi}_{\rm e}} \over e}{\rm \phi}_{{\rm \omega}, k}-\displaystyle{{k_zn_qe} \over {2m{\rm \omega}^2}}{\rm \phi}_{\rm p}} \right]\; \; $$
$${\rm \phi} _{{\rm \omega}, k} = {\rm \phi} _{\rm p}\displaystyle{{{\rm \chi} _{\rm e}} \over {\rm \varepsilon}}, $$where ε = 1 + χ e is the plasma permittivity.
The electric field at ω, k produced by the beating of lasers, is
$$\vec{E}_{{\rm \omega}, k} = -\nabla {\rm \phi} _{{\rm \omega}, k}$$
$$\vec{E}_{{\rm \omega}, k} = -\displaystyle{{ie} \over {\in _0\lpar {1 + {\rm \chi}_{\rm e}} \rpar }}\left( {\displaystyle{{k_zn_qe} \over {2m{\rm \omega}^2}}} \right){\rm \phi} _{\rm p}$$This field is large when permittivity ε(ω, k) = 1 + χ e is small, i.e., the ω, k mode is a quasi-Bernstein mode.
Anomalous heating
The beat wave driven space charge field heats the electrons. The time average heating rate per unit volume is given by
$$H = {\mathop{\rm Re}\nolimits} [-(1/2)n_0^0 e\vec{E}_{{\rm \omega}, k}^{^\ast} \cdot \vec{v}_{{\rm \omega}, k}]$$
where 
$\vec{v}_{{\rm \omega}, k}$ is the electron velocity due to 
$\vec{E}_{{\rm \omega}, k}$.
To obtain 
$\vec{v}_{{\rm \omega}, k}$ we solve the Vlasov equation for electrons,
$$\displaystyle{{\partial f} \over {\partial t}} + \overrightarrow v \cdot \nabla f-e\lpar {{\vec{E}}_{{\rm \omega}, k} + \overrightarrow v \times \mathop B\nolimits_{\rm s} \hat{z}} \rpar \cdot \displaystyle{{\partial f} \over {\partial \overrightarrow v}} = 0$$ In equilibrium 
$f = \mathop f\nolimits_0 $ which we take to be Maxwellian
$$f_0 = n_0\left( {\displaystyle{m \over {2{\rm \pi} T_{\rm e}}}} \right)^{3/2}e^{-v_\bot ^2 /v_{{\rm th}}^2} e^{-v_z^2 /v_{{\rm th}}^2} $$and
$$(J_{l + 1}(x) + J_{l-1}(x)) = \displaystyle{{2l} \over x}J_l(x)$$ Following Kumar and Tripathi (Reference Kumar and Tripathi2010), we expand f as 
$\mathop f\nolimits_0 + \mathop f\nolimits_1 $ and linearize the Vlasov equation, we obtain
$$f_1 = -\displaystyle{{e{\rm \phi}} \over {T_{\rm e}}}f_0\mathop \sum \limits_{l^{\prime}} J_l\left( {\displaystyle{{k_\bot v_\bot} \over {{\rm \omega}_{\rm c}}}} \right)J_{l^{\prime}}\left( {\displaystyle{{k_\bot v_\bot} \over {{\rm \omega}_{\rm c}}}} \right)\displaystyle{{l{\rm \omega} _{\rm c} + k_zv_z} \over {{\rm \omega} -l{\rm \omega} _{\rm c}-k_zv_z}}e^{-i(l-l^{\prime}){\rm \theta}} $$Using the perturbed distribution function we obtain the drift velocity,
$$\vec{v}_{{\rm \omega}, k} = \displaystyle{1 \over {n_0}}\mathop \int \limits_{-\infty} ^\infty \mathop \int \limits_0^{2{\rm \pi}} \mathop \int \limits_0^\infty f_1\vec{v}dv_\bot d{\rm \theta} dv_z$$
$$v_{x \,{\rm \omega}, k} = \displaystyle{{e{\rm \phi} lv_{{\rm th}}} \over {T_{\rm e}{\rm \pi} {\rm \beta}}} \left[ {1 + \displaystyle{{\rm \omega} \over {k_z {v_{\rm th}}}}z\left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z {v_{\rm th}}}}} \right)} \right]\lsqb {I_l\lpar {{\rm \beta}^2/2} \rpar e^{-{\rm \beta}^2/2}} \rsqb $$
$$v_{z \, {\rm \omega}, k} = \displaystyle{{e{\rm \phi} 2{\rm \pi} {\rm \omega}} \over {T_{\rm e}{\rm \pi} k_z{v_{\rm th}}}}\left[ {1 + \displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z{v_{\rm th}}}}z\left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z{v_{\rm th}}}}} \right)} \right]\lsqb {I_l\lpar {{\rm \beta}^2/2} \rpar e^{-{\rm \beta}^2/2}} \rsqb $$Thus the heating rate is:
$$\eqalign{H_{\rm e} & = -\displaystyle{{\mathop n\nolimits_0^0 e} \over 2}\left[ {\displaystyle{{ie} \over {{\rm \varepsilon}_0}}\left( {\displaystyle{{n_qe} \over {2m{\rm \omega}^2}}} \right)} \right]{\rm \phi} _{\rm p}^{^\ast} \left\{ {\lpar {I_l\lpar {{\rm \beta}^2/2} \rpar e^{-{\rm \beta}^2/2}} \rpar \displaystyle{e \over {T_{\rm e}{\rm \pi}}}} \right\} \cr & \quad\left[ {\lpar {k_x + q} \rpar \displaystyle{{lv_{{\rm th}}} \over {\rm \beta}} \left( {1 + \displaystyle{{\rm \omega} \over {k_z{v_{\rm th}}}}z\left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z{v_{\rm th}}}}} \right)} \right)} \right] \cr & \quad + \displaystyle{{2{\rm \pi} {\rm \omega}} \over {k_z}}\left[ {1 + \displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z{v_{\rm th}}}}z\left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_z{v_{\rm th}}}}} \right)} \right]{\rm \phi}} $$We may write χ e = χ er + iχ ei where
$${\rm \chi} _{{\rm e}r} = \displaystyle{{2{\rm \omega} _{\rm p}^2} \over {k^2v_{{\rm th}}^2}} \left[ {1-\displaystyle{{\rm \omega} \over {{\rm \omega} -l{\rm \omega}_{\rm c}}}\mathop {I_l\lpar b \rpar e^{-b}}\limits_{}} \right]$$As
$$\displaystyle{{\chi _{\rm e}} \over \varepsilon }\cong \displaystyle{{\chi _{{\rm e}r}} \over {1 + \chi _{{\rm e}r}}}$$where
$$\displaystyle{{{\rm \chi} _{{\rm e}r}} \over {1 + {\rm \chi} _{{\rm e}r}}} = \left[ {1-\displaystyle{1 \over {1 + \displaystyle{{2\mathop {\rm \omega} \nolimits_{\rm p}^2} \over {k^2\mathop v\nolimits_{{\rm th}}^2}} \left[ {1-\displaystyle{{\rm \omega} \over {{\rm \omega} -l{\rm \omega}_{\rm c}}}I_l\lpar b \rpar e^{-b}} \right]}}} \right]$$The heating rate per electron per second is
$$\eqalign{\displaystyle{H \over {\mathop n\nolimits_0^0}} & = \left( {\displaystyle{{\mathop {\rm \omega} \nolimits_{\rm p}^2} \over {{\rm \omega}^2}}} \right)nq_0\left( {\displaystyle{{eA_1} \over {m{\rm \omega}_1v_{{\rm th}}}}\cdot \displaystyle{{eA_2} \over {m{\rm \omega}_2v_{{\rm th}}}}} \right)^2\displaystyle{{T_{\rm e}} \over {\rm \pi}} \cr & \left[ {I_l{\left( {\displaystyle{1 \over 2}\displaystyle{{k_\bot v_{{\rm th}}} \over {{\rm \omega}_{\rm c}}}} \right)}^2e^{-{\left( {\textstyle{{k_\bot v_{{\rm th}}} \over {2{\rm \omega}_{\rm c}}}} \right)}^2}} \right]\lpar {k_x + q} \rpar \cr & \left[ \displaystyle{{l{\rm \omega}_{\rm c}} \over {k_\bot v_{{\rm th}}}}\cdot v_{{\rm th}}\sqrt {\rm \pi} \displaystyle{{\rm \omega} \over {k_zv_{{\rm th}}}}e^{-\lpar {{\rm \omega} -l{\rm \omega}_{\rm c}} \rpar 2/k_z^2 v_{{\rm th}}^{\rm 2}} \right. \cr &+\left. \displaystyle{{\rm \omega} \over {k_z}}\sqrt {\rm \pi} \left( {\displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_zv_{{\rm th}}}}} \right)e^{{-{\lpar {{\rm \omega} -l{\rm \omega}_{\rm c}} \rpar }^2/k_z^2 v_{{\rm th}}^{\rm 2}}} \right] \cr & \left[ {1-\displaystyle{1 \over {1 + ((2\mathop {\rm \omega} \nolimits_{\rm p}^2 )/(k^2\mathop v\nolimits_{{\rm th}}^2 ))\lsqb {1-({\rm \omega} /({\rm \omega} -l{\rm \omega}_{\rm c}))I_l(b)e^{-b}} \rsqb }}} \right]} $$
$$\eqalign{\displaystyle{H \over {\mathop n\nolimits_0^0}} & = \left( {\displaystyle{{{\rm \omega}_{\rm p}^2} \over {{\rm \omega}^2}}} \right)Nq_0\left( {\displaystyle{{v_1v_2} \over {c^2}}} \right)^2\displaystyle{{mc^2} \over {8{\rm \pi}}} \left[ {I_l\left( {\displaystyle{{{\rm \beta}^2} \over 2}} \right)e^{-{{{\rm \beta^2} /2} }}} \right] \cr & \quad\lpar {k_x + q} \rpar \left[ {\left( {\displaystyle{{l{\rm \omega}_{\rm c}} \over {k_\bot v_{{\rm th}}}} + \displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_zv_{{\rm th}}}}} \right)\displaystyle{{\rm \omega} \over {k_z}}\sqrt {\rm \pi} e^{^{-\lpar {{\rm \omega} -l{\rm \omega}_{\rm c}} \rpar 2/k_z^2 v_{{\rm th}}^2}}} \right]} $$
$$\displaystyle{H \over {\mathop n\nolimits_0^0}} = hmc^2{\rm \omega} $$where
$$\eqalign{ h & = \left( {\displaystyle{{\mathop {\rm \omega} \nolimits_{\rm p}^2} \over {{\rm \omega}^2}}} \right)\displaystyle{{N_{q_0}} \over {8{\rm \pi}}} \left( {\displaystyle{{v_1v_2} \over {c^2}}} \right)^2\displaystyle{{k_\bot} \over {k_z}}\sqrt {\rm \pi} \left[ {I_l\left( {\displaystyle{{{\rm \beta}^2} \over 2}} \right)e^{-{{{\rm \beta^2} /2} }}} \right] \cr & \quad\left[ {\left( {\displaystyle{{l{\rm \omega}_{\rm c}} \over {k_\bot v_{{\rm th}}}} + \displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_zv_{{\rm th}}}}} \right)\displaystyle{{\rm \omega} \over {k_z}}\sqrt {\rm \pi} e^{^{-\lpar {{\rm \omega} -l{\rm \omega}_{\rm c}} \rpar 2/k_z^2 v_{{\rm th}}^2}}} \right]} $$The equation governing the evolution of electron temperature can be written as
$$\eqalign{\displaystyle&{d \over {dt}}\left( {\displaystyle{3 \over 2}T_{\rm e}} \right) = hmc^2{\rm \omega} = C_1\displaystyle{{{\rm \chi} _{{\rm e}i}} \over {{\vert {\rm \varepsilon} \vert } ^2}} \cr &= C_1\left[ {I_l\left( {\displaystyle{{{\rm \beta}^2} \over 2}} \right)e^{-\lpar {{\rm \beta}^2/2} \rpar }} \right]\lpar {k_x + q} \rpar \cr &\left[ {\left( {\displaystyle{{l{\rm \omega}_{\rm c}} \over {k_\bot v_{{\rm th}}}} + \displaystyle{{{\rm \omega} -l{\rm \omega}_{\rm c}} \over {k_zv_{{\rm th}}}}} \right)\displaystyle{{\rm \omega} \over {k_z}}\sqrt {\rm \pi} e^{^{-\lpar {{\rm \omega} -l{\rm \omega}_{\rm c}} \rpar 2/k_z^2 v_{{\rm th}}^2}}} \right] \cr & \left[ {1-\displaystyle{1 \over {1 + ((2\mathop {\rm \omega} \nolimits_{\rm p}^2 )/(k^2\mathop v\nolimits_{{\rm th}}^2 ))\lsqb {1-({\rm \omega} /({\rm \omega} -l{\rm \omega}_{\rm c}))I_l(b)e^{-b}} \rsqb }}} \right]} $$
$$C_1 = \displaystyle{{N_{q_0}} \over {8{\rm \pi}}} \left \vert {\displaystyle{{v_1v_2^{^\ast}} \over {c^2}}} \right \vert ^2\displaystyle{{{\rm \omega} _{\rm p}^2} \over {6{\rm \omega} ^2}}$$ For pulsed lasers, e.g., 
$A_1^2 A_2^2 = A_{10}^2 A_{20}^2 e^{-{{2t^2} / {{\rm \tau} ^2}}}$, C 1 is a function of time and one may solve Eq. (22) numerically to obtain T e as a function of time. As the electron temperature rises the cyclotron damping of electrons (manifested through the rise in χ ei) increases, hence heating rate becomes stronger. We introduce normalized laser amplitudes a 10 = eA 10/mω 1c, a 20 = eA 20/mω 2c and dimensionalize the normalized heating rate h by a quantity h 0.
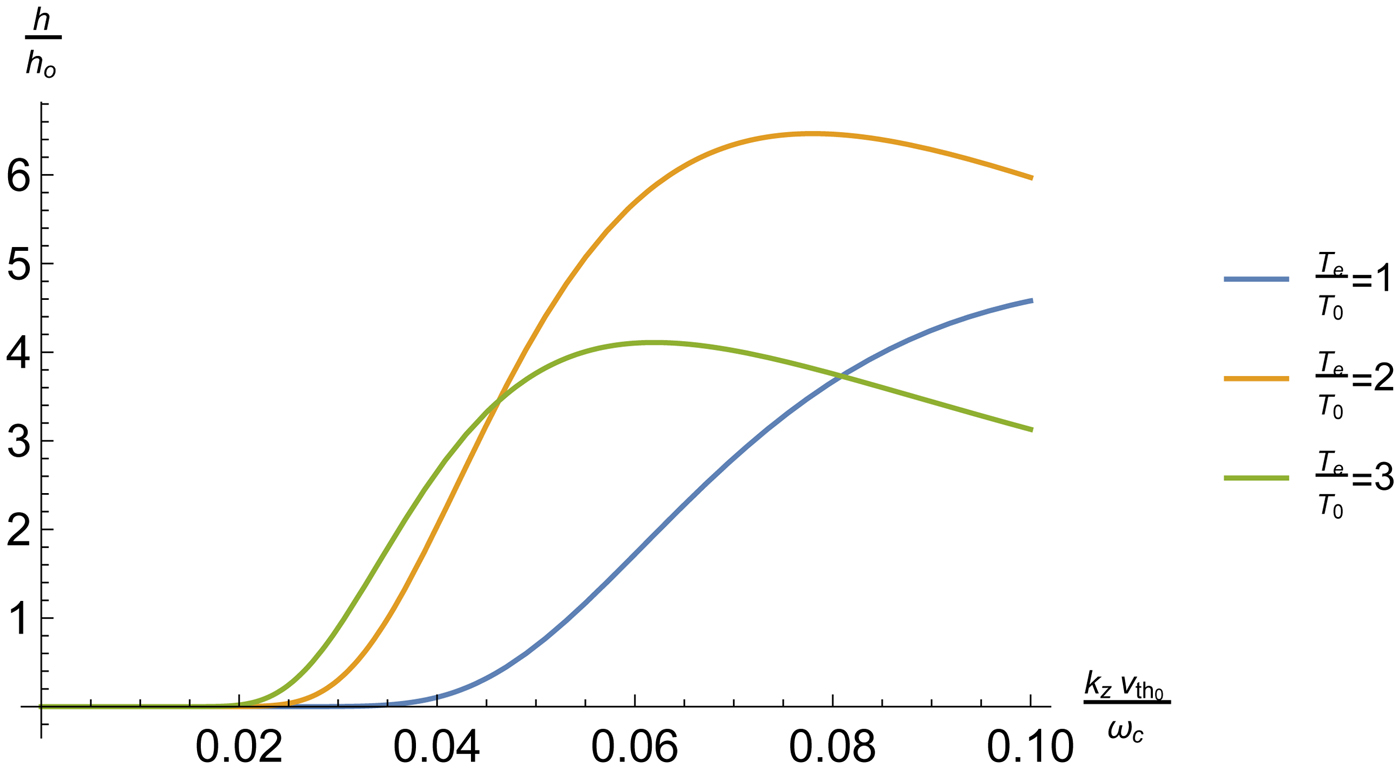
$$h_0 = \left( {\displaystyle{{{\rm \omega}_{\rm p}^2} \over {{\rm \omega}^2}}} \right)\displaystyle{{N_{q_0}} \over {8{\rm \pi}}} \left( {\displaystyle{{v_1v_2} \over {c^2}}} \right)^2\sqrt {\rm \pi}. $$ In Fig. 2, we have plotted the normalized heating rate of electrons h/h 0 as a function of 
$k_zv_{{\rm t}{\rm h}_0}/{\rm \omega} _{\rm c}$, the normalized parallel wave number of the quasi-mode (or beat wave number of the lasers), assuming electron temperature to be clamped. The parameters are (ω − ωc) = 0.1, 
$qv_{{\rm th}}/{\rm \omega} _{\rm c} = \sqrt 2 $.
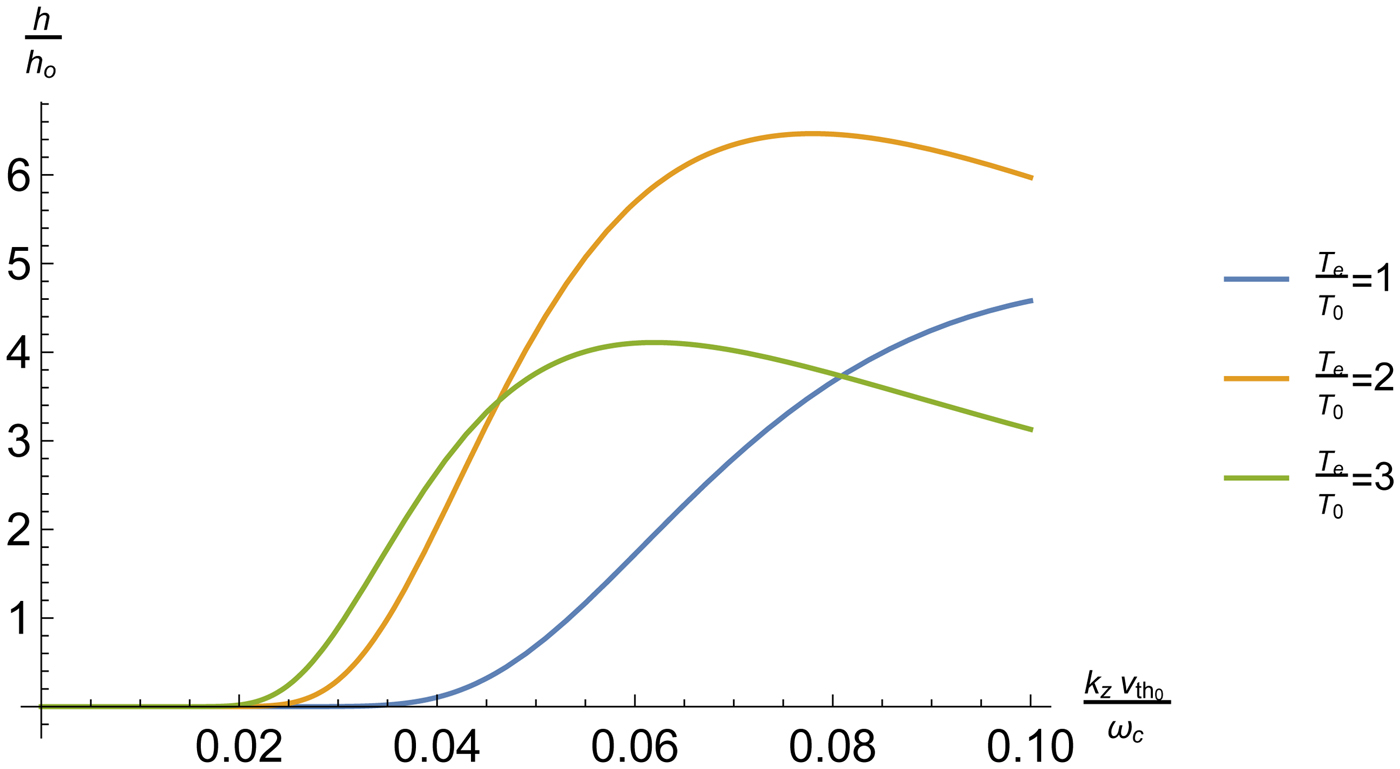
Fig. 2. Normalized heating rate of electrons as a function of normalized wave number 
$k_zv_{{\rm t}{\rm h}_0}/{\rm \omega} _{\rm c}$ of the ripple assuming the electron temperature to be clamped for different T e/T 0.
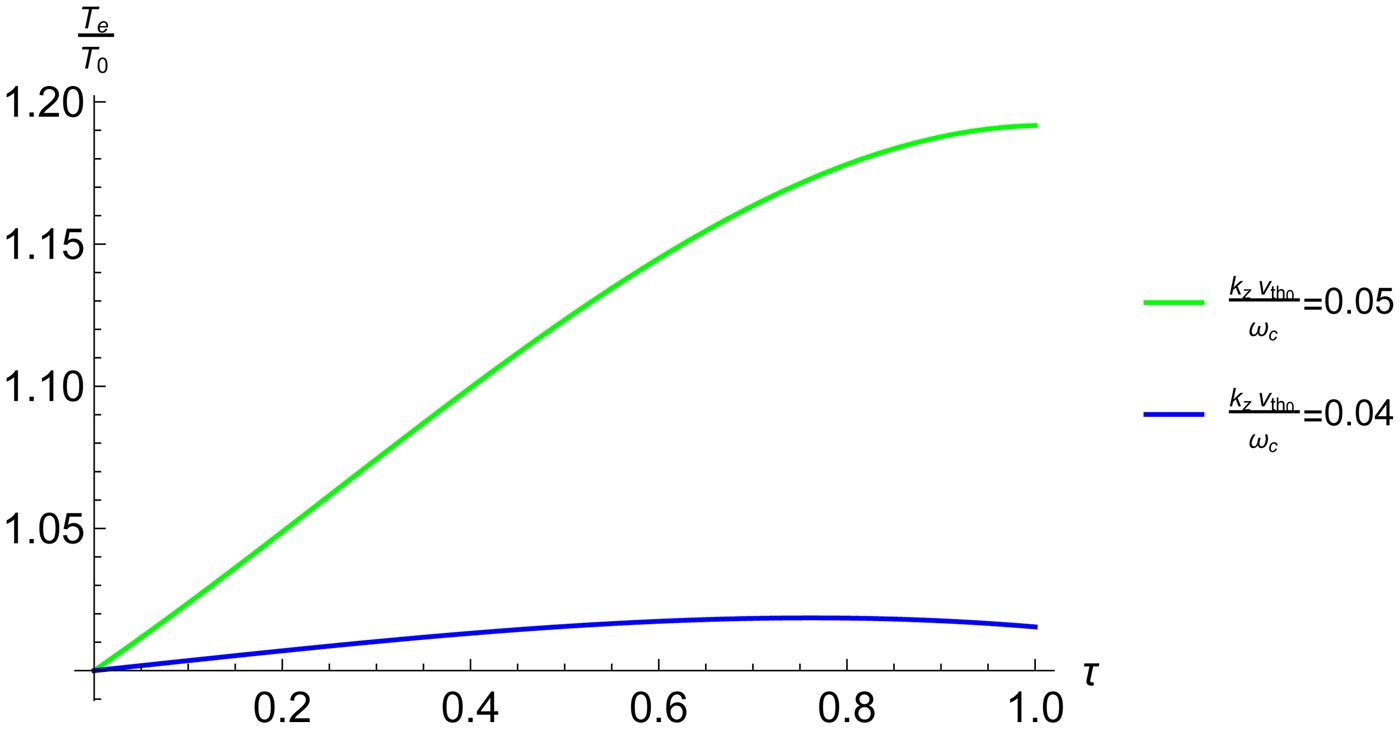
The heating rate increases with 
$k_zv_{{\rm t}{\rm h}_0}/{\rm \omega} _{\rm c}$, attains a maximum when (ω − ωc)/k zv th ≈ 1 and then falls off gradually due to the k z dependence of the factor outside the exponential. Fig. 3 shows the variation of electron temperature as a function of normalized time.
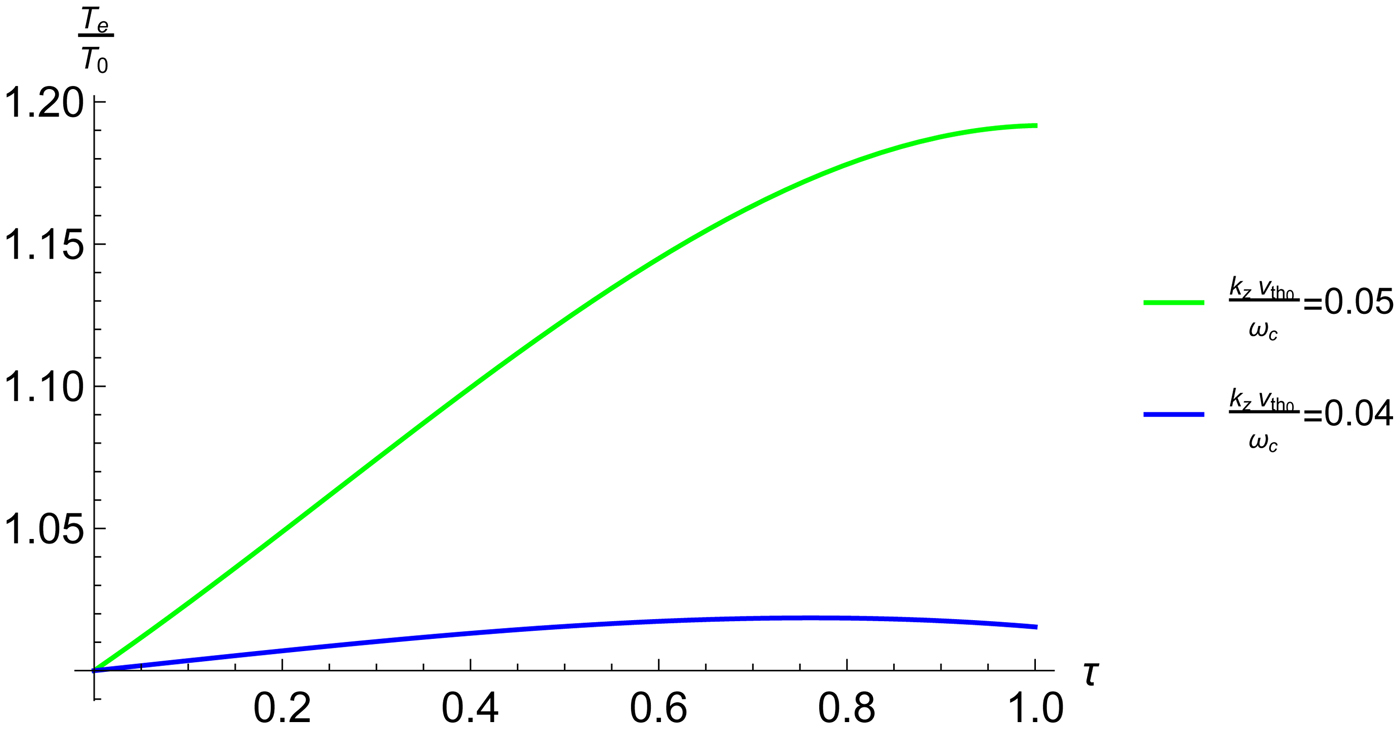
Fig. 3. Variation of electron temperature as a function of normalized time.
The electron temperature initially rises with time more than linearly. As the temperature increases cyclotron damping becomes stronger. Beyond the laser intensity peak the rise ion electron temperature is slow and temperature saturates. gradually and eventually saturates with time.
Discussion
A density ripple of 10% having wavelength few times the laser wavelength is effective for beat wave cyclotron heating of electrons. The ripple could be created by a machining laser beam as done by Milchberg et al. (Reference Milchberg, Mcnaught and Parral2001). The driven beat mode heats the electrons via cyclotron damping. Initially the heating is slow. However, as the electron temperature rises the damping becomes more severe and the heating becomes quite efficient. For Gaussian laser beams, the heating rate rises rapidly as the electron temperature increases. After attaining (ω − ωc)/k zv th ≈ 1, the heating rate slows down. The electron temperature rises with time and saturates in the rear phase of the laser pulse.
Heating rate is a function of wave number of the ripple due to finite Larmor radius effects. The temperature is enhanced on increasing the normalized temperature and the less normalized time is required on increasing the normalized temperature. However, the peak for T e/T 0 = 2 is higher than T e/T 0 = 3 due to the term 
$\lsqb {I_l({\rm \beta}^2/2)e^{-({\rm \beta}^2/2)}} \rsqb $ and exponential term and in Eq. (21).
Acknowledgments
We are thankful to Prof. V. K. Tripathi, IITD New Delhi, India for very useful discussions.
