Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T08:58:04.327Z Has data issue: false hasContentIssue false
  • English
  • Français

Attosecond electron pulses from interference of above-threshold de Broglie waves

Published online by Cambridge University Press:  07 March 2008

S. Varró  and
Gy. Farkas
S. Varró*
Affiliation:
Research Institute for Solid State Physics and Optics of the Hungarian Academy of Sciences, Budapest, Hungary
Gy. Farkas
Affiliation:
Research Institute for Solid State Physics and Optics of the Hungarian Academy of Sciences, Budapest, Hungary
*
Address correspondence and reprint requests to: Sándor Varró, Research Institute for Solid State Physics and Optics of the Hungarian Academy of Sciences, P.O. Box 49, Budapest H-1525, Hungary. E-mails: varro@sunserv.kfki.hu and varro@mail.kfki.hu
Rights & Permissions [Opens in a new window]

Abstract

It is shown that the above-threshold electron de Broglie waves, generated by an intense laser pulse at a metal surface are interfering to yield attosecond electron pulses. This interference of the de Broglie waves is an analog on of the superposition of high harmonics generated from rare gas atoms, resulting in trains of attosecond light pulses. Our model is based on the Floquet analysis of the inelastic electron scattering on the oscillating double-layer potential, generated by the incoming laser field of long duration at the metal surface. Owing to the inherent kinematic dispersion, the propagation of attosecond de Broglie waves in vacuum is very different from that of attosecond light pulses, which propagate without changing shape. The clean attosecond structure of the current at the immediate vicinity of the metal surface is largely degraded due to the propagation, but it partially recovers at certain distances from the surface. Accordingly, above the metal surface, there exist “collapse bands,” where the electron current is erratic or noise-like, and there exist “revival layers,” where the electron current consist of ultrashort pulses of about 250 attosecond durations in the parameter range we considered. The maximum value of the current densities of such ultrashort electron pulses has been estimated to be on order of couple of tenth of mA/cm2. The attosecond structure of the electron photocurrent can perhaps be used for monitoring ultrafast relaxation processes in single atoms or in condensed matter.

Keywords

Charged particle beam sourcesLaser-plasma interactionsMatter wavesPhotoemissionQuantum mechanicsStrong-field excitationSurface plasmas
Type
Research Article
Information
Laser and Particle Beams , Volume 26 , Issue 1 , March 2008 , pp. 9 - 20
Copyright
Copyright © Cambridge University Press 2008

1. INTRODUCTION

The generation of attosecond (10−18 s) light pulses has first been proposed by Farkas and Tóth (Reference Farkas and Tóth1992). The first experimental indication of attosecond localization in time for the high-harmonic signal stemming from the nonlinear response of rare gas jets excited by high-intensity laser pulses was reported by Papadogiannis et al. (Reference Papadogiannis, Witzel, Kalpouzos and Charalambidis1999). The generation of attosecond light pulses is in complete analogy with mode-locking producing picosecond pulse trains through the Fourier synthesis of the laser cavity Eigenmodes. Because the spacing of the high-harmonic components (namely the optical frequency ω = 2πν) is much larger than the spacing of the cavity Eigenmodes (on the order of 1 GHz) for a usual laser, the Fourier synthesis results in a series of spikes whose width can be much smaller than the optical period (which is roughly of the order of 10−15 s), i.e., we receive here a train of sub-femtosecond (attosecond) pulses. At the beginning, it was questionable whether the phases of the high-harmonic components are really locked (i.e., the difference between the phases is a smooth (possibly a constant) function of the harmonic order, which is crucial to have constructive interference), but in the meantime, many thorough analysis have been carried out, e.g., by L'Huillier et al. (Reference L'Huillier, Balcou, Candel, Schafer and Kulander1992), Lewenstein et al. (Reference Lewenstein, Balcou, Ivanov, L'Huillier and Corkum1994), Antoine et al. (Reference Antoine, L'Huillier and Lewenstein1996), and Saliéres (Reference Saliéres, Batani, Joachain, Martellucci and Chester2001), and it has become clear that the phase-locking usually automatically takes place due to the generating mechanism itself. Paul et al. (Reference Paul, Toma, Breger, Mullot, Augé, Balcou, Muller and Agostini2001) have measured first an attosecond pulse train with sub-pulses of 250 attosecond duration, and Tzallas et al. (Reference Tzallas, Charalambidis, Papadogiannis, Witte and Tsakiris2003) repeated a refined version of the earlier experiments by Papadogiannis et al. (Reference Papadogiannis, Witzel, Kalpouzos and Charalambidis1999) for 780 attosecond pulse trains. López-Martens et al. (Reference López-Martens, Varjú, Johnsson, Mauritsson, Mairesse, Saliéres, Gaarde, Schafer, Persson, Svanberg, Wahlström and L'Huillier2005) have produced by now the cleanest attosecond pulse trains of 170 attosecond generated routinely. Christov et al. (Reference Christov, Murname and Kapteyn1997) have predicted theoretically the appearance of a single attosecond pulse, and such a pulse of duration 650 attosecond were first produced by Hentschel et al. (Reference Hentschel, Kienberger, Spielmann, Reider, Milosevic, Brabec, Drescher, Corkum, Heinzmann, Drescher and Krausz2001). Later, Sansone et al. (Reference Sansone, Benedetti, Calegary, Vozzi, Avaldi, Flammini, Poletto, Villoresi, Altucci, Velotta, Stagira, De Silvestri and Nisoli2006) produced one single 120 attosecond pulse by using an optical gate, and it has been predicted by Tsakiris et al. (Reference Tsakiris, Eidmann, Meyer-ter-Vehn and Krausz2006) that from the cut-off region of the high-harmonic spectrum of an overdense plasma layer, where the spectrum is essentially a quasi-continuum, isolated single attosecond light pulses can be obtained.

Recently, there has been much labor put into the classical simulations of various processes (generation of coherent X-rays and laser acceleration of electrons) in laser-plasma interaction (see e.g., Pukhov & Meyer-ter-Vehn, Reference Pukhov and Meyer-ter-Vehn2002, Kiselev et al., Reference Kiselev, Pukhov and Kostyukov2004, Quèrè et al., Reference Quèrè, Thaury, Monot, Dobosz, Martin, Geindre and Audebert2006; Tsakiris et al., Reference Tsakiris, Eidmann, Meyer-ter-Vehn and Krausz2006). Moreover, Hidding et al. (Reference Hidding, Amthor, Liesfeld, Schwoerer, Karsch, Geissler, Veisz, Schmid, Gallacher, Jamison, Jaroszynski, Pretzler and Sauerbrey2006) showed the first experimental results for the generation of quasi-monoenergetic electron bunch by strong laser fields. Eliezer et al. (Reference Eliezer, Eliaz, Grossman, Fisher, Gouzman, Henis, Pecker, Horovitz, Fraenkel, Maman, Ezersky and Eliezer2005) have reported on the production by femtosecond laser pulses on crystal nanoparticles for aluminum and nanotubes for carbon on a transparent heat-insulating glass substrate. Kanapathipillai (Reference Kanapathipillai2006) have worked out a nonlinear oscillator model to describe the nonlinear absorption of ultrashort laser pulses by clusters. Sherlock et al. (Reference Sherlock, Bell and Rozmus2006) have shown by a numerical study that it is necessary to take into account the collisional heat transport into the target to correctly model the absorption rate of laser pulses of duration of 100 fs, and of intensities on the order 1015 W/cm2 at the front of the target surface. According to the theoretical studies on the interaction of a short laser pulse with metals performed by Anwar et al. (Reference Anwar, Latif, Iqbal, Rafique, Khaleeq-Ur-Rahman and Siddique2006), the laser-induced electric field inside the target is responsible for an induction of the current density, which causes, after all, electronic heat conduction. Laser-induced acceleration and manipulation of high-energy charged particle beams are still subjects of extensive theoretical and experimental research. For instance, Lifschitz et al. (Reference Lifschitz, Faure, Glinec, Malka and Mora2006) have recently proposed a new scheme for a compact GeV laser plasma accelerator. According to the simulations performed by these authors, their method would yield the production of high quality, monoenergetic, and sub-50 fs electron bunches at the GeV energy level. Willi et al. (Reference Willi, Toncian, Borghesi, Fuchs, D'humieres, Antici, Audebert, Brambrink, Cecchetti, Pipahl and Romagnani2007) have proposed a novel technique for focusing and energy selection of high-current MeV proton beams. In their scheme, the transient electrostatic field induced by an ultrashort laser pulse is responsible for the “micro-lensing,” i.e., for the focusing and for the selection of a narrow band out of the broadband spectrum of protons generated from a separate laser-irradiated thin foil target. The distortion of the Fermi distribution and the step-like occupation of the energy levels of the electrons due to the influence of a 100 fs strong laser pulse have been recently studied by Schwengelbeck et al. (Reference Schwengelbeck, Plaja, Conejero Jarque, Roso, Varró and Farkas2002), on the basis of a time-dependent exact quantum-mechanical analysis of a many-electron system. Besides these investigations of the interaction of ultrashort but “non-attosecond” laser pulses with matter, there has been a wide experimental and theoretical research carried out concerning attosecond electron pulses, too. Lindner et al. (Reference Lindner, Schaetzel, Walther, Goulielmakis, Krausz, Milosevic, Bauer, Becker and Paulus2005) performed attosecond electron double-slit experiments and Johnsson et al. (Reference Johnsson, López-Martens, Kazamias, Mauritsson, Valentin, Remetter, Varjú, Gaarde, Mairesse, Wabnitz, Saliéres, Balcou, Schafer and L'Huiller2005) studied electron-wave packet dynamics in strong laser fields. A time-dependent calculation has been carried out by Mauritsson et al. (Reference Mauritsson, Gaarde and Schafer2005) in order to study the properties of electron wave packets generated by attosecond laser-pulse trains. In this context, see also the work by Remetter et al. (Reference Remetter, Johsson, Mauritsson, Varjú, Ni, Lépine, Gustafsson, Schafer, Vrakking and L'Huillier2006) on attosecond wave packet interferometer, Breidbach and Cederbaum (Reference Breidbach and Cederbaum2005) on the attosecond response to the removal of an electron, Niikura et al. (Reference Niikura, Villeneuve and Corkum2005) on attosecond electron wave packet motion, Hu and Collins (Reference Hu and Collins2006) on the possibility of attosecond pump-probe experiments for exploring the ultrafast electron motion inside an atom, and Fill et al. (Reference Fill, Veisz, Apolonski and Krausz2006) on sub-fs electron pulses for ultrafast electron diffraction. Quite recently, attosecond real-time observation of electron tunneling in atoms has been reported by Uiberacker et al. (Reference Uiberacker, Uphues, Schultze, Verhoef, Yakovlev, Kling, Rauschenberger, Kabachnik, Schröder, Lezius, Kompa, Muller, Vrakking, Hendel, Kleineberg, Heinzmann, Drescher and Krausz2007).

The above-threshold electron spectra of nonlinear photoionization induced by relatively long laser pulses, analyzed thoroughly, e.g., by Agostini (Reference Agostini, Batani, Joachain, Martellucci and Chester2001), Paulus and Walther (Reference Paulus, Walther, Batani, Joachain, Martellucci and Chester2001), and by Banfi et al. (Reference Banfi, Gianetti, Ferrini, Galimberti, Pagliara, Fausti and Parmigiani2005), have common features with the corresponding high-harmonic spectra. The initial fall-off, the (occasionally rising) plateau and the sharp cut-off are present in each case. In case of multiphoton photoelectric effect of metals, Farkas and Tóth (Reference Farkas and Tóth1990) and Farkas et al. (Reference Farkas, Tóth, Kőházi-Kis, Agostini, Petite, Martin, Berset and Ortega1998) measured very high-order above-threshold electrons coming from metal targets. The theoretical interpretation of these results has been given by Varró and Ehlotzky (Reference Varró and Ehlotzky1998) and recently by Kroó et al. (Reference Kroó, Varró, Farkas, Oszetzky, Nagy and Czitrovszky2007), on the basis of the so-called laser-induced oscillating double-layer potential model. This model is based on a Floquet-type analysis of the inelastic electron scattering on the oscillating double-layer potential generated by the incoming laser field at the metal surface. The model has already been successfully used to interpret the experimental results on very high order surface photoelectric effect in the near infrared (Farkas & Tóth, Reference Farkas and Tóth1990) and in the far infrared regime (Farkas et al., Reference Farkas, Tóth, Kőházi-Kis, Agostini, Petite, Martin, Berset and Ortega1998). By analogy, one may think that if the phases of the above-threshold electron de Broglie waves generated at the metal surface are locked (i.e., the difference in the phases of the neighboring components is a smooth, possibly a constant function on the order, namely the number of absorbed photons), then the Fourier synthesis of these components yields an attosecond electron pulse train emanating perpendicularly from the metal surface, quite similarly to the generation of attosecond light pulses from high harmonics (which, on the other hand, are propagating in the specular direction). This expectation is quite natural; because the spacing of the electron peaks in the frequency space is just the optical frequency hν/h = ν, like in the case of high-harmonic generation.

We emphasize that, owing to the inherent kinematic dispersion, the propagation of the attosecond de Broglie waves in vacuum is very different from that of attosecond light pulses, since the rest mass of the electrons is not zero, in contrast to that of the photons. The clean attosecond structure at the immediate vicinity of the metal surface is largely spoiled due to the propagation, even in vacuum, but it partially recovers at certain distances from the surface. On the basis of the existence of a plateau in the electron spectrum too, as has been discussed, e.g., by Agostini (Reference Agostini, Batani, Joachain, Martellucci and Chester2001), Paulus and Walther (Reference Paulus, Walther, Batani, Joachain, Martellucci and Chester2001), and Kystra et al. (2001), we conjecture that a similar effect of interference of de Broglie waves may exist in the case of the widely studied above-threshold ionization of atoms.

In the present paper, in Section 2, we briefly describe the construction of the laser-induced oscillating double-layer potential (energy) of a test electron scattered by the metal surface, and derive the basic wave function matching equation of the scattered electron. Moreover, we give an approximate analytic expression for the multiphoton scattering amplitudes valid for large final electron energies. This model serves as our basis for studying the high-order multiphoton photoelectric effect. In Section 3, we present the results of the numerical solutions of the matching equations for the scattering amplitudes corresponding to the elementary n-photon absorption of the test electron. The time-averaged above-threshold current components and the phases of the multiphoton transmission amplitudes will be discussed. In Section 4, we study the detailed temporal behavior of the total transmitted current which results from the superposition of the above-threshold de Broglie waves. It will turn out that the ideal attosecond electron pulse train appearing at the immediate vicinity of the metal surface collapses to an almost noise-like signal, by the inherent kinematic dispersion of the electron waves as they perpendicularly propagate from the surface. On the other hand, there are regions quite far from the surface (even at macroscopic distances) where the clean attosecond structure of the electron current revives. Accordingly, in propagation of the electron signal from the metal surface, there appear consecutively “collapse bands” and “revival layers” of a few nanometer thicknesses. In Section 5, a short summary closes our paper.

2. LASER-INDUCED OSCILLATING DOUBLE-LAYER POTENTIAL AT THE METAL SURFACE AND THE ELECTRON'S WAVE FUNCTION MATCHING

In this section, in order to illustrate the appearance of enhanced nonlinearities in the above-threshold electron excitations due to the enlarged electric field of surface inside the metal, let us first calculate the electron displacements in the bulk of the metal caused by the z-component of the penetrating electric field F(x′, z′, t) = F 0exp(z′/δ) sin(ωt − kx′). Here F 0 and ω = 2πν are the peak field strength and the circular frequency of the laser, δ = 1/k metal ≈ c/ωp is the skin depth, and k = (ω/c) sinθ denotes the plasmon wave number, respectively. Moreover, we have introduced the plasma frequency ωp = √(4πn ee 2/m), where e and m are the electron's charge and mass, respectively, and n e denotes the free electron density in the metal. The displacement ξ(x′, z′, t) = α0exp(z′/δ)sin(ωt − kx′) of an electron in the bulk, at an average position (x′, y′, z′) can be obtained from the solution of the corresponding Newton equation, where the amplitude of oscillation is given as α0 = eF 0/mω2. Here we have taken into account parametrically the z′ and x′ dependence of the penetrating electric field, which is a justified approximation at relatively moderate incoming laser intensities to be considered below. The potential energy U d(x, t; x′) of a test electron at position x = (x, y, z) in the joint Coulomb field of a background ionic core at a fixed position x′ = (x′, y′, z′) and of an associated oscillating background electron, is given by U d(x, t; x′) = e 2/|x⃗ − x⃗′(t)| −e 2/|x⃗ − x⃗′|. Here x⃗′(t) = x⃗′ + ɛ⃗zξ(x′, z′, t) is the instantaneous position of the oscillating background electron, with ɛz being a unit vector perpendicular to the metal-vacuum interface, pointing to the positive z-direction. The total potential energy of a test electron is the sum of all the contributions coming from the interactions originating at the positions x′, i.e.,

(1)
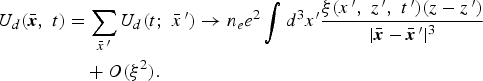
\eqalignno{U_d \lpar \bar{\bi x}\comma \; t\rpar & = \sum_{\bar{x}^{\,\prime}}U_d\lpar t\semicolon \; \bar{x}^{\,\prime}\rpar \rightarrow n_e e^2 \vint d^3 x^{\prime} {\xi \lpar x^{\,\prime}\comma \; z^{\,\prime}\comma \; t^{\,\prime}\rpar \lpar z - z^{\,\prime}\rpar \over \vert \bar{\bi x} - \bar{\bi x}^{\,\prime} \vert^3} \cr & \quad + O \lpar \xi^2\rpar .}

In obtaining Eq. (1), we have used the continuum limit of the summation, and we have expanded the joint Coulomb interaction of the background in powers of the oscillating displacement ξ. The first term on the right-hand side of Eq. (1) can be calculated analytically,

(2)
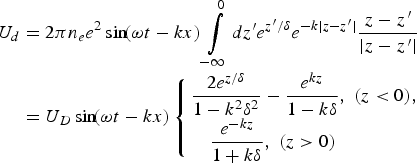
\eqalignno{U_d & = 2\pi n_e e^2 \sin\! \lpar \omega t - kx\rpar \vint\limits_{-\infty}^0 dz^{\prime} e^{z^{\,\prime}/\delta} e^{-k\vert z - z^{\,\prime}\vert} {z - z^{\,\prime} \over \vert z - z^{\,\prime} \vert} \cr & = U_D \sin\! \lpar \omega t - kx\rpar \left\{\matrix{\displaystyle{2e^{z/\delta} \over 1 - k^2 \delta^2} - \displaystyle{e^{kz} \over 1 - k\delta}\comma \; \lpar z \lt 0\rpar\comma \hfill \cr\quad \displaystyle{e^{-kz} \over 1 + k\delta}\comma \; \lpar z \gt 0\rpar \hfill}\right. \; }
(3)
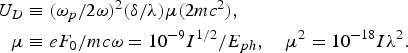
\eqalignno{U_D & \equiv \lpar \omega_p/2\omega\rpar ^2 \lpar \delta/\lambda\rpar \mu \lpar 2mc^2\rpar \comma \cr \mu & \equiv eF_0/mc\omega = 10^{-9} I^{1/2}/E_{ph}\comma \quad \mu^2 = 10^{-18} I\lambda^2.}

In Eq. (3), we have introduced the amplitude U D of the oscillating collective potential energy of the test electron, Eq. (2), which can take on very large values even for relatively moderate laser intensities (notice the factor 2mc 2 being just the pair-creation energy ≈106 eV). The dimensionless intensity parameter μ usually shows up in any strong field calculation, its magnitude governs the nonlinearity of the direct laser-electron interactions. In Eq. (3) I denote the peak laser intensity in W/cm2, E ph is the photon energy measured in eV, and λ is the central wavelength in microns (10−4 cm). We note that the gradient of the potential energy, Eq. (2), essentially equals to the force acting on a test electron due to a corresponding collective electric field. The potential given by Eq. (2) looks very similar to the so-called surface-plasmon polariton potential discussed in detail, e.g., Zayats et al., (Reference Zayats, Smolyaninov and Maradunin2005) in the context of nano-optics. In dipole approximation, i.e., for |kz| and |kx| <<1, the potential energy in Eq. (2), for relatively moderate laser intensity can be well approximated by the following double-layer potential energy U d ≈ sign(z)U Dsin(ωt), where sign (z > 0) = 1 and sign(z < 0) = −1, thus the maximum total jump in the energy equals 2U D. Because of this property, henceforth, we will call U d “laser-induced oscillating double-layer potential,” and describe the scattering of a Sommerfeld electron on this ideal non-conservative potential with the technique of wave function matching. At this point, we have to mention that normal electric field strengths F 0 in the vacuum undergoes a reduction on the order of (ω/ωp)2 by crossing the metal-vacuum interface, but, on the other hand, if we repeat the above same procedure, by using the force term −∂U d/∂z in the Newton equation of an oscillating background electron, in this second iteration, we receive essentially the same expression summarized in Eqs. (1), (2), and (3) with the original field strength F 0. In this way, the reduction factor is completely compensated by the enhancement factor (ωp/ω)2 due to the collective surface plasmon polaritons. So in this “second iteration,” the value of U D is essentially the same as is given by Eq. (3) with the original vacuum amplitude of field strength F 0. The next iteration would be meaningless, because then the amplitude of oscillation of the background electrons α0 would be comparable with the skin depth δ, hence the parametric substitution in Newton's equation could be justified. These details will not be discussed any further in this paper, so henceforth, we are planning to use the idealized laser-induced oscillating double-layer potential (energy) in dipole approximation U d ≈ sign(z)U Dsin(ωt) throughout the paper, where U D is defined in Eq. (3).

The concept of the laser-induced oscillating double-layer potential (energy), outlined above has been first introduced in our earlier study (Varró & Ehlotzky, Reference Varró and Ehlotzky1998), in order to explain a surprising outcome from one of our experiments (Farkas & Tóth, Reference Farkas and Tóth1990), namely, the appearance of very large (~600 eV) energy photoelectrons induced by Nd:Glass laser radiation (hν = 1.17 eV) at moderate intensities of some 10 GW/cm2. The main problem there was that the very large nominal order of the photon absorption processes corresponding to the experimental results (n = 5–600) could not have been deduced even from the usual non-perturbative approach based on Gordon–Volkov states (Kylstra et al., Reference Kylstra, Joachain, Dörr, Batani, Joachain, Martellucci and Chester2001), since the intensity parameter μ = eF 0/mcω was very small, on the order of 10−4 in that case. That time we have realized that instead of μ, another basic dimensionless parameter “a” appears in the analysis in a natural way, when we introduce the interaction with the double-layer potential, which builds up due to the coherent collective excitation of all the electrons within the skin depth. The parameter a is defined as a = 2U D/hν, where U D ≈ (ωp/4ω)μ(2mc 2) is the amplitude of the double layer potential energy of a test electron. The size of this a governing the degree of nonlinearity turned out to be just on the order of 500 for the mentioned experiment, hence we were able to explain the basic features of the measured electron spectra. In the meantime, we have applied the same method (Kroó et al., Reference Kroó, Varró, Farkas, Oszetzky, Nagy and Czitrovszky2007) for the theoretical interpretation of another strange experimental results (Farkas et al., Reference Farkas, Tóth, Kőházi-Kis, Agostini, Petite, Martin, Berset and Ortega1998) concerning electron emission from gold cathodes (work function ~4.7 eV) irradiated by mid-infrared radiation (generated by the Orsay Free Electron Laser) of wavelength up to 12 µm (hν = 0.1 eV) in the I = 10 MW/cm2 intensity regime. The intensity parameter is extremely small in this case: μ ≈ 3 × 10−5. The minimum number of photons required for the deliberation of an electron from the binding is on the order of 50. As was pointed out, both the tunneling model and the multiphoton model predict results many (about 200) orders off the experimental figures.

Now let us turn to the Schrödinger equation of an electron under the joint action of the Sommerfeld step-potential of depth V 0 and the double-layer potential derived above. We restrict our analysis to a one-dimensional scattering in dipole approximation, as in our earlier study (Varró & Ehlotzky, Reference Varró and Ehlotzky1998), which is justified in case of incoming laser intensities on the orders of <109–1011 W/cm2 for Ti:Sa lasers, which we have been using in our numerical calculations. Further, to simplify the following analysis, we shall take the asymptotic amplitude of the double-layer potential for z → −∞ as −U D and for z → +∞ as +U D, thus we get an idealized double-layer potential that oscillates at circular frequency ω between −U D and +U D at a phase difference π between z > 0 and z < 0. For the sake of completeness of the paper, in the following few lines we outline the basic equations presented already in Varró and Ehlotzky (Reference Varró and Ehlotzky1998). The wave function of an electron will then obey the two Schrödinger equations

(4a)
\matrix{\lpar \hat{\,p}^2/2 m - V_0 - U_D \sin \omega t\rpar \Psi_I = i\, \hbar \partial_t \Psi_I \quad \lpar z\lt 0\rpar \comma \; }
(4b)
\matrix{\lpar \hat{p}^2/2 m + U_D \sin \omega t\rpar \Psi_{II} = i\, \hbar \partial_t \Psi_{II} \quad \lpar z\gt 0\rpar \comma \; }

where the subscript I refer to the interior region (metal) and II to the exterior region (vacuum), respectively. In order to fulfill the continuity conditions at the metal surface at z = 0, we make Floquet-type ansätze in terms of the fundamental solutions of Eqs. (4a) and (4b), satisfying the proper mass-shell relations, i.e., the proper free-particle dispersion relations connecting the energies, and the corresponding momenta of the reflected and transmitted components,

(5a)
\eqalignno{\Psi_I & = \left[\chi_0^{\lpar +\rpar } - \chi_0^{\lpar - \rpar } + \sum_{n = - \infty}^{+ \infty} R_n \chi_n^{\lpar - \rpar } \right] \cr & \quad \times \exp\left[- i {U_D \over \hbar\! \omega}\cos \omega t \right]\quad \lpar z \lt 0\rpar \comma \; }
(5b)
\Psi_{II} =\sum\limits_{k=- \infty }^{+\infty } {T_k } \varphi _k^{\lpar +\rpar } \exp \left[{+i{{U_D } \over {\hbar\! \omega }}\cos \omega t} \right]\quad \lpar z \gt 0\rpar \comma

where $\chi\, _n^{\lpar \pm \rpar }=\hbox{exp} \left[{ \pm iq_n z/\hbar - i\left({E_0 + n\hbar\! \omega } \right)\cdot t/\hbar } \right]$ with $q_n=$$\left[{2\, m\left({V_0+E_0+n\hbar\! \omega } \right)} \right]^{1/2}$ and, correspondingly, $\varphi _k^{\lpar +\rpar }=$$\exp \left[{ip_k z/\hbar - i\left({E_0+k\hbar\! \omega } \right)\cdot t/\hbar } \right]$ with $p_k=\left[{2 m\left({E_0+k\hbar\! \omega } \right)} \right]^{1/2}$. Notice the opposite signs in the exponential factors in Eqs. (5a) and (5b), which transforms out the interaction with the double-layer potential in Eqs. (4a) and (4b). Here the energy parameter E 0 denotes the initial energy of the electron impinging from the inner part of the metal onto the metal-vacuum interface. In the numerical calculations, it will be taken as the negative of the work function, i.e., −A, which means that we assume that the test electron starts from the Fermi level. For later convenience, we have separated in Eq. (5a) the trivial elastic back-scattered part χ0(−) from the total back-scattered wave function. The unknown multiphoton reflection and transmission coefficients R n and T k, respectively, can be determined from the matching equations, i.e., from the continuity of the wave function, ΨI (0, t) = ΨII (0, t) and of its spatial derivative, $\partial_{z} \Psi_{I} (0,t) = \partial_{z} \Psi_{II} (0,t) $, which relation must hold for arbitrary instants of time. By using the generating functions of the ordinary Bessel functions of first kind J n(z) of order n (Gradshteyn & Ryzhik, Reference Gradshteyn and Ryzhik2000) to Fourier decompose the time-dependent exponentials in Eqs. (5a) and (5b), the matching equations yield the following infinite set of algebraic equations,

(6a)
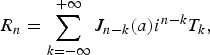
R_n = \sum _{k = - \infty }^{+\infty } {J_{n - k} } \lpar a\rpar i^{n - k} T_{k}\comma \;
(6b)
\delta _{n\comma 0}=\sum_{k=- \infty }^{+\infty } {J_{n - k} } \lpar a\rpar i^{n - k} \left[{\left({q_n+p_k } \right)/2q_0 } \right]T_{k}\comma \;

where we have introduced the dimensionless parameter a, with the definition

(7)
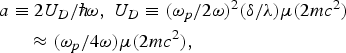
\eqalignno{& a \equiv 2U_D /\hbar\! \omega\comma \; U_D \equiv \lpar \omega _p /2\omega \rpar ^2 \lpar \delta /\lambda \rpar \mu \lpar 2mc^2 \rpar \cr & \quad\ \;\approx \lpar \omega _p /4\omega \rpar \mu \lpar 2mc^2 \rpar \comma \;}

and U D has already been defined in Eq. (3). Thus the dimensionless parameter a given by Eq. (7) is the ratio of the total maximum jump of the oscillating double layer potential (energy) to the photon energy. The last approximate equation is valid if the plasma frequency of the metallic electrons is much larger than the laser frequency, since in this case the skin depth can be approximated as $\delta = c/(\omega_{\,p}^{2} - \omega^{2})^{1/2} \approx $$ c/\omega_{\,p} $. The magnitude of the parameter a governs the extension of the kernel matrix in the sets of algebraic equations (Eqs. (6a) and (6b)), hence it determines the degree of nonlinearity of the multiphoton excitation.

The time-averaged outgoing electron current components (for which p n is real), corresponding to n-photon absorption, can be obtained from ΨII. We normalize these current components with respect to the incoming current, and get the dimensionless quantities

(8a)
\,j_t \lpar n\rpar = \left({\,p_n /q_0 } \right)\cdot \left\vert {T_n } \right\vert ^2 \quad \left({n \geq n_0 } \right)\comma \;

where n 0 is the minimum number of photons to be absorbed in order to yield true free running outgoing waves, i.e., ionization. The corresponding normalized reflected currents are

(8b)
\,j_r \lpar n\rpar =\left({q_n /q_0 } \right)\cdot \left\vert {R_n - \delta _{n\comma 0} } \right\vert ^2 \quad \left({n \geq n_1 } \right)\comma \;

with a similar meaning for n 1 as for n 0. The conservation of probability requires $\sum\nolimits_n {\left[{\,j_t \lpar n\rpar +j_r \lpar n\rpar } \right]}=1$, which condition has been used to check the accuracy of the numerical solutions of the matching equations (Eqs. (6a) and (6b)).

At the end of the present section, we would like to note that for large values of the parameter a given by Eq. (7), an approximate analytic expression has been derived in Varró and Ehlotzky (Reference Varró and Ehlotzky1998) for the transmission coefficients T n, which are particularly accurate for large values of the multiphoton order n. According to this approximation

(9)
\eqalign{T_n & \approx J_n \lpar a\rpar \lpar\! -\! i\rpar ^n\comma \quad j_t \lpar n\rpar \approx \left({\,p_n /q_0 } \right)\cdot J_n^2 \lpar a\rpar \comma \quad \left({a\gt \gt 1} \right)\quad\left({n\gt \gt 1} \right). }

3. THE TIME AVERAGE OF THE ABOVE-THRESHOLD CURRENT COMPONENTS AND THE PHASES OF THE TRANSMISSION COEFFICIENTS. NUMERICAL RESULTS

In this paper, we shall use in the numerical calculations the following input parameters for the incoming laser field and for the gold target. We assume a Ti:Sa laser beam which excites the metal surface at grazing incidence of central wavelength λ = 800 nm, frequency ω = 2.36 × 1015 Hz, photon energy hν = 1.55 eV, and of intensity 109 W/cm2, with its polarization being essentially perpendicular to the metal surface. Moreover, we assume that the pulse duration is much larger than the optical period T = 2.6 fs, so the carrier-envelope phase effects can be neglected in the present case. Concerning the carrier-envelope phase effects (“absolute phase effects”), in case of interactions with ultrashort laser pulses (see the paper by Varró, Reference Varró2007, and the references therein). The depth of the Sommerfeld step potential and the work function of gold are taken to be V 0 = 10.19 eV and A = 4.68 eV, respectively, hence, the Fermi energy equals E F = 5.51 eV. According to Radzig and Smirnov (Reference Radzig and Smirnov1985), the electron density of gold is n e = 5.9 × 1022/cm3, thus the plasma frequency in the bulk equals ωp = 1.37 × 1016 Hz » ω =  2.36 × 1015 Hz. By the definition in Eq. (7), the nonlinearity parameter a equals 60 in the present case. The numerical solution of the infinite set of algebraic equations (Eqs. (6a) and (6b)) is accurate up to a fraction of a percent if we use the truncated kernel in the range of indices {−120 ≤ n ≤ +120, −120 ≤ k ≤ +120}. This can be checked by the conservation of probability displayed after Eq. (8b). We note that the above-mentioned averaging of the multiphoton current means the time-averaging operation$\left\langle f \right\rangle= \hbox{lim} \vint_{ - T_0 }^{+T_0 } {dtf\lpar t\rpar /2T_0 }\comma \; \hbox{as } T_0 \to \infty\comma \; $ thus, of course, the distribution of j t(n) and j r(n) of Eqs. (8a) and (8b) do not reflect back the detailed time behavior of the total current $\lpar \hbar /m\rpar {\mathop{\rm Re}\nolimits} \lsqb \Psi ^ {\ast} \lpar\! -\! i\nabla \rpar \Psi \rsqb $, which will be discussed in the next Section.

At the end of the present Section, the time-averaged above-threshold spectrum and the relative phases of the transmission amplitudes is shown on the basis of our numerical calculations. In Figure 1, it is seen that, owing to the large value (~60) of the parameter a, introduced in Eq. (7), quite high nonlinearities appear even at the relatively moderate laser intensity (~109 W/cm2) we are considering.

Fig. 1. This figure shows the time-averaged spectrum of the above-threshold electron current density for the parameters introduced in the text above. The relative current density components j t(n) = (p n/q 0) · |T n|2 of Eq. (8a) are normalized to their maximum value ~0.02. The discrete points are connected by thick lines in order to guide the eye.

Figure 2 shows the numerical results for the phase differences φn − φn+1(mod 2π) of the transmission amplitudes T n. The detailed structure of the spectrum and the associated phases around the maximum will be summarized in Figure 3.

Fig. 2. This figure shows the dependence of phase differences arg [T n+1*T n] in radians on the number of absorbed photons n, corresponding to the spectrum shown in Figure 1. The discrete points are connected with thin lines in order to guide the eye. For relatively low-order processes the phase difference varies quite irregularly, but for the large energy wing, for 54 < n, it is stationary, which means that these components are strictly locked, which is in complete accord with the first approximate formula in Eq. (9). Based on this figure, we expect that the large-energy Floquet components interfere constructively, because of the regular behavior of their phases.

Fig. 3. This figure shows the large energy wing of the above-threshold spectrum represented by vertical bars (normalized to their maximum value~0.02. This is a magnification of the end of the spectrum shown already in Figure 1, and shows also at the large-energy part of Figure 2, the dependence of phase differences φn − φn+1 in radians on the number of absorbed photons n, at the end of the multiphoton spectrum. These phase differences are represented by points. According to the approximate formula given by Eq. (9) these differences arg [T n+1*] – arg [T n] are quiet uniformly equal about to π/2 ≈ 1.57, as is also seen on the figure.

Fig. 4. This figure shows the detailed time-behavior of the outgoing current density at different distances from the metal surface. Here we have plotted the dimensionless quantity (ℏ $ 4q_0 \rpar {\mathop{\rm Re}\nolimits} \lsqb \Psi _{II}^ {\ast} \lpar\! -\! i\partial _z \Psi _{II} \rpar \rsqb $ by superimposing the large-energy components (54 < n < 66), whose phase are locked, according to Figure 3. At z = 0 we received an ideal T10~250 attosecond pulse train, which is gradually spoiled by the inherent dispersion of de Broglie waves propagating in vacuum (due to the non-trivial z-dependence of the phases), yielding a noise-like electron current density already at the distance of 300 nm from the metal.

4. DETAILED TEMPORAL BEHAVIOR OF THE ABOVE-THRESHOLD CURRENT DENSITY: ATTOSECOND ELECTRON PULSE TRAINS

The superposition of the fundamental solutions describing the outgoing above-threshold de Broglie waves, presented after Eq. (5b), can be brought to the form

(10)
\eqalignno{& \Psi_{II} =\exp \left[+i {U_D \over \hbar\! \omega} \cos \omega t\right]\sum\limits_n T_n \exp \cr & \quad\times\left[-2\pi i \cdot \left({E_0 \over \hbar\! \omega} + n\right){t \over T} + 2\pi i \cdot \sqrt{{2mc^2 \over \hbar\! \omega} \left({E_0 \over \hbar\! \omega} + n\right)} {z \over \lambda}\right]\comma \;}

where we see that a natural unit of time is the opticzal period T (namely 2.6 fs for a Ti:Sa laser), and the unit of length measuring the distance perpendicular from the metal surface is given as $\lambda \sqrt {\hbar \omega /2mc^2}\comma \; $ which with good accuracy, is about 1 nm in the present case. In Figure 4, we shall present the spatial development of the time-behavior of the outgoing current density. The Figure 5 summarizes the spatio-temporal behavior of the outgoing current density.

Fig. 5. This figure shows the spatio-temporal behavior of the outgoing current in the range {0 nm < z < 300 nm, 0 T < t < 5.5 T,}. The white lines represent large values of the current density; on the other hand, the dark (grey or even black) regions indicate low values of the current density. By intersecting the figure vertically at some position z, and projecting the intersection to the time-axis (to the ordinate), we receive a representation of the time behavior at that particular position. It is seen that the ideal attosecond pulse train at the immediate vicinity of the metal surface z = 0, represented by the light lines, is gradually washed out by the propagation from the surface. At z = 300 nm the temporal variation of the electron current density becomes already a noise-like background (represented by the dark band), as is also shown on the last figure in the graphics array of Figure 4.

From the numerical study of contour plots of similar sort in Figure 5, we have realized that revivals of the attosecond structure of the electron current density at very large (even at macroscopic) distances from the metal surface (e.g., we have checked in the spatial range 2 013.985 nm < z < 2 014.015 nm) can take place. The thickness of this “revival layer” is on the order of 10 nm in this case. We have numerically checked for several ranges of the distances z from the metal-vacuum interface, that the “revival layers” are separated usually by wider “collapse bands” where the electron signal has practically an irregular noise-like temporal behavior. The next graphics array shows the temporal behavior of the current in the “collapse bands” and in the “revival layers” in a 555 nm range far from the metal-vacuum interface.

Since we have been discussing the relative current densities so far, at the end of the present Section we would like to make an estimate on the absolute size of the transmission current. According to the Fermi distribution of electrons in the metal, the total incoming current density impinging from inside to the metal-vacuum interface can be written as

(11a)
\eqalignno{& J_{inco \min g}=\lpar e \cdot n_e \cdot \upsilon _F \rpar \cdot \left[{2 \over {\lpar 2\pi \rpar ^3}} \cdot {k_F^3 \over n_e } \right]\cdot \vint\limits_0^\infty d\zeta \cdot \zeta \cdot \vint\limits_{-\infty }^{+\infty } d\xi \cr & \quad \cdot \vint\limits_{-\infty}^{+\infty} d\eta {1 \over \hbox{exp} \lsqb \lpar E_F /kT\rpar \cdot \lpar \zeta^2+\xi^2+\eta^2 - 1\rpar \rsqb +1}\comma }

where we have introduced the dimensionless variables

(11b)
\xi \equiv q_x /m\upsilon _F \comma \; \eta \equiv q_y /m\upsilon _F\quad \hbox{and}\quad \zeta \equiv q_z /m\upsilon _F\comma \;

and the Fermi wave number $k_F \equiv m\upsilon _F /\hbar=1.21 \times 10^8\, cm^{-1}\comma \; $ with ℏ denoting the Planck's constants ℏ ≡ h/2π divided by 2π, as usual. The Fermi velocity υF = 1.40 × 108 cm/s is related to the Fermi energy by the relation E F = mυF2/2 = 5.51eV. For a gold target, the first prefactor yields

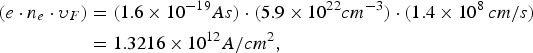
\eqalign{\lpar e \cdot n_e \cdot \upsilon _F \rpar & =\lpar 1.6 \times 10^{-19} As\rpar \cdot \lpar 5.9 \times 10^{22} cm^{ - 3} \rpar \cdot \lpar 1.4 \times 10^8\, cm/s\rpar\cr & =1.3216 \times 10^{12} A/cm^2 \comma \; }

because the electron density equals n e = 5.9 × 1022 cm −3, according to Radzig and Smirnov (Reference Radzig and Smirnov1985). The double integral with respect to ξ and η can be analytically performed, as is shown e.g., by Sokolov (Reference Sokolov1967),

(11c)
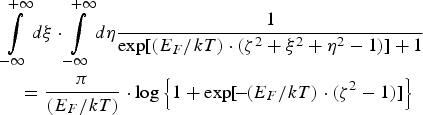
\eqalignno {& \vint\limits_{ - \infty }^{+\infty }{d\xi } \cdot \vint\limits_{-\infty }^{+\infty } {d\eta } {1 \over \exp \lsqb \lpar E_F /kT\rpar \cdot \lpar \zeta ^2+\xi ^2+\eta ^2 - 1\rpar \rsqb +1} \cr & \quad ={\pi \over \lpar E_F /kT\rpar } \cdot \log \left\{{1+\hbox{exp} \lsqb\! -\!\lpar E_F /kT\rpar \cdot \lpar \zeta ^2 - 1\rpar \rsqb } \right\}}

Thus, the incoming current density coming from one cubic centimeter can be expressed as

(11d)
\eqalignno{& J_{inco \min g} = \lpar e \cdot n_e \cdot \upsilon _F\rpar \cdot \left[{2 \over \lpar 2\pi \rpar ^3} \cdot {k_F^3 \over n_e}\right]\cdot {\pi \over \lpar E_F /kT\rpar } \cr & \quad\times \vint\limits_0^\infty d\zeta \cdot \zeta \cdot \log \left\{1 + \exp \lsqb \!-\!\lpar E_F /kT\rpar \cdot \lpar \zeta^2 - 1\rpar \rsqb \right\}}

Since E F/kT = 5.51/0.0236 ≈ 233.5 (where we have taken into account that kT = 0.0236 for T = 273 K), [2/(2π)3] · (k F3/n e) = 0.2421 and [π/(E F/kT)] = 0.01346 we have for the incoming current density from one cubic centimeter,

(12)
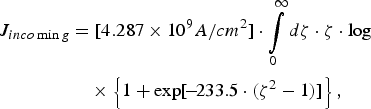
\eqalignno{J_{inco\min g} & =\lsqb 4.287 \times 10^9 A/cm^2 \rsqb \cdot \vint\limits_0^\infty {d\zeta } \cdot \zeta \cdot \log \cr & \quad \times\left\{1+\exp \lsqb\! -\! 233.5 \cdot \lpar \zeta ^2 - 1\rpar \rsqb \right\}\comma }

where ζ ≡ q z0/mυF is the initial scaled momentum of the test electron. Of course, the interaction volume is not one cubic centimeter, but much smaller, on the order of $\delta _{skin} \lambda ^2 \approx \lpar \omega /\omega _p \rpar \lambda ^3=8.82 \times 10^{-14}\, cm^3$, so the numerical prefactor should be reduced accordingly; (8.82 × 10−14) · [4.287 × 109A/cm 2] = 3.78 × 10−4A/cm 2. Since the numerical value of the dimensionless integral in Eq. (12) is 58.3785, the total current density impinging perpendicularly on the metal-vacuum interface from the interior of the metal is about 2.265 × 10−2A/cm 2. As we have seen above, the maximum value of the relative current density is on the order of 2%, hence, the value of the outgoing current density is expected at maximum a few tenth of mA/cm 2, which is, on the other hand, is still a relatively large value for an electron source.

CONCLUSION

In the Introduction of this paper, we have given an overview of the theoretical and experimental research carried out recently on the ultrashort laser pulses with matter. We have also discussed the similarities and differences of the propagation properties of short light pulses and electron pulses. We would like to emphasize that in the scheme discussed in this paper, the production of attosecond electron pulses is a result of interference of de Broglie waves of above-threshold Fourier components of the total electronic wave with the frequency spacing ω, the frequency of the incoming laser field. Thus, the electron pulse train stems from the interference of the “frequency comb” of the above-threshold components. Of course, if an ultrashort (e.g., few-cycle) laser pulse interact with a target (e.g., an atom or a metal surface), then the electron response (ionization or photo effect) is expected to be very short, too. However, this is not the case in our discussion, since we assume relatively long (many-cycle) laser pulses of moderate intensity. Just this assumption allows us to use the Floquet analysis of the Schrödinger equation. In Section 2, we briefly described the construction of the laser-induced oscillating double-layer potential (energy) for a test electron scattered by the metal surface, and derived the basic wave function matching equation of the scattered electron. Moreover, we have given an approximate analytic expression for the multiphoton scattering amplitudes valid for large final electron energies. This model serves as our basis for studying the high-order multiphoton photoelectric effect. In Section 3, we presented the results of the numerical solutions of the matching equations for the scattering amplitudes corresponding to the elementary n-photon absorption of the test electron. The time-averaged above-threshold current components and the phase differences of the multiphoton transmission amplitudes have been discussed (see Fig. 1). The maximum of the relative current density is about 2%. Though the phase differences are erratic for low orders (see Fig. 2), it turned out that in the large-energy wing of the spectrum essentially perfect phase locking is present (see Fig. 3). In Section 4, we studied the detailed temporal behavior of the total transmitted current which results from the superposition (interference) of the above-threshold de Broglie waves. It turned out that the ideal attosecond electron pulse train appearing at the immediate vicinity of the metal surface collapses to an almost noise-like signal by the inherent kinematic dispersion of the electron waves as they perpendicularly propagate from the surface (see Figs. 4 and 5). On the other hand, there are regions quite far from the surface (even at macroscopic distances, see Fig. 6) where the clean attosecond structure of the electron current revives within a spatial range on the order of 555 nm. The attosecond light signals stemming from a single atom propagate in vacuum without changing shape with an intensity distribution of the form f (t − ξ/c), where ξ is the propagation direction. On the other hand, the Fourier components of the electron pulses have a non-trivial spatially dependent phase 2πi(2mc 2/ℏω)½ [(E 0/ℏω) +n]½ (z/λ), which can drastically vary as a function of the distance z from the metal-vacuum interface, resulting in the degradation of the originally clean attosecond pulse train. This is even so, if the phases of the transmission coefficients T n are stricky locked (as has been shown in Fig. 3, for the large-energy wing of the spectrum). At certain spatial region of z, the interference can be constructive, and in other ranges destructive. Accordingly, during the propagation of the electron signal from the metal surface there appear consecutively “collapse bands” (with destructive interference) and “revival layers” (with constructive interference) of a few or more nanometer thickness. By now, no approximate analytic formula has been found by us, which would locate the position and size of the revival layers and the collapse bands. To find such a formula is a subject of our ongoing research. Anyway, we have found by trial (or by chance) the position of a couple of these regions by using spatio-temporal contour plots (similar to Fig. 5) in several domains. At the end of Section 4, it has also been shown that, the value of the outgoing current density can be estimated at maximum a few tenth of mA/cm2, which is still a relatively large value. This is why we think that the mechanism discussed in this paper may serve as a basis for constructing good quality electron injectors for e.g., particle acceleration. The attosecond structure of the electron current can perhaps is used for monitoring of ultrafast relaxation processes in single atoms or in condensed matter.

Fig. 6. This figure Illustrates the formation of the “revival layers” from the “collapse bands” in a 555 nm size range far from the metal surface at macroscopic distances (2 013.700 nm < z < 2 014.255 nm). Here we have again plotted the dimensionless quantity $\lpar \hbar /4q_0 \rpar {\mathop{\rm Re}\nolimits} \lsqb \Psi _{II}^ {\ast} \lpar\! -\! i\partial _z \Psi _{II} \rpar \rsqb $ by superimposing the large-energy components (54 < n < 66), whose phases are locked, according to Figure 3.

Acknowledgment

This work has been supported by the Hungarian National Scientific Research Foundation, OTKA, and Grant No. T048324. S. Varró thanks partial support from the COST P14 Action, Reference Code COST-STSM-P14-02507.

References

REFERENCES

Agostini, P. (2001). Two-color and single-color above threshold ionization. In Atoms, Solids and Plasmas in Super-Intense Laser Fields (Batani, D., Joachain, C.J., Martellucci, S. and Chester, A.N., Eds), pp. 59–80. New York: Kluwer Academic/Plenum Publishers.CrossRefGoogle Scholar
Antoine, Ph., L'Huillier, A. & Lewenstein, M. (1996). Attosecond pulse trains using high-order harmonics. Phys. Rev. Lett. 77, 1234–1237.CrossRefGoogle ScholarPubMed
Anwar, M.S., Latif, A., Iqbal, M., Rafique, M.S., Khaleeq-Ur-Rahman, M. & Siddique, S. (2006). Theoretical model for heat conduction in metals during interaction with ultra short laser pulse. Laser Part. Beams 24, 347–353.CrossRefGoogle Scholar
Banfi, F., Gianetti, C., Ferrini, G., Galimberti, G., Pagliara, S., Fausti, D. & Parmigiani, F. (2005). Experimental evidence of above-threshold photoemission in solids. Phys. Rev. Lett. 94, 037601.CrossRefGoogle ScholarPubMed
Breidbach, J. & Cederbaum, L.S. (2005). Universal attosecond response to the removal of an electron. Phys. Rev. Lett. 94, 033901.CrossRefGoogle Scholar
Christov, I.P., Murname, M.M. & Kapteyn, H.C. (1997). High-harmonic generation of attosecond pulses in the “single-cycle” regime. Phys. Rev. Lett. 78, 1251–1254.CrossRefGoogle Scholar
Eliezer, S., Eliaz, N., Grossman, E., Fisher, D., Gouzman, I., Henis, Z., Pecker, S., Horovitz, Y., Fraenkel, M., Maman, S., Ezersky, V. & Eliezer, D. (2005). Nanoparticles and nanotubes induced by femtosecond lasers. Laser Part. Beams 23, 15–19.CrossRefGoogle Scholar
Farkas, Gy. & Tóth, Cs. (1992). Proposal for attosecond light pulse generation using laser-induced multiple-harmonic conversion processes in rare gases. Phys. Lett. A 168, 447–450.CrossRefGoogle Scholar
Farkas, Gy. & Tóth, Cs. (1990). Energy spectrum of photoelectrons produced by picosecond laser-induced surface multiphoton photoeffect. Phys. Rev. A 41, 4123–4126.CrossRefGoogle ScholarPubMed
Farkas, Gy., Tóth, Cs., Kőházi-Kis, A., Agostini, P., Petite, G., Martin, Ph., Berset, J.M. & Ortega, J.M. (1998). Infrared electron photoemission from a gold surface. J. Phys. B: At. Mol. Opt. Phys. B 31, L461–L468.CrossRefGoogle Scholar
Fill, E., Veisz, L., Apolonski, A. & Krausz, F. (2006). Sub-fs electron pulses for ultrafast diffraction. New J Phys. 8, 272.CrossRefGoogle Scholar
Gradshteyn, I.S. & Ryzhik, I.M. (2000). Table of Integrals, Series and Products. Sixth Edition, page 923, formulas 8.511.3 and 8.511.4. San Diego, CA: Academic Press.Google Scholar
Hentschel, M., Kienberger, R., Spielmann, Ch., Reider, G.A., Milosevic, N., Brabec, Th., Drescher, M., Corkum, P., Heinzmann, U., Drescher, M. & Krausz, F. (2001). Attosecond metrology. Nature 414, 509–513.CrossRefGoogle ScholarPubMed
Hidding, A., Amthor, K.-A., Liesfeld, B., Schwoerer, H., Karsch, S., Geissler, M., Veisz, L., Schmid, K., Gallacher, J.G., Jamison, S.P., Jaroszynski, D., Pretzler, G. & Sauerbrey, R. (2006). Generation of quasimonoenergetic electron bunches with 80-fs laser pulses. Phys. Rev. Lett. 96, 105004.CrossRefGoogle ScholarPubMed
Hu, S.X. & Collins, L.A. (2006). Attosecond pump-probe: Exploring ultrafast electron motion inside an atom. Phys. Rev. Lett. 96, 073004.Google Scholar
Johnsson, P., López-Martens, R., Kazamias, S., Mauritsson, J., Valentin, C., Remetter, T., Varjú, K., Gaarde, M.B., Mairesse, Y., Wabnitz, H., Saliéres, P., Balcou, Ph., Schafer, K.J. & L'Huiller, A. (2005). Attosecond electron wave packet dynamics in strong laser fields. Phys. Rev. Lett. 95, 013001.CrossRefGoogle ScholarPubMed
Kanapathipillai, M. (2006). Nonlinear absorption of ultra-short laser pulses by clusters. Laser Part. Beams 24, 9–14.CrossRefGoogle Scholar
Kiselev, S., Pukhov, A. & Kostyukov, I. (2004). X-ray generation on strongly nonlinear plasma waves. Phys. Rev. Lett. 93, 135004.CrossRefGoogle ScholarPubMed
Kroó, N., Varró, S., Farkas, Gy., Oszetzky, D., Nagy, A. & Czitrovszky, A. (2007). Quantum metal optics. J Modern Opt 54, 2679–2688.CrossRefGoogle Scholar
Kylstra, N., Joachain, C.J. & Dörr, M. (2001). Theory of multiphoton ionization of atoms. In Atoms, Solids and Plasmas in Super-intense Laser Fields (Batani, D., Joachain, C.J., Martellucci, S. and Chester, A.N., Eds), pp 15–36. New York: Kluwer Academic/Plenum Publishers.CrossRefGoogle Scholar
L'Huillier, A., Balcou, Ph., Candel, S., Schafer, K.J. & Kulander, K.C. (1992). Calculation of high-order harmonic-generation processes in xenon at 1064 nm. Phys Rev. A 46, 2778–2790.CrossRefGoogle ScholarPubMed
Lewenstein, M., Balcou, Ph., Ivanov, M.Yu., L'Huillier, A. & Corkum, P.B. (1994). Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 49, 2117–2132.CrossRefGoogle ScholarPubMed
Lifschitz, A.F., Faure, J., Glinec, Y., Malka, V. & Mora, P. (2006). Proposed scheme for compact GeV laser plasma accelerator. Laser Part. Beams 24, 255–259.CrossRefGoogle Scholar
Lindner, F., Schaetzel, M.G., Walther, H., Goulielmakis, E., Krausz, F., Milosevic, D.B., Bauer, D., Becker, W. & Paulus, G.G. (2005). Attosecond double-slit experiment. Phys. Rev. Lett. 95, 040401.CrossRefGoogle ScholarPubMed
López-Martens, R., Varjú, K., Johnsson, P., Mauritsson, J., Mairesse, Y., Saliéres, P., Gaarde, M.B., Schafer, K.J., Persson, A., Svanberg, S., Wahlström, C.-L. & L'Huillier, A. (2005). Amplitude and phase control of attosecond light pulses. Phys. Rev. Lett. 94, 033001.CrossRefGoogle ScholarPubMed
Mauritsson, J., Gaarde, M.B. & Schafer, K.J. (2005). Accessing of electron wave packets generated by attosecond pulse trains through time-dependent calculations. Phys. Rev. A 72, 013401.CrossRefGoogle Scholar
Niikura, H., Villeneuve, D.M. & Corkum, P.B. (2005). Mapping attosecond wave packet motion. Phys. Rev. Lett. 94, 083003.CrossRefGoogle ScholarPubMed
Papadogiannis, N.A., Witzel, B., Kalpouzos, C. & Charalambidis, D. (1999). Observation of attosecond light localization in higher order harmonic generation. Phys. Rev. Lett. 83, 4289–4292.CrossRefGoogle Scholar
Paul, P.M., Toma, E.S., Breger, P., Mullot, G., Augé, F., Balcou, Ph., Muller, H.G. & Agostini, P. (2001). Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692.CrossRefGoogle ScholarPubMed
Paulus, G.G. & Walther, H. (2001). The classical and the quantum face of above-threshold ionization. In Atoms, Solids and Plasmas in Super-Intense Laser Fields (Batani, D., Joachain, C.J., Martellucci, S. and Chester, A.N., Eds.), pp 285–300. New York: Kluwer Academic/Plenum Publishers.CrossRefGoogle Scholar
Pukhov, A. & Meyer-ter-Vehn, J. (2002). Laser wake field accelerator: the highly non-linear broken-wave regime. Appl. Phys. B 74, 355–361.CrossRefGoogle Scholar
Quèrè, F., Thaury, C., Monot, P., Dobosz, P., Martin, Ph., Geindre, J.-P. & Audebert, P. (2006). Coherent wake emission of high-order harmonics from overdense plasmas. Phys. Rev. Lett. 96, 125004.CrossRefGoogle ScholarPubMed
Radzig, A.A. & Smirnov, B.M. (1985). Reference Data on Atoms, Molecules and Ions. Berlin: Springer-Verlag, Berlin.CrossRefGoogle Scholar
Remetter, T., Johsson, P., Mauritsson, J., Varjú, K., Ni, Y., Lépine, F., Gustafsson, E., Schafer, K.J., Vrakking, M.J.J. & L'Huillier, A. (2006). Attosecond electron wave packet interferometry. Nat. Phys. 2, 323–326.CrossRefGoogle Scholar
Saliéres, P. (2001). High-order harmonic generation. In Atoms, Solids and Plasmas in Super-Intense Laser Fields (Batani, D., Joachain, C.J., Martellucci, S. and Chester, A.N., Eds.), pp 83–97. New York: Kluwer Academic/Plenum Publishers.CrossRefGoogle Scholar
Sansone, G., Benedetti, E., Calegary, F., Vozzi, C., Avaldi, L., Flammini, L., Poletto, L., Villoresi, P., Altucci, C., Velotta, R., Stagira, S., De Silvestri, S. & Nisoli, M. (2006). Isolated single-cycle attosecond pulses. Science 314, 443–446.CrossRefGoogle ScholarPubMed
Schwengelbeck, U., Plaja, L., Conejero Jarque, E., Roso, L., Varró, S. & Farkas, Gy. (2002). Prediction of step-like occupation and inversion of states in thin films exposed to laser pulses. J. Phys. B:At. Mol.Opt.Phys. 35, L181–L185.CrossRefGoogle Scholar
Sherlock, M., Bell, A.R. & Rozmus, W. (2006). Absorption of ultra-short laser pulses and particle transport in dense targets. Laser Part. Beams 24, 231–234.CrossRefGoogle Scholar
Sokolov, A.V. (1967). Optical Properties of Metals. London, UK: Blackie and Son Limited.Google Scholar
Tsakiris, G.D., Eidmann, K., Meyer-ter-Vehn, J. & Krausz, F. (2006). Route to intense single attosecond pulses. New J. Phys. 8, 19.CrossRefGoogle Scholar
Tzallas, P.Charalambidis, D., Papadogiannis, N.A., Witte, K. & Tsakiris, G.D. (2003). Direct observation of attosecond light bunching. Nature 426, 267–271.CrossRefGoogle ScholarPubMed
Uiberacker, M., Uphues, Th., Schultze, M., Verhoef, A.J., Yakovlev, V., Kling, M.F., Rauschenberger, J., Kabachnik, N.M., Schröder, H.Lezius, M., Kompa, K.L., Muller, H.-G., Vrakking, M.J.J., Hendel, S., Kleineberg, U., Heinzmann, U., Drescher, M. & Krausz, F. (2007). Attosecond real-time observation of electron tunneling in atoms. Nature 446, 627–632.CrossRefGoogle ScholarPubMed
Varró, S. & Ehlotzky, F. (1998). High-order multiphoton ionization at metal surfaces by laser fields of moderate power. Phys. Rev. A 57, 663–666.CrossRefGoogle Scholar
Varró, S. (2007). Linear and nonlinear absolute phase effects in interaction of ultrashort laser pulses with a metal nano-layer or with a thin plasma layer. Laser Part. Beams 25, 379–390.CrossRefGoogle Scholar
Willi, O., Toncian, T., Borghesi, M., Fuchs, J., D'humieres, E., Antici, P., Audebert, P., Brambrink, E., Cecchetti, C., Pipahl, A. & Romagnani, L. (2007). Laser triggered micro-lens for focusing and energy selection of MeV protons. Laser Part. Beams 25, 71–77.CrossRefGoogle Scholar
Zayats, A.V., Smolyaninov, I.I. & Maradunin, A.A. (2005). Nano-optics of surface plasmon polaritons. Phys. Rept. 408, 131–314.CrossRefGoogle Scholar
Figure 0

Fig. 1. This figure shows the time-averaged spectrum of the above-threshold electron current density for the parameters introduced in the text above. The relative current density components jt(n) = (pn/q0) · |Tn|2 of Eq. (8a) are normalized to their maximum value ~0.02. The discrete points are connected by thick lines in order to guide the eye.

Figure 1

Fig. 2. This figure shows the dependence of phase differences arg [Tn+1*Tn] in radians on the number of absorbed photons n, corresponding to the spectrum shown in Figure 1. The discrete points are connected with thin lines in order to guide the eye. For relatively low-order processes the phase difference varies quite irregularly, but for the large energy wing, for 54 < n, it is stationary, which means that these components are strictly locked, which is in complete accord with the first approximate formula in Eq. (9). Based on this figure, we expect that the large-energy Floquet components interfere constructively, because of the regular behavior of their phases.

Figure 2

Fig. 3. This figure shows the large energy wing of the above-threshold spectrum represented by vertical bars (normalized to their maximum value~0.02. This is a magnification of the end of the spectrum shown already in Figure 1, and shows also at the large-energy part of Figure 2, the dependence of phase differences φn − φn+1 in radians on the number of absorbed photons n, at the end of the multiphoton spectrum. These phase differences are represented by points. According to the approximate formula given by Eq. (9) these differences arg [Tn+1*] – arg [Tn] are quiet uniformly equal about to π/2 ≈ 1.57, as is also seen on the figure.

Figure 3

Fig. 4. This figure shows the detailed time-behavior of the outgoing current density at different distances from the metal surface. Here we have plotted the dimensionless quantity (ℏ$ 4q_0 \rpar {\mathop{\rm Re}\nolimits} \lsqb \Psi _{II}^ {\ast} \lpar\! -\! i\partial _z \Psi _{II} \rpar \rsqb $ by superimposing the large-energy components (54 < n < 66), whose phase are locked, according to Figure 3. At z = 0 we received an ideal T10~250 attosecond pulse train, which is gradually spoiled by the inherent dispersion of de Broglie waves propagating in vacuum (due to the non-trivial z-dependence of the phases), yielding a noise-like electron current density already at the distance of 300 nm from the metal.

Figure 4

Fig. 5. This figure shows the spatio-temporal behavior of the outgoing current in the range {0 nm < z < 300 nm, 0 T < t < 5.5 T,}. The white lines represent large values of the current density; on the other hand, the dark (grey or even black) regions indicate low values of the current density. By intersecting the figure vertically at some position z, and projecting the intersection to the time-axis (to the ordinate), we receive a representation of the time behavior at that particular position. It is seen that the ideal attosecond pulse train at the immediate vicinity of the metal surface z = 0, represented by the light lines, is gradually washed out by the propagation from the surface. At z = 300 nm the temporal variation of the electron current density becomes already a noise-like background (represented by the dark band), as is also shown on the last figure in the graphics array of Figure 4.

Figure 5

Fig. 6. This figure Illustrates the formation of the “revival layers” from the “collapse bands” in a 555 nm size range far from the metal surface at macroscopic distances (2 013.700 nm < z < 2 014.255 nm). Here we have again plotted the dimensionless quantity $\lpar \hbar /4q_0 \rpar {\mathop{\rm Re}\nolimits} \lsqb \Psi _{II}^ {\ast} \lpar\! -\! i\partial _z \Psi _{II} \rpar \rsqb $ by superimposing the large-energy components (54 < n < 66), whose phases are locked, according to Figure 3.