Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T12:14:26.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Pricing Models for German Wine: Hedonic Regression vs. Machine Learning

Published online by Cambridge University Press:  06 August 2020

Britta Niklas  and
Wolfram Rinke
Britta Niklas*
Affiliation:
Institute of Development Research and Development Policy, Ruhr-University Bochum, Universitätsstr.105, 44789Bochum, Germany
Wolfram Rinke
Affiliation:
Department of Information-Technology and Information-Management, Fachhochschule Burgenland GmbH, Campus 1, A-7000Eisenstadt, Austria; e-mail: wolfram.rinke@fh-burgenland.at.
*
e-mail: britta.niklas@rub.de, corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

This article examines whether there are different hedonic price models for different German wines by grape variety, and identifies influential factors that focus on weather variables and direct and indirect quality measures for wine prices. A log linear regression model is first applied only for Riesling, and then machine learning is used to find hedonic price models for Riesling, Silvaner, Pinot Blanc, and Pinot Noir. Machine learning exhibits slightly greater explanatory power, suggests adding additional variables, and allows for a more detailed interpretation of results. Gault&Millau points are shown to have a significant positive impact on German wine prices. The log linear approach suggests a huge effect of different quality categories on the wine prices for Riesling with the highest price premiums for Auslese and “Beerenauslese/Trockenbeerenauslese/Eiswein (Batbaice),” while the machine learning model shows, that additionally the alcohol level has a positive effect on wines in the quality categories “QbA,” “Kabinett,” and “Spätlese,” and a mostly negative one in the categories “Auslese” and “Batbaice.” Weather variables exert different affects per grape variety, but all grape varieties have problems coping with rising maximum temperatures in the winter and with rising minimum and maximum temperatures in the harvest season. (JEL Classifications: C45, L11, Q11)

Keywords

German wine priceshedonic pricingmachine learningweather changes
Type
Articles
Information
Journal of Wine Economics , Volume 15 , Issue 3 , August 2020 , pp. 284 - 311
Copyright
Copyright © American Association of Wine Economists, 2020

I. Introduction and Literature

In the hedonic price approach, the price of a good or service is split into several implied prices that relate to specific characteristics of a good or service for which consumers are willing to pay. In the most common application of the hedonic approach to analyzing wine prices, a log-linear regression is used to estimate the price

(1)$$ln\lpar P \rpar = X\beta + \varepsilon _\comma \;$$

where P is a price vector of a 0.75 liter bottle of wine, X denotes a matrix of characteristics which are supposed to have an influence on the wine price, β is the vector of parameters that are associated to these characteristics, and ɛ is the error term (Thrane, Reference Thrane2004).

There is a growing number of studies dealing with the impact of weather changes on wine quality and wine prices.Footnote 1 Most of these studies suggest that temperature and precipitation during the growing and harvesting seasons may have an important impact on wine prices (e.g., Ashenfelter, Reference Ashenfelter2010; Ashenfelter and Storchmann, Reference Ashenfelter and Storchmann2010; Byron and Ashenfelter, Reference Byron and Ashenfelter1995; Haeger and Storchmann, Reference Haeger and Storchmann2006; Jones and Storchmann, Reference Jones and Storchmann2001; Lecocq and Visser, Reference Lecocq and Visser2006; Oczkowski, Reference Oczkowski2001, Reference Oczkowski2014, Reference Oczkowski2016; Ramirez, Reference Ramirez2008; Storchmann, Reference Storchmann2005, Reference Storchmann2012). As weather information is not given on the wine label, visible quality indicators include the quality categories or the alcohol level as direct measures of quality that are affected by weather (Niklas, Reference Niklas2017), and wine guide scores as indirect measures of wine quality (Schamel, Reference Schamel2000, Reference Schamel2002, Reference Schamel2003; Shapiro, Reference Shapiro1983; Tirole, Reference Tirole1996).

Most of the extant studies use either time series data or cross-sectional data and apply (log)linear regression approaches to identify the impact of the weather, while other disciplines such as engineering or stock exchange trading use machine learning (Shavlik and Diettrich, Reference Shavlik and Diettrich1990) as the core technology for their model building capabilities (Stone et al., Reference Stone, Brooks, Brynjolfsson, Calo, Etzioni, Hager, Hirschberg, Kalyanakrishnan, Kamar, Kraus, Leyton-Brown, Parkes, Press, Saxenian, Shah, Tambe and Teller2016).Footnote 2 There is only one paper to date, that deals with the prediction of wine prices applying machine learning. This paper focuses on time-series analyses required for stock exchange trading (Yeo, Fletcher, and Shawe-Taylor, Reference Yeo, Fletcher and Shawe-Taylor2015).

The current study focuses on separate equations for different German grape varieties, assuming that these grape varieties react differently to weather variables. The results of the log linear regression (and squared forms) and the machine learning are first compared for the Riesling grape variety, then the machine learning is applied for the other grape varieties.

The article is organized as follows. Section II presents the data. Section III describes the methodological approach. Section IV reports the results and Section V draws conclusions.

II. Data on German Weather and Wine Prices

We base our analysis on a dataset that covers farm gate prices for 0.75 liter bottles of wine,Footnote 3 reported by 177 wine producers that we sampled at random for the Riesling, Silvaner, Pinot Blanc, and Pinot Noir grape varieties for the vintages 1998 to 2013, for all 13 German wine regions. We obtained farm gate pricesFootnote 4 from these producers with data on various control variables from “Gault&Millau Weineguide Deutschland” (Diel and Payne, Reference Diel and Payne2002–2009; Payne, Reference Payne2010–2015). Table 1 summarizes all collected variables for the Riesling grape variety.Footnote 5

Table 1 Descriptive Statistics for Riesling

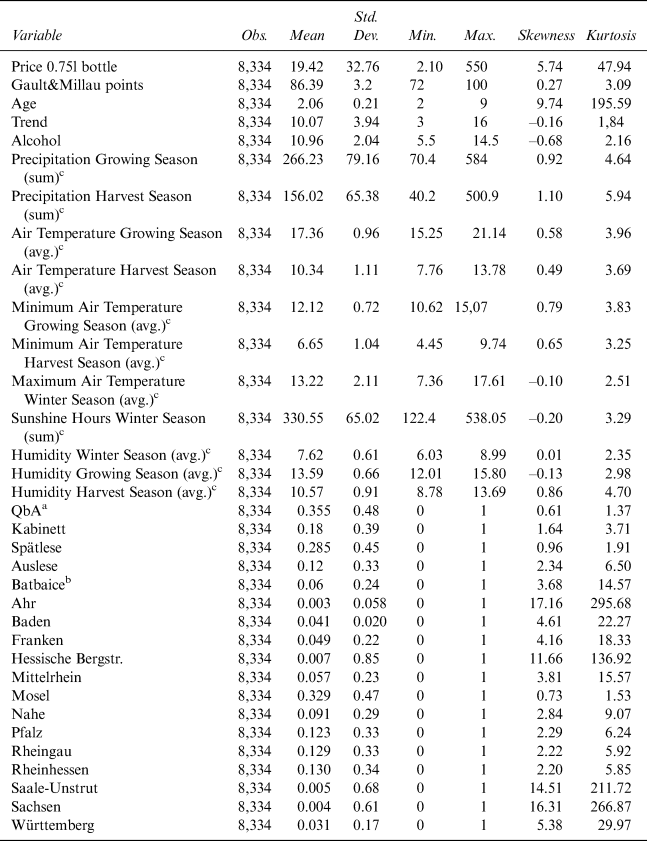
a QbA: Qualitätswein

b Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

c Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors’ calculations.

We use German quality categories as direct measures of quality. German wines are categorized by the degree of ripeness of the grapes, measured as the content of natural sugar in the must (grape juice) at harvest. However, these so called “quality categories” do not measure, per se, whether a wine is of good or bad quality.Footnote 6 The German term is “degree Oechsle”Footnote 7 and the following categories are distinguished: Qualitätswein (QbA),Footnote 8 Kabinett, Spätlese, Auslese, Beerenauslese, Trockenbeerenauslese, and EisweinFootnote 9 (Ashenfelter and Storchmann, Reference Ashenfelter and Storchmann2010).

Instead of collecting data from a single weather station, as shown in the literature (Lecocq and Visser, Reference Lecocq and Visser2006; Haeger and Storchmann, Reference Haeger and Storchmann2006), this study uses daily data (daily average temperature,Footnote 10 average of the daily maximum and daily minimum temperature all in degrees Celsius, sum of precipitation in mm, and daily average humidity in percent) from 13 different local weather stations,Footnote 11 as especially since precipitation varies between German wine regions, which therefore differ in their suitability for grape growing, while one weather station would have been suitable in the case of the temperature due to spatial correlation (Ashenfelter and Storchmann, Reference Ashenfelter and Storchmann2010; Haeger and Storchmann, Reference Haeger and Storchmann2006). Overall, our sample comprises 8,334 observations for Riesling, 2,004 for Pinot Noir, 1,294 for Pinot Blanc, and 917 for Silvaner.

Mainly the regions Mosel (32.9%), Pfalz (12.3%), Rheingau (12.9%), and Rheinhessen (13%) produce Riesling and the quality categories are QbA (35.5%), Spätlese (28.5%), Kabinett (18%), Auslese (12%), and Beerenauslese/Trockenbeerenauslese/Eiswein (Batbaice) (6%). The price of Riesling varies tremendously, from €2.10 to €550.00 per bottle, while Gault&Millau quality points vary between 72 and 100.

III. Methods

In the first step, we run a log linear regression for Riesling and follow the variables employed in the previous literature. The hedonic equation is

(2)$$\eqalignt{ln\lpar {P_i} \rpar &= \beta _0 + \beta _1GMP_{it} + \beta _2age_{it} + \beta _3trend_{it} + \beta _4W_{4it} + \ldots + \beta _kW_{kit} \cr & \quad+ \gamma _1\lpar {Quality} \rpar + \gamma _2\lpar {Region} \rpar + \gamma _3\lpar {Producer} \rpar + \varepsilon _{it}\comma \;$$

where GMP denotes Gault&Millau points (as an indirect measure of quality), age is the age of the wine at the time of purchase, trend is an annual trend variable to capture inflationary trends, W4 ... Wk are various weather variables (average air temperature, squared temperature, sum of precipitation in mm) which we split into the growing and harvest seasons,Footnote 12 Quality is a series of dummy variables for the German quality categories (as a direct measure of quality), Region is a series of dummy variables depicting the region from where the grapes are sourced, and Producer is a series of dummy variables reflecting price policies and other farm specific factors (production cost, capital cost, owner structure, etc.).

In the second step, we substitute the log linear regression algorithm with machine learning (Witten, Eibe, and Hall, Reference Witten, Eibe and Hall2017). We build a non-linear regression model including all variables, which uses a classic feed forward artificial neural network (ANN) algorithm (Witten, Eibe, and Hall, Reference Witten, Eibe and Hall2017; Hornik, Stichcombe, and White, Reference Hornik, Stichcombe and White1990; Rumelhart, Hinton, and Williams, Reference Rumelhart, Hinton and Williams1986) to generate the functional model between environmental and other variables related to logarithmic bottle prices.

An ANN is a mathematical simulation of the biological nervous cell system and consists of many regression units, which are typically non-linear, but could also be linear for scaling purposes. These units are also known in the literature as perceptrons (Rosenblatt, Reference Rosenblatt1958), neurons, or nodes and are organized in layers (Witten, Eibe, and Hall, Reference Witten, Eibe and Hall2017; Hornik, Stichcombe, and White, Reference Hornik, Stichcombe and White1990; Rumelhart, Hinton, and Williams, Reference Rumelhart, Hinton and Williams1986). Each layer is stacked on top of the other and all nodes of the underlying layer have a direct weighted link to each unit in the following layer. Several kinds of architecture exist, where the layers can be skipped or where there are feedback loops between previous layers (Witten, Eibe, and Hall, Reference Witten, Eibe and Hall2017). Feed forward networks, those without any feedback loops or recursions, typically have three types of layers. The input layer type that uses the values of the independent variables as input, the hidden layer type that is responsible for the non-linear functional regression, and the output layer type that performs the final transformation to the dependent variables. Equation (3) describes the general form of the network architecture as

(3)$$ln\lpar {P_i} \rpar = f_o\left({\sum\nolimits_{k\to h} {w_{kh}f_h} \left({\sum\nolimits_{\,j\to k} {w_{\,jk}f_i} \left({\sum\nolimits_{i\to j} {w_{ij}x_i} } \right)} \right)} \right)\comma \;$$

where x i is an independent variable and fi is the transfer function on the input layer, fh is the transfer function of the hidden layer, and fo is the transfer function of the output layer. The transfer function in this case is the logistic sigmoidal function as described in Equation (4).

(4)$$f\lpar x \rpar = \lpar {1 + e^{{-}x}} \rpar ^{{-}1}$$

In the third step, we calculate the dependency matrix (Rinke, Reference Rinke2015) for the previously generated ANN model. We derive the dependency matrix from a sensitivity analyses of the ANN model, which Hashem (Reference Hashem1992) originally presented and Yeh and Cheng (Reference Yeh and Cheng2010) further investigated. It represents a normalized, accumulated Jacobi matrix (Rudin, Reference Rudin1976) over the observed data samples and expresses the relative importance of an independent variable with respect to the dependent variable of the ANN model.

There are two other methods of describing the “importance” of an independent variable with respect to the dependent variable, but these are based only on the learned internal network weights w ij (Olden and Jackson, Reference Olden and Jackson2002; Olden, Joy, and Death, Reference Olden, Joy and Death2004; Garson, Reference Garson1991; Goh, Reference Goh1995; Giam and Olden, Reference Giam and Olden2015). Yeh and Cheng (Reference Yeh and Cheng2010) show that calculating importance as a value, based on the first order partial derivative and further on, the second order partial derivative is more accurate than other common methods.

We calculate the dependency factor (Rinke, Reference Rinke2015) for each independent variable of the model with respect to the dependent variable separately using Equation (5). Yeh and Cheng (Reference Yeh and Cheng2010) call this dependency factor the “average linear importance factor”

(5)$$DF\lpar {y\lpar x \rpar } \rpar = \sqrt {\displaystyle{1 \over n}\mathop \sum \nolimits {\left({{{\partial y} \over {\partial x}}} \right)}^2} $$

where ${{\partial y} \over {\partial x}}$ represents the partial derivative of the function y(x) and n the number of samples.

In addition to the dependency factors, we examine the semi-elasticity ε of y(x) (Owen, Reference Owen2012). Semi-elasticity measures the percentage change in the dependent variable caused by a unit change in the independent variable. In the log-linear-regression model log(y) = ß 0 + ß 1x + u. The variable ß 1 measures the semi-elasticity of the dependent variable in relation to the respective independent variable. Since we use a log-linear specification between the log-price and an independent variable x, a change of one unit of x results in an ε × 100 percent change in y.Footnote 13 We calculate the semi-elasticity following Equation (6) and the average semi-elasticity following Equation (7).

(6)$$\varepsilon _{y\comma x} = \displaystyle{{\partial y} \over {\partial x}}\displaystyle{1 \over y}$$
(7)$$\overline {\varepsilon _{y\comma xi}} = \displaystyle{1 \over n}\mathop \sum \limits_{i = 1..n} \varepsilon _{y\comma xi},$$

for n observations

In the fourth step, we calculate the average semi-elasticity for each independent variable of the model with respect to the dependent variable separately for each German quality category (QbA, Kabinett, Spätlese, Auslese, and Batbaice) and discuss the results. For the remaining grape varieties, Silvaner, Pinot Blanc, and Pinot Noir, we repeat steps two to four and summarize the results (only available online).

IV. Results

A. Riesling Models

(1) Log Linear Regression

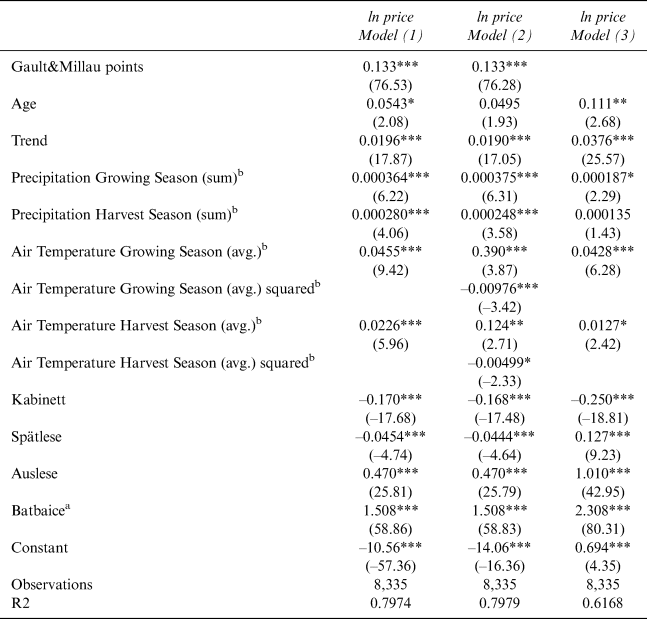
We apply the hedonic Equation (2) using average temperature functions for the growing and harvest seasons in Model 1, squared temperature functions in Model 2, and omitting Gault&Millau points in Model 3 applying robust standard errors.Footnote 14

The reason for using squared temperatures in Model 2 is to check for non-linear temperature effects. The Gault&Millau points are omitted in Model 3 to check whether the weather variables can cover most quality aspects. The results are shown in Table 2 with an R2 of 0.7974 (Model 1), 0.7979 (Model 2), and 0.6168 (Model 3).Footnote 15

Table 2 Comparison of Model 1, 2, and 3 for Riesling (without Regional and Producer Fixed Effects)

Note: Robust t statistics are in parentheses; significance levels are *p < 0.05, **p < 0.01, and ***p < 0.00.

a Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

b Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors’ calculations.

All significant weather variables show a positive impact on wine prices in all three models. Model 3 suggests that average temperatures during the growing and harvest seasons have a significantly positive but decreasing effect, because the squared functions are negative. Based on these results, we calculate the price-maximizing temperature, which is 19.98 degrees Celsius for the growing season and 12.42 degrees Celsius for the harvest season.

Gault&Millau points have the greatest influence on the Riesling price, as the price increases by 13.3% with each additional point in Models 1 and 2. The exclusion of Gault&Millau points leads to less accurate results and a much lower R2.

The price trend has a significantly positive impact in all three models (between 1.9% and 3.76%) and the wine price increases with the age of the wine by 5.43% in Model 1 and 11.1% in Model 3, but is insignificant in Model 2.

Quality categories also have a significant impact. Compared to QbA, the Kabinett category leads to a decline in prices for all three models and Spätlese leads to a decline in prices for Models 1 and 2, while the higher-quality categories lead to much higher prices. The quality Auslese category has a positive price impact from 47% (Models 1 and 2) to 101% (Model 3), and Batbaice from 150.8% (Models 1 and 2) to 230.8% (Model 3).

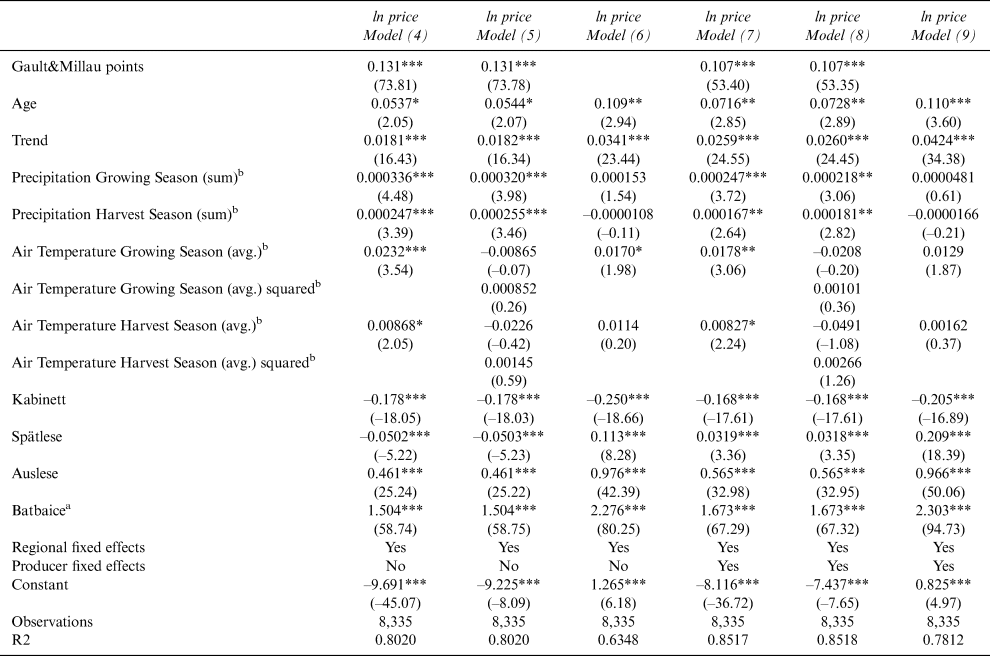
We then estimate the above models applying regional fixed effects to control regional unobserved heterogeneity. Table 3 (left side) shows the results with an R2 of 0.8020 (Model 4), 0.8020 (Model 5), and 0.6348 (Model 6).

Table 3 Models for Riesling

Note: Robust t statistics are in parentheses; significance levels are *p < 0.05, **p < 0.01, and ***p < 0.00.

a Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

b Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors' calculations.

While most of the results are confirmed, Model 5 shows the most obvious change in results. Including squared temperature variables now makes all temperature variables insignificant. One reason might be that non-linear temperature effects are only observed in some regions, so the effects are no longer significant when we apply regional fixed effects. We confirm this assumption when running regressions for regional subsamples: squared temperature variables for both the growing and harvest seasons are only significant for the regions of Baden (in the very south of Germany) and for Mittelrhein (a sunny wine region), while for the harvest season squared temperature variables are only significant for the regions of Nahe and Württemberg (again, in the very south of Germany). The majority of observations (6,504 out of 8,335), however, cover German wine regions with linear temperature effects. Model 6 again has less accurate results than the other two models.

Finally, we estimate the same models applying regional and producer fixed effects that can reflect pricing policies and other farm-specific factors such as production cost, capital cost, or owner structure. Table 3 (right side) shows the results, with an R2 of 0.8517 (Model 7), 0.8518 (Model 8), and 0.7812 (Model 9).

The application of producer fixed effects generally leads to a higher explanatory power of all models. The effect of Gault&Millau points is less strong than before (10.7% instead of 13.1%), while age and trend have stronger effects. Only in Model 7 do all weather variables show a significant and positive effect on wine prices, while the inclusion of squared temperature effects still leads to insignificant results. Similar to the previous explanation, this may be due to the majority of producers in this sample (74.1%) are in regions with linear temperature effects according to the regional subsamples.

Due to the high degree of skewness (5.74) and kurtosis (47.94) in the price data (see Table 1), we assume that marginal effects might vary in different price brackets. Therefore, we finally run a quantile regression for Model 4 (with regional fixed effects without squared temperaturesFootnote 16) and report the results and the corresponding ordinary least square (OLS) results in Table 4 (Column 1), allowing for a direct comparison of results.

Table 4 OLS vs. Quantile Regressions of Model 4 for Riesling

Note: All equations include a full set of regional fixed effects. Robust t statistics are in parentheses; significance levels are *p < 0.05, **p < 0.01, and ***p < 0.00.

a Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

b Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors’ calculations.

Similar to the OLS results, Gault&Millau points have a positive affect on the price. The effect peaks in the 0.75 quantile and then decreases slightly afterwards.

The age of a wine bottle, which is statistically significant in the OLS regression, only exerts a significantly positive price effect in the 0.5 quantile and remains insignificant for all others.

The quantile regression shows significant trend effects like the OLS, but the trend effect decreases with the price quantiles.

Like in the OLS results, wine prices in the growing season are significantly positively affected by precipitation, with a peak in the 0.25 quantile. Precipitation in the harvest season only has a significant positive price effect in the 0.25 quantile and then again in the 0.75 and 0.9 quantiles, the effect increasing with the price quantiles.

The average temperature in the growing season shows a significantly positive price effect only for the 0.25 and 0.5 quantiles, with a peak for the 0.25 quantile. The same holds to the average temperature in the harvest season, which is significantly positive for the 0.9 quantile.

The highest German quality categories, Auslese and Batbaice, show a highly significant positive effect on wine prices. This effect increases with the price quantiles and accounts for a price increase of up to 61% for Auslese and up to 171.1% for Batbaice.

The Kabinett category shows no significant effect for the 0.25 quantile, but for all other quantiles there is an increasing, significantly negative effect on wine prices. For Spätlese, the effect is significantly positive for the 0.25 quantile, but significantly negative for the quantiles 0.5, 0.75, and 0.9.

(2) Machine Learning Approach

All available variables (see Table 1) can be used for the application of ANNsFootnote 17 without a negative impact on the model accuracy, since ANN models are robust with regard to multicollinearity (Dumancas and A Bello, Reference Dumancas and A Bello2015; Garg and Tai, Reference Garg and Tai2013).

First, we investigate a feasible architecture for the ANN model that matches the Riesling dataset. As a result of several experiments with different architectures and the intention to maximize the R2, to minimize root mean squared error (RMSE) and to avoid overfitting, we found a four-layer architecture for the Riesling model. Thus, all 44 input variables, including quality fixed effects and regional fixed effects and, therefore, 44 nodes in the input-layer, 15 nodes in the first hidden layer and one node in the second hidden layer, and finally one output node for our dependent variable. In the next step, we train the Riesling model and calculate the dependency matrix and the semi-elasticity, which gives a sextuple for each independent variable, applying quality fixed effects.

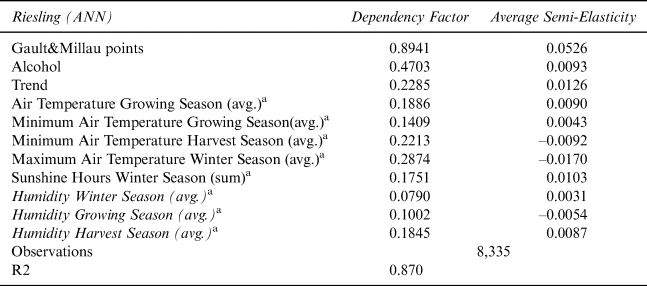
We interpret a variable as important (significant) and influential if it has a high dependency value and a high semi-elasticity value.Footnote 18 Table 5 shows the significant and influential variables for Riesling.Footnote 19 We additionally include Humidity as an independent variable because it has rarely been used in the literature.

Table 5 Significant and Influential Variables for Riesling

a Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors’ calculations.

The ANN model is of higher explanatory power as it is possible to also capture non-linear relationships,Footnote 20 and the resulting R2 is now 0.876. Furthermore, the RMSE with a value of 0.293 shows a better model accuracy (about 18.7% better) than the log linear regression model.

Again, we identify Gault&Millau points as the most important (nonfixed effect) variable with a dependency factor of 0.894, which also shows the highest semi-elasticity, with a price increase of 5.26% for each additional Gault&Millau point.

Like in the log linear regression model, there is a positive price trend, while the age of the wine does not seem to be important for the Riesling prices. The average (and also minimum) temperatures in the growing season again have a positive influence on wine prices, while precipitation does not seem to be relevant.

Some additional variables exert a price effect. The alcohol level has a positive effect on the price, while the rise in the maximum temperatures in the winter season and the minimum temperatures in the harvest season have negative prices effects, so that an increase in extreme weather conditions is, therefore, unfavorable for Riesling.

The ANN model allows the semi-elasticity to be split for each independent variable into a semi-elasticity per fixed effect (here the respective quality category), which improves the interpretation of the results. Table 6 shows the splitting into these semi-elasticities per quality category for Riesling.

Table 6 Average Semi-Elasticity of Significant and Influential Variables for Riesling by Quality Category

a Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

b Qualitätswein

c Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

Source: Authors’ calculations.

The very left column of Table 6 shows the average coefficient (semi-elasticity), while the other 5 columns show the semi-elasticity per quality category. Here, the influence of additional Gault&Millau points on the price for QbA wines (+7.41%) is very high, but only small for wines of the Kabinett quality (+2.67%) and medium for Spätlese (+4.28%), Auslese (+5.85%), and Batbaice (+4.05%). Table 6 shows the positive influence of the alcohol level on the prices of QbA wines (+3.68%), Kabinett (+0.17%), and Spätlese (+0.63%), while the impact is negative regarding the prices of wines of the quality categories Auslese (–3.29%) and Batbaice (–3.02%). A rise in maximum temperatures during the winter season is not favorable for all quality categories of Riesling.

With the scatter plots in Figures 1 and 2, we further split the semi-elasticities and distinguish between the influence on low- and high-priced wines within a single quality category.

Figure 1 Average Semi-Elasticity of Gault&Millau Points for Each Riesling Quality Category

Source: Authors’ calculations.

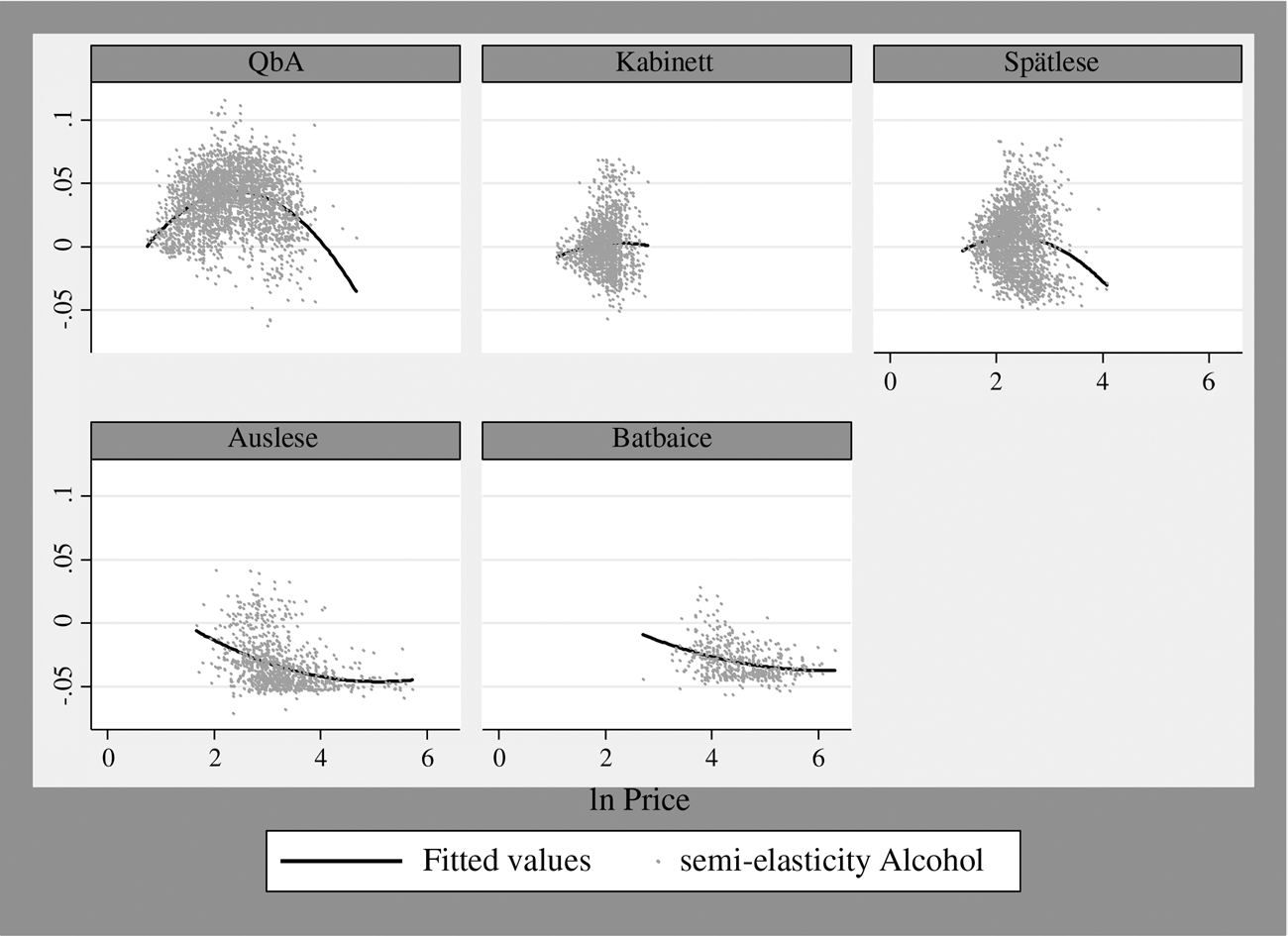
Figure 2 Average Semi-Elasticity of the Alcohol Level for Each Riesling Quality Category

Source: Authors’ calculations.

Figure 1 shows that wines with a lower QbA benefit from additional Gault&Millau points, while wines with a higher price do not. This is the opposite for all other quality categories, since the higher the price, the more positive the price effect.

Figure 2 shows that the influence of the alcohol level is higher for QbA wines with lower prices than for QbA wines with higher prices, and that there is a slightly positive effect on higher-priced Kabinett wines. The scatterplot clearly confirms the negative influence of higher alcohol percentages on wine prices for the quality categories Spätlese, Auslese, and Batbaice.

B. ANN Regression Models for Silvaner, Pinot Blanc, and Pinot Noir

We also conduct the analysis for the Silvaner, Pinot Blanc, and Pinot Noir grape varieties, but as mentioned in Section III, we exclusively apply the machine learning approach due to its better performance. We again build an ANN and apply the same architecture as used for the Riesling model in order to compare the results.

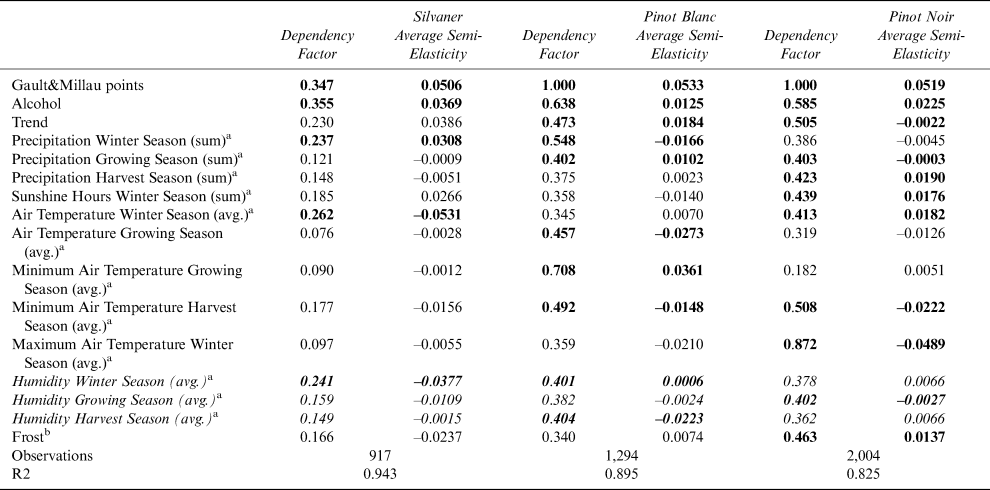
Table 7 shows the dependency matrix and average semi-elasticities for the most important and influential variables for the other three grape varieties.Footnote 21

Table 7 Dependency Matrix and Average Semi-Elasticity for Silvaner, Pinot Blanc, and Pinot Noir

Note: Significant and influential variables for each grape variety in bold letters.

a Winter Season: 12/01–02/28; Growing Season: 03/01–09/15; Harvest Season: 09/15–10/31

b Frost: Sum of days of frost, with soil temperatures < 0 during winter, growing, and harvest seasons.

Source: Authors’ calculations.

Figure 3 (dependency factor) and Figure 4 (average semi-elasticity) visualize the differences between grape varieties regarding dependency factors and average semi-elasticities more easily for all grape varieties, including Riesling.

Figure 3 Dependency Factors for Riesling, Silvaner, Pinot Blanc, and Pinot Noir

Source: Authors’ calculations.

Figure 4 Average Semi-Elasticity for Riesling, Silvaner, Pinot Blanc, and Pinot Noir

Source: Authors’ calculations.

Regarding the dependency factors, Figure 3 clearly shows that the “Gault&Millau points” is the most important independent variable for the prices of all grape varieties and that the various weather variables have differing levels of importance for these prices with the variable “maximum air temperature in the winter season” being the most important one for Pinot Noir prices, and the variable “minimum air temperature in the growing season” for Pinot Blanc prices.

The same applies to the average semi-elasticities (Figure 4) with “Gault&Millau points” and on a lower level “Alcohol” as variables with a highly positive influence on the prices of all grape varieties, the variable “minimum air temperature in the growing season” having a highly positive effect on Pinot Blanc prices, the “air temperature in the winter season” having a highly negative effect on Silvaner prices, and “maximum air temperature in the winter season” on Pinot Noir prices.

We calculate the semi-elasticities per quality category of important (significant) and influential variables for Silvaner, Pinot Blanc, and Pinot Noir as we did for Riesling. The respective scatter plots show whether there is a difference between lower- and higher-priced wines in each quality category for each independent variable.

These results are only addressed in the online publication.

V. Conclusion

The results suggest that a simple hedonic price equation does not exist for all grape varieties. It is more appropriate to use different price equations for each grape variety. The log linear regression model for Riesling finds positive effects especially of Gault&Millau points, but also of age, trend, and average temperatures as well as precipitation on German wine prices. The quality categories Auslese and Batbaice lead to very high-price premiums for Riesling. The non-linear regression using ANNs performs slightly better than the log linear regression model because it delivers better results with respect to R2 and RMSE, suggests some additional explanatory variables (such as alcohol level or minimum and maximum temperatures), and gives a more detailed insight into the interpretation of explanatory variables.

Therefore, the results for Silvaner, Pinot Blanc, and Pinot Noir are based on the machine learning approach. It is shown that the influence of an independent variable on the wine price of a certain grape variety cannot be estimated by a single coefficient, since the influence clearly differs for each quality category (fixed effect) of the respective wine.

The results of the machine learning model also suggest that Gault&Millau points have a significant and high influence on German wine prices, as one additional point increases wine prices by around 5% regarding the average coefficients, but with differences between quality categories. The split analysis shows that the lowest German quality category QbA has the highest premiums, while the highest quality category Batbaice only has high premiums for Pinot Noir. Additional scatter plots show that the higher-priced QbA wines benefit more from additional Gault&Millau points than the lower-priced QbA wines.

The influence of the alcohol level on wine prices is positive with regard to the average coefficient, but the split analysis shows that this influence holds especially to the quality categories QbA, Kabinett, and Spätlese and that the influence is even negative for the quality categories Auslese (except for Pinot Noir) and Batbaice (except for Pinot Blanc).

There are essential differences between grape varieties regarding influential weather variables and their ability to cope with rising temperatures or extreme weather (minimum and maximum temperatures) in different seasons of the ripening process.

Rising average air temperatures during the winter season lead to a decrease in prices for Riesling and Silvaner, while Pinot Blanc copes better with rising winter temperatures and Pinot Noir, the only red variety in the sample, even shows a positive effect of both the rising minimum and average temperatures, but all varieties cannot cope with rising maximum temperatures in the winter season.

During the harvest season, especially higher minimum and maximum temperatures lead to a negative price effect for wines of all grape varieties and quality categories, so that earlier harvest is recommended for all grape varieties in cases of warmer harvest seasons, such as was the case in 2018.

Precipitation does not seem to have as high an impact but is different for each grape variety and quality category.

In the analysis, ripeness levels are used as proxies for quality levels according to the German classification system. Future research may include investigating the effects of climate change on wine prices from regions with distinct quality levels, such as Bordeaux.

Supplementary Material

To view supplementary material for this article, please visit https://doi.org/10.1017/jwe.2020.16.

Appendix

Table A1 Correlation Matrix Between Gault&Millau Points and German Quality Categories

Table A2 Breusch–Pagan/Cook–Weisberg Test for Heteroskedasticity – Model 1, 2, and 3

Breusch–Pagan/Cook–Weisberg test for heteroskedasticity

Ho: Constant variance

Variables: fittes values of logprice075

Table A3 Variance Inflation Tests for Multicollinearity for Model 1, 2, and 3

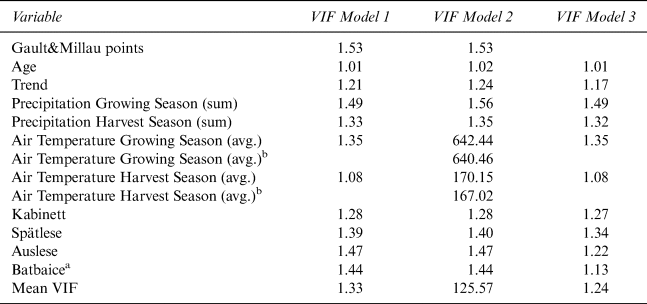
Table A4 Correlation Matrix for Model 1

Footnotes

We are indebted to an anonymous referee and the participants at the 11th Annual AAWE Conference in Padua for many helpful comments.

1 Ashenfelter and Storchmann (Reference Ashenfelter and Storchmann2016) provide a survey of the relevant literature.

2 Autonomous driving, speech recognition, or face recognition technology in modern photographic equipment or video monitoring are other examples for the application of machine learning (National Science and Technology Council, Committee on Technology, 2016).

3 In the Gault&Millau Weinguide Deutschland (Diel and Payne, Reference Diel and Payne2002–2009; Payne, Reference Payne2010–2015), only prices of 0.75 liter bottles are published.

4 Farm gate prices are those prices that consumers pay when visiting the farm and buying in the “farm shop,” but could be related to recommended retail prices.

5 Not all variables are included in all models; further explanations can be found in the methodology Chapter III. The descriptive statistics for Silvaner, Pinot Blanc, and Pinot Noir can be found in the online supplementary material.

6 Hence there is no multicollinearity issue between quality levels and Gault&Millau points. Please see the correlation matrix between Gault&Millau points and quality levels in Table A1 of the Appendix.

7 It denotes the specific weight of the must compared to the weight of the water at a temperature of 20 degrees. One liter of water weighs 1,000 g, which equals 0 degrees Oechsle. Grape must, with a mass of 1,084g per liter, has 84 degrees Oechsle. The mass difference is almost entirely due to the sugar dissolved in the must, so that Oechsle measures the sweetness of the grape juice (Ashenfelter and Storchmann, Reference Ashenfelter and Storchmann2010).

8 Although their production levels are insignificant (less than 1% of total production), there are two categories below the QbA, that is, Tafelwein and Landwein.

9 The Oechsle thresholds vary from region to region. In the region Pfalz (Palatinate), for example, the quality categories fall into the following brackets: Qualitätswein (QbA) (60–72° Oechsle), Kabinett (73–84° Oechsle), Spätlese (85–91° Oechsle), Auslese (92–119° Oechsle), Beerenauslese and Eiswein (120–149° Oechsle), and Trockenbeerenauslese (>150° Oechsle) (Ashenfelter and Storchmann, Reference Ashenfelter and Storchmann2010).

10 The average is calculated from at least 21 hourly measurements each day.

11 The German Weather Service provided the regional weather data from the following weather stations: Ahr: Bad Neuenahr-Ahrweiler – Baden: Karlsruhe/Rheinstetten and Freiburg, Franken: Würzburg as closest station, Hessische Bergstraße: Mannheim – Mittelrhein: Montabaur and Nastätten, Mosel: Bernkastel and Trier Petrisberg, Nahe: Bad Kreuznach, Pfalz: Bad Dürkheim, Rheingau: Geisenheim, Rheinhessen: Alzey, Saale-Unstrut: Osterfeld, Sachsen: Dresden-Hosterwitz, Württemberg: Sachsenheim.

12 The whole season comprises the winter (Dec. 1 to Feb. 28), growing (Mar. 1 to Sep. 15.), and harvest (Sep. 16 to Oct. 31). The growing phase now starts in March, while the majority of grapes are picked from the middle of September to the end of October (Fecke, Reference Fecke2014; Kriener and Mortsiefer, Reference Kriener and Mortsiefer2017; Jones and Storchmann, Reference Jones and Storchmann2001).

13 See Greene (Reference Greene2008) for a more detailed discussion.

14 Since the Breusch–Pagan/Cook–Weisberg test finds heteroscedasticity for all three models, see Table A5 of the Appendix.

15 There is no multicollinearity issue except for the temperature variables and its squared version in Model 2, the respective variance inflation factor test for Models 1, 2, and 3, and the correlation matrix can be found in Tables A6 and A7 of the Appendix.

16 Quantile regressions for models with producer fixed effects cannot be run, since these are underdetermined due to the large number of different producers (177).

17 We use the “Orange: Data Mining Toolbox” version 3.13 for the model building and analyses process (Demsar et al., Reference Demsar, Curk, Erjavec, Gorup, Hocevar, Milutinovic, Mozina, Polajnar, Toplak, Staric, Stajdohar, Umek, Zagar, Zbontar, Zitnik and Zupan2013). Orange is developed by the Bioinformatics Laboratory at the University of Ljubljana, Slovenia, in collaboration with an open source community. Orange is implemented in the Python programming language, with extra Python code developed by the authors to calculate the dependency and semi-elasticity required for proper analysis.

18 Here, variables with a dependency factor > 0.5 are kept independent of the respective semi-elasticity values due to their importance for the whole model.

19 Unless the variable is a fixed effects variable, as due to the definition of fixed effects, their semi-elasticity equals zero.

20 Therefore we do not apply squared functions. The same holds to producer fixed effects that would lead to an underdetermination of the equation system.

21 Numbers in bold, we only include non-bold numbers to allow for comparisons.

a QbA: Qualitätswein

b Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

c Gault&Millau

a Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

b Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

a QbA: Qualitätswein

b Batbaice: Beerenauslese/Trockenbeerenauslese/Eiswein

c Growing Season: 03/01–09/15; Harvest Season: 09/16–10/31

Source: Authors’ calculations.

References

Ashenfelter, O. (2010). Predicting the quality and prices of Bordeaux wines. Journal of Wine Economics, 5(1), 40–52.CrossRefGoogle Scholar
Ashenfelter, O., and Storchmann, K. (2010). Measuring the economic effect of global warming on viticulture using auction, retail and wholesale prices. Review of Industrial Organization, 37(1), 51–64.CrossRefGoogle Scholar
Ashenfelter, O., and Storchmann, K. (2016). Climate change and wine: A review of the economic implications. Journal of Wine Economics, 11(1), 105–138.CrossRefGoogle Scholar
Byron, R. P., and Ashenfelter, O. (1995). Predicting the quality of an unborn Grange. Economic Record, 71(212), 400–414.CrossRefGoogle Scholar
Demsar, J., Curk, T., Erjavec, A., Gorup, C., Hocevar, T., Milutinovic, M., Mozina, M., Polajnar, M., Toplak, M., Staric, A., Stajdohar, M., Umek, L., Zagar, L., Zbontar, J., Zitnik, M., and Zupan, B. (2013). Orange: Data mining toolbox in Python. Journal of Machine Learning Research, 14(Aug.), 2349–2353.Google Scholar
Diel, A., and Payne, J. (eds.). (2002–2009). Gault&Millau Weinguide Deutschland. München: Christian Verlag.Google Scholar
Dumancas, G., and A Bello, G. (2015). Comparison of machine-learning techniques for handling multicollinearity in big data analytics and high performance data mining. Supercomputing 2015: The International Conference for High Performance Computing, Networking, Storage, and Analysis (Austin, TX). doi: 10.13140/RG.2.1.1579.4641.Google Scholar
Fecke, B. (2014). Klimawandel stellt Winzer vor neue Probleme. Deutschlandfunk, 03.11.2014. Available from: http://www.deutschlandfunk.de/weinanbau-klimawandel-stelltwinzer-vor-neue-probleme.697.de.html?dram:article_id=302145 (accessed on November 8, 2017).Google Scholar
Garg, A., and Tai, K. (2013). Comparison of statistical and machine learning methods in modelling of data with multicollinearity. Inter. J. Modelling, Identification and Control, 18(4), 295–312.CrossRefGoogle Scholar
Garson, G. D. (1991). Interpreting neural network connection weights. Artificial Intelligence Expert, 6(4), 46–51.Google Scholar
Giam, X., and Olden, J. D. (2015). A new R2-based metric to shed greater insight on variable importance in artificial neural networks. Elsevier Ecological Modelling 313, 307–313.CrossRefGoogle Scholar
Goh, A. T. C. (1995). Back-propagation neural networks for modelling complex systems. Artificial Intelligence in Engineering, 9(3),143–151.CrossRefGoogle Scholar
Greene, W. H. (2008). Econometric Analysis. 6th ed. Upper Saddle River, NJ: Pearson.Google Scholar
Haeger, J. W., and Storchmann, K. (2006). Prices of American pinot noir wines: Climate, craftsmanship, critics. Agricultural Economics, 35(1), 67–78.CrossRefGoogle Scholar
Hashem, S. (1992). Sensitivity analysis for feedforward artificial neural networks with differentiable activation functions. Proceedings of the International Joint Conference on Neural Networks (Baltimore, MD), 419–424. New York: IEEE Press.Google Scholar
Hornik, K., Stichcombe, M., and White, H. (1990). Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Networks, 3, 551–560.CrossRefGoogle Scholar
Jones, G. V., and Storchmann, K. (2001). Wine market prices and investment under uncertainty. An econometric model for Bordeaux Crus Classés. Agricultural Economics, 26(2), 115–133.Google Scholar
Kriener, M., and Mortsiefer, H. (2017). Weinproduktion sinkt auf 50-Jahres-Tief. Der Tagesspiegel, 2017-10-24. Available from https://www.tagesspiegel.de/wirtschaft/ernte-2017-weinproduktion-sinkt-auf-50-jahres-tief/20497304.html.Google Scholar
Lecocq, S., and Visser, M. (2006). Spatial variations in weather conditions and wines prices in Bordeaux. Journal of Wine Economics, 1(2), 114–124.CrossRefGoogle Scholar
National Science and Technology Council, Committee on Technology (2016). Preparing for the Future of Artificial Intelligence. Available from: https://obamawhitehouse.archives.gov/sites/default/files/whitehouse_files/microsites/ostp/NSTC/preparing_for_the_future_of_ai.pdf.Google Scholar
Niklas, B. (2017). Impact of annual weather fluctuations on wine production in Germany. Journal of Wine Economics, 12(4), 436–445.CrossRefGoogle Scholar
Oczkowski, E. (2001). Hedonic wine price functions and measurement error. Economic Record, 77(239), 374–382.CrossRefGoogle Scholar
Oczkowski, E. (2014). Wine prices and quality ratings: A meta regression analysis. American Journal of Agricultural Economics, 97(1), 103–121.CrossRefGoogle Scholar
Oczkowski, E. (2016). The effect of weather on wine quality and prices: An Australian spatial analysis. Journal of Wine Economics, 11(1), 48–65.CrossRefGoogle Scholar
Olden, J. D., and Jackson, D. A. (2002). Illuminating the “black-box”: A randomization approach for understanding variable contributions in artificial neural networks. Ecological Modelling, 154, 135–150.CrossRefGoogle Scholar
Olden, J. D., Joy, M. K., and Death, R. G. (2004). An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecological Modelling, 178, 389–397.CrossRefGoogle Scholar
Owen, G. W. (2012). Applying point elasticity of demand principles to optimal pricing in management accounting. International Journal of Applied Economics and Finance, 6, 89–99.Google Scholar
Payne, J. (eds.). (2010–2015). Gault&Millau Weinguide Deutschland. München: Christian Verlag.Google Scholar
Ramirez, C. D. (2008). Wine quality, wine prices and the weather: Is Napa “different”? Journal of Wine Economics, 3(2), 114–131.CrossRefGoogle Scholar
Rinke, W. (2015). Calculating the dependency of components of observable nonlinear systems using artificial neural networks. MakeLearn & TIIM Conference Proceedings, 367–374. Available from https://EconPapers.repec.org/RePEc:tkp:mklp15:367-374.Google Scholar
Rosenblatt, F. (1958). The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review, 65(6), 386–408.CrossRefGoogle Scholar
Rudin, W. (1976). Principles of Mathematical Analysis, 3rd edition. New York: McGraw-Hill.Google Scholar
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323, 533–536.CrossRefGoogle Scholar
Schamel, G. (2000). Individual and collective reputation indicators of wine quality. Centre for International Economic Studies, Discussion Paper No. 0009, March. Available from https://www.researchgate.net/publication/228286730_Individual_and_Collective_Repuatation_Indicators_of_Wine_Quality.Google Scholar
Schamel, G. (2002). California wine winners: A hedonic analysis of regional and winery reputation indicators. Paper presented at the AAEA Meeting, July 28–31, Long Beach, CA.Google Scholar
Schamel, G. (2003). A hedonic pricing model for German wine. Agrarwirtschaft, 52(5), 247–254.Google Scholar
Shapiro, C. (1983). Premiums for high quality products as returns to reputation. Quarterly Journal of Economics, 98, 659–679.CrossRefGoogle Scholar
Shavlik, J. W., and Diettrich, T. G. (eds.). (1990). Reading in Machine Learning. San Mateo, CA: Morgan Kaufmann.Google Scholar
Stone, P., Brooks, R., Brynjolfsson, E., Calo, R., Etzioni, O., Hager, G., Hirschberg, J., Kalyanakrishnan, S., Kamar, E., Kraus, S., Leyton-Brown, K., Parkes, D., Press, W., Saxenian, A., Shah, J., Tambe, M., and Teller, A. (2016). Artificial intelligence and life in 2030. One hundred year study on artificial intelligence: Report of the 2015-2016 Study Panel, 8. Available from https://ai100.stanford.edu/sites/default/files/ai100report10032016fnl_singles.pdf.Google Scholar
Storchmann, K. (2005). English weather and Rhine wine quality: An ordered probit approach. Journal of Wine Research, 16(2), 105–119.CrossRefGoogle Scholar
Storchmann, K. (2012). Wine economics. Journal of Wine Economics, 7(1), 1–33.CrossRefGoogle Scholar
Thrane, C. (2004). In defence of the price hedonic model in wine research. Journal of Wine Research, 15(2), 123–134.CrossRefGoogle Scholar
Tirole, J. (1996). A theory of collective reputations (with applications to the persistence of corruption and to firm quality). Review of Economic Studies, 63, 1–22.CrossRefGoogle Scholar
Witten, I., Eibe, F., and Hall, M. (2017). Data Mining – Practical Machine Learning Tools and Techniques, 4th edition, 261–269. New York: Morgan Kaufmann.Google Scholar
Yeh, I.-C., and Cheng, W.-L. (2010). First and second order sensitivity analysis of MLP. Neurocomputing, 73, 2225–2233.CrossRefGoogle Scholar
Yeo, M., Fletcher, T., and Shawe-Taylor, J. (2015). Machine learning in fine wine price prediction. Journal of Wine Economics, 10(2), 151–172.CrossRefGoogle Scholar
Figure 0

Table 1 Descriptive Statistics for Riesling

Figure 1

Table 2 Comparison of Model 1, 2, and 3 for Riesling (without Regional and Producer Fixed Effects)

Figure 2

Table 3 Models for Riesling

Figure 3

Table 4 OLS vs. Quantile Regressions of Model 4 for Riesling

Figure 4

Table 5 Significant and Influential Variables for Riesling

Figure 5

Table 6 Average Semi-Elasticity of Significant and Influential Variables for Riesling by Quality Category

Figure 6

Figure 1 Average Semi-Elasticity of Gault&Millau Points for Each Riesling Quality CategorySource: Authors’ calculations.

Figure 7

Figure 2 Average Semi-Elasticity of the Alcohol Level for Each Riesling Quality CategorySource: Authors’ calculations.

Figure 8

Table 7 Dependency Matrix and Average Semi-Elasticity for Silvaner, Pinot Blanc, and Pinot Noir

Figure 9

Figure 3 Dependency Factors for Riesling, Silvaner, Pinot Blanc, and Pinot NoirSource: Authors’ calculations.

Figure 10

Figure 4 Average Semi-Elasticity for Riesling, Silvaner, Pinot Blanc, and Pinot NoirSource: Authors’ calculations.

Figure 11

Table A1 Correlation Matrix Between Gault&Millau Points and German Quality Categories

Figure 12

Table A2 Breusch–Pagan/Cook–Weisberg Test for Heteroskedasticity – Model 1, 2, and 3Breusch–Pagan/Cook–Weisberg test for heteroskedasticityHo: Constant varianceVariables: fittes values of logprice075

Figure 13

Table A3 Variance Inflation Tests for Multicollinearity for Model 1, 2, and 3

Figure 14

Table A4 Correlation Matrix for Model 1

Supplementary material: File

Niklas and Rinke supplementary material

Niklas and Rinke supplementary material 1

Download Niklas and Rinke supplementary material(File)
File 145.6 KB
Supplementary material: File

Niklas and Rinke supplementary material

Niklas and Rinke supplementary material 2

Download Niklas and Rinke supplementary material(File)
File 162 Bytes