Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-05T09:05:51.703Z Has data issue: false hasContentIssue false
  • English
  • Français

The standard error in the Jacobson and Truax Reliable Change Index: The classical approach to the assessment of reliable change

Published online by Cambridge University Press:  01 October 2004

GERARD H. MAASSEN
GERARD H. MAASSEN
Affiliation:
Department of Methodology and Statistics, Faculty of Social Sciences, Utrecht University, Utrecht, The Netherlands
Rights & Permissions [Opens in a new window]

Abstract

Researchers and clinicians using Jacobson and Truax's index to assess the reliability of change in patients, or its counterpart by Chelune et al., which takes practice effects into account, are confused by the different ways of calculating the standard error encountered in the literature (see the discussion started in this journal by Hinton-Bayre). This article compares the characteristics of (1) the standard error used by Jacobson and Truax, (2) the standard error of difference scores used by Temkin et al. and (3) an adaptation of Jacobson and Truax's approach that accounts for difference between initial and final variance. It is theoretically demonstrated that the last variant is preferable, which is corroborated by real data. (JINS, 2004, 10, 888–893.)

Keywords

Test–retest dataPractice effectsReliable changeStandard error of difference scoresStandard error of measurement of difference scores
Type
CRITICAL REVIEW
Information
Journal of the International Neuropsychological Society , Volume 10 , Issue 6 , October 2004 , pp. 888 - 893
Copyright
© 2004 The International Neuropsychological Society

INTRODUCTION

One of the most frequently applied methods for assessing clinically meaningful change is the procedure of Jacobson and Truax (1991; McGlinchey et al., 2002). An inherent element of this procedure is the assessment of statistically reliable change by means of a so-called reliable change index (RCI). This index is widely known as the JT index, for historical reasons also referred to as the “classical approach” (Maassen, 2000a) since it is actually a reintroduction of a statistic established for some time in psychometric theory (Lord & Novick, 1968; McNemar, 1962). Over the past decade, a series of alternative reliable change indices have been proposed, but in recent articles (Maassen, 2000a, 2000b, 2001) the present author has argued that the advantages of some of those alternatives compared with the classical approach are more apparent than real. This led him to endorse Speer's (1999) plea for a moratorium on the use of adjusted RC methods and the use of the classical approach during this period (Maassen, 2001). Other authors (McGlinchey et al., 2002) agreed with this suggestion and argued for the need to focus on analyzing and improving the methods that exist.

The present article is an attempt to follow this advice and aims at clarifying the confusion associated with the JT index, particularly its standard error. In recent texts, the present author used to denote the standard error by the symbol σED without further explanation of the way this quantity should be calculated, because this could be found in the earlier standard texts referred to (e.g., McNemar, 1969). However, it has since become clear that some researchers are uncertain as to which formula should be used. The point was recently explicitly raised in this journal by Hinton-Bayre (2000) in a letter to the editor responding to texts by Dikmen et al. (1999) and Temkin et al. (1999). The latter authors (Temkin et al., 2000), as well as Abramson (2000), replied to Hinton-Bayre's remarks, albeit very briefly. This article elaborates more thoroughly on this topic, clarifying the assumptions that underlie different forms of the standard error existing in the literature. It will be shown that Temkin et al.'s claim that they used the preferable formula is only theoretically true under restricted circumstances.

Suppose we try to assess the reliability of the change in a given person i using the classical approach. Although the use of this approach (or the JT procedure) is restricted to situations where practice effects can be ignored, it will be convenient in what follows to admit that person i has benefited from an effect πi that may be related to his or her initial score, e.g., a practice effect as a consequence of the repeated testing. The difference score Di observed in a given person i is regarded as an unbiased estimation of the true change. Since within the classical test theory true change is defined as the expected change under the current circumstances, it includes the practice effect. According to classical test theory it can be split into the following components: Di = Yi − Xi = Δi + πi + EXi − EYi. Xi and Yi respectively are the pretest and posttest score observed in person i. Δi, the true difference score excluding the practice effect, and πi, the practice effect, denote fixed parameters of the theoretical score distribution of person i. Within the population of persons as well as within the theoretical score distribution of person i, the following usual assumptions of classical test theory are made: (1) both error components are mutually independent and independent of the true pretest and posttest scores; (2) both error components are normally distributed with zero mean; (3) the standard error of the difference of the two error components is equal for all participants. It should be noted that these assumptions on the error components are questionable in many clinical situations. However, since all the methods compared in this article are based on these assumptions, they will not be challenged within this context. (For situations where the assumption of equal standard deviations of the error components is not met, see, e.g., Mellenbergh & Van den Brink, 1998.) The variance of the observed difference is then equal to the standard error of measurement of the difference (squared), which will be denoted as Var(Di) = σED2 and the statistic

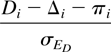
has a standard normal distribution. This expression demonstrates that the practice effect in person i appears only in the numerator, assuming it to be fixed. For methods dealing with practice effects, the reader is further referred to Chelune et al. (1993), who presented an extension of the JT approach, or to Maassen (2003), McSweeny et al. (1993), and Temkin et al. (1999), who presented regression approaches. The statistic (1) boils down to the JT Reliable Change Index (RCI) under the null hypothesis of zero true change and the assumption of zero practice effect in person i:

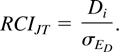
Jacobson and Truax (1991) describe the Reliable Change Index as a psychometric criterion “that tells us whether the change reflects more than the fluctuations of an imprecise instrument” (p. 344). According to Christensen and Mendoza (1986), “RC determines if the pretest to posttest change score exceeds that which would be expected on the basis of measurement error” (p. 305).

How should the standard error (of measurement of the difference score) be calculated? The complete formula is provided by McNemar (1969):

This expression requires knowledge (preferably from external sources) of the standard errors of measurements of the initial and final testing. To circumvent these requisites, Jacobson and Truax (1991) assumed that pretest and posttest are parallel measures, and estimated the common reliability coefficient and the common variance by respectively the test–retest correlation and the variance of the initial testing in the particular study. The expression then simplifies to:

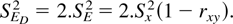
Jacobson and Truax (1991) denoted the standard error of their RCI as Sdiff , following Christensen and Mendoza (1986), who pointed out that the standard error in the RCI earlier proposed by Jacobson et al. (1984) was wrong. Christensen and Mendoza used, however, the following expression:

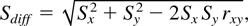
which was called standard error of difference by the authors. This name, the notation Sdiff and Equation (5) may induce misunderstandings among clinicians as we will show, but what was meant by Christensen and Mendoza (1986) is clear in their statement that it “represents the amount of difference which one could expect between two scores obtained on the same test by the same individual as a function of measurement error alone” (p. 307). And indeed, if this person has experienced no actual change, or if the actual change (possibly including a practice effect) is assumed to be fixed, then the only stochastic components of the test scores are the error components. If it is assumed that these components are uncorrelated and that their variances are equal across assessments, then Sdiff2 = 2.SE2. In practice, some authors (e.g., Temkin et al., 1999) have interpreted Expression (5) as referring to the standard deviation of the observed difference scores in the research group at hand. Hereafter, this interpretation will be referred to as Equation (5*).

If the parameter values required for Equation (3) can not be derived from an external source, another option would be to assume only that the reliability coefficients of pretest and posttest are equal, and to estimate this quantity and the variances of the pretest and posttest scores from the research group:

We now have three options for the calculation of the standard error of the RCI within a particular study: Expressions (4), (5*), and (6). What is the relation between these options?

First, it may be noted that Expression (6) is preferable to Expression (4). This is obvious in cases where it is not plausible to assume that the variances of the pretest and posttest scores in the research group are equal. We have already pointed out above that the assumptions underlying the use of Expression (4) imply equality of the variances. In that case the common variance would be better estimated by (Sx2 + Sy2)/2, which is realized by Expression (6) (see also Abramson, 2000). Second, regarding Expressions (5*) and (6) we note a conceptual difference. Equation (5*) indicates what size of an observed change score should be regarded exceptional within the distribution of observed difference scores of the research sample at hand. Equation (6), as derived from Equation (3), indicates what size of an observed change score should be regarded exceptional within the theoretical distribution of a respondent's score distribution under the null hypothesis that no true change occurred. Algebraically, the difference between Expressions (5*) and (6) can be shown to be:

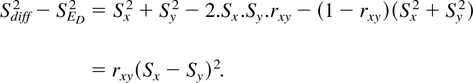
We see that Expression (5*) is never smaller than Expression (6) and that it exceeds Expression (6) to the extent that the test-retest correlation is high and the initial and final variance differ. How this difference can be conceptually explained, is revealed by a division of the variance of the observed differences into two components: a true variance and an error variance component Sdiff2 = Var(Δ + π) + SED2.

Temkin et al. (1999) presented change outcomes observed within a normative sample, where no intervention was conducted and where it is plausible to assume that the true change of all the participants is equal to zero. Thus, any numerical difference between the standard errors (5*) and (6) is induced by differential practice effects. For example, if the practice effects are highly positively correlated with the pretest score, then the pretest and posttest scores will also be highly correlated, while the posttest variance will be greater than the pretest variance, a phenomenon commonly known as fanspread. This reveals the problem with Expression (5*). Differential practice effects increase the posttest variance as compared to the pretest variance, which is clearly accounted for by the standard error calculated according Expression (6). When using Expression (5*) an extra term is implicitly included that, once more, accounts for differential practice effects.

In order to gain more insight into the influence of the practice effects in actual research, we first examine theoretically the regression of the posttest on the pretest within the normative population. Let ξj and ηj respectively be the true pretest and posttest score of a person j belonging to the normative population, and let μξc, μηc and Πc respectively be the population means of the true pretest scores, the true posttest scores and the practice effects. Then ηj = μηc + βc(ξj − μξc) + εj holds, where index c refers to a normative population. Note that βc should be distinguished from the observed regression coefficient bc, the latter being attenuated by imperfect measurement of the initial score, which is expressed by: βc = bc /ρxx (McNemar, 1969, p. 173). The population means are linked as μηc = μξc + Πc, which converts the regression equation into:

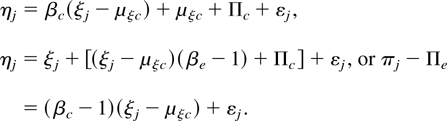
Formula (8) indicates how the practice effect of person j can be estimated from his pretest score. It can be seen that, if βc = 1, there in no better estimation for all the practice effects in the normative population than the population mean Πc. If βc > 1, the estimation of the practice effect is proportional to the value of the pretest score (or Cov(ξ,π) > 0). Note that in this case regression from the mean (fanspread) may very well occur. If βc < 1, the estimation of the practice effect and the pretest score are inversely proportional quantities (or Cov(ξ,π) < 0). In this case regression to the mean probably occurs, induced by practice effects rather than by measurement errors. Thus, when β > 1, as well as when β < 1, the initial and final variance are anticipated to be different, and, considering Equation (7), the standard errors (5*) and (6) are anticipated to be different accordingly.

To examine the practical implications of our discourse, we address the outcomes of two studies, that involve normative samples where no interventions have been conducted, those of McSweeny et al. (1993) and Temkin et al. (1999). In these studies, the authors expected practice effects to occur, which casts doubt on the assumption of equal variances. Hinton-Bayre (2000) has already presented a table, based on the outcomes of the Temkin et al. study, which compares estimations of the RCI interval width according to the Expressions (4) and (5*). In Table 1 the estimations according to Expression (6) are added,1

The reader may notice that the standard errors calculated with Expression (5*) slightly differ from those reported by Temkin et al. (1999). The differences are the consequence of using not entirely identical data. When calculating the standard errors according to Expressions (4), (5*) and (6) we used data provided by Temkin et al. (1999), namely, the standard deviations reported in their Table 2 and the test–retest correlations reported in their Table 3. However, the correlations in Table 3 were derived using individuals who had values for all predictors in the regression analysis and thus may not correspond exactly to the correlations in the entire sample (personal communication).

as well as the outcomes of the McSweeny et al. study. Hinton-Bayre noted that his comparison yielded no clear pattern. This was to be expected since it can be algebraically shown (this will not be done here) that the sign of the difference of the estimations depends on the values of the parameters involved. The comparison of the outcomes of Expressions (5*) and (6) does show a pattern: Consistent with the derivations above, the standard error according to Expression (5*) is always highest. In general, the difference between the initial and final variance is small, and consequently the difference between the estimations of the standard error according to the Expression (5*) and (6) is small and sometimes negligible.

Standard errors calculated according to different approaches for the normative samples of two studies (McSweeny et al., 1993, and Temkin et al., 1999)

Table 1 shows that the posttest variance exceeds the pretest variance in every instance where β > 1 evidencing the phenomenon of fanspread. Regression to the mean, induced by practice effects, is also evidenced by Table 1 showing that the pretest variance exceeds the posttest variance in every instance where β < 1. Two examples are worth noticing. The steepest positive regression coefficient β (= 1.27) is found with regard to the Performance IQ in the McSweeny et al. study. Consequently, the posttest variance is seen to be considerably greater than the pretest variance, and the standard error calculated according to Expression (5*) is 8% greater than according to Expression (6), which is not negligible. The results for the Tactual Performance Total scale in the Temkin et al. study show even more dramatic differences. The two variances differ considerably and the standard error according to Expression (5*) is 25% greater than according to Expression (6). Temkin et al. (1999) anticipated the occurrence of practice effects in their study, implying that according to the classical approach with a 90% confidence interval they would find less “reliable deteriorations” and more “reliable improvements” than the 5% expected on the basis of chance. Indeed, Expression (5*) applied to the TPT Total scale yielded only 1% of the participants showing deterioration. On the other hand, the other scales yielded 7–20% of the participants showing improvement, whereas only 4% showed improvement as measured by the TPT Total scale. These are strong indications, of course, that the confidence interval was too wide.

DISCUSSION

The Reliable Change Index most frequently applied in psychology research is the index proposed by Jacobson and Truax (1991), referred to as the JT index, or, for historical reasons, the classical approach. The counterpart of this index in neuropsychology research is the procedure proposed by Chelune et al. (1993), that, contrary to the JT index, deals with practice effects as a consequence of repeated testing. Both indices incorporate the same standard error; the standard error of measurement of the difference score, which in principle should be borrowed from an external source (e.g., the test manual or the study of a normative population). When the required parameters (such as the reliability coefficient and the variance of the response measure) are estimated from an actual research sample, the researcher should account for sampling fluctuations leading to an increased value of the standard error. If this is not done, a standard normal distribution of the RCI statistic cannot be guaranteed (compare the difference between the t- and the z-statistic). Only a sufficiently large and representative sample then can warrant a satisfactory approximation.

In recent years, base rate information on change gathered within normative populations is being increasingly published (Dikmen et al., 1999; Matarazzo & Herman, 1984; McSweeny et al., 1993; Temkin et al., 1999). The present article discusses three variants of estimating the standard error of the JT and the Chelune et al. indices encountered in research reports. Hinton-Bayre (2000) pointed to the existence of two of the variants: Expression (4) as applied by Jacobson and Truax (1991) and Expression (5), which in the interpretation of Temkin et al. (1999) here is referred to as Expression (5*). Hinton-Bayre showed to be confused by the different outcomes. He adhered to the original source (i.e., Jacobson & Truax, 1991), but, in their reply to Hinton-Bayre, Temkin et al. (2000) stated that their approach is preferable when both the pre- and posttest scores, and thus the difference scores, are available. Abramson (2000), also replying to Hinton-Bayre, took the position that the Temkin et al. approach is correct in cases where the initial and final population variances are equal, and that then the two observed variances should be pooled.

The denominator of the RCI in the classical approach only contains the standard deviation in the measurement error distribution of the person assessed. Estimating this quantity, Jacobson and Truax and Chelune et al. assume that pretest and posttest are parallel measures. Jacobson and Truax proposed to use only the initial variance. However, if the initial and final population variances differ, obviously both the observed initial and final variances should be plugged in. If not, we agree with Abramson (2000) that the two variances should be pooled, thus leading to Expression (6). Consequently, Expression (6) is preferable to Expression (4) in both cases

Regarding Expression (5*), this article firstly pointed out that Temkin et al. (1999) used a notation (Sdiff) consistent with Jacobson and Truax, who adopted it from Christensen and Mendoza (1986). However, they did not use the formula used by Jacobson and Truax, which was (perhaps) the source of Hinton-Bayre's confusion. Second, we pointed out that Temkin et al. did use the original formula of Christensen and Mendoza, but not as intended by these authors. Christensen and Mendoza's formula refers to the theoretical score distribution of a given person; Temkin et al.'s interpretation of the same formula refers to the distribution of difference scores observed within the normative population. The notation of Christensen and Mendoza for the standard error is admittedly susceptible to misunderstanding and therefore, in our view, it should not be used. Third, we pointed out that Temkin et al.'s interpretation boils down to that of Christensen and Mendoza only under the assumption that all the members of the population show the same actual change (including practice effect), possibly equal to zero. Indeed, when this assumption is met, the initial and final variances are equal, and then Abramson's (2000) approval cited above is in place. Fourth, however, it should be noted that Temkin et al. (1999) calculated the RCI intervals in a normative population where (possibly differential) practice effects were anticipated. We pointed out that in the Temkin et al. approach the standard error is increased by an extra term involving the variance of the actual changes in the entire population.

Recapitulating, Temkin et al. did not conduct their study as they reported (Temkin et al., 1999, p. 358), that is, considering the procedure of Jacobson and Truax and that of Chelune et al. What they did is conceptually quite different. The standard error used by Temkin et al. indicates the size of an observed change score that should be regarded exceptional in the distribution of change scores observed in the normative population, whereas the standard error adopted by Jacobson and Truax and by Chelune et al. indicates the size of an observed change score that should be regarded exceptional if it was induced by measurement errors alone. Several authors have already pointed out that the issue of the reliability of a difference should not be confused with the rarity of a patient's difference score (see, e.g., Crawford et al., 1998, and the references therein). The RCI of Jacobson and Truax comprises only a measurement error component in the denominator, whereas the denominator in the Temkin et al. approach also includes the variance of the actual changes in all the members of the population. Thus, the RCI of Temkin et al. accounts twice for differential practice effects, both in the variance component referring to the actual changes, as well as in the variance component referring to measurement error. This clearly hampers the possibility of correctly concluding that the person in question has changed.

Specifically, Expression (6) can be shown to have the attractive characteristic of yielding a narrower RCI interval than does Expression (5*). A narrower RCI interval, as yielded by Expression (6), is not a goal per se but should be statistically sound. The present article provides the mathematical and psychometric arguments underpinning this favorable aspect of Expression (6). Nevertheless, nonstatisticians may rather be convinced by an answer to following question: (1) Does the narrower confidence interval possibly result in excessive numbers of false positive decisions in large populations that are not submitted to an intervention? And apart from statistical soundness, they will like to know (2) how important are the differences between the two approaches.

Beginning with the second question, we note that differences between the results of the two approaches depend on (1) the measure in question and the extent to which it is susceptible to a change of variance (for example, as a consequence of practice effects), and (2) the effectiveness of the (neuropsychological) intervention. In the data sets discussed in the present article, only the TPT Total Scale appears to be seriously affected by variance change. However, other studies with other measures may, of course, show other examples. When the intervention is effective, e.g., when the RCI outcomes with regard to the TPT Total Scale are assumed to be centered at 1.645 and normally distributed, on the basis of the Temkin et al. (1999) data the proportion of patients that will be regarded as reliably changed according to Expression (6) but not according to Expression (5*) is estimated to be 16%, which is quite a substantial difference of power.

Regarding the first question Temkin et al. (1999), whose study involved a large sample not submitted to an intervention, provide comforting results. Using the outcomes of their Tables 2 and 3 concerning the TPT Total Scale, we calculate that Expression (5*) yielded a 90% confidence interval of width 2 × 1.645 × .25 = .83, that Expression (6) yields an interval of width .67, while the interval really delimitating the most extreme 10% of the participants was of width .48 (according to a distribution-free approach, see Temkin et al., 1999, Table 6). Thus, Expression (6) also yields “too few” false positives, but is far closer to reality than was Expression (5*).

In our view, these empirical outcomes corroborate our theoretical reasoning that Expression (6) should be regarded as the preferable standard error among the three variants discussed in this article.

References

REFERENCES

Abramson, I.S. (2000). Reliable Change formula query: A statistician's comments. Journal of the International Neuropsychological Society, 6, 365.CrossRefGoogle Scholar
Chelune, G.J., Naugle, R.I., Lüders, H., Sedlak, J., & Awad, I.A. (1993). Individual change after epilepsy surgery: Practice effects and base-rate information. Neuropsychology, 7, 41–52.CrossRefGoogle Scholar
Christensen, L. & Mendoza, J.L. (1986). A method of assessing change in a single subject: An alteration of the RC index. Behavior Therapy, 17, 305–308.CrossRefGoogle Scholar
Crawford, J.R., Howell, D.C., & Garthwaite, P.H. (1998). Payne and Jones revisited: Estimating the abnormability of test score differences using a modified paired samples t test. Journal of Clinical and Experimental Neuropsychology, 20, 898–905.CrossRefGoogle Scholar
Dikmen, S.S., Heaton, R.K., Grant, I., & Temkin, N.R. (1999). Test-retest reliability and practice effects of Expanded Halstead-Reitan Neuropsychological Test Battery. Journal of the International Neuropsychological Society, 5, 346–356.Google Scholar
Hinton-Bayre, A. (2000). Reliable Change formula query. Journal of the International Neuropsychological Society, 6, 362–363.CrossRefGoogle Scholar
Jacobson, N.S., Follette, W.C., & Revenstorf, D. (1984). Psychotherapy outcome research: Methods for reporting variability and evaluating clinical significance. Behavior Therapy, 15, 336–352.CrossRefGoogle Scholar
Jacobson, N.S. & Truax, P. (1991). Clinical significance: A statistical approach to defining meaningful change in psychotherapy research. Journal of Consulting and Clinical Psychology, 59, 12–19.CrossRefGoogle Scholar
Lord, F.M. & Novick, M.R. (1968). Statistical theories of mental test scores. Reading, MA: Addison-Wesley.
Maassen, G.H. (2000a). Principles of defining reliable change indices. Journal of Clinical and Experimental Neuropsychology, 22, 622–632.Google Scholar
Maassen, G.H. (2000b). Kelley's formula as a basis for the asessment of reliable change. Psychometrika, 65, 187–197.Google Scholar
Maassen, G.H. (2001). The unreliable change of reliable change indices. Behaviour Research and Therapy, 39, 495–498.CrossRefGoogle Scholar
Maassen, G.H. (2003). Principes voor de definitie van reliable change (2): reliable change indices en practice effects [Principles of defining reliable change (2): Reliable Change Indices and practice effects]. Nederlands Tijdschrift voor de Psychologie, 58, 69–79.Google Scholar
Matarazzo, J.D. & Herman, D.O. (1984). Base rate data for the WAIS–R: Test-retest stability and VIQ–PIQ differences. Journal of Clinical Neuropsychology, 6, 351–366.CrossRefGoogle Scholar
McGlinchey, J.B., Atkins, D.C., & Jacobson, N.S. (2002). Clinical significance methods: Which one to use and how useful are they? Behavior Therapy, 33, 529–550.Google Scholar
McNemar, Q. (1962). Psychological statistics (3rd ed.). New York: Wiley.
McNemar, Q. (1969). Psychological statistics (4th ed.). New York: Wiley.
McSweeny, A.J., Naugle, R.I., Chelune, G.J., & Lüders, H. (1993). “T Scores for change”: An illustration of a regression approach to depicting change in clinical neuropsychology. Clinical Neuropsychologist, 7, 300–312.CrossRefGoogle Scholar
Mellenbergh, G.J. & Van den Brink, W.P. (1998). The measurement of individual change. Psychological Methods, 3, 470–485.CrossRefGoogle Scholar
Speer, D.C. (1999). What is the role of two-wave designs in clinical research? Comment on Hageman and Arrindell. Behaviour Research and Therapy, 37, 1203–1210.Google Scholar
Temkin, N.R., Heaton, R.K., Grant, I., & Dikmen, S.S. (1999). Detecting significant change in neuropsychological test performance: A comparison of four models. Journal of the International Neuropsychological Society, 5, 357–369.Google Scholar
Temkin, N.R., Heaton, R.K., Grant, I., & Dikmen, S.S. (2000). Reliable Change formula query: Temkin et al. reply. Journal of the International Neuropsychological Society, 6, 364.CrossRefGoogle Scholar
Figure 0

Standard errors calculated according to different approaches for the normative samples of two studies (McSweeny et al., 1993, and Temkin et al., 1999)