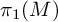1 Introduction
Let F be a field and n a positive integer. An element of
$\mathrm {SL}_n(F)$
is unipotent if it has the same characteristic polynomial as the identity matrix. In [Reference Button9, Reference Button10], Button demonstrated that finitely generated subgroups of
$\mathrm {SL}_n(F)$
containing no infinite-order unipotent elements share some properties with groups acting properly by semisimple isometries on complete
$\mathrm {CAT}(0)$
spaces. Indeed, Button showed that if F has positive characteristic (in which case any unipotent element of
$\mathrm {SL}_n(F)$
has finite order), then any finitely generated subgroup of
$\mathrm {SL}_n(F)$
admits such an action [Reference Button10, Theorem 2.3]. The main theorem of this article is intended to serve as an analogue of the latter result in the characteristic-zero setting. (Note that, since any finitely generated characteristic-zero domain embeds in
$\mathbb {C}$
, one may view any finitely generated subgroup of
$\mathrm {SL}_n(F)$
, where F is a field of characteristic zero, as a subgroup of
$\mathrm {SL}_n(\mathbb {C})$
.)
Theorem 1.1. Let
$\Gamma $
be a finitely generated subgroup of
$\mathrm {SL}_n(\mathbb {C})$
,
$n> 0$
. Then
$\Gamma $
acts on a complete
$\mathrm {CAT}(0)$
space X such that
-
(i) for any subgroup
$H < \Gamma $
containing no nontrivial unipotent matrices, the induced action of H on X is proper; -
(ii) if such a subgroup H is free abelian of finite rank, then H preserves and acts as a lattice of translations on a thick flat in X; in particular, any infinite-order element of such a subgroup H acts ballistically on X;
-
(iii) if
$g \in \Gamma $
is a diagonalizable, then g acts as a semisimple isometry of X.
See Section 2 for the relevant definitions. The space X is a finite product
$\prod _i X_i$
of symmetric spaces of noncompact type and (possibly locally infinite) Euclidean buildings, and
$\Gamma $
acts on X via a product
$\prod _i \mathrm {SL}_n(K_i)$
, where the
$K_i$
are completions of the entry field E of
$\Gamma $
with respect to various absolute values on E. The technique of extracting information about a linear group by varying the absolute value on its entry field is credited to Tits [Reference Tits30] and was employed by Margulis in the latter’s proof of arithmeticity of higher-rank lattices [Reference Margulis24].
We remark that, taken on its own, property (i) in Theorem 1.1 is not so interesting. Indeed, the author is not aware of a finitely generated group that is known to admit no proper action on a complete
$\mathrm {CAT}(0)$
space. On the other hand, there are several constraints on those finitely generated groups
$\Gamma $
admitting proper actions by semisimple isometries on complete
$\mathrm {CAT}(0)$
spaces. For instance, within such
$\Gamma $
, finitely generated abelian subgroups are undistorted (in particular, all polycyclic or Baumslag–Solitar subgroups are virtually abelian), and central finite-rank free abelian subgroups are virtual direct factors; see [Reference Bridson and Haefliger7, Ch. III.
$\Gamma$
, Thm. 1.1(i)-(iv)]. Button [Reference Button10] showed that these properties persist when
$\Gamma $
is replaced with a finitely generated subgroup of
$\mathrm {SL}_n(\mathbb {C})$
lacking nontrivial unipotents. We view Theorem 1.1 as providing geometric context for Button’s results (see Remark 2.3 and Corollary 4.1).
Since an element of
$\mathrm {SL}_n(\mathbb {C})$
that is both diagonalizable and unipotent must be trivial, the following corollary of Theorem 1.1 is immediate.
Corollary 1.2. Any finitely generated subgroup of
$\mathrm {SL}_n(\mathbb {C})$
consisting entirely of diagonalizable matrices acts properly by semisimple isometries on a complete
$\mathrm {CAT}(0)$
space.
Precompact subgroups of
$\mathrm {SL}_n(\mathbb {C})$
are conjugate into
$\mathrm {SU}(n)$
and thus consist entirely of diagonalizable matrices. Furthermore, by the Peter—Weyl theorem, any compact Lie group can be realized as a compact subgroup of
$\mathrm {SL}_n(\mathbb {C})$
for some n [Reference Bröcker and Dieck8, Theorem III.4.1]. Thus, by Corollary 1.2, any finitely generated subgroup of a compact Lie group admits a proper action by semisimple isometries on a complete
$\mathrm {CAT}(0)$
space.
For us, a graph manifold is a connected closed orientable irreducible non-Seifert 3-manifold all of whose Jaco–Shalen–Johannson (JSJ) blocks are Seifert. Property (ii) of the action described in Theorem 1.1 allows us to conclude the following fact about representations of fundamental groups of graph manifolds.
Theorem 1.3. Let M be a graph manifold, and let
$\rho : \pi _1(M) \rightarrow \mathrm {SL}_n(\mathbb {C})$
be any representation. If M does not admit a nonpositively curved Riemannian metric, then there is a JSJ torus S of M and a nontrivial element
$h \in \pi _1(S) < \pi _1(M)$
such that
$\rho (h)$
is unipotent.
A compact manifold is said to be nonpositively curved (NPC) if its interior admits a complete nonpositively curved Riemannian metric. Those non-NPC graph manifolds M that are not Sol
$3$
-manifolds are the only remaining aspherical
$3$
-manifolds whose fundamental groups are not known to admit faithful finite-dimensional linear representations. Such M abound; see Buyalo–Kobel’skii [Reference Buyalo and Kobel’skii11] or Kapovich–Leeb [Reference Kapovich and Leeb20, Section 3.2]. Theorem 1.3, while failing to preclude a characteristic-zero matrix representation of
$\pi _1(M)$
sending no nontrivial element to the identity (i.e., a faithful representation), achieves the weaker objective of ruling out any characteristic-zero matrix representation of
$\pi _1(M)$
mapping no nontrivial element to a unipotent matrix. This indeed distinguishes the non-NPC graph manifolds from their NPC counterparts, as we explain below.
By work of Agol [Reference Agol, Groves and Manning2] (building on work of Bergeron–Wise [Reference Bergeron and Wise5, Thm. 1.5] that used as crucial input a deep result of Kahn–Marković [Reference Kahn and Markovic18]), Przytycki—Wise [Reference Przytycki and Wise26, Reference Przytycki and Wise27], Liu [Reference Liu23] and Wise [Reference Wise31, Thm. 1.5], the fundamental group of any compact NPC
$3$
-manifold is virtually special in the sense of Haglund and Wise [Reference Haglund and Wise17] (for a detailed history of this result, see [Reference Aschenbrenner, Friedl and Wilton4, Ch. 4]). By the theory of special cube complexes developed by the latter two authors, it then follows that the fundamental groups of such manifolds virtually embed into right-angled Coxeter groups. Moreover, Agol [Reference Agol1] showed that any finitely generated right-angled Coxeter group embeds in a compact Lie group (for an elaboration on Agol’s argument, see [Reference Douba13]). Since the property of embedding in some compact Lie group passes to finite-index supergroups via induced representations, one concludes that the fundamental group of any compact NPC
$3$
-manifold embeds in a compact Lie group. On the other hand, if M is a compact aspherical non-NPC 3-manifold, then M is closed [Reference Bridson6, Thm. 4.3], and either M is Seifert, in which case there is a nontrivial element of
$\pi _1(M)$
that gets mapped to a virtually unipotent matrix under any finite-dimensional linear representation of
$\pi _1(M)$
(see, for example, the discussion in the introduction of [Reference Douba14]), or the orientation cover of M is a non-NPC graph manifold. Thus, we obtain from Theorem 1.3 the following corollary.
Corollary 1.4. Let M be a compact aspherical
$3$
-manifold. Then the following are equivalent:
-
(i) the manifold M is nonpositively curved;
-
(ii) the fundamental group
$\pi _1(M)$
embeds in a compact Lie group; -
(iii) there is a faithful finite-dimensional
$\mathbb {C}$
-linear representation of
$\pi _1(M)$
whose image consists entirely of diagonalizable matrices; -
(iv) there is a faithful finite-dimensional
$\mathbb {C}$
-linear representation of
$\pi _1(M)$
whose image contains no nontrivial unipotent matrices.
We remark that a result similar to Theorem 1.1 was announced in [Reference Matsnev25, Theorem 1.4]. However, the proof of [Reference Matsnev25, Theorem 4.8], on which that result rests, contains an error; a
$\mathrm {CAT}(0)$
action of a finitely generated linear group G with proper restrictions to certain subgroups of G is desired, but what is provided is a proper
$\mathrm {CAT}(0)$
action for each such subgroup of G.
Organization
In Section 2, we define the relevant objects, discuss briefly some properties of ballistic isometries of complete
$\mathrm {CAT}(0)$
spaces and introduce the central notion of a ‘thick flat’ in such a space. In Section 3, we prove several lemmas used in the proofs of Theorems 1.1 and 1.3. The latter proofs are contained in Section 4.
2 Preliminaries
2.1 Complete
$\mathrm {CAT}(0)$
spaces
Let X be a complete
$\mathrm {CAT}(0)$
space and
$\partial X$
its visual boundary. We will make references to the cone topology on
$\overline {X} := X \cup \partial X$
, described in [Reference Bridson and Haefliger7]. Under this topology, a sequence of points
$x_n \in X$
converges to
$\xi \in \partial X$
if and only if for some (hence any) point
$x_0 \in X$
, the geodesics joining
$x_0$
to
$x_n$
converge uniformly on compact intervals to the unique geodesic ray emanating from
$x_0$
in the class of
$\xi $
. In addition, we will use the angular metric
$\angle $
on
$\partial X$
, also described in [Reference Bridson and Haefliger7]. Note that the topology on
$\partial X$
induced by the angular metric is in general finer than the cone topology on
$\partial X$
.
An r-dimensional flat in X is an isometrically embedded copy of
$\mathbb {R}^r$
in X. We say X is
$\pi $
-visible if for any
$\xi , \eta \in \partial X$
satisfying
$\angle (\xi , \eta ) = \pi $
, there is a geodesic line in X whose endpoints on
$\partial X$
are
$\xi $
and
$\eta $
. Since Euclidean spaces are
$\pi $
-visible, a complete
$\mathrm {CAT}(0)$
space X with the property that any two points on
$\partial X$
lie on the boundary of a common flat in X is also
$\pi $
-visible. Note that if X is a Euclidean building, a symmetric space of noncompact type, or a product of such spaces, then X possesses the latter property by the building structure on
$\partial X$
so that X is
$\pi $
-visible. For more information on symmetric spaces, we refer the reader to the monograph [Reference Eberlein16].
2.2 Isometries of complete
$\mathrm {CAT}(0)$
spaces
Let
$(X,d_X)$
be a complete
$\mathrm {CAT}(0)$
space, and let
$g \in \mathrm {Isom}(X)$
. The translation length of g is the quantity
$|g|_X := \inf _{x \in X}d_X(x,gx)$
. The isometry g is semisimple if
$|g|_X = d_X(x_0, gx_0)$
for some
$x_0 \in X$
. We say g is ballistic (resp., neutral) if
$|g|_X> 0$
(resp., if
$|g|_X=0$
), and hyperbolic if g is both ballistic and semisimple. A subgroup
$H < \mathrm {Isom}(X)$
acts neutrally on X if each
$h \in H$
is neutral.
Example 2.1. Consider the action of
$\mathrm {SL}_n(\mathbb {C})$
on its associated symmetric space
$X_n := \mathrm {SL}_n(\mathbb {C})/\mathrm {SU}(n)$
, where the latter is endowed with an
$\mathrm {SL}_n(\mathbb {C})$
-invariant Riemannian metric. Under a suitable scaling of this metric, we have that for each
$g \in \mathrm {SL}_n(\mathbb {C})$
, the translation length of g on
$X_n$
is given by
$$\begin{align*}|g|_X = \left(\sum_{k=1}^n (\mathrm{ln}|\lambda_k|)^2\right)^{\frac{1}{2}}, \end{align*}$$
where
$\lambda _1, \ldots , \lambda _n \in \mathbb {C}$
are the eigenvalues of g. In particular, a matrix
$g \in \mathrm {SL}_n(\mathbb {C})$
acts as a ballistic (resp., neutral) isometry of
$X_n$
if and only if g has an eigenvalue of modulus
$\neq 1$
(resp., if and only if all eigenvalues of g are of modulus
$1$
). Moreover, an element
$g \in \mathrm {SL}_n(\mathbb {C})$
acts as a semisimple isometry of
$X_n$
if and only if g is diagonalizable. Thus, for example, the matrix
$$\begin{align*}\begin{pmatrix} 2 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & \frac{1}{4} \end{pmatrix} \end{align*}$$
acts as a ballistic isometry of
$X_3$
that is not hyperbolic.
Returning to the general setting, if
$g \in \mathrm {Isom}(X)$
is ballistic, then there is a point
$\omega _g \in \partial X$
such that for any
$x \in X$
, we have
$g^nx \rightarrow \omega _g$
as
$n \rightarrow \infty $
with respect to the cone topology on
$\overline {X}$
[Reference Caprace and Monod12]; we call
$\omega _g$
the canonical attracting fixed point of g. We use repeatedly the following fact, due to Duchesne [Reference Duchesne15, Prop. 6.2]. For an arbitrary group G and
$g_1, \ldots , g_m \in G$
, we denote by
$\mathcal {Z}_G(g_1, \ldots , g_m)$
the centralizer of
$g_1, \ldots , g_m$
in G.
Theorem 2.2. Let X be a complete
$\pi $
-visible
$\mathrm {CAT}(0)$
space, and suppose
$g \in \mathrm {Isom}(X)$
is ballistic. Then there is a closed convex subspace
$Y \subset X$
and a metric decomposition
$Y = Z \times \mathbb {R}$
such that
-
•
$\mathcal {Z}_{\mathrm {Isom}(X)}(g)$
preserves Y and acts diagonally with respect to the decomposition
$Y = Z \times \mathbb {R}$
, acting by translations on the second factor; -
• the isometry g acts neutrally on the factor Z.
Remark 2.3. Using Theorem 2.2, one can easily adapt the proof of [Reference Bridson and Haefliger7, II.6.12] to show that if
$\Gamma $
is a finitely generated group acting by isometries on a complete
$\pi $
-visible
$\mathrm {CAT}(0)$
space X and H is a central finite-rank free abelian subgroup of
$\Gamma $
all of whose nontrivial elements act ballistically on X, then H is a virtual direct factor of
$\Gamma $
, that is, there is a finite-index subgroup of
$\Gamma $
containing H as a direct factor. (In fact, the
$\pi $
-visibility assumption in the previous sentence can be removed by replacing the map
$\mathcal {Z}_{\mathrm {Isom}(X)}(g) \rightarrow \mathbb {R}$
given by Theorem 2.2 with the Busemann character associated to
$\omega _g$
in the more general setting; see [Reference Caprace and Monod12, page 673].) One then recovers from Theorem 1.1(ii) Button’s result [Reference Button10, Cor. 3.3] that if
$\Gamma $
is a finitely generated subgroup of
$\mathrm {SL}_n(\mathbb {C})$
and H is a central finite-rank free abelian subgroup of
$\Gamma $
lacking nontrivial unipotents, then H is a virtual direct factor of
$\Gamma $
.
In accordance with [Reference Bridson and Haefliger7], we define an isometric action of a group H on a metric space X to be proper if for any point
$x \in X$
, there is a neighborhood
$U \subset X$
of x such that
$\{h \in H \> : \> U \cap h U \neq \emptyset \}$
is finite. In this case, the set
$\{h \in H \> : \> K \cap h K \neq \emptyset \}$
is finite for any compact subset
$K \subset X$
(see, for example, [Reference Bridson and Haefliger7, Remark I.8.3(1)]). Note, however, that if the metric space X is not proper, that is, if X possesses bounded subsets that are not precompact, then X may contain balls B such that
$\{h \in H \> : \> B \cap h B \neq \emptyset \}$
is infinite; that is, the notion of properness for isometric actions used here is strictly weaker than metric properness. We remark that the particular
$\mathrm {CAT}(0)$
space X described in Theorem 1.1 is in general not proper; however, if the entries of the elements of
$\Gamma $
are all algebraic, then one can indeed arrange for X to be proper (in the latter case, one can choose the valuations
$\nu _1, \ldots , \nu _m$
on E in the proof of Theorem 1.1 such that
$E_{\nu _i}$
is a local field for
$i=1,\ldots , m$
).
We will make use of the following well-known theorem [Reference Bridson and Haefliger7, Theorem II.7.1].
Theorem 2.4. Let H be a free abelian group of rank r acting properly by semisimple isometries on a complete
$\mathrm {CAT}(0)$
space X. Then H preserves and acts as a lattice of translations on an r-dimensional flat in X.
2.3 Thick flats
Let
$r \geq 0$
be an integer. A triple
$(Y, Z, \varphi )$
, where
$Z \subset Y \subset X$
are nonempty closed convex subspaces and
$\varphi : Y \rightarrow Z \times \mathbb {R}^r$
is an isometry satisfying
$\varphi (z) = (z,0)$
for all
$z \in Z$
, is called a thick flat of dimension r in X. We say a group H acting isometrically on X preserves the thick flat
$(Y, Z, \varphi )$
if H preserves Y. Such a group H acts as a lattice of translations on the thick flat
$(Y, Z, \varphi )$
if H acts diagonally with respect to the decomposition
$Z \times \mathbb {R}^r$
given by
$\varphi $
, acting neutrally on the first factor and by translations on the second, and in addition the induced map
$\phi : H \rightarrow \mathbb {R}^r$
embeds H as a lattice of
$\mathbb {R}^r$
. We will typically suppress the data of Z and
$\varphi $
and refer to a thick flat
$(Y,Z, \varphi )$
simply as Y.
3 Lemmata
Lemmas 3.1 and 3.2 are probably well known, but we include their proofs for completeness. The objective is to determine the canonical attracting fixed point of a ballistic isometry acting diagonally on a product.
Lemma 3.1. Let
$Y, Z$
be complete
$\mathrm {CAT}(0)$
spaces and
$X = Y \times Z$
. Suppose
$g_Y$
is a neutral isometry of Y and
$g_Z$
a hyperbolic isometry of Z, and let
$g, g' \in \mathrm {Isom}(X)$
be the isometries
$g_Y \times g_Z$
,
$\mathrm {Id}_Y \times g_Z$
of X, respectively. Then
$\omega _g = \omega _{g'}$
.
Proof . There exist a geodesic line
$\gamma _Z: \mathbb {R} \rightarrow Z$
in Z and a positive number
$\ell $
such that
$g_Z(\gamma _Z(t)) = \gamma _Z(t + \ell )$
for any
$t \in \mathbb {R}$
. The point
$\omega _{g'} \in \partial X$
is represented by a geodesic ray of the form
$(y_0, \gamma _Z(t))$
,
$t \geq 0$
,
$y_0 \in Y$
. Thus, we reduce to the case that
$Z = \mathbb {R}$
and
$g_Z$
is a translation by
$\ell> 0$
. Set
$x_0 = (y_0, 0)$
, and for
$n \in \mathbb {N}$
, let
$\gamma ^{(n)} : [0, \infty ) \rightarrow X$
be given by
$$\begin{align*}\gamma^{(n)}(t) = \begin{cases} \overline{\gamma}^{(n)}(t) \quad & 0 \leq t \leq d_X(x_0, g^n x_0) \\ g^n x_0 & t> d_X(x_0, g^n x_0)\end{cases}, \end{align*}$$
where
$\overline {\gamma }^{(n)}$
is the geodesic segment in X from
$x_0$
to
$g^n x_0$
. We show that the
$\gamma ^{(n)}$
converge uniformly on compact subsets as
$n \rightarrow \infty $
to the geodesic ray
$\gamma : [0, \infty ) \rightarrow X$
given by
$t \mapsto (y_0, t)$
.
To that end, let
$R> 0$
, and let n be large enough such that
$d_X(x_0, g^n x_0) \geq R$
. Then
$\gamma ^{(n)}(t) = (\gamma _Y^{(n)}(t), \alpha _n t)$
for
$0 \leq t \leq R$
, where
$\alpha _n> 0$
and
$\gamma ^{(n)}_Y$
is a linearly reparameterized geodesic segment in Y joining
$y_0$
to
$g_Y^ny_0$
. Note that the maximum value of
$d_X(\gamma (t), \gamma ^{(n)}(t))$
on
$[0, R]$
is attained at
$t = R$
; indeed, for
$0 \leq t \leq R$
, we have
$$ \begin{align*} d_X(\gamma(t), \gamma^{(n)}(t))^2 = d_Y(y_0, \gamma_Y^{(n)}(t))^2 + t^2(1-\alpha_n)^2. \end{align*} $$
Thus, it suffices to show that
$d_X(\gamma (R), \gamma ^{(n)}(R)) \rightarrow 0$
. This will follow if we can show that
$d_Y(y_0, \gamma _Y^{(n)}(R)) \rightarrow 0$
since
$$ \begin{align*} R^2 = d_X(x_0, \gamma^{(n)}(R))^2 = d_Y(y_0, \gamma^{(n)}_Y(R))^2 + \alpha_n^2 R^2. \end{align*} $$
To see that
$d_Y(y_0, \gamma _Y^{(n)}(R)) \rightarrow 0$
, note that since
$\gamma ^{(n)}_Y$
is a linearly reparameterized geodesic segment, we have
$$ \begin{align*} \frac{d_Y(y_0, \gamma_Y^{(n)}(R)) }{d_Y(y_0, g_Y^n y_0)} = \frac{R}{d_X(x_0, g^nx_0)} \end{align*} $$
and so
$$\begin{align*}{4} d_Y(y_0, \gamma_Y^{(n)}(R))^2 &= R^2 \frac{d_Y(y_0, g_Y^ny_0)^2}{d_X(x_0, g^nx_0)^2} \\ &= R^2 \frac{d_Y(y_0, g_Y^ny_0)^2}{d_Y(y_0, g_Y^ny_0)^2 + n^2 \ell^2} \\ &= R^2 \frac{\left( \frac{d_Y(y_0, g_Y^ny_0)}{n} \right)^2}{ \left( \frac{d_Y(y_0, g_Y^ny_0)}{n} \right)^2 + \ell^2}. \end{align*}$$
Now, the latter approaches
$0$
as
$n \rightarrow 0$
since
$$ \begin{align*} \lim_{n\rightarrow \infty}\frac{d_Y(y_0, g_Y^ny_0)}{n} \leq |g_Y|_Y \end{align*} $$
and
$|g_Y|_Y = 0$
by assumption.
We bootstrap Lemma 3.1 to prove the following lemma, which features in the proof of Theorem 1.1(ii).
Lemma 3.2. Let
$X_1, X_2$
be complete
$\pi $
-visible CAT(0) spaces, let
$g_i \in \mathrm {Isom}(X_i)$
for
$i=1,2$
and suppose
$g_1$
is ballistic. Let
$X = X_1 \times X_2$
, and let
$g = g_1 \times g_2 \in \mathrm {Isom}(X)$
. Then g acts ballistically on X and
$$\begin{align*}\omega_g = \left(\mathrm{arctan}\left(\frac{|g_2|_{X_2}}{|g_1|_{X_1}}\right), \omega_{g_1}, \omega_{g_2}\right) \end{align*}$$
in the spherical join
$\partial X_1 * \partial X_2 = \partial X$
.
Proof . We suppose first that
$g_1, g_2$
are both ballistic so that we may assume that
$X_i $
admits a decomposition
$X_i = Y_i \times Z_i$
with respect to which
$g_i$
acts diagonally, where
$Z_i$
is isometric to
$\mathbb {R}$
, and where
$g_i$
acts neutrally on the first factor and acts by a translation of
$|g_i|_{X_i}$
on the second factor. Let
$g_i^{\prime } \in \mathrm {Isom}(X_i)$
be the product of the identity on
$Y_i$
with the translation by
$|g_i|_{X_i}$
on
$Z_i$
, and let
$g' = g^{\prime }_1 \times g^{\prime }_2 \in \mathrm {Isom}(X)$
. Note we have
$|g_i|_{X_i} = |g_i^{\prime }|_{X_i}$
, and by Lemma 3.1, we have
$\omega _{g_i} = \omega _{g_i^{\prime }}$
. Moreover, by viewing X as the product
$X = (Y_1 \times Y_2) \times (Z_1 \times Z_2)$
, we also have
$\omega _g = \omega _{g'}$
by Lemma 3.1. Thus, to establish the lemma, it suffices to show
$$\begin{align*}\omega_{g'} = \left(\mathrm{arctan}\left(\frac{|g^{\prime}_2|_{X_2}}{|g^{\prime}_1|_{X_1}}\right), \omega_{g^{\prime}_1}, \omega_{g^{\prime}_2}\right), \end{align*}$$
but this follows from plane geometry since
$g_1^{\prime }, g_2^{\prime }$
preserve and act as translations on the two-dimensional flat
$\{(y_1, y_2)\} \times (Z_1 \times Z_2) \subset X$
, where
$y_i$
is any point in
$Y_i$
.
If
$g_2$
is neutral, then we may only assume that
$X_1$
admits a decomposition
$X_1 = Y_1 \times Z_1$
as above, and now the lemma follows immediately from Lemma 3.1 by viewing X as the product
$X = (Y_1 \times X_2) \times Z_1$
.
We now apply Lemma 3.1 to the special case of matrices acting on symmetric spaces.
Lemma 3.3. Let
$M = \mathrm {GL}_n(\mathbb {C})/\mathrm {U}(n)$
be the symmetric space associated to
$\mathrm {GL}_n(\mathbb {C})$
, endowed with a
$\mathrm {GL}_n(\mathbb {C})$
-invariant Riemannian metric, and let
$g \in \mathrm {GL}_n(\mathbb {C})$
be of the form
$$\begin{align*}g = \mathrm{diag}(\lambda_1 U_1, \ldots, \lambda_m U_m), \end{align*}$$
where
$\lambda _1, \ldots , \lambda _m \in \mathbb {C}^*$
with
$|\lambda _k| \neq 1$
for at least one
$k \in \{1, \ldots , m\}$
, and
$U_k \in \mathrm {SL}_{n_k}(\mathbb {C})$
is an upper unitriangular matrix for
$k \in \{1, \ldots , m\}$
. Then g acts ballistically on M and has the same canonical attracting fixed point as
$$\begin{align*}g' := \mathrm{diag}(\lambda_1 I_{n_1}, \ldots, \lambda_m I_{n_m}) \end{align*}$$
on
$\partial M$
. The same statement holds when
$\mathrm {GL}_n(\mathbb {C})$
is replaced with
$\mathrm {SL}_n(\mathbb {C})$
and M is replaced with
$ \mathrm {SL}_n(\mathbb {C})/\mathrm {SU}(n)$
.
Proof . For
$k = 1, \ldots , m$
, let
$X, X_k, Y_k, Z_k$
be the projections of the subgroups
$$\begin{align*} & \{ \mathrm{diag}(h_1, \ldots, h_m) \> : \> h_k \in \mathrm{GL}_{n_k}(\mathbb{C}) \} \\ & \{ \mathrm{diag}(I_{n_1}, \ldots, I_{n_{k-1}}, \> h, \> I_{n_{k+1}}, \ldots, I_{n_m}) \> : \> h \in \mathrm{GL}_{n_k}(\mathbb{C}) \} \\ & \{ \mathrm{diag}(I_{n_1}, \ldots, I_{n_{k-1}}, \> h, \> I_{n_{k+1}}, \ldots, I_{n_m}) \> : \> h \in \mathrm{SL}_{n_k}(\mathbb{C}) \} \\ & \{ \mathrm{diag}(I_{n_1}, \ldots, I_{n_{k-1}}, \> e^t I_{n_k} , \> I_{n_{k+1}}, \ldots, I_{n_m}) \> : \> t \in \mathbb{R} \} \end{align*}$$
of
$\mathrm {GL}_n(\mathbb {C})$
to M under the quotient map
$\mathrm {GL}_n(\mathbb {C}) \rightarrow M = \mathrm {GL}_n(\mathbb {C})/\mathrm {U}(n)$
, respectively. Then X is a closed convex subspace of M admitting a decomposition
$X = \prod _{k=1}^m X_k$
. The subspace
$X_k$
in turn admits a decomposition
$X_k = Y_k \times Z_k$
, and the factor
$Z_k$
is isometric to
$\mathbb {R}$
. Each of the isometries
$g, g'$
preserves X and acts diagonally with respect to the decomposition
$X = \prod _{k=1}^m X_k$
. On each factor
$X_k$
, each of
$g, g'$
also acts diagonally with respect to the decomposition
$X_k = Y_k \times Z_k$
, acting neutrally on the first factor (via the matrix
$U_k$
in the case of g and via the identity
$I_{n_k}$
in the case of
$g'$
) and as a translation by
$\alpha _k\ln |\lambda _k|$
on the second for some
$\alpha _k> 0$
. The lemma now follows from Lemma 3.1 by setting
$Y = \prod _{k=1}^m Y_k$
and
$Z = \prod _{k=1}^m Z_k$
and viewing X as the product
$Y \times Z$
.
To see that the lemma remains true when
$\mathrm {GL}_n(\mathbb {C})$
is replaced with
$\mathrm {SL}_n(\mathbb {C})$
, note that (up to scaling the metrics) the symmetric space for
$\mathrm {SL}_n(\mathbb {C})$
embeds as a closed convex
$\mathrm {SL}_n(\mathbb {C})$
-invariant subspace of the symmetric space for
$\mathrm {GL}_n(\mathbb {C})$
.
We now observe that a collection of pairwise commuting matrices over
$\mathbb {C}$
can be simultaneously put into the form described in Lemma 3.3.
Lemma 3.4. Let K be an algebraically closed field, and let
$h_\alpha \in \mathrm {M}_n(K)$
be a collection of pairwise commuting matrices. Then there are
$s \in \mathbb {N}$
and
$C \in \mathrm {SL}_n(K)$
such that
$$\begin{align*}Ch_\alpha C^{-1} = \mathrm{diag}(h_{\alpha,1}, \ldots, h_{\alpha,s}), \end{align*}$$
where
$h_{\alpha , \ell } \in \mathrm {M}_{n_\ell }(K)$
is upper triangular and has a single eigenvalue for
$\ell = 1, \ldots , s$
.
Proof . Since K is algebraically closed, it suffices to find such
$C \in \mathrm {GL}_n(K)$
; indeed, we may ultimately replace C with
$\mu C$
, where
$\mu $
is an
$n^{\text {th}}$
root of
$1/\det (C)$
. We now proceed by induction on n. The case
$n=1$
is trivial. Now, let
$n> 1$
and suppose the above claim has been established for matrices of smaller dimension. If each of the
$h_\alpha $
has a single eigenvalue, then the statement follows from the fact that any collection of pairwise commuting elements of
$\mathrm {M}_n(K)$
are simultaneously upper triangularizable [Reference Radjavi and Rosenthal28, Theorem 1.1.5]. Now, suppose a matrix
$h \in \{h_\alpha \}_\alpha $
has more than one eigenvalue. By putting h into Jordan canonical form, for instance, we may assume h is of the form
$$\begin{align*}h = \mathrm{diag}(h_1, h_2), \end{align*}$$
where
$h_i \in \mathrm {M}_{n_i}(K)$
for
$i=1,2$
and
$h_1, h_2$
do not share an eigenvalue. Since the
$h_\alpha $
commute with h, they preserve the generalized eigenspaces of h, and so
$h_\alpha $
also has a block-diagonal structure
$$\begin{align*}h_\alpha = \mathrm{diag}(h_{\alpha,1}, h_{\alpha,2}), \end{align*}$$
where
$h_{\alpha , i} \in \mathrm {M}_{n_i}(K)$
for
$i=1,2$
. The lemma now follows by applying the induction hypothesis to the collections
$\{h_{\alpha ,i}\}_\alpha $
,
$i=1,2$
.
We now prove what one might call a ‘thick flat torus theorem’. This fact is used in the proof of Theorem 1.1(ii).
Theorem 3.5. Suppose X is a complete
$\pi $
-visible CAT(0) space and H is a free abelian subgroup of
$\mathrm {Isom}(X)$
with a basis
$h_1, \ldots , h_r \in H$
consisting of ballistic isometries such that for each
$m \in \{1, \ldots , r\}$
, there is no
$(m-1)$
-dimensional flat in X whose boundary contains the canonical attracting fixed points
$\omega _{h_1}, \ldots , \omega _{h_m}$
. Then H preserves and acts as a lattice of translations on a thick flat of dimension r in X.
Proof . We prove by induction the following statement: For
$m \in \{1, \ldots , r\}$
, there is a closed convex subspace
$Y_m$
of X and a decomposition
$Y_m = Z_m \times \mathbb {R}^m$
such that
-
•
$\mathcal {Z}_{\mathrm {Isom}(X)}(h_1, \ldots , h_m)$
preserves
$Y_m$
and acts diagonally with respect to the decomposition
$Y_m = Z_m \times \mathbb {R}^m$
, acting by translations on the second factor; -
• the subgroup
$\langle h_1, \ldots , h_m \rangle $
acts neutrally on the first factor and as a lattice of translations (in the usual sense) on the second.
The base case
$m=1$
is given by Theorem 2.2 (note that a zero-dimensional flat is just a singleton and hence has empty boundary). Now, suppose the above holds for
$m-1$
, where
$m \in \{2, \ldots , r\}$
. Then since
$h_m \in \mathcal {Z}_{\mathrm {Isom}(X)}(h_1, \ldots , h_{m-1})$
, we have that
$h_m$
preserves
$Y_{m-1}$
and acts diagonally with respect to the decomposition
$Y_{m-1} = Z_{m-1} \times \mathbb {R}^{m-1}$
. Moreover, the action of
$h_m$
on the factor
$Z_{m-1}$
must be ballistic, since otherwise
$\omega _{h_1}, \ldots , \omega _{h_m}$
would be contained in the boundary of
$\{z\} \times \mathbb {R}^{m-1}$
by Lemma 3.1, where z is any point in
$Z_{m-1}$
. Now,
$Z_{m-1}$
is a complete
$\pi $
-visible CAT(0) space so that by Theorem 2.2 there is a closed convex subspace Y of
$Z_{m-1}$
and a decomposition
$Y= Z \times \mathbb {R}$
satisfying
-
•
$\mathcal {Z}_{\mathrm {Isom}(Z_{m-1})}(h_m)$
preserves Y and acts diagonally with respect to the decomposition
$Y = Z \times \mathbb {R}$
, acting by translations on the second factor; -
• the action of
$h_m$
on the first factor Z is neutral.
Then the subspace
$Y_m := Y \times \mathbb {R}^{m-1} \subset Z_{m-1} \times \mathbb {R}^{m-1}$
has the desired properties.
The following observation is used in the proof of Lemma 3.7.
Lemma 3.6. Let X be a complete
$\mathrm {CAT}(0)$
space, and suppose
$H < \mathrm {Isom}(X)$
is a free abelian subgroup with a basis
$h_1, \ldots , h_r \in H$
. Suppose H preserves and acts as a lattice of translations on thick flats
$Y, Y'$
of dimension r in X, and let
$\phi , \phi '$
be the induced maps
$H \rightarrow \mathbb {R}^r$
, respectively. Then the unique linear map
${T: \mathbb {R}^r \rightarrow \mathbb {R}^r}$
satisfying
$T(\phi (h_i)) = \phi '(h_i)$
for
$i = 1, \ldots , r$
is orthogonal.
Proof . We wish to show that T preserves the standard inner product on
$\mathbb {R}^r$
. Since the
$\phi (h_i)$
constitute a basis for
$\mathbb {R}^r$
, it suffices to show that
$\langle \phi '(h_i), \phi '(h_j) \rangle = \langle \phi (h_i), \phi (h_j) \rangle $
for
$i,j \in \{1, \ldots , r\}$
. This is equivalent to saying that for
$i,j \in \{1, \ldots , r\}$
, we have
$\| \phi (h_i) \| = \| \phi '(h_i) \|$
and
$\angle (\phi (h_i), \phi (h_j)) = \angle (\phi '(h_i), \phi '(h_j))$
. The former is true since
$$ \begin{align*} \| \phi (h_i) \| = |h_i|_X = \| \phi' (h_i) \|, \end{align*} $$
and the latter is true since
$\angle (\phi (h_i), \phi (h_j))$
and
$\angle (\phi '(h_i), \phi '(h_j))$
are both equal to the Tits distance between
$\omega _{h_i}$
and
$\omega _{h_j}$
on
$\partial X$
by Lemma 3.1.
The proof of the following lemma borrows heavily from an argument of Leeb; see the proof of Theorem 2.4 in [Reference Kapovich and Leeb20]. Note that we work with the JSJ decomposition of a graph manifold as opposed to its geometric decomposition so that, for example, the twisted circle bundle over the Möbius band may appear as a JSJ block of a graph manifold. For details on the JSJ and geometric decompositions and the distinction between the two, see [Reference Kapovich19, Section 1.7]. Roughly speaking, a nonpositively curved Riemannian orbifold (with totally geodesic boundary) is an orbifold (with boundary) locally modelled on a nonpositively curved Riemannian manifold (with totally geodesic boundary) modulo a finite group of isometries, with transition maps that are equivariant isometries. For precise definitions, see Kleiner and Lott [Reference Kleiner and Lott22, Def. 2.14].
Lemma 3.7. Let M be a graph manifold, and suppose
$\pi _1(M)$
acts by isometries on a complete
$\mathrm {CAT}(0)$
space X such that for each JSJ torus S of M, the subgroup
$\pi _1(S) < \pi _1(M)$
preserves and acts as a lattice of translations on a thick flat in X. Then M admits a nonpositively curved Riemannian metric.
Proof . Let B be a JSJ block of M, and let
$f \in \pi _1(B)$
be an element representing a generic fiber of B. The element f acts ballistically on X since f is a nontrivial element of
$\pi _1(S)$
, where S is a torus boundary component of B, and
$\pi _1(S)$
preserves and acts as a lattice of translations on a thick flat in X by assumption. By Theorem 2.2, there is a closed convex subspace
$Y \subset X$
with a metric decomposition
$Y = Z \times \mathbb {R}$
such that
-
• any element of
$\pi _1(B)$
preserves Y and acts diagonally with respect to the decomposition
$Y = Z \times \mathbb {R}$
, acting as a translation on the second factor; -
• the action of f on the first factor Z is neutral.
Moreover, for each element
$z \in \pi _1(B)$
representing a boundary component of the base orbifold O of B, the action of z on Z is ballistic since the subgroup
$\langle f, z\rangle < \pi _1(B)$
preserves and acts as a lattice of translations on a thick flat in X.
We now realize B as a nonpositively curved Riemannian manifold with totally geodesic flat boundary as follows. Endow the orbifold O with a nonpositively curved Riemannian metric that is flat near the boundary so that the length of each boundary component c of O is equal to the translation length on Z of an element in
$\pi _1(B)$
representing c. We let
$\pi _1(B)$
act on the universal cover
$\tilde {O}$
of O via the projection
$\pi _1(B) \rightarrow \pi _1(O)$
, where
$\pi _1(O)$
acts on
$\tilde {O}$
by deck transformations. The product of this action with the action of
$\pi _1(B)$
on
$\mathbb {R}$
coming from the decomposition
$Y = Z \times \mathbb {R}$
yields a covering space action of
$\pi _1(B)$
on
$\tilde {O} \times \mathbb {R}$
. The quotient of
$\tilde {O} \times \mathbb {R}$
by this action is the desired geometric realization of B. We may do this for each Seifert component of M; the flat metrics on any pair of boundary tori that are matched in M will coincide by Lemma 3.6 so that we may glue the metrics on the Seifert components to obtain a smooth nonpositively curved metric on M.
The following lemma will not be used in the proofs of Theorems 1.1 or 1.3 but will be applied to derive Corollary 4.1 from Theorem 1.1.
Lemma 3.8. Let
$\Gamma $
be a finitely generated group and
$H_0$
a free abelian subgroup of
$\Gamma $
of rank
$r \geq 0$
. Suppose
$\Gamma $
acts on a complete
$\mathrm {CAT}(0)$
space X such that
$H_0$
preserves and acts as a lattice of translations on a thick flat in X. Then
$H_0$
is undistorted in
$\Gamma $
.
Proof . Let
$ \mathcal {B} = \{h_1, \ldots , h_r\} \subset H_0$
be a basis for
$H_0$
, and let
$| \cdot |_{\mathcal {B}}$
be the word metric on
$H_0$
with respect to
$\mathcal {B}$
. Let
$\mathcal {S} \subset \Gamma $
be a finite generating set for
$\Gamma $
, and let
$| \cdot |_{\mathcal {S}}$
be the word metric on
$\Gamma $
with respect to
$\mathcal {S}$
. Let
$\phi : H_0 \rightarrow \mathbb {R}^r$
be the homomorphism to
$\mathbb {R}^r$
induced by the action of
$H_0$
on a thick flat in X. Fix
$x_0 \in X$
,and let
$K = \max _{s \in \mathcal {S}\cup \mathcal {S}^{-1}}d_X(x_0, sx_0)$
. Since any two norms on
$\mathbb {R}^r$
are equivalent, there is some
$C> 0$
such that
$\| \phi (h) \| \geq C |h|_{\mathcal {B}}$
for any
$h \in H_0$
. Thus, for
$h \in H_0$
, we have
$$ \begin{align*} K |h|_{\mathcal{S}} \geq d_X(x_0, hx_0) \geq |h|_X = \| \phi(h) \| \geq C |h|_{\mathcal{B}}, \end{align*} $$
where the first inequality follows from the triangle inequality.
4 Proof of Theorems 1.1 and 1.3
Proof of Theorem 1.1
(i) Since
$\Gamma $
is finitely generated, we have that
$\Gamma \subset \mathrm {SL}_n(A)$
for some finitely generated subdomain
$A \subset \mathbb {C}$
. Let
$E = \mathbb {Q}(A) \subset \mathbb {C}$
so that E is a finitely generated field extension of
$\mathbb {Q}$
. The extension
$E/\mathbb {Q}$
has the structure
$\mathbb {Q} \subset F \subset F(T) \subset E$
, where F is the algebraic closure of
$\mathbb {Q}$
in E, and T is a (possibly empty) transcendence basis for E over F. Since the extension
$E/\mathbb {Q}$
is finitely generated, the set T is finite and the extensions
$F/\mathbb {Q}$
and
$E/F(T)$
are of finite degree.
Let
$d = \mathrm {deg}(F/\mathbb {Q})$
, and let
$\sigma _1, \ldots , \sigma _d$
be the embeddings of F in
$\mathbb {C}$
. Since
$\sigma _j(F)$
is countable but
$\mathbb {C}$
is not, the extension
$\mathbb {C}/\sigma _j(F)$
has infinite transcendence degree, and hence, by mapping T injectively into a transcendence basis for
$\mathbb {C}$
over
$\sigma _j(F)$
, we may extend
$\sigma _j$
to an embedding
$\sigma _j: F(T) \rightarrow \mathbb {C}$
. The latter may in turn be extended to an embedding
${\sigma _j: E \rightarrow \mathbb {C}}$
since
$E/F(T)$
is algebraic and
$\mathbb {C}$
is algebraically closed. The embedding
${\sigma _j: E \rightarrow \mathbb {C}}$
induces an embedding
$\sigma _j: \mathrm {SL}_n(E) \rightarrow \mathrm {SL}_n(\mathbb {C})$
. Let
$$\begin{align*}\sigma: \mathrm{SL}_n(E) \rightarrow G_1 : = \prod_{j=1}^d \mathrm{SL}_n(\mathbb{C}) \end{align*}$$
be the diagonal embedding induced by the maps
$\sigma _j : \mathrm {SL}_n(E) \rightarrow \mathrm {SL}_n(\mathbb {C})$
. Then
$\mathrm {SL}_n(E)$
acts by isometries on the Hadamard manifold
$X_1 := \prod _{j=1}^d M_j$
via the embedding
$\sigma $
, where each
$M_j$
is a copy of the symmetric space (unique up to scaling of the Riemannian metric) associated to
$\mathrm {SL}_n(\mathbb {C})$
.
By [Reference Alperin and Shalen3, Prop. 1.2], there are finitely many discrete valuations
$\nu _1, \ldots , \nu _m$
on E such that
$A \cap \bigcap _{i=1}^m \mathcal {O}_i \subset \mathcal {O}$
, where
$\mathcal {O}$
is the ring of integers of F and
$\mathcal {O}_i$
is the valuation ring of
$\nu _i$
. Let
$B_i$
be the Bruhat—Tits building associated to
$\mathrm {SL}_n(E_{\nu _i})$
, where
$E_{\nu _i}$
is the completion of E with respect to
$\nu _i$
; let
$X_2 = \prod _{i=1}^m B_i$
; and let
$\tau : \mathrm {SL}_n(E) \rightarrow G_2 := \prod _{i=1}^m \mathrm {SL}_n(E_{\nu _i})$
be the diagonal embedding. Then
$\mathrm {SL}_n(E)$
acts by automorphisms on
$X_2$
via the embedding
$\tau $
. We claim that the diagonal action of
$\Gamma $
on
${X := X_1 \times X_2}$
via
$\sigma \times \tau : \mathrm {SL}_n(E) \rightarrow G_1 \times G_2$
has the desired properties.
To that end, let H be a subgroup of
$\Gamma $
containing no nontrivial unipotent elements. We first claim that for any vertex v of
$X_2$
, the subgroup
$\sigma (H_v) < G_1$
is discrete, where
$H_v$
is the stabilizer of v in H. Indeed, let
$h \in H_v$
. Then for
$i=1, \ldots , m$
, the element h fixes a vertex of
$B_i$
and (since
$\mathrm {GL}_n(E)$
acts transitively on the vertices of
$B_i$
) is thus conjugate within
$\mathrm {GL}_n(E)$
into
$\mathrm {SL}_n(\mathcal {O}_i)$
; in particular, the coefficients of the characteristic polynomial
$\chi _h$
of h lie in
$\mathcal {O}_i$
. Since this is true for each
$i \in \{1, \ldots , m\}$
and since
$h \in \mathrm {SL}_n(A)$
, we have that the coefficients of
$\chi _h$
lie in
$A \cap \bigcap _{i=1}^m \mathcal {O}_i$
and hence in
$\mathcal {O}$
. We thus have a commutative diagram
where the function p maps an element
$h \in H_v$
to the n-tuple whose entries are the nonleading coefficients of
$\chi _h$
, the function P is the d-fold product of the analogous map
$\mathrm {SL}_n(\mathbb {C}) \rightarrow \mathbb {C}^n$
and the function
$\hat {\sigma }$
is given by
$$\begin{align*}\hat{\sigma}(\alpha_1, \ldots, \alpha_n) = (\sigma_1(\alpha_1), \ldots, \sigma_1(\alpha_n), \ldots, \sigma_d(\alpha_1), \ldots, \sigma_d(\alpha_n)) \end{align*}$$
for
$\alpha _1, \ldots , \alpha _n \in \mathcal {O}$
. Since
$\hat {\sigma }$
has discrete image (see, for example, Lemma 25.1.10 in [Reference Kargapolov and Merzljakov21]) and the diagram (4.1) is commutative, it follows that
$P(\sigma (H_v))$
is discrete in
$\prod _{j=1}^d \mathbb {C}^n$
. Now, suppose we have a sequence
$(h_k)_{k \in \mathbb {N}}$
in
$H_v$
such that
$\sigma (h_k) \rightarrow 1$
in
$G_1$
. Then, by continuity of the function P, we have
$P(\sigma (h_k)) \rightarrow P(1)$
. By discreteness of
$P(\sigma (H_v))$
, this implies that
$P(\sigma (h_k)) = P(1)$
for k sufficiently large. It follows that for such k the matrix
$h_k$
is unipotent and hence trivial by our assumption that H contains no nontrivial unipotent elements. We conclude that
$\sigma (H_v)$
is indeed discrete in
$G_1$
.
We now argue that, for any
$x \in X_2$
, there is a neighborhood V of x in
$X_2$
such that
$H_V \subset H_v$
for some vertex v of
$X_2$
, where
$$\begin{align*}H_V = \{ h \in H \> : \> V \cap hV \neq \emptyset\}. \end{align*}$$
Let c be the cell of
$X_2$
containing x, and let
$\ell $
be the dimension of c. Let
$\epsilon> 0$
be such that the intersection of the ball
$B_{X_2}(x, \epsilon )$
with the
$\ell $
-skeleton
$X_2^\ell $
of
$X_2$
is contained in c. Then we may take
$V = B_{X_2}(x, \epsilon /2)$
. Indeed, if
$h \in H_V$
, then
$hx \in X_2^\ell \cap B_{X_2}(x, \epsilon ) \subset c$
, and so
$hc = c$
. Since
$\mathrm {SL}_n(E)$
acts on
$B_i$
without permutations, it follows that
$h \in H_v$
for any vertex v of c.
Now, to see that H acts properly on X, we observe that for any point
$x \in X_2$
and any ball
$B \subset X_1$
, the set
$U := B \times V \subset X$
has the property that
$\{ h \in H \> : \> U \cap hU \neq \emptyset \}$
is finite, where
$V \subset X_2$
is as in the preceding paragraph. Indeed, we have
$H_V \subset H_v$
for some vertex v of
$X_2$
, and
$H_v$
acts properly on
$X_1$
since
$\sigma $
embeds
$H_v$
discretely in
$G_1$
.
(ii) Suppose H is free abelian with a basis
$h_1, \ldots , h_r \in H$
. We show that this basis is as in the statement of Theorem 3.5 so that H preserves and acts as a lattice of translations on a thick flat in X. Indeed, by Lemma 3.4, we may assume that for
$j \in \{1, \ldots , d\}$
,
$k \in \{1, \ldots , r\}$
, we have
$$\begin{align*}\sigma_j(h_k) = \mathrm{diag}(h_{j,k,1}, \ldots, h_{j,k, s}), \end{align*}$$
where
$h_{j,k,\ell } \in \mathrm {GL}_{n_\ell }(\mathbb {C})$
is upper triangular with a single eigenvalue for
$\ell \in \{1, \ldots s\}$
. We now have a homomorphism
$\Delta _j: H \rightarrow \mathrm {SL}_n(\mathbb {C})$
that maps
$h \in H$
to the diagonal part of
$\sigma _j(h)$
; note that
$\Delta _j$
is injective since H contains no nontrivial unipotent matrices. The embeddings
$\Delta _j$
produce a diagonal embedding
$\Delta : H \rightarrow G_1$
. Now, let
$\Delta ': H \rightarrow G_1 \times G_2$
be the product of
$\Delta $
with
$\tau \big |_H : H \rightarrow G_2$
. Then, since
$\Delta _j(h)$
has the same characteristic polynomial as
$\sigma _j(h)$
for each
$h \in H$
, and since
$\Delta _j(H)$
contains no nontrivial unipotent matrices, the action of
$\Delta '(H)$
on X is proper by the above arguments. Since the latter action is by semisimple isometries, by Theorem 2.4 there is a genuine r-dimensional flat in X preserved by
$\Delta '(H)$
on which
$\Delta '(H)$
acts as a lattice of translations. Thus, by Lemmas 3.2 and 3.3, each nontrivial
$h \in H$
acts ballistically on X and the canonical attracting fixed point of h on
$\partial X$
is equal to that of
$\Delta '(h)$
; in particular,
$\omega _{h_1}, \ldots , \omega _{h_r}$
must be of the desired form.
(iii) Suppose
$g \in \Gamma $
is diagonalizable (over
$\mathbb {C}$
). Since any isometry of
$X_2$
is semisimple, to show that g acts as a semisimple isometry of X, it suffices to show that
$\sigma _j(g)$
is a semisimple isometry of
$M_j$
for
$j=1, \ldots , d$
. To that end, we show that
$\sigma _j(g)$
is diagonalizable. Indeed, since a diagonalization of g has entries in the splitting field
$\tilde {E} \subset \mathbb {C}$
of
$\chi _g$
over E, we in fact have
${g = CDC^{-1}}$
for some
$C,D \in \mathrm {SL}_n(\tilde {E})$
with D diagonal (see, for example, [Reference Roman29, Theorem 8.11]). Since
$\mathbb {C}$
is algebraically closed, we may extend
$\sigma _j$
to an embedding
$\tilde {\sigma }_j: \tilde {E} \rightarrow \mathbb {C}$
. Now,
$$\begin{align*}\sigma_j(g) = \tilde{\sigma}_j(g) = \tilde{\sigma}_j(C) \> \tilde{\sigma}_j(D) \> \tilde{\sigma}_j(C)^{-1} \end{align*}$$
and
$\tilde {\sigma }_j(D)$
is diagonal.
We recover the following result due to Button [Reference Button9, Theorem 5.2].
Corollary 4.1. Let
$\Gamma $
be a finitely generated group and H a distorted finitely generated abelian subgroup of
$\Gamma $
. Then for any representation
$\rho : \Gamma \rightarrow \mathrm {SL}_n(\mathbb {C})$
, there is an infinite-order element
${h \in H}$
such that
$\rho (h)$
is unipotent.
Proof . Let
$H_0 < H$
be a free abelian subgroup of finite-index, and suppose there is a representation
$\rho _0: \Gamma \rightarrow \mathrm {SL}_n(\mathbb {C})$
that does not map any nontrivial element of
$H_0$
to a unipotent matrix (in particular,
$\rho $
is faithful on
$H_0$
). Then, by Theorem 1.1, there is an action of
$\Gamma $
via
$\rho $
on a complete CAT(0) space X such that
$H_0$
preserves and acts as a lattice of translations on a thick flat in X. By Lemma 3.8, it follows that
$H_0$
is undistorted in
$\Gamma $
, and hence the same is true of H.
Proof of Theorem 1.3
Suppose otherwise so that, for each JSJ torus S of M, the representation
$\rho $
is faithful on
$\pi _1(S) < \pi _1(M)$
and the image
$\rho (\pi _1(S))$
contains no nontrivial unipotent matrices. Then, by Theorem 1.1, there is an action of
$\pi _1(M)$
via
$\rho $
on a complete CAT(0) space X such that for each JSJ torus S of M, the subgroup
$\pi _1(S)$
preserves and acts as a lattice of translations on a thick flat in X. Thus, M admits a nonpositively curved metric by Lemma 3.7.
Acknowledgements
I am deeply grateful to Piotr Przytycki for his encouragement, patience and guidance. I also thank Bruno Duchesne, Zachary Munro and Abdul Zalloum for helpful discussions and the anonymous referees for comments that significantly improved the quality of this article.
Competing interest
None.
