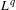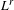Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hishida, Toshiaki
2020.
Decay Estimates of Gradient of a Generalized Oseen Evolution Operator Arising from Time-Dependent Rigid Motions in Exterior Domains.
Archive for Rational Mechanics and Analysis,
Vol. 238,
Issue. 1,
p.
215.
Hishida, Toshiaki
2021.
An alternative proof of $$L^q$$–$$L^r$$ estimates of the Oseen semigroup in higher dimensional exterior domains.
Partial Differential Equations and Applications,
Vol. 2,
Issue. 2,
Takahashi, Tomoki
2021.
Existence of a Stationary Navier–Stokes Flow Past a Rigid Body, with Application to Starting Problem in Higher Dimensions.
Journal of Mathematical Fluid Mechanics,
Vol. 23,
Issue. 2,