Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T05:14:42.805Z Has data issue: false hasContentIssue false
  • English
  • Français

A STABILITY VERSION OF THE GAUSS–LUCAS THEOREM AND APPLICATIONS

Part of: Polynomials, rational functions Geometric function theory

Published online by Cambridge University Press:  05 September 2019

STEFAN STEINERBERGER Open the ORCID record for STEFAN STEINERBERGER [Opens in a new window]
STEFAN STEINERBERGER*
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06511, USA email stefan.steinerberger@yale.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $p:\mathbb{C}\rightarrow \mathbb{C}$ be a polynomial. The Gauss–Lucas theorem states that its critical points, 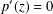$p^{\prime }(z)=0$, are contained in the convex hull of its roots. We prove a stability version whose simplest form is as follows: suppose that $p$ has 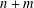$n+m$ roots, where $n$ are inside the unit disk,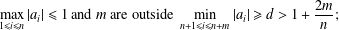

$$\begin{eqnarray}\max _{1\leq i\leq n}|a_{i}|\leq 1~\text{and}~m~\text{are outside}~\min _{n+1\leq i\leq n+m}|a_{i}|\geq d>1+\frac{2m}{n};\end{eqnarray}$$
then $p^{\prime }$ has 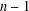$n-1$ roots inside the unit disk and $m$ roots at distance at least 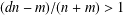$(dn-m)/(n+m)>1$ from the origin and the involved constants are sharp. We also discuss a pairing result: in the setting above, for $n$ sufficiently large, each of the $m$ roots has a critical point at distance 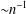${\sim}n^{-1}$.

Keywords

Gauss–Lucas theorempolynomial dynamicsrootszerosderivativescritical points

MSC classification

Primary: 26C10: Polynomials
Secondary: 30C15: Zeros of polynomials, rational functions, and other analytic functions (e.g. zeros of functions with bounded Dirichlet integral)
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 109 , Issue 2 , October 2020 , pp. 262 - 269
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

The author was supported by the NSF (DMS-1763179) and the Alfred P. Sloan Foundation.

References

Aziz, A., ‘On the location of critical points of polynomials’, J. Aust. Math. Soc. 36 (1984), 4–11.Google Scholar
Bray, H. E., ‘On the zeros of a polynomial and of its derivative’, Amer. J. Math. 53(4) (1931), 864–872.Google Scholar
de Bruijn, N. G., ‘On the zeros of a polynomial and of its derivative’, Nederl. Akad. Wetensch. Proc. 49 (1946), 1037–1044; Indag. Math. 8 (1946), 635–642.Google Scholar
de Bruijn, N. G. and Springer, T. A., ‘On the zeros of a polynomial and of its derivative. II’, Nederl. Akad. Wetensch. Proc. 50 (1947), 264–270; Indag. Math. 9 (1947), 458–464.Google Scholar
Curgus, B. and Mascioni, V., ‘A contraction of the Lucas polygon’, Proc. Amer. Math. Soc. 132 (2004), 2973–2981.Google Scholar
Dimitrov, D., ‘A refinement of the Gauss–Lucas theorem’, Proc. Amer. Math. Soc. 126 (1998), 2065–2070.Google Scholar
Gauss, C. F., Werke, Band 3 (Konigliche Gesellschaften der Wissenschaften zu Gottingen, Göttingen, 1866), S. 120:112.Google Scholar
Hanin, B., ‘Pairing of zeros and critical points for random polynomials’, Ann. Inst. Henri Poincaré Probab. Stat. 53 (2017), 1498–1511.Google Scholar
Joyal, A., ‘On the zeros of a polynomial and its derivative’, J. Math. Anal. Appl. 26 (1969), 315–317.Google Scholar
Kabluchko, Z., ‘Critical points of random polynomials with independent and identically distributed roots’, Proc. Amer. Math. Soc. 143(2) (2015), 695–702.Google Scholar
Kalman, D., ‘An elementary proof of Marden’s theorem’, Amer. Math. Monthly 115 (2008), 330–338.Google Scholar
Lucas, F., ‘Sur une application de la mécanique rationnelle à la théorie des équations’, C. R. Acad. Sci. Paris 89 (1879), 224–226.Google Scholar
Malamud, S. M., ‘Inverse spectral problem for normal matrices and the Gauss–Lucas theorem’, Trans. Amer. Math. Soc. 357 (2005), 4043–4064.Google Scholar
Marden, M., ‘A note on the zeroes of the sections of a partial fraction’, Bull. Amer. Math. Soc. 51 (1945), 935–940.Google Scholar
O’Rourke, S. and Williams, N., ‘Pairing between zeros and critical points of random polynomials with independent roots’, Trans. Amer. Math. Soc. 371 (2019), 2343–2381.Google Scholar
Pawlowski, P., ‘On the zeros of a polynomial and its derivatives’, Trans. Amer. Math. Soc. 350 (1998), 4461–4472.Google Scholar
Pemantle, R. and Rivlin, I., ‘The distribution of the zeroes of the derivative of a random polynomial’, in: Advances in Combinatorics (eds. Kotsireas, I. S. and Zima, E. V.) (Springer, Berlin–Heidelberg, 2013), 259–273.Google Scholar
Pereira, R., ‘Differentiators and the geometry of polynomials’, J. Math. Anal. Appl. 285 (2003), 336–348.Google Scholar
Rahman, Q. I., ‘On the zeros of a polynomial and its derivative’, Pacific J. Math. 41 (1972), 525–528.Google Scholar
Ravichandran, M., ‘Principal submatrices, restricted invertibility and a quantitative Gauss–Lucas theorem’, Preprint, 2016, arXiv:1609.04187.Google Scholar
Richards, T., ‘On approximate Gauss–Lucas theorems’, Preprint, 2017, arXiv:1706.05410.Google Scholar
Schmeisser, G., ‘Majorization of the critical points of a polynomial by its zeros’, Comput. Methods Funct. Theory 3(1) (2004), 95–103.Google Scholar
Siebeck, J., ‘Über eine neue analytische Behandlungweise der Brennpunkte’, J. reine angew. Math. 64 (1864), 175–182.Google Scholar
Specht, W., ‘Eine Bemerkung zum Satze von Gauss–Lucas’, Jahresber. Dtsch. Math.-Ver. 62 (1959), 85–92.Google Scholar
Totik, V., ‘The Gauss–Lucas theorem in an asymptotic sense’, Bull. Lond. Math. Soc. 48 (2016), 848–854.Google Scholar
Walsh, J. L., The Location of Critical Points of Analytic and Harmonic Functions, American Mathematical Society Colloquium Publications, 34 (American Mathematical Society, Providence, RI, 1950).Google Scholar