Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-06T09:18:28.382Z Has data issue: false hasContentIssue false
  • English
  • Français

ON POINTS WITH POSITIVE DENSITY OF THE DIGIT SEQUENCE IN INFINITE ITERATED FUNCTION SYSTEMS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Classical measure theory

Published online by Cambridge University Press:  09 September 2016

ZHEN-LIANG ZHANG  and
CHUN-YUN CAO
ZHEN-LIANG ZHANG
Affiliation:
School of Mathematical Sciences, Henan Institute of Science and Technology, 453003 Xinxiang, PR China email zhenliang_zhang@163.com
CHUN-YUN CAO*
Affiliation:
College of Science, Huazhong Agricultural University, 430070 Wuhan, PR China email caochunyun@mail.hzau.edu.cn
*
✉caochunyun@mail.hzau.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 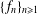$\{f_{n}\}_{n\geq 1}$ be an infinite iterated function system on 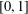$[0,1]$ and let 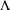$\unicode[STIX]{x1D6EC}$ be its attractor. Then, for any $x\in \unicode[STIX]{x1D6EC}$, it corresponds to a sequence of integers 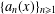$\{a_{n}(x)\}_{n\geq 1}$, called the digit sequence of $x$, in the sense that

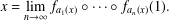$$\begin{eqnarray}x=\lim _{n\rightarrow \infty }f_{a_{1}(x)}\circ \cdots \circ f_{a_{n}(x)}(1).\end{eqnarray}$$
In this note, we investigate the size of the points whose digit sequences are strictly increasing and of upper Banach density one, which improves the work of Tong and Wang and Zhang and Cao.

Keywords

Banach densityHausdorff dimensioninfinite iterated function systems

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 28A80: Fractals
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 102 , Issue 3 , June 2017 , pp. 435 - 443
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the Fundamental Research Funds for the Central University (Grant No. 2662015QC001) and NSFC (Grant Nos. 11426111 and 11501168).

References

Cao, C. Y., Wang, B. W. and Wu, J., ‘The growth speed of digits in infinite iterated function systems’, Stud. Math. 217 (2013), 139–158.Google Scholar
Falconer, K. J., Fractal Geometry, Mathematical Foundations and Applications (John Wiley & Sons, Chichester, 2003).Google Scholar
Fan, A. H., Liao, L. M. and Ma, J. H., ‘The frequency of the digits in continued fractions’, Math. Proc. Cambridge Philos. Soc. 148 (2010), 179–192.Google Scholar
Furstenberg, H., ‘Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions’, J. Anal. Math. 31 (1977), 204–256.Google Scholar
Green, B. and Tao, T., ‘The primes contain arbitrarily long arithmetic progressions’, Ann. of Math. (2) 167 (2008), 481–547.Google Scholar
Jordan, T. and Rams, M., ‘Increasing digit subsystems of infinite iterated function systems’, Proc. Amer. Math. Soc. 140 (2012), 1267–1279.Google Scholar
Liao, L. M., Ma, J. H. and Wang, B. W., ‘Dimension of some non-normal continued fraction sets’, Math. Proc. Cambridge Philos. Soc. 145 (2010), 215–225.Google Scholar
Szemerédi, E., ‘On sets of integers containing no k elements in arithmetic progression’, Acta Arith. 27 (1975), 299–345.Google Scholar
Tong, X. and Wang, B. W., ‘How many points contains arithmetic progressions in continued fraction expansion?’, Acta Arith. 139 (2009), 369–376.Google Scholar
Zhang, Z. L. and Cao, C. Y., ‘On points contain arithmetic progressions in their Lüroth expansion’, Acta Math. Sci. 36B (2016), 257–264.Google Scholar