It is a theorem of Prikry [7] that if κ carries a uniform η-descendingly complete ultrafilter then the stationary reflection property fails. In this paper we will derive similar results, but here from properties of filters (or ideals) rather than ultrafilters.

Throughout κ and η will denote regular cardinals with η < κ (in particular κ will be uncountable), and I will denote an ideal on κ, by which we mean a set I ⊆ P(κ) such that (i) I is closed under taking subsets and finite unions and (ii) αЄ I for each α < κ, but κ ∉ I. I is said to be μ-complete if it is closed under taking unions of size < μ, I* = {X ⊆ κ ∣ κ − X Є I} is the filter dual to I and if A Є I+ (= P(κ) − I), then I∣A is the ideal on κ given by I ∣ A = {X ⊆ κ ∣ X ∩ A Є I}. If h: A → κ then h is said to be (i) unbounded mod I if for each α < κ, h−1(α) = {ξ Є A ∣ h(ξ) < α} Є I and (ii) a least function for I if h is unbounded mod I and whenever g: A → κ is a function, unbounded mod I, then {ξ Є A ∣ g{ξ) < h{ξ)} Є I.

It is shown that the low basis theorem is meaningful and provable in IΣ1 and that the priority-free solution to Post's problem formalizes in this theory.

Because the main difference between combinatory weak equality and λβ-equality is that the rule

is valid for the latter but not the former, it is easy to assume that another way of defining combinatory β-equality is to add rule (ξ) to the postulates for weak equality. However, to make this true, one must choose the definition of combinatory abstraction in (ξ) very carefully. If one tries to use one of the more common abstraction algorithms, the result will be an equality, =ξ, that is either equivalent to βη-equality (and so strictly stronger than β-equality) or else strictly weaker than β-equality. This paper will study the relations =ξ for several commonly used abstraction-algorithms, distinguish between them, and axiomatize them.

I falsely claimed, as an aside remark in [8] and also implicitly in the abstract [9], that the slow-growing hierarchy

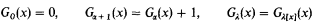
“catches up” with the fast-growing hierarchy

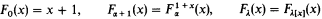
at level Γ0, i.e. that, for all x > 0,

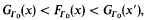
where x′ is some simple (even linear) function of x.

Girard [4] gave the first correct analysis of the deep relationship which exists between G and F, based on his extensive category-theoretic framework for 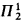-logic. This analysis indicates that the first point at which G catches up with F is the ordinal of the theory ID<ω(0 of arbitrary finite iterations of an inductive definition. This is very far beyond Γ0! In particular, in order to capture F at level ∣IDn∣ the slow-growing hierarchy must be generated up to ∣IDn+1∣, i.e. one extra iteration of an inductive definition is needed in order to generate sufficient new ordinals.