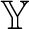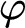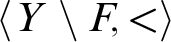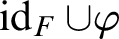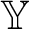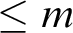1 Introduction
In this article we confirm Vaught’s conjecture for almost chainable theories, extending the result of Reference Kurilić[7], which concerns the smaller class of monomorphic theories. We recall that the Vaught conjecture is related to the number
![]() $I({\mathcal T} ,\omega )$
of non-isomorphic countable models of a countable complete first order theory
$I({\mathcal T} ,\omega )$
of non-isomorphic countable models of a countable complete first order theory
![]() ${\mathcal T}$
. In 1959 Robert Vaught Reference Vaught[14] asked if there is a theory
${\mathcal T}$
. In 1959 Robert Vaught Reference Vaught[14] asked if there is a theory
![]() ${\mathcal T}$
such that the equality
${\mathcal T}$
such that the equality
![]() $I({\mathcal T} ,\omega )=\omega _1$
is provable without the use of the continuum hypothesis; since then, the implication
$I({\mathcal T} ,\omega )=\omega _1$
is provable without the use of the continuum hypothesis; since then, the implication
![]() $I({\mathcal T} ,\omega )> \omega \Rightarrow I({\mathcal T} ,\omega )= {\mathfrak {c}}$
is known as Vaught’s conjecture.
$I({\mathcal T} ,\omega )> \omega \Rightarrow I({\mathcal T} ,\omega )= {\mathfrak {c}}$
is known as Vaught’s conjecture.
The rich history of the investigation related to that (still unresolved) conjecture includes a long list of results confirming the conjecture in particular classes of theories (see, for example, the introduction and references of Reference Puninskaya[9]) and, on the other hand, intriguing results concerning the consequences of the existence of counterexamples and the properties of (potential) counterexamples (see, e.g., Reference Baldwin, Friedman, Koerwien and Laskowski[1]).
The results of this paper are built on the fundament consisting of two (groups of) results. The first one is the basic Rubin’s paper Reference Rubin[11] from 1974 in which the Vaught conjecture is confirmed for theories of linear orders with unary predicates; we will use the following result of Rubin (see Theorem 6.12 of Reference Rubin[11]).
Theorem 1.1 (Rubin)
If
![]() ${\mathcal T}$
is a complete theory of a linear order with a finite set of unary predicates, then
${\mathcal T}$
is a complete theory of a linear order with a finite set of unary predicates, then
![]() $I({\mathcal T}, \omega )\in \{ 1, {\mathfrak {c}}\}$
.
$I({\mathcal T}, \omega )\in \{ 1, {\mathfrak {c}}\}$
.
The second group of results is a part of the fundamental work concerning combinatorial properties of relational structures collected in the book of Roland Fraïssé Reference Fraïssé[2]. We will use Fraïssé’s results related to almost chainable structures, as well as a theorem of Gibson, Pouzet and Woodrow from Reference Gibson, Pouzet and Woodrow[4], describing all linear orders which chain an almost chainable structure over a fixed finite set, which is derived from similar results obtained independently by Frasnay Reference Frasnay[3] and by Hodges et al. [Reference Hodges6]. These results are presented in Section 2.
In Section 3 we show that a complete theory
![]() ${\mathcal T} $
with infinite models has a countable almost chainable model iff all models of
${\mathcal T} $
with infinite models has a countable almost chainable model iff all models of
![]() ${\mathcal T}$
are almost chainable and, so, establish the notion of an almost chainable theory. In Section 4 we prove that for each complete almost chainable theory
${\mathcal T}$
are almost chainable and, so, establish the notion of an almost chainable theory. In Section 4 we prove that for each complete almost chainable theory
![]() ${\mathcal T}$
having infinite models we have
${\mathcal T}$
having infinite models we have
![]() $I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
and, thus, confirm the Vaught conjecture for such theories.
$I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
and, thus, confirm the Vaught conjecture for such theories.
The results of this paper can be regarded as extensions of the existing results concerning Vaught’s conjecture in several ways. First, the role of definability and interpretability in extensions of classes for which Vaught’s conjecture is already confirmed is well known (see Reference Schmerl[12] or [Reference Hodges, Lachlan and Shelah5]); here, taking a specific class
![]() ${\mathcal K}$
of colored linear orders, we confirm the conjecture for the theories of structures which are
${\mathcal K}$
of colored linear orders, we confirm the conjecture for the theories of structures which are
![]() $\Sigma _0$
-definable in structures from
$\Sigma _0$
-definable in structures from
![]() ${\mathcal K}$
. More precisely, if
${\mathcal K}$
. More precisely, if
![]() ${\mathbb X} =\langle X, \vartriangleleft ,\{ a_0\}, \dots ,\{ a_{n-1}\} \rangle $
is a linear order with n unary predicates, where
${\mathbb X} =\langle X, \vartriangleleft ,\{ a_0\}, \dots ,\{ a_{n-1}\} \rangle $
is a linear order with n unary predicates, where
![]() $a_0< \cdots <a_{n-1}$
are the first n elements of
$a_0< \cdots <a_{n-1}$
are the first n elements of
![]() ${\mathbb X}$
, and if
${\mathbb X}$
, and if
![]() $L_n=\langle R, U_0,\dots ,U_{n-1}\rangle $
is the corresponding language, then each quantifier-free
$L_n=\langle R, U_0,\dots ,U_{n-1}\rangle $
is the corresponding language, then each quantifier-free
![]() $L_n$
-formula
$L_n$
-formula
![]() $\varphi (v_0 ,\dots ,v_{m-1})$
defines an m-ary almost chainable relation on the set X. (In this way we obtain “finite modifications” of several relevant monomorphic relations; e.g., betweenness, cyclic-order and dihedral relation, see Reference Fraïssé[2].) More generally, if
$\varphi (v_0 ,\dots ,v_{m-1})$
defines an m-ary almost chainable relation on the set X. (In this way we obtain “finite modifications” of several relevant monomorphic relations; e.g., betweenness, cyclic-order and dihedral relation, see Reference Fraïssé[2].) More generally, if
![]() $L=\langle R_i :i\in I\rangle $
is any relational language and
$L=\langle R_i :i\in I\rangle $
is any relational language and
 $\varphi _i (v_0 ,\dots ,v_{\mathop {\mathrm {ar}}\nolimits (R_i)-1})$
, for
$\varphi _i (v_0 ,\dots ,v_{\mathop {\mathrm {ar}}\nolimits (R_i)-1})$
, for
![]() $i\in I$
, are
$i\in I$
, are
![]() $\Sigma _0$
-formulas of
$\Sigma _0$
-formulas of
![]() $L_n$
defining the relations
$L_n$
defining the relations
 $R_i^{\mathbb Y} \subset X^{\mathop {\mathrm {ar}}\nolimits (R_i)}$
, then the structure
$R_i^{\mathbb Y} \subset X^{\mathop {\mathrm {ar}}\nolimits (R_i)}$
, then the structure
![]() ${\mathbb Y} :=\langle X , \langle R_i^{\mathbb Y} :i\in I\rangle \rangle $
is almost chainable and
${\mathbb Y} :=\langle X , \langle R_i^{\mathbb Y} :i\in I\rangle \rangle $
is almost chainable and
![]() $I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ),\omega )\in \{ 1,{\mathfrak {c}}\}$
. So we obtain a large jungle of theories satisfying Vaught’s conjecture; some simple examples are given in Section 5.
$I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ),\omega )\in \{ 1,{\mathfrak {c}}\}$
. So we obtain a large jungle of theories satisfying Vaught’s conjecture; some simple examples are given in Section 5.
Second, it is known that Vaught’s conjecture is equivalent to its restriction to (the theories of) partial orders (see [Reference Hodges, Lachlan and Shelah5, p. 231]) and, for example, it is confirmed for the theories of trees (Steel Reference Steel[13]) and reticles, that is, the posets which do not embed the four element poset N (Schmerl Reference Schmerl[12]). Here we note that simple infinite almost chainable posets are obtained taking a finite poset
![]() ${\mathbb P}=\langle P ,< \rangle $
and replacing some element
${\mathbb P}=\langle P ,< \rangle $
and replacing some element
![]() $p\in P$
by an infinite linear order
$p\in P$
by an infinite linear order
![]() ${\mathbb L}$
. By Theorem 4.1, the theory of the resulting poset will be
${\mathbb L}$
. By Theorem 4.1, the theory of the resulting poset will be
![]() $\omega $
-categorical iff
$\omega $
-categorical iff
![]() $\mathop {\mathrm {Th}}\nolimits ({\mathbb L})$
has that property; otherwise it will have continuum many non-isomorphic models. We note that in this way we can construct posets of any finite Dushnik–Miller dimension.
$\mathop {\mathrm {Th}}\nolimits ({\mathbb L})$
has that property; otherwise it will have continuum many non-isomorphic models. We note that in this way we can construct posets of any finite Dushnik–Miller dimension.
Third, one combinatorial invariant of a complete theory
![]() ${\mathcal T}$
is its profile function:
${\mathcal T}$
is its profile function:
![]() $\varphi _{\mathcal T} (n)$
is the number of non-isomorphic n-element substructures of models of
$\varphi _{\mathcal T} (n)$
is the number of non-isomorphic n-element substructures of models of
![]() ${\mathcal T}$
. So, in Reference Kurilić[7] Vaught’s conjecture is confirmed for monomorphic theories; namely, the theories having the minimal profile (
${\mathcal T}$
. So, in Reference Kurilić[7] Vaught’s conjecture is confirmed for monomorphic theories; namely, the theories having the minimal profile (
![]() $\varphi _{\mathcal T} (n)=1$
, for all
$\varphi _{\mathcal T} (n)=1$
, for all
![]() $n\in {\mathbb N}$
); here we extend that result for the theories with bounded profile (
$n\in {\mathbb N}$
); here we extend that result for the theories with bounded profile (
![]() $\varphi _{\mathcal T} \leq m$
, for some
$\varphi _{\mathcal T} \leq m$
, for some
![]() $m\in {\mathbb N}$
).
$m\in {\mathbb N}$
).
2 Preliminaries. Almost chainable structures
Throughout the paper we assume that
![]() $L=\langle R_i :i\in I\rangle $
is a relational language, where
$L=\langle R_i :i\in I\rangle $
is a relational language, where
![]() $\mathop {\mathrm {ar}}\nolimits (R_i)=n_i\in {\mathbb N}$
, for
$\mathop {\mathrm {ar}}\nolimits (R_i)=n_i\in {\mathbb N}$
, for
![]() $i\in I$
. If Y is a non-empty set and
$i\in I$
. If Y is a non-empty set and
![]() ${\mathcal T} \subset \mathop {\mathrm {Sent}}\nolimits _L$
an L-theory, then
${\mathcal T} \subset \mathop {\mathrm {Sent}}\nolimits _L$
an L-theory, then
 $\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(Y)$
(resp.
$\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(Y)$
(resp.
![]() $\mathop {\mathrm {Mod}}\nolimits _{L}(Y)$
;
$\mathop {\mathrm {Mod}}\nolimits _{L}(Y)$
;
 $\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }$
) will denote the set of all models of
$\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }$
) will denote the set of all models of
![]() ${\mathcal T}$
with domain Y (resp. the set of all L-structures with domain Y; the class of all models of
${\mathcal T}$
with domain Y (resp. the set of all L-structures with domain Y; the class of all models of
![]() ${\mathcal T}$
). Let
${\mathcal T}$
). Let
![]() ${\mathbb Y} =\langle Y, \langle R_i ^{\mathbb Y} : i\in I\rangle \rangle $
be an L-structure. For a non-empty set
${\mathbb Y} =\langle Y, \langle R_i ^{\mathbb Y} : i\in I\rangle \rangle $
be an L-structure. For a non-empty set
![]() $H\subset Y$
,
$H\subset Y$
,
![]() ${\mathbb H} :=\langle H, \langle R_i ^{\mathbb Y} \upharpoonright H : i\in I\rangle \rangle $
is the corresponding substructure of
${\mathbb H} :=\langle H, \langle R_i ^{\mathbb Y} \upharpoonright H : i\in I\rangle \rangle $
is the corresponding substructure of
![]() ${\mathbb Y}$
. If
${\mathbb Y}$
. If
![]() $J\subset I$
, then
$J\subset I$
, then
![]() $L_J:=\langle R_i : i\in J\rangle $
is the corresponding reduction of L and
$L_J:=\langle R_i : i\in J\rangle $
is the corresponding reduction of L and
![]() ${\mathbb Y} |L_J :=\langle Y, \langle R_i ^{\mathbb Y} : i\in J\rangle \rangle $
the corresponding reduct of
${\mathbb Y} |L_J :=\langle Y, \langle R_i ^{\mathbb Y} : i\in J\rangle \rangle $
the corresponding reduct of
![]() ${\mathbb Y}$
. By
${\mathbb Y}$
. By
![]() $[{\mathbb Y}]$
we will denote the class of all L-structures being isomorphic to
$[{\mathbb Y}]$
we will denote the class of all L-structures being isomorphic to
![]() ${\mathbb Y}$
(the isomorphism type of
${\mathbb Y}$
(the isomorphism type of
![]() ${\mathbb Y}$
).
${\mathbb Y}$
).
If
![]() ${\mathbb X}=\langle X ,<\rangle $
is a linear order, then
${\mathbb X}=\langle X ,<\rangle $
is a linear order, then
![]() ${\mathbb X} ^*$
will denote its reverse,
${\mathbb X} ^*$
will denote its reverse,
![]() $\langle X ,< ^{-1}\rangle $
. By
$\langle X ,< ^{-1}\rangle $
. By
![]() $LO _X$
we denote the set of all linear orders on the set X.
$LO _X$
we denote the set of all linear orders on the set X.
We recall the notions and concepts introduced by Fraïssé which will be used in this paper and fix a convenient notation. For
![]() $n\in {\mathbb N}$
, by
$n\in {\mathbb N}$
, by
![]() $\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
we denote the collection
$\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
we denote the collection
![]() $\{ [{\mathbb H} ]:H\in [Y]^n \}$
of isomorphism types of n-element substructures of
$\{ [{\mathbb H} ]:H\in [Y]^n \}$
of isomorphism types of n-element substructures of
![]() ${\mathbb Y}$
(or, equivalently,
${\mathbb Y}$
(or, equivalently,
![]() $\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )=\{ {\mathbb H} \in \mathop {\mathrm {Mod}}\nolimits _L (n): {\mathbb H}\hookrightarrow {\mathbb Y} \}/\!\cong $
). The age of
$\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )=\{ {\mathbb H} \in \mathop {\mathrm {Mod}}\nolimits _L (n): {\mathbb H}\hookrightarrow {\mathbb Y} \}/\!\cong $
). The age of
![]() ${\mathbb Y} $
is the collection
${\mathbb Y} $
is the collection
 $\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} ):=\bigcup _{n\in {\mathbb N} }\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
. The function
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} ):=\bigcup _{n\in {\mathbb N} }\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
. The function
![]() $\varphi _{\mathbb Y} $
with the domain
$\varphi _{\mathbb Y} $
with the domain
![]() ${\mathbb N}$
defined by
${\mathbb N}$
defined by
![]() $\varphi _{\mathbb Y} (n)=|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|$
, for all
$\varphi _{\mathbb Y} (n)=|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|$
, for all
![]() $n\in {\mathbb N}$
, is the profile of
$n\in {\mathbb N}$
, is the profile of
![]() ${\mathbb Y}$
.
${\mathbb Y}$
.
By
![]() $\mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
we denote the set of all partial automorphisms of
$\mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
we denote the set of all partial automorphisms of
![]() ${\mathbb Y}$
(isomorphisms between substructures of
${\mathbb Y}$
(isomorphisms between substructures of
![]() ${\mathbb Y}$
, or, in Fraïssé’s terminology, local automorphisms). The L-structure
${\mathbb Y}$
, or, in Fraïssé’s terminology, local automorphisms). The L-structure
![]() ${\mathbb Y}$
is freely interpretable in an
${\mathbb Y}$
is freely interpretable in an
![]() $L'$
-structure
$L'$
-structure
![]() ${\mathbb X}$
having the same domain iff
${\mathbb X}$
having the same domain iff
![]() $\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
. We will say that
$\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
. We will say that
![]() ${\mathbb Y}$
is simply definable in
${\mathbb Y}$
is simply definable in
![]() ${\mathbb X}$
iff each relation
${\mathbb X}$
iff each relation
![]() $R_i^{\mathbb Y}$
is definable by a quantifier free
$R_i^{\mathbb Y}$
is definable by a quantifier free
![]() $L'$
-formula in the structure
$L'$
-formula in the structure
![]() ${\mathbb X}$
.
${\mathbb X}$
.
Almost chainable structures. Let
![]() ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
,
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
,
![]() $F\in [Y]^{<\omega }$
and
$F\in [Y]^{<\omega }$
and
![]() $<\in LO _{Y\setminus F}$
. Following Fraïssé (see [Reference Fraïssé2, p. 294]), the structure
$<\in LO _{Y\setminus F}$
. Following Fraïssé (see [Reference Fraïssé2, p. 294]), the structure
![]() ${\mathbb Y}$
is called
${\mathbb Y}$
is called
![]() $(F,<)$
-chainable iff
$(F,<)$
-chainable iff
The structure
![]() ${\mathbb Y}$
is called F-chainable if it is
${\mathbb Y}$
is called F-chainable if it is
![]() $(F,<)$
-chainable for some linear order
$(F,<)$
-chainable for some linear order
![]() $<$
on
$<$
on
![]() $Y\setminus F$
.
$Y\setminus F$
.
![]() ${\mathbb Y}$
is called almost chainable if it is F-chainable for some
${\mathbb Y}$
is called almost chainable if it is F-chainable for some
![]() $F\in [Y]^{<\omega }$
.
$F\in [Y]^{<\omega }$
.
The following four statements are proved in Reference Fraïssé[2] for
![]() $|L|=1$
and have straightforward generalizations for arbitrary relational language L. So, these results of Fraïssé are cited and used in the paper in such, more general, form.
$|L|=1$
and have straightforward generalizations for arbitrary relational language L. So, these results of Fraïssé are cited and used in the paper in such, more general, form.
Generally, if Y is a set,
![]() $F\in [Y]^{n}$
,
$F\in [Y]^{n}$
,
![]() $<\;\in LO _{Y\setminus F}$
and
$<\;\in LO _{Y\setminus F}$
and
![]() $F=\{ a_0,\dots ,a_{n-1}\}$
is an enumeration of the elements of the set F, we introduce the auxiliary language
$F=\{ a_0,\dots ,a_{n-1}\}$
is an enumeration of the elements of the set F, we introduce the auxiliary language
![]() $L_n:=\langle R,U_0,\dots ,U_{n-1}\rangle $
, consisting of new relational symbols, where
$L_n:=\langle R,U_0,\dots ,U_{n-1}\rangle $
, consisting of new relational symbols, where
![]() $\mathop {\mathrm {ar}}\nolimits (R)=2$
and
$\mathop {\mathrm {ar}}\nolimits (R)=2$
and
![]() $\mathop {\mathrm {ar}}\nolimits (U_j)=1$
, for
$\mathop {\mathrm {ar}}\nolimits (U_j)=1$
, for
![]() $j<n$
, and define the linear order
$j<n$
, and define the linear order
![]() $\lhd $
on the set Y and the
$\lhd $
on the set Y and the
![]() $L_n$
-structure (in fact, the linear order with n unary predicates)
$L_n$
-structure (in fact, the linear order with n unary predicates)
![]() ${\mathbb X} $
by
${\mathbb X} $
by
-
(L1)
 $\lhd \upharpoonright (Y\setminus F)=\;<$
,
$\lhd \upharpoonright (Y\setminus F)=\;<$
, -
(L2)
 $\langle Y ,\lhd \rangle = \{a_0\}+\cdots +\{a_{n-1}\}+(Y\setminus F) $
, and
$\langle Y ,\lhd \rangle = \{a_0\}+\cdots +\{a_{n-1}\}+(Y\setminus F) $
, and -
(L3)
 ${\mathbb X} :=\langle Y,\lhd , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
.
${\mathbb X} :=\langle Y,\lhd , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
.
Fact 2.1. Let
![]() ${\mathbb Y}$
be an L-structure,
${\mathbb Y}$
be an L-structure,
![]() $F=\{ a_0,\dots ,a_{n-1}\}\in [Y]^{n}$
and
$F=\{ a_0,\dots ,a_{n-1}\}\in [Y]^{n}$
and
![]() $<\;\in LO _{Y\setminus F}$
. If
$<\;\in LO _{Y\setminus F}$
. If
![]() $\lhd $
and
$\lhd $
and
![]() ${\mathbb X}$
are defined by (L1)–(L3), then the following conditions are equivalent:
${\mathbb X}$
are defined by (L1)–(L3), then the following conditions are equivalent:
-
(a)
 ${\mathbb Y}$
is
${\mathbb Y}$
is
 $(F,<)$
-chainable,
$(F,<)$
-chainable, -
(b)
 ${\mathbb Y}$
is freely interpretable in
${\mathbb Y}$
is freely interpretable in
 ${\mathbb X}$
, (that is,
${\mathbb X}$
, (that is,
 $\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
), and
$\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
), and -
(c)
 ${\mathbb Y}$
is simply definable in
${\mathbb Y}$
is simply definable in
 ${\mathbb X}$
.
${\mathbb X}$
.
Proof (a)
![]() $\Rightarrow $
(b). Let (1) hold and
$\Rightarrow $
(b). Let (1) hold and
![]() $f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )$
. Then, since f preserves
$f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )$
. Then, since f preserves
![]() $U_j$
’s, for each
$U_j$
’s, for each
![]() $y\in \mathop {\mathrm {dom}}\nolimits f$
and each
$y\in \mathop {\mathrm {dom}}\nolimits f$
and each
![]() $j<n$
we have:
$j<n$
we have:
![]() $y=a_j$
iff
$y=a_j$
iff
![]() $f(y)=a_j$
. So, if
$f(y)=a_j$
. So, if
![]() $a_j\in \mathop {\mathrm {dom}}\nolimits f$
, then
$a_j\in \mathop {\mathrm {dom}}\nolimits f$
, then
![]() $f(a_j)=a_j$
and, hence,
$f(a_j)=a_j$
and, hence,
![]() $f \upharpoonright (F\cap \mathop {\mathrm {dom}}\nolimits f)=\mathop {\mathrm {id}}\nolimits _{F\cap \mathop {\mathrm {dom}}\nolimits f}$
. In addition, if
$f \upharpoonright (F\cap \mathop {\mathrm {dom}}\nolimits f)=\mathop {\mathrm {id}}\nolimits _{F\cap \mathop {\mathrm {dom}}\nolimits f}$
. In addition, if
![]() $y\in (\mathop {\mathrm {dom}}\nolimits f )\setminus F$
, then
$y\in (\mathop {\mathrm {dom}}\nolimits f )\setminus F$
, then
![]() $f(y)\not \in F$
and, hence,
$f(y)\not \in F$
and, hence,
![]() $f[(\mathop {\mathrm {dom}}\nolimits f )\setminus F]\subset Y\setminus F$
. So, by (L1),
$f[(\mathop {\mathrm {dom}}\nolimits f )\setminus F]\subset Y\setminus F$
. So, by (L1),
![]() $\varphi :=f \upharpoonright ((\mathop {\mathrm {dom}}\nolimits f )\setminus F)\in \mathop {\mathrm {Pa}}\nolimits (\langle Y\setminus F ,<\rangle ) $
and by (1) we have
$\varphi :=f \upharpoonright ((\mathop {\mathrm {dom}}\nolimits f )\setminus F)\in \mathop {\mathrm {Pa}}\nolimits (\langle Y\setminus F ,<\rangle ) $
and by (1) we have
![]() $g:=\mathop {\mathrm {id}}\nolimits _F \cup \;\varphi \in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
. Finally, since
$g:=\mathop {\mathrm {id}}\nolimits _F \cup \;\varphi \in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
. Finally, since
![]() $f=g\upharpoonright \mathop {\mathrm {dom}}\nolimits f$
, it follows that
$f=g\upharpoonright \mathop {\mathrm {dom}}\nolimits f$
, it follows that
![]() $f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
.
$f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
.
(b)
![]() $\Rightarrow $
(c). Let
$\Rightarrow $
(c). Let
![]() $\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
and
$\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
and
![]() $i\in I$
. Let
$i\in I$
. Let
![]() $\mathop {\mathrm {Lit}}\nolimits _{L_n}(v_0, \dots , v_{n_i-1})$
be the set of all
$\mathop {\mathrm {Lit}}\nolimits _{L_n}(v_0, \dots , v_{n_i-1})$
be the set of all
![]() $L_n$
-literals
$L_n$
-literals
![]() $\eta $
such that
$\eta $
such that
![]() $\mathop {\mathrm {Fv}}\nolimits (\eta )\subset \{ v_0, \dots , v_{n_i-1}\}$
. For
$\mathop {\mathrm {Fv}}\nolimits (\eta )\subset \{ v_0, \dots , v_{n_i-1}\}$
. For
![]() $\bar {y}= \langle y_0, \dots , y_{n_i-1}\rangle \in Y^{n_i}$
let
$\bar {y}= \langle y_0, \dots , y_{n_i-1}\rangle \in Y^{n_i}$
let
 $$ \begin{align*}\textstyle \Phi _{\bar{y}}(\bar{v}):= \Big\{ \eta \in \mathop{\mathrm{Lit}}\nolimits _{L_n}(\bar{v}): {\mathbb X} \models \eta [\bar{y}]\Big\}. \end{align*} $$
$$ \begin{align*}\textstyle \Phi _{\bar{y}}(\bar{v}):= \Big\{ \eta \in \mathop{\mathrm{Lit}}\nolimits _{L_n}(\bar{v}): {\mathbb X} \models \eta [\bar{y}]\Big\}. \end{align*} $$
Since
![]() $|L_n|<\omega $
we have
$|L_n|<\omega $
we have
![]() $|\mathop {\mathrm {Lit}}\nolimits _{L_n}(\bar {v})|<\omega $
, so the relation
$|\mathop {\mathrm {Lit}}\nolimits _{L_n}(\bar {v})|<\omega $
, so the relation
![]() $\sim \subset Y^{n_i}\times Y^{n_i}$
defined by
$\sim \subset Y^{n_i}\times Y^{n_i}$
defined by
![]() $\bar {x} \sim \bar {y}$
iff
$\bar {x} \sim \bar {y}$
iff
![]() $\Phi _{\bar {x}}(\bar {v})=\Phi _{\bar {y}}(\bar {v})$
is an equivalence relation with finitely many equivalence classes, say
$\Phi _{\bar {x}}(\bar {v})=\Phi _{\bar {y}}(\bar {v})$
is an equivalence relation with finitely many equivalence classes, say
![]() $[\bar {y}_k]$
,
$[\bar {y}_k]$
,
![]() $k<m$
. Let
$k<m$
. Let
![]() $\varepsilon _{\bar {y}_k} (\bar {v}):=\bigwedge \Phi _{\bar {y}_k}(\bar {v})$
, for
$\varepsilon _{\bar {y}_k} (\bar {v}):=\bigwedge \Phi _{\bar {y}_k}(\bar {v})$
, for
![]() $k<m$
, and let
$k<m$
, and let
 $$ \begin{align}\textstyle \varphi _i (\bar{v}):= \bigvee \Big\{ \varepsilon _{\bar{y}_k} (\bar{v}): k<m \land \exists \bar{x} \in R_i^{\mathbb Y} \; {\mathbb X} \models \varepsilon _{\bar{y}_k} [\bar{x}]\Big\}. \end{align} $$
$$ \begin{align}\textstyle \varphi _i (\bar{v}):= \bigvee \Big\{ \varepsilon _{\bar{y}_k} (\bar{v}): k<m \land \exists \bar{x} \in R_i^{\mathbb Y} \; {\mathbb X} \models \varepsilon _{\bar{y}_k} [\bar{x}]\Big\}. \end{align} $$
We prove that
 $$ \begin{align} \forall \bar{y} \in Y^{n_i} \;\;\Big(\bar{y}\in R_i^{\mathbb Y} \Leftrightarrow {\mathbb X} \models \varphi _i [\bar{y} ]\Big). \end{align} $$
$$ \begin{align} \forall \bar{y} \in Y^{n_i} \;\;\Big(\bar{y}\in R_i^{\mathbb Y} \Leftrightarrow {\mathbb X} \models \varphi _i [\bar{y} ]\Big). \end{align} $$
Let
![]() $\bar {y}\in R_i^{\mathbb Y}$
and
$\bar {y}\in R_i^{\mathbb Y}$
and
![]() $k<m$
, where
$k<m$
, where
![]() $\bar {y} \sim \bar {y}_k$
. Then
$\bar {y} \sim \bar {y}_k$
. Then
![]() ${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
and
${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
and
![]() $\varepsilon _{\bar {y}_k}(\bar {v})$
appears in
$\varepsilon _{\bar {y}_k}(\bar {v})$
appears in
![]() $\varphi _i (\bar {v})$
. Since
$\varphi _i (\bar {v})$
. Since
![]() ${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
we have
${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
we have
![]() ${\mathbb X} \models \varphi _i [\bar {y} ]$
as well.
${\mathbb X} \models \varphi _i [\bar {y} ]$
as well.
If
![]() ${\mathbb X} \models \varphi _i [\bar {y} ]$
, there are
${\mathbb X} \models \varphi _i [\bar {y} ]$
, there are
![]() $k<m$
and
$k<m$
and
![]() $\bar {x} \in R_i^{\mathbb Y}$
such that
$\bar {x} \in R_i^{\mathbb Y}$
such that
![]() ${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {x}]$
and
${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {x}]$
and
![]() ${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
. Thus
${\mathbb X} \models \varepsilon _{\bar {y}_k} [\bar {y}]$
. Thus
![]() $\bar {x} \sim \bar {y}$
and, hence,
$\bar {x} \sim \bar {y}$
and, hence,
![]() $p:=\{ \langle x_r, y_r\rangle : r < n_i\}\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )\subset \mathop {\mathrm {Pa}}\nolimits (\langle Y, R_i^{\mathbb Y} \rangle )$
. Thus, since
$p:=\{ \langle x_r, y_r\rangle : r < n_i\}\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )\subset \mathop {\mathrm {Pa}}\nolimits (\langle Y, R_i^{\mathbb Y} \rangle )$
. Thus, since
![]() $\bar {x} \in R_i^{\mathbb Y} \upharpoonright \{x_r : r< n_i \}$
, we have
$\bar {x} \in R_i^{\mathbb Y} \upharpoonright \{x_r : r< n_i \}$
, we have
![]() $\bar {y} =p\bar {x} \in R_i^{\mathbb Y} \upharpoonright \{y_r : r < n_i \}$
and, hence,
$\bar {y} =p\bar {x} \in R_i^{\mathbb Y} \upharpoonright \{y_r : r < n_i \}$
and, hence,
![]() $\bar {y}\in R_i^{\mathbb Y}$
.
$\bar {y}\in R_i^{\mathbb Y}$
.
(c)
![]() $\Rightarrow $
(a). For
$\Rightarrow $
(a). For
![]() $i\in I$
, let
$i\in I$
, let
![]() $\varphi _i (v_0, \dots , v_{n_i-1})\in \mathop {\mathrm {Form}}\nolimits _{L_n}$
be a
$\varphi _i (v_0, \dots , v_{n_i-1})\in \mathop {\mathrm {Form}}\nolimits _{L_n}$
be a
![]() $\Sigma _0$
-formula satisfying (3). For a proof of (1) we take
$\Sigma _0$
-formula satisfying (3). For a proof of (1) we take
![]() $\varphi \in \mathop {\mathrm {Pa}}\nolimits (\langle Y\setminus F ,<\rangle )$
and show that
$\varphi \in \mathop {\mathrm {Pa}}\nolimits (\langle Y\setminus F ,<\rangle )$
and show that
![]() $f:=\mathop {\mathrm {id}}\nolimits _F \cup \; \varphi \in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
. By (L1) we have
$f:=\mathop {\mathrm {id}}\nolimits _F \cup \; \varphi \in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} )$
. By (L1) we have
![]() $\varphi \in \mathop {\mathrm {Pa}}\nolimits (\langle Y ,\lhd \rangle )$
; by (L2),
$\varphi \in \mathop {\mathrm {Pa}}\nolimits (\langle Y ,\lhd \rangle )$
; by (L2),
![]() $f \in \mathop {\mathrm {Pa}}\nolimits (\langle Y ,\lhd \rangle )$
and, since
$f \in \mathop {\mathrm {Pa}}\nolimits (\langle Y ,\lhd \rangle )$
and, since
![]() $f(a_j)=a_j$
, for all
$f(a_j)=a_j$
, for all
![]() $j<n$
, we obtain
$j<n$
, we obtain
![]() $f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )$
. So, for
$f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb X} )$
. So, for
![]() $K:=\mathop {\mathrm {dom}}\nolimits f$
and
$K:=\mathop {\mathrm {dom}}\nolimits f$
and
![]() $H:=\mathop {\mathrm {ran}}\nolimits f$
, denoting by
$H:=\mathop {\mathrm {ran}}\nolimits f$
, denoting by
![]() ${\mathbb K}$
and
${\mathbb K}$
and
![]() ${\mathbb H}$
the corresponding substructures of
${\mathbb H}$
the corresponding substructures of
![]() ${\mathbb X} $
, we have
${\mathbb X} $
, we have
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H})$
. Now, for
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H})$
. Now, for
![]() $i\in I$
and
$i\in I$
and
![]() $\bar {y} \in K ^{n_i}$
we have
$\bar {y} \in K ^{n_i}$
we have
![]() $\bar {y}\in R_i ^{\mathbb Y}$
iff (by (3))
$\bar {y}\in R_i ^{\mathbb Y}$
iff (by (3))
![]() ${\mathbb X} \models \varphi _i [\bar {y} ]$
iff (since
${\mathbb X} \models \varphi _i [\bar {y} ]$
iff (since
![]() $\varphi _i$
is a
$\varphi _i$
is a
![]() $\Sigma _0$
-formula)
$\Sigma _0$
-formula)
![]() ${\mathbb K}\models \varphi _i [\bar {y} ]$
iff (since
${\mathbb K}\models \varphi _i [\bar {y} ]$
iff (since
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H})$
)
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H})$
)
![]() ${\mathbb H}\models \varphi _i [f \bar {y} ]$
iff (since
${\mathbb H}\models \varphi _i [f \bar {y} ]$
iff (since
![]() $\varphi _i$
is a
$\varphi _i$
is a
![]() $\Sigma _0$
-formula)
$\Sigma _0$
-formula)
![]() ${\mathbb X}\models \varphi _i [f \bar {y} ]$
iff (by (3))
${\mathbb X}\models \varphi _i [f \bar {y} ]$
iff (by (3))
![]() $f\bar {y}\in R_i ^{\mathbb Y}$
. So
$f\bar {y}\in R_i ^{\mathbb Y}$
. So
![]() $f\in \mathop {\mathrm {Pa}}\nolimits (\langle Y, R_i ^{\mathbb Y} \rangle )$
, for all
$f\in \mathop {\mathrm {Pa}}\nolimits (\langle Y, R_i ^{\mathbb Y} \rangle )$
, for all
![]() $i\in I$
; thus
$i\in I$
; thus
![]() $f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
and (1) is true.⊣
$f\in \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y})$
and (1) is true.⊣
Fact 2.2. If
![]() ${\mathbb Y}$
is an infinite almost chainable L-structure, then there is a minimal finite set
${\mathbb Y}$
is an infinite almost chainable L-structure, then there is a minimal finite set
![]() $F\subset Y$
such that
$F\subset Y$
such that
![]() ${\mathbb Y}$
is F-chainable (the kernel of
${\mathbb Y}$
is F-chainable (the kernel of
![]() ${\mathbb Y}$
, in notation
${\mathbb Y}$
, in notation
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y})$
).
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y})$
).
Proof For
![]() $|L|=1$
, this is 10.9.3 of [Reference Fraïssé2, p. 296]. But the proof of 10.9.3 as well as the proofs of propositions (1), (2) and (3) of 10.9.2, which are used in the proof of 10.9.3 have straightforward generalizations for arbitrary relational language L. We note that the Coherence lemma (2.4.1 of [Reference Fraïssé2, p. 50]) used in the proof of 10.9.2(2) works if, in particular, the language is finite and
$|L|=1$
, this is 10.9.3 of [Reference Fraïssé2, p. 296]. But the proof of 10.9.3 as well as the proofs of propositions (1), (2) and (3) of 10.9.2, which are used in the proof of 10.9.3 have straightforward generalizations for arbitrary relational language L. We note that the Coherence lemma (2.4.1 of [Reference Fraïssé2, p. 50]) used in the proof of 10.9.2(2) works if, in particular, the language is finite and
![]() ${\mathcal I}=[X]^{<\omega }$
for some set X.⊣
${\mathcal I}=[X]^{<\omega }$
for some set X.⊣
Fact 2.3 (Pouzet)
An infinite L-structure
![]() ${\mathbb Y}$
is almost chainable iff its profile is bounded (that is, there is a positive integer m such that
${\mathbb Y}$
is almost chainable iff its profile is bounded (that is, there is a positive integer m such that
![]() $\varphi _{\mathbb Y} (n)\leq m$
, for each
$\varphi _{\mathbb Y} (n)\leq m$
, for each
![]() $n\in {\mathbb N}$
). (See [Reference Pouzet8, Theorem 1.2 in p. 317] or [Reference Fraïssé2, p. 297], for finite L.)
$n\in {\mathbb N}$
). (See [Reference Pouzet8, Theorem 1.2 in p. 317] or [Reference Fraïssé2, p. 297], for finite L.)
Fact 2.4. Let
![]() ${\mathbb Y} $
and
${\mathbb Y} $
and
![]() ${\mathbb Z}$
be L-structures. If
${\mathbb Z}$
be L-structures. If
![]() ${\mathbb Y}$
is almost chainable and
${\mathbb Y}$
is almost chainable and
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )\subset \mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
, then
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )\subset \mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
, then
![]() ${\mathbb Z}$
is almost chainable and
${\mathbb Z}$
is almost chainable and
![]() $|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|\leq |\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.
$|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|\leq |\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.
Proof For
![]() $|L|=1$
, this is Lemma 10.9.6 of [Reference Fraïssé2, p. 297], which has a straightforward generalization for arbitrary relational language L. We note that 10.1.4 of [Reference Fraïssé2, p. 275], which is used in the proof 10.9.6 holds for (in the notation of Reference Fraïssé[2]) R and
$|L|=1$
, this is Lemma 10.9.6 of [Reference Fraïssé2, p. 297], which has a straightforward generalization for arbitrary relational language L. We note that 10.1.4 of [Reference Fraïssé2, p. 275], which is used in the proof 10.9.6 holds for (in the notation of Reference Fraïssé[2]) R and
![]() $R'$
of arbitrary signature and for
$R'$
of arbitrary signature and for
![]() $S'$
of finite signature.⊣
$S'$
of finite signature.⊣
If
![]() $\,{\mathbb Y}\in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
is an infinite
$\,{\mathbb Y}\in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
is an infinite
![]() $(F,<)$
-chainable structure, then the set
$(F,<)$
-chainable structure, then the set
 $$ \begin{align} {\mathcal L} _{\mathbb Y}^F := \Big\{ \langle Y\setminus F, \vartriangleleft \rangle : \;\vartriangleleft \in LO_{Y\setminus F} \mbox{ and }{\mathbb Y} \mbox{ is } (F,\vartriangleleft )\mbox{-chainable} \Big\} \end{align} $$
$$ \begin{align} {\mathcal L} _{\mathbb Y}^F := \Big\{ \langle Y\setminus F, \vartriangleleft \rangle : \;\vartriangleleft \in LO_{Y\setminus F} \mbox{ and }{\mathbb Y} \mbox{ is } (F,\vartriangleleft )\mbox{-chainable} \Big\} \end{align} $$
is a non-empty set of linear orders and it is easy to see that
![]() $\langle Y\setminus F, \vartriangleleft \rangle \in {\mathcal L} _{\mathbb Y}^F$
iff
$\langle Y\setminus F, \vartriangleleft \rangle \in {\mathcal L} _{\mathbb Y}^F$
iff
![]() $\langle Y\setminus F, \vartriangleleft \rangle ^* \in {\mathcal L} _{\mathbb Y}^F$
. Theorem 9 of Reference Gibson, Pouzet and Woodrow[4] gives the following description of the set
$\langle Y\setminus F, \vartriangleleft \rangle ^* \in {\mathcal L} _{\mathbb Y}^F$
. Theorem 9 of Reference Gibson, Pouzet and Woodrow[4] gives the following description of the set
![]() ${\mathcal L} _{\mathbb Y}^F$
.
${\mathcal L} _{\mathbb Y}^F$
.
Theorem 2.5 (Gibson, Pouzet and Woodrow)
If
![]() $\,{\mathbb Y}\in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
is an infinite
$\,{\mathbb Y}\in \mathop {\mathrm {Mod}}\nolimits _L (Y)$
is an infinite
![]() $(F,<)$
-chainable L-structure and
$(F,<)$
-chainable L-structure and
![]() ${\mathbb L} :=\langle Y\setminus F,< \rangle $
, then one of the following holds
${\mathbb L} :=\langle Y\setminus F,< \rangle $
, then one of the following holds
-
(I)
 ${\mathcal L} _{\mathbb Y}^F=LO _{Y\setminus F}$
, that is, each linear order
${\mathcal L} _{\mathbb Y}^F=LO _{Y\setminus F}$
, that is, each linear order
 $\vartriangleleft $
on
$\vartriangleleft $
on
 $Y\setminus F$
chains
$Y\setminus F$
chains
 ${\mathbb Y}$
over F,
${\mathbb Y}$
over F, -
(II)
 ${\mathcal L} _{\mathbb Y} ^F=\bigcup _{{\mathbb L} ={\mathbb I} +{\mathbb F}}\Big \{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\Big \}$
, and
${\mathcal L} _{\mathbb Y} ^F=\bigcup _{{\mathbb L} ={\mathbb I} +{\mathbb F}}\Big \{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\Big \}$
, and -
(III) There are finite subsets K and H of
 $\,Y\setminus F$
such that
$\,Y\setminus F$
such that
 ${\mathbb L} ={\mathbb K} +{\mathbb M} +{\mathbb H}\,$
and
${\mathbb L} ={\mathbb K} +{\mathbb M} +{\mathbb H}\,$
and
 $ {\mathcal L} _{\mathbb Y}^F =\bigcup _{\vartriangleleft _K \in LO_K \atop \vartriangleleft _H \in LO_H} \Big \{ \langle K ,\vartriangleleft _K\rangle + {\mathbb M} +\langle H ,\vartriangleleft _H \rangle , \langle H ,\vartriangleleft _H\rangle ^*+ {\mathbb M} ^* +\langle K ,\vartriangleleft _K \rangle ^*\Big \} $
.
$ {\mathcal L} _{\mathbb Y}^F =\bigcup _{\vartriangleleft _K \in LO_K \atop \vartriangleleft _H \in LO_H} \Big \{ \langle K ,\vartriangleleft _K\rangle + {\mathbb M} +\langle H ,\vartriangleleft _H \rangle , \langle H ,\vartriangleleft _H\rangle ^*+ {\mathbb M} ^* +\langle K ,\vartriangleleft _K \rangle ^*\Big \} $
.
3 Almost chainable theories
A complete theory
![]() ${\mathcal T} \subset \mathop {\mathrm {Sent}}\nolimits _L$
will be called almost chainable iff each model
${\mathcal T} \subset \mathop {\mathrm {Sent}}\nolimits _L$
will be called almost chainable iff each model
![]() ${\mathbb Y}$
of
${\mathbb Y}$
of
![]() ${\mathcal T}$
is almost chainable and this notion is established by the following theorem.
${\mathcal T}$
is almost chainable and this notion is established by the following theorem.
Theorem 3.1. If
![]() ${\mathcal T}$
is a complete L-theory with infinite models, then the following conditions are equivalent:
${\mathcal T}$
is a complete L-theory with infinite models, then the following conditions are equivalent:
(a) All models of
![]() $\;{\mathcal T}$
are almost chainable,
$\;{\mathcal T}$
are almost chainable,
(b)
![]() ${\mathcal T}$
has an almost chainable model, and
${\mathcal T}$
has an almost chainable model, and
(c)
![]() ${\mathcal T}$
has a countable almost chainable model.
${\mathcal T}$
has a countable almost chainable model.
If (a) is true, then there is
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y})|=n$
, for each model
$|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y})|=n$
, for each model
![]() ${\mathbb Y}$
of
${\mathbb Y}$
of
![]() ${\mathcal T}$
.
${\mathcal T}$
.
A proof of the theorem is given at the end of the section.
Claim 3.2. Let
![]() ${\mathcal K} $
be a finite family of non-isomorphic L-structures of size
${\mathcal K} $
be a finite family of non-isomorphic L-structures of size
![]() $n\in {\mathbb N}$
. Then we have
$n\in {\mathbb N}$
. Then we have
(a) For each finite set
![]() $J\subset I$
there is an
$J\subset I$
there is an
![]() $L_J$
-sentence
$L_J$
-sentence
![]() $\psi _{{\mathcal K} ,J}$
such that for each
$\psi _{{\mathcal K} ,J}$
such that for each
![]() ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
we have:
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
we have:
![]() ${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
iff
${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
iff
![]() $\;\{ {\mathbb H} |L_J :H\in [Y]^n\}/\!\cong \; =\{ [ {\mathbb K} |L_J ]:{\mathbb K} \in {\mathcal K}\} $
and
$\;\{ {\mathbb H} |L_J :H\in [Y]^n\}/\!\cong \; =\{ [ {\mathbb K} |L_J ]:{\mathbb K} \in {\mathcal K}\} $
and
(b) For the first-order theory
![]() ${\mathcal T} _{\mathcal K} :=\{ \psi _{{\mathcal K} ,J} :J\in [I]^{<\omega }\}$
and each
${\mathcal T} _{\mathcal K} :=\{ \psi _{{\mathcal K} ,J} :J\in [I]^{<\omega }\}$
and each
![]() ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
we have:
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
we have:
![]() ${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
iff
${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
iff
![]() $\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) = \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\} $
.
$\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) = \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\} $
.
Proof First, without loss of generality we can assume that the domain of each structure
![]() ${\mathbb K} \in {\mathcal K}$
is the same set, say K. Let
${\mathbb K} \in {\mathcal K}$
is the same set, say K. Let
![]() $K=\{ x_0 ,\dots ,x_{n-1}\}$
be an enumeration of its elements and
$K=\{ x_0 ,\dots ,x_{n-1}\}$
be an enumeration of its elements and
![]() $\bar {x}:=\langle x_0 ,\dots ,x_{n-1}\rangle $
.
$\bar {x}:=\langle x_0 ,\dots ,x_{n-1}\rangle $
.
(a) For a structure
![]() ${\mathbb K} \in {\mathcal K}$
, let
${\mathbb K} \in {\mathcal K}$
, let
![]() $\alpha _{{\mathbb K} ,J} (\bar {v}) \!:= \bigwedge \{ \eta \in \mathop {\mathrm {Lit}}\nolimits _{L_J}(\bar {v}): {\mathbb K} \models \eta [\bar {x}]\} $
, where
$\alpha _{{\mathbb K} ,J} (\bar {v}) \!:= \bigwedge \{ \eta \in \mathop {\mathrm {Lit}}\nolimits _{L_J}(\bar {v}): {\mathbb K} \models \eta [\bar {x}]\} $
, where
![]() $\mathop {\mathrm {Lit}}\nolimits _{L_J}(\bar {v})$
is the set of all literals of
$\mathop {\mathrm {Lit}}\nolimits _{L_J}(\bar {v})$
is the set of all literals of
![]() $L_J$
with variables in the set
$L_J$
with variables in the set
![]() $\{ v_0 ,\dots ,v_{n-1}\}$
. Then for
$\{ v_0 ,\dots ,v_{n-1}\}$
. Then for
![]() ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
,
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L$
,
![]() $\bar {y} \in Y^n$
and
$\bar {y} \in Y^n$
and
![]() $H:=\{ y_0 ,\dots ,y_{n-1}\}$
, we have
$H:=\{ y_0 ,\dots ,y_{n-1}\}$
, we have
![]() ${\mathbb Y} \models \alpha _{{\mathbb K} ,J} [\bar {y}]$
iff
${\mathbb Y} \models \alpha _{{\mathbb K} ,J} [\bar {y}]$
iff
![]() $\{ \langle x_k ,y_k\rangle :k<n\}$
is an isomorphism from
$\{ \langle x_k ,y_k\rangle :k<n\}$
is an isomorphism from
![]() ${\mathbb K} |L_J$
onto
${\mathbb K} |L_J$
onto
![]() ${\mathbb H} |L_J$
. If
${\mathbb H} |L_J$
. If
![]() $\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
and
$\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
and
 $\alpha _{{\mathbb K} ,J} ^\pi (\bar {v})$
is the formula obtained from
$\alpha _{{\mathbb K} ,J} ^\pi (\bar {v})$
is the formula obtained from
![]() $\alpha _{{\mathbb K} ,J}$
by replacement of
$\alpha _{{\mathbb K} ,J}$
by replacement of
![]() $v_k$
by
$v_k$
by
![]() $v_{\pi (k)}$
, for all
$v_{\pi (k)}$
, for all
![]() $k<n$
, then
$k<n$
, then
![]() ${\mathbb Y} \models \alpha _{{\mathbb K} ,J} ^\pi [\bar {y}]$
iff
${\mathbb Y} \models \alpha _{{\mathbb K} ,J} ^\pi [\bar {y}]$
iff
![]() ${\mathbb Y} \models \alpha _{{\mathbb K} ,J} [y_{\pi (0)}, \dots ,y_{\pi (n-1)} ]$
iff
${\mathbb Y} \models \alpha _{{\mathbb K} ,J} [y_{\pi (0)}, \dots ,y_{\pi (n-1)} ]$
iff
![]() $p_\pi :=\{ \langle x_k ,y_{\pi (k)}\rangle :k<n\}$
is an isomorphism from
$p_\pi :=\{ \langle x_k ,y_{\pi (k)}\rangle :k<n\}$
is an isomorphism from
![]() ${\mathbb K} |L_J$
onto
${\mathbb K} |L_J$
onto
![]() ${\mathbb H} |L_J$
. So, for the formula
${\mathbb H} |L_J$
. So, for the formula
 $\varphi _{{\mathbb K} ,J} (\bar {v}) := \bigvee _{\pi \in \mathop {\mathrm {Sym}}\nolimits (n) }\alpha _{{\mathbb K} ,J} ^\pi (\bar {v})$
we have
$\varphi _{{\mathbb K} ,J} (\bar {v}) := \bigvee _{\pi \in \mathop {\mathrm {Sym}}\nolimits (n) }\alpha _{{\mathbb K} ,J} ^\pi (\bar {v})$
we have
![]() ${\mathbb Y} \models \varphi _{{\mathbb K} ,J}[\bar {y}]$
iff
${\mathbb Y} \models \varphi _{{\mathbb K} ,J}[\bar {y}]$
iff
![]() ${\mathbb H} |L_J \cong {\mathbb K} |L_J$
, and the equivalence in (a) is true for the formula
${\mathbb H} |L_J \cong {\mathbb K} |L_J$
, and the equivalence in (a) is true for the formula
 $$ \begin{align} \textstyle \psi _{{\mathcal K} ,J} := \bigwedge _{{\mathbb K} \in {\mathcal K}} \exists \bar{v} \;\varphi_{{\mathbb K} ,J} (\bar{v}) \land \forall \bar{v} \; \Big( (\bigwedge _{k<l<n} v_k \neq v_l ) \Rightarrow \bigvee _{{\mathbb K} \in {\mathcal K}}\varphi_{{\mathbb K} ,J} (\bar{v})\Big). \end{align} $$
$$ \begin{align} \textstyle \psi _{{\mathcal K} ,J} := \bigwedge _{{\mathbb K} \in {\mathcal K}} \exists \bar{v} \;\varphi_{{\mathbb K} ,J} (\bar{v}) \land \forall \bar{v} \; \Big( (\bigwedge _{k<l<n} v_k \neq v_l ) \Rightarrow \bigvee _{{\mathbb K} \in {\mathcal K}}\varphi_{{\mathbb K} ,J} (\bar{v})\Big). \end{align} $$
(b) Let
![]() ${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
. Suppose that
${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
. Suppose that
![]() $H=\{ y_0 ,\dots ,y_{n-1}\}\in [Y]^n$
and that
$H=\{ y_0 ,\dots ,y_{n-1}\}\in [Y]^n$
and that
![]() ${\mathbb H} \not \cong {\mathbb K}$
, for all
${\mathbb H} \not \cong {\mathbb K}$
, for all
![]() ${\mathbb K} \in {\mathcal K}$
. Then for each
${\mathbb K} \in {\mathcal K}$
. Then for each
![]() ${\mathbb K} \in {\mathcal K}$
and each
${\mathbb K} \in {\mathcal K}$
and each
![]() $\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
we have
$\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
we have
![]() $p_{{\mathbb K} ,\pi } :=\{ \langle x_k ,y_{\pi (k)}\rangle :k<n\}\not \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H} )$
and, since
$p_{{\mathbb K} ,\pi } :=\{ \langle x_k ,y_{\pi (k)}\rangle :k<n\}\not \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} ,{\mathbb H} )$
and, since
![]() $p_{{\mathbb K} ,\pi } :K\rightarrow H$
is a bijection, there is
$p_{{\mathbb K} ,\pi } :K\rightarrow H$
is a bijection, there is
![]() $i_{{\mathbb K} ,\pi }\in I$
such that
$i_{{\mathbb K} ,\pi }\in I$
such that
 $p_{{\mathbb K} ,\pi } \not \in \mathop {\mathrm {Iso}}\nolimits (\langle K, R_{i_{{\mathbb K} ,\pi }}^{{\mathbb K}}\rangle ,\langle H , R_{i_{{\mathbb K} ,\pi }}^{{\mathbb H} }\rangle )$
.
$p_{{\mathbb K} ,\pi } \not \in \mathop {\mathrm {Iso}}\nolimits (\langle K, R_{i_{{\mathbb K} ,\pi }}^{{\mathbb K}}\rangle ,\langle H , R_{i_{{\mathbb K} ,\pi }}^{{\mathbb H} }\rangle )$
.
Since
![]() $J:=\{ i_{{\mathbb K} ,\pi } : {\mathbb K} \in {\mathcal K} \land \pi \in \mathop {\mathrm {Sym}}\nolimits (n)\}\in [I]^{<\omega }$
and
$J:=\{ i_{{\mathbb K} ,\pi } : {\mathbb K} \in {\mathcal K} \land \pi \in \mathop {\mathrm {Sym}}\nolimits (n)\}\in [I]^{<\omega }$
and
![]() ${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
, by (a) there are
${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
, by (a) there are
![]() ${\mathbb K} _0 \in {\mathcal K}$
and
${\mathbb K} _0 \in {\mathcal K}$
and
![]() $\pi _0\in \mathop {\mathrm {Sym}}\nolimits (n)$
such that
$\pi _0\in \mathop {\mathrm {Sym}}\nolimits (n)$
such that
![]() $p_{{\mathbb K} _0,\pi _0} \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0|L_J ,{\mathbb H} |L_J )$
, which implies that
$p_{{\mathbb K} _0,\pi _0} \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0|L_J ,{\mathbb H} |L_J )$
, which implies that
 $p_{{\mathbb K} _0,\pi _0}\in \mathop {\mathrm {Iso}}\nolimits (\langle K_0, R_{i_{{\mathbb K} _0,\pi _0}}^{{\mathbb K} _0}\rangle ,\langle H , R_{i_{{\mathbb K} _0,\pi _0}}^{{\mathbb H} }\rangle )$
and we have a contradiction. So we have proved
$p_{{\mathbb K} _0,\pi _0}\in \mathop {\mathrm {Iso}}\nolimits (\langle K_0, R_{i_{{\mathbb K} _0,\pi _0}}^{{\mathbb K} _0}\rangle ,\langle H , R_{i_{{\mathbb K} _0,\pi _0}}^{{\mathbb H} }\rangle )$
and we have a contradiction. So we have proved
that is,
![]() $\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) \subset \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}$
. Concerning the inclusion “
$\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) \subset \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}$
. Concerning the inclusion “
![]() $\supset $
,” suppose that for some
$\supset $
,” suppose that for some
![]() ${\mathbb K} _0 \in {\mathcal K}$
${\mathbb K} _0 \in {\mathcal K}$
and let
![]() ${\mathcal K} =\{ {\mathbb K} _0 ,\dots ,{\mathbb K} _{s-1}\}$
be an enumeration. Then, for each
${\mathcal K} =\{ {\mathbb K} _0 ,\dots ,{\mathbb K} _{s-1}\}$
be an enumeration. Then, for each
![]() $0<r<s$
and
$0<r<s$
and
![]() $\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
, since
$\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
, since
![]() ${\mathbb K} _0 \not \cong {\mathbb K} _r$
, we have
${\mathbb K} _0 \not \cong {\mathbb K} _r$
, we have
![]() $p_\pi := \{\langle x_k,x_{\pi (k)}\rangle : k<n \}\not \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0 ,{\mathbb K} _r)$
and, hence, there is
$p_\pi := \{\langle x_k,x_{\pi (k)}\rangle : k<n \}\not \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0 ,{\mathbb K} _r)$
and, hence, there is
![]() $i_{r, \pi } \in I$
such that
$i_{r, \pi } \in I$
such that
 $$ \begin{align} p_\pi \not\in \mathop{\mathrm{Iso}}\nolimits (\langle K, R_{i_{r, \pi}}^{{\mathbb K} _0}\rangle ,\langle K, R_{i_{r, \pi}}^{{\mathbb K} _r}\rangle). \end{align} $$
$$ \begin{align} p_\pi \not\in \mathop{\mathrm{Iso}}\nolimits (\langle K, R_{i_{r, \pi}}^{{\mathbb K} _0}\rangle ,\langle K, R_{i_{r, \pi}}^{{\mathbb K} _r}\rangle). \end{align} $$
Now
![]() $J:= \{i_{r, \pi }: 0<r<s \land \pi \in \mathop {\mathrm {Sym}}\nolimits (n)\}\in [I]^{<\omega }$
and, since
$J:= \{i_{r, \pi }: 0<r<s \land \pi \in \mathop {\mathrm {Sym}}\nolimits (n)\}\in [I]^{<\omega }$
and, since
![]() ${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
, there is
${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
, there is
![]() $H\in [Y]^n$
such that
$H\in [Y]^n$
such that
![]() ${\mathbb H} |L_J \cong {\mathbb K} _0 |L_J $
. By (6) and (7) there is
${\mathbb H} |L_J \cong {\mathbb K} _0 |L_J $
. By (6) and (7) there is
![]() $r>0$
such that
$r>0$
such that
![]() ${\mathbb H} \cong {\mathbb K} _r$
, which implies
${\mathbb H} \cong {\mathbb K} _r$
, which implies
![]() ${\mathbb H} |L_J\cong {\mathbb K} _r |L_J$
and, hence,
${\mathbb H} |L_J\cong {\mathbb K} _r |L_J$
and, hence,
![]() ${\mathbb K} _0 |L_J\cong {\mathbb K} _r |L_J$
. Thus, there is
${\mathbb K} _0 |L_J\cong {\mathbb K} _r |L_J$
. Thus, there is
![]() $\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
such that
$\pi \in \mathop {\mathrm {Sym}}\nolimits (n)$
such that
![]() $p_\pi \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0 |L_J,{\mathbb K} _r|L_J)$
, which in particular gives
$p_\pi \in \mathop {\mathrm {Iso}}\nolimits ({\mathbb K} _0 |L_J,{\mathbb K} _r|L_J)$
, which in particular gives
 $ p_\pi \in \mathop {\mathrm {Iso}}\nolimits (\langle K, R_{i_{r, \pi }}^{{\mathbb K} _0}\rangle ,\langle K, R_{i_{r, \pi }}^{{\mathbb K} _r}\rangle )$
, but this contradicts (8). So for each
$ p_\pi \in \mathop {\mathrm {Iso}}\nolimits (\langle K, R_{i_{r, \pi }}^{{\mathbb K} _0}\rangle ,\langle K, R_{i_{r, \pi }}^{{\mathbb K} _r}\rangle )$
, but this contradicts (8). So for each
![]() ${\mathbb K} \in {\mathcal K}$
there is
${\mathbb K} \in {\mathcal K}$
there is
![]() $H\in [Y]^n$
such that
$H\in [Y]^n$
such that
![]() ${\mathbb H} \cong {\mathbb K}$
; that is,
${\mathbb H} \cong {\mathbb K}$
; that is,
![]() $\{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}\subset \mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
.
$\{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}\subset \mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
.
Conversely, if
![]() $\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) = \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}$
and
$\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} ) = \{ [ {\mathbb K} ]:{\mathbb K} \in {\mathcal K}\}$
and
![]() $J\in [I]^{<\omega }$
, then for each
$J\in [I]^{<\omega }$
, then for each
![]() $H\in [Y]^n$
there is
$H\in [Y]^n$
there is
![]() ${\mathbb K} \in {\mathcal K}$
such that
${\mathbb K} \in {\mathcal K}$
such that
![]() ${\mathbb H} \cong {\mathbb K}$
; so
${\mathbb H} \cong {\mathbb K}$
; so
![]() ${\mathbb H} |L_J\cong {\mathbb K} |L_J$
and, hence,
${\mathbb H} |L_J\cong {\mathbb K} |L_J$
and, hence,
![]() $[{\mathbb H} |L_J]\cong [{\mathbb K} |L_J]$
. In addition, for each
$[{\mathbb H} |L_J]\cong [{\mathbb K} |L_J]$
. In addition, for each
![]() ${\mathbb K} \in {\mathcal K}$
there is
${\mathbb K} \in {\mathcal K}$
there is
![]() $H\in [Y]^n$
such that
$H\in [Y]^n$
such that
![]() ${\mathbb H} \cong {\mathbb K}$
so
${\mathbb H} \cong {\mathbb K}$
so
![]() ${\mathbb H} |L_J\cong {\mathbb K} |L_J$
again and, by (a),
${\mathbb H} |L_J\cong {\mathbb K} |L_J$
again and, by (a),
![]() ${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
. Thus we have
${\mathbb Y} \models \psi _{{\mathcal K} ,J}$
. Thus we have
![]() ${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
.⊣
${\mathbb Y} \models {\mathcal T} _{\mathcal K}$
.⊣
Claim 3.3. Let
![]() ${\mathbb Y} $
be an infinite L-structure and
${\mathbb Y} $
be an infinite L-structure and
![]() $|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|<\omega $
, for each
$|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|<\omega $
, for each
![]() $n\in {\mathbb N}$
. Then for the theory
$n\in {\mathbb N}$
. Then for the theory
![]() ${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}:=\bigcup _{n\in {\mathbb N}}{\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
and any L-structure
${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}:=\bigcup _{n\in {\mathbb N}}{\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
and any L-structure
![]() ${\mathbb Z}$
we have
${\mathbb Z}$
we have
(a)
 ${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}\subset \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
;
${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}\subset \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
;
(b)
![]() ${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}\,$
iff
${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}\,$
iff
![]() $\;\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
; and
$\;\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
; and
(c) If
![]() $\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then
$\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.
Proof (a) By Claim 3.2(b), for
![]() $n\!\in \!{\mathbb N}$
we have
$n\!\in \!{\mathbb N}$
we have
![]() ${\mathbb Y} \!\models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
so
${\mathbb Y} \!\models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
so
 ${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}\subset \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
.
${\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}\subset \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
.
(b)
![]() ${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}$
iff
${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}$
iff
![]() ${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
, for all
${\mathbb Z} \models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits _n({\mathbb Y} )}$
, for all
![]() $n\in {\mathbb N}$
; iff (by Claim 3.2(b))
$n\in {\mathbb N}$
; iff (by Claim 3.2(b))
![]() $\mathop {\mathrm {Age}}\nolimits _n({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
, for all
$\mathop {\mathrm {Age}}\nolimits _n({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )$
, for all
![]() $n\in {\mathbb N}$
; iff
$n\in {\mathbb N}$
; iff
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.
(c) If
![]() $\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then by (a)
$\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then by (a)
![]() ${\mathbb Z}\models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}$
and by (b)
${\mathbb Z}\models {\mathcal T} _{\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )}$
and by (b)
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.⊣
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
.⊣
Claim 3.4. If
![]() ${\mathbb Y}$
is an infinite almost chainable L-structure and
${\mathbb Y}$
is an infinite almost chainable L-structure and
![]() $\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then
$\,{\mathbb Z} \models \mathop {\mathrm {Th}}\nolimits ({\mathbb Y} )$
, then
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
, the structure
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
, the structure
![]() ${\mathbb Z} $
is almost chainable and
${\mathbb Z} $
is almost chainable and
![]() $|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|=|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.
$|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|=|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.
Proof By Fact 2.3 we have
![]() $|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|<\omega $
, for all
$|\mathop {\mathrm {Age}}\nolimits _n ({\mathbb Y} )|<\omega $
, for all
![]() $n\in {\mathbb N}$
. So, by Claim 3.3(c) we have
$n\in {\mathbb N}$
. So, by Claim 3.3(c) we have
![]() $\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
and, by Fact 2.4, the structure
$\mathop {\mathrm {Age}}\nolimits ({\mathbb Z} )=\mathop {\mathrm {Age}}\nolimits ({\mathbb Y} )$
and, by Fact 2.4, the structure
![]() ${\mathbb Z} $
is almost chainable and
${\mathbb Z} $
is almost chainable and
![]() $|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|=|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.⊣
$|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Z} )|=|\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )|$
.⊣
Claim 3.5. If
![]() ${\mathcal T}$
is a complete almost chainable L-theory with infinite models and
${\mathcal T}$
is a complete almost chainable L-theory with infinite models and
![]() $|I|>\omega $
, then
$|I|>\omega $
, then
![]() ${\mathcal T}$
has a countable model and there are a countable language
${\mathcal T}$
has a countable model and there are a countable language
![]() $L_J \subset L$
and a complete almost chainable
$L_J \subset L$
and a complete almost chainable
![]() $L _J$
-theory
$L _J$
-theory
![]() ${\mathcal T} _J$
such that
${\mathcal T} _J$
such that
 $$ \begin{align} \Big|\mathop{\mathrm{Mod}}\nolimits _L ^{\mathcal T} (\omega )/\cong \Big| =\Big|\mathop{\mathrm{Mod}}\nolimits ^{{\mathcal T} _J}_{L_J}(\omega)/\cong \Big|. \end{align} $$
$$ \begin{align} \Big|\mathop{\mathrm{Mod}}\nolimits _L ^{\mathcal T} (\omega )/\cong \Big| =\Big|\mathop{\mathrm{Mod}}\nolimits ^{{\mathcal T} _J}_{L_J}(\omega)/\cong \Big|. \end{align} $$
Proof Let
 ${\mathbb Y} =\langle Y, \langle R_i^{\mathbb Y} :i\in I\rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L$
. By Fact 2.1, there are a finite set
${\mathbb Y} =\langle Y, \langle R_i^{\mathbb Y} :i\in I\rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L$
. By Fact 2.1, there are a finite set
![]() $F=\{ a_0,\dots ,a_{n-1}\}\subset Y$
, a linear order
$F=\{ a_0,\dots ,a_{n-1}\}\subset Y$
, a linear order
![]() $\lhd \mathop {\mathrm {LO}}\nolimits _Y$
and an
$\lhd \mathop {\mathrm {LO}}\nolimits _Y$
and an
![]() $L_n$
-structure
$L_n$
-structure
![]() ${\mathbb X}$
satisfying (L1)–(L3) and for each
${\mathbb X}$
satisfying (L1)–(L3) and for each
![]() $i\in I$
there is a quantifier-free formula
$i\in I$
there is a quantifier-free formula
![]() $\varphi _i (v_0 ,\dots ,v_{n_i -1})$
such that
$\varphi _i (v_0 ,\dots ,v_{n_i -1})$
such that
 $$ \begin{align} \forall \bar{y} \in Y^{n_i} \;\;\Big(\bar{y}\in R_i^{\mathbb Y} \Leftrightarrow {\mathbb X} \models \varphi _i [\bar{y} ]\Big). \end{align} $$
$$ \begin{align} \forall \bar{y} \in Y^{n_i} \;\;\Big(\bar{y}\in R_i^{\mathbb Y} \Leftrightarrow {\mathbb X} \models \varphi _i [\bar{y} ]\Big). \end{align} $$
Since there are countably many
![]() $L_n$
-formulas, there is a partition
$L_n$
-formulas, there is a partition
 $I=\bigcup _{j\in J}I_j$
, where
$I=\bigcup _{j\in J}I_j$
, where
![]() $|J|\leq \omega $
, such that, picking
$|J|\leq \omega $
, such that, picking
![]() $i_j\in I_j$
, for all
$i_j\in I_j$
, for all
![]() $j\in J$
, we have
$j\in J$
, we have
 $R_i^{\mathbb Y} = R_{i_j}^{\mathbb Y}$
, for all
$R_i^{\mathbb Y} = R_{i_j}^{\mathbb Y}$
, for all
![]() $i\in I_j$
. So, for the L-sentences
$i\in I_j$
. So, for the L-sentences
 $\eta _{i,j}:=\forall \bar {v} \; (R_i (\bar {v}) \Leftrightarrow R_{i_j} (\bar {v}))$
, where
$\eta _{i,j}:=\forall \bar {v} \; (R_i (\bar {v}) \Leftrightarrow R_{i_j} (\bar {v}))$
, where
![]() $j\in J$
and
$j\in J$
and
![]() $i\in I_j$
, we have
$i\in I_j$
, we have
 ${\mathcal T} _\eta := \bigcup _{j\in J}\{ \eta _{i,j} : i\in I_j \} \subset \mathop {\mathrm {Th}}\nolimits _L ({\mathbb Y} )={\mathcal T}$
. Now,
${\mathcal T} _\eta := \bigcup _{j\in J}\{ \eta _{i,j} : i\in I_j \} \subset \mathop {\mathrm {Th}}\nolimits _L ({\mathbb Y} )={\mathcal T}$
. Now,
 $L_J :=\langle R_{i_j}:j\in J\rangle \subset L$
and, using recursion, to each L-formula
$L_J :=\langle R_{i_j}:j\in J\rangle \subset L$
and, using recursion, to each L-formula
![]() $\varphi $
we adjoin an
$\varphi $
we adjoin an
![]() $L_J$
-formula
$L_J$
-formula
![]() $\varphi _J$
in the following way:
$\varphi _J$
in the following way:
![]() $(v_k=v_l)_J :=v_k=v_l$
;
$(v_k=v_l)_J :=v_k=v_l$
;
 $(R_i (v_{k_0}, \dots , v_{k_{n_i-1}}))_J := R_{i_j} (v_{k_0}, \dots , v_{k_{n_i -1}})$
, for all
$(R_i (v_{k_0}, \dots , v_{k_{n_i-1}}))_J := R_{i_j} (v_{k_0}, \dots , v_{k_{n_i -1}})$
, for all
![]() $i\in I_j$
;
$i\in I_j$
;
![]() $(\neg \varphi )_J :=\neg \varphi _J $
;
$(\neg \varphi )_J :=\neg \varphi _J $
;
![]() $(\varphi \land \psi )_J :=\varphi _J \land \psi _J$
and
$(\varphi \land \psi )_J :=\varphi _J \land \psi _J$
and
![]() $(\forall v\; \varphi )_J :=\forall v\; \varphi _J $
. A simple induction proves that
$(\forall v\; \varphi )_J :=\forall v\; \varphi _J $
. A simple induction proves that
 $$ \begin{align} \forall {\mathbb Z} \in \mathop{\mathrm{Mod}}\nolimits _L ^{{\mathcal T} _\eta} \;\;\forall \varphi (\bar{v})\in \mathop{\mathrm{Form}}\nolimits _L \forall \bar{z} \in Z\;\; \Big({\mathbb Z} \models \varphi[\bar{z}] \Leftrightarrow {\mathbb Z} |L_J\models \varphi _J[\bar{z}] \Big). \end{align} $$
$$ \begin{align} \forall {\mathbb Z} \in \mathop{\mathrm{Mod}}\nolimits _L ^{{\mathcal T} _\eta} \;\;\forall \varphi (\bar{v})\in \mathop{\mathrm{Form}}\nolimits _L \forall \bar{z} \in Z\;\; \Big({\mathbb Z} \models \varphi[\bar{z}] \Leftrightarrow {\mathbb Z} |L_J\models \varphi _J[\bar{z}] \Big). \end{align} $$
We prove that, in addition, for each
 ${\mathbb Z} _1 ,{\mathbb Z} _2 \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} _\eta }$
we have
${\mathbb Z} _1 ,{\mathbb Z} _2 \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} _\eta }$
we have
The first claim is true since
![]() $\mathop {\mathrm {Iso}}\nolimits ({\mathbb Z} _1 ,{\mathbb Z} _2 )=\mathop {\mathrm {Iso}}\nolimits ({\mathbb Z} _1 |L_J, {\mathbb Z} _2 |L_J )$
. For the second, suppose that
$\mathop {\mathrm {Iso}}\nolimits ({\mathbb Z} _1 ,{\mathbb Z} _2 )=\mathop {\mathrm {Iso}}\nolimits ({\mathbb Z} _1 |L_J, {\mathbb Z} _2 |L_J )$
. For the second, suppose that
![]() ${\mathbb Z} _1 \equiv _L {\mathbb Z} _2$
and
${\mathbb Z} _1 \equiv _L {\mathbb Z} _2$
and
![]() ${\mathbb Z} _1 |L_J \models \psi $
, where
${\mathbb Z} _1 |L_J \models \psi $
, where
![]() $\psi \in \mathop {\mathrm {Sent}}\nolimits _{L_J}$
. Then
$\psi \in \mathop {\mathrm {Sent}}\nolimits _{L_J}$
. Then
![]() $\psi \in \mathop {\mathrm {Sent}}\nolimits _L$
and
$\psi \in \mathop {\mathrm {Sent}}\nolimits _L$
and
![]() ${\mathbb Z} _1 \models \psi $
, which gives
${\mathbb Z} _1 \models \psi $
, which gives
![]() ${\mathbb Z} _2 \models \psi $
so, by (11),
${\mathbb Z} _2 \models \psi $
so, by (11),
![]() ${\mathbb Z} _2 |L_J \models \psi $
, because
${\mathbb Z} _2 |L_J \models \psi $
, because
![]() $\psi _J=\psi $
. Conversely, suppose that
$\psi _J=\psi $
. Conversely, suppose that
![]() ${\mathbb Z} _1 |L_J\equiv _{L_J} {\mathbb Z} _2 |L_J$
and
${\mathbb Z} _1 |L_J\equiv _{L_J} {\mathbb Z} _2 |L_J$
and
![]() ${\mathbb Z} _1\models \varphi $
, where
${\mathbb Z} _1\models \varphi $
, where
![]() $\varphi \in \mathop {\mathrm {Sent}}\nolimits _L$
. Then, by (11),
$\varphi \in \mathop {\mathrm {Sent}}\nolimits _L$
. Then, by (11),
![]() ${\mathbb Z} _1 |L_J \models \varphi _J$
and, hence,
${\mathbb Z} _1 |L_J \models \varphi _J$
and, hence,
![]() ${\mathbb Z} _2 |L_J \models \varphi _J$
so, by (11),
${\mathbb Z} _2 |L_J \models \varphi _J$
so, by (11),
![]() ${\mathbb Z} _2\models \varphi $
.
${\mathbb Z} _2\models \varphi $
.
Let
![]() ${\mathcal T} _J :=\mathop {\mathrm {Th}}\nolimits _{L_J}({\mathbb Y} |L_J)$
. If
${\mathcal T} _J :=\mathop {\mathrm {Th}}\nolimits _{L_J}({\mathbb Y} |L_J)$
. If
 ${\mathbb Z} \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
, that is,
${\mathbb Z} \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
, that is,
![]() ${\mathbb Z} \equiv _L {\mathbb Y}$
, then by (12) we have
${\mathbb Z} \equiv _L {\mathbb Y}$
, then by (12) we have
![]() ${\mathbb Z}|L_J \equiv _{L_J} {\mathbb Y}|L_J $
, which means that
${\mathbb Z}|L_J \equiv _{L_J} {\mathbb Y}|L_J $
, which means that
 ${\mathbb Z}|L_J \in \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
. So we obtain the mapping
${\mathbb Z}|L_J \in \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
. So we obtain the mapping
 $\Lambda : \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} } \rightarrow \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
, where
$\Lambda : \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} } \rightarrow \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
, where
![]() $\Lambda ({\mathbb Z} )= {\mathbb Z} |L_J$
, for all
$\Lambda ({\mathbb Z} )= {\mathbb Z} |L_J$
, for all
 ${\mathbb Z} \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
, which is an injection, because
${\mathbb Z} \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
, which is an injection, because
![]() ${\mathcal T} _\eta \subset {\mathcal T} $
.
${\mathcal T} _\eta \subset {\mathcal T} $
.
If
 ${\mathbb A} \in \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
, then
${\mathbb A} \in \mathop {\mathrm {Mod}}\nolimits _{L_J}^{{\mathcal T} _J }$
, then
 ${\mathbb Z} =\langle A, \langle R_i^{{\mathbb Z} } :i\in I\rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} _\eta }$
, where
${\mathbb Z} =\langle A, \langle R_i^{{\mathbb Z} } :i\in I\rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} _\eta }$
, where
 $R_i^{{\mathbb Z} }=R_{i_j}^{{\mathbb A} }$
, for
$R_i^{{\mathbb Z} }=R_{i_j}^{{\mathbb A} }$
, for
![]() $j\in J$
and
$j\in J$
and
![]() $i\in I_j$
. Now
$i\in I_j$
. Now
![]() ${\mathbb Z} |L_J ={\mathbb A} \equiv _{L_J}{\mathbb Y} |L_J$
and, by (12),
${\mathbb Z} |L_J ={\mathbb A} \equiv _{L_J}{\mathbb Y} |L_J$
and, by (12),
![]() ${\mathbb Z} \equiv _{L}{\mathbb Y} $
, that is,
${\mathbb Z} \equiv _{L}{\mathbb Y} $
, that is,
 ${\mathbb Z}\in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
and
${\mathbb Z}\in \mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T} }$
and
![]() $\Lambda $
is a surjection. Since the mapping
$\Lambda $
is a surjection. Since the mapping
![]() $\Lambda $
preserves cardinalities of structures, we have
$\Lambda $
preserves cardinalities of structures, we have
 $\Lambda [\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )]=\mathop {\mathrm {Mod}}\nolimits ^{{\mathcal T} _J} _{L_J}(\omega )$
. By the Löwenheim–Skolem theorem there is
$\Lambda [\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )]=\mathop {\mathrm {Mod}}\nolimits ^{{\mathcal T} _J} _{L_J}(\omega )$
. By the Löwenheim–Skolem theorem there is
 ${\mathbb A} \in \mathop {\mathrm {Mod}}\nolimits ^{{\mathcal T} _J}_{L_J}(\omega )$
and
${\mathbb A} \in \mathop {\mathrm {Mod}}\nolimits ^{{\mathcal T} _J}_{L_J}(\omega )$
and
![]() $\Lambda ^{-1}({\mathbb A} )$
is a countable model of
$\Lambda ^{-1}({\mathbb A} )$
is a countable model of
![]() ${\mathcal T}$
.
${\mathcal T}$
.
By (12), the mapping
![]() $\Lambda $
preserves the isomorphism relation and (9) is true. By (10) the reduct
$\Lambda $
preserves the isomorphism relation and (9) is true. By (10) the reduct
![]() ${\mathbb Y}|L_J$
is simply definable in
${\mathbb Y}|L_J$
is simply definable in
![]() ${\mathbb X}$
and, by Fact 2.1, it is almost chainable. By Claim 3.4, the theory
${\mathbb X}$
and, by Fact 2.1, it is almost chainable. By Claim 3.4, the theory
![]() ${\mathcal T} _J=\mathop {\mathrm {Th}}\nolimits _{L_J}({\mathbb Y} |L_J)$
is almost chainable.⊣
${\mathcal T} _J=\mathop {\mathrm {Th}}\nolimits _{L_J}({\mathbb Y} |L_J)$
is almost chainable.⊣
Proof of Theorem 3.1 The implication (a)
![]() $\Rightarrow $
(c) follows from Claim 3.5, the implication (c)
$\Rightarrow $
(c) follows from Claim 3.5, the implication (c)
![]() $\Rightarrow $
(b) is trivial and (b)
$\Rightarrow $
(b) is trivial and (b)
![]() $\Rightarrow $
(a) follows from Claim 3.4.⊣
$\Rightarrow $
(a) follows from Claim 3.4.⊣
4 Vaught’s Conjecture
In this section we confirm Vaught’s Conjecture for almost chainable theories. More precisely, the whole section is devoted to a proof of the following statement.
Theorem 4.1. If
![]() ${\mathcal T}$
is a complete almost chainable theory having infinite models, then
${\mathcal T}$
is a complete almost chainable theory having infinite models, then
![]() $I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
. In addition, the theory
$I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
. In addition, the theory
![]() ${\mathcal T}$
is
${\mathcal T}$
is
![]() $\omega $
-categorical iff it has a countable model which is chained by an
$\omega $
-categorical iff it has a countable model which is chained by an
![]() $\omega $
-categorical linear order over its kernel.
$\omega $
-categorical linear order over its kernel.
So, let
![]() ${\mathcal T}$
be a complete almost chainable L-theory having infinite models. By Theorem 3.1, there is
${\mathcal T}$
be a complete almost chainable L-theory having infinite models. By Theorem 3.1, there is
![]() $n\in \omega $
such that each model of
$n\in \omega $
such that each model of
![]() ${\mathcal T}$
has the kernel of size n and, by Claim 3.5, w.l.o.g. we suppose that
${\mathcal T}$
has the kernel of size n and, by Claim 3.5, w.l.o.g. we suppose that
![]() $|L|\leq \omega $
, which gives
$|L|\leq \omega $
, which gives
 $\mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T}} (\omega )\neq \emptyset $
. As above, let
$\mathop {\mathrm {Mod}}\nolimits _L^{{\mathcal T}} (\omega )\neq \emptyset $
. As above, let
![]() $L_n$
denote the language
$L_n$
denote the language
![]() $\langle R, U_0 ,\dots U_{n-1}\rangle $
, where R is a binary and
$\langle R, U_0 ,\dots U_{n-1}\rangle $
, where R is a binary and
![]() $U_j$
’s are unary symbols. In the sequel, for
$U_j$
’s are unary symbols. In the sequel, for
![]() ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L (\omega )$
, by
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _L (\omega )$
, by
![]() $[{\mathbb Y} ]$
we denote the set
$[{\mathbb Y} ]$
we denote the set
![]() $\{ {\mathbb Y} ' \in \mathop {\mathrm {Mod}}\nolimits _L (\omega ): {\mathbb Y} '\cong {\mathbb Y}\}$
and similarly for the structures from
$\{ {\mathbb Y} ' \in \mathop {\mathrm {Mod}}\nolimits _L (\omega ): {\mathbb Y} '\cong {\mathbb Y}\}$
and similarly for the structures from
![]() $\mathop {\mathrm {Mod}}\nolimits _{L_n} (\omega )$
.
$\mathop {\mathrm {Mod}}\nolimits _{L_n} (\omega )$
.
Following the architecture of the proof of the corresponding statement from Reference Kurilić[7] we divide the proof into two subsections. In “Preliminaries” we take an arbitrary countable model
![]() ${\mathbb Y} _0$
of
${\mathbb Y} _0$
of
![]() ${\mathcal T}$
and a linear order with n unary predicates
${\mathcal T}$
and a linear order with n unary predicates
![]() ${\mathbb X} _0$
such that
${\mathbb X} _0$
such that
![]() $\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} _0)\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} _0)$
(see Figure 1) and describe the cardinal argument which will be used in our proof. In “Proof,” distinguishing some cases, taking convenient structures
$\mathop {\mathrm {Pa}}\nolimits ({\mathbb X} _0)\subset \mathop {\mathrm {Pa}}\nolimits ({\mathbb Y} _0)$
(see Figure 1) and describe the cardinal argument which will be used in our proof. In “Proof,” distinguishing some cases, taking convenient structures
![]() ${\mathbb Y} _0$
and
${\mathbb Y} _0$
and
![]() ${\mathbb X} _0$
and using that cardinal argument, we prove Theorem 4.1.
${\mathbb X} _0$
and using that cardinal argument, we prove Theorem 4.1.

Figure 1 The mappings
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
.
$\Psi $
.
4.1 Preliminaries
For convenience, let
![]() $\Delta _n:=\{ \langle x_0,\dots ,x_{n-1}\rangle \in \omega ^n:\bigvee _{k<l<n}x_k=x_l\}$
and, for an n-tuple
$\Delta _n:=\{ \langle x_0,\dots ,x_{n-1}\rangle \in \omega ^n:\bigvee _{k<l<n}x_k=x_l\}$
and, for an n-tuple
![]() $\bar {a}:=\langle a_0,\dots ,a_{n-1}\rangle \in \omega ^n$
, let us define
$\bar {a}:=\langle a_0,\dots ,a_{n-1}\rangle \in \omega ^n$
, let us define
![]() $F_{\bar {a}}:=\{ a_0,\dots ,a_{n-1}\}$
.
$F_{\bar {a}}:=\{ a_0,\dots ,a_{n-1}\}$
.
We fix a model
 ${\mathbb Y} _0=\langle \omega , \langle R _i ^{{\mathbb Y} _0}:i\in I \rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and an enumeration of its kernel,
${\mathbb Y} _0=\langle \omega , \langle R _i ^{{\mathbb Y} _0}:i\in I \rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and an enumeration of its kernel,
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\} $
. By Fact 2.1 there is a linear order
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\} $
. By Fact 2.1 there is a linear order
![]() $\prec \in LO _\omega $
such that, defining
$\prec \in LO _\omega $
such that, defining
![]() $\bar {a} =\langle a_0,\dots ,a_{n-1}\rangle $
and
$\bar {a} =\langle a_0,\dots ,a_{n-1}\rangle $
and
![]() ${\mathbb X} _0:= \langle \omega ,\prec , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
,
${\mathbb X} _0:= \langle \omega ,\prec , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
,
Thus, the structure
![]() ${\mathbb Y} _0$
is
${\mathbb Y} _0$
is
![]() $(F_{\bar {a}},\prec \upharpoonright (\omega \setminus F_{\bar {a}}))$
-chainable. Let
$(F_{\bar {a}},\prec \upharpoonright (\omega \setminus F_{\bar {a}}))$
-chainable. Let
![]() ${\mathcal T} _{{\mathbb X} _0}$
denote the complete theory of
${\mathcal T} _{{\mathbb X} _0}$
denote the complete theory of
![]() ${\mathbb X}_0$
,
${\mathbb X}_0$
,
![]() $\mathop {\mathrm {Th}}\nolimits _{L_n}({\mathbb X} _0)$
. The structure
$\mathop {\mathrm {Th}}\nolimits _{L_n}({\mathbb X} _0)$
. The structure
![]() ${\mathbb X}_0$
has the following properties expressible by first order sentences of the language
${\mathbb X}_0$
has the following properties expressible by first order sentences of the language
![]() $L_n$
:
$L_n$
:
-
(i) The interpretation of R is a linear order,
-
(ii) The interpretations of the relations
 $U_k$
,
$U_k$
,
 $k<n$
, are different singletons,
$k<n$
, are different singletons, -
(iii) These singletons are ordered as the indices of
 $U_k$
’s (that is, the
$U_k$
’s (that is, the
 $L_n$
-sentence
$L_n$
-sentence
 $ \bigwedge _{k<l<n} \forall u,v \; (U_k(u) \land U_l(v)\Rightarrow R(u,v))$
is true in
$ \bigwedge _{k<l<n} \forall u,v \; (U_k(u) \land U_l(v)\Rightarrow R(u,v))$
is true in
 ${\mathbb X} _0$
), and
${\mathbb X} _0$
), and -
(iv) The union of these singletons is an initial segment of the linear order; that is
 ${\mathbb X} _0 \models \forall u,v \; ((U_{n-1}(u)\land \bigwedge _{k<n}\neg U_k(v))\Rightarrow R(u,v))$
.
${\mathbb X} _0 \models \forall u,v \; ((U_{n-1}(u)\land \bigwedge _{k<n}\neg U_k(v))\Rightarrow R(u,v))$
.
So, if
![]() ${\mathcal T} ^*$
is the set of the
${\mathcal T} ^*$
is the set of the
![]() $L_n$
-sentences expressing (i)–(iv), then
$L_n$
-sentences expressing (i)–(iv), then
![]() ${\mathcal T} ^*\subset {\mathcal T} _{{\mathbb X} _0}$
and
${\mathcal T} ^*\subset {\mathcal T} _{{\mathbb X} _0}$
and
 $$ \begin{align*} {\mathbb X} _0 \in {\mathcal M} ^{\bar{a}}_{{\mathbb Y} _0} & := \Big\{ \langle \omega ,\vartriangleleft , \{a_0\},\dots ,\{a_{n-1}\}\rangle \in \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega ):\\ &\qquad \;\;{\mathbb Y} _0 \mbox{ is } (F_{\bar{a}}, \vartriangleleft \upharpoonright (\omega \setminus F_{\bar{a}})) \mbox{-chainable}\Big\}. \end{align*} $$
$$ \begin{align*} {\mathbb X} _0 \in {\mathcal M} ^{\bar{a}}_{{\mathbb Y} _0} & := \Big\{ \langle \omega ,\vartriangleleft , \{a_0\},\dots ,\{a_{n-1}\}\rangle \in \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega ):\\ &\qquad \;\;{\mathbb Y} _0 \mbox{ is } (F_{\bar{a}}, \vartriangleleft \upharpoonright (\omega \setminus F_{\bar{a}})) \mbox{-chainable}\Big\}. \end{align*} $$
By Fact 2.1 the structure
![]() ${\mathbb Y} _0$
is simply definable in the
${\mathbb Y} _0$
is simply definable in the
![]() $L_n$
-structure
$L_n$
-structure
![]() ${\mathbb X} _0$
. Thus, for each
${\mathbb X} _0$
. Thus, for each
![]() $i\in I$
there is a quantifier free
$i\in I$
there is a quantifier free
![]() $L_n$
-formula
$L_n$
-formula
![]() $\varphi _i (v_0 ,\dots ,v_{n_i-1})$
such that
$\varphi _i (v_0 ,\dots ,v_{n_i-1})$
such that
 $$ \begin{align} \forall \bar{x}\in \omega ^{n_i} \;\; \Big(\bar{x}\in R _i ^{{\mathbb Y} _0}\Leftrightarrow {\mathbb X} _0 \models \varphi _i[\bar{x}]\Big). \end{align} $$
$$ \begin{align} \forall \bar{x}\in \omega ^{n_i} \;\; \Big(\bar{x}\in R _i ^{{\mathbb Y} _0}\Leftrightarrow {\mathbb X} _0 \models \varphi _i[\bar{x}]\Big). \end{align} $$
Generally speaking, using the
![]() $L_n$
-formulas
$L_n$
-formulas
![]() $\varphi _i$
,
$\varphi _i$
,
![]() $i\in I$
, to each
$i\in I$
, to each
![]() $L_n$
-structure
$L_n$
-structure
![]() ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
we can adjoin the L-structure
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
we can adjoin the L-structure
 ${\mathbb Y} _{\mathbb X}:=\langle \omega , \langle R _i ^{{\mathbb Y} _{\mathbb X}}:i\in I \rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _{L}(\omega )$
, where, for each
${\mathbb Y} _{\mathbb X}:=\langle \omega , \langle R _i ^{{\mathbb Y} _{\mathbb X}}:i\in I \rangle \rangle \in \mathop {\mathrm {Mod}}\nolimits _{L}(\omega )$
, where, for each
![]() $i\in I$
, the relation
$i\in I$
, the relation
 $R _i ^{{\mathbb Y} _{\mathbb X}}$
is defined in the structure
$R _i ^{{\mathbb Y} _{\mathbb X}}$
is defined in the structure
![]() ${\mathbb X}$
by the formula
${\mathbb X}$
by the formula
![]() $\varphi _i$
, that is,
$\varphi _i$
, that is,
 $$ \begin{align} \forall \bar{x}\in \omega ^{n_i} \;\; \Big(\bar{x}\in R _i ^{{\mathbb Y} _{\mathbb X} }\Leftrightarrow {\mathbb X} \models \varphi _i[\bar{x}]\Big). \end{align} $$
$$ \begin{align} \forall \bar{x}\in \omega ^{n_i} \;\; \Big(\bar{x}\in R _i ^{{\mathbb Y} _{\mathbb X} }\Leftrightarrow {\mathbb X} \models \varphi _i[\bar{x}]\Big). \end{align} $$
Claim 4.2. For each structure
 ${\mathbb Y} _0\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration
${\mathbb Y} _0\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
each structure
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
each structure
 ${\mathbb X}_0 \in {\mathcal M} _{{\mathbb Y} _0}^{\bar {a}}$
and each choice of formulas
${\mathbb X}_0 \in {\mathcal M} _{{\mathbb Y} _0}^{\bar {a}}$
and each choice of formulas
![]() $\varphi _i$
,
$\varphi _i$
,
![]() $i\in I$
, satisfying (13), defining
$i\in I$
, satisfying (13), defining
![]() ${\mathbb Y} _{\mathbb X}$
by (14), for
${\mathbb Y} _{\mathbb X}$
by (14), for
![]() ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
, we have
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
, we have
-
(a) The mapping
 $\Phi : \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )\rightarrow \mathop {\mathrm {Mod}}\nolimits _{L}(\omega )$
, defined by
$\Phi : \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )\rightarrow \mathop {\mathrm {Mod}}\nolimits _{L}(\omega )$
, defined by
 $ \Phi ({\mathbb X} )={\mathbb Y} _{\mathbb X}, $
for each
$ \Phi ({\mathbb X} )={\mathbb Y} _{\mathbb X}, $
for each
 ${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
, preserves elementary equivalence and isomorphism; moreover,
${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
, preserves elementary equivalence and isomorphism; moreover,
 $\mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _1, {\mathbb X} _2)\subset \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X} _1}, {\mathbb Y} _{{\mathbb X} _2})$
, for all
$\mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _1, {\mathbb X} _2)\subset \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X} _1}, {\mathbb Y} _{{\mathbb X} _2})$
, for all
 ${\mathbb X} _1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
and
${\mathbb X} _1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
and -
(b) The mapping
 $\Psi : \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong \;\rightarrow \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/\! \cong $
, given by
$\Psi : \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong \;\rightarrow \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/\! \cong $
, given by
 $ \Psi ([{\mathbb X} ])=[{\mathbb Y} _{\mathbb X}], $
for all
$ \Psi ([{\mathbb X} ])=[{\mathbb Y} _{\mathbb X}], $
for all
 $[{\mathbb X} ]\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong $
, is well defined.
$[{\mathbb X} ]\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong $
, is well defined.
Proof (a) By recursion on the construction of L-formulas to each L-formula
![]() $\varphi (\bar {v})$
we adjoin an
$\varphi (\bar {v})$
we adjoin an
![]() $L_n$
-formula
$L_n$
-formula
![]() $\varphi ^*(\bar {v})$
in the following way:
$\varphi ^*(\bar {v})$
in the following way:
![]() $(v_k=v_l)^* :=v_k=v_l$
,
$(v_k=v_l)^* :=v_k=v_l$
,
 $R_i (v_{k_0}, \dots , v_{k_{n_i-1}})^*:= \varphi _i (v_{k_0}, \dots , v_{k_{n_i-1}})$
(replacement of
$R_i (v_{k_0}, \dots , v_{k_{n_i-1}})^*:= \varphi _i (v_{k_0}, \dots , v_{k_{n_i-1}})$
(replacement of
![]() $v_j$
by
$v_j$
by
![]() $v_{k_j}$
in
$v_{k_j}$
in
![]() $\varphi _i$
),
$\varphi _i$
),
![]() $(\neg \varphi )^* := \neg \varphi ^*$
,
$(\neg \varphi )^* := \neg \varphi ^*$
,
![]() $(\varphi \land \psi )^* := \varphi ^*\land \psi ^*$
and
$(\varphi \land \psi )^* := \varphi ^*\land \psi ^*$
and
![]() $(\exists v_k\; \varphi )^* := \exists v_k\; \varphi ^*$
. A routine induction shows that, writing
$(\exists v_k\; \varphi )^* := \exists v_k\; \varphi ^*$
. A routine induction shows that, writing
![]() $\bar {v}$
instead of
$\bar {v}$
instead of
![]() $v_0,\dots ,v_{n-1}$
, we have (see [Reference Hodges, Lachlan and Shelah5, p. 216])
$v_0,\dots ,v_{n-1}$
, we have (see [Reference Hodges, Lachlan and Shelah5, p. 216])
 $$ \begin{align} \forall {\mathbb X} \in \mathop{\mathrm{Mod}}\nolimits _{L_n}(\omega ) \;\;\forall \varphi (\bar{v})\in \mathop{\mathrm{Form}}\nolimits _L\;\forall \bar{x} \in \omega ^n \; \Big( {\mathbb X} \models \varphi ^*[\bar{x}]\Leftrightarrow {\mathbb Y}_{\mathbb X} \models \varphi[\bar{x}]\Big). \end{align} $$
$$ \begin{align} \forall {\mathbb X} \in \mathop{\mathrm{Mod}}\nolimits _{L_n}(\omega ) \;\;\forall \varphi (\bar{v})\in \mathop{\mathrm{Form}}\nolimits _L\;\forall \bar{x} \in \omega ^n \; \Big( {\mathbb X} \models \varphi ^*[\bar{x}]\Leftrightarrow {\mathbb Y}_{\mathbb X} \models \varphi[\bar{x}]\Big). \end{align} $$
Let
![]() ${\mathbb X} _1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
. If
${\mathbb X} _1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}(\omega )$
. If
![]() ${\mathbb X}_1 \equiv {\mathbb X}_2$
, then for an L-sentence
${\mathbb X}_1 \equiv {\mathbb X}_2$
, then for an L-sentence
![]() $\varphi $
we have:
$\varphi $
we have:
![]() ${\mathbb Y} _{{\mathbb X} _1} \models \varphi $
iff
${\mathbb Y} _{{\mathbb X} _1} \models \varphi $
iff
![]() ${\mathbb X} _1\models \varphi ^*$
(by (15)) iff
${\mathbb X} _1\models \varphi ^*$
(by (15)) iff
![]() ${\mathbb X} _2 \models \varphi ^*$
(since
${\mathbb X} _2 \models \varphi ^*$
(since
![]() ${\mathbb X} _1 \equiv {\mathbb X}_2$
) iff
${\mathbb X} _1 \equiv {\mathbb X}_2$
) iff
![]() ${\mathbb Y} _{{\mathbb X} _2} \models \varphi $
(by (15) again). So,
${\mathbb Y} _{{\mathbb X} _2} \models \varphi $
(by (15) again). So,
![]() ${\mathbb Y} _{{\mathbb X} _1} \equiv {\mathbb Y} _{{\mathbb X}_2} $
and the mapping
${\mathbb Y} _{{\mathbb X} _1} \equiv {\mathbb Y} _{{\mathbb X}_2} $
and the mapping
![]() $\Phi $
preserves elementary equivalence.
$\Phi $
preserves elementary equivalence.
If
![]() $f:{\mathbb X}_1 \rightarrow {\mathbb X} _2$
is an isomorphism, then by (14) and since isomorphisms preserve all formulas in both directions, for each
$f:{\mathbb X}_1 \rightarrow {\mathbb X} _2$
is an isomorphism, then by (14) and since isomorphisms preserve all formulas in both directions, for each
![]() $i\in I$
and
$i\in I$
and
![]() $\bar {x}\in \omega ^{n_i}$
we have:
$\bar {x}\in \omega ^{n_i}$
we have:
 $\bar {x}\in R_i ^{{\mathbb Y}_{{\mathbb X} _1}}$
iff
$\bar {x}\in R_i ^{{\mathbb Y}_{{\mathbb X} _1}}$
iff
![]() ${\mathbb X} _1 \models \varphi _i [\bar {x}]$
iff
${\mathbb X} _1 \models \varphi _i [\bar {x}]$
iff
![]() ${\mathbb X} _2 \models \varphi _i [f\bar {x}]$
iff
${\mathbb X} _2 \models \varphi _i [f\bar {x}]$
iff
 $f \bar {x}\in R_i ^{{\mathbb Y}_{{\mathbb X} _2}}$
. Thus
$f \bar {x}\in R_i ^{{\mathbb Y}_{{\mathbb X} _2}}$
. Thus
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X}_1}, {\mathbb Y} _{ {\mathbb X} _2})$
.
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X}_1}, {\mathbb Y} _{ {\mathbb X} _2})$
.
(b) For
 ${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
![]() ${\mathbb X} \equiv {\mathbb X}_0$
, which, by (a), (13) and (14), implies that
${\mathbb X} \equiv {\mathbb X}_0$
, which, by (a), (13) and (14), implies that
![]() $\Phi ({\mathbb X} )={\mathbb Y} _{\mathbb X} \equiv {\mathbb Y} _{{\mathbb X}_0}={\mathbb Y} _0$
. So, since
$\Phi ({\mathbb X} )={\mathbb Y} _{\mathbb X} \equiv {\mathbb Y} _{{\mathbb X}_0}={\mathbb Y} _0$
. So, since
![]() ${\mathbb Y}_0\models {\mathcal T}$
, we have
${\mathbb Y}_0\models {\mathcal T}$
, we have
 $\Phi ({\mathbb X} )\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and, thus,
$\Phi ({\mathbb X} )\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and, thus,
 $$ \begin{align} \Phi [ \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )] \subset \mathop{\mathrm{Mod}}\nolimits _{L}^{{\mathcal T} }(\omega ). \end{align} $$
$$ \begin{align} \Phi [ \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )] \subset \mathop{\mathrm{Mod}}\nolimits _{L}^{{\mathcal T} }(\omega ). \end{align} $$
Assuming that
 ${\mathbb X}_1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
and
${\mathbb X}_1, {\mathbb X} _2 \in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
and
![]() ${\mathbb X} _1\cong {\mathbb X} _2$
, by (a) we have
${\mathbb X} _1\cong {\mathbb X} _2$
, by (a) we have
![]() ${\mathbb Y}_{{\mathbb X} _1}\cong {\mathbb Y}_{{\mathbb X} _2}$
, that is
${\mathbb Y}_{{\mathbb X} _1}\cong {\mathbb Y}_{{\mathbb X} _2}$
, that is
![]() $[{\mathbb Y}_{{\mathbb X} _1}]=[{\mathbb Y}_{{\mathbb X} _2}]$
. So, the mapping
$[{\mathbb Y}_{{\mathbb X} _1}]=[{\mathbb Y}_{{\mathbb X} _2}]$
. So, the mapping
![]() $\Psi $
is well defined.⊣
$\Psi $
is well defined.⊣
Thus, by Claim 4.2(b), if
![]() $I({\mathcal T} _{{\mathbb X} _0},\omega )={\mathfrak {c}}$
, then for a proof that
$I({\mathcal T} _{{\mathbb X} _0},\omega )={\mathfrak {c}}$
, then for a proof that
![]() $I({\mathcal T} ,\omega )={\mathfrak {c}}$
it is sufficient to show that the mapping
$I({\mathcal T} ,\omega )={\mathfrak {c}}$
it is sufficient to show that the mapping
![]() $\Psi $
is at-most-countable-to-one, which will be true if for each
$\Psi $
is at-most-countable-to-one, which will be true if for each
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
![]() $|\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}]\leq \omega $
. We note that, by Example 4.2 of Reference Kurilić[7], it is possible that
$|\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}]\leq \omega $
. We note that, by Example 4.2 of Reference Kurilić[7], it is possible that
![]() $|\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}]= \omega $
.
$|\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}]= \omega $
.
Now, let
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then we have
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then we have
![]() ${\mathbb X}\models {\mathcal T} ^*$
and, hence, there is
${\mathbb X}\models {\mathcal T} ^*$
and, hence, there is
![]() $\bar {b}:=\langle b_0,\dots ,b_{n-1}\rangle \in \omega ^n \setminus \Delta _n$
such that
$\bar {b}:=\langle b_0,\dots ,b_{n-1}\rangle \in \omega ^n \setminus \Delta _n$
such that
![]() ${\mathbb X}= \langle \omega ,\prec _{\mathbb X}, \{b_0\},\dots ,\{b_{n-1}\}\rangle $
and
${\mathbb X}= \langle \omega ,\prec _{\mathbb X}, \{b_0\},\dots ,\{b_{n-1}\}\rangle $
and
![]() ${\mathbb Y} _{\mathbb X}$
is definable in
${\mathbb Y} _{\mathbb X}$
is definable in
![]() ${\mathbb X}$
by (14). So, by Fact 2.1, the structure
${\mathbb X}$
by (14). So, by Fact 2.1, the structure
![]() ${\mathbb Y} _{\mathbb X}$
is
${\mathbb Y} _{\mathbb X}$
is
![]() $(F_{\bar {b}}, \prec _{\mathbb X}\upharpoonright (\omega \setminus F_{\bar {b}}))$
-chainable and (see (4))
$(F_{\bar {b}}, \prec _{\mathbb X}\upharpoonright (\omega \setminus F_{\bar {b}}))$
-chainable and (see (4))
 $$ \begin{align} {\mathbb L} _{\mathbb X} := \langle \omega \setminus F_{\bar{b}}, \prec _{\mathbb X}\upharpoonright (\omega \setminus F_{\bar{b}}) \rangle\in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{b}}}. \end{align} $$
$$ \begin{align} {\mathbb L} _{\mathbb X} := \langle \omega \setminus F_{\bar{b}}, \prec _{\mathbb X}\upharpoonright (\omega \setminus F_{\bar{b}}) \rangle\in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{b}}}. \end{align} $$
For an n-tuple
![]() $\bar {c}:=\langle c_0,\dots ,c_{n-1}\rangle \in \omega ^n\setminus \Delta _n$
let us define
$\bar {c}:=\langle c_0,\dots ,c_{n-1}\rangle \in \omega ^n\setminus \Delta _n$
let us define
 $$ \begin{align} {\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}} & := \Big\{ \langle \omega ,\prec , \{c_0\},\dots ,\{c_{n-1}\}\rangle \in \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega ):\nonumber \\ & \qquad{\mathbb Y} _{\mathbb X} \mbox{ is } (F_{\bar{c}}, \prec \upharpoonright (\omega \setminus F_{\bar{c}})) \mbox{-chainable}\Big\},\tag{18}\\ {\mathcal M} _{{\mathbb Y} _{\mathbb X}} & := \textstyle \bigcup _{\bar{c}\in \omega ^n\setminus \Delta _n}{\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}}. \tag{19}\end{align} $$
$$ \begin{align} {\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}} & := \Big\{ \langle \omega ,\prec , \{c_0\},\dots ,\{c_{n-1}\}\rangle \in \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega ):\nonumber \\ & \qquad{\mathbb Y} _{\mathbb X} \mbox{ is } (F_{\bar{c}}, \prec \upharpoonright (\omega \setminus F_{\bar{c}})) \mbox{-chainable}\Big\},\tag{18}\\ {\mathcal M} _{{\mathbb Y} _{\mathbb X}} & := \textstyle \bigcup _{\bar{c}\in \omega ^n\setminus \Delta _n}{\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}}. \tag{19}\end{align} $$
Thus,
 ${\mathbb X} \in {\mathcal M} ^{\bar {b}}_{{\mathbb Y} _{\mathbb X}}\subset {\mathcal M} _{{\mathbb Y} _{\mathbb X}}$
. For
${\mathbb X} \in {\mathcal M} ^{\bar {b}}_{{\mathbb Y} _{\mathbb X}}\subset {\mathcal M} _{{\mathbb Y} _{\mathbb X}}$
. For
 ${\mathcal M} \subset \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega )$
, let
${\mathcal M} \subset \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} ^*}(\omega )$
, let
![]() ${\mathcal M} ^{\cong }:=\{ [{\mathbb A} ]:{\mathbb A} \in {\mathcal M}\}$
.
${\mathcal M} ^{\cong }:=\{ [{\mathbb A} ]:{\mathbb A} \in {\mathcal M}\}$
.
Claim 4.3. For each structure
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
 $$ \begin{align*}\Psi ^{-1}\Big[ \{[{\mathbb Y} _{\mathbb X}]\}\Big] \subset {\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong}\cap \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong. \end{align*} $$
$$ \begin{align*}\Psi ^{-1}\Big[ \{[{\mathbb Y} _{\mathbb X}]\}\Big] \subset {\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong}\cap \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong. \end{align*} $$
Proof Let
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then, by (16) we have
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then, by (16) we have
 ${\mathbb Y} _{\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
; so
${\mathbb Y} _{\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
; so
 $\Psi ([{\mathbb X}])=[{\mathbb Y} _{\mathbb X} ]\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/\cong $
and
$\Psi ([{\mathbb X}])=[{\mathbb Y} _{\mathbb X} ]\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/\cong $
and
 $\Psi ^{-1}[\{ [{\mathbb Y} _{\mathbb X}]\}]\subset \mathop {\mathrm {dom}}\nolimits (\Psi )=\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
.
$\Psi ^{-1}[\{ [{\mathbb Y} _{\mathbb X}]\}]\subset \mathop {\mathrm {dom}}\nolimits (\Psi )=\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
.
Let
![]() $[{\mathbb X} _1]\in \Psi ^{-1}[\{[{\mathbb Y} _{\mathbb X}]\}]$
. Then
$[{\mathbb X} _1]\in \Psi ^{-1}[\{[{\mathbb Y} _{\mathbb X}]\}]$
. Then
 $[{\mathbb X} _1]\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
and, since the set
$[{\mathbb X} _1]\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
and, since the set
 $\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
is closed under
$\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
is closed under
![]() $\cong $
, we have
$\cong $
, we have
 ${\mathbb X} _1\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. This implies that
${\mathbb X} _1\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. This implies that
![]() ${\mathbb X} _1 \models {\mathcal T} ^*$
and, hence,
${\mathbb X} _1 \models {\mathcal T} ^*$
and, hence,
![]() ${\mathbb X} _1 =\langle \omega ,\prec _{{\mathbb X} _1}, \{c_0 \},\dots ,\{c_{n-1}\}\rangle $
, for some
${\mathbb X} _1 =\langle \omega ,\prec _{{\mathbb X} _1}, \{c_0 \},\dots ,\{c_{n-1}\}\rangle $
, for some
![]() $\bar {c}:=\langle c_0,\dots ,c_{n-1}\rangle \in \omega ^n\setminus \Delta _n$
. Since
$\bar {c}:=\langle c_0,\dots ,c_{n-1}\rangle \in \omega ^n\setminus \Delta _n$
. Since
 ${\mathbb X} _1\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
, by (14) for
${\mathbb X} _1\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
, by (14) for
![]() $i\in I$
we have
$i\in I$
we have
 $$ \begin{align} \forall \bar{x}\in \omega ^{n_i}\;\;( \bar{x}\in R_i^{{\mathbb Y} _{{\mathbb X} _1}} \Leftrightarrow {\mathbb X} _1 \models \varphi _i [\bar{x}]). \end{align} $$
$$ \begin{align} \forall \bar{x}\in \omega ^{n_i}\;\;( \bar{x}\in R_i^{{\mathbb Y} _{{\mathbb X} _1}} \Leftrightarrow {\mathbb X} _1 \models \varphi _i [\bar{x}]). \end{align} $$
Also we have
![]() $[{\mathbb Y} _{{\mathbb X} _1}]=\Psi ([{\mathbb X} _1])=[{\mathbb Y} _{\mathbb X}] $
, so there is
$[{\mathbb Y} _{{\mathbb X} _1}]=\Psi ([{\mathbb X} _1])=[{\mathbb Y} _{\mathbb X}] $
, so there is
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X} } , {\mathbb Y} _{{\mathbb X} _1})$
and we prove that
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{{\mathbb X} } , {\mathbb Y} _{{\mathbb X} _1})$
and we prove that
 $[{\mathbb X} _1]\in \;{\mathcal M} _{{\mathbb Y} _{{\mathbb X} }} ^{\cong }$
.
$[{\mathbb X} _1]\in \;{\mathcal M} _{{\mathbb Y} _{{\mathbb X} }} ^{\cong }$
.
Clearly,
 ${\mathbb X} _2:=\langle \omega , f^{-1}[\prec _{{\mathbb X} _1}],\{f^{-1}(c_0)\},\dots ,\{f^{-1}(c_{n-1})\} \rangle \cong {\mathbb X}_1$
and
${\mathbb X} _2:=\langle \omega , f^{-1}[\prec _{{\mathbb X} _1}],\{f^{-1}(c_0)\},\dots ,\{f^{-1}(c_{n-1})\} \rangle \cong {\mathbb X}_1$
and
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _2 ,{\mathbb X} _1)$
. For
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _2 ,{\mathbb X} _1)$
. For
![]() $i\in I$
and
$i\in I$
and
![]() $\bar {x}\in \omega ^{n_i}$
we have
$\bar {x}\in \omega ^{n_i}$
we have
 $\bar {x}\in R_i^{{\mathbb Y} _{\mathbb X}}$
iff
$\bar {x}\in R_i^{{\mathbb Y} _{\mathbb X}}$
iff
 $f\bar {x}\in R_i^{{\mathbb Y} _{{\mathbb X} _1}}$
(since
$f\bar {x}\in R_i^{{\mathbb Y} _{{\mathbb X} _1}}$
(since
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{\mathbb X} , {\mathbb Y} _{{\mathbb X} _1})$
), iff
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb Y} _{\mathbb X} , {\mathbb Y} _{{\mathbb X} _1})$
), iff
![]() ${\mathbb X} _1 \models \varphi _i [f\bar {x}]$
(by 20), iff
${\mathbb X} _1 \models \varphi _i [f\bar {x}]$
(by 20), iff
![]() ${\mathbb X} _2\models \varphi _i [\bar {x}]$
(since
${\mathbb X} _2\models \varphi _i [\bar {x}]$
(since
![]() $f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _2 ,{\mathbb X} _1 )$
). Thus
$f\in \mathop {\mathrm {Iso}}\nolimits ({\mathbb X} _2 ,{\mathbb X} _1 )$
). Thus
 $\bar {x}\in R_i^{{\mathbb Y} _{\mathbb X}}$
iff
$\bar {x}\in R_i^{{\mathbb Y} _{\mathbb X}}$
iff
![]() ${\mathbb X} _2\models \varphi _i [\bar {x}]$
, for all
${\mathbb X} _2\models \varphi _i [\bar {x}]$
, for all
![]() $\bar {x}\in \omega ^{n_i}$
, so, by Fact 2.1, the structure
$\bar {x}\in \omega ^{n_i}$
, so, by Fact 2.1, the structure
![]() ${\mathbb Y} _{\mathbb X}$
is
${\mathbb Y} _{\mathbb X}$
is
 $(F_{f^{-1}\bar {c}},f^{-1}[\prec _{{\mathbb X} _1}]\upharpoonright (\omega \setminus F_{f^{-1}\bar {c}}) )$
-chainable. Now,
$(F_{f^{-1}\bar {c}},f^{-1}[\prec _{{\mathbb X} _1}]\upharpoonright (\omega \setminus F_{f^{-1}\bar {c}}) )$
-chainable. Now,
 ${\mathbb X} _2 \in {\mathcal M} _{{\mathbb Y} _{\mathbb X}} ^{f^{-1}\bar {c}}$
and, hence,
${\mathbb X} _2 \in {\mathcal M} _{{\mathbb Y} _{\mathbb X}} ^{f^{-1}\bar {c}}$
and, hence,
 $[{\mathbb X} _1]=[{\mathbb X} _2]\in ({\mathcal M} _{{\mathbb Y} _{\mathbb X}} ^{f^{-1}\bar {c}})^{\cong }\;\subset {\mathcal M} _{{\mathbb Y} _{{\mathbb X} }} ^{\cong }$
. Thus
$[{\mathbb X} _1]=[{\mathbb X} _2]\in ({\mathcal M} _{{\mathbb Y} _{\mathbb X}} ^{f^{-1}\bar {c}})^{\cong }\;\subset {\mathcal M} _{{\mathbb Y} _{{\mathbb X} }} ^{\cong }$
. Thus
 $\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}] \subset {\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }$
.⊣
$\Psi ^{-1}[ \{[{\mathbb Y} _{\mathbb X}]\}] \subset {\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }$
.⊣
The following folklore statement will be used in our case analysis as well.
Claim 4.4. If some structure
 ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
is simply definable in an
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
is simply definable in an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() ${\mathbb X}$
with domain
${\mathbb X}$
with domain
![]() $\omega $
, then
$\omega $
, then
![]() ${\mathbb Y} $
is an
${\mathbb Y} $
is an
![]() $\omega $
-categorical structure and
$\omega $
-categorical structure and
![]() $I({\mathcal T} ,\omega ) = 1$
.
$I({\mathcal T} ,\omega ) = 1$
.
Proof By the theorem of Engeler, Ryll-Nardzewski and Svenonius (see [Reference Hodges, Lachlan and Shelah5, p. 341]), the automorphism group of
![]() ${\mathbb X} $
is oligomorphic; that is, for each
${\mathbb X} $
is oligomorphic; that is, for each
![]() $n\in {\mathbb N}$
we have
$n\in {\mathbb N}$
we have
![]() $|\omega ^n /\!\sim _{{\mathbb X} ,n}|<\omega $
, where
$|\omega ^n /\!\sim _{{\mathbb X} ,n}|<\omega $
, where
![]() $\bar {x} \sim _{{\mathbb X} ,n} \bar {y}$
iff
$\bar {x} \sim _{{\mathbb X} ,n} \bar {y}$
iff
![]() $f\bar {x} =\bar {y}$
, for some
$f\bar {x} =\bar {y}$
, for some
![]() $f\in \mathop {\mathrm {Aut}}\nolimits ({\mathbb X} )$
.
$f\in \mathop {\mathrm {Aut}}\nolimits ({\mathbb X} )$
.
As in Claim 4.2(a) we prove that
![]() $\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Aut}}\nolimits ({\mathbb Y} )$
, which implies that for
$\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} )\subset \mathop {\mathrm {Aut}}\nolimits ({\mathbb Y} )$
, which implies that for
![]() $n\in {\mathbb N}$
and each
$n\in {\mathbb N}$
and each
![]() $\bar {x} , \bar {y} \in \omega ^n$
we have
$\bar {x} , \bar {y} \in \omega ^n$
we have
![]() $\bar {x} \sim _{{\mathbb X} ,n} \bar {y} \Rightarrow \bar {x} \sim _{{\mathbb Y} ,n} \bar {y}$
. Thus
$\bar {x} \sim _{{\mathbb X} ,n} \bar {y} \Rightarrow \bar {x} \sim _{{\mathbb Y} ,n} \bar {y}$
. Thus
![]() $|\omega ^n /\!\sim _{{\mathbb Y} ,n}| \leq |\omega ^n /\!\sim _{{\mathbb X} ,n}|<\omega $
, for all
$|\omega ^n /\!\sim _{{\mathbb Y} ,n}| \leq |\omega ^n /\!\sim _{{\mathbb X} ,n}|<\omega $
, for all
![]() $n\in {\mathbb N}$
, and, since
$n\in {\mathbb N}$
, and, since
![]() $|L|\leq \omega $
, using the same theorem we conclude that
$|L|\leq \omega $
, using the same theorem we conclude that
![]() ${\mathbb Y} $
is an
${\mathbb Y} $
is an
![]() $\omega $
-categorical L-structure.⊣
$\omega $
-categorical L-structure.⊣
4.2 Proof
First we prove that
 $|\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/ \!\cong |\in \{ 1,{\mathfrak {c}}\}$
, using definitions and notation from “Preliminaries” and distinguishing the following cases.
$|\mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )/ \!\cong |\in \{ 1,{\mathfrak {c}}\}$
, using definitions and notation from “Preliminaries” and distinguishing the following cases.
Case A. There exist a structure
 ${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, an enumeration of its kernel,
${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, an enumeration of its kernel,
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and a structure
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and a structure
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
such that the theory
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
such that the theory
![]() ${\mathcal T} _{{\mathbb X} _0}$
is
${\mathcal T} _{{\mathbb X} _0}$
is
![]() $\omega $
-categorical. Then by Fact 2.1 the structure
$\omega $
-categorical. Then by Fact 2.1 the structure
![]() ${\mathbb Y} _0$
is simply definable in
${\mathbb Y} _0$
is simply definable in
![]() ${\mathbb X} _0$
and by Claim 4.4 we have
${\mathbb X} _0$
and by Claim 4.4 we have
![]() $I({\mathcal T} ,\omega ) = 1$
.
$I({\mathcal T} ,\omega ) = 1$
.
In particular, Case A appears if there is a structure
 ${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
satisfying condition (i) of Theorem 2.5:
${\mathbb Y} \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
satisfying condition (i) of Theorem 2.5:
![]() ${\mathbb Y}$
is F-chainable and
${\mathbb Y}$
is F-chainable and
 ${\mathcal L} _{\mathbb Y}^F=LO _{\omega \setminus F}$
. Then, taking an enumeration
${\mathcal L} _{\mathbb Y}^F=LO _{\omega \setminus F}$
. Then, taking an enumeration
![]() $F=\{ a_0,\dots ,a_{n-1}\}$
, the relations
$F=\{ a_0,\dots ,a_{n-1}\}$
, the relations
![]() $R^{\mathbb Y}_i$
of the structure
$R^{\mathbb Y}_i$
of the structure
![]() ${\mathbb Y}$
are definable in the structure
${\mathbb Y}$
are definable in the structure
![]() ${\mathbb X} :=\langle \omega , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
of the unary language
${\mathbb X} :=\langle \omega , \{a_0\},\dots ,\{a_{n-1}\}\rangle $
of the unary language
![]() $L':=\langle U_0,\dots ,U_{n-1}\rangle $
by quantifier free
$L':=\langle U_0,\dots ,U_{n-1}\rangle $
by quantifier free
![]() $L'$
-formulas and, since the structure
$L'$
-formulas and, since the structure
![]() ${\mathbb X}$
is
${\mathbb X}$
is
![]() $\omega $
-categorical,
$\omega $
-categorical,
![]() ${\mathbb Y}$
is
${\mathbb Y}$
is
![]() $\omega $
-categorical as well; so,
$\omega $
-categorical as well; so,
![]() $I({\mathcal T} ,\omega ) = 1$
again. We note that such structures are called finitist by Fraïssé, see [Reference Fraïssé2, p. 292].
$I({\mathcal T} ,\omega ) = 1$
again. We note that such structures are called finitist by Fraïssé, see [Reference Fraïssé2, p. 292].
Case B. For each structure
 ${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration of its kernel
${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration of its kernel
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
and each structure
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
and each structure
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, the theory
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, the theory
![]() ${\mathcal T} _{{\mathbb X} _0}$
is not
${\mathcal T} _{{\mathbb X} _0}$
is not
![]() $\omega $
-categorical; so, by Theorem 1.1,
$\omega $
-categorical; so, by Theorem 1.1,
 $|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0 }}(\omega )/\!\cong |={\mathfrak {c}}$
, for all
$|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0 }}(\omega )/\!\cong |={\mathfrak {c}}$
, for all
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
.
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
.
Then, by the remark from Case A concerning condition (i) of Theorem 2.5, we have
 $$ \begin{align} \forall {\mathbb Y} \in \mathop{\mathrm{Mod}}\nolimits _{L}^{{\mathcal T} }(\omega ) \;\; {\mathcal L} _{\mathbb Y}^{\mathop{\mathrm{Ker}}\nolimits ({\mathbb Y} )} \neq LO _{\omega \setminus \mathop{\mathrm{Ker}}\nolimits ({\mathbb Y} )} , \end{align} $$
$$ \begin{align} \forall {\mathbb Y} \in \mathop{\mathrm{Mod}}\nolimits _{L}^{{\mathcal T} }(\omega ) \;\; {\mathcal L} _{\mathbb Y}^{\mathop{\mathrm{Ker}}\nolimits ({\mathbb Y} )} \neq LO _{\omega \setminus \mathop{\mathrm{Ker}}\nolimits ({\mathbb Y} )} , \end{align} $$
and we prove that
 $|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}$
, distinguishing the following two subcases.
$|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}$
, distinguishing the following two subcases.
Subcase B1. There exist a structure
 ${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, an enumeration of its kernel,
${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, an enumeration of its kernel,
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and a structure
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and a structure
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
such that the linear order
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
such that the linear order
 ${\mathbb L} _{{\mathbb X} _0} := \langle \omega \setminus F_{\bar {a}}, \prec _{{\mathbb X} _0}\upharpoonright (\omega \setminus F_{\bar {a}}) \rangle \in {\mathcal L} _{{\mathbb Y} _0}^{F_{\bar {a}}}$
has at least one end-point.
${\mathbb L} _{{\mathbb X} _0} := \langle \omega \setminus F_{\bar {a}}, \prec _{{\mathbb X} _0}\upharpoonright (\omega \setminus F_{\bar {a}}) \rangle \in {\mathcal L} _{{\mathbb Y} _0}^{F_{\bar {a}}}$
has at least one end-point.
Then we take such
![]() ${\mathbb Y}_0$
,
${\mathbb Y}_0$
,
![]() $\bar {a}$
and
$\bar {a}$
and
![]() ${\mathbb X} _0$
and notice that
${\mathbb X} _0$
and notice that
![]() ${\mathbb X} _0 \models {\mathcal T} ^*$
and that the mentioned property of
${\mathbb X} _0 \models {\mathcal T} ^*$
and that the mentioned property of
![]() ${\mathbb L} _{{\mathbb X} _0}$
gives a first order property of
${\mathbb L} _{{\mathbb X} _0}$
gives a first order property of
![]() ${\mathbb X}_0$
. Namely,
${\mathbb X}_0$
. Namely,
![]() ${\mathbb X} _0\models \theta _0 \lor \theta _1$
, where
${\mathbb X} _0\models \theta _0 \lor \theta _1$
, where
 $$ \begin{align} \theta _0 & := \exists v \;\forall u \;(U_{n-1}(u)\Rightarrow R(u,v)\land \neg \exists w \;(R(u,w) \land R(w,v))),\\ \theta _1 & := \exists v \;\forall u \; (\neg u=v \Rightarrow R(u,v)).\tag{23} \end{align} $$
$$ \begin{align} \theta _0 & := \exists v \;\forall u \;(U_{n-1}(u)\Rightarrow R(u,v)\land \neg \exists w \;(R(u,w) \land R(w,v))),\\ \theta _1 & := \exists v \;\forall u \; (\neg u=v \Rightarrow R(u,v)).\tag{23} \end{align} $$
Now we have
 $|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong |={\mathfrak {c}}$
and, by Claim 4.2(b), for a proof that
$|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong |={\mathfrak {c}}$
and, by Claim 4.2(b), for a proof that
 $|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}$
it is sufficient to show that the mapping
$|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}$
it is sufficient to show that the mapping
![]() $\Psi $
is at-most-countable-to-one. This will follow from the following claim and Claim 4.3.
$\Psi $
is at-most-countable-to-one. This will follow from the following claim and Claim 4.3.
Claim 4.5.
 $\Big |{\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong \Big |\leq \omega $
, for all
$\Big |{\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong \Big |\leq \omega $
, for all
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.
Proof Let
 ${\mathbb X}\!\in \!\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. By (19) it is sufficient to show that for each
${\mathbb X}\!\in \!\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. By (19) it is sufficient to show that for each
![]() $\bar {c}\!\in \omega ^n\setminus \Delta _n$
we have
$\bar {c}\!\in \omega ^n\setminus \Delta _n$
we have
 $$ \begin{align} \Big| ({\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}})^{\cong } \cap \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong\Big| \leq \omega. \end{align} $$
$$ \begin{align} \Big| ({\mathcal M} ^{\bar{c}}_{{\mathbb Y} _{\mathbb X}})^{\cong } \cap \mathop{\mathrm{Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong\Big| \leq \omega. \end{align} $$
Let
 ${\mathbb X} _1= \langle \omega ,\prec _{{\mathbb X} _1}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. Then by (18) and (4) we have
${\mathbb X} _1= \langle \omega ,\prec _{{\mathbb X} _1}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. Then by (18) and (4) we have
 $$ \begin{align*}{\mathbb L} _{{\mathbb X} _1} := \langle \omega \setminus F_{\bar{c}}, \prec _{{\mathbb X} _1}\upharpoonright (\omega \setminus F_{\bar{c}}) \rangle\in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{c}}}. \end{align*} $$
$$ \begin{align*}{\mathbb L} _{{\mathbb X} _1} := \langle \omega \setminus F_{\bar{c}}, \prec _{{\mathbb X} _1}\upharpoonright (\omega \setminus F_{\bar{c}}) \rangle\in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{c}}}. \end{align*} $$
First, if the set
 ${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
satisfies condition (iii) of Theorem 2.5, then we have
${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
satisfies condition (iii) of Theorem 2.5, then we have
 $({\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}})^{\cong }=\{ [{\mathbb L} _{{\mathbb X} _1}], [{\mathbb L} _{{\mathbb X} _1}^*]\}$
(because all “
$({\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}})^{\cong }=\{ [{\mathbb L} _{{\mathbb X} _1}], [{\mathbb L} _{{\mathbb X} _1}^*]\}$
(because all “
![]() ${\mathbb K} +{\mathbb M} +{\mathbb H}$
-sums” are isomorphic and all “
${\mathbb K} +{\mathbb M} +{\mathbb H}$
-sums” are isomorphic and all “
![]() ${\mathbb H} ^* +{\mathbb M} ^* +{\mathbb K} ^*$
-sums” are isomorphic). Thus each structure
${\mathbb H} ^* +{\mathbb M} ^* +{\mathbb K} ^*$
-sums” are isomorphic). Thus each structure
 ${\mathbb X} _2 \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
consists of the initial part,
${\mathbb X} _2 \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
consists of the initial part,
![]() $\{c_0\}+\cdots +\{c_{n-1}\}$
, labeled by the unary relations
$\{c_0\}+\cdots +\{c_{n-1}\}$
, labeled by the unary relations
 $U_j^{{\mathbb X} _2} =\{ c_j \}$
,
$U_j^{{\mathbb X} _2} =\{ c_j \}$
,
![]() $j<n$
, and a final part, which is either isomorphic to the linear order
$j<n$
, and a final part, which is either isomorphic to the linear order
![]() ${\mathbb L} _{{\mathbb X} _1}$
or to its reverse,
${\mathbb L} _{{\mathbb X} _1}$
or to its reverse,
![]() ${\mathbb L} _{{\mathbb X} _1}^*$
. So we have
${\mathbb L} _{{\mathbb X} _1}^*$
. So we have
 $|({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong }|\leq 2$
and (24) is true.
$|({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong }|\leq 2$
and (24) is true.
Otherwise, by (21) and Theorem 2.5,
 ${\mathcal L} _{{\mathbb Y}_{\mathbb X}}^{F_{\bar {c}}} =\bigcup _{{\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}}\{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\}$
.
${\mathcal L} _{{\mathbb Y}_{\mathbb X}}^{F_{\bar {c}}} =\bigcup _{{\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}}\{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\}$
.
Let
 ${\mathbb X} _2= \langle \omega ,\prec _{{\mathbb X} _2}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then
${\mathbb X} _2= \langle \omega ,\prec _{{\mathbb X} _2}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. Then
 ${\mathbb L} _{{\mathbb X} _2} := \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _2}\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle \in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
and, hence, there is a cut
${\mathbb L} _{{\mathbb X} _2} := \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _2}\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle \in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
and, hence, there is a cut
![]() $\{ {\mathbb I},{\mathbb F}\}$
in
$\{ {\mathbb I},{\mathbb F}\}$
in
![]() ${\mathbb L} _{{\mathbb X} _1}$
(i.e. a decomposition
${\mathbb L} _{{\mathbb X} _1}$
(i.e. a decomposition
![]() ${\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}$
) such that
${\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}$
) such that
![]() ${\mathbb L} _{{\mathbb X} _2} ={\mathbb F} +{\mathbb I}$
or
${\mathbb L} _{{\mathbb X} _2} ={\mathbb F} +{\mathbb I}$
or
![]() ${\mathbb L} _{{\mathbb X} _2} ={\mathbb I} ^* +{\mathbb F} ^*$
. Suppose that
${\mathbb L} _{{\mathbb X} _2} ={\mathbb I} ^* +{\mathbb F} ^*$
. Suppose that
![]() ${\mathbb I},{\mathbb F}\neq \emptyset $
, that
${\mathbb I},{\mathbb F}\neq \emptyset $
, that
![]() ${\mathbb I}$
does not have a largest element and that
${\mathbb I}$
does not have a largest element and that
![]() ${\mathbb F}$
does not have a smallest element. Then
${\mathbb F}$
does not have a smallest element. Then
![]() ${\mathbb F} +{\mathbb I}$
and
${\mathbb F} +{\mathbb I}$
and
![]() ${\mathbb I} ^* +{\mathbb F} ^*$
are linear orders without end points. But, since
${\mathbb I} ^* +{\mathbb F} ^*$
are linear orders without end points. But, since
 ${\mathbb X} _2\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
${\mathbb X} _2\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
![]() ${\mathbb X} _2 \models \theta _0 \lor \theta _1$
and, hence, the linear order
${\mathbb X} _2 \models \theta _0 \lor \theta _1$
and, hence, the linear order
![]() ${\mathbb L} _{{\mathbb X} _2}$
must have at least one end-point, which gives a contradiction.
${\mathbb L} _{{\mathbb X} _2}$
must have at least one end-point, which gives a contradiction.
So, for each
 ${\mathbb X} _2\in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
${\mathbb X} _2\in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
we have
![]() ${\mathbb L} _{{\mathbb X} _2} ={\mathbb F} +{\mathbb I}$
or
${\mathbb L} _{{\mathbb X} _2} ={\mathbb F} +{\mathbb I}$
or
![]() ${\mathbb L} _{{\mathbb X} _2} ={\mathbb I} ^* +{\mathbb F} ^*$
, where
${\mathbb L} _{{\mathbb X} _2} ={\mathbb I} ^* +{\mathbb F} ^*$
, where
![]() ${\mathbb I}$
has a largest element or
${\mathbb I}$
has a largest element or
![]() ${\mathbb F}$
has a smallest element. Since such cuts
${\mathbb F}$
has a smallest element. Since such cuts
![]() $\{ {\mathbb I},{\mathbb F}\}$
in
$\{ {\mathbb I},{\mathbb F}\}$
in
![]() ${\mathbb L} _{{\mathbb X} _1}$
are defined by the elements of the set
${\mathbb L} _{{\mathbb X} _1}$
are defined by the elements of the set
![]() $\omega \setminus F_{\bar {c}}$
, there are countably many of them. Thus
$\omega \setminus F_{\bar {c}}$
, there are countably many of them. Thus
 $|{\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )|=\omega $
, which implies (24), since each class from the set
$|{\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )|=\omega $
, which implies (24), since each class from the set
 $({\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\bar {c}})^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
has a representative in
$({\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\bar {c}})^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong $
has a representative in
 ${\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.⊣
${\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.⊣
Subcase B2. For each structure
 ${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration of its kernel,
${\mathbb Y}_0 \in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
, each enumeration of its kernel,
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and each structure
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=\{ a_0,\dots ,a_{n-1}\}$
, and each structure
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, the linear order
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, the linear order
 ${\mathbb L} _{{\mathbb X} _0} := \langle \omega \setminus F_{\bar {a}}, \prec _{{\mathbb X} _0}\upharpoonright (\omega \setminus F_{\bar {a}}) \rangle \in {\mathcal L} _{{\mathbb Y} _0}^{F_{\bar {a}}}$
is a linear order without end points.
${\mathbb L} _{{\mathbb X} _0} := \langle \omega \setminus F_{\bar {a}}, \prec _{{\mathbb X} _0}\upharpoonright (\omega \setminus F_{\bar {a}}) \rangle \in {\mathcal L} _{{\mathbb Y} _0}^{F_{\bar {a}}}$
is a linear order without end points.
Then we fix arbitrary
 ${\mathbb Y}_0\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and
${\mathbb Y}_0\in \mathop {\mathrm {Mod}}\nolimits _{L}^{{\mathcal T} }(\omega )$
and
 ${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, where
${\mathbb X} _0\in {\mathcal M} _{{\mathbb Y} _0} ^{\bar {a}}$
, where
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=F_{\bar {a}}$
.
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} _0)=F_{\bar {a}}$
.
Again we have
 $|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong |={\mathfrak {c}}$
and, as in Subcase B1, the equality
$|\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\!\cong |={\mathfrak {c}}$
and, as in Subcase B1, the equality
 $|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}\,$
will follow from Claims 4.2(b), 4.3 and the next claim.
$|\mathop {\mathrm {Mod}}\nolimits ^{\mathcal T} _L (\omega )/\!\cong |={\mathfrak {c}}\,$
will follow from Claims 4.2(b), 4.3 and the next claim.
Claim 4.6.
 $\Big |{\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong \Big |\leq \omega $
, for all
$\Big |{\mathcal M} _{{\mathbb Y}_{{\mathbb X} }}^{\cong }\cap \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )/\cong \Big |\leq \omega $
, for all
 ${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.
${\mathbb X}\in \mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
.
Proof Let
 ${\mathbb X}\!\in \!\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. By (19) it is sufficient to show that for each
${\mathbb X}\!\in \!\mathop {\mathrm {Mod}}\nolimits _{L_n}^{{\mathcal T} _{{\mathbb X} _0}}(\omega )$
. By (19) it is sufficient to show that for each
![]() $\bar {c}\!\in \omega ^n\setminus \Delta _n$
we have
$\bar {c}\!\in \omega ^n\setminus \Delta _n$
we have
 $| ({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong } | \leq 2$
.
$| ({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong } | \leq 2$
.
Let
 ${\mathbb X} _1= \langle \omega ,\prec _{{\mathbb X} _1}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. Then, by our assumption,
${\mathbb X} _1= \langle \omega ,\prec _{{\mathbb X} _1}, \{c_0\},\dots ,\{c_{n-1}\}\rangle \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. Then, by our assumption,
![]() ${\mathbb L} _{{\mathbb X} _1} = \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _1}\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle $
is a linear order without end points and
${\mathbb L} _{{\mathbb X} _1} = \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _1}\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle $
is a linear order without end points and
 ${\mathbb L} _{{\mathbb X} _1} \in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
.
${\mathbb L} _{{\mathbb X} _1} \in {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
.
Suppose that the set
 ${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
satisfies condition (ii) of Theorem 2.5; that is,
${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}$
satisfies condition (ii) of Theorem 2.5; that is,
 ${\mathcal L} _{{\mathbb Y}_{\mathbb X}}^{F_{\bar {c}}} =\bigcup _{{\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}}\{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\}$
. Then, taking an arbitrary
${\mathcal L} _{{\mathbb Y}_{\mathbb X}}^{F_{\bar {c}}} =\bigcup _{{\mathbb L} _{{\mathbb X} _1}={\mathbb I} +{\mathbb F}}\{ {\mathbb F} + {\mathbb I} ,\, {\mathbb I} ^* +{\mathbb F} ^*\}$
. Then, taking an arbitrary
![]() $x\in \omega \setminus F_{\bar {c}}$
we have
$x\in \omega \setminus F_{\bar {c}}$
we have
 ${\mathbb L} _{{\mathbb X} _1} =(-\infty ,x)_{{\mathbb L} _{{\mathbb X} _1}}+ [x, \infty )_{{\mathbb L} _{{\mathbb X} _1} }=:{\mathbb I} +{\mathbb F}$
; and, since
${\mathbb L} _{{\mathbb X} _1} =(-\infty ,x)_{{\mathbb L} _{{\mathbb X} _1}}+ [x, \infty )_{{\mathbb L} _{{\mathbb X} _1} }=:{\mathbb I} +{\mathbb F}$
; and, since
![]() ${\mathbb L} _{{\mathbb X} _1}$
is a linear order without end points,
${\mathbb L} _{{\mathbb X} _1}$
is a linear order without end points,
![]() ${\mathbb I} ,{\mathbb F}\neq \emptyset $
. Let
${\mathbb I} ,{\mathbb F}\neq \emptyset $
. Let
![]() ${\mathbb X} _2= \langle \omega ,\prec _{{\mathbb X} _2}, \{c_0\},\dots ,\{c_{n-1}\}\rangle $
, where
${\mathbb X} _2= \langle \omega ,\prec _{{\mathbb X} _2}, \{c_0\},\dots ,\{c_{n-1}\}\rangle $
, where
![]() $\prec _{{\mathbb X} _2}$
is the linear order on
$\prec _{{\mathbb X} _2}$
is the linear order on
![]() $\omega $
such that
$\omega $
such that
![]() $\langle \omega , \prec _{{\mathbb X} _2}\rangle =\{c_0\}+\cdots +\{c_{n-1}\}+ {\mathbb F} +{\mathbb I}$
. Then the structure
$\langle \omega , \prec _{{\mathbb X} _2}\rangle =\{c_0\}+\cdots +\{c_{n-1}\}+ {\mathbb F} +{\mathbb I}$
. Then the structure
![]() ${\mathbb Y} _{\mathbb X}$
is
${\mathbb Y} _{\mathbb X}$
is
![]() $(F_{\bar {c}},\prec _{{\mathbb X} _2}\upharpoonright (\omega \setminus F_{\bar {c}}) )$
-chainable and, hence,
$(F_{\bar {c}},\prec _{{\mathbb X} _2}\upharpoonright (\omega \setminus F_{\bar {c}}) )$
-chainable and, hence,
 ${\mathbb X} _2\in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. But the linear order
${\mathbb X} _2\in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
. But the linear order
![]() ${\mathbb L} _{{\mathbb X} _2 } := \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _2 }\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle ={\mathbb F} +{\mathbb I}$
has a smallest element, which contradicts the assumption of Subcase B2.
${\mathbb L} _{{\mathbb X} _2 } := \langle \omega \setminus F_{\bar {c}}, \prec _{{\mathbb X} _2 }\upharpoonright (\omega \setminus F_{\bar {c}}) \rangle ={\mathbb F} +{\mathbb I}$
has a smallest element, which contradicts the assumption of Subcase B2.
Thus there are finite sets
![]() $K,H\subset \omega \setminus F_{\bar {c}}$
such that
$K,H\subset \omega \setminus F_{\bar {c}}$
such that
![]() ${\mathbb L} _{{\mathbb X} _1} ={\mathbb K} +{\mathbb M} +{\mathbb H}\,$
and
${\mathbb L} _{{\mathbb X} _1} ={\mathbb K} +{\mathbb M} +{\mathbb H}\,$
and
 $$ \begin{align*}\textstyle {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{c}}} =\bigcup _{\vartriangleleft _K \in LO_K \atop \vartriangleleft _H \in LO_H} \Big\{ \langle K ,\vartriangleleft _K\rangle + {\mathbb M} +\langle H ,\vartriangleleft _H \rangle, \langle H ,\vartriangleleft _H\rangle ^*+ {\mathbb M} ^* +\langle K ,\vartriangleleft _K \rangle^*\Big\}. \end{align*} $$
$$ \begin{align*}\textstyle {\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar{c}}} =\bigcup _{\vartriangleleft _K \in LO_K \atop \vartriangleleft _H \in LO_H} \Big\{ \langle K ,\vartriangleleft _K\rangle + {\mathbb M} +\langle H ,\vartriangleleft _H \rangle, \langle H ,\vartriangleleft _H\rangle ^*+ {\mathbb M} ^* +\langle K ,\vartriangleleft _K \rangle^*\Big\}. \end{align*} $$
In addition, since each element of
 ${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}} $
is a linear order without end points, we have
${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}} $
is a linear order without end points, we have
![]() $K=H=\emptyset $
and, hence,
$K=H=\emptyset $
and, hence,
![]() ${\mathbb M}={\mathbb L} _{{\mathbb X} _1}$
and
${\mathbb M}={\mathbb L} _{{\mathbb X} _1}$
and
 ${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}=\{ {\mathbb L} _{{\mathbb X} _1} ,{\mathbb L} _{{\mathbb X} _1} ^*\}$
. Thus each structure
${\mathcal L} _{{\mathbb Y} _{\mathbb X}}^{F_{\bar {c}}}=\{ {\mathbb L} _{{\mathbb X} _1} ,{\mathbb L} _{{\mathbb X} _1} ^*\}$
. Thus each structure
 ${\mathbb X} _2 \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
consists of the initial part,
${\mathbb X} _2 \in {\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}}$
consists of the initial part,
![]() $\{c_0\}+\cdots +\{c_{n-1}\}$
, labeled by the unary relations
$\{c_0\}+\cdots +\{c_{n-1}\}$
, labeled by the unary relations
 $U_j^{{\mathbb X} _2} =\{ c_j \}$
,
$U_j^{{\mathbb X} _2} =\{ c_j \}$
,
![]() $j<n$
, and a final part, which is either isomorphic to the linear order
$j<n$
, and a final part, which is either isomorphic to the linear order
![]() ${\mathbb L} _{{\mathbb X} _1}$
or to its reverse,
${\mathbb L} _{{\mathbb X} _1}$
or to its reverse,
![]() ${\mathbb L} _{{\mathbb X} _1}^*$
. So we have
${\mathbb L} _{{\mathbb X} _1}^*$
. So we have
 $|({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong }|\leq 2$
.⊣
$|({\mathcal M} ^{\bar {c}}_{{\mathbb Y} _{\mathbb X}})^{\cong }|\leq 2$
.⊣
Finally we prove the second part of Theorem 4.1. By our analysis, the theory
![]() ${\mathcal T}$
is
${\mathcal T}$
is
![]() $\omega $
-categorical iff Case A appears; so, we have to prove that the
$\omega $
-categorical iff Case A appears; so, we have to prove that the
![]() $L_n$
-structure
$L_n$
-structure
![]() ${\mathbb X} _0 =\langle \omega ,\prec , \{ a_0 \} ,\dots ,\{ a_{n-1 }\}\rangle $
is
${\mathbb X} _0 =\langle \omega ,\prec , \{ a_0 \} ,\dots ,\{ a_{n-1 }\}\rangle $
is
![]() $\omega $
-categorical iff
$\omega $
-categorical iff
![]() ${\mathbb L} _{{\mathbb X} _0}:=\langle \omega \setminus F_{\bar {a}}, \prec \upharpoonright (\omega \setminus F_{\bar {a}})\rangle $
is an
${\mathbb L} _{{\mathbb X} _0}:=\langle \omega \setminus F_{\bar {a}}, \prec \upharpoonright (\omega \setminus F_{\bar {a}})\rangle $
is an
![]() $\omega $
-categorical linear order. Since
$\omega $
-categorical linear order. Since
![]() $\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} _0)=\{ \mathop {\mathrm {id}}\nolimits _{F_{\bar {a}}}\cup \,f : f\in \mathop {\mathrm {Aut}}\nolimits ({\mathbb L} _{{\mathbb X} _0}) \}$
, for
$\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} _0)=\{ \mathop {\mathrm {id}}\nolimits _{F_{\bar {a}}}\cup \,f : f\in \mathop {\mathrm {Aut}}\nolimits ({\mathbb L} _{{\mathbb X} _0}) \}$
, for
![]() $n\in {\mathbb N}$
and
$n\in {\mathbb N}$
and
![]() $\bar {x} ,\bar {y} \in (\omega \setminus F_{\bar {a}})^n$
we have
$\bar {x} ,\bar {y} \in (\omega \setminus F_{\bar {a}})^n$
we have
 $\bar {x} \sim _{{\mathbb L} _{{\mathbb X} _0}}\bar {y} \Leftrightarrow \bar {x} \sim _{{\mathbb X} _0}\bar {y} $
, which implies that
$\bar {x} \sim _{{\mathbb L} _{{\mathbb X} _0}}\bar {y} \Leftrightarrow \bar {x} \sim _{{\mathbb X} _0}\bar {y} $
, which implies that
 $|(\omega \setminus F_{\bar {a}})^n /\sim _{{\mathbb L} _{{\mathbb X} _0}}|\leq |\omega ^n /\sim _{{\mathbb X} _0}|$
. So, if
$|(\omega \setminus F_{\bar {a}})^n /\sim _{{\mathbb L} _{{\mathbb X} _0}}|\leq |\omega ^n /\sim _{{\mathbb X} _0}|$
. So, if
![]() ${\mathbb X} _0$
is
${\mathbb X} _0$
is
![]() $\omega $
-categorical, then
$\omega $
-categorical, then
![]() ${\mathbb L} _{{\mathbb X} _0}$
is
${\mathbb L} _{{\mathbb X} _0}$
is
![]() $\omega $
-categorical (by the theorem of Engeler, Ryll-Nardzewski and Svenonius).
$\omega $
-categorical (by the theorem of Engeler, Ryll-Nardzewski and Svenonius).
On the other hand, if
![]() ${\mathbb L} _{{\mathbb X} _0}$
is
${\mathbb L} _{{\mathbb X} _0}$
is
![]() $\omega $
-categorical, then the linear order
$\omega $
-categorical, then the linear order
![]() $\langle \omega ,\prec \rangle \cong n+ {\mathbb L} _{{\mathbb X} _0}$
is
$\langle \omega ,\prec \rangle \cong n+ {\mathbb L} _{{\mathbb X} _0}$
is
![]() $\omega $
-categorical (see Rosenstein’s theorem, [Reference Rosenstein10, p. 299]) and, since
$\omega $
-categorical (see Rosenstein’s theorem, [Reference Rosenstein10, p. 299]) and, since
![]() $\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} _0)=\mathop {\mathrm {Aut}}\nolimits (\langle \omega ,\prec \rangle )$
,
$\mathop {\mathrm {Aut}}\nolimits ({\mathbb X} _0)=\mathop {\mathrm {Aut}}\nolimits (\langle \omega ,\prec \rangle )$
,
![]() ${\mathbb X} _0$
is
${\mathbb X} _0$
is
![]() $\omega $
-categorical too.
$\omega $
-categorical too.
![]() $\Box $
$\Box $
5 Comments and examples
By Fact 2.3 and Theorems 3.1 and 4.1, if a complete theory
![]() ${\mathcal T}$
has an infinite model
${\mathcal T}$
has an infinite model
![]() ${\mathbb Y}$
with bounded profile, that is
${\mathbb Y}$
with bounded profile, that is
![]() $\varphi _{\mathbb Y} \leq m$
, for some
$\varphi _{\mathbb Y} \leq m$
, for some
![]() $m\in {\mathbb N}$
, then
$m\in {\mathbb N}$
, then
![]() $I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
. In Reference Gibson, Pouzet and Woodrow[4], Gibson et al. have considered the extension of the profile function to infinite cardinals and proved that if
$I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
. In Reference Gibson, Pouzet and Woodrow[4], Gibson et al. have considered the extension of the profile function to infinite cardinals and proved that if
![]() ${\mathbb Y}$
is an L-structure such that
${\mathbb Y}$
is an L-structure such that
![]() $\varphi _{\mathbb Y} (\mu )<\omega $
, for some infinite cardinal
$\varphi _{\mathbb Y} (\mu )<\omega $
, for some infinite cardinal
![]() $\mu \leq |Y|$
, then
$\mu \leq |Y|$
, then
![]() ${\mathbb Y}$
is almost chainable (see Theorem 22 of Reference Gibson, Pouzet and Woodrow[4]). So, by Theorems 3.1 and 4.1 we have
${\mathbb Y}$
is almost chainable (see Theorem 22 of Reference Gibson, Pouzet and Woodrow[4]). So, by Theorems 3.1 and 4.1 we have
Corollary 5.1. If a complete theory
![]() ${\mathcal T}$
has a model
${\mathcal T}$
has a model
![]() ${\mathbb Y}$
such that
${\mathbb Y}$
such that
![]() $\varphi _{\mathbb Y} (\mu )<\omega $
, for some infinite cardinal
$\varphi _{\mathbb Y} (\mu )<\omega $
, for some infinite cardinal
![]() $\mu \leq |Y|$
, then
$\mu \leq |Y|$
, then
![]() $I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
.
$I({\mathcal T} ,\omega )\in \{ 1 , {\mathfrak {c}} \}$
.
We note that Example 4.1 of Reference Kurilić[7] shows that if
![]() ${\mathcal T}$
is the complete theory of the ternary betwenness relation defined on the rational line with doubled integers, then
${\mathcal T}$
is the complete theory of the ternary betwenness relation defined on the rational line with doubled integers, then
![]() ${\mathcal T}$
is a complete monomorphic (and, hence, almost chainable) theory which is unstable, does not have definable Skolem functions and has a countable model which is not bi-interpretable with any linear order. By Theorem 4.1 we have
${\mathcal T}$
is a complete monomorphic (and, hence, almost chainable) theory which is unstable, does not have definable Skolem functions and has a countable model which is not bi-interpretable with any linear order. By Theorem 4.1 we have
![]() $I({\mathcal T} ,\omega )= {\mathfrak {c}} $
.
$I({\mathcal T} ,\omega )= {\mathfrak {c}} $
.
Further, Example 4.2 of Reference Kurilić[7] shows that if
![]() ${\mathcal T}$
is the complete theory of the ternary cyclic-order relation defined on the discrete linear order
${\mathcal T}$
is the complete theory of the ternary cyclic-order relation defined on the discrete linear order
![]() $\omega +\omega ^*$
, then the mapping
$\omega +\omega ^*$
, then the mapping
![]() $\Psi $
defined in Claim 4.2(b) is not finite-to-one. Here we have
$\Psi $
defined in Claim 4.2(b) is not finite-to-one. Here we have
![]() $I({\mathcal T} ,\omega )= {\mathfrak {c}} $
again.
$I({\mathcal T} ,\omega )= {\mathfrak {c}} $
again.
Finally, we give three simple examples of ternary almost chainable structures which are not monomorphic.
Example 5.2. Let
![]() $L=\langle R_0\rangle $
,
$L=\langle R_0\rangle $
,
![]() $\mathop {\mathrm {ar}}\nolimits (R_0)=3$
and let
$\mathop {\mathrm {ar}}\nolimits (R_0)=3$
and let
![]() ${\mathbb X} =\langle \omega , <_\omega , \{0 \} ,\{1 \} ,\{2 \}\rangle $
, where
${\mathbb X} =\langle \omega , <_\omega , \{0 \} ,\{1 \} ,\{2 \}\rangle $
, where
![]() $<_\omega $
is the usual strict linear order on
$<_\omega $
is the usual strict linear order on
![]() $\omega $
. Then we have
$\omega $
. Then we have
![]() ${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_3}(\omega )$
, where
${\mathbb X} \in \mathop {\mathrm {Mod}}\nolimits _{L_3}(\omega )$
, where
![]() $L_3 =\langle < ,U_0,U_1,U_2\rangle $
, and the
$L_3 =\langle < ,U_0,U_1,U_2\rangle $
, and the
![]() $L_3$
-formula
$L_3$
-formula
 $$ \begin{align*} \varphi _0(u,v,w) &:= (v_0<v_1<v_2 )\lor (v_1<v_2<v_0 ) \lor ( v_2<v_0<v_1) \\ & \qquad\textstyle \lor \;\;\Big(U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)\Big) \end{align*} $$
$$ \begin{align*} \varphi _0(u,v,w) &:= (v_0<v_1<v_2 )\lor (v_1<v_2<v_0 ) \lor ( v_2<v_0<v_1) \\ & \qquad\textstyle \lor \;\;\Big(U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)\Big) \end{align*} $$
defines the L-structure
![]() ${\mathbb Y} =\langle \omega , R_0 ^{{\mathbb Y} }\rangle $
in
${\mathbb Y} =\langle \omega , R_0 ^{{\mathbb Y} }\rangle $
in
![]() ${\mathbb X}$
. Clearly,
${\mathbb X}$
. Clearly,
![]() $R_0 ^{{\mathbb Y} }$
is the union of the cyclic-order relation defined on the ordinal
$R_0 ^{{\mathbb Y} }$
is the union of the cyclic-order relation defined on the ordinal
![]() $\langle \omega , <_\omega \rangle $
and the set
$\langle \omega , <_\omega \rangle $
and the set
![]() $\{ \langle 0,0,z\rangle :2<_\omega z\}$
. Thus, for example,
$\{ \langle 0,0,z\rangle :2<_\omega z\}$
. Thus, for example,
![]() $\langle 70,80 ,90 \rangle ,\langle 80 , 90 ,0 \rangle ,\langle 90 , 1 ,3 \rangle ,\langle 0 , 0 ,5 \rangle ,\langle 0 ,0 ,90 \rangle \in R_0 ^{{\mathbb Y} }$
. Since
$\langle 70,80 ,90 \rangle ,\langle 80 , 90 ,0 \rangle ,\langle 90 , 1 ,3 \rangle ,\langle 0 , 0 ,5 \rangle ,\langle 0 ,0 ,90 \rangle \in R_0 ^{{\mathbb Y} }$
. Since
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )= \{ y\in Y : \mathop {\mathrm {Age}}\nolimits (Y \setminus \{ y\})\varsubsetneq \mathop {\mathrm {Age}}\nolimits ({\mathbb Y})\}$
(see [Reference Pouzet8, p. 300]), it is easy to check that
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )= \{ y\in Y : \mathop {\mathrm {Age}}\nolimits (Y \setminus \{ y\})\varsubsetneq \mathop {\mathrm {Age}}\nolimits ({\mathbb Y})\}$
(see [Reference Pouzet8, p. 300]), it is easy to check that
![]() $\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )=3 =\{0,1,2\}$
(for example, for
$\mathop {\mathrm {Ker}}\nolimits ({\mathbb Y} )=3 =\{0,1,2\}$
(for example, for
![]() $K:=\{ 0,1,2,3\}$
we have
$K:=\{ 0,1,2,3\}$
we have
![]() ${\mathbb K} \not \hookrightarrow Y\setminus \{ 1\} $
). Here we have case (iii) of Theorem 2.5 and
${\mathbb K} \not \hookrightarrow Y\setminus \{ 1\} $
). Here we have case (iii) of Theorem 2.5 and
![]() $I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ) ,\omega )= {\mathfrak {c}} $
.
$I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ) ,\omega )= {\mathfrak {c}} $
.
Example 5.3. If in Example 5.2 we take the
![]() $L_3$
-formula
$L_3$
-formula
![]() $\varphi _0' (v_0,v_1,v_2)$
given by
$\varphi _0' (v_0,v_1,v_2)$
given by
 $$ \begin{align*} & \textstyle\Big(\bigwedge _{i,j<3}\neg U_j (v_i) \land ((v_0<v_1<v_2 ) \lor (v_1<v_2<v_0) \lor (v_2<v_0<v_1))\Big) \\ & \textstyle \lor \;\;\Big(U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)\Big), \end{align*} $$
$$ \begin{align*} & \textstyle\Big(\bigwedge _{i,j<3}\neg U_j (v_i) \land ((v_0<v_1<v_2 ) \lor (v_1<v_2<v_0) \lor (v_2<v_0<v_1))\Big) \\ & \textstyle \lor \;\;\Big(U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)\Big), \end{align*} $$
we obtain the ternary almost chainable structure
 ${\mathbb Y} '=\langle \omega , R_0 ^{{\mathbb Y} '}\rangle $
. Now, the relation
${\mathbb Y} '=\langle \omega , R_0 ^{{\mathbb Y} '}\rangle $
. Now, the relation
 $R_0 ^{{\mathbb Y} '}$
is the union of the cyclic-order relation defined on the linear order
$R_0 ^{{\mathbb Y} '}$
is the union of the cyclic-order relation defined on the linear order
![]() $\langle \omega \setminus 3 , <_\omega \rangle $
and the set
$\langle \omega \setminus 3 , <_\omega \rangle $
and the set
![]() $\{ \langle 0,0,z\rangle :z\in \omega \setminus 3\}$
. Here we have case (ii) of Theorem 2.5 and, by Theorem 4.1, the equality
$\{ \langle 0,0,z\rangle :z\in \omega \setminus 3\}$
. Here we have case (ii) of Theorem 2.5 and, by Theorem 4.1, the equality
![]() $I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ') ,\omega )= {\mathfrak {c}} $
holds again.
$I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} ') ,\omega )= {\mathfrak {c}} $
holds again.
Example 5.4. If in Example 5.2 we take
 $\varphi _0'' (v_0,v_1,v_2):= U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)$
, we obtain
$\varphi _0'' (v_0,v_1,v_2):= U_0(v_0)\land U_0(v_1)\land \bigwedge _{j<3}\neg U_j(v_3)$
, we obtain
 ${\mathbb Y} ''=\langle \omega , R_0 ^{{\mathbb Y} ''}\rangle $
, where
${\mathbb Y} ''=\langle \omega , R_0 ^{{\mathbb Y} ''}\rangle $
, where
 $R_0 ^{{\mathbb Y} ''}=\{ \langle 0,0,z\rangle :z\in \omega \setminus 3\}$
. Now we have case (i) of Theorem 2.5 and, by Theorem 4.1,
$R_0 ^{{\mathbb Y} ''}=\{ \langle 0,0,z\rangle :z\in \omega \setminus 3\}$
. Now we have case (i) of Theorem 2.5 and, by Theorem 4.1,
![]() $I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} '') ,\omega )= 1 $
.
$I(\mathop {\mathrm {Th}}\nolimits ({\mathbb Y} '') ,\omega )= 1 $
.
Acknowledgements
The author acknowledges financial support of the Ministry of Education, Science and Technological Development of the Republic of Serbia (Grant No. 451-03-68/2020-14/200125).
The author would like to thank the referee for constructive suggestions.