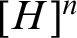1 Introduction
In this paper, we study the computability-theoretic strength of Ramsey’s theorem when we weaken the notion of homogeneous set by allowing more colors. The resulting weakenings are known as thin set theorems. In particular, we show that some thin set theorems are sufficiently weak not to imply the Erdős–Moser theorem in reverse mathematics.
Reverse mathematics is a foundational program which seeks to determine the optimal axioms to prove “ordinary” theorems [Reference Friedman3]. It uses the framework of subsystems of second-order arithmetic, with a base theory called
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, informally capturing “computable mathematics.” When the first-order part consists of the standard integers, the models of
$\operatorname {\mathrm {\sf {RCA}_0}}$
, informally capturing “computable mathematics.” When the first-order part consists of the standard integers, the models of
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
are fully specified by their second-order parts, which are precisely the Turing ideals. A Turing ideal
$\operatorname {\mathrm {\sf {RCA}_0}}$
are fully specified by their second-order parts, which are precisely the Turing ideals. A Turing ideal
![]() $\mathcal {I}$
is a collection of sets which is closed downward under the Turing reduction
$\mathcal {I}$
is a collection of sets which is closed downward under the Turing reduction
![]() $(\forall X \in \mathcal {I})(\forall Y \leq _T X) Y \in \mathcal {I}$
and closed under the effective join
$(\forall X \in \mathcal {I})(\forall Y \leq _T X) Y \in \mathcal {I}$
and closed under the effective join
![]() $(\forall X, Y \in \mathcal {I}) X \oplus Y \in \mathcal {I}$
. We shall only consider such models, called
$(\forall X, Y \in \mathcal {I}) X \oplus Y \in \mathcal {I}$
. We shall only consider such models, called
![]() $\omega $
-models.
$\omega $
-models.
The early study of reverse mathematics has seen the emergence of four subsystems of second-order arithmetic linearly ordered by the provability relation, such that most of the ordinary theorems are either provable in
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, or equivalent in
$\operatorname {\mathrm {\sf {RCA}_0}}$
, or equivalent in
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
to one of them. These subsystems, together with
$\operatorname {\mathrm {\sf {RCA}_0}}$
to one of them. These subsystems, together with
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, form the “Big Five” [Reference Montalbán11]. Among them, let us mention
$\operatorname {\mathrm {\sf {RCA}_0}}$
, form the “Big Five” [Reference Montalbán11]. Among them, let us mention
![]() $\operatorname {\mathrm {\sf {ACA}}}$
, standing for arithmetical comprehension axiom, and
$\operatorname {\mathrm {\sf {ACA}}}$
, standing for arithmetical comprehension axiom, and
![]() $\operatorname {\mathrm {\sf {WKL}}}$
, standing for weak König’s lemma, which states that every infinite binary tree has an infinite path. See Simpson [Reference Simpson20] for a good introduction to reverse mathematics. Among the theorems studied in reverse mathematics, Ramsey’s theorem plays an important role, since Ramsey’s theorem for pairs is historically the first example of statement which does not satisfy this empirical observation.
$\operatorname {\mathrm {\sf {WKL}}}$
, standing for weak König’s lemma, which states that every infinite binary tree has an infinite path. See Simpson [Reference Simpson20] for a good introduction to reverse mathematics. Among the theorems studied in reverse mathematics, Ramsey’s theorem plays an important role, since Ramsey’s theorem for pairs is historically the first example of statement which does not satisfy this empirical observation.
Definition 1.1 (Ramsey’s theorem)
A subset H of
![]() $\omega $
is homogeneous for a coloring
$\omega $
is homogeneous for a coloring
![]() $f : [\omega ]^n \to k$
(or f-homogeneous) if each n-tuple over H is given the same color by f.
$f : [\omega ]^n \to k$
(or f-homogeneous) if each n-tuple over H is given the same color by f.
![]() $\operatorname {\mathrm {\sf {RT}}}^n_k$
is the statement “Every coloring
$\operatorname {\mathrm {\sf {RT}}}^n_k$
is the statement “Every coloring
![]() $f : [\omega ]^n \to k$
has an infinite f-homogeneous set.”
$f : [\omega ]^n \to k$
has an infinite f-homogeneous set.”
 $\operatorname {\mathrm {\sf {RT}}}^1_k$
is nothing but the infinite pigeonhole principle which is provable in
$\operatorname {\mathrm {\sf {RT}}}^1_k$
is nothing but the infinite pigeonhole principle which is provable in
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
. Jockusch [Reference Jockusch6] (see Simpson [Reference Simpson20]) proved that
$\operatorname {\mathrm {\sf {RCA}_0}}$
. Jockusch [Reference Jockusch6] (see Simpson [Reference Simpson20]) proved that
![]() $\operatorname {\mathrm {\sf {RT}}}^n_k$
is equivalent to
$\operatorname {\mathrm {\sf {RT}}}^n_k$
is equivalent to
![]() $\operatorname {\mathrm {\sf {ACA}}}$
over
$\operatorname {\mathrm {\sf {ACA}}}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
whenever
$\operatorname {\mathrm {\sf {RCA}_0}}$
whenever
![]() $n \geq 3$
, and that
$n \geq 3$
, and that
![]() $\operatorname {\mathrm {\sf {WKL}}}$
does not imply
$\operatorname {\mathrm {\sf {WKL}}}$
does not imply
 $\operatorname {\mathrm {\sf {RT}}}^2_2$
over
$\operatorname {\mathrm {\sf {RT}}}^2_2$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
. The computability-theoretic strength of Ramsey’s theorem for pairs was unknown for a long time, until Seetapun [Reference Seetapun and Slaman19] proved that
$\operatorname {\mathrm {\sf {RCA}_0}}$
. The computability-theoretic strength of Ramsey’s theorem for pairs was unknown for a long time, until Seetapun [Reference Seetapun and Slaman19] proved that
 $\operatorname {\mathrm {\sf {RT}}}^2_2$
does not imply
$\operatorname {\mathrm {\sf {RT}}}^2_2$
does not imply
![]() $\operatorname {\mathrm {\sf {ACA}}}$
over
$\operatorname {\mathrm {\sf {ACA}}}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, and that the first author [Reference Liu9] proved that
$\operatorname {\mathrm {\sf {RCA}_0}}$
, and that the first author [Reference Liu9] proved that
 $\operatorname {\mathrm {\sf {RT}}}^2_2$
does not imply
$\operatorname {\mathrm {\sf {RT}}}^2_2$
does not imply
![]() $\operatorname {\mathrm {\sf {WKL}}}$
over
$\operatorname {\mathrm {\sf {WKL}}}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, thereby showing that
$\operatorname {\mathrm {\sf {RCA}_0}}$
, thereby showing that
 $\operatorname {\mathrm {\sf {RT}}}^2_2$
is not even linearly ordered with the Big Five.
$\operatorname {\mathrm {\sf {RT}}}^2_2$
is not even linearly ordered with the Big Five.
This analysis of Ramsey’s theorem naturally started new research axis, among which the search for weakenings of Ramsey’s theorem for arbitrary n-tuples which would not imply
![]() $\operatorname {\mathrm {\sf {ACA}}}$
. Ramsey’s theorem can be seen as a problem, whose instances are k-colorings of
$\operatorname {\mathrm {\sf {ACA}}}$
. Ramsey’s theorem can be seen as a problem, whose instances are k-colorings of
![]() $[\omega ]^n$
, and whose solutions are infinite homogeneous sets. This problem has two explicit parameters, namely, the size n of the n-tuples, and the number k of colors of the coloring. There is one implicit parameter which is the number of colors
$[\omega ]^n$
, and whose solutions are infinite homogeneous sets. This problem has two explicit parameters, namely, the size n of the n-tuples, and the number k of colors of the coloring. There is one implicit parameter which is the number of colors
![]() $\ell $
allowed in the solution. In the case of a homogeneous set,
$\ell $
allowed in the solution. In the case of a homogeneous set,
![]() $\ell = 1$
. In this paper, we give a partial answer to the following question.
$\ell = 1$
. In this paper, we give a partial answer to the following question.
![]() $\bullet $
How does the number of colors allowed in a solution impact the computability-theoretic strength of Ramsey’s theorem?
$\bullet $
How does the number of colors allowed in a solution impact the computability-theoretic strength of Ramsey’s theorem?
We are in particular interested in the case where
![]() $\ell = k-1$
. This yields the notion of thin set.
$\ell = k-1$
. This yields the notion of thin set.
Definition 1.2 (Thin set theorem)
Given a coloring
![]() $f : [\omega ]^n \to k$
(resp.
$f : [\omega ]^n \to k$
(resp.
![]() $f : [\omega ]^n \to \omega $
), a set H is thin for f (or f-thin) if
$f : [\omega ]^n \to \omega $
), a set H is thin for f (or f-thin) if
![]() $|f([H]^n)| \leq k-1$
(resp.
$|f([H]^n)| \leq k-1$
(resp.
![]() $f([H]^n) \neq \omega $
). For every
$f([H]^n) \neq \omega $
). For every
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
is the statement “Every coloring
$\operatorname {\mathrm {\sf {TS}}}^n_k$
is the statement “Every coloring
![]() $f : [\omega ]^n \to k$
has an infinite f-thin set” and
$f : [\omega ]^n \to k$
has an infinite f-thin set” and
![]() $\operatorname {\mathrm {\sf {TS}}}^n_\omega $
is the statement “Every coloring
$\operatorname {\mathrm {\sf {TS}}}^n_\omega $
is the statement “Every coloring
![]() $f : [\omega ]^n \to \omega $
has an infinite f-thin set.”
$f : [\omega ]^n \to \omega $
has an infinite f-thin set.”
In particular,
![]() $\operatorname {\mathrm {\sf {TS}}}^n_2$
is Ramsey’s theorem for n-tuples and two colors. The thin set theorem
$\operatorname {\mathrm {\sf {TS}}}^n_2$
is Ramsey’s theorem for n-tuples and two colors. The thin set theorem
![]() $\operatorname {\mathrm {\sf {TS}}}^n_\omega $
was introduced in reverse mathematics by Friedman [Reference Friedman and James4] and studied by Cholak et al. [Reference Cholak, Giusto, Hirst, Jockusch and Ross2]. Wang [Reference Wang21] proved the surprising result that for every
$\operatorname {\mathrm {\sf {TS}}}^n_\omega $
was introduced in reverse mathematics by Friedman [Reference Friedman and James4] and studied by Cholak et al. [Reference Cholak, Giusto, Hirst, Jockusch and Ross2]. Wang [Reference Wang21] proved the surprising result that for every
![]() $n \geq 1$
and every sufficiently large k (with an explicit upper bound on k),
$n \geq 1$
and every sufficiently large k (with an explicit upper bound on k),
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply
$\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply
![]() $\operatorname {\mathrm {\sf {ACA}}}$
, thereby showing that allowing more colors in the solutions yields a strict weakening of Ramsey’s theorem, which is already reflected in reverse mathematics. The second author refined Wang’s analysis by proving that for every
$\operatorname {\mathrm {\sf {ACA}}}$
, thereby showing that allowing more colors in the solutions yields a strict weakening of Ramsey’s theorem, which is already reflected in reverse mathematics. The second author refined Wang’s analysis by proving that for every
![]() $n,m,\ell \in \omega $
with
$n,m,\ell \in \omega $
with
![]() $m>1$
and every sufficiently large k,
$m>1$
and every sufficiently large k,
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
implies neither
$\operatorname {\mathrm {\sf {TS}}}^n_k$
implies neither
![]() $\operatorname {\mathrm {\sf {WKL}}}$
[Reference Patey13], nor
$\operatorname {\mathrm {\sf {WKL}}}$
[Reference Patey13], nor
![]() $\operatorname {\mathrm {\sf {TS}}}^m_\ell $
[Reference Patey18]. In particular, the statement
$\operatorname {\mathrm {\sf {TS}}}^m_\ell $
[Reference Patey18]. In particular, the statement
![]() $(\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply
$(\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply
 $\operatorname {\mathrm {\sf {RT}}}^2_2$
over
$\operatorname {\mathrm {\sf {RT}}}^2_2$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
. In this paper, we partially answer the following sub-question.
$\operatorname {\mathrm {\sf {RCA}_0}}$
. In this paper, we partially answer the following sub-question.
![]() $\bullet $
What consequences of Ramsey’s theorem for pairs are already consequences of the various thin set theorems in reverse mathematics?
$\bullet $
What consequences of Ramsey’s theorem for pairs are already consequences of the various thin set theorems in reverse mathematics?
The thin set theorem for pairs with
![]() $\omega $
colors (
$\omega $
colors (
 $\operatorname {\mathrm {\sf {TS}}}^2_\omega $
) seems combinatorially very weak, however, it has a diagonalization power similar to Ramsey’s theorem for pairs. For example, there is a computable instance of
$\operatorname {\mathrm {\sf {TS}}}^2_\omega $
) seems combinatorially very weak, however, it has a diagonalization power similar to Ramsey’s theorem for pairs. For example, there is a computable instance of
 $\operatorname {\mathrm {\sf {TS}}}^2_\omega $
with no
$\operatorname {\mathrm {\sf {TS}}}^2_\omega $
with no
![]() $\Sigma ^0_2$
solution [Reference Cholak, Giusto, Hirst, Jockusch and Ross2], and given any low
$\Sigma ^0_2$
solution [Reference Cholak, Giusto, Hirst, Jockusch and Ross2], and given any low
![]() $_2$
set X, there is a computable instance of
$_2$
set X, there is a computable instance of
 $\operatorname {\mathrm {\sf {TS}}}^2_\omega $
with no X-computable solution [Reference Patey14]. One can strengthen the thin set theorem by asking, given a coloring
$\operatorname {\mathrm {\sf {TS}}}^2_\omega $
with no X-computable solution [Reference Patey14]. One can strengthen the thin set theorem by asking, given a coloring
![]() $f : [\omega ]^n \to \omega $
, for an infinite set H such that
$f : [\omega ]^n \to \omega $
, for an infinite set H such that
![]() $H \smallsetminus \{x\}$
is f-thin for every
$H \smallsetminus \{x\}$
is f-thin for every
![]() $x \in H$
. This yields the notion of free set.
$x \in H$
. This yields the notion of free set.
Definition 1.3 (Free set theorem)
Given a coloring
![]() $f : [\omega ]^n \to \omega $
, a set H is free for f (or f-free) if for every
$f : [\omega ]^n \to \omega $
, a set H is free for f (or f-free) if for every
![]() $\sigma \in [H]^n$
,
$\sigma \in [H]^n$
,
![]() $f(\sigma ) \in H \rightarrow f(\sigma ) \in \sigma $
. For every
$f(\sigma ) \in H \rightarrow f(\sigma ) \in \sigma $
. For every
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
is the statement “Every coloring
$\operatorname {\mathrm {\sf {FS}}}^n$
is the statement “Every coloring
![]() $f : [\omega ]^n \to \omega $
has an infinite f-free set.”
$f : [\omega ]^n \to \omega $
has an infinite f-free set.”
The free set theorem is usually studied together with the thin set theorem, as they are combinatorially very close. The standard proof of
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
involves the statement
$\operatorname {\mathrm {\sf {FS}}}^n$
involves the statement
![]() $(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
in a way that propagates most of the computability-theoretic properties of the thin set theorem to the free set theorem. This is why any known proof that
$(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
in a way that propagates most of the computability-theoretic properties of the thin set theorem to the free set theorem. This is why any known proof that
![]() $(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply another statement
$(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
does not imply another statement
![]() $\mathsf {P}$
over
$\mathsf {P}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
empirically yields a proof that
$\operatorname {\mathrm {\sf {RCA}_0}}$
empirically yields a proof that
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
does not imply
$\operatorname {\mathrm {\sf {FS}}}^n$
does not imply
![]() $\mathsf {P}$
[Reference Cholak, Giusto, Hirst, Jockusch and Ross2, Reference Patey13, Reference Patey18, Reference Wang21]. This will again be the case in our paper.
$\mathsf {P}$
[Reference Cholak, Giusto, Hirst, Jockusch and Ross2, Reference Patey13, Reference Patey18, Reference Wang21]. This will again be the case in our paper.
1.1 Main results
Ramsey’s theorem for pairs admits various decompositions into conjunctions of strictly weaker statements. Among them, the decomposition into the Erdős–Moser theorem and the Ascending Descending sequence principle is particularly interesting for various technical reasons.
Definition 1.4 (Erdős–Moser theorem)
A tournament T is an irreflexive binary relation such that for all
![]() $x,y \in \omega $
with
$x,y \in \omega $
with
![]() $x \not = y$
, exactly one of
$x \not = y$
, exactly one of
![]() $T(x,y)$
or
$T(x,y)$
or
![]() $T(y,x)$
holds. A set H is T-transitive if the relation T over H is transitive in the usual sense.
$T(y,x)$
holds. A set H is T-transitive if the relation T over H is transitive in the usual sense.
![]() $\operatorname {\mathrm {\sf {EM}}}$
is the statement “Every infinite tournament T has an infinite transitive subtournament.”
$\operatorname {\mathrm {\sf {EM}}}$
is the statement “Every infinite tournament T has an infinite transitive subtournament.”
Definition 1.5 (Ascending descending sequence)
Given a linear order
![]() $(L, <_L)$
, an ascending (descending) sequence is a set S such that for every
$(L, <_L)$
, an ascending (descending) sequence is a set S such that for every
![]() $x <_{\mathbb {N}} y \in S$
,
$x <_{\mathbb {N}} y \in S$
,
![]() $x <_L y$
(
$x <_L y$
(
![]() $x>_L y$
).
$x>_L y$
).
![]() $\operatorname {\mathrm {\sf {ADS}}}$
is the statement “Every infinite linear order admits an infinite ascending or descending sequence.”
$\operatorname {\mathrm {\sf {ADS}}}$
is the statement “Every infinite linear order admits an infinite ascending or descending sequence.”
Bovykin and Weiermann [Reference Bovykin and Weiermann1] proved Ramsey’s theorem for pairs as follows: Given a coloring
![]() $f : [\mathbb {N}]^2 \to 2$
, we can see f as a tournament T such that whenever
$f : [\mathbb {N}]^2 \to 2$
, we can see f as a tournament T such that whenever
![]() $x <_{\mathbb {N}} y$
,
$x <_{\mathbb {N}} y$
,
![]() $T(x,y)$
holds if and only if
$T(x,y)$
holds if and only if
![]() $f(x,y) = 1$
. Any T-transitive set H can be seen as a linear order
$f(x,y) = 1$
. Any T-transitive set H can be seen as a linear order
![]() $(H, \prec )$
such that for every
$(H, \prec )$
such that for every
![]() $x <_{\mathbb {N}} y$
:
$x <_{\mathbb {N}} y$
:
![]() $x \prec y$
if and only if
$x \prec y$
if and only if
![]() $f(x,y) = 1$
. Any infinite ascending or descending sequence is f-homogeneous. It is therefore natural to study the ascending descending sequence principle together with the Erdős–Moser theorem. Lerman et al. [Reference Lerman, Solomon and Towsner8] proved that
$f(x,y) = 1$
. Any infinite ascending or descending sequence is f-homogeneous. It is therefore natural to study the ascending descending sequence principle together with the Erdős–Moser theorem. Lerman et al. [Reference Lerman, Solomon and Towsner8] proved that
![]() $\operatorname {\mathrm {\sf {EM}}}$
does not imply
$\operatorname {\mathrm {\sf {EM}}}$
does not imply
![]() $\operatorname {\mathrm {\sf {ADS}}}$
over
$\operatorname {\mathrm {\sf {ADS}}}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
, while Hirschfeldt and Shore [Reference Hirschfeldt and Shore5] proved that
$\operatorname {\mathrm {\sf {RCA}_0}}$
, while Hirschfeldt and Shore [Reference Hirschfeldt and Shore5] proved that
![]() $\operatorname {\mathrm {\sf {ADS}}}$
does not imply
$\operatorname {\mathrm {\sf {ADS}}}$
does not imply
![]() $\operatorname {\mathrm {\sf {EM}}}$
. The second author asked [Reference Patey18] whether any of
$\operatorname {\mathrm {\sf {EM}}}$
. The second author asked [Reference Patey18] whether any of
![]() $\operatorname {\mathrm {\sf {FS}}}^2$
,
$\operatorname {\mathrm {\sf {FS}}}^2$
,
 $\operatorname {\mathrm {\sf {TS}}}^2_\omega $
, or
$\operatorname {\mathrm {\sf {TS}}}^2_\omega $
, or
 $\operatorname {\mathrm {\sf {TS}}}^2_3$
implies
$\operatorname {\mathrm {\sf {TS}}}^2_3$
implies
![]() $\operatorname {\mathrm {\sf {EM}}}$
over
$\operatorname {\mathrm {\sf {EM}}}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
. We answer this question negatively, even for stable restrictions of the Erdős–Moser theorem.
$\operatorname {\mathrm {\sf {RCA}_0}}$
. We answer this question negatively, even for stable restrictions of the Erdős–Moser theorem.
Theorem 1.6. Over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
,
$\operatorname {\mathrm {\sf {RCA}_0}}$
,
 $\operatorname {\mathrm {\sf {WKL}}} + \operatorname {\mathrm {\sf {COH}}} + \operatorname {\mathrm {\sf {TS}}}^2_4 + (\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k + (\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
implies none of
$\operatorname {\mathrm {\sf {WKL}}} + \operatorname {\mathrm {\sf {COH}}} + \operatorname {\mathrm {\sf {TS}}}^2_4 + (\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k + (\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
implies none of
![]() $\operatorname {\mathrm {\sf {SEM}}}$
,
$\operatorname {\mathrm {\sf {SEM}}}$
,
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
and
$\operatorname {\mathrm {\sf {STS}}}^2_3$
and
![]() $\operatorname {\mathrm {\sf {SADS}}}$
.
$\operatorname {\mathrm {\sf {SADS}}}$
.
In Theorem 1.6,
 $\operatorname {\mathrm {\sf {STS}}}^2_k$
,
$\operatorname {\mathrm {\sf {STS}}}^2_k$
,
![]() $\operatorname {\mathrm {\sf {SEM}}}$
and
$\operatorname {\mathrm {\sf {SEM}}}$
and
![]() $\operatorname {\mathrm {\sf {SADS}}}$
denote the restriction of
$\operatorname {\mathrm {\sf {SADS}}}$
denote the restriction of
 $\operatorname {\mathrm {\sf {TS}}}^2_k$
,
$\operatorname {\mathrm {\sf {TS}}}^2_k$
,
![]() $\operatorname {\mathrm {\sf {EM}}}$
and
$\operatorname {\mathrm {\sf {EM}}}$
and
![]() $\operatorname {\mathrm {\sf {ADS}}}$
to stable colorings, respectively. A coloring
$\operatorname {\mathrm {\sf {ADS}}}$
to stable colorings, respectively. A coloring
![]() $f : [\omega ]^2 \to k$
is stable if for every
$f : [\omega ]^2 \to k$
is stable if for every
![]() $x \in \omega $
,
$x \in \omega $
,
![]() $\lim _s f(x, s)$
exists. In the case of
$\lim _s f(x, s)$
exists. In the case of
![]() $\operatorname {\mathrm {\sf {SADS}}}$
, this yields the statement “Every linear order of type
$\operatorname {\mathrm {\sf {SADS}}}$
, this yields the statement “Every linear order of type
![]() $\omega +\omega ^{*}$
has an infinite ascending or descending sequence.”
$\omega +\omega ^{*}$
has an infinite ascending or descending sequence.”
![]() $\operatorname {\mathrm {\sf {COH}}}$
is the statement “For every sequence of sets
$\operatorname {\mathrm {\sf {COH}}}$
is the statement “For every sequence of sets
 $\vec R=(R_0, R_1, \dots )$
, there is an infinite set C such that
$\vec R=(R_0, R_1, \dots )$
, there is an infinite set C such that
![]() $C \subseteq ^{*} R_i$
or
$C \subseteq ^{*} R_i$
or
![]() $C \subseteq ^{*} \overline {R}_i$
for every
$C \subseteq ^{*} \overline {R}_i$
for every
![]() $i \in \omega $
.” Such set C is called
$i \in \omega $
.” Such set C is called
![]() $\vec R$
-cohesive.
$\vec R$
-cohesive.
The separation result, Theorem 1.6, shows that although the thin set theorem shares many lower bounds with Ramsey’s theorem, allowing more colors in the solutions yields a statement with strictly weaker computability-theoretic properties. Cholak et al. [Reference Cholak, Giusto, Hirst, Jockusch and Ross2] Question 7.4 asked whether
![]() $\mathsf {FS}^2+\mathsf {CAC}$
implies
$\mathsf {FS}^2+\mathsf {CAC}$
implies
 $\mathsf {RT}_2^2$
. Bovykin and Weiermann [Reference Bovykin and Weiermann1] proved that
$\mathsf {RT}_2^2$
. Bovykin and Weiermann [Reference Bovykin and Weiermann1] proved that
 $\mathsf {RT}_2^2$
is equivalent to
$\mathsf {RT}_2^2$
is equivalent to
![]() $\mathsf {EM}+\mathsf {ADS}$
. It’s well known
$\mathsf {EM}+\mathsf {ADS}$
. It’s well known
![]() $\mathsf {CAC}$
implies
$\mathsf {CAC}$
implies
![]() $\mathsf {ADS}$
. Thus Theorem 1.6 (
$\mathsf {ADS}$
. Thus Theorem 1.6 (
![]() $\mathsf {FS}^2$
does not imply
$\mathsf {FS}^2$
does not imply
![]() $\mathsf {EM}$
) is a partial result towards a negative answer to Cholak et al.’s question.
$\mathsf {EM}$
) is a partial result towards a negative answer to Cholak et al.’s question.
For a problem
![]() $\mathsf {P}$
, a computable
$\mathsf {P}$
, a computable
![]() $\mathsf {P}$
-instance
$\mathsf {P}$
-instance
![]() $I^*$
is universal iff for every computable
$I^*$
is universal iff for every computable
![]() $\mathsf {P}$
-instance I, every solution of
$\mathsf {P}$
-instance I, every solution of
![]() $I^*$
computes a solution of I. The most well known example of a universal instance is for
$I^*$
computes a solution of I. The most well known example of a universal instance is for
![]() $\mathsf {WKL}$
, there is a computable tree
$\mathsf {WKL}$
, there is a computable tree
![]() $T^*\subseteq 2^{<\omega }$
so that every infinite path through
$T^*\subseteq 2^{<\omega }$
so that every infinite path through
![]() $T^*$
is of PA degree. Thus every infinite path through
$T^*$
is of PA degree. Thus every infinite path through
![]() $T^*$
computes an infinite path of a given computable infinite tree
$T^*$
computes an infinite path of a given computable infinite tree
![]() $ T$
. Patey [Reference Patey14] systematically studied which Ramsey type problem admits universal instance. Many Ramsey type problems do not admit a universal instance. Often, if a problem admits a universal instance, it is relatively easy to construct one. The coding is not hard when it exists. For several problems, the question remains. The second author asked in [Reference Patey15] that whether
$ T$
. Patey [Reference Patey14] systematically studied which Ramsey type problem admits universal instance. Many Ramsey type problems do not admit a universal instance. Often, if a problem admits a universal instance, it is relatively easy to construct one. The coding is not hard when it exists. For several problems, the question remains. The second author asked in [Reference Patey15] that whether
![]() $\mathsf {EM}$
admits a universal instance. We answer this question negatively.
$\mathsf {EM}$
admits a universal instance. We answer this question negatively.
Theorem 1.7.
![]() $\mathsf {EM}$
does not have universal instance.
$\mathsf {EM}$
does not have universal instance.
The first author asked a similar question with respect to an arbitrary instance of
 $\mathsf {RT}_2^1$
. Clearly, when an instance is universal, it encodes information about every other computable instance. For a problem
$\mathsf {RT}_2^1$
. Clearly, when an instance is universal, it encodes information about every other computable instance. For a problem
![]() $\mathsf {P}$
, we consider the mass problem generated by instances of
$\mathsf {P}$
, we consider the mass problem generated by instances of
![]() $\mathsf {P}$
. For
$\mathsf {P}$
. For
![]() $\mathsf {P}$
-instances
$\mathsf {P}$
-instances
![]() $I,\hat I$
(not necessarily computable), we say I encodes
$I,\hat I$
(not necessarily computable), we say I encodes
![]() $\hat I$
iff every solution of I computes a solution of
$\hat I$
iff every solution of I computes a solution of
![]() $\hat I$
. That is, the set of solutions of
$\hat I$
. That is, the set of solutions of
![]() $\hat I$
is Muchnick reducible to that of I. Liu [Reference Liu10] asked whether there is a
$\hat I$
is Muchnick reducible to that of I. Liu [Reference Liu10] asked whether there is a
 $\mathsf {RT}_2^1$
instance X that is maximal (in the lattice of the encoding relation) in the sense that for every
$\mathsf {RT}_2^1$
instance X that is maximal (in the lattice of the encoding relation) in the sense that for every
 $\mathsf {RT}_2^1$
instance Y, if Y encodes X, then X encodes Y.
$\mathsf {RT}_2^1$
instance Y, if Y encodes X, then X encodes Y.
1.2 Organization
The paper is divided into two main sections, corresponding to the proofs of Theorems 1.6, 1.7, respectively. In Section 2, we introduce a framework for preservation of 2-hyperimmunity, and develop its basic properties in subsection 2.1. We then prove in subsection 2.3 that
 $\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity, and then generalize the proof to
$\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity, and then generalize the proof to
![]() $(\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
in Section 2.5. We prove that
$(\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k$
in Section 2.5. We prove that
![]() $\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity in Section 2.6, and again generalize it to
$\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity in Section 2.6, and again generalize it to
![]() $(\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
in Section 2.7. In Section 3, we prove Theorem 1.7.
$(\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
in Section 2.7. In Section 3, we prove Theorem 1.7.
1.3 Notation
Given two sets A and B, we write
![]() $A < B$
iff
$A < B$
iff
![]() $x<y$
for all
$x<y$
for all
![]() $x\in A,y\in B$
(
$x\in A,y\in B$
(
![]() $A < \emptyset $
and
$A < \emptyset $
and
![]() $\emptyset < B$
both hold); we write
$\emptyset < B$
both hold); we write
![]() $A>y$
iff
$A>y$
iff
![]() $x>y$
for all
$x>y$
for all
![]() $x\in A$
. We use
$x\in A$
. We use
![]() $|A|$
to denote the cardinal of the set A. Denote by
$|A|$
to denote the cardinal of the set A. Denote by
![]() $[A]^n$
the collection of n-element subsets of A;
$[A]^n$
the collection of n-element subsets of A;
![]() $[A]^{<\omega }$
the collection of finite subsets of A. Usually, we use
$[A]^{<\omega }$
the collection of finite subsets of A. Usually, we use
![]() $F,E,D$
and sometimes
$F,E,D$
and sometimes
![]() $\sigma ,\tau $
to denote finite sets of integers;
$\sigma ,\tau $
to denote finite sets of integers;
![]() $X,Y,Z$
to denote infinite sets of integers;
$X,Y,Z$
to denote infinite sets of integers;
![]() $A,B,H,G$
to denote sets of integers.
$A,B,H,G$
to denote sets of integers.
A Mathias condition is a pair
![]() $(F, X)$
where F is a finite set, X is an infinite set. A condition
$(F, X)$
where F is a finite set, X is an infinite set. A condition
![]() $(E, Y)$
extends
$(E, Y)$
extends
![]() $(F, X)$
(written
$(F, X)$
(written
![]() $(E, Y) \leq (F,X)$
) if
$(E, Y) \leq (F,X)$
) if
 $E\supseteq F, E\smallsetminus F>F, E\smallsetminus F\subseteq X, Y\subseteq X$
. Note that we do not require
$E\supseteq F, E\smallsetminus F>F, E\smallsetminus F\subseteq X, Y\subseteq X$
. Note that we do not require
![]() $F < X$
for a condition
$F < X$
for a condition
![]() $(F, X)$
, but continuity is ensured by the extension relation. A set G satisfies a Mathias condition
$(F, X)$
, but continuity is ensured by the extension relation. A set G satisfies a Mathias condition
![]() $(F, X)$
if
$(F, X)$
if
![]() $F \subseteq G$
,
$F \subseteq G$
,
![]() $G \smallsetminus F \subseteq X, G\smallsetminus F>F$
. A Mathias condition c is seen as the collection
$G \smallsetminus F \subseteq X, G\smallsetminus F>F$
. A Mathias condition c is seen as the collection
![]() $\{G:G\text { satisfies }(F,X)\}$
; we define
$\{G:G\text { satisfies }(F,X)\}$
; we define
![]() $c\leq d$
iff the collection of c is a sub collection of d. We adopt the convention that if
$c\leq d$
iff the collection of c is a sub collection of d. We adopt the convention that if
![]() $\Phi ^F(n)\downarrow $
and
$\Phi ^F(n)\downarrow $
and
![]() $G>F$
, then
$G>F$
, then
![]() $\Phi ^{F\cup G}(n)\downarrow =\Phi ^F(n)$
.
$\Phi ^{F\cup G}(n)\downarrow =\Phi ^F(n)$
.
2 Free and thin sets which are not transitive
This section is devoted to the proof of Theorem 1.6 that we recall now.
Theorem 1.6. Over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
,
$\operatorname {\mathrm {\sf {RCA}_0}}$
,
 $\operatorname {\mathrm {\sf {WKL}}} + \operatorname {\mathrm {\sf {COH}}} + \operatorname {\mathrm {\sf {TS}}}^2_4 + (\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k + (\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
implies none of
$\operatorname {\mathrm {\sf {WKL}}} + \operatorname {\mathrm {\sf {COH}}} + \operatorname {\mathrm {\sf {TS}}}^2_4 + (\forall n)(\exists k)\operatorname {\mathrm {\sf {TS}}}^n_k + (\forall n)\operatorname {\mathrm {\sf {FS}}}^n$
implies none of
![]() $\operatorname {\mathrm {\sf {SEM}}}$
,
$\operatorname {\mathrm {\sf {SEM}}}$
,
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
and
$\operatorname {\mathrm {\sf {STS}}}^2_3$
and
![]() $\operatorname {\mathrm {\sf {SADS}}}$
.
$\operatorname {\mathrm {\sf {SADS}}}$
.
For this, we are going to prove that
![]() $\operatorname {\mathrm {\sf {WKL}}}$
,
$\operatorname {\mathrm {\sf {WKL}}}$
,
![]() $\operatorname {\mathrm {\sf {COH}}}$
,
$\operatorname {\mathrm {\sf {COH}}}$
,
 $\operatorname {\mathrm {\sf {TS}}}^2_4$
and
$\operatorname {\mathrm {\sf {TS}}}^2_4$
and
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserve a computability-theoretic notion that we call 2-hyperimmunity, while none of
$\operatorname {\mathrm {\sf {FS}}}^n$
preserve a computability-theoretic notion that we call 2-hyperimmunity, while none of
![]() $\operatorname {\mathrm {\sf {SEM}}}$
,
$\operatorname {\mathrm {\sf {SEM}}}$
,
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
and
$\operatorname {\mathrm {\sf {STS}}}^2_3$
and
![]() $\operatorname {\mathrm {\sf {SADS}}}$
does (see Lemma 2.3 for why this is enough). We introduce the concept of 2-hyperimmunity preservation next. The required results about 2-hyperimmunity preservation are proved in the remaining sections of this section (see Figure 1 for where they are proved).
$\operatorname {\mathrm {\sf {SADS}}}$
does (see Lemma 2.3 for why this is enough). We introduce the concept of 2-hyperimmunity preservation next. The required results about 2-hyperimmunity preservation are proved in the remaining sections of this section (see Figure 1 for where they are proved).

Figure 1 Diagram of dependencies between the proofs of preservation of 2-hyperimmunity. An arrow from P to Q means that Q depends on P.
Definition 2.1.
-
(1) A bifamily is a collection
 $\mathcal {H}$
of ordered pairs of finite sets which is closed downward under the product subset relation, that is, such that if
$\mathcal {H}$
of ordered pairs of finite sets which is closed downward under the product subset relation, that is, such that if
 $(C, D) \in \mathcal {H}$
and
$(C, D) \in \mathcal {H}$
and
 $E \subseteq C$
and
$E \subseteq C$
and
 $F \subseteq D$
, then
$F \subseteq D$
, then
 $(E, F) \in \mathcal {H}$
.
$(E, F) \in \mathcal {H}$
. -
(2) A biarray is a collection of finite sets
 $(\vec {E},\vec {F}) = \langle E_n, F_{n,m} : n, m \in \omega \rangle $
such that
$(\vec {E},\vec {F}) = \langle E_n, F_{n,m} : n, m \in \omega \rangle $
such that
 $E_n>n$
and
$E_n>n$
and
 $F_{n,m}> m$
for every
$F_{n,m}> m$
for every
 $n, m \in \omega $
. A biarray
$n, m \in \omega $
. A biarray
 $(\vec {E},\vec {F})$
meets a bifamily
$(\vec {E},\vec {F})$
meets a bifamily
 $\mathcal {H}$
if there is some
$\mathcal {H}$
if there is some
 $n, m \in \omega $
such that
$n, m \in \omega $
such that
 $(E_n, F_{n,m}) \in \mathcal {H}$
.
$(E_n, F_{n,m}) \in \mathcal {H}$
. -
(3) A bifamily
 $\mathcal {H}$
is C-2-hyperimmune if every C-computable biarray meets
$\mathcal {H}$
is C-2-hyperimmune if every C-computable biarray meets
 $\mathcal {H}$
.
$\mathcal {H}$
.
We shall relate the notion of 2-hyperimmunity and various notions of immunity in Section 2.1. For notational convenience, in this section we regard each Turing machine
![]() $\Phi $
as computing a biarray. We will therefore assume that whenever
$\Phi $
as computing a biarray. We will therefore assume that whenever
![]() $\Phi (n;1)$
converges, then it will output (the canonical index of) a finite set
$\Phi (n;1)$
converges, then it will output (the canonical index of) a finite set
![]() $E_n> n$
and whenever
$E_n> n$
and whenever
![]() $\Phi (n,m;2)$
converges, then it will output a finite set
$\Phi (n,m;2)$
converges, then it will output a finite set
![]() $F_{n,m}> m$
.
$F_{n,m}> m$
.
Definition 2.2. Fix a problem
![]() $\mathsf {P}$
.
$\mathsf {P}$
.
-
(1)
 $\mathsf {P}$
preserves 2-hyperimmunity if for every bifamily
$\mathsf {P}$
preserves 2-hyperimmunity if for every bifamily
 $\mathcal {H}$
that is C-2-hyperimmune, every C-computable
$\mathcal {H}$
that is C-2-hyperimmune, every C-computable
 $\mathsf {P}$
-instance admit a solution G such that
$\mathsf {P}$
-instance admit a solution G such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $C\oplus G$
-2-hyperimmune.
$C\oplus G$
-2-hyperimmune. -
(2)
 $\mathsf {P}$
strongly preserves 2-hyperimmunity if for every bifamily
$\mathsf {P}$
strongly preserves 2-hyperimmunity if for every bifamily
 $\mathcal {H}$
that is C-2-hyperimmune, every
$\mathcal {H}$
that is C-2-hyperimmune, every
 $\mathsf {P}$
-instance admit a solution G such that
$\mathsf {P}$
-instance admit a solution G such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $C\oplus G$
-2-hyperimmune.
$C\oplus G$
-2-hyperimmune.
The following lemma is a particular case of Lemma 3.4.2 in [Reference Patey17]. We reprove it for the sake of completeness.
Lemma 2.3. If some problems
![]() $\mathsf {P}_1, \mathsf {P}_2, \dots $
preserve 2-hyperimmunity while another problem
$\mathsf {P}_1, \mathsf {P}_2, \dots $
preserve 2-hyperimmunity while another problem
![]() $\mathsf {Q}$
does not, then the conjunction
$\mathsf {Q}$
does not, then the conjunction
![]() $\bigwedge _i \mathsf {P}_i$
does not imply
$\bigwedge _i \mathsf {P}_i$
does not imply
![]() $\mathsf {Q}$
over
$\mathsf {Q}$
over
![]() $\operatorname {\mathrm {\sf {RCA}_0}}$
.
$\operatorname {\mathrm {\sf {RCA}_0}}$
.
Proof. Since
![]() $\mathsf {Q}$
does not preserve 2-hyperimmunity, there is some set C, a bifamily
$\mathsf {Q}$
does not preserve 2-hyperimmunity, there is some set C, a bifamily
![]() $\mathcal {H}$
that is C-2-hyperimmune, and a
$\mathcal {H}$
that is C-2-hyperimmune, and a
![]() $\mathsf {Q}$
-instance B such that for every solution G,
$\mathsf {Q}$
-instance B such that for every solution G,
![]() $\mathcal {H}$
is not
$\mathcal {H}$
is not
![]() $C \oplus G$
-2-hyperimmune. Since each
$C \oplus G$
-2-hyperimmune. Since each
![]() $\mathsf {P}_i$
preserve 2-hyperimmunity, we can define an infinite sequence of sets
$\mathsf {P}_i$
preserve 2-hyperimmunity, we can define an infinite sequence of sets
![]() $C = Z_0 \leq _T Z_1 \leq _T \cdots $
such that
$C = Z_0 \leq _T Z_1 \leq _T \cdots $
such that
-
(i)
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $Z_n$
-2-hyperimmune for every n
$Z_n$
-2-hyperimmune for every n -
(ii) For every
 $i, n \in \omega $
, every
$i, n \in \omega $
, every
 $Z_n$
-computable
$Z_n$
-computable
 $\mathsf {P}_i$
-instance has a
$\mathsf {P}_i$
-instance has a
 $Z_m$
-computable solution for some m
$Z_m$
-computable solution for some m
Consider the
![]() $\omega $
-structure
$\omega $
-structure
![]() $\mathcal {M} = \{ X : (\exists n) X \leq _T Z_n \}$
. By construction,
$\mathcal {M} = \{ X : (\exists n) X \leq _T Z_n \}$
. By construction,
![]() $B \in \mathcal {M}$
, and by (i),
$B \in \mathcal {M}$
, and by (i),
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus G$
-2-hyperimmune for every
$C \oplus G$
-2-hyperimmune for every
![]() $G \in \mathcal {M}$
. It follows that the
$G \in \mathcal {M}$
. It follows that the
![]() $\mathsf {Q}$
-instance
$\mathsf {Q}$
-instance
![]() $B \in \mathcal {M}$
has no solution in
$B \in \mathcal {M}$
has no solution in
![]() $\mathcal {M}$
, so
$\mathcal {M}$
, so
![]() $\mathcal {M} \not \models \mathsf {Q}$
. By (ii),
$\mathcal {M} \not \models \mathsf {Q}$
. By (ii),
![]() $\mathcal {M} \models \mathsf {P}_i$
for every
$\mathcal {M} \models \mathsf {P}_i$
for every
![]() $i \in \omega $
. This completes the proof.⊣
$i \in \omega $
. This completes the proof.⊣
2.1 Relation with immunity notions
Given a pair of infinite sets
![]() $A, B \subseteq \mathbb {N}$
, we let
$A, B \subseteq \mathbb {N}$
, we let
![]() $\mathcal {H}(A,B)$
be the bifamily of all finite pairs
$\mathcal {H}(A,B)$
be the bifamily of all finite pairs
![]() $(E, F)$
such that
$(E, F)$
such that
![]() $E \subseteq \overline {A}$
and
$E \subseteq \overline {A}$
and
![]() $F \subseteq \overline {B}$
. Recall that an infinite set H is C-hyperimmune if for every C-computable arrayFootnote
1
of finite sets
$F \subseteq \overline {B}$
. Recall that an infinite set H is C-hyperimmune if for every C-computable arrayFootnote
1
of finite sets
![]() $V_0, V_1, \dots $
such that
$V_0, V_1, \dots $
such that
![]() $V_n> n$
, there is some n such that
$V_n> n$
, there is some n such that
![]() $V_n \subseteq \overline {H}$
.
$V_n \subseteq \overline {H}$
.
Lemma 2.4. Two sets A and B are C-hyperimmune if and only if
![]() $\mathcal {H}(A, B)$
is C-2-hyperimmune.
$\mathcal {H}(A, B)$
is C-2-hyperimmune.
Proof. For convenience, we assume
![]() $C=\emptyset $
since the result relativizes. Assume that A and B are hyperimmune, and fix a computable biarray
$C=\emptyset $
since the result relativizes. Assume that A and B are hyperimmune, and fix a computable biarray
 $(\vec {E}, \vec {F})$
. By hyperimmunity of A applied to
$(\vec {E}, \vec {F})$
. By hyperimmunity of A applied to
![]() $\vec {E}$
, there is some n such that
$\vec {E}$
, there is some n such that
![]() $E_n \subseteq \overline {A}$
. By hyperimmunity of B applied to
$E_n \subseteq \overline {A}$
. By hyperimmunity of B applied to
![]() $F_{n,0}, F_{n,1}, \dots $
, there is some m such that
$F_{n,0}, F_{n,1}, \dots $
, there is some m such that
![]() $F_{n,m} \subseteq \overline {B}$
. It follows that the biarray
$F_{n,m} \subseteq \overline {B}$
. It follows that the biarray
 $(\vec {E}, \vec {F})$
meets
$(\vec {E}, \vec {F})$
meets
![]() $\mathcal {H}(A,B)$
.
$\mathcal {H}(A,B)$
.
Assume now that either A or B is not hyperimmune. Suppose first that A is not hyperimmune. Let
![]() $E_0, E_1, \dots $
be a computable array of finite sets such that
$E_0, E_1, \dots $
be a computable array of finite sets such that
![]() $E_n> n$
and
$E_n> n$
and
![]() $E_n \cap A \neq \emptyset $
for every n. Then letting
$E_n \cap A \neq \emptyset $
for every n. Then letting
![]() $F_{n,m} = \{m+1\}$
for every m, the computable biarray
$F_{n,m} = \{m+1\}$
for every m, the computable biarray
 $(\vec {E}, \vec {F})$
does not meet
$(\vec {E}, \vec {F})$
does not meet
![]() $\mathcal {H}(A, B)$
. Suppose now that B is not hyperimmune. Let
$\mathcal {H}(A, B)$
. Suppose now that B is not hyperimmune. Let
![]() $D_0, D_1, \dots $
be a computable array of finite sets such that
$D_0, D_1, \dots $
be a computable array of finite sets such that
![]() $D_n> n$
and
$D_n> n$
and
![]() $D_n \cap B \neq \emptyset $
for every n. Then letting
$D_n \cap B \neq \emptyset $
for every n. Then letting
![]() $E_n = \{n+1\}$
and
$E_n = \{n+1\}$
and
![]() $F_{n,m} = D_m$
for every
$F_{n,m} = D_m$
for every
![]() $m, n \in \omega $
, the computable biarray
$m, n \in \omega $
, the computable biarray
 $(\vec {E}, \vec {F})$
does not meet
$(\vec {E}, \vec {F})$
does not meet
![]() $\mathcal {H}(A, B)$
. In both cases,
$\mathcal {H}(A, B)$
. In both cases,
![]() $\mathcal {H}(A,B)$
is not 2-hyperimmune.⊣
$\mathcal {H}(A,B)$
is not 2-hyperimmune.⊣
It follows that if a problem
![]() $\mathsf {P}$
preserves 2-hyperimmunity, then it also preserves two hyperimmunities, in the sense of Definition 6.2.2 in [Reference Patey17]. Since
$\mathsf {P}$
preserves 2-hyperimmunity, then it also preserves two hyperimmunities, in the sense of Definition 6.2.2 in [Reference Patey17]. Since
![]() $\operatorname {\mathrm {\sf {SADS}}}$
is known not to preserve two hyperimmunities (see Corollary 10.3.5 in [Reference Patey17]), we can immediatly conclude that
$\operatorname {\mathrm {\sf {SADS}}}$
is known not to preserve two hyperimmunities (see Corollary 10.3.5 in [Reference Patey17]), we can immediatly conclude that
![]() $\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity. We will nevertheless recall the argument.
$\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity. We will nevertheless recall the argument.
Corollary 2.5.
![]() $\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity.
$\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity.
Proof. Fix any stable linear order of order type
![]() $\omega + \omega ^{*}$
with no computable infinite ascending or descending subsequence. Let A and B be the
$\omega + \omega ^{*}$
with no computable infinite ascending or descending subsequence. Let A and B be the
![]() $\omega $
and
$\omega $
and
![]() $\omega ^{*}$
part, respectively. By Lemma 41 in [Reference Patey16], A and B are hyperimmune. Therefore, by Lemma 2.4,
$\omega ^{*}$
part, respectively. By Lemma 41 in [Reference Patey16], A and B are hyperimmune. Therefore, by Lemma 2.4,
![]() $\mathcal {H}(A, B)$
is 2-hyperimmune. Any infinite ascending or descending sequence G is a subset of A or B, respectively. It follows that either A, or B is not G-hyperimmune, and by Lemma 2.4,
$\mathcal {H}(A, B)$
is 2-hyperimmune. Any infinite ascending or descending sequence G is a subset of A or B, respectively. It follows that either A, or B is not G-hyperimmune, and by Lemma 2.4,
![]() $\mathcal {H}(A, B)$
is not G-2-hyperimmune. It follows that
$\mathcal {H}(A, B)$
is not G-2-hyperimmune. It follows that
![]() $\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity.⊣
$\operatorname {\mathrm {\sf {SADS}}}$
does not preserve 2-hyperimmunity.⊣
Whenever a Turing degree contains no C-hyperimmune set, it is said to be C-hyperimmune-free. A Turing degree
![]() $\mathbf {d}$
is known to be C-hyperimmune-free if and only if every function bounded by
$\mathbf {d}$
is known to be C-hyperimmune-free if and only if every function bounded by
![]() $\mathbf {d}$
is dominated by a C-computable function (see Theorem III.3.8 in [Reference Odifreddi12]).
$\mathbf {d}$
is dominated by a C-computable function (see Theorem III.3.8 in [Reference Odifreddi12]).
Lemma 2.6. Let
![]() $\mathcal {H}$
be a C-2-hyperimmune bifamily and G be of C-hyperimmune-free degree. Then
$\mathcal {H}$
be a C-2-hyperimmune bifamily and G be of C-hyperimmune-free degree. Then
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus G$
-2-hyperimmune.
$C \oplus G$
-2-hyperimmune.
Proof. Again, assume
![]() $C=\emptyset $
since the result relativizes. Fix a bifamily
$C=\emptyset $
since the result relativizes. Fix a bifamily
![]() $\mathcal {H}$
, and a set G of hyperimmune-free degree such that
$\mathcal {H}$
, and a set G of hyperimmune-free degree such that
![]() $\mathcal {H}$
is not
$\mathcal {H}$
is not
![]() $ G$
-2-hyperimmune. We want to show that
$ G$
-2-hyperimmune. We want to show that
![]() $\mathcal {H}$
is not 2-hyperimmune. Let
$\mathcal {H}$
is not 2-hyperimmune. Let
 $(\vec {E}, \vec {F})$
be a
$(\vec {E}, \vec {F})$
be a
![]() $ G$
-computable biarray which does not meet
$ G$
-computable biarray which does not meet
![]() $\mathcal {H}$
. In particular, the function f defined by
$\mathcal {H}$
. In particular, the function f defined by
![]() $f(n, m) = \max E_n, F_{n,m}$
is G-computable, and is therefore dominated by a computable function g. Define the computable biarray
$f(n, m) = \max E_n, F_{n,m}$
is G-computable, and is therefore dominated by a computable function g. Define the computable biarray
 $(\vec {K}, \vec {L})$
by
$(\vec {K}, \vec {L})$
by
![]() $K_n = \{n+1, \dots , g(n, 0) \}$
and
$K_n = \{n+1, \dots , g(n, 0) \}$
and
![]() $L_{n,m} = \{m+1, \dots , g(n, m) \}$
. It is easy to see that
$L_{n,m} = \{m+1, \dots , g(n, m) \}$
. It is easy to see that
![]() $E_n \subseteq K_n$
and
$E_n \subseteq K_n$
and
![]() $F_{n,m} \subseteq L_{n,m}$
for every
$F_{n,m} \subseteq L_{n,m}$
for every
![]() $n, m \in \omega $
. Indeed,
$n, m \in \omega $
. Indeed,
![]() $E_n> n$
and
$E_n> n$
and
![]() $\max E_n \leq f(n, 0) \leq g(n,0)$
so
$\max E_n \leq f(n, 0) \leq g(n,0)$
so
![]() $E_n \subseteq \{n+1, \dots , g(n, 0) \}$
. Similarly,
$E_n \subseteq \{n+1, \dots , g(n, 0) \}$
. Similarly,
![]() $F_{n,m}> m$
and
$F_{n,m}> m$
and
![]() $\max F_{n,m} \leq f(n,m) \leq g(n,m)$
, so
$\max F_{n,m} \leq f(n,m) \leq g(n,m)$
, so
![]() $F_{n,m} \subseteq \{m+1, \dots , g(n, m)\}$
. Since
$F_{n,m} \subseteq \{m+1, \dots , g(n, m)\}$
. Since
 $(\vec {E}, \vec {F})$
does not meet
$(\vec {E}, \vec {F})$
does not meet
![]() $\mathcal {H}$
,
$\mathcal {H}$
,
![]() $(E_n, F_{n,m}) \not \in \mathcal {H}$
, and by downward-closure of
$(E_n, F_{n,m}) \not \in \mathcal {H}$
, and by downward-closure of
![]() $\mathcal {H}$
under the subset relation,
$\mathcal {H}$
under the subset relation,
![]() $(K_n, L_{n,m}) \not \in \mathcal {H}$
. It follows that
$(K_n, L_{n,m}) \not \in \mathcal {H}$
. It follows that
 $(\vec {K}, \vec {L})$
does not meet
$(\vec {K}, \vec {L})$
does not meet
![]() $\mathcal {H}$
and therefore that
$\mathcal {H}$
and therefore that
![]() $\mathcal {H}$
is not 2-hyperimmune.⊣
$\mathcal {H}$
is not 2-hyperimmune.⊣
Corollary 2.7.
![]() $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity.
Proof. Let
![]() $\mathcal {H}$
be a 2-hyperimmune family, and let T be an infinite computable binary tree. By the hyperimmune-free basis theorem [Reference Jockusch and Soare7], there is an infinite path
$\mathcal {H}$
be a 2-hyperimmune family, and let T be an infinite computable binary tree. By the hyperimmune-free basis theorem [Reference Jockusch and Soare7], there is an infinite path
![]() $P \in [T]$
which is C-hyperimmune-free. By Lemma 2.6,
$P \in [T]$
which is C-hyperimmune-free. By Lemma 2.6,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ P$
-2-hyperimmune.⊣
$ P$
-2-hyperimmune.⊣
Given a bifamily
![]() $\mathcal {H}$
, let
$\mathcal {H}$
, let
![]() $\mathcal {B}(\mathcal {H}) \subseteq \omega ^\omega $
be the closed set of all X such that for every
$\mathcal {B}(\mathcal {H}) \subseteq \omega ^\omega $
be the closed set of all X such that for every
![]() $m, n \in \omega $
,
$m, n \in \omega $
,
![]() $X(\langle 0,n\rangle )$
and
$X(\langle 0,n\rangle )$
and
![]() $X(\langle 1,n, m \rangle )$
are finite sets
$X(\langle 1,n, m \rangle )$
are finite sets
![]() $E_n> n$
and
$E_n> n$
and
![]() $F_{n,m}> m$
such that
$F_{n,m}> m$
such that
![]() $(E_n, F_{n,m}) \not \in \mathcal {H}$
.
$(E_n, F_{n,m}) \not \in \mathcal {H}$
.
Lemma 2.8. A bifamily
![]() $\mathcal {H}$
is C-2-hyperimmune if and only if
$\mathcal {H}$
is C-2-hyperimmune if and only if
![]() $\mathcal {B}(\mathcal {H})$
has no C-computable member.
$\mathcal {B}(\mathcal {H})$
has no C-computable member.
Proof. The members of
![]() $\mathcal {B}(\mathcal {H})$
are precisely the biarrays which fail meeting
$\mathcal {B}(\mathcal {H})$
are precisely the biarrays which fail meeting
![]() $\mathcal {H}$
. The equivalence follows immediately.⊣
$\mathcal {H}$
. The equivalence follows immediately.⊣
Corollary 2.9.
![]() $\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity.
Proof. Let
![]() $\mathcal {H}$
be a 2-hyperimmune family, and let
$\mathcal {H}$
be a 2-hyperimmune family, and let
![]() $\vec {R} = R_0, R_1, \dots $
be an infinite computable sequenceFootnote
2
of sets. By Lemma 2.8,
$\vec {R} = R_0, R_1, \dots $
be an infinite computable sequenceFootnote
2
of sets. By Lemma 2.8,
![]() $\mathcal {B}(\mathcal {H})$
has no computable member. By [Reference Patey13, Corollary 2.9], there is an
$\mathcal {B}(\mathcal {H})$
has no computable member. By [Reference Patey13, Corollary 2.9], there is an
![]() $\vec {R}$
-cohesive set G such that
$\vec {R}$
-cohesive set G such that
![]() $\mathcal {B}(\mathcal {H})$
has no
$\mathcal {B}(\mathcal {H})$
has no
![]() $ G$
-computable member. By Lemma 2.8,
$ G$
-computable member. By Lemma 2.8,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G$
-2-hyperimmune.⊣
$ G$
-2-hyperimmune.⊣
2.2
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
and
$\operatorname {\mathrm {\sf {STS}}}^2_3$
and
 $\operatorname {\mathrm {\sf {SEM}}}$
do not preserve 2-hyperimmunity
$\operatorname {\mathrm {\sf {SEM}}}$
do not preserve 2-hyperimmunity
Before proving that
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
and
$\operatorname {\mathrm {\sf {STS}}}^2_3$
and
![]() $\operatorname {\mathrm {\sf {SEM}}}$
do not preserve 2-hyperimmunity, we must first introduce some notation.
$\operatorname {\mathrm {\sf {SEM}}}$
do not preserve 2-hyperimmunity, we must first introduce some notation.
Given a stable coloring
![]() $f : [\omega ]^2 \to 3$
and two sets
$f : [\omega ]^2 \to 3$
and two sets
![]() $E < F$
, we write
$E < F$
, we write
![]() $E \to _i F$
for
$E \to _i F$
for
![]() $(\forall x \in E)(\forall y \in F)f(x, y) = i$
. For every
$(\forall x \in E)(\forall y \in F)f(x, y) = i$
. For every
![]() $i< 3$
, we let
$i< 3$
, we let
![]() $C_i(f) = \{ x : (\forall ^{\infty } y) f(x, y) = i \}$
. Finally, given a stable coloring
$C_i(f) = \{ x : (\forall ^{\infty } y) f(x, y) = i \}$
. Finally, given a stable coloring
![]() $f : [\omega ]^2 \to 3$
, we let
$f : [\omega ]^2 \to 3$
, we let
![]() $\mathcal {H}(f)$
be the bifamily of all pairs
$\mathcal {H}(f)$
be the bifamily of all pairs
![]() $(E, F)$
such that
$(E, F)$
such that
![]() $E < F$
,
$E < F$
,
![]() $E \subseteq C_1(f)$
,
$E \subseteq C_1(f)$
,
![]() $F \subseteq C_2(f)$
, and
$F \subseteq C_2(f)$
, and
![]() $E \to _0 F$
.
$E \to _0 F$
.
Proposition 2.10. There is a stable computable coloring
![]() $f : [\omega ]^2 \to 3$
such that
$f : [\omega ]^2 \to 3$
such that
![]() $\mathcal {H}(f)$
is 2-hyperimmune.
$\mathcal {H}(f)$
is 2-hyperimmune.
Proof. We build the coloring
![]() $f : [\omega ]^2 \to 3$
by a finite injury priority argument. For every
$f : [\omega ]^2 \to 3$
by a finite injury priority argument. For every
![]() $e \in \omega $
, we want to satisfy the following requirement:
$e \in \omega $
, we want to satisfy the following requirement:
 $$ \begin{align} \mathcal{R}_e: &\text{If}\ \Phi_e\ \text{is total, then there is some}\ n, m \in \omega\ \text{such that}\nonumber \\ &\Phi_e(n;1) \subseteq C_1(f), \Phi_e(n,m;2) \subseteq C_2(f)\ \text{and}\ \Phi_e(n;1) \to_0 \Phi_e(n,m;2). \end{align} $$
$$ \begin{align} \mathcal{R}_e: &\text{If}\ \Phi_e\ \text{is total, then there is some}\ n, m \in \omega\ \text{such that}\nonumber \\ &\Phi_e(n;1) \subseteq C_1(f), \Phi_e(n,m;2) \subseteq C_2(f)\ \text{and}\ \Phi_e(n;1) \to_0 \Phi_e(n,m;2). \end{align} $$
The requirements are given the usual priority ordering
![]() $\mathcal {R}_0 < \mathcal {R}_1 < \cdots $
Initially, the requirements are neither partially, nor fully satisfied.
$\mathcal {R}_0 < \mathcal {R}_1 < \cdots $
Initially, the requirements are neither partially, nor fully satisfied.
-
(i) A requirement
 $\mathcal {R}_e$
requires a first attention at stage s if it is not partially satisfied and
$\mathcal {R}_e$
requires a first attention at stage s if it is not partially satisfied and
 $\Phi _{e,s}(n;1) \downarrow = E$
for some set
$\Phi _{e,s}(n;1) \downarrow = E$
for some set
 $E \subseteq \{e+1, \dots , s-1\}$
such that no element in E is restrained by a requirement of higher priority. If it receives attention, then it puts a restrain on E, commit the elements of E to be in
$E \subseteq \{e+1, \dots , s-1\}$
such that no element in E is restrained by a requirement of higher priority. If it receives attention, then it puts a restrain on E, commit the elements of E to be in
 $C_0(f)$
, and is declared partially satisfied.
$C_0(f)$
, and is declared partially satisfied. -
(ii) A requirement
 $\mathcal {R}_e$
requires a second attention at stage s if it is not fully satisfied, and
$\mathcal {R}_e$
requires a second attention at stage s if it is not fully satisfied, and
 $\Phi _{e,s}(n;1) \downarrow = E$
and
$\Phi _{e,s}(n;1) \downarrow = E$
and
 $\Phi _{e,s}(n,m;2) \downarrow = F$
for some sets
$\Phi _{e,s}(n,m;2) \downarrow = F$
for some sets
 $E, F \subseteq \{e+1, \dots , s-1\}$
such that
$E, F \subseteq \{e+1, \dots , s-1\}$
such that
 $E \to _0 F$
and which are not restrained by a requirement of higher priority. If it receives attention, then it puts a restrain on
$E \to _0 F$
and which are not restrained by a requirement of higher priority. If it receives attention, then it puts a restrain on
 $E \cup F$
, commit the elements of E to be in
$E \cup F$
, commit the elements of E to be in
 $C_1(f)$
, the elements of F to be in
$C_1(f)$
, the elements of F to be in
 $C_2(f)$
, and is declared fully satisfied.
$C_2(f)$
, and is declared fully satisfied.
At stage 0, we let
![]() $f = \emptyset $
. Suppose that at stage s, we have defined
$f = \emptyset $
. Suppose that at stage s, we have defined
![]() $f(x, y)$
for every
$f(x, y)$
for every
![]() $x < y < s$
. For every
$x < y < s$
. For every
![]() $x < s$
, if it is committed to be in some
$x < s$
, if it is committed to be in some
![]() $C_i(f)$
, set
$C_i(f)$
, set
![]() $f(x, s) = i$
, and otherwise set
$f(x, s) = i$
, and otherwise set
![]() $f(x, s) = 0$
. Let
$f(x, s) = 0$
. Let
![]() $\mathcal {R}_e$
be the requirement of highest priority which requires attention. If
$\mathcal {R}_e$
be the requirement of highest priority which requires attention. If
![]() $\mathcal {R}_e$
requires a second attention, then execute the second procedure, otherwise execute the first one. In any case, reset all the requirements of lower priorities by setting them unsatisfied, releasing all their restrains, and go to the next stage. This completes the construction. On easily sees by induction that each requirement acts finitely often, and is eventually fully satisfied. This procedure also yields a stable coloring.⊣
$\mathcal {R}_e$
requires a second attention, then execute the second procedure, otherwise execute the first one. In any case, reset all the requirements of lower priorities by setting them unsatisfied, releasing all their restrains, and go to the next stage. This completes the construction. On easily sees by induction that each requirement acts finitely often, and is eventually fully satisfied. This procedure also yields a stable coloring.⊣
Corollary 2.11.
 $\operatorname {\mathrm {\sf {STS}}}^2_3$
does not preserve 2-hyperimmunity.
$\operatorname {\mathrm {\sf {STS}}}^2_3$
does not preserve 2-hyperimmunity.
Proof. Let f be the stable computable coloring of Proposition 2.10. Let
![]() $G = \{ x_0 < x_1 < \cdots \}$
be an infinite f-thin set. We claim that
$G = \{ x_0 < x_1 < \cdots \}$
be an infinite f-thin set. We claim that
![]() $\mathcal {H}(f)$
is not G-2-hyperimmune. Indeed, let
$\mathcal {H}(f)$
is not G-2-hyperimmune. Indeed, let
 $(\vec {E}, \vec {F})$
be the G-computable biarray defined by
$(\vec {E}, \vec {F})$
be the G-computable biarray defined by
![]() $E_n = \{x_n\}$
and
$E_n = \{x_n\}$
and
![]() $F_{n,m} = \{x_{n+m}\}$
. Fix any n. Suppose that
$F_{n,m} = \{x_{n+m}\}$
. Fix any n. Suppose that
![]() $E_n \subseteq C_1(f)$
and
$E_n \subseteq C_1(f)$
and
![]() $F_{n,m} \subseteq C_2(f)$
(if such
$F_{n,m} \subseteq C_2(f)$
(if such
![]() $E_n,F_{n,m}$
does not exist then we are done). In other words, for every sufficiently large k,
$E_n,F_{n,m}$
does not exist then we are done). In other words, for every sufficiently large k,
![]() $f(x_n, x_k) = 1$
and
$f(x_n, x_k) = 1$
and
![]() $f(x_{n+m}, x_k) = 2$
. It follows that G must be f-thin for color 0Footnote
3
, therefore
$f(x_{n+m}, x_k) = 2$
. It follows that G must be f-thin for color 0Footnote
3
, therefore
![]() $E_n \not \to _0 F_{n,m}$
and so
$E_n \not \to _0 F_{n,m}$
and so
![]() $(E_n, F_{n,m}) \not \in \mathcal {H}(f)$
. The G-computable biarray
$(E_n, F_{n,m}) \not \in \mathcal {H}(f)$
. The G-computable biarray
 $(\vec {E}, \vec {F})$
does not meet
$(\vec {E}, \vec {F})$
does not meet
![]() $\mathcal {H}(f)$
, so
$\mathcal {H}(f)$
, so
![]() $\mathcal {H}(f)$
is not G-2-hyperimmune.⊣
$\mathcal {H}(f)$
is not G-2-hyperimmune.⊣
Corollary 2.12.
![]() $\operatorname {\mathrm {\sf {SEM}}}$
does not preserve 2-hyperimmunity.
$\operatorname {\mathrm {\sf {SEM}}}$
does not preserve 2-hyperimmunity.
Proof. Let
![]() $f : [\omega ]^2\rightarrow 3$
be the stable computable coloring of Proposition 2.10. Let T be the stable computable tournament defined for every
$f : [\omega ]^2\rightarrow 3$
be the stable computable coloring of Proposition 2.10. Let T be the stable computable tournament defined for every
![]() $x < y$
by
$x < y$
by
![]() $T(x, y)$
iff
$T(x, y)$
iff
![]() $f(x, y) = 1$
. Let
$f(x, y) = 1$
. Let
![]() $G = \{ x_0 < x_1 < \dots \}$
be an infinite transitive subtournament. We claim that
$G = \{ x_0 < x_1 < \dots \}$
be an infinite transitive subtournament. We claim that
![]() $\mathcal {H}(f)$
is not G-2-hyperimmune. Indeed, let
$\mathcal {H}(f)$
is not G-2-hyperimmune. Indeed, let
 $(\vec {E}, \vec {F})$
be the G-computable biarray defined by
$(\vec {E}, \vec {F})$
be the G-computable biarray defined by
![]() $E_n = \{x_n\}$
and
$E_n = \{x_n\}$
and
![]() $F_{n,m} = \{x_{n+m}\}$
. Fix n. Suppose that
$F_{n,m} = \{x_{n+m}\}$
. Fix n. Suppose that
![]() $E_n \subseteq C_1(f)$
and
$E_n \subseteq C_1(f)$
and
![]() $F_{n,m} \subseteq C_2(f)$
(if such
$F_{n,m} \subseteq C_2(f)$
(if such
![]() $E_n,F_{n,m}$
does not exist then we are done). In other words, for every sufficiently large k,
$E_n,F_{n,m}$
does not exist then we are done). In other words, for every sufficiently large k,
![]() $f(x_n, x_k) = 1$
and
$f(x_n, x_k) = 1$
and
![]() $f(x_{n+m}, x_k) = 2$
, so
$f(x_{n+m}, x_k) = 2$
, so
![]() $T(x_n, x_k)$
and
$T(x_n, x_k)$
and
![]() $T(x_k, x_{n+m})$
will hold. By transitivity of G,
$T(x_k, x_{n+m})$
will hold. By transitivity of G,
![]() $T(x_n, x_{n+m})$
must hold, so
$T(x_n, x_{n+m})$
must hold, so
![]() $f(x_n, x_{n+m}) = 1$
. It follows that
$f(x_n, x_{n+m}) = 1$
. It follows that
![]() $E_n \not \to _0 F_{n,m}$
and so
$E_n \not \to _0 F_{n,m}$
and so
![]() $(E_n, F_{n,m}) \not \in \mathcal {H}(f)$
. The G-computable biarray
$(E_n, F_{n,m}) \not \in \mathcal {H}(f)$
. The G-computable biarray
 $(\vec {E}, \vec {F})$
does not meet
$(\vec {E}, \vec {F})$
does not meet
![]() $\mathcal {H}(f)$
, so
$\mathcal {H}(f)$
, so
![]() $\mathcal {H}(f)$
is not G-2-hyperimmune.⊣
$\mathcal {H}(f)$
is not G-2-hyperimmune.⊣
2.3
 $\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity
$\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity
The purpose of this section is to prove the following theorem.
Theorem 2.13.
 $\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {TS}}}^2_4$
preserves 2-hyperimmunity.
This will be generalized to arbitrary tuples in the next section. The notion of preservation of 2-hyperimmunity for
 $\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
relates to the notion of strong preservation of 2-hyperimmunity for
$\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
relates to the notion of strong preservation of 2-hyperimmunity for
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
in the following sense.
$\operatorname {\mathrm {\sf {TS}}}^n_k$
in the following sense.
Lemma 2.14. Fix some
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $k \geq 2$
. If
$k \geq 2$
. If
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
strongly preserves 2-hyperimmunity, then
$\operatorname {\mathrm {\sf {TS}}}^n_k$
strongly preserves 2-hyperimmunity, then
 $\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
preserves 2-hyperimmunity.
Proof. Let
![]() $\mathcal {H}$
be a 2-hyperimmune family, and
$\mathcal {H}$
be a 2-hyperimmune family, and
![]() $f : [\omega ]^{n+1} \to k$
be a computable instance of
$f : [\omega ]^{n+1} \to k$
be a computable instance of
 $\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
. Let
$\operatorname {\mathrm {\sf {TS}}}^{n+1}_k$
. Let
 $\vec {R} = \langle R_{\sigma ,i} : \sigma \in [\omega ]^n, i < k \rangle $
be the computable family of sets defined for every
$\vec {R} = \langle R_{\sigma ,i} : \sigma \in [\omega ]^n, i < k \rangle $
be the computable family of sets defined for every
![]() $\sigma \in [\omega ]^n$
and
$\sigma \in [\omega ]^n$
and
![]() $i < k$
by
$i < k$
by
Since
![]() $\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity (Corollary 2.9), there is an
$\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity (Corollary 2.9), there is an
![]() $\vec {R}$
-cohesive set G such that
$\vec {R}$
-cohesive set G such that
![]() $\mathcal {H}$
is G-2-hyperimmune. Let
$\mathcal {H}$
is G-2-hyperimmune. Let
![]() $g : [\omega ]^n \to k$
be the
$g : [\omega ]^n \to k$
be the
 $\Delta ^{0,G}_2$
instance of
$\Delta ^{0,G}_2$
instance of
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
defined for every
$\operatorname {\mathrm {\sf {TS}}}^n_k$
defined for every
![]() $\sigma \in [\omega ]^n$
by
$\sigma \in [\omega ]^n$
by
 $$ \begin{align*}g(\sigma) = \lim_{x \in G} f(\sigma, x). \end{align*} $$
$$ \begin{align*}g(\sigma) = \lim_{x \in G} f(\sigma, x). \end{align*} $$
By strong preservation of
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
, there is an infinite g-thin set H such that
$\operatorname {\mathrm {\sf {TS}}}^n_k$
, there is an infinite g-thin set H such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G \oplus H$
-2-hyperimmune. By thinning out the set H, we obtain an infinite
$ G \oplus H$
-2-hyperimmune. By thinning out the set H, we obtain an infinite
![]() $ G \oplus H$
-computable f-thin set
$ G \oplus H$
-computable f-thin set
![]() $\tilde {H}$
. In particular,
$\tilde {H}$
. In particular,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ \tilde {H}$
-2-hyperimmune.⊣
$ \tilde {H}$
-2-hyperimmune.⊣
It therefore remains to prove the following theorem.
Theorem 2.15.
 $\operatorname {\mathrm {\sf {TS}}}^1_4$
strongly preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {TS}}}^1_4$
strongly preserves 2-hyperimmunity.
Proof. For notational convenience, we will prove the non-relativized version, which extends by routine arguments. Let
![]() $\mathcal {H}$
be a 2-hyperimmune bifamily, and let
$\mathcal {H}$
be a 2-hyperimmune bifamily, and let
![]() $f:\omega \rightarrow 4$
be an arbitrary instance of
$f:\omega \rightarrow 4$
be an arbitrary instance of
 $\operatorname {\mathrm {\sf {TS}}}^1_4$
. Without loss of generality, assume that there is no infinite subset H of
$\operatorname {\mathrm {\sf {TS}}}^1_4$
. Without loss of generality, assume that there is no infinite subset H of
![]() $f^{-1}(i)$
such that
$f^{-1}(i)$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ H$
-2-hyperimmune (as otherwise we are done). We are going to
$ H$
-2-hyperimmune (as otherwise we are done). We are going to
 $$ \begin{align*}\nonumber \bullet\ \ &\text{build 4 infinite sets}\ (G_i:i<4)\ \text{such that}\ G_i\ \text{is}\ f\text{-thin for color}\ i\ \text{and}\\ \nonumber &\mathcal{H}\ \text{is} G_i\text{-2-hyperimmune for some}\ i < 4. \end{align*} $$
$$ \begin{align*}\nonumber \bullet\ \ &\text{build 4 infinite sets}\ (G_i:i<4)\ \text{such that}\ G_i\ \text{is}\ f\text{-thin for color}\ i\ \text{and}\\ \nonumber &\mathcal{H}\ \text{is} G_i\text{-2-hyperimmune for some}\ i < 4. \end{align*} $$
We are going to build the sets
![]() $G_i$
by a Mathias forcing whose conditions are tuples
$G_i$
by a Mathias forcing whose conditions are tuples
![]() $(F_0, F_1, F_2, F_3, X)$
, where
$(F_0, F_1, F_2, F_3, X)$
, where
![]() $(F_i,X) $
is a Mathias condition,
$(F_i,X) $
is a Mathias condition,
![]() $F_i$
is f-thin for color i and
$F_i$
is f-thin for color i and
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ X$
-2-hyperimmune. A condition
$ X$
-2-hyperimmune. A condition
![]() $d = (E_0, E_1, E_2, E_3, Y)$
extends
$d = (E_0, E_1, E_2, E_3, Y)$
extends
![]() $c = (F_0, F_1, F_2, F_3, X)$
(written
$c = (F_0, F_1, F_2, F_3, X)$
(written
![]() $d \leq c$
) if
$d \leq c$
) if
![]() $(E_i, Y)$
Mathias extends
$(E_i, Y)$
Mathias extends
![]() $(F_i, X)$
for every
$(F_i, X)$
for every
![]() $i < 4$
.
$i < 4$
.
The first lemma ensures that every sufficiently generic filter for this notion of forcing will induce four infinite sets.
Lemma 2.16. For every condition
![]() $c = (F_0, F_1, F_2, F_3, X)$
and every
$c = (F_0, F_1, F_2, F_3, X)$
and every
![]() $i < 4$
, there is an extension
$i < 4$
, there is an extension
![]() $d = (E_0, E_1, E_2, E_3, Y)$
of c such that
$d = (E_0, E_1, E_2, E_3, Y)$
of c such that
![]() $|E_i|> |F_i|$
.
$|E_i|> |F_i|$
.
Proof. Fix c and
![]() $i < 4$
. Note that
$i < 4$
. Note that
![]() $X \smallsetminus f^{-1}(i)$
is infinite, since otherwise it contradicts with our assumption that
$X \smallsetminus f^{-1}(i)$
is infinite, since otherwise it contradicts with our assumption that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ X$
-2-hyperimmune. Let
$ X$
-2-hyperimmune. Let
![]() $x \in X \smallsetminus f^{-1}(i)$
with
$x \in X \smallsetminus f^{-1}(i)$
with
![]() $x> F_i$
. The condition
$x> F_i$
. The condition
![]() $d = (E_0, E_1, E_2,E_3, X )$
defined by
$d = (E_0, E_1, E_2,E_3, X )$
defined by
![]() $E_i = F_i \cup \{x\}$
, and
$E_i = F_i \cup \{x\}$
, and
![]() $E_j = F_j$
for
$E_j = F_j$
for
![]() $j \neq i$
is the desired extension of c.⊣
$j \neq i$
is the desired extension of c.⊣
A 4-tuple of sets
![]() $G_0, G_1, G_2, G_3$
satisfies a condition
$G_0, G_1, G_2, G_3$
satisfies a condition
![]() $c = (F_0, F_1, F_2, F_3, X)$
if
$c = (F_0, F_1, F_2, F_3, X)$
if
![]() $G_i$
satisfies the Mathias condition
$G_i$
satisfies the Mathias condition
![]() $(F_i, X)$
for every
$(F_i, X)$
for every
![]() $i < 4$
. A condition c forces a formula
$i < 4$
. A condition c forces a formula
![]() $\varphi (G_0, G_1, G_2, G_3)$
if the formula holds for every 4-tuple of sets
$\varphi (G_0, G_1, G_2, G_3)$
if the formula holds for every 4-tuple of sets
![]() $G_0, G_1, G_2, G_3$
satisfying c. Given any
$G_0, G_1, G_2, G_3$
satisfying c. Given any
![]() $e_0, e_1, e_2, e_3$
, we want to satisfy the following requirements:
$e_0, e_1, e_2, e_3$
, we want to satisfy the following requirements:
 $$ \begin{align*}\mathcal{R}_{e_0, e_1, e_2, e_3} \mbox{ : } \mathcal{R}^0_{e_0} \vee \mathcal{R}^1_{e_1} \vee \mathcal{R}^2_{e_2} \vee \mathcal{R}^3_{e_3}, \end{align*} $$
$$ \begin{align*}\mathcal{R}_{e_0, e_1, e_2, e_3} \mbox{ : } \mathcal{R}^0_{e_0} \vee \mathcal{R}^1_{e_1} \vee \mathcal{R}^2_{e_2} \vee \mathcal{R}^3_{e_3}, \end{align*} $$
where
![]() $\mathcal {R}^i_e$
is the requirement:
$\mathcal {R}^i_e$
is the requirement:
Lemma 2.17. For every condition c and every 4-tuple of indices
![]() $e_0, e_1, e_2, e_3$
, there is an extension d of c forcing
$e_0, e_1, e_2, e_3$
, there is an extension d of c forcing
![]() $\mathcal {R}_{e_0, e_1, e_2, e_3}$
.
$\mathcal {R}_{e_0, e_1, e_2, e_3}$
.
Lemmas 2.17, 2.29, 2.38 and 2.46 are main technical lemmas of Theorem 1.6 (where we prove a condition can be extended to force that a given Turing functional meets
![]() $\mathcal {H}$
). We briefly explain one of the ideas of these lemmas (which also appears in the main Lemma 3.9 of Theorem 3.6) a generalization of Seetapun forcing to build weak solution. Usually, given an arbitrary instance f (of a problem), we want to build a solution G to f so that
$\mathcal {H}$
). We briefly explain one of the ideas of these lemmas (which also appears in the main Lemma 3.9 of Theorem 3.6) a generalization of Seetapun forcing to build weak solution. Usually, given an arbitrary instance f (of a problem), we want to build a solution G to f so that
![]() $\Phi ^G$
has a desired behaviour. Since f is not computable, we cannot search computably among initial segments F of solutions to f (call such F finite solution to f) such that
$\Phi ^G$
has a desired behaviour. Since f is not computable, we cannot search computably among initial segments F of solutions to f (call such F finite solution to f) such that
![]() $\Phi ^F$
has that behaviour. The idea of Seetapun forcing is to find sufficiently many F so that
$\Phi ^F$
has that behaviour. The idea of Seetapun forcing is to find sufficiently many F so that
![]() $\Phi ^F$
has that behaviour. By “sufficiently many,” it means whatever f looks like, one of F is, at least, a finite solution to f.
$\Phi ^F$
has that behaviour. By “sufficiently many,” it means whatever f looks like, one of F is, at least, a finite solution to f.
In our case, this means we want to find sufficiently many F such that
![]() $\Phi ^F(n;1)\downarrow $
and
$\Phi ^F(n;1)\downarrow $
and
![]() $\Phi ^F(n,m;2)\downarrow $
. But this is not quite enough. It only gives (by compactness) two sets
$\Phi ^F(n,m;2)\downarrow $
. But this is not quite enough. It only gives (by compactness) two sets
![]() $U_{n,m},V_{n,m}$
so that for every g, there is a finite solution F of g such that
$U_{n,m},V_{n,m}$
so that for every g, there is a finite solution F of g such that
![]() $\Phi ^F(n;1)\subseteq U_{n,m}\wedge \Phi ^F(n,m;2)\subseteq V_{n,m}$
. That is,
$\Phi ^F(n;1)\subseteq U_{n,m}\wedge \Phi ^F(n,m;2)\subseteq V_{n,m}$
. That is,
![]() $U_{n,m}$
depends on m. So one may want to try this: first, search for a sufficient collection
$U_{n,m}$
depends on m. So one may want to try this: first, search for a sufficient collection
![]() $\mathcal {F}$
, so that
$\mathcal {F}$
, so that
![]() $\Phi ^F(n;1)\downarrow $
for each
$\Phi ^F(n;1)\downarrow $
for each
![]() $F\in \mathcal {F}$
; second, search for a sufficient collection
$F\in \mathcal {F}$
; second, search for a sufficient collection
![]() $\mathcal {E}$
each
$\mathcal {E}$
each
![]() $E\in \mathcal {E}$
extends a member of
$E\in \mathcal {E}$
extends a member of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\Phi ^E(n,m;2)\downarrow $
. Let’s see what sufficiency notion
$\Phi ^E(n,m;2)\downarrow $
. Let’s see what sufficiency notion
![]() $\mathcal {F}$
should satisfy. When
$\mathcal {F}$
should satisfy. When
![]() $\mathcal {F}$
exists while
$\mathcal {F}$
exists while
![]() $\mathcal {E}$
does not, we have that for some instance g,
$\mathcal {E}$
does not, we have that for some instance g,
 $$ \begin{align} &\text{there is no finite solution}\ E\ \text{of}\ g\ \text{such that}\ E\ \text{extends a member of}\ \mathcal{F} \nonumber\\ &\text{and}\ \Phi^E(n,m;2)\downarrow. \end{align} $$
$$ \begin{align} &\text{there is no finite solution}\ E\ \text{of}\ g\ \text{such that}\ E\ \text{extends a member of}\ \mathcal{F} \nonumber\\ &\text{and}\ \Phi^E(n,m;2)\downarrow. \end{align} $$
We need to find an appropriate
![]() $F\in \mathcal {F}$
such that F is a finite solution to g and restrict G so that G extends F and G is a solution to g (because by (2.2), for such G,
$F\in \mathcal {F}$
such that F is a finite solution to g and restrict G so that G extends F and G is a solution to g (because by (2.2), for such G,
![]() $\Phi ^G(n,m;2)\uparrow $
). Here “appropriate” means: at least, F is a finite solution to f. The sufficiency notion for
$\Phi ^G(n,m;2)\uparrow $
). Here “appropriate” means: at least, F is a finite solution to f. The sufficiency notion for
![]() $\mathcal {F}$
should guarantee the existence of F. This gives the following sufficiency notion: for every two instances g and h, there is an
$\mathcal {F}$
should guarantee the existence of F. This gives the following sufficiency notion: for every two instances g and h, there is an
![]() $F\in \mathcal {F}$
such that F is a finite solution to both
$F\in \mathcal {F}$
such that F is a finite solution to both
![]() $g,h$
. This is exactly the sufficiency notion we use in Lemma 2.17. For more complex problems, F being a finite solution to f is not enough, but we must ensure that imposing the restriction of F does not cut the candidate space too much. This concern gives rise to the more complex sufficiency notion (Definitions 2.24 and 2.41 and Lemmas 2.42 and 2.25).
$g,h$
. This is exactly the sufficiency notion we use in Lemma 2.17. For more complex problems, F being a finite solution to f is not enough, but we must ensure that imposing the restriction of F does not cut the candidate space too much. This concern gives rise to the more complex sufficiency notion (Definitions 2.24 and 2.41 and Lemmas 2.42 and 2.25).
Proof. Fix
![]() $c = (F_0, F_1, F_2, F_3, X)$
. For notational convenience, we assume
$c = (F_0, F_1, F_2, F_3, X)$
. For notational convenience, we assume
![]() $X=\omega $
and
$X=\omega $
and
![]() $F_i = \emptyset $
. We define a partial computable biarray as follows. To obtain a desired extension of c, we take advantage of the failure of this biarray to meet
$F_i = \emptyset $
. We define a partial computable biarray as follows. To obtain a desired extension of c, we take advantage of the failure of this biarray to meet
![]() $\mathcal {H}$
or its non-totality.
$\mathcal {H}$
or its non-totality.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $n \in \omega $
, search computably for some finite set
$n \in \omega $
, search computably for some finite set
![]() $U_n>n$
Footnote
4
(if it exists) such that for every pair of colorings
$U_n>n$
Footnote
4
(if it exists) such that for every pair of colorings
![]() $g,h:\omega \rightarrow 4$
, there are two colors
$g,h:\omega \rightarrow 4$
, there are two colors
![]() $i_0 < i_1 < 4$
and two sets
$i_0 < i_1 < 4$
and two sets
![]() $E_{i_0}$
and
$E_{i_0}$
and
![]() $E_{i_1}$
such that for every
$E_{i_1}$
such that for every
![]() $i \in \{i_0, i_1 \}$
,
$i \in \{i_0, i_1 \}$
,
![]() $E_i $
is both g-thin and h-thin for color i andFootnote
5
$E_i $
is both g-thin and h-thin for color i andFootnote
5
 $$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
Defining
![]() $V_{n,m}$
. Given
$V_{n,m}$
. Given
![]() $n, m \in \omega $
, search computably for some finite set
$n, m \in \omega $
, search computably for some finite set
![]() $V_{n,m}>m$
(if it exists) such that for every coloring
$V_{n,m}>m$
(if it exists) such that for every coloring
![]() $g:\omega \rightarrow 4 $
, there is an
$g:\omega \rightarrow 4 $
, there is an
![]() $i < 4$
and a finite set
$i < 4$
and a finite set
![]() $E_i g$
-thin for color i such that
$E_i g$
-thin for color i such that
 $$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n \wedge \Phi_{e_i}^{ E_i}(n, m;2) \downarrow \subseteq V_{n,m}. \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n \wedge \Phi_{e_i}^{ E_i}(n, m;2) \downarrow \subseteq V_{n,m}. \end{align*} $$
We now have multiple outcomes, depending on which of
![]() $U_n$
and
$U_n$
and
![]() $V_{n,m}$
is found.
$V_{n,m}$
is found.
-
• Case 1:
 $U_n$
is not found for some
$U_n$
is not found for some
 $n \in \omega $
. By compactness, the following
$n \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of pairs of colorings
$\mathcal {P}$
of pairs of colorings
 $g,h:\omega \rightarrow 4$
is nonempty: there are three indices
$g,h:\omega \rightarrow 4$
is nonempty: there are three indices
 $i_0 < i_1 < i_2 < 4$
such that for every
$i_0 < i_1 < i_2 < 4$
such that for every
 $i \in \{i_0, i_1, i_2\}$
and every finite set
$i \in \{i_0, i_1, i_2\}$
and every finite set
 $E_i$
being both g-thin and h-thin for color i, we have
$E_i$
being both g-thin and h-thin for color i, we have
 $\Phi _{e_i}^{E_i}(n;1) \uparrow $
.
$\Phi _{e_i}^{E_i}(n;1) \uparrow $
.As
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $(g,h)$
of
$(g,h)$
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g\oplus h$
-2-hyperimmune. In particular, there are some
$g\oplus h$
-2-hyperimmune. In particular, there are some
 $i_0 < i_1 < i_2 < 4$
such that for every
$i_0 < i_1 < i_2 < 4$
such that for every
 $i \in \{i_0, i_1, i_2\}$
and every finite
$i \in \{i_0, i_1, i_2\}$
and every finite
 $E_i $
being g-thin and h-thin for color i, we have
$E_i $
being g-thin and h-thin for color i, we have
 $\Phi _{e_i}^{E_i}(n;1) \uparrow $
. There must be an
$\Phi _{e_i}^{E_i}(n;1) \uparrow $
. There must be an
 $i\in \{i_0,i_1,i_2\}$
such that the set
$i\in \{i_0,i_1,i_2\}$
such that the set
 $Y=\{x:g(x)\ne i,h(x)\ne i\}$
is infinite.Footnote
6
Then clearly
$Y=\{x:g(x)\ne i,h(x)\ne i\}$
is infinite.Footnote
6
Then clearly
 $(F_0, F_1, F_2, F_3, Y)$
is an extension of c. For every G satisfying
$(F_0, F_1, F_2, F_3, Y)$
is an extension of c. For every G satisfying
 $(F_i,Y)$
, G is g-thin for color i. Thus
$(F_i,Y)$
, G is g-thin for color i. Thus
 $\Phi _{e_i}^G(n;1)\uparrow $
. That is, d forces
$\Phi _{e_i}^G(n;1)\uparrow $
. That is, d forces
 $\Phi _{e_i}^G(n;1)\uparrow $
, hence
$\Phi _{e_i}^G(n;1)\uparrow $
, hence
 $\mathcal {R}_{e_0, e_1, e_2, e_3}$
.
$\mathcal {R}_{e_0, e_1, e_2, e_3}$
. -
• Case 2:
 $U_n$
is found, but not
$U_n$
is found, but not
 $V_{n,m}$
for some
$V_{n,m}$
for some
 $n, m \in \omega $
. By compactness, the following
$n, m \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of colorings
$\mathcal {P}$
of colorings
 $g:\omega \rightarrow 4$
is nonempty: for every
$g:\omega \rightarrow 4$
is nonempty: for every
 $i < 4$
and every finite set
$i < 4$
and every finite set
 $E_i g$
-thin for color i, (2.3)As
$E_i g$
-thin for color i, (2.3)As $$ \begin{align} \Phi_{e_i}^{E_i}(n;1) \downarrow \subseteq U_n \Rightarrow \Phi_{e_i}^{ E_i}(n, m;2) \uparrow. \end{align} $$
$$ \begin{align} \Phi_{e_i}^{E_i}(n;1) \downarrow \subseteq U_n \Rightarrow \Phi_{e_i}^{ E_i}(n, m;2) \uparrow. \end{align} $$
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $g $
of
$g $
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is g-2-hyperimmune. By definition of
$\mathcal {H}$
is g-2-hyperimmune. By definition of
 $U_n$
(where we take
$U_n$
(where we take
 $h=f$
in the definition of
$h=f$
in the definition of
 $U_n$
), there are some
$U_n$
), there are some
 $i_0 < i_1 < 4$
and some finite sets
$i_0 < i_1 < 4$
and some finite sets
 $E_{i_0}$
and
$E_{i_0}$
and
 $E_{i_1}$
such that for every
$E_{i_1}$
such that for every
 $i \in \{i_0, i_1\}$
,
$i \in \{i_0, i_1\}$
,
 $E_i $
is both g-thin and f-thin for color i and In particular, there must be some
$E_i $
is both g-thin and f-thin for color i and In particular, there must be some $$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
 $i \in \{i_0, i_1\}$
such that the set
$i \in \{i_0, i_1\}$
such that the set
 $Y= \{x :g(x)\ne i\}$
is infinite. Consider the extension
$Y= \{x :g(x)\ne i\}$
is infinite. Consider the extension
 $d = (D_0, D_1, D_2,D_3, Y)$
of c defined by
$d = (D_0, D_1, D_2,D_3, Y)$
of c defined by
 $D_i = F_i \cup E_i$
and
$D_i = F_i \cup E_i$
and
 $D_j = F_j$
for each
$D_j = F_j$
for each
 $j \neq i$
. To see d forces
$j \neq i$
. To see d forces
 $\Phi _{e_i}^{ G_i}(n, m;2) \uparrow $
(hence forces
$\Phi _{e_i}^{ G_i}(n, m;2) \uparrow $
(hence forces
 $\mathcal {R}_{e_0, e_1, e_2, e_3}$
), note that for every G satisfying
$\mathcal {R}_{e_0, e_1, e_2, e_3}$
), note that for every G satisfying
 $(D_i,Y)$
, G is g-thin for color i. But
$(D_i,Y)$
, G is g-thin for color i. But
 $\Phi _{e_i}^{D_i}(n;1)\downarrow \subseteq U_n$
. Thus, by definition of g (namely (2.3)),
$\Phi _{e_i}^{D_i}(n;1)\downarrow \subseteq U_n$
. Thus, by definition of g (namely (2.3)),
 $\Phi _{e_i}^{ G}(n, m;2) \uparrow $
.
$\Phi _{e_i}^{ G}(n, m;2) \uparrow $
.
-
• Case 3:
 $U_n$
and
$U_n$
and
 $V_{n,m}$
are found for every
$V_{n,m}$
are found for every
 $n,m \in \omega $
. By 2-hyperimmunity of
$n,m \in \omega $
. By 2-hyperimmunity of
 $\mathcal {H}$
, there is some
$\mathcal {H}$
, there is some
 $n, m \in \omega $
such that
$n, m \in \omega $
such that
 $(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
$(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
 $V_{n,m}$
(where we take
$V_{n,m}$
(where we take
 $g=f$
in the definition of
$g=f$
in the definition of
 $V_{n,m}$
), there is some
$V_{n,m}$
), there is some
 $i < 4$
and some finite set
$i < 4$
and some finite set
 $E_i $
such that
$E_i $
such that
 $E_i$
is f-thin for color i and The condition
$E_i$
is f-thin for color i and The condition $$ \begin{align*}\Phi_{e_i}^{ E_i }(n;1) \downarrow \subseteq U_n \wedge \Phi_{e_i}^{ E_i }(n, m;2) \downarrow\subseteq V_{n,m}. \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i }(n;1) \downarrow \subseteq U_n \wedge \Phi_{e_i}^{ E_i }(n, m;2) \downarrow\subseteq V_{n,m}. \end{align*} $$
 $(D_0, D_1, D_2, D_3, X)$
defined by
$(D_0, D_1, D_2, D_3, X)$
defined by
 $D_i = F_i \cup E_i$
and
$D_i = F_i \cup E_i$
and
 $D_j = F_j$
for each
$D_j = F_j$
for each
 $j \neq i$
is an extension of c forcing
$j \neq i$
is an extension of c forcing
 $\mathcal {R}_{e_0, e_1, e_2, e_3}$
.
$\mathcal {R}_{e_0, e_1, e_2, e_3}$
.
This completes the proof of Lemma 2.17.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_{0,s}, F_{1,s}, F_{2,s}, F_{3,s}, X_s)$
, and let
$c_s = (F_{0,s}, F_{1,s}, F_{2,s}, F_{3,s}, X_s)$
, and let
![]() $G_i = \bigcup _s F_{i,s}$
. By definition of a condition, for every
$G_i = \bigcup _s F_{i,s}$
. By definition of a condition, for every
![]() $i < 4$
,
$i < 4$
,
![]() $G_i $
is f-thin for color i. By Lemma 2.16,
$G_i $
is f-thin for color i. By Lemma 2.16,
![]() $G_i$
are all infinite, and by Lemma 2.17, there is some
$G_i$
are all infinite, and by Lemma 2.17, there is some
![]() $i < 4$
such that
$i < 4$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G_i$
-2-hyperimmune. This completes the proof of Theorem 2.15.⊣
$ G_i$
-2-hyperimmune. This completes the proof of Theorem 2.15.⊣
For
 $\mathsf {\operatorname {\mathrm {\sf {TS}}}^2_3}$
, its relation with
$\mathsf {\operatorname {\mathrm {\sf {TS}}}^2_3}$
, its relation with
![]() $\mathsf {EM}$
is unclear.
$\mathsf {EM}$
is unclear.
Question 2.18. Does
 $\mathsf {\operatorname {\mathrm {\sf {TS}}}^2_3}$
imply
$\mathsf {\operatorname {\mathrm {\sf {TS}}}^2_3}$
imply
![]() $\mathsf {EM}$
?
$\mathsf {EM}$
?
2.4 Generalized cohesiveness preserves 2-hyperimmunity
In order to prove that
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
and
$\operatorname {\mathrm {\sf {TS}}}^n_k$
and
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserve 2-hyperimmunity for sufficiently large k, we first need to prove the following technical theorem, which thin out colors while preserving 2-hyperimmunity. The proof is a slight adaptation of [Reference Patey13] to 2-hyperimmunity. We however reprove it for the sake of completeness. We will need the case
$\operatorname {\mathrm {\sf {FS}}}^n$
preserve 2-hyperimmunity for sufficiently large k, we first need to prove the following technical theorem, which thin out colors while preserving 2-hyperimmunity. The proof is a slight adaptation of [Reference Patey13] to 2-hyperimmunity. We however reprove it for the sake of completeness. We will need the case
![]() $t = n-1$
for
$t = n-1$
for
![]() $\operatorname {\mathrm {\sf {TS}}}^n_k$
, and the case
$\operatorname {\mathrm {\sf {TS}}}^n_k$
, and the case
![]() $t = n$
for
$t = n$
for
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
. Fix a set C, a bifamily
$\operatorname {\mathrm {\sf {FS}}}^n$
. Fix a set C, a bifamily
![]() $\mathcal {H}$
which is C-2-hyperimmune, an infinite set
$\mathcal {H}$
which is C-2-hyperimmune, an infinite set
![]() $X\leq _T C$
; let
$X\leq _T C$
; let
![]() $f : [\omega ]^n \to k$
be a coloring.
$f : [\omega ]^n \to k$
be a coloring.
Proposition 2.19. Assume
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for each
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for each
![]() $0<s<n$
. Then there exists an infinite set
$0<s<n$
. Then there exists an infinite set
![]() $G\subseteq X$
such that
$G\subseteq X$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus G$
-2-hyperimmune, and for every
$C \oplus G$
-2-hyperimmune, and for every
![]() $\sigma \in [\omega ]^{<\omega }$
such that
$\sigma \in [\omega ]^{<\omega }$
such that
![]() $0< \left | \sigma \right | < n$
, there is a set
$0< \left | \sigma \right | < n$
, there is a set
![]() $I_\sigma \subseteq \{0, \dots , k-1\}$
such that
$I_\sigma \subseteq \{0, \dots , k-1\}$
such that
![]() $|I_\sigma | \leq d_{n-|\sigma |}$
and
$|I_\sigma | \leq d_{n-|\sigma |}$
and
Proof. For notational convenience, assume
![]() $X=\omega $
and
$X=\omega $
and
![]() $C = \emptyset $
. Our forcing conditions are Mathias conditions
$C = \emptyset $
. Our forcing conditions are Mathias conditions
![]() $(F, Y)$
where
$(F, Y)$
where
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ Y$
-2-hyperimmune. The first lemma shows that
$ Y$
-2-hyperimmune. The first lemma shows that
![]() $\mathcal {H}$
will be
$\mathcal {H}$
will be
![]() $ G$
-2-hyperimmune for every sufficiently generic filter. Given e, let
$ G$
-2-hyperimmune for every sufficiently generic filter. Given e, let
![]() $\mathcal {R}_e$
be the requirement:
$\mathcal {R}_e$
be the requirement:
 $$ \begin{align*}\nonumber \text{If}\ \Phi^{ G}_e\ \text{is total, then it meets}\ \mathcal{H}. \end{align*} $$
$$ \begin{align*}\nonumber \text{If}\ \Phi^{ G}_e\ \text{is total, then it meets}\ \mathcal{H}. \end{align*} $$
Lemma 2.20. Given a condition
![]() $c = (F, Y)$
and an index
$c = (F, Y)$
and an index
![]() $e \in \omega $
, there is an extension d forcing
$e \in \omega $
, there is an extension d forcing
![]() $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
Proof. This simply follows by a finite extension argument. Again for notational convenience, assume
![]() $F=\emptyset $
and
$F=\emptyset $
and
![]() $Y=\omega $
. We define a partial computable biarray as follows.
$Y=\omega $
. We define a partial computable biarray as follows.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $n \in \omega $
, search computably for some finite set
$n \in \omega $
, search computably for some finite set
![]() $U_n>n$
(if it exists) and a finite set
$U_n>n$
(if it exists) and a finite set
![]() $E $
such that
$E $
such that
Defining
![]() $V_{n,m}$
. Given
$V_{n,m}$
. Given
![]() $n, m \in \omega $
, search computably for some finite set
$n, m \in \omega $
, search computably for some finite set
![]() $V_{n,m}>m$
(if it exists) and a finite set
$V_{n,m}>m$
(if it exists) and a finite set
![]() $E $
such that
$E $
such that
We now have multiple outcomes, depending on which
![]() $U_n$
and
$U_n$
and
![]() $V_{n,m}$
is found.
$V_{n,m}$
is found.
-
• Case 1:
 $U_n$
is not found for some
$U_n$
is not found for some
 $n \in \omega $
. Then the condition
$n \in \omega $
. Then the condition
 $c = (F, Y)$
already forces
$c = (F, Y)$
already forces
 $\Phi _e^{ G}(n;1) \uparrow $
and therefore forces
$\Phi _e^{ G}(n;1) \uparrow $
and therefore forces
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
. -
• Case 2:
 $U_n$
is found, but not
$U_n$
is found, but not
 $V_{n,m}$
for some
$V_{n,m}$
for some
 $n, m \in \omega $
. By definition of
$n, m \in \omega $
. By definition of
 $U_n$
, there is a finite set
$U_n$
, there is a finite set
 $E $
such that The condition
$E $
such that The condition $$ \begin{align*}\Phi_e^{ E }(n;1) \downarrow = U_n. \end{align*} $$
$$ \begin{align*}\Phi_e^{ E }(n;1) \downarrow = U_n. \end{align*} $$
 $d = ( E, Y)$
is an extension of c forcing
$d = ( E, Y)$
is an extension of c forcing
 $\Phi _e^{ G}(n,m; 2) \uparrow $
.
$\Phi _e^{ G}(n,m; 2) \uparrow $
.
-
• Case 3:
 $U_n$
and
$U_n$
and
 $V_{n,m}$
are found for every
$V_{n,m}$
are found for every
 $n,m \in \omega $
. By 2-hyperimmunity of
$n,m \in \omega $
. By 2-hyperimmunity of
 $\mathcal {H}$
, there is some
$\mathcal {H}$
, there is some
 $n, m \in \omega $
such that
$n, m \in \omega $
such that
 $(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
$(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
 $V_{n,m}$
, there is a finite set
$V_{n,m}$
, there is a finite set
 $E $
such that The condition
$E $
such that The condition $$ \begin{align*}\Phi_e^{ E}(n;1) \downarrow = U_n \wedge \Phi_e^{ E}(n, m;2) \downarrow = V_{n,m}. \end{align*} $$
$$ \begin{align*}\Phi_e^{ E}(n;1) \downarrow = U_n \wedge \Phi_e^{ E}(n, m;2) \downarrow = V_{n,m}. \end{align*} $$
 $d = ( E, Y )$
is an extension of c forcing
$d = ( E, Y )$
is an extension of c forcing
 $\Phi ^{ G}_e$
to meet
$\Phi ^{ G}_e$
to meet
 $\mathcal {H}$
, and therefore forcing
$\mathcal {H}$
, and therefore forcing
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
This completes the proof of Lemma 2.20.⊣
Lemma 2.21. For every condition
![]() $(F, Y)$
and
$(F, Y)$
and
![]() $\sigma \in [\omega ]^{<\omega }$
such that
$\sigma \in [\omega ]^{<\omega }$
such that
![]() $0< \left | \sigma \right | < n$
, there is a finite set
$0< \left | \sigma \right | < n$
, there is a finite set
![]() $I \subseteq \{0, \dots , k-1\}$
with
$I \subseteq \{0, \dots , k-1\}$
with
![]() $|I| \leq d_{n-|\sigma |}$
and an extension
$|I| \leq d_{n-|\sigma |}$
and an extension
![]() $(F, \tilde Y)$
such that
$(F, \tilde Y)$
such that
Proof. This simply follows from strong preservation of
 $\operatorname {\mathrm {\sf {TS}}}^{n - |\sigma |}_{d_{n-|\sigma |}+1}$
. Define the function
$\operatorname {\mathrm {\sf {TS}}}^{n - |\sigma |}_{d_{n-|\sigma |}+1}$
. Define the function
![]() $g : [Y]^{n - |\sigma |} \to k$
by
$g : [Y]^{n - |\sigma |} \to k$
by
![]() $g(\tau ) = f(\sigma , \tau )$
. Since
$g(\tau ) = f(\sigma , \tau )$
. Since
 $\operatorname {\mathrm {\sf {TS}}}^{n - |\sigma |}_{d_{n-|\sigma |}+1}$
strongly preserves 2-hyperimmunity (since
$\operatorname {\mathrm {\sf {TS}}}^{n - |\sigma |}_{d_{n-|\sigma |}+1}$
strongly preserves 2-hyperimmunity (since
![]() $0<n-|\sigma |<n$
), there exists an infinite
$0<n-|\sigma |<n$
), there exists an infinite
![]() $\tilde Y\subseteq Y$
and a finite set
$\tilde Y\subseteq Y$
and a finite set
![]() $I \subseteq \{0, \dots , k-1\}$
such that
$I \subseteq \{0, \dots , k-1\}$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ \tilde {Y}$
-2-hyperimmune,
$ \tilde {Y}$
-2-hyperimmune,
![]() $|I| \leq d_{n-|\sigma |}$
, and
$|I| \leq d_{n-|\sigma |}$
, and
![]() $(\forall \tau \in [\tilde {Y}]^{n-|\sigma |})f(\sigma , \tau ) \in I$
. The condition
$(\forall \tau \in [\tilde {Y}]^{n-|\sigma |})f(\sigma , \tau ) \in I$
. The condition
![]() $(F, \tilde {Y})$
is the desired extension.⊣
$(F, \tilde {Y})$
is the desired extension.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter containing
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter containing
![]() $(\emptyset , \omega )$
, where
$(\emptyset , \omega )$
, where
![]() $c_s = (F_s, X_s)$
. The filter
$c_s = (F_s, X_s)$
. The filter
![]() $\mathcal {F}$
yields a unique infinite set
$\mathcal {F}$
yields a unique infinite set
![]() $G = \bigcup _s F_s$
. By Lemma 2.20,
$G = \bigcup _s F_s$
. By Lemma 2.20,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G$
-2-hyperimmune. By Lemma 2.21, G satisfies the property of the theorem. This completes the proof of Proposition 2.19.⊣
$ G$
-2-hyperimmune. By Lemma 2.21, G satisfies the property of the theorem. This completes the proof of Proposition 2.19.⊣
2.5
 $\operatorname {\mathrm {\sf {TS}}}^n$
preserves 2-hyperimmunity
$\operatorname {\mathrm {\sf {TS}}}^n$
preserves 2-hyperimmunity
Define the sequence
![]() $d_0, d_1, \dots $
by induction as follows:
$d_0, d_1, \dots $
by induction as follows:
 $$ \begin{align*}d_0 = 1 \hspace{1cm} d_{n} = 3\sum_{0 < s < n} d_s d_{n-s} \hspace{20pt} \mbox{ for } n> 1. \end{align*} $$
$$ \begin{align*}d_0 = 1 \hspace{1cm} d_{n} = 3\sum_{0 < s < n} d_s d_{n-s} \hspace{20pt} \mbox{ for } n> 1. \end{align*} $$
The purpose of this section is to prove the following theorem.
Theorem 2.22.
![]() $\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity for every
![]() $n \geq 1$
.
$n \geq 1$
.
Proof. We prove by induction over
![]() $n \geq 1$
that
$n \geq 1$
that
 $\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity, and that
$\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity, and that
![]() $\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity. If
$\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity. If
![]() $n = 1$
,
$n = 1$
,
 $\operatorname {\mathrm {\sf {TS}}}^1_2$
is a computably true statement, that is, every instance has a solution computable in the instance, so
$\operatorname {\mathrm {\sf {TS}}}^1_2$
is a computably true statement, that is, every instance has a solution computable in the instance, so
 $\operatorname {\mathrm {\sf {TS}}}^1_2$
preserves 2-hyperimmunity. On the other hand,
$\operatorname {\mathrm {\sf {TS}}}^1_2$
preserves 2-hyperimmunity. On the other hand,
 $\operatorname {\mathrm {\sf {TS}}}^1_4$
strongly preserves 2-hyperimmunity follow from Theorem 2.15. If
$\operatorname {\mathrm {\sf {TS}}}^1_4$
strongly preserves 2-hyperimmunity follow from Theorem 2.15. If
![]() $n> 1$
, then by the induction hypothesis,
$n> 1$
, then by the induction hypothesis,
 $\operatorname {\mathrm {\sf {TS}}}^{n-1}_{d_{n-1}+1}$
strongly preserves 2-hyperimmunity, so by Lemma 2.14,
$\operatorname {\mathrm {\sf {TS}}}^{n-1}_{d_{n-1}+1}$
strongly preserves 2-hyperimmunity, so by Lemma 2.14,
 $\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity. Assuming by the induction hypothesis that
$\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity. Assuming by the induction hypothesis that
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
![]() $0 < s < n$
, and that
$0 < s < n$
, and that
 $\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity, by Theorem 2.26,
$\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity, by Theorem 2.26,
![]() $\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity.⊣
$\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity.⊣
We need to prove Theorem 2.26 to complete the proof of Theorem 2.22. We start with the following technical lemma which thins out colors while preserving 2-hyperimmune. Fix a set C, a bifamily
![]() $\mathcal {H}$
which is C-2-hyperimmune, an infinite set
$\mathcal {H}$
which is C-2-hyperimmune, an infinite set
![]() $X\leq _T C$
and a coloring
$X\leq _T C$
and a coloring
![]() $f : [\omega ]^n \to k$
.
$f : [\omega ]^n \to k$
.
Lemma 2.23. Assume
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
![]() $0<s <n$
. Then there is an infinite set
$0<s <n$
. Then there is an infinite set
![]() $Y\subseteq X$
so that
$Y\subseteq X$
so that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus Y$
-2-hyperimmune, and a finite set
$C \oplus Y$
-2-hyperimmune, and a finite set
![]() $I \subseteq \{0, \dots , k-1\}$
with
$I \subseteq \{0, \dots , k-1\}$
with
![]() $ |I| \leq \sum _{0 < s < n} d_s d_{n-s} $
such that for each
$ |I| \leq \sum _{0 < s < n} d_s d_{n-s} $
such that for each
![]() $0<s <n$
,
$0<s <n$
,
Proof. For notational convenience, assume
![]() $C=\emptyset $
. Apply Proposition 2.19 to get an infinite set
$C=\emptyset $
. Apply Proposition 2.19 to get an infinite set
![]() $X_0\subseteq X$
so that
$X_0\subseteq X$
so that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $X_0 $
-2-hyperimmune and for every
$X_0 $
-2-hyperimmune and for every
![]() $\sigma \in [\omega ]^{<\omega }$
with
$\sigma \in [\omega ]^{<\omega }$
with
![]() $0<|\sigma |<n$
, there is an
$0<|\sigma |<n$
, there is an
![]() $I_\sigma $
such that
$I_\sigma $
such that
![]() $|I_\sigma | \leq d_{n-|\sigma |}$
and
$|I_\sigma | \leq d_{n-|\sigma |}$
and
For each
![]() $0<s<n$
and
$0<s<n$
and
![]() $\sigma \in [\omega ]^s$
, let
$\sigma \in [\omega ]^s$
, let
![]() $F_s(\sigma ) = I_\sigma $
. Since
$F_s(\sigma ) = I_\sigma $
. Since
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity, for each
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity, for each
![]() $0<s<n$
, there is an infinite set
$0<s<n$
, there is an infinite set
![]() $Y\subseteq X_0$
such that
$Y\subseteq X_0$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $Y $
-2-hyperimmune and such that
$Y $
-2-hyperimmune and such that
![]() $|F_s[Y]^s|\leq d_s$
for all
$|F_s[Y]^s|\leq d_s$
for all
![]() $0<s<n$
. Let
$0<s<n$
. Let
![]() $\mathcal {I}_s = F_s[Y]^s$
for each
$\mathcal {I}_s = F_s[Y]^s$
for each
![]() $0<s<n$
, and let
$0<s<n$
, and let
![]() $I = \bigcup _{J\in \mathcal {I}_s, 0 < s < n} J$
. Then
$I = \bigcup _{J\in \mathcal {I}_s, 0 < s < n} J$
. Then
 $$ \begin{align*}|I| \leq \sum_{0 < s < n} d_s d_{n-s}. \end{align*} $$
$$ \begin{align*}|I| \leq \sum_{0 < s < n} d_s d_{n-s}. \end{align*} $$
We now check that the property is satisfied. Fix an
![]() $0<s<n$
, a
$0<s<n$
, a
![]() $\sigma \in [Y]^s$
and let
$\sigma \in [Y]^s$
and let
![]() $b\in \omega $
be sufficiently large. Because
$b\in \omega $
be sufficiently large. Because
![]() $Y \subseteq X_0$
,
$Y \subseteq X_0$
,
So
![]() $F_s(\sigma ) = I_\sigma $
, but
$F_s(\sigma ) = I_\sigma $
, but
![]() $\sigma \in [Y]^s$
, hence
$\sigma \in [Y]^s$
, hence
![]() $I_\sigma \in \mathcal {I}_s$
. It follows that
$I_\sigma \in \mathcal {I}_s$
. It follows that
This completes the proof.⊣
We need to prove a second lemma saying that if we have sufficiently many finite thin sets, one of them can be extended to an infinite one. This argument is a generalization of case 2 of Lemma 2.17.
Definition 2.24 (
 $\operatorname {\mathrm {\sf {TS}}}$
-sufficient)
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient)
Let
![]() $(\mathcal {F}_i:i<p)$
be a p-tuple of finite collections of finite sets. We say
$(\mathcal {F}_i:i<p)$
be a p-tuple of finite collections of finite sets. We say
![]() $(\mathcal {F}_i:i<p)$
is n-
$(\mathcal {F}_i:i<p)$
is n-
![]() $\operatorname {\mathrm {\sf {TS}}}$
-sufficient iff for every sequence of colorings
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient iff for every sequence of colorings
![]() $(f_{s,j}:[\omega ]^s\rightarrow d_n+1)_{0\leq s<n, j< d_{n-s-1}}$
, there is an
$(f_{s,j}:[\omega ]^s\rightarrow d_n+1)_{0\leq s<n, j< d_{n-s-1}}$
, there is an
![]() $i<p$
, an
$i<p$
, an
![]() $F\in \mathcal {F}_i$
such that F is
$F\in \mathcal {F}_i$
such that F is
![]() $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
![]() $0\leq s<n, j<d_{n-s-1}$
.
$0\leq s<n, j<d_{n-s-1}$
.
In our application, p will be smaller than
![]() $d_n$
. Let
$d_n$
. Let
![]() $(\mathcal {F}_i:i<p)$
be a p-tuple of finite collections of finite sets.
$(\mathcal {F}_i:i<p)$
be a p-tuple of finite collections of finite sets.
Lemma 2.25. Assume
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
![]() $0<s <n$
. Suppose
$0<s <n$
. Suppose
![]() $f\leq _T C$
,
$f\leq _T C$
,
![]() $(\mathcal {F}_i:i<p)$
is n-
$(\mathcal {F}_i:i<p)$
is n-
![]() $\operatorname {\mathrm {\sf {TS}}}$
-sufficient and for every
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient and for every
![]() $i < p$
,
$i < p$
,
![]() $ \mathcal {F}_i$
is f-thin for color i.Footnote
7
Then there exists an
$ \mathcal {F}_i$
is f-thin for color i.Footnote
7
Then there exists an
![]() $i<p$
, an
$i<p$
, an
![]() $F\in \mathcal {F}_i$
and an infinite set
$F\in \mathcal {F}_i$
and an infinite set
![]() $Y\subseteq X$
such that
$Y\subseteq X$
such that
![]() $F\cup Y$
is f-thin for color i and
$F\cup Y$
is f-thin for color i and
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $Y\oplus C$
-2-hyperimmune.
$Y\oplus C$
-2-hyperimmune.
Proof. Again, for notational convenience, assume
![]() $C=\emptyset $
. Let
$C=\emptyset $
. Let
![]() $E=\cup _{F\in \mathcal {F}_i,i<p}F$
. For every
$E=\cup _{F\in \mathcal {F}_i,i<p}F$
. For every
![]() $s<n$
, every
$s<n$
, every
![]() $\sigma \in [E]^s$
, let coloring
$\sigma \in [E]^s$
, let coloring
![]() $f_\sigma :[\omega ]^{n-s}\rightarrow d_n+1$
be defined as
$f_\sigma :[\omega ]^{n-s}\rightarrow d_n+1$
be defined as
![]() $f_\sigma (\tau ) = f(\sigma ,\tau )$
. By Lemma 2.14,
$f_\sigma (\tau ) = f(\sigma ,\tau )$
. By Lemma 2.14,
 $\operatorname {\mathrm {\sf {TS}}}^s_{d_{s-1}+1}$
admits preservation of 2-hyperimmunity for
$\operatorname {\mathrm {\sf {TS}}}^s_{d_{s-1}+1}$
admits preservation of 2-hyperimmunity for
![]() $0\leq s\leq n$
(set
$0\leq s\leq n$
(set
![]() $d_{-1} = 1$
), so there is an infinite set
$d_{-1} = 1$
), so there is an infinite set
![]() $Y\subseteq X$
with
$Y\subseteq X$
with
![]() $\mathcal {H}$
being
$\mathcal {H}$
being
![]() $Y $
-2-hyperimmune such that for every
$Y $
-2-hyperimmune such that for every
![]() $0\leq s<n$
, every
$0\leq s<n$
, every
![]() $\sigma \in [E]^s$
, there is a
$\sigma \in [E]^s$
, there is a
![]() $I_\sigma $
with
$I_\sigma $
with
![]() $|I_\sigma |\leq d_{n -s-1}$
such that
$|I_\sigma |\leq d_{n -s-1}$
such that
For every
![]() $0\leq s<n$
and
$0\leq s<n$
and
![]() $j< d_{n-s-1}$
, let
$j< d_{n-s-1}$
, let
![]() $f_{s,j}$
be the coloring on
$f_{s,j}$
be the coloring on
![]() $[E]^s$
such that
$[E]^s$
such that
![]() $f_{s,j}(\sigma ) $
is the jth element of
$f_{s,j}(\sigma ) $
is the jth element of
![]() $I_\sigma $
.
$I_\sigma $
.
By n-
![]() $\operatorname {\mathrm {\sf {TS}}}$
-sufficient of
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient of
![]() $(\mathcal {F}_i:i<p)$
, there is a
$(\mathcal {F}_i:i<p)$
, there is a
![]() $i<p$
, an
$i<p$
, an
![]() $F\in \mathcal {F}_i$
such that F is
$F\in \mathcal {F}_i$
such that F is
![]() $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
![]() $0\leq s<n$
and
$0\leq s<n$
and
![]() $j<d_{n-s-1}$
. In particular,
$j<d_{n-s-1}$
. In particular,
![]() $i\notin I_\emptyset $
since F is
$i\notin I_\emptyset $
since F is
![]() $f_{0,j}$
-thin for color i (and
$f_{0,j}$
-thin for color i (and
![]() $f_{0,j}\equiv $
the jth element of
$f_{0,j}\equiv $
the jth element of
![]() $I_\emptyset $
). This means Y is f-thin for color i.
$I_\emptyset $
). This means Y is f-thin for color i.
We show that
![]() $F\cup Y$
is f-thin for color i. To see this, let
$F\cup Y$
is f-thin for color i. To see this, let
![]() $\sigma \in [F]^{<\omega },\tau \in [Y]^{<\omega }$
with
$\sigma \in [F]^{<\omega },\tau \in [Y]^{<\omega }$
with
![]() $|\sigma \cup \tau | = n$
. When
$|\sigma \cup \tau | = n$
. When
![]() $|\sigma |=n$
or
$|\sigma |=n$
or
![]() $|\tau | = n$
,
$|\tau | = n$
,
![]() $ f(\sigma ,\tau )\ne i$
follows from f-thin for color i of F and Y respectively. When
$ f(\sigma ,\tau )\ne i$
follows from f-thin for color i of F and Y respectively. When
![]() $|\sigma |=s$
with
$|\sigma |=s$
with
![]() $0<s<n$
, since F is
$0<s<n$
, since F is
![]() $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
![]() $j<d_{n-s-1}$
, we have
$j<d_{n-s-1}$
, we have
![]() $f_{s,j}(\sigma )\ne i$
for all
$f_{s,j}(\sigma )\ne i$
for all
![]() $j<d_{n-s-1}$
. This means
$j<d_{n-s-1}$
. This means
![]() $i\notin I_\sigma $
. Thus
$i\notin I_\sigma $
. Thus
![]() $f(\sigma ,\tau )\ne i$
since
$f(\sigma ,\tau )\ne i$
since
![]() $f(\sigma ,\tau )\in I_\sigma $
(by choice of Y).⊣
$f(\sigma ,\tau )\in I_\sigma $
(by choice of Y).⊣
We are now ready to prove the missing theorem.
Theorem 2.26. Fix some
![]() $n \geq 2$
, and suppose that
$n \geq 2$
, and suppose that
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyperimmunity for every
![]() $0 < s < n$
, and that
$0 < s < n$
, and that
 $\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity. Then
$\operatorname {\mathrm {\sf {TS}}}^n_{d_{n-1}+1}$
preserves 2-hyperimmunity. Then
![]() $\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {TS}}}^n_{d_n+1}$
strongly preserves 2-hyperimmunity.
Proof. Fix a coloring
![]() $f : [\omega ]^n \to d_n+1$
, and a bifamily
$f : [\omega ]^n \to d_n+1$
, and a bifamily
![]() $\mathcal {H}$
which is 2-hyperimmune. Let
$\mathcal {H}$
which is 2-hyperimmune. Let
![]() $q = \sum _{0 < s < n} d_s d_{n-s}$
. By Lemma 2.23, we assume that there exists a finite set
$q = \sum _{0 < s < n} d_s d_{n-s}$
. By Lemma 2.23, we assume that there exists a finite set
![]() $I_f$
of cardinality q such that for every
$I_f$
of cardinality q such that for every
![]() $0<s<n$
,
$0<s<n$
,
Let
 $p = 1+2d_{n-1}+\sum _{0\leq s<n}d_{s-1}d_{n-s-1}$
, so
$p = 1+2d_{n-1}+\sum _{0\leq s<n}d_{s-1}d_{n-s-1}$
, so
![]() $d_n= p+q-1$
. By renaming the colors of f, we can assume without loss of generality that
$d_n= p+q-1$
. By renaming the colors of f, we can assume without loss of generality that
![]() $I_f = \{p, p+1, \dots , d_n\}$
. We will construct simultaneously p infinite sets
$I_f = \{p, p+1, \dots , d_n\}$
. We will construct simultaneously p infinite sets
![]() $G_0, \dots , G_{p -1}$
such that
$G_0, \dots , G_{p -1}$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G_i$
-2-hyperimmune for some
$ G_i$
-2-hyperimmune for some
![]() $i < p$
. We furthermore ensure that for each
$i < p$
. We furthermore ensure that for each
![]() $i < p$
,
$i < p$
,
![]() $G_i$
is f-thin for color i. We construct our sets
$G_i$
is f-thin for color i. We construct our sets
![]() $G_0, \dots , G_{p-1}$
by a Mathias forcing whose conditions are tuples
$G_0, \dots , G_{p-1}$
by a Mathias forcing whose conditions are tuples
![]() $(F_0, \dots , F_{p-1}, X)$
, where
$(F_0, \dots , F_{p-1}, X)$
, where
![]() $(F_i, X)$
is a Mathias condition for each
$(F_i, X)$
is a Mathias condition for each
![]() $i < p$
and the following properties hold:
$i < p$
and the following properties hold:
-
(a)
 $(\forall \sigma \in [F_i]^s) (\forall \tau \in [F_i \cup X]^{n-s}) f(\sigma , \tau ) \geq p$
for every
$(\forall \sigma \in [F_i]^s) (\forall \tau \in [F_i \cup X]^{n-s}) f(\sigma , \tau ) \geq p$
for every
 $0<s<n$
.
$0<s<n$
. -
(b)
 $F_i$
is f-thin for color i for every
$F_i$
is f-thin for color i for every
 $i < p$
.
$i < p$
. -
(c)
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $ X$
-2-hyperimmune.
$ X$
-2-hyperimmune.
A precondition is a tuple of Mathias conditions satisfying (b) and (c). A precondition
![]() $d = (E_0, \dots , E_{p-1}, Y)$
extends a precondition
$d = (E_0, \dots , E_{p-1}, Y)$
extends a precondition
![]() $c = (F_0, \dots , F_{p-1}, X)$
(written
$c = (F_0, \dots , F_{p-1}, X)$
(written
![]() $d \leq c$
) if
$d \leq c$
) if
![]() $(E_i, Y)$
Mathias extends
$(E_i, Y)$
Mathias extends
![]() $(F_i, X)$
for each
$(F_i, X)$
for each
![]() $i < p$
. Obviously,
$i < p$
. Obviously,
![]() $(\emptyset , \dots , \emptyset , \omega )$
is a condition. Therefore, the partial order is non-empty. We note the following simple properties of conditions.
$(\emptyset , \dots , \emptyset , \omega )$
is a condition. Therefore, the partial order is non-empty. We note the following simple properties of conditions.
Lemma 2.27.
-
(1) Every precondition can be extended to a condition.
-
(2) For every condition
 $c = (F_0, \dots , F_{p-1}, X)$
, every
$c = (F_0, \dots , F_{p-1}, X)$
, every
 $i < p$
and every finite set
$i < p$
and every finite set
 $E \subseteq X f$
-thin for color i,
$E \subseteq X f$
-thin for color i,
 $d = (F_0, \dots , F_{i-1}, F_i \cup E, F_{i+1}, \dots , F_{p-1}, X)$
is a precondition extending c.
$d = (F_0, \dots , F_{i-1}, F_i \cup E, F_{i+1}, \dots , F_{p-1}, X)$
is a precondition extending c.
Proof. Item (1) is trivial by (2.4). For item (2), by property (a) and (b) for condition c and by f-thin for color i of E, we have
![]() $i\notin f[F_i\cup E]^n$
, so d is a precondition.⊣
$i\notin f[F_i\cup E]^n$
, so d is a precondition.⊣
The next lemma states that every sufficiently generic filter yields infinite sets
![]() $G_0, \dots , G_{p-1}$
.
$G_0, \dots , G_{p-1}$
.
Lemma 2.28. For every condition
![]() $c = (F_0, \dots , F_{p-1}, X)$
and every
$c = (F_0, \dots , F_{p-1}, X)$
and every
![]() $i < p$
, there is an extension
$i < p$
, there is an extension
![]() $d = (E_0, \dots , E_{p-1}, X)$
of c such that
$d = (E_0, \dots , E_{p-1}, X)$
of c such that
![]() $|E_i|> |F_i|$
.
$|E_i|> |F_i|$
.
Proof. Fix c and some
![]() $i < p$
, and let
$i < p$
, and let
![]() $x\in X\smallsetminus F_i$
. In particular,
$x\in X\smallsetminus F_i$
. In particular,
![]() $[x]^n = \emptyset $
, so
$[x]^n = \emptyset $
, so
![]() $i \not \in f[x]^n$
. Thus, by Lemma 2.27, there is an extension
$i \not \in f[x]^n$
. Thus, by Lemma 2.27, there is an extension
![]() $d = (E_0, \dots , E_{p-1}, X)$
of c such that
$d = (E_0, \dots , E_{p-1}, X)$
of c such that
![]() $E_i = F_i \cup \{x\}$
.
$E_i = F_i \cup \{x\}$
.
A p-tuple of sets
![]() $G_0, \dots , G_{p-1}$
satisfies a condition
$G_0, \dots , G_{p-1}$
satisfies a condition
![]() $c = (F_0, \dots , F_{p-1}, X)$
if
$c = (F_0, \dots , F_{p-1}, X)$
if
![]() $G_i$
satisfies the Mathias condition
$G_i$
satisfies the Mathias condition
![]() $(F_i, X)$
. A condition c forces a formula
$(F_i, X)$
. A condition c forces a formula
![]() $\varphi (G_0, \dots , G_{p-1})$
if the formula holds for every p-tuple of sets
$\varphi (G_0, \dots , G_{p-1})$
if the formula holds for every p-tuple of sets
![]() $G_0, \dots , G_{p-1}$
satisfying c. For every
$G_0, \dots , G_{p-1}$
satisfying c. For every
![]() $e_0, \dots , e_{p-1} \in \omega $
, we want to satisfy the following requirement
$e_0, \dots , e_{p-1} \in \omega $
, we want to satisfy the following requirement
where
![]() $\mathcal {R}_{e_i}$
is the requirement
$\mathcal {R}_{e_i}$
is the requirement
 $$ \begin{align*} \text{If}\ \Phi^{ G_i}_{e_i}\ \text{is a total, then}\ \Phi^{ G_i}_{e_i}\ \text{meets}\ \mathcal{H}. \end{align*} $$
$$ \begin{align*} \text{If}\ \Phi^{ G_i}_{e_i}\ \text{is a total, then}\ \Phi^{ G_i}_{e_i}\ \text{meets}\ \mathcal{H}. \end{align*} $$
Lemma 2.29. For every condition c and every p-tuple of indices
![]() $e_0, \dots , e_{p-1}$
, there is an extension d of c forcing
$e_0, \dots , e_{p-1}$
, there is an extension d of c forcing
![]() $\mathcal {R}_{e_0, \dots , e_{p-1}}$
.
$\mathcal {R}_{e_0, \dots , e_{p-1}}$
.
Proof. Fix
![]() $c = (F_0, \dots , F_{p-1}, X)$
. By Lemma 2.27, for notational convenience, we assume
$c = (F_0, \dots , F_{p-1}, X)$
. By Lemma 2.27, for notational convenience, we assume
![]() $F_i=\emptyset $
and
$F_i=\emptyset $
and
![]() $X=\omega $
Footnote
8
. We define a partial computable biarray as follows.
$X=\omega $
Footnote
8
. We define a partial computable biarray as follows.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $r \in \omega $
, search computably for some finite set
$r \in \omega $
, search computably for some finite set
![]() $U_r>r$
(if it exists) such that for every pair of colorings
$U_r>r$
(if it exists) such that for every pair of colorings
![]() $g, h : [\omega ]^n \to d_n+1$
, there is a n-
$g, h : [\omega ]^n \to d_n+1$
, there is a n-
![]() $\operatorname {\mathrm {\sf {TS}}}$
-sufficient p-tuple
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient p-tuple
![]() $(\mathcal {E}_i:i<p) $
of finite collections of finite sets with
$(\mathcal {E}_i:i<p) $
of finite collections of finite sets with
![]() $\mathcal {E}_i$
being g-thin, h-thin for color i such that for every
$\mathcal {E}_i$
being g-thin, h-thin for color i such that for every
![]() $i<p$
, every
$i<p$
, every
![]() $E\in \mathcal {E}_i$
, we have
$E\in \mathcal {E}_i$
, we have
 $$ \begin{align*}\Phi_{e_i}^{ E }(r;1) \downarrow \subseteq U_r.\\[-15pt] \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E }(r;1) \downarrow \subseteq U_r.\\[-15pt] \end{align*} $$
Defining
![]() $V_{r,m}$
. Given
$V_{r,m}$
. Given
![]() $r, m \in \omega $
, search computably for some finite set
$r, m \in \omega $
, search computably for some finite set
![]() $V_{r,m}>m$
(if it exists) such that for every coloring
$V_{r,m}>m$
(if it exists) such that for every coloring
![]() $g : [\omega ]^n \to d_n+1$
, there is some
$g : [\omega ]^n \to d_n+1$
, there is some
![]() $i < p$
and some
$i < p$
and some
![]() $E_i $
g-thin for color i such that
$E_i $
g-thin for color i such that
 $$ \begin{align*}\Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \wedge \Phi_{e_i}^{E_i }(r, m;2) \downarrow \subseteq V_{r,m}.\\[-15pt] \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \wedge \Phi_{e_i}^{E_i }(r, m;2) \downarrow \subseteq V_{r,m}.\\[-15pt] \end{align*} $$
We now have multiple outcomes, depending on which
![]() $U_r$
and
$U_r$
and
![]() $V_{r,m}$
is found.
$V_{r,m}$
is found.
-
• Case 1:
 $U_r$
is not found for some
$U_r$
is not found for some
 $r \in \omega $
. By compactness, the following
$r \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of pairs of colorings
$\mathcal {P}$
of pairs of colorings
 $g, h : [\omega ]^n \to d_n+1$
is nonempty: there is no n-
$g, h : [\omega ]^n \to d_n+1$
is nonempty: there is no n-
 $\operatorname {\mathrm {\sf {TS}}}$
-sufficient
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient
 $(\mathcal {E}_i:i<p)$
finite collections of finite sets such that
$(\mathcal {E}_i:i<p)$
finite collections of finite sets such that
 $\mathcal {E}_i$
is both g-thin, h-thin for color i and for every
$\mathcal {E}_i$
is both g-thin, h-thin for color i and for every
 $i<p,E\in \mathcal {E}_i$
, we have
$i<p,E\in \mathcal {E}_i$
, we have
 $ \Phi _{e_i}^{ E}(r;1) \downarrow. $
$ \Phi _{e_i}^{ E}(r;1) \downarrow. $
As
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $g, h $
of
$g, h $
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g \oplus h $
-2-hyperimmune. Unfolding the definition of n-
$g \oplus h $
-2-hyperimmune. Unfolding the definition of n-
 $\operatorname {\mathrm {\sf {TS}}}$
-sufficient and using compactness, the following
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient and using compactness, the following
 $\Pi _1^{0,g\oplus h}$
class
$\Pi _1^{0,g\oplus h}$
class
 $\mathcal {Q}$
of sequence
$\mathcal {Q}$
of sequence
 $(f_{s,j}:[\omega ]^s\rightarrow d_n+1)_{0\leq s<n,j<d_{n-s-1}}$
of colorings is nonempty: for every
$(f_{s,j}:[\omega ]^s\rightarrow d_n+1)_{0\leq s<n,j<d_{n-s-1}}$
of colorings is nonempty: for every
 $i<p$
, every finite set E which is both g-thin, h-thin for color i and is
$i<p$
, every finite set E which is both g-thin, h-thin for color i and is
 $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
 $0\leq s<n,j<d_{n-s-1}$
, we have
$0\leq s<n,j<d_{n-s-1}$
, we have
 $ \Phi _{e_i}^{ E}(r;1) \uparrow. $
$ \Phi _{e_i}^{ E}(r;1) \uparrow. $
As
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $(f_{s,j}:0\leq s<n,j<d_{n-s-1})$
of
$(f_{s,j}:0\leq s<n,j<d_{n-s-1})$
of
 $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g\oplus h\oplus _{0\leq s<n,j<d_{n-s-1}}f_{s,j}$
-2-hyperimmune. Since
$g\oplus h\oplus _{0\leq s<n,j<d_{n-s-1}}f_{s,j}$
-2-hyperimmune. Since
 $\operatorname {\mathrm {\sf {TS}}}^s_{d_{s-1}+1}$
preserves 2-hyperimmunity for all
$\operatorname {\mathrm {\sf {TS}}}^s_{d_{s-1}+1}$
preserves 2-hyperimmunity for all
 $0\leq s\leq n$
, there is an infinite set Y such that
$0\leq s\leq n$
, there is an infinite set Y such that
 $|f_{s,j}[Y]^s|\leq d_{s-1}$
for all
$|f_{s,j}[Y]^s|\leq d_{s-1}$
for all
 $0\leq s<n,j<d_{n-s-1}$
,
$0\leq s<n,j<d_{n-s-1}$
,
 $|g[Y]^s|,|h[Y]^s|\leq d_{n-1}$
and
$|g[Y]^s|,|h[Y]^s|\leq d_{n-1}$
and
 $\mathcal {H}$
is Y-2-hyperimmune. Since
$\mathcal {H}$
is Y-2-hyperimmune. Since
 $p> 2d_{n-1}+\sum _{0\leq s<n}d_{s-1}d_{n-s-1}$
, there is an
$p> 2d_{n-1}+\sum _{0\leq s<n}d_{s-1}d_{n-s-1}$
, there is an
 $i<p$
such that Y is
$i<p$
such that Y is
 $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
 $0\leq s<n,j<d_{n-s-1}$
and both g-thin, h-thin for color i.
$0\leq s<n,j<d_{n-s-1}$
and both g-thin, h-thin for color i.Clearly
 $d = (F_0, \dots , F_{p-1}, Y)$
is an extension of c Footnote
9
. We prove that d forces
$d = (F_0, \dots , F_{p-1}, Y)$
is an extension of c Footnote
9
. We prove that d forces
 $\mathcal {R}_{e_0, \dots , e_{p-1}}$
. This is because if
$\mathcal {R}_{e_0, \dots , e_{p-1}}$
. This is because if
 $G_i$
satisfies
$G_i$
satisfies
 $(F_i,Y)$
, then
$(F_i,Y)$
, then
 $G_i$
is both g-thin and h-thin for color i and
$G_i$
is both g-thin and h-thin for color i and
 $f_{s,j}$
-thin for color i for all
$f_{s,j}$
-thin for color i for all
 $0\leq s<n,j<d_{n-s-1}$
. Thus, by definition of
$0\leq s<n,j<d_{n-s-1}$
. Thus, by definition of
 $g,h,(f_{s,j}:0\leq s<n,j<d_{n-s-1}) $
, we have
$g,h,(f_{s,j}:0\leq s<n,j<d_{n-s-1}) $
, we have
 $\Phi _{e_i}^{ G_i}(r;1) \uparrow $
.
$\Phi _{e_i}^{ G_i}(r;1) \uparrow $
. -
• Case 2:
 $U_r$
is found, but not
$U_r$
is found, but not
 $V_{r,m}$
for some
$V_{r,m}$
for some
 $r, m \in \omega $
. By compactness, the following
$r, m \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of colorings
$\mathcal {P}$
of colorings
 $g : [\omega ]^n \to d_n+1$
is nonempty: for every
$g : [\omega ]^n \to d_n+1$
is nonempty: for every
 $i < p$
and every
$i < p$
and every
 $E_i g$
-thin for color i, (2.5)As
$E_i g$
-thin for color i, (2.5)As $$ \begin{align} \Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \Rightarrow \Phi_{e_i}^{ E_i }(r, m;2) \uparrow. \end{align} $$
$$ \begin{align} \Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \Rightarrow \Phi_{e_i}^{ E_i }(r, m;2) \uparrow. \end{align} $$
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $g $
of
$g $
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g $
-2-hyperimmune. By definition of
$g $
-2-hyperimmune. By definition of
 $U_r$
(where we take
$U_r$
(where we take
 $h = f$
), there is a n-
$h = f$
), there is a n-
 $\operatorname {\mathrm {\sf {TS}}}$
-sufficient p-tuple
$\operatorname {\mathrm {\sf {TS}}}$
-sufficient p-tuple
 $(\mathcal {E}_i:i<p)$
of finite collections of finite sets such that
$(\mathcal {E}_i:i<p)$
of finite collections of finite sets such that
 $\mathcal {E}_i$
is both g-thin and f-thin for color i and for every
$\mathcal {E}_i$
is both g-thin and f-thin for color i and for every
 $i<p$
, every
$i<p$
, every
 $ E\in \mathcal {E}_i$
, we have By Lemma 2.25, there is an
$ E\in \mathcal {E}_i$
, we have By Lemma 2.25, there is an $$ \begin{align*}\Phi_{e_i}^{ E}(r;1) \downarrow \subseteq U_r. \\[-20pt]\nonumber \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E}(r;1) \downarrow \subseteq U_r. \\[-20pt]\nonumber \end{align*} $$
 $i<p$
,
$i<p$
,
 $E\in \mathcal {E}_i$
and an infinite set Y such that
$E\in \mathcal {E}_i$
and an infinite set Y such that
 $E\cup Y$
is g-thin for color i and
$E\cup Y$
is g-thin for color i and
 $\mathcal {H}$
is Y-2-hyperimmune. Consider the precondition
$\mathcal {H}$
is Y-2-hyperimmune. Consider the precondition
 $(F_0,\dots ,F_{i-1},F_i\cup E,F_{i+1},\dots F_{p-1},Y)$
.
$(F_0,\dots ,F_{i-1},F_i\cup E,F_{i+1},\dots F_{p-1},Y)$
.
It remains to show that d forces
 $\Phi _{e_i}^{G_i}(n,m;2)\uparrow $
. This is because if
$\Phi _{e_i}^{G_i}(n,m;2)\uparrow $
. This is because if
 $G_i$
satisfies
$G_i$
satisfies
 $(E, Y)$
, then
$(E, Y)$
, then
 $G_i$
is g-thin for color i. But
$G_i$
is g-thin for color i. But
 $\Phi _{e_i}^{ E}(r;1) \downarrow \subseteq U_r$
. Thus, by definition of g (namely (2.5)),
$\Phi _{e_i}^{ E}(r;1) \downarrow \subseteq U_r$
. Thus, by definition of g (namely (2.5)),
 $\Phi _{e_i}^{G_i}(r,m;2) \uparrow $
.
$\Phi _{e_i}^{G_i}(r,m;2) \uparrow $
. -
• Case 3:
 $U_r$
and
$U_r$
and
 $V_{r,m}$
are found for every
$V_{r,m}$
are found for every
 $r,m \in \omega $
. By 2-hyperimmunity of
$r,m \in \omega $
. By 2-hyperimmunity of
 $\mathcal {H}$
, there is some
$\mathcal {H}$
, there is some
 $r, m \in \omega $
such that
$r, m \in \omega $
such that
 $(U_r, V_{r,m}) \in \mathcal {H}$
. In particular, by definition of
$(U_r, V_{r,m}) \in \mathcal {H}$
. In particular, by definition of
 $V_{n,m}$
(where we take
$V_{n,m}$
(where we take
 $g=f$
), there is some
$g=f$
), there is some
 $i < p$
and some
$i < p$
and some
 $E_i f$
-thin for color i such that
$E_i f$
-thin for color i such that  $$ \begin{align*}\Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \wedge \Phi_{e_i}^{E_i }(r, m;2) \downarrow \subseteq V_{r,m}. \end{align*} $$
$$ \begin{align*}\Phi_{e_i}^{ E_i }(r;1) \downarrow \subseteq U_r \wedge \Phi_{e_i}^{E_i }(r, m;2) \downarrow \subseteq V_{r,m}. \end{align*} $$
Since
 $i\notin f[E_i]^n$
, we have
$i\notin f[E_i]^n$
, we have
 $d = (F_0, \dots , F_{i-1}, F_i \cup E_i, F_{i+1}, \dots , F_{p-1}, X)$
is an extension of c. Clearly d forces
$d = (F_0, \dots , F_{i-1}, F_i \cup E_i, F_{i+1}, \dots , F_{p-1}, X)$
is an extension of c. Clearly d forces
 $\mathcal {R}_{e_0, \dots , e_{p-1}}$
.
$\mathcal {R}_{e_0, \dots , e_{p-1}}$
.
This completes the proof of Lemma 2.29.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_{0,s}, \dots , F_{p-1,s}, X_s)$
, and let
$c_s = (F_{0,s}, \dots , F_{p-1,s}, X_s)$
, and let
![]() $G_i = \bigcup _s F_{i,s}$
for every
$G_i = \bigcup _s F_{i,s}$
for every
![]() $i < p$
. By property (b) of a condition, for every
$i < p$
. By property (b) of a condition, for every
![]() $i < p$
,
$i < p$
,
![]() $G_i$
is f-thin for color i. By Lemma 2.28,
$G_i$
is f-thin for color i. By Lemma 2.28,
![]() $G_0, \dots , G_{p-1}$
are all infinite, and by Lemma 2.29, there is some
$G_0, \dots , G_{p-1}$
are all infinite, and by Lemma 2.29, there is some
![]() $i < p$
such that
$i < p$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G_i$
-2-hyperimmune. This completes the proof of Theorem 2.26.⊣
$ G_i$
-2-hyperimmune. This completes the proof of Theorem 2.26.⊣
2.6
 $\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity
$\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity
The purpose of this section is to prove the following theorem.
Theorem 2.30.
![]() $\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {FS}}}^2$
preserves 2-hyperimmunity.
We start with a lemma very similar to Lemma 2.14, which establishes a bridge between strong preservation for a principle over n-tuples and preservation for the same principle over
![]() $(n+1)$
-tuples.
$(n+1)$
-tuples.
Lemma 2.31. Fix some
![]() $n \geq 1$
. If
$n \geq 1$
. If
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
strongly preserves 2-hyperimmunity, then
$\operatorname {\mathrm {\sf {FS}}}^n$
strongly preserves 2-hyperimmunity, then
![]() $\operatorname {\mathrm {\sf {FS}}}^{n+1}$
preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {FS}}}^{n+1}$
preserves 2-hyperimmunity.
Proof. Let
![]() $\mathcal {H}$
be a 2-hyperimmune family, and
$\mathcal {H}$
be a 2-hyperimmune family, and
![]() $f : [\omega ]^{n+1} \to \omega $
be a computable instance of
$f : [\omega ]^{n+1} \to \omega $
be a computable instance of
![]() $\operatorname {\mathrm {\sf {FS}}}^{n+1}$
. Let
$\operatorname {\mathrm {\sf {FS}}}^{n+1}$
. Let
 $\vec {R} = \langle R_{\sigma ,i} : \sigma \in [\omega ]^n, i \in \omega \rangle $
be the computable family of sets defined for every
$\vec {R} = \langle R_{\sigma ,i} : \sigma \in [\omega ]^n, i \in \omega \rangle $
be the computable family of sets defined for every
![]() $\sigma \in [\omega ]^n$
and
$\sigma \in [\omega ]^n$
and
![]() $i \in \omega $
by
$i \in \omega $
by
Since
![]() $\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity (Corollary 2.9), there is an
$\operatorname {\mathrm {\sf {COH}}}$
preserves 2-hyperimmunity (Corollary 2.9), there is an
![]() $\vec {R}$
-cohesive set G
Footnote
10
such that
$\vec {R}$
-cohesive set G
Footnote
10
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G$
-2-hyperimmune. Let
$ G$
-2-hyperimmune. Let
![]() $g : [\omega ]^n \to \omega $
be the instance of
$g : [\omega ]^n \to \omega $
be the instance of
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
defined for every
$\operatorname {\mathrm {\sf {FS}}}^n$
defined for every
![]() $\sigma \in [\omega ]^n$
by
$\sigma \in [\omega ]^n$
by
 $$ \begin{align*}g(\sigma) = \left\{\begin{array}{@{}ll} \lim_{x \in G} f(\sigma, x), & \mbox{if it exists, }\\ 0, & \mbox{otherwise.} \end{array}\right. \end{align*} $$
$$ \begin{align*}g(\sigma) = \left\{\begin{array}{@{}ll} \lim_{x \in G} f(\sigma, x), & \mbox{if it exists, }\\ 0, & \mbox{otherwise.} \end{array}\right. \end{align*} $$
By strong preservation of
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
, there is an infinite g-free set
$\operatorname {\mathrm {\sf {FS}}}^n$
, there is an infinite g-free set
![]() $H\subseteq G$
such that
$H\subseteq G$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G \oplus H$
-2-hyperimmune. By thinning out the set H, we obtain an infinite
$ G \oplus H$
-2-hyperimmune. By thinning out the set H, we obtain an infinite
![]() $G \oplus H$
-computable f-free set
$G \oplus H$
-computable f-free set
![]() $\tilde {H}\subseteq H$
. In particular,
$\tilde {H}\subseteq H$
. In particular,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $\tilde {H}$
-2-hyperimmune.⊣
$\tilde {H}$
-2-hyperimmune.⊣
We shall define a particular kind of function called left trapped function. The notion of trapped function was introduced by Wang in [Reference Wang21] to prove that
![]() $\operatorname {\mathrm {\sf {FS}}}$
does not imply
$\operatorname {\mathrm {\sf {FS}}}$
does not imply
![]() $\operatorname {\mathrm {\sf {ACA}}}$
over
$\operatorname {\mathrm {\sf {ACA}}}$
over
![]() $\omega $
-models. It was later reused by the second author in [Reference Patey13, Reference Patey18].
$\omega $
-models. It was later reused by the second author in [Reference Patey13, Reference Patey18].
Definition 2.32. A function
![]() $f : [\omega ]^n \to \omega $
is left (resp. right) trapped if for every
$f : [\omega ]^n \to \omega $
is left (resp. right) trapped if for every
![]() $\sigma \in [\omega ]^n$
,
$\sigma \in [\omega ]^n$
,
![]() $f(\sigma ) \leq \max \sigma $
(resp.
$f(\sigma ) \leq \max \sigma $
(resp.
![]() $f(\sigma )>\max \sigma $
).
$f(\sigma )>\max \sigma $
).
The following lemma is a particular case of a more general statement proven by the second author in [Reference Patey13]. It follows from the facts that
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for right trapped functions is strongly computably reducible to the diagonally non-computable principle (
$\operatorname {\mathrm {\sf {FS}}}^n$
for right trapped functions is strongly computably reducible to the diagonally non-computable principle (
![]() $\operatorname {\mathrm {\sf {DNR}}}$
), which itself is strongly computably reducible to
$\operatorname {\mathrm {\sf {DNR}}}$
), which itself is strongly computably reducible to
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions.
$\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions.
Lemma 2.33 (Patey in [Reference Patey13])
For each
![]() $n \geq 1$
, if
$n \geq 1$
, if
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions (strongly) preserves 2-hyperimmune, then so does
$\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions (strongly) preserves 2-hyperimmune, then so does
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
.
$\operatorname {\mathrm {\sf {FS}}}^n$
.
It therefore suffices to prove strong preservation of 2-hyperimmunity for
![]() $\operatorname {\mathrm {\sf {FS}}}^1$
restricted to left trapped functions. We first prove a technical lemma thinning out colors while preserving 2-hyperimmunity. Fix a set C, an infinite set
$\operatorname {\mathrm {\sf {FS}}}^1$
restricted to left trapped functions. We first prove a technical lemma thinning out colors while preserving 2-hyperimmunity. Fix a set C, an infinite set
![]() $X\leq _T C$
, a C-2-hyperimmune bifamily
$X\leq _T C$
, a C-2-hyperimmune bifamily
![]() $\mathcal {H}$
and a left trapped coloring
$\mathcal {H}$
and a left trapped coloring
![]() $f : [\omega ]^n \to \omega $
.
$f : [\omega ]^n \to \omega $
.
Lemma 2.34. Assume
![]() $\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
$\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
![]() $0\leq s<n$
. There exists an infinite set
$0\leq s<n$
. There exists an infinite set
![]() $Y\subseteq X$
such that
$Y\subseteq X$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $Y \oplus C$
-2-hyperimmune, and for every
$Y \oplus C$
-2-hyperimmune, and for every
![]() $\sigma \in [Y]^{<\omega }$
such that
$\sigma \in [Y]^{<\omega }$
such that
![]() $0 \leq \left | \sigma \right | < n$
,
$0 \leq \left | \sigma \right | < n$
,
 $$ \begin{align*}(\forall x \in Y \smallsetminus \sigma)(\exists b)(\forall \tau \in [Y \cap (b, +\infty)]^{n-|\sigma|}) f(\sigma, \tau) \neq x. \end{align*} $$
$$ \begin{align*}(\forall x \in Y \smallsetminus \sigma)(\exists b)(\forall \tau \in [Y \cap (b, +\infty)]^{n-|\sigma|}) f(\sigma, \tau) \neq x. \end{align*} $$
Proof. By Proposition 2.19 and since
![]() $\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyper immunity for all
$\operatorname {\mathrm {\sf {TS}}}^s_{d_s+1}$
strongly preserves 2-hyper immunity for all
![]() $s\in \omega $
(Theorem 2.22), there exists a set
$s\in \omega $
(Theorem 2.22), there exists a set
![]() $X_0\subseteq X $
with
$X_0\subseteq X $
with
![]() $\mathcal {H}$
being
$\mathcal {H}$
being
![]() $ X_0$
-2-hyperimmune such that for all
$ X_0$
-2-hyperimmune such that for all
![]() $\sigma \in [\omega ]^{<\omega }$
with
$\sigma \in [\omega ]^{<\omega }$
with
![]() $|\sigma |<n$
, there exists
$|\sigma |<n$
, there exists
![]() $I_\sigma $
with
$I_\sigma $
with
![]() $|I_\sigma |\leq d_{n-|\sigma |}$
such that for every
$|I_\sigma |\leq d_{n-|\sigma |}$
such that for every
![]() $x\notin I_\sigma $
,
$x\notin I_\sigma $
,
For each
![]() $s < n$
and
$s < n$
and
![]() $i < d_{n-s}$
, let
$i < d_{n-s}$
, let
![]() $f_{s,i} : [\omega ]^s \to \omega $
be the coloring such that
$f_{s,i} : [\omega ]^s \to \omega $
be the coloring such that
![]() $f_{s,i}(\sigma )$
is the ith element of
$f_{s,i}(\sigma )$
is the ith element of
![]() $I_\sigma $
. By strong preservation of
$I_\sigma $
. By strong preservation of
![]() $\operatorname {\mathrm {\sf {FS}}}^s$
for each
$\operatorname {\mathrm {\sf {FS}}}^s$
for each
![]() $0\leq s<n$
, there is an infinite set
$0\leq s<n$
, there is an infinite set
![]() $Y\subseteq X_0$
such that Y is
$Y\subseteq X_0$
such that Y is
![]() $f_{s,i}$
-free for all
$f_{s,i}$
-free for all
![]() $0\leq s<n,i<d_{n-s}$
and
$0\leq s<n,i<d_{n-s}$
and
![]() $\mathcal {H}$
is Y-2-hyperimmune.
$\mathcal {H}$
is Y-2-hyperimmune.
We prove that Y is the desired set. Fix
![]() $s < n$
,
$s < n$
,
![]() $\sigma \in [Y]^s$
and
$\sigma \in [Y]^s$
and
![]() $x \in Y \smallsetminus \sigma $
. If
$x \in Y \smallsetminus \sigma $
. If
![]() $(\forall b)(\exists \tau \in [Y \cap (b, +\infty )]^{n - s})f(\sigma , \tau ) = x$
, then by choice of
$(\forall b)(\exists \tau \in [Y \cap (b, +\infty )]^{n - s})f(\sigma , \tau ) = x$
, then by choice of
![]() $X_0$
(and
$X_0$
(and
![]() $Y\subseteq X_0$
), there exists an
$Y\subseteq X_0$
), there exists an
![]() $i < d_{n - s}$
such that
$i < d_{n - s}$
such that
![]() $f_{s, i}(\sigma ) = x$
, contradicting
$f_{s, i}(\sigma ) = x$
, contradicting
![]() $f_{s,i}$
-freeness of Y. So
$f_{s,i}$
-freeness of Y. So
![]() $(\exists b)(\forall \tau \in [Y \cap (b, +\infty )]^{n - s})f(\sigma , \tau ) \neq x$
.⊣
$(\exists b)(\forall \tau \in [Y \cap (b, +\infty )]^{n - s})f(\sigma , \tau ) \neq x$
.⊣
Theorem 2.35.
![]() $\operatorname {\mathrm {\sf {FS}}}^1$
for left trapped functions strongly preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {FS}}}^1$
for left trapped functions strongly preserves 2-hyperimmunity.
Proof. Fix some 2-hyperimmune bifamily
![]() $\mathcal {H}$
, and a left trapped coloring
$\mathcal {H}$
, and a left trapped coloring
![]() $f : \omega \to \omega $
. By Lemma 2.34, we assume
$f : \omega \to \omega $
. By Lemma 2.34, we assume
We will construct an infinite f-free set G such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $G $
-2-hyperimmune by forcing. Our forcing conditions are Mathias conditions
$G $
-2-hyperimmune by forcing. Our forcing conditions are Mathias conditions
![]() $(F, X)$
such that
$(F, X)$
such that
-
(a)
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $X $
-2-hyperimmune.
$X $
-2-hyperimmune. -
(b)
 $(\forall x \in F \cup X) f(x) \not \in F \smallsetminus \{x\}$
.
$(\forall x \in F \cup X) f(x) \not \in F \smallsetminus \{x\}$
.
A Mathias condition
![]() $(F,X)$
is a precondition if it satisfies (a) and F is f-free. Clearly
$(F,X)$
is a precondition if it satisfies (a) and F is f-free. Clearly
![]() $(\emptyset , \omega )$
is a condition. It’s easy to see that:
$(\emptyset , \omega )$
is a condition. It’s easy to see that:
Lemma 2.36.
-
(1) Every precondition can be extended to a condition.
-
(2) For every condition
 $(F,X)$
, every finite f-free set
$(F,X)$
, every finite f-free set
 $E\subseteq X$
with
$E\subseteq X$
with
 $E>F$
,
$E>F$
,
 $(F\cup E, X)$
is a precondition.
$(F\cup E, X)$
is a precondition.
Proof. Item (1) follows from (2.6). For item (2): Since f is left trapped, for every
![]() $x\in F$
,
$x\in F$
,
![]() $f(x)\notin E$
. Combined with f-freeness of F,
$f(x)\notin E$
. Combined with f-freeness of F,
![]() $f(x)\notin (F\cup E)\smallsetminus \{x\}$
. Since E is f-free, for every
$f(x)\notin (F\cup E)\smallsetminus \{x\}$
. Since E is f-free, for every
![]() $x\in E$
,
$x\in E$
,
![]() $f(x)\notin E\smallsetminus \{x\}$
. Combined with property (b) of a condition,
$f(x)\notin E\smallsetminus \{x\}$
. Combined with property (b) of a condition,
![]() $f(x)\notin (F\cup E)\smallsetminus \{x\}$
.⊣
$f(x)\notin (F\cup E)\smallsetminus \{x\}$
.⊣
Lemma 2.37. For every condition
![]() $(F, X)$
there exists an extension
$(F, X)$
there exists an extension
![]() $(E, Y)$
such that
$(E, Y)$
such that
![]() $|E|> |F|$
.
$|E|> |F|$
.
Proof. Pick any
![]() $x \in X$
with
$x \in X$
with
![]() $x>F$
. Clearly
$x>F$
. Clearly
![]() $\{x\}$
is f-free. Thus the conclusion follow from Lemma 2.36.⊣
$\{x\}$
is f-free. Thus the conclusion follow from Lemma 2.36.⊣
For every
![]() $e \in \omega $
, we want to satisfy the requirement
$e \in \omega $
, we want to satisfy the requirement
 $$ \begin{align*} \mathcal{R}_e: \text{If}\ \Phi^{ G}_e\ \text{is total, then}\ \Phi^{ G}_e\ \text{meets}\ \mathcal{H}. \end{align*} $$
$$ \begin{align*} \mathcal{R}_e: \text{If}\ \Phi^{ G}_e\ \text{is total, then}\ \Phi^{ G}_e\ \text{meets}\ \mathcal{H}. \end{align*} $$
Lemma 2.38. For every condition c and every index e, there is an extension d of c forcing
![]() $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
Proof. Fix a condition
![]() $c = (F, X)$
. By Lemma 2.36, for notational convenience, assume
$c = (F, X)$
. By Lemma 2.36, for notational convenience, assume
![]() $F=\emptyset , X=\omega $
. We define a partial computable biarray as follows.
$F=\emptyset , X=\omega $
. We define a partial computable biarray as follows.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $n \in \omega $
, search computably for some finite set
$n \in \omega $
, search computably for some finite set
![]() $U_n>n$
(if it exists) such that for every pair of left trapped colorings
$U_n>n$
(if it exists) such that for every pair of left trapped colorings
![]() $g, h : \omega \to \omega $
, there is a pair of disjoint finite sets
$g, h : \omega \to \omega $
, there is a pair of disjoint finite sets
![]() $E_0, E_1 $
which are both g-free and h-free such that for each
$E_0, E_1 $
which are both g-free and h-free such that for each
![]() $i < 2$
,
$i < 2$
,
 $$ \begin{align*}\Phi_e^{ E_i }(n;1) \downarrow \subseteq U_n. \end{align*} $$
$$ \begin{align*}\Phi_e^{ E_i }(n;1) \downarrow \subseteq U_n. \end{align*} $$
Defining
![]() $V_{n,m}$
. Given
$V_{n,m}$
. Given
![]() $n, m \in \omega $
, search computably for some finite set
$n, m \in \omega $
, search computably for some finite set
![]() $V_{n,m}>m$
(if it exists) such that for every left trapped coloring
$V_{n,m}>m$
(if it exists) such that for every left trapped coloring
![]() $g : \omega \to \omega $
, there is some g-free finite set E such that
$g : \omega \to \omega $
, there is some g-free finite set E such that
We now have multiple outcomes, depending on which
![]() $U_n$
and
$U_n$
and
![]() $V_{n,m}$
is found.
$V_{n,m}$
is found.
-
• Case 1:
 $U_n$
is not found for some
$U_n$
is not found for some
 $n \in \omega $
. By compactness, the following
$n \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of pairs of left trapped colorings
$\mathcal {P}$
of pairs of left trapped colorings
 $g, h : \omega \to \omega $
is nonempty: for every pair of pairwise disjoint finite sets
$g, h : \omega \to \omega $
is nonempty: for every pair of pairwise disjoint finite sets
 $E_0, E_1$
which are both g-free and h-free, there is some
$E_0, E_1$
which are both g-free and h-free, there is some
 $i < 2$
such that
$i < 2$
such that
 $\Phi _e^{ E_i}(n;1) \uparrow $
.
$\Phi _e^{ E_i}(n;1) \uparrow $
.As
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $g, h$
of
$g, h$
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g \oplus h $
-2-hyperimmune. There is an infinite
$g \oplus h $
-2-hyperimmune. There is an infinite
 $g\oplus h$
-computable set Y which is both g-free and h-free. Let
$g\oplus h$
-computable set Y which is both g-free and h-free. Let
 $E_0 $
(if it exists) be g-free, h-free and
$E_0 $
(if it exists) be g-free, h-free and
 $\Phi _e^{E_0}(n;1) \downarrow $
; let
$\Phi _e^{E_0}(n;1) \downarrow $
; let
 $b = \max E_0$
(or
$b = \max E_0$
(or
 $b=0$
if
$b=0$
if
 $E_0$
does not exist). Clearly condition
$E_0$
does not exist). Clearly condition
 $d = (F, Y \smallsetminus [0,b])$
is an extension of c. For every G satisfying d, G is both g-free and h-free, so
$d = (F, Y \smallsetminus [0,b])$
is an extension of c. For every G satisfying d, G is both g-free and h-free, so
 $\Phi _e^G(n;1)\uparrow $
. Thus d forces
$\Phi _e^G(n;1)\uparrow $
. Thus d forces
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
. -
• Case 2:
 $U_n$
is found, but not
$U_n$
is found, but not
 $V_{n,m}$
for some
$V_{n,m}$
for some
 $n, m \in \omega $
. By compactness, the following
$n, m \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of left trapped colorings
$\mathcal {P}$
of left trapped colorings
 $g : \omega \to \omega $
is nonempty: for every g-free set E, (2.7)As
$g : \omega \to \omega $
is nonempty: for every g-free set E, (2.7)As $$ \begin{align} \Phi_e^{ E}(n;1) \downarrow \subseteq U_n \Rightarrow \Phi_e^{ E}(n, m;2) \uparrow. \end{align} $$
$$ \begin{align} \Phi_e^{ E}(n;1) \downarrow \subseteq U_n \Rightarrow \Phi_e^{ E}(n, m;2) \uparrow. \end{align} $$
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member g of
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member g of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is g-2-hyperimmune. There is an infinite g-computable g-free set Y. By definition of
$\mathcal {H}$
is g-2-hyperimmune. There is an infinite g-computable g-free set Y. By definition of
 $U_n$
(where we take
$U_n$
(where we take
 $h = f$
), there is a pair of disjoint finite sets
$h = f$
), there is a pair of disjoint finite sets
 $E_0, E_1 $
which are both g-free and f-free, and such that for every
$E_0, E_1 $
which are both g-free and f-free, and such that for every
 $i < 2$
, Consider the 2-partition
$i < 2$
, Consider the 2-partition $$ \begin{align*}\Phi_e^{E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
$$ \begin{align*}\Phi_e^{E_i}(n;1) \downarrow \subseteq U_n. \end{align*} $$
 $A_0\sqcup A_1$
of
$A_0\sqcup A_1$
of
 $\omega $
defined by
$\omega $
defined by
 $x\in A_i$
if
$x\in A_i$
if
 $g(x)\in E_i$
and
$g(x)\in E_i$
and
 $x\in A_0$
if
$x\in A_0$
if
 $g(x)\notin \cup _{i<2}E_i$
. Since
$g(x)\notin \cup _{i<2}E_i$
. Since
 $\operatorname {\mathrm {\sf {TS}}}^1_2$
is computably true, hence preserves 2-hyperimmunity, there is an
$\operatorname {\mathrm {\sf {TS}}}^1_2$
is computably true, hence preserves 2-hyperimmunity, there is an
 $i < 2$
and an infinite set
$i < 2$
and an infinite set
 $E_i<\tilde Y \subseteq Y$
such that
$E_i<\tilde Y \subseteq Y$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $\tilde Y $
-2-hyperimmune and
$\tilde Y $
-2-hyperimmune and
 $g(\tilde Y)\cap E_i=\emptyset $
. We claim that
$g(\tilde Y)\cap E_i=\emptyset $
. We claim that
 $E_i \cup \tilde Y$
is g-free. Indeed,
$E_i \cup \tilde Y$
is g-free. Indeed,
 $E_i$
and
$E_i$
and
 $\tilde Y$
are both g-free; since g is left trapped,
$\tilde Y$
are both g-free; since g is left trapped,
 $g(E_i) \cap \tilde Y = \emptyset $
; and by choice of
$g(E_i) \cap \tilde Y = \emptyset $
; and by choice of
 $\tilde Y$
,
$\tilde Y$
,
 $g(\tilde Y) \cap E_i = \emptyset $
.
$g(\tilde Y) \cap E_i = \emptyset $
.
By f-free of
 $E_i$
,
$E_i$
,
 $d=(E_i, \tilde Y )$
is a precondition extending c. We prove that the d forces
$d=(E_i, \tilde Y )$
is a precondition extending c. We prove that the d forces
 $\Phi _e^{ G}(n,m;2) \uparrow $
. Because
$\Phi _e^{ G}(n,m;2) \uparrow $
. Because
 $\Phi _e^{E_i}(n;1)\downarrow \subseteq U_n$
and
$\Phi _e^{E_i}(n;1)\downarrow \subseteq U_n$
and
 $E_i \cup \tilde Y$
is g-free (so every G satisfying
$E_i \cup \tilde Y$
is g-free (so every G satisfying
 $(E_i,\tilde Y)$
is g-free), by definition of g (namely (2.7)), d forces
$(E_i,\tilde Y)$
is g-free), by definition of g (namely (2.7)), d forces
 $\Phi _e^{ G}(n, m;2) \uparrow $
.
$\Phi _e^{ G}(n, m;2) \uparrow $
. -
• Case 3:
 $U_n$
and
$U_n$
and
 $V_{n,m}$
are found for every
$V_{n,m}$
are found for every
 $n,m \in \omega $
. By 2-hyperimmunity of
$n,m \in \omega $
. By 2-hyperimmunity of
 $\mathcal {H}$
, there is some
$\mathcal {H}$
, there is some
 $n, m \in \omega $
such that
$n, m \in \omega $
such that
 $(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
$(U_n, V_{n,m}) \in \mathcal {H}$
. In particular, by definition of
 $V_{n,m}$
(where we take
$V_{n,m}$
(where we take
 $g = f$
), there is some f-free finite set
$g = f$
), there is some f-free finite set
 $E $
such that
$E $
such that  $$ \begin{align*}\Phi_e^{E}(n;1) \downarrow \subseteq U_n \wedge \Phi_e^{E}(n, m;2) \downarrow \subseteq V_{n,m}. \end{align*} $$
$$ \begin{align*}\Phi_e^{E}(n;1) \downarrow \subseteq U_n \wedge \Phi_e^{E}(n, m;2) \downarrow \subseteq V_{n,m}. \end{align*} $$
Clearly
 $(E, X)$
is a precondition extending c and forcing
$(E, X)$
is a precondition extending c and forcing
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
This completes the proof of Lemma 2.38.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_s, X_s)$
, and let
$c_s = (F_s, X_s)$
, and let
![]() $G = \bigcup _s F_s$
. By property (b) of a condition, G is f-free. By Lemma 2.37, G is infinite, and by Lemma 2.38,
$G = \bigcup _s F_s$
. By property (b) of a condition, G is f-free. By Lemma 2.37, G is infinite, and by Lemma 2.38,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $ G$
-2-hyperimmune. This completes the proof of Theorem 2.35.⊣
$ G$
-2-hyperimmune. This completes the proof of Theorem 2.35.⊣
2.7
 $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity
The purpose of this section is to prove the following theorem.
Theorem 2.39. For every
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
strongly preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {FS}}}^n$
strongly preserves 2-hyperimmunity.
Proof. We prove by induction over
![]() $n \geq 1$
that
$n \geq 1$
that
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserves and strongly preserves 2-hyperimmunity. If
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves and strongly preserves 2-hyperimmunity. If
![]() $n = 1$
,
$n = 1$
,
![]() $\operatorname {\mathrm {\sf {FS}}}^1$
is a computably true statement, that is, every instance has a solution computable in the instance, so
$\operatorname {\mathrm {\sf {FS}}}^1$
is a computably true statement, that is, every instance has a solution computable in the instance, so
![]() $\operatorname {\mathrm {\sf {FS}}}^1$
preserves 2-hyperimmunity. If
$\operatorname {\mathrm {\sf {FS}}}^1$
preserves 2-hyperimmunity. If
![]() $n> 1$
, then by the induction hypothesis,
$n> 1$
, then by the induction hypothesis,
![]() $\operatorname {\mathrm {\sf {FS}}}^{n-1}$
strongly preserves 2-hyperimmunity, so by Lemma 2.31,
$\operatorname {\mathrm {\sf {FS}}}^{n-1}$
strongly preserves 2-hyperimmunity, so by Lemma 2.31,
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity. Assuming by the induction hypothesis that
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity. Assuming by the induction hypothesis that
![]() $\operatorname {\mathrm {\sf {FS}}}^t$
strongly preserves 2-hyperimmunity for every
$\operatorname {\mathrm {\sf {FS}}}^t$
strongly preserves 2-hyperimmunity for every
![]() $t < n$
, and that
$t < n$
, and that
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, then by Theorem 2.43,
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, then by Theorem 2.43,
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity. By Lemma 2.33, if
$\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity. By Lemma 2.33, if
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity, so does
$\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity, so does
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
. This completes the proof.⊣
$\operatorname {\mathrm {\sf {FS}}}^n$
. This completes the proof.⊣
We first need to prove a technical lemma which will ensure that the reservoirs of our forcing conditions will have good properties, so that the conditions will be extensible. Fix a set C, a C-2-hyperimmune bifamily
![]() $\mathcal {H}$
; a finite set F and an infinite set
$\mathcal {H}$
; a finite set F and an infinite set
![]() $X \leq _T C$
; fix a left trapped coloring
$X \leq _T C$
; fix a left trapped coloring
![]() $f : [\omega ]^n \to \omega $
.
$f : [\omega ]^n \to \omega $
.
Lemma 2.40. Suppose that
![]() $\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
$\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
![]() $0<s<n$
. Then there exists an infinite set
$0<s<n$
. Then there exists an infinite set
![]() $Y \subseteq X$
such that
$Y \subseteq X$
such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $Y \oplus C$
-2-hyperimmune, and for each
$Y \oplus C$
-2-hyperimmune, and for each
![]() $0<s<n$
,
$0<s<n$
,
Proof. For each
![]() $0<s<n$
, each
$0<s<n$
, each
![]() $\sigma \in [F]^s$
consider the coloring
$\sigma \in [F]^s$
consider the coloring
![]() $f_\sigma :[\omega ]^{n-s}\rightarrow \omega $
defined as
$f_\sigma :[\omega ]^{n-s}\rightarrow \omega $
defined as
![]() $f_\sigma (\tau ) = f(\sigma ,\tau )$
. Since
$f_\sigma (\tau ) = f(\sigma ,\tau )$
. Since
![]() $\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
$\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
![]() $0<s<n$
, there is an infinite set
$0<s<n$
, there is an infinite set
![]() $Y \subseteq X$
such that
$Y \subseteq X$
such that
![]() $\mathcal {H}$
is Y-2-hyperimmune and Y is
$\mathcal {H}$
is Y-2-hyperimmune and Y is
![]() $f_\sigma $
-free for all
$f_\sigma $
-free for all
![]() $0<s<n,\sigma \in [F]^s$
. Unfolding the definition of free, Y is desired.⊣
$0<s<n,\sigma \in [F]^s$
. Unfolding the definition of free, Y is desired.⊣
We need to prove a second lemma saying that if we have sufficiently many finite free sets, one of them is extendible into an infinite one. This generalizes the argument of case 2 of Lemma 2.38, where we showed that for every coloring
![]() $g:\omega \rightarrow \omega $
and every pair of disjoint g-free finite sets
$g:\omega \rightarrow \omega $
and every pair of disjoint g-free finite sets
![]() $E_0, E_1$
, there is an
$E_0, E_1$
, there is an
![]() $i<2$
and an infinite set Y such that
$i<2$
and an infinite set Y such that
![]() $E_i\cup Y$
is g-free.
$E_i\cup Y$
is g-free.
Definition 2.41 (
 $\operatorname {\mathrm {\sf {FS}}}$
-sufficient)
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient)
A collection
![]() $\mathcal {F}$
of finite sets is n-
$\mathcal {F}$
of finite sets is n-
![]() $\operatorname {\mathrm {\sf {FS}}}$
-sufficient iff for every sequence
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient iff for every sequence
![]() $(f_{s,i}:[\omega ]^s\rightarrow \omega )_{s< n,i<d_{n-s-1}}$
of left trapped colorings, there exists an
$(f_{s,i}:[\omega ]^s\rightarrow \omega )_{s< n,i<d_{n-s-1}}$
of left trapped colorings, there exists an
![]() $F\in \mathcal {F}$
such that F is
$F\in \mathcal {F}$
such that F is
![]() $f_{s,i}$
-free for all
$f_{s,i}$
-free for all
![]() $s< n,i<d_{n-s-1}$
.
$s< n,i<d_{n-s-1}$
.
In particular, for
![]() $n = 1$
, a collection
$n = 1$
, a collection
![]() $\mathcal {F}$
of finite sets is 1-
$\mathcal {F}$
of finite sets is 1-
![]() $\operatorname {\mathrm {\sf {FS}}}$
-sufficient iff for every left-trapped coloring
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient iff for every left-trapped coloring
![]() $f_{0,0} : [\omega ]^0 \to \omega $
, there exists an
$f_{0,0} : [\omega ]^0 \to \omega $
, there exists an
![]() $F \in \mathcal {F}$
such that F is
$F \in \mathcal {F}$
such that F is
![]() $f_{0,0}$
-free. Note that a coloring
$f_{0,0}$
-free. Note that a coloring
![]() $[\omega ]^\omega \to \omega $
is nothing but the choice of an element in
$[\omega ]^\omega \to \omega $
is nothing but the choice of an element in
![]() $\omega $
, which means that for every
$\omega $
, which means that for every
![]() $x \in \omega $
, there exists an
$x \in \omega $
, there exists an
![]() $F \in \mathcal {F}$
such that
$F \in \mathcal {F}$
such that
![]() $x \not \in F$
. This is true as long as
$x \not \in F$
. This is true as long as
![]() $\mathcal {F}$
contains two disjoint sets.
$\mathcal {F}$
contains two disjoint sets.
Let
![]() $\mathcal {F}$
be a collection of f-free finite sets.
$\mathcal {F}$
be a collection of f-free finite sets.
Lemma 2.42. Assume that
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity and that
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity and that
![]() $\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
$\operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
![]() $0<s<n$
. Suppose
$0<s<n$
. Suppose
![]() $f\leq _T C$
,
$f\leq _T C$
,
![]() $\mathcal {F}$
is n-
$\mathcal {F}$
is n-
![]() $\operatorname {\mathrm {\sf {FS}}}$
-sufficient and f-free.Footnote
11
Then there is an
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient and f-free.Footnote
11
Then there is an
![]() $F\in \mathcal {F}$
and an infinite subset
$F\in \mathcal {F}$
and an infinite subset
![]() $Y \subseteq X$
such that
$Y \subseteq X$
such that
![]() $F \cup Y$
is f-free and
$F \cup Y$
is f-free and
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus Y$
-2-hyperimmune.
$C \oplus Y$
-2-hyperimmune.
Proof. Using a version of Proposition 2.19 and imitating Lemma 2.34 but for preservation instead of strong preservation (which is feasible since
![]() $f \leq _T C$
), there is an infinite set
$f \leq _T C$
), there is an infinite set
![]() $X_0\subseteq X$
with
$X_0\subseteq X$
with
![]() $\mathcal {H}$
being
$\mathcal {H}$
being
![]() $X_0$
-2-hyperimmune such that for every
$X_0$
-2-hyperimmune such that for every
![]() $\sigma \in [\omega ]^{<\omega }$
with
$\sigma \in [\omega ]^{<\omega }$
with
![]() $|\sigma |< n$
, there is a
$|\sigma |< n$
, there is a
![]() $I_\sigma $
with
$I_\sigma $
with
![]() $|I_\sigma |\leq d_{n - |\sigma |-1}$
such that for every
$|I_\sigma |\leq d_{n - |\sigma |-1}$
such that for every
![]() $x\notin I_\sigma $
,
$x\notin I_\sigma $
,
For each
![]() $s< n, i<d_{n-s-1}$
, consider the coloring
$s< n, i<d_{n-s-1}$
, consider the coloring
![]() $f_{s,i}:[\omega ]^s\rightarrow \omega $
such that
$f_{s,i}:[\omega ]^s\rightarrow \omega $
such that
![]() $f_{s,i}(\sigma )$
is the ith element of
$f_{s,i}(\sigma )$
is the ith element of
![]() $I_\sigma $
.
$I_\sigma $
.
Since
![]() $\mathcal {F}$
is n-
$\mathcal {F}$
is n-
![]() $\operatorname {\mathrm {\sf {FS}}}$
-sufficient, there is an
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient, there is an
![]() $F\in \mathcal {F}$
such that F is
$F\in \mathcal {F}$
such that F is
![]() $f_{s,i}$
-free for all
$f_{s,i}$
-free for all
![]() $s< n,i<d_{n-s-1}$
. By choice of
$s< n,i<d_{n-s-1}$
. By choice of
![]() $X_0$
, let
$X_0$
, let
![]() $b\in \omega $
so that for every
$b\in \omega $
so that for every
![]() $\sigma \in [F]^{<\omega }$
with
$\sigma \in [F]^{<\omega }$
with
![]() $|\sigma |<n$
,
$|\sigma |<n$
,
 $$ \begin{align} (\forall \tau\in [X_0\cap (b,\infty)]^{n-|\sigma|}) f(\sigma,\tau)\notin F\smallsetminus I_\sigma. \end{align} $$
$$ \begin{align} (\forall \tau\in [X_0\cap (b,\infty)]^{n-|\sigma|}) f(\sigma,\tau)\notin F\smallsetminus I_\sigma. \end{align} $$
By preservation of 2-hyperimmune of
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
, let infinite f-free set
$\operatorname {\mathrm {\sf {FS}}}^n$
, let infinite f-free set
![]() $X_1\subseteq X_0\cap (b,\infty )$
so that
$X_1\subseteq X_0\cap (b,\infty )$
so that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $X_1$
-2-hyperimmune. By Lemma 2.40, let infinite set
$X_1$
-2-hyperimmune. By Lemma 2.40, let infinite set
![]() $Y\subseteq X_1$
so that
$Y\subseteq X_1$
so that
![]() $\mathcal {H}$
is Y-2-hyperimmune,
$\mathcal {H}$
is Y-2-hyperimmune,
![]() $Y>F$
and for every
$Y>F$
and for every
![]() $0<s<n$
,
$0<s<n$
,
We show that
![]() $F\cup Y$
is f-free. To see this, let
$F\cup Y$
is f-free. To see this, let
![]() $\sigma \in [F]^{<\omega },\tau \in [Y]^{<\omega }$
with
$\sigma \in [F]^{<\omega },\tau \in [Y]^{<\omega }$
with
![]() $|\sigma \cup \tau |=n$
, we need to prove
$|\sigma \cup \tau |=n$
, we need to prove
![]() $f(\sigma ,\tau )\notin F\smallsetminus \sigma $
and
$f(\sigma ,\tau )\notin F\smallsetminus \sigma $
and
![]() $f(\sigma ,\tau )\notin Y\smallsetminus \tau $
. To see
$f(\sigma ,\tau )\notin Y\smallsetminus \tau $
. To see
![]() $f(\sigma ,\tau )\notin Y\smallsetminus \tau $
, when
$f(\sigma ,\tau )\notin Y\smallsetminus \tau $
, when
![]() $|\tau | = n$
, the conclusion follows by f-free of Y; when
$|\tau | = n$
, the conclusion follows by f-free of Y; when
![]() $0<|\tau |<n$
, the conclusion follows from (2.9); when
$0<|\tau |<n$
, the conclusion follows from (2.9); when
![]() $|\tau | = 0$
, the conclusion follows by left trap of f. To see
$|\tau | = 0$
, the conclusion follows by left trap of f. To see
![]() $f(\sigma ,\tau )\notin F\smallsetminus \sigma $
, when
$f(\sigma ,\tau )\notin F\smallsetminus \sigma $
, when
![]() $|\sigma | = n$
, the conclusion follows from f-freeness of F. When
$|\sigma | = n$
, the conclusion follows from f-freeness of F. When
![]() $|\sigma |<n$
, suppose
$|\sigma |<n$
, suppose
![]() $f(\sigma ,\tau )\in F$
(otherwise we are done). By (2.8),
$f(\sigma ,\tau )\in F$
(otherwise we are done). By (2.8),
![]() $f(\sigma ,\tau )=x\in F\cap I_\sigma $
. Since
$f(\sigma ,\tau )=x\in F\cap I_\sigma $
. Since
![]() $x\in I_\sigma $
, it means for
$x\in I_\sigma $
, it means for
![]() $s=n-|\sigma |$
, for some
$s=n-|\sigma |$
, for some
![]() $i<d_{n-s-1}$
,
$i<d_{n-s-1}$
,
![]() $f_{s,i}(\sigma )=x$
. In particular,
$f_{s,i}(\sigma )=x$
. In particular,
![]() $f_{s,i}(\sigma )\in F$
. But F is
$f_{s,i}(\sigma )\in F$
. But F is
![]() $f_{s,i}$
-free, so
$f_{s,i}$
-free, so
![]() $x\notin \sigma $
. Thus we are done.⊣
$x\notin \sigma $
. Thus we are done.⊣
We are now ready to prove the missing theorem.
Theorem 2.43. For each
![]() $n \geq 1$
, if
$n \geq 1$
, if
![]() $\ \operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
$\ \operatorname {\mathrm {\sf {FS}}}^s$
strongly preserves 2-hyperimmunity for each
![]() $0\leq s<n$
and
$0\leq s<n$
and
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, then
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, then
![]() $\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity.
$\operatorname {\mathrm {\sf {FS}}}^n$
for left trapped functions strongly preserves 2-hyperimmunity.
Proof. Fix a left trapped coloring
![]() $f : [\omega ]^n \to \omega $
. By Lemma 2.34, we assume that for every
$f : [\omega ]^n \to \omega $
. By Lemma 2.34, we assume that for every
![]() $s<n$
, every
$s<n$
, every
![]() $\sigma \in [\omega ]^s$
,
$\sigma \in [\omega ]^s$
,
We will construct an infinite f-free set G such that
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $G $
-2-hyperimmune. Our forcing conditions are Mathias conditions
$G $
-2-hyperimmune. Our forcing conditions are Mathias conditions
![]() $(F, X)$
such that
$(F, X)$
such that
-
(a)
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $X $
-2-hyperimmune.
$X $
-2-hyperimmune. -
(b)
 $(\forall \sigma \in [F \cup X]^n) f(\sigma ) \not \in F \smallsetminus \sigma $
.
$(\forall \sigma \in [F \cup X]^n) f(\sigma ) \not \in F \smallsetminus \sigma $
. -
(c)
 $(\forall \sigma \in [F]^s)(\forall \tau \in [X]^{n-s}) f(\sigma , \tau ) \not \in X \smallsetminus \tau $
for each
$(\forall \sigma \in [F]^s)(\forall \tau \in [X]^{n-s}) f(\sigma , \tau ) \not \in X \smallsetminus \tau $
for each
 $0<s<n$
.
$0<s<n$
.
Clearly
![]() $(\emptyset ,\omega )$
is a condition. A precondition
$(\emptyset ,\omega )$
is a condition. A precondition
![]() $(F,X)$
is a Mathias condition satisfying (a) and where F is f-free.
$(F,X)$
is a Mathias condition satisfying (a) and where F is f-free.
Lemma 2.44.
-
(1) Every precondition can be extended to a condition.
-
(2) For every condition
 $(F,X)$
, every f-free set
$(F,X)$
, every f-free set
 $Y\subseteq X$
with
$Y\subseteq X$
with
 $Y>F$
,
$Y>F$
,
 $F\cup Y$
is f-free.
$F\cup Y$
is f-free. -
(3) For every condition
 $(F,X)$
, every finite f-free set
$(F,X)$
, every finite f-free set
 $E\subseteq X$
with
$E\subseteq X$
with
 $E>F$
,
$E>F$
,
 $(F\cup E, X )$
is a precondition.
$(F\cup E, X )$
is a precondition.
Proof. For item (1): Fix a precondition
![]() $(F,X)$
. By (2.10) and f-freeness of F, there is a
$(F,X)$
. By (2.10) and f-freeness of F, there is a
![]() $b\in \omega $
so that for every
$b\in \omega $
so that for every
![]() $\sigma \in [F]^{\leq n}$
,
$\sigma \in [F]^{\leq n}$
,
 $$ \begin{align*}(\forall \tau \in [\omega\cap (b, +\infty)]^{n-|\sigma|}) f(\sigma, \tau) \notin F\smallsetminus \sigma, \end{align*} $$
$$ \begin{align*}(\forall \tau \in [\omega\cap (b, +\infty)]^{n-|\sigma|}) f(\sigma, \tau) \notin F\smallsetminus \sigma, \end{align*} $$
which verifies that
![]() $(F,X\cap (b,\infty ))$
satisfies property (b). By Lemma 2.40, there is a reservoir-extensionFootnote
12
of
$(F,X\cap (b,\infty ))$
satisfies property (b). By Lemma 2.40, there is a reservoir-extensionFootnote
12
of
![]() $(F,X\cap (b,\infty ))$
satisfying property (c) while preserving property (a). Thus we are done (property (b) is preserved by reservoir-extension).
$(F,X\cap (b,\infty ))$
satisfying property (c) while preserving property (a). Thus we are done (property (b) is preserved by reservoir-extension).
For item (2): Let
![]() $\sigma \in [F]^{<\omega }, \tau \in [Y]^{<\omega }$
with
$\sigma \in [F]^{<\omega }, \tau \in [Y]^{<\omega }$
with
![]() $|\sigma \cup \tau | = n$
. We need to show that
$|\sigma \cup \tau | = n$
. We need to show that
![]() $f(\sigma , \tau )\notin F\smallsetminus \sigma $
and
$f(\sigma , \tau )\notin F\smallsetminus \sigma $
and
![]() $ f(\sigma ,\tau )\notin Y\smallsetminus \tau $
. It follows from property (b) of
$ f(\sigma ,\tau )\notin Y\smallsetminus \tau $
. It follows from property (b) of
![]() $(F,X)$
that
$(F,X)$
that
![]() $f(\sigma ,\tau )\notin F\smallsetminus \sigma $
. To see
$f(\sigma ,\tau )\notin F\smallsetminus \sigma $
. To see
![]() $f(\sigma ,\tau )\notin Y\smallsetminus \tau $
, the conclusion follows from property (c) of
$f(\sigma ,\tau )\notin Y\smallsetminus \tau $
, the conclusion follows from property (c) of
![]() $(F,X)$
when
$(F,X)$
when
![]() $|\sigma |,|\tau |>0$
; the conclusion follows by left trap of f when
$|\sigma |,|\tau |>0$
; the conclusion follows by left trap of f when
![]() $|\tau | = 0$
; the conclusion follows from f-freeness of Y when
$|\tau | = 0$
; the conclusion follows from f-freeness of Y when
![]() $|\tau | = n$
.
$|\tau | = n$
.
Item (3) follows from item (2) directly.⊣
Lemma 2.45. For every condition
![]() $(F, X)$
there exists an extension
$(F, X)$
there exists an extension
![]() $(E, Y)$
such that
$(E, Y)$
such that
![]() $|E|> |F|$
.
$|E|> |F|$
.
Proof. Pick any
![]() $x \in X$
so that
$x \in X$
so that
![]() $x>E$
and set
$x>E$
and set
![]() $E = F \cup \{x\}$
. Since
$E = F \cup \{x\}$
. Since
![]() $\{x\}$
is f-free, so by Lemma 2.44,
$\{x\}$
is f-free, so by Lemma 2.44,
![]() $(E,X)$
is a precondition.⊣
$(E,X)$
is a precondition.⊣
For every
![]() $e \in \omega $
, we want to satisfy the requirement
$e \in \omega $
, we want to satisfy the requirement
 $$ \begin{align*} \mathcal{R}_e: \text{If}\ \Phi^{ G}_e\ \text{is a total, then}\ \Phi^{ G}_e\ \text{meets}\ \mathcal{H}. \end{align*} $$
$$ \begin{align*} \mathcal{R}_e: \text{If}\ \Phi^{ G}_e\ \text{is a total, then}\ \Phi^{ G}_e\ \text{meets}\ \mathcal{H}. \end{align*} $$
Lemma 2.46. For every condition c and every index e, there is an extension d of c forcing
![]() $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
Proof. Fix
![]() $c = (F, X)$
. By Lemma 2.44, for notational convenience, assume
$c = (F, X)$
. By Lemma 2.44, for notational convenience, assume
![]() $F=\emptyset $
and
$F=\emptyset $
and
![]() $X=\omega $
. We define a partial computable biarray as follows.
$X=\omega $
. We define a partial computable biarray as follows.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $r \in \omega $
, search computably for some finite set
$r \in \omega $
, search computably for some finite set
![]() $U_r>r$
(if it exists) such that for every pair of left trapped colorings
$U_r>r$
(if it exists) such that for every pair of left trapped colorings
![]() $g, h : [\omega ]^n \to \omega $
, there is a finite n-
$g, h : [\omega ]^n \to \omega $
, there is a finite n-
![]() $\operatorname {\mathrm {\sf {FS}}}$
-sufficient collection
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient collection
![]() $\mathcal {E}$
of finite sets which is both g-free and h-free such that for every
$\mathcal {E}$
of finite sets which is both g-free and h-free such that for every
![]() $E\in \mathcal {E}$
,
$E\in \mathcal {E}$
,
Defining
![]() $V_{r,m}$
. Given
$V_{r,m}$
. Given
![]() $r, m \in \omega $
, search computably for some finite set
$r, m \in \omega $
, search computably for some finite set
![]() $V_{r,m}>m$
(if it exists) such that for every left trapped coloring
$V_{r,m}>m$
(if it exists) such that for every left trapped coloring
![]() $g : [\omega ]^n \to \omega $
, there is some g-free finite set E such that
$g : [\omega ]^n \to \omega $
, there is some g-free finite set E such that
We now have multiple outcomes, depending on which
![]() $U_r$
and
$U_r$
and
![]() $V_{r,m}$
is found.
$V_{r,m}$
is found.
-
• Case 1:
 $U_r$
is not found for some
$U_r$
is not found for some
 $r \in \omega $
. By compactness, the following
$r \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of pairs of left trapped colorings
$\mathcal {P}$
of pairs of left trapped colorings
 $g, h : [\omega ]^n \to \omega $
is nonempty: there is no n-
$g, h : [\omega ]^n \to \omega $
is nonempty: there is no n-
 $\operatorname {\mathrm {\sf {FS}}}$
-sufficient finite collection
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient finite collection
 $\mathcal {E}$
of finite sets which are both g-free and h-free, such that for every
$\mathcal {E}$
of finite sets which are both g-free and h-free, such that for every
 $E\in \mathcal {E}$
, we have
$E\in \mathcal {E}$
, we have
 $\Phi _e^{E}(r;1) \downarrow $
.
$\Phi _e^{E}(r;1) \downarrow $
.As
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $g, h $
of
$g, h $
of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g \oplus h$
-2-hyperimmune. Unfolding the definition of n-
$g \oplus h$
-2-hyperimmune. Unfolding the definition of n-
 $\operatorname {\mathrm {\sf {FS}}}$
-sufficient and use compactness, the following
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient and use compactness, the following
 $\Pi _1^{0,g\oplus h}$
class
$\Pi _1^{0,g\oplus h}$
class
 $\mathcal {Q}$
of sequence
$\mathcal {Q}$
of sequence
 $(f_{s,i}:[\omega ]^s\rightarrow \omega )_{s<n,i<d_{n-s-1}}$
of left trapped colorings is nonempty: (2.11)As
$(f_{s,i}:[\omega ]^s\rightarrow \omega )_{s<n,i<d_{n-s-1}}$
of left trapped colorings is nonempty: (2.11)As $$ \begin{align} &\text{for every finite set}\ E\ \text{which is}\ g\text{-free}, h\text{-free and }\nonumber\\[-3pt] &f_{s,i}\text{-free for each}\ s< n,i<d_{n-s-1}, \Phi_e^{E}(r;1) \uparrow. \end{align} $$
$$ \begin{align} &\text{for every finite set}\ E\ \text{which is}\ g\text{-free}, h\text{-free and }\nonumber\\[-3pt] &f_{s,i}\text{-free for each}\ s< n,i<d_{n-s-1}, \Phi_e^{E}(r;1) \uparrow. \end{align} $$
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member
 $(f_{s,i}:s< n,i<d_{n-s-1})$
of
$(f_{s,i}:s< n,i<d_{n-s-1})$
of
 $\mathcal {Q}$
such that
$\mathcal {Q}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g\oplus h\oplus _{s< n,i<d_{n-s-1}}f_{s,i}$
-2-hyperimmune. As
$g\oplus h\oplus _{s< n,i<d_{n-s-1}}f_{s,i}$
-2-hyperimmune. As
 $\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, there is an infinite set
$\operatorname {\mathrm {\sf {FS}}}^n$
preserves 2-hyperimmunity, there is an infinite set
 $Y $
which is both g-free, h-free and
$Y $
which is both g-free, h-free and
 $f_{s,i}$
-free for each
$f_{s,i}$
-free for each
 $s< n,i<d_{n-s-1}$
and such that
$s< n,i<d_{n-s-1}$
and such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $Y $
-2-hyperimmune. Clearly for every G satisfying condition
$Y $
-2-hyperimmune. Clearly for every G satisfying condition
 $(F,Y)$
, G is g-free, h-free and
$(F,Y)$
, G is g-free, h-free and
 $f_{s,i}$
-free for each
$f_{s,i}$
-free for each
 $s< n,i<d_{n-s-1}$
, so
$s< n,i<d_{n-s-1}$
, so
 $\Phi _e^{ G}(r;1) \uparrow $
. i.e., The condition
$\Phi _e^{ G}(r;1) \uparrow $
. i.e., The condition
 $d = (F, Y)$
is an extension of c forcing
$d = (F, Y)$
is an extension of c forcing
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
-
• Case 2:
 $U_r$
is found, but not
$U_r$
is found, but not
 $V_{r,m}$
for some
$V_{r,m}$
for some
 $r, m \in \omega $
. By compactness, the following
$r, m \in \omega $
. By compactness, the following
 $\Pi ^{0}_1$
class
$\Pi ^{0}_1$
class
 $\mathcal {P}$
of left trapped colorings
$\mathcal {P}$
of left trapped colorings
 $g : [\omega ]^n \to \omega $
is nonempty: for every g-free set
$g : [\omega ]^n \to \omega $
is nonempty: for every g-free set
 $E $
, (2.12)As
$E $
, (2.12)As $$ \begin{align} \Phi_e^{E}(r;1) \downarrow \subseteq U_r\Rightarrow \Phi_e^{E}(r, m;2) \uparrow. \end{align} $$
$$ \begin{align} \Phi_e^{E}(r;1) \downarrow \subseteq U_r\Rightarrow \Phi_e^{E}(r, m;2) \uparrow. \end{align} $$
 $\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member g of
$\operatorname {\mathrm {\sf {WKL}}}$
preserves 2-hyperimmunity (Corollary 2.7), there is a member g of
 $\mathcal {P}$
such that
$\mathcal {P}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $g $
-2-hyperimmune. By definition of
$g $
-2-hyperimmune. By definition of
 $U_r$
(where we take letting
$U_r$
(where we take letting
 $h = f$
), there is a n-
$h = f$
), there is a n-
 $\operatorname {\mathrm {\sf {FS}}}$
-sufficient finite collection
$\operatorname {\mathrm {\sf {FS}}}$
-sufficient finite collection
 $\mathcal {E}$
of finite sets which is both g-free and f-free and such that for each
$\mathcal {E}$
of finite sets which is both g-free and f-free and such that for each
 $E\in \mathcal {E}$
,
$E\in \mathcal {E}$
,  $$ \begin{align*}\Phi_e^{E}(r;1) \downarrow \subseteq U_r. \end{align*} $$
$$ \begin{align*}\Phi_e^{E}(r;1) \downarrow \subseteq U_r. \end{align*} $$
By Lemma 2.42, there is an infinite set Y and some
 $E\in \mathcal {E}$
such that
$E\in \mathcal {E}$
such that
 $\mathcal {H}$
is
$\mathcal {H}$
is
 $Y $
-2-hyperimmune and
$Y $
-2-hyperimmune and
 $E \cup Y$
is g-free. Consider the precondition
$E \cup Y$
is g-free. Consider the precondition
 $d=(E, Y)$
. It remains to prove that d forces
$d=(E, Y)$
. It remains to prove that d forces
 $\Phi _e^{ G}(r, m;2) \uparrow $
. Since
$\Phi _e^{ G}(r, m;2) \uparrow $
. Since
 $E \cup Y$
is g-free, so every G satisfying
$E \cup Y$
is g-free, so every G satisfying
 $(E,Y)$
is g-free. By definition of g (namely (2.12)) and
$(E,Y)$
is g-free. By definition of g (namely (2.12)) and
 $\Phi _e^{E}(r;1)\downarrow \subseteq U_r $
, for every G satisfying
$\Phi _e^{E}(r;1)\downarrow \subseteq U_r $
, for every G satisfying
 $(E,Y)$
,
$(E,Y)$
,
 $\Phi _e^{ G}(r, m;2) \uparrow $
.
$\Phi _e^{ G}(r, m;2) \uparrow $
. -
• Case 3:
 $U_r$
and
$U_r$
and
 $V_{r,m}$
are found for every
$V_{r,m}$
are found for every
 $r,m \in \omega $
. By 2-hyperimmunity of
$r,m \in \omega $
. By 2-hyperimmunity of
 $\mathcal {H}$
, there is some
$\mathcal {H}$
, there is some
 $r, m \in \omega $
such that
$r, m \in \omega $
such that
 $(U_r, V_{r,m}) \in \mathcal {H}$
. In particular, by definition of
$(U_r, V_{r,m}) \in \mathcal {H}$
. In particular, by definition of
 $V_{r,m}$
(where we take
$V_{r,m}$
(where we take
 $g = f$
), there is some f-free finite set E such that Consider the precondition
$g = f$
), there is some f-free finite set E such that Consider the precondition $$ \begin{align*}\Phi_e^{E}(r;1) \downarrow \subseteq U_r \wedge \Phi_e^{E}(r, m;2) \downarrow \subseteq V_{r,m}. \end{align*} $$
$$ \begin{align*}\Phi_e^{E}(r;1) \downarrow \subseteq U_r \wedge \Phi_e^{E}(r, m;2) \downarrow \subseteq V_{r,m}. \end{align*} $$
 $(E, X)$
. Clearly it forces
$(E, X)$
. Clearly it forces
 $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
This completes the proof of Lemma 2.46.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_s, X_s)$
, and let
$c_s = (F_s, X_s)$
, and let
![]() $G = \bigcup _s F_s$
. By property (b) of a condition, G is f-free. By Lemma 2.45, G is infinite, and by Lemma 2.46,
$G = \bigcup _s F_s$
. By property (b) of a condition, G is f-free. By Lemma 2.45, G is infinite, and by Lemma 2.46,
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $C \oplus G$
-2-hyperimmune. This completes the proof of Theorem 2.43.⊣
$C \oplus G$
-2-hyperimmune. This completes the proof of Theorem 2.43.⊣
3 Erdős–Moser theorem has no universal instance
In this section, we prove Theorem 3.6, that
![]() $\mathsf {EM}$
does not have a universal instance. To this end, we construct a pair of computable
$\mathsf {EM}$
does not have a universal instance. To this end, we construct a pair of computable
![]() $\mathsf {EM}$
instances
$\mathsf {EM}$
instances
![]() $T_0,T_1$
such that for every computable
$T_0,T_1$
such that for every computable
![]() $\mathsf {EM}$
instance T, T admits a solution that either computes no solution of
$\mathsf {EM}$
instance T, T admits a solution that either computes no solution of
![]() $T_0$
or computes no solution of
$T_0$
or computes no solution of
![]() $T_1$
. Given an
$T_1$
. Given an
![]() $\mathsf {EM}$
instance T and two sets
$\mathsf {EM}$
instance T and two sets
![]() $A,B$
, we write
$A,B$
, we write
![]() $A\rightarrow _T B$
iff for every
$A\rightarrow _T B$
iff for every
![]() $x\in A, y\in B$
,
$x\in A, y\in B$
,
![]() $T(x,y)$
Footnote
13
; we say T diagonalizes against
$T(x,y)$
Footnote
13
; we say T diagonalizes against
![]() $(A,B)$
if:
$(A,B)$
if:
![]() $A\rightarrow _{T} B$
and for all but finitely many
$A\rightarrow _{T} B$
and for all but finitely many
![]() $x\in \omega $
,
$x\in \omega $
,
![]() $B\rightarrow _{T} x\rightarrow _{T} A$
. The point is, when T diagonalizes against
$B\rightarrow _{T} x\rightarrow _{T} A$
. The point is, when T diagonalizes against
![]() $(A,B)$
, for any set H that has nonempty intersection with both
$(A,B)$
, for any set H that has nonempty intersection with both
![]() $A,B$
, there is no solution to T containing H.
$A,B$
, there is no solution to T containing H.
Definition 3.1.
-
(1) A 4-array is a sequence of
 $4$
-tuple of finite sets (of integers)
$4$
-tuple of finite sets (of integers)
 $\langle E_n,E_{n,m,l}, F_{n,m}, F_{n,m,l}: n,m,l\in \omega \rangle $
such that for every
$\langle E_n,E_{n,m,l}, F_{n,m}, F_{n,m,l}: n,m,l\in \omega \rangle $
such that for every
 $n,m,l\in \omega $
,
$n,m,l\in \omega $
,
 $E_n>n, E_{n,m,l}> m, F_{n,m}>n$
and
$E_n>n, E_{n,m,l}> m, F_{n,m}>n$
and
 $F_{n,m,l}> l$
.
$F_{n,m,l}> l$
. -
(2) A pair of
 $\mathsf {EM}$
instances
$\mathsf {EM}$
instances
 $(T_0,T_1) $
is C-4-hyperimmune if for every C-computable
$(T_0,T_1) $
is C-4-hyperimmune if for every C-computable
 $4$
-array
$4$
-array
 $\langle E_n,E_{n,m,l}, F_{n,m}, F_{n,m,l}: n,m,l\in \omega \rangle $
, there exist
$\langle E_n,E_{n,m,l}, F_{n,m}, F_{n,m,l}: n,m,l\in \omega \rangle $
, there exist
 $n,m,l\in \omega $
such that
$n,m,l\in \omega $
such that
 $T_0$
diagonalizes against
$T_0$
diagonalizes against
 $(E_{n},E_{n,m,l} )$
and
$(E_{n},E_{n,m,l} )$
and
 $T_1$
diagonalizes against
$T_1$
diagonalizes against
 $(F_{n,m},F_{n,m,l})$
.
$(F_{n,m},F_{n,m,l})$
.
For notational convenience, in this section we regard each Turing machine
![]() $\Phi $
as computing a 4-array. We will therefore assume that whenever
$\Phi $
as computing a 4-array. We will therefore assume that whenever
![]() $\Phi (n;1)$
converges, then it will output (the canonical index of) a finite set
$\Phi (n;1)$
converges, then it will output (the canonical index of) a finite set
![]() $E_n> n$
. Similarly for
$E_n> n$
. Similarly for
![]() $\Phi (n,m, l;2)$
,
$\Phi (n,m, l;2)$
,
![]() $\Phi (n,m;3)$
and
$\Phi (n,m;3)$
and
![]() $\Phi (n,m;4)$
with the appropriate lower bound.
$\Phi (n,m;4)$
with the appropriate lower bound.
By finite injury argument (as Proposition 2.10), we have:
Proposition 3.2. There exists a pair of computable stable 4-hyperimmune
![]() $\mathsf {EM}$
instance.
$\mathsf {EM}$
instance.
Proof. We build the tournaments
![]() $T_0$
and
$T_0$
and
![]() $T_1$
by a finite injury priority argument. For simplicity, we see
$T_1$
by a finite injury priority argument. For simplicity, we see
![]() $T_0$
and
$T_0$
and
![]() $T_1$
as functions over
$T_1$
as functions over
![]() $f_0, f_1 : [\omega ]^2 \to 2$
by letting for every
$f_0, f_1 : [\omega ]^2 \to 2$
by letting for every
![]() $x < y$
and
$x < y$
and
![]() $i < 2$
,
$i < 2$
,
![]() $T_i(x, y)$
hold iff
$T_i(x, y)$
hold iff
![]() $f_i(x, y) = 0$
. For every
$f_i(x, y) = 0$
. For every
![]() $e \in \omega $
, we want to satisfy the following requirement:
$e \in \omega $
, we want to satisfy the following requirement:
 $$ \begin{align} \mathcal{R}_e: &\text{If}\ \Phi_e\ \text{is total, then there is some}\ n, m, l \in \omega\ \text{such that}\nonumber\\ &T_0\ \text{diagonalizes against}\ (\Phi_e(n;1), \Phi_e(n, m, l;2))\ \text{and }\nonumber\\ & T_1\ \text{diagonalizes against}\ (\Phi_e(n,m;3), \Phi_e(n, m, l;4)). \end{align} $$
$$ \begin{align} \mathcal{R}_e: &\text{If}\ \Phi_e\ \text{is total, then there is some}\ n, m, l \in \omega\ \text{such that}\nonumber\\ &T_0\ \text{diagonalizes against}\ (\Phi_e(n;1), \Phi_e(n, m, l;2))\ \text{and }\nonumber\\ & T_1\ \text{diagonalizes against}\ (\Phi_e(n,m;3), \Phi_e(n, m, l;4)). \end{align} $$
The requirements are given the usual priority ordering
![]() $\mathcal {R}_0 < \mathcal {R}_1 < \cdots $
Initially, the requirements are neither partially, nor fully satisfied.
$\mathcal {R}_0 < \mathcal {R}_1 < \cdots $
Initially, the requirements are neither partially, nor fully satisfied.
-
(i) A requirement
 $\mathcal {R}_e$
requires a first attention at stage s if it is not first satisfied and
$\mathcal {R}_e$
requires a first attention at stage s if it is not first satisfied and
 $\Phi _{e,s}(n;1) \downarrow = E_n$
for some set
$\Phi _{e,s}(n;1) \downarrow = E_n$
for some set
 $E_n \subseteq \{e+1, \dots , s-1\}$
such that no element in
$E_n \subseteq \{e+1, \dots , s-1\}$
such that no element in
 $E_n$
is restrained by a requirement of higher priority. If it receives attention, then it puts a restraint on
$E_n$
is restrained by a requirement of higher priority. If it receives attention, then it puts a restraint on
 $E_n$
, commits the elements of
$E_n$
, commits the elements of
 $E_n$
to be in
$E_n$
to be in
 $C_0(f_0)$
, and is declared first satisfied.
$C_0(f_0)$
, and is declared first satisfied. -
(ii) A requirement
 $\mathcal {R}_e$
requires a second attention at stage s if it is not second satisfied and
$\mathcal {R}_e$
requires a second attention at stage s if it is not second satisfied and
 $\Phi _{e,s}(n;1) \downarrow = E_n$
and
$\Phi _{e,s}(n;1) \downarrow = E_n$
and
 $\Phi _{e,s}(n,m;3) \downarrow = F_{n,m}$
for some sets
$\Phi _{e,s}(n,m;3) \downarrow = F_{n,m}$
for some sets
 $E_n, F_{n,m} \subseteq \{e+1, \dots , s-1\}$
such that no element in
$E_n, F_{n,m} \subseteq \{e+1, \dots , s-1\}$
such that no element in
 $E_n \cup F_{n,m}$
is restrained by a requirement of higher priority and such that
$E_n \cup F_{n,m}$
is restrained by a requirement of higher priority and such that
 $f_0(x, y) = 0$
for every
$f_0(x, y) = 0$
for every
 $x \in E_n$
and
$x \in E_n$
and
 $y \in \{m+1, m+2, \dots , s-1\}$
. If it receives attention, then it puts a restraint on
$y \in \{m+1, m+2, \dots , s-1\}$
. If it receives attention, then it puts a restraint on
 $E_n \cup F_{n,m}$
, commits the elements of
$E_n \cup F_{n,m}$
, commits the elements of
 $E_n$
to be in
$E_n$
to be in
 $C_0(f_0)$
and the elements of
$C_0(f_0)$
and the elements of
 $F_{n,m}$
to be in
$F_{n,m}$
to be in
 $C_0(f_1)$
. Then the requirement is declared second satisfied.
$C_0(f_1)$
. Then the requirement is declared second satisfied. -
(iii) A requirement
 $\mathcal {R}_e$
requires a third attention at stage s if it is not fully satisfied, and
$\mathcal {R}_e$
requires a third attention at stage s if it is not fully satisfied, and
 $\Phi _{e,s}(n;1) \downarrow = E_n$
,
$\Phi _{e,s}(n;1) \downarrow = E_n$
,
 $\Phi _{e,s}(n, m, l;2) \downarrow = E_{n,m,l}$
,
$\Phi _{e,s}(n, m, l;2) \downarrow = E_{n,m,l}$
,
 $\Phi _{e,s}(n,m;3) \downarrow = F_{n,m}$
and
$\Phi _{e,s}(n,m;3) \downarrow = F_{n,m}$
and
 $\Phi _{e,s}(n,m,l;4) \downarrow = F_{n,m,l}$
for some sets
$\Phi _{e,s}(n,m,l;4) \downarrow = F_{n,m,l}$
for some sets
 $E_n, E_{n,m,l}, F_{n,m}, F_{n,m,l} \subseteq \{e+1, \dots , s-1\}$
which are not restrained by a requirement of higher priority, and such that
$E_n, E_{n,m,l}, F_{n,m}, F_{n,m,l} \subseteq \{e+1, \dots , s-1\}$
which are not restrained by a requirement of higher priority, and such that
 $f_0(x, y) = 0$
for every
$f_0(x, y) = 0$
for every
 $x \in E_n$
and
$x \in E_n$
and
 $y \in \{m+1, m+2, \dots , s-1\}$
, and
$y \in \{m+1, m+2, \dots , s-1\}$
, and
 $f_1(x, y) = 0$
for every
$f_1(x, y) = 0$
for every
 $x \in F_{n,m}$
and
$x \in F_{n,m}$
and
 $y \in \{l+1, l+2, \dots , s-1 \}$
. If it receives attention, then it puts a restraint on
$y \in \{l+1, l+2, \dots , s-1 \}$
. If it receives attention, then it puts a restraint on
 $E_n \cup E_{n,m,l} \cup F_{n,m} \cup F_{n,m,l}$
, commits the elements of
$E_n \cup E_{n,m,l} \cup F_{n,m} \cup F_{n,m,l}$
, commits the elements of
 $E_n$
to be in
$E_n$
to be in
 $C_1(f_0)$
, the elements of
$C_1(f_0)$
, the elements of
 $E_{n,m,l}$
to be in
$E_{n,m,l}$
to be in
 $C_0(f_0)$
, the elements of
$C_0(f_0)$
, the elements of
 $F_{n,m}$
to be in
$F_{n,m}$
to be in
 $C_1(f_1)$
, the elements of
$C_1(f_1)$
, the elements of
 $F_{n,m,l}$
to be in
$F_{n,m,l}$
to be in
 $C_0(f_1)$
, and is declared fully satisfied.
$C_0(f_1)$
, and is declared fully satisfied.
At stage 0, we let
![]() $f_0 = f_1 = \emptyset $
. Suppose that at stage s, we have defined
$f_0 = f_1 = \emptyset $
. Suppose that at stage s, we have defined
![]() $f_0(x, y)$
and
$f_0(x, y)$
and
![]() $f_1(x, y)$
for every
$f_1(x, y)$
for every
![]() $x < y < s$
. For every
$x < y < s$
. For every
![]() $x < s$
and
$x < s$
and
![]() $i < 2$
, if it is committed to be in some
$i < 2$
, if it is committed to be in some
![]() $C_j(f_i)$
, set
$C_j(f_i)$
, set
![]() $f_i(x, s) = j$
, and otherwise set
$f_i(x, s) = j$
, and otherwise set
![]() $f_i(x, s) = 0$
. Let
$f_i(x, s) = 0$
. Let
![]() $\mathcal {R}_e$
be the requirement of highest priority which requires attention. If
$\mathcal {R}_e$
be the requirement of highest priority which requires attention. If
![]() $\mathcal {R}_e$
requires a third attention, then execute the third procedure. Otherwise, if it requires the second attention, then execute the second procedure, and in the last case, execute the first one. In any case, reset all the requirements of lower priorities by setting them unsatisfied, releasing all their restraints, and go to the next stage. This completes the construction. On easily sees by induction that each requirement acts finitely often, and is eventually fully satisfied. This procedure also yields stable colorings, hence stable tournaments.⊣
$\mathcal {R}_e$
requires a third attention, then execute the third procedure. Otherwise, if it requires the second attention, then execute the second procedure, and in the last case, execute the first one. In any case, reset all the requirements of lower priorities by setting them unsatisfied, releasing all their restraints, and go to the next stage. This completes the construction. On easily sees by induction that each requirement acts finitely often, and is eventually fully satisfied. This procedure also yields stable colorings, hence stable tournaments.⊣
Before proving our core argument which will be Theorem 1.7, we prove a few preservation results. These results will be used to assume some good properties on our tournaments.
Proposition 3.3.
![]() $\mathsf {COH}$
preserves 4-hyperimmunity. i.e., For every set C and C-4-hyperimmune
$\mathsf {COH}$
preserves 4-hyperimmunity. i.e., For every set C and C-4-hyperimmune
![]() $\mathsf {EM}$
instance pair
$\mathsf {EM}$
instance pair
![]() $(T_0,T_1)$
, and every C-computable
$(T_0,T_1)$
, and every C-computable
![]() $\mathsf {COH}$
instance
$\mathsf {COH}$
instance
![]() $\vec {R}$
, there exists a solution G of
$\vec {R}$
, there exists a solution G of
![]() $\vec {R}$
such that
$\vec {R}$
such that
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $C\oplus G$
-4-hyperimmune.
$C\oplus G$
-4-hyperimmune.
Proof. Let
![]() $\mathcal {B}$
be the class of all
$\mathcal {B}$
be the class of all
![]() $4$
-arrays such that for every
$4$
-arrays such that for every
![]() $m, n, l \in \omega $
, either
$m, n, l \in \omega $
, either
![]() $T_0$
does not diagonalize against
$T_0$
does not diagonalize against
![]() $(E_{n},E_{n,m,l} )$
or
$(E_{n},E_{n,m,l} )$
or
![]() $T_1$
does not diagonalize against
$T_1$
does not diagonalize against
![]() $(F_{n,m},F_{n,m,l})$
. The class
$(F_{n,m},F_{n,m,l})$
. The class
![]() $\mathcal {B}$
can be coded as a closed set in the Baire space
$\mathcal {B}$
can be coded as a closed set in the Baire space
![]() $\omega ^\omega $
. By hypothesis,
$\omega ^\omega $
. By hypothesis,
![]() $\mathcal {B}$
has no C-computable member. By [Reference Patey13, Corollary 2.9], there is an
$\mathcal {B}$
has no C-computable member. By [Reference Patey13, Corollary 2.9], there is an
![]() $\vec {R}$
-cohesive set G such that
$\vec {R}$
-cohesive set G such that
![]() $\mathcal {B}$
has no
$\mathcal {B}$
has no
![]() $C \oplus G$
-computable member. By definition of
$C \oplus G$
-computable member. By definition of
![]() $\mathcal {B}$
,
$\mathcal {B}$
,
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $C\oplus G$
-4-hyperimmune.⊣
$C\oplus G$
-4-hyperimmune.⊣
We also need the preservation of 4-hyperimmunity of
![]() $\mathsf {WKL}$
.
$\mathsf {WKL}$
.
Proposition 3.4.
![]() $\mathsf {WKL}$
preserves 4-hyperimmunity. i.e., For every set C and C-4-hyperimmune
$\mathsf {WKL}$
preserves 4-hyperimmunity. i.e., For every set C and C-4-hyperimmune
![]() $\mathsf {EM}$
instance pair
$\mathsf {EM}$
instance pair
![]() $(T_0,T_1)$
, every nonempty
$(T_0,T_1)$
, every nonempty
 $\Pi _1^{0,C}$
class
$\Pi _1^{0,C}$
class
![]() $\mathcal {P}\subseteq 2^\omega $
, there is a
$\mathcal {P}\subseteq 2^\omega $
, there is a
![]() $G\in \mathcal {P}$
such that
$G\in \mathcal {P}$
such that
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $C\oplus G$
-4-hyperimmune.
$C\oplus G$
-4-hyperimmune.
Proof. Assume
![]() $C = \emptyset $
, and fix
$C = \emptyset $
, and fix
![]() $(T_0, T_1)$
and a
$(T_0, T_1)$
and a
![]() $\Pi ^0_1$
class
$\Pi ^0_1$
class
![]() $\mathcal {P} \subseteq 2^\omega $
. We will prove our proposition with a forcing with
$\mathcal {P} \subseteq 2^\omega $
. We will prove our proposition with a forcing with
![]() $\Pi ^0_1$
non-empty subclasses of
$\Pi ^0_1$
non-empty subclasses of
![]() $\mathcal {P}$
. We satisfy the requirement:
$\mathcal {P}$
. We satisfy the requirement:
 $$ \begin{align*} \mathcal{R}_e: & \text{If }\Phi_e^G\text{ is total, then for some}\ n,m,l \in \omega, \nonumber\\ & T_0\text{ diagonalizes against}\ (\Phi_e^G(n;1),\Phi_e^G(n,m,l;2))\ \text{and}\nonumber\\ &T_1\ \text{diagonalizes against}\ (\Phi_e^G(n,m;3),\Phi_e^G(n,m,l;4)). \end{align*} $$
$$ \begin{align*} \mathcal{R}_e: & \text{If }\Phi_e^G\text{ is total, then for some}\ n,m,l \in \omega, \nonumber\\ & T_0\text{ diagonalizes against}\ (\Phi_e^G(n;1),\Phi_e^G(n,m,l;2))\ \text{and}\nonumber\\ &T_1\ \text{diagonalizes against}\ (\Phi_e^G(n,m;3),\Phi_e^G(n,m,l;4)). \end{align*} $$
The core of the argument is the following lemma:
Lemma 3.5. For every index e, every condition c admits an extension forcing
![]() $\mathcal {R}_e$
.
$\mathcal {R}_e$
.
Proof. Let
![]() $\mathcal {Q} \subseteq \mathcal {P}$
be a condition. We define a partial computable 4-array as follows.
$\mathcal {Q} \subseteq \mathcal {P}$
be a condition. We define a partial computable 4-array as follows.
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $n \in \omega $
, search computably for some finite set
$n \in \omega $
, search computably for some finite set
![]() $U_n>n$
such that for every
$U_n>n$
such that for every
![]() $X\in \mathcal {Q}$
,
$X\in \mathcal {Q}$
,
Defining
![]() $V_{n,m}$
. Given
$V_{n,m}$
. Given
![]() $n,m\in \omega $
, search computably for some finite set
$n,m\in \omega $
, search computably for some finite set
![]() $ V_{n,m}>n$
such that for every
$ V_{n,m}>n$
such that for every
![]() $X\in \mathcal {Q}$
,
$X\in \mathcal {Q}$
,
Defining
![]() $U_{n,m,l},V_{n,m,l}$
. Given
$U_{n,m,l},V_{n,m,l}$
. Given
![]() $n,m,l\in \omega $
, search computably for some finite sets
$n,m,l\in \omega $
, search computably for some finite sets
![]() $U_{n,m,l}>m, V_{n,m,l}>l$
such that for every
$U_{n,m,l}>m, V_{n,m,l}>l$
such that for every
![]() $X\in \mathcal {Q}$
,
$X\in \mathcal {Q}$
,
We now have multiple outcomes, depending on which
![]() $U_n$
and
$U_n$
and
![]() $V_{n,m}$
is found.
$V_{n,m}$
is found.
-
• Case 1:
 $U_n$
is not found for some
$U_n$
is not found for some
 $n \in \omega $
. Then by compactness, the
$n \in \omega $
. Then by compactness, the
 $\Pi _1^0$
class
$\Pi _1^0$
class
 $\mathcal {W}$
of
$\mathcal {W}$
of
 $X\in \mathcal {Q}$
so that
$X\in \mathcal {Q}$
so that
 $\Phi _e^X(n;1)\uparrow $
is nonempty. Thus
$\Phi _e^X(n;1)\uparrow $
is nonempty. Thus
 $\mathcal {W}$
is the desired extension.
$\mathcal {W}$
is the desired extension. -
• Case 2:
 $V_{n,m}$
is not found for some
$V_{n,m}$
is not found for some
 $n, m \in \omega $
. Then by compactness, the
$n, m \in \omega $
. Then by compactness, the
 $\Pi _1^0$
class
$\Pi _1^0$
class
 $\mathcal {W}$
of
$\mathcal {W}$
of
 $X\in \mathcal {Q}$
so that
$X\in \mathcal {Q}$
so that
 $\Phi _{e}^{X}(n, m;2) \uparrow $
is nonempty. Thus
$\Phi _{e}^{X}(n, m;2) \uparrow $
is nonempty. Thus
 $\mathcal {W}$
is the desired extension.
$\mathcal {W}$
is the desired extension. -
• Case 3:
 $U_n$
or
$U_n$
or
 $V_{n,m}$
is not found for some
$V_{n,m}$
is not found for some
 $n,m \in \omega $
. Then by compactness, the
$n,m \in \omega $
. Then by compactness, the
 $\Pi _1^0$
class
$\Pi _1^0$
class
 $\mathcal {W}$
of
$\mathcal {W}$
of
 $X\in \mathcal {Q}$
so that is nonempty. Thus
$X\in \mathcal {Q}$
so that is nonempty. Thus $$ \begin{align*} &\Phi_e^X(n,m,l;3)\uparrow\vee \Phi_e^X(n,m,l;4)\uparrow \end{align*} $$
$$ \begin{align*} &\Phi_e^X(n,m,l;3)\uparrow\vee \Phi_e^X(n,m,l;4)\uparrow \end{align*} $$
 $\mathcal {W}$
is the desired extension.
$\mathcal {W}$
is the desired extension.
-
• Case 4:
 $U_n, V_{n,m},U_{n,m,l},V_{n,m,l}$
are found for every
$U_n, V_{n,m},U_{n,m,l},V_{n,m,l}$
are found for every
 $n,m \in \omega $
. Since
$n,m \in \omega $
. Since
 $(T_0,T_1)$
is 4-hyperimmune, there exist
$(T_0,T_1)$
is 4-hyperimmune, there exist
 $n, m,l$
such that
$n, m,l$
such that
 $T_0$
,
$T_0$
,
 $T_1$
diagonalizes against
$T_1$
diagonalizes against
 $(U_{n},U_{n,m,l})$
and
$(U_{n},U_{n,m,l})$
and
 $(V_{n, m},V_{n, m,l})$
respectively. Thus
$(V_{n, m},V_{n, m,l})$
respectively. Thus
 $\mathcal {Q}$
already forces
$\mathcal {Q}$
already forces
 $\mathcal {R}_e$
.⊣
$\mathcal {R}_e$
.⊣
Let
![]() $\mathcal {F} = \{\mathcal {P}_0, \mathcal {P}_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{\mathcal {P}_0, \mathcal {P}_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_s, X_s)$
, and let
$c_s = (F_s, X_s)$
, and let
![]() $G \in \bigcap _s \mathcal {P}_s$
. In particular,
$G \in \bigcap _s \mathcal {P}_s$
. In particular,
![]() $G \in \mathcal {P}$
and by Lemma 3.5,
$G \in \mathcal {P}$
and by Lemma 3.5,
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $C\oplus G$
-4-hyperimmune. This completes the proof of Theorem 3.4.⊣
$C\oplus G$
-4-hyperimmune. This completes the proof of Theorem 3.4.⊣
The rest of this section will be dedicated to the proof of Theorem 3.6, from which Theorem 1.7 follows.
Theorem 3.6. If a pair of
![]() $\mathsf {EM}$
instance
$\mathsf {EM}$
instance
![]() $(T_0,T_1)$
is C-4-hyperimmune, then for every C-computable
$(T_0,T_1)$
is C-4-hyperimmune, then for every C-computable
![]() $\mathsf {EM}$
instance T, there exists a solution G to T such that either
$\mathsf {EM}$
instance T, there exists a solution G to T such that either
![]() $C\oplus G$
does not compute a solution to
$C\oplus G$
does not compute a solution to
![]() $T_0$
, or
$T_0$
, or
![]() $C\oplus G$
does not compute a solution to
$C\oplus G$
does not compute a solution to
![]() $T_1$
.
$T_1$
.
Proof. For notational convenience, we assume
![]() $C=\emptyset $
. Fix
$C=\emptyset $
. Fix
![]() $(T_0,T_1)$
and T as in Theorem 3.6. By Proposition 3.3, we may assume that T is stable (for every
$(T_0,T_1)$
and T as in Theorem 3.6. By Proposition 3.3, we may assume that T is stable (for every
![]() $x\in \omega $
, either
$x\in \omega $
, either
![]() $x\rightarrow _T y$
for all but finitely many y, or
$x\rightarrow _T y$
for all but finitely many y, or
![]() $y\rightarrow _T x$
for all but finitely many y).
$y\rightarrow _T x$
for all but finitely many y).
In the rest of the proof, every Turing functional
![]() $\Phi ^G$
is computing a set of integers, namely
$\Phi ^G$
is computing a set of integers, namely
![]() $\{n: \Phi ^G(n)\downarrow =1\}$
; so it makes sense to write
$\{n: \Phi ^G(n)\downarrow =1\}$
; so it makes sense to write
![]() $\Phi ^G\cap A$
. Let
$\Phi ^G\cap A$
. Let
![]() $A_0\sqcup A_1$
be a 2-partition (of
$A_0\sqcup A_1$
be a 2-partition (of
![]() $\omega $
) such that
$\omega $
) such that
![]() $x\in A_0$
if and only if
$x\in A_0$
if and only if
![]() $x\rightarrow _T y$
for all but finitely many
$x\rightarrow _T y$
for all but finitely many
![]() $y\in \omega $
(which is well defined since T is stable). This automatically ensures that
$y\in \omega $
(which is well defined since T is stable). This automatically ensures that
![]() $x\in A_1$
iff
$x\in A_1$
iff
![]() $y\rightarrow _T x$
for all but finitely many
$y\rightarrow _T x$
for all but finitely many
![]() $y\in \omega $
. For a set
$y\in \omega $
. For a set
![]() $Z\subseteq \omega $
, a
$Z\subseteq \omega $
, a
![]() $2$
-partition
$2$
-partition
![]() $X_0\sqcup X_1$
of
$X_0\sqcup X_1$
of
![]() $\omega $
, we say Z is compatible with
$\omega $
, we say Z is compatible with
![]() $X_0\sqcup X_1$
if
$X_0\sqcup X_1$
if
![]() $Z\cap X_0\rightarrow _T Z\cap X_1$
. Note that if
$Z\cap X_0\rightarrow _T Z\cap X_1$
. Note that if
![]() $Z\subseteq X_i$
for some i, then Z is compatible with
$Z\subseteq X_i$
for some i, then Z is compatible with
![]() $X_0\sqcup X_1$
.
$X_0\sqcup X_1$
.
A condition is a Mathias condition
![]() $(F,X)$
with the following properties:
$(F,X)$
with the following properties:
-
(a) F is T-transitive and compatible with
 $A_0\sqcup A_1$
;
$A_0\sqcup A_1$
; -
(b)
 $F\cap A_0\rightarrow _T X\rightarrow _T F\cap A_1$
; and
$F\cap A_0\rightarrow _T X\rightarrow _T F\cap A_1$
; and -
(c)
 $(T_0,T_1)$
is X-4-hyperimmune.
$(T_0,T_1)$
is X-4-hyperimmune.
A precondition is a Mathias condition satisfying (a)(c).
Lemma 3.7. Let
![]() $(F,X)$
be a condition and
$(F,X)$
be a condition and
![]() $Y\subseteq X$
.
$Y\subseteq X$
.
-
(1) If Y is T-transitive, then
 $F\cup Y$
is T-transitive.
$F\cup Y$
is T-transitive. -
(2) If Y is compatible with
 $A_0\sqcup A_1$
, then
$A_0\sqcup A_1$
, then
 $F\cup Y$
is compatible with
$F\cup Y$
is compatible with
 $A_0\sqcup A_1$
.
$A_0\sqcup A_1$
. -
(3) For every precondition
 $(E,Y)$
, there is a
$(E,Y)$
, there is a
 $b\in \omega $
so that
$b\in \omega $
so that
 $(E,Y\cap (b,\infty ))$
is a condition.
$(E,Y\cap (b,\infty ))$
is a condition.
Proof. Items (1) and (2) follow from property (b) of
![]() $(F,X)$
. Item (3) follows from definition of
$(F,X)$
. Item (3) follows from definition of
![]() $A_0,A_1$
.⊣
$A_0,A_1$
.⊣
Lemma 3.8. For every condition
![]() $(F, X)$
there exists an extension
$(F, X)$
there exists an extension
![]() $(E, Y)$
such that
$(E, Y)$
such that
![]() $|E|> |F|$
.
$|E|> |F|$
.
Proof. Let
![]() $x\in X\smallsetminus F$
. Clearly
$x\in X\smallsetminus F$
. Clearly
![]() $\{x\}$
is T-transitive and compatible with
$\{x\}$
is T-transitive and compatible with
![]() $A_0\sqcup A_1$
. By Lemma 3.7 item (1)(2),
$A_0\sqcup A_1$
. By Lemma 3.7 item (1)(2),
![]() $(F\cup \{x\}, X)$
is a precondition.⊣
$(F\cup \{x\}, X)$
is a precondition.⊣
For
![]() $e\in \omega $
,
$e\in \omega $
,
![]() $i\in 2$
, let
$i\in 2$
, let
![]() $\mathcal {R}_e^i$
denote the requirement:
$\mathcal {R}_e^i$
denote the requirement:
 $$ \begin{align*}\Phi_e^G\text{ is not a solution to }T_i.\end{align*} $$
$$ \begin{align*}\Phi_e^G\text{ is not a solution to }T_i.\end{align*} $$
We will construct a solution G of T satisfying:
 $$ \begin{align*}\mathcal{R}_{e_0,e_1}: \mathcal{R}_{e_0}^0\vee \mathcal{R}_{e_1}^1\end{align*} $$
$$ \begin{align*}\mathcal{R}_{e_0,e_1}: \mathcal{R}_{e_0}^0\vee \mathcal{R}_{e_1}^1\end{align*} $$
for all
![]() $e_0,e_1\in \omega $
. A condition
$e_0,e_1\in \omega $
. A condition
![]() $(F,X)$
forces
$(F,X)$
forces
![]() $\mathcal {R}_{e_0,e_1}$
if: for every solution G of T satisfying
$\mathcal {R}_{e_0,e_1}$
if: for every solution G of T satisfying
![]() $(F,X)$
, G satisfies
$(F,X)$
, G satisfies
![]() $\mathcal {R}_{e_0,e_1}$
. Note that the definition of forcing is slightly different from that in Section 2, that we restrict to T-transitive set. This restriction cannot be applied in Section 2 since there we deal with arbitrary instance instead of computable instance.
$\mathcal {R}_{e_0,e_1}$
. Note that the definition of forcing is slightly different from that in Section 2, that we restrict to T-transitive set. This restriction cannot be applied in Section 2 since there we deal with arbitrary instance instead of computable instance.
Lemma 3.9. For every condition c and indices
![]() $e_0,e_1\in \omega $
, there is an extension of c forcing
$e_0,e_1\in \omega $
, there is an extension of c forcing
![]() $\mathcal {R}_{e_0,e_1}$
.
$\mathcal {R}_{e_0,e_1}$
.
Proof. Fix
![]() $c=(D,X)$
. By Lemma 3.7, for notational convenience, we assume
$c=(D,X)$
. By Lemma 3.7, for notational convenience, we assume
![]() $D=\emptyset $
and
$D=\emptyset $
and
![]() $X=\omega $
. We firstly describe a process to partially compute a
$X=\omega $
. We firstly describe a process to partially compute a
![]() $4$
-array. Then we show that if the computation diverges, we obtain an extension
$4$
-array. Then we show that if the computation diverges, we obtain an extension
![]() $d\leq c $
forcing
$d\leq c $
forcing
![]() $\mathcal {R}_{e_0,e_1}$
in the
$\mathcal {R}_{e_0,e_1}$
in the
![]() $\Pi _1^0$
way: one of
$\Pi _1^0$
way: one of
 $\Phi _{e_i}^{G}$
is not infinite; and if the computation converges, we obtain
$\Phi _{e_i}^{G}$
is not infinite; and if the computation converges, we obtain
![]() $d\leq c$
forcing
$d\leq c$
forcing
![]() $\mathcal {R}_{e_0,e_1}$
in a
$\mathcal {R}_{e_0,e_1}$
in a
![]() $\Sigma _1^0$
way: for some
$\Sigma _1^0$
way: for some
![]() $n,m,l$
so that
$n,m,l$
so that
![]() $T_0,T_1$
diagonalizes against
$T_0,T_1$
diagonalizes against
![]() $(V_n,V_{n,m}), (U_{n,m},U_{n,m,l})$
respectively, either
$(V_n,V_{n,m}), (U_{n,m},U_{n,m,l})$
respectively, either
 $\Phi _{e_0}^G\cap U_n\ne \emptyset \wedge \Phi _{e_0}^G\cap U_{n,m}\ne \emptyset $
; or
$\Phi _{e_0}^G\cap U_n\ne \emptyset \wedge \Phi _{e_0}^G\cap U_{n,m}\ne \emptyset $
; or
 $\Phi _{e_1}^G\cap V_{n,m}\ne \emptyset \wedge \Phi _{e_1}^G\cap V_{n,m,l}\ne \emptyset $
(which means for some
$\Phi _{e_1}^G\cap V_{n,m}\ne \emptyset \wedge \Phi _{e_1}^G\cap V_{n,m,l}\ne \emptyset $
(which means for some
![]() $i<2$
,
$i<2$
,
 $\Phi _{e_i}^G$
is not a solution to
$\Phi _{e_i}^G$
is not a solution to
![]() $T_i$
).
$T_i$
).
Defining
![]() $U_n$
. Given
$U_n$
. Given
![]() $n \in \omega $
, search computably for some finite set
$n \in \omega $
, search computably for some finite set
![]() $U_n>n$
such that for every
$U_n>n$
such that for every
![]() $8$
-partition
$8$
-partition
![]() $X_0\sqcup \cdots \sqcup X_7 = \omega $
, there exists an
$X_0\sqcup \cdots \sqcup X_7 = \omega $
, there exists an
![]() $i< 8$
, a finite T-transitive set
$i< 8$
, a finite T-transitive set
![]() $E\subseteq X_i$
such that
$E\subseteq X_i$
such that
 $\Phi _{e_0}^E\cap U_n\ne \emptyset $
.
$\Phi _{e_0}^E\cap U_n\ne \emptyset $
.
Defining
![]() $U_{n,m},V_{n,m}$
. Given
$U_{n,m},V_{n,m}$
. Given
![]() $n,m\in \omega $
, search computably for some finite set
$n,m\in \omega $
, search computably for some finite set
![]() $U_{n,m}>m, V_{n,m}>n$
such that for every
$U_{n,m}>m, V_{n,m}>n$
such that for every
![]() $4$
-partition
$4$
-partition
![]() $X_0\sqcup \cdots \sqcup X_3$
:
$X_0\sqcup \cdots \sqcup X_3$
:
-
(a) either there exists an
 $i< 4$
, a finite T-transitive set
$i< 4$
, a finite T-transitive set
 $E\subseteq X_i$
such that
$E\subseteq X_i$
such that
 $\Phi _{e_0}^{E}\cap U_n \neq \emptyset $
and
$\Phi _{e_0}^{E}\cap U_n \neq \emptyset $
and
 $\Phi _{e_0}^E\cap U_{n,m}\ne \emptyset $
and
$\Phi _{e_0}^E\cap U_{n,m}\ne \emptyset $
and -
(b) or there exist
 $j\ne i<4$
and two finite T-transitive sets
$j\ne i<4$
and two finite T-transitive sets
 $F\subseteq X_j, E\subseteq X_i$
such that
$F\subseteq X_j, E\subseteq X_i$
such that
 $\Phi _{e_0}^E\cap U_n \neq \emptyset $
and
$\Phi _{e_0}^E\cap U_n \neq \emptyset $
and
 $\Phi _{e_1}^{F}\cap V_{n,m}\ne \emptyset $
.
$\Phi _{e_1}^{F}\cap V_{n,m}\ne \emptyset $
.
Defining
![]() $U_{n,m,l},V_{n,m,l}$
. Given
$U_{n,m,l},V_{n,m,l}$
. Given
![]() $n,m\in \omega $
, search computably for some finite sets
$n,m\in \omega $
, search computably for some finite sets
![]() $U_{n,m,l}>m, V_{n,m,l}>l$
such that for every
$U_{n,m,l}>m, V_{n,m,l}>l$
such that for every
![]() $2$
-partition
$2$
-partition
![]() $X_0\sqcup X_1$
, there exists a finite T-transitive set
$X_0\sqcup X_1$
, there exists a finite T-transitive set
![]() $E $
compatible with
$E $
compatible with
![]() $X_0\sqcup X_1$
such that:
$X_0\sqcup X_1$
such that:
-
(p) either
 $\Phi _{e_0}^E\cap U_n \neq \emptyset $
and
$\Phi _{e_0}^E\cap U_n \neq \emptyset $
and
 $\Phi _{e_0}^E\cap U_{n,m,l}\ne \emptyset $
;
$\Phi _{e_0}^E\cap U_{n,m,l}\ne \emptyset $
; -
(q) or
 $\Phi _{e_1}^E\cap V_{n,m} \neq \emptyset $
and
$\Phi _{e_1}^E\cap V_{n,m} \neq \emptyset $
and
 $\Phi _{e_1}^E\cap V_{n,m,l}\ne \emptyset $
.
$\Phi _{e_1}^E\cap V_{n,m,l}\ne \emptyset $
.
Case 1:
![]() $U_n$
is not found for n.
$U_n$
is not found for n.
This is straightforward. By compactness, the following
![]() $\Pi _1^0$
class
$\Pi _1^0$
class
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $8$
-partitions
$8$
-partitions
![]() $X_0\sqcup \cdots \sqcup X_7$
is nonempty: for every
$X_0\sqcup \cdots \sqcup X_7$
is nonempty: for every
![]() $i< 8$
, every T-transitive finite set
$i< 8$
, every T-transitive finite set
![]() $E\subseteq X_i$
,
$E\subseteq X_i$
,
 $\Phi _{e_0}^E\cap (n,\infty )=\emptyset $
. As
$\Phi _{e_0}^E\cap (n,\infty )=\emptyset $
. As
![]() $\mathsf {WKL}$
preserves 4-hyperimmunity (Proposition 3.4), there exists a member
$\mathsf {WKL}$
preserves 4-hyperimmunity (Proposition 3.4), there exists a member
![]() $X_0\sqcup \cdots \sqcup X_7$
of
$X_0\sqcup \cdots \sqcup X_7$
of
![]() $\mathcal {P}$
so that
$\mathcal {P}$
so that
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $\oplus _{i<8} X_i$
-4-hyperimmune. Fix any
$\oplus _{i<8} X_i$
-4-hyperimmune. Fix any
![]() $i < 8$
such that
$i < 8$
such that
![]() $X_i$
is infinite. Then
$X_i$
is infinite. Then
![]() $(D,X_i) $
is an extension of c forcing
$(D,X_i) $
is an extension of c forcing
![]() $\mathcal {R}_{e_0,e_1}$
.
$\mathcal {R}_{e_0,e_1}$
.
Case 2:
![]() $U_n$
is found but not
$U_n$
is found but not
![]() $(U_{n,m},V_{n,m})$
for some
$(U_{n,m},V_{n,m})$
for some
![]() $n,m$
.
$n,m$
.
By compactness, the following
![]() $\Pi _1^0$
class
$\Pi _1^0$
class
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $4$
-partitions
$4$
-partitions
![]() $X_0\sqcup \cdots \sqcup X_3$
is nonempty:
$X_0\sqcup \cdots \sqcup X_3$
is nonempty:
-
(a) for every
 $i< 4$
, every finite T-transitive set
$i< 4$
, every finite T-transitive set
 $E\subseteq X_i$
, we have
$E\subseteq X_i$
, we have
 $\Phi _{e_0}^{E}\cap U_n=\emptyset \vee \Phi _{e_0}^E\cap ( m,\infty )=\emptyset $
and
$\Phi _{e_0}^{E}\cap U_n=\emptyset \vee \Phi _{e_0}^E\cap ( m,\infty )=\emptyset $
and -
(b) for every
 $j\ne i<4$
and every two finite T-transitive sets
$j\ne i<4$
and every two finite T-transitive sets
 $F\subseteq X_j, E\subseteq X_i$
, we have
$F\subseteq X_j, E\subseteq X_i$
, we have
 $\Phi _{e_0}^E\cap U_n=\emptyset \vee \Phi _{e_1}^{F}\cap (n,\infty )=\emptyset $
.
$\Phi _{e_0}^E\cap U_n=\emptyset \vee \Phi _{e_1}^{F}\cap (n,\infty )=\emptyset $
.
As
![]() $\mathsf {WKL}$
preserves 4-hyperimmunity (Proposition 3.4), there exists a member
$\mathsf {WKL}$
preserves 4-hyperimmunity (Proposition 3.4), there exists a member
![]() $X_0\sqcup \cdots \sqcup X_3$
of
$X_0\sqcup \cdots \sqcup X_3$
of
![]() $\mathcal {P}$
so that
$\mathcal {P}$
so that
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $\oplus _{i<4} X_i$
-4-hyperimmune. Consider the
$\oplus _{i<4} X_i$
-4-hyperimmune. Consider the
![]() $8$
-partition
$8$
-partition
![]() $(X_i\cap A_k: i<4,k<2)$
. By definition of
$(X_i\cap A_k: i<4,k<2)$
. By definition of
![]() $U_n$
, there exist
$U_n$
, there exist
![]() $i<4,k<2$
and a finite T-transitive set
$i<4,k<2$
and a finite T-transitive set
![]() $E\subseteq X_i\cap A_k$
, such that
$E\subseteq X_i\cap A_k$
, such that
 $\Phi _{e_0}^E\cap U_n\ne \emptyset $
.
$\Phi _{e_0}^E\cap U_n\ne \emptyset $
.
Subcase 1:
![]() $X_i$
is infinite.
$X_i$
is infinite.
Since
![]() $E\subseteq A_k$
, E is compatible with
$E\subseteq A_k$
, E is compatible with
![]() $A_0\sqcup A_1$
. So
$A_0\sqcup A_1$
. So
![]() $d=(E,X_i )$
is a precondition extending c. Note that by property (a) of
$d=(E,X_i )$
is a precondition extending c. Note that by property (a) of
![]() $X_0\sqcup \cdots \sqcup X_3$
, for every T-transitive set G satisfying d (so
$X_0\sqcup \cdots \sqcup X_3$
, for every T-transitive set G satisfying d (so
![]() $G\subseteq X_i$
), we have
$G\subseteq X_i$
), we have
 $\Phi _{e_0}^G\cap ( m,\infty )=\emptyset $
(since
$\Phi _{e_0}^G\cap ( m,\infty )=\emptyset $
(since
 $\Phi _{e_0}^G\cap U_n\ne \emptyset $
). Thus, d forces
$\Phi _{e_0}^G\cap U_n\ne \emptyset $
). Thus, d forces
![]() $\mathcal {R}_{e_0,e_1}$
.
$\mathcal {R}_{e_0,e_1}$
.
Subcase 2:
![]() $X_i$
is finite.
$X_i$
is finite.
Then there exists a
![]() $j\ne i $
such that
$j\ne i $
such that
![]() $X_j$
is infinite. Note that by property (b) of
$X_j$
is infinite. Note that by property (b) of
![]() $X_0\sqcup \cdots \sqcup X_3$
, for every T-transitive set
$X_0\sqcup \cdots \sqcup X_3$
, for every T-transitive set
![]() $G\subseteq X_j$
, we have
$G\subseteq X_j$
, we have
 $\Phi _{e_1}^G\cap (n,\infty )=\emptyset $
. Thus the condition
$\Phi _{e_1}^G\cap (n,\infty )=\emptyset $
. Thus the condition
![]() $(D,X_j)$
extends c and forces
$(D,X_j)$
extends c and forces
![]() $\mathcal {R}_{e_0,e_1}$
.
$\mathcal {R}_{e_0,e_1}$
.
Case 3:
![]() $U_n,U_{n,m},V_{n,m}$
are found but not
$U_n,U_{n,m},V_{n,m}$
are found but not
![]() $(U_{n,m,l},V_{n,m,l})$
for some
$(U_{n,m,l},V_{n,m,l})$
for some
![]() $n,m,l\in \omega $
.
$n,m,l\in \omega $
.
By compactness, the following
![]() $\Pi _1^0$
class
$\Pi _1^0$
class
![]() $\mathcal {P}$
of
$\mathcal {P}$
of
![]() $2$
-partitions
$2$
-partitions
![]() $X_0\sqcup X_1$
is nonempty: for every finite T-transitive finite set
$X_0\sqcup X_1$
is nonempty: for every finite T-transitive finite set
![]() $E $
compatible with
$E $
compatible with
![]() $X_0\sqcup X_1$
, we have
$X_0\sqcup X_1$
, we have
-
(p)
 $\Phi _{e_0}^E\cap U_n=\emptyset \vee \Phi _{e_0}^E\cap ( m,\infty )=\emptyset $
and
$\Phi _{e_0}^E\cap U_n=\emptyset \vee \Phi _{e_0}^E\cap ( m,\infty )=\emptyset $
and -
(q)
 $\Phi _{e_1}^E\cap V_{n,m}=\emptyset \vee \Phi _{e_1}^E\cap ( l,\infty )=\emptyset $
.
$\Phi _{e_1}^E\cap V_{n,m}=\emptyset \vee \Phi _{e_1}^E\cap ( l,\infty )=\emptyset $
.
By Proposition 3.4, there exists a member
![]() $X_0\sqcup X_1$
of
$X_0\sqcup X_1$
of
![]() $\mathcal {P}$
so that
$\mathcal {P}$
so that
![]() $(T_0,T_1)$
is
$(T_0,T_1)$
is
![]() $\oplus _{j<2} X_j$
-4-hyperimmune. Consider the
$\oplus _{j<2} X_j$
-4-hyperimmune. Consider the
![]() $4$
-partition
$4$
-partition
![]() $(X_j\cap A_k:j,k<2)$
. By property (p) of
$(X_j\cap A_k:j,k<2)$
. By property (p) of
![]() $X_0\sqcup X_1$
, for every
$X_0\sqcup X_1$
, for every
![]() $j,k<2$
and
$j,k<2$
and
![]() $E\subseteq X_j\cap A_k$
(so E is compatible with
$E\subseteq X_j\cap A_k$
(so E is compatible with
![]() $X_0\sqcup X_1$
),
$X_0\sqcup X_1$
),
 $$ \begin{align} \Phi_{e_0}^E\cap U_n=\emptyset\vee \Phi_{e_0}^E\cap( m,\infty)=\emptyset. \end{align} $$
$$ \begin{align} \Phi_{e_0}^E\cap U_n=\emptyset\vee \Phi_{e_0}^E\cap( m,\infty)=\emptyset. \end{align} $$
Combine with the definition of
![]() $U_{n,m},V_{n,m}$
(where we take the 4-partition to be
$U_{n,m},V_{n,m}$
(where we take the 4-partition to be
![]() $(X_j\cap A_k:j,k<2)$
and note that by (3.2), property (a) fails, so property (b) occurs), we have: there are
$(X_j\cap A_k:j,k<2)$
and note that by (3.2), property (a) fails, so property (b) occurs), we have: there are
 $(j,k)\ne (\hat j,\hat k)$
and finite T-transitive sets
$(j,k)\ne (\hat j,\hat k)$
and finite T-transitive sets
 $E\subseteq X_j\cap A_k, F\subseteq X_{\hat j}\cap A_{\hat k} $
such that
$E\subseteq X_j\cap A_k, F\subseteq X_{\hat j}\cap A_{\hat k} $
such that
 $$ \begin{align*}\Phi_{e_0}^E\cap U_n, \Phi_{e_1}^{F}\cap V_{n,m}\ne\emptyset.\end{align*} $$
$$ \begin{align*}\Phi_{e_0}^E\cap U_n, \Phi_{e_1}^{F}\cap V_{n,m}\ne\emptyset.\end{align*} $$
Subcase 1: Either
![]() $X_j$
or
$X_j$
or
![]() $X_{\hat j}$
is infinite.
$X_{\hat j}$
is infinite.
Suppose
![]() $X_j$
is infinite. Consider the precondition
$X_j$
is infinite. Consider the precondition
![]() $d=(E,X_j)$
extending c. Note that for every T-transitive set
$d=(E,X_j)$
extending c. Note that for every T-transitive set
![]() $G $
satisfying d,
$G $
satisfying d,
![]() $ G$
is compatible with
$ G$
is compatible with
![]() $X_0\sqcup X_1$
(since
$X_0\sqcup X_1$
(since
![]() $G\subseteq X_j$
). Thus by property (p) of
$G\subseteq X_j$
). Thus by property (p) of
![]() $X_0\sqcup X_1$
and
$X_0\sqcup X_1$
and
 $\Phi _{e_0}^E\cap U_n\ne \emptyset $
, for every T-transitive set
$\Phi _{e_0}^E\cap U_n\ne \emptyset $
, for every T-transitive set
![]() $G $
satisfying d, we have
$G $
satisfying d, we have
 $\Phi _{e_0}^G\cap (m,\infty )=\emptyset $
. Thus d forces
$\Phi _{e_0}^G\cap (m,\infty )=\emptyset $
. Thus d forces
![]() $\mathcal {R}_{e_0,e_1}$
. Suppose now
$\mathcal {R}_{e_0,e_1}$
. Suppose now
![]() $X_{\hat j}$
is infinite. Then, taking
$X_{\hat j}$
is infinite. Then, taking
 $d = (F, X_{\hat j})$
, a similar argument shows that by property (q) of
$d = (F, X_{\hat j})$
, a similar argument shows that by property (q) of
![]() $X_0\sqcup X_1$
, for every T-transitive set
$X_0\sqcup X_1$
, for every T-transitive set
![]() $G $
satisfying d, we have
$G $
satisfying d, we have
 $\Phi _{e_1}^G\cap (l,\infty )=\emptyset $
. Thus d forces
$\Phi _{e_1}^G\cap (l,\infty )=\emptyset $
. Thus d forces
![]() $\mathcal {R}_{e_0,e_1}$
. Thus we are done in this subcase.
$\mathcal {R}_{e_0,e_1}$
. Thus we are done in this subcase.
Subcase 2: Both
![]() $X_j$
,
$X_j$
,
![]() $X_{\hat j}$
are finite.
$X_{\hat j}$
are finite.
This implies
![]() $j=\hat j$
since
$j=\hat j$
since
![]() $X_0 \sqcup X_1 = \omega $
, and then
$X_0 \sqcup X_1 = \omega $
, and then
 $k\ne \hat k$
since
$k\ne \hat k$
since
 $(j,k)\ne (\hat j,\hat k)$
. Let b be sufficiently large to witness the limits of the elements of F and E with respect to the tournament.
$(j,k)\ne (\hat j,\hat k)$
. Let b be sufficiently large to witness the limits of the elements of F and E with respect to the tournament.
If
![]() $j=\hat j=0$
(so
$j=\hat j=0$
(so
![]() $X_1$
is infinite) and
$X_1$
is infinite) and
![]() $\hat k=0, k=1$
, consider the condition
$\hat k=0, k=1$
, consider the condition
![]() $d= (F,X_1\smallsetminus [0,b])$
. Since
$d= (F,X_1\smallsetminus [0,b])$
. Since
![]() $F\subseteq A_{\hat k}=A_0$
, we have
$F\subseteq A_{\hat k}=A_0$
, we have
![]() $F\rightarrow _T X_1\smallsetminus [0,b]$
. Therefore for every
$F\rightarrow _T X_1\smallsetminus [0,b]$
. Therefore for every
![]() $G\subseteq X_1\smallsetminus [0,b]$
,
$G\subseteq X_1\smallsetminus [0,b]$
,
![]() $F\cup G$
is compatible with
$F\cup G$
is compatible with
![]() $X_0\sqcup X_1$
(since
$X_0\sqcup X_1$
(since
![]() $F\subseteq X_0$
). Thus for every T-transitive set G satisfying d, by property (q) of
$F\subseteq X_0$
). Thus for every T-transitive set G satisfying d, by property (q) of
![]() $X_0\sqcup X_1$
and since
$X_0\sqcup X_1$
and since
 $\Phi _{e_1}^F\cap V_{n,m}\ne \emptyset $
, we have
$\Phi _{e_1}^F\cap V_{n,m}\ne \emptyset $
, we have
 $\Phi _{e_1}^{G}\cap (l,\infty )=\emptyset $
. Thus d forces
$\Phi _{e_1}^{G}\cap (l,\infty )=\emptyset $
. Thus d forces
 $\mathcal {R}_{e_1}^1$
.
$\mathcal {R}_{e_1}^1$
.
If
![]() $j=\hat j=1$
(so
$j=\hat j=1$
(so
![]() $X_0$
is infinite) and
$X_0$
is infinite) and
![]() $\hat k=0, k=1$
, consider the condition
$\hat k=0, k=1$
, consider the condition
![]() $d=(E,X_0 \smallsetminus [0,b])$
. Since
$d=(E,X_0 \smallsetminus [0,b])$
. Since
![]() $E\subseteq A_k=A_1 $
, we have
$E\subseteq A_k=A_1 $
, we have
![]() $X_0\smallsetminus [0,b]\rightarrow _T E$
. Therefore for every set
$X_0\smallsetminus [0,b]\rightarrow _T E$
. Therefore for every set
![]() $G\subseteq X_0\smallsetminus [0,b]$
,
$G\subseteq X_0\smallsetminus [0,b]$
,
![]() $E\cup G$
is compatible with
$E\cup G$
is compatible with
![]() $X_0\sqcup X_1$
(since
$X_0\sqcup X_1$
(since
![]() $E\subseteq X_1$
). Thus for every T-transitive set G satisfying d, by property (p) of
$E\subseteq X_1$
). Thus for every T-transitive set G satisfying d, by property (p) of
![]() $X_0\sqcup X_1$
and
$X_0\sqcup X_1$
and
 $\Phi _{e_0}^E\cap U_n\ne \emptyset $
, we have
$\Phi _{e_0}^E\cap U_n\ne \emptyset $
, we have
 $\Phi _{e_0}^G\cap (m,\infty )=\emptyset $
. Thus d forces
$\Phi _{e_0}^G\cap (m,\infty )=\emptyset $
. Thus d forces
 $\mathcal {R}_{e_0}^0$
.
$\mathcal {R}_{e_0}^0$
.
If
![]() $j=\hat j=0$
(so
$j=\hat j=0$
(so
![]() $X_1$
is infinite) and
$X_1$
is infinite) and
![]() $\hat k=1, k=0$
, then the condition
$\hat k=1, k=0$
, then the condition
![]() $(E, X_1 \smallsetminus [0, b])$
forces
$(E, X_1 \smallsetminus [0, b])$
forces
 $\mathcal {R}_{e_0}^0$
by a similar argument using property (p) of
$\mathcal {R}_{e_0}^0$
by a similar argument using property (p) of
![]() $X_0\sqcup X_1$
.
$X_0\sqcup X_1$
.
If
![]() $j=\hat j=1$
(so
$j=\hat j=1$
(so
![]() $X_0$
is infinite) and
$X_0$
is infinite) and
![]() $\hat k=1, k=0$
, then the condition
$\hat k=1, k=0$
, then the condition
![]() $(F, X_0 \smallsetminus [0, b])$
forces
$(F, X_0 \smallsetminus [0, b])$
forces
 $\mathcal {R}_{e_1}^1$
by a similar argument using property (q) of
$\mathcal {R}_{e_1}^1$
by a similar argument using property (q) of
![]() $X_0\sqcup X_1$
.
$X_0\sqcup X_1$
.
Case 4:
![]() $U_n,U_{n,m},V_{n,m},U_{n,m,l},V_{n,m,l}$
is found for all
$U_n,U_{n,m},V_{n,m},U_{n,m,l},V_{n,m,l}$
is found for all
![]() $n,m,l$
.
$n,m,l$
.
Since
![]() $(T_0,T_1)$
is 4-hyperimmune, there exist
$(T_0,T_1)$
is 4-hyperimmune, there exist
![]() $n, m,l$
such that
$n, m,l$
such that
![]() $T_0$
and
$T_0$
and
![]() $T_1$
diagonalize against
$T_1$
diagonalize against
![]() $(U_{n},U_{n,m,l})$
and
$(U_{n},U_{n,m,l})$
and
![]() $(V_{n, m},V_{n, m,l})$
, respectively. By definition of
$(V_{n, m},V_{n, m,l})$
, respectively. By definition of
![]() $U_{n,m,l},V_{n,m,l}$
(where we take
$U_{n,m,l},V_{n,m,l}$
(where we take
![]() $X_0\sqcup X_1$
to be
$X_0\sqcup X_1$
to be
![]() $A_0\sqcup A_1$
), there exists a finite T-transitive set
$A_0\sqcup A_1$
), there exists a finite T-transitive set
![]() $F $
compatible with
$F $
compatible with
![]() $A_0\sqcup A_1$
such that
$A_0\sqcup A_1$
such that
-
(p) either
 $\Phi _{e_0}^{F}\cap U_{n} \neq \emptyset $
and
$\Phi _{e_0}^{F}\cap U_{n} \neq \emptyset $
and
 $\Phi _{e_0}^{F}\cap U_{n,m,l}\ne \emptyset $
and
$\Phi _{e_0}^{F}\cap U_{n,m,l}\ne \emptyset $
and -
(q) or
 $\Phi _{e_1}^{F}\cap V_{n,m} \neq \emptyset $
and
$\Phi _{e_1}^{F}\cap V_{n,m} \neq \emptyset $
and
 $\Phi _{e_1}^{F}\cap V_{n,m,l}\ne \emptyset $
.
$\Phi _{e_1}^{F}\cap V_{n,m,l}\ne \emptyset $
.
Let
![]() $d=(F,X)$
. We claim that d forces
$d=(F,X)$
. We claim that d forces
![]() $\mathcal {R}_{e_0,e_1}$
by forcing
$\mathcal {R}_{e_0,e_1}$
by forcing
 $\mathcal {R}^0_{e_0}$
on case (p) and
$\mathcal {R}^0_{e_0}$
on case (p) and
 $\mathcal {R}^1_{e_1}$
on case (q). Let G be a set satisfying d. In the case (p),
$\mathcal {R}^1_{e_1}$
on case (q). Let G be a set satisfying d. In the case (p),
 $\Phi _{e_0}^G$
has a non-empty intersection with both
$\Phi _{e_0}^G$
has a non-empty intersection with both
![]() $U_{n}$
and
$U_{n}$
and
![]() $U_{n,m,l}$
, in which case
$U_{n,m,l}$
, in which case
 $\Phi _{e_0}^G$
is not a solution to
$\Phi _{e_0}^G$
is not a solution to
![]() $T_0$
(recall the definition of diagonalizes against); and in the case (q),
$T_0$
(recall the definition of diagonalizes against); and in the case (q),
 $\Phi _{e_1}^G$
has non-empty intersection with both
$\Phi _{e_1}^G$
has non-empty intersection with both
![]() $V_{n,m}$
and
$V_{n,m}$
and
![]() $V_{n,m,l}$
, in which case
$V_{n,m,l}$
, in which case
 $\Phi _{e_1}^G$
is not a solution to
$\Phi _{e_1}^G$
is not a solution to
![]() $T_1$
. This completes the proof of the lemma.⊣
$T_1$
. This completes the proof of the lemma.⊣
Let
![]() $\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
$\mathcal {F} = \{c_0, c_1, \dots \}$
be a sufficiently generic filter for this notion of forcing, where
![]() $c_s = (F_s, X_s)$
, and let
$c_s = (F_s, X_s)$
, and let
![]() $G = \bigcup _s F_s$
. By property (a) of a condition, G is T-transitive. By Lemma 3.8, G is infinite, and by Lemma 3.9, G satisfies
$G = \bigcup _s F_s$
. By property (a) of a condition, G is T-transitive. By Lemma 3.8, G is infinite, and by Lemma 3.9, G satisfies
![]() $\mathcal {R}_{e_0,e_1}$
for all
$\mathcal {R}_{e_0,e_1}$
for all
![]() $e_0,e_1$
. By pairing argument, this means either G does not compute a solution to
$e_0,e_1$
. By pairing argument, this means either G does not compute a solution to
![]() $T_0$
, or
$T_0$
, or
![]() $G $
does not compute a solution to
$G $
does not compute a solution to
![]() $T_1$
. This completes the proof of Theorem 3.6.⊣
$T_1$
. This completes the proof of Theorem 3.6.⊣
Acknowledgements
The second author was partially supported by grant ANR “ACTC” #ANR-19-CE48-0012-01.