Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T08:09:54.077Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE DEFINABILITY OF n-GENERICS

Published online by Cambridge University Press:  21 December 2018

WEI WANG
WEI WANG*
Affiliation:
INSTITUTE OF LOGIC AND COGNITION AND DEPARTMENT OF PHILOSOPHY SUN YAT-SEN UNIVERSITY 135 XINGANG XI ROAD GUANGZHOU 510275, P.R. CHINAE-mail: wwang.cn@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A set 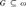$G \subseteq \omega$ is n-generic for a positive integer n if and only if every 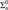${\rm{\Sigma }}_n^0$ formula of G is decided by a finite initial segment of G in the sense of Cohen forcing. It is shown here that every n-generic set G is properly ${\rm{\Sigma }}_n^0$ in some G-recursive X. As a corollary, we also prove that for every $n > 1$ and every n-generic set G there exists a G-recursive X which is generalized ${\rm{lo}}{{\rm{w}}_n}$ but not generalized ${\rm{lo}}{{\rm{w}}_{n - 1}}$. Thus we confirm two conjectures of Jockusch [4].

Keywords

03D2803D25Turing degreesgeneric
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1345 - 1362
Copyright
Copyright © The Association for Symbolic Logic 2018 

References

REFERENCES

Anderson, B. A., Relatively computably enumerable reals. Archive for Mathematical Logic, vol. 50 (2011), no. 3–4, pp. 361–365.CrossRefGoogle Scholar
Cai, M. and Shore, R., Domination, forcing, array nonrecursiveness and relative recursive enumerability, this Journal, vol. 77 (2012), pp. 226–239.Google Scholar
Downey, R. and Hirschfeldt, D., Algorithmic Randomness and Complexity, Theory and Applications of Computability, Springer, 2010.CrossRefGoogle Scholar
Jockusch, C. G. Jr., Degrees of generic sets, Recursion Theory: Its Generalizations and Applications, Proceedings of Logic Colloquium ’79 (Drake, F. R. and Wainer, S. S., editors), Cambridge University Press, Cambridge, 1980, pp. 110–139.CrossRefGoogle Scholar
Kumabe, M., Relative recursive enumerability of generic degrees, this Journal, vol. 56 (1991), no. 3, pp. 1075–1084.Google Scholar
Kumabe, M., Degrees of generic sets, Computability, Enumerability, Unsolvability (Cooper, S. B., Slaman, T. A., and Wainer, S. S., editors), London Mathematical Society, Lecture Notes Series, vol. 224, Cambridge University Press, Cambridge, 1996, pp. 167–183.CrossRefGoogle Scholar
Kurtz, S., Randomness and genericty in the degrees of unsolvability, Ph.D. thesis, University of Illinios at Urbana-Champaign, 1981.Google Scholar
Yates, C. E. M., Initial segments of the degrees of unsolvability, part II: Minimal degrees, this Journal, vol. 35 (1970), pp. 243–266.Google Scholar