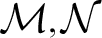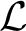1. Introduction
o-minimality is not preserved under ultraproducts, as shown in the following example:
Example 1.1. Let
$\mathcal {L}= \{<, U\}$
where
$<$
is a binary relation symbol and U is a unary predicate. For every
$n\in \mathbb {N}$
, let
$\mathcal {M}_n$
be a structure interpreting
$<$
as a dense linear order without end points and U as a set of points of size n. Then each
$\mathcal {M}_n$
is o-minimal. But for any nonprincipal ultrafilter
$\mathcal {U}$
on
$\mathbb {N}$
, in the ultraproduct
$\prod _{\mathbb {N}} \mathcal {M}_n / \mathcal {U}$
, the definable set U is infinite and discrete, thus the ultraproduct of o-minimal structures need not be o-minimal.
Example 1.1 can be generalized to any first-order language
$\mathcal {L}\supsetneq \{<\}$
. So By Łos’ Theorem, given a first-order language
$\mathcal {L}\supsetneq \{<\}$
, there is no first-order theory T, such that
$\mathcal {M}\models T\iff \mathcal {M}$
is o-minimal for every
$\mathcal {L}$
-structure
$\mathcal {M}$
.
Here we focus our attention on some properties implied by o-minimality which are first-order, that is, those properties which both hold in all o-minimal structures, and, given a language
$\mathcal {L}=\{<,\dots\}$
, can be axiomatized by a set of
$\mathcal {L}$
-sentences. Rigorously, we follow the conventions from [Reference Schoutens12], defined below:
Definition 1.2. Given a language
$\mathcal {L}=\{<,\dots \}$
, let
$T^{omin}_{\mathcal {L}}$
be the set of all
$\mathcal {L}$
-sentences satisfied in every o-minimal
$\mathcal {L}$
-structure.
An
$\mathcal {L}$
-structure
$\mathcal {M}$
for
$\mathcal {L}= \{<,\dots \}$
is pseudo-o-minimal if
$\mathcal {M}\models T_{\mathcal {L}}^{omin}$
.
Fact 1.3 ([Reference Schoutens12, Corollary 10.2])
An
$\mathcal {L}$
-structure
$\mathcal {M}$
for
$\mathcal {L}=\{<,\dots \}$
is pseudo-o-minimal if and only if
$\mathcal {M}$
is elementarily equivalent to an ultraproduct of o-minimal structures.
The following two definitions are examples of first-order weakenings of o-minimality.
Definition 1.4. An expansion of a dense linear order without endpoints
$\mathcal {M} = \langle M;\, <,\dots \kern-0.1pt\rangle$
is definably complete if every definable subset of M has a least upper bound.
Definition 1.5. An expansion of a dense linear order without endpoints
$\mathcal {M} = \langle M;\, <,\dots \kern-0.1pt\rangle$
is locally o-minimal if for any definable subset
$A\subseteq M$
and any
$a\in M$
there are
$b_1,b_2\in M$
such that
$b_1<a<b_2$
and if
$I=(b_1,a)$
or
$(a,b_2)$
then either
$I\subset A$
or
$I\cap A=\emptyset $
.
Notice that both definable completeness and local o-minimality, in a given language
$\mathcal {L}$
, are axiomatized by first-order schemes which hold in any o-minimal structure. Thus, any pseudo-o-minimal
$\mathcal {L}$
-structure is definably complete and locally o-minimal.
Fornasiero, Hieronymi, Miller, Schoutens, Servi and others proved many tameness properties for definably complete and for locally o-minimal structures. (See, e.g., [ Reference Huntington8, 2–7, Reference Schoutens12].) Citing all tameness properties proved in this area will be longer than this paper, so we give two elementary examples by Miller:
Fact 1.6 ([Reference Miller9, Corollary 1.5])
Let
$\mathcal {M} = \langle M;\, <,\dots \kern-0.1pt\rangle$
be an expansion of a dense linear order without endpoints. Then the following are equivalent:
-
1.
$\mathcal {M}$
is definably complete. -
2.
$\mathcal {M}$
has the intermediate value property, that is, the image of an interval under a definable continuous map is an interval. -
3. Intervals in M are definably connected, that is, for every interval
$A\subseteq M$
and every disjoint open definable subsets
$U,V\subseteq M$
, if
$A=(A\cap U) \cup (A\cap V)$
, then either
$A\cap U=\emptyset $
or
$A\cap V=\emptyset $
. -
4. M is definably connected.
Fact 1.7 ([Reference Miller9, Proposition 1.10])
Let
$\mathcal {M}=\langle M;\, <,\dots \kern-0.1pt\rangle$
be definably complete. Let
$f:A\to M^n$
be definable and continuous with A closed and bounded. Then
$f(A)$
is closed and bounded. In particular, If
$f:A\to M$
is definable and continuous with A closed and bounded, then f achieves a maximum and a minimum on A.
In [Reference Schoutens12], Schoutens presented a strengthening of local o-minimality by the name of type completeness, as defined below. In a sense this strengthening extends the locality to
$\pm \infty $
:
Definition 1.8. An expansion of a dense linear order without endpoints
$\mathcal {M} = \langle M;\, <,\dots \kern-0.1pt\rangle$
is type complete if it is locally o-minimal and, in addition, for any definable subset
$A\subseteq M$
there are
$c_1,c_2\in M$
such that if
$I=(-\infty ,c_1)$
or
$(c_2,+\infty )$
, then either
$I\subset A$
or
$I\cap A=\emptyset $
.
Type completeness is a first-order scheme, and therefore satisfied by any pseudo-o-minimal structure.
Several tameness results were proved for definably complete type complete structures in [Reference Schoutens12]. For example, a version of o-minimal cell decomposition called quasi-cell decomposition ([Reference Schoutens12, Theorem 8.10]) and the following monotonicity theorem:
Fact 1.9 ([Reference Schoutens12, Theorem 3.2])
Let
$\mathcal {M}=\langle M;\, <,\dots \kern-0.1pt\rangle$
be a definably complete type complete structure. The set of discontinuities of a one-variable definable map
$f: Y\to M$
is discrete, closed, and bounded, and consists entirely of jump discontinuities. Moreover, there is a definable discrete, closed, bounded subset
$D\subseteq Y$
so that in between any two consecutive points of
$D\cup \{\,\pm \infty \,\}$
, the map is monotone, that is to say, either strictly increasing, strictly decreasing, or constant.
Of particular importance in the study of definably complete structures are the definable pseudo-finite sets, as defined below.
Definition 1.10. Let
$\mathcal {M}=\langle M;\, <,\dots \kern-0.1pt\rangle$
be a definably complete structure. A definable subset
$A\subset M^n$
is pseudo-finite if it is closed, bounded, and discrete.
These definable sets play a role in each of the papers cited above. We follow the convention in [Reference Fornasiero2, Reference Fornasiero3], where there is an extensive study of pseudo-finite sets and their tameness properties. In [Reference Fornasiero2], the wording was justified in the definably complete context by saying that pseudo-finite sets are first-order analogue of finite subsets of
$\mathbb {R}^n$
, with evidence given by numerous tameness properties of such sets.
One must not confuse pseudo-finite sets defined above with pseudo-o-finite sets, as we define below, coined in [Reference Schoutens12]. Though, as we will see in Fact 1.12 the two definitions coincide if
$\mathcal {M}$
is assumed to be pseudo-o-minimal.
Definition 1.11. Let
$\mathcal {M}=\langle M;\, <,\dots \kern-0.1pt\rangle$
be a pseudo-o-minimal structure. A definable set
$X\subseteq M^n$
is pseudo-o-finite if
$(\mathcal {M},X)$
satisfies the common theory of o-minimal structures expanded by a unary predicate for a distinguished finite subset.
The following fact can be immediately extracted from [Reference Schoutens12, Corollary 12.6] together with [Reference Schoutens12, Theorem 12.7].
Fact 1.12. Let
$\mathcal {M}=\langle M;\, <,\dots \kern-0.1pt\rangle$
be a pseudo-o-minimal structure. A definable set
$A\subset M^n$
is pseudo-finite if and only if it is pseudo-o-finite.
A tameness property of pseudo-finite sets occurring naturally is “the discrete pigeonhole principle” [Reference Schoutens12]. (Or just “the pigeonhole principle” in [Reference Fornasiero2, Reference Fornasiero3].)
Definition 1.13. An expansion of a dense linear order without endpoints
$\mathcal {M} = \langle M;\, <,\dots \kern-0.1pt\rangle$
has the pigeonhole principle if for any pseudo-finite
$X\subset K^n$
and definable
$f:X\to X$
, if f is injective, then it is surjective.
We remark that the pigeonhole principle can be formulated as “every pseudo-finite set is definably Dedekind finite”, and as this is a first-order scheme, every pseudo-o-minimal structure has the pigeonhole principle.
In [Reference Fornasiero3] and [Reference Fornasiero2], Fornasiero conjectured the following:
Conjecture 1.14. If
$\mathcal {K} = \langle K,+,\cdot ,<,\dots \kern-0.1pt\rangle $
is a definably complete expansion of a real closed field, then
$\mathcal {K}$
has the pigeonhole principle.
This conjecture remained open even for
$\mathcal {K}$
a definably complete expansion of a dense linear order. Clearly, the conjecture holds for
$\mathcal {K}$
pseudo-o-minimal. Consequently, it is connected to two other questions asked by Schoutens in [Reference Schoutens12]:
Question 1.15. Does every definably complete type complete structure have the pigeonhole principle?
Question 1.16. Is there an axiomatization of pseudo-o-minimality by first-order conditions on one-variable formulae only?
To clarify the meaning of a first-order conditions on one-variable formulae only, this does not mean a first-order sentence conditioned on a specific one-variable formula, as the following example demonstrates how any first-order theory is axiomatized by such sentences, in particular
$T^{omin}$
.
Example 1.17. Let
$\mathcal {L}$
be any language and T be any
$\mathcal {L}$
-theory (not necessarily complete). For every sentence
$\sigma \in T$
, let
$\psi _\sigma (x):= x=x\land \sigma $
and let
$\phi _\sigma := \exists x\, \psi _\sigma (x)$
. Then
$\phi _\sigma $
is a first order condition on
$\psi _\sigma $
, however
$\vdash \psi _\sigma \iff \sigma $
, so
$\{\,\psi _\sigma \ {|}\ \sigma \in T\,\}$
is an axiomatization of T.
Clearly, this is not the intended meaning in the question. Rather, following the terminology of [Reference Schoutens12], we interpret a first-order condition on one-variable formulae as a first-order scheme ranging over all one-variable formulae. Rigorously, a first-order condition on one-variable formulae is obtained as follows:
-
• Let
$\tau $
be a first-order sentence in the language
$\{<,U\}$
where U is a unary predicate. -
• Let
$\Phi $
be the set of all partitioned
$\mathcal {L}$
-formulae
$\varphi (x;\overline {y})$
where x is a single variable and
$\overline {y}$
is a finite tuple of variables not appearing in
$\tau $
. -
• For every
$\varphi (x;\overline {y})\in \Phi $
, let
$\tau _\varphi (x;\overline {y})$
be the
$\mathcal {L}$
-formula obtained by replacing any instance of
$U(x)$
by
$\varphi (x;\overline {y})$
. -
•
${{\Delta _\tau }} := \{\, \forall\, \overline {y} \,\tau _\varphi (x;\overline {y}) \ {|}\ \varphi (x;\overline {y}) \in \Phi \,\} $
.
For example, definable completeness is axiomatized by
$\Delta _\tau $
in the above fashion by setting
$\tau $
to be
$$ \begin{align*} & \exists v\, \forall w\, \big(U(w)\rightarrow w<v\big) \rightarrow \\ & \exists v \big( \forall w\, \big(U(w)\rightarrow w<v\big) \land \forall v'\big(\forall w\, \big(U(w)\rightarrow w<v\big)\big)\rightarrow v\leq v' \big). \end{align*} $$
Namely,
$\tau $
is the
$\{\,<,U\,\}$
-sentence stating if U is bounded, then it has a least upper bound. Following the same terminology, an axiomatization of pseudo-o-minimality by first-order conditions on one-variable formulae only is an
$\mathcal {L}$
-theory
$T'$
such that
$T'$
and
$T^{omin}$
have the same models, and
$$ \begin{align*} T'\subseteq \cup\{\,\Delta_\tau \ {|}\ \tau \text{ is an } \{<,U\}-\text{sentence}\,\}. \end{align*} $$
In [Reference Rennet11], Rennet showed that there is no recursive first-order axiomatization of pseudo-o-minimality in the language of rings
$\{\,+,-,\cdot ,0,1\,\}$
. In particular, as definable completeness and type completeness are both recursive first-order schemes, given a recursive language, they cannot axiomatize pseudo-o-minimality.
In this paper, we show a stronger result (with respect to one-variable definable sets) by constructing two ordered structures
$\mathcal {M},\ \mathcal {N}$
on the same universe, in the same language, with the same definable subsets in one variable, where
$\mathcal {M}$
is pseudo-o-minimal and
$\mathcal {N}$
does not have the pigeonhole principle. This gives a negative answer to both Questions 1.15 and 1.16, as well as a partial answer to Conjecture 1.14. Furthermore, this gives a stronger result than a negative answer to Question 1.16. It shows that not only is there no first order axiomatization
$T'$
as above, but also there is no second order theory in the language
$\mathcal {L}_{ \operatorname {\mathrm {Def}}}:=\{<, \operatorname {\mathrm {Def}}\}$
where
$ \operatorname {\mathrm {Def}}$
is a unary predicate on subsets interpreted as the definable subsets. This result is strictly stronger as any axiomatization
$T'$
as above is equivalent to a second order theory in
$\mathcal {L}_{ \operatorname {\mathrm {Def}}}$
, but not vice-versa.
This also implies that there is no result analogous to Fact 1.12 in the theory of definably complete type complete structures, namely there is a definably complete type complete structure
$\mathcal {M}$
and a pseudo-finite subset
$X\subset M$
such that
$(\mathcal {M},X)$
does not satisfy the common theory of definably complete type complete structures expanded by a unary predicate for a finite set.
It is still open whether we can extend this result to the case where
$\mathcal {M}_0$
is an expansion of a real closed field and fully answer Conjecture 1.14.
Outline. The construction is done as follows: In Section 3, the theory
$T_0$
is constructed as an expansion of a dense linear without endpoints by a predicate for a discrete, closed, and bounded set Z and some extra structure in the language
$\mathcal {L}_0$
such that
$T_0\supseteq T_{\mathcal {L}_0}^{omin}$
. We then introduce an expansion
$\mathcal {L}_1\supset \mathcal {L}_0$
and
$T_1\supset T_0$
an
$\mathcal {L}_1$
-theory containing a function symbol f which is bijective on Z. We show
$T_0$
and
$T_1$
are consistent. In Section 4 we prove quantifier elimination for
$T_0$
.
In Section 5, we give the construction of
$\mathcal {M}_2$
which will be an expansion of some model
$\mathcal {M}_0$
of
$T_0$
to
$\mathcal {L}_1$
with the same one-variable definable sets as
$\mathcal {M}_0$
such that
$\mathcal {M}_2$
does not have the pigeonhole principle. This is done by tweaking a given model
$\mathcal {M}_1$
of
$T_1$
expanding
$\mathcal {M}_0$
so that f is now injective but not surjective. It is done carefully enough, so that any definable set in
$\mathcal {M}_2$
differs from a set definable in
$\mathcal {M}_1$
by finitely many constant terms. In Section 6 we show quantifier elimination in
$\mathcal {M}_2$
and deduce that any definable subset of
$\mathcal {M}_2$
is definable in
$\mathcal {M}_0$
. We then define
$\mathcal {M}$
to be a trivial expansion of
$\mathcal {M}_0$
to
$\mathcal {L}_0$
and
$\mathcal {N}$
to be
$\mathcal {M}_2$
and show that
$\mathcal {M},\ \mathcal {N}$
possess the properties proclaimed in the introduction.
2. Preliminaries—cyclic orders
In this section, we present the standard definition of a cyclic order, as defined below, and present some of its properties needed for the construction following.
Definition 2.1. A cyclic order on a set A is a ternary relation C satisfying the following axioms:
-
1. Cyclicity: If
$C(a,b,c)$
, then
$C(b,c,a)$
. -
2. Asymmetry: If
$C(a,b,c)$
, then not
$C(c,b,a)$
. -
3. Transitivity: If
$C(a,b,c)$
and
$C(a,c,d)$
, then
$C(a,b,d)$
. -
4. Totality: If
$a,b,c$
are distinct, then either
$C(a,b,c)$
or
$C(c,b,a)$
.
The following fact is folklore (e.g., [Reference Huntington8] and [Reference Čech1, Part I, Section 4]) and can be easily verified:
Fact 2.2. If
$\langle A,<\kern-0.1pt\rangle$
is a linearly ordered set, then the relation defined by
$$ \begin{align*} C_<(a,b,c) \iff (a<b<c) \lor (b<c<a) \lor (c<a<b) \end{align*} $$
is a cyclic order on A.
We call
$C_<$
the cyclic order induced by
$<$
.
Definition 2.3. Let
$(X,<)$
be a linearly ordered set. A
$<$
-cut in X is a pair of subsets
$(A,B)$
of X such that
and
$a<b$
for every
$a\in A$
and
$b\in B$
.
Fact 2.4 ([Reference Novák10, Corollary 3.9])
Let X be a set with
$|X|>2$
. Let
$<_1,<_2$
be distinct linear orders on X. Then
$C_{<_1}=C_{<_2}$
holds if and only if there exist nonempty disjoint subsets
$A,B$
of X such that
$(A,<_1)=(A,<_2)$
,
$(B,<_1)=(B,<_2)$
,
$(A,B)$
is a
$<_1$
-cut in X and
$(B,A)$
is a
$<_2$
-cut in X.
Definition 2.5. Let C be a cyclic order on a set A. For any
$a,b\in A$
, denote
$$ \begin{align*} C(a,-,b):=\{\,x\in A \ {|}\ C(a,x,b)\,\}. \end{align*} $$
Lemma 2.6. Let C be a cyclic order on a set A and let
$a,b,c\in A$
. If
$C(a,b,c)$
then
$$ \begin{align*} C(a,-,c) = C(a,-,b)\cup \{\,b\,\}\cup C(b,-,c). \end{align*} $$
Proof.
-
• To prove
$C(a,-,c) \supseteq C(a,-,b)\cup \{\,b\,\}\cup C(b,-,c)$
:-
– By definition,
$b\in C(a,-,c)$
. -
– If
$C(a,x,b)$
, then together with
$C(a,b,c)$
, and transitivity, we get
$C(a,x,c)$
. -
– If
$C(b,x,c)$
, then by cyclicity,
$C(c,b,x)$
. By cyclicity again,
$C(c,a,b)$
. Now by transitivity,
$C(c,a,x)$
, which is equivalent by cyclicity to
$C(a,x,c)$
.
-
-
• To prove
$C(a,-,c) \subseteq C(a,-,b)\cup \{\,b\,\}\cup C(b,-,c)$
, if then
$$ \begin{align*} x\notin \big(C(a,-,b)\cup \{\,b\,\}\cup C(b,-,c)\big), \end{align*} $$
$x\notin \{a,b,c\}$
and by totality,
$C(b,x,a)$
and
$C(c,x,b)$
. By cyclicity, we get that
$C(x,a,b)$
and
$C(x,b,c)$
, which in turn, by transitivity, implies
$C(x,a,c)$
which by cyclicity is equivalent to
$C(c,x,a)$
which by asymmetry, implies that
$x\notin C(a,-,c)$
. ⊣
Definition 2.7. Let C be a cyclic order on a set A and let
$X\subseteq A$
. Two elements
$a,b\in A$
are X-close if either
$X\cap C(a,-,b)$
or
$X\cap C(b,-,a)$
is finite.
Denote
$a\sim _X b$
if
$a,b\in A$
are X-close.
Lemma 2.8. Let C be a cyclic order on a set A and let
$X\subseteq A$
. Then
$\sim _X$
is an equivalence relation on A.
Proof.
-
•
$X\cap C(a,-,a) =\emptyset $
for all
$a\in A$
, so reflexivity holds. -
• Symmetry is obvious by definition.
-
• To prove transitivity, let
$a,b,c\in A$
such that
$a\sim _X b$
and
$b\sim _X c$
. Assume towards a contradiction that
$X\cap C(a,-,c)$
and
$X\cap C(c,-,a)$
are both infinite. We may further assume, without loss of generality, that
$C(a,b,c)$
. So by cyclicity, also
$ C(c,a,b)$
and
$ C(b,c,a)$
. By Lemma 2.6, (1)
$$ \begin{align} \kern-13pt X\cap C(a,-,c) = \big(X\cap C(a,-,b)\big)\cup \big(X\cap \{\,b\,\}\kern1pt\big)\cup \big(X\cap C(b,-,c)\big), \end{align} $$
(2)
$$ \begin{align} X\cap C(c,-,b) = \big(X\cap C(c,-,a)\big)\cup \big(X\cap \{\,a\,\}\kern1pt\big)\cup \big(X\cap C(a,-,b)\big), \end{align} $$
(3)By Equation 2,
$$ \begin{align} \hspace{12pt}X\cap C(b,-,a) = \big(X\cap C(b,-,c)\big)\cup \big(X\cap \{\,c\,\}\kern1pt\big)\cup \big(X\cap C(c,-,a)\big).\kern13pt \end{align} $$
$X \cap C(c,-,b)$
is infinite and by Equation 3,
$X\cap C(b,-,a)$
is infinite. But by Equation 1, either
$X\cap C(a,-,b)$
or
$X\cap C(b,-,c)$
is infinite, so either
$a\not \sim _X b$
or
$b\not \sim _X c$
. ⊣
Lemma 2.9. Let C be a cyclic order on a set A. Let
$a,a',b,b',c,c'\in A$
and let
$X\subseteq A$
such that
$$ \begin{align*} &a\sim_X a',\ b\sim_X b',\ c\sim_X c', \\ &a\not\sim_X b,\ a\not\sim_X c,\ b\not\sim_X c. \end{align*} $$
Then
$C(a,b,c)\iff C(a',b',c')$
.
Proof. By symmetry of
$\sim _X$
and cyclicity of C, it suffices to show that
$C(a,b,c)\implies C(a,b,c')$
. So assume towards a contradiction
$$ \begin{align} C(a,b,c), \end{align} $$
$$ \begin{align} C(c',b,a). \end{align} $$
By cyclicity on (5), we get
$$ \begin{align} C(a,c',b). \end{align} $$
By transitivity applied to (4) and (6) we get
$C(a,c',c)$
, which in turn by cyclicity is equivalent to (7) below. By cyclicity and transitivity applied to (4) and (5), we get (8) below.
$$ \begin{align} C(c,a,c'), \end{align} $$
$$ \begin{align} C(c',b,c). \end{align} $$
By the assumption of the lemma, either
$C(c',-,c)$
or
$C(c,-,c')$
is finite. By Lemma 2.6 and by (7) and (8), this implies that at least one of the following is finite:
$C(c',-,b),C(b,-,c),C(c,-,a),C(a,-,c')$
. By transitivity of
$\sim _X$
(Lemma 2.8),
$a\sim _X c$
or
$b\sim _X c$
. Contradiction. ⊣
3. Definitions of
$T_0$
and
$T_1$
Definition 3.1. Let
$\mathcal {L}_0:=\langle<, Z; S,P,\pi ; c_1,c_2,c_3,c_4\kern-0.1pt\rangle$
where
$<$
is a binary relation symbol, Z is a unary predicate,
$S,P, \pi $
are function symbols and
$c_1,c_2,c_3,c_4$
are constant symbols. Let
$T_0$
be the
$\mathcal {L}_0$
-theory consisting of the following axioms:
-
1.
$<$
is a dense linear order without end points. -
2.
$T^{omin}_{\mathcal {L}_{{0}}}$
. -
3. Z is discretely ordered, that is, every nonmaximal (respectively, nonminimal) element in Z has an immediate successor (respectively, predecessor) in Z.
-
4. Z is closed, that is, for all
$x\notin Z$
, there is an interval disjoint from Z containing x. -
5.
$\min (Z) = c_1, \max (Z)=c_4$
. -
6.
$c_2,c_3 \in Z$
are such that
$c_1<c_2<c_3<c_4$
and there are infinitely many elements in Z between any two of them. -
7.
$\pi $
is the cyclic forward projection on Z:
$$ \begin{align*} \big(\forall x\big)\ \ \ (\pi(x)\in Z)\land (\forall y\in Z \big(\neg C_<(x,y,\pi(x))\big)). \end{align*} $$
-
8. S is defined as the cyclic successor function on Z, and as the identity outside of Z:
P is defined as
$$ \begin{align*} S(x)=y \leftrightarrow \big(x\notin Z \land x=y\big)\lor \big(x\in Z \land y\in Z \land \neg \exists z\in Z\,\big(C_<\big(x,z,y\big)\big)\big). \end{align*} $$
$S^{-1}$
.
The consistency of
$T_0$
will be proven together with the consistency of
$T_1$
defined in Definition 3.2 below.
Definition 3.2. Let
$\mathcal {L}_1:=\mathcal {L}_0\cup \{ f, g \}$
where
$f,g$
are unary function symbols.
Let
$T_1$
be
$T_0$
together with the following axioms:
-
9. f is bijective and
$g=f^{-1}$
. -
10.
$f(Z\cap [c_1,c_2])= Z\cap [c_3,c_4]$
and
$f\upharpoonright \big (Z\cap [c_1,c_2]\big )$
is a partial order isomorphism. -
11.
$f(Z\cap (c_2,c_4]) = Z\cap [c_1,c_3)$
and
$f\upharpoonright \big (Z\cap (c_2,c_4]\big )$
is a partial order isomorphisms. -
12. For all
$n> 1$
and for every
$z\in Z$
are infinite, that is,
$$ \begin{align*} Z\cap C_<\big(z,-,f^n(z)\big)\text{ and }Z\cap C_<\big(f^n(z),-,z\big) \end{align*} $$
$z\not \sim _Z f^n(z)$
. Notice that this is a first-order scheme.
-
13.
$f(x)=x$
for every
$x\notin Z$
-
14.
$C_<\big (f^m(z),f^n(z),z\big ) $
for all
$m>n>0$
and for every
$z\in Z$
.
Proposition 3.3.
$T_1$
is consistent.
Proof. To prove finite satisfiability of
$T_1$
take some sufficiently large natural number N. Take
$Z=\{\,0,\dots ,N\,\}\times \{\,0,\dots ,N\,\}$
with the lexicographic order and consider a structure
$\mathcal {M}$
which is a DLO containing Z as an ordered subset.
Let
$c_1:= (0,0), c_2 := (0,N), c_3 := (N,0), c_4 :=(N,N)$
.
Let
$$ \begin{align*} f((a,b)): = \left\{ \begin{array}{ll} (a-1 \mod (N+1),b) & \mbox{if } x=(a,b)\in Z, \\ x & \mbox{if } x\notin Z \end{array}\right. \end{align*} $$
and let
$g := f^{-1}$
.
Let
$\pi $
the circular projection, as defined in Axiom 7.
Let S be the circular successor function, as defined in Axiom 8 and let
$P:=S^{-1}$
.
Then
$\mathcal {M}$
satisfies Axioms 1 to 5, 7 to 11 and 13 by definition. As for Axioms 6
, 12 and 14:
Any finite segment of Axiom 6 is contained in the following axiomatization, for a fixed
$k\in \mathbb {N}$
:
-
6 k .
$c_2,c_3 \in Z$
are such that
$c_1<c_2<c_3<c_4$
and there are at least k elements in Z between any two of them. -
12 k . For all
$k>n>0$
and for every
$z\in Z$
.-
(a) There are at least k elements in
$Z\cap C_<\big (z,-,f^n(z)\big )$
. -
(b) There are at least k elements in
$Z\cap C_<\big (f^n(z),-,z\big )$
.
-
-
14 k .
$C_<\big (f^m(z),f^n(z),z\big )$
for all
$k>m>n>0$
.
If
$N>k$
then
$\mathcal {M}$
satisfies Axioms 6
$_k$
and 12
$_k$
, by definition.
Under the assumption
$N>k$
, we prove that
$\mathcal {M}$
satisfies Axiom 14
$_k$
, thus
$T_1$
is finitely satisfiable.
For all
$(x,y)\in Z$
:
$$ \begin{align*} f^m((x,y)) = (x-m \mod (N+1),y), \\ f^n((x,y)) = (x-n \mod (N+1),y). \end{align*} $$
So proving Axiom 14
$_k$
reduces to proving that for any
$x\in \{\,0,\dots ,N\,\}$
and
$0<n<m<N$
one of the following holds:
-
(a)
$ x\ominus m < x\ominus n < x,$
-
(b)
$ x\ominus n < x < x\ominus m, $
-
(c)
$ x < x\ominus m < x\ominus n, $
where
$\ominus $
is subtraction modulo
$N+1$
.
If
$m\leq x$
then (a) holds.
If
$n\leq x<m$
then (b) holds.
If
$x<n$
then (c) holds. ⊣
4. Quantifier elimination in
$T_0$
We now show that
$T_0$
eliminates quantifiers:
Remark 4.1. Let
$\mathcal {M}\models T_0$
and
$\tau , a\in \mathcal {M}$
. Then the following hold:
-
1.
$ S(\tau ) \in Z \iff \tau \in Z, $
-
2.
$ P(\tau )\in Z\iff \tau \in Z, $
-
3.
$ S(\tau ) = a \iff \tau = P(a), $
-
4.
$\hspace{-5pt}\begin{array}[t]{l}S(\tau ) < a \iff \big [\tau < P(a) \land \tau \neq c_4 \land a\neq c_1\big ] \lor\\ \big [\tau = c_4 \land S(c_4)<a\big ] \lor \big [a = c_1 \land \tau <c_1\big ], \end{array} $
-
5.
$\hspace{-5pt}\begin{array}[t]{l}P(\tau )> a \iff \big [\tau > S(a) \land \tau \neq c_1 \land a\neq c_4\big ] \lor\\ \big [\tau = c_1 \land P(c_1)>a\big ] \lor \big [a = c_4 \land \tau >c_4\big ], \end{array} $
-
6.
$ \pi (\tau ) \in Z \iff c_1\in Z, $
-
7.
$ \pi (\tau ) = a \iff \big [\tau \leq c_4 \land a\in Z\land P(a)<\tau \leq a\big ]\lor \big [ \tau>c_4 \land c_1=a \big ], $
-
8.
$ \pi (\tau )< a \iff \big [\tau \leq c_4 \land \tau \leq P\circ \pi (a)\big ]\lor \big [ \tau>c_4 \land c_1<a \big ], $
-
9.
$ \pi (\tau )> a \iff \big [\tau \leq c_4 \land \tau \geq P\circ \pi \circ S(a)\big ]\lor \big [ \tau >c_4 \land c_1>a \big ]. $
Remark 4.2. If
$x\in Z$
then:
-
1.
$S^{m_1}\circ \pi ^{n_1} \circ \dots \circ S^{m_{k}}\circ \pi ^{n_k}\circ S^{l}(x) = S^{m_1+\dots +m_k+l}(x) $
. -
2.
$P^{m}(x) = S^{-m}(x)$
and
$P^{-m}(x)=S^m(x)$
for all
$m\in \mathbb {N}$
. -
3.
$ S^{m}(x)\square x \iff S^{m}(c_2)\square c_2$
for all
$m\in \mathbb {N},\ \square \in \{<,>,=\}x\notin\{c_4, P(c_4),\dots $
,
$P^m(c_4),\} $
.
$ P^{m}(x)\square x \iff S^{m}(c_2)\square c_2$
for all
$m\in \mathbb {N},\ \square \in \{<,>,=\}$
,
$x\notin \{\,c_1, S(c_1),\dots , S^m(c_1),\,\} $
.
If
$x\notin Z$
:
-
1.
$ S^{m_1}\circ \pi ^{n_1} \circ \dots \circ S^{m_{k}}\circ \pi ^{n_k}\circ S^{l}(x) = S^{m_1+\dots +m_k}\circ \pi (x) $
. -
2.
$S^m(x) \square x \iff c_1\square c_1$
for all
$m\in \mathbb {Z},\ \square \in \{<,>,=\}$
. -
3.
$S^m\circ \pi (x) = x \iff c_1\neq c_1$
for
$m\neq 0$
. -
4.
$S^m\circ \pi (x)>x\iff S^{m+1}\circ \pi (x)> \pi (x) $
. -
5.
$S^m\circ \pi (x)<x\iff S^m\circ \pi (x)<\pi (x) $
.
Lemma 4.3. For any
$\mathcal {M}\models T_0$
and
$a,b\in \mathcal {M}$
,
$$ \begin{align*} \mathcal{M}\models \big[\exists x\in Z (a<x<b)\big]\leftrightarrow \big[\pi\circ S(a)<b\big]. \end{align*} $$
Proof. If
$a\in Z$
then
$ \mathcal {M}\models \big [\exists x\in Z (a<x<b)\big ]\leftrightarrow \big [S(a)<b\big ] $
and
$S(a) = \pi \circ S(a)$
.
If
$a\notin Z$
then
$ \mathcal {M}\models \big [\exists x\in Z (a<x<b)\big ]\leftrightarrow \big [\pi (a)<b\big ] $
and
$\pi (a) = \pi \circ S(a)$
. ⊣
Proposition 4.4.
$T_0$
admits quantifier elimination.
Proof. Let
$\phi = \exists x \bigwedge _{i\in I} \theta _i\big (\overline {y},x\big ) $
such that
$\{\theta _i\}_{i\in I}$
are atomic and negated atomic formulae. We need to find a quantifier-free
$\mathcal {L}_0$
-formula
$\varphi $
such
$$ \begin{align*} T_0\models \forall\, \overline{y}\left[ \bigg(\exists x \bigwedge_{i\in I} \theta_i\big(\overline{y},x\bigg) \bigg)\leftrightarrow \varphi(\overline{y})\right]. \end{align*} $$
First, since
$\vdash \exists x \big ( \chi \big (\overline {y},x\big ) \land \theta \big (\overline {y}\big ) \big ) \leftrightarrow \exists x \big ( \chi \big (\overline {y},x\big )\big ) \land \theta \big (\overline {y}\big )$
we may assume that x occurs in
$\theta _i$
for all
$i\in I$
. Second,
$$ \begin{align*} \vdash \bigg[\exists x \bigwedge_{i\in I} \theta_i(\overline{y},x)\bigg] \leftrightarrow \bigg[\exists x \bigg( \bigwedge_{i\in I} \theta_i\big(\overline{y},x\big) \land \big( x\in Z \lor x\notin Z \big)\bigg)\bigg]\leftrightarrow \end{align*} $$
$$ \begin{align*} \bigg[ \bigg(\exists x \bigg( \bigwedge_{i\in I} \theta_i\big(\overline{y},x\big) \land x\in Z \bigg)\bigg)\lor \bigg(\exists x \bigg( \bigwedge_{i\in I} \theta_i\big(\overline{y},x\big) \land x\notin Z \bigg)\bigg)\bigg] . \end{align*} $$
So we may assume
$\phi $
is either of the form
$ \exists x \big ( \bigwedge _{i\in I} \theta _i\big (\overline {y},x\big ) \land x\in Z \big )$
or of the form
$\exists x \big ( \bigwedge _{i\in I} \theta _i\big (\overline {y},x\big ) \land x\notin Z \big )$
where
$\theta _i$
are atomic and negated atomic formulae such that x occurs in each
$\theta _i$
. We may assume that
$\theta _i$
is neither ‘
$x\in Z$
’ nor ‘
$x\notin Z$
’ for any
$i\in I$
, as such occurrence would be either superfluous or inconsistent. So each
$\theta _i$
is of the form
$t_1\square t_2$
where
$t_1,t_2$
are terms with variables in
$x,\overline {y}$
.
By Remark 4.1, we may assume either
$$ \begin{align*} \phi(\overline{y}) = \exists x \Bigg(\bigwedge_{i=1}^k t_i\square_{i} x \land {{x \in Z}} \Bigg) \end{align*} $$
or
$$ \begin{align*} \phi(\overline{y}) = \exists x \Bigg(\bigwedge_{i=1}^k t_i\square_{i} x \land x\notin Z \Bigg), \end{align*} $$
where
$t_i$
are with variables from
$\{x,\ \overline {y}\}$
,
$\square \in \{<,>,=,\leq ,\geq ,\neq\}$
. By Remark 4.2, we may assume that x does not occur in any
$t_i$
. Next, notice that
$\geq, \leq, \neq $
are positive Boolean combinations of
$<,>,=$
and if
$\square _i$
is
$``="$
for some i we can just replace x with
$t_i$
. So we may assume
$\square _i\in \{<,>\}$
, that is, either
$$ \begin{align} \phi(\overline{y}) = \exists x \bigg(\bigwedge_{i=1}^m l_i < x \land \bigwedge_{j=1}^n u_i> x \land x\in Z \bigg) \end{align} $$
or
$$ \begin{align} \phi(\overline{y}) = \exists x \bigg(\bigwedge_{i=1}^m l_i < x \land \bigwedge_{j=1}^n u_i> x \land x\notin Z \bigg), \end{align} $$
where
$l_i, u_i$
are terms not containing x.
If
$\phi $
is as in (9), then by Lemma 4.3,
$\phi (\overline {y})$
is equivalent to
$$ \begin{align*} \bigwedge_{i=1}^n\bigwedge_{j=1}^m \big(\pi\circ S(l_i)<u_j\big). \end{align*} $$
If
$\phi $
is as in (10), then since Z is co-dense,
$\phi (\overline {y})$
is equivalent to
$$ \begin{align*} \bigwedge_{i=1}^n\bigwedge_{j=1}^m \big(l_i<u_j\big). \end{align*} $$
⊣
5. Definition of
$T_2$
and the relation to
$T_1$
Definition 5.1. Let
$\mathcal {M}_1\models T_1$
be arbitrary, with universe M.
Let
$\mathcal {M}_0$
be the restriction of
$\mathcal {M}$
to
$\mathcal {L}_0$
, that is,
$\mathcal {M}_0 =\mathcal {M}_1\upharpoonright \mathcal {L}_0$
. Consequently,
$\mathcal {M}_0\models T_0$
.
Let
$\mathcal {M}_2$
be the same
$\mathcal {L}_1$
-structure as
$\mathcal {M}$
with a slight modification on f and g, as follows.
$$ \begin{align*} & f^{\mathcal{M}_2}(x):= \bigg\{ \begin{array}{ll} P\circ f^{\mathcal{M}_1}(x) & \mbox{if } S^n(x)=c_4\text{ for some }n\in \mathbb{N}, \\ f^{\mathcal{M}_1}(x) & \mbox{if } S^n(x)\neq c_4\text{ for all }n\in \mathbb{N}. \end{array} \big. \\ & g^{\mathcal{M}_2}(x):= \bigg\{ \begin{array}{ll} g^{\mathcal{M}_1}\circ S(x) & \mbox{if } S^n(x)=P(c_3)\text{ for some }n\in \mathbb{N}, \\ g^{\mathcal{M}_1} & \mbox{if } S^n(x)\neq P(c_3)\text{ for all }n\in \mathbb{N}. \end{array} \big. \end{align*} $$
In words, there is some convex set X with maximum
$c_4$
such that the order type of
$X\cap Z$
is
$\omega ^{*}$
.
$f^{\mathcal {M}_1}$
maps
$X\cap Z$
to a convex subset
$f^{\mathcal {M}_1}(X\cap Z)$
of Z of order type
$\omega ^*$
with maximum
$P(c_3)$
, by Axiom 11 in Definition 3.2.
Then
$f^{\mathcal {M}_2},g^{\mathcal {M}_2}$
are obtained from
$f^{\mathcal {M}_1},g^{\mathcal {M}_1}$
by applying a shift by one element in
$X\cap Z$
,
$f(X\cap Z)$
respectively.
Lemma 5.2.
$f^{\mathcal {M}_1}$
preserves the cyclic order on Z, that is,
$$ \begin{align*}T_1\models \big(\forall z_1,z_2,z_3\in Z\big)\big[C_<\big(z_1,z_2,z_3\big)\leftrightarrow C_<\big(f(z_1),f(z_2),f(z_3)\big)\big]. \end{align*} $$
Proof. Define a new ordering
$<'$
on Z by
$$ \begin{align*} x<'y \iff & \big(x,y \in [c_3,c_4] \land x<y\big)\ \lor \\ & \big(x,y \in [c_1,c_3) \land x<y\big)\ \lor \\ & \big(x\in [c_3,c_4], y \in [c_1,c_3) \big). \end{align*} $$
By Axioms 10 and 11 in Definition 3.2,
$\big([c_1,c_2], < \big) \cong ([c_3,c_4],<')$
and
$\big((c_2,c_4], {<} \big) \cong ([c_1,c_3),<')$
and
$$ \begin{align*}T_0\models \big(\forall x,y\in Z\big) \big[x<y \leftrightarrow f(x)<'f(y)\big]. \end{align*} $$
Additionally, by definition of
$<'$
, it follows that
$\big ([c_3,c_4],[c_1,c_3) \big )$
is a
$<'$
-cut in Z and
$\big ([c_1,c_3), [c_3,c_4] \big )$
is a
$<$
-cut in Z. So by Fact 2.4,
$C_{<'} = C_<$
. In conclusion
$$ \begin{align*} T_0\models \big(\forall z_1,z_2,z_3\in Z\big)\ \Big[ &C_<\big(z_1,z_2,z_3\big)\leftrightarrow \\ & C_{<'}\big(f(z_1),f(z_2),f(z_3)\big) \leftrightarrow \\ & C_<\big(f(z_1),f(z_2),f(z_3)\big)\Big]. \end{align*} $$
⊣
Lemma 5.3. Let
$f,g, S, P$
be as in Definition 3.2. Then
$\langle f,g,S,P\kern-0.1pt\rangle_{cl}$
, the closure of
$\{\,f,g,S,P\,\}$
under composition is an Abelian group.
Proof. By definition,
$g\circ f = I = P\circ S$
, so
$f,S$
are invertible and
$\langle f,g,S,P\kern-0.1pt\rangle_{cl} = \langle f,S\kern-0.1pt\rangle_{grp}$
where
$\langle f,S\kern-0.1pt\rangle_{grp}$
is the group generated by
$\{\,f,S\,\}$
.
Since S is definable by the cyclic order on Z (Axiom 8 in Definition 3.1) and f preserves the cyclic order on Z (Lemma 5.2), it follows that
$f\circ S(x)=S\circ f(x)$
. Now
$\langle f,S\kern-0.1pt\rangle_{grp}$
is Abelian, as the group defined by
$\langle a,b \,{|}\, ab=ba\kern-0.1pt\rangle$
is Abelian. ⊣
Corollary 5.4. Let
$n\geq 1$
and
$x\in Z$
.
$$ \begin{align*} \big(g^{\mathcal{M}_1}\big)^n(x)\not\sim_Z x. \end{align*} $$
Proof. Since
$x\in Z$
, so is
$\big (g^{\mathcal {M}_1}\big )^n(x)$
. Therefore, by Axiom 12,
$$ \begin{align*} \big(f^{\mathcal{M}_1}\big)^n\circ \big(g^{\mathcal{M}_1}\big)^n(x) \not\sim_Z \big(g^{\mathcal{M}_1}\big)^n(x). \end{align*} $$
By Lemma 5.3,
$\big (f^{\mathcal {M}_1}\big )^n\circ \big (g^{\mathcal {M}_1}\big )^n(x)=x$
. ⊣
Lemma 5.5. Let
$x\in M$
and
$n\in \mathbb {N}$
. There are
$k_1,k_2\in \mathbb {N}$
such that
$$ \begin{align*} \big(f^{\mathcal{M}_2}\big)^n(x) &= P^{k_1}\circ \big(f^{\mathcal{M}_1}\big)^n(x) \text{ and } \\ \big(g^{\mathcal{M}_2}\big)^n(x) &= S^{k_2}\circ \big(g^{\mathcal{M}_1}\big)^n(x). \end{align*} $$
Proof. By definition of
$f^{\mathcal {M}_2}, g^{\mathcal {M}_2}$
(Definition 5.1), there are
$\varepsilon _1,\dots ,\varepsilon _n, \nu _1,\dots , \nu _k\in \{0,1\}$
such that
$$ \begin{align} & \big(f^{\mathcal{M}_2}\big)^n (x) = P^{\varepsilon_1}\circ f^{\mathcal{M}_1}\circ \dots \circ P^{\varepsilon_n}\circ f^{\mathcal{M}_1}(x), \end{align} $$
$$ \begin{align} & \big(g^{\mathcal{M}_2}\big)^n (x) = S^{\nu_1}\circ g^{\mathcal{M}_1}\circ \dots \circ S^{\nu_n}\circ g^{\mathcal{M}_1}(x). \end{align} $$
By Lemma 5.3, the right hand side in Equation 11 is equal to
$$ \begin{align*}P^{\varepsilon_1+\dots+\varepsilon_n}\circ \big(f^{\mathcal{M}_1}\big)^n(x)\end{align*} $$
and the right hand side in Equation 12 is equal to
$$ \begin{align*}S^{\nu_1+\dots+\nu_n}\circ \big(f^{\mathcal{M}_1}\big)^n(x).\end{align*} $$
⊣
Corollary 5.6. For all
$n\in \mathbb {N}$
and every
$x\in M$
:
$$ \begin{align*}\big(f^{\mathcal{M}_1}\big)^n(x)\sim_Z \big(f^{\mathcal{M}_2}\big)^n(x) \text{ and } \big(g^{\mathcal{M}_1}\big)^n(x)\sim_Z \big(g^{\mathcal{M}_2}\big)^n(x),\end{align*} $$
6. Quantifier elimination in
$T_2$
In this section, unless otherwise specified, we work inside
$\mathcal {M}_2$
, so f is
$f^{\mathcal {M}_2}$
and g is
$g^{\mathcal {M}_2}$
.
Lemma 6.1.
$\mathcal {M}_2$
satisfies the following:
-
1.
$f(Z\cap [c_1,c_2])= Z\cap [c_3,c_4]$
and
$f\upharpoonright \big (Z\cap [c_1,c_2]\big )$
is a partial order isomorphism, and its inverse is
$g\upharpoonright Z\cap [c_3,c_4]$
. -
2.
$f(Z\cap (c_2,c_4]) = Z\cap [c_1,P(c_3))$
and
$f\upharpoonright \big (Z\cap (c_2,c_4]\big )$
is a partial order isomorphisms, and its inverse is
$g\upharpoonright Z\cap [c_1,P(c_3))$
. -
3.
$g(x) = f(x)=x$
for every
$x\notin Z.$
-
4. f is injective and not surjective on Z. Moreover,
$f(Z)= Z\setminus \{P(c_3)\}$
. -
5.
$g\circ f(x)=x$
for all
$x\in M$
. -
6.
$f\circ g(x)=x$
for all
$x\in M\setminus \{P(c_3)\}$
. -
7. For all
$n\geq 1$
and for every
$z\in Z$
are infinite, that is,
$$ \begin{align*}Z\cap C_<\big(z,-,f^n(z)\big)\text{ and }Z\cap C_<\big(f^n(z),-,z\big)\end{align*} $$
$z\not \sim _Z f^n(z)$
.
-
8. For all
$n\geq 1$
and for every
$z\in Z$
are infinite, that is,
$$ \begin{align*}Z\cap C_<\big(z,-,g^n(z)\big)\text{ and }Z\cap C_<\big(g^n(z),-,z\big)\end{align*} $$
$z\not \sim _Z g^n(z)$
.
Proof.
-
• Items 1 to 3 follow by definition of
$f^{\mathcal {M}_2}$
and by Axioms 10
, 11 and 13 in Definition 3.2. -
• Item 4 follows from Items 1 and 2, as
-
• To prove Item 5, we separate into two cases:
-
– if
$S^n(x)=c_4$
for some
$n\in \mathbb {N}$
, then
$S^n\circ f^{\mathcal {M}_1}(x) =P(c_3)$
, so So by definition of
$$ \begin{align*}S^{n+1}\circ f^{\mathcal{M}_2}(x)= S^{n} \circ S\circ P\circ f^{\mathcal{M}_1}(x) = S^{n} \circ f^{\mathcal{M}_1}(x) = P(c_3).\end{align*} $$
$g^{\mathcal {M}_2}$
,
$$ \begin{align*} g^{\mathcal{M}_2}\circ f^{\mathcal{M}_2}(x) = g^{\mathcal{M}_1}\circ S\circ P\circ f^{\mathcal{M}_1}(x) = x. \end{align*} $$
-
– if
$S^n(x)\neq c_4$
for all
$n\in \mathbb {N}$
, then
$S^n\circ f^{\mathcal {M}_1}(x)\neq P(c_3)$
for all
$n\in \mathbb {N}$
. So
$$ \begin{align*} g^{\mathcal{M}_2}\circ f^{\mathcal{M}_2}(x) = g^{\mathcal{M}_1}\circ f^{\mathcal{M}_1} (x) = x. \end{align*} $$
-
-
• To prove Item 6, by Items 3 and 4, for all
$x\in M\setminus \{\,P(c_3)\,\}$
,
$x = f(y)$
for some
$y\in M$
, therefore by Item 5
$$ \begin{align*} f\circ g(x) = f\circ g\circ f(y) = f(y) = x. \end{align*} $$
-
• Item 7 follows from Axiom 12 in Definition 3.2 and Corollary 5.6.
Corollary 6.2. Let
$a,b\in Z$
,
$\square \in \{<,>,=\}$
-
1. If
$a\in [c_1,c_2]$
and
$b\in [c_3, c_4]$
, then
$\mathcal {M}_2\models f(a)\square b \iff a\square g(b)$
. -
2. If
$a\in [c_1,c_2]$
and
$b\notin [c_3, c_4]$
, then
$\mathcal {M}_2\models f(a)\square b \iff c_3\square b$
. -
3. If
$a\in (c_2,c_4]$
and
$b\in [c_1, P(c_3))$
, then
$\mathcal {M}_2\models f(a)\square b \iff a\square g(b)$
. -
4. If
$a\in (c_2,c_4]$
and
$b\notin [c_1, P(c_3))$
, then
$\mathcal {M}_2\models f(a)\square b \iff c_1\square b$
. -
5. If
$a\in [c_1,P(c_3))$
and
$b\notin (c_2, c_4]$
, then
$\mathcal {M}_2\models g(a)\square b \iff c_4\square b$
. -
6. If
$a\in [c_3,c_4]$
and
$b\notin [c_1, c_2]$
, then
$\mathcal {M}_2\models g(a)\square b \iff c_1\square b$
.
Proof.
$(1)$
and
$(2)$
follow from Lemma 6.1, Items 1 and 6.
$(3)$
and
$(4)$
follow from Lemma 6.1, Items 2 and 6.
Corollary 6.3. Let
$x\in M, y\in Z$
,
$\square \in \{<,>,=\}$
.
$$ \begin{align*} & \mathcal{M}_2\models f(x)\square y \leftrightarrow \begin{pmatrix} \Big(& \big(x\notin Z \big) & \land & x\square y & \Big) & \lor \\ \Big(& \big(x\in Z \cap [c_1, c_2] \land y\in [c_3,c_4]\big) & \land & x\square g(y) & \Big) & \lor \\ \Big(& \big(x\in Z \cap [c_1, c_2] \land y\notin [c_3,c_4]\big) & \land & c_3\square y & \Big) & \lor \\ \Big(& \big(x\in Z \cap (c_2, c_4] \land y\in [c_1, P(c_3))\big) & \land & x\square g(y) & \Big) & \lor \\ \Big(& \big(x\in Z \cap (c_2, c_4] \land y\notin [c_1, P(c_3))\big) & \land & c_1\square y & \Big) & \end{pmatrix}, \\ & \mathcal{M}_2\models g(x)\square y \leftrightarrow \begin{pmatrix} \Big(& \big(x\notin Z \big) & \land & x\square y & \Big) & \lor \\ \Big(& \big(x\in Z\cap [c_3,c_4]\land y\in [c_1, c_2]\big) & \land & x\square f(y) & \Big) & \lor \\ \Big(& \big(x\in Z\cap [c_3,c_4]\land y\notin [c_1, c_2]\big) & \land & c_1\square y & \Big) & \lor \\ \Big(& \big(x\in Z\cap [c_1,P(c_3))\land y\in (c_2, c_4]\big) & \land & x\square f(y) & \Big) & \lor \\ \Big(& \big(x\in Z\cap [c_1,P(c_3))\land y\notin (c_2, c_4]\big) & \land & c_4\square y & \Big) & \lor \\ \Big(& \big(x=P(c_3)\big) & \land & P(c_3)\square y & \Big) & \end{pmatrix}. \end{align*} $$
Remark 6.4. If
$x\notin Z$
then
$\mathcal {M}_2\models f(x)=g(x)=x$
. In particular,
-
•
$\mathcal {M}_2\models f(x)\in Z\leftrightarrow x\in Z$
for all
$x\in M$
. -
•
$\mathcal {M}_2\models g(x)\in Z\leftrightarrow x\in Z$
for all
$x\in M$
. -
•
$\mathcal {M}_2\models f(x)\square y \leftrightarrow g(x)\square y\leftrightarrow x\square y $
for any
$x\in M\setminus Z, y\in M$
,
$\square \in \{<,>,=\}$
.
Remark 6.5. If
$x\in Z, y\notin Z$
then:
-
•
$\mathcal {M}_2\models x>y \leftrightarrow x\geq \pi (y)$
. -
•
$\mathcal {M}_2\models x< y \leftrightarrow x\leq P\circ \pi (y)$
.
Corollary 6.6.
$$ \begin{align*} & T_2\models \big[ x\in Z\land y\notin Z \land x>y \big]\leftrightarrow \big[ x\in Z\land y\notin Z \land x\geq \pi(y)\land \pi(y)\in Z \big], \\ & T_2\models \big[ x\in Z\land y\notin Z \land x<y \big]\leftrightarrow \big[ x\in Z\land y\notin Z \land x\leq P\circ\pi(y)\land P\circ\pi(y)\in Z \big], \\ & T_2\models \big[ x\in Z\land y\notin Z \land x=y \big]\leftrightarrow \big[ x\in Z\land y\notin Z \land c_1\neq c_1\big]. \end{align*} $$
Definition 6.7. Following standard terminology, a constant term is a term with no free variables.
Definition 6.8. Given two
$\mathcal {L}_1$
-definable maps
$F,G:M\to M$
, denote
$F\approx G$
if there are finitely many constant terms
$\tau _1,\dots , \tau _k$
, such that
$$ \begin{align*} T_2\models (\forall x)\ \Bigg[F(x)=G(x)\lor \bigvee_{i=1}^k x=\tau_i\Bigg]. \end{align*} $$
$\approx $
is an equivalence relation. For any
$\mathcal {L}_1$
-definable map
$F:M\to M$
, let
$[F]$
be its equivalence class.
Lemma 6.9.
$f\circ S\approx S\circ f$
.
Proof.
-
• If
$x\notin Z$
then both S and f are the identity on x, so the equality
$f\circ S(x)= S\circ f(x)$
is trivial. -
• If
$x\in Z$
and
$c_1< x<c_2$
or
$c_2<x<c_4$
then the equality
$f\circ S(x)= S\circ f(x)$
follows by Items 1 and 2 in Lemma 6.1.
In conclusion, the equality
$f\circ S(x)= S\circ f(x)$
holds for all
$x\neq c_1, c_2,c_4$
. ⊣
For any finite-to-one map
$F,F',G,G':M\to M$
, if
$F\approx F'$
and
$G\approx G'$
then
$F\circ G\approx {{F'\circ G'}}$
. Since
$f,S,P$
are injective and g is injective outside
$\{P(c_3)\}$
, the composition
$[F]\circ [G]:=[F\circ G]$
is well defined, for any composition of
$f,g,S,P$
.
Proposition 6.10.
$\langle[f],\ [g],\ [S],\ [P]\kern-0.1pt\rangle_{cl}$
, the closure of
$\{[f],\ [g],\ [S],\ [P]\}$
under composition is an Abelian group.
Proof.
$$ \begin{align*} T_2\supset T_0 &\models P\circ S(x) = S\circ P = x \\ T_2 &\models \forall (x\neq P(c_3)) g\circ f(x) =f\circ g (x) = x. \end{align*} $$
So
$[g][f]=[f][g]=[P][S]=[S][P]=1$
. In particular
$[f],[S]$
are invertible and
$\langle [f],\ [g],\ [S],\ [P]\kern-0.1pt\rangle = \langle [f],\ [S]\kern-0.1pt\rangle_{grp}$
where
$\langle[f],\ [S]\kern-0.1pt\rangle_{grp}$
is the group generated by
$\{[f],\ [g]\}$
. By Lemma 6.9,
$[f][S]=[S][f]$
. The claim now follows from the fact the group defined by
$\langle a,b \,{|}\, ab=ba\kern-0.1pt\rangle$
is Abelian. ⊣
Remark 6.11. Let
$x\in M$
and
$F\in \{S,\ P,\ \pi \}$
. If there are infinitely many elements in Z between x and
$F(x)$
, then
$F(x)\in \{c_1,\ c_4\}$
.
By infinitely many elements in Z between x and
$F(x)$
, we mean with respect to the order
$<$
and not the cyclic order
$C_<$
, that is, either
$x<F(x)$
and
$Z\cap [x,F(x)]\geq \aleph _0$
, or
$F(x)<x$
and
$Z\cap [F(x),x]\geq \aleph _0$
.
This is weaker than
$x\not \sim _Z F(x)$
; for example,
$c_1\sim _Z c_4$
but there are infinitely many elements in Z between
$c_1$
and
$c_4$
.
Lemma 6.12. Let
$F,G\in \langle S,P,\pi \kern-0.1pt\rangle_{cl}$
. Then there are finitely many constant terms
$\tau _1,\dots , \tau _k$
, such that if
$F(x)\notin \{\tau _1,\dots , \tau _k\}$
, then there are only finitely many elements in Z between x and
$F(x)$
.
Proof. Let
$F=G_k\circ \dots \circ G_1$
where
$G_1,\dots , G_k\in \{S,\ P,\ \pi \}$
. Let
${{F_0:= \operatorname {\mathrm {Id}}}}$
,
$F_i:= G_i\circ \dots \circ G_1$
for any
$1\leq i\leq k$
, so
$F=F_k$
. If there are infinitely many elements in Z between x and
$F(x)$
, then there is some
$1\leq i\leq k$
with infinitely many elements in Z between
$F_i(x)$
and
$F_{i-1}(x)$
, so by Remark 6.11,
$F_i(x)\in \{c_1,\ c_4\}$
and thus
$F(x)= F_k(x) = F_{k-i}\circ F_i(x) \in \{\,F_{k-i}(c_1), F_{k-i}(c_4)\,\}$
. So if
$$ \begin{align*}F(x)\notin \{F_i(c) | 0\leq i\leq k-1, c\in\{c_1,\ c_4\} \}\end{align*} $$
then there are finitely many elements in Z between x and
$F(x)$
. ⊣
Lemma 6.13.
$C_<\big (f^m(z),f^n(z),z\big ) $
for all
$m>n>0$
and for every
$z\in Z$
.
Proof. Let
$m>n>0$
and
$z\in Z$
. By Axiom 14 in Definition 3.2,
$$ \begin{align*}C_<\big(\big(f^{\mathcal{M}_1}\big)^m(z),\big(f^{\mathcal{M}_1}\big)^n(z),z\big).\end{align*} $$
By Corollary 5.6,
$$ \begin{align*}\big(f^{\mathcal{M}_2}\big)^n(z)\sim_Z\big(f^{\mathcal{M}_1}\big)^n(z)\text{ and }\big(f^{\mathcal{M}_2}\big)^m(z)\sim_Z\big(f^{\mathcal{M}_1}\big)^m(z).\end{align*} $$
and the lemma follows from Lemma 2.9. ⊣
Lemma 6.14. for any
$n\in \mathbb {N}$
and
$z\in Z$
:
$$ \begin{align*}\mathcal{M}_2\models f^{n+1}(z)<z\leftrightarrow\bigwedge_{i=0}^n ( f^{i}(z)>c_2).\end{align*} $$
Proof. We prove the lemma by induction on n. For
$n=0$
the claim holds by definition of f. For
$n\geq 1$
, By Lemma 6.13,
$C_<(f^{n+1}(z),f^n(z),z)$
. So
$$ \begin{align*}\mathcal{M}_2\models f^{n+1}(z)<z \leftrightarrow f^{n+1}(z)<f^n(z)<z. \end{align*} $$
By the induction hypothesis,
$f^n(z)<z$
is equivalent to
$\bigwedge _{i=0}^{n-1} ( f^{i}(z)> c_2)$
and
$f^{n+1}(z)<f^n(z)$
is equivalent to
$f^n(z)>c_2$
. ⊣
Definition 6.15.
-
1.
$ \Phi :=\{\,\phi ^n \ {|}\ \phi \in \{f,\ g\},\ n\in \mathbb {N}\,\}$
. -
2.
$\Sigma :=\{\, \sigma ^m \ {|}\ \sigma \in \{S,\ P\}, m\in \mathbb {N} \,\}$
. -
3.
$\Pi : = \{\,\pi ^{\epsilon } \ {|}\ \epsilon \in \{0,\ 1\} \,\}$
. -
4. For any functions
$h_1,\dots , h_n$
and
$A,B\subseteq \langle h_1,\dots , h_n\kern-0.1pt\rangle_{cl}$
, let
$AB:=\{a\circ b | a{\,\in\,} A, b$
${\in\,} B\}$
.
Lemma 6.16. Let
$n\geq 1$
,
$\psi _1,\psi _2\in \Sigma \Pi $
, and
$\square \in \{\,<,>,=\,\}$
. Then
-
1. There are constant terms
$\tau _1,\dots , \tau _k$
such that
$$ \begin{align*}& T_2\models f^n\circ\psi_1(x)\square \psi_2(x)\\&\quad\leftrightarrow \begin{bmatrix} \big( \psi_1(x)\notin Z\land \psi_1(x)\square\psi_2(x) \big) & \lor \\ \big( \psi_1(x)\in Z, \psi_1(x),\psi_2(x)\notin \{\,\tau_1,\dots, \tau_k\,\} \land f^n\circ\psi_1(x)\square\psi_1(x) \big) & \lor \\ \big( \bigvee_{i=1}^k \big(\psi_1(x)=\tau_i \land f^n(\tau_i)\square\psi_2(x)\big) \big) & \lor \\ \big( \bigvee_{i=1}^k \big(\psi_2(x)=\tau_i \land f^n\circ\psi_1(x)\square\tau_i\big) \big) \\ \end{bmatrix}. \end{align*} $$
-
2. There are constant terms
$\sigma _1,\dots , \sigma _l$
such that
$$ \begin{align*}&T_2\models g^n\circ\psi_1(x)\square \psi_2(x) \\&\quad \leftrightarrow \begin{bmatrix} \big( \psi_1(x)\notin Z\land \psi_1(x)\square\psi_2(x) \big) & \lor \\ \big( \psi_1(x),\psi_2(x)\in Z\setminus \{\sigma_1,\dots, \sigma_l\} \land g^n\circ\psi_1(x)\square\psi_1(x) \big) & \lor \\ \big( \bigvee_{i=1}^l \big(\psi_1(x)=\sigma_i \land g^n(\sigma_i)\square\psi_2(x)\big) \big) & \lor \\ \big( \bigvee_{i=1}^l \big(\psi_2(x)=\sigma_i \land g^n\circ\psi_1(x)\square\sigma_i\big) \big) \\ \end{bmatrix}. \end{align*} $$
Proof.
-
1. By Lemma 6.12 applied twice, there are constant terms
$\tau _1,\dots ,\tau _k$
such that whenever
$\psi (x)_1,\psi _2(x)\notin \{\tau _1,\dots , \tau _k\}$
, there are finitely many elements in Z between
$\psi (x)_1$
and
$\psi _2(x)$
.-
• If
$\psi _1(x)\notin Z$
, then by Item 3 of Lemma 6.1,
$f^n\circ \psi _1(x)=\psi _1(x)$
. In particular,
$$ \begin{align*}\mathcal{M}_2\models f^n\circ \psi_1(x)\square \psi_2(x) \leftrightarrow \psi_1(x)\square \psi_2(x). \end{align*} $$
-
• If
$\psi _1(x)\in Z$
,
$\psi _1(x),\psi _2(x)\notin \{\tau _1,\dots , \tau _k\}$
, then by Lemma 6.1, Item 7 there are infinitely many elements in Z between
$\psi _1(x)$
and
$f^n\circ \psi _1(x)$
. As there are only finitely many elements in Z between
$\psi _1(x)$
and
$\psi _2(x)$
, it follows that
$$ \begin{align*}\mathcal{M}_2\models f^n\circ \psi_1(x)\square \psi_2(x) \leftrightarrow f^n\circ \psi_1(x)\square \psi_1(x). \end{align*} $$
-
-
2. The proof is similar. ⊣
Definition 6.17.
-
1. We define
$\deg (F)$
for
$F\in \langle f,\ g,\ S,\ P,\ \pi \kern-0.1pt\rangle_{cl}$
inductively, as follows:-
•
$\deg ( \operatorname {\mathrm {Id}})=\deg (S)=\deg (P)=\deg (\pi ) = 0.$
-
•
$\deg (f)=\deg (g) = 1$
. -
•
$\deg (F\circ G) = \deg (F)+\deg (G)$
for all
$F,G\in \langle f,\ g,\ S,\ P,\ \pi \kern-0.1pt\rangle_{cl}$
.
Notice that this is a syntactic definition, for example,
$\deg (F\circ G) = 2$
. -
-
2. For any quantifier free
$\mathcal {L}_1$
-formula
$\theta (x,\overline {y})$
and variable x we define
$ \operatorname {\mathrm {rank}}(\theta , x)\in \big (\{-\infty \}\cup \mathbb {N}\big )^2$
by induction on the complexity of
$\theta $
:-
• If x does not occur in
$\theta $
, then
$ \operatorname {\mathrm {rank}}(\theta ,x) = (-\infty , -\infty )$
. -
• If
$\theta $
is atomic of the form
$F(x)\in Z$
then
$ \operatorname {\mathrm {rank}}(\theta ,\ x) = (-\infty , \deg (F))$
. -
• If
$\theta $
is atomic of the form
$F(x)\square \tau $
where
$F\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
,
$\square \in \{<,>,=\}$
, and
$\tau $
is an
$\mathcal {L}_1$
-term such that x does not occur in
$\tau $
, then
$ \operatorname {\mathrm {rank}}(\theta ,x) = (-\infty , \deg (F))$
. -
• If
$\theta $
is atomic of the form
$F(x)\square G(x)$
where
$F, G\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
,
$\square \in \{<, >,=\}$
, and
$\deg (F)\leq \deg (G)$
, then
$ \operatorname {\mathrm {rank}}(\theta ,x) = (\deg (F), \deg (G))$
. -
• If
$\theta $
is a Boolean combination of atomic formulae
$\theta _1,\dots , \theta _k$
, then
$ \operatorname {\mathrm {rank}}(\theta ,x)$
is the lexicographic maximum of
$\{\, \operatorname {\mathrm {rank}}(\theta _i,x)\,\}_{i=1}^k$
. -
• ranks are endowed with the lexicographic order on pairs, that is,
$(n,\ m)\leq (n',\ m')$
if either
$n\leq n'$
or both
$n=n'$
and
$m\leq m'$
. Notice that if
$ \operatorname {\mathrm {rank}}(\theta , x) = (n,\ m)$
then
$n\leq m$
.
-
Definition 6.18. A quantifier free
$\mathcal {L}_1$
-formula
$\theta (x,\ \overline {y})$
is x-corrected if any term
$F(x)$
appearing in
$\theta $
belongs to
$\Phi \Sigma \Pi $
.
Lemma 6.19. For any quantifier free
$\mathcal {L}_1$
-formula
$\varphi $
and variable x, there is some x-corrected formula
${{\psi }}$
such that
$ \operatorname {\mathrm {rank}}({{\psi }},\ x)\leq \operatorname {\mathrm {rank}}(\varphi ,\ x)$
and
$T_2\models \varphi \leftrightarrow {{\psi }}$
.
Proof. A Boolean combination of x-corrected formulae is x-corrected, so we may assume
$\varphi $
is atomic.
-
• If
$\varphi $
is of the form
$F(x)\in Z$
for some
${{F}}\in \langle f,\ g,\ S,\ P,\ \pi \kern-0.1pt\rangle_{cl}\setminus \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
then
$T_2\models F(x)\in Z \leftrightarrow \pi (x)\in Z$
. -
• If
$\varphi $
is of the form
$F(x)\in Z$
for some
${{F}}\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{{cl}}$
then
$T_2\models {{F}}(x)\in Z \leftrightarrow x\in Z$
. -
• If
$\varphi $
of the form
$F(x)\square \tau $
for some term
$\tau $
and
$\square \in \{<,>,=\}$
:-
– If
$F\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
, then by Proposition 6.10, there is some
$F'\in \Phi \Sigma $
with
$\deg (F')=\deg (F)$
, and constant terms
$\tau _1,\dots , \tau _k$
such that
$F(x)=F'(x)$
for all
$x\notin \{\tau _1,\dots ,\tau _k\}$
.So
$$ \begin{align*}\begin{matrix} T_2\models & \big[F(x)\square\tau\big]\leftrightarrow & \begin{bmatrix} \big(\bigwedge_{i=1}^k x\neq \tau_k \land F'(x)\square \tau\big) & \lor \\ \bigvee_{i=1}^k \big( x=\tau_i \land F(\tau_i)\square \tau \big) \end{bmatrix} \end{matrix}. \end{align*} $$
-
– If
$F\in \langle f,\ g,\ S,\ P,\ \pi \kern-0.1pt\rangle_{cl}\setminus \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
, then there are
$F_1,\ F_2\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
such that
$\mathcal {M}_2\models F(x) = F_1\circ \pi \circ F_2(x)$
for all
$x\in M$
and
$\deg (F_1)\leq \deg (F_1\circ F_2)=\deg (F)$
. So
$\mathcal {M}_2\models F(x)=F_1\circ F_2(x)$
for all
$x\in Z$
and
$\mathcal {M}_2\models F(x)=F_1\circ \pi (x)$
for all
$x\notin Z$
. So and
$$ \begin{align*}\begin{matrix} T_2\models & \big[F(x)\square \tau\big]\leftrightarrow & \begin{bmatrix} \big(x\in Z \land F_1\circ F_2(x)\square \tau\big) \lor \\ \big(x\notin Z \land F_1\circ\pi(x)\square \tau\big) \\ \end{bmatrix} \end{matrix}\end{align*} $$
$F_1,\ F_1\circ F_2\in \langle f,\ g,\ S,\ P\kern-0.1pt\rangle_{cl}$
, so we can apply the previous case to get a formula where every term
$F(x)$
to the left of
$\square $
belongs to
$\Phi \Sigma \Pi $
.
Finally, if x does not appear in
$\tau $
we are done. Otherwise, if
$\tau =G(x)$
for some term G, a symmetric argument applied to G will yield an x-corrected formula
$\psi $
equivalent to
$\varphi $
as needed. ⊣ -
Lemma 6.20. Let
$\varphi $
be an x-corrected atomic formula of rank
$(-\infty ,\ n+1)$
or of rank
$(n+1,\ k)$
for some
$n, k\in \mathbb {N}$
. Then there is some quantifier free formula
${{\psi }}$
such that
$ \operatorname {\mathrm {rank}}({{\psi }},\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
and
$T_2\models \varphi \leftrightarrow {{\psi }}$
.
Proof.
-
(1) Assume
$ \operatorname {\mathrm {rank}}(\varphi ,x) = (-\infty ,\ n+1)$
.If
$\varphi $
is of the form
$F\circ H(x)\in Z$
where
$F\in \Phi ,\ H\in \Sigma \Pi $
, by Remark 6.4,
$\mathcal {M}_2 \models F\circ H(x)\in Z\iff H(x)\in Z$
and
$ \operatorname {\mathrm {rank}}(H(x)\in Z,\ x)=(-\infty ,\ 0)$
.If
$\varphi $
is of the form
$F\circ H(x)\square \tau $
where
$F\in \Phi ,\ H\in \Phi \Sigma \Pi $
,
$\deg (F)=1,\deg (H)=n$
, and
$\tau $
is some
$\mathcal {L}_1$
-term not containing xIn which case,
$F\in \{f,\ g\}$
and So it suffices to show that each of the disjuncts above is equivalent to an x-corrected formula of rank
$$ \begin{align*}\mathcal{M}_2\models \big[F\circ H(x)\square \tau \big] \leftrightarrow \begin{bmatrix} \big(F\circ H(x)\square \tau \land \tau\in Z \big)& \lor \\ \big(F\circ H(x)\square \tau \land \tau\notin Z\land H(x)\notin Z\big) & \lor \\ \big(F\circ H(x)\square \tau \land \tau\notin Z\land H(x)\in Z\big) \end{bmatrix}. \end{align*} $$
$<(-\infty ,\ n+1)$
.-
(a) Applying Corollary 6.3 to
$H(x)$
and
$\tau $
, there is some x-corrected formula
${{\psi }}'(x,\tau )$
of rank
$(-\infty ,\ n)$
such that
$\mathcal {M}_2\models {{\psi }}'(x,\ \tau )\leftrightarrow F\circ H(x)\square \tau $
for all
$\tau \in Z$
. So
$$ \begin{align*} \mathcal{M}_2\models {{\psi}}'(x,\ \tau)\land \tau\in Z \leftrightarrow F\circ H(x)\square \tau \land \tau\in Z. \end{align*} $$
-
(b) By Remark 6.4,
$\big (F\circ H(x)\square \tau \land \tau \notin Z\land H(x)\notin Z\big )$
is equivalent to and the latter is an x-corrected formula of rank
$$ \begin{align*}\big( H(x)\square \tau \land \tau\notin Z\land H(x)\notin Z\big)\end{align*} $$
$(-\infty ,\ n)$
.
-
(c) Applying Corollary 6.6 to
$F\circ H(x)$
and
$\tau $
, we obtain that (13)is equivalent to one of the following:
$$ \begin{align} \big(F\circ H(x)\square \tau \land \tau\notin Z\land H(x)\in Z\big) \end{align} $$
(14)
$$ \begin{align} & F\circ H(x) \in Z\land \tau \notin Z \land F\circ H(x)\geq \pi(\tau)\land \pi(\tau)\in Z, \end{align} $$
(15)
$$ \begin{align} & F\circ H(x)\in Z\land \tau\notin Z \land F\circ H(x)\leq P\circ\pi(\tau)\land P\circ\pi(\tau)\in Z, \end{align} $$
(16)As in 1a, there are
$$ \begin{align} & F\circ H(x)\in Z\land \tau\notin Z \land c_1=\tau. \end{align} $$
${{\psi }}^{\prime }_1(x,\ \pi (\tau ))$
and
${{\psi }}^{\prime }_2(x,P\circ \pi (\tau ))$
of rank
$(-\infty ,\ n)$
equivalent to
$F\circ H(x)\geq \pi (\tau )\land \pi (\tau )\in Z$
and
$F\circ H(x)\leq P\circ \pi (\tau )\land P\circ \pi (\tau )\in Z$
, respectively. So (13) is equivalent to one of the following: (17)
$$ \begin{align} & H(x) \in Z\land \tau \notin Z \land {{\psi}}^{\prime}_1(x,\ \pi(\tau)) \land \pi(\tau)\in Z, \end{align} $$
(18)
$$ \begin{align} & H(x)\in Z\land \tau\notin Z \land {{\psi}}^{\prime}_2(x,\ P\circ\pi(\tau)) \land P\circ\pi(\tau)\in Z, \end{align} $$
(19)
$$ \begin{align} & H(x)\in Z\land \tau\notin Z \land c_1=\tau \end{align} $$
an each is x-corrected of rank
$(-\infty ,\ n)$
. -
-
(2) Assume
$ \operatorname {\mathrm {rank}}(\varphi ,\ x) = (n+1,\ k)$
. Then
$\varphi $
is of the form
$F\circ H(x)\square G(x)$
where
$F\in \Phi , H, G\in \Phi \Sigma \Pi $
,
$\deg (F)=1,\deg (H)=n, \deg (G)=k$
and
$n<k$
. We repeat an argument similar to that in Item (1) of this lemma, with
$\tau $
replaced by
$G(x)$
: So it suffices to show that each of the disjuncts above is equivalent to an x-corrected formula of rank
$$ \begin{align*}\mathcal{M}_2\models \big[F\circ H(x)\square G(x) \big] \leftrightarrow \begin{bmatrix} \big(F\circ H(x)\square G(x) \land G(x)\in Z \big)& \lor \\ \big(F\circ H(x)\square G(x) \land G(x)\notin Z\land H(x)\notin Z\big) & \lor \\ \big(F\circ H(x)\square G(x) \land G(x)\notin Z\land H(x)\in Z\big) \end{bmatrix}. \end{align*} $$
$<(n+1,\ k)$
.
-
(a) Applying Corollary 6.3 to
$H(x)$
and
$G(x)$
, there is some quantifier-free formula
${{\psi }}'(x)$
of rank
$\leq (n,\ k+1)$
such that
$\mathcal {M}_2\models {{\psi }}'(x)\leftrightarrow F\circ H(x)\square G(x)$
whenever
$G(x)\in Z$
. So
$$ \begin{align*} \mathcal{M}_2\models {{\psi}}'(x)\land G(x)\in Z \leftrightarrow F\circ H(x)\square G(x) \land G(x)\in Z. \end{align*} $$
-
(b) By Remark 6.4,
$\big (F\circ H(x)\square G(x) \land G(x)\notin Z\land H(x)\notin Z\big )$
is equivalent to and the latter is an x-corrected formula of rank
$$ \begin{align*}\big( H(x)\square G(x) \land G(x)\notin Z\land H(x)\notin Z\big)\end{align*} $$
$(n,\ k)$
.
-
(c) Applying Corollary 6.6 to
$F\circ H(x)$
and
$G(x)$
, we obtain that (20)is equivalent to one of the following:
$$ \begin{align} \big(F\circ H(x)\square G(x) \land G(x)\notin Z\land H(x)\in Z\big) \end{align} $$
(21)
$$ \begin{align} & F\circ H(x)\in Z\land G(x) \notin Z \land F\circ H(x)\geq \pi\circ G(x)\land \pi\circ G(x)\in Z, \end{align} $$
(22)
$$ \begin{align} & F\circ H(x)\in Z\land G(x)\notin Z \land F\circ H(x) \nonumber \\ & \leq P\circ\pi\circ G(x)\land P\circ\pi\circ G(x)\in Z, \end{align} $$
(23)As in 2a, applying Corollary 6.3 to
$$ \begin{align} & F\circ H(x)\in Z\land G(x)\notin Z \land c_1=G(x). \end{align} $$
$H(x), \pi \circ G(x)$
and to
$H(x),P\circ \pi \circ G(x)$
, there are
${{\psi }}^{\prime }_1(x)$
and
${{\psi }}^{\prime }_2(x)$
of rank
$\leq (n,\ k+1)$
equivalent to
$F\circ H(x)\geq \pi \circ G(x)\land \pi \circ G(x)\in Z$
and
$F\circ H(x)\leq P\circ \pi \circ G(x)\land P\circ \pi \circ G(x)\in Z$
, respectively. So (20) is equivalent to one of the following: (24)
$$ \begin{align} & H(x) \in Z\land G(x) \notin Z \land {{\psi}}^{\prime}_1(x)) \land \pi\circ G(x)\in Z, \end{align} $$
(25)
$$ \begin{align} & H(x)\in Z\land G(x)\notin Z \land {{\psi}}^{\prime}_2(x) \land P\circ\pi\circ G(x)\in Z, \end{align} $$
(26)an each is quantifier-free of rank
$$ \begin{align} & H(x)\in Z\land G(x)\notin Z \land c_1=G(x) \end{align} $$
$\leq (n,\ k+1)$
. To finally obtain an x-corrected formula of rank
$\leq (n,\ k+1)$
, apply Lemma 6.19. ⊣
-
Lemma 6.21. Let
$\varphi $
be an x-corrected atomic formula of rank
$(0,\ k+1)$
for some
$k\in \mathbb {N}$
. Then there is some quantifier free formula
${{\psi }}$
such that
$ \operatorname {\mathrm {rank}}({{\psi }},\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
and
$T_2\models \varphi \leftrightarrow {{\psi }}$
.
Proof. By Lemma 6.16, we may assume
$\varphi $
is either of the form
$f^{k+1}\circ {{\sigma }}(x)\square {{\sigma }}(x)$
or of the form
$g^{k+1}\circ {{\sigma }}(x)\square {{\sigma }}(x)$
for some
${{\sigma }}\in \Sigma \Pi ,\ \square \in \{<,>,=\}$
.
-
1. In case
$\varphi $
is
$f^{k+1}\circ {{\sigma }}(x)\square {{\sigma }}(x)$
:-
• If
$\phi (x)\notin Z$
, then, by Lemma 6.1, Item 3,
$f^{k+1}\circ \phi (x)=\phi (x)$
. -
• If
$\phi (x)\in Z$
, then, by Lemma 6.1, Item 7,
$f^{k+1}\circ \phi (x)\neq \phi (x)$
. So
$f^{k+1}\circ \phi (x)>\phi (x)$
is equivalent to
$f^{k+1}\circ \phi (x)\nless \phi (x)$
. By Lemma 6.14, (27)
$$ \begin{align} T_2\models &{{\phi(x)\in Z \land }} f^{k+1}\circ {{\sigma}}(x)< {{\sigma}}(x) \leftrightarrow \end{align} $$
(28)and the formula in (28) is of rank
$$ \begin{align} & \Bigg(\phi(x)\in Z\land \bigvee_{i=0}^{k}(c_1\leq f^{i}\circ {{\sigma}}(x)\leq c_2)\Bigg) \end{align} $$
$(0,0)$
. In conclusion, for this case
$\varphi $
is a Boolean combination of formulae of the form
$\varphi (x)\in Z$
,
$\varphi (x)\square \varphi (x)$
, and formula (28) above, all of which are of rank
$(0,\ 0)$
.
-
-
2. In case
$\varphi $
is
$g^{k+1}\circ \sigma (x)\square \sigma (x)$
, by Proposition 6.10, there are finitely many constant terms
$\tau _1,\dots , \tau _m$
such that
$f^{k+1}\circ g^{k+1}(x)=x$
for all
$x\notin \{\tau _1,\dots ,\tau _m\}$
. So and
$$ \begin{align*} T_2\models & g^{k+1}\circ {{\sigma}}(x)\square {{\sigma}}(x) \leftrightarrow \\ & \begin{bmatrix} \big({{\sigma}}(x)\notin \{\tau_1,\dots, \tau_m\}\land g^{k+1}\circ{{\sigma}}(x)\square f^{k+1}\circ g^{k+1}\circ {{\sigma}}(x)\big) & \lor \\ \big(\bigvee_{i=1}^m \big({{\sigma}}(x)=\tau_i\land g^{k+1} (\tau_i)=\tau_i \big)\big) \end{bmatrix} \end{align*} $$
$ \operatorname {\mathrm {rank}}\big (\bigvee _{i=0}^k (c_1\leq f^{i}\circ {{\sigma }}(x)\leq c_2),\ x\big ) = (-\infty ,\ k-1)$
Now, replacing
${{\sigma }}(x)$
with
$g^{k+1}\circ {{\sigma }}(x)$
in (27), we get (29)
$$ \begin{align} T_2\models & f^{k+1}\circ g^{k+1}\circ {{\sigma}}(x)\square g^{k+1}\circ {{\sigma}}(x) \leftrightarrow \end{align} $$
(30)By noticing that
$$ \begin{align} & \begin{bmatrix} \big(g^k\circ {{\sigma}}(x)\in Z\land \bigvee_{i=0}^{k}(c_1\leq f^{i}\circ g^{k+1}\circ {{\sigma}}(x)\leq c_2)\big) & \lor \\ \big(g^k \circ {{\sigma}}(x)\notin Z\land g^{k+1}\circ{{\sigma}}(x)=g^{k+1}\circ {{\sigma}}(x) \big) \end{bmatrix}. \end{align} $$
$\vdash g^{k+1}\circ {{\sigma }}(x)=g^{k+1}\circ {{\sigma }}(x) \leftrightarrow x=x$
, the formula in (30) is of rank
$(0,\ 0)$
. ⊣
Lemma 6.22. Let
$\varphi $
be an x-corrected atomic formula of rank
$(0,\ 0)$
. Then there is some quantifier free formula
${{\psi }}$
such that
$ \operatorname {\mathrm {rank}}({{\psi }},x)< \operatorname {\mathrm {rank}}(\varphi ,x)$
and
$T_2\models \varphi \leftrightarrow {{\psi }}$
.
Proof. By Remarks 4.1 and 4.2 we may assume
$\varphi $
is of the form
${{\sigma }}(x)\square x$
where
${{\sigma }}\in \Sigma \Pi $
and
$\square \in \{<,>,=\}$
. Now
$$ \begin{align*}\vdash \big[{{\sigma}}(x)\square x\big] \leftrightarrow \big[\big({{\sigma}}(x)\square x \land x\in Z\big) \lor \big({{\sigma}}(x)\square x \land x\notin Z\big) \big].\end{align*} $$
By Remark 4.2, the right hand side is equivalent to a quantifier free formula of rank
$(-\infty ,-\infty )$
. ⊣
Lemma 6.23. Let
$\varphi $
be a quantifier free formula with free variable x. Then there is some x-corrected formula
$\phi $
such that
$ \operatorname {\mathrm {rank}}(\phi ,\ x)\leq (-\infty ,\ 0)$
for some
$k\in \mathbb {N}$
and
$T_2\models \varphi \leftrightarrow \phi $
.
Proof. By Lemma 6.19 we may assume
$\varphi $
is x-corrected. Since the lexicographic order on well-ordered sets is well-ordered, by induction it suffices to show that if
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)>(-\infty ,\ 0)$
, then there is some x-corrected
$\phi $
such that
$ \operatorname {\mathrm {rank}}(\phi ,\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
and
$T_2\models \varphi \leftrightarrow \phi $
. As a Boolean combination of formulae of rank at most
$(-\infty ,\ 0)$
is of rank at most
$(-\infty ,\ 0)$
as well, we may further assume that
$\varphi $
is atomic.
-
• If
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)=(n+1,\ k)$
for some
$n,\ k\in \mathbb {N}$
, then by Lemma 6.20 there is some quantifier free formula
$\phi '$
such that
$ \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
. -
• If
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)=(0,\ k+1)$
for some
$k\in \mathbb {N}$
, then by Lemma 6.21 there is some quantifier free formula
$\phi '$
such that
$ \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
. -
• If
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)=(0,\ 0)$
for some
$k\in \mathbb {N}$
, then by Lemma 6.22 there is some quantifier free formula
$\phi '$
such that
$ \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
. -
• If
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)=(-\infty ,\ n+1)$
for some
$k\in \mathbb {N}$
, then by Lemma 6.20 there is some quantifier free formula
$\phi '$
such that
$ \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
.
So in conclusion, whenever
$\varphi $
is x-corrected and
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)>(-\infty ,\ 0)$
, there is some quantifier free formula
$\phi '$
such that
$T_2\models \varphi \leftrightarrow \phi '$
and
$ \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
. By Lemma 6.19, there is some x-corrected formula
$\phi $
such that
$T_2\models \varphi \leftrightarrow \phi '\leftrightarrow \phi $
and
$ \operatorname {\mathrm {rank}}(\phi ,\ x)= \operatorname {\mathrm {rank}}(\phi ',\ x)< \operatorname {\mathrm {rank}}(\varphi ,\ x)$
. ⊣
Theorem 6.24.
$T_2$
admits quantifier elimination.
Proof. Let
$\varphi (x,y_1,\dots , y_k)$
be a quantifier free
$\mathcal {L}_1$
-formula. It suffices to find a quantifier free formula
$\phi (y_1,\dots , y_k)$
such that
$ T_2\models \exists x\varphi (x,y_1,\dots , y_k)\leftrightarrow \phi (y_1,\dots , y_k)$
. By Lemma 6.23, we may assume
$\varphi $
is x-corrected and
$ \operatorname {\mathrm {rank}}(\varphi ,x)=(-\infty ,\ 0)$
. Since
$ \operatorname {\mathrm {rank}}(\varphi ,\ x)=(-\infty ,\ 0)$
, there is some quantifier-free
$\mathcal {L}_0$
-formula
$\varphi '(x,z_1,\dots , z_l)$
and
$\mathcal {L}_1$
-terms
$t_1,\dots ,t_l$
with variables in
$\{y_1,\dots , y_k\}$
such that
$$ \begin{align*}\varphi(x,y_1,\dots, y_k) = \varphi'(x,t_1,\dots,t_k).\end{align*} $$
Now by Proposition 4.4, there is some quantifier-free formula
$\phi (z_1,\dots ,z_k)$
such that
$$ \begin{align*}T_0\models \exists x \varphi'(x,z_1,\dots,z_l)\leftrightarrow \phi(x,z_1,\dots,z_l).\end{align*} $$
As
$T_2\supset T_0$
, in conclusion,
$$ \begin{align*} T_0\models \exists x \varphi(x,y_1,\dots,y_k) \leftrightarrow \exists x \varphi'(x,t_1,\dots,t_l)\leftrightarrow \phi(t_1,\dots,t_l) \end{align*} $$
and
$\phi (t_1,\dots ,t_l)$
is a quantifier-free
$\mathcal {L}_1$
-formula with variables from
$\{y_1,\dots , y_k\}$
. ⊣
Corollary 6.25. Every one-variable set definable in
$\mathcal {M}_2$
is definable in
$\mathcal {M}_0$
.
Proof. By Theorem 6.24, every definable set in
$\mathcal {M}_2$
is quantifier-free definable. By Lemma 6.23, every quantifier-free one-variable set definable in
$\mathcal {M}_2$
is equivalent to an x-corrected formula of rank
$\leq (-\infty ,\ 0)$
, which in turn is definable (with parameters) in
$\mathcal {M}_0$
. ⊣
We conclude by articulating the answers to Questions 1.15 and 1.16.
Theorem 6.26. There is a definably complete type complete structure without the pigeonhole property.
Proof. The failure of the pigeonhole principle in
$\mathcal {M}_2$
is witnessed by Z and
$f \upharpoonright Z$
. But by Corollary 6.25,
$\mathcal {M}_0$
and
$\mathcal {M}_2$
have the same definable sets in one free variable. In particular,
$\mathcal {M}_2$
is definably complete and type complete. ⊣
Theorem 6.27. There are two ordered structures in the same language
$\mathcal {M},\ \mathcal {N}$
on the same universe, admitting the same order and the same definable subsets with
$\mathcal {M}$
being pseudo-o-minimal and
$\mathcal {N}$
not.
In particular, the answer to Question 1.16
is negative and there is no axiomatization of pseudo-o-minimality by first-order conditions on one-variable formulae only. Furthermore, there is no axiomatization of pseudo-o-minimality by any second order theory in the language
$\mathcal {L}_{ \operatorname {\mathrm {Def}}}:=\{<, \operatorname {\mathrm {Def}}\}$
where
$ \operatorname {\mathrm {Def}}$
is interpreted as the definable one-variable subsets.
Proof.
$\mathcal {M}_0$
is pseudo-o-minimal and
$\mathcal {M}_2$
is not pseudo-o-minimal as the failure of the pigeonhole principle is witnessed by Z and
$f \upharpoonright Z$
. But
$\mathcal {M}_0\upharpoonright \{<\} = \mathcal {M}_2\upharpoonright \{<\}$
and by Corollary 6.25,
$\mathcal {M}_0$
and
$\mathcal {M}_2$
have the same definable sets in one free variable. We may now define
$\mathcal {N}$
to be
$\mathcal {M}_2$
and
$\mathcal {M}$
to be a trivial expansion of
$\mathcal {M}_0$
to
$\mathcal {L}_1$
(letting every function symbol be interpreted as the identity map and any relation symbol be interpreted as the
$\emptyset $
). ⊣
Acknowledgments
The author is grateful to Phillip Hieronymi for presenting the question which motivated this paper, as well as for the fruitful discussions. The author is grateful to Assaf Hasson for the fruitful discussions and the warm support along the way. The author thanks Itay Kaplan for his helpful comments on a preliminary version of this paper and for the discussion which helped clarify and strengthen the main result.
The work in this paper is part of the author’s Ph.D. studies at the Department of Mathematics, Ben-Gurion University of the Negev under the supervision of Assaf Hasson.
The author was partially supported by ISF Grant 181/16 and the Hillel Gauchman scholarship. The author was partially supported by Leverhulme Trust grant number RPG – 2017 – 179. The author is supported by National Science Center, Poland, grant 2016/22/E/ST1/00450.
