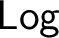1 Introduction
Universal algebra [Reference Bergman3, Reference Burris and Sankappanavar7] and abstract algebraic logic [Reference Czelakowski10, Reference Font15] are two disciplines that study, respectively, general algebraic structures and propositional logics. One of their main achievements is the development of two parallel taxonomies, one of varieties (a.k.a. equational classes) of algebras, and the other one of propositional logics.
More precisely, the Maltsev hierarchy of universal algebra is a classification of varieties in terms of syntactic principles (called Maltsev conditions) intended to describe the structure of the congruence lattices of algebras [Reference Hobby and McKenzie25, Reference Kearnes and Kiss29, Reference Pixley41, Reference Taylor49, Reference Wille50]. The first, and perhaps most celebrated, example of a Maltsev condition is the requirement that a variety
![]() $\mathsf {K}$
is congruence permutable, equivalent to the syntactic requirement of the existence of a minority term for
$\mathsf {K}$
is congruence permutable, equivalent to the syntactic requirement of the existence of a minority term for
![]() $\mathsf {K}$
[Reference Mal’cev31], i.e., a ternary term
$\mathsf {K}$
[Reference Mal’cev31], i.e., a ternary term
![]() $\varphi (x, y, z)$
such that
$\varphi (x, y, z)$
such that
Similarly, in abstract algebraic logic, the Leibniz hierarchy is a taxonomy of propositional logics in terms of rule schemata (here called Leibniz conditions) whose aim is to govern the interplay between lattices of deductive filters (a.k.a. theories) of logics and lattices of congruences of algebras [Reference Blok and Pigozzi4, Reference Blok and Pigozzi5, Reference Czelakowski10, Reference Czelakowski and Jansana12, Reference Moraschini36, Reference Raftery44]. One of the most fundamental examples of a Leibniz condition is the requirement that a logic
![]() $\vdash $
possesses a set
$\vdash $
possesses a set
![]() $\varDelta (x, y)$
of binary formulas satisfying the rules
$\varDelta (x, y)$
of binary formulas satisfying the rules
which generalize the behavior of most implication connectives. Notably, this requirement is equivalent to the property that the Leibniz operator of the logic
![]() $\vdash $
is monotone [Reference Blok and Pigozzi4].
$\vdash $
is monotone [Reference Blok and Pigozzi4].
From this point of view, it is natural to wonder whether the Maltsev and Leibniz hierarchies are two faces of the same coin (see for instance [Reference Moraschini37, Reference Raftery45]). In the series of papers constituted by the present one and [Reference Jansana and Moraschini27, Reference Jansana and Moraschini28], we show that this is indeed the case. More in detail, it turns out that the Maltsev hierarchy is a sort of finitary companion of the Leibniz hierarchy of the two-deductive systems [Reference Blok, Pigozzi, Romanowska and Smith6], i.e., substitution-invariant consequence relations between pairs of terms understood as equations. One of the main obstacles to establish this result is that, while there exists a precise definition of Maltsev condition, this is not the case for what concerns Leibniz conditions (which until now were recognized solely on empirical grounds).
To clarify the notion of a Leibniz condition, we adopt an order-theoretic perspective inspired by the theory of the Maltsev hierarchy, in which varieties are ordered by means of the existence of interpretations between them [Reference Neumann39, Reference Taylor47] (see also [Reference Lawvere30]). A variety
![]() $\mathsf {K}$
is said to be interpretable [Reference Taylor47] into another variety
$\mathsf {K}$
is said to be interpretable [Reference Taylor47] into another variety
![]() $\mathsf {V}$
, when
$\mathsf {V}$
, when
![]() $\mathsf {V}$
is term-equivalent to some variety
$\mathsf {V}$
is term-equivalent to some variety
![]() $\mathsf {V}^{\ast }$
whose reducts (in a smaller signature) belong to
$\mathsf {V}^{\ast }$
whose reducts (in a smaller signature) belong to
![]() $\mathsf {K}$
. When this is true we write
$\mathsf {K}$
. When this is true we write
![]() ${\mathsf {K}} \leqslant {\mathsf {V}}$
. For instance, the variety of distributive lattices is interpretable into the one of Boolean algebras, while the variety of sets (lacking non-trivial operations) is interpretable in any variety. It is clear that the interpretability relation
${\mathsf {K}} \leqslant {\mathsf {V}}$
. For instance, the variety of distributive lattices is interpretable into the one of Boolean algebras, while the variety of sets (lacking non-trivial operations) is interpretable in any variety. It is clear that the interpretability relation
![]() $\leqslant $
is a preorder on the collection of all varieties. More interestingly, the poset
$\leqslant $
is a preorder on the collection of all varieties. More interestingly, the poset
![]() $\mathsf {Var}$
associated with
$\mathsf {Var}$
associated with
![]() $\leqslant $
happens to be a lattice, sometimes called the lattice of interpretability types of varieties [Reference García and Taylor20, Reference Neumann39]. The study of the lattice
$\leqslant $
happens to be a lattice, sometimes called the lattice of interpretability types of varieties [Reference García and Taylor20, Reference Neumann39]. The study of the lattice
![]() $\mathsf {Var}$
allowed to identify the classes of models of Maltsev conditions with the filters of
$\mathsf {Var}$
allowed to identify the classes of models of Maltsev conditions with the filters of
![]() $\mathsf {Var}$
that are generated by finitely presentable varieties [Reference Baldwin and Berman2, Reference Grätzer21, Reference Neumann39, Reference Taylor47].
$\mathsf {Var}$
that are generated by finitely presentable varieties [Reference Baldwin and Berman2, Reference Grätzer21, Reference Neumann39, Reference Taylor47].
As we mentioned, we will export this order-theoretic perspective to the realm of propositional logics that, when ordered under a suitable notion of interpretability, form the poset of all logics
![]() $\mathsf {Log}$
. Accordingly, the aim of this paper is to describe the structure of the poset
$\mathsf {Log}$
. Accordingly, the aim of this paper is to describe the structure of the poset
![]() $\mathsf {Log}$
, which will be exploited to define and investigate Leibniz conditions in general in [Reference Jansana and Moraschini27, Reference Jansana and Moraschini28]. The main results of this paper can be summarized as follows. First we establish that
$\mathsf {Log}$
, which will be exploited to define and investigate Leibniz conditions in general in [Reference Jansana and Moraschini27, Reference Jansana and Moraschini28]. The main results of this paper can be summarized as follows. First we establish that
![]() $\mathsf {Log}$
is a set-complete meet-semilattice in which binary joins may fail to exist (Theorems 4.6 and 5.1). Then we show that the proper submeet-semilattice
$\mathsf {Log}$
is a set-complete meet-semilattice in which binary joins may fail to exist (Theorems 4.6 and 5.1). Then we show that the proper submeet-semilattice
![]() $\mathsf {Equiv}$
of
$\mathsf {Equiv}$
of
![]() $\mathsf {Log}$
, whose elements are equivalential logics, happens to have joins and to be a set-complete lattice (Theorem 6.5). We conclude by investigating the bottom and the top parts of
$\mathsf {Log}$
, whose elements are equivalential logics, happens to have joins and to be a set-complete lattice (Theorem 6.5). We conclude by investigating the bottom and the top parts of
![]() $\mathsf {Log}$
and by comparing the poset of all logics
$\mathsf {Log}$
and by comparing the poset of all logics
![]() $\mathsf {Log}$
with the lattice of interpretability types of varieties
$\mathsf {Log}$
with the lattice of interpretability types of varieties
![]() $\mathsf {Var}$
.
$\mathsf {Var}$
.
2 Propositional logics
For general informations on abstract algebraic logic, we refer the reader to [Reference Blok and Pigozzi4, Reference Blok and Pigozzi5, Reference Blok, Pigozzi, Romanowska and Smith6, Reference Czelakowski10, Reference Font15, Reference Font and Jansana16, Reference Font, Jansana and Pigozzi17, Reference Jansana and Moraschini26, Reference Wójcicki51]. We fix a proper class of (propositional) variables
![]() $\{ x_{\alpha } \colon \alpha \in \mathsf {OR} \}$
indexed in a one-to-one way by the ordinals. Given an algebraic language
$\{ x_{\alpha } \colon \alpha \in \mathsf {OR} \}$
indexed in a one-to-one way by the ordinals. Given an algebraic language
![]() $\mathscr {L}$
(from now on, simply a language), and an infinite cardinal
$\mathscr {L}$
(from now on, simply a language), and an infinite cardinal
![]() $\kappa $
, we denote by
$\kappa $
, we denote by
![]() $Fm_{\mathscr {L}}(\kappa )$
the set of formulas of
$Fm_{\mathscr {L}}(\kappa )$
the set of formulas of
![]() $\mathscr {L}$
with variables among
$\mathscr {L}$
with variables among
![]() $\{x_{\alpha } \colon \alpha < \kappa \}$
, and by
$\{x_{\alpha } \colon \alpha < \kappa \}$
, and by
![]() $\boldsymbol {Fm}_{\mathscr {L}}(\kappa )$
the corresponding algebra. When the language
$\boldsymbol {Fm}_{\mathscr {L}}(\kappa )$
the corresponding algebra. When the language
![]() $\mathscr {L}$
is clear from the context, we simply write
$\mathscr {L}$
is clear from the context, we simply write
![]() $Fm(\kappa )$
. For the sake of simplicity, we assume that languages have no nullary operation.Footnote
1
Note that the cardinality of
$Fm(\kappa )$
. For the sake of simplicity, we assume that languages have no nullary operation.Footnote
1
Note that the cardinality of
![]() $Fm_{\mathscr {L}}(\kappa )$
is the maximum of
$Fm_{\mathscr {L}}(\kappa )$
is the maximum of
![]() $\kappa $
and the cardinality of
$\kappa $
and the cardinality of
![]() $\mathscr {L}$
.
$\mathscr {L}$
.
A logic
![]() $\vdash $
is then a consequence relation on the set
$\vdash $
is then a consequence relation on the set
![]() $Fm_{\mathscr {L}}(\kappa )$
, for some language
$Fm_{\mathscr {L}}(\kappa )$
, for some language
![]() $\mathscr {L}$
and infinite cardinal
$\mathscr {L}$
and infinite cardinal
![]() $\kappa $
, that is substitution invariant in the sense that for every substitution
$\kappa $
, that is substitution invariant in the sense that for every substitution
![]() $\sigma $
on
$\sigma $
on
![]() $Fm_{\mathscr {L}}(\kappa )$
and
$Fm_{\mathscr {L}}(\kappa )$
and
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm_{\mathscr {L}}(\kappa )$
,
$\varGamma \cup \{ \varphi \} \subseteq Fm_{\mathscr {L}}(\kappa )$
,
Given a logic
![]() $\vdash $
, we denote by
$\vdash $
, we denote by
![]() $\mathscr {L}_{\vdash }$
(resp.
$\mathscr {L}_{\vdash }$
(resp.
![]() $\kappa _{\vdash }$
) the language (resp. the cardinality of the set of variables) in which
$\kappa _{\vdash }$
) the language (resp. the cardinality of the set of variables) in which
![]() $\vdash $
is formulated. Moreover, we write
$\vdash $
is formulated. Moreover, we write
![]() $Fm(\vdash )$
as a shorthand for
$Fm(\vdash )$
as a shorthand for
![]() $Fm_{\mathscr {L}_{\vdash }}(\kappa _{\vdash })$
. A theorem of
$Fm_{\mathscr {L}_{\vdash }}(\kappa _{\vdash })$
. A theorem of
![]() $\vdash $
is a formula
$\vdash $
is a formula
![]() $\varphi $
such that
$\varphi $
such that
![]() $\emptyset \vdash \varphi $
.
$\emptyset \vdash \varphi $
.
Given an algebra
![]() $\boldsymbol {A}$
and a logic
$\boldsymbol {A}$
and a logic
![]() $\vdash $
in the same language, a set
$\vdash $
in the same language, a set
![]() $F \subseteq A$
is said to be a deductive filter of
$F \subseteq A$
is said to be a deductive filter of
![]() $\vdash $
on
$\vdash $
on
![]() $\boldsymbol {A}$
when for every
$\boldsymbol {A}$
when for every
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
such that
$\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
such that
![]() $\varGamma \vdash \varphi $
and every homomorphism
$\varGamma \vdash \varphi $
and every homomorphism
![]() $h \colon \boldsymbol {Fm}(\vdash ) \to \boldsymbol {A}$
, if
$h \colon \boldsymbol {Fm}(\vdash ) \to \boldsymbol {A}$
, if
![]() $h[\varGamma ] \subseteq F$
, then
$h[\varGamma ] \subseteq F$
, then
![]() $h(\varphi ) \in F$
. The set of deductive filters of
$h(\varphi ) \in F$
. The set of deductive filters of
![]() $\vdash $
on
$\vdash $
on
![]() $\boldsymbol {A}$
is a closure system, whose closure operator is denoted by
$\boldsymbol {A}$
is a closure system, whose closure operator is denoted by
 $\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(\cdot ) \colon \mathcal {P}(A) \to \mathcal {P}(A)$
. Given
$\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(\cdot ) \colon \mathcal {P}(A) \to \mathcal {P}(A)$
. Given
![]() $X \cup \{ a \} \subseteq A$
, we write
$X \cup \{ a \} \subseteq A$
, we write
 $\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X, a)$
as a shorthand for
$\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X, a)$
as a shorthand for
 $\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X \cup \{ a\})$
. Given an algebra
$\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X \cup \{ a\})$
. Given an algebra
![]() $\boldsymbol {B}$
, we also write
$\boldsymbol {B}$
, we also write
![]() $\boldsymbol {B} \subseteq \boldsymbol {A}$
when
$\boldsymbol {B} \subseteq \boldsymbol {A}$
when
![]() $\boldsymbol {B}$
is a subalgebra of
$\boldsymbol {B}$
is a subalgebra of
![]() $\boldsymbol {A}$
, and
$\boldsymbol {A}$
, and
![]() $\boldsymbol {B} \leqslant \boldsymbol {A}$
when
$\boldsymbol {B} \leqslant \boldsymbol {A}$
when
![]() $\boldsymbol {B}$
is isomorphic to a subalgebra of
$\boldsymbol {B}$
is isomorphic to a subalgebra of
![]() $\boldsymbol {A}$
.
$\boldsymbol {A}$
.
Lemma 2.1. Let
![]() $\vdash $
be a logic formulated on
$\vdash $
be a logic formulated on
![]() $Fm(\kappa )$
and
$Fm(\kappa )$
and
![]() $\boldsymbol {A}$
an algebra.
$\boldsymbol {A}$
an algebra.
-
(i) If
 $\boldsymbol {B} \subseteq \boldsymbol {A}$
and
$\boldsymbol {B} \subseteq \boldsymbol {A}$
and
 $X \subseteq A$
, then
$X \subseteq A$
, then
 $\textrm {Fg}_{\vdash }^{\boldsymbol {B}}(X \cap B) \subseteq \textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X)$
.
$\textrm {Fg}_{\vdash }^{\boldsymbol {B}}(X \cap B) \subseteq \textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X)$
. -
(ii) Let
 $\lambda \geqslant \vert Fm(\kappa ) \vert $
and
$\lambda \geqslant \vert Fm(\kappa ) \vert $
and
 $X \cup Z \cup \{ a \} \subseteq A$
be such that
$X \cup Z \cup \{ a \} \subseteq A$
be such that
 $\vert Z \vert \leqslant \lambda $
. If
$\vert Z \vert \leqslant \lambda $
. If
 $a \in \textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X)$
, then there is an algebra
$a \in \textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X)$
, then there is an algebra
 $\boldsymbol {B} \subseteq \boldsymbol {A}$
such that
$\boldsymbol {B} \subseteq \boldsymbol {A}$
such that
 $\vert B \vert \leqslant \lambda $
,
$\vert B \vert \leqslant \lambda $
,
 $Z \subseteq B$
, and
$Z \subseteq B$
, and
 $a \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(X \cap B)$
.
$a \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(X \cap B)$
.
Proof. Condition (i) is straightforward. Hence we detail only the proof of (ii).
It is well-known that
 $$ \begin{align*} \textrm{Fg}_{\vdash}^{\boldsymbol{A}}(X) = \bigcup_{\alpha < \lambda^{+}}V_{\alpha}, \end{align*} $$
$$ \begin{align*} \textrm{Fg}_{\vdash}^{\boldsymbol{A}}(X) = \bigcup_{\alpha < \lambda^{+}}V_{\alpha}, \end{align*} $$
where the various
![]() $V_{\alpha }$
are defined in the following way. First we set
$V_{\alpha }$
are defined in the following way. First we set
![]() $V_{0} := X$
, and at limit ordinals we take unions. At successor ordinals we proceed as follows. If
$V_{0} := X$
, and at limit ordinals we take unions. At successor ordinals we proceed as follows. If
![]() $\alpha < \lambda $
, then
$\alpha < \lambda $
, then
 $$ \begin{align*} V_{\alpha+1} := V_{\alpha} \cup \{ & c \in C \colon c = f(\varphi)\text{ for some homomorphism }f \colon \boldsymbol{Fm}(\kappa) \to \boldsymbol{A} \\ &\text{and }\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa) \text{ such that }\varGamma \vdash \varphi \text{ and } v[\varGamma] \subseteq V_{\alpha}\}. \end{align*} $$
$$ \begin{align*} V_{\alpha+1} := V_{\alpha} \cup \{ & c \in C \colon c = f(\varphi)\text{ for some homomorphism }f \colon \boldsymbol{Fm}(\kappa) \to \boldsymbol{A} \\ &\text{and }\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa) \text{ such that }\varGamma \vdash \varphi \text{ and } v[\varGamma] \subseteq V_{\alpha}\}. \end{align*} $$
We claim that for every
![]() $\alpha < \lambda ^{+}$
and
$\alpha < \lambda ^{+}$
and
![]() $b \in V_{\alpha }$
, there is an algebra
$b \in V_{\alpha }$
, there is an algebra
![]() $\boldsymbol {B}[b, \alpha ] \leqslant \boldsymbol {A}$
such that
$\boldsymbol {B}[b, \alpha ] \leqslant \boldsymbol {A}$
such that
![]() $\vert B[b, \alpha ] \vert \leqslant \lambda $
,
$\vert B[b, \alpha ] \vert \leqslant \lambda $
,
![]() $Z \subseteq B[b, \alpha ]$
, and
$Z \subseteq B[b, \alpha ]$
, and
 $b \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
. To prove this, we reason by induction on
$b \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
. To prove this, we reason by induction on
![]() $\alpha \leqslant \lambda ^{+}$
. In the case where
$\alpha \leqslant \lambda ^{+}$
. In the case where
![]() $\alpha = 0$
we take the subalgebra of
$\alpha = 0$
we take the subalgebra of
![]() $\boldsymbol {A}$
generated by
$\boldsymbol {A}$
generated by
![]() $X \cup Z$
. If
$X \cup Z$
. If
![]() $\alpha $
is a limit ordinal and
$\alpha $
is a limit ordinal and
![]() $b \in V_{\alpha }$
, then
$b \in V_{\alpha }$
, then
![]() $b \in V_{\beta }$
for some
$b \in V_{\beta }$
for some
![]() $\beta < \alpha $
. Therefore, with an application of the inductive hypothesis, we are done.
$\beta < \alpha $
. Therefore, with an application of the inductive hypothesis, we are done.
Then we consider the case where
![]() $\alpha = \beta +1$
. Since
$\alpha = \beta +1$
. Since
![]() $b \in V_{\beta + 1}$
, there are a homomorphism
$b \in V_{\beta + 1}$
, there are a homomorphism
![]() $f \colon \boldsymbol {Fm}(\kappa ) \to \boldsymbol {A}$
and
$f \colon \boldsymbol {Fm}(\kappa ) \to \boldsymbol {A}$
and
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa )$
such that
$\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa )$
such that
![]() $\varGamma \vdash \varphi $
,
$\varGamma \vdash \varphi $
,
![]() $b = f(\varphi )$
, and
$b = f(\varphi )$
, and
![]() $v[\varGamma ] \subseteq V_{\beta }$
. Now, for every
$v[\varGamma ] \subseteq V_{\beta }$
. Now, for every
![]() $\gamma \in \varGamma $
, we consider the algebra
$\gamma \in \varGamma $
, we consider the algebra
![]() $\boldsymbol {B}[ \kern 0.4pt f(\gamma ), \beta ]$
given by the inductive hypothesis. Let
$\boldsymbol {B}[ \kern 0.4pt f(\gamma ), \beta ]$
given by the inductive hypothesis. Let
![]() $\boldsymbol {B}[b, \alpha ]$
be the subalgebra of
$\boldsymbol {B}[b, \alpha ]$
be the subalgebra of
![]() $\boldsymbol {A}$
generated by
$\boldsymbol {A}$
generated by
 $$ \begin{align*} Z \cup f[Fm(\kappa)] \cup \bigcup_{\gamma \in \varGamma} B[\kern 0.4pt f(\gamma), \beta ]. \end{align*} $$
$$ \begin{align*} Z \cup f[Fm(\kappa)] \cup \bigcup_{\gamma \in \varGamma} B[\kern 0.4pt f(\gamma), \beta ]. \end{align*} $$
The fact that
![]() $\vert Z \vert + \vert Fm(\kappa ) \vert \leqslant \lambda $
, and that
$\vert Z \vert + \vert Fm(\kappa ) \vert \leqslant \lambda $
, and that
![]() $\vert B[\kern 0.4pt f(\gamma ), \beta ] \vert \leqslant \lambda $
for every
$\vert B[\kern 0.4pt f(\gamma ), \beta ] \vert \leqslant \lambda $
for every
![]() $\gamma \in \varGamma $
ensures that
$\gamma \in \varGamma $
ensures that
![]() $\vert B[b, \alpha ] \vert \leqslant \lambda $
.
$\vert B[b, \alpha ] \vert \leqslant \lambda $
.
It only remains to show that
 $b \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
. To this end, consider
$b \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
. To this end, consider
![]() $\gamma \in \varGamma $
. By the inductive hypothesis and condition (i) we obtain
$\gamma \in \varGamma $
. By the inductive hypothesis and condition (i) we obtain
 $$ \begin{align} f(\gamma) \in \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\kern 0.4pt f(\gamma), \beta]}(X \cap B[\kern 0.4pt f(\gamma), \beta]) \subseteq \textrm{Fg}_{\vdash}^{\boldsymbol{B}[b, \alpha]}(X \cap B[b, \alpha]). \end{align} $$
$$ \begin{align} f(\gamma) \in \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\kern 0.4pt f(\gamma), \beta]}(X \cap B[\kern 0.4pt f(\gamma), \beta]) \subseteq \textrm{Fg}_{\vdash}^{\boldsymbol{B}[b, \alpha]}(X \cap B[b, \alpha]). \end{align} $$
Since
![]() $f[Fm(\kappa )] \subseteq B[b, \alpha ]$
, the homomorphism
$f[Fm(\kappa )] \subseteq B[b, \alpha ]$
, the homomorphism
![]() $f \colon \boldsymbol {Fm}(\kappa ) \to \boldsymbol {B}[b, \alpha ]$
is well defined. Together with the fact that
$f \colon \boldsymbol {Fm}(\kappa ) \to \boldsymbol {B}[b, \alpha ]$
is well defined. Together with the fact that
![]() $\varGamma \vdash \varphi $
and that
$\varGamma \vdash \varphi $
and that
 $f[\varGamma ] \subseteq \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
by (1), this implies that
$f[\varGamma ] \subseteq \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
by (1), this implies that
 $b = f(\varphi ) \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
, as desired. This establishes the claim.
$b = f(\varphi ) \in \textrm {Fg}_{\vdash }^{\boldsymbol {B}[b, \alpha ]}(X \cap B[b, \alpha ])$
, as desired. This establishes the claim.
Together with the fact that
 $\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X) = \bigcup _{\alpha < \lambda ^{+}}V_{\alpha }$
, the claim concludes the proof.⊣
$\textrm {Fg}_{\vdash }^{\boldsymbol {A}}(X) = \bigcup _{\alpha < \lambda ^{+}}V_{\alpha }$
, the claim concludes the proof.⊣
Given an algebra
![]() $\boldsymbol {A}$
, we denote by
$\boldsymbol {A}$
, we denote by
![]() $\textrm {Con} \boldsymbol {A}$
its congruence lattice. Moreover, a congruence
$\textrm {Con} \boldsymbol {A}$
its congruence lattice. Moreover, a congruence
![]() $\theta \in \textrm {Con} \boldsymbol {A}$
is compatible with a set
$\theta \in \textrm {Con} \boldsymbol {A}$
is compatible with a set
![]() $F \subseteq A$
when for every
$F \subseteq A$
when for every
![]() $a, b\in A$
,
$a, b\in A$
,
The Leibniz congruence
![]() $\boldsymbol {\varOmega }^{\boldsymbol {A}}F$
of F is the largest congruence on
$\boldsymbol {\varOmega }^{\boldsymbol {A}}F$
of F is the largest congruence on
![]() $\boldsymbol {A}$
compatible with F. Similarly, given a logic
$\boldsymbol {A}$
compatible with F. Similarly, given a logic
![]() $\vdash $
(in the same language as
$\vdash $
(in the same language as
![]() $\boldsymbol {A}$
), we set
$\boldsymbol {A}$
), we set

The relation

is often called the Suszko congruence of F. The congruences
![]() $\boldsymbol {\varOmega }^{\boldsymbol {A}} F$
and
$\boldsymbol {\varOmega }^{\boldsymbol {A}} F$
and

can de described as follows [Reference Font15, Theorems 4.23 and 5.32]:
Proposition 2.2. Let
![]() $\vdash $
be a logic,
$\vdash $
be a logic,
![]() $\boldsymbol {A}$
an algebra,
$\boldsymbol {A}$
an algebra,
![]() $F \subseteq A$
, and
$F \subseteq A$
, and
![]() $a, b\in A$
.
$a, b\in A$
.
-
(i)
 $\langle a, b \rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F\Longleftrightarrow (p(a)\in F\ \text { if and only if }\ p(b)\in F)$
, for every unary polynomial function p of
$\langle a, b \rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F\Longleftrightarrow (p(a)\in F\ \text { if and only if }\ p(b)\in F)$
, for every unary polynomial function p of
 $\boldsymbol {A}$
.
$\boldsymbol {A}$
. -
(ii)
 , for every unary polynomial function p of
, for every unary polynomial function p of
 $\boldsymbol {A}$
.
$\boldsymbol {A}$
.
A matrix is a pair
![]() $\langle \boldsymbol {A}, F\rangle $
such that
$\langle \boldsymbol {A}, F\rangle $
such that
![]() $\boldsymbol {A}$
is an algebra and
$\boldsymbol {A}$
is an algebra and
![]() $F \subseteq A$
. A matrix
$F \subseteq A$
. A matrix
![]() $\langle \boldsymbol {A}, F \rangle $
is said to be reduced when
$\langle \boldsymbol {A}, F \rangle $
is said to be reduced when
![]() $\boldsymbol {\varOmega }^{\boldsymbol {A}}F$
is the identity relation. Moreover, we set
$\boldsymbol {\varOmega }^{\boldsymbol {A}}F$
is the identity relation. Moreover, we set
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle^{\ast} := \langle \boldsymbol{A} / \boldsymbol{\varOmega}^{\boldsymbol{A}}F, F/ \boldsymbol{\varOmega}^{\boldsymbol{A}}F\rangle. \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle^{\ast} := \langle \boldsymbol{A} / \boldsymbol{\varOmega}^{\boldsymbol{A}}F, F/ \boldsymbol{\varOmega}^{\boldsymbol{A}}F\rangle. \end{align*} $$
Similarly, given a class of matrices
![]() $\mathsf {K}$
, we set
$\mathsf {K}$
, we set
where
![]() $\mathbb {I}$
is the class operator of closing under isomorphic copies. A matrix
$\mathbb {I}$
is the class operator of closing under isomorphic copies. A matrix
![]() $\langle \boldsymbol {A}, F \rangle $
is said to be trivial when
$\langle \boldsymbol {A}, F \rangle $
is said to be trivial when
![]() $\boldsymbol {A}$
is the trivial algebra (which we denote by
$\boldsymbol {A}$
is the trivial algebra (which we denote by
![]() ${\textbf {1}}$
) and
${\textbf {1}}$
) and
![]() $F = \{ 1 \}$
.
$F = \{ 1 \}$
.
The logic in
![]() $\kappa $
variables induced by a class of similar matrices
$\kappa $
variables induced by a class of similar matrices
![]() $\mathsf {K}$
is the consequence relation
$\mathsf {K}$
is the consequence relation
![]() $\vdash $
on
$\vdash $
on
![]() $Fm(\kappa )$
defined for every
$Fm(\kappa )$
defined for every
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa )$
as follows:
$\varGamma \cup \{ \varphi \} \subseteq Fm(\kappa )$
as follows:
 $$ \begin{align*} \varGamma \vdash \varphi \Longleftrightarrow&\text{ for every}\ \langle \boldsymbol{A}, F \rangle \in \mathsf{K}\ \text{and homomorphism }h \colon \boldsymbol{Fm}(\kappa) \to \boldsymbol{A}, \\ &\text{ if }h[\varGamma] \subseteq F\text{, then }h(\varphi)\in F. \end{align*} $$
$$ \begin{align*} \varGamma \vdash \varphi \Longleftrightarrow&\text{ for every}\ \langle \boldsymbol{A}, F \rangle \in \mathsf{K}\ \text{and homomorphism }h \colon \boldsymbol{Fm}(\kappa) \to \boldsymbol{A}, \\ &\text{ if }h[\varGamma] \subseteq F\text{, then }h(\varphi)\in F. \end{align*} $$
A matrix
![]() $\langle \boldsymbol {A}, F \rangle $
is said to be a model of a logic
$\langle \boldsymbol {A}, F \rangle $
is said to be a model of a logic
![]() $\vdash $
(in the same language as
$\vdash $
(in the same language as
![]() $\boldsymbol {A}$
) when F is a deductive filter of
$\boldsymbol {A}$
) when F is a deductive filter of
![]() $\vdash $
on
$\vdash $
on
![]() $\boldsymbol {A}$
. We set
$\boldsymbol {A}$
. We set

Observe that
![]() $\vdash $
is the logic induced both by
$\vdash $
is the logic induced both by
![]() $\mathsf {Mod}(\vdash )$
and
$\mathsf {Mod}(\vdash )$
and
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
[Reference Font15, Theorem 4.16].
$\mathsf {Mod}^{\equiv }(\vdash )$
[Reference Font15, Theorem 4.16].
We denote by
![]() $\mathbb {S}, \mathbb {P}, \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}$
and
$\mathbb {S}, \mathbb {P}, \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}$
and
 $\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}$
the class operators for substructures, direct products, subdirect products, and reduced products over
$\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}$
the class operators for substructures, direct products, subdirect products, and reduced products over
![]() $\kappa $
-complete filters. We assume that their application produces classes closed under isomorphic copies. Moreover, we assume that the product-style operators, when applied to empty sets of indexes, produce trivial matrices. We also consider the following class operator: given a class of matrices
$\kappa $
-complete filters. We assume that their application produces classes closed under isomorphic copies. Moreover, we assume that the product-style operators, when applied to empty sets of indexes, produce trivial matrices. We also consider the following class operator: given a class of matrices
![]() $\mathsf {K}$
and an infinite cardinal
$\mathsf {K}$
and an infinite cardinal
![]() $\kappa $
, we define
$\kappa $
, we define
Lemma 2.3. If
![]() $\vdash $
is a logic, then
$\vdash $
is a logic, then
![]() $\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {R}(\mathsf {Mod}(\vdash ))$
.
$\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {R}(\mathsf {Mod}(\vdash ))$
.
Proof. See [Reference Czelakowski11, Theorem 5.3].⊣
The first equality of the following result is taken from [Reference Dellunde and Jansana14, Reference Přenosil42], and generalizes a previous result in [Reference Czelakowski8].
Theorem 2.4. Let
![]() $\mathsf {K}$
be a class of matrices. If
$\mathsf {K}$
be a class of matrices. If
![]() $\vdash $
is the logic induced by
$\vdash $
is the logic induced by
![]() $\mathsf {K}$
on
$\mathsf {K}$
on
![]() $Fm(\kappa )$
and
$Fm(\kappa )$
and
![]() $\vert Fm(\kappa ) \vert \leqslant \kappa $
, then
$\vert Fm(\kappa ) \vert \leqslant \kappa $
, then
 $\mathbb {R}(\mathsf {Mod}(\vdash )) = \mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K}) = \mathbb {R}\mathbb {U}_{\kappa }\mathbb {S}\mathbb {P}(\mathsf {K})$
.
$\mathbb {R}(\mathsf {Mod}(\vdash )) = \mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K}) = \mathbb {R}\mathbb {U}_{\kappa }\mathbb {S}\mathbb {P}(\mathsf {K})$
.
Proof. Under the assumption that the cardinality of the language of a class of matrices
![]() $\mathsf {K}$
is
$\mathsf {K}$
is
![]() $\leqslant \kappa $
, the proof of the equality
$\leqslant \kappa $
, the proof of the equality
 $\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K}) = \mathbb {U}_{\kappa }\mathbb {S}\mathbb {P}(\mathsf {K})$
is routinary.⊣
$\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K}) = \mathbb {U}_{\kappa }\mathbb {S}\mathbb {P}(\mathsf {K})$
is routinary.⊣
Corollary 2.5. Let
![]() $\mathsf {K}$
be a class of matrices. If
$\mathsf {K}$
be a class of matrices. If
![]() $\vdash $
is the logic induced by
$\vdash $
is the logic induced by
![]() $\mathsf {K}$
on
$\mathsf {K}$
on
![]() $Fm(\kappa )$
and
$Fm(\kappa )$
and
![]() $\vert Fm(\kappa ) \vert \leqslant \kappa $
, then
$\vert Fm(\kappa ) \vert \leqslant \kappa $
, then
 $\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K})$
.
$\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {K})$
.
Corollary 2.6. Let
![]() $\vdash $
be the logic induced by a class of matrices
$\vdash $
be the logic induced by a class of matrices
![]() $\mathsf {K}$
on
$\mathsf {K}$
on
![]() $Fm(\kappa )$
. Then the algebraic reducts of the matrices in
$Fm(\kappa )$
. Then the algebraic reducts of the matrices in
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
belong to the variety generated by the algebraic reducts of the matrices in
$\mathsf {Mod}^{\equiv }(\vdash )$
belong to the variety generated by the algebraic reducts of the matrices in
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
A logic
![]() $\vdash $
is said to be equivalential [Reference Blok and Pigozzi4, Reference Czelakowski9] if there is a non-emptyFootnote
2
set of formulas
$\vdash $
is said to be equivalential [Reference Blok and Pigozzi4, Reference Czelakowski9] if there is a non-emptyFootnote
2
set of formulas
![]() $\varDelta (x, y)$
such that for every
$\varDelta (x, y)$
such that for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash )$
and
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash )$
and
![]() $a, b \in A$
,
$a, b \in A$
,
 $$ \begin{align*} \langle a, b \rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}}F \Longleftrightarrow \varDelta^{\boldsymbol{A}}(a, b) \subseteq F. \end{align*} $$
$$ \begin{align*} \langle a, b \rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}}F \Longleftrightarrow \varDelta^{\boldsymbol{A}}(a, b) \subseteq F. \end{align*} $$
In this case we say that
![]() $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
![]() $\vdash $
. Examples of equivalential logics comprise all the so-called algebraizable logics [Reference Blok and Pigozzi5], as well as a wide range of non-algebraizable ones such as the local consequence of the normal modal system
$\vdash $
. Examples of equivalential logics comprise all the so-called algebraizable logics [Reference Blok and Pigozzi5], as well as a wide range of non-algebraizable ones such as the local consequence of the normal modal system
![]() ${\textbf {K}}$
[Reference Malinowski32]. For further information about equivalential logics, see [Reference Czelakowski10, Reference Font15, Reference Herrmann22–Reference Herrmann24].
${\textbf {K}}$
[Reference Malinowski32]. For further information about equivalential logics, see [Reference Czelakowski10, Reference Font15, Reference Herrmann22–Reference Herrmann24].
Theorem 2.7. A logic
![]() $\vdash $
is equivalential if and only if there is a non-empty set of formulas
$\vdash $
is equivalential if and only if there is a non-empty set of formulas
![]() $\varDelta (x, y)$
such that for every n-ary connective
$\varDelta (x, y)$
such that for every n-ary connective
![]() $\ast $
,
$\ast $
,
 $$ \begin{align*} \emptyset \vdash &\varDelta(x, x), \qquad x, \varDelta(x, y) \vdash y,\\ \bigcup_{1 \leqslant i \leqslant n}\varDelta(x_{i}, y_{i}) &\vdash \varDelta(\ast(x_{1}, \dots, x_{n}), \ast(y_{1}, \dots, y_{n})). \end{align*} $$
$$ \begin{align*} \emptyset \vdash &\varDelta(x, x), \qquad x, \varDelta(x, y) \vdash y,\\ \bigcup_{1 \leqslant i \leqslant n}\varDelta(x_{i}, y_{i}) &\vdash \varDelta(\ast(x_{1}, \dots, x_{n}), \ast(y_{1}, \dots, y_{n})). \end{align*} $$
In this case,
![]() $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
![]() $\vdash $
and
$\vdash $
and
![]() $\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {R}(\mathsf {Mod}(\vdash ))$
.
$\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {R}(\mathsf {Mod}(\vdash ))$
.
Proof. See [Reference Font15, Theorems 6.17 and 6.60].⊣
For equivalential logics we have the following improvement of Corollary 2.5:
Lemma 2.8. Let
![]() $\vdash $
be the logic induced by a class of reduced matrices
$\vdash $
be the logic induced by a class of reduced matrices
![]() $\mathsf {K}$
on
$\mathsf {K}$
on
![]() $Fm(\kappa )$
. If
$Fm(\kappa )$
. If
![]() $\vdash $
is equivalential, then
$\vdash $
is equivalential, then
![]() $\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {U}_{\kappa }\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {S}(\mathsf {K})$
.
$\mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {U}_{\kappa }\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {S}(\mathsf {K})$
.
Proof. This result is essentially [Reference Raftery46, Theorem 5.6].⊣
A tuple of elements of a set A is a finite sequence of elements of A.
Lemma 2.9. If
![]() $\vdash $
is a logic on
$\vdash $
is a logic on
![]() $Fm(\kappa )$
and
$Fm(\kappa )$
and
![]() $\lambda \geqslant \vert Fm(\kappa ) \vert $
, then
$\lambda \geqslant \vert Fm(\kappa ) \vert $
, then
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
is closed under
$\mathsf {Mod}^{\equiv }(\vdash )$
is closed under
![]() $\mathbb {U}_{\lambda }$
.
$\mathbb {U}_{\lambda }$
.
Proof. Suppose, with a view to contradiction, that there is a matrix
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\lambda }(\mathsf {Mod}^{\equiv }(\vdash ))$
such that
$\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\lambda }(\mathsf {Mod}^{\equiv }(\vdash ))$
such that
![]() $\langle \boldsymbol {A}, F \rangle \notin \mathsf {Mod}^{\equiv }(\vdash )$
. First observe that
$\langle \boldsymbol {A}, F \rangle \notin \mathsf {Mod}^{\equiv }(\vdash )$
. First observe that
![]() $\langle \boldsymbol {A}, F \rangle $
is a model of
$\langle \boldsymbol {A}, F \rangle $
is a model of
![]() $\vdash $
, since
$\vdash $
, since
![]() $\lambda \geqslant \kappa $
and
$\lambda \geqslant \kappa $
and
![]() $\vdash $
is defined on
$\vdash $
is defined on
![]() $Fm(\kappa )$
. Then the congruence
$Fm(\kappa )$
. Then the congruence
 is not the identity relation. Together with Proposition 2.2(ii), this implies that there are two different
is not the identity relation. Together with Proposition 2.2(ii), this implies that there are two different
![]() $a, b \in A$
such that for every
$a, b \in A$
such that for every
![]() $\varphi (x, \vec {y}) \in Fm(\omega )$
, and every tuple
$\varphi (x, \vec {y}) \in Fm(\omega )$
, and every tuple
![]() $\vec {c} \in A$
,
$\vec {c} \in A$
,
 $$ \begin{align} \textrm{Fg}_{\vdash}^{\boldsymbol{A}}(F, \varphi(a, \vec{c})) = \textrm{Fg}_{\vdash}(F, \varphi^{\boldsymbol{A}}(b, \vec{c})). \end{align} $$
$$ \begin{align} \textrm{Fg}_{\vdash}^{\boldsymbol{A}}(F, \varphi(a, \vec{c})) = \textrm{Fg}_{\vdash}(F, \varphi^{\boldsymbol{A}}(b, \vec{c})). \end{align} $$
We define a chain (under the subalgebra relation)
![]() $\langle \boldsymbol {B}_{\alpha } \colon \alpha < \lambda \rangle $
of subalgebras of
$\langle \boldsymbol {B}_{\alpha } \colon \alpha < \lambda \rangle $
of subalgebras of
![]() $\boldsymbol {A}$
as follows. First we let
$\boldsymbol {A}$
as follows. First we let
![]() $\boldsymbol {B}_{0}$
be the subalgebra of
$\boldsymbol {B}_{0}$
be the subalgebra of
![]() $\boldsymbol {A}$
generated by
$\boldsymbol {A}$
generated by
![]() $\{ a, b \}$
. At limit ordinals we take unions. Now, suppose that
$\{ a, b \}$
. At limit ordinals we take unions. Now, suppose that
![]() $\boldsymbol {B}_{\alpha }$
has already been defined and that
$\boldsymbol {B}_{\alpha }$
has already been defined and that
![]() $\alpha < \lambda $
. Consider a formula
$\alpha < \lambda $
. Consider a formula
![]() $\varphi (x, \vec {y}) \in Fm(\omega )$
and a tuple
$\varphi (x, \vec {y}) \in Fm(\omega )$
and a tuple
![]() $\vec {c} \in B_{\alpha }$
. By Lemma 2.1 and (2) there is a subalgebra
$\vec {c} \in B_{\alpha }$
. By Lemma 2.1 and (2) there is a subalgebra
![]() $\boldsymbol {B}[\varphi , \vec {c}, \alpha ] \leqslant \boldsymbol {A}$
such that
$\boldsymbol {B}[\varphi , \vec {c}, \alpha ] \leqslant \boldsymbol {A}$
such that
![]() $\vert B[\varphi , \vec {c}, \alpha ] \vert \leqslant \lambda $
,
$\vert B[\varphi , \vec {c}, \alpha ] \vert \leqslant \lambda $
,
![]() $a, b, \vec {c} \in B[\varphi , \vec {c}]$
and
$a, b, \vec {c} \in B[\varphi , \vec {c}]$
and
 $$ \begin{align} \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(a, \vec{c})) = \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c})). \end{align} $$
$$ \begin{align} \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(a, \vec{c})) = \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c})). \end{align} $$
Then we let
![]() $\boldsymbol {B}_{\alpha +1}^{\ast }$
be the subalgebra of
$\boldsymbol {B}_{\alpha +1}^{\ast }$
be the subalgebra of
![]() $\boldsymbol {A}$
generated by the union of the various
$\boldsymbol {A}$
generated by the union of the various
![]() $B[\varphi , \vec {c}, \alpha ]$
, and
$B[\varphi , \vec {c}, \alpha ]$
, and
![]() $\boldsymbol {B}_{\alpha }$
the subalgebra of
$\boldsymbol {B}_{\alpha }$
the subalgebra of
![]() $\boldsymbol {A}$
generated by
$\boldsymbol {A}$
generated by
![]() $B_{\alpha } \cup B_{\alpha +1}^{\ast }$
.
$B_{\alpha } \cup B_{\alpha +1}^{\ast }$
.
Now we set
 $$ \begin{align*} \langle \boldsymbol{B}, G \rangle := \langle \bigcup_{\alpha < \lambda} \boldsymbol{B}_{\alpha}, F \cap \bigcup_{\alpha < \lambda}B_{\alpha} \rangle. \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{B}, G \rangle := \langle \bigcup_{\alpha < \lambda} \boldsymbol{B}_{\alpha}, F \cap \bigcup_{\alpha < \lambda}B_{\alpha} \rangle. \end{align*} $$
Bearing in mind that
![]() $\vert B[\varphi , \vec {c}, \alpha ] \vert + \vert Fm(\kappa ) \vert \leqslant \lambda $
, an easy induction shows that
$\vert B[\varphi , \vec {c}, \alpha ] \vert + \vert Fm(\kappa ) \vert \leqslant \lambda $
, an easy induction shows that
![]() $\vert B_{\alpha } \vert \leqslant \lambda $
for every
$\vert B_{\alpha } \vert \leqslant \lambda $
for every
![]() $\alpha < \lambda $
. As a consequence, we obtain that
$\alpha < \lambda $
. As a consequence, we obtain that
![]() $\vert B \vert \leqslant \lambda $
and, therefore, that
$\vert B \vert \leqslant \lambda $
and, therefore, that
![]() $\boldsymbol {B}$
is
$\boldsymbol {B}$
is
![]() $\lambda $
-generated. Together with
$\lambda $
-generated. Together with
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\lambda }(\mathsf {Mod}^{\equiv }(\vdash ))$
, this implies that
$\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\lambda }(\mathsf {Mod}^{\equiv }(\vdash ))$
, this implies that
![]() $\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
.
$\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
.
Now, the fact that
![]() $\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
implies that
$\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
implies that
 is the identity relation and, therefore, that
is the identity relation and, therefore, that
 . By Lemma 2.2(ii) we can assume without loss of generality that there are a formula
. By Lemma 2.2(ii) we can assume without loss of generality that there are a formula
![]() $\varphi (x, \vec {y}) \in Fm(\omega )$
and a tuple
$\varphi (x, \vec {y}) \in Fm(\omega )$
and a tuple
![]() $\vec {c} \in B$
such that
$\vec {c} \in B$
such that
 $\varphi (a, \vec {c}) \notin \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(G, \varphi (b, \vec {c}))$
. Observe that there is
$\varphi (a, \vec {c}) \notin \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(G, \varphi (b, \vec {c}))$
. Observe that there is
![]() $\alpha < \lambda $
such that
$\alpha < \lambda $
such that
![]() $\vec {c} \in B_{\alpha }$
. By (3) and Lemma 2.1(i) we obtain that
$\vec {c} \in B_{\alpha }$
. By (3) and Lemma 2.1(i) we obtain that
 $$ \begin{align*} \varphi(a, \vec{c}) &\in \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c}))\\ &= \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(G \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c}))\\ & \subseteq \textrm{Fg}_{\vdash}^{\boldsymbol{B}}(G, \varphi(b, \vec{c})). \end{align*} $$
$$ \begin{align*} \varphi(a, \vec{c}) &\in \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(F \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c}))\\ &= \textrm{Fg}_{\vdash}^{\boldsymbol{B}[\varphi, \vec{c}, \alpha]}(G \cap B[\varphi, \vec{c}, \alpha], \varphi(b, \vec{c}))\\ & \subseteq \textrm{Fg}_{\vdash}^{\boldsymbol{B}}(G, \varphi(b, \vec{c})). \end{align*} $$
But this contradicts the fact that
 $\varphi (a, \vec {c}) \notin \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(G, \varphi (b, \vec {c}))$
. Hence we reached a contradiction, as desired.⊣
$\varphi (a, \vec {c}) \notin \textrm {Fg}_{\vdash }^{\boldsymbol {B}}(G, \varphi (b, \vec {c}))$
. Hence we reached a contradiction, as desired.⊣
3 Interpretations
Definition 3.1. Let
![]() $\mathscr {L}$
and
$\mathscr {L}$
and
![]() $\mathscr {L}'$
be two languages. A translation
$\mathscr {L}'$
be two languages. A translation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathscr {L}$
into
$\mathscr {L}$
into
![]() $\mathscr {L}'$
is a map that associates an n-ary formula
$\mathscr {L}'$
is a map that associates an n-ary formula
![]() $\boldsymbol {\tau }(\ast )$
of
$\boldsymbol {\tau }(\ast )$
of
![]() $\mathscr {L}'$
in variables
$\mathscr {L}'$
in variables
![]() $x_{1}, \dots , x_{n}$
to every n-ary function symbol
$x_{1}, \dots , x_{n}$
to every n-ary function symbol
![]() $\ast $
of
$\ast $
of
![]() $\mathscr {L}$
.
$\mathscr {L}$
.
Let
![]() $\boldsymbol {\tau }$
be a translation of
$\boldsymbol {\tau }$
be a translation of
![]() $\mathscr {L}$
into
$\mathscr {L}$
into
![]() $\mathscr {L}'$
. Given two infinite cardinals
$\mathscr {L}'$
. Given two infinite cardinals
![]() $\kappa \leqslant \lambda $
and a formula
$\kappa \leqslant \lambda $
and a formula
![]() $\varphi \in Fm_{\mathscr {L}}(\kappa )$
, we define a formula
$\varphi \in Fm_{\mathscr {L}}(\kappa )$
, we define a formula
![]() $\boldsymbol {\tau }(\varphi ) \in Fm_{\mathscr {L}'}(\lambda )$
by recursion as follows. If
$\boldsymbol {\tau }(\varphi ) \in Fm_{\mathscr {L}'}(\lambda )$
by recursion as follows. If
![]() $\varphi = x_{\alpha }$
for some
$\varphi = x_{\alpha }$
for some
![]() $\alpha < \kappa $
, then
$\alpha < \kappa $
, then
![]() $\boldsymbol {\tau }(\varphi ) := x_{\alpha }$
. Moreover, if
$\boldsymbol {\tau }(\varphi ) := x_{\alpha }$
. Moreover, if
![]() $\varphi = \ast (\psi _{1}, \dots , \psi _{n})$
for some n-ary function symbol
$\varphi = \ast (\psi _{1}, \dots , \psi _{n})$
for some n-ary function symbol
![]() $\ast $
of
$\ast $
of
![]() $\mathscr {L}$
, then
$\mathscr {L}$
, then
![]() $\boldsymbol {\tau }(\varphi ) := \boldsymbol {\tau }(\ast )(\boldsymbol {\tau }(\psi _{1}), \dots , \boldsymbol {\tau }(\psi _{n}))$
. We extend this notation to sets of formulas
$\boldsymbol {\tau }(\varphi ) := \boldsymbol {\tau }(\ast )(\boldsymbol {\tau }(\psi _{1}), \dots , \boldsymbol {\tau }(\psi _{n}))$
. We extend this notation to sets of formulas
![]() $\varGamma \subseteq Fm_{\mathscr {L}}(\kappa )$
, by setting
$\varGamma \subseteq Fm_{\mathscr {L}}(\kappa )$
, by setting
![]() $\boldsymbol {\tau }[\varGamma ] := \{ \boldsymbol {\tau }(\gamma ) \colon \gamma \in \varGamma \}$
. Note that the variables of
$\boldsymbol {\tau }[\varGamma ] := \{ \boldsymbol {\tau }(\gamma ) \colon \gamma \in \varGamma \}$
. Note that the variables of
![]() $\boldsymbol {\tau }(\varphi )$
are among the variables in
$\boldsymbol {\tau }(\varphi )$
are among the variables in
![]() $\varphi $
.
$\varphi $
.
Moreover, given an
![]() $\mathscr {L}'$
-algebra
$\mathscr {L}'$
-algebra
![]() $\boldsymbol {A}$
, we let
$\boldsymbol {A}$
, we let
![]() $\boldsymbol {A}^{\boldsymbol {\tau }}$
be the
$\boldsymbol {A}^{\boldsymbol {\tau }}$
be the
![]() $\mathscr {L}$
-algebra, whose universe is A, and whose n-ary operations
$\mathscr {L}$
-algebra, whose universe is A, and whose n-ary operations
![]() $\ast $
are interpreted as follows:
$\ast $
are interpreted as follows:
 $$ \begin{align*} \ast^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_1, \ldots, a_n) := \boldsymbol{\tau}(\ast)^{\boldsymbol{A}}(a_1, \ldots, a_n), \text{ for every }a_{1}, \dots, a_{n} \in A. \end{align*} $$
$$ \begin{align*} \ast^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_1, \ldots, a_n) := \boldsymbol{\tau}(\ast)^{\boldsymbol{A}}(a_1, \ldots, a_n), \text{ for every }a_{1}, \dots, a_{n} \in A. \end{align*} $$
By induction on the construction of the formulas we obtain that for every
![]() $\varphi (z_1, \ldots , z_n) \in Fm_{\mathscr {L}}(\kappa )$
and every
$\varphi (z_1, \ldots , z_n) \in Fm_{\mathscr {L}}(\kappa )$
and every
![]() $a_1, \ldots , a_n \in A$
,
$a_1, \ldots , a_n \in A$
,
 $$ \begin{align*} \boldsymbol{\tau}(\varphi)^{\boldsymbol{A}}(a_1, \ldots, a_n) = \varphi^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_1, \ldots, a_n). \end{align*} $$
$$ \begin{align*} \boldsymbol{\tau}(\varphi)^{\boldsymbol{A}}(a_1, \ldots, a_n) = \varphi^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_1, \ldots, a_n). \end{align*} $$
Definition 3.2. Let
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
be two logics. An interpretation of
$\vdash '$
be two logics. An interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
is a translation
$\vdash '$
is a translation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathscr {L}_{\vdash }$
into
$\mathscr {L}_{\vdash }$
into
![]() $\mathscr {L}_{\vdash '}$
such that
$\mathscr {L}_{\vdash '}$
such that
For instance, for every given logic the identity map is an interpretation of it into any of its extensions.
Proposition 3.3. If
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\ \vdash $
into
$\ \vdash $
into
![]() $\vdash '$
, and
$\vdash '$
, and
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
, then
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
, then
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}(\vdash )$
. Moreover, if
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}(\vdash )$
. Moreover, if
![]() $\lambda \leqslant \kappa _{\vdash } \leqslant \kappa _{\vdash '}$
, then for every
$\lambda \leqslant \kappa _{\vdash } \leqslant \kappa _{\vdash '}$
, then for every
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm_{\mathscr {L}_{\vdash }}(\lambda )$
,
$\varGamma \cup \{ \varphi \} \subseteq Fm_{\mathscr {L}_{\vdash }}(\lambda )$
,
Proposition 3.4. Let
![]() $\vdash $
and
$\vdash $
and
![]() $\ \vdash '$
be two logics and
$\ \vdash '$
be two logics and
![]() $\boldsymbol {\tau }$
be a translation of
$\boldsymbol {\tau }$
be a translation of
![]() $\mathscr {L}_{\vdash }$
into
$\mathscr {L}_{\vdash }$
into
![]() $\mathscr {L}_{\vdash '}$
. Then
$\mathscr {L}_{\vdash '}$
. Then
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
if and only if
$\vdash '$
if and only if
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash '))$
.
$\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash '))$
.
Proof. The “only if” part is immediate. The “if” one is a consequence of Lemma 2.3.⊣
When there is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
we write
$\vdash '$
we write
![]() ${\vdash } \leqslant {\vdash '}$
and say that
${\vdash } \leqslant {\vdash '}$
and say that
![]() $\vdash $
is interpretable into
$\vdash $
is interpretable into
![]() $\vdash '$
. Similarly, we say that
$\vdash '$
. Similarly, we say that
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
are equi-interpretable if
$\vdash '$
are equi-interpretable if
![]() ${\vdash } \leqslant {\vdash '}$
and
${\vdash } \leqslant {\vdash '}$
and
![]() ${\vdash '} \leqslant {\vdash }$
. Given a logic
${\vdash '} \leqslant {\vdash }$
. Given a logic
![]() $\vdash $
, we denote by
$\vdash $
, we denote by
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
the class of all logics which are equi-interpretable with
$[\kern-1pt[ \vdash ]\kern-1pt] $
the class of all logics which are equi-interpretable with
![]() $\vdash $
. It is clear that the relation
$\vdash $
. It is clear that the relation
![]() $\leqslant $
is a preorder on the proper class of all logics, and that it induces a partial order on the collection of all classes of the form
$\leqslant $
is a preorder on the proper class of all logics, and that it induces a partial order on the collection of all classes of the form
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
. The latter poset constitutes the object of study of this work.
$[\kern-1pt[ \vdash ]\kern-1pt] $
. The latter poset constitutes the object of study of this work.
Definition 3.5. We denote by
![]() $\mathsf {Log}$
the poset of all logics, i.e., the poset whose universe is
$\mathsf {Log}$
the poset of all logics, i.e., the poset whose universe is
![]() $\{ [\kern-1pt[ \vdash ]\kern-1pt] \colon {\vdash } \text { is a logic}\}$
equipped with the partial order
$\{ [\kern-1pt[ \vdash ]\kern-1pt] \colon {\vdash } \text { is a logic}\}$
equipped with the partial order
![]() $\leqslant $
, defined as follows:
$\leqslant $
, defined as follows:
Remark 3.6. The reader may feel reassured by learning that, despite our reference to classes and collections, the results of this work can be formulated entirely in ZFC. This is because our statements can be phrased equivalently as speaking about logics ordered under the preorder
![]() $\leqslant $
by modifying the statements about posets to statements about preorders in the natural way. It is therefore only for the sake of simplicity that we found convenient to work with the poset
$\leqslant $
by modifying the statements about posets to statements about preorders in the natural way. It is therefore only for the sake of simplicity that we found convenient to work with the poset
![]() $\mathsf {Log}$
whose elements are, strictly speaking, proper classes.
$\mathsf {Log}$
whose elements are, strictly speaking, proper classes.
The notion of interpretability can be broken into two halves as follows:
Definition 3.7. Let
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
be logics.
$\vdash '$
be logics.
-
(i)
 $\vdash $
and
$\vdash $
and
 $\vdash '$
are term-equivalent if there are interpretations
$\vdash '$
are term-equivalent if there are interpretations
 $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
 $\vdash $
into
$\vdash $
into
 $\vdash '$
and
$\vdash '$
and
 $\boldsymbol {\rho }$
of
$\boldsymbol {\rho }$
of
 $\vdash '$
into
$\vdash '$
into
 $\vdash $
such that for every
$\vdash $
such that for every $$ \begin{align*} \langle \boldsymbol{A}, F \rangle =\langle \boldsymbol{A}^{\boldsymbol{\tau}\boldsymbol{\rho}}, F \rangle \; \text{ and } \; \langle \boldsymbol{B}, G \rangle = \langle \boldsymbol{B}^{\boldsymbol{\rho}\boldsymbol{\tau}}, G \rangle \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle =\langle \boldsymbol{A}^{\boldsymbol{\tau}\boldsymbol{\rho}}, F \rangle \; \text{ and } \; \langle \boldsymbol{B}, G \rangle = \langle \boldsymbol{B}^{\boldsymbol{\rho}\boldsymbol{\tau}}, G \rangle \end{align*} $$
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
and
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
and
 $\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
.
$\langle \boldsymbol {B}, G \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
.
-
(ii)
 $\vdash '$
is a compatible expansion of
$\vdash '$
is a compatible expansion of
 $\vdash $
if
$\vdash $
if
 $\mathscr {L}_{\vdash } \subseteq \mathscr {L}_{\vdash '}$
and the
$\mathscr {L}_{\vdash } \subseteq \mathscr {L}_{\vdash '}$
and the
 $\mathscr {L}_{\vdash }$
-reducts of the structures in
$\mathscr {L}_{\vdash }$
-reducts of the structures in
 $\mathsf {Mod}^{\equiv }(\vdash ')$
belong to
$\mathsf {Mod}^{\equiv }(\vdash ')$
belong to
 $\mathsf {Mod}^{\equiv }(\vdash )$
.
$\mathsf {Mod}^{\equiv }(\vdash )$
.
Proposition 3.8. Let
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
be logics. Then
$\vdash '$
be logics. Then
![]() ${\vdash } \leqslant {\vdash '}$
if and only if
${\vdash } \leqslant {\vdash '}$
if and only if
![]() $\vdash '$
is term-equivalent to a compatible expansion of
$\vdash '$
is term-equivalent to a compatible expansion of
![]() $\vdash $
.
$\vdash $
.
Proof. The “if” part is immediate. To prove the “only if” part, suppose that there is an interpretation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
. We can assume without loss of generality that the sets of function symbols of
$\vdash '$
. We can assume without loss of generality that the sets of function symbols of
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
are disjoint. Then let
$\vdash '$
are disjoint. Then let
![]() $\mathscr {L}$
be the language extending
$\mathscr {L}$
be the language extending
![]() $\mathscr {L}_{\vdash '}$
with the symbols of
$\mathscr {L}_{\vdash '}$
with the symbols of
![]() $\vdash $
. Given a matrix
$\vdash $
. Given a matrix
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
, we denote by
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
, we denote by
![]() $\boldsymbol {A}_{\mathscr {L}}$
the
$\boldsymbol {A}_{\mathscr {L}}$
the
![]() $\mathscr {L}$
-algebra obtained by enriching
$\mathscr {L}$
-algebra obtained by enriching
![]() $\boldsymbol {A}$
with the following interpretation of the n-ary symbols
$\boldsymbol {A}$
with the following interpretation of the n-ary symbols
![]() $\ast $
of
$\ast $
of
![]() $\vdash $
: for every
$\vdash $
: for every
![]() $a_{1}, \dots , a_{n} \in A$
,
$a_{1}, \dots , a_{n} \in A$
,
Then consider the class of matrices
![]() $\mathsf {K} := \{ \langle \boldsymbol {A}_{\mathscr {L}}, F \rangle \colon \langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ') \}$
, and let
$\mathsf {K} := \{ \langle \boldsymbol {A}_{\mathscr {L}}, F \rangle \colon \langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ') \}$
, and let
![]() $\vdash ''$
be the logic on
$\vdash ''$
be the logic on
![]() $Fm_{\mathscr {L}}(\kappa _{\vdash '})$
induced by
$Fm_{\mathscr {L}}(\kappa _{\vdash '})$
induced by
![]() $\mathsf {K}$
. It is not hard to see that
$\mathsf {K}$
. It is not hard to see that
![]() $\mathsf {Mod}^{\equiv }(\vdash '') = \mathsf {K}$
. Together with the fact that
$\mathsf {Mod}^{\equiv }(\vdash '') = \mathsf {K}$
. Together with the fact that
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
, this implies that
$\vdash '$
, this implies that
![]() $\vdash ''$
is a compatible expansion of
$\vdash ''$
is a compatible expansion of
![]() $\vdash $
. As it is clear that
$\vdash $
. As it is clear that
![]() $\vdash '$
and
$\vdash '$
and
![]() $\vdash ''$
are term-equivalent, we are done.⊣
$\vdash ''$
are term-equivalent, we are done.⊣
The following is instrumental to construct concrete interpretations.
Proposition 3.9. Let
![]() $\mathsf {K}$
be a class of reduced matrices that induces an equivalential logic
$\mathsf {K}$
be a class of reduced matrices that induces an equivalential logic
![]() $\vdash '$
. Moreover, let
$\vdash '$
. Moreover, let
![]() $\vdash $
be a logic such that
$\vdash $
be a logic such that
![]() $\kappa _{\vdash '} \geqslant \vert Fm(\vdash ) \vert $
. A translation
$\kappa _{\vdash '} \geqslant \vert Fm(\vdash ) \vert $
. A translation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\mathscr {L}_{\vdash }$
into
$\mathscr {L}_{\vdash }$
into
![]() $\mathscr {L}_{\vdash '}$
is an interpretation of
$\mathscr {L}_{\vdash '}$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
if and only if
$\vdash '$
if and only if
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {S}(\mathsf {K})$
.
$\langle \boldsymbol {A}, F \rangle \in \mathbb {S}(\mathsf {K})$
.
Proof. The “if” part follows from the fact that
![]() $\mathbb {S}(\mathsf {K}) \subseteq \mathsf {Mod}^{\equiv }(\vdash ')$
by Lemma 2.8.
$\mathbb {S}(\mathsf {K}) \subseteq \mathsf {Mod}^{\equiv }(\vdash ')$
by Lemma 2.8.
To prove the “only if” part, suppose that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {S}(\mathsf {K})$
. By Lemmas 2.3 and 2.9 this yields that
$\langle \boldsymbol {A}, F \rangle \in \mathbb {S}(\mathsf {K})$
. By Lemmas 2.3 and 2.9 this yields that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\kappa _{\vdash '}}\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {S}(\mathsf {K})$
. With an application of Lemma 2.8, we conclude that
$\langle \boldsymbol {A}, F \rangle \in \mathbb {U}_{\kappa _{\vdash '}}\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}\mathbb {S}(\mathsf {K})$
. With an application of Lemma 2.8, we conclude that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
and, therefore, that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
and, therefore, that
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
.⊣
$\vdash '$
.⊣
4 Existence of infima of sets
A basic question about the poset
![]() $\mathsf {Log}$
is whether it is a lattice or not. It turns out that
$\mathsf {Log}$
is whether it is a lattice or not. It turns out that
![]() $\mathsf {Log}$
has infima of arbitrarily large sets, but unfortunately may lack even finite suprema. In this section we describe a construction that supplies an explicit description of infima.
$\mathsf {Log}$
has infima of arbitrarily large sets, but unfortunately may lack even finite suprema. In this section we describe a construction that supplies an explicit description of infima.
Definition 4.1. Given a family
![]() $\{\mathscr {L}_i \colon i \in I \}$
of languages, we denote by
$\{\mathscr {L}_i \colon i \in I \}$
of languages, we denote by
![]() $\bigotimes _{i \in I}\mathscr {L}_i$
the language whose n-ary symbols
$\bigotimes _{i \in I}\mathscr {L}_i$
the language whose n-ary symbols
![]() $\ast $
are sequences of the form
$\ast $
are sequences of the form
where
![]() $\varphi _{i}(x_{1}, \dots , x_{n}) \in Fm_{\mathscr {L}_{i}}(\omega )$
for every
$\varphi _{i}(x_{1}, \dots , x_{n}) \in Fm_{\mathscr {L}_{i}}(\omega )$
for every
![]() $i \in I$
. Keeping this in mind, consider a family
$i \in I$
. Keeping this in mind, consider a family
![]() $J = \{ \boldsymbol {A}_{i} \colon i \in I \}$
in which
$J = \{ \boldsymbol {A}_{i} \colon i \in I \}$
in which
![]() $\boldsymbol {A}_{i}$
is an
$\boldsymbol {A}_{i}$
is an
![]() $\mathscr {L}_{i}$
-algebra, for every
$\mathscr {L}_{i}$
-algebra, for every
![]() $i \in I$
. The non-indexed product
$i \in I$
. The non-indexed product
![]() $\bigotimes _{i \in I}\boldsymbol {A}_i$
of J is the
$\bigotimes _{i \in I}\boldsymbol {A}_i$
of J is the
![]() $\bigotimes _{i \in I}\mathscr {L}_i$
-algebra defined as follows:
$\bigotimes _{i \in I}\mathscr {L}_i$
-algebra defined as follows:
-
(i) the universe of
 $\bigotimes _{i \in I}\boldsymbol {A}_i$
is the Cartesian product
$\bigotimes _{i \in I}\boldsymbol {A}_i$
is the Cartesian product
 $\prod _{i \in I}A_{i}$
, and
$\prod _{i \in I}A_{i}$
, and -
(ii) the n-ary symbols
 $\ast = \langle \varphi _{i}(x_1, \ldots , x_n) \colon i \in I \rangle $
are interpreted as
$\ast = \langle \varphi _{i}(x_1, \ldots , x_n) \colon i \in I \rangle $
are interpreted as  $$ \begin{align*} \ast^{\bigotimes_{i \in I} \boldsymbol{A}_{i}}(\vec{a}_{1}, \dots, \vec{a}_{n}) := \langle \varphi_{i}^{\boldsymbol{A}_{i}}(\vec{a}_{1}(i), \dots, \vec{a}_{n}(i)) \colon i \in I \rangle, \end{align*} $$
$$ \begin{align*} \ast^{\bigotimes_{i \in I} \boldsymbol{A}_{i}}(\vec{a}_{1}, \dots, \vec{a}_{n}) := \langle \varphi_{i}^{\boldsymbol{A}_{i}}(\vec{a}_{1}(i), \dots, \vec{a}_{n}(i)) \colon i \in I \rangle, \end{align*} $$
for every
![]() $\vec {a}_{1}, \dots , \vec {a}_{n} \in \prod _{i \in I}A_{i}$
.
$\vec {a}_{1}, \dots , \vec {a}_{n} \in \prod _{i \in I}A_{i}$
.
Non-indexed products of algebras found various applications in universal algebra, especially in the theory of Maltsev conditions [Reference Baldwin and Berman2, Reference García and Taylor20, Reference Grätzer21, Reference Neumann39, Reference Taylor47]. We use the terminology of these papers and extend it to families of matrices and logics.
Definition 4.2. The non-indexed product of a family
![]() $\{ \langle \boldsymbol {A}_{i}, F_{i}\rangle \colon i \in I\}$
of matrices is defined in a similar fashion, by setting
$\{ \langle \boldsymbol {A}_{i}, F_{i}\rangle \colon i \in I\}$
of matrices is defined in a similar fashion, by setting
 $$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle := \langle \bigotimes_{i \in I}\boldsymbol{A}_{i}, \prod_{i \in I}F_{i}\rangle. \end{align*} $$
$$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle := \langle \bigotimes_{i \in I}\boldsymbol{A}_{i}, \prod_{i \in I}F_{i}\rangle. \end{align*} $$
Remark 4.3. If
![]() $\{ {\vdash _{i}} \colon i \in I \}$
is a family of logics, then the cardinal of
$\{ {\vdash _{i}} \colon i \in I \}$
is a family of logics, then the cardinal of
![]() $\bigotimes _{i \in I}{\mathscr {L}_{\vdash _i}}$
is lesser than or equal to
$\bigotimes _{i \in I}{\mathscr {L}_{\vdash _i}}$
is lesser than or equal to
 $\prod _{i \in I}\vert Fm(\vdash _{i})\vert $
. Moreover, if
$\prod _{i \in I}\vert Fm(\vdash _{i})\vert $
. Moreover, if
 $\kappa \geqslant \prod _{i \in I}\vert Fm(\vdash _{i})\vert $
and
$\kappa \geqslant \prod _{i \in I}\vert Fm(\vdash _{i})\vert $
and
![]() $Fm(\kappa )$
is the set of formulas of
$Fm(\kappa )$
is the set of formulas of
![]() $\bigotimes _{i \in I}{\mathscr {L}_{\vdash _i}}$
in
$\bigotimes _{i \in I}{\mathscr {L}_{\vdash _i}}$
in
![]() $\kappa $
variables, then
$\kappa $
variables, then
![]() $\vert Fm(\kappa )\vert \leqslant \kappa $
.
$\vert Fm(\kappa )\vert \leqslant \kappa $
.
Given a collection
![]() $\{ \mathsf {K}_{i} \colon i \in I \}$
in which
$\{ \mathsf {K}_{i} \colon i \in I \}$
in which
![]() $\mathsf {K}_{i}$
is a class of
$\mathsf {K}_{i}$
is a class of
![]() $\mathscr {L}_{i}$
-matrices and I is a set, we define
$\mathscr {L}_{i}$
-matrices and I is a set, we define
 $$ \begin{align*} \bigotimes_{i \in I} \mathsf{K}_{i} := \mathbb{I} \{ \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \colon \langle \boldsymbol{A}_{i}, F_{i}\rangle \in \mathsf{K}_{i} \}. \end{align*} $$
$$ \begin{align*} \bigotimes_{i \in I} \mathsf{K}_{i} := \mathbb{I} \{ \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \colon \langle \boldsymbol{A}_{i}, F_{i}\rangle \in \mathsf{K}_{i} \}. \end{align*} $$
A submatrix
![]() $\langle \boldsymbol {A}, F \rangle \subseteq \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
is said to be a non-indexed subdirect product of
$\langle \boldsymbol {A}, F \rangle \subseteq \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
is said to be a non-indexed subdirect product of
![]() $\{ \langle \boldsymbol {A}_{i}, F_{i}\rangle \colon i \in I\}$
, in symbols
$\{ \langle \boldsymbol {A}_{i}, F_{i}\rangle \colon i \in I\}$
, in symbols
![]() $\langle \boldsymbol {A}, F \rangle \subseteq _{\;\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
, if the projection maps
$\langle \boldsymbol {A}, F \rangle \subseteq _{\;\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
, if the projection maps
![]() $\pi _{i} \colon A \to A_{i}$
are surjective. We write
$\pi _{i} \colon A \to A_{i}$
are surjective. We write
![]() $\langle \boldsymbol {A}, F \rangle \leqslant _{\; \textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
to indicate that
$\langle \boldsymbol {A}, F \rangle \leqslant _{\; \textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
to indicate that
![]() $\langle \boldsymbol {A}, F \rangle $
is isomorphic to a matrix
$\langle \boldsymbol {A}, F \rangle $
is isomorphic to a matrix
![]() $\langle \boldsymbol {B}, G\rangle $
such that
$\langle \boldsymbol {B}, G\rangle $
such that
![]() $\langle \boldsymbol {B}, G \rangle \subseteq _{\;\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
.
$\langle \boldsymbol {B}, G \rangle \subseteq _{\;\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
.
Definition 4.4. Let
![]() $\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The non-indexed product
$\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The non-indexed product
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
of
$\bigotimes _{i \in I}{\vdash _{i}}$
of
![]() $\{ \vdash _{i} \colon i \in I \}$
is the logic in the language
$\{ \vdash _{i} \colon i \in I \}$
is the logic in the language
![]() $\bigotimes _{i \in I}\mathscr {L}_i$
formulated in
$\bigotimes _{i \in I}\mathscr {L}_i$
formulated in
![]() $\kappa $
variables and induced by the class of matrices
$\kappa $
variables and induced by the class of matrices
 $\bigotimes _{i \in I}\mathsf {Mod}^{\equiv }(\vdash _{i})$
, where
$\bigotimes _{i \in I}\mathsf {Mod}^{\equiv }(\vdash _{i})$
, where
 $$ \begin{align*} \kappa := \prod_{i \in I}\vert Fm(\vdash_{i}) \vert. \end{align*} $$
$$ \begin{align*} \kappa := \prod_{i \in I}\vert Fm(\vdash_{i}) \vert. \end{align*} $$
When
![]() $I = \emptyset $
, we stipulate that
$I = \emptyset $
, we stipulate that
![]() $\bigotimes _{i \in I} {\vdash _{i}}$
is the logic in the empty language formulated in countably many variables and induced by the trivial matrix
$\bigotimes _{i \in I} {\vdash _{i}}$
is the logic in the empty language formulated in countably many variables and induced by the trivial matrix
![]() $\langle \boldsymbol {1}, \{ 1 \}\rangle $
.
$\langle \boldsymbol {1}, \{ 1 \}\rangle $
.
Our aim is to prove that
![]() $[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is the infimum of
$[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is the infimum of
![]() $\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
in
$\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
in
![]() $\mathsf {Log}$
. To this end, we rely on the following characterization of
$\mathsf {Log}$
. To this end, we rely on the following characterization of
 $\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
, to be established later on.
$\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
, to be established later on.
Proposition 4.5. If
![]() $\{ \vdash _{i} \colon i \in I \}$
is a family of logics, then
$\{ \vdash _{i} \colon i \in I \}$
is a family of logics, then
 $$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) =\mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))) = \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
$$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) =\mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))) = \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
Moreover,
 $$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) = \{\langle \boldsymbol{A}, F\rangle:\langle \boldsymbol{A}, F\rangle \leqslant_{\textrm{sd}} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \text{ for some } \langle \boldsymbol{A}_{i}, F_{i}\rangle\in \mathsf{Mod}^{\equiv}(\vdash_i)\}. \end{align*} $$
$$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) = \{\langle \boldsymbol{A}, F\rangle:\langle \boldsymbol{A}, F\rangle \leqslant_{\textrm{sd}} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \text{ for some } \langle \boldsymbol{A}_{i}, F_{i}\rangle\in \mathsf{Mod}^{\equiv}(\vdash_i)\}. \end{align*} $$
As we promised, we obtain the following:
Theorem 4.6. The infimum of a set
![]() $\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \} \subseteq \mathsf {Log}$
is
$\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \} \subseteq \mathsf {Log}$
is
![]() $[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
. Thus
$[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
. Thus
![]() $\mathsf {Log}$
is a set-complete meet-semilattice, i.e., infima of subsets of
$\mathsf {Log}$
is a set-complete meet-semilattice, i.e., infima of subsets of
![]() $\mathsf {Log}$
exist.
$\mathsf {Log}$
exist.
Proof. First we show that
![]() ${\bigotimes _{i \in I}{\vdash _{i}}}\leqslant {\vdash _{j}}$
for every
${\bigotimes _{i \in I}{\vdash _{i}}}\leqslant {\vdash _{j}}$
for every
![]() $j \in I$
. To this end, consider the map
$j \in I$
. To this end, consider the map
![]() $\boldsymbol {\tau }$
that sends every n-ary basic operation of
$\boldsymbol {\tau }$
that sends every n-ary basic operation of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
to its j-th component (which is an n-ary term of
$\bigotimes _{i \in I}{\vdash _{i}}$
to its j-th component (which is an n-ary term of
![]() $\vdash _{j}$
). Consider
$\vdash _{j}$
). Consider
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{j})$
. It is clear that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{j})$
. It is clear that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \cong \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
where
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \cong \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
where
![]() $\langle \boldsymbol {A}_{i}, F_{i}\rangle $
is the trivial
$\langle \boldsymbol {A}_{i}, F_{i}\rangle $
is the trivial
![]() $\mathscr {L}_{i}$
-matrix for every
$\mathscr {L}_{i}$
-matrix for every
![]() $i \in I \smallsetminus \{ j \}$
, and
$i \in I \smallsetminus \{ j \}$
, and
![]() $\langle \boldsymbol {A}_{j}, F_{j} \rangle := \langle \boldsymbol {A}, F \rangle $
. By Proposition 4.5 we have
$\langle \boldsymbol {A}_{j}, F_{j} \rangle := \langle \boldsymbol {A}, F \rangle $
. By Proposition 4.5 we have
 $$ \begin{align*} \langle \boldsymbol{A}^{\boldsymbol{\tau}}, F \rangle \, \cong\, \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \in \bigotimes_{i \in I}\mathsf{Mod}^{\equiv}(\vdash_{i}) \subseteq \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}). \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}^{\boldsymbol{\tau}}, F \rangle \, \cong\, \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle \in \bigotimes_{i \in I}\mathsf{Mod}^{\equiv}(\vdash_{i}) \subseteq \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}). \end{align*} $$
In particular, this means that
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
into
$\bigotimes _{i \in I}{\vdash _{i}}$
into
![]() $\vdash _{j}$
, thus
$\vdash _{j}$
, thus
![]() $\bigotimes _{i \in I}{\vdash _{i}} \leqslant {\vdash _{j}}$
. As a consequence,
$\bigotimes _{i \in I}{\vdash _{i}} \leqslant {\vdash _{j}}$
. As a consequence,
![]() $[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is a lower bound of
$[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is a lower bound of
![]() $\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
.
$\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
.
To prove that
![]() $\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
is the greatest lower bound of
$\{ [\kern-1pt[ \vdash _{i} ]\kern-1pt] \colon i \in I \}$
is the greatest lower bound of
![]() $[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
, consider a logic
$[\kern-1pt[ \bigotimes _{i \in I}{\vdash _{i}} ]\kern-1pt] $
, consider a logic
![]() $\vdash $
such that
$\vdash $
such that
![]() ${\vdash } \leqslant {\vdash _{i}}$
for every
${\vdash } \leqslant {\vdash _{i}}$
for every
![]() $i \in I$
. Then for each
$i \in I$
. Then for each
![]() $i \in I$
there is an interpretation
$i \in I$
there is an interpretation
![]() $\boldsymbol {\tau }_{i} $
of
$\boldsymbol {\tau }_{i} $
of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{i}$
. Let
$\vdash _{i}$
. Let
![]() $\boldsymbol {\tau }$
be the map that associates with every basic n-ary symbol
$\boldsymbol {\tau }$
be the map that associates with every basic n-ary symbol
![]() $\ast $
of
$\ast $
of
![]() $\vdash $
the following n-ary term of
$\vdash $
the following n-ary term of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
:
$\bigotimes _{i \in I}{\vdash _{i}}$
:
Now, consider a matrix
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. From Proposition 4.5 it follows that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. From Proposition 4.5 it follows that
 $\langle \boldsymbol {A}, F \rangle \leqslant \prod _{j \in J} (\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle )$
is a subdirect product for some
$\langle \boldsymbol {A}, F \rangle \leqslant \prod _{j \in J} (\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle )$
is a subdirect product for some
 $\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
. It is easy to see that
$\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
. It is easy to see that
 $$ \begin{align*} \langle \boldsymbol{A}^{\boldsymbol{\tau}}, F \rangle \; \leqslant\; \prod_{j \in J} \Big(\prod_{i \in I}\langle (\boldsymbol{A}_{i}^{j})^{\boldsymbol{\tau}_{i}}, F_{i}^{j}\rangle \Big) \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}^{\boldsymbol{\tau}}, F \rangle \; \leqslant\; \prod_{j \in J} \Big(\prod_{i \in I}\langle (\boldsymbol{A}_{i}^{j})^{\boldsymbol{\tau}_{i}}, F_{i}^{j}\rangle \Big) \end{align*} $$
is also a subdirect product. Since each
![]() $\boldsymbol {\tau }_{i}$
is an interpretation of
$\boldsymbol {\tau }_{i}$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{i}$
, we conclude that
$\vdash _{i}$
, we conclude that
Together with the fact that
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
is closed under subdirect products by Lemma 2.3, this yields that
$\mathsf {Mod}^{\equiv }(\vdash )$
is closed under subdirect products by Lemma 2.3, this yields that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
. Hence we conclude that
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
. Hence we conclude that
![]() $\bigotimes _{i \in I}{\vdash _{i}} \leqslant {\vdash }$
.⊣
$\bigotimes _{i \in I}{\vdash _{i}} \leqslant {\vdash }$
.⊣
The remaining part of this section is devoted to prove Proposition 4.5. The proof proceeds through a series of technical observations.
Lemma 4.7. If
![]() $\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
and
$\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
and
![]() $F \ne \emptyset $
, then for every
$F \ne \emptyset $
, then for every
![]() $\vec {a}, \vec {c} \in A$
,
$\vec {a}, \vec {c} \in A$
,
 $$ \begin{align*} \langle \vec{a}, \vec{c} \kern 0.4pt \rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}}F \Longleftrightarrow \text{ for every }i \in I, \langle \vec{a}(i), \vec{c}(i)\rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}_{i}}F_{i}. \end{align*} $$
$$ \begin{align*} \langle \vec{a}, \vec{c} \kern 0.4pt \rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}}F \Longleftrightarrow \text{ for every }i \in I, \langle \vec{a}(i), \vec{c}(i)\rangle \in \boldsymbol{\varOmega}^{\boldsymbol{A}_{i}}F_{i}. \end{align*} $$
Proof. The right-to-left direction is an easy exercise. To prove the left-to-right direction, suppose that
 $\langle \vec {a}, \vec {c}\rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F$
. By Lemma 2.2(i), given an arbitrary
$\langle \vec {a}, \vec {c}\rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F$
. By Lemma 2.2(i), given an arbitrary
![]() $j \in I$
, we need to show that
$j \in I$
, we need to show that
![]() $p(\vec {a}(j)) \in F$
iff
$p(\vec {a}(j)) \in F$
iff
![]() $p(\vec {c}(j)) \in F$
, for every unary polynomial function
$p(\vec {c}(j)) \in F$
, for every unary polynomial function
![]() $p(x)$
of
$p(x)$
of
![]() $\boldsymbol {A}_{j}$
. To this end, consider a formula
$\boldsymbol {A}_{j}$
. To this end, consider a formula
![]() $\varphi (x, y_{1}, \dots , y_{n})$
of
$\varphi (x, y_{1}, \dots , y_{n})$
of
![]() $\boldsymbol {A}_{j}$
and elements
$\boldsymbol {A}_{j}$
and elements
![]() $e_{1}, \dots , e_{n} \in A_{j}$
such that
$e_{1}, \dots , e_{n} \in A_{j}$
such that
 $$ \begin{align} \varphi^{\boldsymbol{A}_{j}}(\vec{a}(j), e_{1}, \dots, e_{n}) \in F_{j}. \end{align} $$
$$ \begin{align} \varphi^{\boldsymbol{A}_{j}}(\vec{a}(j), e_{1}, \dots, e_{n}) \in F_{j}. \end{align} $$
Since
![]() $\pi _{j} \colon A \to A_{j}$
is surjective, there are
$\pi _{j} \colon A \to A_{j}$
is surjective, there are
![]() $\vec {e}_{1}, \dots , \vec {e}_{n} \in A$
whose j-th components are respectively
$\vec {e}_{1}, \dots , \vec {e}_{n} \in A$
whose j-th components are respectively
![]() $e_{1}, \dots , e_{n}$
. Moreover, as
$e_{1}, \dots , e_{n}$
. Moreover, as
![]() $F \ne \emptyset $
, we can choose an element
$F \ne \emptyset $
, we can choose an element
![]() $\vec {e} \in F$
. Then consider the basic operation
$\vec {e} \in F$
. Then consider the basic operation
of
![]() $\boldsymbol {A}$
, where
$\boldsymbol {A}$
, where
![]() $\psi _{j} = \varphi $
, and
$\psi _{j} = \varphi $
, and
![]() $\psi _{i} = z$
for every
$\psi _{i} = z$
for every
![]() $i \in J \smallsetminus \{ j \}$
. We have that for every
$i \in J \smallsetminus \{ j \}$
. We have that for every
![]() $i \in I$
,
$i \in I$
,
 $$ \begin{align*} \psi(\vec{a}, \vec{e}_{1}, \dots, \vec{e}_{n}, \vec{e})(i)= \left\{ \begin{array}{ll} \varphi^{\boldsymbol{A}_{j}}(\vec{a}(j), e_{1}, \dots, e_{n}) & \text{if}\ i= j,\\ \vec{e}(i) & \text{otherwise.}\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \psi(\vec{a}, \vec{e}_{1}, \dots, \vec{e}_{n}, \vec{e})(i)= \left\{ \begin{array}{ll} \varphi^{\boldsymbol{A}_{j}}(\vec{a}(j), e_{1}, \dots, e_{n}) & \text{if}\ i= j,\\ \vec{e}(i) & \text{otherwise.}\\ \end{array} \right. \end{align*} $$
Together with (4) and
![]() $\vec {e} \in F$
, this implies that
$\vec {e} \in F$
, this implies that
![]() $\psi (\vec {a}, \vec {e}_{1}, \dots , \vec {e}_{n}, \vec {e}) \in F$
. Since
$\psi (\vec {a}, \vec {e}_{1}, \dots , \vec {e}_{n}, \vec {e}) \in F$
. Since
 $\langle \vec {a}, \vec {c }\kern 0.4pt \rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F$
, we obtain that
$\langle \vec {a}, \vec {c }\kern 0.4pt \rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}}F$
, we obtain that
![]() $\psi (\vec {c}, \vec {e}_{1}, \dots , \vec {e}_{n}, \vec {e}) \in F$
as well. In particular, this means that
$\psi (\vec {c}, \vec {e}_{1}, \dots , \vec {e}_{n}, \vec {e}) \in F$
as well. In particular, this means that
 $$ \begin{align*} \varphi^{\boldsymbol{A}_{j}}(\vec{c}(j), e_{1}, \dots, e_{n}) = \psi(\vec{c}, \vec{e}_{1}, \dots, \vec{e}_{n}, \vec{e})(j) \in F_{j}. \end{align*} $$
$$ \begin{align*} \varphi^{\boldsymbol{A}_{j}}(\vec{c}(j), e_{1}, \dots, e_{n}) = \psi(\vec{c}, \vec{e}_{1}, \dots, \vec{e}_{n}, \vec{e})(j) \in F_{j}. \end{align*} $$
Hence we conclude that
 $\langle \vec {a}(j), \vec {c}(j)\rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}_{j}}F_{j}$
, as desired.⊣
$\langle \vec {a}(j), \vec {c}(j)\rangle \in \boldsymbol {\varOmega }^{\boldsymbol {A}_{j}}F_{j}$
, as desired.⊣
Corollary 4.8. If
![]() $\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
and
$\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
and
![]() $F \ne \emptyset $
, then
$F \ne \emptyset $
, then
-
(i) if the matrices in
 $\{\langle \boldsymbol {A}_{i}, F_{i}\rangle : i \in I\}$
are reduced, then so is
$\{\langle \boldsymbol {A}_{i}, F_{i}\rangle : i \in I\}$
are reduced, then so is
 $\langle \boldsymbol {A}, F \rangle $
and
$\langle \boldsymbol {A}, F \rangle $
and -
(ii)
 $\langle \boldsymbol {A}, F \rangle ^{\ast } \leqslant _{\textrm {sd}}\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
.
$\langle \boldsymbol {A}, F \rangle ^{\ast } \leqslant _{\textrm {sd}}\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
.
Proof. Condition (i) is an immediate consequence of Lemma 4.7. To prove condition (ii), consider the map
![]() $f \colon \langle \boldsymbol {A}, F \rangle ^{\ast } \to \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
defined as
$f \colon \langle \boldsymbol {A}, F \rangle ^{\ast } \to \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
defined as
 $$ \begin{align*} f(a/\boldsymbol{\varOmega}^{\boldsymbol{A}}F) := \langle a(i)/\boldsymbol{\varOmega}^{\boldsymbol{A}_{i}}F_{i} \colon i \in I\rangle \end{align*} $$
$$ \begin{align*} f(a/\boldsymbol{\varOmega}^{\boldsymbol{A}}F) := \langle a(i)/\boldsymbol{\varOmega}^{\boldsymbol{A}_{i}}F_{i} \colon i \in I\rangle \end{align*} $$
for every
![]() $a \in A$
. From Lemma 4.7 it follows that f is a well-defined embedding. Together with the fact that
$a \in A$
. From Lemma 4.7 it follows that f is a well-defined embedding. Together with the fact that
![]() $\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
, this implies that
$\langle \boldsymbol {A}, F \rangle \subseteq _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
, this implies that
![]() $\langle \boldsymbol {A}, F \rangle ^{\ast } \leqslant _{\textrm {sd}}\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
.⊣
$\langle \boldsymbol {A}, F \rangle ^{\ast } \leqslant _{\textrm {sd}}\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\ast }$
.⊣
Proposition 4.9. Let
![]() $\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The logic
$\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The logic
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
has theorems if and only if each
$\bigotimes _{i \in I}{\vdash _{i}}$
has theorems if and only if each
![]() $\vdash _{i}$
has theorems.
$\vdash _{i}$
has theorems.
Proof. The “only if” part is immediate. To prove the “if” one, suppose that each
![]() $\vdash _{i}$
has a theorem
$\vdash _{i}$
has a theorem
![]() $\varphi _{i}$
. By substitution invariance, we can assume that
$\varphi _{i}$
. By substitution invariance, we can assume that
![]() $\varphi _{i} = \varphi _{i}(x)$
. Then the formula
$\varphi _{i} = \varphi _{i}(x)$
. Then the formula
![]() $\varphi (x) := \langle \varphi _{i}(x) \colon i \in I \rangle $
is a theorem of
$\varphi (x) := \langle \varphi _{i}(x) \colon i \in I \rangle $
is a theorem of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
.⊣
$\bigotimes _{i \in I}{\vdash _{i}}$
.⊣
Lemma 4.10. Let
![]() $\{ \vdash _{i} \colon i \in I \}$
be a family of logics, and
$\{ \vdash _{i} \colon i \in I \}$
be a family of logics, and
![]() $\langle \boldsymbol {A}, F \rangle $
a matrix such that
$\langle \boldsymbol {A}, F \rangle $
a matrix such that
![]() $F \ne \emptyset $
. The following conditions are equivalent:
$F \ne \emptyset $
. The following conditions are equivalent:
-
(i)
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
.
$\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
. -
(ii)
 $\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm{sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
, for some
$\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm{sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
, for some
 $\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
.
$\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
.
Proof. (i)
![]() $\Rightarrow $
(ii): Let
$\Rightarrow $
(ii): Let
 $\kappa := \prod _{i \in I}\vert Fm(\vdash _{i}) \vert $
and
$\kappa := \prod _{i \in I}\vert Fm(\vdash _{i}) \vert $
and
![]() $Fm(\kappa )$
the set of formulas of
$Fm(\kappa )$
the set of formulas of
![]() $\bigotimes _{i \in I} {\vdash _{i}}$
in
$\bigotimes _{i \in I} {\vdash _{i}}$
in
![]() $\kappa $
variables. We know that
$\kappa $
variables. We know that
![]() $\kappa \geqslant \vert Fm(\kappa ) \vert $
. Since
$\kappa \geqslant \vert Fm(\kappa ) \vert $
. Since
![]() $\bigotimes _{i \in I} \vdash _{i}$
is the logic on
$\bigotimes _{i \in I} \vdash _{i}$
is the logic on
![]() $Fm(\kappa )$
induced by
$Fm(\kappa )$
induced by
 $\bigotimes _{i \in I}\mathsf {Mod}^{\equiv }(\vdash _{i})$
, we can apply Theorem 2.4 yielding
$\bigotimes _{i \in I}\mathsf {Mod}^{\equiv }(\vdash _{i})$
, we can apply Theorem 2.4 yielding
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle \in \mathbb{R}\mathbb{S}\mathbb{P}_{\!{\scriptstyle \textrm{R}}_{\kappa^{+}}}^{}(\bigotimes_{i \in I}\mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle \in \mathbb{R}\mathbb{S}\mathbb{P}_{\!{\scriptstyle \textrm{R}}_{\kappa^{+}}}^{}(\bigotimes_{i \in I}\mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
Then there are a matrix
![]() $\langle \boldsymbol {B}, G \rangle $
, a family of matrices
$\langle \boldsymbol {B}, G \rangle $
, a family of matrices
 $\{ \langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \colon i \in I, j \in J \}$
, and a
$\{ \langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \colon i \in I, j \in J \}$
, and a
![]() $\kappa ^{+}$
-complete filter F on J such that
$\kappa ^{+}$
-complete filter F on J such that
![]() $\langle \boldsymbol {B}, G \rangle ^{\ast } = \langle \boldsymbol {A}, F \rangle $
,
$\langle \boldsymbol {B}, G \rangle ^{\ast } = \langle \boldsymbol {A}, F \rangle $
,
 $\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
, and
$\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
, and
 $$ \begin{align} \langle \boldsymbol{B}, G \rangle \leqslant \Big(\prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) \Big)/ F{\kern -1pt}. \end{align} $$
$$ \begin{align} \langle \boldsymbol{B}, G \rangle \leqslant \Big(\prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) \Big)/ F{\kern -1pt}. \end{align} $$
It is easy to see that the map
 $$ \begin{align*} f \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) \to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle), \end{align*} $$
$$ \begin{align*} f \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) \to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle), \end{align*} $$
defined by the rule
is an isomorphism. We shall see that also the map
 $$ \begin{align*} g \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) / F \to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle / F), \end{align*} $$
$$ \begin{align*} g \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) / F \to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle / F), \end{align*} $$
defined by the rule
is an isomorphism. The proof that g is a well-defined surjective homomorphism is routinary. To prove that g is also injective, consider
 $\vec {a}, \vec {c} \in \prod _{j \in J} (\bigotimes _{i \in I} \langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle ) $
such that
$\vec {a}, \vec {c} \in \prod _{j \in J} (\bigotimes _{i \in I} \langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle ) $
such that
![]() $g(\vec {a}/ F) = g(\vec {c}/ F)$
, i.e., that
$g(\vec {a}/ F) = g(\vec {c}/ F)$
, i.e., that
![]() $f(\vec {a})(i) / F = f(\vec {c}) / F$
for every
$f(\vec {a})(i) / F = f(\vec {c}) / F$
for every
![]() $i \in I$
. Since
$i \in I$
. Since
![]() $\kappa \geqslant \vert I \vert $
and F is
$\kappa \geqslant \vert I \vert $
and F is
![]() $\kappa ^{+}$
-complete, we have
$\kappa ^{+}$
-complete, we have
 $$ \begin{align*} \{ j \in J \colon \vec{a}(j) = \vec{c}(j) \} &= \bigcap_{i \in I} \{ j \in J \colon \vec{a}(j)(i) = \vec{c}(j)(i) \}\\ & = \bigcap_{i \in I} \{ j \in J \colon f(\vec{a})(i)(j) = f(\vec{c})(i)(j) \}\\ & \in F{\kern -1pt}. \end{align*} $$
$$ \begin{align*} \{ j \in J \colon \vec{a}(j) = \vec{c}(j) \} &= \bigcap_{i \in I} \{ j \in J \colon \vec{a}(j)(i) = \vec{c}(j)(i) \}\\ & = \bigcap_{i \in I} \{ j \in J \colon f(\vec{a})(i)(j) = f(\vec{c})(i)(j) \}\\ & \in F{\kern -1pt}. \end{align*} $$
Hence
![]() $\vec {a}/ F = \vec {c}/ F$
and, therefore, g is injective. This establishes that g is an isomorphism.
$\vec {a}/ F = \vec {c}/ F$
and, therefore, g is injective. This establishes that g is an isomorphism.
Together with (5), this yields that
 $\langle \boldsymbol {B}, G \rangle \leqslant \bigotimes _{i \in I} (\prod _{j \in J}\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle / F)$
. As a consequence, there are
$\langle \boldsymbol {B}, G \rangle \leqslant \bigotimes _{i \in I} (\prod _{j \in J}\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle / F)$
. As a consequence, there are
 $\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i}))$
such that
$\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i}))$
such that
![]() $\langle \boldsymbol {B}, G \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
. Together with Corollary 4.8, this implies that
$\langle \boldsymbol {B}, G \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
. Together with Corollary 4.8, this implies that
 $$ \begin{align*} \langle \boldsymbol{A}, F\rangle \leqslant_{\; \textrm{sd}} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle^{\ast}, \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F\rangle \leqslant_{\; \textrm{sd}} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i}\rangle^{\ast}, \end{align*} $$
where
 $\langle \boldsymbol {A}_{i}, F_{i} \rangle ^{\ast } \in \mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i}))$
. As
$\langle \boldsymbol {A}_{i}, F_{i} \rangle ^{\ast } \in \mathbb {R}\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i}))$
. As
![]() $\kappa \geqslant \vert Fm(\vdash _{i})\vert $
, it is not hard to see that
$\kappa \geqslant \vert Fm(\vdash _{i})\vert $
, it is not hard to see that
 $\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}(\vdash _{i})$
. In particular, this implies that
$\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}(\vdash _{i})$
. In particular, this implies that
 $\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}(\vdash _{i})$
and, therefore, that
$\mathbb {S}\mathbb {P}_{\!{\scriptstyle \textrm {R}}_{\kappa ^{+}}}^{}(\mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}(\vdash _{i})$
and, therefore, that
![]() $\langle \boldsymbol {A}_{i}, F_{i} \rangle ^{\ast } \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
.
$\langle \boldsymbol {A}_{i}, F_{i} \rangle ^{\ast } \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
.
(ii)
![]() $\Rightarrow $
(i): From the definition of
$\Rightarrow $
(i): From the definition of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
it follows that
$\bigotimes _{i \in I}{\vdash _{i}}$
it follows that
![]() $\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
is a model of
$\bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
is a model of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
. As submatrices of models are still models, this implies that
$\bigotimes _{i \in I}{\vdash _{i}}$
. As submatrices of models are still models, this implies that
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}})$
. Finally, the matrix
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}})$
. Finally, the matrix
![]() $\langle \boldsymbol {A}, F \rangle $
is reduced by Corollary 4.8.⊣
$\langle \boldsymbol {A}, F \rangle $
is reduced by Corollary 4.8.⊣
The following observation is well-known [Reference Font15, p. 205].
Lemma 4.11. Let
![]() $\vdash $
be a logic, and
$\vdash $
be a logic, and
![]() $\boldsymbol {A}$
an algebra.
$\boldsymbol {A}$
an algebra.
-
(i) If
 $\langle \boldsymbol {A}, \emptyset \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash ))$
, then
$\langle \boldsymbol {A}, \emptyset \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash ))$
, then
 $\boldsymbol {A}$
is the trivial algebra
$\boldsymbol {A}$
is the trivial algebra
 $\boldsymbol{1}$
.
$\boldsymbol{1}$
. -
(ii) A logic
 $\vdash $
has theorems if and only if
$\vdash $
has theorems if and only if
 $\langle \boldsymbol{1}, \emptyset \rangle \notin \mathsf {Mod}^{\equiv }(\vdash )$
or, equivalently, if
$\langle \boldsymbol{1}, \emptyset \rangle \notin \mathsf {Mod}^{\equiv }(\vdash )$
or, equivalently, if
 $\langle \boldsymbol {1}, \emptyset \rangle \notin \mathbb {R}(\mathsf {Mod}(\vdash ))$
.
$\langle \boldsymbol {1}, \emptyset \rangle \notin \mathbb {R}(\mathsf {Mod}(\vdash ))$
.
As a consequence we obtain a transparent description of
 $\mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
:
$\mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
:
Proposition 4.12. Let
![]() $\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The class
$\{ \vdash _{i} \colon i \in I \}$
be a family of logics. The class
 $\mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
consists of the matrices satisfying condition (ii) of Lemma 4.10, plus
$\mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
consists of the matrices satisfying condition (ii) of Lemma 4.10, plus
![]() $\langle \boldsymbol {1}, \emptyset \rangle $
in case some
$\langle \boldsymbol {1}, \emptyset \rangle $
in case some
![]() $\vdash _{i}$
has no theorems.
$\vdash _{i}$
has no theorems.
Let
![]() $\{ \mathscr {L}_{i} \colon i \in I \}$
be a family of languages and
$\{ \mathscr {L}_{i} \colon i \in I \}$
be a family of languages and
![]() $\langle \boldsymbol {A}, F \rangle $
be a
$\langle \boldsymbol {A}, F \rangle $
be a
![]() $\mathscr {L}_{j}$
-matrix for some
$\mathscr {L}_{j}$
-matrix for some
![]() $j \in I$
. We denote by
$j \in I$
. We denote by
![]() $\langle \boldsymbol {A}, F \rangle ^{\flat }$
the
$\langle \boldsymbol {A}, F \rangle ^{\flat }$
the
![]() $\bigotimes _{i \in I}\mathscr {L}_{i}$
-matrix
$\bigotimes _{i \in I}\mathscr {L}_{i}$
-matrix
![]() $\bigotimes _{i \in I} \langle \boldsymbol {A}^{-}_{i}, F^{-}_{i}\rangle $
, where
$\bigotimes _{i \in I} \langle \boldsymbol {A}^{-}_{i}, F^{-}_{i}\rangle $
, where
 $$ \begin{align*} \langle \boldsymbol{A}^{-}_{i}, F^{-}_{i}\rangle := \left\{ \begin{array}{ll} \langle \boldsymbol{A}, F \rangle & \text{if}\ i= j\\ \langle \boldsymbol{1}, \{ 1 \} \rangle& \text{otherwise.}\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}^{-}_{i}, F^{-}_{i}\rangle := \left\{ \begin{array}{ll} \langle \boldsymbol{A}, F \rangle & \text{if}\ i= j\\ \langle \boldsymbol{1}, \{ 1 \} \rangle& \text{otherwise.}\\ \end{array} \right. \end{align*} $$
Note that if
![]() $\langle \boldsymbol {A}, F \rangle $
is reduced, then
$\langle \boldsymbol {A}, F \rangle $
is reduced, then
![]() $\langle \boldsymbol {A}, F \rangle ^{\flat }$
is reduced as well.
$\langle \boldsymbol {A}, F \rangle ^{\flat }$
is reduced as well.
Lemma 4.13. If
![]() $\{ \vdash _{i} \colon i \in I \}$
is a family of logics,
$\{ \vdash _{i} \colon i \in I \}$
is a family of logics,
 $$ \begin{align*} \mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) \subseteq \mathbb{P}_{\!{\scriptstyle {\textrm{SD}}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i})))\subseteq \mathbb{P}_{\!{\scriptstyle {\textrm{SD}}}}^{}\mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})). \end{align*} $$
$$ \begin{align*} \mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) \subseteq \mathbb{P}_{\!{\scriptstyle {\textrm{SD}}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i})))\subseteq \mathbb{P}_{\!{\scriptstyle {\textrm{SD}}}}^{}\mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})). \end{align*} $$
Proof. We detail only the proof of the first inclusion, since the proof of the second one exploits similar ideas. Consider a matrix
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
. First we consider the case where
$\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigotimes _{i \in I}{\vdash _{i}}))$
. First we consider the case where
![]() $F = \emptyset $
. As the matrix
$F = \emptyset $
. As the matrix
![]() $\langle \boldsymbol {A}, F \rangle $
is reduced, we know that
$\langle \boldsymbol {A}, F \rangle $
is reduced, we know that
![]() $\boldsymbol {A}$
is trivial by Lemma 4.11(i). Now, the fact that F is empty implies that
$\boldsymbol {A}$
is trivial by Lemma 4.11(i). Now, the fact that F is empty implies that
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
has no theorems. From Proposition 4.9 it follows that there is
$\bigotimes _{i \in I}{\vdash _{i}}$
has no theorems. From Proposition 4.9 it follows that there is
![]() $j \in I$
such that
$j \in I$
such that
![]() $\vdash _{j}$
has no theorems. Therefore by Lemma 4.11(ii) the
$\vdash _{j}$
has no theorems. Therefore by Lemma 4.11(ii) the
![]() $\mathscr {L}_{j}$
-matrix
$\mathscr {L}_{j}$
-matrix
![]() $\langle \boldsymbol {1}, \emptyset \rangle $
belongs to
$\langle \boldsymbol {1}, \emptyset \rangle $
belongs to
![]() $\mathbb {R}(\mathsf {Mod}( \vdash _{j}))$
. As a consequence we obtain that
$\mathbb {R}(\mathsf {Mod}( \vdash _{j}))$
. As a consequence we obtain that
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle = \langle \boldsymbol{1}, \emptyset \rangle^{\flat} \in \bigotimes_{i \in I}(\mathbb{R}(\mathsf{Mod}(\vdash_{i})). \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle = \langle \boldsymbol{1}, \emptyset \rangle^{\flat} \in \bigotimes_{i \in I}(\mathbb{R}(\mathsf{Mod}(\vdash_{i})). \end{align*} $$
Then we consider the case where
![]() $F \ne \emptyset $
. From Lemma 4.10 we know that
$F \ne \emptyset $
. From Lemma 4.10 we know that
![]() $\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
for some
$\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
for some
![]() $\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
. Moreover, it is easy to see that the map
$\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
. Moreover, it is easy to see that the map
 $$ \begin{align*} f \colon \prod_{i \in I} \langle \boldsymbol{A}_{i}, F_{i}\rangle^{\flat} \to \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \end{align*} $$
$$ \begin{align*} f \colon \prod_{i \in I} \langle \boldsymbol{A}_{i}, F_{i}\rangle^{\flat} \to \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \end{align*} $$
defined by the rule
is an isomorphism. Together with the fact that
![]() $\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
, this implies that
$\langle \boldsymbol {A}, F \rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i} \rangle $
, this implies that
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle \leqslant \prod_{i \in I} \langle \boldsymbol{A}_{i}, F_{i}\rangle^{\flat} \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle \leqslant \prod_{i \in I} \langle \boldsymbol{A}_{i}, F_{i}\rangle^{\flat} \end{align*} $$
is a subdirect product. Hence we conclude that
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathbb {R}(\mathsf {Mod}(\vdash _{i})))$
.⊣
$\langle \boldsymbol {A}, F \rangle \in \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathbb {R}(\mathsf {Mod}(\vdash _{i})))$
.⊣
Proof of Proposition 4.5. We begin by proving the first part. From Lemmas 2.3 and 4.13 it follows that
 $$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) &= \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} \mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}\mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} (\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i})))\\ &= \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} (\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))). \end{align*} $$
$$ \begin{align*} \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}) &= \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} \mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}\mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} (\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i})))\\ &= \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{} (\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))). \end{align*} $$
Moreover, since
![]() $\mathbb {R}(\mathsf {Mod}(\vdash _{i})) \subseteq \mathsf {Mod}^{\equiv }(\vdash _{i})$
for every
$\mathbb {R}(\mathsf {Mod}(\vdash _{i})) \subseteq \mathsf {Mod}^{\equiv }(\vdash _{i})$
for every
![]() $i \in I$
, we have
$i \in I$
, we have
 $$ \begin{align*} \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
$$ \begin{align*} \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathbb{R}(\mathsf{Mod}(\vdash_{i}))) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I} \mathsf{Mod}^{\equiv}(\vdash_{i})). \end{align*} $$
It only remains to prove that
 $\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. Since the class
$\mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. Since the class
 $\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
is closed under subdirect products by Lemma 2.3, it suffices to show that
$\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
is closed under subdirect products by Lemma 2.3, it suffices to show that
 $\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. To this end, consider a matrix
$\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
. To this end, consider a matrix
![]() $\langle \boldsymbol {A}_{i}, F_{i} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
for each
$\langle \boldsymbol {A}_{i}, F_{i} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i})$
for each
![]() $i \in I$
. By Lemma 2.3, for every
$i \in I$
. By Lemma 2.3, for every
![]() $i \in I$
there is a family
$i \in I$
there is a family
 $\{ \langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle \colon j \in J_{i} \} \subseteq \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
such that
$\{ \langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle \colon j \in J_{i} \} \subseteq \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
such that
 $\langle \boldsymbol {A}_{i}, F_{i} \rangle \leqslant \prod _{j \in J_{i}}\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle $
is a subdirect product. We can assume without loss of generality that
$\langle \boldsymbol {A}_{i}, F_{i} \rangle \leqslant \prod _{j \in J_{i}}\langle \boldsymbol {A}_{i}^{j}, F_{i}^{j}\rangle $
is a subdirect product. We can assume without loss of generality that
![]() $J_{i} = J_{j}$
for every
$J_{i} = J_{j}$
for every
![]() $i, j \in I$
(for instance, by adding trivial matrices to the factors of products when necessary). Accordingly, we drop the index i in each
$i, j \in I$
(for instance, by adding trivial matrices to the factors of products when necessary). Accordingly, we drop the index i in each
![]() $J_{i}$
, and write simply J. Under this convention, it is easy to see that
$J_{i}$
, and write simply J. Under this convention, it is easy to see that
 $$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \leqslant \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{A}_{i}^{j}, F_{i}^{j}\rangle) \end{align*} $$
$$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \leqslant \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{A}_{i}^{j}, F_{i}^{j}\rangle) \end{align*} $$
is a subdirect product. Together with Lemmas 4.13 and 2.3, this yields
 $$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \in \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I}\mathbb{R}(\mathsf{Mod}(\vdash_{i}))) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}\mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) = \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}). \end{align*} $$
$$ \begin{align*} \bigotimes_{i \in I}\langle \boldsymbol{A}_{i}, F_{i} \rangle \in \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}(\bigotimes_{i \in I}\mathbb{R}(\mathsf{Mod}(\vdash_{i}))) \subseteq \mathbb{P}_{\!{\scriptstyle \textrm{SD}}}^{}\mathbb{R}(\mathsf{Mod}(\bigotimes_{i \in I}{\vdash_{i}})) = \mathsf{Mod}^{\equiv}(\bigotimes_{i \in I}{\vdash_{i}}). \end{align*} $$
Hence we conclude that
 $\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
, as desired.
$\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}) \subseteq \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
, as desired.
To prove the second part, we rely on the first one. Consider a matrix
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}}) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}))$
. We can assume without loss of generality that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}}) = \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}))$
. We can assume without loss of generality that
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle \subseteq \prod_{j \in J} \bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle \subseteq \prod_{j \in J} \bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle \end{align*} $$
is a subdirect product for some families
 $\{\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \colon j \in J\} \subseteq \mathsf {Mod}^{\equiv }(\vdash _{i})$
, one for each
$\{\langle \boldsymbol {B}_{i}^{j}, G_{i}^{j}\rangle \colon j \in J\} \subseteq \mathsf {Mod}^{\equiv }(\vdash _{i})$
, one for each
![]() $i \in I$
. Then for every
$i \in I$
. Then for every
![]() $i \in I$
, let
$i \in I$
, let
 $$ \begin{align*} f \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) &\to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle),\\ \pi_i \colon \prod_{i \in I}\prod_{j \in J}B_{i}^{j} &\to \prod_{j \in J}B_{i}^{j} \end{align*} $$
$$ \begin{align*} f \colon \prod_{j \in J} (\bigotimes_{i \in I} \langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle) &\to \bigotimes_{i \in I} (\prod_{j \in J}\langle \boldsymbol{B}_{i}^{j}, G_{i}^{j}\rangle),\\ \pi_i \colon \prod_{i \in I}\prod_{j \in J}B_{i}^{j} &\to \prod_{j \in J}B_{i}^{j} \end{align*} $$
be, respectively, the isomorphism defined in the proof of Lemma 4.10, and the natural projection on the i-th component. Bearing this in mind, for every
![]() $i \in I$
let
$i \in I$
let
![]() $\langle \boldsymbol {C}_{i}, H_{i}\rangle $
be the matrix where
$\langle \boldsymbol {C}_{i}, H_{i}\rangle $
be the matrix where
![]() $\boldsymbol {C}_i$
is the subalgebra
$\boldsymbol {C}_i$
is the subalgebra
 $\pi _i[f[\boldsymbol {A}]] \subseteq \prod _{j \in J}\boldsymbol {B}_{i}^{j}$
and
$\pi _i[f[\boldsymbol {A}]] \subseteq \prod _{j \in J}\boldsymbol {B}_{i}^{j}$
and
![]() $H_i = \pi _i[f[F]]$
.
$H_i = \pi _i[f[F]]$
.
The restriction
![]() $f{\upharpoonright }_A \colon \langle \boldsymbol {A}, F \rangle \to \bigotimes _{i \in I} \langle \boldsymbol {C}_{i}, H_{i}\rangle $
is a well-defined matrix embedding such that
$f{\upharpoonright }_A \colon \langle \boldsymbol {A}, F \rangle \to \bigotimes _{i \in I} \langle \boldsymbol {C}_{i}, H_{i}\rangle $
is a well-defined matrix embedding such that
![]() $\pi _i[f{\upharpoonright }_A [A]] = C_i$
for every
$\pi _i[f{\upharpoonright }_A [A]] = C_i$
for every
![]() $i \in I$
. Hence, we conclude that
$i \in I$
. Hence, we conclude that
 $$ \begin{align*} \langle \boldsymbol{A}, F\rangle \leqslant_{\textrm{sd}} \bigotimes_{i \in I} \langle \boldsymbol{C}_{i}, H_{i}\rangle. \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F\rangle \leqslant_{\textrm{sd}} \bigotimes_{i \in I} \langle \boldsymbol{C}_{i}, H_{i}\rangle. \end{align*} $$
Now, it is not hard to see that
![]() $\langle \boldsymbol {C}_{i}, H_{i}\rangle $
is a subdirect product of
$\langle \boldsymbol {C}_{i}, H_{i}\rangle $
is a subdirect product of
 $\prod _{j \in J}\langle \boldsymbol {B}_i^{j}, G_{i}^{j}\rangle $
, for every
$\prod _{j \in J}\langle \boldsymbol {B}_i^{j}, G_{i}^{j}\rangle $
, for every
![]() $i \in I$
. Since each
$i \in I$
. Since each
![]() $\mathsf {Mod}^{\equiv }(\vdash _{i})$
is closed under subdirect products, this implies that
$\mathsf {Mod}^{\equiv }(\vdash _{i})$
is closed under subdirect products, this implies that
![]() $\langle \boldsymbol {C}_{i}, H_{i}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _i)$
for every
$\langle \boldsymbol {C}_{i}, H_{i}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _i)$
for every
![]() $i \in I$
. This proves the inclusion from left to right.
$i \in I$
. This proves the inclusion from left to right.
To prove the other inclusion, let
![]() $\langle \boldsymbol {A}, F\rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
where
$\langle \boldsymbol {A}, F\rangle \leqslant _{\textrm {sd}} \bigotimes _{i \in I}\langle \boldsymbol {A}_{i}, F_{i}\rangle $
where
![]() $\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathsf {Mod}^{\equiv } (\vdash _i)$
for every
$\langle \boldsymbol {A}_{i}, F_{i}\rangle \in \mathsf {Mod}^{\equiv } (\vdash _i)$
for every
![]() $i \in I$
. Then, as in the proof of Lemma 4.13, we have that
$i \in I$
. Then, as in the proof of Lemma 4.13, we have that
![]() $\langle \boldsymbol {A}, F \rangle $
is a subdirect product of
$\langle \boldsymbol {A}, F \rangle $
is a subdirect product of
 $\prod _{i \in I} \langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\flat }$
. From the fact that
$\prod _{i \in I} \langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\flat }$
. From the fact that
 $\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\flat } \in \bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})$
for every
$\langle \boldsymbol {A}_{i}, F_{i}\rangle ^{\flat } \in \bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})$
for every
![]() $i \in I$
, we obtain that
$i \in I$
, we obtain that
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}))$
.
$\langle \boldsymbol {A}, F \rangle \in \mathbb {P}_{\!{\scriptstyle \textrm {SD}}}^{}(\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i}))$
.
The characterization of
 $\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
given in Proposition 4.5 has a particularly appealing simplification in the case where the index set I is finite.
$\mathsf {Mod}^{\equiv }(\bigotimes _{i \in I}{\vdash _{i}})$
given in Proposition 4.5 has a particularly appealing simplification in the case where the index set I is finite.
Corollary 4.14. If
![]() $\ \vdash $
and
$\ \vdash $
and
![]() $\ \vdash '$
are logics, then
$\ \vdash '$
are logics, then
 $$ \begin{align*} \mathsf{Mod}^{\equiv}({\vdash} \bigotimes {\vdash'}) = \mathsf{Mod}^{\equiv}(\vdash) \bigotimes \mathsf{Mod}^{\equiv}(\vdash'). \end{align*} $$
$$ \begin{align*} \mathsf{Mod}^{\equiv}({\vdash} \bigotimes {\vdash'}) = \mathsf{Mod}^{\equiv}(\vdash) \bigotimes \mathsf{Mod}^{\equiv}(\vdash'). \end{align*} $$
Proof. As shown essentially in [Reference Taylor47, Lemma 1.9 and 1.10], if
![]() $\mathsf {K}_{1}$
and
$\mathsf {K}_{1}$
and
![]() $\mathsf {K}_{2}$
are classes of matrices (resp. algebras) closed under subdirect products, then so is
$\mathsf {K}_{2}$
are classes of matrices (resp. algebras) closed under subdirect products, then so is
![]() $\mathsf {K}_{1} \bigotimes \mathsf {K}_{2}$
. Together with Lemma 2.3, this implies that the class
$\mathsf {K}_{1} \bigotimes \mathsf {K}_{2}$
. Together with Lemma 2.3, this implies that the class
![]() $\mathsf {Mod}^{\equiv }(\vdash ) \bigotimes \mathsf {Mod}^{\equiv }(\vdash ')$
is closed under subdirect products. By Proposition 4.5 we conclude that
$\mathsf {Mod}^{\equiv }(\vdash ) \bigotimes \mathsf {Mod}^{\equiv }(\vdash ')$
is closed under subdirect products. By Proposition 4.5 we conclude that
![]() $\mathsf {Mod}^{\equiv }({\vdash } \bigotimes {\vdash '}) = \mathsf {Mod}^{\equiv }(\vdash ) \bigotimes \mathsf {Mod}^{\equiv }(\vdash ')$
.⊣
$\mathsf {Mod}^{\equiv }({\vdash } \bigotimes {\vdash '}) = \mathsf {Mod}^{\equiv }(\vdash ) \bigotimes \mathsf {Mod}^{\equiv }(\vdash ')$
.⊣
5 Finite suprema need not exist
It is well known that if
![]() $\mathbb {A}$
is a poset whose universe is a set and in which infima of sets exist, then
$\mathbb {A}$
is a poset whose universe is a set and in which infima of sets exist, then
![]() $\mathbb {A}$
is a complete lattice. Unfortunately, the proof of this fact relies on the assumption that the universe of
$\mathbb {A}$
is a complete lattice. Unfortunately, the proof of this fact relies on the assumption that the universe of
![]() $\mathbb {A}$
is a set and, therefore, cannot be applied to the poset
$\mathbb {A}$
is a set and, therefore, cannot be applied to the poset
![]() $\mathsf {Log}$
(which is known to have infima of sets by Theorem 4.6). The situation is entirely different for
$\mathsf {Log}$
(which is known to have infima of sets by Theorem 4.6). The situation is entirely different for
![]() $\mathsf {Log}$
. This section is devoted to prove the following:
$\mathsf {Log}$
. This section is devoted to prove the following:
Theorem 5.1. Finite suprema need not exist in
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
The proof of this theorem builds on a counterexample. Let
![]() $\boldsymbol {A} = \langle A; \lor , \textbf {a}, \textbf {b}, \textbf {0}\rangle $
be the join-semilattice, expanded with constants,Footnote
3
depicted below:
$\boldsymbol {A} = \langle A; \lor , \textbf {a}, \textbf {b}, \textbf {0}\rangle $
be the join-semilattice, expanded with constants,Footnote
3
depicted below:

Then let
![]() $\vdash _{\lor }$
be the logic in countably many variables induced by the set of matrices
$\vdash _{\lor }$
be the logic in countably many variables induced by the set of matrices
Fact 1. We have that
![]() $\langle \boldsymbol {A}, \{ 1 \}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lor })$
.
$\langle \boldsymbol {A}, \{ 1 \}\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lor })$
.
Proof. It is clear that
![]() $\langle \boldsymbol {A}, \{ 1 \}\rangle $
is a model of
$\langle \boldsymbol {A}, \{ 1 \}\rangle $
is a model of
![]() $\vdash _{\lor }$
. Hence it will be enough to prove that
$\vdash _{\lor }$
. Hence it will be enough to prove that

is the identity relation on A. From the definition of
![]() $\vdash _{\lor }$
it follows that
$\vdash _{\lor }$
it follows that
![]() $\{ c, 1\}$
is a deductive filter of
$\{ c, 1\}$
is a deductive filter of
![]() $\vdash _{\lor }$
on
$\vdash _{\lor }$
on
![]() $\boldsymbol {A}$
. Now, an easy computation shows that:
$\boldsymbol {A}$
. Now, an easy computation shows that:
-
(i) The blocks of
 $\boldsymbol {\varOmega }^{\boldsymbol {A}}\{ 1 \}$
are
$\boldsymbol {\varOmega }^{\boldsymbol {A}}\{ 1 \}$
are
 $\{ a, e, c \}, \{ 0, d\}, \{ b \}, \{ 1\}$
.
$\{ a, e, c \}, \{ 0, d\}, \{ b \}, \{ 1\}$
. -
(ii) The blocks of
 $\boldsymbol {\varOmega }^{\boldsymbol {A}}\{ c, 1 \}$
are
$\boldsymbol {\varOmega }^{\boldsymbol {A}}\{ c, 1 \}$
are
 $\{ 0\}, \{ a\}, \{e \}, \{ b, d\}, \{ c, 1\}$
.
$\{ 0\}, \{ a\}, \{e \}, \{ b, d\}, \{ c, 1\}$
.
Together with the fact

this implies that

is the identity relation on A.⊣
Fact 2. The algebraic reducts of the matrices in
![]() $\mathsf {Mod}^{\equiv }(\vdash _{\lor })$
are either trivial or have at least four elements.
$\mathsf {Mod}^{\equiv }(\vdash _{\lor })$
are either trivial or have at least four elements.
Proof. In this proof we assume that semilattices are equipped with the join-order. Consider a matrix
![]() $\langle \boldsymbol {B}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lor })$
such that
$\langle \boldsymbol {B}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lor })$
such that
![]() $\boldsymbol {B}$
is non-trivial. By Corollary 2.6 we know that
$\boldsymbol {B}$
is non-trivial. By Corollary 2.6 we know that
![]() $\boldsymbol {B}$
is a semilattice with constants
$\boldsymbol {B}$
is a semilattice with constants
![]() $\textbf {a}, \textbf {b}, \textbf {0}$
such that
$\textbf {a}, \textbf {b}, \textbf {0}$
such that
Now, since
![]() $\boldsymbol {B}$
is non-trivial, we know that
$\boldsymbol {B}$
is non-trivial, we know that
![]() $F \ne B$
. Together with the fact that
$F \ne B$
. Together with the fact that
this implies that
![]() $\textbf {a}, \textbf {b}, \textbf {0} \notin F$
. Observe that
$\textbf {a}, \textbf {b}, \textbf {0} \notin F$
. Observe that
![]() $\textbf {a} \lor \textbf {b} \in F$
, since
$\textbf {a} \lor \textbf {b} \in F$
, since
![]() $\emptyset \vdash _{\lor }\textbf {a} \lor \textbf {b}$
. Hence, to conclude that B has at least four elements, it will be enough to check that
$\emptyset \vdash _{\lor }\textbf {a} \lor \textbf {b}$
. Hence, to conclude that B has at least four elements, it will be enough to check that
![]() $\textbf {a}, \textbf {b}, \textbf {0}$
are different one from the other. From the fact that
$\textbf {a}, \textbf {b}, \textbf {0}$
are different one from the other. From the fact that
![]() $\textbf {a}, \textbf {b} \notin F$
and
$\textbf {a}, \textbf {b} \notin F$
and
![]() $\textbf {a} \lor \textbf {b} \in F$
, it follows that
$\textbf {a} \lor \textbf {b} \in F$
, it follows that
![]() $\textbf {a}$
and
$\textbf {a}$
and
![]() $\textbf {b}$
are incomparable in the order of
$\textbf {b}$
are incomparable in the order of
![]() $\boldsymbol {B}$
. Together with (6), this implies that
$\boldsymbol {B}$
. Together with (6), this implies that
![]() $\textbf {0}$
is different from
$\textbf {0}$
is different from
![]() $\textbf {a}$
and
$\textbf {a}$
and
![]() $\textbf {b}$
.⊣
$\textbf {b}$
.⊣
We say that a negation algebra is an algebra
![]() $\boldsymbol {B} = \langle B; \lnot \rangle $
where
$\boldsymbol {B} = \langle B; \lnot \rangle $
where
![]() $\lnot $
is a unary operation with at most one fix point, and such that
$\lnot $
is a unary operation with at most one fix point, and such that
![]() $\lnot \lnot a = a $
for all
$\lnot \lnot a = a $
for all
![]() $a \in B$
. We denote by
$a \in B$
. We denote by
![]() $\mathsf {NA}$
the class of negation algebras, and by
$\mathsf {NA}$
the class of negation algebras, and by
![]() $\vdash _{\lnot }$
be the negation fragment of classical propositional logic (formulated in countably many variables). The relation between
$\vdash _{\lnot }$
be the negation fragment of classical propositional logic (formulated in countably many variables). The relation between
![]() $\vdash _{\lnot }$
and
$\vdash _{\lnot }$
and
![]() $\mathsf {NA}$
is captured by the following result:
$\mathsf {NA}$
is captured by the following result:
Fact 3.
![]() $\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is the class of matrices
$\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is the class of matrices
![]() $\langle \boldsymbol {B}, F\rangle $
such that either
$\langle \boldsymbol {B}, F\rangle $
such that either
![]() $\boldsymbol {B}$
is trivial or
$\boldsymbol {B}$
is trivial or
![]() $\boldsymbol {B}$
is a negation algebra and in this case either
$\boldsymbol {B}$
is a negation algebra and in this case either
![]() $F= \emptyset $
or
$F= \emptyset $
or
![]() $F= \{ a \}$
for some
$F= \{ a \}$
for some
![]() $a \in B$
that is not a fixed point of
$a \in B$
that is not a fixed point of
![]() $\lnot $
.
$\lnot $
.
Proof. The interested reader may consult the Appendix for the details.⊣
Now, given a cardinal
![]() $\kappa> 0$
and
$\kappa> 0$
and
![]() $\alpha < \kappa $
, we let
$\alpha < \kappa $
, we let
![]() $\boldsymbol {A}_{\alpha , \kappa }$
be the expansion of
$\boldsymbol {A}_{\alpha , \kappa }$
be the expansion of
![]() $\boldsymbol {A}$
with a constant for every element of A, a unary operation
$\boldsymbol {A}$
with a constant for every element of A, a unary operation
![]() $\lnot $
defined as
$\lnot $
defined as
and with a set of binary operations
![]() $\{ \multimap _{\beta } \colon \beta < \kappa \}$
defined for every
$\{ \multimap _{\beta } \colon \beta < \kappa \}$
defined for every
![]() $\beta < \kappa $
and
$\beta < \kappa $
and
![]() $p, q \in A$
as follows:
$p, q \in A$
as follows:
 $$ \begin{align*} p \multimap_{\beta}q:= \left\{\begin{array}{@{\,}ll} 1 & \text{if}\ p=q\ \text{or}\ \beta \ne \alpha,\\ 0 & \text{if}\ p \ne q\ \text{and}\ \beta = \alpha.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} p \multimap_{\beta}q:= \left\{\begin{array}{@{\,}ll} 1 & \text{if}\ p=q\ \text{or}\ \beta \ne \alpha,\\ 0 & \text{if}\ p \ne q\ \text{and}\ \beta = \alpha.\\ \end{array} \right. \end{align*} $$
Then let
![]() $\vdash _{\kappa }$
be the logic formulated in countably many variables induced by the class of matrices
$\vdash _{\kappa }$
be the logic formulated in countably many variables induced by the class of matrices
![]() $\{ \langle \boldsymbol {A}_{\alpha , \kappa }, \{ 1 \} \rangle \colon \alpha < \kappa \}$
.
$\{ \langle \boldsymbol {A}_{\alpha , \kappa }, \{ 1 \} \rangle \colon \alpha < \kappa \}$
.
Fact 4. For every
![]() $\kappa> 0$
, the logic
$\kappa> 0$
, the logic
![]() $\vdash _{\kappa }$
is equivalential.
$\vdash _{\kappa }$
is equivalential.
Proof. Consider the set
It is easy to see that
![]() $\varDelta $
witnesses the validity of the rules in Theorem 2.7. Hence we conclude that
$\varDelta $
witnesses the validity of the rules in Theorem 2.7. Hence we conclude that
![]() $\vdash _{\kappa }$
is equivalential.⊣
$\vdash _{\kappa }$
is equivalential.⊣
Fact 5. For every
![]() $\kappa> 0$
,
$\kappa> 0$
,
![]() $[\kern-1pt[ \vdash _{\kappa }]\kern-1pt] $
is an upper bound of
$[\kern-1pt[ \vdash _{\kappa }]\kern-1pt] $
is an upper bound of
![]() $[\kern-1pt[ \vdash _{\lor }]\kern-1pt] $
and
$[\kern-1pt[ \vdash _{\lor }]\kern-1pt] $
and
![]() $[\kern-1pt[ \vdash _{\lnot }]\kern-1pt] $
in
$[\kern-1pt[ \vdash _{\lnot }]\kern-1pt] $
in
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
Proof. Consider the class of matrices
![]() $\mathsf {K} := \{ \langle \boldsymbol {A}_{\alpha , \kappa }, \{ 1 \} \rangle \colon \alpha < \kappa \}$
. It is clear that
$\mathsf {K} := \{ \langle \boldsymbol {A}_{\alpha , \kappa }, \{ 1 \} \rangle \colon \alpha < \kappa \}$
. It is clear that
![]() $\vdash _{\kappa }$
is the logic induced by
$\vdash _{\kappa }$
is the logic induced by
![]() $\mathsf {K}$
and that
$\mathsf {K}$
and that
![]() $\mathbb {S}(\mathsf {K}) = \mathsf {K}$
. Then let
$\mathbb {S}(\mathsf {K}) = \mathsf {K}$
. Then let
![]() $\boldsymbol {\tau }$
be the identity translation of
$\boldsymbol {\tau }$
be the identity translation of
![]() $\mathscr {L}_{\vdash _{\lor }}$
into
$\mathscr {L}_{\vdash _{\lor }}$
into
![]() $\mathscr {L}_{\vdash _{\kappa }}$
. By Fact 1 we have
$\mathscr {L}_{\vdash _{\kappa }}$
. By Fact 1 we have
for every
![]() $\langle \boldsymbol {B}, F \rangle \in \mathsf {K}$
. Together with Fact 4 and Proposition 3.9, this implies that
$\langle \boldsymbol {B}, F \rangle \in \mathsf {K}$
. Together with Fact 4 and Proposition 3.9, this implies that
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash _{\lor }$
into
$\vdash _{\lor }$
into
![]() $\vdash _{\kappa }$
.
$\vdash _{\kappa }$
.
A similar argument (requiring Fact 3) shows that
![]() $\vdash _{\lor }$
is also interpretable in
$\vdash _{\lor }$
is also interpretable in
![]() $\vdash _{\kappa }$
.⊣
$\vdash _{\kappa }$
.⊣
Suppose, with a view to contradiction, that there exists the supremum of
![]() $[\kern-1pt[ \vdash _{\lor } ]\kern-1pt] $
and
$[\kern-1pt[ \vdash _{\lor } ]\kern-1pt] $
and
![]() $[\kern-1pt[ \vdash _{\lnot } ]\kern-1pt] $
in
$[\kern-1pt[ \vdash _{\lnot } ]\kern-1pt] $
in
![]() $\mathsf {Log}$
, i.e., that there exists a logic
$\mathsf {Log}$
, i.e., that there exists a logic
![]() $\vdash $
such that
$\vdash $
such that
From now on, our aim is to obtain a contradiction.
Fact 6. For every
![]() $\kappa>0$
, we have
$\kappa>0$
, we have
![]() $[\kern-1pt[ \vdash ]\kern-1pt] \leqslant [\kern-1pt[ \vdash _{\kappa }]\kern-1pt] $
.
$[\kern-1pt[ \vdash ]\kern-1pt] \leqslant [\kern-1pt[ \vdash _{\kappa }]\kern-1pt] $
.
Proof. This is a direct consequence of Fact 5.⊣
Now, since
![]() $\vdash $
is a logic, its language is a set, say of cardinality
$\vdash $
is a logic, its language is a set, say of cardinality
![]() $\kappa $
. We can assume without loss of generality that
$\kappa $
. We can assume without loss of generality that
![]() $\kappa $
is infinite (if it is not, then we can add to it infinitely many unary operations whose interpretation in
$\kappa $
is infinite (if it is not, then we can add to it infinitely many unary operations whose interpretation in
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
would be the identity map). By Fact 6 there is an interpretation
$\mathsf {Mod}^{\equiv }(\vdash )$
would be the identity map). By Fact 6 there is an interpretation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{\kappa ^{+}}$
.
$\vdash _{\kappa ^{+}}$
.
Fact 7. There is
![]() $\alpha < \kappa ^{+}$
such that the symbol
$\alpha < \kappa ^{+}$
such that the symbol
![]() $\multimap _{\alpha }$
does not appear in the terms
$\multimap _{\alpha }$
does not appear in the terms
![]() $\{ \boldsymbol {\tau }(\varphi ) \colon \varphi \in \mathscr {L}_{\vdash } \}$
.
$\{ \boldsymbol {\tau }(\varphi ) \colon \varphi \in \mathscr {L}_{\vdash } \}$
.
Proof. Straightforward.⊣
From now on we will work with the special
![]() $\alpha < \kappa ^{+}$
provided by Fact 7. Let
$\alpha < \kappa ^{+}$
provided by Fact 7. Let
 $ \skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
be the
$ \skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
be the
![]() $\{ \multimap _{\alpha } \}$
-free reduct of
$\{ \multimap _{\alpha } \}$
-free reduct of
![]() $\boldsymbol {A}_{\alpha , \kappa ^{+}}$
.
$\boldsymbol {A}_{\alpha , \kappa ^{+}}$
.
Fact 8. The algebra
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
is term-equivalent to
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
is term-equivalent to
 $$ \begin{align*} \langle A; \lor^{\boldsymbol{A}_{\alpha, \kappa^{+}}}, \lnot^{\boldsymbol{A}_{\alpha, \kappa^{+}}}, \textbf{a}, \textbf{b}, \textbf{0}, e\rangle. \end{align*} $$
$$ \begin{align*} \langle A; \lor^{\boldsymbol{A}_{\alpha, \kappa^{+}}}, \lnot^{\boldsymbol{A}_{\alpha, \kappa^{+}}}, \textbf{a}, \textbf{b}, \textbf{0}, e\rangle. \end{align*} $$
Proof. Using negation, it is easy to see that all constants from
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
are definable in the displayed algebra. Moreover, if
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
are definable in the displayed algebra. Moreover, if
![]() $\beta \ne \alpha $
, then
$\beta \ne \alpha $
, then
 $\multimap _{\beta }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}$
is a constant map. This shows that all term-functions of
$\multimap _{\beta }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}$
is a constant map. This shows that all term-functions of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
are also term-functions of the algebra in the display. The converse is obvious.⊣
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
are also term-functions of the algebra in the display. The converse is obvious.⊣
In what follows we will work under the identification of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
with the algebra displayed in Fact 8.
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
with the algebra displayed in Fact 8.
Fact 9. If
![]() $\gamma (x)$
is a formula of
$\gamma (x)$
is a formula of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
such that
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
such that
 $\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra, then
$\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra, then
![]() $\gamma $
can be obtained as a composition of
$\gamma $
can be obtained as a composition of
![]() $\lor $
and
$\lor $
and
![]() $\lnot $
.
$\lnot $
.
Proof. Assume that
 $\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra. Suppose, with a view to contradiction, that either
$\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra. Suppose, with a view to contradiction, that either
![]() $\textbf {0}$
or
$\textbf {0}$
or
![]() $\textbf {a}$
or
$\textbf {a}$
or
![]() $\textbf {b}$
occur in
$\textbf {b}$
occur in
![]() $\gamma $
. It is not hard to see that this implies that
$\gamma $
. It is not hard to see that this implies that
 $e \notin \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}[A]$
. However, since
$e \notin \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}[A]$
. However, since
 $\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\rangle $
is a negation algebra, we know that
$\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\rangle $
is a negation algebra, we know that
 $$ \begin{align*} e = \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}} \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}}(e) \in \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}}[A], \end{align*} $$
$$ \begin{align*} e = \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}} \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}}(e) \in \gamma^{\hat{\boldsymbol{A}}_{\alpha, \kappa^{+}}}[A], \end{align*} $$
which is false. Hence we conclude that
![]() $\textbf {0}$
,
$\textbf {0}$
,
![]() $\textbf {a}$
, and
$\textbf {a}$
, and
![]() $\textbf {b}$
do not occur in
$\textbf {b}$
do not occur in
![]() $\gamma $
.
$\gamma $
.
It only remains to prove that e does not occur in
![]() $\gamma $
. Suppose the contrary, with a view to contradiction. An easy induction on the construction of formulas shows that if
$\gamma $
. Suppose the contrary, with a view to contradiction. An easy induction on the construction of formulas shows that if
![]() $\varphi (x)$
is a formula of
$\varphi (x)$
is a formula of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
in which
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
in which
![]() $\textbf {0}$
,
$\textbf {0}$
,
![]() $\textbf {a}$
, and
$\textbf {a}$
, and
![]() $\textbf {b}$
do not occur and in which e occurs, then
$\textbf {b}$
do not occur and in which e occurs, then
 $\varphi ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}(0) \in \{ e, \textbf {a}, c \}$
. As
$\varphi ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}(0) \in \{ e, \textbf {a}, c \}$
. As
![]() $\textbf {0}$
,
$\textbf {0}$
,
![]() $\textbf {a}$
, and
$\textbf {a}$
, and
![]() $\textbf {b}$
do not occur in the composition
$\textbf {b}$
do not occur in the composition
![]() $\gamma (\gamma (x))$
, this means that
$\gamma (\gamma (x))$
, this means that
 $\gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}(0) \ne 0$
. But this contradicts the fact that
$\gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}(0) \ne 0$
. But this contradicts the fact that
 $\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\rangle $
is a negation algebra, as desired.⊣
$\langle A; \gamma ^{\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}}\rangle $
is a negation algebra, as desired.⊣
Fact 10. The blocks of
 $\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
are
$\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
are
![]() $\{ 0, d \}, \{a, c, e \}, \{ b \}, \{ 1 \}$
.
$\{ 0, d \}, \{a, c, e \}, \{ b \}, \{ 1 \}$
.
Proof. By Fact 7 we know that the term-functions of
![]() $\boldsymbol {A}^{\boldsymbol {\tau }}_{\alpha , \kappa ^{+}}$
are also term-functions of
$\boldsymbol {A}^{\boldsymbol {\tau }}_{\alpha , \kappa ^{+}}$
are also term-functions of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. In particular, this means that
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. In particular, this means that
 $\textrm {Con} \skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}} \subseteq \textrm {Con} \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}$
.
$\textrm {Con} \skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}} \subseteq \textrm {Con} \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}$
.
Consider the equivalence relation
![]() $\theta $
on A determined by the partition in the statement. Using for instance Fact 8, it is easy to see that
$\theta $
on A determined by the partition in the statement. Using for instance Fact 8, it is easy to see that
![]() $\theta $
is a congruence of
$\theta $
is a congruence of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. Then
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. Then
![]() $\theta $
is also a congruence of
$\theta $
is also a congruence of
![]() $\boldsymbol {A}^{\boldsymbol {\tau }}_{\alpha , \kappa ^{+}}$
. As
$\boldsymbol {A}^{\boldsymbol {\tau }}_{\alpha , \kappa ^{+}}$
. As
![]() $\theta $
is compatible with
$\theta $
is compatible with
![]() $\{ 1 \}$
, this implies that
$\{ 1 \}$
, this implies that
 $\theta \subseteq \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
.
$\theta \subseteq \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
.
As a consequence, we obtain that
 $A / \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
is a set of at most four elements. Moreover, since
$A / \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
is a set of at most four elements. Moreover, since
 $\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
is compatible with
$\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
is compatible with
![]() $\{ 1\}$
, we know that
$\{ 1\}$
, we know that
 $\langle 0, 1 \rangle \notin \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
. Therefore we have
$\langle 0, 1 \rangle \notin \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
. Therefore we have
 $$ \begin{align} 2 \leqslant \vert A / \boldsymbol{\varOmega}^{\boldsymbol{A}_{\alpha, \kappa^{+}}^{\boldsymbol{\tau}}}\{ 1 \} \vert \leqslant 4. \end{align} $$
$$ \begin{align} 2 \leqslant \vert A / \boldsymbol{\varOmega}^{\boldsymbol{A}_{\alpha, \kappa^{+}}^{\boldsymbol{\tau}}}\{ 1 \} \vert \leqslant 4. \end{align} $$
Now, it is easy to see that
![]() $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathbb {R}(\mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}}))$
. Since
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathbb {R}(\mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}}))$
. Since
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{\kappa ^{+}}$
, this implies that
$\vdash _{\kappa ^{+}}$
, this implies that
 $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle \in \mathsf {Mod}(\vdash )$
and, therefore, that
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle \in \mathsf {Mod}(\vdash )$
and, therefore, that
 $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle ^{\ast } \in \mathsf {Mod}^{\equiv }(\vdash )$
. Together with Fact 2 and
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle ^{\ast } \in \mathsf {Mod}^{\equiv }(\vdash )$
. Together with Fact 2 and
![]() ${\vdash _{\lor }} \leqslant {\vdash }$
, this implies that either the matrix
${\vdash _{\lor }} \leqslant {\vdash }$
, this implies that either the matrix
![]() $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle ^{\ast }$
is trivial, or the congruence
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \} \rangle ^{\ast }$
is trivial, or the congruence
 $\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
has at least four blocks. By (8) we conclude that
$\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
has at least four blocks. By (8) we conclude that
 $\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
has exactly four blocks. Together with the fact that
$\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
has exactly four blocks. Together with the fact that
 $\theta \subseteq \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
, this implies that
$\theta \subseteq \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
, this implies that
 $\theta = \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
.⊣
$\theta = \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
.⊣
We are now ready to produce the desired contradiction. To this end, recall that there is an interpretation
![]() $\boldsymbol {\rho }$
of
$\boldsymbol {\rho }$
of
![]() $\vdash _{\lnot }$
into
$\vdash _{\lnot }$
into
![]() $\vdash $
. Since
$\vdash $
. Since
![]() $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
, we can apply Fact 3 obtaining that
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
, we can apply Fact 3 obtaining that
 $\langle A; \boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra. By Fact 7 we know that the function
$\langle A; \boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}} \rangle $
is a negation algebra. By Fact 7 we know that the function
 $\boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}\colon A \to A$
is a term-function of
$\boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}\colon A \to A$
is a term-function of
 $\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. Hence we can apply Fact 9 obtaining that
$\skew6\hat {\boldsymbol{A}}_{\alpha , \kappa ^{+}}$
. Hence we can apply Fact 9 obtaining that
 $\boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}$
can be produced as a composition of the functions
$\boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}}$
can be produced as a composition of the functions
This yields that
 $$ \begin{align} \boldsymbol{\tau}\boldsymbol{\rho}(\lnot)^{\boldsymbol{A}_{\alpha, \kappa^{+}}}(0) \in \{ 0, d\} \text{ and }\boldsymbol{\tau}\boldsymbol{\rho}(\lnot)^{\boldsymbol{A}_{\alpha, \kappa^{+}}}(e) = e. \end{align} $$
$$ \begin{align} \boldsymbol{\tau}\boldsymbol{\rho}(\lnot)^{\boldsymbol{A}_{\alpha, \kappa^{+}}}(0) \in \{ 0, d\} \text{ and }\boldsymbol{\tau}\boldsymbol{\rho}(\lnot)^{\boldsymbol{A}_{\alpha, \kappa^{+}}}(e) = e. \end{align} $$
From the fact that
![]() $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
it follows that
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}, \{ 1 \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
it follows that
 $\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \}\rangle \in \mathsf {Mod}(\vdash )$
. In particular, this implies that
$\langle \boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}, \{ 1 \}\rangle \in \mathsf {Mod}(\vdash )$
. In particular, this implies that
where
 $\theta := \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
. Together with Fact 3, this yields that
$\theta := \boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha , \kappa ^{+}}^{\boldsymbol {\tau }}}\{ 1 \}$
. Together with Fact 3, this yields that
 $\langle A/ \theta; \boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}/ \theta }\rangle $
is a negation algebra. However, by Fact 10 and (9) this negation algebra has two distinct fixed points for negation (namely
$\langle A/ \theta; \boldsymbol {\tau }\boldsymbol {\rho }(\lnot )^{\boldsymbol {A}_{\alpha , \kappa ^{+}}/ \theta }\rangle $
is a negation algebra. However, by Fact 10 and (9) this negation algebra has two distinct fixed points for negation (namely
![]() $0/\theta $
and
$0/\theta $
and
![]() $e/ \theta $
), which is impossible. Hence we reached a contradiction, establishing Theorem 5.1.
$e/ \theta $
), which is impossible. Hence we reached a contradiction, establishing Theorem 5.1.
6 The lattice of equivalential logics
Even if suprema need not exist in
![]() $\mathsf {Log}$
there is an important subsemilattice of
$\mathsf {Log}$
there is an important subsemilattice of
![]() $\mathsf {Log}$
where suprema exist, i.e., the lattice of equivalential logics.
$\mathsf {Log}$
where suprema exist, i.e., the lattice of equivalential logics.
Proposition 6.1.
-
(i) Let
 $\vdash $
and
$\vdash $
and
 $\vdash '$
be logics. If
$\vdash '$
be logics. If
 $\vdash $
is equivalential and
$\vdash $
is equivalential and
 ${\vdash } \leqslant {\vdash '}$
, then
${\vdash } \leqslant {\vdash '}$
, then
 $\vdash '$
is also equivalential.
$\vdash '$
is also equivalential. -
(ii) If
 $\{ \vdash _{i} \colon i \in I \}$
is a family of equivalential logics, then
$\{ \vdash _{i} \colon i \in I \}$
is a family of equivalential logics, then
 $\bigotimes _{i \in I} {\vdash _{i}}$
is equivalential.
$\bigotimes _{i \in I} {\vdash _{i}}$
is equivalential.
Proof. (i): Let
![]() $\varDelta (x, y)$
be the set of formulas witnessing the fact that
$\varDelta (x, y)$
be the set of formulas witnessing the fact that
![]() $\vdash $
is equivalential, as in Theorem 2.7. Moreover, let
$\vdash $
is equivalential, as in Theorem 2.7. Moreover, let
![]() $\boldsymbol {\tau }$
be an interpretation of
$\boldsymbol {\tau }$
be an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash '$
. We consider the set
$\vdash '$
. We consider the set
![]() $\varSigma (x, y) := \boldsymbol {\tau }[\varDelta ]$
of formulas of
$\varSigma (x, y) := \boldsymbol {\tau }[\varDelta ]$
of formulas of
![]() $\mathscr {L}_{\vdash '}$
. In order to establish that
$\mathscr {L}_{\vdash '}$
. In order to establish that
![]() $\vdash '$
is equivalential, it will be enough to show that
$\vdash '$
is equivalential, it will be enough to show that
![]() $\varSigma $
and
$\varSigma $
and
![]() $\vdash '$
satisfy the conditions in Theorem 2.7.
$\vdash '$
satisfy the conditions in Theorem 2.7.
From Proposition 3.3 it follows that
![]() $\emptyset \vdash ' \varSigma (x, x)$
and
$\emptyset \vdash ' \varSigma (x, x)$
and
![]() $x, \varSigma (x, y) \vdash ' y$
. It only remains to prove that for every n-ary connective
$x, \varSigma (x, y) \vdash ' y$
. It only remains to prove that for every n-ary connective
![]() $\ast $
of
$\ast $
of
![]() $\vdash '$
,
$\vdash '$
,
 $$ \begin{align} \bigcup_{1 \leqslant i \leqslant n}\varSigma(x_{i}, y_{i}) \vdash' \varSigma(\ast(x_{1}, \dots, x_{n}), \ast(y_{1}, \dots, y_{n})). \end{align} $$
$$ \begin{align} \bigcup_{1 \leqslant i \leqslant n}\varSigma(x_{i}, y_{i}) \vdash' \varSigma(\ast(x_{1}, \dots, x_{n}), \ast(y_{1}, \dots, y_{n})). \end{align} $$
To this end, consider an n-ary connective
![]() $\ast $
of
$\ast $
of
![]() $\vdash '$
, a matrix
$\vdash '$
, a matrix
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
, and tuples
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ')$
, and tuples
![]() $\vec {a}, \vec {c} \in A^{n}$
such that
$\vec {a}, \vec {c} \in A^{n}$
such that
 $$ \begin{align*} \bigcup_{1 \leqslant i \leqslant n}\varSigma^{\boldsymbol{A}}(a_{i}, c_{i}) \subseteq F{\kern -1pt}. \end{align*} $$
$$ \begin{align*} \bigcup_{1 \leqslant i \leqslant n}\varSigma^{\boldsymbol{A}}(a_{i}, c_{i}) \subseteq F{\kern -1pt}. \end{align*} $$
Since
![]() $\varSigma = \boldsymbol {\tau }[\varDelta ]$
, we have
$\varSigma = \boldsymbol {\tau }[\varDelta ]$
, we have
 $$ \begin{align*} \bigcup_{1 \leqslant i \leqslant n}\varDelta^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_{i}, c_{i}) \subseteq F{\kern -1pt}. \end{align*} $$
$$ \begin{align*} \bigcup_{1 \leqslant i \leqslant n}\varDelta^{\boldsymbol{A}^{\boldsymbol{\tau}}}(a_{i}, c_{i}) \subseteq F{\kern -1pt}. \end{align*} $$
As
![]() $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
![]() $\vdash $
, and
$\vdash $
, and
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {R}(\mathsf {Mod}(\vdash ))$
, the above display implies that
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash ) = \mathbb {R}(\mathsf {Mod}(\vdash ))$
, the above display implies that
![]() $\vec {a} = \vec {c}$
. As a consequence, we obtain that
$\vec {a} = \vec {c}$
. As a consequence, we obtain that
![]() $\ast ^{\boldsymbol {A}}(\vec {a}) = \ast ^{\boldsymbol {A}}(\vec {c}\kern 0.4pt )$
. Since
$\ast ^{\boldsymbol {A}}(\vec {a}) = \ast ^{\boldsymbol {A}}(\vec {c}\kern 0.4pt )$
. Since
![]() $\emptyset \vdash ' \varSigma (x, x)$
and
$\emptyset \vdash ' \varSigma (x, x)$
and
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
, this yields
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
, this yields
Hence we conclude that (10) holds.
(ii): Given
![]() $i \in I$
, let
$i \in I$
, let
![]() $\varDelta _{i}(x, y)$
be a set of congruence formulas for
$\varDelta _{i}(x, y)$
be a set of congruence formulas for
![]() $\vdash _{i}$
. Observe that the Cartesian product
$\vdash _{i}$
. Observe that the Cartesian product
![]() $\prod _{i \in I} \varDelta _{i}$
can be viewed as a set
$\prod _{i \in I} \varDelta _{i}$
can be viewed as a set
![]() $\varDelta (x, y)$
of formulas of
$\varDelta (x, y)$
of formulas of
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
. Since the various
$\bigotimes _{i \in I}{\vdash _{i}}$
. Since the various
![]() $\varDelta _{i}$
satisfy the rules in Theorem 2.7, and
$\varDelta _{i}$
satisfy the rules in Theorem 2.7, and
![]() $\bigotimes _{i \in I}{\vdash _{i}}$
is the logic induced by
$\bigotimes _{i \in I}{\vdash _{i}}$
is the logic induced by
 $\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})$
, it is easy to see that the set
$\bigotimes _{i \in I} \mathsf {Mod}^{\equiv }(\vdash _{i})$
, it is easy to see that the set
![]() $\varDelta $
satisfies the rules in Theorem 2.7 as well. As a consequence, we conclude that
$\varDelta $
satisfies the rules in Theorem 2.7 as well. As a consequence, we conclude that
![]() $\bigotimes _{i \in I} {\vdash _{i}}$
is an equivalential logic.⊣
$\bigotimes _{i \in I} {\vdash _{i}}$
is an equivalential logic.⊣
The above result motivates the following definition:
Definition 6.2. Let
![]() $\mathsf {Equiv}$
be the subposet of
$\mathsf {Equiv}$
be the subposet of
![]() $\mathsf {Log}$
that contains the classes
$\mathsf {Log}$
that contains the classes
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
such that
$[\kern-1pt[ \vdash ]\kern-1pt] $
such that
![]() $\vdash $
is an equivalential logic.
$\vdash $
is an equivalential logic.
From Proposition 6.1 it follows that
![]() $\mathsf {Equiv}$
is a set-complete filter of
$\mathsf {Equiv}$
is a set-complete filter of
![]() $\mathsf {Log}$
, i.e., an upset that is closed under infima of sets. Moreover, we shall prove that in
$\mathsf {Log}$
, i.e., an upset that is closed under infima of sets. Moreover, we shall prove that in
![]() $\mathsf {Equiv}$
suprema of sets exist.
$\mathsf {Equiv}$
suprema of sets exist.
Definition 6.3. Given a family
![]() $\{\mathscr {L}_i \colon i \in I \}$
of languages, we let
$\{\mathscr {L}_i \colon i \in I \}$
of languages, we let
![]() $\bigoplus _{i \in I}{\mathscr {L}_i}$
be the language consisting of the disjoint union of the various
$\bigoplus _{i \in I}{\mathscr {L}_i}$
be the language consisting of the disjoint union of the various
![]() $\mathscr {L}_{i}$
. Moreover, given a family
$\mathscr {L}_{i}$
. Moreover, given a family
![]() $\{ \vdash _{i} \colon i \in I \}$
of equivalential logics, we let
$\{ \vdash _{i} \colon i \in I \}$
of equivalential logics, we let
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
be the logic in the language
$\bigoplus _{i \in I}{\vdash _{i}}$
be the logic in the language
![]() $\bigoplus _{i \in I}{\mathscr {L}_i}$
formulated in
$\bigoplus _{i \in I}{\mathscr {L}_i}$
formulated in
![]() $\varSigma _{i \in I} \kappa _{\vdash _{i}}$
variables and induced by the following class of
$\varSigma _{i \in I} \kappa _{\vdash _{i}}$
variables and induced by the following class of
![]() $\bigoplus _{i \in I}{\mathscr {L}_{\vdash _{i}}}$
-matrices:
$\bigoplus _{i \in I}{\mathscr {L}_{\vdash _{i}}}$
-matrices:
We will show that
![]() $[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}}]\kern-1pt] $
is the supremum of
$[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}}]\kern-1pt] $
is the supremum of
![]() $\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I \}$
both in
$\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I \}$
both in
![]() $\mathsf {Log}$
and
$\mathsf {Log}$
and
![]() $\mathsf {Equiv}$
.
$\mathsf {Equiv}$
.
Lemma 6.4. Let
![]() $\{ \vdash _{i} \colon i \in I \}$
be a family of equivalential logics.
$\{ \vdash _{i} \colon i \in I \}$
be a family of equivalential logics.
-
(i) If
 $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
 $\vdash _{i}$
, then so it is for
$\vdash _{i}$
, then so it is for
 $\bigoplus _{i \in I}{\vdash _{i}}$
.
$\bigoplus _{i \in I}{\vdash _{i}}$
. -
(ii) The logic
 $\bigoplus _{i \in I}{\vdash _{i}}$
is equivalential.
$\bigoplus _{i \in I}{\vdash _{i}}$
is equivalential. -
(iii)
 $\mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
is the class of matrices in (11).
$\mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
is the class of matrices in (11). -
(iv)
 $[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is the supremum of
$[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}} ]\kern-1pt] $
is the supremum of
 $\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I\}$
both in
$\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I\}$
both in
 $\mathsf {Equiv}$
and in
$\mathsf {Equiv}$
and in
 $\mathsf {Log}$
.
$\mathsf {Log}$
.
Proof. (i): Observe that the
![]() $\mathscr {L}_{\vdash _{i}}$
-reducts of the matrices in (11) are reduced. Together with the fact that
$\mathscr {L}_{\vdash _{i}}$
-reducts of the matrices in (11) are reduced. Together with the fact that
![]() $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
![]() $\vdash _{i}$
, this easily implies that
$\vdash _{i}$
, this easily implies that
![]() $\varDelta $
satisfies the conditions of Theorem 2.7 for
$\varDelta $
satisfies the conditions of Theorem 2.7 for
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
. As a consequence, we conclude that
$\bigoplus _{i \in I}{\vdash _{i}}$
. As a consequence, we conclude that
![]() $\varDelta $
is a set of congruence formulas for
$\varDelta $
is a set of congruence formulas for
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
.
$\bigoplus _{i \in I}{\vdash _{i}}$
.
(ii): Immediate from (i). (iii): Let
![]() $\mathsf {M}$
be the class of matrices in (11). It is easy to see that the matrices in
$\mathsf {M}$
be the class of matrices in (11). It is easy to see that the matrices in
![]() $\mathsf {M}$
are reduced and, therefore, that
$\mathsf {M}$
are reduced and, therefore, that
 $\mathsf {M} \subseteq \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
. To prove the other inclusion, consider
$\mathsf {M} \subseteq \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
. To prove the other inclusion, consider
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
. As
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
. As
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
is equivalential by (ii), we can apply Theorem 2.7 obtaining that
$\bigoplus _{i \in I}{\vdash _{i}}$
is equivalential by (ii), we can apply Theorem 2.7 obtaining that
 $\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigoplus _{i \in I}{\vdash _{i}}))$
. It will be enough to show that (for every
$\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\bigoplus _{i \in I}{\vdash _{i}}))$
. It will be enough to show that (for every
![]() $i \in I$
) the
$i \in I$
) the
![]() $\mathscr {L}_{\vdash _{i}}$
-reduct
$\mathscr {L}_{\vdash _{i}}$
-reduct
![]() $\langle \boldsymbol {A}^{-}, F \rangle $
of
$\langle \boldsymbol {A}^{-}, F \rangle $
of
![]() $\langle \boldsymbol {A}, F \rangle $
is a reduced model of
$\langle \boldsymbol {A}, F \rangle $
is a reduced model of
![]() $\vdash _{i}$
. The fact that
$\vdash _{i}$
. The fact that
![]() $\langle \boldsymbol {A}^{-}, F\rangle $
is a model of
$\langle \boldsymbol {A}^{-}, F\rangle $
is a model of
![]() $\vdash _{i}$
is clear. To prove that it is reduced, let
$\vdash _{i}$
is clear. To prove that it is reduced, let
![]() $\varDelta $
be a set of congruence formulas of
$\varDelta $
be a set of congruence formulas of
![]() $\vdash _{i}$
. By (i) we know that
$\vdash _{i}$
. By (i) we know that
![]() $\varDelta $
is also a set of congruence formulas for
$\varDelta $
is also a set of congruence formulas for
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
. Together with the fact that
$\bigoplus _{i \in I}{\vdash _{i}}$
. Together with the fact that
![]() $\langle \boldsymbol {A}, F \rangle $
is a reduced model of
$\langle \boldsymbol {A}, F \rangle $
is a reduced model of
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
, this implies that for every
$\bigoplus _{i \in I}{\vdash _{i}}$
, this implies that for every
![]() $a, b \in A$
,
$a, b \in A$
,
Since
![]() $\langle \boldsymbol {A}^{-}, F \rangle $
is a model of
$\langle \boldsymbol {A}^{-}, F \rangle $
is a model of
![]() $\vdash _{i}$
, this implies that the matrix
$\vdash _{i}$
, this implies that the matrix
![]() $\langle \boldsymbol {A}^{-}, F \rangle $
is reduced.
$\langle \boldsymbol {A}^{-}, F \rangle $
is reduced.
(iv): By (i) we know that
![]() $[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}} ]\kern-1pt] $
belongs to
$[\kern-1pt[ \bigoplus _{i \in I}{\vdash _{i}} ]\kern-1pt] $
belongs to
![]() $\mathsf {Equiv}$
. Hence it will be enough to show that it is the supremum of
$\mathsf {Equiv}$
. Hence it will be enough to show that it is the supremum of
![]() $\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I\}$
in
$\{ [\kern-1pt[ \vdash _{i}]\kern-1pt] \colon i \in I\}$
in
![]() $\mathsf {Log}$
. Recall from Theorem 2.7 that
$\mathsf {Log}$
. Recall from Theorem 2.7 that
![]() $\mathsf {Mod}^{\equiv }(\vdash _{i}) = \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
for all
$\mathsf {Mod}^{\equiv }(\vdash _{i}) = \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
for all
![]() $i \in I$
. Together with (iii), this implies that
$i \in I$
. Together with (iii), this implies that
![]() ${\vdash _{j}} \leqslant {\bigoplus _{i \in I}{\vdash _{i}}}$
for all
${\vdash _{j}} \leqslant {\bigoplus _{i \in I}{\vdash _{i}}}$
for all
![]() $j \in I$
.
$j \in I$
.
Now, consider a logic
![]() $\vdash $
such that
$\vdash $
such that
![]() ${\vdash _{i}} \leqslant {\vdash }$
for every
${\vdash _{i}} \leqslant {\vdash }$
for every
![]() $i \in I$
. Then for every
$i \in I$
. Then for every
![]() $i \in I$
, there is an interpretation
$i \in I$
, there is an interpretation
![]() $\boldsymbol {\tau }_{i}$
of
$\boldsymbol {\tau }_{i}$
of
![]() $\vdash _{i}$
into
$\vdash _{i}$
into
![]() $\vdash $
. Observe that all these
$\vdash $
. Observe that all these
![]() $\boldsymbol {\tau }_{i}$
can be joined together into a translation
$\boldsymbol {\tau }_{i}$
can be joined together into a translation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\bigoplus _{i \in I}{\mathscr {L}_{i}}$
into
$\bigoplus _{i \in I}{\mathscr {L}_{i}}$
into
![]() $\mathscr {L}_{\vdash }$
. We will show that
$\mathscr {L}_{\vdash }$
. We will show that
![]() $\boldsymbol {\tau }$
is also an interpretation of
$\boldsymbol {\tau }$
is also an interpretation of
![]() $\bigoplus _{i \in I}{\vdash _{i}}$
into
$\bigoplus _{i \in I}{\vdash _{i}}$
into
![]() $\vdash $
. To this end, consider a matrix
$\vdash $
. To this end, consider a matrix
![]() $\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
. We know that
$\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
. We know that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }_{i}}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i}) = \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }_{i}}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash _{i}) = \mathbb {R}(\mathsf {Mod}(\vdash _{i}))$
for every
![]() $i \in I$
. This implies that the matrix
$i \in I$
. This implies that the matrix
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F\rangle $
belongs to the class in (11). By (iii) we conclude that
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F\rangle $
belongs to the class in (11). By (iii) we conclude that
 $\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
.⊣
$\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\bigoplus _{i \in I}{\vdash _{i}})$
.⊣
As a consequence, we obtain the following:
Theorem 6.5.
![]() $\mathsf {Equiv}$
is a set-complete lattice, i.e., infima and suprema of subsets of
$\mathsf {Equiv}$
is a set-complete lattice, i.e., infima and suprema of subsets of
![]() $\mathsf {Equiv}$
exist. Moreover, these infima and suprema coincide with those of
$\mathsf {Equiv}$
exist. Moreover, these infima and suprema coincide with those of
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
Problem 1. Do suprema of protoalgebraic logics [Reference Font15] exist as well?
An adaptation of an argument given in [Reference García and Taylor20, p. 34] shows that the lattice
![]() $\mathsf {Equiv}$
is not modular. However, to our knowledge, the following problem remains open:
$\mathsf {Equiv}$
is not modular. However, to our knowledge, the following problem remains open:
Problem 2. Do
![]() $\mathsf {Equiv}$
and
$\mathsf {Equiv}$
and
![]() $\mathsf {Var}$
satisfy any non-trivial lattice equation?
$\mathsf {Var}$
satisfy any non-trivial lattice equation?
7 The top and the bottom
In this section we will describe the top and the bottom parts of
![]() $\mathsf {Log}$
. To this end, recall that a logic
$\mathsf {Log}$
. To this end, recall that a logic
![]() $\vdash $
is inconsistent if
$\vdash $
is inconsistent if
![]() $\varGamma \vdash \varphi $
for every
$\varGamma \vdash \varphi $
for every
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
. Similarly,
$\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
. Similarly,
![]() $\vdash $
is said to be almost inconsistent if it lacks theorems and
$\vdash $
is said to be almost inconsistent if it lacks theorems and
![]() $\varGamma \vdash \varphi $
for every
$\varGamma \vdash \varphi $
for every
![]() $\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
such that
$\varGamma \cup \{ \varphi \} \subseteq Fm(\vdash )$
such that
![]() $\varGamma \ne \emptyset $
. The following result is part of the folklore.
$\varGamma \ne \emptyset $
. The following result is part of the folklore.
Lemma 7.1. A logic
![]() $\vdash $
is inconsistent (resp. almost inconsistent) if and only if
$\vdash $
is inconsistent (resp. almost inconsistent) if and only if
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
is the class of isomorphic copies of
$\mathsf {Mod}^{\equiv }(\vdash )$
is the class of isomorphic copies of
![]() $\langle {\boldsymbol {1}}, \{ 1 \} \rangle $
(resp. of
$\langle {\boldsymbol {1}}, \{ 1 \} \rangle $
(resp. of
![]() $\langle {\boldsymbol {1}}, \{ 1 \} \rangle $
and
$\langle {\boldsymbol {1}}, \{ 1 \} \rangle $
and
![]() $\langle {\boldsymbol {1}}, \emptyset \rangle $
).
$\langle {\boldsymbol {1}}, \emptyset \rangle $
).
The lemma easily implies that any two inconsistent (resp. almost inconsistent) logics are equi-interpretable (since any translation between their languages is necessarily an interpretation).
Corollary 7.2. The class of all inconsistent (resp. almost inconsistent) logics is a member of
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
In the light of the above corollary, the main results of this section can be summarized as follows:
Theorem 7.3. The poset
![]() $\mathsf {Log}$
lacks a minimum. Moreover, its maximum is the class of all inconsistent logics, and its unique coatom is the class
$\mathsf {Log}$
lacks a minimum. Moreover, its maximum is the class of all inconsistent logics, and its unique coatom is the class
![]() $\mathcal {K}$
of all almost inconsistent logics. In particular, a logic
$\mathcal {K}$
of all almost inconsistent logics. In particular, a logic
![]() $\vdash $
lacks theorems if and only if
$\vdash $
lacks theorems if and only if
![]() $[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
.
$[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
.
Proof. We first prove that
![]() $\mathsf {Log}$
has no minimum. Suppose, with a view to contradiction, that
$\mathsf {Log}$
has no minimum. Suppose, with a view to contradiction, that
![]() $\mathsf {Log}$
has a minimum
$\mathsf {Log}$
has a minimum
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
. Then let
$[\kern-1pt[ \vdash ]\kern-1pt] $
. Then let
![]() $\kappa := \vert Fm(\vdash ) \vert $
and consider the language
$\kappa := \vert Fm(\vdash ) \vert $
and consider the language
![]() $\mathscr {L}$
that consists in
$\mathscr {L}$
that consists in
![]() $k^{+}$
binary connectives
$k^{+}$
binary connectives
![]() $\{ \multimap _{\alpha } \colon \alpha < \kappa ^{+}\}$
. For every
$\{ \multimap _{\alpha } \colon \alpha < \kappa ^{+}\}$
. For every
![]() $\alpha < \kappa ^{+}$
, let
$\alpha < \kappa ^{+}$
, let
![]() $\boldsymbol {A}_{\alpha }$
be the
$\boldsymbol {A}_{\alpha }$
be the
![]() $\mathscr {L}$
-algebra with universe
$\mathscr {L}$
-algebra with universe
![]() $\{ 1, 0, a \}$
and operations defined for every
$\{ 1, 0, a \}$
and operations defined for every
![]() $p , q \in A$
and
$p , q \in A$
and
![]() $\beta < \kappa ^{+}$
as follows:
$\beta < \kappa ^{+}$
as follows:
 $$ \begin{align*} p \multimap_{\beta} q:= \left\{\begin{array}{@{\,}ll} 1 & \text{if}\ p=q\ \text{or}\ \beta \ne \alpha,\\ 0 & \text{if}\ p \ne q\ \text{and}\ \beta = \alpha.\\ \end{array} \right. \end{align*} $$
$$ \begin{align*} p \multimap_{\beta} q:= \left\{\begin{array}{@{\,}ll} 1 & \text{if}\ p=q\ \text{or}\ \beta \ne \alpha,\\ 0 & \text{if}\ p \ne q\ \text{and}\ \beta = \alpha.\\ \end{array} \right. \end{align*} $$
Let also
![]() $\vdash _{\kappa ^{+}}$
be the logic (formulated in a countable set of variables) induced by the class of reduced matrices
$\vdash _{\kappa ^{+}}$
be the logic (formulated in a countable set of variables) induced by the class of reduced matrices
Clearly,
![]() $\mathsf {M} \subseteq \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
.
$\mathsf {M} \subseteq \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
.
Since
![]() $\vdash $
is the minimum of
$\vdash $
is the minimum of
![]() $\mathsf {Log}$
, there is an interpretation
$\mathsf {Log}$
, there is an interpretation
![]() $\boldsymbol {\tau }$
of
$\boldsymbol {\tau }$
of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{\kappa ^{+}}$
. On cardinality grounds, there is
$\vdash _{\kappa ^{+}}$
. On cardinality grounds, there is
![]() $\alpha < \kappa ^{+}$
such that the symbol
$\alpha < \kappa ^{+}$
such that the symbol
![]() $\multimap _{\alpha }$
does not occur in the formulas
$\multimap _{\alpha }$
does not occur in the formulas
![]() $\{ \boldsymbol {\tau }(\varphi ) \colon \varphi \in \mathscr {L} \}$
. In particular, this implies that the matrix
$\{ \boldsymbol {\tau }(\varphi ) \colon \varphi \in \mathscr {L} \}$
. In particular, this implies that the matrix
![]() $\langle \boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}, \{ 1, a \} \rangle $
is not reduced.
$\langle \boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}, \{ 1, a \} \rangle $
is not reduced.
On the other hand, we know that

is the identity relation, since
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash _{\kappa ^{+}}$
and
$\vdash _{\kappa ^{+}}$
and
![]() $\langle \boldsymbol {A}_{\alpha }, \{ 1, a \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
. Now, since
$\langle \boldsymbol {A}_{\alpha }, \{ 1, a \} \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\kappa ^{+}})$
. Now, since
![]() $A_{\alpha }= \{ 1, 0, a \}$
, the only deductive filter of
$A_{\alpha }= \{ 1, 0, a \}$
, the only deductive filter of
![]() $\vdash $
on
$\vdash $
on
![]() $\boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}$
extending properly
$\boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}$
extending properly
![]() $\{ 1, a \}$
is forcefully
$\{ 1, a \}$
is forcefully
![]() $\{ 1, 0, a \}$
. Hence we obtain that
$\{ 1, 0, a \}$
. Hence we obtain that

But this implies that
 $\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}} \{ 1, a \}$
is the identity relation, which is false.
$\boldsymbol {\varOmega }^{\boldsymbol {A}_{\alpha }^{\boldsymbol {\tau }}} \{ 1, a \}$
is the identity relation, which is false.
Now, from Lemma 7.1 it follows easily that the class of inconsistent (resp. almost inconsistent) logics is the maximum (resp. a coatom) of
![]() $\mathsf {Log}$
. Hence, in order to establish the second part of the theorem it only remains to show that the class
$\mathsf {Log}$
. Hence, in order to establish the second part of the theorem it only remains to show that the class
![]() $\mathcal {K}$
of all almost inconsistent logics is the unique coatom of
$\mathcal {K}$
of all almost inconsistent logics is the unique coatom of
![]() $\mathsf {Log}$
, and that a logic
$\mathsf {Log}$
, and that a logic
![]() $\vdash $
lacks theorems if and only if
$\vdash $
lacks theorems if and only if
![]() $[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
.
$[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
.
By Lemmas 4.11(ii) and 7.1 a logic
![]() $\vdash $
lacks theorems if and only if
$\vdash $
lacks theorems if and only if
![]() $[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
. Hence it only remains to show that
$[\kern-1pt[ \vdash ]\kern-1pt] \leqslant {\mathcal {K}}$
. Hence it only remains to show that
![]() $\mathcal {K}$
is the unique coatom of
$\mathcal {K}$
is the unique coatom of
![]() $\mathsf {Log}$
. Suppose, with a view to contradiction, that there is a coatom
$\mathsf {Log}$
. Suppose, with a view to contradiction, that there is a coatom
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
in
$[\kern-1pt[ \vdash ]\kern-1pt] $
in
![]() $\mathsf {Log}$
such that
$\mathsf {Log}$
such that
![]() $\vdash $
is not almost inconsistent. Since
$\vdash $
is not almost inconsistent. Since
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
is neither the maximum of nor comparable with
$[\kern-1pt[ \vdash ]\kern-1pt] $
is neither the maximum of nor comparable with
![]() $\mathcal {K}$
, we know that
$\mathcal {K}$
, we know that
![]() $\vdash $
is not inconsistent and that it has theorems. Then there is a matrix
$\vdash $
is not inconsistent and that it has theorems. Then there is a matrix
![]() $\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
such that
$\langle \boldsymbol {A}, F\rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
such that
![]() $F \in \mathcal {P}(A) \smallsetminus \{ \emptyset , A \}$
. In particular, this implies that
$F \in \mathcal {P}(A) \smallsetminus \{ \emptyset , A \}$
. In particular, this implies that
![]() $\vert A \vert \geqslant 2$
. Now, consider the matrix
$\vert A \vert \geqslant 2$
. Now, consider the matrix
 $$ \begin{align*} \langle \boldsymbol{B}, G \rangle := \langle \boldsymbol{A}, F \rangle^{\vert A \vert} \in \mathbb{P}(\mathsf{Mod}^{\equiv}(\vdash)) \subseteq \mathsf{Mod}^{\equiv}(\vdash) \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{B}, G \rangle := \langle \boldsymbol{A}, F \rangle^{\vert A \vert} \in \mathbb{P}(\mathsf{Mod}^{\equiv}(\vdash)) \subseteq \mathsf{Mod}^{\equiv}(\vdash) \end{align*} $$
and observe that
![]() $\vert B \vert> \vert A \vert $
by Cantor’s Theorem.
$\vert B \vert> \vert A \vert $
by Cantor’s Theorem.
Let
![]() $\boldsymbol {B}^{+}$
be the expansion of
$\boldsymbol {B}^{+}$
be the expansion of
![]() $\boldsymbol {B}$
with all finitary operations on B, and consider the logic
$\boldsymbol {B}$
with all finitary operations on B, and consider the logic
![]() $\vdash ^{+}$
formulated in
$\vdash ^{+}$
formulated in
![]() $\vert Fm(\vdash ) \vert $
variables induced by the matrix
$\vert Fm(\vdash ) \vert $
variables induced by the matrix
![]() $\langle \boldsymbol {B}^{+}, G \rangle $
.
$\langle \boldsymbol {B}^{+}, G \rangle $
.
Bering in mind that all finitary operations on B are term-function of
![]() $\boldsymbol {B}^{+}$
, it is not hard to see that the matrix
$\boldsymbol {B}^{+}$
, it is not hard to see that the matrix
![]() $\langle \boldsymbol {B}^{+}, G \rangle $
is reduced and that the logic
$\langle \boldsymbol {B}^{+}, G \rangle $
is reduced and that the logic
![]() $\vdash ^{+}$
is equivalential (see [Reference Moraschini34, Lemma 3.2] if necessary). Moreover, we have that
$\vdash ^{+}$
is equivalential (see [Reference Moraschini34, Lemma 3.2] if necessary). Moreover, we have that
![]() $\mathbb {S}(\boldsymbol {B}^{+}) = \{ \boldsymbol {B}^{+} \}$
. Together with Proposition 3.9, this implies that the identity map is a translation of
$\mathbb {S}(\boldsymbol {B}^{+}) = \{ \boldsymbol {B}^{+} \}$
. Together with Proposition 3.9, this implies that the identity map is a translation of
![]() $\vdash $
into
$\vdash $
into
![]() $\vdash ^{+}$
. Since
$\vdash ^{+}$
. Since
![]() $\vdash $
is a coatom of
$\vdash $
is a coatom of
![]() $\mathsf {Log}$
, this implies that either
$\mathsf {Log}$
, this implies that either
![]() $\vdash ^{+}$
is inconsistent or it is equi-interpretable with
$\vdash ^{+}$
is inconsistent or it is equi-interpretable with
![]() $\vdash $
. As
$\vdash $
. As
![]() $G \ne B$
and
$G \ne B$
and
![]() $\langle \boldsymbol {B}^{+}, G \rangle $
is a model of
$\langle \boldsymbol {B}^{+}, G \rangle $
is a model of
![]() $\vdash ^{+}$
, we know that
$\vdash ^{+}$
, we know that
![]() $\vdash ^{+}$
is not inconsistent, whence
$\vdash ^{+}$
is not inconsistent, whence
![]() ${\vdash ^{+}} \leqslant {\vdash }$
.
${\vdash ^{+}} \leqslant {\vdash }$
.
Together with the fact that
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
, this implies that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
, this implies that
![]() $\mathsf {Mod}^{\equiv }(\vdash ^{+})$
contains a matrix of size
$\mathsf {Mod}^{\equiv }(\vdash ^{+})$
contains a matrix of size
![]() $\vert A \vert $
. However, from Lemma 2.8 it follows that every non-trivial member of
$\vert A \vert $
. However, from Lemma 2.8 it follows that every non-trivial member of
![]() $\mathsf {Mod}^{\equiv }(\vdash ^{+})$
has cardinality
$\mathsf {Mod}^{\equiv }(\vdash ^{+})$
has cardinality
![]() $\geqslant \vert B \vert $
. Together with the fact that
$\geqslant \vert B \vert $
. Together with the fact that
![]() $\vert A \vert < \vert B \vert $
, this implies that
$\vert A \vert < \vert B \vert $
, this implies that
![]() $\boldsymbol {A}$
is trivial, which is false.⊣
$\boldsymbol {A}$
is trivial, which is false.⊣
Remark 7.4. The proof above of the first part of Theorem 7.3 suggests that the lack of a minimum in
![]() $\mathsf {Log}$
can be amended if we impose restrictions on the cardinality of the languages in which logics are formulated.Footnote
4
To be more precise, we will show that the following poset has a minimum for every infinite cardinal
$\mathsf {Log}$
can be amended if we impose restrictions on the cardinality of the languages in which logics are formulated.Footnote
4
To be more precise, we will show that the following poset has a minimum for every infinite cardinal
![]() $\kappa $
:
$\kappa $
:
To this end, recall that the basic logic
![]() $\vdash _{\mathsf {V}}$
of a variety
$\vdash _{\mathsf {V}}$
of a variety
![]() $\mathsf {V}$
[Reference Font and Moraschini18, Reference Font and Moraschini19] is the logic in the language of
$\mathsf {V}$
[Reference Font and Moraschini18, Reference Font and Moraschini19] is the logic in the language of
![]() $\mathsf {V}$
(formulated in a countable set of variables) induced by the following class of matrices
$\mathsf {V}$
(formulated in a countable set of variables) induced by the following class of matrices
Given an infinite cardinal
![]() $\kappa $
, we consider the language
$\kappa $
, we consider the language
![]() $\mathscr {L}_{\kappa }$
comprising
$\mathscr {L}_{\kappa }$
comprising
![]() $\kappa $
different n-ary symbols for every
$\kappa $
different n-ary symbols for every
![]() $n \in \omega $
. Then let
$n \in \omega $
. Then let
![]() $\mathsf {V}_{\kappa }$
be the variety of all
$\mathsf {V}_{\kappa }$
be the variety of all
![]() $\mathscr {L}_{\kappa }$
-algebras. Clearly
$\mathscr {L}_{\kappa }$
-algebras. Clearly
![]() $[\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] \in \mathsf {Log}_{\kappa }$
. More interestingly, we shall prove that
$[\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] \in \mathsf {Log}_{\kappa }$
. More interestingly, we shall prove that
![]() $[\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] $
is indeed the minimum of
$[\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] $
is indeed the minimum of
![]() $\mathsf {Log}_{\kappa }$
.
$\mathsf {Log}_{\kappa }$
.
Consider a logic
![]() $\vdash $
such that
$\vdash $
such that
![]() $\vert \mathscr {L}_{\vdash } \vert \leqslant \kappa $
. We can assume without loss of generality that the language of
$\vert \mathscr {L}_{\vdash } \vert \leqslant \kappa $
. We can assume without loss of generality that the language of
![]() $\vdash $
is of size
$\vdash $
is of size
![]() $\kappa $
. Then there is a surjective translation
$\kappa $
. Then there is a surjective translation
![]() $\boldsymbol {\tau } \colon \mathscr {L}_{\kappa } \to \mathscr {L}_{\vdash }$
. We will show that
$\boldsymbol {\tau } \colon \mathscr {L}_{\kappa } \to \mathscr {L}_{\vdash }$
. We will show that
![]() $\boldsymbol {\tau }$
is an interpretation of
$\boldsymbol {\tau }$
is an interpretation of
![]() $\vdash _{\mathsf {V}_{\kappa }}$
into
$\vdash _{\mathsf {V}_{\kappa }}$
into
![]() $\vdash $
. To this end, consider
$\vdash $
. To this end, consider
![]() $\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash ))$
. Since
$\langle \boldsymbol {A}, F \rangle \in \mathbb {R}(\mathsf {Mod}(\vdash ))$
. Since
![]() $\boldsymbol {\tau }$
is surjective, the algebras
$\boldsymbol {\tau }$
is surjective, the algebras
![]() $\boldsymbol {A}$
and
$\boldsymbol {A}$
and
![]() $\boldsymbol {A}^{\boldsymbol {\tau }}$
are term-equivalent. In particular, this implies that the matrix
$\boldsymbol {A}^{\boldsymbol {\tau }}$
are term-equivalent. In particular, this implies that the matrix
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle $
is reduced. Together with the fact that
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle $
is reduced. Together with the fact that
![]() $\boldsymbol {A}^{\boldsymbol {\tau }} \in \mathsf {V}_{\kappa }$
, this implies that
$\boldsymbol {A}^{\boldsymbol {\tau }} \in \mathsf {V}_{\kappa }$
, this implies that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\mathsf {V}_{\kappa }})$
. Hence, with an application of Proposition 3.4, we conclude that
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\mathsf {V}_{\kappa }})$
. Hence, with an application of Proposition 3.4, we conclude that
![]() $\boldsymbol {\tau }$
is an interpretation.
$\boldsymbol {\tau }$
is an interpretation.
As a consequence of the remark we have:
Corollary 7.5. The upset of
![]() $\mathsf {Log}$
generated by the set
$\mathsf {Log}$
generated by the set
![]() $\{ [\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] \colon \kappa \text { is an infinite} \text{cardinal}\}$
is
$\{ [\kern-1pt[ \vdash _{\mathsf {V}_{\kappa }}]\kern-1pt] \colon \kappa \text { is an infinite} \text{cardinal}\}$
is
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
8 Relations with the lattice of varieties
For
![]() $\kappa \in \omega $
, a k-deductive system
$\kappa \in \omega $
, a k-deductive system
![]() $\vdash $
[Reference Blok, Pigozzi, Romanowska and Smith6] is a consequence relation over
$\vdash $
[Reference Blok, Pigozzi, Romanowska and Smith6] is a consequence relation over
![]() $Fm_{\mathscr {L}}(\kappa )^{k}$
(for some language
$Fm_{\mathscr {L}}(\kappa )^{k}$
(for some language
![]() $\mathscr {L}$
and infinite cardinal
$\mathscr {L}$
and infinite cardinal
![]() $\kappa $
) that, moreover, is substitution invariant in the sense that for every substitution
$\kappa $
) that, moreover, is substitution invariant in the sense that for every substitution
![]() $\sigma $
,
$\sigma $
,
for every
![]() $\varGamma \cup \{ \langle \varphi _{1}, \dots , \varphi _{k}\rangle \} \subseteq Fm_{\mathscr {L}}(\kappa )^{k}$
.
$\varGamma \cup \{ \langle \varphi _{1}, \dots , \varphi _{k}\rangle \} \subseteq Fm_{\mathscr {L}}(\kappa )^{k}$
.
Example 8.1. Observe that one-deductive systems coincide with logics. Moreover, every variety
![]() $\mathsf {K}$
can be associated with a
$\mathsf {K}$
can be associated with a
![]() $2$
-deductive system
$2$
-deductive system
![]() $\vDash _{\mathsf {K}}$
formulated over
$\vDash _{\mathsf {K}}$
formulated over
![]() $Fm(\omega )^{2}$
as follows. For every
$Fm(\omega )^{2}$
as follows. For every
![]() $\varGamma \cup \langle \varphi , \psi \rangle \subseteq Fm(\omega )^{2}$
we set
$\varGamma \cup \langle \varphi , \psi \rangle \subseteq Fm(\omega )^{2}$
we set
 $$ \begin{align*} \varGamma \vDash_{\mathsf{K}} \langle \varphi, \psi \rangle \Longleftrightarrow& \text{ for every}\ \boldsymbol{A} \in \mathsf{K}\ \text{and homomorphism }f \colon \boldsymbol{Fm}(\omega) \to \boldsymbol{A}\\ & \text{ if }f(\varepsilon) = f(\delta) \text{ for all }\langle \varepsilon, \delta \rangle \in \varGamma\text{, then }f(\varphi) = f(\psi). \end{align*} $$
$$ \begin{align*} \varGamma \vDash_{\mathsf{K}} \langle \varphi, \psi \rangle \Longleftrightarrow& \text{ for every}\ \boldsymbol{A} \in \mathsf{K}\ \text{and homomorphism }f \colon \boldsymbol{Fm}(\omega) \to \boldsymbol{A}\\ & \text{ if }f(\varepsilon) = f(\delta) \text{ for all }\langle \varepsilon, \delta \rangle \in \varGamma\text{, then }f(\varphi) = f(\psi). \end{align*} $$
The relation
![]() $\vDash _{\mathsf {K}}$
is presented as a notational variant of the standard equational consequence relative to
$\vDash _{\mathsf {K}}$
is presented as a notational variant of the standard equational consequence relative to
![]() $\mathsf {K}$
(formulated in countably many variables).
$\mathsf {K}$
(formulated in countably many variables).
The theory of k-deductive systems is a smooth generalization of that of logics (for the details, see for instance [Reference Blok, Pigozzi, Romanowska and Smith6, Reference Raftery43]). In particular, every k-deductive system
![]() $\vdash $
can be associated with a class
$\vdash $
can be associated with a class
![]() $\mathsf {Mod}^{\equiv }(\vdash )$
of models of the form
$\mathsf {Mod}^{\equiv }(\vdash )$
of models of the form
![]() $\langle \boldsymbol {A}, F \rangle $
where
$\langle \boldsymbol {A}, F \rangle $
where
![]() $\boldsymbol {A}$
is an algebra and
$\boldsymbol {A}$
is an algebra and
![]() $F \subseteq A^{k}$
. Bearing this in mind, we say that an interpretation of a k-deductive system
$F \subseteq A^{k}$
. Bearing this in mind, we say that an interpretation of a k-deductive system
![]() $\vdash $
into another k-deductive system
$\vdash $
into another k-deductive system
![]() $\vdash '$
is a translation
$\vdash '$
is a translation
![]() $\boldsymbol {\tau }$
of the language of
$\boldsymbol {\tau }$
of the language of
![]() $\vdash $
into that of
$\vdash $
into that of
![]() $\vdash '$
such that
$\vdash '$
such that
![]() $\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
, for every
$\langle \boldsymbol {A}^{\boldsymbol {\tau }}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash )$
, for every
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
. We denote by
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash ')$
. We denote by
![]() $\mathsf {Syst}(k)$
the poset of classes
$\mathsf {Syst}(k)$
the poset of classes
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
of equi-interpretable k-deductive systems, under interpretability. Let also
$[\kern-1pt[ \vdash ]\kern-1pt] $
of equi-interpretable k-deductive systems, under interpretability. Let also
![]() $\mathsf {Equiv}(k)$
be the subposet of
$\mathsf {Equiv}(k)$
be the subposet of
![]() $\mathsf {Syst}(k)$
that contains the classes
$\mathsf {Syst}(k)$
that contains the classes
![]() $[\kern-1pt[ \vdash ]\kern-1pt] $
such that
$[\kern-1pt[ \vdash ]\kern-1pt] $
such that
![]() $\vdash $
is an equivalential k-deductive system. A straightforward adaptation of the proof of Theorem 6.5 shows that
$\vdash $
is an equivalential k-deductive system. A straightforward adaptation of the proof of Theorem 6.5 shows that
![]() $\mathsf {Equiv}(k)$
is a set-complete lattice.
$\mathsf {Equiv}(k)$
is a set-complete lattice.
Recall from §1 that a variety
![]() $\mathsf {K}$
is interpretable [Reference Taylor47] into another variety
$\mathsf {K}$
is interpretable [Reference Taylor47] into another variety
![]() $\mathsf {V}$
, when
$\mathsf {V}$
, when
![]() $\mathsf {V}$
is term-equivalent to some variety
$\mathsf {V}$
is term-equivalent to some variety
![]() $\mathsf {V}^{\ast }$
whose reducts (in a smaller signature) belong to
$\mathsf {V}^{\ast }$
whose reducts (in a smaller signature) belong to
![]() $\mathsf {K}$
, in which case we write
$\mathsf {K}$
, in which case we write
![]() ${\mathsf {K}} \leqslant {\mathsf {V}}$
. When
${\mathsf {K}} \leqslant {\mathsf {V}}$
. When
![]() ${\mathsf {K}} \leqslant {\mathsf {V}}$
and
${\mathsf {K}} \leqslant {\mathsf {V}}$
and
![]() ${\mathsf {V}} \leqslant {\mathsf {K}}$
we say that
${\mathsf {V}} \leqslant {\mathsf {K}}$
we say that
![]() ${\mathsf {K}}$
and
${\mathsf {K}}$
and
![]() ${\mathsf {V}}$
are equi-interpretable. The class of all varieties equi-interpretable with
${\mathsf {V}}$
are equi-interpretable. The class of all varieties equi-interpretable with
![]() $\mathsf {K}$
is denoted by
$\mathsf {K}$
is denoted by
![]() $[\kern-1pt[ \mathsf {K}]\kern-1pt] $
and is called the interpretability type of
$[\kern-1pt[ \mathsf {K}]\kern-1pt] $
and is called the interpretability type of
![]() $\mathsf {K}$
. Moreover, we denote by
$\mathsf {K}$
. Moreover, we denote by
![]() $\mathsf {Var}$
the lattice of interpretability types of varieties ordered by the relation
$\mathsf {Var}$
the lattice of interpretability types of varieties ordered by the relation
![]() $\leqslant $
defined as follows:
$\leqslant $
defined as follows:
![]() $[\kern-1pt[ \mathsf {K}]\kern-1pt] \leqslant [\kern-1pt[ \mathsf {V}]\kern-1pt] $
if and only if
$[\kern-1pt[ \mathsf {K}]\kern-1pt] \leqslant [\kern-1pt[ \mathsf {V}]\kern-1pt] $
if and only if
![]() ${\mathsf {K}} \leqslant {\mathsf {V}}$
. The next result draws a relation between
${\mathsf {K}} \leqslant {\mathsf {V}}$
. The next result draws a relation between
![]() $\mathsf {Syst}(2)$
, and the lattice
$\mathsf {Syst}(2)$
, and the lattice
![]() $\mathsf {Var}$
of interpretability types of varieties.
$\mathsf {Var}$
of interpretability types of varieties.
Proposition 8.2. The map given by the rule
![]() $[\kern-1pt[ \mathsf {K}]\kern-1pt] \longmapsto [\kern-1pt[ \vDash _{\mathsf {K}} ]\kern-1pt] $
is a lattice-embedding of
$[\kern-1pt[ \mathsf {K}]\kern-1pt] \longmapsto [\kern-1pt[ \vDash _{\mathsf {K}} ]\kern-1pt] $
is a lattice-embedding of
![]() $\mathsf {Var}$
into into
$\mathsf {Var}$
into into
![]() $\mathsf {Equiv}(2)$
.
$\mathsf {Equiv}(2)$
.
Proof sketch. It is well known that if
![]() $\mathsf {K}$
is a variety, then
$\mathsf {K}$
is a variety, then
![]() $\vDash _{\mathsf {K}}$
is an algebraizable [Reference Blok and Pigozzi5] (and, therefore, equivalential)
$\vDash _{\mathsf {K}}$
is an algebraizable [Reference Blok and Pigozzi5] (and, therefore, equivalential)
![]() $2$
-deductive system such that
$2$
-deductive system such that
As a consequence, a variety
![]() $\mathsf {K}$
is interpretable into another variety
$\mathsf {K}$
is interpretable into another variety
![]() $\mathsf {V}$
if and only if
$\mathsf {V}$
if and only if
![]() $\vDash _{\mathsf {K}}$
is interpretable into
$\vDash _{\mathsf {K}}$
is interpretable into
![]() $\vDash _{\mathsf {V}}$
. Hence, the map in the statement is an order-embedding. The fact that it is a lattice homomorphism follows from the description of infima and suprema in
$\vDash _{\mathsf {V}}$
. Hence, the map in the statement is an order-embedding. The fact that it is a lattice homomorphism follows from the description of infima and suprema in
![]() $\mathsf {Var}$
[Reference García and Taylor20, Reference Neumann39], and from a straightforward adaptation of the description of infima and suprema of equivalential logics given here to the case of two-deductive systems.⊣
$\mathsf {Var}$
[Reference García and Taylor20, Reference Neumann39], and from a straightforward adaptation of the description of infima and suprema of equivalential logics given here to the case of two-deductive systems.⊣
The above result gives a logical explanation of some known facts about
![]() $\mathsf {Var}$
. For instance, the fact that
$\mathsf {Var}$
. For instance, the fact that
![]() $\mathsf {Var}$
is a lattice (as opposed to a poset only) can be viewed as a consequence of the fact that equivalential two-deductive systems form a lattice. Similarly, the fact that
$\mathsf {Var}$
is a lattice (as opposed to a poset only) can be viewed as a consequence of the fact that equivalential two-deductive systems form a lattice. Similarly, the fact that
![]() $\mathsf {Var}$
has no coatoms [Reference García and Taylor20, Chapter 2] follows from a variant of Theorem 7.3, and the observation that every two-deductive system of the form
$\mathsf {Var}$
has no coatoms [Reference García and Taylor20, Chapter 2] follows from a variant of Theorem 7.3, and the observation that every two-deductive system of the form
![]() $\vDash _{\mathsf {K}}$
has at least one theorem, namely
$\vDash _{\mathsf {K}}$
has at least one theorem, namely
![]() $\langle x, x \rangle $
.
$\langle x, x \rangle $
.
We conclude this section by showing that there is a meet-homomorphism from
![]() $\mathsf {Var}$
to
$\mathsf {Var}$
to
![]() $\mathsf {Log}$
(Theorem 8.4). To this end, given a language
$\mathsf {Log}$
(Theorem 8.4). To this end, given a language
![]() $\mathcal {L}$
we denote by
$\mathcal {L}$
we denote by
![]() $T_{m}(\mathcal {L})$
the set of all its m-ary terms in the variables
$T_{m}(\mathcal {L})$
the set of all its m-ary terms in the variables
![]() $x_1, \ldots , x_m$
. Then, for every
$x_1, \ldots , x_m$
. Then, for every
![]() $\mathcal {L}$
-algebra
$\mathcal {L}$
-algebra
![]() $\boldsymbol {A}$
and
$\boldsymbol {A}$
and
![]() $n>0$
, the n-th matrix power of
$n>0$
, the n-th matrix power of
![]() $\boldsymbol {A}$
is the algebra
$\boldsymbol {A}$
is the algebra
 $$ \begin{align*} \boldsymbol{A}^{[n]} := \langle A^{n}; \{ m_{t} \colon t \in T_{kn}(\boldsymbol{A})^{n} \text{ for some positive }k \in \omega \}\rangle, \end{align*} $$
$$ \begin{align*} \boldsymbol{A}^{[n]} := \langle A^{n}; \{ m_{t} \colon t \in T_{kn}(\boldsymbol{A})^{n} \text{ for some positive }k \in \omega \}\rangle, \end{align*} $$
where for each
![]() $t = \langle t_{1}, \dots , t_{n}\rangle \in T_{kn}(\boldsymbol {A})^{n}$
, we define
$t = \langle t_{1}, \dots , t_{n}\rangle \in T_{kn}(\boldsymbol {A})^{n}$
, we define
![]() $m_{t} \colon (A^{n})^{k} \to A^{n}$
as follows: if
$m_{t} \colon (A^{n})^{k} \to A^{n}$
as follows: if
![]() $a_{j} = \langle a_{j1}, \dots , a_{jn}\rangle \in A^{n}$
for
$a_{j} = \langle a_{j1}, \dots , a_{jn}\rangle \in A^{n}$
for
![]() $j = 1, \dots , k$
, then
$j = 1, \dots , k$
, then
 $$ \begin{align*} m_{t}(a_{1}, \dots, a_{k}) = \langle t^{\boldsymbol{A}}_{i}(a_{11}, \dots, a_{1n}, \dots, a_{k1}, \dots, a_{kn}) :1 \leqslant i \leqslant n \rangle. \end{align*} $$
$$ \begin{align*} m_{t}(a_{1}, \dots, a_{k}) = \langle t^{\boldsymbol{A}}_{i}(a_{11}, \dots, a_{1n}, \dots, a_{k1}, \dots, a_{kn}) :1 \leqslant i \leqslant n \rangle. \end{align*} $$
For
![]() $0<n\in \omega $
, the n-th matrix power of a class
$0<n\in \omega $
, the n-th matrix power of a class
![]() $\mathsf {K}$
of similar algebras is the class
$\mathsf {K}$
of similar algebras is the class
 $\mathsf {K}^{[n]} := \mathbb {I} \{ \boldsymbol {A}^{[n]} : \boldsymbol {A} \in \mathsf {K} \}$
. Applications of the matrix power construction range from the algebraic study of category equivalences and adjunctions [Reference Davey, Werner and Bolyai13, Reference McKenzie, Aglianò and Magari33, Reference Moraschini35] to the study of clones [Reference Neumann40], Maltsev conditions [Reference Taylor48, Reference García and Taylor20], and finite algebras [Reference Hobby and McKenzie25].
$\mathsf {K}^{[n]} := \mathbb {I} \{ \boldsymbol {A}^{[n]} : \boldsymbol {A} \in \mathsf {K} \}$
. Applications of the matrix power construction range from the algebraic study of category equivalences and adjunctions [Reference Davey, Werner and Bolyai13, Reference McKenzie, Aglianò and Magari33, Reference Moraschini35] to the study of clones [Reference Neumann40], Maltsev conditions [Reference Taylor48, Reference García and Taylor20], and finite algebras [Reference Hobby and McKenzie25].
Given a variety
![]() $\mathsf {K}$
, we denote by
$\mathsf {K}$
, we denote by
![]() $\vdash _{\mathsf {K}}^{2}$
the logic formulated in countably many variables induced by the class of matrices
$\vdash _{\mathsf {K}}^{2}$
the logic formulated in countably many variables induced by the class of matrices
 $$ \begin{align} \mathbb{I} \{ \langle \boldsymbol{A}^{[2]}, \{ \langle a, a \rangle \colon a \in A \}\rangle \colon \boldsymbol{A} \in \mathsf{K}\}. \end{align} $$
$$ \begin{align} \mathbb{I} \{ \langle \boldsymbol{A}^{[2]}, \{ \langle a, a \rangle \colon a \in A \}\rangle \colon \boldsymbol{A} \in \mathsf{K}\}. \end{align} $$
We rely on the following observation [Reference Moraschini and Raftery38, Theorem 8]:
Theorem 8.3. If
![]() $\mathsf {K}$
is variety, then
$\mathsf {K}$
is variety, then
![]() $\mathsf {Mod}^{\equiv }(\vdash ^{2}_{\mathsf {K}})$
is the class in (12).
$\mathsf {Mod}^{\equiv }(\vdash ^{2}_{\mathsf {K}})$
is the class in (12).
As a consequence we obtain the desired result (cf. [Reference García and Taylor20, Proposition 7]):
Theorem 8.4. The map defined by the rule
 $[\kern-1pt[ \mathsf {K}]\kern-1pt] \longmapsto [\kern-1pt[ \vdash _{\mathsf {K}}^{[2]}]\kern-1pt] $
is a meet-homomorphism from
$[\kern-1pt[ \mathsf {K}]\kern-1pt] \longmapsto [\kern-1pt[ \vdash _{\mathsf {K}}^{[2]}]\kern-1pt] $
is a meet-homomorphism from
![]() $\mathsf {Var}$
into
$\mathsf {Var}$
into
![]() $\mathsf {Log}$
.
$\mathsf {Log}$
.
Proof. We claim that if
![]() $\mathsf {K}$
and
$\mathsf {K}$
and
![]() $\mathsf {V}$
are varieties such that
$\mathsf {V}$
are varieties such that
![]() ${\mathsf {K}} \leqslant {\mathsf {V}}$
, then
${\mathsf {K}} \leqslant {\mathsf {V}}$
, then
 ${\vdash _{\mathsf {K}}^{[2]}} \leqslant {\vdash _{\mathsf {V}}^{[2]}}$
. To prove this, let
${\vdash _{\mathsf {K}}^{[2]}} \leqslant {\vdash _{\mathsf {V}}^{[2]}}$
. To prove this, let
![]() $\boldsymbol {\tau }$
be an interpretation of
$\boldsymbol {\tau }$
be an interpretation of
![]() $\mathsf {K}$
into
$\mathsf {K}$
into
![]() $\mathsf {V}$
. It is not hard to see that the map
$\mathsf {V}$
. It is not hard to see that the map
![]() $\boldsymbol {\tau }^{\ast }$
, defined by the rule
$\boldsymbol {\tau }^{\ast }$
, defined by the rule
![]() $\langle t_{1}, t_{2}\rangle \longmapsto \langle \boldsymbol {\tau }(t_{1}), \boldsymbol {\tau }(t_{2})\rangle $
, is an interpretation of
$\langle t_{1}, t_{2}\rangle \longmapsto \langle \boldsymbol {\tau }(t_{1}), \boldsymbol {\tau }(t_{2})\rangle $
, is an interpretation of
![]() $\mathsf {K}^{[2]}$
into
$\mathsf {K}^{[2]}$
into
![]() $\mathsf {V}^{[2]}$
. We will show that
$\mathsf {V}^{[2]}$
. We will show that
![]() $\boldsymbol {\tau }^{\ast }$
is also an interpretation of
$\boldsymbol {\tau }^{\ast }$
is also an interpretation of
 $\vdash _{\mathsf {K}}^{[2]}$
into
$\vdash _{\mathsf {K}}^{[2]}$
into
 $\vdash _{\mathsf {V}}^{[2]}$
. To this end, consider
$\vdash _{\mathsf {V}}^{[2]}$
. To this end, consider
 $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\mathsf {V}}^{[2]})$
. By Theorem 8.3 there is
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\mathsf {V}}^{[2]})$
. By Theorem 8.3 there is
![]() $\boldsymbol {B} \in \mathsf {V}^{[2]}$
such that
$\boldsymbol {B} \in \mathsf {V}^{[2]}$
such that
![]() $\langle \boldsymbol {A}, F \rangle \cong \langle \boldsymbol {B}, \{ \langle b, b \rangle \colon b \in B \} \rangle $
. As
$\langle \boldsymbol {A}, F \rangle \cong \langle \boldsymbol {B}, \{ \langle b, b \rangle \colon b \in B \} \rangle $
. As
![]() $\boldsymbol {\tau }^{\ast }$
is an interpretation of
$\boldsymbol {\tau }^{\ast }$
is an interpretation of
![]() $\mathsf {K}^{[2]}$
into
$\mathsf {K}^{[2]}$
into
![]() $\mathsf {V}^{[2]}$
, this yields
$\mathsf {V}^{[2]}$
, this yields
![]() $\boldsymbol {B}^{\boldsymbol {\tau }^{\ast }} \in \mathsf {K}^{[2]}$
. Hence, by Theorem 8.3 we obtain
$\boldsymbol {B}^{\boldsymbol {\tau }^{\ast }} \in \mathsf {K}^{[2]}$
. Hence, by Theorem 8.3 we obtain
 $$ \begin{align*} \langle \boldsymbol{A}, F \rangle \in \mathbb{I}(\langle \boldsymbol{B}^{\boldsymbol{\tau}^{\ast}}, \{ \langle b, b \rangle \colon b \in B \} \rangle) \subseteq \mathsf{Mod}^{\equiv}(\vdash_{\mathsf{K}}^{[2]}). \end{align*} $$
$$ \begin{align*} \langle \boldsymbol{A}, F \rangle \in \mathbb{I}(\langle \boldsymbol{B}^{\boldsymbol{\tau}^{\ast}}, \{ \langle b, b \rangle \colon b \in B \} \rangle) \subseteq \mathsf{Mod}^{\equiv}(\vdash_{\mathsf{K}}^{[2]}). \end{align*} $$
We conclude that
![]() $\boldsymbol {\tau }^{\ast }$
is an interpretation of
$\boldsymbol {\tau }^{\ast }$
is an interpretation of
 $\vdash _{\mathsf {K}}^{[2]}$
into
$\vdash _{\mathsf {K}}^{[2]}$
into
 $\vdash _{\mathsf {V}}^{[2]}$
, establishing the claim.
$\vdash _{\mathsf {V}}^{[2]}$
, establishing the claim.
Let
![]() $\mu \colon \mathsf {Var} \to \mathsf {Log}$
be the map in the statement. From the claim it follows that
$\mu \colon \mathsf {Var} \to \mathsf {Log}$
be the map in the statement. From the claim it follows that
![]() $\mu $
is well-defined. Then we turn to prove that it is a meet-homomorphism. To this end, given two varieties
$\mu $
is well-defined. Then we turn to prove that it is a meet-homomorphism. To this end, given two varieties
![]() $\mathsf {K}$
and
$\mathsf {K}$
and
![]() $\mathsf {V}$
, we set
$\mathsf {V}$
, we set
![]() $\mathsf {K} \bigotimes \mathsf {V} := \mathbb {I} \{ \boldsymbol {A} \bigotimes \boldsymbol {B} \colon \boldsymbol {A} \in \mathsf {K} \text { and }\boldsymbol {B} \in \mathsf {V} \}$
. It is easy to see that
$\mathsf {K} \bigotimes \mathsf {V} := \mathbb {I} \{ \boldsymbol {A} \bigotimes \boldsymbol {B} \colon \boldsymbol {A} \in \mathsf {K} \text { and }\boldsymbol {B} \in \mathsf {V} \}$
. It is easy to see that
![]() $\mathsf {K} \bigotimes \mathsf {V}$
is a variety. Moreover, recall that
$\mathsf {K} \bigotimes \mathsf {V}$
is a variety. Moreover, recall that
![]() $[\kern-1pt[ \mathsf {K} \bigotimes \mathsf {V} ]\kern-1pt] $
is the meet of
$[\kern-1pt[ \mathsf {K} \bigotimes \mathsf {V} ]\kern-1pt] $
is the meet of
![]() $[\kern-1pt[ \mathsf {K}]\kern-1pt] $
and
$[\kern-1pt[ \mathsf {K}]\kern-1pt] $
and
![]() $[\kern-1pt[ \mathsf {V} ]\kern-1pt] $
in
$[\kern-1pt[ \mathsf {V} ]\kern-1pt] $
in
![]() $\mathsf {Var}$
, and that
$\mathsf {Var}$
, and that
![]() $(\mathsf {K} \bigotimes \mathsf {V})^{[2]}$
is term-equivalent to
$(\mathsf {K} \bigotimes \mathsf {V})^{[2]}$
is term-equivalent to
![]() $\mathsf {K}^{[2]} \bigotimes \mathsf {V}^{[2]}$
(see for instance [Reference García and Taylor20]). Together with Corollary 4.14 and Theorem 8.3, this implies that
$\mathsf {K}^{[2]} \bigotimes \mathsf {V}^{[2]}$
(see for instance [Reference García and Taylor20]). Together with Corollary 4.14 and Theorem 8.3, this implies that
 $\vdash _{\mathsf {K} \bigotimes \mathsf {V}}^{[2]}$
is term-equivalent to
$\vdash _{\mathsf {K} \bigotimes \mathsf {V}}^{[2]}$
is term-equivalent to
 $\vdash _{\mathsf {K}}^{[2]}\bigotimes \vdash _{\mathsf {V}}^{[2]}$
as well. Hence we have that
$\vdash _{\mathsf {K}}^{[2]}\bigotimes \vdash _{\mathsf {V}}^{[2]}$
as well. Hence we have that
 $$ \begin{align*} \mu([\kern-1pt[ \mathsf{K}]\kern-1pt]) \land \mu([\kern-1pt[ \mathsf{V}]\kern-1pt]) &= [\kern-1pt[ \vdash_{\mathsf{K}}^{[2]}]\kern-1pt] \land [\kern-1pt[ \vdash_{\mathsf{V}}^{[2]}]\kern-1pt] = [\kern-1pt[ \vdash_{\mathsf{K}}^{[2]}\bigotimes \vdash_{\mathsf{V}}^{[2]} ]\kern-1pt] = [\kern-1pt[\vdash_{\mathsf{K} \bigotimes \mathsf{V}}^{[2]} ]\kern-1pt] \\ &= \mu ([\kern-1pt[ \mathsf{K} \bigotimes \mathsf{V} ]\kern-1pt]) = \mu([\kern-1pt[ \mathsf{K}]\kern-1pt] \land [\kern-1pt[ \mathsf{V}]\kern-1pt]). \end{align*} $$
$$ \begin{align*} \mu([\kern-1pt[ \mathsf{K}]\kern-1pt]) \land \mu([\kern-1pt[ \mathsf{V}]\kern-1pt]) &= [\kern-1pt[ \vdash_{\mathsf{K}}^{[2]}]\kern-1pt] \land [\kern-1pt[ \vdash_{\mathsf{V}}^{[2]}]\kern-1pt] = [\kern-1pt[ \vdash_{\mathsf{K}}^{[2]}\bigotimes \vdash_{\mathsf{V}}^{[2]} ]\kern-1pt] = [\kern-1pt[\vdash_{\mathsf{K} \bigotimes \mathsf{V}}^{[2]} ]\kern-1pt] \\ &= \mu ([\kern-1pt[ \mathsf{K} \bigotimes \mathsf{V} ]\kern-1pt]) = \mu([\kern-1pt[ \mathsf{K}]\kern-1pt] \land [\kern-1pt[ \mathsf{V}]\kern-1pt]). \end{align*} $$
This shows that
![]() $\mu $
is a meet-homomorphism, as desired.⊣
$\mu $
is a meet-homomorphism, as desired.⊣
Appendix A
Recall that
![]() $\vdash _{\lnot }$
is the negation fragment of classical propositional logic. The following result is part of the folklore:
$\vdash _{\lnot }$
is the negation fragment of classical propositional logic. The following result is part of the folklore:
Proposition 8.5. The logic
![]() $\vdash _{\lnot }$
is axiomatized by the following rules:
$\vdash _{\lnot }$
is axiomatized by the following rules:
Theorem 8.6.
![]() $\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is the class of matrices
$\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is the class of matrices
![]() $\langle \boldsymbol {A}, F\rangle $
such that either
$\langle \boldsymbol {A}, F\rangle $
such that either
![]() $\boldsymbol {A}$
is trivial or (
$\boldsymbol {A}$
is trivial or (
![]() $\boldsymbol {A} \in \mathsf {NA}$
and either
$\boldsymbol {A} \in \mathsf {NA}$
and either
![]() $F= \emptyset $
or
$F= \emptyset $
or
![]() $F= \{ a \}$
for some
$F= \{ a \}$
for some
![]() $a \in A$
that is not a fixed point of
$a \in A$
that is not a fixed point of
![]() $\lnot $
).
$\lnot $
).
Proof. We begin by proving the inclusion from left to right. To this end, observe that
![]() $\vdash _{\lnot }$
is determined the the matrix
$\vdash _{\lnot }$
is determined the the matrix
![]() $\langle {\textbf {2}}, \{ 1 \} \rangle $
where
$\langle {\textbf {2}}, \{ 1 \} \rangle $
where
![]() ${\textbf {2}}$
is the negation reduct of the two-element Boolean algebra with universe
${\textbf {2}}$
is the negation reduct of the two-element Boolean algebra with universe
![]() $\{ 0, 1 \}$
. Then consider a matrix
$\{ 0, 1 \}$
. Then consider a matrix
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
such that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
such that
![]() $\boldsymbol {A}$
is non-trivial. First we show that
$\boldsymbol {A}$
is non-trivial. First we show that
![]() $\boldsymbol {A} \in \mathsf {NA}$
. The fact that
$\boldsymbol {A} \in \mathsf {NA}$
. The fact that
![]() ${\textbf {2}} \vDash x \thickapprox \lnot \lnot x$
, together with Corollary 2.5, implies that
${\textbf {2}} \vDash x \thickapprox \lnot \lnot x$
, together with Corollary 2.5, implies that
![]() $\boldsymbol {A} \vDash x \thickapprox \lnot \lnot x$
.
$\boldsymbol {A} \vDash x \thickapprox \lnot \lnot x$
.
It only remains to prove that
![]() $\boldsymbol {A}$
has at most one fixed point of
$\boldsymbol {A}$
has at most one fixed point of
![]() $\lnot $
. Suppose that
$\lnot $
. Suppose that
![]() $a, b \in A$
are fixed points of
$a, b \in A$
are fixed points of
![]() $\lnot $
. We prove that
$\lnot $
. We prove that
 $\textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(a)) = \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(b))$
for every unary polynomial function p of
$\textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(a)) = \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(b))$
for every unary polynomial function p of
![]() $\boldsymbol {A}$
. This implies that
$\boldsymbol {A}$
. This implies that
 by Proposition 2.2(ii) and, since
by Proposition 2.2(ii) and, since
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
, we that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
, we that
![]() $a = b$
. Let p be a unary polynomial function of
$a = b$
. Let p be a unary polynomial function of
![]() $\boldsymbol {A}$
. Because of the poor language of
$\boldsymbol {A}$
. Because of the poor language of
![]() $\boldsymbol {A}$
, every polynomial function
$\boldsymbol {A}$
, every polynomial function
![]() $q(x)$
of
$q(x)$
of
![]() $\boldsymbol {A}$
has the form
$\boldsymbol {A}$
has the form
 $$ \begin{align*} q(x) =\underbrace{\lnot \dots \lnot}_{n\text{-times}}x \quad \text{ or } \quad q(x) =\underbrace{\lnot \dots \lnot}_{n\text{-times}}c \end{align*} $$
$$ \begin{align*} q(x) =\underbrace{\lnot \dots \lnot}_{n\text{-times}}x \quad \text{ or } \quad q(x) =\underbrace{\lnot \dots \lnot}_{n\text{-times}}c \end{align*} $$
for some
![]() $n \in \omega $
and
$n \in \omega $
and
![]() $c \in A$
. If p is of the first shape, then since
$c \in A$
. If p is of the first shape, then since
![]() $a, b$
are fixed points of
$a, b$
are fixed points of
![]() $\lnot $
, it easily follows that
$\lnot $
, it easily follows that
![]() $p(a) = a$
and
$p(a) = a$
and
![]() $p(b) = b$
; then using the rule
$p(b) = b$
; then using the rule
![]() $x, \lnot x \rhd y$
, which holds in the logic, it follows that
$x, \lnot x \rhd y$
, which holds in the logic, it follows that
 $b \in \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, a)$
and
$b \in \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, a)$
and
 $a \in \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, b)$
and, therefore,
$a \in \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, b)$
and, therefore,
 $\textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(a)) = \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(b))$
. If p is of the second shape, then there is nothing to prove. Hence we conclude that
$\textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(a)) = \textrm {Fg}^{\boldsymbol {A}}_{\vdash _{\lnot }}(F, p(b))$
. If p is of the second shape, then there is nothing to prove. Hence we conclude that
![]() $\boldsymbol {A}$
is a negation algebra.
$\boldsymbol {A}$
is a negation algebra.
Now, recall that
![]() $\vdash _{\lnot }$
is determined by a matrix
$\vdash _{\lnot }$
is determined by a matrix
![]() $\langle {\textbf {2}}, \{ 1 \} \rangle $
, whose set of designated elements is a singleton. By a minor variant of [Reference Albuquerque, Font, Jansana, Moraschini and Czelakowski1, Theorem 8], this implies that
$\langle {\textbf {2}}, \{ 1 \} \rangle $
, whose set of designated elements is a singleton. By a minor variant of [Reference Albuquerque, Font, Jansana, Moraschini and Czelakowski1, Theorem 8], this implies that
![]() $\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is a class of matrices
$\mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
is a class of matrices
![]() $\langle \boldsymbol {A}, F \rangle $
such that F is either empty or a singleton. Then consider a matrix
$\langle \boldsymbol {A}, F \rangle $
such that F is either empty or a singleton. Then consider a matrix
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
such that
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
such that
![]() $\boldsymbol {A}$
is non-trivial. We know that
$\boldsymbol {A}$
is non-trivial. We know that
![]() $\boldsymbol {A}$
is a negation algebra and that F is either empty or a singleton. Suppose, with a view to contradiction, that
$\boldsymbol {A}$
is a negation algebra and that F is either empty or a singleton. Suppose, with a view to contradiction, that
![]() $F = \{ a \}$
for a fixed point a of
$F = \{ a \}$
for a fixed point a of
![]() $\lnot $
. Since
$\lnot $
. Since
![]() $x, \lnot x \vdash _{\lnot } y$
, this implies that
$x, \lnot x \vdash _{\lnot } y$
, this implies that
![]() $F = A$
and, therefore, that
$F = A$
and, therefore, that
![]() $\boldsymbol {A}$
is trivial which is false. This establishes the inclusion from left to right.
$\boldsymbol {A}$
is trivial which is false. This establishes the inclusion from left to right.
To prove the reverse inclusion, consider a matrix
![]() $\langle \boldsymbol {A}, F \rangle $
satisfying the conditions in the statement. If
$\langle \boldsymbol {A}, F \rangle $
satisfying the conditions in the statement. If
![]() $\boldsymbol {A} = {\textbf {1}}$
, then either
$\boldsymbol {A} = {\textbf {1}}$
, then either
![]() $F = \emptyset $
or
$F = \emptyset $
or
![]() $F = \{ 1 \}$
. In both cases,
$F = \{ 1 \}$
. In both cases,
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
, since
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}^{\equiv }(\vdash _{\lnot })$
, since
![]() $\vdash _{\lnot }$
has no theorems. Then we suppose that
$\vdash _{\lnot }$
has no theorems. Then we suppose that
![]() $\boldsymbol {A}$
is non-trivial, in which case
$\boldsymbol {A}$
is non-trivial, in which case
![]() $\boldsymbol {A} \in \mathsf {NA}$
and either
$\boldsymbol {A} \in \mathsf {NA}$
and either
![]() $F = \emptyset $
or
$F = \emptyset $
or
![]() $F = \{ a \}$
for some
$F = \{ a \}$
for some
![]() $a \in A$
that is not a fixed point of
$a \in A$
that is not a fixed point of
![]() $\lnot $
. Together with Proposition 8.5, this implies that
$\lnot $
. Together with Proposition 8.5, this implies that
![]() $\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash _{\lnot })$
.
$\langle \boldsymbol {A}, F \rangle \in \mathsf {Mod}(\vdash _{\lnot })$
.
It only remains to prove that
 is the identity relation. To prove this, consider two different elements
is the identity relation. To prove this, consider two different elements
![]() $b, c \in A$
. First we consider the case where
$b, c \in A$
. First we consider the case where
![]() $F = \emptyset $
. Since
$F = \emptyset $
. Since
![]() $\boldsymbol {A}$
is a negation algebra, it has at most one fixed point of
$\boldsymbol {A}$
is a negation algebra, it has at most one fixed point of
![]() $\lnot $
. Thus we can assume without loss of generality that b is not a fixed point of
$\lnot $
. Thus we can assume without loss of generality that b is not a fixed point of
![]() $\lnot $
. Together with Proposition 8.5, this implies that
$\lnot $
. Together with Proposition 8.5, this implies that
![]() $\langle \boldsymbol {A}, \{ b \} \rangle \in \mathsf {Mod}(\vdash _{\lnot })$
. Moreover, clearly we have that
$\langle \boldsymbol {A}, \{ b \} \rangle \in \mathsf {Mod}(\vdash _{\lnot })$
. Moreover, clearly we have that
![]() $F = \emptyset \subseteq \{ b \}$
and
$F = \emptyset \subseteq \{ b \}$
and
 .
.
Then we consider the case in which
![]() $F = \{ a \}$
for some
$F = \{ a \}$
for some
![]() $a \in A$
that is not a fixed point of
$a \in A$
that is not a fixed point of
![]() $\lnot $
. Since
$\lnot $
. Since
![]() $\boldsymbol {A}$
has at most one fixed point of
$\boldsymbol {A}$
has at most one fixed point of
![]() $\lnot $
,
$\lnot $
,
![]() $\boldsymbol {A} \vDash x \thickapprox \lnot \lnot x$
, and
$\boldsymbol {A} \vDash x \thickapprox \lnot \lnot x$
, and
![]() $b \ne c$
one of the following conditions holds:
$b \ne c$
one of the following conditions holds:
-
(i) Either (
 $b \ne \lnot b$
and
$b \ne \lnot b$
and
 $b \ne \lnot a$
) or (
$b \ne \lnot a$
) or (
 $c \ne \lnot c$
and
$c \ne \lnot c$
and
 $c \ne \lnot a$
).
$c \ne \lnot a$
). -
(ii) Either (
 $b = \lnot b$
and
$b = \lnot b$
and
 $c = \lnot a$
) or (
$c = \lnot a$
) or (
 $c = \lnot c$
and
$c = \lnot c$
and
 $b = \lnot a$
).
$b = \lnot a$
).
If condition (i) holds, we can assume without loss of generality that
![]() $b \ne \lnot b$
and
$b \ne \lnot b$
and
![]() $b \ne \lnot a$
. If
$b \ne \lnot a$
. If
![]() $c = a$
, then
$c = a$
, then
 . Then consider the case where
. Then consider the case where
![]() $c \ne a$
. By Proposition 8.5 we know that
$c \ne a$
. By Proposition 8.5 we know that
![]() $\{ a, b \}$
is a deductive filter of
$\{ a, b \}$
is a deductive filter of
![]() $\vdash _{\lnot }$
. Hence we have that
$\vdash _{\lnot }$
. Hence we have that
 . Then suppose that the condition (ii) holds. We can assume without loss of generality that
. Then suppose that the condition (ii) holds. We can assume without loss of generality that
![]() $b = \lnot b$
and
$b = \lnot b$
and
![]() $c = \lnot a$
. In this case we have that
$c = \lnot a$
. In this case we have that
![]() $\lnot b \notin \{ a \}$
and
$\lnot b \notin \{ a \}$
and
![]() $\lnot c \in \{ a \}$
which, by Proposition 2.2(ii), implies that
$\lnot c \in \{ a \}$
which, by Proposition 2.2(ii), implies that
 .
.
This concludes the proof that
 is the identity relation.⊣
is the identity relation.⊣
B
We close the paper with an observation on languages with constant symbols. If a logic
![]() $\vdash $
has constants in its language, then we can obtain a new language by keeping all the connectives of
$\vdash $
has constants in its language, then we can obtain a new language by keeping all the connectives of
![]() $\mathscr {L}_\vdash $
and replacing each constant c by a unary operation
$\mathscr {L}_\vdash $
and replacing each constant c by a unary operation
![]() $\ast _c$
. Then we can transform every algebra
$\ast _c$
. Then we can transform every algebra
![]() $\boldsymbol {A}$
for the language
$\boldsymbol {A}$
for the language
![]() $\mathscr {L}_\vdash $
into an algebra
$\mathscr {L}_\vdash $
into an algebra
![]() $\boldsymbol {A}^{co}$
for the new language, where
$\boldsymbol {A}^{co}$
for the new language, where
 $\ast _c^{\boldsymbol {A}^{co}}$
is the unary constant map to
$\ast _c^{\boldsymbol {A}^{co}}$
is the unary constant map to
![]() $c^{\boldsymbol {A}}$
. The logic
$c^{\boldsymbol {A}}$
. The logic
![]() $\vdash ^{co}$
in the new language induced by the class of matrices
$\vdash ^{co}$
in the new language induced by the class of matrices
is the incarnation of the logic
![]() $\vdash $
in our setting of logics with languages without constants.
$\vdash $
in our setting of logics with languages without constants.
Note that if the language of
![]() $\vdash $
has no constant symbols, then
$\vdash $
has no constant symbols, then
![]() ${\vdash } = {\vdash ^{co}}$
. It is therefore natural to say of any two logics
${\vdash } = {\vdash ^{co}}$
. It is therefore natural to say of any two logics
![]() $\vdash $
and
$\vdash $
and
![]() $\vdash '$
, possibly with constants, that
$\vdash '$
, possibly with constants, that
![]() $\vdash $
is interpretable into
$\vdash $
is interpretable into
![]() $\vdash '$
if
$\vdash '$
if
![]() $\vdash ^{co}$
is interpretable into
$\vdash ^{co}$
is interpretable into
![]() ${\vdash ^{\prime }}^{co}$
in the sense of Definition 3.2. Alternatively, and with similar ideas to the ones used in the paper, the reader can easily figure out how to modify our notion of a concrete interpretation to accommodate interpretations between languages possibly with constants.
${\vdash ^{\prime }}^{co}$
in the sense of Definition 3.2. Alternatively, and with similar ideas to the ones used in the paper, the reader can easily figure out how to modify our notion of a concrete interpretation to accommodate interpretations between languages possibly with constants.
Acknowledgements
Thanks are due to James G. Raftery for rising the question about whether the theory of the Maltsev and Leibniz hierarchy could be, to some extent, unified. The authors were supported by the research grant
![]() $2017$
SGR
$2017$
SGR
![]() $95$
of the AGAUR from the Generalitat de Catalunya and by the I+D+i research project PID2019-110843GA-I00 La geometria de las logicas no-clasicas funded by the Ministry of Science and Innovation of Spain. The second author was also supported by the Beatriz Galindo grant BEAGAL
$95$
of the AGAUR from the Generalitat de Catalunya and by the I+D+i research project PID2019-110843GA-I00 La geometria de las logicas no-clasicas funded by the Ministry of Science and Innovation of Spain. The second author was also supported by the Beatriz Galindo grant BEAGAL
![]() $18$
/
$18$
/
![]() $00040$
funded by the Ministry of Science and Innovation of Spain and by the grant CZ.
$00040$
funded by the Ministry of Science and Innovation of Spain and by the grant CZ.
![]() $02$
.
$02$
.
![]() $2$
.
$2$
.
![]() $69$
/
$69$
/
![]() $0$
.
$0$
.
![]() $0$
/
$0$
/
![]() $0$
.
$0$
.
![]() $0$
/
$0$
/
![]() $17$
_
$17$
_
![]() $050$
/
$050$
/
![]() $0008361$
, OPVVV MŠMT, MSCA-IF Lidské zdroje v teoretické informatice funded by the Ministry of Education, Youth and Sports of the Czech Republic.
$0008361$
, OPVVV MŠMT, MSCA-IF Lidské zdroje v teoretické informatice funded by the Ministry of Education, Youth and Sports of the Czech Republic.