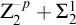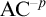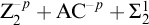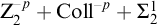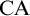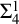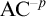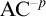1 Introduction
The strength of a second-order arithmetic theory depends mostly on the amount of comprehension that the theory admits. A comprehension scheme specifies which formulas give collections that turn out to be sets in the model. At the lower extreme, the second-order theory
![]() $\mathrm {ACA}_0$
includes comprehension for all first-order formulas and at the higher extreme, full second-order arithmetic
$\mathrm {ACA}_0$
includes comprehension for all first-order formulas and at the higher extreme, full second-order arithmetic
![]() $\mathrm {Z}_2$
includes comprehension for all (second-order) formulas. In between, we have
$\mathrm {Z}_2$
includes comprehension for all (second-order) formulas. In between, we have
![]() $\Sigma ^1_n$
-comprehension schemes for second-order formulas of complexity
$\Sigma ^1_n$
-comprehension schemes for second-order formulas of complexity
![]() $\Sigma ^1_n$
(n alternations of set quantifiers followed by a first-order formula). A precise formulation of these comprehension schemes should mention that the specified formulas are allowed to use set parameters from the model. But how significant really are parameters in comprehension? What if we formulate the comprehension schemes without parameters, do we get equivalent theories, perhaps, equiconsistent theories?
$\Sigma ^1_n$
(n alternations of set quantifiers followed by a first-order formula). A precise formulation of these comprehension schemes should mention that the specified formulas are allowed to use set parameters from the model. But how significant really are parameters in comprehension? What if we formulate the comprehension schemes without parameters, do we get equivalent theories, perhaps, equiconsistent theories?
Let
![]() $\mathrm {Z}_2^{-p}$
be the version of full second-order arithmetic
$\mathrm {Z}_2^{-p}$
be the version of full second-order arithmetic
![]() $\mathrm {Z}_2$
, where we do not allow parameters in the comprehension scheme. Friedman showed in [Reference Friedman3, Lemma 3.1.7] that given a model of
$\mathrm {Z}_2$
, where we do not allow parameters in the comprehension scheme. Friedman showed in [Reference Friedman3, Lemma 3.1.7] that given a model of
![]() $\mathrm {Z}_2^{-p}$
, we can appropriately restrict its sets to get a model of
$\mathrm {Z}_2^{-p}$
, we can appropriately restrict its sets to get a model of
![]() $\mathrm {Z}_2$
. Thus, the theories
$\mathrm {Z}_2$
. Thus, the theories
![]() $\mathrm {Z}_2$
and
$\mathrm {Z}_2$
and
![]() $\mathrm {Z}_2^{-p}$
are equiconsistent. In a recent work [Reference Kanovei and Lyubetsky8], Lyubetsky and Kanovei separated the theories
$\mathrm {Z}_2^{-p}$
are equiconsistent. In a recent work [Reference Kanovei and Lyubetsky8], Lyubetsky and Kanovei separated the theories
![]() $\mathrm {Z}_2$
and
$\mathrm {Z}_2$
and
![]() $\mathrm {Z}_2^{-p}$
by constructing models of
$\mathrm {Z}_2^{-p}$
by constructing models of
![]() $\mathrm {Z}_2^{-p}$
with various failures of comprehension with parameters. They constructed a model of
$\mathrm {Z}_2^{-p}$
with various failures of comprehension with parameters. They constructed a model of
![]() $\mathrm {Z}_2^{-p}$
in which the sets were not even closed under complement, showing that comprehension without parameters does not even give comprehension with parameters for
$\mathrm {Z}_2^{-p}$
in which the sets were not even closed under complement, showing that comprehension without parameters does not even give comprehension with parameters for
![]() $\Sigma ^0_0$
-assertions. They next considered whether it was possible to have a model of
$\Sigma ^0_0$
-assertions. They next considered whether it was possible to have a model of
![]() $\mathrm {Z}_2^{-p}$
with enough comprehension with parameters to carry out most standard constructions, but still have comprehension with parameters fail somewhere above. They argued that a reasonable amount of comprehension with parameters for general mathematical purposes is the
$\mathrm {Z}_2^{-p}$
with enough comprehension with parameters to carry out most standard constructions, but still have comprehension with parameters fail somewhere above. They argued that a reasonable amount of comprehension with parameters for general mathematical purposes is the
![]() $\Sigma ^1_2$
-comprehension scheme and constructed a model of
$\Sigma ^1_2$
-comprehension scheme and constructed a model of
![]() $\mathrm {Z}_2^{-p}$
with the
$\mathrm {Z}_2^{-p}$
with the
![]() $\Sigma ^1_2$
-comprehension scheme and a failure of
$\Sigma ^1_2$
-comprehension scheme and a failure of
![]() $\Sigma ^1_4$
-comprehension. The model was constructed in a forcing extension by a (non-linear) tree iteration of Sacks forcing. Lyubetsky and Kanovei asked whether the result can be improved to obtain the optimal failure of
$\Sigma ^1_4$
-comprehension. The model was constructed in a forcing extension by a (non-linear) tree iteration of Sacks forcing. Lyubetsky and Kanovei asked whether the result can be improved to obtain the optimal failure of
![]() $\Sigma ^1_3$
-comprehension [Reference Kanovei and Lyubetsky8, Problem 8.2].
$\Sigma ^1_3$
-comprehension [Reference Kanovei and Lyubetsky8, Problem 8.2].
In this article, we answer their question positively by constructing a model with the required properties, similarly to how the model of [Reference Kanovei and Lyubetsky8] was constructed, in a forcing extension by a tree iteration of Jensen’s forcing. Jensen’s forcing is a subposet of Sacks forcing constructed in L using the
![]() $\diamondsuit $
-principle. Jensen’s forcing has the ccc and adds a unique generic real whose singleton is
$\diamondsuit $
-principle. Jensen’s forcing has the ccc and adds a unique generic real whose singleton is
![]() $\Pi ^1_2$
-definable.Footnote
1
Jensen originally introduced the forcing because it gives a forcing extension of L in which there is a
$\Pi ^1_2$
-definable.Footnote
1
Jensen originally introduced the forcing because it gives a forcing extension of L in which there is a
![]() $\Pi ^1_2$
-definable non-constructible singleton real [Reference Jensen5].
$\Pi ^1_2$
-definable non-constructible singleton real [Reference Jensen5].
Theorem 1.1. It is consistent that there is a model of
![]() $\mathrm {Z}_2^{-p}$
together with
$\mathrm {Z}_2^{-p}$
together with
![]() $\Sigma ^1_2$
-comprehension and a failure of
$\Sigma ^1_2$
-comprehension and a failure of
![]() $\Sigma ^1_3$
-comprehension.
$\Sigma ^1_3$
-comprehension.
Theorem 1.1 is proved in Section 3.
If the first-order part of a second-order arithmetic model satisfies
![]() $\mathrm {PA}$
, then via Gödel’s pairing function, we can view any set in the model as a collection of n-tuples, for some
$\mathrm {PA}$
, then via Gödel’s pairing function, we can view any set in the model as a collection of n-tuples, for some
![]() $n<\omega $
, of elements of the model. Among these collections are orderings of the first-order domain of the model, which the model believes are well-orders. In a model of
$n<\omega $
, of elements of the model. Among these collections are orderings of the first-order domain of the model, which the model believes are well-orders. In a model of
![]() $\mathrm {Z}_2$
, these well-orders are comparable in that given any two of them, there is a set coding an isomorphism of one of them with an initial segment of the other. Using coding, a model of
$\mathrm {Z}_2$
, these well-orders are comparable in that given any two of them, there is a set coding an isomorphism of one of them with an initial segment of the other. Using coding, a model of
![]() $\mathrm {Z}_2$
can construct an initial segment of the L-hierarchy along any of its well-orders, and these initial segments are similarly coherent (for details of the construction, see [Reference Simpson10], Chapter VII). We will call a real of a model of
$\mathrm {Z}_2$
can construct an initial segment of the L-hierarchy along any of its well-orders, and these initial segments are similarly coherent (for details of the construction, see [Reference Simpson10], Chapter VII). We will call a real of a model of
![]() $\mathrm {Z}_2$
constructible if it appears in an initial segment of the L-hierarchy of the model. Similarly, in a model of
$\mathrm {Z}_2$
constructible if it appears in an initial segment of the L-hierarchy of the model. Similarly, in a model of
![]() $\mathrm {Z}_2^{-p}$
, we can show that any two definable without parameters well-orders are comparable and we can construct an initial segment of the L-hierarchy along any such well-order so that the resulting structures are coherent. We will call a real of a model of
$\mathrm {Z}_2^{-p}$
, we can show that any two definable without parameters well-orders are comparable and we can construct an initial segment of the L-hierarchy along any such well-order so that the resulting structures are coherent. We will call a real of a model of
![]() $\mathrm {Z}_2^{-p}$
constructible if it appears in an initial segment of the L-hierarchy constructed along a definable without parameters well-order.
$\mathrm {Z}_2^{-p}$
constructible if it appears in an initial segment of the L-hierarchy constructed along a definable without parameters well-order.
The theory
![]() $\mathrm {Z}_2$
can be further strengthened by adding the choice scheme
$\mathrm {Z}_2$
can be further strengthened by adding the choice scheme
![]() $\mathrm {AC}$
, which is a set choice principle asserting for every second-order formula
$\mathrm {AC}$
, which is a set choice principle asserting for every second-order formula
![]() $\varphi (n,X,A)$
(with set parameter A) that if for every n, there is a set X such that
$\varphi (n,X,A)$
(with set parameter A) that if for every n, there is a set X such that
![]() $\varphi (n,X,A)$
holds, then there is a single set Y whose n-th slice
$\varphi (n,X,A)$
holds, then there is a single set Y whose n-th slice
![]() $Y_n$
is a witness for n. It is not difficult to see that the scheme
$Y_n$
is a witness for n. It is not difficult to see that the scheme
![]() $\mathrm {AC}$
actually implies
$\mathrm {AC}$
actually implies
![]() $\mathrm {Z}_2$
over
$\mathrm {Z}_2$
over
![]() $\mathrm {ACA}_0$
. The collection of the constructible reals of a model of
$\mathrm {ACA}_0$
. The collection of the constructible reals of a model of
![]() $\mathrm {Z}_2$
satisfies
$\mathrm {Z}_2$
satisfies
![]() $\mathrm {Z}_2+\mathrm {AC}$
(see [Reference Simpson10, Section VII.6]), giving that the two theories are equiconsistent. Friedman’s sub-collection of a model of
$\mathrm {Z}_2+\mathrm {AC}$
(see [Reference Simpson10, Section VII.6]), giving that the two theories are equiconsistent. Friedman’s sub-collection of a model of
![]() $\mathrm {Z}_2^{-p}$
, which he showed satisfies
$\mathrm {Z}_2^{-p}$
, which he showed satisfies
![]() $\mathrm {Z}_2$
, was precisely the constructible reals of the model, as defined above, coming from the initial segments of the L-hierarchy constructed along definable without parameters well-orders. His argument additionally showed that the collection of the constructible reals satisfies
$\mathrm {Z}_2$
, was precisely the constructible reals of the model, as defined above, coming from the initial segments of the L-hierarchy constructed along definable without parameters well-orders. His argument additionally showed that the collection of the constructible reals satisfies
![]() $\mathrm {AC}$
. Thus, the theories
$\mathrm {AC}$
. Thus, the theories
![]() $\mathrm {Z}_2^{-p}$
and
$\mathrm {Z}_2^{-p}$
and
![]() $\mathrm {Z}_2+\mathrm {AC}$
are equiconsistent.
$\mathrm {Z}_2+\mathrm {AC}$
are equiconsistent.
Let
![]() $\mathrm {AC}^{-p}$
denote the parameter-free choice scheme. Because standard arguments that the choice scheme
$\mathrm {AC}^{-p}$
denote the parameter-free choice scheme. Because standard arguments that the choice scheme
![]() $\mathrm {AC}$
implies comprehension over
$\mathrm {AC}$
implies comprehension over
![]() $\mathrm {ACA}_0$
require parameters, it is probably not the case that
$\mathrm {ACA}_0$
require parameters, it is probably not the case that
![]() $\mathrm {AC}^{-p}$
implies
$\mathrm {AC}^{-p}$
implies
![]() $\mathrm {Z}_2^{-p}$
over
$\mathrm {Z}_2^{-p}$
over
![]() $\mathrm {ACA}_0$
. The reals of the Feferman–Lévy model of
$\mathrm {ACA}_0$
. The reals of the Feferman–Lévy model of
![]() $\mathrm {ZF}$
(a symmetric submodel of a forcing extension), in which
$\mathrm {ZF}$
(a symmetric submodel of a forcing extension), in which
![]() $\omega _1^L$
is countable for every
$\omega _1^L$
is countable for every
![]() $n<\omega $
and
$n<\omega $
and
![]() $\omega _\omega ^L$
is the first uncountable cardinal [Reference Lévy9], is a model of
$\omega _\omega ^L$
is the first uncountable cardinal [Reference Lévy9], is a model of
![]() $\mathrm {Z}_2$
in which
$\mathrm {Z}_2$
in which
![]() $\mathrm {AC}^{-p}$
fails. In this model (the code of)
$\mathrm {AC}^{-p}$
fails. In this model (the code of)
![]() $L_{\omega _n^L}$
exists for every
$L_{\omega _n^L}$
exists for every
![]() $n<\omega $
, but (the code of)
$n<\omega $
, but (the code of)
![]() $L_{\omega _\omega ^L}$
does not exist, because
$L_{\omega _\omega ^L}$
does not exist, because
![]() $\omega _\omega ^L$
is uncountable in the Feferman–Lévy model, and therefore cannot be coded by a real. Guzicki constructed a model of
$\omega _\omega ^L$
is uncountable in the Feferman–Lévy model, and therefore cannot be coded by a real. Guzicki constructed a model of
![]() $\mathrm {ZF}$
(again a symmetric submodel of a forcing extension) whose reals are a model satisfying
$\mathrm {ZF}$
(again a symmetric submodel of a forcing extension) whose reals are a model satisfying
![]() $\mathrm {Z}_2+\mathrm {AC}^{-p}$
in which
$\mathrm {Z}_2+\mathrm {AC}^{-p}$
in which
![]() $\mathrm {AC}$
fails [Reference Guzicki4], separating the two principles.Footnote
2
$\mathrm {AC}$
fails [Reference Guzicki4], separating the two principles.Footnote
2
Vladimir Kanovei suggested to try to construct a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}$
together with
$\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}$
together with
![]() $\Sigma ^1_2$
-comprehension in which there is a failure of
$\Sigma ^1_2$
-comprehension in which there is a failure of
![]() $\Sigma ^1_3$
-comprehension. However, the best we were able to get is the following theorem.
$\Sigma ^1_3$
-comprehension. However, the best we were able to get is the following theorem.
Theorem 1.2. It is consistent that there is a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}$
together with
$\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}$
together with
![]() $\Sigma ^1_2$
-comprehension in which there is a failure of
$\Sigma ^1_2$
-comprehension in which there is a failure of
![]() $\Sigma ^1_4$
-comprehension.
$\Sigma ^1_4$
-comprehension.
Theorem 1.3 is proved in Section 5.
A set existence principle closely related to the choice scheme is the collection scheme
![]() $\mathrm {Coll}$
, which asserts for every second-order formula
$\mathrm {Coll}$
, which asserts for every second-order formula
![]() $\varphi (n,X,A)$
(with set parameter A) that if for every n, there is a set X such that
$\varphi (n,X,A)$
(with set parameter A) that if for every n, there is a set X such that
![]() $\varphi (n,X,A)$
holds, then there is a set Y whose slices are a collecting set for the witnesses X. A slice of Y may not be one of the witnesses and a witness for n may be on some slice
$\varphi (n,X,A)$
holds, then there is a set Y whose slices are a collecting set for the witnesses X. A slice of Y may not be one of the witnesses and a witness for n may be on some slice
![]() $m\neq n$
. It is easy to see that over
$m\neq n$
. It is easy to see that over
![]() $\mathrm {Z}_2$
,
$\mathrm {Z}_2$
,
![]() $\mathrm {Coll}$
is equivalent to
$\mathrm {Coll}$
is equivalent to
![]() $\mathrm {AC}$
. Over
$\mathrm {AC}$
. Over
![]() $\mathrm {ACA}_0$
,
$\mathrm {ACA}_0$
,
![]() $\mathrm {Coll}$
implies
$\mathrm {Coll}$
implies
![]() $\mathrm {Z}_2$
, and hence, over
$\mathrm {Z}_2$
, and hence, over
![]() $\mathrm {ACA}_0$
,
$\mathrm {ACA}_0$
,
![]() $\mathrm {Coll}$
is equivalent to
$\mathrm {Coll}$
is equivalent to
![]() $\mathrm {AC}$
. Let
$\mathrm {AC}$
. Let
![]() $\mathrm {Coll}^{-p}$
be the parameter-free collection scheme. I separate the schemes
$\mathrm {Coll}^{-p}$
be the parameter-free collection scheme. I separate the schemes
![]() $\mathrm {Coll}^{-p}$
and
$\mathrm {Coll}^{-p}$
and
![]() $\mathrm {AC}^{-p}$
over
$\mathrm {AC}^{-p}$
over
![]() $\mathrm {Z}_2^{-p}$
.
$\mathrm {Z}_2^{-p}$
.
Theorem 1.3. It is consistent that there is a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}$
together with
$\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}$
together with
![]() $\Sigma ^1_2$
-comprehension in which there is a failure of
$\Sigma ^1_2$
-comprehension in which there is a failure of
![]() $\Sigma ^1_4$
-comprehension and a failure of
$\Sigma ^1_4$
-comprehension and a failure of
![]() $\mathrm {AC}^{-p}$
.
$\mathrm {AC}^{-p}$
.
Theorem 1.3 is proved in Section 5. Thus, we get
Theorem 1.4. The schemes
![]() $\mathrm {Coll}^{-p}$
and
$\mathrm {Coll}^{-p}$
and
![]() $\mathrm {AC}^{-p}$
are not equivalent over
$\mathrm {AC}^{-p}$
are not equivalent over
![]() ${\mathrm {Z}}_2^{-p}$
.
${\mathrm {Z}}_2^{-p}$
.
2 Preliminaries
2.1 Second-order arithmetic
Second-order arithmetic has two types of objects: numbers and sets of numbers, which we think of as the reals of the model. It is formalized in a two-sorted logic, which has two separate sorts of variables and corresponding quantifiers. By convention, we use lower-case variables for numbers and upper-case variables for sets. The language of second-order arithmetic consists of the language of
![]() $\mathrm {PA}$
together with a membership relation
$\mathrm {PA}$
together with a membership relation
![]() $\in $
used to determine which numbers belong to which sets. A model of second-order arithmetic is a structure
$\in $
used to determine which numbers belong to which sets. A model of second-order arithmetic is a structure
![]() $\mathcal M=\langle M,+,\times ,<,0,1,\in ,\mathcal S\rangle $
, where M is the universe of numbers and
$\mathcal M=\langle M,+,\times ,<,0,1,\in ,\mathcal S\rangle $
, where M is the universe of numbers and
![]() $\mathcal S$
is the universe of sets. We associate each set A with a subset of M consisting of those
$\mathcal S$
is the universe of sets. We associate each set A with a subset of M consisting of those
![]() $a\in M$
such that
$a\in M$
such that
![]() $a\in A$
. This interpretation is formalized by the extensionality axiom for sets. The second-order arithmetic theories we consider include the
$a\in A$
. This interpretation is formalized by the extensionality axiom for sets. The second-order arithmetic theories we consider include the
![]() $\mathrm {PA}$
axioms for the first-order part together with the extensionality axiom for sets and a single induction axiom
$\mathrm {PA}$
axioms for the first-order part together with the extensionality axiom for sets and a single induction axiom
asserting that induction holds for every set. The theories then differ by which sets are posited to exist. The most common set existence axioms are the comprehension schemes. The
![]() $\Sigma ^1_n$
-comprehension scheme,
$\Sigma ^1_n$
-comprehension scheme,
![]() $\Sigma ^1_n$
-
$\Sigma ^1_n$
-
![]() $\mathrm {CA}$
, asserts that every
$\mathrm {CA}$
, asserts that every
![]() $\Sigma ^1_n$
-formula with parameters defines a set. Formally,
$\Sigma ^1_n$
-formula with parameters defines a set. Formally,
![]() $\Sigma ^1_n$
-
$\Sigma ^1_n$
-
![]() $\mathrm {CA}$
asserts for every
$\mathrm {CA}$
asserts for every
![]() $\Sigma ^1_n$
-formula
$\Sigma ^1_n$
-formula
![]() $\varphi (n,A)$
, with set parameter A, that there is a set
$\varphi (n,A)$
, with set parameter A, that there is a set
![]() $X\in \mathcal S$
such that
$X\in \mathcal S$
such that
![]() $X=\{n\mid \varphi (n,A)\}$
.Footnote
3
One of the strongest second-order arithmetic theories is full second-order arithmetic
$X=\{n\mid \varphi (n,A)\}$
.Footnote
3
One of the strongest second-order arithmetic theories is full second-order arithmetic
![]() $\mathrm {Z}_2$
, which includes the comprehension scheme asserting that every second-order formula with parameters defines a set, namely
$\mathrm {Z}_2$
, which includes the comprehension scheme asserting that every second-order formula with parameters defines a set, namely
![]() $\Sigma ^1_n$
-
$\Sigma ^1_n$
-
![]() $\mathrm {CA}$
for every
$\mathrm {CA}$
for every
![]() $n<\omega $
. If we exclude parameters from the comprehension scheme, we get the theory
$n<\omega $
. If we exclude parameters from the comprehension scheme, we get the theory
![]() $\mathrm {Z}_2^{-p}$
, which is the focus of this article.
$\mathrm {Z}_2^{-p}$
, which is the focus of this article.
Other common set existence principles are the set choice principles. The choice scheme
![]() $\mathrm {AC}$
asserts for every second-order formula
$\mathrm {AC}$
asserts for every second-order formula
![]() $\varphi (n,X,A )$
that if
$\varphi (n,X,A )$
that if
![]() $\forall n\exists X\,\varphi (n,X)$
holds, then there is a set Y such that
$\forall n\exists X\,\varphi (n,X)$
holds, then there is a set Y such that
![]() $\forall n\,\varphi (n,Y_n,A)$
holds, where
$\forall n\,\varphi (n,Y_n,A)$
holds, where
is the n-th slice of Y. We will denote by
![]() $\mathrm {AC}^{-p}$
the parameter-free choice scheme. Closely related to the choice scheme is the collection scheme, which asserts for every second-order formula
$\mathrm {AC}^{-p}$
the parameter-free choice scheme. Closely related to the choice scheme is the collection scheme, which asserts for every second-order formula
![]() $\varphi (n,X,A )$
that if
$\varphi (n,X,A )$
that if
![]() $\forall n\exists X\,\varphi (n,X)$
holds, then there is a set Y such that
$\forall n\exists X\,\varphi (n,X)$
holds, then there is a set Y such that
![]() $\forall n\exists m\,\varphi (n,Y_m,A)$
holds. We will denote by
$\forall n\exists m\,\varphi (n,Y_m,A)$
holds. We will denote by
![]() $\mathrm {Coll}^{-p}$
the parameter-free collection scheme.
$\mathrm {Coll}^{-p}$
the parameter-free collection scheme.
2.2 Tree iterations of Jensen’s forcing
Recall that a perfect tree is a subtree of
![]() $2^{{<}\omega }$
in which every node has a splitting node above it. Also recall that given a tree T and a node
$2^{{<}\omega }$
in which every node has a splitting node above it. Also recall that given a tree T and a node
![]() $s\in T$
, we denote by
$s\in T$
, we denote by
![]() $T_s$
the subtree of T consisting of all nodes compatible with s. If T and S are perfect trees whose intersection includes a perfect tree, then there is a maximal such perfect tree, which we call the meet of T and S and denote by
$T_s$
the subtree of T consisting of all nodes compatible with s. If T and S are perfect trees whose intersection includes a perfect tree, then there is a maximal such perfect tree, which we call the meet of T and S and denote by
![]() $T\wedge S$
. A perfect poset
$T\wedge S$
. A perfect poset
![]() $\mathbb {P}$
is a collection of perfect trees ordered by the subtree relation satisfying the following closure properties:
$\mathbb {P}$
is a collection of perfect trees ordered by the subtree relation satisfying the following closure properties:
-
(1)
 $(2^{{<}\omega })_s\in \mathbb {P}$
for every
$(2^{{<}\omega })_s\in \mathbb {P}$
for every
 $s\in 2^{{<}\omega }$
,
$s\in 2^{{<}\omega }$
, -
(2) if
 $T,S\in \mathbb {P}$
, then
$T,S\in \mathbb {P}$
, then
 $T\wedge S\in \mathbb {P}$
,
$T\wedge S\in \mathbb {P}$
, -
(3) finite unions of trees in
 $\mathbb {P}$
are in
$\mathbb {P}$
are in
 $\mathbb {P}$
.
$\mathbb {P}$
.
Perfect posets are subposets of Sacks forcing and they share many of the properties of Sacks forcing such as that the generic filter is determined by a single generic real that is precisely the intersection of all the trees in the generic filter. While Sacks forcing is the largest perfect poset, the smallest perfect poset, which I will denote by
![]() $\mathbb {P}_{\text {min}}$
, is the closure under finite unions of the collection of all trees
$\mathbb {P}_{\text {min}}$
, is the closure under finite unions of the collection of all trees
![]() $(2^{{<}\omega })_s$
for some
$(2^{{<}\omega })_s$
for some
![]() $s\in 2^{{<}\omega }$
(it is easy to see that this collection is closed under meets).
$s\in 2^{{<}\omega }$
(it is easy to see that this collection is closed under meets).
Given a perfect poset
![]() $\mathbb {P}$
, let
$\mathbb {P}$
, let
![]() $\mathbb {Q}(\mathbb {P})$
be the poset whose elements are pairs
$\mathbb {Q}(\mathbb {P})$
be the poset whose elements are pairs
![]() $(T,n)$
, where
$(T,n)$
, where
![]() $T\in \mathbb {P}$
and
$T\in \mathbb {P}$
and
![]() $n<\omega $
, ordered so that
$n<\omega $
, ordered so that
![]() $(S,m)\leq (T,n)$
whenever S is a subtree of T such that S and T agree up to level n and
$(S,m)\leq (T,n)$
whenever S is a subtree of T such that S and T agree up to level n and
![]() $m\geq n$
. Forcing with
$m\geq n$
. Forcing with
![]() $\mathbb {Q}(\mathbb {P})$
adds a generic perfect tree. Let
$\mathbb {Q}(\mathbb {P})$
adds a generic perfect tree. Let
![]() $\mathbb {Q}(\mathbb {P})^{{<}\omega }$
be the finite-support
$\mathbb {Q}(\mathbb {P})^{{<}\omega }$
be the finite-support
![]() $\omega $
-length product of the
$\omega $
-length product of the
![]() $\mathbb {Q}(\mathbb {P})$
and let
$\mathbb {Q}(\mathbb {P})$
and let
![]() $G\subseteq \mathbb {Q}(\mathbb {P})^{{<}\omega }$
be V-generic. In the forcing extension
$G\subseteq \mathbb {Q}(\mathbb {P})^{{<}\omega }$
be V-generic. In the forcing extension
![]() $V[G]$
, let
$V[G]$
, let
![]() $\{\mathscr T_n\mid n<\omega \}$
be the
$\{\mathscr T_n\mid n<\omega \}$
be the
![]() $\omega $
-many generic perfect trees added by G. Finally, let
$\omega $
-many generic perfect trees added by G. Finally, let
![]() $\mathbb {P}^*$
be the closure of
$\mathbb {P}^*$
be the closure of
![]() $\mathbb {P}$
and
$\mathbb {P}$
and
![]() $\{\mathscr T_n\mid n<\omega \}$
under finite meets and unions. In
$\{\mathscr T_n\mid n<\omega \}$
under finite meets and unions. In
![]() $V[G]$
, the perfect poset
$V[G]$
, the perfect poset
![]() $\mathbb {P}^*$
has the following two key properties:
$\mathbb {P}^*$
has the following two key properties:
-
(1)
 $\{\mathscr T_n\mid n<\omega \}$
is a maximal antichain,
$\{\mathscr T_n\mid n<\omega \}$
is a maximal antichain, -
(2) every maximal antichain of
 $\mathbb {P}$
from V remains maximal in
$\mathbb {P}$
from V remains maximal in
 $\mathbb {P}^*$
$\mathbb {P}^*$
(see [Reference Friedman, Gitman and Kanovei2] for details). Let us now work in the constructible universe L. Let
![]() $\vec D=\langle D_\xi \mid \xi <\omega _1\rangle $
be the canonical
$\vec D=\langle D_\xi \mid \xi <\omega _1\rangle $
be the canonical
![]() $\diamondsuit $
-sequence obtained by letting
$\diamondsuit $
-sequence obtained by letting
![]() $D_{\alpha +1}$
be the least counterexample if one exists. Let us call a countable level
$D_{\alpha +1}$
be the least counterexample if one exists. Let us call a countable level
![]() $L_\alpha $
of L suitable if
$L_\alpha $
of L suitable if
For example, the collapse of any countable elementary substructure of
![]() $L_{\omega _2}$
is suitable. Observe also that, by canonicity of the
$L_{\omega _2}$
is suitable. Observe also that, by canonicity of the
![]() $\diamondsuit $
-sequence
$\diamondsuit $
-sequence
![]() $\vec D$
, if
$\vec D$
, if
![]() $L_\alpha $
is suitable and
$L_\alpha $
is suitable and
![]() $\delta =(\omega _1)^{L_\alpha }$
, then
$\delta =(\omega _1)^{L_\alpha }$
, then
![]() $\vec D\upharpoonright \delta \in L_\alpha $
. We will use suitable models
$\vec D\upharpoonright \delta \in L_\alpha $
. We will use suitable models
![]() $L_\alpha $
handed to us by
$L_\alpha $
handed to us by
![]() $\vec D$
to construct Jensen’s forcing
$\vec D$
to construct Jensen’s forcing
![]() $\mathbb J$
in
$\mathbb J$
in
![]() $\omega _1$
-many steps as a continuous chain of length
$\omega _1$
-many steps as a continuous chain of length
![]() $\omega _1$
of countable perfect posets. Let
$\omega _1$
of countable perfect posets. Let
![]() $\mathbb {P}_0=\mathbb {P}_{\text {min}}$
. At limit ordinals, we will take unions. So suppose we have constructed a countable perfect poset
$\mathbb {P}_0=\mathbb {P}_{\text {min}}$
. At limit ordinals, we will take unions. So suppose we have constructed a countable perfect poset
![]() $\mathbb {P}_\xi $
. We let
$\mathbb {P}_\xi $
. We let
![]() $\mathbb {P}_{\xi +1}=\mathbb {P}_\xi $
unless the following happens. Suppose that
$\mathbb {P}_{\xi +1}=\mathbb {P}_\xi $
unless the following happens. Suppose that
![]() $D_\xi $
codes a suitable model
$D_\xi $
codes a suitable model
![]() $L_{\alpha _\xi }$
such that
$L_{\alpha _\xi }$
such that
![]() $\mathbb {P}_\xi \in L_{\alpha _\xi }$
and
$\mathbb {P}_\xi \in L_{\alpha _\xi }$
and
![]() $(\omega _1)^{L_{\alpha _\xi }}=\xi $
. Then we let
$(\omega _1)^{L_{\alpha _\xi }}=\xi $
. Then we let
![]() $G_\xi $
be the L-least
$G_\xi $
be the L-least
![]() $L_{\alpha _\xi }$
-generic filter for
$L_{\alpha _\xi }$
-generic filter for
![]() $\mathbb {Q}(\mathbb {P}_\xi )^{{<}\omega }$
and let
$\mathbb {Q}(\mathbb {P}_\xi )^{{<}\omega }$
and let
![]() $\mathbb {P}_{\xi +1}=\mathbb {P}_\xi ^*$
as constructed in
$\mathbb {P}_{\xi +1}=\mathbb {P}_\xi ^*$
as constructed in
![]() $L_{\alpha _\xi }[G_\xi ]$
. Notice that by our observations above, we seal maximal antichains ensuring that the resulting union poset will have the ccc. We let
$L_{\alpha _\xi }[G_\xi ]$
. Notice that by our observations above, we seal maximal antichains ensuring that the resulting union poset will have the ccc. We let
![]() $\mathbb J=\bigcup _{\xi <\omega _1}\mathbb {P}_\xi $
. Jensen showed that the poset
$\mathbb J=\bigcup _{\xi <\omega _1}\mathbb {P}_\xi $
. Jensen showed that the poset
![]() $\mathbb J$
has the ccc and adds a unique generic real, whose singleton is
$\mathbb J$
has the ccc and adds a unique generic real, whose singleton is
![]() $\Pi ^1_2$
-definable [Reference Jensen5]. Products and iterations of Jensen’s forcing also turned out to have “unique generics” properties.
$\Pi ^1_2$
-definable [Reference Jensen5]. Products and iterations of Jensen’s forcing also turned out to have “unique generics” properties.
Lyubetsky and Kanovei showed that in a forcing extension by a finite-support
![]() $\alpha $
-length product of Jensen’s forcing the only L-generic reals for
$\alpha $
-length product of Jensen’s forcing the only L-generic reals for
![]() $\mathbb J$
are those explicitly added by the (
$\mathbb J$
are those explicitly added by the (
![]() $\alpha $
-many) slices of the generic filter [Reference Kanovei and Lyubetsky6].
$\alpha $
-many) slices of the generic filter [Reference Kanovei and Lyubetsky6].
As mentioned in footnote 1, a forcing with the same properties as
![]() $\mathbb J$
, minus the low complexity of the generic singleton, can be constructed in any model of the
$\mathbb J$
, minus the low complexity of the generic singleton, can be constructed in any model of the
![]() $\diamondsuit $
-principle. In particular, since ccc posets of size
$\diamondsuit $
-principle. In particular, since ccc posets of size
![]() $\omega _1$
preserve the
$\omega _1$
preserve the
![]() $\diamondsuit $
-principle, any forcing extension of L by
$\diamondsuit $
-principle, any forcing extension of L by
![]() $\mathbb J$
continues to satisfy the
$\mathbb J$
continues to satisfy the
![]() $\diamondsuit $
-principle, and we can construct a Jensen-like poset again in it. In this way, we can make sense of iterating Jensen’s forcing and define finite n-length iterations
$\diamondsuit $
-principle, and we can construct a Jensen-like poset again in it. In this way, we can make sense of iterating Jensen’s forcing and define finite n-length iterations
![]() $\mathbb J_n$
of
$\mathbb J_n$
of
![]() $\mathbb J$
. The iterations
$\mathbb J$
. The iterations
![]() $\mathbb J_n$
are constructed, analogously to Jensen’s forcing, as a chain of length
$\mathbb J_n$
are constructed, analogously to Jensen’s forcing, as a chain of length
![]() $\omega _1$
of iterations
$\omega _1$
of iterations
![]() $\mathbb {P}_n^{\xi }=\mathbb {Q}_0^\xi * \dot {\mathbb {Q}}_1^\xi *\cdots *\dot {\mathbb {Q}}_{n-1}^\xi $
for
$\mathbb {P}_n^{\xi }=\mathbb {Q}_0^\xi * \dot {\mathbb {Q}}_1^\xi *\cdots *\dot {\mathbb {Q}}_{n-1}^\xi $
for
![]() $\xi <\omega _1$
, where
$\xi <\omega _1$
, where
![]() $\mathbb {P}_0^\xi $
is a countable perfect poset, and for
$\mathbb {P}_0^\xi $
is a countable perfect poset, and for
![]() $i<n-1$
,
$i<n-1$
,
We start with
![]() $\mathbb {P}^0_n$
in which
$\mathbb {P}^0_n$
in which
![]() $\mathbb {Q}^0_0=\mathbb {P}_{\text {min}}$
and for
$\mathbb {Q}^0_0=\mathbb {P}_{\text {min}}$
and for
![]() $i<n-1$
,
$i<n-1$
,
![]() $\dot {\mathbb {Q}}^0_i=\check {\mathbb {P}}_{\text {min}}$
. At stages
$\dot {\mathbb {Q}}^0_i=\check {\mathbb {P}}_{\text {min}}$
. At stages
![]() $\xi +1$
at which the canonical
$\xi +1$
at which the canonical
![]() $\diamondsuit $
-sequence
$\diamondsuit $
-sequence
![]() $\vec D$
codes a suitable model
$\vec D$
codes a suitable model
![]() $L_{\alpha _\xi }$
, we construct
$L_{\alpha _\xi }$
, we construct
![]() $\mathbb {P}_n^{\xi +1}$
in a generic extension of
$\mathbb {P}_n^{\xi +1}$
in a generic extension of
![]() $L_{\alpha _\xi }$
(by a poset generalizing
$L_{\alpha _\xi }$
(by a poset generalizing
![]() $\mathbb {Q}(\mathbb {P})^{{<}\omega }$
which adds
$\mathbb {Q}(\mathbb {P})^{{<}\omega }$
which adds
![]() $\omega $
-many generic perfect trees to every iterate in
$\omega $
-many generic perfect trees to every iterate in
![]() $\mathbb {P}_n^\xi $
). As in the case of the construction of Jensen’s forcing
$\mathbb {P}_n^\xi $
). As in the case of the construction of Jensen’s forcing
![]() $\mathbb J$
, every maximal antichain of
$\mathbb J$
, every maximal antichain of
![]() $\mathbb {P}_n^\xi $
remains maximal in
$\mathbb {P}_n^\xi $
remains maximal in
![]() $\mathbb J_n$
(see [Reference Friedman, Gitman and Kanovei2] for details). Abraham showed that the finite iterations
$\mathbb J_n$
(see [Reference Friedman, Gitman and Kanovei2] for details). Abraham showed that the finite iterations
![]() $\mathbb J_n$
have the ccc and add a unique n-length generic sequence of reals [Reference Abraham1, Lemmas 2.3 and 2.4].
$\mathbb J_n$
have the ccc and add a unique n-length generic sequence of reals [Reference Abraham1, Lemmas 2.3 and 2.4].
In [Reference Friedman, Gitman and Kanovei2], together with Friedman and Kanovei, we studied the properties of the (non-linear) tree iterations of
![]() $\mathbb J$
. Suppose that
$\mathbb J$
. Suppose that
![]() $\mathcal T$
is a tree of height at most
$\mathcal T$
is a tree of height at most
![]() $\omega $
. We will call the following poset
$\omega $
. We will call the following poset
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
, the tree iteration of
$\mathbb {P}(\mathbb J,\mathcal T)$
, the tree iteration of
![]() $\mathbb J$
along
$\mathbb J$
along
![]() $\mathcal T$
. Elements of
$\mathcal T$
. Elements of
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
are functions p from a finite subtree
$\mathbb {P}(\mathbb J,\mathcal T)$
are functions p from a finite subtree
![]() $D_p$
of
$D_p$
of
![]() $\mathcal T$
into
$\mathcal T$
into
![]() $\bigcup _{n<\omega }\mathbb J_n$
such that for every node
$\bigcup _{n<\omega }\mathbb J_n$
such that for every node
![]() $s\in D_p$
,
$s\in D_p$
,
![]() $p(s)\in \mathbb J_{\text {len}(s)}$
and whenever
$p(s)\in \mathbb J_{\text {len}(s)}$
and whenever
![]() $s\subseteq t$
in
$s\subseteq t$
in
![]() $D_p$
, then
$D_p$
, then
![]() $p(s)=p(t)\upharpoonright \text {len}(s)$
. In other words, a condition is a tree isomorphic to a finite subtree of
$p(s)=p(t)\upharpoonright \text {len}(s)$
. In other words, a condition is a tree isomorphic to a finite subtree of
![]() $\mathcal T$
whose level n nodes are elements of the n-length iteration
$\mathcal T$
whose level n nodes are elements of the n-length iteration
![]() $\mathbb J_n$
and the assignment is coherent in the sense that conditions on the lower nodes are restrictions of the conditions on the higher nodes. The elements are ordered so that
$\mathbb J_n$
and the assignment is coherent in the sense that conditions on the lower nodes are restrictions of the conditions on the higher nodes. The elements are ordered so that
![]() $q\leq p$
if
$q\leq p$
if
![]() $D_p\subseteq D_q$
and for every node
$D_p\subseteq D_q$
and for every node
![]() $s\in D_p$
,
$s\in D_p$
,
![]() $q(s)\leq p(s)$
. A generic filter G for
$q(s)\leq p(s)$
. A generic filter G for
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
adds a tree
$\mathbb {P}(\mathbb J,\mathcal T)$
adds a tree
![]() $\mathcal T^G$
isomorphic to
$\mathcal T^G$
isomorphic to
![]() $\mathcal T$
whose nodes on level n are mutually generic sequences for
$\mathcal T$
whose nodes on level n are mutually generic sequences for
![]() $\mathbb J_n$
.
$\mathbb J_n$
.
Theorem 2.1 [Reference Friedman, Gitman and Kanovei2].
Suppose that
![]() $\mathcal T=\omega ^{{<}\omega }$
or
$\mathcal T=\omega ^{{<}\omega }$
or
![]() $\mathcal T=\omega _1^{{<}\omega }$
. Then the tree iteration
$\mathcal T=\omega _1^{{<}\omega }$
. Then the tree iteration
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
has the ccc.
$\mathbb {P}(\mathbb J,\mathcal T)$
has the ccc.
The tree iterations of
![]() $\mathbb J$
also have a “uniqueness of generics” property generalizing Lyubetsky and Kanovei’s result for finite-support products of
$\mathbb J$
also have a “uniqueness of generics” property generalizing Lyubetsky and Kanovei’s result for finite-support products of
![]() $\mathbb J$
.
$\mathbb J$
.
Theorem 2.2 [Reference Friedman, Gitman and Kanovei2].
Suppose that
![]() $\mathcal T=\omega ^{{<}\omega }$
or
$\mathcal T=\omega ^{{<}\omega }$
or
![]() $\mathcal T=\omega _1^{{<}\omega }$
and
$\mathcal T=\omega _1^{{<}\omega }$
and
![]() $G\subseteq \mathbb {P}(\mathbb J,\mathcal T)$
is L-generic. In
$G\subseteq \mathbb {P}(\mathbb J,\mathcal T)$
is L-generic. In
![]() $L[G]$
:
$L[G]$
:
-
(1) The only L-generic sequences of reals for
 $\mathbb J_n$
are those coming from the nodes of
$\mathbb J_n$
are those coming from the nodes of
 $\mathcal T^G$
on level n.
$\mathcal T^G$
on level n. -
(2) The collection of all L-generic n-length sequences of reals for
 $\mathbb J_n$
is
$\mathbb J_n$
is
 $\Pi ^1_2$
-definable.
$\Pi ^1_2$
-definable.
The following two easy propositions will be useful in later arguments. Given a condition
![]() $p\in \mathbb {P}(\mathbb J,\mathcal T)$
and a subtree T of
$p\in \mathbb {P}(\mathbb J,\mathcal T)$
and a subtree T of
![]() $\mathcal T$
, let
$\mathcal T$
, let
![]() $p\upharpoonright T$
be the restriction of p to the domain
$p\upharpoonright T$
be the restriction of p to the domain
![]() $D_p\cap T$
.
$D_p\cap T$
.
Proposition 2.3. Suppose that T is a subtree of
![]() $\mathcal T$
,
$\mathcal T$
,
![]() $a\in \mathbb {P}(\mathbb J, T)$
,
$a\in \mathbb {P}(\mathbb J, T)$
,
![]() $p\in \mathbb {P}(\mathbb J,\mathcal T)$
, and a is compatible with
$p\in \mathbb {P}(\mathbb J,\mathcal T)$
, and a is compatible with
![]() $p\upharpoonright T$
in
$p\upharpoonright T$
in
![]() $\mathbb {P}(\mathbb J,T)$
, then a is compatible with p in
$\mathbb {P}(\mathbb J,T)$
, then a is compatible with p in
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
.
$\mathbb {P}(\mathbb J,\mathcal T)$
.
Proof. Let
![]() $q\in \mathbb {P}(\mathbb J,T)$
be such that
$q\in \mathbb {P}(\mathbb J,T)$
be such that
![]() $q\leq a,p\upharpoonright T$
. Define a condition
$q\leq a,p\upharpoonright T$
. Define a condition
![]() $q'$
with domain
$q'$
with domain
![]() $D_{q'}=D_q\cup D_p$
as follows. If
$D_{q'}=D_q\cup D_p$
as follows. If
![]() $s\in T$
, then
$s\in T$
, then
![]() $q'(s)=q(s)$
. If
$q'(s)=q(s)$
. If
![]() $s\in D_{q'}\setminus T$
, then let i be largest such that
$s\in D_{q'}\setminus T$
, then let i be largest such that
![]() $s\upharpoonright i\in D_p$
and let
$s\upharpoonright i\in D_p$
and let
![]() $q'(s)$
be
$q'(s)$
be
![]() $q(s\upharpoonright i)$
concatenated with the tail of
$q(s\upharpoonright i)$
concatenated with the tail of
![]() $p(s)$
from i. It is easy to see that
$p(s)$
from i. It is easy to see that
![]() $q'\leq p,a$
in
$q'\leq p,a$
in
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
.
$\mathbb {P}(\mathbb J,\mathcal T)$
.
Suppose that
![]() $G\subseteq \mathbb {P}(\mathbb J,\mathcal T)$
is L-generic. Given a subtree T of
$G\subseteq \mathbb {P}(\mathbb J,\mathcal T)$
is L-generic. Given a subtree T of
![]() $\mathcal T$
, let
$\mathcal T$
, let
![]() $G_T$
consist of all conditions
$G_T$
consist of all conditions
![]() $p\in G$
with domain
$p\in G$
with domain
![]() $D_p\subseteq T$
.
$D_p\subseteq T$
.
Proposition 2.4. Suppose that T is a subtree of
![]() $\mathcal T$
. Then
$\mathcal T$
. Then
![]() $G_T$
is L-generic for
$G_T$
is L-generic for
![]() $\mathbb {P}(\mathbb J,T)$
.
$\mathbb {P}(\mathbb J,T)$
.
Proof. Suppose that
![]() $p\in G_T$
and
$p\in G_T$
and
![]() $q\geq p$
in
$q\geq p$
in
![]() $\mathbb {P}(\mathbb J,T)$
. Then
$\mathbb {P}(\mathbb J,T)$
. Then
![]() $q\geq p$
in
$q\geq p$
in
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
. So
$\mathbb {P}(\mathbb J,\mathcal T)$
. So
![]() $q\in G$
, and hence
$q\in G$
, and hence
![]() $q\in G_T$
. Next, suppose that
$q\in G_T$
. Next, suppose that
![]() $p,q\in G_T$
. Since
$p,q\in G_T$
. Since
![]() $p,q\in G$
, there is
$p,q\in G$
, there is
![]() $r\in G$
such that
$r\in G$
such that
![]() $r\leq p,q$
, and hence
$r\leq p,q$
, and hence
![]() $r\upharpoonright T\leq p,q$
. Observe that
$r\upharpoonright T\leq p,q$
. Observe that
![]() $r\upharpoonright T$
is compatible with every condition in G because r is compatible with every condition in G. Thus,
$r\upharpoonright T$
is compatible with every condition in G because r is compatible with every condition in G. Thus,
![]() $r\upharpoonright T\in G$
, and hence
$r\upharpoonright T\in G$
, and hence
![]() $r\upharpoonright T\in G_T$
. Finally, suppose that
$r\upharpoonright T\in G_T$
. Finally, suppose that
![]() $\mathcal A$
is a maximal antichain of
$\mathcal A$
is a maximal antichain of
![]() $\mathbb {P}(\mathbb J,T)$
. Let’s argue that
$\mathbb {P}(\mathbb J,T)$
. Let’s argue that
![]() $\mathcal A$
is also a maximal antichain of
$\mathcal A$
is also a maximal antichain of
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
. Let
$\mathbb {P}(\mathbb J,\mathcal T)$
. Let
![]() $p\in \mathbb {P}(\mathbb J,\mathcal T)$
. Then there is
$p\in \mathbb {P}(\mathbb J,\mathcal T)$
. Then there is
![]() $a\in \mathcal A$
that is compatible with
$a\in \mathcal A$
that is compatible with
![]() $p\upharpoonright T$
in
$p\upharpoonright T$
in
![]() $\mathbb {P}(\mathbb J,T)$
, but then a is also compatible with p in
$\mathbb {P}(\mathbb J,T)$
, but then a is also compatible with p in
![]() $\mathbb {P}(\mathbb J,\mathcal T)$
by Proposition 2.3. Thus, there is
$\mathbb {P}(\mathbb J,\mathcal T)$
by Proposition 2.3. Thus, there is
![]() $p\in G\cap \mathcal A$
. This completes the argument that
$p\in G\cap \mathcal A$
. This completes the argument that
![]() $G_T$
is L-generic for
$G_T$
is L-generic for
![]() $\mathbb {P}(\mathbb J,T)$
.
$\mathbb {P}(\mathbb J,T)$
.
2.3 Automorphisms of forcing notions
Suppose that
![]() $\mathbb {P}$
is a partial order,
$\mathbb {P}$
is a partial order,
![]() $\pi $
is an automorphism of
$\pi $
is an automorphism of
![]() $\mathbb {P}$
, and
$\mathbb {P}$
, and
![]() $G\subseteq \mathbb {P}$
is V-generic. We can apply
$G\subseteq \mathbb {P}$
is V-generic. We can apply
![]() $\pi $
recursively to any
$\pi $
recursively to any
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\sigma $
to obtain the
$\sigma $
to obtain the
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\pi (\sigma )$
defined by
$\pi (\sigma )$
defined by
![]() $\langle \tau ,p\rangle \in \sigma $
if and only if
$\langle \tau ,p\rangle \in \sigma $
if and only if
![]() $\langle \pi (\tau ),\pi (p)\rangle \in \pi (\sigma )$
. Standard arguments then show that for a condition
$\langle \pi (\tau ),\pi (p)\rangle \in \pi (\sigma )$
. Standard arguments then show that for a condition
![]() $p\in \mathbb {P}$
,
$p\in \mathbb {P}$
,
![]() $p\Vdash \varphi (\sigma )$
if and only if
$p\Vdash \varphi (\sigma )$
if and only if
![]() $\pi (p)\Vdash \varphi (\pi (\sigma ))$
. It is also easy to see that
$\pi (p)\Vdash \varphi (\pi (\sigma ))$
. It is also easy to see that ![]() is V-generic. We will use the following standard proposition later, and we include the proof here for completeness.
is V-generic. We will use the following standard proposition later, and we include the proof here for completeness.
Proposition 2.5. Suppose that
![]() $\sigma $
is a
$\sigma $
is a
![]() $\mathbb {P}$
-name. Then
$\mathbb {P}$
-name. Then ![]() .
.
Proof. We can assume recursively that we already showed the conclusion for all
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\tau $
of rank less than
$\tau $
of rank less than
![]() $\sigma $
. Suppose that
$\sigma $
. Suppose that ![]() . Then there is a
. Then there is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot b$
such that
$\dot b$
such that ![]() ,
,
![]() $\langle \dot b,p\rangle \in \sigma $
, and
$\langle \dot b,p\rangle \in \sigma $
, and ![]() . Let
. Let
![]() $\pi ^{-1}(\bar p)=p$
. Then
$\pi ^{-1}(\bar p)=p$
. Then
![]() $\langle \pi (\dot b),\bar p\rangle \in \pi (\sigma )$
and
$\langle \pi (\dot b),\bar p\rangle \in \pi (\sigma )$
and
![]() $\bar p\in G$
. Thus,
$\bar p\in G$
. Thus,
![]() $\pi (\dot b)_G\in \pi (\sigma )_G$
, and by our recursive assumption, since
$\pi (\dot b)_G\in \pi (\sigma )_G$
, and by our recursive assumption, since
![]() $\dot b$
has rank less than
$\dot b$
has rank less than
![]() $\sigma $
,
$\sigma $
, ![]() , and so,
, and so,
![]() $b\in \pi (\sigma )_G$
. Reversing the steps of this argument shows that if
$b\in \pi (\sigma )_G$
. Reversing the steps of this argument shows that if
![]() $b\in \pi (\sigma )_G$
, then
$b\in \pi (\sigma )_G$
, then ![]() , verifying the equality.
, verifying the equality.
3 A model of
 $\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
 $\mathrm {CA}$
+
$\mathrm {CA}$
+
 $\neg \Sigma ^1_3$
-
$\neg \Sigma ^1_3$
-
 $\mathrm {CA.}$
$\mathrm {CA.}$
In this section, we construct a model of
![]() $\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
in which
$\mathrm {CA}$
in which
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm {CA}$
fails.
$\mathrm {CA}$
fails.
Let
![]() $G\subseteq \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
be L-generic. We work in
$G\subseteq \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
be L-generic. We work in
![]() $L[G]$
. Let
$L[G]$
. Let
![]() $\dot \varphi $
be the canonical name for the isomorphism between
$\dot \varphi $
be the canonical name for the isomorphism between
![]() $\omega ^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic n-length sequences of reals for
$\omega ^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic n-length sequences of reals for
![]() $\mathbb J_n$
.
$\mathbb J_n$
.
Observe that any automorphism
![]() $\pi $
of the tree
$\pi $
of the tree
![]() $\omega ^{{<}\omega }$
gives rise to the obvious corresponding automorphism
$\omega ^{{<}\omega }$
gives rise to the obvious corresponding automorphism
![]() $\pi ^*$
of the poset
$\pi ^*$
of the poset
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
.
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
.
Theorem 3.1. Suppose that T is a finite subtree of
![]() $\omega ^{{<}\omega }$
. Then the only L-generic sequences for
$\omega ^{{<}\omega }$
. Then the only L-generic sequences for
![]() $\mathbb J_n$
in
$\mathbb J_n$
in
![]() $L[G_T]$
are the sequences
$L[G_T]$
are the sequences
![]() $\dot \varphi _G(s)$
for
$\dot \varphi _G(s)$
for
![]() $s\in T$
.
$s\in T$
.
Proof. Let
![]() $r\in L[G_T]$
be an n-length sequence of reals L-generic for
$r\in L[G_T]$
be an n-length sequence of reals L-generic for
![]() $\mathbb J_n$
. Then by Theorem 2.2 (1),
$\mathbb J_n$
. Then by Theorem 2.2 (1),
![]() $r=\dot \varphi _G(s)$
for some node s on level n of
$r=\dot \varphi _G(s)$
for some node s on level n of
![]() $\omega ^{{<}\omega }$
. Suppose towards a contradiction that
$\omega ^{{<}\omega }$
. Suppose towards a contradiction that
![]() $s\notin T$
. Let
$s\notin T$
. Let
![]() $i\geq 1$
be least such that
$i\geq 1$
be least such that
![]() $s\upharpoonright i\notin T$
. Let
$s\upharpoonright i\notin T$
. Let
![]() $\dot r$
be a
$\dot r$
be a
![]() $\mathbb {P}(\mathbb J,T)$
-name for r. Let
$\mathbb {P}(\mathbb J,T)$
-name for r. Let
![]() $p\in G$
be such that
$p\in G$
be such that
![]() $p\Vdash \dot r=\dot \varphi (\check s)$
. Fix any condition
$p\Vdash \dot r=\dot \varphi (\check s)$
. Fix any condition
![]() $q\leq p$
. Let
$q\leq p$
. Let
![]() $t\in \omega ^{{<}\omega }$
be a node on the same level as s such that
$t\in \omega ^{{<}\omega }$
be a node on the same level as s such that
![]() $t\upharpoonright i-1=s\upharpoonright i-1$
and
$t\upharpoonright i-1=s\upharpoonright i-1$
and
![]() $t\notin D_q\cup T\cup \{s\}$
. Many such nodes t must exist since
$t\notin D_q\cup T\cup \{s\}$
. Many such nodes t must exist since
![]() $D_q$
and T are both finite. Let
$D_q$
and T are both finite. Let
![]() $\pi $
be an automorphism of
$\pi $
be an automorphism of
![]() $\omega ^{{<}\omega }$
which maps
$\omega ^{{<}\omega }$
which maps
![]() $(\omega ^{{<}\omega })_s$
onto
$(\omega ^{{<}\omega })_s$
onto
![]() $(\omega ^{{<}\omega })_t$
, while fixing everything outside these subtrees. In particular,
$(\omega ^{{<}\omega })_t$
, while fixing everything outside these subtrees. In particular,
![]() $\pi $
fixes T and
$\pi $
fixes T and
![]() $\pi (s)=t$
. Let
$\pi (s)=t$
. Let ![]() and let
and let
![]() $\bar q$
be the condition defined so that for
$\bar q$
be the condition defined so that for
![]() $a\in D_q$
,
$a\in D_q$
,
![]() $\bar q(a)=\bar q(\pi (a))=q(a)$
. In other words, conditions on nodes in
$\bar q(a)=\bar q(\pi (a))=q(a)$
. In other words, conditions on nodes in
![]() $D_q\cap (\omega ^{{<}\omega })_s$
are copied over to
$D_q\cap (\omega ^{{<}\omega })_s$
are copied over to
![]() $(\omega ^{{<}\omega })_t$
. This means, in particular, that
$(\omega ^{{<}\omega })_t$
. This means, in particular, that
![]() $\pi ^*(\bar q)=\bar q$
. We have just argued that such conditions
$\pi ^*(\bar q)=\bar q$
. We have just argued that such conditions
![]() $\bar q$
are dense below p, and so some such
$\bar q$
are dense below p, and so some such
![]() $\bar q\in G$
. Let
$\bar q\in G$
. Let ![]() , which is also L-generic for
, which is also L-generic for
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, and note that
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, and note that
![]() $\pi ^*(\bar q)=\bar q\in H$
. Observe that
$\pi ^*(\bar q)=\bar q\in H$
. Observe that
![]() $\dot r_H=\dot r_G=r$
since the name
$\dot r_H=\dot r_G=r$
since the name
![]() $\dot r$
only mentioned conditions with domain contained in T, and
$\dot r$
only mentioned conditions with domain contained in T, and
![]() $\pi $
fixes T. Since
$\pi $
fixes T. Since
![]() $p\geq \bar q$
,
$p\geq \bar q$
,
![]() $p\in H$
. So it must be the case that
$p\in H$
. So it must be the case that
![]() $r=\dot \varphi _H(s)$
. But this is impossible because
$r=\dot \varphi _H(s)$
. But this is impossible because
![]() $\dot \varphi _H(s)=\dot \varphi _G(t)$
and, by genericity,
$\dot \varphi _H(s)=\dot \varphi _G(t)$
and, by genericity,
![]() $\dot \varphi _G(s)\neq \dot \varphi _G(t)$
.
$\dot \varphi _G(s)\neq \dot \varphi _G(t)$
.
It is not clear how to make the argument above work for infinite subtrees
![]() $T\in L$
, and I suspect that the result will turn out to be false for these.
$T\in L$
, and I suspect that the result will turn out to be false for these.
We now follow the ideas in [Reference Kanovei and Lyubetsky8] to define the following subtree
![]() $\mathcal T$
of
$\mathcal T$
of
![]() $\omega ^{{<}\omega }$
in
$\omega ^{{<}\omega }$
in
![]() $L[G]$
. For
$L[G]$
. For
![]() $1\leq m<\omega $
, let
$1\leq m<\omega $
, let
![]() $\vec 0_m$
denote the m-length sequence of zeroes. We have for every
$\vec 0_m$
denote the m-length sequence of zeroes. We have for every
![]() $n<\omega $
and
$n<\omega $
and
![]() $1\leq m<\omega $
:
$1\leq m<\omega $
:
-
(1)
 $\langle n\rangle \in \mathcal T$
,
$\langle n\rangle \in \mathcal T$
, -
(2)
 ,
, -
(3)
 if and only if
if and only if
 $\dot \varphi _G(\langle n,1 \rangle )(1)(m)=1$
.
$\dot \varphi _G(\langle n,1 \rangle )(1)(m)=1$
.
Condition (1) puts all level 1 nodes of
![]() $\omega ^{{<}\omega }$
into
$\omega ^{{<}\omega }$
into
![]() $\mathcal T$
. Condition (2) puts all left-most branches of
$\mathcal T$
. Condition (2) puts all left-most branches of
![]() $\omega ^{{<}\omega }$
above level 1 nodes into
$\omega ^{{<}\omega }$
above level 1 nodes into
![]() $\mathcal T$
. Condition (3) says that a node on level
$\mathcal T$
. Condition (3) says that a node on level
![]() $m+1$
of the left-most branch above
$m+1$
of the left-most branch above
![]() $\langle n\rangle $
splits in
$\langle n\rangle $
splits in
![]() $\mathcal T$
if and only if the mth bit of the second real in the pair of reals
$\mathcal T$
if and only if the mth bit of the second real in the pair of reals
![]() $\dot \varphi _G(\langle n,1\rangle )$
is 1. Condition (3) is coding the reals
$\dot \varphi _G(\langle n,1\rangle )$
is 1. Condition (3) is coding the reals
![]() $\dot \varphi _G(\langle n,1\rangle )(1)$
into the tree
$\dot \varphi _G(\langle n,1\rangle )(1)$
into the tree
![]() $\mathcal T$
. Let
$\mathcal T$
. Let
![]() $\dot {\mathcal T}$
be the canonical
$\dot {\mathcal T}$
be the canonical
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
-name for
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
-name for
![]() $\mathcal T$
.
$\mathcal T$
.
Let
be the union of the powersets of
![]() $\omega $
from all submodels
$\omega $
from all submodels
![]() $L[G_T]$
with T a finite subtree of
$L[G_T]$
with T a finite subtree of
![]() $\mathcal T$
, and let
$\mathcal T$
, and let
be a model of second-order arithmetic in
![]() $L[G]$
. We will argue that the model
$L[G]$
. We will argue that the model
![]() $\mathcal M$
has all the required properties.
$\mathcal M$
has all the required properties.
Proposition 3.2.
![]() $\mathcal S=\{A\in P^{L[\{\dot \varphi _G(s)\mid s\in X\}]}(\omega )\mid X\subseteq \mathcal T\text { is finite}\}.$
$\mathcal S=\{A\in P^{L[\{\dot \varphi _G(s)\mid s\in X\}]}(\omega )\mid X\subseteq \mathcal T\text { is finite}\}.$
Proof. Suppose that
![]() $A\in P^{L[\{\dot \varphi _G(s)\mid s\in X\}]}(\omega )$
for some finite
$A\in P^{L[\{\dot \varphi _G(s)\mid s\in X\}]}(\omega )$
for some finite
![]() $X\subseteq \mathcal T$
. Let
$X\subseteq \mathcal T$
. Let
![]() $X\subseteq T$
, where T is a finite subtree of
$X\subseteq T$
, where T is a finite subtree of
![]() $\mathcal T$
. Then
$\mathcal T$
. Then
![]() $A\in L[\{\dot \varphi _G(s)\mid s\in X\}]\subseteq L[G_T]$
. Next, suppose that
$A\in L[\{\dot \varphi _G(s)\mid s\in X\}]\subseteq L[G_T]$
. Next, suppose that
![]() $A\in L[G_T]$
for some finite subtree T of
$A\in L[G_T]$
for some finite subtree T of
![]() $\mathcal T$
. The generic
$\mathcal T$
. The generic
![]() $G_T$
is clearly inter-definable with the collection
$G_T$
is clearly inter-definable with the collection
![]() $\{\dot \varphi _G(s)\mid s\in T\}$
, which means that
$\{\dot \varphi _G(s)\mid s\in T\}$
, which means that
![]() $A\in L[G_T]=L[\{\dot \varphi _G(s)\mid s\in T\}]$
.
$A\in L[G_T]=L[\{\dot \varphi _G(s)\mid s\in T\}]$
.
In other words,
![]() $\mathcal S$
depends only on the collection
$\mathcal S$
depends only on the collection
![]() $\bar {\mathcal T}=\{\dot \varphi _G(s)\mid s\in \mathcal T\}$
. Let
$\bar {\mathcal T}=\{\dot \varphi _G(s)\mid s\in \mathcal T\}$
. Let
![]() $\dot {\mathcal S}$
be the canonical
$\dot {\mathcal S}$
be the canonical
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
-name for
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
-name for
![]() $\mathcal S$
. Since, via coding, we can view L-generic sequences for
$\mathcal S$
. Since, via coding, we can view L-generic sequences for
![]() $\mathbb J_n$
as subsets of
$\mathbb J_n$
as subsets of
![]() $\omega $
, we can talk about these sequences internally to the model
$\omega $
, we can talk about these sequences internally to the model
![]() $\mathcal M$
. In particular, clearly
$\mathcal M$
. In particular, clearly
![]() $\bar {\mathcal T}\subseteq \mathcal S$
.
$\bar {\mathcal T}\subseteq \mathcal S$
.
Lemma 3.3. For every n-length sequence of reals
![]() $r\in \mathcal S$
, we have that r is L-generic for
$r\in \mathcal S$
, we have that r is L-generic for
![]() $\mathbb J_n$
if and only if
$\mathbb J_n$
if and only if
![]() $r\in \bar { \mathcal T}$
. Hence
$r\in \bar { \mathcal T}$
. Hence
![]() $\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
$\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
Proof. Suppose that
![]() $r\in \mathcal S$
is an n-length sequence L-generic for
$r\in \mathcal S$
is an n-length sequence L-generic for
![]() $\mathbb J_n$
. Then
$\mathbb J_n$
. Then
![]() $r\in L[G_T]$
for some finite tree
$r\in L[G_T]$
for some finite tree
![]() $T\subseteq \mathcal T$
. But then, by Theorem 3.1,
$T\subseteq \mathcal T$
. But then, by Theorem 3.1,
![]() $r=\dot \varphi _G(s)$
for some
$r=\dot \varphi _G(s)$
for some
![]() $s\in T$
. Since
$s\in T$
. Since
![]() $\langle 0,1\rangle \notin \mathcal T$
, it follows that
$\langle 0,1\rangle \notin \mathcal T$
, it follows that
![]() $\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
$\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
Observe that any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega $
gives rise to the automorphism
$\omega $
gives rise to the automorphism
![]() $\pi _f$
of the tree
$\pi _f$
of the tree
![]() $\omega ^{{<}\omega }$
which correspondingly permutes the trees
$\omega ^{{<}\omega }$
which correspondingly permutes the trees
![]() $(\omega ^{{<}\omega })_{\langle n\rangle }$
for
$(\omega ^{{<}\omega })_{\langle n\rangle }$
for
![]() $n<\omega $
. More precisely
$n<\omega $
. More precisely
![]() $\pi _f(\langle n_0,n_1,\ldots , n_{\text {len}(s)-1}\rangle )=\langle f(n_0),n_1,\ldots , n_{\text {len}(s)-1}\rangle )$
. Given any two conditions
$\pi _f(\langle n_0,n_1,\ldots , n_{\text {len}(s)-1}\rangle )=\langle f(n_0),n_1,\ldots , n_{\text {len}(s)-1}\rangle )$
. Given any two conditions
![]() $p,q\in \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, there is a permutation
$p,q\in \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, there is a permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega $
such that p and
$\omega $
such that p and
![]() $\pi _f^*(q)$
are compatible, namely, let f be any permutation such that for every
$\pi _f^*(q)$
are compatible, namely, let f be any permutation such that for every
![]() $\langle n\rangle \in D_p\cap D_q$
,
$\langle n\rangle \in D_p\cap D_q$
,
![]() $f(n)=m$
for some m such that
$f(n)=m$
for some m such that
![]() $\langle m\rangle \notin D_p$
. We will argue that the collection
$\langle m\rangle \notin D_p$
. We will argue that the collection
![]() $\bar {\mathcal T}$
is not affected by applying automorphisms
$\bar {\mathcal T}$
is not affected by applying automorphisms
![]() $\pi ^*_f$
to the generic filter G, and hence neither is the collection
$\pi ^*_f$
to the generic filter G, and hence neither is the collection
![]() $\mathcal S$
.
$\mathcal S$
.
Lemma 3.4. For any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega $
, if
$\omega $
, if ![]() , then
, then ![]() , and hence
, and hence
![]() $\mathcal S=\dot {\mathcal S}_H$
.
$\mathcal S=\dot {\mathcal S}_H$
.
Proof. Suppose that
![]() $s=\langle n\rangle $
for some
$s=\langle n\rangle $
for some
![]() $n<\omega $
and let
$n<\omega $
and let
![]() $r=\dot \varphi _G(s)$
. Then
$r=\dot \varphi _G(s)$
. Then
![]() $r=\dot \varphi _H(\langle f(n)\rangle )$
by the definition of
$r=\dot \varphi _H(\langle f(n)\rangle )$
by the definition of
![]() $\pi _f$
, and hence
$\pi _f$
, and hence ![]() . Next, suppose that
. Next, suppose that ![]() for some
for some
![]() $n<\omega $
and
$n<\omega $
and
![]() $1\leq m<\omega $
, and
$1\leq m<\omega $
, and
![]() $r=\dot \varphi _G(s)$
. Then
$r=\dot \varphi _G(s)$
. Then ![]() by the definition of
by the definition of
![]() $\pi _f$
, and hence
$\pi _f$
, and hence ![]() . Finally, suppose that
. Finally, suppose that ![]() for some
for some
![]() $n<\omega $
and
$n<\omega $
and
![]() $1\leq m<\omega $
, and
$1\leq m<\omega $
, and
![]() $r=\dot \varphi _G(s)$
. Then
$r=\dot \varphi _G(s)$
. Then
![]() $\dot \varphi _G(\langle n,1 \rangle )(1)(m)=1$
by the definition of
$\dot \varphi _G(\langle n,1 \rangle )(1)(m)=1$
by the definition of
![]() $\mathcal T$
, and hence
$\mathcal T$
, and hence
![]() $\dot \varphi _H(\langle f(n),1\rangle )(1)(m)=1$
by the definition of
$\dot \varphi _H(\langle f(n),1\rangle )(1)(m)=1$
by the definition of
![]() $\pi _f$
. Thus,
$\pi _f$
. Thus, ![]() by the definition of
by the definition of
![]() $\dot {\mathcal T}$
. Since
$\dot {\mathcal T}$
. Since
![]() $f^{-1}$
is also a permutation of
$f^{-1}$
is also a permutation of
![]() $\omega $
, the same argument shows that
$\omega $
, the same argument shows that ![]() . Since
. Since
![]() $\mathcal S$
depends only on
$\mathcal S$
depends only on ![]() , it follows immediately that
, it follows immediately that
![]() $\mathcal S=\dot {\mathcal S}_H$
.
$\mathcal S=\dot {\mathcal S}_H$
.
Corollary 3.5. For any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega $
,
$\omega $
,
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega ^{{<}\omega })}\dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega ^{{<}\omega })}\dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
Proof. We need to show that for any L-generic filter
![]() $\bar G$
for
$\bar G$
for
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
,
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
,
![]() $\dot {\mathcal S}_{\bar G}=\pi ^*_f(\dot {\mathcal S})_{\bar G}$
. By Lemma 3.4, we know that
$\dot {\mathcal S}_{\bar G}=\pi ^*_f(\dot {\mathcal S})_{\bar G}$
. By Lemma 3.4, we know that ![]() . Since, clearly,
. Since, clearly,
![]() $\pi _{f^{-1}}=\pi ^{-1}_f$
, we have
$\pi _{f^{-1}}=\pi ^{-1}_f$
, we have ![]() . By Proposition 2.5, we have
. By Proposition 2.5, we have ![]() .
.
Lemma 3.6. The model
![]() $\mathcal M=\langle \omega ,+,\times ,<,0,1,\mathcal S\rangle \models \mathrm {Z}_2^{-p}$
.
$\mathcal M=\langle \omega ,+,\times ,<,0,1,\mathcal S\rangle \models \mathrm {Z}_2^{-p}$
.
Proof. Suppose that
![]() $\psi (x)$
is a second-order arithmetic formula. We need to argue that
$\psi (x)$
is a second-order arithmetic formula. We need to argue that
Indeed, we will argue that
![]() $A\in L$
by showing that if
$A\in L$
by showing that if
![]() $\mathcal M\models \psi (n)$
for some
$\mathcal M\models \psi (n)$
for some
![]() $n<\omega $
, then
$n<\omega $
, then
Suppose toward a contradiction that
![]() $p,q\in \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
and
$p,q\in \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
and
![]() $n<\omega $
such that
$n<\omega $
such that
and
Let
![]() $f\in L$
be a permutation of
$f\in L$
be a permutation of
![]() $\omega $
such that p and
$\omega $
such that p and
![]() $\pi ^*_f(q)$
are compatible. We have
$\pi ^*_f(q)$
are compatible. We have
But since by Corollary 3.5,
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega ^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*_f(\dot {\mathcal S})$
,
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega ^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*_f(\dot {\mathcal S})$
,
Let
![]() $r\leq p, \pi ^*_f(q)$
. Then
$r\leq p, \pi ^*_f(q)$
. Then
and
which is the desired contradiction.
Lemma 3.7. The collection
![]() $\bar {\mathcal T}=\{\dot \varphi _G(s)\mid s\in \mathcal T\}$
is definable in
$\bar {\mathcal T}=\{\dot \varphi _G(s)\mid s\in \mathcal T\}$
is definable in
![]() $\mathcal M$
by a
$\mathcal M$
by a
![]() $\Pi ^1_2$
-formula.
$\Pi ^1_2$
-formula.
Proof. By Lemma 3.3, for every n-length sequence
![]() $r\in \mathcal S$
,
$r\in \mathcal S$
,
![]() $r\in \bar {\mathcal T}$
if and only if r is an n-length sequence of reals L-generic for some
$r\in \bar {\mathcal T}$
if and only if r is an n-length sequence of reals L-generic for some
![]() $\mathbb J_n$
. Thus, it suffices to argue that
$\mathbb J_n$
. Thus, it suffices to argue that
![]() $\mathcal M$
can recognize in a
$\mathcal M$
can recognize in a
![]() $\Pi ^1_2$
-way whether an n-length sequence of reals is L-generic for
$\Pi ^1_2$
-way whether an n-length sequence of reals is L-generic for
![]() $\mathbb J_n$
. Recall, from Section 2.2, that the iteration
$\mathbb J_n$
. Recall, from Section 2.2, that the iteration
![]() $\mathbb J_n$
is constructed as the union of the
$\mathbb J_n$
is constructed as the union of the
![]() $\omega _1$
-length chain of iterations
$\omega _1$
-length chain of iterations
![]() $\mathbb {P}_n^\xi $
for
$\mathbb {P}_n^\xi $
for
![]() $\xi <\omega _1$
, and every maximal antichain of
$\xi <\omega _1$
, and every maximal antichain of
![]() $\mathbb {P}_n^\xi $
remains maximal in
$\mathbb {P}_n^\xi $
remains maximal in
![]() $\mathbb J_n$
(for the precise result, see Lemma 6.11 (4) in [Reference Friedman, Gitman and Kanovei2]). Thus, any n-length L-generic sequence of reals for
$\mathbb J_n$
(for the precise result, see Lemma 6.11 (4) in [Reference Friedman, Gitman and Kanovei2]). Thus, any n-length L-generic sequence of reals for
![]() $\mathbb J_n$
is also
$\mathbb J_n$
is also
![]() $L_{\alpha _\xi }$
-generic for
$L_{\alpha _\xi }$
-generic for
![]() $\mathbb {P}_n^\xi $
, where
$\mathbb {P}_n^\xi $
, where
![]() $\xi +1$
is a non-trivial stage in the construction of
$\xi +1$
is a non-trivial stage in the construction of
![]() $\mathbb J_n$
. Since each iteration
$\mathbb J_n$
. Since each iteration
![]() $\mathbb J_n$
has the ccc, the converse holds as well: if an n-length sequence of reals is
$\mathbb J_n$
has the ccc, the converse holds as well: if an n-length sequence of reals is
![]() $L_{\alpha _\xi }$
-generic for
$L_{\alpha _\xi }$
-generic for
![]() $\mathbb {P}_n^\xi $
for all non-trivial stages
$\mathbb {P}_n^\xi $
for all non-trivial stages
![]() $\xi +1$
in the construction of
$\xi +1$
in the construction of
![]() $\mathbb J_n$
, then it is fully L-generic for
$\mathbb J_n$
, then it is fully L-generic for
![]() $\mathbb J_n$
. Next, observe that whether an n-length sequence of reals r is
$\mathbb J_n$
. Next, observe that whether an n-length sequence of reals r is
![]() $L_{\alpha _\xi }$
-generic for
$L_{\alpha _\xi }$
-generic for
![]() $\mathbb {P}_n^\xi $
can be verified in any
$\mathbb {P}_n^\xi $
can be verified in any
![]() $L_\alpha [r]\models \mathrm {ZFC}^-$
with
$L_\alpha [r]\models \mathrm {ZFC}^-$
with
![]() $\alpha>\xi $
. Notice also that any
$\alpha>\xi $
. Notice also that any
![]() $L_\alpha \models \mathrm {ZFC}^-$
can verify whether
$L_\alpha \models \mathrm {ZFC}^-$
can verify whether
![]() $\xi +1<\alpha $
is a non-trivial stage in the construction of
$\xi +1<\alpha $
is a non-trivial stage in the construction of
![]() $\mathbb J_n$
. Putting it all together, we get that an n-length sequence r of reals is L-generic for
$\mathbb J_n$
. Putting it all together, we get that an n-length sequence r of reals is L-generic for
![]() $\mathbb J_n$
if and only if for every
$\mathbb J_n$
if and only if for every
![]() $\alpha <\omega _1$
such that
$\alpha <\omega _1$
such that
![]() $L_\alpha [r]\models \mathrm {ZFC}^-$
, if
$L_\alpha [r]\models \mathrm {ZFC}^-$
, if
![]() $\xi <\alpha $
is such that
$\xi <\alpha $
is such that
![]() $\xi +1$
is a non-trivial stage in the construction of
$\xi +1$
is a non-trivial stage in the construction of
![]() $\mathbb J_n$
, then
$\mathbb J_n$
, then
![]() $L_\alpha [r]$
satisfies that r is
$L_\alpha [r]$
satisfies that r is
![]() $L_{\alpha _\xi }$
-generic for
$L_{\alpha _\xi }$
-generic for
![]() $\mathbb {P}_n^\xi $
. Because
$\mathbb {P}_n^\xi $
. Because
![]() $\mathcal S$
is the union powersets of
$\mathcal S$
is the union powersets of
![]() $\omega $
for models of the form
$\omega $
for models of the form
![]() $L[A]$
, given any
$L[A]$
, given any
![]() $r\in \mathcal S$
,
$r\in \mathcal S$
,
![]() $\mathcal S$
has (a code for)
$\mathcal S$
has (a code for)
![]() $L_\alpha [r]$
for any countable
$L_\alpha [r]$
for any countable
![]() $\alpha $
and
$\alpha $
and
![]() $r\in \mathcal S$
. Thus, an n-length sequence
$r\in \mathcal S$
. Thus, an n-length sequence
![]() $r\in \mathcal S$
of reals is L-generic for
$r\in \mathcal S$
of reals is L-generic for
![]() $\mathbb J_n$
if and only if
$\mathbb J_n$
if and only if
![]() $\mathcal M$
satisfies that for every class X, Y, Z, if X is a well-order and Y codes
$\mathcal M$
satisfies that for every class X, Y, Z, if X is a well-order and Y codes
![]() $L_X[r]$
and Z is a truth predicate for
$L_X[r]$
and Z is a truth predicate for
![]() $L_X[r]$
and
$L_X[r]$
and
![]() $L_X[r]\models \mathrm {ZFC}^-$
(according to Z), then r is
$L_X[r]\models \mathrm {ZFC}^-$
(according to Z), then r is
![]() $L_{\alpha _\xi }$
-generic for
$L_{\alpha _\xi }$
-generic for
![]() $\mathbb {P}_n^\xi $
for every non-trivial successor stage
$\mathbb {P}_n^\xi $
for every non-trivial successor stage
![]() $\xi +1$
in
$\xi +1$
in
![]() $L_X$
. The formula is
$L_X$
. The formula is
![]() $\Pi ^1_2$
because being a well-order is
$\Pi ^1_2$
because being a well-order is
![]() $\Pi ^1_1$
.
$\Pi ^1_1$
.
Lemma 3.8.
![]() $\dot \varphi _G(\langle 0,1\rangle )$
is definable in
$\dot \varphi _G(\langle 0,1\rangle )$
is definable in
![]() $\mathcal M$
from the parameter
$\mathcal M$
from the parameter
![]() $\dot \varphi _G(\langle 0\rangle )$
by a
$\dot \varphi _G(\langle 0\rangle )$
by a
![]() $\Sigma ^1_3$
-formula. Thus,
$\Sigma ^1_3$
-formula. Thus,
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm {CA}$
fails in
$\mathrm {CA}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Proof. We have that
![]() $m\in \dot \varphi _G(\langle 0,1\rangle )(1)$
if and only if there are two L-generic
$m\in \dot \varphi _G(\langle 0,1\rangle )(1)$
if and only if there are two L-generic
![]() $m+1$
-length sequences of reals generic for
$m+1$
-length sequences of reals generic for
![]() $\mathbb J_{m+1}$
whose first coordinate is
$\mathbb J_{m+1}$
whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
. By Lemma 3.7, this is a
$\dot \varphi _G(\langle 0\rangle )$
. By Lemma 3.7, this is a
![]() $\Sigma ^1_3$
-formula with parameter
$\Sigma ^1_3$
-formula with parameter
![]() $\dot \varphi _G(\langle 0\rangle )$
. Since
$\dot \varphi _G(\langle 0\rangle )$
. Since
![]() $\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
,
$\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
,
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm {CA}$
fails in
$\mathrm {CA}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Lemma 3.9.
![]() $\Sigma ^1_2$
-
$\Sigma ^1_2$
-
![]() $\mathrm {CA}$
holds in
$\mathrm {CA}$
holds in
![]() $\mathcal M$
.
$\mathcal M$
.
Proof. Since
![]() $\mathcal S$
is clearly closed under complement, it suffices to show that
$\mathcal S$
is clearly closed under complement, it suffices to show that
![]() $\Pi ^1_2$
-
$\Pi ^1_2$
-
![]() $\mathrm {CA}$
holds in
$\mathrm {CA}$
holds in
![]() $\mathcal M$
. Let
$\mathcal M$
. Let
![]() $A\in \mathcal S$
and fix a formula
$A\in \mathcal S$
and fix a formula
![]() $\psi (x,A):=\forall X\exists Y\,\varphi (x,X,Y,A)$
, where
$\psi (x,A):=\forall X\exists Y\,\varphi (x,X,Y,A)$
, where
![]() $\varphi $
is a first-order formula. We will argue that
$\varphi $
is a first-order formula. We will argue that
This suffices since if
![]() $A\in \mathcal S$
, then
$A\in \mathcal S$
, then
![]() $A\in L[G_T]$
for some finite subtree T of
$A\in L[G_T]$
for some finite subtree T of
![]() $\mathcal T$
, and hence the set
$\mathcal T$
, and hence the set
![]() $\{n\in \omega \mid L[A]\models \psi (n,A)\}$
is in
$\{n\in \omega \mid L[A]\models \psi (n,A)\}$
is in
![]() $L[G_T]$
as well.
$L[G_T]$
as well.
Suppose
![]() $L[A]\models \psi (n,A)$
for some
$L[A]\models \psi (n,A)$
for some
![]() $n<\omega $
. Let
$n<\omega $
. Let
![]() $C\in \mathcal S$
. By Shoenfield’s absoluteness,
$C\in \mathcal S$
. By Shoenfield’s absoluteness,
Thus, there is
![]() $B\in L[A,C]$
such that
$B\in L[A,C]$
such that
Since
![]() $A,C\in \mathcal S$
,
$A,C\in \mathcal S$
,
![]() $P^{L[A,C]}(\omega )\subseteq \mathcal S$
, and so
$P^{L[A,C]}(\omega )\subseteq \mathcal S$
, and so
![]() $B\in \mathcal S$
. Thus,
$B\in \mathcal S$
. Thus,
![]() $\mathcal M\models \varphi (n,C,B,A)$
. Since
$\mathcal M\models \varphi (n,C,B,A)$
. Since
![]() $C\in \mathcal S$
was arbitrary,
$C\in \mathcal S$
was arbitrary,
![]() $\mathcal M\models \psi (n,A)$
. Next, suppose that
$\mathcal M\models \psi (n,A)$
. Next, suppose that
![]() $\mathcal M\models \psi (n,A)$
. Fix
$\mathcal M\models \psi (n,A)$
. Fix
![]() $C\in L[A]$
. Then
$C\in L[A]$
. Then
![]() $\mathcal M\models \exists Y\,\varphi (n,C,Y,A)$
. Fix
$\mathcal M\models \exists Y\,\varphi (n,C,Y,A)$
. Fix
![]() $B\in \mathcal S$
such that
$B\in \mathcal S$
such that
![]() $\mathcal M\models \varphi (n,C,B,A)$
. Then
$\mathcal M\models \varphi (n,C,B,A)$
. Then
![]() $L[A,C,B]\models \varphi (n,C,B,A)$
, and so
$L[A,C,B]\models \varphi (n,C,B,A)$
, and so
![]() $L[A,C,B]\models \exists Y\,\varphi (n,C,Y,A)$
. But then by Shoenfield’s absoluteness,
$L[A,C,B]\models \exists Y\,\varphi (n,C,Y,A)$
. But then by Shoenfield’s absoluteness,
![]() $L[A]\models \exists Y\,\varphi (n,C,Y,A)$
. Since
$L[A]\models \exists Y\,\varphi (n,C,Y,A)$
. Since
![]() $C\in L[A]$
was arbitrary,
$C\in L[A]$
was arbitrary,
![]() $L[A]\models \psi (n,A)$
.
$L[A]\models \psi (n,A)$
.
This finishes the argument that
![]() $\mathcal M\models \mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
$\mathcal M\models \mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
+
$\mathrm {CA}$
+
![]() $\neg \Sigma ^1_3$
-
$\neg \Sigma ^1_3$
-
![]() $\mathrm {CA}$
. Finally, let’s observe that the parameter-free collection scheme fails in
$\mathrm {CA}$
. Finally, let’s observe that the parameter-free collection scheme fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Proposition 3.10.
![]() $\mathrm {Coll}^{-p}$
fails in
$\mathrm {Coll}^{-p}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Proof. The model
![]() $\mathcal M$
satisfies that for every n, there is an n-length L-generic sequence of reals for
$\mathcal M$
satisfies that for every n, there is an n-length L-generic sequence of reals for
![]() $\mathbb J_n$
. But there cannot be a single set
$\mathbb J_n$
. But there cannot be a single set
![]() $X\in \mathcal S$
collecting on its slices n-length L-generic sequences of reals for
$X\in \mathcal S$
collecting on its slices n-length L-generic sequences of reals for
![]() $\mathbb J_n$
for every
$\mathbb J_n$
for every
![]() $n<\omega $
because X has to come from some
$n<\omega $
because X has to come from some
![]() $L[G_T]$
, where T is a finite tree. Since T is finite, by the uniqueness Theorem 3.1, there is some
$L[G_T]$
, where T is a finite tree. Since T is finite, by the uniqueness Theorem 3.1, there is some
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $L[G_T]$
cannot have an L-generic sequence of reals for
$L[G_T]$
cannot have an L-generic sequence of reals for
![]() $\mathbb J_n$
.
$\mathbb J_n$
.
4 A model of
 $\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
 $\mathrm {CA}+\neg \Sigma ^1_4$
-
$\mathrm {CA}+\neg \Sigma ^1_4$
-
 $\mathrm {CA}+\neg \mathrm {AC}^{-p}$
$\mathrm {CA}+\neg \mathrm {AC}^{-p}$
In this section, we construct a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
in which
$\mathrm {CA}$
in which
![]() $\Sigma ^1_4$
-
$\Sigma ^1_4$
-
![]() $\mathrm {CA}$
fails and
$\mathrm {CA}$
fails and
![]() $\mathrm {AC}^{-p}$
fails. We do this by using a more complicated version of the construction in Section 3 working in a forcing extension of L by
$\mathrm {AC}^{-p}$
fails. We do this by using a more complicated version of the construction in Section 3 working in a forcing extension of L by
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
instead of
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
instead of
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
.
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
.
Let
![]() $G\subseteq \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
be L-generic. We work in
$G\subseteq \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
be L-generic. We work in
![]() $L[G]$
. Let
$L[G]$
. Let
![]() $\dot \varphi $
be the canonical name for the isomorphism between
$\dot \varphi $
be the canonical name for the isomorphism between
![]() $\omega _1^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic sequences of reals for
$\omega _1^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic sequences of reals for
![]() $\mathbb J_n$
.
$\mathbb J_n$
.
We start with the following generalization of Theorem 3.1.
Theorem 4.1. Suppose that
![]() $T\in L$
that is a countable subtree of
$T\in L$
that is a countable subtree of
![]() $\omega _1^{{<}\omega }$
. Then the only L-generic sequences for
$\omega _1^{{<}\omega }$
. Then the only L-generic sequences for
![]() $\mathbb J_n$
in
$\mathbb J_n$
in
![]() $L[G_T]$
are the sequences
$L[G_T]$
are the sequences
![]() $\dot \varphi _G(s)$
for
$\dot \varphi _G(s)$
for
![]() $s\in T$
.
$s\in T$
.
The proof is analogous to the proof of Theorem 3.1, using that
![]() $\omega _1^{{<}\omega }$
is uncountable and the tree T is countable to have enough room to find the required node t for the automorphism.
$\omega _1^{{<}\omega }$
is uncountable and the tree T is countable to have enough room to find the required node t for the automorphism.
We define the following subtree
![]() $\mathcal T$
of
$\mathcal T$
of
![]() $\omega _1^{{<}\omega }$
in
$\omega _1^{{<}\omega }$
in
![]() $L[G]$
. We have for every
$L[G]$
. We have for every
![]() $\xi <\omega _1$
,
$\xi <\omega _1$
,
![]() $1\leq m<\omega $
,
$1\leq m<\omega $
,
![]() $n<\omega $
:
$n<\omega $
:
-
(1)
 $\langle \xi \rangle \in \mathcal T$
,
$\langle \xi \rangle \in \mathcal T$
, -
(2)
 ,
, -
(3)

-
(4)
 for all
for all
 $\eta <\omega _1$
if and only if
$\eta <\omega _1$
if and only if
 $\dot \varphi _G(\langle \xi ,1 \rangle )(1)(m)=1$
.
$\dot \varphi _G(\langle \xi ,1 \rangle )(1)(m)=1$
.
Conditions (3) and (4) say that whether a node ![]() of a left-most branch above a level 1 node splits into
of a left-most branch above a level 1 node splits into
![]() $\omega $
-many or
$\omega $
-many or
![]() $\omega _1$
-many nodes depends on whether
$\omega _1$
-many nodes depends on whether
![]() $\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
.
$\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
.
Let
be the union of the powersets of
![]() $\omega $
from all submodels
$\omega $
from all submodels
![]() $L[G_T]$
with T a countable subtree of
$L[G_T]$
with T a countable subtree of
![]() $\mathcal T$
from L, and let
$\mathcal T$
from L, and let
We will argue that the model
![]() $\mathcal M$
has all the required properties. As before, let
$\mathcal M$
has all the required properties. As before, let
![]() $\bar {\mathcal {T}}=\{\dot\varphi_G(s)\mid s\in \mathcal {T}\}$
and let
$\bar {\mathcal {T}}=\{\dot\varphi_G(s)\mid s\in \mathcal {T}\}$
and let
![]() $\dot{\mathcal {S}}$
be the canonical
$\dot{\mathcal {S}}$
be the canonical
![]() $\mathbb{P}(\mathbb{J},\omega_1^{{<}\omega})$
-name for
$\mathbb{P}(\mathbb{J},\omega_1^{{<}\omega})$
-name for
![]() $\mathcal {S}$
. Using Theorem 4.1, we show
$\mathcal {S}$
. Using Theorem 4.1, we show
Lemma 4.2. For every n-length sequence of reals
![]() $r\in \mathcal S$
, we have that r is L-generic for
$r\in \mathcal S$
, we have that r is L-generic for
![]() $\mathbb J_n$
if and only if
$\mathbb J_n$
if and only if
![]() $r\in \bar { \mathcal T}$
. Hence
$r\in \bar { \mathcal T}$
. Hence
![]() $\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
$\dot \varphi _G(\langle 0,1\rangle )\notin \mathcal S$
.
Observe that any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega _1$
gives rise to the automorphism
$\omega _1$
gives rise to the automorphism
![]() $\pi _f$
of the tree
$\pi _f$
of the tree
![]() $\omega _1^{{<}\omega }$
which correspondingly permutes the trees
$\omega _1^{{<}\omega }$
which correspondingly permutes the trees
![]() $(\omega _1^{{<}\omega })_{\langle \xi \rangle }$
for
$(\omega _1^{{<}\omega })_{\langle \xi \rangle }$
for
![]() $\xi <\omega _1$
. More precisely
$\xi <\omega _1$
. More precisely
![]() $\pi _f(\langle \xi _0,\xi _1,\ldots , \xi _{\text {len}(s)-1}\rangle )=\langle f(\xi _0),\xi _1,\ldots , \xi _{\text {len}(s)-1}\rangle )$
. As before, given any two conditions
$\pi _f(\langle \xi _0,\xi _1,\ldots , \xi _{\text {len}(s)-1}\rangle )=\langle f(\xi _0),\xi _1,\ldots , \xi _{\text {len}(s)-1}\rangle )$
. As before, given any two conditions
![]() $p,q\in \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
, there is a permutation
$p,q\in \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
, there is a permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega _1$
such that p and
$\omega _1$
such that p and
![]() $\pi _f^*(q)$
are compatible. We will argue that the collection
$\pi _f^*(q)$
are compatible. We will argue that the collection
![]() $\mathcal S$
is not affected by applying automorphisms
$\mathcal S$
is not affected by applying automorphisms
![]() $\pi ^*_f$
to the generic filter G.
$\pi ^*_f$
to the generic filter G.
Lemma 4.3. For any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega _1$
, we have
$\omega _1$
, we have ![]() . Thus,
. Thus,
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
Proof. Let ![]() . Suppose that
. Suppose that
![]() $T\in L$
is a countable subtree of
$T\in L$
is a countable subtree of
![]() $\mathcal T$
. Let
$\mathcal T$
. Let ![]() . Let’s argue that
. Let’s argue that
![]() $T'\subseteq \dot {\mathcal T}_H$
. It suffices to focus on nodes
$T'\subseteq \dot {\mathcal T}_H$
. It suffices to focus on nodes ![]() , where
, where
![]() $\eta \notin \omega $
. So suppose
$\eta \notin \omega $
. So suppose
![]() $s\in T$
. It follows that
$s\in T$
. It follows that
![]() $\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
, and so
$\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
, and so
![]() $\dot \varphi _H(\langle f(\xi ),1\rangle )(m)=1$
, which means that
$\dot \varphi _H(\langle f(\xi ),1\rangle )(m)=1$
, which means that ![]() . Since
. Since
![]() $f^{-1}$
is also a permutation of
$f^{-1}$
is also a permutation of
![]() $\omega _1$
, we have that if
$\omega _1$
, we have that if
![]() $T'\in L$
is a countable subtree of
$T'\in L$
is a countable subtree of
![]() $\dot {\mathcal T}_H$
, then
$\dot {\mathcal T}_H$
, then ![]() is a subtree of
is a subtree of
![]() $\mathcal T$
. Next, observe that given such trees T and
$\mathcal T$
. Next, observe that given such trees T and
![]() $T'$
, we have that
$T'$
, we have that
![]() $L[G_T]=L[H_{T'}]$
because the trees T and
$L[G_T]=L[H_{T'}]$
because the trees T and
![]() $T'$
are isomorphic by
$T'$
are isomorphic by
![]() $\pi _f$
, making the posets
$\pi _f$
, making the posets
![]() $\mathbb {P}(\mathbb J,T)$
and
$\mathbb {P}(\mathbb J,T)$
and
![]() $\mathbb {P}(\mathbb J,T')$
isomorphic by
$\mathbb {P}(\mathbb J,T')$
isomorphic by
![]() $\pi ^*_f$
, and the isomorphism takes
$\pi ^*_f$
, and the isomorphism takes
![]() $G_T$
to
$G_T$
to
![]() $H_{T'}$
. It follows that
$H_{T'}$
. It follows that ![]() .
.
Analogs of Lemma 3.6 and Lemma 3.9 in Section 3 give that
![]() $\mathcal M$
satisfies
$\mathcal M$
satisfies
![]() $\mathrm {Z}^{-p}_2+\Sigma ^1_2$
-
$\mathrm {Z}^{-p}_2+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
.
$\mathrm {CA}$
.
Lemma 4.4.
![]() $\dot \varphi _G(\langle 0,1\rangle )$
is definable in
$\dot \varphi _G(\langle 0,1\rangle )$
is definable in
![]() $\mathcal M$
from the parameter
$\mathcal M$
from the parameter
![]() $\dot \varphi _G(\langle 0\rangle )$
by a
$\dot \varphi _G(\langle 0\rangle )$
by a
![]() $\Pi ^1_4$
-formula. Thus,
$\Pi ^1_4$
-formula. Thus,
![]() $\Sigma ^1_4$
-
$\Sigma ^1_4$
-
![]() $\mathrm {CA}$
fails in
$\mathrm {CA}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Proof. Recall that for
![]() $m<\omega $
,
$m<\omega $
,
![]() $\dot \varphi _G(\langle 0,1\rangle )(1)(m)=1$
if and only if
$\dot \varphi _G(\langle 0,1\rangle )(1)(m)=1$
if and only if
![]() $\mathcal T$
splits
$\mathcal T$
splits
![]() $\omega _1$
-many times above the node
$\omega _1$
-many times above the node ![]() . In this case,
. In this case,
![]() $\mathcal S$
does not have a maximal set of L-generic sequences for
$\mathcal S$
does not have a maximal set of L-generic sequences for
![]() $\mathbb J_{m+1}$
whose first coordinate is
$\mathbb J_{m+1}$
whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
. More formally, there is no set
$\dot \varphi _G(\langle 0\rangle )$
. More formally, there is no set
![]() $A\in \mathcal S$
such that each slice
$A\in \mathcal S$
such that each slice
![]() $A_n$
is an L-generic
$A_n$
is an L-generic
![]() $m+1$
-length sequence for
$m+1$
-length sequence for
![]() $\mathbb J_{m+1}$
whose first coordinate is
$\mathbb J_{m+1}$
whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
and whenever R is an L-generic
$\dot \varphi _G(\langle 0\rangle )$
and whenever R is an L-generic
![]() $m+1$
-length sequence for
$m+1$
-length sequence for
![]() $\mathbb J_{m+1}$
whose first coordinate is
$\mathbb J_{m+1}$
whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
, then
$\dot \varphi _G(\langle 0\rangle )$
, then
![]() $R=A_n$
for some
$R=A_n$
for some
![]() $n<\omega $
. The assertion that each slice
$n<\omega $
. The assertion that each slice
![]() $A_n$
is an L-generic
$A_n$
is an L-generic
![]() $m+1$
-length sequence for
$m+1$
-length sequence for
![]() $\mathbb J_{m+1}$
whose first coordinate is
$\mathbb J_{m+1}$
whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
is
$\dot \varphi _G(\langle 0\rangle )$
is
![]() $\Pi ^1_2$
and the assertion that every L-generic
$\Pi ^1_2$
and the assertion that every L-generic
![]() $m+1$
-length sequence R for
$m+1$
-length sequence R for
![]() $\mathbb J_{m+1}$
, whose first coordinate is
$\mathbb J_{m+1}$
, whose first coordinate is
![]() $\dot \varphi _G(\langle 0\rangle )$
, is
$\dot \varphi _G(\langle 0\rangle )$
, is
![]() $A_n$
for some
$A_n$
for some
![]() $n<\omega $
is
$n<\omega $
is
![]() $\Pi ^1_3$
. Thus, the assertion that A is maximal as above is
$\Pi ^1_3$
. Thus, the assertion that A is maximal as above is
![]() $\Pi ^1_3$
, and therefore, the assertion that there is no such A is
$\Pi ^1_3$
, and therefore, the assertion that there is no such A is
![]() $\Pi _4^1$
.
$\Pi _4^1$
.
Next, we verify that
![]() $\mathcal M\models \mathrm {Coll}^{-p}$
.
$\mathcal M\models \mathrm {Coll}^{-p}$
.
We will call a countable subtree
![]() $T\in L$
of
$T\in L$
of
![]() $\mathcal T$
full if whenever it contains a node
$\mathcal T$
full if whenever it contains a node
![]() $\langle \xi \rangle $
, then it contains all nodes
$\langle \xi \rangle $
, then it contains all nodes ![]() for
for
![]() $1\leq m<\omega $
and all nodes
$1\leq m<\omega $
and all nodes ![]() for
for
![]() $n<\omega $
and
$n<\omega $
and
![]() $1\leq m<\omega $
. We will call a countable tree
$1\leq m<\omega $
. We will call a countable tree
![]() $T\in L$
undecided if the only nodes in T are of the form
$T\in L$
undecided if the only nodes in T are of the form
![]() $\langle \xi \rangle $
for some
$\langle \xi \rangle $
for some
![]() $\xi <\omega _1$
or
$\xi <\omega _1$
or ![]() for some
for some
![]() $m<\omega $
or
$m<\omega $
or ![]() for some
for some
![]() $n<\omega $
and
$n<\omega $
and
![]() $1\leq m<\omega $
. Observe that every undecided tree T is automatically contained in
$1\leq m<\omega $
. Observe that every undecided tree T is automatically contained in
![]() $\mathcal T$
. As the name suggests, we cannot tell from an undecided tree whether
$\mathcal T$
. As the name suggests, we cannot tell from an undecided tree whether
![]() $\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
for any
$\dot \varphi _G(\langle \xi ,1\rangle )(1)(m)=1$
for any
![]() $\xi <\omega _1$
and
$\xi <\omega _1$
and
![]() $m<\omega $
.
$m<\omega $
.
Lemma 4.5. Suppose that
![]() $T\in L$
is a full countable subtree of
$T\in L$
is a full countable subtree of
![]() $\mathcal T$
,
$\mathcal T$
,
![]() $\varphi (x,X)$
is a second-order formula, and there is
$\varphi (x,X)$
is a second-order formula, and there is
![]() $A\in L[G_T]$
such that
$A\in L[G_T]$
such that
![]() $\mathcal M\models \varphi (n,A)$
. Then there is a full undecided countable tree
$\mathcal M\models \varphi (n,A)$
. Then there is a full undecided countable tree
![]() $\bar T\in L$
and
$\bar T\in L$
and
![]() $\bar A\in L[G_{\bar T}]$
such that
$\bar A\in L[G_{\bar T}]$
such that
![]() $\mathcal M\models \varphi (n,\bar A)$
.
$\mathcal M\models \varphi (n,\bar A)$
.
Proof. Let
![]() $p\in G$
be such that
$p\in G$
be such that
Let’s argue that there can only be finitely many
![]() $\xi <\omega _1$
such that
$\xi <\omega _1$
such that ![]() for some
for some
![]() $\eta \notin \omega $
. Since
$\eta \notin \omega $
. Since
![]() $T\subseteq \mathcal T$
, there is some condition
$T\subseteq \mathcal T$
, there is some condition
![]() $q\in G$
such that
$q\in G$
such that
![]() $q\Vdash T\subseteq \dot {\mathcal T}$
. Thus, for every node
$q\Vdash T\subseteq \dot {\mathcal T}$
. Thus, for every node ![]() with
with
![]() $\eta \notin \omega $
,
$\eta \notin \omega $
,
But this is clearly only possible for
![]() $\xi $
such that
$\xi $
such that
![]() $\langle \xi \rangle \in D_q$
, and
$\langle \xi \rangle \in D_q$
, and
![]() $D_q$
is finite. So let
$D_q$
is finite. So let
![]() $\{\xi _0,\ldots ,\xi _{n-1}\}$
be a finite set such that if
$\{\xi _0,\ldots ,\xi _{n-1}\}$
be a finite set such that if ![]() with
with
![]() $\eta \notin \omega $
, then
$\eta \notin \omega $
, then
![]() $\xi =\xi _i$
for some
$\xi =\xi _i$
for some
![]() $i<n$
. By strengthening the condition p, we can assume that
$i<n$
. By strengthening the condition p, we can assume that
-
(1)
 $\{\langle \xi _i\rangle \mid i<n\}$
are exactly the level 1 nodes in
$\{\langle \xi _i\rangle \mid i<n\}$
are exactly the level 1 nodes in
 $D_p$
,
$D_p$
, -
(2) for
 $i<n$
,
$i<n$
,
 $\langle \xi _i,1\rangle \in D_p$
,
$\langle \xi _i,1\rangle \in D_p$
, -
(3) for every
 with
with
 $\eta \notin \omega $
,
$\eta \notin \omega $
,
 $p(\langle \xi _i\rangle )\Vdash p(\langle \xi _i,1\rangle )(1)(m)=1.$
$p(\langle \xi _i\rangle )\Vdash p(\langle \xi _i,1\rangle )(1)(m)=1.$
Fix some
![]() $\vec \eta =\{\eta _i\mid i<n\}$
such that for
$\vec \eta =\{\eta _i\mid i<n\}$
such that for
![]() $i<n$
,
$i<n$
,
![]() $\langle \eta _i\rangle \notin T\cup \{\langle \xi _i\rangle \mid i<n\}$
, which is possible since T is countable. Let
$\langle \eta _i\rangle \notin T\cup \{\langle \xi _i\rangle \mid i<n\}$
, which is possible since T is countable. Let
![]() $f:\omega _1\to \omega _1$
such that
$f:\omega _1\to \omega _1$
such that
![]() $f(\xi _i)=\eta _i$
,
$f(\xi _i)=\eta _i$
,
![]() $f(\eta _i)=\xi _i$
for
$f(\eta _i)=\xi _i$
for
![]() $i<n$
and
$i<n$
and
![]() $f(\xi )=\xi $
otherwise. For each
$f(\xi )=\xi $
otherwise. For each
![]() $i<n$
and
$i<n$
and
![]() $1\leq m<\omega $
, let
$1\leq m<\omega $
, let
![]() $f_{i,m}:\omega _1\to \omega _1$
be a bijection which maps the set
$f_{i,m}:\omega _1\to \omega _1$
be a bijection which maps the set
onto
![]() $\omega $
. Let
$\omega $
. Let
![]() $\pi _{\vec \eta }$
be the following automorphism of
$\pi _{\vec \eta }$
be the following automorphism of
![]() $\omega _1^{{<}\omega }$
. If
$\omega _1^{{<}\omega }$
. If
![]() $t=\langle \alpha _0,\alpha _1\ldots ,\alpha _n\rangle $
does not end-extend a node
$t=\langle \alpha _0,\alpha _1\ldots ,\alpha _n\rangle $
does not end-extend a node ![]() with
with
![]() $\alpha =\xi _i$
or
$\alpha =\xi _i$
or
![]() $\alpha =\eta _i$
for some
$\alpha =\eta _i$
for some
![]() $i<n$
, then
$i<n$
, then
![]() $\pi _{\vec \eta }(t)=\langle f(\alpha _0),\alpha _1,\ldots ,\alpha _n\rangle $
. Suppose
$\pi _{\vec \eta }(t)=\langle f(\alpha _0),\alpha _1,\ldots ,\alpha _n\rangle $
. Suppose ![]() , where
, where
![]() $\alpha =\xi _i$
or
$\alpha =\xi _i$
or
![]() $\alpha =\eta _i$
. If
$\alpha =\eta _i$
. If
![]() $\alpha =\xi _i$
, then
$\alpha =\xi _i$
, then ![]() and if
and if
![]() $\alpha =\eta _i$
, then
$\alpha =\eta _i$
, then ![]() . To summarize,
. To summarize,
![]() $\pi _{\vec \eta }$
switches the tree
$\pi _{\vec \eta }$
switches the tree
![]() $(\omega _1^{{<}\omega })_{\xi _i}$
with the tree
$(\omega _1^{{<}\omega })_{\xi _i}$
with the tree
![]() $(\omega _1^{{<}\omega })_{\eta _i}$
for
$(\omega _1^{{<}\omega })_{\eta _i}$
for
![]() $i<n$
, keeping everything the same other than mapping nodes of the form
$i<n$
, keeping everything the same other than mapping nodes of the form ![]() to nodes of the form
to nodes of the form ![]() such that if
such that if
![]() $s\in T$
, then
$s\in T$
, then
![]() $\bar \eta <\omega $
. This ensures that the image of T under
$\bar \eta <\omega $
. This ensures that the image of T under
![]() $\pi _{\vec \eta }$
is an undecided tree.
$\pi _{\vec \eta }$
is an undecided tree.
By density, we can find such a set of nodes
![]() $\vec \eta $
and a condition
$\vec \eta $
and a condition
![]() $q\in G$
with
$q\in G$
with ![]() such that for nodes
such that for nodes
![]() $s\in D_p$
,
$s\in D_p$
,
![]() $q(s)=p(s)$
and
$q(s)=p(s)$
and
![]() $q(\pi _{\vec \eta }(s))=p(s)$
. In particular,
$q(\pi _{\vec \eta }(s))=p(s)$
. In particular,
![]() $q\leq p$
. By the definition of
$q\leq p$
. By the definition of
![]() $\pi _{\vec \eta }$
, this means that
$\pi _{\vec \eta }$
, this means that
![]() $\pi ^*_{\vec \eta }(q)=q$
. Let
$\pi ^*_{\vec \eta }(q)=q$
. Let ![]() . It is easy to see that if
. It is easy to see that if
![]() $S\in L$
is a subtree of
$S\in L$
is a subtree of
![]() $\mathcal T$
, then
$\mathcal T$
, then ![]() is a subtree of
is a subtree of
![]() $\dot {\mathcal T}_H$
. So let’s argue that if
$\dot {\mathcal T}_H$
. So let’s argue that if
![]() $S'\in L$
is a subtree of
$S'\in L$
is a subtree of
![]() $\dot {\mathcal T}_H$
, then
$\dot {\mathcal T}_H$
, then ![]() is a subtree of
is a subtree of
![]() $\mathcal T$
. The main concern is to show that if
$\mathcal T$
. The main concern is to show that if
![]() $\dot \varphi _H(\langle \eta _i,1\rangle )(m)(1)=0$
, then for every
$\dot \varphi _H(\langle \eta _i,1\rangle )(m)(1)=0$
, then for every ![]() with
with
![]() $n<\omega $
,
$n<\omega $
, ![]() with
with
![]() $k<\omega $
. But this is true because, according to
$k<\omega $
. But this is true because, according to
![]() $\pi _{\vec \eta }$
, the only situation in which k might end up outside of
$\pi _{\vec \eta }$
, the only situation in which k might end up outside of
![]() $\omega $
is when
$\omega $
is when
![]() $\pi ^{-1}_{\vec \eta }(t)\in T$
, and in this case, by our assumption on p,
$\pi ^{-1}_{\vec \eta }(t)\in T$
, and in this case, by our assumption on p,
![]() $q(\langle \eta _i\rangle )=p(\langle \xi _i\rangle )\Vdash p(\langle \xi _i,1\rangle )(1)(m)=1$
, and
$q(\langle \eta _i\rangle )=p(\langle \xi _i\rangle )\Vdash p(\langle \xi _i,1\rangle )(1)(m)=1$
, and
![]() $p(\langle \xi _i,1\rangle )=q(\langle \eta _i,1\rangle )$
, which means that
$p(\langle \xi _i,1\rangle )=q(\langle \eta _i,1\rangle )$
, which means that
![]() $\dot \varphi _H(\langle \eta _i,1\rangle )(1)(m)=1$
.
$\dot \varphi _H(\langle \eta _i,1\rangle )(1)(m)=1$
.
Thus, by our usual arguments, the automorphism
![]() $\pi ^*_{\vec \eta }$
does not affect
$\pi ^*_{\vec \eta }$
does not affect
![]() $\mathcal S$
. Next, observe that
$\mathcal S$
. Next, observe that ![]() is a full undecided subtree of
is a full undecided subtree of
![]() $\dot {\mathcal T}_H$
. Since
$\dot {\mathcal T}_H$
. Since
![]() $q\leq p$
,
$q\leq p$
,
Since
![]() $q=\pi ^*_{\vec \eta }(q)\in H$
and
$q=\pi ^*_{\vec \eta }(q)\in H$
and
![]() $\pi ^*_{\vec \eta }$
does not affect
$\pi ^*_{\vec \eta }$
does not affect
![]() $\mathcal S$
, there is
$\mathcal S$
, there is
![]() $A\in L[H_T]$
such that
$A\in L[H_T]$
such that
![]() $\mathcal M\models \varphi (n,A)$
. But now since T is isomorphic to
$\mathcal M\models \varphi (n,A)$
. But now since T is isomorphic to
![]() $T'$
via
$T'$
via
![]() $\pi _{\vec \eta }$
, the posets
$\pi _{\vec \eta }$
, the posets
![]() $\mathbb {P}(\mathbb J,T)$
and
$\mathbb {P}(\mathbb J,T)$
and
![]() $\mathbb {P}(\mathbb J,T')$
are isomorphic via
$\mathbb {P}(\mathbb J,T')$
are isomorphic via
![]() $\pi ^*_{\vec \eta }$
, which means that
$\pi ^*_{\vec \eta }$
, which means that
![]() $L[H_T]=L[G_{T'}]$
. Since
$L[H_T]=L[G_{T'}]$
. Since
![]() $T'$
is undecided, we have proved what we promised.
$T'$
is undecided, we have proved what we promised.
Lemma 4.6.
![]() $\mathcal M\models {\mathrm {Coll}}^{-p}$
.
$\mathcal M\models {\mathrm {Coll}}^{-p}$
.
Proof. Suppose that
![]() $\mathcal M\models \forall n\exists X\,\varphi (n,X)$
for some second-order arithmetic formula
$\mathcal M\models \forall n\exists X\,\varphi (n,X)$
for some second-order arithmetic formula
![]() $\varphi (n,X)$
. Given
$\varphi (n,X)$
. Given
![]() $n<\omega $
, by Lemma 4.5, there is a full undecided countable subtree
$n<\omega $
, by Lemma 4.5, there is a full undecided countable subtree
![]() $T_n\in L$
and
$T_n\in L$
and
![]() $X\in L[G_{T_n}]$
such that
$X\in L[G_{T_n}]$
such that
![]() $\mathcal M\models \varphi (n,X)$
. By extending
$\mathcal M\models \varphi (n,X)$
. By extending
![]() $T_n$
to a larger tree, if necessary, we can assume that
$T_n$
to a larger tree, if necessary, we can assume that
![]() $\{\xi <\omega _1\mid \langle \xi \rangle \in T_n\}$
is an ordinal
$\{\xi <\omega _1\mid \langle \xi \rangle \in T_n\}$
is an ordinal
![]() $\alpha _n$
. Let
$\alpha _n$
. Let
![]() $\alpha =\bigcup _{n<\omega }\alpha _n$
and let T be the full undecided tree whose level 1 nodes are precisely
$\alpha =\bigcup _{n<\omega }\alpha _n$
and let T be the full undecided tree whose level 1 nodes are precisely
![]() $\langle \xi \rangle $
for
$\langle \xi \rangle $
for
![]() $\xi <\alpha $
. Then each
$\xi <\alpha $
. Then each
![]() $T_n$
is contained in T. Thus, for every
$T_n$
is contained in T. Thus, for every
![]() $n<\omega $
, there is some
$n<\omega $
, there is some
![]() $X\in L[G_T]$
such that
$X\in L[G_T]$
such that
![]() $\mathcal M\models \varphi (n,X)$
.
$\mathcal M\models \varphi (n,X)$
.
Since
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
has the ccc by Theorem 2.1, all
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
has the ccc by Theorem 2.1, all
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
-nice names for reals are in
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
-nice names for reals are in
![]() $L_{\omega _1}$
. Thus, there is a countable ordinal
$L_{\omega _1}$
. Thus, there is a countable ordinal
![]() $\beta $
such that
$\beta $
such that
![]() $L_\beta $
already has, for every
$L_\beta $
already has, for every
![]() $n<\omega $
, a
$n<\omega $
, a
![]() $\mathbb {P}(\mathbb J,T)$
-name
$\mathbb {P}(\mathbb J,T)$
-name
![]() $\dot X_n$
such that
$\dot X_n$
such that
![]() $\mathcal M\models \varphi (n,(\dot X_n)_G)$
. It follows that
$\mathcal M\models \varphi (n,(\dot X_n)_G)$
. It follows that
![]() $\{\dot X_{G_T}\mid \dot X\in L_\beta \text { is a } \mathbb {P}(\mathbb J,T)\text {-name}\}$
is a countable set of reals in
$\{\dot X_{G_T}\mid \dot X\in L_\beta \text { is a } \mathbb {P}(\mathbb J,T)\text {-name}\}$
is a countable set of reals in
![]() $L[G_T]$
having a witness to
$L[G_T]$
having a witness to
![]() $\mathcal M\models \varphi (n,X)$
for every
$\mathcal M\models \varphi (n,X)$
for every
![]() $n<\omega $
, and this set is in
$n<\omega $
, and this set is in
![]() $\mathcal S$
.
$\mathcal S$
.
This finishes the argument that
![]() $\mathcal M\models \mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
$\mathcal M\models \mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
+
$\mathrm {CA}$
+
![]() $\neg \Sigma ^1_4$
-
$\neg \Sigma ^1_4$
-
![]() $\mathrm {CA}$
.
$\mathrm {CA}$
.
Finally, let’s observe that
![]() $\mathrm {AC}^{-p}$
fails in
$\mathrm {AC}^{-p}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
Lemma 4.7.
![]() $\mathrm {AC}^{-p}$
fails in
$\mathrm {AC}^{-p}$
fails in
![]() $\mathcal M.$
$\mathcal M.$
Proof. The model
![]() $\mathcal M$
satisfies that for every
$\mathcal M$
satisfies that for every
![]() $n<\omega $
, there is an L-generic real Y for
$n<\omega $
, there is an L-generic real Y for
![]() $\mathbb J$
and
$\mathbb J$
and
![]() $s\in 2^n$
such that for
$s\in 2^n$
such that for
![]() $m<n$
,
$m<n$
,
![]() $s(m)=1$
if and only if for every set coding
$s(m)=1$
if and only if for every set coding
![]() $\omega $
-many
$\omega $
-many
![]() $m+1$
-length L-generic sequences for
$m+1$
-length L-generic sequences for
![]() $\mathbb J_{m+1}$
with Y as the first coordinate, there is another
$\mathbb J_{m+1}$
with Y as the first coordinate, there is another
![]() $m+1$
-length L-generic sequence for
$m+1$
-length L-generic sequence for
![]() $\mathbb J_{m+1}$
not in the set. In other words,
$\mathbb J_{m+1}$
not in the set. In other words,
![]() $Y=\dot \varphi _G(\langle \xi \rangle )$
for some
$Y=\dot \varphi _G(\langle \xi \rangle )$
for some
![]() $\xi <\omega _1$
and
$\xi <\omega _1$
and
![]() $s= \dot \varphi _G(\langle \xi ,1\rangle )\upharpoonright n$
.
$s= \dot \varphi _G(\langle \xi ,1\rangle )\upharpoonright n$
.
Suppose that
![]() $\mathcal M\models \mathrm {AC}^{-p}$
. Then
$\mathcal M\models \mathrm {AC}^{-p}$
. Then
![]() $\mathcal S$
has a set A such that
$\mathcal S$
has a set A such that
![]() $A_n$
codes
$A_n$
codes
![]() $Y_n$
and
$Y_n$
and
![]() $s_n$
witnessing the statement above. Let
$s_n$
witnessing the statement above. Let
![]() $T\in L$
be a countable subtree of
$T\in L$
be a countable subtree of
![]() $\mathcal T$
such that
$\mathcal T$
such that
![]() $A\in L[G_T]$
. First, let’s observe that there cannot be cofinally many
$A\in L[G_T]$
. First, let’s observe that there cannot be cofinally many
![]() $n<\omega $
such that
$n<\omega $
such that
![]() $A_n$
codes the same real Y because if this was the case and
$A_n$
codes the same real Y because if this was the case and
![]() $Y=\dot \varphi _G(\langle \xi \rangle )$
, then using
$Y=\dot \varphi _G(\langle \xi \rangle )$
, then using
![]() $\Sigma ^1_2$
-
$\Sigma ^1_2$
-
![]() $\mathrm {CA}$
, we could argue that
$\mathrm {CA}$
, we could argue that
![]() $\dot \varphi _G(\langle \xi ,1\rangle )\in \mathcal S$
. Thus, there are countably many different reals Y coded on the slices of A. Next, we fix a condition p and a
$\dot \varphi _G(\langle \xi ,1\rangle )\in \mathcal S$
. Thus, there are countably many different reals Y coded on the slices of A. Next, we fix a condition p and a
![]() $\mathbb {P}(\mathbb J,T)$
-name
$\mathbb {P}(\mathbb J,T)$
-name
![]() $\dot A$
such that p forces that for all
$\dot A$
such that p forces that for all
![]() $n<\omega $
,
$n<\omega $
,
![]() $\dot A_n$
codes, for some
$\dot A_n$
codes, for some
![]() $\xi <\omega _1$
,
$\xi <\omega _1$
,
![]() $\dot \varphi (\langle \xi \rangle )$
and
$\dot \varphi (\langle \xi \rangle )$
and
![]() $\dot \varphi (\langle \xi ,1\rangle )\upharpoonright n$
. Choose some
$\dot \varphi (\langle \xi ,1\rangle )\upharpoonright n$
. Choose some
![]() $Y_n=\dot \varphi _G(\langle \alpha \rangle )$
with
$Y_n=\dot \varphi _G(\langle \alpha \rangle )$
with
![]() $\langle \alpha \rangle \notin D_p$
, which is possible since there are infinitely many different Y and p is finite. Next choose some
$\langle \alpha \rangle \notin D_p$
, which is possible since there are infinitely many different Y and p is finite. Next choose some
![]() $1\leq \eta <\omega _1$
such that
$1\leq \eta <\omega _1$
such that
![]() $\dot \varphi _G(\langle \alpha ,\eta \rangle )\upharpoonright n\neq \dot \varphi _G(\langle \alpha ,1\rangle )\upharpoonright n$
, which must exist by density. Let
$\dot \varphi _G(\langle \alpha ,\eta \rangle )\upharpoonright n\neq \dot \varphi _G(\langle \alpha ,1\rangle )\upharpoonright n$
, which must exist by density. Let
![]() $\pi $
be an automorphism of
$\pi $
be an automorphism of
![]() $\omega _1^{{<}\omega }$
which switches the trees
$\omega _1^{{<}\omega }$
which switches the trees
![]() $(\omega _1^{{<}\omega })_{\langle \alpha ,1\rangle }$
and
$(\omega _1^{{<}\omega })_{\langle \alpha ,1\rangle }$
and
![]() $(\omega _1^{{<}\omega })_{\langle \alpha ,\eta \rangle }$
, while preserving everything else, and note that
$(\omega _1^{{<}\omega })_{\langle \alpha ,\eta \rangle }$
, while preserving everything else, and note that
![]() $\pi $
fixes T and p by our choice of
$\pi $
fixes T and p by our choice of
![]() $\alpha $
and
$\alpha $
and
![]() $\eta $
. Let
$\eta $
. Let ![]() , and note that
, and note that
![]() $\pi ^*(p)=p\in H$
. Also,
$\pi ^*(p)=p\in H$
. Also,
![]() $\pi ^*(p)=p$
forces that for all
$\pi ^*(p)=p$
forces that for all
![]() $n<\omega $
,
$n<\omega $
,
![]() $\pi ^*(\dot A)_n=\dot A_n$
codes, for some
$\pi ^*(\dot A)_n=\dot A_n$
codes, for some
![]() $\xi <\omega _1$
,
$\xi <\omega _1$
,
![]() $\dot \varphi (\langle \xi \rangle )$
and
$\dot \varphi (\langle \xi \rangle )$
and
![]() $\dot \varphi (\langle \xi ,1\rangle )\upharpoonright n$
. Now we have that
$\dot \varphi (\langle \xi ,1\rangle )\upharpoonright n$
. Now we have that
![]() $\dot A_G=\dot A_H$
, but
$\dot A_G=\dot A_H$
, but
![]() $\dot \varphi _H(\langle \alpha ,1\rangle )=\dot \varphi _G(\langle \alpha ,\eta \rangle )$
, and, by construction,
$\dot \varphi _H(\langle \alpha ,1\rangle )=\dot \varphi _G(\langle \alpha ,\eta \rangle )$
, and, by construction,
![]() $\dot \varphi _G(\langle \alpha ,1\rangle )\upharpoonright n\neq \dot \varphi _G(\langle \alpha ,\eta \rangle )\upharpoonright n$
. Thus, we have reached a contradiction, showing that such a set A cannot exist.
$\dot \varphi _G(\langle \alpha ,1\rangle )\upharpoonright n\neq \dot \varphi _G(\langle \alpha ,\eta \rangle )\upharpoonright n$
. Thus, we have reached a contradiction, showing that such a set A cannot exist.
Corollary 4.8. The schemes
![]() $\mathrm {AC}^{-p}$
and
$\mathrm {AC}^{-p}$
and
![]() $\mathrm {Coll}^{-p}$
are not equivalent over
$\mathrm {Coll}^{-p}$
are not equivalent over
![]() ${\mathrm {Z}}_2^{-p}$
or even over
${\mathrm {Z}}_2^{-p}$
or even over
![]() ${\mathrm {Z}}_2^{-p}+\Sigma ^1_2$
-
${\mathrm {Z}}_2^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
.
$\mathrm {CA}$
.
5 A model of
 $\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
 $\mathrm {CA}+\neg \Sigma ^1_4$
-
$\mathrm {CA}+\neg \Sigma ^1_4$
-
 $\mathrm {CA.}$
$\mathrm {CA.}$
In this section, we construct a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
in which
$\mathrm {CA}$
in which
![]() $\Sigma ^1_4$
-
$\Sigma ^1_4$
-
![]() $\mathrm {CA}$
fails. We will again be working in a forcing extension of L by
$\mathrm {CA}$
fails. We will again be working in a forcing extension of L by
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
, but we are going to change the tree
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
, but we are going to change the tree
![]() $\mathcal T$
to code in a different set to witness the failure of comprehension with parameters in our model.
$\mathcal T$
to code in a different set to witness the failure of comprehension with parameters in our model.
Let
![]() $G\subseteq \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
be L-generic. We work in
$G\subseteq \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
be L-generic. We work in
![]() $L[G]$
. Let
$L[G]$
. Let
![]() $\dot \varphi $
be the canonical name for the isomorphism between
$\dot \varphi $
be the canonical name for the isomorphism between
![]() $\omega _1^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic sequences of reals for
$\omega _1^{{<}\omega }$
and the tree, added by G, whose nodes on level n are mutually generic sequences of reals for
![]() $\mathbb J_n$
.
$\mathbb J_n$
.
In this construction, we are going to define a tree
![]() $\mathcal T$
similarly to how we defined it in the previous sections, but instead of coding, for every
$\mathcal T$
similarly to how we defined it in the previous sections, but instead of coding, for every
![]() $\xi <\omega _1$
, the sets
$\xi <\omega _1$
, the sets
![]() $\dot \varphi _G(\langle \xi ,1\rangle )(1)$
into
$\dot \varphi _G(\langle \xi ,1\rangle )(1)$
into
![]() $\mathcal T$
, we are going to code in, for every
$\mathcal T$
, we are going to code in, for every
![]() $\xi <\omega _1$
, the finite fragments
$\xi <\omega _1$
, the finite fragments
![]() $\dot \varphi _G(\langle \xi ,n\rangle )(1)\upharpoonright n$
for
$\dot \varphi _G(\langle \xi ,n\rangle )(1)\upharpoonright n$
for
![]() $n<\omega $
. Let
$n<\omega $
. Let
![]() $p_n$
, for
$p_n$
, for
![]() $n<\omega $
, denote the n-th prime. For
$n<\omega $
, denote the n-th prime. For
![]() $n<\omega $
, we will code the n-length fragment
$n<\omega $
, we will code the n-length fragment
![]() $\dot \varphi _G(\langle \xi ,n\rangle )(1)\upharpoonright n$
so that
$\dot \varphi _G(\langle \xi ,n\rangle )(1)\upharpoonright n$
so that
![]() $\dot \varphi _G(\langle \xi ,n\rangle )(1)(m)=1$
if and only if the node
$\dot \varphi _G(\langle \xi ,n\rangle )(1)(m)=1$
if and only if the node ![]() splits
splits
![]() $\omega _1$
-many times in
$\omega _1$
-many times in
![]() $\mathcal T$
.
$\mathcal T$
.
We define the following subtree
![]() $\mathcal T$
of
$\mathcal T$
of
![]() $\omega _1^{{<}\omega }$
in
$\omega _1^{{<}\omega }$
in
![]() $L[G]$
. We have for every
$L[G]$
. We have for every
![]() $\xi <\omega _1$
,
$\xi <\omega _1$
,
![]() $1\leq m<\omega $
,
$1\leq m<\omega $
,
![]() $n<\omega $
:
$n<\omega $
:
-
(1)
 $\langle \xi \rangle \in \mathcal T$
,
$\langle \xi \rangle \in \mathcal T$
, -
(2)
 ,
, -
(3)

-
(4)
 for all
for all
 $\eta <\omega _1$
if and only if
$\eta <\omega _1$
if and only if
 $\dot \varphi _G(\langle \xi ,n \rangle )(1)(m)=1$
and
$\dot \varphi _G(\langle \xi ,n \rangle )(1)(m)=1$
and
 $m<n$
.
$m<n$
.
Let
and let
We will argue that the model
![]() $\mathcal M$
has all the required properties.
$\mathcal M$
has all the required properties.
As before, let
![]() $\dot {\mathcal S}$
be the canonical
$\dot {\mathcal S}$
be the canonical
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
-name for
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
-name for
![]() $\mathcal S$
. An analogous proof to the proof of Lemma 4.3 gives
$\mathcal S$
. An analogous proof to the proof of Lemma 4.3 gives
Lemma 5.1. For any permutation
![]() $f\in L$
of
$f\in L$
of
![]() $\omega _1$
, we have
$\omega _1$
, we have ![]() . Thus,
. Thus,
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
.
Analogs of Lemma 3.6 and Lemma 3.9 in Section 3 give that
![]() $\mathcal M$
satisfies
$\mathcal M$
satisfies
![]() $\mathrm {Z}^{-p}_2+\Sigma ^1_2$
-
$\mathrm {Z}^{-p}_2+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
.
$\mathrm {CA}$
.
Let
It is easy to see using the proof of Lemma 4.4 that C is
![]() $\Pi ^1_4$
-definable in
$\Pi ^1_4$
-definable in
![]() $\mathcal M$
from the parameter
$\mathcal M$
from the parameter
![]() $\dot \varphi _G(\langle 0\rangle )$
.
$\dot \varphi _G(\langle 0\rangle )$
.
Lemma 5.2. The set
![]() $C\notin \mathcal S$
.
$C\notin \mathcal S$
.
Proof. Suppose towards a contradiction that
![]() $C\in \mathcal S$
, and fix a countable subtree
$C\in \mathcal S$
, and fix a countable subtree
![]() $T\in L$
of
$T\in L$
of
![]() $\mathcal T$
such that
$\mathcal T$
such that
![]() $C\in L[G_T]$
. Let
$C\in L[G_T]$
. Let
![]() $\dot C$
be a
$\dot C$
be a
![]() $\mathbb {P}(\mathbb J,T)$
-name such that
$\mathbb {P}(\mathbb J,T)$
-name such that
![]() $\dot C_G=C$
and fix a condition
$\dot C_G=C$
and fix a condition
Fix some
![]() $1\leq k<\omega $
such that
$1\leq k<\omega $
such that
![]() $\langle 0,k\rangle \notin D_p$
, which is possible since
$\langle 0,k\rangle \notin D_p$
, which is possible since
![]() $D_p$
is finite. Fix some
$D_p$
is finite. Fix some
![]() $1\leq \eta <\omega _1$
such that
$1\leq \eta <\omega _1$
such that
![]() $\dot \varphi _G(\langle 0,\eta \rangle )\upharpoonright k\neq \dot \varphi _G(\langle 0,k\rangle )\upharpoonright k$
, which must exist by density. Let
$\dot \varphi _G(\langle 0,\eta \rangle )\upharpoonright k\neq \dot \varphi _G(\langle 0,k\rangle )\upharpoonright k$
, which must exist by density. Let
![]() $\pi $
be an automorphism of the tree
$\pi $
be an automorphism of the tree
![]() $\omega _1^{{<}\omega }$
which switches the trees
$\omega _1^{{<}\omega }$
which switches the trees
![]() $(\omega _1^{{<}\omega })_{\langle 0,k\rangle }$
and
$(\omega _1^{{<}\omega })_{\langle 0,k\rangle }$
and
![]() $(\omega _1^{{<}\omega })_{\langle 0,\eta \rangle }$
and fixes everything else. Observe that
$(\omega _1^{{<}\omega })_{\langle 0,\eta \rangle }$
and fixes everything else. Observe that
![]() $\pi $
fixes every node in the tree T. By construction,
$\pi $
fixes every node in the tree T. By construction,
![]() $\pi ^*(p)=p$
, and since
$\pi ^*(p)=p$
, and since
![]() $\pi $
fixes the tree T,
$\pi $
fixes the tree T,
![]() $\pi ^*(\dot C)=\dot C$
. Let
$\pi ^*(\dot C)=\dot C$
. Let ![]() . Since
. Since
![]() $\pi ^*(p)=p$
,
$\pi ^*(p)=p$
,
![]() $p\in H$
. Thus,
$p\in H$
. Thus,
because of the statement forced by p. But, we have
while
which is impossible by our choice of
![]() $\eta $
. Thus, we have reached the desired contradiction showing that
$\eta $
. Thus, we have reached the desired contradiction showing that
![]() $C\notin \mathcal S$
.
$C\notin \mathcal S$
.
Combining our observation about the complexity of the definition of the set C in the model
![]() $\mathcal M$
with the fact that
$\mathcal M$
with the fact that
![]() $C\not \in \mathcal S$
, we obtain the following lemma.
$C\not \in \mathcal S$
, we obtain the following lemma.
Lemma 5.3. The set C is definable in
![]() $\mathcal M$
from the parameter
$\mathcal M$
from the parameter
![]() $\dot \varphi _G(\langle 0\rangle )$
by a
$\dot \varphi _G(\langle 0\rangle )$
by a
![]() $\Pi ^1_4$
-formula. Thus,
$\Pi ^1_4$
-formula. Thus,
![]() $\Sigma ^1_4$
-
$\Sigma ^1_4$
-
![]() $\mathrm {CA}$
fails in
$\mathrm {CA}$
fails in
![]() $\mathcal M$
.
$\mathcal M$
.
It remains to verify that
![]() $\mathrm {AC}^{-p}$
holds in
$\mathrm {AC}^{-p}$
holds in
![]() $\mathcal M$
.
$\mathcal M$
.
We will use the definitions of a full and undecided tree from Section 4 verbatim. An analogous proof to that of Lemma 4.5 gives
Lemma 5.4. Suppose that
![]() $T\in L$
is a full countable subtree of
$T\in L$
is a full countable subtree of
![]() $\mathcal T$
,
$\mathcal T$
,
![]() $\varphi (x,X)$
is a second-order formula, and there is
$\varphi (x,X)$
is a second-order formula, and there is
![]() $A\in L[G_T]$
such that
$A\in L[G_T]$
such that
![]() $\mathcal M\models \varphi (n,A)$
. Then there is a full undecided countable tree
$\mathcal M\models \varphi (n,A)$
. Then there is a full undecided countable tree
![]() $\bar T\in L$
and
$\bar T\in L$
and
![]() $\bar A\in L[G_{\bar T}]$
such that
$\bar A\in L[G_{\bar T}]$
such that
![]() $\mathcal M\models \varphi (n,\bar A)$
.
$\mathcal M\models \varphi (n,\bar A)$
.
Lemma 5.5. Suppose that
![]() $T\in L$
is a full undecided countable subtree of
$T\in L$
is a full undecided countable subtree of
![]() $\mathcal T$
and
$\mathcal T$
and
![]() $p,q\in \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
are such that
$p,q\in \mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
are such that
![]() $q\leq p\upharpoonright T$
. Then there is an automorphism
$q\leq p\upharpoonright T$
. Then there is an automorphism
![]() $\pi $
of
$\pi $
of
![]() $\omega _1^{{<}\omega }$
fixing all nodes in T such that p is compatible with
$\omega _1^{{<}\omega }$
fixing all nodes in T such that p is compatible with
![]() $\pi ^*(q)$
and
$\pi ^*(q)$
and ![]() . Thus,
. Thus,
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*(\dot {\mathcal S})$
.
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*(\dot {\mathcal S})$
.
Proof. We define the automorphism
![]() $\pi $
as follows. Suppose that
$\pi $
as follows. Suppose that
![]() $s\in D_p\cap D_q$
and
$s\in D_p\cap D_q$
and
![]() $s\notin T$
. We first handle nodes of the form
$s\notin T$
. We first handle nodes of the form
![]() $s=\langle \xi \rangle $
. In this case,
$s=\langle \xi \rangle $
. In this case,
![]() $\pi $
switches the tree
$\pi $
switches the tree
![]() $(\omega _1^{{<}\omega })_{\langle \xi \rangle }$
with a tree
$(\omega _1^{{<}\omega })_{\langle \xi \rangle }$
with a tree
![]() $(\omega _1^{{<}\omega })_{\langle \eta \rangle }$
for some
$(\omega _1^{{<}\omega })_{\langle \eta \rangle }$
for some
![]() $\eta <\omega _1$
such that
$\eta <\omega _1$
such that
![]() $\langle \eta \rangle \notin T\cup D_p\cup D_q$
. Next, we handle nodes of the form
$\langle \eta \rangle \notin T\cup D_p\cup D_q$
. Next, we handle nodes of the form
![]() $s=\langle \xi ,n\rangle $
, for some
$s=\langle \xi ,n\rangle $
, for some
![]() $n<\omega $
, which weren’t handled in the previous case (this must have been because
$n<\omega $
, which weren’t handled in the previous case (this must have been because
![]() $\langle \xi \rangle \in T$
). In this case,
$\langle \xi \rangle \in T$
). In this case,
![]() $\pi $
switches the tree
$\pi $
switches the tree
![]() $(\omega _1^{{<}\omega })_{s}$
with a tree
$(\omega _1^{{<}\omega })_{s}$
with a tree
![]() $(\omega _1^{{<}\omega })_{t}$
, where
$(\omega _1^{{<}\omega })_{t}$
, where
![]() $t=\langle \xi ,\beta \rangle \notin T\cup D_p\cup D_q$
,
$t=\langle \xi ,\beta \rangle \notin T\cup D_p\cup D_q$
,
![]() $\beta \geq \omega $
and
$\beta \geq \omega $
and
Note that such a node t must exist by density. Finally, if a node
![]() $s=\langle \alpha _0,\ldots ,\alpha _n\rangle $
was not handled by one of the above cases, then
$s=\langle \alpha _0,\ldots ,\alpha _n\rangle $
was not handled by one of the above cases, then
![]() $\pi $
switches the tree
$\pi $
switches the tree
![]() $(\omega _1^{{<}\omega })_{s}$
with a tree
$(\omega _1^{{<}\omega })_{s}$
with a tree
![]() $(\omega _1^{{<}\omega })_{t}$
, where
$(\omega _1^{{<}\omega })_{t}$
, where
![]() $t=\langle \alpha _0,\ldots ,\beta \rangle \notin T\cup D_p\cup D_q$
was not yet placed in the image of
$t=\langle \alpha _0,\ldots ,\beta \rangle \notin T\cup D_p\cup D_q$
was not yet placed in the image of
![]() $\pi $
by the above cases. All other nodes are fixed by
$\pi $
by the above cases. All other nodes are fixed by
![]() $\pi $
. In particular, all nodes in T are fixed by
$\pi $
. In particular, all nodes in T are fixed by
![]() $\pi $
.
$\pi $
.
Suppose that ![]() . Then it should be clear that
. Then it should be clear that
![]() $T\in L$
is a countable subtree of
$T\in L$
is a countable subtree of
![]() $\mathcal T$
if and only if
$\mathcal T$
if and only if ![]() is a countable subtree of
is a countable subtree of
![]() $\dot {\mathcal T}_H$
, which implies that
$\dot {\mathcal T}_H$
, which implies that ![]() .
.
Lemma 5.6.
![]() $\mathcal M\models \mathrm {AC}^{-p}$
.
$\mathcal M\models \mathrm {AC}^{-p}$
.
Proof. Suppose that
![]() $\mathcal M\models \forall n\exists X\,\varphi (n,X)$
for some second-order arithmetic formula
$\mathcal M\models \forall n\exists X\,\varphi (n,X)$
for some second-order arithmetic formula
![]() $\varphi (n,X)$
. Given
$\varphi (n,X)$
. Given
![]() $n<\omega $
, by Lemma 5.4, there is a full undecided countable subtree
$n<\omega $
, by Lemma 5.4, there is a full undecided countable subtree
![]() $T_n\in L$
and
$T_n\in L$
and
![]() $X\in L[G_{T_n}]$
such that
$X\in L[G_{T_n}]$
such that
![]() $\mathcal M\models \varphi (n,X)$
. By extending
$\mathcal M\models \varphi (n,X)$
. By extending
![]() $T_n$
to a larger tree, if necessary, we can assume that
$T_n$
to a larger tree, if necessary, we can assume that
![]() $\{\xi <\omega _1\mid \langle \xi \rangle \in T_n\}$
is an ordinal
$\{\xi <\omega _1\mid \langle \xi \rangle \in T_n\}$
is an ordinal
![]() $\alpha _n$
. Let
$\alpha _n$
. Let
![]() $\alpha =\bigcup _{n<\omega }\alpha _n$
and let T be the full undecided tree whose level 1 nodes are precisely
$\alpha =\bigcup _{n<\omega }\alpha _n$
and let T be the full undecided tree whose level 1 nodes are precisely
![]() $\langle \xi \rangle $
for
$\langle \xi \rangle $
for
![]() $\xi <\alpha $
. Then each
$\xi <\alpha $
. Then each
![]() $T_n$
is contained in T. Thus, for every
$T_n$
is contained in T. Thus, for every
![]() $n<\omega $
, there is some
$n<\omega $
, there is some
![]() $X\in L[G_T]$
such that
$X\in L[G_T]$
such that
![]() $\mathcal M\models \varphi (n,X)$
.
$\mathcal M\models \varphi (n,X)$
.
Fix a condition
Let’s argue that this statement is already forced by
![]() $p\upharpoonright T$
. Suppose towards a contradiction that this is not the case. Then there is a condition
$p\upharpoonright T$
. Suppose towards a contradiction that this is not the case. Then there is a condition
![]() $q\leq p\upharpoonright T$
such that
$q\leq p\upharpoonright T$
such that
![]() $q\Vdash \neg \psi (\dot G_T,\dot {\mathcal S})$
. By Lemma 5.5, there is an automorphism
$q\Vdash \neg \psi (\dot G_T,\dot {\mathcal S})$
. By Lemma 5.5, there is an automorphism
![]() $\pi $
of
$\pi $
of
![]() $\omega _1^{{<}\omega }$
fixing all nodes in T such that p is compatible with
$\omega _1^{{<}\omega }$
fixing all nodes in T such that p is compatible with
![]() $\pi ^*(q)$
and
$\pi ^*(q)$
and
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*(\dot {\mathcal S})$
. Observe that the condition
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi ^*(\dot {\mathcal S})$
. Observe that the condition
![]() $\pi ^*(q)\Vdash \psi (\dot G_T,\dot {\mathcal S})$
because
$\pi ^*(q)\Vdash \psi (\dot G_T,\dot {\mathcal S})$
because
![]() $\pi ^*$
fixes
$\pi ^*$
fixes
![]() $\dot G_T$
and
$\dot G_T$
and
![]() $\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
. Thus, we have reached the desired contradiction showing that
$\mathop {1\hskip -2.5pt \mathrm {l}}_{\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })}\Vdash \dot {\mathcal S}=\pi _f^*(\dot {\mathcal S})$
. Thus, we have reached the desired contradiction showing that
![]() $p\upharpoonright T\Vdash \psi (\dot G_T,\dot {\mathcal S})$
. We can now assume without loss of generality that
$p\upharpoonright T\Vdash \psi (\dot G_T,\dot {\mathcal S})$
. We can now assume without loss of generality that
![]() $D_p\subseteq T$
.
$D_p\subseteq T$
.
Fix
![]() $n<\omega $
. We will construct a mixed
$n<\omega $
. We will construct a mixed
![]() $\mathbb {P}(\mathbb J,T)$
-name
$\mathbb {P}(\mathbb J,T)$
-name
![]() $\dot X_n$
such that
$\dot X_n$
such that
For every
![]() $r\leq p$
, there is a condition
$r\leq p$
, there is a condition
![]() $q\leq r$
and a
$q\leq r$
and a
![]() $\mathbb {P}(\mathbb J,T)$
-name
$\mathbb {P}(\mathbb J,T)$
-name
![]() $\dot X^{q}_n$
such that
$\dot X^{q}_n$
such that
An analogous automorphism argument to above shows that actually
and so we can assume without loss of generality that
![]() $D_q\subseteq T$
. Thus, we can construct a maximal antichain
$D_q\subseteq T$
. Thus, we can construct a maximal antichain
![]() $\mathcal A_n$
of such conditions q with
$\mathcal A_n$
of such conditions q with
![]() $D_q\subseteq T$
below p. By Proposition 2.3, it easy to see that
$D_q\subseteq T$
below p. By Proposition 2.3, it easy to see that
![]() $\mathcal A_n$
is a maximal antichain of
$\mathcal A_n$
is a maximal antichain of
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
below p.
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
below p.
Let
Clearly,
![]() $\dot X_n$
is a
$\dot X_n$
is a
![]() $\mathbb {P}(\mathbb J,T)$
-name. Since
$\mathbb {P}(\mathbb J,T)$
-name. Since
![]() $\mathcal A_n$
is an antichain, if
$\mathcal A_n$
is an antichain, if
![]() $(\tau ,r)\in \dot X_n$
, then there is a unique
$(\tau ,r)\in \dot X_n$
, then there is a unique
![]() $q\in \mathcal A_n$
such that
$q\in \mathcal A_n$
such that
![]() $r\leq q$
. Fix an L-generic filter
$r\leq q$
. Fix an L-generic filter
![]() $\bar G$
for
$\bar G$
for
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
with
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
with
![]() $p\in \bar G$
. Let
$p\in \bar G$
. Let
![]() $q\in \bar G\cap \mathcal A_n$
. We will argue that
$q\in \bar G\cap \mathcal A_n$
. We will argue that
![]() $(\dot X_n)_{\bar G}=(\dot X^{q}_n)_{\bar G}$
. Suppose that
$(\dot X_n)_{\bar G}=(\dot X^{q}_n)_{\bar G}$
. Suppose that
![]() $a\in (\dot X_n)_{\bar G}$
. Then
$a\in (\dot X_n)_{\bar G}$
. Then
![]() $( \tau ,r)\in \dot X_n$
such that
$( \tau ,r)\in \dot X_n$
such that
![]() $\tau _{\bar G}=a$
and
$\tau _{\bar G}=a$
and
![]() $r\in \bar G$
. It follows that r is compatible with q, which, since
$r\in \bar G$
. It follows that r is compatible with q, which, since
![]() $\mathcal A_n$
is an antichain, means that
$\mathcal A_n$
is an antichain, means that
![]() $r\leq q$
. By definition of
$r\leq q$
. By definition of
![]() $\dot X_n$
,
$\dot X_n$
,
![]() $r\Vdash \tau \in \dot X^{q}_n$
, which implies that
$r\Vdash \tau \in \dot X^{q}_n$
, which implies that
![]() $a\in (\dot X^{q}_n)_{\bar G}$
. Next, suppose that
$a\in (\dot X^{q}_n)_{\bar G}$
. Next, suppose that
![]() $a\in (\dot X^{q}_n)_{\bar G}$
. Then
$a\in (\dot X^{q}_n)_{\bar G}$
. Then
![]() $(\tau ,r)\in \dot X^{q}_n$
such that
$(\tau ,r)\in \dot X^{q}_n$
such that
![]() $a=\tau _{\bar G}$
and
$a=\tau _{\bar G}$
and
![]() $r\in G$
. Let
$r\in G$
. Let
![]() $r'\in \bar G$
such that
$r'\in \bar G$
such that
![]() $r'\leq r,q$
. Observe that
$r'\leq r,q$
. Observe that
![]() $r'\upharpoonright T\leq r,q$
and
$r'\upharpoonright T\leq r,q$
and
![]() $r'\upharpoonright T\in \bar G$
because it is above
$r'\upharpoonright T\in \bar G$
because it is above
![]() $r'$
. Thus, we can assume without loss of generality that
$r'$
. Thus, we can assume without loss of generality that
![]() $D_{r'}\subseteq T$
. Also, since
$D_{r'}\subseteq T$
. Also, since
![]() $r'\leq r$
,
$r'\leq r$
,
![]() $r'\Vdash \tau \in \dot X^{q}_n$
. Thus,
$r'\Vdash \tau \in \dot X^{q}_n$
. Thus,
![]() $(\tau ,r')\in \dot X_n$
, and so
$(\tau ,r')\in \dot X_n$
, and so
![]() $a\in (\dot X_n)_{\bar G}$
. Since
$a\in (\dot X_n)_{\bar G}$
. Since
![]() $\mathcal A_n$
was a maximal antichain below p, it follows that
$\mathcal A_n$
was a maximal antichain below p, it follows that
Now, let
![]() $\dot Y$
be a
$\dot Y$
be a
![]() $\mathbb {P}(\mathbb J,T)$
-name for the set whose n-th slice is
$\mathbb {P}(\mathbb J,T)$
-name for the set whose n-th slice is
![]() $\dot X_n$
. Then clearly,
$\dot X_n$
. Then clearly,
and
![]() $\dot Y_G\in L[G_T]$
. Hence
$\dot Y_G\in L[G_T]$
. Hence
![]() $\dot Y_G\in \mathcal S$
.
$\dot Y_G\in \mathcal S$
.
6 Questions
In Sections 3 and 4, we obtained models
![]() $\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
with a failure of
$\mathrm {CA}$
with a failure of
![]() $\Sigma ^1_4$
-
$\Sigma ^1_4$
-
![]() $\mathrm {CA}$
in which
$\mathrm {CA}$
in which
![]() $\mathrm {Coll}^{-p}$
and
$\mathrm {Coll}^{-p}$
and
![]() $\mathrm {AC}^{-p}$
holds respectively. Is it possible to obtain such models with an optimal failure of
$\mathrm {AC}^{-p}$
holds respectively. Is it possible to obtain such models with an optimal failure of
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm { CA}$
?
$\mathrm { CA}$
?
Question 6.1. Can we obtain a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
in which, optimally,
$\mathrm {CA}$
in which, optimally,
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm {CA}$
fails?
$\mathrm {CA}$
fails?
Question 6.2. Can we obtain a model of
![]() $\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
$\mathrm {Z}_2^{-p}+\mathrm {AC}^{-p}+\Sigma ^1_2$
-
![]() $\mathrm {CA}$
in which, optimally,
$\mathrm {CA}$
in which, optimally,
![]() $\Sigma ^1_3$
-
$\Sigma ^1_3$
-
![]() $\mathrm {CA}$
fails?
$\mathrm {CA}$
fails?
Since standard arguments showing that
![]() $\mathrm {AC}$
implies
$\mathrm {AC}$
implies
![]() $\mathrm {Z}_2$
over
$\mathrm {Z}_2$
over
![]() $\mathrm {ACA}_0$
rely on parameters, it is most likely not the case that
$\mathrm {ACA}_0$
rely on parameters, it is most likely not the case that
![]() $\mathrm {AC}^{-p}$
implies
$\mathrm {AC}^{-p}$
implies
![]() $\mathrm {Z}_2^{-p}$
over
$\mathrm {Z}_2^{-p}$
over
![]() $\mathrm {ACA}_0$
.
$\mathrm {ACA}_0$
.
Question 6.3. Can we obtain a model
![]() $\mathrm {ACA}_0+\mathrm {AC}^{-p}$
in which
$\mathrm {ACA}_0+\mathrm {AC}^{-p}$
in which
![]() $\mathrm {Z}_2^{-p}$
fails?
$\mathrm {Z}_2^{-p}$
fails?
This is not directly relevant to the results in this article, but for the complete understanding of forcing extensions by
![]() $\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, it is interesting to know whether the uniqueness result of Theorem 3.1 holds for countable trees and an analogous question applies to the forcing
$\mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
, it is interesting to know whether the uniqueness result of Theorem 3.1 holds for countable trees and an analogous question applies to the forcing
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
.
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
.
Question 6.4. Suppose that
![]() $G\subseteq \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
is L-generic and that
$G\subseteq \mathbb {P}(\mathbb J,\omega ^{{<}\omega })$
is L-generic and that
![]() $T\in L$
is a countable subtree of
$T\in L$
is a countable subtree of
![]() $\omega ^{{<}\omega }$
. Is it true that the only L-generic sequences for
$\omega ^{{<}\omega }$
. Is it true that the only L-generic sequences for
![]() $\mathbb J_n$
in
$\mathbb J_n$
in
![]() $L[G_T]$
are the sequences
$L[G_T]$
are the sequences
![]() $\dot \varphi _G(s)$
for
$\dot \varphi _G(s)$
for
![]() $s\in T$
? What about an analogous question for uncountable subtrees and forcing extensions by
$s\in T$
? What about an analogous question for uncountable subtrees and forcing extensions by
![]() $\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
?
$\mathbb {P}(\mathbb J,\omega _1^{{<}\omega })$
?