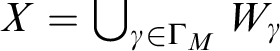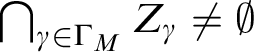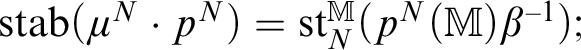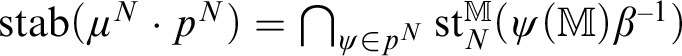1 Introduction
In [Reference Peterzil and Steinhorn16], Peterzil and Steinhorn prove that if G is a definable group in an o-minimal structure M, and G is not definably compact, then G has a definable one-dimensional subgroup H that is not definably compact. To prove this, they take a continuous unbounded definable curve
![]() $I : [0,+\infty ) \to G$
and take H to be the “tangent line at
$I : [0,+\infty ) \to G$
and take H to be the “tangent line at
![]() $\infty $
.” This can be made precise using the language of
$\infty $
.” This can be made precise using the language of
![]() $\mu $
-types and
$\mu $
-types and
![]() $\mu $
-stabilizers developed later by Peterzil and Starchenko [Reference Peterzil and Starchenko15]. Say that two complete types
$\mu $
-stabilizers developed later by Peterzil and Starchenko [Reference Peterzil and Starchenko15]. Say that two complete types
![]() $q, r \in S_G(M)$
are “infinitesimally close” if there are realizations
$q, r \in S_G(M)$
are “infinitesimally close” if there are realizations
![]() $a \models q$
and
$a \models q$
and
![]() $b \models r$
such that
$b \models r$
such that
![]() $ab^{-1}$
is infinitesimally close to
$ab^{-1}$
is infinitesimally close to
![]() $\operatorname {\mathrm {id}}_G$
(that is,
$\operatorname {\mathrm {id}}_G$
(that is,
![]() $ab^{-1}$
is contained in every M-definable neighborhood of
$ab^{-1}$
is contained in every M-definable neighborhood of
![]() $\operatorname {\mathrm {id}}_G$
). This is an equivalence relation on
$\operatorname {\mathrm {id}}_G$
). This is an equivalence relation on
![]() $S_G(M)$
, and equivalence classes are called “
$S_G(M)$
, and equivalence classes are called “
![]() $\mu $
-types.” The “
$\mu $
-types.” The “
![]() $\mu $
-stabilizer”
$\mu $
-stabilizer”
![]() $\operatorname {\mathrm {stab}}^\mu (q)$
of
$\operatorname {\mathrm {stab}}^\mu (q)$
of
![]() $q \in S_G(M)$
is the stabilizer of the
$q \in S_G(M)$
is the stabilizer of the
![]() $\mu $
-type of q.
$\mu $
-type of q.
With these definitions, the “tangent line of I at
![]() $\infty $
” is simply the
$\infty $
” is simply the
![]() $\mu $
-stabilizer of the type on I at infinity, an unbounded one-dimensional definable type. (Here, we say that a type
$\mu $
-stabilizer of the type on I at infinity, an unbounded one-dimensional definable type. (Here, we say that a type
![]() $q \in S_G(M)$
is “unbounded” if no formula in q defines a definably compact subset of G.) Peterzil and Steinhorn essentially show that the
$q \in S_G(M)$
is “unbounded” if no formula in q defines a definably compact subset of G.) Peterzil and Steinhorn essentially show that the
![]() $\mu $
-stabilizer of an unbounded one-dimensional definable type is a torsion-free non-compact definable subgroup of dimension 1. More generally, in [Reference Peterzil and Starchenko15], Peterzil and Starchenko consider a general definable type
$\mu $
-stabilizer of an unbounded one-dimensional definable type is a torsion-free non-compact definable subgroup of dimension 1. More generally, in [Reference Peterzil and Starchenko15], Peterzil and Starchenko consider a general definable type
![]() $q \in S_G(M)$
, showing that
$q \in S_G(M)$
, showing that
![]() $\operatorname {\mathrm {stab}}^\mu (q)$
is a torsion-free definable group of a certain dimension.
$\operatorname {\mathrm {stab}}^\mu (q)$
is a torsion-free definable group of a certain dimension.
It is natural to ask whether analogous results hold in the theory pCF (p-adically closed fields). There are many formal similarities between pCF and o-minimal theories, especially RCF (real closed fields). In both settings, definable groups can be regarded as real or p-adic Lie groups [Reference Pillay17, Reference Pillay18], and are locally isomorphic to real or p-adic algebraic groups [Reference Hrushovski, Peterzil and Pillay8]. In both the real and p-adic contexts, definable sets have a dimension which has a topological description as well as an algebraic description (the algebro-geometric dimension of the Zariski closure). On the other hand, definable connectedness behaves very differently in the two settings.
In this paper, we restrict our attention to one-dimensional definable types, as in the original work of Peterzil and Steinhorn [Reference Peterzil and Steinhorn16]. Unfortunately, we must also assume that G is “nearly abelian” for most of our theorems.
Definition 1.1. Let G be a definable group in a model of pCF. G is nearly abelian if there is a definably compact definable normal subgroup
![]() $K \subseteq G$
with
$K \subseteq G$
with
![]() $G/K$
abelian.
$G/K$
abelian.
See Definition 2.1 for a precise definition of “definable compactness,” and Propositions 2.16 and 2.24 for some equivalent conditions.
Our main results are as follows:
Theorem 1.2. Let G be a definable group over a p-adically closed field M. If G is not definably compact and G is nearly abelian, then there is a one-dimensional definable subgroup
![]() $H \subseteq G$
that is not definably compact.
$H \subseteq G$
that is not definably compact.
We plan to generalize Theorem 1.2 to non-abelian groups in a future paper.
Theorem 1.3. Suppose that G is a definable group over an
![]() $\aleph _1$
-saturated p-adically closed field M. Then for any definable unbounded one-dimensional type
$\aleph _1$
-saturated p-adically closed field M. Then for any definable unbounded one-dimensional type
![]() $r \in S_G(M)$
, the
$r \in S_G(M)$
, the
![]() $\mu $
-stabilizer
$\mu $
-stabilizer
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is a one-dimensional type-definable subgroup of G. If G is abelian
$\operatorname {\mathrm {stab}}^\mu (r)$
is a one-dimensional type-definable subgroup of G. If G is abelian
![]() $($
or nearly abelian
$($
or nearly abelian
![]() $)$
, then
$)$
, then
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is unbounded.
$\operatorname {\mathrm {stab}}^\mu (r)$
is unbounded.
Here, a set or type is “bounded” if it is contained in a definably compact set, and “unbounded” otherwise (Definition 2.9). The assumption on saturation is necessary. For example, suppose
![]() $M = {\mathbb Q}_p$
, G is the multiplicative group, and
$M = {\mathbb Q}_p$
, G is the multiplicative group, and
![]() $r \in S_G({\mathbb Q}_p)$
is one of the definable types consistent with
$r \in S_G({\mathbb Q}_p)$
is one of the definable types consistent with
![]() $\{x \mid v(x) < \mathbb {Z}\}$
. Then
$\{x \mid v(x) < \mathbb {Z}\}$
. Then
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is the intersection of all n-th powers
$\operatorname {\mathrm {stab}}^\mu (r)$
is the intersection of all n-th powers
![]() $P_n=\{x \mid x\neq 0\wedge \exists (x=y^n)\}$
, which is the trivial group
$P_n=\{x \mid x\neq 0\wedge \exists (x=y^n)\}$
, which is the trivial group
![]() $\{1\}$
.
$\{1\}$
.
We can also say something when M is not saturated, but we will need a few more definitions from [Reference Peterzil and Starchenko15]. Fix a group G definable in a p-adically closed field M. For any partial type
![]() $\Sigma (x)$
in G, and any
$\Sigma (x)$
in G, and any
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\phi (x;y)$
, let
$\phi (x;y)$
, let
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma )$
denote
$\operatorname {\mathrm {stab}}_\phi (\Sigma )$
denote
 $$ \begin{align*} \bigcap_{b \in M^k} \operatorname{\mathrm{stab}} \{ g \in G(M) \mid \Sigma \vdash \phi(g x; b) \}. \end{align*} $$
$$ \begin{align*} \bigcap_{b \in M^k} \operatorname{\mathrm{stab}} \{ g \in G(M) \mid \Sigma \vdash \phi(g x; b) \}. \end{align*} $$
(This can be understood as the stabilizer of the
![]() $\phi (z \cdot x; y)$
-type generated by
$\phi (z \cdot x; y)$
-type generated by
![]() $\Sigma (x)$
.) It turns out that
$\Sigma (x)$
.) It turns out that
 $\operatorname {\mathrm {stab}}(\Sigma ) = \bigcap _{\phi \in \mathcal {L}} \operatorname {\mathrm {stab}}_\phi (\Sigma )$
. Now suppose that r is a type in
$\operatorname {\mathrm {stab}}(\Sigma ) = \bigcap _{\phi \in \mathcal {L}} \operatorname {\mathrm {stab}}_\phi (\Sigma )$
. Now suppose that r is a type in
![]() $S_G(M)$
. Let
$S_G(M)$
. Let
![]() $\mu $
be the partial type of “infinitesimals,” that is, the set of
$\mu $
be the partial type of “infinitesimals,” that is, the set of
![]() $\mathcal {L}_M$
-formulas defining neighborhoods of
$\mathcal {L}_M$
-formulas defining neighborhoods of
![]() $\operatorname {\mathrm {id}}_G$
. Let
$\operatorname {\mathrm {id}}_G$
. Let
![]() $\mu \cdot r$
be the partial type such that
$\mu \cdot r$
be the partial type such that
![]() $(\mu \cdot r)(N) = \mu (N) \cdot r(N)$
for sufficiently saturated
$(\mu \cdot r)(N) = \mu (N) \cdot r(N)$
for sufficiently saturated
![]() $N \succ M$
. It turns out that
$N \succ M$
. It turns out that
 $$ \begin{align*} \operatorname{\mathrm{stab}}^\mu(r) = \operatorname{\mathrm{stab}}(\mu \cdot r) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi(\mu \cdot r). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}^\mu(r) = \operatorname{\mathrm{stab}}(\mu \cdot r) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi(\mu \cdot r). \end{align*} $$
Moreover, when r is definable, the groups
![]() $\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
are definable, and
$\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
are definable, and
![]() $\operatorname {\mathrm {stab}}(\mu \cdot r)$
is type-definable. (This is the reason why
$\operatorname {\mathrm {stab}}(\mu \cdot r)$
is type-definable. (This is the reason why
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is type-definable in Theorem 1.3. In the o-minimal case, there is a descending chain condition on definable groups, which ensures that
$\operatorname {\mathrm {stab}}^\mu (r)$
is type-definable in Theorem 1.3. In the o-minimal case, there is a descending chain condition on definable groups, which ensures that
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is definable in [Reference Peterzil and Starchenko15].)
$\operatorname {\mathrm {stab}}^\mu (r)$
is definable in [Reference Peterzil and Starchenko15].)
Theorem 1.4. Suppose that G is a definable group over a p-adically closed field M. Let
![]() $r \in S_G(M)$
be a definable unbounded one-dimensional type. Then there is a formula
$r \in S_G(M)$
be a definable unbounded one-dimensional type. Then there is a formula
![]() $\phi \in \mathcal {L}$
such that
$\phi \in \mathcal {L}$
such that
![]() $\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
is a one-dimensional definable subgroup of G. When G is abelian
$\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
is a one-dimensional definable subgroup of G. When G is abelian
![]() $($
or nearly abelian
$($
or nearly abelian
![]() $)$
,
$)$
,
![]() $\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
is unbounded.
$\operatorname {\mathrm {stab}}_\phi (\mu \cdot r)$
is unbounded.
Our proofs of these theorems are based on the original proofs of Peterzil and Steinhorn [Reference Peterzil and Steinhorn16], though several important changes are necessary. First of all, the
![]() $\mu $
-stabilizer
$\mu $
-stabilizer
![]() $\operatorname {\mathrm {stab}}^\mu (r)$
is no longer definable, but merely type-definable, as mentioned above. For this reason, it is necessary to compute the stabilizers in an
$\operatorname {\mathrm {stab}}^\mu (r)$
is no longer definable, but merely type-definable, as mentioned above. For this reason, it is necessary to compute the stabilizers in an
![]() $|M|^+$
-saturated elementary extension
$|M|^+$
-saturated elementary extension
![]() $N \succ M$
.
$N \succ M$
.
A more serious problem arises when trying to generalize [Reference Peterzil and Steinhorn16, Lemma 3.8]. This lemma, which is used to show that
![]() $\operatorname {\mathrm {stab}}^\mu (p) \ne \{\operatorname {\mathrm {id}}_G\}$
, roughly says the following: if I is a curve tending to infinity and B is an annulus around
$\operatorname {\mathrm {stab}}^\mu (p) \ne \{\operatorname {\mathrm {id}}_G\}$
, roughly says the following: if I is a curve tending to infinity and B is an annulus around
![]() $\operatorname {\mathrm {id}}_G$
, then
$\operatorname {\mathrm {id}}_G$
, then
![]() $g \cdot B \cap I \ne \emptyset $
for all
$g \cdot B \cap I \ne \emptyset $
for all
![]() $g \in I$
. This follows by a simple connectedness argument (I is connected, so it must cut across the annulus
$g \in I$
. This follows by a simple connectedness argument (I is connected, so it must cut across the annulus
![]() $g \cdot B$
on its way from g to infinity). This argument fails critically in the totally disconnected p-adic context. In Section 4 we develop an alternative argument to replace [Reference Peterzil and Steinhorn16, Lemma 3.8]. Unfortunately, the argument only works properly in the abelian (or near-abelian) case.
$g \cdot B$
on its way from g to infinity). This argument fails critically in the totally disconnected p-adic context. In Section 4 we develop an alternative argument to replace [Reference Peterzil and Steinhorn16, Lemma 3.8]. Unfortunately, the argument only works properly in the abelian (or near-abelian) case.
1.1 Notation and conventions
We shall assume a basic knowledge of model theory, including basic notions such as definable types, saturation, heirs, and so on. Good references are [Reference Marker12, Reference Poizat21]. We refer to the excellent survey [Reference Belair1] as well as [Reference Hrushovski, Peterzil and Pillay8, Reference Onshuus and Pillay13] for the model theory of the p-adic field
![]() $({\mathbb Q}_p, +, \times , 0, 1)$
. In fact, [Reference Hrushovski, Peterzil and Pillay8, Reference Onshuus and Pillay13] are also good references for the model-theoretic background required for the current paper.
$({\mathbb Q}_p, +, \times , 0, 1)$
. In fact, [Reference Hrushovski, Peterzil and Pillay8, Reference Onshuus and Pillay13] are also good references for the model-theoretic background required for the current paper.
Let T be a theory in some language
![]() $\mathcal {L}$
. We write
$\mathcal {L}$
. We write
![]() $\mathbb M$
for a monster model of T, in which every type over a small subset
$\mathbb M$
for a monster model of T, in which every type over a small subset
![]() $A\subseteq \mathbb M$
is realized, where “small” means
$A\subseteq \mathbb M$
is realized, where “small” means
![]() $|A|< \kappa $
for some big enough cardinal
$|A|< \kappa $
for some big enough cardinal
![]() $\kappa $
. The letters
$\kappa $
. The letters
![]() $M,N, M^{\prime }$
, and
$M,N, M^{\prime }$
, and
![]() $ N'$
will denote small elementary submodels of
$ N'$
will denote small elementary submodels of
![]() $\mathbb M$
. We will use
$\mathbb M$
. We will use
![]() $x, y, z$
to mean arbitrary n-tuples of variables and
$x, y, z$
to mean arbitrary n-tuples of variables and
![]() $a, b, c \in \mathbb M$
to denote n-tuples in
$a, b, c \in \mathbb M$
to denote n-tuples in
![]() $\mathbb M^n$
with
$\mathbb M^n$
with
![]() $n\in \mathbb N$
. Every formula is an
$n\in \mathbb N$
. Every formula is an
![]() $\mathcal {L}_{\mathbb M}$
-formula. For an
$\mathcal {L}_{\mathbb M}$
-formula. For an
![]() $\mathcal {L}_{M}$
-formula
$\mathcal {L}_{M}$
-formula
![]() $\phi (x)$
,
$\phi (x)$
,
![]() $\phi (M)$
denotes the definable subset of
$\phi (M)$
denotes the definable subset of
![]() $M^{|x|}$
defined by
$M^{|x|}$
defined by
![]() $\phi $
, and a set
$\phi $
, and a set
![]() $X\subseteq M^n$
is definable if there is an
$X\subseteq M^n$
is definable if there is an
![]() $\mathcal {L}_M$
-formula
$\mathcal {L}_M$
-formula
![]() $\phi (x)$
such that
$\phi (x)$
such that
![]() $X=\phi (M)$
. If
$X=\phi (M)$
. If
![]() $M\prec N\prec \mathbb M$
, and
$M\prec N\prec \mathbb M$
, and
![]() $X\subseteq N^n$
is defined by a formula
$X\subseteq N^n$
is defined by a formula
![]() $\psi $
with parameters from M, then
$\psi $
with parameters from M, then
![]() $X(M)$
and
$X(M)$
and
![]() $X(\mathbb M)$
will denote
$X(\mathbb M)$
will denote
![]() $\psi (M)$
and
$\psi (M)$
and
![]() $\psi (\mathbb M)$
, respectively; these are clearly definable subsets of
$\psi (\mathbb M)$
, respectively; these are clearly definable subsets of
![]() $M^n$
and
$M^n$
and
![]() $\mathbb M^n$
, respectively.
$\mathbb M^n$
, respectively.
Following [Reference Peterzil and Starchenko15, Definition 2.12], we say that a partial type
![]() $\Sigma $
is A-definable or definable over A if for every formula
$\Sigma $
is A-definable or definable over A if for every formula
![]() $\phi (x;y)$
, there is an
$\phi (x;y)$
, there is an
![]() $\mathcal {L}_A$
-formula
$\mathcal {L}_A$
-formula
![]() $\psi (y)$
such that
$\psi (y)$
such that
for all
![]() $b \in M$
. We will denote the formula
$b \in M$
. We will denote the formula
![]() $\psi (y)$
by
$\psi (y)$
by
![]() $(d_\Sigma x) \phi (x,y)$
, thinking of
$(d_\Sigma x) \phi (x,y)$
, thinking of
![]() $d_\Sigma $
as a quantifier. The map
$d_\Sigma $
as a quantifier. The map
![]() $\phi (x;y) \mapsto (d_\Sigma x) \phi (x,y)$
is called the definition schema of
$\phi (x;y) \mapsto (d_\Sigma x) \phi (x,y)$
is called the definition schema of
![]() $\Sigma (x)$
.
$\Sigma (x)$
.
If
![]() $\Sigma (x)$
is a definable partial type over M, and
$\Sigma (x)$
is a definable partial type over M, and
![]() $N\succ M$
, then
$N\succ M$
, then
![]() $\Sigma ^N$
will denote the canonical extension of
$\Sigma ^N$
will denote the canonical extension of
![]() $\Sigma $
by definitions, i.e., the following partial type over N:
$\Sigma $
by definitions, i.e., the following partial type over N:
When p is a complete definable type over M, the canonical extension
![]() $p^N$
is the same thing as the unique heir of p over N.
$p^N$
is the same thing as the unique heir of p over N.
For a definable set
![]() $D\subseteq M^n$
, and
$D\subseteq M^n$
, and
![]() $\phi (x)$
an
$\phi (x)$
an
![]() $\mathcal {L}_{\mathbb M}$
-formula, we say that
$\mathcal {L}_{\mathbb M}$
-formula, we say that
![]() $\phi (x)$
is a D-formula if
$\phi (x)$
is a D-formula if
![]() $\mathbb M\models \phi (x) \implies x\in D(\mathbb M)$
. A partial type
$\mathbb M\models \phi (x) \implies x\in D(\mathbb M)$
. A partial type
![]() $q(x)$
(over a small subset) is a D-type if
$q(x)$
(over a small subset) is a D-type if
![]() $q(x)\vdash x\in D(\mathbb M)$
. We write
$q(x)\vdash x\in D(\mathbb M)$
. We write
![]() $S_D(M)$
for the space of complete D-types over M.
$S_D(M)$
for the space of complete D-types over M.
We consider
![]() ${\mathbb Q}_p$
as a structure in the language of rings
${\mathbb Q}_p$
as a structure in the language of rings
![]() $\mathcal {L} = \mathcal {L}_r =\{+,\times ,-,0,1\}$
. The valuation ring
$\mathcal {L} = \mathcal {L}_r =\{+,\times ,-,0,1\}$
. The valuation ring
![]() ${\mathbb Z}_p$
is definable in
${\mathbb Z}_p$
is definable in
![]() ${\mathbb Q}_p$
. The valuation group
${\mathbb Q}_p$
. The valuation group
![]() $(\mathbb Z,+,<)$
and the valuation
$(\mathbb Z,+,<)$
and the valuation
![]() $v:{\mathbb Q}_p\rightarrow \mathbb Z\cup \{\infty \} $
are interpretable. A p-adically closed field is a model of
$v:{\mathbb Q}_p\rightarrow \mathbb Z\cup \{\infty \} $
are interpretable. A p-adically closed field is a model of
![]() $p\mathrm {CF} := \operatorname {\mathrm {Th}}({\mathbb Q}_p)$
. For any
$p\mathrm {CF} := \operatorname {\mathrm {Th}}({\mathbb Q}_p)$
. For any
![]() $M\models p\mathrm {CF}$
,
$M\models p\mathrm {CF}$
,
![]() $R(M)$
will denote the valuation ring, and
$R(M)$
will denote the valuation ring, and
![]() $\Gamma _M$
will denote the value group. By [Reference Macintyre11], pCF admits quantifier elimination after adjoining predicates
$\Gamma _M$
will denote the value group. By [Reference Macintyre11], pCF admits quantifier elimination after adjoining predicates
![]() $P_n$
for the n-th power of the multiplicative group for all
$P_n$
for the n-th power of the multiplicative group for all
![]() $n\in \mathbb N^+$
. The theory pCF also has definable Skolem functions [Reference Dolich, Goodrick and Lippel3].
$n\in \mathbb N^+$
. The theory pCF also has definable Skolem functions [Reference Dolich, Goodrick and Lippel3].
The p-adic field
![]() ${\mathbb Q}_p$
is a locally compact topological field, with basis given by the sets
${\mathbb Q}_p$
is a locally compact topological field, with basis given by the sets
for
![]() $a\in {\mathbb Q}_p$
and
$a\in {\mathbb Q}_p$
and
![]() $n\in \mathbb Z$
. The valuation ring
$n\in \mathbb Z$
. The valuation ring
![]() ${\mathbb Z}_p$
is compact. The topology is definable (as in Section 2.1 below), so it extends to any p-adically closed field M, making M a topological field (usually not locally compact). Any definable set
${\mathbb Z}_p$
is compact. The topology is definable (as in Section 2.1 below), so it extends to any p-adically closed field M, making M a topological field (usually not locally compact). Any definable set
![]() $X\subseteq M^n$
has a topological dimension, denoted by
$X\subseteq M^n$
has a topological dimension, denoted by
![]() $\dim (X)$
, which is the maximal
$\dim (X)$
, which is the maximal
![]() $k\leq n$
such that the image of the projection
$k\leq n$
such that the image of the projection
![]() $\pi : X\rightarrow M^n$
;
$\pi : X\rightarrow M^n$
;
![]() $(x_1, \ldots , x_n) \mapsto (x_{r_1} , \ldots , x_{r_k} )$
has interior, for suitable
$(x_1, \ldots , x_n) \mapsto (x_{r_1} , \ldots , x_{r_k} )$
has interior, for suitable
![]() $1 \leq r_1 < \cdots < r_k \leq n$
. As model-theoretic algebraic closure coincides with the field-theoretic algebraic closure, algebraic closure gives a pregeometry on M, and the algebraic dimension
$1 \leq r_1 < \cdots < r_k \leq n$
. As model-theoretic algebraic closure coincides with the field-theoretic algebraic closure, algebraic closure gives a pregeometry on M, and the algebraic dimension
![]() $\dim _{\operatorname {\mathrm {alg}}}(X)$
of X can be calculated in the usual way. The topological dimension coincides with the algebraic dimension.
$\dim _{\operatorname {\mathrm {alg}}}(X)$
of X can be calculated in the usual way. The topological dimension coincides with the algebraic dimension.
1.2 Outline
In Section 2, we review the notion of definable compactness, and how it behaves in definable manifolds and definable groups in pCF. In Section 3 we review the theory of dp-rank, which is used in Section 4. In Section 4, we prove a technical statement about “gaps” in unbounded sets, which replaces the use of connectedness in Peterzil–Steinhorn [Reference Peterzil and Steinhorn16, Lemma 3.8]. In Section 5, we review the theory of stabilizers and
![]() $\mu $
-stabilizers from [Reference Peterzil and Starchenko15]. Finally, we prove the main theorems in Section 6.
$\mu $
-stabilizers from [Reference Peterzil and Starchenko15]. Finally, we prove the main theorems in Section 6.
2 Definable compactness
In this section, we review the notion of definable compactness for definable manifolds and definable groups in p-adically closed fields. The treatment of (p-adic) definable compactness in the literature is questionable, so we build up the theory from scratch, out of an abundance of caution.
In Section 2.1 we recall an abstract definition of definable compactness, which behaves well in any definable topological space. In the next two sections, we restrict our attention to p-adic definable manifolds. In Section 2.2 we show that our definition agrees with the definition in the literature in terms of curve completion. In Section 2.3 we give another characterization using specialization of definable types. Finally, in Section 2.4 we list some consequences for definable groups.
2.1 Abstract definable compactness
Let M be an arbitrary structure. A definable topology on a definable set
![]() $X \subseteq M^n$
is a topology with a (uniformly) definable basis of opens. A definable topological space is a definable set with a definable topology.
$X \subseteq M^n$
is a topology with a (uniformly) definable basis of opens. A definable topological space is a definable set with a definable topology.
Recall that a topological space is compact if any filtered intersection of non-empty closed sets is non-empty.
Definition 2.1. Let X be a definable topological space in a structure M. Say that X is definably compact if the following holds: for any definable family
![]() $\mathcal {F} = \{Y_t : t \in T\}$
of non-empty closed sets
$\mathcal {F} = \{Y_t : t \in T\}$
of non-empty closed sets
![]() $Y_t \subseteq X$
, if
$Y_t \subseteq X$
, if
![]() $\mathcal {F}$
is downwards directed, then
$\mathcal {F}$
is downwards directed, then
![]() $\bigcap \mathcal {F} \ne \emptyset $
.
$\bigcap \mathcal {F} \ne \emptyset $
.
More generally, say that a definable set
![]() $Y \subseteq X$
is definably compact if it is definably compact with respect to the induced subspace topology.
$Y \subseteq X$
is definably compact if it is definably compact with respect to the induced subspace topology.
Definable compactness has many of the expected properties:
Fact 2.2.
-
1. If X is a compact definable topological space, then X is definably compact.
-
2. If
 $X, Y$
are definably compact, then
$X, Y$
are definably compact, then
 $X \times Y$
is definably compact.
$X \times Y$
is definably compact. -
3. If
 $f : X \to Y$
is definable and continuous, and X is definably compact, then the image
$f : X \to Y$
is definable and continuous, and X is definably compact, then the image
 $f(X) \subseteq Y$
is definably compact.
$f(X) \subseteq Y$
is definably compact. -
4. If X is a Hausdorff definable topological space and
 $Y \subseteq X$
is definably compact, then Y is closed.
$Y \subseteq X$
is definably compact, then Y is closed. -
5. If X is definably compact and
 $Y \subseteq X$
is closed and definable, then Y is definably compact.
$Y \subseteq X$
is closed and definable, then Y is definably compact. -
6. If X is a definable topological space and
 $Y_1, Y_2 \subseteq X$
are definably compact, then
$Y_1, Y_2 \subseteq X$
are definably compact, then
 $Y_1 \cup Y_2$
is definably compact.
$Y_1 \cup Y_2$
is definably compact.
Definition 2.1 and Fact 2.2 are due independently to Fornasiero [Reference Fornasiero4] and the first author [Reference Johnson9, Section 3.1].
Remark 2.3. Suppose X is a definable topological space in a structure M, and
![]() $N \succ M$
. Then
$N \succ M$
. Then
![]() $X(N)$
is naturally a definable topological space in the structure N, and
$X(N)$
is naturally a definable topological space in the structure N, and
![]() $X(N)$
is definably compact if and only if X is definably compact. In other words, definable compactness is invariant in elementary extensions.
$X(N)$
is definably compact if and only if X is definably compact. In other words, definable compactness is invariant in elementary extensions.
2.2 Definable compactness and definable manifolds in pCF
Let M be a p-adically closed field with valuation group
![]() $\Gamma _M$
. Each power
$\Gamma _M$
. Each power
![]() $M^n$
is a definable topological space. We first characterize definable compactness for subsets of
$M^n$
is a definable topological space. We first characterize definable compactness for subsets of
![]() $M^n$
.
$M^n$
.
Lemma 2.4. If
![]() $X \subseteq M^n$
is definably compact, then X is closed and bounded.
$X \subseteq M^n$
is definably compact, then X is closed and bounded.
Proof For
![]() $t \in M {\setminus} \{0\}$
, let
$t \in M {\setminus} \{0\}$
, let
![]() $O_t$
be the n-dimensional ball
$O_t$
be the n-dimensional ball
![]() ${\cal B}(0,v(t))^n$
. Each
${\cal B}(0,v(t))^n$
. Each
![]() $O_t$
is clopen in
$O_t$
is clopen in
![]() $M^n$
. Therefore
$M^n$
. Therefore
![]() $\{X {\setminus} O_t : t \in M {\setminus} \{0\}\}$
is a downwards-directed definable family of closed subsets of X, with empty intersection. By definable compactness, there is some t such that
$\{X {\setminus} O_t : t \in M {\setminus} \{0\}\}$
is a downwards-directed definable family of closed subsets of X, with empty intersection. By definable compactness, there is some t such that
![]() $X {\setminus} O_t = \emptyset $
, or equivalently,
$X {\setminus} O_t = \emptyset $
, or equivalently,
![]() $X \subseteq O_t$
. Then X is bounded.
$X \subseteq O_t$
. Then X is bounded.
Lemma 2.5. If
![]() $X \subseteq M^n$
is closed and bounded, then X is definably compact.
$X \subseteq M^n$
is closed and bounded, then X is definably compact.
Proof Equivalently, if
![]() $\{Y_t\}$
is a downwards-directed definable family of non-empty, closed, bounded sets, then
$\{Y_t\}$
is a downwards-directed definable family of non-empty, closed, bounded sets, then
![]() $\bigcap _t Y_t \ne \emptyset $
. This claim can be expressed as a countable conjunction of
$\bigcap _t Y_t \ne \emptyset $
. This claim can be expressed as a countable conjunction of
![]() $\mathcal {L}$
-sentences. (We need infinitely many sentences because there is no bound on the complexity of the definable family
$\mathcal {L}$
-sentences. (We need infinitely many sentences because there is no bound on the complexity of the definable family
![]() $\{Y_t\}$
.) As a countable conjunction of
$\{Y_t\}$
.) As a countable conjunction of
![]() $\mathcal {L}$
-sentences, the claim holds in M if and only if it holds in
$\mathcal {L}$
-sentences, the claim holds in M if and only if it holds in
![]() ${\mathbb Q}_p$
. Therefore, we may assume that
${\mathbb Q}_p$
. Therefore, we may assume that
![]() $M = {\mathbb Q}_p$
. In this case, the set X will be compact, and hence definably compact by Fact 2.2(1).
$M = {\mathbb Q}_p$
. In this case, the set X will be compact, and hence definably compact by Fact 2.2(1).
Definition 2.6. Let X be a definable topological space. A
![]() $\Gamma $
-exhaustion is a definable family
$\Gamma $
-exhaustion is a definable family
![]() $\{W_\gamma \mid \gamma \in \Gamma _M\}$
such that
$\{W_\gamma \mid \gamma \in \Gamma _M\}$
such that
-
• Each
 $W_\gamma $
is an open, definably compact subset of X. In particular,
$W_\gamma $
is an open, definably compact subset of X. In particular,
 $W_\gamma $
is clopen.
$W_\gamma $
is clopen. -
• If
 $\gamma \le \gamma '$
, then
$\gamma \le \gamma '$
, then
 $W_\gamma \subseteq W_{\gamma '}$
.
$W_\gamma \subseteq W_{\gamma '}$
. -
•
 $X = \bigcup _{\gamma \in \Gamma _M} W_\gamma $
.
$X = \bigcup _{\gamma \in \Gamma _M} W_\gamma $
.
Lemma 2.7. If
![]() $U \subseteq M^n$
is definable and open, then U has a
$U \subseteq M^n$
is definable and open, then U has a
![]() $\Gamma $
-exhaustion.
$\Gamma $
-exhaustion.
Proof For any
![]() $\bar {x} = (x_1,\ldots ,x_n) \in M^n$
and
$\bar {x} = (x_1,\ldots ,x_n) \in M^n$
and
![]() $\gamma \in \Gamma _M$
, let
$\gamma \in \Gamma _M$
, let
![]() ${\cal B}(\bar {x},\gamma )$
denote the ball of valuative radius
${\cal B}(\bar {x},\gamma )$
denote the ball of valuative radius
![]() $\gamma $
around
$\gamma $
around
![]() $\bar {x}$
, i.e.,
$\bar {x}$
, i.e.,
![]() $\prod _{i = 1}^n {\cal B}(x_i,\gamma )$
.
$\prod _{i = 1}^n {\cal B}(x_i,\gamma )$
.
Let
![]() $W_{\gamma }$
be the set of
$W_{\gamma }$
be the set of
![]() $x \in U$
such that
$x \in U$
such that
![]() ${\cal B}(x,\gamma ) \subseteq U$
and
${\cal B}(x,\gamma ) \subseteq U$
and
![]() $\bar {0} \in {\cal B}(x,-\gamma )$
. We claim that the family
$\bar {0} \in {\cal B}(x,-\gamma )$
. We claim that the family
![]() $W_{\gamma }$
is a
$W_{\gamma }$
is a
![]() $\Gamma $
-exhaustion.
$\Gamma $
-exhaustion.
First of all, for all
![]() $x'$
sufficiently close to x, we have
$x'$
sufficiently close to x, we have
![]() ${\cal B}(x,\gamma ) = {\cal B}(x',\gamma )$
and
${\cal B}(x,\gamma ) = {\cal B}(x',\gamma )$
and
![]() ${\cal B}(x,-\gamma ) = {\cal B}(x',-\gamma )$
, and so
${\cal B}(x,-\gamma ) = {\cal B}(x',-\gamma )$
, and so
![]() $x \in W_\gamma \iff x' \in W_\gamma $
. Therefore
$x \in W_\gamma \iff x' \in W_\gamma $
. Therefore
![]() $W_\gamma $
is clopen. Additionally,
$W_\gamma $
is clopen. Additionally,
 $$ \begin{align*} x \in W_\gamma \implies \bar{0} \in {\cal B}(x,-\gamma) \iff x \in {\cal B}(\bar{0},-\gamma). \end{align*} $$
$$ \begin{align*} x \in W_\gamma \implies \bar{0} \in {\cal B}(x,-\gamma) \iff x \in {\cal B}(\bar{0},-\gamma). \end{align*} $$
Therefore
![]() $W_\gamma $
is bounded. By Lemma 2.5,
$W_\gamma $
is bounded. By Lemma 2.5,
![]() $W_\gamma $
is definably compact.
$W_\gamma $
is definably compact.
If
![]() $\gamma ' \ge \gamma $
, then
$\gamma ' \ge \gamma $
, then
![]() ${\cal B}(x,\gamma ') \subseteq {\cal B}(x,\gamma )$
and
${\cal B}(x,\gamma ') \subseteq {\cal B}(x,\gamma )$
and
![]() ${\cal B}(x,-\gamma ') \supseteq {\cal B}(x,-\gamma )$
. Therefore
${\cal B}(x,-\gamma ') \supseteq {\cal B}(x,-\gamma )$
. Therefore
and the family
![]() $\{W_\gamma \}$
is monotone.
$\{W_\gamma \}$
is monotone.
Lastly, if
![]() $x \in U$
, then for sufficiently large
$x \in U$
, then for sufficiently large
![]() $\gamma $
, we have
$\gamma $
, we have
![]() ${\cal B}(x,\gamma ) \subseteq U$
, because U is open. Also,
${\cal B}(x,\gamma ) \subseteq U$
, because U is open. Also,
![]() $\bar {0} \in {\cal B}(x,-\gamma )$
for sufficiently large
$\bar {0} \in {\cal B}(x,-\gamma )$
for sufficiently large
![]() $\gamma $
. Thus
$\gamma $
. Thus
![]() $x \in W_\gamma $
for all sufficiently large
$x \in W_\gamma $
for all sufficiently large
![]() $\gamma $
. This shows
$\gamma $
. This shows
 $U = \bigcup _\gamma W_\gamma $
.
$U = \bigcup _\gamma W_\gamma $
.
An n-dimensional definable manifold over M is a Hausdorff definable topological space X with a covering by finitely many open subsets
![]() $U_1$
,…,
$U_1$
,…,
![]() $U_m$
, and a definable homeomorphism from
$U_m$
, and a definable homeomorphism from
![]() $U_i$
to an open set
$U_i$
to an open set
![]() $V_i \subseteq M^n$
for each i.
$V_i \subseteq M^n$
for each i.
Proposition 2.8. Let X be a definable manifold in M. Then X has a
![]() $\Gamma $
-exhaustion.
$\Gamma $
-exhaustion.
Proof Cover X with finitely many open sets
![]() $U_i$
homeomorphic to open subsets of
$U_i$
homeomorphic to open subsets of
![]() $M^n$
. For each i, let
$M^n$
. For each i, let
![]() $\{W_{i,\gamma }\}_{\gamma \in \Gamma _M}$
be a
$\{W_{i,\gamma }\}_{\gamma \in \Gamma _M}$
be a
![]() $\Gamma $
-exhaustion of
$\Gamma $
-exhaustion of
![]() $U_i$
. Let
$U_i$
. Let
![]() $V_\gamma = \bigcup _i W_{i,\gamma }$
. Then the family
$V_\gamma = \bigcup _i W_{i,\gamma }$
. Then the family
![]() $\{V_\gamma \}$
is a
$\{V_\gamma \}$
is a
![]() $\Gamma $
-exhaustion of X.
$\Gamma $
-exhaustion of X.
Definition 2.9. Let X be a definable manifold. An arbitrary subset
![]() $Y \subseteq X$
is bounded if
$Y \subseteq X$
is bounded if
![]() $Y \subseteq D$
for some definably compact subset
$Y \subseteq D$
for some definably compact subset
![]() $D \subseteq X$
.
$D \subseteq X$
.
Proposition 2.10(1) gives a more concrete definition of “bounded” in terms of
![]() $\Gamma $
-exhaustions.
$\Gamma $
-exhaustions.
Proposition 2.10. Let X be a definable manifold and
![]() $Y \subseteq X$
be an arbitrary subset.
$Y \subseteq X$
be an arbitrary subset.
-
1. Let
 $\{W_\gamma \}$
be a
$\{W_\gamma \}$
be a
 $\Gamma $
-exhaustion of X. Then Y is bounded if and only if there is
$\Gamma $
-exhaustion of X. Then Y is bounded if and only if there is
 $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
 $Y \subseteq W_\gamma $
.
$Y \subseteq W_\gamma $
. -
2. Suppose Y is definable. Then Y is definably compact if and only if Y is closed and bounded.
-
3. Suppose Y is definable. Then Y is bounded if and only if the closure
 $\overline {Y}$
is definably compact.
$\overline {Y}$
is definably compact.
Proof
-
1. If
 $Y \subseteq W_\gamma $
, then Y is contained in the definably compact set
$Y \subseteq W_\gamma $
, then Y is contained in the definably compact set
 $W_\gamma $
. Conversely, suppose Y is bounded, witnessed by a definably compact set
$W_\gamma $
. Conversely, suppose Y is bounded, witnessed by a definably compact set
 $Z \subseteq X$
with
$Z \subseteq X$
with
 $Y \subseteq Z$
. The filtered intersection is empty, so there is some
$Y \subseteq Z$
. The filtered intersection is empty, so there is some $$ \begin{align*} \bigcap_\gamma (Z {\setminus} W_\gamma) \end{align*} $$
$$ \begin{align*} \bigcap_\gamma (Z {\setminus} W_\gamma) \end{align*} $$
 $\gamma $
such that
$\gamma $
such that
 $W_\gamma \supseteq Z \supseteq Y$
.
$W_\gamma \supseteq Z \supseteq Y$
.
-
2. If Y is definably compact, then Y is closed (Fact 2.2(4)), and Y is bounded because
 $Y \subseteq Y$
. Conversely, suppose that Y is closed and bounded. Then Y is a definable closed subset of a definably compact set, so Y is definably compact by Fact 2.2(5).
$Y \subseteq Y$
. Conversely, suppose that Y is closed and bounded. Then Y is a definable closed subset of a definably compact set, so Y is definably compact by Fact 2.2(5). -
3. If
 $\overline {Y}$
is definably compact, then Y is bounded because
$\overline {Y}$
is definably compact, then Y is bounded because
 $Y \subseteq \overline {Y}$
. Conversely, suppose that Y is bounded. Then
$Y \subseteq \overline {Y}$
. Conversely, suppose that Y is bounded. Then
 $Y \subseteq Z$
for some definably compact set
$Y \subseteq Z$
for some definably compact set
 $Z \subseteq X$
. The closure
$Z \subseteq X$
. The closure
 $\overline {Y}$
is a definable closed subset of Z, so
$\overline {Y}$
is a definable closed subset of Z, so
 $\overline {Y}$
is definably compact by Fact 2.2(5).
$\overline {Y}$
is definably compact by Fact 2.2(5).
Remark 2.11. Definable compactness is a definable property: Let
![]() $X_t$
be a definable manifold depending definably on some parameter
$X_t$
be a definable manifold depending definably on some parameter
![]() $t \in T$
. Then
$t \in T$
. Then
is definable. This can be proved from Proposition 2.10(1,2) by compactness, using Remark 2.3 to reduce to the case where M is highly saturated.
Remark 2.12. When
![]() $M = {\mathbb Q}_p$
, a definable manifold X is definably compact if and only if it is compact. One direction is Fact 2.2(1). Conversely, suppose X is definably compact. Cover X by definable open subsets
$M = {\mathbb Q}_p$
, a definable manifold X is definably compact if and only if it is compact. One direction is Fact 2.2(1). Conversely, suppose X is definably compact. Cover X by definable open subsets
![]() $U_1, \ldots , U_n$
, each homeomorphic to an open subset of
$U_1, \ldots , U_n$
, each homeomorphic to an open subset of
![]() $M^n$
. As in the proof of Proposition 2.8, let
$M^n$
. As in the proof of Proposition 2.8, let
![]() $\{W_{i,\gamma }\}_{\gamma \in \mathbb {Z}}$
be a
$\{W_{i,\gamma }\}_{\gamma \in \mathbb {Z}}$
be a
![]() $\Gamma $
-exhaustion of
$\Gamma $
-exhaustion of
![]() $U_i$
, and let
$U_i$
, and let
![]() $V_\gamma = \bigcup _{i = 1}^n W_{i,\gamma }$
, so that
$V_\gamma = \bigcup _{i = 1}^n W_{i,\gamma }$
, so that
![]() $\{V_\gamma \}_{\gamma \in \mathbb {Z}}$
is a
$\{V_\gamma \}_{\gamma \in \mathbb {Z}}$
is a
![]() $\Gamma $
-exhaustion of X. By Proposition 2.10, there is some
$\Gamma $
-exhaustion of X. By Proposition 2.10, there is some
![]() $\gamma \in \mathbb {Z}$
such that
$\gamma \in \mathbb {Z}$
such that
![]() $X = V_\gamma $
. Then
$X = V_\gamma $
. Then
![]() $X = \bigcup _{i = 1}^n W_{i,\gamma }$
, where each
$X = \bigcup _{i = 1}^n W_{i,\gamma }$
, where each
![]() $W_{i,\gamma }$
is definably compact. Lemmas 2.4 and 2.5 imply that definable compactness is equivalent to compactness for definable subsets of
$W_{i,\gamma }$
is definably compact. Lemmas 2.4 and 2.5 imply that definable compactness is equivalent to compactness for definable subsets of
![]() $M^n$
. Therefore each
$M^n$
. Therefore each
![]() $W_{i,\gamma }$
is compact. As X is covered by finitely many compact sets, X itself is compact.
$W_{i,\gamma }$
is compact. As X is covered by finitely many compact sets, X itself is compact.
We now try to relate our notion of definable compactness to the more familiar notions appearing in [Reference Onshuus and Pillay13].
Definition 2.13. Let X be a definable manifold. Let D be a definable subset of
![]() $M {\setminus} \{0\}$
with
$M {\setminus} \{0\}$
with
![]() $0 \in \overline {D}$
. Let
$0 \in \overline {D}$
. Let
![]() $f : D \to X$
be a definable function. Then
$f : D \to X$
be a definable function. Then
![]() $a \in X$
is a cluster point of f if
$a \in X$
is a cluster point of f if
![]() $(0,a)$
is in the closure of the graph of f. In other words, for every neighborhood
$(0,a)$
is in the closure of the graph of f. In other words, for every neighborhood
![]() $U_1$
of 0 and every neighborhood
$U_1$
of 0 and every neighborhood
![]() $U_2$
of a, there is
$U_2$
of a, there is
![]() $x \in U_1 \cap D$
such that
$x \in U_1 \cap D$
such that
![]() $f(x) \in U_2$
.
$f(x) \in U_2$
.
Lemma 2.14. Let X be a definable manifold. Let
![]() $f : R(M) {\setminus} \{0\} \to X$
be a definable function. Then f is continuous at all but finitely many points of
$f : R(M) {\setminus} \{0\} \to X$
be a definable function. Then f is continuous at all but finitely many points of
![]() $R(M)$
.
$R(M)$
.
Proof An exercise using the fact that any definable function
![]() $M \to M^n$
is continuous off a finite set.
$M \to M^n$
is continuous off a finite set.
Lemma 2.15. Let X be a definable manifold. Let Y be a definable subset. The following are equivalent
![]() $:$
$:$
-
1. Y is definably compact.
-
2. If D is a definable subset of
 $M {\setminus} \{0\}$
with
$M {\setminus} \{0\}$
with
 $0 \in \overline {D}$
, then every definable function
$0 \in \overline {D}$
, then every definable function
 $f : D \to Y$
has a cluster point.
$f : D \to Y$
has a cluster point. -
3. Any definable continuous function
 $f : R(M) {\setminus} \{0\} \to Y$
has a cluster point in Y.
$f : R(M) {\setminus} \{0\} \to Y$
has a cluster point in Y. -
4. Any definable continuous function
 $f : {\cal B}(0,\gamma ) {\setminus} \{0\} \to Y$
has a cluster point in Y.
$f : {\cal B}(0,\gamma ) {\setminus} \{0\} \to Y$
has a cluster point in Y. -
5. Let
 $\{Z_\gamma \}_{\gamma \in \Gamma _M}$
be a definable family of non-empty closed subsets of Y, such that
$\{Z_\gamma \}_{\gamma \in \Gamma _M}$
be a definable family of non-empty closed subsets of Y, such that
 $\gamma \le \gamma ' \implies Z_{\gamma } \supseteq Z_{\gamma '}$
. Then
$\gamma \le \gamma ' \implies Z_{\gamma } \supseteq Z_{\gamma '}$
. Then
 $\bigcap _{\gamma \in \Gamma _M} Z_\gamma \ne \emptyset $
.
$\bigcap _{\gamma \in \Gamma _M} Z_\gamma \ne \emptyset $
.
Proof (1)
![]() $\Rightarrow $
(2): The set of cluster points is the intersection
$\Rightarrow $
(2): The set of cluster points is the intersection
 $$ \begin{align*} \bigcap_{\gamma \in \Gamma_M} \overline{f({\cal B}(0,\gamma) \cap D)}. \end{align*} $$
$$ \begin{align*} \bigcap_{\gamma \in \Gamma_M} \overline{f({\cal B}(0,\gamma) \cap D)}. \end{align*} $$
This is non-empty by definable compactness of Y.
(2)
![]() $\Rightarrow $
(3) is trivial, and (3)
$\Rightarrow $
(3) is trivial, and (3)
![]() $\Rightarrow $
(4) follows by rescaling.
$\Rightarrow $
(4) follows by rescaling.
(4)
![]() $\Rightarrow $
(5): By definable Skolem functions, there is some definable function
$\Rightarrow $
(5): By definable Skolem functions, there is some definable function
![]() $f : M {\setminus} \{0\} \to Y$
such that
$f : M {\setminus} \{0\} \to Y$
such that
![]() $f(x) \in Z_{v(x)}$
for all
$f(x) \in Z_{v(x)}$
for all
![]() $x \in M {\setminus} \{0\}$
. By Lemma 2.14, there is some
$x \in M {\setminus} \{0\}$
. By Lemma 2.14, there is some
![]() $\delta \in \Gamma _M$
such that f is continuous on
$\delta \in \Gamma _M$
such that f is continuous on
![]() ${\cal B}(0,\delta ) {\setminus} \{0\}$
. By (4), f has a cluster point
${\cal B}(0,\delta ) {\setminus} \{0\}$
. By (4), f has a cluster point
![]() $a \in Y$
. Then
$a \in Y$
. Then
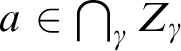 $a \in \bigcap _{\gamma } Z_\gamma $
. Otherwise, take
$a \in \bigcap _{\gamma } Z_\gamma $
. Otherwise, take
![]() $\gamma $
large enough that
$\gamma $
large enough that
![]() $a \notin Z_\gamma $
. Because a is a cluster point and
$a \notin Z_\gamma $
. Because a is a cluster point and
![]() $Z_\gamma $
is closed in Y, there is some
$Z_\gamma $
is closed in Y, there is some
![]() $x \ne 0$
such that
$x \ne 0$
such that
![]() $v(x) \ge \gamma $
and
$v(x) \ge \gamma $
and
![]() $f(x) \notin Z_\gamma $
. By choice of f,
$f(x) \notin Z_\gamma $
. By choice of f,
![]() $f(x) \in Z_{v(x)} \subseteq Z_\gamma $
, a contradiction.
$f(x) \in Z_{v(x)} \subseteq Z_\gamma $
, a contradiction.
(5)
![]() $\Rightarrow $
(1): We first claim that Y is closed. Take
$\Rightarrow $
(1): We first claim that Y is closed. Take
![]() $p \in \overline {Y}$
. Because X is a definable manifold, we can identify a neighborhood of p in X with the closed ball
$p \in \overline {Y}$
. Because X is a definable manifold, we can identify a neighborhood of p in X with the closed ball
![]() $R(M)^n$
in
$R(M)^n$
in
![]() $M^n$
. For
$M^n$
. For
![]() $\gamma \ge 0$
, let
$\gamma \ge 0$
, let
![]() $B_\gamma $
be the closed ball of radius
$B_\gamma $
be the closed ball of radius
![]() $\gamma $
around p. For
$\gamma $
around p. For
![]() $\gamma \le 0$
let
$\gamma \le 0$
let
![]() $B_\gamma = B_0$
. Then
$B_\gamma = B_0$
. Then
![]() $B_\gamma \cap Y$
is a non-empty closed subset of Y for any
$B_\gamma \cap Y$
is a non-empty closed subset of Y for any
![]() $\gamma $
, because
$\gamma $
, because
![]() $p \in \overline {Y}$
. By (4), the intersection
$p \in \overline {Y}$
. By (4), the intersection
 $\bigcap _{\gamma } (B_\gamma \cap Y)$
is non-empty, and so
$\bigcap _{\gamma } (B_\gamma \cap Y)$
is non-empty, and so
![]() $p \in Y$
. Therefore Y is closed.
$p \in Y$
. Therefore Y is closed.
Similarly, Y is bounded. Take a
![]() $\Gamma $
-exhaustion
$\Gamma $
-exhaustion
![]() $\{U_\gamma \}_{\gamma \in \Gamma _M}$
of the definable manifold X. If Y is unbounded, then
$\{U_\gamma \}_{\gamma \in \Gamma _M}$
of the definable manifold X. If Y is unbounded, then
![]() $Y {\setminus} U_\gamma $
is a closed non-empty subset of Y for each
$Y {\setminus} U_\gamma $
is a closed non-empty subset of Y for each
![]() $\gamma $
. Applying (5) to the family of sets
$\gamma $
. Applying (5) to the family of sets
![]() $Y {\setminus} U_\gamma $
, we see that
$Y {\setminus} U_\gamma $
, we see that
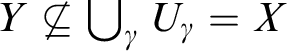 $Y \not \subseteq \bigcup _{\gamma } U_\gamma = X$
, a contradiction. Therefore Y is closed and bounded. By Proposition 2.10(2), Y is definably compact.
$Y \not \subseteq \bigcup _{\gamma } U_\gamma = X$
, a contradiction. Therefore Y is closed and bounded. By Proposition 2.10(2), Y is definably compact.
Therefore, we could alternatively define definable compactness as follows:
Proposition 2.16. Let Y be a definable subset of a definable manifold X. Then Y is definably compact if and only if every definable continuous function
![]() $f : R(M) {\setminus} \{0\} \to Y$
has a cluster point.
$f : R(M) {\setminus} \{0\} \to Y$
has a cluster point.
This is essentially the definition of “definable compactness” appearing in [Reference Onshuus and Pillay13] (with the mistake fixed).
2.3 Definable compactness and definable one-dimensional types
Suppose that
![]() $N \succ M$
. Let X be a definable manifold in M.
$N \succ M$
. Let X be a definable manifold in M.
Definition 2.17. For
![]() $a \in X(M)$
and
$a \in X(M)$
and
![]() $b \in X(N)$
, say that a and b are infinitesimally close over M if b is contained in every M-definable neighborhood of a.
$b \in X(N)$
, say that a and b are infinitesimally close over M if b is contained in every M-definable neighborhood of a.
Suppose that
![]() $X, Y$
are M-definable manifolds and
$X, Y$
are M-definable manifolds and
![]() $f : X \to Y$
is an M-definable continuous function. If
$f : X \to Y$
is an M-definable continuous function. If
![]() $a \in X(M)$
is infinitesimally close to
$a \in X(M)$
is infinitesimally close to
![]() $b \in X(N)$
, then
$b \in X(N)$
, then
![]() $f(a)$
is infinitesimally close to
$f(a)$
is infinitesimally close to
![]() $f(b)$
.
$f(b)$
.
Definition 2.18.
-
• We let
 $\mathcal {O}_{X(M)}(N)$
denote the set of
$\mathcal {O}_{X(M)}(N)$
denote the set of
 $b \in X(N)$
such that b is infinitesimally close to at least one
$b \in X(N)$
such that b is infinitesimally close to at least one
 $a \in X(M)$
.
$a \in X(M)$
. -
• There is a function
 $\operatorname {\mathrm {st}}_M^N : \mathcal {O}_{X(M)}(N) \to X(M)$
sending each b to the unique
$\operatorname {\mathrm {st}}_M^N : \mathcal {O}_{X(M)}(N) \to X(M)$
sending each b to the unique
 $a \in X(M)$
such that b and a are infinitesimally close. This is well defined because X is Hausdorff.
$a \in X(M)$
such that b and a are infinitesimally close. This is well defined because X is Hausdorff.
The map
![]() $\operatorname {\mathrm {st}}_M^N$
is the “standard part” map from
$\operatorname {\mathrm {st}}_M^N$
is the “standard part” map from
![]() $\mathcal {O}_{X(M)}(N)$
to
$\mathcal {O}_{X(M)}(N)$
to
![]() $X(M)$
.
$X(M)$
.
Definition 2.19. If p is a complete X-type over M, we say that p specializes to
![]() $a \in X(M)$
if
$a \in X(M)$
if
![]() $p(x) \vdash x \in U$
for every M-definable neighborhood
$p(x) \vdash x \in U$
for every M-definable neighborhood
![]() $U \ni a$
.
$U \ni a$
.
If
![]() $b \in X(N)$
is a realization of p, then p specializes to a if and only if
$b \in X(N)$
is a realization of p, then p specializes to a if and only if
![]() $\operatorname {\mathrm {st}}_M^N(b) = a$
.
$\operatorname {\mathrm {st}}_M^N(b) = a$
.
Fact 2.20. If
![]() $a'\in N\backslash M$
is infinitesimally close to
$a'\in N\backslash M$
is infinitesimally close to
![]() $ a\in M$
over M, then there is a coset
$ a\in M$
over M, then there is a coset
![]() $C\subseteq N\backslash \{0\}$
of
$C\subseteq N\backslash \{0\}$
of
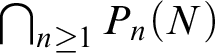 $\bigcap _{n\geq 1}P_n(N)$
such that
$\bigcap _{n\geq 1}P_n(N)$
such that
![]() $\operatorname {\mathrm {tp}}(a'/M)$
is determined by the partial type
$\operatorname {\mathrm {tp}}(a'/M)$
is determined by the partial type
and
![]() $\operatorname {\mathrm {tp}}(a'/M)$
is definable over M.
$\operatorname {\mathrm {tp}}(a'/M)$
is definable over M.
This follows by a similar argument to Lemma 2.1 in [Reference Penazzi, Pillay and Yao14].
Lemma 2.21. Let
![]() $\mathcal {C}$
be a definable
$\mathcal {C}$
be a definable
![]() $($
i.e., interpretable
$($
i.e., interpretable
![]() $)$
family of balls
$)$
family of balls
![]() $B \subseteq M$
. Suppose the following conditions hold
$B \subseteq M$
. Suppose the following conditions hold
![]() $:$
$:$
-
1.
 $\mathcal {C}$
is non-empty.
$\mathcal {C}$
is non-empty. -
2.
 $\mathcal {C}$
is a chain
$\mathcal {C}$
is a chain
 $:$
it is linearly ordered by
$:$
it is linearly ordered by
 $\subseteq $
.
$\subseteq $
. -
3.
 $\mathcal {C}$
is upwards-closed
$\mathcal {C}$
is upwards-closed
 $:$
if
$:$
if
 $B \supseteq B' \in \mathcal {C}$
for balls
$B \supseteq B' \in \mathcal {C}$
for balls
 $B, B'$
, then
$B, B'$
, then
 $B \in \mathcal {C}$
.
$B \in \mathcal {C}$
. -
4.
 $\mathcal {C}$
has no minimal element.
$\mathcal {C}$
has no minimal element.
Then there is
![]() $d \in M$
such that
$d \in M$
such that
![]() $\mathcal {C}$
is the set of balls containing d.
$\mathcal {C}$
is the set of balls containing d.
Proof We may assume
![]() $M = {\mathbb Q}_p$
, in which case the lemma is an easy exercise using spherical completeness of
$M = {\mathbb Q}_p$
, in which case the lemma is an easy exercise using spherical completeness of
![]() ${\mathbb Q}_p$
.
${\mathbb Q}_p$
.
Lemma 2.22. Let X be an M-definable set, and p be a one-dimensional definable type over M in X. Then there is an elementary extension
![]() $N \succ M$
and elements
$N \succ M$
and elements
![]() $a \in M$
,
$a \in M$
,
![]() $b \in X(M)$
, such that a is infinitesimally close to 0,
$b \in X(M)$
, such that a is infinitesimally close to 0,
![]() $b \in \operatorname {\mathrm {dcl}}(Ma)$
, and
$b \in \operatorname {\mathrm {dcl}}(Ma)$
, and
![]() $p = \operatorname {\mathrm {tp}}(b/M)$
.
$p = \operatorname {\mathrm {tp}}(b/M)$
.
Proof Take
![]() $N \succ M$
containing a realization b of p. Because p is one-dimensional, there is some singleton
$N \succ M$
containing a realization b of p. Because p is one-dimensional, there is some singleton
![]() $c \in N$
such that
$c \in N$
such that
![]() $\operatorname {\mathrm {dcl}}(Mb) = \operatorname {\mathrm {dcl}}(Mc)$
. (In fact, we can take c to be a coordinate of the tuple b.) Replacing c with
$\operatorname {\mathrm {dcl}}(Mb) = \operatorname {\mathrm {dcl}}(Mc)$
. (In fact, we can take c to be a coordinate of the tuple b.) Replacing c with
![]() $1/c$
if necessary, we may assume that
$1/c$
if necessary, we may assume that
![]() $v(c) \ge 0$
. Then
$v(c) \ge 0$
. Then
![]() $\operatorname {\mathrm {tp}}(c/M)$
is definable and one-dimensional. Let
$\operatorname {\mathrm {tp}}(c/M)$
is definable and one-dimensional. Let
![]() $\mathcal {C}$
be the family of M-definable balls which contain c. Then
$\mathcal {C}$
be the family of M-definable balls which contain c. Then
![]() $\mathcal {C}$
is definable, because
$\mathcal {C}$
is definable, because
![]() $\operatorname {\mathrm {tp}}(c/M)$
is definable. Moreover,
$\operatorname {\mathrm {tp}}(c/M)$
is definable. Moreover,
![]() $\mathcal {C}$
satisfies the four conditions of Lemma 2.21:
$\mathcal {C}$
satisfies the four conditions of Lemma 2.21:
-
1.
 $\mathcal {C}$
is non-empty, because it contains the ball
$\mathcal {C}$
is non-empty, because it contains the ball
 $R(M)$
of radius 0.
$R(M)$
of radius 0. -
2.
 $\mathcal {C}$
is a chain, because any two balls which intersect are comparable, and
$\mathcal {C}$
is a chain, because any two balls which intersect are comparable, and
 $\mathcal {C}$
cannot contain two disjoint balls.
$\mathcal {C}$
cannot contain two disjoint balls. -
3.
 $\mathcal {C}$
is upwards-closed, trivially.
$\mathcal {C}$
is upwards-closed, trivially. -
4.
 $\mathcal {C}$
has no least element. Otherwise, if B were the smallest M-definable ball containing c, then we could write B as a disjoint union of smaller balls
$\mathcal {C}$
has no least element. Otherwise, if B were the smallest M-definable ball containing c, then we could write B as a disjoint union of smaller balls
 $B = B_1 \cup \cdots \cup B_p$
, and one of the
$B = B_1 \cup \cdots \cup B_p$
, and one of the
 $B_i$
would belong to
$B_i$
would belong to
 $\mathcal {C}$
.
$\mathcal {C}$
.
By Lemma 2.21,
![]() $\mathcal {C}$
is the class of balls around some point d. So there is some
$\mathcal {C}$
is the class of balls around some point d. So there is some
![]() $d \in M$
such that c is contained in every M-definable ball around d. Therefore, c is infinitesimally close to d over M. Take
$d \in M$
such that c is contained in every M-definable ball around d. Therefore, c is infinitesimally close to d over M. Take
![]() $a = c - d$
.
$a = c - d$
.
Lemma 2.23. Let X be a definable manifold over M. Let Y be a definably compact definable subset of X. Let p be a definable one-dimensional complete Y-type over M. Then p specializes to a point in Y.
Proof Let N be an
![]() $\aleph _1$
-saturated elementary extension of M, and let
$\aleph _1$
-saturated elementary extension of M, and let
![]() $\mathbb M$
be a monster model extending N. Let
$\mathbb M$
be a monster model extending N. Let
![]() $p^N$
be the heir of p over N. We first show that
$p^N$
be the heir of p over N. We first show that
![]() $p^N$
specializes to a point in
$p^N$
specializes to a point in
![]() $Y(N)$
. Take
$Y(N)$
. Take
![]() $c \in Y(\mathbb M)$
realizing
$c \in Y(\mathbb M)$
realizing
![]() $p^N$
. By Lemma 2.22, we can write c as
$p^N$
. By Lemma 2.22, we can write c as
![]() $g(a)$
for some N-definable function
$g(a)$
for some N-definable function
![]() $g : \mathbb M \to Y(\mathbb M)$
and some
$g : \mathbb M \to Y(\mathbb M)$
and some
![]() $a \in \mathbb M$
infinitesimally close to 0 over N. Because N is
$a \in \mathbb M$
infinitesimally close to 0 over N. Because N is
![]() $\aleph _1$
-saturated, there is some
$\aleph _1$
-saturated, there is some
![]() $u \in N$
such that
$u \in N$
such that
![]() $a/u \in P_n(\mathbb M)$
for all n. Replacing a with
$a/u \in P_n(\mathbb M)$
for all n. Replacing a with
![]() $a/u$
, we may assume that
$a/u$
, we may assume that
![]() $a \in P_n(\mathbb M)$
for all n. For each n, let
$a \in P_n(\mathbb M)$
for all n. For each n, let
![]() $S_n \subseteq Y(N)$
be the definable set of cluster points of
$S_n \subseteq Y(N)$
be the definable set of cluster points of
![]() $g \restriction P_{n}(N)$
. Each
$g \restriction P_{n}(N)$
. Each
![]() $S_n$
is closed, and non-empty by Lemma 2.15(2). The intersection
$S_n$
is closed, and non-empty by Lemma 2.15(2). The intersection
![]() $\bigcap _n S_n$
is filtered, and therefore non-empty by
$\bigcap _n S_n$
is filtered, and therefore non-empty by
![]() $\aleph _1$
-saturation. Take
$\aleph _1$
-saturation. Take
![]() $b \in \bigcap _n S_n$
. Let
$b \in \bigcap _n S_n$
. Let
![]() $\Sigma (x)$
be the partial type saying that x is infinitesimally close to 0,
$\Sigma (x)$
be the partial type saying that x is infinitesimally close to 0,
![]() $g(x)$
is infinitesimally close to b, and
$g(x)$
is infinitesimally close to b, and
![]() $x \in P_n$
for all n. Then
$x \in P_n$
for all n. Then
![]() $\Sigma (x)$
is finitely satisfiable, by choice of b. Take
$\Sigma (x)$
is finitely satisfiable, by choice of b. Take
![]() $a' \in \mathbb M$
realizing
$a' \in \mathbb M$
realizing
![]() $\Sigma (x)$
. By Fact 2.20,
$\Sigma (x)$
. By Fact 2.20,
![]() $\operatorname {\mathrm {tp}}(a'/N) = \operatorname {\mathrm {tp}}(a/N)$
. Therefore a satisfies
$\operatorname {\mathrm {tp}}(a'/N) = \operatorname {\mathrm {tp}}(a/N)$
. Therefore a satisfies
![]() $\Sigma (x)$
, and so
$\Sigma (x)$
, and so
![]() $g(a)$
is infinitesimally close to b. It follows that
$g(a)$
is infinitesimally close to b. It follows that
![]() $p^N(x)$
specializes to b.
$p^N(x)$
specializes to b.
Let Z be the set of
![]() $b \in Y(N)$
such that
$b \in Y(N)$
such that
![]() $p^N$
specializes to b. The set Z is M-definable, because
$p^N$
specializes to b. The set Z is M-definable, because
![]() $p^N$
is definable over M. The above argument shows
$p^N$
is definable over M. The above argument shows
![]() $|Z|> 0$
. On the other hand,
$|Z|> 0$
. On the other hand,
![]() $|Z| \le 1$
because
$|Z| \le 1$
because
![]() $Y(N)$
is Hausdorff. Therefore Z is a singleton
$Y(N)$
is Hausdorff. Therefore Z is a singleton
![]() $\{b\}$
, and the element b lies in
$\{b\}$
, and the element b lies in
![]() $Y(M)$
. Then p specializes to b.
$Y(M)$
. Then p specializes to b.
Proposition 2.24. Work in a model M. Let X be a definable manifold and Y be a definable subset. Then Y is definably compact if and only if every one-dimensional definable Y-type specializes to a point of Y.
Proof One direction is Lemma 2.23. Conversely, suppose every one-dimensional definable type in Y specializes to a point. We claim that Y is definably compact. We use criterion (3) of Lemma 2.15. Let
![]() $f : R(M) {\setminus} \{0\} \to Y$
be a definable continuous function. Take a monster model
$f : R(M) {\setminus} \{0\} \to Y$
be a definable continuous function. Take a monster model
![]() $\mathbb M \succ M$
and a non-zero
$\mathbb M \succ M$
and a non-zero
![]() $a \in \mathbb M$
infinitesimally close to 0 over M. Let
$a \in \mathbb M$
infinitesimally close to 0 over M. Let
![]() $b = f(a)$
. By Fact 2.20,
$b = f(a)$
. By Fact 2.20,
![]() $\operatorname {\mathrm {tp}}(a/M)$
is definable. Therefore
$\operatorname {\mathrm {tp}}(a/M)$
is definable. Therefore
![]() $\operatorname {\mathrm {tp}}(b/M)$
is one-dimensional and definable. Then
$\operatorname {\mathrm {tp}}(b/M)$
is one-dimensional and definable. Then
![]() $\operatorname {\mathrm {tp}}(b/M)$
specializes to a point
$\operatorname {\mathrm {tp}}(b/M)$
specializes to a point
![]() $c \in Y(M)$
. We claim that c is a cluster point of f. For any M-definable neighborhoods
$c \in Y(M)$
. We claim that c is a cluster point of f. For any M-definable neighborhoods
![]() $U_1 \ni 0$
and
$U_1 \ni 0$
and
![]() $U_2 \ni c$
, we have
$U_2 \ni c$
, we have
![]() $(a,f(a)) = (a,b) \in U_1 \times U_2$
. As
$(a,f(a)) = (a,b) \in U_1 \times U_2$
. As
![]() $M \prec \mathbb M$
, there must be some
$M \prec \mathbb M$
, there must be some
![]() $(a',f(a')) \in U_1(M) \times U_2(M)$
. This shows that c is a cluster point of f.
$(a',f(a')) \in U_1(M) \times U_2(M)$
. This shows that c is a cluster point of f.
Lemma 2.25. Let X be an M-definable manifold and
![]() $\{O_t\}_{t \in \Gamma _M}$
be a
$\{O_t\}_{t \in \Gamma _M}$
be a
![]() $\Gamma $
-exhaustion. Let p be a definable one-dimensional type in X over M, such that p does not concentrate on
$\Gamma $
-exhaustion. Let p be a definable one-dimensional type in X over M, such that p does not concentrate on
![]() $O_t$
for any
$O_t$
for any
![]() $t \in \Gamma _M$
. Suppose
$t \in \Gamma _M$
. Suppose
![]() $\mathbb M \succ N \succ M$
. Suppose that
$\mathbb M \succ N \succ M$
. Suppose that
![]() $b \in X(\mathbb M)$
realizes p, and
$b \in X(\mathbb M)$
realizes p, and
![]() $b \notin O_t(\mathbb M)$
for any
$b \notin O_t(\mathbb M)$
for any
![]() $t \in \Gamma _N$
. Then b realizes
$t \in \Gamma _N$
. Then b realizes
![]() $p^N\kern-1pt ,$
the heir of p over N.
$p^N\kern-1pt ,$
the heir of p over N.
Proof By Lemma 2.22, we have
![]() $b = f(a)$
for some M-definable function
$b = f(a)$
for some M-definable function
![]() $f : \mathbb M \to X$
and some
$f : \mathbb M \to X$
and some
![]() $a \in \mathbb M$
infinitesimally close to 0 over M. By Lemma 2.14, f is continuous on
$a \in \mathbb M$
infinitesimally close to 0 over M. By Lemma 2.14, f is continuous on
![]() ${\cal B}(0,\gamma _0)$
for some sufficiently large
${\cal B}(0,\gamma _0)$
for some sufficiently large
![]() $\gamma _0 \in \Gamma _M$
; note that
$\gamma _0 \in \Gamma _M$
; note that
![]() $v(a)> \gamma _0$
. We claim that a is infinitesimally close to 0 over N. Otherwise, there is some
$v(a)> \gamma _0$
. We claim that a is infinitesimally close to 0 over N. Otherwise, there is some
![]() $\gamma \in \Gamma _N$
such that
$\gamma \in \Gamma _N$
such that
![]() $v(a) < \gamma $
. Let A be the definable set of
$v(a) < \gamma $
. Let A be the definable set of
![]() $x \in \mathbb M$
such that
$x \in \mathbb M$
such that
![]() $\gamma _0 < v(x) < \gamma $
; note that
$\gamma _0 < v(x) < \gamma $
; note that
![]() $a \in A$
. The set A is definably compact and N-definable. Also, f is N-definable and continuous on A. Therefore, the image
$a \in A$
. The set A is definably compact and N-definable. Also, f is N-definable and continuous on A. Therefore, the image
![]() $f(A)$
is N-definable, and definably compact. By Proposition 2.10, there is some
$f(A)$
is N-definable, and definably compact. By Proposition 2.10, there is some
![]() $t \in \Gamma _N$
such that
$t \in \Gamma _N$
such that
![]() $f(A) \subseteq O_t$
. Then
$f(A) \subseteq O_t$
. Then
![]() $b = f(a) \in f(A) \subseteq O_t(\mathbb M)$
, contradicting the assumptions.
$b = f(a) \in f(A) \subseteq O_t(\mathbb M)$
, contradicting the assumptions.
This shows that a is infinitesimally close to 0 over N. By Fact 2.20,
![]() $\operatorname {\mathrm {tp}}(a/N)$
is the heir of
$\operatorname {\mathrm {tp}}(a/N)$
is the heir of
![]() $\operatorname {\mathrm {tp}}(a/M)$
, implying that
$\operatorname {\mathrm {tp}}(a/M)$
, implying that
![]() $\operatorname {\mathrm {tp}}(b/N) = \operatorname {\mathrm {tp}}(f(a)/N)$
is the heir of
$\operatorname {\mathrm {tp}}(b/N) = \operatorname {\mathrm {tp}}(f(a)/N)$
is the heir of
![]() $\operatorname {\mathrm {tp}}(f(a)/M) = p$
.
$\operatorname {\mathrm {tp}}(f(a)/M) = p$
.
2.4 Definable groups in pCF
By a definable group over M, we mean a definable set with a definable group operation. By [Reference Pillay18], any group G definable in M admits a unique definable manifold structure making the group operations be continuous.
Remark 2.26. In particular, there is a canonical notion of “definable compactness” for abstract definable groups and their definable subsets. As in Remarks 2.3 and 2.11, one can show that these notions are definable in families and invariant in elementary extensions.
Definition 2.27. A good neighborhood basis is a definable neighborhood basis of the form
![]() $\{O_t : t \in \Gamma _M\}$
which is also a
$\{O_t : t \in \Gamma _M\}$
which is also a
![]() $\Gamma $
-exhaustion, and such that
$\Gamma $
-exhaustion, and such that
![]() $O_t = O_t^{-1}$
for each
$O_t = O_t^{-1}$
for each
![]() $t \in \Gamma _M$
.
$t \in \Gamma _M$
.
Proposition 2.28. Every definable group has a good neighborhood basis.
Proof By Proposition 2.8, the group G admits a
![]() $\Gamma $
-exhaustion
$\Gamma $
-exhaustion
![]() $\{W_t : t \in \Gamma _M\}$
. Replacing
$\{W_t : t \in \Gamma _M\}$
. Replacing
![]() $\{W_t\}$
with
$\{W_t\}$
with
![]() $\{W_{t + \gamma }\}$
, we may assume that
$\{W_{t + \gamma }\}$
, we may assume that
![]() $W_0$
is non-empty. Replacing
$W_0$
is non-empty. Replacing
![]() $\{W_t\}$
with
$\{W_t\}$
with
![]() $\{a \cdot W_t\}$
, we may assume that
$\{a \cdot W_t\}$
, we may assume that
![]() $\operatorname {\mathrm {id}}_G \in W_0$
.
$\operatorname {\mathrm {id}}_G \in W_0$
.
Because G is a definable manifold, there is some definable neighborhood basis
![]() $\{N_t : t \in \Gamma _M,\ t < 0\}$
such that each
$\{N_t : t \in \Gamma _M,\ t < 0\}$
such that each
![]() $N_t$
is clopen, and
$N_t$
is clopen, and
![]() $N_t$
depends monotonically on t. Define
$N_t$
depends monotonically on t. Define
 $$ \begin{align*} B_t = \begin{cases} W_t & t \ge 0, \\ W_0 \cap N_t & t < 0. \end{cases} \end{align*} $$
$$ \begin{align*} B_t = \begin{cases} W_t & t \ge 0, \\ W_0 \cap N_t & t < 0. \end{cases} \end{align*} $$
Then
![]() $\{B_t : t \in \Gamma _M\}$
is a definable neighborhood basis and a
$\{B_t : t \in \Gamma _M\}$
is a definable neighborhood basis and a
![]() $\Gamma $
-exhaustion. Lastly, define
$\Gamma $
-exhaustion. Lastly, define
![]() $O_t = B_t \cap B_t^{-1}$
. Then
$O_t = B_t \cap B_t^{-1}$
. Then
![]() $\{O_t : t \in \Gamma _M\}$
has all the desired properties.
$\{O_t : t \in \Gamma _M\}$
has all the desired properties.
Proposition 2.29. Let
![]() $\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis of a definable group G.
$\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis of a definable group G.
-
1. For any
 $t \in \Gamma _M$
, there is
$t \in \Gamma _M$
, there is
 $t' \in \Gamma _M$
such that
$t' \in \Gamma _M$
such that
 $O_{t'} \cdot O_{t'} \subseteq O_t$
.
$O_{t'} \cdot O_{t'} \subseteq O_t$
. -
2. For any
 $t \in \Gamma _M$
, there is
$t \in \Gamma _M$
, there is
 $t'' \in \Gamma _M$
such that
$t'' \in \Gamma _M$
such that
 $O_t \cdot O_t \subseteq O_{t''}$
.
$O_t \cdot O_t \subseteq O_{t''}$
.
Proof (1) is by continuity. For (2), note that the set
![]() $O_t \cdot O_t$
is an image of the definably compact space
$O_t \cdot O_t$
is an image of the definably compact space
![]() $O_t \times O_t$
under the definable continuous map
$O_t \times O_t$
under the definable continuous map
![]() $(x,y) \mapsto x \cdot y$
. Therefore
$(x,y) \mapsto x \cdot y$
. Therefore
![]() $O_t \cdot O_t$
is definably compact. Then
$O_t \cdot O_t$
is definably compact. Then
![]() $t''$
exists by Proposition 2.10.
$t''$
exists by Proposition 2.10.
Lemma 2.30. Let
![]() $\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis of a definable group G. For every
$\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis of a definable group G. For every
![]() $t, \epsilon \in \Gamma _M$
, there is
$t, \epsilon \in \Gamma _M$
, there is
![]() $\delta \in \Gamma _M$
such that if
$\delta \in \Gamma _M$
such that if
![]() $a \in O_\delta $
and
$a \in O_\delta $
and
![]() $b \in O_t$
, then
$b \in O_t$
, then
![]() ${b^{-1} a b \in O_\epsilon }$
.
${b^{-1} a b \in O_\epsilon }$
.
Proof Define
![]() $S_\delta = \{(a,b) \in O_\delta \times O_t : b^{-1} a b \notin O_\epsilon \}$
. Suppose for the sake of contradiction that
$S_\delta = \{(a,b) \in O_\delta \times O_t : b^{-1} a b \notin O_\epsilon \}$
. Suppose for the sake of contradiction that
![]() $S_\delta \ne \emptyset $
for all
$S_\delta \ne \emptyset $
for all
![]() $\delta $
. The family
$\delta $
. The family
![]() $S_\delta $
is definable, and depends monotonically on
$S_\delta $
is definable, and depends monotonically on
![]() $\delta $
. Each set
$\delta $
. Each set
![]() $S_\delta $
is closed, because
$S_\delta $
is closed, because
![]() $O_\epsilon , O_\delta $
, and
$O_\epsilon , O_\delta $
, and
![]() $O_t$
are clopen. By definable compactness of
$O_t$
are clopen. By definable compactness of
![]() $O_{\delta } \times O_t$
, the intersection
$O_{\delta } \times O_t$
, the intersection
![]() $\bigcap _\delta S_\delta $
is non-empty. Therefore there are
$\bigcap _\delta S_\delta $
is non-empty. Therefore there are
![]() $a, b \in G$
such that
$a, b \in G$
such that
-
1.
 $a \in O_\delta $
for all
$a \in O_\delta $
for all
 $\delta $
.
$\delta $
. -
2.
 $b \in O_t$
.
$b \in O_t$
. -
3.
 $b^{-1} a b \notin O_\epsilon $
.
$b^{-1} a b \notin O_\epsilon $
.
The first point implies
![]() $a = \operatorname {\mathrm {id}}_G$
, which then implies
$a = \operatorname {\mathrm {id}}_G$
, which then implies
![]() $b^{-1} a b = \operatorname {\mathrm {id}}_G \in O_\epsilon $
, a contradiction.
$b^{-1} a b = \operatorname {\mathrm {id}}_G \in O_\epsilon $
, a contradiction.
3 Review of dp-rank
In Section 4 we will make extensive use of dp-rank, so we review its basic properties here.
Definition 3.1. Let
![]() $\kappa $
be a cardinal and
$\kappa $
be a cardinal and
![]() $\Sigma (x)$
be a partial type. An ict-pattern of depth
$\Sigma (x)$
be a partial type. An ict-pattern of depth
![]() $\kappa $
in
$\kappa $
in
![]() $\Sigma (x)$
consists of
$\Sigma (x)$
consists of
-
• a family of formulas
 $\{\phi _\alpha (x,y_\alpha )\}_{\alpha < \kappa }$
,
$\{\phi _\alpha (x,y_\alpha )\}_{\alpha < \kappa }$
, -
• an array of parameters
 $\{b_{\alpha ,i}\}_{\alpha < \kappa ,~i < \omega }$
with
$\{b_{\alpha ,i}\}_{\alpha < \kappa ,~i < \omega }$
with
 $|b_{\alpha ,i}| = |y_\alpha |$
,
$|b_{\alpha ,i}| = |y_\alpha |$
,
such that for any function
![]() $\eta : \kappa \to \omega $
, the following type is consistent:
$\eta : \kappa \to \omega $
, the following type is consistent:
Definition 3.2. The dp-rank of a partial type
![]() $\Sigma (x)$
is the supremum of cardinals
$\Sigma (x)$
is the supremum of cardinals
![]() $\kappa $
such that, in some elementary extension
$\kappa $
such that, in some elementary extension
![]() $N \succeq M$
, there is an ict-pattern of depth
$N \succeq M$
, there is an ict-pattern of depth
![]() $\kappa $
in
$\kappa $
in
![]() $\Sigma (x)$
. When there is no supremum, the dp-rank is defined to be
$\Sigma (x)$
. When there is no supremum, the dp-rank is defined to be
![]() $\infty $
, a formal symbol greater than all cardinals.
$\infty $
, a formal symbol greater than all cardinals.
We write the dp-rank of
![]() $\Sigma (x)$
as
$\Sigma (x)$
as
![]() $\operatorname {\mathrm {dp-rk}}(\Sigma )$
. When
$\operatorname {\mathrm {dp-rk}}(\Sigma )$
. When
![]() $\Sigma (x)$
is a complete type
$\Sigma (x)$
is a complete type
![]() $\operatorname {\mathrm {tp}}(b/A)$
, we write the dp-rank as
$\operatorname {\mathrm {tp}}(b/A)$
, we write the dp-rank as
![]() $\operatorname {\mathrm {dp-rk}}(b/A)$
.
$\operatorname {\mathrm {dp-rk}}(b/A)$
.
The following facts can be found in [Reference Kaplan, Onshuus and Usvyatsov10], or alternatively [Reference Simon22, Chapter 4].
Fact 3.3. The following are equivalent in a structure
![]() $M{\kern-3pt}:$
$M{\kern-3pt}:$
-
1. M is NIP.
-
2.
 $\operatorname {\mathrm {dp-rk}}(x=x) < \infty $
.
$\operatorname {\mathrm {dp-rk}}(x=x) < \infty $
. -
3. Every partial type has dp-rank
 $< \infty $
.
$< \infty $
.
Fact 3.4. If
![]() $\Sigma (x)$
is a partial type over A, and if the ambient model M is
$\Sigma (x)$
is a partial type over A, and if the ambient model M is
![]() $|A|^+$
-saturated, then
$|A|^+$
-saturated, then
![]() $\operatorname {\mathrm {dp-rk}}(\Sigma )$
is the supremum of
$\operatorname {\mathrm {dp-rk}}(\Sigma )$
is the supremum of
![]() $\operatorname {\mathrm {dp-rk}}(b/A)$
as b ranges over realizations of
$\operatorname {\mathrm {dp-rk}}(b/A)$
as b ranges over realizations of
![]() $\Sigma (x)$
.
$\Sigma (x)$
.
Fact 3.5. If
![]() $b \in \operatorname {\mathrm {acl}}(A)$
, then
$b \in \operatorname {\mathrm {acl}}(A)$
, then
![]() $\operatorname {\mathrm {dp-rk}}(b/A) = 0$
. If
$\operatorname {\mathrm {dp-rk}}(b/A) = 0$
. If
![]() $b \notin \operatorname {\mathrm {acl}}(A)$
, then
$b \notin \operatorname {\mathrm {acl}}(A)$
, then
![]() $\operatorname {\mathrm {dp-rk}}(b/A)> 0$
.
$\operatorname {\mathrm {dp-rk}}(b/A)> 0$
.
Fact 3.6. For any
![]() $b, c, A$
, we have
$b, c, A$
, we have
It is also helpful to view dp-rank as a property of definable sets:
Definition 3.7. If D is a definable set, then the dp-rank of D, written
![]() $\operatorname {\mathrm {dp-rk}}(D)$
, is
$\operatorname {\mathrm {dp-rk}}(D)$
, is
![]() $\operatorname {\mathrm {dp-rk}}(\phi (x))$
for any formula
$\operatorname {\mathrm {dp-rk}}(\phi (x))$
for any formula
![]() $\phi (x)$
defining D.
$\phi (x)$
defining D.
The following facts are easy exercises using Facts 3.3–3.6.
Fact 3.8.
![]() $\operatorname {\mathrm {dp-rk}}(D)> 0$
if and only if D is infinite.
$\operatorname {\mathrm {dp-rk}}(D)> 0$
if and only if D is infinite.
Fact 3.9. If
![]() $D_1, D_2$
are definable sets, then
$D_1, D_2$
are definable sets, then
![]() $\operatorname {\mathrm {dp-rk}}(D_1 \times D_2) = \operatorname {\mathrm {dp-rk}}(D_1) + \operatorname {\mathrm {dp-rk}}(D_2)$
.
$\operatorname {\mathrm {dp-rk}}(D_1 \times D_2) = \operatorname {\mathrm {dp-rk}}(D_1) + \operatorname {\mathrm {dp-rk}}(D_2)$
.
Fact 3.10. If
![]() $f : D_1 \to D_2$
is a definable injection, then
$f : D_1 \to D_2$
is a definable injection, then
![]() $\operatorname {\mathrm {dp-rk}}(D_1) \le \operatorname {\mathrm {dp-rk}}(D_2)$
. If
$\operatorname {\mathrm {dp-rk}}(D_1) \le \operatorname {\mathrm {dp-rk}}(D_2)$
. If
![]() $f : D_1 \to D_2$
is a definable surjection, then
$f : D_1 \to D_2$
is a definable surjection, then
![]() $\operatorname {\mathrm {dp-rk}}(D_1) \ge \operatorname {\mathrm {dp-rk}}(D_2)$
.
$\operatorname {\mathrm {dp-rk}}(D_1) \ge \operatorname {\mathrm {dp-rk}}(D_2)$
.
We will need the following about dp-rank in p-adically closed fields:
Fact 3.11 ([Reference van den Dries2, Theorem 6.6])
If M is a p-adically closed field, then
![]() $\operatorname {\mathrm {dp-rk}}(M) = 1$
.
$\operatorname {\mathrm {dp-rk}}(M) = 1$
.
Corollary 3.12. If M is a p-adically closed field, then every n-type in M has dp-rank at most n.
In fact, dp-rank in pCF agrees with the natural notion of dimension (topological dimension or
![]() $\operatorname {\mathrm {acl}}$
-dimension), by [Reference Simon22, Exercise 4.38]. We will not need this fact, however.
$\operatorname {\mathrm {acl}}$
-dimension), by [Reference Simon22, Exercise 4.38]. We will not need this fact, however.
4 Large gaps
In order to apply the strategy of Peterzil and Steinhorn, we need a technical statement about “gaps” in unbounded curves:
Conjecture 4.1. Let G be a definable group over a p-adically closed field M, with a good neighborhood basis
![]() $\{O_t \mid t \in \Gamma _M\}$
. Let I be a one-dimensional unbounded definable subset of G. Then for every
$\{O_t \mid t \in \Gamma _M\}$
. Let I be a one-dimensional unbounded definable subset of G. Then for every
![]() $t_0 \in \Gamma _M$
, there is
$t_0 \in \Gamma _M$
, there is
![]() $t \in \Gamma _M$
such that
$t \in \Gamma _M$
such that
is bounded.
The o-minimal analogue of Conjecture 4.1 holds by an easy connectedness argument [Reference Peterzil and Steinhorn16, Lemma 3.8]. But in a p-adically closed field, everything is totally disconnected and we need a completely different approach. In the end, we will prove Conjecture 4.1 only in a special case (Proposition 4.14), namely when G is nearly abelian (Definition 1.1).
Remark 4.2. It is useful to consider what a counterexample to Conjecture 4.1 would look like. For each
![]() $t \gg t_0$
, there would be unboundedly many
$t \gg t_0$
, there would be unboundedly many
![]() $g \in I$
such that
$g \in I$
such that
or equivalently
![]() $g O_t \cap I = g O_{t_0} \cap I$
. Around g, the set I looks like an “island”
$g O_t \cap I = g O_{t_0} \cap I$
. Around g, the set I looks like an “island”
![]() $g O_{t_0} \cap I$
surrounded by a very large empty space
$g O_{t_0} \cap I$
surrounded by a very large empty space
![]() $g (O_t {\setminus} O_{t_0})$
. Since I is unbounded, there must be infinitely many of these “islands.” Because this holds for any t, the gaps between the islands must become greater and greater as we move towards “
$g (O_t {\setminus} O_{t_0})$
. Since I is unbounded, there must be infinitely many of these “islands.” Because this holds for any t, the gaps between the islands must become greater and greater as we move towards “
![]() $\infty $
.”
$\infty $
.”
The behavior described above is reminiscent of the behavior of the set
![]() $2^{\mathbb {Z}}$
in the group
$2^{\mathbb {Z}}$
in the group
![]() $(\mathbb R,+,<)$
. The structure
$(\mathbb R,+,<)$
. The structure
![]() $(\mathbb R,+,<,2^{\mathbb {Z}})$
is NIP [Reference Günaydin and Hieronymi5, Theorem 6.5] but it does not have finite dp-rank, and this is a direct consequence of the “large gaps” in
$(\mathbb R,+,<,2^{\mathbb {Z}})$
is NIP [Reference Günaydin and Hieronymi5, Theorem 6.5] but it does not have finite dp-rank, and this is a direct consequence of the “large gaps” in
![]() $2^{\mathbb {Z}}$
. In a non-standard elementary extension, by choosing
$2^{\mathbb {Z}}$
. In a non-standard elementary extension, by choosing
![]() $a_1 < b_1 < a_2 < b_2 < \cdots < a_n < b_n$
carefully, one can ensure that the map
$a_1 < b_1 < a_2 < b_2 < \cdots < a_n < b_n$
carefully, one can ensure that the map
 $$ \begin{align*} \prod_{i = 1}^n (2^{\mathbb{Z}} \cap [a_i, b_i]) \to \mathbb R \\ (x_1,\ldots,x_n) \mapsto \sum_{i = 1}^n x_i \end{align*} $$
$$ \begin{align*} \prod_{i = 1}^n (2^{\mathbb{Z}} \cap [a_i, b_i]) \to \mathbb R \\ (x_1,\ldots,x_n) \mapsto \sum_{i = 1}^n x_i \end{align*} $$
is injective and each set
![]() $2^{\mathbb {Z}} \cap [a_i,b_i]$
is infinite, showing that the model has dp-rank at least n (for arbitrary finite n).
$2^{\mathbb {Z}} \cap [a_i,b_i]$
is infinite, showing that the model has dp-rank at least n (for arbitrary finite n).
Our approach for attacking Conjecture 4.1 is based on this line of argument: take a set I with large gaps and obtain infinite dp-rank. Unfortunately, the argument only works in the nearly abelian case (Proposition 4.14), though we can salvage a much weaker statement in the non-abelian case (Proposition 4.15).
4.1 Notation
Let G be a group. If H is a subgroup of G, we let
![]() $G/H$
denote the set of left cosets of H. If
$G/H$
denote the set of left cosets of H. If
![]() $A \subseteq G$
, we will write
$A \subseteq G$
, we will write
![]() $A/H$
to indicate the image of A in
$A/H$
to indicate the image of A in
![]() $G/H$
. If
$G/H$
. If
![]() $A, B \subseteq G$
, we let
$A, B \subseteq G$
, we let
![]() $A^B$
indicate
$A^B$
indicate
![]() $\{b^{-1}ab : a \in A, ~ b \in B\}$
. Notation like “
$\{b^{-1}ab : a \in A, ~ b \in B\}$
. Notation like “
![]() $X {\setminus} Y$
” will always mean set subtraction, rather than quotienting by a group action on the left.
$X {\setminus} Y$
” will always mean set subtraction, rather than quotienting by a group action on the left.
Definition 4.3. Let
![]() $X, Y$
be subsets of a group G. Define
$X, Y$
be subsets of a group G. Define
Note that
![]() $X \diamond Y$
depends negatively on Y. We will write “
$X \diamond Y$
depends negatively on Y. We will write “
![]() $A \diamond B {\setminus} C$
” to mean “
$A \diamond B {\setminus} C$
” to mean “
![]() $A \diamond (B {\setminus} C)$
.”
$A \diamond (B {\setminus} C)$
.”
Remark 4.4. Suppose
![]() $X, Y$
are subgroups of G,
$X, Y$
are subgroups of G,
![]() $S\subseteq G$
, and
$S\subseteq G$
, and
![]() $a, b \in S \diamond X {\setminus} Y$
. Then
$a, b \in S \diamond X {\setminus} Y$
. Then
Otherwise,
![]() $b = a \delta $
for some
$b = a \delta $
for some
![]() $\delta \in X {\setminus} Y$
, and so
$\delta \in X {\setminus} Y$
, and so
![]() $b \in a (X {\setminus} Y) \cap S$
, contradicting the fact that
$b \in a (X {\setminus} Y) \cap S$
, contradicting the fact that
![]() $a (X {\setminus} Y) \cap S = \emptyset $
.
$a (X {\setminus} Y) \cap S = \emptyset $
.
4.2 The bad gap configuration
Recall that an externally definable set X in a structure M is a set of the form
![]() $Y \cap M^n$
for some elementary extension
$Y \cap M^n$
for some elementary extension
![]() $N \succ M$
and definable set
$N \succ M$
and definable set
![]() $Y \subseteq N^n$
. The Shelah expansion
$Y \subseteq N^n$
. The Shelah expansion
![]() $M^{Sh}$
is the expansion of M by all externally definable sets. When M is NIP, the Shelah expansion
$M^{Sh}$
is the expansion of M by all externally definable sets. When M is NIP, the Shelah expansion
![]() $M^{Sh}$
has elimination of quantifiers [Reference Simon22, Proposition 3.23]. Using this, it is easy to see that
$M^{Sh}$
has elimination of quantifiers [Reference Simon22, Proposition 3.23]. Using this, it is easy to see that
![]() $M^{Sh}$
has the same dp-rank as M.
$M^{Sh}$
has the same dp-rank as M.
Remark 4.5. Let
![]() $\mathcal {F}$
be a collection of definable subsets of
$\mathcal {F}$
be a collection of definable subsets of
![]() $M^n$
. If the sets in
$M^n$
. If the sets in
![]() $\mathcal {F}$
are uniformly definable, and
$\mathcal {F}$
are uniformly definable, and
![]() $\mathcal {F}$
is linearly ordered by inclusion, then the sets
$\mathcal {F}$
is linearly ordered by inclusion, then the sets
![]() $\bigcup \mathcal {F}$
and
$\bigcup \mathcal {F}$
and
![]() $\bigcap \mathcal {F}$
are externally definable [Reference Halevi, Hasson and Jahnke6, Kaplan’s Lemma 3.4].
$\bigcap \mathcal {F}$
are externally definable [Reference Halevi, Hasson and Jahnke6, Kaplan’s Lemma 3.4].
Later, we will use Remark 4.5 in conjunction with Proposition 2.29 to construct externally definable subgroups of definable groups.
Definition 4.6. Let G be a definable group in a structure M. A bad gap configuration in G consists of the following:
-
• a finite subgroup
 $F \subseteq G$
,
$F \subseteq G$
, -
• externally definable subgroups,
 $$ \begin{align*} \cdots \subseteq Y_2 \subseteq Y_1 \subseteq Y_0 \subseteq X_0 \subseteq X_1 \subseteq \cdots \subseteq G, \end{align*} $$
$$ \begin{align*} \cdots \subseteq Y_2 \subseteq Y_1 \subseteq Y_0 \subseteq X_0 \subseteq X_1 \subseteq \cdots \subseteq G, \end{align*} $$
-
• an externally definable subset
 $I \subseteq G$
,
$I \subseteq G$
,
such that the following conditions hold:
-
•
 $Y_i^F \subseteq Y_i$
, for all i.
$Y_i^F \subseteq Y_i$
, for all i. -
•
 $Y_i^{X_i} \subseteq Y_{i-1}$
, for
$Y_i^{X_i} \subseteq Y_{i-1}$
, for
 $i> 0$
.
$i> 0$
. -
•
 $(X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1}))/X_{i-1}$
is infinite, for
$(X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1}))/X_{i-1}$
is infinite, for
 $i> 0$
.
$i> 0$
.
We say that a bad gap configuration is
![]() $($
A-
$($
A-
![]() $)$
definable if all of F, the
$)$
definable if all of F, the
![]() $X_i$
,
$X_i$
,
![]() $Y_i$
, and I are (A-)definable.
$Y_i$
, and I are (A-)definable.
Lemma 4.7. If G has finite dp-rank, then there is no bad gap configuration in G.
Proof Let
![]() $(F,\{Y_i\},\{X_i\},I)$
be a bad gap configuration. Replacing M with the Shelah expansion
$(F,\{Y_i\},\{X_i\},I)$
be a bad gap configuration. Replacing M with the Shelah expansion
![]() $M^{Sh}$
, we may assume that the bad gap configuration is definable. Passing to an elementary extension and naming parameters, we may assume that M is
$M^{Sh}$
, we may assume that the bad gap configuration is definable. Passing to an elementary extension and naming parameters, we may assume that M is
![]() $\aleph _1$
-saturated and the bad gap configuration is
$\aleph _1$
-saturated and the bad gap configuration is
![]() $\emptyset $
-definable.
$\emptyset $
-definable.
Note that
![]() $FY_i = Y_iF$
is a subgroup of G, and that the index of
$FY_i = Y_iF$
is a subgroup of G, and that the index of
![]() $Y_i$
if
$Y_i$
if
![]() $FY_i$
is finite, no more than
$FY_i$
is finite, no more than
![]() $|F|$
. Let
$|F|$
. Let
![]() $D_i$
be the definable set
$D_i$
be the definable set
![]() $X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1})$
. By assumption,
$X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1})$
. By assumption,
![]() $D_i/X_{i-1}$
is infinite.
$D_i/X_{i-1}$
is infinite.
Claim 1. Suppose
![]() $a_i, a^{\prime }_i \in D_i$
for
$a_i, a^{\prime }_i \in D_i$
for
![]() $i = 1, \ldots , n$
, and suppose
$i = 1, \ldots , n$
, and suppose
Then
![]() $a_n F Y_{n-1} = a^{\prime }_n F Y_{n-1}$
. If moreover
$a_n F Y_{n-1} = a^{\prime }_n F Y_{n-1}$
. If moreover
![]() $a_n Y_{n-1} = a^{\prime }_n Y_{n-1}$
, then
$a_n Y_{n-1} = a^{\prime }_n Y_{n-1}$
, then
Proof Note that
![]() $a_i, a_i' \in X_i$
. Equation (1) implies that
$a_i, a_i' \in X_i$
. Equation (1) implies that
for some
![]() $\epsilon \in Y_n$
. Then
$\epsilon \in Y_n$
. Then
![]() $\epsilon ^{a_n} \in Y_n^{X_n} \subseteq Y_{n-1} \subseteq X_{n-1}$
. For
$\epsilon ^{a_n} \in Y_n^{X_n} \subseteq Y_{n-1} \subseteq X_{n-1}$
. For
![]() $i < n$
, we have
$i < n$
, we have
![]() $a_i, a^{\prime }_i \in X_i \subseteq X_{n-1}$
. Therefore (3) implies that
$a_i, a^{\prime }_i \in X_i \subseteq X_{n-1}$
. Therefore (3) implies that
![]() $a^{\prime }_n X_{n-1} = a_n X_{n-1}$
. Both
$a^{\prime }_n X_{n-1} = a_n X_{n-1}$
. Both
![]() $a^{\prime }_n$
and
$a^{\prime }_n$
and
![]() $a_n$
are in
$a_n$
are in
![]() $I \diamond X_{n-1} {\setminus} F Y_{n-1}$
, so by Remark 4.4 we have
$I \diamond X_{n-1} {\setminus} F Y_{n-1}$
, so by Remark 4.4 we have
![]() $a^{\prime }_n F Y_{n-1} = a_n F Y_{n-1}$
as desired. Now suppose that
$a^{\prime }_n F Y_{n-1} = a_n F Y_{n-1}$
as desired. Now suppose that
![]() $a_n Y_{n-1} = a^{\prime }_n Y_{n-1}$
. Then
$a_n Y_{n-1} = a^{\prime }_n Y_{n-1}$
. Then
![]() $a^{\prime }_n = a_n \delta $
for some
$a^{\prime }_n = a_n \delta $
for some
![]() $\delta \in Y_{n-1}$
. Then Equation (3) implies
$\delta \in Y_{n-1}$
. Then Equation (3) implies
 $$ \begin{align*} a_n \epsilon^{a_n} a_{n-1} \cdots a_1 &= a_n \delta a^{\prime}_{n-1} a^{\prime}_{n-2} \cdots a^{\prime}_1, \\ \epsilon^{a_n} a_{n-1} \cdots a_1 &= \delta a^{\prime}_{n-1} a^{\prime}_{n-2} \cdots a^{\prime}_1. \end{align*} $$
$$ \begin{align*} a_n \epsilon^{a_n} a_{n-1} \cdots a_1 &= a_n \delta a^{\prime}_{n-1} a^{\prime}_{n-2} \cdots a^{\prime}_1, \\ \epsilon^{a_n} a_{n-1} \cdots a_1 &= \delta a^{\prime}_{n-1} a^{\prime}_{n-2} \cdots a^{\prime}_1. \end{align*} $$
Both
![]() $\epsilon ^{a_n}$
and
$\epsilon ^{a_n}$
and
![]() $\delta $
are in
$\delta $
are in
![]() $Y_{n-1}$
, so Equation (2) holds.
$Y_{n-1}$
, so Equation (2) holds.
For any
![]() $n \in \mathbb N$
, we claim that
$n \in \mathbb N$
, we claim that
![]() $\operatorname {\mathrm {dp-rk}}(G) \ge n$
. By assumption, the interpretable set
$\operatorname {\mathrm {dp-rk}}(G) \ge n$
. By assumption, the interpretable set
![]() $D_i/X_{i-1}$
is infinite. The interpretable set
$D_i/X_{i-1}$
is infinite. The interpretable set
![]() $D_i/Y_{i-1}$
is even bigger, because
$D_i/Y_{i-1}$
is even bigger, because
![]() $Y_{i-1} \subseteq X_{i-1}$
. By the properties of dp-rank in Section 3,
$Y_{i-1} \subseteq X_{i-1}$
. By the properties of dp-rank in Section 3,
![]() $\prod _{i = 1}^n D_i/Y_{i-1}$
has dp-rank at least n. Take a tuple
$\prod _{i = 1}^n D_i/Y_{i-1}$
has dp-rank at least n. Take a tuple
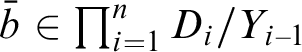 $\bar {b} \in \prod _{i = 1}^n D_i/Y_{i-1}$
such that
$\bar {b} \in \prod _{i = 1}^n D_i/Y_{i-1}$
such that
![]() $\operatorname {\mathrm {dp-rk}}(\bar {b}/\emptyset ) \ge n$
. Each
$\operatorname {\mathrm {dp-rk}}(\bar {b}/\emptyset ) \ge n$
. Each
![]() $b_i$
is a coset
$b_i$
is a coset
![]() $a_iY_{i-1}$
for some
$a_iY_{i-1}$
for some
![]() $a_i \in D_i$
. Let
$a_i \in D_i$
. Let
![]() $c = a_na_{n-1} \cdots a_1 \in G$
.
$c = a_na_{n-1} \cdots a_1 \in G$
.
Claim 2. For each i, we have
![]() $b_i \in \operatorname {\mathrm {acl}}(c, b_{i+1}, \ldots , b_n)$
.
$b_i \in \operatorname {\mathrm {acl}}(c, b_{i+1}, \ldots , b_n)$
.
Proof Let S be the set of
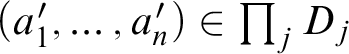 $(a^{\prime }_1,\ldots ,a^{\prime }_n) \in \prod _j D_j$
such that
$(a^{\prime }_1,\ldots ,a^{\prime }_n) \in \prod _j D_j$
such that
-
•
 $a^{\prime }_n a^{\prime }_{n-1} \cdots a^{\prime }_1 = c$
.
$a^{\prime }_n a^{\prime }_{n-1} \cdots a^{\prime }_1 = c$
. -
•
 $a^{\prime }_j Y_{j-1} = b_j = a_j Y_{j-1}$
, for
$a^{\prime }_j Y_{j-1} = b_j = a_j Y_{j-1}$
, for
 $j> i$
.
$j> i$
.
Then
![]() $(a_1,\ldots ,a_n) \in S$
and S is definable over
$(a_1,\ldots ,a_n) \in S$
and S is definable over
![]() $c, b_{i+1}, \ldots , b_n$
. If
$c, b_{i+1}, \ldots , b_n$
. If
![]() $(a^{\prime }_1,\ldots ,a^{\prime }_n) \in S$
, then
$(a^{\prime }_1,\ldots ,a^{\prime }_n) \in S$
, then
By Claim 1 applied
![]() $(n-i+1)$
times, we see that
$(n-i+1)$
times, we see that
![]() $a_i F Y_{i-1} = a^{\prime }_i F Y_{i-1}$
. We have shown
$a_i F Y_{i-1} = a^{\prime }_i F Y_{i-1}$
. We have shown
It follows that
![]() $a_i F Y_{i-1}$
is definable over
$a_i F Y_{i-1}$
is definable over
![]() $c, b_{i+1}, \ldots , b_n$
. The fibers of the map
$c, b_{i+1}, \ldots , b_n$
. The fibers of the map
![]() $G/Y_{i-1} \to G/(FY_{i-1})$
are finite, and so
$G/Y_{i-1} \to G/(FY_{i-1})$
are finite, and so
![]() $a_i Y_{i-1} = b_i$
is algebraic over
$a_i Y_{i-1} = b_i$
is algebraic over
![]() $c, b_{i+1}, \ldots , b_n$
.
$c, b_{i+1}, \ldots , b_n$
.
By Claim 2 and induction,
![]() $\bar {b} \in \operatorname {\mathrm {acl}}(c)$
. Therefore
$\bar {b} \in \operatorname {\mathrm {acl}}(c)$
. Therefore
 $$ \begin{align*}n \le \operatorname{\mathrm{dp-rk}}(\bar{b}/\emptyset) \le \operatorname{\mathrm{dp-rk}}(c/\emptyset) \le \operatorname{\mathrm{dp-rk}}(G).\end{align*} $$
$$ \begin{align*}n \le \operatorname{\mathrm{dp-rk}}(\bar{b}/\emptyset) \le \operatorname{\mathrm{dp-rk}}(c/\emptyset) \le \operatorname{\mathrm{dp-rk}}(G).\end{align*} $$
As n was arbitrary, G has infinite dp-rank, a contradiction.
4.3 The saturated case
Until Section 4.4, we will work in a monster model
![]() $\mathbb M \models p\mathrm {CF}$
. Fix a definable group G, not definably compact, and fix a good neighborhood basis
$\mathbb M \models p\mathrm {CF}$
. Fix a definable group G, not definably compact, and fix a good neighborhood basis
![]() $\{O_t : t \in \Gamma _{\mathbb M}\}$
in the sense of Definition 2.27.
$\{O_t : t \in \Gamma _{\mathbb M}\}$
in the sense of Definition 2.27.
Lemma 4.8. There is no bad gap configuration in G.
Proof For definable sets in pCF, dp-rank agrees with dimension. In particular, dp-rank is finite. Therefore Lemma 4.7 applies to G.
Recall from Definition 2.9 and Proposition 2.10(1) that a subset
![]() $S \subseteq G(\mathbb M)$
is bounded if
$S \subseteq G(\mathbb M)$
is bounded if
![]() $S \subseteq O_t$
for some
$S \subseteq O_t$
for some
![]() $t \in \Gamma _{\mathbb M}$
.
$t \in \Gamma _{\mathbb M}$
.
Lemma 4.9. If
![]() $S \subseteq G(\mathbb M)$
is bounded, then
$S \subseteq G(\mathbb M)$
is bounded, then
![]() $S \subseteq X$
for some bounded externally definable subgroup
$S \subseteq X$
for some bounded externally definable subgroup
![]() $X \subseteq G(\mathbb M)$
.
$X \subseteq G(\mathbb M)$
.
Proof Take
![]() $t_0 \in \Gamma _{\mathbb M}$
such that
$t_0 \in \Gamma _{\mathbb M}$
such that
![]() $S \subseteq O_{t_0}$
. By Proposition 2.29, we can build an ascending sequence
$S \subseteq O_{t_0}$
. By Proposition 2.29, we can build an ascending sequence
in
![]() $\Gamma _{\mathbb M}$
such that
$\Gamma _{\mathbb M}$
such that
![]() $O_{t_i} \cdot O_{t_i} \subseteq O_{t_{i+1}}$
for each i. By saturation, we can also find some
$O_{t_i} \cdot O_{t_i} \subseteq O_{t_{i+1}}$
for each i. By saturation, we can also find some
![]() $t_\omega> t_i$
for all finite i. Set
$t_\omega> t_i$
for all finite i. Set
![]() $X = \bigcup _{i < \omega } O_{t_i}$
. The set X is externally definable (Remark 4.5). The set X is bounded, because
$X = \bigcup _{i < \omega } O_{t_i}$
. The set X is externally definable (Remark 4.5). The set X is bounded, because
![]() $X \subseteq O_{t_\omega }$
. We have
$X \subseteq O_{t_\omega }$
. We have
![]() $X = X^{-1}$
because
$X = X^{-1}$
because
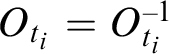 $O_{t_i} = O_{t_i}^{-1}$
for each i. Lastly, X is closed under the group operation by choice of the
$O_{t_i} = O_{t_i}^{-1}$
for each i. Lastly, X is closed under the group operation by choice of the
![]() $t_i$
’s.
$t_i$
’s.
Lemma 4.10. Let I be an unbounded subset of G. Let
![]() $X \subseteq G(\mathbb M)$
be a bounded subgroup. Then there is an externally definable bounded subgroup
$X \subseteq G(\mathbb M)$
be a bounded subgroup. Then there is an externally definable bounded subgroup
![]() $X' \supseteq X$
such that
$X' \supseteq X$
such that
![]() $(X' \cap I)/X$
is infinite.
$(X' \cap I)/X$
is infinite.
Proof We claim that
![]() $I/X$
is infinite. Otherwise, I is contained in a finite union of cosets:
$I/X$
is infinite. Otherwise, I is contained in a finite union of cosets:
![]() $I \subseteq \bigcup _{i = 1}^n a_i X$
. Take
$I \subseteq \bigcup _{i = 1}^n a_i X$
. Take
![]() $t \in \Gamma _M$
such that
$t \in \Gamma _M$
such that
![]() $X \subseteq O_t$
. Then I is a subset of the definably compact set
$X \subseteq O_t$
. Then I is a subset of the definably compact set
![]() $\bigcup _{i = 1}^n a_i O_t$
, so I is bounded, a contradiction.
$\bigcup _{i = 1}^n a_i O_t$
, so I is bounded, a contradiction.
Now take
![]() $a_1, a_2, a_3, \ldots \in I$
such that the cosets
$a_1, a_2, a_3, \ldots \in I$
such that the cosets
![]() $a_iX$
are pairwise distinct. By saturation, there is some
$a_iX$
are pairwise distinct. By saturation, there is some
![]() $t \in \Gamma $
such that
$t \in \Gamma $
such that
![]() $\{a_1,a_2,\ldots \} \subseteq O_t$
. Then
$\{a_1,a_2,\ldots \} \subseteq O_t$
. Then
![]() $\{a_1,a_2,\ldots \}$
and X are bounded. By Lemma 4.9, there is an externally definable bounded subgroup
$\{a_1,a_2,\ldots \}$
and X are bounded. By Lemma 4.9, there is an externally definable bounded subgroup
![]() $X'$
containing
$X'$
containing
![]() $\{a_1,a_2,\ldots \} \cup X$
. Then
$\{a_1,a_2,\ldots \} \cup X$
. Then
![]() $(X' \cap I)/X$
is infinite, witnessed by the
$(X' \cap I)/X$
is infinite, witnessed by the
![]() $a_iX$
.
$a_iX$
.
Recall from Definition 1.1 that G is nearly abelian if there is a definably compact definable normal subgroup
![]() $K \subseteq G$
with
$K \subseteq G$
with
![]() $G/K$
abelian. Equivalently, G is nearly abelian if there is a definably compact subgroup K containing the derived group
$G/K$
abelian. Equivalently, G is nearly abelian if there is a definably compact subgroup K containing the derived group
![]() $[G,G]$
.
$[G,G]$
.
Lemma 4.11. Suppose that G is nearly abelian. Let I be an unbounded definable subset of
![]() $G(\mathbb M)$
. For any bounded set A, there is
$G(\mathbb M)$
. For any bounded set A, there is
![]() $t \in \Gamma _{\mathbb M}$
such that
$t \in \Gamma _{\mathbb M}$
such that
![]() $I \diamond O_t {\setminus} A$
is bounded.
$I \diamond O_t {\setminus} A$
is bounded.
Proof Suppose not.
Claim. For any bounded sets
![]() $C \supseteq B \supseteq A$
, the set
$C \supseteq B \supseteq A$
, the set
![]() $I \diamond C {\setminus} B$
is unbounded.
$I \diamond C {\setminus} B$
is unbounded.
Proof Take
![]() $t \in \Gamma _{\mathbb M}$
such that
$t \in \Gamma _{\mathbb M}$
such that
![]() $C \subseteq O_t$
. Then
$C \subseteq O_t$
. Then
![]() $I \diamond C {\setminus} B$
contains the unbounded set
$I \diamond C {\setminus} B$
contains the unbounded set
![]() $I \diamond O_t {\setminus} A$
, because
$I \diamond O_t {\setminus} A$
, because
![]() $O_t {\setminus} A \supseteq C {\setminus} B$
.
$O_t {\setminus} A \supseteq C {\setminus} B$
.
Let K be the normal subgroup witnessing near-abelianity. By Lemma 4.9, there is a bounded externally definable subgroup
![]() $X_0 \supseteq A \cup K$
. By Lemma 4.10 we can recursively build an increasing chain of bounded externally definable subgroups
$X_0 \supseteq A \cup K$
. By Lemma 4.10 we can recursively build an increasing chain of bounded externally definable subgroups
such that
-
•
 $(X_1 \cap I)/X_0$
is infinite.
$(X_1 \cap I)/X_0$
is infinite. -
• For
 $n> 1$
,
$n> 1$
,
 $(X_n \cap (I \diamond X_{n-1} {\setminus} X_0))/X_{n-1}$
is infinite. This is possible because
$(X_n \cap (I \diamond X_{n-1} {\setminus} X_0))/X_{n-1}$
is infinite. This is possible because
 $I \diamond X_{n-1} {\setminus} X_0$
is unbounded by the claim.
$I \diamond X_{n-1} {\setminus} X_0$
is unbounded by the claim.
Let
![]() $Y_i = X_0$
for all i, and let
$Y_i = X_0$
for all i, and let
![]() $F = \{\operatorname {\mathrm {id}}_G\}$
. Note
$F = \{\operatorname {\mathrm {id}}_G\}$
. Note
![]() $X_0$
is normal, because it contains K which contains
$X_0$
is normal, because it contains K which contains
![]() $[G,G]$
. We have constructed a bad gap configuration in G, contradicting Lemma 4.8.
$[G,G]$
. We have constructed a bad gap configuration in G, contradicting Lemma 4.8.
Lemma 4.12. If
![]() $S \subseteq G(\mathbb M)$
is a neighborhood of
$S \subseteq G(\mathbb M)$
is a neighborhood of
![]() $\operatorname {\mathrm {id}}_G$
, then
$\operatorname {\mathrm {id}}_G$
, then
![]() $S \supseteq X$
for some externally definable open subgroup
$S \supseteq X$
for some externally definable open subgroup
![]() $X \subseteq G(\mathbb M)$
. If, in addition,
$X \subseteq G(\mathbb M)$
. If, in addition,
![]() $B \subseteq G(\mathbb M)$
is a bounded set, then we can choose the group X to ensure
$B \subseteq G(\mathbb M)$
is a bounded set, then we can choose the group X to ensure
![]() $X^B \subseteq X$
.
$X^B \subseteq X$
.
Proof Take
![]() $t_0 \in \Gamma _M$
such that
$t_0 \in \Gamma _M$
such that
![]() $S \supseteq O_{t_0}$
. By Proposition 2.29 and Lemma 2.30, there is a descending sequence
$S \supseteq O_{t_0}$
. By Proposition 2.29 and Lemma 2.30, there is a descending sequence
in
![]() $\Gamma _{\mathbb M}$
such that
$\Gamma _{\mathbb M}$
such that
![]() $O_{t_{i+1}} \cdot O_{t_{i+1}} \subseteq O_{t_i}$
and also
$O_{t_{i+1}} \cdot O_{t_{i+1}} \subseteq O_{t_i}$
and also
 $O_{t_{i+1}}^B \subseteq O_{t_i}$
. Take
$O_{t_{i+1}}^B \subseteq O_{t_i}$
. Take
![]() $X = \bigcap _{i = 1}^\infty O_{t_i}$
. Then X is an externally definable subgroup with
$X = \bigcap _{i = 1}^\infty O_{t_i}$
. Then X is an externally definable subgroup with
![]() $X^B \subseteq X$
. We can take some
$X^B \subseteq X$
. We can take some
![]() $t_\omega $
less than all the
$t_\omega $
less than all the
![]() $t_i$
’s, and then
$t_i$
’s, and then
![]() $O_{t_\omega } \subseteq X$
. Therefore X has interior, and is an open subgroup.
$O_{t_\omega } \subseteq X$
. Therefore X has interior, and is an open subgroup.
Lemma 4.13. Let I be an unbounded definable subset of
![]() $G(\mathbb M)$
. Let F be a finite subgroup of
$G(\mathbb M)$
. Let F be a finite subgroup of
![]() $G(\mathbb M)$
. Then there exist
$G(\mathbb M)$
. Then there exist
![]() $t, t' \in \Gamma _{\mathbb M}$
such that
$t, t' \in \Gamma _{\mathbb M}$
such that
![]() $I \diamond O_t {\setminus} (F \cdot O_{t'})$
is bounded.
$I \diamond O_t {\setminus} (F \cdot O_{t'})$
is bounded.
Proof Suppose not.
Claim. For any neighborhood
![]() $A \ni id_G$
and any bounded set
$A \ni id_G$
and any bounded set
![]() $B \subseteq G$
, the set
$B \subseteq G$
, the set
![]() $I \diamond B {\setminus} FA$
is unbounded.
$I \diamond B {\setminus} FA$
is unbounded.
Proof Take
![]() $t, t'$
such that
$t, t'$
such that
 $$ \begin{gather*} O_{t'} \subseteq A \text{ and } B \subseteq O_t, \\ O_t {\setminus} (F \cdot O_{t'}) \supseteq B {\setminus} (F \cdot A), \\ I \diamond O_t {\setminus} (F \cdot O_{t'}) \subseteq I \diamond B {\setminus} (F \cdot A). \\[-36pt]\end{gather*} $$
$$ \begin{gather*} O_{t'} \subseteq A \text{ and } B \subseteq O_t, \\ O_t {\setminus} (F \cdot O_{t'}) \supseteq B {\setminus} (F \cdot A), \\ I \diamond O_t {\setminus} (F \cdot O_{t'}) \subseteq I \diamond B {\setminus} (F \cdot A). \\[-36pt]\end{gather*} $$
Take any bounded open externally definable subgroup
![]() $X_0 \subseteq G$
. By Lemma 4.12 there is an externally definable open subgroup
$X_0 \subseteq G$
. By Lemma 4.12 there is an externally definable open subgroup
![]() $Y_0 \subseteq X_0$
such that
$Y_0 \subseteq X_0$
such that
![]() $Y_0^F \subseteq Y_0$
. Recursively build chains
$Y_0^F \subseteq Y_0$
. Recursively build chains
 $$ \begin{align*} X_0 \subseteq X_1 \subseteq \cdots, \\ Y_0 \supseteq Y_1 \supseteq \cdots, \end{align*} $$
$$ \begin{align*} X_0 \subseteq X_1 \subseteq \cdots, \\ Y_0 \supseteq Y_1 \supseteq \cdots, \end{align*} $$
where
-
•
 $X_i$
is a bounded externally definable subgroup, chosen large enough to ensure that
$X_i$
is a bounded externally definable subgroup, chosen large enough to ensure that
 $(X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1}))/X_{i-1}$
is infinite (Lemma 4.10).
$(X_i \cap (I \diamond X_{i-1} {\setminus} F Y_{i-1}))/X_{i-1}$
is infinite (Lemma 4.10). -
•
 $Y_i$
is an open externally definable subgroup with
$Y_i$
is an open externally definable subgroup with
 $Y_i^F = Y_i$
, chosen small enough that
$Y_i^F = Y_i$
, chosen small enough that
 $Y_i^{X_i} \subseteq Y_{i-1}$
(Lemma 4.12).
$Y_i^{X_i} \subseteq Y_{i-1}$
(Lemma 4.12).
This gives a bad gap configuration in G, contradicting Lemma 4.8.
4.4 The general case
Proposition 4.14. Let M be any model of pCF. Let G be a definable non-compact group and
![]() $\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis. Suppose that G is nearly abelian. Let I be an unbounded definable set. Then for any
$\{O_t : t \in \Gamma _M\}$
be a good neighborhood basis. Suppose that G is nearly abelian. Let I be an unbounded definable set. Then for any
![]() $t \in \Gamma _M$
, there is
$t \in \Gamma _M$
, there is
![]() $t' \in \Gamma _M$
such that
$t' \in \Gamma _M$
such that
![]() $I \diamond O_{t'} {\setminus} O_t$
is bounded.
$I \diamond O_{t'} {\setminus} O_t$
is bounded.
Proof We may replace M with a monster model, and then apply Lemma 4.11.
Proposition 4.15. Let M be any model of pCF. Let G be a definable non-compact group. Let I be an unbounded definable set. Let F be a finite subgroup of G. Then for any sufficiently small s and sufficiently large t, the set
![]() $I \diamond O_t {\setminus} (F O_s)$
is bounded.
$I \diamond O_t {\setminus} (F O_s)$
is bounded.
Proof We may replace M with a monster model, and then apply Lemma 4.13.
5 Stabilizers and
 $\mu $
-stabilizers
$\mu $
-stabilizers
In this section we review some notation and facts from [Reference Peterzil and Starchenko15].
5.1 Stabilizers
Let G be a group definable in a structure M.
Notation 5.1.
-
(1) If
 $\phi (x)$
and
$\phi (x)$
and
 $\psi (x)$
are G-formulas then
$\psi (x)$
are G-formulas then
 $\phi \cdot \psi $
denotes the G-formula Thus
$\phi \cdot \psi $
denotes the G-formula Thus $$ \begin{align*} (\phi\cdot \psi)(x):= \exists u\exists v(\phi(u)\wedge \psi(v)\wedge x=u\cdot v). \end{align*} $$
$$ \begin{align*} (\phi\cdot \psi)(x):= \exists u\exists v(\phi(u)\wedge \psi(v)\wedge x=u\cdot v). \end{align*} $$
 $(\phi \cdot \psi )(M) = \phi (M) \cdot \psi (M)$
.
$(\phi \cdot \psi )(M) = \phi (M) \cdot \psi (M)$
.
-
(2) More generally, if
 $q(x)$
and
$q(x)$
and
 $r(x)$
are partial G-types then
$r(x)$
are partial G-types then
 $q\cdot r$
denotes the G-type Thus
$q\cdot r$
denotes the G-type Thus $$ \begin{align*} (q\cdot r)(x):= \{\phi\cdot \psi(x) \mid q(x)\vdash \phi(x),~ r(x)\vdash \psi(x)\}. \end{align*} $$
$$ \begin{align*} (q\cdot r)(x):= \{\phi\cdot \psi(x) \mid q(x)\vdash \phi(x),~ r(x)\vdash \psi(x)\}. \end{align*} $$
 $(q \cdot r)(N) = q(N) \cdot r(N)$
for an
$(q \cdot r)(N) = q(N) \cdot r(N)$
for an
 $|M|^+$
-saturated elementary extension
$|M|^+$
-saturated elementary extension
 $N \succ M$
.
$N \succ M$
.
-
(3) If
 $g \in G(M)$
and
$g \in G(M)$
and
 $\phi (x)$
is a G-formula, then
$\phi (x)$
is a G-formula, then
 $g \cdot \phi $
denotes the G-formula Thus
$g \cdot \phi $
denotes the G-formula Thus $$ \begin{align*} (g \cdot \phi)(x) := \exists u (\phi(u) \wedge x = g \cdot u). \end{align*} $$
$$ \begin{align*} (g \cdot \phi)(x) := \exists u (\phi(u) \wedge x = g \cdot u). \end{align*} $$
 $(g \cdot \phi )(M) = g \cdot \phi (M)$
.
$(g \cdot \phi )(M) = g \cdot \phi (M)$
.
-
(4) If
 $g \in G(M)$
and
$g \in G(M)$
and
 $p(x)$
is a partial G-type then
$p(x)$
is a partial G-type then
 $g \cdot p$
denotes the G-type Thus
$g \cdot p$
denotes the G-type Thus $$ \begin{align*} (g \cdot p)(x) := \{g \cdot \phi(x) \mid p(x) \vdash \phi(x)\}. \end{align*} $$
$$ \begin{align*} (g \cdot p)(x) := \{g \cdot \phi(x) \mid p(x) \vdash \phi(x)\}. \end{align*} $$
 $(g \cdot p)(N) = g \cdot p(N)$
for an
$(g \cdot p)(N) = g \cdot p(N)$
for an
 $|M|^+$
-saturated
$|M|^+$
-saturated
 $N \succ M$
.
$N \succ M$
.
Note that for partial G-types
![]() $q_1, q_2, q_3$
over M, we have
$q_1, q_2, q_3$
over M, we have
as
![]() $((q_1 \cdot q_2) \cdot q_3)(N) = q_1(N) \cdot q_2(N) \cdot q_3(N) = (q_1 \cdot (q_2 \cdot q_3))(N)$
for
$((q_1 \cdot q_2) \cdot q_3)(N) = q_1(N) \cdot q_2(N) \cdot q_3(N) = (q_1 \cdot (q_2 \cdot q_3))(N)$
for
![]() $|M|^+$
-saturated
$|M|^+$
-saturated
![]() $N \succ M$
.
$N \succ M$
.
Definition 5.2. Given a partial type
![]() $\Sigma (x)$
over M, define
$\Sigma (x)$
over M, define
![]() $\operatorname {\mathrm {stab}}(\Sigma )$
to be the stabilizer, i.e.,
$\operatorname {\mathrm {stab}}(\Sigma )$
to be the stabilizer, i.e.,
where
![]() $\Sigma \equiv \Sigma '$
if
$\Sigma \equiv \Sigma '$
if
![]() $\Sigma (x) \vdash \Sigma '(x)$
and
$\Sigma (x) \vdash \Sigma '(x)$
and
![]() $\Sigma '(x) \vdash \Sigma (x)$
. Equivalently,
$\Sigma '(x) \vdash \Sigma (x)$
. Equivalently,
![]() $\operatorname {\mathrm {stab}}(\Sigma )$
is
$\operatorname {\mathrm {stab}}(\Sigma )$
is
![]() $\{g \in G(M) \mid g \Sigma (N) = \Sigma (N)\}$
for
$\{g \in G(M) \mid g \Sigma (N) = \Sigma (N)\}$
for
![]() $|M|^+$
-saturated
$|M|^+$
-saturated
![]() $N \succeq M$
.
$N \succeq M$
.
Definition 5.3. Given a partial type
![]() $\Sigma (x)$
over M and an
$\Sigma (x)$
over M and an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\phi (x,y)$
, we define
$\phi (x,y)$
, we define
 $$ \begin{align*} \operatorname{\mathrm{stab}}_\phi(\Sigma)=\bigcap_{b\in M^k}X_{\phi,b}, \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}_\phi(\Sigma)=\bigcap_{b\in M^k}X_{\phi,b}, \end{align*} $$
where each
![]() $X_{\phi ,b}$
is the stabilizer of
$X_{\phi ,b}$
is the stabilizer of
![]() $\{g\in G(M) \mid \Sigma \vdash (g\phi )(x,b)\}$
.
$\{g\in G(M) \mid \Sigma \vdash (g\phi )(x,b)\}$
.
Remark 5.4. Given
![]() $\phi (x;y)$
, let
$\phi (x;y)$
, let
![]() $\phi '(x;y,z)$
be the formula
$\phi '(x;y,z)$
be the formula
![]() $\phi (z \cdot x; y)$
. Then G acts on
$\phi (z \cdot x; y)$
. Then G acts on
![]() $\phi '$
-types by left translation, and
$\phi '$
-types by left translation, and
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma )$
is the stabilizer of the
$\operatorname {\mathrm {stab}}_\phi (\Sigma )$
is the stabilizer of the
![]() $\phi '$
-type generated by
$\phi '$
-type generated by
![]() $\Sigma $
.
$\Sigma $
.
Remark 5.5. Note that our
![]() $\operatorname {\mathrm {stab}}_\phi $
is slightly different from the
$\operatorname {\mathrm {stab}}_\phi $
is slightly different from the
![]() $\operatorname {\mathrm {Stab}}_\phi $
considered in [Reference Peterzil and Starchenko15], which is more like the set
$\operatorname {\mathrm {Stab}}_\phi $
considered in [Reference Peterzil and Starchenko15], which is more like the set
![]() $X_{\phi ,b}$
appearing in Definition 5.3 above.
$X_{\phi ,b}$
appearing in Definition 5.3 above.
The following two facts are easy exercises.
Fact 5.6.
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma )$
is a definable subgroup of G if
$\operatorname {\mathrm {stab}}_\phi (\Sigma )$
is a definable subgroup of G if
![]() $\Sigma $
is definable.
$\Sigma $
is definable.
Fact 5.7. For every partial type
![]() $\Sigma $
over M,
$\Sigma $
over M,
 $$ \begin{align*} \operatorname{\mathrm{stab}}(\Sigma)=\bigcap_{ \phi\in \mathcal{L}}\operatorname{\mathrm{stab}}_\phi(\Sigma). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}(\Sigma)=\bigcap_{ \phi\in \mathcal{L}}\operatorname{\mathrm{stab}}_\phi(\Sigma). \end{align*} $$
In particular, if
![]() $\Sigma $
is definable then
$\Sigma $
is definable then
![]() $\operatorname {\mathrm {stab}}(\Sigma )$
is an intersection of definable subgroups.
$\operatorname {\mathrm {stab}}(\Sigma )$
is an intersection of definable subgroups.
Recall the notation
![]() $\Sigma ^N$
for the canonical extension of a definable type
$\Sigma ^N$
for the canonical extension of a definable type
![]() $\Sigma $
to an elementary extension
$\Sigma $
to an elementary extension
![]() $N \succ M$
, and the notation
$N \succ M$
, and the notation
![]() $(d_\Sigma x)\phi (x;y)$
for the
$(d_\Sigma x)\phi (x;y)$
for the
![]() $\phi $
-definition of
$\phi $
-definition of
![]() $\Sigma $
.
$\Sigma $
.
Lemma 5.8. If
![]() $\Sigma $
is definable and
$\Sigma $
is definable and
![]() $N \succ M$
, then
$N \succ M$
, then
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma ^N) = \operatorname {\mathrm {stab}}_\phi (\Sigma )(N)$
, and so
$\operatorname {\mathrm {stab}}_\phi (\Sigma ^N) = \operatorname {\mathrm {stab}}_\phi (\Sigma )(N)$
, and so
 $$ \begin{align*} \operatorname{\mathrm{stab}}(\Sigma^N) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi(\Sigma)(N). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}(\Sigma^N) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi(\Sigma)(N). \end{align*} $$
Proof Indeed,
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma )(M)$
is defined by the formula
$\operatorname {\mathrm {stab}}_\phi (\Sigma )(M)$
is defined by the formula
and
![]() $\operatorname {\mathrm {stab}}_\phi (\Sigma ^N)$
is defined by the same formula, because
$\operatorname {\mathrm {stab}}_\phi (\Sigma ^N)$
is defined by the same formula, because
![]() $\Sigma ^N$
and
$\Sigma ^N$
and
![]() $\Sigma $
have the same definition schema.
$\Sigma $
have the same definition schema.
5.2
 $\mu $
-types and
$\mu $
-types and
 $\mu $
-stabilizers
$\mu $
-stabilizers
In this section we assume that G is a Hausdorff topological group definable in M with a uniformly definable basis
![]() $\{O_t \mid t\in T\}$
of open neighborhoods of the identity. For each
$\{O_t \mid t\in T\}$
of open neighborhoods of the identity. For each
![]() $N\succ M$
, the group
$N\succ M$
, the group
![]() $G(N)$
is again a topological group and the definable family
$G(N)$
is again a topological group and the definable family
![]() $\{O_t(N) \mid t\in T(N)\}$
again forms a basis for the open neighborhoods of
$\{O_t(N) \mid t\in T(N)\}$
again forms a basis for the open neighborhoods of
![]() $\operatorname {\mathrm {id}}_G$
.
$\operatorname {\mathrm {id}}_G$
.
Definition 5.9. The infinitesimal type of G, denoted
![]() $\mu (x)$
, is the partial type consisting of all formulas
$\mu (x)$
, is the partial type consisting of all formulas
![]() $x \in U$
with U an M-definable neighborhood of
$x \in U$
with U an M-definable neighborhood of
![]() $\operatorname {\mathrm {id}}_G$
.
$\operatorname {\mathrm {id}}_G$
.
Thus, if
![]() $N \succeq M$
, then
$N \succeq M$
, then
![]() $\mu (N)$
is the set of elements of
$\mu (N)$
is the set of elements of
![]() $G(N)$
which are infinitesimally close to
$G(N)$
which are infinitesimally close to
![]() $\operatorname {\mathrm {id}}_G$
:
$\operatorname {\mathrm {id}}_G$
:
 $$ \begin{align*} \mu(N) &= \bigcap \{U(N) \mid U \text{ is an }M\text{-definable neighborhood of } \operatorname{\mathrm{id}}_G\} \\ &= \bigcap_{t \in T(M)} O_t(N). \end{align*} $$
$$ \begin{align*} \mu(N) &= \bigcap \{U(N) \mid U \text{ is an }M\text{-definable neighborhood of } \operatorname{\mathrm{id}}_G\} \\ &= \bigcap_{t \in T(M)} O_t(N). \end{align*} $$
Fact 5.10 ([Reference Peterzil and Starchenko15, Corollary 2.5 and Claim 2.15])
-
1. If
 $N \succ M$
, then
$N \succ M$
, then
 $\mu (N)$
is a subgroup of
$\mu (N)$
is a subgroup of
 $G(N)$
normalized by
$G(N)$
normalized by
 $G(M)$
.
$G(M)$
. -
2. For any definable
 $q \in S_G(M)$
, the partial type
$q \in S_G(M)$
, the partial type
 $\mu \cdot q$
is definable.
$\mu \cdot q$
is definable.
Partial types of the form
![]() $\mu \cdot q$
for
$\mu \cdot q$
for
![]() $q \in S_G(M)$
are called
$q \in S_G(M)$
are called
![]() $\mu $
-types. The
$\mu $
-types. The
![]() $\mu $
-stabilizer of
$\mu $
-stabilizer of
![]() $q \in S_G(M)$
is the stabilizer of the associated
$q \in S_G(M)$
is the stabilizer of the associated
![]() $\mu $
-type:
$\mu $
-type:
Note that if
![]() $\mu $
is the infinitesimal type of
$\mu $
is the infinitesimal type of
![]() $G = G(M)$
, and
$G = G(M)$
, and
![]() $N \succeq M$
, then the canonical extension
$N \succeq M$
, then the canonical extension
![]() $\mu ^N$
is the infinitesimal type of
$\mu ^N$
is the infinitesimal type of
![]() $G(N)$
.
$G(N)$
.
Fact 5.11 ([Reference Peterzil and Starchenko15, Remark 2.16])
If p is a definable type over M and
![]() $N \succ M$
, then the product of the canonical extensions is equal to the canonical extension of the product
$N \succ M$
, then the product of the canonical extensions is equal to the canonical extension of the product
![]() $:$
$:$
Remark 5.12. Let N be an
![]() $|M|^+$
-saturated extension of M, and
$|M|^+$
-saturated extension of M, and
![]() $\mu ^N$
and
$\mu ^N$
and
![]() $p^N$
be the canonical extensions of
$p^N$
be the canonical extensions of
![]() $\mu $
and p. Then
$\mu $
and p. Then
 $$ \begin{align*} \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) = \operatorname{\mathrm{stab}}(({\mu\cdot p })^N) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) = \operatorname{\mathrm{stab}}(({\mu\cdot p })^N) = \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N), \end{align*} $$
By Fact 5.10,
![]() $\mu (N)\cdot G(M)$
is a subgroup of
$\mu (N)\cdot G(M)$
is a subgroup of
![]() $G(N)$
as
$G(N)$
as
![]() $\mu (N)\subseteq G(N)$
is normalized by
$\mu (N)\subseteq G(N)$
is normalized by
![]() $G(M)$
. This subgroup is the
$G(M)$
. This subgroup is the
![]() ${\cal O}_{G(M)}(N)$
of Definition 2.18. Because
${\cal O}_{G(M)}(N)$
of Definition 2.18. Because
![]() $\mu (N)\cap G(M)=\{\operatorname {\mathrm {id}}_G\}$
, the group
$\mu (N)\cap G(M)=\{\operatorname {\mathrm {id}}_G\}$
, the group
![]() $\mu (N) \cdot G(M)$
is a semidirect product of
$\mu (N) \cdot G(M)$
is a semidirect product of
![]() $\mu (N)$
and
$\mu (N)$
and
![]() $G(M)$
, and there is a natural homomorphism
$G(M)$
, and there is a natural homomorphism
This map is exactly the “standard part” map
![]() $\operatorname {\mathrm {st}}_M^N$
of Definition 2.18. For
$\operatorname {\mathrm {st}}_M^N$
of Definition 2.18. For
![]() $Y\subseteq G(N)$
, we will write
$Y\subseteq G(N)$
, we will write
![]() $\operatorname {\mathrm {st}}_M^N(Y)$
as a shorthand for
$\operatorname {\mathrm {st}}_M^N(Y)$
as a shorthand for
 $\operatorname {\mathrm {st}}_M^N(Y \cap \mathcal {O}_{G(M)}(N))$
, following [Reference Peterzil and Starchenko15].
$\operatorname {\mathrm {st}}_M^N(Y \cap \mathcal {O}_{G(M)}(N))$
, following [Reference Peterzil and Starchenko15].
Lemma 5.13. Let
![]() $p\in S_G(M)$
be a definable type and let
$p\in S_G(M)$
be a definable type and let
![]() $\beta \in G(\mathbb M)$
realize
$\beta \in G(\mathbb M)$
realize
![]() $p^N$
. Then
$p^N$
. Then
-
1.
 $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})={\operatorname {\mathrm {st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta ^{-1});$
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})={\operatorname {\mathrm {st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta ^{-1});$
-
2.
 $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})=\bigcap _{\psi \in p^N}{\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})$
.
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})=\bigcap _{\psi \in p^N}{\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})$
.
Proof Clause (1) is by Claim 2.22 in [Reference Peterzil and Starchenko15].
For (2), we must show
 $$ \begin{align*} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta^{-1}) = \bigcap_{\psi\in p^N}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
$$ \begin{align*} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta^{-1}) = \bigcap_{\psi\in p^N}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
The
![]() $\subseteq $
direction is clear. For
$\subseteq $
direction is clear. For
![]() $\supseteq $
, suppose that
$\supseteq $
, suppose that
 $g \in \bigcap _{\psi \in p^N}{\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})$
. Then for any
$g \in \bigcap _{\psi \in p^N}{\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})$
. Then for any
![]() $\psi \in p^N$
, there is
$\psi \in p^N$
, there is
![]() $h_\psi \in \psi (\mathbb M)$
such that
$h_\psi \in \psi (\mathbb M)$
such that
![]() $h_\psi \cdot \beta ^{-1} \cdot g^{-1}$
satisfies
$h_\psi \cdot \beta ^{-1} \cdot g^{-1}$
satisfies
![]() $\mu ^N$
. By compactness there is
$\mu ^N$
. By compactness there is
![]() $h \in p^N(\mathbb M)$
such that
$h \in p^N(\mathbb M)$
such that
![]() $h \cdot \beta ^{-1} \cdot g^{-1}$
satisfies
$h \cdot \beta ^{-1} \cdot g^{-1}$
satisfies
![]() $\mu ^N$
. Then
$\mu ^N$
. Then
 $g \in {\operatorname {\mathrm {st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta ^{-1})$
.
$g \in {\operatorname {\mathrm {st}}_N^{\mathbb M}}(p^N(\mathbb M)\beta ^{-1})$
.
6 Proof of main theorems
From now on M is a p-adically closed field,
![]() $\mathbb M\succ M$
is the monster model,
$\mathbb M\succ M$
is the monster model,
![]() $G\subseteq M^n$
denotes a group definable in M, and
$G\subseteq M^n$
denotes a group definable in M, and
![]() $\mu $
denotes the infinitesimal type of G over M. All formulas and types will be G-formulas and G-types. We assume G is not definably compact. Fix a good neighborhood basis
$\mu $
denotes the infinitesimal type of G over M. All formulas and types will be G-formulas and G-types. We assume G is not definably compact. Fix a good neighborhood basis
![]() $\{O_t : t \in \Gamma _M\}$
of G.
$\{O_t : t \in \Gamma _M\}$
of G.
Fix a one-dimensional definable type
![]() $p \in S_G(M)$
which does not specialize to any point of
$p \in S_G(M)$
which does not specialize to any point of
![]() $G(M)$
. Such a type p exists by Proposition 2.24. Fix a small
$G(M)$
. Such a type p exists by Proposition 2.24. Fix a small
![]() $|M|^+$
-saturated model N with
$|M|^+$
-saturated model N with
![]() $M \prec N \prec \mathbb M$
. As usual,
$M \prec N \prec \mathbb M$
. As usual,
![]() $p^N$
and
$p^N$
and
![]() $\mu ^N$
denote the canonical extensions to N. Fix an element
$\mu ^N$
denote the canonical extensions to N. Fix an element
![]() $\beta \in G(\mathbb M)$
realizing
$\beta \in G(\mathbb M)$
realizing
![]() $p^N$
.
$p^N$
.
Remark 6.1. The types p and
![]() $p^N$
are “unbounded” in the following sense:
$p^N$
are “unbounded” in the following sense:
-
1. If
 $t \in \Gamma _M$
, then
$t \in \Gamma _M$
, then
 $O_t \notin p$
.
$O_t \notin p$
. -
2. If
 $t \in \Gamma _N$
, then
$t \in \Gamma _N$
, then
 $O_t \notin p^N$
.
$O_t \notin p^N$
. -
3. If X is a bounded M-definable subset of
 $G(M)$
, then
$G(M)$
, then
 $X \notin p$
.
$X \notin p$
. -
4. If X is a bounded N-definable subset of
 $G(N)$
, then
$G(N)$
, then
 $X \notin p^N$
.
$X \notin p^N$
.
Point (1) follows by Proposition 2.24: if
![]() $O_t \in p$
then p specializes to a point in
$O_t \in p$
then p specializes to a point in
![]() $O_t(M)$
, because
$O_t(M)$
, because
![]() $O_t$
is definably compact. Point (2) then follows because
$O_t$
is definably compact. Point (2) then follows because
![]() $p^N$
is the heir of p. Points (3) and (4) reduce to (1) and (2), respectively.
$p^N$
is the heir of p. Points (3) and (4) reduce to (1) and (2), respectively.
Lemma 6.2.
 $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) = \bigcap _{\phi \in p} {\operatorname {\mathrm {st}}_N^{\mathbb M}}(\phi (N)\beta ^{-1})$
.
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) = \bigcap _{\phi \in p} {\operatorname {\mathrm {st}}_N^{\mathbb M}}(\phi (N)\beta ^{-1})$
.
Proof By Lemma 5.13, it suffices to show
 $$ \begin{align*} \bigcap_{\phi \in p}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(\mathbb M)\beta^{-1}) \subseteq \bigcap_{\phi \in p^N}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(\mathbb M)\beta^{-1}). \end{align*} $$
$$ \begin{align*} \bigcap_{\phi \in p}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(\mathbb M)\beta^{-1}) \subseteq \bigcap_{\phi \in p^N}{\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(\mathbb M)\beta^{-1}). \end{align*} $$
Suppose g belongs to the left-hand side. In particular,
![]() $g \in G(N)$
. By a compactness argument similar to Lemma 5.13, we see that
$g \in G(N)$
. By a compactness argument similar to Lemma 5.13, we see that
![]() $g = \epsilon b \beta ^{-1}$
for some
$g = \epsilon b \beta ^{-1}$
for some
![]() $\epsilon \in \mu ^N(\mathbb M)$
and
$\epsilon \in \mu ^N(\mathbb M)$
and
![]() $b \in p(\mathbb M)$
. It suffices to show
$b \in p(\mathbb M)$
. It suffices to show
![]() $b \in p^N(\mathbb M)$
. By Lemma 2.25, it suffices to show
$b \in p^N(\mathbb M)$
. By Lemma 2.25, it suffices to show
![]() $b \notin O_t(\mathbb M)$
for any
$b \notin O_t(\mathbb M)$
for any
![]() $t \in \Gamma _N$
. Suppose
$t \in \Gamma _N$
. Suppose
![]() $b \in O_t(\mathbb M)$
. Since
$b \in O_t(\mathbb M)$
. Since
![]() $g \in N$
, there is some
$g \in N$
, there is some
![]() $t' \in \Gamma _N$
such that
$t' \in \Gamma _N$
such that
![]() $g^{-1} \cdot O_0(\mathbb M) \cdot O_t(\mathbb M) \subseteq O_{t'}(\mathbb M)$
. Then
$g^{-1} \cdot O_0(\mathbb M) \cdot O_t(\mathbb M) \subseteq O_{t'}(\mathbb M)$
. Then
contradicting the fact that
![]() $\operatorname {\mathrm {tp}}(\beta /N)$
is unbounded.
$\operatorname {\mathrm {tp}}(\beta /N)$
is unbounded.
Note that a similar argument to the proof of Lemma 2.31 of [Reference Yao23] shows the following:
Fact 6.3. Suppose that
![]() $b\in \mathbb M^k$
and
$b\in \mathbb M^k$
and
![]() $\operatorname {\mathrm {tp}}(b/N)$
is definable. If
$\operatorname {\mathrm {tp}}(b/N)$
is definable. If
![]() $Y\subseteq G(\mathbb M)$
is definable over b then
$Y\subseteq G(\mathbb M)$
is definable over b then
![]() ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(Y)\subseteq G(N)$
is definable and
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(Y)\subseteq G(N)$
is definable and
Lemma 6.4. There is an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\phi $
such that
$\phi $
such that
![]() $\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p }))\leq 1$
.
$\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p }))\leq 1$
.
Proof Take
![]() $\psi \in p$
such that
$\psi \in p$
such that
![]() $\dim (\psi (\mathbb M)) = 1$
. Then
$\dim (\psi (\mathbb M)) = 1$
. Then
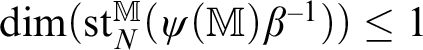 $\dim ({\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})) \le 1$
by Fact 6.3. By Remark 5.12 and Lemma 5.13,
$\dim ({\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})) \le 1$
by Fact 6.3. By Remark 5.12 and Lemma 5.13,
 $$ \begin{align*} \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) \subseteq {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
$$ \begin{align*} \bigcap_{\phi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) \subseteq {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
The intersection on the left is directed, and the set on the right is definable, so by
![]() $|M|^+$
-saturation of N there is some
$|M|^+$
-saturation of N there is some
![]() $\phi \in \mathcal {L}$
such that
$\phi \in \mathcal {L}$
such that
 $$ \begin{align*} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) \subseteq {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) \subseteq {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(\mathbb M)\beta^{-1}). \end{align*} $$
Then
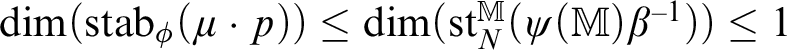 $\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \le \dim ({\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})) \le 1$
.
$\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \le \dim ({\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (\mathbb M)\beta ^{-1})) \le 1$
.
To finish our main result, we now show that each
![]() $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is not definably compact.
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is not definably compact.
Lemma 6.5. Assume G is nearly abelian
![]() $($
Definition 1.1
$($
Definition 1.1
![]() $)$
. For any N-definable set I containing
$)$
. For any N-definable set I containing
![]() $\beta $
, the set
$\beta $
, the set
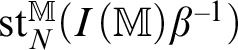 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
is unbounded.
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
is unbounded.
Proof Suppose
 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
is bounded. Then
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
is bounded. Then
 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1}) \subseteq O_t(N)$
for some
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1}) \subseteq O_t(N)$
for some
![]() $t \in \Gamma _N$
. By Remark 6.1, I is unbounded. By Proposition 4.14, there is some
$t \in \Gamma _N$
. By Remark 6.1, I is unbounded. By Proposition 4.14, there is some
![]() $t' \in \Gamma _N$
such that the set
$t' \in \Gamma _N$
such that the set
![]() $I^{-1} \diamond O_{t'} {\setminus} O_t$
is bounded. Then
$I^{-1} \diamond O_{t'} {\setminus} O_t$
is bounded. Then
 $$ \begin{align*} \beta^{-1} \notin (I^{-1} \diamond O_{t'} {\setminus} O_t)(\mathbb M)\end{align*} $$
$$ \begin{align*} \beta^{-1} \notin (I^{-1} \diamond O_{t'} {\setminus} O_t)(\mathbb M)\end{align*} $$
by Remark 6.1. This means that
![]() $\beta ^{-1} (O_{t'}(\mathbb M) {\setminus} O_t(\mathbb M)) \cap I(\mathbb M)^{-1} \ne \emptyset $
. Therefore there is
$\beta ^{-1} (O_{t'}(\mathbb M) {\setminus} O_t(\mathbb M)) \cap I(\mathbb M)^{-1} \ne \emptyset $
. Therefore there is
![]() $a \in O_{t'}(\mathbb M) {\setminus} O_t(\mathbb M)$
such that
$a \in O_{t'}(\mathbb M) {\setminus} O_t(\mathbb M)$
such that
![]() $a \beta \in I(\mathbb M)$
. By definable Skolem functions, we can take
$a \beta \in I(\mathbb M)$
. By definable Skolem functions, we can take
![]() $a \in \operatorname {\mathrm {dcl}}(N \beta )$
. Note
$a \in \operatorname {\mathrm {dcl}}(N \beta )$
. Note
![]() $a \in I(\mathbb M)\beta ^{-1}$
. By Lemma 2.23,
$a \in I(\mathbb M)\beta ^{-1}$
. By Lemma 2.23,
![]() ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
exists. Because
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
exists. Because
![]() $O_{t'} {\setminus} O_t$
is closed, we see that
$O_{t'} {\setminus} O_t$
is closed, we see that
![]() ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a) \in O_{t'}(N) {\setminus} O_t(N)$
. This contradicts the fact that
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a) \in O_{t'}(N) {\setminus} O_t(N)$
. This contradicts the fact that
 $$ \begin{align*} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(a) \in {\operatorname{\mathrm{st}}_N^{\mathbb M}}(I(\mathbb M)\beta^{-1}) \subseteq O_t(N). \\[-32pt] \end{align*} $$
$$ \begin{align*} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(a) \in {\operatorname{\mathrm{st}}_N^{\mathbb M}}(I(\mathbb M)\beta^{-1}) \subseteq O_t(N). \\[-32pt] \end{align*} $$
Lemma 6.6. If G is nearly abelian, then the type-definable group
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) \subseteq G(N)$
is one-dimensional and unbounded.
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) \subseteq G(N)$
is one-dimensional and unbounded.
Proof The dimension of
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is at most 1 by Lemma 6.4 and Remark 5.12. If
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is at most 1 by Lemma 6.4 and Remark 5.12. If
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is bounded, then
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is bounded, then
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) \subseteq O_t(N)$
for some
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N}) \subseteq O_t(N)$
for some
![]() $t \in \Gamma _N$
. By Lemma 6.2, we have
$t \in \Gamma _N$
. By Lemma 6.2, we have
 $$ \begin{align*} \bigcap_{\psi \in p} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(N)\beta^{-1}) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) \subseteq O_t(N). \end{align*} $$
$$ \begin{align*} \bigcap_{\psi \in p} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\psi(N)\beta^{-1}) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) \subseteq O_t(N). \end{align*} $$
The intersection on the left is a filtered intersection of definable sets. There are at most
![]() $|M|$
sets in the intersection, and N is
$|M|$
sets in the intersection, and N is
![]() $|M|^+$
-saturated. Therefore there is some
$|M|^+$
-saturated. Therefore there is some
![]() $\psi \in p$
such that
$\psi \in p$
such that
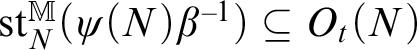 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (N)\beta ^{-1}) \subseteq O_t(N)$
, contradicting Lemma 6.5. Therefore
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(\psi (N)\beta ^{-1}) \subseteq O_t(N)$
, contradicting Lemma 6.5. Therefore
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is unbounded. In particular, it is infinite, so it has dimension at least 1.
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is unbounded. In particular, it is infinite, so it has dimension at least 1.
Lemma 6.7. Suppose G is nearly abelian. Then there is
![]() $\phi \in \mathcal {L}$
such that the M-definable group
$\phi \in \mathcal {L}$
such that the M-definable group
![]() $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is not definably compact and has dimension
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is not definably compact and has dimension
![]() $1$
.
$1$
.
Proof By Lemma 6.4 there is an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\phi $
such that
$\phi $
such that
![]() $\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \le 1$
. By Remark 5.12, we have
$\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \le 1$
. By Remark 5.12, we have
 $$ \begin{align*} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) \supseteq \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{stab}}_\phi({\mu\cdot p })(N) \supseteq \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}), \end{align*} $$
and therefore
![]() $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is unbounded by Lemma 6.6. In particular,
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is unbounded by Lemma 6.6. In particular,
![]() $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is infinite, and
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is infinite, and
![]() $\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \ge 1$
.
$\dim (\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })) \ge 1$
.
Theorem 6.8. Let G be a definable group in a p-adically closed field M. Suppose G is nearly abelian, and not definably compact.
-
1. G has a one-dimensional definable subgroup which is not definably compact.
-
2. If
 $p \in S_G(M)$
is a definable unbounded one-dimensional type, then there is
$p \in S_G(M)$
is a definable unbounded one-dimensional type, then there is
 $\phi \in \mathcal {L}$
such that
$\phi \in \mathcal {L}$
such that
 $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is a one-dimensional definable subgroup of G which is not definably compact.
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
is a one-dimensional definable subgroup of G which is not definably compact. -
3. Suppose in addition that M is
 $\aleph _1$
-saturated. If
$\aleph _1$
-saturated. If
 $p \in S_G(M)$
is a definable unbounded one-dimensional type, then
$p \in S_G(M)$
is a definable unbounded one-dimensional type, then
 $\operatorname {\mathrm {stab}}^\mu (p)$
is a one-dimensional type-definable subgroup of G which is unbounded.
$\operatorname {\mathrm {stab}}^\mu (p)$
is a one-dimensional type-definable subgroup of G which is unbounded.
Proof Part (2) is Lemma 6.7. Part (1) then follows because there is at least one unbounded one-dimensional definable type by Proposition 2.24. For Part (3), take a countable model
![]() $M_0 \preceq M$
such that G and p are
$M_0 \preceq M$
such that G and p are
![]() $M_0$
-definable. Then apply Lemma 6.6 to M and
$M_0$
-definable. Then apply Lemma 6.6 to M and
![]() $M_0$
in place of N and M (respectively), to see that
$M_0$
in place of N and M (respectively), to see that
![]() $\operatorname {\mathrm {stab}}({\mu \cdot p })$
is one-dimensional and unbounded. Type-definability is by Fact 5.7.
$\operatorname {\mathrm {stab}}({\mu \cdot p })$
is one-dimensional and unbounded. Type-definability is by Fact 5.7.
Recall from [Reference Pillay and Yao19] that in an NIP context, a global type
![]() $p\in S_G(\mathbb M)$
is said to be a definable f-generic, abbreviated as dfg, if there is a small submodel
$p\in S_G(\mathbb M)$
is said to be a definable f-generic, abbreviated as dfg, if there is a small submodel
![]() $M_0$
such that every left G-translate of p is definable over
$M_0$
such that every left G-translate of p is definable over
![]() $M_0$
. In [Reference Pillay and Yao19], Pillay and the second author showed that:
$M_0$
. In [Reference Pillay and Yao19], Pillay and the second author showed that:
Fact 6.9. A group G definable over
![]() ${\mathbb Q}_p$
has dfg iff there is a normal sequence of definable subgroups
${\mathbb Q}_p$
has dfg iff there is a normal sequence of definable subgroups
such that
![]() $G_0$
is finite,
$G_0$
is finite,
![]() $G_n$
is a finite index subgroup of G, and each
$G_n$
is a finite index subgroup of G, and each
![]() $G_{i+1}/G_{i}$
is definably isomorphic to either the additive group
$G_{i+1}/G_{i}$
is definably isomorphic to either the additive group
![]() $\mathbb G_a$
, or a finite index subgroup of the multiplicative group
$\mathbb G_a$
, or a finite index subgroup of the multiplicative group
![]() $\mathbb G_m$
.
$\mathbb G_m$
.
The intuition is that “dfg” means “totally non-compact” in the p-adic context.
Lemma 6.10. Let G be a one-dimensional definable group. If G is not definably compact, then G has dfg.
Proof Recall from [Reference Hrushovski and Pillay7, Section 4] that G has finitely satisfiable generics (fsg) if there is a small model
![]() $M_0$
and a global type
$M_0$
and a global type
![]() $p(x)$
in G such that every left G-translate of p is finitely satisfiable in
$p(x)$
in G such that every left G-translate of p is finitely satisfiable in
![]() $M_0$
. By [Reference Pillay and Yao19, Lemma 2.9], G has fsg or dfg.Footnote
1
It suffices to show that G does not have fsg. Suppose otherwise, witnessed by p and
$M_0$
. By [Reference Pillay and Yao19, Lemma 2.9], G has fsg or dfg.Footnote
1
It suffices to show that G does not have fsg. Suppose otherwise, witnessed by p and
![]() $M_0$
. Recall that a definable set
$M_0$
. Recall that a definable set
![]() $X \subseteq G$
is generic if finitely many left translates cover G. By [Reference Hrushovski and Pillay7, Proposition 4.2], the complement of a non-generic set is generic, and every generic set intersects
$X \subseteq G$
is generic if finitely many left translates cover G. By [Reference Hrushovski and Pillay7, Proposition 4.2], the complement of a non-generic set is generic, and every generic set intersects
![]() $G(M_0)$
. Let
$G(M_0)$
. Let
![]() $\{W_\gamma \}_{\gamma }$
be a
$\{W_\gamma \}_{\gamma }$
be a
![]() $\Gamma $
-exhaustion of G. By taking
$\Gamma $
-exhaustion of G. By taking
![]() $\gamma $
sufficiently large, we can arrange for
$\gamma $
sufficiently large, we can arrange for
![]() $G(M_0) \subseteq W_\gamma $
, because
$G(M_0) \subseteq W_\gamma $
, because
![]() $M_0$
is small. Then
$M_0$
is small. Then
![]() $G {\setminus} W_\gamma $
does not intersect
$G {\setminus} W_\gamma $
does not intersect
![]() $G(M_0)$
, so it is not generic. Therefore the complement
$G(M_0)$
, so it is not generic. Therefore the complement
![]() $W_\gamma $
is generic. A finite union of left translates of
$W_\gamma $
is generic. A finite union of left translates of
![]() $W_\gamma $
will be definably compact, so it cannot be all of G. We conclude that G does not have fsg, and instead has dfg.
$W_\gamma $
will be definably compact, so it cannot be all of G. We conclude that G does not have fsg, and instead has dfg.
The following is then a corollary of Theorem 6.8.
Corollary 6.11. Let
![]() $G\subseteq M^k$
be a nearly abelian definable group. If G is not definably compact, then G has a one-dimensional dfg subgroup.
$G\subseteq M^k$
be a nearly abelian definable group. If G is not definably compact, then G has a one-dimensional dfg subgroup.
Next, we consider the general non-abelian case. Let
![]() $G, M, N, \mathbb M, p, \beta $
be as in the start of this section.
$G, M, N, \mathbb M, p, \beta $
be as in the start of this section.
Lemma 6.12. For any N-definable set I containing
![]() $\beta $
, and any finite N-definable subgroup
$\beta $
, and any finite N-definable subgroup
![]() $F \subseteq G$
, the set
$F \subseteq G$
, the set
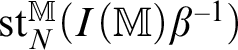 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
contains a point outside of F.
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(I(\mathbb M)\beta ^{-1})$
contains a point outside of F.
Proof As in Lemma 6.5, I is unbounded. Let J be the unbounded set
![]() $I^{-1}$
. By Proposition 4.15, there are
$I^{-1}$
. By Proposition 4.15, there are
![]() $s, t \in \Gamma _N$
such that
$s, t \in \Gamma _N$
such that
![]() $J \diamond O_t {\setminus} F O_s$
is bounded. Then
$J \diamond O_t {\setminus} F O_s$
is bounded. Then
![]() $\beta ^{-1} \notin J \diamond O_t {\setminus} F O_s$
. Therefore
$\beta ^{-1} \notin J \diamond O_t {\setminus} F O_s$
. Therefore
 $$ \begin{align*} \beta^{-1} (O_t {\setminus} F O_s) \cap J \ne \emptyset, \end{align*} $$
$$ \begin{align*} \beta^{-1} (O_t {\setminus} F O_s) \cap J \ne \emptyset, \end{align*} $$
or equivalently
Therefore there is
![]() $a \in O_t(\mathbb M) {\setminus} O_s(\mathbb M) F(\mathbb M)$
such that
$a \in O_t(\mathbb M) {\setminus} O_s(\mathbb M) F(\mathbb M)$
such that
![]() $a \beta \in I(\mathbb M)$
. By definable Skolem functions, we can take
$a \beta \in I(\mathbb M)$
. By definable Skolem functions, we can take
![]() $a \in \operatorname {\mathrm {dcl}}(N \beta )$
. Note
$a \in \operatorname {\mathrm {dcl}}(N \beta )$
. Note
![]() $a \in I(\mathbb M)\beta ^{-1}$
. Because
$a \in I(\mathbb M)\beta ^{-1}$
. Because
![]() $O_{t} {\setminus} O_s F$
is definably compact, Lemma 2.23 implies that
$O_{t} {\setminus} O_s F$
is definably compact, Lemma 2.23 implies that
![]() ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
exists and is in
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
exists and is in
![]() $O_t {\setminus} O_s F$
. Then
$O_t {\setminus} O_s F$
. Then
![]() ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
is not in F, since
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(a)$
is not in F, since
![]() $F \subseteq O_s F$
.
$F \subseteq O_s F$
.
Lemma 6.13. The group
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is one-dimensional. In particular, it is infinite.
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is one-dimensional. In particular, it is infinite.
Proof As in Lemma 6.6, the dimension is at most 1. If
![]() $\dim (\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})) = 0$
, then
$\dim (\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})) = 0$
, then
![]() $\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is a finite subgroup F. By Lemma 6.2, we have
$\operatorname {\mathrm {stab}}({\mu ^N\cdot p^N})$
is a finite subgroup F. By Lemma 6.2, we have
 $$ \begin{align*} \bigcap_{\phi \in p} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(N)\beta^{-1}) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) = F. \end{align*} $$
$$ \begin{align*} \bigcap_{\phi \in p} {\operatorname{\mathrm{st}}_N^{\mathbb M}}(\phi(N)\beta^{-1}) = \operatorname{\mathrm{stab}}({\mu^N\cdot p^N}) = F. \end{align*} $$
As in Lemma 6.6, there is some
![]() $\phi \in p$
such that
$\phi \in p$
such that
 ${\operatorname {\mathrm {st}}_N^{\mathbb M}}(\phi (N)\beta ^{-1}) \subseteq F$
. This contradicts Lemma 6.12
${\operatorname {\mathrm {st}}_N^{\mathbb M}}(\phi (N)\beta ^{-1}) \subseteq F$
. This contradicts Lemma 6.12
By Lemma 6.4 and Remark 5.12, we obtain the following conclusion.
Lemma 6.14. There is
![]() $\phi \in \mathcal {L}$
such that the M-definable group
$\phi \in \mathcal {L}$
such that the M-definable group
![]() $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
has dimension 1.
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
has dimension 1.
We summarize the non-abelian case in the following theorem.
Theorem 6.15. Let G be a definable group in a p-adically closed field M. Suppose G is not definably compact. Let
![]() $p \in S_G(M)$
be a definable unbounded one-dimensional type.
$p \in S_G(M)$
be a definable unbounded one-dimensional type.
-
1. There is
 $\phi \in \mathcal {L}$
such that
$\phi \in \mathcal {L}$
such that
 $\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
has dimension 1.
$\operatorname {\mathrm {stab}}_\phi ({\mu \cdot p })$
has dimension 1. -
2. If M is
 $\aleph _1$
-saturated, then
$\aleph _1$
-saturated, then
 $\operatorname {\mathrm {stab}}^\mu (p)$
is a one-dimensional type-definable subgroup of G.
$\operatorname {\mathrm {stab}}^\mu (p)$
is a one-dimensional type-definable subgroup of G.
Acknowledgments
The first author was supported by the National Natural Science Foundation of China (Grant No. 12101131). The second author was supported by the National Social Science Fund of China (Grant No. 20CZX050).