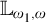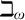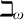1 Introduction
The upward Löwenheim–Skolem theorem says that any first-order theory with an infinite model has models of arbitrarily large cardinalities. This result is no longer true outside of first-order logics, for example for theories in
![]() $\mathbb {L}_{\omega _1, \omega }$
. For this more general case, it is reasonable to ask which properties of small models guarantee existence of bigger models. In that light, the following early result of Shelah [She87a] is remarkable:
$\mathbb {L}_{\omega _1, \omega }$
. For this more general case, it is reasonable to ask which properties of small models guarantee existence of bigger models. In that light, the following early result of Shelah [She87a] is remarkable:
Fact 1.1. An
![]() $\mathbb {L}_{\omega _1, \omega }$
sentence which is categorical in both
$\mathbb {L}_{\omega _1, \omega }$
sentence which is categorical in both
![]() $\aleph _0$
and
$\aleph _0$
and
![]() $\aleph _1$
has a model of size
$\aleph _1$
has a model of size
![]() $\aleph _2$
.
$\aleph _2$
.
Shelah proved in fact a more general theorem, valid for any “reasonably definable” abstract elementary class (AEC) with countable Löwenheim–Skolem number (see [Reference ShelahShe09a, I.3.11] for the details). In particular, he answered in the negative Baldwin’s question: can a sentence in
![]() $\mathbb {L} (\exists ^{\ge \aleph _1})$
have exactly one uncountable model? See for example [Reference GrossbergGro02, §4] for a more detailed history.
$\mathbb {L} (\exists ^{\ge \aleph _1})$
have exactly one uncountable model? See for example [Reference GrossbergGro02, §4] for a more detailed history.
It is natural to ask whether Fact 1.1 generalizes to any AEC. More specifically:
Question 1.2. Assume
![]() $\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
$\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
![]() $\lambda $
. If
$\lambda $
. If
![]() $\mathbf {K}$
is categorical in both
$\mathbf {K}$
is categorical in both
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda ^+$
, must it have a model of cardinality
$\lambda ^+$
, must it have a model of cardinality
![]() $\lambda ^{++}$
?
$\lambda ^{++}$
?
Question 1.2 is still open. Partial approximations immensely stimulated the field: Shelah [Reference ShelahShe01] has shown assuming some set-theoretic hypotheses that categoricity in three successive cardinals suffices:
Fact 1.3. AssumeFootnote
1
![]() $2^{\lambda } < 2^{\lambda ^+} < 2^{\lambda ^{++}}$
. Let
$2^{\lambda } < 2^{\lambda ^+} < 2^{\lambda ^{++}}$
. Let
![]() $\mathbf {K}$
be an AEC with Löwenheim–Skolem–Tarski number
$\mathbf {K}$
be an AEC with Löwenheim–Skolem–Tarski number
![]() $\lambda $
. If
$\lambda $
. If
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\lambda $
,
$\lambda $
,
![]() $\lambda ^+$
, and
$\lambda ^+$
, and
![]() $\lambda ^{++}$
, then it has a model of size
$\lambda ^{++}$
, then it has a model of size
![]() $\lambda ^{+3}$
.
$\lambda ^{+3}$
.
Remark 1.4. One of the byproduct of Shelah’s proof is the machinery of good frames , developed in Shelah’s two volume book [Reference ShelahShe09a]. Essentially, an AEC has a good
![]() $\lambda $
- frame if
$\lambda $
- frame if
![]() ${\mathbf {K}}_\lambda $
, its class of models of cardinality
${\mathbf {K}}_\lambda $
, its class of models of cardinality
![]() $\lambda $
, behaves “well” in the sense that it has several structural properties, including a superstable-like forking notion. Good frames have subsequently been used in many results, for example in the author’s proof of the eventual categoricity conjecture for universal classes [Reference VaseyVas17b, Reference VaseyVas17c], in the recent proof of the eventual categoricity conjecture from large cardinals [Reference Shelah and VaseySV], and in the full analysis of the categoricity spectrum of AECs with amalgamation [Reference VaseyVas19].
$\lambda $
, behaves “well” in the sense that it has several structural properties, including a superstable-like forking notion. Good frames have subsequently been used in many results, for example in the author’s proof of the eventual categoricity conjecture for universal classes [Reference VaseyVas17b, Reference VaseyVas17c], in the recent proof of the eventual categoricity conjecture from large cardinals [Reference Shelah and VaseySV], and in the full analysis of the categoricity spectrum of AECs with amalgamation [Reference VaseyVas19].
More ambitiously, one can ask when it is possible not only to prove the existence of a model from successive categoricity, but to prove the existence of arbitrarily large models, or even the existence of a unique model in all cardinalities. Another milestone result of Shelah in that direction is [Reference ShelahShe83a, Reference ShelahShe83b]:
Fact 1.5. Assume
![]() $2^{\aleph _n} < 2^{\aleph _{n + 1}}$
for all
$2^{\aleph _n} < 2^{\aleph _{n + 1}}$
for all
![]() $n < \omega $
. If an
$n < \omega $
. If an
![]() $\mathbb {L}_{\omega _1, \omega }$
sentence is categorical in every
$\mathbb {L}_{\omega _1, \omega }$
sentence is categorical in every
![]() $\aleph _n$
, then it is categorical in every infinite cardinal.
$\aleph _n$
, then it is categorical in every infinite cardinal.
This has recently been generalized to AECs by Shelah and the author [Reference Shelah and VaseySV]. An example of Hart and Shelah [Reference Hart and ShelahHS90, Reference Baldwin and KolesnikovBK09] shows that one needs in general to assume categoricity at all
![]() $\aleph _n$
’s to deduce categoricity further up. However, Mazari-Armida and the author [Reference Mazari-Armida and VaseyMAV18] showed that this restriction does not apply to “simple” AECs, and in particular to universal classes (classes of structures closed under isomorphisms, unions of chains, and substructures, see for example [Reference VaseyVas17b]). The reader may argue that there are relatively few interesting examples of universal classes, so let us work in the much broader (but slightly harder to define—see Section 2 for the details) framework of tame AECs with intersections, encompassing multiuniversal classes [Reference Ackerman, Boney and VaseyABV19], and Zilber’s quasiminimal classes [Reference Zilber, Blass and ZhangZil05]:
$\aleph _n$
’s to deduce categoricity further up. However, Mazari-Armida and the author [Reference Mazari-Armida and VaseyMAV18] showed that this restriction does not apply to “simple” AECs, and in particular to universal classes (classes of structures closed under isomorphisms, unions of chains, and substructures, see for example [Reference VaseyVas17b]). The reader may argue that there are relatively few interesting examples of universal classes, so let us work in the much broader (but slightly harder to define—see Section 2 for the details) framework of tame AECs with intersections, encompassing multiuniversal classes [Reference Ackerman, Boney and VaseyABV19], and Zilber’s quasiminimal classes [Reference Zilber, Blass and ZhangZil05]:
Fact 1.6. Assume
![]() $2^{\aleph _0} < 2^{\aleph _1}$
. If
$2^{\aleph _0} < 2^{\aleph _1}$
. If
![]() $\mathbf {K}$
is an AEC with
$\mathbf {K}$
is an AEC with
![]() $\text {LS} (\mathbf {K}) = \aleph _0$
which has intersections, is
$\text {LS} (\mathbf {K}) = \aleph _0$
which has intersections, is
![]() $\aleph _0$
-tame, and is categorical in both
$\aleph _0$
-tame, and is categorical in both
![]() $\aleph _0$
and
$\aleph _0$
and
![]() $\aleph _1$
, then it is categorical in all infinite cardinals.
$\aleph _1$
, then it is categorical in all infinite cardinals.
Proof. By [Reference Boney and VaseyBV19, 3.14],
![]() ${\mathbf {K}}_{\le \aleph _0}$
is analytic, so the result follows from [Reference Mazari-Armida and VaseyMAV18, 4.4]. ⊣
${\mathbf {K}}_{\le \aleph _0}$
is analytic, so the result follows from [Reference Mazari-Armida and VaseyMAV18, 4.4]. ⊣
In the present paper, we aim to prove results along the ones above but in ZFC. The broad idea is to develop a new, local, model theory that relies only on very weak consequences of the compactness theorem. In essence, using cardinal arithmetic makes it “too easy” by allowing set-theoretic tools (such as the weak diamond) to be used instead of model theory. While removing a minor-looking assumption such as “
![]() $2^{\aleph _0} < 2^{\aleph _1}$
” may not seem very impressive, it is the author’s thesis that in fact proving such results in ZFC is much harder and yields to interesting new mathematics.
$2^{\aleph _0} < 2^{\aleph _1}$
” may not seem very impressive, it is the author’s thesis that in fact proving such results in ZFC is much harder and yields to interesting new mathematics.
One specific challenge is that it is harder to obtain amalgamation when one does not assume set-theoretic hypotheses: Shelah [Reference ShelahShe09a, I.3.8] has shown that categoricity in
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda ^+$
implies amalgamation in
$\lambda ^+$
implies amalgamation in
![]() $\lambda $
assuming that
$\lambda $
assuming that
![]() $2^\lambda < 2^{\lambda ^+}$
. However, the set-theoretic hypothesis cannot in general be removed:
$2^\lambda < 2^{\lambda ^+}$
. However, the set-theoretic hypothesis cannot in general be removed:
Example 1.7 ([Reference ShelahShe09a, §I.6])
Assuming Martin’s axiom, there is an AEC (axiomatizable in
![]() $\mathbb {L} (\exists ^{\ge \aleph _1})$
) that is categorical in every cardinal in
$\mathbb {L} (\exists ^{\ge \aleph _1})$
) that is categorical in every cardinal in
![]() $[\aleph _0, 2^{\aleph _0})$
, fails amalgamation everywhere below
$[\aleph _0, 2^{\aleph _0})$
, fails amalgamation everywhere below
![]() $2^{\aleph _0}$
, and has no model of cardinality
$2^{\aleph _0}$
, and has no model of cardinality
![]() $\left (2^{\aleph _0}\right )^+$
.
$\left (2^{\aleph _0}\right )^+$
.
This example leads to the following weakening of Question 1.2, which is also open:
Question 1.8. Assume
![]() $\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
$\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
![]() $\lambda $
, categorical in every cardinal in
$\lambda $
, categorical in every cardinal in
![]() $[\lambda , 2^{\lambda }]$
. Must
$[\lambda , 2^{\lambda }]$
. Must
![]() $\mathbf {K}$
have a model of cardinality
$\mathbf {K}$
have a model of cardinality
![]() $\left (2^\lambda \right )^+$
?
$\left (2^\lambda \right )^+$
?
Similarly, looking at Fact 1.5 suggests that to replace
![]() $\aleph _\omega $
by
$\aleph _\omega $
by
![]() $\beth _\omega $
may be interesting:
$\beth _\omega $
may be interesting:
Question 1.9. Assume
![]() $\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
$\mathbf {K}$
is an AEC with Löwenheim–Skolem–Tarski number
![]() $\lambda $
, categorical in every cardinal in
$\lambda $
, categorical in every cardinal in
![]() $[\lambda , \beth _\omega (\lambda ))$
. Must
$[\lambda , \beth _\omega (\lambda ))$
. Must
![]() $\mathbf {K}$
be categorical everywhere above
$\mathbf {K}$
be categorical everywhere above
![]() $\lambda $
?
$\lambda $
?
The present paper makes the following contributions:
-
(1) By a very short proof, putting together several results of Shelah, we observe (Corollary 3.7) that if
 $\mu> \text {LS} (\mathbf {K})$
is limit and
$\mu> \text {LS} (\mathbf {K})$
is limit and
 $\mathbf {K}$
is categorical everywhere in
$\mathbf {K}$
is categorical everywhere in
 $[\text {LS} (\mathbf {K}), \mu ]$
, then
$[\text {LS} (\mathbf {K}), \mu ]$
, then
 $\mathbf {K}$
has a model of cardinality
$\mathbf {K}$
has a model of cardinality
 $\mu ^+$
. This is a very partial approximation to Questions 1.8 and 1.9, but perhaps it can awaken interest in these general cases again.
$\mu ^+$
. This is a very partial approximation to Questions 1.8 and 1.9, but perhaps it can awaken interest in these general cases again. -
(2) We give a positive answer to Question 1.9 in the special case where
 $\mathbf {K}$
is a tame AEC with intersections (hence in particular when it is a universal class, see Corollary 5.10). This gives a ZFC version of the Facts presented above, and partially answers [Reference Mazari-Armida and VaseyMAV18, Question 4.3] (where we worked near
$\mathbf {K}$
is a tame AEC with intersections (hence in particular when it is a universal class, see Corollary 5.10). This gives a ZFC version of the Facts presented above, and partially answers [Reference Mazari-Armida and VaseyMAV18, Question 4.3] (where we worked near
 $\aleph _1$
and assumed the weak continuum hypothesis, see Fact 1.6). We more generally answer Question 1.9 in the broader framework of tame AECs with weak amalgamation and coherent sequences (see §2 for the definitions):
$\aleph _1$
and assumed the weak continuum hypothesis, see Fact 1.6). We more generally answer Question 1.9 in the broader framework of tame AECs with weak amalgamation and coherent sequences (see §2 for the definitions):Corollary 5.9. Assume
 $\mathbf {K}$
is a
$\mathbf {K}$
is a
 $\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences. If
$\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences. If
 $\mathbf {K}$
is categorical everywhere in
$\mathbf {K}$
is categorical everywhere in
 $[\text {LS} (\mathbf {K}), \beth _\omega (\text {LS} (\mathbf {K})))$
, then
$[\text {LS} (\mathbf {K}), \beth _\omega (\text {LS} (\mathbf {K})))$
, then
 $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
 $\text {LS} (\mathbf {K})$
.
$\text {LS} (\mathbf {K})$
.Interestingly, even in the case of tame AECs with (full) amalgamation, the result is new and not trivial: it was only known [Reference Grossberg and VanDierenGV06c, Reference Grossberg and VanDierenGV06a] in case the AEC also has arbitrarily large models.
The proof of Corollary 5.9 proceeds as follows: we use tameness and the weak amount of amalgamation to build a good
![]() $\beth _\omega (\lambda )$
-frame (we have set
$\beth _\omega (\lambda )$
-frame (we have set
![]() $\lambda := \text {LS} (\mathbf {K})$
). The very rough idea is to follow the construction in [Reference VaseyVas16a] (where amalgamation and arbitrarily large models were assumed), but there are many nontrivial difficulties because of the lack of amalgamation. We develop new, more local tools to get around this. One key is a local character theorem (Lemma 4.6), generalizing [Reference VaseyVas18, 4.12] which was instrumental in studying the stability spectrum for tame AECs. An important problem is how to build “free” (nonsplitting) extensions of types. The notion of a nicely fitrable model (Definition 4.9) is a new definition for a “good” saturated models in this amalgamationless context. In a sense, nicely filtrable models form the bases over which types behave well. They have independent interest and may play a role in future investigations.
$\lambda := \text {LS} (\mathbf {K})$
). The very rough idea is to follow the construction in [Reference VaseyVas16a] (where amalgamation and arbitrarily large models were assumed), but there are many nontrivial difficulties because of the lack of amalgamation. We develop new, more local tools to get around this. One key is a local character theorem (Lemma 4.6), generalizing [Reference VaseyVas18, 4.12] which was instrumental in studying the stability spectrum for tame AECs. An important problem is how to build “free” (nonsplitting) extensions of types. The notion of a nicely fitrable model (Definition 4.9) is a new definition for a “good” saturated models in this amalgamationless context. In a sense, nicely filtrable models form the bases over which types behave well. They have independent interest and may play a role in future investigations.
Once the good frame is built, a known upward transfer of good frames in tame AECs with weak amalgamation (see [Reference BoneyBon14] and [Reference VaseyVas17b, 4.16]) is used to prove that the AEC has arbitrarily large models and eventual amalgamation. After some more work, it then becomes possible to use the result of Grossberg and VanDieren [Reference Grossberg and VanDierenGV06a] showing that in tame AECs with amalgamation and arbitrarily large models, categoricity in two successive cardinals implies categoricity above those cardinals.
We assume the reader has some basic knowledge of AECs (see e.g. [Reference ShelahShe09a, Reference BaldwinBal09, Reference GrossbergGro02]), although we briefly repeat the main definitions in the preliminaries. In the last section, we will also assume some familiarity with the material in [Reference VaseyVas16a] regarding good frames. Other results we use can be regarded as black boxes.
The author would like to thank John T. Baldwin for some interesting discussions (while on a research visit at UIC) that led to §3 of the present paper. The author also thanks Marcos Mazari-Armida and a referee for helpful feedback on this paper.
2 Preliminaries
2.1 Abstract elementary classes
Given a structure M, write
![]() $|M|$
for its universe and
$|M|$
for its universe and
![]() $\|M\|$
for the cardinality of its universe. We usually do not distinguish between M and
$\|M\|$
for the cardinality of its universe. We usually do not distinguish between M and
![]() $|M|$
, writing e.g.
$|M|$
, writing e.g.
![]() $a \in M$
instead of
$a \in M$
instead of
![]() $a \in |M|$
and
$a \in |M|$
and
![]() $A \subseteq M$
instead of
$A \subseteq M$
instead of
![]() $A \subseteq |M|$
. An abstract class is a pair
$A \subseteq |M|$
. An abstract class is a pair
![]() $\mathbf {K} = (K, \le _{\mathbf {K}})$
, where K is a class of structures in a fixed (here will all arities finite) vocabulary
$\mathbf {K} = (K, \le _{\mathbf {K}})$
, where K is a class of structures in a fixed (here will all arities finite) vocabulary
![]() $\tau = \tau (\mathbf {K})$
and
$\tau = \tau (\mathbf {K})$
and
![]() $\le _{\mathbf {K}}$
is a partial order,
$\le _{\mathbf {K}}$
is a partial order,
![]() $M \le _{\mathbf {K}} N$
implies that M is a
$M \le _{\mathbf {K}} N$
implies that M is a
![]() $\tau $
-substructure of N, and both K and
$\tau $
-substructure of N, and both K and
![]() $\le _{\mathbf {K}}$
respect isomorphisms (the definition is due to Grossberg). We often do not distinguish between K (the class of structures) and
$\le _{\mathbf {K}}$
respect isomorphisms (the definition is due to Grossberg). We often do not distinguish between K (the class of structures) and
![]() $\mathbf {K}$
(the ordered class of structures). Any abstract class admits a notion of
$\mathbf {K}$
(the ordered class of structures). Any abstract class admits a notion of
![]() $\mathbf {K}$
-embedding: these are the functions
$\mathbf {K}$
-embedding: these are the functions
![]() $f: M \rightarrow N$
such that
$f: M \rightarrow N$
such that
![]() $f: M \cong f[M]$
and
$f: M \cong f[M]$
and
![]() $f[M] \le _{\mathbf {K}} N$
. Thus one can naturally see
$f[M] \le _{\mathbf {K}} N$
. Thus one can naturally see
![]() $\mathbf {K}$
as a category. Unless explicitly stated, any map
$\mathbf {K}$
as a category. Unless explicitly stated, any map
![]() $f: M \rightarrow N$
in this paper will be a
$f: M \rightarrow N$
in this paper will be a
![]() $\mathbf {K}$
-embedding. We write
$\mathbf {K}$
-embedding. We write
![]() $f: M \xrightarrow [A]{} N$
to mean that f is a
$f: M \xrightarrow [A]{} N$
to mean that f is a
![]() $\mathbf {K}$
-embedding from M into N which fixes the set A pointwise (so
$\mathbf {K}$
-embedding from M into N which fixes the set A pointwise (so
![]() $A \subseteq M$
). We similarly write
$A \subseteq M$
). We similarly write
![]() $f: M \cong _A N$
for isomorphisms from M onto N fixing A.
$f: M \cong _A N$
for isomorphisms from M onto N fixing A.
For
![]() $\lambda $
a cardinal, we will write
$\lambda $
a cardinal, we will write
![]() ${\mathbf {K}}_\lambda $
for the restriction of
${\mathbf {K}}_\lambda $
for the restriction of
![]() $\mathbf {K}$
to models of cardinality
$\mathbf {K}$
to models of cardinality
![]() $\lambda $
. Similarly define
$\lambda $
. Similarly define
![]() ${\mathbf {K}}_{\ge \lambda }$
,
${\mathbf {K}}_{\ge \lambda }$
,
![]() ${\mathbf {K}}_{<\lambda }$
, or more generally
${\mathbf {K}}_{<\lambda }$
, or more generally
![]() ${\mathbf {K}}_{\Theta }$
, where
${\mathbf {K}}_{\Theta }$
, where
![]() $\Theta $
is a class of cardinals.
$\Theta $
is a class of cardinals.
For an abstract class
![]() $\mathbf {K}$
, we denote by
$\mathbf {K}$
, we denote by
![]() $\mathbb {I} (\mathbf {K})$
the number of models in
$\mathbb {I} (\mathbf {K})$
the number of models in
![]() $\mathbf {K}$
up to isomorphism (i.e. the cardinality of
$\mathbf {K}$
up to isomorphism (i.e. the cardinality of
![]() $\mathbf {K} /_{\cong }$
). We write
$\mathbf {K} /_{\cong }$
). We write
![]() $\mathbb {I} (\mathbf {K}, \lambda )$
instead of
$\mathbb {I} (\mathbf {K}, \lambda )$
instead of
![]() $\mathbb {I} ({\mathbf {K}}_\lambda )$
. When
$\mathbb {I} ({\mathbf {K}}_\lambda )$
. When
![]() $\mathbb {I} (\mathbf {K}) = 1$
, we say that
$\mathbb {I} (\mathbf {K}) = 1$
, we say that
![]() $\mathbf {K}$
is categorical. We say that
$\mathbf {K}$
is categorical. We say that
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\lambda $
if
$\lambda $
if
![]() ${\mathbf {K}}_\lambda $
is categorical, i.e.
${\mathbf {K}}_\lambda $
is categorical, i.e.
![]() $\mathbb {I} (\mathbf {K}, \lambda ) = 1$
.
$\mathbb {I} (\mathbf {K}, \lambda ) = 1$
.
We say that
![]() $\mathbf {K}$
has amalgamation if for any
$\mathbf {K}$
has amalgamation if for any
![]() $M_0 \le _{\mathbf {K}} M_\ell $
,
$M_0 \le _{\mathbf {K}} M_\ell $
,
![]() $\ell = 1,2$
, there is
$\ell = 1,2$
, there is
![]() $M_3 \in \mathbf {K}$
and
$M_3 \in \mathbf {K}$
and
![]() $\mathbf {K}$
-embeddings
$\mathbf {K}$
-embeddings
![]() $f_\ell : M_\ell \xrightarrow [M_0]{} M_3$
,
$f_\ell : M_\ell \xrightarrow [M_0]{} M_3$
,
![]() $\ell = 1,2$
.
$\ell = 1,2$
.
![]() $\mathbf {K}$
has joint embedding if any two models can be
$\mathbf {K}$
has joint embedding if any two models can be
![]() $\mathbf {K}$
-embedded in a common model.
$\mathbf {K}$
-embedded in a common model.
![]() $\mathbf {K}$
has no maximal models if for any
$\mathbf {K}$
has no maximal models if for any
![]() $M \in \mathbf {K}$
there exists
$M \in \mathbf {K}$
there exists
![]() $N \in \mathbf {K}$
with
$N \in \mathbf {K}$
with
![]() $M \le _{\mathbf {K}} N$
and
$M \le _{\mathbf {K}} N$
and
![]() $M \neq N$
(we write
$M \neq N$
(we write
![]() $M <_{\mathbf {K}} N$
). Localized concepts such as amalgamation in
$M <_{\mathbf {K}} N$
). Localized concepts such as amalgamation in
![]() $\lambda $
mean that
$\lambda $
mean that
![]() ${\mathbf {K}}_\lambda $
has amalgamation.
${\mathbf {K}}_\lambda $
has amalgamation.
The definition of an abstract elementary class is due to Shelah [Reference Shelah and BaldwinShe87a]:
Definition 2.1. An abstract elementary class (AEC) is an abstract class
![]() $\mathbf {K}$
satisfying:
$\mathbf {K}$
satisfying:
-
(1) Coherence: if
 $M_0, M_1, M_2 \in \mathbf {K}$
,
$M_0, M_1, M_2 \in \mathbf {K}$
,
 $M_0 \subseteq M_1 \le _{\mathbf {K}} M_2$
and
$M_0 \subseteq M_1 \le _{\mathbf {K}} M_2$
and
 $M_0 \le _{\mathbf {K}} M_2$
, then
$M_0 \le _{\mathbf {K}} M_2$
, then
 $M_0 \le _{\mathbf {K}} M_1$
.
$M_0 \le _{\mathbf {K}} M_1$
. -
(2) Tarski-Vaught chain axioms: if
 $\langle M_i : i \in I \rangle $
is a
$\langle M_i : i \in I \rangle $
is a
 $\le _{\mathbf {K}}$
-directed system and
$\le _{\mathbf {K}}$
-directed system and
 $M := \bigcup _{i \in I} M_i$
, then:
$M := \bigcup _{i \in I} M_i$
, then:-
(a)
 $M \in \mathbf {K}$
.
$M \in \mathbf {K}$
. -
(b)
 $M_i \le _{\mathbf {K}} M$
for all
$M_i \le _{\mathbf {K}} M$
for all
 $i \in I$
.
$i \in I$
. -
(c) If
 $N \in \mathbf {K}$
is such that
$N \in \mathbf {K}$
is such that
 $M_i \le _{\mathbf {K}} N$
for all
$M_i \le _{\mathbf {K}} N$
for all
 $i \in I$
, then
$i \in I$
, then
 $M \le _{\mathbf {K}} N$
.
$M \le _{\mathbf {K}} N$
.
-
-
(3) Löwenheim–Skolem–Tarski axiom: there exists a cardinal
 $\lambda \ge |\tau (\mathbf {K})| + \aleph _0$
such that for any
$\lambda \ge |\tau (\mathbf {K})| + \aleph _0$
such that for any
 $N \in \mathbf {K}$
and any
$N \in \mathbf {K}$
and any
 $A \subseteq N$
, there exists
$A \subseteq N$
, there exists
 $M \in \mathbf {K}$
with
$M \in \mathbf {K}$
with
 $M \le _{\mathbf {K}} N$
,
$M \le _{\mathbf {K}} N$
,
 $A \subseteq M$
, and
$A \subseteq M$
, and
 $\|M\| \le |A| + \lambda $
. We write
$\|M\| \le |A| + \lambda $
. We write
 $\text {LS} (\mathbf {K})$
for the least such
$\text {LS} (\mathbf {K})$
for the least such
 $\lambda $
.
$\lambda $
.
2.2 Types
In any abstract class
![]() $\mathbf {K}$
, we can define a semantic notion of type (the definition was first given by Shelah in [Reference Shelah and BaldwinShe87b]). We give the full definition here for convenience, but the reader can also check [Reference VaseyVas16b, 2.16] for more details. First, define a relation
$\mathbf {K}$
, we can define a semantic notion of type (the definition was first given by Shelah in [Reference Shelah and BaldwinShe87b]). We give the full definition here for convenience, but the reader can also check [Reference VaseyVas16b, 2.16] for more details. First, define a relation
![]() $E_{at}$
(atomic equivalence) on the class of triples
$E_{at}$
(atomic equivalence) on the class of triples
![]() $(b, A, N)$
with
$(b, A, N)$
with
![]() $N \in \mathbf {K}$
,
$N \in \mathbf {K}$
,
![]() $A \subseteq N$
, and
$A \subseteq N$
, and
![]() $b \in N$
as follows:
$b \in N$
as follows:
![]() $(b_1, A, N_1) E_{at} (b_2, B, N_2)$
if
$(b_1, A, N_1) E_{at} (b_2, B, N_2)$
if
![]() $A = B$
and there exists
$A = B$
and there exists
![]() $N \in \mathbf {K}$
and
$N \in \mathbf {K}$
and
![]() $\mathbf {K}$
-embeddings
$\mathbf {K}$
-embeddings
![]() $f: N_1 \xrightarrow [A]{} N$
,
$f: N_1 \xrightarrow [A]{} N$
,
![]() $g: N_2 \xrightarrow [A]{} N$
so that
$g: N_2 \xrightarrow [A]{} N$
so that
![]() $f (b_1) = g (b_2)$
. Note that
$f (b_1) = g (b_2)$
. Note that
![]() $E_{at}$
is a symmetric and reflexive relation. Let E denote its transitive closure (if
$E_{at}$
is a symmetric and reflexive relation. Let E denote its transitive closure (if
![]() $\mathbf {K}$
has amalgamation, it is easy to check that
$\mathbf {K}$
has amalgamation, it is easy to check that
![]() $E_{at}$
is in fact already transitive, so
$E_{at}$
is in fact already transitive, so
![]() $E = E_{at}$
in this case). For
$E = E_{at}$
in this case). For
![]() $N \in \mathbf {K}$
,
$N \in \mathbf {K}$
,
![]() $A \subseteq N$
, and
$A \subseteq N$
, and
![]() $b \in N$
, we define the type of b over A in N, written
$b \in N$
, we define the type of b over A in N, written
![]() $\mathbf {tp}_{\mathbf {K}} (b / A; N)$
, to be the E-equivalence class of the triple
$\mathbf {tp}_{\mathbf {K}} (b / A; N)$
, to be the E-equivalence class of the triple
![]() $(b, A, N)$
. Usually
$(b, A, N)$
. Usually
![]() $\mathbf {K}$
will be clear from context and we will omit it from the notation. These semantic types are called Galois (or orbital) types in the literature, but they coincide with the first-order syntactic types in elementary classes (and we will never use syntactic types anyway) so we simply call them “types”. For
$\mathbf {K}$
will be clear from context and we will omit it from the notation. These semantic types are called Galois (or orbital) types in the literature, but they coincide with the first-order syntactic types in elementary classes (and we will never use syntactic types anyway) so we simply call them “types”. For
![]() $M \in \mathbf {K}$
, we write
$M \in \mathbf {K}$
, we write
![]() $\mathbf {S}_{\mathbf {K}} (M) = \mathbf {S} (M)$
for
$\mathbf {S}_{\mathbf {K}} (M) = \mathbf {S} (M)$
for
![]() $\{\mathbf {tp} (b / M; N) \mid M \le _{\mathbf {K}} N\}$
, the classFootnote
2
of all types over M. Also define, for
$\{\mathbf {tp} (b / M; N) \mid M \le _{\mathbf {K}} N\}$
, the classFootnote
2
of all types over M. Also define, for
![]() $M \le _{\mathbf {K}} N$
,
$M \le _{\mathbf {K}} N$
,
![]() $\mathbf {S} (M; N) = \{\mathbf {tp} (b / M; N) \mid b \in N\}$
, the class of all types over M realized inside N. We define in the expected way what it means for a type to extend another type or to take the image of a type by a
$\mathbf {S} (M; N) = \{\mathbf {tp} (b / M; N) \mid b \in N\}$
, the class of all types over M realized inside N. We define in the expected way what it means for a type to extend another type or to take the image of a type by a
![]() $\mathbf {K}$
-embedding. We call a type p algebraic if it can be written as
$\mathbf {K}$
-embedding. We call a type p algebraic if it can be written as
![]() $p = \mathbf {tp} (a / M; N)$
, with
$p = \mathbf {tp} (a / M; N)$
, with
![]() $a \in M$
.
$a \in M$
.
As mentioned before, when
![]() $\mathbf {K}$
is an elementary class,
$\mathbf {K}$
is an elementary class,
![]() $\mathbf {tp} (b / A; N)$
contains the same information as the usual notion of
$\mathbf {tp} (b / A; N)$
contains the same information as the usual notion of
![]() $\mathbb {L}_{\omega , \omega }$
-syntactic type. In particular, types in an elementary class are determined by their restrictions to finite sets. In [Reference Grossberg and VanDierenGV06b], this fact was built into the following definition: for
$\mathbb {L}_{\omega , \omega }$
-syntactic type. In particular, types in an elementary class are determined by their restrictions to finite sets. In [Reference Grossberg and VanDierenGV06b], this fact was built into the following definition: for
![]() $\chi $
an infinite cardinal, an abstract class
$\chi $
an infinite cardinal, an abstract class
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $(<\chi )$
-tame if for any
$(<\chi )$
-tame if for any
![]() $M \in \mathbf {K}$
and any distinct
$M \in \mathbf {K}$
and any distinct
![]() $p, q \in \mathbf {S} (M)$
, there exists
$p, q \in \mathbf {S} (M)$
, there exists
![]() $A \subseteq M$
such that
$A \subseteq M$
such that
![]() $|A| < \chi $
and
$|A| < \chi $
and
![]() $p \upharpoonright A \neq q \upharpoonright A$
. We say that
$p \upharpoonright A \neq q \upharpoonright A$
. We say that
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\chi $
-tame if it is
$\chi $
-tame if it is
![]() $(<\chi ^+)$
-tame. Thus elementary classes are
$(<\chi ^+)$
-tame. Thus elementary classes are
![]() $(<\aleph _0)$
-tame, but there are examples of nontame AECs, see e.g. [Reference Boney, Vasey and IovinoBV17a, 3.2.2].
$(<\aleph _0)$
-tame, but there are examples of nontame AECs, see e.g. [Reference Boney, Vasey and IovinoBV17a, 3.2.2].
2.3 Weak amalgamation, intersections, and coherent sequences of types
Weak amalgamation was first introduced in [Reference VaseyVas17b, 4.11]. It can be seen as a common weakening of amalgamation and having certain kinds of prime models.
Definition 2.2. Let
![]() $\mathbf {K}$
be an abstract class and let
$\mathbf {K}$
be an abstract class and let
![]() $M \in \mathbf {K}$
. We say that M is a weak amalgamation base (in
$M \in \mathbf {K}$
. We say that M is a weak amalgamation base (in
![]() $\mathbf {K}$
) if for any
$\mathbf {K}$
) if for any
![]() $N_1, N_2 \in \mathbf {K}$
with
$N_1, N_2 \in \mathbf {K}$
with
![]() $M \le _{\mathbf {K}} N_1$
,
$M \le _{\mathbf {K}} N_1$
,
![]() $M \le _{\mathbf {K}} N_2$
, and any
$M \le _{\mathbf {K}} N_2$
, and any
![]() $a_1 \in N_1$
,
$a_1 \in N_1$
,
![]() $a_2 \in N_2$
, if
$a_2 \in N_2$
, if
![]() $\mathbf {tp} (a_1 / M; N_1) = \mathbf {tp} (a_2 / M; N_2)$
, then there exists
$\mathbf {tp} (a_1 / M; N_1) = \mathbf {tp} (a_2 / M; N_2)$
, then there exists
![]() $N_1^0, N_2^{\prime }, f$
such that:
$N_1^0, N_2^{\prime }, f$
such that:
-
(1)
 $M \le _{\mathbf {K}} N_1^0 \le _{\mathbf {K}} N_1$
.
$M \le _{\mathbf {K}} N_1^0 \le _{\mathbf {K}} N_1$
. -
(2)
 $a_1 \in N_1^0$
.
$a_1 \in N_1^0$
. -
(3)
 $N_2 \le _{\mathbf {K}} N_2^{\prime }$
.
$N_2 \le _{\mathbf {K}} N_2^{\prime }$
. -
(4)
 $f: N_1^0 \xrightarrow [M]{} N_2^{\prime }$
.
$f: N_1^0 \xrightarrow [M]{} N_2^{\prime }$
. -
(5)
 $f (a_1) = a_2$
.
$f (a_1) = a_2$
.
We say that
![]() $\mathbf {K}$
has weak amalgamation if every object of
$\mathbf {K}$
has weak amalgamation if every object of
![]() $\mathbf {K}$
is a weak amalgamation base.
$\mathbf {K}$
is a weak amalgamation base.
Note that amalgamation implies weak amalgamation (see Fact 2.5 below). Another example of abstract classes with weak amalgamation are those that have intersections:
Definition 2.3. An abstract class
![]() $\mathbf {K}$
has intersections if for any
$\mathbf {K}$
has intersections if for any
![]() $N \in \mathbf {K}$
and any
$N \in \mathbf {K}$
and any
![]() $A \subseteq N$
, the set
$A \subseteq N$
, the set
![]() $\bigcap \{M \in \mathbf {K} \mid M \le _{\mathbf {K}} N, A \subseteq M\}$
induces a
$\bigcap \{M \in \mathbf {K} \mid M \le _{\mathbf {K}} N, A \subseteq M\}$
induces a
![]() $\mathbf {K}$
-substructure of N. We write
$\mathbf {K}$
-substructure of N. We write
![]() $\operatorname {cl}^N (A)$
for this substructure.
$\operatorname {cl}^N (A)$
for this substructure.
Remark 2.4. By [Reference Baldwin and ShelahBS08, 1.3] or [Reference VaseyVas17b, 2.18], in an abstract class with intersections,
![]() $\mathbf {tp} (a_1 / M; N_1) = \mathbf {tp} (a_2 / M; N_2)$
if and only if there exists an isomorphism
$\mathbf {tp} (a_1 / M; N_1) = \mathbf {tp} (a_2 / M; N_2)$
if and only if there exists an isomorphism
![]() $f: \operatorname {cl}^{N_1} (a_1 M) \cong _M \operatorname {cl}^{N_2} (a_2 M)$
such that
$f: \operatorname {cl}^{N_1} (a_1 M) \cong _M \operatorname {cl}^{N_2} (a_2 M)$
such that
![]() $f (a_1) = a_2$
. In particular, abstract classes with intersections have weak amalgamation.
$f (a_1) = a_2$
. In particular, abstract classes with intersections have weak amalgamation.
The following characterizes when weak amalgamation implies amalgamation.
Fact 2.5 ([Reference VaseyVas17b, 4.14])
Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\lambda \ge \text {LS} (\mathbf {K})$
. The following are equivalent:
$\lambda \ge \text {LS} (\mathbf {K})$
. The following are equivalent:
-
(1)
 ${\mathbf {K}}_\lambda $
has weak amalgamation and for any
${\mathbf {K}}_\lambda $
has weak amalgamation and for any
 $M \le _{\mathbf {K}} N$
both in
$M \le _{\mathbf {K}} N$
both in
 ${\mathbf {K}}_\lambda $
, any
${\mathbf {K}}_\lambda $
, any
 $p \in \mathbf {S} (M)$
can be extended to a type in
$p \in \mathbf {S} (M)$
can be extended to a type in
 $\mathbf {S} (N)$
.
$\mathbf {S} (N)$
. -
(2)
 ${\mathbf {K}}_\lambda $
has amalgamation.
${\mathbf {K}}_\lambda $
has amalgamation.
The definitions below are well known in AECs with amalgamation, see [Reference BaldwinBal09, §11].
Definition 2.6. Let
![]() $\mathbf {K}$
be an abstract class,
$\mathbf {K}$
be an abstract class,
![]() $\bar {M} = \langle M_i : i < \alpha \rangle $
be increasing continuous, and let
$\bar {M} = \langle M_i : i < \alpha \rangle $
be increasing continuous, and let
![]() $\bar {p} = \langle p_i : i < \alpha \rangle $
be an increasing chain of types with
$\bar {p} = \langle p_i : i < \alpha \rangle $
be an increasing chain of types with
![]() $p_i \in \mathbf {S} (M_i)$
for all
$p_i \in \mathbf {S} (M_i)$
for all
![]() $i < \alpha $
.
$i < \alpha $
.
-
(1) We say that
 $\bar {p}$
is local if for any limit
$\bar {p}$
is local if for any limit
 $i < \alpha $
and any
$i < \alpha $
and any
 $q \in \mathbf {S} (M_i)$
, if
$q \in \mathbf {S} (M_i)$
, if
 $q \upharpoonright M_j = p_j$
for all
$q \upharpoonright M_j = p_j$
for all
 $j < i$
, then
$j < i$
, then
 $q = p_i$
. We say that
$q = p_i$
. We say that
 $\bar {M}$
is local if any increasing chain of types
$\bar {M}$
is local if any increasing chain of types
 $\bar {p}$
as above is local.
$\bar {p}$
as above is local. -
(2) We say that
 $\bar {p}$
is coherent if there exists
$\bar {p}$
is coherent if there exists
 $\langle N_i : i < \alpha \rangle $
increasing continuous,
$\langle N_i : i < \alpha \rangle $
increasing continuous,
 $\langle a_i : i < \alpha \rangle $
, and
$\langle a_i : i < \alpha \rangle $
, and
 $\langle f_{ij} : i \le j < \alpha \rangle $
such that for all
$\langle f_{ij} : i \le j < \alpha \rangle $
such that for all
 $i \le j \le k < \alpha $
:
$i \le j \le k < \alpha $
:-
(a)
 $M_i \le _{\mathbf {K}} N_i$
.
$M_i \le _{\mathbf {K}} N_i$
. -
(b)
 $a_i \in N_i$
.
$a_i \in N_i$
. -
(c)
 $p_i = \mathbf {tp} (a_i / M_i; N_i)$
.
$p_i = \mathbf {tp} (a_i / M_i; N_i)$
. -
(d)
 $f_{ij} : N_i \xrightarrow [M_i]{} N_{j}$
.
$f_{ij} : N_i \xrightarrow [M_i]{} N_{j}$
. -
(e)
 $f_{ii} = \text {id}_{N_i}$
.
$f_{ii} = \text {id}_{N_i}$
. -
(f)
 $f_{jk} \circ f_{ij} = f_{ik}$
.
$f_{jk} \circ f_{ij} = f_{ik}$
. -
(g)
 $f_{ij} (a_i) = a_{j}$
.
$f_{ij} (a_i) = a_{j}$
.
-
We say that
![]() $\bar {M}$
is coherent if any local
$\bar {M}$
is coherent if any local
![]() $\bar {p}$
as above is coherent. Finally, we say that
$\bar {p}$
as above is coherent. Finally, we say that
![]() $\mathbf {K}$
has coherent sequences if any
$\mathbf {K}$
has coherent sequences if any
![]() $\bar {M}$
as above is coherent.
$\bar {M}$
as above is coherent.
The following is immediate from the definitions (take a directed colimit). See [Reference BaldwinBal09, 11.5].
Fact 2.7. Let
![]() $\mathbf {K}$
be an AEC. Let
$\mathbf {K}$
be an AEC. Let
![]() $\delta $
be a limit ordinal, let
$\delta $
be a limit ordinal, let
![]() $\bar {M} = \langle M_i : i < \delta \rangle $
be increasing continuous in
$\bar {M} = \langle M_i : i < \delta \rangle $
be increasing continuous in
![]() $\mathbf {K}$
, and let
$\mathbf {K}$
, and let
![]() $\bar {p} = \langle p_i : i < \delta \rangle $
be an increasing chain of types with
$\bar {p} = \langle p_i : i < \delta \rangle $
be an increasing chain of types with
![]() $p_i \in \mathbf {S} (M_i)$
for all
$p_i \in \mathbf {S} (M_i)$
for all
![]() $i < \delta $
. If
$i < \delta $
. If
![]() $\bar {p}$
is coherent, then there exists
$\bar {p}$
is coherent, then there exists
![]() $q \in \mathbf {S} (\bigcup _{i < \delta } M_i)$
so that
$q \in \mathbf {S} (\bigcup _{i < \delta } M_i)$
so that
![]() $q \upharpoonright M_i = q_i$
for all
$q \upharpoonright M_i = q_i$
for all
![]() $i < \delta $
.
$i < \delta $
.
We finish by proving some easy results about building coherent sequences of types: it can be done assuming amalgamation or assuming the AEC has intersections.
Lemma 2.8. Let
![]() $\mathbf {K}$
be an AEC. Let
$\mathbf {K}$
be an AEC. Let
![]() $\delta $
be a limit ordinal, let
$\delta $
be a limit ordinal, let
![]() $\bar {M} = \langle M_i : i < \delta \rangle $
be increasing continuous in
$\bar {M} = \langle M_i : i < \delta \rangle $
be increasing continuous in
![]() $\mathbf {K}$
, and let
$\mathbf {K}$
, and let
![]() $\bar {p} = \langle p_i : i < \delta \rangle $
be an increasing chain of types with
$\bar {p} = \langle p_i : i < \delta \rangle $
be an increasing chain of types with
![]() $p_i \in \mathbf {S} (M_i)$
for all
$p_i \in \mathbf {S} (M_i)$
for all
![]() $i < \delta $
. Assume that
$i < \delta $
. Assume that
![]() $\bar {p}$
is local.
$\bar {p}$
is local.
-
(1) If
 ${\mathbf {K}}_{<\mathrm {sup}_{i < \delta }(\|M_i\| + \text {LS} (\mathbf {K}))^+}$
has amalgamation, then
${\mathbf {K}}_{<\mathrm {sup}_{i < \delta }(\|M_i\| + \text {LS} (\mathbf {K}))^+}$
has amalgamation, then
 $\bar {p}$
is coherent.
$\bar {p}$
is coherent. -
(2) If
 $\mathbf {K}$
has intersections, then
$\mathbf {K}$
has intersections, then
 $\bar {p}$
is coherent.
$\bar {p}$
is coherent.
In particular, AECs with amalgamation and AECs with intersections both have coherent sequences.
-
(1) Straightforward and well known. See the proof of [Reference BaldwinBal09, 11.5].
-
(2) We build the coherence witnesses
 $\langle N_i : i < \alpha \rangle $
,
$\langle N_i : i < \alpha \rangle $
,
 $\langle a_i : i < \alpha \rangle $
,
$\langle a_i : i < \alpha \rangle $
,
 $\langle f_{ij} : i \le j < \alpha \rangle $
inductively such that for all
$\langle f_{ij} : i \le j < \alpha \rangle $
inductively such that for all
 $i < \alpha $
,
$i < \alpha $
,
 $N_i = \operatorname {cl}^{N_i} (M_i a_i)$
. The base case is trivial, and at limits we can take directed colimits (and use locality to see type equality is preserved; the closure condition will be preserved by finite character of the closure operator [Reference VaseyVas17b, 2.14(6)]). At successors, we are given
$N_i = \operatorname {cl}^{N_i} (M_i a_i)$
. The base case is trivial, and at limits we can take directed colimits (and use locality to see type equality is preserved; the closure condition will be preserved by finite character of the closure operator [Reference VaseyVas17b, 2.14(6)]). At successors, we are given
 $N_i$
and
$N_i$
and
 $a_i$
and want to build
$a_i$
and want to build
 $N_{i + 1}$
,
$N_{i + 1}$
,
 $a_{i + 1}$
, and
$a_{i + 1}$
, and
 $f_{i(i + 1)}$
. Pick
$f_{i(i + 1)}$
. Pick
 $N_{i + 1}^{\prime }$
and
$N_{i + 1}^{\prime }$
and
 $a_{i + 1}$
such that
$a_{i + 1}$
such that
 $p_{i + 1} = \mathbf {tp} (a_{i + 1} / M_{i + 1}; N_{i + 1}^{\prime })$
. Then
$p_{i + 1} = \mathbf {tp} (a_{i + 1} / M_{i + 1}; N_{i + 1}^{\prime })$
. Then
 $p_{i + 1} \upharpoonright M_i = p_i$
, so there exists an isomorphism
$p_{i + 1} \upharpoonright M_i = p_i$
, so there exists an isomorphism
 $f_{i} : N_i \cong \operatorname {cl}^{N_{i + 1}^{\prime }} (M_i a_{i + 1})$
such that
$f_{i} : N_i \cong \operatorname {cl}^{N_{i + 1}^{\prime }} (M_i a_{i + 1})$
such that
 $f (a_i) = a_{i + 1}$
. Let
$f (a_i) = a_{i + 1}$
. Let
 $N_{i + 1} := \operatorname {cl}^{N_{i + 1}^{\prime }} (M_{i + 1} a_{i + 1})$
. By the coherence axiom of AECs,
$N_{i + 1} := \operatorname {cl}^{N_{i + 1}^{\prime }} (M_{i + 1} a_{i + 1})$
. By the coherence axiom of AECs,
 $\operatorname {cl}^{N_{i + 1}^{\prime }} (M_i a_{i + 1}) \le _{\mathbf {K}} N_{i + 1}$
. Thus composing
$\operatorname {cl}^{N_{i + 1}^{\prime }} (M_i a_{i + 1}) \le _{\mathbf {K}} N_{i + 1}$
. Thus composing
 $f_i$
with the inclusion gives the desired
$f_i$
with the inclusion gives the desired
 $\mathbf {K}$
-embedding
$\mathbf {K}$
-embedding
 $f_{i(i + 1)}$
of
$f_{i(i + 1)}$
of
 $N_i$
into
$N_i$
into
 $N_{i + 1}$
.
$N_{i + 1}$
.
⊣
3 Existence from successive categoricity below a limit
In this section, we work in an arbitrary AEC (i.e. we do not assume tameness or weak amalgamation) and prove some relatively easy results about deriving no maximal models from categoricity below a limit.
The following easy observation will be used in the later sections:
Lemma 3.1. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a limit cardinal of countable cofinality. If
$\mu> \text {LS} (\mathbf {K})$
be a limit cardinal of countable cofinality. If
![]() $\mathbf {K}$
is categorical in unboundedly-many cardinals below
$\mathbf {K}$
is categorical in unboundedly-many cardinals below
![]() $\mu $
, then
$\mu $
, then
![]() ${\mathbf {K}}_\mu \neq \emptyset $
.
${\mathbf {K}}_\mu \neq \emptyset $
.
Proof. Since
![]() $\mu $
has countable cofinality, we can pick
$\mu $
has countable cofinality, we can pick
![]() $\langle \mu _i : i < \omega \rangle $
increasing cofinal in
$\langle \mu _i : i < \omega \rangle $
increasing cofinal in
![]() $\mu $
such that
$\mu $
such that
![]() $\mu _0 \ge \text {LS} (\mathbf {K})$
and
$\mu _0 \ge \text {LS} (\mathbf {K})$
and
![]() $\mu _i$
is a categoricity cardinal for each
$\mu _i$
is a categoricity cardinal for each
![]() $i < \omega $
. Now we build an increasing chain
$i < \omega $
. Now we build an increasing chain
![]() $\langle M_i : i < \omega \rangle $
such that
$\langle M_i : i < \omega \rangle $
such that
![]() $M_i \in {\mathbf {K}}_{\mu _i}$
for all
$M_i \in {\mathbf {K}}_{\mu _i}$
for all
![]() $i < \omega $
. Then the union of the chain will be in
$i < \omega $
. Then the union of the chain will be in
![]() ${\mathbf {K}}_\mu $
. For
${\mathbf {K}}_\mu $
. For
![]() $i = 0$
, take any
$i = 0$
, take any
![]() $M_0 \in {\mathbf {K}}_{\mu _0}$
. For
$M_0 \in {\mathbf {K}}_{\mu _0}$
. For
![]() $i = j + 1$
, given
$i = j + 1$
, given
![]() $M_j$
, first pick any
$M_j$
, first pick any
![]() $N_i \in {\mathbf {K}}_{\mu _i}$
. Pick
$N_i \in {\mathbf {K}}_{\mu _i}$
. Pick
![]() $N_i^0 \le _{\mathbf {K}} N_i$
with
$N_i^0 \le _{\mathbf {K}} N_i$
with
![]() $N_i^0 \in {\mathbf {K}}_{\mu _j}$
. By categoricity, there is an isomorphism
$N_i^0 \in {\mathbf {K}}_{\mu _j}$
. By categoricity, there is an isomorphism
![]() $f: N_i^0 \cong M_j$
. With some renaming, we can extend this isomorphism to
$f: N_i^0 \cong M_j$
. With some renaming, we can extend this isomorphism to
![]() $g: N_i \cong M_i$
, for some
$g: N_i \cong M_i$
, for some
![]() $M_i$
with
$M_i$
with
![]() $M_j \le _{\mathbf {K}} M_i$
. Then
$M_j \le _{\mathbf {K}} M_i$
. Then
![]() $M_i \in {\mathbf {K}}_{\mu _i}$
, as desired. ⊣
$M_i \in {\mathbf {K}}_{\mu _i}$
, as desired. ⊣
The next two definitions are due to Shelah [Reference ShelahShe01].
Definition 3.2. An existence triple in an abstract class
![]() $\mathbf {K}$
is a triple
$\mathbf {K}$
is a triple
![]() $(a, M, N)$
with
$(a, M, N)$
with
![]() $M \le _{\mathbf {K}} N$
both in
$M \le _{\mathbf {K}} N$
both in
![]() $\mathbf {K}$
and
$\mathbf {K}$
and
![]() $a \in N \backslash M$
.
$a \in N \backslash M$
.
Definition 3.3. We say an abstract class
![]() $\mathbf {K}$
has weak extension if for any existence triple in
$\mathbf {K}$
has weak extension if for any existence triple in
![]() $(a, M, N)$
in
$(a, M, N)$
in
![]() $\mathbf {K}$
, there exists an existence triple
$\mathbf {K}$
, there exists an existence triple
![]() $(b, M', N')$
in
$(b, M', N')$
in
![]() $\mathbf {K}$
with
$\mathbf {K}$
with
![]() $a = b$
,
$a = b$
,
![]() $M <_{\mathbf {K}} M'$
, and
$M <_{\mathbf {K}} M'$
, and
![]() $N <_{\mathbf {K}} N'$
. We say that
$N <_{\mathbf {K}} N'$
. We say that
![]() $(b, M', N')$
is a strict extension of
$(b, M', N')$
is a strict extension of
![]() $(a, M, N)$
.
$(a, M, N)$
.
The next two results are essentially due to Shelah, see [Reference ShelahShe09a, §VI.1]. We give full proofs here because they are short and (for the second one) slightly simpler than Shelah’s.
Lemma 3.4. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
. If:
$\mu> \text {LS} (\mathbf {K})$
. If:
-
(1) There exists an existence triple in
 ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
.
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
. -
(2) For every
 $\lambda \in [\text {LS} (\mathbf {K}), \mu )$
,
$\lambda \in [\text {LS} (\mathbf {K}), \mu )$
,
 ${\mathbf {K}}_\lambda $
has weak extension.
${\mathbf {K}}_\lambda $
has weak extension.
Then not every element of
![]() ${\mathbf {K}}_\mu $
is maximal.
${\mathbf {K}}_\mu $
is maximal.
Proof. Pick an existence triple
![]() $(a, M, N)$
in
$(a, M, N)$
in
![]() ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
. Now build
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
. Now build
![]() $\langle M_i : i \le \mu \rangle $
,
$\langle M_i : i \le \mu \rangle $
,
![]() $\langle N_i : i \le \mu \rangle $
both increasing continuous such that for every
$\langle N_i : i \le \mu \rangle $
both increasing continuous such that for every
![]() $i < \mu $
:
$i < \mu $
:
-
(1)
 $M_0 = M$
,
$M_0 = M$
,
 $N_0 = N$
.
$N_0 = N$
. -
(2)
 $M_i, N_i \in {\mathbf {K}}_{|i| + \text {LS} (\mathbf {K})}$
.
$M_i, N_i \in {\mathbf {K}}_{|i| + \text {LS} (\mathbf {K})}$
. -
(3)
 $M_i \le _{\mathbf {K}} N_i$
.
$M_i \le _{\mathbf {K}} N_i$
. -
(4)
 $a \in N_i \backslash M_i$
.
$a \in N_i \backslash M_i$
. -
(5)
 $M_{i} <_{\mathbf {K}} M_{i + 1}$
.
$M_{i} <_{\mathbf {K}} M_{i + 1}$
.
This is possible using the weak extension property at successor stages and taking unions at limit stages. In the end,
![]() $M_\mu <_{\mathbf {K}} N_\mu $
, since
$M_\mu <_{\mathbf {K}} N_\mu $
, since
![]() $a \in N_\mu \backslash M_\mu $
. Thus
$a \in N_\mu \backslash M_\mu $
. Thus
![]() $M_\mu $
is not maximal. Since
$M_\mu $
is not maximal. Since
![]() $\langle M_i : i \le \mu \rangle $
was strictly increasing,
$\langle M_i : i \le \mu \rangle $
was strictly increasing,
![]() $M_\mu \in {\mathbf {K}}_\mu $
.⊣
$M_\mu \in {\mathbf {K}}_\mu $
.⊣
Lemma 3.5. Let
![]() $\mathbf {K}$
be an AEC. If
$\mathbf {K}$
be an AEC. If
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\text {LS} (\mathbf {K})$
and
$\text {LS} (\mathbf {K})$
and
![]() ${\mathbf {K}}_{\text {LS} (\mathbf {K})^+}$
has no maximal models, then
${\mathbf {K}}_{\text {LS} (\mathbf {K})^+}$
has no maximal models, then
![]() ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has weak extension.
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has weak extension.
Proof. Let
![]() $\lambda := \text {LS} (\mathbf {K})$
. Let
$\lambda := \text {LS} (\mathbf {K})$
. Let
![]() $(a, M, N)$
be an existence triple in
$(a, M, N)$
be an existence triple in
![]() ${\mathbf {K}}_{\lambda }$
. We want to find a strict extension of
${\mathbf {K}}_{\lambda }$
. We want to find a strict extension of
![]() $(a, M, N)$
. We build
$(a, M, N)$
. We build
![]() $\langle M_i : i \le \lambda ^+ \rangle $
increasing continuous and
$\langle M_i : i \le \lambda ^+ \rangle $
increasing continuous and
![]() $\langle a_i : i < \lambda ^+ \rangle $
such that for all
$\langle a_i : i < \lambda ^+ \rangle $
such that for all
![]() $i < \lambda ^+$
:
$i < \lambda ^+$
:
-
(1)
 $(a_i, M_i, M_{i + 1})$
is an existence triple in
$(a_i, M_i, M_{i + 1})$
is an existence triple in
 ${\mathbf {K}}_{\lambda }$
.
${\mathbf {K}}_{\lambda }$
. -
(2) There exists an isomorphism
 $f_i : N\hspace{-1.5pt} \cong\hspace{-1.5pt} M_{i + 1}$
so that
$f_i : N\hspace{-1.5pt} \cong\hspace{-1.5pt} M_{i + 1}$
so that
 $f_i[M]\hspace{-1.5pt} = \hspace{-1.5pt}M_i$
and
$f_i[M]\hspace{-1.5pt} = \hspace{-1.5pt}M_i$
and
 $f_i (a)\hspace{-1.5pt} =\hspace{-1.5pt} a_i$
.
$f_i (a)\hspace{-1.5pt} =\hspace{-1.5pt} a_i$
.
This is possible by categoricity. This is enough: since
![]() ${\mathbf {K}}_{\lambda ^+}$
has no maximal models, there exists
${\mathbf {K}}_{\lambda ^+}$
has no maximal models, there exists
![]() $M' \in {\mathbf {K}}_{\lambda ^+}$
with
$M' \in {\mathbf {K}}_{\lambda ^+}$
with
![]() $M_{\lambda ^+} <_{\mathbf {K}} M'$
. Let
$M_{\lambda ^+} <_{\mathbf {K}} M'$
. Let
![]() $\langle M_i^{\prime } : i \le \lambda ^+ \rangle $
be an increasing continuous resolution of
$\langle M_i^{\prime } : i \le \lambda ^+ \rangle $
be an increasing continuous resolution of
![]() $M'$
. Let
$M'$
. Let
![]() $C \subseteq \lambda ^+$
be a club such that
$C \subseteq \lambda ^+$
be a club such that
![]() $i \in C$
implies
$i \in C$
implies
![]() $M_i \le _{\mathbf {K}} M_i^{\prime }$
and moreover
$M_i \le _{\mathbf {K}} M_i^{\prime }$
and moreover
![]() $M_{\lambda ^+} \cap M_i^{\prime } = M_i$
. Pick
$M_{\lambda ^+} \cap M_i^{\prime } = M_i$
. Pick
![]() $b \in M' \backslash M_{\lambda ^+}$
and pick
$b \in M' \backslash M_{\lambda ^+}$
and pick
![]() $i \in C$
so that
$i \in C$
so that
![]() $b \in M_i^{\prime }$
. Then
$b \in M_i^{\prime }$
. Then
![]() $M_i <_{\mathbf {K}} M_i^{\prime }$
and one can pick
$M_i <_{\mathbf {K}} M_i^{\prime }$
and one can pick
![]() $j < \lambda ^+$
so that
$j < \lambda ^+$
so that
![]() $M_{i + 1} <_{\mathbf {K}} M_j^{\prime }$
. Then
$M_{i + 1} <_{\mathbf {K}} M_j^{\prime }$
. Then
![]() $(a_i, M_i^{\prime }, M_j^{\prime })$
is a strict extension of
$(a_i, M_i^{\prime }, M_j^{\prime })$
is a strict extension of
![]() $(a_i, M_i, M_{i + 1})$
. Taking an isomorphic copy, we obtain a strict extension of the original triple
$(a_i, M_i, M_{i + 1})$
. Taking an isomorphic copy, we obtain a strict extension of the original triple
![]() $(a, M, N)$
.⊣
$(a, M, N)$
.⊣
Putting the two lemmas together, we obtain:
Theorem 3.6. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a limit cardinal. If
$\mu> \text {LS} (\mathbf {K})$
be a limit cardinal. If
![]() $\mathbf {K}$
is categorical in every cardinal in
$\mathbf {K}$
is categorical in every cardinal in
![]() $[\text {LS} (\mathbf {K}), \mu )$
, then not every element of
$[\text {LS} (\mathbf {K}), \mu )$
, then not every element of
![]() ${\mathbf {K}}_\mu $
is maximal.
${\mathbf {K}}_\mu $
is maximal.
Proof. Note that for every
![]() $\lambda \in [\text {LS} (\mathbf {K}), \mu )$
, both
$\lambda \in [\text {LS} (\mathbf {K}), \mu )$
, both
![]() ${\mathbf {K}}_{\lambda }$
and
${\mathbf {K}}_{\lambda }$
and
![]() ${\mathbf {K}}_{\lambda ^+}$
are not empty and have no maximal models (we are using that
${\mathbf {K}}_{\lambda ^+}$
are not empty and have no maximal models (we are using that
![]() $\mu $
is limit to deduce this for
$\mu $
is limit to deduce this for
![]() ${\mathbf {K}}_{\lambda ^+}$
). In particular, there is an existence triple in
${\mathbf {K}}_{\lambda ^+}$
). In particular, there is an existence triple in
![]() ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
. Moreover by Lemma 3.5 (applied to
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
. Moreover by Lemma 3.5 (applied to
![]() ${\mathbf {K}}_{\ge \lambda }$
), for any
${\mathbf {K}}_{\ge \lambda }$
), for any
![]() $\lambda \in [\text {LS} (\mathbf {K}), \mu )$
,
$\lambda \in [\text {LS} (\mathbf {K}), \mu )$
,
![]() ${\mathbf {K}}_\lambda $
has the weak extension property. By Lemma 3.4, we get the result. ⊣
${\mathbf {K}}_\lambda $
has the weak extension property. By Lemma 3.4, we get the result. ⊣
Corollary 3.7. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a limit cardinal. If
$\mu> \text {LS} (\mathbf {K})$
be a limit cardinal. If
![]() $\mathbf {K}$
is categorical in every cardinal in
$\mathbf {K}$
is categorical in every cardinal in
![]() $[\text {LS} (\mathbf {K}), \mu ]$
, then
$[\text {LS} (\mathbf {K}), \mu ]$
, then
![]() ${\mathbf {K}}_{\mu ^+} \neq \emptyset $
.
${\mathbf {K}}_{\mu ^+} \neq \emptyset $
.
Proof. By Theorem 3.6, not every model in
![]() ${\mathbf {K}}_\mu $
is maximal. By categoricity in
${\mathbf {K}}_\mu $
is maximal. By categoricity in
![]() $\mu $
, this implies that
$\mu $
, this implies that
![]() ${\mathbf {K}}_\mu $
has no maximal models, hence that
${\mathbf {K}}_\mu $
has no maximal models, hence that
![]() ${\mathbf {K}}_{\mu ^+} \neq \emptyset $
. ⊣
${\mathbf {K}}_{\mu ^+} \neq \emptyset $
. ⊣
4 Local saturation and splitting
The present section is the core of the paper. We adapt known results about saturated models and splitting to setups without amalgamation (but often with weak amalgamation and/or tameness). For several results, categoricity is not needed, but in the end we will use it to put everything together.
The following are localized definitions of the well known variations of saturation:
Definition 4.1. Let
![]() $\mathbf {K}$
be an AEC. For
$\mathbf {K}$
be an AEC. For
![]() $\theta $
an infinite cardinal, a model M is locally
$\theta $
an infinite cardinal, a model M is locally
![]() $\theta $
- saturated if for any
$\theta $
- saturated if for any
![]() $N \ge _{\mathbf {K}} M$
and any
$N \ge _{\mathbf {K}} M$
and any
![]() $A \subseteq M$
with
$A \subseteq M$
with
![]() $|A| < \theta $
, we have that
$|A| < \theta $
, we have that
![]() $\mathbf {S} (A; N) = \mathbf {S} (A; M)$
. For
$\mathbf {S} (A; N) = \mathbf {S} (A; M)$
. For
![]() $M_0 \le _{\mathbf {K}} M$
, we say that M is locally
$M_0 \le _{\mathbf {K}} M$
, we say that M is locally
![]() $\theta $
- universal over
$\theta $
- universal over
![]() $M_0$
if for any
$M_0$
if for any
![]() $M_0 \le _{\mathbf {K}} N_0 \le _{\mathbf {K}} N$
with
$M_0 \le _{\mathbf {K}} N_0 \le _{\mathbf {K}} N$
with
![]() $M \le _{\mathbf {K}} N$
and
$M \le _{\mathbf {K}} N$
and
![]() $\|N_0\| < \theta $
,
$\|N_0\| < \theta $
,
![]() $N_0$
embeds into M over
$N_0$
embeds into M over
![]() $M_0$
. M is locally
$M_0$
. M is locally
![]() $\theta $
- model-homogeneous if it is
$\theta $
- model-homogeneous if it is
![]() $\theta $
-universal over
$\theta $
-universal over
![]() $M_0$
for any
$M_0$
for any
![]() $M_0 \le _{\mathbf {K}} M$
with
$M_0 \le _{\mathbf {K}} M$
with
![]() $\|M_0\| < \theta $
. We say that M is locally saturated when it is locally
$\|M_0\| < \theta $
. We say that M is locally saturated when it is locally
![]() $\|M\|$
-saturated, and similarly for locally model-homogeneous. We say that M is locally universal over
$\|M\|$
-saturated, and similarly for locally model-homogeneous. We say that M is locally universal over
![]() $M_0$
if it is locally
$M_0$
if it is locally
![]() $\|M_0\|^+$
-universal over
$\|M_0\|^+$
-universal over
![]() $M_0$
.
$M_0$
.
The usual exhaustion argument shows that locally model-homogeneous model can be built assuming some cardinal arithmetic. See for example the proof of [Reference RosickýRos97, Theorem 1].
Fact 4.2. Let
![]() $\mathbf {K}$
be an AEC. For any
$\mathbf {K}$
be an AEC. For any
![]() $M \in \mathbf {K}$
and any regular cardinal
$M \in \mathbf {K}$
and any regular cardinal
![]() $\theta> \text {LS} (\mathbf {K})$
, there exists
$\theta> \text {LS} (\mathbf {K})$
, there exists
![]() $N \in \mathbf {K}$
such that
$N \in \mathbf {K}$
such that
![]() $M \le _{\mathbf {K}} N$
, N is locally
$M \le _{\mathbf {K}} N$
, N is locally
![]() $\theta $
-model-homogeneous, and
$\theta $
-model-homogeneous, and
![]() $\|N\| \le \|M\|^{<\theta }$
.
$\|N\| \le \|M\|^{<\theta }$
.
Assuming categoricity in a suitable unbounded set, we can build locally model-homogeneous models.
Lemma 4.3. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal. If for every
$\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal. If for every
![]() $\theta < \mu $
there exists
$\theta < \mu $
there exists
![]() $\lambda < \mu $
such that
$\lambda < \mu $
such that
![]() $\lambda = \lambda ^\theta $
and
$\lambda = \lambda ^\theta $
and
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\lambda $
, then every object of
$\lambda $
, then every object of
![]() ${\mathbf {K}}_\mu $
is locally model-homogeneous.
${\mathbf {K}}_\mu $
is locally model-homogeneous.
Proof. Let
![]() $M \in {\mathbf {K}}_\mu $
. Fix
$M \in {\mathbf {K}}_\mu $
. Fix
![]() $\theta < \mu $
,
$\theta < \mu $
,
![]() $N \in {\mathbf {K}}_\mu $
with
$N \in {\mathbf {K}}_\mu $
with
![]() $M \le _{\mathbf {K}} N$
, and
$M \le _{\mathbf {K}} N$
, and
![]() $M_0, N_0 \in {\mathbf {K}}_{\le \theta }$
with
$M_0, N_0 \in {\mathbf {K}}_{\le \theta }$
with
![]() $M_0 \le _{\mathbf {K}} M$
,
$M_0 \le _{\mathbf {K}} M$
,
![]() $M_0 \le _{\mathbf {K}} N_0 \le _{\mathbf {K}} N$
. We have to see that
$M_0 \le _{\mathbf {K}} N_0 \le _{\mathbf {K}} N$
. We have to see that
![]() $N_0$
embeds inside M over
$N_0$
embeds inside M over
![]() $M_0$
. Without loss of generality,
$M_0$
. Without loss of generality,
![]() $\theta \ge \text {LS} (\mathbf {K})$
. By assumption, we can pick a categoricity cardinal
$\theta \ge \text {LS} (\mathbf {K})$
. By assumption, we can pick a categoricity cardinal
![]() $\lambda < \mu $
such that
$\lambda < \mu $
such that
![]() $\lambda = \lambda ^\theta $
. Let
$\lambda = \lambda ^\theta $
. Let
![]() $M_0^{\prime } \le _{\mathbf {K}} M$
be such that
$M_0^{\prime } \le _{\mathbf {K}} M$
be such that
![]() $M_0 \le _{\mathbf {K}} M_0^{\prime }$
and
$M_0 \le _{\mathbf {K}} M_0^{\prime }$
and
![]() $M_0^{\prime } \in {\mathbf {K}}_{\lambda }$
. By categoricity in
$M_0^{\prime } \in {\mathbf {K}}_{\lambda }$
. By categoricity in
![]() $\lambda $
and Fact 4.2,
$\lambda $
and Fact 4.2,
![]() $M_0^{\prime }$
is locally
$M_0^{\prime }$
is locally
![]() $\theta ^+$
-model-homogeneous. In particular,
$\theta ^+$
-model-homogeneous. In particular,
![]() $N_0$
embeds into
$N_0$
embeds into
![]() $M_0^{\prime }$
over
$M_0^{\prime }$
over
![]() $M_0$
. Thus
$M_0$
. Thus
![]() $N_0$
embeds into M over
$N_0$
embeds into M over
![]() $M_0$
, as desired. ⊣
$M_0$
, as desired. ⊣
The following notion was introduced by Shelah [Reference ShelahShe99, 3.2] for AECs with amalgamation.
Definition 4.4 (Splitting)
Let
![]() $\mathbf {K}$
be an AEC, let
$\mathbf {K}$
be an AEC, let
![]() $N \in \mathbf {K}$
,
$N \in \mathbf {K}$
,
![]() $A \subseteq N$
, let
$A \subseteq N$
, let
![]() $p \in \mathbf {S} (N)$
, and let
$p \in \mathbf {S} (N)$
, and let
![]() $\theta $
be an infinite cardinal with
$\theta $
be an infinite cardinal with
![]() $|A| < \theta $
. We say that
$|A| < \theta $
. We say that
![]() $p (<\theta )$
- splits over A if there exists
$p (<\theta )$
- splits over A if there exists
![]() $M_1, M_2 \in {\mathbf {K}}_{<\theta }$
such that
$M_1, M_2 \in {\mathbf {K}}_{<\theta }$
such that
![]() $A \subseteq M_\ell \le _{\mathbf {K}} N$
for
$A \subseteq M_\ell \le _{\mathbf {K}} N$
for
![]() $\ell = 1,2$
and
$\ell = 1,2$
and
![]() $f: M_1 \cong _A M_2$
so that
$f: M_1 \cong _A M_2$
so that
![]() $f (p \upharpoonright M_1) \neq p \upharpoonright M_2$
. We say that
$f (p \upharpoonright M_1) \neq p \upharpoonright M_2$
. We say that
![]() $p \theta $
- splits over A if it
$p \theta $
- splits over A if it
![]() $(<\theta ^+)$
-splits over A. We say that p splits over A if it
$(<\theta ^+)$
-splits over A. We say that p splits over A if it
![]() $(|A| + \aleph _0)$
-splits over A.
$(|A| + \aleph _0)$
-splits over A.
Remark 4.5. Let
![]() $N \in \mathbf {K}$
,
$N \in \mathbf {K}$
,
![]() $A \subseteq N$
, let
$A \subseteq N$
, let
![]() $p \in \mathbf {S} (N)$
and let
$p \in \mathbf {S} (N)$
and let
![]() $\theta $
be an infinite cardinal with
$\theta $
be an infinite cardinal with
![]() $|A| < \theta $
. If
$|A| < \theta $
. If
![]() $p (<\theta )$
-splits over A, then there exists
$p (<\theta )$
-splits over A, then there exists
![]() $N_0 \le _{\mathbf {K}} N$
with
$N_0 \le _{\mathbf {K}} N$
with
![]() $A \subseteq N_0$
and
$A \subseteq N_0$
and
![]() $\|N_0\| < \theta $
such that
$\|N_0\| < \theta $
such that
![]() $p \upharpoonright N_0 (<\theta )$
-splits over A.
$p \upharpoonright N_0 (<\theta )$
-splits over A.
The following is a generalization of [Reference VaseyVas18, 4.12].
Lemma 4.6 (Local character)
Let
![]() $\mathbf {K}$
be an AEC, let
$\mathbf {K}$
be an AEC, let
![]() $M \in {\mathbf {K}}_{\ge \aleph _0}$
, let
$M \in {\mathbf {K}}_{\ge \aleph _0}$
, let
![]() $\delta $
be a regular cardinal, and let
$\delta $
be a regular cardinal, and let
![]() $\langle A_i : i \le \delta \rangle $
be an increasing continuous chain of sets with
$\langle A_i : i \le \delta \rangle $
be an increasing continuous chain of sets with
![]() $A_\delta = M$
. Let
$A_\delta = M$
. Let
![]() $\theta $
be either
$\theta $
be either
![]() $\|M\|^+$
or
$\|M\|^+$
or
![]() $\mathrm {sup}_{i < \delta } |A_i|^+$
. Let
$\mathrm {sup}_{i < \delta } |A_i|^+$
. Let
![]() $p \in \mathbf {S} (M)$
. If there exists a regular
$p \in \mathbf {S} (M)$
. If there exists a regular
![]() $\chi \le \|M\|$
such that:
$\chi \le \|M\|$
such that:
-
(1)
 ${\mathbf {K}}_{<\theta }$
is
${\mathbf {K}}_{<\theta }$
is
 $(<\chi )$
-tame.
$(<\chi )$
-tame. -
(2) M is locally
 $(\chi + \delta ^+)$
-saturated.
$(\chi + \delta ^+)$
-saturated.
Then there exists
![]() $i < \delta $
such that p does not
$i < \delta $
such that p does not
![]() $(<\theta )$
-split over
$(<\theta )$
-split over
![]() $A_i$
.
$A_i$
.
Proof. Suppose not. Then for each
![]() $i < \delta $
, there exists
$i < \delta $
, there exists
![]() $M_i^1, M_i^2 \in {\mathbf {K}}_{<\theta }$
and
$M_i^1, M_i^2 \in {\mathbf {K}}_{<\theta }$
and
![]() $f_i : M_i^1 \cong _{A_i} M_i^2$
so that
$f_i : M_i^1 \cong _{A_i} M_i^2$
so that
![]() $A_i \subseteq M_i^\ell \le _{\mathbf {K}} M$
,
$A_i \subseteq M_i^\ell \le _{\mathbf {K}} M$
,
![]() $\ell = 1,2$
and
$\ell = 1,2$
and
![]() $f_i (p \upharpoonright M_i^1) \neq p \upharpoonright M_i^2$
.
$f_i (p \upharpoonright M_i^1) \neq p \upharpoonright M_i^2$
.
By
![]() $(<\chi )$
-tameness, we can find
$(<\chi )$
-tameness, we can find
![]() $A_i^1 \subseteq M_i^1$
of cardinality strictly less than
$A_i^1 \subseteq M_i^1$
of cardinality strictly less than
![]() $\chi $
so that
$\chi $
so that
![]() $f_i (p \upharpoonright A_i^1) \neq p \upharpoonright A_i^2$
(we have set
$f_i (p \upharpoonright A_i^1) \neq p \upharpoonright A_i^2$
(we have set
![]() $A_i^2 := f_i[A_i^1])$
.
$A_i^2 := f_i[A_i^1])$
.
Let
![]() $A := \bigcup _{i < \delta } (A_i^1 \cup A_i^2)$
. Recall that p is realized in an extension of M. Moreover, if
$A := \bigcup _{i < \delta } (A_i^1 \cup A_i^2)$
. Recall that p is realized in an extension of M. Moreover, if
![]() $\delta < \chi $
then
$\delta < \chi $
then
![]() $|A| < \chi $
and if
$|A| < \chi $
and if
![]() $\delta \ge \chi $
then
$\delta \ge \chi $
then
![]() $|A| \le \delta $
. In either case, M is locally
$|A| \le \delta $
. In either case, M is locally
![]() $|A|^+$
-saturated, so
$|A|^+$
-saturated, so
![]() $p \upharpoonright A$
is realized in M, say by a. Since
$p \upharpoonright A$
is realized in M, say by a. Since
![]() $\delta $
is a limit ordinal, there exists
$\delta $
is a limit ordinal, there exists
![]() $i < \delta $
such that
$i < \delta $
such that
![]() $a \in A_i$
. Now, fix an extension
$a \in A_i$
. Now, fix an extension
![]() $g_i : M \cong M'$
of
$g_i : M \cong M'$
of
![]() $f_i$
(so
$f_i$
(so
![]() $M_i^2 \le _{\mathbf {K}} M'$
). We have:
$M_i^2 \le _{\mathbf {K}} M'$
). We have:
Where we have used that
![]() $g_i$
fixes
$g_i$
fixes
![]() $A_i$
, so
$A_i$
, so
![]() $g_i (a) = a$
. On the other hand, since
$g_i (a) = a$
. On the other hand, since
![]() $A_i^2 \subseteq A$
,
$A_i^2 \subseteq A$
,
Finally, observe that
![]() $M_i^2 \le _{\mathbf {K}} M$
and
$M_i^2 \le _{\mathbf {K}} M$
and
![]() $M_i^2 \le _{\mathbf {K}} M'$
by construction. Therefore since
$M_i^2 \le _{\mathbf {K}} M'$
by construction. Therefore since
![]() $a \in A_i \subseteq M_i^2$
,
$a \in A_i \subseteq M_i^2$
,
![]() $\mathbf {tp} (a / A_i^2; M') = \mathbf {tp} (a / A_i^2; M_i^2) = \mathbf {tp} (a / A_i^2; M)$
. We have shown that
$\mathbf {tp} (a / A_i^2; M') = \mathbf {tp} (a / A_i^2; M_i^2) = \mathbf {tp} (a / A_i^2; M)$
. We have shown that
![]() $f_i (p \upharpoonright A_i^1) = p \upharpoonright A_i^2$
, contradicting the definition of
$f_i (p \upharpoonright A_i^1) = p \upharpoonright A_i^2$
, contradicting the definition of
![]() $A_i^1, A_i^2$
, and
$A_i^1, A_i^2$
, and
![]() $f_i$
.⊣
$f_i$
.⊣
We now generalize the weak uniqueness and extension properties of splitting first isolated by VanDieren [Reference VanDierenVan06, I.4.10].
Lemma 4.7 (Weak uniqueness)
Let
![]() $M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} N$
all be in
$M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} N$
all be in
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
. Let
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
. Let
![]() $p, q \in \mathbf {S} (N)$
. If
$p, q \in \mathbf {S} (N)$
. If
![]() $M_1$
is locally universal over
$M_1$
is locally universal over
![]() $M_0$
, p and q both do not split over
$M_0$
, p and q both do not split over
![]() $M_0$
, and
$M_0$
, and
![]() $p \upharpoonright M_1 = q \upharpoonright M_1$
, then
$p \upharpoonright M_1 = q \upharpoonright M_1$
, then
![]() $p \upharpoonright A = q \upharpoonright A$
for any
$p \upharpoonright A = q \upharpoonright A$
for any
![]() $A \subseteq N$
with
$A \subseteq N$
with
![]() $|A| \le \|M_0\|$
.
$|A| \le \|M_0\|$
.
Proof. Fix
![]() $A \subseteq N$
with
$A \subseteq N$
with
![]() $|A| \le \|M_0\|$
. Pick
$|A| \le \|M_0\|$
. Pick
![]() $N_0 \le _{\mathbf {K}} N$
with
$N_0 \le _{\mathbf {K}} N$
with
![]() $A \subseteq N_0$
and
$A \subseteq N_0$
and
![]() $\|N_0\| \le \|M_0\|$
. Since
$\|N_0\| \le \|M_0\|$
. Since
![]() $M_1$
is locally universal over
$M_1$
is locally universal over
![]() $M_0$
, there exists
$M_0$
, there exists
![]() $f: N_0 \xrightarrow [M_0]{} M_1$
. By the definition of nonsplitting (where
$f: N_0 \xrightarrow [M_0]{} M_1$
. By the definition of nonsplitting (where
![]() $M_1, M_2$
there stand for
$M_1, M_2$
there stand for
![]() $N_0$
,
$N_0$
,
![]() $f[N_0]$
here), we must have that
$f[N_0]$
here), we must have that
![]() $f (p \upharpoonright N_0) = p \upharpoonright f[N_0]$
and
$f (p \upharpoonright N_0) = p \upharpoonright f[N_0]$
and
![]() $f (q \upharpoonright N_0) = q \upharpoonright f[N_0]$
. Since
$f (q \upharpoonright N_0) = q \upharpoonright f[N_0]$
. Since
![]() $p \upharpoonright M_1 = q \upharpoonright M_1$
,
$p \upharpoonright M_1 = q \upharpoonright M_1$
,
![]() $f \upharpoonright f[N_0] = q \upharpoonright f[N_0]$
. Therefore
$f \upharpoonright f[N_0] = q \upharpoonright f[N_0]$
. Therefore
![]() $f (p \upharpoonright N_0) = f (q \upharpoonright N_0)$
, hence
$f (p \upharpoonright N_0) = f (q \upharpoonright N_0)$
, hence
![]() $p \upharpoonright N_0 = q \upharpoonright N_0$
. ⊣
$p \upharpoonright N_0 = q \upharpoonright N_0$
. ⊣
Lemma 4.8 (Weak extension)
Let
![]() $M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} M$
all be in
$M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} M$
all be in
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
and let
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
and let
![]() $p \in \mathbf {S} (M)$
. Let
$p \in \mathbf {S} (M)$
. Let
![]() $N_0 \in \mathbf {K}$
be such that
$N_0 \in \mathbf {K}$
be such that
![]() $M_1 \le _{\mathbf {K}} N_0$
. If:
$M_1 \le _{\mathbf {K}} N_0$
. If:
-
(1) p does not split over
 $M_0$
.
$M_0$
. -
(2)
 $N_0$
embeds into M over
$N_0$
embeds into M over
 $M_1$
.
$M_1$
.
Then there exists
![]() $q_0 \in \mathbf {S} (N_0)$
such that
$q_0 \in \mathbf {S} (N_0)$
such that
![]() $q_0$
extends
$q_0$
extends
![]() $p \upharpoonright M_1$
and
$p \upharpoonright M_1$
and
![]() $q_0$
does not split over
$q_0$
does not split over
![]() $M_0$
. Moreover, if p is not algebraic then
$M_0$
. Moreover, if p is not algebraic then
![]() $q_0$
can be taken to be nonalgebraic.
$q_0$
can be taken to be nonalgebraic.
Proof. Use the hypothesis to fix
![]() $f: N_0 \xrightarrow [M_1]{} M$
. Let
$f: N_0 \xrightarrow [M_1]{} M$
. Let
![]() $q_0 := f^{-1} (p \upharpoonright f[N_0])$
. By invariance,
$q_0 := f^{-1} (p \upharpoonright f[N_0])$
. By invariance,
![]() $q_0$
does not split over
$q_0$
does not split over
![]() $M_0$
and
$M_0$
and
![]() $q_0 \upharpoonright M_1 = p \upharpoonright M_1$
. To see the moreover part, assume that
$q_0 \upharpoonright M_1 = p \upharpoonright M_1$
. To see the moreover part, assume that
![]() $q_0$
is algebraic. Then
$q_0$
is algebraic. Then
![]() $p \upharpoonright f[N_0]$
is algebraic, hence p is algebraic. ⊣
$p \upharpoonright f[N_0]$
is algebraic, hence p is algebraic. ⊣
We now work toward improving the statement of weak extension. Roughly, we would like to prove that if M is model-homogeneous and N is an extension of M of the same cardinality, then types over M have nonsplitting extensions over N. This is not immediate from Lemma 4.8 because without amalgamation we do not know whether N embeds into M. Instead, we will first build small approximations of the type we want to build, and then use tameness and existence of coherent sequences of types to take the limit of these approximations. The following technical definition will be key (one can think of it as a replacement for the notion of a “good saturated model”—or limit model—in this context, see Remark 4.10):
Definition 4.9. Let
![]() $\mathbf {K}$
be an AEC. We call
$\mathbf {K}$
be an AEC. We call
![]() $N \in \mathbf {K}$
nicely filtrable over M if there exists a limit ordinal
$N \in \mathbf {K}$
nicely filtrable over M if there exists a limit ordinal
![]() $\delta $
and an increasing continuous chain
$\delta $
and an increasing continuous chain
![]() $\bar {N} = \langle N_i : i < \delta \rangle $
such that:
$\bar {N} = \langle N_i : i < \delta \rangle $
such that:
-
(1)
 $N = \bigcup _{i < \delta } N_i$
,
$N = \bigcup _{i < \delta } N_i$
,
 $N_0 = M$
.
$N_0 = M$
. -
(2)
 $\|N_i\| < \|N\|$
for all
$\|N_i\| < \|N\|$
for all
 $i < \delta $
.
$i < \delta $
. -
(3)
 $N_{i + 1}$
is locally universal over
$N_{i + 1}$
is locally universal over
 $N_i$
for all
$N_i$
for all
 $i < \delta $
.
$i < \delta $
. -
(4)
 $\bar {N}$
is local and coherent (Definition 2.6).
$\bar {N}$
is local and coherent (Definition 2.6). -
(5) For any
 $p \in \mathbf {S} (\bigcup _{i < \delta } N_i)$
, there exists
$p \in \mathbf {S} (\bigcup _{i < \delta } N_i)$
, there exists
 $i < \delta $
so that p does not split over
$i < \delta $
so that p does not split over
 $N_i$
.
$N_i$
.
We call
![]() $\langle N_i : i < \delta \rangle $
a nice filtration of N (over M).
$\langle N_i : i < \delta \rangle $
a nice filtration of N (over M).
Remark 4.10. It is not clear whether in general if N is nicely filtrable over M, then N is nicely filtrable over any
![]() $M'$
with
$M'$
with
![]() $\|M'\| < \|N\|$
, although this seems to happen in reasonable cases. For example, if
$\|M'\| < \|N\|$
, although this seems to happen in reasonable cases. For example, if
![]() $\mathbf {K}$
is the class of models of a superstable first-order theory T (ordered by elementary substructure), then a model N is nicely filtrable (over some base) if and only if it is saturated. This holds even if T is only stable with
$\mathbf {K}$
is the class of models of a superstable first-order theory T (ordered by elementary substructure), then a model N is nicely filtrable (over some base) if and only if it is saturated. This holds even if T is only stable with
![]() $\text {cf} (\|N\|) \ge \kappa (T)$
, and generalizes (in high-enough cardinals) to tame AECs with amalgamation, see for example [Reference VaseyVas18, §6].
$\text {cf} (\|N\|) \ge \kappa (T)$
, and generalizes (in high-enough cardinals) to tame AECs with amalgamation, see for example [Reference VaseyVas18, §6].
From categoricity in a suitable unbounded set of cardinals below a strong limit of countable cofinality
![]() $\mu $
, we can get nice filtrations. Note that Lemma 3.1 tells us that from the hypotheses of Lemma 4.11 there will be a model in
$\mu $
, we can get nice filtrations. Note that Lemma 3.1 tells us that from the hypotheses of Lemma 4.11 there will be a model in
![]() ${\mathbf {K}}_\mu $
.
${\mathbf {K}}_\mu $
.
Lemma 4.11. Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal of countable cofinality. If:
$\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal of countable cofinality. If:
-
(1) For any
 $\theta < \mu $
there exists
$\theta < \mu $
there exists
 $\lambda < \mu $
such that
$\lambda < \mu $
such that
 $\lambda = \lambda ^\theta $
and
$\lambda = \lambda ^\theta $
and
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\lambda $
.
$\lambda $
. -
(2)
 ${\mathbf {K}}_{<\mu }$
is
${\mathbf {K}}_{<\mu }$
is
 $\text {LS} (\mathbf {K})$
-tame.
$\text {LS} (\mathbf {K})$
-tame. -
(3)
 ${\mathbf {K}}_{<\mu }$
has coherent sequences.
${\mathbf {K}}_{<\mu }$
has coherent sequences.
Then for any
![]() $N \in {\mathbf {K}}_{\mu }$
and any
$N \in {\mathbf {K}}_{\mu }$
and any
![]() $M \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}),\mu )}$
with
$M \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}),\mu )}$
with
![]() $M \le _{\mathbf {K}} N$
, N is nicely filtrable over M.
$M \le _{\mathbf {K}} N$
, N is nicely filtrable over M.
Proof. Let
![]() $N \in {\mathbf {K}}_{\mu }$
and let
$N \in {\mathbf {K}}_{\mu }$
and let
![]() $M \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}), \mu )}$
with
$M \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}), \mu )}$
with
![]() $M \le _{\mathbf {K}} N$
. Pick an increasing sequence
$M \le _{\mathbf {K}} N$
. Pick an increasing sequence
![]() $\langle \mu _i : i < \omega \rangle $
cofinal in
$\langle \mu _i : i < \omega \rangle $
cofinal in
![]() $\mu $
with
$\mu $
with
![]() $\|M\| \le \mu _0$
and so that for any
$\|M\| \le \mu _0$
and so that for any
![]() $i < \omega $
,
$i < \omega $
,
![]() $\mu _{i + 1}^{\mu _i} = \mu _{i + 1}$
and
$\mu _{i + 1}^{\mu _i} = \mu _{i + 1}$
and
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\mu _i$
. This is possible by assumption. By increasing M if needed, we can assume without loss of generality that
$\mu _i$
. This is possible by assumption. By increasing M if needed, we can assume without loss of generality that
![]() $M \in {\mathbf {K}}_{\mu _0}$
. Now pick any increasing sequence
$M \in {\mathbf {K}}_{\mu _0}$
. Now pick any increasing sequence
![]() $\langle N_i : i < \omega \rangle $
such that
$\langle N_i : i < \omega \rangle $
such that
![]() $N_0 = M$
,
$N_0 = M$
,
![]() $\bigcup _{i < \omega } N_i = N$
, and
$\bigcup _{i < \omega } N_i = N$
, and
![]() $N_i \in {\mathbf {K}}_{\mu _i}$
for all
$N_i \in {\mathbf {K}}_{\mu _i}$
for all
![]() $i < \omega $
. We claim this is a nice filtration of N over M.
$i < \omega $
. We claim this is a nice filtration of N over M.
As in the proof of Lemma 4.3, for any
![]() $i < \omega $
,
$i < \omega $
,
![]() $N_{i + 1}$
is locally universal over
$N_{i + 1}$
is locally universal over
![]() $N_i$
. Also,
$N_i$
. Also,
![]() $\bar {N} = \langle N_i : i < \omega \rangle $
is trivially local since there are no limit ordinals below
$\bar {N} = \langle N_i : i < \omega \rangle $
is trivially local since there are no limit ordinals below
![]() $\omega $
. Furthermore,
$\omega $
. Furthermore,
![]() $\bar {N}$
is coherent because by assumption
$\bar {N}$
is coherent because by assumption
![]() ${\mathbf {K}}_{<\mu }$
has coherent sequences. Finally, pick
${\mathbf {K}}_{<\mu }$
has coherent sequences. Finally, pick
![]() $p \in \mathbf {S} (N)$
. Note that by Lemma 4.3, N is locally model-homogeneous, hence locally saturated. Thus Lemma 4.6 (where
$p \in \mathbf {S} (N)$
. Note that by Lemma 4.3, N is locally model-homogeneous, hence locally saturated. Thus Lemma 4.6 (where
![]() $\delta , \chi $
there stands for
$\delta , \chi $
there stands for
![]() $\omega , \text {LS} (\mathbf {K})^+$
here) implies there exists
$\omega , \text {LS} (\mathbf {K})^+$
here) implies there exists
![]() $i < \omega $
so that p does not split over
$i < \omega $
so that p does not split over
![]() $N_i$
. ⊣
$N_i$
. ⊣
From the existence of nice filtrations, we can now prove the desired extension property:
Lemma 4.12 (Extension)
Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} M \le _{\mathbf {K}} N$
all be in
$M_0 \le _{\mathbf {K}} M_1 \le _{\mathbf {K}} M \le _{\mathbf {K}} N$
all be in
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
. Let
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
. Let
![]() $p \in \mathbf {S} (M)$
. If:
$p \in \mathbf {S} (M)$
. If:
-
(1) p does not split over
 $M_0$
.
$M_0$
. -
(2)
 $M_1$
is locally universal over
$M_1$
is locally universal over
 $M_0$
.
$M_0$
. -
(3) M is
 $(\|M\|)$
-locally universal over
$(\|M\|)$
-locally universal over
 $M_1$
.
$M_1$
. -
(4)
 $\|N\| = \|M\|$
.
$\|N\| = \|M\|$
. -
(5) N is nicely filtrable over
 $M_1$
.
$M_1$
. -
(6)
 ${\mathbf {K}}_{\le \|N\|}$
is
${\mathbf {K}}_{\le \|N\|}$
is
 $\|M_0\|$
-tame.
$\|M_0\|$
-tame.
Then there exists
![]() $q \in \mathbf {S} (N)$
which extends p and does not split over
$q \in \mathbf {S} (N)$
which extends p and does not split over
![]() $M_0$
. Moreover, q is not algebraic if p is not algebraic.
$M_0$
. Moreover, q is not algebraic if p is not algebraic.
Proof. Fix
![]() $\bar {N} = \langle N_i : i < \delta \rangle $
a nice filtration of N over
$\bar {N} = \langle N_i : i < \delta \rangle $
a nice filtration of N over
![]() $M_1$
. For
$M_1$
. For
![]() $i < \delta $
, let
$i < \delta $
, let
![]() $q_i \in \mathbf {S} (N_i)$
be as given by weak extension: it extends
$q_i \in \mathbf {S} (N_i)$
be as given by weak extension: it extends
![]() $p \upharpoonright M_1$
and does not split over
$p \upharpoonright M_1$
and does not split over
![]() $M_0$
. Moreover it is nonalgebraic if p is nonalgebraic. By weak uniqueness (and tameness),
$M_0$
. Moreover it is nonalgebraic if p is nonalgebraic. By weak uniqueness (and tameness),
![]() $q_j \upharpoonright N_i = q_i$
for
$q_j \upharpoonright N_i = q_i$
for
![]() $i < j < \delta $
. By Fact 2.7, there exists
$i < j < \delta $
. By Fact 2.7, there exists
![]() $q \in \mathbf {S} (N)$
such that
$q \in \mathbf {S} (N)$
such that
![]() $q \upharpoonright N_i = q_i$
for all
$q \upharpoonright N_i = q_i$
for all
![]() $i < \delta $
. Note that q cannot be algebraic if all the
$i < \delta $
. Note that q cannot be algebraic if all the
![]() $q_i$
’s are nonalgebraic. By the properties of
$q_i$
’s are nonalgebraic. By the properties of
![]() $\bar {N}$
, there exists
$\bar {N}$
, there exists
![]() $i < \delta $
so that q does not split over
$i < \delta $
so that q does not split over
![]() $N_i$
.
$N_i$
.
Claim: q does not split over
![]() $M_0$
.
$M_0$
.
Proof of Claim: By Remark 4.5, it suffices to see that
![]() $q \upharpoonright N_0^{\prime }$
does not split over
$q \upharpoonright N_0^{\prime }$
does not split over
![]() $M_0$
for any
$M_0$
for any
![]() $N_0^{\prime } \in {\mathbf {K}}_{<\|N\|}$
with
$N_0^{\prime } \in {\mathbf {K}}_{<\|N\|}$
with
![]() $N_{i + 1} \le _{\mathbf {K}} N_0^{\prime } \le _{\mathbf {K}} N$
. So let
$N_{i + 1} \le _{\mathbf {K}} N_0^{\prime } \le _{\mathbf {K}} N$
. So let
![]() $q_0^{\prime } \in \mathbf {S} (N_0^{\prime })$
be as given by weak extension (extending
$q_0^{\prime } \in \mathbf {S} (N_0^{\prime })$
be as given by weak extension (extending
![]() $p \upharpoonright M_1$
and not splitting over
$p \upharpoonright M_1$
and not splitting over
![]() $M_0$
). By weak uniqueness,
$M_0$
). By weak uniqueness,
![]() $q_0^{\prime } \upharpoonright N_{i + 1} = q_{i + 1}$
. Since q does not split over
$q_0^{\prime } \upharpoonright N_{i + 1} = q_{i + 1}$
. Since q does not split over
![]() $N_i$
,
$N_i$
,
![]() $q \upharpoonright N_0^{\prime }$
does not split over
$q \upharpoonright N_0^{\prime }$
does not split over
![]() $N_i$
. By monotonicity, also
$N_i$
. By monotonicity, also
![]() $q_0^{\prime }$
does not split over
$q_0^{\prime }$
does not split over
![]() $N_i$
. By weak uniqueness again (recalling that by definition
$N_i$
. By weak uniqueness again (recalling that by definition
![]() $N_{i + 1}$
is locally universal over
$N_{i + 1}$
is locally universal over
![]() $N_i$
),
$N_i$
),
![]() $q_0^{\prime } = q \upharpoonright N_0^{\prime }$
. In particular,
$q_0^{\prime } = q \upharpoonright N_0^{\prime }$
. In particular,
![]() $q \upharpoonright N_0^{\prime }$
does not split over
$q \upharpoonright N_0^{\prime }$
does not split over
![]() $M_0$
.⊣
$M_0$
.⊣
Now since
![]() $q \upharpoonright M_1 = p \upharpoonright M_1$
, weak uniqueness and tameness imply that
$q \upharpoonright M_1 = p \upharpoonright M_1$
, weak uniqueness and tameness imply that
![]() $q \upharpoonright M = p$
, as desired. ⊣
$q \upharpoonright M = p$
, as desired. ⊣
5 Good frames and the main theorem
We use the tools of the previous section to build a good frame, a local forking-like notion. We assume some familiarity with good frames (see [Reference ShelahShe09a, Chapter 2]) here. We will use the definition and notation from [Reference VaseyVas16a, §2.4] (which we do not repeat here). Recall that a
![]() $\text {good}^{-S} \lambda $
-frame is a good frame, except that it may fail the symmetry property. The following key result tells us that good frame can be transferred up in tame AECs with weak amalgamation:
$\text {good}^{-S} \lambda $
-frame is a good frame, except that it may fail the symmetry property. The following key result tells us that good frame can be transferred up in tame AECs with weak amalgamation:
Fact 5.1. Let
![]() $\mathfrak {s}$
be a
$\mathfrak {s}$
be a
![]() $\text {good}^{-S} \lambda $
-frame on an AEC
$\text {good}^{-S} \lambda $
-frame on an AEC
![]() $\mathbf {K}$
. If
$\mathbf {K}$
. If
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\lambda $
-tame and has weak amalgamation, then
$\lambda $
-tame and has weak amalgamation, then
![]() $\mathfrak {s}$
is a good
$\mathfrak {s}$
is a good
![]() $\lambda $
-frame and extends to a good
$\lambda $
-frame and extends to a good
![]() $[\lambda , \infty )$
-frame on all of
$[\lambda , \infty )$
-frame on all of
![]() ${\mathbf {K}}_{\ge \lambda }$
. In particular,
${\mathbf {K}}_{\ge \lambda }$
. In particular,
![]() ${\mathbf {K}}_{\ge \lambda }$
has amalgamation and arbitrarily large models.
${\mathbf {K}}_{\ge \lambda }$
has amalgamation and arbitrarily large models.
Proof. By [Reference VaseyVas17b, 4.16],
![]() ${\mathbf {K}}_{\ge \lambda }$
has amalgamation. By [Reference BoneyBon14],
${\mathbf {K}}_{\ge \lambda }$
has amalgamation. By [Reference BoneyBon14],
![]() $\mathfrak {s}$
extends to a
$\mathfrak {s}$
extends to a
![]() $\text {good}^{-S} [\lambda , \infty )$
-frame
$\text {good}^{-S} [\lambda , \infty )$
-frame
![]() $\mathfrak {t}$
on
$\mathfrak {t}$
on
![]() $\mathbf {K}$
. By [Reference VaseyVas16a, 6.14],
$\mathbf {K}$
. By [Reference VaseyVas16a, 6.14],
![]() $\mathfrak {t}$
, and hence
$\mathfrak {t}$
, and hence
![]() $\mathfrak {s}$
, also has symmetry.Footnote
3
The “in particular” part follows from the definition of a good
$\mathfrak {s}$
, also has symmetry.Footnote
3
The “in particular” part follows from the definition of a good
![]() $[\lambda , \infty )$
-frame. ⊣
$[\lambda , \infty )$
-frame. ⊣
For
![]() $\mathbf {K}$
an AEC and
$\mathbf {K}$
an AEC and
![]() $M \in \mathbf {K}$
, we let
$M \in \mathbf {K}$
, we let
![]() ${\mathbf {K}}_M$
denote the AEC obtained by adding constant symbols for M (see [Reference VaseyVas17b, 2.20] for the precise definition). Roughly speaking, it is the AEC of models above M.
${\mathbf {K}}_M$
denote the AEC obtained by adding constant symbols for M (see [Reference VaseyVas17b, 2.20] for the precise definition). Roughly speaking, it is the AEC of models above M.
Lemma 5.2 (Main lemma)
Let
![]() $\mathbf {K}$
be an AEC and let
$\mathbf {K}$
be an AEC and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal of countable cofinality. If :
$\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal of countable cofinality. If :
-
(1)
 ${\mathbf {K}}_{\mu }$
has weak amalgamation.
${\mathbf {K}}_{\mu }$
has weak amalgamation. -
(2)
 ${\mathbf {K}}_{<\mu }$
has coherent sequences.
${\mathbf {K}}_{<\mu }$
has coherent sequences. -
(3)
 ${\mathbf {K}}_{\le \mu }$
is
${\mathbf {K}}_{\le \mu }$
is
 $\text {LS} (\mathbf {K})$
-tame.
$\text {LS} (\mathbf {K})$
-tame. -
(4) For every
 $\theta < \mu $
, there exists
$\theta < \mu $
, there exists
 $\lambda < \mu $
such that
$\lambda < \mu $
such that
 $\lambda = \lambda ^\theta $
and
$\lambda = \lambda ^\theta $
and
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\lambda $
.
$\lambda $
.
Then for any nonmaximal
![]() $M \in {\mathbf {K}}_\mu $
,
$M \in {\mathbf {K}}_\mu $
,
![]() ${\mathbf {K}}_M$
has a type-full
${\mathbf {K}}_M$
has a type-full
![]() $\text {good}^{-S} \mu $
-frame.
$\text {good}^{-S} \mu $
-frame.
Proof. For
![]() $N_1 \le _{\mathbf {K}} N_2$
both in
$N_1 \le _{\mathbf {K}} N_2$
both in
![]() ${\mathbf {K}}_\mu $
and
${\mathbf {K}}_\mu $
and
![]() $p \in \mathbf {S} (N_2)$
, we say that p does not fork over
$p \in \mathbf {S} (N_2)$
, we say that p does not fork over
![]() $N_1$
if there exists
$N_1$
if there exists
![]() $N_1^0 \in {\mathbf {K}}_{<\mu }$
with
$N_1^0 \in {\mathbf {K}}_{<\mu }$
with
![]() $N_1^0 \le _{\mathbf {K}} N_1$
such that p does not split over
$N_1^0 \le _{\mathbf {K}} N_1$
such that p does not split over
![]() $N_1^0$
. We prove several claims:
$N_1^0$
. We prove several claims:
-
• Nonforking is invariant under isomorphisms, and if
 $N_1 \le _{\mathbf {K}} N_2 \le _{\mathbf {K}} N_3$
are all in
$N_1 \le _{\mathbf {K}} N_2 \le _{\mathbf {K}} N_3$
are all in
 ${\mathbf {K}}_\mu $
and
${\mathbf {K}}_\mu $
and
 $p \in \mathbf {S} (N_3)$
does not fork over
$p \in \mathbf {S} (N_3)$
does not fork over
 $N_1$
, then
$N_1$
, then
 $p \upharpoonright N_2$
does not fork over
$p \upharpoonright N_2$
does not fork over
 $N_1$
and p does not fork over
$N_1$
and p does not fork over
 $N_2$
. This is immediate from the definition and the basic properties of splitting.
$N_2$
. This is immediate from the definition and the basic properties of splitting. -
• If
 $N_1 \le _{\mathbf {K}} N_2$
are both in
$N_1 \le _{\mathbf {K}} N_2$
are both in
 ${\mathbf {K}}_\mu $
,
${\mathbf {K}}_\mu $
,
 $p, q \in \mathbf {S} (N_2)$
both do not fork over
$p, q \in \mathbf {S} (N_2)$
both do not fork over
 $N_1$
and
$N_1$
and
 $p \upharpoonright N_1 = q \upharpoonright N_1$
, then
$p \upharpoonright N_1 = q \upharpoonright N_1$
, then
 $p = q$
. To see this use the Löwenheim–Skolem axiom, fix
$p = q$
. To see this use the Löwenheim–Skolem axiom, fix
 $N_1^0 \le _{\mathbf {K}} N_1$
such that
$N_1^0 \le _{\mathbf {K}} N_1$
such that
 $N_1^0 \in {\mathbf {K}}_{<\mu }$
and both p and q do not split over
$N_1^0 \in {\mathbf {K}}_{<\mu }$
and both p and q do not split over
 $N_1^0$
. By Lemma 4.3, all the models in
$N_1^0$
. By Lemma 4.3, all the models in
 ${\mathbf {K}}_\mu $
are locally model-homogeneous, so in particular
${\mathbf {K}}_\mu $
are locally model-homogeneous, so in particular
 $N_1$
is locally universal over
$N_1$
is locally universal over
 $N_1^0$
, so by tameness and weak uniqueness (Lemma 4.7),
$N_1^0$
, so by tameness and weak uniqueness (Lemma 4.7),
 $p = q$
.
$p = q$
. -
• If
 $N \in {\mathbf {K}}_\mu $
and
$N \in {\mathbf {K}}_\mu $
and
 $p \in \mathbf {S} (N)$
, then p does not fork over N. This follows directly from the definition of nice filtrations and Lemma 4.11.
$p \in \mathbf {S} (N)$
, then p does not fork over N. This follows directly from the definition of nice filtrations and Lemma 4.11. -
• If
 $N_1 \le _{\mathbf {K}} N_2$
are both in
$N_1 \le _{\mathbf {K}} N_2$
are both in
 ${\mathbf {K}}_\mu $
and
${\mathbf {K}}_\mu $
and
 $p \in \mathbf {S} (N_1)$
, then there exists
$p \in \mathbf {S} (N_1)$
, then there exists
 $q \in \mathbf {S} (N_2)$
such that q extends p and q does not fork over
$q \in \mathbf {S} (N_2)$
such that q extends p and q does not fork over
 $N_1$
. Moreover, q can be taken to be nonalgebraic if p is nonalgebraic. To see this, first note that we have observed previously that p does not fork over
$N_1$
. Moreover, q can be taken to be nonalgebraic if p is nonalgebraic. To see this, first note that we have observed previously that p does not fork over
 $N_1$
, hence there is
$N_1$
, hence there is
 $M_0 \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}), \mu )}$
such that
$M_0 \in {\mathbf {K}}_{[\text {LS} (\mathbf {K}), \mu )}$
such that
 $M_0 \le _{\mathbf {K}} N_1$
and p does not split over
$M_0 \le _{\mathbf {K}} N_1$
and p does not split over
 $M_0$
. Now we can pick
$M_0$
. Now we can pick
 $M_1 \le _{\mathbf {K}} N_1$
with
$M_1 \le _{\mathbf {K}} N_1$
with
 $M_0 \le _{\mathbf {K}} M_1$
,
$M_0 \le _{\mathbf {K}} M_1$
,
 $\|M_0\| < \|M_1\| < \|N_1\|$
, and
$\|M_0\| < \|M_1\| < \|N_1\|$
, and
 $\|M_1\|^{\|M_0\|} = \|M_1\|$
, and
$\|M_1\|^{\|M_0\|} = \|M_1\|$
, and
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\|M_1\|$
. Then it follows that
$\|M_1\|$
. Then it follows that
 $M_1$
is locally universal over
$M_1$
is locally universal over
 $M_0$
(see Fact 4.2). Also, Lemma 4.11 implies that
$M_0$
(see Fact 4.2). Also, Lemma 4.11 implies that
 $N_1$
is nicely filtrable over
$N_1$
is nicely filtrable over
 $M_1$
. Now apply Lemma 4.12, where
$M_1$
. Now apply Lemma 4.12, where
 $M, N$
there stand for
$M, N$
there stand for
 $N_1, N_2$
here.
$N_1, N_2$
here. -
• If
 $\delta < \mu ^+$
is a limit ordinal,
$\delta < \mu ^+$
is a limit ordinal,
 $\langle N_i : i \le \delta \rangle $
is increasing continuous in
$\langle N_i : i \le \delta \rangle $
is increasing continuous in
 ${\mathbf {K}}_\mu $
, and
${\mathbf {K}}_\mu $
, and
 $p \in \mathbf {S} (N_\delta )$
, then there exists
$p \in \mathbf {S} (N_\delta )$
, then there exists
 $i < \delta $
such that p does not fork over
$i < \delta $
such that p does not fork over
 $N_i$
. Indeed, suppose not. Assume without loss of generality that
$N_i$
. Indeed, suppose not. Assume without loss of generality that
 $\delta $
is regular. In particular,
$\delta $
is regular. In particular,
 $\delta < \mu $
and so
$\delta < \mu $
and so
 $\delta ^+ < \mu $
. Let
$\delta ^+ < \mu $
. Let
 $\theta := \text {LS} (\mathbf {K})^+ + \delta ^+$
. Pick
$\theta := \text {LS} (\mathbf {K})^+ + \delta ^+$
. Pick
 $\lambda < \mu $
such that
$\lambda < \mu $
such that
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\lambda $
and
$\lambda $
and
 $\lambda ^\theta = \lambda $
. By Fact 4.2, the model in
$\lambda ^\theta = \lambda $
. By Fact 4.2, the model in
 ${\mathbf {K}}_\lambda $
is locally
${\mathbf {K}}_\lambda $
is locally
 $\theta ^+$
-model-homogeneous. Build
$\theta ^+$
-model-homogeneous. Build
 $\langle N_i^0 : i < \delta \rangle $
and
$\langle N_i^0 : i < \delta \rangle $
and
 $\langle N_i^1 : i < \delta \rangle $
increasing in
$\langle N_i^1 : i < \delta \rangle $
increasing in
 ${\mathbf {K}}_{\lambda }$
such that for all
${\mathbf {K}}_{\lambda }$
such that for all
 $i < \delta $
,
$i < \delta $
,
 $N_i^0 \le _{\mathbf {K}} N_i$
,
$N_i^0 \le _{\mathbf {K}} N_i$
,
 $N_i^0 \le _{\mathbf {K}} N_i^1 \le _{\mathbf {K}} N_\delta $
,
$N_i^0 \le _{\mathbf {K}} N_i^1 \le _{\mathbf {K}} N_\delta $
,
 $N_{i}^1 \cap N_i \subseteq N_{i + 1}^0$
,
$N_{i}^1 \cap N_i \subseteq N_{i + 1}^0$
,
 $p \upharpoonright N_i^1$
splits over
$p \upharpoonright N_i^1$
splits over
 $N_i^0$
. This is possible (see [Reference VaseyVas16a, 4.11] for a very similar construction). At the end, let
$N_i^0$
. This is possible (see [Reference VaseyVas16a, 4.11] for a very similar construction). At the end, let
 $N_\delta ^\ell := \bigcup _{i < \delta } N_i^\ell $
. Observe that
$N_\delta ^\ell := \bigcup _{i < \delta } N_i^\ell $
. Observe that
 $N_\delta ^1 = N_\delta ^0$
so by Lemma 4.6, there exists
$N_\delta ^1 = N_\delta ^0$
so by Lemma 4.6, there exists
 $i < \delta $
so that
$i < \delta $
so that
 $p \upharpoonright N_\delta ^1$
does not split over
$p \upharpoonright N_\delta ^1$
does not split over
 $N_i^0$
. This is a contradiction, since we assumed that
$N_i^0$
. This is a contradiction, since we assumed that
 $p \upharpoonright N_i^1$
splits over
$p \upharpoonright N_i^1$
splits over
 $N_i^0$
.
$N_i^0$
. -
• For any
 $N \in {\mathbf {K}}_\mu $
,
$N \in {\mathbf {K}}_\mu $
,
 $|\mathbf {S} (N)| \le \mu $
. Indeed, if
$|\mathbf {S} (N)| \le \mu $
. Indeed, if
 $\langle p_i : i < \mu ^+ \rangle $
are types in
$\langle p_i : i < \mu ^+ \rangle $
are types in
 $\mathbf {S} (N)$
, we can first use Lemma 4.11 to find a nice filtration
$\mathbf {S} (N)$
, we can first use Lemma 4.11 to find a nice filtration
 $\langle N_j : j < \omega \rangle $
of N. In particular, for all
$\langle N_j : j < \omega \rangle $
of N. In particular, for all
 $i < \mu ^+$
there exists
$i < \mu ^+$
there exists
 $j_i < \omega $
with p not splitting over
$j_i < \omega $
with p not splitting over
 $N_{j_i}$
. By the usual pruning argument (using that
$N_{j_i}$
. By the usual pruning argument (using that
 $\mu $
is strong limit to see that
$\mu $
is strong limit to see that
 $|\mathbf {S} (N_j)| < \mu $
for each
$|\mathbf {S} (N_j)| < \mu $
for each
 $j < \mu $
), there exists
$j < \mu $
), there exists
 $j < \omega $
and an unbounded subset
$j < \omega $
and an unbounded subset
 $X \subseteq \mu ^+$
such that for
$X \subseteq \mu ^+$
such that for
 $i_1, i_2 \in X$
,
$i_1, i_2 \in X$
,
 $p_{i_1}$
,
$p_{i_1}$
,
 $p_{i_2}$
both do not split over
$p_{i_2}$
both do not split over
 $N_j$
and have the same restriction to
$N_j$
and have the same restriction to
 $N_{j + 1}$
. By weak uniqueness,
$N_{j + 1}$
. By weak uniqueness,
 $p_{i_1} = p_{i_2}$
. This shows that
$p_{i_1} = p_{i_2}$
. This shows that
 $|\mathbf {S} (N)| \le \mu $
.
$|\mathbf {S} (N)| \le \mu $
.
Now fix a nonmaximal
![]() $M \in {\mathbf {K}}_\mu $
. We identify any
$M \in {\mathbf {K}}_\mu $
. We identify any
![]() $N \in {\mathbf {K}}_\mu $
such that
$N \in {\mathbf {K}}_\mu $
such that
![]() $M \le _{\mathbf {K}} N$
with the corresponding member of
$M \le _{\mathbf {K}} N$
with the corresponding member of
![]() ${\mathbf {K}}_M$
(this will not yield to confusion). We define nonforking in the frame using the nonforking relation defined above. The basic types are the nonalgebraic types. We have just established that invariance, monotonicity, uniqueness, extension, and local character hold in the frame. Therefore transitivity and continuity automatically follow (see [Reference ShelahShe09a, II.2.17, II.2.18]). Also note that
${\mathbf {K}}_M$
(this will not yield to confusion). We define nonforking in the frame using the nonforking relation defined above. The basic types are the nonalgebraic types. We have just established that invariance, monotonicity, uniqueness, extension, and local character hold in the frame. Therefore transitivity and continuity automatically follow (see [Reference ShelahShe09a, II.2.17, II.2.18]). Also note that
![]() ${\mathbf {K}}_M$
is not empty (it contains a copy of M) and has no maximal models of cardinality
${\mathbf {K}}_M$
is not empty (it contains a copy of M) and has no maximal models of cardinality
![]() $\mu $
: given
$\mu $
: given
![]() $M \le _{\mathbf {K}} N$
in
$M \le _{\mathbf {K}} N$
in
![]() ${\mathbf {K}}_\mu $
, we can fix a nonalgebraic
${\mathbf {K}}_\mu $
, we can fix a nonalgebraic
![]() $p \in \mathbf {S} (M)$
(which exists as M is not maximal) and take its nonforking extension to
$p \in \mathbf {S} (M)$
(which exists as M is not maximal) and take its nonforking extension to
![]() $\mathbf {S} (N)$
. We have observed this extension is not algebraic, hence N cannot be maximal either. We have also seen that
$\mathbf {S} (N)$
. We have observed this extension is not algebraic, hence N cannot be maximal either. We have also seen that
![]() $\mathbf {K}$
(hence
$\mathbf {K}$
(hence
![]() ${\mathbf {K}}_M$
) is stable in
${\mathbf {K}}_M$
) is stable in
![]() $\mu $
. Finally,
$\mu $
. Finally,
![]() $\mathbf {K}$
has amalgamation in
$\mathbf {K}$
has amalgamation in
![]() $\mu $
. This follows from Fact 2.5 and the extension property of nonforking. We deduce that
$\mu $
. This follows from Fact 2.5 and the extension property of nonforking. We deduce that
![]() ${\mathbf {K}}_M$
has amalgamation in
${\mathbf {K}}_M$
has amalgamation in
![]() $\mu $
and also joint embedding in
$\mu $
and also joint embedding in
![]() $\mu $
.⊣
$\mu $
.⊣
Remark 5.3. By Lemma 3.1, any AEC satisfying the hypotheses of Lemma 5.2 will have a model in
![]() ${\mathbf {K}}_\mu $
, but we do not in general know how to find a nonmaximal one. Theorem 3.6 gives a way by assuming categoricity in more cardinals.
${\mathbf {K}}_\mu $
, but we do not in general know how to find a nonmaximal one. Theorem 3.6 gives a way by assuming categoricity in more cardinals.
We deduce arbitrarily large models from categoricity in enough small cardinals:
Theorem 5.4. Let
![]() $\mathbf {K}$
be an
$\mathbf {K}$
be an
![]() $\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences, and let
$\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences, and let
![]() $\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal. If :
$\mu> \text {LS} (\mathbf {K})$
be a strong limit cardinal. If :
-
(1) Not every element of
 ${\mathbf {K}}_{\mu }$
is maximal.
${\mathbf {K}}_{\mu }$
is maximal. -
(2) For every
 $\theta < \mu $
there exists
$\theta < \mu $
there exists
 $\lambda < \mu $
such that
$\lambda < \mu $
such that
 $\lambda = \lambda ^{\theta }$
and
$\lambda = \lambda ^{\theta }$
and
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\lambda $
.
$\lambda $
.
Then
![]() ${\mathbf {K}}_{\ge \mu }$
has amalgamation and arbitrarily large models.
${\mathbf {K}}_{\ge \mu }$
has amalgamation and arbitrarily large models.
Proof. Assume without loss of generality that
![]() $\mu $
has countable cofinality (otherwise, it is easy to find a smaller cardinal which has countable cofinality and still satisfies the hypotheses). Fix a nonmaximal
$\mu $
has countable cofinality (otherwise, it is easy to find a smaller cardinal which has countable cofinality and still satisfies the hypotheses). Fix a nonmaximal
![]() $M \in {\mathbf {K}}_\mu $
. By Lemma 5.2, there is a
$M \in {\mathbf {K}}_\mu $
. By Lemma 5.2, there is a
![]() $\text {good}^{-S} \mu $
-frame on
$\text {good}^{-S} \mu $
-frame on
![]() ${\mathbf {K}}_M$
. It is easy to check that
${\mathbf {K}}_M$
. It is easy to check that
![]() ${\mathbf {K}}_M$
has weak amalgamation and is
${\mathbf {K}}_M$
has weak amalgamation and is
![]() $\mu $
-tame. Therefore by Fact 5.1,
$\mu $
-tame. Therefore by Fact 5.1,
![]() ${\mathbf {K}}_M$
has amalgamation and arbitrarily large model. In particular,
${\mathbf {K}}_M$
has amalgamation and arbitrarily large model. In particular,
![]() $\mathbf {K}$
has arbitrarily large models and M is an amalgamation base in
$\mathbf {K}$
has arbitrarily large models and M is an amalgamation base in
![]() $\mathbf {K}$
. Since any maximal model is an amalgamation base, we deduce that
$\mathbf {K}$
. Since any maximal model is an amalgamation base, we deduce that
![]() ${\mathbf {K}}_{\ge \mu }$
has amalgamation. ⊣
${\mathbf {K}}_{\ge \mu }$
has amalgamation. ⊣
We now work toward transferring categoricity assuming arbitrarily large models. We will use the following upward categoricity transfer of Grossberg and VanDieren for tame AECs with both amalgamation and arbitrarily large models.
Fact 5.5 ([Reference Grossberg and VanDierenGV06a, 6.3])
Let
![]() $\mathbf {K}$
be an
$\mathbf {K}$
be an
![]() $\text {LS} (\mathbf {K})$
-tame AEC with amalgamation and arbitrarily large models. If
$\text {LS} (\mathbf {K})$
-tame AEC with amalgamation and arbitrarily large models. If
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\text {LS} (\mathbf {K})$
and in
$\text {LS} (\mathbf {K})$
and in
![]() $\text {LS} (\mathbf {K})^+$
, then
$\text {LS} (\mathbf {K})^+$
, then
![]() $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
![]() $\text {LS} (\mathbf {K})$
.
$\text {LS} (\mathbf {K})$
.
Toward deriving global amalgamation, we show how to build a good frame assuming arbitrarily large models and enough categoricity, tameness, and amalgamation in low cardinals. We will use recent results from [Reference Boney, Grossberg, Vandieren and VaseyBGVV17] and [Reference VaseyVas17a], but the reader can regard them as black boxes.
Lemma 5.6. Let
![]() $\mathbf {K}$
be an AEC. If :
$\mathbf {K}$
be an AEC. If :
-
(1)
 $\mathbf {K}$
has arbitrarily large models.
$\mathbf {K}$
has arbitrarily large models. -
(2)
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\text {LS} (\mathbf {K})$
.
$\text {LS} (\mathbf {K})$
. -
(3)
 $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
 $\text {LS} (\mathbf {K})^+$
.
$\text {LS} (\mathbf {K})^+$
. -
(4)
 ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has amalgamation.
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has amalgamation. -
(5)
 ${\mathbf {K}}_{\text {LS} (\mathbf {K})^+}$
has weak amalgamation.
${\mathbf {K}}_{\text {LS} (\mathbf {K})^+}$
has weak amalgamation. -
(6)
 ${\mathbf {K}}_{\le \text {LS} (\mathbf {K})^+}$
is
${\mathbf {K}}_{\le \text {LS} (\mathbf {K})^+}$
is
 $\text {LS} (\mathbf {K})$
-tame.
$\text {LS} (\mathbf {K})$
-tame.
Then
![]() $\mathbf {K}$
has a good
$\mathbf {K}$
has a good
![]() $\text {LS} (\mathbf {K})^+$
-frame.
$\text {LS} (\mathbf {K})^+$
-frame.
Proof. Let
![]() $\lambda := \text {LS} (\mathbf {K})$
. By [Reference Boney, Grossberg, Vandieren and VaseyBGVV17],
$\lambda := \text {LS} (\mathbf {K})$
. By [Reference Boney, Grossberg, Vandieren and VaseyBGVV17],
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\lambda $
-superstable (essentially, this means that splitting has what is called the
$\lambda $
-superstable (essentially, this means that splitting has what is called the
![]() $\aleph _0$
-local character for universal chains in [Reference VaseyVas16a]) and by [Reference VaseyVas17a, 5.7(1)],
$\aleph _0$
-local character for universal chains in [Reference VaseyVas16a]) and by [Reference VaseyVas17a, 5.7(1)],
![]() $\mathbf {K}$
has
$\mathbf {K}$
has
![]() $\lambda $
-symmetry. We now attempt to build a
$\lambda $
-symmetry. We now attempt to build a
![]() $\text {good}^{-S}$
-frame as in [Reference VaseyVas16a]. We can prove extension without using amalgamation in
$\text {good}^{-S}$
-frame as in [Reference VaseyVas16a]. We can prove extension without using amalgamation in
![]() $\lambda ^+$
, hence by Fact 2.5 we obtain amalgamation in
$\lambda ^+$
, hence by Fact 2.5 we obtain amalgamation in
![]() $\lambda ^+$
, and hence obtain a
$\lambda ^+$
, and hence obtain a
![]() $\text {good}^{-S} \lambda ^+$
-frame. Symmetry is then proven as in [Reference Boney and VaseyBV17b, 6.8] (and is not needed for the present paper).⊣
$\text {good}^{-S} \lambda ^+$
-frame. Symmetry is then proven as in [Reference Boney and VaseyBV17b, 6.8] (and is not needed for the present paper).⊣
We can now prove a generalization of Fact 5.5 for tame AECs with only weak amalgamation (but still with arbitrarily large models).
Theorem 5.7. Let
![]() $\mathbf {K}$
be an
$\mathbf {K}$
be an
![]() $\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and arbitrarily large models. If
$\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and arbitrarily large models. If
![]() ${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has amalgamation, and
${\mathbf {K}}_{\text {LS} (\mathbf {K})}$
has amalgamation, and
![]() $\mathbf {K}$
is categorical in both
$\mathbf {K}$
is categorical in both
![]() $\text {LS} (\mathbf {K})$
and
$\text {LS} (\mathbf {K})$
and
![]() $\text {LS} (\mathbf {K})^+$
, then
$\text {LS} (\mathbf {K})^+$
, then
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
has amalgamation and
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
has amalgamation and
![]() $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
![]() $\text {LS} (\mathbf {K})$
.
$\text {LS} (\mathbf {K})$
.
Proof. By Lemma 5.6,
![]() $\mathbf {K}$
has a good
$\mathbf {K}$
has a good
![]() $\text {LS} (\mathbf {K})^+$
-frame. By Fact 5.1, it follows that
$\text {LS} (\mathbf {K})^+$
-frame. By Fact 5.1, it follows that
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})^+}$
(and hence
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})^+}$
(and hence
![]() ${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
) has amalgamation. Now apply Fact 5.5. ⊣
${\mathbf {K}}_{\ge \text {LS} (\mathbf {K})}$
) has amalgamation. Now apply Fact 5.5. ⊣
Lemma 5.6 still asked for full amalgamation in one cardinal. However we can use the weak diamond to derive it from successive categoricity:
Corollary 5.8. Let
![]() $\mathbf {K}$
be an
$\mathbf {K}$
be an
![]() $\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and arbitrarily large models. Let
$\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and arbitrarily large models. Let
![]() $\theta> \text {LS} (\mathbf {K})$
be least such that
$\theta> \text {LS} (\mathbf {K})$
be least such that
![]() $2^{\text {LS} (\mathbf {K})} < 2^\theta $
. If
$2^{\text {LS} (\mathbf {K})} < 2^\theta $
. If
![]() $\mathbf {K}$
is categorical in every cardinal in
$\mathbf {K}$
is categorical in every cardinal in
![]() $[\text {LS} (\mathbf {K}), \theta ]$
, then
$[\text {LS} (\mathbf {K}), \theta ]$
, then
![]() $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
![]() $\text {LS} (\mathbf {K})$
. Moreover, there exists
$\text {LS} (\mathbf {K})$
. Moreover, there exists
![]() $\lambda \in [\text {LS} (\mathbf {K}), \theta )$
such that
$\lambda \in [\text {LS} (\mathbf {K}), \theta )$
such that
![]() ${\mathbf {K}}_{\ge \lambda }$
has amalgamation.
${\mathbf {K}}_{\ge \lambda }$
has amalgamation.
Proof. Generalizing [Reference ShelahShe09a, I.3.8] (using the corresponding generalization of the Devlin–Shelah weak diamond [Reference Devlin and ShelahDS78] as in [Reference Shelah and VillavecesSV99, 1.2.4]), we can find
![]() $\lambda \in [\text {LS} (\mathbf {K}), \theta )$
such that
$\lambda \in [\text {LS} (\mathbf {K}), \theta )$
such that
![]() ${\mathbf {K}}_\lambda $
has amalgamation. Now apply Theorem 5.7 to
${\mathbf {K}}_\lambda $
has amalgamation. Now apply Theorem 5.7 to
![]() ${\mathbf {K}}_{\ge \lambda }$
. ⊣
${\mathbf {K}}_{\ge \lambda }$
. ⊣
Putting together all the results proven so far, we obtain the main result of the paper:
Corollary 5.9. Let
![]() $\mathbf {K}$
be an
$\mathbf {K}$
be an
![]() $\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences. If
$\text {LS} (\mathbf {K})$
-tame AEC with weak amalgamation and coherent sequences. If
![]() $\mathbf {K}$
is categorical in every cardinal in
$\mathbf {K}$
is categorical in every cardinal in
![]() $[\text {LS} (\mathbf {K}), \beth _\omega (\text {LS} (\mathbf {K})))$
, then
$[\text {LS} (\mathbf {K}), \beth _\omega (\text {LS} (\mathbf {K})))$
, then
![]() $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
![]() $\text {LS} (\mathbf {K})$
.
$\text {LS} (\mathbf {K})$
.
Proof. Let
![]() $\mu := \beth _\omega (\text {LS} (\mathbf {K}))$
. By Theorem 3.6, not every element of
$\mu := \beth _\omega (\text {LS} (\mathbf {K}))$
. By Theorem 3.6, not every element of
![]() ${\mathbf {K}}_\mu $
is maximal. By Theorem 5.4,
${\mathbf {K}}_\mu $
is maximal. By Theorem 5.4,
![]() $\mathbf {K}$
has arbitrarily large models. Now apply Corollary 5.8. ⊣
$\mathbf {K}$
has arbitrarily large models. Now apply Corollary 5.8. ⊣
Specializing to universal classes, we get:
Corollary 5.10. If a universal
![]() $\mathbb {L}_{\omega _1, \omega }$
sentence is categorical in an end segment of cardinals strictly below
$\mathbb {L}_{\omega _1, \omega }$
sentence is categorical in an end segment of cardinals strictly below
![]() $\beth _\omega $
, then it is also categorical everywhere above
$\beth _\omega $
, then it is also categorical everywhere above
![]() $\beth _\omega $
.
$\beth _\omega $
.
Proof. Let
![]() $\phi $
be a universal
$\phi $
be a universal
![]() $\mathbb {L}_{\omega _1, \omega }$
sentence and let
$\mathbb {L}_{\omega _1, \omega }$
sentence and let
![]() $\mathbf {K}$
be its the class of models (ordered with substructure). Note that
$\mathbf {K}$
be its the class of models (ordered with substructure). Note that
![]() $\mathbf {K}$
has intersections (the closure operator computed inside N is the closure under the functions of N). By Lemma 2.8,
$\mathbf {K}$
has intersections (the closure operator computed inside N is the closure under the functions of N). By Lemma 2.8,
![]() $\mathbf {K}$
has coherent sequences. By Remark 2.4,
$\mathbf {K}$
has coherent sequences. By Remark 2.4,
![]() $\mathbf {K}$
has weak amalgamation. By [Reference VaseyVas17b, 3.7],
$\mathbf {K}$
has weak amalgamation. By [Reference VaseyVas17b, 3.7],
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\text {LS} (\mathbf {K})$
-tame. Let
$\text {LS} (\mathbf {K})$
-tame. Let
![]() $\chi \in [\aleph _0, \beth _\omega )$
be such that
$\chi \in [\aleph _0, \beth _\omega )$
be such that
![]() $\mathbf {K}$
is categorical in every cardinal in
$\mathbf {K}$
is categorical in every cardinal in
![]() $[\chi , \beth _\omega )$
. Now apply Corollary 5.9 to
$[\chi , \beth _\omega )$
. Now apply Corollary 5.9 to
![]() ${\mathbf {K}}_{\ge \chi }$
. ⊣
${\mathbf {K}}_{\ge \chi }$
. ⊣
For completeness, we also point out that the last two results can be drastically improved assuming the weak GCH (see also [Reference Mazari-Armida and VaseyMAV18] for how to improve even more when the Löwenheim–Skolem–Tarski number is
![]() $\aleph _0$
). On
$\aleph _0$
). On
![]() $\mu _{\text {unif}}$
, see [Reference ShelahShe09b, VII.0.4] for a definition and [Reference ShelahShe09b, VII.9.4] for what is known. It seems that for all practical purposes the reader can take
$\mu _{\text {unif}}$
, see [Reference ShelahShe09b, VII.0.4] for a definition and [Reference ShelahShe09b, VII.9.4] for what is known. It seems that for all practical purposes the reader can take
![]() $\mu _{\text {unif}} (\lambda ^{++}, 2^{\lambda ^+})$
to mean
$\mu _{\text {unif}} (\lambda ^{++}, 2^{\lambda ^+})$
to mean
![]() $2^{\lambda ^{++}}$
.
$2^{\lambda ^{++}}$
.
Theorem 5.11. Let
![]() $\mathbf {K}$
be an AEC with Löwenheim–Skolem–Tarski number
$\mathbf {K}$
be an AEC with Löwenheim–Skolem–Tarski number
![]() $\lambda $
. Assume that
$\lambda $
. Assume that
![]() $\mathbf {K}$
is
$\mathbf {K}$
is
![]() $\lambda ^+$
-tame and has weak amalgamation. Assume further that
$\lambda ^+$
-tame and has weak amalgamation. Assume further that
![]() $2^{\lambda } < 2^{\lambda ^+} < 2^{\lambda ^{++}}$
. If
$2^{\lambda } < 2^{\lambda ^+} < 2^{\lambda ^{++}}$
. If
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\lambda $
,
$\lambda $
,
![]() $\mathbf {K}$
is categorical in
$\mathbf {K}$
is categorical in
![]() $\lambda ^+$
, and
$\lambda ^+$
, and
![]() $1 \le \mathbb {I} (\mathbf {K}, \lambda ^{++}) < \mu _{\text {unif}} (\lambda ^{++}, 2^{\lambda ^+})$
, then
$1 \le \mathbb {I} (\mathbf {K}, \lambda ^{++}) < \mu _{\text {unif}} (\lambda ^{++}, 2^{\lambda ^+})$
, then
![]() $\mathbf {K}$
is categorical everywhere above
$\mathbf {K}$
is categorical everywhere above
![]() $\lambda $
.
$\lambda $
.
Proof. By results of Shelah on building good frames, there is a good
![]() $\lambda $
-frame on
$\lambda $
-frame on
![]() $\mathbf {K}$
and
$\mathbf {K}$
and
![]() ${\mathbf {K}}_{\le \lambda ^+}$
is
${\mathbf {K}}_{\le \lambda ^+}$
is
![]() $\lambda $
-tame (see [Reference VaseyVas20, 7.1] for an outline of the proof). By Fact 5.1,
$\lambda $
-tame (see [Reference VaseyVas20, 7.1] for an outline of the proof). By Fact 5.1,
![]() $\mathbf {K}$
has arbitrarily large models. Now apply Corollary 5.8. ⊣
$\mathbf {K}$
has arbitrarily large models. Now apply Corollary 5.8. ⊣