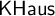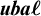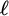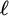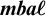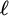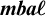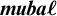1 Introduction
In modal logic there is a well-established duality theory between categories of Kripke frames and the corresponding categories of boolean algebras with operators, which forms the backbone of modern studies of modal logic. One of the most fundamental such dualities establishes that the category of modal algebras is dually equivalent to the category of descriptive frames. This duality is often called Jónsson-Tarski duality because it originates in the work of Jónsson and Tarski [Reference Jónsson and Tarski24] (see also Kripke [Reference Kripke29]). In its current form it was developed by Halmos [Reference Halmos19], Esakia [Reference Esakia14], and Goldblatt [Reference Goldblatt18]. For a modern account we refer to [Reference Sambin and Vaccaro35] or the textbooks [Reference Blackburn, de Rijke and Venema9, Reference Chagrov and Zakharyaschev11, Reference Kracht27].
This duality generalizes the celebrated Stone duality between the categories of boolean algebras and Stone spaces (zero-dimensional compact Hausdorff spaces). Descriptive frames are Stone spaces equipped with a continuous relation. It is well known that a binary relation R on a Stone space X is continuous iff the corresponding map from X to the Vietoris space
$\mathcal {V}X$
, given by sending each
$x\in X$
to its R-image, is a well-defined continuous map (see [Reference Esakia14, Section 1] or [Reference Kupke, Kurz and Venema30, Section 3]). Since the Vietoris space
$\mathcal {V}X$
of a compact Hausdorff space X is compact Hausdorff, the consideration above allows us to generalize the notion of a descriptive frame to what we call a compact Hausdorff frame; that is, a compact Hausdorff space equipped with a continuous relation. The category
${\sf KHF}$
of compact Hausdorff frames was studied in [Reference Bezhanishvili, Bezhanishvili and Harding4], under the name of modal compact Hausdorff spaces, where Isbell [Reference Isbell21] and de Vries [Reference de Vries12] dualities for the category
${\sf KHaus}$
of compact Hausdorff spaces were generalized to
${\sf KHF}$
.
One of the best known (and oldest) dualities for
${\sf KHaus}$
goes back to the 1930s–1940s and is known under various names. The basic idea is to work with the ring of continuous functions on a compact Hausdorff space, but we arrive at different algebras depending on whether we work with complex-valued or real-valued functions. Gelfand and Naimark [Reference Gelfand and Neumark16] worked with continuous complex-valued functions and established that
${\sf KHaus}$
is dually equivalent to the category of commutative unital
$C^*$
-algebras. Independently, Stone [Reference Stone36] worked with continuous real-valued functions and established that
${\sf KHaus}$
is dually equivalent to the category of uniformly complete bounded archimedean
$\ell $
-algebras. These two categories of algebras are equivalent, which can be seen directly without passing to
${\sf KHaus}$
. Indeed, the self-adjoint elements of a commutative unital
$C^*$
-algebra form a uniformly complete bounded archimedean
$\ell $
-algebra, and each such algebra A gives rise to a commutative unital
$C^*$
-algebra by taking the complexification
$A\otimes _{\mathbb R}\mathbb C$
(see [Reference Bezhanishvili, Morandi and Olberding6, Section 7] for details).
Yet another duality for
${\sf KHaus}$
can be obtained by dropping multiplication from the signature of
$\ell $
-algebras, thus giving rise to the notion of a vector lattice, also called a Riesz space [Reference Luxemburg and Zaanen31]. It follows from the work of Kakutani [Reference Kakutani25, Reference Kakutani26], Krein and Krein [Reference Krein and Krein28], and Yosida [Reference Yosida37] that
${\sf KHaus}$
is dually equivalent to the category of uniformly complete bounded archimedean vector lattices.
These dualities for
${\sf KHaus}$
are often collectively referred to as Gelfand duality (see, e.g., [Reference Johnstone23, Section IV.4]), the terminology that we will follow in this paper. The version of Gelfand duality we will work with is obtained by associating to each compact Hausdorff space X the ring
$C(X)$
of continuous real-valued functions on X. For some time now there has been a desire to generalize Gelfand duality to a duality for
${\sf KHF}$
, but it remained elusive for at least two reasons. On the conceptual side, there was no agreement on what should be the definition of modal operators on the ring
$C(X)$
. On the technical side, it was unclear how to axiomatize attempted definitions of modal operators.
The goal of this paper is to resolve these issues. After recalling Gelfand duality, we define a modal operator on the ring
$C(X)$
for each compact Hausdorff frame
$(X,R)$
, and study its basic properties. This motivates the definition of a modal operator on an arbitrary bounded archimedean
$\ell $
-algebra, which is the main definition of the paper, giving rise to the category
$\boldsymbol {\mathit {mba}\ell }$
of modal bounded archimedean
$\ell $
-algebras. We show that there is a contravariant functor
$C:{\sf KHF}\to \boldsymbol {\mathit {mba}\ell }$
.
Next we define a contravariant functor
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
in the opposite direction. Proving that
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
is well defined is technically the most challenging part of the paper. Our main result establishes that the contravariant functors C and Y yield a dual adjunction between
$\boldsymbol {\mathit {mba}\ell }$
and
${\sf KHF}$
, which restricts to a dual equivalence between
${\sf KHF}$
and the reflective subcategory
$\boldsymbol {\mathit {muba}\ell }$
of
$\boldsymbol {\mathit {mba}\ell }$
consisting of uniformly complete objects of
$\boldsymbol {\mathit {mba}\ell }$
.
Our result generalizes both Gelfand duality and Jónsson-Tarski duality. We also take first steps in developing correspondence theory for
$\boldsymbol {\mathit {mba}\ell }$
by characterizing the classes of algebras in
$\boldsymbol {\mathit {mba}\ell }$
such that the corresponding relations on the dual side are serial, reflexive, transitive, or symmetric. We conclude the paper outlining several possible future directions of this line of research.
In the future, it would be of interest to develop the logical formalisms that can be modeled by modal bounded archimedean
$\ell $
-algebras. This can be done along the same lines as in [Reference Diaconescu, Metcalfe and Schnüriger13] where a modal extension of Abelian logic [Reference Casari10, Reference Meyer and Slaney33] is developed. Another approach can be found in [Reference Furber, Mardare and Mio15] with applications to probabilistic logic and Markov processes. This would give rise to novel modal logics based on compact Hausdorff spaces (rather than Stone spaces), and could serve as an alternative to the approaches developed in [Reference Bezhanishvili, Bezhanishvili and Harding4, Reference Bezhanishvili, Bezhanishvili, Santoli and Venema5].
2 Gelfand duality
In this section we give a brief outline of Gelfand duality. We start by recalling several basic definitions (see [Reference Birkhoff8, Chapter XIII and onwards] or [Reference Bezhanishvili, Morandi and Olberding6]). All rings that we will consider in this paper are commutative and unital (have multiplicative identity
$1$
).
Definition 2.1.
-
1. A ring A with a partial order
$\le $
is an
$\ell $
-ring (that is, a lattice-ordered ring) if
$(A,\le )$
is a lattice,
$a\le b$
implies
$a+c \le b+c$
for each c, and
$0 \leq a, b$
implies
$0 \le ab$
. -
2. An
$\ell $
-ring A is bounded if for each
$a \in A$
there is
$n \in \mathbb {N}$
such that
$a \le n\cdot 1$
(that is,
$1$
is a strong order unit). -
3. An
$\ell $
-ring A is archimedean if for each
$a,b \in A$
, whenever
$n\cdot a \le b$
for each
$n \in \mathbb {N}$
, then
$a \le 0$
. -
4. An
$\ell $
-ring A is an
$\ell $
-algebra if it is an
$\mathbb R$
-algebra and for each
$0 \le a\in A$
and
$0\le \lambda \in \mathbb R$
we have
$0 \le \lambda \cdot a$
. -
5. Let
$\boldsymbol {\mathit {ba}\ell }$
be the category of bounded archimedean
$\ell $
-algebras and unital
$\ell $
-algebra homomorphisms.
Let
$A\in \boldsymbol {\mathit {ba}\ell }$
. For
$a\in A$
, define the absolute value of a by
$$ \begin{align*} |a|=a\vee(-a) \end{align*} $$
and the norm of a by
$$ \begin{align*} ||a||=\inf\{\lambda\in\mathbb R \mid |a|\le \lambda\}, \end{align*} $$
where we view
$\mathbb {R}$
as an
$\ell $
-subalgebra of A by identifying
$\lambda \in \mathbb R$
with
$\lambda \cdot 1\in A$
. Then A is uniformly complete if the norm is complete. Let
$\boldsymbol {\mathit {uba}\ell }$
be the full subcategory of
$\boldsymbol {\mathit {ba}\ell }$
consisting of uniformly complete
$\ell $
-algebras.
Theorem 2.2 (Gelfand duality [Reference Gelfand and Neumark16, Reference Stone36])
There is a dual adjunction between
$\boldsymbol {\mathit {ba}\ell }$
and
${\sf KHaus}$
which restricts to a dual equivalence between
${\sf KHaus}$
and
$\boldsymbol {\mathit {uba}\ell }$
.
We describe briefly the functors
$C:{\sf KHaus} \to \boldsymbol {\mathit {ba}\ell }$
and
$Y:\boldsymbol {\mathit {ba}\ell }\to {\sf KHaus}$
yielding the dual adjunction. The functor C is defined in an obvious way. It associates with each compact Hausdorff space X the ring
$C(X)$
of (necessarily bounded) continuous real-valued functions on X, and with each continuous map
$\varphi :X\to Y$
the unital
$\ell $
-algebra homomorphism
$C(\varphi ):C(Y)\to C(X)$
given by
$C(\varphi )(f)=f\circ \varphi $
for each
$f\in C(Y)$
. It is straightforward to check that
$C:{\sf KHaus}\to \boldsymbol {\mathit {ba}\ell }$
is a well-defined contravariant functor.
To define the functor
$Y:\boldsymbol {\mathit {ba}\ell }\to {\sf KHaus}$
, we recall that an ideal I of
$A\in \boldsymbol {\mathit {ba}\ell }$
is an
$\ell $
-ideal if
$|a|\le |b|$
and
$b\in I$
imply
$a\in I$
. It is well known that
$\ell $
-ideals are exactly the kernels of
$\ell $
-algebra homomorphisms. An
$\ell $
-ideal I of A is proper if
$I\ne A$
, and a maximal
$\ell $
-ideal is a proper
$\ell $
-ideal that is maximal with respect to inclusion. A standard Zorn’s lemma argument yields that each proper
$\ell $
-ideal is contained in a maximal
$\ell $
-ideal.
Let
$Y_A$
be the space of maximal
$\ell $
-ideals of A, whose closed sets are exactly sets of the form
$$ \begin{align*} Z_\ell(I) = \{x\in Y_A\mid I\subseteq x\}, \end{align*} $$
where I is an
$\ell $
-ideal of A. The space
$Y_A$
is often referred to as the Yosida space of A in honor of Yosida’s fundamental work, which in particular implies that
$Y_A\in {\sf KHaus}$
(see [Reference Yosida37]).
The functor
$Y : \boldsymbol {\mathit {ba}\ell } \to {\sf KHaus}$
is defined by associating with each
$A \in \boldsymbol {\mathit {ba}\ell }$
the Yosida space
$Y_A$
and with each morphism
$\alpha : A \to B$
in
$\boldsymbol {\mathit {ba}\ell }$
the continuous map
$Y(\alpha )=\alpha ^{-1} : Y_B \to Y_A$
. It is well known that Y is a well-defined contravariant functor, and that the functors Y and C yield a dual adjunction between
$\boldsymbol {\mathit {ba}\ell }$
and
${\sf KHaus}$
.
For
$X\in {\sf KHaus}$
and
$x\in X$
let
$M_x:=\{f\in C(X) \mid f(x)=0\}$
be the
$\ell $
-ideal of
$C(X)$
consisting of functions that vanish at
$x\in X$
. Then
$M_x$
is a maximal
$\ell $
-ideal of
$C(X)$
, and since X is compact, every maximal
$\ell $
-ideal of
$C(X)$
is of this form (see, e.g., [Reference Gillman and Jerison17, Theorem 7.2]). Thus,
$\varepsilon _X:X\to Y_{C(X)}$
given by
$$ \begin{align*} \varepsilon_X(x)=M_x \end{align*} $$
is a homeomorphism.
Let
$A\in \boldsymbol {\mathit {ba}\ell }$
. In order to define
$\zeta _A:A\to C(Y_A)$
we require Hölder’s well-known theorem that a totally ordered archimedean
$\ell $
-group is isomorphic to a subgroup of
$\mathbb {R}$
. If
$x\in Y_A$
, then the quotient
$A/x$
is a totally ordered archimedean
$\ell $
-group, so
$A/x$
is isomorphic to a subgroup of
$\mathbb {R}$
by Hölder’s theorem. Since
$A/x$
is also an
$\mathbb {R}$
-algebra, we conclude that
$A/x \cong \mathbb {R}$
. Therefore, for each
$a\in A$
there is a unique
$\lambda \in \mathbb R$
with
$a+x=\lambda +x$
(as usual,
$a+x\in A/x$
denotes the coset of a with respect to x). Thus, we may define
$\zeta _A :A\to C(Y_A)$
by
$$ \begin{align*} \zeta_A(a)(x)=\lambda \end{align*} $$
for each
$x\in Y_A$
. Since
$\bigcap Y_A = 0$
(see [Reference Johnson22, Theorem II.2.11]),
$\zeta _A$
is a monomorphism in
$\boldsymbol {\mathit {ba}\ell }$
. In addition,
$\zeta _A$
separates points of
$Y_A$
, meaning that if
$x, y \in Y_A$
are distinct, then there is
$a \in A$
with
$\zeta _A(a)(x) \ne \zeta _A(a)(y)$
. Consequently, the Stone-Weierstrass theorem yields:
Proposition 2.3. The uniform completion of
$A \in \boldsymbol {\mathit {ba}\ell }$
is
$\zeta _A : A \to C(Y_A)$
. Therefore, if A is uniformly complete, then
$\zeta _A$
is an isomorphism.
We abuse the terminology and call
$C(Y_A)$
the uniform completion of
$A$
. Recalling that a subcategory
$\sf D$
of a category
$\sf C$
is a reflective subcategory if the inclusion functor
${\sf D}\hookrightarrow {\sf C}$
has a left adjoint, the above result yields:
Corollary 2.4.
$\boldsymbol {\mathit {uba}\ell }$
is a reflective subcategory of
$\boldsymbol {\mathit {ba}\ell }$
, and the reflector assigns to each
$A \in \boldsymbol {\mathit {ba}\ell }$
its uniform completion
$C(Y_A) \in \boldsymbol {\mathit {uba}\ell }$
.
As a result, we obtain that the dual adjunction between
$\boldsymbol {\mathit {ba}\ell }$
and
${\sf KHaus}$
restricts to a dual equivalence between
$\boldsymbol {\mathit {uba}\ell }$
and
${\sf KHaus}$
, yielding Gelfand duality.
Remark 2.5. It follows from Gelfand duality that each
$A\in \boldsymbol {\mathit {ba}\ell }$
is isomorphic to a subalgebra of
$C(Y_A)$
. Thus, each
$A\in \boldsymbol {\mathit {ba}\ell }$
is a function ring or f-ring for short (see, e.g., [Reference Birkhoff8, Section XVII.5]). We will use this in Section 6.
3 Modal operators on
$C(X)$
In this section we define modal operators on rings of continuous real-valued functions on compact Hausdorff frames and study their basic properties. This motivates the definition of a modal operator on
$A\in \boldsymbol {\mathit {ba}\ell }$
, giving rise to the category
$\boldsymbol {\mathit {mba}\ell }$
of modal bounded archimedean
$\ell $
-algebras. We end the section by describing a contravariant functor from
${\sf KHF}$
to
$\boldsymbol {\mathit {mba}\ell }$
.
We recall that a Kripke frame is a pair
$\mathfrak F=(X,R)$
where X is a set and R is a binary relation on X. As usual, for
$x\in X$
we write
$$ \begin{align*} R[x]=\{y\in X \mid xRy\} \quad\mbox{and} \quad R^{-1}[x]=\{y\in X \mid yRx\}, \end{align*} $$
and for
$U\subseteq X$
we write
$$ \begin{align*} R[U]=\bigcup\{R[u] \mid u\in U\} \quad\mbox{and}\quad R^{-1}[U]=\bigcup\{R^{-1}[u] \mid u\in U\}. \end{align*} $$
Definition 3.1. [Reference Bezhanishvili, Bezhanishvili and Harding4] A binary relation R on a compact Hausdorff space X is continuous if:
-
1.
$R[x]$
is closed for each
$x\in X$
. -
2.
$F\subseteq X$
closed implies
$R^{-1}[F]$
is closed. -
3.
$U\subseteq X$
open implies
$R^{-1}[U]$
is open.
If R is a continuous relation on X, we call
$(X, R)$
a compact Hausdorff frame.
Notation 3.2. For a binary relation R on a set X let
$$ \begin{align*} D &= \{ x \in X \mid R[x] \ne \varnothing \} = R^{-1}[X],\\ E &= X \setminus D = \{ x \in X \mid R[x] = \varnothing\}. \end{align*} $$
The next lemma is straightforward and we omit the proof.
Lemma 3.3. If
$(X,R)$
is a compact Hausdorff frame, then D and E are clopen subsets of X.
Definition 3.4. For a compact Hausdorff frame
$(X,R)$
, define
$\Box _R$
on
$C(X)$
by
$$ \begin{align*} (\Box_Rf)(x) = \left\{\begin{array}{ll}\inf fR[x] & \text{if }x \in D,\\ 1 & \text{if }x \in E.\end{array}\right. \end{align*} $$
Remark 3.5. We define
$\Diamond _R$
by
$$ \begin{align*} (\Diamond_R f)(x) = \left\{\begin{array}{ll}\sup fR[x] & \text{if }x \in D,\\ 0 & \text{if }x \in E.\end{array}\right. \end{align*} $$
We have
$$ \begin{align*} \Diamond_R f = 1 -\Box_R (1-f) \quad\mbox{and}\quad \Box_Rf = 1 -\Diamond_R(1-f). \end{align*} $$
For, if
$x \in D$
, then
$$ \begin{align*} 1 - \Box_R(1-f)(x) &= 1 -\inf\{ 1-f(y) \mid xRy\} = 1 -(1 - \sup\{ f(y) \mid xRy\}) \\ &= \sup \{ f(y) \mid xRy\} = \Diamond_Rf(x). \end{align*} $$
If
$x \in E$
, then
$$\begin{align*}(1 - \Box _R (1-f))(x) = 1 - 1 = 0 = (\Diamond _Rf)(x). \end{align*}$$
Thus,
$\Diamond _R f = 1 - \Box _R(1-f)$
, as desired. A similar argument will show that
$\Box _Rf = 1 - \Diamond _R(1-f)$
. Therefore, each of
$\Box _R$
and
$\Diamond _R$
can be determined from the other.
Remark 3.6. Let
$(X,R)$
be a compact Hausdorff frame,
$f \in C(X)$
, and
$x \in X$
with
$R[x] \ne \varnothing $
. Then
$fR[x]$
is a nonempty compact subset of
$\mathbb {R}$
, and so it has least and greatest elements. Thus, we have
$$ \begin{align*} (\Box_Rf)(x) = \min fR[x] \quad\mbox{and}\quad (\Diamond_R f)(x) = \max fR[x]. \end{align*} $$
A version of the next result goes back to Michael [Reference Michael34]. Let
$X\in {\sf KHaus}$
and
$f \in C(X)$
. Denoting by
$\mathcal V^*X$
the space of nonempty closed subsets of X with the Vietoris topology, it follows from [Reference Michael34, Proposition 4.7] that the map
$\mathcal {V}^* X \to \mathbb {R}$
that sends F to
$\inf f(F)$
is continuous.
Lemma 3.7. Suppose that
$(X,R)$
is a compact Hausdorff frame. If
$f \in C(X)$
, then
$\Box _R f \in C(X)$
.
Proof. To see that
$\Box _R f$
is continuous, it is sufficient to show that for each
$\lambda \in \mathbb {R}$
, both
$(\Box _R f)^{-1}(\lambda , \infty )$
and
$(\Box _R f)^{-1}(-\infty , \lambda )$
are open in X. We first show that
$(\Box _R f)^{-1}(\lambda , \infty )$
is open. Let
$x \in X$
and first suppose that
$x \in D$
. Then
$fR[x]$
is a nonempty compact subset of
$\mathbb {R}$
, so it has a least element. Therefore,
$$ \begin{align*} x \in (\Box_R f)^{-1}(\lambda, \infty) & \mbox{ iff } (\Box_R f)(x)> \lambda \\ & \mbox{ iff } \min fR[x] > \lambda \\ & \mbox{ iff } R[x] \subseteq f^{-1}(\lambda, \infty) \\ & \mbox{ iff } x \in X \setminus R^{-1}[X \setminus f^{-1}(\lambda, \infty)]. \end{align*} $$
Next suppose that
$x \in E$
. Then
$(\Box _R f)(x) = 1$
. Thus,
$E \subseteq (\Box _R f)^{-1}(\lambda , \infty )$
if
$\lambda < 1$
, and
$E \cap (\Box _R f)^{-1}(\lambda , \infty ) = \varnothing $
otherwise. Consequently,
$$ \begin{align*} (\Box_R f)^{-1}(\lambda, \infty) = \left[D \cap (X \setminus R^{-1}[X \setminus f^{-1}(\lambda, \infty)]) \right]\cup E \end{align*} $$
if
$\lambda < 1$
, and
$$ \begin{align*} (\Box_R f)^{-1}(\lambda, \infty) = D \cap (X \setminus R^{-1}[X \setminus f^{-1}(\lambda, \infty)]) \end{align*} $$
if
$1 \le \lambda $
. Since
$f\in C(X)$
and R is continuous,
$X \setminus R^{-1}[X \setminus f^{-1}(\lambda , \infty )]$
is open. Thus,
$(\Box _R f)^{-1}(\lambda , \infty )$
is open by Lemma 3.3.
We next show that
$(\Box _R f)^{-1}(-\infty , \lambda )$
is open. If
$x \in D$
, then
$$ \begin{align*} x \in (\Box_R f)^{-1}(-\infty, \lambda) & \mbox{ iff } (\Box_R f)(x) < \lambda \\ & \mbox{ iff } \min fR[x] < \lambda \\ & \mbox{ iff } R[x] \cap f^{-1}(-\infty, \lambda) \ne \varnothing \\ & \mbox{ iff } x \in R^{-1}[f^{-1}(-\infty, \lambda)]. \end{align*} $$
If
$\lambda \le 1$
, then
$E \cap (\Box _R f)^{-1}(-\infty , \lambda ) = \varnothing $
. On the other hand, if
$1 < \lambda $
, then
$E \subseteq (\Box _R f)^{-1}(-\infty , \lambda )$
. Therefore,
$$ \begin{align*} (\Box_R f)^{-1}(-\infty, \lambda) = D \cap R^{-1}[f^{-1}(-\infty, \lambda)] \end{align*} $$
if
$\lambda \le 1$
, and
$$ \begin{align*} (\Box_R f)^{-1}(-\infty, \lambda) =\left[D \cap (R^{-1}[f^{-1}(-\infty, \lambda)])\right] \cup E \end{align*} $$
if
$\lambda> 1$
. Since
$f\in C(X)$
and R is continuous,
$R^{-1}[f^{-1}(-\infty , \lambda )]$
is open. Consequently,
$(\Box _R f)^{-1}(-\infty , \lambda )$
is open by Lemma 3.3. This completes the proof that if
$f \in C(X)$
, then
$\Box _R f \in C(X)$
.⊣
In the next lemma we describe the properties of
$\Box _R$
. For this we recall (see, e.g., [Reference Bezhanishvili, Morandi and Olberding6, Remark 2.2]) that if
$A\in \boldsymbol {\mathit {ba}\ell }$
and
$a\in A$
, then the positive and negative parts of a are defined as
$$ \begin{align*} a^+=a\vee 0 \quad \mbox{and}\quad a^-={-}\ (a\wedge 0)=(-a)\vee 0. \end{align*} $$
Then
$a^+,a^- \ge 0$
,
$a^+ \wedge a^-=0$
,
$a=a^+ - a^-$
, and
$|a|=a^+ + a^-$
.
Lemma 3.8. Let
$(X,R)$
be a compact Hausdorff frame,
$f,g \in C(X)$
, and
$\lambda \in \mathbb {R}$
.
-
1.
$\Box _R(f\wedge g) = \Box _R f \wedge \Box _R g$
. In particular,
$\Box _R$
is order preserving. -
2.
$\Box _R \lambda = \lambda + (1-\lambda )(\Box _R 0)$
. In particular,
$\Box _R 1 = 1$
. -
3.
$\Box _R (f^+) = (\Box _R f)^+$
. -
4.
$\Box _R(f + \lambda ) = \Box _R f + \Box _R\lambda - \Box _R 0$
. -
5. If
$0 \le \lambda $
, then
$\Box _R (\lambda f) = (\Box _R\lambda )( \Box _R f)$
.
Proof. (1) For
$x \in D$
, we have
$$ \begin{align*} \Box_R (f \wedge g )(x) &= \inf \{ (f \wedge g)(y) \mid y \in R[x] \} = \inf \{ \min \{ f(y), g(y) \} \mid y \in R[x] \} \\ &= \min \{ \inf \{ f(y) \mid y \in R[x] \}, \inf \{ g(y) \mid y \in R[x] \} \}\\ & = \min \{ (\Box_R f)(x), (\Box_R g)(x) \} \\ &= (\Box_R f \wedge \Box_R g)(x). \end{align*} $$
If
$x \in E$
, then
$$ \begin{align*} \Box _R (f \wedge g)(x) = 1 = (\Box _R f \wedge \Box _R g)(x). \end{align*} $$
Thus,
$\Box _R(f\wedge g) = \Box _R f \wedge \Box _R g$
.
(2) For
$x \in D$
, if
$\mu \in \mathbb {R}$
, we have
$(\Box _R \mu )(x) = \inf \{ \mu \mid y \in R[x] \} = \mu $
. From this we see that
$(\Box _R \lambda )(x) = \lambda = (\lambda + (1-\lambda )(\Box _R 0))(x)$
. If
$x \in E$
, then
$(\Box _R \lambda )(x) = 1 = (\lambda + (1-\lambda )(\Box _R 0))(x)$
. Thus,
$\Box _R \lambda = \lambda + (1-\lambda )(\Box _R 0)$
. Setting
$\lambda =1$
yields
$\Box _R 1 = 1$
.
(3) For
$x \in D$
, we have
$$ \begin{align*} (\Box_R (f^+))(x) &= \Box_R (f \lor 0)(x) =\inf \{ \max\{f(y),0 \} \mid y \in R[x] \} \\ &=\max\{\inf \{ f(y) \mid y \in R[x] \},0\} = \max \{ \Box_R f(x), 0\}\\ &= (\Box_R f \vee 0)(x) = (\Box_R f)^+(x). \end{align*} $$
If
$x \in E$
, then
$(\Box _R (f^+))(x) = 1 = (\Box _R f)^+(x)$
. Thus,
$\Box _R (f^+) = (\Box _R f)^+$
.
(4) For
$x \in D$
, we have
$$ \begin{align*} \Box_R (f+\lambda)(x) &=\inf \{ f(y)+\lambda \mid y \in R[x] \}\\ &=\inf \{ f(y) \mid y \in R[x] \}+\lambda \\ &= \Box_R f(x) + \lambda. \end{align*} $$
On the other hand,
$$ \begin{align*} (\Box_R f + \Box_R \lambda - \Box_R 0)(x) = (\Box_R f)(x) + (\Box_R \lambda)(x) - (\Box_R 0)(x) = (\Box_R f)(x) + \lambda. \end{align*} $$
Therefore,
$\Box _R (f+\lambda )(x) = (\Box _R f + \Box _R \lambda - \Box _R 0)(x)$
. If
$x \in E$
, then
$$ \begin{align*} \Box_R (f+\lambda)(x) = 1 = (\Box_Rf + \Box_R \lambda - \Box_R 0)(x). \end{align*} $$
Thus,
$\Box _R(f + \lambda ) = \Box _Rf + \Box _R \lambda - \Box _R 0$
.
(5) Let
$0 \le \lambda $
. For
$x \in D$
, we have
$$ \begin{align*} (\Box_R \lambda f )(x) &=\inf \{ \lambda f(y) \mid y \in R[x] \}= \lambda \inf \{ f(y) \mid y \in R[x] \} \\ &= \lambda (\Box_R f)(x) = (\Box_R\lambda)(x)(\Box_R f)(x) = (\Box_R\lambda \Box_R f)(x). \end{align*} $$
If
$x \in E$
, then
$$ \begin{align*} (\Box _R \lambda f)(x) = 1 = (\Box _R \lambda )(\Box _R f)(x). \end{align*} $$
Thus,
$\Box _R (\lambda f) = (\Box _R\lambda )(\Box _R f)$
.⊣
Remark 3.9. Lemma 3.8 can be stated dually in terms of
$\Diamond _R$
as follows. Let
$(X,R)$
be a compact Hausdorff frame,
$f,g \in C(X)$
, and
$\lambda \in \mathbb {R}$
.
-
1.
$\Diamond _R (f \vee g)=\Diamond _R f \vee \Diamond _R g$
. In particular,
$\Diamond _R$
is order preserving. -
2.
$\Diamond _R \lambda = \lambda (\Diamond _R 1)$
. In particular,
$\Diamond _R 0 = 0$
. -
3.
$\Diamond _R (f \wedge 1) = (\Diamond _R f) \wedge 1$
. -
4.
$\Diamond _R(f+\lambda )=\Diamond _R f + \Diamond _R\lambda $
. -
5. If
$0 \le \lambda $
, then
$\Diamond _R (\lambda f) = \Diamond _R\lambda \Diamond _R f$
.
The identities (1), (3), and (5) are direct translations of the corresponding identities for
$\Box _R$
. However, the identities (2) and (4) are simpler. We next show why
$\Diamond _R$
affords such simplifications.
For (2), since
$\Diamond _R 1 = 1 - \Box _R 0$
, by Lemma 3.8(2),
$$ \begin{align*} \Diamond_R \lambda = 1 - \Box_R(1-\lambda) = 1 - (1 - \lambda + \lambda\Box_R 0) = \lambda(1 - \Box_R 0) = \lambda\Diamond_R 1. \end{align*} $$
For (4), by using (4) and (2) of Lemma 3.8, we have
$$ \begin{align*} \Diamond_R(f + \lambda) &= 1 - \Box_R(1- (f + \lambda)) = 1 - \Box_R((1-f) - \lambda) \\ &= 1 - (\Box_R(1-f) + \Box_R(-\lambda) - \Box_R 0) = \Diamond_R f - \Box_R(-\lambda) + \Box_R 0 \\ &= \Diamond_R f - (-\lambda + (1+\lambda)\Box_R 0) + \Box_R 0 = \Diamond_R f + \lambda(1 - \Box_R 0) \\ &= \Diamond_R f + \Diamond_R \lambda. \end{align*} $$
In Remark 4.2 we will explain why we prefer to work with
$\Box _R$
.
Lemmas 3.7 and 3.8 motivate the main definition of this paper.
Definition 3.10.
-
1. Let
$A \in \boldsymbol {\mathit {ba}\ell }$
. We say that a unary function
$\Box : A \to A$
is a modal operator on A provided
$\Box $
satisfies the following axioms for each
$a,b \in A$
and
$\lambda \in \mathbb {R}$
:-
(M1)
$\Box (a \land b) = \Box a \land \Box b$
. -
(M2)
$\Box \lambda = \lambda + (1 - \lambda )\Box 0$
. -
(M3)
$\Box (a^+)=(\Box a)^+$
. -
(M4)
$\Box (a+\lambda )=\Box a + \Box \lambda - \Box 0$
. -
(M5)
$\Box (\lambda a)= (\Box \lambda )(\Box a)$
provided
$\lambda \ge 0$
.
-
-
2. If
$\Box $
is a modal operator on
$A\in \boldsymbol {\mathit {ba}\ell }$
, then we call the pair
$\mathfrak {A} = (A, \Box )$
a modal bounded archimedean
$\ell $
-algebra. -
3. Let
$\boldsymbol {\mathit {mba}\ell }$
be the category of modal bounded archimedean
$\ell $
-algebras and unital
$\ell $
-algebra homomorphisms preserving
$\Box $
.
Remark 3.11. We can define
$\Diamond :A \to A$
dual to
$\Box $
by
$\Diamond a = 1 - \Box (1 - a)$
for each
$a \in A$
. Then
$(A,\Diamond )$
satisfies the axioms for
$\Diamond $
dual to the ones for
$\Box $
in Definition 3.10(1) (see Remark 3.9). While algebras in
$\boldsymbol {\mathit {mba}\ell }$
can be axiomatized either in the signature of
$\Box $
or
$\Diamond $
, we prefer to work with
$\Box $
for the reasons given in Remark 4.2.
Remark 3.12. If
$\Box 0 = 0$
, then (M2), (M4), and (M5) simplify to the following:
-
(M2')
$\Box \lambda = \lambda $
. -
(M4')
$\Box (a + \lambda ) = \Box a + \lambda $
. -
(M5')
$\Box (\lambda a) = \lambda \Box a$
provided
$\lambda \ge 0$
.
Moreover, assuming
$\Box 0=0$
and (M4
${}'$
), we obtain (M2
${}'$
) by setting
$a = 0$
in (M4
${}'$
). Furthermore,
$\Diamond a =\, -\Box (-a)$
. In Section 7 we will see that
$\Box 0 = 0$
holds iff the binary relation
$R_\Box $
given in Definition 4.1 is serial.
Lemma 3.13. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
,
$a,b\in A$
, and
$\lambda \in \mathbb R$
.
-
1.
$a \leq b$
implies
$\Box a \leq \Box b$
. -
2.
$\Box 1 = 1$
. -
3.
$a \ge 0$
implies
$\Box a \ge 0$
. -
4.
$(\Box 0)(\Box a) = \Box 0$
. In particular,
$\Box 0$
is an idempotent. -
5.
$\Box (a + \lambda ) = \Box a + \lambda (1-\Box 0)$
. -
6.
$\Diamond a =\, -\Box (-a)(1 - \Box 0)$
. -
7.
$(\Diamond a)(\Box 0) = 0$
.
Proof. (1) If
$a \leq b$
, then
$a \land b=a$
. Therefore, by (M1), we have
$\Box a = \Box (a \land b)= \Box a \land \Box b$
. Thus,
$\Box a \leq \Box b$
.
(2) This follows by substituting
$\lambda =1$
in (M2).
(3) From (M3) and
$a \ge 0$
we have
$\Box a = \Box (a^+) = (\Box a)^+ \ge 0$
.
(4) By (M5),
$\Box 0 = \Box (0a) = (\Box 0)(\Box a)$
. Setting
$a = 0$
gives
$(\Box 0)^2 = \Box 0$
.
(5) By (M4),
$\Box (a + \lambda ) = \Box a + \Box \lambda - \Box 0$
. By (M2),
$$ \begin{align*} \Box \lambda = \lambda + (1-\lambda )(\Box 0) = \lambda (1 - \Box 0) + \Box 0. \end{align*} $$
Therefore,
$\Box \lambda - \Box 0 = \lambda (1 - \Box 0)$
, and so (5) follows.
(6) By (M4), (2), and (4) we have
$$ \begin{align*} \Diamond a &= 1 - \Box(1-a) = 1 - (\Box(-a) + \Box 1 - \Box 0) \\ &=\, -\Box(-a) + \Box 0 =\, -\Box(-a) + \Box(-a)\Box 0 \\ &=\, -\Box(-a)(1- \Box 0). \end{align*} $$
(7) Since
$\Box 0$
is an idempotent by (4), we have
$(1 - \Box 0)\Box 0 = 0$
. Multiplying both sides of (6) by
$\Box 0$
yields
$\Diamond a \Box 0 = 0$
.⊣
As follows from Lemmas 3.7 and 3.8, if
$(X,R)$
is a compact Hausdorff frame, then
$(C(X),\Box _R)\in \boldsymbol {\mathit {mba}\ell }$
. We now extend this correspondence to a contravariant functor. For this we recall the definition of a bounded morphism.
Definition 3.14.
-
1. A bounded morphism (or p-morphism) between Kripke frames
$\mathfrak F=(X,R)$
and
$\mathfrak G=(Y,S)$
is a map
$f:X\to Y$
satisfying
$f(R[x])=S[f(x)]$
for each
$x\in X$
(equivalently,
$f^{-1} (S^{-1}[y]) = R^{-1}[f^{-1}(y)]$
for each
$y \in Y$
). -
2. Let
${\sf KHF}$
be the category of compact Hausdorff frames and continuous bounded morphisms.
Lemma 3.15. If
$\mathfrak F=(X,R)$
and
$\mathfrak G=(Y,S)$
are compact Hausdorff frames and
$\varphi : X \to Y$
is a continuous bounded morphism, then
$C(\varphi )$
is a morphism in
$\boldsymbol {\mathit {mba}\ell }$
.
Proof. That
$C(\varphi )$
is a
$\boldsymbol {\mathit {ba}\ell }$
-morphism follows from Gelfand duality. Therefore, it is sufficient to prove that
$C(\varphi )$
preserves
$\Box $
; that is,
$C(\varphi )(\Box _S f) = \Box _R C(\varphi )(f)$
for each
$f\in C(Y)$
. Since
$\varphi $
is a bounded morphism,
$\varphi (R[x]) = S[\varphi (x)]$
for each
$x \in X$
. Let
$x \in X$
and
$f\in C(Y)$
. If
$R[x] \ne \varnothing $
, then
$S[\varphi (x)] \ne \varnothing $
, so
$$ \begin{align*} C(\varphi)(\Box_S f)(x) &= (\Box_S f \circ \varphi)(x)=(\Box_S f)(\varphi(x)) =\inf (f(S[\varphi(x)]))\\ &=\inf (f(\varphi(R[x])))= \inf ((f \circ \varphi)(R[x])) =\Box_R(f \circ \varphi)(x) \\ &= \Box_R(C(\varphi)(f))(x). \end{align*} $$
If
$R[x] = \varnothing $
, then
$S[\varphi (x)] = \varnothing $
, so
$$ \begin{align*} C(\varphi )(\Box _S f)(x) = (\Box _S f)(\varphi (x)) = 1 = (\Box _R C(\varphi )(f))(x). \end{align*} $$
Thus,
$C(\varphi )(\Box _S f) = \Box _R C(\varphi )(f)$
.⊣
Theorem 3.16. There is a contravariant functor
$C:{\sf KHF}\to \boldsymbol {\mathit {mba}\ell }$
which sends
$\mathfrak F=(X,R)$
to
$C(\mathfrak F) = (C(X),\Box _R)$
and a morphism
$\varphi $
in
${\sf KHF}$
to
$C(\varphi )$
.
Proof. If
$\mathfrak F \in {\sf KHF}$
, then
$C(\mathfrak F) \in \boldsymbol {\mathit {mba}\ell }$
by Lemmas 3.7 and 3.8. If
$\varphi $
is a morphism in
${\sf KHF}$
, then
$C(\varphi )$
is a morphism in
$\boldsymbol {\mathit {mba}\ell }$
by Lemma 3.15. It follows from Gelfand duality that
$C(\psi \circ \varphi ) = C(\varphi )\circ C(\psi )$
and that C preserves identity morphisms. Thus, C is a contravariant functor.⊣
4 Continuous relations on the Yosida space
In this section we define a contravariant functor
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
in the other direction, which is technically the most involved part of the paper.
Let
$A\in \boldsymbol {\mathit {ba}\ell }$
. For
$S \subseteq A$
let
$$ \begin{align*} S^+=\{a \in S \mid a \geq 0 \}. \end{align*} $$
We point out that if I is an
$\ell $
-ideal of A, then
$I^+ = \{ a^+ \mid a \in I\}$
.
Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
. For
$S \subseteq A$
we use the following standard notation from modal logic
$$ \begin{align*} \Box S := \{ \Box a \mid a \in S \} \mbox{ and } \Box^{-1} S := \{ a \mid \Box a \in S \}. \end{align*} $$
Definition 4.1. Let
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
and let
$Y_A$
be the Yosida space of A. Define
$R_\Box $
on
$Y_A$
by
$$ \begin{align*} x R_\Box y \quad\mbox{iff}\quad \Box y^+ \subseteq x, \quad\mbox{iff}\quad y^+ \subseteq \Box^{-1}x. \end{align*} $$
Remark 4.2. Comparing the definition above of
$R_\Box $
to the definition of
$R_\Box $
on the space of ultrafilters of a modal algebra in Jónsson-Tarski duality, we see that the inclusion is reversed because here we work with ideals rather than filters.
We have that
$$ \begin{align*} xR_\Box y \text{ iff } (\forall a \ge 0)(a+y = 0+y \Rightarrow \Box a + x = 0 + x). \end{align*} $$
If we work with
$\Diamond $
instead of
$\Box $
, since
$\Diamond a=1-\Box (1-a)$
, the definition becomes
$$ \begin{align*} x R_\Box y \text{ iff } (\forall b \le 1)(b + y = 1 + y \Rightarrow \Diamond b + x = 1 + x).\end{align*} $$
Thus,
$x R_\Box y$
iff
$\{ 1 - \Diamond b \mid 1-b \in y, b \le 1\} \subseteq x$
. This more complicated definition is one reason why we prefer to work with
$\Box $
rather than
$\Diamond $
. Another is that, as is standard in working with ordered algebras, using
$\Box $
allows us to work with the positive cone rather than the set of elements below 1.
Let
$A \in \boldsymbol {\mathit {ba}\ell }$
. We recall that the zero set of
$a \in A$
is defined as
$$ \begin{align*} Z_{\ell}(a) = \{ x \in Y_A \mid a \in x \}. \end{align*} $$
If
$S \subseteq A$
, then we set
$$ \begin{align*} Z_{\ell}(S) = \bigcap \{ Z_{\ell}(a) \mid a \in S\} = \{ x \in Y_A \mid S \subseteq x\}. \end{align*} $$
It is easy to see that if I is the
$\ell $
-ideal generated by S, then
$Z_{\ell }(S) = Z_{\ell }(I)$
. We define the cozero set of S as
$$ \begin{align*} \operatorname{coz}_{\ell}(S)=Y_A \setminus Z_{\ell}(S)=\{ x \in Y_A \mid S \not\subseteq x \}. \end{align*} $$
Since the zero sets are exactly the closed sets, the cozero sets are exactly the open sets of
$Y_A$
. The family
$\{ \operatorname {coz}_{\ell }(a) \mid a \in A \}$
then constitutes a basis for the topology on
$Y_A$
.
Remark 4.3. Let
$A \in \boldsymbol {\mathit {ba}\ell }$
,
$Y_A$
be the Yosida space of A,
$x \in Y_A$
, and
$a \in A$
.
-
1. x is a prime ideal of A because
$A/x \cong \mathbb {R}$
(see, e.g., [Reference Henriksen and Johnson20, Corollary 2.7]). -
2. Either
$a^+ \in x$
or
$a^- \in x$
. This follows from (1) and
$a^+ a^- = 0$
. -
3.
$a^+ \in x$
and
$a^- \notin x$
iff
$a + x < 0 + x$
(see [Reference Bezhanishvili, Morandi and Olberding7, Remark 2.11]). -
4.
$a^+ \in x$
iff
$a + x \le 0 + x$
. For, if
$a^+ \in x$
, thensince
$$ \begin{align*} a + x = (a^+ - a^-) + x =\ -a^- + x \le 0 + x \end{align*} $$
$a^- \ge 0$
. Conversely, if
$a + x \le 0 + x$
, then either
$a + x < 0 + x$
, in which case
$a^+ \in x$
by (3), or
$a + x = 0 + x$
, in which case
$a \in x$
, so
$a^+ \in x$
.
-
5.
$a^- \in x$
and
$a^+ \notin x$
iff
$a + x> 0 + x$
(see [Reference Bezhanishvili, Morandi and Olberding7, Remark 2.11]). -
6.
$a^- \in x$
iff
$a + x \ge 0 + x$
. The proof is similar to that of (4) but uses (5) instead of (3).
Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
and
$R_\Box $
be defined on
$Y_A$
as in Definition 4.1. Recalling Notation 3.2, we denote
$R_\Box ^{-1}[Y_A]$
by
$D_A$
and
$Y_A \setminus D_A$
by
$E_A$
.
Lemma 4.4. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
,
$a \in A$
,
$\lambda \in \mathbb {R}$
, and
$x \in Y_A$
.
-
1. If
$x \in D_A$
, then
$\Box 0 \in x$
. -
2. If
$\Box 0 \in x$
, then
$\Box (a + \lambda ) + x = (\Box a + \lambda ) + x$
. -
3. If
$\Box 0 \in x$
, then
$\Box ((a - \lambda )^+) \in x$
iff
$(\Box a - \lambda )^+ \in x$
. -
4. If
$\Box 0 \in x$
, then
$\Diamond a + x =\, -\Box (-a) + x$
. -
5. If
$\Box 0 \notin x$
, then
$1 - \Box a \in x$
. -
6. If
$\Diamond a \notin x$
, then
$\Box 0 \in x$
.
Proof. (1) If
$x \in D_A$
, then there is y with
$x R_\Box y$
. Therefore, since
$0 \in y^+$
, we have
$\Box 0 \in x$
.
(2) By (M4) and (M2),
$\Box (a + \lambda ) = \Box a + \lambda - \lambda \Box 0$
. Therefore, if
$\Box 0 \in x$
, then
$\Box (a + \lambda ) + x = (\Box a + \lambda ) + x$
.
(3) This follows from (M3), Remark 4.3(4), and (2).
(4) Apply Lemma 3.13(6).
(5) By Lemma 3.13(4),
$\Box 0 = (\Box 0)(\Box a)$
, so
$(\Box 0)(1 - \Box a) = 0 \in x$
. Since
$\Box 0 \notin x$
and x is a prime ideal,
$1 - \Box a \in x$
.
(6) By Lemma 3.13(7),
$(\Diamond a)(\Box 0) = 0 \in x$
. Since x is a prime ideal and
$\Diamond a \notin x$
, we have
$\Box 0 \in x$
.⊣
Proposition 4.5.
$R_\Box [x]$
is closed for every
$x \in Y_A$
.
Proof. We prove that
$Y_A \setminus R_\Box [x]$
is open for every
$x \in Y_A$
. Let
$y \notin R_\Box [x]$
, so
$y^+ \nsubseteq \Box ^{-1} x$
. Therefore, there is
$a \geq 0$
such that
$a \in y$
and
$\Box a \notin x$
. By Lemma 3.13(3),
$\Box a \geq 0$
, so there exists
$0 \le \lambda \in \mathbb {R}$
such that
$(\Box a -\lambda ) +x> 0+x$
but
$(a-\lambda )+y < 0+y$
. By Remark 4.3(3,5),
$(a-\lambda )^- \notin y$
and
$(\Box a - \lambda )^+ \notin x$
. Thus,
$y\in \operatorname {coz}_{\ell }((a-\lambda )^-)$
, and it remains to show that
$\operatorname {coz}_{\ell }((a-\lambda )^-) \cap R_\Box [x]= \varnothing $
. Suppose not. Then there is z such that
$x R_\Box z$
and
$z \in \operatorname {coz}_{\ell }((a-\lambda )^-)$
. Since
$(a-\lambda )^- \notin z$
, we have
$(a-\lambda )^+ \in z$
(see Remark 4.3(2)). But
$x R_\Box z$
means
$z^+ \subseteq \Box ^{-1} x$
, so
$\Box 0, \Box ((a-\lambda )^+) \in x$
. Thus, by Lemma 4.4(3),
$(\Box a - \lambda )^+ \in x$
, hence
$(\Box a - \lambda ) + x \le 0 + x$
. This is a contradiction. Consequently, we have that
$\operatorname {coz}_{\ell }((a-\lambda )^-) \cap R_\Box [x]= \varnothing $
, completing the proof.⊣
Remark 4.6. Since
$R_\Box [x]$
is closed for each
$x \in Y_A$
, it is of the form
$Z_\ell (S)$
for some
$S \subseteq A$
. In fact,
$R_\Box [x] = Z_\ell (S)$
where
$S = \{ a \in A \mid a \ge 0 \text{ and } \Diamond a \in x\}$
.
For a topological space X and a continuous real-valued function f on X, we recall that the zero set of f is
$$ \begin{align*} Z(f)=\{x\in X \mid f(x)=0\} \end{align*} $$
and the cozero set of f is
$$ \begin{align*} \mathrm{coz}(f) = X \setminus Z(f) = \{x\in X \mid f(x) \ne 0\}. \end{align*} $$
The following lemma is a consequence of [Reference Gillman and Jerison17, Problem 1D, p. 21].
Lemma 4.7. Let
$A\in \boldsymbol {\mathit {ba}\ell }$
and
$a,s \in A$
. If
$Z_{\ell }(a) \subseteq \operatorname {int} Z_{\ell }(s)$
, then there is
$f \in C(Y_A)$
such that
$\zeta _A(s)=\zeta _A(a)f$
in
$C(Y_A)$
.
Proof. Observe that for each
$t\in A$
we have
$Z_{\ell }(t)=Z(\zeta _A(t))$
. Therefore,
$Z_{\ell }(a) \subseteq \operatorname {int} Z_{\ell }(s)$
implies
$Z(\zeta _A(a)) \subseteq \operatorname {int} Z(\zeta _A(s))$
. Now apply [Reference Gillman and Jerison17, Problem 1D, p. 21].⊣
Lemma 4.8. Let
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
,
$x \in Y_A$
,
$S=(A \setminus \Box ^{-1} x)^+$
, and
$a \in (\Box ^{-1} x)^+$
.
-
1.
$\bigcap \{ \operatorname {coz}_{\ell }(s) \mid s \in S \} = \bigcap \{ \overline {\operatorname {coz}_{\ell }(s)} \mid s \in S \}$
. -
2.
$\overline {\operatorname {coz}_{\ell }(s)} \cap Z_{\ell }(a) \neq \varnothing $
for every
$s \in S$
. -
3. The family
$\{ \overline {\operatorname {coz}_{\ell }(s)} \cap Z_{\ell }(a) \mid s \in S \}$
has the finite intersection property.
Proof. (1) The inclusion
$\subseteq $
is clear. To prove the reverse inclusion, it is sufficient to prove that for each
$s \in S$
there is
$t \in S$
such that
$\overline {\operatorname {coz}_{\ell }(t)} \subseteq \operatorname {coz}_{\ell }(s)$
. Since
$s \in S$
, we have
$\Box s \notin x$
, so there is
$\varepsilon \in \mathbb {R}$
with
$\Box s + x> \varepsilon + x > 0 + x$
. Set
$t=(s-\varepsilon )^+$
. Then
$t \geq 0$
and
$$ \begin{align*} \Box t = \Box (s-\varepsilon)^+ = (\Box (s - \varepsilon))^+ \end{align*} $$
by (M3). If
$\Box t \in x$
, then
$\Box (s - \varepsilon ) + x \le 0 + x$
, so
$\Box s - \varepsilon (1-\Box 0) + x \le 0 + x$
by Lemma 3.13(5). We have
$\Box 0 \in x$
by Lemma 4.4(5) as
$\Box a \in x$
. Therefore,
$(\Box s - \varepsilon) + x \le 0 + x$
, and hence
$\Box s + x \le \varepsilon + x$
. The obtained contradiction shows
$\Box t \notin x$
, so
$t \in S$
. Let
$ z \in Z_{\ell }(s)$
. Then
$z \in \zeta _A(s)^{-1}(- \varepsilon , \varepsilon )$
, an open set. But
$\zeta _A(s)^{-1}(- \varepsilon , \varepsilon ) \subseteq Z_{\ell }(t)$
by the definition of t and Remark 4.3(3), so
$Z_{\ell }(s) \subseteq \operatorname {int} Z_{\ell }(t)$
. Thus,
$\overline {\operatorname {coz}_{\ell }(t)} \subseteq \operatorname {coz}_{\ell }(s)$
.
(2) Note that
$\overline {\operatorname {coz}_{\ell }(s)} \cap Z_{\ell }(a) \neq \varnothing $
means that
$Z_{\ell }(a) \nsubseteq \operatorname {int} Z_{\ell }(s)$
. We argue by contradiction. Suppose
$Z_{\ell }(a) \subseteq \operatorname {int} Z_{\ell }(s)$
. Then by Lemma 4.7, there is
$f \in C(Y_A)$
such that
$\zeta _A(s)=\zeta _A(a)f$
in
$C(Y_A)$
. Since
$C(Y_A)$
is the uniform completion of A (see Proposition 2.3), there is a sequence
$\{ b_n \} \subseteq A$
such that
$f= \lim \zeta _A(b_n)$
. It is well known that multiplication is continuous with respect to the norm, so we have
$\lim \zeta _A(ab_n)= \zeta _A(a)f =\zeta _A(s)$
. Since
$s \in S$
, there is
$\varepsilon>0$
such that
$\Box s + x> \varepsilon + x$
, so
$(\Box s - \varepsilon ) + x> 0 + x$
. There is N such that
$||s-ab_N||< \varepsilon $
. Therefore,
$s < ab_N+\varepsilon $
. Take
$0 < \lambda \in \mathbb {R}$
such that
$b_N \leq \lambda $
. Then
$s < \lambda a + \varepsilon $
. Since
$0 \le \Box 0 \le \Box a \in x$
, we have
$\Box 0 \in x$
. Thus by Lemmas 3.13(1) and 4.4(2), and (M5),
$$ \begin{align*} \Box s + x \leq \Box (\lambda a +\varepsilon) + x = (\Box (\lambda a) + \varepsilon) + x = (\Box\lambda\Box a + \varepsilon) + x. \end{align*} $$
But
$\Box a \in x$
, so
$\Box s + x \le \varepsilon + x$
, contradicting
$\varepsilon + x < \Box s +x$
.
(3) We first show that the intersection of any two members of the family contains another member of the family. Let
$s,t \in S$
. Then
$\Box s, \Box t \notin x$
. Since x is a maximal
$\ell $
-ideal,
$A/x \cong \mathbb {R}$
is totally ordered, so
$$ \begin{align*} (\Box s \wedge \Box t) + x = \min\{ \Box s + x, \Box t + x\} \ne 0 + x, \end{align*} $$
and hence
$\Box s \wedge \Box t \notin x$
. By (M1), this shows
$\Box (s \wedge t) \notin x$
, which gives
$s \wedge t \in S$
. Since
$\operatorname {coz}_{\ell }(s\wedge t)= \operatorname {coz}_{\ell }(s) \cap \operatorname {coz}_{\ell }(t)$
, we have:
$$ \begin{align*} (\overline{\operatorname{coz}_{\ell}(s)}\cap Z_{\ell}(a)) \cap (\overline{\operatorname{coz}_{\ell}(t)}\cap Z_{\ell}(a)) & = \overline{\operatorname{coz}_{\ell}(s)} \cap \overline{\operatorname{coz}_{\ell}(t)} \cap Z_{\ell}(a) \\ & \supseteq \overline{\operatorname{coz}_{\ell}(s) \cap \operatorname{coz}_{\ell}(t)} \cap Z_{\ell}(a)\\ & = \overline{\operatorname{coz}_{\ell}(s\wedge t)} \cap Z_{\ell}(a). \end{align*} $$
Because
$s\wedge t \in S$
, we have that
$\overline {\operatorname {coz}_{\ell }(s\wedge t)} \cap Z_{\ell }(a)$
is in the family. An easy induction argument then completes the proof because every element of the family is nonempty by (2).⊣
Proposition 4.9. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
and
$x \in Y_A$
. Then
$$ \begin{align*} (\Box ^{-1} x)^+ = \bigcup \{ y^+ \mid y \in R_\Box [x] \}. \end{align*} $$
Proof. The right-to-left inclusion follows from the definition of
$R_\Box $
. For the left-to-right inclusion, let
$a \in (\Box ^{-1} x)^+$
. By Lemma 4.8(1),
$$ \begin{align*} \bigcap \{\operatorname{coz}_{\ell}(s) \cap Z_{\ell}(a) \mid s \in S \} = \bigcap \{ \overline{\operatorname{coz}_{\ell}(s)} \cap Z_{\ell}(a) \mid s \in S \}. \end{align*} $$
By Lemma 4.8(3) and compactness of
$Y_A$
, this intersection is nonempty. Therefore, there is
$y \in \bigcap \{ \operatorname {coz}_{\ell }(s) \cap Z_{\ell }(a) \mid s \in S \}$
. This means that
$a \in y$
and
$y \cap S= \varnothing $
, so
$y^+ \subseteq \Box ^{-1} x$
. Thus, a is contained in some
$y \in R_\Box [x]$
, completing the proof.⊣
Lemma 4.10. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
.
-
1.
$R_\Box ^{-1}[Z_{\ell }(a)]=Z_{\ell }(\Box a)$
for every
$0\le a \in A$
. -
2.
$D_A = Z_{\ell }(\Box 0)$
.
Proof. (1) Let
$x \in R_\Box ^{-1}[Z_{\ell }(a)]$
. Then there is
$y \in Y_A$
such that
$x R_\Box y$
and
$a \in y$
. Therefore,
$a \in y^+ \subseteq \Box ^{-1} x$
. Thus,
$\Box a \in x$
, and so
$x \in Z_{\ell }(\Box a)$
.
For the other inclusion, let
$x \in Z_{\ell }(\Box a)$
. Since
$\Box a \in x$
and
$\Box a \geq 0$
, we have
$a \in (\Box ^{-1}x)^+$
. By Proposition 4.9, there is
$y \in Y_A$
such that
$x R_\Box y$
and
$a \in y$
. Thus,
$x \in R_\Box ^{-1}[Z_{\ell }(a)]$
.
(2) This follows from (1) by setting
$a = 0$
and using
$Y_A = Z_{\ell }(0)$
.⊣
We will use Lemma 4.10 to prove that
$R_\Box ^{-1}[F]$
is closed for each closed subset F of
$Y_A$
. For this we require Esakia’s lemma, which is an important tool in modal logic (see, e.g., [Reference Chagrov and Zakharyaschev11, Section 10.3]). The original statement is for descriptive frames, but it has a straightforward generalization to the setting of compact Hausdorff frames (see [Reference Bezhanishvili, Bezhanishvili and Harding4, Lemma 2.17]). We call a relation R on a compact Hausdorff space X point-closed if
$R[x]$
is closed for each
$x\in X$
.
Lemma 4.11 (Esakia’s lemma)
If R is a point-closed relation on a compact Hausdorff space X, then for each
$($
nonempty
$)$
down-directed family
$\{ F_i \mid i\in I \}$
of closed subsets of X we have
$$ \begin{align*} R^{-1}\left[\bigcap\{ F_i \mid i\in I\}\right] = \bigcap \{ R^{-1}[F_i] \mid i\in I\}. \end{align*} $$
Remark 4.12. Let
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
and S be a set of nonnegative elements of A closed under addition. Since
$Z_{\ell }(a+b) \subseteq Z_{\ell }(a) \cap Z_{\ell }(b)$
for each
$a,b \in S$
, we have that
$\{ Z_{\ell }(a) \mid a \in S \}$
is a down-directed family of closed subsets of
$Y_A$
. Then, by Esakia’s lemma and Lemma 4.10, we have:
$$ \begin{align*} R_\Box^{-1}[Z_{\ell}(S)] & = R_\Box^{-1} \left[ \bigcap \{Z_{\ell}(a) \mid a \in S \} \right] = \bigcap \{ R_\Box^{-1}[Z_{\ell}(a)] \mid a \in S \}\\ & = \bigcap \{ Z_{\ell}(\Box a) \mid a \in S \} = Z_{\ell}(\Box S). \end{align*} $$
In particular, for an
$\ell $
-ideal I, since
$Z_\ell (I) = Z_\ell (I^+)$
, we have
$$ \begin{align*} R_\Box^{-1} Z_{\ell}(I)=R_\Box^{-1} Z_{\ell}(I^+)=\bigcap \{ Z_{\ell}(\Box a) \mid a \in I^+ \}. \end{align*} $$
Proposition 4.13.
$R_\Box ^{-1}[F]$
is closed for every closed subset F of
$Y_A$
.
Proof. Since F is a closed subset of
$Y_A$
, there is an
$\ell $
-ideal I such that
$F=Z_{\ell }(I)$
. By Remark 4.12,
$$ \begin{align*} R_\Box^{-1} Z_{\ell}(I)=\bigcap \{ Z_{\ell}(\Box a) \mid a \in I^+ \}, \end{align*} $$
which is closed because it is an intersection of closed subsets of
$Y_A$
.⊣
Lemma 4.14. If
$\Diamond a \in x$
and
$x R_\Box y$
, then
$a^+ \in y$
.
Proof. Suppose that
$x R_\Box y$
and
$a^+ \notin y$
. By Remark 4.3(4)
$a + y> 0 + y$
, so there is
$0 < \lambda \in \mathbb {R}$
such that
$a + y = \lambda + y$
. Therefore,
$\lambda -a \in y$
, so
$(\lambda -a)^+ \in y$
. Since
$y^+ \subseteq \Box ^{-1}x$
, we have
$\Box ((\lambda - a)^+ ) \in x$
. By Lemma 4.4(1)
$\Box 0 \in x$
, so
$(\lambda + \Box (- a))^+ \in x$
by Lemma 4.4(3). Thus,
$(\lambda + \Box (-a)) + x \le 0 + x$
, so
$\lambda + x \le\ -\Box (-a) + x$
, and hence
$\lambda + x \le \Diamond a + x$
by Lemma 4.4(4). Since
$\lambda + x> 0 + x$
, this shows
$\Diamond a \notin x$
.⊣
Lemma 4.15.
$R_\Box ^{-1}[\operatorname {coz}_{\ell }(a)]=\operatorname {coz}_{\ell }(\Diamond a)$
for every
$0 \le a \in A$
.
Proof. For the left-to-right inclusion, suppose
$x \notin \operatorname {coz}_{\ell }(\Diamond a)$
. Then
$\Diamond a \in x$
. Consider
$y \in R_\Box [x]$
. By Lemma 4.14,
$a=a^+ \in y$
, so
$y \notin \operatorname {coz}_{\ell } (a)$
. Therefore,
$x \notin R_\Box ^{-1}[\operatorname {coz}_{\ell }(a)]$
.
For the right-to-left inclusion, let
$x \in \operatorname {coz}_{\ell }(\Diamond a)$
. Then
$\Diamond a \notin x$
, so
$\Box 0 \in x$
by Lemma 4.4(6). Therefore, by Lemma 4.4(4),
$0 + x \ne \Diamond a + x =\, -\Box (-a) + x$
, and hence
$\Box (-a) \notin x$
. Since
$-a \leq 0$
, we have
$\Box (-a) + x \leq \Box 0 + x = 0 + x$
. Thus, there is
$\lambda \in \mathbb {R}$
with
$\lambda < 0$
and
$\Box (-a)+x= \lambda +x$
, so
$\Box (-a) - \lambda \in x$
. By Lemma 4.4(3), we have
$$ \begin{align*} \Box((-a-\lambda)^+) \in x \mbox{ iff } (\Box(-a)-\lambda)^+ \in x. \end{align*} $$
Consequently, by Proposition 4.9,
$$ \begin{align*} (-a-\lambda)^+ \in (\Box^{-1}x)^+ = \bigcup \{ y^+ \mid y \in R_\Box[x] \}. \end{align*} $$
Hence, there is
$y \in R_\Box [x]$
such that
$(-a-\lambda )^+ \in y$
. This means that
$(-a-\lambda )+y \leq 0+y$
, so
$a+y \geq\ -\lambda +y>0+y$
. Therefore,
$a \notin y$
, and so
$y \in \operatorname {coz}_{\ell }(a)$
. Thus,
$x \in R_\Box ^{-1}[\operatorname {coz}_{\ell }(a)]$
.⊣
Proposition 4.16.
$R_\Box ^{-1}[U]$
is open for every open subset U of
$Y_A$
.
Proof. Open subsets of
$Y_A$
are of the form
$\operatorname {coz}_{\ell }(I)=\bigcup \{ \operatorname {coz}_{\ell } (a) \mid a \in I \}$
for some
$\ell $
-ideal I. Since
$\operatorname {coz}_{\ell }(I)=\bigcup \{ \operatorname {coz}_{\ell } (a) \mid a \in I, \, a \geq 0 \}$
and
$R_\Box ^{-1}$
commutes with arbitrary unions, by Lemma 4.15, we have
$$ \begin{align*} R_\Box^{-1}\operatorname{coz}_{\ell}(I) & =R_\Box^{-1}\bigcup \{ \operatorname{coz}_{\ell} (a) \mid a \in I, \, a \geq 0 \}\\ & =\bigcup \{ R_\Box^{-1}\operatorname{coz}_{\ell} (a) \mid a \in I, \, a \geq 0 \}\\ & =\bigcup \{ \operatorname{coz}_{\ell} (\Diamond a) \mid a \in I, \, a \geq 0 \}, \end{align*} $$
which is open because it is a union of open subsets of
$Y_A$
.⊣
Putting Propositions 4.5, 4.13, and 4.16 together yields:
Theorem 4.17. If
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
, then
$(Y_A,R_\Box )\in {\sf KHF}$
.
We finish the section by showing how to extend the object correspondence of Theorem 4.17 to a contravariant functor
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
.
Lemma 4.18. Let
$(A,\Box ),(B,\Box ) \in \boldsymbol {\mathit {mba}\ell }$
and
$\alpha :A \to B$
be a morphism in
$\boldsymbol {\mathit {mba}\ell }$
. Then
$Y(\alpha ) : (Y_B, R_\Box ) \to (Y_A, R_\Box )$
is a bounded morphism.
Proof. For each
$y \in Y_A$
, we have that
$y^+$
and
$\alpha (y^+)$
are sets of nonnegative elements closed under addition, so Remark 4.12 applies. Therefore, since
$Z_\ell(y^+) = \{y\}$
,
$$ \begin{align*} Y(\alpha)^{-1}(R_\Box^{-1}[y]) =Y(\alpha)^{-1}(R_\Box^{-1}[Z_{\ell}(y^+)])=Y(\alpha)^{-1}(Z_{\ell}(\Box y^+)) \end{align*} $$
and
$$ \begin{align*} Z_{\ell}(\Box \alpha(y^+))=R_\Box^{-1}[Z_{\ell}(\alpha(y^+))]. \end{align*} $$
The definition of
$Y(\alpha )$
shows that
$$ \begin{align*} Y(\alpha)^{-1}(Z_{\ell}(\Box y^+))=Z_{\ell}(\alpha(\Box y^+)) \quad \mbox{and} \quad Y(\alpha)^{-1}(Z_{\ell}(y^+)) = Z_{\ell}(\alpha(y^+)). \end{align*} $$
This yields
$$ \begin{align*} Y(\alpha)^{-1}(R_\Box^{-1}[y]) = Y(\alpha)^{-1}(Z_{\ell}(\Box y^+)) = Z_{\ell}(\alpha(\Box y^+)) \end{align*} $$
and
$$ \begin{align*} R_\Box^{-1}[Y(\alpha)^{-1}(y)] = R_\Box^{-1}[Y(\alpha)^{-1}(Z_{\ell}(y^+))] = R_\Box^{-1}[Z_{\ell}(\alpha(y^+))] = Z_{\ell}(\Box \alpha(y^+)). \end{align*} $$
Consequently, since
$\alpha $
commutes with
$\Box $
, we have
$$ \begin{align*} Y(\alpha)^{-1}(R_\Box^{-1}[y]) = R_\Box^{-1}[Y(\alpha)^{-1}(y)], \end{align*} $$
which proves that
$Y(\alpha )$
is a bounded morphism.⊣
Putting Theorem 4.17 and Lemma 4.18 together and remembering that
$Y : \boldsymbol {\mathit {ba}\ell }\to {\sf KHaus}$
is a contravariant functor yields:
Theorem 4.19.
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
is a contravariant functor.
5 Duality
In this section we prove our main results. We show that Y and C yield a dual adjunction between
$\boldsymbol {\mathit {mba}\ell }$
and
${\sf KHF}$
which restricts to a dual equivalence between the category of uniformly complete members of
$\boldsymbol {\mathit {mba}\ell }$
and
${\sf KHF}$
.
Definition 5.1. Let
$\boldsymbol {\mathit {muba}\ell }$
be the full subcategory of
$\boldsymbol {\mathit {mba}\ell }$
consisting of uniformly complete objects of
$\boldsymbol {\mathit {mba}\ell }$
.
Proposition 5.2.
$\boldsymbol {\mathit {muba}\ell }$
is a reflective subcategory of
$\boldsymbol {\mathit {mba}\ell }$
.
Proof. By Corollary 2.4,
$\boldsymbol {\mathit {uba}\ell }$
is a reflective subcategory of
$\boldsymbol {\mathit {ba}\ell }$
, where
$CY :\boldsymbol {\mathit {ba}\ell }\to \boldsymbol {\mathit {uba}\ell }$
is the reflector. We first show that
$\zeta _A$
is an
$\boldsymbol {\mathit {mba}\ell }$
-morphism for each
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
. Let
$x \in Y_A$
. Recall that
$$ \begin{align*} (\Box_{R_\Box}\zeta_A(a))(x) = \left\{\begin{array}{ll}\inf \{ \zeta_A(a)(y) \mid x R_\Box y \} & \mbox{if }x \in D_A,\\ 1 & \text{if } x \in E_A.\end{array}\right. \end{align*} $$
If
$x \in E_A$
, then
$\Box 0 \notin x$
by Lemma 4.10(2). Therefore,
$\Box a - 1 \in x$
by Lemma 4.4(5), and hence
$\zeta _A(\Box a)(x) = 1 = (\Box _{R_\Box }\zeta _A(a))(x)$
. Now let
$x \in D_A$
. Then
$(\Box _{R_\Box }\zeta _A(a))(x) = \inf \{ \zeta _A(a)(y) \mid x R_\Box y \}$
. We first show that
$\zeta _A(\Box a)(x) \leq \inf \{ \zeta _A(a)(y) \mid x R_\Box y \}$
. Suppose that
$x R_\Box y$
, so
$y^+ \subseteq \Box ^{-1} x$
. Let
$\lambda = \zeta _A(a)(y)$
. Then
$a - \lambda \in y$
, so
$(a-\lambda )^+ \in y^+ \subseteq \Box ^{-1} x$
, and hence
$(\Box a -\lambda )^+ \in x$
by Lemma 4.4(1,3). Therefore,
$$ \begin{align*} 0=\zeta_A((\Box a -\lambda)^+)(x)=\max \{ \zeta_A(\Box a)(x)-\lambda ,0 \}, \end{align*} $$
so
$\zeta _A(\Box a)(x)-\lambda \leq 0$
, and hence
$\zeta _A(\Box a)(x) \leq \lambda =\zeta _A(a)(y)$
. Thus,
$\zeta _A(\Box a)(x) \leq \inf \{ \zeta _A(a)(y) \mid x R_\Box y \}$
.
We next show that
$\zeta _A(\Box a)(x) \geq \inf \{ \zeta _A(a)(y) \mid x R_\Box y \}$
. Let
$\mu = \zeta _A(\Box a)(x)$
. Then
$(\Box a - \mu)^+ \in x$
, and hence
$\Box((a-\mu)^+) \in x$
. Therefore, by Proposition 4.9,
$$ \begin{align*} (a-\mu)^+ \in (\Box^{-1}x)^+{=}\bigcup \{ y^+ \mid x R_\Box y \}. \end{align*} $$
So there is
$y \in R_\Box [x]$
such that
$(a-\mu )^+ \in y$
. Thus, by Remark 4.3(4),
$\zeta _A(a)(y) \leq \mu =\zeta _A(\Box a)(x)$
. Consequently,
$\inf \{ \zeta _A(a)(y) \mid y \in R_\Box [x] \} \leq \zeta _A(\Box a)(x)$
, and hence
$\zeta_A(\Box a) = \Box_{R_\Box} \zeta(a)$
. This yields that
$\zeta_A$
is an
$\boldsymbol {\mathit {mba}\ell }$
-morphism.
Next, let
$\alpha : A \to B$
be an
$\boldsymbol {\mathit {mba}\ell }$
-morphism with
$B \in \boldsymbol {\mathit {muba}\ell }$
. Since
$\alpha $
is a
$\boldsymbol {\mathit {ba}\ell }$
-morphism, there is a unique
$\boldsymbol {\mathit {ba}\ell }$
-morphism
$\gamma : C(Y_A) \to B$
such that
$\gamma \circ \zeta _A = \alpha $
. Since
$\zeta$
is a natural transformation and
$\zeta_B$
is an isomorphism, it follows that
$\gamma=\zeta_B^{-1} \circ CY(\alpha)$
.
As we saw in the paragraph above,
$\zeta _B$
is an
$\boldsymbol {\mathit {mba}\ell }$
-morphism. Also,
$CY(\alpha ) : C(Y_A) \to C(Y_B)$
is an
$\boldsymbol {\mathit {mba}\ell }$
-morphism by Lemmas 4.18 and 3.15. Therefore,
$\gamma $
is an
$\boldsymbol {\mathit {mba}\ell }$
-morphism, concluding the proof.⊣
Theorem 5.3. The functors
$Y:\boldsymbol {\mathit {mba}\ell }\to {\sf KHF}$
and
$C:{\sf KHF}\to \boldsymbol {\mathit {mba}\ell }$
yield a dual adjunction of the categories, which restricts to a dual equivalence between
$\boldsymbol {\mathit {muba}\ell }$
and
${\sf KHF}$
.
Proof. By Gelfand duality, the functors
$Y:\boldsymbol {\mathit {ba}\ell }\to {\sf KHaus}$
and
$C:{\sf KHaus}\to \boldsymbol {\mathit {ba}\ell }$
yield a dual adjunction between
$\boldsymbol {\mathit {ba}\ell }$
and
${\sf KHaus}$
that restricts to a dual equivalence between
$\boldsymbol {\mathit {uba}\ell }$
and
${\sf KHaus}$
. The natural transformations are given by
$\zeta :1_{\boldsymbol {\mathit {ba}\ell }}\to CY$
and
$\varepsilon :1_{{\sf KHaus}}\to YC$
where we recall from Section 2 that
$\varepsilon _X: X \to X_{C(X)}$
is defined by
$$ \begin{align*} \varepsilon_X(x) = M_x = \{f \in C(X) \mid f(x)=0 \}. \end{align*} $$
Therefore, it is sufficient to show that
$\zeta _A$
is a morphism in
$\boldsymbol {\mathit {mba}\ell }$
for each
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
and that
$\varepsilon _X$
is a bounded morphism for each
$(X, R) \in {\sf KHF}$
. We showed in the proof of Proposition 5.2 that
$\zeta _A$
is a morphism in
$\boldsymbol {\mathit {mba}\ell }$
, and hence it remains to show that
$xRy$
iff
$\varepsilon _X(x) R_{\Box _R} \varepsilon _X(y)$
for each
$(X,R)\in {\sf KHF}$
.
To see this recall that
$\varepsilon _X(x) R_{\Box _R} \varepsilon _X(y)$
means that
$M_y^+ \subseteq \Box _R^{-1} M_x$
. First suppose that
$x R y$
and
$f \in M_y^+$
. Then
$f(y)=0$
and
$f \geq 0$
. By the definition of
$\Box_R$
we have
$(\Box _R f) (x)= \inf \{ f(z) \mid x R z \}=0$
. Therefore,
$\Box _R f \in M_x$
, and so
$f \in \Box _R^{-1} M_x$
. This gives
$M_y^+ \subseteq \Box _R^{-1} M_x$
. Next suppose that
, so
$y \notin R[x]$
. If
$R[x] = \varnothing $
, then
$(\Box _R0)(x) = 1$
, so
$0 \in M_y^+$
but
$\Box _R 0 \notin M_x$
, yielding
$M_y^+ \not \subseteq \Box _R^{-1} M_x$
. On the other hand, if
$R[x] \ne \varnothing $
, since
$R[x]$
is closed, by Urysohn’s Lemma there is
$f \geq 0$
such that
$f(y)=0$
and
$f(R[x]) = \{1\}$
. Thus,
$f \in M_y^+$
and
$\Box _R f \notin M_x$
. Consequently,
$M_y^+ \nsubseteq \Box _R^{-1}M_x$
.⊣
6 Connection to modal algebras and Jónsson-Tarski duality
In this section we connect Theorem 5.3 to Jónsson-Tarski duality. Recall that a modal algebra is a pair
$\mathfrak A=(A,\Box )$
where A is a boolean algebra and
$\Box $
is a unary function on A preserving finite meets (including 1). As usual, the dual function
$\Diamond $
is defined by
$\Diamond a=\neg \Box \neg a$
, and is axiomatized as a unary function preserving finite joins (including 0). Let
${\sf MA}$
be the category of modal algebras and modal homomorphisms (boolean homomorphisms preserving
$\Box $
).
We recall from the Introduction that a descriptive frame is a pair
$\mathfrak F=(X,R)$
where X is a Stone space and R is a continuous relation on X, and that
${\sf DF}$
is the category of descriptive frames and continuous bounded morphisms. As we already pointed out, Stone duality generalizes to the following duality:
Theorem 6.1 (Jónsson–Tarski duality)
${\sf MA}$
is dually equivalent to
${\sf DF}$
.
The functors
$(-)^*:{\sf DF}\to {\sf MA}$
and
$(-)_*:{\sf MA}\to {\sf DF}$
are defined as follows. For a descriptive Kripke frame
$\mathfrak F=(X,R)$
let
$\mathfrak F^*=({\sf Clop}(X),\Box _R)$
where
${\sf Clop}(X)$
is the boolean algebra of clopen subsets of X and
$\Box _R U = X \setminus R^{-1}[X \setminus U]$
(alternatively,
$\Diamond _R U = R^{-1}[U]$
). For a bounded morphism f let
$f^*=f^{-1}$
. Then
$(-)^*:{\sf DF}\to {\sf MA}$
is a well-defined contravariant functor.
For a modal algebra
$\mathfrak A=(A,\Box )$
let
$\mathfrak A_*=(Y_A,R_\Box )$
where
$Y_A$
is the set of ultrafilters of A with the Stone topology and
$$ \begin{align*} x R_\Box y \quad\mbox{iff}\quad (\forall a\in A)(\Box a \in x \Rightarrow a \in y) \quad\mbox{iff}\quad \Box^{-1}x \subseteq y \end{align*} $$
(alternatively,
$x R_\Box y$
iff
$(\forall a\in A)(a \in y \Rightarrow \Diamond a\in x)$
iff
$y \subseteq \Diamond ^{-1}x$
). For a modal algebra homomorphism h let
$h_*=h^{-1}$
. Then
$(-)_*:{\sf MA}\to {\sf DF}$
is a well-defined contravariant functor, and the functors
$(-)_*$
and
$(-)^*$
yield a dual equivalence of
${\sf MA}$
and
${\sf DF}$
.
To define a functor from
$\boldsymbol {\mathit {mba}\ell }$
to
${\sf MA}$
we recall that for each commutative ring A with
$1$
, the idempotents of A form a boolean algebra
$\operatorname {Id}(A)$
, where the boolean operations on
$\operatorname {Id}(A)$
are defined as follows:
$$ \begin{align*} e \wedge f = ef, \ \ \ e \vee f = e + f - ef, \ \ \ \neg e = 1 - e. \end{align*} $$
We point out that if
$A \in \boldsymbol {\mathit {ba}\ell }$
, then the lattice operations on A restrict to those on
$\operatorname {Id}(A)$
.
Remark 6.2. Since each
$A\in \boldsymbol {\mathit {ba}\ell }$
is an f-ring (see Remark 2.5), we will freely use the following two identities of f-rings (see [Reference Birkhoff8, Section XIII.3] and [Reference Birkhoff8, Corollary XVII.5.1]):
$$ \begin{align*} (a \wedge b) + c = (a + c) \wedge (b + c) \quad\mbox{and}\quad (a \wedge b) d = (ad) \wedge (bd) \mbox{ for } d \ge 0. \end{align*} $$
Lemma 6.3. If
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
, then
$\Box $
sends idempotents to idempotents.
Proof. First observe that
$e \in A$
is an idempotent iff
$1 \wedge 2e = e$
. To see this, if e is an idempotent, by Remark 6.2,
$$ \begin{align*} (1 \wedge 2e) - e = (1-e) \wedge e = \lnot e \wedge e = 0. \end{align*} $$
Therefore,
$1 \wedge 2e = e$
. Conversely, suppose that
$1 \wedge 2e = e$
. Then
$(1-e) \wedge e = 0$
by the same calculation. Since each
$A \in \boldsymbol {\mathit {ba}\ell }$
is an f-ring, from
$(1-e) \wedge e = 0$
it follows that
$(1-e)e = 0$
(see, e.g., [Reference Birkhoff8, Lemma XVII.5.1]). Thus,
$e^2 = e$
, and hence e is an idempotent.
For each
$a \in A$
, by (M5), (M2), and Lemma 3.13(4) we have
$$ \begin{align*} \Box (2 a) = \Box 2 \Box a=(2-\Box 0)\Box a=(2-2\Box 0+\Box 0)\Box a=2 \Box a (1-\Box 0)+\Box 0. \end{align*} $$
By Lemma 3.13(3),
$\Box 0 \ge 0$
, so Lemma 3.13(4) and Remark 6.2 imply
$$ \begin{align*} (1 \wedge 2 \Box a)\Box 0=\Box 0 \wedge 2\Box a \Box 0=\Box 0 \wedge 2\Box 0=\Box 0. \end{align*} $$
Now suppose e is an idempotent, so
$e = 1 \wedge 2e$
. Since
$\Box 0\le \Box 1=1$
, we have that
$1-\Box 0 \ge 0$
. Thus, by Remark 6.2 and the two identities just proved,
$$ \begin{align*} \Box e &= \Box (1 \wedge 2e)=1 \wedge \Box(2e) \\ &= ((1-\Box 0)+\Box 0) \wedge \Box(2e) \\ &= ((1-\Box 0)+\Box 0) \wedge (2 \Box e (1-\Box 0)+\Box 0) \\ &= ((1-\Box 0) \wedge 2 \Box e (1-\Box 0))+\Box 0 \\ &= (1 \wedge 2 \Box e)(1-\Box 0)+\Box 0 \\ &= (1 \wedge 2 \Box e)(1-\Box 0)+(1 \wedge 2 \Box e)\Box 0 \\ &= 1 \wedge 2 \Box e. \end{align*} $$
Therefore,
$\Box e$
is an idempotent.⊣
Lemma 6.4. If
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
, then
$(\operatorname {Id}(A),\Box )\in {\sf MA}$
.
Proof. Since
$A\in \boldsymbol {\mathit {ba}\ell }$
, we have that
$\operatorname {Id}(A)$
is a boolean algebra. That
$\Box $
is well defined on
$\operatorname {Id}(A)$
follows from Lemma 6.3. That
$\Box $
preserves finite meets in
$\operatorname {Id}(A)$
follows from (M1) and Lemma 3.13(2). Thus,
$(\operatorname {Id}(A),\Box )\in {\sf MA}$
.⊣
Define
$\operatorname {Id}:\boldsymbol {\mathit {mba}\ell }\to {\sf MA}$
by sending
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
to
$(\operatorname {Id}(A),\Box )\in {\sf MA}$
and a morphism
$A\to B$
in
$\boldsymbol {\mathit {mba}\ell }$
to its restriction
$\operatorname {Id}(A)\to \operatorname {Id}(B)$
. The next lemma is an easy consequence of Lemma 6.4.
Lemma 6.5.
$\operatorname {Id}:\boldsymbol {\mathit {mba}\ell }\to {\sf MA}$
is a well-defined covariant functor.
We recall (see [Reference McGovern32] and the references therein) that a commutative ring A is clean if each element is the sum of an idempotent and a unit.
Definition 6.6. Let
$\boldsymbol {\mathit {cuba}\ell }$
be the full subcategory of
$\boldsymbol {\mathit {uba}\ell }$
consisting of those
$A \in \boldsymbol {\mathit {uba}\ell }$
where A is clean.
Remark 6.7. By Stone duality, the category
$\mathsf{BA}$
of boolean algebras and boolean homomorphisms is dually equivalent to the category
$\mathsf{Stone}$
of Stone spaces and continuous maps. Thus, by [Reference Bezhanishvili, Morandi and Olberding6, Proposition 5.20], the following diagram commutes (up to natural isomorphism), and the functor
$\operatorname {Id}$
yields an equivalence of
$\boldsymbol {\mathit {cuba}\ell }$
and
${\sf BA}$
.
Definition 6.8. Let
$\boldsymbol {\mathit {mcuba}\ell }$
be the full subcategory of
$\boldsymbol {\mathit {muba}\ell }$
consisting of those
$(A,\Box ) \in \boldsymbol {\mathit {muba}\ell }$
where A is clean.
As a corollary of Theorems 5.3, 6.1 and Remark 6.7, we obtain:
Theorem 6.9. The diagram below commutes (up to natural isomorphism) and the functor
$\operatorname {Id}$
yields an equivalence of
$\boldsymbol {\mathit {mcuba}\ell }$
and
${\sf MA}$
.
7 Some correspondence results
In this section we take the first steps towards the correspondence theory for
$\boldsymbol {\mathit {mba}\ell }$
by characterizing algebraically what it takes for the relation
$R_\Box $
to satisfy additional first-order properties, such as seriality, reflexivity, transitivity, and symmetry.
We recall that a relation R on X is serial if
$R[x] \ne \varnothing $
for each
$x \in X$
.
Lemma 7.1. Let
$(X,R)\in {\sf KHF}$
.
-
1. If R is serial, then
$\Box _R 0=0$
in
$C(X)$
. -
2. If R is reflexive, then
$\Box _R f \le f$
for each
$f \in C(X)$
. -
3. If R is transitive, then
$\Box _R f \le \Box _R(\Box _R f(1-\Box _R 0)+f\Box _R 0)$
for each
$f\in C(X)$
. -
4. If R is symmetric, then
$(\Diamond _R \Box _R f) (1-\Box _R 0) \le f(1-\Box _R 0) $
for each
$f\in C(X)$
.
Proof. (1) Suppose that R is serial. Then
$R[x] \ne \varnothing $
, so
$(\Box _{R} 0)(x)= 0$
for each
$x \in Y$
. Thus,
$\Box _{R} 0 = 0$
.
(2) Suppose that R is reflexive and
$f \in C(Y)$
. For each
$x \in Y$
, we have
$x \in R[x]$
. Thus,
$(\Box _{R} f)(x) = \inf fR[x] \le f(x)$
.
(3) Suppose that R is transitive. Let
$f \in C(Y)$
and
$x \in Y$
. If
$R[x] = \varnothing $
, then by the definition of
$\Box _R$
,
$$ \begin{align*} (\Box_R f)(x)=1=\Box_R(\Box_R f(1-\Box_R 0)+f\Box_R 0)(x). \end{align*} $$
Suppose that
$R[x] \ne \varnothing $
. Then
$(\Box _R f)(x)= \inf fR[x]$
and
$$ \begin{align*} \Box_R(\Box_R f(1-\Box_R 0) &+f\Box_R 0)(x) \\ &= \inf \{(\Box_R f)(y)(1-\Box_R 0)(y)+f(y)(\Box_R 0)(y) \mid xRy \}. \end{align*} $$
We have
$$ \begin{align*} (\Box_R f)(y)(1-\Box_R 0)(y)+f(y)(\Box_R 0)(y) = \left\{\begin{array}{ll} f(y) & \mbox{if }R[y]=\varnothing,\\ (\Box_R f)(y) & \mbox{if }R[y]\ne \varnothing.\end{array}\right. \end{align*} $$
It is therefore sufficient to prove that, for each
$y \in R[x]$
, if
$R[y]=\varnothing $
then
$(\Box _R f)(x) \le f(y)$
and if
$R[y] \ne \varnothing $
then
$(\Box _R f)(x) \le (\Box _R f)(y)$
. Suppose
$R[y]=\varnothing $
. Since
$R[x] \ne \varnothing $
, we have
$$ \begin{align*} (\Box_R f)(x)= \inf \{ f(z) \mid z \in R[x] \} \le f(y). \end{align*} $$
If
$R[y] \ne \varnothing $
, then by transitivity of R we have
$R[y] \subseteq R[x]$
, so
$$ \begin{align*} (\Box_R f)(x)= \inf \{ f(z) \mid z \in R[x] \} \le \inf \{ f(w) \mid w \in R[y] \} = (\Box_R f)(y). \end{align*} $$
Thus,
$\Box _R f \le \Box _R(\Box _R f(1-\Box _R 0)+f\Box _R 0)$
.
(4) Suppose that R is symmetric. Let
$f \in C(Y)$
and
$x \in Y$
. If
$R[x] = \varnothing $
, then
$(1-\Box _R 0)(x)=0$
so
$$ \begin{align*} (\Diamond_R \Box_R f)(x)(1-\Box_R 0)(x) = 0 = f(x)(1-\Box_R 0)(x). \end{align*} $$
If
$R[x] \ne \varnothing $
, then
$(1-\Box _R 0)(x)=1$
, so it is sufficient to prove that
$(\Diamond _R \Box _R f)(x)\le f(x)$
. For any
$y \in R[x]$
we have
$x \in R[y]$
by symmetry. Therefore,
$$ \begin{align*} (\Box_R f)(y) = \inf\{f(z) \mid z \in R[y] \} \le f(x). \end{align*} $$
Thus, recalling Remark 3.5, we have
$$ \begin{align*} (\Diamond_R \Box_R f)(x) = \sup \{(\Box_R f)(y) \mid y \in R[x] \} \le f(x). \\[-34pt] \end{align*} $$
⊣
Since each
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
is isomorphic to a subalgebra of
$(C(Y),\Box _R)$
and equations satisfied by an algebra are also satisfied by a subalgebra, as an immediate consequence of Lemma 7.1 we obtain:
Proposition 7.2. Let
$(A,\Box )\in \boldsymbol {\mathit {mba}\ell }$
and
$(Y_A,R_\Box )$
be its dual.
-
1. If
$R_\Box $
is serial, then
$\Box 0=0$
in A. -
2. If
$R_\Box $
is reflexive, then
$\Box a \le a$
for each
$a \in A$
. -
3. If
$R_\Box $
is transitive, then
$\Box a \le \Box (\Box a(1-\Box 0)+a\Box 0)$
for each
$a\in A$
. -
4. If
$R_\Box $
is symmetric, then
$\Diamond \Box a(1-\Box 0) \le a(1-\Box 0)$
for each
$a\in A$
.
Proposition 7.3. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
and
$(Y_A, R_\Box )$
be its dual.
-
1. If
$\Box 0 = 0$
, then
$R_\Box $
is serial. -
2. If
$\Box a \le a$
for each
$a \in A$
, then
$R_\Box $
is reflexive. -
3. If
$\Box a \le \Box (\Box a(1-\Box 0)+a\Box 0)$
for each
$a\in A$
, then
$R_\Box $
is transitive. -
4. If
$\Diamond \Box a(1-\Box 0) \le a(1-\Box 0) $
for each
$a\in A$
, then
$R_\Box $
is symmetric.
Proof. (1) Suppose that
$\Box 0 = 0$
in A. Since
$Y_A=Z_{\ell }(0)$
, by Lemma 4.10(2), we have
$D_A=Z_{\ell }(\Box 0)=Z_{\ell }(0)=Y_A$
. Thus,
$R_\Box $
is serial.
(2) Suppose
$\Box a \le a$
for each
$a\in A$
. Let
$x \in Y_A$
and
$a \in x^+$
. We then have
$0 \le \Box a \le a \in x$
. Thus,
$x^+ \subseteq \Box ^{-1} x$
, and so
$x R_\Box x$
.
(3) Suppose
$\Box a \le \Box (\Box a(1-\Box 0)+a\Box 0)$
for each
$a\in A$
. Let
$x,y,z \in Y_A$
with
$x R_\Box y$
and
$y R_\Box z$
. Then
$y^+ \subseteq \Box ^{-1} x$
and
$z^+ \subseteq \Box ^{-1} y$
. Let
$a \in z^+$
. Then
$\Box a \in y^+$
. As
$0 \in z^+$
, we have
$\Box 0 \in y^+$
. Thus, since y is an ideal,
$\Box a(1-\Box 0)+a \Box 0 \in y$
. Because
$\Box a(1-\Box 0)+a \Box 0 \ge 0$
, we have
$\Box (\Box a(1-\Box 0)+a \Box 0) \in x$
. By hypothesis,
$0 \le \Box a \le \Box (\Box a(1-\Box 0)+a\Box 0) \in x$
. Thus,
$\Box a \in x$
. This shows that
$z^+ \subseteq \Box ^{-1} x$
, and hence
$x R_\Box z$
.
(4) Suppose
$\Diamond \Box a(1-\Box 0) \le a(1-\Box 0)$
for each
$a\in A$
. Let
$x,y \in Y_A$
with
$x R_\Box y$
. Then
$y^+ \subseteq \Box ^{-1} x$
, so
$0 \in y^+$
implies
$\Box 0 \in x$
. Thus,
$$ \begin{align*} \Diamond \Box a+ x = \Diamond \Box a(1-\Box 0) + x \le a(1-\Box 0) + x = a + x. \end{align*} $$
To see that
$y R_\Box x$
, let
$a \in x^+$
. If
$\Box a \notin y$
, then
$0+y < \Box a +y$
because
$\Box a \ge 0$
. So there is
$0 < \lambda \in \mathbb {R}$
such that
$\lambda - \Box a \in y$
. Thus,
$(\lambda - \Box a)^+ \in y^+$
. Since
$x R_\Box y$
, by (2) and (4) of Lemma 4.4, we have
$$ \begin{align*} (\lambda-\Diamond \Box a)^+ +x &= (\lambda + \Box (- \Box a))^+ +x=(\Box (\lambda - \Box a))^+ + x\\ &=\Box (\lambda - \Box a)^+ +x=0+x. \end{align*} $$
Because
$\Diamond \Box a +x \le a+x$
we have
$(\lambda - a) +x \le (\lambda - \Diamond \Box a) +x $
. Therefore,
$$ \begin{align*} 0 + x \le (\lambda-a)^+ + x \le (\lambda-\Diamond \Box a)^+ +x =0+x. \end{align*} $$
This implies
$(\lambda -a)^+ \in x$
. Thus, by Remark 4.3(4),
$0+x < \lambda +x \le a+x$
, which contradicts
$a \in x^+$
. Therefore,
$\Box a \in y$
, which yields
$x^+ \subseteq \Box ^{-1} y$
. Thus,
$y R_\Box x$
.⊣
Putting Propositions 7.2 and 7.3 together yields:
Theorem 7.4. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
and
$(Y_A,R_\Box )$
be its dual.
-
1.
$R_\Box $
is serial iff
$\Box 0=0$
in A. -
2.
$R_\Box $
is reflexive iff
$\Box a \le a$
for each
$a \in A$
. -
3.
$R_\Box $
is transitive iff
$\Box a \le \Box (\Box a(1-\Box 0)+a\Box 0)$
for each
$a\in A$
. -
4.
$R_\Box $
is symmetric iff
$\Diamond \Box a(1-\Box 0) \le a(1-\Box 0)$
for each
$a\in A$
.
Remark 7.5. If we work with
$\Diamond $
instead of
$\Box $
, then Theorem 7.4 can be stated as follows.
-
1.
$R_\Box $
is serial iff
$\Diamond 1 = 1$
. -
2.
$R_\Box $
is reflexive iff
$a \le \Diamond a$
for each
$a \in A$
. -
3.
$R_\Box $
is transitive iff
$\Diamond (\Diamond a +a(1-\Diamond 1)) \le \Diamond a$
for each
$a \in A$
. -
4.
$R_\Box $
is symmetric iff
$\Diamond \Box a \le a\Diamond 1$
for each
$a \in A$
.
Remark 7.6. Let
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
. If
$\Box 0 = 0$
, then the transitivity and symmetry axioms simplify to
$\Box a \le \Box \Box a$
and
$\Diamond \Box a \le a$
, which are standard transitivity and symmetry axioms in modal logic.
Definition 7.7.
-
1. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf D}$
be the full subcategory of
$\boldsymbol {\mathit {mba}\ell }$
consisting of objects
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
satisfying
$\Box 0 = 0$
. -
2. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf T}$
be the full subcategory of
$\boldsymbol {\mathit {mba}\ell }$
consisting of objects
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
satisfying
$\Box a \le a$
. -
3. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf K4}$
be the full subcategory of
$\boldsymbol {\mathit {mba}\ell }$
consisting of objects
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
satisfying
$\Box a \le \Box (\Box a(1-\Box 0)+a\Box 0)$
. -
4. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf B}$
be the full subcategory of
$\boldsymbol {\mathit {mba}\ell }$
consisting of objects
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }$
satisfying
$\Diamond \Box a(1-\Box 0) \le a(1-\Box 0)$
. -
5. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf S4} = \boldsymbol {\mathit {mba}\ell }^{\sf T} \cap \boldsymbol {\mathit {mba}\ell }^{\sf K4}$
. -
6. Let
$\boldsymbol {\mathit {mba}\ell }^{\sf S5} = \boldsymbol {\mathit {mba}\ell }^{\sf S4} \cap \boldsymbol {\mathit {mba}\ell }^{\sf B}$
.
Remark 7.8. Since the reflexivity axiom implies the seriality axiom, we obtain that
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }^{\sf S4}$
iff
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }^{\sf T}$
and
$\Box a \le \Box \Box a$
for each
$a \in A$
. Similarly,
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }^{\sf S5}$
iff
$(A, \Box ) \in \boldsymbol {\mathit {mba}\ell }^{\sf S4}$
and
$\Diamond \Box a \le a$
for each
$a \in A$
.
Remark 7.9. The notation of Definition 7.7 is motivated by the standard notation in modal logic:
-
1.
$\sf D$
denotes the least normal modal logic containing the axiom
$\Diamond \top $
. -
2.
$\sf T$
denotes the least normal modal logic containing the axiom
$\Box p\to p$
. -
3.
$\sf K4$
denotes the least normal modal logic containing the axiom
$\Box p\to \Box \Box p$
. -
4.
$\sf B$
denotes the least normal modal logic containing the axiom
$\Diamond \Box p \to p$
. -
5.
$\sf S4$
denotes the join of
$\sf T$
and
$\sf K4$
. -
6.
$\sf S5$
denotes the join of
$\sf S4$
and
$\sf B$
.
The inclusions between the subclasses of algebras in
$\boldsymbol {\mathit {mba}\ell }$
given in Definition 7.7 are the same as for the corresponding classes of modal algebras; see Figure 1. Similarly to Definition 7.7, for
$\sf X \in \{ D, T, K4, B, S4, S5 \}$
we define the following categories:
-
• The categories
$\boldsymbol {\mathit {muba}\ell }^{\sf X}$
are defined similarly to
$\boldsymbol {\mathit {mba}\ell }^{\sf X}$
but with
$\boldsymbol {\mathit {mba}\ell }$
replaced by
$\boldsymbol {\mathit {muba}\ell }$
. -
• The categories
$\boldsymbol {\mathit {mcuba}\ell }^{\sf X}$
are defined similarly to
$\boldsymbol {\mathit {mba}\ell }^{\sf X}$
but with
$\boldsymbol {\mathit {mba}\ell }$
replaced by
$\boldsymbol {\mathit {mcuba}\ell }$
. -
• The categories
${\sf MA}^{\sf X}$
are defined similarly to
$\boldsymbol {\mathit {mba}\ell }^{\sf X}$
but with
$\boldsymbol {\mathit {mba}\ell }$
replaced by
${\sf MA}$
. -
• The categories
${\sf KHF}^{\sf X}$
are defined by adding the corresponding properties of the relation R to the definition of
${\sf KHF}$
. -
• The categories
${\sf DF}^{\sf X}$
are defined as
${\sf KHF}^{\sf X}$
by restricting
${\sf KHF}$
to
${\sf DF}$
.
Figure 1 Inclusion relationships between some subcategories of
$\boldsymbol {\mathit {mba}\ell }$
.
Theorems 5.3, 6.9, and 7.4, and the corresponding versions of Theorem 6.1 yield the following result.
Theorem 7.10. Suppose that
$\sf X \in \{ D, T, K4, B, S4, S5 \}$
.
-
1. The category
$\boldsymbol {\mathit {muba}\ell }^{\sf X}$
is dually equivalent to
${\sf KHF}^{\sf X}$
. -
2. The categories
$\boldsymbol {\mathit {mcuba}\ell }^{\sf X}$
and
${\sf MA}^{\sf X}$
are dually equivalent to
${\sf DF}^{\sf X}$
, and hence are equivalent.
8 Concluding remarks
We finish the paper with several remarks, which indicate a number of possible directions for future research.
Remark 8.1.
-
1. As we pointed out in the Introduction, there are other dualities for
${\sf KHaus}$
. For example, in pointfree topology we have Isbell duality [Reference Isbell21] (see also [Reference Banaschewski and Mulvey1] or [Reference Johnstone23, Section III.1]) and de Vries duality [Reference de Vries12] (see also [Reference Bezhanishvili2]). The two are closely related, see [Reference Bezhanishvili3]. Isbell and de Vries dualities were generalized to the setting of
${\sf KHF}$
in [Reference Bezhanishvili, Bezhanishvili and Harding4]. We plan to compare the results of [Reference Bezhanishvili, Bezhanishvili and Harding4] to the ones obtained in this paper. -
2. As we pointed out in the Introduction, another relevant duality was established by Kakutani [Reference Kakutani25, Reference Kakutani26], the Krein brothers [Reference Krein and Krein28], and Yosida [Reference Yosida37], who worked in the signature of vector lattices. Gelfand duality has a natural counterpart in this setting. Let
$\boldsymbol {\mathit {bav}}$
be the category of bounded archimedean vector lattices and let
$\boldsymbol {\mathit {ubav}}$
be its reflective subcategory consisting of uniformly complete objects. Then there is a dual adjunction between
$\boldsymbol {\mathit {bav}}$
and
${\sf KHaus}$
, which restricts to a dual equivalence between
$\boldsymbol {\mathit {ubav}}$
and
${\sf KHaus}$
. This duality is sometimes referred to as Yosida duality (or Kakutani–Krein–Yosida duality). In our axiomatization of
$\boldsymbol {\mathit {mba}\ell }$
(see Definition 3.10), the only axiom involving multiplication is (M5). In the serial case (M5) simplifies to (M5
${}'$
) of Remark 3.12, which only involves scalar multiplication. In the non-serial case, (M5) can be replaced by the following two axioms-
•
$\Box (\lambda a) = \lambda \Box a + (1-\lambda ) \Box 0$
provided
$\lambda \ge 0$
, -
•
$\Box 0 \wedge (1-\Box a)^+ = 0$
,
which again only involve vector lattice operations. This yields the category
$\boldsymbol {\mathit {mbav}}$
of modal bounded archimedean vector lattices and its reflective subcategory
$\boldsymbol {\mathit {mubav}}$
consisting of uniformly complete objects. The results of Section 5 then generalize to the setting of
$\boldsymbol {\mathit {mbav}}$
and
$\boldsymbol {\mathit {mubav}}$
, and provide a generalization of Yosida duality. -
-
3. Our definition of a modal operator on a bounded archimedean
$\ell $
-algebra can be further adjusted to the settings of
$\ell $
-rings,
$\ell $
-groups, and MV-algebras. In this regard, it would be interesting to develop logical systems corresponding to these algebras. As we pointed out in the introduction, this can be done along the same lines as in [Reference Diaconescu, Metcalfe and Schnüriger13] (see also [Reference Furber, Mardare and Mio15]). -
4. It would be natural to develop the correspondence theory for
$\boldsymbol {\mathit {mba}\ell }$
by generalizing the results of Section 7, with the final goal towards a Sahlqvist type correspondence (see, e.g., [Reference Blackburn, de Rijke and Venema9, Chapter 3]).
Acknowledgement
We would like to thank the referee for careful reading and for useful comments which have improved our presentation.
