Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-11T17:56:02.405Z Has data issue: false hasContentIssue false
  • English
  • Français

A METRIC VERSION OF SCHLICHTING’S THEOREM

Part of: Connections with logic Algebraic combinatorics Ordered sets Structure and classification of infinite or finite groups Algebraic logic Semigroups

Published online by Cambridge University Press:  07 September 2020

ITAÏ BEN YAACOV  and
FRANK O. WAGNER
ITAÏ BEN YAACOV
Affiliation:
UNIVERSITÉ DE LYON, CNRS UNIVERSITÉ CLAUDE BERNARD LYON 1 INSTITUT CAMILLE JORDAN UMR5208 43 BD DU 11 NOVEMBRE 1918 69622 VILLEURBANNE CEDEX, FRANCEE-mail: benyaacov@math.univ-lyon1.frE-mail: wagner@math.univ-lyon1.frURL: http://math.univ-lyon1.fr/~wagner/URL: http://math.univ-lyon1.fr/~begnac/
FRANK O. WAGNER
Affiliation:
UNIVERSITÉ DE LYON, CNRS UNIVERSITÉ CLAUDE BERNARD LYON 1 INSTITUT CAMILLE JORDAN UMR5208 43 BD DU 11 NOVEMBRE 1918 69622 VILLEURBANNE CEDEX, FRANCEE-mail: benyaacov@math.univ-lyon1.frE-mail: wagner@math.univ-lyon1.frURL: http://math.univ-lyon1.fr/~wagner/URL: http://math.univ-lyon1.fr/~begnac/
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 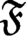${\mathfrak {F}}$ is a type-definable family of commensurable subsets, subgroups or subvector spaces in a metric structure, then there is an invariant subset, subgroup or subvector space commensurable with ${\mathfrak {F}}$. This in particular applies to type-definable or hyper-definable objects in a classical first-order structure.

Keywords

Schlichting’s Theoremuniformly commensurableclose-knit familycontinuous logicinvariant

MSC classification

Primary: 03G10: Lattices and related structures
Secondary: 05E15: Combinatorial aspects of groups and algebras 20M10: General structure theory 06A12: Semilattices 12L12: Model theory 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 4 , December 2020 , pp. 1607 - 1613
Check for updates
Copyright
© The Association for Symbolic Logic 2020

References

REFERENCES

Bergman, G. M. and Lenstra, H. W. Jr., Subgroups close to normal subgroups. Journal of Algebra, vol. 127 (1989), pp. 80–97.CrossRefGoogle Scholar
Brailovsky, L., Pasechnik, D. V., and Praeger, C. E., Subsets close to invariant subsets for group actions. Proceedings of the American Mathematical Society, vol. 123 (1995), pp. 2283–2295.CrossRefGoogle Scholar
Hrushovski, E., Stable group theory and approximate subgroups. Journal of the American Mathematical Society, vol. 25 (2012), no. 1, pp. 189–243.CrossRefGoogle Scholar
Neumann, P., Permutation groups and close–knit families of sets. Archiv der Mathematik, vol. 67 (1996), pp. 265–274.CrossRefGoogle Scholar
Schlichting, G., Operationen mit periodischen Stabilisatoren. Archiv der Mathematik, vol. 34 (1980), pp. 97–99.CrossRefGoogle Scholar
Wagner, F. O., Almost invariant families. Bulletin of the London Mathematical Society, vol. 30 (1998), pp. 235–240.CrossRefGoogle Scholar
Wagner, F. O., Simple Theories. Mathematics and Its Applications, vol. 503. Kluwer Academic Publishers, Dordrecht, 2000.Google Scholar
Wagner, F. O., The right angle to look at orthogonal sets, this Journal, vol. 81 (2016), no. 4, pp. 1298–1314.Google Scholar
Waterhouse, W. C., Intersections of two cofinite subfields. Archiv der Mathematik, vol. 82 (2004), no. 4, pp. 298–300.CrossRefGoogle Scholar