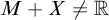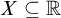1 Introduction
More than 100 years ago Borel [Reference Borel4] defined the notion of strong measure zero: a metric space X has strong measure zero (hereafter
${\boldsymbol {\mathsf {Smz}}}$
) if for any sequence
$\langle {\varepsilon _n} \rangle $
of positive numbers there is a cover
$\{U_n\}$
of X such that
$\operatorname {\textrm {diam}} U_n\leqslant \varepsilon _n$
for all n. In the same paper, Borel conjectured that every
${\boldsymbol {\mathsf {Smz}}}{}$
set of reals is countable. This statement, known as the Borel Conjecture, attracted a lot of attention. It is well-known that the Borel Conjecture is independent of ZFC, the usual axioms of set theory. The proof of consistency of its failure was settled by 1948 by Sierpiński [Reference Sierpiński24], who proved in 1928 that the Luzin set (that exists under the Continuum Hypothesis) is a counterexample, and Gödel [Reference Gödel8], who proved in 1948 the consistency of the Continuum Hypothesis. The consistency of the Borel Conjecture was proved in 1976 in Laver’s ground-breaking paper [Reference Laver13].
Over time numerous characterizations of
${\boldsymbol {\mathsf {Smz}}}{}$
were discovered. Maybe the most interesting is the Galvin–Mycielski–Solovay Theorem: Confirming Prikry’s conjecture, Galvin et al. [Reference Galvin, Mycielski and Solovay6] proved the following:
Theorem [Reference Galvin, Mycielski and Solovay6].
A set
$X\subseteq \mathbb {R}$
is
${\boldsymbol {\mathsf {Smz}}}{}$
if and only if
$M+X\neq 2^\omega $
for each meager set
$M\subseteq 2^\omega $
.
This theorem led to the study of small sets defined in a similar manner. We focus on the meager-additive sets. By definition, a set
$X\subseteq \mathbb {R}$
is meager-additive if
$M+X$
is meager for each meager set M. The definition easily extends to any topological group. Meager-additive sets in
$2^\omega $
have received a lot of attention. They were investigated by many, most notably by Bartoszyński and Judah [Reference Bartoszyński and Judah1], Pawlikowski [Reference Pawlikowski20] and Shelah [Reference Shelah23].
In a recent paper [Reference Zindulka28], the author of the present paper used combinatorial properties of meager-additive sets described by Shelah [Reference Shelah23] and Pawlikowski [Reference Pawlikowski20] to characterize meager-additive sets in
$2^\omega $
in a way that nicely parallels Borel’s definition of strong measure zero, thus obtaining a theorem that is very similar to the Galvin–Mycielski–Solovay Theorem.
In more detail, a set X has sharp measure zero (thereinafter
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
) if for any sequence
$\langle {\varepsilon _n} \rangle $
of positive numbers there is a
$\gamma$
-groupable cover
$\{U_n\}$
of X such that
$\operatorname {\textrm {diam}} U_n\leqslant \varepsilon _n$
for all n. Note that the only difference between strong measure zero and sharp measure zero is that the cover is required to be
$\gamma $
-groupable (the notion is defined below). With these definitions, the theorem reads
Theorem [Reference Zindulka28, Theorem 5.1].
A set
$X\subseteq 2^\omega $
has sharp measure zero if and only if it is meager-additive.
With some effort, the theorem was shown to hold also in
$\mathbb {R}$
and Euclidean spaces. In the present paper we attempt to extend it to a wider class of Polish groups.
The inspiration comes from recent results on strong measure zero: Kysiak [Reference Kysiak12] and Fremlin [Reference Fremlin5] showed that the Galvin–Mycielski–Solovay Theorem holds in all locally compact Polish groups. Hrušák et al. [Reference Hrušák, Wohofsky and Zindulka9] and Hrušák and Zapletal [Reference Hrušák and Zapletal10] (see also [Reference Hrušák and Zindulka11]) found that among Polish groups admitting an invariant metric, under the Continuum Hypothesis the Galvin–Mycielski–Solovay Theorem fails for groups that are not locally compact.
This of course raises questions about the scope of the above theorem. Does it hold for locally compact metric groups? Does it consistently fail for other Polish groups? We give partial answers to the former questions; to date, the latter remains a mystery.
It turns out that in addition to sharp measure zero and meager-additive sets it is handy to consider a subfamily of meager-additive sets, the so called sharply meager-additive sets (see Section 3 for the definition).
The following are the main results of the paper.
Theorem 1.1. Let
$\mathbb {G}$
be a Polish group equipped with a right-invariant metric. Then every sharply
$\mathcal M$
-additive set in
$\mathbb {G}$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
.
Theorem 1.2. Let
$\mathbb {G}$
be a locally compact Polish group and
$S\subseteq \mathbb {G}$
. Then S is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
if and only if S is sharply
$\mathcal M$
-additive.
Theorem 1.3. Let
$\mathbb {G}$
be a Polish group admitting an invariant metric. If
$X\subseteq \mathbb {G}$
is
$\mathcal M$
-additive, then X is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
(in any metric on
$\mathbb {G}$
).
As a corollary to these theorems, we get an equivalence of the three properties in locally compact groups admitting an invariant metric. This class of groups includes all compact or locally compact abelian Polish groups.
Theorem 1.4. Let
$\mathbb {G}$
be a locally compact group admitting an invariant metric. Let
$X\subseteq \mathbb {G}$
. The following are equivalent:
-
(i) X is
$\mathcal M$
-additive, -
(ii) X is sharply
$\mathcal M$
-additive, -
(iii) X is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
.
Consequences include, for instance:
-
• Meager-additive sets are preserved by continuous mappings between groups (Theorem 6.1).
-
• A product of two meager-additive sets is meager-additive (Theorem 6.2).
-
• Meager-additive sets are universally meager and transitively meager (Propositions 6.5 and 6.6).
-
• All
$\gamma $
-sets are meager-additive (Proposition 6.8).
We also calculate the uniformity number of the ideal of meager-additive sets in any Polish group admitting an invariant metric (Theorem 7.1).
The paper is organized as follows. In Section 2 we recall elementary material on sharp measure zero and a few technical facts. In Section 3 we introduce sharply meager-additive sets and prove Theorem 1.1. In Section 4 we show that in locally compact groups the classes of sharp measure zero and sharply meager-additive sets coincide, i.e., we prove Theorem 1.2. In Section 5 Theorems 1.3 and 1.4 are proved. In Section 6 we derive the aforementioned consequences and in Section 7 we calculate the uniformity number of meager-additive sets. The last section lists some open problems that we consider interesting.
Some common notation used throughout the paper includes
$|{A}|$
for the cardinality of a set A,
$\omega $
for the set of natural numbers,
$\omega ^\omega $
for the family of all sequences of natural numbers. We also write
$E_n{\nearrow } E$
to denote that
$\langle {E_n} \rangle $
is an increasing sequence of sets with union E. All metric spaces and topological groups we consider are separable. The diameter of a set E in a metric space is denoted
$\operatorname {\textrm {diam}} E$
. A closed ball of radius r centered at x is denoted by
$B(x,r)$
.
2 Sharp measure zero: review
In this section we review a few facts from the theory of sharp measure zero, as developed in [Reference Zindulka28]. There are many equivalent definitions listed there. We will make use of two of them.
Let’s recall once again that by Borel’s definition [Reference Borel4] a metric space X has strong measure zero (abbreviated as
${\boldsymbol {\mathsf {Smz}}}$
) if for every sequence
$\langle {\varepsilon _n} \rangle $
of positive reals there is a cover
$\langle {U_n} \rangle $
of X such that
$\operatorname {\textrm {diam}} U_n\leqslant \varepsilon _n$
for all n. Our first goal is to describe sharp measure zero in a way that parallels this definition.
We need to recall a few notions regarding covers. Let
$\langle {U_n} \rangle $
be a sequence of subsets of a set X.
-
• A sequence of sets
$\langle {U_n} \rangle $
is called a
$\gamma $
-cover if each
$x\in X$
belongs to all but finitely many
$U_n$
. -
• A sequence of sets
$\langle {U_n} \rangle $
is called a
$\gamma $
-groupable cover if there is a partition
$\omega =I_0\cup I_1\cup I_2\cup \cdots $
into consecutive finite intervals (i.e.,
$I_{j+1}$
is on the right of
$I_j$
for all j) such that the sequence
$\langle {\bigcup _{n\in I_j}U_n:j\in \omega } \rangle $
is a
$\gamma $
-cover. The partition
$\langle {I_j} \rangle $
will be occasionally called witnessing and the finite families
$\{U_n:n\in I_j\}$
will be occasionally called witnessing families.
Definition 2.1. A metric space X has sharp measure zero (abbreviated as
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
) if for every sequence
$\langle {\varepsilon _n} \rangle $
of positive reals there is a
$\gamma$
-groupable cover
$\langle {U_n} \rangle $
of X such that
$\operatorname {\textrm {diam}} U_n\leqslant \varepsilon _n$
for all n.
For a metric space X, the family of all
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
subsets of X will be denoted
${\boldsymbol {\mathsf {Smz}}^{\sharp }}(X)$
.
Sharp measure zero is a
$\sigma $
-additive property and it is preserved by uniformly continuous maps:
Proposition 2.2 [Reference Zindulka28, 1.2].
-
(i) For a metric space X, the family
${\boldsymbol {\mathsf {Smz}}^{\sharp }}(X)$
is a
$\sigma $
-ideal. -
(ii) If
$f:X\to Y$
is a uniformly continuous mapping and
$S\subseteq X$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, then
$f(S)$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
.
The latter yields another property of
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
that is worth mentioning:
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
is a uniform property: it depends only on the uniformity induced by a metric, not the metric itself. Also, it is not a topological property; we prove that in Remark 7.2.
Lemma 2.3 [Reference Zindulka28, 3.4].
-
(i) Every
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
set admits a countable cover by totally bounded sets. -
(ii) In particular, every
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
set S in a complete metric space is contained in a
$\sigma $
-compact set.
This lets us relax the uniform continuity condition in Proposition 2.2(ii):
Proposition 2.4. Let X be a complete or
$\sigma $
- compact metric space and
$f:X\to Y$
a continuous mapping. If
$S\subseteq X$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, then so is
$f(S)$
.
Proof Lemma 2.3 yields, in either case, a countable cover
$\{K_n\}$
of S by compact sets. The maps
$f{\restriction } K_n$
are thus uniformly continuous for all
$n\in \omega $
. Hence
$f(S\cap K_n)$
are
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
by 2.2(ii) and
$f(S)$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
by 2.2(i).
2.1 Hausdorff measures
The other definition of
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
that we will utilize is set up in terms of Hausdorff measure and its modification. We recall the definitions and basic facts.
A non-decreasing, right-continuous function
$h:[0,\infty )\to [0,\infty )$
such that
$h(0)=0$
and
$h(r)>0$
if
$r>0$
is called a gauge.
If
$\delta>0$
, a cover
$\mathcal {A}$
of a set
$E\subseteq X$
is termed
$\delta $
-fine if
$\operatorname {\textrm {diam}} A\leqslant \delta $
for all
$A\in \mathcal {A}$
. Let h be a gauge. For each
$\delta>0$
set
$$ \begin{align*}\mathcal H^h_\delta(E)= \inf\left\{\sum_{n\in\omega}h(\operatorname{\textrm{diam}} E_n): \{E_n\}\ \text{is a countable}\ \delta\text{-fine cover of}\ E\right\} \end{align*} $$
and define
$$ \begin{align*}\mathcal H^h(E)=\mathop{\textrm{sup}}\limits_{\delta>0}\mathcal H^h_\delta(E). \end{align*} $$
The set function
$\mathcal H^h$
is called the h-dimensional Hausdorff measure. Properties of Hausdorff measures are well-known. The following, including the two lemmas, can be found e.g., in [Reference Rogers22]. The restriction of
$\mathcal H^h$
to Borel sets is a
$G_\delta $
-regular Borel measure.
Sharp measure zero requires a slight modification of Hausdorff measure, as it was introduced in [Reference Zindulka28]. Let h be a gauge. For each
$\delta>0$
set
$$ \begin{align*}\overline{\mathcal H}^h_\delta(E)= \inf\left\{\sum_{n=0}^N h(\operatorname{\textrm{diam}} E_n): \{E_n\}\ \text{is a}\ \textit{finite}\ \delta\text{-fine cover of}\ E\right\}. \end{align*} $$
Note that the only difference is that only finite covers are taken in account, as opposed to countable covers in the definition of
$\mathcal H^h_\delta (E)$
. Then let
$$ \begin{align*}\overline{\mathcal H}_0^h(E)=\mathop{\textrm{sup}}\limits_{\delta>0}\overline{\mathcal H}^h_\delta(E). \end{align*} $$
It is easy to check that
$\overline {\mathcal H}_0^h$
is a finitely subadditive set function. However, it is not a measure, since it need not be
$\sigma $
-additive. That is why another step is required: we need to apply the operation known as Munroe’s Method I construction (cf. [Reference Munroe16] or [Reference Rogers22]):
$$ \begin{align*}\overline{\mathcal H}^h(E)=\inf\left\{\sum_{n\in\omega}\overline{\mathcal H}^h_0(E_n): E\subseteq\bigcup_{n\in\omega}E_n\right\}. \end{align*} $$
Thus defined set function is indeed an outer measure whose restriction to Borel sets is a Borel measure. It is called the h-dimensional upper Hausdorff measure.
Detailed information on the upper Hausdorff measure is provided in [Reference Zindulka28], see also [Reference Zindulka27]. Here we only recall two properties that we will make use of.
Lemma 2.5 [Reference Zindulka28, Lemma 3.4].
Let h be a gauge and E a set in a metric space. If E is
$\sigma $
- compact, then
$\overline {\mathcal H}^h(E)=\mathcal H^h(E)$
.
Lemma 2.6 [Reference Zindulka28, Lemma 3.9].
Let h be a gauge and E a set in a metric space. If E has a
$\gamma $
-groupable cover
$\langle {U_n} \rangle $
such that
$\sum _{n\in \omega }h(\operatorname {\textrm {diam}} U_n)<\infty $
, then
$\overline {\mathcal H}^h(E)=0$
.
By a classical result of Besicovitch [Reference Besicovitch2, Reference Besicovitch3] (cf. [Reference Zindulka28] for detailed proofs), a metric space X is
${\boldsymbol {\mathsf {Smz}}}$
if and only if
$\mathcal H^h(X)=0$
for all gauges h. It is nice that
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
sets are characterized in exactly the same way, only that the upper Hausdorff measures are used in place of Hausdorff measures:
Theorem 2.7 [Reference Zindulka28, Theorem 3.7].
A metric space X is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
if and only if
$\overline {\mathcal H}^h(X)=0$
for each gauge h.
3 Sharply
$\mathcal{M}$
-additive sets
Given a metric space X, we write
$\mathcal M(X)$
to denote the family of all meager sets in X, and likewise for a topological group. In most cases there is no danger of confusion, so we write only
$\mathcal M$
instead.
Let us clarify our terminology regarding Polish groups first. A Polish group is a topological group that is homeomorphic to a Polish space, i.e., a completely metrizable separable topological space. (A metric on a group is a metric whose induced topology is the group topology.) Trivially, every Polish group admits a complete metric. It also admits a right-invariant metric. The two metrics, though, do not have to coincide: there are Polish groups that do not have a metric that is simultaneously right-invariant and complete. Also, not every Polish group has a (two-sided) invariant metric. However, if the group is abelian or compact, then it has an invariant metric. Any invariant metric on a Polish group is complete.
Recall that Prikry [Reference Prikry21] proved that if
$\mathbb {G}$
is a separable group with a right-invariant metric and
$X\subseteq \mathbb {G}$
is a set satisfying
$\forall M\in \mathcal M\ MX\neq \mathbb {G}$
, then X has strong measure zero. This is the easy part of the Galvin–Mycielski–Solovay Theorem discussed above. In this section we prove a counterpart of Prikry’s result for sharp measure zero. We first provide a formal definition of an
$\mathcal M$
-additive set.
Definition 3.1. Let
$\mathbb {G}$
be a Polish group and
$X\subseteq \mathbb {G}$
. The set X is called
$\mathcal M$
-additive (or meager-additive) if for every meager set
$M\subseteq \mathbb {G}$
, the set
$MX$
is meager.
We will write
$\mathcal M^*(\mathbb {G})$
for the
$\sigma $
-ideal of
$\mathcal M$
-additive sets in
$\mathbb {G}$
.
$\mathcal M$
-additive sets are difficult to deal with in a general Polish group. The following property, though appearing more complex, is much easier, as we shall see.
Proposition 3.2. Let
$\mathbb {G}$
be a Polish group and
$X\subseteq \mathbb {G}$
. The following are equivalent.
-
(i)
$\forall M\in \mathcal M\ \exists K\supseteq X \sigma \text {-compact } MK\neq \mathbb {G}$
and -
(ii)
$\forall M\in \mathcal M\ \exists K\supseteq X \sigma \text {-compact } MK\in \mathcal M$
.
Proof Let X satisfy (i) and
$M\in \mathcal M$
. We may suppose M is
$F_\sigma $
. Let
$Q\subseteq \mathbb {G}$
be countable and dense. Then
$QM$
is meager, hence there is a
$\sigma $
-compact set
$K\supseteq X$
and
$z\notin QMK$
. The latter yields
$Q^{-1}z\cap MK=\emptyset $
. Since Q is dense, so is
$Q^{-1}z$
, thus
$MK$
is disjoint with a dense set. If we prove that
$MK$
is
$F_\sigma $
, we are done. To that end it is enough show that if C is compact and F is closed, then
$FC$
is closed. Suppose
$y\notin FC$
. Let d be a left-invariant metric on
$\mathbb {G}$
. Define a function on C by
$f(x)=\underline {d}(Fx,y)=\underline {d}(x,F^{-1}y)$
. Since
$Fx$
is closed for each
$x\in C$
, f positive and it is clearly continuous. Therefore there is
$\delta>0$
such that
$\inf _{x\in C}f(x)>\delta $
. Hence
$\underline {d}(Fx,y)>\delta $
for all
$x\in C$
and
$\underline {d}(FC,y)\geqslant \delta>0$
follows. We proved that
$\underline {d}(FC,y)>0$
for each
$y\notin FC$
, i.e.,
$FC$
is closed, which concludes the proof.
It is clear that the property described by this proposition is stronger than
$\mathcal M$
-additivity. We capture it in the following definition.
Definition 3.3. Let
$\mathbb {G}$
be a Polish group and
$X\subseteq \mathbb {G}$
. The set X is called sharply
$\mathcal M$
-additive if for every meager set
$M\subseteq \mathbb {G}$
there is a
$\sigma $
-compact set
$K\supseteq X$
such that
$MK$
is meager.
We will write
$\mathcal M^\sharp (\mathbb {G})$
for the
$\sigma $
-ideal of sharply
$\mathcal M$
-additive sets in
$\mathbb {G}$
.
As proved in [Reference Zindulka28], in
$2^\omega $
and
$\mathbb {R}$
and its finite powers, every
$\mathcal M$
-additive set is sharply
$\mathcal M$
-additive. We shall see later that the same remains true in a wide class of locally compact Polish groups.
Our first theorem shows that sharply
$\mathcal M$
-additive sets are of sharp measure zero.
Theorem 3.4. Let
$\mathbb {G}$
be a Polish group equipped with a right-invariant metric. Then every sharply
$\mathcal M$
-additive set in
$\mathbb {G}$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
.
Proof Let d be a right-invariant metric on
$\mathbb {G}$
and let
$X\subseteq \mathbb {G}$
be a sharply
$\mathcal M$
-additive set. Let g be an arbitrary gauge. We want to show that
$\overline {\mathcal H}^g(X)=0$
. Let
$Q\subseteq \mathbb {G}$
be a countable dense symmetric set. Since Hausdorff measures are
$G_\delta $
- regular, there is a
$G_\delta $
-set
$H\supseteq Q$
such that
$\mathcal H^g(H)=0$
. Since Q is symmetric, we may, replacing H with
$H\cap H^{-1}$
if necessary, suppose that H is symmetric as well. The set
$M=\mathbb {G}\setminus H$
is obviously meager. Since X is sharply
$\mathcal M$
-additive, there is a
$\sigma $
-compact set
$K\kern-1pt\supseteq\kern-1pt X$
and
$z\notin MK$
. Routine manipulation leads to
$K\subseteq H^{-1}z \kern-1pt = \kern-1pt Hz$
. Since the underlying metric is right-invariant, with the aid of Lemma 2.5 we get
$$ \begin{align*}\overline{\mathcal H}^g(X)\leqslant\overline{\mathcal H}^g(K)=\mathcal H^g(K)\leqslant\mathcal H^g(Hz)=\mathcal H^g(H)=0, \end{align*} $$
as required.
4 Sharply
$\mathcal{M}$
-additive sets in locally compact groups
In this section we prove that in locally compact Polish groups, sharp meager-additivity and sharp measure zero are equivalent notions. The following theorem may be regarded a “Galvin–Mycielski–Solovay theorem for
$\mathcal M$
-additive sets.”
Theorem 4.1. Let
$\mathbb {G}$
be a locally compact Polish group and
$S\subseteq \mathbb {G}$
. Then S is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
if and only if S is sharply
$\mathcal M$
-additive.
It turns out that this theorem is a particular case of a more general result. Its proof is postponed until the end of the section. Let us first note that it follows from Proposition 2.4 that the notion of sharp measure zero in a locally compact metric group is independent of the choice of metric.
Proposition 4.2. Let
$d_1$
and
$d_2$
be two metrics on a locally compact metrizable group
$\mathbb {G}$
. If
$X\subseteq \mathbb {G}$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
with respect to
$d_1$
, then so it is with respect to
$d_2$
.
Thus we may refer to a
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
set in a locally compact group without referring to a metric on
$\mathbb {G}$
.
The following theorem is a group-free version of Theorem 4.1.
Theorem 4.3. Let Y be a Polish metric space and X a separable locally compact metric space. Let
$\phi :Y\times X\to X$
be a continuous mapping such that for each
$y\in Y$
and every compact nowhere dense set
$P\subseteq X$
the image
$\phi (\{y\}\times P)$
is nowhere dense. If
$S\subseteq Y$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
and
$M\subseteq X$
is meager, then there is a
$\sigma $
-compact set
$\widehat S\supseteq S$
such that
$\phi (\widehat S\times M)$
is meager.
Proof We need the following combinatorial lemma.
Lemma 4.4 [Reference Hrušák and Zapletal10, Lemma 6.2].
Let K be a compact metric space and X a separable locally compact metric space. Let
$U\subseteq X$
be an open set with compact closure
$C=\overline {U}$
and
$P\subseteq X$
be compact nowhere dense. Let
$\phi :K\times X\to X$
be a continuous mapping such that for each
$y\in K$
the image
$\phi (\{y\}\times P)$
is nowhere dense. Then
$$ \begin{align*}\forall\varepsilon>0\ \exists\delta>0\ \forall x\in C\ \forall y\in K\ \exists z\in C \quad B(z,\delta)\subseteq B(x,\varepsilon)\setminus\phi(B(y,\delta)\times P). \end{align*} $$
Since S is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
and Y is complete, S is contained in a
$\sigma $
-compact subset of Y, so we may suppose Y is
$\sigma $
- compact. Let
$K_n$
be compact sets in Y with
$K_n{\nearrow } Y$
and let
$P_n$
be compact nowhere dense sets with
$P_n{\nearrow } M$
. Let
$\{U_k\}$
be a countable base of X. For each k choose
$x_0^k\in X$
and
$\varepsilon _0^k>0$
such that
$B(x_0^k,\varepsilon _0^k)\subseteq U_k$
is compact, and let
$C_k=B(x_0^k,\varepsilon _0^k)$
. Use Lemma 4.4 to recursively construct a sequence
$\langle {\varepsilon _n} \rangle \in (0,\infty )^\omega $
such that
$$ \begin{align} \forall n\ \forall i\leqslant n\ & \forall x\in C_i \forall y\in K_n\ \exists z\in C_i\nonumber\\ &\qquad\qquad\qquad B(z,\varepsilon_n)\subseteq B(x,\varepsilon_{n-1})\setminus\phi((B(y,\varepsilon_n)\cap K_n)\times P_n). \end{align} $$
Since S is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, there is an
$\gamma $
-groupable cover
$\{E_n\}$
of S such that
$\operatorname {\textrm {diam}} E_n<\varepsilon _n$
for all n. Hence for each n there is y such that
$E_n\subseteq B(y,\varepsilon _n)$
. Therefore we may use (1) to construct sequences
$\langle {x_n^k:n\in \omega } \rangle $
such that for all k
$$ \begin{align} B(x_{n+1}^k,\varepsilon_{n+1})\subseteq B(x_n^k,\varepsilon_n) \setminus \phi((E_{n+1}\cap K_{n+1})\times P_{n+1}). \end{align} $$
It is easy to check that since
$\{E_n\}$
is a
$\gamma $
-groupable cover of S and
$K_n{\nearrow } Y$
, the family
$\{E_n\cap K_n\}$
is also a
$\gamma $
-groupable cover of S. Thus we might have supposed that
$E_n\subseteq K_n$
, and also that all
$E_n$
’s are closed. Therefore (2) simplifies to
$$ \begin{align} B(x_{n+1}^k,\varepsilon_{n+1})\subseteq B(x_n^k,\varepsilon_n) \setminus \phi(E_{n+1}\times P_{n+1}). \end{align} $$
In particular,
$B(x_n^k,\varepsilon _n)$
is a decreasing sequence of compact balls for all k and thus there is a point
$x^k\in U_k$
such that
$$ \begin{align} x^k\notin \bigcup_{n\in\omega}\phi(E_n\times P_n). \end{align} $$
The set
$\widehat S$
is constructed as follows: Let
$\mathcal {G}_j$
be the families of
$E_n$
’s witnessing the
$\gamma $
-groupability of
$\{E_n\}$
. Put
$G_n=\bigcup _{n\in \mathcal {G}_j}E_n$
and let
$F_n=\bigcap _{i<n}G_i$
and
$\widehat S=\bigcup _{n\in \omega }F_n$
. It is clear that since
$E_n$
’s are closed, the set
$\widehat S$
is
$F_\sigma $
, and clearly
$S\subseteq \widehat S$
. Moreover, routine calculation shows that
$\widehat S\times M\subseteq \bigcup _n E_n\times P_n$
. Therefore (4) yields
$x^k\notin \phi (\widehat S\times M)$
for all k. So letting
$D=\{x^k:k\in \omega \}$
, the set D is disjoint with
$\phi (\widehat S\times M)$
and it is dense in X. Since
$\widehat S$
and M are
$\sigma $
-compact, so is
$\phi (\widehat S\times M)$
. Therefore
$\phi (\widehat S\times M)$
is an
$F_\sigma $
set disjoint with a dense set, and is thus meager.
The following is obviously a particular case of the theorem.
Corollary 4.5. Let
$\phi :\mathbb {G}\curvearrowright X$
be an action of a Polish group
$\mathbb {G}$
on a
$\sigma $
-compact space X. If
$S\subseteq \mathbb {G}$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, then there is
$\sigma $
- compact set
$\widehat S\supseteq S$
such that
$\phi (\widehat S\times M)$
is meager.
Proof of Theorem 4.1 Let
$X=\mathbb {G}$
, define
$\phi :\mathbb {G}\curvearrowright \mathbb {G}$
by
$\phi (x,y)=yx$
and apply the corollary to get the forward implication. The reverse implication follows from Theorem 3.4.
5 Meager-additive sets
In the previous sections we linked sharp measure zero to sharp meager-additivity. In this section we investigate
$\mathcal M$
-additive sets in the hope that we can link them to sharp measure zero sets as well.
We first note that if a set in a Polish group is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
in some complete metric, then it is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
in any other metric as well. This follows at once from Proposition 2.4. Thus in the following theorem the particular metric does not matter.
Theorem 5.1. Let
$\mathbb {G}$
be a Polish group admitting an invariant metric. If
$X\subseteq \mathbb {G}$
is
$\mathcal M$
-additive, then X is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
(in any metric on
$\mathbb {G}$
).
Let us recall once again that not every Polish group admits an invariant metric, but if it is compact or abelian, then it does. Also, any invariant metric on a Polish group is complete. Polish groups that admit an invariant metric are referred to as
${\mathsf {TSI}}$
groups.
The following easily follows from Theorems 5.1 and 4.1.
Theorem 5.2. Let
$\mathbb {G}$
be a locally compact
${\mathsf {TSI}}$
group. Let
$X\subseteq \mathbb {G}$
. The following are equivalent:
-
(i) X is
$\mathcal M$
-additive, -
(ii) X is sharply
$\mathcal M$
-additive, -
(iii) X is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
.
The rest of this section is devoted to the proof of Theorem 5.1.
The symbol
$\mathbb {G}$
stands for the Polish group. We suppose it is equipped with an invariant (and thus complete) metric throughout this section. The metric will be denoted by d. We will use additive notation for the group operation, though
$\mathbb {G}$
is not a priori assumed to be abelian.
We shall deal with series in
$\mathbb {G}$
. Write
$\|{x}\|=d(0,x)$
. Suppose that
$\langle {x_n} \rangle $
is a sequence in
$\mathbb {G}$
such that
$\sum _{n\in \omega }\|{x_n}\|<\infty $
. Then the sequence of partial sums is Cauchy and therefore converges. We will thus write
$\sum _{n\in \omega }x_n$
for
$\lim _{n\to \infty }(x_0+x_1+\cdots +x_n)$
.
Given
$\varepsilon>0$
, a set
$B\subseteq \mathbb {G}$
is
$\varepsilon $
-separated if
$d(p,q)\geqslant \varepsilon $
for any two distinct points in B.
The grid
For each
$n\in \omega $
set
$\varepsilon _n=2^{-n}$
. We use this notation throughout. Define a system of grids in
$\mathbb {G}$
as follows.
-
• Let
$Q_0$
be a set that is maximal among all
$\varepsilon _0$
-separated sets in
$\mathbb {G}$
containing
$0$
. -
• For
$n\geqslant 1$
let
$Q_n$
be a set that is maximal among all
$\varepsilon _n$
-separated subsets of the closed ball
$B(0,\varepsilon _{n-1})$
containing
$0$
.
The maximality ensures that any point in
$B(0,\varepsilon _{n-1})$
is within distance
$\varepsilon _n$
from some point of
$Q_n$
.
Each
$Q_n$
is finite or countable. Provide it with a well-ordering so that
$0$
is the first point in the order and
-
• let
$Q_{n,m}$
be the set of the first m points in
$Q_n$
.
Then set
-
•
$Q_n^*=Q_{0,n}+Q_{1,n}+\cdots +Q_{n,n}$
and -
•
$Q=\bigcup _{n\in \omega }Q_n^*$
.
It is easy to check that Q is a dense set.
Base for meager sets
Next we define canonical meager sets in
$\mathbb {G}$
. We will use the following notation:
$\omega ^\omega $
is the family of all sequences of natural numbers;
$\omega ^{\uparrow \omega }\subseteq \omega ^\omega $
is the family of nondecreasing unbounded sequences of natural numbers. The quantifiers
$\forall ^\infty $
and
$\exists ^\infty $
have the usual meaning: “for all except finitely many” and “for infinitely many.” The symbol
$\underline {d}$
denotes the lower distance.
Definition 5.3. Let
$f\in \omega ^{\uparrow \omega }$
,
$x\in \mathbb {G}$
and
$c>0$
. Let
$$ \begin{align*}H(f,x,c)=\{z\in\mathbb{G}:\forall^\infty n\ \underline{d}(z,Q^*_{f(n)}+x)\geqslant c\,\varepsilon_{f(n+1)}\}. \end{align*} $$
Lemma 5.4. The set
$H(f,x,c)$
is meager for any
$f\in \omega ^{\uparrow \omega }$
,
$x\in \mathbb {G}$
and
$c>0$
.
Proof
$H(f,x,c)$
is disjoint with the set
$$ \begin{align*}\{z\in\mathbb{G}:\exists^\infty n\ z\in Q^*_{f(n)}+x\}=\bigcap_{n\in\omega}\bigcup_{m\geqslant n}(Q^*_{f(m)}+x)=Q+x. \end{align*} $$
Since Q is dense in
$\mathbb {G}$
, so is
$Q+x$
. On the other hand,
$H(f,x,c)$
is obviously
$F_\sigma $
. Hence it is meager.
Not only that the sets
$H(f,x,c)$
are meager, they actually form a base for meager sets in
$\mathbb {G}$
. We need yet a little more:
Lemma 5.5.
$\forall M\in \mathcal M\ \forall f\in \omega ^{\uparrow \omega }\ \exists g\in \omega ^{\uparrow \omega }\ \exists x\in \mathbb {G}\ M\subseteq H(f{\circ } g,x,1)$
Proof Suppose
$F_n$
are closed nowhere dense sets such that
$F_n{\nearrow } M$
. Write
$G_n=\mathbb {G}\setminus F_n$
.
We recursively define a sequence
$\langle {x_n} \rangle $
in
$\mathbb {G}$
and an increasing sequence
$\langle {k_n} \rangle $
of integers subject to the following conditions. Write
$y_n=x_0+x_1+\cdots +x_n$
.
$$ \begin{align} &x_{n+1}\in Q_{f(k_n)+1}+Q_{f(k_n)+2}+\cdots+Q_{f(k_{n+1})}, \end{align} $$
$$ \begin{align} &\underline{d}(F_n,Q^*_{f(k_n)}+y_{n+1})>3\varepsilon_{f(k_{n+1})}. \end{align} $$
Let
$k_0=0$
and
$x_0=0$
and proceed by induction. Suppose that
$x_n$
and
$k_n$
are defined. The sets
$-x_n-q-G_n$
are open dense for each
$q\in \mathbb {G}$
. Since
$Q^*_{f(k_n)}$
is finite, there is
$z\in \mathbb {G}$
and
$\delta>0$
such that
$$ \begin{align} B(z,\delta)\subseteq\bigcap_{q\in Q^*_{f(k_n)}}(-y_n-q+G_n)\cap B(0,\varepsilon_{f(k_n)}). \end{align} $$
Choose
$k_{n+1}>k_n$
large enough to satisfy
$4\varepsilon _{f(k_{n+1})}<\delta $
.
Denote for the moment
$m=f(k_n)$
and
$j=f(k_{n+1})-m$
.
-
• Since
$\|{z}\|\leqslant \varepsilon _m$
, there is
$t_1\in Q_{m+1}$
such that
$d(t_1,z)\leqslant \varepsilon _{m+1}$
.
$\vdots $
-
• Since
$\|{-t_1+z}\|\leqslant \varepsilon _{m+1}$
, there is
$t_2\in Q_{m+2}$
such that
$d(t_2,-t_1+z)\leqslant \varepsilon _{m+2}$
. -
• Proceed by induction up to
$m+j$
to get, for each
$i\in [1,j]$
,
$t_i\in Q_{m+i}$
such that (8)
$$\begin{align} \|{-t_j-t_{j-1}-\cdots-t_1+z}\|\leqslant\varepsilon_{m+j}. \end{align} $$
Put
$x_{n+1}=t_1+t_2+\cdots +t_j$
. Condition (5) is clearly satisfied.
Using left invariance of the metric, inequality (8) reads
$d(z,x_{n+1})\leqslant \varepsilon _{f(k_{n+1})}$
. Therefore
$4\varepsilon _{f(k_{n+1})}<\delta $
and (7) yield
$$ \begin{align*}B(x_{n+1},3\varepsilon_{f(k_{n+1})})\subseteq B(z,4\varepsilon_{f(k_{n+1})}) \subseteq B(z,\delta)\subseteq-y_n-q+G_n \end{align*} $$
for all
$q\in Q^*_{f(k_n)}$
. Using left invariance of the metric again, we get
$B(q+y_{n+1},3\varepsilon _{f(k_{n+1})})\cap F_n=\emptyset $
and (6) follows. Since
$Q_{j+1}\subseteq B(0,\varepsilon _j)$
for all j, (5) yields
$\|{x_{n+1}}\|\leqslant \sum _{j=f(k_n)}^\infty \varepsilon _j=2\varepsilon _{f(k_n)}$
. In particular,
$\sum \|{x_n}\|<\infty $
, whence the series
$\sum x_n$
converges. Set
$x=\sum x_n=\lim y_n$
and
$g(n)=k_n$
.
(5) also yields
$d(x,y_{n+1})\leqslant 2\varepsilon _{f(k_{n+1})}$
. Combine this inequality with (6) and the triangle inequality to get, for each
$q\in Q^*_{f(k_n)}$
,
$$ \begin{align*} \underline{d}(F_n,q+x)&\geqslant\underline{d}(F_n,q+y_{n+1})-d(q+y_{n+1},q+x)\\ &\geqslant 3\varepsilon_{f(k_{n+1})}-d(y_{n+1},x)\varepsilon_{f(k_{n+1})}=\varepsilon_{fg(n+1)}. \end{align*} $$
It follows that
$\underline {d}(F_n,Q^*_{f(k_n)}+x)\geqslant \varepsilon _{fg(n+1)}$
for all n, which is enough.
Key lemma
We now prove an important combinatorial lemma on the canonical meager sets.
Lemma 5.6. Let
$x,y\in \mathbb {G}$
and
$f,g\in \omega ^{\uparrow \omega }$
. Suppose that for each
$k\in \omega $
$$ \begin{align} & |{Q_{f(k)}}|>1, \end{align} $$
$$ \begin{align} & Q^*_{f(k)}\ \text{is}\ 3\varepsilon_{f(k+1)}\text{-separated}, \end{align} $$
$$ \begin{align} & f(k+1)\geqslant f(k)+4. \end{align} $$
If
$H(f,x,\frac 14)\subseteq H(f{\circ } g,y,1)$
, then
$$ \begin{align*}\forall^\infty n\in\omega\ \exists k\in[g(n),g(n+1))\quad \underline{d}(Q^*_{f(k)}+x,Q^*_{f(k)}+y)\leqslant\varepsilon_{f(k+1)}. \end{align*} $$
Proof Using right invariance of the metric we may assume
$y=0$
. Set
$$ \begin{align*}S=\{n\in\omega:\forall k\in[g(n),g(n+1))\quad \underline{d}(Q^*_{f(k)}+x,Q^*_{f(k)})>\varepsilon_{f(k+1)}\}. \end{align*} $$
We need to prove that S is finite. So aiming towards contradiction suppose that
$|{S}|=\omega $
. Our goal is to construct
$\tau \in \mathbb {G}$
such that
$$ \begin{align} &\forall n\in S\quad \underline{d}(\tau,Q^*_{fg(n)})<\varepsilon_{fg(n+1)}, \end{align} $$
$$ \begin{align} &\forall^\infty k\in\omega\quad \underline{d}(\tau,Q^*_{f(k)}+x)\geqslant\frac14\varepsilon_{f(k+1)}. \end{align} $$
Once we have such a
$\tau $
, since
$|{S}|=\omega $
, condition (12) will ensure that
$\tau \notin H(f{\circ } g,0,1)$
. On the other hand, condition (13) will ensure that
$\tau \in H(f,x,\frac 14)$
: the desired contradiction.
$\tau $
will be defined as a sum of a series. For each
$k\in \omega $
we shall choose
$\tau _k\in Q_{f(k+1)}$
according to the following rules, and then we let
$\tau =\sum _{k\in \omega }\tau _k$
.
For any k put
$T_k=\sum _{i<k}\tau _i$
and
$t_k=\sum _{i\geqslant k}\tau _i$
.
The rules for recursive construction of
$\tau _k$
’s are as follows:
-
(a) If there is
$n\in S$
such that
$k\in [g(n),g(n+1))$
, put
$\tau _k=0$
. -
(b) If there is
$n\notin S$
such that
$k\in [g(n),g(n+1))$
and
$\underline {d}(T_k,Q^*_{f(k)}+x)\geqslant \frac 12\varepsilon _{f(k+1)}$
, put
$\tau _k=0$
. -
(c) If there is
$n\notin S$
such that
$k\in [g(n),g(n+1))$
and
$\underline {d}(T_k,Q^*_{f(k)}+x)<\frac 12\varepsilon _{f(k+1)}$
, let
$\tau _k$
be the first nonzero element of
$Q_{f(k+1)}$
. Condition (9) ensures that such a choice is possible.
The rules ensure that
$$ \begin{align} T_k\in Q_{f(1),2}+Q_{f(2),2}+\cdots+Q_{f(k),2}\subseteq Q^*_{f(k)}. \end{align} $$
Notice also that since
$\tau _i\in Q_{f(i+1)}$
, we have
$\|{\tau _i}\|\leqslant 2\varepsilon _{f(i+1)}$
and thus condition (11) yields
$$ \begin{align} \|{t_k}\|\leqslant\frac{2}{15}\varepsilon_{f(k)}. \end{align} $$
We prove (12) first. Suppose
$n\in S$
. Since
$T_{g(n)}\in Q^*_{fg(n)}$
by (14), we have
$$ \begin{align*}\underline{d}(\tau,Q^*_{fg(n)})\leqslant d(T_{g(n)}+t_{g(n)},T_{g(n)})=\|{t_{g(n)}}\|. \end{align*} $$
Since
$n\in S$
, rule (a) yields
$t_{g(n)}=t_{g(n+1)}$
and thus (15) gives
$$ \begin{align*}\underline{d}(\tau,Q^*_{fg(n)})\leqslant\|{t_{g(n+1)}}\|\leqslant \frac{2}{15}\varepsilon_{fg(n+1)} <\varepsilon_{fg(n+1)}. \end{align*} $$
Thus (12) is proved. The proof of (13) is split into three cases corresponding to the three rules (a)–(c).
Claim 1. If
$n\in S$
and
$k\in [g(n),g(n+1))$
, then
$\underline {d}(\tau ,Q^*_{f(k)}+x)\geqslant \frac 14\varepsilon _{f(k+1)}$
.
Proof Since
$n\in S$
, (14) implies
$ \underline {d}(Q^*_{f(k)}+x,T_k)>\varepsilon _{f(k+1)}. $
Rule (a) yields
$t_k=t_{g(n+1)}$
. Hence
$ \|{t_k}\|=\|{t_{g(n+1)}}\|\leqslant \frac {2}{15}\varepsilon _{fg(n+1)}\leqslant \frac {2}{15}\varepsilon _{f(k+1)}. $
Combine and use triangle inequality and left invariance of the metric to get
$$ \begin{align*} \underline{d}(Q^*_{f(k)}+x,\tau) &\geqslant\underline{d}(Q^*_{f(k)}+x,T_k)-\underline{d}(T_k,\tau) \\ &>\varepsilon_{f(k+1)}-\|{t_k}\|\geqslant\varepsilon_{f(k+1)}-\frac{2}{15}\varepsilon_{f(k+1)} >\frac14\varepsilon_{f(k+1)}.\\[-36pt] \end{align*} $$
Claim 2. If
$n\notin S$
,
$k\in [g(n),g(n+1))$
and
$\underline {d}(T_k,Q^*_{f(k)}+x)\geqslant \frac 12\varepsilon _{f(k+1)}$
, then
$\underline {d}(\tau ,Q^*_{f(k)}+x)\geqslant \frac 14\varepsilon _{f(k+1)}$
Proof This time rule (b) applies. Since
$\tau _k=0$
, we have
$t_k=t_{k+1}$
. Use the same arguments as before and the assumption.
$$ \begin{align*} \underline{d}(Q^*_{f(k)}+x,\tau) &\geqslant\underline{d}(Q^*_{f(k)}+x,T_k)-\underline{d}(T_k,\tau) \\ &\geqslant\frac12\varepsilon_{f(k+1)}-\|{t_k}\|=\frac12\varepsilon_{f(k+1)}-\|{t_{k+1}}\|\\ &\geqslant\frac12\varepsilon_{f(k+1)}-\frac{2}{15}\varepsilon_{f(k+1)}>\frac14\varepsilon_{f(k+1)}.\\[-36pt] \end{align*} $$
Claim 3. If
$n\notin S$
,
$k\in [g(n),g(n+1))$
and
$\underline {d}(T_k,Q^*_{f(k)}+x)<\frac 12\varepsilon _{f(k+1)}$
, then
$\underline {d}(\tau ,Q^*_{f(k)}+x)\geqslant \frac 14\varepsilon _{f(k+1)}$
.
Proof This is the only nontrivial case. Geometrically, an approximation
$T_k$
of
$\tau $
is close to some point of
$Q^*_{f(k)}+x$
, so that the next term
$\tau _k$
in the sequence is chosen large enough to move the new approximation
$T_{k+1}$
of
$\tau $
away from that point. We however have to make sure that
$T_{k+1}$
does not get close to another point of
$Q^*_{f(k)}+x$
. That is why condition (10) is required.
Write
$\tau =T_k+\tau _k+t_{k+1}$
. We know that
$\|{t_{k+1}}\|\leqslant \frac {2}{15}\varepsilon _{f(k+1)}$
. Since
$\tau _k\neq 0$
, we also have
$\varepsilon _{f(k+1)}\leqslant \|{\tau _k}\|\leqslant 2\varepsilon _{f(k+1)}$
.
By assumption, there is
$q_0\in Q^*_{f(k)}$
such that
$d(q_0+x,T_k)<\frac 12\varepsilon _{f(k+1)}$
. First estimate
$d(q_0+x,\tau )$
from above:
$$ \begin{align*} d(q_0+x,\tau)&\leqslant d(q_0+x,T_k)+\|{\tau_k}\|+\|{t_{k+1}}\|\\ &\leqslant\left(\frac12+2+\frac{2}{15}\right)\varepsilon_{f(k+1)}<\frac83\varepsilon_{f(k+1)}. \end{align*} $$
Use this inequality to estimate
$d(p+x,\tau )$
from below for any
$p\in Q^*_{f(k)}$
,
$p\neq q_0$
. Here condition (10) gets in play: it yields
$d(p+x,q_0+x)=d(p,q_0)\geqslant 3\varepsilon _{f(k+1)}$
and thus
$$ \begin{align*} d(p+x,\tau)&\geqslant d(p+x,q_0+x)-d(q_0+x,\tau) \\ &\geqslant 3\varepsilon_{f(k+1)}-\frac83\varepsilon_{f(k+1)}>\frac14\varepsilon_{f(k+1)}. \end{align*} $$
It remains to show that
$d(q_0+x,\tau )>\frac 14\varepsilon _{f(k+1)}$
:
$$ \begin{align*} d(q_0+x,\tau)&\geqslant \|{\tau_k}\|-d(q_0+x,T_k)-\|{t_{k+1}}\|\\ &\geqslant\varepsilon_{f(k+1)}-\frac12\varepsilon_{f(k+1)}-\frac{2}{15}\varepsilon_{f(k+1)}>\frac14\varepsilon_{f(k+1)}.\\[-36pt] \end{align*} $$
We can now finish the proof of Lemma 5.6: Claims 1–3 yield (13). Therefore
$\tau \in H(f,x,\frac 14)\setminus H(f{\circ } g,0,1)$
: the required contradiction.
Proof of Theorem 5.1 Let
$X\subseteq \mathbb {G}$
be
$\mathcal M$
-additive. We will show that
$\overline {\mathcal H}^h(X)=0$
for every gauge h.
Begin by recursively building
$f\in \omega ^{\uparrow \omega }$
subject to conditions (9)–(11) and
$$ \begin{align} \forall k\in\omega\quad h\bigl(2\varepsilon_{f(k+1)}\bigr)<\frac{2^{-k}}{|{Q^*_{f(k)}}|^2}. \end{align} $$
Consider the set
$H(f,0,\frac 14)$
. It is meager by Lemma 5.4. Therefore
$H(f,0,\frac 14)+X$
is meager as well. By virtue of Lemma 5.5 there thus exists
$g\in \omega ^{\uparrow \omega }$
and
$y\in \mathbb {G}$
such that
$H(f,0,\frac 14)+x\subseteq H(f{\circ } g,y,1)$
for all
$x\in X$
. Right invariance of the metric gives
$H(f,0,\frac 14)+x=H(f,x,\frac 14)$
. It follows that
$H(f,x,\frac 14)\subseteq H(f{\circ } g,y,1)$
for all
$x\in X$
. Lemma 5.6 thus yields
$$ \begin{align} \forall x\in X\, \forall^\infty n\in\omega\, \exists k\in[g(n),g(n+1)) \ \underline{d}(Q^*_{f(k)}+x,Q^*_{f(k)}+y)\leqslant\varepsilon_{f(k+1)}. \end{align} $$
The latter inequality means that there are
$p,q\in Q^*_{f(k)}$
such that
$d(p+x,q+y)\leqslant \varepsilon _{f(k+1)}$
which is, via left invariance of the metric, equivalent to
$$ \begin{align*}x\in B(-p+q+y,\varepsilon_{f(k+1)}). \end{align*} $$
Therefore (17) can be phrased as follows:
$$ \begin{align} \forall x\in X\ \forall^\infty n\in\omega\ \exists k\in[g(n),\ g(n+1))&\ \exists p,\ q\in Q^*_{f(k)}\nonumber\\ & x\in B(-\!p+q+y,\varepsilon_{f(k+1)}). \end{align} $$
Set
$$ \begin{align*}{2} &\mathcal{B}_k =\{B(-{p}+q+y,\varepsilon_{f(k+1)}):p,q\in Q^*_{f(k)}\},\qquad k\in\omega,\\&\mathcal{G}_n =\bigcup\{\mathcal{B}_k:g(n)\leqslant k<g(n+1)\},\qquad n\in\omega,\\&\mathcal{G} =\bigcup_{k\in\omega}\mathcal{B}_k=\bigcup_{n\in\omega}\mathcal{G}_n. \end{align*} $$
With this setting, (18) reads
$$ \begin{align*}\forall x\in X\ \forall^\infty n\in\omega\ \exists G\in\mathcal{G}_n\quad x\in G. \end{align*} $$
For all
$k\in \omega $
we have
$|{\mathcal {B}_k}|\leqslant |{Q^*_{f(k)}}|^2$
. In particular, the families
$\mathcal {G}_n$
are finite, witnessing that
$\mathcal {G}$
is a
$\gamma $
-groupable cover of X.
By Lemma 2.6, in order to prove that
$\overline {\mathcal H}^h(X)=0$
it is enough to show that
$\sum _{G\in \mathcal {G}}h(\operatorname {\textrm {diam}} G)$
is finite. Clearly
$\operatorname {\textrm {diam}} B(-\!p+q+y,\varepsilon _{f(k+1)})\leqslant 2\varepsilon _{f(k+1)}$
. Therefore (16) yields
$$ \begin{align*} \sum_{G\in\mathcal{G}}h(\operatorname{\textrm{diam}} G)&= \sum_{k\in\omega}\sum_{G\in\mathcal{B}_k}h(\operatorname{\textrm{diam}} G)\\ &= \sum_{k\in\omega}\sum_{p,q\in Q^*_{f(k)}}h(\operatorname{\textrm{diam}} B(-\!p+q+y,\varepsilon_{f(k+1)}))\\ &\leqslant \sum_{k\in\omega}|{Q^*_{f(k)}}|^2\, h(2\varepsilon_{f(k+1)}) \leqslant \sum_{k\in\omega}2^{-k}<\infty. \end{align*} $$
The proof of Theorem 5.1 is complete.
6 Some consequences
Continuous images and cartesian products
Meager-additive sets are preserved by continuous mappings between Polish groups and by cartesian products as follows:
Theorem 6.1. Let
$\mathbb {G}_1$
be a
${\mathsf {TSI}}$
Polish group and
$\mathbb {G}_2$
a locally compact Polish group. Let
$f:\mathbb {G}_1\to \mathbb {G}_2$
a continuous mapping. If
$X\subseteq \mathbb {G}_1$
is
$\mathcal M$
-additive, then so is
$f(X)$
.
Proof Since X is
$\mathcal M$
-additive it is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
by Theorem 5.1. By Proposition 2.4,
$f(X)$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
as well. By Theorem 4.1,
$f(X)$
is
$\mathcal M$
-additive.
Theorem 6.2. Let
$\mathbb {G}_1,\mathbb {G}_2$
be
${\mathsf {TSI}}$
locally compact groups. Let
$X_1\subseteq \mathbb {G}_1$
,
$X_2\subseteq \mathbb {G}_2$
.
-
(i) If
$X_1$
is
${\boldsymbol {\mathsf {Smz}}}$
and
$X_2$
is
$\mathcal M$
-additive, then
$X_1\times X_2$
is
${\boldsymbol {\mathsf {Smz}}}$
. -
(ii) If
$X_1$
and
$X_2$
are
$\mathcal M$
-additive, then so is
$X_1\times X_2$
.
Proof (i) By Theorem 5.2,
$X_2$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
. By [Reference Zindulka28, Theorem 3.14], a product of a
${\boldsymbol {\mathsf {Smz}}}$
and
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
sets is
${\boldsymbol {\mathsf {Smz}}}$
.
(ii) By Theorem 5.2, both
$X_1$
and
$X_2$
are
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
. By [Reference Zindulka28, Theorem 3.14], a product of two
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
sets is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
. Now apply Theorem 5.2 to conclude that
$X_1\times X_2$
is
$\mathcal M$
-additive.
Corollary 6.3. Let
$\mathbb {G}_1,\mathbb {G}_2$
be
${\mathsf {TSI}}$
locally compact groups. Let
$X\subseteq \mathbb {G}_1\times \mathbb {G}_2$
. The following are equivalent.
-
(i) X is
$\mathcal M$
-additive, -
(ii)
$\operatorname {\textrm {proj}}_1X$
and
$\operatorname {\textrm {proj}}_2X$
are
$\mathcal M$
-additive, and -
(iii)
$\operatorname {\textrm {proj}}_1X\times \operatorname {\textrm {proj}}_2X$
is
$\mathcal M$
-additive.
Proof Write
$X_1=\operatorname {\textrm {proj}}_1 X$
,
$X_2=\operatorname {\textrm {proj}}_2 X$
. (iii)
${\Rightarrow }$
(i) is trivial.
(i)
${\Rightarrow }$
(ii) Suppose X is
$\mathcal M$
additive. Then by Theorem 6.1 both
$X_1$
and
$X_2$
are
$\mathcal M$
additive.
(ii)
${\Rightarrow }$
(iii) Suppose
$X_1$
and
$X_2$
are
$\mathcal M$
additive. Then by Theorem 6.2
$X_1\times X_2$
is
$\mathcal M$
additive.
Binary operations
Theorems 4.1 and 5.2 reveal a surprising fact about
$\mathcal M$
-additive sets in
${\mathsf {TSI}}$
locally compact groups:
Corollary 6.4. Let
$\mathbb {G}$
be a
${\mathsf {TSI}}$
locally compact group. Let
$\star $
be a continuous binary operation on
$\mathbb {G}$
such that
$N\star x$
is nowhere dense for each nowhere dense set N and
$x\in \mathbb {G}$
. If
$X\subseteq \mathbb {G}$
is
$\mathcal M$
-additive, then
$M\star X$
is meager for each meager set M.
In particular, this holds for any action
$\phi :\mathbb {G}\curvearrowright \mathbb {G}$
.
Universally meager sets
Recall that a separable metric space E is termed universally meager [Reference Zakrzewski25, Reference Zakrzewski26] if for any perfect Polish spaces
$Y,X$
such that
$E\subseteq X$
and every continuous one–to–one mapping
$f:Y\to X$
the set
$f^{-1}(E)$
is meager in Y. By [Reference Zindulka28, Proposition 6.11] every
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
set is universally meager. Thus Theorem 5.2 yields
Proposition 6.5. Every
$\mathcal M$
-additive set in a
${\mathsf {TSI}}$
Polish group is universally meager.
Transitively meager sets
Nowik et al. [Reference Nowik, Scheepers and Weiss17] studied the notion of transitively meager sets on the line. By the definition, a set
$S\subseteq \mathbb {G}$
in a Polish group is transitively meager if
$$ \begin{align*}\forall P\subseteq\mathbb{G}\text{ perfect }\exists F\supseteq S\ \sigma\text{-compact } \forall x\in\mathbb{G}\ P\cap xF\text{ is meager in}\ P. \end{align*} $$
Proposition 6.6. Every
$\mathcal M$
-additive set in a
${\mathsf {TSI}}$
Polish group is transitively meager.
Proof This is an easy consequence of a technical [Reference Zindulka28, Lemma 6.10]:
Lemma 6.7 [Reference Zindulka28, Lemma 6.10].
Let
$X,Y,Z$
be perfect Polish spaces and
$\phi :Y\to X$
a continuous one–to–one mapping. Let
$\mathcal {F}$
be an equicontinuous family of uniformly continuous mappings of Z into X. If
$E\subseteq Z$
is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
, then there is a
$\sigma $
-compact set
$F\supseteq E$
such that
$\phi ^{-1}f(F)$
is meager in Y for all
$f\in \mathcal {F}$
.
Let S be an
$\mathcal M$
-additive set in
$\mathbb {G}$
. By Theorem 5.1 it is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
. Now apply the lemma with
$Y=P$
,
$X=Z=\mathbb {G}$
,
$\phi :P\to \mathbb {G}$
the identity inclusion, and
$\mathcal {F}$
the family of all left translates.
$\gamma $
-sets
Recall the notion of
$\gamma $
-set, as introduced by Gerlits and Nagy [Reference Gerlits and Nagy7]. A family
$\mathcal {U}$
of open sets in a separable metric space X is called an
$\omega $
\!-cover of X if every finite subset of X is contained in some
$U\in \mathcal {U}$
. A metric space X is a
$\gamma $
-set if every
$\omega $
-cover of X contains a
$\gamma $
-cover. Generalizing a result of Nowik and Weiss [Reference Nowik and Weiss18, Proposition 3.7], [Reference Zindulka28, Proposition 6.6] proved that every
$\gamma $
-set is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}{}$
. This, together with Theorem 4.1, yields
Proposition 6.8. Every
$\gamma $
-set in a locally compact Polish group is sharply
$\mathcal M$
-additive.
7 Uniformity number of meager-additive sets
Let
$\mathbb {G}$
be a Polish group. We have considered the following
$\sigma $
-ideals of small sets:
-
•
$\mathcal M^*(\mathbb {G})$
, the ideal of
$\mathcal M$
-additive sets in
$\mathbb {G}$
, -
•
$\mathcal M^\sharp (\mathbb {G})$
, the ideal of sharply
$\mathcal M$
-additive sets in
$\mathbb {G}$
, and -
•
${\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
, the ideal of sharp measure zero sets in
$\mathbb {G}$
. This notion may depend, unlike the other two, on the metric.
We will calculate uniformity numbers of
$\mathcal M^*(\mathbb {G})$
and
${\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
for
${\mathsf {TSI}}$
Polish groups. Recall that if
$\mathcal J$
is an ideal of subsets of a set X, then
-
•
$\operatorname {\mathsf {non}}\mathcal J=\min \{|{A}|:A\notin \mathcal J\}$
(uniformity of
$\mathcal J$
), -
•
$\operatorname {\mathsf {add}}\mathcal J=\min \{|{\mathcal {A}}|:\mathcal {A}\subseteq \mathcal J,\bigcup \mathcal {A}\notin \mathcal J\}$
(additivity of
$\mathcal J$
), -
•
$\operatorname {\mathsf {cov}}\mathcal J=\min \{|{\mathcal {A}}|:\mathcal {A}\subseteq \mathcal J,\bigcup \mathcal {A}=\mathbb {G}\}$
(covering of
$\mathcal J$
).
The invariants
$\operatorname {{\mathsf {non}}}\mathcal M(2^\omega )$
,
$\operatorname {{\mathsf {add}}}\mathcal M(2^\omega )$
and
$\operatorname {{\mathsf {cov}}}\mathcal M(2^\omega )$
are commonly denoted just
$\operatorname {{\mathsf {non}}}\mathcal M$
,
$\operatorname {{\mathsf {add}}}\mathcal M$
and
$\operatorname {{\mathsf {cov}}}\mathcal M$
.
The cardinal invariant
$\operatorname {{\mathsf {non}}}\mathcal M^*(2^\omega )$
is termed transitive additivity of
$\mathcal M$
and denoted
$\operatorname {{\mathsf {add}}}^*\mathcal M$
in [Reference Bartoszyński and Judah1, Reference Pawlikowski19], where a combinatorial characterization of
$\operatorname {{\mathsf {add}}}^*\mathcal M$
is also provided [Reference Bartoszyński and Judah1, Theorem 2.7.14].
Theorem 7.1. Let
$\mathbb {G}$
be a
${\mathsf {TSI}}$
Polish group.
-
(i) If
$\mathbb {G}$
is locally compact, then
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})=\operatorname {{\mathsf {non}}}\mathcal M^*(\mathbb {G})=\operatorname {{\mathsf {add}}}^*\mathcal M$
. -
(ii) If
$\mathbb {G}$
is not locally compact, then
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})=\operatorname {{\mathsf {non}}}\mathcal M^*(\mathbb {G})=\operatorname {{\mathsf {add}}}\mathcal M$
.
Proof (i) Let
$K_n{\nearrow }\mathbb {G}$
be a sequence of compact sets. Let
$X\subseteq \mathbb {G}$
be a not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
set such that
$|{X}|=\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
. There is n such that
$X\cap K_n$
is not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, therefore
$|{X\cap K_n}|=\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
. Since
$K_n$
is compact, it is dyadic: there is a continuous mapping
$f:2^\omega \to K_n$
onto
$K_n$
. For each
$x\in X\cap K_n$
pick
$\widehat x\in f^{-1}(x)$
and set
$\widehat X=\{\widehat x:x\in X\cap K_n\}$
. Then
$f(\widehat X)=X\cap K_n$
, hence
$\widehat X$
is by Proposition 2.4 not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
, and clearly
$|{\widehat X}|=|{X\cap K_n}|=\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
. It follows that
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(2^\omega )\leqslant \operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
.
On the other hand, by the Perfect set theorem,
$\mathbb {G}$
contains a copy of
$2^\omega $
. It follows that
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(2^\omega )\geqslant \operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
.
Combine the two inequalities to get
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(2^\omega )=\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
. By Theorem 5.2 we have
${\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})=\mathcal M^*(\mathbb {G})$
and likewise for
$2^\omega $
. Thus
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(2^\omega )=\operatorname {{\mathsf {non}}}\mathcal M^*(2^\omega )=\operatorname {{\mathsf {add}}}^*\mathcal M$
and
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})=\operatorname {{\mathsf {non}}}\mathcal M^*(\mathbb {G})$
and the result follows.
(ii) We will consider
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
sets in
$\omega ^\omega $
. The metric on
$\omega ^\omega $
is the usual least difference metric: for distinct
$f,g\in \omega ^\omega $
we let
$d(f,g)=2^{-n}$
, where n is the first number for which
$f(n)\neq g(n)$
.
Recall that a set
$X\subseteq \omega ^\omega $
is bounded if
$\exists g\in \omega ^\omega \ \forall f\in X\ \forall ^\infty n\in \omega \ f(n)\leqslant g(n)$
. Let
$\mathfrak b=\min \{|{X}|:X\subseteq \omega ^\omega \text { is not bounded}\}$
denote the bounding number.
Let
$X\subseteq \omega ^\omega $
be an unbounded set such that
$|{X}|=\mathfrak b$
. Since X is not bounded, it is not contained in a
$\sigma $
- compact set and in particular (by Lemma 2.3) it is not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
. It follows that
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\omega ^\omega )\leqslant \mathfrak b$
.
Miller and Fremlin [Reference Miller and Fremlin15] constructed a set
$X\subseteq \omega ^\omega $
that is not
${\boldsymbol {\mathsf {Smz}}}$
and
$|{X}|=\operatorname {{\mathsf {cov}}}\mathcal M$
. This set is clearly not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
and thus
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\omega ^\omega )\leqslant \operatorname {{\mathsf {cov}}}\mathcal M$
.
It follows that
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\omega ^\omega )\leqslant \min (\operatorname {{\mathsf {cov}}}\mathcal M,\mathfrak b)$
. Miller [Reference Miller14] proved that
$\min (\operatorname {{\mathsf {cov}}}\mathcal M,\mathfrak b)=\operatorname {{\mathsf {add}}}\mathcal M$
(see also [Reference Bartoszyński and Judah1, 2.2.9]). Overall we have
$$ \begin{align} \operatorname{{\mathsf{non}}}{\boldsymbol{\mathsf{Smz}}^{\sharp}}(\omega^\omega)\leqslant\operatorname{{\mathsf{add}}}\mathcal M. \end{align} $$
Our group
$\mathbb {G}$
is not locally compact and is equipped with an invariant metric. By [Reference Hrušák, Wohofsky and Zindulka9, Lemma 5.4], such a group contains a uniform copy of
$\omega ^\omega $
and thus
$\operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})\leqslant \operatorname {{\mathsf {non}}}{\boldsymbol {\mathsf {Smz}}^{\sharp }}(\omega ^\omega )$
. Combine with (19) to get
$$ \begin{align} \operatorname{{\mathsf{non}}}{\boldsymbol{\mathsf{Smz}}^{\sharp}}(\mathbb{G})\leqslant\operatorname{{\mathsf{add}}}\mathcal M. \end{align} $$
It is well-known that
$\operatorname {{\mathsf {add}}}\mathcal M(X)=\operatorname {{\mathsf {add}}}\mathcal M$
for every uncountable Polish space. Thus if X is a set in
$\mathbb {G}$
such that
$|{X}|<\operatorname {{\mathsf {add}}}\mathcal M$
, then for each meager set
$M\subseteq \mathbb {G}$
the set
$MX$
is a union of less than
$\operatorname {{\mathsf {add}}}\mathcal M$
many meager sets and is thus meager. It follows that
$$ \begin{align} \operatorname{{\mathsf{non}}}\mathcal M^*(\mathbb{G})\geqslant\operatorname{{\mathsf{add}}}\mathcal M. \end{align} $$
Finally, by Theorem 5.1,
$\mathcal M^*(\mathbb {G})\subseteq {\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
and hence
$$ \begin{align} \operatorname{{\mathsf{non}}}\mathcal M^*(\mathbb{G})\leqslant\operatorname{{\mathsf{non}}}{\boldsymbol{\mathsf{Smz}}^{\sharp}}(\mathbb{G}). \end{align} $$
Now combine (21), (22), and (20):
$$ \begin{align*}\operatorname{{\mathsf{add}}}\mathcal M\leqslant\operatorname{{\mathsf{non}}}\mathcal M^*(\mathbb{G})\leqslant\operatorname{{\mathsf{non}}}{\boldsymbol{\mathsf{Smz}}^{\sharp}}(\mathbb{G})\leqslant\operatorname{{\mathsf{add}}}\mathcal M \end{align*} $$
and the result follows.
Remark 7.2. Theorem 7.1 provides a simple argument proving that
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
is consistently not a topological property. (Remind that under Borel Conjecture
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
is a topological property for a trivial reason.)
The Baer–Specker group
$\mathbb {Z}^\omega $
is a
${\mathsf {TSI}}$
Polish group. On the other hand, it is homeomorphic to the set of irrational numbers, so regard it as a subset of
$\mathbb {R}$
. By Theorem 7.1(ii) there is a set
$X\subseteq \mathbb {Z}^\omega $
such that
$|{X}|=\operatorname {{\mathsf {add}}}\mathcal M$
and that is not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
in the invariant metric. On the other hand, if
$\operatorname {{\mathsf {add}}}\mathcal M<\operatorname {{\mathsf {add}}}^*\mathcal M$
, then X is by Theorem 7.1(i)
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
in the metric of the real line. Since
$\operatorname {{\mathsf {add}}}\mathcal M<\operatorname {{\mathsf {add}}}^*\mathcal M$
is relatively consistent with ZFC (as proved by Pawlikowski [Reference Pawlikowski19]), X is consistently a set that is
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
is one metric on
$\mathbb {Z}^\omega $
and not
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
in another homeomorphic metric.
8 Questions
We conclude with a few open problems.
$\mathcal M$
-additive vs.
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
under the Continuum Hypothesis
As to
${\boldsymbol {\mathsf {Smz}}}$
sets in groups, let us recall that Galvin–Mycielski–Solovay Theorem has been extended to all locally compact Polish groups by Kysiak [Reference Kysiak12] and Fremlin [Reference Fremlin5]. Further extension of the theorem to Polish groups has been proven to be impossible: Hrušák et al. [Reference Hrušák, Wohofsky and Zindulka9] and Hrušák and Zapletal [Reference Hrušák and Zapletal10] found that under the Continuum Hypothesis the Galvin–Mycielski–Solovay Theorem fails for all
${\mathsf {TSI}}$
Polish groups that are not locally compact.
We ask if an analogous situation occurs for
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
sets. We know from Theorem 5.1 that for a
${\mathsf {TSI}}$
Polish group we have
$\mathcal M^*(\mathbb {G})\subseteq {\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
. Does the converse inclusion hold?
Question 8.1. Assume the Continuum Hypothesis. Is there a
${\mathsf {TSI}}$
, not locally compact Polish group
$\mathbb {G}$
such that
$\mathcal M^*(\mathbb {G})\neq {\boldsymbol {\mathsf {Smz}}^{\sharp }}(\mathbb {G})$
?
We conjecture the answer to be negative. More specifically, we may ask about the Baer–Specker group:
Question 8.2. Assume the Continuum Hypothesis. Is there a
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
set in
$\mathbb {Z}^\omega $
that is not
$\mathcal M$
-additive?
${\mathsf {TSI}}$
condition
The proof of Theorem 5.1 relies on the two-sided invariance of the metric. Can we do better?
$\mathcal E$
-additive sets
Let
$\mathbb {G}$
be locally compact Polish group. Denote by
$\mathcal E$
the
$\sigma $
- ideal consisting of sets that are contained in an
$F_\sigma $
-set of Haar measure zero. A set
$X\subseteq \mathbb {G}$
is
$\mathcal E$
\!-additive if
$EX\in \mathcal E$
for every
$E\in \mathcal E$
. The notion of sharply
$\mathcal E$
\!-additive sets can be defined, too, in the obvious manner.
In [Reference Zindulka28, Theorem 5.2] it is shown that a set
$X\subseteq 2^\omega $
is
$\mathcal M$
-additive if and only if it is
$\mathcal E$
-additive if and only if it is sharply
$\mathcal E$
-additive. The proofs heavily depend on the combinatorics of sets in
$\mathcal E$
. We have no idea if this theorem or at least some inclusions extend to other locally compact groups.
Question 8.4.
-
(i) In what locally compact Polish groups is every
$\mathcal M$
-additive set
$\mathcal E$
-additive (or sharply
$\mathcal E$
-additive)? -
(ii) In what locally compact Polish groups is every
$\mathcal E$
-additive (or sharply
$\mathcal E$
-additive) set
$\mathcal M$
-additive? -
(iii) In what locally compact Polish groups is every
$\mathcal E$
-additive sharply
$\mathcal E$
-additive?
The two new classes extend the family of ideals that we are interested in to five:
${\boldsymbol {\mathsf {Smz}}^{\sharp }}$
,
$\mathcal M^*$
,
$\mathcal M^\sharp $
,
$\mathcal E^*$
and
$\mathcal E^\sharp $
, leading to a number of questions about possible inclusions. For
${\mathsf {TSI}}$
locally compact groups, the twelve questions reduce, due to Theorem 5.2, to the five listed in Question 8.4.
Acknowledgments
I would like to thank Michael Hrušák for his kind support and help while I was visiting Instituto de Matemáticas, Unidad Morelia, Universidad Nacional Autonóma de México; and Piotr Szewczak and Boaz Tsaban who encouraged me to write the paper.
Work on this project was partially conducted during the author’s sabbatical stay at the Instituto de matemáticas, Unidad Morelia, Universidad Nacional Autonóma de México supported by CONACyT grant no. 125108. The author was supported from European Regional Development Fund-Project “Center for Advanced Applied Science” (No. CZ.02.1.01/0.0/0.0/16_019/0000778).
