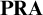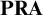1 Introduction
1.1 Brouwer’s Intuitionism and Hilbert’s Finitism
Brouwer’s Intuitionism is considered as the precursor of many varieties of constructivism and finitism which reject the law of excluded middle (LEM) for statements concerning infinite objects. It is said that even Hilbert, a most severe opponent of Brouwer’s, adopted a part of Brouwer’s idea in his proposal for meta-mathematics or proof theory, and this partial adoption is now called Hilbert’s Finitism. However, there are several essential differences between these two varieties of constructivism or finitism.
First, they are different in their original aims. Brouwer’s Intuitionism is a claim how mathematics in its entirety should be, and the mathematics practiced according to this is called Intuitionistic Mathematics (INT). On the other hand, Hilbert’s Finitism was intended to apply only to a particular part of mathematics, called proof theory or meta-mathematics. The aim of this part was “saving” the entirety of mathematics from the fear of inconsistency. The “entirety of mathematics” in Hilbert’s idea is far beyond finitism and now called Classical Mathematics (CLASS) in the context of comparison among kinds of mathematics.
This difference might explain why Hilbert’s Finitism is stricter than Brouwer’s Intuitionism: for example, the induction schema on numbers is granted for free in the latter whereas it is allowed only if restricted to finitely checkable statements in the former. The acceptance of the schema for properties not finitely checkable (even though LEM for such properties is not allowed) seems to be reason enough not to call Brouwer’s Intuitionism a finitism, and moreover Brouwer’s Intuitionism requires transcendental assumptions which basically assert that everything is to be constructed (cf. the notion of choice sequence) contradicting CLASS.
It is worth mentioning Bishop’s constructivism, a third variety of constructivism. Bishop-style constructive mathematics (BISH) is considered to be completely constructive, in the sense that it does not assume any transcendental assertion. Thus all the theorems of BISH, as formal sentences, are contained in those of CLASS and INT. Nonetheless, it does not seem plausible to call it a finitism either, for it also accepts the induction schema applied to properties not finitely checkable. It accepts the axiom of choice applied to such properties as well, which is also beyond the finitistically justifiable part of CLASS.
Another contrast between Brouwer and Hilbert is in their attitudes towards formalization: while Brouwer did not formalize INT, Hilbert tried to formalize CLASS and since then his Finitism (now identified with what is formalizable in Primitive Recursive Arithmetic
![]() $\textbf {PRA}$
; see [Reference Tait47]Footnote
1
) has been established as the meta-theory of handling formalization, or, in which proof theory is practiced. This contrast has, however, been gradually losing significance: followers of Brouwer formalized INT, and now our interest is in how different it is, as a formal theory,Footnote
2
from CLASS and from BISH as well as from Russian Recursive Mathematics RUSS. The last requires a different transcendental assumption asserting that everything is computable.
$\textbf {PRA}$
; see [Reference Tait47]Footnote
1
) has been established as the meta-theory of handling formalization, or, in which proof theory is practiced. This contrast has, however, been gradually losing significance: followers of Brouwer formalized INT, and now our interest is in how different it is, as a formal theory,Footnote
2
from CLASS and from BISH as well as from Russian Recursive Mathematics RUSS. The last requires a different transcendental assumption asserting that everything is computable.
Unfortunately a difference is also in popularity: CLASS has been investigated extensively, e.g., identifying the finitistically secured part, while there seems to have been no similar systematic investigation for INT.
Given these contrasts, the aim of the present series of articles, the identification of the part of INT and addable axioms that Hilbert would recognize as secured, has multi-fold motivations. To repeat: from the viewpoint that Brouwer’s Intuitionism is the precursor of various kinds of constructivism and finitism; from the historical perspective that Brouwer and Hilbert were severe opponents of each other; and from the necessity of the identification as has been done for CLASS in order to develop INT in parallel to CLASS.
1.2 Reducibility and interpretability
By what criterion would Hilbert recognize a fragment of mathematics as secured according to his Finitism? We may distinguish two criteria: a fragment is said to be (i) finitistically guaranteed if it is consistent provably in
![]() $\textbf {PRA}$
; and (ii) finitistically justifiable if it is consistent relative to
$\textbf {PRA}$
; and (ii) finitistically justifiable if it is consistent relative to
![]() $\textbf {PRA}$
provably in
$\textbf {PRA}$
provably in
![]() $\textbf {PRA}$
. It is likely that these were not distinguished in Hilbert’s original intention prior to Gödel’s incompleteness theorem.
$\textbf {PRA}$
. It is likely that these were not distinguished in Hilbert’s original intention prior to Gödel’s incompleteness theorem.
Proof theory, to which Hilbert’s Finitism was originally intended to apply, has refined (ii) above (see [Reference Rathjen32, Section 2.5]): a formal theory
![]() $T_1$
is (proof theoretically) reducible to another
$T_1$
is (proof theoretically) reducible to another
![]() $T_2$
over a class
$T_2$
over a class
![]() $\mathcal {C}$
of sentences if there is a primitive recursive function f such that provably within
$\mathcal {C}$
of sentences if there is a primitive recursive function f such that provably within
![]() $\textbf {PRA}$
, for any sentence A from
$\textbf {PRA}$
, for any sentence A from
![]() $\mathcal {C}$
, if x is a proof of A in
$\mathcal {C}$
, if x is a proof of A in
![]() $T_1$
then
$T_1$
then
![]() $f(x)$
is a proof of A in
$f(x)$
is a proof of A in
![]() $T_2$
. Usually
$T_2$
. Usually
![]() $\mathcal {C}$
contains the absurdum
$\mathcal {C}$
contains the absurdum
![]() $\bot $
and so this notion yields the comparison of externally defined consistency strengths (namely, the consistency of
$\bot $
and so this notion yields the comparison of externally defined consistency strengths (namely, the consistency of
![]() $T_2$
implies that of
$T_2$
implies that of
![]() $T_1$
or consistency-wise implication) provably in
$T_1$
or consistency-wise implication) provably in
![]() $\textbf {PRA}$
. In many interesting cases, the theories essentially contain a fragment of arithmetic and we can assume
$\textbf {PRA}$
. In many interesting cases, the theories essentially contain a fragment of arithmetic and we can assume
![]() $\mathcal {C}$
includes
$\mathcal {C}$
includes
![]() $\Pi ^0_1$
or
$\Pi ^0_1$
or
![]() $\Pi ^0_2$
sentences. As the Gödel sentence (of a reasonable theory) is
$\Pi ^0_2$
sentences. As the Gödel sentence (of a reasonable theory) is
![]() $\Pi ^0_1$
, it also yields the comparison of internally defined consistency strength: any reasonable formal theory consistent provably in
$\Pi ^0_1$
, it also yields the comparison of internally defined consistency strength: any reasonable formal theory consistent provably in
![]() $T_1$
is consistent provably also in
$T_1$
is consistent provably also in
![]() $T_2$
. Now
$T_2$
. Now
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
,
$\textbf {I}\boldsymbol {\Sigma }_1$
,
![]() $\textbf {RCA}_0$
and
$\textbf {RCA}_0$
and
![]() $\mathbf{WKL}_0$
are parts of Classical Mathematics that are known to be proof theoretically reducible to
$\mathbf{WKL}_0$
are parts of Classical Mathematics that are known to be proof theoretically reducible to
![]() $\textbf {PRA}$
. As a subtheory is trivially reducible to a supertheory, these four theories are proof theoretically equivalent.
$\textbf {PRA}$
. As a subtheory is trivially reducible to a supertheory, these four theories are proof theoretically equivalent.
For our purposes, however, we can use a stronger notion, interpretability. We will prove reducibility results by giving concrete interpretations, among which are Gödel–Gentzen negative interpretation and realizability interpretation. Our notion of interpretability is slightly broader than that in some literature, in the sense that logical connectives can be interpreted non-trivially (as in the aforementioned examples).Footnote
3
An interpretation I is called
![]() $\mathcal {C}$
-preserving, if any
$\mathcal {C}$
-preserving, if any
![]() $\mathcal {C}$
sentence A is implied by its interpretation
$\mathcal {C}$
sentence A is implied by its interpretation
![]() $A^I$
in the interpreting theory
$A^I$
in the interpreting theory
![]() $T_2$
. All interpretations in the present article are
$T_2$
. All interpretations in the present article are
![]() $\Pi ^0_1$
-preserving, and so imply reducibility with
$\Pi ^0_1$
-preserving, and so imply reducibility with
![]() $\mathcal {C} = \Pi ^0_1$
. Whereas reducibility concerns only proofs ending with sentences in
$\mathcal {C} = \Pi ^0_1$
. Whereas reducibility concerns only proofs ending with sentences in
![]() $\mathcal {C}$
, interpretability means that all mathematical practice formalized in one theory can be simulated in another. As each step of proofs in
$\mathcal {C}$
, interpretability means that all mathematical practice formalized in one theory can be simulated in another. As each step of proofs in
![]() $T_1$
is transformed into a uniformly bounded number of steps in
$T_1$
is transformed into a uniformly bounded number of steps in
![]() $T_2$
, the induced transformation f of proofs belongs to even lower complexity, and so the consistency-wise implication is proved in meta-theories weaker than
$T_2$
, the induced transformation f of proofs belongs to even lower complexity, and so the consistency-wise implication is proved in meta-theories weaker than
![]() $\textbf {PRA}$
.
$\textbf {PRA}$
.
The difference between reducibility and interpretability becomes essential when we talk about the relations between finitistically guaranteed theories (hence weaker than
![]() $\textbf {PRA}$
): while the reducibility is proved typically by cut elimination, which requires commitment to superexponential functions, such a commitment yields the consistency of
$\textbf {PRA}$
): while the reducibility is proved typically by cut elimination, which requires commitment to superexponential functions, such a commitment yields the consistency of
![]() $\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
,
$\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
,
![]() $\textbf {RCA}_0^*$
and
$\textbf {RCA}_0^*$
and
![]() $\mathbf{WKL}_0^*$
, typical finitistically guaranteed theories, and so collapses the hierarchy of the externally defined consistency strengths of such weaker theories.
$\mathbf{WKL}_0^*$
, typical finitistically guaranteed theories, and so collapses the hierarchy of the externally defined consistency strengths of such weaker theories.
1.3 Characteristic axioms of Intuitionistic Mathematics
Up to the present, there seems to be a consensus on what axiomatizes (the characteristic part of) INT. An informal explanation of such characterizing axioms is as follows, where the terminology might differ from Brouwer’s original.
-
Intuitionistic logic neither the law of excluded middle (
 $A\lor \neg A$
) nor double negation elimination (
$A\lor \neg A$
) nor double negation elimination (
 $\neg \neg A \to A$
) is accepted unless A is finitely checkable (while the explosion axiom
$\neg \neg A \to A$
) is accepted unless A is finitely checkable (while the explosion axiom
 $\bot \to A$
is accepted);
$\bot \to A$
is accepted); -
Basic arithmetic basic properties, which are finitely checkable and which govern the natural numbers and fundamental operations, are accepted;
-
Induction on natural numbers the induction schema on
 $\omega $
for all the legitimate propertiesFootnote
4
(not necessarily finitely checkable) is accepted;
$\omega $
for all the legitimate propertiesFootnote
4
(not necessarily finitely checkable) is accepted; -
Bar induction transfinite induction along the well-founded tree (coded by a bar, which intersects any infinite sequence) of finite sequences of numbers, with various restriction, Footnote 5 is accepted;
-
Fan theorem classically equivalent to a form of König’s lemma or weak fan theorem, restricted to binary trees but defined by any legitimate properties, is an important consequence of bar induction in many applications; either of them is taken as an axiom of INT instead of bar induction in some literature;
-
Axiom of choice for any legitimate property A of sorts i and j, if for any x of sort i there is y of j such that
 $A[x,y]$
holds then there exists a function f of sort
$A[x,y]$
holds then there exists a function f of sort
 $i \to j$
such that
$i \to j$
such that
 $A[x,f(x)]$
holds for any x of i;
$A[x,f(x)]$
holds for any x of i; -
Continuity principle a function on Baire space
 $\omega ^\omega $
defined by any legitimate property is locally continuous.
$\omega ^\omega $
defined by any legitimate property is locally continuous.
The last contradicts CLASS, and the others, except the first two and weak fan theorem, are classically beyond Finitism. Since Heyting arithmetic, consisting only of the first three, is mutually interpretable with Peano arithmetic, and hence already beyond Finitism, we need to restrict these axioms, as in CLASS.
The first half of the main purpose of the present series of articles is thus to clarify how large fragments of these axioms are jointly reducible to Hilbert’s Finitism (i.e., finitistically justifiable) or jointly consistent provably in Finitism (i.e., finitistically guaranteed). This article, the first in the series, addresses this question, in the language
![]() $\mathcal {L}_{\mathrm{F}}$
of function-based second order arithmetic (similar to that of
$\mathcal {L}_{\mathrm{F}}$
of function-based second order arithmetic (similar to that of
![]() $\textbf {EL}$
from [Reference Troelstra and van Dalen50, Chapter 3, 6.2]), where we need some twist to state the existence of choice functions on Baire space (see Section 2.5.5) or where we could say that the axiom of choice for such sorts is illegitimate at all (see f.n.12).
$\textbf {EL}$
from [Reference Troelstra and van Dalen50, Chapter 3, 6.2]), where we need some twist to state the existence of choice functions on Baire space (see Section 2.5.5) or where we could say that the axiom of choice for such sorts is illegitimate at all (see f.n.12).
The expositions of axioms here are informal or pre-formal, and it is quite delicate how to formalize them. We follow a standard way, but some discussions are unavoidable and will be addressed in Section 2.
We define fragments of the axioms basically by requiring the relevant properties to be in classes of formulae, e.g.,
![]() $\Sigma ^0_n$
’s and
$\Sigma ^0_n$
’s and
![]() $\Pi ^0_n$
’s (which however do not exhaust all arithmetical formulae because of the lack of prenex normal form theorem), and by controlling the sorts in the axiom of choice.
$\Pi ^0_n$
’s (which however do not exhaust all arithmetical formulae because of the lack of prenex normal form theorem), and by controlling the sorts in the axiom of choice.
1.4 Finitistically justifiable and guaranteed parts of Intuitionistic Mathematics
We will see that the following with
![]() $\textbf {EL}_0^-$
(i.e., the logic and basic arithmetic) are jointly reducible to
$\textbf {EL}_0^-$
(i.e., the logic and basic arithmetic) are jointly reducible to
![]() $\textbf {PRA}$
:
$\textbf {PRA}$
:
-
• induction on natural numbers restricted to
 $\Sigma ^0_2$
properties (
$\Sigma ^0_2$
properties (
 $\Sigma ^0_2\textsf {-Ind}$
);
$\Sigma ^0_2\textsf {-Ind}$
); -
• bar induction restricted to
 $\Pi ^0_1$
properties (
$\Pi ^0_1$
properties (
 $\Pi ^0_1\textsf {-BI}$
, see the exact formulation in Definition 2.26);
$\Pi ^0_1\textsf {-BI}$
, see the exact formulation in Definition 2.26); -
• fan theorem for fans (decidable by definition) and bars defined by any legitimate properties (
 $\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
);
$\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
); -
• axiom of choice for all legitimate properties and dependent choice of numbers for
 $\Sigma ^0_2$
ones (
$\Sigma ^0_2$
ones (
 $\Sigma ^0_2\textsf {-DC}^0$
);
$\Sigma ^0_2\textsf {-DC}^0$
); -
• continuity principle for functions defined by any legitimate properties (
 $\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^0$
and
$\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^0$
and
 $\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^1$
),
$\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^1$
),
and that, with the following further restrictions, jointly consistent provably in
![]() $\textbf {PRA}$
: induction on numbers to decidable properties; dependent choice and bar induction omitted; fans to be complete binary (
$\textbf {PRA}$
: induction on numbers to decidable properties; dependent choice and bar induction omitted; fans to be complete binary (
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-WFT}$
).
$\mathcal {L}_{\mathrm{F}}\textsf {-WFT}$
).
Besides the well known contrast with the classical situation concerning the continuity principle, we see further contrasts, as any of the following is, classically, beyond
![]() $\textbf {PRA}$
:
$\textbf {PRA}$
:
![]() $\Sigma ^0_2\textsf {-Ind}$
; fan theorem restricted either to decidable bars
$\Sigma ^0_2\textsf {-Ind}$
; fan theorem restricted either to decidable bars
![]() $\Delta ^0_0\textsf {-FT}$
or to complete binary fans and
$\Delta ^0_0\textsf {-FT}$
or to complete binary fans and
![]() $\Pi ^0_1$
bars
$\Pi ^0_1$
bars
![]() $\Pi ^0_1\textsf {-WFT}$
; and
$\Pi ^0_1\textsf {-WFT}$
; and
![]() $\Pi ^0_1$
axiom of choice.
$\Pi ^0_1$
axiom of choice.
Our method is Kleene’s functional realizability, known to be able to interpret most part of INT in CLASS. We examine which fragments of INT are interpreted by this in
![]() $\mathbf{WKL}_0$
or
$\mathbf{WKL}_0$
or
![]() $\mathbf{WKL}_0^*$
. As it is based on a
$\mathbf{WKL}_0^*$
. As it is based on a
![]() $\Pi ^0_2$
-definable application “
$\Pi ^0_2$
-definable application “
![]() $\,|\,$
” for functions, unlike the number realizability, naïve attempts of proof easily rely on
$\,|\,$
” for functions, unlike the number realizability, naïve attempts of proof easily rely on
![]() $\Pi ^0_2$
or higher induction. The proof is, in general, not straightforward from previously known one.
$\Pi ^0_2$
or higher induction. The proof is, in general, not straightforward from previously known one.
As a byproduct, we can add Markov’s principle
![]() $\textsf {MP}$
(i.e.,
$\textsf {MP}$
(i.e.,
![]() $\Sigma ^0_1\textsf {-DNE}$
double negation elimination restricted to
$\Sigma ^0_1\textsf {-DNE}$
double negation elimination restricted to
![]() $\Sigma _1$
assertions) to the combinations above.
$\Sigma _1$
assertions) to the combinations above.
![]() $\textsf {MP}$
is accepted from some constructive views and called semi-constructive. While it seems agreed not to accept
$\textsf {MP}$
is accepted from some constructive views and called semi-constructive. While it seems agreed not to accept
![]() $\textsf {MP}$
in Intuitionism, it is not agreed to accept its negation.Footnote
6
We need no interpretations that exclude
$\textsf {MP}$
in Intuitionism, it is not agreed to accept its negation.Footnote
6
We need no interpretations that exclude
![]() $\textsf {MP}$
, as the interpretability of
$\textsf {MP}$
, as the interpretability of
![]() $T{+}\textsf { MP}$
trivially implies that of T.
$T{+}\textsf { MP}$
trivially implies that of T.
Moreover, we will see that these fragments are optimal: none of
![]() $\Pi ^0_2\textsf {-Ind}$
,
$\Pi ^0_2\textsf {-Ind}$
,
![]() $\Sigma ^0_1\textsf {-BI}_D$
(restricted to decidable bars),
$\Sigma ^0_1\textsf {-BI}_D$
(restricted to decidable bars),
![]() $\Pi ^0_2\textsf {-DC}!^0$
(with uniqueness in the premise) and
$\Pi ^0_2\textsf {-DC}!^0$
(with uniqueness in the premise) and
![]() $\Pi ^0_1\textsf {-DC}!^1$
(dependent choice of functions) can only with
$\Pi ^0_1\textsf {-DC}!^1$
(dependent choice of functions) can only with
![]() $\textbf {EL}_0^-$
be reducible to
$\textbf {EL}_0^-$
be reducible to
![]() $\textbf {PRA}$
; none of
$\textbf {PRA}$
; none of
![]() $\Pi ^0_1\textsf {-Ind}$
,
$\Pi ^0_1\textsf {-Ind}$
,
![]() $\Sigma ^0_1\textsf {-Ind}$
,
$\Sigma ^0_1\textsf {-Ind}$
,
![]() $\Delta ^0_0\textsf {-BI}_D$
,
$\Delta ^0_0\textsf {-BI}_D$
,
![]() $\Delta ^0_0\textsf {-DC}!^0$
and
$\Delta ^0_0\textsf {-DC}!^0$
and
![]() $\Delta ^0_0\textsf {-FT}$
only with
$\Delta ^0_0\textsf {-FT}$
only with
![]() $\textbf {EL}_0^-$
is consistent provably in
$\textbf {EL}_0^-$
is consistent provably in
![]() $\textbf {PRA}$
. For the former, we interpret
$\textbf {PRA}$
. For the former, we interpret
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
, which proves the consistency of
$\textbf {I}\boldsymbol {\Sigma }_2$
, which proves the consistency of
![]() $\textbf {PRA}$
, by generalizing Coquand and Hofmann’s method [Reference Coquand and Hofmann11]. For the latter, we interpret
$\textbf {PRA}$
, by generalizing Coquand and Hofmann’s method [Reference Coquand and Hofmann11]. For the latter, we interpret
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
which is equiconsistent with
$\textbf {I}\boldsymbol {\Sigma }_1$
which is equiconsistent with
![]() $\textbf {PRA}$
.
$\textbf {PRA}$
.
Note that, by Gödel’s second incompleteness, if a theory
![]() $T_1$
proves the consistency
$T_1$
proves the consistency
![]() $\textrm {Con}(T_2)$
of another
$\textrm {Con}(T_2)$
of another
![]() $T_2$
, then
$T_2$
, then
![]() $T_1$
is not reducible to (nor interpretable in)
$T_1$
is not reducible to (nor interpretable in)
![]() $T_2$
, since otherwise
$T_2$
, since otherwise
![]() $T_1$
proves its own consistency.
$T_1$
proves its own consistency.
1.5 Effects of semi-constructive or semi-classical principles
Hilbert’s Finitism did not intend to restrict the mathematics, but to maximize the set of acceptable axioms that are in the direct sense beyond Finitism but that are secured on his Finitistic ground through meta-mathematics. So we should continue to clarify which axioms beyond Intuitionism can be added to the secure parts of INT without losing finitistic guaranteedness or justifiability. The aforementioned byproduct on
![]() $\textsf {MP}$
is a part of answer, and it is natural to try to answer more generally: which part of classical logic, or even of CLASS, is finitistically guaranteed or justifiable jointly with major partsFootnote
7
of INT? As many classically valid principles are known not to imply full classical logic, the other half of our purpose is to ask: how does the secured part change from the intuitionistic situation to classical one, along the hierarchy of such semi-classical principles?Footnote
8
$\textsf {MP}$
is a part of answer, and it is natural to try to answer more generally: which part of classical logic, or even of CLASS, is finitistically guaranteed or justifiable jointly with major partsFootnote
7
of INT? As many classically valid principles are known not to imply full classical logic, the other half of our purpose is to ask: how does the secured part change from the intuitionistic situation to classical one, along the hierarchy of such semi-classical principles?Footnote
8
Among famous ones are limited principle of omniscience
![]() $\textsf {LPO}$
(i.e.,
$\textsf {LPO}$
(i.e.,
![]() $\Sigma ^0_1\textsf {-LEM}$
the law of excluded middle for
$\Sigma ^0_1\textsf {-LEM}$
the law of excluded middle for
![]() $\Sigma ^0_1$
) and lesser limited principle of omniscience
$\Sigma ^0_1$
) and lesser limited principle of omniscience
![]() $\textsf {LLPO}$
(i.e.,
$\textsf {LLPO}$
(i.e.,
![]() $\Pi ^0_1{\lor }\Pi ^0_1\textsf {-DNE}$
double negation elimination for
$\Pi ^0_1{\lor }\Pi ^0_1\textsf {-DNE}$
double negation elimination for
![]() $\Pi ^0_1{\lor }\Pi ^0_1$
).
$\Pi ^0_1{\lor }\Pi ^0_1$
).
![]() $\textsf {LLPO}$
is implied by
$\textsf {LLPO}$
is implied by
![]() $\textsf {LPO}$
and, as shown in [Reference Akama, Berardi, Hayashi and Kohlenbach1], independent of
$\textsf {LPO}$
and, as shown in [Reference Akama, Berardi, Hayashi and Kohlenbach1], independent of
![]() $\textsf {MP}$
. In the presence of full induction,
$\textsf {MP}$
. In the presence of full induction,
![]() $\textsf {LLPO}$
is equivalent to
$\textsf {LLPO}$
is equivalent to
![]() $\textsf {B}\Sigma ^0_2\textsf {-DNE}$
and to
$\textsf {B}\Sigma ^0_2\textsf {-DNE}$
and to
![]() $\Sigma ^0_1\textsf {-GDM}$
, generalized De Morgan’s law
$\Sigma ^0_1\textsf {-GDM}$
, generalized De Morgan’s law
![]() $\neg (\forall x < y)A \to (\exists x\,{<}\,y)\neg A$
for
$\neg (\forall x < y)A \to (\exists x\,{<}\,y)\neg A$
for
![]() $\Sigma ^0_1$
properties. With restricted induction, however, all the implications we know among these are as follows.
$\Sigma ^0_1$
properties. With restricted induction, however, all the implications we know among these are as follows.

Unlike
![]() $\textsf {MP}$
, by weak counterexample argument
Footnote
9
we can presume that Brouwer would reject the idea of
$\textsf {MP}$
, by weak counterexample argument
Footnote
9
we can presume that Brouwer would reject the idea of
![]() $\textsf {LLPO}$
(and hence all principles above it). Thus the status of
$\textsf {LLPO}$
(and hence all principles above it). Thus the status of
![]() $\textsf {LLPO}$
in Intuitionism is as that of WKL in Finitism, since WKL is definitely directly unacceptable in Finitism, and actually they are equivalent in the presence of axiom of choice (cf. 3.9). Because accepting WKL indirectly by consistency proof was the core of Simpson’s “partial realizations of Hilbert’s Program” from [Reference Simpson44],
$\textsf {LLPO}$
in Intuitionism is as that of WKL in Finitism, since WKL is definitely directly unacceptable in Finitism, and actually they are equivalent in the presence of axiom of choice (cf. 3.9). Because accepting WKL indirectly by consistency proof was the core of Simpson’s “partial realizations of Hilbert’s Program” from [Reference Simpson44],
![]() $\textsf {LLPO}$
should be of particular interest in our context.
$\textsf {LLPO}$
should be of particular interest in our context.
We show that adding
![]() $\Sigma ^0_1\textsf {-GDM}$
(and so
$\Sigma ^0_1\textsf {-GDM}$
(and so
![]() $\textsf {LLPO}$
), even jointly with
$\textsf {LLPO}$
), even jointly with
![]() $\textsf {MP}$
, does not change the intuitionistic situation described in Section 1.4, except the axiom of function-number and function-function choice. Though these choices cannot be formalized in
$\textsf {MP}$
, does not change the intuitionistic situation described in Section 1.4, except the axiom of function-number and function-function choice. Though these choices cannot be formalized in
![]() $\mathcal {L}_{\mathrm{F}}$
, continuous choice (CC), whose
$\mathcal {L}_{\mathrm{F}}$
, continuous choice (CC), whose
![]() $\Pi ^0_1$
fragment contradicts
$\Pi ^0_1$
fragment contradicts
![]() $\textsf {LLPO}$
, could be seen as conjunctions of them and continuity principle (cf. Section 2.5.5). Our main tool is van Oosten’s Lifschitz-style functional realizability from [Reference van Oosten31], in the definition of which, a bounded
$\textsf {LLPO}$
, could be seen as conjunctions of them and continuity principle (cf. Section 2.5.5). Our main tool is van Oosten’s Lifschitz-style functional realizability from [Reference van Oosten31], in the definition of which, a bounded
![]() $\Sigma ^0_2$
property plays a central role. Thus the arguments on the finitistic ground is much more delicate than in van Oosten’s original context.
$\Sigma ^0_2$
property plays a central role. Thus the arguments on the finitistic ground is much more delicate than in van Oosten’s original context.
On the other hand, we will see that
![]() $\textsf {LPO}$
already makes the situation completely classical, that is, any of the following separately, but together with
$\textsf {LPO}$
already makes the situation completely classical, that is, any of the following separately, but together with
![]() $\textbf {EL}_0^-\,{+}\textsf {LPO}$
, is already non-reducible to
$\textbf {EL}_0^-\,{+}\textsf {LPO}$
, is already non-reducible to
![]() $\textbf {PRA}$
:
$\textbf {PRA}$
:
-
•
 $\Sigma ^0_2$
induction on numbers (
$\Sigma ^0_2$
induction on numbers (
 $\Sigma ^0_2\textsf {-Ind}$
);
$\Sigma ^0_2\textsf {-Ind}$
); -
• fan theorem restricted to
 $\Delta ^0_0$
bars but without the binary constraint (
$\Delta ^0_0$
bars but without the binary constraint (
 $\Delta ^0_0\textsf {-FT}$
);
$\Delta ^0_0\textsf {-FT}$
); -
• weak fan theorem restricted to (complete binary fans and)
 $\Pi ^0_1$
-bars (
$\Pi ^0_1$
-bars (
 $\Pi ^0_1\textsf {-WFT}$
); and
$\Pi ^0_1\textsf {-WFT}$
); and -
•
 $\Pi ^0_1$
axiom of choice even with the uniqueness assumption in the premise (
$\Pi ^0_1$
axiom of choice even with the uniqueness assumption in the premise (
 $\Pi ^0_1\textsf {-AC!}^{00}$
).
$\Pi ^0_1\textsf {-AC!}^{00}$
).
For the second and fourth we will show the interpretability of
![]() $\textbf {ACA}_0$
with Gödel–Gentzen negative interpretation. For the others, we need the combination with intuitionistic forcing to interpret
$\textbf {ACA}_0$
with Gödel–Gentzen negative interpretation. For the others, we need the combination with intuitionistic forcing to interpret
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
or
$\textbf {I}\boldsymbol {\Sigma }_2$
or
![]() $\textbf {ACA}_0$
.
$\textbf {ACA}_0$
.
1.6 Constructive reverse mathematics on consistency strength
Our study also contributes to the research field, called constructive reverse mathematics (cf. e.g., [Reference Ishihara19, Reference Ishihara20]). There implications, on a constructive ground, between (fragments of) axioms from CLASS, INT and RUSS, are investigated and, for the unprovability of these implications, questions of the following type are of interest:
which combination of axioms (from different kinds of mathematics) is consistent and which is not?
Namely, it has been asked only whether a combination is consistent or inconsistent.
Now our investigation is on the proof theoretic or consistency strengths of combinations. In other words, we ask how consistent (or to which extent consistent) the combination is. Thus the question becomes refined:
which combination of axioms (from different kinds of mathematics) is how much consistent?
The proof theoretic investigation of intuitionistic theories seems much less developed than classical ones.
Even the consistency strengths of
![]() $\Sigma _n$
or
$\Sigma _n$
or
![]() $\Pi _n$
induction schemata, the most basic targets of the study, were identified only in 1990s. Then Visser (in his unpublished note, see [Reference Wehmeier56]) pointed out that
$\Pi _n$
induction schemata, the most basic targets of the study, were identified only in 1990s. Then Visser (in his unpublished note, see [Reference Wehmeier56]) pointed out that
![]() $\textbf {i}\boldsymbol {\Sigma }_{\infty }\,{=}\,\textbf {i}\boldsymbol {\Pi }_{\infty }$
, Heyting arithmetic with induction restricted to prenex formulae, is mutually
$\textbf {i}\boldsymbol {\Sigma }_{\infty }\,{=}\,\textbf {i}\boldsymbol {\Pi }_{\infty }$
, Heyting arithmetic with induction restricted to prenex formulae, is mutually
![]() $\Pi _2$
-preservingly interpretable with
$\Pi _2$
-preservingly interpretable with
![]() $\textbf {i}\boldsymbol {\Pi }_2$
, and so with classical
$\textbf {i}\boldsymbol {\Pi }_2$
, and so with classical
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
. This shows the drastic contrast with the classical situation, as classical
$\textbf {I}\boldsymbol {\Sigma }_2$
. This shows the drastic contrast with the classical situation, as classical
![]() $\textbf {I}\boldsymbol {\Sigma }_n$
’s form a strict hierarchy exhausting Peano arithmetic
$\textbf {I}\boldsymbol {\Sigma }_n$
’s form a strict hierarchy exhausting Peano arithmetic
![]() $\textbf {PA}$
.
$\textbf {PA}$
.
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
and
$\textbf {i}\boldsymbol {\Sigma }_1$
and
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
are mutually
$\textbf {I}\boldsymbol {\Sigma }_1$
are mutually
![]() $\Pi _2$
-preservingly interpretable (see [Reference Coquand and Hofmann11, Reference Avigad3]), and so are
$\Pi _2$
-preservingly interpretable (see [Reference Coquand and Hofmann11, Reference Avigad3]), and so are
![]() $\textbf {i}\boldsymbol {\Pi }_1$
and
$\textbf {i}\boldsymbol {\Pi }_1$
and
![]() $\textbf {I}\boldsymbol {\Pi }_1\,{=}\,\textbf {I}\boldsymbol {\Sigma }_1$
as shown easily by Gödel–Gentzen negative interpretation (but only
$\textbf {I}\boldsymbol {\Pi }_1\,{=}\,\textbf {I}\boldsymbol {\Sigma }_1$
as shown easily by Gödel–Gentzen negative interpretation (but only
![]() $\Pi _1$
-preserving, as shown in [Reference Wehmeier56]). Thus any of
$\Pi _1$
-preserving, as shown in [Reference Wehmeier56]). Thus any of
![]() $\textbf {i}\boldsymbol {\Sigma }_n$
(
$\textbf {i}\boldsymbol {\Sigma }_n$
(
![]() $n\,{\geq }\, 3$
) and
$n\,{\geq }\, 3$
) and
![]() $\textbf {i}\boldsymbol {\Pi }_n$
(
$\textbf {i}\boldsymbol {\Pi }_n$
(
![]() $n\,{\geq }\, 2$
) has the same strength as classical
$n\,{\geq }\, 2$
) has the same strength as classical
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
, and both
$\textbf {I}\boldsymbol {\Sigma }_2$
, and both
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
and
$\textbf {i}\boldsymbol {\Sigma }_1$
and
![]() $\textbf {i}\boldsymbol {\Pi }_1$
as classical
$\textbf {i}\boldsymbol {\Pi }_1$
as classical
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
(and so
$\textbf {I}\boldsymbol {\Sigma }_1$
(and so
![]() $\textbf {PRA}$
). What remains is
$\textbf {PRA}$
). What remains is
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
, which [Reference Burr10, Corollary 2.27] interpreted in a fragment of Gödel’s
$\textbf {i}\boldsymbol {\Sigma }_2$
, which [Reference Burr10, Corollary 2.27] interpreted in a fragment of Gödel’s
![]() $\textbf {T}$
of the same proof theoretic strength as
$\textbf {T}$
of the same proof theoretic strength as
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
by Dialectica interpretation. We will show these results by realizability but also that these strengths are not affected by adding the fragments of Brouwerian axioms. While for this goal we need functional realizability, our proof also shows that Kleene’s number realizability, used in [Reference Wehmeier56], interprets intuitionistic
$\textbf {I}\boldsymbol {\Sigma }_1$
by Dialectica interpretation. We will show these results by realizability but also that these strengths are not affected by adding the fragments of Brouwerian axioms. While for this goal we need functional realizability, our proof also shows that Kleene’s number realizability, used in [Reference Wehmeier56], interprets intuitionistic
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
in classical
$\textbf {i}\boldsymbol {\Sigma }_2$
in classical
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
. Here, realizing in a classical theory is essential; we do not know if
$\textbf {I}\boldsymbol {\Sigma }_1$
. Here, realizing in a classical theory is essential; we do not know if
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
is realizable in intuitionistic
$\textbf {i}\boldsymbol {\Sigma }_2$
is realizable in intuitionistic
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
.
$\textbf {i}\boldsymbol {\Sigma }_1$
.

As mentioned in Section 1.5,
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
and
$\textbf {i}\boldsymbol {\Sigma }_2$
and
![]() $\textsf {LPO}$
jointly have the same strength as classical
$\textsf {LPO}$
jointly have the same strength as classical
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
. Generally, our method shows that
$\textbf {I}\boldsymbol {\Sigma }_2$
. Generally, our method shows that
![]() $\textbf {i}\boldsymbol {\Sigma }_{n+1}{+}\Sigma _n\textsf {-LEM}$
is mutually
$\textbf {i}\boldsymbol {\Sigma }_{n+1}{+}\Sigma _n\textsf {-LEM}$
is mutually
![]() $\Pi _{n+2}$
-preservingly interpretable with
$\Pi _{n+2}$
-preservingly interpretable with
![]() $\textbf {I}\boldsymbol {\Sigma }_{n+1}$
, whereas Gödel–Gentzen negative interpretation needs stronger
$\textbf {I}\boldsymbol {\Sigma }_{n+1}$
, whereas Gödel–Gentzen negative interpretation needs stronger
![]() $\textbf {i}\boldsymbol {\Sigma }_{n+1}{+}\Sigma _{n+1}\textsf {-DNE}$
to interpret
$\textbf {i}\boldsymbol {\Sigma }_{n+1}{+}\Sigma _{n+1}\textsf {-DNE}$
to interpret
![]() $\textbf {I}\boldsymbol {\Sigma }_{n+1}$
.
$\textbf {I}\boldsymbol {\Sigma }_{n+1}$
.
Besides induction, there seem to have been no proof theoretic studies (in the sense of Section 1.2) on intuitionistic theories of the strength below
![]() $\textbf {HA}$
.Footnote
10
The present article leads to this large field of proof theoretic study.
$\textbf {HA}$
.Footnote
10
The present article leads to this large field of proof theoretic study.
1.7 Conclusions
Although bar induction (BI) was accepted in Brouwer’s original idea, the accumulation of studies has shown that weak fan theorem (WFT), a consequence of BI, and continuous choice (CC) suffice in most cases. These two have been perceived even to characterize Intuitionistic Mathematics (INT) in constructive reverse mathematics (see [Reference Bridges and Richman9, Chapter 5], [Reference Ishihara20, p.44, l.
![]() $-$
7] or [Reference Diener and Loeb12, Section 4] where WFT is called fan theorem). If we agree with this perception,Footnote
11
we could conclude that Brouwer’s Intuitionism is compatible with Hilbert’s Finitism, for WFT and CC both for arbitrary formulae are jointly reducible to, and, even provably consistent in
$-$
7] or [Reference Diener and Loeb12, Section 4] where WFT is called fan theorem). If we agree with this perception,Footnote
11
we could conclude that Brouwer’s Intuitionism is compatible with Hilbert’s Finitism, for WFT and CC both for arbitrary formulae are jointly reducible to, and, even provably consistent in
![]() $\textbf {PRA}$
.
$\textbf {PRA}$
.
Moreover, some semi-classical principles, e.g., Markov’s principle
![]() $\textsf {MP}$
and lesser limited principle of omniscience
$\textsf {MP}$
and lesser limited principle of omniscience
![]() $\textsf {LLPO}$
, do not destroy the compatibility and are hence consistent with Intuitionism and FinitismFootnote
12
(Figure 1) even though Brouwer did not accept them. Thus
$\textsf {LLPO}$
, do not destroy the compatibility and are hence consistent with Intuitionism and FinitismFootnote
12
(Figure 1) even though Brouwer did not accept them. Thus
![]() $\textsf {MP}$
and
$\textsf {MP}$
and
![]() $\textsf {LLPO}$
are acceptable in the same (indirect) sense as WKL is acceptable in Hilbert’s Finitism. On the other hand, limited principle of omniscience
$\textsf {LLPO}$
are acceptable in the same (indirect) sense as WKL is acceptable in Hilbert’s Finitism. On the other hand, limited principle of omniscience
![]() $\textsf {LPO}$
is, by no means, consistent with Intuitionism and Finitism: it is finitistically consistent only with those fragments of Brouwerian axioms with which the entire classical logic is finitistically consistent (Figure 2).
$\textsf {LPO}$
is, by no means, consistent with Intuitionism and Finitism: it is finitistically consistent only with those fragments of Brouwerian axioms with which the entire classical logic is finitistically consistent (Figure 2).

Figure 1 “Intuitionisitic Situation” – over any base theory between
![]() $\textbf {EL}^-_0$
and
$\textbf {EL}^-_0$
and
![]() $\textbf {EL}^-_0{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-GDM}$
.
$\textbf {EL}^-_0{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-GDM}$
.

Figure 2 “Classical Situation” – over any base theory between
![]() $\textbf {EL}_0^-{+}\textsf {LPO}$
and
$\textbf {EL}_0^-{+}\textsf {LPO}$
and
![]() $\textbf {EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
$\textbf {EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
1.8 A marriage of Brouwer’s Intuitionism and an ultrafinitism
After Hilbert’s Finitism in the early 20th century, ultrafinitisms, stricter kinds of finitism than Hilbert’s, have been proposed. Some are motivated by the development of computational complexity theory in the latter half of the century: only functions of a certain complexity are admitted, in the same sense as Hilbert’s (formalized as
![]() $\textbf {PRA}$
) admits only primitive recursive ones. Which part of INT, with which semi-classical principle, is justifiable or guaranteed with respect to them? An abundance of complexity classes (not yet proved to be identical), and hence of ultrafinitisms, makes this question too big to answer in one article.
$\textbf {PRA}$
) admits only primitive recursive ones. Which part of INT, with which semi-classical principle, is justifiable or guaranteed with respect to them? An abundance of complexity classes (not yet proved to be identical), and hence of ultrafinitisms, makes this question too big to answer in one article.
Here we consider only the easiest kind, which admits only Kalmár’s elementary functions.Footnote
13
This could be formalized as
![]() $\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
. All our finitistic guaranteedness results yield justifiability with respect to this kind of ultrafinitism, as they are proved via interpretability in
$\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
. All our finitistic guaranteedness results yield justifiability with respect to this kind of ultrafinitism, as they are proved via interpretability in
![]() $\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
. Recall that the notion of proof theoretic reducibility collapses the consistency of such weak theories but that of interpretability does not.
$\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
. Recall that the notion of proof theoretic reducibility collapses the consistency of such weak theories but that of interpretability does not.
Theories for even stricter kinds of ultrafinitism require the distinction between large and small numbers (i.e., x’s and
![]() $|x|$
’s), and therefore, in such a context, the natural formulations of some axioms, e.g., fan theorem, are not clear. The authors hope that they could treat these topics somewhere in the near future.
$|x|$
’s), and therefore, in such a context, the natural formulations of some axioms, e.g., fan theorem, are not clear. The authors hope that they could treat these topics somewhere in the near future.
1.9 Outline and prerequisites
Section 2 introduces our base theory
![]() $\textbf {EL}_0^-$
and some variants, as well as semi-classical principles and Brouwerian axioms whose strengths we will investigate, with basic properties. Section 3 gives upper bounds of the strengths of combinations of them, with Kleene’s functional realizability and van Oosten’s variant for Lifschitz-style, whose characterization by axioms will be generalized extensively. Folklore results from classical arithmetic, refined in Section 3.1, play vital roles. Section 4 gives lower bounds, with Gödel–Gentzen negative interpretation and by generalizing Coquand–Hofmann forcing interpretation. Section 5 will present the results in final forms, with supplementary results, further problems and related works.
$\textbf {EL}_0^-$
and some variants, as well as semi-classical principles and Brouwerian axioms whose strengths we will investigate, with basic properties. Section 3 gives upper bounds of the strengths of combinations of them, with Kleene’s functional realizability and van Oosten’s variant for Lifschitz-style, whose characterization by axioms will be generalized extensively. Folklore results from classical arithmetic, refined in Section 3.1, play vital roles. Section 4 gives lower bounds, with Gödel–Gentzen negative interpretation and by generalizing Coquand–Hofmann forcing interpretation. Section 5 will present the results in final forms, with supplementary results, further problems and related works.
While Section 2 summarizes basic definitions and results on function-based second order arithmetic, the readers are assumed to be familiar with set-based counterpart from, e.g., [Reference Simpson45]. They are supposed to know the systems
![]() $\textbf {RCA}_0^*$
,
$\textbf {RCA}_0^*$
,
![]() $\mathbf{WKL}_0^*$
,
$\mathbf{WKL}_0^*$
,
![]() $\textbf {RCA}_0$
,
$\textbf {RCA}_0$
,
![]() $\mathbf{WKL}_0$
and
$\mathbf{WKL}_0$
and
![]() $\textbf {ACA}_0$
as well as the axiom schema
$\textbf {ACA}_0$
as well as the axiom schema
![]() $\Pi ^1_m\textsf {-TI}$
, which is known to be equivalent over
$\Pi ^1_m\textsf {-TI}$
, which is known to be equivalent over
![]() $\textbf {ACA}_0$
to the transfinite induction along well-founded trees represented by sets. Comprehension axioms below are central in defining theories. By convention, we always assume that there are no collisions of free variables with bound ones. Thus below we implicitly assume that X is not free in
$\textbf {ACA}_0$
to the transfinite induction along well-founded trees represented by sets. Comprehension axioms below are central in defining theories. By convention, we always assume that there are no collisions of free variables with bound ones. Thus below we implicitly assume that X is not free in
![]() $A[x]$
.
$A[x]$
.
-
(
 $\mathcal {C}\textsf {-CA}$
)
$\mathcal {C}\textsf {-CA}$
)
 $\exists X\forall x(x\,{\in }\,X\,{\leftrightarrow }\, A[x])$
for A from
$\exists X\forall x(x\,{\in }\,X\,{\leftrightarrow }\, A[x])$
for A from
 $\mathcal {C}$
.
$\mathcal {C}$
.
2 Preliminaries
2.1 The system
 $\textbf {EL}_0^-$
of basic arithmetic
$\textbf {EL}_0^-$
of basic arithmetic
Definition 2.1 (languages
 $\mathcal {L}_1$
and
$\mathcal {L}_1$
and
 $\mathcal {L}_{\mathrm{F}}$
)
$\mathcal {L}_{\mathrm{F}}$
)
-
(1) The language
 $\mathcal {L}_1$
is a one-sorted first order language with equality
$\mathcal {L}_1$
is a one-sorted first order language with equality
 $=$
consisting of constants
$=$
consisting of constants
 $0$
and
$0$
and
 $1$
, binary function symbols
$1$
, binary function symbols
 $+$
,
$+$
,
 $\cdot $
and
$\cdot $
and
 $\exp $
and a binary predicate
$\exp $
and a binary predicate
 $<$
.
$<$
. -
(2) The language
 $\mathcal {L}_{\mathrm{F}}$
of elementary analysis is the two-sorted first order language, whose sorts are called number and function, which includes
$\mathcal {L}_{\mathrm{F}}$
of elementary analysis is the two-sorted first order language, whose sorts are called number and function, which includes
 $\mathcal {L}_1$
as the part of the number sort, and which, additionally, has two function symbols
$\mathcal {L}_1$
as the part of the number sort, and which, additionally, has two function symbols
 $\textrm {Ev}$
and
$\textrm {Ev}$
and
 $\text {Rest}$
of arity one function and one number and of value number.
$\text {Rest}$
of arity one function and one number and of value number.
Notice that
![]() $\mathcal {L}_{\mathrm{F}}$
does not have the equality for the function sort as a primitive symbol. We call the systems on this language function-based second order arithmetic, in order to distinguish them from set-based second order arithmetic, systems on the language
$\mathcal {L}_{\mathrm{F}}$
does not have the equality for the function sort as a primitive symbol. We call the systems on this language function-based second order arithmetic, in order to distinguish them from set-based second order arithmetic, systems on the language
![]() $\mathcal {L}_{\textrm {S}}$
(called
$\mathcal {L}_{\textrm {S}}$
(called
![]() $\textrm {L}_2$
in [Reference Simpson45]), which has been common in classical reverse mathematics.
$\textrm {L}_2$
in [Reference Simpson45]), which has been common in classical reverse mathematics.
Notation 2.2. Variables of the number sort are denoted by lower-case Latin letters
![]() $x,y,z,u,v,$
etc., and those of the function are by Greek ones
$x,y,z,u,v,$
etc., and those of the function are by Greek ones
![]() $\alpha ,\beta ,$
etc.
$\alpha ,\beta ,$
etc.
Let
![]() $\alpha (x)\,{:=}\,\textrm {Ev}(\alpha ,x)$
and
$\alpha (x)\,{:=}\,\textrm {Ev}(\alpha ,x)$
and
![]() $\alpha {\upharpoonright } x\,{:=}\,\textrm {Rest}(\alpha ,x)$
. Furthermore,
$\alpha {\upharpoonright } x\,{:=}\,\textrm {Rest}(\alpha ,x)$
. Furthermore,
![]() $(\exists x\,{<}\,t)A$
stands for
$(\exists x\,{<}\,t)A$
stands for
![]() $\exists x(x\,{<}\, t\land A)$
,
$\exists x(x\,{<}\, t\land A)$
,
![]() $(\forall x\,{<}\,t)A$
for
$(\forall x\,{<}\,t)A$
for
![]() $\forall x(x\,{<}\, t\,{\to }\, A)$
,
$\forall x(x\,{<}\, t\,{\to }\, A)$
,
![]() $\alpha \,{<}\,\beta $
for
$\alpha \,{<}\,\beta $
for
![]() $\forall x(\alpha (x)\,{<}\,\beta (x))$
and
$\forall x(\alpha (x)\,{<}\,\beta (x))$
and
![]() $\alpha \,{=}\,\beta $
for
$\alpha \,{=}\,\beta $
for
![]() $\forall x(\alpha (x)\,{=}\,\beta (x))$
.
$\forall x(\alpha (x)\,{=}\,\beta (x))$
.
We let
![]() $\exists !xA[x]\,{:\equiv }\,\exists xA[x]\land \forall y,z(A[y]\land A[z]\,{\to }\,y\,{=}\,z)$
and similarly we also let
$\exists !xA[x]\,{:\equiv }\,\exists xA[x]\land \forall y,z(A[y]\land A[z]\,{\to }\,y\,{=}\,z)$
and similarly we also let
![]() $\exists !\alpha A[\alpha ]\,{:\equiv }\,\exists \alpha A[\alpha ]\land \forall \beta ,\gamma (A[\beta ]\land A[\gamma ]\,{\to }\,\beta \,{=}\,\gamma )$
.
$\exists !\alpha A[\alpha ]\,{:\equiv }\,\exists \alpha A[\alpha ]\land \forall \beta ,\gamma (A[\beta ]\land A[\gamma ]\,{\to }\,\beta \,{=}\,\gamma )$
.
Definition 2.3 (
 $\mathcal {C}{\land }\mathcal {D}$
,
$\mathcal {C}{\land }\mathcal {D}$
,
 $\mathcal {C}{\lor }\mathcal {D}$
,
$\mathcal {C}{\lor }\mathcal {D}$
,
 $\mathcal {C}{\to }\mathcal {D}$
,
$\mathcal {C}{\to }\mathcal {D}$
,
 $\neg \mathcal {C}$
,
$\neg \mathcal {C}$
,
 $\textsf {B}\forall ^i\mathcal {C}$
,
$\textsf {B}\forall ^i\mathcal {C}$
,
 $\textsf {B}\exists ^i\mathcal {C}$
,
$\textsf {B}\exists ^i\mathcal {C}$
,
 $\forall ^i\mathcal {C}$
and
$\forall ^i\mathcal {C}$
and
 $\exists ^i\mathcal {C}$
)
$\exists ^i\mathcal {C}$
)
Let
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
be classes of formulae.
$\mathcal {D}$
be classes of formulae.
![]() $\mathcal {C}\,\Box \,\mathcal {D}$
consists of all formulae of the form
$\mathcal {C}\,\Box \,\mathcal {D}$
consists of all formulae of the form
![]() $A\,\Box \, B$
with A and B from
$A\,\Box \, B$
with A and B from
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
, respectively, for
$\mathcal {D}$
, respectively, for
![]() $\Box \equiv {\land },{\to },{\lor }$
.
$\Box \equiv {\land },{\to },{\lor }$
.
Moreover
![]() $\neg \mathcal {C}$
,
$\neg \mathcal {C}$
,
![]() $\textsf {B}\forall ^0\mathcal {C}$
,
$\textsf {B}\forall ^0\mathcal {C}$
,
![]() $\textsf {B}\exists ^0\mathcal {C}$
,
$\textsf {B}\exists ^0\mathcal {C}$
,
![]() $\forall ^0\mathcal {C}$
,
$\forall ^0\mathcal {C}$
,
![]() $\exists ^0\mathcal {C}$
,
$\exists ^0\mathcal {C}$
,
![]() $\textsf {B}\forall ^1\mathcal {C}$
,
$\textsf {B}\forall ^1\mathcal {C}$
,
![]() $\textsf {B}\exists ^1\mathcal {C}$
,
$\textsf {B}\exists ^1\mathcal {C}$
,
![]() $\forall ^1\mathcal {C}$
and
$\forall ^1\mathcal {C}$
and
![]() $\exists ^1\mathcal {C}$
consist of all those formulae of the forms
$\exists ^1\mathcal {C}$
consist of all those formulae of the forms
![]() $\neg A$
,
$\neg A$
,
![]() $(\forall x\,{<}\,t)A$
,
$(\forall x\,{<}\,t)A$
,
![]() $(\exists x\,{<}\,t)A$
,
$(\exists x\,{<}\,t)A$
,
![]() $\forall xA$
,
$\forall xA$
,
![]() $\exists xA$
,
$\exists xA$
,
![]() $(\forall \xi \,{<}\,\alpha )A$
,
$(\forall \xi \,{<}\,\alpha )A$
,
![]() $(\exists \xi \,{<}\,\alpha )A$
,
$(\exists \xi \,{<}\,\alpha )A$
,
![]() $\forall \xi A$
and
$\forall \xi A$
and
![]() $\exists \xi A$
, respectively, with A from
$\exists \xi A$
, respectively, with A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Definition 2.4 (
 $\Delta ^0_0$
,
$\Delta ^0_0$
,
 $\textsf {B}\Pi ^0_{n+1}$
,
$\textsf {B}\Pi ^0_{n+1}$
,
 $\textsf {B}\Sigma ^0_{n+1}$
,
$\textsf {B}\Sigma ^0_{n+1}$
,
 $\Pi ^0_n$
,
$\Pi ^0_n$
,
 $\Sigma ^0_n$
,
$\Sigma ^0_n$
,
 $\Pi ^0_{\infty }$
,
$\Pi ^0_{\infty }$
,
 $\Sigma ^0_{\infty }$
,
$\Sigma ^0_{\infty }$
,
 $\Delta ^1_0$
)
$\Delta ^1_0$
)
A formula of
![]() $\mathcal {L}_{\mathrm{F}}$
is called
$\mathcal {L}_{\mathrm{F}}$
is called
![]() $\Delta ^0_0$
(as well as
$\Delta ^0_0$
(as well as
![]() $\Sigma ^0_0$
and
$\Sigma ^0_0$
and
![]() $\Pi ^0_0$
) if all the quantifiers in it are number and bounded, i.e., only in the forms
$\Pi ^0_0$
) if all the quantifiers in it are number and bounded, i.e., only in the forms
![]() $\forall x<t$
and
$\forall x<t$
and
![]() $\exists x<t$
.
$\exists x<t$
.
Let
![]() $\textsf {B}\Pi ^0_{n+1}\,{:\equiv }\,\textsf {B}\forall ^0\Sigma ^0_n$
;
$\textsf {B}\Pi ^0_{n+1}\,{:\equiv }\,\textsf {B}\forall ^0\Sigma ^0_n$
;
![]() $\textsf {B}\Sigma ^0_{n+1}\,{:\equiv }\,\textsf {B}\exists ^0\Pi ^0_n$
;
$\textsf {B}\Sigma ^0_{n+1}\,{:\equiv }\,\textsf {B}\exists ^0\Pi ^0_n$
;
![]() $\Pi ^0_{n+1}\,{:\equiv }\,\forall ^0\Sigma ^0_n$
; and
$\Pi ^0_{n+1}\,{:\equiv }\,\forall ^0\Sigma ^0_n$
; and
![]() $\Sigma ^0_{n+1}\,{:\equiv }\,\exists ^0\Pi ^0_n$
. A formula is called arithmetically prenex (
$\Sigma ^0_{n+1}\,{:\equiv }\,\exists ^0\Pi ^0_n$
. A formula is called arithmetically prenex (
![]() $\Pi ^0_{\infty }$
and
$\Pi ^0_{\infty }$
and
![]() $\Sigma ^0_{\infty }$
) if it is
$\Sigma ^0_{\infty }$
) if it is
![]() $\Pi ^0_n$
or
$\Pi ^0_n$
or
![]() $\Sigma ^0_n$
for some n; and called
$\Sigma ^0_n$
for some n; and called
![]() $\Delta ^1_0$
if it contains no function quantifiers.
$\Delta ^1_0$
if it contains no function quantifiers.
Definition 2.5 (
 $\textbf {iQex}$
)
$\textbf {iQex}$
)
The intuitionistic
![]() $\mathcal {L}_1$
-theory
$\mathcal {L}_1$
-theory
![]() $\textbf {iQex}$
is generated by the equality axioms and
$\textbf {iQex}$
is generated by the equality axioms and
 $$ \begin{align*} \text{(a0)}\;&x\,{+}\,0\,{=}\,x;&\text{(a1)}\;& x\,{+}\,(y\,{+}\,1)\,{=}\,(x\,{+}\,y)\,{+}\,1;\\ \text{(m0)}\;&x\,{\cdot}\, 0\,{=}\,0;&\text{(m1)}\;& x\,{\cdot}\,(y\,{+}\,1)\,{=}\,(x\,{\cdot}\, y)\,{+}\,x;\\ \text{(e0)}\;&\exp(x,0)\,{=}\,1;&\text{(e1)}\;& \exp(x,y\,{+}\,1)\,{=}\,\exp(x,y)\,{\cdot}\, x;\\ \text{(ir)}\;&\neg(x\,{<}\,x);& \text{(tr)}\;&x\,{<}\,y\land y\,{<}\,z\,\to\,x\,{<}\,z;\\ \text{(s0)}\;&x\,{<}\,x\,{+}\,1;& \text{(s1)}\;&x\,{<}\,y\,\to\,(x\,{+}\,1\,{<}\,y)\,{\lor}\,(x\,{+}\,1\,{=}\,y). \end{align*} $$
$$ \begin{align*} \text{(a0)}\;&x\,{+}\,0\,{=}\,x;&\text{(a1)}\;& x\,{+}\,(y\,{+}\,1)\,{=}\,(x\,{+}\,y)\,{+}\,1;\\ \text{(m0)}\;&x\,{\cdot}\, 0\,{=}\,0;&\text{(m1)}\;& x\,{\cdot}\,(y\,{+}\,1)\,{=}\,(x\,{\cdot}\, y)\,{+}\,x;\\ \text{(e0)}\;&\exp(x,0)\,{=}\,1;&\text{(e1)}\;& \exp(x,y\,{+}\,1)\,{=}\,\exp(x,y)\,{\cdot}\, x;\\ \text{(ir)}\;&\neg(x\,{<}\,x);& \text{(tr)}\;&x\,{<}\,y\land y\,{<}\,z\,\to\,x\,{<}\,z;\\ \text{(s0)}\;&x\,{<}\,x\,{+}\,1;& \text{(s1)}\;&x\,{<}\,y\,\to\,(x\,{+}\,1\,{<}\,y)\,{\lor}\,(x\,{+}\,1\,{=}\,y). \end{align*} $$
Definition 2.6 (
 $\mathcal {C}\textsf {-Ind}$
,
$\mathcal {C}\textsf {-Ind}$
,
 $\mathcal {C}\textsf {-Bdg}$
,
$\mathcal {C}\textsf {-Bdg}$
,
 $\mathcal {C}\textsf {-LNP}$
,
$\mathcal {C}\textsf {-LNP}$
,
 $\mathcal {C}\textsf {-LEM}$
and
$\mathcal {C}\textsf {-LEM}$
and
 $\mathcal {C}\textsf {-DNE}$
)
$\mathcal {C}\textsf {-DNE}$
)
For a class
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $\mathcal {L}_1$
or
$\mathcal {L}_1$
or
![]() $\mathcal {L}_{\mathrm{F}}$
formulae, define the following axiom schemata:
$\mathcal {L}_{\mathrm{F}}$
formulae, define the following axiom schemata:
-
(
 $\mathcal {C}\textsf {-Ind}$
):
$\mathcal {C}\textsf {-Ind}$
):
 $A[0]\land (\forall x\,{<}\,n)(A[x]\,{\to }\, A[x{+}1])\,{\to }\,A[n]$
;
$A[0]\land (\forall x\,{<}\,n)(A[x]\,{\to }\, A[x{+}1])\,{\to }\,A[n]$
; -
(
 $\mathcal {C}\textsf {-Bdg}$
):
$\mathcal {C}\textsf {-Bdg}$
):
 $(\forall x\,{<}\,n)\exists yA[x,y,n]\,\to \,\exists u(\forall x\,{<}\,n)(\exists y\,{<}\,u) A[x,y,n]$
;
$(\forall x\,{<}\,n)\exists yA[x,y,n]\,\to \,\exists u(\forall x\,{<}\,n)(\exists y\,{<}\,u) A[x,y,n]$
; -
(
 $\mathcal {C}\textsf {-LNP}$
):
$\mathcal {C}\textsf {-LNP}$
):
 $A[x]{{\kern-1pt}\to{\kern-1pt}}(\exists y\,{\leq }\,x)(A[y]{\land}(\forall z\,{<}\,y)\neg A[z])$
, where
$A[x]{{\kern-1pt}\to{\kern-1pt}}(\exists y\,{\leq }\,x)(A[y]{\land}(\forall z\,{<}\,y)\neg A[z])$
, where
 $y\, {\leq } \,x$
stands for
$y\, {\leq } \,x$
stands for
 $y\,{<}\,x{+}1$
;
$y\,{<}\,x{+}1$
; -
(
 $\mathcal {C}\textsf {-LEM}$
):
$\mathcal {C}\textsf {-LEM}$
):
 $A\lor \neg A$
;
$A\lor \neg A$
; -
(
 $\mathcal {C}\textsf {-DNE}$
):
$\mathcal {C}\textsf {-DNE}$
):
 $\neg \neg A \to A$
,
$\neg \neg A \to A$
,
for any formula A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Definition 2.7 (
 $\textbf {i}\boldsymbol {\Pi }_{n+1}$
,
$\textbf {i}\boldsymbol {\Pi }_{n+1}$
,
 $\textbf {i}\boldsymbol {\Sigma }_{n+1}$
,
$\textbf {i}\boldsymbol {\Sigma }_{n+1}$
,
 $\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
,
$\textbf {B}\boldsymbol {\Sigma }_1\textbf {ex}$
,
 $\textbf {I}\boldsymbol {\Sigma }_{n+1}$
)
$\textbf {I}\boldsymbol {\Sigma }_{n+1}$
)
Define
 $$ \begin{align*} \textbf{i}\boldsymbol{\Pi}_{n+1}:&\equiv\textbf{iQex}{+}\Pi_{n+1}\textsf{-Ind}; & \textbf{i}\boldsymbol{\Sigma}_{n+1}:&\equiv\textbf{iQex}{+}\Sigma_{n+1}\textsf{-Ind};\\ \textbf{I}\boldsymbol{\Delta}_0\textbf{ex}:&\equiv \textbf{iQex}{+}\mathcal{L}_1\textsf{-LEM}{+}\Delta_0\textsf{-Ind}; & \textbf{B}\boldsymbol{\Sigma}_1\textbf{ex}:&\equiv \textbf{I}\boldsymbol{\Delta}_0\textbf{ex}{+}\Sigma_1\textsf{-Bdg};\\ \textbf{I}\boldsymbol{\Sigma}_{n+1}:&\equiv \textbf{i}\boldsymbol{\Sigma}_{n+1}{+}\mathcal{L}_1\textsf{-LEM}, \end{align*} $$
$$ \begin{align*} \textbf{i}\boldsymbol{\Pi}_{n+1}:&\equiv\textbf{iQex}{+}\Pi_{n+1}\textsf{-Ind}; & \textbf{i}\boldsymbol{\Sigma}_{n+1}:&\equiv\textbf{iQex}{+}\Sigma_{n+1}\textsf{-Ind};\\ \textbf{I}\boldsymbol{\Delta}_0\textbf{ex}:&\equiv \textbf{iQex}{+}\mathcal{L}_1\textsf{-LEM}{+}\Delta_0\textsf{-Ind}; & \textbf{B}\boldsymbol{\Sigma}_1\textbf{ex}:&\equiv \textbf{I}\boldsymbol{\Delta}_0\textbf{ex}{+}\Sigma_1\textsf{-Bdg};\\ \textbf{I}\boldsymbol{\Sigma}_{n+1}:&\equiv \textbf{i}\boldsymbol{\Sigma}_{n+1}{+}\mathcal{L}_1\textsf{-LEM}, \end{align*} $$
where
![]() $\Delta _0\,{:\equiv }\,\Delta ^0_0\,{\cap }\,\mathcal {L}_1$
,
$\Delta _0\,{:\equiv }\,\Delta ^0_0\,{\cap }\,\mathcal {L}_1$
,
![]() $\Sigma _n\,{:\equiv }\,\Sigma ^0_n\,{\cap }\,\mathcal {L}_1$
and
$\Sigma _n\,{:\equiv }\,\Sigma ^0_n\,{\cap }\,\mathcal {L}_1$
and
![]() $\Pi _n\,{:\equiv }\,\Pi ^0_n\,{\cap }\,\mathcal {L}_1$
.
$\Pi _n\,{:\equiv }\,\Pi ^0_n\,{\cap }\,\mathcal {L}_1$
.
Proposition 2.8.
-
(1) (i)
 $0\,{<}\,x{+}1$
; (ii)
$0\,{<}\,x{+}1$
; (ii)
 $x\,{<}\,y\lor x\,{=}\,y\lor y\,{<}\,x$
; and (iii)
$x\,{<}\,y\lor x\,{=}\,y\lor y\,{<}\,x$
; and (iii)
 $\Delta _0\textsf {-LEM}$
, are provable in
$\Delta _0\textsf {-LEM}$
, are provable in
 $\mathbf{iQex}+\Delta _0\textsf {-Ind}$
.
$\mathbf{iQex}+\Delta _0\textsf {-Ind}$
. -
(2) (i)
 $\mathbf{iQex}\,{+}\, \textsf {B}\forall ^0\neg \mathcal {C}\textsf {-Ind}\,{+}\,\textsf {B}\exists ^0(\mathcal {C}\,{\land }\,\textsf {B}\forall ^0\neg \mathcal {C})\textsf {-DNE}\vdash \mathcal {C}\textsf {-LNP}$
. In particular, (ii)
$\mathbf{iQex}\,{+}\, \textsf {B}\forall ^0\neg \mathcal {C}\textsf {-Ind}\,{+}\,\textsf {B}\exists ^0(\mathcal {C}\,{\land }\,\textsf {B}\forall ^0\neg \mathcal {C})\textsf {-DNE}\vdash \mathcal {C}\textsf {-LNP}$
. In particular, (ii)
 $\mathbf{iQex}\,{+}\,\Delta _0\textsf {-Ind}\vdash \Delta _0\textsf {-LNP}$
.
$\mathbf{iQex}\,{+}\,\Delta _0\textsf {-Ind}\vdash \Delta _0\textsf {-LNP}$
. -
(3) (i)
 $\textsf {B}\forall ^0\Sigma _{n}\subseteq \Sigma _{n}$
up to equivalence over
$\textsf {B}\forall ^0\Sigma _{n}\subseteq \Sigma _{n}$
up to equivalence over
 $\mathbf{iQex}{+}\Sigma _{n}\textsf {-Bdg}$
; and (ii)
$\mathbf{iQex}{+}\Sigma _{n}\textsf {-Bdg}$
; and (ii)
 $\mathbf{iQex}{+}\Sigma _{n}\textsf {-Ind} \vdash \Sigma _{n}\textsf {-Bdg}\ \text{for}\ n\geq 1 $
.
$\mathbf{iQex}{+}\Sigma _{n}\textsf {-Ind} \vdash \Sigma _{n}\textsf {-Bdg}\ \text{for}\ n\geq 1 $
.
Proof (1) (i) is by
![]() $\Delta _0\textsf {-Ind}$
, (s0) and (tr).
$\Delta _0\textsf {-Ind}$
, (s0) and (tr).
For (ii), let
![]() $A[x,y]\,:\equiv \,(x\,{<}\,y\lor x\,{=}\,y\lor y\,{<}\,x)$
. Now
$A[x,y]\,:\equiv \,(x\,{<}\,y\lor x\,{=}\,y\lor y\,{<}\,x)$
. Now
![]() $A[0,0]$
and, by (i),
$A[0,0]$
and, by (i),
![]() $A[0,y]\,{\to }\, A[0,y{+}1]$
. Thus
$A[0,y]\,{\to }\, A[0,y{+}1]$
. Thus
![]() $\Delta _0\textsf {-Ind}$
yields
$\Delta _0\textsf {-Ind}$
yields
![]() $\forall yA[0,y]$
. Because of
$\forall yA[0,y]$
. Because of
![]() $\Delta _0\textsf {-Ind}$
it remains to show
$\Delta _0\textsf {-Ind}$
it remains to show
![]() $A[x,y]\,{\to }\, A[x{+}1,y]$
.
$A[x,y]\,{\to }\, A[x{+}1,y]$
.
![]() $x\,{<}\,y\,{\to }\, A[x{+}1,y]$
is by (s1),
$x\,{<}\,y\,{\to }\, A[x{+}1,y]$
is by (s1),
![]() $x\,{=}\,y\,{\to }\, A[x{+}1,y]$
by (s0) and
$x\,{=}\,y\,{\to }\, A[x{+}1,y]$
by (s0) and
![]() $y\,{<}\,x\,{\to }\, A[x{+}1,y]$
by (s0) and (tr).
$y\,{<}\,x\,{\to }\, A[x{+}1,y]$
by (s0) and (tr).
We see (iii) by induction on A. The atomic cases are by (ii), where (ir) implies
![]() $x\,{<}\,y\,{\lor }\, y\,{<}\,x\to \neg (x\,{=}\,y)$
and (ir) and (tr) imply
$x\,{<}\,y\,{\lor }\, y\,{<}\,x\to \neg (x\,{=}\,y)$
and (ir) and (tr) imply
![]() $x\,{<}\,y\,{\lor }\, x\,{=}\,y\to \neg (y\,{<}\,x)$
. The cases of
$x\,{<}\,y\,{\lor }\, x\,{=}\,y\to \neg (y\,{<}\,x)$
. The cases of
![]() $\land $
and
$\land $
and
![]() $\to $
logically follow from the induction hypothesis. For
$\to $
logically follow from the induction hypothesis. For
![]() $Q\,{\equiv }\,\exists ,\forall $
, let
$Q\,{\equiv }\,\exists ,\forall $
, let
![]() $B[n]:\equiv (Q x\,{<}\,n)A[x]\lor \neg (Q x\,{<}\,n)A[x]$
. By (s1), (i) and (tr), if
$B[n]:\equiv (Q x\,{<}\,n)A[x]\lor \neg (Q x\,{<}\,n)A[x]$
. By (s1), (i) and (tr), if
![]() $x\,{<}\,0$
then
$x\,{<}\,0$
then
![]() $x{+}1\,{<}\,0\,{\lor }\,x{+}1\,{=}\,0$
and
$x{+}1\,{<}\,0\,{\lor }\,x{+}1\,{=}\,0$
and
![]() $x{+}1\,{<}\,x{+}1$
contradicting (ir). Thus
$x{+}1\,{<}\,x{+}1$
contradicting (ir). Thus
![]() $\neg (x\,{<}\,0)$
and
$\neg (x\,{<}\,0)$
and
![]() $B[0]$
. Now
$B[0]$
. Now
![]() $x\,{<}\,n{+}1\,{\to }\,x\,{<}\,n\,{\lor }\,x\,{=}\,n$
by (s1) and (ii).
$x\,{<}\,n{+}1\,{\to }\,x\,{<}\,n\,{\lor }\,x\,{=}\,n$
by (s1) and (ii).
![]() $B[n]\,{\land }\,(A[n]\,{\lor }\,\neg A[n])\,{\to }\, B[n{+}1]$
and
$B[n]\,{\land }\,(A[n]\,{\lor }\,\neg A[n])\,{\to }\, B[n{+}1]$
and
![]() $B[n]\,{\to }\,B[n{+}1]$
by the hypothesis for A. Apply
$B[n]\,{\to }\,B[n{+}1]$
by the hypothesis for A. Apply
![]() $\Delta _0\textsf {-Ind}$
.
$\Delta _0\textsf {-Ind}$
.
(2) Let A be
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $B[y]:\equiv (\forall z\,{\leq }\,y)\neg A[z]$
.
$B[y]:\equiv (\forall z\,{\leq }\,y)\neg A[z]$
.
![]() $\neg (\exists y\,{\leq }\,x)(A[y]\land (\forall z\,{<}\,y)\neg A[z])$
, i.e.,
$\neg (\exists y\,{\leq }\,x)(A[y]\land (\forall z\,{<}\,y)\neg A[z])$
, i.e.,
![]() $(\forall y\,{\leq }\,x)((\forall z\,{<}\,y)\neg A[z]\,{\to }\neg A[y])$
implies
$(\forall y\,{\leq }\,x)((\forall z\,{<}\,y)\neg A[z]\,{\to }\neg A[y])$
implies
![]() $B[0] \land (\forall y < x)(B[y] \to B[y{+}1])$
and
$B[0] \land (\forall y < x)(B[y] \to B[y{+}1])$
and
![]() $B[x]$
by
$B[x]$
by
![]() $\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-Ind}$
. So
$\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-Ind}$
. So
![]() $A[x]\,{\to }\,\neg \neg (\exists y\,{\leq }\,x)(A[y]\land (\forall z\,{<}\,y)\neg A[z])$
.
$A[x]\,{\to }\,\neg \neg (\exists y\,{\leq }\,x)(A[y]\land (\forall z\,{<}\,y)\neg A[z])$
.
(3) (ii) Let A be
![]() $\Pi _{n-1}$
. If
$\Pi _{n-1}$
. If
![]() $(\forall x\,{<}\,m)\exists y,zA[x,y,z]$
, by
$(\forall x\,{<}\,m)\exists y,zA[x,y,z]$
, by
![]() $\Sigma _{n}\textsf {-Ind}$
on
$\Sigma _{n}\textsf {-Ind}$
on
![]() $k\,{\leq }\,m$
, we have
$k\,{\leq }\,m$
, we have
![]() $\exists u(\forall x\,{<}\,k)(\exists y,z\,{<}\,u)A[x,y,z]$
.
$\exists u(\forall x\,{<}\,k)(\exists y,z\,{<}\,u)A[x,y,z]$
.
Notation 2.9. (1) While
![]() $\mathcal {L}_{\mathrm{F}}$
has no function symbols besides
$\mathcal {L}_{\mathrm{F}}$
has no function symbols besides
![]() $+$
,
$+$
,
![]() $\cdot $
and
$\cdot $
and
![]() $\exp $
, we can treat a bounded
$\exp $
, we can treat a bounded
![]() $\Delta ^0_0$
definable function f (i.e., defined by
$\Delta ^0_0$
definable function f (i.e., defined by
![]() $A[\vec {x},\vec {\alpha },y]$
from
$A[\vec {x},\vec {\alpha },y]$
from
![]() $\Delta ^0_0$
and bounded by a term
$\Delta ^0_0$
and bounded by a term
![]() $t[\vec {x},\vec {\alpha }]$
) as follows: for a formula
$t[\vec {x},\vec {\alpha }]$
) as follows: for a formula
![]() $B[y]$
, by
$B[y]$
, by
![]() $B[f(\vec {x},\vec {\alpha })]$
we mean
$B[f(\vec {x},\vec {\alpha })]$
we mean
![]() $(\exists y\,{<}\,t[\vec {x},\vec {\alpha }])(A[\vec {x},\vec {\alpha },y] \land B[y])$
. If
$(\exists y\,{<}\,t[\vec {x},\vec {\alpha }])(A[\vec {x},\vec {\alpha },y] \land B[y])$
. If
![]() $B[y]$
is
$B[y]$
is
![]() $\Delta ^0_0$
, so is
$\Delta ^0_0$
, so is
![]() $B[f(\vec {x},\vec {\alpha })]$
. In this way, we can introduce fundamental operations on pairing and sequences of numbers without affecting the complexity: we fix, for each standard n, a bounded
$B[f(\vec {x},\vec {\alpha })]$
. In this way, we can introduce fundamental operations on pairing and sequences of numbers without affecting the complexity: we fix, for each standard n, a bounded
![]() $\Delta ^0_0$
definable bijection
$\Delta ^0_0$
definable bijection
![]() $(\text {-},\ldots ,\text {-}):\mathbb {N}^n\,{\to }\, \mathbb {N}$
and the associated projections
$(\text {-},\ldots ,\text {-}):\mathbb {N}^n\,{\to }\, \mathbb {N}$
and the associated projections
![]() $(\text {-})^n_i$
satisfying
$(\text {-})^n_i$
satisfying
![]() $(x)^n_i\,{\leq }\, x$
; and also a bijection
$(x)^n_i\,{\leq }\, x$
; and also a bijection
![]() $\mathbb {N}^{<\omega }\,{\to }\,\mathbb {N}$
so that evaluation
$\mathbb {N}^{<\omega }\,{\to }\,\mathbb {N}$
so that evaluation
![]() $[u,x]\,{\mapsto }\,u(x)$
; concatenation
$[u,x]\,{\mapsto }\,u(x)$
; concatenation
![]() $[u,v]\,{\mapsto }\,u{*}v$
and
$[u,v]\,{\mapsto }\,u{*}v$
and
![]() $[u,x,\alpha ]\,{\mapsto }\,(u{*}\alpha )(x)$
; length-1 sequence
$[u,x,\alpha ]\,{\mapsto }\,(u{*}\alpha )(x)$
; length-1 sequence
![]() $x\,{\mapsto }\,\langle x\rangle $
; length
$x\,{\mapsto }\,\langle x\rangle $
; length
![]() $u\,{\mapsto }\, |u|$
; and restriction
$u\,{\mapsto }\, |u|$
; and restriction
![]() $[u,n]\,{\mapsto }\, u{\upharpoonright } n$
are bounded
$[u,n]\,{\mapsto }\, u{\upharpoonright } n$
are bounded
![]() $\Delta ^0_0$
definable. Assume
$\Delta ^0_0$
definable. Assume
![]() $\max (u(x),|u|,u{\upharpoonright } n)\,{\leq }\,u$
.
$\max (u(x),|u|,u{\upharpoonright } n)\,{\leq }\,u$
.
(2) Define
![]() $(\beta )^n_i = \lambda x.(\beta (x))^n_i$
,
$(\beta )^n_i = \lambda x.(\beta (x))^n_i$
,
![]() $(\beta ,\gamma ) =\lambda x.(\beta (x),\gamma (x))$
,
$(\beta ,\gamma ) =\lambda x.(\beta (x),\gamma (x))$
,
![]() $(\beta )_y = \lambda x.\beta ((y,x))$
,
$(\beta )_y = \lambda x.\beta ((y,x))$
,
![]() $\beta {\ominus }y=\lambda x.\beta (y{+}x)$
and
$\beta {\ominus }y=\lambda x.\beta (y{+}x)$
and
![]() $\underline {z} = \lambda x.z$
, which are all bounded
$\underline {z} = \lambda x.z$
, which are all bounded
![]() $\Delta ^0_0$
definable. Alternatively, for example,
$\Delta ^0_0$
definable. Alternatively, for example,
![]() $A[(\beta )^n_i]$
is the result of replacing all the occurrences of
$A[(\beta )^n_i]$
is the result of replacing all the occurrences of
![]() $\alpha (t)$
in
$\alpha (t)$
in
![]() $A[\alpha ]$
by
$A[\alpha ]$
by
![]() $(\beta (t))^n_i$
and those of
$(\beta (t))^n_i$
and those of
![]() $\alpha {\upharpoonright } t$
by corresponding bounded
$\alpha {\upharpoonright } t$
by corresponding bounded
![]() $\Delta ^0_0$
definable terms.
$\Delta ^0_0$
definable terms.
(3) We assume that classes of formulae are closed under (i) conjunctions and disjunctions with
![]() $\Delta ^0_0$
, and (ii) substitutions of the expressions from (1) and (2). The operations in Definition 2.3 preserve these closure properties.
$\Delta ^0_0$
, and (ii) substitutions of the expressions from (1) and (2). The operations in Definition 2.3 preserve these closure properties.
Definition 2.10 (
 $\textbf {EL}_0^-$
)
$\textbf {EL}_0^-$
)
The
![]() $\mathcal {L}_{\mathrm{F}}$
-theory
$\mathcal {L}_{\mathrm{F}}$
-theory
![]() $\textbf {EL}_0^-$
is generated over intuitionistic logic with equality for numbers, by (a) the axiom of
$\textbf {EL}_0^-$
is generated over intuitionistic logic with equality for numbers, by (a) the axiom of
![]() $\textbf {iQex}$
, (b)
$\textbf {iQex}$
, (b)
![]() $\Delta ^0_0\textsf {-Ind}$
, (c)
$\Delta ^0_0\textsf {-Ind}$
, (c)
![]() $\alpha {\upharpoonright } 0 = \langle \,\rangle $
,
$\alpha {\upharpoonright } 0 = \langle \,\rangle $
,
![]() $\alpha {\upharpoonright }(x{+}1) = (\alpha {\upharpoonright } x){*}\langle \alpha (x)\rangle $
; and (d)
$\alpha {\upharpoonright }(x{+}1) = (\alpha {\upharpoonright } x){*}\langle \alpha (x)\rangle $
; and (d)
![]() $\Delta ^0_0$
bounded search defined below:
$\Delta ^0_0$
bounded search defined below:
-
(
 $\mathcal {C}$
bounded search):
$\mathcal {C}$
bounded search):
 $\exists \beta \forall x( (\exists y < t[x])A[x,y]\,{\to }\, \beta (x) < t[x]\land A[x,\beta (x)])$
for A from
$\exists \beta \forall x( (\exists y < t[x])A[x,y]\,{\to }\, \beta (x) < t[x]\land A[x,\beta (x)])$
for A from
 $\mathcal {C}$
and a term
$\mathcal {C}$
and a term
 $t[x]$
.
$t[x]$
.
![]() $\textbf {EL}_0^-$
is almost equivalent to
$\textbf {EL}_0^-$
is almost equivalent to
![]() $\textbf {EL}_{\textrm {ELEM}}$
from [Reference Ishihara19], which however has terms for all elementary functions by the help of functionals. Our
$\textbf {EL}_{\textrm {ELEM}}$
from [Reference Ishihara19], which however has terms for all elementary functions by the help of functionals. Our
![]() $\textbf {EL}_0^-$
proves the existence of those functions by the axiom (d) but shares the important feature with
$\textbf {EL}_0^-$
proves the existence of those functions by the axiom (d) but shares the important feature with
![]() $\mathcal {L}_{\textrm {S}}$
from classical reverse mathematics that second order terms are only variables.
$\mathcal {L}_{\textrm {S}}$
from classical reverse mathematics that second order terms are only variables.
Since
![]() $\Sigma ^0_n$
is
$\Sigma ^0_n$
is
![]() $\Sigma _n$
with
$\Sigma _n$
with
![]() $\mathcal {L}_\mathrm{F}$
-terms substituted for x’s, 2.8 holds with
$\mathcal {L}_\mathrm{F}$
-terms substituted for x’s, 2.8 holds with
![]() $\Delta _0$
and
$\Delta _0$
and
![]() $\Sigma _n$
replaced by
$\Sigma _n$
replaced by
![]() $\Delta ^0_0$
and
$\Delta ^0_0$
and
![]() $\Sigma ^0_n$
.
$\Sigma ^0_n$
.
Lemma 2.11. For any A and B, in
![]() $\mathbf{iQex}{+}\Delta ^0_0\textsf {-Ind}$
or
$\mathbf{iQex}{+}\Delta ^0_0\textsf {-Ind}$
or
![]() $\mathbf{EL}_0^-$
,
$\mathbf{EL}_0^-$
,
![]() $A\,{\lor }\,B$
is equivalent to
$A\,{\lor }\,B$
is equivalent to
A key fact in second order arithmetic is a formal version of famous Kleene’s normal form theorem. While in references (e.g., [Reference Simpson45, Theorem II.2.7]) the proof is omitted or very sketchy, we give a little details.
Definition 2.12 (
 $\textrm {D}_C$
,
$\textrm {D}_C$
,
 $\textrm {B}_C$
)
$\textrm {B}_C$
)
For a
![]() $\Delta ^0_0$
formula
$\Delta ^0_0$
formula
![]() $C[\vec {x},\vec {\alpha }]$
, we define
$C[\vec {x},\vec {\alpha }]$
, we define
![]() $\textrm {D}_C$
and
$\textrm {D}_C$
and
![]() $\text {B}_C$
as follows.
$\text {B}_C$
as follows.
-
(1)
 $\textrm {D}_C[\vec {x},\vec {u}]$
is the result of replacing
$\textrm {D}_C[\vec {x},\vec {u}]$
is the result of replacing
 $\alpha _i(s)$
and
$\alpha _i(s)$
and
 $\alpha _i{\upharpoonright }s$
by
$\alpha _i{\upharpoonright }s$
by
 $u_i(s)$
and
$u_i(s)$
and
 $u_i{\upharpoonright }s$
, respectively, in C.
$u_i{\upharpoonright }s$
, respectively, in C. -
(2) (i) For atomic C, let
 $\text {B}_C[\vec {x},v,\vec {\alpha }]\,{:\equiv }\,\bigwedge _{i}(v\,{>}\, t_i[\vec {x},\vec {\alpha }])$
where
$\text {B}_C[\vec {x},v,\vec {\alpha }]\,{:\equiv }\,\bigwedge _{i}(v\,{>}\, t_i[\vec {x},\vec {\alpha }])$
where
 $t_i[\vec {x},\vec {\alpha }]$
’s are all subterms in C;
$t_i[\vec {x},\vec {\alpha }]$
’s are all subterms in C;(ii) for
 $\Box \equiv \land ,{\to },\lor $
, let
$\Box \equiv \land ,{\to },\lor $
, let
 $\textrm {B}_{C_1\Box C_2}[\vec {x},v,\vec {\alpha }]\,{:\equiv }\, \bigwedge _{i=1,2}\textrm {B}_{C_i}[\vec {x},v,\vec {\alpha }]$
;
$\textrm {B}_{C_1\Box C_2}[\vec {x},v,\vec {\alpha }]\,{:\equiv }\, \bigwedge _{i=1,2}\textrm {B}_{C_i}[\vec {x},v,\vec {\alpha }]$
;(iii)
 $\textrm {B}_{(Qz<t)C}[\vec {x},v,\vec {\alpha }]\,{:\equiv }\, (\forall z\,{<}\,t[\vec {x},\vec {\alpha }])\textrm {B}_C[z,\vec {x},v,\vec {\alpha }] \land \textrm {B}_{0<t[\vec {x},\vec {\alpha }]}[\vec {x},v,\vec {\alpha }]$
.
$\textrm {B}_{(Qz<t)C}[\vec {x},v,\vec {\alpha }]\,{:\equiv }\, (\forall z\,{<}\,t[\vec {x},\vec {\alpha }])\textrm {B}_C[z,\vec {x},v,\vec {\alpha }] \land \textrm {B}_{0<t[\vec {x},\vec {\alpha }]}[\vec {x},v,\vec {\alpha }]$
.
![]() $\textrm {B}_C[\vec {x},v,\vec {\alpha }]$
means “
$\textrm {B}_C[\vec {x},v,\vec {\alpha }]$
means “
![]() $C[\vec {x},\vec {\alpha }]$
refers
$C[\vec {x},\vec {\alpha }]$
refers
![]() $\alpha $
only below
$\alpha $
only below
![]() $v$
”. So we take ‘
$v$
”. So we take ‘
![]() $\bigwedge _{i=1,2}$
’ even for
$\bigwedge _{i=1,2}$
’ even for
![]() ${\to },\lor $
and ‘
${\to },\lor $
and ‘
![]() $(\forall z\,{<}\,t[\vec {x},\vec {\alpha }])$
’ for
$(\forall z\,{<}\,t[\vec {x},\vec {\alpha }])$
’ for
![]() $\exists $
. In
$\exists $
. In
![]() $\mathcal {L}_{\textrm {S}}$
,
$\mathcal {L}_{\textrm {S}}$
,
![]() $v\,{>}\,t_C[\vec {x}]$
can play the role of
$v\,{>}\,t_C[\vec {x}]$
can play the role of
![]() $\textrm {B}_C$
for a suitable
$\textrm {B}_C$
for a suitable
![]() $t_C$
(cf. [Reference Nemoto26, Lemma 2.13], where
$t_C$
(cf. [Reference Nemoto26, Lemma 2.13], where
![]() $t(i,\vec {k})$
on p.162, l.9 is a typo of
$t(i,\vec {k})$
on p.162, l.9 is a typo of
![]() $t''(i,\vec {k})$
). Below
$t''(i,\vec {k})$
). Below
![]() $\beta (x_0,\dots ,x_n)$
stands for
$\beta (x_0,\dots ,x_n)$
stands for
![]() $\beta ((x_0,\dots ,x_n))$
where the inner
$\beta ((x_0,\dots ,x_n))$
where the inner
![]() $(\dots )$
is from 2.9(1).
$(\dots )$
is from 2.9(1).
Lemma 2.13. For a
![]() $\Delta ^0_0$
formula
$\Delta ^0_0$
formula
![]() $C[\vec {x},\vec {\alpha }]$
, the following are provable in
$C[\vec {x},\vec {\alpha }]$
, the following are provable in
![]() $\mathbf{EL}_0^-$
:
$\mathbf{EL}_0^-$
:
-
(i)
 $\textrm {B}_C[\vec {x},u,\vec {\alpha }]\land u\,{\leq }\,v\,{\to }\,\text {B}_C[\vec {x},v,\vec {\alpha }]$
(upward closure);
$\textrm {B}_C[\vec {x},u,\vec {\alpha }]\land u\,{\leq }\,v\,{\to }\,\text {B}_C[\vec {x},v,\vec {\alpha }]$
(upward closure); -
(ii)
 $\exists \beta \forall \vec {x}\,\textrm {B}_C[\vec {x},\beta (\vec {x}),\vec {\alpha }] \land \forall u,\vec {x}(\textrm {B}_C[\vec {x},u,\vec {\alpha }]\,{\to }\, (C[\vec {x},\vec {\alpha }]\,{\leftrightarrow }\,\textrm {D}_C[\vec {x},\vec {\alpha }{\upharpoonright } u])).$
$\exists \beta \forall \vec {x}\,\textrm {B}_C[\vec {x},\beta (\vec {x}),\vec {\alpha }] \land \forall u,\vec {x}(\textrm {B}_C[\vec {x},u,\vec {\alpha }]\,{\to }\, (C[\vec {x},\vec {\alpha }]\,{\leftrightarrow }\,\textrm {D}_C[\vec {x},\vec {\alpha }{\upharpoonright } u])).$
Proof As we can prove (i) by easy induction on C, we concentrate on (ii).
First let C be atomic, whose all subterms are
![]() $t_i[\vec {x}, \vec {\alpha }]$
’s. By Axiom (d), take
$t_i[\vec {x}, \vec {\alpha }]$
’s. By Axiom (d), take
![]() $\beta $
with
$\beta $
with
![]() $\beta (\vec {x}) = 1{+}\sum _{i}t_i[\vec {x}, \vec {\alpha }]$
. Then
$\beta (\vec {x}) = 1{+}\sum _{i}t_i[\vec {x}, \vec {\alpha }]$
. Then
![]() $\textrm {B}_C[\vec {x}, \beta (\vec {x}), \vec {\alpha }]$
. For the latter conjunct, assume
$\textrm {B}_C[\vec {x}, \beta (\vec {x}), \vec {\alpha }]$
. For the latter conjunct, assume
![]() $\textrm {B}_C[\vec {x},u,\vec {\alpha }]$
. Now
$\textrm {B}_C[\vec {x},u,\vec {\alpha }]$
. Now
![]() $t_i[\vec {x}, \vec {\alpha }]\,{<}\,u$
and so
$t_i[\vec {x}, \vec {\alpha }]\,{<}\,u$
and so
![]() $\alpha _j(t_i[\vec {x},\vec {\alpha }]) = (\alpha _j{\upharpoonright } u)(t_i[\vec {x}, \vec {\alpha }])$
. Thus we can show
$\alpha _j(t_i[\vec {x},\vec {\alpha }]) = (\alpha _j{\upharpoonright } u)(t_i[\vec {x}, \vec {\alpha }])$
. Thus we can show
![]() $t_i[\vec {x},\vec {\alpha }] = t_i[\vec {x},\vec {\alpha }{\upharpoonright } u]$
by induction on
$t_i[\vec {x},\vec {\alpha }] = t_i[\vec {x},\vec {\alpha }{\upharpoonright } u]$
by induction on
![]() $t_i$
and hence
$t_i$
and hence
![]() $C[\vec {x},\vec {\alpha }]\,{\leftrightarrow }\, \textrm {D}_C[\vec {x},\vec {\alpha }{\upharpoonright } u]$
.
$C[\vec {x},\vec {\alpha }]\,{\leftrightarrow }\, \textrm {D}_C[\vec {x},\vec {\alpha }{\upharpoonright } u]$
.
In the quantifier case, the induction hypotheses for C and
![]() $0<t[\vec {x},\vec {\alpha }]$
yield
$0<t[\vec {x},\vec {\alpha }]$
yield
![]() $\gamma ,\delta $
with
$\gamma ,\delta $
with
![]() $\forall \vec {x},z\,\textrm {B}_C[z,\vec {x},\gamma (z,\vec {x}),\vec {\alpha }]$
and
$\forall \vec {x},z\,\textrm {B}_C[z,\vec {x},\gamma (z,\vec {x}),\vec {\alpha }]$
and
![]() $\forall \vec {x}\text {B}_{0<t[\vec {x},\vec {\alpha }]}[\vec {x},\delta (\vec {x}),\vec {\alpha }]$
. Therefore,
$\forall \vec {x}\text {B}_{0<t[\vec {x},\vec {\alpha }]}[\vec {x},\delta (\vec {x}),\vec {\alpha }]$
. Therefore,
![]() $\beta $
with
$\beta $
with
![]() $\beta (\vec {x}) := \gamma {\upharpoonright }(t[\vec {x},\vec {\alpha }],\vec {x}){+}\delta (\vec {x})$
yielded by Axiom (c) gives us
$\beta (\vec {x}) := \gamma {\upharpoonright }(t[\vec {x},\vec {\alpha }],\vec {x}){+}\delta (\vec {x})$
yielded by Axiom (c) gives us
![]() $\forall \vec {x}\,\textrm {B}_{(Qz<t)C}[\vec {x},\beta (\vec {x}),\vec {\alpha }]$
. For the latter conjunct, assume
$\forall \vec {x}\,\textrm {B}_{(Qz<t)C}[\vec {x},\beta (\vec {x}),\vec {\alpha }]$
. For the latter conjunct, assume
![]() $\textrm {B}_{(Qz<t)C}[\vec {x}, u, \vec {\alpha }]$
. Then
$\textrm {B}_{(Qz<t)C}[\vec {x}, u, \vec {\alpha }]$
. Then
![]() $(\forall z < t[\vec {x},\vec {\alpha }])\textrm {B}_C[z,\vec {x},u, \alpha ]$
and, since
$(\forall z < t[\vec {x},\vec {\alpha }])\textrm {B}_C[z,\vec {x},u, \alpha ]$
and, since
![]() $C[z, \vec {x},\vec {\alpha }]\,{\leftrightarrow }\,\textrm {D}_C[z,\vec {x}, \vec {\alpha }{\upharpoonright } u]$
for each
$C[z, \vec {x},\vec {\alpha }]\,{\leftrightarrow }\,\textrm {D}_C[z,\vec {x}, \vec {\alpha }{\upharpoonright } u]$
for each
![]() $z\,{<}\,t[\vec {x},\vec {\alpha }]$
by the induction hypothesis, we have
$z\,{<}\,t[\vec {x},\vec {\alpha }]$
by the induction hypothesis, we have
![]() $(Qz\,{<}\,t[\vec {x},\vec {\alpha }])C[z,\vec {x},\vec {\alpha }]\leftrightarrow \textrm {D}_{(Qz<t)C}[z, \vec {x},\vec {\alpha }{\upharpoonright } u]$
.
$(Qz\,{<}\,t[\vec {x},\vec {\alpha }])C[z,\vec {x},\vec {\alpha }]\leftrightarrow \textrm {D}_{(Qz<t)C}[z, \vec {x},\vec {\alpha }{\upharpoonright } u]$
.
The other cases are proved similarly.
Theorem 2.14. For any
![]() $A[\vec {\alpha }]$
from
$A[\vec {\alpha }]$
from
![]() $\Sigma ^0_1$
there is
$\Sigma ^0_1$
there is
![]() $D[\vec {u}]$
from
$D[\vec {u}]$
from
![]() $\Delta ^0_0$
without
$\Delta ^0_0$
without
![]() $\vec {\alpha }$
with
$\vec {\alpha }$
with
![]() $\mathbf{EL}_0^-\vdash \forall \vec {\alpha }(A[\vec {\alpha }]\,{\leftrightarrow }\,\exists nD[\vec {\alpha }{\upharpoonright } n])$
.
$\mathbf{EL}_0^-\vdash \forall \vec {\alpha }(A[\vec {\alpha }]\,{\leftrightarrow }\,\exists nD[\vec {\alpha }{\upharpoonright } n])$
.
Proof For simplicity, let
![]() $\vec {\alpha }\,{=}\,\alpha $
. Define
$\vec {\alpha }\,{=}\,\alpha $
. Define
for
![]() $A[\alpha ]\,{\equiv }\,\exists xC[x,\alpha ]$
. Note
$A[\alpha ]\,{\equiv }\,\exists xC[x,\alpha ]$
. Note
![]() $\textrm {B}_C[x,n,\alpha ]\,{\to }\,\forall \beta \,\textrm {B}_C[x,n,(\alpha {\upharpoonright } n){*}\beta ]$
. If
$\textrm {B}_C[x,n,\alpha ]\,{\to }\,\forall \beta \,\textrm {B}_C[x,n,(\alpha {\upharpoonright } n){*}\beta ]$
. If
![]() $\exists nD[\alpha {\upharpoonright } n]$
, say
$\exists nD[\alpha {\upharpoonright } n]$
, say
![]() $x\,{<}\,n\land \textrm {B}_C[x, n, (\alpha {\upharpoonright } n){*}\,\underline {0}]\land \textrm {D}_C[x,\alpha {\upharpoonright } n]$
, then, by 2.13,
$x\,{<}\,n\land \textrm {B}_C[x, n, (\alpha {\upharpoonright } n){*}\,\underline {0}]\land \textrm {D}_C[x,\alpha {\upharpoonright } n]$
, then, by 2.13,
![]() $C[x,\alpha ]$
. Conversely, if
$C[x,\alpha ]$
. Conversely, if
![]() $C[x,\alpha ]$
, 2.13 yields
$C[x,\alpha ]$
, 2.13 yields
![]() $n\,{>}\,x$
with
$n\,{>}\,x$
with
![]() $\textrm {B}_C[x,n,\alpha ]$
and so
$\textrm {B}_C[x,n,\alpha ]$
and so
![]() $\textrm {D}_C[x,\alpha {\upharpoonright } n]$
.
$\textrm {D}_C[x,\alpha {\upharpoonright } n]$
.
2.2 Choice axioms along numbers
Besides the existence of some specific functions and the closure conditions 2.10(d),
![]() $\textbf {EL}_0^-$
has no constraints on the second order domain. It seems common to use choice axioms to govern the domain in the function-based setting, while in the set-based one comprehension axioms are more common.
$\textbf {EL}_0^-$
has no constraints on the second order domain. It seems common to use choice axioms to govern the domain in the function-based setting, while in the set-based one comprehension axioms are more common.
Among several variants of dependent choice, we decide to set the premise to be
![]() $\textrm {Ran}(R)\subseteq \textrm {Dom}(R)$
for the relation R.
$\textrm {Ran}(R)\subseteq \textrm {Dom}(R)$
for the relation R.
Definition 2.15 (choice schema)
For a class
![]() $\mathcal {C}$
of formulae, define the following axiom schemata.
$\mathcal {C}$
of formulae, define the following axiom schemata.
-
(
 $\mathcal {C}\textsf {-AC}^{00}$
):
$\mathcal {C}\textsf {-AC}^{00}$
):
 $\forall x\exists yA[x,y]\,{\to }\,\exists \alpha \forall xA[x,\alpha (x)]$
;
$\forall x\exists yA[x,y]\,{\to }\,\exists \alpha \forall xA[x,\alpha (x)]$
; -
(
 $\mathcal {C}\textsf {-AC}^{01}$
):
$\mathcal {C}\textsf {-AC}^{01}$
):
 $\forall x\exists \beta A[x,\beta ]\,{\to }\,\exists \alpha \forall xA[x,(\alpha )_x]$
;
$\forall x\exists \beta A[x,\beta ]\,{\to }\,\exists \alpha \forall xA[x,(\alpha )_x]$
; -
(
 $\mathcal {C}\textsf {-DC}^{0}$
):
$\mathcal {C}\textsf {-DC}^{0}$
):
 $\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])\\ \phantom{AAAAAA..} {\to }\,\forall x,y(A[x,y]\,{\to }\,\exists \alpha (\alpha (0)\,{=}\,x\land \forall zA[\alpha (z),\alpha (z{+}1)]))$
;
$\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])\\ \phantom{AAAAAA..} {\to }\,\forall x,y(A[x,y]\,{\to }\,\exists \alpha (\alpha (0)\,{=}\,x\land \forall zA[\alpha (z),\alpha (z{+}1)]))$
; -
(
 $\mathcal {C}\textsf {-DC}^1$
):
$\mathcal {C}\textsf {-DC}^1$
):
 $\forall \beta ,\gamma (A[\beta ,\gamma ]\,{\to }\,\exists \delta A[\gamma ,\delta ])\\ \phantom{AAAAAA..} {\to }\,\forall \beta ,\gamma (A[\beta ,\gamma ]\,{\to }\,\exists \alpha ((\alpha )_0\,{=}\,\beta \land \forall zA[(\alpha )_z,(\alpha )_{z+1}]))$
,
$\forall \beta ,\gamma (A[\beta ,\gamma ]\,{\to }\,\exists \delta A[\gamma ,\delta ])\\ \phantom{AAAAAA..} {\to }\,\forall \beta ,\gamma (A[\beta ,\gamma ]\,{\to }\,\exists \alpha ((\alpha )_0\,{=}\,\beta \land \forall zA[(\alpha )_z,(\alpha )_{z+1}]))$
,
for any A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Moreover
![]() $\mathcal {C}\textsf {-AC!}^{0i}$
and
$\mathcal {C}\textsf {-AC!}^{0i}$
and
![]() $\mathcal {C}\textsf {-DC!}^{i}$
for
$\mathcal {C}\textsf {-DC!}^{i}$
for
![]() $i\,{=}\,0,1$
are defined with
$i\,{=}\,0,1$
are defined with
![]() $\exists $
replaced by
$\exists $
replaced by
![]() $\exists !$
in the premises.
$\exists !$
in the premises.
Lemma 2.16.
-
(1) Over
 $\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-LNP}$
, (i)
$\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-LNP}$
, (i)
 $(\mathcal {C}\land \textsf {B}\forall ^0\neg \mathcal {C})\textsf {-AC!}^{00}$
implies
$(\mathcal {C}\land \textsf {B}\forall ^0\neg \mathcal {C})\textsf {-AC!}^{00}$
implies
 $\mathcal {C}\textsf {-AC}^{00}$
;
$\mathcal {C}\textsf {-AC}^{00}$
;(ii)
 $(\mathcal {C}\land \textsf {B}\forall ^0\neg \mathcal {C})\textsf {-DC!}^{0}$
implies
$(\mathcal {C}\land \textsf {B}\forall ^0\neg \mathcal {C})\textsf {-DC!}^{0}$
implies
 $\mathcal {C}\textsf {-DC}^{0}$
.
$\mathcal {C}\textsf {-DC}^{0}$
. -
(2) Over
 $\mathbf{EL}_0^-$
, for
$\mathbf{EL}_0^-$
, for
 $j\,{\leq }\,i\,{\in }\,\{0,1\}$
, (i)
$j\,{\leq }\,i\,{\in }\,\{0,1\}$
, (i)
 $\mathcal {C}\textsf {-DC}^{i}$
yields
$\mathcal {C}\textsf {-DC}^{i}$
yields
 $\exists ^i\mathcal {C}\textsf {-DC}^{j}$
;
$\exists ^i\mathcal {C}\textsf {-DC}^{j}$
;(ii)
 $\mathcal {C}\textsf {-DC}^{i}$
yields
$\mathcal {C}\textsf {-DC}^{i}$
yields
 $\mathcal {C}\textsf {-AC}^{0j}$
; (iii)
$\mathcal {C}\textsf {-AC}^{0j}$
; (iii)
 $\mathcal {C}\textsf {-AC}^{0i}$
yields
$\mathcal {C}\textsf {-AC}^{0i}$
yields
 $\exists ^i\mathcal {C}\textsf {-AC}^{0j}\!$
;
$\exists ^i\mathcal {C}\textsf {-AC}^{0j}\!$
;(iv)
 $\mathcal {C}\textsf {-DC}!^{i}$
yields
$\mathcal {C}\textsf {-DC}!^{i}$
yields
 $\mathcal {C}\textsf {-AC}!^{0i}$
; (v)
$\mathcal {C}\textsf {-AC}!^{0i}$
; (v)
 $\mathcal {C}{\land }\Pi ^0_1\textsf {-DC}!^{1}$
yields
$\mathcal {C}{\land }\Pi ^0_1\textsf {-DC}!^{1}$
yields
 $\mathcal {C}\textsf {-DC}!^0$
;
$\mathcal {C}\textsf {-DC}!^0$
;(vi)
 $\mathcal {C}{\land }\Pi ^0_1\textsf {-AC}!^{01}$
yields
$\mathcal {C}{\land }\Pi ^0_1\textsf {-AC}!^{01}$
yields
 $\mathcal {C}\textsf {-AC}!^{00}$
.
$\mathcal {C}\textsf {-AC}!^{00}$
. -
(3) (i)
 $\mathbf{EL}_0^-\!{+}\mathcal {C}\textsf {-DC!}^0\,{\vdash } \,\mathcal {C}\textsf {-Ind}$
; (ii)
$\mathbf{EL}_0^-\!{+}\mathcal {C}\textsf {-DC!}^0\,{\vdash } \,\mathcal {C}\textsf {-Ind}$
; (ii)
 $\mathbf{EL}_0^-\!{+}\mathcal {C}\textsf {-AC}^{00}\,{\vdash } \,\mathcal {C}\textsf {-Bdg}$
.
$\mathbf{EL}_0^-\!{+}\mathcal {C}\textsf {-AC}^{00}\,{\vdash } \,\mathcal {C}\textsf {-Bdg}$
. -
(4)
 $\mathbf{EL}^-_0 {+}\,\textsf {B}\forall ^0\mathcal {C}\textsf {-AC!}^{00}{+}\,\exists ^0(\textsf{B}\forall ^0\mathcal {C})\textsf {-Ind} \vdash \mathcal {C}\textsf {-DC!}^0$
.
$\mathbf{EL}^-_0 {+}\,\textsf {B}\forall ^0\mathcal {C}\textsf {-AC!}^{00}{+}\,\exists ^0(\textsf{B}\forall ^0\mathcal {C})\textsf {-Ind} \vdash \mathcal {C}\textsf {-DC!}^0$
. -
(5)
 $\mathbf{EL}_0^-{+}\forall ^0(\mathcal {C}{\land } \neg \mathcal {C})\textsf {-DC!}^1{+}\mathcal {C}\textsf {-LNP} \vdash \forall ^0\exists ^0\mathcal {C}\textsf {-DC!}^1$
.
$\mathbf{EL}_0^-{+}\forall ^0(\mathcal {C}{\land } \neg \mathcal {C})\textsf {-DC!}^1{+}\mathcal {C}\textsf {-LNP} \vdash \forall ^0\exists ^0\mathcal {C}\textsf {-DC!}^1$
.
Proof In what follows, let A be
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(2)(i) First consider the case of
![]() $i=0$
. If
$i=0$
. If
![]() $\forall x,y(\exists uA[x,y,u] \to \exists z,vA[y,z,v]))$
then
$\forall x,y(\exists uA[x,y,u] \to \exists z,vA[y,z,v]))$
then
![]() $\forall x,y(B[x,y] \to \exists zB[y,z])$
where
$\forall x,y(B[x,y] \to \exists zB[y,z])$
where
![]() $B[x,y]\equiv A[(x)^2_0,(y)^2_0,(y)^2_1]$
. For any
$B[x,y]\equiv A[(x)^2_0,(y)^2_0,(y)^2_1]$
. For any
![]() $x,y$
such that
$x,y$
such that
![]() $\exists uA[x,y,u]$
, since
$\exists uA[x,y,u]$
, since
![]() $\exists y,uB[(x,0),(y,u)]$
,
$\exists y,uB[(x,0),(y,u)]$
,
![]() $\mathcal {C}\textsf {-DC}^0$
yields
$\mathcal {C}\textsf {-DC}^0$
yields
![]() $\beta $
with
$\beta $
with
![]() $\beta (0) = (x,0)$
and
$\beta (0) = (x,0)$
and
![]() $\forall zB[\beta (z), \beta (z{+}1)]$
. Define
$\forall zB[\beta (z), \beta (z{+}1)]$
. Define
![]() $\alpha $
by
$\alpha $
by
![]() $\alpha (x)=(\beta (x))^2_0$
. The case of
$\alpha (x)=(\beta (x))^2_0$
. The case of
![]() $i=1$
is similarly proved.
$i=1$
is similarly proved.
(ii) First consider the case of
![]() $i=0$
. If
$i=0$
. If
![]() $\forall x\exists yA[x,y]$
then
$\forall x\exists yA[x,y]$
then
and
![]() $\mathcal {C}\textsf {-DC}^0$
yields
$\mathcal {C}\textsf {-DC}^0$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha (0)=(0,0)$
and
$\alpha (0)=(0,0)$
and
![]() $\Delta ^0_0\textsf {-Ind}$
shows
$\Delta ^0_0\textsf {-Ind}$
shows
![]() $(\alpha (x))^2_0=x$
and so
$(\alpha (x))^2_0=x$
and so
![]() $\forall xA[x,(\alpha (x{+}1))^2_1]$
.
$\forall xA[x,(\alpha (x{+}1))^2_1]$
.
Next consider the case of
![]() $i=1$
. If
$i=1$
. If
![]() $\forall x\exists \gamma A[x,\gamma ]$
,
$\forall x\exists \gamma A[x,\gamma ]$
,
![]() $\mathcal {C}\textsf {-DC}^1$
yields
$\mathcal {C}\textsf {-DC}^1$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $(\alpha )_0=\underline {0}$
and
$(\alpha )_0=\underline {0}$
and
(v)(vi) If
![]() $\exists !z A[z]$
then
$\exists !z A[z]$
then
![]() $\exists !\gamma (A[\gamma (0)]\land \gamma {\ominus } 1=\underline {0})$
and vice versa, where
$\exists !\gamma (A[\gamma (0)]\land \gamma {\ominus } 1=\underline {0})$
and vice versa, where
![]() $\gamma {\ominus } 1=\underline {0}$
is
$\gamma {\ominus } 1=\underline {0}$
is
![]() $\Pi ^0_1$
.
$\Pi ^0_1$
.
(3)(i) Let
![]() $B[x,y]:\equiv y = x\,{+}\,1\land (y \leq n \to A[y])$
which is also in
$B[x,y]:\equiv y = x\,{+}\,1\land (y \leq n \to A[y])$
which is also in
![]() $\mathcal {C}$
by 2.9(3). If
$\mathcal {C}$
by 2.9(3). If
![]() $A[0]\land (\forall x < n)(A[x] \to A[x{+}1])$
, since
$A[0]\land (\forall x < n)(A[x] \to A[x{+}1])$
, since
![]() $\forall x,y(B[x,y] \to \exists ! zB[y,z])$
and
$\forall x,y(B[x,y] \to \exists ! zB[y,z])$
and
![]() $B[0,1]$
,
$B[0,1]$
,
![]() $\mathcal {C}\textsf {-DC!}^0$
yields
$\mathcal {C}\textsf {-DC!}^0$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $\forall xB[\alpha (x),\alpha (x{+}1)]$
and
$\forall xB[\alpha (x),\alpha (x{+}1)]$
and
![]() $\alpha (0) = 0$
. By
$\alpha (0) = 0$
. By
![]() $\Delta ^0_0\textsf {-Ind}$
we have
$\Delta ^0_0\textsf {-Ind}$
we have
![]() $(\forall x\,{\leq }\,n)(x = \alpha (x))$
and
$(\forall x\,{\leq }\,n)(x = \alpha (x))$
and
![]() $A[n]$
.
$A[n]$
.
(4) Let
![]() $\forall x,y(A[x,y] \to \exists !zA[y,z])$
and
$\forall x,y(A[x,y] \to \exists !zA[y,z])$
and
![]() $A[x,y]$
. By
$A[x,y]$
. By
![]() $\exists ^0(\textsf {B}\forall ^0\mathcal {C})\textsf {-Ind}$
we can show
$\exists ^0(\textsf {B}\forall ^0\mathcal {C})\textsf {-Ind}$
we can show
![]() $\forall n\exists ! uC[n,u]$
where
$\forall n\exists ! uC[n,u]$
where
![]() $\textsf {B}\forall ^0\mathcal {C}\textsf {-AC!}^{00}$
yields
$\textsf {B}\forall ^0\mathcal {C}\textsf {-AC!}^{00}$
yields
![]() $\beta $
with
$\beta $
with
![]() $\forall nC[n,\beta (n)]$
. We can easily see
$\forall nC[n,\beta (n)]$
. We can easily see
![]() $\beta (n)\,{\subset }\,\beta (n{+}1)$
by
$\beta (n)\,{\subset }\,\beta (n{+}1)$
by
![]() $\Delta ^0_0\textsf {-Ind}$
. Thus
$\Delta ^0_0\textsf {-Ind}$
. Thus
![]() $\forall kA[\alpha (k),\alpha (k{+}1)]$
for
$\forall kA[\alpha (k),\alpha (k{+}1)]$
for
![]() $\alpha (k)\,{=}\,\beta (k)(k)$
.
$\alpha (k)\,{=}\,\beta (k)(k)$
.
(5) Since
![]() $\Pi ^0_1{\land }\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})\,{\subseteq }\,\forall ^0(\Delta ^0_0{\land }\mathcal {C}{\land }\neg \mathcal {C}) \,{\subseteq }\,\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})$
, (2)(iv)(v) and
$\Pi ^0_1{\land }\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})\,{\subseteq }\,\forall ^0(\Delta ^0_0{\land }\mathcal {C}{\land }\neg \mathcal {C}) \,{\subseteq }\,\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})$
, (2)(iv)(v) and
![]() $\mathcal {C}\textsf {-LNP}$
yield
$\mathcal {C}\textsf {-LNP}$
yield
 $$ \begin{align*} &\exists!\eta\forall x\exists yA[\xi,\eta,x,y] \leftrightarrow\exists!\eta B[\xi,\eta]\\ &\text{ where } B[\xi,\eta]\,{:\equiv}\,\forall x(\forall y\,{<}\,(\eta)^2_1(x))(A[\xi,(\eta)^2_0,x,(\eta)^2_1(x))]{\land}\neg A[\xi,(\eta)^2_0,x,y]). \end{align*} $$
$$ \begin{align*} &\exists!\eta\forall x\exists yA[\xi,\eta,x,y] \leftrightarrow\exists!\eta B[\xi,\eta]\\ &\text{ where } B[\xi,\eta]\,{:\equiv}\,\forall x(\forall y\,{<}\,(\eta)^2_1(x))(A[\xi,(\eta)^2_0,x,(\eta)^2_1(x))]{\land}\neg A[\xi,(\eta)^2_0,x,y]). \end{align*} $$
Assume
![]() $\forall \beta ,\gamma (\forall x\exists yA[\beta ,\gamma ,x,y]\,{\to }\,\exists !\delta \forall x\exists y A[\gamma ,\delta ,x,y])$
. Then, by the equivalence, we have
$\forall \beta ,\gamma (\forall x\exists yA[\beta ,\gamma ,x,y]\,{\to }\,\exists !\delta \forall x\exists y A[\gamma ,\delta ,x,y])$
. Then, by the equivalence, we have
![]() $\forall \beta ,\gamma (B[(\beta )^2_0,\gamma ]\,{\to }\,\exists !\delta B[(\gamma )^2_0,\delta ])$
, and
$\forall \beta ,\gamma (B[(\beta )^2_0,\gamma ]\,{\to }\,\exists !\delta B[(\gamma )^2_0,\delta ])$
, and
![]() $\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})\textsf {-DC!}^1$
yields
$\forall ^0(\mathcal {C}{\land }\neg \mathcal {C})\textsf {-DC!}^1$
yields
![]() $\gamma $
such that
$\gamma $
such that
![]() $\forall zB[((\gamma )_z)^2_0,(\gamma )_{z+1}]$
which implies
$\forall zB[((\gamma )_z)^2_0,(\gamma )_{z+1}]$
which implies
![]() $\forall z,x\exists yA[((\gamma )_z)^2_0,((\gamma )_{z+1})^2_0,x,y]$
.
$\forall z,x\exists yA[((\gamma )_z)^2_0,((\gamma )_{z+1})^2_0,x,y]$
.
Definition 2.17 (
 $\textbf {EL}^*_0$
,
$\textbf {EL}^*_0$
,
 $\textbf {EL}_0$
and
$\textbf {EL}_0$
and
 $\textbf {EL}$
)
$\textbf {EL}$
)
By 2.8(2)(ii) and 2.16(1),
![]() $\textbf {EL}_0^-\,{\vdash }\,\Delta ^0_0\textsf {-DC}^0 \,{\leftrightarrow }\,\Delta ^0_0\textsf {-DC!}^0$
. By 2.16(2)(i)(ii)(3)(i)(4),
$\textbf {EL}_0^-\,{\vdash }\,\Delta ^0_0\textsf {-DC}^0 \,{\leftrightarrow }\,\Delta ^0_0\textsf {-DC!}^0$
. By 2.16(2)(i)(ii)(3)(i)(4),
![]() $\textbf {EL}_0=\textbf {EL}_0^-{+}\Delta ^0_0\textsf {-DC}^0$
.
$\textbf {EL}_0=\textbf {EL}_0^-{+}\Delta ^0_0\textsf {-DC}^0$
.
2.3 Relation to set-based systems
One might consider that the study of our function-based second order arithmetic is equivalent to that of the famous set-based one (extensively done, e.g., in [Reference Simpson45]), since functions are coded by sets as graphs and sets are coded by functions as characteristic functions. This expectation is true if we consider only classical systems not sensitive to arithmetical complexity. Otherwise there are several delicate differences. We first clarify the correspondence between the two settings along which we consider similarity and dissimilarity.
Definition 2.18 (characteristic function interpretation
 $\mathfrak {ch}$
)
$\mathfrak {ch}$
)
Assign injectively function variables
![]() $\alpha _X$
of
$\alpha _X$
of
![]() $\mathcal {L}_{\mathrm{F}}$
to set variables X of
$\mathcal {L}_{\mathrm{F}}$
to set variables X of
![]() $\mathcal {L}_{\textrm {S}}$
. For an
$\mathcal {L}_{\textrm {S}}$
. For an
![]() $\mathcal {L}_{\textrm {S}}$
formula A, define an
$\mathcal {L}_{\textrm {S}}$
formula A, define an
![]() $\mathcal {L}_{\mathrm{F}}$
formula
$\mathcal {L}_{\mathrm{F}}$
formula
![]() $A^{\mathfrak {ch}}$
by
$A^{\mathfrak {ch}}$
by
 $$ \begin{align*} \bot^{\mathfrak{ch}}\,{:\equiv}\,\bot;&\quad (t\,{\in}\,X)^{\mathfrak{ch}}\,{:\equiv}\,\alpha_X(t)\,{=}\,0; &\! (s \mathbin{\mathrm{R}} t)^{\mathfrak{ch}}\,&{:\equiv}\,s\mathbin{\mathrm{R}} t\text{ for }\mathrm{R}\equiv{=},{<};\\ (A\Box B)^{\mathfrak{ch}}\,{:\equiv}&\,A^{\mathfrak{ch}} \Box B^{\mathfrak{ch}} \text{ for }\Box\,{\equiv}\,{\land},{\to},{\lor};&\! (QxA)^{\mathfrak{ch}}\,&{:\equiv}\,QxA^{\mathfrak{ch}} \text{ for }Q\,{\equiv}\,{\forall},{\exists};\\[2pt] (\forall X A)^{\mathfrak{ch}}\,&{:\equiv}\, \forall \alpha_X(\alpha_X\,{<}\,\underline{2} \,{\to}\, A^{\mathfrak{ch}});&\! (\exists X A)^{\mathfrak{ch}}\,&{:\equiv}\, \exists \alpha_X(\alpha_X\,{<}\,\underline{2} \land A^{\mathfrak{ch}}). \end{align*} $$
$$ \begin{align*} \bot^{\mathfrak{ch}}\,{:\equiv}\,\bot;&\quad (t\,{\in}\,X)^{\mathfrak{ch}}\,{:\equiv}\,\alpha_X(t)\,{=}\,0; &\! (s \mathbin{\mathrm{R}} t)^{\mathfrak{ch}}\,&{:\equiv}\,s\mathbin{\mathrm{R}} t\text{ for }\mathrm{R}\equiv{=},{<};\\ (A\Box B)^{\mathfrak{ch}}\,{:\equiv}&\,A^{\mathfrak{ch}} \Box B^{\mathfrak{ch}} \text{ for }\Box\,{\equiv}\,{\land},{\to},{\lor};&\! (QxA)^{\mathfrak{ch}}\,&{:\equiv}\,QxA^{\mathfrak{ch}} \text{ for }Q\,{\equiv}\,{\forall},{\exists};\\[2pt] (\forall X A)^{\mathfrak{ch}}\,&{:\equiv}\, \forall \alpha_X(\alpha_X\,{<}\,\underline{2} \,{\to}\, A^{\mathfrak{ch}});&\! (\exists X A)^{\mathfrak{ch}}\,&{:\equiv}\, \exists \alpha_X(\alpha_X\,{<}\,\underline{2} \land A^{\mathfrak{ch}}). \end{align*} $$
Definition 2.19 (graph interpretation
 $\mathfrak {g}$
)
$\mathfrak {g}$
)
Assign injectively variables
![]() $X_{\alpha }$
of
$X_{\alpha }$
of
![]() $\mathcal {L}_{\textrm {S}}$
to variables
$\mathcal {L}_{\textrm {S}}$
to variables
![]() $\alpha $
of
$\alpha $
of
![]() $\mathcal {L}_{\mathrm{F}}$
. For an
$\mathcal {L}_{\mathrm{F}}$
. For an
![]() $\mathcal {L}_{\mathrm{F}}$
-term t, define
$\mathcal {L}_{\mathrm{F}}$
-term t, define
![]() $[\![t]\!]^{\mathfrak {g}}(x)$
:
$[\![t]\!]^{\mathfrak {g}}(x)$
:
 $$ \begin{align*} &[\![x]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,x\,{=}\,y;\\ &[\![c]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,c\,{=}\,y\text{ for } c\equiv 0,1;\\ &[\![t{\circ}t']\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,\exists x,x'([\![t]\!]^{\mathfrak{g}}(x)\,{\land}\,[\![t']\!]^{\mathfrak{g}}(x') \,{\land}\,y\,{=}\,x{\circ}x')\text{ for }{\circ}\,{\equiv}\,{+},{\cdot},\exp;\\ &[\![\alpha(t)]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,\exists z([\![t]\!]^{\mathfrak{g}}(z) \land(z,y)\,{\in}\,X_{\alpha});\\ &[\![\alpha{\upharpoonright} t]\!]^{\mathfrak{g}}(u)\,{:}{\equiv}\,[\![t]\!]^{\mathfrak{g}}(|u|)\land(\forall x\,{<}\,|u|) ( (x,u(x))\,{\in}\,X_{\alpha})). \end{align*} $$
$$ \begin{align*} &[\![x]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,x\,{=}\,y;\\ &[\![c]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,c\,{=}\,y\text{ for } c\equiv 0,1;\\ &[\![t{\circ}t']\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,\exists x,x'([\![t]\!]^{\mathfrak{g}}(x)\,{\land}\,[\![t']\!]^{\mathfrak{g}}(x') \,{\land}\,y\,{=}\,x{\circ}x')\text{ for }{\circ}\,{\equiv}\,{+},{\cdot},\exp;\\ &[\![\alpha(t)]\!]^{\mathfrak{g}}(y)\,{:}{\equiv}\,\exists z([\![t]\!]^{\mathfrak{g}}(z) \land(z,y)\,{\in}\,X_{\alpha});\\ &[\![\alpha{\upharpoonright} t]\!]^{\mathfrak{g}}(u)\,{:}{\equiv}\,[\![t]\!]^{\mathfrak{g}}(|u|)\land(\forall x\,{<}\,|u|) ( (x,u(x))\,{\in}\,X_{\alpha})). \end{align*} $$
For A in
![]() $\mathcal {L}_{\mathrm{F}}$
, define
$\mathcal {L}_{\mathrm{F}}$
, define
![]() $A^{\mathfrak {g}}$
in
$A^{\mathfrak {g}}$
in
![]() $\mathcal {L}_{\textrm {S}}$
as follows, where
$\mathcal {L}_{\textrm {S}}$
as follows, where
![]() $\textrm {Func}[X]\,{:\equiv }\,\forall x\exists !y((x,y)\,{\in }\,X)$
:
$\textrm {Func}[X]\,{:\equiv }\,\forall x\exists !y((x,y)\,{\in }\,X)$
:
 $$ \begin{align*} \bot^{\mathfrak{g}}\,{:\equiv}\,&\bot;\quad (s\mathbin{\mathrm{R}} t)^{\mathfrak{g}}\,{:\equiv}\,\exists x,y([\![s]\!]^{\mathfrak{g}}(x)\,{\land}\, [\![t]\!]^{\mathfrak{g}}(y)\,{\land}\,x\mathbin{\mathrm{R}}y)\text{ for }\mathrm{R}\equiv{=},{<};\\ (A\Box B)^{\mathfrak{g}}\,&{:\equiv}\,A^{\mathfrak{g}} \Box B^{\mathfrak{g}} \text{ for }\Box\,{\equiv}\,{\land},{\to},{\lor};\quad (QxA)^{\mathfrak{g}}\,{:\equiv}\,QxA^{\mathfrak{g}} \text{ for }Q\,{\equiv}\,{\forall},{\exists};\\ (\forall\alpha A)^{\mathfrak{g}}\,&{:\equiv}\, \forall X_{\alpha}(\mathrm{Func}[X_{\alpha}]{\to}\, A^{\mathfrak{g}});\quad (\exists\alpha A)^{\mathfrak{g}}\,{:\equiv}\, \exists X_{\alpha}(\mathrm{Func}[X_{\alpha}]\,{\land}\, A^{\mathfrak{g}}). \end{align*} $$
$$ \begin{align*} \bot^{\mathfrak{g}}\,{:\equiv}\,&\bot;\quad (s\mathbin{\mathrm{R}} t)^{\mathfrak{g}}\,{:\equiv}\,\exists x,y([\![s]\!]^{\mathfrak{g}}(x)\,{\land}\, [\![t]\!]^{\mathfrak{g}}(y)\,{\land}\,x\mathbin{\mathrm{R}}y)\text{ for }\mathrm{R}\equiv{=},{<};\\ (A\Box B)^{\mathfrak{g}}\,&{:\equiv}\,A^{\mathfrak{g}} \Box B^{\mathfrak{g}} \text{ for }\Box\,{\equiv}\,{\land},{\to},{\lor};\quad (QxA)^{\mathfrak{g}}\,{:\equiv}\,QxA^{\mathfrak{g}} \text{ for }Q\,{\equiv}\,{\forall},{\exists};\\ (\forall\alpha A)^{\mathfrak{g}}\,&{:\equiv}\, \forall X_{\alpha}(\mathrm{Func}[X_{\alpha}]{\to}\, A^{\mathfrak{g}});\quad (\exists\alpha A)^{\mathfrak{g}}\,{:\equiv}\, \exists X_{\alpha}(\mathrm{Func}[X_{\alpha}]\,{\land}\, A^{\mathfrak{g}}). \end{align*} $$
Lemma 2.20.
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg} {+}\Delta ^0_0\textsf {-AC}^{00}{+}\Sigma ^0_n\textsf {-Ind}$
is interpreted by the graph interpretation
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg} {+}\Delta ^0_0\textsf {-AC}^{00}{+}\Sigma ^0_n\textsf {-Ind}$
is interpreted by the graph interpretation
![]() $\mathfrak {g}$
in
$\mathfrak {g}$
in
![]() $\mathbf{RCA}_0^*{+}\Sigma ^0_n\textsf {-Ind}$
.
$\mathbf{RCA}_0^*{+}\Sigma ^0_n\textsf {-Ind}$
.
Proof As
![]() $\textbf {RCA}_0^*$
proves
$\textbf {RCA}_0^*$
proves
![]() $\Sigma ^0_1\textsf {-Bdg}$
, we have, for any term t,
$\Sigma ^0_1\textsf {-Bdg}$
, we have, for any term t,
Thus we can show
![]() $\exists !x[\![t]\!]^{\mathfrak {g}}(x)$
by induction on t, and hence
$\exists !x[\![t]\!]^{\mathfrak {g}}(x)$
by induction on t, and hence
![]() $(s \mathbin {\textrm {R}} t)^{\mathfrak {g}}$
is equivalent to
$(s \mathbin {\textrm {R}} t)^{\mathfrak {g}}$
is equivalent to
![]() $\forall x,y([\![s]\!]^{\mathfrak {g}}(x)\,{\land }\,[\![t]\!]^{\mathfrak {g}}(y)\,{\to }\,x\textrm {R}y)$
. Thus, if A is
$\forall x,y([\![s]\!]^{\mathfrak {g}}(x)\,{\land }\,[\![t]\!]^{\mathfrak {g}}(y)\,{\to }\,x\textrm {R}y)$
. Thus, if A is
![]() $\Delta ^0_0$
, then
$\Delta ^0_0$
, then
![]() $A^{\mathfrak {g}}$
is
$A^{\mathfrak {g}}$
is
![]() $\Delta ^0_1$
and
$\Delta ^0_1$
and
![]() $\textbf {RCA}_0^*$
yields
$\textbf {RCA}_0^*$
yields
![]() $X_{\alpha }\,{=}\,\{(x,y)\,{:}\, A[x,y]^{\mathfrak {g}} \land (\forall z\,{<}\,y)\neg A[x,y]^{\mathfrak {g}}\}$
.
$X_{\alpha }\,{=}\,\{(x,y)\,{:}\, A[x,y]^{\mathfrak {g}} \land (\forall z\,{<}\,y)\neg A[x,y]^{\mathfrak {g}}\}$
.
If
![]() $(\forall x\exists yA[x,y])^{\mathfrak {g}}$
, then
$(\forall x\exists yA[x,y])^{\mathfrak {g}}$
, then
![]() $\forall x\exists !y ((x,y)\,{\in }\,X_{\alpha })$
by
$\forall x\exists !y ((x,y)\,{\in }\,X_{\alpha })$
by
![]() $\Delta ^0_0\textsf {-LNP}$
, which is provable in
$\Delta ^0_0\textsf {-LNP}$
, which is provable in
![]() $\textbf {RCA}_0^*$
. Now
$\textbf {RCA}_0^*$
. Now
![]() $\forall x\exists y((x,y)\,{\in }\,X_{\alpha }\,{\land }\, A[x,y]^{\mathfrak {g}})$
i.e.,
$\forall x\exists y((x,y)\,{\in }\,X_{\alpha }\,{\land }\, A[x,y]^{\mathfrak {g}})$
i.e.,
![]() $(\forall xA[x,\alpha (x)])^{\mathfrak {g}}$
. Thus
$(\forall xA[x,\alpha (x)])^{\mathfrak {g}}$
. Thus
![]() $(\Delta ^0_0\textsf {-AC}^{00})^{\mathfrak {g}}$
. The interpretability of the remaining axioms by
$(\Delta ^0_0\textsf {-AC}^{00})^{\mathfrak {g}}$
. The interpretability of the remaining axioms by
![]() $\mathfrak {g}$
is obvious.
$\mathfrak {g}$
is obvious.
Thus
![]() $\mathfrak {g}$
seems to require
$\mathfrak {g}$
seems to require
![]() $\Delta ^0_1\textsf {-CA}$
in
$\Delta ^0_1\textsf {-CA}$
in
![]() $\mathcal {L}_{\textrm {S}}$
. To interpret it,
$\mathcal {L}_{\textrm {S}}$
. To interpret it,
![]() $\mathfrak {ch}$
seems to require
$\mathfrak {ch}$
seems to require
![]() $\Delta ^0_0\textsf {-AC}^{00}$
and hence
$\Delta ^0_0\textsf {-AC}^{00}$
and hence
![]() $\textbf {EL}_0^*$
.
$\textbf {EL}_0^*$
.
The delicate differences are mainly caused by the clauses
![]() $\forall x\exists !y((x,y)\,{\in }\,X_{\alpha })$
of the totality (which is known to be
$\forall x\exists !y((x,y)\,{\in }\,X_{\alpha })$
of the totality (which is known to be
![]() $\Pi ^0_2$
complete in recursion theory) and of
$\Pi ^0_2$
complete in recursion theory) and of
![]() $\forall x(\alpha _X(x)\,{<}\,2)$
. For example, the premise
$\forall x(\alpha _X(x)\,{<}\,2)$
. For example, the premise
![]() $\forall x\exists \alpha A[x,\alpha ]$
of the number-function choice
$\forall x\exists \alpha A[x,\alpha ]$
of the number-function choice
![]() $\mathcal {C}\textsf {-AC}^{01}$
is interpreted by
$\mathcal {C}\textsf {-AC}^{01}$
is interpreted by
![]() $\mathfrak {g}$
as
$\mathfrak {g}$
as
![]() $\forall x\exists X_{\alpha }( \textrm {Func}[X_{\alpha }]\land A[x,\alpha ]^{\mathfrak {g}})$
and so we cannot apply the number-set choice, unless the class is closed under conjunctions with
$\forall x\exists X_{\alpha }( \textrm {Func}[X_{\alpha }]\land A[x,\alpha ]^{\mathfrak {g}})$
and so we cannot apply the number-set choice, unless the class is closed under conjunctions with
![]() $\Pi ^0_2$
formulae. Conversely,
$\Pi ^0_2$
formulae. Conversely,
![]() $(\forall x\exists XA[x,X])^{\mathfrak {ch}}$
is
$(\forall x\exists XA[x,X])^{\mathfrak {ch}}$
is
![]() $\forall x(\exists \alpha _X\,{<}\,\underline {2})A[x,X]^{\mathfrak {ch}}$
and therefore we could say that the number-set choice is only a fragment of number-function choice, or bounded version of the latter. This motivates the following.
$\forall x(\exists \alpha _X\,{<}\,\underline {2})A[x,X]^{\mathfrak {ch}}$
and therefore we could say that the number-set choice is only a fragment of number-function choice, or bounded version of the latter. This motivates the following.
Definition 2.21 (bounded choice schema)
For a class
![]() $\mathcal {C}$
of formulae, define the following axiom schemata:
$\mathcal {C}$
of formulae, define the following axiom schemata:
-
(
 $\mathcal {C}\textsf {-BAC}^{01}$
):
$\mathcal {C}\textsf {-BAC}^{01}$
):
 $\forall x(\exists \beta \,{<}\,(\gamma )_x) A[x,\beta ] \,{\to }\,(\exists \alpha \,{<}\,\gamma )\forall xA[x,(\alpha )_x]$
;
$\forall x(\exists \beta \,{<}\,(\gamma )_x) A[x,\beta ] \,{\to }\,(\exists \alpha \,{<}\,\gamma )\forall xA[x,(\alpha )_x]$
; -
(
 $\mathcal {C}\textsf {-BAC}^{00}$
):
$\mathcal {C}\textsf {-BAC}^{00}$
):
 $\forall x(\exists y\,{<}\,\beta (x)) A[x,y]\,{\to }\, (\exists \alpha \,{<}\,\beta )\forall xA[x,\alpha (x)]$
;
$\forall x(\exists y\,{<}\,\beta (x)) A[x,y]\,{\to }\, (\exists \alpha \,{<}\,\beta )\forall xA[x,\alpha (x)]$
; -
(
 $\mathcal {C}\textsf {-2AC}^{01}$
):
$\mathcal {C}\textsf {-2AC}^{01}$
):
 $\forall x(\exists \beta \,{<}\,\underline {2}) A[x,\beta ]\,{\to }\, (\exists \alpha \,{<}\,\underline {2})\forall xA[x,(\alpha )_x]$
;
$\forall x(\exists \beta \,{<}\,\underline {2}) A[x,\beta ]\,{\to }\, (\exists \alpha \,{<}\,\underline {2})\forall xA[x,(\alpha )_x]$
; -
(
 $\mathcal {C}\textsf {-2AC}^{00}$
):
$\mathcal {C}\textsf {-2AC}^{00}$
):
 $\forall x(\exists y\,{<}\,2) A[x,y]\,{\to }\, (\exists \alpha \,{<}\,\underline {2})\forall xA[x,\alpha (x)]$
,
$\forall x(\exists y\,{<}\,2) A[x,y]\,{\to }\, (\exists \alpha \,{<}\,\underline {2})\forall xA[x,\alpha (x)]$
,
for any A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
2.4 Semi-classical or semi-constructive principles
Definition 2.22 (
 $\textsf {MP}$
,
$\textsf {MP}$
,
 $\textsf {LPO}$
,
$\textsf {LPO}$
,
 $\mathcal {C}\textsf {-DM}$
,
$\mathcal {C}\textsf {-DM}$
,
 $\mathcal {C}\textsf {-GDM}$
and
$\mathcal {C}\textsf {-GDM}$
and
 $\textsf {LLPO}$
)
$\textsf {LLPO}$
)
![]() $\textsf {MP}$
and
$\textsf {MP}$
and
![]() $\textsf {LPO}$
denote
$\textsf {LPO}$
denote
![]() $\Sigma ^0_1\textsf {-DNE}$
and
$\Sigma ^0_1\textsf {-DNE}$
and
![]() $\Sigma ^0_1\textsf {-LEM}$
both from 2.6, respectively.
$\Sigma ^0_1\textsf {-LEM}$
both from 2.6, respectively.
![]() $\textsf {LLPO}$
denotes
$\textsf {LLPO}$
denotes
![]() $\Sigma ^0_1\textsf {-DM}$
, where for a class
$\Sigma ^0_1\textsf {-DM}$
, where for a class
![]() $\mathcal {C}$
of formulae, define the schemata:
$\mathcal {C}$
of formulae, define the schemata:
-
(
 $\mathcal {C}\textsf {-DM}$
):
$\mathcal {C}\textsf {-DM}$
):
 $\neg (A\,{\land }\, B)\to \neg A\,{\lor }\,\neg B$
;
$\neg (A\,{\land }\, B)\to \neg A\,{\lor }\,\neg B$
; -
(
 $\mathcal {C}\textsf {-GDM}$
):
$\mathcal {C}\textsf {-GDM}$
):
 $\neg (\forall x\,{<}\,y)A \to (\exists x\,{<}\,y)\neg A$
,
$\neg (\forall x\,{<}\,y)A \to (\exists x\,{<}\,y)\neg A$
,
for any
![]() $A,B$
from
$A,B$
from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 2.23.
-
(1)
 $\mathcal {C}\textsf {-LEM}$
yields
$\mathcal {C}\textsf {-LEM}$
yields
 $A\,{\lor }\,\neg A$
and
$A\,{\lor }\,\neg A$
and
 $\neg \neg A\,{\to }\,A$
for any A built from
$\neg \neg A\,{\to }\,A$
for any A built from
 $\mathcal {C}$
formulae by
$\mathcal {C}$
formulae by
 ${\land }$
,
${\land }$
,
 ${\lor }$
,
${\lor }$
,
 ${\to }$
and
${\to }$
and
 $\neg $
.
$\neg $
. -
(2) (i)
 $\textsf {B}\exists ^0(\forall ^0\neg \mathcal {C})\subseteq \neg \exists ^0\textsf {B}\forall ^0\textsf {B}\exists ^0\mathcal {C}$
over
$\textsf {B}\exists ^0(\forall ^0\neg \mathcal {C})\subseteq \neg \exists ^0\textsf {B}\forall ^0\textsf {B}\exists ^0\mathcal {C}$
over
 $\mathbf{EL}_0^-{+}\exists ^0\mathcal {C}\textsf {-GDM}{+}\,\mathcal {C}\textsf {-Bdg}$
;
$\mathbf{EL}_0^-{+}\exists ^0\mathcal {C}\textsf {-GDM}{+}\,\mathcal {C}\textsf {-Bdg}$
;(ii)
 $\mathbf{EL}_0^-\vdash \,(\neg \mathcal {C}\lor \neg \mathcal {C})\textsf {-DNE} \,{\leftrightarrow }\,\mathcal {C}\textsf {-DM}$
.
$\mathbf{EL}_0^-\vdash \,(\neg \mathcal {C}\lor \neg \mathcal {C})\textsf {-DNE} \,{\leftrightarrow }\,\mathcal {C}\textsf {-DM}$
. -
(3)
 $\mathbf{EL}_0^-{+}\,\mathcal {C} \textsf {-GDM}\vdash \textsf {B}\exists ^0(\neg \mathcal {C})\textsf {-DNE}$
and
$\mathbf{EL}_0^-{+}\,\mathcal {C} \textsf {-GDM}\vdash \textsf {B}\exists ^0(\neg \mathcal {C})\textsf {-DNE}$
and
 $\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-DNE}{+}\, \textsf {B}\exists ^0(\neg \mathcal {C})\textsf {-DNE}\vdash \mathcal {C} \textsf {-GDM}$
.
$\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-DNE}{+}\, \textsf {B}\exists ^0(\neg \mathcal {C})\textsf {-DNE}\vdash \mathcal {C} \textsf {-GDM}$
. -
(4)
 $\mathbf{EL}_0^-{+}\,\mathcal {C} \textsf {-GDM}\vdash \mathcal {C}\textsf {-DM}$
.
$\mathbf{EL}_0^-{+}\,\mathcal {C} \textsf {-GDM}\vdash \mathcal {C}\textsf {-DM}$
.
Proof Let A and B be
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(2) (i)
![]() $\neg \exists u(\forall x\,{<}\,t)(\exists y\,{<}\,u) A[x,y]$
is equivalent to
$\neg \exists u(\forall x\,{<}\,t)(\exists y\,{<}\,u) A[x,y]$
is equivalent to
![]() $\neg (\forall x\,{<}\,t)\exists yA[x,y]$
by
$\neg (\forall x\,{<}\,t)\exists yA[x,y]$
by
![]() $\mathcal {C}\textsf {-Bdg}$
and to
$\mathcal {C}\textsf {-Bdg}$
and to
![]() $(\exists x\,{<}\,t)\forall y\neg A[x,y]$
by
$(\exists x\,{<}\,t)\forall y\neg A[x,y]$
by
![]() $\exists ^0\mathcal {C}\textsf {-GDM}$
. (ii)
$\exists ^0\mathcal {C}\textsf {-GDM}$
. (ii)
![]() $\neg \neg (\neg A{\lor }\neg B)$
,
$\neg \neg (\neg A{\lor }\neg B)$
,
![]() $(\neg \neg A{\land }\neg \neg B)\,{\to }\,\bot $
and
$(\neg \neg A{\land }\neg \neg B)\,{\to }\,\bot $
and
![]() $\neg (A{\land } B)$
are equivalent.
$\neg (A{\land } B)$
are equivalent.
(3)
![]() $\neg \neg (\exists x\,{<}\,y)\neg A$
is equivalent to
$\neg \neg (\exists x\,{<}\,y)\neg A$
is equivalent to
![]() $\neg (\forall x\,{<}\,y)\neg \neg A$
and implies
$\neg (\forall x\,{<}\,y)\neg \neg A$
and implies
![]() $\neg (\forall x\,{<}\,y)A$
. Thus
$\neg (\forall x\,{<}\,y)A$
. Thus
![]() $\mathcal {C}\textsf {-DNE}$
yields the converse.
$\mathcal {C}\textsf {-DNE}$
yields the converse.
Lemma 2.24.
-
(1) Over
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}$
, (i)
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}$
, (i)
 $\neg \Pi ^0_{n}=\Sigma ^0_{n}$
; (ii)
$\neg \Pi ^0_{n}=\Sigma ^0_{n}$
; (ii)
 $\neg \Sigma ^0_{n+1}=\Pi ^0_{n+1}$
; and so (iii)
$\neg \Sigma ^0_{n+1}=\Pi ^0_{n+1}$
; and so (iii)
 $\Pi ^0_{n+1}\textsf {-DNE}$
holds.
$\Pi ^0_{n+1}\textsf {-DNE}$
holds. -
(2) Over
 $\mathbf{EL}_0^-$
, the following hold.
$\mathbf{EL}_0^-$
, the following hold.-
(i)
 $\Sigma ^0_{n+1}\textsf {-DNE}$
yields
$\Sigma ^0_{n+1}\textsf {-DNE}$
yields
 $\Sigma ^0_{n}\textsf {-GDM}$
;
$\Sigma ^0_{n}\textsf {-GDM}$
; -
(ii)
 $\Sigma ^0_{n}\textsf {-GDM}\land \Sigma ^0_{n-1}\textsf {-DNE}$
yields
$\Sigma ^0_{n}\textsf {-GDM}\land \Sigma ^0_{n-1}\textsf {-DNE}$
yields
 $\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
;
$\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
; -
(iii)
 $\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
yields
$\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
yields
 $\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
;
$\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
; -
(iv) both
 $\Sigma ^0_{n+1}\textsf {-DNE}$
and
$\Sigma ^0_{n+1}\textsf {-DNE}$
and
 $\Pi ^0_{n+1}{\lor }\Pi ^0_{n+1}\textsf {-DNE}$
yield
$\Pi ^0_{n+1}{\lor }\Pi ^0_{n+1}\textsf {-DNE}$
yield
 $\Sigma ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
;
$\Sigma ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
; -
(v)
 $\Sigma ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
is equivalent to
$\Sigma ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
is equivalent to
 $\Sigma ^0_{n}\textsf {-LEM}$
;
$\Sigma ^0_{n}\textsf {-LEM}$
; -
(vi)
 $\Sigma ^0_{n}\textsf {-LEM}$
yields
$\Sigma ^0_{n}\textsf {-LEM}$
yields
 $\Sigma ^0_{n}\textsf {-DNE}$
and
$\Sigma ^0_{n}\textsf {-DNE}$
and
 $\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
.
$\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
.
-
Proof (1) By induction,
![]() $\neg \Pi ^0_{n} \,{=}\,\neg \forall ^0\neg \neg \Sigma ^0_{n-1} \,{=}\,\neg \neg \exists ^0\neg \Sigma ^0_{n-1} \,{=}\,\neg \neg \exists ^0\Pi ^0_{n-1} \,{=}\,\Sigma ^0_{n}$
, and
$\neg \Pi ^0_{n} \,{=}\,\neg \forall ^0\neg \neg \Sigma ^0_{n-1} \,{=}\,\neg \neg \exists ^0\neg \Sigma ^0_{n-1} \,{=}\,\neg \neg \exists ^0\Pi ^0_{n-1} \,{=}\,\Sigma ^0_{n}$
, and
![]() $\neg \Sigma ^0_{n+1} \,{=}\,\forall ^0\neg \Pi ^0_{n}\,{=}\,\forall ^0\Sigma ^0_{n}$
.
$\neg \Sigma ^0_{n+1} \,{=}\,\forall ^0\neg \Pi ^0_{n}\,{=}\,\forall ^0\Sigma ^0_{n}$
.
(2) (i) and (ii) are by 2.23(3), since
![]() $\Sigma ^0_{n-1}\textsf {-DNE}$
implies
$\Sigma ^0_{n-1}\textsf {-DNE}$
implies
![]() $\neg \Sigma ^0_{n}\,{=}\,\Pi ^0_{n}$
and since
$\neg \Sigma ^0_{n}\,{=}\,\Pi ^0_{n}$
and since
![]() $\textsf {B}\exists ^0(\neg \Sigma ^0_{n}) \,{=}\,\textsf {B}\Sigma ^0_{n+1}\,{\subseteq }\,\Sigma ^0_{n+1}$
. (iii) and (iv) are by 2.11. For (v), for A from
$\textsf {B}\exists ^0(\neg \Sigma ^0_{n}) \,{=}\,\textsf {B}\Sigma ^0_{n+1}\,{\subseteq }\,\Sigma ^0_{n+1}$
. (iii) and (iv) are by 2.11. For (v), for A from
![]() $\Sigma ^0_{n-1}$
,
$\Sigma ^0_{n-1}$
,
![]() $\Sigma ^0_{n-1}\textsf {-DNE}$
applied to
$\Sigma ^0_{n-1}\textsf {-DNE}$
applied to
![]() $\neg ((\forall xA)\land \neg \forall xA)$
yields
$\neg ((\forall xA)\land \neg \forall xA)$
yields
![]() $\neg ((\forall x\neg \neg A)\land \neg \forall xA)$
and hence
$\neg ((\forall x\neg \neg A)\land \neg \forall xA)$
and hence
![]() $\neg \neg (\exists x\neg A \lor \forall xA)$
where
$\neg \neg (\exists x\neg A \lor \forall xA)$
where
![]() $\neg \Sigma ^0_{n-1} =\Pi ^0_{n-1}$
. The rest of (v) and (vi) are by 2.23(1).
$\neg \Sigma ^0_{n-1} =\Pi ^0_{n-1}$
. The rest of (v) and (vi) are by 2.23(1).
We thus obtain the diagram in Section 1.5. [Reference Akama, Berardi, Hayashi and Kohlenbach1] showed the independence of
![]() $\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
and
$\Pi ^0_{n}{\lor }\Pi ^0_{n}\textsf {-DNE}$
and
![]() $\Sigma ^0_{n}\textsf {-DNE}$
, and the non-reversibility of (2) (i), (iv) and (vi) for
$\Sigma ^0_{n}\textsf {-DNE}$
, and the non-reversibility of (2) (i), (iv) and (vi) for
![]() $n\,{>}\,0$
. While (ii) and (iii) are reversible with
$n\,{>}\,0$
. While (ii) and (iii) are reversible with
![]() $\Delta ^1_0\textsf {-Ind}$
, we do not know over
$\Delta ^1_0\textsf {-Ind}$
, we do not know over
![]() $\textbf {EL}_0^-$
if they are nor if
$\textbf {EL}_0^-$
if they are nor if
![]() $\Pi ^0_{n+1}{\lor }\Pi ^0_{n+1}\textsf {-DNE}$
or
$\Pi ^0_{n+1}{\lor }\Pi ^0_{n+1}\textsf {-DNE}$
or
![]() $\Sigma ^0_{n}\textsf {-LEM}$
implies
$\Sigma ^0_{n}\textsf {-LEM}$
implies
![]() $\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
or
$\textsf {B}\Sigma ^0_{n+1}\textsf {-DNE}$
or
![]() $\Sigma ^0_{n}\textsf {-GDM}$
.
$\Sigma ^0_{n}\textsf {-GDM}$
.
2.5 Brouwerian axioms
2.5.1 Bar induction
Definition 2.25 (
 $\textsf {Bar}$
)
$\textsf {Bar}$
)
Let
Definition 2.26 (
 $\mathcal {C}\textsf {-BI}_D$
,
$\mathcal {C}\textsf {-BI}_D$
,
 $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
,
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
,
 $\mathcal {C}\textsf {-BI}$
)
$\mathcal {C}\textsf {-BI}$
)
Define the following axiom schemata:
-
(
 $\mathcal {C}\textsf {-BI}_D$
):
$\mathcal {C}\textsf {-BI}_D$
):
 $\textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \,{\land }\,\forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\land }\,\forall u(\alpha (u)\,{=}\,0\,{\to }\,A[u])\\ \phantom{\textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \, \, \, \,\, \textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \,{\land }\,} {\to }\, A[\langle \,\rangle ]$
;
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \,{\land }\,\forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\land }\,\forall u(\alpha (u)\,{=}\,0\,{\to }\,A[u])\\ \phantom{\textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \, \, \, \,\, \textsf {Bar}[\,\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}] \,{\land }\,} {\to }\, A[\langle \,\rangle ]$
; -
(
 $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
):
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
):
 $\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}] \,{\land }\,\forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\land }\,\forall u(B[u]\,{\to }\,A[u])\\ \phantom{AAAAAAAAAAAA} {\to }\,(\forall u,v(B[u]\,{\to }\,B[u{*}v])\,{\to }\, A[\langle \,\rangle ])$
;
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}] \,{\land }\,\forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\land }\,\forall u(B[u]\,{\to }\,A[u])\\ \phantom{AAAAAAAAAAAA} {\to }\,(\forall u,v(B[u]\,{\to }\,B[u{*}v])\,{\to }\, A[\langle \,\rangle ])$
; -
(
 $\mathcal {C}\textsf {-BI}$
):
$\mathcal {C}\textsf {-BI}$
):
 $\textsf {Bar}[\,\underline {0},\left \{u{:}\,A[u]\right \}] \land \forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\to }\, A[\langle \,\rangle ]$
,
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,A[u]\right \}] \land \forall u(\forall xA[u{*}\langle x\rangle ]\,{\to }\, A[u]) \,{\to }\, A[\langle \,\rangle ]$
,
for any A from
![]() $\mathcal {C}$
and B from
$\mathcal {C}$
and B from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Note that, in
![]() $\mathcal {C}\textsf {-BI}$
we do not distinguish B from A, since
$\mathcal {C}\textsf {-BI}$
we do not distinguish B from A, since
![]() $\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}]$
and
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}]$
and
![]() $\forall u(B[u]\,{\to }\,A[u])$
imply
$\forall u(B[u]\,{\to }\,A[u])$
imply
![]() $\textsf {Bar}[\,\underline {0},\left \{u{:}\,A[u]\right \}]$
.
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,A[u]\right \}]$
.
As
![]() $\textsf {LPO}$
is absolutely against Brouwer’s philosophy, 2.27 below shows that
$\textsf {LPO}$
is absolutely against Brouwer’s philosophy, 2.27 below shows that
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BI}$
cannot be a Brouwerian axiom though Brouwer’s original texts look to accept it. Whereas Kleene presumed that Brouwer had meant
$\mathcal {L}_{\mathrm{F}}\textsf {-BI}$
cannot be a Brouwerian axiom though Brouwer’s original texts look to accept it. Whereas Kleene presumed that Brouwer had meant
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
, it seems more common to consider
$\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
, it seems more common to consider
![]() $(\mathcal {L}_{\mathrm{F}},\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
(see, e.g., [Reference Veldman53]), which are, as will be shown in 2.28(1)(iii) and 2.39(4), equivalent to
$(\mathcal {L}_{\mathrm{F}},\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
(see, e.g., [Reference Veldman53]), which are, as will be shown in 2.28(1)(iii) and 2.39(4), equivalent to
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
under another Brouwerian axiom. Yet, there seems to be no positive argument for this presumption in the literature (for, monotonicity was not mentioned explicitly in the original texts and there might be other ways to restrict bar induction consistently with other Brouwerian axioms) and
$\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
under another Brouwerian axiom. Yet, there seems to be no positive argument for this presumption in the literature (for, monotonicity was not mentioned explicitly in the original texts and there might be other ways to restrict bar induction consistently with other Brouwerian axioms) and
![]() $\mathcal {C}\textsf {-BI}$
for
$\mathcal {C}\textsf {-BI}$
for
![]() $\mathcal {C}\,{\not \supseteq }\,\Sigma ^0_1{\lor }\Pi ^0_1$
is still not refuted. However we do not need to enter into such discussion, since our result will be same for
$\mathcal {C}\,{\not \supseteq }\,\Sigma ^0_1{\lor }\Pi ^0_1$
is still not refuted. However we do not need to enter into such discussion, since our result will be same for
![]() $\mathcal {C}\textsf {-BI}$
and
$\mathcal {C}\textsf {-BI}$
and
![]() $\mathcal {C}\textsf {-BI}_D$
, and hence for any variant inbetween, including
$\mathcal {C}\textsf {-BI}_D$
, and hence for any variant inbetween, including
![]() $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
. Actually below we see:
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
. Actually below we see:
![]() $\Pi ^0_1\textsf {-BI}$
is finitistically justifiable and this is optimal in the sense that
$\Pi ^0_1\textsf {-BI}$
is finitistically justifiable and this is optimal in the sense that
![]() $\Sigma ^0_1\textsf {-BI}_D$
is not.
$\Sigma ^0_1\textsf {-BI}_D$
is not.
Lemma 2.27.
![]() $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-LEM}{+}(\exists ^0\mathcal {C}\,{\lor }\,\forall ^0\neg \mathcal {C}) \textsf {-BI}\,{\vdash }\,\exists ^0\mathcal {C}\textsf {-LEM}$
.
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-LEM}{+}(\exists ^0\mathcal {C}\,{\lor }\,\forall ^0\neg \mathcal {C}) \textsf {-BI}\,{\vdash }\,\exists ^0\mathcal {C}\textsf {-LEM}$
.
In particular
![]() $\mathbf{EL}_0^-{+}(\Sigma ^0_1\,{\lor }\,\Pi ^0_1)\textsf {-BI}\vdash \textsf {LPO}$
.
$\mathbf{EL}_0^-{+}(\Sigma ^0_1\,{\lor }\,\Pi ^0_1)\textsf {-BI}\vdash \textsf {LPO}$
.
Proof Let
![]() $C[x]$
be
$C[x]$
be
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
If
![]() $\forall xB[u{*}\langle x\rangle ]$
then
$\forall xB[u{*}\langle x\rangle ]$
then
![]() $|u|\,{=}\,0\land \forall x\neg C[x]$
and
$|u|\,{=}\,0\land \forall x\neg C[x]$
and
![]() $B[u]$
.
$B[u]$
.
![]() $\mathcal {C}\textsf {-LEM}$
yields
$\mathcal {C}\textsf {-LEM}$
yields
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
by
$\textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
by
![]() $C[\alpha (0)]\,{\to }\,B[\alpha {\upharpoonright }0]$
and
$C[\alpha (0)]\,{\to }\,B[\alpha {\upharpoonright }0]$
and
![]() $\neg C[\alpha (0)]\,{\to }\,B[\alpha {\upharpoonright }1]$
.
$\neg C[\alpha (0)]\,{\to }\,B[\alpha {\upharpoonright }1]$
.
Lemma 2.28.
-
(1) (i)
 $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}\,{\vdash }\,(\mathcal {C},\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
;
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}\,{\vdash }\,(\mathcal {C},\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
;(ii)
 $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D\,{\vdash }\,(\mathcal {C},\Delta ^0_0)\textsf {-BI}_M$
;
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D\,{\vdash }\,(\mathcal {C},\Delta ^0_0)\textsf {-BI}_M$
;(iii)
 $\mathbf{EL}_0^-{+}(\mathcal {C},\Delta ^0_0)\textsf {-BI}_M\,{\vdash }\,\mathcal {C}\textsf {-BI}_D$
.
$\mathbf{EL}_0^-{+}(\mathcal {C},\Delta ^0_0)\textsf {-BI}_M\,{\vdash }\,\mathcal {C}\textsf {-BI}_D$
. -
(2)
 $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D \,{\vdash }\,\mathcal {C}\textsf {-Ind}$
.
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D \,{\vdash }\,\mathcal {C}\textsf {-Ind}$
. -
(3)
 $\mathbf{EL}_0^-{+} \exists ^0\mathcal {C}\textsf {-DNE} {+}\mathcal {C}\textsf {-DC}^0 \vdash \neg \mathcal {C}\textsf {-BI}$
.
$\mathbf{EL}_0^-{+} \exists ^0\mathcal {C}\textsf {-DNE} {+}\mathcal {C}\textsf {-DC}^0 \vdash \neg \mathcal {C}\textsf {-BI}$
. -
(4)
 $\mathbf{EL}_0^-{+}(\mathcal {D},\textsf {B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash (\mathcal {D},\exists ^0\mathcal {C})\textsf {-BI}_M$
.
$\mathbf{EL}_0^-{+}(\mathcal {D},\textsf {B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash (\mathcal {D},\exists ^0\mathcal {C})\textsf {-BI}_M$
. -
(5) (i)
 $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D\vdash \forall ^0\mathcal {C}\textsf {-BI}_D$
;
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}_D\vdash \forall ^0\mathcal {C}\textsf {-BI}_D$
;(ii)
 $\mathbf{EL}_0^-{+}(\mathcal {C},\mathcal {D})\textsf {-BI}_M\vdash (\forall ^0\mathcal {C},\mathcal {D})\textsf {-BI}_M$
; and
$\mathbf{EL}_0^-{+}(\mathcal {C},\mathcal {D})\textsf {-BI}_M\vdash (\forall ^0\mathcal {C},\mathcal {D})\textsf {-BI}_M$
; and(iii)
 $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}\vdash \forall ^0\mathcal {C}\textsf {-BI}$
.
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-BI}\vdash \forall ^0\mathcal {C}\textsf {-BI}$
.
Proof (1) (i) Trivial. (ii) Easy by 2.10(d). (iii) Let
Then
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
implies
$\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
implies
![]() $\textsf { Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, and also
$\textsf { Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, and also
![]() $B[u{*}\langle x\rangle ]$
implies
$B[u{*}\langle x\rangle ]$
implies
![]() $B[u]\,{\lor }\,\alpha (u{*}\langle x\rangle )\,{=}\,0$
and
$B[u]\,{\lor }\,\alpha (u{*}\langle x\rangle )\,{=}\,0$
and
![]() $B[u]\,{\lor }\,A[u{*}\langle x\rangle ]$
if
$B[u]\,{\lor }\,A[u{*}\langle x\rangle ]$
if
![]() $\forall u(\alpha (u)\,{=}\,0\,{\to }\,A[u])$
. Thus we can see that
$\forall u(\alpha (u)\,{=}\,0\,{\to }\,A[u])$
. Thus we can see that
![]() $\forall x(B[u{*}\langle x\rangle ]\,{\lor }\,A[u{*}\langle x\rangle ])$
implies
$\forall x(B[u{*}\langle x\rangle ]\,{\lor }\,A[u{*}\langle x\rangle ])$
implies
![]() $B[u]\,{\lor }\,\forall xA[u{*}\langle x\rangle ]$
and
$B[u]\,{\lor }\,\forall xA[u{*}\langle x\rangle ]$
and
![]() $B[u]\,{\lor }\,A[u]$
if
$B[u]\,{\lor }\,A[u]$
if
![]() $\forall xA[u{*}\langle x\rangle ]\,{\to }\,A[u]$
.
$\forall xA[u{*}\langle x\rangle ]\,{\to }\,A[u]$
.
In what follows, let C be
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(2) Assume
![]() $C[0]$
and
$C[0]$
and
![]() $(\forall x\,{<}\,n)(C[x]\,{\to }\,C[x{+}1])$
. Take
$(\forall x\,{<}\,n)(C[x]\,{\to }\,C[x{+}1])$
. Take
(3) Assume (a)
![]() $\textsf {Bar}[\,\underline {0},\left \{u{:}\,\neg C[u]\right \}]$
and (b)
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,\neg C[u]\right \}]$
and (b)
![]() $\forall u(\forall x\neg C[u{*}\langle x\rangle ]\,{\to }\,\neg C[u])$
. Let
$\forall u(\forall x\neg C[u{*}\langle x\rangle ]\,{\to }\,\neg C[u])$
. Let
By
![]() $\exists ^0\mathcal {C}\textsf {-DNE}$
with (b),
$\exists ^0\mathcal {C}\textsf {-DNE}$
with (b),
![]() $\forall u,v(B[u,v]{\to }\exists wB[v,w])$
. If
$\forall u,v(B[u,v]{\to }\exists wB[v,w])$
. If
![]() $C[\langle \,\rangle ]$
, as
$C[\langle \,\rangle ]$
, as
![]() $\exists vB[\langle \,\rangle ,v]$
,
$\exists vB[\langle \,\rangle ,v]$
,
![]() $\mathcal {C}\textsf {-DC}^0$
yields
$\mathcal {C}\textsf {-DC}^0$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $\forall nB[\alpha (n),\alpha (n{+}1)]$
and
$\forall nB[\alpha (n),\alpha (n{+}1)]$
and
![]() $\alpha (0)\,{=}\,\langle \,\rangle $
and, for
$\alpha (0)\,{=}\,\langle \,\rangle $
and, for
![]() $\beta (n)\,{:=}\,(\alpha (n{+}1))(n)$
,
$\beta (n)\,{:=}\,(\alpha (n{+}1))(n)$
,
![]() $\Delta ^0_0\textsf {-Ind}$
shows
$\Delta ^0_0\textsf {-Ind}$
shows
![]() $\alpha (n)\,{=}\,\beta {\upharpoonright } n$
and so
$\alpha (n)\,{=}\,\beta {\upharpoonright } n$
and so
![]() $\forall nC[\beta {\upharpoonright } n]$
contradicting (a).
$\forall nC[\beta {\upharpoonright } n]$
contradicting (a).
(4) Let
![]() $B[u]\,{:\equiv }\,(\exists x,y\,{<}\,|u|)C[u{\upharpoonright }y,x]$
. Obviously
$B[u]\,{:\equiv }\,(\exists x,y\,{<}\,|u|)C[u{\upharpoonright }y,x]$
. Obviously
![]() $B[u]\,{\to }\,B[u{*}v]$
.
$B[u]\,{\to }\,B[u{*}v]$
.
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\exists xC[u,x]\right \}]$
implies
$\textsf {Bar}[\underline {0},\left \{u{:}\,\exists xC[u,x]\right \}]$
implies
![]() $\textsf { Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, and
$\textsf { Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, and
![]() $B[u]$
implies
$B[u]$
implies
![]() $\exists xC[u,x]$
, if
$\exists xC[u,x]$
, if
![]() $\forall u,v(\exists xC[u,x]\,{\to }\,\exists xC[u{*}v,x])$
.
$\forall u,v(\exists xC[u,x]\,{\to }\,\exists xC[u{*}v,x])$
.
(5)(i) Let
![]() $[v]^2_0\, {:=}\,\langle (v(0))^2_0,\dots ,(v(|v|{-}1))^2_0\rangle $
and
$[v]^2_0\, {:=}\,\langle (v(0))^2_0,\dots ,(v(|v|{-}1))^2_0\rangle $
and
![]() $A[y,u]\,{:\equiv }\,C[[u]^2_0,((\langle y\rangle {*}u)(|u|))^2_1]$
. If
$A[y,u]\,{:\equiv }\,C[[u]^2_0,((\langle y\rangle {*}u)(|u|))^2_1]$
. If
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
and
$\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
and
![]() $\forall u(\alpha (u)\,{=}\,0\,{\to }\,\forall zC[u,z])$
then
$\forall u(\alpha (u)\,{=}\,0\,{\to }\,\forall zC[u,z])$
then
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha ([u]^2_0)\,{=}\,0\right \}]$
and
$\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha ([u]^2_0)\,{=}\,0\right \}]$
and
![]() $\forall u(\alpha ([u]^2_0)\,{=}\,0\,{\to }\,A[y,u])$
.
$\forall u(\alpha ([u]^2_0)\,{=}\,0\,{\to }\,A[y,u])$
.
Moreover if
![]() $\forall u(\forall x,zC[u{*}\langle x\rangle ,z] \to \forall zC[u,z])$
, then
$\forall u(\forall x,zC[u{*}\langle x\rangle ,z] \to \forall zC[u,z])$
, then
![]() $\forall xA[y,u{*}\langle x\rangle ]$
, i.e.,
$\forall xA[y,u{*}\langle x\rangle ]$
, i.e.,
![]() $\forall xC[[u]^2_0{*}\langle (x)^2_0\rangle , (x)^2_1]$
yields
$\forall xC[[u]^2_0{*}\langle (x)^2_0\rangle , (x)^2_1]$
yields
![]() $\forall zC[[u]^2_0,z]$
, and so
$\forall zC[[u]^2_0,z]$
, and so
![]() $A[y,u]$
.
$A[y,u]$
.
Thus
![]() $A[y,\langle \,\rangle ]$
by
$A[y,\langle \,\rangle ]$
by
![]() $\mathcal {C}\textsf {-BI}_D$
for any y. Hence
$\mathcal {C}\textsf {-BI}_D$
for any y. Hence
![]() $\forall zC[\langle \,\rangle ,z]$
. (ii) (iii) Similar.
$\forall zC[\langle \,\rangle ,z]$
. (ii) (iii) Similar.
Corollary 2.29.
-
(1)
 $\mathbf{EL}_0{+}\textsf {MP}\,{\vdash }\,\Pi ^0_1\textsf {-BI}$
.
$\mathbf{EL}_0{+}\textsf {MP}\,{\vdash }\,\Pi ^0_1\textsf {-BI}$
. -
(2)
 $\mathbf{EL}_0^- {+}\Sigma ^0_n\textsf {-BI}_D\,{\vdash }\,\Pi ^0_{n+1}\textsf {-Ind}$
.
$\mathbf{EL}_0^- {+}\Sigma ^0_n\textsf {-BI}_D\,{\vdash }\,\Pi ^0_{n+1}\textsf {-Ind}$
. -
(3)
 $\mathbf{EL}_0^-\vdash \mathcal {C}\textsf {-BI}_D\leftrightarrow (\mathcal {C},\Sigma ^0_1)\textsf {-BI}_M$
.
$\mathbf{EL}_0^-\vdash \mathcal {C}\textsf {-BI}_D\leftrightarrow (\mathcal {C},\Sigma ^0_1)\textsf {-BI}_M$
.
2.5.2 Fan theorem
Definition 2.30 (
 $\textsf {Fan}$
)
$\textsf {Fan}$
)
Let
![]() $u\,{<}\,\beta \,{:\equiv }\, (\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
and
$u\,{<}\,\beta \,{:\equiv }\, (\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
and
Definition 2.31 (
 $\mathcal {C}\textsf {-FT}$
,
$\mathcal {C}\textsf {-FT}$
,
 $\mathcal {C}\textsf {-BFT}$
,
$\mathcal {C}\textsf {-BFT}$
,
 $\mathcal {C}\textsf {-WFT}$
)
$\mathcal {C}\textsf {-WFT}$
)
For a class
![]() $\mathcal {C}$
of formulae, define the following axiom schemata:
$\mathcal {C}$
of formulae, define the following axiom schemata:
-
(
 $\mathcal {C}\textsf {-FT}$
):
$\mathcal {C}\textsf {-FT}$
):
 $\textsf {Fan}[\gamma ]\,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}] \to \exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) {{\kern-2pt}\to{\kern-2pt}} (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n])$
;
$\textsf {Fan}[\gamma ]\,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}] \to \exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) {{\kern-2pt}\to{\kern-2pt}} (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n])$
; -
(
 $\mathcal {C}\textsf {-BFT}$
):
$\mathcal {C}\textsf {-BFT}$
):
 $\textsf {Fan}[\gamma ]\, {\land }\,\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\beta )\,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]\\ \phantom{\hspace{120pt}}{\to }\;\exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) {{\kern-2pt}\to{\kern-2pt}} (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n])$
;
$\textsf {Fan}[\gamma ]\, {\land }\,\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\beta )\,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]\\ \phantom{\hspace{120pt}}{\to }\;\exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) {{\kern-2pt}\to{\kern-2pt}} (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n])$
; -
(
 $\mathcal {C}\textsf {-WFT}$
):
$\mathcal {C}\textsf {-WFT}$
):
 $(\forall \alpha \,{<}\,\underline {2})\exists nB[\alpha {\upharpoonright } n] \to \exists m(\forall \alpha \,{<}\,\underline {2})(\exists n\,{<}\,m)B[\alpha {\upharpoonright } n]$
,
$(\forall \alpha \,{<}\,\underline {2})\exists nB[\alpha {\upharpoonright } n] \to \exists m(\forall \alpha \,{<}\,\underline {2})(\exists n\,{<}\,m)B[\alpha {\upharpoonright } n]$
,
for any B from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
![]() $\mathcal {C}\textsf {-WFT}$
consists of the instances of
$\mathcal {C}\textsf {-WFT}$
consists of the instances of
![]() $\mathcal {C}\textsf {-FT}$
with
$\mathcal {C}\textsf {-FT}$
with
![]() $\gamma $
defined by
$\gamma $
defined by
![]() $\gamma (u)\,{=}\,0$
iff
$\gamma (u)\,{=}\,0$
iff
![]() $u\,{<}\,\underline {2}$
. This is a classical contrapositive of weak König’s lemma. 2.20 is enhanced as (1) in the following (cf. [Reference Simpson45, X.4 and IV.1.4]).
$u\,{<}\,\underline {2}$
. This is a classical contrapositive of weak König’s lemma. 2.20 is enhanced as (1) in the following (cf. [Reference Simpson45, X.4 and IV.1.4]).
Lemma 2.32.
-
(1)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Bdg} {+}\Delta ^0_0\textsf {-AC}^{00} {+}\Delta ^0_0\textsf {-BFT}$
is interpreted by
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Bdg} {+}\Delta ^0_0\textsf {-AC}^{00} {+}\Delta ^0_0\textsf {-BFT}$
is interpreted by
 $\mathfrak {g}$
in
$\mathfrak {g}$
in
 $\mathbf{WKL}_0^*$
.
$\mathbf{WKL}_0^*$
. -
(2) (i)
 $\mathbf{EL}_0^-{+}(\exists ^0\forall ^0\textsf {B}\exists ^0\mathcal {C},\textsf { B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash \mathcal {C}\textsf {-FT}$
; and
$\mathbf{EL}_0^-{+}(\exists ^0\forall ^0\textsf {B}\exists ^0\mathcal {C},\textsf { B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash \mathcal {C}\textsf {-FT}$
; and(ii)
 $\mathbf{EL}_0^-{+}(\exists ^0\textsf {B}\forall ^0\textsf {B}\exists ^0\mathcal {C},\textsf { B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash \mathcal {C}\textsf {-WFT}$
.
$\mathbf{EL}_0^-{+}(\exists ^0\textsf {B}\forall ^0\textsf {B}\exists ^0\mathcal {C},\textsf { B}\exists ^0\mathcal {C})\textsf {-BI}_M\vdash \mathcal {C}\textsf {-WFT}$
. -
(3) (i)
 $\mathbf{EL}_0^-{+}\textsf {B}\exists ^0\mathcal {C}\textsf {-FT}\,{\vdash }\, \exists ^0\mathcal {C}\textsf {-FT}$
and (ii)
$\mathbf{EL}_0^-{+}\textsf {B}\exists ^0\mathcal {C}\textsf {-FT}\,{\vdash }\, \exists ^0\mathcal {C}\textsf {-FT}$
and (ii)
 $\mathbf{EL}_0^-{+}\textsf {B}\exists ^0\mathcal {C}\textsf {-BFT}\,{\vdash }\, \exists ^0\mathcal {C}\textsf {-BFT}$
.
$\mathbf{EL}_0^-{+}\textsf {B}\exists ^0\mathcal {C}\textsf {-BFT}\,{\vdash }\, \exists ^0\mathcal {C}\textsf {-BFT}$
. -
(4)
 $\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-WFT}\,{\vdash }\, \mathcal {C}\textsf {-Bdg}$
.
$\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-WFT}\,{\vdash }\, \mathcal {C}\textsf {-Bdg}$
.
Proof In what follows, let C be from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(2) (i) Define A as follows, which is in
![]() $\exists ^0\forall ^0\textsf{B}\exists ^0\mathcal {C}$
:
$\exists ^0\forall ^0\textsf{B}\exists ^0\mathcal {C}$
:
If
![]() $\textsf {Fan}[\gamma ]$
then
$\textsf {Fan}[\gamma ]$
then
![]() $\forall ^0\textsf {B}\exists ^0\mathcal {C}\textsf {-Bdg}$
, which is by 2.28(2), yields
$\forall ^0\textsf {B}\exists ^0\mathcal {C}\textsf {-Bdg}$
, which is by 2.28(2), yields
![]() $\forall xA[u{*}\langle x\rangle ,\gamma ]\,{\to }\,A[u,\gamma ]$
.
$\forall xA[u{*}\langle x\rangle ,\gamma ]\,{\to }\,A[u,\gamma ]$
.
(ii) Similar.
(3) Let
![]() $B[u]:\equiv (\exists x,k\,{<}\,|u|)C[u{\upharpoonright } k,x]$
. As
$B[u]:\equiv (\exists x,k\,{<}\,|u|)C[u{\upharpoonright } k,x]$
. As
![]() $\exists k,xC[\alpha {\upharpoonright } k,x]$
implies
$\exists k,xC[\alpha {\upharpoonright } k,x]$
implies
![]() $\exists nB[\alpha {\upharpoonright } n]$
, if
$\exists nB[\alpha {\upharpoonright } n]$
, if
![]() $\textsf {Bar}[\gamma ,\left \{u{:}\,\exists xC[u,x]\right \}]$
then
$\textsf {Bar}[\gamma ,\left \{u{:}\,\exists xC[u,x]\right \}]$
then
![]() $\textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]$
.
$\textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]$
.
(4) Let
![]() $B[u,m]:\equiv |u|\,{\geq }\, m\land (\forall x\,{<}\,m)(u{\upharpoonright } x\,{=}\,\underline {0}{\upharpoonright } x\land u(x)\,{>}\,0 \,{\to }\, C[x,|u|{-}m])$
. Then
$B[u,m]:\equiv |u|\,{\geq }\, m\land (\forall x\,{<}\,m)(u{\upharpoonright } x\,{=}\,\underline {0}{\upharpoonright } x\land u(x)\,{>}\,0 \,{\to }\, C[x,|u|{-}m])$
. Then
![]() $(\forall x\,{<}\,m)\exists yC[x,y]$
implies
$(\forall x\,{<}\,m)\exists yC[x,y]$
implies
![]() $(\forall \alpha \,{<}\,\underline {2})\exists kB[\alpha {\upharpoonright } k,m]$
and, by
$(\forall \alpha \,{<}\,\underline {2})\exists kB[\alpha {\upharpoonright } k,m]$
and, by
![]() $\textsf {B}\forall ^0\mathcal {C}\textsf {-WFT}$
, it also implies
$\textsf {B}\forall ^0\mathcal {C}\textsf {-WFT}$
, it also implies
![]() $\exists n(\forall \alpha \,{<}\,\underline {2})(\exists k\,{<}\,n)B[\alpha {\upharpoonright } k,m]$
, and so
$\exists n(\forall \alpha \,{<}\,\underline {2})(\exists k\,{<}\,n)B[\alpha {\upharpoonright } k,m]$
, and so
![]() $\exists n(\forall x\,{<}\,m)(\exists y\,{<}\,n)C[x,y]$
.
$\exists n(\forall x\,{<}\,m)(\exists y\,{<}\,n)C[x,y]$
.
Thus, classically
![]() $\Sigma ^0_1\textsf {-BFT}$
is finitistically justifiable. This is optimal in the sense that
$\Sigma ^0_1\textsf {-BFT}$
is finitistically justifiable. This is optimal in the sense that
![]() $(\textbf {ACA}_0)^{\mathfrak {ch}}$
classically follows from
$(\textbf {ACA}_0)^{\mathfrak {ch}}$
classically follows from
![]() $\Pi ^0_1\textsf {-WFT}$
as shown in [Reference Berger7] (cf. 4.8(1)); and from
$\Pi ^0_1\textsf {-WFT}$
as shown in [Reference Berger7] (cf. 4.8(1)); and from
![]() $\Delta ^0_0\textsf {-FT}$
as in [Reference Simpson45, Theorem III.7.2] (cf. 4.9(1)). Though [Reference Simpson45, Theorem III.7.2] relies on
$\Delta ^0_0\textsf {-FT}$
as in [Reference Simpson45, Theorem III.7.2] (cf. 4.9(1)). Though [Reference Simpson45, Theorem III.7.2] relies on
![]() $\Sigma ^0_1\textsf {-Ind}$
, it does not matter as seen in the next proposition.
$\Sigma ^0_1\textsf {-Ind}$
, it does not matter as seen in the next proposition.
Proposition 2.33.
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
proves
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
proves
![]() $\Sigma ^0_1\textsf {-Ind}$
.
$\Sigma ^0_1\textsf {-Ind}$
.
Proof Let C be
![]() $\Delta ^0_0$
. Assume
$\Delta ^0_0$
. Assume
![]() $\exists yC[0,y]$
and
$\exists yC[0,y]$
and
![]() $(\forall x\, {<} \,n)(\exists yC[x,y]\, {\to } \,\exists yC[x{+}1,y])$
. With
$(\forall x\, {<} \,n)(\exists yC[x,y]\, {\to } \,\exists yC[x{+}1,y])$
. With
![]() $\Delta ^0_0\textsf {-LNP}$
, by replacing
$\Delta ^0_0\textsf {-LNP}$
, by replacing
![]() $C[x,y]$
with
$C[x,y]$
with
![]() $C[x,y]\,{\land }\,(\forall z\,{<}\,y)\neg C[x,z]$
we may assume
$C[x,y]\,{\land }\,(\forall z\,{<}\,y)\neg C[x,z]$
we may assume
![]() $(C[x,y]\,{\land }\, C[x,z])\,{\to }\, y\,{=}\,z$
. Define
$(C[x,y]\,{\land }\, C[x,z])\,{\to }\, y\,{=}\,z$
. Define
![]() $\gamma $
and
$\gamma $
and
![]() $B[x,u]$
by
$B[x,u]$
by
 $$ \begin{align*} &\gamma(u)\,{=}\,0\,\leftrightarrow\,(\forall k\,{<}\,|u|) (u(k)\,{\neq}\, 0\to k\,{\leq}\,n\land(\forall l\,{\leq}\,k) (u(l)\,{\neq}\, 0\land C[l,u(l){-}1]));\\ &B[x,u]\,{:\equiv}\,|u|\,{>}\,u{\upharpoonright}(x{+}1). \end{align*} $$
$$ \begin{align*} &\gamma(u)\,{=}\,0\,\leftrightarrow\,(\forall k\,{<}\,|u|) (u(k)\,{\neq}\, 0\to k\,{\leq}\,n\land(\forall l\,{\leq}\,k) (u(l)\,{\neq}\, 0\land C[l,u(l){-}1]));\\ &B[x,u]\,{:\equiv}\,|u|\,{>}\,u{\upharpoonright}(x{+}1). \end{align*} $$
Assume
![]() $\gamma (u)\,{=}\,0$
. We prove
$\gamma (u)\,{=}\,0$
. We prove
![]() $\textsf {Fan}[\gamma ]$
by case-distinction:
$\textsf {Fan}[\gamma ]$
by case-distinction:
-
• if
 $(\forall k\,{<}\,|u|)(u(k)\,{\neq }\,0) \land |u|\,{\leq }\,n$
, then
$(\forall k\,{<}\,|u|)(u(k)\,{\neq }\,0) \land |u|\,{\leq }\,n$
, then
 $\forall x(\gamma (u{*}\langle x\rangle )\,{=}\,0\,{\leftrightarrow }\, x\,{=}\,0\,{\lor }\, x\,{=}\,y{+}1)$
for y with
$\forall x(\gamma (u{*}\langle x\rangle )\,{=}\,0\,{\leftrightarrow }\, x\,{=}\,0\,{\lor }\, x\,{=}\,y{+}1)$
for y with
 $C[|u|,y]$
, yielded by
$C[|u|,y]$
, yielded by
 $C[|u|{-}1,u(|u|{-}1){-}1]$
if
$C[|u|{-}1,u(|u|{-}1){-}1]$
if
 $|u|\,{>}\,0$
;
$|u|\,{>}\,0$
; -
• otherwise
 $\forall x(\gamma (u{*}\langle x\rangle )\,{=}\,0\,{\leftrightarrow }\, x\,{=}\,0)$
.
$\forall x(\gamma (u{*}\langle x\rangle )\,{=}\,0\,{\leftrightarrow }\, x\,{=}\,0)$
.
As
![]() $\forall \alpha \exists mB[n,\alpha {\upharpoonright } m]$
,
$\forall \alpha \exists mB[n,\alpha {\upharpoonright } m]$
,
![]() $\Delta ^0_0\textsf {-FT}$
yields m with
$\Delta ^0_0\textsf {-FT}$
yields m with
![]() $\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\, {=}\,0) \, {\to } \,(\exists k\,{<}\,m)B[n,\alpha {\upharpoonright } k])$
. By
$\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\, {=}\,0) \, {\to } \,(\exists k\,{<}\,m)B[n,\alpha {\upharpoonright } k])$
. By
![]() $\Delta ^0_0\textsf {-Ind}$
on
$\Delta ^0_0\textsf {-Ind}$
on
![]() $k\,{\leq }\, n{+}1$
we prove
$k\,{\leq }\, n{+}1$
we prove
![]() $(\exists u\,{<}\,m)D[k,u]$
for
$(\exists u\,{<}\,m)D[k,u]$
for
If
![]() $D[k,v]$
, the assumption yields y with
$D[k,v]$
, the assumption yields y with
![]() $C[k,y]$
; then
$C[k,y]$
; then
![]() $D[k{+}1,u]$
for
$D[k{+}1,u]$
for
![]() $u\,{:=}\,v{*}\langle y{+}1\rangle $
, and
$u\,{:=}\,v{*}\langle y{+}1\rangle $
, and
![]() $(\exists \ell \,{<}\,m)B[n,(u{*}\underline {0}){\upharpoonright } \ell ]$
which implies
$(\exists \ell \,{<}\,m)B[n,(u{*}\underline {0}){\upharpoonright } \ell ]$
which implies
![]() $u\,{\leq }\,(u{*}\underline {0}){\upharpoonright }(n{+}1)\,{<}\,\ell \,{<}\,m$
.
$u\,{\leq }\,(u{*}\underline {0}){\upharpoonright }(n{+}1)\,{<}\,\ell \,{<}\,m$
.
2.5.3 (Weak) continuity principles
Definition 2.34 (
 $\mathcal {C}\textsf {-WC}^i$
,
$\mathcal {C}\textsf {-WC}^i$
,
 $\mathcal {C}\textsf {-WC!}^i$
)
$\mathcal {C}\textsf {-WC!}^i$
)
For a class
![]() $\mathcal {C}$
of formulae and
$\mathcal {C}$
of formulae and
![]() $i\,{=}\,0,1$
,
$i\,{=}\,0,1$
,
![]() $\mathcal {C}\textsf {-WC}^i$
is defined as follows, and
$\mathcal {C}\textsf {-WC}^i$
is defined as follows, and
![]() $\mathcal {C}\textsf {-WC!}^i$
is defined with
$\mathcal {C}\textsf {-WC!}^i$
is defined with
![]() $\exists $
replaced by
$\exists $
replaced by
![]() $\exists !$
in the premises.
$\exists !$
in the premises.
-
(
 $\mathcal {C}\textsf {-WC}^0$
):
$\mathcal {C}\textsf {-WC}^0$
):
 $\forall \alpha \exists xA[\alpha ,x] \,{\to }\,\forall \alpha \exists x,m\forall \beta A[(\alpha {\upharpoonright } m){*}\beta ,x]$
;
$\forall \alpha \exists xA[\alpha ,x] \,{\to }\,\forall \alpha \exists x,m\forall \beta A[(\alpha {\upharpoonright } m){*}\beta ,x]$
; -
(
 $\mathcal {C}\textsf {-WC}^1$
):
$\mathcal {C}\textsf {-WC}^1$
):
 $\forall \alpha \exists \gamma A[\alpha ,\gamma ] \,{\to }\,\forall \alpha \exists \gamma (A[\alpha ,\gamma ]\land \forall n\exists m\forall \beta \exists \delta A[(\alpha {\upharpoonright } m){*}\beta ,(\gamma {\upharpoonright } n){*}\,\delta ])$
,Footnote
14
$\forall \alpha \exists \gamma A[\alpha ,\gamma ] \,{\to }\,\forall \alpha \exists \gamma (A[\alpha ,\gamma ]\land \forall n\exists m\forall \beta \exists \delta A[(\alpha {\upharpoonright } m){*}\beta ,(\gamma {\upharpoonright } n){*}\,\delta ])$
,Footnote
14
for A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
We can see that
![]() $(\exists ^1\mathcal {C})\textsf {-WC!}^0$
implies
$(\exists ^1\mathcal {C})\textsf {-WC!}^0$
implies
![]() $(\exists ^1\mathcal {C})\textsf {-WC!}^1$
, by considering
$(\exists ^1\mathcal {C})\textsf {-WC!}^1$
, by considering
Thus, with 2.35(1)(iii) below,
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^1$
and
$\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^1$
and
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^0$
are equivalent.Footnote
15
Informally this is an easy consequence of the universality (in the sense of category theory) of the product topology with which Baire space is equipped.
$\mathcal {L}_{\mathrm{F}}\textsf {-WC!}^0$
are equivalent.Footnote
15
Informally this is an easy consequence of the universality (in the sense of category theory) of the product topology with which Baire space is equipped.
![]() $\mathcal {C}\textsf {-WC}^i$
asserts the existence of a continuous branch cut, not the continuity of all branch cuts. We cannot show the equivalence between
$\mathcal {C}\textsf {-WC}^i$
asserts the existence of a continuous branch cut, not the continuity of all branch cuts. We cannot show the equivalence between
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-WC}^1$
and
$\mathcal {L}_{\mathrm{F}}\textsf {-WC}^1$
and
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-WC}^0$
, because of the results mentioned in f.n.15.
$\mathcal {L}_{\mathrm{F}}\textsf {-WC}^0$
, because of the results mentioned in f.n.15.
By 2.14,
![]() $\Sigma ^0_1\textsf {-WC!}^1$
is vacuous and
$\Sigma ^0_1\textsf {-WC!}^1$
is vacuous and
![]() $\mathbf{EL}_0^- \vdash \Sigma ^0_1\textsf {-WC}^1$
. Classically this is optimal by 2.35(2)(ii) below.
$\mathbf{EL}_0^- \vdash \Sigma ^0_1\textsf {-WC}^1$
. Classically this is optimal by 2.35(2)(ii) below.
Lemma 2.35.
-
(1) Over
 $\mathbf{EL}_0^-$
,
$\mathbf{EL}_0^-$
,-
(i)
 $\Sigma ^0_1\textsf {-WC}^1$
holds;
$\Sigma ^0_1\textsf {-WC}^1$
holds; -
(ii)
 $\mathcal {C}\textsf {-WC}^1$
implies
$\mathcal {C}\textsf {-WC}^1$
implies
 $\mathcal {C}\textsf {-WC}^0$
; and
$\mathcal {C}\textsf {-WC}^0$
; and -
(iii)
 $(\mathcal {C}\land \Pi ^0_1)\textsf {-WC!}^1$
implies
$(\mathcal {C}\land \Pi ^0_1)\textsf {-WC!}^1$
implies
 $\mathcal {C}\textsf {-WC!}^0$
.
$\mathcal {C}\textsf {-WC!}^0$
.
-
-
(2) (i)
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-WC}^0{+}\textsf {LLPO}$
is inconsistent; and
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-WC}^0{+}\textsf {LLPO}$
is inconsistent; and(ii)
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-WC!}^0{+}\textsf {LPO}$
is inconsistent.
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-WC!}^0{+}\textsf {LPO}$
is inconsistent.
Proof (1) As (ii) is easier, we prove (iii). For A from
![]() $\mathcal {C}$
, let
$\mathcal {C}$
, let
Then
![]() $\forall \alpha \exists ! xA[\alpha ,x]$
implies
$\forall \alpha \exists ! xA[\alpha ,x]$
implies
![]() $\forall \alpha \exists !\gamma B[\alpha ,\gamma ]$
. By applying
$\forall \alpha \exists !\gamma B[\alpha ,\gamma ]$
. By applying
![]() $(\mathcal {C}{\land }\Pi ^0_1)\textsf {-WC!}^1$
to the latter, we have
$(\mathcal {C}{\land }\Pi ^0_1)\textsf {-WC!}^1$
to the latter, we have
![]() $\forall \alpha \exists \gamma ,m(B[\alpha ,\gamma ]\land \forall \beta \exists \delta B[(\alpha {\upharpoonright } m){*}\beta ,(\gamma {\upharpoonright } 1){*}\delta ])$
.
$\forall \alpha \exists \gamma ,m(B[\alpha ,\gamma ]\land \forall \beta \exists \delta B[(\alpha {\upharpoonright } m){*}\beta ,(\gamma {\upharpoonright } 1){*}\delta ])$
.
(2)(i) Let
![]() $A[\alpha ,i]\,{:\equiv }\, \exists n(\alpha {\upharpoonright } n\,{=}\, \underline {0}{\upharpoonright } n\land \alpha (n)\,{>}\,0\land n\,{=}\,2{\cdot }\lfloor n/2\rfloor {+}\,i)$
which is
$A[\alpha ,i]\,{:\equiv }\, \exists n(\alpha {\upharpoonright } n\,{=}\, \underline {0}{\upharpoonright } n\land \alpha (n)\,{>}\,0\land n\,{=}\,2{\cdot }\lfloor n/2\rfloor {+}\,i)$
which is
![]() $\Sigma ^0_1$
. Since
$\Sigma ^0_1$
. Since
![]() $\neg (A[\alpha ,0]\land A[\alpha ,1])$
, by applying
$\neg (A[\alpha ,0]\land A[\alpha ,1])$
, by applying
![]() $\textsf { LLPO}$
, we have
$\textsf { LLPO}$
, we have
![]() $\forall \alpha \exists i\neg A[\alpha ,i]$
.
$\forall \alpha \exists i\neg A[\alpha ,i]$
.
![]() $\Pi ^0_1\textsf {-WC}^0$
yields i and n with
$\Pi ^0_1\textsf {-WC}^0$
yields i and n with
![]() $\forall \beta \neg A[(\underline {0}{\upharpoonright } n){*}\beta ,i]$
. Thus
$\forall \beta \neg A[(\underline {0}{\upharpoonright } n){*}\beta ,i]$
. Thus
![]() $\neg A[(\underline {0}{\upharpoonright } n){*}\underline {1},i]\land \neg A[(\underline {0}{\upharpoonright } (n{+}1)){*}\underline {1},i]$
, a contradiction.
$\neg A[(\underline {0}{\upharpoonright } n){*}\underline {1},i]\land \neg A[(\underline {0}{\upharpoonright } (n{+}1)){*}\underline {1},i]$
, a contradiction.
(ii) Let
![]() $A[\alpha ,n]\,{:\equiv }\, (n\,{=}\,0\,{\to }\,\alpha \,{=}\,\underline {0}) \land (n\,{>}\,0\,{\to }\,\alpha (n{-}1)\,{>}\,0\land \alpha {\upharpoonright }(n{-}1)\,{=}\, \underline {0}{\upharpoonright }(n{-}1))$
.
$A[\alpha ,n]\,{:\equiv }\, (n\,{=}\,0\,{\to }\,\alpha \,{=}\,\underline {0}) \land (n\,{>}\,0\,{\to }\,\alpha (n{-}1)\,{>}\,0\land \alpha {\upharpoonright }(n{-}1)\,{=}\, \underline {0}{\upharpoonright }(n{-}1))$
.
![]() $\textsf {LPO}$
and
$\textsf {LPO}$
and
![]() $\Delta ^0_0\textsf {-LNP}$
imply
$\Delta ^0_0\textsf {-LNP}$
imply
![]() $\forall \alpha \exists !nA[\alpha ,n]$
.
$\forall \alpha \exists !nA[\alpha ,n]$
.
![]() $\Pi ^0_1\textsf {-WC!}^0$
, applied to
$\Pi ^0_1\textsf {-WC!}^0$
, applied to
![]() $\underline {0}$
, leads a contradiction similarly.
$\underline {0}$
, leads a contradiction similarly.
2.5.4 Summary: maximal fragments in the classical setting
Proposition 2.36.
-
(i)
 $\mathbf{CFG}$
is interpreted by
$\mathbf{CFG}$
is interpreted by
 $\mathfrak {g}$
in
$\mathfrak {g}$
in
 $\mathbf{WKL}_0^*$
; and
$\mathbf{WKL}_0^*$
; and -
(ii)
 $\mathbf{CFG} {+}\Pi ^0_1\{\textsf {-BI},\textsf {-Ind}\} {+}\Sigma ^0_1\{\textsf {-DC}^1\!,\textsf {-DC}^0\!,\textsf {-Ind}\}$
is interpreted by
$\mathbf{CFG} {+}\Pi ^0_1\{\textsf {-BI},\textsf {-Ind}\} {+}\Sigma ^0_1\{\textsf {-DC}^1\!,\textsf {-DC}^0\!,\textsf {-Ind}\}$
is interpreted by
 $\mathfrak {g}$
in
$\mathfrak {g}$
in
 $\mathbf{WKL}_0$
,
$\mathbf{WKL}_0$
,
where
![]() $\mathbf{CFG} :\equiv \mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_1\{\textsf {-Bdg}, \textsf {-BFT}, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\!, \textsf {-WC}^0\!, \textsf {-WC}^1\}$
.
$\mathbf{CFG} :\equiv \mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_1\{\textsf {-Bdg}, \textsf {-BFT}, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\!, \textsf {-WC}^0\!, \textsf {-WC}^1\}$
.
Proof
![]() $\Sigma ^0_1\textsf {-AC}^{00}\!,\textsf {-DC}^{0}$
yield
$\Sigma ^0_1\textsf {-AC}^{00}\!,\textsf {-DC}^{0}$
yield
![]() $\Sigma ^0_1\textsf {-AC}^{01}\!,\textsf {-DC}^{1}$
by 2.14. The rest is by 2.32(1)(3),2.16(1)(2)(i)(4),2.29(1)(2),2.35(1).
$\Sigma ^0_1\textsf {-AC}^{01}\!,\textsf {-DC}^{1}$
by 2.14. The rest is by 2.32(1)(3),2.16(1)(2)(i)(4),2.29(1)(2),2.35(1).
These fragments are optimal (in the classical setting) in the following sense:
![]() $\Delta ^0_0\textsf {-DC}^i$
yields
$\Delta ^0_0\textsf {-DC}^i$
yields
![]() $\Sigma ^0_1\textsf {-Ind}$
by 2.16(2)(i)(3)(i);
$\Sigma ^0_1\textsf {-Ind}$
by 2.16(2)(i)(3)(i);
![]() $\Sigma ^0_1\textsf {-DC}!^1$
is vacuous by 2.14;
$\Sigma ^0_1\textsf {-DC}!^1$
is vacuous by 2.14;
![]() $\Pi ^0_1\textsf {-AC}!^{00}$
,
$\Pi ^0_1\textsf {-AC}!^{00}$
,
![]() $\Pi ^0_1\textsf {-BFT}$
and
$\Pi ^0_1\textsf {-BFT}$
and
![]() $\Delta ^0_0\textsf {-FT}$
imply
$\Delta ^0_0\textsf {-FT}$
imply
![]() $(\textbf {ACA}_0)^{\mathfrak {ch}}$
as mentioned before 2.33 where all
$(\textbf {ACA}_0)^{\mathfrak {ch}}$
as mentioned before 2.33 where all
![]() $\Pi ^0_1\textsf {-DC}!^1$
,
$\Pi ^0_1\textsf {-DC}!^1$
,
![]() $\Pi ^0_1\textsf {-DC}!^0$
and
$\Pi ^0_1\textsf {-DC}!^0$
and
![]() $\Pi ^0_1\textsf {-AC}!^{01}$
imply
$\Pi ^0_1\textsf {-AC}!^{01}$
imply
![]() $\Pi ^0_1\textsf {-AC}!^{00}$
by 2.16(2)(iv)(v)(vi) and
$\Pi ^0_1\textsf {-AC}!^{00}$
by 2.16(2)(iv)(v)(vi) and
![]() $\Sigma ^0_1\textsf {-BI}_D$
implies
$\Sigma ^0_1\textsf {-BI}_D$
implies
![]() $\Delta ^0_0\textsf {-FT}$
by 2.32(2)(i) and 2.28(1)(ii); and
$\Delta ^0_0\textsf {-FT}$
by 2.32(2)(i) and 2.28(1)(ii); and
![]() $\Pi ^0_1\textsf {-WC!}^0$
is inconsistent by 2.35(2)(ii).
$\Pi ^0_1\textsf {-WC!}^0$
is inconsistent by 2.35(2)(ii).
One of our main results is that for this optimality
![]() $\textsf {LPO}$
suffices instead of the full classical logic or
$\textsf {LPO}$
suffices instead of the full classical logic or
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
$\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
2.5.5 Continuous choice and remarks on choice axioms along functions
Notation 2.37.
![]() $\alpha \,{=}\,\beta |\gamma $
denotes a
$\alpha \,{=}\,\beta |\gamma $
denotes a
![]() $\Pi ^0_2$
formula
$\Pi ^0_2$
formula
Definition 2.38 (generalized continuous choice/bounding;
 $\mathcal {C}\textsf {-CC}^i$
,
$\mathcal {C}\textsf {-CC}^i$
,
 $\mathcal {C}\textsf {-CB}^i$
and
$\mathcal {C}\textsf {-CB}^i$
and
 $\mathcal {C}\textsf {-CC!}^i$
)
$\mathcal {C}\textsf {-CC!}^i$
)
For classes
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
of formulae, define the following axiom schemata:
$\mathcal {D}$
of formulae, define the following axiom schemata:
-
(
 $(\mathcal {C},\mathcal {D})\textsf {-GCC}^0$
):
$(\mathcal {C},\mathcal {D})\textsf {-GCC}^0$
):
 $\forall \alpha (B[\alpha ]{{\kern-2pt}\to{\kern-2pt}}\exists x A[\alpha ,x]) {{\kern-2pt}\to{\kern-2pt}} \exists \gamma \forall \alpha (B[\alpha ]{{\kern-2pt}\to{\kern-2pt}} \exists \delta (\delta \,{=}\,\gamma |\alpha {{\kern-2pt}\land{\kern-2pt}} A[\alpha ,\delta (0)]))$
;
$\forall \alpha (B[\alpha ]{{\kern-2pt}\to{\kern-2pt}}\exists x A[\alpha ,x]) {{\kern-2pt}\to{\kern-2pt}} \exists \gamma \forall \alpha (B[\alpha ]{{\kern-2pt}\to{\kern-2pt}} \exists \delta (\delta \,{=}\,\gamma |\alpha {{\kern-2pt}\land{\kern-2pt}} A[\alpha ,\delta (0)]))$
; -
(
 $(\mathcal {C},\mathcal {D})\textsf {-GCB}^0$
):
$(\mathcal {C},\mathcal {D})\textsf {-GCB}^0$
):
 $\forall \alpha (B[\alpha ]\,{\to }\,\exists x A[\alpha ,x])\\\phantom{\hspace{110pt}} {\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land (\exists y\,{<}\,\delta (0))A[\alpha ,y]))$
;
$\forall \alpha (B[\alpha ]\,{\to }\,\exists x A[\alpha ,x])\\\phantom{\hspace{110pt}} {\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land (\exists y\,{<}\,\delta (0))A[\alpha ,y]))$
; -
(
 $(\mathcal {C},\mathcal {D})\textsf {-GCC}^1$
):
$(\mathcal {C},\mathcal {D})\textsf {-GCC}^1$
):
 $\forall \alpha (B[\alpha ]\,{\to }\,\exists \beta A[\alpha ,\beta ]) \,{\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land A[\alpha ,\delta ]))$
;
$\forall \alpha (B[\alpha ]\,{\to }\,\exists \beta A[\alpha ,\beta ]) \,{\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land A[\alpha ,\delta ]))$
; -
(
 $(\mathcal {C},\mathcal {D})\textsf {-GCB}^1$
):
$(\mathcal {C},\mathcal {D})\textsf {-GCB}^1$
):
 $\forall \alpha (B[\alpha ]\,{\to }\,\exists \beta A[\alpha ,\beta ])\\ \phantom{\hspace{130pt}} {\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land (\exists \beta \,{<}\,\delta )A[\alpha ,\beta ]))$
,
$\forall \alpha (B[\alpha ]\,{\to }\,\exists \beta A[\alpha ,\beta ])\\ \phantom{\hspace{130pt}} {\to }\, \exists \gamma \forall \alpha (B[\alpha ]\,{\to }\, \exists \delta (\delta \,{=}\,\gamma |\alpha \land (\exists \beta \,{<}\,\delta )A[\alpha ,\beta ]))$
,
for any A from
![]() $\mathcal {C}$
and B from
$\mathcal {C}$
and B from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
![]() $(\mathcal {C},\mathcal {D})\textsf {-GCC!}^i$
is defined with
$(\mathcal {C},\mathcal {D})\textsf {-GCC!}^i$
is defined with
![]() $\exists $
replaced by
$\exists $
replaced by
![]() $\exists !$
in the premise;
$\exists !$
in the premise;
![]() $\mathcal {C}\textsf {-CC}^i$
,
$\mathcal {C}\textsf {-CC}^i$
,
![]() $\mathcal {C}\textsf {-CB}^i$
and
$\mathcal {C}\textsf {-CB}^i$
and
![]() $\mathcal {C}\textsf {-CC!}^i$
are by setting
$\mathcal {C}\textsf {-CC!}^i$
are by setting
![]() $B\,{\equiv }\,\top $
.
$B\,{\equiv }\,\top $
.
![]() $\mathcal {C}\textsf {-CC}^1$
could be seen as the conjunction of
$\mathcal {C}\textsf {-CC}^1$
could be seen as the conjunction of
![]() $\mathcal {C}\textsf {-AC}^{11}$
the axiom of function-function choice for
$\mathcal {C}\textsf {-AC}^{11}$
the axiom of function-function choice for
![]() $\mathcal {C}$
properties and
$\mathcal {C}$
properties and
![]() $\mathcal {C}\textsf {-CC!}^1$
asserting that any
$\mathcal {C}\textsf {-CC!}^1$
asserting that any
![]() $\mathcal {C}$
-definable functional is represented as
$\mathcal {C}$
-definable functional is represented as
![]() $\alpha \mapsto \gamma |\alpha $
for some
$\alpha \mapsto \gamma |\alpha $
for some
![]() $\gamma $
.
$\gamma $
.
Even while
![]() $\mathcal {C}\textsf {-AC}^{1i}$
’s are not formalizable in our
$\mathcal {C}\textsf {-AC}^{1i}$
’s are not formalizable in our
![]() $\mathcal {L}_{\mathrm{F}}$
, it is plausible to think: (1)
$\mathcal {L}_{\mathrm{F}}$
, it is plausible to think: (1)
![]() $\mathcal {C}\textsf {-AC}!^{1i}$
implies
$\mathcal {C}\textsf {-AC}!^{1i}$
implies
![]() $\mathcal {C}\textsf {-AC}!^{0i}$
; and (2)
$\mathcal {C}\textsf {-AC}!^{0i}$
; and (2)
![]() $\mathcal {C}\textsf {-AC}^{1i}$
’s follow from
$\mathcal {C}\textsf {-AC}^{1i}$
’s follow from
![]() $\mathcal {C}\textsf {-CC}^i$
and
$\mathcal {C}\textsf {-CC}^i$
and
![]() $\mathcal {C}\textsf {-AC}!^{1i}$
’s from
$\mathcal {C}\textsf {-AC}!^{1i}$
’s from
![]() $\mathcal {C}\textsf {-CC}!^i$
if all the classes in the axioms of the system are closed under
$\mathcal {C}\textsf {-CC}!^i$
if all the classes in the axioms of the system are closed under
![]() $\Sigma ^0_1$
definable total functions. For, “imaginary” choice functionals would be of the base complexity but, for (2), be coded by
$\Sigma ^0_1$
definable total functions. For, “imaginary” choice functionals would be of the base complexity but, for (2), be coded by
![]() $\alpha |\beta $
, which is
$\alpha |\beta $
, which is
![]() $\Sigma ^0_1$
definable as far as
$\Sigma ^0_1$
definable as far as
![]() $(\alpha |\beta ){\downarrow }$
. As
$(\alpha |\beta ){\downarrow }$
. As
![]() $\Sigma ^0_1\textsf {-AC}^{00}$
makes
$\Sigma ^0_1\textsf {-AC}^{00}$
makes
![]() $\mathbf{EL}_0^-$
satisfy this condition by overwriting 2.10(d), we can “imaginarily” evaluate the strength of
$\mathbf{EL}_0^-$
satisfy this condition by overwriting 2.10(d), we can “imaginarily” evaluate the strength of
![]() $\mathcal {C}\textsf {-AC}^{1i}$
, by that of
$\mathcal {C}\textsf {-AC}^{1i}$
, by that of
![]() $\mathcal {C}\textsf {-CC}^i{+}\Sigma ^0_1\textsf {-AC}^{00}$
from above and
$\mathcal {C}\textsf {-CC}^i{+}\Sigma ^0_1\textsf {-AC}^{00}$
from above and
![]() $\mathcal {C}\textsf {-AC}!^{0i}$
from below. We could thus add
$\mathcal {C}\textsf {-AC}!^{0i}$
from below. We could thus add
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{1i}$
’s (as we can add
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{1i}$
’s (as we can add
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-CC}^i$
) in Section 1.4;
$\mathcal {L}_{\mathrm{F}}\textsf {-CC}^i$
) in Section 1.4;
![]() $\Sigma ^0_1\textsf {-AC}^{1i}$
’s in Section 2.5.4 by 2.39(1); and claim that
$\Sigma ^0_1\textsf {-AC}^{1i}$
’s in Section 2.5.4 by 2.39(1); and claim that
![]() $\textsf {LPO}{+}\Pi ^0_1\textsf {-AC}!^{1i}$
’s are non-justifiable by 4.9(iii) and 2.16(2)(vi).
$\textsf {LPO}{+}\Pi ^0_1\textsf {-AC}!^{1i}$
’s are non-justifiable by 4.9(iii) and 2.16(2)(vi).
Similarly, we could consider that
![]() $\mathcal {C}\textsf {-AC}^{10}$
(and so
$\mathcal {C}\textsf {-AC}^{10}$
(and so
![]() $\mathcal {C}\textsf {-AC}^{11}$
) makes
$\mathcal {C}\textsf {-AC}^{11}$
) makes
![]() $\mathcal {C}\textsf {-WC}^0$
and
$\mathcal {C}\textsf {-WC}^0$
and
![]() $\mathcal {C}\textsf {-WC}!^0$
be equivalent. From 2.35(2)(i) we could claim that neither
$\mathcal {C}\textsf {-WC}!^0$
be equivalent. From 2.35(2)(i) we could claim that neither
![]() $\Pi ^0_1\textsf {-AC}^{11}$
nor
$\Pi ^0_1\textsf {-AC}^{11}$
nor
![]() $\Pi ^0_1\textsf {-AC}^{10}$
can be added to the combination of Brouwerian axioms finitistically justifiable or guaranteed jointly with
$\Pi ^0_1\textsf {-AC}^{10}$
can be added to the combination of Brouwerian axioms finitistically justifiable or guaranteed jointly with
![]() $\textsf {LLPO}$
, while
$\textsf {LLPO}$
, while
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}!^{1i}$
can with
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}!^{1i}$
can with
![]() $\Sigma ^0_1\textsf {-GDM}$
and
$\Sigma ^0_1\textsf {-GDM}$
and
![]() $\textsf {MP}$
.
$\textsf {MP}$
.
Lemma 2.39.
-
(1)
 $\mathbf{EL}_0^-\vdash \Sigma ^0_1\textsf {-CC}^1$
.
$\mathbf{EL}_0^-\vdash \Sigma ^0_1\textsf {-CC}^1$
. -
(2) Over
 $\mathbf{EL}_0^-$
, (i)
$\mathbf{EL}_0^-$
, (i)
 $\mathcal {C}\textsf {-CC}^1$
implies
$\mathcal {C}\textsf {-CC}^1$
implies
 $\mathcal {C}\textsf {-WC}^0$
; (ii)
$\mathcal {C}\textsf {-WC}^0$
; (ii)
 $(\mathcal {C}{\land }\Pi ^0_1)\textsf {-CC!}^1$
implies
$(\mathcal {C}{\land }\Pi ^0_1)\textsf {-CC!}^1$
implies
 $\mathcal {C}\textsf {-WC!}^0$
.
$\mathcal {C}\textsf {-WC!}^0$
. -
(3) Over
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
, (i)
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
, (i)
 $\mathcal {C}\textsf {-CC}^1$
yields
$\mathcal {C}\textsf {-CC}^1$
yields
 $\mathcal {C}\textsf {-WC}^1$
; (ii)
$\mathcal {C}\textsf {-WC}^1$
; (ii)
 $\mathcal {C}\textsf {-CC!}^1$
yields
$\mathcal {C}\textsf {-CC!}^1$
yields
 $\mathcal {C}\textsf {-WC!}^1$
.
$\mathcal {C}\textsf {-WC!}^1$
. -
(4)
 $\mathbf{EL}_0^-{+}\mathcal {D}\textsf {-CB}^0{+}\mathcal {C}\textsf {-BI}_D\,{\vdash }\, (\mathcal {C},\mathcal {D})\textsf {-BI}_M$
.
$\mathbf{EL}_0^-{+}\mathcal {D}\textsf {-CB}^0{+}\mathcal {C}\textsf {-BI}_D\,{\vdash }\, (\mathcal {C},\mathcal {D})\textsf {-BI}_M$
.
Proof (1) For A from
![]() $\Sigma ^0_1$
, let
$\Sigma ^0_1$
, let
![]() $\forall \alpha \exists \beta A[\alpha ,\beta ]$
. Take D by 2.14 and
$\forall \alpha \exists \beta A[\alpha ,\beta ]$
. Take D by 2.14 and
![]() $\gamma $
as follows. Then
$\gamma $
as follows. Then
![]() $\forall \alpha \exists \beta (\beta \,{=}\,\gamma |\alpha \,{\land }\, A[\alpha ,\beta ])$
.
$\forall \alpha \exists \beta (\beta \,{=}\,\gamma |\alpha \,{\land }\, A[\alpha ,\beta ])$
.
 $$ \begin{align*} \gamma(y)\,{=}\,\begin{cases} (v{*}\underline{0})(z){+}1 & \text{if }y\,{=}\,\langle z\rangle{*}u\text{ and if }v\,{:=}\,|u|\text{ satisfies }D[u{\upharpoonright} |v|,v]\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \gamma(y)\,{=}\,\begin{cases} (v{*}\underline{0})(z){+}1 & \text{if }y\,{=}\,\langle z\rangle{*}u\text{ and if }v\,{:=}\,|u|\text{ satisfies }D[u{\upharpoonright} |v|,v]\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
(2) Easy.
(3) Let
![]() $C[x,y]\,{:\equiv }\,\gamma (\langle x\rangle {*} (\alpha {\upharpoonright } y)) \, {>} \,0\,{\land }\,(\forall z\,{<}\,y)(\gamma (\langle x\rangle {*}(\alpha {\upharpoonright } z))\,{=}\,0)$
. If
$C[x,y]\,{:\equiv }\,\gamma (\langle x\rangle {*} (\alpha {\upharpoonright } y)) \, {>} \,0\,{\land }\,(\forall z\,{<}\,y)(\gamma (\langle x\rangle {*}(\alpha {\upharpoonright } z))\,{=}\,0)$
. If
![]() $\exists \delta (\delta \,{=}\,\gamma |\alpha )$
, then
$\exists \delta (\delta \,{=}\,\gamma |\alpha )$
, then
![]() $(\forall x\,{<}\,n)\exists yC[x,y]$
and
$(\forall x\,{<}\,n)\exists yC[x,y]$
and
![]() $\Sigma ^0_1\textsf {-Bdg}$
yields m with
$\Sigma ^0_1\textsf {-Bdg}$
yields m with
![]() $(\forall x\,{<}\,n)(\exists y\,{<}\,m)C[x,y]$
. Then
$(\forall x\,{<}\,n)(\exists y\,{<}\,m)C[x,y]$
. Then
![]() $\forall \beta (\beta {\upharpoonright } m\,{=}\,\alpha {\upharpoonright } m\to (\gamma |\beta ){\upharpoonright } n\,{=}\, (\gamma |\alpha ){\upharpoonright } n)$
.
$\forall \beta (\beta {\upharpoonright } m\,{=}\,\alpha {\upharpoonright } m\to (\gamma |\beta ){\upharpoonright } n\,{=}\, (\gamma |\alpha ){\upharpoonright } n)$
.
(4) Let B from
![]() $\mathcal {D}$
and assume
$\mathcal {D}$
and assume
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]\,{\equiv }\,\forall \alpha \exists nB[\alpha {\upharpoonright } n]$
.
$\textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]\,{\equiv }\,\forall \alpha \exists nB[\alpha {\upharpoonright } n]$
.
![]() $\mathcal {D}\textsf {-CB}^0$
yields
$\mathcal {D}\textsf {-CB}^0$
yields
![]() $\gamma $
with
$\gamma $
with
![]() $\forall \alpha (\exists k\,{<}(\gamma |\alpha )(0)) B[\alpha {\upharpoonright } k]$
. Define
$\forall \alpha (\exists k\,{<}(\gamma |\alpha )(0)) B[\alpha {\upharpoonright } k]$
. Define
![]() $\beta $
by
$\beta $
by
Then
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\beta (u)\,{=}\,0\right \}]$
. Now
$\textsf {Bar}[\underline {0},\left \{u{:}\,\beta (u)\,{=}\,0\right \}]$
. Now
![]() $\beta(u)\,{=}\,0$
implies
$\beta(u)\,{=}\,0$
implies
![]() $|u| \,{\geq}\, (\gamma| u*\underline{0})(0)$
and so
$|u| \,{\geq}\, (\gamma| u*\underline{0})(0)$
and so
![]() $B[u]$
, if
$B[u]$
, if
![]() $\forall u,v(B[u]\,{\to}\,B[u*v])$
.
$\forall u,v(B[u]\,{\to}\,B[u*v])$
.
2.5.6 Remarks on axiom schemata for decidable properties
In the context of Intuitionism, one of the most important constraints on properties is decidability: A is called decidable or detachable if
![]() $\forall x(A[x]\,{\lor }\,\neg A[x])$
. In other words, we can decide, for any x, if
$\forall x(A[x]\,{\lor }\,\neg A[x])$
. In other words, we can decide, for any x, if
![]() $A[x]$
holds or not.
$A[x]$
holds or not.
This is not syntactical and so inadequate for our way of defining axiom schemata, similarly to the non-syntactical constraints
![]() $\Delta ^0_{n+1}$
in classical arithmetic. For, it might be the case that
$\Delta ^0_{n+1}$
in classical arithmetic. For, it might be the case that
![]() $\forall x(A[x,y]\,{\lor }\,\neg A[x,y])$
holds for some y but, for another z,
$\forall x(A[x,y]\,{\lor }\,\neg A[x,y])$
holds for some y but, for another z,
![]() $\forall x(A[x,z]\,{\lor }\,\neg A[x,z])$
does not. Thus the constraint is on the abstract
$\forall x(A[x,z]\,{\lor }\,\neg A[x,z])$
does not. Thus the constraint is on the abstract
![]() $\left \{x{:}\,A[x,y]\right \}$
rather than on the formula A, as the constraint
$\left \{x{:}\,A[x,y]\right \}$
rather than on the formula A, as the constraint
![]() $\textsf {Bar}$
(Definition 2.25), where an abstract
$\textsf {Bar}$
(Definition 2.25), where an abstract
![]() $\left \{\vec {x}{:}\,B[\vec {x},\vec {y}]\right \}$
is a formula
$\left \{\vec {x}{:}\,B[\vec {x},\vec {y}]\right \}$
is a formula
![]() $B[\vec {x},\vec {y}]$
with designated free variables
$B[\vec {x},\vec {y}]$
with designated free variables
![]() $\vec {x}$
. By 2.8(1),
$\vec {x}$
. By 2.8(1),
![]() $\Delta ^0_0$
abstracts are decidable, but not vice versa.
$\Delta ^0_0$
abstracts are decidable, but not vice versa.
Below are some related schemata, where
![]() $\textsf {D}$
,
$\textsf {D}$
,
![]() $\textsf {E}$
and
$\textsf {E}$
and
![]() $\textsf {U}$
stand for ‘decidable’, ‘existential’ and ‘universal’, respectively. In some literature MP and LLPO refer to
$\textsf {U}$
stand for ‘decidable’, ‘existential’ and ‘universal’, respectively. In some literature MP and LLPO refer to
![]() $\textsf {E}\textsf {-DNE}$
and
$\textsf {E}\textsf {-DNE}$
and
![]() $\textsf {E}\textsf {-GDM}$
(restricted to
$\textsf {E}\textsf {-GDM}$
(restricted to
![]() $z\,{=}\,2$
), respectively.
$z\,{=}\,2$
), respectively.
Definition 2.40.
![]() $A[\vec {x},\vec {y}]$
is called decidable in
$A[\vec {x},\vec {y}]$
is called decidable in
![]() $\vec {x}$
if
$\vec {x}$
if
Define the following axiom schemata:
-
(
 $\textsf {E}\textsf {-DNE}$
):
$\textsf {E}\textsf {-DNE}$
):
 $\textsf {D}[\left \{x{:}\,A[x]\right \}] \to (\neg \neg \exists xA[x]\to \exists xA[x])$
;
$\textsf {D}[\left \{x{:}\,A[x]\right \}] \to (\neg \neg \exists xA[x]\to \exists xA[x])$
; -
(
 $\textsf {E}\textsf {-GDM}$
):
$\textsf {E}\textsf {-GDM}$
):
 $\textsf {D}[\left \{x,y{:}\,A[x,y,z]\right \}] {{\kern-2pt}\to{\kern-2pt}} (\neg (\forall x < z)\exists yA[x,y,z] {{\kern-2pt}\to{\kern-2pt}} (\exists x\,{<}\,z)\forall y\neg A[x,y,z])$
;
$\textsf {D}[\left \{x,y{:}\,A[x,y,z]\right \}] {{\kern-2pt}\to{\kern-2pt}} (\neg (\forall x < z)\exists yA[x,y,z] {{\kern-2pt}\to{\kern-2pt}} (\exists x\,{<}\,z)\forall y\neg A[x,y,z])$
; -
(
 $\textsf {EU}\textsf {-Ind}$
):
$\textsf {EU}\textsf {-Ind}$
):
 $\textsf {D}[\left \{x,y,z{:}\,A[x,y,z]\right \}] \,{\land }\,\exists y\forall zA[0,y,z]\\\phantom{\hspace{47pt}} {\to }\,((\forall x\,{<}\,n)(\exists y\forall zA[x,y,z] \,{\to }\,\exists y\forall zA[x{+}1,y,z])\,{\to }\,\exists y\forall zA[n,y,z])$
;
$\textsf {D}[\left \{x,y,z{:}\,A[x,y,z]\right \}] \,{\land }\,\exists y\forall zA[0,y,z]\\\phantom{\hspace{47pt}} {\to }\,((\forall x\,{<}\,n)(\exists y\forall zA[x,y,z] \,{\to }\,\exists y\forall zA[x{+}1,y,z])\,{\to }\,\exists y\forall zA[n,y,z])$
; -
(
 $\textsf {U}\textsf {-BI}$
):
$\textsf {U}\textsf {-BI}$
):
 $\textsf {D}[\left \{u,y{:}\,B[u,y]\right \}]\land \textsf {Bar}[\,\underline {0},\left \{u{:}\,\forall yB[u,y]\right \}] \\\phantom{\hspace{55pt}}\to \,(\forall u(\forall x,yB[u{*}\langle x\rangle ,y]\,{\to}\, \forall yB[u,y]) \,{\to }\,\forall yB[\langle \,\rangle ,y])$
.
$\textsf {D}[\left \{u,y{:}\,B[u,y]\right \}]\land \textsf {Bar}[\,\underline {0},\left \{u{:}\,\forall yB[u,y]\right \}] \\\phantom{\hspace{55pt}}\to \,(\forall u(\forall x,yB[u{*}\langle x\rangle ,y]\,{\to}\, \forall yB[u,y]) \,{\to }\,\forall yB[\langle \,\rangle ,y])$
.
In what follows, however, we will not consider these schemata for the following reason. In the upper bound proofs, we always have full choice
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
, with which decidable properties are equivalently
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
, with which decidable properties are equivalently
![]() $\Delta ^0_0$
, in other words,
$\Delta ^0_0$
, in other words,
![]() $\textsf {D}(\left \{x{:}\,A[x,\vec {y}]\right \})$
implies
$\textsf {D}(\left \{x{:}\,A[x,\vec {y}]\right \})$
implies
![]() $\exists \alpha \forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\, A[x,\vec {y}])$
. For lower bounds, we can obtain all the expected results for the corresponding weaker syntactical classes (e.g.,
$\exists \alpha \forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\, A[x,\vec {y}])$
. For lower bounds, we can obtain all the expected results for the corresponding weaker syntactical classes (e.g.,
![]() $\Delta ^0_0$
instead of
$\Delta ^0_0$
instead of
![]() $\textsf {D}$
,
$\textsf {D}$
,
![]() $\Sigma ^0_1$
instead of
$\Sigma ^0_1$
instead of
![]() $\textsf {E}$
). Thus our results for syntactic classes can automatically be enhanced for these schemata. So the schemata listed above (as well as
$\textsf {E}$
). Thus our results for syntactic classes can automatically be enhanced for these schemata. So the schemata listed above (as well as
![]() $\textsf { EU-DC}^0$
and
$\textsf { EU-DC}^0$
and
![]() $\textsf { E-DC}^1$
defined similarly) are all finitistically justifiable jointly with
$\textsf { E-DC}^1$
defined similarly) are all finitistically justifiable jointly with
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{0i}\ (i\,{=}\,0,1)$
,
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{0i}\ (i\,{=}\,0,1)$
,
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
and
$\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
and
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-CC!}^{1}$
.
$\mathcal {L}_{\mathrm{F}}\textsf {-CC!}^{1}$
.
3 Upper Bounds: Functional Realizability
3.1 Preliminaries for upper bound proofs
We will need two equivalences, which are among the folklore in classical second order arithmetic. We here sharpen these in the intuitionistic context (Corollaries 3.3 and 3.9) with some related fundamental results.
3.1.1 Bounded comprehension
The first equivalence to be sharpened is between induction and bounded comprehension. This was mentioned in [Reference Simpson45, Exercise II.3.13]. For this equivalence, we need a semi-classical principle. For the equivalence in the purely intuitionistic setting, we need to replace the induction
![]() $\mathcal {C}\textsf {-Ind}$
by the least number principle
$\mathcal {C}\textsf {-Ind}$
by the least number principle
![]() $\mathcal {C}\textsf {-LNP}$
.
$\mathcal {C}\textsf {-LNP}$
.
Definition 3.1 (
 $\mathcal {C}\textsf {-BCA}$
,
$\mathcal {C}\textsf {-BCA}$
,
 $\Delta ^0_0(\mathcal {C})$
,
$\Delta ^0_0(\mathcal {C})$
,
 $\Sigma ^0_1(\mathcal {C})$
,
$\Sigma ^0_1(\mathcal {C})$
,
 $\Pi ^0_1(\mathcal {C})$
)
$\Pi ^0_1(\mathcal {C})$
)
For a class
![]() $\mathcal {C}$
of formulae,
$\mathcal {C}$
of formulae,
-
(
 $\mathcal {C}\textsf {-BCA}$
):
$\mathcal {C}\textsf {-BCA}$
):
 $\exists u(|u|\,{=}\,n\land (\forall k\,{<}\,n)(u(k)\,{=}\,0\leftrightarrow A[k]))$
for any A from
$\exists u(|u|\,{=}\,n\land (\forall k\,{<}\,n)(u(k)\,{=}\,0\leftrightarrow A[k]))$
for any A from
 $\mathcal {C}$
.
$\mathcal {C}$
.
![]() $\Delta ^0_0(\mathcal {C})$
denotes the smallest class
$\Delta ^0_0(\mathcal {C})$
denotes the smallest class
![]() $\mathcal {D}\supseteq \mathcal {C}$
closed under
$\mathcal {D}\supseteq \mathcal {C}$
closed under
![]() $\land ,\lor ,\to , \textsf {B}\exists ^0\!,\textsf {B}\forall ^0\!$
. Analogously
$\land ,\lor ,\to , \textsf {B}\exists ^0\!,\textsf {B}\forall ^0\!$
. Analogously
![]() $\Sigma ^0_1(\mathcal {C})\,{\equiv }\,\exists ^0\!\Delta ^0_0(\mathcal {C})$
and
$\Sigma ^0_1(\mathcal {C})\,{\equiv }\,\exists ^0\!\Delta ^0_0(\mathcal {C})$
and
![]() $\Pi ^0_1(\mathcal {C})\,{\equiv }\,\forall ^0\!\Delta ^0_0(\mathcal {C})$
.
$\Pi ^0_1(\mathcal {C})\,{\equiv }\,\forall ^0\!\Delta ^0_0(\mathcal {C})$
.
Lemma 3.2.
-
(1)
 $\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-LNP}$
proves
$\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-LNP}$
proves
 $\mathcal {C}\textsf {-BCA}$
.
$\mathcal {C}\textsf {-BCA}$
. -
(2)
 $\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-BCA}$
proves
$\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-BCA}$
proves
 $\mathcal {C}\textsf {-Ind}$
,
$\mathcal {C}\textsf {-Ind}$
,
 $\mathcal {C}\textsf {-LEM}$
and
$\mathcal {C}\textsf {-LEM}$
and
 $\mathcal {C}\textsf {-LNP}$
.
$\mathcal {C}\textsf {-LNP}$
. -
(3)
 $\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-BCA}$
proves
$\mathbf{EL}_0^-{+}\,\mathcal {C}\textsf {-BCA}$
proves
 $\Delta ^0_0(\mathcal {C})\textsf {-BCA}$
.
$\Delta ^0_0(\mathcal {C})\textsf {-BCA}$
. -
(4) Hence
 $\mathcal {C}\textsf {-BCA}$
and
$\mathcal {C}\textsf {-BCA}$
and
 $\textsf { B}\forall ^0\mathcal {C}\textsf {-LNP}$
are equivalent over
$\textsf { B}\forall ^0\mathcal {C}\textsf {-LNP}$
are equivalent over
 $\mathbf{EL}_0^-$
.
$\mathbf{EL}_0^-$
.
Proof In this proof, let A be from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(1) We may assume
![]() $|u|\,{\leq }\,|v|\,{\land }\,(\forall k\,{<}\,|u|)(u(k)\,{\leq }\,v(k))\,{\to }\,u\,{\leq }\, v$
by changing way of coding if necessary. Let
$|u|\,{\leq }\,|v|\,{\land }\,(\forall k\,{<}\,|u|)(u(k)\,{\leq }\,v(k))\,{\to }\,u\,{\leq }\, v$
by changing way of coding if necessary. Let
![]() $B[u]\,{:\equiv }\,|u|\,{=}\,n\,{\land }\,(\forall k\,{<}\,n)(u(k)\,{=}\,0\,{\to }\,A[k])$
which is
$B[u]\,{:\equiv }\,|u|\,{=}\,n\,{\land }\,(\forall k\,{<}\,n)(u(k)\,{=}\,0\,{\to }\,A[k])$
which is
![]() $\textsf {B}\forall ^0\mathcal {C}$
(cf. Notation 2.9(3)).
$\textsf {B}\forall ^0\mathcal {C}$
(cf. Notation 2.9(3)).
![]() $\textsf {B}\forall ^0\mathcal {C}\textsf {-LNP}$
yields
$\textsf {B}\forall ^0\mathcal {C}\textsf {-LNP}$
yields
![]() $v$
with
$v$
with
![]() $B[v]\,{\land }\,(\forall u\,{<}\,v)\neg B[u]$
. It remains to show
$B[v]\,{\land }\,(\forall u\,{<}\,v)\neg B[u]$
. It remains to show
![]() $(\forall k\,{<}\,n)(A[k]\,{\to }\,v(k)\,{=}\,0)$
. For
$(\forall k\,{<}\,n)(A[k]\,{\to }\,v(k)\,{=}\,0)$
. For
![]() $k\,{<}\,n$
with
$k\,{<}\,n$
with
![]() $A[k]$
, if
$A[k]$
, if
![]() $v(k)\,{\neq }\,0$
, then u defined by
$v(k)\,{\neq }\,0$
, then u defined by
![]() $u(k)\,{=}\,0$
and
$u(k)\,{=}\,0$
and
![]() $u(l)\,{=}\,v(l)$
for
$u(l)\,{=}\,v(l)$
for
![]() $l\,{\neq }\,k$
satisfies
$l\,{\neq }\,k$
satisfies
![]() $u\,{<}\,v$
and
$u\,{<}\,v$
and
![]() $B[u]$
, a contradiction.
$B[u]$
, a contradiction.
(2) By
![]() $\mathcal {C}\textsf {-BCA}$
we can take u such that
$\mathcal {C}\textsf {-BCA}$
we can take u such that
![]() $(\forall x\,{\leq }\,n)(u(x)\,{=}\,0\,{\leftrightarrow }\, A[x])$
. If
$(\forall x\,{\leq }\,n)(u(x)\,{=}\,0\,{\leftrightarrow }\, A[x])$
. If
![]() $A[0]$
and
$A[0]$
and
![]() $(\forall x < n)(A[x] \to A[x{+}1])$
, then
$(\forall x < n)(A[x] \to A[x{+}1])$
, then
![]() $u(0) = 0$
and
$u(0) = 0$
and
![]() $(\forall x < n)(u(x) = 0 \to u(x{+}1) = 0)$
which, with
$(\forall x < n)(u(x) = 0 \to u(x{+}1) = 0)$
which, with
![]() $\Delta ^0_0\textsf {-Ind}$
, yields
$\Delta ^0_0\textsf {-Ind}$
, yields
![]() $u(n)\,{=}\,0$
and so
$u(n)\,{=}\,0$
and so
![]() $A[n]$
. The others are similar.
$A[n]$
. The others are similar.
(3) We show
![]() $\forall n \exists u(|u|\,{=}\,n \,{\land }\,(\forall x\,{<}\,n)(u(x)\,{=}\,0\,{\leftrightarrow }\, A[(x)^k_0,\dots ,(x)^k_{k-1}]))$
by induction on A. Consider the case of
$\forall n \exists u(|u|\,{=}\,n \,{\land }\,(\forall x\,{<}\,n)(u(x)\,{=}\,0\,{\leftrightarrow }\, A[(x)^k_0,\dots ,(x)^k_{k-1}]))$
by induction on A. Consider the case of
![]() $A[\vec {x}]\,{\equiv }\,(Q y\,{<}\,t[\vec {x}])B[\vec {x},y]$
. The induction hypothesis yields
$A[\vec {x}]\,{\equiv }\,(Q y\,{<}\,t[\vec {x}])B[\vec {x},y]$
. The induction hypothesis yields
![]() $v$
with
$v$
with
Then
![]() $(\forall x < n)(\forall y < (|v|)^2_1) (v(((x)^k_0,\dots ,(x)^k_{k-1},y)) = 0 \leftrightarrow B[(x)^k_0,\dots ,(x)^k_{k-1},y])$
. Take u with
$(\forall x < n)(\forall y < (|v|)^2_1) (v(((x)^k_0,\dots ,(x)^k_{k-1},y)) = 0 \leftrightarrow B[(x)^k_0,\dots ,(x)^k_{k-1},y])$
. Take u with
This is what we need.
Corollary 3.3.
-
(1)
 $\mathbf{EL}_0^-\vdash \Pi ^0_n\textsf {-BCA}\,{\leftrightarrow }\,\Pi ^0_n\textsf {-LNP}$
.
$\mathbf{EL}_0^-\vdash \Pi ^0_n\textsf {-BCA}\,{\leftrightarrow }\,\Pi ^0_n\textsf {-LNP}$
. -
(2)
 $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_{n+1}\textsf {-DNE} \vdash \Sigma ^0_n\textsf {-BCA}\,{\land }\,\Delta ^0_0(\Sigma ^0_n)\textsf {-Ind}$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_{n+1}\textsf {-DNE} \vdash \Sigma ^0_n\textsf {-BCA}\,{\land }\,\Delta ^0_0(\Sigma ^0_n)\textsf {-Ind}$
. -
(3)
 $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM} \,{\subseteq }\,\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-BCA} \,{\subseteq }\,\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+} \Sigma ^0_{n+1}\textsf {-DNE}$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM} \,{\subseteq }\,\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-BCA} \,{\subseteq }\,\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+} \Sigma ^0_{n+1}\textsf {-DNE}$
.
Proof (1) This is by 3.2(1)(2). (2) We have
![]() $\textsf {B}\forall ^0\neg \Pi ^0_n\,{\subseteq }\,\Sigma ^0_n$
by 2.8(3)(i)(ii) and 2.24(1)(i), and
$\textsf {B}\forall ^0\neg \Pi ^0_n\,{\subseteq }\,\Sigma ^0_n$
by 2.8(3)(i)(ii) and 2.24(1)(i), and
![]() $\textsf {B}\exists ^0(\Pi ^0_n\,{\land }\,\textsf { B}\forall ^0\neg \Pi ^0_n)\,{\subseteq }\,\Sigma ^0_{n+1}$
. By 2.8(2)(i),
$\textsf {B}\exists ^0(\Pi ^0_n\,{\land }\,\textsf { B}\forall ^0\neg \Pi ^0_n)\,{\subseteq }\,\Sigma ^0_{n+1}$
. By 2.8(2)(i),
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_{n+1}\textsf {-DNE}$
proves
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-Ind}{+}\Sigma ^0_{n+1}\textsf {-DNE}$
proves
![]() $\Pi ^0_n\textsf {-LNP}$
and so
$\Pi ^0_n\textsf {-LNP}$
and so
![]() $\Pi ^0_n\textsf {-BCA}$
which with
$\Pi ^0_n\textsf {-BCA}$
which with
![]() $\Sigma ^0_n\textsf {-DNE}$
implies
$\Sigma ^0_n\textsf {-DNE}$
implies
![]() $\Sigma ^0_n\textsf {-BCA}$
.
$\Sigma ^0_n\textsf {-BCA}$
.
The statements (2) and (3) refine the corresponding classical results:
![]() $\Sigma ^0_n\textsf {-Ind}$
implies
$\Sigma ^0_n\textsf {-Ind}$
implies
![]() $\Delta ^0_0(\Sigma ^0_n)\textsf {-Ind}$
(e.g., [Reference Hájek and Pudlák18, Chapter I, 2.14 Lemma]); and
$\Delta ^0_0(\Sigma ^0_n)\textsf {-Ind}$
(e.g., [Reference Hájek and Pudlák18, Chapter I, 2.14 Lemma]); and
![]() $\Sigma ^0_n\textsf {-Ind}$
is equivalent to
$\Sigma ^0_n\textsf {-Ind}$
is equivalent to
![]() $\Sigma ^0_n\textsf {-BCA}$
. Since
$\Sigma ^0_n\textsf {-BCA}$
. Since
![]() $\Sigma ^0_n\textsf {-BCA}$
easily follows from
$\Sigma ^0_n\textsf {-BCA}$
easily follows from
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM}$
, in the usual intuitionistic context with full induction,
$\mathcal {L}_{\mathrm{F}}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM}$
, in the usual intuitionistic context with full induction,
![]() $\Sigma ^0_n\textsf {-BCA}$
is equivalent to
$\Sigma ^0_n\textsf {-BCA}$
is equivalent to
![]() $\Sigma ^0_n\textsf {-LEM}$
. In our context however we need some trick to adjust the proof above to
$\Sigma ^0_n\textsf {-LEM}$
. In our context however we need some trick to adjust the proof above to
![]() $\Sigma ^0_n$
to show this (cf. [Reference Nemoto28, Corollary 84]) while we saw that it is equivalent to
$\Sigma ^0_n$
to show this (cf. [Reference Nemoto28, Corollary 84]) while we saw that it is equivalent to
![]() $\textsf {B}\Pi ^0_{n+1}\textsf {-LNP}$
, to
$\textsf {B}\Pi ^0_{n+1}\textsf {-LNP}$
, to
![]() $\Delta ^0_0(\Sigma ^0_n)\textsf {-LNP}$
and to
$\Delta ^0_0(\Sigma ^0_n)\textsf {-LNP}$
and to
![]() $\Pi ^0_n\textsf {-LNP}{+}\Sigma ^0_n\textsf {-DNE}$
. As
$\Pi ^0_n\textsf {-LNP}{+}\Sigma ^0_n\textsf {-DNE}$
. As
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM}$
is known not to imply
$\mathcal {L}_{\mathrm{F}}\textsf {-Ind}{+}\Sigma ^0_n\textsf {-LEM}$
is known not to imply
![]() $\Sigma ^0_{n+1}\textsf {-DNE}$
(by [Reference Akama, Berardi, Hayashi and Kohlenbach1]), the second
$\Sigma ^0_{n+1}\textsf {-DNE}$
(by [Reference Akama, Berardi, Hayashi and Kohlenbach1]), the second
![]() $\subseteq $
in (3) is proper. We do not know if so is the first.
$\subseteq $
in (3) is proper. We do not know if so is the first.
Our proof refines [Reference Hájek and Pudlák18, Chapter I, 2.13 Lemma] and differs from that suggested in [Reference Simpson45]. The latter proof is based on pigeon-hole principle (PHP), and does not solve the question above either. Whereas we applied the least number principle to sequence u’s or large numbers in the sense of Section 1.8, in the proof by PHP the induction is applied to k’s with
![]() $k\,{<}\,|u|$
or small numbers.Footnote
16
Thus the difference between these two proofs could be essential in the further studies mentioned in Section 1.8,Footnote
17
but not so essential for the purpose of the present article.
$k\,{<}\,|u|$
or small numbers.Footnote
16
Thus the difference between these two proofs could be essential in the further studies mentioned in Section 1.8,Footnote
17
but not so essential for the purpose of the present article.
3.1.2 Bounded König’s lemma
The other equivalence is between weak König’s lemma (WKL) and
![]() $\Pi ^0_1$
axiom of choice (for sets) which is mentioned in [Reference Simpson45, p.54, f.n.1]. The implication from the former to the latter was in [Reference Nemoto26, Lemma 3.6], and the converse is proved as follows: similarly to [Reference Simpson45, Lemma VII.6.6.1],
$\Pi ^0_1$
axiom of choice (for sets) which is mentioned in [Reference Simpson45, p.54, f.n.1]. The implication from the former to the latter was in [Reference Nemoto26, Lemma 3.6], and the converse is proved as follows: similarly to [Reference Simpson45, Lemma VII.6.6.1],
![]() $\Pi ^0_1$
axiom of choice implies
$\Pi ^0_1$
axiom of choice implies
![]() $\Sigma ^0_1$
separation which is known to be equivalent to WKL by [Reference Simpson45, Lemma IV.4.4]. We refine this equivalence in our
$\Sigma ^0_1$
separation which is known to be equivalent to WKL by [Reference Simpson45, Lemma IV.4.4]. We refine this equivalence in our
![]() $\mathbf{EL}_0^-$
.
$\mathbf{EL}_0^-$
.
Definition 3.4 (
 $u\,{<}\,\alpha $
,
$u\,{<}\,\alpha $
,
 $\mathcal {C}\textsf {-BKL}$
,
$\mathcal {C}\textsf {-BKL}$
,
 $\mathcal {C}\textsf {-WKL}$
)
$\mathcal {C}\textsf {-WKL}$
)
Let
![]() $u\,{<}\,\alpha \,:\equiv \, (\forall k\,{<}\,|u|)(u(k)\,{<}\,\alpha (k))$
. For a class
$u\,{<}\,\alpha \,:\equiv \, (\forall k\,{<}\,|u|)(u(k)\,{<}\,\alpha (k))$
. For a class
![]() $\mathcal {C}$
of formulae define the following schemata:
$\mathcal {C}$
of formulae define the following schemata:
-
(
 $\mathcal {C}\textsf {-BKL}$
):
$\mathcal {C}\textsf {-BKL}$
):
 $\forall n(\exists u\,{<}\,\alpha )(|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k]) \,\to \,(\exists \gamma \,{<}\,\alpha )\forall nA[\gamma {\upharpoonright } n]$
;
$\forall n(\exists u\,{<}\,\alpha )(|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k]) \,\to \,(\exists \gamma \,{<}\,\alpha )\forall nA[\gamma {\upharpoonright } n]$
; -
(
 $\mathcal {C}\textsf {-WKL}$
):
$\mathcal {C}\textsf {-WKL}$
):
 $\forall n(\exists u\,{<}\,\underline {2})(|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k]) \,\to \,(\exists \gamma \,{<}\,\underline {2})\forall nA[\gamma {\upharpoonright } n]$
,
$\forall n(\exists u\,{<}\,\underline {2})(|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k]) \,\to \,(\exists \gamma \,{<}\,\underline {2})\forall nA[\gamma {\upharpoonright } n]$
,
for any A from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 3.5.
-
(1) For A from
 $\forall ^0\mathcal {C}$
there is a formula B from
$\forall ^0\mathcal {C}$
there is a formula B from
 $\textsf {B}\forall ^0\mathcal {C}$
such that
$\textsf {B}\forall ^0\mathcal {C}$
such that-
(a)
 $\forall nB[\beta {\upharpoonright } n] \to \forall nA[\beta {\upharpoonright } n]$
and
$\forall nB[\beta {\upharpoonright } n] \to \forall nA[\beta {\upharpoonright } n]$
and -
(b)
 $\forall n(\exists u < \alpha )(|u| = n\land (\forall k \leq n)A[u{\upharpoonright } k])\\ \phantom{\hspace{55pt}}\to \forall n(\exists u < \alpha )(|u| = n \land (\forall k\leq n)B[u{\upharpoonright } k])$
.
$\forall n(\exists u < \alpha )(|u| = n\land (\forall k \leq n)A[u{\upharpoonright } k])\\ \phantom{\hspace{55pt}}\to \forall n(\exists u < \alpha )(|u| = n \land (\forall k\leq n)B[u{\upharpoonright } k])$
.
-
-
(2) Over
 $\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL}$
, (i)
$\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL}$
, (i)
 $\forall ^0\mathcal {C}\textsf {-BKL}$
holds; (ii)
$\forall ^0\mathcal {C}\textsf {-BKL}$
holds; (ii)
 $(\exists \beta \,{<}\,\alpha )\forall nA[\beta {\upharpoonright } n]$
is
$(\exists \beta \,{<}\,\alpha )\forall nA[\beta {\upharpoonright } n]$
is
 $\forall ^0(\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C})$
if A is
$\forall ^0(\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C})$
if A is
 $\forall ^0\mathcal {C}$
.
$\forall ^0\mathcal {C}$
. -
(3)
 $\mathbf{EL}_0^-{+}\mathcal {D}\textsf {-BKL} {+}\textsf {B}\exists ^0\mathcal {D}\textsf {-Ind} {+}\textsf {B}\exists ^0\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-LEM} {+}\textsf {B}\exists ^0\mathcal {C}\textsf {-DNE} \vdash \mathcal {C}\textsf {-BFT}$
,
$\mathbf{EL}_0^-{+}\mathcal {D}\textsf {-BKL} {+}\textsf {B}\exists ^0\mathcal {D}\textsf {-Ind} {+}\textsf {B}\exists ^0\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-LEM} {+}\textsf {B}\exists ^0\mathcal {C}\textsf {-DNE} \vdash \mathcal {C}\textsf {-BFT}$
,where
 $\mathcal {D}\equiv \textsf {B}\forall ^0(\mathcal {C}\,{\to }\,\textsf { B}\exists ^0\mathcal {C})$
.
$\mathcal {D}\equiv \textsf {B}\forall ^0(\mathcal {C}\,{\to }\,\textsf { B}\exists ^0\mathcal {C})$
.
Proof Let C be
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(1) Say
![]() $A[u]\equiv \forall xC[u,x]$
. Define
$A[u]\equiv \forall xC[u,x]$
. Define
![]() $B[u]:\equiv (\forall x,k\,{<}\,|u|)C[u{\upharpoonright } k,x]$
.
$B[u]:\equiv (\forall x,k\,{<}\,|u|)C[u{\upharpoonright } k,x]$
.
For (a), if
![]() $\forall nB[\beta {\upharpoonright } n]$
, then, for n and x,
$\forall nB[\beta {\upharpoonright } n]$
, then, for n and x,
![]() $B[\beta {\upharpoonright }(n{+}x{+}1)]$
implies
$B[\beta {\upharpoonright }(n{+}x{+}1)]$
implies
![]() $C[\beta {\upharpoonright } n,x]$
.
$C[\beta {\upharpoonright } n,x]$
.
As
![]() $\forall u((\forall k\,{\leq }\,|u|)A[u{\upharpoonright } k] \,{\to }\,(\forall k\,{\leq }\,|u|)B[u{\upharpoonright } k])$
, (b) holds.
$\forall u((\forall k\,{\leq }\,|u|)A[u{\upharpoonright } k] \,{\to }\,(\forall k\,{\leq }\,|u|)B[u{\upharpoonright } k])$
, (b) holds.
(2) This follows from (1).
(3) Define the following, where B is in
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
 $$ \begin{align*} D[v]\,&{:\equiv}\,(\exists k\,{\leq}\,|v|) C[v{\upharpoonright} k]\\ B[u]\,&{:\equiv}\,\gamma(u)\,{=}\,0\land(\forall v\,{<}\,\beta) (\gamma(v)\,{=}\,0\,{\land}\,|v|\,{=}\,|u|\,{\land}\, D[u]\to D[v]). \end{align*} $$
$$ \begin{align*} D[v]\,&{:\equiv}\,(\exists k\,{\leq}\,|v|) C[v{\upharpoonright} k]\\ B[u]\,&{:\equiv}\,\gamma(u)\,{=}\,0\land(\forall v\,{<}\,\beta) (\gamma(v)\,{=}\,0\,{\land}\,|v|\,{=}\,|u|\,{\land}\, D[u]\to D[v]). \end{align*} $$
Assume
![]() $\textsf {Fan}[\gamma ]$
,
$\textsf {Fan}[\gamma ]$
,
![]() $\textsf {Bar}[\gamma ,C]$
and
$\textsf {Bar}[\gamma ,C]$
and
![]() $\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\alpha )$
.
$\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\alpha )$
.
We show
![]() $\exists u(\gamma (u)\,{=}\,0\land |u|\,{=}\,n\land (\forall k\,{\leq }\, n)B[u{\upharpoonright } k])$
by
$\exists u(\gamma (u)\,{=}\,0\land |u|\,{=}\,n\land (\forall k\,{\leq }\, n)B[u{\upharpoonright } k])$
by
![]() $\textsf {B}\exists ^0\mathcal {D}\textsf {-Ind}$
on n. If
$\textsf {B}\exists ^0\mathcal {D}\textsf {-Ind}$
on n. If
![]() $n\,{=}\,0$
this is trivial. Assume
$n\,{=}\,0$
this is trivial. Assume
![]() $|v|\,{=}\,n\,{\land }\,(\forall k\,{\leq }\, n)B[v{\upharpoonright } k]$
.
$|v|\,{=}\,n\,{\land }\,(\forall k\,{\leq }\, n)B[v{\upharpoonright } k]$
.
![]() $\textsf {B}\exists ^0\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-LEM}$
gives two cases: if
$\textsf {B}\exists ^0\textsf {B}\forall ^0\neg \mathcal {C}\textsf {-LEM}$
gives two cases: if
![]() $\gamma (w)\,{=}\,0\land |w|\,{=}\,n{+}1\land \neg D[w]$
then
$\gamma (w)\,{=}\,0\land |w|\,{=}\,n{+}1\land \neg D[w]$
then
![]() $(\forall k\,{\leq }\, n{+}1)\neg D[w{\upharpoonright } k]$
and
$(\forall k\,{\leq }\, n{+}1)\neg D[w{\upharpoonright } k]$
and
![]() $(\forall k\,{\leq }\, n{+}1)B[w{\upharpoonright } k]$
; if no such
$(\forall k\,{\leq }\, n{+}1)B[w{\upharpoonright } k]$
; if no such
![]() $w$
exists, as
$w$
exists, as
![]() $\forall w(\gamma (w)\,{=}\,0{\land }|w|\,{=}\,n{+}1\,{\to }\, D[w])$
by
$\forall w(\gamma (w)\,{=}\,0{\land }|w|\,{=}\,n{+}1\,{\to }\, D[w])$
by
![]() $\textsf { B}\exists ^0\mathcal {C}\textsf {-DNE}$
,
$\textsf { B}\exists ^0\mathcal {C}\textsf {-DNE}$
,
![]() $\textsf {Fan}[\gamma ]$
yields x with
$\textsf {Fan}[\gamma ]$
yields x with
![]() $\gamma (v{*}\langle x\rangle )\,{=}\,0\,{\land }\, B[v{*}\langle x\rangle ]$
.
$\gamma (v{*}\langle x\rangle )\,{=}\,0\,{\land }\, B[v{*}\langle x\rangle ]$
.
Now
![]() $\mathcal {D}\textsf {-BKL}$
yields
$\mathcal {D}\textsf {-BKL}$
yields
![]() $\beta < \alpha$
with
$\beta < \alpha$
with
![]() $\forall kB[\beta {\upharpoonright } k]$
. By
$\forall kB[\beta {\upharpoonright } k]$
. By
![]() $\textsf {Bar}[\gamma ,C]$
we have n with
$\textsf {Bar}[\gamma ,C]$
we have n with
![]() $C[\beta {\upharpoonright } n]$
. Then
$C[\beta {\upharpoonright } n]$
. Then
![]() $\forall v(\gamma (v)\,{=}\,0\land |v|\,{=}\,n\to (\exists k\,{\leq }\, n)C[v{\upharpoonright } k])$
by
$\forall v(\gamma (v)\,{=}\,0\land |v|\,{=}\,n\to (\exists k\,{\leq }\, n)C[v{\upharpoonright } k])$
by
![]() $B[\beta {\upharpoonright } n]$
.
$B[\beta {\upharpoonright } n]$
.
Compare (2)(i) with 2.32(3)(ii). A similar argument was also used for 2.28(4) (and will be in 3.56(2)).
As an instance of (3) with
![]() $\mathcal {C}\,{\equiv }\,\Delta ^0_0$
,
$\mathcal {C}\,{\equiv }\,\Delta ^0_0$
,
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BKL}\,{\vdash }\,\Delta ^0_0\textsf {-BFT}$
. This was shown in [Reference Ishihara21], but the essentially same proof had been given: e.g., the proof of [Reference Kohlenbach24, 4.7 Proposition 2) “
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BKL}\,{\vdash }\,\Delta ^0_0\textsf {-BFT}$
. This was shown in [Reference Ishihara21], but the essentially same proof had been given: e.g., the proof of [Reference Kohlenbach24, 4.7 Proposition 2) “
![]() $\to$
”] with g instantiated with the particular g defined just below (++) on p.1263 is exactly the same proof, and there might be earlier proofs.
$\to$
”] with g instantiated with the particular g defined just below (++) on p.1263 is exactly the same proof, and there might be earlier proofs.
Lemma 3.6.
-
(1)
 $\mathbf{EL}_0^-{+} \neg \mathcal {C}\textsf {-BKL} {+}\textsf {B}\exists ^0\mathcal {C}\textsf {-GDM} \vdash \exists ^0\mathcal {C}\textsf {-GDM}$
;
$\mathbf{EL}_0^-{+} \neg \mathcal {C}\textsf {-BKL} {+}\textsf {B}\exists ^0\mathcal {C}\textsf {-GDM} \vdash \exists ^0\mathcal {C}\textsf {-GDM}$
; -
(2)
 $\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL} {+}\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}\textsf {-Ind} \vdash \forall ^0\mathcal {C}\textsf {-BAC}^{00}$
;
$\mathbf{EL}_0^-{+}\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL} {+}\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}\textsf {-Ind} \vdash \forall ^0\mathcal {C}\textsf {-BAC}^{00}$
; -
(3)
 $\mathbf{EL}_0^- {+}\mathcal {D}\textsf {-DNE} {+}\mathcal {D}\textsf {-Ind} {+}\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00} {+}\exists ^0\mathcal {E}\textsf {-DM} \vdash \mathcal {C}\textsf {-WKL}$
for
$\mathbf{EL}_0^- {+}\mathcal {D}\textsf {-DNE} {+}\mathcal {D}\textsf {-Ind} {+}\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00} {+}\exists ^0\mathcal {E}\textsf {-DM} \vdash \mathcal {C}\textsf {-WKL}$
for
 $\mathcal {D}\equiv \textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}$
and
$\mathcal {D}\equiv \textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}$
and
 $\mathcal {E}\equiv \mathcal {D}{\land }\neg \mathcal {D}$
.
$\mathcal {E}\equiv \mathcal {D}{\land }\neg \mathcal {D}$
.
Proof Let A be
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
(1) Let
![]() $C[u]:\equiv |u|> 0 \to \neg A[u(0),|u|{-}1]$
. Assume
$C[u]:\equiv |u|> 0 \to \neg A[u(0),|u|{-}1]$
. Assume
![]() $\neg (\forall x\,{<}\,m)\exists y A[x,y]$
. Then, for any n, we have
$\neg (\forall x\,{<}\,m)\exists y A[x,y]$
. Then, for any n, we have
![]() $\neg (\forall x <m)(\exists y < n) A[x,y]$
and therefore by
$\neg (\forall x <m)(\exists y < n) A[x,y]$
and therefore by
![]() $(\textsf {B}\exists ^0\mathcal {C})\textsf {-GDM}$
,
$(\textsf {B}\exists ^0\mathcal {C})\textsf {-GDM}$
,
![]() $(\exists x < m) (\forall y < n)\neg A[x,y]$
. For such
$(\exists x < m) (\forall y < n)\neg A[x,y]$
. For such
![]() $x\,{<}\,m$
it is easy to see that
$x\,{<}\,m$
it is easy to see that
![]() $\langle x\rangle {*}(\underline {0}{\upharpoonright } (n{-}1))$
witnesses
$\langle x\rangle {*}(\underline {0}{\upharpoonright } (n{-}1))$
witnesses
![]() $\exists u(u\,{<}\,\underline {m} \land |u|\,{=}\,n\land (\forall k\,{\leq }\, n)C[u{\upharpoonright } k])$
.
$\exists u(u\,{<}\,\underline {m} \land |u|\,{=}\,n\land (\forall k\,{\leq }\, n)C[u{\upharpoonright } k])$
.
![]() $\neg \mathcal {C}\textsf {-BKL}$
yields
$\neg \mathcal {C}\textsf {-BKL}$
yields
![]() $\beta \,{<}\,\underline {m}$
with
$\beta \,{<}\,\underline {m}$
with
![]() $\forall nC[\beta {\upharpoonright } n]$
, and
$\forall nC[\beta {\upharpoonright } n]$
, and
![]() $\forall y\neg A[\beta (0),y]$
.
$\forall y\neg A[\beta (0),y]$
.
(2) Assume
![]() $\forall x(\exists y\,{<}\,\alpha (x))\forall zA[x,y,z]$
. Let
$\forall x(\exists y\,{<}\,\alpha (x))\forall zA[x,y,z]$
. Let
![]() $B[u]:\equiv (\forall x,z\,{<}\,|u|)A[x,u(x),z]$
. For n,
$B[u]:\equiv (\forall x,z\,{<}\,|u|)A[x,u(x),z]$
. For n,
![]() $\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}\textsf {-Ind}$
on
$\textsf {B}\exists ^0\textsf {B}\forall ^0\mathcal {C}\textsf {-Ind}$
on
![]() $k \leq n$
shows
$k \leq n$
shows
![]() $\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL}$
yields
$\textsf {B}\forall ^0\mathcal {C}\textsf {-BKL}$
yields
![]() $\beta <\alpha $
with
$\beta <\alpha $
with
![]() $\forall xB[\beta {\upharpoonright } x]$
. So
$\forall xB[\beta {\upharpoonright } x]$
. So
![]() $\forall x,zA[x,\beta (x),z]$
.
$\forall x,zA[x,\beta (x),z]$
.
(3) Assume
![]() $\forall n(\exists u\,{<}\,\underline {2}) (|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k])$
. Define a
$\forall n(\exists u\,{<}\,\underline {2}) (|u|\,{=}\,n\land (\forall k\,{\leq }\, n)A[u{\upharpoonright } k])$
. Define a
![]() $\mathcal {D}$
formula B and an
$\mathcal {D}$
formula B and an
![]() $\mathcal {E}$
formula C by
$\mathcal {E}$
formula C by
 $$ \begin{align*} B[k,u]\,&{:\equiv}\,(\exists v<\underline{2})(|v|\,{=}\,k\land(\forall l\,{\leq}\, |u|{+}k)A[(u{*}v){\upharpoonright} l]);\\ C[n,u,x]\,&{:\equiv}\,B[n,u{*}\langle 1{-}x\rangle] \land\neg B[n,u{*}\langle x\rangle]. \end{align*} $$
$$ \begin{align*} B[k,u]\,&{:\equiv}\,(\exists v<\underline{2})(|v|\,{=}\,k\land(\forall l\,{\leq}\, |u|{+}k)A[(u{*}v){\upharpoonright} l]);\\ C[n,u,x]\,&{:\equiv}\,B[n,u{*}\langle 1{-}x\rangle] \land\neg B[n,u{*}\langle x\rangle]. \end{align*} $$
Suppose
![]() $\exists n C[n,u,0]\land \exists nC[n,u,1]$
, say
$\exists n C[n,u,0]\land \exists nC[n,u,1]$
, say
![]() $C[n,u,0]\land C[m,u,1]$
. Now we may assume
$C[n,u,0]\land C[m,u,1]$
. Now we may assume
![]() $n\geq m$
.
$n\geq m$
.
![]() $C[n,u,0]$
implies
$C[n,u,0]$
implies
![]() $B[n,u{*}\langle 1\rangle ]$
and so
$B[n,u{*}\langle 1\rangle ]$
and so
![]() $B[m,u{*}\langle 1\rangle ]$
contradicting
$B[m,u{*}\langle 1\rangle ]$
contradicting
![]() $C[m,u,1]$
. Thus
$C[m,u,1]$
. Thus
![]() $\exists ^0\mathcal {E}\textsf {-DM}$
yields
$\exists ^0\mathcal {E}\textsf {-DM}$
yields
![]() $\forall n\neg C[n,u,0]\lor \forall n\neg C[n,u,1]$
.
$\forall n\neg C[n,u,0]\lor \forall n\neg C[n,u,1]$
.
![]() $\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00}$
yields
$\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00}$
yields
![]() $\gamma \,{<}\,\underline {2}$
with
$\gamma \,{<}\,\underline {2}$
with
![]() $\forall u,n\neg C[n,u,\gamma (u)]$
. By induction on n, we can show
$\forall u,n\neg C[n,u,\gamma (u)]$
. By induction on n, we can show
![]() $(\exists v < \underline {2}{\upharpoonright } n)(\forall k < n)(v(k) = \gamma (v{\upharpoonright } k))$
. Thus
$(\exists v < \underline {2}{\upharpoonright } n)(\forall k < n)(v(k) = \gamma (v{\upharpoonright } k))$
. Thus
![]() $\Delta ^0_0\textsf {-2AC}^{00}$
yields
$\Delta ^0_0\textsf {-2AC}^{00}$
yields
![]() $\beta < \underline {2}$
with
$\beta < \underline {2}$
with
![]() ${\forall k(\beta (k) = \gamma (\beta {\upharpoonright } k))}$
and so
${\forall k(\beta (k) = \gamma (\beta {\upharpoonright } k))}$
and so
![]() $\forall n,k\neg C[n,\beta {\upharpoonright } k,\beta (k)]$
.
$\forall n,k\neg C[n,\beta {\upharpoonright } k,\beta (k)]$
.
We prove
![]() $B[n{-}k,\beta {\upharpoonright } k]$
by
$B[n{-}k,\beta {\upharpoonright } k]$
by
![]() $\mathcal {D}\textsf {-Ind}$
on
$\mathcal {D}\textsf {-Ind}$
on
![]() $k \leq n$
. For
$k \leq n$
. For
![]() $k = 0$
, this is by assumption. For
$k = 0$
, this is by assumption. For
![]() $k < n$
, if
$k < n$
, if
![]() $B[n{-}k,\beta {\upharpoonright } k]$
, say
$B[n{-}k,\beta {\upharpoonright } k]$
, say
![]() $|v| = n{-}k\land (\forall l\leq n)A[((\beta {\upharpoonright } k){*}v){\upharpoonright } l]$
then
$|v| = n{-}k\land (\forall l\leq n)A[((\beta {\upharpoonright } k){*}v){\upharpoonright } l]$
then
![]() $B[n{-}k{-}1,(\beta {\upharpoonright } k){*}\langle v(0)\rangle ]$
. We may assume
$B[n{-}k{-}1,(\beta {\upharpoonright } k){*}\langle v(0)\rangle ]$
. We may assume
![]() $v(0) = 1{-}\beta (k)$
. By
$v(0) = 1{-}\beta (k)$
. By
![]() $\neg C[n{-}k{-}1,\beta {\upharpoonright } k,\beta (k)]$
we have
$\neg C[n{-}k{-}1,\beta {\upharpoonright } k,\beta (k)]$
we have
![]() $\neg \neg B[n{-}k{-}1,(\beta {\upharpoonright } k){*}\langle \beta (k)\rangle ]$
. Apply
$\neg \neg B[n{-}k{-}1,(\beta {\upharpoonright } k){*}\langle \beta (k)\rangle ]$
. Apply
![]() $\mathcal {D}\textsf {-DNE}$
. Thus
$\mathcal {D}\textsf {-DNE}$
. Thus
![]() $B[0,\beta {\upharpoonright } n]$
, and
$B[0,\beta {\upharpoonright } n]$
, and
![]() $A[\beta {\upharpoonright } n]$
.
$A[\beta {\upharpoonright } n]$
.
Via
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $\mathfrak {ch}$
from Section 2.3,
$\mathfrak {ch}$
from Section 2.3,
![]() $\Pi ^0_1\textsf {-2AC}^{01}$
corresponds to
$\Pi ^0_1\textsf {-2AC}^{01}$
corresponds to
![]() $\Pi ^0_1\textsf {-AC}$
and
$\Pi ^0_1\textsf {-AC}$
and
![]() $\Pi ^0_1\textsf {-2AC}^{00}$
to
$\Pi ^0_1\textsf {-2AC}^{00}$
to
![]() $\Sigma ^0_1$
separation. Hence (3) with
$\Sigma ^0_1$
separation. Hence (3) with
![]() $\mathcal {C}\,{\equiv }\,\Delta ^0_0$
refines the classical fact that
$\mathcal {C}\,{\equiv }\,\Delta ^0_0$
refines the classical fact that
![]() $\Sigma ^0_1$
separation implies WKL (cf. [Reference Simpson45, Lemma IV.4.4]).
$\Sigma ^0_1$
separation implies WKL (cf. [Reference Simpson45, Lemma IV.4.4]).
Replacing
![]() $\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00}$
and
$\forall ^0\neg \mathcal {E}\textsf {-2AC}^{00}$
and
![]() $\exists ^0\mathcal {E}\textsf {-DM}$
by
$\exists ^0\mathcal {E}\textsf {-DM}$
by
![]() $\forall ^0\neg \mathcal {E}\textsf {-BAC}^{00}$
and
$\forall ^0\neg \mathcal {E}\textsf {-BAC}^{00}$
and
![]() $\exists ^0\mathcal {E}\textsf {-GDM}$
in (iii), we can prove
$\exists ^0\mathcal {E}\textsf {-GDM}$
in (iii), we can prove
![]() $\mathcal {C}\textsf {-BKL}$
. However, in a straightforward manner (or as in [Reference Simpson45, Lemma IV.1.4]) we can show
$\mathcal {C}\textsf {-BKL}$
. However, in a straightforward manner (or as in [Reference Simpson45, Lemma IV.1.4]) we can show
![]() $\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-WKL}\,{\vdash }\,\mathcal {C}\textsf {-BKL}$
.
$\mathbf{EL}_0^-{+}\mathcal {C}\textsf {-WKL}\,{\vdash }\,\mathcal {C}\textsf {-BKL}$
.
Corollary 3.7. Over
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0(\mathcal {C})\{\textsf {-DNE},\textsf {-GDM}, \textsf {-Ind}\}$
, the following are equivalent:
$\mathbf{EL}_0^-{+}\Delta ^0_0(\mathcal {C})\{\textsf {-DNE},\textsf {-GDM}, \textsf {-Ind}\}$
, the following are equivalent:
-
(a)
 $\Pi ^0_1(\mathcal {C})\textsf {-BKL}$
;
$\Pi ^0_1(\mathcal {C})\textsf {-BKL}$
; -
(b)
 $\Delta ^0_0(\mathcal {C})\textsf {-BKL}$
;
$\Delta ^0_0(\mathcal {C})\textsf {-BKL}$
; -
(c)
 $\Sigma ^0_1(\mathcal {C})\textsf {-GDM}+\Pi ^0_1(\mathcal {C})\textsf {-BAC}^{00}$
;
$\Sigma ^0_1(\mathcal {C})\textsf {-GDM}+\Pi ^0_1(\mathcal {C})\textsf {-BAC}^{00}$
; -
(d)
 $\Sigma ^0_1(\mathcal {C})\textsf {-DM}+\Pi ^0_1(\mathcal {C})\textsf {-2AC}^{00}$
;
$\Sigma ^0_1(\mathcal {C})\textsf {-DM}+\Pi ^0_1(\mathcal {C})\textsf {-2AC}^{00}$
; -
(e)
 $\Delta ^0_0(\mathcal {C})\textsf {-WKL}$
.
$\Delta ^0_0(\mathcal {C})\textsf {-WKL}$
.
Lemma 3.8.
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BKL}$
proves
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BKL}$
proves
![]() $\Pi ^0_1\textsf {-BAC}^{01}$
.
$\Pi ^0_1\textsf {-BAC}^{01}$
.
Proof Let A be
![]() $\Pi ^0_1$
. By 2.14, we may assume
$\Pi ^0_1$
. By 2.14, we may assume
![]() $A[x,\beta ]\equiv \forall yC[x,\beta {\upharpoonright } y]$
where C is
$A[x,\beta ]\equiv \forall yC[x,\beta {\upharpoonright } y]$
where C is
![]() $\Delta ^0_0$
. Let
$\Delta ^0_0$
. Let
![]() $(u)_x(y)=u((x,y))$
for
$(u)_x(y)=u((x,y))$
for
![]() $(x,y)\,{<}\,|u|$
and define
$(x,y)\,{<}\,|u|$
and define
 $$ \begin{align*} B[u]\,&{:\equiv}\,(\forall x\,{<}\,|u|)(\forall y\,{<}\,|(u)_x|) C[x,(u)_x{\upharpoonright} y];\\ D[x,n,v]\,&{:\equiv}\, v\,{<}\,(\gamma)_x\land |v|\,{=}\,n\land(\forall y\,{<}\,n) C[x,v{\upharpoonright} y]. \end{align*} $$
$$ \begin{align*} B[u]\,&{:\equiv}\,(\forall x\,{<}\,|u|)(\forall y\,{<}\,|(u)_x|) C[x,(u)_x{\upharpoonright} y];\\ D[x,n,v]\,&{:\equiv}\, v\,{<}\,(\gamma)_x\land |v|\,{=}\,n\land(\forall y\,{<}\,n) C[x,v{\upharpoonright} y]. \end{align*} $$
Assume
![]() $\forall x(\exists \beta \,{<}\,(\gamma )_x)A[x,\beta ]$
.
$\forall x(\exists \beta \,{<}\,(\gamma )_x)A[x,\beta ]$
.
By assumption,
![]() $(\forall x\,{<}\,n)(\exists v)D[x,n,v]$
. By induction on
$(\forall x\,{<}\,n)(\exists v)D[x,n,v]$
. By induction on
![]() $m\,{\leq }\, n$
, we can show
$m\,{\leq }\, n$
, we can show
![]() $(\exists w\,{<}\,\gamma {\upharpoonright }(m,n))(w\,{<}\,\gamma \,{\land }\,(\forall x\,{<}\,m)D[x,n,(w)_x])$
. We have
$(\exists w\,{<}\,\gamma {\upharpoonright }(m,n))(w\,{<}\,\gamma \,{\land }\,(\forall x\,{<}\,m)D[x,n,(w)_x])$
. We have
![]() $(\exists u\,{<}\,\gamma )(|u|\,{=}\,n\land B[u])$
by setting
$(\exists u\,{<}\,\gamma )(|u|\,{=}\,n\land B[u])$
by setting
![]() $m\,{=}\,n$
.
$m\,{=}\,n$
.
![]() $\Delta ^0_0\textsf {-BKL}$
yields
$\Delta ^0_0\textsf {-BKL}$
yields
![]() $\beta \,{<}\,\gamma $
with
$\beta \,{<}\,\gamma $
with
![]() $\forall nB[\beta {\upharpoonright } n]$
, and
$\forall nB[\beta {\upharpoonright } n]$
, and
![]() $\forall x,yC[x,(\beta )_x{\upharpoonright } y]$
, i.e.,
$\forall x,yC[x,(\beta )_x{\upharpoonright } y]$
, i.e.,
![]() $\forall xA[x,(\beta )_x]$
.
$\forall xA[x,(\beta )_x]$
.
Corollary 3.9.
![]() $\Pi ^0_1\textsf {-BKL}$
;
$\Pi ^0_1\textsf {-BKL}$
;
![]() $\Pi ^0_1\textsf {-BAC}^{01}\!{+}\Sigma ^0_1\textsf {-GDM}$
;
$\Pi ^0_1\textsf {-BAC}^{01}\!{+}\Sigma ^0_1\textsf {-GDM}$
;
![]() $\Pi ^0_1\textsf {-2AC}^{00}\!{+}\textsf {LLPO}$
; and
$\Pi ^0_1\textsf {-2AC}^{00}\!{+}\textsf {LLPO}$
; and
![]() $\Delta ^0_0\textsf {-WKL}$
are equivalent over
$\Delta ^0_0\textsf {-WKL}$
are equivalent over
![]() $\mathbf{EL}_0^-$
.
$\mathbf{EL}_0^-$
.
Remark 3.10. If we define
![]() $\mathcal {C}\textsf {-BDC}^i$
, bounded dependence choice, similarly to
$\mathcal {C}\textsf {-BDC}^i$
, bounded dependence choice, similarly to
![]() $\Pi ^0_1\textsf {-BAC}^1$
, 3.8 can be enhanced to
$\Pi ^0_1\textsf {-BAC}^1$
, 3.8 can be enhanced to
![]() $\Pi ^0_1\textsf {-BDC}^1$
with the essentially same proof (see also the proof of 3.56(2)), and
$\Pi ^0_1\textsf {-BDC}^1$
with the essentially same proof (see also the proof of 3.56(2)), and
![]() $\Pi ^0_1\textsf {-BDC}^{01}\!{+}\Sigma ^0_1\textsf {-GDM}$
can be added to 3.9. This will play an essential role in the second author’s next work [Reference Sato41].
$\Pi ^0_1\textsf {-BDC}^{01}\!{+}\Sigma ^0_1\textsf {-GDM}$
can be added to 3.9. This will play an essential role in the second author’s next work [Reference Sato41].
3.2 Functional realizability
3.2.1 General theory of Lifschitz’s realizability
A general and abstract machinery for Lifschitz’s realizability is provided by a theory
![]() $\textbf {CDL}$
of combinators and
$\textbf {CDL}$
of combinators and
![]() $\in _{\texttt {L}}$
. This could be seen as a subsystem of explicit mathematics with classesFootnote
18
from [Reference Feferman16]: all individuals are also classes and comprehension is much more restricted than elementary, with some modification on case distinction. Since the use of undefined terms is essential, we have to modify the first order logic as follows.
$\in _{\texttt {L}}$
. This could be seen as a subsystem of explicit mathematics with classesFootnote
18
from [Reference Feferman16]: all individuals are also classes and comprehension is much more restricted than elementary, with some modification on case distinction. Since the use of undefined terms is essential, we have to modify the first order logic as follows.
Definition 3.11 (logic of partial terms (cf. [Reference Beeson5, VI.1]))
The first order logic of partial terms is formulated by the usual axioms and inference rules of the first order (intuitionistic or classical) logic, but
-
(i) a new unary predicate (treated as a logical symbol)
 $\downarrow $
, called definedness predicate, is added;
$\downarrow $
, called definedness predicate, is added; -
(ii) the usual
 $\forall $
- and
$\forall $
- and
 $\exists $
-axioms (if formulated in Hilbert-style) are replaced by
$\exists $
-axioms (if formulated in Hilbert-style) are replaced by
 $\forall xA[x]\,{\land }\, t{\downarrow }\,{\to }\, A[t]$
and
$\forall xA[x]\,{\land }\, t{\downarrow }\,{\to }\, A[t]$
and
 $A[t]\,{\land }\, t{\downarrow }\,{\to }\,\exists xA[x]$
, respectively;
$A[t]\,{\land }\, t{\downarrow }\,{\to }\,\exists xA[x]$
, respectively; -
(iii) the equality axioms are formulated only with free variables and only for atomic formulae;
-
(iv) so-called strictness axiom:
 $A[t]\,{\to }\,t{\downarrow }$
for any atomic formula
$A[t]\,{\to }\,t{\downarrow }$
for any atomic formula
 $A[x]$
in which x actually occurs (which includes
$A[x]$
in which x actually occurs (which includes
 $t[s]{\downarrow }\to s{\downarrow }$
for any term
$t[s]{\downarrow }\to s{\downarrow }$
for any term
 $t[x]$
in which x actually occurs).
$t[x]$
in which x actually occurs).
Notice that (iii) includes
![]() $x\,{=}\,x$
and so (iv) yields
$x\,{=}\,x$
and so (iv) yields
![]() $x{\downarrow }$
. Thus free variables vary only over “defined” objects. This logic is called
$x{\downarrow }$
. Thus free variables vary only over “defined” objects. This logic is called
![]() $E^+$
-logic with equality in [Reference Troelstra and van Dalen50, Chapter 1, 2.4], where
$E^+$
-logic with equality in [Reference Troelstra and van Dalen50, Chapter 1, 2.4], where
![]() $\downarrow $
is called the existence predicate.
$\downarrow $
is called the existence predicate.
Definition 3.12 (
 $\mathcal {L}_{\textrm {Cb}}$
,
$\mathcal {L}_{\textrm {Cb}}$
,
 $\mathcal {L}_{\textrm {CD}}$
,
$\mathcal {L}_{\textrm {CD}}$
,
 $\mathcal {L}_{\textrm {CDL}}$
)
$\mathcal {L}_{\textrm {CDL}}$
)
-
(1) The language
 $\mathcal {L}_{\textrm {Cb}}$
has
$\mathcal {L}_{\textrm {Cb}}$
has
 $=$
as the only predicate symbol (besides
$=$
as the only predicate symbol (besides
 $\downarrow$
); one binary function symbol
$\downarrow$
); one binary function symbol
 $|$
; constant symbols
$|$
; constant symbols
 $\textsf {k}$
,
$\textsf {k}$
,
 $\textsf {s}$
,
$\textsf {s}$
,
 $\textsf {p}$
,
$\textsf {p}$
,
 $\textsf {p}_0$
and
$\textsf {p}_0$
and
 $\textsf {p}_1$
.
$\textsf {p}_1$
.
 $\mathcal {L}_{\textrm {CD}}$
is the expansion with constants
$\mathcal {L}_{\textrm {CD}}$
is the expansion with constants
 $\textsf {z}$
,
$\textsf {z}$
,
 $\textsf {o}$
and
$\textsf {o}$
and
 $\textsf {d}$
; and a unary relation symbol
$\textsf {d}$
; and a unary relation symbol
 $\mathrm{Bo}$
.
$\mathrm{Bo}$
.
 $\mathcal {L}_{\textrm {CDL}}$
expands
$\mathcal {L}_{\textrm {CDL}}$
expands
 $\mathcal {L}_{\textrm {CD}}$
with a binary predicate symbol
$\mathcal {L}_{\textrm {CD}}$
with a binary predicate symbol
 $\in _{\texttt {L}}$
and constant symbols
$\in _{\texttt {L}}$
and constant symbols
 $\textsf {g}$
,
$\textsf {g}$
,
 $\textsf {u}$
,
$\textsf {u}$
,
 $\textsf {r}$
,
$\textsf {r}$
,
 $\textsf {f}$
and
$\textsf {f}$
and
 $\textsf {c}$
. Variables of these languages are denoted by
$\textsf {c}$
. Variables of these languages are denoted by
 $\alpha ,\beta ,\gamma ,\dots ,\xi ,\eta ,\dots $
(except
$\alpha ,\beta ,\gamma ,\dots ,\xi ,\eta ,\dots $
(except
 $\lambda $
) possibly with subscripts.
$\lambda $
) possibly with subscripts. -
(2) (i)
 $st:\equiv s|t$
;
$st:\equiv s|t$
;
 $st_0\dots t_n:\equiv (\dots (st_0)\dots )t_n$
;
$st_0\dots t_n:\equiv (\dots (st_0)\dots )t_n$
;
 $\langle s,t\rangle :=\textsf {p}st$
and
$\langle s,t\rangle :=\textsf {p}st$
and
 $\langle s,t,t'\rangle :=\textsf {p}s(\textsf {p}tt')$
. (ii)
$\langle s,t,t'\rangle :=\textsf {p}s(\textsf {p}tt')$
. (ii)
 $s\simeq t:\equiv \,(s{\downarrow })\,{\lor }\,(t{\downarrow })\,{\to }\, s\,{=}\,t$
.
$s\simeq t:\equiv \,(s{\downarrow })\,{\lor }\,(t{\downarrow })\,{\to }\, s\,{=}\,t$
. -
(3) (i) For a term t and a variable
 $\xi $
, another term
$\xi $
, another term
 $\lambda \xi .t$
, without occurrences of
$\lambda \xi .t$
, without occurrences of
 $\xi $
, is defined inductively:
$\xi $
, is defined inductively:-
(a)
 $\lambda \xi .\eta :\equiv \textsf {k}\eta $
if
$\lambda \xi .\eta :\equiv \textsf {k}\eta $
if
 $\xi \,{\not \equiv }\,\eta $
;
$\xi \,{\not \equiv }\,\eta $
; -
(b)
 $\lambda \xi .\xi :\equiv \textsf {s}\textsf {k}\textsf {k}$
;
$\lambda \xi .\xi :\equiv \textsf {s}\textsf {k}\textsf {k}$
; -
(c)
 $\lambda \xi .c:\equiv \textsf {k}c$
for a constant c;
$\lambda \xi .c:\equiv \textsf {k}c$
for a constant c; -
(d)
 $\lambda \xi .st:\equiv \,\textsf {s}(\lambda \xi .s)(\lambda \xi .t)$
;
$\lambda \xi .st:\equiv \,\textsf {s}(\lambda \xi .s)(\lambda \xi .t)$
;
-
-
(4) (i)
 $\lambda \eta _0\cdots \eta _n.t\,{:\equiv }\, \lambda \eta _0.(\dots (\lambda \eta _n.t)\dots )$
; (ii)
$\lambda \eta _0\cdots \eta _n.t\,{:\equiv }\, \lambda \eta _0.(\dots (\lambda \eta _n.t)\dots )$
; (ii)
 $\textsf { fix}\,{:=}\,\lambda \zeta .(\lambda \xi \eta .\zeta (\xi \xi )\eta )(\lambda \xi \eta .\zeta (\xi \xi )\eta )$
.
$\textsf { fix}\,{:=}\,\lambda \zeta .(\lambda \xi \eta .\zeta (\xi \xi )\eta )(\lambda \xi \eta .\zeta (\xi \xi )\eta )$
.
Definition 3.13 (
 $\textbf {Cb}$
,
$\textbf {Cb}$
,
 $\textbf {CD}$
,
$\textbf {CD}$
,
 $\textbf {CDL}$
)
$\textbf {CDL}$
)
The theory
![]() $\textbf {Cb}$
of
$\textbf {Cb}$
of
![]() $\mathcal {L}_{\textrm {Cb}}$
is generated over intuitionistic logic of partial terms by axioms (k), (s), (p).
$\mathcal {L}_{\textrm {Cb}}$
is generated over intuitionistic logic of partial terms by axioms (k), (s), (p).
![]() $\textbf {CD}$
is
$\textbf {CD}$
is
![]() $\textbf {Cb}{+}\mathrm {(zo)}{+}\mathrm {(d)}$
in
$\textbf {Cb}{+}\mathrm {(zo)}{+}\mathrm {(d)}$
in
![]() $\mathcal {L}_{\textrm {CD}}$
, and
$\mathcal {L}_{\textrm {CD}}$
, and
![]() $\textbf {CDL}$
is
$\textbf {CDL}$
is
![]() $\textbf {Cb}{+}\mathrm {(g)}{+}\mathrm {(u)}{+}\mathrm {(r)}$
in
$\textbf {Cb}{+}\mathrm {(g)}{+}\mathrm {(u)}{+}\mathrm {(r)}$
in
![]() $\mathcal {L}_{\textrm {CDL}}$
.Footnote
19
$\mathcal {L}_{\textrm {CDL}}$
.Footnote
19
 $$ \begin{align*} (\textrm{k})\;&\textsf{k}\alpha\beta\,{=}\, \alpha; \qquad\qquad\qquad\quad \qquad(\textrm{s})\; \textsf{s}\alpha\beta{\downarrow}\land\, \textsf{s}\alpha\beta\gamma\,{\simeq}\, \alpha\gamma(\beta\gamma);\\ (\textrm{p})\;&\textsf{p}_0(\textsf{p}\alpha\beta)\,{=}\, \alpha \land\textsf{p}_1(\textsf{p}\alpha\beta)\,{=}\, \beta \land\textsf{p}_0\alpha{\downarrow} \land\textsf{p}_1\alpha{\downarrow};\\ (\textrm{zo})\;&\textrm{Bo}[\alpha]\,{\leftrightarrow}\,(\alpha\,{=}\,\textsf{z}\ {\lor}\ \alpha\,{=}\,\textsf{o});\ \qquad(\textrm{d})\; \textsf{d}\beta\gamma\textsf{z}\,{=}\,\beta\,{\land}\,\textsf{d}\beta\gamma\textsf{o}\,{=}\,\gamma;\\ (\textrm{g})\;&\textsf{g}\alpha{\downarrow}\land \,(\xi\,{\in_{\texttt{L}}}\,\textsf{g}\alpha\leftrightarrow\xi\,{=}\,\alpha); \qquad(\textrm{u})\;\textsf{u}\alpha{\downarrow}\land\, (\xi\,{\in_{\texttt{L}}}\,\textsf{u}\alpha\leftrightarrow(\exists\beta\,{\in_{\texttt{L}}}\,\alpha)(\xi\,{\in_{\texttt{L}}}\,\beta));\\ (\textrm{r})\;&(\forall\eta\,{\in_{\texttt{L}}}\,\alpha)(\beta\eta{\downarrow})\,{\to}\, \textsf{r}\alpha\beta{\downarrow} \land\forall\xi (\xi\,{\in_{\texttt{L}}}\,\textsf{r}\alpha\beta \,{\leftrightarrow}\,(\exists\eta\,{\in_{\texttt{L}}}\,\alpha)(\xi\,{=}\,\beta\eta)). \end{align*} $$
$$ \begin{align*} (\textrm{k})\;&\textsf{k}\alpha\beta\,{=}\, \alpha; \qquad\qquad\qquad\quad \qquad(\textrm{s})\; \textsf{s}\alpha\beta{\downarrow}\land\, \textsf{s}\alpha\beta\gamma\,{\simeq}\, \alpha\gamma(\beta\gamma);\\ (\textrm{p})\;&\textsf{p}_0(\textsf{p}\alpha\beta)\,{=}\, \alpha \land\textsf{p}_1(\textsf{p}\alpha\beta)\,{=}\, \beta \land\textsf{p}_0\alpha{\downarrow} \land\textsf{p}_1\alpha{\downarrow};\\ (\textrm{zo})\;&\textrm{Bo}[\alpha]\,{\leftrightarrow}\,(\alpha\,{=}\,\textsf{z}\ {\lor}\ \alpha\,{=}\,\textsf{o});\ \qquad(\textrm{d})\; \textsf{d}\beta\gamma\textsf{z}\,{=}\,\beta\,{\land}\,\textsf{d}\beta\gamma\textsf{o}\,{=}\,\gamma;\\ (\textrm{g})\;&\textsf{g}\alpha{\downarrow}\land \,(\xi\,{\in_{\texttt{L}}}\,\textsf{g}\alpha\leftrightarrow\xi\,{=}\,\alpha); \qquad(\textrm{u})\;\textsf{u}\alpha{\downarrow}\land\, (\xi\,{\in_{\texttt{L}}}\,\textsf{u}\alpha\leftrightarrow(\exists\beta\,{\in_{\texttt{L}}}\,\alpha)(\xi\,{\in_{\texttt{L}}}\,\beta));\\ (\textrm{r})\;&(\forall\eta\,{\in_{\texttt{L}}}\,\alpha)(\beta\eta{\downarrow})\,{\to}\, \textsf{r}\alpha\beta{\downarrow} \land\forall\xi (\xi\,{\in_{\texttt{L}}}\,\textsf{r}\alpha\beta \,{\leftrightarrow}\,(\exists\eta\,{\in_{\texttt{L}}}\,\alpha)(\xi\,{=}\,\beta\eta)). \end{align*} $$
In
![]() $\textbf {CDL}$
we can consider an object as a code of a set of objects with
$\textbf {CDL}$
we can consider an object as a code of a set of objects with
![]() $\in _{\texttt {L}}$
, and
$\in _{\texttt {L}}$
, and
![]() $\textsf {g}$
,
$\textsf {g}$
,
![]() $\textsf {u}$
and
$\textsf {u}$
and
![]() $\textsf {r}$
give the codes of singletons, unions and direct images under operations, respectively. The constants
$\textsf {r}$
give the codes of singletons, unions and direct images under operations, respectively. The constants
![]() $\textsf {f}$
and
$\textsf {f}$
and
![]() $\textsf {c}$
are used only in the extensions.
$\textsf {c}$
are used only in the extensions.
Definition 3.14 (
 $\textbf {CDL}\textsf {c}$
,
$\textbf {CDL}\textsf {c}$
,
 $\textbf {CDL}\textsf {f}$
)
$\textbf {CDL}\textsf {f}$
)
-
(1)
 $\textbf {CDL}\textsf {c}$
is an extension of
$\textbf {CDL}\textsf {c}$
is an extension of
 $\textbf {CDL}$
by the additional axiom
$\textbf {CDL}$
by the additional axiom
 $\exists !\xi (\xi \,{\in _{\texttt {L}}}\,\alpha ) \,{\to }\,(\textsf {c}\alpha {\downarrow }\land \textsf {c}\alpha \,{\in _{\texttt {L}}}\,\alpha )$
.
$\exists !\xi (\xi \,{\in _{\texttt {L}}}\,\alpha ) \,{\to }\,(\textsf {c}\alpha {\downarrow }\land \textsf {c}\alpha \,{\in _{\texttt {L}}}\,\alpha )$
. -
(2)
 $\textbf {CDL}\textsf {f}$
is an extension of
$\textbf {CDL}\textsf {f}$
is an extension of
 $\textbf {CDL}$
by
$\textbf {CDL}$
by  $$ \begin{align*} (\exists\xi\,{\in_{\texttt{L}}}\,\alpha)(\textsf{p}_0\xi\,{=}\,\eta)\to \textsf{f}\alpha\eta{\downarrow} \land \forall\xi(\xi\,{\in_{\texttt{L}}}\,\textsf{f}\alpha\eta \leftrightarrow\xi\,{\in_{\texttt{L}}}\,\alpha\land\textsf{p}_0\xi\,{=}\,\eta). \end{align*} $$
$$ \begin{align*} (\exists\xi\,{\in_{\texttt{L}}}\,\alpha)(\textsf{p}_0\xi\,{=}\,\eta)\to \textsf{f}\alpha\eta{\downarrow} \land \forall\xi(\xi\,{\in_{\texttt{L}}}\,\textsf{f}\alpha\eta \leftrightarrow\xi\,{\in_{\texttt{L}}}\,\alpha\land\textsf{p}_0\xi\,{=}\,\eta). \end{align*} $$
Thus
![]() $\textsf {c}$
“chooses” an element if the set is a singleton and
$\textsf {c}$
“chooses” an element if the set is a singleton and
![]() $\textsf {f}$
gives the code of inverse images along projection if inhabited. While these are not needed in the definition nor in the proofs of basic properties below, they will be essential to generalize the “featured” properties of Lifschitz’s realizability (
$\textsf {f}$
gives the code of inverse images along projection if inhabited. While these are not needed in the definition nor in the proofs of basic properties below, they will be essential to generalize the “featured” properties of Lifschitz’s realizability (
![]() $\textsf {c}$
in 3.32 and
$\textsf {c}$
in 3.32 and
![]() $\textsf {f}$
in 3.34).
$\textsf {f}$
in 3.34).
Lemma 3.15.
-
(1)
 $\mathbf{Cb}\vdash (\lambda \xi .t[\xi ]){\downarrow } \land (s{\downarrow } \to (\lambda \xi .t[\xi ])s \simeq t[s])$
for any
$\mathbf{Cb}\vdash (\lambda \xi .t[\xi ]){\downarrow } \land (s{\downarrow } \to (\lambda \xi .t[\xi ])s \simeq t[s])$
for any
 $\mathcal {L}_{\mathrm{Cb}}$
term
$\mathcal {L}_{\mathrm{Cb}}$
term
 $t[\xi ]$
.
$t[\xi ]$
. -
(2)
 $\mathbf{Cb}\vdash \textsf {fix}\,\zeta {\downarrow } \land \textsf { fix}\,\zeta \eta \simeq \zeta (\textsf {fix}\,\zeta )\eta $
.
$\mathbf{Cb}\vdash \textsf {fix}\,\zeta {\downarrow } \land \textsf { fix}\,\zeta \eta \simeq \zeta (\textsf {fix}\,\zeta )\eta $
.
![]() $\mathbb {N}$
with Kleene bracket
$\mathbb {N}$
with Kleene bracket
![]() $nm\,{\simeq }\,\{n\}(m)$
is a model of
$nm\,{\simeq }\,\{n\}(m)$
is a model of
![]() $\textbf {CD}$
. We can trivially expand it to
$\textbf {CD}$
. We can trivially expand it to
![]() $\textbf {CDL}$
by interpreting
$\textbf {CDL}$
by interpreting
![]() $\in _{\texttt {L}}$
as
$\in _{\texttt {L}}$
as
![]() $=$
(only singletons are codable), but also by interpreting
$=$
(only singletons are codable), but also by interpreting
![]() $n\,{\in _{\texttt {L}}}\,m$
as
$n\,{\in _{\texttt {L}}}\,m$
as
![]() $n\,{<}\,(m)^2_1\land \pi [(m)^2_0,n]$
where
$n\,{<}\,(m)^2_1\land \pi [(m)^2_0,n]$
where
![]() $\pi $
is universal
$\pi $
is universal
![]() $\Pi _1$
(the codable are bounded
$\Pi _1$
(the codable are bounded
![]() $\Pi ^0_1$
), and we can interpret
$\Pi ^0_1$
), and we can interpret
![]() $\textsf {g}$
,
$\textsf {g}$
,
![]() $\textsf {u}$
and
$\textsf {u}$
and
![]() $\textsf {r}$
accordingly, as well as
$\textsf {r}$
accordingly, as well as
![]() $\textsf {c}$
and
$\textsf {c}$
and
![]() $\textsf {f}$
.
$\textsf {f}$
.
In
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability defined below, a realizer of existence statement is a (code of) inhabited sets of pairs of witnesses and realizers of the instantiated statements. Within the trivial model of
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability defined below, a realizer of existence statement is a (code of) inhabited sets of pairs of witnesses and realizers of the instantiated statements. Within the trivial model of
![]() $\textbf {CDL}$
,
$\textbf {CDL}$
,
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability is the usual number-realizability; and in the other aforementioned model it is Lifschitz’s (number) realizability.
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability is the usual number-realizability; and in the other aforementioned model it is Lifschitz’s (number) realizability.
Below let
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {L}'$
be first order languages sharing the set of variables, and let
$\mathcal {L}'$
be first order languages sharing the set of variables, and let
![]() $\mathcal {L}'$
expand
$\mathcal {L}'$
expand
![]() $\mathcal {L}_{\textrm {CDL}}$
.
$\mathcal {L}_{\textrm {CDL}}$
.
Definition 3.16 (
 $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
,
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
,
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable)
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable)
For atomic
![]() $\mathcal {L}$
formulae A, fix
$\mathcal {L}$
formulae A, fix
![]() $\mathcal {L}'$
formulae
$\mathcal {L}'$
formulae
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
whose free variables are
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
whose free variables are
![]() $\alpha $
and those in A, where
$\alpha $
and those in A, where
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\bot \,:\equiv \,\bot $
. Extend
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\bot \,:\equiv \,\bot $
. Extend
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
for an arbitrary
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
for an arbitrary
![]() $\mathcal {L}$
formula A by
$\mathcal {L}$
formula A by
 $$ \begin{align*} \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\land B) &:\equiv (\textsf{p}_0\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A)\land(\textsf{p}_1\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} B);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\,{\to}\, B) &:\equiv \forall\beta(\beta\mathbin{{\textbf{r}_{\texttt{L}}}} A\to \alpha\beta{\downarrow}\land\,\alpha\beta\mathbin{{\textbf{r}_{\texttt{L}}}} B);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\,{\lor}\, B) &:\equiv \\ \ \quad\exists\eta(\eta\,{\in_{\texttt{L}}}\,\alpha)\,{\land}\, &(\forall\xi\,{\in_{\texttt{L}}}\,\alpha)(\textrm{Bo}[\textsf{p}_0\xi]\,{\land}\, (\textsf{p}_0\xi\,{=}\,\textsf{z}\,{\to}\,\textsf{p}_1\xi\mathbin{{\textbf{r}_{\texttt{L}}}} A)\,{\land}\,(\textsf{p}_0\xi\,{=}\,\textsf{o}\,{\to}\,\textsf{p}_1\xi\mathbin{{\textbf{r}_{\texttt{L}}}} B));\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}}\forall \xi A[\xi] &:\equiv \forall\xi(\alpha\xi{\downarrow} \land\,\alpha\xi\mathbin{{\textbf{r}_{\texttt{L}}}} A[\xi]);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}}\exists \xi A[\xi] &:\equiv \exists\eta(\eta\,{\in_{\texttt{L}}}\,\alpha)\land (\forall\xi\,{\in_{\texttt{L}}}\,\alpha) (\textsf{p}_1\xi \mathbin{{\textbf{r}_{\texttt{L}}}} A[\textsf{p}_0\xi]). \end{align*} $$
$$ \begin{align*} \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\land B) &:\equiv (\textsf{p}_0\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A)\land(\textsf{p}_1\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} B);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\,{\to}\, B) &:\equiv \forall\beta(\beta\mathbin{{\textbf{r}_{\texttt{L}}}} A\to \alpha\beta{\downarrow}\land\,\alpha\beta\mathbin{{\textbf{r}_{\texttt{L}}}} B);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}} (A\,{\lor}\, B) &:\equiv \\ \ \quad\exists\eta(\eta\,{\in_{\texttt{L}}}\,\alpha)\,{\land}\, &(\forall\xi\,{\in_{\texttt{L}}}\,\alpha)(\textrm{Bo}[\textsf{p}_0\xi]\,{\land}\, (\textsf{p}_0\xi\,{=}\,\textsf{z}\,{\to}\,\textsf{p}_1\xi\mathbin{{\textbf{r}_{\texttt{L}}}} A)\,{\land}\,(\textsf{p}_0\xi\,{=}\,\textsf{o}\,{\to}\,\textsf{p}_1\xi\mathbin{{\textbf{r}_{\texttt{L}}}} B));\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}}\forall \xi A[\xi] &:\equiv \forall\xi(\alpha\xi{\downarrow} \land\,\alpha\xi\mathbin{{\textbf{r}_{\texttt{L}}}} A[\xi]);\\ \alpha\mathbin{{\textbf{r}_{\texttt{L}}}}\exists \xi A[\xi] &:\equiv \exists\eta(\eta\,{\in_{\texttt{L}}}\,\alpha)\land (\forall\xi\,{\in_{\texttt{L}}}\,\alpha) (\textsf{p}_1\xi \mathbin{{\textbf{r}_{\texttt{L}}}} A[\textsf{p}_0\xi]). \end{align*} $$
An
![]() $\mathcal {L}$
theory T is called
$\mathcal {L}$
theory T is called
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in an
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in an
![]() $\mathcal {L}'$
theory
$\mathcal {L}'$
theory
![]() $T'$
if
$T'$
if
![]() $T'\vdash \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
for any A in T.
$T'\vdash \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
for any A in T.
Definition 3.17 (operator
 $\textsf {b}_A$
)
$\textsf {b}_A$
)
Fix
![]() $\mathcal {L}_{\textrm {CDL}}$
terms
$\mathcal {L}_{\textrm {CDL}}$
terms
![]() $\textsf {b}_{A[\vec {\eta }]}$
for atomic
$\textsf {b}_{A[\vec {\eta }]}$
for atomic
![]() $A[\vec {\eta }]$
’s. Extend
$A[\vec {\eta }]$
’s. Extend
![]() $\textsf {b}_A$
to arbitrary A by
$\textsf {b}_A$
to arbitrary A by
 $$ \begin{align*} \textsf{b}_{A\land B} & :\equiv \lambda\vec{\eta}\alpha.\textsf{p}(\textsf{b}_{A}\vec{\eta}(\textsf{r}\alpha\textsf{p}_0))(\textsf{b}_{B}\vec{\eta}(\textsf{r}\alpha\textsf{p}_1));\\ \textsf{b}_{B\to A} & :\equiv \lambda\vec{\eta}\alpha\beta.\textsf{b}_{A}\vec{\eta}(\textsf{r}\alpha(\lambda\zeta.\zeta\beta));\\ \textsf{b}_{\forall\xi A[\vec{\eta},\xi]} & :\equiv \lambda\vec{\eta}\alpha\xi.\textsf{b}_{A[\vec{\eta},\xi]}\vec{\eta}\xi(\textsf{r}\alpha(\lambda\zeta.\zeta\xi));\\ \textsf{b}_{\exists\xi A[\vec{\eta},\xi]}, \textsf{b}_{A\lor B} & :\equiv \lambda\vec{\eta}\alpha.\textsf{u}\alpha. \end{align*} $$
$$ \begin{align*} \textsf{b}_{A\land B} & :\equiv \lambda\vec{\eta}\alpha.\textsf{p}(\textsf{b}_{A}\vec{\eta}(\textsf{r}\alpha\textsf{p}_0))(\textsf{b}_{B}\vec{\eta}(\textsf{r}\alpha\textsf{p}_1));\\ \textsf{b}_{B\to A} & :\equiv \lambda\vec{\eta}\alpha\beta.\textsf{b}_{A}\vec{\eta}(\textsf{r}\alpha(\lambda\zeta.\zeta\beta));\\ \textsf{b}_{\forall\xi A[\vec{\eta},\xi]} & :\equiv \lambda\vec{\eta}\alpha\xi.\textsf{b}_{A[\vec{\eta},\xi]}\vec{\eta}\xi(\textsf{r}\alpha(\lambda\zeta.\zeta\xi));\\ \textsf{b}_{\exists\xi A[\vec{\eta},\xi]}, \textsf{b}_{A\lor B} & :\equiv \lambda\vec{\eta}\alpha.\textsf{u}\alpha. \end{align*} $$
Strictly,
![]() $\textsf {b}_A$
is defined for abstracts A rather than formulae. We write
$\textsf {b}_A$
is defined for abstracts A rather than formulae. We write
![]() $\textsf {b}_{C[\vec {\alpha }]}$
also for
$\textsf {b}_{C[\vec {\alpha }]}$
also for
![]() $\textsf {b}_{C[\vec {\alpha }]}\vec {\eta }$
with the free variables
$\textsf {b}_{C[\vec {\alpha }]}\vec {\eta }$
with the free variables
![]() $\vec {\eta }$
implicit (i.e., other than
$\vec {\eta }$
implicit (i.e., other than
![]() $\vec {\alpha }$
’s) in
$\vec {\alpha }$
’s) in
![]() ${C[\vec {\alpha }]}$
. We will not need the definition of
${C[\vec {\alpha }]}$
. We will not need the definition of
![]() $\textsf {b}_A$
but the following.
$\textsf {b}_A$
but the following.
Lemma 3.18. For an
![]() $\mathcal {L}'$
theory
$\mathcal {L}'$
theory
![]() $T'$
, if
$T'$
, if
for any atomic
![]() $\mathcal {L}$
formula A, then it holds for an arbitrary
$\mathcal {L}$
formula A, then it holds for an arbitrary
![]() $\mathcal {L}$
formula A.
$\mathcal {L}$
formula A.
Proposition 3.19. Assume the premise of 3.18. If
![]() $A[\vec {\eta }]$
follows from sentences
$A[\vec {\eta }]$
follows from sentences
![]() $B_1, \dots , B_n$
intuitionistically, then there is a closed
$B_1, \dots , B_n$
intuitionistically, then there is a closed
![]() $\mathcal {L}_{\mathrm{CDL}}$
-term t such that
$\mathcal {L}_{\mathrm{CDL}}$
-term t such that
Proof Consider a Hilbert-style calculus. The axioms in the negative parts are realizable as follows.
![]() $\lambda \vec {\eta }.\textsf {k}$
,
$\lambda \vec {\eta }.\textsf {k}$
,
![]() $\lambda \vec {\eta }.\textsf {s}$
,
$\lambda \vec {\eta }.\textsf {s}$
,
![]() $\lambda \vec {\eta }.\textsf {p}_i$
,
$\lambda \vec {\eta }.\textsf {p}_i$
,
![]() $\lambda \vec {\eta }.\textsf {p}$
and
$\lambda \vec {\eta }.\textsf {p}$
and
![]() $\lambda \vec {\eta }\xi \alpha .\alpha \xi $
realize the universal closures of the axioms
$\lambda \vec {\eta }\xi \alpha .\alpha \xi $
realize the universal closures of the axioms
![]() $\forall \vec {\eta }(A{\to } B{\to } A)$
,
$\forall \vec {\eta }(A{\to } B{\to } A)$
,
![]() $\forall \vec {\eta }((A{\to } (B{\to } C)){\to }(A{\to } B){\to }(A{\to } C))$
,
$\forall \vec {\eta }((A{\to } (B{\to } C)){\to }(A{\to } B){\to }(A{\to } C))$
,
![]() $\forall \vec {\eta }(A_0{\land } A_1{\to } A_i)$
,
$\forall \vec {\eta }(A_0{\land } A_1{\to } A_i)$
,
![]() $\forall \vec {\eta }(A_0{\to } A_1{\to } A_0{\land } A_1)$
and
$\forall \vec {\eta }(A_0{\to } A_1{\to } A_0{\land } A_1)$
and
![]() $\forall \vec {\eta },\xi (\forall \zeta A[\zeta ]\,{\to }\, A[\xi ])$
, respectively. For the inference rules for the negative part, if
$\forall \vec {\eta },\xi (\forall \zeta A[\zeta ]\,{\to }\, A[\xi ])$
, respectively. For the inference rules for the negative part, if
![]() $s\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(C{\to } A)$
and
$s\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(C{\to } A)$
and
![]() $t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }C$
then
$t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }C$
then
![]() $\lambda \vec {\eta }.s\vec {\eta }(t\vec {\eta })\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }A$
, and if
$\lambda \vec {\eta }.s\vec {\eta }(t\vec {\eta })\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }A$
, and if
![]() $t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\zeta (C{\to } A[\zeta ])$
then
$t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\zeta (C{\to } A[\zeta ])$
then
![]() $\lambda \vec {\eta }\alpha \zeta .t\vec {\eta }\zeta \alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(C\,{\to }\,\forall \zeta A[\zeta ])$
.
$\lambda \vec {\eta }\alpha \zeta .t\vec {\eta }\zeta \alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(C\,{\to }\,\forall \zeta A[\zeta ])$
.
For the
![]() $\exists $
-axiom, it is easy to see
$\exists $
-axiom, it is easy to see
![]() $\lambda \vec {\eta }\xi \gamma .\textsf {g}(\langle \xi ,\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\xi (A[\xi ]\,{\to }\,\exists \zeta A[\zeta ])$
. For the
$\lambda \vec {\eta }\xi \gamma .\textsf {g}(\langle \xi ,\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\xi (A[\xi ]\,{\to }\,\exists \zeta A[\zeta ])$
. For the
![]() $\exists $
-rule, we show that if
$\exists $
-rule, we show that if
![]() $t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\zeta (A[\zeta ]\,{\to }\, C)$
then
$t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta },\zeta (A[\zeta ]\,{\to }\, C)$
then
![]() $\lambda \vec {\eta }\gamma .\textsf {b}_C\vec {\eta } (\textsf {r}\gamma (\lambda \xi .t\vec {\eta } (\textsf {p}_0\xi )(\textsf {p}_1\xi )))$
realizes
$\lambda \vec {\eta }\gamma .\textsf {b}_C\vec {\eta } (\textsf {r}\gamma (\lambda \xi .t\vec {\eta } (\textsf {p}_0\xi )(\textsf {p}_1\xi )))$
realizes
![]() $\forall \vec {\eta }(\exists \zeta A[\zeta ]\,{\to }\, C)$
as follows. Take
$\forall \vec {\eta }(\exists \zeta A[\zeta ]\,{\to }\, C)$
as follows. Take
![]() $\gamma $
such that
$\gamma $
such that
![]() $\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \zeta A[\zeta ]$
. Then we have
$\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \zeta A[\zeta ]$
. Then we have
![]() $(\forall \xi \,{\in _{\texttt {L}}}\,\gamma )(\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\textsf {p}_0\xi ])$
and
$(\forall \xi \,{\in _{\texttt {L}}}\,\gamma )(\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\textsf {p}_0\xi ])$
and
![]() $(\forall \xi \,{\in _{\texttt {L}}}\,\gamma )(t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi ){\downarrow }\land \,t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )\mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
, i.e.,
$(\forall \xi \,{\in _{\texttt {L}}}\,\gamma )(t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi ){\downarrow }\land \,t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )\mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
, i.e.,
![]() $(\forall \xi '\,{\in _{\texttt {L}}}\,\textsf {r}\gamma (\lambda \xi .t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )))(\xi '\mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
. Similarly
$(\forall \xi '\,{\in _{\texttt {L}}}\,\textsf {r}\gamma (\lambda \xi .t\vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )))(\xi '\mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
. Similarly
![]() $\exists \xi '(\xi '\,{\in _{\texttt {L}}}\,\textsf {r}\gamma (\lambda \xi .\beta \vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )))$
. Now we can apply 3.18.
$\exists \xi '(\xi '\,{\in _{\texttt {L}}}\,\textsf {r}\gamma (\lambda \xi .\beta \vec {\eta }(\textsf {p}_0\xi )(\textsf {p}_1\xi )))$
. Now we can apply 3.18.
For the
![]() $\lor $
-axioms, it is easy to see
$\lor $
-axioms, it is easy to see
![]() $\lambda \vec {\eta }\gamma .\textsf {g}(\langle \textsf {z},\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(A\,{\to }\,A\,{\lor }\,B)$
and also
$\lambda \vec {\eta }\gamma .\textsf {g}(\langle \textsf {z},\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(A\,{\to }\,A\,{\lor }\,B)$
and also
![]() $\lambda \vec {\eta }\gamma .\textsf {g}(\langle \textsf {o},\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(B{{\kern-2pt}\to{\kern-2pt}}A\,{\lor }\,B)$
. For the
$\lambda \vec {\eta }\gamma .\textsf {g}(\langle \textsf {o},\gamma \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(B{{\kern-2pt}\to{\kern-2pt}}A\,{\lor }\,B)$
. For the
![]() $\lor $
-rule, if
$\lor $
-rule, if
![]() $s\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(A{{\kern-2pt}\to{\kern-2pt}}C)$
and
$s\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(A{{\kern-2pt}\to{\kern-2pt}}C)$
and
![]() $t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(B{{\kern-2pt}\to{\kern-2pt}}C)$
then, similarly we can show that
$t\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \vec {\eta }(B{{\kern-2pt}\to{\kern-2pt}}C)$
then, similarly we can show that
![]() $\lambda \vec {\eta }\alpha .\textsf {b}_C\vec {\eta }(\textsf {r}\alpha (\lambda \xi .\textsf {d}(s\vec {\eta }(\textsf {p}_1\xi ))(t\vec {\eta }(\textsf {p}_1\xi )) (\textsf {p}_0\xi )))$
realizes
$\lambda \vec {\eta }\alpha .\textsf {b}_C\vec {\eta }(\textsf {r}\alpha (\lambda \xi .\textsf {d}(s\vec {\eta }(\textsf {p}_1\xi ))(t\vec {\eta }(\textsf {p}_1\xi )) (\textsf {p}_0\xi )))$
realizes
![]() $\forall \vec {\eta }(A\,{\lor }\,B\,{\to }\, C)$
.
$\forall \vec {\eta }(A\,{\lor }\,B\,{\to }\, C)$
.
Therefore
![]() $A\mapsto \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
can be considered as an interpretation of intuitionistic logic (i.e., the theory axiomatized by
$A\mapsto \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
can be considered as an interpretation of intuitionistic logic (i.e., the theory axiomatized by
![]() $\emptyset $
) over
$\emptyset $
) over
![]() $\mathcal {L}$
to extensions of
$\mathcal {L}$
to extensions of
![]() $\textbf {CDL}$
in the sense of Section 1.2. The theme of this section is to clarify: with which axioms in
$\textbf {CDL}$
in the sense of Section 1.2. The theme of this section is to clarify: with which axioms in
![]() $\mathcal {L}'$
, which axioms in
$\mathcal {L}'$
, which axioms in
![]() $\mathcal {L}$
can be interpreted in this way.
$\mathcal {L}$
can be interpreted in this way.
3.2.2 Kleene’s second model
 $\mathfrak {k}$
$\mathfrak {k}$
We will need functional realizability and so a functional model of
![]() $\textbf {CD}$
, called Kleene’s second model. Though [Reference Troelstra and van Dalen51, Chapter 9, 4.1] gave a construction in an abstract way, it seems easier for us to give an explicit definition, in order to check if the construction is possible in our context of weak induction.
$\textbf {CD}$
, called Kleene’s second model. Though [Reference Troelstra and van Dalen51, Chapter 9, 4.1] gave a construction in an abstract way, it seems easier for us to give an explicit definition, in order to check if the construction is possible in our context of weak induction.
Notation 3.20 (
 $u|v$
)
$u|v$
)
The expression
![]() $(u|v)(x)$
denotes
$(u|v)(x)$
denotes
![]() $u(\langle x\rangle {*}(v{\upharpoonright } y))-1$
if
$u(\langle x\rangle {*}(v{\upharpoonright } y))-1$
if
![]() ${y= \min \{z:u(\langle x\rangle {*}(v{\upharpoonright } z))> 0\}}$
, and is undefined if there is no such y. Now “
${y= \min \{z:u(\langle x\rangle {*}(v{\upharpoonright } z))> 0\}}$
, and is undefined if there is no such y. Now “
![]() $(u|v)(x)$
is defined” is
$(u|v)(x)$
is defined” is
![]() $\Delta ^0_0$
. If
$\Delta ^0_0$
. If
![]() $u\subseteq u'$
,
$u\subseteq u'$
,
![]() $v\subseteq v'$
and
$v\subseteq v'$
and
![]() $(u|v)(k)$
is defined, then
$(u|v)(k)$
is defined, then
![]() $(u|v)(k)=(u'|v')(k)$
.
$(u|v)(k)=(u'|v')(k)$
.
Definition 3.21 (
 $A^{\mathfrak {k}}$
)
$A^{\mathfrak {k}}$
)
For an
![]() $\mathcal {L}_{\mathrm{Cb}}$
term t and
$\mathcal {L}_{\mathrm{Cb}}$
term t and
![]() $\mathcal {L}_{\mathrm{Cb}}$
formula A, define
$\mathcal {L}_{\mathrm{Cb}}$
formula A, define
![]() $\mathcal {L}_{\mathrm{F}}$
formulae
$\mathcal {L}_{\mathrm{F}}$
formulae
![]() $[\![t]\!]^{\mathfrak {k}}(\xi )$
and
$[\![t]\!]^{\mathfrak {k}}(\xi )$
and
![]() $A^{\mathfrak {k}}$
by
$A^{\mathfrak {k}}$
by
 $$ \begin{align*} [\![\alpha]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\xi\,{=}\,\alpha;\; &[\![c]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\xi\,{=}\,c^{\mathfrak{k}}\text{ for a constant }c;\\ [\![st]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\exists\eta,\zeta([\![s]\!]^{\mathfrak{k}}(\eta) \land [\![t]\!]^{\mathfrak{k}}(\zeta)\land\xi\,{=}\,\eta|\zeta); \end{align*} $$
$$ \begin{align*} [\![\alpha]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\xi\,{=}\,\alpha;\; &[\![c]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\xi\,{=}\,c^{\mathfrak{k}}\text{ for a constant }c;\\ [\![st]\!]^{\mathfrak{k}}(\xi)\,&{:\equiv}\,\exists\eta,\zeta([\![s]\!]^{\mathfrak{k}}(\eta) \land [\![t]\!]^{\mathfrak{k}}(\zeta)\land\xi\,{=}\,\eta|\zeta); \end{align*} $$
and by
 $$ \begin{align*} (s{\downarrow})^{\mathfrak{k}}\,&{:\equiv}\,\exists\xi([\![s]\!]^{\mathfrak{k}}(\xi)); & (s\,{=}\,t)^{\mathfrak{k}}\,&{:\equiv}\,\exists\xi([\![s]\!]^{\mathfrak{k}}(\xi)\land[\![t]\!]^{\mathfrak{k}}(\xi));& \bot^{\mathfrak{k}}\,&{:\equiv}\,\bot;\\ (A\Box B)^{\mathfrak{k}}\,&{:\equiv}\, A^{\mathfrak{k}}\Box B^{\mathfrak{k}}\;(\Box\equiv{\land},{\to},{\lor}); & (Q\xi A)^{\mathfrak{k}}\,&{:\equiv}\, Q\xi A^{\mathfrak{k}}\;(Q\equiv\forall,\exists). \end{align*} $$
$$ \begin{align*} (s{\downarrow})^{\mathfrak{k}}\,&{:\equiv}\,\exists\xi([\![s]\!]^{\mathfrak{k}}(\xi)); & (s\,{=}\,t)^{\mathfrak{k}}\,&{:\equiv}\,\exists\xi([\![s]\!]^{\mathfrak{k}}(\xi)\land[\![t]\!]^{\mathfrak{k}}(\xi));& \bot^{\mathfrak{k}}\,&{:\equiv}\,\bot;\\ (A\Box B)^{\mathfrak{k}}\,&{:\equiv}\, A^{\mathfrak{k}}\Box B^{\mathfrak{k}}\;(\Box\equiv{\land},{\to},{\lor}); & (Q\xi A)^{\mathfrak{k}}\,&{:\equiv}\, Q\xi A^{\mathfrak{k}}\;(Q\equiv\forall,\exists). \end{align*} $$
where
![]() $\xi \,{=}\,\eta |\zeta $
is from 2.37 and where
$\xi \,{=}\,\eta |\zeta $
is from 2.37 and where
![]() $c^{\mathfrak {k}}$
’s are defined as follows by
$c^{\mathfrak {k}}$
’s are defined as follows by
![]() $\Delta ^0_0$
bounded search in
$\Delta ^0_0$
bounded search in
![]() $\mathbf{EL}_0^-$
from 2.10:
$\mathbf{EL}_0^-$
from 2.10:
 $$ \begin{align*} & {\textsf{p}_i}^{\mathfrak{k}}(x)= \begin{cases} (w(y))^2_i\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle {*} w \text{ and } |w|\,{=}\,y\,{+}\,1;\\ 0 & \text{otherwise}. \end{cases}\\ &\textsf{p}^{\mathfrak{k}}(x)= \begin{cases} (u(y),v(y))\,{+}\,2 & \text{if } x\,{=}\,\langle \langle y\rangle {*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,y\,{+}\,1; \\ 0 & \text{if } x\,{=}\,\langle \langle y\rangle {*}v\rangle {*}u \text{ and }|u|\,{\neq}\,|v|\,{=}\,y\,{+}\,1; \\ 1 & \text{otherwise.} \end{cases}\\ & \textsf{k}^{\mathfrak{k}}(x)= \begin{cases} u(y)\,{+}\,2 & \text{if } x\,{=}\,\langle\langle y\rangle\rangle{*}u \text{ and } |u|\,{=}\,y\,{+}\,1; \\ 1 & \text{if } x\,{=}\,\langle v\rangle \text{ and } |v|\,{\neq}\,1; \\ 0 & \text{otherwise}. \end{cases}\\ &\textsf{s}^{\mathfrak{k}}(x)= \begin{cases} ((u|w)|(v|w))(y)\,{+}\,3 & \text{if } x\,{=}\,\langle\langle \langle y\rangle {*}w\rangle{*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,|w|\\ &\text{ and }(\forall z\leq y)\begin{pmatrix}(u|w)(z)\text{, }(v|w)(z)\text{ and }\\ ((u|w)|(v|w))(z)\text{ are defined}\end{pmatrix}; \\ 2 & \hspace{-28pt}\text{if } x\,{=}\,\langle\langle \langle y\rangle {*}w\rangle{*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,|w| \text{ but otherwise};\\ 1 &\hspace{-28pt}\text{if } x\,{=}\,\langle \langle \langle y\rangle {*}w\rangle{*}v\rangle, 0\,{<}\,|w| \text{ and } |v|\,{\neq}\,|w|;\\ 2 & \hspace{-28pt}\text{if } x\,{=}\,\langle \langle \langle y\rangle\rangle{*}v\rangle \text{ with } |v|\,{>}\,0 \text{ or } x\,{=}\,\langle \langle \langle \rangle \rangle{*}v\rangle \text{ or } x\,{=}\,\langle\langle \rangle\rangle; \\ 0 & \hspace{-28pt}\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} & {\textsf{p}_i}^{\mathfrak{k}}(x)= \begin{cases} (w(y))^2_i\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle {*} w \text{ and } |w|\,{=}\,y\,{+}\,1;\\ 0 & \text{otherwise}. \end{cases}\\ &\textsf{p}^{\mathfrak{k}}(x)= \begin{cases} (u(y),v(y))\,{+}\,2 & \text{if } x\,{=}\,\langle \langle y\rangle {*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,y\,{+}\,1; \\ 0 & \text{if } x\,{=}\,\langle \langle y\rangle {*}v\rangle {*}u \text{ and }|u|\,{\neq}\,|v|\,{=}\,y\,{+}\,1; \\ 1 & \text{otherwise.} \end{cases}\\ & \textsf{k}^{\mathfrak{k}}(x)= \begin{cases} u(y)\,{+}\,2 & \text{if } x\,{=}\,\langle\langle y\rangle\rangle{*}u \text{ and } |u|\,{=}\,y\,{+}\,1; \\ 1 & \text{if } x\,{=}\,\langle v\rangle \text{ and } |v|\,{\neq}\,1; \\ 0 & \text{otherwise}. \end{cases}\\ &\textsf{s}^{\mathfrak{k}}(x)= \begin{cases} ((u|w)|(v|w))(y)\,{+}\,3 & \text{if } x\,{=}\,\langle\langle \langle y\rangle {*}w\rangle{*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,|w|\\ &\text{ and }(\forall z\leq y)\begin{pmatrix}(u|w)(z)\text{, }(v|w)(z)\text{ and }\\ ((u|w)|(v|w))(z)\text{ are defined}\end{pmatrix}; \\ 2 & \hspace{-28pt}\text{if } x\,{=}\,\langle\langle \langle y\rangle {*}w\rangle{*}v\rangle {*}u \text{ and } |u|\,{=}\,|v|\,{=}\,|w| \text{ but otherwise};\\ 1 &\hspace{-28pt}\text{if } x\,{=}\,\langle \langle \langle y\rangle {*}w\rangle{*}v\rangle, 0\,{<}\,|w| \text{ and } |v|\,{\neq}\,|w|;\\ 2 & \hspace{-28pt}\text{if } x\,{=}\,\langle \langle \langle y\rangle\rangle{*}v\rangle \text{ with } |v|\,{>}\,0 \text{ or } x\,{=}\,\langle \langle \langle \rangle \rangle{*}v\rangle \text{ or } x\,{=}\,\langle\langle \rangle\rangle; \\ 0 & \hspace{-28pt}\text{otherwise}. \end{cases} \end{align*} $$
Proposition 3.22.
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00} \vdash (\mathbf{Cb})^{\mathfrak {k}}\land ((\textsf {p}\alpha \beta )^{\mathfrak {k}} \,{=}\,(\alpha ,\beta ))$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00} \vdash (\mathbf{Cb})^{\mathfrak {k}}\land ((\textsf {p}\alpha \beta )^{\mathfrak {k}} \,{=}\,(\alpha ,\beta ))$
.
Proof Let
![]() $\overline {\alpha }n$
denote
$\overline {\alpha }n$
denote
![]() $\alpha {\upharpoonright } n$
. We can easily see
$\alpha {\upharpoonright } n$
. We can easily see
![]() $(\textsf {p}_i\alpha )^{\mathfrak {k}}(x)=(\alpha (x))^2_i$
, and using the following we can show
$(\textsf {p}_i\alpha )^{\mathfrak {k}}(x)=(\alpha (x))^2_i$
, and using the following we can show
![]() $(\textsf {k}\alpha \beta )^{\mathfrak {k}}(x)=\alpha (x)$
and
$(\textsf {k}\alpha \beta )^{\mathfrak {k}}(x)=\alpha (x)$
and
![]() $(\textsf{p}\alpha \beta )^{\mathfrak {k}}(x)= (\alpha (x), \beta (x))$
and the first conjunct of (s).
$(\textsf{p}\alpha \beta )^{\mathfrak {k}}(x)= (\alpha (x), \beta (x))$
and the first conjunct of (s).
 $$ \begin{align*} &(\textsf{p}\alpha)^{\mathfrak{k}}(x)= \begin{cases} (\alpha(y), v(y))\,{+}\,1 & \text{if } x\,{=}\, \langle y\rangle{*}v\land |v|\,{=}\,y\,{+}\,1; \\ 0 & \text{otherwise}. \end{cases}\\ & (\textsf{k}\alpha)^{\mathfrak{k}}(x)= \begin{cases} \alpha(y)\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle;\\ 0 & \text{otherwise}. \end{cases};\\ & (\textsf{s}\alpha)^{\mathfrak{k}}(x)= \begin{cases} ((\overline{\alpha}k|w)|(v|w))(y)\,{+}\,2 & \text{if } x\,{=}\,\langle \langle y\rangle{*}w\rangle{*}v \text{ and, for } k\,{:=}\,|v|\,{=}\,|w|,\\ &(\forall z\leq y)\!\begin{pmatrix}(\overline{\alpha}k|w)(z)\text{, } (v|w)(z)\text{ and }\\ ((\overline{\alpha}k|w)|(v|w))(z)\text{ are defined}\end{pmatrix}\! ;\\ 1 & \hspace{-25pt}\text{if } x\,{=}\,\langle \langle y\rangle {*}w\rangle{*}v \text{ and } |v|\,{=}\,|w| \text{ but otherwise};\\[-2pt] 0 & \hspace{-25pt}\text{if } x\,{=}\, \langle \langle y\rangle {*}w\rangle{*}v, 0\,{<}\,|w| \text{ and } |v|\,{\neq}\,|w|;\\[-2pt] 1 & \hspace{-25pt}\text{if } x\,{=}\,\langle \langle y\rangle \rangle{*}v \text{ with } |v|\,{>}\,0 \text{ or } x\,{=}\,\langle \langle \rangle \rangle{*}v \text{ or } x\,{=}\,\langle\,\rangle. \end{cases}\\ & (\textsf{s}\alpha\beta)^{\mathfrak{k}}(x)= \begin{cases} ((\overline{\alpha}k|w)|(\overline{\beta}k|w))(y)\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle{*}w \text{ and, for } k\,{:=}\,|w|,\\[-2pt] &\hspace{-25pt}(\forall z\leq y)\begin{pmatrix}(\overline{\alpha}k|w)(z), (\overline{\beta}k|w)(z)\text{ and }\\ ((\overline{\alpha}k|w)|(\overline{\beta}k|w))(z)\text{ are defined}\end{pmatrix}\!;\\ 0 & \hspace{-25pt}\text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} &(\textsf{p}\alpha)^{\mathfrak{k}}(x)= \begin{cases} (\alpha(y), v(y))\,{+}\,1 & \text{if } x\,{=}\, \langle y\rangle{*}v\land |v|\,{=}\,y\,{+}\,1; \\ 0 & \text{otherwise}. \end{cases}\\ & (\textsf{k}\alpha)^{\mathfrak{k}}(x)= \begin{cases} \alpha(y)\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle;\\ 0 & \text{otherwise}. \end{cases};\\ & (\textsf{s}\alpha)^{\mathfrak{k}}(x)= \begin{cases} ((\overline{\alpha}k|w)|(v|w))(y)\,{+}\,2 & \text{if } x\,{=}\,\langle \langle y\rangle{*}w\rangle{*}v \text{ and, for } k\,{:=}\,|v|\,{=}\,|w|,\\ &(\forall z\leq y)\!\begin{pmatrix}(\overline{\alpha}k|w)(z)\text{, } (v|w)(z)\text{ and }\\ ((\overline{\alpha}k|w)|(v|w))(z)\text{ are defined}\end{pmatrix}\! ;\\ 1 & \hspace{-25pt}\text{if } x\,{=}\,\langle \langle y\rangle {*}w\rangle{*}v \text{ and } |v|\,{=}\,|w| \text{ but otherwise};\\[-2pt] 0 & \hspace{-25pt}\text{if } x\,{=}\, \langle \langle y\rangle {*}w\rangle{*}v, 0\,{<}\,|w| \text{ and } |v|\,{\neq}\,|w|;\\[-2pt] 1 & \hspace{-25pt}\text{if } x\,{=}\,\langle \langle y\rangle \rangle{*}v \text{ with } |v|\,{>}\,0 \text{ or } x\,{=}\,\langle \langle \rangle \rangle{*}v \text{ or } x\,{=}\,\langle\,\rangle. \end{cases}\\ & (\textsf{s}\alpha\beta)^{\mathfrak{k}}(x)= \begin{cases} ((\overline{\alpha}k|w)|(\overline{\beta}k|w))(y)\,{+}\,1 & \text{if } x\,{=}\,\langle y\rangle{*}w \text{ and, for } k\,{:=}\,|w|,\\[-2pt] &\hspace{-25pt}(\forall z\leq y)\begin{pmatrix}(\overline{\alpha}k|w)(z), (\overline{\beta}k|w)(z)\text{ and }\\ ((\overline{\alpha}k|w)|(\overline{\beta}k|w))(z)\text{ are defined}\end{pmatrix}\!;\\ 0 & \hspace{-25pt}\text{otherwise}. \end{cases} \end{align*} $$
Let
![]() $(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}{\downarrow }$
. Then
$(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}{\downarrow }$
. Then
![]() $(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}(y)\,{=}\, ((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
, where k is a least such that
$(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}(y)\,{=}\, ((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
, where k is a least such that
![]() $(\overline {\alpha }k|\overline {\gamma }k)(z)|(\overline {\beta }k|\overline {\gamma }k)(z)$
and
$(\overline {\alpha }k|\overline {\gamma }k)(z)|(\overline {\beta }k|\overline {\gamma }k)(z)$
and
![]() $((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(z)$
are defined for all
$((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(z)$
are defined for all
![]() $z\,{\leq }\, y$
. By 3.20,
$z\,{\leq }\, y$
. By 3.20,
![]() $((\alpha |\gamma )|(\beta |\gamma ))(y)$
is defined and is
$((\alpha |\gamma )|(\beta |\gamma ))(y)$
is defined and is
![]() $((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
.
$((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
.
![]() $\Sigma ^0_1\textsf {-AC}^{00}$
yields
$\Sigma ^0_1\textsf {-AC}^{00}$
yields
![]() $(\alpha |\gamma ){\downarrow }$
,
$(\alpha |\gamma ){\downarrow }$
,
![]() $(\beta |\gamma ){\downarrow }$
,
$(\beta |\gamma ){\downarrow }$
,
![]() $((\alpha |\gamma )|(\beta |\gamma )){\downarrow }$
and
$((\alpha |\gamma )|(\beta |\gamma )){\downarrow }$
and
![]() $(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}\,{=}\,((\alpha |\gamma )|(\beta |\gamma ))$
. Conversely let
$(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}\,{=}\,((\alpha |\gamma )|(\beta |\gamma ))$
. Conversely let
![]() $((\alpha |\gamma )|(\beta |\gamma )){\downarrow }$
, which implies
$((\alpha |\gamma )|(\beta |\gamma )){\downarrow }$
, which implies
![]() $(\alpha |\gamma ){\downarrow }$
and
$(\alpha |\gamma ){\downarrow }$
and
![]() $(\beta |\gamma ){\downarrow }$
. For x, by 2.16(3)(ii),
$(\beta |\gamma ){\downarrow }$
. For x, by 2.16(3)(ii),
![]() $\Delta ^0_0\textsf {-AC}^{00}$
yields k with
$\Delta ^0_0\textsf {-AC}^{00}$
yields k with
![]() $(\overline {\alpha }k|\overline {\gamma }k)(y)$
,
$(\overline {\alpha }k|\overline {\gamma }k)(y)$
,
![]() $(\overline {\beta }k|\overline {\gamma }k)(y)$
and
$(\overline {\beta }k|\overline {\gamma }k)(y)$
and
![]() $((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
are defined for all
$((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(y)$
are defined for all
![]() $y\leq x$
. Then
$y\leq x$
. Then
![]() $(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}(x)\,{=}\, ((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(x)$
. Thus
$(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}(x)\,{=}\, ((\overline {\alpha }k|\overline {\gamma }k)|(\overline {\beta }k|\overline {\gamma }k))(x)$
. Thus
![]() $(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}{\downarrow }$
.
$(\textsf {s}\alpha \beta \gamma )^{\mathfrak {k}}{\downarrow }$
.
Lemma 3.23.
-
(1) (i) For a
 $\Sigma ^0_1$
formula A,
$\Sigma ^0_1$
formula A,
 $\mathbf{EL}_0^-$
proves that:and (ii) for a
$\mathbf{EL}_0^-$
proves that:and (ii) for aif
 $\forall x,y,z,\alpha ( A[x,y,\alpha ]\land A[x,z,\alpha ]\,{\to }\,y\,{=}\,z)$
$\forall x,y,z,\alpha ( A[x,y,\alpha ]\land A[x,z,\alpha ]\,{\to }\,y\,{=}\,z)$
then there is
 $\gamma _A$
such that (a)
$\gamma _A$
such that (a)
 $\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\leftrightarrow }\, \exists \beta \forall xA[x,\beta (x),\alpha ]\,)$
and that (b)
$\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\leftrightarrow }\, \exists \beta \forall xA[x,\beta (x),\alpha ]\,)$
and that (b)
 $\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\to }\, \forall xA[x,(\gamma _A|\alpha )(x),\alpha ]\,)$
;
$\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\to }\, \forall xA[x,(\gamma _A|\alpha )(x),\alpha ]\,)$
; $\Sigma ^0_1$
formula A,
$\Sigma ^0_1$
formula A,
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
proves that there is
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
proves that there is
 $\gamma _A$
with (b) and
$\gamma _A$
with (b) and
 $\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\leftrightarrow }\, \forall x\exists yA[x,y,\alpha ])$
.
$\forall \alpha ((\gamma _A|\alpha ){\downarrow } \,{\leftrightarrow }\, \forall x\exists yA[x,y,\alpha ])$
.
-
(2) For a
 $\Pi ^0_1$
formula
$\Pi ^0_1$
formula
 $B[\xi ,\eta ,\gamma ]$
,
$B[\xi ,\eta ,\gamma ]$
,
 $\mathbf{EL}_0^- {+}\Delta ^0_0\textsf {-BKL}$
proves that there is
$\mathbf{EL}_0^- {+}\Delta ^0_0\textsf {-BKL}$
proves that there is
 $\chi _B$
such that for any
$\chi _B$
such that for any
 $\alpha ,\beta ,\xi $
,
$\alpha ,\beta ,\xi $
,
 $(\chi _B|\alpha |\beta ){\downarrow } \land \,\forall \xi ((\exists \eta \,{<}\,\alpha )B[\xi ,\eta ,\beta ] \leftrightarrow \forall n((\chi _B|\alpha |\beta )(\xi {\upharpoonright } n)=0))$
.
$(\chi _B|\alpha |\beta ){\downarrow } \land \,\forall \xi ((\exists \eta \,{<}\,\alpha )B[\xi ,\eta ,\beta ] \leftrightarrow \forall n((\chi _B|\alpha |\beta )(\xi {\upharpoonright } n)=0))$
.
Proof (1)(ii) follows from (i) and
![]() $\Delta ^0_0\textsf {-LNP}$
. (i) By 2.14, take C from
$\Delta ^0_0\textsf {-LNP}$
. (i) By 2.14, take C from
![]() $\Delta ^0_0$
with
$\Delta ^0_0$
with
![]() $A[x,y,\alpha ]\,{\leftrightarrow }\,\exists kC[x,y,\alpha {\upharpoonright } k]$
. Let
$A[x,y,\alpha ]\,{\leftrightarrow }\,\exists kC[x,y,\alpha {\upharpoonright } k]$
. Let
 $$ \begin{align*} \gamma_A(w)=\left\{\begin{array}{ll} y{+}1 & \text{if } w\,{=}\,\langle x\rangle{*}v \text{ and }y\,{<}\,|v|\land (\exists k\,{<}\,|v|)C[x,y,v{\upharpoonright} k];\\[-0pt] 0 & \text{if there are no such }x,v,y. \end{array}\right. \end{align*} $$
$$ \begin{align*} \gamma_A(w)=\left\{\begin{array}{ll} y{+}1 & \text{if } w\,{=}\,\langle x\rangle{*}v \text{ and }y\,{<}\,|v|\land (\exists k\,{<}\,|v|)C[x,y,v{\upharpoonright} k];\\[-0pt] 0 & \text{if there are no such }x,v,y. \end{array}\right. \end{align*} $$
(2) By 3.5(2)(ii) and 2.14, let
![]() $\forall \xi ,\alpha ,\beta ((\exists \eta \,{<}\,\alpha )B[\xi ,\eta ,\beta ] \,{\leftrightarrow }\,\neg \exists nC[\xi {\upharpoonright } n,(\alpha ,\beta )])$
where C is
$\forall \xi ,\alpha ,\beta ((\exists \eta \,{<}\,\alpha )B[\xi ,\eta ,\beta ] \,{\leftrightarrow }\,\neg \exists nC[\xi {\upharpoonright } n,(\alpha ,\beta )])$
where C is
![]() $\Delta ^0_0$
. By (1)(i) with 2.10(d) we can take
$\Delta ^0_0$
. By (1)(i) with 2.10(d) we can take
![]() $\gamma $
with
$\gamma $
with
![]() $(\gamma |(\alpha ,\beta )){\downarrow }$
and
$(\gamma |(\alpha ,\beta )){\downarrow }$
and
![]() $\forall u((\gamma |(\alpha ,\beta ))(u) = 0 \leftrightarrow \neg C[u,(\alpha ,\beta )])$
. Set
$\forall u((\gamma |(\alpha ,\beta ))(u) = 0 \leftrightarrow \neg C[u,(\alpha ,\beta )])$
. Set
![]() $\chi _B\,{:=}\,\lambda \alpha \beta .\gamma |(\textsf {p}|\alpha |\beta )$
.
$\chi _B\,{:=}\,\lambda \alpha \beta .\gamma |(\textsf {p}|\alpha |\beta )$
.
Here (1) formalizes the famous fact: any continuous functional can be represented by an operation in Kleene’s second model (cf. [Reference Jäger, Rosebrock and Sato23, Section 5.2]). (2) is a preliminary for van Oosten’s model treated in 3.2.3.
Definition 3.24 (
 $\mathfrak {k}$
)
$\mathfrak {k}$
)
Expand
![]() $\mathfrak {k}$
to
$\mathfrak {k}$
to
![]() $\mathcal {L}_{\mathrm{CDL}}$
by
$\mathcal {L}_{\mathrm{CDL}}$
by
![]() $\mathrm{Bo}[\alpha ]^{\mathfrak {k}}\,{:\equiv }\,\alpha \,{<}\,\underline {2}\,{\land }\,\forall x,y(\alpha (x)\,{=}\,\alpha (y))$
and
$\mathrm{Bo}[\alpha ]^{\mathfrak {k}}\,{:\equiv }\,\alpha \,{<}\,\underline {2}\,{\land }\,\forall x,y(\alpha (x)\,{=}\,\alpha (y))$
and
![]() $\xi \,{\in _{\texttt {L}}^{\mathfrak {k}}}\,\alpha \,{:\equiv }\,\alpha \,{=}\,\xi $
with
$\xi \,{\in _{\texttt {L}}^{\mathfrak {k}}}\,\alpha \,{:\equiv }\,\alpha \,{=}\,\xi $
with
![]() $\textsf {z}^{\mathfrak {k}}\,{:=}\,\underline {0}$
;
$\textsf {z}^{\mathfrak {k}}\,{:=}\,\underline {0}$
;
![]() $\textsf {o}^{\mathfrak {k}}\,{:=}\,\underline {1}$
;
$\textsf {o}^{\mathfrak {k}}\,{:=}\,\underline {1}$
;
![]() $\textsf {d}^{\mathfrak {k}}\,{:=}\,\lambda \xi \eta \zeta .\gamma _A(\textsf {p}\xi (\textsf {p}\eta \zeta ))$
;
$\textsf {d}^{\mathfrak {k}}\,{:=}\,\lambda \xi \eta \zeta .\gamma _A(\textsf {p}\xi (\textsf {p}\eta \zeta ))$
;
![]() $\textsf {g}^{\mathfrak {k}},\textsf {u}^{\mathfrak {k}},\textsf {c}^{\mathfrak {k}}\,{:=}\,\lambda \xi .\xi $
;
$\textsf {g}^{\mathfrak {k}},\textsf {u}^{\mathfrak {k}},\textsf {c}^{\mathfrak {k}}\,{:=}\,\lambda \xi .\xi $
;
![]() $\textsf {f}^{\mathfrak {k}}\,{:=}\,\textsf {k}^{\mathfrak {k}}$
; and
$\textsf {f}^{\mathfrak {k}}\,{:=}\,\textsf {k}^{\mathfrak {k}}$
; and
![]() $\textsf {r}^{\mathfrak {k}}\,{:=}\,\lambda \xi \eta .\eta |\xi $
, where
$\textsf {r}^{\mathfrak {k}}\,{:=}\,\lambda \xi \eta .\eta |\xi $
, where
![]() $\gamma _A$
is as in 3.23(1)(i) above applied to A from
$\gamma _A$
is as in 3.23(1)(i) above applied to A from
![]() $\Delta ^0_0$
such that
$\Delta ^0_0$
such that
![]() $A[x,y,\textsf {p}^{\mathfrak {k}}\xi (\textsf {p}^{\mathfrak {k}}\eta \zeta )] \,{\leftrightarrow }\,((\zeta (0)\,{=}\,0\,{\to }\,y\,{=}\,\xi (x))\,{\land }\,(\zeta (0)\,{\neq }\,0\,{\to }\,y\,{=}\,\eta (x)))$
.
$A[x,y,\textsf {p}^{\mathfrak {k}}\xi (\textsf {p}^{\mathfrak {k}}\eta \zeta )] \,{\leftrightarrow }\,((\zeta (0)\,{=}\,0\,{\to }\,y\,{=}\,\xi (x))\,{\land }\,(\zeta (0)\,{\neq }\,0\,{\to }\,y\,{=}\,\eta (x)))$
.
Proposition 3.25.
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}\vdash (\mathbf{CDL}\textsf{c})^{\mathfrak {k}}\,{+}\,(\mathbf{CDL}\textsf {f})^{\mathfrak {k}}$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}\vdash (\mathbf{CDL}\textsf{c})^{\mathfrak {k}}\,{+}\,(\mathbf{CDL}\textsf {f})^{\mathfrak {k}}$
.
3.2.3 Van Oosten’s model
 $\mathfrak {o}$
$\mathfrak {o}$
Under
![]() $\mathfrak {k}$
, only singletons are codable and so
$\mathfrak {k}$
, only singletons are codable and so
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability is the usual functional realizability. On the other hand, under
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizability is the usual functional realizability. On the other hand, under
![]() $\mathfrak {o}$
due to van Oosten [Reference van Oosten31, Section 5],
$\mathfrak {o}$
due to van Oosten [Reference van Oosten31, Section 5],
![]() $\alpha $
codes the sets of infinite paths through the “bounded” tree
$\alpha $
codes the sets of infinite paths through the “bounded” tree
![]() $\left \{u\,{<}\,(\alpha )^2_1{:}\,\forall n((\alpha )^2_0(u{\upharpoonright } n)\,{=}\,0)\right \}$
so that bounded König’s lemma could be
$\left \{u\,{<}\,(\alpha )^2_1{:}\,\forall n((\alpha )^2_0(u{\upharpoonright } n)\,{=}\,0)\right \}$
so that bounded König’s lemma could be
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable. We have to check if it works in our context of weak induction. This is not easy. Indeed Dorais [Reference Dorais13, Remark 4.10] tried to weaken induction in van Oosten’s argument but required
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable. We have to check if it works in our context of weak induction. This is not easy. Indeed Dorais [Reference Dorais13, Remark 4.10] tried to weaken induction in van Oosten’s argument but required
![]() $\Pi ^0_1\textsf {-Bdg}$
. We show that it is not needed and
$\Pi ^0_1\textsf {-Bdg}$
. We show that it is not needed and
![]() $\Delta ^0_0\textsf {-Ind}$
suffices.
$\Delta ^0_0\textsf {-Ind}$
suffices.
Definition 3.26 (
 $\mathfrak {o}$
and
$\mathfrak {o}$
and
 $\pi _A$
)
$\pi _A$
)
-
(1) Let
 $\mathfrak {o}$
coincide with
$\mathfrak {o}$
coincide with
 $\mathfrak {k}$
on
$\mathfrak {k}$
on
 $\mathcal {L}_{\textrm {CD}}$
, and
$\mathcal {L}_{\textrm {CD}}$
, and  $$ \begin{align*} \xi\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha\,{:\equiv}\,\xi\,{<}\,(\alpha)^2_1\land\forall n((\alpha)^2_0(\xi{\upharpoonright} n)\,{=}\,0).\end{align*} $$
$$ \begin{align*} \xi\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha\,{:\equiv}\,\xi\,{<}\,(\alpha)^2_1\land\forall n((\alpha)^2_0(\xi{\upharpoonright} n)\,{=}\,0).\end{align*} $$
-
(2) For any
 $\Pi ^0_1$
formula
$\Pi ^0_1$
formula
 $A[\xi ,\eta ,\gamma ]$
, define
$A[\xi ,\eta ,\gamma ]$
, define
 $\pi _A\,{:\equiv }\,\lambda \alpha \beta \gamma .\textsf {p}| (\chi _A|\beta |\gamma )|\alpha $
where
$\pi _A\,{:\equiv }\,\lambda \alpha \beta \gamma .\textsf {p}| (\chi _A|\beta |\gamma )|\alpha $
where
 $\chi _A$
is from 3.23(2).
$\chi _A$
is from 3.23(2).
Then
![]() $\pi _A|\alpha |\beta |\gamma $
codes the bounded
$\pi _A|\alpha |\beta |\gamma $
codes the bounded
![]() $\Pi ^0_1$
set
$\Pi ^0_1$
set
![]() $\left \{\xi \,{<}\,\alpha {:}\,(\exists \eta \,{<}\,\beta )A[\xi ,\eta ,\gamma ]\right \}$
, as stated in the next lemma (2), whereas (1) gives us the necessary bound to make the arguments (for 3.28) work only with
$\left \{\xi \,{<}\,\alpha {:}\,(\exists \eta \,{<}\,\beta )A[\xi ,\eta ,\gamma ]\right \}$
, as stated in the next lemma (2), whereas (1) gives us the necessary bound to make the arguments (for 3.28) work only with
![]() $\Delta ^0_0\textsf {-Ind}$
. This will be essential to define the interpretation of
$\Delta ^0_0\textsf {-Ind}$
. This will be essential to define the interpretation of
![]() $\textsf {r}$
in 3.28, and, in later parts,
$\textsf {r}$
in 3.28, and, in later parts,
![]() $\textsf {r}$
will gives the necessary bounds.
$\textsf {r}$
will gives the necessary bounds.
Lemma 3.27.
-
(1)
 $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00} {+}\Delta ^0_0\textsf {-BKL}$
proves that there is
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00} {+}\Delta ^0_0\textsf {-BKL}$
proves that there is
 $\zeta $
such that, for any
$\zeta $
such that, for any
 $\alpha $
and
$\alpha $
and
 $\beta $
,
$\beta $
,  $$ \begin{align*} \begin{array}{l} (\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta){\downarrow}) \to \zeta|(\alpha,\beta){\downarrow}\land{}\\ \quad(\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta)\,{<}\,\zeta|(\alpha,\beta) \land\forall k(\exists n\,{<}\,(\zeta|(\alpha,\beta))(k)) (\beta(\langle k\rangle{*}(\eta{\upharpoonright} n))\,{>}\,0)). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} (\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta){\downarrow}) \to \zeta|(\alpha,\beta){\downarrow}\land{}\\ \quad(\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta)\,{<}\,\zeta|(\alpha,\beta) \land\forall k(\exists n\,{<}\,(\zeta|(\alpha,\beta))(k)) (\beta(\langle k\rangle{*}(\eta{\upharpoonright} n))\,{>}\,0)). \end{array} \end{align*} $$
-
(2) For A from
 $\Pi ^0_1$
,
$\Pi ^0_1$
,
 $\mathbf{EL}_0^- {+}\Delta ^0_0\textsf {-BKL}$
proves
$\mathbf{EL}_0^- {+}\Delta ^0_0\textsf {-BKL}$
proves  $$ \begin{align*} \forall\alpha,\beta,\gamma( (\pi_A|\alpha|\beta|\gamma){\downarrow} \land\,\forall\xi( \xi\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\pi_A|\alpha|\beta|\gamma\,\leftrightarrow\, \xi\,{<}\,\alpha\land(\exists\eta\,{<}\,\beta)A[\xi,\eta,\gamma] )).\end{align*} $$
$$ \begin{align*} \forall\alpha,\beta,\gamma( (\pi_A|\alpha|\beta|\gamma){\downarrow} \land\,\forall\xi( \xi\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\pi_A|\alpha|\beta|\gamma\,\leftrightarrow\, \xi\,{<}\,\alpha\land(\exists\eta\,{<}\,\beta)A[\xi,\eta,\gamma] )).\end{align*} $$
Proof Since (2) is immediate, we prove (1). Let
and
![]() $D[k,y,\alpha ,\beta ]\,{:\equiv }\,(\forall u\,{<}\,(\alpha )^2_1)( |u|\,{=}\,y\,{\to }\,(\exists l\,{\leq }\,|u|) C[u{\upharpoonright } l,k,\alpha ,\beta ])$
, where
$D[k,y,\alpha ,\beta ]\,{:\equiv }\,(\forall u\,{<}\,(\alpha )^2_1)( |u|\,{=}\,y\,{\to }\,(\exists l\,{\leq }\,|u|) C[u{\upharpoonright } l,k,\alpha ,\beta ])$
, where
![]() $u\,{<}\,\gamma $
is defined in 3.4. Now we have
$u\,{<}\,\gamma $
is defined in 3.4. Now we have
 $$ \begin{align*} &(\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta){\downarrow})\\ \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)(\, \forall x((\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0) \to\exists w (\beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{>}\,0))\\ &&\hspace{-80pt}(\text{by }\Delta^0_0\textsf{-AC}^{00})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\neg(\, \forall x((\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0) \land\neg\exists w (\beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{>}\,0))\\ &&\hspace{-160pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\exists x,w \neg(\,(\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0\land \beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{=}\,0\,)\\ &&\hspace{-80pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\exists lC[\eta{\upharpoonright} l,k,\alpha,\beta] \,\leftrightarrow\,\forall k\neg(\exists\eta\,{<}\,(\alpha)^2_1)\forall l\neg C[\eta{\upharpoonright} l,k,\alpha,\beta] \\ &&\hspace{-160pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k\neg\forall y(\exists u\,{<}\,(\alpha)^2_1) (|u|\,{=}\,y\land(\forall l\,{\leq}\,y)\neg C[u{\upharpoonright} l,k,\alpha,\beta]) \,\leftrightarrow\, \forall k\exists yD[k,y,\alpha,\beta]\\ &&\hspace{-80pt}(\text{by }\Delta^0_0\textsf{-BKL},\textsf{MP}). \end{align*} $$
$$ \begin{align*} &(\forall\eta\,{\in_{\texttt{L}}^{\mathfrak{o}}}\,\alpha)((\beta|\eta){\downarrow})\\ \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)(\, \forall x((\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0) \to\exists w (\beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{>}\,0))\\ &&\hspace{-80pt}(\text{by }\Delta^0_0\textsf{-AC}^{00})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\neg(\, \forall x((\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0) \land\neg\exists w (\beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{>}\,0))\\ &&\hspace{-160pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\exists x,w \neg(\,(\alpha)^2_0(\eta{\upharpoonright} x)\,{=}\,0\land \beta(\langle k\rangle{*}(\eta{\upharpoonright} w))\,{=}\,0\,)\\ &&\hspace{-80pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k(\forall\eta\,{<}\,(\alpha)^2_1)\exists lC[\eta{\upharpoonright} l,k,\alpha,\beta] \,\leftrightarrow\,\forall k\neg(\exists\eta\,{<}\,(\alpha)^2_1)\forall l\neg C[\eta{\upharpoonright} l,k,\alpha,\beta] \\ &&\hspace{-160pt}(\text{by }\textsf{ MP})\\[2pt] \,&\leftrightarrow\,\forall k\neg\forall y(\exists u\,{<}\,(\alpha)^2_1) (|u|\,{=}\,y\land(\forall l\,{\leq}\,y)\neg C[u{\upharpoonright} l,k,\alpha,\beta]) \,\leftrightarrow\, \forall k\exists yD[k,y,\alpha,\beta]\\ &&\hspace{-80pt}(\text{by }\Delta^0_0\textsf{-BKL},\textsf{MP}). \end{align*} $$
3.23(1)(ii) yields
![]() $\gamma $
with
$\gamma $
with
![]() $\forall kD[k,(\gamma |(\alpha ,\beta ))(k),\alpha ,\beta ]$
. Then
$\forall kD[k,(\gamma |(\alpha ,\beta ))(k),\alpha ,\beta ]$
. Then
Thus
![]() $\zeta $
with the following is what we need:
$\zeta $
with the following is what we need:
Proposition 3.28.
![]() $\mathbf{EL}_0^-{+}\textsf { MP}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\Delta ^0_0\textsf {-BKL} \vdash (\mathbf{CDL}\textsf {c}\,{+}\,\mathbf{CDL}\textsf {f})^{\mathfrak {o}}$
with suitable
$\mathbf{EL}_0^-{+}\textsf { MP}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\Delta ^0_0\textsf {-BKL} \vdash (\mathbf{CDL}\textsf {c}\,{+}\,\mathbf{CDL}\textsf {f})^{\mathfrak {o}}$
with suitable
![]() $\textsf {g}^{\mathfrak {o}}$
,
$\textsf {g}^{\mathfrak {o}}$
,
![]() $\textsf {u}^{\mathfrak {o}}$
,
$\textsf {u}^{\mathfrak {o}}$
,
![]() $\textsf { r}^{\mathfrak {o}}$
,
$\textsf { r}^{\mathfrak {o}}$
,
![]() $\textsf {c}^{\mathfrak {o}}$
and
$\textsf {c}^{\mathfrak {o}}$
and
![]() $\textsf {f}^{\mathfrak {o}}$
.
$\textsf {f}^{\mathfrak {o}}$
.
Proof First
![]() $\alpha \,{=}\,\xi $
is
$\alpha \,{=}\,\xi $
is
![]() $\Pi ^0_1$
. Next notice that
$\Pi ^0_1$
. Next notice that
-
•
 $(\exists \beta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )(\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\beta )$
is equivalent to
$(\exists \beta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )(\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\beta )$
is equivalent to
 $\xi \,{<}\,\alpha \land (\exists \beta \,{<}\,\alpha )((\beta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )\land (\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\beta ))$
,
$\xi \,{<}\,\alpha \land (\exists \beta \,{<}\,\alpha )((\beta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )\land (\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\beta ))$
, -
•
 $(\exists \eta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )(\xi \,{=}\,\beta |\eta )$
is equivalent to
$(\exists \eta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )(\xi \,{=}\,\beta |\eta )$
is equivalent to
 $\xi <\zeta |(\alpha ,\beta )\land (\exists \eta \in _{\texttt {L}}^{\mathfrak {o}}\alpha )(\xi =\beta |\eta )$
under
$\xi <\zeta |(\alpha ,\beta )\land (\exists \eta \in _{\texttt {L}}^{\mathfrak {o}}\alpha )(\xi =\beta |\eta )$
under
 $(\forall \eta \,{\in }^{\mathfrak {o}}_{\texttt {L}}\,\alpha )(\beta |\eta {\downarrow })$
and
$(\forall \eta \,{\in }^{\mathfrak {o}}_{\texttt {L}}\,\alpha )(\beta |\eta {\downarrow })$
and -
•
 $\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \land \textsf {p}_0|\xi \,{=}\,\eta $
is equivalent to
$\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \land \textsf {p}_0|\xi \,{=}\,\eta $
is equivalent to
 $\xi \,{<}\,\alpha \land \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \land (\xi )^2_0\,{=}\,\eta $
,
$\xi \,{<}\,\alpha \land \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \land (\xi )^2_0\,{=}\,\eta $
,
where
![]() $\zeta $
is from 3.27(1) and
$\zeta $
is from 3.27(1) and
![]() $\xi =\beta |\eta $
is equivalently
$\xi =\beta |\eta $
is equivalently
![]() $\Pi ^0_1$
with the bound
$\Pi ^0_1$
with the bound
![]() $\zeta |(\alpha ,\beta )$
. 3.27(2) yields
$\zeta |(\alpha ,\beta )$
. 3.27(2) yields
![]() $\textsf {g}^{\mathfrak {o}}$
,
$\textsf {g}^{\mathfrak {o}}$
,
![]() $\textsf {u}^{\mathfrak {o}}$
,
$\textsf {u}^{\mathfrak {o}}$
,
![]() $\textsf {r}^{\mathfrak {o}}$
and
$\textsf {r}^{\mathfrak {o}}$
and
![]() $\textsf {f}^{\mathfrak {o}}$
.
$\textsf {f}^{\mathfrak {o}}$
.
Let
![]() $u\,\bot \,\xi \,:\equiv \,(\exists k\,{<}\,|u|)(u(k)\,{\neq }\,\xi (k))$
; recall
$u\,\bot \,\xi \,:\equiv \,(\exists k\,{<}\,|u|)(u(k)\,{\neq }\,\xi (k))$
; recall
![]() $u\,{<}\,\beta \,:\equiv \,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
and
$u\,{<}\,\beta \,:\equiv \,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
and
![]() $(\beta {\ominus } n)(k)\,{=}\,\beta (k{+}n)$
.
$(\beta {\ominus } n)(k)\,{=}\,\beta (k{+}n)$
.
Assume
![]() $\exists !\xi (\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )$
and
$\exists !\xi (\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )$
and
![]() $\xi \in _{\texttt {L}}^{\mathfrak {o}}\alpha $
. Then
$\xi \in _{\texttt {L}}^{\mathfrak {o}}\alpha $
. Then
By
![]() $\Delta ^0_0\textsf {-BKL}$
, we have
$\Delta ^0_0\textsf {-BKL}$
, we have
 $$ \begin{align*} (\forall u\,{<}\,(\alpha)^2_1) \left( u\,\bot\,\xi\to\neg\forall m(\exists v\,{<}\,(\alpha)^2_1{\ominus}|u|) \begin{pmatrix} |v| = m\land{}\\ (\forall n\,{<}\,m{+}|u|)((\alpha)^2_0((u{*}v){\upharpoonright} n)\,{=}\,0) \end{pmatrix} \!\right) , \end{align*} $$
$$ \begin{align*} (\forall u\,{<}\,(\alpha)^2_1) \left( u\,\bot\,\xi\to\neg\forall m(\exists v\,{<}\,(\alpha)^2_1{\ominus}|u|) \begin{pmatrix} |v| = m\land{}\\ (\forall n\,{<}\,m{+}|u|)((\alpha)^2_0((u{*}v){\upharpoonright} n)\,{=}\,0) \end{pmatrix} \!\right) , \end{align*} $$
and, by
![]() $\textsf {MP}$
,
$\textsf {MP}$
,
![]() $(\forall u<(\alpha )^2_1)(u\bot \xi {\to } B[u,\alpha ])$
where
$(\forall u<(\alpha )^2_1)(u\bot \xi {\to } B[u,\alpha ])$
where
Thus
![]() $\xi {\upharpoonright } n$
is the only
$\xi {\upharpoonright } n$
is the only
![]() $w$
with
$w$
with
since
![]() $\forall n\neg B[\xi {\upharpoonright } n,\alpha ]$
. C is equivalently
$\forall n\neg B[\xi {\upharpoonright } n,\alpha ]$
. C is equivalently
![]() $\Sigma ^0_1$
with
$\Sigma ^0_1$
with
![]() $\Sigma ^0_1\textsf {-Bdg}$
which is by
$\Sigma ^0_1\textsf {-Bdg}$
which is by
![]() $\Delta ^0_0\textsf {-AC}^{00}$
with 2.16(3)(ii). Apply 3.23(1)(ii) to
$\Delta ^0_0\textsf {-AC}^{00}$
with 2.16(3)(ii). Apply 3.23(1)(ii) to
![]() $D[n,y,\alpha ]:\equiv \exists w (C[n{+}1,w,\alpha ]\land w(n)\,{=}\,y)$
; then
$D[n,y,\alpha ]:\equiv \exists w (C[n{+}1,w,\alpha ]\land w(n)\,{=}\,y)$
; then
![]() $\forall nD[n,(\gamma _D|\alpha )(n),\alpha ]$
, i.e.,
$\forall nD[n,(\gamma _D|\alpha )(n),\alpha ]$
, i.e.,
![]() $(\gamma _D|\alpha )(n)\,{=}\,\xi (n)$
. Set
$(\gamma _D|\alpha )(n)\,{=}\,\xi (n)$
. Set
![]() $\textsf {c}^{\mathfrak {o}}\,{=}\,\gamma _D$
.
$\textsf {c}^{\mathfrak {o}}\,{=}\,\gamma _D$
.
3.2.4 Characterizing axioms of realizability
As in Section 3.2.1 let
![]() $\mathcal {L}'$
expand
$\mathcal {L}'$
expand
![]() $\mathcal {L}_{\mathrm{CDL}}$
via some interpretation, but atomic
$\mathcal {L}_{\mathrm{CDL}}$
via some interpretation, but atomic
![]() $\mathcal {L}_{\mathrm{CDL}}$
formulae may be non-atomic in
$\mathcal {L}_{\mathrm{CDL}}$
formulae may be non-atomic in
![]() $\mathcal {L}'$
, as in
$\mathcal {L}'$
, as in
![]() $\mathfrak {k}$
or
$\mathfrak {k}$
or
![]() $\mathfrak {o}$
. As
$\mathfrak {o}$
. As
![]() $\Delta ^0_0$
is non-sense, 2.9(3) is not applicable here. General treatment here will help us in [Reference Nemoto and Sato30].
$\Delta ^0_0$
is non-sense, 2.9(3) is not applicable here. General treatment here will help us in [Reference Nemoto and Sato30].
Definition 3.29 (
 $A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
, canonicalized,
$A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
, canonicalized,
 $N(\mathcal {C})$
,
$N(\mathcal {C})$
,
 $\mathit {RH}(\mathcal {C})$
,
$\mathit {RH}(\mathcal {C})$
,
 $\mathcal {R}$
)
$\mathcal {R}$
)
-
(1) To an
 $\mathcal {L}$
formula A, assign an
$\mathcal {L}$
formula A, assign an
 $\mathcal {L}'$
formula
$\mathcal {L}'$
formula
 $A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
by
$A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
by  $$ \begin{align*} A^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&\,:\equiv\,\exists\alpha(\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A)\text{ for atomic }A;\\ (A\Box B)^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&:\equiv\,A^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\Box B^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\text{ for }\Box\equiv{\land},\to,{\lor};\\ (QxA)^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&:\equiv\,QxA^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\text{ for }Q\equiv\forall,\exists. \end{align*} $$
$$ \begin{align*} A^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&\,:\equiv\,\exists\alpha(\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A)\text{ for atomic }A;\\ (A\Box B)^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&:\equiv\,A^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\Box B^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\text{ for }\Box\equiv{\land},\to,{\lor};\\ (QxA)^{\mathbin{{\textbf{r}_{\texttt{L}}}}}&:\equiv\,QxA^{\mathbin{{\textbf{r}_{\texttt{L}}}}}\text{ for }Q\equiv\forall,\exists. \end{align*} $$
-
(2)
 $A[\vec {\eta }]$
, without other parameters, is called
$A[\vec {\eta }]$
, without other parameters, is called
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized by
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized by
 $c_{A}$
(in a theory) if
$c_{A}$
(in a theory) if
 $\forall \vec {\eta },\alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }] \,{\rightarrow }\, c_{A}\vec {\eta }{\downarrow } \,{\land }\, c_{A}\vec {\eta }\mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }])$
(is provable in the theory).
$\forall \vec {\eta },\alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }] \,{\rightarrow }\, c_{A}\vec {\eta }{\downarrow } \,{\land }\, c_{A}\vec {\eta }\mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }])$
(is provable in the theory). -
(3) A formula is called (i)
 $N(\mathcal {C})$
or negative in
$N(\mathcal {C})$
or negative in
 $\mathcal {C}$
if it is built up from
$\mathcal {C}$
if it is built up from
 $\mathcal {C}$
formulae by
$\mathcal {C}$
formulae by
 $\land $
,
$\land $
,
 $\to $
and
$\to $
and
 $\forall $
; and (ii)
$\forall $
; and (ii)
 $\mathit {RH}(\mathcal {C})$
or Rasiowa–Harrop in
$\mathit {RH}(\mathcal {C})$
or Rasiowa–Harrop in
 $\mathcal {C}$
if it is built up from
$\mathcal {C}$
if it is built up from
 $\mathcal {C}$
by
$\mathcal {C}$
by
 $\land $
,
$\land $
,
 $\forall $
and
$\forall $
and
 $A\,{\to }\,\text {-}$
with arbitrary formulae A.
$A\,{\to }\,\text {-}$
with arbitrary formulae A. -
(4)
 $\mathcal {R}$
is the class of
$\mathcal {R}$
is the class of
 $\mathcal {L}'$
formulae negative in
$\mathcal {L}'$
formulae negative in  $$ \begin{align*} \{\exists\xi(\xi\,{\in_{\texttt{L}}}\,\alpha),\;\xi\,{\in_{\texttt{L}}}\,\alpha,\;\alpha\beta{\downarrow},\;\gamma\,{=}\,\alpha\beta, \;\textrm{Bo}[\alpha]\} \,\cup\,\{\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A\,|\, A\text{ is }\mathcal{L}\text{-atomic}\}. \end{align*} $$
$$ \begin{align*} \{\exists\xi(\xi\,{\in_{\texttt{L}}}\,\alpha),\;\xi\,{\in_{\texttt{L}}}\,\alpha,\;\alpha\beta{\downarrow},\;\gamma\,{=}\,\alpha\beta, \;\textrm{Bo}[\alpha]\} \,\cup\,\{\alpha\mathbin{{\textbf{r}_{\texttt{L}}}} A\,|\, A\text{ is }\mathcal{L}\text{-atomic}\}. \end{align*} $$
Definition 3.30 (Generalized choice schemata
 $(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
and
$(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
and
 $(\mathcal {C},\mathcal {D})\textsf {-GC!}$
)
$(\mathcal {C},\mathcal {D})\textsf {-GC!}$
)
For classes
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\mathcal {L}'$
formulae, define the following axiom schemata:
$\mathcal {L}'$
formulae, define the following axiom schemata:
-
(
 $(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
):
$(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
):
 $\forall \alpha (D[\alpha ]\,{\to }\,\exists \beta C[\alpha ,\beta ])\\\phantom{\hspace{89pt}} {{\kern-2pt}\to{\kern-2pt}}\exists \gamma \forall \alpha (D[\alpha ]{{\kern-2pt}\to{\kern-2pt}}\gamma \alpha {\downarrow } {{\kern-2pt}\land{\kern-2pt}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\gamma \alpha ) {{\kern-2pt}\land{\kern-2pt}} (\forall \xi \,{\in _{\texttt {L}}}\,\gamma \alpha )C[\alpha ,\xi ])$
;
$\forall \alpha (D[\alpha ]\,{\to }\,\exists \beta C[\alpha ,\beta ])\\\phantom{\hspace{89pt}} {{\kern-2pt}\to{\kern-2pt}}\exists \gamma \forall \alpha (D[\alpha ]{{\kern-2pt}\to{\kern-2pt}}\gamma \alpha {\downarrow } {{\kern-2pt}\land{\kern-2pt}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\gamma \alpha ) {{\kern-2pt}\land{\kern-2pt}} (\forall \xi \,{\in _{\texttt {L}}}\,\gamma \alpha )C[\alpha ,\xi ])$
; -
(
 $(\mathcal {C},\mathcal {D})\textsf {-GC!}$
):
$(\mathcal {C},\mathcal {D})\textsf {-GC!}$
):
 $\forall \alpha (D[\alpha ]\,{\to }\,\exists !\beta C[\alpha ,\beta ]) \to \exists \gamma \forall \alpha (D[\alpha ]\,{\to }\,\gamma \alpha {\downarrow } \land C[\alpha ,\gamma \alpha ])$
,
$\forall \alpha (D[\alpha ]\,{\to }\,\exists !\beta C[\alpha ,\beta ]) \to \exists \gamma \forall \alpha (D[\alpha ]\,{\to }\,\gamma \alpha {\downarrow } \land C[\alpha ,\gamma \alpha ])$
,
for any C from
![]() $\mathcal {C}$
and D from
$\mathcal {C}$
and D from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 3.31. Assume the premise of 3.18.
-
(1) If
 $\mathcal {C}$
formulae are
$\mathcal {C}$
formulae are
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized, then so are
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized, then so are
 $\mathit {RH}(\mathcal {C})$
ones.
$\mathit {RH}(\mathcal {C})$
ones. -
(2) (i)
 $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
is in
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
is in
 $\mathcal {R}$
; and (ii)
$\mathcal {R}$
; and (ii)
 $\mathbf{CDL}{+}(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}} \vdash A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}{\leftrightarrow }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
, for an
$\mathbf{CDL}{+}(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}} \vdash A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}{\leftrightarrow }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
, for an
 $\mathcal {L}$
formula A.
$\mathcal {L}$
formula A.
Proof It is easy to see (1) and (2)(i). We prove (2)(ii) by induction on A. The atomic,
![]() ${\land }$
,
${\land }$
,
![]() ${\lor }$
cases are obvious.
${\lor }$
cases are obvious.
By induction hypothesis,
![]() $(B{\to } C)^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
is equivalent to
$(B{\to } C)^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
is equivalent to
![]() $\exists \beta (\beta \mathbin {{\mathbf{r}_{\texttt {L}}}} B)\to \exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
, i.e.,
$\exists \beta (\beta \mathbin {{\mathbf{r}_{\texttt {L}}}} B)\to \exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} C)$
, i.e.,
![]() $\forall \beta ((\beta \mathbin {{\mathbf{r}_{\texttt {L}}}} B){\to }\exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} C))$
. Obviously
$\forall \beta ((\beta \mathbin {{\mathbf{r}_{\texttt {L}}}} B){\to }\exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} C))$
. Obviously
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}(B\,{\to }\, C)$
implies this. Conversely, by (2)(i), the above with
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}(B\,{\to }\, C)$
implies this. Conversely, by (2)(i), the above with
![]() $(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
yields
$(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
yields
![]() $\alpha $
such that
$\alpha $
such that
Thus
![]() $\lambda \beta .\textsf {b}_C(\alpha \beta )\mathbin {{\mathbf{r}_{\texttt {L}}}} (B\,{\to }\, C)$
.
$\lambda \beta .\textsf {b}_C(\alpha \beta )\mathbin {{\mathbf{r}_{\texttt {L}}}} (B\,{\to }\, C)$
.
If
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \xi A[\xi ]$
then
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \xi A[\xi ]$
then
![]() $\forall \xi (\alpha \xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\xi ])$
and so
$\forall \xi (\alpha \xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\xi ])$
and so
![]() $\forall \xi A[\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
by induction hypothesis. If
$\forall \xi A[\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
by induction hypothesis. If
![]() $\forall \xi A[\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
then
$\forall \xi A[\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
then
![]() $\forall \xi \exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\xi ])$
and so
$\forall \xi \exists \gamma (\gamma \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\xi ])$
and so
![]() $(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
yields
$(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
yields
![]() $\alpha $
with
$\alpha $
with
Thus
![]() $\lambda \xi .\textsf {b}_A\xi (\alpha \xi )\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \xi A[\xi ]$
.
$\lambda \xi .\textsf {b}_A\xi (\alpha \xi )\mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \xi A[\xi ]$
.
If
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \xi A[\xi ]$
, then
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \xi A[\xi ]$
, then
![]() $(\exists \xi \,{\in _{\texttt {L}}}\,\alpha ) (\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\textsf {p}_0\xi ])$
and by induction hypothesis
$(\exists \xi \,{\in _{\texttt {L}}}\,\alpha ) (\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\textsf {p}_0\xi ])$
and by induction hypothesis
![]() $A[\textsf {p}_0\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
for some
$A[\textsf {p}_0\xi ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
for some
![]() $\xi $
and so
$\xi $
and so
![]() $\exists \eta A[\eta ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
. Conversely, if
$\exists \eta A[\eta ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
. Conversely, if
![]() $A[\eta ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
, the induction hypothesis yields
$A[\eta ]^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
, the induction hypothesis yields
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\eta ]$
and so
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\eta ]$
and so
![]() $\textsf {g}(\textsf {p}\eta \alpha )\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \xi A[\xi ]$
.
$\textsf {g}(\textsf {p}\eta \alpha )\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \xi A[\xi ]$
.
Lemma 3.32. In
![]() $\mathbf{CDL}\textsf {c}$
, under the assumption of 3.18 if
$\mathbf{CDL}\textsf {c}$
, under the assumption of 3.18 if
![]() $(\xi \,{=}\,\eta )^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}{\to }\,\xi \,{=}\,\eta $
and
$(\xi \,{=}\,\eta )^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}{\to }\,\xi \,{=}\,\eta $
and
![]() $\mathcal {D}$
formulae are canonicalized, then
$\mathcal {D}$
formulae are canonicalized, then
![]() $(\mathcal {L},\mathcal {D})\textsf {-GC!}$
is realizable.
$(\mathcal {L},\mathcal {D})\textsf {-GC!}$
is realizable.
Proof Assume
![]() $\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \alpha (D[\alpha ]{\to }\exists !\beta C[\alpha ,\beta ])$
. For
$\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \alpha (D[\alpha ]{\to }\exists !\beta C[\alpha ,\beta ])$
. For
![]() $\alpha $
with
$\alpha $
with
![]() $\zeta '\mathbin {{\mathbf{r}_{\texttt {L}}}} D[\alpha ]$
, we have
$\zeta '\mathbin {{\mathbf{r}_{\texttt {L}}}} D[\alpha ]$
, we have
-
(a)
 $\zeta \alpha (c_D\alpha ){\downarrow }$
,
$\zeta \alpha (c_D\alpha ){\downarrow }$
, -
(b)
 $\textsf {p}_0(\zeta \alpha (c_D\alpha ))\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \beta C[\alpha ,\beta ]$
and
$\textsf {p}_0(\zeta \alpha (c_D\alpha ))\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \beta C[\alpha ,\beta ]$
and -
(c)
 $\textsf {p}_1(\zeta \alpha (c_D\alpha ))\mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \beta ,\beta '(C[\alpha ,\beta ]\land C[\alpha ,\beta ']\,{\to }\,\beta \,{=}\,\beta ')$
.
$\textsf {p}_1(\zeta \alpha (c_D\alpha ))\mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \beta ,\beta '(C[\alpha ,\beta ]\land C[\alpha ,\beta ']\,{\to }\,\beta \,{=}\,\beta ')$
.
Let
![]() $\gamma \,{:=}\,\lambda \alpha .\textsf {c}(\textsf {r} (\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_0)$
.
$\gamma \,{:=}\,\lambda \alpha .\textsf {c}(\textsf {r} (\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_0)$
.
If
![]() $\eta ,\eta '\,{\in _{\texttt {L}}}\,\textsf {p}_0(\zeta \alpha (c_D\alpha ))$
, by (b)(c),
$\eta ,\eta '\,{\in _{\texttt {L}}}\,\textsf {p}_0(\zeta \alpha (c_D\alpha ))$
, by (b)(c),
![]() $(\textsf {p}_0\eta =\textsf {p}_0\eta ')^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
. By the assumption, we have
$(\textsf {p}_0\eta =\textsf {p}_0\eta ')^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}$
. By the assumption, we have
![]() $\exists !\eta (\eta \,{\in _{\texttt {L}}} \,\textsf {r}(\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_0)$
and
$\exists !\eta (\eta \,{\in _{\texttt {L}}} \,\textsf {r}(\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_0)$
and
![]() $\gamma \alpha {\downarrow }$
. For
$\gamma \alpha {\downarrow }$
. For
![]() $\xi \,{\in _{\texttt {L}}}\,\textsf {p}_0(\zeta \alpha (c_D\alpha ))$
, by
$\xi \,{\in _{\texttt {L}}}\,\textsf {p}_0(\zeta \alpha (c_D\alpha ))$
, by
![]() $\textsf {p}_0\xi =\gamma \alpha $
and (b), we have
$\textsf {p}_0\xi =\gamma \alpha $
and (b), we have
![]() $\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\gamma \alpha ]$
. So
$\textsf {p}_1\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\gamma \alpha ]$
. So
![]() $\textsf {b}_C\alpha (\gamma \alpha )(\textsf {r}(\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_1) \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\gamma \alpha ]$
.
$\textsf {b}_C\alpha (\gamma \alpha )(\textsf {r}(\textsf {p}_0(\zeta \alpha (c_D\alpha )))\textsf {p}_1) \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\gamma \alpha ]$
.
Thus
![]() $\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \alpha (D[\alpha ]{\to }\exists !\beta C[\alpha ,\beta ])$
implies
$\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \alpha (D[\alpha ]{\to }\exists !\beta C[\alpha ,\beta ])$
implies
Below we additionally assume
![]() $\mathcal {L}\,{\equiv }\,\mathcal {L}'$
. The notions of canonicalizedness, actualizedness and completedness (the last two being defined below) are, although not implying “being realized”, called “having a canonical realizer” in the literature, where the three notions do not seem to be distinguished clearly. The last two make sense only when the formula belongs to both the realized and realizing languages (i.e.,
$\mathcal {L}\,{\equiv }\,\mathcal {L}'$
. The notions of canonicalizedness, actualizedness and completedness (the last two being defined below) are, although not implying “being realized”, called “having a canonical realizer” in the literature, where the three notions do not seem to be distinguished clearly. The last two make sense only when the formula belongs to both the realized and realizing languages (i.e.,
![]() $A\,{\in }\,\mathcal {L}\,{\cap }\,\mathcal {L}'$
), while the first is free from such an assumption. By definition,
$A\,{\in }\,\mathcal {L}\,{\cap }\,\mathcal {L}'$
), while the first is free from such an assumption. By definition,
![]() $A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}\,{\leftrightarrow }\, A$
if all the atomic are
$A^{\mathbin {{\mathbf{r}_{\texttt {L}}}}}\,{\leftrightarrow }\, A$
if all the atomic are
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed.
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed.
Definition 3.33 (actualized, completed)
![]() $A[\vec {\eta }]$
is (i)
$A[\vec {\eta }]$
is (i)
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-actualized by
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-actualized by
![]() $d_A$
if
$d_A$
if
![]() $\forall \vec {\eta }(A[\vec {\eta }] \leftrightarrow (d_{A}\vec {\eta }{\downarrow } \land d_{A}\vec {\eta }\mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }]))$
; (ii)
$\forall \vec {\eta }(A[\vec {\eta }] \leftrightarrow (d_{A}\vec {\eta }{\downarrow } \land d_{A}\vec {\eta }\mathbin {{\mathbf{r}_{\texttt {L}}}} A[\vec {\eta }]))$
; (ii)
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed by
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed by
![]() $c_A$
if it is
$c_A$
if it is
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized and
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-canonicalized and
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-actualized by the same
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-actualized by the same
![]() $c_A$
.
$c_A$
.
Lemma 3.34.
-
(1) If
 ${\in _{\texttt {L}}}$
is completed, so is
${\in _{\texttt {L}}}$
is completed, so is
 $\exists \xi (\xi \,{\in _{\texttt {L}}}\,\text {-})$
.
$\exists \xi (\xi \,{\in _{\texttt {L}}}\,\text {-})$
. -
(2) If
 $\mathcal {C}$
formulae are completed, so are
$\mathcal {C}$
formulae are completed, so are
 $N(\mathcal {C})$
ones.
$N(\mathcal {C})$
ones. -
(3)
 $(\mathcal {L},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
is
$(\mathcal {L},\mathcal {D})\textsf {-GC}_{\texttt {L}}$
is
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in
 $\mathbf{CDL}\textsf {f}$
if
$\mathbf{CDL}\textsf {f}$
if
 $\in _{\texttt {L}}$
is completed,
$\in _{\texttt {L}}$
is completed,
 $(\mbox{-}|\mbox{-}){\downarrow}$
actualized, and
$(\mbox{-}|\mbox{-}){\downarrow}$
actualized, and
 $\mathcal {D}$
formulae canonicalized under the assumption of 3.18.
$\mathcal {D}$
formulae canonicalized under the assumption of 3.18.
Proof (1) For
![]() $\xi \,{\in _{\texttt {L}}}\,\alpha $
, we have
$\xi \,{\in _{\texttt {L}}}\,\alpha $
, we have
![]() $c_{\in _{\texttt {L}}}\xi \alpha {\downarrow }$
and
$c_{\in _{\texttt {L}}}\xi \alpha {\downarrow }$
and
![]() $\langle \xi ,c_{\in _{\texttt {L}}}\xi \alpha \rangle {\downarrow }$
. Therefore
$\langle \xi ,c_{\in _{\texttt {L}}}\xi \alpha \rangle {\downarrow }$
. Therefore
![]() $\exists \xi (\xi \,{\in _{\texttt {L}}}\,\alpha )$
iff
$\exists \xi (\xi \,{\in _{\texttt {L}}}\,\alpha )$
iff
![]() $\textsf {r}\alpha (\lambda \xi .\langle \xi ,c_{\in _{\texttt {L}}}\xi \alpha \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \xi (\xi \,{\in _{\texttt {L}}}\,\alpha )$
.
$\textsf {r}\alpha (\lambda \xi .\langle \xi ,c_{\in _{\texttt {L}}}\xi \alpha \rangle ) \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \xi (\xi \,{\in _{\texttt {L}}}\,\alpha )$
.
(2) By induction on
![]() $N(\mathcal {C})$
formulae. Consider
$N(\mathcal {C})$
formulae. Consider
![]() $\to $
only. If
$\to $
only. If
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} (A\,{\to }\,B)$
, A implies
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} (A\,{\to }\,B)$
, A implies
![]() $\alpha c_A \mathbin {{\mathbf{r}_{\texttt {L}}}} B$
,
$\alpha c_A \mathbin {{\mathbf{r}_{\texttt {L}}}} B$
,
![]() $c_B \mathbin {{\mathbf{r}_{\texttt {L}}}} B$
and B. If
$c_B \mathbin {{\mathbf{r}_{\texttt {L}}}} B$
and B. If
![]() $A\,{\to }\,B$
then
$A\,{\to }\,B$
then
![]() $\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
implies
$\xi \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
implies
![]() $c_A \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
and A whence B, which means
$c_A \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
and A whence B, which means
![]() $\lambda \xi .c_B \mathbin {{\mathbf{r}_{\texttt {L}}}} (A\,{\to }\,B)$
.
$\lambda \xi .c_B \mathbin {{\mathbf{r}_{\texttt {L}}}} (A\,{\to }\,B)$
.
(3) Assume
![]() $\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \alpha (D[\alpha ]{\to }\exists \beta C[\alpha ,\beta ])$
. Then, for
$\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}}\forall \alpha (D[\alpha ]{\to }\exists \beta C[\alpha ,\beta ])$
. Then, for
![]() $\alpha $
with
$\alpha $
with
![]() $\zeta ' \mathbin {{\mathbf{r}_{\texttt {L}}}} D[\alpha ]$
, we have
$\zeta ' \mathbin {{\mathbf{r}_{\texttt {L}}}} D[\alpha ]$
, we have
![]() $\zeta \alpha (c_D\alpha ){\downarrow } \land (\zeta \alpha (c_D\alpha )\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \beta C[\alpha ,\beta ])$
. Let
$\zeta \alpha (c_D\alpha ){\downarrow } \land (\zeta \alpha (c_D\alpha )\mathbin {{\mathbf{r}_{\texttt {L}}}}\exists \beta C[\alpha ,\beta ])$
. Let
For
![]() $\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha $
, by
$\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha $
, by
![]() $(\forall \eta \,{\in _{\texttt {L}}}\,\textsf {f}(\zeta \alpha (c_D\alpha ))\xi ) (\textsf {p}_1\eta \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\xi ])$
and 3.18, we can imply that
$(\forall \eta \,{\in _{\texttt {L}}}\,\textsf {f}(\zeta \alpha (c_D\alpha ))\xi ) (\textsf {p}_1\eta \mathbin {{\mathbf{r}_{\texttt {L}}}} C[\alpha ,\xi ])$
and 3.18, we can imply that
![]() $\textsf {b}_C\alpha \xi (\textsf {r}(\textsf {f}(\zeta \alpha (c_D\alpha ))\xi )\textsf {p}_1)$
realizes
$\textsf {b}_C\alpha \xi (\textsf {r}(\textsf {f}(\zeta \alpha (c_D\alpha ))\xi )\textsf {p}_1)$
realizes
![]() $C[\alpha ,\xi ]$
. Since
$C[\alpha ,\xi ]$
. Since
![]() $\in _{\texttt {L}}$
is completed,
$\in _{\texttt {L}}$
is completed,
realizes
![]() $(\forall \xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )C[\alpha ,\xi ]$
.
$(\forall \xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )C[\alpha ,\xi ]$
.
As
![]() $\exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )$
, (1) yields
$\exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )$
, (1) yields
![]() $d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha ) \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )$
. The triple of
$d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha ) \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha )$
. The triple of
![]() $d_{(\mbox{-}|\mbox{-}){\downarrow}}(\delta \zeta )\alpha $
,
$d_{(\mbox{-}|\mbox{-}){\downarrow}}(\delta \zeta )\alpha $
,
![]() $d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha )$
and (
$d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha )$
and (
![]() $*$
) realizes
$*$
) realizes
![]() $\delta \zeta \alpha {\downarrow } {{\kern-1pt}\land{\kern-1pt}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha ) {\land} (\forall \xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha ) C[\alpha ,\xi ]$
. Thus
$\delta \zeta \alpha {\downarrow } {{\kern-1pt}\land{\kern-1pt}} \exists \xi (\xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha ) {\land} (\forall \xi \,{\in _{\texttt {L}}}\,\delta \zeta \alpha ) C[\alpha ,\xi ]$
. Thus
![]() $\exists \gamma \forall \alpha (D[\alpha ]\,\,{\to }\,\, \gamma \alpha {\downarrow } \land \exists \xi (\xi \,{\in _{\texttt {L}}}\,\gamma \alpha ) \land (\forall \xi \,{\in _{\texttt {L}}}\,\gamma \alpha )C[\alpha ,\xi ])$
is realized by
$\exists \gamma \forall \alpha (D[\alpha ]\,\,{\to }\,\, \gamma \alpha {\downarrow } \land \exists \xi (\xi \,{\in _{\texttt {L}}}\,\gamma \alpha ) \land (\forall \xi \,{\in _{\texttt {L}}}\,\gamma \alpha )C[\alpha ,\xi ])$
is realized by
![]() ${\textsf {g}(\langle \delta \zeta ,\lambda \alpha \zeta '. \langle d_{(\mbox{-}|\mbox{-}){\downarrow}} (\delta \zeta )\alpha ,d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha), \lambda \xi \xi '.\textsf {b}_C\alpha \xi (\textsf {r}(\textsf {f}(\zeta \alpha (c_D\alpha ))\xi )\textsf {p}_1)\rangle \rangle )}$
. Take
${\textsf {g}(\langle \delta \zeta ,\lambda \alpha \zeta '. \langle d_{(\mbox{-}|\mbox{-}){\downarrow}} (\delta \zeta )\alpha ,d_{\exists \xi (\xi {\in _{\texttt {L}}}\text {-})}(\delta \zeta \alpha), \lambda \xi \xi '.\textsf {b}_C\alpha \xi (\textsf {r}(\textsf {f}(\zeta \alpha (c_D\alpha ))\xi )\textsf {p}_1)\rangle \rangle )}$
. Take
![]() $\lambda \zeta .$
of this term.
$\lambda \zeta .$
of this term.
Corollary 3.35. Assume
-
• all the following formulae are
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed in
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-completed in
 $\mathbf{CDL}\textsf {f}{+}T$
:
$\mathbf{CDL}\textsf {f}{+}T$
:
 $\xi \,{\in _{\texttt {L}}}\,\alpha $
,
$\xi \,{\in _{\texttt {L}}}\,\alpha $
,
 $\alpha \beta {\downarrow }$
,
$\alpha \beta {\downarrow }$
,
 $\gamma \,{=}\,\alpha \beta $
,
$\gamma \,{=}\,\alpha \beta $
,
 $\mathrm{Bo}[\alpha ]$
and both A itself and
$\mathrm{Bo}[\alpha ]$
and both A itself and
 $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
for atomic A;
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A$
for atomic A; -
•
 $\mathbf{CDL}\textsf {f}{+}T$
is
$\mathbf{CDL}\textsf {f}{+}T$
is
 $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realizable in
 $\mathbf{CDL}\textsf {f}{+}T$
itself;
$\mathbf{CDL}\textsf {f}{+}T$
itself; -
•
 $\mathit {RH}(\mathcal {R})\,{\supseteq }\,\mathcal {D}\,{\supseteq }\,\mathcal {R}$
and
$\mathit {RH}(\mathcal {R})\,{\supseteq }\,\mathcal {D}\,{\supseteq }\,\mathcal {R}$
and
 $\mathcal {C}\,{\supseteq }\,\mathcal {R}$
; and
$\mathcal {C}\,{\supseteq }\,\mathcal {R}$
; and -
• the premise of 3.18 is satisfied.
Then
![]() $\mathbf{CDL}\textsf {f}{+}T\,{\vdash }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
iff
$\mathbf{CDL}\textsf {f}{+}T\,{\vdash }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)$
iff
![]() $\mathbf{CDL}\textsf {f}{+}T{+}(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}\,{\vdash }\, A$
.
$\mathbf{CDL}\textsf {f}{+}T{+}(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}\,{\vdash }\, A$
.
This generalizes the characterizations of Kleene’s number realizability (by ECT); Lifschitz’s (number) realizability; Kleene’s functional realizability (by
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
) and van Oosten’s functional realizability.
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
) and van Oosten’s functional realizability.
Moreover, this shows that
![]() $(\mathcal {L},\mathit {RH}(\mathcal {R}))\textsf {-GC}_{\texttt {L}}$
follows from
$(\mathcal {L},\mathit {RH}(\mathcal {R}))\textsf {-GC}_{\texttt {L}}$
follows from
![]() $(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
over
$(\mathcal {R},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
over
![]() $\textbf {CDL}\textsf {f}$
.
$\textbf {CDL}\textsf {f}$
.
We used
![]() $\textsf {f}$
only in the proof of the last lemma and we do not know if it is definable from other constants.
$\textsf {f}$
only in the proof of the last lemma and we do not know if it is definable from other constants.
3.3 Realizability of intuitionistic systems
We apply the results from the last subsection to our situation:
![]() $\mathcal {L}\,{\equiv }\,\mathcal {L}' \,{\equiv }\,\mathcal {L}_{\mathrm{F}}$
where
$\mathcal {L}\,{\equiv }\,\mathcal {L}' \,{\equiv }\,\mathcal {L}_{\mathrm{F}}$
where
![]() $\mathcal {L}_{\mathrm{F}}$
is considered to include
$\mathcal {L}_{\mathrm{F}}$
is considered to include
![]() $\mathcal {L}_{\mathrm{CDL}}$
via either
$\mathcal {L}_{\mathrm{CDL}}$
via either
![]() $\mathfrak {k}$
or
$\mathfrak {k}$
or
![]() $\mathfrak {o}$
. Setting
$\mathfrak {o}$
. Setting
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A\,:\equiv \,A$
and
$\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A\,:\equiv \,A$
and
![]() $\textsf {b}_A\,{:=}\,\lambda \vec {\eta }\alpha .\underline {0}$
for atomic
$\textsf {b}_A\,{:=}\,\lambda \vec {\eta }\alpha .\underline {0}$
for atomic
![]() $A[\vec {\eta }]$
, we have 3.19.
$A[\vec {\eta }]$
, we have 3.19.
Definition 3.36 (
 $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
,
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
,
 $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
)
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
)
Let
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A\,{:\equiv }\,(\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)^{\mathfrak {k}}$
and
$\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A\,{:\equiv }\,(\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)^{\mathfrak {k}}$
and
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A\,{:\equiv }\,(\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)^{\mathfrak {o}}$
, where
$\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A\,{:\equiv }\,(\alpha \mathbin {{\mathbf{r}_{\texttt {L}}}} A)^{\mathfrak {o}}$
, where
![]() $QxA[x]$
is treated as
$QxA[x]$
is treated as
![]() $Q\xi A[\xi (0)]$
.
$Q\xi A[\xi (0)]$
.
3.3.1 Realizability of base theories
Recall
![]() $\mathbf{EL}^*_0\,{=}\,\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
. As seen in 3.2.3, for
$\mathbf{EL}^*_0\,{=}\,\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
. As seen in 3.2.3, for
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizability, it is convenient to define the following.
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizability, it is convenient to define the following.
Definition 3.37 (
 ${\mathbf{EL}_0^{\prime }\!}^*$
,
${\mathbf{EL}_0^{\prime }\!}^*$
,
 $\mathbf{EL}_0^{\prime }$
)
$\mathbf{EL}_0^{\prime }$
)
Define
Lemma 3.38.
-
(1)
 $N(\Sigma ^0_1)$
formulae are
$N(\Sigma ^0_1)$
formulae are
 $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-completed in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-completed in
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
. -
(2)
 $N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
are
$N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
are
 $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed in
 ${\mathbf{EL}_0^{\prime }\!}^*$
.
${\mathbf{EL}_0^{\prime }\!}^*$
.
Proof The atomic are trivially completed. Let B from
![]() $\Delta ^0_0$
be completed by
$\Delta ^0_0$
be completed by
![]() $c_B$
.
$c_B$
.
![]() $\exists zB[\vec {\eta },z]$
, i.e.,
$\exists zB[\vec {\eta },z]$
, i.e.,
![]() $\exists \beta \forall xB[\vec {\eta },\beta (0)]$
implies
$\exists \beta \forall xB[\vec {\eta },\beta (0)]$
implies
![]() $(\gamma _B|\vec {\eta }){\downarrow }\land B[\vec {\eta },(\gamma _B|\vec {\eta })(0)]$
by 3.23(1)(i), i.e.,
$(\gamma _B|\vec {\eta }){\downarrow }\land B[\vec {\eta },(\gamma _B|\vec {\eta })(0)]$
by 3.23(1)(i), i.e.,
![]() $\textsf {g}|\langle \gamma _B|\vec {\eta },c_B|\vec {\eta }|(\gamma _B|\vec {\eta })\rangle \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists z B[\vec {\eta },z]$
. By the hypothesis on
$\textsf {g}|\langle \gamma _B|\vec {\eta },c_B|\vec {\eta }|(\gamma _B|\vec {\eta })\rangle \mathbin {{\mathbf{r}_{\texttt {L}}}}\exists z B[\vec {\eta },z]$
. By the hypothesis on
![]() $c_B$
, we have
$c_B$
, we have
This suffices for (1) by 3.34(2) with 2.11. For (2), for A from
![]() $\Pi ^0_1$
, 3.27(2) yields
$\Pi ^0_1$
, 3.27(2) yields
![]() $\forall \xi (\xi \,{\in ^{\mathfrak {o}}_{\texttt {L}}}\,\pi _A|\alpha |\underline {1}|\gamma \,{\leftrightarrow }\,\xi \,{<}\,\alpha \land A[\xi ,\gamma ])$
. Thus,
$\forall \xi (\xi \,{\in ^{\mathfrak {o}}_{\texttt {L}}}\,\pi _A|\alpha |\underline {1}|\gamma \,{\leftrightarrow }\,\xi \,{<}\,\alpha \land A[\xi ,\gamma ])$
. Thus,
Theorem 3.39.
-
(1)
 $\mathbf{EL}_0^* {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
is
$\mathbf{EL}_0^* {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
is
 $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
 $\mathbf{EL}_0^*$
.
$\mathbf{EL}_0^*$
. -
(2)
 ${\mathbf{EL}_0^{\prime }\!}^* {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)) \{\textsf {-GCC!}^1\!, \textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}\}$
is
${\mathbf{EL}_0^{\prime }\!}^* {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)) \{\textsf {-GCC!}^1\!, \textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}\}$
is
 $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
 ${\mathbf{EL}_0^{\prime }\!}^*$
, and so is
${\mathbf{EL}_0^{\prime }\!}^*$
, and so is
 $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1))\textsf {-GCB}^1$
.
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1))\textsf {-GCB}^1$
.
Proof Since
![]() $\in _{\texttt {L}}^{\mathfrak {k}}$
and
$\in _{\texttt {L}}^{\mathfrak {k}}$
and
![]() $\in _{\texttt {L}}^{\mathfrak {o}}$
are
$\in _{\texttt {L}}^{\mathfrak {o}}$
are
![]() $N(\Sigma ^0_1)$
, they are completed. Also
$N(\Sigma ^0_1)$
, they are completed. Also
![]() $\alpha \beta {\downarrow }$
is completed by
$\alpha \beta {\downarrow }$
is completed by
![]() $\textsf { g}|\langle \alpha |\beta ,c_{\delta \,{=}\,\alpha |\beta }|(\alpha |\beta )|\alpha |\beta \rangle $
. Thus, by 3.32 and 3.34(3),
$\textsf { g}|\langle \alpha |\beta ,c_{\delta \,{=}\,\alpha |\beta }|(\alpha |\beta )|\alpha |\beta \rangle $
. Thus, by 3.32 and 3.34(3),
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
in (1) and
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
in (1) and
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf { B}\exists ^1\Pi ^0_1))\{\textsf {-GCC!}^1,\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}\}$
in (2) are realizable, and so are
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\cup \textsf { B}\exists ^1\Pi ^0_1))\{\textsf {-GCC!}^1,\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}\}$
in (2) are realizable, and so are
![]() $N(\Sigma ^0_1)$
axioms of
$N(\Sigma ^0_1)$
axioms of
![]() $\mathbf{EL}_0^-$
. Moreover
$\mathbf{EL}_0^-$
. Moreover
![]() $\textsf {MP}$
and
$\textsf {MP}$
and
![]() $\Delta ^0_0\textsf {-BKL}$
are
$\Delta ^0_0\textsf {-BKL}$
are
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable by 3.38(2) as they are
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable by 3.38(2) as they are
![]() $N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
. Obviously
$N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
. Obviously
![]() $(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}$
implies
$(\mathcal {C},\mathcal {D})\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}}$
implies
![]() $(\mathcal {C},\mathcal {D})\textsf {-GCB}^1$
.
$(\mathcal {C},\mathcal {D})\textsf {-GCB}^1$
.
It remains to realize (d) (in 2.10) of
![]() $\mathbf{EL}_0^-$
and
$\mathbf{EL}_0^-$
and
![]() $\Delta ^0_0\textsf {-AC}^{00}$
. As (d) is of the form
$\Delta ^0_0\textsf {-AC}^{00}$
. As (d) is of the form
![]() $\exists \delta \forall xA[x,\delta (x),\alpha ]$
with A from
$\exists \delta \forall xA[x,\delta (x),\alpha ]$
with A from
![]() $\Delta ^0_0$
, 3.23(1)(i) yields
$\Delta ^0_0$
, 3.23(1)(i) yields
![]() $\gamma _A$
with
$\gamma _A$
with
![]() $\Delta ^0_0\textsf {-AC}^{00}$
is realized similarly by 3.23(1)(ii) (or see more general 3.42(ii) below).
$\Delta ^0_0\textsf {-AC}^{00}$
is realized similarly by 3.23(1)(ii) (or see more general 3.42(ii) below).
Corollary 3.40.
-
(1)
 $\mathbf{EL}_0^* {+}\textsf {S}\,{\vdash }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A)$
iff
$\mathbf{EL}_0^* {+}\textsf {S}\,{\vdash }\,\exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A)$
iff
 $\mathbf{EL}_0^* {+}\textsf {S} {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1\,{\vdash }\,A$
for any schema
$\mathbf{EL}_0^* {+}\textsf {S} {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1\,{\vdash }\,A$
for any schema
 $\textsf {S}$
consisting of
$\textsf {S}$
consisting of
 $N(\Sigma ^0_1)$
formulae.
$N(\Sigma ^0_1)$
formulae. -
(2)
 ${\mathbf{EL}_0^{\prime }\!}^*\!{+}\textsf {S} \vdash \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A)$
iff
${\mathbf{EL}_0^{\prime }\!}^*\!{+}\textsf {S} \vdash \exists \alpha (\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A)$
iff
 ${\mathbf{EL}_0^{\prime }\!}^*\!{+}\textsf {S}{+} (\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\,{\cup }\,\textsf {B}\exists ^1\Pi ^0_1))\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}} \vdash A$
for any schema
${\mathbf{EL}_0^{\prime }\!}^*\!{+}\textsf {S}{+} (\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1\,{\cup }\,\textsf {B}\exists ^1\Pi ^0_1))\textsf {-GC}_{\texttt {L}}^{\mathfrak {o}} \vdash A$
for any schema
 $\textsf {S}$
consisting of
$\textsf {S}$
consisting of
 $N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
formulae.
$N(\Sigma ^0_1\cup \textsf {B}\exists ^1\Pi ^0_1)$
formulae.
These characterizations follow from 3.35. Among
![]() $N(\Sigma ^0_1)$
schemata are
$N(\Sigma ^0_1)$
schemata are
![]() $\textsf {MP}$
,
$\textsf {MP}$
,
![]() $\Sigma ^0_1\textsf {-Ind}$
and
$\Sigma ^0_1\textsf {-Ind}$
and
![]() $\Pi ^0_2\textsf {-Ind}$
.
$\Pi ^0_2\textsf {-Ind}$
.
3.3.2 Realizability of the axioms of Intuitionism with the weakest induction
While 3.40 reduces realizability to the derivability from
![]() $(\mathcal {L}_{\mathrm{F}},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
, showing the latter is often as demanding as showing the former directly, as below. The folklore result 3.8 will be essential in the proof of 3.42(ii).
$(\mathcal {L}_{\mathrm{F}},\mathcal {R})\textsf {-GC}_{\texttt {L}}$
, showing the latter is often as demanding as showing the former directly, as below. The folklore result 3.8 will be essential in the proof of 3.42(ii).
Proposition 3.41.
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BFT}$
is (i)
$\mathcal {L}_{\mathrm{F}}\textsf {-BFT}$
is (i)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*{+}\Delta ^0_0\textsf {-BFT}$
; (ii)
$\mathbf{EL}_0^*{+}\Delta ^0_0\textsf {-BFT}$
; (ii)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() ${\mathbf{EL}_0^{\prime }\!}^*$
.
${\mathbf{EL}_0^{\prime }\!}^*$
.
Proof As
![]() $\Delta ^0_0\textsf {-BFT}$
is equivalently
$\Delta ^0_0\textsf {-BFT}$
is equivalently
![]() $N(\Sigma ^0_1)$
, by 3.40 it suffices to derive
$N(\Sigma ^0_1)$
, by 3.40 it suffices to derive
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BFT}$
from
$\mathcal {L}_{\mathrm{F}}\textsf {-BFT}$
from
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GC}_{\texttt {L}}$
in the respective systems.
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GC}_{\texttt {L}}$
in the respective systems.
Assume
![]() $\textsf {Fan}[\gamma ]$
,
$\textsf {Fan}[\gamma ]$
,
![]() $\forall u(\gamma (u) = 0 \to u < \beta )$
and
$\forall u(\gamma (u) = 0 \to u < \beta )$
and
![]() $\textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]$
, namely
$\textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}]$
, namely
Then
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GC}_{\texttt {L}}$
yields
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GC}_{\texttt {L}}$
yields
![]() $\zeta $
with
$\zeta $
with
Particularly, for
![]() $\alpha \,{<}\,\beta $
, if
$\alpha \,{<}\,\beta $
, if
![]() $\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0)$
then both (a)
$\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0)$
then both (a)
![]() $\exists mC[\alpha {\upharpoonright } m]$
and (b)
$\exists mC[\alpha {\upharpoonright } m]$
and (b)
![]() $\forall m (C[\alpha {\upharpoonright } m]\,{\to }\,(\exists k\,{<}\,m)B[\alpha {\upharpoonright } k])$
hold, where
$\forall m (C[\alpha {\upharpoonright } m]\,{\to }\,(\exists k\,{<}\,m)B[\alpha {\upharpoonright } k])$
hold, where
![]() $C[u]\,{:\equiv }\, |u|\,{>}\,(\zeta |u)(0)$
which is
$C[u]\,{:\equiv }\, |u|\,{>}\,(\zeta |u)(0)$
which is
![]() $\Sigma ^0_1$
, and where
$\Sigma ^0_1$
, and where
![]() $\zeta |u$
is defined analogously to 3.20.
$\zeta |u$
is defined analogously to 3.20.
Since (a) means
![]() $\textsf {Bar}[\gamma ,C]$
,
$\textsf {Bar}[\gamma ,C]$
,
![]() $\Sigma ^0_1\textsf {-BFT}$
with 2.32(3)(ii) yields n with
$\Sigma ^0_1\textsf {-BFT}$
with 2.32(3)(ii) yields n with
which, with (b), implies
![]() $(\forall \alpha \,{<}\,\beta ) (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0)\,{\to }\, (\exists k\,{<}\,n)B[\alpha {\upharpoonright } k])$
. Here, note
$(\forall \alpha \,{<}\,\beta ) (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0)\,{\to }\, (\exists k\,{<}\,n)B[\alpha {\upharpoonright } k])$
. Here, note
![]() ${\mathbf{EL}_0^{\prime }\!}^*\vdash \Delta ^0_0\textsf {-BFT}$
by 3.5(3).
${\mathbf{EL}_0^{\prime }\!}^*\vdash \Delta ^0_0\textsf {-BFT}$
by 3.5(3).
Proposition 3.42. Both
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
and
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
and
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{01}$
are (i)
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{01}$
are (i)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*$
; (ii)
$\mathbf{EL}_0^*$
; (ii)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() ${\mathbf{EL}_0^{\prime }\!}^*$
.
${\mathbf{EL}_0^{\prime }\!}^*$
.
Proof As
![]() $\mathcal {C}\textsf {-AC}^{01}$
yields
$\mathcal {C}\textsf {-AC}^{01}$
yields
![]() $\mathcal {C}\textsf {-AC}^{00}$
, it suffices to derive
$\mathcal {C}\textsf {-AC}^{00}$
, it suffices to derive
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{01}$
from
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{01}$
from
![]() $(\mathcal {L}_{\mathrm{F}},\{\top \})\textsf {-GC}_{\texttt {L}}$
(uniformly for (i) and (ii)).
$(\mathcal {L}_{\mathrm{F}},\{\top \})\textsf {-GC}_{\texttt {L}}$
(uniformly for (i) and (ii)).
Assume
![]() $\forall x\exists \beta A[x,\beta ]$
, i.e.,
$\forall x\exists \beta A[x,\beta ]$
, i.e.,
![]() $\forall \xi \exists \beta A[\xi (0),\beta ]$
. By
$\forall \xi \exists \beta A[\xi (0),\beta ]$
. By
![]() $(\mathcal {L}_{\mathrm{F}},\{\top \})\textsf {-GC}_{\texttt {L}}$
, we have
$(\mathcal {L}_{\mathrm{F}},\{\top \})\textsf {-GC}_{\texttt {L}}$
, we have
![]() $\zeta $
with
$\zeta $
with
![]() $\forall x((\zeta |\underline {x}){\downarrow } \land \exists \eta (\eta \,{\in _{\texttt {L}}}\,\zeta |\underline {x})\land (\forall \eta \,{\in _{\texttt {L}}}\,\zeta |\underline {x})A[x,\eta ])$
. Therefore 3.23(1)(ii) applied to
$\forall x((\zeta |\underline {x}){\downarrow } \land \exists \eta (\eta \,{\in _{\texttt {L}}}\,\zeta |\underline {x})\land (\forall \eta \,{\in _{\texttt {L}}}\,\zeta |\underline {x})A[x,\eta ])$
. Therefore 3.23(1)(ii) applied to
![]() ${y = (\zeta |\underline {(x)^2_0})((x)^2_1)}$
yields
${y = (\zeta |\underline {(x)^2_0})((x)^2_1)}$
yields
![]() $\gamma $
with
$\gamma $
with
![]() $(\gamma |\zeta ){\downarrow }$
and
$(\gamma |\zeta ){\downarrow }$
and
![]() $\forall x((\gamma |\zeta )_x\,{=}\,(\zeta |\underline {x}))$
.
$\forall x((\gamma |\zeta )_x\,{=}\,(\zeta |\underline {x}))$
.
We then treat (i) and (ii) separately. (i) For
![]() ${\in _{\texttt {L}}}\,\equiv \,{\in _{\texttt {L}}^{\mathfrak {k}}}$
, obviously
${\in _{\texttt {L}}}\,\equiv \,{\in _{\texttt {L}}^{\mathfrak {k}}}$
, obviously
![]() $\forall xA[x,(\gamma |\zeta )_x]$
. (ii) For
$\forall xA[x,(\gamma |\zeta )_x]$
. (ii) For
![]() ${\in _{\texttt {L}}}\,\equiv \,{\in _{\texttt {L}}^{\mathfrak {o}}}$
,
${\in _{\texttt {L}}}\,\equiv \,{\in _{\texttt {L}}^{\mathfrak {o}}}$
,
![]() $\Pi ^0_1\textsf {-BAC}^{01}$
, with 3.8, applied to
$\Pi ^0_1\textsf {-BAC}^{01}$
, with 3.8, applied to
![]() $\forall x\exists \eta (\eta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,(\gamma |\zeta )_x)$
yields
$\forall x\exists \eta (\eta \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,(\gamma |\zeta )_x)$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $\forall x((\alpha )_x\,{\in _{\texttt {L}}^{\mathfrak {o}}}\, (\gamma |\zeta )_x)$
, which implies
$\forall x((\alpha )_x\,{\in _{\texttt {L}}^{\mathfrak {o}}}\, (\gamma |\zeta )_x)$
, which implies
![]() $\forall xA[x,(\alpha )_x]$
.
$\forall xA[x,(\alpha )_x]$
.
Theorem 3.43.
-
(1)
 $\mathbf{EL}_0^-{+}\textsf {MP}{+} \mathcal {L}_{\mathrm{F}}\{ \textsf {-CC}^{1}\!, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\!, \textsf {-BFT}\}$
is
$\mathbf{EL}_0^-{+}\textsf {MP}{+} \mathcal {L}_{\mathrm{F}}\{ \textsf {-CC}^{1}\!, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\!, \textsf {-BFT}\}$
is
 $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
 $\mathbf{EL}_0^-\!{+}\textsf { MP}{+}\Delta ^0_0\textsf {-AC}^{00}\!{+}\Delta ^0_0\textsf {-BFT}$
.
$\mathbf{EL}_0^-\!{+}\textsf { MP}{+}\Delta ^0_0\textsf {-AC}^{00}\!{+}\Delta ^0_0\textsf {-BFT}$
. -
(2)
 ${{\mathbf{EL}_0^{\prime }}^-+}\textsf {MP}{+}\Sigma ^0_1\textsf {-GDM}{+} \mathcal {L}_{\mathrm{F}}\{\textsf {-CB}^{1},\textsf {-CC!}^{1}, \textsf {-AC}^{00}, \textsf {-AC}^{01}, \textsf {-BFT}\}$
is
${{\mathbf{EL}_0^{\prime }}^-+}\textsf {MP}{+}\Sigma ^0_1\textsf {-GDM}{+} \mathcal {L}_{\mathrm{F}}\{\textsf {-CB}^{1},\textsf {-CC!}^{1}, \textsf {-AC}^{00}, \textsf {-AC}^{01}, \textsf {-BFT}\}$
is
 $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
 ${\mathbf{EL}_0^{\prime }}^*$
.
${\mathbf{EL}_0^{\prime }}^*$
.
As a byproduct, we have the following upper bound result for the semi-Russian axiom
![]() $\textsf {NCT}$
(cf. f.n.8).
$\textsf {NCT}$
(cf. f.n.8).
Definition 3.44 (Church’s thesis
 $\textsf {CT}$
and negative Church’s thesis
$\textsf {CT}$
and negative Church’s thesis
 $\textsf {NCT}$
)
$\textsf {NCT}$
)
Let
![]() $\{e\}(k) = n$
abbreviate the
$\{e\}(k) = n$
abbreviate the
![]() $\Sigma ^0_1$
formula asserting that the value of the recursive function with index e at k is n (Kleene bracket).
$\Sigma ^0_1$
formula asserting that the value of the recursive function with index e at k is n (Kleene bracket).
-
(
 $\textsf {CT}$
):
$\textsf {CT}$
):
 $\forall \alpha \exists e\forall k(\alpha (k)\,{=}\,\{e\}(k))$
;
$\forall \alpha \exists e\forall k(\alpha (k)\,{=}\,\{e\}(k))$
; -
(
 $\textsf {NCT}$
):
$\textsf {NCT}$
):
 $\forall \alpha \neg \forall e\neg \forall k(\alpha (k)\,{=}\,\{e\}(k))$
.
$\forall \alpha \neg \forall e\neg \forall k(\alpha (k)\,{=}\,\{e\}(k))$
.
Corollary 3.45.
![]() $\mathbf{EL}_0^-{+}\textsf {MP}{+} \mathcal {L}_{\mathrm{F}}\{ \textsf {-CC}^{1}\!, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\}{+}\textsf {NCT}$
is
$\mathbf{EL}_0^-{+}\textsf {MP}{+} \mathcal {L}_{\mathrm{F}}\{ \textsf {-CC}^{1}\!, \textsf {-AC}^{00}\!, \textsf {-AC}^{01}\}{+}\textsf {NCT}$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^-\!{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00}\!{+}\textsf {CT}$
.
$\mathbf{EL}_0^-\!{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00}\!{+}\textsf {CT}$
.
3.3.3 Realizability with
 $\Sigma ^0_1$
induction
$\Sigma ^0_1$
induction
One may wonder if
![]() $\mathcal {C}\textsf {-FT}$
follows from
$\mathcal {C}\textsf {-FT}$
follows from
![]() $\mathcal {C}\textsf {-BFT}$
with
$\mathcal {C}\textsf {-BFT}$
with
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
, as we can take a function bounding the number n of branching in
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
, as we can take a function bounding the number n of branching in
![]() $\textsf {Fan}[\gamma ]$
. This is not the case when
$\textsf {Fan}[\gamma ]$
. This is not the case when
![]() $\mathcal {C}\,{\equiv }\,\Delta ^0_0$
by 3.43(1) and 2.33. Here we have to distinguish two ways of bounding:
$\mathcal {C}\,{\equiv }\,\Delta ^0_0$
by 3.43(1) and 2.33. Here we have to distinguish two ways of bounding:
-
• (locally bound) depending on nodes
 $\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
as defined below, and
$\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
as defined below, and -
• (uniformly bound) depending only on heights
 $\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\delta )$
.
$\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\delta )$
.
Now
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
yields the former, and we need
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
yields the former, and we need
![]() $\Sigma ^0_1\textsf {-Ind}$
or primitive recursion to enhance it to the latter. This seems analogous to the classical fact mentioned before 2.33 that KL (König’s lemma) or
$\Sigma ^0_1\textsf {-Ind}$
or primitive recursion to enhance it to the latter. This seems analogous to the classical fact mentioned before 2.33 that KL (König’s lemma) or
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Delta ^0_0\textsf {-FT}$
is consistency-wise stronger than
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Delta ^0_0\textsf {-FT}$
is consistency-wise stronger than
![]() $\mathbf{WKL}_0$
(but also than
$\mathbf{WKL}_0$
(but also than
![]() $\mathbf{EL}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
or
$\mathbf{EL}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
or
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
).
$\textbf {I}\boldsymbol {\Sigma }_1$
).
Definition 3.46 (
 $\mathcal {C}\textsf {-LBFT}$
)
$\mathcal {C}\textsf {-LBFT}$
)
Let
![]() $\textsf {LBFan}[\gamma, \delta]\;{:\equiv }\;\textsf {Fan}[\gamma ] \,{\land }\,\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
where
$\textsf {LBFan}[\gamma, \delta]\;{:\equiv }\;\textsf {Fan}[\gamma ] \,{\land }\,\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
where
![]() $u\,{\ll }\,\delta \,{:\equiv }\,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\delta (u{\upharpoonright } k))$
. For a class
$u\,{\ll }\,\delta \,{:\equiv }\,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\delta (u{\upharpoonright } k))$
. For a class
![]() $\mathcal {C}$
of formulae, define the following axiom schema:
$\mathcal {C}$
of formulae, define the following axiom schema:
-
(
 $\mathcal {C}\textsf {-LBFT}$
):
$\mathcal {C}\textsf {-LBFT}$
):
 $\textsf {LBFan}[\gamma, \delta] \,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}] \\\phantom{\hspace{130pt}}{\to }\,\exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) \,{\to }\, (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n]),$
$\textsf {LBFan}[\gamma, \delta] \,{\land }\, \textsf {Bar}[\gamma ,\left \{u{:}\,B[u]\right \}] \\\phantom{\hspace{130pt}}{\to }\,\exists m\forall \alpha (\forall k(\gamma (\alpha {\upharpoonright } k)\,{=}\,0) \,{\to }\, (\exists n\,{<}\,m)B[\alpha {\upharpoonright } n]),$
for any B from
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 3.47.
-
(1)
 $\mathbf{EL}_0{+}\mathcal {C}\textsf {-BFT} \,{\vdash }\,\mathcal {C}\textsf {-LBFT}$
.
$\mathbf{EL}_0{+}\mathcal {C}\textsf {-BFT} \,{\vdash }\,\mathcal {C}\textsf {-LBFT}$
. -
(2)
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{00}{+}\mathcal {C}\textsf {-LBFT} \,{\vdash }\,\mathcal {C}\textsf {-FT}$
.
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{00}{+}\mathcal {C}\textsf {-LBFT} \,{\vdash }\,\mathcal {C}\textsf {-FT}$
.
Proof (1) Defined the following, which is equivalently
![]() $\Delta ^0_0$
.
$\Delta ^0_0$
.
Since
![]() $\forall d\exists v(|v|\,{=}\,|d|{+}1\,{\land }\,d\,{\subset }\,v\,{\land }\,C[d,v(|d|),\delta ])$
, by
$\forall d\exists v(|v|\,{=}\,|d|{+}1\,{\land }\,d\,{\subset }\,v\,{\land }\,C[d,v(|d|),\delta ])$
, by
![]() $\Delta ^0_0\textsf {-DC}^0$
we can take
$\Delta ^0_0\textsf {-DC}^0$
we can take
![]() $\beta $
such that
$\beta $
such that
![]() $\forall nC[\beta {\upharpoonright } n,\beta (n),\delta ]$
. Then
$\forall nC[\beta {\upharpoonright } n,\beta (n),\delta ]$
. Then
![]() $\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
implies
$\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{\ll }\,\delta )$
implies
![]() $\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\beta )$
.
$\forall u(\gamma (u)\,{=}\,0\,{\to }\, u\,{<}\,\beta )$
.
(2)
![]() $\Pi ^0_1\textsf {-AC}^{00}$
, applied to
$\Pi ^0_1\textsf {-AC}^{00}$
, applied to
![]() $\textsf {Fan}[\gamma ]$
, yields
$\textsf {Fan}[\gamma ]$
, yields
![]() $\delta $
with
$\delta $
with
![]() $\forall u(\gamma (u)\,{=}\,0\,{\to }\,u\,{\ll }\,\delta )$
.
$\forall u(\gamma (u)\,{=}\,0\,{\to }\,u\,{\ll }\,\delta )$
.
Next let us realize
![]() $\Sigma ^0_2\textsf {-DC}^0$
, which implies
$\Sigma ^0_2\textsf {-DC}^0$
, which implies
![]() $\Sigma ^0_1\textsf {-DC}^1$
by 2.14 and
$\Sigma ^0_1\textsf {-DC}^1$
by 2.14 and
![]() $\Sigma ^0_2\textsf {-Ind}$
by 2.16(3)(i). This might be the most non-trivial part of the present article. The trick is the use of semi-classical principle. For, the realizing theory does not need to be intuitionistic since
$\Sigma ^0_2\textsf {-Ind}$
by 2.16(3)(i). This might be the most non-trivial part of the present article. The trick is the use of semi-classical principle. For, the realizing theory does not need to be intuitionistic since
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
and
$\textbf {i}\boldsymbol {\Sigma }_1$
and
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
are known to be mutually interpretable. We do not know if
$\textbf {I}\boldsymbol {\Sigma }_1$
are known to be mutually interpretable. We do not know if
![]() $\Sigma ^0_2\textsf {-Ind}$
(or
$\Sigma ^0_2\textsf {-Ind}$
(or
![]() $\Sigma ^0_2\textsf {-DC}^0$
) can be realizable directly in
$\Sigma ^0_2\textsf {-DC}^0$
) can be realizable directly in
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
. Let us start with
$\textbf {i}\boldsymbol {\Sigma }_1$
. Let us start with
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizability.
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizability.
Definition 3.48 (closure under
 $\mathcal {C}$
functions)
$\mathcal {C}$
functions)
A class
![]() $\mathcal {S}$
is called closed under
$\mathcal {S}$
is called closed under
![]() $\mathcal {C}$
functions iff (i)
$\mathcal {C}$
functions iff (i)
![]() $\mathcal {S}\land \mathcal {C}\land \neg \mathcal {C}\,{\subseteq }\,\mathcal {S}$
and (ii) for C from
$\mathcal {S}\land \mathcal {C}\land \neg \mathcal {C}\,{\subseteq }\,\mathcal {S}$
and (ii) for C from
![]() $\mathcal {C}$
and D from
$\mathcal {C}$
and D from
![]() $\mathcal {S}$
, there is
$\mathcal {S}$
, there is
![]() $D_C$
from
$D_C$
from
![]() $\mathcal {S}$
with
$\mathcal {S}$
with
![]() $\mathbf{EL}_0^-\vdash \exists !yC[x,y]\,{\to }\,(D_C[x]\,{\leftrightarrow }\, \exists y(C[x,y]{\land } D[x,y])).$
$\mathbf{EL}_0^-\vdash \exists !yC[x,y]\,{\to }\,(D_C[x]\,{\leftrightarrow }\, \exists y(C[x,y]{\land } D[x,y])).$
Proposition 3.49.
-
(1)
 $\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1)$
is closed under
$\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1)$
is closed under
 $\Sigma ^0_1$
functions.
$\Sigma ^0_1$
functions. -
(2) If
 $\mathcal {S}\,{\subseteq }\,N(\Sigma ^0_1)$
and is closed under
$\mathcal {S}\,{\subseteq }\,N(\Sigma ^0_1)$
and is closed under
 $\Sigma ^0_1$
functions, both
$\Sigma ^0_1$
functions, both
 $\exists ^0\mathcal {S}\textsf {-DC}^0$
and
$\exists ^0\mathcal {S}\textsf {-DC}^0$
and
 $\exists ^0\mathcal {S}\textsf {-Ind}$
are
$\exists ^0\mathcal {S}\textsf {-Ind}$
are
 $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
 $\mathbf{EL}_0{+}\mathcal {S}\textsf {-Ind}$
.
$\mathbf{EL}_0{+}\mathcal {S}\textsf {-Ind}$
.
Proof (1) is by induction on D:
![]() $\exists !yC[x,y]$
yields
$\exists !yC[x,y]$
yields
(2) As
![]() $\mathcal {S}\textsf {-Ind}$
is
$\mathcal {S}\textsf {-Ind}$
is
![]() $N(\Sigma ^0_1)$
, it suffices to derive
$N(\Sigma ^0_1)$
, it suffices to derive
![]() $\mathcal {S}\textsf {-DC}^0$
in
$\mathcal {S}\textsf {-DC}^0$
in
![]() $\mathbf{EL}_0{+}(\mathcal {L}_{\mathrm{F}}, N(\Sigma ^0_1))\textsf {-GCC}^1 {+}\mathcal {S}\textsf {-Ind}$
by 2.16(2)(i)(3)(i), 3.40(1) and 3.42(i)
. Let
$\mathbf{EL}_0{+}(\mathcal {L}_{\mathrm{F}}, N(\Sigma ^0_1))\textsf {-GCC}^1 {+}\mathcal {S}\textsf {-Ind}$
by 2.16(2)(i)(3)(i), 3.40(1) and 3.42(i)
. Let
![]() $\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])$
with A from
$\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])$
with A from
![]() $\mathcal {S}$
, say
$\mathcal {S}$
, say
![]() $\forall x,y(A[x,y]\to (\gamma |\underline {x}|\underline {y}){\downarrow } \land A[\underline {y},(\gamma |\underline {x}|\underline {y})(0)])$
by
$\forall x,y(A[x,y]\to (\gamma |\underline {x}|\underline {y}){\downarrow } \land A[\underline {y},(\gamma |\underline {x}|\underline {y})(0)])$
by
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
. Fix
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\textsf {-GCC}^1$
. Fix
![]() $x,y$
with
$x,y$
with
![]() $A[x,y]$
. We prove
$A[x,y]$
. We prove
![]() $\exists !uC[n,u]\land D_C[n]$
by
$\exists !uC[n,u]\land D_C[n]$
by
![]() $\mathcal {S}\textsf {-Ind}$
on n, where
$\mathcal {S}\textsf {-Ind}$
on n, where
 $$ \begin{align*} C[n,u]&\,{:\equiv}\, |u|\,{=}\,n{+}2\land u{\upharpoonright}2\,{=}\,\langle x\rangle{*}\langle y\rangle \land(\forall k\,{<}\,n) (u(k{+}2)\,{=}\,(\gamma|\underline{u(k)}|\underline{u(k{+}1)})(0)); \\ D[k,u]&\,{:\equiv}\, A[u(k),u(k{+}1)], \end{align*} $$
$$ \begin{align*} C[n,u]&\,{:\equiv}\, |u|\,{=}\,n{+}2\land u{\upharpoonright}2\,{=}\,\langle x\rangle{*}\langle y\rangle \land(\forall k\,{<}\,n) (u(k{+}2)\,{=}\,(\gamma|\underline{u(k)}|\underline{u(k{+}1)})(0)); \\ D[k,u]&\,{:\equiv}\, A[u(k),u(k{+}1)], \end{align*} $$
and
![]() $D_C$
is
$D_C$
is
![]() $\mathcal {S}$
by 3.48. If it is done,
$\mathcal {S}$
by 3.48. If it is done,
![]() $\Sigma ^0_1\textsf {-AC}^{00}$
yields
$\Sigma ^0_1\textsf {-AC}^{00}$
yields
![]() $\beta $
with
$\beta $
with
![]() $\forall n\exists u(C[n,u]\land u(n)\,{=}\,\beta (n))$
.
$\forall n\exists u(C[n,u]\land u(n)\,{=}\,\beta (n))$
.
As
![]() $C[0,\langle x\rangle {*}\langle y\rangle ]$
,
$C[0,\langle x\rangle {*}\langle y\rangle ]$
,
![]() $D_C[0]$
is by
$D_C[0]$
is by
![]() $A[x,y]$
. If
$A[x,y]$
. If
![]() $\exists ! uC[n,u]\land D_C[n]$
, say
$\exists ! uC[n,u]\land D_C[n]$
, say
![]() $C[n,v]$
, then
$C[n,v]$
, then
![]() $D_C[n]$
means
$D_C[n]$
means
![]() $A[v(n),v(n{+}1)]$
and hence
$A[v(n),v(n{+}1)]$
and hence
![]() $(\gamma |\underline {v(n)}|\underline {v(n{+}1)}){\downarrow } \,{\land }\, A[v(n{+}1),z]$
with
$(\gamma |\underline {v(n)}|\underline {v(n{+}1)}){\downarrow } \,{\land }\, A[v(n{+}1),z]$
with
![]() $z\,{=}\,(\gamma |\underline {v(n)}|\underline {v(n{+}1)})(0)$
. Thus
$z\,{=}\,(\gamma |\underline {v(n)}|\underline {v(n{+}1)})(0)$
. Thus
![]() $C[n{+}1,v{*}\langle z\rangle ]$
and so
$C[n{+}1,v{*}\langle z\rangle ]$
and so
![]() $D_C[n{+}1]$
.
$D_C[n{+}1]$
.
As
![]() $\Pi ^0_1\,{\subseteq }\,\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1)$
,
$\Pi ^0_1\,{\subseteq }\,\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1)$
,
![]() $\Sigma ^0_2\{\textsf {-DC}^0,\textsf {-Ind}\}$
is
$\Sigma ^0_2\{\textsf {-DC}^0,\textsf {-Ind}\}$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0{+}\Sigma ^0_2\textsf {-DNE}$
, by 3.3(2), the other folklore.
$\mathbf{EL}_0{+}\Sigma ^0_2\textsf {-DNE}$
, by 3.3(2), the other folklore.
For this argument functionality is not essential: ECT in Kleene’s number realizability can substitute GCC, and so
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
is realizable in
$\textbf {i}\boldsymbol {\Sigma }_2$
is realizable in
![]() $\textbf {I}\boldsymbol {\Sigma }_1$
. Wehmeier [Reference Wehmeier56] identified the strengths of
$\textbf {I}\boldsymbol {\Sigma }_1$
. Wehmeier [Reference Wehmeier56] identified the strengths of
![]() $\textbf {i}\boldsymbol {\Sigma }_1$
,
$\textbf {i}\boldsymbol {\Sigma }_1$
,
![]() $\textbf {i}\boldsymbol {\Pi }_{n+2}$
and
$\textbf {i}\boldsymbol {\Pi }_{n+2}$
and
![]() $\textbf {i}\boldsymbol {\Sigma }_{n+3}$
by this realizability, but left
$\textbf {i}\boldsymbol {\Sigma }_{n+3}$
by this realizability, but left
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
. Burr [Reference Burr10] identified it by another method. Our argument shows that Wehmeier’s method could deal with
$\textbf {i}\boldsymbol {\Sigma }_2$
. Burr [Reference Burr10] identified it by another method. Our argument shows that Wehmeier’s method could deal with
![]() $\textbf {i}\boldsymbol {\Sigma }_2$
. If we expand this number realizability to
$\textbf {i}\boldsymbol {\Sigma }_2$
. If we expand this number realizability to
![]() $\mathcal {L}_{\mathrm{F}}$
in an obvious manner,
$\mathcal {L}_{\mathrm{F}}$
in an obvious manner,
![]() $\Sigma ^0_2\textsf {-DC}^0$
and
$\Sigma ^0_2\textsf {-DC}^0$
and
![]() $\textsf {CT}$
are also realizable. By allowing
$\textsf {CT}$
are also realizable. By allowing
![]() $\Sigma _n$
oracle, we can interpret
$\Sigma _n$
oracle, we can interpret
![]() $\textbf {i}\boldsymbol {\Sigma }_{n+2}{+}\Sigma _{n+1}\textsf {-DNE}$
in
$\textbf {i}\boldsymbol {\Sigma }_{n+2}{+}\Sigma _{n+1}\textsf {-DNE}$
in
![]() $\textbf {I}\boldsymbol {\Sigma }_{n+1}$
.
$\textbf {I}\boldsymbol {\Sigma }_{n+1}$
.
For
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizability, this does not seem to work well. We employ a more elaborated way, which works also in the first order setting, i.e., Lifschitz’s number realizability, with recursive indices substituting functions. However, in this case we do not know if we can enhance
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizability, this does not seem to work well. We employ a more elaborated way, which works also in the first order setting, i.e., Lifschitz’s number realizability, with recursive indices substituting functions. However, in this case we do not know if we can enhance
![]() $\Sigma ^0_2$
to
$\Sigma ^0_2$
to
![]() $\exists ^0(\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1))$
as in the previous case.
$\exists ^0(\Delta ^0_0(\Sigma ^0_1)\,{\cap }\, N(\Sigma ^0_1))$
as in the previous case.
Definition 3.50 (
 $(\mathcal {C},\mathcal {D})\textsf {-EUB}$
)
$(\mathcal {C},\mathcal {D})\textsf {-EUB}$
)
The schema of extended uniform bounding
![]() $(\mathcal {C},\mathcal {D})\textsf {-EUB}$
is defined as follows.
$(\mathcal {C},\mathcal {D})\textsf {-EUB}$
is defined as follows.
-
(
 $(\mathcal {C},\mathcal {D})\textsf {-EUB}$
):
$(\mathcal {C},\mathcal {D})\textsf {-EUB}$
):
 $\forall x(D[x]{{\kern-2pt}\to{\kern-2pt}}\exists yC[x,y]){{\kern-2pt}\to{\kern-2pt}}\exists \alpha \forall n(\forall x\,{<}\,n)(D[x]{{\kern-2pt}\to{\kern-2pt}} (\exists y{{\kern-2pt}<{\kern-2pt}}\alpha (n))C[x,y]),$
$\forall x(D[x]{{\kern-2pt}\to{\kern-2pt}}\exists yC[x,y]){{\kern-2pt}\to{\kern-2pt}}\exists \alpha \forall n(\forall x\,{<}\,n)(D[x]{{\kern-2pt}\to{\kern-2pt}} (\exists y{{\kern-2pt}<{\kern-2pt}}\alpha (n))C[x,y]),$
for any C from
![]() $\mathcal {C}$
and any D from
$\mathcal {C}$
and any D from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 3.51.
![]() $(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
is
$(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}_0^{\prime }{+}\textsf {LPO}$
.
$\mathbf{EL}_0^{\prime }{+}\textsf {LPO}$
.
Proof Let C and D be
![]() $\Pi ^0_1$
. Let D be
$\Pi ^0_1$
. Let D be
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed by
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed by
![]() $c_D$
, by 3.38(2). Define A and B as follows:
$c_D$
, by 3.38(2). Define A and B as follows:
 $$ \begin{align*} A[n,m,\zeta]\,&{:\equiv}\,(\forall x\,{<}\,n)(D[x]\,{\to}\,(\zeta|\underline{x}|(c_D|\underline{x}))(0)\,{\leq}\,m); \\ B[\alpha]\,&{:\equiv}\,\forall n (\forall x\,{<}\,n)(D[x]\,{\to}\,(\exists y\,{<}\,\alpha(n))C[x,y]). \end{align*} $$
$$ \begin{align*} A[n,m,\zeta]\,&{:\equiv}\,(\forall x\,{<}\,n)(D[x]\,{\to}\,(\zeta|\underline{x}|(c_D|\underline{x}))(0)\,{\leq}\,m); \\ B[\alpha]\,&{:\equiv}\,\forall n (\forall x\,{<}\,n)(D[x]\,{\to}\,(\exists y\,{<}\,\alpha(n))C[x,y]). \end{align*} $$
As A is equivalently
![]() $\Sigma ^0_1$
by
$\Sigma ^0_1$
by
![]() $\textsf {LPO}$
, 3.23(1)(ii) yields
$\textsf {LPO}$
, 3.23(1)(ii) yields
![]() $\gamma _A$
with
$\gamma _A$
with
Let
![]() $\zeta \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} \forall x(D[x]\,{\to }\,\exists yC[x,y])$
. We prove
$\zeta \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} \forall x(D[x]\,{\to }\,\exists yC[x,y])$
. We prove
![]() $\exists mA[n,m,\zeta ]$
by induction on n. Obviously
$\exists mA[n,m,\zeta ]$
by induction on n. Obviously
![]() $A[0,0,\zeta ]$
. If
$A[0,0,\zeta ]$
. If
![]() $A[n,m,\zeta ]$
and
$A[n,m,\zeta ]$
and
![]() $D[n]$
, then
$D[n]$
, then
![]() $c_D|\underline {n} \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} D[n]$
and so
$c_D|\underline {n} \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} D[n]$
and so
![]() $(\zeta |\underline {n}|(c_D|\underline {n})){\downarrow }$
which implies
$(\zeta |\underline {n}|(c_D|\underline {n})){\downarrow }$
which implies
![]() $A[n{+}1,m^{\prime },\zeta ]$
for
$A[n{+}1,m^{\prime },\zeta ]$
for
![]() $m^{\prime }\,{:=}\,m\,{+}\, (\zeta |\underline {n}|(c_D|\underline {n}))(0)$
. If
$m^{\prime }\,{:=}\,m\,{+}\, (\zeta |\underline {n}|(c_D|\underline {n}))(0)$
. If
![]() $A[n,m,\zeta ]$
and
$A[n,m,\zeta ]$
and
![]() $\neg D[n]$
, then
$\neg D[n]$
, then
![]() $A[n{+}1,m,\zeta ]$
. By
$A[n{+}1,m,\zeta ]$
. By
![]() $\Pi ^0_1\textsf {-LEM}$
, we have
$\Pi ^0_1\textsf {-LEM}$
, we have
![]() $\exists mA[n,m,\zeta ]\,{\to }\,\exists mA[n{+}1,m,\zeta ]$
.
$\exists mA[n,m,\zeta ]\,{\to }\,\exists mA[n{+}1,m,\zeta ]$
.
Thus
![]() $\forall n A[n,(\gamma _A|\zeta )(n),\zeta ]$
. Then
$\forall n A[n,(\gamma _A|\zeta )(n),\zeta ]$
. Then
and so
![]() $B[\gamma _A|\zeta ]$
. As B is
$B[\gamma _A|\zeta ]$
. As B is
![]() $N(\textsf {B}\exists ^1\Pi ^0_1)$
, by 3.38(2), let B be
$N(\textsf {B}\exists ^1\Pi ^0_1)$
, by 3.38(2), let B be
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed by
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-completed by
![]() $c_B$
. Then
$c_B$
. Then
![]() $\textsf {g}|\langle \gamma _A|\zeta ,c_B|(\gamma _A|\zeta )\rangle \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} \exists \alpha B[\alpha ]$
.
$\textsf {g}|\langle \gamma _A|\zeta ,c_B|(\gamma _A|\zeta )\rangle \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} \exists \alpha B[\alpha ]$
.
Therefore
![]() $\lambda \zeta .\textsf {g}|\langle \gamma _A|\zeta ,c_B|(\gamma _A|\zeta )\rangle \ \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizes the instance of
$\lambda \zeta .\textsf {g}|\langle \gamma _A|\zeta ,c_B|(\gamma _A|\zeta )\rangle \ \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizes the instance of
![]() $(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
.
$(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
.
Proposition 3.52.
![]() $\Pi ^0_1\textsf {-DC}^0$
is
$\Pi ^0_1\textsf {-DC}^0$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}^{\prime }_0{+}\textsf { LPO}$
. Hence so are
$\mathbf{EL}^{\prime }_0{+}\textsf { LPO}$
. Hence so are
![]() $\Sigma ^0_2\textsf {-DC}^0$
,
$\Sigma ^0_2\textsf {-DC}^0$
,
![]() $\Sigma ^0_1\textsf {-DC}^1$
and
$\Sigma ^0_1\textsf {-DC}^1$
and
![]() $\Sigma ^0_2\textsf {-Ind}$
.
$\Sigma ^0_2\textsf {-Ind}$
.
Proof By 3.39(2) and 3.51, it suffices to derive
![]() $\Pi ^0_1\textsf {-DC}^0$
in
$\Pi ^0_1\textsf {-DC}^0$
in
![]() $\mathbf{EL}^{\prime }_0{+}(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
. Let A be
$\mathbf{EL}^{\prime }_0{+}(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
. Let A be
![]() $\Pi ^0_1$
, and assume
$\Pi ^0_1$
, and assume
![]() $\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])$
. Then
$\forall x,y(A[x,y]\,{\to }\,\exists zA[y,z])$
. Then
![]() $(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
yields
$(\Pi ^0_1,\Pi ^0_1)\textsf {-EUB}$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $(\forall v\,{<}\,n) (A[(v)^2_0,(v)^2_1]\,{\to }\,(\exists z\,{<}\,\alpha (n))A[(v)^2_1,z])$
.
$(\forall v\,{<}\,n) (A[(v)^2_0,(v)^2_1]\,{\to }\,(\exists z\,{<}\,\alpha (n))A[(v)^2_1,z])$
.
Fix
![]() $x,y$
with
$x,y$
with
![]() $A[x,y]$
.
$A[x,y]$
.
![]() $\Delta ^0_0\textsf {-DC}^{0}$
yields
$\Delta ^0_0\textsf {-DC}^{0}$
yields
![]() $\beta $
with
$\beta $
with
Define the following, where
![]() $u\,{<}\,\beta \,{:\equiv }\,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
.
$u\,{<}\,\beta \,{:\equiv }\,(\forall k\,{<}\,|u|)(u(k)\,{<}\,\beta (k))$
.
 $$ \begin{align*} B[n,\beta]\,&{:\equiv}\,(\exists u\,{<}\,\beta)C[u,n]; \\ C[u,n]\,&{:\equiv}\,|u|\,{=}\,n{+}2\land u(0)\,{=}\,x\land (\forall k\,{\leq}\,n)A[u(k),u(k{+}1)]. \end{align*} $$
$$ \begin{align*} B[n,\beta]\,&{:\equiv}\,(\exists u\,{<}\,\beta)C[u,n]; \\ C[u,n]\,&{:\equiv}\,|u|\,{=}\,n{+}2\land u(0)\,{=}\,x\land (\forall k\,{\leq}\,n)A[u(k),u(k{+}1)]. \end{align*} $$
B is
![]() $\Pi ^0_1$
by 2.23(2)(i) and 3.7.
$\Pi ^0_1$
by 2.23(2)(i) and 3.7.
![]() $\Sigma ^0_1\textsf {-Ind}$
and
$\Sigma ^0_1\textsf {-Ind}$
and
![]() $\textsf {MP}$
yield
$\textsf {MP}$
yield
![]() $\Pi ^0_1\textsf {-Ind}$
. It remains to see
$\Pi ^0_1\textsf {-Ind}$
. It remains to see
![]() $\forall nB[n,\beta ]$
by
$\forall nB[n,\beta ]$
by
![]() $\Pi ^0_1\textsf {-Ind}$
, as it implies
$\Pi ^0_1\textsf {-Ind}$
, as it implies
![]() $\exists \gamma (\gamma (0)\,{=}\,x\land \forall kA[\gamma (k),\gamma (k{+}1)])$
by
$\exists \gamma (\gamma (0)\,{=}\,x\land \forall kA[\gamma (k),\gamma (k{+}1)])$
by
![]() $\Pi ^0_1\textsf {-BKL}$
with 3.5(2)(i).
$\Pi ^0_1\textsf {-BKL}$
with 3.5(2)(i).
Obviously
![]() $\langle x\rangle {*}\langle y\rangle $
witnesses
$\langle x\rangle {*}\langle y\rangle $
witnesses
![]() $B[0,\beta ]$
. Let
$B[0,\beta ]$
. Let
![]() $B[n,\beta ]$
, say
$B[n,\beta ]$
, say
![]() $u\,{<}\,\beta \land C[u,n]$
. Since
$u\,{<}\,\beta \land C[u,n]$
. Since
![]() $(u(n),u(n{+}1))\,{<}\,(\beta (n),\beta (n{+}1))$
,
$(u(n),u(n{+}1))\,{<}\,(\beta (n),\beta (n{+}1))$
,
![]() $A[u(n),u(n{+}1)]$
yields
$A[u(n),u(n{+}1)]$
yields
So
![]() $C[u{*}\langle z\rangle ,n{+}1]\land u{*}\langle z\rangle \,{<}\,\beta $
.
$C[u{*}\langle z\rangle ,n{+}1]\land u{*}\langle z\rangle \,{<}\,\beta $
.
Theorem 3.53. (1)
![]() $\mathbf{EL}_0{+}\Sigma ^0_1\textsf {-DC}^1{+}\Sigma ^0_2\{\textsf {-DC}^0\!,\textsf {-Ind}\} {+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
is
$\mathbf{EL}_0{+}\Sigma ^0_1\textsf {-DC}^1{+}\Sigma ^0_2\{\textsf {-DC}^0\!,\textsf {-Ind}\} {+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0 {+}\Delta ^0_0\textsf {-BFT}{+}\Sigma ^0_2\textsf {-DNE}$
.
$\mathbf{EL}_0 {+}\Delta ^0_0\textsf {-BFT}{+}\Sigma ^0_2\textsf {-DNE}$
.
(2)
![]() $\mathbf{EL}_0^{\prime }{+}\Sigma ^0_1\{\textsf {-GDM},\textsf {-DC}^1\}{+}\Sigma ^0_2\{\textsf {-DC}^0\!,\textsf {-Ind}\} {+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
is
$\mathbf{EL}_0^{\prime }{+}\Sigma ^0_1\{\textsf {-GDM},\textsf {-DC}^1\}{+}\Sigma ^0_2\{\textsf {-DC}^0\!,\textsf {-Ind}\} {+}\mathcal {L}_{\mathrm{F}}\textsf {-FT}$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}_0^{\prime } {+}\textsf {LPO}$
.
$\mathbf{EL}_0^{\prime } {+}\textsf {LPO}$
.
3.3.4 Realizability with
 $\Pi ^0_2$
induction
$\Pi ^0_2$
induction
It is natural to ask how to realize
![]() $\Pi ^0_{n+2}\textsf {-Ind}$
and
$\Pi ^0_{n+2}\textsf {-Ind}$
and
![]() $\Sigma ^0_{n+3}\textsf {-Ind}$
. As Wehmeier [Reference Wehmeier56] mentioned, they are all realizable in
$\Sigma ^0_{n+3}\textsf {-Ind}$
. As Wehmeier [Reference Wehmeier56] mentioned, they are all realizable in
![]() $\textbf {I}\boldsymbol {\Sigma }_2$
by Kleene’s number realizability. This remains to hold for our two kinds of functional realizability. It is technically convenient to introduce the following schema.
$\textbf {I}\boldsymbol {\Sigma }_2$
by Kleene’s number realizability. This remains to hold for our two kinds of functional realizability. It is technically convenient to introduce the following schema.
Definition 3.54 (
 $(\mathcal {C},\mathcal {D})\textsf {-RDC}$
)
$(\mathcal {C},\mathcal {D})\textsf {-RDC}$
)
For classes
![]() $\mathcal {C}$
,
$\mathcal {C}$
,
![]() $\mathcal {D}$
of formulae, define the following axiom schemata:
$\mathcal {D}$
of formulae, define the following axiom schemata:
-
 $((\mathcal {C},\mathcal {D})\textsf {-RDC}^1) : \forall \alpha (D[\alpha ]\,{\to }\,\exists \beta (D[\beta ]\,{\land }\,C[\alpha ,\beta ])) $
$((\mathcal {C},\mathcal {D})\textsf {-RDC}^1) : \forall \alpha (D[\alpha ]\,{\to }\,\exists \beta (D[\beta ]\,{\land }\,C[\alpha ,\beta ])) $
 ${\to }\,\forall \gamma (D[\gamma ]\,{\to }\,\exists \delta ((\delta )_0\,{=}\,\gamma \,{\land }\,\forall n\,C[(\delta )_n,(\delta )_{n+1}])),$
${\to }\,\forall \gamma (D[\gamma ]\,{\to }\,\exists \delta ((\delta )_0\,{=}\,\gamma \,{\land }\,\forall n\,C[(\delta )_n,(\delta )_{n+1}])),$
for any C from
![]() $\mathcal {C}$
and D from
$\mathcal {C}$
and D from
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 3.55.
-
(1)
 $\mathbf{EL}_0^-{+}(\mathcal {C},\exists ^1\mathcal {C})\textsf {-RDC}^1\vdash \mathcal {C}\textsf {-DC}^1$
.
$\mathbf{EL}_0^-{+}(\mathcal {C},\exists ^1\mathcal {C})\textsf {-RDC}^1\vdash \mathcal {C}\textsf {-DC}^1$
. -
(2)
 $\mathbf{EL}_0^-{+}(\mathcal {C},\mathcal {D})\textsf {-RDC}^1\vdash (\mathcal {C},\exists ^1\mathcal {D})\textsf {-RDC}^1$
.
$\mathbf{EL}_0^-{+}(\mathcal {C},\mathcal {D})\textsf {-RDC}^1\vdash (\mathcal {C},\exists ^1\mathcal {D})\textsf {-RDC}^1$
.
Proof As (1) is easy, we show (2).
Assume
![]() $\forall \alpha (\exists \xi D[\alpha ,\xi ] \to \exists \beta (\exists \eta D[\beta ,\eta ] \land C[\alpha ,\beta ]))$
. For
$\forall \alpha (\exists \xi D[\alpha ,\xi ] \to \exists \beta (\exists \eta D[\beta ,\eta ] \land C[\alpha ,\beta ]))$
. For
![]() $\gamma $
with
$\gamma $
with
![]() $\exists \eta D[\gamma ,\eta ]$
, say
$\exists \eta D[\gamma ,\eta ]$
, say
![]() $D[\gamma ,\eta ]$
,
$D[\gamma ,\eta ]$
,
![]() $(\mathcal {C},\mathcal {D})\textsf {-RDC}^1$
applied to
$(\mathcal {C},\mathcal {D})\textsf {-RDC}^1$
applied to
yields
![]() $\delta $
such that
$\delta $
such that
![]() $(\delta )_0\,{=}\,(\gamma ,\eta )$
and
$(\delta )_0\,{=}\,(\gamma ,\eta )$
and
![]() $\forall n\,C[((\delta )_n)^2_0,((\delta )_{n+1})^2_0]$
.
$\forall n\,C[((\delta )_n)^2_0,((\delta )_{n+1})^2_0]$
.
Our goal is to show the realizability of
![]() $\exists ^1\Pi ^0_{\infty }\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
. By 2.16(2)(i)(3)(i) and the last lemma, it suffices to realize
$\exists ^1\Pi ^0_{\infty }\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
. By 2.16(2)(i)(3)(i) and the last lemma, it suffices to realize
![]() $(\exists ^1\Pi ^0_{\infty },\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
.
$(\exists ^1\Pi ^0_{\infty },\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
.
Lemma 3.56.
-
(1) (i)
 $\Pi ^0_{n}\!{\to }\Pi ^0_{n+1}\!\subseteq \!\forall ^0\neg \Pi ^0_{n}$
over
$\Pi ^0_{n}\!{\to }\Pi ^0_{n+1}\!\subseteq \!\forall ^0\neg \Pi ^0_{n}$
over
 $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-DNE}$
; and
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-DNE}$
; and(ii)
 $(\forall \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )A[\xi ,\alpha ]$
is
$(\forall \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )A[\xi ,\alpha ]$
is
 $\Pi ^0_2$
over
$\Pi ^0_2$
over
 ${\mathbf{EL}_0^{\prime }\!}^*$
if A is
${\mathbf{EL}_0^{\prime }\!}^*$
if A is
 $\Pi ^0_2$
.
$\Pi ^0_2$
. -
(2) For B from
 $\Pi ^0_1$
,
$\Pi ^0_1$
,
 $\mathbf{EL}^-_0{+}\Delta ^0_0\textsf {-BKL}$
proves
$\mathbf{EL}^-_0{+}\Delta ^0_0\textsf {-BKL}$
proves  $$ \begin{align*} \forall n(\exists \eta\,{<}\,\alpha)(\forall k\,{<}\,n)B[k,(\eta)_k,(\eta)_{k+1}] \,{\to}\,(\exists \eta\,{<}\,\alpha)\forall kB[k,(\eta)_k,(\eta)_{k+1}].\end{align*} $$
$$ \begin{align*} \forall n(\exists \eta\,{<}\,\alpha)(\forall k\,{<}\,n)B[k,(\eta)_k,(\eta)_{k+1}] \,{\to}\,(\exists \eta\,{<}\,\alpha)\forall kB[k,(\eta)_k,(\eta)_{k+1}].\end{align*} $$
-
(3) (i)
 $\Pi ^0_{\infty }\,{\subseteq }\,\exists ^1\Pi ^0_1$
over
$\Pi ^0_{\infty }\,{\subseteq }\,\exists ^1\Pi ^0_1$
over
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{01}$
. Hence (ii)
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{01}$
. Hence (ii)
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{01}\vdash \exists ^1\Pi ^0_{\infty }\textsf {-AC}^{01}$
,
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-AC}^{01}\vdash \exists ^1\Pi ^0_{\infty }\textsf {-AC}^{01}$
,
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC}^{1}\vdash \exists ^1\Pi ^0_{\infty }\textsf {-DC}^1$
and
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC}^{1}\vdash \exists ^1\Pi ^0_{\infty }\textsf {-DC}^1$
and
 $\mathbf{EL}_0^-{+}(\mathcal {C},\Pi ^0_1)\textsf {-RDC}^{1}\vdash (\mathcal {C},\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
.
$\mathbf{EL}_0^-{+}(\mathcal {C},\Pi ^0_1)\textsf {-RDC}^{1}\vdash (\mathcal {C},\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
.
Proof (1)(i) By 2.24(1)(ii),
![]() $\Sigma ^0_{n}\textsf {-DNE}$
yields
$\Sigma ^0_{n}\textsf {-DNE}$
yields
(ii) Take B from
![]() $\Pi ^0_1$
with
$\Pi ^0_1$
with
![]() $(\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \,{\to }\, A[\xi ,\alpha ]) \leftrightarrow \forall x\neg B[x,\xi ,\alpha ]$
by (i). Then
$(\xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha \,{\to }\, A[\xi ,\alpha ]) \leftrightarrow \forall x\neg B[x,\xi ,\alpha ]$
by (i). Then
![]() $(\forall \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )A[\xi ,\alpha ]$
is equivalent to
$(\forall \xi \,{\in _{\texttt {L}}^{\mathfrak {o}}}\,\alpha )A[\xi ,\alpha ]$
is equivalent to
![]() $(\forall \xi \,{<}\,(\alpha )^2_0)\forall x\neg B[x,\xi ,\alpha ]$
, and therefore to
$(\forall \xi \,{<}\,(\alpha )^2_0)\forall x\neg B[x,\xi ,\alpha ]$
, and therefore to
![]() $\forall x\neg (\exists \xi \,{<}\,(\alpha )^2_0) B[x,\xi ,\alpha ]$
which is equivalently
$\forall x\neg (\exists \xi \,{<}\,(\alpha )^2_0) B[x,\xi ,\alpha ]$
which is equivalently
![]() $\Pi ^0_2$
by 3.5(2)(ii) and
$\Pi ^0_2$
by 3.5(2)(ii) and
![]() $\textsf {MP}$
.
$\textsf {MP}$
.
(2) Let C be
![]() $\Delta ^0_0$
such that
$\Delta ^0_0$
such that
![]() $\forall \eta ,k(B[k,\eta ,\eta ^{\prime }]\,{\leftrightarrow }\,\forall \ell C[k,\eta {\upharpoonright }\ell , \eta ^{\prime }{\upharpoonright }\ell ])$
by 2.14. The premise implies
$\forall \eta ,k(B[k,\eta ,\eta ^{\prime }]\,{\leftrightarrow }\,\forall \ell C[k,\eta {\upharpoonright }\ell , \eta ^{\prime }{\upharpoonright }\ell ])$
by 2.14. The premise implies
![]() $\forall z(\exists u\,{<}\,\alpha )(|u|\,{=}\,z\,{\land }\,(\forall k,\ell \,{<}\,z)C[k,(u)_k{\upharpoonright }\ell ,(u)_{k+1}{\upharpoonright }\ell ])$
, where
$\forall z(\exists u\,{<}\,\alpha )(|u|\,{=}\,z\,{\land }\,(\forall k,\ell \,{<}\,z)C[k,(u)_k{\upharpoonright }\ell ,(u)_{k+1}{\upharpoonright }\ell ])$
, where
![]() $(u)_k$
is as in 3.8. Apply
$(u)_k$
is as in 3.8. Apply
![]() $\Delta ^0_0\textsf {-BKL}$
.
$\Delta ^0_0\textsf {-BKL}$
.
(3)
![]() $\Pi ^0_1\textsf {-AC}^{01}$
yields the Skolem functions for any
$\Pi ^0_1\textsf {-AC}^{01}$
yields the Skolem functions for any
![]() $\Pi ^0_{\infty }$
formula under the necessary existence assumption. More precisely, we can show, by meta-induction on
$\Pi ^0_{\infty }$
formula under the necessary existence assumption. More precisely, we can show, by meta-induction on
![]() $k\,{\leq }\, n$
with
$k\,{\leq }\, n$
with
![]() $\Pi ^0_1\textsf {-AC}^{01}$
, that
$\Pi ^0_1\textsf {-AC}^{01}$
, that
![]() $\forall x_k\exists y_k\dots \forall x_0\exists y_0 C[x_n,\dots ,x_0,y_n,\dots ,y_0]$
is equivalent to
$\forall x_k\exists y_k\dots \forall x_0\exists y_0 C[x_n,\dots ,x_0,y_n,\dots ,y_0]$
is equivalent to
![]() $\exists \alpha \forall x_k,\dots ,x_0 C[x_n,\dots ,x_0,y_n,\dots ,y_{k+1},(\alpha )_k(x_k),\dots ,(\alpha )_0(x_k,\dots x_0)]$
, for any
$\exists \alpha \forall x_k,\dots ,x_0 C[x_n,\dots ,x_0,y_n,\dots ,y_{k+1},(\alpha )_k(x_k),\dots ,(\alpha )_0(x_k,\dots x_0)]$
, for any
![]() $\Delta ^0_0$
-formula C.
$\Delta ^0_0$
-formula C.
Definition 3.57 (
 $\textsf {rec}$
)
$\textsf {rec}$
)
Let
![]() $\textsf {rec}$
be such that
$\textsf {rec}$
be such that
The existence of
![]() $\textsf {rec}$
is directly by 3.23(1)(ii), but it can also be constructed by
$\textsf {rec}$
is directly by 3.23(1)(ii), but it can also be constructed by
![]() $\textsf {fix}$
and
$\textsf {fix}$
and
![]() $\textsf {d}$
as in the usual theories of operations and numbers (cf. [Reference Beeson5, VI.2.8] and [Reference Troelstra and van Dalen51, Chapter 9, 3.8]). However, we need
$\textsf {d}$
as in the usual theories of operations and numbers (cf. [Reference Beeson5, VI.2.8] and [Reference Troelstra and van Dalen51, Chapter 9, 3.8]). However, we need
![]() $\Pi ^0_2\textsf {-Ind}$
as well as
$\Pi ^0_2\textsf {-Ind}$
as well as
![]() $\Delta ^0_0\textsf {-AC}^{00}$
to imply
$\Delta ^0_0\textsf {-AC}^{00}$
to imply
![]() $\forall z((\textsf{rec}|\xi |\eta |\underline {z}){\downarrow })$
from
$\forall z((\textsf{rec}|\xi |\eta |\underline {z}){\downarrow })$
from
![]() $\forall z((\textsf{rec}|\xi |\eta |\underline {z}){\downarrow }\,{\to }\,(\textsf{rec}|\xi |\eta |\underline {z{+}1}){\downarrow })$
. This is why we need
$\forall z((\textsf{rec}|\xi |\eta |\underline {z}){\downarrow }\,{\to }\,(\textsf{rec}|\xi |\eta |\underline {z{+}1}){\downarrow })$
. This is why we need
![]() $\Pi ^0_2\textsf {-Ind}$
.
$\Pi ^0_2\textsf {-Ind}$
.
In the following, (i) is just by constructing the realizer in this way, whereas (ii) requires further tricks.
Theorem 3.58.
![]() $(\mathcal {L}_{\mathrm{F}},\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
is (i)
$(\mathcal {L}_{\mathrm{F}},\exists ^1\Pi ^0_{\infty })\textsf {-RDC}^1$
is (i)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*{+} \Pi ^0_2\textsf {-Ind}$
; and (ii)
$\mathbf{EL}_0^*{+} \Pi ^0_2\textsf {-Ind}$
; and (ii)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}_0^{\prime }{+}\Pi ^0_2\textsf {-Ind}$
.
$\mathbf{EL}_0^{\prime }{+}\Pi ^0_2\textsf {-Ind}$
.
Proof By 3.55(2) and 3.56(3)(ii), it suffices to realize
![]() $(\mathcal {L}_{\mathrm{F}},\Pi ^0_1)\textsf {-RDC}^1$
. Let A be
$(\mathcal {L}_{\mathrm{F}},\Pi ^0_1)\textsf {-RDC}^1$
. Let A be
![]() $\Pi^0_1$
, which is by Lemma 3.38 completed by
$\Pi^0_1$
, which is by Lemma 3.38 completed by
![]() $c_A$
, and B an arbitrary
$c_A$
, and B an arbitrary
![]() $\mathcal{L}_\mathrm{F}$
formula. By 3.23(1)(ii) construct
$\mathcal{L}_\mathrm{F}$
formula. By 3.23(1)(ii) construct
![]() $\epsilon $
so that, for any
$\epsilon $
so that, for any
![]() $\zeta ,\zeta ^{\prime },\gamma $
,
$\zeta ,\zeta ^{\prime },\gamma $
,
where
![]() $\theta \,{:=}\,\lambda \zeta \xi .\zeta |(\xi )^2_0|(c_A|(\xi)^2_0)$
. The last
$\theta \,{:=}\,\lambda \zeta \xi .\zeta |(\xi )^2_0|(c_A|(\xi)^2_0)$
. The last
![]() $\simeq $
means that, as far as
$\simeq $
means that, as far as
![]() $\theta|\zeta$
is defined on
$\theta|\zeta$
is defined on
![]() $\varepsilon | \zeta | \zeta' | \gamma | \underline{z}$
, for any
$\varepsilon | \zeta | \zeta' | \gamma | \underline{z}$
, for any
![]() $\eta $
,
$\eta $
,
Note that
![]() $(\alpha |\dots |\beta ){\downarrow }$
is
$(\alpha |\dots |\beta ){\downarrow }$
is
![]() $\Pi ^0_2$
by
$\Pi ^0_2$
by
![]() $\Delta ^0_0\textsf {-AC}^{00}$
. By 3.23(1)(ii), we can take
$\Delta ^0_0\textsf {-AC}^{00}$
. By 3.23(1)(ii), we can take
![]() $\epsilon ^{\prime \prime }$
such that, for any
$\epsilon ^{\prime \prime }$
such that, for any
![]() $\zeta ,\zeta ^{\prime },\gamma $
,
$\zeta ,\zeta ^{\prime },\gamma $
,
For (i), set
![]() $\epsilon ^{\prime }\,{=}\,\epsilon ^{\prime \prime }$
and, for (ii), by 3.27(2) take also
$\epsilon ^{\prime }\,{=}\,\epsilon ^{\prime \prime }$
and, for (ii), by 3.27(2) take also
![]() $\epsilon ^{\prime }$
so that, for any
$\epsilon ^{\prime }$
so that, for any
![]() $\zeta ,\zeta ^{\prime },\gamma $
,
$\zeta ,\zeta ^{\prime },\gamma $
,
 $$ \begin{align*} \forall z(\epsilon|\zeta|\zeta^{\prime}|\gamma|\underline{z}{\downarrow}){{\kern-2pt}\to{\kern-2pt}} \begin{pmatrix}\epsilon^{\prime}|\zeta|\zeta^{\prime}|\gamma{\downarrow} \,{\land}\\ \forall\eta\left(\eta\,{\in_{\texttt{L}}}\,\epsilon^{\prime}|\zeta|\zeta^{\prime}|\gamma\;{\leftrightarrow}\; \begin{pmatrix}\eta\,{\leq}\,\epsilon^{\prime\prime}|\zeta|\zeta^{\prime}|\gamma\,{\land}\, \forall z\left((\eta)_{z+1}\,{\in_{\texttt{L}}}\,\theta|\zeta|(\eta)_z\right)\end{pmatrix}\right) \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \forall z(\epsilon|\zeta|\zeta^{\prime}|\gamma|\underline{z}{\downarrow}){{\kern-2pt}\to{\kern-2pt}} \begin{pmatrix}\epsilon^{\prime}|\zeta|\zeta^{\prime}|\gamma{\downarrow} \,{\land}\\ \forall\eta\left(\eta\,{\in_{\texttt{L}}}\,\epsilon^{\prime}|\zeta|\zeta^{\prime}|\gamma\;{\leftrightarrow}\; \begin{pmatrix}\eta\,{\leq}\,\epsilon^{\prime\prime}|\zeta|\zeta^{\prime}|\gamma\,{\land}\, \forall z\left((\eta)_{z+1}\,{\in_{\texttt{L}}}\,\theta|\zeta|(\eta)_z\right)\end{pmatrix}\right) \end{pmatrix}. \end{align*} $$
We
![]() $\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realize
$\mathbin {{\mathbf{r}_{\texttt {L}}}}$
-realize
![]() $(\{B\},\{A\})\textsf {-RDC}^1$
. By 2.8(1)(iii), 3.19 and 3.39, we may assume that A contains no
$(\{B\},\{A\})\textsf {-RDC}^1$
. By 2.8(1)(iii), 3.19 and 3.39, we may assume that A contains no
![]() ${\to }$
except
${\to }$
except
![]() $\neg $
applied to atomic subformulae. Then obviously
$\neg $
applied to atomic subformulae. Then obviously
![]() $c_A|(\eta)^2_0 \,{{\mathbf{r}_{\texttt {L}}}}\,A[(\eta)^2_0]$
is equivalent to
$c_A|(\eta)^2_0 \,{{\mathbf{r}_{\texttt {L}}}}\,A[(\eta)^2_0]$
is equivalent to
![]() $A[(\eta)^2_0]$
, a
$A[(\eta)^2_0]$
, a
![]() $\Pi^0_1$
formula.
$\Pi^0_1$
formula.
Assume
![]() $\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \alpha (A[\alpha ]\,{\to }\,\exists \beta (A[\beta ]\,{\land }\,B[\alpha ,\beta ]))$
and
$\zeta \mathbin {{\mathbf{r}_{\texttt {L}}}} \forall \alpha (A[\alpha ]\,{\to }\,\exists \beta (A[\beta ]\,{\land }\,B[\alpha ,\beta ]))$
and
![]() $\zeta ^{\prime } \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\gamma ]$
. By
$\zeta ^{\prime } \mathbin {{\mathbf{r}_{\texttt {L}}}} A[\gamma ]$
. By
![]() $\Pi ^0_2\textsf {-Ind}$
on z we can show:
$\Pi ^0_2\textsf {-Ind}$
on z we can show:
-
(a)
 $\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z}{\downarrow } \,{\land } (\forall \eta \,{\in }_{\texttt {L}}\,\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z})(c_A|(\eta)^2_0 \mathbin {{\mathbf{r}_{\texttt {L}}}} A[(\eta )^2_0])$
$\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z}{\downarrow } \,{\land } (\forall \eta \,{\in }_{\texttt {L}}\,\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z})(c_A|(\eta)^2_0 \mathbin {{\mathbf{r}_{\texttt {L}}}} A[(\eta )^2_0])$
-
(b)
 $(\exists \eta \,{\leq }\,\epsilon ^{\prime \prime }|\zeta |\zeta ^{\prime }|\gamma ) ((\eta )_z\,{\in _{\texttt {L}}}\,\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z}\,{\land }\, (\forall k\,{<}\,z)((\eta )_{k+1}\,{\in _{\texttt {L}}}\,\theta |\zeta |(\eta )_k))$
and
$(\exists \eta \,{\leq }\,\epsilon ^{\prime \prime }|\zeta |\zeta ^{\prime }|\gamma ) ((\eta )_z\,{\in _{\texttt {L}}}\,\epsilon |\zeta |\zeta ^{\prime }|\gamma |\underline {z}\,{\land }\, (\forall k\,{<}\,z)((\eta )_{k+1}\,{\in _{\texttt {L}}}\,\theta |\zeta |(\eta )_k))$
and -
(c)
 $(\forall \eta \,{\in _{\texttt {L}}}\,\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma ) (c_A | (\textsf{p}_0| (\eta)_z)) \mathbin {{\mathbf{r}_{\texttt {L}}}} A[ \textsf {p}_0 | (\eta)_z])$
$(\forall \eta \,{\in _{\texttt {L}}}\,\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma ) (c_A | (\textsf{p}_0| (\eta)_z)) \mathbin {{\mathbf{r}_{\texttt {L}}}} A[ \textsf {p}_0 | (\eta)_z])$
By 3.23(1)(ii) take
![]() $\nu $
such that
$\nu $
such that
![]() $(\textsf {p}_0|(\nu |\eta ))_z = \textsf {p}_0|(\eta )_z$
,
$(\textsf {p}_0|(\nu |\eta ))_z = \textsf {p}_0|(\eta )_z$
,
![]() $(\textsf {p}_0|(\textsf {p}_1|(\nu |\eta )) = \lambda \xi .\underline {0}$
and
$(\textsf {p}_0|(\textsf {p}_1|(\nu |\eta )) = \lambda \xi .\underline {0}$
and
![]() $(\textsf {p}_1|(\textsf {p}_1|(\nu |\eta )))|\underline {z} = \textsf {p}_1|(\textsf {p}_1|(\eta )_{z+1})$
for any
$(\textsf {p}_1|(\textsf {p}_1|(\nu |\eta )))|\underline {z} = \textsf {p}_1|(\textsf {p}_1|(\eta )_{z+1})$
for any
![]() $\eta ,z$
. Now (c) yields
$\eta ,z$
. Now (c) yields
To show
![]() $\textsf {r}|(\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma )|\nu \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \eta ((\eta )_0 = \gamma \land \forall zB[(\eta )_z,(\eta )_{z+1}])$
, it remains to show
$\textsf {r}|(\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma )|\nu \mathbin {{\mathbf{r}_{\texttt {L}}}} \exists \eta ((\eta )_0 = \gamma \land \forall zB[(\eta )_z,(\eta )_{z+1}])$
, it remains to show
![]() $\exists \eta (\eta \,{\in _{\texttt {L}}}\,\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma )$
.
$\exists \eta (\eta \,{\in _{\texttt {L}}}\,\epsilon ^{\prime }|\zeta |\zeta ^{\prime }|\gamma )$
.
![]() $\Sigma ^0_1\textsf {-AC}^{00}$
yields
$\Sigma ^0_1\textsf {-AC}^{00}$
yields
![]() $\alpha \,{=}\,\epsilon ^{\prime \prime }|\zeta |\zeta ^{\prime }|\gamma $
. (i) is done. For (ii) apply 3.56(2) to (b).
$\alpha \,{=}\,\epsilon ^{\prime \prime }|\zeta |\zeta ^{\prime }|\gamma $
. (i) is done. For (ii) apply 3.56(2) to (b).
By 2.16(2)(i)(3)(i) and 3.55(1), the next corollary follows.
Corollary 3.59.
![]() $\exists ^1\Pi ^0_{\infty }\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
are (i)
$\exists ^1\Pi ^0_{\infty }\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
are (i)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*{+}\Pi ^0_2\textsf {-Ind}$
; (ii)
$\mathbf{EL}_0^*{+}\Pi ^0_2\textsf {-Ind}$
; (ii)
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}_0^{\prime }{+}\Pi ^0_2\textsf {-Ind}$
.
$\mathbf{EL}_0^{\prime }{+}\Pi ^0_2\textsf {-Ind}$
.
3.3.5 Realizability with full induction and full bar induction
For the sake of completeness, let us realize even stronger induction schemata, beyond
![]() $\Pi ^0_{\infty }\textsf {-Ind}\,{=}\,\Sigma ^0_{\infty }\textsf {-Ind}$
. The self-realizability of full induction
$\Pi ^0_{\infty }\textsf {-Ind}\,{=}\,\Sigma ^0_{\infty }\textsf {-Ind}$
. The self-realizability of full induction
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-Ind}$
was known (e.g., from [Reference van Oosten31]). Here we recall and hierarchize it.
$\mathcal {L}_{\mathrm{F}}\textsf {-Ind}$
was known (e.g., from [Reference van Oosten31]). Here we recall and hierarchize it.
Definition 3.60.
-
(1)
 $\Lambda ^i_{n,0}\,{:\equiv }\,\forall ^i\Sigma ^0_{n}$
;
$\Lambda ^i_{n,0}\,{:\equiv }\,\forall ^i\Sigma ^0_{n}$
;
 $\Lambda ^i_{n,m+1}\,{:\equiv }\,\forall ^i(\Lambda ^i_{n,m}\!{\to }\Sigma ^0_n)$
for
$\Lambda ^i_{n,m+1}\,{:\equiv }\,\forall ^i(\Lambda ^i_{n,m}\!{\to }\Sigma ^0_n)$
for
 $i\,{<}\,2$
.
$i\,{<}\,2$
. -
(2)
 $\Xi _{n,0}\,{:\equiv }\,\Pi ^0_{n+1}$
;
$\Xi _{n,0}\,{:\equiv }\,\Pi ^0_{n+1}$
;
 $\Xi _{n,m+1}\,{:\equiv }\,\forall ^1(\Xi _{n,m}{\to }\Sigma ^0_{n})$
.
$\Xi _{n,m+1}\,{:\equiv }\,\forall ^1(\Xi _{n,m}{\to }\Sigma ^0_{n})$
. -
(3)
 $\Theta ^1_0$
is the closure of
$\Theta ^1_0$
is the closure of
 $\Delta ^0_0$
under
$\Delta ^0_0$
under
 ${\land },{\lor },\forall ^0\!,\exists ^0$
and
${\land },{\lor },\forall ^0\!,\exists ^0$
and
 $\exists ^1$
;
$\exists ^1$
;
 $\Theta ^1_{m+1}$
is that of
$\Theta ^1_{m+1}$
is that of
 $\Theta ^1_m$
under
$\Theta ^1_m$
under
 ${\land },{\lor },\forall ^0\!,\exists ^0\!,\forall ^1\!,\exists ^1$
and
${\land },{\lor },\forall ^0\!,\exists ^0\!,\forall ^1\!,\exists ^1$
and
 $\Theta ^1_m{\to }(\text {-})$
.
$\Theta ^1_m{\to }(\text {-})$
.
![]() $\Theta ^1_m$
is the second order analogue of Burr’s
$\Theta ^1_m$
is the second order analogue of Burr’s
![]() $\Theta _m$
from [Reference Burr10]. Note that
$\Theta _m$
from [Reference Burr10]. Note that
![]() $\Theta ^1_m$
’s exhaust
$\Theta ^1_m$
’s exhaust
![]() $\mathcal {L}_{\mathrm{F}}$
and
$\mathcal {L}_{\mathrm{F}}$
and
![]() $\Xi _{n,m}\,{\subseteq }\,\Theta ^1_m$
. Moreover,
$\Xi _{n,m}\,{\subseteq }\,\Theta ^1_m$
. Moreover,
![]() $\Xi _{n,m+1}$
is equivalent to
$\Xi _{n,m+1}$
is equivalent to
![]() $\Lambda ^1_{n+1,m}$
over
$\Lambda ^1_{n+1,m}$
over
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_{n+1}\textsf {-DNE}$
. The next is enough to generalize 3.58.
$\mathbf{EL}_0^-{+}\Sigma ^0_{n+1}\textsf {-DNE}$
. The next is enough to generalize 3.58.
Lemma 3.61. Let
![]() $m\,{>}\,0$
. If A is
$m\,{>}\,0$
. If A is
![]() $\Theta ^1_m$
whose
$\Theta ^1_m$
whose
![]() $\Delta ^0_0$
subformulae contain no
$\Delta ^0_0$
subformulae contain no
![]() ${\to }$
except
${\to }$
except
![]() $\neg $
applied to atomic subformulae, then both
$\neg $
applied to atomic subformulae, then both
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A$
and
$\alpha \mathbin {{\mathbf{r}_{\texttt {f}}}} A$
and
![]() $\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A$
are equivalently
$\alpha \mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}} A$
are equivalently
![]() $\Xi _{1,m}$
over
$\Xi _{1,m}$
over
![]() $\mathbf{EL}_0^*$
and
$\mathbf{EL}_0^*$
and
![]() ${\mathbf{EL}_0^{\prime }\!}^*$
, respectively.
${\mathbf{EL}_0^{\prime }\!}^*$
, respectively.
Proof
![]() $(\alpha |\dots |\beta ){\downarrow }$
is
$(\alpha |\dots |\beta ){\downarrow }$
is
![]() $\Pi ^0_2$
by
$\Pi ^0_2$
by
![]() $\Delta ^0_0\textsf {-AC}^{00}$
. For
$\Delta ^0_0\textsf {-AC}^{00}$
. For
![]() $\exists $
,
$\exists $
,
![]() $\lor $
in the case of
$\lor $
in the case of
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
with
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
with
![]() $m\,{=}\,0$
, use 3.5(2)(ii) and 3.56(1)(ii).
$m\,{=}\,0$
, use 3.5(2)(ii) and 3.56(1)(ii).
![]() $\Xi _{n,m}$
is closed under
$\Xi _{n,m}$
is closed under
![]() $\land $
, as
$\land $
, as
![]() $(A\,{\to }\,B)\land (C\,{\to }\,D)$
is equivalent to
$(A\,{\to }\,B)\land (C\,{\to }\,D)$
is equivalent to
![]() $\forall n((n\,{=}\,0\,{\to }\,A){\land }(n\,{>}\,0\,{\to }\,C) \,{\to }\,(n\,{=}\,0\,{\to }\,B){\land }(n\,{>}\,0\,{\to }\,D))$
.
$\forall n((n\,{=}\,0\,{\to }\,A){\land }(n\,{>}\,0\,{\to }\,C) \,{\to }\,(n\,{=}\,0\,{\to }\,B){\land }(n\,{>}\,0\,{\to }\,D))$
.
Here
![]() $m\,{>}\,0$
is required only because of our treatment of first order quantifiers in the definition of realizability. If
$m\,{>}\,0$
is required only because of our treatment of first order quantifiers in the definition of realizability. If
![]() $\alpha\, {{\textbf{r}_{\texttt{L}}}}\, \forall xA[x]$
and
$\alpha\, {{\textbf{r}_{\texttt{L}}}}\, \forall xA[x]$
and
![]() $\alpha\, {{\textbf{r}_{\texttt{L}}}}\, \exists xA[x]$
were defined by
$\alpha\, {{\textbf{r}_{\texttt{L}}}}\, \exists xA[x]$
were defined by
![]() $\forall x (\alpha | \underline{x}{\downarrow}\,{\land}\,\alpha | \underline{x}\; {{\textbf{r}_{\texttt{L}}}}\, A[x])$
and
$\forall x (\alpha | \underline{x}{\downarrow}\,{\land}\,\alpha | \underline{x}\; {{\textbf{r}_{\texttt{L}}}}\, A[x])$
and
![]() $\exists x( (\alpha)^2_0 = \underline{x} \,{\land}\,(\alpha)^2_1\; {{\textbf{r}_{\texttt{L}}}}\, A[x])$
respectively,then this lemma would be the case also for
$\exists x( (\alpha)^2_0 = \underline{x} \,{\land}\,(\alpha)^2_1\; {{\textbf{r}_{\texttt{L}}}}\, A[x])$
respectively,then this lemma would be the case also for
![]() $m\,{=}\,0$
.
$m\,{=}\,0$
.
Theorem 3.62.
![]() $(\mathcal {L}_{\mathrm{F}},\Theta ^1_m)\textsf {-RDC}^1$
, and hence
$(\mathcal {L}_{\mathrm{F}},\Theta ^1_m)\textsf {-RDC}^1$
, and hence
![]() $\Theta ^1_m\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
, are
$\Theta ^1_m\{\textsf {-DC}^1,\textsf {-DC}^0,\textsf {-Ind}\}$
, are
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*{+}\Xi _{1,m}\textsf {-Ind}$
, and
$\mathbf{EL}_0^*{+}\Xi _{1,m}\textsf {-Ind}$
, and
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $ \mathbf{EL}^{\prime }_0{+}\Xi _{1,m}\textsf {-Ind}$
.
$ \mathbf{EL}^{\prime }_0{+}\Xi _{1,m}\textsf {-Ind}$
.
Proof Note
![]() $\exists ^1\Pi ^0_1 = \Theta ^1_0$
over
$\exists ^1\Pi ^0_1 = \Theta ^1_0$
over
![]() $\mathbf{EL}_0^*{+}\Pi ^0_1\textsf {-AC}^{01}$
by 2.11 and 3.56(3). Thus, the case of
$\mathbf{EL}_0^*{+}\Pi ^0_1\textsf {-AC}^{01}$
by 2.11 and 3.56(3). Thus, the case of
![]() $m\,{=}\,0$
is already proved in Theorem 3.58. Now assume
$m\,{=}\,0$
is already proved in Theorem 3.58. Now assume
![]() $m\,{>}\,0$
. The proof is the same as 3.58, but now
$m\,{>}\,0$
. The proof is the same as 3.58, but now
![]() $c_A | (\xi)^2_0$
,
$c_A | (\xi)^2_0$
,
![]() $c_A | (\eta)^2_0$
and
$c_A | (\eta)^2_0$
and
![]() $c_A | (\textsf {p}_0 | (\eta)_z)$
being replaced with
$c_A | (\textsf {p}_0 | (\eta)_z)$
being replaced with
![]() $((\xi)^2_1)^2_0$
,
$((\xi)^2_1)^2_0$
,
![]() $((\eta)^2_1)^2_0$
and
$((\eta)^2_1)^2_0$
and
![]() $\textsf {p}_0 | ( \textsf {p}_1 | (\eta)_z )$
respectively, which guarantees that (a) and (c) are
$\textsf {p}_0 | ( \textsf {p}_1 | (\eta)_z )$
respectively, which guarantees that (a) and (c) are
![]() $\Xi _{1,m}$
if A is
$\Xi _{1,m}$
if A is
![]() $\Theta ^1_m$
.
$\Theta ^1_m$
.
Remark 3.63. As
![]() $\exists ^1\Pi ^0_1\,{=}\,\exists ^1\neg \Sigma ^0_1$
has a universal formula over
$\exists ^1\Pi ^0_1\,{=}\,\exists ^1\neg \Sigma ^0_1$
has a universal formula over
![]() $\mathbf{EL}_0^-$
, so does
$\mathbf{EL}_0^-$
, so does
![]() $\Theta ^1_0$
over
$\Theta ^1_0$
over
![]() $\mathbf{EL}_0^*{+}\Pi ^0_1\textsf {-AC}^{01}$
.
$\mathbf{EL}_0^*{+}\Pi ^0_1\textsf {-AC}^{01}$
.
For
![]() $m\,{>}\,0$
, since
$m\,{>}\,0$
, since
![]() $\exists ^1\Xi _{1,m}$
has a universal formula (defined easily from a universal
$\exists ^1\Xi _{1,m}$
has a universal formula (defined easily from a universal
![]() $\Sigma ^0_1$
formula) over
$\Sigma ^0_1$
formula) over
![]() $\mathbf{EL}_0^-$
, 3.31(2)(ii) and 3.61 tell us that
$\mathbf{EL}_0^-$
, 3.31(2)(ii) and 3.61 tell us that
![]() $\Theta ^1_m$
has a universal formula over
$\Theta ^1_m$
has a universal formula over
![]() $\mathbf{EL}^*_0 {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\text {-}\mathsf {GCC}^1$
. By a close look at the proof of 3.31(2)(ii), we see that
$\mathbf{EL}^*_0 {+}(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\text {-}\mathsf {GCC}^1$
. By a close look at the proof of 3.31(2)(ii), we see that
![]() $(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\text {-}\mathsf {GCC}^1$
can actually be weakened to
$(\mathcal {L}_{\mathrm{F}},N(\Sigma ^0_1))\text {-}\mathsf {GCC}^1$
can actually be weakened to
![]() $(\Xi _{1,m},\Xi _{1,m-1})\text {-}\mathsf {GCC}^1$
.
$(\Xi _{1,m},\Xi _{1,m-1})\text {-}\mathsf {GCC}^1$
.
As
![]() $\neg \Theta _m\,{\subseteq }\,\Theta _{m+1}$
, by the usual diagonalization, the formalized strict hierarchy theorem can be proved.
$\neg \Theta _m\,{\subseteq }\,\Theta _{m+1}$
, by the usual diagonalization, the formalized strict hierarchy theorem can be proved.
Similarly, Burr’s
![]() $\Theta _{m+1}$
has a universal formula in the presence of ECT. This suggests that, in certain contexts,
$\Theta _{m+1}$
has a universal formula in the presence of ECT. This suggests that, in certain contexts,
![]() $\Theta _m$
’s and
$\Theta _m$
’s and
![]() $\Theta ^1_m$
’s behave as nicely as essential
$\Theta ^1_m$
’s behave as nicely as essential
![]() $\Sigma ^i_m$
’s and essential
$\Sigma ^i_m$
’s and essential
![]() $\Pi ^i_m$
’s do in the classical context with AC.
$\Pi ^i_m$
’s do in the classical context with AC.
A similar strategy by 3.61 applies to bar induction. This is the last Brouwerian axiom that we realize.
Theorem 3.64.
![]() $(\Theta ^1_m,\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
is
$(\Theta ^1_m,\mathcal {L}_{\mathrm{F}})\textsf {-BI}_M$
is
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}}}$
-realizable in
![]() $\mathbf{EL}_0^*{+}\Xi _{1,m}\textsf {-BI}_D$
, and
$\mathbf{EL}_0^*{+}\Xi _{1,m}\textsf {-BI}_D$
, and
![]() $\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
$\mathbin {{\mathbf{r}_{\texttt {f}}^{\prime }}}$
-realizable in
![]() $\mathbf{EL}^{\prime }_0{+}\Xi _{1,m}\textsf {-BI}_D$
.
$\mathbf{EL}^{\prime }_0{+}\Xi _{1,m}\textsf {-BI}_D$
.
Proof First assume
![]() $m\,{>}\,0$
. As
$m\,{>}\,0$
. As
![]() $(\mathcal {L}_{\mathrm{F}},\Delta ^0_0)\textsf {-GCB}^1$
implies
$(\mathcal {L}_{\mathrm{F}},\Delta ^0_0)\textsf {-GCB}^1$
implies
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-CB}^0$
, it suffices to realize
$\mathcal {L}_{\mathrm{F}}\textsf {-CB}^0$
, it suffices to realize
![]() $\Theta ^1_m\textsf {-BI}_D$
, by 2.39(4) and 3.39. Assume
$\Theta ^1_m\textsf {-BI}_D$
, by 2.39(4) and 3.39. Assume
3.23(1)(ii) yields
![]() $\gamma ,\delta ,\epsilon $
with
$\gamma ,\delta ,\epsilon $
with
 $$ \begin{align*} &\gamma|\xi|\underline{u}|\eta\,{\simeq}\,\xi|\underline{u{*}\langle \eta(0)\rangle}; \\ &\delta|\zeta|\alpha|\xi|\underline{u}\,{\simeq}\, \begin{cases} (\zeta)^3_1|\underline{u}|(c_{\alpha(u)\,{=}\,0}|\alpha|\underline{u}) &\text{ if }\alpha(u)\,{=}\,0;\\[-1pt] (\zeta)^3_2|\underline{u}|(\lambda\eta.\gamma|\xi|\underline{u}|\eta) &\text{ otherwise;} \end{cases}\\ &\epsilon\,{:=}\,\lambda\alpha\zeta.\textsf{fix}|(\delta|\zeta|\alpha). \end{align*} $$
$$ \begin{align*} &\gamma|\xi|\underline{u}|\eta\,{\simeq}\,\xi|\underline{u{*}\langle \eta(0)\rangle}; \\ &\delta|\zeta|\alpha|\xi|\underline{u}\,{\simeq}\, \begin{cases} (\zeta)^3_1|\underline{u}|(c_{\alpha(u)\,{=}\,0}|\alpha|\underline{u}) &\text{ if }\alpha(u)\,{=}\,0;\\[-1pt] (\zeta)^3_2|\underline{u}|(\lambda\eta.\gamma|\xi|\underline{u}|\eta) &\text{ otherwise;} \end{cases}\\ &\epsilon\,{:=}\,\lambda\alpha\zeta.\textsf{fix}|(\delta|\zeta|\alpha). \end{align*} $$
Let
![]() $B[u]\,{:\equiv }\,(\varepsilon|\alpha |\zeta |\underline {u}){\downarrow }\,{\land }\,(\varepsilon|\alpha |\zeta |\underline {u}\mathbin {{\mathbf{r}_{\texttt {L}}}} A[u])$
. If
$B[u]\,{:\equiv }\,(\varepsilon|\alpha |\zeta |\underline {u}){\downarrow }\,{\land }\,(\varepsilon|\alpha |\zeta |\underline {u}\mathbin {{\mathbf{r}_{\texttt {L}}}} A[u])$
. If
![]() $\alpha (u)\,{=}\,0$
then
$\alpha (u)\,{=}\,0$
then
![]() $\varepsilon|\alpha |\zeta |\underline {u} \mathbin {{\mathbf{r}_{\texttt {L}}}} A[u]\,{\equiv }\,B[u]$
. As
$\varepsilon|\alpha |\zeta |\underline {u} \mathbin {{\mathbf{r}_{\texttt {L}}}} A[u]\,{\equiv }\,B[u]$
. As
![]() $\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
by 3.38, it remains to show
$\textsf {Bar}[\underline {0},\left \{u{:}\,\alpha (u)\,{=}\,0\right \}]$
by 3.38, it remains to show
![]() $\forall xB[u{*}\langle x\rangle ]\,{\to }\,B[u]$
: we may assume
$\forall xB[u{*}\langle x\rangle ]\,{\to }\,B[u]$
: we may assume
![]() $\alpha (u)\,{\neq }\,0$
, and
$\alpha (u)\,{\neq }\,0$
, and
![]() $\varepsilon|\alpha |\zeta |\underline {u}\,{\simeq }\,(\zeta )^3_2|\underline {u}|(\lambda \eta . \varepsilon|\alpha |\zeta |\underline {u{*}\langle \eta (0)\rangle })$
. Thus
$\varepsilon|\alpha |\zeta |\underline {u}\,{\simeq }\,(\zeta )^3_2|\underline {u}|(\lambda \eta . \varepsilon|\alpha |\zeta |\underline {u{*}\langle \eta (0)\rangle })$
. Thus
![]() $\forall xB[u{*}\langle x\rangle ]$
, i.e.,
$\forall xB[u{*}\langle x\rangle ]$
, i.e.,
![]() $(\lambda \eta .\varepsilon|\alpha |\zeta |\underline {u{*}\langle \eta (0)\rangle })\mathbin {{\mathbf{r}_{\texttt {L}}}} \forall xA[u{*}\langle x\rangle ]$
yields
$(\lambda \eta .\varepsilon|\alpha |\zeta |\underline {u{*}\langle \eta (0)\rangle })\mathbin {{\mathbf{r}_{\texttt {L}}}} \forall xA[u{*}\langle x\rangle ]$
yields
![]() $\varepsilon|\alpha |\zeta |\underline {u}\mathbin {{\mathbf{r}_{\texttt {L}}}} A[u]$
. Hence
$\varepsilon|\alpha |\zeta |\underline {u}\mathbin {{\mathbf{r}_{\texttt {L}}}} A[u]$
. Hence
![]() $\lambda\alpha\zeta.(\varepsilon|\alpha |\zeta |\langle \,\rangle )$
realizes
$\lambda\alpha\zeta.(\varepsilon|\alpha |\zeta |\langle \,\rangle )$
realizes
![]() $\{A\}\textsf {-BI}_D$
.
$\{A\}\textsf {-BI}_D$
.
For
![]() $m\,{=}\,0$
, as in Theorem 3.62 we can consider
$m\,{=}\,0$
, as in Theorem 3.62 we can consider
![]() $\Theta^1_0 \,{\equiv}\, \exists^1\Pi^0_1$
, say
$\Theta^1_0 \,{\equiv}\, \exists^1\Pi^0_1$
, say
![]() $A[u] \,{\equiv}\, \exists\eta C[\eta,u]$
with C being
$A[u] \,{\equiv}\, \exists\eta C[\eta,u]$
with C being
![]() $\Pi^0_1$
. We can modify the argument above by replacing
$\Pi^0_1$
. We can modify the argument above by replacing
![]() $(\zeta)^3_1$
and
$(\zeta)^3_1$
and
![]() $(\zeta)^3_2$
with
$(\zeta)^3_2$
with
![]() $\textsf {p} | ((\zeta)^3_1)^2_0 | (c_C | \underline{u} )$
and
$\textsf {p} | ((\zeta)^3_1)^2_0 | (c_C | \underline{u} )$
and
![]() $\textsf {p} | ((\zeta)^3_2)^2_0 | (c_C | \underline{u} )$
respectivelyin the definition of
$\textsf {p} | ((\zeta)^3_2)^2_0 | (c_C | \underline{u} )$
respectivelyin the definition of
![]() $\delta$
, so that B is equivalently
$\delta$
, so that B is equivalently
![]() $\Pi^0_2$
.
$\Pi^0_2$
.
One may wonder if this can be extended to the “bar version” of dependent choice, defined as follows:
-
(
 $(\mathcal {C},\mathcal {D})\textsf {-BarDC}_M$
):
$(\mathcal {C},\mathcal {D})\textsf {-BarDC}_M$
):
 $\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}] \,{\land }\,\forall u,v(B[u]\,{\to }\,B[u{*}v])\,{\land }\,\forall u,\beta \exists \gamma A[u,\beta ,\gamma ]\\ {{\kern70pt}\land }\, (\forall u(B[u]\,{\to }\,A[u,(\alpha )_{\prec u},(\alpha )_u])$
$\textsf {Bar}[\,\underline {0},\left \{u{:}\,B[u]\right \}] \,{\land }\,\forall u,v(B[u]\,{\to }\,B[u{*}v])\,{\land }\,\forall u,\beta \exists \gamma A[u,\beta ,\gamma ]\\ {{\kern70pt}\land }\, (\forall u(B[u]\,{\to }\,A[u,(\alpha )_{\prec u},(\alpha )_u])$
 ${\to }\,\exists \delta \forall u (A[u,(\delta )_{\prec u},(\delta )_u]\land (B[u]\,{\to }\,(\delta )_u\,{=}\,(\alpha )_u))$
${\to }\,\exists \delta \forall u (A[u,(\delta )_{\prec u},(\delta )_u]\land (B[u]\,{\to }\,(\delta )_u\,{=}\,(\alpha )_u))$
where
 $(\gamma )_{\prec u}$
is such that
$(\gamma )_{\prec u}$
is such that
 $((\gamma )_{\prec u})_x\,{=}\,(\gamma )_{u*\langle x\rangle }$
and A is from
$((\gamma )_{\prec u})_x\,{=}\,(\gamma )_{u*\langle x\rangle }$
and A is from
 $\mathcal {C}$
and B from
$\mathcal {C}$
and B from
 $\mathcal {D}$
.
$\mathcal {D}$
.
Among similar axioms are transfinite dependent choice [Reference Rüede35, Reference Rüede36] and bar recursion [Reference Avigad and Feferman4, Section 6.4]. In our context, this extension is not proper, since
We can show this by applying
![]() $\exists ^1\forall ^0\mathcal {C}\textsf {-BI}_D$
to the following:
$\exists ^1\forall ^0\mathcal {C}\textsf {-BI}_D$
to the following:
4 Lower Bounds: Forcing and Negative Interpretations
4.1 Gödel–Gentzen negative interpretation
Gödel–Gentzen negative interpretation N, sometimes called double negation translation, is the standard way of interpreting logical symbols of classical logic intuitionistically. In arithmetic, since
![]() $\neg \neg A$
is equivalent to A for atomic A, if we consider the classical
$\neg \neg A$
is equivalent to A for atomic A, if we consider the classical
![]() $\vee $
and
$\vee $
and
![]() $\exists $
as abbreviations defined from
$\exists $
as abbreviations defined from
![]() ${\land },{\to },\bot ,\forall $
, we may identify
${\land },{\to },\bot ,\forall $
, we may identify
![]() $A^N$
with A, and intuitionistic theories are extensions of classical ones with new logical symbols
$A^N$
with A, and intuitionistic theories are extensions of classical ones with new logical symbols
![]() $\lor $
and
$\lor $
and
![]() $\exists $
in the same sense as modal logics are extensions with
$\exists $
in the same sense as modal logics are extensions with
![]() $\Box $
and
$\Box $
and
![]() $\Diamond $
. Here, however, we consider
$\Diamond $
. Here, however, we consider
![]() $\lor $
and
$\lor $
and
![]() $\exists $
are primitive symbols even in the classical theories, which extend intuitionistic ones only by the axiom schema
$\exists $
are primitive symbols even in the classical theories, which extend intuitionistic ones only by the axiom schema
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
$\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
.
Definition 4.1 (N)
For a formula A, define
 $$ \begin{align*} A^N\,&{:\equiv}\,\neg\neg A\text{ for atomic }A;\\ (A\Box B)^N\,&{:\equiv}\,A^N\Box B^N\text{ for }\Box\equiv\land,{\to}; &(\forall\xi A)^N\,&{:\equiv}\,\forall\xi A^N;\\ (A\,{\lor}\,B)^N\,&{:\equiv}\,\neg(\neg A^N{\land}\neg B^N); &(\exists\xi A)^N\,&{:\equiv}\,\neg\forall\xi\neg A^N, \end{align*} $$
$$ \begin{align*} A^N\,&{:\equiv}\,\neg\neg A\text{ for atomic }A;\\ (A\Box B)^N\,&{:\equiv}\,A^N\Box B^N\text{ for }\Box\equiv\land,{\to}; &(\forall\xi A)^N\,&{:\equiv}\,\forall\xi A^N;\\ (A\,{\lor}\,B)^N\,&{:\equiv}\,\neg(\neg A^N{\land}\neg B^N); &(\exists\xi A)^N\,&{:\equiv}\,\neg\forall\xi\neg A^N, \end{align*} $$
where
![]() $Q xA[x]$
is considered as
$Q xA[x]$
is considered as
![]() $Q\xi A[\xi (0)]$
.
$Q\xi A[\xi (0)]$
.
Lemma 4.2.
-
(1)
 $A^N$
intuitionistically follows from
$A^N$
intuitionistically follows from
 ${B_1}^N, \dots , {B_n}^N$
, if A classically follows from
${B_1}^N, \dots , {B_n}^N$
, if A classically follows from
 $B_1, \dots , B_n$
.
$B_1, \dots , B_n$
. -
(2)
 $((\exists x < y)A)^N$
and
$((\exists x < y)A)^N$
and
 $((\forall x < y)A)^N$
are equivalent to
$((\forall x < y)A)^N$
are equivalent to
 $\neg (\forall x < y)\neg A^N$
and
$\neg (\forall x < y)\neg A^N$
and
 $(\forall x < y)A^N$
, respectively.
$(\forall x < y)A^N$
, respectively. -
(3)
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}\vdash A^N\,{\leftrightarrow }\, A$
if A is negative in
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}\vdash A^N\,{\leftrightarrow }\, A$
if A is negative in
 $\Pi ^0_{n+1}$
, i.e., built up by
$\Pi ^0_{n+1}$
, i.e., built up by
 $\land $
,
$\land $
,
 $\to $
and
$\to $
and
 $\forall $
from
$\forall $
from
 $\Pi ^0_{n+1}$
formulae.
$\Pi ^0_{n+1}$
formulae. -
(4)
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}\vdash A\,{\to }\, A^N$
if A is built up by
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}\vdash A\,{\to }\, A^N$
if A is built up by
 $\land $
,
$\land $
,
 $\lor, \forall $
and
$\lor, \forall $
and
 $\exists $
from those formulae negative in
$\exists $
from those formulae negative in
 $\Pi ^0_{n+1}$
.
$\Pi ^0_{n+1}$
.
Corollary 4.3.
-
(1)
 $\mathbf{EL}_0^-\vdash (\mathbf{EL}_0^-)^N$
; and
$\mathbf{EL}_0^-\vdash (\mathbf{EL}_0^-)^N$
; and
 $\Pi ^0_{n+1}$
-preservingly N interprets
$\Pi ^0_{n+1}$
-preservingly N interprets
 $\mathbf{EL}_0^-{+} \mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
in
$\mathbf{EL}_0^-{+} \mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-DNE}$
. -
(2) Over
 $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-DNE}$
, (i)
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-DNE}$
, (i)
 $\Pi ^0_{n+1}\textsf {-Ind}$
, (ii)
$\Pi ^0_{n+1}\textsf {-Ind}$
, (ii)
 $\Sigma ^0_{n}\textsf {-Ind}$
are equivalent to their N-interpretations; if
$\Sigma ^0_{n}\textsf {-Ind}$
are equivalent to their N-interpretations; if
 $n\,{\geq }\,1$
, so are (iii)
$n\,{\geq }\,1$
, so are (iii)
 $\Sigma^0_n\textsf {-Bdg}$
, (iv)
$\Sigma^0_n\textsf {-Bdg}$
, (iv)
 $\mathcal {C}\textsf {-BI}_D$
and (v)
$\mathcal {C}\textsf {-BI}_D$
and (v)
 $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
for
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
for
 $\mathcal {C}\,{\in }\,\{\Sigma _k,\Lambda ^i_{k,m},\Xi _{k,m}\,|\,k\,{\leq }\,n\}$
,
$\mathcal {C}\,{\in }\,\{\Sigma _k,\Lambda ^i_{k,m},\Xi _{k,m}\,|\,k\,{\leq }\,n\}$
,
 $\mathcal {D}\,{\in }\,\{\Pi ^0_\ell ,\Sigma ^0_{\ell +1}\,|\,\ell \,{<}\,n\}$
.
$\mathcal {D}\,{\in }\,\{\Pi ^0_\ell ,\Sigma ^0_{\ell +1}\,|\,\ell \,{<}\,n\}$
.
In this corollary (2), only (ii) cannot be proved instance-wise, but the equivalence between the schemata by meta-induction on n.
Recall 3.60, the definitions of
![]() $\Lambda ^i_{n,m},\Xi _{n,m}$
.
$\Lambda ^i_{n,m},\Xi _{n,m}$
.
![]() $\Lambda ^1_{1,m}$
is the N-interpretation of
$\Lambda ^1_{1,m}$
is the N-interpretation of
![]() $\Pi ^1_{m+1}$
normal form, over
$\Pi ^1_{m+1}$
normal form, over
![]() $\textsf {MP}$
.
$\textsf {MP}$
.
While N will be one of our main tools for lower bound proof, it yields some result for a semi-Russian axiom
![]() $\textsf {KA}$
, introduced by Veldman [Reference Veldman53]. This asserts the existence of counterexample of
$\textsf {KA}$
, introduced by Veldman [Reference Veldman53]. This asserts the existence of counterexample of
![]() $\Delta ^0_0\textsf {-WFT}$
.
$\Delta ^0_0\textsf {-WFT}$
.
Definition 4.4 (
 $\textsf {KA}$
)
$\textsf {KA}$
)
Let
![]() $\textsf {KA}\,{:\equiv }\,\exists \gamma \textrm {KA}[\gamma ]$
where
$\textsf {KA}\,{:\equiv }\,\exists \gamma \textrm {KA}[\gamma ]$
where
Proposition 4.5.
![]() $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\textsf {NCT}\vdash \textsf { KA}$
.
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\textsf {NCT}\vdash \textsf { KA}$
.
Proof Let
![]() $\{c\}$
be the computable counterexample, i.e.,
$\{c\}$
be the computable counterexample, i.e.,
Applying N to this, with 4.2(3) with
![]() $n\,{=}\,1$
, we have
$n\,{=}\,1$
, we have
![]() $\Delta ^0_0\textsf {-AC}^{00}$
yields
$\Delta ^0_0\textsf {-AC}^{00}$
yields
![]() $\gamma $
with
$\gamma $
with
![]() $\{c\}\,{=}\,\gamma $
.
$\{c\}\,{=}\,\gamma $
.
Classically
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
implies
$\mathcal {L}_{\mathrm{F}}\textsf {-AC}^{00}$
implies
![]() $(\mathcal {L}_{\mathrm{F}}\textsf {-CA})^{\mathfrak {ch}}$
. As a refinement, it is known that, even intuitionistically with LPO,
$(\mathcal {L}_{\mathrm{F}}\textsf {-CA})^{\mathfrak {ch}}$
. As a refinement, it is known that, even intuitionistically with LPO,
![]() $\Pi ^0_1\textsf {-AC}^{00}$
implies
$\Pi ^0_1\textsf {-AC}^{00}$
implies
![]() $(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
and hence it is of the strength of
$(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
and hence it is of the strength of
![]() $\textbf {ACA}_0$
. Here
$\textbf {ACA}_0$
. Here
![]() $\Pi ^0_1\textsf {-AC}^{00}$
can be weakened to
$\Pi ^0_1\textsf {-AC}^{00}$
can be weakened to
![]() $\Pi ^0_1\textsf {-AC}!^{00}$
, and even to
$\Pi ^0_1\textsf {-AC}!^{00}$
, and even to
![]() $\textsf {SBAC}!$
defined below, which restricts the
$\textsf {SBAC}!$
defined below, which restricts the
![]() $\Pi ^0_1$
formulae to be of a special form. With
$\Pi ^0_1$
formulae to be of a special form. With
![]() $\textsf {SBAC}$
, we can refine the classical implication from KL (König’s lemma) to
$\textsf {SBAC}$
, we can refine the classical implication from KL (König’s lemma) to
![]() $\textbf {ACA}_0$
(cf. [Reference Simpson45, Theorem III.7.2]) as follows.
$\textbf {ACA}_0$
(cf. [Reference Simpson45, Theorem III.7.2]) as follows.
Definition 4.6 (semi-bounded axiom of choice
 $\textsf {SBAC}$
and
$\textsf {SBAC}$
and
 $\textsf {SBAC}!$
)
$\textsf {SBAC}!$
)
![]() $\textsf {SBAC}$
is defined as follows and
$\textsf {SBAC}$
is defined as follows and
![]() $\textsf {SBAC}!$
is defined with
$\textsf {SBAC}!$
is defined with
![]() $\exists $
replaced by
$\exists $
replaced by
![]() $\exists !$
in the premise.
$\exists !$
in the premise.
-
(
 $\textsf {SBAC}$
):
$\textsf {SBAC}$
):
 $\forall x\exists y\,\textrm {SB}_{C,D,t}[x,y] \,{\to }\,\exists \alpha \forall x\,\textrm {SB}_{C,D,t}[x,\alpha (x)]$
, for C and D both from
$\forall x\exists y\,\textrm {SB}_{C,D,t}[x,y] \,{\to }\,\exists \alpha \forall x\,\textrm {SB}_{C,D,t}[x,\alpha (x)]$
, for C and D both from
 $\Delta ^0_0$
, where
$\Delta ^0_0$
, where
 $\textrm {SB}_{C,D,t}[x,y]\,{:\equiv }\,C[x,y]\,{\lor }\,(y\,{<}\,t[x]\,{\land }\,\forall zD[x,y,z])$
.
$\textrm {SB}_{C,D,t}[x,y]\,{:\equiv }\,C[x,y]\,{\lor }\,(y\,{<}\,t[x]\,{\land }\,\forall zD[x,y,z])$
.
Lemma 4.7.
-
(1)
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT} \vdash (\textsf {SBAC})^N$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT} \vdash (\textsf {SBAC})^N$
. -
(2)
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\textsf { SBAC}!\vdash (\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\textsf { SBAC}!\vdash (\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
.
Proof (1) As in the proof of 2.33, we may assume
![]() $C[x,y]\,{\land }\, C[x,z]\,{\to }\, y\,{=}\,z$
and
$C[x,y]\,{\land }\, C[x,z]\,{\to }\, y\,{=}\,z$
and
![]() $D[x,y,z] \,{\to }\, y<t[x]$
. Let
$D[x,y,z] \,{\to }\, y<t[x]$
. Let
![]() $A\,{:\equiv }\,\textrm {SB}_{C,D,t}$
. Define
$A\,{:\equiv }\,\textrm {SB}_{C,D,t}$
. Define
![]() $\gamma $
by
$\gamma $
by
 $$ \begin{align*} &\gamma(u)\,{=}\,0\leftrightarrow {}\\ &\exists k(|u|=k{+}1 {{\kern-2pt}\land{\kern-2pt}} (\forall x\leq k)( u(x)>0 {{\kern-2pt}\to{\kern-2pt}} ( C[x,u(x){-}1] {{\kern-2pt}\lor{\kern-2pt}} (\forall z<|u|)D[x,u(x){-}1,z] ))). \end{align*} $$
$$ \begin{align*} &\gamma(u)\,{=}\,0\leftrightarrow {}\\ &\exists k(|u|=k{+}1 {{\kern-2pt}\land{\kern-2pt}} (\forall x\leq k)( u(x)>0 {{\kern-2pt}\to{\kern-2pt}} ( C[x,u(x){-}1] {{\kern-2pt}\lor{\kern-2pt}} (\forall z<|u|)D[x,u(x){-}1,z] ))). \end{align*} $$
We prove
![]() $\textsf {Fan}[\gamma ]$
. By
$\textsf {Fan}[\gamma ]$
. By
![]() $\textsf {LPO}$
, there are two cases:
$\textsf {LPO}$
, there are two cases:
-
• if
 $\neg \exists yC[|u|,y]$
then
$\neg \exists yC[|u|,y]$
then
 $\forall z(\gamma (u{*}\langle z\rangle )\,{=}\,0 \,{\to }\, z\,{\leq }\,t[x])$
;
$\forall z(\gamma (u{*}\langle z\rangle )\,{=}\,0 \,{\to }\, z\,{\leq }\,t[x])$
; -
• if
 $C[|u|,y]$
for some y then
$C[|u|,y]$
for some y then
 $\forall z(\gamma (u{*}\langle z\rangle )\,{=}\,0\,{\to }\, z\,{\leq }\,\max (y{+}1,t[x]))$
.
$\forall z(\gamma (u{*}\langle z\rangle )\,{=}\,0\,{\to }\, z\,{\leq }\,\max (y{+}1,t[x]))$
.
Obviously
![]() $\gamma (u)\,{=}\,0\,{\to }\, \gamma (u{*}\langle 0\rangle )\,{=}\,0$
.
$\gamma (u)\,{=}\,0\,{\to }\, \gamma (u{*}\langle 0\rangle )\,{=}\,0$
.
If
![]() $\forall k(\gamma (\beta {\upharpoonright } k)\,{=}\,0)$
and
$\forall k(\gamma (\beta {\upharpoonright } k)\,{=}\,0)$
and
![]() $\forall x(\beta (x)\,{\neq }\, 0)$
, then we have
$\forall x(\beta (x)\,{\neq }\, 0)$
, then we have
for
![]() $\alpha (x)\,{:=}\,\beta (x){-}1$
, and, as “
$\alpha (x)\,{:=}\,\beta (x){-}1$
, and, as “
![]() $\forall k(\forall x\,{\leq }\,k)$
” is same as “
$\forall k(\forall x\,{\leq }\,k)$
” is same as “
![]() $\forall x(\forall k\,{\geq }\,x)$
”, we also have
$\forall x(\forall k\,{\geq }\,x)$
”, we also have
![]() $\forall x(C[x,\alpha (x)]\lor (\alpha (x)\,{<}\, t[x]\land \forall zD[x,\alpha (x),z])$
and so
$\forall x(C[x,\alpha (x)]\lor (\alpha (x)\,{<}\, t[x]\land \forall zD[x,\alpha (x),z])$
and so
![]() $\forall xA^N[x,\alpha (x)]$
.
$\forall xA^N[x,\alpha (x)]$
.
Thus
![]() $\forall \alpha \neg \forall xA^N[x,\alpha (x)]\to \forall \beta (\forall k(\gamma (\beta {\upharpoonright } k)\,{=}\,0) \,{\to }\,(\forall x(\beta (x)\,{\neq }\,0)\to \bot ))$
and, by
$\forall \alpha \neg \forall xA^N[x,\alpha (x)]\to \forall \beta (\forall k(\gamma (\beta {\upharpoonright } k)\,{=}\,0) \,{\to }\,(\forall x(\beta (x)\,{\neq }\,0)\to \bot ))$
and, by
![]() $\textsf {MP}$
,
$\textsf {MP}$
,
Assume
![]() $(\forall x\exists yA[x,y])^N$
. Fix arbitrary n. Then obviously we have
$(\forall x\exists yA[x,y])^N$
. Fix arbitrary n. Then obviously we have
![]() $\forall x\neg \forall y\neg (C[x,y]\lor (y < t[x]\land (\forall z < n)D[x,y,z]))^N$
and, by using
$\forall x\neg \forall y\neg (C[x,y]\lor (y < t[x]\land (\forall z < n)D[x,y,z]))^N$
and, by using
![]() $\textsf {MP}$
, also
$\textsf {MP}$
, also
![]() $(\forall x < n)\exists y (C[x,y]\lor (y < t[x]\land (\forall z < n)D[x,y,z]))$
. With
$(\forall x < n)\exists y (C[x,y]\lor (y < t[x]\land (\forall z < n)D[x,y,z]))$
. With
![]() $\Sigma ^0_1\textsf {-Ind}$
yielded by 2.33, we can show
$\Sigma ^0_1\textsf {-Ind}$
yielded by 2.33, we can show
![]() $\exists u(|u|\,{=}\,k{+}1\land \gamma (u)\,{=}\,0\land (\forall \ell \,{\leq }\,k)(u(\ell )\,{\neq }\,0)))$
for
$\exists u(|u|\,{=}\,k{+}1\land \gamma (u)\,{=}\,0\land (\forall \ell \,{\leq }\,k)(u(\ell )\,{\neq }\,0)))$
for
![]() $k\,{<}\,n$
. Particularly,
$k\,{<}\,n$
. Particularly,
![]() $\exists v(|v|\,{=}\,n \land (\forall k\,{<}\,n)(v(k)\,{\neq }\,0) \land \gamma (v)\,{=}\,0)$
. Now by
$\exists v(|v|\,{=}\,n \land (\forall k\,{<}\,n)(v(k)\,{\neq }\,0) \land \gamma (v)\,{=}\,0)$
. Now by
![]() $\Delta ^0_0\textsf {-FT}$
this means
$\Delta ^0_0\textsf {-FT}$
this means
![]() $\neg \textsf {Bar}[\gamma ,\big\{u{:}\,(\exists k\,{<} |u|)(u(k)\,{=}\,0)\big \}]$
, and hence, by (
$\neg \textsf {Bar}[\gamma ,\big\{u{:}\,(\exists k\,{<} |u|)(u(k)\,{=}\,0)\big \}]$
, and hence, by (
![]() $*$
),
$*$
),
![]() $\neg \forall \alpha \neg \forall xA^N[x,\alpha (x)]$
, i.e.,
$\neg \forall \alpha \neg \forall xA^N[x,\alpha (x)]$
, i.e.,
![]() $(\exists \alpha \forall xA[x,\alpha (x)])^N$
.
$(\exists \alpha \forall xA[x,\alpha (x)])^N$
.
(2) Let B be
![]() $\Sigma ^0_1$
of
$\Sigma ^0_1$
of
![]() $\mathcal {L}_{\textrm {S}}$
, say
$\mathcal {L}_{\textrm {S}}$
, say
![]() $B^{\mathfrak {ch}}[x]\,{\equiv }\,\exists yC[x,y]$
. As before, now we may assume
$B^{\mathfrak {ch}}[x]\,{\equiv }\,\exists yC[x,y]$
. As before, now we may assume
![]() $C[x,y]\land C[x,z]\,{\to }\, y\,{=}\,z$
.
$C[x,y]\land C[x,z]\,{\to }\, y\,{=}\,z$
.
![]() $\textsf {LPO}$
yields
$\textsf {LPO}$
yields
![]() $\forall x\exists ! y(C[x,y]\lor (y\,{=}\,0\land \forall z\neg C[x,z]))$
. Now
$\forall x\exists ! y(C[x,y]\lor (y\,{=}\,0\land \forall z\neg C[x,z]))$
. Now
![]() $\textsf {SBAC!}$
yields
$\textsf {SBAC!}$
yields
![]() $\alpha $
with
$\alpha $
with
![]() $\forall x(C[x,\alpha (x)]\lor (\alpha (x)\,{=}\,0\land \forall z\neg C[x,z]))$
. Because
$\forall x(C[x,\alpha (x)]\lor (\alpha (x)\,{=}\,0\land \forall z\neg C[x,z]))$
. Because
![]() $\forall x(\exists i\,{<}\,2)(i\,{=}\,0\,{\leftrightarrow }\, C[x,\alpha (x)])$
, there is
$\forall x(\exists i\,{<}\,2)(i\,{=}\,0\,{\leftrightarrow }\, C[x,\alpha (x)])$
, there is
![]() $\beta $
with
$\beta $
with
![]() $\forall x(\beta (x)\,{=}\,0\,{\leftrightarrow }\, C[x,\alpha (x)])$
. Then
$\forall x(\beta (x)\,{=}\,0\,{\leftrightarrow }\, C[x,\alpha (x)])$
. Then
![]() $\forall x(\beta (x)\,{=}\,0\,{\leftrightarrow }\, B^{\mathfrak {ch}}[x])$
.
$\forall x(\beta (x)\,{=}\,0\,{\leftrightarrow }\, B^{\mathfrak {ch}}[x])$
.
Thus in the presence of
![]() $\textsf {LPO}$
, we cannot strengthen
$\textsf {LPO}$
, we cannot strengthen
![]() $\Delta ^0_0\textsf {-WFT}$
to
$\Delta ^0_0\textsf {-WFT}$
to
![]() $\Delta ^0_0\textsf {-FT}$
unless going beyond Finitism.
$\Delta ^0_0\textsf {-FT}$
unless going beyond Finitism.
How about
![]() $\mathcal {C}\textsf {-WFT}$
,
$\mathcal {C}\textsf {-WFT}$
,
![]() $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
or
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
or
![]() $\mathcal {C}\textsf {-BI}_D$
? By 2.32(3)(ii) and 2.29(1), the first to ask are
$\mathcal {C}\textsf {-BI}_D$
? By 2.32(3)(ii) and 2.29(1), the first to ask are
![]() $\Pi ^0_1\textsf {-WFT}$
and
$\Pi ^0_1\textsf {-WFT}$
and
![]() $\Sigma ^0_1\textsf {-BI}_D$
. The below answers this with help of
$\Sigma ^0_1\textsf {-BI}_D$
. The below answers this with help of
![]() $\Sigma ^0_2\textsf {-DNE}$
or
$\Sigma ^0_2\textsf {-DNE}$
or
![]() $\textsf {MP}$
. (1) refines Berger’s [Reference Berger7], where he relies on classical logic but with a slightly weaker variant of WFT. We weaken
$\textsf {MP}$
. (1) refines Berger’s [Reference Berger7], where he relies on classical logic but with a slightly weaker variant of WFT. We weaken
![]() $\Sigma ^0_2\textsf {-DNE}$
and
$\Sigma ^0_2\textsf {-DNE}$
and
![]() $\textsf {MP}$
in the next subsections.
$\textsf {MP}$
in the next subsections.
Lemma 4.8.
-
(1)
 $\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+} \Pi^0_1 \textsf {-WFT} \vdash ((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+} \Pi^0_1 \textsf {-WFT} \vdash ((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N$
. -
(2)
 $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-BI}_D \vdash ((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N$
.
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-BI}_D \vdash ((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N$
.
Proof (1) Let A be
![]() $\Sigma ^0_1$
, say
$\Sigma ^0_1$
, say
![]() $A[x]^{\mathfrak {ch}}\,{\equiv }\,\exists yC[x,y]$
with C being
$A[x]^{\mathfrak {ch}}\,{\equiv }\,\exists yC[x,y]$
with C being
![]() $\Delta ^0_0$
. Recall
$\Delta ^0_0$
. Recall
![]() $v\,{<}\,\underline {2}\,{:\equiv }\,(\forall k\,{<}\,|v|)(v(k)\,{<}\,2)$
. Define
$v\,{<}\,\underline {2}\,{:\equiv }\,(\forall k\,{<}\,|v|)(v(k)\,{<}\,2)$
. Define
 $$ \begin{align*} &D[u]\,{:\equiv}\,(\forall x\,{<}\,|u|)(u(x)\,{=}\,0\,{\leftrightarrow}\,(\exists y\,{<}\,|u|)C[x,y]);\\ &B[u]\,{:\equiv}\,(\forall v\,{<}\,\underline{2})\neg D[u{*}v]. \end{align*} $$
$$ \begin{align*} &D[u]\,{:\equiv}\,(\forall x\,{<}\,|u|)(u(x)\,{=}\,0\,{\leftrightarrow}\,(\exists y\,{<}\,|u|)C[x,y]);\\ &B[u]\,{:\equiv}\,(\forall v\,{<}\,\underline{2})\neg D[u{*}v]. \end{align*} $$
We show
![]() $(\forall \alpha \,{<}\,\underline {2})(\forall k\neg B[\alpha {\upharpoonright } k] \to \forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists yC[x,y]))$
. Let
$(\forall \alpha \,{<}\,\underline {2})(\forall k\neg B[\alpha {\upharpoonright } k] \to \forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists yC[x,y]))$
. Let
![]() $\forall k\neg B[\alpha {\upharpoonright } k]$
, i.e.,
$\forall k\neg B[\alpha {\upharpoonright } k]$
, i.e.,
![]() $\forall k\neg (\forall v\,{<}\,\underline {2})\neg D[(\alpha {\upharpoonright } k){*}v]$
. By
$\forall k\neg (\forall v\,{<}\,\underline {2})\neg D[(\alpha {\upharpoonright } k){*}v]$
. By
![]() $\textsf {MP}$
, we have
$\textsf {MP}$
, we have
![]() $\forall k(\exists v\,{<}\,\underline {2})D[(\alpha {\upharpoonright } k){*}v].$
If
$\forall k(\exists v\,{<}\,\underline {2})D[(\alpha {\upharpoonright } k){*}v].$
If
![]() $\alpha (x)\,{=}\,0$
, taking
$\alpha (x)\,{=}\,0$
, taking
![]() $v\,{<}\,\underline {2}$
with
$v\,{<}\,\underline {2}$
with
![]() $D[(\alpha {\upharpoonright }(x{+}1)){*}v]$
, as
$D[(\alpha {\upharpoonright }(x{+}1)){*}v]$
, as
![]() $((\alpha {\upharpoonright }(x{+}1)){*}v)(x)\,{=}\,\alpha (x)\,{=}\,0$
, we now have
$((\alpha {\upharpoonright }(x{+}1)){*}v)(x)\,{=}\,\alpha (x)\,{=}\,0$
, we now have
![]() $(\exists y\,{<}\,|(\alpha {\upharpoonright }(x{+}1)){*}v|)C[x,y]$
, and
$(\exists y\,{<}\,|(\alpha {\upharpoonright }(x{+}1)){*}v|)C[x,y]$
, and
![]() $\exists yC[x,y]$
. Conversely if
$\exists yC[x,y]$
. Conversely if
![]() $C[x,y]$
, taking
$C[x,y]$
, taking
![]() $v\,{<}\,\underline {2}$
with
$v\,{<}\,\underline {2}$
with
![]() $D[(\alpha {\upharpoonright }(x{+}y{+}1)){*}v]$
, since
$D[(\alpha {\upharpoonright }(x{+}y{+}1)){*}v]$
, since
![]() $(\exists z\,{<}\,|(\alpha {\upharpoonright }(x{+}y{+}1)){*}v|)C[x,z]$
we can conclude
$(\exists z\,{<}\,|(\alpha {\upharpoonright }(x{+}y{+}1)){*}v|)C[x,z]$
we can conclude
![]() $\alpha (x)\,{=}\,((\alpha {\upharpoonright }(x{+}y{+}1)){*}v)(x)\,{=}\,0$
.
$\alpha (x)\,{=}\,((\alpha {\upharpoonright }(x{+}y{+}1)){*}v)(x)\,{=}\,0$
.
We show
![]() $((\exists \alpha \,{<}\,\underline {2})\forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists yC[x,y]))^N$
, which is, by
$((\exists \alpha \,{<}\,\underline {2})\forall x(\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists yC[x,y]))^N$
, which is, by
![]() $\textsf {MP}$
, equivalent to
$\textsf {MP}$
, equivalent to
Suppose for contradiction
![]() $(\forall \alpha \,{<}\,\underline {2})\neg \forall x (\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists y C[x,y])$
. Then, by the above,
$(\forall \alpha \,{<}\,\underline {2})\neg \forall x (\alpha (x)\,{=}\,0\,{\leftrightarrow }\,\exists y C[x,y])$
. Then, by the above,
![]() $(\forall \alpha \,{<}\,\underline {2})\neg \forall k\neg B[\alpha {\upharpoonright } k]$
and, by
$(\forall \alpha \,{<}\,\underline {2})\neg \forall k\neg B[\alpha {\upharpoonright } k]$
and, by
![]() $\Sigma ^0_2\textsf {-DNE}$
,
$\Sigma ^0_2\textsf {-DNE}$
,
![]() $(\forall \alpha \,{<}\,\underline {2})\exists k B[\alpha {\upharpoonright } k]$
.
$(\forall \alpha \,{<}\,\underline {2})\exists k B[\alpha {\upharpoonright } k]$
.
![]() $\Pi ^0_1\textsf {-WFT}$
yields n with
$\Pi ^0_1\textsf {-WFT}$
yields n with
![]() $(\forall \alpha \,{<}\,\underline {2})(\exists k\,{<}\,n)B[\alpha {\upharpoonright } k]$
and so
$(\forall \alpha \,{<}\,\underline {2})(\exists k\,{<}\,n)B[\alpha {\upharpoonright } k]$
and so
![]() $(\forall \alpha \,{<}\,\underline {2})\neg D[\alpha {\upharpoonright } n]$
. However we can construct
$(\forall \alpha \,{<}\,\underline {2})\neg D[\alpha {\upharpoonright } n]$
. However we can construct
![]() $u\,{<}\,\underline {2}$
with
$u\,{<}\,\underline {2}$
with
![]() $|u|=n$
and
$|u|=n$
and
![]() $(\forall k\,{<}\,n)(u(k)\,{=}\,0 \,{\leftrightarrow }\,(\exists y\,{<}\,n)C[x,y])$
, a contradiction.
$(\forall k\,{<}\,n)(u(k)\,{=}\,0 \,{\leftrightarrow }\,(\exists y\,{<}\,n)C[x,y])$
, a contradiction.
(2) By 4.3(1)(2)(iv), it suffices to show
![]() $(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
in
$(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
in
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-BI}_D$
. We prove
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-BI}_D$
. We prove
![]() $\Pi ^0_1\textsf {-AC}^{00}$
classically by 4.7(2). Let A be
$\Pi ^0_1\textsf {-AC}^{00}$
classically by 4.7(2). Let A be
![]() $\Pi ^0_1$
and
$\Pi ^0_1$
and
![]() $B[u]\,{:\equiv }\,(\exists k\,{<}\,|u|)\neg A[k,u(k)]$
. Then
$B[u]\,{:\equiv }\,(\exists k\,{<}\,|u|)\neg A[k,u(k)]$
. Then
![]() $\neg B[\langle \,\rangle ]$
and
$\neg B[\langle \,\rangle ]$
and
![]() $B[u]\,{\to }\,B[u{*}v]$
. Now
$B[u]\,{\to }\,B[u{*}v]$
. Now
![]() $\forall k\exists xA[k,x]$
yields
$\forall k\exists xA[k,x]$
yields
![]() $\forall xB[u{*}\langle x\rangle ]\,{\to }\,B[u]$
, and, by
$\forall xB[u{*}\langle x\rangle ]\,{\to }\,B[u]$
, and, by
![]() $(\Sigma ^0_1,\Sigma ^0_1)\textsf {-BI}_M$
with 2.29(3), also
$(\Sigma ^0_1,\Sigma ^0_1)\textsf {-BI}_M$
with 2.29(3), also
![]() $\neg \textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, i.e.,
$\neg \textsf {Bar}[\underline {0},\left \{u{:}\,B[u]\right \}]$
, i.e.,
![]() $\exists \alpha \forall n\neg B[\alpha {\upharpoonright }n]$
.
$\exists \alpha \forall n\neg B[\alpha {\upharpoonright }n]$
.
Thus, only with this famous negative interpretation N, we have the following lower bound results. For the lower bounds of
![]() $\Sigma ^0_1\textsf {-Ind}$
,
$\Sigma ^0_1\textsf {-Ind}$
,
![]() $\Sigma ^0_1\textsf {-BI}_D$
(without (
$\Sigma ^0_1\textsf {-BI}_D$
(without (
![]() $\textsf {MP}$
)) and
$\textsf {MP}$
)) and
![]() $\Pi^0_1-\textsf {WFT} + \textsf {LPO}$
, more works are required as in the next subsections.
$\Pi^0_1-\textsf {WFT} + \textsf {LPO}$
, more works are required as in the next subsections.
Corollary 4.9.
![]() $\mathbf{ACA}_0$
is interpretable
$\mathbf{ACA}_0$
is interpretable
-
(i)
 $\Pi ^0_2$
-preservingly in
$\Pi ^0_2$
-preservingly in
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT}$
and in
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT}$
and in
 $\mathbf{EL}_0^-{+}\textsf { MP}{+}\Sigma ^0_1\textsf {-BI}_D$
;
$\mathbf{EL}_0^-{+}\textsf { MP}{+}\Sigma ^0_1\textsf {-BI}_D$
; -
(ii)
 $\Pi ^0_3$
-preservingly in
$\Pi ^0_3$
-preservingly in
 $\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Pi ^0_1\textsf {-WFT}$
; and
$\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Pi ^0_1\textsf {-WFT}$
; and -
(iii)
 $\Delta ^1_0$
-preservingly in
$\Delta ^1_0$
-preservingly in
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
Proof (i) By 4.7, 4.8(2) and 4.3(1) with
![]() $n\,{=}\,1$
. (ii) Similar.
$n\,{=}\,1$
. (ii) Similar.
(iii)
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
trivially includes
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
trivially includes
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\textsf {SBAC!}$
and, by 4.7(2), also includes
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\textsf {SBAC!}$
and, by 4.7(2), also includes
![]() $\mathbf{EL}_0^-{+}(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
. As
$\mathbf{EL}_0^-{+}(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
. As
![]() $(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
implies
$(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
implies
![]() $\Pi ^0_{\infty }\textsf {-LEM}$
and so
$\Pi ^0_{\infty }\textsf {-LEM}$
and so
![]() $\Delta ^1_0\textsf {-LEM}$
,
$\Delta ^1_0\textsf {-LEM}$
,
![]() $\mathbf{EL}_0^-{+}(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
proves
$\mathbf{EL}_0^-{+}(\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}}$
proves
![]() $((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N\,{\land }\,\Delta ^1_0\textsf {-LEM}$
, and so interprets
$((\Sigma ^0_1\textsf {-CA})^{\mathfrak {ch}})^N\,{\land }\,\Delta ^1_0\textsf {-LEM}$
, and so interprets
![]() $\Delta ^1_0$
-preservingly
$\Delta ^1_0$
-preservingly
![]() $(\mathbf{ACA}_0)^{\mathfrak {ch}}$
by N.
$(\mathbf{ACA}_0)^{\mathfrak {ch}}$
by N.
4.2 Coquand–Hofmann forcing interpretation
Gödel–Gentzen negative interpretation N yields the
![]() $\Pi _1$
conservation of
$\Pi _1$
conservation of
![]() $\textbf {PA}$
over
$\textbf {PA}$
over
![]() $\textbf {HA}$
. Friedman–Dragalin translation (also known as Friedman’s A-translation) was introduced to enhance it to
$\textbf {HA}$
. Friedman–Dragalin translation (also known as Friedman’s A-translation) was introduced to enhance it to
![]() $\Pi _2$
conservation, or equivalently to show the admissibility of
$\Pi _2$
conservation, or equivalently to show the admissibility of
![]() $\textsf {MP}$
-rule. We start by recalling this well-known technique:
$\textsf {MP}$
-rule. We start by recalling this well-known technique:
 $$ \begin{align*} C^A\,&:{\equiv}\,C\,{\lor}\, A\text{ if }C\text{ is atomic};\\ (C\Box D)^A\,&:{\equiv}\,C^A\Box D^A\text{ for }\Box\,{\equiv}\,\land,{\to},\lor;\\ (QxC)^A\,&:{\equiv}\,Qx(C^A)\text{ for }Q\,{\equiv}\,\forall,\exists. \end{align*} $$
$$ \begin{align*} C^A\,&:{\equiv}\,C\,{\lor}\, A\text{ if }C\text{ is atomic};\\ (C\Box D)^A\,&:{\equiv}\,C^A\Box D^A\text{ for }\Box\,{\equiv}\,\land,{\to},\lor;\\ (QxC)^A\,&:{\equiv}\,Qx(C^A)\text{ for }Q\,{\equiv}\,\forall,\exists. \end{align*} $$
For any
![]() $\Sigma _1$
formula
$\Sigma _1$
formula
![]() $A[x]$
, since
$A[x]$
, since
![]() $\textbf {HA}\vdash A[x]^N\,{\leftrightarrow }\,\neg \neg A[x]$
, if
$\textbf {HA}\vdash A[x]^N\,{\leftrightarrow }\,\neg \neg A[x]$
, if
![]() $\textbf {PA}\vdash \forall xA(x)$
then
$\textbf {PA}\vdash \forall xA(x)$
then
![]() $\textbf {HA}\vdash \neg \neg A[x]$
, to which by applying
$\textbf {HA}\vdash \neg \neg A[x]$
, to which by applying
![]() $A[x]$
-translation, we have
$A[x]$
-translation, we have
![]() $\textbf {HA}\vdash (\neg \neg A[x])^{A[x]}$
, i.e.,
$\textbf {HA}\vdash (\neg \neg A[x])^{A[x]}$
, i.e.,
![]() $\textbf {HA}\vdash (A[x]\,{\lor }\, A[x]\,{\to }\,A[x])\,{\to }\,A[x]$
and hence
$\textbf {HA}\vdash (A[x]\,{\lor }\, A[x]\,{\to }\,A[x])\,{\to }\,A[x]$
and hence
![]() $\textbf {HA}\vdash \forall xA[x]$
. However, this combination of the negative interpretation N and
$\textbf {HA}\vdash \forall xA[x]$
. However, this combination of the negative interpretation N and
![]() $A[x]$
-translation does not necessarily preserve another
$A[x]$
-translation does not necessarily preserve another
![]() $\Pi _2$
sentence
$\Pi _2$
sentence
![]() $\forall xB[x]$
. Thus, it does not uniformly preserve
$\forall xB[x]$
. Thus, it does not uniformly preserve
![]() $\Pi _2$
sentences. Moreover, A-translation is not
$\Pi _2$
sentences. Moreover, A-translation is not
![]() $\{\bot \}$
-preserving, unless A is equivalent to
$\{\bot \}$
-preserving, unless A is equivalent to
![]() $\bot $
, and so does not yield the consistency-wise implication. Coquand–Hofmann forcing overcomes this disadvantage, by replacing single A with a finite set of such A’s. We further generalize this technique to general
$\bot $
, and so does not yield the consistency-wise implication. Coquand–Hofmann forcing overcomes this disadvantage, by replacing single A with a finite set of such A’s. We further generalize this technique to general
![]() $\exists ^0\mathcal {C}$
but assuming
$\exists ^0\mathcal {C}$
but assuming
![]() $\mathcal {C}\textsf {-LEM}$
.
$\mathcal {C}\textsf {-LEM}$
.
Below we consider any
![]() $\alpha $
to code a finite set of
$\alpha $
to code a finite set of
![]() $(x,\xi )$
’s: e.g.,
$(x,\xi )$
’s: e.g.,
and also
![]() $(x,\xi )$
to code
$(x,\xi )$
to code
![]() $\exists uP[x,u,\xi ]$
. (Thus
$\exists uP[x,u,\xi ]$
. (Thus
![]() $\exists u\textrm {Tr}_P[u,\alpha ]$
means the disjunction of all formulae “belonging to”
$\exists u\textrm {Tr}_P[u,\alpha ]$
means the disjunction of all formulae “belonging to”
![]() $\alpha $
.) As an example, we can take P from
$\alpha $
.) As an example, we can take P from
![]() $\Pi ^0_n$
so that
$\Pi ^0_n$
so that
![]() $\exists uP[x,u,\xi ]$
is a universal
$\exists uP[x,u,\xi ]$
is a universal
![]() $\Sigma ^0_{n+1}$
formula.
$\Sigma ^0_{n+1}$
formula.
Definition 4.10 (
 $\textrm {Tr}_P$
,
$\textrm {Tr}_P$
,
 $\Vvdash _P$
)
$\Vvdash _P$
)
-
(1)
 $\textrm {Tr}_P[u,\alpha ]:\equiv (\exists (x,\xi )\,{\in }\,\alpha )P[x,u,\xi ]$
.
$\textrm {Tr}_P[u,\alpha ]:\equiv (\exists (x,\xi )\,{\in }\,\alpha )P[x,u,\xi ]$
. -
(2)
 $\alpha \!\Vvdash _P\! A\,:\equiv \,A\lor \exists u\textrm {Tr}_P[u,\alpha ]$
.
$\alpha \!\Vvdash _P\! A\,:\equiv \,A\lor \exists u\textrm {Tr}_P[u,\alpha ]$
.
Since
![]() $\textrm {Tr}_P[u,\alpha ]$
is
$\textrm {Tr}_P[u,\alpha ]$
is
![]() $(\exists k\,{<}\,\alpha (0))P[(\alpha {\ominus }1)_k(0),u, (\alpha {\ominus }1)_k{\ominus }1]$
, we see that
$(\exists k\,{<}\,\alpha (0))P[(\alpha {\ominus }1)_k(0),u, (\alpha {\ominus }1)_k{\ominus }1]$
, we see that
![]() $\exists u\textrm {Tr}_P[u,\alpha ]$
is
$\exists u\textrm {Tr}_P[u,\alpha ]$
is
![]() $\Sigma ^0_{n+1}$
if P is
$\Sigma ^0_{n+1}$
if P is
![]() $\Pi ^0_n$
.
$\Pi ^0_n$
.
Definition 4.11 (
 $\Vdash _P$
)
$\Vdash _P$
)
To an
![]() $\mathcal {L}_{\mathrm{F}}$
formula B, assign
$\mathcal {L}_{\mathrm{F}}$
formula B, assign
![]() $\alpha \!\Vdash _P\!B$
as follows:
$\alpha \!\Vdash _P\!B$
as follows:
 $$ \begin{align*} &\alpha\!\Vdash_P\! B\,:\equiv\,\alpha\!\Vvdash_P\! B\text{ for atomic };\\ &\alpha\!\Vdash_P\! B\,{\to}\, C\,:\equiv\,(\forall\beta\supseteq\alpha)((\beta\!\Vdash_P\! B) \,{\to}\,(\beta\!\Vdash_P\!C));\\ &\alpha\!\Vdash_P\! B\Box C\,:\equiv\,(\alpha\!\Vdash_P\! B)\Box(\alpha\!\Vdash_P\!C)\text{ for }\Box\,{\equiv}\,\land,\lor;\\ &\alpha\!\Vdash_P\!Q\xi B\,:\equiv\,Q\xi(\alpha\!\Vdash_P\!B) \text{ for }Q\,{\equiv}\,\forall,\exists, \end{align*} $$
$$ \begin{align*} &\alpha\!\Vdash_P\! B\,:\equiv\,\alpha\!\Vvdash_P\! B\text{ for atomic };\\ &\alpha\!\Vdash_P\! B\,{\to}\, C\,:\equiv\,(\forall\beta\supseteq\alpha)((\beta\!\Vdash_P\! B) \,{\to}\,(\beta\!\Vdash_P\!C));\\ &\alpha\!\Vdash_P\! B\Box C\,:\equiv\,(\alpha\!\Vdash_P\! B)\Box(\alpha\!\Vdash_P\!C)\text{ for }\Box\,{\equiv}\,\land,\lor;\\ &\alpha\!\Vdash_P\!Q\xi B\,:\equiv\,Q\xi(\alpha\!\Vdash_P\!B) \text{ for }Q\,{\equiv}\,\forall,\exists, \end{align*} $$
where
![]() $QxB[x]$
is treated as
$QxB[x]$
is treated as
![]() $Q\xi B[\xi (0)]$
.
$Q\xi B[\xi (0)]$
.
The connection to Friedman’s A-translation is clear in the atomic case. The extension to compound formulae is by Kripke semantics, where the monotonicity is (1)(ii) of the next lemma. (2) in the lemma, asserting the
![]() $\Vdash _P$
respects intuitionistic reasonings, easily follows, and (3) corresponds to the assertion that
$\Vdash _P$
respects intuitionistic reasonings, easily follows, and (3) corresponds to the assertion that
![]() $B^A\,{\leftrightarrow }\,B\lor A$
if B is
$B^A\,{\leftrightarrow }\,B\lor A$
if B is
![]() $\Sigma _1$
, which allowed us to show
$\Sigma _1$
, which allowed us to show
![]() $A[x]^{A[x]}\,{\leftrightarrow }\,A[x]\lor A[x]$
, the key fact to show
$A[x]^{A[x]}\,{\leftrightarrow }\,A[x]\lor A[x]$
, the key fact to show
![]() $\textsf {MP}$
-rule.
$\textsf {MP}$
-rule.
Lemma 4.12.
-
(1)
 $\mathbf{EL}_0^-$
proves
$\mathbf{EL}_0^-$
proves  $$ \begin{align*} \mathrm{(i) }B\,{\leftrightarrow}\,(\emptyset\,{\Vvdash_P}\,\! B)\text{ and } \mathrm{(ii)}\ \alpha\,{\subseteq}\, \beta\,{\to}\,(\alpha\,{\Vvdash_P}\,\! B\,{\to}\,\beta\,{\Vvdash_P}\,\! B)\land (\alpha\,{\Vdash_P}\,\! B\,{\to}\,\beta\,{\Vdash_P}\,\! B).\end{align*} $$
$$ \begin{align*} \mathrm{(i) }B\,{\leftrightarrow}\,(\emptyset\,{\Vvdash_P}\,\! B)\text{ and } \mathrm{(ii)}\ \alpha\,{\subseteq}\, \beta\,{\to}\,(\alpha\,{\Vvdash_P}\,\! B\,{\to}\,\beta\,{\Vvdash_P}\,\! B)\land (\alpha\,{\Vdash_P}\,\! B\,{\to}\,\beta\,{\Vdash_P}\,\! B).\end{align*} $$
-
(2) If C intuitionistically follows from
 $B_1, \dots , B_n$
, then
$B_1, \dots , B_n$
, then  $$ \begin{align*} \mathbf{EL}_0^-\vdash(\alpha\,{\Vdash_P}B_1)\land\dots\land(\alpha\,{\Vdash_P}B_n) \,{\to}\,(\alpha\,{\Vdash_P}C).\end{align*} $$
$$ \begin{align*} \mathbf{EL}_0^-\vdash(\alpha\,{\Vdash_P}B_1)\land\dots\land(\alpha\,{\Vdash_P}B_n) \,{\to}\,(\alpha\,{\Vdash_P}C).\end{align*} $$
-
(3) If
 $C,D,\exists x\neg E,E\in \mathcal {C}$
for all subformulae
$C,D,\exists x\neg E,E\in \mathcal {C}$
for all subformulae
 $C\,{\to }\, D$
and
$C\,{\to }\, D$
and
 $\forall xE$
of B, then
$\forall xE$
of B, then  $$ \begin{align*}\mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash(\alpha\,{\Vdash_P}\,\! B)\,{\leftrightarrow}\,(\alpha\,{\Vvdash_P}\,\!B).\end{align*} $$
$$ \begin{align*}\mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash(\alpha\,{\Vdash_P}\,\! B)\,{\leftrightarrow}\,(\alpha\,{\Vvdash_P}\,\!B).\end{align*} $$
-
(4) If F is built up by
 $\land ,\lor ,\forall ,\exists $
from those B’s which satisfy the condition of (3), then
$\land ,\lor ,\forall ,\exists $
from those B’s which satisfy the condition of (3), then  $$ \begin{align*}\mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash F\,{\leftrightarrow}\,(\emptyset\,{\Vdash_P}\, F).\end{align*} $$
$$ \begin{align*}\mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash F\,{\leftrightarrow}\,(\emptyset\,{\Vdash_P}\, F).\end{align*} $$
-
(5) If B is as in (3), then
Hence, $$ \begin{align*} \mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash\alpha\,{\Vdash_P}(B{\to} G)\,{\leftrightarrow}\,(B\,{\to}\,\alpha\,{\Vdash_P}G). \end{align*} $$
$$ \begin{align*} \mathbf{EL}_0^-{+}\mathcal{C}\textsf{-LEM} \vdash\alpha\,{\Vdash_P}(B{\to} G)\,{\leftrightarrow}\,(B\,{\to}\,\alpha\,{\Vdash_P}G). \end{align*} $$
 $\alpha \,{\Vdash _P}((\forall x\,{<}\,y)G)\,{\leftrightarrow }\,(\forall x\,{<}\,y) (\alpha \,{\Vdash _P}G)$
.
$\alpha \,{\Vdash _P}((\forall x\,{<}\,y)G)\,{\leftrightarrow }\,(\forall x\,{<}\,y) (\alpha \,{\Vdash _P}G)$
.
Proof (3) By induction on B. The atomic case is trivial. The case of
![]() $\land $
is by
$\land $
is by
![]() $(C\lor F)\land (D\lor F)\leftrightarrow (C\land D)\lor F$
.
$(C\lor F)\land (D\lor F)\leftrightarrow (C\land D)\lor F$
.
![]() $\alpha \,{\Vdash _P}\, C\,{\to }\, D$
is, by induction hypothesis, equivalent to
$\alpha \,{\Vdash _P}\, C\,{\to }\, D$
is, by induction hypothesis, equivalent to
to
![]() $C\,{\to }\,(\forall \beta \,{\supseteq }\,\alpha )(D\lor \exists u\textrm {Tr}_P[u,\beta ])$
, by
$C\,{\to }\,(\forall \beta \,{\supseteq }\,\alpha )(D\lor \exists u\textrm {Tr}_P[u,\beta ])$
, by
![]() $\mathcal {C}\textsf {-LEM}$
to
$\mathcal {C}\textsf {-LEM}$
to
![]() $\neg C\lor D\lor (\forall \beta \,{\supseteq }\,\alpha ) \exists u\textrm {Tr}_P[u,\beta ]$
and to
$\neg C\lor D\lor (\forall \beta \,{\supseteq }\,\alpha ) \exists u\textrm {Tr}_P[u,\beta ]$
and to
![]() $(C\,{\to }\, D)\lor \exists u\textrm {Tr}_P[u,\alpha ]$
.
$(C\,{\to }\, D)\lor \exists u\textrm {Tr}_P[u,\alpha ]$
.
By induction hypothesis,
![]() $\alpha \,{\Vdash _P}\,\!\exists x E$
is equivalent to
$\alpha \,{\Vdash _P}\,\!\exists x E$
is equivalent to
![]() $\exists x(E\lor \exists u\textrm {Tr}_P[u,\alpha ])$
and to
$\exists x(E\lor \exists u\textrm {Tr}_P[u,\alpha ])$
and to
![]() $(\exists x E)\lor \exists u\textrm {Tr}_P[u,\alpha ]$
. Similarly
$(\exists x E)\lor \exists u\textrm {Tr}_P[u,\alpha ]$
. Similarly
![]() $\alpha \,{\Vdash _P}\,\!\forall x E$
is to
$\alpha \,{\Vdash _P}\,\!\forall x E$
is to
![]() $\forall x(E\lor \exists u\textrm {Tr}_P[u,\alpha ])$
and to
$\forall x(E\lor \exists u\textrm {Tr}_P[u,\alpha ])$
and to
![]() $(\forall x E)\lor \exists u\textrm {Tr}_P[u,\alpha ,u]$
, but by
$(\forall x E)\lor \exists u\textrm {Tr}_P[u,\alpha ,u]$
, but by
![]() $\exists x\neg E\lor \forall x E$
.
$\exists x\neg E\lor \forall x E$
.
(5) If
![]() $\alpha \,{\Vdash _P}\,(B\,{\to }\,G)$
and B then, by (4) and (1)(ii),
$\alpha \,{\Vdash _P}\,(B\,{\to }\,G)$
and B then, by (4) and (1)(ii),
![]() $\alpha \,{\Vdash _P}B$
and
$\alpha \,{\Vdash _P}B$
and
![]() $\alpha \,{\Vdash _P}G$
. If
$\alpha \,{\Vdash _P}G$
. If
![]() $B\,{\to }\,(\alpha \,{\Vdash _P}G)$
then, for
$B\,{\to }\,(\alpha \,{\Vdash _P}G)$
then, for
![]() $\beta \,{\supseteq }\,\alpha $
, we can see that
$\beta \,{\supseteq }\,\alpha $
, we can see that
![]() $\beta \,{\Vdash _P}B$
implies
$\beta \,{\Vdash _P}B$
implies
![]() $B\lor \exists u\textrm {Tr}_P[u,\beta ]$
by (3),
$B\lor \exists u\textrm {Tr}_P[u,\beta ]$
by (3),
![]() $(\alpha \,{\Vdash _P}G)\lor (\beta \,{\Vdash _P}\bot )$
and so, by (1)(ii) and (2),
$(\alpha \,{\Vdash _P}G)\lor (\beta \,{\Vdash _P}\bot )$
and so, by (1)(ii) and (2),
![]() $\beta \,{\Vdash _P}G$
, i.e.,
$\beta \,{\Vdash _P}G$
, i.e.,
![]() $\alpha \,{\Vdash _P}\,(B\,{\to }\,G)$
.
$\alpha \,{\Vdash _P}\,(B\,{\to }\,G)$
.
Corollary 4.13. (1) If B is
![]() $\Pi ^0_{\infty }$
,
$\Pi ^0_{\infty }$
,
![]() $\mathbf{EL}_0^-\vdash B\,{\leftrightarrow }\,(\emptyset \!\Vdash _P\!B)$
;
$\mathbf{EL}_0^-\vdash B\,{\leftrightarrow }\,(\emptyset \!\Vdash _P\!B)$
;
(2) if B is
![]() $\Sigma ^0_{n+1}$
, then
$\Sigma ^0_{n+1}$
, then
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} \vdash (\alpha \!\Vdash _P\! B){\leftrightarrow }(\alpha \!\Vvdash _P\!B)$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} \vdash (\alpha \!\Vdash _P\! B){\leftrightarrow }(\alpha \!\Vvdash _P\!B)$
.
Definition 4.14 (self-forcible)
A schema
![]() $\textsf {S}$
is called self-forcible for
$\textsf {S}$
is called self-forcible for
![]() $\mathcal {C}$
if, for any
$\mathcal {C}$
if, for any
![]() $P\in \mathcal {C}$
,
$P\in \mathcal {C}$
,
![]() $\textsf {S}$
implies
$\textsf {S}$
implies
![]() $\emptyset \!\Vdash _P\!\textsf {S}$
.
$\emptyset \!\Vdash _P\!\textsf {S}$
.
Corollary 4.15. (i)
![]() $\mathbf{EL}_0^-{\vdash }(\emptyset \,{\Vdash _P}\,\mathbf{EL}_0^-)$
; (ii) in
$\mathbf{EL}_0^-{\vdash }(\emptyset \,{\Vdash _P}\,\mathbf{EL}_0^-)$
; (ii) in
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_{k+1}\textsf {-LEM}$
,
$\mathbf{EL}_0^-{+}\Sigma ^0_{k+1}\textsf {-LEM}$
,
![]() $\Sigma ^0_k\textsf {-Ind}$
and
$\Sigma ^0_k\textsf {-Ind}$
and
![]() $\Pi ^0_k\textsf {-Ind}$
are self-forcible for
$\Pi ^0_k\textsf {-Ind}$
are self-forcible for
![]() $\mathcal {L}_{\mathrm{F}}$
.
$\mathcal {L}_{\mathrm{F}}$
.
Lemma 4.16. Over
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-LEM}$
, the following are self-forcible for
$\mathbf{EL}_0^-{+}\Sigma ^0_{n}\textsf {-LEM}$
, the following are self-forcible for
![]() $\Pi ^0_n$
:
$\Pi ^0_n$
:
-
(i)
 $\Pi ^0_n\textsf {-WFT}$
if
$\Pi ^0_n\textsf {-WFT}$
if
 $n\,{>}\,0$
;
$n\,{>}\,0$
; -
(ii) for
 $\mathcal {C},\mathcal {D}\,{\in }\, \{\Sigma ^0_{n+2k+1},\Pi ^0_{n+2k+2},\Lambda ^1_{n+2k+1,m},\Xi _{n+2k+1,m},\Theta ^1_m\}$
, (a)
$\mathcal {C},\mathcal {D}\,{\in }\, \{\Sigma ^0_{n+2k+1},\Pi ^0_{n+2k+2},\Lambda ^1_{n+2k+1,m},\Xi _{n+2k+1,m},\Theta ^1_m\}$
, (a)
 $\mathcal {C}\textsf {-Ind}$
, (b)
$\mathcal {C}\textsf {-Ind}$
, (b)
 $\mathcal {C}\textsf {-Bdg}$
, (c)
$\mathcal {C}\textsf {-Bdg}$
, (c)
 $\mathcal {C}\textsf {-AC}^{0i}$
, (d)
$\mathcal {C}\textsf {-AC}^{0i}$
, (d)
 $\mathcal {C}\textsf {-DC}^{i}$
, (e)
$\mathcal {C}\textsf {-DC}^{i}$
, (e)
 $(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
and (f)
$(\mathcal {C},\mathcal {D})\textsf {-BI}_M$
and (f)
 $\mathcal {C}\textsf {-BI}_D$
(if
$\mathcal {C}\textsf {-BI}_D$
(if
 $n\,{=}\,0$
).
$n\,{=}\,0$
).
Proof We may assume
![]() $\exists u\textrm {Tr}_P[u,\alpha ] \,{\equiv }\,\exists lC[l,\alpha ]$
with C being
$\exists u\textrm {Tr}_P[u,\alpha ] \,{\equiv }\,\exists lC[l,\alpha ]$
with C being
![]() $\Pi ^0_n$
.
$\Pi ^0_n$
.
(i) If
![]() $\alpha \,{\Vdash _P}\,\! (\forall \xi \,{<}\,\underline {2})\exists kB[\xi {\upharpoonright } k]$
where B is
$\alpha \,{\Vdash _P}\,\! (\forall \xi \,{<}\,\underline {2})\exists kB[\xi {\upharpoonright } k]$
where B is
![]() $\Pi ^0_n$
, then
$\Pi ^0_n$
, then
![]() $(\forall \xi \,{<}\,\underline {2}) \exists k(\alpha \,{\Vvdash _P}\,B[\xi {\upharpoonright } k])$
by 4.13(2), i.e.,
$(\forall \xi \,{<}\,\underline {2}) \exists k(\alpha \,{\Vvdash _P}\,B[\xi {\upharpoonright } k])$
by 4.13(2), i.e.,
![]() $(\forall \xi \,{<}\, \underline {2})\exists k(B[\xi {\upharpoonright } k]\lor \exists lC[l,\alpha ])$
. Thus
$(\forall \xi \,{<}\, \underline {2})\exists k(B[\xi {\upharpoonright } k]\lor \exists lC[l,\alpha ])$
. Thus
![]() $(\forall \xi \,{<}\,\underline {2})\exists k D[\xi {\upharpoonright } k]$
where
$(\forall \xi \,{<}\,\underline {2})\exists k D[\xi {\upharpoonright } k]$
where
is
![]() $\Pi ^0_n{\lor }\Pi ^0_n\subseteq \Pi ^0_n$
by
$\Pi ^0_n{\lor }\Pi ^0_n\subseteq \Pi ^0_n$
by
![]() $\Sigma ^0_n\textsf {-LEM}$
. Then
$\Sigma ^0_n\textsf {-LEM}$
. Then
![]() $\Pi ^0_n\textsf {-WFT}$
yields m with
$\Pi ^0_n\textsf {-WFT}$
yields m with
![]() $(\forall \xi \,{<}\,\underline {2})(\exists k\,{<}\,m) D[\xi {\upharpoonright } k]$
and so
$(\forall \xi \,{<}\,\underline {2})(\exists k\,{<}\,m) D[\xi {\upharpoonright } k]$
and so
![]() $(\forall \xi \,{<}\,\underline {2}) (\exists k\,{<}\,m)(\alpha \!\Vvdash _P\!B[\xi {\upharpoonright } k])$
. As
$(\forall \xi \,{<}\,\underline {2}) (\exists k\,{<}\,m)(\alpha \!\Vvdash _P\!B[\xi {\upharpoonright } k])$
. As
![]() $\xi \,{<}\,\underline {2}$
is
$\xi \,{<}\,\underline {2}$
is
![]() $\Pi ^0_1$
, by 4.12(3)(5) with
$\Pi ^0_1$
, by 4.12(3)(5) with
![]() $n\,{>}\,0$
,
$n\,{>}\,0$
,
![]() $\alpha \,{\Vdash _P}(\forall \xi \,{<}\,\underline {2})(\exists k\,{<}\,m)B[\xi {\upharpoonright } k]$
.
$\alpha \,{\Vdash _P}(\forall \xi \,{<}\,\underline {2})(\exists k\,{<}\,m)B[\xi {\upharpoonright } k]$
.
(ii) If B is
![]() $\Pi ^0_{n}$
, then
$\Pi ^0_{n}$
, then
![]() $\beta \!\Vdash _P\!Q y_{n+2k(+1\,\textrm {or}\, 2)}\dots \exists y_{n+1}B[x,y_{n+2},\dots ]$
is equivalent to
$\beta \!\Vdash _P\!Q y_{n+2k(+1\,\textrm {or}\, 2)}\dots \exists y_{n+1}B[x,y_{n+2},\dots ]$
is equivalent to
![]() $Q\dots \exists y_{n+1}(\beta \!\Vdash _P\!B[x,y_{n+1},\dots ])$
and, by 4.13(2), also to
$Q\dots \exists y_{n+1}(\beta \!\Vdash _P\!B[x,y_{n+1},\dots ])$
and, by 4.13(2), also to
By
![]() $\Sigma ^0_n\textsf {-LEM}$
, if A is equivalently
$\Sigma ^0_n\textsf {-LEM}$
, if A is equivalently
![]() $\mathcal {C}$
, so is
$\mathcal {C}$
, so is
![]() $\beta \!\Vdash _P\!A[x]$
.
$\beta \!\Vdash _P\!A[x]$
.
-
(a) Assume
 $\alpha \!\Vdash _P\!A[0] \land (\forall x < n)(A[x] \to A[x{+}1])$
. Then we have
$\alpha \!\Vdash _P\!A[0] \land (\forall x < n)(A[x] \to A[x{+}1])$
. Then we have
 $\alpha \!\Vdash _P\!A[0]$
and
$\alpha \!\Vdash _P\!A[0]$
and
 $(\forall x < n)(\alpha \!\Vdash _P\!A[x] \to \alpha \!\Vdash _P\!A[x{+}1])$
. Thus, by
$(\forall x < n)(\alpha \!\Vdash _P\!A[x] \to \alpha \!\Vdash _P\!A[x{+}1])$
. Thus, by
 $\mathcal {C}\textsf {-Ind}$
, we can get
$\mathcal {C}\textsf {-Ind}$
, we can get
 $ \alpha \!\Vdash _P\!A[n]$
.
$ \alpha \!\Vdash _P\!A[n]$
. -
(b) Assume
 $\alpha \!\Vdash _P\!(\forall x < m)\exists yA[x,y]$
. Then
$\alpha \!\Vdash _P\!(\forall x < m)\exists yA[x,y]$
. Then
 $(\forall x < m)\exists y(\alpha \!\Vdash _P\!A[x,y])$
and, by
$(\forall x < m)\exists y(\alpha \!\Vdash _P\!A[x,y])$
and, by
 $\mathcal {C}\textsf {-Bdg}$
, also
$\mathcal {C}\textsf {-Bdg}$
, also
 $\exists u(\forall x < m)(\exists y < u)(\alpha \!\Vdash _P\!A[x,y])$
. Therefore, by 4.12(5), we have
$\exists u(\forall x < m)(\exists y < u)(\alpha \!\Vdash _P\!A[x,y])$
. Therefore, by 4.12(5), we have
 $\exists u(\alpha \!\Vdash _P\!(\forall x < m)(\exists y < u)A[x,y])$
.
$\exists u(\alpha \!\Vdash _P\!(\forall x < m)(\exists y < u)A[x,y])$
. -
(c) (d) (e) Similar.
-
(f) Use (e) and 2.29(3).
In the lemma, (ii)(f) seems to require
![]() $n\,{=}\,0$
: a bar
$n\,{=}\,0$
: a bar
![]() $\left \{v{:}\,\beta (v)\,{=}\,0\right \}$
is interpreted as
$\left \{v{:}\,\beta (v)\,{=}\,0\right \}$
is interpreted as
![]() $\left \{v{:}\,\alpha \Vdash _P\beta (v)\,{=}\,0\right \}$
, i.e.,
$\left \{v{:}\,\alpha \Vdash _P\beta (v)\,{=}\,0\right \}$
, i.e.,
![]() $\left \{v{:}\,\beta (v)\,{=}\,0\lor \exists u\textrm {Tr}[u,\alpha ]\right \}$
, to which we cannot apply
$\left \{v{:}\,\beta (v)\,{=}\,0\lor \exists u\textrm {Tr}[u,\alpha ]\right \}$
, to which we cannot apply
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
even if
$\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
even if
![]() $\textsf {Bar}[\underline {0},\left \{v{:}\,\beta (v)\,{=}\,0\lor \exists u\textrm {Tr}[u,\alpha ]\right \}]$
.
$\textsf {Bar}[\underline {0},\left \{v{:}\,\beta (v)\,{=}\,0\lor \exists u\textrm {Tr}[u,\alpha ]\right \}]$
.
The following is the central trick corresponding to that of A-translation, namely
![]() $(\neg \neg A[x])^{A[x]}\,{\leftrightarrow }\,A[x]$
.
$(\neg \neg A[x])^{A[x]}\,{\leftrightarrow }\,A[x]$
.
Proposition 4.17. For P from
![]() $\Pi ^0_n$
,
$\Pi ^0_n$
,
Proof
![]() $\Pi ^0_n\textsf {-LEM}$
yields
$\Pi ^0_n\textsf {-LEM}$
yields
![]() $\forall v\exists u(\neg P[x,v,\xi ]\lor P[x,u,\xi ])$
, which is equivalent to
$\forall v\exists u(\neg P[x,v,\xi ]\lor P[x,u,\xi ])$
, which is equivalent to
![]() $\forall v(\neg P[x,v,\xi ]\lor \exists u P[x,u,\xi ])$
, i.e.,
$\forall v(\neg P[x,v,\xi ]\lor \exists u P[x,u,\xi ])$
, i.e.,
![]() $\forall v(\{(x,\xi )\}\!\Vvdash _P\! \neg P[x,v,\xi ])$
. By 4.13(2) and 4.12(3), we have
$\forall v(\{(x,\xi )\}\!\Vvdash _P\! \neg P[x,v,\xi ])$
. By 4.13(2) and 4.12(3), we have
![]() $\{(x,\xi )\}\!\Vdash _P\!\forall v\neg P[x,v,\xi ]$
.
$\{(x,\xi )\}\!\Vdash _P\!\forall v\neg P[x,v,\xi ]$
.
Thus, if
![]() $\alpha \!\Vdash _P\!\neg \forall v\neg P[v,x,\xi ]$
then
$\alpha \!\Vdash _P\!\neg \forall v\neg P[v,x,\xi ]$
then
![]() $\alpha \,{\cup }\,\{(x,\xi )\}\!\Vdash _P\!\bot $
, i.e.,
$\alpha \,{\cup }\,\{(x,\xi )\}\!\Vdash _P\!\bot $
, i.e.,
![]() $\exists u\textrm {Tr}_P[\alpha \,{\cup }\,\{(x,\xi )\},u]$
which is equivalent to
$\exists u\textrm {Tr}_P[\alpha \,{\cup }\,\{(x,\xi )\},u]$
which is equivalent to
![]() $\exists u(\textrm {Tr}_P[\alpha ,u]\lor P[x,u,\xi ])$
, to
$\exists u(\textrm {Tr}_P[\alpha ,u]\lor P[x,u,\xi ])$
, to
![]() $\exists u(\alpha \!\Vvdash _P\!P[x,u,\xi ])$
, and, again by 4.13(2), to
$\exists u(\alpha \!\Vvdash _P\!P[x,u,\xi ])$
, and, again by 4.13(2), to
![]() $\alpha \!\Vdash _P\!\exists uP[x,u,\xi ]$
.
$\alpha \!\Vdash _P\!\exists uP[x,u,\xi ]$
.
Theorem 4.18. There is a
![]() $\Pi ^0_n$
formula P such that
$\Pi ^0_n$
formula P such that
Proof Let
![]() $P[x,u,\xi ]\,{:\equiv }\,\forall y_n\exists y_{n-1}\dots Qy_1(\xi (x,u,y_n,y_{n-1},\ldots ,y_1)\,{=}\,0)$
. Fix A from
$P[x,u,\xi ]\,{:\equiv }\,\forall y_n\exists y_{n-1}\dots Qy_1(\xi (x,u,y_n,y_{n-1},\ldots ,y_1)\,{=}\,0)$
. Fix A from
![]() $\Sigma ^0_{n+1}$
. Take C from
$\Sigma ^0_{n+1}$
. Take C from
![]() $\Delta ^0_0$
with
$\Delta ^0_0$
with
Take
![]() $\xi $
with
$\xi $
with
![]() $(\forall x,u,\vec {y})( \xi (x,u,\vec {y})\,{=}\,0\,{\leftrightarrow }\, C[x,u,\vec {y},\alpha ])$
by 2.10(d). Then we have
$(\forall x,u,\vec {y})( \xi (x,u,\vec {y})\,{=}\,0\,{\leftrightarrow }\, C[x,u,\vec {y},\alpha ])$
by 2.10(d). Then we have
![]() $\forall x(A[x,\alpha ]\,{\leftrightarrow }\, \exists uP[x,u,\xi ])$
.
$\forall x(A[x,\alpha ]\,{\leftrightarrow }\, \exists uP[x,u,\xi ])$
.
As this argument is possible in
![]() $\mathbf{EL}_0^-$
,
$\mathbf{EL}_0^-$
,
![]() $\emptyset \Vdash _P\exists \xi \forall x(A[x,\alpha ]\,{\leftrightarrow }\, \exists uP[x,u,\xi ])$
by 4.12(2) and 4.15(i)
. By 4.17 with 4.12(2), we finally get
$\emptyset \Vdash _P\exists \xi \forall x(A[x,\alpha ]\,{\leftrightarrow }\, \exists uP[x,u,\xi ])$
by 4.12(2) and 4.15(i)
. By 4.17 with 4.12(2), we finally get
![]() $\emptyset \Vdash _P\neg \neg A[x,\alpha ]\,{\to } A[x,\alpha ]$
.
$\emptyset \Vdash _P\neg \neg A[x,\alpha ]\,{\to } A[x,\alpha ]$
.
4.3 Combining negative and forcing interpretations
Coquand–Hofmann [Reference Coquand and Hofmann11] and Avigad [Reference Avigad3] combined the interpretation
![]() $A\mapsto \emptyset \!\Vdash _P\! A$
with the negative interpretation N. We follow this way, with the following enhancement. While they considered only the first order case where P in
$A\mapsto \emptyset \!\Vdash _P\! A$
with the negative interpretation N. We follow this way, with the following enhancement. While they considered only the first order case where P in
![]() $\Vdash _P$
is
$\Vdash _P$
is
![]() $\Delta ^0_0$
, we have considered second order cases with P being
$\Delta ^0_0$
, we have considered second order cases with P being
![]() $\Pi ^0_n$
but assuming
$\Pi ^0_n$
but assuming
![]() $\Sigma ^0_n\textsf {-LEM}$
.
$\Sigma ^0_n\textsf {-LEM}$
.
Theorem 4.19.
-
(1) (a)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
and so
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
and so
 $\mathbf{I}\boldsymbol {\Delta }_0\mathbf{ex}$
(and
$\mathbf{I}\boldsymbol {\Delta }_0\mathbf{ex}$
(and
 $\mathbf{EFA}$
) are
$\mathbf{EFA}$
) are
 $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
 $\mathbf{EL}_0^-$
and (b) so are
$\mathbf{EL}_0^-$
and (b) so are
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Bdg}$
and
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Bdg}$
and
 $\mathbf{B}\boldsymbol {\Delta }_0\mathbf{ex}$
in
$\mathbf{B}\boldsymbol {\Delta }_0\mathbf{ex}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
and hence in
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
and hence in
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
. -
(2)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Ind}$
and so
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Ind}$
and so
 $\mathbf{I}\boldsymbol {\Sigma }_1\,{=}\,\mathbf{I}\boldsymbol {\Pi }_1$
(as well as
$\mathbf{I}\boldsymbol {\Sigma }_1\,{=}\,\mathbf{I}\boldsymbol {\Pi }_1$
(as well as
 $\mathbf{PRA}$
) are interpretable (a)
$\mathbf{PRA}$
) are interpretable (a)
 $\Pi ^0_1$
-preservingly in
$\Pi ^0_1$
-preservingly in
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and hence in
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and hence in
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
; (b)
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
; (b)
 $\Pi ^0_2$
-preservingly in
$\Pi ^0_2$
-preservingly in
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
and hence in
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
and hence in
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
. -
(3)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_2\textsf {-Ind}$
and so
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_2\textsf {-Ind}$
and so
 $\mathbf{I}\boldsymbol {\Sigma }_2\,{=}\,\mathbf{I}\boldsymbol {\Pi }_2$
are interpretable (a)
$\mathbf{I}\boldsymbol {\Sigma }_2\,{=}\,\mathbf{I}\boldsymbol {\Pi }_2$
are interpretable (a)
 $\Pi ^0_2$
-preservingly in
$\Pi ^0_2$
-preservingly in
 $\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-Ind}$
and hence in
$\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-Ind}$
and hence in
 $\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-DC!}^0$
and in
$\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-DC!}^0$
and in
 $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC!}^1$
and (b)
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC!}^1$
and (b)
 $\Pi ^0_3$
-preservingly in
$\Pi ^0_3$
-preservingly in
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
. -
(4)
 $\mathbf{ACA}_0$
is interpretable (a)
$\mathbf{ACA}_0$
is interpretable (a)
 $\Pi ^0_2$
-preservingly in
$\Pi ^0_2$
-preservingly in
 $\mathbf{EL}_0^-+\Sigma ^0_1\textsf {-BI}_D$
, and also in
$\mathbf{EL}_0^-+\Sigma ^0_1\textsf {-BI}_D$
, and also in
 $\mathbf{EL}_0^-{+} \textsf { LPO}{+}\Delta ^0_0\textsf {-FT}$
; (b)
$\mathbf{EL}_0^-{+} \textsf { LPO}{+}\Delta ^0_0\textsf {-FT}$
; (b)
 $\Pi ^0_3$
-preservingly in
$\Pi ^0_3$
-preservingly in
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
; and (c)
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
; and (c)
 $\Delta ^1_0$
-preservingly in
$\Delta ^1_0$
-preservingly in
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
Proof (1) By 4.3(1) with
![]() $n\,{=}\,1$
,
$n\,{=}\,1$
,
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
is
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
is
![]() $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\textsf {MP}$
. The latter is
$\mathbf{EL}_0^-{+}\textsf {MP}$
. The latter is
![]() $\Pi ^0_{\infty }$
-preservingly interpretable in
$\Pi ^0_{\infty }$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-$
by 4.13(1) and 4.18 with
$\mathbf{EL}_0^-$
by 4.13(1) and 4.18 with
![]() $n\,{=}\,0$
. For (b) use additionally 4.3(2)(iii) with
$n\,{=}\,0$
. For (b) use additionally 4.3(2)(iii) with
![]() $n\,{=}\,1$
and 4.16(ii)(b) with
$n\,{=}\,1$
and 4.16(ii)(b) with
![]() $n\,{=}\,k\,{=}\,0$
, where we can easily see
$n\,{=}\,k\,{=}\,0$
, where we can easily see
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}\vdash \Sigma ^0_1\textsf {-Bdg}$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}\vdash \Sigma ^0_1\textsf {-Bdg}$
.
(2) (a)
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Ind} \,{=}\, \mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+} \Pi ^0_1\textsf {-Ind}$
is
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_1\textsf {-Ind} \,{=}\, \mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+} \Pi ^0_1\textsf {-Ind}$
is
![]() $\Pi ^0_1$
-preservingly interpretable in
$\Pi ^0_1$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
by 4.3(1)(2)(i) with
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
by 4.3(1)(2)(i) with
![]() $n\,{=}\,0$
, and by 2.29(2) further in
$n\,{=}\,0$
, and by 2.29(2) further in
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
.
(b) By 4.3(1)(2)(ii) with
![]() $n\,{=}\,1$
,
$n\,{=}\,1$
,
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+} \Sigma ^0_1\textsf {-Ind}$
is
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+} \Sigma ^0_1\textsf {-Ind}$
is
![]() $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-Ind}$
. The latter is
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-Ind}$
. The latter is
![]() $\Pi ^0_{\infty }$
-preservingly interpretable in
$\Pi ^0_{\infty }$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
by 4.13(1), 4.16(ii)(a) with
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
by 4.13(1), 4.16(ii)(a) with
![]() $n\,{=}\,k\,{=}\,0$
and 4.18 with
$n\,{=}\,k\,{=}\,0$
and 4.18 with
![]() $n\,{=}\,0$
, and hence in
$n\,{=}\,0$
, and hence in
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
by 2.33.
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
by 2.33.
(3) (a) By 4.3(1)(2)(i) with
![]() $n\,{=}\,1$
,
$n\,{=}\,1$
,
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Pi ^0_2\textsf {-Ind}$
is
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Pi ^0_2\textsf {-Ind}$
is
![]() $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\textsf { MP}{+}\Pi ^0_2\textsf {-Ind}$
, and, by 4.13(1), 4.16(ii)(a) with
$\mathbf{EL}_0^-{+}\textsf { MP}{+}\Pi ^0_2\textsf {-Ind}$
, and, by 4.13(1), 4.16(ii)(a) with
![]() $n\,{=}\,k\,{=}\,0$
and 4.18, further in
$n\,{=}\,k\,{=}\,0$
and 4.18, further in
![]() $\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-Ind}$
. The latter is included in
$\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-Ind}$
. The latter is included in
![]() $\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-DC!}^0$
by 2.16(3)(i), and in
$\mathbf{EL}_0^-{+}\Pi ^0_2\textsf {-DC!}^0$
by 2.16(3)(i), and in
![]() $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC!}^1$
by 2.16(5) with
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-DC!}^1$
by 2.16(5) with
![]() $\mathcal {C}\,{\equiv }\,\Delta ^0_0$
and 2.16(2)(v).
$\mathcal {C}\,{\equiv }\,\Delta ^0_0$
and 2.16(2)(v).
(b) By 4.3(1)(2)(ii) with
![]() $n\,{=}\,2$
,
$n\,{=}\,2$
,
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_2\textsf {-Ind}$
is
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Sigma ^0_2\textsf {-Ind}$
is
![]() $\Pi ^0_3$
-preservingly interpretable in
$\Pi ^0_3$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Sigma ^0_2\textsf {-Ind}$
and further in
$\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Sigma ^0_2\textsf {-Ind}$
and further in
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
by 4.13(1), 4.16(ii)(a) with
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
by 4.13(1), 4.16(ii)(a) with
![]() $(n,k)\,{=}\,(1,0)$
and 4.18 with
$(n,k)\,{=}\,(1,0)$
and 4.18 with
![]() $n\,{=}\,1$
.
$n\,{=}\,1$
.
(4) (a)(b)(c) follow from 4.9(i)(ii)(iii), respectively, since
![]() $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-BI}_D$
is interpretable
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Sigma ^0_1\textsf {-BI}_D$
is interpretable
![]() $\Pi ^0_{\infty }$
-preservingly in
$\Pi ^0_{\infty }$
-preservingly in
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-BI}_D$
by 4.13(1), 4.16(ii)(f) with
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-BI}_D$
by 4.13(1), 4.16(ii)(f) with
![]() $n\,{=}\,k\,{=}\,0$
and 4.18 with
$n\,{=}\,k\,{=}\,0$
and 4.18 with
![]() $n\,{=}\,0$
; and so is
$n\,{=}\,0$
; and so is
![]() $\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Pi ^0_1\textsf {-WFT}$
in
$\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}{+}\Pi ^0_1\textsf {-WFT}$
in
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
by 4.13(1), 4.16(i)
with
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
by 4.13(1), 4.16(i)
with
![]() $n\,{=}\,1$
and 4.18 with
$n\,{=}\,1$
and 4.18 with
![]() $n\,{=}\,1$
.
$n\,{=}\,1$
.
With the hierarchy of
![]() $\Lambda ^i_{n,m}$
’s from 3.60, we can hierarchize the interpretability as in 4.20 below. For (e),
$\Lambda ^i_{n,m}$
’s from 3.60, we can hierarchize the interpretability as in 4.20 below. For (e),
![]() $(\Pi ^0_{n+2+m})^N\,{\subseteq }\,\Lambda ^1_{n+1,m}$
under
$(\Pi ^0_{n+2+m})^N\,{\subseteq }\,\Lambda ^1_{n+1,m}$
under
![]() $\Sigma ^0_{n+1}\textsf {-DNE}$
and if
$\Sigma ^0_{n+1}\textsf {-DNE}$
and if
![]() $m>0$
by recursive indices we can interpret
$m>0$
by recursive indices we can interpret
![]() $\Lambda ^1_{n+1,m}$
in
$\Lambda ^1_{n+1,m}$
in
![]() $\Lambda ^0_{n+1,m}$
.
$\Lambda ^0_{n+1,m}$
.
Corollary 4.20. Let
![]() $k\,{<}\,n$
or
$k\,{<}\,n$
or
![]() $k\,{=}\,n{+}1$
. We can interpret
$k\,{=}\,n{+}1$
. We can interpret
![]() $\Pi ^0_{n+2}$
-preservingly
$\Pi ^0_{n+2}$
-preservingly
-
(a)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM}$
;
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM}$
; -
(b)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Bdg}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Bdg}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Bdg}$
;
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Bdg}$
; -
(c)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Ind}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Ind}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Ind}$
;
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Sigma ^0_k\textsf {-Ind}$
; -
(d)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Pi ^0_{n+2}\textsf {-Ind}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Pi ^0_{n+2}\textsf {-Ind}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+} \Pi^0_{n+2}\textsf {-Ind}$
;
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+} \Pi^0_{n+2}\textsf {-Ind}$
; -
(e)
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Pi ^0_{n+m+3}\textsf {-Ind}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Pi ^0_{n+m+3}\textsf {-Ind}$
in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Lambda ^1_{n+1,m+1}\textsf {-Ind}$
and hence in
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Lambda ^1_{n+1,m+1}\textsf {-Ind}$
and hence in
 $\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Lambda ^0_{n+1,m+1}\textsf {-Ind}$
.
$\mathbf{EL}_0^-{+}\Sigma ^0_n\textsf {-LEM} {+}\Lambda ^0_{n+1,m+1}\textsf {-Ind}$
.
In the first order setting, by letting
![]() $\exists uP[x,u]$
be universal
$\exists uP[x,u]$
be universal
![]() $\Sigma _{n+1}$
, we obtain the analogous
$\Sigma _{n+1}$
, we obtain the analogous
![]() $\Pi _{n+2}$
-preserving interpretability results where
$\Pi _{n+2}$
-preserving interpretability results where
![]() $\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex} \mathbin {:\equiv } \textbf {iQex}\,{+}\,\Delta _0\textsf {-Ind}$
: (a)
$\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex} \mathbin {:\equiv } \textbf {iQex}\,{+}\,\Delta _0\textsf {-Ind}$
: (a)
![]() $\mathbf{I}\boldsymbol {\Delta }_{0}\textbf {ex}{+}\Sigma _{n+1}\textsf {-Bdg}$
in
$\mathbf{I}\boldsymbol {\Delta }_{0}\textbf {ex}{+}\Sigma _{n+1}\textsf {-Bdg}$
in
![]() $\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+}\Sigma _{n+1}\textsf {-Bdg}{+}\Sigma _n\textsf {-LEM}$
; (b)
$\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+}\Sigma _{n+1}\textsf {-Bdg}{+}\Sigma _n\textsf {-LEM}$
; (b)
![]() $\mathbf{I}\boldsymbol {\Sigma }_{n+1}$
in
$\mathbf{I}\boldsymbol {\Sigma }_{n+1}$
in
![]() $\mathbf{i}\boldsymbol {\Sigma }_{n+1} {+}\Sigma _n\textsf {-LEM}$
; and (c)
$\mathbf{i}\boldsymbol {\Sigma }_{n+1} {+}\Sigma _n\textsf {-LEM}$
; and (c)
![]() $\mathbf{I}\boldsymbol {\Pi }_{n+m+2}$
in
$\mathbf{I}\boldsymbol {\Pi }_{n+m+2}$
in
![]() $\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+} (\Lambda ^0_{n+1,m}{\cap }\,\mathcal {L}_1)\textsf {-Ind} {+}\Sigma _n\textsf {-LEM}$
; and (d)
$\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+} (\Lambda ^0_{n+1,m}{\cap }\,\mathcal {L}_1)\textsf {-Ind} {+}\Sigma _n\textsf {-LEM}$
; and (d)
![]() $\textbf {PA}$
in
$\textbf {PA}$
in
![]() $\textbf {HA}{+}\Sigma _n\textsf {-LEM}$
. However, this does not work for
$\textbf {HA}{+}\Sigma _n\textsf {-LEM}$
. However, this does not work for
![]() $\mathbf{I}\boldsymbol {\Delta }_{0}\textbf {ex}$
in
$\mathbf{I}\boldsymbol {\Delta }_{0}\textbf {ex}$
in
![]() $\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+}\Sigma _n\textsf {-LEM}$
, since
$\mathbf{i}\boldsymbol {\Delta }_0\textbf {ex}{+}\Sigma _n\textsf {-LEM}$
, since
![]() $\Sigma _{1}\textsf {-Bdg}$
seems necessary for universal formula.
$\Sigma _{1}\textsf {-Bdg}$
seems necessary for universal formula.
We can go further to stronger theories, where
![]() $\Pi ^1_{m} {\textsf{-}\textbf {TI}}_0\,{:\equiv }\,\mathbf{ACA}_0{+}\Pi ^1_{m}\textsf{-}\textsf{TI}$
and
$\Pi ^1_{m} {\textsf{-}\textbf {TI}}_0\,{:\equiv }\,\mathbf{ACA}_0{+}\Pi ^1_{m}\textsf{-}\textsf{TI}$
and
![]() $\Pi ^1_{\infty } {\textsf{-}\textbf {TI}}_0\,{:\equiv }\bigcup _m\Pi ^1_m {\textsf{-}\textbf {TI}}_0$
.
$\Pi ^1_{\infty } {\textsf{-}\textbf {TI}}_0\,{:\equiv }\bigcup _m\Pi ^1_m {\textsf{-}\textbf {TI}}_0$
.
Theorem 4.21.
![]() $\Pi ^1_{m+1} {\textsf{-}\textbf {TI}}_0$
is
$\Pi ^1_{m+1} {\textsf{-}\textbf {TI}}_0$
is
![]() $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
. So is
$\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
. So is
![]() $\Pi ^1_{\infty } {\textsf{-}\textbf {TI}}_0$
in
$\Pi ^1_{\infty } {\textsf{-}\textbf {TI}}_0$
in
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
.
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
.
Proof By
![]() $\Pi ^1_1$
normal form, we may consider
$\Pi ^1_1$
normal form, we may consider
![]() $(\Pi ^1_{m+1})^N\,{\subseteq }\,\Lambda ^1_{1,m}$
over
$(\Pi ^1_{m+1})^N\,{\subseteq }\,\Lambda ^1_{1,m}$
over
![]() $\mathbf{EL}_0^-{+}\textsf {MP}$
. Thus, by 4.3(1)(2)(iv) with
$\mathbf{EL}_0^-{+}\textsf {MP}$
. Thus, by 4.3(1)(2)(iv) with
![]() $n\,{=}\,1$
and 4.8(2),
$n\,{=}\,1$
and 4.8(2),
![]() $\Pi ^1_{m+1} {\textsf{-}\textbf {TI}}_0$
is
$\Pi ^1_{m+1} {\textsf{-}\textbf {TI}}_0$
is
![]() $\Pi ^0_2$
-preservingly interpretable in
$\Pi ^0_2$
-preservingly interpretable in
![]() $\mathbf{EL}_0^-{+}\textsf {MP}{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
. The latter is interpretable
$\mathbf{EL}_0^-{+}\textsf {MP}{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
. The latter is interpretable
![]() $\Pi ^0_{\infty }$
-preservingly in
$\Pi ^0_{\infty }$
-preservingly in
![]() $\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
by 4.13(1), 4.16(ii)(f) with
$\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
by 4.13(1), 4.16(ii)(f) with
![]() $\mathcal {C}\,{\equiv }\,\Lambda ^1_{1,m}$
and 4.18 with
$\mathcal {C}\,{\equiv }\,\Lambda ^1_{1,m}$
and 4.18 with
![]() $n\,{=}\,0$
.
$n\,{=}\,0$
.
Actually Coquand and Hofmann [Reference Coquand and Hofmann11] mentioned the combination of their interpretation of
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
into
$\mathbf{I}\boldsymbol {\Sigma }_1$
into
![]() $\mathbf{i}\boldsymbol {\Sigma }_1$
further with the modified realizability of
$\mathbf{i}\boldsymbol {\Sigma }_1$
further with the modified realizability of
![]() $\mathbf{i}\boldsymbol {\Sigma }_1$
in
$\mathbf{i}\boldsymbol {\Sigma }_1$
in
![]() $\mathbf{PRA}^\omega $
, the higher order version of primitive recursive arithmetic, as an alternative proof of Parson’s Theorem: the
$\mathbf{PRA}^\omega $
, the higher order version of primitive recursive arithmetic, as an alternative proof of Parson’s Theorem: the
![]() $\Pi ^0_2$
conservation of
$\Pi ^0_2$
conservation of
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
over
$\mathbf{I}\boldsymbol {\Sigma }_1$
over
![]() $\mathbf{PRA}$
. However we need cut elimination to reduce
$\mathbf{PRA}$
. However we need cut elimination to reduce
![]() $\mathbf{PRA}^\omega $
to
$\mathbf{PRA}^\omega $
to
![]() $\mathbf{PRA}$
.Footnote
20
This kind of longer combination (of negative, forcing and realizability interpretations in this order) is called making-a-detour method in Section 5.4.
$\mathbf{PRA}$
.Footnote
20
This kind of longer combination (of negative, forcing and realizability interpretations in this order) is called making-a-detour method in Section 5.4.
5 Final Remarks
5.1 Summary of results
Corollary 5.2 below is by 3.43 and 3.53, with 2.29(1). [Reference Avigad2] gave a
![]() $\Pi ^1_1$
-preserving interpretation of
$\Pi ^1_1$
-preserving interpretation of
![]() $\mathbf{WKL}_0$
in
$\mathbf{WKL}_0$
in
![]() $\textbf {RCA}_0$
, which also
$\textbf {RCA}_0$
, which also
![]() $\Pi ^1_1$
-preservingly interprets
$\Pi ^1_1$
-preservingly interprets
![]() $\mathbf{WKL}_0^*$
in
$\mathbf{WKL}_0^*$
in
![]() $\textbf {RCA}_0^*$
(where we need to show that
$\textbf {RCA}_0^*$
(where we need to show that
![]() $\Sigma ^0_1\textsf {-Bdg}$
is
$\Sigma ^0_1\textsf {-Bdg}$
is
![]() $\frac {1}{2}$
-forced by formalizing the argument of [Reference Simpson and Smith46, 4.5 Lemma]). By recursive indices we can
$\frac {1}{2}$
-forced by formalizing the argument of [Reference Simpson and Smith46, 4.5 Lemma]). By recursive indices we can
![]() $\Delta ^1_0$
-preservingly interpret
$\Delta ^1_0$
-preservingly interpret
![]() $\textbf {RCA}_0$
in
$\textbf {RCA}_0$
in
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
and
$\mathbf{I}\boldsymbol {\Sigma }_1$
and
![]() $\textbf {RCA}_0^*$
in
$\textbf {RCA}_0^*$
in
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
. Moreover
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
. Moreover
![]() $\mathbf{PRA}\vdash \textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
and
$\mathbf{PRA}\vdash \textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
and
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
is
$\mathbf{I}\boldsymbol {\Sigma }_1$
is
![]() $\Pi _2$
reducible to
$\Pi _2$
reducible to
![]() $\mathbf{PRA}$
(see Section 5.2). Hence the combinations in 5.2(1) are finitistically guaranteed and those in 5.2(2) are finitistically justifiable.
$\mathbf{PRA}$
(see Section 5.2). Hence the combinations in 5.2(1) are finitistically guaranteed and those in 5.2(2) are finitistically justifiable.
Definition 5.1 (functionally realizable analysis
 $\textbf {FR}_0^*$
,
$\textbf {FR}_0^*$
,
 $\textbf {FR}_0$
,
$\textbf {FR}_0$
,
 $\textbf {FR}^+_m$
,
$\textbf {FR}^+_m$
,
 $\textbf {FR}^{++}_m$
)
$\textbf {FR}^{++}_m$
)
 $$ \begin{align*} &\textbf{FR}_0^-\,{:\equiv}\,\mathbf{EL}_0^-{+}\textsf{MP}{+} \mathcal{L}_{\textrm{F}}\{\textsf{-CB}^1\!,\textsf{-CC!}^1\};\\ &\textbf{FR}_0^*\,{:\equiv}\,\textbf{FR}_0^-{+} \mathcal{L}_{\textrm{F}}\{\textsf{-AC}^{00}\!, \textsf{-AC}^{01}\!, \textsf{-WFT}\};\\ &\textbf{FR}_0\,{:\equiv}\, \textbf{FR}_0^*{+}\Sigma^0_1\textsf{-DC}^1 {+}\Sigma^0_2\{\textsf{-Ind},\textsf{-DC}^0\} {+}\Pi^0_1\textsf{-BI} {+}\mathcal{L}_{\textrm{F}}\textsf{-FT};\\ &\textbf{FR}^+_m\,{:\equiv}\,\textbf{FR}_0{+}\Theta^1_m\{\textsf{-Ind},\textsf{-DC}^0\!,\textsf{-DC}^1\};\\ &\textbf{FR}^{++}_m\,{:\equiv}\,\textbf{FR}^+_m {+}(\Theta^1_m,\mathcal{L}_{\textrm{F}})\textsf{-BI}_M \text{ (cf.\ 3.60 for the definition of } \Theta^1_m). \end{align*} $$
$$ \begin{align*} &\textbf{FR}_0^-\,{:\equiv}\,\mathbf{EL}_0^-{+}\textsf{MP}{+} \mathcal{L}_{\textrm{F}}\{\textsf{-CB}^1\!,\textsf{-CC!}^1\};\\ &\textbf{FR}_0^*\,{:\equiv}\,\textbf{FR}_0^-{+} \mathcal{L}_{\textrm{F}}\{\textsf{-AC}^{00}\!, \textsf{-AC}^{01}\!, \textsf{-WFT}\};\\ &\textbf{FR}_0\,{:\equiv}\, \textbf{FR}_0^*{+}\Sigma^0_1\textsf{-DC}^1 {+}\Sigma^0_2\{\textsf{-Ind},\textsf{-DC}^0\} {+}\Pi^0_1\textsf{-BI} {+}\mathcal{L}_{\textrm{F}}\textsf{-FT};\\ &\textbf{FR}^+_m\,{:\equiv}\,\textbf{FR}_0{+}\Theta^1_m\{\textsf{-Ind},\textsf{-DC}^0\!,\textsf{-DC}^1\};\\ &\textbf{FR}^{++}_m\,{:\equiv}\,\textbf{FR}^+_m {+}(\Theta^1_m,\mathcal{L}_{\textrm{F}})\textsf{-BI}_M \text{ (cf.\ 3.60 for the definition of } \Theta^1_m). \end{align*} $$
Corollary 5.2.
-
(1) Both
 $\mathbf{FR}_0^*{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
and
$\mathbf{FR}_0^*{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
and
 $\mathbf{FR}_0^*{+}\Sigma ^0_1\textsf {-GDM}$
are
$\mathbf{FR}_0^*{+}\Sigma ^0_1\textsf {-GDM}$
are
 $\Pi ^0_{\infty }$
-preservingly interpretable in
$\Pi ^0_{\infty }$
-preservingly interpretable in
 $\mathbf{WKL}^*_0$
.
$\mathbf{WKL}^*_0$
. -
(2) Both
 $\mathbf{FR}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
and
$\mathbf{FR}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
and
 $\mathbf{FR}_0{+}\Sigma ^0_1\textsf {-GDM}$
are
$\mathbf{FR}_0{+}\Sigma ^0_1\textsf {-GDM}$
are
 $\Pi ^0_{\infty }$
-preservingly interpretable in
$\Pi ^0_{\infty }$
-preservingly interpretable in
 $\mathbf{WKL}_0$
.
$\mathbf{WKL}_0$
.
Moreover these combinations are optimal in the sense of the hierarchies of Brouwerian axioms and of semi-classical principles: by 4.19(2) with 2.16(2)(i)(3)(i),
![]() $\mathbf{EL}_0^-$
together with any of
$\mathbf{EL}_0^-$
together with any of
![]() $\Pi ^0_1\textsf {-Ind}$
,
$\Pi ^0_1\textsf {-Ind}$
,
![]() $\Delta ^0_0\textsf {-BI}_D$
,
$\Delta ^0_0\textsf {-BI}_D$
,
![]() $\Sigma ^0_1\textsf {-Ind}$
,
$\Sigma ^0_1\textsf {-Ind}$
,
![]() $\Delta ^0_0\textsf {-DC}!^0\!$
and
$\Delta ^0_0\textsf {-DC}!^0\!$
and
![]() $\Delta ^0_0\textsf {-FT}$
interprets
$\Delta ^0_0\textsf {-FT}$
interprets
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
and hence is not provably consistent in
$\mathbf{I}\boldsymbol {\Sigma }_1$
and hence is not provably consistent in
![]() $\mathbf{PRA}$
; by 4.19(3)(4)(a),
$\mathbf{PRA}$
; by 4.19(3)(4)(a),
![]() $\mathbf{EL}_0^-$
with any of
$\mathbf{EL}_0^-$
with any of
![]() $\Pi ^0_2\textsf {-Ind}$
,
$\Pi ^0_2\textsf {-Ind}$
,
![]() $\Pi ^0_2\textsf {-DC}!^0\!$
,
$\Pi ^0_2\textsf {-DC}!^0\!$
,
![]() $\Pi ^0_1\textsf {-DC}!^1\!$
,
$\Pi ^0_1\textsf {-DC}!^1\!$
,
![]() $\Sigma ^0_1\textsf {-BI}_D$
and
$\Sigma ^0_1\textsf {-BI}_D$
and
![]() $\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
interprets
$\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
interprets
![]() $\mathbf{I}\boldsymbol {\Sigma }_2$
and hence is not reducible to
$\mathbf{I}\boldsymbol {\Sigma }_2$
and hence is not reducible to
![]() $\mathbf{PRA}$
; by 4.19(4) with 2.16(2)(iv),
$\mathbf{PRA}$
; by 4.19(4) with 2.16(2)(iv),
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}$
with any of
$\mathbf{EL}_0^-{+}\textsf {LPO}$
with any of
![]() $\Pi ^0_1\textsf {-AC}!^{00}\!$
,
$\Pi ^0_1\textsf {-AC}!^{00}\!$
,
![]() $\Pi ^0_1\textsf {-DC}!^0\!$
,
$\Pi ^0_1\textsf {-DC}!^0\!$
,
![]() $\Delta ^0_0\textsf {-FT}$
and
$\Delta ^0_0\textsf {-FT}$
and
![]() $\Pi ^0_1\textsf {-WFT}$
interprets
$\Pi ^0_1\textsf {-WFT}$
interprets
![]() $\mathbf{ACA}_0$
; as shown in 2.35(2),
$\mathbf{ACA}_0$
; as shown in 2.35(2),
![]() $\mathbf{EL}_0^-{+}\textsf {LLPO}{+}\Pi ^0_1\textsf {-WC}^0$
and
$\mathbf{EL}_0^-{+}\textsf {LLPO}{+}\Pi ^0_1\textsf {-WC}^0$
and
![]() $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WC!}^0$
are both inconsistent. (See also Section 2.5.5.)
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WC!}^0$
are both inconsistent. (See also Section 2.5.5.)
Classically,
![]() $\mathbf{CFG}\,{:\equiv }\,\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_1\{\textsf {-AC}^{00}\!,\textsf {-AC}^{01}\!, \textsf {-WFT},\textsf {-WC}^{0}\!,\textsf {-WC}^{1}\}$
is finitistically guaranteed, and
$\mathbf{CFG}\,{:\equiv }\,\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM} {+}\Sigma ^0_1\{\textsf {-AC}^{00}\!,\textsf {-AC}^{01}\!, \textsf {-WFT},\textsf {-WC}^{0}\!,\textsf {-WC}^{1}\}$
is finitistically guaranteed, and
![]() $\mathbf{CFG}{+}\Pi ^0_1\{\textsf {-BI},\textsf {-Ind}\} {+}\Sigma ^0_1\{\textsf {-Ind},\textsf {-DC}^{0}\!, \textsf {-DC}^{1}\}$
is finitistically justifiable; and these are optimal, as seen in Section 2.5.4.
$\mathbf{CFG}{+}\Pi ^0_1\{\textsf {-BI},\textsf {-Ind}\} {+}\Sigma ^0_1\{\textsf {-Ind},\textsf {-DC}^{0}\!, \textsf {-DC}^{1}\}$
is finitistically justifiable; and these are optimal, as seen in Section 2.5.4.
Thus we have completed Figures 1 and 2. Moreover 5.2, 3.62, 3.64, and 4.19 with the uses of
![]() $\mathfrak {g}$
, yield the below (some pairs in (d) have stronger preserving as 4.19(4)) as Avigad’s [Reference Avigad2] method preserves
$\mathfrak {g}$
, yield the below (some pairs in (d) have stronger preserving as 4.19(4)) as Avigad’s [Reference Avigad2] method preserves
![]() $\Pi ^0_2\textsf {-Ind}$
.
$\Pi ^0_2\textsf {-Ind}$
.
Corollary 5.3. The following are, in each case, mutually interpretable
![]() $\Pi ^0_2$
-preservingly:
$\Pi ^0_2$
-preservingly:
-
(a)
 $\mathbf{B}\boldsymbol {\Sigma }_1\mathbf{ex}$
,
$\mathbf{B}\boldsymbol {\Sigma }_1\mathbf{ex}$
,
 $\mathbf{FR}_0^*{{\kern-3pt}+{\kern-3pt}}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
,
$\mathbf{FR}_0^*{{\kern-3pt}+{\kern-3pt}}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
,
 $\mathbf{FR}_0^*{{\kern-3pt}+{\kern-3pt}}\Sigma ^0_1\textsf {-GDM}$
,
$\mathbf{FR}_0^*{{\kern-3pt}+{\kern-3pt}}\Sigma ^0_1\textsf {-GDM}$
,
 $\mathbf{EL}_0^*\,{\equiv }\,\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
and
$\mathbf{EL}_0^*\,{\equiv }\,\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-AC}^{00}$
and
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
;
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Bdg}$
; -
(b)
 $\mathbf{I}\boldsymbol {\Sigma }_1$
,
$\mathbf{I}\boldsymbol {\Sigma }_1$
,
 $\mathbf{FR}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
,
$\mathbf{FR}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1$
,
 $\mathbf{FR}_0{+}\Sigma ^0_1\textsf {-GDM}$
,
$\mathbf{FR}_0{+}\Sigma ^0_1\textsf {-GDM}$
,
 $\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
,
$\mathbf{EL}_0^-{+}\Sigma ^0_1\textsf {-Ind}$
,
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
,
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-FT}$
,
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-DC!}^0$
and
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-DC!}^0$
and
 $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-DC}^1$
;
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-DC}^1$
; -
(c)
 $\mathbf{I}\boldsymbol {\Sigma }_2$
,
$\mathbf{I}\boldsymbol {\Sigma }_2$
,
 $\mathbf{FR}^+_0{{\kern-3pt}+{\kern-3pt}}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^+_0{{\kern-3pt}+{\kern-3pt}}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^+_0{{\kern-3pt}+{\kern-3pt}}\Sigma ^0_1\textsf {-GDM}$
,
$\mathbf{FR}^+_0{{\kern-3pt}+{\kern-3pt}}\Sigma ^0_1\textsf {-GDM}$
,
 $\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}}\Pi ^0_2\textsf {-Ind}$
,
$\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}}\Pi ^0_2\textsf {-Ind}$
,
 $\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}}\Pi ^0_2\textsf {-DC}!^0\!$
,
$\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}}\Pi ^0_2\textsf {-DC}!^0\!$
,
 $\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}} \Pi ^0_1\textsf {-DC}!^1$
and
$\mathbf{EL}^-_0{{\kern-3pt}+{\kern-3pt}} \Pi ^0_1\textsf {-DC}!^1$
and
 $\mathbf{EL}^-_0{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
;
$\mathbf{EL}^-_0{+}\textsf {LPO}{+}\Sigma ^0_2\textsf {-Ind}$
; -
(d)
 $\mathbf{ACA}_0$
,
$\mathbf{ACA}_0$
,
 $\mathbf{FR}^{++}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^{++}_0{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^{++}_0{+}\Sigma ^0_1\textsf {-GDM}$
,
$\mathbf{FR}^{++}_0{+}\Sigma ^0_1\textsf {-GDM}$
,
 $\mathbf{EL}^-_0{+}\Sigma ^0_1\textsf {-BI}_D$
,
$\mathbf{EL}^-_0{+}\Sigma ^0_1\textsf {-BI}_D$
,
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT}$
,
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Delta ^0_0\textsf {-FT}$
,
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
and
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-WFT}$
and
 $\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
$\mathbf{EL}_0^-{+}\textsf {LPO}{+}\Pi ^0_1\textsf {-AC!}^{00}$
.
Moreover, so are theories in (b) with
![]() $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and
![]() $\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
but only
$\mathbf{EL}_0^-{+}\Delta ^0_0\textsf {-BI}_D$
but only
![]() $\Pi ^0_1$
-preservingly.
$\Pi ^0_1$
-preservingly.
Thus we determined the “interpretability strengths” of fragments of Brouwerian axioms for all
![]() $\Sigma ^0_n$
and
$\Sigma ^0_n$
and
![]() $\Pi ^0_n$
with semi-classical principles below
$\Pi ^0_n$
with semi-classical principles below
![]() $\Sigma ^0_1\textsf {-GDM}$
. For classes beyond
$\Sigma ^0_1\textsf {-GDM}$
. For classes beyond
![]() $\Pi ^0_{\infty }$
, we have the following hierarchized interpretability, since Avigad’s [Reference Avigad2] preserves also
$\Pi ^0_{\infty }$
, we have the following hierarchized interpretability, since Avigad’s [Reference Avigad2] preserves also
![]() $\Xi _{1,m}\textsf {-Ind}$
, which is interpreted in
$\Xi _{1,m}\textsf {-Ind}$
, which is interpreted in
![]() $\mathbf{I}\boldsymbol {\Sigma }_{m+2}$
by recursive indices.
$\mathbf{I}\boldsymbol {\Sigma }_{m+2}$
by recursive indices.
Corollary 5.4. The following are, in each case, mutually interpretable
![]() $\Pi ^0_2$
-preservingly:
$\Pi ^0_2$
-preservingly:
-
(a)
 $\mathbf{I}\boldsymbol {\Sigma }_{m+2}$
,
$\mathbf{I}\boldsymbol {\Sigma }_{m+2}$
,
 $\mathbf{FR}^+_{m}{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^+_{m}{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^+_{m}{+}\Sigma ^0_1\textsf {-GDM}$
,
$\mathbf{FR}^+_{m}{+}\Sigma ^0_1\textsf {-GDM}$
,
 $\mathbf{EL}^-_0{+}\Lambda ^0_{1,m}\textsf {-Ind}$
and
$\mathbf{EL}^-_0{+}\Lambda ^0_{1,m}\textsf {-Ind}$
and
 $\mathbf{EL}^-_0{+}\Lambda ^0_{1,m}\textsf {-DC!}^i$
;
$\mathbf{EL}^-_0{+}\Lambda ^0_{1,m}\textsf {-DC!}^i$
; -
(b)
 $\Pi ^1_{m+1} {\mathbf{-TI}}_0\,{:\equiv }\,\mathbf{ACA}_0{+}\Pi ^1_{m+1}\textsf {-TI}$
,
$\Pi ^1_{m+1} {\mathbf{-TI}}_0\,{:\equiv }\,\mathbf{ACA}_0{+}\Pi ^1_{m+1}\textsf {-TI}$
,
 $\mathbf{FR}^{++}_{m+1}{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^{++}_{m+1}{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^{++}_{m+1}{+}\Sigma ^0_1\textsf {-GDM}$
and
$\mathbf{FR}^{++}_{m+1}{+}\Sigma ^0_1\textsf {-GDM}$
and
 $\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
;
$\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D$
; -
(c)
 $\Pi ^1_{m+1} {\mathbf{-TI}}_0{+}\Pi ^1_{n+1}\textsf {-Ind}$
,
$\Pi ^1_{m+1} {\mathbf{-TI}}_0{+}\Pi ^1_{n+1}\textsf {-Ind}$
,
 $\mathbf{FR}^{++}_{m+1}\!{+}\mathbf{FR}^+_{n+1}\!{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^{++}_{m+1}\!{+}\mathbf{FR}^+_{n+1}\!{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^{++}_{m+1}\!{+}\mathbf{FR}^+_{n+1}\!{+}\Sigma ^0_1\textsf {-GDM}$
and
$\mathbf{FR}^{++}_{m+1}\!{+}\mathbf{FR}^+_{n+1}\!{+}\Sigma ^0_1\textsf {-GDM}$
and
 $\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D{+}\Lambda ^1_{1,n}\textsf {-Ind}$
;
$\mathbf{EL}_0^-{+}\Lambda ^1_{1,m}\textsf {-BI}_D{+}\Lambda ^1_{1,n}\textsf {-Ind}$
; -
(d)
 $\Pi ^1_{\infty } {\mathbf{-TI}}_0$
,
$\Pi ^1_{\infty } {\mathbf{-TI}}_0$
,
 $\mathbf{FR}^{++}_{\infty }{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
$\mathbf{FR}^{++}_{\infty }{+}\mathcal {L}_{\mathrm{F}}\textsf {-CC}^1\!$
,
 $\mathbf{FR}^{++}_{\infty }{+}\Sigma ^0_1\textsf {-GDM}$
and
$\mathbf{FR}^{++}_{\infty }{+}\Sigma ^0_1\textsf {-GDM}$
and
 $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
.
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-BI}_D$
.
Note that
![]() $\mathbf{ACA}_0$
is not interpretable in
$\mathbf{ACA}_0$
is not interpretable in
![]() $\textbf {PA}\,{\equiv }\,\mathbf{I}\boldsymbol {\Sigma }_{\infty }$
by f.n.20.
$\textbf {PA}\,{\equiv }\,\mathbf{I}\boldsymbol {\Sigma }_{\infty }$
by f.n.20.
![]() $\Pi ^1_{\infty } {\mathbf{-TI}}_0$
is known to be mutually interpretable with
$\Pi ^1_{\infty } {\mathbf{-TI}}_0$
is known to be mutually interpretable with
![]() $\textbf {ID}_1$
,
$\textbf {ID}_1$
,
![]() $\textbf {KP}$
and
$\textbf {KP}$
and
![]() $\textbf {CZF}$
, theories of generalized predicativity. (The interpretations of
$\textbf {CZF}$
, theories of generalized predicativity. (The interpretations of
![]() $\Pi ^1_{\infty } {\mathbf{-TI}}_0$
in
$\Pi ^1_{\infty } {\mathbf{-TI}}_0$
in
![]() $\textbf {ID}_1$
and of
$\textbf {ID}_1$
and of
![]() $\textbf {ID}_1$
in
$\textbf {ID}_1$
in
![]() $\textbf {KP}$
can be found in [Reference Sato42, Section 8]; that of
$\textbf {KP}$
can be found in [Reference Sato42, Section 8]; that of
![]() $\textbf {ID}_1$
in
$\textbf {ID}_1$
in
![]() $\Pi ^1_{\infty } {\mathbf{-TI}}_0$
is in [Reference Rathjen34, Lemma 3.2]; that of
$\Pi ^1_{\infty } {\mathbf{-TI}}_0$
is in [Reference Rathjen34, Lemma 3.2]; that of
![]() $\textbf {KP}$
in
$\textbf {KP}$
in
![]() $\textbf {ID}_1$
is in [Reference Tapp49] or [Reference Fujimoto17, Section 9.2]; that of
$\textbf {ID}_1$
is in [Reference Tapp49] or [Reference Fujimoto17, Section 9.2]; that of
![]() $\textbf {KP}$
in
$\textbf {KP}$
in
![]() $\textbf {CZF}$
is in [Reference Avigad3]; and that of
$\textbf {CZF}$
is in [Reference Avigad3]; and that of
![]() $\textbf {CZF}$
in
$\textbf {CZF}$
in
![]() $\textbf {KP}$
is in [Reference Rathjen33, Theorem 7.1].) As
$\textbf {KP}$
is in [Reference Rathjen33, Theorem 7.1].) As
![]() $\mathbf{FR}^{++}_{\infty }$
contains all the Brouwerian axioms formulated in
$\mathbf{FR}^{++}_{\infty }$
contains all the Brouwerian axioms formulated in
![]() $\mathcal {L}_{\mathrm{F}}$
except
$\mathcal {L}_{\mathrm{F}}$
except
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-CC}^i$
(see f.n.12), this could be “a marriage of Intuitionism and generalized predicativity”. However, these are beyond predicativity in Feferman’s [Reference Feferman15] sense, as
$\mathcal {L}_{\mathrm{F}}\textsf {-CC}^i$
(see f.n.12), this could be “a marriage of Intuitionism and generalized predicativity”. However, these are beyond predicativity in Feferman’s [Reference Feferman15] sense, as
![]() $\Pi ^1_{2} {\mathbf{-TI}}_0\vdash \textrm {Con}(\textbf {ATR}_0)$
(cf. [Reference Simpson45, Exercise VII.2.32]). With bar induction restricted to
$\Pi ^1_{2} {\mathbf{-TI}}_0\vdash \textrm {Con}(\textbf {ATR}_0)$
(cf. [Reference Simpson45, Exercise VII.2.32]). With bar induction restricted to
![]() $\Theta ^1_1$
, (c) with
$\Theta ^1_1$
, (c) with
![]() $(m,n)\,{=}\,(0,\infty )$
is in the predicative bound, or “a marriage of Intuitionism and predicativism”, as
$(m,n)\,{=}\,(0,\infty )$
is in the predicative bound, or “a marriage of Intuitionism and predicativism”, as
![]() $\Pi ^1_{1} {\mathbf{-TI}}_0\,{=}\,\Sigma ^1_1 {\textbf {-DC}}_0$
by [Reference Simpson45, Theorem VIII.5.12].
$\Pi ^1_{1} {\mathbf{-TI}}_0\,{=}\,\Sigma ^1_1 {\textbf {-DC}}_0$
by [Reference Simpson45, Theorem VIII.5.12].
For the semi-Russian axioms, 3.45 yields the first interpretability below, where by coding functions as recursive indices we interpret
![]() $\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\textsf {CT}$
in
$\mathbf{EL}_0^-{+}\mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Delta ^0_0\textsf {-AC}^{00}{+}\textsf {CT}$
in
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
. By additionally 3.49, 3.62 and 2.29(1), we have the other two. The converses are proved in Corollaries 5.3 and 5.4(a).
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
. By additionally 3.49, 3.62 and 2.29(1), we have the other two. The converses are proved in Corollaries 5.3 and 5.4(a).
![]() $\textsf {NCT}$
is consistent with
$\textsf {NCT}$
is consistent with
![]() $\mathcal {L}_{\mathrm{F}}\textsf {-CC}^0$
which contradicts
$\mathcal {L}_{\mathrm{F}}\textsf {-CC}^0$
which contradicts
![]() $\textsf {CT}$
(see f.n.8). Thus,
$\textsf {CT}$
(see f.n.8). Thus,
![]() $\textsf {CT}$
is strictly stronger than
$\textsf {CT}$
is strictly stronger than
![]() $\textsf {NCT}$
and than Veldman’s
$\textsf {NCT}$
and than Veldman’s
![]() $\textsf {KA}$
by 4.5.
$\textsf {KA}$
by 4.5.
Definition 5.5 (semi-Russian analysis
 $\textbf {SR}^-_0$
,
$\textbf {SR}^-_0$
,
 $\textbf {SR}^*_0$
,
$\textbf {SR}^*_0$
,
 $\textbf {SR}_0$
,
$\textbf {SR}_0$
,
 $\textbf {SR}^+_m$
)
$\textbf {SR}^+_m$
)
 $$ \begin{align*} &\textbf{SR}^-_0{:\equiv}\,\mathbf{EL}_0^-{+}\textsf{NCT}{+}\textsf{MP}{+} \mathcal{L}_{\textrm{F}}\textsf{-CC}^1;\\ &\textbf{SR}^*_0{:\equiv}\,\textbf{SR}^-_0{+}\mathcal{L}_{\textrm{F}}\{\textsf{-AC}^{00}\!, \textsf{-AC}^{01}\};\\ &\textbf{SR}_0{:\equiv}\,\textbf{SR}^*_0 {+}\Sigma^0_1\textsf{-DC}^1 {+}\Sigma^0_2\{\textsf{-Ind},\textsf{-DC}^0\} {+}\Pi^0_1\textsf{-BI};\\ &\textbf{SR}^+_m{:\equiv}\,\textbf{SR}_0{+}\Theta^1_m\{\textsf{-Ind},\textsf{-DC}^0\!,\textsf{-DC}^1\}. \end{align*} $$
$$ \begin{align*} &\textbf{SR}^-_0{:\equiv}\,\mathbf{EL}_0^-{+}\textsf{NCT}{+}\textsf{MP}{+} \mathcal{L}_{\textrm{F}}\textsf{-CC}^1;\\ &\textbf{SR}^*_0{:\equiv}\,\textbf{SR}^-_0{+}\mathcal{L}_{\textrm{F}}\{\textsf{-AC}^{00}\!, \textsf{-AC}^{01}\};\\ &\textbf{SR}_0{:\equiv}\,\textbf{SR}^*_0 {+}\Sigma^0_1\textsf{-DC}^1 {+}\Sigma^0_2\{\textsf{-Ind},\textsf{-DC}^0\} {+}\Pi^0_1\textsf{-BI};\\ &\textbf{SR}^+_m{:\equiv}\,\textbf{SR}_0{+}\Theta^1_m\{\textsf{-Ind},\textsf{-DC}^0\!,\textsf{-DC}^1\}. \end{align*} $$
Corollary 5.6.
![]() $\mathbf{SR}^*_0$
,
$\mathbf{SR}^*_0$
,
![]() $\mathbf{SR}_0$
and
$\mathbf{SR}_0$
and
![]() $\mathbf{SR}^+_m$
are interpretable in
$\mathbf{SR}^+_m$
are interpretable in
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\mathbf{ex}$
,
$\mathbf{B}\boldsymbol {\Sigma }_1\mathbf{ex}$
,
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
and
$\mathbf{I}\boldsymbol {\Sigma }_1$
and
![]() $\mathbf{I}\,\boldsymbol {\Sigma }_{m+2}$
, resp.,
$\mathbf{I}\,\boldsymbol {\Sigma }_{m+2}$
, resp.,
![]() $\Pi ^0_{\infty }$
-preservingly.
$\Pi ^0_{\infty }$
-preservingly.
5.2 Supplement:
 $\mathbf{I}\boldsymbol {\Sigma }_1 \vdash \mathrm{Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
as well as
$\mathbf{I}\boldsymbol {\Sigma }_1 \vdash \mathrm{Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
as well as
 $\mathbf{I}\boldsymbol {\Sigma }_1\,{\equiv }_{\Pi ^0_2}\,\mathbf{PRA}$
and
$\mathbf{I}\boldsymbol {\Sigma }_1\,{\equiv }_{\Pi ^0_2}\,\mathbf{PRA}$
and
 $\mathbf{I}\boldsymbol {\Sigma }_2 \vdash \mathrm{Con}(\mathbf{I}\boldsymbol {\Sigma }_1)$
$\mathbf{I}\boldsymbol {\Sigma }_2 \vdash \mathrm{Con}(\mathbf{I}\boldsymbol {\Sigma }_1)$
To conclude that theories interpretable in
![]() $\mathbf{WKL}_0^*$
are finitistically guaranteed, we used a folklore result
$\mathbf{WKL}_0^*$
are finitistically guaranteed, we used a folklore result
![]() $\mathbf{I}\boldsymbol {\Sigma }_1 \,{\vdash }\,\textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
(and hence
$\mathbf{I}\boldsymbol {\Sigma }_1 \,{\vdash }\,\textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
(and hence
![]() $\mathbf{PRA} \,{\vdash }\,\textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
by
$\mathbf{PRA} \,{\vdash }\,\textrm {Con}(\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex})$
by
![]() $\Pi _2$
-reducibility).
$\Pi _2$
-reducibility).
![]() $\mathbf{I}\boldsymbol {\Sigma }_1\,{\vdash }\,\textrm {Con}(\mathbf{EFA})$
and the
$\mathbf{I}\boldsymbol {\Sigma }_1\,{\vdash }\,\textrm {Con}(\mathbf{EFA})$
and the
![]() $\Pi ^0_2$
conservation of
$\Pi ^0_2$
conservation of
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
over
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
over
![]() $\mathbf{EFA}$
are stated in [Reference Simpson45, II.8.11, X.4.2], and the version without
$\mathbf{EFA}$
are stated in [Reference Simpson45, II.8.11, X.4.2], and the version without
![]() $\exp $
is proved in [Reference Hájek and Pudlák18, Chapter IV, Section 4(b)]. As we cannot find a reference for the folklore, we briefly sketch a proof with some byproducts.
$\exp $
is proved in [Reference Hájek and Pudlák18, Chapter IV, Section 4(b)]. As we cannot find a reference for the folklore, we briefly sketch a proof with some byproducts.
We formalize
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
by the following rules on the base of one-sided sequent calculus (in which
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
by the following rules on the base of one-sided sequent calculus (in which
![]() $\neg $
is a syntactical operation) for classical logic, where C is
$\neg $
is a syntactical operation) for classical logic, where C is
![]() $\Delta ^0_0$
and where z is an eigenvariable in (ind).
$\Delta ^0_0$
and where z is an eigenvariable in (ind).

By the standard partial cut elimination, we may assume that all cut formulae are
![]() $\Sigma ^0_1$
,
$\Sigma ^0_1$
,
![]() $\Pi ^0_1$
or
$\Pi ^0_1$
or
![]() $\Delta ^0_0$
. For a (one-sided) sequent
$\Delta ^0_0$
. For a (one-sided) sequent
![]() $\Gamma $
, we write
$\Gamma $
, we write
![]() $\Gamma ^{(n,m)}$
for the result of replacing all the unbounded quantifiers
$\Gamma ^{(n,m)}$
for the result of replacing all the unbounded quantifiers
![]() $\forall x$
and
$\forall x$
and
![]() $\exists y$
by
$\exists y$
by
![]() $(\forall x\,{<}\,n)$
and
$(\forall x\,{<}\,n)$
and
![]() $(\exists y\,{<}\,m)$
, respectively, in
$(\exists y\,{<}\,m)$
, respectively, in
![]() $\Gamma $
. By induction on derivation with free variables at most
$\Gamma $
. By induction on derivation with free variables at most
![]() $\vec {x}$
, we can show that there is an elementary function f with
$\vec {x}$
, we can show that there is an elementary function f with
![]() $\forall n(\forall \vec {x}\,{<}\,n)(\bigvee \Gamma ^{(n,f(n))})$
. Thus, if
$\forall n(\forall \vec {x}\,{<}\,n)(\bigvee \Gamma ^{(n,f(n))})$
. Thus, if
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}\vdash \bot $
then
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}\vdash \bot $
then
![]() $\bot $
.
$\bot $
.
While cut elimination increases the size of proofs by superexponential, it can be executed in
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
. Indices of elementary function can also be dealt with in
$\mathbf{I}\boldsymbol {\Sigma }_1$
. Indices of elementary function can also be dealt with in
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
, and the required f is constructed elementarily in the sense of indices from derivation. As
$\mathbf{I}\boldsymbol {\Sigma }_1$
, and the required f is constructed elementarily in the sense of indices from derivation. As
![]() $\forall n(\forall \vec {x}\,{<}\,n)(\bigvee \Gamma ^{(n,f(n))})$
is
$\forall n(\forall \vec {x}\,{<}\,n)(\bigvee \Gamma ^{(n,f(n))})$
is
![]() $\Pi ^0_1$
, we can formalize this argument in
$\Pi ^0_1$
, we can formalize this argument in
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
.
$\mathbf{I}\boldsymbol {\Sigma }_1$
.
Since
![]() $\mathcal {E}^n$
indices can also be dealt with,
$\mathcal {E}^n$
indices can also be dealt with,
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
proves the consistency of
$\mathbf{I}\boldsymbol {\Sigma }_1$
proves the consistency of
![]() $\mathbf{B}\boldsymbol {\Sigma }_1(\mathcal {E}^n)$
, defined similarly with function symbols for
$\mathbf{B}\boldsymbol {\Sigma }_1(\mathcal {E}^n)$
, defined similarly with function symbols for
![]() $\mathcal {E}^n$
(cf. f.n.13). If we allow C to be
$\mathcal {E}^n$
(cf. f.n.13). If we allow C to be
![]() $\Sigma ^0_1$
in (ind), such f’s can be primitive recursive, whose indices can be used in
$\Sigma ^0_1$
in (ind), such f’s can be primitive recursive, whose indices can be used in
![]() $\mathbf{I}\boldsymbol {\Sigma }_2$
. Thus
$\mathbf{I}\boldsymbol {\Sigma }_2$
. Thus
![]() $\mathbf{I}\boldsymbol {\Sigma }_1$
is reducible to
$\mathbf{I}\boldsymbol {\Sigma }_1$
is reducible to
![]() $\mathbf{PRA}$
over
$\mathbf{PRA}$
over
![]() $\Pi _2$
, and consistent provably in
$\Pi _2$
, and consistent provably in
![]() $\mathbf{I}\boldsymbol {\Sigma }_2$
.
$\mathbf{I}\boldsymbol {\Sigma }_2$
.
It is worth mentioning that, by cut elimination, we can easily show the equivalence between first-order formulation of
![]() $\mathbf{PRA}$
and quantifier-free formulation of
$\mathbf{PRA}$
and quantifier-free formulation of
![]() $\mathbf{PRA}$
: proving exactly same quantifier-free formulae with free variables. Tait’s [Reference Tait47] identification of Hilbert’s Finitism is with the latter, rather than the former.
$\mathbf{PRA}$
: proving exactly same quantifier-free formulae with free variables. Tait’s [Reference Tait47] identification of Hilbert’s Finitism is with the latter, rather than the former.
Notice that this subsection is the only part in which we use cut elimination method, and that the results do not survive for ultrafinitism mentioned in Section 1.8 (but survive for those accepting
![]() $\mathcal {E}^4$
from f.n.13). Actually, it is known [Reference Hájek and Pudlák18, Chapter V, 5.29 Corollary] that
$\mathcal {E}^4$
from f.n.13). Actually, it is known [Reference Hájek and Pudlák18, Chapter V, 5.29 Corollary] that
![]() $\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
cannot prove even the consistency of Robinson Arithmetic
$\mathbf{B}\boldsymbol {\Sigma }_1\textbf {ex}$
cannot prove even the consistency of Robinson Arithmetic
![]() $\textbf {Q}$
, and hence nor of the intuitionistic variant. Thus ultrafinitistically guaranteed parts must be even weaker.
$\textbf {Q}$
, and hence nor of the intuitionistic variant. Thus ultrafinitistically guaranteed parts must be even weaker.
It is interesting that forcing and realizability, which are sometimes seen as model construction methods, require only weaker meta-theories than cut elimination, the central technique in proof theory. For, it has been considered that proof theoretic arguments require weaker meta-theories than model theoretic ones.
5.3 Further problems
-
Strength of c-WFT: 4.8(1) actually shows that
 $c\textsf {-WFT}$
, a restriction of WFT to c-bars (
$c\textsf {-WFT}$
, a restriction of WFT to c-bars (
 $B[u]$
’s of the form
$B[u]$
’s of the form
 $\forall v(\beta (u{*}v)\,{=}\,0)$
), with
$\forall v(\beta (u{*}v)\,{=}\,0)$
), with
 $\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}$
, interprets
$\mathbf{EL}_0^-{+}\Sigma ^0_2\textsf {-DNE}$
, interprets
 $\mathbf{ACA}_0$
. Can
$\mathbf{ACA}_0$
. Can
 $\textsf {LPO}$
replace
$\textsf {LPO}$
replace
 $\Sigma ^0_2\textsf {-DNE}$
?
$\Sigma ^0_2\textsf {-DNE}$
?
 $c\textsf {-WFT}$
has a particular significance [Reference Berger6, Reference Berger and Bridges8], and is known to be strictly between
$c\textsf {-WFT}$
has a particular significance [Reference Berger6, Reference Berger and Bridges8], and is known to be strictly between
 $\Delta ^0_0\textsf {-WFT}$
and
$\Delta ^0_0\textsf {-WFT}$
and
 $\Pi ^0_1\textsf {-WFT}$
(where the border lies; Fig. 2).
$\Pi ^0_1\textsf {-WFT}$
(where the border lies; Fig. 2). -
Hierarchy of WWFT and LPO: In the constructive context, weak weak König’s lemma investigated in, e.g., the first author [Reference Nemoto27], should be called weak weak fan theorem
 $\mathcal {C}\textsf {-WWFT}$
, since it is a weakened version of
$\mathcal {C}\textsf {-WWFT}$
, since it is a weakened version of
 $\mathcal {C}\textsf {-WFT}$
rather than of
$\mathcal {C}\textsf {-WFT}$
rather than of
 $\mathcal {C}\textsf {-WKL}$
. What is the strength of
$\mathcal {C}\textsf {-WKL}$
. What is the strength of
 $\mathcal {C}\textsf {-WWFT}{+}\textsf {LPO}$
, especially for
$\mathcal {C}\textsf {-WWFT}{+}\textsf {LPO}$
, especially for
 $\mathcal {C}\equiv \Pi ^0_1$
?
$\mathcal {C}\equiv \Pi ^0_1$
? -
 $\Pi ^0_3$
conservation of
$\Pi ^0_3$
conservation of
 $\Delta ^0_0$
-FT: Whereas 4.19(4)(b) asserts the
$\Delta ^0_0$
-FT: Whereas 4.19(4)(b) asserts the
 $\Pi ^0_3$
conservation of
$\Pi ^0_3$
conservation of
 $\mathbf{EL}_0^-{+} \mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Pi ^0_1\textsf {-WFT}$
over
$\mathbf{EL}_0^-{+} \mathcal {L}_{\mathrm{F}}\textsf {-LEM}{+}\Pi ^0_1\textsf {-WFT}$
over
 $\mathbf{EL}_0^-{+} \textsf { LPO}{+}\Pi ^0_1\textsf {-WFT}$
, (a) asserts similar but only
$\mathbf{EL}_0^-{+} \textsf { LPO}{+}\Pi ^0_1\textsf {-WFT}$
, (a) asserts similar but only
 $\Pi ^0_2$
one for
$\Pi ^0_2$
one for
 $\Delta ^0_0\textsf {-FT}$
. Can it be enhanced to
$\Delta ^0_0\textsf {-FT}$
. Can it be enhanced to
 $\Pi ^0_3$
?
$\Pi ^0_3$
? -
Effect of WLPO: We classified the axioms of Intuitionistic Mathematics into the three categories, finitistically non-justifiable, justifiable and guaranteed ones, in the presence of any semi-classical principle beyond
 $\textsf {LPO}$
or below
$\textsf {LPO}$
or below
 $\Sigma ^0_1\textsf {-GDM}$
. Among those in the gap is
$\Sigma ^0_1\textsf {-GDM}$
. Among those in the gap is
 $\textsf {WLPO}\,{\equiv }\,\Pi ^0_1\textsf {-LEM}$
. How is the classification in the presence of it?
$\textsf {WLPO}\,{\equiv }\,\Pi ^0_1\textsf {-LEM}$
. How is the classification in the presence of it?
 $\textsf {LPO}$
seems essential in the lower bound proofs (i.e., 4.7(2), 4.12(3) and 2.35(2)(ii)).
$\textsf {LPO}$
seems essential in the lower bound proofs (i.e., 4.7(2), 4.12(3) and 2.35(2)(ii)). -
Effect of Baire’s category theorem: It is mentioned in Section 1.5 that the effect of the semi-classical principle
 $\textsf {LLPO}$
is of our special interest because of its similar status as WKL, which plays a central role in Simpson’s “partial realizations of Hilbert’s Program”. Simpson [Reference Simpson44] also mentioned the role of Baire’s category theorem (BCT).Footnote
21
What is to BCT that
$\textsf {LLPO}$
is of our special interest because of its similar status as WKL, which plays a central role in Simpson’s “partial realizations of Hilbert’s Program”. Simpson [Reference Simpson44] also mentioned the role of Baire’s category theorem (BCT).Footnote
21
What is to BCT that
 $\textsf {LLPO}$
is to WKL? And how is the effect of it in the sense of last paragraph?
$\textsf {LLPO}$
is to WKL? And how is the effect of it in the sense of last paragraph?
5.4 Related works
Similar investigations in set theory
While we considered the axioms in the language
![]() $\mathcal {L}_{\mathrm{F}}$
, the authors are preparing an article [Reference Nemoto and Sato30] on the same questions in the language of set theory. The abstract treatment in Section 3.2 will be helpful. The axiom of choice along functions can now be formulated without twist, and it is natural to consider also some set theoretic principles, e.g., replacement, collection, subset collection, extensionality and regularity or foundation. Whereas the first two correspond to unique and non-unique axioms of choice, respectively, the others seem specific to set theory. As we want to have
$\mathcal {L}_{\mathrm{F}}$
, the authors are preparing an article [Reference Nemoto and Sato30] on the same questions in the language of set theory. The abstract treatment in Section 3.2 will be helpful. The axiom of choice along functions can now be formulated without twist, and it is natural to consider also some set theoretic principles, e.g., replacement, collection, subset collection, extensionality and regularity or foundation. Whereas the first two correspond to unique and non-unique axioms of choice, respectively, the others seem specific to set theory. As we want to have
![]() $\omega $
and to stay within the strength of
$\omega $
and to stay within the strength of
![]() $\mathbf{PRA}$
, we shall consider “weak weak” set theory in the sense of the second author [Reference Sato37].
$\mathbf{PRA}$
, we shall consider “weak weak” set theory in the sense of the second author [Reference Sato37].
Independence of negated premise
Our use of realizability allowed us to add Markov’s principle
![]() $\textsf {MP}$
to the upper bound results, for the realizing system
$\textsf {MP}$
to the upper bound results, for the realizing system
![]() $\textbf {CDL}$
was untyped. With typed systems we can add independence of negated premise
$\textbf {CDL}$
was untyped. With typed systems we can add independence of negated premise
-
(
 $\mathcal {C}\textsf {-INP}$
):
$\mathcal {C}\textsf {-INP}$
):
 $(\neg A\,{\to }\,\exists xB[x]) \,{\to }\,\exists x(\neg A\,{\to }\,B[x])$
for A from
$(\neg A\,{\to }\,\exists xB[x]) \,{\to }\,\exists x(\neg A\,{\to }\,B[x])$
for A from
 $\mathcal {C}$
$\mathcal {C}$
instead, from which follows Vesley’s [Reference Vesley55] alternative formalization of creative subject mentioned in f.n.14. In this way, we could have a marriage of “subjective Intuitionism” and Hilbert’s Finitism. Ishihara and the first author [Reference Ishihara and Nemoto22] used a translation
![]() $*$
for
$*$
for
![]() $\textsf {INP}$
-rule in the same sense as Friedman’s A-translation is for
$\textsf {INP}$
-rule in the same sense as Friedman’s A-translation is for
![]() $\textsf {MP}$
-rule. Following the way from A-translation to Coquand–Hofmann forcing (cf. Section 4.2), we can define, from
$\textsf {MP}$
-rule. Following the way from A-translation to Coquand–Hofmann forcing (cf. Section 4.2), we can define, from
![]() $*$
, a forcing interpreting
$*$
, a forcing interpreting
![]() $\mathcal {C}\textsf {-INP}$
for reasonable
$\mathcal {C}\textsf {-INP}$
for reasonable
![]() $\mathcal {C}$
. Avigad’s forcing from [Reference Avigad3] can be seen as such an interpretation.
$\mathcal {C}$
. Avigad’s forcing from [Reference Avigad3] can be seen as such an interpretation.
Constructive reverse mathematics based on our base theories
In this article, we have introduced theories
![]() $\mathbf{EL}_0^-$
,
$\mathbf{EL}_0^-$
,
![]() $\mathbf{EL}_0^*$
,
$\mathbf{EL}_0^*$
,
![]() $\mathbf{EL}_0$
and
$\mathbf{EL}_0$
and
![]() $\mathbf{EL}$
, which are intended to be base theories of constructive reverse mathematics. During unusually delayed publishing procedure of this article, the authors have conducted some studies based on these base theories, e.g., [Reference Nemoto29] and [Reference Sato40].
$\mathbf{EL}$
, which are intended to be base theories of constructive reverse mathematics. During unusually delayed publishing procedure of this article, the authors have conducted some studies based on these base theories, e.g., [Reference Nemoto29] and [Reference Sato40].
Complexity of Kleene’s second model
In the context of
![]() $\mathbf{EL}$
, Kleene’s second model
$\mathbf{EL}$
, Kleene’s second model
![]() $\mathfrak {k}$
can be seen as a definable extension, as the systems are not sensitive to the complexity below arithmetic
$\mathfrak {k}$
can be seen as a definable extension, as the systems are not sensitive to the complexity below arithmetic
![]() $\Delta ^1_0$
. However, if the system is sensitive (like those we considered), it cannot be seen so, since the atomic formulae
$\Delta ^1_0$
. However, if the system is sensitive (like those we considered), it cannot be seen so, since the atomic formulae
![]() $(\alpha |\beta ){\downarrow }$
and
$(\alpha |\beta ){\downarrow }$
and
![]() $\alpha \,{=}\,\beta |\gamma $
are not in the base complexity. Recently Jäger, Rosebrock and the second author [Reference Jäger, Rosebrock and Sato23] makes use of this unusual complexity, to separate: enumerable by operation; being the domain of an operation; and being the image of an operation. They are equivalent if we interpret ‘operation’ as ‘partial recursive function’.
$\alpha \,{=}\,\beta |\gamma $
are not in the base complexity. Recently Jäger, Rosebrock and the second author [Reference Jäger, Rosebrock and Sato23] makes use of this unusual complexity, to separate: enumerable by operation; being the domain of an operation; and being the image of an operation. They are equivalent if we interpret ‘operation’ as ‘partial recursive function’.
Making-a-detour method
We used realizability interpretations (as upper bound proofs) to embed intuitionistic systems into classical
![]() $\mathbf{WKL}_0^*$
and
$\mathbf{WKL}_0^*$
and
![]() $\mathbf{WKL}_0$
, and a combination of negative and forcing interpretations (as lower bound proofs) to embed classical ones into intuitionistic ones. The composition of both the directions results in an interpretation of classical ones in classical ones, of the same kind as that the second author [Reference Sato and Zumbrunnen43] (with Zumbrunnen) and [Reference Sato38] introduced under the name of “making a detour via intuitionistic systems”. This is the third kind of such model construction methods for classical theories that logical connectives are interpreted non-trivially (see Section 1.2), after Cohen’s classical forcing and Krivine’s classical realizability. We would like to stress that interpretations between intuitionistic ones could help studies of classical theories. In the next paper [Reference Sato41] in this series, the second author uses the results of the present article and the making-a-detour method, in order to get interpretations among classical theories of second order arithmetic that are standard in classical reverse mathematics. A further paper [Reference Sato42] follows.
$\mathbf{WKL}_0$
, and a combination of negative and forcing interpretations (as lower bound proofs) to embed classical ones into intuitionistic ones. The composition of both the directions results in an interpretation of classical ones in classical ones, of the same kind as that the second author [Reference Sato and Zumbrunnen43] (with Zumbrunnen) and [Reference Sato38] introduced under the name of “making a detour via intuitionistic systems”. This is the third kind of such model construction methods for classical theories that logical connectives are interpreted non-trivially (see Section 1.2), after Cohen’s classical forcing and Krivine’s classical realizability. We would like to stress that interpretations between intuitionistic ones could help studies of classical theories. In the next paper [Reference Sato41] in this series, the second author uses the results of the present article and the making-a-detour method, in order to get interpretations among classical theories of second order arithmetic that are standard in classical reverse mathematics. A further paper [Reference Sato42] follows.
Relation to Veldman’s work
While we discussed the strength of fan theorem analogously to that of König’s lemma in the classical setting at the beginning of Section 3.3.3, the former is not as strong as the latter. The branching
![]() $\left \{x{:}\,\gamma (u{*}\langle x\rangle )\,{=}\,0\right \}$
of the fan
$\left \{x{:}\,\gamma (u{*}\langle x\rangle )\,{=}\,0\right \}$
of the fan
![]() $\gamma $
in 4.7(1) has at most
$\gamma $
in 4.7(1) has at most
![]() $t[|u|]{+}2$
elements, and hence is almost-finite and bounded-in-number (both from [Reference Veldman53, Section 10.2]). With these notions Veldman looks for an axiom which is intuitionistically to (weak) fan theorem as König’s lemma is classically to weak König’s lemma.
$t[|u|]{+}2$
elements, and hence is almost-finite and bounded-in-number (both from [Reference Veldman53, Section 10.2]). With these notions Veldman looks for an axiom which is intuitionistically to (weak) fan theorem as König’s lemma is classically to weak König’s lemma.
Proof theoretic ordinals
In proof theory, the strength of a formal theory is measured by the so-called proof theoretic ordinal. While there are various definitions, the standard definitions 1, 2, 6 from [Reference Sato39, Section 1.2] assign the same ordinal to the theories that are
![]() $\Pi ^0_2$
-equivalent provably in
$\Pi ^0_2$
-equivalent provably in
![]() $\mathbf{PRA}$
. Particularly,
$\mathbf{PRA}$
. Particularly,
![]() $\omega ^\omega $
is assigned to the theories in Corollary 5.2(2) and in Corollary 5.3(b) as well as
$\omega ^\omega $
is assigned to the theories in Corollary 5.2(2) and in Corollary 5.3(b) as well as
![]() $\mathbf{SR}_0$
;
$\mathbf{SR}_0$
;
![]() $\omega ^{\omega ^\omega }$
to those in Corollary 5.3(c) and as well as
$\omega ^{\omega ^\omega }$
to those in Corollary 5.3(c) and as well as
![]() $\mathbf{SR}_0^+$
; and
$\mathbf{SR}_0^+$
; and
![]() $\varepsilon _0\,{=}\,\sup \{\omega ,\omega ^\omega ,\omega ^{\omega ^\omega },\ldots \}$
to those in Corollary 5.3(d). Although these are well-known facts, the second author [Reference Sato39] has recently given proofs to them. The ordinal assigned to the theories in Corollary 5.3(a) and in Corollary 5.2(1) as well as
$\varepsilon _0\,{=}\,\sup \{\omega ,\omega ^\omega ,\omega ^{\omega ^\omega },\ldots \}$
to those in Corollary 5.3(d). Although these are well-known facts, the second author [Reference Sato39] has recently given proofs to them. The ordinal assigned to the theories in Corollary 5.3(a) and in Corollary 5.2(1) as well as
![]() $\mathbf{SR}_0^*$
is said to be sometimes
$\mathbf{SR}_0^*$
is said to be sometimes
![]() $\omega ^2$
and sometimes
$\omega ^2$
and sometimes
![]() $\omega ^3$
(as well as
$\omega ^3$
(as well as
![]() $\omega $
,
$\omega $
,
![]() $0$
, etc.), depending on which definition of proof theoretic ordinal we take, as discussed in [Reference Sato39, Appendix B]. The ordinal assigned to
$0$
, etc.), depending on which definition of proof theoretic ordinal we take, as discussed in [Reference Sato39, Appendix B]. The ordinal assigned to
![]() $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-Ind}$
and
![]() $\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-BI}$
, the other theories in Corollary 5.3, also depends, as we have only
$\mathbf{EL}_0^-{+}\Pi ^0_1\textsf {-BI}$
, the other theories in Corollary 5.3, also depends, as we have only
![]() $\Pi ^0_1$
-equivalence with those in Corollary 5.3(b).
$\Pi ^0_1$
-equivalence with those in Corollary 5.3(b).
Acknowledgements
The authors are deeply indebted to Timotej Rosebrock for checking and correcting the definition of Kleene’s second model
![]() $\mathfrak {k}$
, and they are very grateful to François Dorais for having an invaluable discussion with the second author about one of our main methods, van Oosten’s Lifschitz-style functional realizability with weak induction. They also thank Lev Gordeev, Danko Ilik, Hajime Ishihara, Dick de Jongh, Tatsuji Kawai, Graham Leigh, Stephen Simpson, Wim Veldman and the two anonymous referees for their careful reading and invaluable comments on earlier versions of this article. Their special appreciation goes to Reinhard Kahle for his patience and kind help during the typesetting procedure.
$\mathfrak {k}$
, and they are very grateful to François Dorais for having an invaluable discussion with the second author about one of our main methods, van Oosten’s Lifschitz-style functional realizability with weak induction. They also thank Lev Gordeev, Danko Ilik, Hajime Ishihara, Dick de Jongh, Tatsuji Kawai, Graham Leigh, Stephen Simpson, Wim Veldman and the two anonymous referees for their careful reading and invaluable comments on earlier versions of this article. Their special appreciation goes to Reinhard Kahle for his patience and kind help during the typesetting procedure.
The second author was supported by the John Templeton Foundation during revisions of this article. This publication was made possible through the support of a grant from the John Templeton Foundation. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.