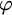1 Introduction
In this article, we introduce the notion of many-one reducibility for sets with witnesses and reanalyze the arithmetical/Borel/projective hierarchy under this new reducibility notion. In computational complexity theory, the notion of polytime many-one reducibility for sets with witnesses (i.e., search problems or function problems) is known as Levin reducibility [Reference Levin4], but strangely enough, it seems that its computable analogue has never been studied.
Definition 1.1 (Levin [Reference Levin4])
Let
![]() $\Sigma $
be a finite alphabet. A search problem (or a set with witnesses) is a binary relation
$\Sigma $
be a finite alphabet. A search problem (or a set with witnesses) is a binary relation
![]() $R\subseteq \Sigma ^\ast \times \Sigma ^\ast $
, and any y satisfying
$R\subseteq \Sigma ^\ast \times \Sigma ^\ast $
, and any y satisfying
![]() $R(x,y)$
is called a witness (or a certificate) for
$R(x,y)$
is called a witness (or a certificate) for
![]() $x\in |R|$
, where
$x\in |R|$
, where
![]() $|R|=\{x:\exists yR(x,y)\}$
. For a complexity class
$|R|=\{x:\exists yR(x,y)\}$
. For a complexity class
![]() $\mathcal {C}$
and search problems A and B, we say that A is
$\mathcal {C}$
and search problems A and B, we say that A is
![]() $\mathcal {C}$
-Levin reducible to B if there exist
$\mathcal {C}$
-Levin reducible to B if there exist
![]() $\mathcal {C}$
-functions
$\mathcal {C}$
-functions
![]() $\varphi ,r_-,r_+$
such that for any
$\varphi ,r_-,r_+$
such that for any
![]() $x,y,z\in \Sigma ^\ast $
the following holds:
$x,y,z\in \Sigma ^\ast $
the following holds:
-
1.
 $x\in |A|$
if and only if
$x\in |A|$
if and only if
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
2. If y is a witness for
 $x\in |A|$
then
$x\in |A|$
then
 $r_-(x,y)$
is a witness for
$r_-(x,y)$
is a witness for
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
3. If z is a witness for
 $\varphi (x)\in |B|$
then
$\varphi (x)\in |B|$
then
 $r_+(x,z)$
is a witness for
$r_+(x,z)$
is a witness for
 $x\in |A|$
.
$x\in |A|$
.
As a closer look at the definition shows, Levin reducibility is nothing more than the realizability interpretation of many-one reducibility. In this article, we introduce the notion of many-one reducibility for subobjects in any category having pullbacks, and observe that the same definition as computable Levin reducibility is restored as many-one reducibility in the category of represented spaces. This perspective unexpectedly connects the notion of Levin reducibility with the study of arithmetical/Borel/projective hierarchy in intuitionistic systems.
The notion of many-one reducibility in intuitionistic/constructive systems was first studied exhaustively by Veldman [Reference Veldman9, Reference Veldman10, Reference Veldman12, Reference Veldman13] and later more recently by [Reference Forster and Jahn3] and others. According to Veldman, the intuitionistic Borel/projective hierarchy behaves differently from the classical hierarchy. For instance, Veldman showed that, under a certain intuitionistic system, the union of two
![]() $\Pi ^0_1$
sets is not necessarily
$\Pi ^0_1$
sets is not necessarily
![]() $\Pi ^0_1$
[Reference Veldman9], the set
$\Pi ^0_1$
[Reference Veldman9], the set
![]() $\mathsf {Fin}$
of all sequences which is eventually zero is not
$\mathsf {Fin}$
of all sequences which is eventually zero is not
![]() $\Sigma ^0_2$
-complete [Reference Veldman12], and the set
$\Sigma ^0_2$
-complete [Reference Veldman12], and the set
![]() $\mathsf {IFKB}$
of all trees which are ill-founded w.r.t. the Kleene–Brouwer ordering is not
$\mathsf {IFKB}$
of all trees which are ill-founded w.r.t. the Kleene–Brouwer ordering is not
![]() $\Sigma ^1_1$
-complete [Reference Veldman13].
$\Sigma ^1_1$
-complete [Reference Veldman13].
We see that these seemingly strange results can be clearly understood using Levin reducibility. The category of represented spaces has the natural numbers object
![]() $\omega $
, the exponential object
$\omega $
, the exponential object
![]() $\omega ^\omega $
, and the interpretation of first-order logic, so one can introduce the notion of arithmetic/Borel/projective subobjects by interpreting their defining formulas in the internal logic. Moreover, in this category, a subobject is nothing but a subset with witnesses. Based on these observations, for instance, one can understand Veldman’s result as meaning that the witnessed version of
$\omega ^\omega $
, and the interpretation of first-order logic, so one can introduce the notion of arithmetic/Borel/projective subobjects by interpreting their defining formulas in the internal logic. Moreover, in this category, a subobject is nothing but a subset with witnesses. Based on these observations, for instance, one can understand Veldman’s result as meaning that the witnessed version of
![]() $\mathsf {Fin}$
is simply not Levin-complete among the witnessed
$\mathsf {Fin}$
is simply not Levin-complete among the witnessed
![]() $\Sigma ^0_2$
subsets (in classical mathematics). The same applies to
$\Sigma ^0_2$
subsets (in classical mathematics). The same applies to
![]() $\mathsf {IFKB}$
. In this way, even classical mathematicians can clearly understand Veldman’s results on the intuitionistic hierarchy.
$\mathsf {IFKB}$
. In this way, even classical mathematicians can clearly understand Veldman’s results on the intuitionistic hierarchy.
Of course, merely giving an interpretation of the existing results is not very interesting, so we push this point of view forward with further analysis of many-one/Levin degrees of witnessed sets. In this article, we focus in particular on
![]() $\Sigma ^0_2$
sets with their existential witnesses. Our results are summarized in Figure 1.
$\Sigma ^0_2$
sets with their existential witnesses. Our results are summarized in Figure 1.

Figure 1 The fine analysis of classical
![]() $\Sigma ^0_2$
-complete sets.
$\Sigma ^0_2$
-complete sets.
For example,
![]() $\mathsf {Fin}$
is many-one/Levin complete among
$\mathsf {Fin}$
is many-one/Levin complete among
![]() $\Sigma ^0_2$
sets defined by formulas of the form
$\Sigma ^0_2$
sets defined by formulas of the form
![]() $\exists n\forall m\geq n.\varphi (m,x)$
, where
$\exists n\forall m\geq n.\varphi (m,x)$
, where
![]() $\varphi $
is decidable. The decision of boundedness for posets
$\varphi $
is decidable. The decision of boundedness for posets
![]() $\mathsf {BddPO}$
is also at the same level. The decision of boundedness for sequences
$\mathsf {BddPO}$
is also at the same level. The decision of boundedness for sequences
![]() $\mathsf {BddSeq}$
is many-one/Levin complete among
$\mathsf {BddSeq}$
is many-one/Levin complete among
![]() $\Sigma ^0_2$
sets defined by formulas of the form
$\Sigma ^0_2$
sets defined by formulas of the form
![]() $\exists n\forall m\geq n\forall k.\varphi (m,k,x)$
, where
$\exists n\forall m\geq n\forall k.\varphi (m,k,x)$
, where
![]() $\varphi $
is decidable. The decision of finiteness for width
$\varphi $
is decidable. The decision of finiteness for width
![]() $\mathsf {FinWidth}$
and height
$\mathsf {FinWidth}$
and height
![]() $\mathsf {FinHeight}$
for posets are also at the same level. The decision of non-density of linear orders
$\mathsf {FinHeight}$
for posets are also at the same level. The decision of non-density of linear orders
![]() $\mathsf {NonDense}$
is truly
$\mathsf {NonDense}$
is truly
![]() $\Sigma ^0_2$
-complete. In this way, the focus on (existential) witnesses leads us to the discovery of a previously unknown classification of
$\Sigma ^0_2$
-complete. In this way, the focus on (existential) witnesses leads us to the discovery of a previously unknown classification of
![]() $\Sigma ^0_2$
sets.
$\Sigma ^0_2$
sets.
2 Preliminaries
2.1 Represented space
A coding system is a set
![]() $\mathtt {Code}$
of symbols for coding various mathematical objects, with a prior specification of which functions on
$\mathtt {Code}$
of symbols for coding various mathematical objects, with a prior specification of which functions on
![]() $\mathtt {Code}$
are realizable. There are three typical coding systems:
$\mathtt {Code}$
are realizable. There are three typical coding systems:
-
1. Kleene’s first algebra
 $\mathsf {K}_1$
:
$\mathsf {K}_1$
:
 $\mathtt {Code}=\omega $
, and
$\mathtt {Code}=\omega $
, andrealizable functions
 $=$
computable functions on
$=$
computable functions on
 $\omega $
.
$\omega $
. -
2. Kleene’s second algebra
 $\mathsf {K}_2$
:
$\mathsf {K}_2$
:
 $\mathtt {Code}=\omega ^\omega $
, and
$\mathtt {Code}=\omega ^\omega $
, andrealizable functions
 $=$
continuous functions on
$=$
continuous functions on
 $\omega ^\omega $
.
$\omega ^\omega $
. -
3. Kleene-Vesley algebra
 $\mathsf {KV}$
:
$\mathsf {KV}$
:
 $\mathtt {Code}=\omega ^\omega $
, and
$\mathtt {Code}=\omega ^\omega $
, andrealizable functions
 $=$
computable functions on
$=$
computable functions on
 $\omega ^\omega $
.
$\omega ^\omega $
.
Here,
![]() $\omega $
denotes the set of all natural numbers.
$\omega $
denotes the set of all natural numbers.
Notation. We write
![]() $p\ast x$
as the output result of feeding an input x to the realizable function coded by p. For instance,
$p\ast x$
as the output result of feeding an input x to the realizable function coded by p. For instance,
![]() $e\ast x$
in
$e\ast x$
in
![]() $\mathsf {K}_1$
stands for
$\mathsf {K}_1$
stands for
![]() $\{e\}(x)$
or
$\{e\}(x)$
or
![]() $\varphi _e(x)$
in traditional notation.
$\varphi _e(x)$
in traditional notation.
Hereafter we assume that a coding system
![]() $\mathtt {Code}$
is one of
$\mathtt {Code}$
is one of
![]() $\mathsf {K}_1$
,
$\mathsf {K}_1$
,
![]() $\mathsf {K}_2$
, or
$\mathsf {K}_2$
, or
![]() $\mathsf {KV}$
. Of course, it is obviously possible to consider an arbitrary relative partial combinatory algebra (or more) as a coding system [Reference van Oosten6]. However, in order to lower the threshold for reading, we avoid unnecessary generalizations as much as possible.
$\mathsf {KV}$
. Of course, it is obviously possible to consider an arbitrary relative partial combinatory algebra (or more) as a coding system [Reference van Oosten6]. However, in order to lower the threshold for reading, we avoid unnecessary generalizations as much as possible.
Definition 2.1. A represented space X consists of an underlying set
![]() $|X|$
and a partial surjection
$|X|$
and a partial surjection
![]() $\delta _X\colon \!\!\!\subseteq \mathtt {Code}\to |X|$
. We sometimes use the symbol
$\delta _X\colon \!\!\!\subseteq \mathtt {Code}\to |X|$
. We sometimes use the symbol
![]() $p\vdash _Xx$
to denote
$p\vdash _Xx$
to denote
![]() $\delta _X(p)=x$
, and say that p is an X-name of x or p is a name of
$\delta _X(p)=x$
, and say that p is an X-name of x or p is a name of
![]() $x\in X$
.
$x\in X$
.
We sometimes use
![]() $E_X(x)$
to denote the set of all names of
$E_X(x)$
to denote the set of all names of
![]() $x\in X$
.
$x\in X$
.
Example 2.2.
![]() $\mathtt {Code}$
itself is a represented space via the identity map
$\mathtt {Code}$
itself is a represented space via the identity map
![]() $\mathrm {id}\colon \mathtt {Code}\to \mathtt {Code}$
.
$\mathrm {id}\colon \mathtt {Code}\to \mathtt {Code}$
.
Example 2.3. The terminal space
![]() $\mathbf {1}$
is defined as follows: The underlying set is
$\mathbf {1}$
is defined as follows: The underlying set is
![]() $|\mathbf {1}|=\{\bullet \}$
, and any
$|\mathbf {1}|=\{\bullet \}$
, and any
![]() $p\in \mathtt {Code}$
is a name of its unique element
$p\in \mathtt {Code}$
is a name of its unique element
![]() $\bullet $
.
$\bullet $
.
Example 2.4. The space of natural numbers
![]() $\mathsf {Nat}$
is defined as follows: The underlying set is
$\mathsf {Nat}$
is defined as follows: The underlying set is
![]() $|\mathsf {Nat}|=\omega $
. In
$|\mathsf {Nat}|=\omega $
. In
![]() $\mathsf {K}_1$
,
$\mathsf {K}_1$
,
![]() $n\in \omega $
is a name of
$n\in \omega $
is a name of
![]() $n\in \mathsf {Nat}$
. In
$n\in \mathsf {Nat}$
. In
![]() $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
![]() $\mathsf {KV}$
,
$\mathsf {KV}$
,
![]() $n0^\infty \in \omega ^\omega $
is a name of
$n0^\infty \in \omega ^\omega $
is a name of
![]() $n\in \mathsf {Nat}$
, where
$n\in \mathsf {Nat}$
, where
![]() $n0^\infty $
is the infinite string resulting from concatenating n followed by the zero sequence
$n0^\infty $
is the infinite string resulting from concatenating n followed by the zero sequence
![]() $0^\infty $
; that is,
$0^\infty $
; that is,
![]() $(n0^\infty )(0)=n$
and
$(n0^\infty )(0)=n$
and
![]() $(n0^\infty )(k)=0$
for any
$(n0^\infty )(k)=0$
for any
![]() $k>0$
. By an abuse of notation, we often use
$k>0$
. By an abuse of notation, we often use
![]() $\omega $
to denote
$\omega $
to denote
![]() $\mathsf {Nat}$
.
$\mathsf {Nat}$
.
Example 2.5. The represented Sierpiński space
![]() $\mathbb {S}$
is defined as follows:
$\mathbb {S}$
is defined as follows:
-
• The underlying set is
 $|\mathbb {S}|=\{\top ,\bot \}$
.
$|\mathbb {S}|=\{\top ,\bot \}$
. -
• (
 $\mathsf {K}_1$
) If
$\mathsf {K}_1$
) If
 $p\ast 0\downarrow $
then p is a name of
$p\ast 0\downarrow $
then p is a name of
 $\top $
else p is a name of
$\top $
else p is a name of
 $\bot $
.
$\bot $
. -
• (
 $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
 $\mathsf {KV}$
) The zero sequence
$\mathsf {KV}$
) The zero sequence
 $0^\infty $
is a name of
$0^\infty $
is a name of
 $\bot $
and the other sequences are names of
$\bot $
and the other sequences are names of
 $\top $
.
$\top $
.
See also Bauer [Reference Bauer1] for a common construction of the Sierpiński space (a.k.a. the Rosolini dominance) in general coding systems.
Definition 2.6. Let X and Y be represented spaces. A morphism
![]() $f\colon X\to Y$
is a function
$f\colon X\to Y$
is a function
![]() $f\colon |X|\to |Y|$
such that there exists a partial realizable function F on
$f\colon |X|\to |Y|$
such that there exists a partial realizable function F on
![]() $\mathtt {Code}$
such that if p is a name of
$\mathtt {Code}$
such that if p is a name of
![]() $x\in X$
then
$x\in X$
then
![]() $F(p)$
is a name of
$F(p)$
is a name of
![]() $f(x)\in Y$
. We often call F a tracker of f.
$f(x)\in Y$
. We often call F a tracker of f.
Definition 2.7. For represented spaces
![]() $X,Y$
, a morphism
$X,Y$
, a morphism
![]() $f\colon X\to Y$
is mono if it is injective on underlying sets.
$f\colon X\to Y$
is mono if it is injective on underlying sets.
3 The structure of subobjects
3.1 Witnessed subset
Our aim is to consider an arithmetic hierarchy over a represented space. For this purpose, we carefully consider what a subset of a represented space is.
Definition 3.1. A subspace of a represented space X is a represented space A such that
![]() $|A|\subseteq |X|$
and
$|A|\subseteq |X|$
and
![]() $\delta _A=\delta _X{\upharpoonright _{|A|}}$
; that is, the A- and X-names of
$\delta _A=\delta _X{\upharpoonright _{|A|}}$
; that is, the A- and X-names of
![]() $x\in |A|$
are the same.
$x\in |A|$
are the same.
The notion of a subspace seems most appropriate when viewing a subset of a represented space as a represented space again. However, there could be another possibility.
Definition 3.2. A subobject of a represented space X is a represented space A such that
![]() $|A|\subseteq |X|$
and there exists a partial realizable function which, given an A-name of
$|A|\subseteq |X|$
and there exists a partial realizable function which, given an A-name of
![]() $x\in |A|$
, returns its X-name.
$x\in |A|$
, returns its X-name.
A regular subobject of a represented space X is a subobject A of X such that there exists a partial realizable function which, given an X-name of
![]() $x\in |A|$
, returns its A-name.
$x\in |A|$
, returns its A-name.
Observation 3.3. A represented space A is a subobject of X iff
![]() $|A|\subseteq |X|$
and the inclusion map
$|A|\subseteq |X|$
and the inclusion map
![]() $i\colon A\rightarrowtail X$
is a morphism.
$i\colon A\rightarrowtail X$
is a morphism.
A represented space A is a regular subobject of X iff it is a subobject of X and the inclusion morphism
![]() $i\colon A\rightarrowtail X$
has a partial inverse morphism
$i\colon A\rightarrowtail X$
has a partial inverse morphism
![]() $i^{-1}\colon \!\!\!\subseteq X\to A$
; that is,
$i^{-1}\colon \!\!\!\subseteq X\to A$
; that is,
![]() $i^{-1}(i(x))=x$
for any
$i^{-1}(i(x))=x$
for any
![]() $x\in |A|$
.
$x\in |A|$
.
The most basic relation between subsets is the inclusion relation. We introduce the inclusion relation between subobjects as follows:
Definition 3.4. For subobjects
![]() $A,B$
of a represented space X, we say that A is included in B (written
$A,B$
of a represented space X, we say that A is included in B (written
![]() $A\subseteq B$
) if
$A\subseteq B$
) if
![]() $|A|\subseteq |B|$
and the inclusion map
$|A|\subseteq |B|$
and the inclusion map
![]() $i\colon A\hookrightarrow B$
is a morphism. If
$i\colon A\hookrightarrow B$
is a morphism. If
![]() $A\subseteq B$
and
$A\subseteq B$
and
![]() $B\subseteq A$
we say that A is equivalent to B and write
$B\subseteq A$
we say that A is equivalent to B and write
![]() $A\equiv B$
.
$A\equiv B$
.
Observation 3.5. A subspace of X is a regular subobject of X. Conversely, every regular subobject of X is equivalent to a subspace of X.
Thus, one can understand that a regular subobject is a represented space obtained by taking a subset of a represented space. What then is the value of non-regular subobjects? To answer this, it is better to think of the notion of a (non-regular) subobject as a subset with additional information, such as a subset with witnesses, rather than just a subset.
Definition 3.6. A witnessed subset A of a represented space X is a represented space such that
![]() $|A|\subseteq |X|$
and every name of
$|A|\subseteq |X|$
and every name of
![]() $x\in A$
is a pair
$x\in A$
is a pair
![]() $\langle w,p\rangle $
of an X-name p of x and some
$\langle w,p\rangle $
of an X-name p of x and some
![]() $w\in \mathtt {Code}$
. In this case, w is called a witness for
$w\in \mathtt {Code}$
. In this case, w is called a witness for
![]() $x\in A$
.
$x\in A$
.
One can see that a subobject of a represented space is nothing more than a witnessed subset:
Observation 3.7. A witnessed subset of X is a subobject of X. Conversely, every subobject of X is equivalent to a witnessed subset of X.
Proof. For a witnessed subset A of X, the inclusion map
![]() $i\colon A\hookrightarrow X$
is clearly tracked by the projection map
$i\colon A\hookrightarrow X$
is clearly tracked by the projection map
![]() $\pi _1\colon \langle w,p\rangle \mapsto p$
. Conversely, if A is a subobject of X, that is,
$\pi _1\colon \langle w,p\rangle \mapsto p$
. Conversely, if A is a subobject of X, that is,
![]() $i\colon A\hookrightarrow X$
is tracked by some f, then consider the following represented space
$i\colon A\hookrightarrow X$
is tracked by some f, then consider the following represented space
![]() $A_f$
: The underlying set is
$A_f$
: The underlying set is
![]() $|A_f|=|A|$
, and
$|A_f|=|A|$
, and
![]() $\langle w,p\rangle $
is a name of
$\langle w,p\rangle $
is a name of
![]() $x\in A_f$
iff w is a name of
$x\in A_f$
iff w is a name of
![]() $x\in A$
and
$x\in A$
and
![]() $p=f(w)$
. Then,
$p=f(w)$
. Then,
![]() $A_f$
is clearly a witnessed subset of X. Moreover,
$A_f$
is clearly a witnessed subset of X. Moreover,
![]() $A_f\subseteq A$
is tracked by
$A_f\subseteq A$
is tracked by
![]() $\pi _0\colon \langle w,p\rangle \mapsto w$
, and
$\pi _0\colon \langle w,p\rangle \mapsto w$
, and
![]() $A\subseteq A_f$
is tracked by
$A\subseteq A_f$
is tracked by
![]() $w\mapsto \langle w,f(w)\rangle $
.
$w\mapsto \langle w,f(w)\rangle $
.
Then we will quickly realize that there are numerous natural examples of non-regular subobjects.
Example 3.8 (
 $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
 $\mathsf {KV}$
)
$\mathsf {KV}$
)
In
![]() $\mathsf {K}_2$
and
$\mathsf {K}_2$
and
![]() $\mathsf {KV}$
, the space
$\mathsf {KV}$
, the space
![]() $\omega ^\omega $
is represented by the identity map as in Example 2.2. Then a subobject
$\omega ^\omega $
is represented by the identity map as in Example 2.2. Then a subobject
![]() $\mathsf {Fin}$
of
$\mathsf {Fin}$
of
![]() $\omega ^\omega $
is defined as follows:
$\omega ^\omega $
is defined as follows:
-
• The underlying set is
 $|\mathsf {Fin}|=\{x\in \omega ^\omega :(\exists n)(\forall m\geq n)\;x(m)=0\}$
.
$|\mathsf {Fin}|=\{x\in \omega ^\omega :(\exists n)(\forall m\geq n)\;x(m)=0\}$
. -
• A name of
 $x\in \mathsf {Fin}$
is a pair
$x\in \mathsf {Fin}$
is a pair
 $\langle n,x\rangle $
of
$\langle n,x\rangle $
of
 $x\in \omega ^\omega $
and its witness n; that is,
$x\in \omega ^\omega $
and its witness n; that is,
 $x(m)=0$
for any
$x(m)=0$
for any
 $m\geq n$
.
$m\geq n$
.
Note that the inclusion map
![]() $\mathsf {Fin}\rightarrowtail \omega ^\omega $
is a morphism, tracked by the projection
$\mathsf {Fin}\rightarrowtail \omega ^\omega $
is a morphism, tracked by the projection
![]() $\pi _1\colon \langle n,x\rangle \mapsto x$
.
$\pi _1\colon \langle n,x\rangle \mapsto x$
.
Proposition 3.9.
![]() $\mathsf {Fin}$
is a non-regular subobject of
$\mathsf {Fin}$
is a non-regular subobject of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proof. Suppose that
![]() $\mathsf {Fin}$
is regular. Then, there exists a partial realizable function F which, given
$\mathsf {Fin}$
is regular. Then, there exists a partial realizable function F which, given
![]() $x\in |\mathsf {Fin}|$
, returns an
$x\in |\mathsf {Fin}|$
, returns an
![]() $\mathsf {Fin}$
-name of x, say
$\mathsf {Fin}$
-name of x, say
![]() $F(x)=\langle n,x\rangle $
. By the continuity of F, the witness n is determined after reading a finite initial segment
$F(x)=\langle n,x\rangle $
. By the continuity of F, the witness n is determined after reading a finite initial segment
![]() $x\upharpoonright s$
of x. Put
$x\upharpoonright s$
of x. Put
![]() $t=\max \{n,s\}$
, and consider
$t=\max \{n,s\}$
, and consider
![]() $y=(x\upharpoonright t)\text {}^\smallfrown 1\text {}^\smallfrown 0^\infty $
. Then
$y=(x\upharpoonright t)\text {}^\smallfrown 1\text {}^\smallfrown 0^\infty $
. Then
![]() $y\in |\mathsf {Fin}|$
, so
$y\in |\mathsf {Fin}|$
, so
![]() $F(y)$
returns a name of
$F(y)$
returns a name of
![]() $y\in \mathsf {Fin}$
; that is,
$y\in \mathsf {Fin}$
; that is,
![]() $F(y)$
is of the form
$F(y)$
is of the form
![]() $\langle m,y\rangle $
. As y extends
$\langle m,y\rangle $
. As y extends
![]() $x\upharpoonright s$
, the first value of
$x\upharpoonright s$
, the first value of
![]() $F(y)$
must be n; hence
$F(y)$
must be n; hence
![]() $F(y)=\langle n,y\rangle $
. However, we have
$F(y)=\langle n,y\rangle $
. However, we have
![]() $t\geq n$
and
$t\geq n$
and
![]() $y(t)=1$
, which means that
$y(t)=1$
, which means that
![]() $\langle n,y\rangle $
is not an
$\langle n,y\rangle $
is not an
![]() $\mathsf {Fin}$
-name of y.
$\mathsf {Fin}$
-name of y.
One of the most typical ways to obtain a set is to describe a formula
![]() $\varphi $
to define a subset
$\varphi $
to define a subset
![]() $\{x\in X:\varphi (x)\}$
of X. Then, it is sometimes desirable to keep information behind the construction of the subset, for example, a witness of an existential quantification within
$\{x\in X:\varphi (x)\}$
of X. Then, it is sometimes desirable to keep information behind the construction of the subset, for example, a witness of an existential quantification within
![]() $\varphi $
. In such a case, non-regular subobjects can appear, as described above. Our goal is to classify such “subsets with witnesses”.
$\varphi $
. In such a case, non-regular subobjects can appear, as described above. Our goal is to classify such “subsets with witnesses”.
Remark. Let us give some more background on Definition 3.2. In the case of sets, one can identify an injection
![]() $m\colon S\rightarrowtail X$
with its image, which is a subset of X. Then the inclusion relation between subsets of X can be characterized using injections as follows. A monomorphism
$m\colon S\rightarrowtail X$
with its image, which is a subset of X. Then the inclusion relation between subsets of X can be characterized using injections as follows. A monomorphism
![]() $i\colon A\rightarrowtail X$
is included in
$i\colon A\rightarrowtail X$
is included in
![]() $j\colon B\rightarrowtail X$
if there exists a morphism
$j\colon B\rightarrowtail X$
if there exists a morphism
![]() $k\colon A\to B$
such that
$k\colon A\to B$
such that
![]() $i=j\circ k$
. If i is included in j and vice versa, we write
$i=j\circ k$
. If i is included in j and vice versa, we write
![]() $i\equiv j$
. Formally, a subobject is the
$i\equiv j$
. Formally, a subobject is the
![]() $\equiv $
-equivalence class of a mono. In the category of represented spaces, any
$\equiv $
-equivalence class of a mono. In the category of represented spaces, any
![]() $\equiv $
-equivalence class of a mono contains an inclusion map, which leads us to Definition 3.2. Similarly, a regular subobject is the
$\equiv $
-equivalence class of a mono contains an inclusion map, which leads us to Definition 3.2. Similarly, a regular subobject is the
![]() $\equiv $
-equivalence class of a regular mono.
$\equiv $
-equivalence class of a regular mono.
Remark. One may also call a regular subobject of X a
![]() $\neg \neg $
-closed subobject of X. For
$\neg \neg $
-closed subobject of X. For
![]() $j\colon \mathcal {P}(\mathtt {Code})\to \mathcal {P}(\mathtt {Code})$
, the j-closure
$j\colon \mathcal {P}(\mathtt {Code})\to \mathcal {P}(\mathtt {Code})$
, the j-closure
![]() $A^j$
of a subobject
$A^j$
of a subobject
![]() $A\rightarrowtail X$
is defined as follows:
$A\rightarrowtail X$
is defined as follows:
where recall that
![]() $E_A(x)$
is the set of all names of
$E_A(x)$
is the set of all names of
![]() $x\in A$
. A subobject
$x\in A$
. A subobject
![]() $A\rightarrowtail X$
is j-closed if the j-closure
$A\rightarrowtail X$
is j-closed if the j-closure
![]() $A^j\rightarrowtail X$
is equivalent to
$A^j\rightarrowtail X$
is equivalent to
![]() $A\rightarrowtail X$
.
$A\rightarrowtail X$
.
Then consider
![]() $\neg \neg \colon \mathcal {P}(\mathtt {Code})\to \mathcal {P}(\mathtt {Code})$
defined by
$\neg \neg \colon \mathcal {P}(\mathtt {Code})\to \mathcal {P}(\mathtt {Code})$
defined by
![]() $\neg \neg U=\mathcal {P}(\mathtt {Code})$
if
$\neg \neg U=\mathcal {P}(\mathtt {Code})$
if
![]() $U\not =\emptyset $
; otherwise
$U\not =\emptyset $
; otherwise
![]() $\neg \neg U=\emptyset $
. One can easily see that a subobject is
$\neg \neg U=\emptyset $
. One can easily see that a subobject is
![]() $\neg \neg $
-closed iff it is regular. To comment on the background of this notion, it is the closure by the universal closure operator obtained from the double negation topology.
$\neg \neg $
-closed iff it is regular. To comment on the background of this notion, it is the closure by the universal closure operator obtained from the double negation topology.
Remark. Example 3.8 gives a direct definition of the function space
![]() $\omega ^\omega $
. Alternatively, one may introduce
$\omega ^\omega $
. Alternatively, one may introduce
![]() $\omega ^\omega $
as the exponential object
$\omega ^\omega $
as the exponential object
![]() $\mathsf {Nat}^{\mathsf {Nat}}$
. The notion of
$\mathsf {Nat}^{\mathsf {Nat}}$
. The notion of
![]() $\omega ^\omega $
then makes sense even in
$\omega ^\omega $
then makes sense even in
![]() $\mathsf {K}_1$
since the category of
$\mathsf {K}_1$
since the category of
![]() $\mathsf {K}_1$
-represented spaces is cartesian closed, and in this case,
$\mathsf {K}_1$
-represented spaces is cartesian closed, and in this case,
![]() $\mathsf {Nat}^{\mathsf {Nat}}$
is the space of all total computable functions. Then one can formulate the definition of
$\mathsf {Nat}^{\mathsf {Nat}}$
is the space of all total computable functions. Then one can formulate the definition of
![]() $\mathsf {Fin}$
within the system
$\mathsf {Fin}$
within the system
![]() $\mathsf {K_1}$
. In fact, Proposition 3.9 holds in
$\mathsf {K_1}$
. In fact, Proposition 3.9 holds in
![]() $\mathsf {K}_1$
as well. The details of this argument will be given later.
$\mathsf {K}_1$
as well. The details of this argument will be given later.
3.2 Lattice of subobjects
Next, let us go a little further into the structure of the inclusion relation among subobjects. Let us denote by
![]() $\mathrm {Sub}(X)$
the set of all subobjects of X. One can easily check the following:
$\mathrm {Sub}(X)$
the set of all subobjects of X. One can easily check the following:
Observation 3.10.
![]() $(\mathrm {Sub}(X),\subseteq )$
is a poset.
$(\mathrm {Sub}(X),\subseteq )$
is a poset.
In fact, in the category of represented spaces, one can see that a subobject poset is always a Heyting algebra.
Proposition 3.11. The poset
![]() $(\mathrm {Sub}(X),\subseteq )$
of subobjects of a represented space X forms a Heyting algebra.
$(\mathrm {Sub}(X),\subseteq )$
of subobjects of a represented space X forms a Heyting algebra.
This is a consequence of the fact that the category of represented spaces is a Heyting category, but it is important to give an explicit description of what the lattice and Heyting operations actually are. Of course, as is well known, they are given in a form corresponding to the realizability interpretation.
Definition 3.12. Let
![]() $X,Y$
be subobjects of a represented space Z. Then their witnessed union
$X,Y$
be subobjects of a represented space Z. Then their witnessed union
![]() $X\uplus Y$
is defined as follows:
$X\uplus Y$
is defined as follows:
-
• The underlying set is
 $|X\uplus Y|=|X|\cup |Y|$
.
$|X\uplus Y|=|X|\cup |Y|$
. -
•
 $\langle i,p\rangle $
is a name of
$\langle i,p\rangle $
is a name of
 $x\in X\uplus Y$
iff, if
$x\in X\uplus Y$
iff, if
 $i=0$
then p is a name of
$i=0$
then p is a name of
 $x\in X$
else p is a name of
$x\in X$
else p is a name of
 $x\in Y$
.
$x\in Y$
.
Definition 3.13. Let
![]() $X,Y$
be subobjects of a represented space Z. Then their witnessed intersection
$X,Y$
be subobjects of a represented space Z. Then their witnessed intersection ![]() is defined as follows:
is defined as follows:
-
• The underlying set is
 .
. -
•
 $\langle p,q\rangle $
is a name of
$\langle p,q\rangle $
is a name of  iff p is a name of
iff p is a name of
 $x\in X$
and q is a name of
$x\in X$
and q is a name of
 $x\in Y$
.
$x\in Y$
.
Definition 3.14. Let
![]() $X,Y$
be subobjects of a represented space Z. Then the implication
$X,Y$
be subobjects of a represented space Z. Then the implication ![]() is defined as follows:
is defined as follows:
-
•
 $\langle p,q\rangle $
is a name of
$\langle p,q\rangle $
is a name of  iff p is a name of
iff p is a name of
 $x\in Z$
, and if a is a name of
$x\in Z$
, and if a is a name of
 $x\in X$
then
$x\in X$
then
 $q\ast a$
is a name of
$q\ast a$
is a name of
 $x\in Y$
.
$x\in Y$
. -
• The underlying set is the set of all
 $x\in |Z|$
having
$x\in |Z|$
having  -names.
-names.
Proof of Proposition 3.11
We show that the witnessed union
![]() $\uplus $
and the intersection
$\uplus $
and the intersection ![]() give the join and the meet in any subobject poset. Let
give the join and the meet in any subobject poset. Let
![]() $X,Y$
be subobjects of Z. Then the inclusion maps
$X,Y$
be subobjects of Z. Then the inclusion maps
![]() $X\hookrightarrow X\uplus Y$
and
$X\hookrightarrow X\uplus Y$
and
![]() $Y\hookrightarrow X\uplus Y$
are tracked by
$Y\hookrightarrow X\uplus Y$
are tracked by
![]() $a\mapsto \langle 0,a\rangle $
and
$a\mapsto \langle 0,a\rangle $
and
![]() $b\mapsto \langle 1,b\rangle $
, respectively. Now, let
$b\mapsto \langle 1,b\rangle $
, respectively. Now, let
![]() $S\rightarrowtail Z$
be such that
$S\rightarrowtail Z$
be such that
![]() $X,Y\subseteq S$
. Then the inclusion maps
$X,Y\subseteq S$
. Then the inclusion maps
![]() $X\hookrightarrow S$
and
$X\hookrightarrow S$
and
![]() $Y\hookrightarrow S$
are tracked by some u and v, respectively. Then consider the process that, given a name
$Y\hookrightarrow S$
are tracked by some u and v, respectively. Then consider the process that, given a name
![]() $\langle i,p\rangle $
of
$\langle i,p\rangle $
of
![]() $x\in X\uplus Y$
, if
$x\in X\uplus Y$
, if
![]() $i=0$
then returns
$i=0$
then returns
![]() $u(p)$
else
$u(p)$
else
![]() $v(p)$
. Note that if
$v(p)$
. Note that if
![]() $i=0$
then
$i=0$
then
![]() $p\vdash _X x$
, so
$p\vdash _X x$
, so
![]() $u(p)\vdash _S x$
. Similarly, if
$u(p)\vdash _S x$
. Similarly, if
![]() $i\not =0$
then
$i\not =0$
then
![]() $p\vdash _Y x$
, so
$p\vdash _Y x$
, so
![]() $v(p)\vdash _Sx$
. Thus, in any case, the above process yields a name of
$v(p)\vdash _Sx$
. Thus, in any case, the above process yields a name of
![]() $x\in S$
. This means that
$x\in S$
. This means that
![]() $X\uplus Y$
is included in S. Hence,
$X\uplus Y$
is included in S. Hence,
![]() $X\uplus Y$
is the join of X and Y in the poset of subobjects of Z.
$X\uplus Y$
is the join of X and Y in the poset of subobjects of Z.
Next, the inclusion maps ![]() and
and ![]() are tracked by projections
are tracked by projections
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
, respectively. Now, let
$\pi _1$
, respectively. Now, let
![]() $S\rightarrowtail Z$
be such that
$S\rightarrowtail Z$
be such that
![]() $S\subseteq X,Y$
. Then the inclusion maps
$S\subseteq X,Y$
. Then the inclusion maps
![]() $S\hookrightarrow X$
and
$S\hookrightarrow X$
and
![]() $S\hookrightarrow Y$
are tracked by some u and v, respectively. Then
$S\hookrightarrow Y$
are tracked by some u and v, respectively. Then
![]() $p\mapsto \langle u(p),v(p)\rangle $
tracks the inclusion map
$p\mapsto \langle u(p),v(p)\rangle $
tracks the inclusion map ![]() . To see this, if
. To see this, if
![]() $p\vdash _S x$
then
$p\vdash _S x$
then
![]() $u(p)\vdash _Xx$
and
$u(p)\vdash _Xx$
and
![]() $v(p)\vdash _Yx$
, so
$v(p)\vdash _Yx$
, so ![]() . This means that S is included in
. This means that S is included in ![]() . Hence,
. Hence, ![]() is the meet of X and Y in the poset of subobjects of Z.
is the meet of X and Y in the poset of subobjects of Z.
To see that ![]() is the Heyting operation, for subobjects
is the Heyting operation, for subobjects
![]() $A,B,C\rightarrowtail Z$
, first assume
$A,B,C\rightarrowtail Z$
, first assume ![]() , which is realized by u. If
, which is realized by u. If
![]() $\langle p,q \rangle $
is a name of
$\langle p,q \rangle $
is a name of ![]() then, since p is an A-name of x,
then, since p is an A-name of x,
![]() $u(p)$
is a
$u(p)$
is a ![]() -name of x by our assumption. If
-name of x by our assumption. If
![]() $u(p)$
is of the form
$u(p)$
is of the form
![]() $\langle u_0(p),u_1(p) \rangle $
, as q is a B-name of x,
$\langle u_0(p),u_1(p) \rangle $
, as q is a B-name of x,
![]() $u_1(p)\ast q$
is a C-name of x. This shows
$u_1(p)\ast q$
is a C-name of x. This shows ![]() . Conversely, assume
. Conversely, assume ![]() , which is realized by u. Assume that p is a name of
, which is realized by u. Assume that p is a name of
![]() $x\in A$
. As A is a subobject of Z, the inclusion map
$x\in A$
. As A is a subobject of Z, the inclusion map
![]() $A\rightarrowtail Z$
is tracked by some i, so
$A\rightarrowtail Z$
is tracked by some i, so
![]() $i(p)$
is a Z-name of x. If
$i(p)$
is a Z-name of x. If
![]() $x\not \in B$
then anything is a
$x\not \in B$
then anything is a ![]() -name of x. If q is a name of
-name of x. If q is a name of
![]() $x\in B$
then
$x\in B$
then
![]() $\langle p,q\rangle $
is a
$\langle p,q\rangle $
is a ![]() -name of x, so
-name of x, so
![]() $u(p,q)$
is a C-name of x. Hence,
$u(p,q)$
is a C-name of x. Hence,
![]() $\langle i(p),\lambda q.u(p,q) \rangle $
is a
$\langle i(p),\lambda q.u(p,q) \rangle $
is a ![]() -name of x. Note that
-name of x. Note that
![]() $\lambda q.u(p,q)$
is always defined, and thus
$\lambda q.u(p,q)$
is always defined, and thus
![]() $\lambda p.\langle i(p),\lambda q.u(p,q) \rangle $
tracks the inclusion
$\lambda p.\langle i(p),\lambda q.u(p,q) \rangle $
tracks the inclusion ![]() .
.
3.3 Quantifier
One of our objectives is to analyze arithmetical and Borel hierarchies, especially in the latter case, it is useful to have the notion of countable union and countable intersection. If a subobject lattice were complete, we could automatically obtain infinitary operations. Of course, a lattice of regular subobjects in the category of represented spaces is always a complete Boolean algebra (since regular subobjects are merely subsets); however, the completeness of a subobject lattice strongly depends on what is chosen as a coding system.
Proposition 3.15 (
 $\mathsf {K}_1$
)
$\mathsf {K}_1$
)
The poset
![]() $(\mathrm {Sub}(X),\subseteq )$
of subobjects of a represented space X is not necessarily a
$(\mathrm {Sub}(X),\subseteq )$
of subobjects of a represented space X is not necessarily a
![]() $\sigma $
-complete lattice. Indeed,
$\sigma $
-complete lattice. Indeed,
![]() $(\mathrm {Sub}(\omega ),\subseteq )$
has neither
$(\mathrm {Sub}(\omega ),\subseteq )$
has neither
![]() $\sigma $
-join nor
$\sigma $
-join nor
![]() $\sigma $
-meet.
$\sigma $
-meet.
Proof. For the non-existence of
![]() $\sigma $
-join, for each
$\sigma $
-join, for each
![]() $n\in \omega $
, think of the singleton
$n\in \omega $
, think of the singleton
![]() $\{n\}$
as a subspace of
$\{n\}$
as a subspace of
![]() $\omega $
. Let
$\omega $
. Let
![]() $I\rightarrowtail \omega $
be such that
$I\rightarrowtail \omega $
be such that
![]() $\{n\}\subseteq I$
in
$\{n\}\subseteq I$
in
![]() $\mathrm {Sub}(\omega )$
for any
$\mathrm {Sub}(\omega )$
for any
![]() $n\in \omega $
. Then
$n\in \omega $
. Then
![]() $|I|=\omega $
. Let
$|I|=\omega $
. Let
![]() $E_I(n)$
be the set of all I-names of
$E_I(n)$
be the set of all I-names of
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $E_I(n)\not =\emptyset $
for all
$E_I(n)\not =\emptyset $
for all
![]() $n\in \omega $
, take the least element
$n\in \omega $
, take the least element
![]() $s(n)\in E_I(n)$
. Construct a new subobject
$s(n)\in E_I(n)$
. Construct a new subobject
![]() $J\rightarrowtail \omega $
as follows: The underlying set is
$J\rightarrowtail \omega $
as follows: The underlying set is
![]() $|J|=\omega $
, and the only J-name of
$|J|=\omega $
, and the only J-name of
![]() $n\in \omega $
is
$n\in \omega $
is
![]() $s'(n)$
, where
$s'(n)$
, where
![]() $s'$
is the Turing jump of s. Clearly,
$s'$
is the Turing jump of s. Clearly,
![]() $\{n\}\subseteq J$
holds in
$\{n\}\subseteq J$
holds in
![]() $\mathrm {Sub}(\omega )$
for any
$\mathrm {Sub}(\omega )$
for any
![]() $n\in \omega $
. If
$n\in \omega $
. If
![]() $I\subseteq J$
in
$I\subseteq J$
in
![]() $\mathrm {Sub}(\omega )$
then some computable function f tracks the inclusion
$\mathrm {Sub}(\omega )$
then some computable function f tracks the inclusion
![]() $I\hookrightarrow J$
. Since
$I\hookrightarrow J$
. Since
![]() $s(n)$
is an I-name of n,
$s(n)$
is an I-name of n,
![]() $f(s(n))$
must be a J-name of n, which means
$f(s(n))$
must be a J-name of n, which means
![]() $f(s(n))=s'(n)$
. This implies that the jump
$f(s(n))=s'(n)$
. This implies that the jump
![]() $s'$
is Turing reducible to s, a contradiction. Hence,
$s'$
is Turing reducible to s, a contradiction. Hence,
![]() $I\not \subseteq J$
, which shows that any I cannot be a
$I\not \subseteq J$
, which shows that any I cannot be a
![]() $\sigma $
-join of the singletons
$\sigma $
-join of the singletons
![]() $\{n\}$
.
$\{n\}$
.
For the non-existence of
![]() $\sigma $
-meet, consider a sequence
$\sigma $
-meet, consider a sequence
![]() $g_0<_Tg_1<_T\dots $
, where
$g_0<_Tg_1<_T\dots $
, where
![]() $\leq _T$
is Turing reducibility. For each
$\leq _T$
is Turing reducibility. For each
![]() $i\in \omega $
, consider a subobject
$i\in \omega $
, consider a subobject
![]() $A_i\rightarrowtail \omega $
such that its underlying set is
$A_i\rightarrowtail \omega $
such that its underlying set is
![]() $|A_i|=\omega $
and
$|A_i|=\omega $
and
![]() $g_i(n)$
is a unique name of
$g_i(n)$
is a unique name of
![]() $n\in A_i$
. Assume that
$n\in A_i$
. Assume that
![]() $B\rightarrowtail \omega $
is a subobject such that
$B\rightarrowtail \omega $
is a subobject such that
![]() $B\subseteq A_i$
for any
$B\subseteq A_i$
for any
![]() $i\in \omega $
. We construct a subobject
$i\in \omega $
. We construct a subobject
![]() $C\rightarrowtail \omega $
such that
$C\rightarrowtail \omega $
such that
![]() $C\subseteq A_i$
for any
$C\subseteq A_i$
for any
![]() $i\in \omega $
but
$i\in \omega $
but
![]() $C\not \subseteq B$
. Put
$C\not \subseteq B$
. Put
![]() $|C|=\omega $
. We inductively define an increasing sequence
$|C|=\omega $
. We inductively define an increasing sequence
![]() $(n_e)_{e\in \omega }$
with
$(n_e)_{e\in \omega }$
with
![]() $n_0=0$
. Assume that
$n_0=0$
. Assume that
![]() $n_e$
has already been defined. If the eth partial computable function
$n_e$
has already been defined. If the eth partial computable function
![]() $\varphi _e$
is not total then put
$\varphi _e$
is not total then put
![]() $n_{e+1}=n_e+1$
. If
$n_{e+1}=n_e+1$
. If
![]() $\varphi _e$
is total, we claim that there exists
$\varphi _e$
is total, we claim that there exists
![]() $n\geq n_e$
such that
$n\geq n_e$
such that
![]() $\varphi _e(\langle g_i(n)\rangle _{i\leq e})$
is not a name of
$\varphi _e(\langle g_i(n)\rangle _{i\leq e})$
is not a name of
![]() $n\in B$
. This is because, since
$n\in B$
. This is because, since
![]() $B\subseteq A_{e+1}$
, if one knows a name of
$B\subseteq A_{e+1}$
, if one knows a name of
![]() $n\in B$
one can compute
$n\in B$
one can compute
![]() $g_{e+1}(n)$
. Thus, if the claim fails then we get
$g_{e+1}(n)$
. Thus, if the claim fails then we get
![]() $g_{e+1}\leq _T\bigoplus _{i\leq e}g_i\equiv _T g_e$
, a contradiction. Define
$g_{e+1}\leq _T\bigoplus _{i\leq e}g_i\equiv _T g_e$
, a contradiction. Define
![]() $n_{e+1}=n+1$
where n is a number in the above claim. Then declare that, if
$n_{e+1}=n+1$
where n is a number in the above claim. Then declare that, if
![]() $n_e\leq n<n_{e+1}$
, then
$n_e\leq n<n_{e+1}$
, then
![]() $\langle g_i(n)\rangle _{i\leq e}$
is a unique name of
$\langle g_i(n)\rangle _{i\leq e}$
is a unique name of
![]() $n\in C$
. For almost all n, the ith coordinate of a name of
$n\in C$
. For almost all n, the ith coordinate of a name of
![]() $n\in C$
yields a name of
$n\in C$
yields a name of
![]() $A_i$
, so we have
$A_i$
, so we have
![]() $C\subseteq A_i$
. Moreover, the above construction ensures that
$C\subseteq A_i$
. Moreover, the above construction ensures that
![]() $\varphi _e$
cannot be a tracker of the inclusion
$\varphi _e$
cannot be a tracker of the inclusion
![]() $C\subseteq B$
for any e, which means that
$C\subseteq B$
for any e, which means that
![]() $C\not \subseteq B$
. Consequently, any B cannot be a
$C\not \subseteq B$
. Consequently, any B cannot be a
![]() $\sigma $
-meet of
$\sigma $
-meet of
![]() $(A_i)_{i\in \omega }$
.
$(A_i)_{i\in \omega }$
.
Of course, this only states that there are no external countable operations, and there is no problem if one uses internal countable operations or quantifiers. In fact, the arithmetical hierarchy is usually defined as the hierarchy of number quantifiers.
It is known that the existential quantifier and the universal quantifier are characterized by the following adjoint rules:
 $$ \begin{align*} A(x,y)\vdash B(y)&\iff \exists xA(x,y)\vdash B(y)\\ B(y)\vdash A(x,y)&\iff B(y)\vdash\forall xA(x,y). \end{align*} $$
$$ \begin{align*} A(x,y)\vdash B(y)&\iff \exists xA(x,y)\vdash B(y)\\ B(y)\vdash A(x,y)&\iff B(y)\vdash\forall xA(x,y). \end{align*} $$
In categorical logic, the existential quantification and the universal quantification are introduced as follows: If A is a subobject of
![]() $X\times Y$
, then
$X\times Y$
, then
![]() $\exists ^XA$
and
$\exists ^XA$
and
![]() $\forall ^XA$
are subobjects of Y such that for any subobject
$\forall ^XA$
are subobjects of Y such that for any subobject
![]() $B\rightarrowtail Y$
the following holds in the subobject posets:
$B\rightarrowtail Y$
the following holds in the subobject posets:
 $$ \begin{align*} A\subseteq X\times B&\iff \exists^XA\subseteq B\\ X\times B\subseteq A&\iff B\subseteq\forall^XA. \end{align*} $$
$$ \begin{align*} A\subseteq X\times B&\iff \exists^XA\subseteq B\\ X\times B\subseteq A&\iff B\subseteq\forall^XA. \end{align*} $$
As already mentioned, the category of represented spaces is a Heyting category, so it has interpretations of the existential quantification and the universal quantification. To develop our theory, it is useful to have explicit descriptions of these notions.
Definition 3.16. Let X be a subobject of a represented space
![]() $I\times Z$
. Then its witnessed projection
$I\times Z$
. Then its witnessed projection
![]() $\exists ^IX\rightarrowtail Z$
is defined as follows:
$\exists ^IX\rightarrowtail Z$
is defined as follows:
-
• The underlying set is
 $|\exists ^IX|=\{z\in Z:(\exists i\in I)\;(i,z)\in X\}$
.
$|\exists ^IX|=\{z\in Z:(\exists i\in I)\;(i,z)\in X\}$
. -
•
 $\langle p,q\rangle $
is a name of
$\langle p,q\rangle $
is a name of
 $z\in \exists ^IX$
iff p is a name of some
$z\in \exists ^IX$
iff p is a name of some
 $i\in I$
and q is a name of
$i\in I$
and q is a name of
 $z\in Z$
such that
$z\in Z$
such that
 $(i,z)\in X$
.
$(i,z)\in X$
.
From a practical standpoint, we also want to use the notation
![]() $\exists ^ZX$
for the projection of
$\exists ^ZX$
for the projection of
![]() $X\rightarrowtail I\times Z$
into I. Then, however, the notation
$X\rightarrowtail I\times Z$
into I. Then, however, the notation
![]() $\exists ^IX$
for
$\exists ^IX$
for
![]() $X\rightarrowtail I\times I$
is ambiguous as to what it is quantifying. In order to describe it unambiguously, we need to specify a projection, but it is often cumbersome and unintuitive. In some cases, rather, a collection
$X\rightarrowtail I\times I$
is ambiguous as to what it is quantifying. In order to describe it unambiguously, we need to specify a projection, but it is often cumbersome and unintuitive. In some cases, rather, a collection
![]() $(X_i)_{i\in I}$
of subobjects is given first, and the existential quantification is defined as its (witnessed) union. To be more explicit:
$(X_i)_{i\in I}$
of subobjects is given first, and the existential quantification is defined as its (witnessed) union. To be more explicit:
Definition 3.17. Let I be a represented space, and for each
![]() $i\in I$
let
$i\in I$
let
![]() $X_i$
be a subobject of a represented space Z. Then their witnessed union
$X_i$
be a subobject of a represented space Z. Then their witnessed union
![]() $\biguplus _{i\in I}X_i$
is defined as follows:
$\biguplus _{i\in I}X_i$
is defined as follows:
-
• The underlying set is
 $|\biguplus _{i\in I}X_i|=\bigcup _{i\in I}|X_i|$
.
$|\biguplus _{i\in I}X_i|=\bigcup _{i\in I}|X_i|$
. -
•
 $\langle u,p\rangle $
is a name of
$\langle u,p\rangle $
is a name of
 $x\in \biguplus _{i\in I}X_i$
iff, if u is a name of
$x\in \biguplus _{i\in I}X_i$
iff, if u is a name of
 $j\in I$
then p is a name of
$j\in I$
then p is a name of
 $x\in X_j$
.
$x\in X_j$
.
Note that for a subobject
![]() $X\rightarrowtail I\times Z$
, we have
$X\rightarrowtail I\times Z$
, we have
![]() $\exists ^IX=\biguplus _{i\in I}X_i$
, where
$\exists ^IX=\biguplus _{i\in I}X_i$
, where
![]() $X_i$
is the subspace of
$X_i$
is the subspace of
![]() $I\times Z$
whose underlying set is
$I\times Z$
whose underlying set is
![]() $\{z\in Z:(i,z)\in X\}$
.
$\{z\in Z:(i,z)\in X\}$
.
Definition 3.18. Let I be a represented space, and for each
![]() $i\in I$
let
$i\in I$
let
![]() $X_i$
be a subobject of a represented space Z. Then their witnessed intersection
$X_i$
be a subobject of a represented space Z. Then their witnessed intersection ![]() is defined as follows:
is defined as follows:
-
• p is a name of
 iff, if z is a name of
iff, if z is a name of
 $i\in I$
then
$i\in I$
then
 $p\ast z$
is a name of
$p\ast z$
is a name of
 $x\in X_i$
.
$x\in X_i$
. -
• The underlying set is the set of all
 $x\in |Z|$
having
$x\in |Z|$
having  -names.
-names.
These notions play the roles of the existential quantification and the universal quantification, respectively; that is, for any subobjects
![]() $A\rightarrowtail I\times Z$
and
$A\rightarrowtail I\times Z$
and
![]() $B\rightarrowtail Z$
,
$B\rightarrowtail Z$
,

where
![]() $A_i$
is the subobject of Z such that
$A_i$
is the subobject of Z such that
![]() $|A_i|=\{z\in |Z|:(i,z)\in |A|\}$
and a name of
$|A_i|=\{z\in |Z|:(i,z)\in |A|\}$
and a name of
![]() $z\in A_i$
is a name of
$z\in A_i$
is a name of
![]() $(i,z)\in A$
.
$(i,z)\in A$
.
3.4 Reducibility
We will see later, for example, that
![]() $\mathsf {Fin}$
is not
$\mathsf {Fin}$
is not
![]() $\Sigma ^0_2$
-complete. Of course, in order to define the notion of completeness, we need a notion of reducibility, which requires some discussion.
$\Sigma ^0_2$
-complete. Of course, in order to define the notion of completeness, we need a notion of reducibility, which requires some discussion.
Definition 3.19. For subsets
![]() $A,B\subseteq \omega $
, we say that A is many-one reducible to B (written
$A,B\subseteq \omega $
, we say that A is many-one reducible to B (written
![]() $A\leq _mB$
) if there exists a computable function
$A\leq _mB$
) if there exists a computable function
![]() $\varphi \colon \omega \to \omega $
such that for any
$\varphi \colon \omega \to \omega $
such that for any
![]() $n\in \omega $
$n\in \omega $
For a collection
![]() $\Gamma $
of subsets of
$\Gamma $
of subsets of
![]() $\omega $
, a set
$\omega $
, a set
![]() $A\subseteq \omega $
is
$A\subseteq \omega $
is
![]() $\Gamma $
-hard if
$\Gamma $
-hard if
![]() $B\leq _mA$
for any
$B\leq _mA$
for any
![]() $B\in \Gamma $
. If
$B\in \Gamma $
. If
![]() $A\in \Gamma $
also holds, then A is called
$A\in \Gamma $
also holds, then A is called
![]() $\Gamma $
-complete.
$\Gamma $
-complete.
Definition 3.20. For subsets
![]() $A,B\subseteq \omega ^\omega $
, we say that A is Wadge reducible to B (written
$A,B\subseteq \omega ^\omega $
, we say that A is Wadge reducible to B (written
![]() $A\leq _WB$
) if there exists a continuous function
$A\leq _WB$
) if there exists a continuous function
![]() $\varphi \colon \omega ^\omega \to \omega ^\omega $
such that for any
$\varphi \colon \omega ^\omega \to \omega ^\omega $
such that for any
![]() $x\in \omega ^\omega $
$x\in \omega ^\omega $
For a collection
![]() $\Gamma $
of subsets of
$\Gamma $
of subsets of
![]() $\omega ^\omega $
, a set
$\omega ^\omega $
, a set
![]() $A\subseteq \omega $
is
$A\subseteq \omega $
is
![]() $\Gamma $
-hard if
$\Gamma $
-hard if
![]() $B\leq _WA$
for any
$B\leq _WA$
for any
![]() $B\in \Gamma $
. If
$B\in \Gamma $
. If
![]() $A\in \Gamma $
also holds, then A is called
$A\in \Gamma $
also holds, then A is called
![]() $\Gamma $
-complete.
$\Gamma $
-complete.
These notions of reducibility are for subsets and can be easily extended to subspaces (or regular subobjects) of represented spaces, but it is less clear how to extend them to non-regular subobjects. After a short time of gazing at the definitions, one may find that both definitions of reducibility can be rewritten as
![]() $A=\varphi ^{-1}[B]$
. That is, this is just a pullback. Using the notion of pullback, it is natural to extend the notion of many-one/Wadge reducibility as follows:
$A=\varphi ^{-1}[B]$
. That is, this is just a pullback. Using the notion of pullback, it is natural to extend the notion of many-one/Wadge reducibility as follows:
Definition 3.21. Let
![]() $X,Y$
be objects in a category
$X,Y$
be objects in a category
![]() $\mathcal {C}$
having pullbacks. A mono
$\mathcal {C}$
having pullbacks. A mono
![]() $A\overset {i}{\rightarrowtail } X$
is many-one reducible to
$A\overset {i}{\rightarrowtail } X$
is many-one reducible to
![]() $B\overset {j}{\rightarrowtail }Y$
if
$B\overset {j}{\rightarrowtail }Y$
if
![]() $A\overset {i}{\rightarrowtail }X$
is a pullback of
$A\overset {i}{\rightarrowtail }X$
is a pullback of
![]() $B\overset {j}{\rightarrowtail }Y$
along some morphism
$B\overset {j}{\rightarrowtail }Y$
along some morphism
![]() $\varphi \colon X\to Y$
.
$\varphi \colon X\to Y$
.

Recall an explicit description of pullback in the category of represented spaces:
Definition 3.22. For represented spaces X and Y, for a subobject
![]() $B\rightarrowtail Y$
and a morphism
$B\rightarrowtail Y$
and a morphism
![]() $\varphi \colon X\to Y$
, the pullback
$\varphi \colon X\to Y$
, the pullback
![]() $\varphi ^\ast B$
of B along
$\varphi ^\ast B$
of B along
![]() $\varphi $
is defined as follows:
$\varphi $
is defined as follows:
-
• The underlying set is
 $|\varphi ^\ast B|=\varphi ^{-1}[|B|]=\{x\in |X|:\varphi (x)\in |B|\}$
.
$|\varphi ^\ast B|=\varphi ^{-1}[|B|]=\{x\in |X|:\varphi (x)\in |B|\}$
. -
• A name of
 $x\in \varphi ^\ast B$
is a pair
$x\in \varphi ^\ast B$
is a pair
 $\langle p,q\rangle $
of a name p of
$\langle p,q\rangle $
of a name p of
 $x\in X$
and a name q of
$x\in X$
and a name q of
 $\varphi (x)\in B$
.
$\varphi (x)\in B$
.
If
![]() $B\rightarrowtail Y$
is regular, then so is
$B\rightarrowtail Y$
is regular, then so is
![]() $\varphi ^\ast B\rightarrowtail X$
, and the information of q in the name of
$\varphi ^\ast B\rightarrowtail X$
, and the information of q in the name of
![]() $\varphi ^\ast B$
is unnecessary.
$\varphi ^\ast B$
is unnecessary.
The definition of many-one reducibility in the category of represented spaces can be explicitly written as follows:
Definition 3.23. Let X and Y be represented spaces. A subobject
![]() $A\rightarrowtail X$
is many-one reducible to
$A\rightarrowtail X$
is many-one reducible to
![]() $B\rightarrowtail Y$
if there exist a morphism
$B\rightarrowtail Y$
if there exist a morphism
![]() $\varphi \colon X\to Y$
and partial realizable functions
$\varphi \colon X\to Y$
and partial realizable functions
![]() $r_-,r_+\colon \!\!\!\subseteq \mathtt {Code}\to \mathtt {Code}$
such that the following hold:
$r_-,r_+\colon \!\!\!\subseteq \mathtt {Code}\to \mathtt {Code}$
such that the following hold:
-
1. For any
 $x\in |X|$
,
$x\in |X|$
,
 $x\in |A|$
if and only if
$x\in |A|$
if and only if
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
2. If p is an A-name of
 $x\in |A|$
then
$x\in |A|$
then
 $r_-(p)$
is a B-name of
$r_-(p)$
is a B-name of
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
3. If p is an X-name of
 $x\in |A|$
and q is a B-name of
$x\in |A|$
and q is a B-name of
 $\varphi (x)\in |B|$
then
$\varphi (x)\in |B|$
then
 $r_+(p,q)$
is an A-name of
$r_+(p,q)$
is an A-name of
 $x\in |A|$
.
$x\in |A|$
.
In this case, we write
![]() $A\leq _{\mathsf {m}}B$
. One can think of this as the realizability interpretation of many-one reducibility; that is,
$A\leq _{\mathsf {m}}B$
. One can think of this as the realizability interpretation of many-one reducibility; that is,
![]() $r_-$
is a realizer for “
$r_-$
is a realizer for “
![]() $x\in A\implies \varphi (x)\in B$
”, and
$x\in A\implies \varphi (x)\in B$
”, and
![]() $r_+$
is a realizer for “
$r_+$
is a realizer for “
![]() $\varphi (x)\in B\implies x\in A$
”.
$\varphi (x)\in B\implies x\in A$
”.
Observation 3.24. Definition 3.23 is equivalent to Definition 3.21 in the category of represented spaces.
Proof. Definition 3.23 states that the subobject
![]() $A\rightarrowtail X$
is equivalent to the pullback
$A\rightarrowtail X$
is equivalent to the pullback
![]() $\varphi ^\ast B\rightarrowtail X$
in Definition 3.22. Indeed, if u is a tracker of
$\varphi ^\ast B\rightarrowtail X$
in Definition 3.22. Indeed, if u is a tracker of
![]() $\varphi $
, then
$\varphi $
, then
![]() $p\mapsto \langle u(p),r_-(p) \rangle $
tracks
$p\mapsto \langle u(p),r_-(p) \rangle $
tracks
![]() $A\subseteq \varphi ^\ast B$
, and
$A\subseteq \varphi ^\ast B$
, and
![]() $r_+$
tracks
$r_+$
tracks
![]() $\varphi ^\ast B\subseteq A$
. Thus,
$\varphi ^\ast B\subseteq A$
. Thus,
![]() $A\rightarrowtail X$
is also a pullback of
$A\rightarrowtail X$
is also a pullback of
![]() $B\rightarrowtail Y$
along
$B\rightarrowtail Y$
along
![]() $\varphi $
. Conversely, if a subobject
$\varphi $
. Conversely, if a subobject
![]() $A\rightarrowtail X$
is a pullback of
$A\rightarrowtail X$
is a pullback of
![]() $B\rightarrowtail Y$
along
$B\rightarrowtail Y$
along
![]() $\varphi $
, then one can easily see that A is equivalent to
$\varphi $
, then one can easily see that A is equivalent to
![]() $\varphi ^\ast B$
.
$\varphi ^\ast B$
.
Example 3.25. Let
![]() $\mathbf {Rep}(\mathsf {K}_1)$
be the category of represented spaces over Kleene’s first algebra
$\mathbf {Rep}(\mathsf {K}_1)$
be the category of represented spaces over Kleene’s first algebra
![]() $\mathsf {K}_1$
. Then many-one reducibility for regular subobjects of
$\mathsf {K}_1$
. Then many-one reducibility for regular subobjects of
![]() $\omega $
in
$\omega $
in
![]() $\mathbf {Rep}(K_1)$
is exactly the usual many-one reducibility.
$\mathbf {Rep}(K_1)$
is exactly the usual many-one reducibility.
Example 3.26. Let
![]() $\mathbf {Rep}(\mathsf {K}_2)$
be the category of represented spaces over Kleene’s second algebra
$\mathbf {Rep}(\mathsf {K}_2)$
be the category of represented spaces over Kleene’s second algebra
![]() $\mathsf {K}_2$
. Then many-one reducibility for regular subobjects of
$\mathsf {K}_2$
. Then many-one reducibility for regular subobjects of
![]() $\omega ^\omega $
in
$\omega ^\omega $
in
![]() $\mathbf {Rep}(K_2)$
is exactly the Wadge reducibility.
$\mathbf {Rep}(K_2)$
is exactly the Wadge reducibility.
Example 3.27. Many-one reducibility for subobjects of
![]() $\omega $
in
$\omega $
in
![]() $\mathbf {Rep}(K_1)$
can be thought of as computable Levin reducibility (cf. Definition 1.1).
$\mathbf {Rep}(K_1)$
can be thought of as computable Levin reducibility (cf. Definition 1.1).
To be more explicit, a witnessed subset
![]() $A\rightarrowtail X$
is many-one reducible to a witnessed subset
$A\rightarrowtail X$
is many-one reducible to a witnessed subset
![]() $B\rightarrowtail Y$
if and only if there exist a morphism
$B\rightarrowtail Y$
if and only if there exist a morphism
![]() $\varphi \colon X\to Y$
and partial realizable functions
$\varphi \colon X\to Y$
and partial realizable functions
![]() $r_-,r_+$
such that for any name p of
$r_-,r_+$
such that for any name p of
![]() $x\in X$
and
$x\in X$
and
![]() $v,w\in \mathsf {Code}$
the following holds:
$v,w\in \mathsf {Code}$
the following holds:
-
1.
 $x\in |A|$
if and only if
$x\in |A|$
if and only if
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
2. If v is a witness for
 $x\in |A|$
then
$x\in |A|$
then
 $r_-(v,p)$
is a witness for
$r_-(v,p)$
is a witness for
 $\varphi (x)\in |B|$
.
$\varphi (x)\in |B|$
. -
3. If w is a witness for
 $\varphi (x)\in |B|$
then
$\varphi (x)\in |B|$
then
 $r_+(w,p)$
is a witness for
$r_+(w,p)$
is a witness for
 $x\in |A|$
.
$x\in |A|$
.
Next, let us discuss an alternative to the definition of many-one reducibility. Considering the “meaning” of many-one reducibility, it might be a bit questionable whether Definition 3.23 is appropriate. The “meaning” of many-one reducibility
![]() $A\leq _mB$
is that it is sufficient to know information about B in order to compute information about A. That is, the computationally correct understanding of
$A\leq _mB$
is that it is sufficient to know information about B in order to compute information about A. That is, the computationally correct understanding of
![]() $A\leq _mB$
might not be “
$A\leq _mB$
might not be “
![]() $x\in A\iff \varphi (x)\in B$
,” but
$x\in A\iff \varphi (x)\in B$
,” but
The conditions (1) and (3) of Definition 3.23 reflect that meaning, but the condition (2) is the opposite. Therefore, from a computational point of view, it would be correct to remove the condition (2). In fact, for reducibility for function problems in computational complexity theory (e.g., the definition of FNP-completeness), this form of reducibility is often considered instead of Levin reducibility.
Definition 3.28. We say that a subobject
![]() $A\rightarrowtail X$
is demi-many-one reducible to
$A\rightarrowtail X$
is demi-many-one reducible to
![]() $B\rightarrowtail Y$
(written
$B\rightarrowtail Y$
(written
![]() $A\leq _{\mathsf {m}}'B$
) if the conditions (1) and (3) in Definition 3.23 hold.
$A\leq _{\mathsf {m}}'B$
) if the conditions (1) and (3) in Definition 3.23 hold.
Observation 3.29.
![]() $A\leq _{\mathsf {m}}B\implies A\leq _{\mathsf {m}}'B$
.
$A\leq _{\mathsf {m}}B\implies A\leq _{\mathsf {m}}'B$
.
Of course, removing the condition (2) would be unnatural in the categorical setting. Recall that the
![]() $\neg \neg $
-closure
$\neg \neg $
-closure
![]() $A^{\neg \neg }\rightarrowtail X$
of a subobject
$A^{\neg \neg }\rightarrowtail X$
of a subobject
![]() $A\rightarrowtail X$
as the unique regular subobject with
$A\rightarrowtail X$
as the unique regular subobject with
![]() $|A^{\neg \neg }|=|A|$
. In other words, it is the
$|A^{\neg \neg }|=|A|$
. In other words, it is the
![]() $\subseteq $
-least regular subobject including A.
$\subseteq $
-least regular subobject including A.
Observation 3.30.
![]() $A\leq _{\mathsf {m}}'B$
iff there exists a morphism
$A\leq _{\mathsf {m}}'B$
iff there exists a morphism
![]() $\varphi $
such that
$\varphi $
such that
![]() $\varphi ^\ast B\subseteq A\subseteq (\varphi ^\ast B)^{\neg \neg }$
.
$\varphi ^\ast B\subseteq A\subseteq (\varphi ^\ast B)^{\neg \neg }$
.
Observation 3.31. If
![]() $A,B\rightarrowtail X$
are regular then
$A,B\rightarrowtail X$
are regular then
![]() $A\leq _{\mathsf {m}}B$
iff
$A\leq _{\mathsf {m}}B$
iff
![]() $A\leq _{\mathsf {m}}'B$
.
$A\leq _{\mathsf {m}}'B$
.
Remark. One may notice that demi-many-one reducibility closely resembles Weihrauch reducibility [Reference Brattka, Gherardi and Pauly2], which has been studied in depth in computable analysis. In fact, demi-many-one reducibility corresponds to Weihrauch reducibility for “hardest totalizations”. Here, the hardest totalization
![]() $F^{ht}$
of
$F^{ht}$
of
![]() $F\colon \!\!\!\subseteq X\rightrightarrows Y$
is the totalization of F such that if
$F\colon \!\!\!\subseteq X\rightrightarrows Y$
is the totalization of F such that if
![]() $x\not \in \mathrm {dom}(F)$
then
$x\not \in \mathrm {dom}(F)$
then
![]() $F^{ht}(x)=\emptyset $
.
$F^{ht}(x)=\emptyset $
.
3.5 Structure
Let us analyze the structure of many-one reducibility.
Observation 3.32.
![]() $\leq _{\mathsf {m}}$
and
$\leq _{\mathsf {m}}$
and
![]() $\leq _{\mathsf {m}}'$
form preorders.
$\leq _{\mathsf {m}}'$
form preorders.
Proof. The proof for the many-one case follows from a general argument, but we give an explicit description applicable to the demi-many-one case. Reflexivity is trivial. For transitivity, for subobjects
![]() $A,B,C$
of
$A,B,C$
of
![]() $X,Y,Z$
, assume
$X,Y,Z$
, assume
![]() $A\leq _{\mathsf {m}}B$
via
$A\leq _{\mathsf {m}}B$
via
![]() $\varphi ,r_-,r_+$
and
$\varphi ,r_-,r_+$
and
![]() $B\leq _{\mathsf {m}}C$
via
$B\leq _{\mathsf {m}}C$
via
![]() $\psi ,s_-,s_+$
. Only an outer reduction is nontrivial. Let p be a tracker of
$\psi ,s_-,s_+$
. Only an outer reduction is nontrivial. Let p be a tracker of
![]() $\varphi $
. Given a name a of
$\varphi $
. Given a name a of
![]() $x\in X$
we know that
$x\in X$
we know that
![]() $p\ast a$
is a name of
$p\ast a$
is a name of
![]() $\varphi (x)\in Y$
. Thus, given a name c of
$\varphi (x)\in Y$
. Thus, given a name c of
![]() $\psi (\varphi (x))\in C$
,
$\psi (\varphi (x))\in C$
,
![]() $s^+(p\ast a,c)$
is a name of
$s^+(p\ast a,c)$
is a name of
![]() $\varphi (x)\in B$
, and
$\varphi (x)\in B$
, and
![]() $r^+(a,s^+(p\ast a,c))$
is a name of
$r^+(a,s^+(p\ast a,c))$
is a name of
![]() $x\in A$
. This process gives an outer reduction for
$x\in A$
. This process gives an outer reduction for
![]() $A\leq _{\mathsf {m}}C$
. This actually shows that
$A\leq _{\mathsf {m}}C$
. This actually shows that
![]() $\leq _{\mathsf {m}}'$
is a preorder.
$\leq _{\mathsf {m}}'$
is a preorder.
The poset reflections of
![]() $\leq _{\mathsf {m}}$
and
$\leq _{\mathsf {m}}$
and
![]() $\leq _{\mathsf {m}}'$
are called the many-one degrees and the demi-many-one degrees, respectively. It is easy to show the following property similar to many order degree structures.
$\leq _{\mathsf {m}}'$
are called the many-one degrees and the demi-many-one degrees, respectively. It is easy to show the following property similar to many order degree structures.
Proposition 3.33. The (demi-)many-one degrees on represented spaces form an upper semilattice.
Proof. Again, the proof for the many-one case follows from a general argument, but we give an explicit description applicable to the demi-many-one case. We construct a join of subobjects
![]() $A\rightarrowtail X$
and
$A\rightarrowtail X$
and
![]() $B\rightarrowtail Y$
. The coproduct
$B\rightarrowtail Y$
. The coproduct
![]() $X+Y$
of represented spaces X and Y are defined as follows:
$X+Y$
of represented spaces X and Y are defined as follows:
-
• The underlying set is
 $|X+Y|=\{(0,x):x\in X\}\cup \{(1,y):y\in Y\}$
.
$|X+Y|=\{(0,x):x\in X\}\cup \{(1,y):y\in Y\}$
. -
•
 $\langle i,p \rangle $
is a name of
$\langle i,p \rangle $
is a name of
 $(j,z)$
iff
$(j,z)$
iff
 $i=j$
and if
$i=j$
and if
 $i=0$
then p is a name of
$i=0$
then p is a name of
 $z\in X$
else p is a name of
$z\in X$
else p is a name of
 $z\in Y$
.
$z\in Y$
.
One can think of
![]() $A+B$
as a subobject of
$A+B$
as a subobject of
![]() $X+Y$
. Clearly,
$X+Y$
. Clearly,
![]() $A,B\leq _{\mathsf {m}}A+B$
. Assume that C is a subobject of Z such that
$A,B\leq _{\mathsf {m}}A+B$
. Assume that C is a subobject of Z such that
![]() $A\leq _{\mathsf {m}}C$
via
$A\leq _{\mathsf {m}}C$
via
![]() $\varphi ,r_-,r_+$
and
$\varphi ,r_-,r_+$
and
![]() $B\leq _{\mathsf {m}}C$
via
$B\leq _{\mathsf {m}}C$
via
![]() $\psi ,s_-,s_+$
. Let
$\psi ,s_-,s_+$
. Let
![]() $[\varphi ,\psi ]\colon X+Y\to Z$
be a morphism such that, for any
$[\varphi ,\psi ]\colon X+Y\to Z$
be a morphism such that, for any
![]() $(i,x)\in X+Y$
, if
$(i,x)\in X+Y$
, if
![]() $i=0$
then
$i=0$
then
![]() $[\varphi ,\psi ](i,x)=\varphi (x)$
else
$[\varphi ,\psi ](i,x)=\varphi (x)$
else
![]() $[\varphi ,\psi ](i,x)=\psi (x)$
. Given
$[\varphi ,\psi ](i,x)=\psi (x)$
. Given
![]() $\langle i,u \rangle \vdash _{A+B}(i,x)$
, if
$\langle i,u \rangle \vdash _{A+B}(i,x)$
, if
![]() $i=0$
then
$i=0$
then
![]() $r_-(u)\vdash _C\varphi (x)=[\varphi ,\psi ](i,x)$
else
$r_-(u)\vdash _C\varphi (x)=[\varphi ,\psi ](i,x)$
else
![]() $s_-(u)\vdash _C\psi (x)=[\varphi ,\psi ](i,x)$
. Given
$s_-(u)\vdash _C\psi (x)=[\varphi ,\psi ](i,x)$
. Given
![]() $\langle i,u \rangle \vdash _{X+Y}(i,x)$
and
$\langle i,u \rangle \vdash _{X+Y}(i,x)$
and
![]() $c\vdash _C[\varphi ,\psi ](i,x)$
, if
$c\vdash _C[\varphi ,\psi ](i,x)$
, if
![]() $i=0$
then
$i=0$
then
![]() $[\varphi ,\psi ](i,x)=\varphi (x)$
, so
$[\varphi ,\psi ](i,x)=\varphi (x)$
, so
![]() $r_+(u,c)\vdash _Ax$
; thus
$r_+(u,c)\vdash _Ax$
; thus
![]() $\langle 0,r_+(u,c) \rangle \vdash _{A+B}(i,x)$
. Similarly, if
$\langle 0,r_+(u,c) \rangle \vdash _{A+B}(i,x)$
. Similarly, if
![]() $i\not =0$
then
$i\not =0$
then
![]() $\langle 1,r_+(u,c) \rangle \vdash _{A+B}(i,x)$
. This shows
$\langle 1,r_+(u,c) \rangle \vdash _{A+B}(i,x)$
. This shows
![]() $A+B\leq _{\mathsf {m}}C$
. By a similar argument, one can show that
$A+B\leq _{\mathsf {m}}C$
. By a similar argument, one can show that
![]() $\leq _{\mathsf {m}}'$
also yields an upper semilattice.
$\leq _{\mathsf {m}}'$
also yields an upper semilattice.
The many-one degree structure has the following good property that other degree structures do not have very often.
Theorem 3.34. The (demi-)many-one degrees on represented spaces form a distributive lattice.
Proof. First consider
![]() $\leq _{\mathsf {m}}'$
. Given subobjects
$\leq _{\mathsf {m}}'$
. Given subobjects
![]() $A\rightarrowtail X$
and
$A\rightarrowtail X$
and
![]() $B\rightarrowtail Y$
, we define the space
$B\rightarrowtail Y$
, we define the space
![]() $A\odot B$
of common information of A and B as follows: First consider the subspace
$A\odot B$
of common information of A and B as follows: First consider the subspace
![]() $C(A,B)$
of
$C(A,B)$
of
![]() $\mathtt {Code}$
such that
$\mathtt {Code}$
such that
![]() $\langle p,q,n \rangle \in |C(A,B)|$
iff
$\langle p,q,n \rangle \in |C(A,B)|$
iff
Then the equivalence relation
![]() $\sim $
on
$\sim $
on
![]() $C(A,B)$
is defined as follows:
$C(A,B)$
is defined as follows:
Then let
![]() $A\odot B$
be the quotient space
$A\odot B$
be the quotient space
![]() $C(A,B)/{\sim }$
; that is, an
$C(A,B)/{\sim }$
; that is, an
![]() $(A\odot B)$
-name of a
$(A\odot B)$
-name of a
![]() $\sim $
-equivalence class
$\sim $
-equivalence class
![]() $[p,q,n]$
is of the form
$[p,q,n]$
is of the form
![]() $\langle p,q,m \rangle $
for some
$\langle p,q,m \rangle $
for some
![]() $\langle p,q,m \rangle \in [p,q,n]$
. Then we define a subobject
$\langle p,q,m \rangle \in [p,q,n]$
. Then we define a subobject
![]() $A\Cap B\rightarrowtail A\odot B$
as follows:
$A\Cap B\rightarrowtail A\odot B$
as follows:
-
•
 $[p,q,n] \in |A\Cap B|$
iff
$[p,q,n] \in |A\Cap B|$
iff
 $[p,q,n]\in |A\odot B|$
and
$[p,q,n]\in |A\odot B|$
and
 $\delta _X(p\ast n)\in |A|$
.
$\delta _X(p\ast n)\in |A|$
. -
•
 $\langle i,u,v\rangle $
is a name of
$\langle i,u,v\rangle $
is a name of
 $[p,q,n]\in A\Cap B$
iff u is a name of
$[p,q,n]\in A\Cap B$
iff u is a name of
 $[p,q,n]\in A\odot B$
and if
$[p,q,n]\in A\odot B$
and if
 $i=0$
then v is a name of
$i=0$
then v is a name of
 $\delta _X(p\ast n)\in A$
else v is a name of
$\delta _X(p\ast n)\in A$
else v is a name of
 $\delta _Y(q\ast n)\in B$
.
$\delta _Y(q\ast n)\in B$
.
To see that
![]() $A\Cap B\leq _{\mathsf {m}}' A$
, consider
$A\Cap B\leq _{\mathsf {m}}' A$
, consider
![]() $\varphi \colon [p,q,n]\mapsto \delta _X(p\ast n)$
, which is well-defined. If
$\varphi \colon [p,q,n]\mapsto \delta _X(p\ast n)$
, which is well-defined. If
![]() $[p,q,n]\in |A\odot B|$
then
$[p,q,n]\in |A\odot B|$
then
![]() ${\varphi ([p,q,n])\downarrow }\in X$
since
${\varphi ([p,q,n])\downarrow }\in X$
since
![]() $\langle p,q,n \rangle \in C(A,B)$
. Thus,
$\langle p,q,n \rangle \in C(A,B)$
. Thus,
![]() $[p,q,n]\in |A\Cap B|$
iff
$[p,q,n]\in |A\Cap B|$
iff
![]() $\varphi ([p,q,n])\in |A|$
. Moreover, if
$\varphi ([p,q,n])\in |A|$
. Moreover, if
![]() $\langle p,q,m \rangle $
is a name of
$\langle p,q,m \rangle $
is a name of
![]() $[p,q,m]\in A\odot B$
and v is a name of
$[p,q,m]\in A\odot B$
and v is a name of
![]() $\varphi ([p,q,n])\in A$
then
$\varphi ([p,q,n])\in A$
then
![]() $\langle 0,p,q,m,v\rangle $
is a name of
$\langle 0,p,q,m,v\rangle $
is a name of
![]() $[p,q,n]\in A\Cap B$
.
$[p,q,n]\in A\Cap B$
.
Similarly, to see that
![]() $A\Cap B\leq _{\mathsf {m}}' B$
, consider
$A\Cap B\leq _{\mathsf {m}}' B$
, consider
![]() $\varphi \colon [p,q,n]\mapsto \delta _Y(q\ast n)$
, which is well-defined. If
$\varphi \colon [p,q,n]\mapsto \delta _Y(q\ast n)$
, which is well-defined. If
![]() $[p,q,n]\in |A\odot B|$
then
$[p,q,n]\in |A\odot B|$
then
![]() ${\varphi ([p,q,n])\downarrow }\in Y$
. By definition,
${\varphi ([p,q,n])\downarrow }\in Y$
. By definition,
![]() $[p,q,n]\in |A\Cap B|$
iff
$[p,q,n]\in |A\Cap B|$
iff
![]() $\delta _X(p\ast n)\in |A|$
, iff
$\delta _X(p\ast n)\in |A|$
, iff
![]() $\varphi ([p,q,n])=\delta _X(q\ast n)\in |B|$
since
$\varphi ([p,q,n])=\delta _X(q\ast n)\in |B|$
since
![]() $\langle p,q,n\rangle \in C(A,B)$
. Moreover, if
$\langle p,q,n\rangle \in C(A,B)$
. Moreover, if
![]() $\langle p,q,m \rangle $
is a name of
$\langle p,q,m \rangle $
is a name of
![]() $[p,q,m]\in A\odot B$
and v is a name of
$[p,q,m]\in A\odot B$
and v is a name of
![]() $\varphi ([p,q,n])\in B$
then
$\varphi ([p,q,n])\in B$
then
![]() $\langle 1,p,q,m,v\rangle $
is a name of
$\langle 1,p,q,m,v\rangle $
is a name of
![]() $[p,q,n]\in A\Cap B$
.
$[p,q,n]\in A\Cap B$
.
For a subobject
![]() $C\rightarrowtail Z$
, if
$C\rightarrowtail Z$
, if
![]() $C\leq _{\mathsf {m}}'A,B$
then there are
$C\leq _{\mathsf {m}}'A,B$
then there are
![]() $\varphi ,\psi $
such that, for any
$\varphi ,\psi $
such that, for any
![]() $x\in |Z|$
,
$x\in |Z|$
,
![]() $x\in |C|$
iff
$x\in |C|$
iff
![]() $\varphi (x)\in |A|$
and
$\varphi (x)\in |A|$
and
![]() $\psi (x)\in |B|$
. We also have
$\psi (x)\in |B|$
. We also have
![]() $r,s$
such that if u is a name of
$r,s$
such that if u is a name of
![]() $\varphi (x)\in A$
then
$\varphi (x)\in A$
then
![]() $r\ast u$
is a name of
$r\ast u$
is a name of
![]() $x\in C$
, and if v is a name of
$x\in C$
, and if v is a name of
![]() $\psi (x)\in B$
then
$\psi (x)\in B$
then
![]() $s\ast v$
is a name of
$s\ast v$
is a name of
![]() $x\in C$
.
$x\in C$
.
To show
![]() $C\leq _{\mathsf {m}}'A\Cap B$
, let p and q be trackers of
$C\leq _{\mathsf {m}}'A\Cap B$
, let p and q be trackers of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively. Then if k is a name of some
$\psi $
, respectively. Then if k is a name of some
![]() $x\in Z$
, then
$x\in Z$
, then
![]() $k\vdash _Z x\in |C|$
iff
$k\vdash _Z x\in |C|$
iff
![]() ${p\ast k\downarrow }\vdash _X\varphi (x)\in |A|$
iff
${p\ast k\downarrow }\vdash _X\varphi (x)\in |A|$
iff
![]() ${q\ast k\downarrow }\vdash _Y\psi (x)\in |B|$
. Hence,
${q\ast k\downarrow }\vdash _Y\psi (x)\in |B|$
. Hence,
![]() $[p,q,k]\in |A\odot B|$
, and moreover,
$[p,q,k]\in |A\odot B|$
, and moreover,
![]() $k\vdash _Z x\in |C|$
iff
$k\vdash _Z x\in |C|$
iff
![]() $[p,q,k]\in |A\Cap B|$
. Moreover, if k and
$[p,q,k]\in |A\Cap B|$
. Moreover, if k and
![]() $\ell $
are names of
$\ell $
are names of
![]() $x\in Z$
, then
$x\in Z$
, then
![]() $\delta _X(p\ast k)=\delta _X(p\ast \ell )=\varphi (x)$
and
$\delta _X(p\ast k)=\delta _X(p\ast \ell )=\varphi (x)$
and
![]() $\delta _Y(q\ast k)=\delta _Y(q\ast \ell )=\psi (x)$
; hence
$\delta _Y(q\ast k)=\delta _Y(q\ast \ell )=\psi (x)$
; hence
![]() $[p,q,k]=[p,q,\ell ]$
. Therefore,
$[p,q,k]=[p,q,\ell ]$
. Therefore,
![]() $k\mapsto \langle p,q,k\rangle $
tracks some morphism
$k\mapsto \langle p,q,k\rangle $
tracks some morphism
![]() $\theta \colon Z\to A\odot B$
such that
$\theta \colon Z\to A\odot B$
such that
![]() $x\in |C|$
iff
$x\in |C|$
iff
![]() $[p,q,k]\in |A\Cap B|$
. Given a name
$[p,q,k]\in |A\Cap B|$
. Given a name
![]() $\langle i,u,v\rangle $
of
$\langle i,u,v\rangle $
of
![]() $[p,q,k]\in A\Cap B$
, if
$[p,q,k]\in A\Cap B$
, if
![]() $i=0$
then v is a name of
$i=0$
then v is a name of
![]() $\delta _X(p\ast k)=\varphi (x)\in A$
, so
$\delta _X(p\ast k)=\varphi (x)\in A$
, so
![]() $r\ast v$
is a name of
$r\ast v$
is a name of
![]() $x\in C$
. If
$x\in C$
. If
![]() $i\not =0$
then v is a name of
$i\not =0$
then v is a name of
![]() $\delta _Y(q\ast k)=\psi (x)\in B$
, so
$\delta _Y(q\ast k)=\psi (x)\in B$
, so
![]() $s\ast v$
is a name of
$s\ast v$
is a name of
![]() $x\in C$
. This completes the proof.
$x\in C$
. This completes the proof.
The proof for
![]() $\leq _{\mathsf {m}}$
is almost the same, but the construction is a little more complicated. Consider the subspace
$\leq _{\mathsf {m}}$
is almost the same, but the construction is a little more complicated. Consider the subspace
![]() $D(A,B)$
of
$D(A,B)$
of
![]() $\mathtt {Code}$
such that
$\mathtt {Code}$
such that
![]() $\langle p,q,a,b,c,d,n \rangle \in |D(A,B)|$
iff
$\langle p,q,a,b,c,d,n \rangle \in |D(A,B)|$
iff
![]() $\langle p,q,n \rangle \in |C(A,B)|$
and the following hold:
$\langle p,q,n \rangle \in |C(A,B)|$
and the following hold:
-
• If v is a name of
 $\delta _X(p\ast n)\in A$
then
$\delta _X(p\ast n)\in A$
then
 $a\ast (c\ast v)$
is a name of
$a\ast (c\ast v)$
is a name of
 $\delta _X(p\ast n)\in A$
and
$\delta _X(p\ast n)\in A$
and
 $b\ast (c\ast v)$
is a name of
$b\ast (c\ast v)$
is a name of
 $\delta _Y(q\ast n)\in B$
.
$\delta _Y(q\ast n)\in B$
. -
• If v is a name of
 $\delta _Y(q\ast n)\in B$
then
$\delta _Y(q\ast n)\in B$
then
 $a\ast (d\ast v)$
is a name of
$a\ast (d\ast v)$
is a name of
 $\delta _X(p\ast n)\in A$
and
$\delta _X(p\ast n)\in A$
and
 $b\ast (d\ast v)$
is a name of
$b\ast (d\ast v)$
is a name of
 $\delta _Y(q\ast n)\in B$
.
$\delta _Y(q\ast n)\in B$
.
The construction after this is exactly the same as in the previous one, except for the additional information
![]() $\alpha =(a,b,c,d)$
.
$\alpha =(a,b,c,d)$
.
To see that
![]() $A\Cap B\leq _{\mathsf {m}} A$
, consider
$A\Cap B\leq _{\mathsf {m}} A$
, consider
![]() $\varphi \colon [p,q,\alpha ,n]\mapsto \delta _X(p\ast n)$
, which is well-defined. If
$\varphi \colon [p,q,\alpha ,n]\mapsto \delta _X(p\ast n)$
, which is well-defined. If
![]() $[p,q,\alpha ,n]\in |A\odot B|$
then
$[p,q,\alpha ,n]\in |A\odot B|$
then
![]() ${\varphi ([p,q,\alpha ,n])\downarrow }\in X$
since
${\varphi ([p,q,\alpha ,n])\downarrow }\in X$
since
![]() $\langle p,q,n \rangle \in C(A,B)$
. Thus,
$\langle p,q,n \rangle \in C(A,B)$
. Thus,
![]() $[p,q,\alpha ,n]\in |A\Cap B|$
iff
$[p,q,\alpha ,n]\in |A\Cap B|$
iff
![]() $\varphi ([p,q,\alpha ,n])\in |A|$
. Moreover, if
$\varphi ([p,q,\alpha ,n])\in |A|$
. Moreover, if
![]() $\langle p,q,\alpha ,m \rangle $
is a name of
$\langle p,q,\alpha ,m \rangle $
is a name of
![]() $[p,q,\alpha ,m]\in A\odot B$
and v is a name of
$[p,q,\alpha ,m]\in A\odot B$
and v is a name of
![]() $\varphi ([p,q,\alpha ,n])\in A$
then
$\varphi ([p,q,\alpha ,n])\in A$
then
![]() $\langle 0,p,q,\alpha ,m,v\rangle $
is a name of
$\langle 0,p,q,\alpha ,m,v\rangle $
is a name of
![]() $[p,q,\alpha ,n]\in A\Cap B$
. Conversely, assume that
$[p,q,\alpha ,n]\in A\Cap B$
. Conversely, assume that
![]() $\langle 0,p,q,\alpha ,m,v\rangle $
is a name of
$\langle 0,p,q,\alpha ,m,v\rangle $
is a name of
![]() $[p,q,\alpha ,n]\in A\Cap B$
. If
$[p,q,\alpha ,n]\in A\Cap B$
. If
![]() $i=0$
then v is a name of
$i=0$
then v is a name of
![]() $\delta _X(p\ast n)\in A$
. If
$\delta _X(p\ast n)\in A$
. If
![]() $i=1$
then v is a name of
$i=1$
then v is a name of
![]() $\delta _Y(q\ast n)\in B$
, so
$\delta _Y(q\ast n)\in B$
, so
![]() $a\ast (d\ast v)$
is a name of
$a\ast (d\ast v)$
is a name of
![]() $\delta _X(p\ast n)\in A$
. By the same argument, one can also show
$\delta _X(p\ast n)\in A$
. By the same argument, one can also show
![]() $A\Cap B\leq _{\mathsf {m}} B$
.
$A\Cap B\leq _{\mathsf {m}} B$
.
For a subobject
![]() $C\rightarrowtail Z$
, if
$C\rightarrowtail Z$
, if
![]() $C\leq _{\mathsf {m}}A,B$
then there are
$C\leq _{\mathsf {m}}A,B$
then there are
![]() $\varphi ,\psi $
such that, for any
$\varphi ,\psi $
such that, for any
![]() $x\in |Z|$
,
$x\in |Z|$
,
![]() $x\in |C|$
iff
$x\in |C|$
iff
![]() $\varphi (x)\in |A|$
and
$\varphi (x)\in |A|$
and
![]() $\psi (x)\in |B|$
. Let p and q be trackers of
$\psi (x)\in |B|$
. Let p and q be trackers of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively. Then if k is a name of some
$\psi $
, respectively. Then if k is a name of some
![]() $x\in Z$
, then
$x\in Z$
, then
![]() $k\vdash _Z x\in |C|$
iff
$k\vdash _Z x\in |C|$
iff
![]() ${p\ast k\downarrow }\vdash _X\varphi (x)\in |A|$
iff
${p\ast k\downarrow }\vdash _X\varphi (x)\in |A|$
iff
![]() ${q\ast k\downarrow }\vdash _Y\psi (x)\in |B|$
. We also have
${q\ast k\downarrow }\vdash _Y\psi (x)\in |B|$
. We also have
![]() $a,b,c,d$
such that
$a,b,c,d$
such that
![]() $v\vdash _A\varphi (x)$
implies
$v\vdash _A\varphi (x)$
implies
![]() $c\ast v\vdash _Cx$
;
$c\ast v\vdash _Cx$
;
![]() $v\vdash _B\psi (x)$
implies
$v\vdash _B\psi (x)$
implies
![]() $d\ast v\vdash _Cx$
; and
$d\ast v\vdash _Cx$
; and
![]() $v\vdash _Cx$
implies
$v\vdash _Cx$
implies
![]() $a\ast v\vdash _A\varphi (x)$
and
$a\ast v\vdash _A\varphi (x)$
and
![]() $b\ast v\vdash _B\psi (x)$
. In particular,
$b\ast v\vdash _B\psi (x)$
. In particular,
![]() $v\vdash _A\varphi (x)$
implies
$v\vdash _A\varphi (x)$
implies
![]() $a\ast (c\ast v)\vdash _A\varphi (x)$
and
$a\ast (c\ast v)\vdash _A\varphi (x)$
and
![]() $b\ast (c\ast v)\vdash _B\psi (x)$
, and
$b\ast (c\ast v)\vdash _B\psi (x)$
, and
![]() $v\vdash _B\psi (x)$
implies
$v\vdash _B\psi (x)$
implies
![]() $a\ast (d\ast v)\vdash _A\varphi (x)$
and
$a\ast (d\ast v)\vdash _A\varphi (x)$
and
![]() $b\ast (d\ast v)\vdash _B\psi (x)$
. As
$b\ast (d\ast v)\vdash _B\psi (x)$
. As
![]() $\varphi (x)=\delta _X(p\ast k)$
and
$\varphi (x)=\delta _X(p\ast k)$
and
![]() $\psi (x)=\delta _Y(q\ast k)$
, this implies
$\psi (x)=\delta _Y(q\ast k)$
, this implies
![]() $\langle p,q,\alpha ,n\rangle \in D(A,B)$
. The rest of the proof of
$\langle p,q,\alpha ,n\rangle \in D(A,B)$
. The rest of the proof of
![]() $C\leq _{\mathsf {m}}A\Cap B$
is the same as before.
$C\leq _{\mathsf {m}}A\Cap B$
is the same as before.
To show distributivity, first consider
![]() $\leq _{\mathsf {m}}'$
. For subobjects
$\leq _{\mathsf {m}}'$
. For subobjects
![]() $A,B,C$
of
$A,B,C$
of
![]() $X,Y,Z$
, it suffices to show
$X,Y,Z$
, it suffices to show
![]() $(A+B)\Cap (A+C)\leq _{\mathsf {m}}' A+(B\Cap C)$
. We construct a reduction
$(A+B)\Cap (A+C)\leq _{\mathsf {m}}' A+(B\Cap C)$
. We construct a reduction
![]() $\varphi $
as follows: Given
$\varphi $
as follows: Given
![]() $[p,q,n]\in |(A+B)\odot (A+C)|$
, assume that
$[p,q,n]\in |(A+B)\odot (A+C)|$
, assume that
![]() $p\ast n$
and
$p\ast n$
and
![]() $q\ast n$
are of the forms
$q\ast n$
are of the forms
![]() $\langle i,u\rangle $
and
$\langle i,u\rangle $
and
![]() $\langle j,v\rangle $
, respectively. If
$\langle j,v\rangle $
, respectively. If
![]() $i=0$
then define
$i=0$
then define
![]() $\varphi ([p,q,n])=\langle 0,\delta _X(u) \rangle $
else if
$\varphi ([p,q,n])=\langle 0,\delta _X(u) \rangle $
else if
![]() $j=0$
then
$j=0$
then
![]() $\varphi ([p,q,n])=\langle 0,\delta _X(v) \rangle $
. For instance, if
$\varphi ([p,q,n])=\langle 0,\delta _X(v) \rangle $
. For instance, if
![]() $i=1$
and
$i=1$
and
![]() $j=0$
then
$j=0$
then
![]() $\delta _Y(u)\in |B|$
iff
$\delta _Y(u)\in |B|$
iff
![]() $\delta _X(v)\in |A|$
; hence
$\delta _X(v)\in |A|$
; hence
![]() $[p,q,n]\in |(A+B)\Cap (A+C)|$
iff
$[p,q,n]\in |(A+B)\Cap (A+C)|$
iff
![]() $\delta _X(v)\in |A|$
iff
$\delta _X(v)\in |A|$
iff
![]() $\varphi ([p,q,n])=\langle 0,\delta _X(v) \rangle \in |A+(B\Cap C)|$
. If
$\varphi ([p,q,n])=\langle 0,\delta _X(v) \rangle \in |A+(B\Cap C)|$
. If
![]() $i\not =0$
and
$i\not =0$
and
![]() $j\not =0$
then let
$j\not =0$
then let
![]() $p_1$
and
$p_1$
and
![]() $q_1$
be such that
$q_1$
be such that
![]() $p_1\ast n=u$
and
$p_1\ast n=u$
and
![]() $q_1\ast n=v$
and then define
$q_1\ast n=v$
and then define
![]() $\varphi ([p,q,n])=\langle 1,[p_1,q_1,n]\rangle $
. As
$\varphi ([p,q,n])=\langle 1,[p_1,q_1,n]\rangle $
. As
![]() $\delta _Y(u)\in |B|$
iff
$\delta _Y(u)\in |B|$
iff
![]() $\delta _Z(v)\in |C|$
iff
$\delta _Z(v)\in |C|$
iff
![]() $[p_1,q_1,n]\in |B\Cap C|$
iff
$[p_1,q_1,n]\in |B\Cap C|$
iff
![]() $\varphi ([p,q,n])\in |A+(B\Cap C)|$
. For an outer reduction, given a name
$\varphi ([p,q,n])\in |A+(B\Cap C)|$
. For an outer reduction, given a name
![]() $\langle p,q,m \rangle $
of
$\langle p,q,m \rangle $
of
![]() $[p,q,n]\in (A+B)\odot (A+C)$
and a name
$[p,q,n]\in (A+B)\odot (A+C)$
and a name
![]() $\langle k,w\rangle $
of
$\langle k,w\rangle $
of
![]() $\varphi [p,q,n]\in A+(B\Cap C)$
, if
$\varphi [p,q,n]\in A+(B\Cap C)$
, if
![]() $i=0$
or
$i=0$
or
![]() $j=0$
then
$j=0$
then
![]() $k=0$
and w is an A-name of
$k=0$
and w is an A-name of
![]() $\delta _X(u)$
or
$\delta _X(u)$
or
![]() $\delta _X(v)$
, so one can compute a name of
$\delta _X(v)$
, so one can compute a name of
![]() $[p,q,n]\in (A+B)\Cap (A+C)$
. If
$[p,q,n]\in (A+B)\Cap (A+C)$
. If
![]() $i\not =0$
and
$i\not =0$
and
![]() $j\not =0$
then w is of the form
$j\not =0$
then w is of the form
![]() $\langle \ell ,p_1,q_1,m',z \rangle $
, where if
$\langle \ell ,p_1,q_1,m',z \rangle $
, where if
![]() $\ell =0$
then
$\ell =0$
then
![]() $z\vdash _B\delta _Y(u)$
else
$z\vdash _B\delta _Y(u)$
else
![]() $z\vdash _C\delta _Z(v)$
. Thus, if
$z\vdash _C\delta _Z(v)$
. Thus, if
![]() $\ell =0$
then
$\ell =0$
then
![]() $\langle 1,z\rangle \vdash _{A+B}(1,\delta _Y(u))$
else
$\langle 1,z\rangle \vdash _{A+B}(1,\delta _Y(u))$
else
![]() $\langle 1,z\rangle \vdash _{A+C}(1,\delta _Z(v))$
, so one can compute a name of
$\langle 1,z\rangle \vdash _{A+C}(1,\delta _Z(v))$
, so one can compute a name of
![]() $[p,q,n]\in (A+B)\Cap (A+C)$
.
$[p,q,n]\in (A+B)\Cap (A+C)$
.
For
![]() $\leq _{\mathsf {m}}$
, if
$\leq _{\mathsf {m}}$
, if
![]() $i\not =0$
and
$i\not =0$
and
![]() $j\not =0$
then transform
$j\not =0$
then transform
![]() $\alpha =(a,b,c,d)$
into
$\alpha =(a,b,c,d)$
into
![]() $\alpha '=(a',b',c',d')$
, where
$\alpha '=(a',b',c',d')$
, where
![]() $a'=\lambda x.\pi _1(a\ast x)$
,
$a'=\lambda x.\pi _1(a\ast x)$
,
![]() $b'=\lambda x.\pi _1(b\ast x)$
,
$b'=\lambda x.\pi _1(b\ast x)$
,
![]() $c'=\lambda x.c(1,x)$
and
$c'=\lambda x.c(1,x)$
and
![]() $d'=\lambda x.d(1,x)$
. Then define
$d'=\lambda x.d(1,x)$
. Then define
![]() $\varphi ([p,q,\alpha ,n])=\langle 1,[p_1,q_1,\alpha ',n]\rangle $
. The rest of the discussion is the same as above.
$\varphi ([p,q,\alpha ,n])=\langle 1,[p_1,q_1,\alpha ',n]\rangle $
. The rest of the discussion is the same as above.
However, if one focuses only on subobjects of a single represented space, it is generally not a lattice.
Proposition 3.35 (
 $\mathsf {K}_1$
)
$\mathsf {K}_1$
)
Both
![]() $(\mathrm {Sub}(\omega ),\leq _{\mathsf {m}})$
and
$(\mathrm {Sub}(\omega ),\leq _{\mathsf {m}})$
and
![]() $(\mathrm {Sub}(\omega ),\leq _{\mathsf {m}}')$
do not have binary meet.
$(\mathrm {Sub}(\omega ),\leq _{\mathsf {m}}')$
do not have binary meet.
Let us prepare a lemma to prove this. A general argument shows that regular subobjects are
![]() $\leq _{\mathsf {m}}$
-downward closed.
$\leq _{\mathsf {m}}$
-downward closed.
Lemma 3.36. If a mono
![]() $i\colon A\rightarrowtail X$
is many-one reducible to a regular mono
$i\colon A\rightarrowtail X$
is many-one reducible to a regular mono
![]() $j\colon B\rightarrowtail Y$
, then
$j\colon B\rightarrowtail Y$
, then
![]() $i\colon A\rightarrowtail X$
is also a regular mono.
$i\colon A\rightarrowtail X$
is also a regular mono.
Proof. Regular monos are stable under pullback.
This can also easily be shown using explicit descriptions. In fact, explicit descriptions lead us to more than that.
Lemma 3.37. If a mono
![]() $i\colon A\rightarrowtail X$
is demi-many-one reducible to a regular mono
$i\colon A\rightarrowtail X$
is demi-many-one reducible to a regular mono
![]() $j\colon B\rightarrowtail Y$
, then
$j\colon B\rightarrowtail Y$
, then
![]() $i\colon A\rightarrowtail X$
is also a regular mono.
$i\colon A\rightarrowtail X$
is also a regular mono.
Proof. Assume
![]() $A\leq _{\mathsf {m}}' B$
via
$A\leq _{\mathsf {m}}' B$
via
![]() $\varphi ,r_+$
. Given an X-name p of
$\varphi ,r_+$
. Given an X-name p of
![]() $x\in |A|$
, using a tracker of
$x\in |A|$
, using a tracker of
![]() $\varphi $
, one can find an X-name of
$\varphi $
, one can find an X-name of
![]() $\varphi (x)\in |B|$
. As B is regular, we get a B-name q of
$\varphi (x)\in |B|$
. As B is regular, we get a B-name q of
![]() $\varphi (x)$
. Then
$\varphi (x)$
. Then
![]() $r_+(p,q)$
is an A-name of x. Thus, A is regular.
$r_+(p,q)$
is an A-name of x. Thus, A is regular.
Proof of Proposition 3.35
For the non-existence of meet, it is known that every increasing sequence of many-one degrees has an exact pair [Reference Odifreddi5, Theorem VI.3.4]; that is, for any sequence
![]() $A_0<_mA_1<_m\dots $
of subsets of
$A_0<_mA_1<_m\dots $
of subsets of
![]() $\omega $
there exists
$\omega $
there exists
![]() $B,C\subseteq \omega $
such that
$B,C\subseteq \omega $
such that
![]() $A\leq _m B,C$
if and only if
$A\leq _m B,C$
if and only if
![]() $A\leq _m A_i$
for some
$A\leq _m A_i$
for some
![]() $i\in \omega $
, where
$i\in \omega $
, where
![]() $\leq _m$
is many-one reducibility in the classical sense (Definition 3.19). Now note that if
$\leq _m$
is many-one reducibility in the classical sense (Definition 3.19). Now note that if
![]() $R,S$
are regular subobjects of
$R,S$
are regular subobjects of
![]() $\omega $
then
$\omega $
then
![]() $R\leq _{\mathsf {m}}S$
iff
$R\leq _{\mathsf {m}}S$
iff
![]() $R\leq _{\mathsf {m}}'S$
iff
$R\leq _{\mathsf {m}}'S$
iff
![]() $|R|\leq _m|S|$
. For each
$|R|\leq _m|S|$
. For each
![]() $i\in \omega $
, let us think of
$i\in \omega $
, let us think of
![]() $A_i,B,C$
as regular subobjects of
$A_i,B,C$
as regular subobjects of
![]() $\omega $
. We claim that B and C do not have meet. If
$\omega $
. We claim that B and C do not have meet. If
![]() $A\leq _{\mathsf {m}}' B,C$
then, by Lemma 3.37, A is also regular. Thus, the above property shows
$A\leq _{\mathsf {m}}' B,C$
then, by Lemma 3.37, A is also regular. Thus, the above property shows
![]() $A\leq _{\mathsf {m}}A_i$
for some
$A\leq _{\mathsf {m}}A_i$
for some
![]() $i\in \omega $
. Then we get
$i\in \omega $
. Then we get
![]() $A<_{\mathsf {m}}A_{i+1}<_{\mathsf {m}}B,C$
, which means that A is not a meet of B and C.
$A<_{\mathsf {m}}A_{i+1}<_{\mathsf {m}}B,C$
, which means that A is not a meet of B and C.
4 Hierarchy
4.1 Sierpiński dominance
Our objective is to analyze the arithmetical/Borel hierarchy in the category of represented spaces. For this, we first need to define the notion of
![]() $\Sigma ^0_1$
and
$\Sigma ^0_1$
and
![]() $\Pi ^0_1$
subobjects. Let us first explain these notions for subobjects of
$\Pi ^0_1$
subobjects. Let us first explain these notions for subobjects of
![]() $\omega ^\omega $
in
$\omega ^\omega $
in
![]() $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
![]() $\mathsf {KV}$
, followed by the general definitions.
$\mathsf {KV}$
, followed by the general definitions.
Definition 4.1 (
 $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
 $\mathsf {KV}$
)
$\mathsf {KV}$
)
A subobject
![]() $A\rightarrowtail \omega ^\omega $
is open or
$A\rightarrowtail \omega ^\omega $
is open or
![]() $\Sigma ^0_1$
if there exists a morphism
$\Sigma ^0_1$
if there exists a morphism
![]() $\varphi \colon \omega ^\omega \times \omega \to \omega $
such that A is equivalent to the following subspace
$\varphi \colon \omega ^\omega \times \omega \to \omega $
such that A is equivalent to the following subspace
![]() $E_\varphi $
of
$E_\varphi $
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
Similarly, a subobject
![]() $A\rightarrowtail \omega ^\omega $
is closed or
$A\rightarrowtail \omega ^\omega $
is closed or
![]() $\Pi ^0_1$
if there exists a morphism
$\Pi ^0_1$
if there exists a morphism
![]() $\varphi \colon \omega ^\omega \times \omega \to \omega $
such that A is equivalent to the subspace of
$\varphi \colon \omega ^\omega \times \omega \to \omega $
such that A is equivalent to the subspace of
![]() $\omega ^\omega $
whose underlying set is
$\omega ^\omega $
whose underlying set is
![]() $\omega ^\omega \setminus E_\varphi $
.
$\omega ^\omega \setminus E_\varphi $
.
Via currying, a
![]() $\Sigma ^0_1$
subobject is a subspace of the form
$\Sigma ^0_1$
subobject is a subspace of the form
![]() $\{x\in \omega ^\omega :\varphi (x)\not =0^\infty \}$
, and a
$\{x\in \omega ^\omega :\varphi (x)\not =0^\infty \}$
, and a
![]() $\Pi ^0_1$
subobject is a subspace of the form
$\Pi ^0_1$
subobject is a subspace of the form
![]() $\{x\in \omega ^\omega :\varphi (x)=0^\infty \}$
. We would like to consider a similar notion for
$\{x\in \omega ^\omega :\varphi (x)=0^\infty \}$
. We would like to consider a similar notion for
![]() $\mathsf {K}_1$
, but we need to give a formal definition of
$\mathsf {K}_1$
, but we need to give a formal definition of
![]() $\omega ^\omega $
in
$\omega ^\omega $
in
![]() $\mathsf {K}_1$
.
$\mathsf {K}_1$
.
Definition 4.2. By an abuse of notation, we use
![]() $\omega ^\omega $
to denote the exponential object
$\omega ^\omega $
to denote the exponential object
![]() $\mathsf {Nat}^{\mathsf {Nat}}$
. To be more explicit:
$\mathsf {Nat}^{\mathsf {Nat}}$
. To be more explicit:
-
• In
 $\mathsf {K}_2$
and
$\mathsf {K}_2$
and
 $\mathsf {KV}$
, the underlying set
$\mathsf {KV}$
, the underlying set
 $|\mathsf {Nat}^{\mathsf {Nat}}|$
is the set of all functions on
$|\mathsf {Nat}^{\mathsf {Nat}}|$
is the set of all functions on
 $\mathbb {N}$
. A name of
$\mathbb {N}$
. A name of
 $f\in \mathsf {Nat}^{\mathsf {Nat}}$
is f itself (as in Examples 2.2 and 3.8).
$f\in \mathsf {Nat}^{\mathsf {Nat}}$
is f itself (as in Examples 2.2 and 3.8). -
• In
 $\mathsf {K}_1$
, the underlying set
$\mathsf {K}_1$
, the underlying set
 $|\mathsf {Nat}^{\mathsf {Nat}}|$
is the set of all total computable functions on
$|\mathsf {Nat}^{\mathsf {Nat}}|$
is the set of all total computable functions on
 $\mathbb {N}$
. A name of
$\mathbb {N}$
. A name of
 $f\in \mathsf {Nat}^{\mathsf {Nat}}$
is any program
$f\in \mathsf {Nat}^{\mathsf {Nat}}$
is any program
 $p\in \mathtt {Code}$
computing f.
$p\in \mathtt {Code}$
computing f.
By adopting this definition, Definition 4.1 makes sense for
![]() $\mathsf {K}_1$
as well. Since most of the concrete examples in this article are subobjects of
$\mathsf {K}_1$
as well. Since most of the concrete examples in this article are subobjects of
![]() $\omega ^\omega $
, it is sufficient to understand the above as definitions of open and closed subobjects. However, for the sake of uniform discussion, we also give general definitions.
$\omega ^\omega $
, it is sufficient to understand the above as definitions of open and closed subobjects. However, for the sake of uniform discussion, we also give general definitions.
Definition 4.3. A subobject
![]() $A\rightarrowtail X$
is open or
$A\rightarrowtail X$
is open or
![]() $\Sigma ^0_1$
if there exists a partial realizable function F such that A is equivalent to the following subspace
$\Sigma ^0_1$
if there exists a partial realizable function F such that A is equivalent to the following subspace
![]() $E_F$
of X:
$E_F$
of X:
 $$ \begin{align*} x\in |E_F|&\iff \text{if }p\text{ is an }X\text{-name of }x\text{ then }F(p)\text{ is an }\omega^\omega\text{-name of }0^\infty,\\ x\not\in |E_F|&\iff \text{if }p\text{ is an }X\text{-name of }x\text{ then }F(p)\text{ is an }\omega^\omega\text{-name of some }\alpha\not=0^\infty. \end{align*} $$
$$ \begin{align*} x\in |E_F|&\iff \text{if }p\text{ is an }X\text{-name of }x\text{ then }F(p)\text{ is an }\omega^\omega\text{-name of }0^\infty,\\ x\not\in |E_F|&\iff \text{if }p\text{ is an }X\text{-name of }x\text{ then }F(p)\text{ is an }\omega^\omega\text{-name of some }\alpha\not=0^\infty. \end{align*} $$
Similarly, a subobject
![]() $A\rightarrowtail \omega ^\omega $
is closed or
$A\rightarrowtail \omega ^\omega $
is closed or
![]() $\Pi ^0_1$
if there exists a partial realizable function such that A is equivalent to the subspace of X whose underlying set is
$\Pi ^0_1$
if there exists a partial realizable function such that A is equivalent to the subspace of X whose underlying set is
![]() $|X|\setminus |E_F|$
.
$|X|\setminus |E_F|$
.
Let us explain the general theory behind this definition. Recall from Example 2.5 that
![]() $\mathbb {S}$
is the represented Sierpiński space. Here, (an
$\mathbb {S}$
is the represented Sierpiński space. Here, (an
![]() $\omega ^\omega $
-name of) the sequence
$\omega ^\omega $
-name of) the sequence
![]() $0^\infty $
is a name of
$0^\infty $
is a name of
![]() $\top \in \mathbb {S}$
and any other sequence is a name of
$\top \in \mathbb {S}$
and any other sequence is a name of
![]() $\bot \in \mathbb {S}$
.
$\bot \in \mathbb {S}$
.
It is well-known that an open set in a topological space can be identified with a continuous map to the (topological) Sierpiński space
![]() $\mathbb {S}$
, which consists of the open point
$\mathbb {S}$
, which consists of the open point
![]() $\top $
and the closed point
$\top $
and the closed point
![]() $\bot $
. To be precise, an open subset A of a topological space X is exactly a set of the form
$\bot $
. To be precise, an open subset A of a topological space X is exactly a set of the form
![]() $\varphi ^{-1}\{\top \}$
for some continuous map
$\varphi ^{-1}\{\top \}$
for some continuous map
![]() $\varphi \colon X\to \mathbb {S}$
. This idea can be generalized as follows:
$\varphi \colon X\to \mathbb {S}$
. This idea can be generalized as follows:
Definition 4.4. A subobject
![]() $A\rightarrowtail X$
is open if it is a pullback of
$A\rightarrowtail X$
is open if it is a pullback of
![]() $\top \colon \mathbf {1}\rightarrowtail \mathbb {S}$
along some morphism
$\top \colon \mathbf {1}\rightarrowtail \mathbb {S}$
along some morphism
![]() $\varphi \colon X\to \mathbb {S}$
. Similarly, a subobject
$\varphi \colon X\to \mathbb {S}$
. Similarly, a subobject
![]() $A\rightarrowtail X$
is closed if it is a pullback of
$A\rightarrowtail X$
is closed if it is a pullback of
![]() $\bot \colon \mathbf {1}\rightarrowtail \mathbb {S}$
along some morphism
$\bot \colon \mathbf {1}\rightarrowtail \mathbb {S}$
along some morphism
![]() $\varphi \colon X\to \mathbb {S}$
.
$\varphi \colon X\to \mathbb {S}$
.
To be more explicit, the pullback
![]() $\varphi ^\ast \top $
can be written as follows:
$\varphi ^\ast \top $
can be written as follows:
-
• The underlying set is
 $|\varphi ^\ast \top |=\{x\in X:\varphi (x)=\top \}$
.
$|\varphi ^\ast \top |=\{x\in X:\varphi (x)=\top \}$
. -
• A name of
 $x\in \varphi ^\ast \top $
is a name of
$x\in \varphi ^\ast \top $
is a name of
 $x\in X$
.
$x\in X$
.
Note that fixing a name of
![]() $\top \in \mathbb {S}$
in advance makes it possible to omit the information on a name of
$\top \in \mathbb {S}$
in advance makes it possible to omit the information on a name of
![]() $\top $
form the above description of
$\top $
form the above description of
![]() $\varphi ^\ast \top $
. By definition of the representation of
$\varphi ^\ast \top $
. By definition of the representation of
![]() $\mathbb {S}$
, it is easy to verify that this definition is consistent with Definition 4.3. Also note, by definition, that
$\mathbb {S}$
, it is easy to verify that this definition is consistent with Definition 4.3. Also note, by definition, that
![]() $A\rightarrowtail X$
is open iff
$A\rightarrowtail X$
is open iff
![]() $A\leq _{\mathsf {m}}(\top \colon \mathbf {1}\rightarrowtail \mathbb {S})$
, and
$A\leq _{\mathsf {m}}(\top \colon \mathbf {1}\rightarrowtail \mathbb {S})$
, and
![]() $A\rightarrowtail X$
is closed iff
$A\rightarrowtail X$
is closed iff
![]() $A\leq _{\mathsf {m}}(\bot \colon \mathbf {1}\rightarrowtail \mathbb {S})$
.
$A\leq _{\mathsf {m}}(\bot \colon \mathbf {1}\rightarrowtail \mathbb {S})$
.
Observation 4.5. An open subobject is regular. Similarly, a closed subobject is regular.
Proof. This is because an open subobject is a pullback of a regular subobject
![]() $\top \colon \mathbf {1}\rightarrowtail \mathbb {S}$
. The same applies to a closed subobject. See also the above explicit description of the pullback.
$\top \colon \mathbf {1}\rightarrowtail \mathbb {S}$
. The same applies to a closed subobject. See also the above explicit description of the pullback.
Example 4.6.
-
1. In
 $\mathsf {K}_1$
: An open subobject of
$\mathsf {K}_1$
: An open subobject of
 $\omega $
is exactly a
$\omega $
is exactly a
 $\Sigma ^0_1$
subset of
$\Sigma ^0_1$
subset of
 $\omega $
, and a closed subobject of
$\omega $
, and a closed subobject of
 $\omega $
is exactly a
$\omega $
is exactly a
 $\Pi ^0_1$
subset of
$\Pi ^0_1$
subset of
 $\omega $
.
$\omega $
. -
2. In
 $\mathsf {KV}$
: An open subobject of
$\mathsf {KV}$
: An open subobject of
 $\omega ^\omega $
is exactly a
$\omega ^\omega $
is exactly a
 $\Sigma ^0_1$
subset of
$\Sigma ^0_1$
subset of
 $\omega ^\omega $
, and a closed subobject of
$\omega ^\omega $
, and a closed subobject of
 $\omega ^\omega $
is exactly a
$\omega ^\omega $
is exactly a
 $\Pi ^0_1$
subset of
$\Pi ^0_1$
subset of
 $\omega ^\omega $
.
$\omega ^\omega $
. -
3. In
 $\mathsf {K}_2$
: An open subobject of
$\mathsf {K}_2$
: An open subobject of
 $\omega ^\omega $
is exactly an open subset of
$\omega ^\omega $
is exactly an open subset of
 $\omega ^\omega $
, and a closed subobject of
$\omega ^\omega $
, and a closed subobject of
 $\omega ^\omega $
is exactly a closed subset of
$\omega ^\omega $
is exactly a closed subset of
 $\omega ^\omega $
.
$\omega ^\omega $
.
One can generalize these equivalences to (computable) Polish spaces and more, under appropriate (admissible) representations.
4.2 Arithmetical hierarchy
One of the main ingredients of the theory of hierarchies is the extraction of subsets using formulas. This idea is common to both arithmetic and Borel hierarchies.
Let
![]() $\Gamma $
be a class of subobjects. A sequence
$\Gamma $
be a class of subobjects. A sequence
![]() $(A_i)_{i\in I}$
of subobjects of X is uniformly
$(A_i)_{i\in I}$
of subobjects of X is uniformly
![]() $\Gamma $
if there exists a
$\Gamma $
if there exists a
![]() $\Gamma $
-subobject
$\Gamma $
-subobject
![]() $A\rightarrowtail I\times X$
such that
$A\rightarrowtail I\times X$
such that
![]() $A_i$
is the ith projection of A for each
$A_i$
is the ith projection of A for each
![]() $i\in I$
.
$i\in I$
.
Definition 4.7. Let A be a subobject of a represented space X.
-
1. A subobject A is
 ${\Sigma }^0_1$
if it is an open subobject of X.
${\Sigma }^0_1$
if it is an open subobject of X. -
2. A subobject A is
 ${\Pi }^0_1$
if it is a closed subobject of X.
${\Pi }^0_1$
if it is a closed subobject of X. -
3. A subobject A is
 ${\Sigma }^0_{n+1}$
if there exists a uniformly
${\Sigma }^0_{n+1}$
if there exists a uniformly
 $\Pi ^0_n$
sequence
$\Pi ^0_n$
sequence
 $(B_n)_{n\in \omega }$
of subobjects of X such that
$(B_n)_{n\in \omega }$
of subobjects of X such that
 $A\equiv \biguplus _{n\in \omega }B_n$
.
$A\equiv \biguplus _{n\in \omega }B_n$
. -
4. A subobject A is
 ${\Pi }^0_{n+1}$
if there exists a uniformly
${\Pi }^0_{n+1}$
if there exists a uniformly
 $\Sigma ^0_n$
sequence
$\Sigma ^0_n$
sequence
 $(B_n)_{n\in \omega }$
of subobjects of X such that
$(B_n)_{n\in \omega }$
of subobjects of X such that  .
.
In
![]() $\mathsf {K}_2$
, this definition coincides with the standard definition of the Borel hierarchy. In
$\mathsf {K}_2$
, this definition coincides with the standard definition of the Borel hierarchy. In
![]() $\mathsf {K}_1$
, this is the arithmetical hierarchy with witnesses.
$\mathsf {K}_1$
, this is the arithmetical hierarchy with witnesses.
Example 4.8. Recall from Example 3.8 that
![]() $\mathsf {Fin}$
is the subobject of
$\mathsf {Fin}$
is the subobject of
![]() $\omega ^\omega $
consisting of sequences which are eventually zero. Then
$\omega ^\omega $
consisting of sequences which are eventually zero. Then
![]() $\mathsf {Fin}$
is a
$\mathsf {Fin}$
is a
![]() ${\Sigma }^0_2$
subobject of
${\Sigma }^0_2$
subobject of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
This is because
![]() $F=\{(n,x)\in \omega \times \omega ^\omega :(\forall m\geq n)\;x(m)=0\}$
is a closed subobject of
$F=\{(n,x)\in \omega \times \omega ^\omega :(\forall m\geq n)\;x(m)=0\}$
is a closed subobject of
![]() $\omega \times \omega ^\omega $
; hence
$\omega \times \omega ^\omega $
; hence
![]() $\mathsf {Fin}=\exists ^\omega F=\biguplus _{n\in \omega }F_n$
is
$\mathsf {Fin}=\exists ^\omega F=\biguplus _{n\in \omega }F_n$
is
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
Observation 4.9. Every
![]() ${\Pi }^0_2$
subobject of a represented space X is regular.
${\Pi }^0_2$
subobject of a represented space X is regular.
Proof. Every
![]() $\Pi ^0_2$
subobject
$\Pi ^0_2$
subobject
![]() $A\rightarrowtail X$
is of the form
$A\rightarrowtail X$
is of the form ![]() for some open subobject
for some open subobject
![]() $B\rightarrowtail \omega \times X$
. By Observation 4.5, B is regular, so a name of
$B\rightarrowtail \omega \times X$
. By Observation 4.5, B is regular, so a name of
![]() $(n,x)\in B$
is just the pair of
$(n,x)\in B$
is just the pair of
![]() $n\in \omega $
and an X-name of x. By definition, a name of
$n\in \omega $
and an X-name of x. By definition, a name of
![]() $x\in A$
is a name of a function that, given
$x\in A$
is a name of a function that, given
![]() $n\in \omega $
, returns an name of
$n\in \omega $
, returns an name of
![]() $(n,x)\in B$
. In particular, if p is a name of
$(n,x)\in B$
. In particular, if p is a name of
![]() $x\in X$
then the constant function
$x\in X$
then the constant function
![]() $n\mapsto p$
gives a name of
$n\mapsto p$
gives a name of
![]() $x\in A$
. This means that
$x\in A$
. This means that
![]() $A\rightarrowtail X$
is regular.
$A\rightarrowtail X$
is regular.
4.3 Internal logic
It is also useful to introduce a method of defining a subobject of a represented space using a first order formula. It is often easier to read the meaning of a construction of a subobject by using a formula than by combining set operations.
Definition 4.10. Given a sequence
![]() $(X_i)_{i\leq n}$
of represented spaces, let
$(X_i)_{i\leq n}$
of represented spaces, let
![]() $x_i$
be a variable symbol of type
$x_i$
be a variable symbol of type
![]() $X_i$
. Put a subobject
$X_i$
. Put a subobject
![]() $R_i\rightarrowtail X_i$
as a relation symbol of type
$R_i\rightarrowtail X_i$
as a relation symbol of type
![]() $X_i$
in our language. Then inductively define a subobject
$X_i$
in our language. Then inductively define a subobject ![]() of
of
![]() $X_1\times \dots \times X_n$
as follows:
$X_1\times \dots \times X_n$
as follows:
-
1.
 .
. -
2.
 .
. -
3.
 .
. -
4.
 .
.
Moreover, for a represented space I,
-
5.
 .
. -
6.
 .
.
Thereafter, a relation symbol
![]() $R(x)$
in a formula is sometimes abbreviated to
$R(x)$
in a formula is sometimes abbreviated to
![]() $x\in R$
. Also, we sometimes use a notation such as
$x\in R$
. Also, we sometimes use a notation such as
![]() $s(x)=t(y)$
in a formula, which determines the subspace whose underlying set is
$s(x)=t(y)$
in a formula, which determines the subspace whose underlying set is
![]() $\{(x,y):s(x)=t(y)\}$
.
$\{(x,y):s(x)=t(y)\}$
.
Hereafter, we mainly focus on the subobjects of
![]() $\omega ^\omega $
. As already noted, in
$\omega ^\omega $
. As already noted, in
![]() $\mathsf {K}_2$
and
$\mathsf {K}_2$
and
![]() $\mathsf {KV}$
, the object
$\mathsf {KV}$
, the object
![]() $\omega ^\omega $
literally means the set of all infinite sequences of natural numbers, while in
$\omega ^\omega $
literally means the set of all infinite sequences of natural numbers, while in
![]() $\mathsf {K}_1$
, the exponential object
$\mathsf {K}_1$
, the exponential object
![]() $\omega ^\omega $
is the space of all total computable functions. Thus, our theory on many-one reducibility for subobjects of
$\omega ^\omega $
is the space of all total computable functions. Thus, our theory on many-one reducibility for subobjects of
![]() $\omega ^\omega $
in
$\omega ^\omega $
in
![]() $\mathsf {K}_1$
correspond to the witnessed version of many-one reducibility for index sets within
$\mathsf {K}_1$
correspond to the witnessed version of many-one reducibility for index sets within
![]() $\mathrm {Tot}$
in classical terms, where
$\mathrm {Tot}$
in classical terms, where
![]() $\mathrm {Tot}$
is the set of all indices of total computable functions on
$\mathrm {Tot}$
is the set of all indices of total computable functions on
![]() $\omega $
.
$\omega $
.
5 The structure of
 $\Sigma ^0_2$
sets
$\Sigma ^0_2$
sets
5.1 Union of closed sets
According to Veldman [Reference Veldman9], in certain intuitionistic systems, interestingly, the union of two
![]() $\Pi ^0_1$
sets is not necessarily
$\Pi ^0_1$
sets is not necessarily
![]() $\Pi ^0_1$
. We first see that this strange phenomenon can be given a clear interpretation even in classical logic by using reducibility for non-regular subobjects.
$\Pi ^0_1$
. We first see that this strange phenomenon can be given a clear interpretation even in classical logic by using reducibility for non-regular subobjects.
Example 5.1. Let I be a represented space, and
![]() $X,Y\subseteq I$
be its subspaces. Then the tartan
$X,Y\subseteq I$
be its subspaces. Then the tartan
![]() $\uplus _I(X,Y)$
is defined as the witnessed union
$\uplus _I(X,Y)$
is defined as the witnessed union
![]() $(X\times I)\uplus (I\times Y)$
. In other words,
$(X\times I)\uplus (I\times Y)$
. In other words, ![]() .
.
Example 5.2. For the closed subspace
![]() $\{0^\infty \}\subseteq \omega ^\omega $
, consider the tartan
$\{0^\infty \}\subseteq \omega ^\omega $
, consider the tartan
![]() $\mathsf {L}=\uplus _{\omega ^\omega }(\{0^\infty \},\{0^\infty \})$
. In other words,
$\mathsf {L}=\uplus _{\omega ^\omega }(\{0^\infty \},\{0^\infty \})$
. In other words, ![]() .
.
Let
![]() $\Sigma _{\pi \cup \pi }$
be the class of subobjects which can be written as a witnessed union of two
$\Sigma _{\pi \cup \pi }$
be the class of subobjects which can be written as a witnessed union of two
![]() $\Pi ^0_1$
sets.
$\Pi ^0_1$
sets.
Observation 5.3.
![]() $\mathsf {L}\in \Sigma _{\pi \cup \pi }$
.
$\mathsf {L}\in \Sigma _{\pi \cup \pi }$
.
A typical way to show the non-regularity of a subobject in
![]() $\mathsf {K}_2$
or
$\mathsf {K}_2$
or
![]() $\mathsf {KV}$
can be to use the following notion.
$\mathsf {KV}$
can be to use the following notion.
Definition 5.4. For a subobject
![]() $A\rightarrowtail X$
, we say that
$A\rightarrowtail X$
, we say that
![]() $x\in A$
is non-regular if, for some
$x\in A$
is non-regular if, for some
![]() $\ell \in \omega $
, for any A-name p of x and X-name q of x, there exists a sequence
$\ell \in \omega $
, for any A-name p of x and X-name q of x, there exists a sequence
![]() $(y_n)_{n\in \omega }$
of points in A such that
$(y_n)_{n\in \omega }$
of points in A such that
-
1.
 $p\upharpoonright \ell $
cannot be extended to an A-name of
$p\upharpoonright \ell $
cannot be extended to an A-name of
 $y_n$
for any
$y_n$
for any
 $n\in \omega $
.
$n\in \omega $
. -
2. for any m,
 $q\upharpoonright m$
can be extended to an X-name of
$q\upharpoonright m$
can be extended to an X-name of
 $y_n$
for some
$y_n$
for some
 $n\in \omega $
.
$n\in \omega $
.
Example 5.5.
![]() $\mathsf {L}$
has a non-regular point. We claim that
$\mathsf {L}$
has a non-regular point. We claim that
![]() $z=(0^\infty ,0^\infty )$
is a non-regular point of
$z=(0^\infty ,0^\infty )$
is a non-regular point of
![]() $\mathsf {L}$
. To see this, note that a name of
$\mathsf {L}$
. To see this, note that a name of
![]() $z\in \mathsf {L}$
is of the form
$z\in \mathsf {L}$
is of the form
![]() $q_i=(i,0^\infty ,0^\infty )$
for some
$q_i=(i,0^\infty ,0^\infty )$
for some
![]() $i<2$
. Then, put
$i<2$
. Then, put
![]() $\ell =1$
,
$\ell =1$
,
![]() $y_m^0=(0^{m}1^\infty ,0^\infty )$
and
$y_m^0=(0^{m}1^\infty ,0^\infty )$
and
![]() $y_m^1=(0^\infty ,0^m1^\infty )$
. Then
$y_m^1=(0^\infty ,0^m1^\infty )$
. Then
![]() $q_i\upharpoonright \ell $
cannot be extended to an
$q_i\upharpoonright \ell $
cannot be extended to an
![]() $\mathsf {L}$
-name of
$\mathsf {L}$
-name of
![]() $y_m^i$
for each
$y_m^i$
for each
![]() $i<2$
, while
$i<2$
, while
![]() $z\upharpoonright m$
can be extended to X-names of both
$z\upharpoonright m$
can be extended to X-names of both
![]() $y_m^0$
and
$y_m^0$
and
![]() $y_m^1$
.
$y_m^1$
.
Lemma 5.6. If a subobject
![]() $A\rightarrowtail X$
has a non-regular point, then A is not regular.
$A\rightarrowtail X$
has a non-regular point, then A is not regular.
Proof. Assume that
![]() $A\rightarrowtail X$
is regular. Then the inclusion map
$A\rightarrowtail X$
is regular. Then the inclusion map
![]() $A\rightarrowtail X$
has a partial left-inverse morphism, so let r be its tracker. That is, if q is an X-name of
$A\rightarrowtail X$
has a partial left-inverse morphism, so let r be its tracker. That is, if q is an X-name of
![]() $x\in |A|$
, then
$x\in |A|$
, then
![]() $r(q)$
is an A-name of x. Now, suppose that A has a non-regular point
$r(q)$
is an A-name of x. Now, suppose that A has a non-regular point
![]() $x\in A$
, and let
$x\in A$
, and let
![]() $\ell $
be a length for its non-regularity. For an X-name q of x and an A-name
$\ell $
be a length for its non-regularity. For an X-name q of x and an A-name
![]() $r(q)$
of x, we get a witness
$r(q)$
of x, we get a witness
![]() $(y_t)_{t\in \omega }$
for non-regularity. By continuity, after reading some m bits of q, the first
$(y_t)_{t\in \omega }$
for non-regularity. By continuity, after reading some m bits of q, the first
![]() $\ell $
bits of
$\ell $
bits of
![]() $r(q)$
are determined. Then
$r(q)$
are determined. Then
![]() $q\upharpoonright m$
can be extended to an X-name
$q\upharpoonright m$
can be extended to an X-name
![]() $q'$
of
$q'$
of
![]() $y_t\in |A|$
, so
$y_t\in |A|$
, so
![]() $r(q')$
must be an A-name of
$r(q')$
must be an A-name of
![]() $y_t$
. However,
$y_t$
. However,
![]() $r(q')$
extends
$r(q')$
extends
![]() $r(q)\upharpoonright \ell $
, which cannot be an A-name of
$r(q)\upharpoonright \ell $
, which cannot be an A-name of
![]() $y_t$
.
$y_t$
.
Corollary 5.7. A union of two
![]() $\Pi ^0_1$
subobjects of
$\Pi ^0_1$
subobjects of
![]() $\omega ^\omega $
is not necessarily
$\omega ^\omega $
is not necessarily
![]() $\Pi ^0_1$
. Indeed,
$\Pi ^0_1$
. Indeed,
![]() $\mathsf {L}$
is not
$\mathsf {L}$
is not
![]() ${\Pi }^0_2$
, and thus
${\Pi }^0_2$
, and thus
![]() $\Sigma _{\pi \cup \pi }\not \subseteq {\Pi }^0_2$
.
$\Sigma _{\pi \cup \pi }\not \subseteq {\Pi }^0_2$
.
5.2 Non-complete
 $\Sigma ^0_2$
sets
$\Sigma ^0_2$
sets
Classically, it is well-known that
![]() $\mathrm {Fin}=\{x\in \omega ^\omega :(\exists n)(\forall m\geq n)\;x(m)=0\}$
is
$\mathrm {Fin}=\{x\in \omega ^\omega :(\exists n)(\forall m\geq n)\;x(m)=0\}$
is
![]() $\Sigma ^0_2$
-complete. Surprisingly, Veldman [Reference Veldman12] showed that this does not hold in certain intuitionistic systems. His insightful work suggests that its witnessed counterpart is not
$\Sigma ^0_2$
-complete. Surprisingly, Veldman [Reference Veldman12] showed that this does not hold in certain intuitionistic systems. His insightful work suggests that its witnessed counterpart is not
![]() $\Sigma ^0_2$
-complete in our setting.
$\Sigma ^0_2$
-complete in our setting.
For the explicit description, recall Example 3.8. Our first goal is to show the following:
Theorem 5.8.
![]() $\mathsf {Fin}$
is not
$\mathsf {Fin}$
is not
![]() $\Sigma ^0_2$
-complete; indeed,
$\Sigma ^0_2$
-complete; indeed,
![]() $\mathsf {L}\not \leq _{\mathsf {m}}\mathsf {Fin}$
.
$\mathsf {L}\not \leq _{\mathsf {m}}\mathsf {Fin}$
.
To prove this, let us introduce a few notions. We say that a subobject
![]() $A\rightarrowtail Z$
is almost
$A\rightarrowtail Z$
is almost
![]() $\Pi ^0_1$
if it is a finite witnessed union of
$\Pi ^0_1$
if it is a finite witnessed union of
![]() $\Pi ^0_1$
subobjects of Z. We say that a subobject
$\Pi ^0_1$
subobjects of Z. We say that a subobject
![]() $A\rightarrowtail Z$
is amalgamable if there exists
$A\rightarrowtail Z$
is amalgamable if there exists
![]() $A'\equiv A$
and there exists a partial realizable function F that, given a Z-name of
$A'\equiv A$
and there exists a partial realizable function F that, given a Z-name of
![]() $x\in |A'|$
and a finite sequence
$x\in |A'|$
and a finite sequence
![]() $(p_1,\dots ,p_n)$
, returns a name of
$(p_1,\dots ,p_n)$
, returns a name of
![]() $x\in A'$
, whenever there exists
$x\in A'$
, whenever there exists
![]() $i\leq n$
such that
$i\leq n$
such that
![]() $p_i$
is a name of
$p_i$
is a name of
![]() $x\in A'$
.
$x\in A'$
.
Proposition 5.9.
![]() $\mathsf {Fin}$
is an amalgamable subobject of
$\mathsf {Fin}$
is an amalgamable subobject of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proof. Let
![]() $x\in |\mathsf {Fin}|$
and
$x\in |\mathsf {Fin}|$
and
![]() $(p_1,\dots ,p_n)$
be given. Assume that
$(p_1,\dots ,p_n)$
be given. Assume that
![]() $p_i$
is a name of
$p_i$
is a name of
![]() $x\in \mathsf {Fin}$
for some
$x\in \mathsf {Fin}$
for some
![]() $i\leq n$
. As a name of an element of
$i\leq n$
. As a name of an element of
![]() $\mathsf {Fin}$
is of the form
$\mathsf {Fin}$
is of the form
![]() $\langle s,z\rangle $
, it does not lose generality to assume that each
$\langle s,z\rangle $
, it does not lose generality to assume that each
![]() $p_i$
is of the form
$p_i$
is of the form
![]() $\langle s_i,z_i\rangle $
. By our assumption, at least one of these is a correct name of
$\langle s_i,z_i\rangle $
. By our assumption, at least one of these is a correct name of
![]() $x\in \mathsf {Fin}$
, so it is of the form
$x\in \mathsf {Fin}$
, so it is of the form
![]() $p_j=\langle s_j,x\rangle $
for some j. Here, recall that
$p_j=\langle s_j,x\rangle $
for some j. Here, recall that
![]() $\langle s_j,x\rangle $
is a name of
$\langle s_j,x\rangle $
is a name of
![]() $x\in \mathsf {Fin}$
if and only if
$x\in \mathsf {Fin}$
if and only if
![]() $x(t)=0$
for any
$x(t)=0$
for any
![]() $t\geq s_j$
. Note that, if we put
$t\geq s_j$
. Note that, if we put
![]() $m=\max _{i\leq n}s_i$
, then
$m=\max _{i\leq n}s_i$
, then
![]() $\langle m,x\rangle $
is also a name of
$\langle m,x\rangle $
is also a name of
![]() $x\in \mathsf {Fin}$
. This is because we have
$x\in \mathsf {Fin}$
. This is because we have
![]() $s_j\leq m$
, which implies
$s_j\leq m$
, which implies
![]() $x(t)=0$
for any
$x(t)=0$
for any
![]() $t\geq m$
. In summary,
$t\geq m$
. In summary,
![]() $F(x,p_1,\dots ,p_n)=\langle \max _{i\leq n}\pi _0(p_i),x\rangle $
gives a name of
$F(x,p_1,\dots ,p_n)=\langle \max _{i\leq n}\pi _0(p_i),x\rangle $
gives a name of
![]() $x\in \mathsf {Fin}$
. Hence,
$x\in \mathsf {Fin}$
. Hence,
![]() $\mathsf {Fin}$
is amalgamable.
$\mathsf {Fin}$
is amalgamable.
Lemma 5.10. If an almost
![]() $\Pi ^0_1$
subobject
$\Pi ^0_1$
subobject
![]() $A\rightarrowtail X$
is many-one reducible to an amalgamable subobject
$A\rightarrowtail X$
is many-one reducible to an amalgamable subobject
![]() $B\rightarrowtail Y$
, then A is regular.
$B\rightarrowtail Y$
, then A is regular.
Proof. Assume that
![]() $A\leq _{\mathsf {m}}B$
is witnessed by
$A\leq _{\mathsf {m}}B$
is witnessed by
![]() $\varphi \colon X\to Y$
and
$\varphi \colon X\to Y$
and
![]() $r_-,r_+$
. To show that
$r_-,r_+$
. To show that
![]() $A\rightarrowtail Z$
is regular, suppose that an X-name p of
$A\rightarrowtail Z$
is regular, suppose that an X-name p of
![]() $x\in |A|$
is given. Since A is almost
$x\in |A|$
is given. Since A is almost
![]() $\Pi ^0_1$
and any
$\Pi ^0_1$
and any
![]() $\Pi ^0_1$
subobject is regular, we may assume that a name of
$\Pi ^0_1$
subobject is regular, we may assume that a name of
![]() $x\in A$
is of the form
$x\in A$
is of the form
![]() $(k,p)$
for some
$(k,p)$
for some
![]() $k<n$
. Then
$k<n$
. Then
![]() $(r_-(k,p))_{k<n}$
is a sequence of candidates of names of
$(r_-(k,p))_{k<n}$
is a sequence of candidates of names of
![]() $\varphi (x)\in B$
. That is, since
$\varphi (x)\in B$
. That is, since
![]() $(k,p)$
is a correct name of
$(k,p)$
is a correct name of
![]() $x\in A$
for some
$x\in A$
for some
![]() $k<n$
,
$k<n$
,
![]() $r_-(k,p)$
must be a correct name of
$r_-(k,p)$
must be a correct name of
![]() $\varphi (x)\in B$
. Here, note that
$\varphi (x)\in B$
. Here, note that
![]() $r_-(k,p)$
may be undefined, but the condition
$r_-(k,p)$
may be undefined, but the condition
![]() $x\in |A_k|$
is
$x\in |A_k|$
is
![]() $\Pi ^0_1(p)$
, so once we see that this is refuted, we modify it to output some value. In this way, we can assume that
$\Pi ^0_1(p)$
, so once we see that this is refuted, we modify it to output some value. In this way, we can assume that
![]() $r_-(k,p)$
is defined.
$r_-(k,p)$
is defined.
A tracker of
![]() $\varphi $
transforms an X-name of x into an Y-name of
$\varphi $
transforms an X-name of x into an Y-name of
![]() $\varphi (x)$
, which, together with the above candidates, can be used to obtain a correct B-name q of
$\varphi (x)$
, which, together with the above candidates, can be used to obtain a correct B-name q of
![]() $\varphi (x)$
by the assumption that B is amalgamable. Then,
$\varphi (x)$
by the assumption that B is amalgamable. Then,
![]() $r_+(p,q)$
is an A-name of
$r_+(p,q)$
is an A-name of
![]() $x\in A$
. This concludes that A is regular.
$x\in A$
. This concludes that A is regular.
Proof of Theorem 5.8
By Proposition 5.9,
![]() $\mathsf {Fin}$
is amalgamable. Obviously,
$\mathsf {Fin}$
is amalgamable. Obviously,
![]() $\mathsf {L}$
is almost
$\mathsf {L}$
is almost
![]() $\Pi ^0_1$
. Hence, by Lemma 5.10, if
$\Pi ^0_1$
. Hence, by Lemma 5.10, if
![]() $\mathsf {L}\leq _{\mathsf {m}}\mathsf {Fin}$
then
$\mathsf {L}\leq _{\mathsf {m}}\mathsf {Fin}$
then
![]() $\mathsf {L}$
is regular, which is impossible by Lemma 5.6 and Example 5.5.
$\mathsf {L}$
is regular, which is impossible by Lemma 5.6 and Example 5.5.
As in classical reducibility, one can see that
![]() $\mathsf {Fin}$
is
$\mathsf {Fin}$
is
![]() $\Sigma ^0_2$
-complete w.r.t. demi-many-one-reducibility.
$\Sigma ^0_2$
-complete w.r.t. demi-many-one-reducibility.
Observation 5.11. For any
![]() $\Sigma ^0_2$
subobject
$\Sigma ^0_2$
subobject
![]() $A\rightarrowtail \omega ^\omega $
, we have
$A\rightarrowtail \omega ^\omega $
, we have
![]() $A\leq _{\mathsf {m}}'\mathsf {Fin}$
.
$A\leq _{\mathsf {m}}'\mathsf {Fin}$
.
Proof. The argument is similar to the classical
![]() $\Sigma ^0_2$
-completeness proof of
$\Sigma ^0_2$
-completeness proof of
![]() $\mathsf {Fin}$
. Let
$\mathsf {Fin}$
. Let ![]() be given, where
be given, where
![]() $\theta $
is decidable. Given x, we construct
$\theta $
is decidable. Given x, we construct
![]() $\varphi (x)$
. In order to determine the value of
$\varphi (x)$
. In order to determine the value of
![]() $\varphi (x)(s)$
, we first calculate the largest
$\varphi (x)(s)$
, we first calculate the largest
![]() $n_s\leq s$
fulfilling the following condition: For any
$n_s\leq s$
fulfilling the following condition: For any
![]() $k\leq n_s$
there exists
$k\leq n_s$
there exists
![]() $m\leq s-n_s$
such that
$m\leq s-n_s$
such that
![]() $\neg \theta (k,m,x)$
. If
$\neg \theta (k,m,x)$
. If
![]() $n_s>n_{s-1}$
then put
$n_s>n_{s-1}$
then put
![]() $\varphi (x)(s)=1$
; otherwise
$\varphi (x)(s)=1$
; otherwise
![]() $\varphi (x)(s)=0$
. Note that if
$\varphi (x)(s)=0$
. Note that if
![]() $x\in A$
and if n is the least witness for
$x\in A$
and if n is the least witness for
![]() $x\in A$
, then we have
$x\in A$
, then we have
![]() $n_s\leq n$
for any s. Hence, for the least s such that
$n_s\leq n$
for any s. Hence, for the least s such that
![]() $n_s=n$
, the value
$n_s=n$
, the value
![]() $s+1$
must be a witness for
$s+1$
must be a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
. Conversely, if s is a witness for
$\varphi (x)\in \mathsf {Fin}$
. Conversely, if s is a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
, then
$\varphi (x)\in \mathsf {Fin}$
, then
![]() $n_t=n_s$
for any
$n_t=n_s$
for any
![]() $t\geq s$
. Then it is easy to see that
$t\geq s$
. Then it is easy to see that
![]() $n_s+1$
is a witness for
$n_s+1$
is a witness for
![]() $x\in A$
.
$x\in A$
.
The above proof shows that given the least witness for
![]() $x\in A$
, one can compute a witness for
$x\in A$
, one can compute a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
. Of course, there may also be a non-least witness for
$\varphi (x)\in \mathsf {Fin}$
. Of course, there may also be a non-least witness for
![]() $x\in A$
, but if it is always possible to obtain the least witness for any
$x\in A$
, but if it is always possible to obtain the least witness for any
![]() $x\in A$
, this suggests that A be many-one reducible to
$x\in A$
, this suggests that A be many-one reducible to
![]() $\mathsf {Fin}$
. Let us explore this idea further.
$\mathsf {Fin}$
. Let us explore this idea further.
5.3 Classification of
 $\Sigma ^0_2$
-complete sets
$\Sigma ^0_2$
-complete sets
A closer look at classical
![]() $\Sigma ^0_2$
-complete sets reveals that there are in fact various qualitative differences among them. A
$\Sigma ^0_2$
-complete sets reveals that there are in fact various qualitative differences among them. A
![]() $\Sigma ^0_2$
set is a countable union of
$\Sigma ^0_2$
set is a countable union of
![]() $\Pi ^0_1$
sets, but there are various types of “countable union,” such as separated union, disjoint union, increasing union, and ordinary union. In classical theory, separated union (coproduct) and ordinary union are distinguished, but others are not.
$\Pi ^0_1$
sets, but there are various types of “countable union,” such as separated union, disjoint union, increasing union, and ordinary union. In classical theory, separated union (coproduct) and ordinary union are distinguished, but others are not.
This situation can also be understood as a classification of
![]() $\Sigma ^0_2$
formulas. First note that
$\Sigma ^0_2$
formulas. First note that
![]() $\mathsf {Fin}$
is defined by a
$\mathsf {Fin}$
is defined by a
![]() $\Sigma ^0_2$
formula of the form
$\Sigma ^0_2$
formula of the form
![]() $\exists n\forall m\geq n.\varphi (m,x)$
, where
$\exists n\forall m\geq n.\varphi (m,x)$
, where
![]() $\varphi $
is decidable. For such a formula, if a witness n is given, one can effectively find the smallest witness
$\varphi $
is decidable. For such a formula, if a witness n is given, one can effectively find the smallest witness
![]() $n_0$
by checking
$n_0$
by checking
![]() $\varphi (m,x)$
holds for any
$\varphi (m,x)$
holds for any
![]() $n_0\leq m\leq n$
. This means that such a formula can be replaced with a
$n_0\leq m\leq n$
. This means that such a formula can be replaced with a
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\exists n\psi (n,x)$
having the following “unique witness property”:
$\exists n\psi (n,x)$
having the following “unique witness property”:
Also, many
![]() $\Sigma ^0_2$
sets can be written as an increasing union of
$\Sigma ^0_2$
sets can be written as an increasing union of
![]() $\Pi ^0_1$
sets. Expressed as a formula
$\Pi ^0_1$
sets. Expressed as a formula
![]() $\exists n\psi (n,x)$
, this means that they have the following “increasing witness property”:
$\exists n\psi (n,x)$
, this means that they have the following “increasing witness property”:
Of course, having the increasing witness property is precisely being defined by a
![]() $\Sigma ^0_2$
formula of the form
$\Sigma ^0_2$
formula of the form
![]() $\exists n\forall m\geq n.\varphi (m,x)$
, where
$\exists n\forall m\geq n.\varphi (m,x)$
, where
![]() $\varphi $
is a
$\varphi $
is a
![]() $\Pi ^0_1$
formula.
$\Pi ^0_1$
formula.
The notion of classical
![]() $\Sigma ^0_2$
-completeness makes no distinction between these special and general
$\Sigma ^0_2$
-completeness makes no distinction between these special and general
![]() $\Sigma ^0_2$
-formulas. The notion of many-one reducibility for nonregular subobjects helps to clarify these qualitative differences.
$\Sigma ^0_2$
-formulas. The notion of many-one reducibility for nonregular subobjects helps to clarify these qualitative differences.
Definition 5.12. Let
![]() $A\rightarrowtail X$
be a
$A\rightarrowtail X$
be a
![]() ${\Sigma }^0_2$
subobject.
${\Sigma }^0_2$
subobject.
-
1. A has the unique witness property iff there exists a uniformly
 ${\Pi }^0_1$
sequence
${\Pi }^0_1$
sequence
 $(A_n)_{n\in \omega }$
of subobjects of X such that
$(A_n)_{n\in \omega }$
of subobjects of X such that
 $A\equiv \biguplus _{n\in \omega }A_n$
and
$A\equiv \biguplus _{n\in \omega }A_n$
and
 $|A_n|\cap |A_m|=\emptyset $
whenever
$|A_n|\cap |A_m|=\emptyset $
whenever
 $n\not =m$
.
$n\not =m$
. -
2. A has the increasing witness property iff there exists a uniformly
 ${\Pi }^0_1$
sequence
${\Pi }^0_1$
sequence
 $(A_n)_{n\in \omega }$
of subobjects of X such that
$(A_n)_{n\in \omega }$
of subobjects of X such that
 $A\equiv \biguplus _{n\in \omega }A_n$
and
$A\equiv \biguplus _{n\in \omega }A_n$
and
 $|A_n|\subseteq |A_m|$
whenever
$|A_n|\subseteq |A_m|$
whenever
 $n\leq m$
.
$n\leq m$
.
Observation 5.13. Let
![]() $A\rightarrowtail X$
be a
$A\rightarrowtail X$
be a
![]() $\Sigma ^0_2$
subobject such that
$\Sigma ^0_2$
subobject such that ![]() for some morphism
for some morphism
![]() $f\colon \omega \times X\to 2$
. Then A has the unique witness property.
$f\colon \omega \times X\to 2$
. Then A has the unique witness property.
Proof. Define ![]() . Then,
. Then,
![]() $(A_n)_{n\in \omega }$
is a uniform
$(A_n)_{n\in \omega }$
is a uniform
![]() $\Pi ^0_1$
sequence, and
$\Pi ^0_1$
sequence, and
![]() $|A_n|\cap |A_m|=\emptyset $
for
$|A_n|\cap |A_m|=\emptyset $
for
![]() $n\not =m$
. Clearly, we have
$n\not =m$
. Clearly, we have
![]() $\biguplus _nA_n\subseteq A$
. To see
$\biguplus _nA_n\subseteq A$
. To see
![]() $A\subseteq \biguplus _nA_n$
, if n is a witness for
$A\subseteq \biguplus _nA_n$
, if n is a witness for
![]() $x\in A$
, then search for the least
$x\in A$
, then search for the least
![]() $n_0\leq n$
such that
$n_0\leq n$
such that
![]() $f(m,x)=1$
for any
$f(m,x)=1$
for any
![]() $n_0\leq m\leq n$
. By our assumption on n, one can see that
$n_0\leq m\leq n$
. By our assumption on n, one can see that
![]() $n_0$
is the least witness for
$n_0$
is the least witness for
![]() $x\in A$
. Therefore,
$x\in A$
. Therefore,
![]() $x\in A_{n_0}$
. As
$x\in A_{n_0}$
. As
![]() $n\mapsto n_0$
is computable, we have
$n\mapsto n_0$
is computable, we have
![]() $A\subseteq \biguplus _nA_n$
.
$A\subseteq \biguplus _nA_n$
.
Observation 5.14. A
![]() $\Sigma ^0_2$
subobject
$\Sigma ^0_2$
subobject
![]() $A\rightarrowtail X$
has the increasing witness property iff there exists a
$A\rightarrowtail X$
has the increasing witness property iff there exists a
![]() $\Pi ^0_1$
subobject
$\Pi ^0_1$
subobject
![]() $P\rightarrowtail \omega \times X$
such that
$P\rightarrowtail \omega \times X$
such that ![]() .
.
Proof. For the forward direction,
![]() $x\in A$
iff
$x\in A$
iff
![]() $x\in A_n$
for some n, and for such n,
$x\in A_n$
for some n, and for such n,
![]() $x\in A_m$
for any
$x\in A_m$
for any
![]() $m\geq n$
. For the backward direction, consider
$m\geq n$
. For the backward direction, consider ![]() , where
, where
![]() $P_m\rightarrowtail X$
is the mth projection of P. Then
$P_m\rightarrowtail X$
is the mth projection of P. Then
![]() $(A_n)_{n\in \omega }$
is a uniform
$(A_n)_{n\in \omega }$
is a uniform
![]() $\Pi ^0_1$
sequence, and
$\Pi ^0_1$
sequence, and
![]() $|A_n|\subseteq |A_m|$
whenever
$|A_n|\subseteq |A_m|$
whenever
![]() $n\leq m$
. Note that n is a witness for
$n\leq m$
. Note that n is a witness for
![]() $x\in A$
iff
$x\in A$
iff
![]() $x\in A_n$
, so it is also a witness for
$x\in A_n$
, so it is also a witness for
![]() $x\in \biguplus _{n\in \omega }A_n$
. Thus,
$x\in \biguplus _{n\in \omega }A_n$
. Thus,
![]() $A\equiv \biguplus _{n\in \omega }A_n$
.
$A\equiv \biguplus _{n\in \omega }A_n$
.
Observation 5.15. Let
![]() $A\rightarrowtail X$
and
$A\rightarrowtail X$
and
![]() $B\rightarrowtail Y$
be
$B\rightarrowtail Y$
be
![]() ${\Sigma }^0_2$
subobjects such that
${\Sigma }^0_2$
subobjects such that
![]() $A\leq _{\mathsf {m}}B$
.
$A\leq _{\mathsf {m}}B$
.
-
1. If B has the unique witness property, so does A.
-
2. If B has the increasing witness property, so does A.
Proof. (1) Assume
![]() $B\equiv \biguplus _{n\in \omega }B_n$
. If
$B\equiv \biguplus _{n\in \omega }B_n$
. If
![]() $A\leq _{\mathsf {m}}B$
via
$A\leq _{\mathsf {m}}B$
via
![]() $\varphi $
then we have
$\varphi $
then we have
![]() $A\equiv \varphi ^\ast B$
. Note that
$A\equiv \varphi ^\ast B$
. Note that
![]() $\varphi ^\ast (\biguplus _nB_n)\equiv \biguplus _n\varphi ^\ast B_n$
. Hence,
$\varphi ^\ast (\biguplus _nB_n)\equiv \biguplus _n\varphi ^\ast B_n$
. Hence,
![]() $|B_n|\cap |B_m|=\emptyset $
implies
$|B_n|\cap |B_m|=\emptyset $
implies
![]() $|\varphi ^\ast B_n|\cap |\varphi ^\ast B_m|=\varphi ^{-1}[|B_n|]\cap \varphi ^{-1}[|B_n|]=\varphi ^{-1}[|B_n|\cap |B_m|]=\emptyset $
. Thus,
$|\varphi ^\ast B_n|\cap |\varphi ^\ast B_m|=\varphi ^{-1}[|B_n|]\cap \varphi ^{-1}[|B_n|]=\varphi ^{-1}[|B_n|\cap |B_m|]=\emptyset $
. Thus,
![]() $\varphi ^\ast (\biguplus _nB_n)$
has the unique witness property. Now,
$\varphi ^\ast (\biguplus _nB_n)$
has the unique witness property. Now,
![]() $B\equiv \biguplus _nB_n$
implies
$B\equiv \biguplus _nB_n$
implies
![]() $A\equiv \varphi ^\ast B\equiv \varphi ^\ast (\biguplus _nB_n)$
; hence, A also has the unique witness property.
$A\equiv \varphi ^\ast B\equiv \varphi ^\ast (\biguplus _nB_n)$
; hence, A also has the unique witness property.
(2) Note that
![]() $|B_n|\subseteq |B_m|$
implies
$|B_n|\subseteq |B_m|$
implies
![]() $|\varphi ^\ast B_n|=\varphi ^{-1}[|B_n|]\subseteq \varphi ^{-1}[|B_m|]=|\varphi ^\ast B_m|$
. Thus, by the same argument as above, one can see that A has the increasing witness property.
$|\varphi ^\ast B_n|=\varphi ^{-1}[|B_n|]\subseteq \varphi ^{-1}[|B_m|]=|\varphi ^\ast B_m|$
. Thus, by the same argument as above, one can see that A has the increasing witness property.
Proposition 5.16. If a
![]() ${\Sigma }^0_2$
subobject
${\Sigma }^0_2$
subobject
![]() $A\rightarrowtail X$
has the unique witness property then it has the increasing witness property.
$A\rightarrowtail X$
has the unique witness property then it has the increasing witness property.
Proof. Assume
![]() $A\equiv \biguplus _{n\in \omega }A_n$
, and consider
$A\equiv \biguplus _{n\in \omega }A_n$
, and consider
![]() $A_m'=\biguplus _{k\leq m}A_k$
. Obviously,
$A_m'=\biguplus _{k\leq m}A_k$
. Obviously,
![]() $m\leq n$
implies
$m\leq n$
implies
![]() $|A_m'|\subseteq |A_n'|$
. One can see
$|A_m'|\subseteq |A_n'|$
. One can see
![]() $A\equiv \biguplus _{m\in \omega }A_m'$
. This is because, if
$A\equiv \biguplus _{m\in \omega }A_m'$
. This is because, if
![]() $(n,p)$
is a name of
$(n,p)$
is a name of
![]() $x\in \biguplus _{n\in \omega }A_n$
then
$x\in \biguplus _{n\in \omega }A_n$
then
![]() $(n,n,p)$
is a name of
$(n,n,p)$
is a name of
![]() $x\in \biguplus _{m}\biguplus _{k\leq m}A_k$
, and if
$x\in \biguplus _{m}\biguplus _{k\leq m}A_k$
, and if
![]() $(m,k,p)$
is a name of
$(m,k,p)$
is a name of
![]() $x\in \biguplus _{m}\biguplus _{k\leq m}A_k$
then
$x\in \biguplus _{m}\biguplus _{k\leq m}A_k$
then
![]() $(k,p)$
is a name of
$(k,p)$
is a name of
![]() $x\in \biguplus _{n\in \omega }A_n$
.
$x\in \biguplus _{n\in \omega }A_n$
.
Now note that, in general, even if
![]() $A_n$
is
$A_n$
is
![]() ${\Pi }^0_1$
for each n,
${\Pi }^0_1$
for each n,
![]() $A_m'$
is not necessarily
$A_m'$
is not necessarily
![]() ${\Pi }^0_1$
. However, the unique witness property solves this problem. In this case, we claim that
${\Pi }^0_1$
. However, the unique witness property solves this problem. In this case, we claim that
![]() $A_m'$
is equivalent to a subspace
$A_m'$
is equivalent to a subspace
![]() $B_m$
of X whose underlying set is
$B_m$
of X whose underlying set is
![]() $|A_m'|$
. Clearly,
$|A_m'|$
. Clearly,
![]() $A_m'\subseteq B_m$
. Given a name p of
$A_m'\subseteq B_m$
. Given a name p of
![]() $x\in B_m$
, by the unique witness property, there exists a unique
$x\in B_m$
, by the unique witness property, there exists a unique
![]() $k\leq m$
such that
$k\leq m$
such that
![]() $x\in A_k$
. Now wait for
$x\in A_k$
. Now wait for
![]() $x\not \in A_n$
to be recognized for all
$x\not \in A_n$
to be recognized for all
![]() $n\leq m$
except one k. By continuity of trackers of co-characteristic functions of
$n\leq m$
except one k. By continuity of trackers of co-characteristic functions of
![]() $A_n$
’s, one can recognize this after reading a finite initial segment on p. Then we must have
$A_n$
’s, one can recognize this after reading a finite initial segment on p. Then we must have
![]() $x\in A_k$
. Now, as p is an X-name of x, by regularity, one can recover its
$x\in A_k$
. Now, as p is an X-name of x, by regularity, one can recover its
![]() $A_k$
-name
$A_k$
-name
![]() $p_k$
. Then
$p_k$
. Then
![]() $(k,p_k)$
is a name of
$(k,p_k)$
is a name of
![]() $x\in A_m'$
.
$x\in A_m'$
.
It remains to check that
![]() $B_m$
is a
$B_m$
is a
![]() ${\Pi }^0_1$
subobject of X. This is because p is not a name of an element of
${\Pi }^0_1$
subobject of X. This is because p is not a name of an element of
![]() $B_m$
iff
$B_m$
iff
![]() $p_k$
is not a name of an element of
$p_k$
is not a name of an element of
![]() $A_k$
for any
$A_k$
for any
![]() $k\leq m$
, which is recognizable.
$k\leq m$
, which is recognizable.
As an argument for modifying a given formula, let us introduce Veldman’s notion of “perhaps” [Reference Veldman11, Reference Veldman12]. Given a
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\psi \equiv \exists a\forall b\theta (a,b,x)$
, consider the following:
$\psi \equiv \exists a\forall b\theta (a,b,x)$
, consider the following:
Note that the above has the same many-one degree as ![]() , where
, where
![]() $\eta (a,x)\equiv \exists z\neg \theta (a,z,x)$
. Veldman [Reference Veldman11, Theorem 3.8] proved that
$\eta (a,x)\equiv \exists z\neg \theta (a,z,x)$
. Veldman [Reference Veldman11, Theorem 3.8] proved that
![]() $\mathsf {Perhaps}(\mathsf {Fin})$
is
$\mathsf {Perhaps}(\mathsf {Fin})$
is
![]() $\Sigma ^0_4$
but not
$\Sigma ^0_4$
but not
![]() $\Pi ^0_4$
, and in particular, it jumps out of
$\Pi ^0_4$
, and in particular, it jumps out of
![]() $\Sigma ^0_2$
. Here, we consider its totalized version that falls into the framework of
$\Sigma ^0_2$
. Here, we consider its totalized version that falls into the framework of
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
To be more explicit, for a
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\psi \equiv \exists a\forall z\theta (a,z,x)$
, the subobject
$\psi \equiv \exists a\forall z\theta (a,z,x)$
, the subobject
![]() $\mathsf {Half}(\psi )\rightarrowtail \omega ^\omega $
is given as follows:
$\mathsf {Half}(\psi )\rightarrowtail \omega ^\omega $
is given as follows:
-
• The underlying set is
 $\{x\in \omega ^\omega :\psi (x)\}$
.
$\{x\in \omega ^\omega :\psi (x)\}$
. -
•
 $(a,b,x)$
is a name of
$(a,b,x)$
is a name of
 $x\in \mathsf {Half}(\psi )$
iff either
$x\in \mathsf {Half}(\psi )$
iff either
 $\forall z\theta (a,z,x)$
or
$\forall z\theta (a,z,x)$
or
 $\forall z\theta (b,z,x)$
holds.
$\forall z\theta (b,z,x)$
holds.
Definition 5.17. A subobject
![]() $A\rightarrowtail \omega ^\omega $
is half
$A\rightarrowtail \omega ^\omega $
is half
![]() $\Sigma ^0_2$
-hard if
$\Sigma ^0_2$
-hard if
![]() $\mathsf {Half}(\psi )\leq _{\mathsf {m}}A$
for any
$\mathsf {Half}(\psi )\leq _{\mathsf {m}}A$
for any
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\psi $
.
$\psi $
.
Later we will show that no half
![]() $\Sigma ^0_2$
-hard subobject has the increasing witness property.
$\Sigma ^0_2$
-hard subobject has the increasing witness property.
5.4 Examples
We give some natural examples of witnessed sets whose underlying sets are classically
![]() $\Sigma ^0_2$
-complete. The examples listed below seem to fall into four groups.
$\Sigma ^0_2$
-complete. The examples listed below seem to fall into four groups.
5.4.1 Unique witness property
The first group consists of examples of the “unique witness” type.
Example 5.18. A binary relation
![]() $R\subseteq \omega \times \omega $
is coded by its characteristic function
$R\subseteq \omega \times \omega $
is coded by its characteristic function
![]() $\chi _R\in 2^{\omega \times \omega }$
. Let
$\chi _R\in 2^{\omega \times \omega }$
. Let
![]() $(P_x,\leq _x)\in \mathsf {PO}$
denote the partial order coded by
$(P_x,\leq _x)\in \mathsf {PO}$
denote the partial order coded by
![]() $x\in \omega ^\omega $
, where
$x\in \omega ^\omega $
, where
![]() $P_x=\{a\in \omega :a\leq _xa\}$
. In this way, the space
$P_x=\{a\in \omega :a\leq _xa\}$
. In this way, the space
![]() $\mathsf {PO}$
of partial orders on a subset of
$\mathsf {PO}$
of partial orders on a subset of
![]() $\omega $
can be introduced as a
$\omega $
can be introduced as a
![]() $\Pi ^0_1$
subspace of
$\Pi ^0_1$
subspace of
![]() $2^{\omega \times \omega }$
. Consider the following subobject
$2^{\omega \times \omega }$
. Consider the following subobject
![]() $\mathsf {PO}_{\mathsf {top}}$
of
$\mathsf {PO}_{\mathsf {top}}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all partial orders having greatest elements; that is,
 $|\mathsf {PO}_{\mathsf {top}}|=\{x\in \omega ^\omega :(\exists a\in P_x)(\forall b\in P_x)\;b\leq _xa\}$
.
$|\mathsf {PO}_{\mathsf {top}}|=\{x\in \omega ^\omega :(\exists a\in P_x)(\forall b\in P_x)\;b\leq _xa\}$
. -
•
 $(a,p)$
is a name of
$(a,p)$
is a name of
 $x\in \mathsf {PO}_{\mathsf {top}}$
iff
$x\in \mathsf {PO}_{\mathsf {top}}$
iff
 $p=x$
and a is the greatest element in
$p=x$
and a is the greatest element in
 $(P_x,\leq _x)$
.
$(P_x,\leq _x)$
.
Since the greatest element is unique if it exists, it is obvious that it has the unique witness property.
Proposition 5.19.
![]() $\mathsf {Fin}\equiv _{\mathsf {m}}\mathsf {PO}_{\mathsf {top}}$
.
$\mathsf {Fin}\equiv _{\mathsf {m}}\mathsf {PO}_{\mathsf {top}}$
.
Proof.
![]() $\mathsf {PO}_{\mathsf {top}}\leq _{\mathsf {m}}\mathsf {Fin}$
: Given
$\mathsf {PO}_{\mathsf {top}}\leq _{\mathsf {m}}\mathsf {Fin}$
: Given
![]() $P=P_x$
, consider
$P=P_x$
, consider
![]() $P[s]=\{p\leq s:p\leq _Pp\}$
. If
$P[s]=\{p\leq s:p\leq _Pp\}$
. If
![]() $\max P[s]=\max P[s+1]$
then put
$\max P[s]=\max P[s+1]$
then put
![]() $\varphi (x)(s)=0$
; otherwise
$\varphi (x)(s)=0$
; otherwise
![]() $\varphi (x)(s)=1$
. If p is the
$\varphi (x)(s)=1$
. If p is the
![]() $\leq _P$
-greatest element, then we have
$\leq _P$
-greatest element, then we have
![]() $p=\max P[p]=\max P$
, so
$p=\max P[p]=\max P$
, so
![]() $\varphi (x)(s)=0$
for any
$\varphi (x)(s)=0$
for any
![]() $s\geq p$
. Hence, p is a witness for
$s\geq p$
. Hence, p is a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
. Conversely, if s is a witness for
$\varphi (x)\in \mathsf {Fin}$
. Conversely, if s is a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
, then
$\varphi (x)\in \mathsf {Fin}$
, then
![]() $\varphi (x)(t)=0$
for any
$\varphi (x)(t)=0$
for any
![]() $t\geq s$
. This means
$t\geq s$
. This means
![]() $\max P[s]=\max P$
, so compute the
$\max P[s]=\max P$
, so compute the
![]() $\leq _P$
-greatest element p among the finite set
$\leq _P$
-greatest element p among the finite set
![]() $P[s]$
. Then p is a witness for
$P[s]$
. Then p is a witness for
![]() $x\in \mathsf {PO}_{\mathsf {top}}$
.
$x\in \mathsf {PO}_{\mathsf {top}}$
.
![]() $\mathsf {Fin}\leq _{\mathsf {m}}\mathsf {PO}_{\mathsf {top}}$
: Given
$\mathsf {Fin}\leq _{\mathsf {m}}\mathsf {PO}_{\mathsf {top}}$
: Given
![]() $x\in \omega ^\omega $
, we construct a poset
$x\in \omega ^\omega $
, we construct a poset
![]() $P=P_{\varphi (x)}$
. Whenever
$P=P_{\varphi (x)}$
. Whenever
![]() $x(s)\not =0$
happens, we add a new top element to P; that is, if
$x(s)\not =0$
happens, we add a new top element to P; that is, if
![]() $x(s)\not =0$
, put
$x(s)\not =0$
, put
![]() $t<_Ps\leq _Ps$
for any
$t<_Ps\leq _Ps$
for any
![]() $t<s$
; otherwise we do not add anything to P. If s is a witness for
$t<s$
; otherwise we do not add anything to P. If s is a witness for
![]() $x\in \mathsf {Fin}$
then search for the
$x\in \mathsf {Fin}$
then search for the
![]() $\leq _P$
-greatest element p among the finite set
$\leq _P$
-greatest element p among the finite set
![]() $\{t\in P:t\leq s\}$
. Since nothing is added to P after stage s, this p remains the
$\{t\in P:t\leq s\}$
. Since nothing is added to P after stage s, this p remains the
![]() $\leq _P$
-greatest element in P, so p is a witness for
$\leq _P$
-greatest element in P, so p is a witness for
![]() $\varphi (x)\in \mathsf {PO}_{\mathsf {top}}$
. Conversely, if p is the
$\varphi (x)\in \mathsf {PO}_{\mathsf {top}}$
. Conversely, if p is the
![]() $\leq _P$
-greatest element in P then there is no
$\leq _P$
-greatest element in P then there is no
![]() $s>p$
such that
$s>p$
such that
![]() $x(s)\not =0$
. Otherwise, we add a new top element
$x(s)\not =0$
. Otherwise, we add a new top element
![]() $s>_Pp$
, which is impossible. Thus, p is a witness for
$s>_Pp$
, which is impossible. Thus, p is a witness for
![]() $x\in \mathsf {Fin}$
.
$x\in \mathsf {Fin}$
.
Of course, partial orders may be changed to linear orders, and top elements may be changed to bottom elements. This means that the decision of boundedness
![]() $\mathsf {BddPO}$
of posets is also
$\mathsf {BddPO}$
of posets is also
![]() $\mathsf {m}$
-equivalent to
$\mathsf {m}$
-equivalent to
![]() $\mathsf {Fin}$
. Here are some other examples.
$\mathsf {Fin}$
. Here are some other examples.
Example 5.20. Consider the following subobject
![]() $\mathsf {Conv}$
of
$\mathsf {Conv}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all convergent sequences on
 $\omega $
; that is,
$\omega $
; that is,
 $|\mathsf {Conv}|=\{x\in \omega ^\omega :\lim _{n\to \infty }x(n)\text { exists}\}$
.
$|\mathsf {Conv}|=\{x\in \omega ^\omega :\lim _{n\to \infty }x(n)\text { exists}\}$
. -
•
 $(s,p)$
is a name of
$(s,p)$
is a name of
 $x\in \mathsf {Conv}$
iff
$x\in \mathsf {Conv}$
iff
 $p=x$
and
$p=x$
and
 $x(t)=x(s)$
for all
$x(t)=x(s)$
for all
 $t\geq s$
.
$t\geq s$
.
Example 5.21. We consider a decision problem for real numbers, where a real number is presented by accuracy-guaranteed rational approximations, so we deal with a decision problem for such rational approximations. A pre-real is a rational sequence
![]() $(q_n)_{n\in \omega }$
such that
$(q_n)_{n\in \omega }$
such that
![]() $|q_n-q_m|\leq 2^{-n}$
for any
$|q_n-q_m|\leq 2^{-n}$
for any
![]() $m\geq n$
. Here, rational numbers are coded by natural numbers in an obvious manner, so we can consider
$m\geq n$
. Here, rational numbers are coded by natural numbers in an obvious manner, so we can consider
![]() $\mathbb {R}_{\mathsf {pre}}$
to be a
$\mathbb {R}_{\mathsf {pre}}$
to be a
![]() $\Pi ^0_1$
subobject of
$\Pi ^0_1$
subobject of
![]() $\omega ^\omega $
. In the following, we often identify a pre-real
$\omega ^\omega $
. In the following, we often identify a pre-real
![]() $(q_n)_{n\in \omega }$
with the real number
$(q_n)_{n\in \omega }$
with the real number
![]() $\lim _{n\to \infty }q_n$
. If the limit is rational, we say that it is a pre-rational. Consider the following subobject
$\lim _{n\to \infty }q_n$
. If the limit is rational, we say that it is a pre-rational. Consider the following subobject
![]() $\mathbb {Q}_{\mathsf {pre}}$
of
$\mathbb {Q}_{\mathsf {pre}}$
of
![]() $\mathbb {R}_{\mathsf {pre}}$
:
$\mathbb {R}_{\mathsf {pre}}$
:
-
• The underlying set is the set of all pre-rationals.
-
•
 $(m,n,p)$
is a name of
$(m,n,p)$
is a name of
 $x\in \mathbb {Q}_{\mathsf {pre}}$
iff p is an
$x\in \mathbb {Q}_{\mathsf {pre}}$
iff p is an
 $\mathbb {R}_{\mathsf {pre}}$
-name of x, and
$\mathbb {R}_{\mathsf {pre}}$
-name of x, and
 $x=\frac {k}{m}$
where
$x=\frac {k}{m}$
where
 $m\in \omega \setminus \{0\}$
, and n is a
$m\in \omega \setminus \{0\}$
, and n is a
 $\mathbb {Z}$
-name of k.
$\mathbb {Z}$
-name of k.
Here, for example, although there can be more than one witness
![]() $\frac {k}{m}$
for
$\frac {k}{m}$
for
![]() $x\in \mathbb {Q}_{\mathsf {pre}}$
, if restricted to only irreducible fractions, the witness for
$x\in \mathbb {Q}_{\mathsf {pre}}$
, if restricted to only irreducible fractions, the witness for
![]() $x\in \mathbb {Q}_{\mathsf {pre}}$
is unique. Thus,
$x\in \mathbb {Q}_{\mathsf {pre}}$
is unique. Thus,
![]() $\mathbb {Q}_{\mathsf {pre}}\rightarrowtail \mathbb {R}_{\mathsf {pre}}$
can be described by a formula with the unique witness property without changing the intrinsic complexity. In this sense,
$\mathbb {Q}_{\mathsf {pre}}\rightarrowtail \mathbb {R}_{\mathsf {pre}}$
can be described by a formula with the unique witness property without changing the intrinsic complexity. In this sense,
![]() $\mathbb {Q}_{\mathsf {pre}}\rightarrowtail \mathbb {R}_{\mathsf {pre}}$
is an object of the unique witness type.
$\mathbb {Q}_{\mathsf {pre}}\rightarrowtail \mathbb {R}_{\mathsf {pre}}$
is an object of the unique witness type.
The case of
![]() $\mathsf {Conv}$
is a little more difficult. At first glance,
$\mathsf {Conv}$
is a little more difficult. At first glance,
![]() $\mathsf {Conv}$
appears to be of the increasing type, but closer analysis reveals that it is in fact of the unique witness type. We will discuss this in detail later, but first let us see the following:
$\mathsf {Conv}$
appears to be of the increasing type, but closer analysis reveals that it is in fact of the unique witness type. We will discuss this in detail later, but first let us see the following:
Observation 5.22.
![]() $\mathsf {Conv}\equiv _{\mathsf {m}}\mathsf {Fin}\equiv _{\mathsf {m}}\mathbb {Q}_{\mathsf {pre}}$
.
$\mathsf {Conv}\equiv _{\mathsf {m}}\mathsf {Fin}\equiv _{\mathsf {m}}\mathbb {Q}_{\mathsf {pre}}$
.
Proof.
![]() $\mathsf {Conv}\leq _{\mathsf {m}}\mathsf {Fin}$
: Given
$\mathsf {Conv}\leq _{\mathsf {m}}\mathsf {Fin}$
: Given
![]() $x\in \omega ^\omega $
, define
$x\in \omega ^\omega $
, define
![]() $\varphi (x)\in \omega ^\omega $
as follows: If
$\varphi (x)\in \omega ^\omega $
as follows: If
![]() $x(s+1)\not =x(s)$
, put
$x(s+1)\not =x(s)$
, put
![]() $\varphi (x)(s)=1$
; otherwise
$\varphi (x)(s)=1$
; otherwise
![]() $\varphi (x)(s)=0$
. Note that s is a witness for
$\varphi (x)(s)=0$
. Note that s is a witness for
![]() $x\in \mathsf {Conv}$
iff
$x\in \mathsf {Conv}$
iff
![]() $x(t+1)=x(t)$
for any
$x(t+1)=x(t)$
for any
![]() $t\geq s$
iff
$t\geq s$
iff
![]() $\varphi (x)(t)=0$
for any
$\varphi (x)(t)=0$
for any
![]() $t\geq s$
iff s is a witness for
$t\geq s$
iff s is a witness for
![]() $\varphi (x)\in \mathsf {Fin}$
. Thus, using
$\varphi (x)\in \mathsf {Fin}$
. Thus, using
![]() $r_-(s,x)=s$
and
$r_-(s,x)=s$
and
![]() $r_+(s,x)=s$
work.
$r_+(s,x)=s$
work.
![]() $\mathsf {Fin}\leq _{\mathsf {m}}\mathbb {Q}_{\mathsf {pre}}$
: For
$\mathsf {Fin}\leq _{\mathsf {m}}\mathbb {Q}_{\mathsf {pre}}$
: For
![]() $f(n)=n^2$
, the sum
$f(n)=n^2$
, the sum
![]() $\sum _{n=0}^\infty 2^{-f(n)}$
is irrational. Given
$\sum _{n=0}^\infty 2^{-f(n)}$
is irrational. Given
![]() $x\in \omega ^\omega $
, consider
$x\in \omega ^\omega $
, consider
![]() $\varphi (x):=\sum _{x(n)\not =0}2^{-f(n)}$
. Note that
$\varphi (x):=\sum _{x(n)\not =0}2^{-f(n)}$
. Note that
![]() $x\in \mathsf {Fin}$
iff the binary expansion of
$x\in \mathsf {Fin}$
iff the binary expansion of
![]() $\varphi (x)$
is eventually periodic iff
$\varphi (x)$
is eventually periodic iff
![]() $\varphi (x)$
is rational. Given a witness s for
$\varphi (x)$
is rational. Given a witness s for
![]() $x\in \mathsf {Fin}$
, the value
$x\in \mathsf {Fin}$
, the value
![]() $\varphi (x)$
can be written as
$\varphi (x)$
can be written as
![]() $\sum _{n\leq s}2^{f(s)-f(n)}/2^{f(s)}$
. The denominator and numerator are both natural numbers, so the pair is a witness for
$\sum _{n\leq s}2^{f(s)-f(n)}/2^{f(s)}$
. The denominator and numerator are both natural numbers, so the pair is a witness for
![]() $\varphi (x)\in \mathbb {Q}_{\mathsf {pre}}$
. Conversely, if
$\varphi (x)\in \mathbb {Q}_{\mathsf {pre}}$
. Conversely, if
![]() $\varphi (x)$
is of the form
$\varphi (x)$
is of the form
![]() $a/b$
, the denominator b must be a multiple of some
$a/b$
, the denominator b must be a multiple of some
![]() $2^{f(s)}$
. If
$2^{f(s)}$
. If
![]() $x(t)\not =0$
for some
$x(t)\not =0$
for some
![]() $t>s$
, then
$t>s$
, then
![]() $2^{-f(t)}$
is added to
$2^{-f(t)}$
is added to
![]() $\varphi (x)$
, which makes it impossible to express
$\varphi (x)$
, which makes it impossible to express
![]() $\varphi (x)$
as a multiple of
$\varphi (x)$
as a multiple of
![]() $2^{-f(s)}$
. Thus,
$2^{-f(s)}$
. Thus,
![]() $s+1$
is a witness for
$s+1$
is a witness for
![]() $x\in \mathsf {Fin}$
.
$x\in \mathsf {Fin}$
.
![]() $\mathbb {Q}_{\mathsf {pre}}\leq _{\mathsf {m}}\mathsf {Conv}$
: Given
$\mathbb {Q}_{\mathsf {pre}}\leq _{\mathsf {m}}\mathsf {Conv}$
: Given
![]() $x\in \mathbb {R}_{\mathsf {pre}}$
, we first get its rational approximation with accuracy
$x\in \mathbb {R}_{\mathsf {pre}}$
, we first get its rational approximation with accuracy
![]() $1$
, from which we can compute a positive integer b that is an upper bound of
$1$
, from which we can compute a positive integer b that is an upper bound of
![]() $|x|$
, so we get
$|x|$
, so we get
![]() $y=x/b\in [-1,1]$
. We define
$y=x/b\in [-1,1]$
. We define
![]() $\varphi (x)(s)$
as the prediction of the denominator of y at stage s; that is, the current prediction is n iff the prediction that
$\varphi (x)(s)$
as the prediction of the denominator of y at stage s; that is, the current prediction is n iff the prediction that
![]() $y=k/n$
for some
$y=k/n$
for some
![]() $-n\leq k\leq n$
is not refuted at that stage. Here, the prediction that
$-n\leq k\leq n$
is not refuted at that stage. Here, the prediction that
![]() $y=k/n$
is refuted at stage s means that
$y=k/n$
is refuted at stage s means that
![]() $|q_s-k/n|>2^{-s}$
is confirmed by looking at the information on a rational approximation
$|q_s-k/n|>2^{-s}$
is confirmed by looking at the information on a rational approximation
![]() $q_s$
of y with accuracy
$q_s$
of y with accuracy
![]() $2^{-s}$
. If the prediction n is refuted at s, change the prediction at stage
$2^{-s}$
. If the prediction n is refuted at s, change the prediction at stage
![]() $s+1$
to
$s+1$
to
![]() $\varphi (x)(s+1)=n+1$
.
$\varphi (x)(s+1)=n+1$
.
If x is a rational number of the form
![]() $a/b$
, then rewrite this into irreducible fraction
$a/b$
, then rewrite this into irreducible fraction
![]() $k/n$
. One can see that the denominator n is equal to
$k/n$
. One can see that the denominator n is equal to
![]() $\lim _{s\to \infty }\varphi (x)(s)$
. We search for the first s such that
$\lim _{s\to \infty }\varphi (x)(s)$
. We search for the first s such that
![]() $\varphi (x)(s)=n$
. This s is a witness for
$\varphi (x)(s)=n$
. This s is a witness for
![]() $\varphi (x)\in \mathsf {Conv}$
since
$\varphi (x)\in \mathsf {Conv}$
since
![]() $\varphi (x)$
is monotone. Conversely, if s is a witness for
$\varphi (x)$
is monotone. Conversely, if s is a witness for
![]() $\varphi (x)\in \mathsf {Conv}$
, then compute
$\varphi (x)\in \mathsf {Conv}$
, then compute
![]() $\varphi (x)(s)=n$
. By our construction, x must be of the form
$\varphi (x)(s)=n$
. By our construction, x must be of the form
![]() $k/n$
for some
$k/n$
for some
![]() $-n\leq k\leq n$
. Looking at an approximation of x with accuracy
$-n\leq k\leq n$
. Looking at an approximation of x with accuracy
![]() $2^{-n}$
, the equation
$2^{-n}$
, the equation
![]() $x=k/n$
is refuted except for one k, so the last remaining k is the numerator of x.
$x=k/n$
is refuted except for one k, so the last remaining k is the numerator of x.
The reason why we introduced the notion of pre-real here is in the proof of
![]() $\mathbb {Q}_{\mathsf {pre}}\leq _{\mathsf {m}}\mathsf {Conv}$
. By our definition, a many-one reduction
$\mathbb {Q}_{\mathsf {pre}}\leq _{\mathsf {m}}\mathsf {Conv}$
. By our definition, a many-one reduction
![]() $\varphi $
must be well-defined on represented spaces; however, observe that there are few morphisms
$\varphi $
must be well-defined on represented spaces; however, observe that there are few morphisms
![]() $\mathbb {R}\to \omega ^\omega $
, while there are many morphisms
$\mathbb {R}\to \omega ^\omega $
, while there are many morphisms
![]() $\mathbb {R}_{\mathsf {pre}}\to \omega ^\omega $
. In the context of Wadge reducibility (topological many-one reducibility; Definition 3.20), the difference between the structures of
$\mathbb {R}_{\mathsf {pre}}\to \omega ^\omega $
. In the context of Wadge reducibility (topological many-one reducibility; Definition 3.20), the difference between the structures of
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\omega ^\omega $
is examined in depth [Reference Schlicht8]. If we change the definition to a form that allows a many-one reduction
$\omega ^\omega $
is examined in depth [Reference Schlicht8]. If we change the definition to a form that allows a many-one reduction
![]() $\varphi $
on the name space
$\varphi $
on the name space
![]() $\mathtt {Code}$
, as in Pequignot-style Wadge reducibility [Reference Pequignot7] or Weihrauch reducibility [Reference Brattka, Gherardi and Pauly2], there is no need to introduce the notion of pre-real.
$\mathtt {Code}$
, as in Pequignot-style Wadge reducibility [Reference Pequignot7] or Weihrauch reducibility [Reference Brattka, Gherardi and Pauly2], there is no need to introduce the notion of pre-real.
5.4.2 Increasing witnes s property
Next, let us discuss examples that are of the “increasing” type.
Example 5.23. Consider the following subobject
![]() $\mathsf {BddSeq}_\omega $
of
$\mathsf {BddSeq}_\omega $
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all bounded sequences on
 $\omega $
; that is,
$\omega $
; that is,
 $|\mathsf {BddSeq}_\omega |=\{x\in \omega ^\omega :(\exists b)(\forall n)\;x(n)\leq b\}$
.
$|\mathsf {BddSeq}_\omega |=\{x\in \omega ^\omega :(\exists b)(\forall n)\;x(n)\leq b\}$
. -
•
 $(b,p)$
is a name of
$(b,p)$
is a name of
 $x\in \mathsf {BddSeq}_\omega $
iff
$x\in \mathsf {BddSeq}_\omega $
iff
 $p=x$
and
$p=x$
and
 $x(n)\leq b$
for all n.
$x(n)\leq b$
for all n.
![]() $\mathsf {BddSeq}_{\mathbb {Q}}\rightarrowtail \mathbb {Q}^\omega $
and
$\mathsf {BddSeq}_{\mathbb {Q}}\rightarrowtail \mathbb {Q}^\omega $
and
![]() $\mathsf {BddSeq}_{\mathbb {R}}\rightarrowtail \mathbb {R}^\omega $
can be defined in a similar manner.
$\mathsf {BddSeq}_{\mathbb {R}}\rightarrowtail \mathbb {R}^\omega $
can be defined in a similar manner.
It is not difficult to verify that these examples can be written as increasing sequences of
![]() $\Pi ^0_1$
sets.
$\Pi ^0_1$
sets.
Observation 5.24.
![]() $\mathsf {BddSeq}_\omega \equiv _{\mathsf {m}}\mathsf {BddSeq}_{\mathbb {Q}}\equiv _{\mathsf {m}}\mathsf {BddSeq}_{\mathbb {R}}$
.
$\mathsf {BddSeq}_\omega \equiv _{\mathsf {m}}\mathsf {BddSeq}_{\mathbb {Q}}\equiv _{\mathsf {m}}\mathsf {BddSeq}_{\mathbb {R}}$
.
Proof. A natural number is clearly a rational number, which is clearly a real number. Given an upper bound b of a sequence
![]() $(x_n)_{n\in \omega }$
of real numbers, first extract a rational approximation
$(x_n)_{n\in \omega }$
of real numbers, first extract a rational approximation
![]() $m/n$
of b with precision
$m/n$
of b with precision
![]() $2^{-1}$
. Then the natural number
$2^{-1}$
. Then the natural number
![]() $|m|+1$
is an upper bound of
$|m|+1$
is an upper bound of
![]() $(x_n)_{n\in \omega }$
.
$(x_n)_{n\in \omega }$
.
An example other than decision problems on sequences is the decision that a partial order has a finite height/width. Here, the height (width, resp.) of a poset P is the supremum of the cardinality of chains (antichains, resp.) in P.
If one attempts to describe finiteness of the size of something by a
![]() $\Sigma ^0_2$
-formula, it is natural to write it as the existence of a finite upper bound of the size. Therefore, it is appropriate to consider the witness of this formula as the value of an upper bound of the size.
$\Sigma ^0_2$
-formula, it is natural to write it as the existence of a finite upper bound of the size. Therefore, it is appropriate to consider the witness of this formula as the value of an upper bound of the size.
Example 5.25. Recall that
![]() $P_x$
is the poset coded by
$P_x$
is the poset coded by
![]() $x\in \omega ^\omega $
. Consider the following subobjects
$x\in \omega ^\omega $
. Consider the following subobjects
![]() $\mathsf {FinHeight}$
and
$\mathsf {FinHeight}$
and
![]() $\mathsf {FinWidth}$
of
$\mathsf {FinWidth}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
•
 $|\mathsf {FinHeight}|=\{x\in \omega ^\omega :\text {the height of} P_x \text {is finite}\}$
.
$|\mathsf {FinHeight}|=\{x\in \omega ^\omega :\text {the height of} P_x \text {is finite}\}$
. -
•
 $|\mathsf {FinWidth}|=\{x\in \omega ^\omega :\text {the width of} P_x \text {is finite}\}$
.
$|\mathsf {FinWidth}|=\{x\in \omega ^\omega :\text {the width of} P_x \text {is finite}\}$
. -
•
 $(b,p)$
is a name of
$(b,p)$
is a name of
 $x\in \mathsf {FinHeight}$
iff
$x\in \mathsf {FinHeight}$
iff
 $p=x$
and the height of
$p=x$
and the height of
 $P_x$
is at most b.
$P_x$
is at most b. -
•
 $(b,p)$
is a name of
$(b,p)$
is a name of
 $x\in \mathsf {FinWidth}$
iff
$x\in \mathsf {FinWidth}$
iff
 $p=x$
and the width of
$p=x$
and the width of
 $P_x$
is at most b.
$P_x$
is at most b.
Observation 5.26.
![]() $\mathsf {BddSeq}_\omega \equiv _{\mathsf {m}}\mathsf {FinHeight}\equiv _{\mathsf {m}}\mathsf {FinWidth}$
.
$\mathsf {BddSeq}_\omega \equiv _{\mathsf {m}}\mathsf {FinHeight}\equiv _{\mathsf {m}}\mathsf {FinWidth}$
.
Proof.
![]() $\mathsf {FinHeight},\mathsf {FinWidth}\leq _{\mathsf {m}}\mathsf {BddSeq}_\omega $
: Given
$\mathsf {FinHeight},\mathsf {FinWidth}\leq _{\mathsf {m}}\mathsf {BddSeq}_\omega $
: Given
![]() $P=P_x$
, consider the cardinality
$P=P_x$
, consider the cardinality
![]() $\varphi (x)(n)$
of a maximal chain or antichain in the finite set
$\varphi (x)(n)$
of a maximal chain or antichain in the finite set
![]() $P[n]=\{p\leq n: p\leq _Pp\}$
.
$P[n]=\{p\leq n: p\leq _Pp\}$
.
![]() $\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {FinHeight}$
: Given
$\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {FinHeight}$
: Given
![]() $x\in \omega ^\omega $
, we construct a poset
$x\in \omega ^\omega $
, we construct a poset
![]() $P=P_{\varphi (x)}$
. Whenever a previously unseen large value appears in x, we add a new top element to P. To be precise, let the underlying set of P be
$P=P_{\varphi (x)}$
. Whenever a previously unseen large value appears in x, we add a new top element to P. To be precise, let the underlying set of P be
![]() $\{\langle n,t \rangle :x(t)\geq n\text { and }\forall s<t.\;x(s)<n\}$
. Here,
$\{\langle n,t \rangle :x(t)\geq n\text { and }\forall s<t.\;x(s)<n\}$
. Here,
![]() $n<m$
implies
$n<m$
implies
![]() $\langle n,t \rangle <_P\langle m,s \rangle $
for any
$\langle n,t \rangle <_P\langle m,s \rangle $
for any
![]() $s,t$
. Note that for each n, P has at most one element of the form
$s,t$
. Note that for each n, P has at most one element of the form
![]() $\langle n,t \rangle $
.
$\langle n,t \rangle $
.
If b is a witness for
![]() $x\in \mathsf {BddSeq}_\omega $
, then
$x\in \mathsf {BddSeq}_\omega $
, then
![]() $x(t)\leq n$
for any t. Thus,
$x(t)\leq n$
for any t. Thus,
![]() $\langle m,s \rangle \in P$
implies
$\langle m,s \rangle \in P$
implies
![]() $m\leq n$
. Then P can contain at most
$m\leq n$
. Then P can contain at most
![]() $n+1$
elements as noted above, so the height of P is at most
$n+1$
elements as noted above, so the height of P is at most
![]() $n+1$
. Therefore,
$n+1$
. Therefore,
![]() $n+1$
is a witness for
$n+1$
is a witness for
![]() $\varphi (x)\in \mathsf {FinHeight}$
. Conversely, if n is a witness for
$\varphi (x)\in \mathsf {FinHeight}$
. Conversely, if n is a witness for
![]() $\varphi (x)\in \mathsf {FinHeight}$
then we claim that n is a witness for
$\varphi (x)\in \mathsf {FinHeight}$
then we claim that n is a witness for
![]() $x\in \mathsf {BddSeq}_\omega $
. Otherwise, there exists t such that
$x\in \mathsf {BddSeq}_\omega $
. Otherwise, there exists t such that
![]() $x(t)>n$
. Hence, for any
$x(t)>n$
. Hence, for any
![]() $m\geq n$
, let
$m\geq n$
, let
![]() $t(m)$
be the least number such that
$t(m)$
be the least number such that
![]() $x(t(m))\geq n$
. By definition, we have
$x(t(m))\geq n$
. By definition, we have
![]() $\langle m,t(m) \rangle \in P$
. In particular,
$\langle m,t(m) \rangle \in P$
. In particular,
![]() $(a^m_{t(m)})_{m\leq n}$
is a chain of length
$(a^m_{t(m)})_{m\leq n}$
is a chain of length
![]() $n+1$
; thus the height of P is at least
$n+1$
; thus the height of P is at least
![]() $n+1$
. This contradicts our assumption, so n is a witness for
$n+1$
. This contradicts our assumption, so n is a witness for
![]() $x\in \mathsf {BddSeq}_\omega $
.
$x\in \mathsf {BddSeq}_\omega $
.
![]() $\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {FinWidth}$
: Given
$\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {FinWidth}$
: Given
![]() $x\in \omega ^\omega $
, we construct a poset
$x\in \omega ^\omega $
, we construct a poset
![]() $P=P_{\varphi (x)}$
. The underlying set is the same as above. Now we declare that all distinct elements in P are incomparable. The rest of the proof is exactly the same as above.
$P=P_{\varphi (x)}$
. The underlying set is the same as above. Now we declare that all distinct elements in P are incomparable. The rest of the proof is exactly the same as above.
5.4.3 Half
 $\Sigma ^0_2$
-hard
$\Sigma ^0_2$
-hard
Let us discuss
![]() $\Sigma ^0_2$
subobjects that are half
$\Sigma ^0_2$
subobjects that are half
![]() $\Sigma ^0_2$
-hard. Obviously, there exists a subobject of
$\Sigma ^0_2$
-hard. Obviously, there exists a subobject of
![]() $\omega ^\omega $
which is complete w.r.t. the ones of the form
$\omega ^\omega $
which is complete w.r.t. the ones of the form
![]() $\mathsf {Half}(\psi )\rightarrowtail \omega ^\omega $
for some
$\mathsf {Half}(\psi )\rightarrowtail \omega ^\omega $
for some
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\psi $
. To see this, just take a universal
$\psi $
. To see this, just take a universal
![]() $\Sigma ^0_2$
formula
$\Sigma ^0_2$
formula
![]() $\psi $
.
$\psi $
.
Example 5.27. Consider the following subobject
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}\rightarrowtail \omega ^\omega $
:
$\mathsf {HalfTruth}_{\Sigma ^0_2}\rightarrowtail \omega ^\omega $
:
-
• The underlying set is
 $\{(x_n)_{n\in \omega }\in (\omega ^\omega )^\omega :(\exists n\in \omega )\;x_n=0^\infty \}$
.
$\{(x_n)_{n\in \omega }\in (\omega ^\omega )^\omega :(\exists n\in \omega )\;x_n=0^\infty \}$
. -
•
 $(n,m,p)$
is a name of
$(n,m,p)$
is a name of
 $x=(x_n)_{n\in \omega }\in \mathsf {DisConn}$
iff
$x=(x_n)_{n\in \omega }\in \mathsf {DisConn}$
iff
 $p=x$
and either
$p=x$
and either
 $x_n=0^\infty $
or
$x_n=0^\infty $
or
 $x_m=0^\infty $
holds.
$x_m=0^\infty $
holds.
Observation 5.28.
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}$
is half
$\mathsf {HalfTruth}_{\Sigma ^0_2}$
is half
![]() $\Sigma ^0_2$
-hard.
$\Sigma ^0_2$
-hard.
However, this is just a meta-mathematical example of a half
![]() $\Sigma ^0_2$
-complete subobject. A natural example of a half
$\Sigma ^0_2$
-complete subobject. A natural example of a half
![]() $\Sigma ^0_2$
-hard subobject may be presented from graph theory.
$\Sigma ^0_2$
-hard subobject may be presented from graph theory.
There are two ways to formalize the notion of a graph. One is to introduce edges as pairs of vertices. That is, a directed graph is a pair
![]() $G=(V,E)$
satisfying
$G=(V,E)$
satisfying
![]() $E\subseteq V^2$
. We call this a subset presentation of a directed graph.
$E\subseteq V^2$
. We call this a subset presentation of a directed graph.
The other is to treat edges as data with specified source and target vertices. In other words, a directed multigraph is a map
![]() $\langle d,c\rangle \colon E\to V^2$
, where
$\langle d,c\rangle \colon E\to V^2$
, where
![]() $d(e)$
denotes the source vertex (tail) of edge e and
$d(e)$
denotes the source vertex (tail) of edge e and
![]() $c(e)$
denotes the target vertex (head) of edge e. This is also a very standard way of presenting a directed multigraph, which we call a function presentation of a graph. We sometime use the symbol
$c(e)$
denotes the target vertex (head) of edge e. This is also a very standard way of presenting a directed multigraph, which we call a function presentation of a graph. We sometime use the symbol
![]() $u\overset {e}{\longrightarrow }v$
to denote an edge e with
$u\overset {e}{\longrightarrow }v$
to denote an edge e with
![]() $d(e)=u$
and
$d(e)=u$
and
![]() $c(e)=v$
.
$c(e)=v$
.
From here on, we only deal with undirected graphs. In the case of a presentation of an undirected graph, we consider
![]() $E\subseteq [V]^2$
and
$E\subseteq [V]^2$
and
![]() $\gamma \colon E\to [V]^2$
. Here,
$\gamma \colon E\to [V]^2$
. Here,
![]() $[V]^2=\{(u,v)\in V^2:u<v\}$
for
$[V]^2=\{(u,v)\in V^2:u<v\}$
for
![]() $V\subseteq \omega $
, and each
$V\subseteq \omega $
, and each
![]() $(u,v)\in [V]^2$
is often written as
$(u,v)\in [V]^2$
is often written as
![]() $\{u,v\}$
or
$\{u,v\}$
or
![]() $\{v,u\}$
; that is, we do not distinguish between
$\{v,u\}$
; that is, we do not distinguish between
![]() $\{u,v\}$
and
$\{u,v\}$
and
![]() $\{v,u\}$
as usual.
$\{v,u\}$
as usual.
Note that subset and function presentations (even restricted to undirected simple graphs) are not computability–theoretically equivalent in a certain sense, but they are equivalent as far as the following disconnectedness problem is concerned.
Example 5.29. A subset presentation of a graph
![]() $G=(V,E)$
with
$G=(V,E)$
with
![]() $V\subseteq \omega $
and
$V\subseteq \omega $
and
![]() $E\subseteq [V]^2$
is coded as their characteristic functions
$E\subseteq [V]^2$
is coded as their characteristic functions
![]() $\chi _V\in 2^\omega $
and
$\chi _V\in 2^\omega $
and
![]() $\chi _E\in 2^{(\omega ^2)}\simeq 2^\omega $
. Let
$\chi _E\in 2^{(\omega ^2)}\simeq 2^\omega $
. Let
![]() $G_x=(V_x,E_x)$
be the subset presentation of the graph coded by x. Consider the following subobject
$G_x=(V_x,E_x)$
be the subset presentation of the graph coded by x. Consider the following subobject
![]() $\mathsf {DisConn}$
of
$\mathsf {DisConn}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all subset presentations of disconnected graphs; that is,
 $x\in |\mathsf {DisConn}|$
iff not every two vertices are connected by a finite path in
$x\in |\mathsf {DisConn}|$
iff not every two vertices are connected by a finite path in
 $G_x$
.
$G_x$
. -
•
 $(a,b,p)$
is a name of
$(a,b,p)$
is a name of
 $x\in \mathsf {DisConn}$
iff
$x\in \mathsf {DisConn}$
iff
 $p=x$
and
$p=x$
and
 $a,b\in V_x$
are not connected by any finite path in
$a,b\in V_x$
are not connected by any finite path in
 $G_x$
.
$G_x$
.
Example 5.30. A function presentation of a graph
![]() $\gamma \colon E\to [V]^2$
with
$\gamma \colon E\to [V]^2$
with
![]() $V\subseteq \omega $
and
$V\subseteq \omega $
and
![]() $E\subseteq \omega $
is coded as the triple
$E\subseteq \omega $
is coded as the triple
![]() $(\gamma ,\chi _V,\chi _E)$
. Let
$(\gamma ,\chi _V,\chi _E)$
. Let
![]() $\gamma _x\colon E_x\to [V_x]^2$
be the function presentation of the graph coded by x. Consider the following subobject
$\gamma _x\colon E_x\to [V_x]^2$
be the function presentation of the graph coded by x. Consider the following subobject
![]() $\mathsf {DisConn}_{\mathsf {fun}}$
of
$\mathsf {DisConn}_{\mathsf {fun}}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all function presentations of disconnected graphs; that is,
 $x\in |\mathsf {DisConn}_{\mathsf {fun}}|$
iff not every two vertices are connected by a finite path in
$x\in |\mathsf {DisConn}_{\mathsf {fun}}|$
iff not every two vertices are connected by a finite path in
 $\gamma _x$
.
$\gamma _x$
. -
•
 $(a,b,p)$
is a name of
$(a,b,p)$
is a name of
 $x\in \mathsf {DisConn}_{\mathsf {fun}}$
iff
$x\in \mathsf {DisConn}_{\mathsf {fun}}$
iff
 $p=x$
and
$p=x$
and
 $a,b\in V_x$
are not connected by any finite path in
$a,b\in V_x$
are not connected by any finite path in
 $\gamma _x$
.
$\gamma _x$
.
These are clearly
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
. A function presentation of a graph may appear, for example, in the context of group actions.
$\omega ^\omega $
. A function presentation of a graph may appear, for example, in the context of group actions.
Example 5.31. An action
![]() $\alpha \colon G\times S\to S$
of a countable group
$\alpha \colon G\times S\to S$
of a countable group
![]() $G\subseteq \omega $
on a set
$G\subseteq \omega $
on a set
![]() $S\subseteq \omega $
is coded via their characteristic functions, where a code of
$S\subseteq \omega $
is coded via their characteristic functions, where a code of
![]() $G\subseteq \omega $
also involves the operation
$G\subseteq \omega $
also involves the operation
![]() $\ast \in \omega ^{\omega \times \omega }$
and the inverse
$\ast \in \omega ^{\omega \times \omega }$
and the inverse
![]() $\circ ^{-1}\in \omega ^\omega $
. Let
$\circ ^{-1}\in \omega ^\omega $
. Let
![]() $(G_x,S_x,\alpha _x)$
denote the countable group action coded by
$(G_x,S_x,\alpha _x)$
denote the countable group action coded by
![]() $x\in \omega ^\omega $
. Consider the following subobject
$x\in \omega ^\omega $
. Consider the following subobject
![]() $\mathsf {Orbit}_{\geq 2}$
of
$\mathsf {Orbit}_{\geq 2}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all countable group actions on subsets of
 $\omega $
; that is,
$\omega $
; that is,
 $x\in |\mathsf {Orbit}_{\geq 2}|$
iff
$x\in |\mathsf {Orbit}_{\geq 2}|$
iff
 $\alpha _x\colon G_x\times S_x\to S_x$
has at least two orbits.
$\alpha _x\colon G_x\times S_x\to S_x$
has at least two orbits. -
•
 $(a,b,p)$
is a name of
$(a,b,p)$
is a name of
 $x\in \mathsf {Orbit}_{\geq 2}$
iff
$x\in \mathsf {Orbit}_{\geq 2}$
iff
 $p=x$
and
$p=x$
and
 $a,b\in S_x$
belong to different orbits; that is, there is no
$a,b\in S_x$
belong to different orbits; that is, there is no
 $g\in G_x$
such that
$g\in G_x$
such that
 $\alpha _x(g,a)=b$
.
$\alpha _x(g,a)=b$
.
When a group action
![]() $\alpha $
is given,
$\alpha $
is given,
![]() $\alpha (g,a)$
is often abbreviated as
$\alpha (g,a)$
is often abbreviated as
![]() $g\cdot a$
.
$g\cdot a$
.
Proposition 5.32.
![]() $\mathsf {DisConn}\equiv _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}\equiv _{\mathsf {m}}\mathsf {Orbit}_{\geq 2}$
.
$\mathsf {DisConn}\equiv _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}\equiv _{\mathsf {m}}\mathsf {Orbit}_{\geq 2}$
.
Proof.
![]() $\mathsf {DisConn}\leq _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}$
: It is obvious since any subset
$\mathsf {DisConn}\leq _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}$
: It is obvious since any subset
![]() $E\subseteq [V]^2$
can be thought of as an inclusion map
$E\subseteq [V]^2$
can be thought of as an inclusion map
![]() $E\hookrightarrow [V]^2$
.
$E\hookrightarrow [V]^2$
.
![]() $\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {DisConn}$
: Let a function presentation of a graph
$\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {DisConn}$
: Let a function presentation of a graph
![]() $\gamma \colon E\to [V]^2$
is given. For each
$\gamma \colon E\to [V]^2$
is given. For each
![]() $v\in V$
, put
$v\in V$
, put
![]() $2v\in V'$
. If
$2v\in V'$
. If
![]() $\gamma (a)=\{u,v\}$
then put
$\gamma (a)=\{u,v\}$
then put
![]() $\{2u,2\langle u,v,a\rangle +1\},\{2\langle u,v,a\rangle +1,2v\}\in E'$
. Note that the graph
$\{2u,2\langle u,v,a\rangle +1\},\{2\langle u,v,a\rangle +1,2v\}\in E'$
. Note that the graph
![]() $\phi (\gamma )=(V',E')$
is the result of adding one vertex to the midpoint of each edge of the graph
$\phi (\gamma )=(V',E')$
is the result of adding one vertex to the midpoint of each edge of the graph
![]() $(V,E)$
. For the forward reduction, clearly
$(V,E)$
. For the forward reduction, clearly
![]() $\{u,v\}$
is disconnected in
$\{u,v\}$
is disconnected in
![]() $(V,E)$
iff
$(V,E)$
iff
![]() $\{2u,2v\}$
is disconnected in
$\{2u,2v\}$
is disconnected in
![]() $(V',E')$
. For the backward reduction, assume that
$(V',E')$
. For the backward reduction, assume that
![]() $\{2u,2\langle v,w,a\rangle +1\}$
is disconnected in
$\{2u,2\langle v,w,a\rangle +1\}$
is disconnected in
![]() $(V',E')$
. By definition,
$(V',E')$
. By definition,
![]() $2v$
is adjacent to
$2v$
is adjacent to
![]() $2\langle v,w,a\rangle +1$
, so
$2\langle v,w,a\rangle +1$
, so
![]() $\{2u,2v\}$
must also be disconnected; hence
$\{2u,2v\}$
must also be disconnected; hence
![]() $\{u,v\}$
is disconnected in
$\{u,v\}$
is disconnected in
![]() $(V,E)$
. Similarly, if
$(V,E)$
. Similarly, if
![]() $\{2\langle u,v,a\rangle +1,2\langle u',v',a'\rangle +1\}$
is disconnected in
$\{2\langle u,v,a\rangle +1,2\langle u',v',a'\rangle +1\}$
is disconnected in
![]() $(V',E')$
, so is
$(V',E')$
, so is
![]() $(2u,2u')$
; hence
$(2u,2u')$
; hence
![]() $(u,u')$
is disconnected in
$(u,u')$
is disconnected in
![]() $(V,E)$
.
$(V,E)$
.
![]() $\mathsf {Orbit}_{\geq 2}\leq _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}$
: Given a group action
$\mathsf {Orbit}_{\geq 2}\leq _{\mathsf {m}}\mathsf {DisConn}_{\mathsf {fun}}$
: Given a group action
![]() $G\times S\to S$
, consider the (directed) graph
$G\times S\to S$
, consider the (directed) graph
![]() $\gamma \colon G\times S\to S^2$
defined by
$\gamma \colon G\times S\to S^2$
defined by
![]() $\gamma (g,a)=(a,g\cdot a)$
. Intuitively,
$\gamma (g,a)=(a,g\cdot a)$
. Intuitively,
![]() $\gamma $
consists of edges of the form
$\gamma $
consists of edges of the form
![]() $a\overset {g}{\longrightarrow }g\cdot a$
, but this must be distinguished from
$a\overset {g}{\longrightarrow }g\cdot a$
, but this must be distinguished from
![]() $b\overset {g}{\longrightarrow }g\cdot b$
for
$b\overset {g}{\longrightarrow }g\cdot b$
for
![]() $b\not =a$
, so we add the information on tails to the names of these edges; that is, the name of the former is
$b\not =a$
, so we add the information on tails to the names of these edges; that is, the name of the former is
![]() $(g,a)$
and the latter is
$(g,a)$
and the latter is
![]() $(g,b)$
. Now every
$(g,b)$
. Now every
![]() $g\in G$
is invertible, so we have
$g\in G$
is invertible, so we have
![]() $\gamma (g^{-1},g\cdot a)=(g\cdot a,a)$
. As the information of
$\gamma (g^{-1},g\cdot a)=(g\cdot a,a)$
. As the information of
![]() $\circ ^{-1}$
is contained in a code of G, given an edge
$\circ ^{-1}$
is contained in a code of G, given an edge
![]() $u\overset {e}{\longrightarrow }v$
in
$u\overset {e}{\longrightarrow }v$
in
![]() $\gamma $
, one can always effectively find an edge
$\gamma $
, one can always effectively find an edge
![]() $v\overset {c}{\longrightarrow }u$
in
$v\overset {c}{\longrightarrow }u$
in
![]() $\gamma $
; that is, if
$\gamma $
; that is, if
![]() $e=(g,a)$
then
$e=(g,a)$
then
![]() $c=(g^{-1},g\cdot a)$
. Hence
$c=(g^{-1},g\cdot a)$
. Hence
![]() $\gamma $
can be modified to an undirected graph
$\gamma $
can be modified to an undirected graph
![]() $\gamma '\colon G\times S\to [S]^2$
. Now, it is easy to see that
$\gamma '\colon G\times S\to [S]^2$
. Now, it is easy to see that
![]() $a,b\in S$
belong to the same orbit iff a and b are connected by a finite path in
$a,b\in S$
belong to the same orbit iff a and b are connected by a finite path in
![]() $\gamma '$
.
$\gamma '$
.
![]() $\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {Orbit}_{\geq 2}$
: Given a function presentation of a graph
$\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {Orbit}_{\geq 2}$
: Given a function presentation of a graph
![]() $\gamma \colon E\to [V]^2$
, consider the free group
$\gamma \colon E\to [V]^2$
, consider the free group
![]() $F_E$
over the set E. Then define the
$F_E$
over the set E. Then define the
![]() $F_E$
-action on V as follows: For
$F_E$
-action on V as follows: For
![]() $a\in E$
, if
$a\in E$
, if
![]() $\gamma (a)=\{u,v\}$
then put
$\gamma (a)=\{u,v\}$
then put
![]() $a\cdot u=v$
and
$a\cdot u=v$
and
![]() $a\cdot v=u$
. For
$a\cdot v=u$
. For
![]() $w\in V\setminus \{u,v\}$
, put
$w\in V\setminus \{u,v\}$
, put
![]() $a\cdot w=w$
. Then a and b are connected by a finite path in
$a\cdot w=w$
. Then a and b are connected by a finite path in
![]() $\gamma $
iff
$\gamma $
iff
![]() $a,b\in S$
belong to the same orbit.
$a,b\in S$
belong to the same orbit.
Interestingly, as we will see later,
![]() $\mathsf {DisConn}$
is half
$\mathsf {DisConn}$
is half
![]() $\Sigma ^0_2$
-hard, but not
$\Sigma ^0_2$
-hard, but not
![]() $\Sigma ^0_2$
-complete.
$\Sigma ^0_2$
-complete.
5.4.4
 $\Sigma ^0_2$
-complete
$\Sigma ^0_2$
-complete
The last group consists of “genuine”
![]() $\Sigma ^0_2$
-complete sets. Of course, a meta-mathematical example of a
$\Sigma ^0_2$
-complete sets. Of course, a meta-mathematical example of a
![]() $\Sigma ^0_2$
-complete subobject of
$\Sigma ^0_2$
-complete subobject of
![]() $\omega ^\omega $
is
$\omega ^\omega $
is ![]() , where
, where
![]() $\exists a\forall b\theta (a,b,x)$
is a universal
$\exists a\forall b\theta (a,b,x)$
is a universal
![]() $\Sigma ^0_2$
formula. This is equivalent to the following:
$\Sigma ^0_2$
formula. This is equivalent to the following:
Example 5.33. Consider the following subobject
![]() $\mathsf {Truth}_{\Sigma ^0_2}\rightarrowtail \omega ^\omega $
:
$\mathsf {Truth}_{\Sigma ^0_2}\rightarrowtail \omega ^\omega $
:
-
• The underlying set is
 $\{(x_n)_{n\in \omega }\in (\omega ^\omega )^\omega :(\exists n\in \omega )\;x_n=0^\infty \}$
.
$\{(x_n)_{n\in \omega }\in (\omega ^\omega )^\omega :(\exists n\in \omega )\;x_n=0^\infty \}$
. -
•
 $(n,p)$
is a name of
$(n,p)$
is a name of
 $x=(x_n)_{n\in \omega }\in \mathsf {Truth}_{\Sigma ^0_2}$
iff
$x=(x_n)_{n\in \omega }\in \mathsf {Truth}_{\Sigma ^0_2}$
iff
 $p=x$
and
$p=x$
and
 $x_n=0^\infty $
holds.
$x_n=0^\infty $
holds.
Observation 5.34.
![]() $\mathsf {Truth}_{\Sigma ^0_2}$
is complete w.r.t.
$\mathsf {Truth}_{\Sigma ^0_2}$
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Next, we give some order-theoretic examples of
![]() $\Sigma ^0_2$
-complete subobjects.
$\Sigma ^0_2$
-complete subobjects.
Example 5.35. The space of linear orders
![]() $\mathsf {LO}$
on a subset of
$\mathsf {LO}$
on a subset of
![]() $\omega $
is a
$\omega $
is a
![]() $\Pi ^0_1$
subspace of
$\Pi ^0_1$
subspace of
![]() $2^{\omega \times \omega }$
. Let
$2^{\omega \times \omega }$
. Let
![]() $(L_x,\leq _x)\in \mathsf {LO}$
denote the linear order coded by
$(L_x,\leq _x)\in \mathsf {LO}$
denote the linear order coded by
![]() $x\in \omega ^\omega $
, where
$x\in \omega ^\omega $
, where
![]() $L_x=\{a\in \omega :a\leq _xa\}$
. Consider the following subobject
$L_x=\{a\in \omega :a\leq _xa\}$
. Consider the following subobject
![]() $\mathsf {NonDense}$
of
$\mathsf {NonDense}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all non-dense linear orders; that is,
 $|\mathsf {NonDense}|=\{x\in \omega ^\omega :\neg (\forall a,b\in L_x)\;[a<_xb\to (\exists c\in L_x)\;a<_xc<_xa]\}$
.
$|\mathsf {NonDense}|=\{x\in \omega ^\omega :\neg (\forall a,b\in L_x)\;[a<_xb\to (\exists c\in L_x)\;a<_xc<_xa]\}$
. -
•
 $(a,b,p)$
is a name of
$(a,b,p)$
is a name of
 $x\in \mathsf {NonDense}$
iff
$x\in \mathsf {NonDense}$
iff
 $p=x$
,
$p=x$
,
 $a<_xb$
and for any
$a<_xb$
and for any
 $c\in P_x$
either
$c\in P_x$
either
 $c\leq _xa$
or
$c\leq _xa$
or
 $b\leq _xc$
holds.
$b\leq _xc$
holds.
Example 5.36. A bottomed poset is a tuple
![]() $(P,\leq _P,\bot _P)$
, where
$(P,\leq _P,\bot _P)$
, where
![]() $(P,\leq _P)$
is a poset, and
$(P,\leq _P)$
is a poset, and
![]() $\bot _P$
is the least element in P. An atom of a bottomed poset P is an element which is minimal among non-bottom elements in P. For
$\bot _P$
is the least element in P. An atom of a bottomed poset P is an element which is minimal among non-bottom elements in P. For
![]() $P\subseteq \omega $
, a bottomed poset
$P\subseteq \omega $
, a bottomed poset
![]() $(P,\leq _P,\bot _P)$
is coded by the pair of the characteristic function of
$(P,\leq _P,\bot _P)$
is coded by the pair of the characteristic function of
![]() $\leq _P$
and the natural number
$\leq _P$
and the natural number
![]() $\bot _P\in P\subseteq \omega $
. In this way, the space of bottomed posets
$\bot _P\in P\subseteq \omega $
. In this way, the space of bottomed posets
![]() $\mathsf {PO}_\bot $
on a subset of
$\mathsf {PO}_\bot $
on a subset of
![]() $\omega $
can be introduced as a
$\omega $
can be introduced as a
![]() $\Pi ^0_1$
subspace of
$\Pi ^0_1$
subspace of
![]() $2^{\omega \times \omega }\times \omega $
.
$2^{\omega \times \omega }\times \omega $
.
Let
![]() $(P_x,\leq _x,\bot _x)\in \mathsf {PO}_\bot $
denote the bottomed poset coded by
$(P_x,\leq _x,\bot _x)\in \mathsf {PO}_\bot $
denote the bottomed poset coded by
![]() $x\in \omega ^\omega $
, where
$x\in \omega ^\omega $
, where
![]() $P_x=\{a\in \omega :a\leq _xa\}$
. Consider the following subobject
$P_x=\{a\in \omega :a\leq _xa\}$
. Consider the following subobject
![]() $\mathsf {PO}_{\mathsf {atom}}$
of
$\mathsf {PO}_{\mathsf {atom}}$
of
![]() $\omega ^\omega $
:
$\omega ^\omega $
:
-
• The underlying set is the set of all partial orders having atoms; that is,
 $|\mathsf {PO}_{\mathsf {atom}}|=\{x\in \omega ^\omega :(\exists a\in P_x)(\forall b\in P_x)\;b<_xa\to b=\bot _x\}$
.
$|\mathsf {PO}_{\mathsf {atom}}|=\{x\in \omega ^\omega :(\exists a\in P_x)(\forall b\in P_x)\;b<_xa\to b=\bot _x\}$
. -
•
 $(a,p)$
is a name of
$(a,p)$
is a name of
 $x\in \mathsf {PO}_{\mathsf {atom}}$
iff
$x\in \mathsf {PO}_{\mathsf {atom}}$
iff
 $p=x$
, for any
$p=x$
, for any
 $c\in P_x$
either
$c\in P_x$
either
 $c\leq _xa$
or
$c\leq _xa$
or
 $b\leq _xc$
holds.
$b\leq _xc$
holds.
Proposition 5.37.
![]() $\mathsf {NonDense}$
is complete w.r.t.
$\mathsf {NonDense}$
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proof. It suffices to show
![]() $\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {NonDense}$
. Given
$\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {NonDense}$
. Given
![]() $x=(x_n)_{n\in \omega }$
, we construct a linear order
$x=(x_n)_{n\in \omega }$
, we construct a linear order
![]() $L=L_{\varphi (x)}$
. First put
$L=L_{\varphi (x)}$
. First put
![]() $(n,0)<_L(n+1,0)$
for any
$(n,0)<_L(n+1,0)$
for any
![]() $n\in \omega $
. As long as
$n\in \omega $
. As long as
![]() $x_n=0^\infty $
is true, nothing is enumerated between
$x_n=0^\infty $
is true, nothing is enumerated between
![]() $(n,0)$
and
$(n,0)$
and
![]() $(n+1,0)$
. If we see
$(n+1,0)$
. If we see
![]() $x_n\not =0^\infty $
at stage s, we enumerate elements of the form
$x_n\not =0^\infty $
at stage s, we enumerate elements of the form
![]() $(n,t)$
for
$(n,t)$
for
![]() $t\geq s$
between
$t\geq s$
between
![]() $(n,0)$
and
$(n,0)$
and
![]() $(n+1,0)$
so that the
$(n+1,0)$
so that the
![]() $\leq _L$
-interval
$\leq _L$
-interval
![]() $[(n,0),(n+1,0)]$
eventually becomes dense.
$[(n,0),(n+1,0)]$
eventually becomes dense.
If n is a witness for
![]() $x\in \mathsf {Truth}_{\Sigma ^0_2}$
, i.e.,
$x\in \mathsf {Truth}_{\Sigma ^0_2}$
, i.e.,
![]() $x_n=0^\infty $
, then there is no element between
$x_n=0^\infty $
, then there is no element between
![]() $(n,0)$
and
$(n,0)$
and
![]() $(n+1,0)$
, so this pair is a witness for
$(n+1,0)$
, so this pair is a witness for
![]() $\varphi (x)\in \mathsf {NonDense}$
. Conversely, let
$\varphi (x)\in \mathsf {NonDense}$
. Conversely, let
![]() $\langle (n,i),(m,j) \rangle $
be a witness for
$\langle (n,i),(m,j) \rangle $
be a witness for
![]() $\varphi (x)\in \mathsf {NonDense}$
. We may assume
$\varphi (x)\in \mathsf {NonDense}$
. We may assume
![]() $n\leq m$
. If
$n\leq m$
. If
![]() $n+1<m$
then we have
$n+1<m$
then we have
![]() $(n,i)<(n+1,0)<(m,j)$
, so
$(n,i)<(n+1,0)<(m,j)$
, so
![]() $\langle (n,i),(m,j) \rangle $
cannot be a witness. If
$\langle (n,i),(m,j) \rangle $
cannot be a witness. If
![]() $n=m$
and
$n=m$
and
![]() $i\not =j$
, then either
$i\not =j$
, then either
![]() $i\not =0$
or
$i\not =0$
or
![]() $j\not =0$
; that is, some
$j\not =0$
; that is, some
![]() $(n,k)$
for
$(n,k)$
for
![]() $k\not =0$
is enumerated into L. By our construction, this means that the
$k\not =0$
is enumerated into L. By our construction, this means that the
![]() $\leq _L$
-interval
$\leq _L$
-interval
![]() $[(n,0),(n+1)]$
becomes dense, and any element of the form
$[(n,0),(n+1)]$
becomes dense, and any element of the form
![]() $(n,k)$
is enumerated into this interval. In particular,
$(n,k)$
is enumerated into this interval. In particular,
![]() $(n,i)$
and
$(n,i)$
and
![]() $(n,j)$
are contained in the
$(n,j)$
are contained in the
![]() $\leq _L$
-dense interval
$\leq _L$
-dense interval
![]() $[(n,0),(n+1)]$
, so some
$[(n,0),(n+1)]$
, so some
![]() $(n,k)$
is enumerated between
$(n,k)$
is enumerated between
![]() $(n,0)$
and
$(n,0)$
and
![]() $(n+1,0)$
; hence
$(n+1,0)$
; hence
![]() $\langle (n,i),(m,j) \rangle $
cannot be a witness. Therefore, we have
$\langle (n,i),(m,j) \rangle $
cannot be a witness. Therefore, we have
![]() $m=n+1$
, but there is no element between
$m=n+1$
, but there is no element between
![]() $(n,i)$
and
$(n,i)$
and
![]() $(n+1,j)$
then we must have
$(n+1,j)$
then we must have
![]() $i=j=0$
, which means
$i=j=0$
, which means
![]() $x_n=0^\infty $
; that is, n is a witness for
$x_n=0^\infty $
; that is, n is a witness for
![]() $x\in \mathsf {Truth}_{\Sigma ^0_2}$
.
$x\in \mathsf {Truth}_{\Sigma ^0_2}$
.
Proposition 5.38.
![]() $\mathsf {PO}_{\mathsf {atom}}$
is complete w.r.t.
$\mathsf {PO}_{\mathsf {atom}}$
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proof. It suffices to show
![]() $\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {PO}_{\mathsf {atom}}$
. Given
$\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {PO}_{\mathsf {atom}}$
. Given
![]() $x=(x_n)_{n\in \omega }$
, we construct a partially ordered set
$x=(x_n)_{n\in \omega }$
, we construct a partially ordered set
![]() $P=P_\varphi (x)$
. Put
$P=P_\varphi (x)$
. Put
![]() $\bot \in P$
and
$\bot \in P$
and
![]() $(n,0)\in P$
for each
$(n,0)\in P$
for each
![]() $n\in \omega $
. As long as
$n\in \omega $
. As long as
![]() $x_n=0^\infty $
is true, nothing other than
$x_n=0^\infty $
is true, nothing other than
![]() $\bot $
is enumerated below
$\bot $
is enumerated below
![]() $(n,0)$
, which becomes an atom in P. If we see
$(n,0)$
, which becomes an atom in P. If we see
![]() $x_n\not =0^\infty $
at stage s, we enumerate an infinite decreasing sequence
$x_n\not =0^\infty $
at stage s, we enumerate an infinite decreasing sequence
![]() $(n,0)>_P(n,s)>_P(n,s+1)>_P\dots $
.
$(n,0)>_P(n,s)>_P(n,s+1)>_P\dots $
.
If n is a witness for
![]() $x\in \mathsf {Truth}_{\Sigma ^0_2}$
, i.e.,
$x\in \mathsf {Truth}_{\Sigma ^0_2}$
, i.e.,
![]() $x_n=0^\infty $
, then
$x_n=0^\infty $
, then
![]() $(n,0)$
is an atom in P. Conversely, if
$(n,0)$
is an atom in P. Conversely, if
![]() $(n,s)$
is an atom in P, we must have
$(n,s)$
is an atom in P, we must have
![]() $s=0$
and
$s=0$
and
![]() $x_n=0^\infty $
; that is, n is a witness for
$x_n=0^\infty $
; that is, n is a witness for
![]() $x\in \mathsf {Truth}_{\Sigma ^0_2}$
.
$x\in \mathsf {Truth}_{\Sigma ^0_2}$
.
We also introduce a
![]() $\Sigma ^0_2$
-complete subobject concerning trees.
$\Sigma ^0_2$
-complete subobject concerning trees.
Example 5.39. Let
![]() $\mathsf {Tr}_2$
be the represented space of binary trees. Consider the following subobject
$\mathsf {Tr}_2$
be the represented space of binary trees. Consider the following subobject
![]() $\mathsf {Tr}_2(\geq 2)$
of
$\mathsf {Tr}_2(\geq 2)$
of
![]() $\mathsf {Tr}_2$
:
$\mathsf {Tr}_2$
:
-
• The underlying set is the set of all binary trees which have at least two infinite paths.
-
•
 $(\sigma ,\tau ,p)$
is a name of
$(\sigma ,\tau ,p)$
is a name of
 $T\in \mathsf {Tr}_2(\geq 2)$
iff p is a
$T\in \mathsf {Tr}_2(\geq 2)$
iff p is a
 $\mathsf {Tr}_2$
-name of T, and
$\mathsf {Tr}_2$
-name of T, and
 $\sigma $
and
$\sigma $
and
 $\tau $
are incomparable finite strings which are extendible to infinite paths in T.
$\tau $
are incomparable finite strings which are extendible to infinite paths in T.
Proposition 5.40.
![]() $\mathsf {Tr}_2(\geq 2)$
is complete w.r.t.
$\mathsf {Tr}_2(\geq 2)$
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proof. It suffices to show
![]() $\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {Tr}_2(\geq 2)$
. Given
$\mathsf {Truth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {Tr}_2(\geq 2)$
. Given
![]() $x\in \omega ^\omega $
, construct a tree
$x\in \omega ^\omega $
, construct a tree
![]() $T_x$
such that
$T_x$
such that
![]() $0^m\in T_x$
for any
$0^m\in T_x$
for any
![]() $m\in \omega $
and
$m\in \omega $
and
![]() $0^n1^s\in T_x$
iff
$0^n1^s\in T_x$
iff
![]() $x_n=0^\infty $
is not yet recognized when x is read up to s. Note that
$x_n=0^\infty $
is not yet recognized when x is read up to s. Note that
![]() $0^\infty $
is always an infinite path through
$0^\infty $
is always an infinite path through
![]() $T_x$
, and
$T_x$
, and
![]() $0^n1^\infty $
is an infinite path through
$0^n1^\infty $
is an infinite path through
![]() $T_x$
iff
$T_x$
iff
![]() $x_n\not =0^\infty $
. Therefore,
$x_n\not =0^\infty $
. Therefore,
![]() $x\in |A|$
iff
$x\in |A|$
iff
![]() $T_x$
has at least two infinite paths, i.e.,
$T_x$
has at least two infinite paths, i.e.,
![]() $T_x\in |\mathsf {Tr}_2(\geq 2)|$
.
$T_x\in |\mathsf {Tr}_2(\geq 2)|$
.
Given a witness n for
![]() $x\in A$
, we know
$x\in A$
, we know
![]() $x_n\not =0^\infty $
, so
$x_n\not =0^\infty $
, so
![]() $(0^{n+1},0^n1)$
is an incomparable extendible pair in
$(0^{n+1},0^n1)$
is an incomparable extendible pair in
![]() $T_x$
; hence
$T_x$
; hence
![]() $r_-(n,x):=(0^{n+1},0^n1)$
is a witness for
$r_-(n,x):=(0^{n+1},0^n1)$
is a witness for
![]() $T_x\in \mathsf {Tr}_2(\geq 2)$
. Conversely, if
$T_x\in \mathsf {Tr}_2(\geq 2)$
. Conversely, if
![]() $(\sigma ,\tau )$
is a witness for
$(\sigma ,\tau )$
is a witness for
![]() $T_x\in \mathsf {Tr}_2(\geq 2)$
, either
$T_x\in \mathsf {Tr}_2(\geq 2)$
, either
![]() $\sigma $
or
$\sigma $
or
![]() $\tau $
is of the form
$\tau $
is of the form
![]() $0^m1^k$
, and in this case, we have
$0^m1^k$
, and in this case, we have
![]() $x_m\not =0^\infty $
; hence
$x_m\not =0^\infty $
; hence
![]() $r_+(\sigma ,\tau ,x):=m$
is a witness for
$r_+(\sigma ,\tau ,x):=m$
is a witness for
![]() $x\in A$
.
$x\in A$
.
5.5 Many-one degree structure
5.5.1 Completeness and hardness
Let us first confirm that each of the first two levels of
![]() $\Sigma ^0_2$
subobjects has a complete subobject.
$\Sigma ^0_2$
subobjects has a complete subobject.
Theorem 5.41.
![]() $\mathsf {Fin}$
is complete w.r.t.
$\mathsf {Fin}$
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
having the unique witness property.
$\omega ^\omega $
having the unique witness property.
Proof. We first check that
![]() $\mathsf {Fin}$
has the unique witness property. The idea is to use a process to search for the least witness for
$\mathsf {Fin}$
has the unique witness property. The idea is to use a process to search for the least witness for
![]() $x\in \mathsf {Fin}$
using its name. First, we divide
$x\in \mathsf {Fin}$
using its name. First, we divide
![]() $\mathsf {Fin}$
according to what its least witness is. Namely, let
$\mathsf {Fin}$
according to what its least witness is. Namely, let
![]() $F_n$
be a subspace of
$F_n$
be a subspace of
![]() $\omega ^\omega $
whose underlying set is:
$\omega ^\omega $
whose underlying set is:
Then we claim that
![]() $\mathsf {Fin}\equiv \biguplus _nF_n$
. One can easily observe that
$\mathsf {Fin}\equiv \biguplus _nF_n$
. One can easily observe that
![]() $|\mathsf {Fin}|=|\biguplus _nF_n|$
, and any name of
$|\mathsf {Fin}|=|\biguplus _nF_n|$
, and any name of
![]() $x\in \biguplus _nF_n$
is also a name of
$x\in \biguplus _nF_n$
is also a name of
![]() $x\in \mathsf {Fin}$
. Given a name
$x\in \mathsf {Fin}$
. Given a name
![]() $(n,x)$
of
$(n,x)$
of
![]() $x\in \mathsf {Fin}$
, search for its least witness; that is, the least
$x\in \mathsf {Fin}$
, search for its least witness; that is, the least
![]() $m\leq n$
such that
$m\leq n$
such that
![]() $x(k)=0$
for any
$x(k)=0$
for any
![]() $m\leq k\leq n$
. One can see that
$m\leq k\leq n$
. One can see that
![]() $x\in F_m$
for such m. Then
$x\in F_m$
for such m. Then
![]() $(m,x)$
is a name of
$(m,x)$
is a name of
![]() $x\in \biguplus _nF_n$
.
$x\in \biguplus _nF_n$
.
For the completeness, assume that A has the unique witness property via
![]() $A\equiv \biguplus _nA_n$
. Let
$A\equiv \biguplus _nA_n$
. Let
![]() $f_n$
be a witness for closedness of
$f_n$
be a witness for closedness of
![]() $A_n$
; that is,
$A_n$
; that is,
![]() $x\in A_n$
iff
$x\in A_n$
iff
![]() $f_n(x)=0^\infty $
. Given
$f_n(x)=0^\infty $
. Given
![]() $x\in \omega ^\omega $
, by continuity of
$x\in \omega ^\omega $
, by continuity of
![]() $f_n$
, if
$f_n$
, if
![]() $x\not \in A_n$
(i.e.,
$x\not \in A_n$
(i.e.,
![]() $f_n(x)$
returns some nonzero value), that can be recognized after reading a finite initial segment of x. Starting from
$f_n(x)$
returns some nonzero value), that can be recognized after reading a finite initial segment of x. Starting from
![]() $n=0$
,
$n=0$
,
![]() $\varphi (x)$
keeps outputting
$\varphi (x)$
keeps outputting
![]() $0$
until
$0$
until
![]() $f_n$
recognizes
$f_n$
recognizes
![]() $x\not \in A_n$
. When it recognizes
$x\not \in A_n$
. When it recognizes
![]() $x\not \in A_n$
,
$x\not \in A_n$
,
![]() $\varphi (x)$
outputs
$\varphi (x)$
outputs
![]() $1$
, and then repeat the same procedure with
$1$
, and then repeat the same procedure with
![]() $n+1$
. This reduction is exactly the same as the proof of the classical
$n+1$
. This reduction is exactly the same as the proof of the classical
![]() $\Sigma ^0_2$
-completeness, which shows that
$\Sigma ^0_2$
-completeness, which shows that
![]() $x\in |\biguplus _nA_n|$
iff
$x\in |\biguplus _nA_n|$
iff
![]() $\varphi (x)\in |\mathsf {Fin}|$
.
$\varphi (x)\in |\mathsf {Fin}|$
.
Given a name
![]() $(n,x)$
of
$(n,x)$
of
![]() $x\in \biguplus _nA_n$
, we have
$x\in \biguplus _nA_n$
, we have
![]() $x\in A_n$
. By uniqueness, we also have
$x\in A_n$
. By uniqueness, we also have
![]() $x\not \in A_m$
for any
$x\not \in A_m$
for any
![]() $m<n$
. Therefore, the above procedure eventually recognizes
$m<n$
. Therefore, the above procedure eventually recognizes
![]() $x\not \in A_m$
for each
$x\not \in A_m$
for each
![]() $m<n$
, and thus, it arrives at a state waiting for
$m<n$
, and thus, it arrives at a state waiting for
![]() $f_n$
to recognize
$f_n$
to recognize
![]() $x\not \in A_n$
at some stage
$x\not \in A_n$
at some stage
![]() $s_n$
. Since
$s_n$
. Since
![]() $x\in A_n$
, it is never recognized, so
$x\in A_n$
, it is never recognized, so
![]() $\varphi (x)$
continues to output
$\varphi (x)$
continues to output
![]() $0$
forever after stage
$0$
forever after stage
![]() $s_n$
. Therefore,
$s_n$
. Therefore,
![]() $r_-(n,x)=(s_n,\varphi (x))$
is a name of
$r_-(n,x)=(s_n,\varphi (x))$
is a name of
![]() $x\in \mathsf {Fin}$
.
$x\in \mathsf {Fin}$
.
Given a name
![]() $(s,p)$
of
$(s,p)$
of
![]() $\varphi (x)\in \mathsf {Fin}$
, run the above procedure for s steps. At that point, the process is waiting for
$\varphi (x)\in \mathsf {Fin}$
, run the above procedure for s steps. At that point, the process is waiting for
![]() $f_k$
to recognize
$f_k$
to recognize
![]() $x\not \in A_k$
for some k. If it is ever recognized,
$x\not \in A_k$
for some k. If it is ever recognized,
![]() $\varphi (x)$
outputs
$\varphi (x)$
outputs
![]() $1$
at somewhere after the sth bit, which is impossible because of the assumption that
$1$
at somewhere after the sth bit, which is impossible because of the assumption that
![]() $(s,p)$
is the name of
$(s,p)$
is the name of
![]() $\varphi (x)\in \mathsf {Fin}$
. Therefore,
$\varphi (x)\in \mathsf {Fin}$
. Therefore,
![]() $x\not \in A_k$
is never recognized, that is,
$x\not \in A_k$
is never recognized, that is,
![]() $x\in A_k$
. Therefore,
$x\in A_k$
. Therefore,
![]() $r_+(x,(s,p))=(k,x)$
is a name of
$r_+(x,(s,p))=(k,x)$
is a name of
![]() $x\in \biguplus _nA_n$
.
$x\in \biguplus _nA_n$
.
Combining with Observation 5.13, this verifies our claim that
![]() $\mathsf {Fin}$
is complete among
$\mathsf {Fin}$
is complete among
![]() $\Sigma ^0_2$
subobjects defined by a formula of the form
$\Sigma ^0_2$
subobjects defined by a formula of the form
![]() $\forall n\exists m\geq n.\varphi (m,x)$
, where
$\forall n\exists m\geq n.\varphi (m,x)$
, where
![]() $\varphi $
is decidable.
$\varphi $
is decidable.
Theorem 5.42.
![]() $\mathsf {BddSeq}_\omega $
is complete w.r.t.
$\mathsf {BddSeq}_\omega $
is complete w.r.t.
![]() $\Sigma ^0_2$
subobjects of
$\Sigma ^0_2$
subobjects of
![]() $\omega ^\omega $
having the increasing witness property.
$\omega ^\omega $
having the increasing witness property.
Proof. For each
![]() $k\in \omega $
, consider
$k\in \omega $
, consider ![]() . Then clearly
. Then clearly
![]() $|B_k|\subseteq |B_{k+1}|$
and
$|B_k|\subseteq |B_{k+1}|$
and
![]() $\mathsf {BddSeq}_\omega =\biguplus _{k\in \omega }B_k$
. Hence,
$\mathsf {BddSeq}_\omega =\biguplus _{k\in \omega }B_k$
. Hence,
![]() $\mathsf {BddSeq}_\omega $
has the increasing witness property.
$\mathsf {BddSeq}_\omega $
has the increasing witness property.
For the completeness, assume that A has the increasing witness property via
![]() $A\equiv \biguplus _nA_n$
. Let
$A\equiv \biguplus _nA_n$
. Let
![]() $f_n$
be a witness for closedness of
$f_n$
be a witness for closedness of
![]() $A_n$
; that is,
$A_n$
; that is,
![]() $x\in A_n$
iff
$x\in A_n$
iff
![]() $f_n(x)=0^\infty $
. Given
$f_n(x)=0^\infty $
. Given
![]() $x\in \omega ^\omega $
, by continuity of
$x\in \omega ^\omega $
, by continuity of
![]() $f_n$
, if
$f_n$
, if
![]() $x\not \in A_n$
, that can be recognized after reading a finite initial segment of x. Starting from
$x\not \in A_n$
, that can be recognized after reading a finite initial segment of x. Starting from
![]() $n=0$
,
$n=0$
,
![]() $\varphi (x)$
keeps outputting
$\varphi (x)$
keeps outputting
![]() $0$
until
$0$
until
![]() $f_n$
recognizes
$f_n$
recognizes
![]() $x\not \in A_n$
. When it recognizes
$x\not \in A_n$
. When it recognizes
![]() $x\not \in A_n$
,
$x\not \in A_n$
,
![]() $\varphi (x)$
outputs n, and then repeat the same procedure with
$\varphi (x)$
outputs n, and then repeat the same procedure with
![]() $n+1$
. This reduction is exactly the same as the proof of the classical
$n+1$
. This reduction is exactly the same as the proof of the classical
![]() $\Sigma ^0_2$
-completeness, which shows that
$\Sigma ^0_2$
-completeness, which shows that
![]() $x\in |\biguplus _nA_n|$
iff
$x\in |\biguplus _nA_n|$
iff
![]() $\varphi (x)\in |\mathsf {BddSeq}_\omega |$
.
$\varphi (x)\in |\mathsf {BddSeq}_\omega |$
.
Given a name
![]() $(k,x)$
of
$(k,x)$
of
![]() $x\in \biguplus _nA_n$
, we have
$x\in \biguplus _nA_n$
, we have
![]() $x\in A_k$
. For the least
$x\in A_k$
. For the least
![]() $n\leq k$
such that
$n\leq k$
such that
![]() $x\in A_n$
, we have
$x\in A_n$
, we have
![]() $x\not \in A_m$
for any
$x\not \in A_m$
for any
![]() $m<n$
. Therefore, the above procedure eventually recognizes
$m<n$
. Therefore, the above procedure eventually recognizes
![]() $x\not \in A_m$
for each
$x\not \in A_m$
for each
![]() $m<n$
, and thus, it arrives at a state waiting for
$m<n$
, and thus, it arrives at a state waiting for
![]() $f_n$
to recognize
$f_n$
to recognize
![]() $x\not \in A_n$
at some stage. Since
$x\not \in A_n$
at some stage. Since
![]() $x\in A_n$
, it is never recognized, so
$x\in A_n$
, it is never recognized, so
![]() $\varphi (x)$
continues to output
$\varphi (x)$
continues to output
![]() $0$
forever after the stage. This means, in particular, that
$0$
forever after the stage. This means, in particular, that
![]() $\varphi (x)$
only outputs values less than n. Now, since
$\varphi (x)$
only outputs values less than n. Now, since
![]() $n\leq k$
, k gives an upper bound of
$n\leq k$
, k gives an upper bound of
![]() $\varphi (x)$
. Therefore,
$\varphi (x)$
. Therefore,
![]() $r_-(n,x)=(k,\varphi (x))$
is a name of
$r_-(n,x)=(k,\varphi (x))$
is a name of
![]() $x\in \mathsf {BddSeq}_\omega $
.
$x\in \mathsf {BddSeq}_\omega $
.
Given a name
![]() $(b,p)$
of
$(b,p)$
of
![]() $\varphi (x)\in \mathsf {BddSeq}_\omega $
, note that b is an upper bound of
$\varphi (x)\in \mathsf {BddSeq}_\omega $
, note that b is an upper bound of
![]() $\varphi (x)$
, so let
$\varphi (x)$
, so let
![]() $k\leq b$
the least upper bound of
$k\leq b$
the least upper bound of
![]() $\varphi (x)$
. In particular, during the above process,
$\varphi (x)$
. In particular, during the above process,
![]() $\varphi (x)$
outputs k at some stage, but never output
$\varphi (x)$
outputs k at some stage, but never output
![]() $k+1$
. This means that
$k+1$
. This means that
![]() $f_k$
recognizes
$f_k$
recognizes
![]() $x\not \in A_k$
, but
$x\not \in A_k$
, but
![]() $f_{k+1}$
never recognizes
$f_{k+1}$
never recognizes
![]() $x\not \in A_{k+1}$
; hence,
$x\not \in A_{k+1}$
; hence,
![]() $x\in A_{k+1}$
. As
$x\in A_{k+1}$
. As
![]() $k+1\leq b+1$
,
$k+1\leq b+1$
,
![]() $r_+(x,(b,p))=(b+1,x)$
is a name of
$r_+(x,(b,p))=(b+1,x)$
is a name of
![]() $x\in \biguplus _nA_n$
.
$x\in \biguplus _nA_n$
.
Next, we show that a half
![]() $\Sigma ^0_2$
-hard subobject bounds these two levels. For this purpose, we compare these notions with amalgamability.
$\Sigma ^0_2$
-hard subobject bounds these two levels. For this purpose, we compare these notions with amalgamability.
Observation 5.43. If a
![]() ${\Sigma }^0_2$
subobject
${\Sigma }^0_2$
subobject
![]() $A\rightarrowtail X$
has the increasing witness property, then A is amalgamable.
$A\rightarrowtail X$
has the increasing witness property, then A is amalgamable.
Proof. Assume that A has the increasing witness property via
![]() $A\equiv \biguplus _{n\in \omega }A_n$
. Let p be a name of
$A\equiv \biguplus _{n\in \omega }A_n$
. Let p be a name of
![]() $x\in \biguplus _nA_n$
. Given
$x\in \biguplus _nA_n$
. Given
![]() $(n_1,p_1),\dots ,(n_k,p_k)$
, if at least one of them, say
$(n_1,p_1),\dots ,(n_k,p_k)$
, if at least one of them, say
![]() $(n_i,p_i)$
, is a correct name of
$(n_i,p_i)$
, is a correct name of
![]() $x\in \biguplus _nA_n$
then
$x\in \biguplus _nA_n$
then
![]() $x\in |A_{n_i}|$
, and thus
$x\in |A_{n_i}|$
, and thus
![]() $x\in |A_m|$
for any
$x\in |A_m|$
for any
![]() $m\geq n_i$
by the increasing witness property. Hence,
$m\geq n_i$
by the increasing witness property. Hence,
![]() $(m,p)$
is also a name of
$(m,p)$
is also a name of
![]() $x\in \biguplus _nA_n$
. Thus, if we put
$x\in \biguplus _nA_n$
. Thus, if we put
![]() $m=\max _{j\leq k}n_j$
then
$m=\max _{j\leq k}n_j$
then
![]() $(m,p)$
is a name of
$(m,p)$
is a name of
![]() $x\in \biguplus _nA_n$
.
$x\in \biguplus _nA_n$
.
Proposition 5.44. If
![]() $A\rightarrowtail \omega ^\omega $
is half
$A\rightarrowtail \omega ^\omega $
is half
![]() $\Sigma ^0_2$
-hard, then
$\Sigma ^0_2$
-hard, then
![]() $B\leq _{\mathsf {m}}A$
for any amalgamable
$B\leq _{\mathsf {m}}A$
for any amalgamable
![]() $\Sigma ^0_2$
subobject
$\Sigma ^0_2$
subobject
![]() $B\rightarrowtail \omega ^\omega $
.
$B\rightarrowtail \omega ^\omega $
.
Proof. Let
![]() $\psi (x)\equiv \exists a\theta (a,x)$
be a
$\psi (x)\equiv \exists a\theta (a,x)$
be a
![]() $\Sigma ^0_2$
formula defining B, where
$\Sigma ^0_2$
formula defining B, where
![]() $\theta $
is
$\theta $
is
![]() $\Pi ^0_1$
. Then, for each witness a for
$\Pi ^0_1$
. Then, for each witness a for
![]() $x\in B$
,
$x\in B$
,
![]() $(a,a)$
is a witness for
$(a,a)$
is a witness for
![]() $x\in \mathsf {Half}(\psi )$
. Conversely, if
$x\in \mathsf {Half}(\psi )$
. Conversely, if
![]() $(a,b)$
is a witness for
$(a,b)$
is a witness for
![]() $x\in \mathsf {Half}(\psi )$
, then either a or b is a witness for
$x\in \mathsf {Half}(\psi )$
, then either a or b is a witness for
![]() $x\in B$
. As B is amalgamable, from the information on
$x\in B$
. As B is amalgamable, from the information on
![]() $(a,b,x)$
, one can compute a correct witness for
$(a,b,x)$
, one can compute a correct witness for
![]() $x\in B$
. Hence,
$x\in B$
. Hence,
![]() $B\leq _{\mathsf {m}}\mathsf {Half}(\psi )\leq _{\mathsf {m}}A$
.
$B\leq _{\mathsf {m}}\mathsf {Half}(\psi )\leq _{\mathsf {m}}A$
.
By Observation 5.43 and Proposition 5.44, we get
![]() $\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
. We next show
$\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
. We next show
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {DisConn}$
.
$\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {DisConn}$
.
Proposition 5.45.
![]() $\mathsf {DisConn}$
is half
$\mathsf {DisConn}$
is half
![]() $\Sigma ^0_2$
-hard.
$\Sigma ^0_2$
-hard.
Proof. We show that
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {DisConn}$
. Given
$\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}\mathsf {DisConn}$
. Given
![]() $x\in \omega ^\omega $
, we construct a graph
$x\in \omega ^\omega $
, we construct a graph
![]() $G=(V,E)$
. First put a special vertex
$G=(V,E)$
. First put a special vertex
![]() $v_0\in V$
. As long as
$v_0\in V$
. As long as
![]() $x_n=0^\infty $
is true, we enumerate a path
$x_n=0^\infty $
is true, we enumerate a path
![]() $(n,0)\to (n,1)\to (n,2)\to \dots $
into E. If we see
$(n,0)\to (n,1)\to (n,2)\to \dots $
into E. If we see
![]() $x_n\not =0^\infty $
at some stage s, terminate the construction of this path at
$x_n\not =0^\infty $
at some stage s, terminate the construction of this path at
![]() $(n,s)$
and then enumerate the edge
$(n,s)$
and then enumerate the edge
![]() $(n,s)\to v_0$
into E. Note that if
$(n,s)\to v_0$
into E. Note that if
![]() $x_n=0^\infty $
holds then
$x_n=0^\infty $
holds then
![]() $\{(n,i):n\in \omega \}$
is a connected component in G; otherwise
$\{(n,i):n\in \omega \}$
is a connected component in G; otherwise
![]() $(n,i)$
is connected to
$(n,i)$
is connected to
![]() $v_0$
.
$v_0$
.
Now assume that
![]() $(n,m)$
be a witness for
$(n,m)$
be a witness for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Then either
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Then either
![]() $x_n=0^\infty $
or
$x_n=0^\infty $
or
![]() $x_m=0^\infty $
holds. If
$x_m=0^\infty $
holds. If
![]() $n=m$
then
$n=m$
then
![]() $x_n=0^\infty $
, so
$x_n=0^\infty $
, so
![]() $(n,0)$
is not connected to
$(n,0)$
is not connected to
![]() $v_0$
by a finite path, so
$v_0$
by a finite path, so
![]() $\langle (n,0),v_0 \rangle $
is a witness for
$\langle (n,0),v_0 \rangle $
is a witness for
![]() $G\in \mathsf {DisConn}$
. Assume
$G\in \mathsf {DisConn}$
. Assume
![]() $n\not =m$
. If
$n\not =m$
. If
![]() $x_n=0^\infty $
then
$x_n=0^\infty $
then
![]() $\{(n,i):i\in \omega \}$
is a connected component in G which does not contain
$\{(n,i):i\in \omega \}$
is a connected component in G which does not contain
![]() $(m,0)$
since
$(m,0)$
since
![]() $n\not =m$
. If
$n\not =m$
. If
![]() $x_n\not =0^\infty $
then we must have
$x_n\not =0^\infty $
then we must have
![]() $x_m=0^\infty $
, so
$x_m=0^\infty $
, so
![]() $\{(m,i):i\in \omega \}$
is a connected component which does not contain
$\{(m,i):i\in \omega \}$
is a connected component which does not contain
![]() $(n,0)$
. Thus,
$(n,0)$
. Thus,
![]() $(n,0)$
and
$(n,0)$
and
![]() $(m,0)$
are not connected by a finite path; that is,
$(m,0)$
are not connected by a finite path; that is,
![]() $\langle (n,0),(m,0) \rangle $
is a witness for
$\langle (n,0),(m,0) \rangle $
is a witness for
![]() $G\in \mathsf {DisConn}$
.
$G\in \mathsf {DisConn}$
.
Conversely, assume that a witness for
![]() $G\in \mathsf {DisConn}$
is given. First consider the case that the witness is of the form
$G\in \mathsf {DisConn}$
is given. First consider the case that the witness is of the form
![]() $\langle (n,i),(m,j) \rangle $
. If both
$\langle (n,i),(m,j) \rangle $
. If both
![]() $x_n\not =0^\infty $
and
$x_n\not =0^\infty $
and
![]() $x_m\not =0^\infty $
hold then both
$x_m\not =0^\infty $
hold then both
![]() $(n,i)$
and
$(n,i)$
and
![]() $(m,j)$
are connected to
$(m,j)$
are connected to
![]() $v_0$
. This is impossible. Hence, either
$v_0$
. This is impossible. Hence, either
![]() $x_n=0^\infty $
or
$x_n=0^\infty $
or
![]() $x_m=0^\infty $
holds; that is,
$x_m=0^\infty $
holds; that is,
![]() $(n,m)$
is a witness for
$(n,m)$
is a witness for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Next, if the witness is of the form
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Next, if the witness is of the form
![]() $\langle (n,i),v_0 \rangle $
, then
$\langle (n,i),v_0 \rangle $
, then
![]() $(n,i)$
is not connected to
$(n,i)$
is not connected to
![]() $v_0$
, so we must have
$v_0$
, so we must have
![]() $x_n=0^\infty $
. Therefore,
$x_n=0^\infty $
. Therefore,
![]() $(n,n)$
is a witness for
$(n,n)$
is a witness for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
.
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
.
5.5.2 Separation
We will see that these levels of
![]() $\Sigma ^0_2$
subobjects have different strengths. In other words, our goal here is to prove the following:
$\Sigma ^0_2$
subobjects have different strengths. In other words, our goal here is to prove the following:
Theorem 5.46.
![]() $\mathsf {Fin}<_{\mathsf {m}}\mathsf {BddSeq}<_{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}<_{\mathsf {m}}\mathsf {DisConn}<_{\mathsf {m}}\mathsf {Truth}_{\Sigma ^0_2}$
.
$\mathsf {Fin}<_{\mathsf {m}}\mathsf {BddSeq}<_{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}<_{\mathsf {m}}\mathsf {DisConn}<_{\mathsf {m}}\mathsf {Truth}_{\Sigma ^0_2}$
.
For this purpose, we first show a technical lemma. An element
![]() $x\in |A|$
of a subobject
$x\in |A|$
of a subobject
![]() $A\rightarrowtail X$
is splittable if for any
$A\rightarrowtail X$
is splittable if for any
![]() $\ell \in \omega $
and
$\ell \in \omega $
and
![]() $j,k$
there exists
$j,k$
there exists
![]() $x'\in |A|$
extending
$x'\in |A|$
extending
![]() $x\upharpoonright \ell $
such that j is no longer a witness for
$x\upharpoonright \ell $
such that j is no longer a witness for
![]() $x'\in A$
, but if
$x'\in A$
, but if
![]() $k\not =j$
is a witness for
$k\not =j$
is a witness for
![]() $x\in A$
, then k is still a witness for
$x\in A$
, then k is still a witness for
![]() $x'\in A$
.
$x'\in A$
.
Lemma 5.47 (Split Lemma)
For subobjects
![]() $A\rightarrowtail X$
and
$A\rightarrowtail X$
and
![]() $B\rightarrowtail Y$
, assume that
$B\rightarrowtail Y$
, assume that
![]() $A\leq _{\mathsf {m}}B$
holds via
$A\leq _{\mathsf {m}}B$
holds via
![]() $\varphi ,r_-,r_+$
(in the sense of Example 3.27). If k is a witness for
$\varphi ,r_-,r_+$
(in the sense of Example 3.27). If k is a witness for
![]() $x\in A$
for some splittable element
$x\in A$
for some splittable element
![]() $x\in |A|$
then
$x\in |A|$
then
![]() $r_+(r_-(k,x),x)=k$
holds.
$r_+(r_-(k,x),x)=k$
holds.
Proof. Let
![]() $B\rightarrowtail Y$
be given, and assume that
$B\rightarrowtail Y$
be given, and assume that
![]() $A\leq _{\mathsf {m}}B$
via
$A\leq _{\mathsf {m}}B$
via
![]() $\varphi ,r_-,r_+$
. If j is a witness for
$\varphi ,r_-,r_+$
. If j is a witness for
![]() $x\in A$
, then
$x\in A$
, then
![]() $r_-(j,x)$
is a witness for
$r_-(j,x)$
is a witness for
![]() $\varphi (x)\in B$
. Hence,
$\varphi (x)\in B$
. Hence,
![]() $r_+(r_-(k,x),x)$
must be a witness for
$r_+(r_-(k,x),x)$
must be a witness for
![]() $x\in A$
. Suppose for the sake of contradiction that we have
$x\in A$
. Suppose for the sake of contradiction that we have
![]() $r_+(r_-(k,x),x)=j\not =k$
for some k.
$r_+(r_-(k,x),x)=j\not =k$
for some k.
By continuity, we have
![]() $r_+(r_-(k,x)\upharpoonright \ell ,x\upharpoonright \ell )=j$
for sufficiently large
$r_+(r_-(k,x)\upharpoonright \ell ,x\upharpoonright \ell )=j$
for sufficiently large
![]() $\ell $
. Similarly, for sufficiently large
$\ell $
. Similarly, for sufficiently large
![]() $\ell '\geq \ell $
, the sequence
$\ell '\geq \ell $
, the sequence
![]() $r_-(k,x\upharpoonright \ell ')$
extends
$r_-(k,x\upharpoonright \ell ')$
extends
![]() $r_-(k,x)\upharpoonright \ell $
. By splittability of
$r_-(k,x)\upharpoonright \ell $
. By splittability of
![]() $x\in A$
, there exists
$x\in A$
, there exists
![]() $x'\in |A|$
extending
$x'\in |A|$
extending
![]() $x\upharpoonright \ell '$
such that j is not a witness for
$x\upharpoonright \ell '$
such that j is not a witness for
![]() $x'\in A$
, but k is a witness for
$x'\in A$
, but k is a witness for
![]() $x'\in A$
. By our choice of
$x'\in A$
. By our choice of
![]() $\ell '$
, we have
$\ell '$
, we have
![]() $r_+(r_-(k,x'),x')=j$
. As k is a witness for
$r_+(r_-(k,x'),x')=j$
. As k is a witness for
![]() $x'\in A$
,
$x'\in A$
,
![]() $r_-(k,x')$
is a witness for
$r_-(k,x')$
is a witness for
![]() $\varphi (x')\in B$
, so
$\varphi (x')\in B$
, so
![]() $r_+(r_-(k,x'),x')=j$
must be a witness for
$r_+(r_-(k,x'),x')=j$
must be a witness for
![]() $x'\in A$
, which leads to a contradiction.
$x'\in A$
, which leads to a contradiction.
Abstractly speaking, this roughly says that, if x is splittable,
![]() $r_-(\cdot ,x)$
and
$r_-(\cdot ,x)$
and
![]() $r_+(\cdot ,x)$
form a section-retraction pair; in particular,
$r_+(\cdot ,x)$
form a section-retraction pair; in particular,
![]() $r_-(\cdot ,x)$
is a split mono. We first separate
$r_-(\cdot ,x)$
is a split mono. We first separate
![]() $\mathsf {BddSeq}$
from
$\mathsf {BddSeq}$
from
![]() $\mathsf {Fin}$
.
$\mathsf {Fin}$
.
Proposition 5.48.
![]() $\mathsf {BddSeq}_\omega $
does not have the unique witness property.
$\mathsf {BddSeq}_\omega $
does not have the unique witness property.
Proof. Suppose that
![]() $\mathsf {BddSeq}_\omega $
has the unique witness property via
$\mathsf {BddSeq}_\omega $
has the unique witness property via
![]() $\mathsf {BddSeq}_\omega \equiv \biguplus _{n\in \omega }A_n$
. We may assume that
$\mathsf {BddSeq}_\omega \equiv \biguplus _{n\in \omega }A_n$
. We may assume that
![]() $A_n$
is a subspace of
$A_n$
is a subspace of
![]() $\omega ^\omega $
. Let
$\omega ^\omega $
. Let
![]() $i,j$
be trackers of
$i,j$
be trackers of
![]() $\mathsf {BddSeq}_\omega \subseteq \biguplus _nA_n$
and
$\mathsf {BddSeq}_\omega \subseteq \biguplus _nA_n$
and
![]() $\biguplus _nA_n\subseteq \mathsf {BddSeq}_\omega $
. For any
$\biguplus _nA_n\subseteq \mathsf {BddSeq}_\omega $
. For any
![]() $x\in |\mathsf {BddSeq}_\omega |$
there exists a unique n such that
$x\in |\mathsf {BddSeq}_\omega |$
there exists a unique n such that
![]() $x\in |A_n|$
. Thus, if
$x\in |A_n|$
. Thus, if
![]() $(m,x)$
is a name of
$(m,x)$
is a name of
![]() $x\in \mathsf {BddSeq}_\omega $
, we must have
$x\in \mathsf {BddSeq}_\omega $
, we must have
![]() $i(m,x)=(n,x)$
. Moreover, as
$i(m,x)=(n,x)$
. Moreover, as
![]() $(n,x)$
is a name of
$(n,x)$
is a name of
![]() $x\in \biguplus _{n\in \omega }A_n$
,
$x\in \biguplus _{n\in \omega }A_n$
,
![]() $j(n,x)$
is a name of
$j(n,x)$
is a name of
![]() $x\in \mathsf {BddSeq}_\omega $
, which is of the form
$x\in \mathsf {BddSeq}_\omega $
, which is of the form
![]() $(b,x)$
.
$(b,x)$
.
Of course,
![]() $(b+1,x)$
is also a name of
$(b+1,x)$
is also a name of
![]() $x\in \mathsf {BddSeq}_\omega $
, and we have
$x\in \mathsf {BddSeq}_\omega $
, and we have
![]() $j\circ i(b+1,x)=j(n,x)=(b,x)$
. By continuity of i and j, the first value b is determined after reading
$j\circ i(b+1,x)=j(n,x)=(b,x)$
. By continuity of i and j, the first value b is determined after reading
![]() $b+1$
and a finite initial segment
$b+1$
and a finite initial segment
![]() $x\upharpoonright t$
of x. However,
$x\upharpoonright t$
of x. However,
![]() $x\upharpoonright t$
has an extension which is bounded by
$x\upharpoonright t$
has an extension which is bounded by
![]() $b+1$
, but not by b. For instance, consider an extension y of x such that
$b+1$
, but not by b. For instance, consider an extension y of x such that
![]() $y(k)=b$
for any
$y(k)=b$
for any
![]() $k\geq t$
. Again,
$k\geq t$
. Again,
![]() $\langle b+1,y\rangle $
is a correct name of
$\langle b+1,y\rangle $
is a correct name of
![]() $y\in \mathsf {BddSeq}_\omega $
, but nevertheless the first value
$y\in \mathsf {BddSeq}_\omega $
, but nevertheless the first value
![]() $j\circ i(b+1,y)$
must be b, which is not an upper bound of y. In particular,
$j\circ i(b+1,y)$
must be b, which is not an upper bound of y. In particular,
![]() $j\circ i(b+1,y)$
cannot be a name of
$j\circ i(b+1,y)$
cannot be a name of
![]() $y\in \mathsf {BddSeq}_\omega $
.
$y\in \mathsf {BddSeq}_\omega $
.
We next separate
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}$
from
$\mathsf {HalfTruth}_{\Sigma ^0_2}$
from
![]() $\mathsf {BddSeq}$
.
$\mathsf {BddSeq}$
.
Proposition 5.49. If a
![]() $\Sigma ^0_2$
subobject
$\Sigma ^0_2$
subobject
![]() $A\rightarrowtail \omega ^\omega $
is amalgamable, then
$A\rightarrowtail \omega ^\omega $
is amalgamable, then
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}\not \leq _{\mathsf {m}}A$
. In particular,
$\mathsf {HalfTruth}_{\Sigma ^0_2}\not \leq _{\mathsf {m}}A$
. In particular,
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}$
is not amalgamable.
$\mathsf {HalfTruth}_{\Sigma ^0_2}$
is not amalgamable.
Proof. Suppose that
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}A$
via
$\mathsf {HalfTruth}_{\Sigma ^0_2}\leq _{\mathsf {m}}A$
via
![]() $\varphi ,r_-,r_+$
. Since
$\varphi ,r_-,r_+$
. Since
![]() $A\rightarrowtail \omega ^\omega $
is amalgamable, there exists a partial morphism F such that if either a or
$A\rightarrowtail \omega ^\omega $
is amalgamable, there exists a partial morphism F such that if either a or
![]() $a'$
is a witness for
$a'$
is a witness for
![]() $\varphi (x)\in A$
, then
$\varphi (x)\in A$
, then
![]() $F(a,a',x)$
is a witness for
$F(a,a',x)$
is a witness for
![]() $\varphi (x)\in A$
. First put
$\varphi (x)\in A$
. First put
![]() $x_n=0^\infty $
for each
$x_n=0^\infty $
for each
![]() $n\in \omega $
. For
$n\in \omega $
. For
![]() $x=(x_n)_{n\in \omega }$
, both
$x=(x_n)_{n\in \omega }$
, both
![]() $\{0,1\}$
and
$\{0,1\}$
and
![]() $\{2,3\}$
are witnesses for
$\{2,3\}$
are witnesses for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
, so both
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
, so both
![]() $a:=r_-(\{0,1\},x)$
and
$a:=r_-(\{0,1\},x)$
and
![]() $a':=r_-(\{2,3\},x)$
are witnesses for
$a':=r_-(\{2,3\},x)$
are witnesses for
![]() $\varphi (x)\in A$
. By amalgamability,
$\varphi (x)\in A$
. By amalgamability,
![]() $F(a,a',x)$
returns a witness b for
$F(a,a',x)$
returns a witness b for
![]() $\varphi (x)\in A$
. Then
$\varphi (x)\in A$
. Then
![]() $r_+(b,x)$
returns a witness
$r_+(b,x)$
returns a witness
![]() $\{j,k\}$
for
$\{j,k\}$
for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
.
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
.
Note that this b is a natural number since A is
![]() $\Sigma ^0_2$
. Hence, the above mentioned computations are determined after reading a finite initial segment of x. By changing only sufficiently large values, modify
$\Sigma ^0_2$
. Hence, the above mentioned computations are determined after reading a finite initial segment of x. By changing only sufficiently large values, modify
![]() $x_j$
and
$x_j$
and
![]() $x_k$
to
$x_k$
to
![]() $x_j'$
and
$x_j'$
and
![]() $x_j'$
so that
$x_j'$
so that
![]() $x^{\prime }_j\not =0^\infty $
and
$x^{\prime }_j\not =0^\infty $
and
![]() $x^{\prime }_k\not =0^\infty $
respectively while keeping
$x^{\prime }_k\not =0^\infty $
respectively while keeping
![]() $x_i'=0^\infty $
for each
$x_i'=0^\infty $
for each
![]() $i\not \in \{j,k\}$
. In particular,
$i\not \in \{j,k\}$
. In particular,
![]() $x_i'=0^\infty $
holds for some
$x_i'=0^\infty $
holds for some
![]() $i<4$
. Hence, either
$i<4$
. Hence, either
![]() $\{0,1\}$
or
$\{0,1\}$
or
![]() $\{2,3\}$
is a witness for
$\{2,3\}$
is a witness for
![]() $x'\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
, so either
$x'\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
, so either
![]() $a=r_-(\{0,1\},x')$
or
$a=r_-(\{0,1\},x')$
or
![]() $a'=r_-(\{2,3\},x')$
is still a witness for
$a'=r_-(\{2,3\},x')$
is still a witness for
![]() $\varphi (x')\in A$
. Since only sufficiently large values of x are modified to
$\varphi (x')\in A$
. Since only sufficiently large values of x are modified to
![]() $x'$
, we maintain
$x'$
, we maintain
![]() $F(a,a',x')=b$
, which must be a witness for
$F(a,a',x')=b$
, which must be a witness for
![]() $\varphi (x')\in A$
by amalgamability. However,
$\varphi (x')\in A$
by amalgamability. However,
![]() $r_+(b,x')=\{j,k\}$
is not a witness for
$r_+(b,x')=\{j,k\}$
is not a witness for
![]() $x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
since our construction makes
$x\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
since our construction makes
![]() $x^{\prime }_j\not =0^\infty $
and
$x^{\prime }_j\not =0^\infty $
and
![]() $x^{\prime }_k\not =0^\infty $
.
$x^{\prime }_k\not =0^\infty $
.
We next show that
![]() $\mathsf {DisConn}$
is not only half
$\mathsf {DisConn}$
is not only half
![]() $\Sigma ^0_2$
-hard, but is strictly stronger than any half
$\Sigma ^0_2$
-hard, but is strictly stronger than any half
![]() $\Sigma ^0_2$
subobject of
$\Sigma ^0_2$
subobject of
![]() $\omega ^\omega $
.
$\omega ^\omega $
.
Proposition 5.50.
![]() $\mathsf {DisConn}_{\mathsf {fun}}\not \leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
.
$\mathsf {DisConn}_{\mathsf {fun}}\not \leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
.
Proof. Assume
![]() $\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
via
$\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
via
![]() $\varphi ,r_-,r_+$
. A witness for
$\varphi ,r_-,r_+$
. A witness for
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}$
is in the form of a pair
$\mathsf {HalfTruth}_{\Sigma ^0_2}$
is in the form of a pair
![]() $(a,b)$
, but since it is symmetric, we may write it as
$(a,b)$
, but since it is symmetric, we may write it as
![]() $\{a,b\}$
; that is, we always have
$\{a,b\}$
; that is, we always have
![]() $r_-(\{u,v\},\alpha ),r_+(\{a,b\},\alpha )\in [\omega ]^2$
.
$r_-(\{u,v\},\alpha ),r_+(\{a,b\},\alpha )\in [\omega ]^2$
.
Begin with the edgeless graph
![]() $\alpha \colon E\to V^2$
with
$\alpha \colon E\to V^2$
with
![]() $V=\mathbb {N}$
and
$V=\mathbb {N}$
and
![]() $E=\emptyset $
. Note that
$E=\emptyset $
. Note that
![]() $\alpha \in \mathsf {Disconn}_{\mathsf {fun}}$
is splittable since even if some finite information
$\alpha \in \mathsf {Disconn}_{\mathsf {fun}}$
is splittable since even if some finite information
![]() $\alpha \upharpoonright \ell $
of
$\alpha \upharpoonright \ell $
of
![]() $\alpha $
is fixed, for each pair
$\alpha $
is fixed, for each pair
![]() $(u,v)$
of V, by putting
$(u,v)$
of V, by putting
![]() $u\overset {e}{\longrightarrow }v$
for
$u\overset {e}{\longrightarrow }v$
for
![]() $e\in E$
larger than
$e\in E$
larger than
![]() $\ell $
, only
$\ell $
, only
![]() $(u,v)$
is made connected and all other pairs are maintained to be disconnected.
$(u,v)$
is made connected and all other pairs are maintained to be disconnected.
Now, for three distinct vertices
![]() $u_0,u_1,u_2\in V$
,
$u_0,u_1,u_2\in V$
,
![]() $\{u_j,u_k\}$
is a witness for disconnectedness for any
$\{u_j,u_k\}$
is a witness for disconnectedness for any
![]() $j\not =k$
. Let us consider
$j\not =k$
. Let us consider
![]() $r_-(\{u_j,u_k\},\alpha )=\{z^0_{jk},z^1_{jk}\}$
, which is a witness for
$r_-(\{u_j,u_k\},\alpha )=\{z^0_{jk},z^1_{jk}\}$
, which is a witness for
![]() $\varphi (\alpha )\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Here,
$\varphi (\alpha )\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. Here,
![]() $\varphi (\alpha )$
is a sequence in
$\varphi (\alpha )$
is a sequence in
![]() $\omega ^\omega $
. By abuse of notation, we write its nth term as
$\omega ^\omega $
. By abuse of notation, we write its nth term as
![]() $\varphi (n,\alpha )$
. Note that if
$\varphi (n,\alpha )$
. Note that if
![]() $j\not =k$
then either
$j\not =k$
then either
![]() $\varphi (z^0_{jk},\alpha )=0^\infty $
or
$\varphi (z^0_{jk},\alpha )=0^\infty $
or
![]() $\varphi (z^1_{jk},\alpha )=0^\infty $
holds.
$\varphi (z^1_{jk},\alpha )=0^\infty $
holds.

Figure 2 (left) A reduction pair for
![]() $\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
if it exists; (right) An example of our action if
$\mathsf {DisConn}_{\mathsf {fun}}\leq _{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
if it exists; (right) An example of our action if
![]() $r_+$
moves a pair
$r_+$
moves a pair
![]() $\{z^\ell _{mn},z^p_{qr}\}$
out of the triangle
$\{z^\ell _{mn},z^p_{qr}\}$
out of the triangle
![]() $\{u_0,u_1,u_2\}$
.
$\{u_0,u_1,u_2\}$
.
We are now in the situation shown in the left half of Figure 2: We have six candidates
![]() $\{z^0_{01},z^{1}_{01},z^0_{02},z^1_{02},z^0_{12},z^1_{12}\}$
for witnesses for
$\{z^0_{01},z^{1}_{01},z^0_{02},z^1_{02},z^0_{12},z^1_{12}\}$
for witnesses for
![]() $\varphi (\alpha )\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. We analyze to which pair of vertices
$\varphi (\alpha )\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. We analyze to which pair of vertices
![]() $r_+$
moves each pair of these six candidates.
$r_+$
moves each pair of these six candidates.
Claim 1. For any
![]() $\ell ,m,n,p,q,r$
, if
$\ell ,m,n,p,q,r$
, if
![]() $\langle \ell ,\{m,n\}\rangle \not =\langle p,\{q,r\}\rangle $
then
$\langle \ell ,\{m,n\}\rangle \not =\langle p,\{q,r\}\rangle $
then
![]() $r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )\subseteq \{u_0,u_1,u_2\}$
.
$r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )\subseteq \{u_0,u_1,u_2\}$
.
Proof. Otherwise,
![]() $\{v,v'\}:=r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )\not \subseteq \{u_0,u_1,u_2\}$
. If
$\{v,v'\}:=r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )\not \subseteq \{u_0,u_1,u_2\}$
. If
![]() $\{m,n\}=\{q,r\}$
then
$\{m,n\}=\{q,r\}$
then
![]() $\ell \not =p$
, so by Split Lemma 5.47, we must have
$\ell \not =p$
, so by Split Lemma 5.47, we must have
![]() $\{v,v'\}=r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )=r_+(\{z^0_{mn},z^1_{mn}\},\alpha )=\{u_m,u_n\}$
, which is impossible by our assumption. Therefore,
$\{v,v'\}=r_+(\{z^\ell _{mn},z^p_{qr}\},\alpha )=r_+(\{z^0_{mn},z^1_{mn}\},\alpha )=\{u_m,u_n\}$
, which is impossible by our assumption. Therefore,
![]() $\{m,n\}\not =\{q,r\}$
.
$\{m,n\}\not =\{q,r\}$
.
Next, we assume that either
![]() $\varphi (z_{mn}^{1-\ell },\alpha )\not =0^\infty $
or
$\varphi (z_{mn}^{1-\ell },\alpha )\not =0^\infty $
or
![]() $\varphi (z_{qr}^{1-p},\alpha )\not =0^\infty $
holds. In the former case, by reading
$\varphi (z_{qr}^{1-p},\alpha )\not =0^\infty $
holds. In the former case, by reading
![]() $\alpha $
up to a sufficiently large t, we recognize
$\alpha $
up to a sufficiently large t, we recognize
![]() $\varphi (z_{mn}^{1-\ell },\alpha \upharpoonright t)\not =0^\infty $
, so connect vertices v and
$\varphi (z_{mn}^{1-\ell },\alpha \upharpoonright t)\not =0^\infty $
, so connect vertices v and
![]() $v'$
by an edge
$v'$
by an edge
![]() $e\in E$
larger than t. Then,
$e\in E$
larger than t. Then,
![]() $\{v,v'\}$
is not a witness for disconnectedness of the new graph
$\{v,v'\}$
is not a witness for disconnectedness of the new graph
![]() $\alpha '$
, but as t is large,
$\alpha '$
, but as t is large,
![]() $r_+(z^\ell _{mn},z^p_{qr},\alpha ')=\{v,v'\}$
is maintained. This forces
$r_+(z^\ell _{mn},z^p_{qr},\alpha ')=\{v,v'\}$
is maintained. This forces
![]() $\{z^\ell _{mn},z^p_{qr}\}$
not to be a witness for
$\{z^\ell _{mn},z^p_{qr}\}$
not to be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
; in particular,
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
; in particular,
![]() $\varphi (z_{mn}^{\ell },\alpha ')\not =0^\infty $
. Therefore, this construction forces
$\varphi (z_{mn}^{\ell },\alpha ')\not =0^\infty $
. Therefore, this construction forces
![]() $\varphi (z_{mn}^i,\alpha ')\not =0^\infty $
for each
$\varphi (z_{mn}^i,\alpha ')\not =0^\infty $
for each
![]() $i<2$
. However,
$i<2$
. However,
![]() $\{u_m,u_n\}$
is maintained to be disconnected, so
$\{u_m,u_n\}$
is maintained to be disconnected, so
![]() $r_-(\{u_m,u_n\},\alpha ')=\{z_{mn}^0,z_{mn}^1\}$
still returns a witness, which means that
$r_-(\{u_m,u_n\},\alpha ')=\{z_{mn}^0,z_{mn}^1\}$
still returns a witness, which means that
![]() $\varphi (z_{mn}^i,\alpha ')=0^\infty $
must be true for some
$\varphi (z_{mn}^i,\alpha ')=0^\infty $
must be true for some
![]() $i<2$
, which is impossible. The same argument applies in the case that
$i<2$
, which is impossible. The same argument applies in the case that
![]() $\varphi (z_{qr}^{1-p},\alpha )\not =0^\infty $
holds. Hence, both
$\varphi (z_{qr}^{1-p},\alpha )\not =0^\infty $
holds. Hence, both
![]() $\varphi (z_{mn}^{1-\ell },\alpha )=0^\infty $
and
$\varphi (z_{mn}^{1-\ell },\alpha )=0^\infty $
and
![]() $\varphi (z_{qr}^{1-p},\alpha )=0^\infty $
are true.
$\varphi (z_{qr}^{1-p},\alpha )=0^\infty $
are true.
By our assumption, the intersection
![]() $\{v,v'\}\cap \{u_0,u_1,u_2\}$
has at most one element, and
$\{v,v'\}\cap \{u_0,u_1,u_2\}$
has at most one element, and
![]() $\{m,n\}\not =\{q,r\}$
, so we have either
$\{m,n\}\not =\{q,r\}$
, so we have either
![]() $\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
or
$\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
or
![]() $\{v,v'\}\cap \{u_q,u_r\}=\emptyset $
. We assume that the former holds. The argument is the same for the latter case.
$\{v,v'\}\cap \{u_q,u_r\}=\emptyset $
. We assume that the former holds. The argument is the same for the latter case.
Then, consider the case that for any
![]() $i,j,k$
if
$i,j,k$
if
![]() $r_+(z^{1-\ell }_{mn},z^i_{jk},\alpha )$
is defined then this value is included in
$r_+(z^{1-\ell }_{mn},z^i_{jk},\alpha )$
is defined then this value is included in
![]() $\{u_m,u_n\}$
. Since both
$\{u_m,u_n\}$
. Since both
![]() $\varphi (z_{mn}^{1-\ell },\alpha )=0^\infty $
and
$\varphi (z_{mn}^{1-\ell },\alpha )=0^\infty $
and
![]() $\varphi (z_{qr}^{1-p},\alpha )=0^\infty $
are true,
$\varphi (z_{qr}^{1-p},\alpha )=0^\infty $
are true,
![]() $r_+(z^{1-\ell }_{mn},z^{1-p}_{qr},\alpha )$
is defined, so this value is included in
$r_+(z^{1-\ell }_{mn},z^{1-p}_{qr},\alpha )$
is defined, so this value is included in
![]() $\{u_m,u_n\}$
by our assumption. Indeed, this value must be
$\{u_m,u_n\}$
by our assumption. Indeed, this value must be
![]() $\{u_m,u_n\}$
since it is a witness for disconnectedness. Consider a graph
$\{u_m,u_n\}$
since it is a witness for disconnectedness. Consider a graph
![]() $\alpha '$
with sufficiently large edges
$\alpha '$
with sufficiently large edges
![]() $v\to v'$
and
$v\to v'$
and
![]() $u_m\to u_n$
so that
$u_m\to u_n$
so that
![]() $r_+(z^{\ell }_{mn},z^p_{qr},\alpha ')=\{v,v'\}$
and
$r_+(z^{\ell }_{mn},z^p_{qr},\alpha ')=\{v,v'\}$
and
![]() $r_+(z^{1-\ell }_{mn},z^{1-p}_{qr},\alpha ')=\{u_m,u_n\}$
are maintained. This makes
$r_+(z^{1-\ell }_{mn},z^{1-p}_{qr},\alpha ')=\{u_m,u_n\}$
are maintained. This makes
![]() $\{v,v'\}$
and
$\{v,v'\}$
and
![]() $\{u_m,u_n\}$
connected, but the assumption
$\{u_m,u_n\}$
connected, but the assumption
![]() $\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
guarantees that no other pair is connected in
$\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
guarantees that no other pair is connected in
![]() $\alpha '$
. See the right half of Figure 2. Now
$\alpha '$
. See the right half of Figure 2. Now
![]() $\{v,v'\}$
and
$\{v,v'\}$
and
![]() $\{u_m,u_n\}$
are not witnesses for disconnectedness of
$\{u_m,u_n\}$
are not witnesses for disconnectedness of
![]() $\alpha '$
, so this forces
$\alpha '$
, so this forces
![]() $\{z^{\ell }_{mn},z^p_{qr}\}$
and
$\{z^{\ell }_{mn},z^p_{qr}\}$
and
![]() $\{z^{1-\ell }_{mn},z^{1-p}_{qr}\}$
not to be witnesses for
$\{z^{1-\ell }_{mn},z^{1-p}_{qr}\}$
not to be witnesses for
![]() $\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
. In particular, we get
$\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
. In particular, we get
![]() $\varphi (z_{qr}^{i},\alpha ')\not =0^\infty $
for each
$\varphi (z_{qr}^{i},\alpha ')\not =0^\infty $
for each
![]() $i<2$
. Since
$i<2$
. Since
![]() $\{m,n\}\not =\{q,r\}$
, the assumption
$\{m,n\}\not =\{q,r\}$
, the assumption
![]() $\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
guarantees that
$\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
guarantees that
![]() $\{u_q,u_r\}$
is maintained to be disconnected in
$\{u_q,u_r\}$
is maintained to be disconnected in
![]() $\alpha '$
as mentioned above, so
$\alpha '$
as mentioned above, so
![]() $r_-(\{u_q,u_r\},\alpha ')=\{z^0_{qr},z^1_{qr}\}$
must be a witness for
$r_-(\{u_q,u_r\},\alpha ')=\{z^0_{qr},z^1_{qr}\}$
must be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
![]() $\varphi (z_{qr}^{i},\alpha ')=0^\infty $
for some
$\varphi (z_{qr}^{i},\alpha ')=0^\infty $
for some
![]() $i<2$
, which is impossible.
$i<2$
, which is impossible.
Hence, there exists
![]() $i,j,k$
such that
$i,j,k$
such that
![]() $r_+(z^{1-\ell }_{mn},z^i_{jk},\alpha )$
is defined, but the value
$r_+(z^{1-\ell }_{mn},z^i_{jk},\alpha )$
is defined, but the value
![]() $\{w,w'\}$
is not included in
$\{w,w'\}$
is not included in
![]() $\{u_m,u_n\}$
. Then consider a graph
$\{u_m,u_n\}$
. Then consider a graph
![]() $\alpha '$
with sufficiently large edges
$\alpha '$
with sufficiently large edges
![]() $v\to v'$
and
$v\to v'$
and
![]() $w\to w'$
so that necessary computations are maintained. Now
$w\to w'$
so that necessary computations are maintained. Now
![]() $\{v,v'\}$
and
$\{v,v'\}$
and
![]() $\{w,w'\}$
are not witnesses for disconnectedness of
$\{w,w'\}$
are not witnesses for disconnectedness of
![]() $\alpha '$
, so this forces
$\alpha '$
, so this forces
![]() $\{z^{\ell }_{mn},z^p_{qr}\}$
and
$\{z^{\ell }_{mn},z^p_{qr}\}$
and
![]() $\{z^{1-\ell }_{mn},z^i_{jk}\}$
not to be witnesses for
$\{z^{1-\ell }_{mn},z^i_{jk}\}$
not to be witnesses for
![]() $\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
as before. In particular, we get
$\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
as before. In particular, we get
![]() $\varphi (z_{mn}^{i},\alpha ')\not =0^\infty $
for each
$\varphi (z_{mn}^{i},\alpha ')\not =0^\infty $
for each
![]() $i<2$
. Since
$i<2$
. Since
![]() $\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
and
$\{v,v'\}\cap \{u_m,u_n\}=\emptyset $
and
![]() $\{w,w'\}\not \subseteq \{u_m,u_n\}$
, the intersection
$\{w,w'\}\not \subseteq \{u_m,u_n\}$
, the intersection
![]() $\{v,v',w,w'\}\cap \{u_m,u_n\}$
has at most one element, so
$\{v,v',w,w'\}\cap \{u_m,u_n\}$
has at most one element, so
![]() $\{u_m,u_n\}$
is maintained to be disconnected in
$\{u_m,u_n\}$
is maintained to be disconnected in
![]() $\alpha '$
. Thus,
$\alpha '$
. Thus,
![]() $r_-(\{u_m,u_n\},\alpha ')=\{z_{mn}^0,z_{mn}^1\}$
must be a witness for
$r_-(\{u_m,u_n\},\alpha ')=\{z_{mn}^0,z_{mn}^1\}$
must be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
![]() $\varphi (z_{mn}^{i},\alpha ')=0^\infty $
for some
$\varphi (z_{mn}^{i},\alpha ')=0^\infty $
for some
![]() $i<2$
, which is impossible.
$i<2$
, which is impossible.
Claim 2.
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
for some
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
for some
![]() $j,k<2$
.
$j,k<2$
.
Proof. Suppose not. First consider the case that for each j if
![]() $\varphi (z^j_{01},\alpha )=0^\infty $
then there exists k such that
$\varphi (z^j_{01},\alpha )=0^\infty $
then there exists k such that
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_1,u_2\}$
. In this case, consider a graph
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_1,u_2\}$
. In this case, consider a graph
![]() $\alpha '$
with a sufficiently large edge
$\alpha '$
with a sufficiently large edge
![]() $u_1\overset {e}{\longrightarrow } u_2$
so that necessary computations are maintained. Then
$u_1\overset {e}{\longrightarrow } u_2$
so that necessary computations are maintained. Then
![]() $\{u_1,u_2\}$
is not a witness for disconnectedness of
$\{u_1,u_2\}$
is not a witness for disconnectedness of
![]() $\alpha '$
, so if
$\alpha '$
, so if
![]() $\varphi (z^j_{01},\alpha )=0^\infty $
, by our assumption, this forces
$\varphi (z^j_{01},\alpha )=0^\infty $
, by our assumption, this forces
![]() $\{z^j_{01},z^k_{02}\}$
not to be a witness for
$\{z^j_{01},z^k_{02}\}$
not to be a witness for
![]() $\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
as before. In particular, we get
$\varphi (\alpha ')\in \mathsf { HalfTruth}_{\Sigma ^0_2}$
as before. In particular, we get
![]() $\varphi (z_{01}^{j},\alpha ')\not =0^\infty $
and
$\varphi (z_{01}^{j},\alpha ')\not =0^\infty $
and
![]() $\varphi (z_{02}^{k},\alpha ')\not =0^\infty $
. If
$\varphi (z_{02}^{k},\alpha ')\not =0^\infty $
. If
![]() $\varphi (z^{j}_{01},\alpha )\not =\infty $
, then this still holds for
$\varphi (z^{j}_{01},\alpha )\not =\infty $
, then this still holds for
![]() $\alpha '$
since e above is sufficiently large. Therefore, in any case, we obtain
$\alpha '$
since e above is sufficiently large. Therefore, in any case, we obtain
![]() $\varphi (z^{j}_{01},\alpha ')\not =0^\infty $
for each
$\varphi (z^{j}_{01},\alpha ')\not =0^\infty $
for each
![]() $j<2$
. However,
$j<2$
. However,
![]() $\{u_0,u_1\}$
is still a witness for disconnectedness of
$\{u_0,u_1\}$
is still a witness for disconnectedness of
![]() $\alpha '$
, so
$\alpha '$
, so
![]() $r_-(\{u_0,u_1\},\alpha ')=\{z^0_{01},z^1_{01}\}$
must be a witness for
$r_-(\{u_0,u_1\},\alpha ')=\{z^0_{01},z^1_{01}\}$
must be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
![]() $\varphi (z^i_{01},\alpha ')=0^\infty $
for some
$\varphi (z^i_{01},\alpha ')=0^\infty $
for some
![]() $i<2$
, which is impossible.
$i<2$
, which is impossible.
Hence, there exists j such that
![]() $\varphi (z^j_{01},\alpha )=0^\infty $
and
$\varphi (z^j_{01},\alpha )=0^\infty $
and
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\not \subseteq \{u_1,u_2\}$
for any k. Note that
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\not \subseteq \{u_1,u_2\}$
for any k. Note that
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )$
is defined for each
$r_+(\{z^j_{01},z^k_{02}\},\alpha )$
is defined for each
![]() $k<2$
since
$k<2$
since
![]() $\varphi (z^j_{01},\alpha )=0^\infty $
. By our assumption, we also have
$\varphi (z^j_{01},\alpha )=0^\infty $
. By our assumption, we also have
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\not \subseteq \{u_0,u_2\}$
; hence by Claim 1, this value must be
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\not \subseteq \{u_0,u_2\}$
; hence by Claim 1, this value must be
![]() $\{u_0,u_1\}$
. In this case, consider a graph
$\{u_0,u_1\}$
. In this case, consider a graph
![]() $\alpha '$
with a sufficiently large edge
$\alpha '$
with a sufficiently large edge
![]() $u_0\to u_1$
so that necessary computations are maintained. Then
$u_0\to u_1$
so that necessary computations are maintained. Then
![]() $\{u_0,u_1\}$
is not a witness for disconnectedness of
$\{u_0,u_1\}$
is not a witness for disconnectedness of
![]() $\alpha '$
, which forces
$\alpha '$
, which forces
![]() $\{z^j_{01},z^k_{02}\}$
not to be a witness for
$\{z^j_{01},z^k_{02}\}$
not to be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
for each
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
for each
![]() $k<2$
. In particular, we get
$k<2$
. In particular, we get
![]() $\varphi (z_{02}^{k},\alpha ')\not =0^\infty $
for each
$\varphi (z_{02}^{k},\alpha ')\not =0^\infty $
for each
![]() $k<2$
. However,
$k<2$
. However,
![]() $\{u_0,u_2\}$
is still a witness for disconnectedness of
$\{u_0,u_2\}$
is still a witness for disconnectedness of
![]() $\alpha '$
, so
$\alpha '$
, so
![]() $r_-(\{u_0,u_2\},\alpha ')=\{z^0_{02},z^1_{02}\}$
must be a witness for
$r_-(\{u_0,u_2\},\alpha ')=\{z^0_{02},z^1_{02}\}$
must be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
![]() $\varphi (z^k_{02},\alpha ')=0^\infty $
for some
$\varphi (z^k_{02},\alpha ')=0^\infty $
for some
![]() $k<2$
, which is impossible.
$k<2$
, which is impossible.
Fix
![]() $j,k<2$
satisfying the condition in Claim 2. Now, choose a new vertex
$j,k<2$
satisfying the condition in Claim 2. Now, choose a new vertex
![]() $u_3\in V$
, and focus on
$u_3\in V$
, and focus on
![]() $\{u_0,u_1,u_3\}$
. As in Claim 2, one can see
$\{u_0,u_1,u_3\}$
. As in Claim 2, one can see
![]() $r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
for some
$r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
for some
![]() $\ell ,m$
. We first assume
$\ell ,m$
. We first assume
![]() $j\not =\ell $
. Then, consider a graph
$j\not =\ell $
. Then, consider a graph
![]() $\alpha '$
with sufficiently large edges
$\alpha '$
with sufficiently large edges
![]() $u_0\to u_2$
and
$u_0\to u_2$
and
![]() $u_1\to u_3$
so that necessary computations are maintained. See the leftmost part of Figure 3. Since
$u_1\to u_3$
so that necessary computations are maintained. See the leftmost part of Figure 3. Since
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
and
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
and
![]() $r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
, this forces
$r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
, this forces
![]() $\varphi (z,\alpha ')\not =0^\infty $
for each
$\varphi (z,\alpha ')\not =0^\infty $
for each
![]() $z\in \{z^j_{01},z^k_{02},z^\ell _{01},z^m_{13}\}$
. In particular,
$z\in \{z^j_{01},z^k_{02},z^\ell _{01},z^m_{13}\}$
. In particular,
![]() $\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
$\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
![]() $i<2$
since
$i<2$
since
![]() $j\not =\ell $
. Since we have taken different vertices,
$j\not =\ell $
. Since we have taken different vertices,
![]() $\{u_0,u_2\}\cap \{u_1,u_3\}=\emptyset $
. Hence,
$\{u_0,u_2\}\cap \{u_1,u_3\}=\emptyset $
. Hence,
![]() $\{u_0,u_1\}$
is still a witness for disconnectedness of
$\{u_0,u_1\}$
is still a witness for disconnectedness of
![]() $\alpha '$
, so
$\alpha '$
, so
![]() $r_-(\{u_0,u_1\},\alpha ')=\{z^0_{01},z^1_{01}\}$
must be a witness for
$r_-(\{u_0,u_1\},\alpha ')=\{z^0_{01},z^1_{01}\}$
must be a witness for
![]() $\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
$\varphi (\alpha ')\in \mathsf {HalfTruth}_{\Sigma ^0_2}$
. This means
![]() $\varphi (z^i_{01},\alpha ')=0^\infty $
for some
$\varphi (z^i_{01},\alpha ')=0^\infty $
for some
![]() $i<2$
, which is impossible.
$i<2$
, which is impossible.

Figure 3 Some examples of our actions.
Thus, we now assume
![]() $j=\ell $
. If
$j=\ell $
. If
![]() $\varphi (z^{1-j}_{01},\alpha )\not =0^\infty $
, then consider a graph
$\varphi (z^{1-j}_{01},\alpha )\not =0^\infty $
, then consider a graph
![]() $\alpha '$
with a sufficiently large edge
$\alpha '$
with a sufficiently large edge
![]() $u_0\to u_2$
so that necessary computations are maintained. Since
$u_0\to u_2$
so that necessary computations are maintained. Since
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
, which is maintained in
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
, which is maintained in
![]() $\alpha '$
, this forces
$\alpha '$
, this forces
![]() $\varphi (z^{i}_{01},\alpha ')\not =0^\infty $
for each
$\varphi (z^{i}_{01},\alpha ')\not =0^\infty $
for each
![]() $i<2$
. However,
$i<2$
. However,
![]() $\{u_0,u_1\}$
is still disconnected in
$\{u_0,u_1\}$
is still disconnected in
![]() $\alpha '$
, so we get
$\alpha '$
, so we get
![]() $\varphi (z^i_{01},\alpha ')=0^\infty $
for some
$\varphi (z^i_{01},\alpha ')=0^\infty $
for some
![]() $i<2$
as before, which is impossible. Hence, we get
$i<2$
as before, which is impossible. Hence, we get
![]() $\varphi (z^{1-j}_{01},\alpha )=0^\infty $
. Thus,
$\varphi (z^{1-j}_{01},\alpha )=0^\infty $
. Thus,
![]() $r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )$
is defined for each
$r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )$
is defined for each
![]() $p<2$
.
$p<2$
.
If
![]() $r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )\subseteq \{u_0,u_1\}$
for each
$r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )\subseteq \{u_0,u_1\}$
for each
![]() $p<2$
, then consider a graph
$p<2$
, then consider a graph
![]() $\alpha '$
with a sufficiently large edge
$\alpha '$
with a sufficiently large edge
![]() $u_0\to u_1$
so that necessary computations are maintained. In particular, this forces
$u_0\to u_1$
so that necessary computations are maintained. In particular, this forces
![]() $\varphi (z^{p}_{02},\alpha ')\not =0^\infty $
for each
$\varphi (z^{p}_{02},\alpha ')\not =0^\infty $
for each
![]() $p<2$
; however,
$p<2$
; however,
![]() $\{u_{0},u_2\}$
is still disconnected in
$\{u_{0},u_2\}$
is still disconnected in
![]() $\alpha $
, this is impossible as before. Therefore, we obtain
$\alpha $
, this is impossible as before. Therefore, we obtain
![]() $r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )\not \subseteq \{u_0,u_1\}$
for some
$r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )\not \subseteq \{u_0,u_1\}$
for some
![]() $p<2$
.
$p<2$
.
Assume
![]() $r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )=\{v,v'\}$
. If
$r_+(\{z_{01}^{1-j},z_{02}^p\},\alpha )=\{v,v'\}$
. If
![]() $\{v,v'\}=\{u_1,u_2\}$
, then consider a graph
$\{v,v'\}=\{u_1,u_2\}$
, then consider a graph
![]() $\alpha '$
with sufficiently large edges
$\alpha '$
with sufficiently large edges
![]() $u_1\to u_2$
and
$u_1\to u_2$
and
![]() $u_1\to u_3$
so that necessary computations are maintained. See the middle part of Figure 3. Since
$u_1\to u_3$
so that necessary computations are maintained. See the middle part of Figure 3. Since
![]() $r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
, this forces
$r_+(\{z^\ell _{01},z^m_{13}\},\alpha )\subseteq \{u_1,u_3\}$
, this forces
![]() $\varphi (z,\alpha ')\not =0^\infty $
for each
$\varphi (z,\alpha ')\not =0^\infty $
for each
![]() $z\in \{z^{1-j}_{01},z^p_{02},z^\ell _{01},z^m_{13}\}$
. In particular,
$z\in \{z^{1-j}_{01},z^p_{02},z^\ell _{01},z^m_{13}\}$
. In particular,
![]() $\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
$\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
![]() $i<2$
since
$i<2$
since
![]() $j=\ell $
. However,
$j=\ell $
. However,
![]() $\{u_0,u_1\}$
is still disconnected in
$\{u_0,u_1\}$
is still disconnected in
![]() $\alpha '$
, which is impossible as in the previous argument.
$\alpha '$
, which is impossible as in the previous argument.
If
![]() $\{v,v'\}\not =\{u_1,u_2\}$
, then consider a graph
$\{v,v'\}\not =\{u_1,u_2\}$
, then consider a graph
![]() $\alpha '$
with sufficiently large edges
$\alpha '$
with sufficiently large edges
![]() $v\to v'$
and
$v\to v'$
and
![]() $u_0\to u_2$
so that necessary computations are maintained. See the rightmost part of Figure 3. Since
$u_0\to u_2$
so that necessary computations are maintained. See the rightmost part of Figure 3. Since
![]() $r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
, this forces
$r_+(\{z^j_{01},z^k_{02}\},\alpha )\subseteq \{u_0,u_2\}$
, this forces
![]() $\varphi (z,\alpha ')\not =0^\infty $
for each
$\varphi (z,\alpha ')\not =0^\infty $
for each
![]() $z\in \{z^{1-j}_{01},z^p_{02},z^j_{01},z^k_{02}\}$
. In particular,
$z\in \{z^{1-j}_{01},z^p_{02},z^j_{01},z^k_{02}\}$
. In particular,
![]() $\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
$\varphi (z^i_{01},\alpha ')\not =0^\infty $
for each
![]() $i<2$
. Now note that
$i<2$
. Now note that
![]() $\{u_0,u_1\}$
is still disconnected in
$\{u_0,u_1\}$
is still disconnected in
![]() $\alpha '$
since
$\alpha '$
since
![]() $\{v,v'\}\not =\{u_1,u_2\}$
. Thus, this leads to a contradiction as before.
$\{v,v'\}\not =\{u_1,u_2\}$
. Thus, this leads to a contradiction as before.
Finally, we show that
![]() $\mathsf {DisConn}$
is not
$\mathsf {DisConn}$
is not
![]() $\Sigma ^0_2$
-complete. In fact,
$\Sigma ^0_2$
-complete. In fact,
![]() $\mathsf {DisConn}$
cannot even reduce
$\mathsf {DisConn}$
cannot even reduce
![]() $\mathsf {L}$
, even though it is not amalgamable. Here, recall that
$\mathsf {L}$
, even though it is not amalgamable. Here, recall that
![]() $\mathsf {L}$
is a
$\mathsf {L}$
is a
![]() $\Sigma _{\pi \cup \pi }$
subobject of
$\Sigma _{\pi \cup \pi }$
subobject of
![]() $\omega ^\omega $
introduced in Example 5.2.
$\omega ^\omega $
introduced in Example 5.2.
Proposition 5.51.
![]() $\mathsf {L}\not \leq _{\mathsf {m}}\mathsf {DisConn}$
.
$\mathsf {L}\not \leq _{\mathsf {m}}\mathsf {DisConn}$
.
Proof. Otherwise,
![]() $\mathsf {L}\leq _{\mathsf {m}}\mathsf {DisConn}$
via some
$\mathsf {L}\leq _{\mathsf {m}}\mathsf {DisConn}$
via some
![]() $\varphi ,r_-,r_+$
. Begin with
$\varphi ,r_-,r_+$
. Begin with
![]() $x_0=x_1=0^\infty $
. Clearly,
$x_0=x_1=0^\infty $
. Clearly,
![]() $x:=(x_0,x_1)\in \mathsf {L}$
is splittable. Then
$x:=(x_0,x_1)\in \mathsf {L}$
is splittable. Then
![]() $r_-(i,x)=\{u^i_0,u^i_1\}$
is a witness for disconnectedness of the graph
$r_-(i,x)=\{u^i_0,u^i_1\}$
is a witness for disconnectedness of the graph
![]() $G_x:=\varphi (x)$
. By Split Lemma 5.47, we get
$G_x:=\varphi (x)$
. By Split Lemma 5.47, we get
![]() $r_+(\{u^i_0,u^i_1\},x)=i$
. Now, consider
$r_+(\{u^i_0,u^i_1\},x)=i$
. Now, consider
![]() $r_+(\{u^i_k,u^j_\ell \},x)=a^{ij}_{k\ell }$
for each
$r_+(\{u^i_k,u^j_\ell \},x)=a^{ij}_{k\ell }$
for each
![]() $i,j,k,\ell $
. Let t be a sufficiently large value such that
$i,j,k,\ell $
. Let t be a sufficiently large value such that
![]() $r_-(i,x\upharpoonright t)=\{u^i_0,u^i_1\}$
and
$r_-(i,x\upharpoonright t)=\{u^i_0,u^i_1\}$
and
![]() $r_+(\{u^i_k,u^j_\ell \},x\upharpoonright t)=a^{ij}_{k\ell }$
are determined. Similarly, if
$r_+(\{u^i_k,u^j_\ell \},x\upharpoonright t)=a^{ij}_{k\ell }$
are determined. Similarly, if
![]() $\{u^i_k,u^j_\ell \}$
is connected in
$\{u^i_k,u^j_\ell \}$
is connected in
![]() $G_x$
, restrain
$G_x$
, restrain
![]() $x\upharpoonright t$
so that
$x\upharpoonright t$
so that
![]() $\varphi (x\upharpoonright t)$
contains a path connecting these vertices.
$\varphi (x\upharpoonright t)$
contains a path connecting these vertices.
Assume that
![]() $\{a_{00}^{01},a_{11}^{01}\}$
is at most singleton; that is, there exists
$\{a_{00}^{01},a_{11}^{01}\}$
is at most singleton; that is, there exists
![]() $i<2$
such that if
$i<2$
such that if
![]() $a_{kk}^{01}$
is defined then
$a_{kk}^{01}$
is defined then
![]() $a_{kk}^{01}=i$
for any
$a_{kk}^{01}=i$
for any
![]() $k<2$
. Then set
$k<2$
. Then set
![]() $x_{i}'\not =0^\infty $
by changing some value of
$x_{i}'\not =0^\infty $
by changing some value of
![]() $x_{i}$
greater than t. Since
$x_{i}$
greater than t. Since
![]() $r_+(\{u^{i}_0,u^{i}_1\},x')=i$
, this forces
$r_+(\{u^{i}_0,u^{i}_1\},x')=i$
, this forces
![]() $\{u^{i}_0,u^{i}_1\}$
to be connected in
$\{u^{i}_0,u^{i}_1\}$
to be connected in
![]() $G_{x'}$
. Given
$G_{x'}$
. Given
![]() $k<2$
, if
$k<2$
, if
![]() $a_{kk}^{01}$
is defined, then
$a_{kk}^{01}$
is defined, then
![]() $r_+(\{u^0_k,u^1_k\},x')=a_{kk}^{01}=i$
, so
$r_+(\{u^0_k,u^1_k\},x')=a_{kk}^{01}=i$
, so
![]() $\{u_{k}^0,u_{k}^1\}$
must also be connected in
$\{u_{k}^0,u_{k}^1\}$
must also be connected in
![]() $G_{x'}$
. If
$G_{x'}$
. If
![]() $a_{kk}^{01}$
is undefined, this means that
$a_{kk}^{01}$
is undefined, this means that
![]() $r_+(\{u^0_k,u^1_k\},x)$
is undefined, so
$r_+(\{u^0_k,u^1_k\},x)$
is undefined, so
![]() $\{u_{k}^0,u_{k}^1\}$
must be connected in
$\{u_{k}^0,u_{k}^1\}$
must be connected in
![]() $G_x$
. By our choice of t,
$G_x$
. By our choice of t,
![]() $\{u_{k}^0,u_{k}^1\}$
is still connected in
$\{u_{k}^0,u_{k}^1\}$
is still connected in
![]() $G_{x'}$
. As k is arbitrary, now note that each of
$G_{x'}$
. As k is arbitrary, now note that each of
![]() $\{u_\ell ^{1-i},u_\ell ^{i}\}$
,
$\{u_\ell ^{1-i},u_\ell ^{i}\}$
,
![]() $\{u^i_\ell ,u^i_{1-\ell }\}$
and
$\{u^i_\ell ,u^i_{1-\ell }\}$
and
![]() $\{u^i_{1-\ell },u^{1-i}_{1-\ell }\}$
is connected in
$\{u^i_{1-\ell },u^{1-i}_{1-\ell }\}$
is connected in
![]() $G_{x'}$
; see Figure 4 for
$G_{x'}$
; see Figure 4 for
![]() $i=1$
. By connecting all of these paths, we conclude that
$i=1$
. By connecting all of these paths, we conclude that
![]() $\{u_\ell ^{1-i},u^{1-i}_{1-\ell }\}$
is connected in
$\{u_\ell ^{1-i},u^{1-i}_{1-\ell }\}$
is connected in
![]() $G_{x'}$
. However, since
$G_{x'}$
. However, since
![]() $x_{1-i}'=0^\infty $
,
$x_{1-i}'=0^\infty $
,
![]() $r_-(1-i,x')=\{u^{1-i}_0,u^{1-i}_1\}$
must be a witness for disconnectedness of
$r_-(1-i,x')=\{u^{1-i}_0,u^{1-i}_1\}$
must be a witness for disconnectedness of
![]() $G_{x'}$
, which is impossible. Hence, we must have
$G_{x'}$
, which is impossible. Hence, we must have
![]() $a_{00}^{01}\not =a_{11}^{01}$
, both of which are defined. By the same argument, one can see
$a_{00}^{01}\not =a_{11}^{01}$
, both of which are defined. By the same argument, one can see
![]() $a_{01}^{01}\not =a_{10}^{01}$
, both of which are defined; see also the left side of Figure 5, where different values are represented by different types of lines.
$a_{01}^{01}\not =a_{10}^{01}$
, both of which are defined; see also the left side of Figure 5, where different values are represented by different types of lines.

Figure 4 If
![]() $\{a^{01}_{00},a^{01}_{11}\}\subseteq \{1\}$
, our action forces
$\{a^{01}_{00},a^{01}_{11}\}\subseteq \{1\}$
, our action forces
![]() $\{u^0_0,u^1_0\}$
,
$\{u^0_0,u^1_0\}$
,
![]() $\{u^1_0,u^1_1\}$
and
$\{u^1_0,u^1_1\}$
and
![]() $\{u^1_1,u^0_1\}$
to be connected.
$\{u^1_1,u^0_1\}$
to be connected.

Figure 5 If
![]() $a^{01}_{00}=a^{01}_{01}=0$
, our action forces
$a^{01}_{00}=a^{01}_{01}=0$
, our action forces
![]() $\{u^0_0,u^1_0\}$
,
$\{u^0_0,u^1_0\}$
,
![]() $\{u^0_0,u^1_1\}$
and
$\{u^0_0,u^1_1\}$
and
![]() $\{u^1_1,u^0_1\}$
to be connected.
$\{u^1_1,u^0_1\}$
to be connected.
Now assume
![]() $a^{01}_{k0}=a^{01}_{k1}$
for some
$a^{01}_{k0}=a^{01}_{k1}$
for some
![]() $k<2$
. Let i be this value. Then we get
$k<2$
. Let i be this value. Then we get
![]() $a^{01}_{1-k,1}\not =a^{01}_{k0}=a^{01}_{k1}\not =a^{01}_{1-k,0}$
, so
$a^{01}_{1-k,1}\not =a^{01}_{k0}=a^{01}_{k1}\not =a^{01}_{1-k,0}$
, so
![]() $a^{01}_{1-k,0}=a^{01}_{1-k,1}=1-i$
holds. Hence, we get
$a^{01}_{1-k,0}=a^{01}_{1-k,1}=1-i$
holds. Hence, we get
![]() $a^{01}_{k0}=a^{01}_{k1}=0$
for some k. Then set
$a^{01}_{k0}=a^{01}_{k1}=0$
for some k. Then set
![]() $x_{0}'\not =0^\infty $
by changing some value of
$x_{0}'\not =0^\infty $
by changing some value of
![]() $x_{0}$
greater than t. Since
$x_{0}$
greater than t. Since
![]() $r_+(\{u^0_k,u^1_\ell \},x')=a_{k\ell }^{01}=0$
, this forces
$r_+(\{u^0_k,u^1_\ell \},x')=a_{k\ell }^{01}=0$
, this forces
![]() $\{u^0_k,u^1_0\}$
and
$\{u^0_k,u^1_0\}$
and
![]() $\{u^0_k,u^1_1\}$
to be connected in
$\{u^0_k,u^1_1\}$
to be connected in
![]() $G_{x'}$
. Similarly, since
$G_{x'}$
. Similarly, since
![]() $r_+(\{u^{0}_0,u^{0}_1\},x')=0$
, this also forces
$r_+(\{u^{0}_0,u^{0}_1\},x')=0$
, this also forces
![]() $\{u^{0}_0,u^{0}_1\}$
to be connected in
$\{u^{0}_0,u^{0}_1\}$
to be connected in
![]() $G_{x'}$
. This implies that
$G_{x'}$
. This implies that
![]() $\{u^1_0,u^1_1\}$
is also connected in
$\{u^1_0,u^1_1\}$
is also connected in
![]() $G_{x'}$
; see Figure 5 for
$G_{x'}$
; see Figure 5 for
![]() $k=0$
. However, since
$k=0$
. However, since
![]() $x_{1}'=0^\infty $
,
$x_{1}'=0^\infty $
,
![]() $r_-(1,x')=\{u^{1}_0,u^{1}_1\}$
must be a witness for disconnectedness of
$r_-(1,x')=\{u^{1}_0,u^{1}_1\}$
must be a witness for disconnectedness of
![]() $G_{x'}$
, which is impossible.
$G_{x'}$
, which is impossible.
Thus,
![]() $a^{01}_{k0}\not =a^{01}_{k1}$
for any
$a^{01}_{k0}\not =a^{01}_{k1}$
for any
![]() $k<2$
. Then we have
$k<2$
. Then we have
![]() $a^{01}_{0\ell }\not =a^{01}_{0,1-\ell }\not =a^{01}_{1\ell }$
, which implies
$a^{01}_{0\ell }\not =a^{01}_{0,1-\ell }\not =a^{01}_{1\ell }$
, which implies
![]() $a^{01}_{0\ell }=a^{01}_{1\ell }$
. As in the above argument, we get
$a^{01}_{0\ell }=a^{01}_{1\ell }$
. As in the above argument, we get
![]() $a^{01}_{0\ell }=a^{01}_{1\ell }=1$
for some
$a^{01}_{0\ell }=a^{01}_{1\ell }=1$
for some
![]() $\ell $
. Then set
$\ell $
. Then set
![]() $x_{1}'\not =0^\infty $
by changing some value of
$x_{1}'\not =0^\infty $
by changing some value of
![]() $x_{1}$
greater than t. Since
$x_{1}$
greater than t. Since
![]() $r_+(\{u^0_k,u^1_\ell \},x')=a_{k\ell }^{01}=1$
, this forces
$r_+(\{u^0_k,u^1_\ell \},x')=a_{k\ell }^{01}=1$
, this forces
![]() $\{u^0_0,u^1_\ell \}$
and
$\{u^0_0,u^1_\ell \}$
and
![]() $\{u^0_1,u^1_\ell \}$
to be connected in
$\{u^0_1,u^1_\ell \}$
to be connected in
![]() $G_{x'}$
. Similarly, since
$G_{x'}$
. Similarly, since
![]() $r_+(\{u^{1}_0,u^{1}_1\},x')=1$
, this also forces
$r_+(\{u^{1}_0,u^{1}_1\},x')=1$
, this also forces
![]() $\{u^{1}_0,u^{1}_1\}$
to be connected in
$\{u^{1}_0,u^{1}_1\}$
to be connected in
![]() $G_{x'}$
. This implies that
$G_{x'}$
. This implies that
![]() $\{u^0_0,u^0_1\}$
is also connected in
$\{u^0_0,u^0_1\}$
is also connected in
![]() $G_{x'}$
. However, since
$G_{x'}$
. However, since
![]() $x_{0}'=0^\infty $
,
$x_{0}'=0^\infty $
,
![]() $r_-(0,x')=\{u^{0}_0,u^{0}_1\}$
must be a witness for disconnectedness of
$r_-(0,x')=\{u^{0}_0,u^{0}_1\}$
must be a witness for disconnectedness of
![]() $G_{x'}$
, which is impossible.
$G_{x'}$
, which is impossible.
Proof of Theorem 5.46
By Theorem 5.41 and Proposition 5.48,
![]() $\mathsf {Fin}$
has the unique witness property, but
$\mathsf {Fin}$
has the unique witness property, but
![]() $\mathsf {BddSeq}_\omega $
does not. By Observation 5.15, if
$\mathsf {BddSeq}_\omega $
does not. By Observation 5.15, if
![]() $\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {Fin}$
, then
$\mathsf {BddSeq}_\omega \leq _{\mathsf {m}}\mathsf {Fin}$
, then
![]() $\mathsf {BddSeq}_\omega $
must have the unique witness property, which is false; hence
$\mathsf {BddSeq}_\omega $
must have the unique witness property, which is false; hence
![]() $\mathsf { BddSeq}_\omega \not \leq _{\mathsf {m}}\mathsf {Fin}$
. By Proposition 5.16,
$\mathsf { BddSeq}_\omega \not \leq _{\mathsf {m}}\mathsf {Fin}$
. By Proposition 5.16,
![]() $\mathsf {Fin}$
has the increasing witness property; hence Theorem 5.42 implies
$\mathsf {Fin}$
has the increasing witness property; hence Theorem 5.42 implies
![]() $\mathsf {Fin}<_{\mathsf {m}}\mathsf {BddSeq}_\omega $
. Again by Proposition 5.48,
$\mathsf {Fin}<_{\mathsf {m}}\mathsf {BddSeq}_\omega $
. Again by Proposition 5.48,
![]() $\mathsf {BddSeq}_\omega $
is amalgamable, so by Propositions 5.44 and 5.49, we get
$\mathsf {BddSeq}_\omega $
is amalgamable, so by Propositions 5.44 and 5.49, we get
![]() $\mathsf { BddSeq}_\omega <_{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
. By Propositions 5.45 and 5.45, we obtain
$\mathsf { BddSeq}_\omega <_{\mathsf {m}}\mathsf {HalfTruth}_{\Sigma ^0_2}$
. By Propositions 5.45 and 5.45, we obtain
![]() $\mathsf {HalfTruth}_{\Sigma ^0_2}<_{\mathsf {m}}\mathsf {DisConn}$
. Finally, by Proposition 5.51,
$\mathsf {HalfTruth}_{\Sigma ^0_2}<_{\mathsf {m}}\mathsf {DisConn}$
. Finally, by Proposition 5.51,
![]() $\mathsf {DisConn}$
is not
$\mathsf {DisConn}$
is not
![]() $\Sigma ^0_2$
-complete; hence
$\Sigma ^0_2$
-complete; hence
![]() $\mathsf {DisConn}<_{\mathsf {m}}\mathsf {Truth}_{\Sigma ^0_2}$
.
$\mathsf {DisConn}<_{\mathsf {m}}\mathsf {Truth}_{\Sigma ^0_2}$
.
Finally, let us recall that we are free to choose
![]() $\mathsf {K_1}$
,
$\mathsf {K_1}$
,
![]() $\mathsf {K}_2$
, or
$\mathsf {K}_2$
, or
![]() $\mathsf {KV}$
as our coding system. This means that the results we have presented in this section are for the witnessed version of any of “many-one reducibility for index sets within
$\mathsf {KV}$
as our coding system. This means that the results we have presented in this section are for the witnessed version of any of “many-one reducibility for index sets within
![]() $\mathrm {Tot}$
,” “Wadge reducibility,” and “effective Wadge reducibility.”
$\mathrm {Tot}$
,” “Wadge reducibility,” and “effective Wadge reducibility.”
In conclusion, the notion of many-one reducibility for witnessed subsets is expected to bring new perspectives for finer analysis of definable subsets. In this article, we have only classified
![]() $\Sigma ^0_2$
subobjects, but the author and his colleagues have already started to classify higher levels of the arithmetic hierarchy, the
$\Sigma ^0_2$
subobjects, but the author and his colleagues have already started to classify higher levels of the arithmetic hierarchy, the
![]() $\Sigma ^1_1$
level, and the difference hierarchy.
$\Sigma ^1_1$
level, and the difference hierarchy.
Acknowledgements
The author wishes to thank Koki Hashimoto for valuable discussions.
Funding
The author’s research was partially supported by JSPS KAKENHI Grant Numbers 21H03392, 22K03401 and 23H03346.