No CrossRef data available.
Published online by Cambridge University Press: 03 May 2016
We show that isomorphism is not a complete 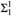 ${\rm{\Sigma }}_1^1$ equivalence relation even when restricted to the hyperarithmetic reals: If E1 denotes the
${\rm{\Sigma }}_1^1$ equivalence relation even when restricted to the hyperarithmetic reals: If E1 denotes the 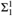 ${\rm{\Sigma }}_1^1$ (even
${\rm{\Sigma }}_1^1$ (even  ${\rm{\Delta }}_1^1$) equivalence relation of [4] then for no Hyp function f do we have xEy iff f(x) is isomorphic to f(y) for all Hyp reals x,y. As a corollary to the proof we provide for each computable limit ordinal α a hyperarithmetic reduction of
${\rm{\Delta }}_1^1$) equivalence relation of [4] then for no Hyp function f do we have xEy iff f(x) is isomorphic to f(y) for all Hyp reals x,y. As a corollary to the proof we provide for each computable limit ordinal α a hyperarithmetic reduction of 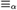 ${ \equiv _\alpha }$ (elementary-equivalence for sentences of quantifier-rank less than α) on arbitrary countable structures to isomorphism on countable structures of Scott rank at most α.
${ \equiv _\alpha }$ (elementary-equivalence for sentences of quantifier-rank less than α) on arbitrary countable structures to isomorphism on countable structures of Scott rank at most α.